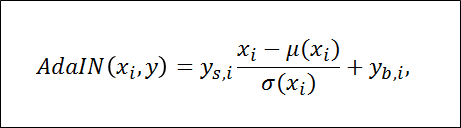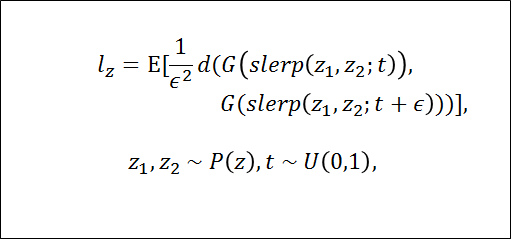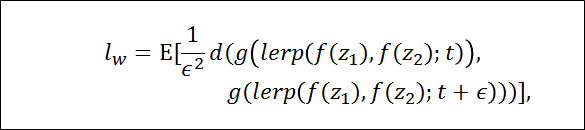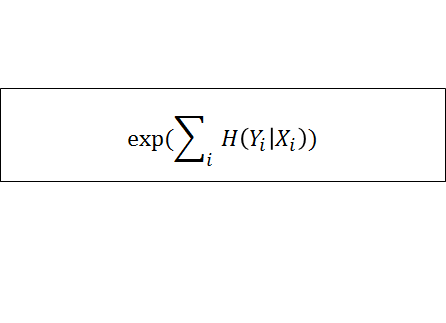- 投稿日:2019-02-11T18:44:08+09:00
im2col関数の理解
書籍「ゼロから作るディープラーニング」をもとに
畳み込みニューラルネットワーク(CNN、Convolutional Neural Network)を勉強しているのですが、途中に出てくるim2col関数というものについて理解が難しかったため、
自分なりの噛み砕きの経緯を書いてみました。もしもどなたかの参考になれば幸いです。
im2col関数について
CNNの畳み込み演算において複雑なループ処理を避けるため、
フィルター適用領域ごとに一列のデータになるよう変換する関数です。入力データとフィルターにこの関数を適用することで、
行列のドット演算で一気に畳み込み演算が行えます。オリジナルの実装
「ゼロから作る〜」で紹介されている実装はこのようなものです。
def im2col(input_data, filter_h, filter_w, stride=1, pad=0): N, C, H, W = input_data.shape out_h = (H + 2*pad - filter_h)//stride + 1 out_w = (W + 2*pad - filter_w)//stride + 1 img = np.pad(input_data, [(0,0), (0,0), (pad, pad), (pad, pad)], 'constant') col = np.zeros((N, C, filter_h, filter_w, out_h, out_w)) for y in range(filter_h): y_max = y + stride*out_h for x in range(filter_w): x_max = x + stride*out_w col[:, :, y, x, :, :] = img[:, :, y:y_max:stride, x:x_max:stride] col = col.transpose(0, 4, 5, 1, 2, 3).reshape(N*out_h*out_w, -1) return col書籍の説明を見ると目指すところは理解できるのですが、
このループ処理部分で行っている事がどうにも理解できませんでした。引っかかった点
y_maxとx_maxが何を意味しているのかよくわからない- imgのスライスで何を取り出しているのかよくわからない
y:y_max:stride,、x:x_max:strideって何?- フィルターサイズについてのループだけで処理できる理由がよくわからない
そこで、まずは自分なりに素朴な発想で実装してみました。
素朴な実装
フィルターを移動させるループ
→フィルタ内の各画素をコピーするループ
の順でx方向・y方向、4重ループ処理すればいけるはず...
という発想でforループ部分のみ変更してみたのが以下のim2col_slowです。def im2col_slow(input_data, filter_h, filter_w, stride=1, pad=0): N, C, H, W = input_data.shape out_h = (H + 2*pad - filter_h)//stride + 1 out_w = (W + 2*pad - filter_w)//stride + 1 img = np.pad(input_data, [(0,0), (0,0), (pad, pad), (pad, pad)], 'constant') col = np.zeros((N, C, filter_h, filter_w, out_h, out_w)) for move_y in range(out_h): for move_x in range(out_w): for y in range(filter_h): for x in range(filter_w): col[:, :, y, x, move_y, move_x] = \ img[:, :, y + stride * move_y, x + stride * move_x] col = col.transpose(0, 4, 5, 1, 2, 3).reshape(N*out_h*out_w, -1) return col実行してみます。
(見やすくするためにデータ数1、チャンネル数1に絞ってます)data = np.random.rand(1, 1, 7, 7) * 100 // 1 print('========== input ==========\n', data) print('=====================') filter_h = 3 filter_w = 3 stride = 2 pad = 0 col = im2col(data, filter_h=filter_h, filter_w=filter_w, stride=stride, pad=pad) col2 = im2col_slow(data, filter_h=filter_h, filter_w=filter_w, stride=stride, pad=pad) print('========== col ==========\n', col) print('=====================') print('========== col2 ==========\n', col2) print('=====================')同様の結果を得られました。
========== input ========== [[[[30. 91. 11. 13. 52. 44. 98.] [99. 6. 35. 41. 97. 72. 79.] [ 5. 92. 15. 95. 72. 8. 10.] [68. 5. 86. 25. 69. 46. 70.] [95. 32. 98. 49. 51. 19. 46.] [32. 15. 39. 44. 76. 58. 49.] [43. 47. 95. 1. 1. 12. 21.]]]] ===================== ========== col ========== [[30. 91. 11. 99. 6. 35. 5. 92. 15.] [11. 13. 52. 35. 41. 97. 15. 95. 72.] [52. 44. 98. 97. 72. 79. 72. 8. 10.] [ 5. 92. 15. 68. 5. 86. 95. 32. 98.] [15. 95. 72. 86. 25. 69. 98. 49. 51.] [72. 8. 10. 69. 46. 70. 51. 19. 46.] [95. 32. 98. 32. 15. 39. 43. 47. 95.] [98. 49. 51. 39. 44. 76. 95. 1. 1.] [51. 19. 46. 76. 58. 49. 1. 12. 21.]] ===================== ========== col2 ========== [[30. 91. 11. 99. 6. 35. 5. 92. 15.] [11. 13. 52. 35. 41. 97. 15. 95. 72.] [52. 44. 98. 97. 72. 79. 72. 8. 10.] [ 5. 92. 15. 68. 5. 86. 95. 32. 98.] [15. 95. 72. 86. 25. 69. 98. 49. 51.] [72. 8. 10. 69. 46. 70. 51. 19. 46.] [95. 32. 98. 32. 15. 39. 43. 47. 95.] [98. 49. 51. 39. 44. 76. 95. 1. 1.] [51. 19. 46. 76. 58. 49. 1. 12. 21.]] =====================オリジナルとの比較
自分で実装してみたおかげで、オリジナルの実装は
上記の素朴版で行っているフィルター移動分の2重ループをしなくて済むよう効率化したものだと気づきました。
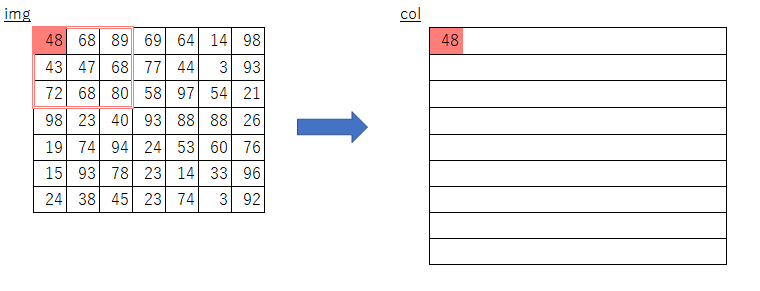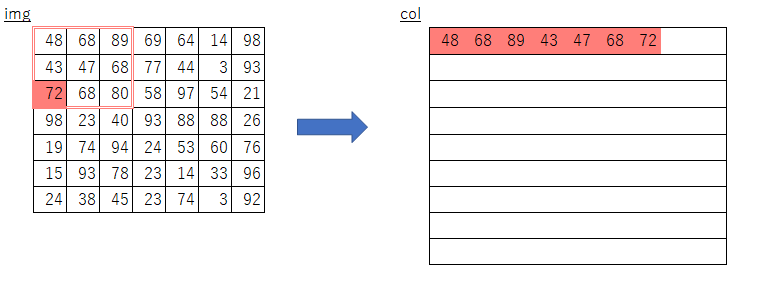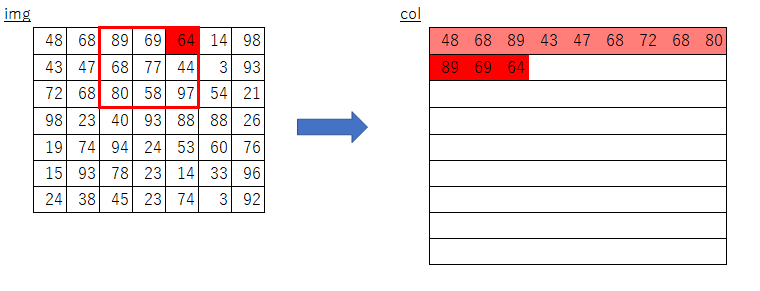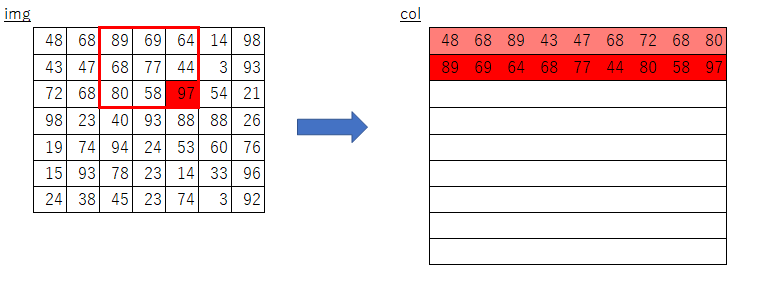
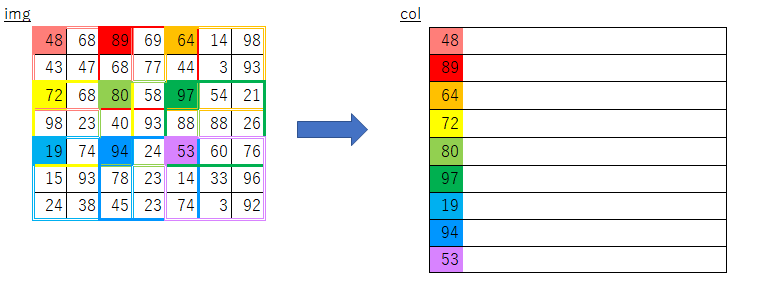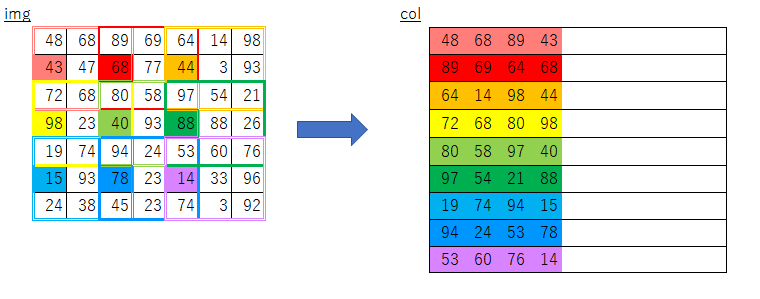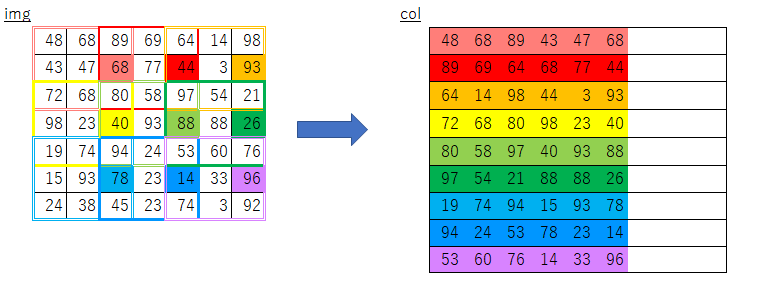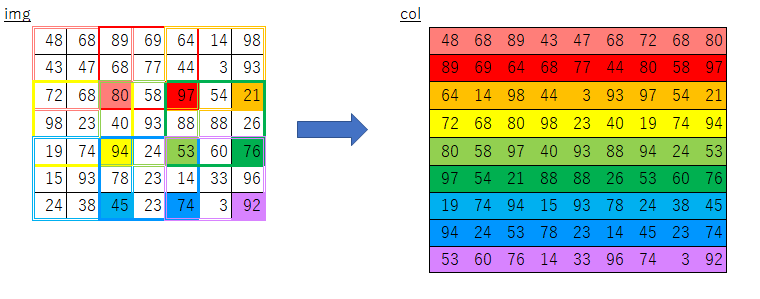
(ストライド幅刻みでスライスすることで、フィルタを移動させて取得する分を一気に取得・コピーしている)絵にしてみるとこんな感じになるかと思います。
素朴版の実装におけるimgからcolへのコピー
オリジナルim2colにおけるimgからcolへのコピー
ループ処理が効率化された結果、あのような実装になっているのだなぁ...
という感じで自分の理解は落ち着きました。
- 投稿日:2019-02-11T18:23:46+09:00
ディープラーニングを実装から学ぶ(9-1)CNNの実装
CNNは、画像認識に用いられます。MNISTも画像ですので、CNNを適用することにより、大幅な精度向上が期待できます。CNNの実装について考えてみましょう。
ここでは、CNN自体の詳細な説明は行いませんので、詳しく知りたい方は、他で確認してください。実装は、「ディープラーニングを実装から学ぶ(8)実装変更」をベースに行います。データは、MNISTを利用します。
畳み込み
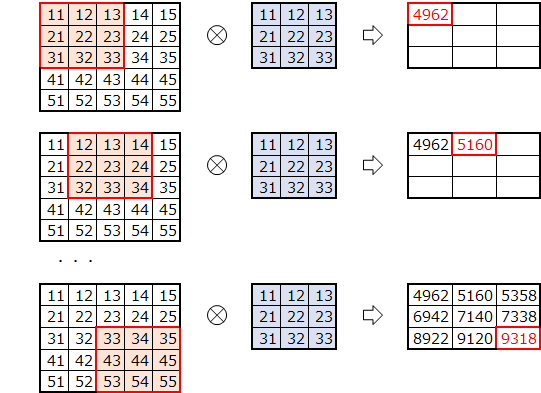
畳み込みは、画像に対して、フィルタを動かしながら画像のデータとフィルタを掛けた和をとります。
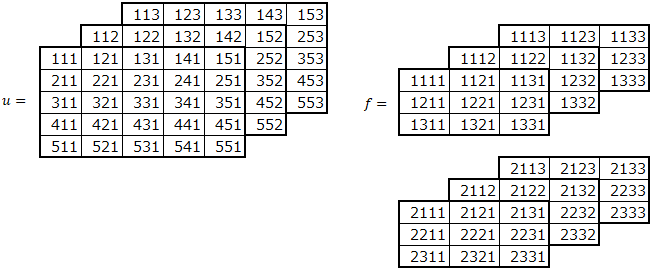
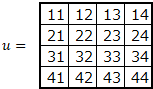
たとえば、画像$ u $とフィルタ$ f $の畳み込みを行うと、以下のような結果となります。\begin{align} u &= \begin{pmatrix} u_{11} & u_{12} & u_{13} \\ u_{21} & u_{22} & u_{23} \\ u_{31} & u_{32} & u_{33} \end{pmatrix} \\ \\ f &= \begin{pmatrix} w_{11} & w_{12} \\ w_{21} & w_{22} \end{pmatrix} \\ \\ z &= \begin{pmatrix} u_{11}w_{11}+u_{12}w_{12}+u_{21}w_{21}+u_{22}w_{22} & u_{12}w_{11}+u_{13}w_{12}+u_{22}w_{21}+u_{23}w_{22} \\ u_{21}w_{11}+u_{22}w_{12}+u_{31}w_{21}+u_{32}w_{22} & u_{22}w_{11}+u_{23}w_{12}+u_{32}w_{21}+u_{33}w_{22} \end{pmatrix} \end{align}数式で表すと以下です。
z_{ij} = \sum_{k,l=0}^{2}u_{i+k,j+l}w_{kl}畳み込みの実装
一度に全部を実装するのは難しいため、1ステップごとに考えます。
フィルタ
画像サイズが$ 5\times5 $、フィルタサイズが$ 3\times3 $の場合を考えます。
このように、フィルタをひとつづつ、ずらしながら掛けて和をとります。
実装
畳み込み後のサイズを考えます。
画像$ u $の高さと幅を$ uh, uw $、フィルタ$ f $の高さ、幅を$ fh, fw $とします。
畳み込み後の高さ($ zh $)、幅($ zw $)は、以下となります。
元のサイズより、フィルタ-1個分、小さくなります。
- 畳み込み後のサイズ
zh = uh-fh+1\\ zw = uw-fw+1畳み込みのプログラムを考えます。
画像の左上から順に、ひとつずつずらしながらフィルタサイズ分切り出します。
切り出した画像とフィルタの内積を計算します。
2次元のままでは、内積を計算できないため、flattenで1次元に変換しています。
プログラムです。def conv(u, f): # 画像の高さ、幅 uh, uw = u.shape # フィルタの高さ、幅 fh, fw = f.shape # 畳み込み後の高さ、幅 zh, zw = uh-fh+1, uw-fw+1 # 畳み込み後の格納領域確保 z = np.zeros((zh, zw)) # 畳み込み後の高さ、幅分ループ for i in range(zh): for j in range(zw): # 画像からフィルタサイズ分切り出し ud = u[i:i+fh,j:j+fw] # 切り出した画像とフィルタの内積の計算 z[i,j] = np.dot(ud.flatten(),f.flatten()) return z実行例
先ほどの例で確認します。
import numpy as np u55 = np.array([[11,12,13,14,15],[21,22,23,24,25],[31,32,33,34,35],[41,42,43,44,45],[51,52,53,54,55]]) f33 = np.array([[11,12,13],[21,22,23],[31,32,33]]) print("u55.shape=", u55.shape) print("f33.shape=", f33.shape) print("u55=") print(u55) print("f33=") print(f33)u55.shape= (5, 5) f33.shape= (3, 3) u55= [[11 12 13 14 15] [21 22 23 24 25] [31 32 33 34 35] [41 42 43 44 45] [51 52 53 54 55]] f33= [[11 12 13] [21 22 23] [31 32 33]]conv(u55, f33)array([[ 4962., 5160., 5358.], [ 6942., 7140., 7338.], [ 8922., 9120., 9318.]])パディング
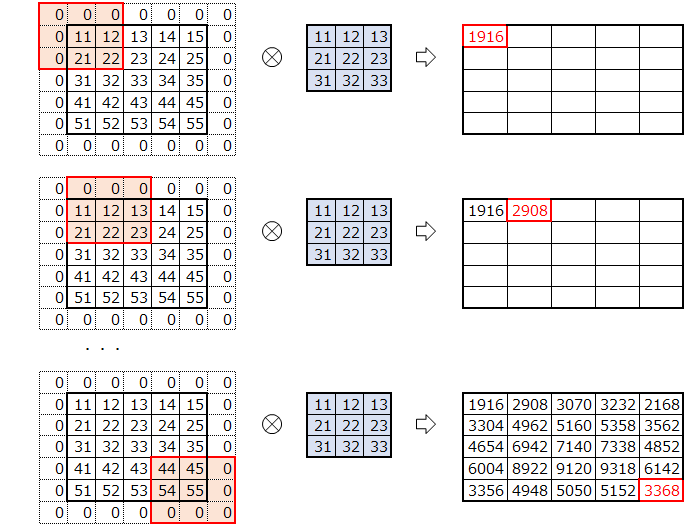
畳み込みを行うと元の画像サイズより小さくなります。画像の周りにパディングを行い、畳み込み後も元の画像の大きさを維持できるようにします。通常は、0で埋めるゼロパディングを行います。
ここでは、ゼロパディングのみ対応します。
パディングサイズ1の場合は、$ pu $のようになります。パディング後、畳み込みを実行します。
この場合は、畳み込み、前後で高さ、幅は同じになりました。
実装
パディングサイズが1の場合、パディング後の画像サイズは、左右、上下にパディングを行うため、高さ、幅とも+2となります。画像サイズがパディングによって増加した分、パディング後のサイズも大きくなります。
パディングの幅、高さを$ ph,pw $とし、画像のパディング後の高さ、幅を$ puh,puw $とします。
- パディング後のサイズ
puh = uh+2*ph\\ puw = uw+2*pw畳み込み後のサイズは、パディング後の画像サイズより、以下となります。
- 畳み込み後のサイズ
zh = puh-fh+1\\ zw = puw-fw+1パディング対応のプログラムです。元の画像にパディングを施した上で、畳み込みを実行しています。
def convp(u, f, p=(0,0)): # 画像の高さ、幅 uh, uw = u.shape # フィルタの高さ、幅 fh, fw = f.shape # パディングの高さ、幅 ph, pw = p # パディング後のデータ puh, puw = uh+2*ph,uw+2*pw pu = np.zeros((puh,puw)) pu[ph:ph+uh,pw:pw+uw] = u # 畳み込み後の高さ、幅 zh, zw = puh-fh+1, puw-fw+1 # 畳み込み後の格納領域確保 z = np.zeros((zh, zw)) # 畳み込み後の高さ、幅分ループ for i in range(zh): for j in range(zw): # 画像からフィルタサイズ分切り出し ud = pu[i:i+fh,j:j+fw] # 切り出した画像とフィルタの内積の計算 z[i,j] = np.dot(ud.flatten(),f.flatten()) return z実行例
先ほどのデータにパディングサイズ=1で実行します。
convp(u55, f33, p=(1,1))array([[ 1916., 2908., 3070., 3232., 2168.], [ 3304., 4962., 5160., 5358., 3562.], [ 4654., 6942., 7140., 7338., 4852.], [ 6004., 8922., 9120., 9318., 6142.], [ 3356., 4948., 5050., 5152., 3368.]])畳み込み後も元のサイズと同じになりました。
ストライド
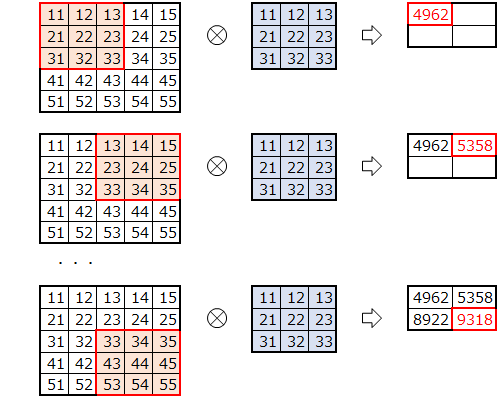
今までは、フィルタを1ずつずらしていました。フィルタをずらす幅を指定してみます。
ストライドを2とし、2つずつずらしてみます。
実装
畳み込み後のサイズを考えます。
ストライドずつ移動するため、ストライドで割ります。
画像のパディング後の高さ、幅を$ puh,puw$、ストライドの高さ、幅を$ sh,sw $とします。
- 畳み込み後のサイズ
zh = (puh-fh)/sh+1\\ zw = (puw-fw)/sw+1プログラムです。畳み込みをストライド分ずらして実行していきます。
def convps(u, f, p=(0,0), s=(1,1)): # 画像の高さ、幅 uh, uw = u.shape # フィルタの高さ、幅 fh, fw = f.shape # パディングの高さ、幅 ph, pw = p # ストライドの高さ、幅 sh, sw = s # パディング後のデータ puh, puw = uh+2*ph,uw+2*pw pu = np.zeros((puh,puw)) pu[ph:ph+uh,pw:pw+uw] = u # 畳み込み後の高さ、幅 zh, zw = int((puh-fh)/sh)+1, int((puw-fw)/sw)+1 # 畳み込み後の格納領域確保 z = np.zeros((zh, zw)) # 畳み込み後の高さ、幅分ループ for i in range(zh): for j in range(zw): # 画像からフィルタサイズ分切り出し ud = pu[i*sh:i*sh+fh,j*sw:j*sw+fw] # 切り出した画像とフィルタの内積の計算 z[i,j] = np.dot(ud.flatten(),f.flatten()) return z実行例
先ほどのデータにストライド=2で実行します
convps(u55, f33, s=(2,2))array([[ 4962., 5358.], [ 8922., 9318.]])チャネル
MNISTは、単色のため2次元のデータでした。カラー画像では、RGBの色のデータを加えて3次元となります。カラー画像への対応を考えます。
フィルタもチャネルを加えて、3次元となります。画像とフィルタのチャネル数は同じにします。
色を1次元目にするか3次元目にするか、両方のデータが存在するようですが、ここでは、色のデータは、3次元目とします。
画像、フィルタの各次元は、以下を表します。
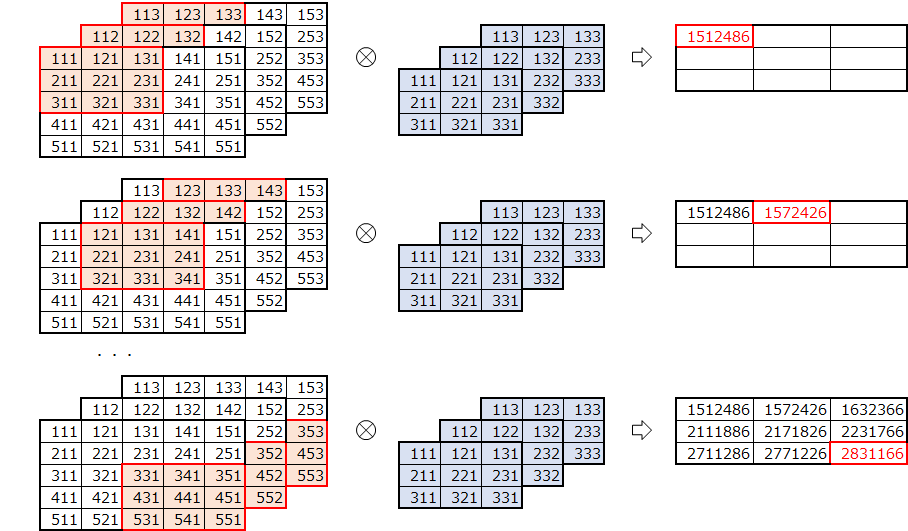
(高さ、幅、チャネル)畳み込みを行います。
各チャネルごとに、画像をフィルタサイズ分抽出し、各フィルタと掛けてすべてのチャネル分足し合わせます。実装
基本的に、3次元目にチャネルが増えただけです。
def convpsc(u, f, p=(0,0), s=(1,1)): # 画像の高さ、幅、チャネル uh, uw, uc = u.shape # フィルタの高さ、幅、チャネル fh, fw, fc = f.shape # パディングの高さ、幅 ph, pw = p # ストライドの高さ、幅 sh, sw = s # パディング後のデータ puh, puw = uh+2*ph,uw+2*pw pu = np.zeros((puh,puw,uc)) pu[ph:ph+uh,pw:pw+uw,:] = u # 畳み込み後の高さ、幅 zh, zw = int((puh-fh)/sh)+1, int((puw-fw)/sw)+1 # 畳み込み後の格納領域確保 z = np.zeros((zh, zw)) # 畳み込み後の高さ、幅分ループ for i in range(zh): for j in range(zw): # 画像からフィルタサイズ分切り出し ud = pu[i*sh:i*sh+fh,j*sw:j*sw+fw,:] # 切り出した画像とフィルタの内積の計算 z[i,j] = np.dot(ud.flatten(),f.flatten()) return z実行例
チャネルを3としたデータ例です。
import numpy as np u553 = np.array([[[111,112,113],[121,122,123],[131,132,133],[141,142,143],[151,152,153]], [[211,212,213],[221,222,223],[231,232,233],[241,242,243],[251,252,253]], [[311,312,313],[321,322,323],[331,332,333],[341,342,343],[351,352,353]], [[411,412,413],[421,422,423],[431,432,433],[441,442,443],[451,452,453]], [[511,512,513],[521,522,523],[531,532,533],[541,542,543],[551,552,553]]]) f333 = np.array([[[111,112,113],[121,122,123],[131,132,133]], [[211,212,213],[221,222,223],[231,232,233]], [[311,312,313],[321,322,323],[331,332,333]]]) print("u553.shape=", u553.shape) print("f333.shape=", f333.shape) print("u553=") for i in range(3): print(u553[:,:,i]) print("f333=") for i in range(3): print(f333[:,:,i])u553.shape= (5, 5, 3) f333.shape= (3, 3, 3) u553= [[111 121 131 141 151] [211 221 231 241 251] [311 321 331 341 351] [411 421 431 441 451] [511 521 531 541 551]] [[112 122 132 142 152] [212 222 232 242 252] [312 322 332 342 352] [412 422 432 442 452] [512 522 532 542 552]] [[113 123 133 143 153] [213 223 233 243 253] [313 323 333 343 353] [413 423 433 443 453] [513 523 533 543 553]] f333= [[111 121 131] [211 221 231] [311 321 331]] [[112 122 132] [212 222 232] [312 322 332]] [[113 123 133] [213 223 233] [313 323 333]]畳み込みの実行
convpsc(u553, f333)array([[ 1512486., 1572426., 1632366.], [ 2111886., 2171826., 2231766.], [ 2711286., 2771226., 2831166.]])フィルタ数
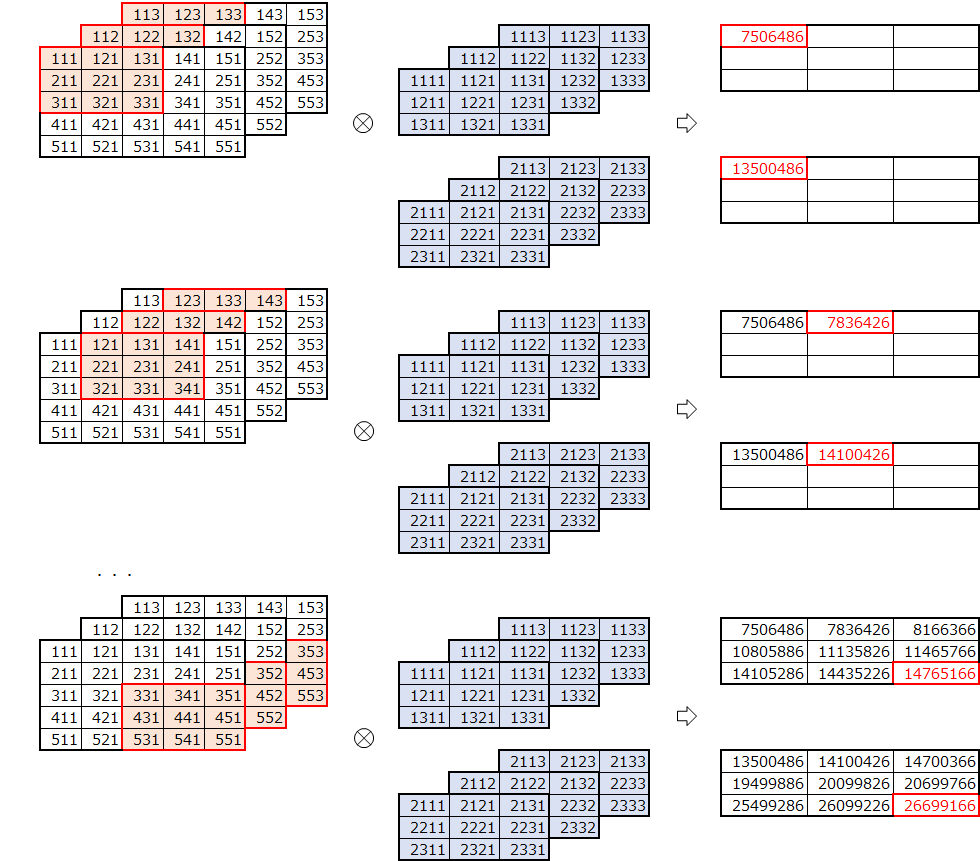
今度は、フィルタ数を複数にしてみます。フィルターは、以下の4次元となります。
(フィルタ、高さ、幅、チャネル)
フィルタ数2の例です。フィルタごとに畳み込みを行います。
畳み込み後は、フィルタ数分のデータとなり、3次元になります。
実装
基本は、同じですが、内積の部分に注意が必要です。
フィルタのひとつひとつと内積をとるため、フィルタをreshapeしています。その後、内積を行えるように転置します。def convpscf(u, f, p=(0,0), s=(1,1)): # 画像の高さ、幅、チャネル uh, uw, uc = u.shape # フィルタの数、高さ、幅、チャネル fn, fh, fw, fc = f.shape # パディングの高さ、幅 ph, pw = p # ストライドの高さ、幅 sh, sw = s # パディング後のデータ puh, puw = uh+2*ph,uw+2*pw pu = np.zeros((puh,puw,uc)) pu[ph:ph+uh,pw:pw+uw,:] = u # 畳み込み後の高さ、幅 zh, zw = int((puh-fh)/sh)+1, int((puw-fw)/sw)+1 # 畳み込み後の格納領域確保 z = np.zeros((zh, zw, fn)) # 畳み込み後の高さ、幅分ループ for i in range(zh): for j in range(zw): # 画像からフィルタサイズ分切り出し ud = pu[i*sh:i*sh+fh,j*sw:j*sw+fw,:] # 切り出した画像とフィルタの内積の計算 z[i,j,:] = np.dot(ud.flatten(),f.reshape((fn,fh*fw*fc)).T) return z実行例
フィルタ数を2とした場合の例です。
import numpy as np f2333 = np.array([[[[1111,1112,1113],[1121,1122,1123],[1131,1132,1133]], [[1211,1212,1213],[1221,1222,1223],[1231,1232,1233]], [[1311,1312,1313],[1321,1322,1323],[1331,1332,1333]]], [[[2111,2112,2113],[2121,2122,2123],[2131,2132,2133]], [[2211,2212,2213],[2221,2222,2223],[2231,2232,2233]], [[2311,2312,2313],[2321,2322,2323],[2331,2332,2333]]]]) print("f2333.shape=", f2333.shape) print("f2333=") for i in range(2): for j in range(3): print(f2333[i,:,:,j])f2333.shape= (2, 3, 3, 3) f2333= [[1111 1121 1131] [1211 1221 1231] [1311 1321 1331]] [[1112 1122 1132] [1212 1222 1232] [1312 1322 1332]] [[1113 1123 1133] [1213 1223 1233] [1313 1323 1333]] [[2111 2121 2131] [2211 2221 2231] [2311 2321 2331]] [[2112 2122 2132] [2212 2222 2232] [2312 2322 2332]] [[2113 2123 2133] [2213 2223 2233] [2313 2323 2333]]畳み込みの実行
z = convpscf(u553, f2333) print("z=") for i in range(2): print(z[:,:,i])z= [[ 7506486. 7836426. 8166366.] [ 10805886. 11135826. 11465766.] [ 14105286. 14435226. 14765166.]] [[ 13500486. 14100426. 14700366.] [ 19499886. 20099826. 20699766.] [ 25499286. 26099226. 26699166.]]データ数
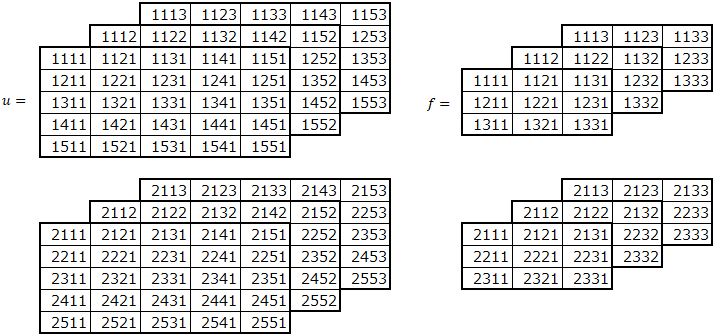
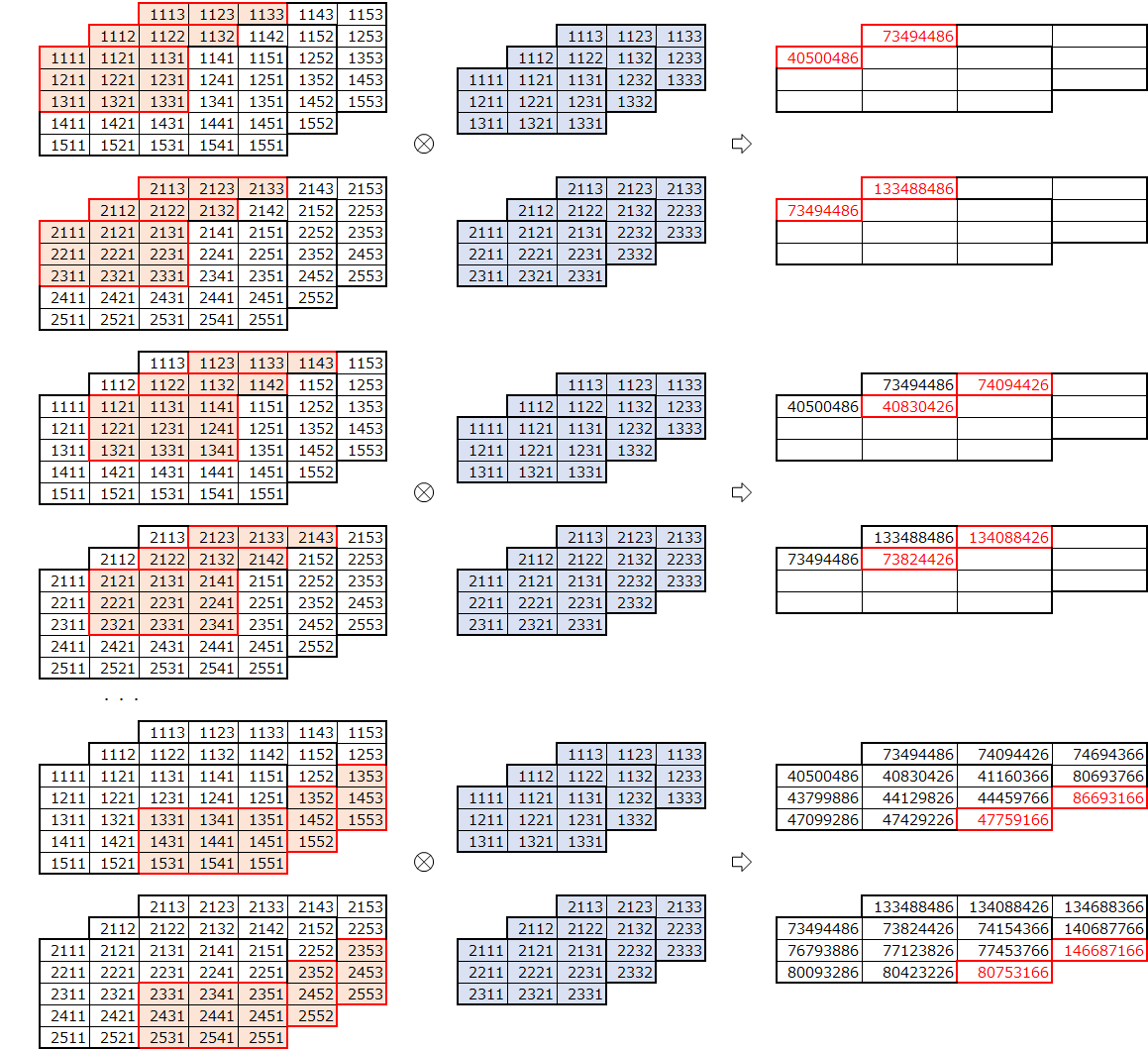
最後に、データを複数にしてみます。バッチサイズ分のデータを一度に畳み込みする必要があります。
データは、以下の4次元となります。
(データ、高さ、幅、チャネル)
データ数2の例です。畳み込みを行います。
畳み込みは、各データとフィルターの組み合わせで行います。
実装
フィルター数の対応を行った場合と同様に、内積の部分に注意が必要です。
データのひとつひとつと内積をとるため、データをフィルターと内積が取れるようにreshapeしています。def convpscfu(u, f, p=(0,0), s=(1,1)): # 画像の数、高さ、幅、チャネル un, uh, uw, uc = u.shape # フィルタの数、高さ、幅、チャネル fn, fh, fw, fc = f.shape # パディングの高さ、幅 ph, pw = p # ストライドの高さ、幅 sh, sw = s # パディング後のデータ puh, puw = uh+2*ph,uw+2*pw pu = np.zeros((un,puh,puw,uc)) pu[:,ph:ph+uh,pw:pw+uw,:] = u # 畳み込み後の高さ、幅 zh, zw = int((puh-fh)/sh)+1, int((puw-fw)/sw)+1 # 畳み込み後の格納領域確保 z = np.zeros((un, zh, zw, fn)) # 畳み込み後の高さ、幅分ループ for i in range(zh): for j in range(zw): # 画像からフィルタサイズ分切り出し ud = pu[:,i*sh:i*sh+fh,j*sw:j*sw+fw,:] # 切り出した画像とフィルタの内積の計算 z[:,i,j,:] = np.dot(ud.reshape((un,fh*fw*uc)),f.reshape((fn,fh*fw*fc)).T) return z実行例
データ数を2とした場合の例です。
import numpy as np u2553 = np.array([[[[1111,1112,1113],[1121,1122,1123],[1131,1132,1133],[1141,1142,1143],[1151,1152,1153]], [[1211,1212,1213],[1221,1222,1223],[1231,1232,1233],[1241,1242,1243],[1251,1252,1253]], [[1311,1312,1313],[1321,1322,1323],[1331,1332,1333],[1341,1342,1343],[1351,1352,1353]], [[1411,1412,1413],[1421,1422,1423],[1431,1432,1433],[1441,1442,1443],[1451,1452,1453]], [[1511,1512,1513],[1521,1522,1523],[1531,1532,1533],[1541,1542,1543],[1551,1552,1553]]], [[[2111,2112,2113],[2121,2122,2123],[2131,2132,2133],[2141,2142,2143],[2151,2152,2153]], [[2211,2212,2213],[2221,2222,2223],[2231,2232,2233],[2241,2242,2243],[2251,2252,2253]], [[2311,2312,2313],[2321,2322,2323],[2331,2332,2333],[2341,2342,2343],[2351,2352,2353]], [[2411,2412,2413],[2421,2422,2423],[2431,2432,2433],[2441,2442,2443],[2451,2452,2453]], [[2511,2512,2513],[2521,2522,2523],[2531,2532,2533],[2541,2542,2543],[2551,2552,2553]]]]) print("u2553.shape=", u2553.shape) print("u2553=") for i in range(2): for j in range(3): print(u2553[i,:,:,j])u2553.shape= (2, 5, 5, 3) u2553= [[1111 1121 1131 1141 1151] [1211 1221 1231 1241 1251] [1311 1321 1331 1341 1351] [1411 1421 1431 1441 1451] [1511 1521 1531 1541 1551]] [[1112 1122 1132 1142 1152] [1212 1222 1232 1242 1252] [1312 1322 1332 1342 1352] [1412 1422 1432 1442 1452] [1512 1522 1532 1542 1552]] [[1113 1123 1133 1143 1153] [1213 1223 1233 1243 1253] [1313 1323 1333 1343 1353] [1413 1423 1433 1443 1453] [1513 1523 1533 1543 1553]] [[2111 2121 2131 2141 2151] [2211 2221 2231 2241 2251] [2311 2321 2331 2341 2351] [2411 2421 2431 2441 2451] [2511 2521 2531 2541 2551]] [[2112 2122 2132 2142 2152] [2212 2222 2232 2242 2252] [2312 2322 2332 2342 2352] [2412 2422 2432 2442 2452] [2512 2522 2532 2542 2552]] [[2113 2123 2133 2143 2153] [2213 2223 2233 2243 2253] [2313 2323 2333 2343 2353] [2413 2423 2433 2443 2453] [2513 2523 2533 2543 2553]]畳み込みの実行
z = convpscfu(u2553, f2333) for i in range(2): print("z[",i,"]=") for j in range(2): print(z[i,:,:,j])z[ 0 ]= [[ 40500486. 40830426. 41160366.] [ 43799886. 44129826. 44459766.] [ 47099286. 47429226. 47759166.]] [[ 73494486. 74094426. 74694366.] [ 79493886. 80093826. 80693766.] [ 85493286. 86093226. 86693166.]] z[ 1 ]= [[ 73494486. 73824426. 74154366.] [ 76793886. 77123826. 77453766.] [ 80093286. 80423226. 80753166.]] [[ 1.33488486e+08 1.34088426e+08 1.34688366e+08] [ 1.39487886e+08 1.40087826e+08 1.40687766e+08] [ 1.45487286e+08 1.46087226e+08 1.46687166e+08]]データの値は、分かりやすくするため、データの添え字にしましたが、大きな値になり、指数表現になってしまいました。分かりやすくしたつもりが、分かりにくくなっていますね。
順伝播
最終的に4次元の配列どうしの演算となるため、混乱しないように、ひとつひとつ次元を増やしながら確認しました。
ここからは、正式な対応を行います。
今までは、バイアスを考慮していませんでした。バイアスを追加します。バイアスは、フィルタごとに1つです。\begin{align} u &= \begin{pmatrix} u_{11} & u_{12} & u_{13} \\ u_{21} & u_{22} & u_{23} \\ u_{31} & u_{32} & u_{33} \end{pmatrix} \\ \\ f &= \begin{pmatrix} w_{11} & w_{12} \\ w_{21} & w_{22} \end{pmatrix} \\ \\ z &= \begin{pmatrix} u_{11}w_{11}+u_{12}w_{12}+u_{21}w_{21}+u_{22}w_{22}+b & u_{12}w_{11}+u_{13}w_{12}+u_{22}w_{21}+u_{23}w_{22}+b \\ u_{21}w_{11}+u_{22}w_{12}+u_{31}w_{21}+u_{32}w_{22}+b & u_{22}w_{11}+u_{23}w_{12}+u_{32}w_{21}+u_{33}w_{22}+b \end{pmatrix} \end{align}実装
パディングとストライドは、整数を設定すれば、高さ、幅に同じ値を設定されるように変更しました。高さ、幅の値を変えたい場合は、高さ、幅をタプルで指定します。
def convolution2d(u, W, b, padding=0, strides=1): # パディング if type(padding) == int: padding_h, padding_w = padding, padding else: padding_h, padding_w = padding # ストライド if type(strides) == int: strides_h, strides_w = strides, strides else: strides_h, strides_w = strides # 画像の数、高さ、幅、チャネル un, uh, uw, uc = u.shape # フィルタの数、高さ、幅、チャネル fn, fh, fw, fc = W.shape # パディング後の高さ、幅 ph, pw = uh + padding_h*2, uw + padding_w*2 # パディング pu = np.zeros((un, ph, pw, uc)) pu[:, padding_h:padding_h+uh, padding_w:padding_w+uw, :] = u # 畳み込み後の高さ、幅 zh, zw = int((ph-fh)/strides_h)+1, int((pw-fw)/strides_w)+1 # 畳み込み後の格納領域確保 z = np.zeros((un, zh, zw, fn)) # 畳み込み後の高さ、幅分ループ for i in range(zh): for j in range(zw): # 画像からフィルタサイズ分切り出し # ud - (un, fh, fw, uc) ud = pu[:, i*strides_h:i*strides_h+fh, j*strides_w:j*strides_w+fw, :] # 切り出した画像とフィルタの内積の計算 # (un, fh*fw*fc) @ (fh*fw*fx, fn) => (un, fn) z[:, i, j, :] = np.dot(ud.reshape(un, fh*fw*fc), W.reshape(fn, fh*fw*fc).T) + b return z逆伝播
順伝播は、以下のように計算しました。
\begin{align} u &= \begin{pmatrix} u_{11} & u_{12} & u_{13} \\ u_{21} & u_{22} & u_{23} \\ u_{31} & u_{32} & u_{33} \end{pmatrix} \\ \\ f &= \begin{pmatrix} w_{11} & w_{12} \\ w_{21} & w_{22} \end{pmatrix} \\ \\ z &= \begin{pmatrix} u_{11}w_{11}+u_{12}w_{12}+u_{21}w_{21}+u_{22}w_{22} & u_{12}w_{11}+u_{13}w_{12}+u_{22}w_{21}+u_{23}w_{22} \\ u_{21}w_{11}+u_{22}w_{12}+u_{31}w_{21}+u_{32}w_{22} & u_{22}w_{11}+u_{23}w_{12}+u_{32}w_{21}+u_{33}w_{22} \end{pmatrix} \end{align}後ろからの勾配は、以下とします。
dz = \begin{pmatrix} dz_{11} & dz_{12} \\ dz_{21} & dz_{22} \end{pmatrix}$ z_{11} $について、勾配を考えます。
z_{11} = u_{11}w_{11}+u_{12}w_{12}+u_{21}w_{21}+u_{22}w_{22}+b$ u_{11} $方向
{\frac{\partial z_{11}}{\partial u_{11}} = w_{11}}後ろからの勾配$ dz_{11} $を掛けた値$ w_{11}dz_{11} $が勾配になります。
$ w_{11} $方向
{\frac{\partial z_{11}}{\partial w_{11}} = u_{11}}後ろからの勾配$ dz_{11} $を掛けた値$ u_{11}dz_{11} $が勾配になります。
$ b $方向
{\frac{\partial z_{11}}{\partial b} = 1}後ろからの勾配$ dz_{11} $を掛けた値$ dz_{11} $が勾配になります。
全体の勾配を考えます。
- $ u $の勾配$ du $
まずは、$ dz_{11} $についてです。$ z_{11} $に関係する場所に影響します。
\begin{pmatrix} w_{11}dz_{11} & w_{12}dz_{11} & 0 \\ w_{21}dz_{11} & w_{22}dz_{11} & 0 \\ 0 & 0 & 0 \end{pmatrix}次に、$ dz_{12} $についてです。
\begin{pmatrix} 0 & w_{11}dz_{12} & w_{12}dz_{12} \\ 0 & w_{21}dz_{12} & w_{22}dz_{12} \\ 0 & 0 & 0 \end{pmatrix}$ f $と各$ dz $の内積をとり、もとの位置に戻します。
最終的には、同じ場所は加え以下となります。\begin{pmatrix} w_{11}dz_{11} & w_{12}dz_{11}+w_{11}dz_{12} & w_{12}dz_{12} \\ w_{21}dz_{11}+w_{11}dz_{21} & w_{22}dz_{11}+w_{21}dz_{12}+w_{12}dz_{21}+w_{11}dz_{22} & w_{22}dz_{12}+w_{12}dz_{22} \\ w_{21}dz_{21} & w_{22}dz_{21}+w_{21}dz_{22} & w_{22}dz_{22} \end{pmatrix}
- $ w $の勾配$ dw $
まずは、$ dz_{11} $についてです。$ z_{11} $に関係する場所に影響します。
\begin{pmatrix} u_{11}dz_{11} & u_{12}dz_{11} \\ u_{21}dz_{11} & u_{22}dz_{11} \end{pmatrix}次に、$ dz_{12} $についてです。
\begin{pmatrix} u_{12}dz_{12} & u_{13}dz_{12} \\ u_{22}dz_{12} & u_{23}dz_{12} \end{pmatrix}$ z $のもとになった$ u $と$ dz $の内積となります。
最終的には、それぞれ加え以下となります。\begin{pmatrix} u_{11}dz_{11}+u_{12}dz_{12}+u_{21}dz_{21}+u_{22}dz_{22} & u_{12}dz_{11}+u_{13}dz_{12}+u_{22}dz_{21}+u_{23}dz_{22} \\ u_{21}dz_{11}+u_{22}dz_{12}+u_{31}dz_{21}+u_{32}dz_{22} & u_{22}dz_{11}+u_{23}dz_{12}+u_{32}dz_{21}+u_{33}dz_{22} \end{pmatrix}
- $ b $の勾配$ db $
$ dz_{11} $は、$ b $方向の勾配が1のため、そのままの値です。
$ 1 \times dz_{11} = dz_{11} $
最終的には、すべて足した値となります。dz_{11} + dz_{12} + dz_{21} + dz_{22}実装
勾配は、単純な2次元で説明しましたが、4次元となっても同様です。内積を行うためreshapeが必要です。
def convolution2d_back(dz, u, W, b, padding=0, strides=1): # パディング if type(padding) == int: padding_h, padding_w = padding, padding else: padding_h, padding_w = padding # ストライド if type(strides) == int: strides_h, strides_w = strides, strides else: strides_h, strides_w = strides # 画像の数、高さ、幅、チャネル un, uh, uw, uc = u.shape # フィルターの数、高さ、幅、チャネル fn, fh, fw, fc = W.shape # パディング後の高さ、幅 ph, pw = uh + padding_h*2, uw + padding_w*2 # パディング pu = np.zeros((un, ph, pw, uc)) pu[:, padding_h:padding_h+uh, padding_w:padding_w+uw, :] = u # 畳み込み後の高さ、幅 zh, zw = int((ph-fh)/strides_h)+1, int((pw-fw)/strides_w)+1 # 勾配格納領域確保 dpu = np.zeros((un, ph, pw, uc)) dW = np.zeros((fn, fh, fw, fc)) # 畳み込み後の高さ、幅分ループ for i in range(zh): for j in range(zw): # dzijの取り出し # dzs - (un, fn) dzs = dz[:,i,j,:] # u方向の勾配計算 # dpusr - (un,fn) @ (fn, fh*fw*fc) => (un, fh*fw*fc) dpusr = np.dot(dzs, W.reshape(fn, fh*fw*fc)) # dpus - (un, fh, fw, uc) dpus = dpusr.reshape(un, fh, fw, uc) dpu[:, i*strides_h:i*strides_h+fh, j*strides_w:j*strides_w+fw, :] += dpus # W方向の勾配計算 # pus - (un, fh*fw*uc) pus = pu[:, i*strides_h:i*strides_h+fh, j*strides_w:j*strides_w+fw, :] # pudr - (un, fh*fw*uc) pusr = pus.reshape(un, fh*fw*uc) # dWsr - (fn, un) @ (un, fh*fw*uc) => (fn, fh*fw*uc) dWsr = np.dot(dzs.T, pusr) # dWs - (fn, fh, fw, fc=uc) dWs = dWsr.reshape(fn, fh, fw, fc) dW = dW + dWs # パディング部分の除去 du = dpu[:, padding_h:padding_h+uh, padding_w:padding_w+uw, :] # b方向の勾配計算 db = np.sum(dz.reshape(un*zh*zw, fn), axis=0) return du, dW, dbプーリング
プーリング層では、画像の圧縮を行います。圧縮方式としては、一定範囲の最大値を取る、マックスプーリングが一般的に用いられます。ここは、マックスプーリングと平均を取る平均プーリングについて考えます。
マックスプーリングの実装
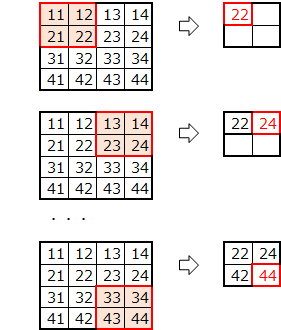
一定の範囲の最大値をデータとして抽出します。範囲は、プールサイズとして指定します。畳み込みと同様に、パディング、ストライドにも対応します。ストライドは、基本的にプールサイズと同じにします。すなわち、範囲が重ならないように移動しながら最大値を計算します。
プーリングは、チャネルごとに行います。プーリング後もチャネル数は変わりません。マックスプーリングの適用例です。
ここでは、プールサイズ=2分移動しながら最大値を抽出しています。
順伝播
プーリング後のサイズは、以下のように、元のサイズをプールサイズで割ったものとなります。
zh = uh/pool\_size\_h\\ zw = uw/pool\_size\_wパディングを適用した場合のサイズです。パディング後のサイズを$ ph,pw $とすると以下のようになります。
zh = ph/pool\_size\_h\\ zw = pw/pool\_size\_w最後にストライド適用後のサイズを考えます。今までは、プールサイズ=ストライドで考えていました。プールサイズとは別に、ストライドを設定した場合を考えます。以下のようになります。
zh = (ph-pool\_size\_h)/strides\_h + 1\\ zw = (pw-pool\_size\_w)/strides\_w + 1実装は、基本的に畳み込みと同じですが、フィルタとの内積を取るのではなく、maxで最大値を抽出します。
def max_pooling2d(u, pool_size=2, padding=0, strides=None): # ストライド設定 if strides is None: strides = pool_size # プールサイズ if type(pool_size) == int: pool_size_h, pool_size_w = pool_size, pool_size else: pool_size_h, pool_size_w = pool_size # パディング if type(padding) == int: padding_h, padding_w = padding, padding else: padding_h, padding_w = padding # ストライド if type(strides) == int: strides_h, strides_w = strides, strides else: strides_h, strides_w = strides # 画像の数、高さ、幅、チャネル un, uh, uw, uc = u.shape # パディング後の高さ、幅 ph, pw = uh + padding_h*2, uw + padding_w*2 # パディング pu = np.zeros((un, ph, pw, uc)) pu[:, padding_h:padding_h+uh, padding_w:padding_w+uw, :] = u # プーリング後の高さ、幅 zh, zw = int((ph-pool_size_h)/strides_h)+1, int((pw-pool_size_w)/strides_w)+1 # プーリング後の格納領域確保 z = np.zeros((un, zh, zw, uc)) # プーリング後の高さ、幅分ループ for i in range(zh): for j in range(zw): # 画像からプーリングサイズ分切り出し # pus - (un, pool_size_h, pool_size_w, uc) pus = pu[:, i*strides_h:i*strides_h+pool_size_h, j*strides_w:j*strides_w+pool_size_w, :] # 切り出した画像の最大 z[:, i, j, :] = np.max(pus.reshape(un, pool_size_h*pool_size_w, uc), axis=1) return z逆伝播
最大の値をそのまま後ろに流しているため、逆伝播では、最大値のところに、dzの値をそのまま返します。
argmaxで最大値の位置を取得します。データごとに最大値の位置が違うので、forループで、データ数、チャネル分ひとつずつ設定しています。def max_pooling2d_back(dz, u, z, pool_size=2, padding=0, strides=None): # ストライド設定 if strides is None: strides = pool_size # プールサイズ if type(pool_size) == int: pool_size_h, pool_size_w = pool_size, pool_size else: pool_size_h, pool_size_w = pool_size # パディング if type(padding) == int: padding_h, padding_w = padding, padding else: padding_h, padding_w = padding # ストライド if type(strides) == int: strides_h, strides_w = strides, strides else: strides_h, strides_w = strides # 画像の数、高さ、幅、チャネル un, uh, uw, uc = u.shape # パディング後の高さ、幅 ph, pw = uh + padding_h*2, uw + padding_w*2 # パディング pu = np.zeros((un, ph, pw, uc)) pu[:, padding_h:padding_h+uh, padding_w:padding_w+uw, :] = u # プーリング後のデータ格納用 zh, zw = int((ph-pool_size_h)/strides_h)+1, int((pw-pool_size_w)/strides_w)+1 # 勾配格納領域確保 dpu = np.zeros((un, ph, pw, uc)) # プーリング後の高さ、幅分ループ for i in range(zh): for j in range(zw): # dzijの取り出し # dzs - (un, fn) dzs = dz[:,i,j,:] # 最大の要素 pus = pu[:, i*strides_h:i*strides_h+pool_size_h, j*strides_w:j*strides_w+pool_size_w, :] z_argmax = np.argmax(pus.reshape(un, pool_size_h*pool_size_w, uc), axis=1) # 勾配格納領域確保 dusr = np.zeros((un, pool_size_h*pool_size_w, uc)) # データ数、チャネル分ループ for k in range(un): for l in range(uc): # 最大の要素にdzを設定 dusr[k, z_argmax[k,l], l] = dzs[k, l] # 勾配設定 dus = dusr.reshape(un, pool_size_h, pool_size_w, uc) dpu[:, i*strides_h:i*strides_h+pool_size_h, j*strides_w:j*strides_w+pool_size_w, :] += dus # パディング部分の除去 du = dpu[:, padding_h:padding_h+uh, padding_w:padding_w+uw, :] return du本当は、forループは使用せず、一気に設定したかったのですが、良い方法が分かりませんでした。
実際に、実行してみると、性能が遅く使いものになりませんでした。その後、検討の結果、transposeによって、配列の順番を変えれば対応できることがわかりました。
最大値の場所への代入ですが、データとチャネル部分が離れていて、一度に代入することができませんでした。transposeにより、データ、チャネル、高さ、幅の順に並び変えることにより、データ・チャネルごとに最大の高さ・幅の位置に代入できます。代入後に、再度、transposeを行い、位置を元に戻します。def max_pooling2d_back(dz, u, z, pool_size=2, padding=0, strides=None): # ストライド設定 if strides is None: strides = pool_size # プールサイズ if type(pool_size) == int: pool_size_h, pool_size_w = pool_size, pool_size else: pool_size_h, pool_size_w = pool_size # パディング if type(padding) == int: padding_h, padding_w = padding, padding else: padding_h, padding_w = padding # ストライド if type(strides) == int: strides_h, strides_w = strides, strides else: strides_h, strides_w = strides # 画像の数、高さ、幅、チャネル un, uh, uw, uc = u.shape # パディング後の高さ、幅 ph, pw = uh + padding_h*2, uw + padding_w*2 # パディング pu = np.zeros((un, ph, pw, uc)) pu[:, padding_h:padding_h+uh, padding_w:padding_w+uw, :] = u # プーリング後のデータ格納用 zh, zw = int((ph-pool_size_h)/strides_h)+1, int((pw-pool_size_w)/strides_w)+1 # 勾配格納領域確保 dpu = np.zeros((un, ph, pw, uc)) # プーリング後の高さ、幅分ループ for i in range(zh): for j in range(zw): # dzijの取り出し # dzs - (un, fn) dzs = dz[:,i,j,:] # 最大の要素 pus = pu[:, i*strides_h:i*strides_h+pool_size_h, j*strides_w:j*strides_w+pool_size_w, :] # 順番並び替え pustr = pus.transpose(0, 3, 1, 2) # 最大の要素 z_argmax = np.argmax(pustr.reshape(un*uc, pool_size_h*pool_size_w), axis=1) # 勾配格納 dudrtr = np.zeros((un*uc, pool_size_h*pool_size_w)) dudrtr[np.arange(un*uc), z_argmax.ravel()] = dzs.ravel() dudtr = dudrtr.reshape(un, uc, pool_size_h, pool_size_w) # 順番元に戻す dud = dudtr.transpose(0, 2, 3, 1) # 勾配設定 dpu[:, i*strides_h:i*strides_h+pool_size_h, j*strides_w:j*strides_w+pool_size_w, :] += dud du = dpu[:, padding_h:padding_h+uh, padding_w:padding_w+uw, :] return duかなり性能改善できました。
平均プーリングの実装
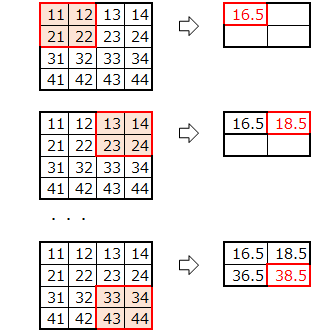
マックスプーリングは、プールサイズ分の画像から最大値を抽出していたのに対して、平均プーリングでは、平均を行います。
平均プーリングの適用例です。
ここでは、プールサイズ=2分移動しながら平均値を求めています。
順伝播
マックスプーリングとの違いは、プーリングの関数をmaxからmeanに変更するのみです。
def average_pooling2d(u, pool_size=2, padding=0, strides=None): # ストライド設定 if strides is None: strides = pool_size # プールサイズ if type(pool_size) == int: pool_size_h, pool_size_w = pool_size, pool_size else: pool_size_h, pool_size_w = pool_size # パディング if type(padding) == int: padding_h, padding_w = padding, padding else: padding_h, padding_w = padding # ストライド if type(strides) == int: strides_h, strides_w = strides, strides else: strides_h, strides_w = strides # 画像の数、高さ、幅、チャネル un, uh, uw, uc = u.shape # パディング後の高さ、幅 ph, pw = uh + padding_h*2, uw + padding_w*2 # パディング pu = np.zeros((un, ph, pw, uc)) pu[:, padding_h:padding_h+uh, padding_w:padding_w+uw, :] = u # プーリング後の高さ、幅 zh, zw = int((ph-pool_size_h)/strides_h)+1, int((pw-pool_size_w)/strides_w)+1 # プーリング後の格納領域確保 z = np.zeros((un, zh, zw, uc)) # プーリング後の高さ、幅分ループ for i in range(zh): for j in range(zw): # 画像からプーリングサイズ分切り出し # pus - (un, pool_size_h, pool_size_w, uc) pus = pu[:, i*strides_h:i*strides_h+pool_size_h, j*strides_w:j*strides_w+pool_size_w, :] # 切り出した画像の平均 z[:, i, j, :] = np.mean(pus.reshape(un, pool_size_h*pool_size_w, uc), axis=1) return z逆伝播
順伝播は、以下のように決定していました。
\begin{align} u &= \begin{pmatrix} u_{11} & u_{12} & u_{13} & u_{14}\\ u_{21} & u_{22} & u_{23} & u_{24}\\ u_{31} & u_{32} & u_{33} & u_{34}\\ u_{41} & u_{42} & u_{43} & u_{44} \end{pmatrix} \\ \\ z &= \begin{pmatrix} \frac{u_{11}+u_{12}+u_{21}+u_{22}}{4} & \frac{u_{13}+u_{14}+u_{23}+u_{24}}{4} \\ \frac{u_{31}+u_{32}+u_{41}+u_{42}}{4} & \frac{u_{33}+u_{34}+u_{43}+u_{44}}{4} \end{pmatrix} \end{align}$ z_{11} $について、勾配を考えます。
z_{11} = \frac{u_{11}+u_{12}+u_{21}+u_{22}}{4}$ u_{11} $方向
{\frac{\partial z_{11}}{\partial u_{11}} = \frac{1}{4}}後ろからの勾配$ dz_{11} $を掛けた値$ dz_{11}/4 $が勾配になります。
$ dz $をpool_size_h $ \times $ pool_size_wで割ります。それを、平均を求めた元の場所に加えます。def average_pooling2d_back(dz, u, z, pool_size=2, padding=0, strides=None): # ストライド設定 if strides is None: strides = pool_size # プールサイズ if type(pool_size) == int: pool_size_h, pool_size_w = pool_size, pool_size else: pool_size_h, pool_size_w = pool_size # パディング if type(padding) == int: padding_h, padding_w = padding, padding else: padding_h, padding_w = padding # ストライド if type(strides) == int: strides_h, strides_w = strides, strides else: strides_h, strides_w = strides # 画像の数、高さ、幅、チャネル un, uh, uw, uc = u.shape # パディング後の高さ、幅 ph, pw = uh + padding_h*2, uw + padding_w*2 # パディング pu = np.zeros((un, ph, pw, uc)) pu[:, padding_h:padding_h+uh, padding_w:padding_w+uw, :] = u # プーリング後のデータ格納用 zh, zw = int((ph-pool_size_h)/strides_h)+1, int((pw-pool_size_w)/strides_w)+1 # 勾配格納領域確保 dpu = np.zeros((un, ph, pw, uc)) # プーリング後の高さ、幅分ループ for i in range(zh): for j in range(zw): # dzijをプールサイズで割る # dzs - (un, uc) dzs = dz[:,i,j,:]/(pool_size_h*pool_size_w) dzs = dzs.reshape(un, 1, 1, uc) # プールサイズの高さ、幅分ループ for k in range(pool_size_h): for l in range(pool_size_w): # 勾配設定 dpu[:, i*strides_h+k:i*strides_h+k+1, j*strides_w+l:j*strides_w+l+1, :] += dzs # パディング部分の除去 du = dpu[:, padding_h:padding_h+uh, padding_w:padding_w+uw, :] return dufor分の入れ子になりましたが、特に性能上の問題はありませんでした。
np.tileを利用しすれば、プールサイズの高さ、幅分のループは不要になることが分かりましたが、ほとんど性能が変わらなかったため分かりやすさの観点からこのままにしています。flatten
最後に、畳み込み後の4次元データを全結合(Affine)で扱えるように、2次元に変換を行います。
flattenの実装
順伝播
高さ、幅、チャネル部分を1次元に変換します。reshapeするのみです。
def flatten2d(u): # 画像の数、高さ、幅、チャネル un, uh, uw, uc = u.shape z = u.reshape(un, uh*uw*uc) return z逆伝播
逆伝播は、逆に、3次元の高さ、幅、チャネルに戻します。
def flatten2d_back(dz, u, z): du = dz.reshape(u.shape) return du組み込み
「ディープラーニングを実装から学ぶ(8)実装変更」の実装に、CNNを組み込みます。
畳み込み
層の追加
畳み込み時にフィルタは、add_layerのunitにフィルタ数を、設定し、filter_sizeにフィルタ、paddinにパディング、stridesにストライドを設定するようにします。
フィルタ数を8とし、フィルタサイズ=5、パディング=2、ストライド=1を設置した例です。model = add_layer(model, "conv", convolution2d, d=8, filter_size=5, padding=2, strides=1)初期化
重さとして、フィルタサイズ$ \times $フィルタ数分を確保し初期化を行います。
def convolution2d_init_layer(d_prev, d, filter_size=2, padding=0, strides=1, weight_init_func=he_normal, weight_init_params={}, bias_init_func=zeros_b, bias_init_params={}): # フィルタサイズ if type(filter_size) == int: filter_size_h, filter_size_w = filter_size, filter_size else: filter_size_h, filter_size_w = filter_size # パディング if type(padding) == int: padding_h, padding_w = padding, padding else: padding_h, padding_w = padding # ストライド if type(strides) == int: strides_h, strides_w = strides, strides else: strides_h, strides_w = strides # 画像の高さ、幅、チャネル uh, uw, uc = d_prev # フィルターの数、高さ、幅、チャネル fn, fh, fw, fc = d, filter_size_h, filter_size_w, d_prev[2] # パディング後の高さ、幅 ph, pw = uh + padding_h*2, uw + padding_w*2 # 畳み込み後のデータ格納用 zh, zw = int((ph-fh)/strides_h)+1, int((pw-fw)/strides_w)+1 d_next = (zh, zw, fn) # W - fn, fh, fw, fc #fn, fh, fw, fc = d, filter_size_h, filter_size_w, d_prev.shape[2] W = weight_init_func(fh*fw*fc, fn, **weight_init_params) W = W.reshape((fn, fh, fw, fc)) b = bias_init_func(fn, **bias_init_params) return d_next, {"W":W, "b":b, "padding":padding, "strides":strides} def convolution2d_init_optimizer(): sW = {} sb = {} return {"sW":sW, "sb":sb}順伝播、逆伝播、重みの更新
順伝播、逆伝播では、それぞれの関数を呼び出すようにします。update_weightで、重み、バイアスの更新を行います。
重み減衰にも対応します。対応方法は、affineと同じです。def convolution2d_propagation(func, u, weights, weight_decay, learn_flag, **params): z = func(u, weights["W"], weights["b"], padding=weights["padding"], strides=weights["strides"]) # 重み減衰対応 weight_decay_r = 0 if weight_decay is not None: weight_decay_r = weight_decay["func"](weights["W"], **weight_decay["params"]) return {"u":u, "z":z}, weight_decay_r def convolution2d_back_propagation(back_func, dz, us, weights, weight_decay, calc_du_flag, **params): du, dW, db = back_func(dz, us["u"], weights["W"], weights["b"], padding=weights["padding"], strides=weights["strides"], calc_du_flag=calc_du_flag) # 重み減衰対応 if weight_decay is not None: dW = dW + weight_decay["back_func"](weights["W"], **weight_decay["params"]) return {"du":du, "dW":dW, "db":db} def convolution2d_update_weight(func, du, weights, optimizer_stats, **params): weights["W"], optimizer_stats["sW"] = func(weights["W"], du["dW"], **params, **optimizer_stats["sW"]) weights["b"], optimizer_stats["sb"] = func(weights["b"], du["db"], **params, **optimizer_stats["sb"]) return weights, optimizer_statsプーリング
プーリングの層の定義例です。
マックスプーリングをプールサイズ=2、パディング=1、ストライド=2で設定しています。model = add_layer(model, "max_pooling", max_pooling2d, pool_size=2, padding=1, strides=2)プーリング層は、重さを持たないため、初期化で、プーリング後のサイズを求めるだけです。
def max_pooling2d_init_layer(d_prev, d, pool_size=2, padding=0, strides=None): # ストライド設定 if strides is None: strides = pool_size # プールサイズ if type(pool_size) == int: pool_size_h, pool_size_w = pool_size, pool_size else: pool_size_h, pool_size_w = pool_size # パディング if type(padding) == int: padding_h, padding_w = padding, padding else: padding_h, padding_w = padding # ストライド if type(strides) == int: strides_h, strides_w = strides, strides else: strides_h, strides_w = strides # 画像の高さ、幅、チャネル uh, uw, uc = d_prev # パディング後の高さ、幅 ph, pw = uh + padding_h*2, uw + padding_w*2 # プーリング後のデータ格納用 zh, zw = int((ph-pool_size_h)/strides_h)+1, int((pw-pool_size_w)/strides_w)+1 d_next = (zh, zw, uc) return d_next, {} def average_pooling2d_init_layer(d_prev, d, pool_size=2, padding=0, strides=None): # ストライド設定 if strides is None: strides = pool_size # プールサイズ if type(pool_size) == int: pool_size_h, pool_size_w = pool_size, pool_size else: pool_size_h, pool_size_w = pool_size # パディング if type(padding) == int: padding_h, padding_w = padding, padding else: padding_h, padding_w = padding # ストライド if type(strides) == int: strides_h, strides_w = strides, strides else: strides_h, strides_w = strides # 画像の高さ、幅、チャネル uh, uw, uc = d_prev # パディング後の高さ、幅 ph, pw = uh + padding_h*2, uw + padding_w*2 # プーリング後のデータ格納用 zh, zw = int((ph-pool_size_h)/strides_h)+1, int((pw-pool_size_w)/strides_w)+1 d_next = (zh, zw, uc) return d_next, {}flatten
層の定義です。flattenは、パラメータはありません。
model = add_layer(model, "flatten", flatten2d)flattenも重さを持たないため、初期化でflatten後のサイズを求めるだけです。
def flatten2d_init_layer(d_prev, d): d_next = d_prev[0]*d_prev[1]*d_prev[2] return d_next, {}実行例
CNNを実行してみます。
データ(画像)
画像データは、1次元で処理していました。
高さ、幅、チャネルの3次元で処理するため、あらかじめデータをreshapeします。MNISTは、白黒のため、チャネルは、1です。nx_train = nx_train.reshape((nx_train.shape[0], 28, 28, 1)) nx_test = nx_test.reshape((nx_test.shape[0], 28, 28, 1))モデル
畳み込み、マックスプーリング、全結合によるモデルを作成します。
例として、畳み込み部分は、フィルタ数を6、フィルタサイズを7としています。活性化関数は、ReLUです。
マックスプーリングは、プールサイズ=2(既定値)とします。
全結合は、今まで行っていた、100-50-10の階層モデルをそのまま利用しています。model = create_model((28,28,1)) model = add_layer(model, "conv1", convolution2d, 6, filter_size=7) model = add_layer(model, "reluc1", relu) model = add_layer(model, "pooling1", max_pooling2d) model = add_layer(model, "flatten", flatten2d) model = add_layer(model, "affine1", affine, 100) model = add_layer(model, "relua1", relu) model = add_layer(model, "affine2", affine, 50) model = add_layer(model, "relua2", relu) model = add_layer(model, "affine3", affine, 10) model = set_output(model, softmax) model = set_error(model, cross_entropy_error)学習
バッチサイズは、100として、30エポック学習してみます。
epoch = 30 batch_size = 100 np.random.seed(10) model, optimizer, learn_info = learn(model, nx_train, t_train, nx_test, t_test, batch_size=batch_size, epoch=epoch)実行結果
input - 0 (28, 28, 1) conv1 convolution2d (28, 28, 1) (22, 22, 6) reluc1 relu (22, 22, 6) (22, 22, 6) pooling1 max_pooling2d (22, 22, 6) (11, 11, 6) flatten flatten2d (11, 11, 6) 726 affine1 affine 726 100 relua1 relu 100 100 affine2 affine 100 50 relua2 relu 50 50 affine3 affine 50 10 output softmax 10 error cross_entropy_error 0 0.07975 2.58034561588 0.0773 2.58935648296 1 0.912583333333 0.283821423709 0.9667 0.104532411461 2 0.97325 0.0871521629503 0.9807 0.0617759030541 3 0.981733333333 0.0599540945957 0.9835 0.0506263259402 4 0.98515 0.0478125171804 0.9824 0.0544197303191 5 0.98755 0.0387084821671 0.9857 0.0431286090129 6 0.990516666667 0.0308306128231 0.9875 0.0372474273481 7 0.9915 0.0268400314089 0.9864 0.0425423202775 8 0.993316666667 0.0220682303396 0.9872 0.0392856988624 9 0.994633333333 0.0180485538536 0.9879 0.0378849975895 10 0.995483333333 0.0150215339979 0.9885 0.0400400907118 11 0.995866666667 0.0133006690729 0.9889 0.0371786578452 12 0.996966666667 0.0106675351944 0.9878 0.0431819648487 13 0.9973 0.00950805570707 0.9894 0.0378315592841 14 0.998016666667 0.00741429101193 0.9875 0.0425102406285 15 0.9985 0.00618680262641 0.9897 0.0383318882663 16 0.998616666667 0.00543502302013 0.9898 0.0382562129824 17 0.999133333333 0.00435419902991 0.9879 0.0414861122906 18 0.999016666667 0.00405959291219 0.9898 0.0413239474756 19 0.999483333333 0.00290562351368 0.9897 0.0397207654605 20 0.9997 0.00210381824759 0.9896 0.04057246413 21 0.999616666667 0.00204826697134 0.9901 0.0424649254543 22 0.999783333333 0.00167668925789 0.9902 0.0418876835005 23 0.99985 0.0013869041977 0.9894 0.0415403854871 24 0.999766666667 0.0014446994155 0.9904 0.040863073686 25 0.999883333333 0.00103046478336 0.9903 0.0407925786511 26 0.999883333333 0.0010185068358 0.9901 0.0427330248162 27 0.9999 0.000865082113849 0.9897 0.0431897308844 28 0.999916666667 0.000680996876102 0.9897 0.0426519497202 29 0.999966666667 0.000537026205558 0.9899 0.0422285960568 30 0.999983333333 0.000458706804451 0.9901 0.0433974335546 所要時間 = 38 分 19 秒なんと、テストデータの正解率は、99%を超えました。
ただし、学習には、38分もかかりました。
時間はかかりましたが、CNNを利用することで、大幅に精度が向上しました。参考
関数仕様
畳み込み関連の関数を追加しました。
# 層追加関数 model = add_layer(model, name, func, d=None, **kwargs) # 引数 # model : モデル # name : レイヤの名前 # func : 中間層の関数 # affine,sigmoid,tanh,relu,leaky_relu,prelu,rrelu,relun,srelu,elu,maxout, # identity,softplus,softsign,step,dropout,batch_normalization, # convolution2d,max_pooling2d,average_pooling2d,flatten2d # d : ノード数 # affine,maxout,convolution2dの場合指定 # convolution2dの場合は、フィルタ数 # kwargs: 中間層の関数のパラメータ # affine - weight_init_func=he_normal, weight_init_params={}, bias_init_func=zeros_b, bias_init_params={} # weight_init_func - lecun_normal,lecun_uniform,glorot_normal,glorot_uniform,he_normal,he_uniform,normal_w,uniform_w,zeros_w,ones_w # weight_init_params # normal_w - mean=0, var=1 # uniform_w - min=0, max=1 # bias_init_func - normal_b,uniform_b,zeros_b,ones_b # bias_init_params # normal_b - mean=0, var=1 # uniform_b - min=0, max=1 # leaky_relu - alpha # rrelu - min=0.0, max=0.1 # relun - n # srelu - alpha # elu - alpha # maxout - unit=1, weight_init_func=he_normal, weight_init_params={}, bias_init_func=zeros_b, bias_init_params={} # dropout - dropout_ratio=0.9 # batch_normalization - batch_norm_node=True, use_gamma_beta=True, use_train_stats=True, alpha=0.1 # convolution2d - padding=0, strides=1, weight_init_func=he_normal, weight_init_params={}, bias_init_func=zeros_b, bias_init_params={} # max_pooling2d - pool_size=2, padding=0, strides=None # average_pooling2d - pool_size=2, padding=0, strides=None # 戻り値 # モデルプログラム
「ディープラーニングを実装から学ぶ(8)実装変更」の追加分です。
基本的には、上で記述した通りですが、一部効率化のため見直しをしています。# 畳み込み def convolution2d(u, W, b, padding=0, strides=1): # パディング if type(padding) == int: padding_h, padding_w = padding, padding else: padding_h, padding_w = padding # ストライド if type(strides) == int: strides_h, strides_w = strides, strides else: strides_h, strides_w = strides # 画像の数、高さ、幅、チャネル un, uh, uw, uc = u.shape # フィルタの数、高さ、幅、チャネル fn, fh, fw, fc = W.shape # パディング後の高さ、幅 ph, pw = uh + padding_h*2, uw + padding_w*2 # パディング pu = np.zeros((un, ph, pw, uc)) pu[:, padding_h:padding_h+uh, padding_w:padding_w+uw, :] = u # 畳み込み後の高さ、幅 zh, zw = int((ph-fh)/strides_h)+1, int((pw-fw)/strides_w)+1 # 畳み込み後の格納領域確保 z = np.zeros((un, zh, zw, fn)) # Wを事前にreshape&転置 # (fn, fh, fw, fc) => (fh*fw*fc, fn) Wrt = W.reshape(fn, fh*fw*fc).T # 畳み込み後の高さ、幅分ループ for i in range(zh): for j in range(zw): # 画像からフィルタサイズ分切り出し # ud - (un, fh, fw, uc) ud = pu[:, i*strides_h:i*strides_h+fh, j*strides_w:j*strides_w+fw, :] # 切り出した画像とフィルタの内積の計算 # (un, fh*fw*fc) @ (fh*fw*fx, fn) => (un, fn) z[:, i, j, :] = np.dot(ud.reshape(un, fh*fw*fc), Wrt) + b return z def convolution2d_back(dz, u, W, b, padding=0, strides=1, calc_du_flag=True): # パディング if type(padding) == int: padding_h, padding_w = padding, padding else: padding_h, padding_w = padding # ストライド if type(strides) == int: strides_h, strides_w = strides, strides else: strides_h, strides_w = strides # 画像の数、高さ、幅、チャネル un, uh, uw, uc = u.shape # フィルターの数、高さ、幅、チャネル fn, fh, fw, fc = W.shape # パディング後の高さ、幅 ph, pw = uh + padding_h*2, uw + padding_w*2 # パディング pu = np.zeros((un, ph, pw, uc)) pu[:, padding_h:padding_h+uh, padding_w:padding_w+uw, :] = u # 畳み込み後の高さ、幅 zh, zw = int((ph-fh)/strides_h)+1, int((pw-fw)/strides_w)+1 # 勾配格納領域確保 dpu = np.zeros((un, ph, pw, uc)) dW = np.zeros((fn, fh, fw, fc)) # Wを事前にreshape # (fn, fh, fw, fc) => (fn, fh*fw*fc) Wr = W.reshape(fn, fh*fw*fc) # (fn, fh, fw, fc) => (fn, fh*fw*fc) dWr = dW.reshape(fn, fh*fw*fc) # 畳み込み後の高さ、幅分ループ for i in range(zh): for j in range(zw): # dzijの取り出し # dzs - (un, fn) dzs = dz[:,i,j,:] if calc_du_flag: # u方向の勾配計算 # dpusr - (un,fn) @ (fn, fh*fw*fc) => (un, fh*fw*fc) dpusr = np.dot(dzs, Wr) # dpus - (un, fh, fw, uc) dpus = dpusr.reshape(un, fh, fw, uc) dpu[:, i*strides_h:i*strides_h+fh, j*strides_w:j*strides_w+fw, :] += dpus # W方向の勾配計算 # pus - (un, fh*fw*uc) pus = pu[:, i*strides_h:i*strides_h+fh, j*strides_w:j*strides_w+fw, :] # pudr - (un, fh*fw*uc) pusr = pus.reshape(un, fh*fw*uc) # dWsr - (fn, un) @ (un, fh*fw*uc) => (fn, fh*fw*uc=fc) dWsr = np.dot(dzs.T, pusr) dWr += dWsr # (fn, fh*fw*fc) => (fn, fh, fw, fc) dW = dWr.reshape(fn, fh, fw, fc) # パディング部分の除去 du = dpu[:, padding_h:padding_h+uh, padding_w:padding_w+uw, :] # b方向の勾配計算 db = np.sum(dz.reshape(un*zh*zw, fn), axis=0) return du, dW, db def max_pooling2d(u, pool_size=2, padding=0, strides=None): # ストライド設定 if strides is None: strides = pool_size # プールサイズ if type(pool_size) == int: pool_size_h, pool_size_w = pool_size, pool_size else: pool_size_h, pool_size_w = pool_size # パディング if type(padding) == int: padding_h, padding_w = padding, padding else: padding_h, padding_w = padding # ストライド if type(strides) == int: strides_h, strides_w = strides, strides else: strides_h, strides_w = strides # 画像の数、高さ、幅、チャネル un, uh, uw, uc = u.shape # パディング後の高さ、幅 ph, pw = uh + padding_h*2, uw + padding_w*2 # パディング pu = np.zeros((un, ph, pw, uc)) pu[:, padding_h:padding_h+uh, padding_w:padding_w+uw, :] = u # プーリング後の高さ、幅 zh, zw = int((ph-pool_size_h)/strides_h)+1, int((pw-pool_size_w)/strides_w)+1 # プーリング後の格納領域確保 z = np.zeros((un, zh, zw, uc)) # プーリング後の高さ、幅分ループ for i in range(zh): for j in range(zw): # 画像からプーリングサイズ分切り出し # pus - (un, pool_size_h, pool_size_w, uc) pus = pu[:, i*strides_h:i*strides_h+pool_size_h, j*strides_w:j*strides_w+pool_size_w, :] # 切り出した画像の最大 z[:, i, j, :] = np.max(pus.reshape(un, pool_size_h*pool_size_w, uc), axis=1) return z def max_pooling2d_back(dz, u, z, pool_size=2, padding=0, strides=None): # ストライド設定 if strides is None: strides = pool_size # プールサイズ if type(pool_size) == int: pool_size_h, pool_size_w = pool_size, pool_size else: pool_size_h, pool_size_w = pool_size # パディング if type(padding) == int: padding_h, padding_w = padding, padding else: padding_h, padding_w = padding # ストライド if type(strides) == int: strides_h, strides_w = strides, strides else: strides_h, strides_w = strides # 画像の数、高さ、幅、チャネル un, uh, uw, uc = u.shape # パディング後の高さ、幅 ph, pw = uh + padding_h*2, uw + padding_w*2 # パディング pu = np.zeros((un, ph, pw, uc)) pu[:, padding_h:padding_h+uh, padding_w:padding_w+uw, :] = u # プーリング後のデータ格納用 zh, zw = int((ph-pool_size_h)/strides_h)+1, int((pw-pool_size_w)/strides_w)+1 # 勾配格納領域確保 dpu = np.zeros((un, ph, pw, uc)) # プーリング後の高さ、幅分ループ for i in range(zh): for j in range(zw): # dzijの取り出し # dzs - (un, fn) dzs = dz[:,i,j,:] # 最大の要素 pus = pu[:, i*strides_h:i*strides_h+pool_size_h, j*strides_w:j*strides_w+pool_size_w, :] # 順番並び替え pustr = pus.transpose(0, 3, 1, 2) # 最大の要素 z_argmax = np.argmax(pustr.reshape(un*uc, pool_size_h*pool_size_w), axis=1) # 勾配格納 dudrtr = np.zeros((un*uc, pool_size_h*pool_size_w)) dudrtr[np.arange(un*uc), z_argmax.ravel()] = dzs.ravel() dudtr = dudrtr.reshape(un, uc, pool_size_h, pool_size_w) # 順番元に戻す dud = dudtr.transpose(0, 2, 3, 1) # 勾配設定 dpu[:, i*strides_h:i*strides_h+pool_size_h, j*strides_w:j*strides_w+pool_size_w, :] += dud du = dpu[:, padding_h:padding_h+uh, padding_w:padding_w+uw, :] return du def average_pooling2d(u, pool_size=2, padding=0, strides=None): # ストライド設定 if strides is None: strides = pool_size # プールサイズ if type(pool_size) == int: pool_size_h, pool_size_w = pool_size, pool_size else: pool_size_h, pool_size_w = pool_size # パディング if type(padding) == int: padding_h, padding_w = padding, padding else: padding_h, padding_w = padding # ストライド if type(strides) == int: strides_h, strides_w = strides, strides else: strides_h, strides_w = strides # 画像の数、高さ、幅、チャネル un, uh, uw, uc = u.shape # パディング後の高さ、幅 ph, pw = uh + padding_h*2, uw + padding_w*2 # パディング pu = np.zeros((un, ph, pw, uc)) pu[:, padding_h:padding_h+uh, padding_w:padding_w+uw, :] = u # プーリング後の高さ、幅 zh, zw = int((ph-pool_size_h)/strides_h)+1, int((pw-pool_size_w)/strides_w)+1 # プーリング後の格納領域確保 z = np.zeros((un, zh, zw, uc)) # プーリング後の高さ、幅分ループ for i in range(zh): for j in range(zw): # 画像からプーリングサイズ分切り出し # pus - (un, pool_size_h, pool_size_w, uc) pus = pu[:, i*strides_h:i*strides_h+pool_size_h, j*strides_w:j*strides_w+pool_size_w, :] # 切り出した画像の平均 z[:, i, j, :] = np.mean(pus.reshape(un, pool_size_h*pool_size_w, uc), axis=1) return z def average_pooling2d_back(dz, u, z, pool_size=2, padding=0, strides=None): # ストライド設定 if strides is None: strides = pool_size # プールサイズ if type(pool_size) == int: pool_size_h, pool_size_w = pool_size, pool_size else: pool_size_h, pool_size_w = pool_size # パディング if type(padding) == int: padding_h, padding_w = padding, padding else: padding_h, padding_w = padding # ストライド if type(strides) == int: strides_h, strides_w = strides, strides else: strides_h, strides_w = strides # 画像の数、高さ、幅、チャネル un, uh, uw, uc = u.shape # パディング後の高さ、幅 ph, pw = uh + padding_h*2, uw + padding_w*2 # パディング pu = np.zeros((un, ph, pw, uc)) pu[:, padding_h:padding_h+uh, padding_w:padding_w+uw, :] = u # プーリング後のデータ格納用 zh, zw = int((ph-pool_size_h)/strides_h)+1, int((pw-pool_size_w)/strides_w)+1 # 勾配格納領域確保 dpu = np.zeros((un, ph, pw, uc)) # プーリング後の高さ、幅分ループ for i in range(zh): for j in range(zw): # dzijをプールサイズで割る # dzs - (un, uc) dzs = dz[:,i,j,:]/(pool_size_h*pool_size_w) dzs = dzs.reshape(un, 1, 1, uc) # プールサイズの高さ、幅分ループ for k in range(pool_size_h): for l in range(pool_size_w): # 勾配設定 dpu[:, i*strides_h+k:i*strides_h+k+1, j*strides_w+l:j*strides_w+l+1, :] += dzs # パディング部分の除去 du = dpu[:, padding_h:padding_h+uh, padding_w:padding_w+uw, :] return du def flatten2d(u): # 画像の数、高さ、幅、チャネル un, uh, uw, uc = u.shape z = u.reshape(un, uh*uw*uc) return z def flatten2d_back(dz, u, z): du = dz.reshape(u.shape) return du# convolution2d def convolution2d_init_layer(d_prev, d, filter_size=2, padding=0, strides=1, weight_init_func=he_normal, weight_init_params={}, bias_init_func=zeros_b, bias_init_params={}): # フィルタサイズ if type(filter_size) == int: filter_size_h, filter_size_w = filter_size, filter_size else: filter_size_h, filter_size_w = filter_size # パディング if type(padding) == int: padding_h, padding_w = padding, padding else: padding_h, padding_w = padding # ストライド if type(strides) == int: strides_h, strides_w = strides, strides else: strides_h, strides_w = strides # 画像の高さ、幅、チャネル uh, uw, uc = d_prev # フィルターの数、高さ、幅、チャネル fn, fh, fw, fc = d, filter_size_h, filter_size_w, d_prev[2] # パディング後の高さ、幅 ph, pw = uh + padding_h*2, uw + padding_w*2 # 畳み込み後のデータ格納用 zh, zw = int((ph-fh)/strides_h)+1, int((pw-fw)/strides_w)+1 d_next = (zh, zw, fn) # W - fn, fh, fw, fc #fn, fh, fw, fc = d, filter_size_h, filter_size_w, d_prev.shape[2] W = weight_init_func(fh*fw*fc, fn, **weight_init_params) W = W.reshape((fn, fh, fw, fc)) b = bias_init_func(fn, **bias_init_params) return d_next, {"W":W, "b":b, "padding":padding, "strides":strides} def convolution2d_init_optimizer(): sW = {} sb = {} return {"sW":sW, "sb":sb} def convolution2d_propagation(func, u, weights, weight_decay, learn_flag, **params): z = func(u, weights["W"], weights["b"], padding=weights["padding"], strides=weights["strides"]) # 重み減衰対応 weight_decay_r = 0 if weight_decay is not None: weight_decay_r = weight_decay["func"](weights["W"], **weight_decay["params"]) return {"u":u, "z":z}, weight_decay_r def convolution2d_back_propagation(back_func, dz, us, weights, weight_decay, calc_du_flag, **params): du, dW, db = back_func(dz, us["u"], weights["W"], weights["b"], padding=weights["padding"], strides=weights["strides"], calc_du_flag=calc_du_flag) # 重み減衰対応 if weight_decay is not None: dW = dW + weight_decay["back_func"](weights["W"], **weight_decay["params"]) return {"du":du, "dW":dW, "db":db} def convolution2d_update_weight(func, du, weights, optimizer_stats, **params): weights["W"], optimizer_stats["sW"] = func(weights["W"], du["dW"], **params, **optimizer_stats["sW"]) weights["b"], optimizer_stats["sb"] = func(weights["b"], du["db"], **params, **optimizer_stats["sb"]) return weights, optimizer_stats # max_pooling2d def max_pooling2d_init_layer(d_prev, d, pool_size=2, padding=0, strides=None): # ストライド設定 if strides is None: strides = pool_size # プールサイズ if type(pool_size) == int: pool_size_h, pool_size_w = pool_size, pool_size else: pool_size_h, pool_size_w = pool_size # パディング if type(padding) == int: padding_h, padding_w = padding, padding else: padding_h, padding_w = padding # ストライド if type(strides) == int: strides_h, strides_w = strides, strides else: strides_h, strides_w = strides # 画像の高さ、幅、チャネル uh, uw, uc = d_prev # パディング後の高さ、幅 ph, pw = uh + padding_h*2, uw + padding_w*2 # プーリング後のデータ格納用 zh, zw = int((ph-pool_size_h)/strides_h)+1, int((pw-pool_size_w)/strides_w)+1 d_next = (zh, zw, uc) return d_next, {} # average_pooling2d def average_pooling2d_init_layer(d_prev, d, pool_size=2, padding=0, strides=None): # ストライド設定 if strides is None: strides = pool_size # プールサイズ if type(pool_size) == int: pool_size_h, pool_size_w = pool_size, pool_size else: pool_size_h, pool_size_w = pool_size # パディング if type(padding) == int: padding_h, padding_w = padding, padding else: padding_h, padding_w = padding # ストライド if type(strides) == int: strides_h, strides_w = strides, strides else: strides_h, strides_w = strides # 画像の高さ、幅、チャネル uh, uw, uc = d_prev # パディング後の高さ、幅 ph, pw = uh + padding_h*2, uw + padding_w*2 # プーリング後のデータ格納用 zh, zw = int((ph-pool_size_h)/strides_h)+1, int((pw-pool_size_w)/strides_w)+1 d_next = (zh, zw, uc) return d_next, {} # flatten2d def flatten2d_init_layer(d_prev, d): d_next = d_prev[0]*d_prev[1]*d_prev[2] return d_next, {}
- 投稿日:2019-02-11T18:00:08+09:00
StyleGAN 「写真が証拠になる時代は終わった」
StyleGAN
スタイル変換の技術を基にGeneratorのアーキテクチャを設計し直したことで
画像合成の過程をコントロールすることができるようになった
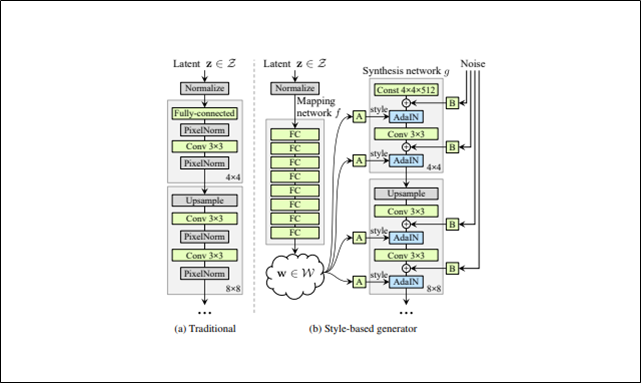
Style-based generator
StyleGANのGenerator
図のAはアフィン変換、Bは足し合わせができるようにノイズのチャンネル変換を行うことを意味する構成
Style-based generatorではこれまでのような入力層をまるごとなくして全結合層を連ねたものにする
Mapping network fは8層で構成されSynthesis network gは18層で構成されている流れ(上図の矢印を追う)
Mapping network fで入力である潜在変数zを一度潜在空間Wにマッピングする。
潜在変数wはアフィン変換されることでスタイルyになる
スタイルyは各convolution層後でのAdaIn処理で使われ、Generatorをコントロールする。
ガウシアンノイズをAdaInと各convolution層の間に加える。
最終層の出力は1×1のconvolution層を使ってRGBに変換する
解像度は4×4で始まり、最終的に1024×1024
Style-based generatorの合計パラメーター数は26.2M
従来のGeneratorの合計パラメーター数は23.1Mこれまでの改良の流れ
様々な改良をすることで画像のクオリティを上げてきた
評価指標はFID
FIDはGANの生成分布と真のデータ分布の距離を表す指標
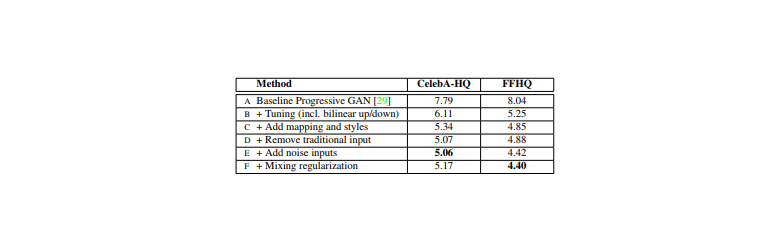
数値は低いほど良いことを意味する(A)
ベースラインとして設定したのはProgressive GAN
ネットワークとハイパーパラメーターの変更はしておらず、提案されたままを使った(B)
ベースラインの改良として、bilinear up/downsamplingとハイパーパラメーターチューニングをした(C)
更にベースラインの改良として、マッピングネットワークとAdaIN処理を加えた
この時点で、従来通り最初のconvolution層に潜在変数を与えるネットワークでは改善の余地がないという見解に至った(D)
これまでの入力層を取り除き4×4×512のconstant tensorで画像生成を始めるというシンプルなアーキテクチャにしたsynthesis network(Generator)は
AdaINをコントロールするスタイルのみの入力で素晴らしい生成ができることがわかった(E)
ノイズを入れることで更に改善(F)
mixing regularizationを導入により
隣接したスタイルの相互関係をなくし、より洗練された画像を生成することができるStyle mixing
スタイルを細部にも適用できるようにmixing regularizationを導入する
訓練時、画像の指定範囲分(%)の生成を
1つのランダム潜在変数ではなく2つのランダム潜在変数を使ってすること
テスト時は下記結果表が示すように3つ以上でも実行されているSynthesis networkのランダムに選ばれたところで潜在変数を他のものに切り替える(これをstyle mixingと呼ぶ)
具体的には、Mapping networkではz1とz2という2つの潜在変数を実行する
Synthesis networkではw1を適用して、その後ランダムに選ばれたところからw2を適用するこの正則化手法により、隣り合ったスタイルは相互に関連しているということをネットワークが仮定せずに生成することができる
テスト結果
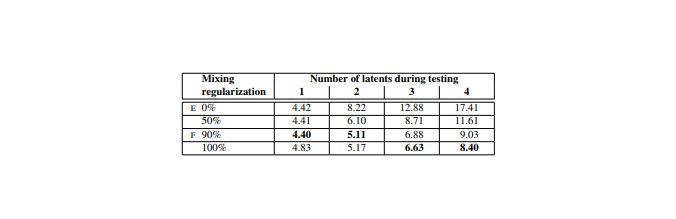
潜在変数の数(Number of latents during testing)と潜在変数を混ぜて生成する比率(Mixing regularization)を変えて結果を表にして示している
評価指標はFID
FIDはGANの生成分布と真のデータ分布の距離を表す指標
数値は低い方が良い結果表のE,Fは最初に見た表のE,Fと対応している
Mixing regularizationの比率を大きくすることで結果が良くなっているのがわかる
2つの潜在変数を混ぜて生成された画像
1つの潜在変数で生成されたスタイル(source)に、同じく1つの潜在変数から生成されたスタイル(destination)を合わせると画像はどのように変化していくのかを可視化している・解像度が粗い段階で合わせた場合(4×4 ~ 8×8)
顔の向き・髪型・顔の形・眼鏡のような大まかな特徴はsourceの要素が画像で表現されている一方で、目・髪・明暗のような色や顔の特徴はdestinationの要素が表現されている・解像度(16×16 ~ 32×32)の場合
顔の特徴・髪型・目の特徴がsourceの要素で
顔の向きや顔の形や眼鏡がdestinationの要素で構成されている・高解像度(64×64 ~ 1024×1024)の場合
配色や細部のデザインはsource由来になっているノイズの効果
・確率的特徴
正しい分布に従って生成されていれば、ランダムに生成しても画像の見た目に大きな影響を与えない特徴
例)髪質や髪の流れ、ヒゲ、そばかす、肌質従来のジェネレーターが確率的特徴を生成する場合、
入力層への入力のみになるため、ネットワークは必要となったら以前のアクティベーションから
空間的に変化する疑似乱数を生成しなくてはならないこれはネットワーク容量を消費し、周期性がなく本当にランダムな乱数を生成することは困難で成功する保証はない
本研究のアーキテクチャでは各convolution層の後に、ピクセルごとのノイズを加えることでこれらの問題を解決する
例1
上図はベースとなる生成画像は同じでノイズだけを変えた場合の結果である
ノイズは確率的特徴(毛の流れ)だけを変化させて、その他の高レベルな特徴(顔の特徴や向きなど)はそのままである
上図右の白黒の画像はどこがノイズの影響を受けているかを表している
白い部分がノイズの影響を受けている部分ほとんどが髪の毛、輪郭、背景だが、目の反射も白くなっているのは興味深い点
例2
この図もノイズがどのように生成画像を変化させるかについてである
男性の生成画像も同じように(a)(b)(c)(d)で分割して見てほしい(a)すべての層でノイズを加えた場合
(b)ノイズを全く加えない場合
(c)ノイズを解像度がきれいな層(64×64 ~ 1024×1024)でのみノイズを加える場合
(d)ノイズを解像度が粗い層(4×4 ~ 32×32)でのみノイズを加える場合(a)と(b)を比較するとわかるが、
ノイズを加えないことで特徴のない絵画っぽい(リアルではない)画像が生成される(d)ノイズを解像度が粗い層(4×4 ~ 32×32)でのみノイズを加える場合、
髪の毛のカールが大きくなっていたり、背景の特徴が大きく表現されている(c)ノイズを解像度がきれいな層(64×64 ~ 1024×1024)でのみノイズを加える場合、
髪の毛のカール、背景、肌質が細かくきれいに描かれていているスタイルとノイズのまとめ
スタイルを変化させることは全体的な影響(姿勢、向き、顔の特徴を変える)を与えるのに対して、
ノイズはそこまで重要ではない部分(髪の毛の流れやヒゲ)に影響を与えるスタイルが画像全体に影響を与えるのはすべての特徴マップが同じ値でスケール変換、バイアス変換されるからである(AdaIn処理)
そのため、画像全体への影響(姿勢、明暗、背景)は一貫してコントロールされる一方ノイズは独立的にピクセルごとに加えられ、確率的な変化をコントロールするには理想的である
もし生成画像の姿勢を変えたいときにノイズの使ってしまったら、
矛盾した選択でありDiscriminatorに見破られてしまうネットワークは明確な指示がなくても、適切にスタイルとノイズを使えるように学習する
潜在空間Wの必要性
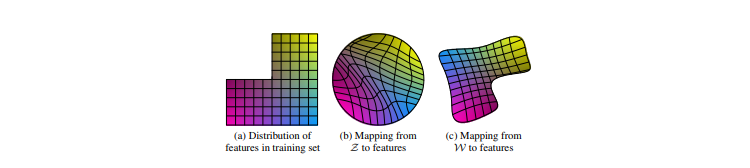
(a)訓練データの特徴分布
長い髪の男性など一部の組み合わせが存在しない訓練データ(b)Zから特徴表現へのマッピング(従来のやり方)
訓練データになかった組み合わせ(長い髪の男性)がサンプリングされないようにするため
Zから画像特徴へのマッピングは曲線になる(c)Wから特徴表現へのマッピング(本研究)
ZからWへのマッピングは学習されたマッピングであるため、このゆがみを元に戻すことができる仮定
特徴が絡み合っている表現に基づいてリアルな画像を生成するよりも、
それぞれの特徴がしっかり分解されている表現に基づいてリアルな画像を生成する方が容易であるはず例)人の顔を生成したいとき
・特徴が絡み合っている
→この軸を調整すると、目が大きくなって髪が長くなって輪郭が丸くなるみたいになると
各軸が複雑に影響し合って生成しづらい・特徴がしっかり分解されている
→この軸は目の大きさ、この軸は髪の長さ、この軸は輪郭みたいに特徴が独立していると
生成がしやすい目標
線形部分空間(それぞれの線形部分空間が1つの変動要因をコントロールする)を用意する
変動要因が事前にわかっていない状況の中で、学習によって可能な限り特徴が分解されたWができることが理想問題
ただし、従来のGANのようなアーキテクチャでは
Z内の各要因の組み合わせのサンプリング確率は、学習データ内の対応する密度と一致する必要がある
そのため、各要因がデータセットの分布と入力潜在分布から完全に分解することができない対策
本研究のGeneratorが優れている点は
中間潜在空間Wは任意の固定分布に従ってサンプリングする必要がないことWのサンプリング密度は学習された区分的連続写像f(z)(線形変換である全結合層を8つ重ねて計算する)によってできたものを使う
このマッピングによって、変動要因はより線形になりゆがみのない潜在空間Wができる
指標
「特徴が分解されている」ということを定量化するための指標が最近提案されたのだが、
残念なことにその指標を使うには入力画像を潜在変数にマッピングするエンコーダーがなくてはならない
本研究ではそういったエンコーダーは使っていないため適した指標とは言えない
そのためにエンコーダーをわざわざ追加することもできるが、根本的解決にはならないのでやらないその代りに新しい定量化手法を2つ提案する
その指標の場合はエンコーダーを必要とせず、変動要因を事前に知らなくていいため
どんな画像データセットやGeneratorでも問題ない新指標1:Perceptual path length
潜在空間のinterpolation(上図)をすると両端の画像(①や⑨)にはない特徴が中間の画像(④、⑤、⑥)に現れるという非線形な変化が起こることがある
これは潜在空間が絡み合っていて変動要因が適切に分離されていないことを示す潜在空間でinterpolationをしたときに、どれだけ急激に画像が変化するかを測ることでこの効果を定量化することができる
直感的には、曲りの大きい曲線の潜在空間よりも曲りの少ない曲線の潜在空間の方が画像がなめらかに変化していくと考えられる
方法
2枚の画像の距離を測定する
この計算はVGG16のembeddingで計算されるため、人間が2枚の画像を見たときに感じる画像の類似性と一致するようになっている定義上は潜在空間のinterpolation pathを線形セグメントに無限に細分化した状況で計測することになっているが、
実際にはepsilon(10のマイナス4乗)を用いて近似計算する潜在空間Zの取り得るすべての両端(①や⑨)の平均距離(perceptual path length)の定義は以下のようになる
G・・・Generator
D・・・画像間の距離を計測
slerp・・・標準化された入力潜在空間のinterpolationに最も適した球状interpolation
潜在空間Wの場合は以下のようになる
Wのベクトルは標準化されていないため線形interpolation(lerp)
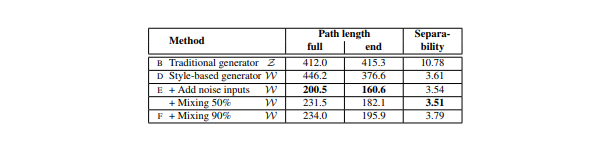
結果1
・ノイズありのStyle-based generator(本研究のgenerator)が最もpath lengthが短くなった
これはWがZよりも知覚的に線形であることを意味している・Style mixingができるようなネットワークにすると中間潜在空間Wを多少ゆがませてしまうようだ
・Style mixingによって、Wが複数のスケールにわたる変動要因をエンコードすることを困難にしていると仮定できる結果2
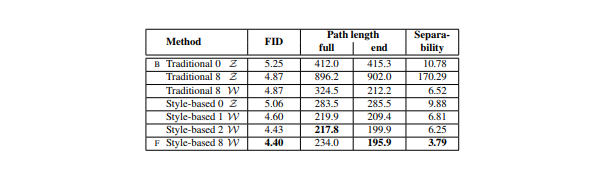
Path lengthがマッピングネットワークからどのように影響を受けているかを示している従来のGeneratorでも本研究のstyle-based generatorでもマッピングネットワークを持つことは有益である
深さを増すこともほとんどのPath lengthとFIDで良い結果につながっている従来のGeneratorのlwは向上しているのに対し、lzは悪化している点を見ると
これまでの様々なGANモデルの入力潜在空間が無作為に絡み合っていることがわかる新指標2:Linear separability
潜在空間が十分に分解されていれば、個々の変動要因に対応した方向ベクトルを見つけることができるはず
この効果を定量化する指標がLinear separability
どれだけ上手に潜在空間の点を線形超平面で2つに分けられるかを計測する
分けられた2つはそれぞれ、画像のバイナリ属性に対応する(例:片方は男性、もう片方は女性)方法
①生成画像にラベルを付けるために、画像の二値分類(男性と女性の顔を見分ける)ができる補助ネットワーク(Discriminatorと同じアーキテクチャ)を訓練する
②訓練データはCelebA-Hデータセット(元のCelebAデータセットの中の40属性を保持するデータセット)
属性の分離度を測るために20万枚の画像を生成し補助ネットワークを使って分類する
分類器のスコアが高い10万枚だけをラベル付きの潜在空間ベクトルとする③各属性について、潜在空間点(従来の場合はz, style-basedではw)に基づいたラベルを予測するために線形SVMで学習する
④超平面がどれほど正確に点を分類できたかを条件付きエントロピーH(Y|X)で計算する
X・・・SVMで予測したクラス
Y・・・補助ネットワークが決めたクラス条件付きエントロピーは正しいクラス分類をするために、どれほど追加情報が必要かを示している
もし変動要因が矛盾した潜在空間の方向を持っていたら、サンプル点を超平面でわけるのは一層難しいため
条件付きエントロピーは高い数値になる低い数値になるということは簡単に分けられたということを示す
すなわち属性が対応する要因と潜在空間の方向が一致したことを意味する潜在空間Wについてのまとめ
・結果1と結果2からWはZよりも分離しやすい(表現が絡み合っていない)ことがわかる
・マッピングネットワークの深さを増すことは画質とWの分離性を向上させる
これは合成ネットワーク(Synthesis network)がもつれを解消した入力表現を好むという仮説と一致している・従来のジェネレータの前にマッピングネットワークを追加するとZの分離性が大幅に失われるが、中間潜在空間Wの状況は改善されFIDの結果も良くなる
これは訓練データの分布に従わなくてよい中間潜在空間を導入すると、従来のジェネレータアーキテクチャでもパフォーマンスが向上することを示している全体まとめ
・従来のGANアーキテクチャは様々な点でStyleGANよりも劣っていることが明らかになった
・高レベルの属性(スタイル)と確率的効果(ノイズ)の分離、中間潜在空間の線形性に対する調査が
StyleGANの理解を深める上で有益であると確信している・Path length指標とLinear separability指標が訓練時の正則化として容易に使えることも示した
・訓練時に直接、中間潜在空間を形成する方法が今後の研究のキーになっていくと考えている
FFHQデータセット
FlickrFaces-HQ (FFHQ)という顔画像のデータセットを提供する
・70000枚
・解像度:1024×1024
・データセットは年齢・民族・視点・明暗・画像の背景に関して多様な種類がある
・眼鏡・サングラス・帽子などを身に着けた画像も十分に用意されている論文
画像引用
https://users.aalto.fi/~laines9/publications/laine2018iclr_paper.pdf
- 投稿日:2019-02-11T18:00:08+09:00
StyleGAN「写真が証拠になる時代は終わった。」
StyleGAN
スタイル変換の技術を基にGeneratorのアーキテクチャを設計し直したことで
画像合成の過程をコントロールすることができるようになった
Style-based generator
StyleGANのGenerator
図のAはアフィン変換、Bは足し合わせができるようにノイズのチャンネル変換を行うことを意味する構成
Style-based generatorではこれまでのような入力層をまるごとなくして全結合層を連ねたものにする
Mapping network fは8層で構成されSynthesis network gは18層で構成されている流れ(上図の矢印を追う)
Mapping network fで入力である潜在変数zを一度潜在空間Wにマッピングする。
潜在変数wはアフィン変換されることでスタイルyになる
スタイルyは各convolution層後でのAdaIn処理で使われ、Generatorをコントロールする。
ガウシアンノイズをAdaInと各convolution層の間に加える。
最終層の出力は1×1のconvolution層を使ってRGBに変換する
解像度は4×4で始まり、最終的に1024×1024
Style-based generatorの合計パラメーター数は26.2M
従来のGeneratorの合計パラメーター数は23.1Mこれまでの改良の流れ
様々な改良をすることで画像のクオリティを上げてきた
評価指標はFID
FIDはGANの生成分布と真のデータ分布の距離を表す指標
数値は低いほど良いことを意味する(A)
ベースラインとして設定したのはProgressive GAN
ネットワークとハイパーパラメーターの変更はしておらず、提案されたままを使った(B)
ベースラインの改良として、bilinear up/downsamplingとハイパーパラメーターチューニングをした(C)
更にベースラインの改良として、マッピングネットワークとAdaIN処理を加えた
この時点で、従来通り最初のconvolution層に潜在変数を与えるネットワークでは改善の余地がないという見解に至った(D)
これまでの入力層を取り除き4×4×512のconstant tensorで画像生成を始めるというシンプルなアーキテクチャにしたsynthesis network(Generator)は
AdaINをコントロールするスタイルのみの入力で素晴らしい生成ができることがわかった(E)
ノイズを入れることで更に改善(F)
mixing regularizationを導入により
隣接したスタイルの相互関係をなくし、より洗練された画像を生成することができるStyle mixing
スタイルを細部にも適用できるようにmixing regularizationを導入する
訓練時、画像の指定範囲分(%)の生成を
1つのランダム潜在変数ではなく2つのランダム潜在変数を使ってすること
テスト時は下記結果表が示すように3つ以上でも実行されているSynthesis networkのランダムに選ばれたところで潜在変数を他のものに切り替える(これをstyle mixingと呼ぶ)
具体的には、Mapping networkではz1とz2という2つの潜在変数を実行する
Synthesis networkではw1を適用して、その後ランダムに選ばれたところからw2を適用するこの正則化手法により、隣り合ったスタイルは相互に関連しているということをネットワークが仮定せずに生成することができる
テスト結果
潜在変数の数(Number of latents during testing)と潜在変数を混ぜて生成する比率(Mixing regularization)を変えて結果を表にして示している
評価指標はFID
FIDはGANの生成分布と真のデータ分布の距離を表す指標
数値は低い方が良い結果表のE,Fは最初に見た表のE,Fと対応している
Mixing regularizationの比率を大きくすることで結果が良くなっているのがわかる
2つの潜在変数を混ぜて生成された画像
1つの潜在変数で生成されたスタイル(source)に、同じく1つの潜在変数から生成されたスタイル(destination)を合わせると画像はどのように変化していくのかを可視化している・解像度が粗い段階で合わせた場合(4×4 ~ 8×8)
顔の向き・髪型・顔の形・眼鏡のような大まかな特徴はsourceの要素が画像で表現されている一方で、目・髪・明暗のような色や顔の特徴はdestinationの要素が表現されている・解像度(16×16 ~ 32×32)の場合
顔の特徴・髪型・目の特徴がsourceの要素で
顔の向きや顔の形や眼鏡がdestinationの要素で構成されている・高解像度(64×64 ~ 1024×1024)の場合
配色や細部のデザインはsource由来になっているノイズの効果
・確率的特徴
正しい分布に従って生成されていれば、ランダムに生成しても画像の見た目に大きな影響を与えない特徴
例)髪質や髪の流れ、ヒゲ、そばかす、肌質従来のジェネレーターが確率的特徴を生成する場合、
入力層への入力のみになるため、ネットワークは必要となったら以前のアクティベーションから
空間的に変化する疑似乱数を生成しなくてはならないこれはネットワーク容量を消費し、周期性がなく本当にランダムな乱数を生成することは困難で成功する保証はない
本研究のアーキテクチャでは各convolution層の後に、ピクセルごとのノイズを加えることでこれらの問題を解決する
例1
上図はベースとなる生成画像は同じでノイズだけを変えた場合の結果である
ノイズは確率的特徴(毛の流れ)だけを変化させて、その他の高レベルな特徴(顔の特徴や向きなど)はそのままである
上図右の白黒の画像はどこがノイズの影響を受けているかを表している
白い部分がノイズの影響を受けている部分ほとんどが髪の毛、輪郭、背景だが、目の反射も白くなっているのは興味深い点
例2
この図もノイズがどのように生成画像を変化させるかについてである
男性の生成画像も同じように(a)(b)(c)(d)で分割して見てほしい(a)すべての層でノイズを加えた場合
(b)ノイズを全く加えない場合
(c)ノイズを解像度がきれいな層(64×64 ~ 1024×1024)でのみノイズを加える場合
(d)ノイズを解像度が粗い層(4×4 ~ 32×32)でのみノイズを加える場合(a)と(b)を比較するとわかるが、
ノイズを加えないことで特徴のない絵画っぽい(リアルではない)画像が生成される(d)ノイズを解像度が粗い層(4×4 ~ 32×32)でのみノイズを加える場合、
髪の毛のカールが大きくなっていたり、背景の特徴が大きく表現されている(c)ノイズを解像度がきれいな層(64×64 ~ 1024×1024)でのみノイズを加える場合、
髪の毛のカール、背景、肌質が細かくきれいに描かれていているスタイルとノイズのまとめ
スタイルを変化させることは全体的な影響(姿勢、向き、顔の特徴を変える)を与えるのに対して、
ノイズはそこまで重要ではない部分(髪の毛の流れやヒゲ)に影響を与えるスタイルが画像全体に影響を与えるのはすべての特徴マップが同じ値でスケール変換、バイアス変換されるからである(AdaIn処理)
そのため、画像全体への影響(姿勢、明暗、背景)は一貫してコントロールされる一方ノイズは独立的にピクセルごとに加えられ、確率的な変化をコントロールするには理想的である
もし生成画像の姿勢を変えたいときにノイズを使ってしまったら、
矛盾した選択であるためDiscriminatorに見破られてしまうネットワークは明確な指示がなくても、適切にスタイルとノイズを使えるように学習する
潜在空間Wの必要性
(a)訓練データの特徴分布
長い髪の男性など一部の組み合わせが存在しない訓練データ(b)Zから特徴表現へのマッピング(従来のやり方)
訓練データになかった組み合わせ(長い髪の男性)がサンプリングされないようにするため
Zから画像特徴へのマッピングは曲線になる(c)Wから特徴表現へのマッピング(本研究)
ZからWへのマッピングは学習されたマッピングであるため、このゆがみを元に戻すことができる仮定
特徴が絡み合っている表現に基づいてリアルな画像を生成するよりも、
それぞれの特徴がしっかり分解されている表現に基づいてリアルな画像を生成する方が容易であるはず例)人の顔を生成したいとき
・特徴が絡み合っている
→この軸を調整すると、目が大きくなって髪が長くなって輪郭が丸くなるみたいになると
各軸が複雑に影響し合って生成しづらい・特徴がしっかり分解されている
→この軸は目の大きさ、この軸は髪の長さ、この軸は輪郭みたいに特徴が独立していると
生成がしやすい目標
線形部分空間(それぞれの線形部分空間が1つの変動要因をコントロールする)を用意する
変動要因が事前にわかっていない状況の中で、学習によって可能な限り特徴が分解されたWができることが理想問題
ただし、従来のGANのようなアーキテクチャでは
Z内の各要因の組み合わせのサンプリング確率は、学習データ内の対応する密度と一致する必要がある
そのため、各要因がデータセットの分布と入力潜在分布から完全に分解することができない対策
本研究のGeneratorが優れている点は
中間潜在空間Wは任意の固定分布に従ってサンプリングする必要がないことWのサンプリング密度は学習された区分的連続写像f(z)(線形変換である全結合層を8つ重ねて計算する)によってできたものを使う
このマッピングによって、変動要因はより線形になりゆがみのない潜在空間Wができる
指標
「特徴が分解されている」ということを定量化するための指標が最近提案されたのだが、
残念なことにその指標を使うには入力画像を潜在変数にマッピングするエンコーダーがなくてはならない
本研究ではそういったエンコーダーは使っていないため適した指標とは言えない
そのためにエンコーダーをわざわざ追加することもできるが、根本的解決にはならないのでやらないその代りに新しい定量化手法を2つ提案する
その指標の場合はエンコーダーを必要とせず、変動要因を事前に知らなくていいため
どんな画像データセットやGeneratorでも問題ない新指標1:Perceptual path length
潜在空間のinterpolation(上図)をすると両端の画像(①や⑨)にはない特徴が中間の画像(④、⑤、⑥)に現れるという非線形な変化が起こることがある
これは潜在空間が絡み合っていて変動要因が適切に分離されていないことを示す潜在空間でinterpolationをしたときに、どれだけ急激に画像が変化するかを測ることでこの効果を定量化することができる
直感的には、曲りの大きい曲線の潜在空間よりも曲りの少ない曲線の潜在空間の方が画像がなめらかに変化していくと考えられる
方法
2枚の画像の距離を測定する
この計算はVGG16のembeddingで計算されるため、人間が2枚の画像を見たときに感じる画像の類似性と一致するようになっている定義上は潜在空間のinterpolation pathを線形セグメントに無限に細分化した状況で計測することになっているが、
実際にはepsilon(10のマイナス4乗)を用いて近似計算する潜在空間Zの取り得るすべての両端(①や⑨)の平均距離(perceptual path length)の定義は以下のようになる
G・・・Generator
D・・・画像間の距離を計測
slerp・・・標準化された入力潜在空間のinterpolationに最も適した球状interpolation
潜在空間Wの場合は以下のようになる
Wのベクトルは標準化されていないため線形interpolation(lerp)
結果1
・ノイズありのStyle-based generator(本研究のgenerator)が最もpath lengthが短くなった
これはWがZよりも知覚的に線形であることを意味している・Style mixingができるようなネットワークにすると中間潜在空間Wを多少ゆがませてしまうようだ
・Style mixingによって、Wが複数のスケールにわたる変動要因をエンコードすることを困難にしていると仮定できる結果2
Path lengthがマッピングネットワークからどのように影響を受けているかを示している従来のGeneratorでも本研究のstyle-based generatorでもマッピングネットワークを持つことは有益である
深さを増すこともほとんどのPath lengthとFIDで良い結果につながっている従来のGeneratorのlwは向上しているのに対し、lzは悪化している点を見ると
これまでの様々なGANモデルの入力潜在空間が無作為に絡み合っていることがわかる新指標2:Linear separability
潜在空間が十分に分解されていれば、個々の変動要因に対応した方向ベクトルを見つけることができるはず
この効果を定量化する指標がLinear separability
どれだけ上手に潜在空間の点を線形超平面で2つに分けられるかを計測する
分けられた2つはそれぞれ、画像のバイナリ属性に対応する(例:片方は男性、もう片方は女性)方法
①生成画像にラベルを付けるために、画像の二値分類(男性と女性の顔を見分ける)ができる補助ネットワーク(Discriminatorと同じアーキテクチャ)を訓練する
②訓練データはCelebA-Hデータセット(元のCelebAデータセットの中の40属性を保持するデータセット)
属性の分離度を測るために20万枚の画像を生成し補助ネットワークを使って分類する
分類器のスコアが高い10万枚だけをラベル付きの潜在空間ベクトルとする③各属性について、潜在空間点(従来の場合はz, style-basedではw)に基づいたラベルを予測するために線形SVMで学習する
④超平面がどれほど正確に点を分類できたかを条件付きエントロピーH(Y|X)で計算する
X・・・SVMで予測したクラス
Y・・・補助ネットワークが決めたクラス条件付きエントロピーは正しいクラス分類をするために、どれほど追加情報が必要かを示している
もし変動要因が矛盾した潜在空間の方向を持っていたら、サンプル点を超平面でわけるのは一層難しいため
条件付きエントロピーは高い数値になる低い数値になるということは簡単に分けられたということを示す
すなわち属性が対応する要因と潜在空間の方向が一致したことを意味する潜在空間Wのまとめ
・結果1と結果2からWはZよりも分離しやすい(表現が絡み合っていない)ことがわかる
・マッピングネットワークの深さを増すことは画質とWの分離性を向上させる
これは合成ネットワーク(Synthesis network)がもつれを解消した入力表現を好むという仮説と一致している・従来のジェネレータの前にマッピングネットワークを追加するとZの分離性が大幅に失われるが、中間潜在空間Wの状況は改善されFIDの結果も良くなる
これは訓練データの分布に従わなくてよい中間潜在空間を導入すると、従来のジェネレータアーキテクチャでもパフォーマンスが向上することを示している全体まとめ
・従来のGANアーキテクチャは様々な点でStyleGANよりも劣っていることが明らかになった
・高レベルの属性(スタイル)と確率的効果(ノイズ)の分離、中間潜在空間の線形性に対する調査が
StyleGANの理解を深める上で有益であると確信している・Path length指標とLinear separability指標が訓練時の正則化として容易に使えることも示した
・訓練時に直接、中間潜在空間を形成する方法が今後の研究のキーになっていくと考えている
FFHQデータセット
FlickrFaces-HQ (FFHQ)という顔画像のデータセットを提供する
・70000枚
・解像度:1024×1024
・データセットは年齢・民族・視点・明暗・画像の背景に関して多様な種類がある
・眼鏡・サングラス・帽子などを身に着けた画像も十分に用意されている論文
画像引用
https://arxiv.org/abs/1812.04948
https://users.aalto.fi/~laines9/publications/laine2018iclr_paper.pdf
- 投稿日:2019-02-11T16:59:46+09:00
【論文読み】Semi-convolutional Operators for Instance Segmentation
Instance Segmentation のタスクに対する手法を整理・分解し、精度をより向上する
Semi-convolutional operatorsを提案した論文です。この記事は、Wantedlyの勉強会で取り上げられた論文・技術をまとめたものです。
2018年に読んだ機械学習系論文・技術まとめ at Wantedly Advent Calendar 2018 - QiitaReference
- Semi-convolutional Operators for Instance Segmentation [David Novotny, Samuel Albanie, Diane Larlus, and Andrea Vedaldi. ECCV 2018]
- https://arxiv.org/abs/1807.10712
(文中の図表は論文より引用しています)
Instance Segmentation
まずはじめに簡単に Instance Segmentation というタスクと、現在主流とされているアプローチについて述べます。
Instance Segmentation とは、画像の各 Pixel について、 どのクラスに属すか、どのインスタンスに属するか を予測するタスクです。
入力画像を「この領域は人、この領域は車、...」というように色塗りしていくタスクです。Instance Segmentation において重要なのが どのインスタンスに属するか も予測しなければならないという点です。
たとえば人が 3 人で肩を組んでいるような画像の場合、どこからどこまでが 1 人目かを予測しなければなりません。
一方、インスタンスを考慮せず色塗りをしていくようなタスクを Semantic Segmentation といいます。Semantic Segmentation の場合は、入力画像の各 Pixel について多クラス分類を行えば Segmentation の完成になります。
Instance Segmentation ではそれに加えて個々のインスタンスを区別するような仕組みが必要になります。propose & verify
Instance Segmentation タスクへのアプローチとして、現在主流とされているのは Mask R-CNN 1 に代表される Region based な手法です。
(Mask R-CNN は FAIR から出ている論文で、 OSS として公開されている Detectron に実装が含まれています。 https://github.com/facebookresearch/Detectron )Mask R-CNN は、物体のクラスと bounding box だけを予測する Object Detection タスクへのアプローチを応用しています。
まず Object Detection をすることで「この bounding box に人間が 1 人いる」ということを予測し、その後 bounding box 内を色塗りしていきます。
Object Detection として bounding box を予測している時点で Instance を分離することが出来ています。色塗りのフェーズでは、すでに Instance が分離されているので単なる Pixel 単位の 2 クラス分類をやればよいことになります。はじめに Region を提案し、その中を精査するこれらの手法を、この論文では propose & verify (P&V) と呼んでいます。
ここで、 P&V は必ず一度矩形で切り取ってから色塗りをしなければならない という点が問題になります。
予測したい物体は必ずしも矩形で近似できるような形状をしているとは限りません。
実際の形状と極端にかけ離れた場合、bounding box を予測すること自体が難しく、また Instance の分離も難しくなります。instance coloring
P&V の問題点を解決する方法として、Pixel ごとに ラベル + Instance の identifier となる何か を予測する方法があります。
これらをこの論文では instance coloring (IC) と呼んでいます。「Instance の identifier となる何か」 は、連番などではうまく学習できません(どの Object が ID 1 なのか ID 2 なのかわからない)。
そこで、 Pixel ごとに低次元の embedding を出力し、同じ Instance に所属する Pixel の embedding たちが似たものになるように学習します。
入力画像に対して、Pixel ごとのラベルと embedding を出力し、embedding を基に Pixel たちをクラスタリングすることで Instance を分離します。IC の良いところは、典型的な image-to-image の問題と同じネットワーク構造を利用できるところです。
Semantic Segmetation, Style Transfer など、画像を入力とし同じサイズの feature map を出力とするタスクは他にも数多くあり、それらと同じ構造をシンプルに流用できるのは大きな利点になります。
(P&V の場合は Region Proposal + Region ごとの Coloring が必要で、ネットワーク構造としてはかなり複雑かつ独特なものになります)一方、IC であまり精度が出ない大きな理由の一つに 画像的に似た領域が繰り返されると Instance の分離に失敗する という問題があります。
image-to-image のネットワークは通常 Convolutional operators をベースにしていますが、CNN の出力は、入力である pixel の特徴量にのみ依存し、 座標は全く結果に影響を及ぼしません 。
そのため、画像的にそっくりな領域が複数あると、それらの pixel に対する embedding は同じような値になってしまい、クラスタリングがうまくいきません。Semi-convolutional operators
一般的な IC では、出力された embedding が次の条件をみたすことを目標とします。
ここで、 $\Omega$ は全 Pixel の集合、 $x$ は入力画像、 $\Phi$ は学習したい関数(NN)、 $S_k$ はクラス k の segmentation mask、 $M$ はマージン (hyperparameter) です。
言葉で説明すると、 同じクラスに属する Pixel $u$, $v$ の embedding の距離をより近づけ、違うクラスに属する場合はより遠ざける という感じです。
$M$ は分離境界をよりくっきりさせるためのパラメータです。さきほど述べたように $\Phi$ は CNN であり、座標情報を加味できません。
Semi-convolutinal 版では、 $\Phi$ の代わりに次のような $\Psi$ を考えます。\Psi_u(x) = f(\Phi_u(x), u)ここで、 $u$ は Pixel の座標を表し、 $f$ は $\Phi$ の結果と座標情報を合成するなんらかの関数です。
$f$ の簡単な例としては、単純な足し算が考えられます。
$\Psi$ は、CNN の結果に加えて座標情報も持ち合わせているため、IC の弱点を克服できています。
$f$ を単純な加算とし、うまく学習が成功した場合、各 Instance ごとに centroid $c_k$ が決定され、\forall u \in S_k: \Phi_u(x) + u = c_kとなるように $\Phi$ が学習されます。
これを可視化すると次の画像のようになります。各インスタンス内の Pixel から、なんとなく中心っぽい場所へベクトルが伸びているのがわかります。
実際の学習の際の損失関数は次のようになります。
同じインスタンスに属する Pixel の embedding たちを平均値になるべく近づける、というのが損失関数になります。
(マージンの考えも含まれていないし、「違うインスタンスとの距離を取る」という損失も含まれていないですが、これで十分に良い学習ができたと述べられています。)実際にはもうちょっと複雑な $\Psi$ や距離の定義を使っていますが、概要としては上記のようなものを Semi-convolutional operators として提案しています。
Experiments
Mask R-CNN との統合もこの論文の重要な topic なのですが、ぶっちゃけ論文を読んだほうがわかりやすいので飛ばして実験結果をざーっと眺めてみます。
まずはじめに、 画像的にそっくりな領域が繰り返されてもうまく Instance を分離できることを確認しています。
(c) は通常の Conv. のみを使って IC を行った場合の結果です。クラスタリングに大失敗していることがわかります。
一方 (d) の Semi-conv. 版ではきれいな分離が実現されています。つぎに線虫の segmentation です。こちらは P&V のように矩形で認識するタイプの手法がニガテとするようなタスクです。
現在主流である Mask RCNN よりも良い結果が示されています。より一般的なデータである PASCAL VOC2012 に対しても Mask RCNN より良い結果となっています(Mask RCNN に Semi-conv. の仕組みを組み込んだもので比較しています。)
まとめと感想
instance coloring の手法をまったく知らなかったのですが、 CornerNet: Detecting Objects as Paired Keypoints で Pixel ごとの embedding をクラスタリングしてペアを作るという手法を知り、興味を持ったのでその関連で読んでみた論文です。
P&V 形式はかなり複雑な構造になるので、それを避けられるならすごく面白いなと思ったのですが、この論文では Mask R-CNN と組み合わせることで精度向上と言っているので、まだまだ IC 単体で勝てる感じではないのでしょうか?同じタスクに対して全く違う 2 つのアプローチが(比較対象になるくらいには)同じような成果を出しているのも面白いところです。segmentation は主流ではなかった分、まだまだ改善がありそうで楽しみです。
K. He, et al., https://arxiv.org/abs/1703.06870 ↩
- 投稿日:2019-02-11T10:55:45+09:00
Ubuntu18_04でMT4と、DeepLearning環境を構築
今回は、近い将来に構築するであろう、Server環境について、実運用を兼ねて実験的にローカル環境で構築を行ってみる。
やりたいこと
- ServerはVPSサーバをレンタル(を想定)
- MT4を動かせる環境
- OSはUbuntuを前提(ネットを見たらMT4も、DeepLearningの構築実績が多そうだったから)
VPSサーバの選定
過去に何度もやってきているが、時代は変わる、、、そんなこんなで2019年、改めてVPSサーバを調べてみた。
ちなみに、現在は、ABLENETのWin1と言うプランでMT4を1つ動かしている。
以前は、2つ契約をし、多いときはそれぞれ5枚ずつぐらい運用していたが、色々あって今の状態に。
月額1,600円(年払い用)だが、この費用も抑えたいので、「やりたいこと」に記載した条件となった。いくつかあったが、費用面とスペックで下記に絞った
お名前.com VPS(https://www.onamae-server.com/vps/)
GMOクラウド(https://vps.gmocloud.com/)
WebAREA(https://web.arena.ne.jp/vps-cloud/)
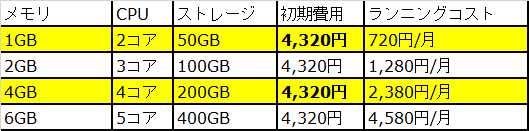
これらのスペックと料金を調べたところ、2コア、4コアではGMOクラウドの月額が少ないことがわかったが、初期費用が、、、と言うのが気になった。
これらの他、https://www.gamehuntblog.com/entry/vps-compare-recommendation のサイトを参考に調べたが、とりあえず、現在の料金より安く、スペックアップを望む程度として、
お名前.com VPSの2コアのプランを前提に環境を構築してみる。VMware
仮想環境と言えば、VMwareと昔は思っていたのだが、最近、VirtualBOXもちらほら見え隠れしている。が、VirtualBOXは32bitしかインストールできず(私が知らないだけだろうが)、コアも変更できそうなのに、変更できなかったので、使い慣れたVMwareにした。
しかし、インストール時に、例の問題が、、、
Hyper-Vの問題は、( https://soma-engineering.com/cloud/vmware-workstation/error-poweron-vm/2018/05/04/ )この辺のサイトを参考にさせていただき解除Ubuntu
Let's Install
さて、まずはUbuntuのInstall。
UbuntuのDownloadは、( https://www.ubuntulinux.jp/download )からISOファイルをダウンロードして、VMwareからインストールwine
次に、MT4を動かすためにwineなどをインストールする
まぁ、基本的にコピペですべてを済ませてきたので、今回もググって実施
( https://bitcoin-with.com/ubuntu_mt4_install/ )
- ubuntuにsshをInstallして、ローカルのWindowsからVMwareに接続できるようにする
sudo apt install -y net-tools ssh service ssh start
- puttyなどを使って、sshでVMware上のUbuntuに接続
- UbuntuにwineをInstall. 文字化け対策も一緒に施す.
sudo dpkg --add-architecture i386 sudo apt install -y wine-development winetricks winetricks ' このあと、https://symfoware.blog.fc2.com/blog-entry-2228.htmlを参考に色々やってみた
- 普段TitanFXを使っているので、VMware上でTitanFXのサイトからMT4をDownload.
- VMwareのコマンドプロンプト上でwineと打ったあとに、DownloadしたexeファイルをD&D
とりあえず、これでUbuntuでMT4を動かすことができた!!
最後に
忘れちゃいけないのが、Ubuntuログイン時のMT4の自動起動。
Windowsと違って、OSのパッチに伴い再起動することは少ないと思うが、ログイン時に自動起動するように設定
(https://sicklylife.jp/ubuntu/1804/help/startup-applications.html)