- 投稿日:2019-06-07T22:34:38+09:00
【画像生成】AutoencoderでDenoising, Coloring, そして拡大カラー画像生成♬
今回は、「AutoencoderでDenoising, Coloring, そして拡大画像生成」を取り上げます。
大切なことはこの3つ(元々のAutoencoder含め4つ)のことは、ほぼ同じプログラムでデータをそのように用意すればできるというところがミソです。
いつもなんとなく別々に説明されるので、難しいことかと思いがちですが、基本はAutoencoderなので簡単です。
【参考】
・畳み込みオートエンコーダによる画像の再現、ノイズ除去、セグメンテーション簡単に今回の記事を要約すると以下のようになります。
すなわち、autoencoder-decoderの学習部分のfit関数を示します。
vae.fit(x_train_gray,x_train_size, epochs=epochs, batch_size=batch_size, callbacks=callbacks, validation_data=(x_test_gray, x_test_size))これは、
入力;x_train_gray(32,32,1)のgray画像 出力;x_train_size(64,64,3)のcolor画像として学習し、
入力;x_test_gray(32,32,1)のテストgray画像 出力;x_test_size(64,64,3)のテストcolor画像で検証することになります。
すなわち、絵にすると以下のような感じです。
問題は、入力と出力を何にするかということです
そして、ドメイン間を変換する関数がencoder-decoderということになり、ドメインの性質に合わせて適切なモデルを配置すればよいことになります。
ということで、いろいろなドメイン間の変換ができることを意味しています。今回やったこと
①入力:ノイズあり画像、出力;ノイズ無し画像
②入力;Gray画像、出力;カラー画像
③入力;32x32サイズGray画像、出力;64x64サイズカラー画像基本のコードは以下に置きました
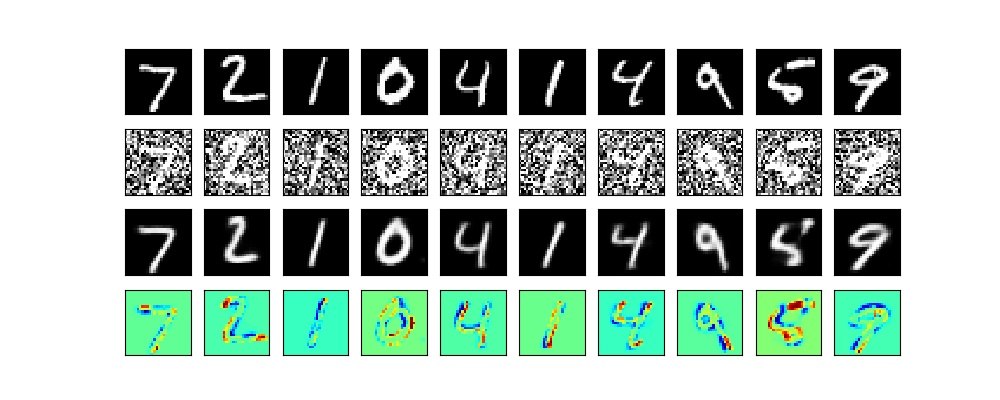
以下はMNISTのノイズ除去のコードです
・VAE/keras_conv2d_noise_reduction.py①入力:ノイズあり画像、出力;ノイズ無し画像
Denoisingのコード解説
一応、簡単に上記のコードの骨の部分を解説します。
以下のとおり、encoder-decoder-modelは前回と同様です。# encoder model inputs = Input(shape=input_shape, name='encoder_input') x = Conv2D(32, (3, 3), activation='relu', strides=2, padding='same')(inputs) x = Conv2D(64, (3, 3), activation='relu', strides=2, padding='same')(x) shape = K.int_shape(x) print("shape[1], shape[2], shape[3]",shape[1], shape[2], shape[3]) x = Flatten()(x) z_mean = Dense(latent_dim, name='z_mean')(x) encoder = Model(inputs, z_mean, name='encoder') encoder.summary() # decoder model latent_inputs = Input(shape=(latent_dim,), name='z_sampling') x = Dense(shape[1] * shape[2] * shape[3], activation='relu')(latent_inputs) x = Reshape((shape[1], shape[2], shape[3]))(x) x = Conv2DTranspose(64, (3, 3), activation='relu', strides=2, padding='same')(x) x = Conv2DTranspose(32, (3, 3), activation='relu', strides=2, padding='same')(x) outputs = Conv2DTranspose(1, (3, 3), activation='sigmoid', padding='same')(x) decoder = Model(latent_inputs, outputs, name='decoder') decoder.summary() outputs = decoder(encoder(inputs)) vae = Model(inputs, outputs, name='vae_mlp') vae.compile(loss='binary_crossentropy',optimizer='adam')変更は、以下のように入力データとしてノイズを重畳します。
【参考】
・numpy.random.normal@SciPy.org
loc;Mean (“centre”) of the distribution.
scale;Standard deviation (spread or “width”) of the distribution.
size;Output shape
np.clip;0,1を下回るまたは上回る場合に0,1に制限しますnoise_train = np.random.normal(loc=0.5, scale=0.5, size=x_train.shape) noise_test = np.random.normal(loc=0.5, scale=0.5, size=x_test.shape) # 学習に使うデータを限定する x_train_noisy = np.clip(x_train + noise_train, 0, 1) x_test_noisy = np.clip(x_test+ noise_test, 0, 1)一番大切なのは、学習のとき、入力;x_train_noisy, 出力;x_trainで学習し、検証も入力;x_test_noisy, 出力;x_testで実施しています。
実は、今回の3つのテーマではこの入力と出力を変更し、それらに合わせてネットワークなどをちょっと変更するだけで、いろいろな変換ができることがミソです。class Check_layer(keras.callbacks.Callback): def on_epoch_end(self, epoch, logs={}): if epoch%2==0: ... decoded_imgs = vae.predict(x_test_noisy[:n]) plot_irregular(x_test,x_test_noisy,decoded_imgs,epoch=epoch) ch_layer = Check_layer() callbacks = [ch_layer] # 学習 vae.fit(x_train_noisy,x_train, epochs=epochs, batch_size=batch_size, callbacks=callbacks, validation_data=(x_test_noisy, x_test))Denoisingの結果
以下のとおり、潜在空間10次元で100epochだと完全にノイズ除去してくれました。
もう少し、見ると以下のとおり、綺麗に出力できました。
②入力;Gray画像、出力;カラー画像
Coloring
同じように、カラー画像であるCifr10でgray-colorの変換を実施してみます。
コード全体は、以下のとおりです。
・VAE/keras_conv2d_coloring.py
そして、コードの大きな変更部分は、以下のとおりです。
1.描画サイズは慎重に変更しましょう
2.入力は(32,32,1)のGray画像で、出力は(32,32,3)のカラー画像
3.描画の中で、以下のとおり、カテゴリの色指定を以下のとおり1-Dに変換していますy_test1 = np.ravel(y_test) sc=plt.scatter(z_mean[:, 0], z_mean[:, 1], c=y_test1,s=50,cmap=plt.cm.jet) plt.colorbar(sc)4.学習と検証に使うGray画像変換は以下の関数を使っています
def rgb2gray(rgb): return np.dot(rgb[...,:3], [0.299, 0.587, 0.114]) x_train_gray = rgb2gray(x_train).reshape(len(x_train),32,32,1) x_test_gray = rgb2gray(x_test).reshape(len(x_test),32,32,1)5.モデルは入出力に注意して、以下のようにしました
# encoder model inputs = Input(shape=input_shape, name='encoder_input') x = Conv2D(32, (3, 3), activation='relu', strides=2, padding='same')(inputs) x = Conv2D(64, (3, 3), activation='relu', strides=2, padding='same')(x) shape = K.int_shape(x) print("shape[1], shape[2], shape[3]",shape[1], shape[2], shape[3]) x = Flatten()(x) z_mean = Dense(latent_dim, name='z_mean')(x) encoder = Model(inputs, z_mean, name='encoder') encoder.summary() # decoder model latent_inputs = Input(shape=(latent_dim,), name='z_sampling') x = Dense(shape[1] * shape[2] * shape[3], activation='relu')(latent_inputs) x = Reshape((shape[1], shape[2], shape[3]))(x) x = Conv2DTranspose(64, (3, 3), activation='relu', strides=2, padding='same')(x) x = Conv2DTranspose(32, (3, 3), activation='relu', strides=2, padding='same')(x) outputs = Conv2DTranspose(3, (3, 3), activation='sigmoid', padding='same')(x) decoder = Model(latent_inputs, outputs, name='decoder') decoder.summary() outputs = decoder(encoder(inputs)) vae = Model(inputs, outputs, name='vae_mlp') vae.compile(loss='binary_crossentropy',optimizer='adam')6.学習は以下のようにしています
入力;x_train_gray,出力;x_train、そして検証は、入力;x_test_gray, 出力;x_testで学習しています。
相変わらず、vae.compile(loss='binary_crossentropy',optimizer='adam')
として、loss='binary_crossentropy'or 'mse'で実施しました。class Check_layer(keras.callbacks.Callback): def on_epoch_end(self, epoch, logs={}): if epoch%20==0: ... n=10 decoded_imgs = vae.predict(x_test_gray[:n]) plot_irregular(x_test,x_test_gray,decoded_imgs,epoch=epoch) ch_layer = Check_layer() callbacks = [ch_layer] # autoencoderの実行 vae.fit(x_train_gray,x_train, epochs=epochs, batch_size=batch_size, callbacks=callbacks, validation_data=(x_test_gray, x_test))Coloringの結果
上段が元の絵で、中断が入力のGray画像、そして下段が色付けされた画像。
まあ、元の絵とは配色が異なりますが、一応塗れています。
100epoch
③入力;32x32サイズGray画像、出力;64x64サイズカラー画像
Grayから拡大カラー画像生成
コード全体は以下のとおりです。
・VAE/keras_conv2d_x4coloring.py
複雑な変換のようみ見えますが、上記と大きな違いは、元のCifar10画像を拡大して学習データを作成するところです。
入力のGray画像は上記のものを使います。
そして、カラー画像の拡大は以下のコードで実施します。
※本来は高精細画像を縮小して学習すればもっと高精細な変換器が作成できるはずですが、ここではさぼりました
そのためのコードは以下のとおりです。cv2.resizeを使います。
※サイズは今回は1060で計算したのでメモリーの関係で(64,64)としました
ここには示しませんが1080、8MB だと(256,256)まで拡大できました。
ただし、batch_size=8(128@1080マシン)など小さな値にしていますimg_rows, img_cols=64,64 #256,256 #128,128 X_train =[] X_test = [] for i in range(len(x_train)): dst = cv2.resize(x_train[i], (img_rows, img_cols), interpolation=cv2.INTER_CUBIC) X_train.append(dst) for i in range(len(x_test)): dst = cv2.resize(x_test[i], (img_rows, img_cols), interpolation=cv2.INTER_CUBIC) X_test.append(dst) x_train_size = np.array(X_train) x_test_size = np.array(X_test)モデルは以下のとおりとしています。
# encoder model inputs = Input(shape=input_shape, name='encoder_input') x = Conv2D(32, (3, 3), activation='relu', strides=2, padding='same')(inputs) x = Conv2D(64, (3, 3), activation='relu', strides=2, padding='same')(x) shape = K.int_shape(x) print("shape[1], shape[2], shape[3]",shape[1], shape[2], shape[3]) x = Flatten()(x) z_mean = Dense(latent_dim, name='z_mean')(x) encoder = Model(inputs, z_mean, name='encoder') encoder.summary() # decoder model latent_inputs = Input(shape=(latent_dim,), name='z_sampling') x = Dense(shape[1] * shape[2] * shape[3], activation='relu')(latent_inputs) x = Reshape((shape[1], shape[2], shape[3]))(x) x = Conv2DTranspose(64, (3, 3), activation='relu', strides=2, padding='same')(x) x = Conv2DTranspose(32, (3, 3), activation='relu', strides=2, padding='same')(x) x = Conv2DTranspose(16, (3, 3), activation='relu', strides=2, padding='same')(x) outputs = Conv2DTranspose(3, (3, 3), activation='sigmoid', padding='same')(x) decoder = Model(latent_inputs, outputs, name='decoder') decoder.summary() outputs = decoder(encoder(inputs)) vae = Model(inputs, outputs, name='vae_mlp') vae.compile(loss='mse',optimizer='adam')拡大カラー画像生成
描画時点で拡大の効果は消えちゃいますが、それぞれ拡大して上記の画像と比較すると、ギザギザが消えて少し綺麗になったように思います。以下、20epochと100epoch時点の出力です。
20epoch
100epoch
まとめ
・Autoencoder-decoderでDenoising、Coloring、そして画像拡大をやってみた
・ほぼ同じ仕組みで実施できることを示した
・精度はまだまだだが、潜在空間の次元を増やして一定精度がえられた・さらなる精度改善を実施する
・アニメ画像やコマ補間から動画生成も同様な方法で実施できるのでやってみようと思うおまけ
綺麗な画像生成するためには、潜在空間の次元をなるべく大きくするとより綺麗な画像が生成できます。ということで、今回は以下のように4096次元としています。
_________________________________________________________________ Layer (type) Output Shape Param # ================================================================= encoder_input (InputLayer) (None, 32, 32, 1) 0 _________________________________________________________________ conv2d_1 (Conv2D) (None, 16, 16, 32) 320 _________________________________________________________________ conv2d_2 (Conv2D) (None, 8, 8, 64) 18496 _________________________________________________________________ flatten_1 (Flatten) (None, 4096) 0 _________________________________________________________________ z_mean (Dense) (None, 4096) 16781312 ================================================================= Total params: 16,800,128 Trainable params: 16,800,128 Non-trainable params: 0 _________________________________________________________________ _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= z_sampling (InputLayer) (None, 4096) 0 _________________________________________________________________ dense_1 (Dense) (None, 4096) 16781312 _________________________________________________________________ reshape_1 (Reshape) (None, 8, 8, 64) 0 _________________________________________________________________ conv2d_transpose_1 (Conv2DTr (None, 16, 16, 64) 36928 _________________________________________________________________ conv2d_transpose_2 (Conv2DTr (None, 32, 32, 32) 18464 _________________________________________________________________ conv2d_transpose_3 (Conv2DTr (None, 64, 64, 16) 4624 _________________________________________________________________ conv2d_transpose_4 (Conv2DTr (None, 64, 64, 3) 435 ================================================================= Total params: 16,841,763 Trainable params: 16,841,763 Non-trainable params: 0 _________________________________________________________________
- 投稿日:2019-06-07T18:01:49+09:00
【論文紹介】 条件付き模倣学習によるEnd-to-Endナビゲーション
紹介する論文
論文の要約
- 観測(入力)から行動(出力)を直接学習する方法を模倣学習(imitation learning)と呼ぶ
- 模倣学習は「観測から最適な行動が決まると仮定している」ため,なかなか実用的な性能になりえない(実際この様な仮定は基本的には成り立たない)
- もう少し条件(右左折や直進などの行動という情報)を加えて学習を行う条件付き模倣学習(conditional imitation learning)を提案する
- 行動に従って使用するネットワークを変えることで,性能が上がることを検証した
はじめに
模倣学習(imitation learning)という言葉が最近良く使われています.カメラ画像など(入力)から行動(出力)を学習していくというものです(End-to-End学習でロボットを動かすというニュアンスで使われると思いますが,最近の言葉で定義が曖昧な気がするので,確かではありません).この模倣学習は観測から最適な行動が決定されると仮定しています.なぜなら,観測値のみを入力として使い行動を予測するからです.しかし,実際このような仮定が成り立つことはあまりありえません.例えば自動運転の文脈で考えた場合,交差点に近づいたとき,その際のカメラの画像だけから直進するか右左折するかなどは判断できません.なぜなら,「向かいたい目的地に到達するための行動(直進や右左折などの情報)を知らないから」です.なお論文では以下の様に問題提起されています.
Why has imitation learning not scaled up to fully autonomous urban driving? One limitation is in the assumption that the optimal action can be inferred from the perceptual input alone. This assumption often does not hold in practice: for instance, when a car approaches an intersection, the camera input is not sufficient to predict whether the car should turn left, right, or go straight.
(訳)
なぜ模倣学習が市街地での完全自動までスケールアップできないのか?模倣学習の限界は,ある瞬間における最適な行動を視覚的な入力だけで決定できるという仮定に基づいているために発生する.当然,この仮定は常に正しいとは限らず,例えば交差点に近づいている際のカメラからの映像だけを見ても,右折すべきか,左折すべきか,もしくは直進すべきかは判断できない.そこで本論文では,もう少し条件を加えて模倣学習を行う条件付き模倣学習(conditional imitation learning)を提案します.
条件付き模倣学習(conditional imitation learning)
模倣学習は,時刻$t$におけるある観測${\bf o}{t}$に対する行動${\bf a}{t}$をマッピングするためのモデルを学習します.特に,熟練者(expert)の行動を模倣する,というニュアンスで使われるので,模倣学習と言われます.模倣学習は以下の最適化問題を解くことで実行されます(論文中式1).
\mathop{\rm minimize}\limits_{\boldsymbol{\theta}}\sum_{i}l(F({\bf o}_{i};\boldsymbol{\theta}),{\bf a}_{i})ここで$F$は観測を行動へマッピングする関数であり,$\boldsymbol{\theta}$はそのパラメータ,$l$はマッピングされた値と実際の行動によって定義されるロスになります.この式は,熟練者の行動は観測のみからマッピングできることを仮定しているということを意味しています.
そこで本論文では,熟練者の内部状態(意図や目的地や事前知識など)を表現したベクトル${\bf h}$を導入し,上式のコスト関数を以下の様に修正します(論文中式2).
\mathop{\rm minimize}\limits_{\boldsymbol{\theta}}\sum_{i}l(F({\bf o}_{i};\boldsymbol{\theta}),E({\bf o}_{i},{\bf h}_{i}))ここで$E$は,観測と内部状態から行動をマッピングする関数です.
しかし,実際に熟練者の内部状態を正確に取得することは困難です.そこで本論文では,新たな制御入力${\bf c}={\bf c}({\bf h})$を加えることとしています.${\bf c}$はデシジョンメイキングに相当し,${\rm continue}$,${\rm left}$,${\rm straight}$,${\rm right}$といった行動の指示を与えます.そして,実際に最適化するコスト関数を以下の様にしています(論文中式3).
\mathop{\rm minimize}\limits_{\boldsymbol{\theta}}\sum_{i}l(F({\bf o}_{i}, {\bf c}_{i};\boldsymbol{\theta}),{\bf a}_{i})おそらくオンラインのテスト時には,トポロジカルな位置推定(あまり精度の高くない位置推定)を行い,予め指定した経路を追従するための入力${\bf c}$を求めているのだと思います.
ネットワーク構造
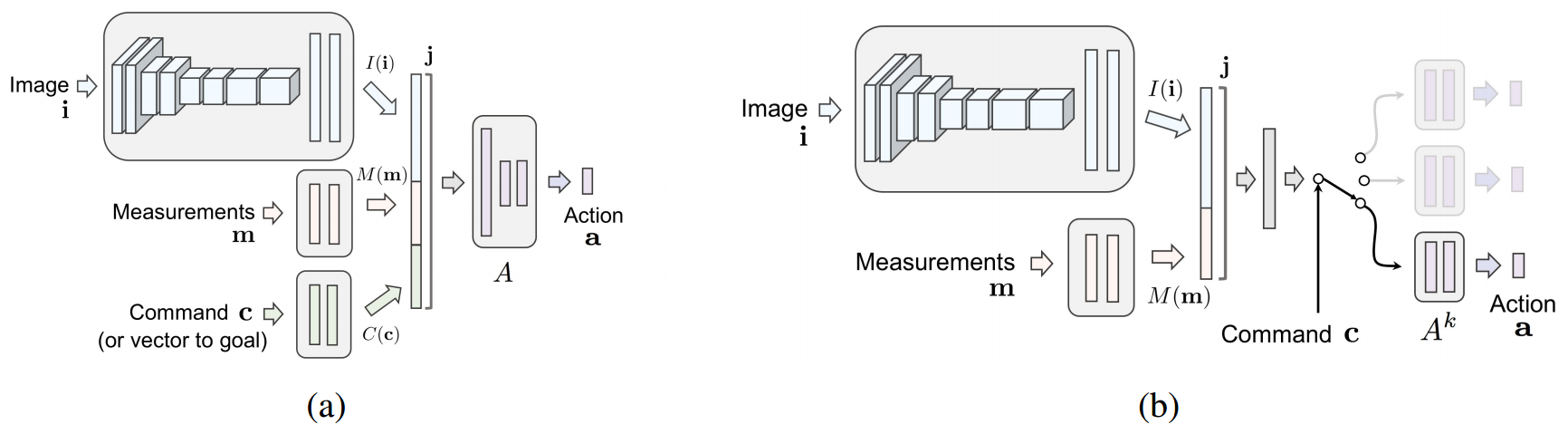
上述の行動のマッピング関数を深層学習によりモデル化します.本論文では,以下に示す2種類のネットワークが提案されています(論文中図3).なお,Image ${\bf i}$とMeasurements ${\bf m}$が観測${\bf o}_{t}$に,Command ${\bf c}$が制御入力${\bf c}$にそれぞれ相当しています.
(a)のネットワークでは,すべての値が入力として用いれ,1つのネットワークで行動${\bf a}{t}$を出力します.一方(b)のネットワークでは,Commandがスイッチの様に用いられます.すなわち,Command毎に行動を出力するネットワークの学習を行います.なお行動${\bf a}{t}$は,ステアリング角$s_{t}$とアクセル$a_{t}$で構成されています.
実験
実験はCARLAを用いたシミュレーション実験と,実車と比べて1/5スケールのラジコン(Traxxas Maxx)を用いた実環境実験を行っています.
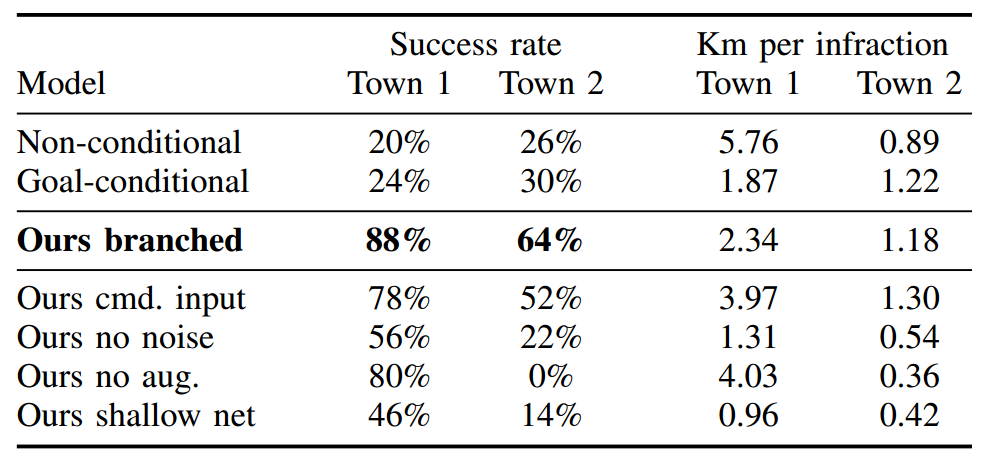
まずシミュレーション結果が以下の様になっています(論文中表1).
「1km走行するあたりの交通違反率」を指標とし,Commandによって使用するネットワークを変更する方法(Ours branched)が最も良い性能となっています.
また実環境実験の結果は以下の様になっています(論文中表2).
「右左折の失敗割合」,「平均介入回数」,および「走行時間」で評価されており,これにおいても提案法(Ours branched)が最も良い結果となっています.
感想
「模倣学習は観測から最適な行動が推定できると仮定している」というのは,改めて聞くとその通りだと思いました.そしてそれでうまくナビゲーションができないのもその通りだと思いました.やはり「End-to-End」ではなく,「最低限必要な情報はあるよな」と思えました.
- 投稿日:2019-06-07T18:01:49+09:00
【論文紹介】 Conditional Imitation LearningによるEnd-to-Endナビゲーション
紹介する論文
論文の要約
- 観測(入力)から行動(出力)を直接学習する方法を模倣学習(imitation learning)と呼ぶ
- 模倣学習は「観測から最適な行動が決まると仮定している」ため,なかなか実用的な性能になりえない(実際この様な仮定は基本的には成り立たない)
- もう少し条件(右左折や直進などの行動という情報)を加えて学習を行う条件付き模倣学習(conditional imitation learning)を提案する
- 行動に従って使用するネットワークを変えることで,性能が上がることを検証した
はじめに
模倣学習(imitation learning)という言葉が最近良く使われています.カメラ画像など(入力)から行動(出力)を学習していくというものです(End-to-End学習でロボットを動かすというニュアンスで使われると思いますが,最近の言葉で定義が曖昧な気がするので,確かではありません).この模倣学習は観測から最適な行動が決定されると仮定しています.なぜなら,観測値のみを入力として使い行動を予測するからです.しかし,実際このような仮定が成り立つことはあまりありえません.例えば自動運転の文脈で考えた場合,交差点に近づいたとき,その際のカメラの画像だけから直進するか右左折するかなどは判断できません.なぜなら,「向かいたい目的地に到達するための行動(直進や右左折などの情報)を知らないから」です.なお論文では以下の様に問題提起されています.
Why has imitation learning not scaled up to fully autonomous urban driving? One limitation is in the assumption that the optimal action can be inferred from the perceptual input alone. This assumption often does not hold in practice: for instance, when a car approaches an intersection, the camera input is not sufficient to predict whether the car should turn left, right, or go straight.
(訳)
なぜ模倣学習が市街地での完全自動までスケールアップできないのか?模倣学習の限界は,ある瞬間における最適な行動を視覚的な入力だけで決定できるという仮定に基づいているために発生する.当然,この仮定は常に正しいとは限らず,例えば交差点に近づいている際のカメラからの映像だけを見ても,右折すべきか,左折すべきか,もしくは直進すべきかは判断できない.そこで本論文では,もう少し条件を加えて模倣学習を行う条件付き模倣学習(conditional imitation learning)を提案します.
条件付き模倣学習(conditional imitation learning)
模倣学習は,時刻$t$におけるある観測${\bf o}{t}$に対する行動${\bf a}{t}$をマッピングするためのモデルを学習します.特に,熟練者(expert)の行動を模倣する,というニュアンスで使われるので,模倣学習と言われます.模倣学習は以下の最適化問題を解くことで実行されます(論文中式1).
\mathop{\rm minimize}\limits_{\boldsymbol{\theta}}\sum_{i}l(F({\bf o}_{i};\boldsymbol{\theta}),{\bf a}_{i})ここで$F$は観測を行動へマッピングする関数であり,$\boldsymbol{\theta}$はそのパラメータ,$l$はマッピングされた値と実際の行動によって定義されるロスになります.この式は,熟練者の行動は観測のみからマッピングできることを仮定しているということを意味しています.
そこで本論文では,熟練者の内部状態(意図や目的地や事前知識など)を表現したベクトル${\bf h}$を導入し,上式のコスト関数を以下の様に修正します(論文中式2).
\mathop{\rm minimize}\limits_{\boldsymbol{\theta}}\sum_{i}l(F({\bf o}_{i};\boldsymbol{\theta}),E({\bf o}_{i},{\bf h}_{i}))ここで$E$は,観測と内部状態から行動をマッピングする関数です.
しかし,実際に熟練者の内部状態を正確に取得することは困難です.そこで本論文では,新たな制御入力${\bf c}={\bf c}({\bf h})$を加えることとしています.${\bf c}$はデシジョンメイキングに相当し,${\rm continue}$,${\rm left}$,${\rm straight}$,${\rm right}$といった行動の指示を与えます.そして,実際に最適化するコスト関数を以下の様にしています(論文中式3).
\mathop{\rm minimize}\limits_{\boldsymbol{\theta}}\sum_{i}l(F({\bf o}_{i}, {\bf c}_{i};\boldsymbol{\theta}),{\bf a}_{i})おそらくオンラインのテスト時には,トポロジカルな位置推定(あまり精度の高くない位置推定)を行い,予め指定した経路を追従するための入力${\bf c}$を求めているのだと思います.
ネットワーク構造
上述の行動のマッピング関数を深層学習によりモデル化します.本論文では,以下に示す2種類のネットワークが提案されています(論文中図3).なお,Image ${\bf i}$とMeasurements ${\bf m}$が観測${\bf o}_{t}$に,Command ${\bf c}$が制御入力${\bf c}$にそれぞれ相当しています.
(a)のネットワークでは,すべての値が入力として用いれ,1つのネットワークで行動${\bf a}{t}$を出力します.一方(b)のネットワークでは,Commandがスイッチの様に用いられます.すなわち,Command毎に行動を出力するネットワークの学習を行います.なお行動${\bf a}{t}$は,ステアリング角$s_{t}$とアクセル$a_{t}$で構成されています.
実験
実験はCARLAを用いたシミュレーション実験と,実車と比べて1/5スケールのラジコン(Traxxas Maxx)を用いた実環境実験を行っています.
まずシミュレーション結果が以下の様になっています(論文中表1).
「1km走行するあたりの交通違反率」を指標とし,Commandによって使用するネットワークを変更する方法(Ours branched)が最も良い性能となっています.
また実環境実験の結果は以下の様になっています(論文中表2).
「右左折の失敗割合」,「平均介入回数」,および「走行時間」で評価されており,これにおいても提案法(Ours branched)が最も良い結果となっています.
感想
「模倣学習は観測から最適な行動が推定できると仮定している」というのは,改めて聞くとその通りだと思いました.そしてそれでうまくナビゲーションができないのもその通りだと思いました.やはり「End-to-End」ではなく,「最低限必要な情報はあるよな」と思えました.
- 投稿日:2019-06-07T09:27:28+09:00
既存のChainerコードをChainerXに対応させる
chainerx 対応:コード変換部分早見表
とうとうChainer version 6.0.0 がリリースされましたね。本記事ではこれまでの Chainer v5 以前までに書かれていたモデル訓練用コードを、 Chainer v6 で導入されたChainerXへ対応させるための変更点についてまとめます。
(上記コードの変換をしなくても今まで通り v5 のコードを v6で動作させることは可能です。)
本題に飛びたい方は v5 のコードを v6 のChainerX対応コードに変換する からご覧ください。ChainerX とは
先日Chainer version 6.0.0 が正式リリースされました。
#Chainer/#CuPy v6.0.0 をリリースしました。変更点の概要はブログをご覧ください。 https://t.co/1k7VXirOFC https://t.co/Rf7GxJCZyKhttps://t.co/leNCHR6bdU
— ChainerJP (@ChainerJP) May 16, 2019V6で追加された機能で注目したいのは何といってもChainerXです。
ChainerXはC++で実装されており、
- 多次元配列の計算 Operators:numpy arrayのように使える
- Device management :さまざまなDevice (CPU/GPUなど) を切り替えて使える
- 自動微分機能 :chainer Variableが行っていた、微分機能の機能を合わせもつ Array を提供しています。
これまで numpy or cupy という CPUかGPUか、→他のDeviceは考えていないというコードを書いていましたが、ChainerXの導入により将来新しく出てくるDeviceに対してもアプリケーション側のコードは同じまま、計算を扱えるようになりました。
つまり、CPU だろうがGPUだろうが、理論的には "
Backendさえ追加で実装されれば" (計算で使用する関数など)、 IOTに使用される格安チップで使われるFPGA、スマホなどで使われる Arm 専用などなどにも対応できる仕組みということです。ChainerXに変えることによる大きなメリットは以下二つです
・高速:C++で書かれているため、python のOverheadを少なくすることができます。※
・hetero device への対応:Backend さえ実装すれば、組み込みなどへの対応も可能です!※ ただし、現状はBLASなどの実装が最適化されていない関数もあり、絶対に numpy/cupy より速い!とは限らないようです。
より詳しい説明は以下のslideshareやブログをご覧ください
- ChainerX and How to Take Part
- N次元配列の自動微分をC++で実装したChainerXをリリース。Chainer v6(β版)に統合し、計算パフォーマンスを向上インストール方法
ChainerXはDefaultではBuildされません。
Linux では以下のように環境変数を設定してからChainerをインストールすることで、ChainerXもBuild されます。$ export CHAINER_BUILD_CHAINERX=1 $ export CHAINERX_BUILD_CUDA=1 # Only when you have GPU and CUDA installed $ export MAKEFLAGS=-j8 # Using 8 parallel jobs. $ pip install chainerDockerfileを使いたい場合は、以下のように書くとよいでしょう。
FROM nvidia/cuda:10.0-cudnn7-devel-ubuntu16.04 ... # Install from source is expected, to align cudnn version between cupy & chainerx RUN pip install cupy==6.0.0 # chainer & chainerx ENV CHAINER_BUILD_CHAINERX 1 ENV CHAINERX_BUILD_CUDA 1 ENV CUDNN_ROOT_DIR=/usr/include ENV MAKEFLAGS -j8 RUN pip install chainer==6.0.0 #RUN git clone https://github.com/chainer/chainer && pip install -e chainer # To use ChainerMN # RUN pip install mpi4pyGPUを使わない場合は
cupyのインストールと、CHAINERX_BUILD_CUDA,CUDNN_ROOT_DIRの設定の行を抜かしてください。v5 のコードを v6 のChainerX対応コードに変換する
いよいよ本題です。
一番BasicなOfficial Example であるtrain_mnist.pyを、 v5のコードとv6のコード で比較してみればその違いはすぐに分かります。一番の大きな違いは以下の部分です。
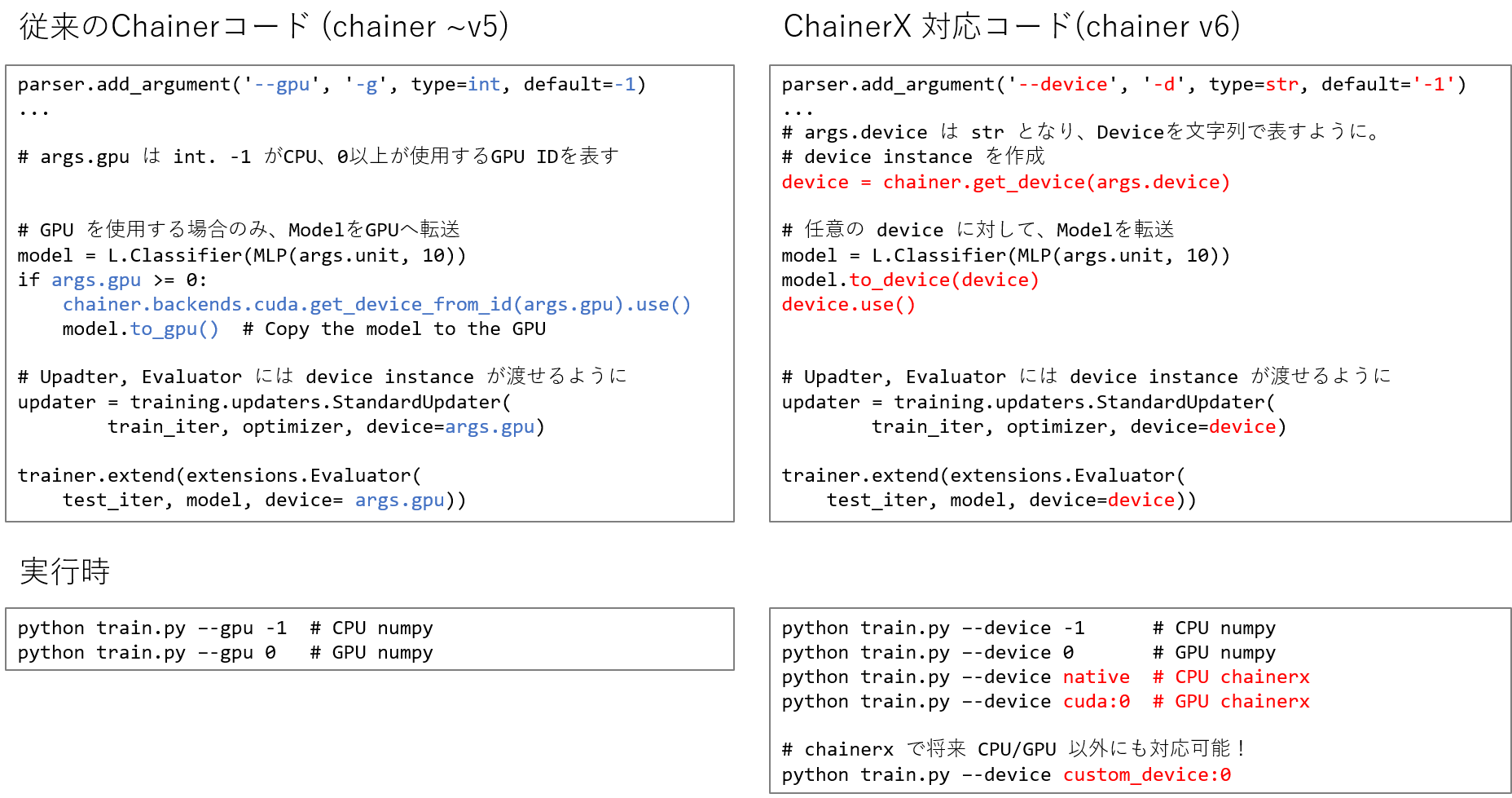
~v5: CPUかGPUかを、
parser.add_argument('--gpu', '-g', type=int, default=-1) ... # args.gpu は int. -1 がCPU、0以上が使用するGPU IDを表す。 model = L.Classifier(MLP(args.unit, 10)) if args.gpu >= 0: # Make a specified GPU current chainer.backends.cuda.get_device_from_id(args.gpu).use() model.to_gpu() # Copy the model to the GPUv6
parser.add_argument('--device', '-d', type=str, default='-1') ... # args.device は str となり、Deviceを文字列で表すように。 device = chainer.get_device(args.device) model = L.Classifier(MLP(args.unit, 10)) model.to_device(device) device.use()基本的にはこの部分を変更するだけでOKです。
上記コードの変換をするとChainerXに対応した動作ができるようになるということなので、変換をしなくても今まで通り v5 のコードを v6で動作させることは可能です。以下、コード上は変化ありませんが、関数の引数が変化している部分です。
これまでdeviceとして -1 or 0 といった int を引数としていたところが、 chainerのDevice instance を受け取るように変化しています。
- Updater
- Evaluator
~v5
device = args.gpu # type: int updater = training.updaters.StandardUpdater( train_iter, optimizer, device=device) trainer.extend(extensions.Evaluator( test_iter, model, device=device))v6
device = chainer.get_device(args.device) # type: chainer._backend.Device updater = training.updaters.StandardUpdater( train_iter, optimizer, device=device) trainer.extend(extensions.Evaluator( test_iter, model, device=device))また、
converterをカスタマイズして使っている方はその部分も変更が入っています。実行時の option の指定方法
これまで、
--gpu -1→ CPU, numpy
--gpu 0→ GPU, cupyと int 型を指定してCPU or GPUを切り替えていたののが、
--device -1→ CPU, numpy
--device 0→ GPU, cupy
--device native→ CPU (native backend), chainerx
--device cuda:0→ GPU (CUDA backend), chainerxというように
str型を渡すことで任意のDeviceを使えるような設計に変わっています。
'-1' や '0' といった int に変換できる文字列を渡した場合には これまでどおりの挙動と同じく numpy/cupy が使われます。今後新しいDeviceに対しても Backend が実装されれば、アプリケーション側のコードは同じまま、
--device custom_device:0などと指定することで動かせることができるようになっています。まとめ
以上をまとめると冒頭に張った図のように変換するだけでChainerXを動かせるということになります。
chainerx 対応:コード変換部分早見表
時間がとれれば次は少しコードリーディングや device class/backend 機構について追記したいと思っています。
皆さんもぜひChainerXを使ってみてください。
- 投稿日:2019-06-07T09:27:28+09:00
ChainerX移行ガイド
chainerx 対応:コード変換部分早見表
とうとうChainer version 6.0.0 がリリースされましたね。本記事ではこれまでの Chainer v5 以前までに書かれていたモデル訓練用コードを、 Chainer v6 で導入されたChainerXへ対応させるための変更点についてまとめます。
(上記コードの変換をしなくても今まで通り v5 のコードを v6で動作させることは可能です。)
本題に飛びたい方は v5 のコードを v6 のChainerX対応コードに変換する からご覧ください。ChainerX とは
先日Chainer version 6.0.0 が正式リリースされました。
#Chainer/#CuPy v6.0.0 をリリースしました。変更点の概要はブログをご覧ください。 https://t.co/1k7VXirOFC https://t.co/Rf7GxJCZyKhttps://t.co/leNCHR6bdU
— ChainerJP (@ChainerJP) May 16, 2019V6で追加された機能で注目したいのは何といってもChainerXです。
ChainerXはC++で実装されており、
- 多次元配列の計算 Operators:numpy arrayのように使える
- Device management :さまざまなDevice (CPU/GPUなど) を切り替えて使える
- 自動微分機能 :chainer Variableが行っていた、微分機能の機能を合わせもつ Array を提供しています。
これまで numpy or cupy という CPUかGPUか、→他のDeviceは考えていないというコードを書いていましたが、ChainerXの導入により将来新しく出てくるDeviceに対してもアプリケーション側のコードは同じまま、計算を扱えるようになりました。
つまり、CPU だろうがGPUだろうが、理論的には "
Backendさえ追加で実装されれば" (計算で使用する関数など)、 IOTに使用される格安チップで使われるFPGA、スマホなどで使われる Arm 専用などなどにも対応できる仕組みということです。ChainerXに変えることによる大きなメリットは以下二つです
・高速:C++で書かれているため、python のOverheadを少なくすることができます。※
・hetero device への対応:Backend さえ実装すれば、組み込みなどへの対応も可能です!※ ただし、現状はBLASなどの実装が最適化されていない関数もあり、絶対に numpy/cupy より速い!とは限らないようです。
より詳しい説明は以下のslideshareやブログをご覧ください
- ChainerX and How to Take Part
- N次元配列の自動微分をC++で実装したChainerXをリリース。Chainer v6(β版)に統合し、計算パフォーマンスを向上インストール方法
ChainerXはDefaultではBuildされません。
Linux では以下のように環境変数を設定してからChainerをインストールすることで、ChainerXもBuild されます。$ export CHAINER_BUILD_CHAINERX=1 $ export CHAINERX_BUILD_CUDA=1 # Only when you have GPU and CUDA installed $ export MAKEFLAGS=-j8 # Using 8 parallel jobs. $ pip install chainerDockerfileを使いたい場合は、以下のように書くとよいでしょう。
FROM nvidia/cuda:10.0-cudnn7-devel-ubuntu16.04 ... # Install from source is expected, to align cudnn version between cupy & chainerx RUN pip install cupy==6.0.0 # chainer & chainerx ENV CHAINER_BUILD_CHAINERX 1 ENV CHAINERX_BUILD_CUDA 1 ENV CUDNN_ROOT_DIR=/usr/include ENV MAKEFLAGS -j8 RUN pip install chainer==6.0.0 #RUN git clone https://github.com/chainer/chainer && pip install -e chainer # To use ChainerMN # RUN pip install mpi4pyGPUを使わない場合は
cupyのインストールと、CHAINERX_BUILD_CUDA,CUDNN_ROOT_DIRの設定の行を抜かしてください。v5 のコードを v6 のChainerX対応コードに変換する
いよいよ本題です。既存のChainerコードをChainerXに対応させるためにコードのどの部分を変換すればよいかを紹介します。
一番BasicなOfficial Example である
train_mnist.pyを、 v5のコードとv6のコード で比較してみればその違いはすぐに分かります。一番の大きな違いは以下の部分です。
~v5: CPUかGPUかを、args.gpu として int で指定。 GPUの場合のみ Deviceへ送る処理を書く。
parser.add_argument('--gpu', '-g', type=int, default=-1) ... # args.gpu は int. -1 がCPU、0以上が使用するGPU IDを表す。 model = L.Classifier(MLP(args.unit, 10)) if args.gpu >= 0: # Make a specified GPU current chainer.backends.cuda.get_device_from_id(args.gpu).use() model.to_gpu() # Copy the model to the GPUv6: どの deviceをつかうかを、args.device として str で指定。 任意の
deviceへ送る処理を書く。parser.add_argument('--device', '-d', type=str, default='-1') ... # args.device は str となり、Deviceを文字列で表すように。 device = chainer.get_device(args.device) model = L.Classifier(MLP(args.unit, 10)) model.to_device(device) device.use()基本的にはこの部分を変更するだけでOKです。
上記コードの変換をするとChainerXに対応した動作ができるようになるということなので、変換をしなくても今まで通り v5 のコードを v6で動作させることは可能です。
device.use()は必須ではなく省略可能のようです。
また有効範囲としては、thread local な機能なので、別スレッドでは効果がないということに注意してください。以下、コード上は変化ありませんが、関数の引数が変化している部分です。
これまでdeviceとして -1 or 0 といった int を引数としていたところが、 chainerのDevice instance を受け取るように変化しています。
- Updater
- Evaluator
~v5
device = args.gpu # type: int updater = training.updaters.StandardUpdater( train_iter, optimizer, device=device) trainer.extend(extensions.Evaluator( test_iter, model, device=device))v6
device = chainer.get_device(args.device) # type: chainer._backend.Device updater = training.updaters.StandardUpdater( train_iter, optimizer, device=device) trainer.extend(extensions.Evaluator( test_iter, model, device=device))また、
converterをカスタマイズして使っている方はその部分も変更が入っています。実行時の option の指定方法
これまで、
--gpu -1→ CPU, numpy
--gpu 0→ GPU, cupyと int 型を指定してCPU or GPUを切り替えていたののが、
--device -1→ CPU, numpy
--device 0→ GPU, cupy
--device native→ CPU (native backend), chainerx
--device cuda:0→ GPU (CUDA backend), chainerxというように
str型を渡すことで任意のDeviceを使えるような設計に変わっています。
'-1' や '0' といった int に変換できる文字列を渡した場合には これまでどおりの挙動と同じく numpy/cupy が使われます。今後新しいDeviceに対しても Backend が実装されれば、アプリケーション側のコードは同じまま、
--device custom_device:0などと指定することで動かせることができるようになっています。まとめ
以上をまとめると冒頭に張った図のように変換するだけでChainerXを動かせるということになります。
chainerx 対応:コード変換部分早見表
時間がとれれば次は少しコードリーディングや device class/backend 機構について追記したいと思っています。
皆さんもぜひChainerXを使ってみてください。
chainer レポジトリから、コードをpull して /examples/mnist で
python train_mnist.py --device cuda:0
などと実行してみれば動かせるはずです!
- 投稿日:2019-06-07T05:53:57+09:00
論文まとめ:JointFlow: Temporal Flow Fields for Multi Person Pose Tracking
はじめに
BMVC 2018 から以下の論文のまとめ
A. Doering, et. al, "JointFlow: Temporal Flow Fields for Multi Person Pose Tracking"arXiv:
https://arxiv.org/abs/1805.04596コードの場所は不明
概要
- 単眼RGBビデオカメラからの映像から同時に複数人に対して姿勢推定・トラッキングを行うモデル
- real timeで行うことが可能
- 時間軸方向への関節の推移を表すベクトル場であるTFF(temporal flow fields) を用いる
以下がtrackingの例。
いずれもposetrack dataset に対する推論。上2つの行が車道のシーン、下2つの行がサッカーのシーン。
各列は左から右への時間推移だと思うが、同じ人に対して同じ色の骨格が塗られているので、同一の人物と推定されているだろう。
アーキテクチャ
アーキテクチャの全体像
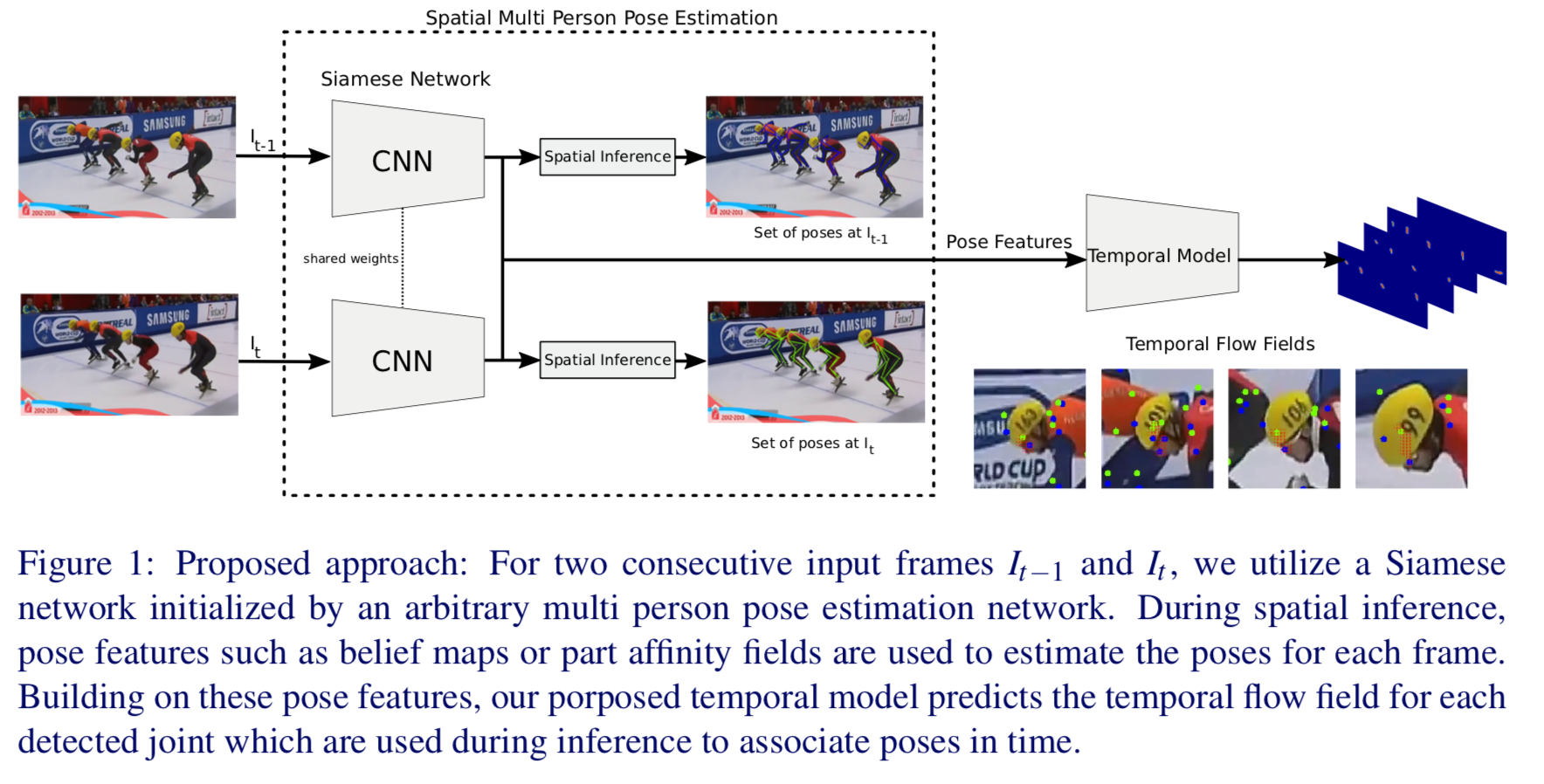
以下の図が全体像。
1)左から t-1 時の画像 $I_{t-1}$ と t 時の画像 $I_t$ を入力する。
2)それぞれに対してCNNで特徴量を抽出する。
3)特徴量から各時間において関節の位置と四肢のベクトルを推定し、骨格を推定する。
4)一方で各時間における関節位置から関節の推移を推定する。
定義等
$p_j = (x_j, y_j)$ :関節 j の2次元座標
$P= \left\{ p_j \right\}_{i:J} $ :ある人の J 個ある関節群
$I_t$ : ビデオの t フレーム目の画像
$N_t$ :ビデオの t フレーム目の画像内における人の数
$\mathcal{P}_t = \{ P^{1}_t, \cdots , P^{N}t \}$ :t フレーム目の姿勢群
temporal flow fields
TFF(temporal flow fields) はこの論文の中核である。
中身は、OpenPoseのPAF(part affinity fields)とほぼ同じ。
PAFはあるフレーム内における関節 j から関節 j' への単位ベクトルを表す場だったが、TFFは t-1 フレームにおける関節 j から t フレームにおける関節 j への単位ベクトルを表す場に変わっただけ。
まず t フレームにおける k 番目の人の関節 j を
p^t_{j,k} \in P^k_tで表す。単位ベクトル $\nu$ を k さんの j 関節におけるフレーム間の移動を正規化したものと考えると
\begin{eqnarray*} \nu &=& \frac{p^t_{j,k} - p^{t-1}_{j,k}}{\| p^t_{j,k} - p^{t-1}_{j,k} \|_2}\\ &=& \frac{p^t_{j,k} - p^{t-1}_{j,k}}{\lambda_{j,k}}\\ \end{eqnarray*}次に以下の図のように $\nu$ と垂直な $\nu_{\perp}$ を定義する。
以下のような領域 $\Omega_{j,k}$ を用いて、画像上の点 p がTFFに属する($p \in \Omega_{j,k}$)か否かを判別する。
\Omega_{j,k} = \left\{ p | 0 \leq \nu \cdot (p-p^{t-1}_{j,k}) \leq \lambda_{j,k} \land | \nu_{\perp} \cdot (p-p^{t-1}_{j,k}) | \leq \sigma \right\}$\sigma$ はパラメータ。
つまり、$\Omega_{j,k}$ は
こんな感じの領域。この領域内に p が入る時に値を $\nu$ とし、他を0とする。
T^{*}_{j,k}(p) = \begin{cases} \nu & if \ p \in \Omega_{j,k} \\ 0 & otherwise. \end{cases}1チャンネルの feature map に全ての人の関節 j に関するTFF をのせるので、関節 j のTFF は
T^{*}_{j}(p) = \frac{1}{n_t (p)} \sum^K_{k=1} T^{*}_{j,k}(p)となる。 $n_t (p)$ は non-zero となる $\nu$ の個数。
アーキテクチャの詳細
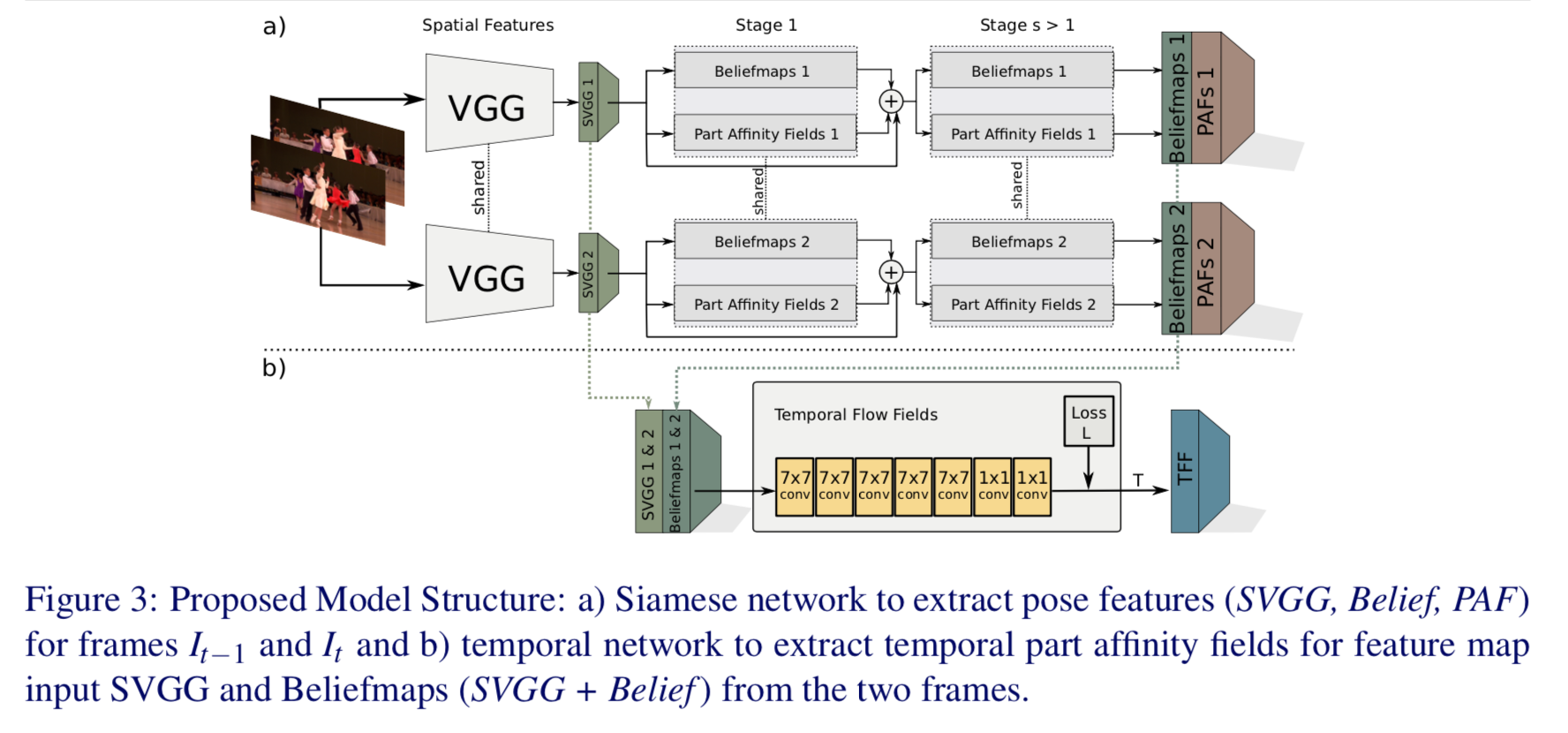
以下が詳細図。
上側(a)部分に関してはほぼOpenPose。
本論文の中核(b)部分では、VGGからの特徴量(SVGG)とheatmapを入力とし、7x7 convで5回、1x1 convで2回畳み込んだ後にTFFを推定する。
loss
(b)部分の loss は以下のようにL2で求める。
\mathcal{L} = \sum^J_{j=1} \sum_{p\in \Omega} M(p) \cdot \| T^{*}_j (p) - T_j(p) \|^2_2$T^{*}_j (p)$ は ground truthの TFF、$M(p)$ はバイナリーマスクで、アノテーションされてない領域に対して0とする。
推論時の骨格トラッキング
問題設定
求まったTFFなどから骨格形成、およびトラッキングを行うロジックは、以下のように $P_t \in \mathcal{P}_t \ $ と $ \ P'_{t-1} \in \mathcal{P}_{t-1}$ からなる bipartite graph $\mathcal{G}$ に関するエネルギー最大化問題を解くことで達成する。
\newcommand{\argmax}{\mathop{\rm arg~max}\limits} \begin{eqnarray} \hat{z} &=& \argmax_z \sum_{P_t \in \mathcal{P}_t} \sum_{P'_{t-1} \in \mathcal{P}_{t-1}} \Psi_{P_t, P'_{t-1}} \cdot z_{P_t, P'_{t-1}} \\ &s.t.& \forall P_t \in \mathcal{P}_t, \sum_{P'_{t-1} \in \mathcal{P}_{t-1}} z_{P_t,P'_{t-1}} \leq 1 \ and \ \forall P'_{t-1} \in \mathcal{P}_{t-1}, \sum_{P_{t} \in \mathcal{P}_{t}} z_{P_t,P'_{t-1}} \leq 1\\ \end{eqnarray}ここで $z_{P_t, P'_{t-1}} \in \{ 0,1 \}$ はindicator関数で、$P_t \in \mathcal{P}_t \ $ と $ \ P'_{t-1} \in \mathcal{P}_{t-1}$ とが対応している時に1、他は0となる。
また binary potential $\Psi_{P_t, P'_{t-1}}$ は $P_t$ と $P'_{t-1}$ との類似度を表す。
よって、このエネルギー関数を最大化させることは $P_t$ と $P'_{t-1}$ とが対応している組に関して、その類似度を最大化させること。
ただし、条件から対応する $P_t$ と $P'_{t-1}$ とはそれぞれの点において1つ以下である。
最適化の手法
上記のエネルギー最大化問題を解くため、
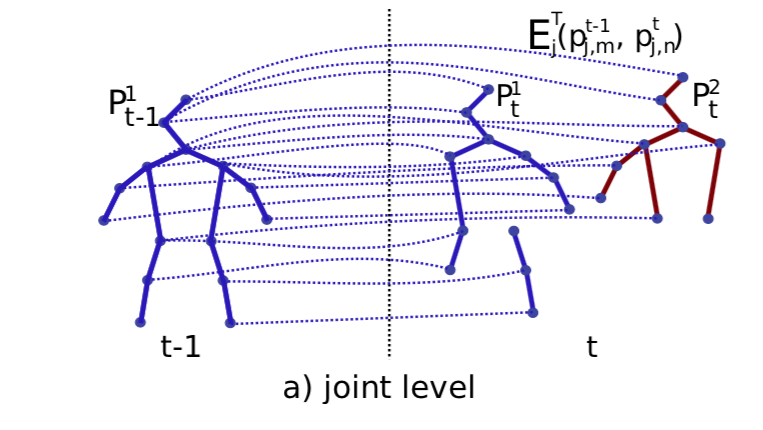
Z^t_j = \left\{ z^{p_{t-1},p_t}_j \mid P_t \in \mathcal{P}_t, P_{t-1} \in \mathcal{P}_{t-1} \right\}なる edge から構成される subgraph $\mathcal{G}_j$ を考える。つまり以下の図のようにフレーム t および t-1 において関節 j と推定された全ての点に関するグラフである。
この組み合わせに関して以下を求める。
E_{aggr}(p^{t-1}_{j,m}, p^t_{j,n}) = \int_{o=0}^{o=1} T_j(i(o))^T \frac{p^t_{j,n} - p^{t-1}_{j,m}}{\| p^t_{j,n} - p^{t-1}_{j,m} \|_2} do,ここで $i(o) = (1-o)\cdot p^{t-1}_{j,m} + o\cdot p^t_{j,n}$ とする。つまり $p^{t-1}_{j,m} $ から $p^t_{j,n}$ への直線経路。これに沿ってTFFとedgeの単位ベクトルとの内積を線積分するので、TFFが両nodeを対応すると考えているなら1に近い大きな値になるハズ。
ただこれだとTFFに基づいて対応するnodeを求めるため、対象の人の関節位置が動いてないと計算できない。そこで両node間のユークリッド距離 $\Delta p^t_{j,m,n} = \left| p^t_{j,n} - p^{t-1}_{j,m} \right|_2$ を用いて
E_j ( p^{t-1}_{j,m}, p^t]{j,n}) = \begin{cases} E^T_{aggr} (p^{t-1}_{j,m}, p^t_{j,n}) & if \ \Delta p^t_{j,m,n} \geq \tau_{\Delta} \\ 1 & if \ \Delta p^t_{j,m,n} < \tau_{\Delta} \end{cases}とする。 $\tau_{\Delta}$ は閾値。
つまり、両nodeの距離が閾値を下回る時は1(対応)とし、上回る時は $E_{aggr}$ を計算する。
こうして骨格 $j$ ごとに求まった $E_j$ の大小で t-1 フレームと t フレームの骨格を対応づけると、t-1 フレームの k さんの右肩と t フレームの m さんの右肩が対応づけられる一方で、t-1 フレームの k さんの左肩と t フレーム目の n さんの左肩が対応づけられるという状況も生じうる。
そこで、PAFにより定まった m さんの骨格、 n さんの骨格を基準として、人ベースでの対応づけとする。
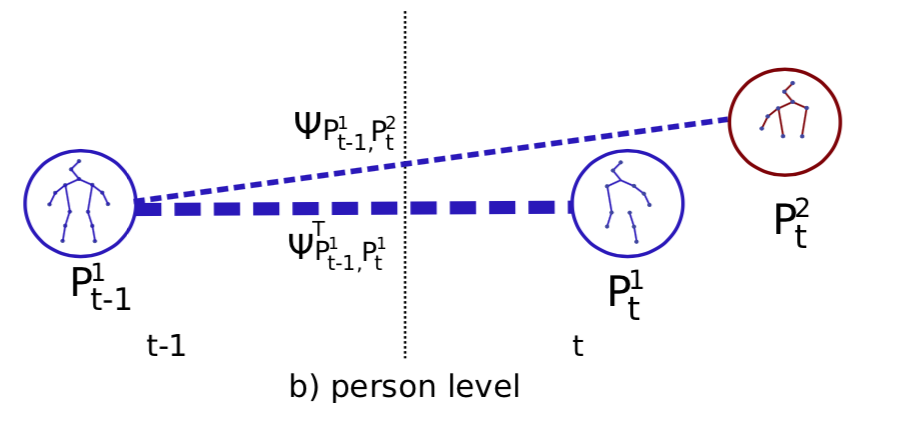
$\Psi_{P^m_{t-1},P^t_{t}}$ を $P^m_{t-1}$ さんと $P^t_{t}$ さんとの全ての骨格の対応づけと考えて、
\Psi_{P^m_{t-1},P^t_{t}} = \sum^J_{j=1} \mathbb{1} (P^{t-1}_{j,m}, P^t_{j,n}) \cdot E_j(P^{t-1}_{j,m}, P^t_{j,n})とする。ここで indicator関数 $\mathbb{1} (P^{t-1}_{j,m}, P^t_{j,n})$ は両方の関節が検出された場合に1、他を0とする。
そうすると以下の図のように人と人との対応関係ごとに $\Psi_{P^m_{t-1},P^t_{t}}$ が求まるので、この値の大小で正しい対応関係を決めればいい。
実装時のポイント
実装時のポイントは以下
1. ベースはOpenPoseのアーキテクチャだが、特徴量抽出部分でVGG19の10層を12層に変更する
2. 出力する関節の heat map は閾値 $\tau_{NMS}$ により切り捨てる
3. まずOpenPose部分をMicrosoft COCO datasetと PoseTrack datasetの個々の画像で学習させる
4. 次にPoseTrack dataset をシーケンシャルに用いてTFF部分を学習させる
5. 推論時には4つのスケール(0.5, 1, 1.5, 2)の画像を入力し、その出力を平均して用いる他の手法との比較
PoseTrack dataset での他の手法との比較結果は以下。
下段 test data で見ると、FlowTrackに次いで2番目のMOTAとなっている。ちなみに現在(19/6/9)ではtopdown方式のPOINetがMOTA=58.41で最もよい。