概要

• API GatewayとLambdaでS3にある画像を返却する
• クライアント側からは単にURLにアクセスしたら画像が表示されるように見える
• S3をpublicにすることなく画像を表示することができる (限定公開などが可能)
• pythonでの実装

仕様がよく分からずハマったのでメモを残します．

やること

1. Lambdaの作成
2. API Gatewayの作成

S3は作成済みとします．

1. Lambdaの作成

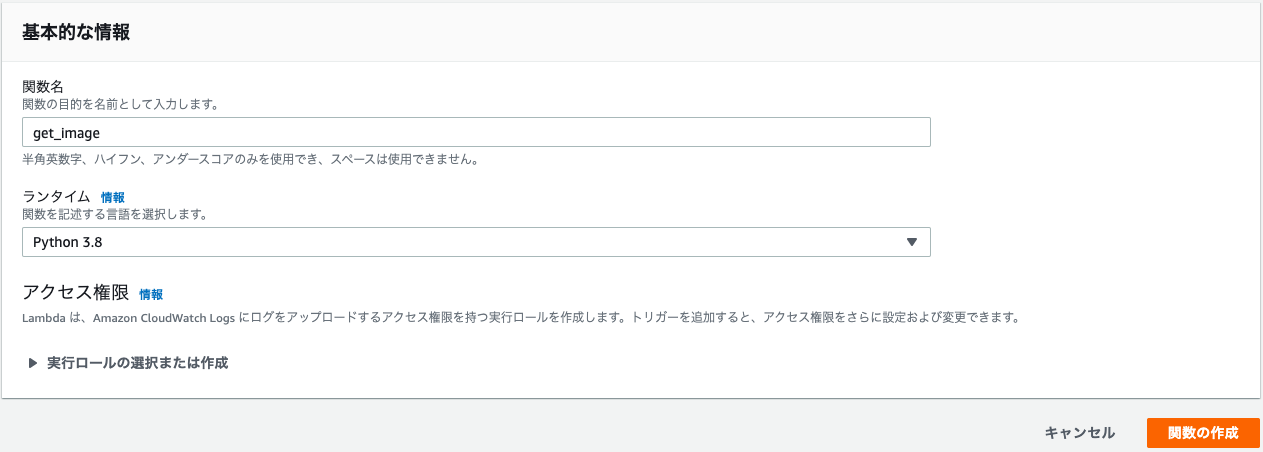
Lambdaを適当な名前で作成します．ここではget_imageとしました．

また，ランタイムはPython 3.8を選択しました．

そして関数コードに
以下のコードを登録します．

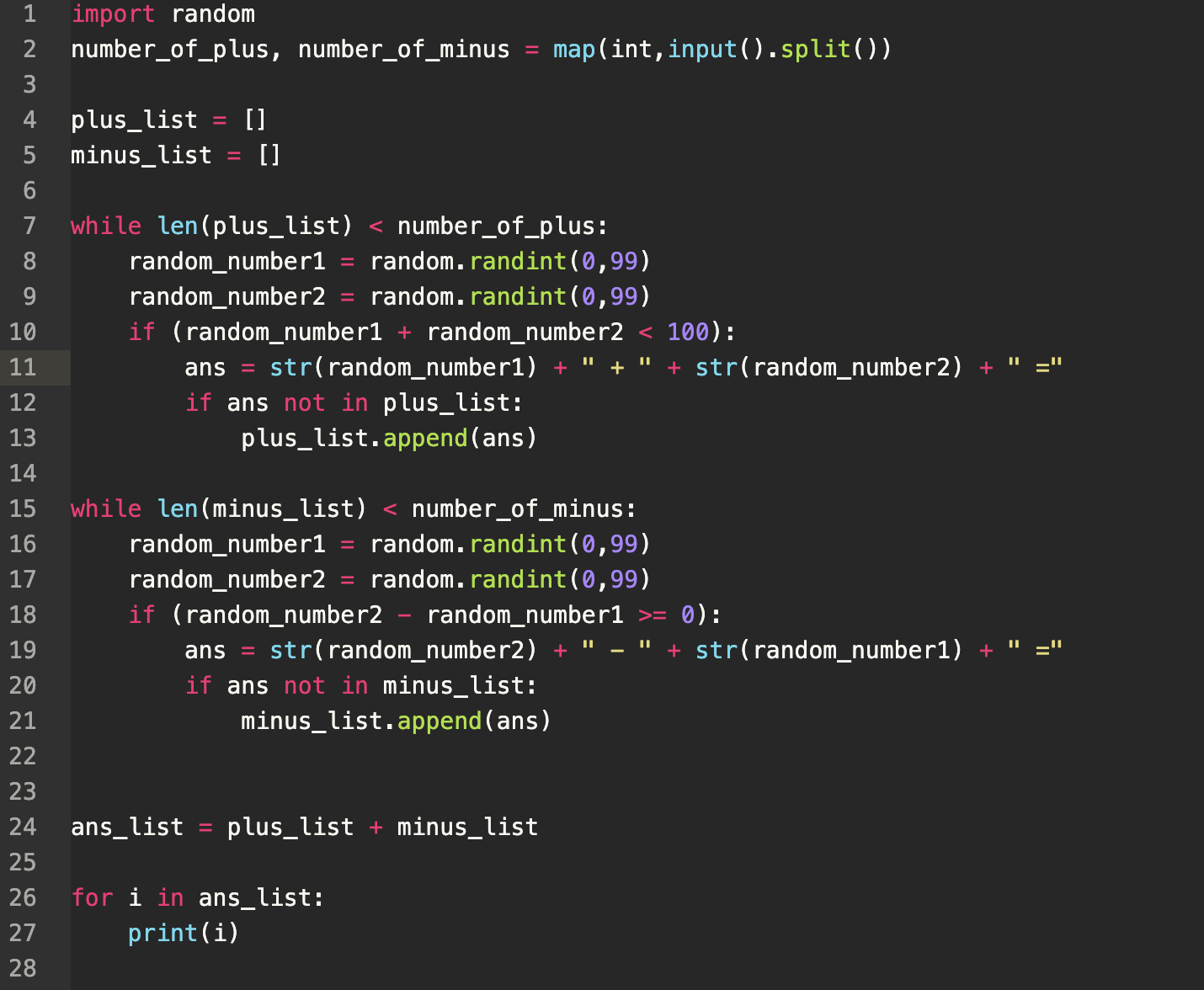
import boto3
import base64

def get_img_from_s3():
    s3 = boto3.client('s3')
    bucket_name = 'BUCKET_NAME'
    file_path = 'FILE_PATH'
    responce = s3.get_object(Bucket=bucket_name, Key=file_path)
    body = responce['Body'].read()
    body = base64.b64encode(body)
    return body


def lambda_handler(event, context):
    img = get_img_from_s3()
    return img

bucket_nameにS3のバケットの名前，file_nameに読み込みたいS3のオブジェクト(画像)のパスを渡しS3からオブジェクトを読み込みます．

LambdaにS3へのアクセス権限を付与

作成したLambdaはS3へのアクセス権限を持っておらず，このままだとアクセスが拒否されてしまうのでS3へのアクセス権限を付与します．

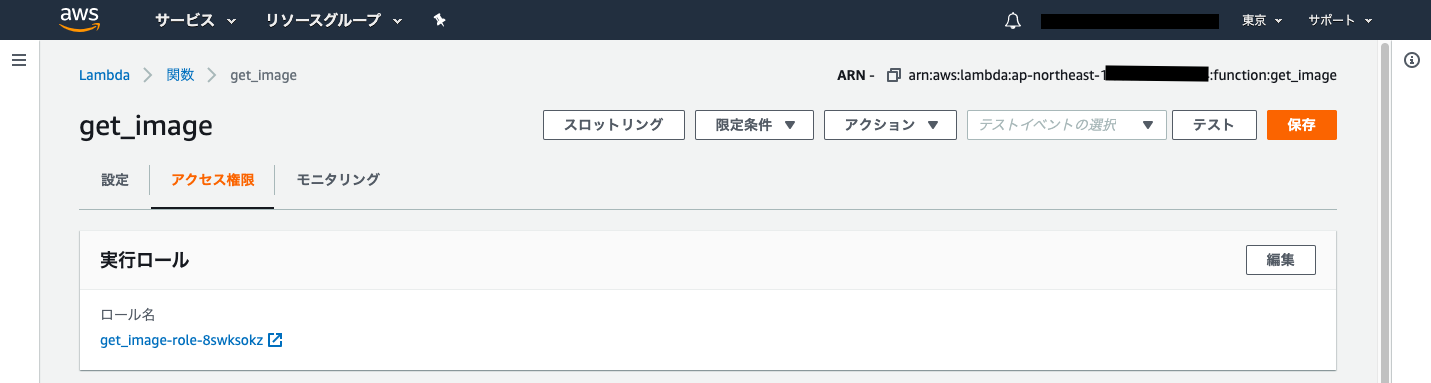
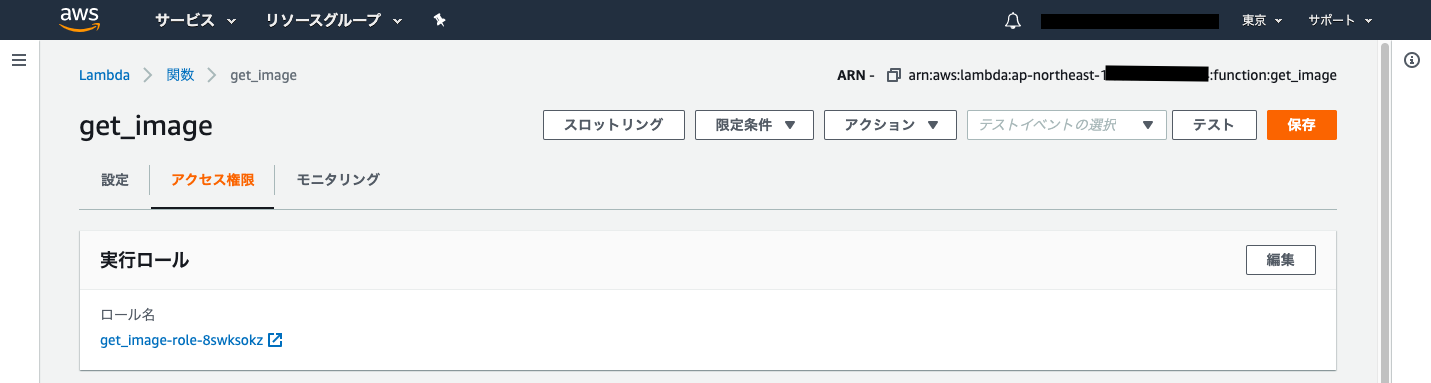
まず作成したLambdaのアクセス権限のページを開きます．

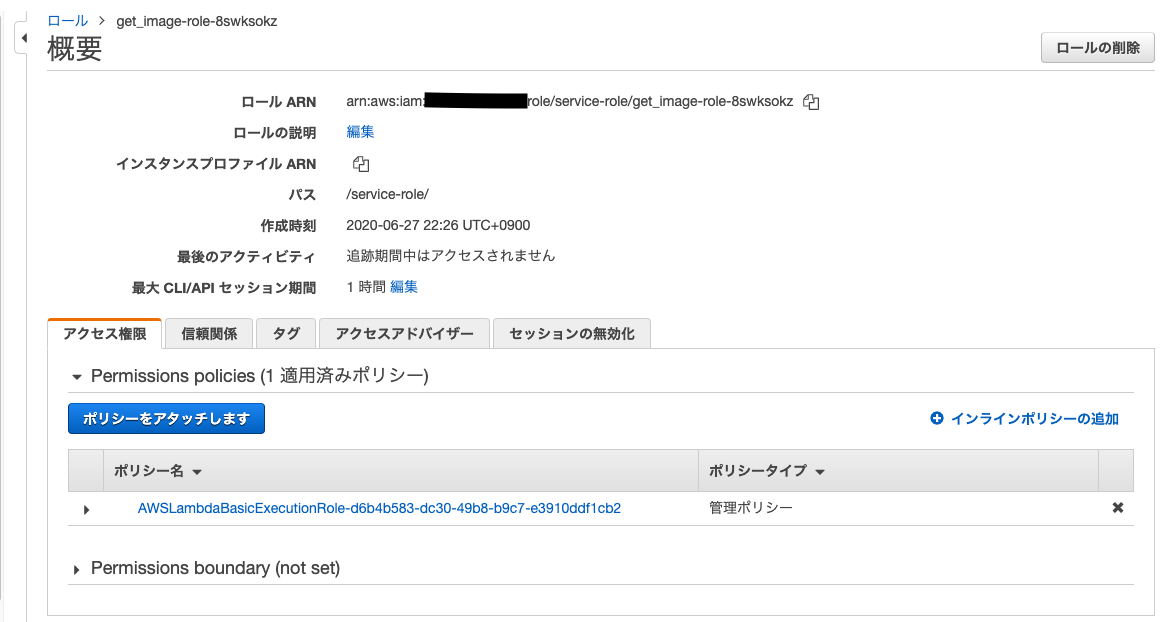
ここに自動で作成された実行ロールが割り当てられているので，この実行ロールのページを開きます．

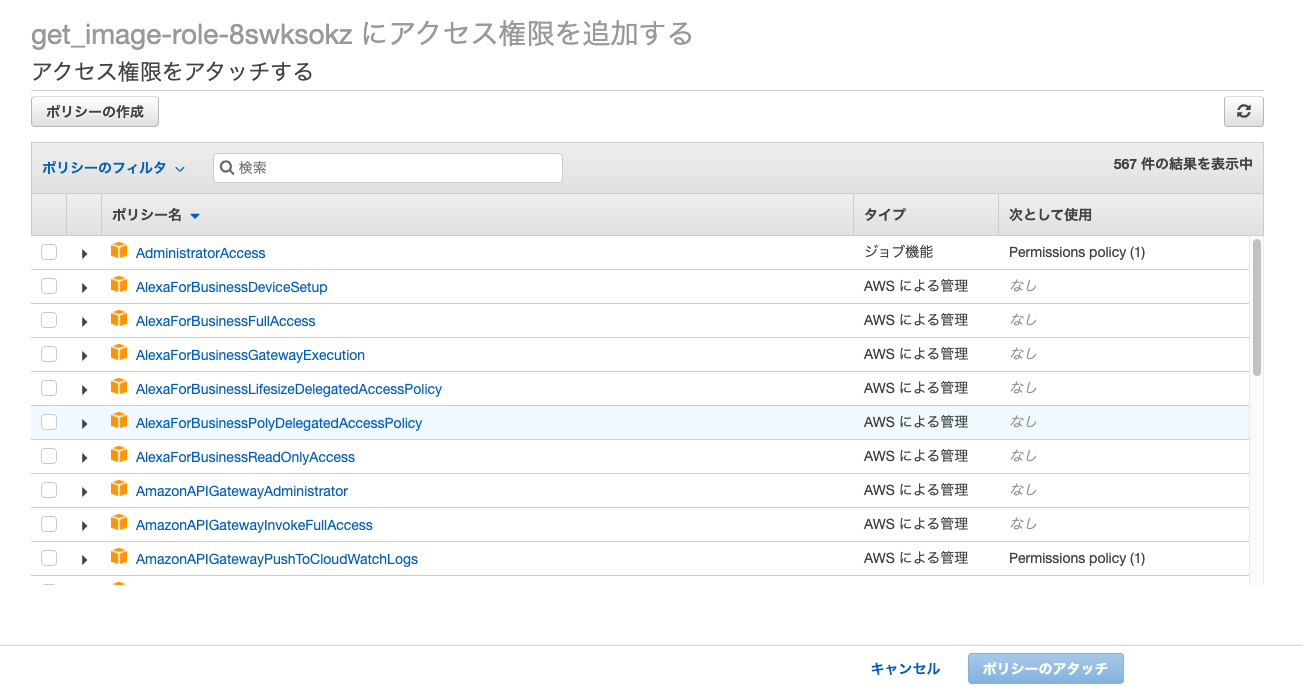
ページ中央の青いポリシーをアタッチしますというボタンを押します．

このようにいろいろなポリシーが出てきます．

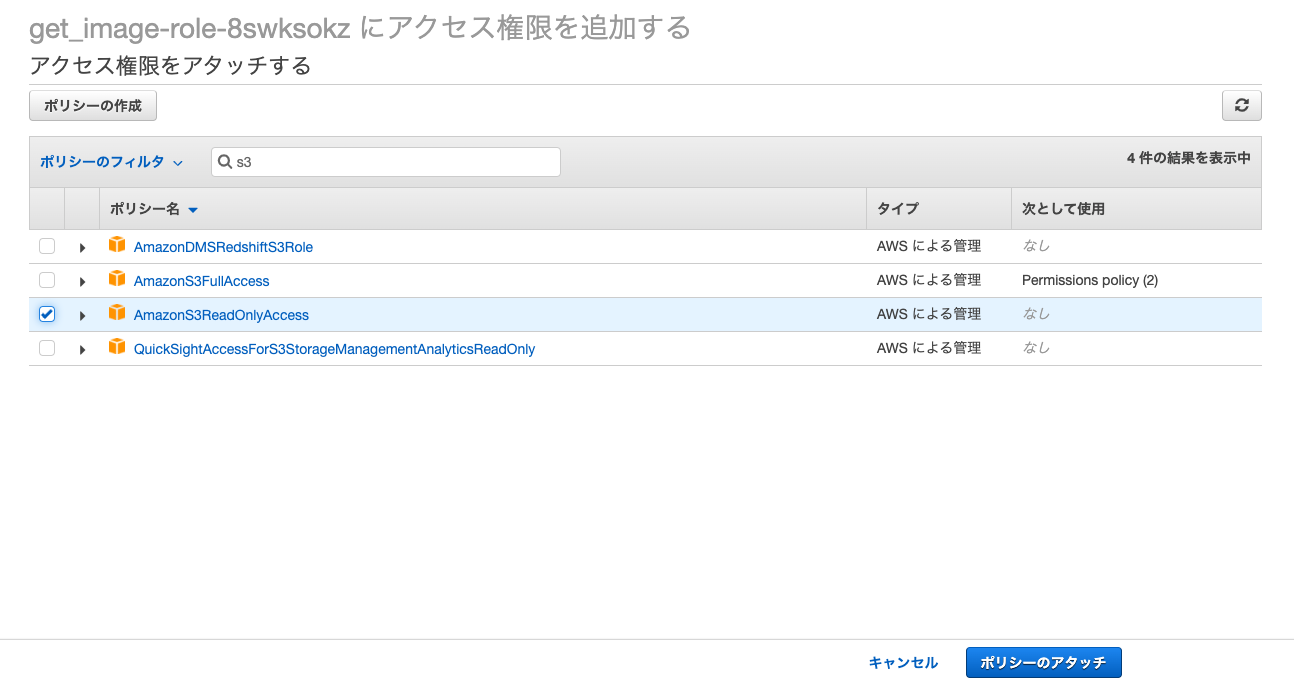
S3で検索するとS3に関するポリシーが出てきます．
今回はS3から画像を読み込むのでAmazonS3ReadOnlyAccessというポリシーをアタッチします．
これでLambdaからS3に保存されているファイルを読むことができるようになります．

以上でLambdaの設定は終了です．

2. API Gatewayの作成

続いてAPI Gatewayの作成をします．

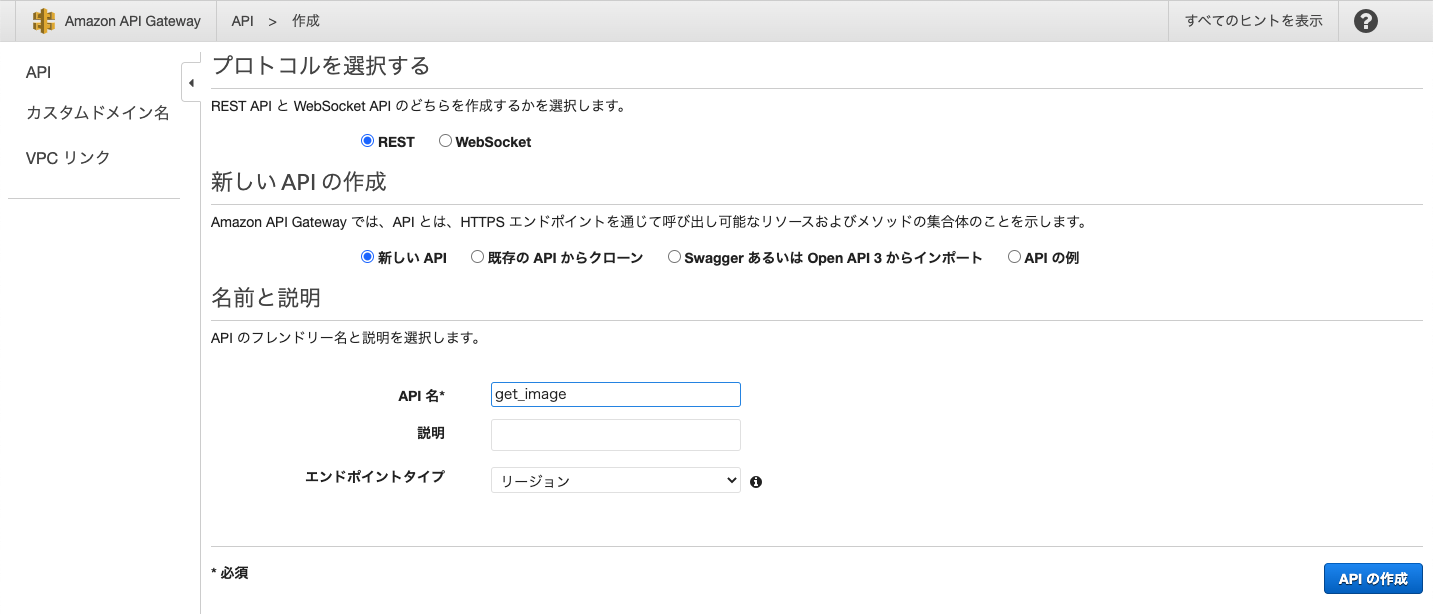
APIタイプはREST APIを選択し，API名は適当にget_imageとしました．

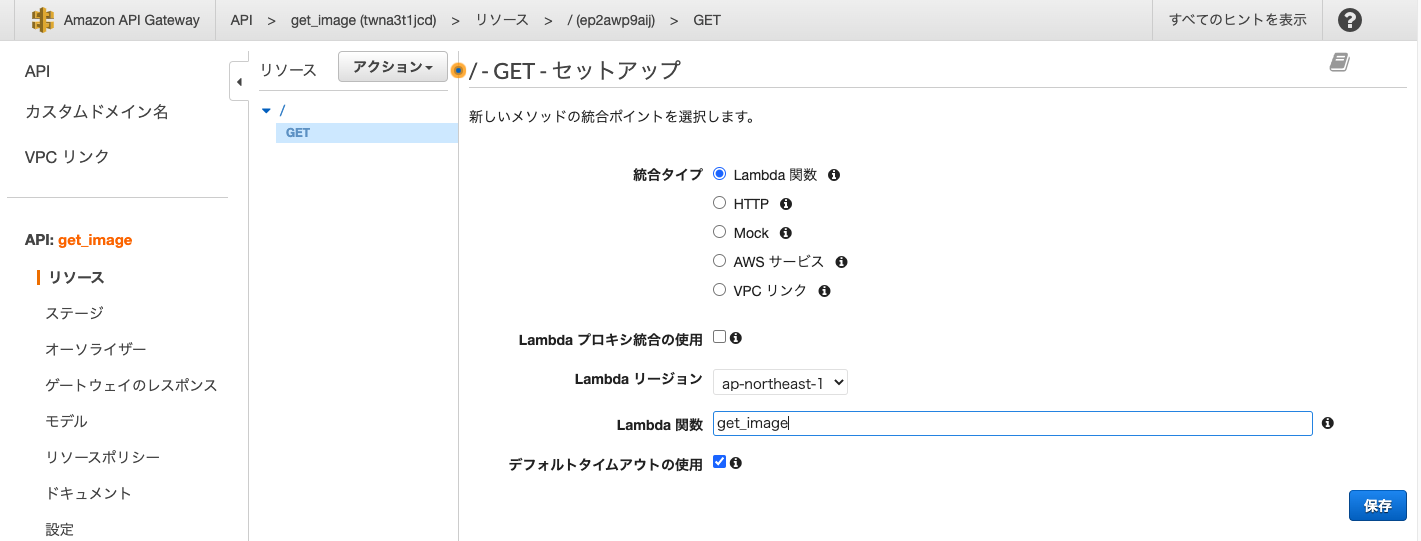
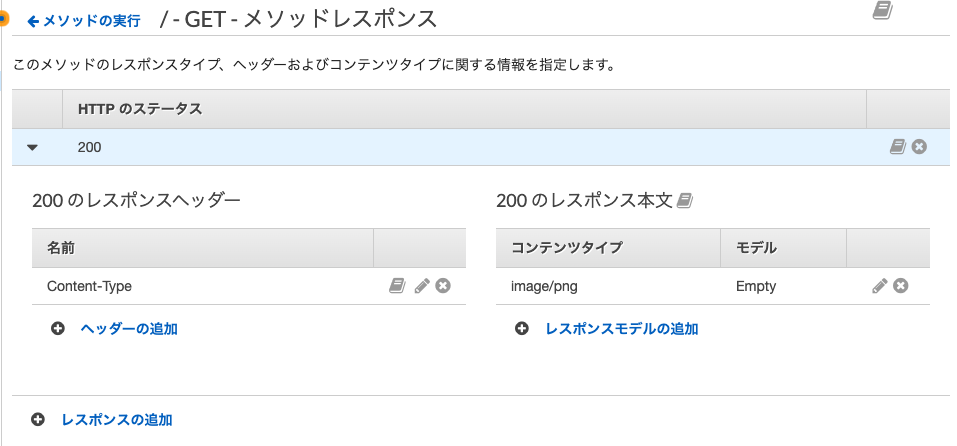
続いてGETメソッドを追加し，統合タイプにはLambdaを，Lambda関数には先ほど作成したget_imageというLambda関数を指定しました．

これでAPI Gatewayが作成できたのでメソッドレスポンスの設定を行います．

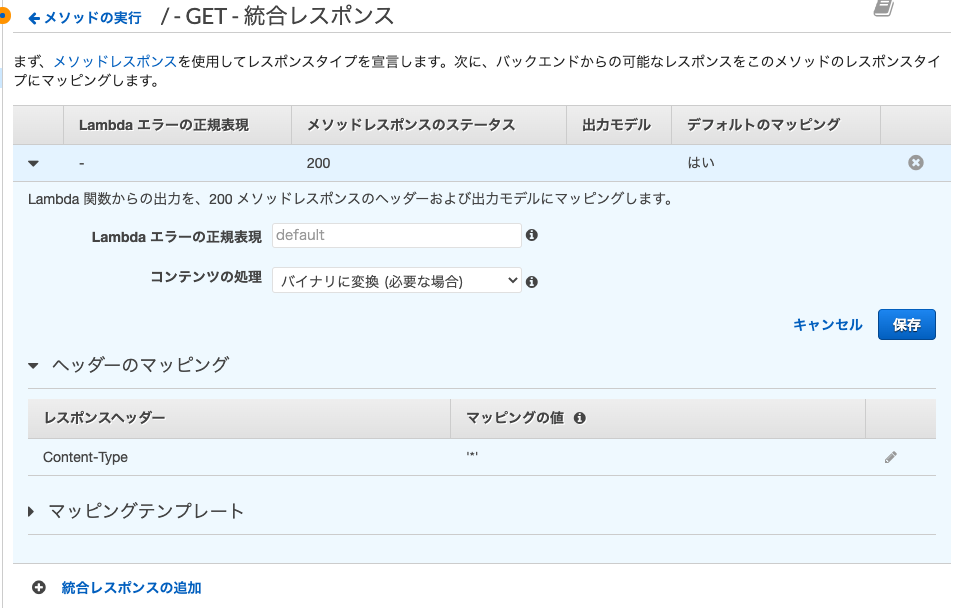
まずレスポンスヘッダーにContent-Typeを追加し，レスポンス本文のコンテンツタイプにはimage/pngを追加しました．(今回はpngを読み込んだのでimage/pngにしました．)

次に統合レスポンスの設定を行います．

コンテンツの処理方法をデフォルトではパススルーになっていますが，バイナリに変換（必要な場合）を選択します．
またヘッダーのマッピングのマッピングの値を'*'とします．

以上でAPI Gatewayの設定も終了です．

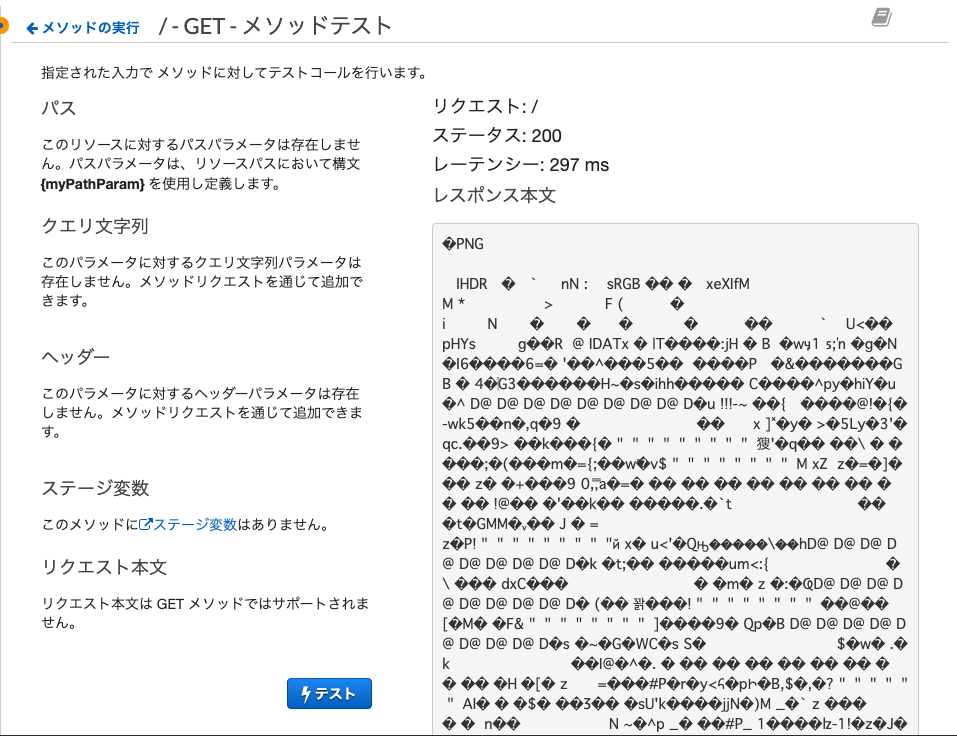
最後にAPIのテストを行うと

このようにpngのバイナリを返すことができました！

実際にAPIをデプロイしてURLにアクセスすると画像が表示されます．

参考

Node.jsによる実装　Lambda + API Gateway入門。画像のDL

AtCoder Beginner Contest 172 参戦記

前回はE問題まで20分で行ってF問題を100分考えて駄目だったけど、今回は30分でD問題まで行ってE問題を90分考えたけど駄目だった. そもそもC問題で制限を見ながら計算量の緩和をすることが珍しいのに、2重で緩和しないといけないのってやっぱり ABC C問題にしては難しいような. 前回の阿鼻叫喚の EXCEL 列名C問題でも半分弱解いているのに、今回のC問題は3割弱しか解けていない時点で難しいことは確かなんだけど.

ABC172A - Calc

2分くらい?で突破. コードテストが動かなくて、B問題を書いたあとに提出した. 書くだけ.

a = int(input())

print(a + a * a + a * a * a)

ABC172B - Minor Change

2分くらい?で突破. 書くだけ. 違うところの数ですね.

S = input()
T = input()

result = 0
for i in range(len(S)):
    if S[i] == T[i]:
        continue
    result += 1
print(result)

ABC172C - Tsundoku

9分半で突破. 累積和+二分探索で O(NlogN). 二分探索で境界値バグを出さないように気を揉んだので、解説の O(N+M) 解はスマートだなあって思いました.

from itertools import accumulate
from bisect import bisect_right

N, M, K = map(int, input().split())
A = list(map(int, input().split()))
B = list(map(int, input().split()))

a = [0] + list(accumulate(A))
b = [0] + list(accumulate(B))

result = 0
for i in range(N + 1):
    if a[i] > K:
        break
    j = bisect_right(b, K - a[i])
    result = max(result, i + j - 1)
print(result)

追記: 解説は累積和は使って、二分探索は使わないコードだったが、累積和を使わなくても書ける.

N, M, K = map(int, input().split())
A = list(map(int, input().split()))
B = list(map(int, input().split()))

b_sum = sum(B)
for i in range(M - 1, -1, -1):
    if b_sum <= K:
        j = i
        break
    b_sum -= B[i]
else:
    j = -1
result = j + 1

a_sum = 0
for i in range(N):
    a_sum += A[i]
    if a_sum > K:
        break
    while a_sum + b_sum > K:
        b_sum -= B[j]
        j -= 1
    result = max(result, (i + 1) + (j + 1))
print(result)

ABC172D - Sum of Divisors

14分で突破. 半分くらいは ABC152E - Flatten のコードと同じ. エラトステネスの篩で素因数分解して、各素数の個数 + 1 を積算すると素数の数が出る. それを使って f(X) を書いて、後は問題文通りに∑^N_K=1K×f(K) を求めるだけ. PyPy で2.8秒なので割と制限ギリギリだった.

N = int(input())

sieve = [0] * (N + 1)
sieve[0] = -1
sieve[1] = -1
for i in range(2, N + 1):
    if sieve[i] != 0:
        continue
    sieve[i] = i
    for j in range(i * i, N + 1, i):
        if sieve[j] == 0:
            sieve[j] = i


def f(X):
    t = []
    a = X
    while a != 1:
        if len(t) != 0 and t[-1][0] == sieve[a]:
            t[-1][1] += 1
        else:
            t.append([sieve[a], 1])
        a //= sieve[a]
    result = 1
    for _, n in t:
        result *= n + 1
    return result


result = 0
for K in range(1, N + 1):
    result += K * f(K)
print(result)

ABC172E - NEQ

90分考えたけど解けず.

準備

herokuにログイン

heroku login

アプリケーションの作成

heroku create APPNAME

gitの設定

heroku git:remote -a APPNAME

buildpacksの設定（Pythonアプリ）

heroku buildpacks:set heroku/python 

デプロイ

デプロイ

git push heroku master

アプリケーション起動

heroku open

その他

heroku上でコマンド実行

heroku run COMMAND

コマンドの中断: heroku run:detached COMMAND

ログ

heroku logs --t

アプリケーションの一覧

heroku list

アプリケーション毎のコマンド実行

heroku COMMAND --app APPNAME

準備

herokuにログイン

heroku login

アプリケーションの作成

heroku create APPNAME

gitの設定

heroku git:remote -a APPNAME

buildpacksの設定

heroku buildpacks:set heroku/python 

デプロイ

デプロイ

git push heroku master

アプリケーション起動

heroku open

その他

heroku上でコマンド実行

heroku run COMMAND

コマンドの中断: heroku run:detached COMMAND

ログ

heroku logs --t

アプリケーションの一覧

heroku list

アプリケーション毎のコマンド実行

heroku COMMAND --app APPNAME

はじめに

ここでは、Pythonの例外処理について解説します。

例外処理の基本

例外処理は、プログラムを実行中に何らかのエラーが発生した場合の処理を記述するものです。
tryとexceptを用いて、以下のように記述します。

import pandas as pd

try:
    df = pd.read_csv('sample.csv')
except FileNotFoundError:
    print('File not found.')

tryに続けてエラー（例外）が発生する可能性のある処理を、exceptに続けてエラーが発生した場合の処理を記述します。
exceptに続けてエラーの種類を書いておくと、指定したエラーが発生した場合に例外処理が実行されます。
ここで示した例では、FileNotFoundError（指定されたファイルが見つからないという例外）が発生した場合のみ、except節の処理が実行されます。
exceptの直後に何も記述しなかった場合は全てのエラーに対して、except節の処理が実行されますが、予期せぬエラーに対しても処理が実行されてしまうため、推奨されません。

else節

elseを入れると、エラーが発生しなかった場合に、続けて行いたい処理を記述することができます。

import pandas as pd

try:
    df = pd.read_csv('sample.csv')
except FileNotFoundError:
    print('File not found.')
else:
    df.to_excel('sample.xlsx', index=False)

上の例では、読み込んだファイルと同じ内容をエクセルファイルとして保存するようにしています。

finally節

finallyを使うと、エラーが発生したかどうかに関係なく実行したい処理を記述できます。

import pandas as pd

try:
    df = pd.read_csv('sample.csv')
except FileNotFoundError:
    print('File not found.')
finally:
    print('finished.')

上の例では、ファイルが読み込めても読み込めなくても、最後にfinished.という文字列が出力されます。

まとめ

ここでは、Pythonの例外処理について解説しました。
ユーザーからの入力を求めたり、データベースに接続したりする場合には例外処理を入れておくと良いでしょう。

1 目的

CAGRの説明とCAGRを計算するコードを記載する。

2 内容

2-1 CAGRの計算式

ある株式銘柄の価格について、基準日の銘柄価格をS_0 , 開始日からn営業日後の銘柄価格をS_nとする。このときCAGR(compound average growth rate)を下記式で計算する。

CAGR = \biggl({\frac{S_n}{S_0}} \biggl)^{\frac{1}{years}}-1

ただし、years= n/(1年間の取引日総数)　となる。

2-2 CAGRの意味は?

CAGR（年平均成長率）とは、複数年にわたる成長率から、1年あたりの幾何平均を求めたもの。
例えば、100百万円の売上高が3年間で160百万円に伸びたときの、3年間の平均成長率を考える。
この問題に対して、3年間で160÷100＝1.6　すなわち60％増だから、1年あたりの平均成長率は60÷3＝20で20％という考え方は誤りである。一般のビジネスの考え方では年平均成長率というとき、複利の考え方を前提にしており、100×（1＋x）×（1＋x）×（1＋x）＝160となるようなxを求めないといけない。
従って、3√1.6＝1.1696･･･　すなわち17.0％が正解となる。

出典：https://mba.globis.ac.jp/about_mba/glossary/detail-11621.html

2-3 CAGR計算するコード

test.py

#CAGR(年率成長率)を計算する
def CAGR(DF):
    df = DF.copy()
    df["daily_ret"] = DF["Close"].pct_change() #株価終値の前日との変化率を計算する。
    df["cum_return"] = (1 + df["daily_ret"]).cumprod() #cumprod(全要素の累積積を スカラーyに返します.
    n = len(df)/252
    CAGR = (df["cum_return"][-1])**(1/n) - 1
    return CAGR

はじめに

おひさしぶりです。100ページ越えの化学の宿題や数学の課題に追われていたので、なかなか競プロの時間が取れませんでした。久し振りにABCに出ましたが、結果は惨敗でした。ほんとうにありがとうございました。
ABの二完でした。

A問題

問題

考えたこと
やるだけ

a = int(input())
print(a+a**2+a**3)

B問題

問題

考えたこと
文字列を並び変えていいものだと誤読してタイムロスしました。前から順番に調べるだけ

s = input()
t = input()

ans = 0
for i in range(len(s)):
    if s[i] != t[i]:
        ans += 1

print(ans)

C問題

問題

考えたこと
DPで解けそう。knapsack-DP風にメモリに気をつかえば解けそうだと思いました。

D問題

問題

考えたこと
約数の個数を高速に列挙する方法が分りません。$O(N\sqrt N)$から減らす方法が分かりませんでした。

まとめ

少しやってないだけで、衰えが顕著に出て自分でも驚いています。課題も一段落したので、†精進†します。

参考URL

内容	URL
公式HP	https://www.tensorflow.org/probability
TFP入門チュートリアル	https://www.tensorflow.org/probability/examples/A_Tour_of_TensorFlow_Probability
Bayesian Methods for Hackersのipynbファイル	https://github.com/CamDavidsonPilon/Probabilistic-Programming-and-Bayesian-Methods-for-Hackers
Youtubeチャンネル	https://www.youtube.com/channel/UC0rqucBdTuFTjJiefW5t-IQ/search?query=probability
公式ブログ	https://blog.tensorflow.org/search?label=TensorFlow+Probability&max-results=20
githubレポジトリ	https://github.com/tensorflow/probability
Jupyter Notebook形式チュートリアル	https://github.com/tensorflow/probability/tree/master/tensorflow_probability/examples/jupyter_notebooks

※本記事は個人用のメモです。

ちょっと作ってみたくなったので調べてみた。
参考にさせていただいたのは以下のページ

https://qiita.com/Gen6/items/c153d562e757d88aa5c1
https://stackoverflow.com/questions/35588873/how-to-logout-in-python-bottle
http://www.denzow.me/entry/2017/12/09/103828
https://qiita.com/yoskmr/items/8d35b6c7a15cfa275dfc

コード

こんな感じになった。ほとんど参考ページのスクリプトを流用させていただいた。感謝。

login.py

#!/user/bin/env python
# -*- coding: utf-8 -*-

from bottle import route, run, template, request, static_file, url, get, post, response, error
from bottle import redirect
import sys, codecs
sys.stdout = codecs.getwriter("utf-8")(sys.stdout)

SECRET_KEY = 'some-secret-key'
LIFE_TIME = 120

@route("/")
def html_index():
    user_id = request.get_cookie('account', secret=SECRET_KEY)
    if user_id is None:
        redirect('/login')
    else:
        return template('index',url=url)


@route("/static/<filepath:path>", name="static_file")
def static(filepath):   
    user_id = request.get_cookie('account', secret=SECRET_KEY)
    if user_id is None:
        redirect('/login')
    else:
        return static_file(filepath, root="./static")


@get("/login")
def login():
    return """
        <form action="/login" method="post">
            Username: <input name="username" type="text" />
            Password: <input name="password" type="password" />
            <input value="Login" type="submit" />
        </form>
    """

@route("/login", method="POST")
def do_login():
    username = request.forms.get("username")
    password = request.forms.get("password")
    if check_login(username, password):
        response.set_cookie("account", username, secret=SECRET_KEY, path='/', max_age=LIFE_TIME )
        redirect('/')
    else:
        redirect('/login')

def check_login(username, password):
  if username == "admin" and password=="password":
    return True
  else:
    return False


@route('/logout')
@route('/logout', method="POST")
def logout():
    response.delete_cookie('account')
    redirect('/login')

@error(404)
def error404(error):
    return template("404")

run(host="localhost", port=8080, debug=True, reloader=True)

これで、
・最初の状態はログイン画面に遷移する。
・ログインしたらcookieにユーザー情報を登録し、以後のアクセスはそちらを見て行う。
・/logoutにアクセスしたらcookieの情報を削除してログアウトした状態になる。
・指定時間たったらcookieが無効になる。
ってことができた。

ディレクトリ構造はこんな感じで。

├─static
│  ├─css
│  ├─img
│  └─js
└─views

viewsの下にtemplateで使うファイルを入れてあげればよいはず。
templateはこちらのページに詳しく解説されているので、ここを参照のこと。
http://www.denzow.me/entry/2018/03/03/220942

Templateの中でmicro Pythonも使えそうなのでとっても便利そう。

この方法で一般的なお作法にのっとっているかは？？？
いろいろ難しいなぁ。

背景

近頃、ある一定の境界条件を満たす多項式の解析解を必要とすることがありました。
解析解を求めるのは、苦労しそうだったので、SymPyを使って楽にできないか検討してみました。

SymPy

SymPyはシンボリック演算をするためのpythonライブラリです。
以下のようなことができます。

たとえば以下のうような連立方程式の解析解を求めたいとします。
$ bx + ay = ab $
$ x - cy = c$
この連立方程式の解は、

import sympy
a = sympy.symbols("a")
b = sympy.symbols("b")
c = sympy.symbols("c")
x = sympy.symbols("x")
y = sympy.symbols("y")
sympy.solve([b*x+a*y-b*a,x-c*y-c],(x,y))

この結果は、$\frac{a c \left(b + 1\right)}{a + b c},\frac{b \left(a - c\right)}{a + b c}$となって正しい結果が得られます。

多項式の係数

ここでは、多項式

$f(x) = A_{0}+A_{1} x+A_{1} x^{2} + A_{3} x^{3} + A_{4} x^{4} + A_{5} x^{5}$

の中で、

$f(0) = 0$
$f(1) = S_{1}$
$f'(0) = 0$
$f'(1) = 0$
$f''(0) = 0$
$f''(1) = 0$
を満たす係数を求めたいとします。

for i in range(6):
    exec(f"A{i} = sympy.Symbol(\"A{i}\")")
S1 = sympy.Symbol("S1")
x = sympy.Symbol("x")

f = A0 + A1*(x) + A2*(x)**2 + A3*(x)**3 + A4*(x)**4 + A5*(x)**5
f1 = sympy.diff(f, x)
f2 = sympy.diff(f1, x)

まず上記のように変数と求めたい関数を用意して、

$f(0) = 0$の条件は

cond0 = f.subs(x, 0) - 0

のように表現します。
同様に残りすべての条件を

cond1 = f.subs(x, 1) - S1
cond2 = f1.subs(x, 0) - 0
cond3 = f1.subs(x, 1) - 0
cond4 = f2.subs(x, 0) - 0
cond5 = f2.subs(x, 1) - 0

で定義します。

このすべての条件を満たす$A_{0},A_{1},A_{2},A_{3},A_{4},A_{5}$は

solution = sympy.solve([cond0, cond1, cond2, cond3, cond4, cond5],(A0,A1,A2,A3,A4,A5))

とすると、答えは
$(A_{0},A_{1},A_{2},A_{3},A_{4},A_{5}) = (0, 0, 0, 10 S_{1}, - 15 S_{1}, 6 S_{1})$
と求まりました。

この結果を$f(x)$に再代入すると、

for i in range(6):
    exec(f"f = f.subs(A{i}, solution[A{i}])")

$f(x) = 10S_{1}x^{3} -15S_{1}x^{4} + 6S_{1}x^{5}$
$f'(x) = 30S_{1}x^{2} -60S_{1}x^{3} + 30S_{1}x^{4}$
$f''(x) = 60S_{1}x -180S_{1}x^{2} + 120S_{1}x^{3}$

となり、求めたい関数$f(x)$が分かりました。

前回挑戦時。笑

今回挑戦時。

多少成長したけど、独学に少し限界を感じてきた。

v2使用時にv1の関数を使用したい場合

.compat.v1.を付け加える

>>> tf.get_variable_scope()
AttributeError: module 'tensorflow' has no attribute 'variable_scope'

>>> tf.compat.v1.get_variable_scope()
<tensorflow.python.ops.variable_scope.VariableScope at 0x7f41e7efb198>

v2使用時にv1の関数を使用したい場合

.compat.v1.を付け加える

>>> tf.get_variable_scope()
AttributeError: module 'tensorflow' has no attribute 'variable_scope'

>>> tf.compat.v1.get_variable_scope()
<tensorflow.python.ops.variable_scope.VariableScope at 0x7f41e7efb198>

使用バージョン

• LibreOffice 6.4.4
• Python 3.7.7

概要

LibreOffice を操作する Python でモジュールを import する際には、通常に加えて以下のモジュール検索を行う。
- マクロ実行時に<LibreOffice インストールディレクトリ>/program ディレクトリが自動的にモジュール検索パス sys.path に追加されている。
- マクロ実行時には、とマクロ設置ディレクトリの pythonpath サブディレクトリと pythonpath.zip ファイルがもし存在すれば自動的に sys.path に追加されている。
- マクロもしくは <LibreOffice インストールディレクトリ>/program/uno.py を import したプログラムからは　com.sun.star で始まる UNO 固有モジュールからの import が行える。モジュール自体の import はできない。

マクロの sys.path

<LibreOffice インストールディレクトリ>/program ディレクトリ

Python マクロの実行時には、<LibreOffice インストールディレクトリ>/program ディレクトリが sys.path に含まれる。
<LibreOffice インストールディレクトリ> は、FreeBSD の場合 /usr/local/lib/libreoffice、Microsoft Windows の場合 %PROGRAMFILES%\LibreOffice。
uno, unohelper, pythonscript, msgbox はここから import する。

pythonpath ディレクトリと pythonpath.zip ファイル

マクロを設置したディレクトリの pythonpath サブディレクトリもしくは pythonpath.zip ファイルが存在すれば sys.path に追加されてモジュール検索の対称となる。

ユーザーマクロの場合,

• Microsoft Windows の場合

%APPDATA%\LibreOffice\4\user\Scripts\python\pythonpath
%APPDATA%\LibreOffice\4\user\Scripts\python\pythonpath.zip

• FreeBSD もしくは UNIX 類似システムの場合

${HOME}/.config/libreoffice/4/user/Scripts/python/pythonpath
${HOME}/.config/libreoffice/4/user/Scripts/python/pythonpath.zip

となる。
これらのパスは、マクロ終了後も LibreOffice を終了するまで維持される。
保持しているのは <LibreOffice インストールディレクトリ>/program/pythonloader.py の Loader クラスと推測される。
同じファイル中の checkForPythonPathBesideComponent() 関数が存在のチェックと sys.path への追加に使用されている。

システム共有マクロや機能拡張の場合でもそれぞれ追加されるのでマクロ呼び出し時に不必要なディレクトリが sys.path に含まれている可能性がある。

例えば sys.path の内容をメッセージボックスに表示するのに以下のマクロを実行してみる。

syspath.py

import sys
from msgbox import MsgBox

def syspath_msgbox():
    ctx = XSCRIPTCONTEXT.getComponentContext()
    sys_path_box = MsgBox(ctx)
    sys_path_box.addButton('oK')
    sys_path_box.renderFromBoxSize(300)
    sys_path = '\n'.join(sys.path)
    sys_path_box.show(sys_path, 0, 'sys.path')

表示されるのは以下のとおり。この時 pythonpath サブディレクトリは作ってあるが pythonpath.zip ファイルは存在しない。
2 番目に表示された /home/shota243 は LibreOffice 起動時のカレントディレクトリ。この時 PYTHONPATH 環境変数は設定していない。

/usr/local/lib/libreoffice/program
/home/shota243
/usr/local/lib/python37.zip
/usr/local/lib/python3.7
/usr/local/lib/python3.7/lib-dynload
/home/shota243/.local/lib/python3.7/site-packages
/usr/local/lib/python3.7/site-packages
/home/shota/.config/libreoffice/4/user/Scripts/python/pythonpath

APSO - Alternative Script Organizer for Python 拡張機能の Python インタープリタコンソールから sys.path を表示した場合は以下のとおり。

APSO python console [LibreOffice]
3.7.7 (default, Jun 21 2020, 22:27:00) 
[Clang 8.0.0 (tags/RELEASE_800/final 356365)]
Type "help", "copyright", "credits" or "license" for more information.
>>> import sys
>>> for p in sys.path:
...  print(p)
... 
/usr/local/lib/libreoffice/program
/home/shota243
/usr/local/lib/python37.zip
/usr/local/lib/python3.7
/usr/local/lib/python3.7/lib-dynload
/home/shota243/.local/lib/python3.7/site-packages
/usr/local/lib/python3.7/site-packages
/home/shota243/.config/libreoffice/4/user/uno_packages/cache/uno_packages/lu2030qffpne.tmp_/apso.oxt/python/pythonpath
>>> 

APSO 拡張機能のインストール先が　/home/shota243/.config/libreoffice/4/user/uno_packages/cache/uno_packages/lu2030qffpne.tmp_。
(前略)lu2030qffpne.tmp_/apso.oxt/python/apso.py が本体で (前略)lu2030qffpne.tmp_/apso.oxt/python/pythonpath ディレクトリ下の
apso_debug.py, apso_utils.py, theconsole.py がモジュール。

UNO 固有モジュールからの import

マクロもしくは uno を import したプログラムでは、com.sun.star. で始まるモジュールから識別子を import できる。

これは、import の実態である __import__() 関数が <LibreOffice インストールディレクトリ>/program/uno.py 内の _uno_import() 関数で置き換えられていることによる。
com はモジュール検索パスのどこにも存在しない。
_uno_import() 関数では、標準の __import__() 関数でのモジュール検索に失敗すると pyuno.getClass() 関数で取得を試みる。
この際に from <モジュール名> import <識別子> の <モジュール名> と <識別子> は連結して getClass() を呼ぶので <モジュール名> 全体の import や from <モジュール名> import * での一括 import は例外となる。

例：

mike% export PYTHONPATH="${PYTHONPATH}:/usr/local/lib/libreoffice/program"
mike% export LD_LIBRARY_PATH="${LD_LIBRARY_PATH}:/usr/local/lib/libreoffice/program"
mike% export PATH="${PATH}:/usr/local/lib/libreoffice/program"
mike% python
python
Python 3.7.7 (default, Jun 21 2020, 22:27:00) 
[Clang 8.0.0 (tags/RELEASE_800/final 356365)] on freebsd11
Type "help", "copyright", "credits" or "license" for more information.
>>> import uno
import uno
>>> from com.sun.star.uno import RuntimeException
from com.sun.star.uno import RuntimeException
>>> import com.sun.start.uno.RuntimeException
import com.sun.start.uno.RuntimeException
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
  File "/usr/local/lib/libreoffice/program/uno.py", line 356, in _uno_import
    return _builtin_import(name, *optargs, **kwargs)
ModuleNotFoundError: No module named 'com'
>>> from com.sun.star.uno import *
from com.sun.star.uno import *
from com.sun.star.uno import *
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
  File "/usr/local/lib/libreoffice/program/uno.py", line 434, in _uno_import
    raise uno_import_exc
  File "/usr/local/lib/libreoffice/program/uno.py", line 356, in _uno_import
    return _builtin_import(name, *optargs, **kwargs)
ImportError: No module named 'com' (or 'com.sun.star.uno.*' is unknown)
>>> 

import できるモジュール、識別子のリファレンスはcom::sun::star Module Reference と考えられる。

はじめに

動機：関数内でグローバル変数の動的な定義＆値の代入がしたい！

（こんなことホイホイとやっちゃダメですが…。）

def dainyuu(val_name):
    global val
    val = 123  # ここで指定された名前の変数に代入したい

dainyuu("val")
print(val)  # 関数外で参照

exec() によって動的な変数の定義や代入が可能ですが、グローバル変数への代入で少し手間取ったのでまとめました。

なお、検証は Python 3.7.3 です。

• 公式リファレンス：組み込み関数#exec

パターン１：グローバル変数のシンプルな定義

• exec の第2引数に globals() を渡す
• 第3引数を渡さない

exec に globals() のみを渡すことによって、文字列中の代入はグローバル変数への代入になります。

# 特に指定がない場合、ローカル変数の定義になる
def define_variable_test1(var_name):
    exec(f"{var_name} = 123")
    eval(f"print('{var_name} (in): ' + str({var_name}))")

# globals() を渡すとグローバル変数の定義になる
def define_variable_test2(var_name):
    exec(f"{var_name} = 345", globals())
    eval(f"print('{var_name} (in): ' + str({var_name}))")


define_variable_test1("val1")
try:
    print(f"val1(out): {val1}\n")
except NameError:
    print("val1(out): not defined\n")

define_variable_test2("val2")
try:
    print(f"val2(out): {val2}\n")
except NameError:
    print("val2(out): not defined\n")

out

val1 (in): 123
val1(out): not defined

val2 (in): 345
val2(out): 345

パターン２：グローバル変数の定義にローカル変数を使う

• exec に globals() と locals() を渡す
• 評価文中で global 変数宣言を行う

exec に locals() を渡すと文字列中の代入はローカル変数になりますが、同じ文字列中で global 宣言を行っておくことでグローバル変数への代入が行えます。

# locals() も渡すとローカル変数の定義になってしまう
def define_variable_test3(var_name):
    local_val = 12345
    exec(f"{var_name} = local_val", globals(), locals())
    eval(f"print('{var_name} (in): ' + str({var_name}))")

# exec 内でのグローバル変数宣言によってグローバル変数の定義になる
def define_variable_test4(var_name):
    local_val = 34567
    exec(f"global {var_name}\n{var_name} = local_val", globals(), locals())
    eval(f"print('{var_name} (in): ' + str({var_name}))")


define_variable_test3("val3")
try:
    print(f"val3(out): {val3}\n")
except NameError:
    print("val3(out): not defined\n")

define_variable_test4("val4")
try:
    print(f"val4(out): {val4}\n")
except NameError:
    print("val4(out): not defined\n")

out

val3 (in): 12345
val3(out): not defined

val4 (in): 34567
val4(out): 34567

当たり前と言えば当たり前ですが、引数として global() とかを渡せるのもあって無駄に悩みました…

というか、こんな邪道を歩む行為やめようねって話です。

$$
\def\bra#1{\mathinner{\left\langle{#1}\right|}}
\def\ket#1{\mathinner{\left|{#1}\right\rangle}}
\def\braket#1#2{\mathinner{\left\langle{#1}\middle|#2\right\rangle}}
$$

はじめに

前回までで一通り「誤り訂正符号」について理解できました。これで量子コンピュータに多少のノイズが加わっても誤りを訂正して正しく計算結果を得ることができる！（少なくとも理論的には！）と言いたいところなのですが、実は全然そうではありません！という話をこれからします。ノイズは量子計算プロセスのあらゆる箇所に発生する可能性があって、その各々について特別な手当てをしてあげる必要があります。それらを実施してはじめて誤りがあったとしても正しく動作する誤り耐性のある量子計算＝フォールトトレラント量子計算(fault-tolerant quantum computation)が実現できたと言えます。

この後の節で何を説明しようとしているか最初に言っておきます。まず、「理論説明」ではフォールトトレラントであるとは一体どういうことなのかを述べた後、具体的にフォールトトレラントな量子ゲートや測定や初期状態作成の実現方法を紹介し、連結符号としきい値定理について説明します。「動作確認」では、フォールトトレラント量子計算のとても簡単な例を取り上げて、量子計算シミュレータqlazyを使ってその動作を確認してみます。

参考にさせていただいたのは、以下の文献です。

1. ニールセン、チャン「量子コンピュータと量子通信（３）」オーム社（2005年）

理論説明

フォールトトレラントの定義

誤り訂正符号は量子状態を蓄積・伝送する際に発生するノイズに対応するものでした。実際の量子計算は「初期状態作成」「ゲート演算」「測定」といった一連のプロセスから成り立っていますので、誤り訂正符号だけでは十分ではありません。例えば、ゲート演算はどうやって実行すれば良いでしょうか。符号状態を一旦復号化してゲート演算を実行して完了したらすかさず再度符号化すればいいんじゃない？と思われたかもしれませんが、その考えは良くないです。復号化して符号化するプロセスやゲート演算の最中にノイズが紛れ込む可能性があります。したがって、より良い方法は符号化状態のままゲート演算をすることなのですが、単に復号化しないで済むようにゲートを構成しました、というだけではこれまた不十分です。どこかに発生したノイズが伝搬し増殖しないように構成しないといけません。例えば、制御NOTゲート（CNOTゲート）はあらゆる場面で大活躍するゲートですが、$U_{1,2}$を制御NOT演算とすると$U_{1,2}X_{1}=X_{1}X_{2}U_{1,2}$が成り立つので、入力の制御側に発生したビット反転ノイズは出力の制御側と標的側の両方に伝搬します。一方、$U_{1,2}Z_{2}=Z_{1}Z_{2}U_{1,2}$が成り立つので、入力の標的側に発生した位相反転ノイズは出力の制御側と標的側に伝搬します。図で書くと以下のように伝搬することになります。

＜制御側のビット反転[X]は制御・標的に伝搬＞

--[X]--*----     ----*--[X]--
       |      =>     |
-------X----     ----X--[X]--


＜標的側の位相反転[Z]は制御・標的に伝搬＞

-------*----     ----*--[Z]--
       |      =>     |
--[Z]--X----     ----X--[Z]--

符号状態に対するゲート演算の中にこのような部品があるととてもマズイです。誤り訂正は一つの符号ブロックの中で高々1回だけ発生するのであれば訂正可能ですが、上記のような構成があると1個のノイズが2個に増えますので、訂正不能となります。したがって、このようなことにならないように構成しないといけません。さらにゲート演算だけでなく、誤り訂正の手続き自体にもノイズが発生する可能性もあるので、この対策も必要です。さらに初期状態作成や測定のプロセスにもノイズが紛れ込む可能性があります。

等々、、ということを考えると、フォールトトレラントなんて不可能なのでは、という気分にだんだんなってきます。だってCNOTがノイズを伝搬させるのですよ。果たしてCNOTを使わないで符号状態に対するCNOTが実現できるでしょうか？またCNOTなしで誤り訂正を実現できるでしょうか？、、でも、ご安心ください。実はCNOTを絶対に使ってはいけないということではありません。ある条件を満たした伝搬であれば問題ないのです。その条件（＝フォールトトレラントの定義）というのは、「量子計算を実行するシステムの中で1個ノイズが発生したときに各符号ブロックの中に高々1個のノイズしか発生しない状態になっている」というものです。各符号ブロックあたり1個のノイズであれば訂正できるので、ノイズが発生したのと同じ符号ブロックへの伝搬はダメですが（ブロックあたりのノイズが2個になるので）、他のブロックへの伝搬であれば許されます（1個のノイズであれば訂正できるので）。そのように量子計算システムが構成されていればフォールトトレラントであると言うことができます。

残念ながら、ノイズは2箇所以上同時に発生する場合があります¹。そして、不幸にして、伝搬の結果同じ符号ブロックにノイズが2個紛れ込むことがあります。その場合は計算結果が間違ってしまいます。しかし、その確率は1箇所にノイズが発生する確率を$p$とすると高々$O(p^{2})$にまで抑えられているはずです。誤りに関して何も対策を施さない場合、計算結果が間違う確率は$O(p)$であり、それが$O(p^{2})$になるということなので、これはフォールトトレラントの明白な効果です。すなわち、計算誤り率が高々$O(p^{2})$になっていることが、フォールトトレラント量子計算のひとつの特徴と考えることもできそうです。

フォールトトレラント量子計算の構成

それでは、具体的に「ゲート演算」「測定」「初期状態作成」をどのようにフォールトトレラントに構成できるかについて見ていきます。7量子ビットのSteane符号で考えるのがもっともわかりやすいということなので、以降の議論はすべてSteane符号を前提にします²。

ゲート演算

パウリゲート:X,Y,Z

まずパウリ$Z$からはじめます。Steane符号の論理$Z$は、6個ある生成元すべてと可換なものとして、

\bar{Z} = Z_{1} Z_{2} Z_{3} Z_{4} Z_{5} Z_{6} Z_{7}  \tag{1}

と定義できます。生成元は、

生成元	演算子
$g_1$	$I \space I \space I \space X \space X \space X \space X$
$g_2$	$I \space X \space X \space I \space I \space X \space X$
$g_3$	$X \space I \space X \space I \space X \space I \space X$
$g_4$	$I \space I \space I \space Z \space Z \space Z \space Z$
$g_5$	$I \space Z \space Z \space I \space I \space Z \space Z$
$g_6$	$Z \space I \space Z \space I \space Z \space I \space Z$

だったので、式(1)の定義で良いことがわかると思います³。

6個の生成元に$\bar{Z}$を加えた7個の演算子によってユニークに決まるスタビライザー状態を$\ket{0_L}$とし、$\bar{Z}$を$-\bar{Z}$に変えたときにユニークに決まるスタビライザー状態を$\ket{1_L}$とします。そうすると、

\bar{Z} \ket{0_L} = \ket{0_L}, \space \bar{Z} \ket{1_L} = - \ket{1_L}  \tag{2}

となり、$\bar{Z}$を論理基底$\{ \ket{0_L}, \ket{1_L} \}$で表現すると、

\bar{Z} = 
\begin{pmatrix}
1 & 0\\
0 & -1
\end{pmatrix}  \tag{3}

という具合に見慣れた格好になります。ここまでは誤り訂正符号のときにやったことを思い出すための復習です。ここで注目したいのは式(1)の形です。量子回路で書くと、

--Z--
--Z--
--Z--
--Z--
--Z--
--Z--
--Z--

となります。見てわかる通り、ビットごとに$Z$演算を実行するという形になっており、どこかのビットにノイズが発生しても符号ブロック内の他のビットに影響を及ぼすことはありません。このように符号化ゲートがビットごとのゲート演算で実現できる性質のことを「トランスバーサル性(transversality)」といい、こうなっていればフォールトトレラントなゲート演算であるということが直ちに言えます。

次にパウリ$X$についてです。

\bar{X} \bar{Z} \bar{X} = -\bar{Z}  \tag{4}

を満たすように$\bar{X}$を決めれば良いです。例えば、

\bar{X} = X_{1} X_{2} X_{3} X_{4} X_{5} X_{6} X_{7}  \tag{5}

でいけますね。そうすると、

\bar{X} \ket{0_L} = \ket{1_L}, \space \bar{X} \ket{1_L} = \ket{0_L}  \tag{6}

なので⁴、論理基底での行列表現は、

\bar{X} =
\begin{pmatrix}
0 & 1\\
1 & 0
\end{pmatrix}  \tag{7}

です。式(5)の形を見ればわかる通りこれもトランスバーサル型になっていますので、これでフォールトトレラントなパウリ$X$が実現できたことになります。

パウリ$Y$については、

\bar{Y} = i\bar{X}\bar{Z} = Y_{1} Y_{2} Y_{3} Y_{4} Y_{5} Y_{6} Y_{7}  \tag{8}

としておけば万事丸く収まります。すなわち、$\bar{Y}$は$\bar{X}$および$\bar{Z}$と反可換で$\bar{Y}$自身はエルミートになり、

\bar{Y}\ket{0_L} = -i\ket{1_L}, \space \bar{Y}\ket{1_L} = i\ket{0_L} \tag{9}

なので、行列表現は、

\bar{Y} =
\begin{pmatrix}
0 & -i\\
1 & 0
\end{pmatrix}  \tag{10}

となります。式(8)はトランスバーサル型なので、これでフォールトトレラントなパウリ$Y$が実現できたことになります。

アダマールゲート:H

$\bar{X},\bar{Y},\bar{Z}$に基づき、符号状態に対するアダマールゲートをフォールトトレラントに構成してみます。

\bar{H} \bar{X} \bar{H} = \bar{Z}, \space \bar{H} \bar{Z} \bar{H} = \bar{X}  \tag{11}

を満たす$\bar{H}$を決めれば良いのですが、

\bar{H} = H_{1} H_{2} H_{3} H_{4} H_{5} H_{6} H_{7}  \tag{12}

としてみると式(11)を満たすことがわかります。

\begin{align}
\bar{H}\ket{0_L} &= \bar{H}\bar{Z}\ket{0_L} = \bar{X}\bar{H}\ket{0_L} \\
\bar{H}\ket{1_L} &= -\bar{H}\bar{Z}\ket{1_1} = -\bar{X}\bar{H}\ket{1_L} \tag{13}
\end{align}

からわかるように、$\bar{H}\ket{0_L}$は$\bar{X}$の固有値$+1$の固有状態で$\bar{H}\ket{1_L}$は$\bar{X}$の固有値$-1$の固有状態です。したがって、各々、

\begin{align}
\bar{H}\ket{0_L} &= \frac{1}{\sqrt{2}} (\ket{0_L} + \ket{1_L}) \\
\bar{H}\ket{1_L} &= \frac{1}{\sqrt{2}} (\ket{0_L} - \ket{1_L}) \tag{14}
\end{align}

のように書けて、行列表現は、

\bar{H} = \frac{1}{\sqrt{2}}
\begin{pmatrix}
1 & 1\\
1 & -1
\end{pmatrix}  \tag{15}

となります。式(12)からわかるようにトランスバーサル型になっているので、これでフォールトトレラントなアダマールゲートが実現できたことになります。

位相シフトゲート:S

\bar{S}\bar{X}\bar{S}^{\dagger} = \bar{Y}, \space \bar{S}\bar{Z}\bar{S}^{\dagger} = \bar{Z} \tag{16}

を満たすように$\bar{S}$を決めます。

\bar{S} = S_{1} S_{2} S_{3} S_{4} S_{5} S_{6} S_{7}  \tag{17}

でいけるのではと一瞬思うのですが、これでは式(16)は成り立ちません。

\bar{S} = (Z_{1}S_{1}) (Z_{2}S_{2}) (Z_{3}S_{3}) (Z_{4}S_{4}) (Z_{5}S_{5}) (Z_{6}S_{6}) (Z_{7}S_{7})  \tag{18}

とすればＯＫです（簡単に確認できると思います）。式(16)を満たすための行列表現は、

\bar{S} =
\begin{pmatrix}
1 & 0\\
0 & -i
\end{pmatrix}  \tag{19}

です（これも簡単に確認できると思います）。式(18)からわかるようにトランスバーサル型になっているので、これでフォールトトレラントな位相シフトゲートが実現できたことになります。

間違えないと思いますが、念のため回路図を書くと、

--S-Z--
--S-Z--
--S-Z--
--S-Z--
--S-Z--
--S-Z--
--S-Z--

です。数式で書いたときの演算子の順番と回路図で書いたときの演算子の順番が左右逆だというのは、この業界の常識ですが、うっかりすると間違って実装してしまいます（自分のことです、汗）。

制御NOTゲート:CNOT

さて、問題の制御NOTゲートです。果たして同一符号ブロック内に伝搬しないようにうまく構成できるのでしょうか、、。符号ブロック$A$を制御ビット、符号ブロック$B$を標的ビットとみなした符号状態に対する制御NOT演算子を$\bar{U}_{A,B}$と書くことにします。このとき、

\begin{align}
\bar{U}_{A,B} \bar{X_A} \bar{U}_{A,B} &= \bar{X_A} \bar{X_B} \\
\bar{U}_{A,B} \bar{X_B} \bar{U}_{A,B} &= \bar{X_B} \\
\bar{U}_{A,B} \bar{Z_A} \bar{U}_{A,B} &= \bar{Z_A} \\
\bar{U}_{A,B} \bar{Z_B} \bar{U}_{A,B} &= \bar{Z_A}\bar{Z_B} \tag{20}
\end{align}

を満たすように制御NOT演算を決めることを考えます。符号ブロックAの中に含まれる7個のビット番号を$A_{1},A_{2},A_{3},A_{4},A_{5},A_{6},A_{7}$とおき、符号ブロックBの中に含まれる7個のビット番号を$B_{1},B_{2},B_{3},B_{4},B_{5},B_{6},B_{7}$とおき、$i$番目のビットを制御、$j$番目のビットを標的とする単なる制御NOT演算子を$U_{i,j}$と書くことにします。そうすると、式(18)を満たす$\bar{U}_{A,B}$は、

\bar{U}_{A,B} = U_{A_1,B_1} U_{A_2,B_2} U_{A_3,B_3} U_{A_4,B_4} U_{A_5,B_5} U_{A_6,B_6} U_{A_7,B_7}  \tag{21}

であることがわかります。確かめるのは、簡単です。式(20)の1番目の式は、

\begin{align}
\bar{U}_{A,B} \bar{X_A} \bar{U}_{A,B} &= (U_{A_1,B_1} \cdots U_{A_7,B_7}) (X_{A_1} \cdots X_{A_7}) (U_{A_1,B_1} \cdots U_{A_7,B_7}) \\
&= (U_{A_1,B_1} X_{A_1} U_{A_1,B_1}) \cdots (U_{A_7,B_7} X_{A_7} U_{A_7,B_7}) \\
&= (X_{A_1} X_{B_1}) \cdots (X_{A_7} X_{B_7}) \\
&= (X_{A_1} \cdots X_{A_7}) (X_{B_1} \cdots X_{B_7}) = \bar{X_A} \bar{X_B} \tag{22}
\end{align}

となるので式(21)でＯＫです。2番目、3番目、4番目も同様に確認できます。ちょっと身構えてしまっていましたが、結局とても簡単な形になりました。回路図で書くと、

           A1 --*--------------------
[block A]  A2 --|--*-----------------
           A3 --|--|--*--------------
           A4 --|--|--|--*-----------
           A5 --|--|--|--|--*--------
           A6 --|--|--|--|--|--*-----
           A7 --|--|--|--|--|--|--*--
                |  |  |  |  |  |  |
           B1 --X--|--|--|--|--|--|--
[block B]  B2 -----X--|--|--|--|--|--
           B3 --------X--|--|--|--|--
           B4 -----------X--|--|--|--
           B5 --------------X--|--|--
           B6 -----------------X--|--
           B7 --------------------X--

というきれいな形になり、これでフォールトトレラントな制御NOTが実現できたことになります。見ての通り、符号ブロックAに発生したビット反転ノイズは符号ブロックBに伝搬します。が、同じブロック内に伝搬するわけではないので大丈夫です。符号ブロックBに発生した位相反転ノイズは符号ブロックAにも伝搬しますがこれも同じブロックに伝搬するわけではないので大丈夫です（各ブロックで各々誤り訂正が可能です）。

位相シフトゲート:T

以上でCliffordゲートが出揃いました。量子計算をユニバーサルにするためには、もうひとつの位相シフトゲート$T$ゲートが必要です。$T$ゲートは、

T =
\begin{pmatrix}
1 & 0\\
0 & e^{i\pi /4}
\end{pmatrix}  \tag{23}

で定義されるので、符号状態$\ket{\psi}=a\ket{0_L} + b\ket{1_L}$を入力して$\ket{\psi^{\prime}}=a\ket{0_L} + b e^{i\pi /4}\ket{1_L}$を出力するような演算をフォールトトレラントに構成できれば良いです。が、これはそれほど簡単ではありません。ちょっとわかりにくい巧妙なやり方⁵なので、答えを先に言います。回路図は、

               |C>
                v
|0L>  --/--H--T----*----SX-- T|psi>
                   |    |
|psi> --/----------X----M

です。1番目の符号ブロックの中にこれから定義しようとしてる$T$が入っているのはどういうこと？と思われたかもしれません。この1番目の符号ブロックの最初のアダマールと$T$ゲートは、このように演算したのと同じような状態を吐き出すなんらかの作用を表していると思ってください。図では$\ket{C}$と書きましたが、

\ket{C} = \frac{1}{\sqrt{2}} (\ket{0_L} + e^{i\pi /4} \ket{1_L})  \tag{24}

となります。どうやってこの状態をつくるかはこの後に説明するとして、こういう状態ができた前提でその次の演算について説明します。まず制御NOTを作用させます。これは先ほど構成したフォールトトレラントな制御NOTです。フォールトトレラントな制御NOTは、数式上は基底を論理基底にしたものとして扱えば良いだけなので、単なる制御NOTと同じように、

\ket{0_L} \bra{0_L} \otimes I + \ket{1_L} \bra{1_L} \otimes \bar{X}  \tag{25}

と書けます。したがって、$\ket{C}\ket{\psi}$に対するCNOTの効果は、

\begin{align}
\ket{C}\ket{\psi} &\rightarrow \frac{1}{\sqrt{2}} (\ket{0_L} \bra{0_L} \otimes I + \ket{1_L} \bra{1_L} \otimes \bar{X}) \ket{C}\ket{\psi} \\
&= \frac{1}{2} (\ket{0_L} \bra{0_L} \otimes I + \ket{1_L} \bra{1_L} \otimes \bar{X}) (\ket{0_L} + e^{i\pi /4} \ket{1_L}) (a\ket{0_L} + b\ket{1_L}) \\
&= \frac{1}{2} (\ket{0_L} (a\ket{0_L}+b\ket{1_L}) + e^{i\pi /4} \ket{1_L} (a\ket{1_L}+b\ket{0_L})) \\
&= \frac{1}{2} ((a\ket{0_L}+b e^{i\pi /4} \ket{1_L}) \ket{0_L} + (b\ket{0_L}+a e^{i\pi /4} \ket{1_L}) \ket{1_L}) \tag{26}
\end{align}

となります。2番目の符号ブロックを測定して測定値が$1(\ket{0_L})$だった場合、何もしないので、1番目の符号ブロックの出力は、

\ket{\psi^{\prime}} = a\ket{0_L}+b e^{i\pi /4} \ket{1_L} = \bar{T} \ket{\psi}  \tag{27}

となります。測定値が$-1(\ket{1_L})$だった場合、$SX$を演算するので、同じく式(27)の状態にグローバル位相がかかったものが1番目の符号状態として出力されます。

さて、式(24)のような状態をどうやって吐き出させるかの説明が残っていました。スタビライザー形式で考えると$\ket{0_L}$から$TH\ket{0_L}$への変換は$\bar{Z} \rightarrow \bar{T}\bar{H}\bar{Z}\bar{H}\bar{T}^{\dagger}$と表すことができ、$\bar{T}\bar{H}\bar{Z}\bar{H}\bar{T}^{\dagger}$は、

\begin{align}
\bar{T}\bar{H}\bar{Z}\bar{H}\bar{T}^{\dagger} &= \bar{T}\bar{X}\bar{T}^{\dagger}  \\
&=
\begin{pmatrix}
1 & 0\\
0 & e^{i\pi /4}
\end{pmatrix}
\begin{pmatrix}
0 & 1\\
1 & 0
\end{pmatrix}
\begin{pmatrix}
1 & 0\\
0 & e^{-i\pi /4}
\end{pmatrix} \\
&= e^{-i\pi /4} \bar{S} \bar{X}  \tag{28}
\end{align}

のように書き換えることができます。したがって、状態$\ket{C}$は演算子$e^{-i\pi /4} \bar{S} \bar{X}$の固有値$+1$に対する固有状態になります。ということは$e^{-i\pi /4} \bar{S} \bar{X}$を間接測定して、測定値$+1$が得られればそれを$\ket{C}$として良いということになります。もし測定値が$-1$だった場合は、$\bar{Z}$を適用します。そうすると、固有値$+1$の状態に変化します⁶。

ここで注意事項がひとつあります。$e^{-i\pi /4} \bar{S} \bar{X}$を間接測定すると言いましたが、ちょっとした工夫が必要です。模式的には、

|0>  -----H--*--*----*-----------H-- M
             |  |    |
|0L> --/-----X--S--exp(-i pi/4)-----

という測定なのですが、制御つきの$e^{-i\pi /4} I$ゲートが問題です。これは、

|0>  ----*-----------    ---T---
         |             = 
|0L> --exp(-i pi/4)--    -------

という等式を使って、

|0>  -----H--*--*--T--H-- M
             |  |
|0L> --/-----X--S--------

という形に変形するのが良いです。この図における$T$ゲートは単なる$T$ゲートです。

というわけで、これで符号状態に対する$T$ゲートを構成することができました。$CNOT,S,X$というゲートはすべてトランスバーサル型にできるので、全体としてフォールトトレラントであると言えます。ただし、測定については何も配慮していませんでした。本当は測定部分もフォールトトレラントにできてはじめて本当の意味でフォールトトレラントな$T$ゲートが実現できたということができます。

というわけで、次にフォールトトレラントな測定について説明します。

測定

符号状態に働く演算子$ABC$の間接測定は、

|0> --H--*--*--*--H-- M
         |  |  |
    -----A--|--|-----
    --------B--|-----
    -----------C-----

とやればできます（Steane符号前提なので本当は符号ブロックには線が7本必要なのですが、説明を簡単にするため省略して3本にしています）。ところが、フォールトトレラントを実現する観点からするとこれは非常にマズイやり方です。補助ビットにノイズが発生した場合、符号ブロックを構成するすべてのビットにそのノイズが伝搬する可能性があります。これを避けるため、以下のような構成にすれば良いということがわかっています。

|0> --H--*----*----------*--H-- M
    -----X----|--*-------X-----
    -----X----|--|--*----X-----
              |  |  |
    ----------A--|--|----------
    -------------B--|----------
    ----------------C----------

補助ビットを3ビットにして、

|0> --H--*--
    -----X--
    -----X--

この回路で、いわゆるcat状態$(\ket{000}+\ket{111})/\sqrt{2}$を作ります。こうすると間接測定が実現できますし、補助ビットにノイズが発生したとしても、符号ブロックのどれか1個のビットにしかノイズが伝搬しません。

これはこれで良いのですが、最初のcat状態を作成する際にノイズが発生する可能性があります。補助ビット3ビットのどれかにノイズが発生すると簡単にブロック内をノイズが伝搬します。さて、どうしましょう？というわけで、こんな場合はcat状態を作成したら正しくできているかをどうか検査して正しくなかったらその状態を捨てて、もう一回作成をトライするという方針でいくしかないです。具体的には、cat状態を作成した直後にパリティ検査の回路を入れます。

       パリティ検査
      |0> --X--X-- M
            |  |
|0> --H--*--*--|--*----------*--H-- M
    -----X-----*--|--*-------X-----
    -----X--------|--|--*----X-----
                  |  |  |
    --------------A--|--|----------
    -----------------A--|----------
    --------------------A----------

こんな具合です。簡単のためパリティ検査は1つしか書いていませんが、すべてのビットの組み合わせで確認すべきなので、2番目と3番目のビットのパリティ検査も必要です。すべてのパリティが偶パリティになるまでcat状態の作成を繰り返します。

ちょっと大変ですがこれでフォールトトレラントになりました！と言いたいところなのですが、もうひとつ問題があります。パリティ検査のために追加した補助ビットに位相反転ノイズが発生することも考えておかないといけません。この場合間接測定のための3ビットブロックの2つのビットに伝搬してしまいます。これでは誤り訂正できないです。結果として、一番右の測定は間違った結果を出力することになります。この場合も仕方ないので、測定を3回繰り返して多数決をとるようにします。そうすると、誤り発生率を$O(p^2)$に抑えることができます（ノイズ発生の確率を$p$とすると）。

これで誤り耐性のある測定を構成することができました。測定は単に計算結果を取得するときだけでなく、誤り訂正のためのシンドローム測定や先ほど説明した$T$ゲート作成にも必要な部品ですし、次に説明する初期状態を作成する際にも必要になるものです。

初期状態作成

というわけで、初期状態作成をフォールトトレラントに構成する方法について説明します。前回、前々回の記事で5量子ビット符号の初期状態（論理基底状態$\ket{0_L}$）を作成する方法について詳細に述べました。それをSteane符号に置き換えて、間接測定の部分をたったいま説明したフォールトトレラントな測定に置き換えるだけです。

Steane符号の6個の生成元と論理$Z$演算子は先ほど提示していました。初期状態作成にはこの７個の演算子を順に測定していき固有値$+1$の固有空間への射影を次々に行っていくのですが、固有値$-1$の固有空間に射影されてしまう場合もあるので、その時は当該生成元と反可換で他の生成元と可換な演算子を適用すれば良かったです。Steane符号の場合、以下の7個の演算子になります⁷。後の動作確認の際に必要になるので、ここに掲載しておきます。

生成元	演算子
$g_{1}^{\prime}$	$Z \space Z \space Z \space Z \space I \space I \space I$
$g_{2}^{\prime}$	$Z \space Z \space I \space I \space Z \space Z \space I$
$g_{3}^{\prime}$	$I \space I \space Z \space I \space Z \space I \space Z$
$g_{4}^{\prime}$	$X \space X \space X \space X \space I \space I \space I$
$g_{5}^{\prime}$	$X \space X \space I \space I \space X \space X \space I$
$g_{6}^{\prime}$	$I \space I \space X \space I \space X \space I \space X$
$g_{7}^{\prime}$	$X \space X \space X \space X \space X \space X \space X$

これで量子計算に必要な一連のプロセス（初期状態作成、ゲート演算、測定）のすべてをフォールトトレラントに構成する方法がわかりました。

さて、次に気になるのは、その量子計算の誤り率をどの程度まで小さくできるかということです。システムを構成する各部品が誤る確率を$p$とすると、計算結果の誤り率は高々$O(p^2)$に抑えることができるということでしたが、それをどの程度にまで小さくできるのかということです。実は、$p$があるしきい値以下であれば、いくらでも小さくできる方法があります。それについて以下で説明します。

連結符号としきい値定理

量子計算システムを構成する部品としては、量子ビット、それを制御する制御デバイス、量子状態を測定するための測定デバイス等々があり、その各々が動作不良や外界からの雑音を受ける等で、所定の動作をしないことが一定の確率で発生します。非常に単純にその平均的な確率を$p$としてみます。前節までで説明したように、各符号ブロックあたり高々1個の誤りであれば訂正することができます。問題は2箇所に同時に誤りが発生して、伝搬することによって特定の符号ブロックに2つの誤りが入り込む場合です。その確率は$p^2$に比例していて$cp^2$となります。この比例係数$c$は「特定の符号ブロックに2つの誤りをもたらす」という場合の数です。ニールセン、チャンには、簡単な量子回路を例に非常に大雑把な見積もりとして$c \approx 10^{4}$という値が掲載されています。

この誤り率をもっと小さくするために符号ブロックや誤り訂正のための補助ブロックを構成する各量子ビットをさらに符号化することを考えます。もとのシステムの1ビットがSteane符号によって7倍+$\alpha$になっていたので、さらにその7倍+$\alpha$になります。システムの規模は大きくなるのですが、このお陰で誤り率は$c(cp^2)^2=c^{3}p^{4}$になります。もう一度、各ビットをSteane符号で符号化するとさらにシステム規模はその7倍+$\alpha$となり、誤り率は$c(c(cp^2)^2)^2=c^{7}p^{8}$になります。この操作を$k$回繰り返すと、システムの規模（必要なビット数）は、元のシステム規模を$d$としたとき$d^k$になり、誤り率は$(cp)^{2^k}/c$となります。このように符号化を階層的に構成することを「連結符号(concatenated code)」と呼びます。

いま考えている量子計算システムに$p(n)$個のゲートが元々あったとします。ここで$n$はある問題の大きさを表しており$p(n)$は$n$についての多項式関数であるとします。最終的に達成したい誤り率を$\epsilon$とすると、

\frac{(cp)^{2^k}}{c} \leq \frac{\epsilon}{p(n)}  \tag{29}

という関係が成り立っていなければなりません。これを見てわかる通り、$p$がある閾値$p_{th} < 1/c$を満たしているなら$k$の値を十分大きくすることで、いくらでも誤り率を小さくできます。大雑把な見積もりとして$c \approx 10^{4}$だったので、$p_{th} \approx 10^{-4} = 0.01\%$ということになります。

では、誤り率$\epsilon$を達成するために必要なシステムの規模（ビット数）$d^k$はどの程度になるでしょうか。式(27)の不等号を近似に置き換えて、以下のように変形することでわかります。

d^k \approx (\frac{\log(p(n)/c\epsilon)}{\log(1/pc)})^{\log d} = O(poly(\log p(n)/\epsilon))  \tag{30}

この中に含まれるゲート数は、

O(poly(\log p(n)/\epsilon) p(n))  \tag{31} 

と見積もることができます。つまり、$p(n)$個のゲートを含む量子回路は、部品の誤り確率が高々$p$であるハードウェアによる、

O(poly(\log p(n)/\epsilon) p(n))  \tag{32} 

個のゲートを用いて$\epsilon$の誤り率を達成することができます。ただし、$p$はある一定の閾値より小さくなっている必要があります。これを「しきい値定理」と呼んでいます。

動作確認

理論がわかったところで、フォールトトレラント量子計算の非常に簡単な例を取り上げて、量子計算シミュレータqlazyで動作確認してみたいと思います。$T$ゲートをフォールトトレラントに実現する方法について上で説明しましたが、ちょっとトリッキーな回路構成になっていると感じたので、これが本当に正しい働きをするものなのか確認してみます。$\ket{0_L}$状態に対して$T$ゲートを作用させても$\ket{0_L}$のままで全然面白くないので前後にアダマールをかけて、$\bar{H}\bar{T}\bar{H}\ket{0_L}$という演算を実施して最後に$\bar{Z}$基底で測定してみます。一応すべてのゲート演算と測定をフォールトトレラントに構成しました。が、何らかのノイズを加えて誤り訂正を行うような処理は省略しました（前回やったので）。さらに、cat状態が正しくできているか検査するパリティ検査や何度も測定して多数決をとるという方式も省略しました。とにかく、今回は、符号状態に対する演算および測定がフォールトトレラントな構成で正しく実現できていることの確認のみに注力しました。

実装

それでは、全体のPythonコードを示します。

from qlazypy import QState

def logical_zero():

    anc = [0,1,2,3,4,5,6]     # registers for ancila
    cod = [7,8,9,10,11,12,13] # registers for steane code
    qs_total = QState(14)

    # g1
    qs_total.h(anc[0])
    [qs_total.cx(anc[0], anc[i]) for i in range(1,4)]
    qs_total.cx(anc[0], cod[3]).cx(anc[1], cod[4]).cx(anc[2], cod[5]).cx(anc[3], cod[6])
    [qs_total.cx(anc[0], anc[i]) for i in range(1,4)]
    qs_total.h(anc[0])
    mval = qs_total.m(qid=[anc[0]]).last
    if mval == '1': qs_total.z(cod[0]).z(cod[1]).z(cod[2]).z(cod[3])
    qs_total.reset(qid=anc)

    # g2
    qs_total.h(anc[0])
    [qs_total.cx(anc[0], anc[i]) for i in range(1,4)]
    qs_total.cx(anc[0], cod[1]).cx(anc[1], cod[2]).cx(anc[2], cod[5]).cx(anc[3], cod[6])
    [qs_total.cx(anc[0], anc[i]) for i in range(1,4)]
    qs_total.h(anc[0])
    mval = qs_total.m(qid=[anc[0]]).last
    if mval == '1': qs_total.z(cod[0]).z(cod[1]).z(cod[4]).z(cod[5])
    qs_total.reset(qid=anc)

    # g3
    qs_total.h(anc[0])
    [qs_total.cx(anc[0], anc[i]) for i in range(1,4)]
    qs_total.cx(anc[0], cod[0]).cx(anc[1], cod[2]).cx(anc[2], cod[4]).cx(anc[3], cod[6])
    [qs_total.cx(anc[0], anc[i]) for i in range(1,4)]
    qs_total.h(anc[0])
    mval = qs_total.m(qid=[anc[0]]).last
    if mval == '1': qs_total.z(cod[2]).z(cod[4]).z(cod[6])
    qs_total.reset(qid=anc)

    # g4
    qs_total.h(anc[0])
    [qs_total.cx(anc[0], anc[i]) for i in range(1,4)]
    qs_total.cz(anc[0], cod[3]).cz(anc[1], cod[4]).cz(anc[2], cod[5]).cz(anc[3], cod[6])
    [qs_total.cx(anc[0], anc[i]) for i in range(1,4)]
    qs_total.h(anc[0])
    mval = qs_total.m(qid=[anc[0]]).last
    if mval == '1': qs_total.x(cod[0]).x(cod[1]).x(cod[2]).x(cod[3])
    qs_total.reset(qid=anc)

    # g5
    qs_total.h(anc[0])
    [qs_total.cx(anc[0], anc[i]) for i in range(1,4)]
    qs_total.cz(anc[0], cod[1]).cz(anc[1], cod[2]).cz(anc[2], cod[5]).cz(anc[3], cod[6])
    [qs_total.cx(anc[0], anc[i]) for i in range(1,4)]
    qs_total.h(anc[0])
    mval = qs_total.m(qid=[anc[0]]).last
    if mval == '1': qs_total.x(cod[0]).x(cod[1]).x(cod[4]).x(cod[5])
    qs_total.reset(qid=anc)

    # g6
    qs_total.h(anc[0])
    [qs_total.cx(anc[0], anc[i]) for i in range(1,4)]
    qs_total.cz(anc[0], cod[0]).cz(anc[1], cod[2]).cz(anc[2], cod[4]).cz(anc[3], cod[6])
    [qs_total.cx(anc[0], anc[i]) for i in range(1,4)]
    qs_total.h(anc[0])
    mval = qs_total.m(qid=[anc[0]]).last
    if mval == '1': qs_total.x(cod[2]).x(cod[4]).x(cod[6])
    qs_total.reset(qid=anc)

    # g7
    qs_total.h(anc[0])
    [qs_total.cx(anc[0], anc[i]) for i in range(1,7)]
    [qs_total.cz(anc[i], cod[i]) for i in range(7)]
    [qs_total.cx(anc[0], anc[i]) for i in range(1,7)]
    qs_total.h(anc[0])
    mval = qs_total.m(qid=[anc[0]]).last
    if mval == '1': [qs_total.x(q) for q in cod]
    qs_total.reset(qid=anc)

    qs = qs_total.partial(qid=cod)
    qs_total.free()

    return qs

def faulttolerant_t(qs_in):

    A = [0,1,2,3,4,5,6]         # registers for ancila
    B = [7,8,9,10,11,12,13]     # registers for output quantum state
    C = [14,15,16,17,18,19,20]  # registers for input quantum state
    qs_A = QState(7)
    qs_B = logical_zero()
    qs_AB = qs_A.tenspro(qs_B)
    qs_ABC = qs_AB.tenspro(qs_in)

    # -H-T-
    qs_ABC.h(A[0])
    [qs_ABC.cx(A[0], A[i]) for i in range(1,7)]
    [qs_ABC.cx(A[i],B[i]).cs(A[i],B[i]).cz(A[i],B[i]).t_dg(A[i]) for i in range(7)]
    [qs_ABC.cx(A[0], A[i]) for i in range(1,7)]
    qs_ABC.h(A[0])
    mval = qs_ABC.m(qid=[A[0]]).last
    if mval == '1': [qs_ABC.z(q) for q in B]
    qs_ABC.reset(qid=A)

    # -CNOT-
    [qs_ABC.cx(B[i], C[i]) for i in range(7)]

    # -M-, -SX-
    qs_ABC.h(A[0])
    [qs_ABC.cx(A[0], A[i]) for i in range(1,7)]
    [qs_ABC.cz(A[i],C[i]) for i in range(7)]
    [qs_ABC.cx(A[0], A[i]) for i in range(1,7)]
    qs_ABC.h(A[0])
    mval = qs_ABC.m(qid=[A[0]]).last
    if mval == '1': [qs_ABC.x(q).s(q).z(q) for q in B]

    qs_out = qs_ABC.partial(qid=B)
    QState.free_all(qs_A, qs_B, qs_AB, qs_ABC)

    return qs_out

def faulttolerant_m(qs_in):

    anc = [0,1,2,3,4,5,6]      # ancila
    cod = [7,8,9,10,11,12,13]  # steane code
    qs_anc = QState(7)
    qs_total = qs_anc.tenspro(qs_in)

    qs_total.h(anc[0])
    [qs_total.cx(anc[0], anc[i]) for i in range(1,7)]
    [qs_total.cz(anc[i], cod[i]) for i in range(7)]
    [qs_total.cx(anc[0], anc[i]) for i in range(1,7)]
    qs_total.h(anc[0])
    md = qs_total.m(qid=[0], shots=10000)
    QState.free_all(qs_anc, qs_total)

    return md

if __name__ == '__main__':

    qs = QState(1).h(0).t(0).h(0)    # not fault-tolerant -HTH-
    qs.show()

    qs_ini = logical_zero()          # make initial state (logical zero)
    [qs_ini.h(i) for i in range(7)]  # operate fault-tolerant H
    qs_fin = faulttolerant_t(qs_ini) # operate fault-tlerant T
    [qs_fin.h(i) for i in range(7)]  # operate fault-tolerant H
    md = faulttolerant_m(qs_fin)     # execute fault-tolerant measurement
    print(md.frequency)

    QState.free_all(qs, qs_ini, qs_fin)

何をやっているか簡単に説明します。まず、メイン処理部を見てください。

qs_ini = logical_zero()          # make initial state (logical zero)

で、Steane符号の論理基底状態$\ket{0_L}$を作成しています。詳細は関数logical_zeroの中身なのですが、とても長くてわかりにくいかもしれません。が、基本は簡単で、

# g1
qs_total.h(anc[0])
[qs_total.cx(anc[0], anc[i]) for i in range(1,4)]
qs_total.cx(anc[0], cod[3]).cx(anc[1], cod[4]).cx(anc[2], cod[5]).cx(anc[3], cod[6])
[qs_total.cx(anc[0], anc[i]) for i in range(1,4)]
qs_total.h(anc[0])
mval = qs_total.m(qid=[anc[0]]).last
if mval == '1': qs_total.z(cod[0]).z(cod[1]).z(cod[2]).z(cod[3])
qs_total.reset(qid=anc)

のようなコードの繰り返しになっています。補助ビットをcat状態にして生成元を間接測定します。測定結果が1（つまり$\ket{1_L}$）だった場合、当該生成元と反可換な演算子を適用します。7個の演算子についてすべて完了したらば、その状態を（補助ビットを除いて）リターンします。ここで、測定値を得るためのメソッドlastは2進数の文字列を得るためのものです(v0.0.41で追加)。次に、

[qs_ini.h(i) for i in range(7)]  # operate fault-tolerant H

で、フォールトトレラントなアダマールを適用しています。トランスバーサル型なので簡単です。

qs_fin = faulttolerant_t(qs_ini) # operate fault-tlerant T

で、フォールトトレラントな$T$ゲートを実行しています。関数faulttolerant_tの中身を見てみます。上で説明した1番目の符号ブロックをB、2番目の符号ブロックをCと名付け、測定に必要となる補助ブロックをAと名付けています。各々7個のビットから成り立っています。という前提で見ていただければと思います。

# -H-T-
qs_ABC.h(A[0])
[qs_ABC.cx(A[0], A[i]) for i in range(1,7)]
[qs_ABC.cx(A[i],B[i]).cs(A[i],B[i]).cz(A[i],B[i]).t_dg(A[i]) for i in range(7)]
[qs_ABC.cx(A[0], A[i]) for i in range(1,7)]
qs_ABC.h(A[0])
mval = qs_ABC.m(qid=[A[0]]).last
if mval == '1': [qs_ABC.z(q) for q in B]
qs_ABC.reset(qid=A)

で、$H$と$T$を適用したのと同じ符号状態を作成しています。補助ビットをcat状態にして、演算子$e^{-i \pi /4}SX$を測定するのですが$S$のトランスバーサル型は$ZS$だったので$ZSX$を制御化するようにします。さらに、位相$e^{-i \pi /4}$は制御側の$T$ゲートに等しいということだったので、その演算も忘れず入れています。

# -CNOT-
[qs_ABC.cx(B[i], C[i]) for i in range(7)]

で、トランスバーサルなCNOTを実行して、

# -M-, -SX-
qs_ABC.h(A[0])
[qs_ABC.cx(A[0], A[i]) for i in range(1,7)]
[qs_ABC.cz(A[i],C[i]) for i in range(7)]
[qs_ABC.cx(A[0], A[i]) for i in range(1,7)]
qs_ABC.h(A[0])
mval = qs_ABC.m(qid=[A[0]]).last
if mval == '1': [qs_ABC.x(q).s(q).z(q) for q in B]

で、符号ブロックCを測定して測定結果が1であれば、符号ブロックAに$SX$を適用します。このときも$S$のトランスバーサル型が$ZS$だったことを忘れずに考慮しています。結果は符号ブロックBに入っているはずなので、

qs_out = qs_ABC.partial(qid=B)

で、符号ブロックBに対応した部分系をpartialメソッドで取り出しています。これをリターンします。

メイン処理部に戻ります。

$T$ゲートの結果に対して、

[qs_fin.h(i) for i in range(7)]  # operate fault-tolerant H

で、再びアダマールをフォールトトレラントに演算して、最後に、

md = faulttolerant_m(qs_fin)     # execute fault-tolerant measurement
print(md.frequency)

で、測定を実施します。詳細は関数faulttolerant_mの中身を見てください。補助ビットをcat状態にして間接測定しているだけです。測定結果を変数md(MDataクラスのインスタンス)として取得し、frequencyメソッド(v0.0.41で追加)で頻度データをCounter形式で得るようにしています。以上です。

結果

実行結果を以下に示します。

c[0] = +0.9239-0.0000*i : 0.8536 |++++++++++
c[1] = +0.0000-0.3827*i : 0.1464 |++
Counter({'1': 8524, '0': 1476})

最初の2行はフォールトトレラントではない普通の-H-T-H-の結果です。これが答えになります。つまり$\ket{0_L}$状態と$\ket{1_L}$状態の確率は各々0.8536と0.1464になるということです。3行目のCounterがフォールトトレラントの-H-T-H-を実行して10000回測定シミュレーションした結果になります。答えの確率に大体一致していると思います（思ってください！）。

おわりに

フォールトトレラント量子計算というのは、いろんなテクニックを駆使しながら実現するとても大変な技術だということがわかりました。本当に実用的な量子コンピュータをつくるには、やはりこのような地道な蓄積が大事なのですね。しきい値定理は、その努力がきっと必ず報われるということを保証してくれる心の支えとも言える超重要な理論成果でありました。それにしても$10^{-4}=0.01\%$という誤り率は厳しい要求です。スタビライザー符号のような誤り訂正符号と連結符号を想定すると、どうしてもこのくらいの精度が必要なのです。が、もっと別の符号化方式を使えば、このしきい値を上げることができるようです。次回は、そんな符号方式のひとつである「トポロジカル符号（表面符号）」について勉強してみたいと思います。

以上

---

1. 「同時に」というのは1個のノイズに対する誤り訂正実行前に、別のノイズが発生することだと思えば良いです（と思います）。 ↩

2. 5量子ビット符号の場合ゲート演算をフォールトトレラントにするのは結構難しいとのことです。が、$X$も$Z$も後の説明ででてくるトランスバーサル型にできそうですし、それほど難しくないのでは？という気がするのですが、、おそらく自分自身とんでもない勘違いをしているか、まだ理解が及んでいないところに壁ががあるのだと思います。5量子ビットで誤り耐性を考えてみるのは今後の宿題としておきます。 ↩

3. 同じ演算子を$X_{1}Z_{2}X_{3}$と書いたり$X \otimes Z \otimes X$と書いたり$XZX$と書いたりしますが、実体は同じですので混乱しないようにしてください。 ↩

4. $\bar{X}\ket{0_L}=\bar{X}\bar{Z}\ket{0_L}=-\bar{Z}\bar{X}\ket{0_L}$なので$\bar{X}\ket{0_L}$は$\bar{X}$の固有値$-1$に対する固有状態です。つまり、$\bar{X}\ket{0_L}=\ket{1_L}$です。両辺に$\bar{X}$を演算すると$\bar{X}\ket{1_L}=\ket{0_L}$が得られます。細かいことを言うと$\bar{X}\ket{0_L}=e^{i\alpha}\ket{1_L}$という定義でも良いような気もしますが、$\alpha=0$とするのが習わしということなのだと思います。 ↩

5. ニールセン、チャンの「演習10.65」「演習10.66」にこの回路をどうやって導いたかが書かれています。この演習をやってみると、なるほど！という感じになります。また、「演習10.68」には、同じような考え方でToffoliゲートをフォールトトレラントに構成する方法が書かれています。 ↩

6. $\bar{Z}$は$e^{-i\pi /4} \bar{S}\bar{X}$と反可換なので、$\bar{Z} \frac{1}{2} (I-e^{-i\pi /4} \bar{S}\bar{X})\ket{0_L} = \frac{1}{2} (I+e^{-i\pi /4} \bar{S}\bar{X})\ket{0_L}$となり、固有値を逆転させることができます。 ↩

7. これ以外にも選択肢はあると思いますが、簡単に思いついたものを一つの例として並べてみました。 ↩

MacOS の VirtualBox に Ubuntu をインストールする

やっとできた！MacのVirtualBox上にUbuntuをインストールする方法
https://tomslifestylelab.com/mac-virtualbox-ubuntu/

とりあえず

sudo apt-get update
sudo apt-get upgrade

MacでUbuntuを快適に使う
https://qiita.com/ryoheimorimoto/items/a82369a83c100a646cce

Ubuntu に SSH でアクセスできるようにする

Mac 上のVirtual Box のUbuntu にSSH でアクセスしX転送する
https://withfpga.com/?p=78

Virtualboxでアダプタ2,アダプタ3,アダプタ4が選択できない
https://teratail.com/questions/164319

SSH で Docker をインストールする

Ubuntu に Docker をインストールする
https://docs.docker.com/engine/install/ubuntu/

Dockerコマンドをsudoなしで実行する方法
https://qiita.com/DQNEO/items/da5df074c48b012152ee

Docker 上で Jupyter notebook を作成してアクセスする

Dockerで基本的なData Science環境(Jupyter, Python, R, Julia, 定番ライブラリ)を構築する。
https://qiita.com/y4m3/items/c2703d4e131e05084b7b

サーバーのDockerで起動したJupyter Notebookを他のパソコンからアクセスできるようにした話
https://qiita.com/yamasakih/items/d23ac0bf773e9b1b4d9d

pip3 install psutil時にfatal error: Python.h: そのようなファイルやディレクトリはありません

pip3 install psutil時にエラー

$ pip3 install psutil
Collecting psutil
  Downloading psutil-5.7.0.tar.gz (449 kB)
     |????????????????????????????????| 449 kB 3.6 MB/s
Building wheels for collected packages: psutil
  Building wheel for psutil (setup.py) ... error
  ERROR: Command errored out with exit status 1:
   command: /usr/bin/python3 -u -c 'import sys, setuptools, tokenize; sys.argv[0] = '"'"'/tmp/pip-install-ep62l8yz/psutil/setup.py'"'"'; __file__='"'"'/tmp/pip-install-ep62l8yz/psutil/setup.py'"'"';f=getattr(tokenize, '"'"'open'"'"', open)(__file__);code=f.read().replace('"'"'\r\n'"'"', '"'"'\n'"'"');f.close();exec(compile(code, __file__, '"'"'exec'"'"'))' bdist_wheel -d /tmp/pip-wheel-ctube83k
       cwd: /tmp/pip-install-ep62l8yz/psutil/
  Complete output (42 lines):
...
  running build_ext
  building 'psutil._psutil_linux' extension
  creating build/temp.linux-x86_64-3.5
  creating build/temp.linux-x86_64-3.5/psutil
  x86_64-linux-gnu-gcc -pthread -DNDEBUG -g -fwrapv -O2 -Wall -Wstrict-prototypes -g -fstack-protector-strong -Wformat -Werror=format-security -Wdate-time -D_FORTIFY_SOURCE=2 -fPIC -DPSUTIL_POSIX=1 -DPSUTIL_SIZEOF_PID_T=4 -DPSUTIL_VERSION=570 -DPSUTIL_LINUX=1 -I/usr/include/python3.5m -c psutil/_psutil_common.c -o build/temp.linux-x86_64-3.5/psutil/_psutil_common.o
  psutil/_psutil_common.c:9:20: fatal error: Python.h: そのようなファイルやディレクトリはありません
  compilation terminated.
  error: command 'x86_64-linux-gnu-gcc' failed with exit status 1
  ----------------------------------------
  ERROR: Failed building wheel for psutil
  Running setup.py clean for psutil
Failed to build psutil
Installing collected packages: psutil
    Running setup.py install for psutil ... error
    ERROR: Command errored out with exit status 1:
...

    building 'psutil._psutil_linux' extension
    creating build/temp.linux-x86_64-3.5
    creating build/temp.linux-x86_64-3.5/psutil
    x86_64-linux-gnu-gcc -pthread -DNDEBUG -g -fwrapv -O2 -Wall -Wstrict-prototypes -g -fstack-protector-strong -Wformat -Werror=format-security -Wdate-time -D_FORTIFY_SOURCE=2 -fPIC -DPSUTIL_POSIX=1 -DPSUTIL_SIZEOF_PID_T=4 -DPSUTIL_VERSION=570 -DPSUTIL_LINUX=1 -I/usr/include/python3.5m -c psutil/_psutil_common.c -o build/temp.linux-x86_64-3.5/psutil/_psutil_common.o
    psutil/_psutil_common.c:9:20: fatal error: Python.h: そのようなファイルやディレクトリはありません
    compilation terminated.
    error: command 'x86_64-linux-gnu-gcc' failed with exit status 1
    ----------------------------------------
ERROR: Command errored out with exit status 1: /usr/bin/python3 -u -c 'import sys, setuptools, tokenize; sys.argv[0] = '"'"'/tmp/pip-install-ep62l8yz/psutil/setup.py'"'"'; __file__='"'"'/tmp/pip-install-ep62l8yz/psutil/setup.py'"'"';f=getattr(tokenize, '"'"'open'"'"', open)(__file__);code=f.read().replace('"'"'\r\n'"'"', '"'"'\n'"'"');f.close();exec(compile(code, __file__, '"'"'exec'"'"'))' install --record /tmp/pip-record-vtubkrgc/install-record.txt --single-version-externally-managed --compile --install-headers /usr/local/include/python3.5/psutil Check the logs for full command output.

以下で解決

sudo add-apt-repository ppa:deadsnakes/ppa
sudo apt-get update
sudo apt-get install -y python3-dev
sudo pip3 install psutil

参考

giampaolo psutil
Why can't I install python3.6-dev on Ubuntu16.04
Ubuntu 16.04 で python3.6-dev のインストールに失敗する場合の対処法

目次

1. 共通の設定
2. Googleアカウントでの認証機能
3. Facebookアカウントでの認証機能

1. 共通の設定

ライブラリをインストールします。

$ pip install social-auth-app-django

settings.pyを編集します。

settings.py

SOCIAL_AUTH_GOOGLE_OAUTH2_KEY = '[クライアントID]'  ?これを追加。
SOCIAL_AUTH_GOOGLE_OAUTH2_SECRET = '[クライアント シークレット]' ?これを追加。

INSTALLED_APPS = [
    ...省略...
    'social_django',  ?これを追加。
]

MIDDLEWARE_CLASSES = [
    ...省略...
    'social_django.middleware.SocialAuthExceptionMiddleware',  ?これを追加。
]

TEMPLATES = [
    {
        'BACKEND': 'django.template.backends.django.DjangoTemplates',
        'DIRS': [
            PROJECT_DIR.child('templates'),
        ],
        'APP_DIRS': True,
        'OPTIONS': {
            'context_processors': [
                ...省略...
                'social_django.context_processors.backends',  ?これを追加。
                'social_django.context_processors.login_redirect', ?これを追加。
            ]
        },
    },
]

マイグレーションを実行します。

$ python manage.py migrate

Operations to perform:
  Apply all migrations: admin, auth, contenttypes, sessions, social_django
Running migrations:
  Applying social_django.0001_initial... OK
  Applying social_django.0002_add_related_name... OK
  Applying social_django.0003_alter_email_max_length... OK
  Applying social_django.0004_auto_20160423_0400... OK
  Applying social_django.0005_auto_20160727_2333... OK
  Applying social_django.0006_partial... OK
...

プロジェクト全体を管理する、urls.pyを編集します。

urls.py

urlpatterns = [
    ...省略...
    path('oauth/', include('social_django.urls', namespace='social')),   ?これを追加
]

2. Googleアカウントでの認証機能

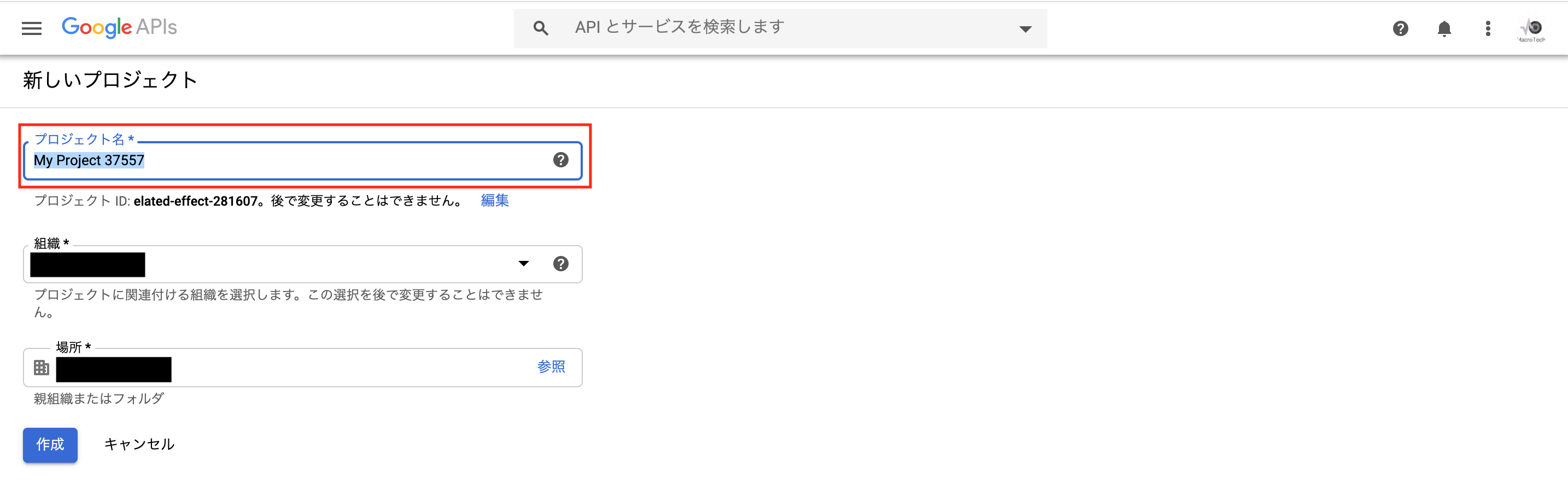
クライアントキーとクライアントシークレットを取得する為、Goolge Developers Consoleへアクセスし「プロジェクトを作成」を選択します。

「プロジェクト名」に適当な名称を入力し、「作成」を押下します。

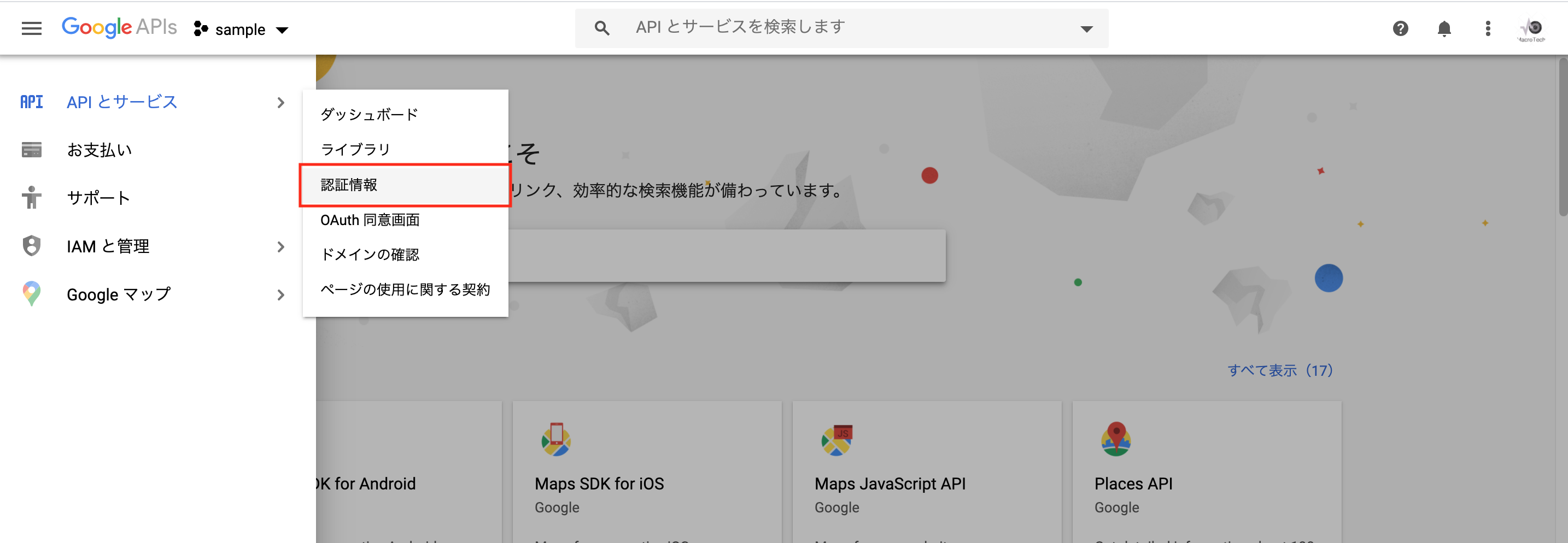
「認証情報」を選択します。

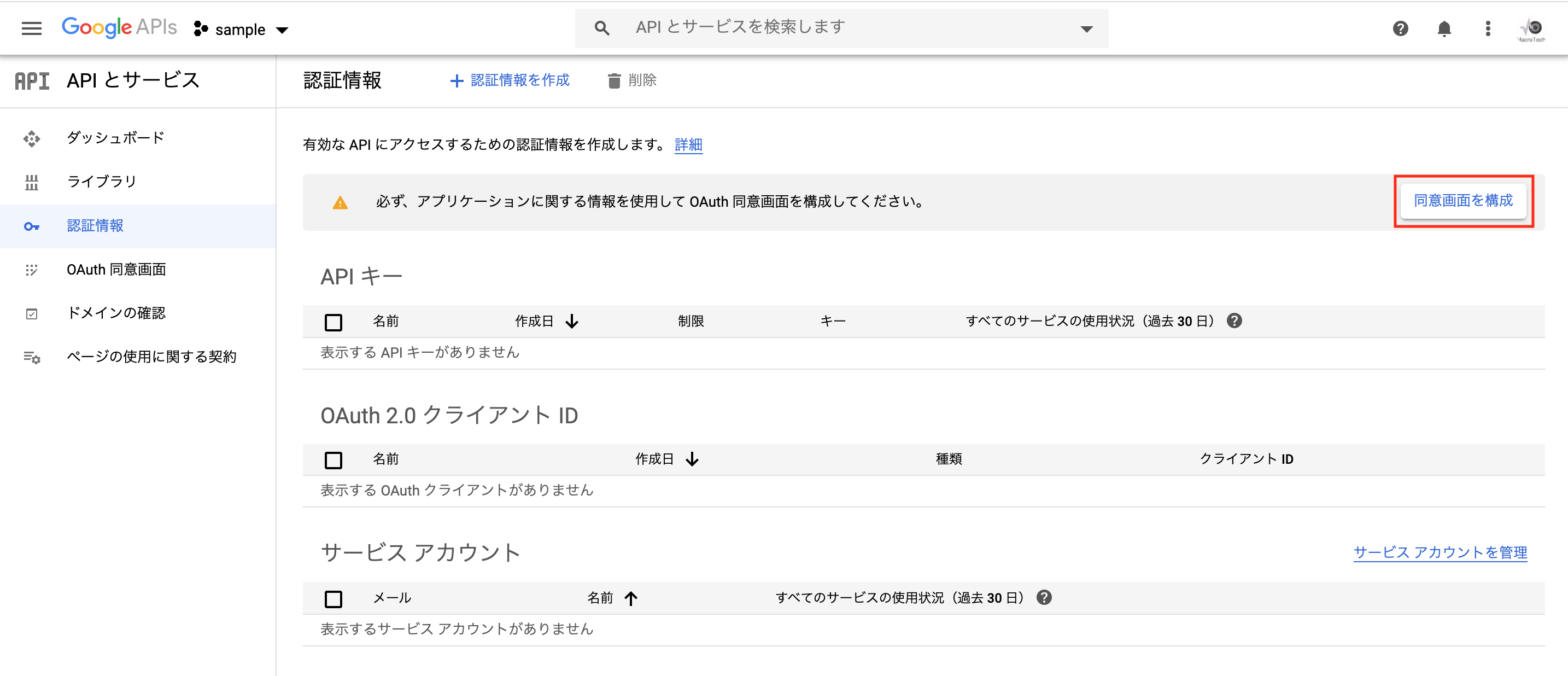
「同意画面を構成」を選択します。

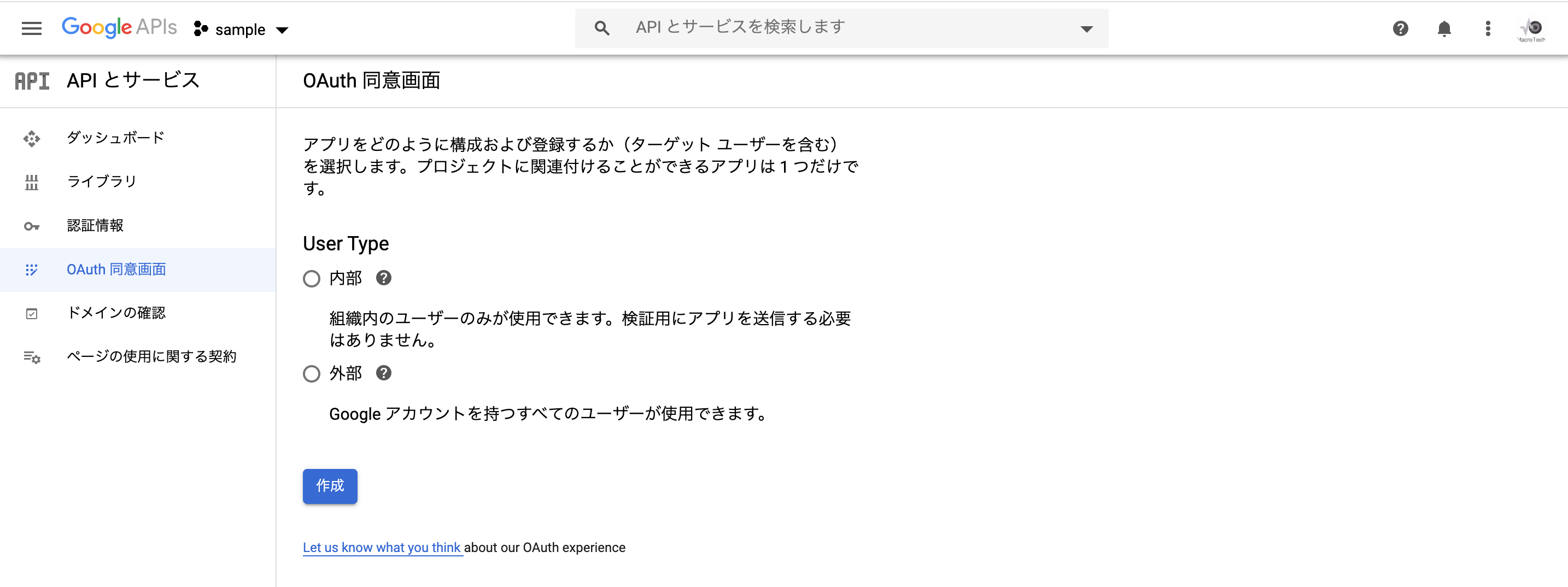
UserTypeを「内部」又は「外部」を選択し、「作成」をクリックします。
テスト環境では「内部」、本番環境では「外部」がいいかと思います。（特に理由はないです笑）

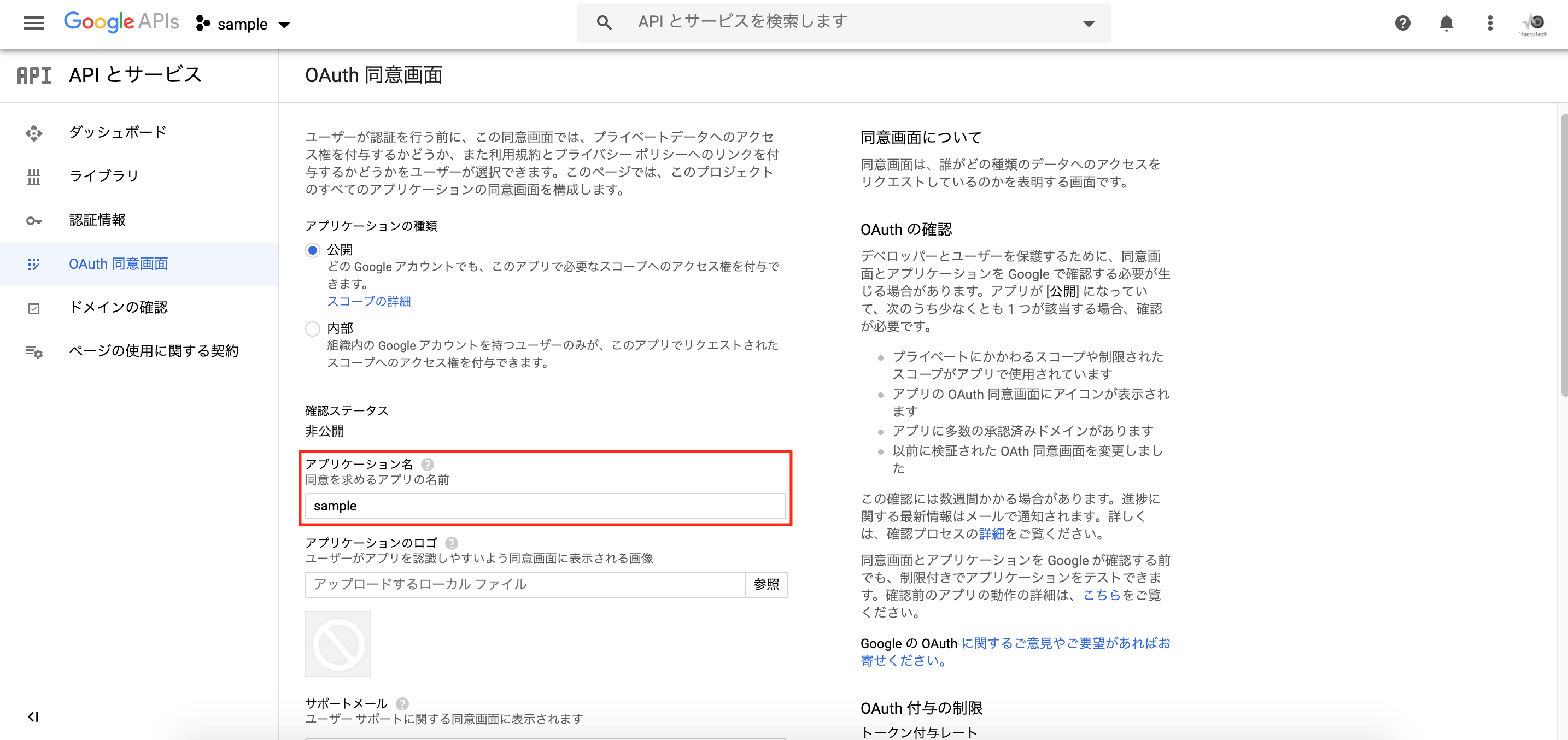
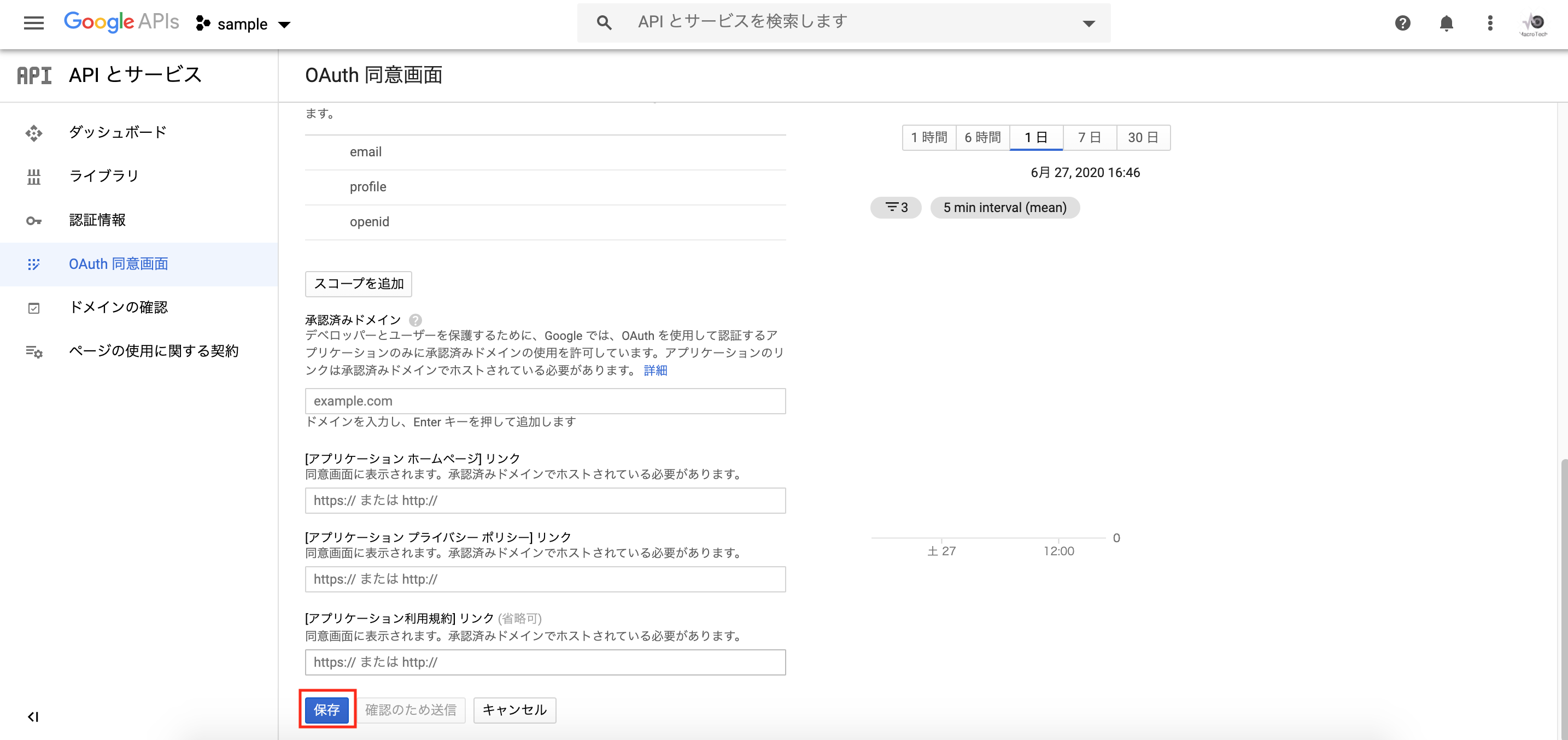
「アプリケーション名」に適当な値を入力し、「作成」をクリックします。


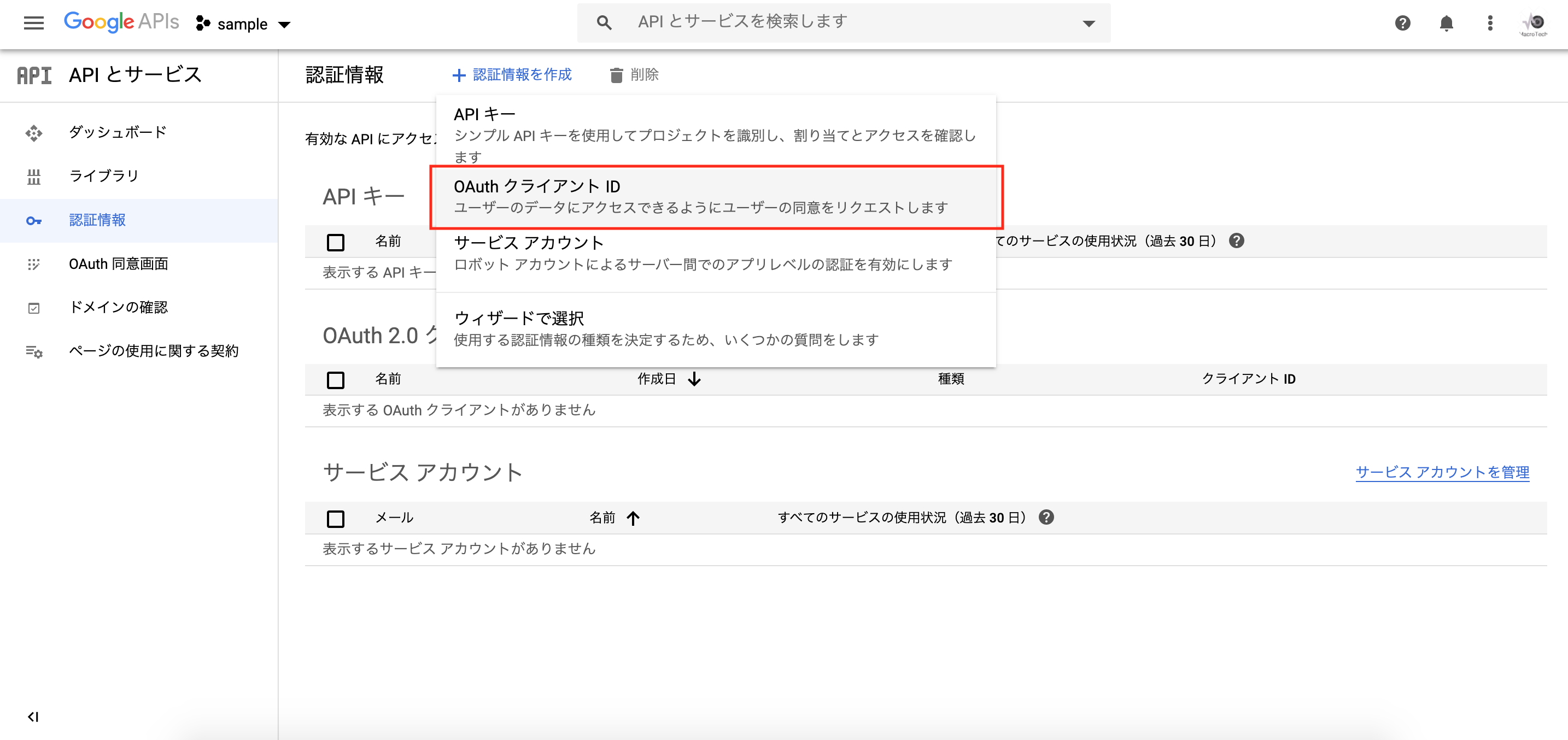
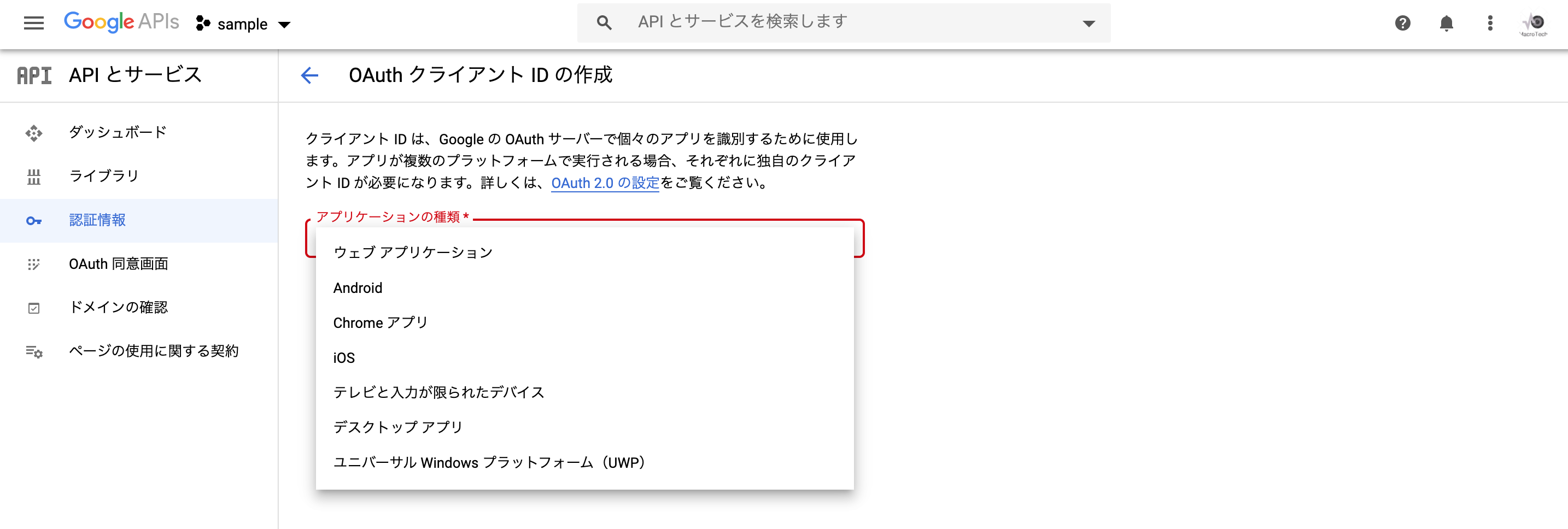
「認証情報を作成」をクリックし、「OAuthクライアントID」を選択します。

「アプリケーションの種類」から「ウェブアプリケーション」を選択します。
※使用用途によって適当なアプリケーションを選択します。

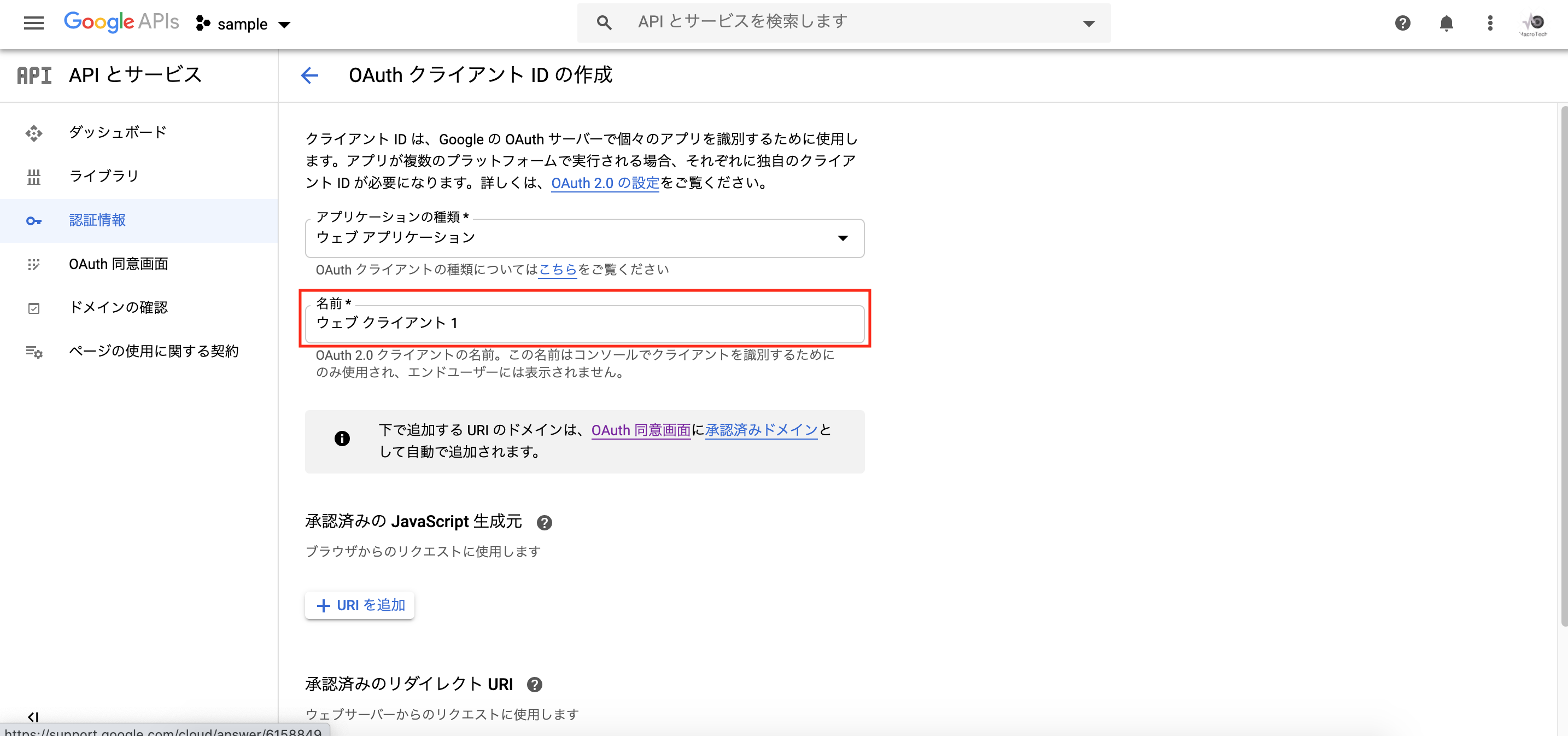
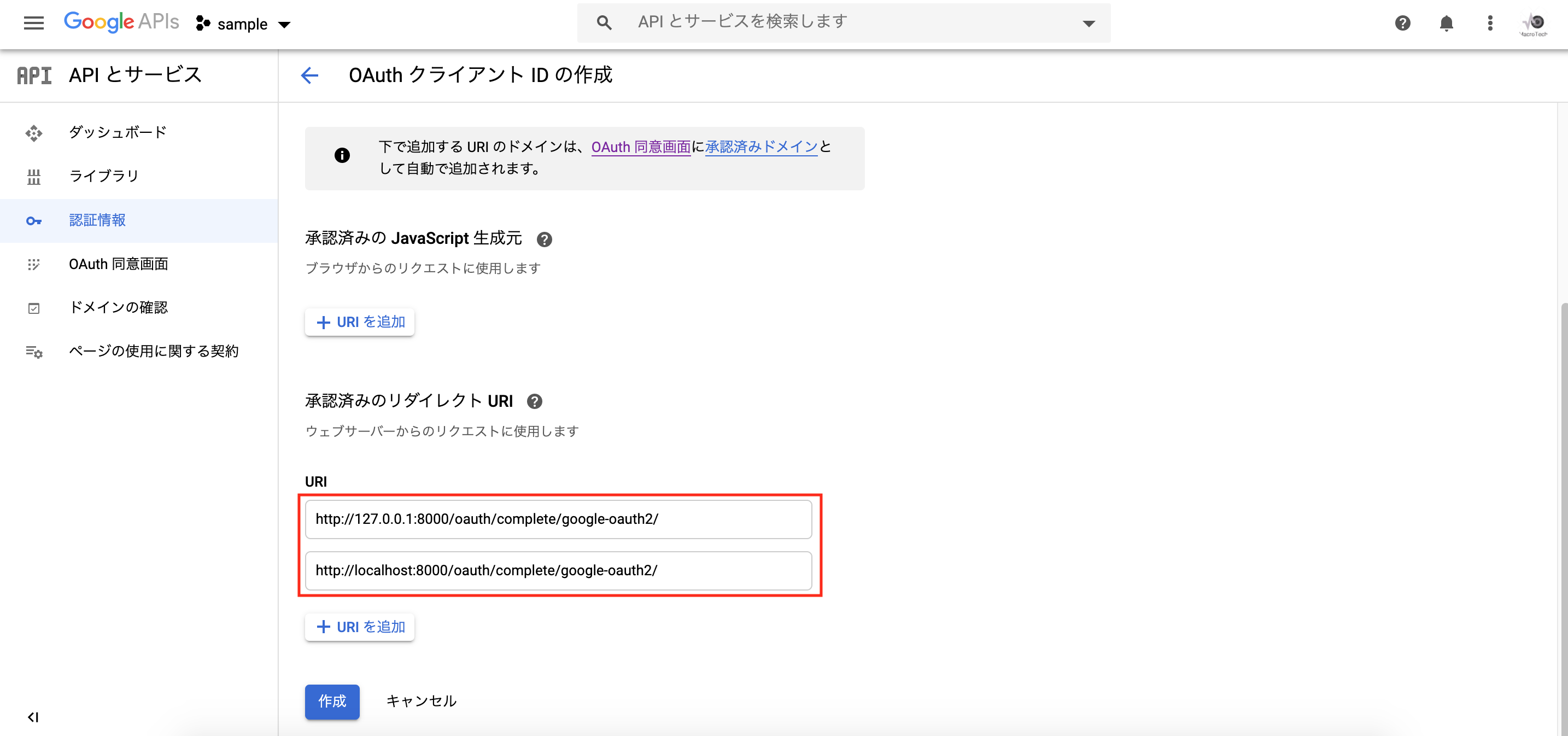
「名前」に適当な値を入力、承認済みのリダイレクトURIに以下のURLを追加し、「作成」をクリックします。
・http://127.0.0.1:8000/oauth/complete/google-oauth2/
・http://localhost:8000/oauth/complete/google-oauth2/


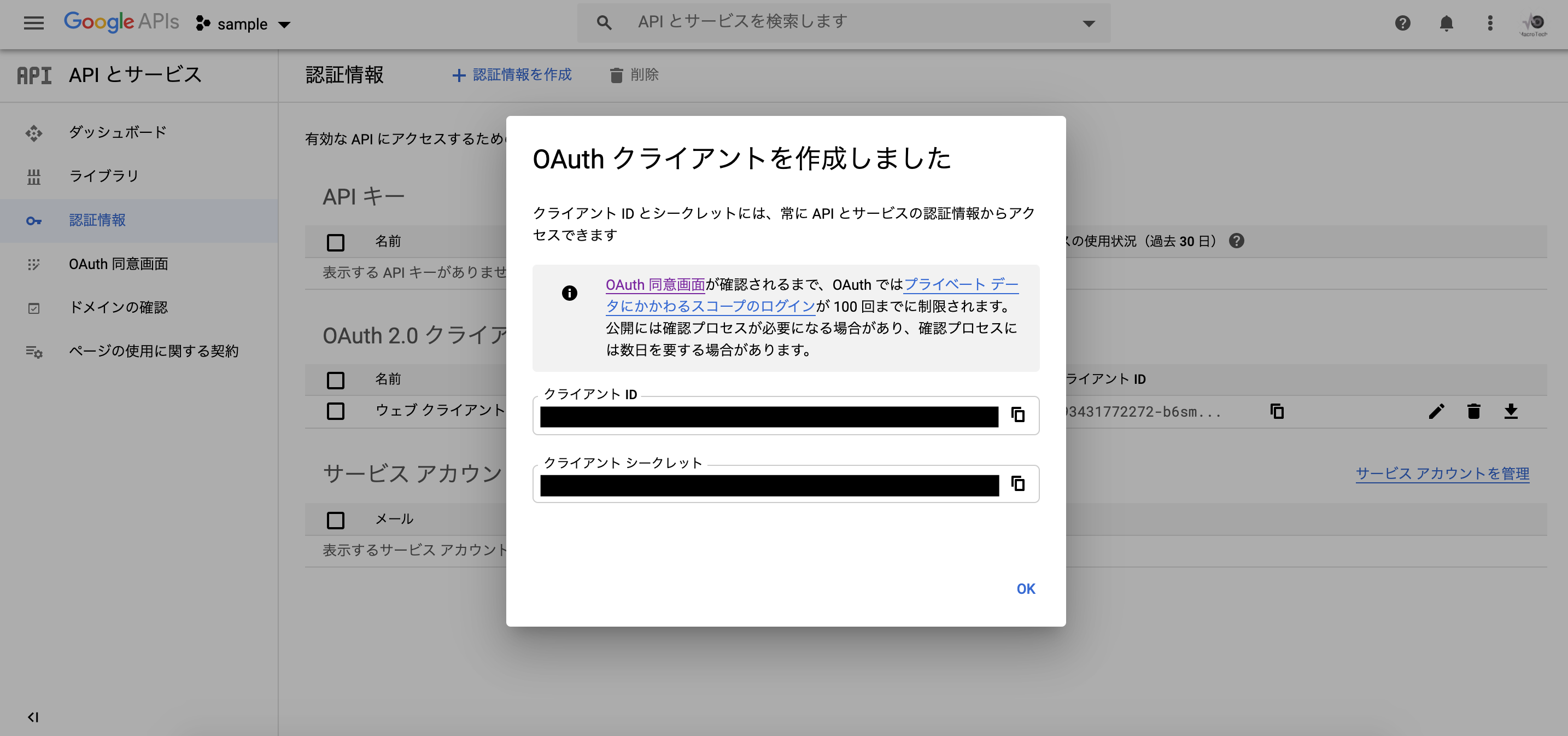
「クライアントID」と「クライアントシークレット」を、settings.pyに設定します。

settings.py

SOCIAL_AUTH_GOOGLE_OAUTH2_KEY = ''  ?ここにクライアントIDを追加。
SOCIAL_AUTH_GOOGLE_OAUTH2_SECRET = '' ?ここにクライアントシークレットを追加。
...省略...
AUTHENTICATION_BACKENDS = (
    'social_core.backends.open_id.OpenIdAuth',  ?これを追加。
    'social_core.backends.google.GoogleOpenId',　　?これを追加。
    'social_core.backends.google.GoogleOAuth2',　　?これを追加。
    'django.contrib.auth.backends.ModelBackend',　　?これを追加。
)

htmlでの、ログインリンクは以下のように作成することができます。

login.html

...省略...
<a href="{% url 'social:begin' 'google-oauth2' %}">Googleでログイン</a>
...省略...

3. Facebookアカウントでの認証機能

現在、作成中。（実装中の為、後に追加します）

最近の不甲斐ない競プロの成績を鑑みて再び精進の量を増やしていくことにしました。水diff以上の問題が時間内に解けるように精進をしたいと思います。

とりあえず、Sセメスターの授業が全て終わるまでは水diff~黄diffの問題を毎日1AC以上していくつもりです。頑張ります。

1日目

ABC128-E Roadwork

かかった時間

1時間半程度(今度から時間を測ります)

考察

それぞれの人がどの道路工事で通行止めにさせられるかを一回ずつ判定すると$O(NQ)$なので、それぞれの道路工事がどの人を通行止めにするか考えれば効率よくできそうです。

ここで、i番目の道路工事は$[S_i,T_i-1]$の間に座標$X_i$を通る人を通行止めにしますが、座標は時間にまとめることができます。つまり、速度1で歩くことから、$[S_i-X_i,T_i-X_i-1]$の間に出発する人を通行止めにすると言い換えることができます。

先ほどの時間に出発する人は二分探索で探すことができるので、二分探索で求めた区間の更新を$N$回行うことを考えますが、区間の更新を効率よく行う必要があります。区間の更新を効率よく行うデータ構造として遅延セグ木があり、通行止めにされる道路工事で最も近い座標のものを求めるには座標が遠いものから順に更新を行えば良いのではと考えました。しかし、遅延セグ木を使ったことがなくバグらせるのが怖かったのでこの解法は避けました。

ここで、区間更新で重要なのは両端のみを保存して最後に累積して考えるということです(imos法や遅延セグ木でも同じ)。したがって、ans_sectl[i]:i番目の人が左端となるような区間のインデックスを保存するdequeとans_sectr[i]:i番目の人が右端となるような区間のインデックスを保存するdequeを用意します。($\because$dequeにしたのは$O(1)$で取り出せるからです。)

また、再掲ではありますが、通行止めにされる道路工事で最も近い座標のものが実際に通行止めにするので、はじめに$S_i,T_i,X_i$を受け取る際に$X_i$の値で昇順ソートしておきます(xst)。…①

このもとで、それぞれの人の出発時間が含まれる区間のインデックス(=それぞれの人が通行止めにされる可能性のある道路工事のインデックス)を保存するコンテナ(ans)を用意して、番号の小さい人から順にans_sectlに含まれる場合はinsertしてans_sectrに含まれる場合はeraseすることを繰り返せば、ansは求めるような挙動を高速にします。

さらに、ansに含まれる区間のインデックスはC++のmapやsetであれば昇順で保存され、求めるべきはansに含まれる中で最も近い座標の道路工事なのでコンテナの先頭の要素に対応する通行止めの地点の距離を出力すれば良いです($\because$①)。

また、$[S_i-X_i,T_i-X_i-1]$に出発時間が含まれるような人を閉区間で求める際に、左端をL=(lower_bound(ALL(d),s-x)-d.begin())で右端をR=(upper_bound(ALL(d),t-x-1)-d.begin())-1で求める必要がありますが、$[S_i-X_i,T_i-X_i-1]$に出発時間が含まれるような人が存在しない場合は$L>R$となるので、このような場合は除く必要があります。

コード

abc128e.cc

#include<algorithm>//sort,二分探索,など
#include<bitset>//固定長bit集合
#include<cmath>//pow,logなど
#include<complex>//複素数
#include<deque>//両端アクセスのキュー
#include<functional>//sortのgreater
#include<iomanip>//setprecision(浮動小数点の出力の誤差)
#include<iostream>//入出力
#include<iterator>//集合演算(積集合,和集合,差集合など)
#include<map>//map(辞書)
#include<numeric>//iota(整数列の生成),gcdとlcm(c++17)
#include<queue>//キュー
#include<set>//集合
#include<stack>//スタック
#include<string>//文字列
#include<unordered_map>//イテレータあるけど順序保持しないmap
#include<unordered_set>//イテレータあるけど順序保持しないset
#include<utility>//pair
#include<vector>//可変長配列

using namespace std;
typedef long long ll;

//マクロ
//forループ関係
//引数は、(ループ内変数,動く範囲)か(ループ内変数,始めの数,終わりの数)、のどちらか
//Dがついてないものはループ変数は1ずつインクリメントされ、Dがついてるものはループ変数は1ずつデクリメントされる
#define REP(i,n) for(ll i=0;i<(ll)(n);i++)
#define REPD(i,n) for(ll i=n-1;i>=0;i--)
#define FOR(i,a,b) for(ll i=a;i<=(ll)(b);i++)
#define FORD(i,a,b) for(ll i=a;i>=(ll)(b);i--)
//xにはvectorなどのコンテナ
#define ALL(x) x.begin(),x.end() //sortなどの引数を省略したい
#define SIZE(x) ll(x.size()) //sizeをsize_tからllに直しておく
//定数
#define INF 1000000000000 //10^12:極めて大きい値,∞
#define MOD 1000000007 //10^9+7:合同式の法
#define MAXR 100000 //10^5:配列の最大のrange(素数列挙などで使用)
//略記
#define PB push_back //vectorヘの挿入
#define MP make_pair //pairのコンストラクタ
#define F first //pairの一つ目の要素
#define S second //pairの二つ目の要素
#define Umap unordered_map
#define Uset unordered_set

//最後のところの処理がいい加減になっていた、こういう詰めの甘い実装がダメなんだよカス
signed main(){
    //入力の高速化用のコード
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    ll n,q;cin>>n>>q;

    vector<vector<ll>> xst(n);
    REP(i,n){
        ll s,t,x;cin>>s>>t>>x;
        xst[i]={x,s,t};
    }
    sort(ALL(xst));

    vector<ll> d(q);
    REP(i,q)cin>>d[i];

    vector<deque<ll>> ans_sectl(q);
    vector<deque<ll>> ans_sectr(q);
    REP(i,n){
        ll s,t,x;x=xst[i][0];s=xst[i][1];t=xst[i][2];
        ll L=(lower_bound(ALL(d),s-x)-d.begin());
        ll R=(upper_bound(ALL(d),t-x-1)-d.begin())-1;
        //lower,upper気を付ける
        //2RE
        if(L<=R){ans_sectl[L].PB(i);ans_sectr[R].PB(i);}
        //cout << L << " " << R << endl;
    }

    map<ll,ll> ans;
    REP(i,q){
        ll sl=SIZE(ans_sectl[i]);
        ll sr=SIZE(ans_sectr[i]);
        REP(_,sl){
            ans[*(ans_sectl[i].begin())]+=1;
            ans_sectl[i].pop_front();
        }
        if(ans.empty()){
            cout<<-1<<"\n";
        }else{
            cout<<xst[ans.begin()->F][0]<<"\n";
        }
        REP(_,sr){
            ans[*(ans_sectr[i].begin())]-=1;
            if(ans[*(ans_sectr[i].begin())]==0)ans.erase(*(ans_sectr[i].begin()));
            ans_sectr[i].pop_front();
        }
    }
}

abc128e_set.cc

#include<algorithm>//sort,二分探索,など
#include<bitset>//固定長bit集合
#include<cmath>//pow,logなど
#include<complex>//複素数
#include<deque>//両端アクセスのキュー
#include<functional>//sortのgreater
#include<iomanip>//setprecision(浮動小数点の出力の誤差)
#include<iostream>//入出力
#include<iterator>//集合演算(積集合,和集合,差集合など)
#include<map>//map(辞書)
#include<numeric>//iota(整数列の生成),gcdとlcm(c++17)
#include<queue>//キュー
#include<set>//集合
#include<stack>//スタック
#include<string>//文字列
#include<unordered_map>//イテレータあるけど順序保持しないmap
#include<unordered_set>//イテレータあるけど順序保持しないset
#include<utility>//pair
#include<vector>//可変長配列

using namespace std;
typedef long long ll;

//マクロ
//forループ関係
//引数は、(ループ内変数,動く範囲)か(ループ内変数,始めの数,終わりの数)、のどちらか
//Dがついてないものはループ変数は1ずつインクリメントされ、Dがついてるものはループ変数は1ずつデクリメントされる
#define REP(i,n) for(ll i=0;i<(ll)(n);i++)
#define REPD(i,n) for(ll i=n-1;i>=0;i--)
#define FOR(i,a,b) for(ll i=a;i<=(ll)(b);i++)
#define FORD(i,a,b) for(ll i=a;i>=(ll)(b);i--)
//xにはvectorなどのコンテナ
#define ALL(x) x.begin(),x.end() //sortなどの引数を省略したい
#define SIZE(x) ll(x.size()) //sizeをsize_tからllに直しておく
//定数
#define INF 1000000000000 //10^12:極めて大きい値,∞
#define MOD 1000000007 //10^9+7:合同式の法
#define MAXR 100000 //10^5:配列の最大のrange(素数列挙などで使用)
//略記
#define PB push_back //vectorヘの挿入
#define MP make_pair //pairのコンストラクタ
#define F first //pairの一つ目の要素
#define S second //pairの二つ目の要素
#define Umap unordered_map
#define Uset unordered_set

//最後のところの処理がいい加減になっていた、こういう詰めの甘い実装がダメなんだよカス
signed main(){
    //入力の高速化用のコード
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    ll n,q;cin>>n>>q;

    vector<vector<ll>> xst(n);
    REP(i,n){
        ll s,t,x;cin>>s>>t>>x;
        xst[i]={x,s,t};
    }
    sort(ALL(xst));

    vector<ll> d(q);
    REP(i,q)cin>>d[i];

    vector<deque<ll>> ans_sectl(q);
    vector<deque<ll>> ans_sectr(q);
    REP(i,n){
        ll s,t,x;x=xst[i][0];s=xst[i][1];t=xst[i][2];
        ll L=(lower_bound(ALL(d),s-x)-d.begin());
        ll R=(upper_bound(ALL(d),t-x-1)-d.begin())-1;
        //lower,upper気を付ける
        //2RE
        if(L<=R){ans_sectl[L].PB(i);ans_sectr[R].PB(i);}
        //cout << L << " " << R << endl;
    }

    set<ll> ans;
    REP(i,q){
        ll sl=SIZE(ans_sectl[i]);
        ll sr=SIZE(ans_sectr[i]);
        REP(_,sl){
            ans.insert(*(ans_sectl[i].begin()));
            ans_sectl[i].pop_front();
        }
        if(ans.empty()){
            cout<<-1<<"\n";
        }else{
            cout<<xst[*ans.begin()][0]<<"\n";
        }
        REP(_,sr){
            ans.erase(*(ans_sectr[i].begin()));
            ans_sectr[i].pop_front();
        }
    }
}

2日目

ABC128-D equeue

かかった時間

1時間程度(今度から時間を測ります)

考察

「K回まで行う」を「K回ちょうど行う」と誤読して難易度の高くなった問題を解いていました。全然だめですね…。

まずは$N$と$K$があまり大きくないので、計算量にある程度余裕がありそうであることを把握する必要があります。

ここで、貪欲に外側の価値の高い宝石から取るという方法をまず試しますが、内側に価値の高い宝石がある可能性があるので却下します。また、詰める操作の後に同じ側で取り出す操作を行うとその二つの操作には無駄があるので、取り出す操作を行った後に詰める操作を行えば良いこともわかります(操作を入れ替えて考えやすくする！)。

ここで、取り出す回数を決めれば詰める回数も決まるので、取り出す回数を$i$回と決めることにしました(最初の誤読のせいでこの辺りで方針が迷走し始めましたが、落ち着いて問題文を読む必要がありました。)。$i$が0の場合は詰める操作もできず操作終了後の宝石の価値の合計の最大値は0なので、$i$は1から$min(k,n)$で考えます。また、取り出す操作の回数が$i$回の時も外側の価値の高い宝石から順に貪欲に取ろうと思ったのですが内側に価値の高い宝石がある可能性があるのでこの方針は却下します。

したがって、まだ計算量的に余裕があることと合わせて、左から$m$個,右から$i-m$個取り出す場合の$m$を全て試すようにしました($m=0$~$i$で取り出したものはスライスして配列$s$に格納)。また、取り出したもののうち価値が低いものから順に詰めていけば良いので(ただし、その価値は0以下)、$s$をソートして最大$min(k-i,i)$回詰めれば良いです。また、詰めたものを0として$s$の合計が求める最大値の候補になります。

以上で計算量は$X=min(N,K)$として$O(X^3\log{X})$でありこれ以上高速化する必要もないので、実装して以下のようになります。

コード

abc128d.py

import math
from collections import deque
n,k=map(int,input().split())
v=list(map(int,input().split()))
#k回までだったー誤読
ans=0
for i in range(1,min(k,n)+1):
    #取るところ(大きい方とは限らないのか)
    for m in range(i+1):
        s=v[:m]+v[n-(i-m):]
        s.sort()
        #取った個数より多く詰めようとしないように！
        #残りk-i回ある
        for j in range(i,min(k,2*i)):#それ以上詰められない場合
            #0より小さい場合は書き換える
            if s[j-i]<0:s[j-i]=0
        #取り出したやつの最大(戻す場合は0)
        ans=max(ans,sum(s))
        #残りk-j回ある(breakの時のjはやってないので)
        #ここからはいい感じに出すのと入れるのを繰り返す(偶数の場合はこのままか)
        #必要すらない、k回を使い切らなくていいので
        #print(sum(s))
print(ans)

3日目

ABC129-E Sum Equals Xor

かかった時間

今回もまとまった時間が取れませんでしたが、合計で1時間程度で解けました。

考察

二つある条件のうち考えやすい$a+b=a\oplus b$から考察しました。これは少し考えればわかりますが、$XOR$はそれぞれのビットが独立に計算できる$\leftrightarrow$2進数の計算での繰り上がりがないので、aとbの任意のbitについて(0,1),(1,0),(0,0)の三組のみがあることがわかります。…①

このもとで、一つ目の条件である$a+b\leqq L$を処理しますが、ここで「1番目の桁が0or1なら,2番目の桁が0or1なら,…と考えなきゃなあ」「どこかの桁で下回ったらそのあとの桁はなんでも良いなあ」などと雑に考えていたのですが、このようなパターンの問題では桁DPの考えが当てはまることをだいぶ経ってから思い出しました…。

桁DPについての軽いまとめ

ARMERIAさんの記事やけんちょんさんの記事を参照するなら、以下の二つの性質がある場合は桁DPを用いることができると一般化できるのではないでしょうか。

1:上限値$L$以下で〇〇を満たすような値の個数(〇〇の最大値や最小値)を求めたい(しかも$L$は大きい)
2:桁に関する条件が存在する

このもとでは、次のようにDPの状態を決めることができます。
$DP[i][smaller]:=$上から$i$桁目までを決めた時のなんらかの値
(ただし、$smaller=0$の時は$i$桁目までで$L$より小さな桁が存在し、$smaller=1$の時はi桁目までの全ての桁が$L$と同じ、と言えます。)

さらに、DPの遷移も毎回以下のようになります。
・$DP[i][0]$からは$DP[i+1][0]$にしか遷移せず、$i$桁目は何を選んでもよい。
・$DP[i][1]$から$DP[i+1][0]$の遷移では、$i$桁目は$L$の$i$桁目より小さい全ての数を選ぶことができる。
・$DP[i][1]$から$DP[i+1][1]$の遷移では、$i$桁目は$L$の$i$桁目と同じでなければならない。

---

以上で桁DPの動きを確認すれば今回の問題は簡単で、下記のようにDPの状態を決めることができます。

$DP[i][smaller]:=$上から$i$ビット目までを決めた時の$(a,b)$の組の個数
(ただし、$smaller$が0の時は上から$i$ビット目までで$L$より小さいビットが$a+b$に存在し,$smaller$が1の時は上から$i$ビット目までの全てのビットが$L$と等しい)

また、DPの遷移は以下の3通りです(\because$①$)。

・$DP[i+1][0]=3×DP[i][0](\because a+b$の$i$ビット目は0でも1でも良い$)$
・$L$の$i+1$桁目が0の時
　$DP[i+1][1]=DP[i][1](\because a+b$の$i$ビット目も0しかない$)$
・$L$の$i+1$桁目が1の時
　$DP[i+1][0]=DP[i][1](\because a+b$の$i$ビット目が0の時は$(a$と$b$のiビット目$)=(0,0))$
　$DP[i+1][1]=2*DP[i][1](\because a+b$の$i$ビット目が1の時は$(a$と$b$のiビット目$)=(0,1),(1,0))$

この遷移を実装して以下のようなコードになります。桁DPをすぐに発想できるかが勝負だったのでもう少し解けたはずです。悔しいです。

コード

abc129e.py

mod=10**9+7
l=input()
bit=[int(i) for i in l]
m=len(bit)

#適当にやりすぎたけど、桁DP
#小さい方と同じ方
dp=[[0,0] for i in range(m)]
dp[0]=[1,2]
for i in range(m-1):
    dp[i+1][0]=3*dp[i][0]%mod
    if bit[i+1]==0:
        dp[i+1][1]+=dp[i][1]
        dp[i+1][1]%=mod
    else:
        dp[i+1][0]+=dp[i][1]
        dp[i+1][1]+=(2*dp[i][1])
        dp[i+1][0]%=mod
        dp[i+1][1]%=mod
print(sum(dp[m-1])%mod)

2020/6/26(日本時間)にcx_Oracleが7.3から8.0にバージョンアップされました。
以下、8.0の新機能、変更点のおおまかな解説です。メジャーバージョンアップだけあって、大きな(と筆者が感じる)変更が含まれています。以下、番号はcx_Oracleのリリースノートに対応しています。

1. Python2のサポート終了

サポートするPythonのバージョンが3.5以降となりました。Python2で利用したい場合は7.3を使用する必要があります。

2. ODPI-Cのバージョン変更

cx_OracleはODPI-CというOSSのC言語のOracleアクセスドライバを用いて作成されています。バージョン8.0は、ODPI-C 4.0.1をベースにビルドされています。

3. 型マネジメントの変更

以下の通り、大幅に見直されています。

• 型の定数の体系が以下の通りに整理されました。
  • DB API Type : DB APIに準拠した型
  • Database Type : Oracle Databaseのデータ型に対応した型。7.3と名称が異なる
  • Database Type Synonym : 7.3時代の型。8.0以降は非推奨で将来廃止予定
  • Other Type : 上記に含まれない型
• 7.3では一部のOralce Databaseデータ型に対し、対応するcx_Oracleデータ型定数が存在しませんでした。8.0で不足していたデータ型への対応として、以下を追加しています。
  • cx_Oracle.DB_TYPE_BINARY_FLOAT
  • cx_Oracle.DB_TYPE_INTERVAL_YM
  • cx_Oracle.DB_TYPE_TIMESTAMP_LTZ
  • cx_Oracle.DB_TYPE_TIMESTAMP_TZ
• Variableオブジェクトのtype属性に対する変更
  • Oracle Databaseのオブジェクト型にバインドされていない場合、NoneではなくDatabase Typeを使用するように変更
  • LOBに対応
  • Oracle Databaseのオブジェクト型の属性を取得可能に
• Object Typeオブジェクトにelement_type属性を追加
• 同一セッションないしコネクションプール使用時において、Object Typeオブジェクトの名前やスキーマの比較が可能に
• すべての変数が同一クラスのインスタンスとなった
• 変数の文字列表現に、値に加えて型が追加

4. cx_Oracle.init_oracle_client()の追加

Oracle Clientライブラリの初期化を行う関数cx_Oracle.init_oracle_client()が追加されました。

5. デフォルトエンコーディングの変更

7.3ではNoneでしたが、8.0ではUTF-8になりました。NLS_LANG環境変数のキャラクタおセットの指定は無視されます。

6. Soda Documentクラスへのメソッド追加

SodaCollectionオブジェクトにsave(), saveAndGet(), truncate()メソッドが追加されました。これらの機能を利用するためには、Oracle Client 20以降が必要です。

7. SodaOperation.fetchArraySize()の追加

SODAドキュメントのフェッチ件数を設定するSodaOperation.fetchArraySize()が追加されました。この機能を利用するためには、Oracle Client 19.5以降が必要です。

8. Cursor.prefetchrowsの追加

結果セットのプリフェッチを行うCursor.prefetchrowsが追加されました。

9. Connection.versionの初回実行に伴うラウンドトリップの回避

データベースのバージョン番号を取得するConnection.versionの初回実行に伴うラウンドトリップを回避するために、新しいモードの追加行っています。この機能を利用するためには、Oracle Client 20以降が必要です。

10. PFILE対応

PFILEを使用したデータベースの起動に対応しました。7.3まではSPFILEのみの対応でした。

11. Cursor.getbatcherrors()のバッファオーバーフローの修正

オフセットが65536を超えた場合、Cursor.getbatcherrors()でバッファオーバーフローが発生する問題を修正しました。

12. Cursor.lastrowidの挙動の変更

INSERT ALL文を実行した後にCursor.lastrowidを実行した場合にエラーが発生しないように変更されました。

13. Alex Henrie氏のpull requestの受け入れ

主にコードの改善(冗長なコーディングの改善等)に関する6つのpull requestを取り込んでいます。

14. boolean変数にバインドされたPythonオブジェクトの挙動

boolean変数にバインドされたPythonオブジェクトは、Pythonのif文の中でTrueかFalseとみなされるかに従ってTrue/Falseに変換されるようになりました。従来はTrueのみTrueに変換され、それ以外はFalseに変換されていました。

15. 本体コード以外の改善

ドキュメント、サンプル、テストを改善しています。

DjangoをAWS Lambdaにデプロイできました。Serverless Frameworkを使うと簡単です。
URLとレポジトリはこちらです。
https://django-sls-helloworld.umihi.co/
https://github.com/umihico/django-sls-helloworld

slsのデフォルトプロジェクトを作成し、f1a13ba
動作確認したらカスタムドメインをプラグインをインストールします。0970afe
API GatewayはURL末端につくstage名を外せず、djangoのルーティングと相性が悪いようで、カスタムドメインを先に整えました。

$ serverless create --template aws-python3 --path django-sls-helloworld # プロジェクト作成 
$ cd django-sls-helloworld
$ serverless deploy #　一度デプロイ
$ serverless invoke -f hello # 正常に動くかテスト
{
    "statusCode": 200,
    "body": "{\"message\": \"Go Serverless v1.0! Your function executed successfully!\", \"input\": {}}"
}
$ sls plugin install -n serverless-domain-manager #　ドメイン設定のためのプラグインインストール

serverless.ymlを編集します。603753b

serverless.yml

+ custom:
+   customDomain:
+     domainName: django-sls-helloworld.umihi.co
+     certificateName: umihi.co
+     basePath: ''
+     stage: ${opt:stage, self:provider.stage}
+     createRoute53Record: true
+     endpointType: 'edge'
+     securityPolicy: tls_1_2

provider:
  name: aws
  runtime: python3.8

$ sls create_domain
# 最大４０分かかると言われるが、次のデプロイコマンドはすぐにできる。ただドメイン適用に時間がかかるだけ。
$ sls deploy

これで、カスタムドメイン設定されたWEBページが完成しました。次にDjangoに必要なライブラリをインストールします。80e8f1b

$ sls plugin install -n serverless-python-requirements

以下のファイルを追加し、不要ですがインポートされてるかテストのため、handler.pyも編集しました。ec47570

requirements.py

import os
import sys

requirements = os.path.join(
    os.path.split(__file__)[0],
    '.requirements',
)

if requirements not in sys.path:
    sys.path.append(requirements)

requirements.txt

Django
Werkzeug
PyMySQL

handler.py

import json
+ import requirements

def hello(event, context):
+     # testing import libraries
+     import django
+     import werkzeug
+     import pymysql
    body = {
        "message": "Go Serverless v1.0! Your function executed successfully!",

デプロイし、serverless invoke -f helloが正常であれば、importは成功です。
次に、Djangoのプロジェクトを作成します。930a0c2
そして、サーバレスライブラリ用のWSGIプラグインをインストールします。52386e4

$ django-admin startproject django_sls_helloworld .
$ sls plugin install -n serverless-wsgi

最後に、
MySQLdbの代わりにPyMySQLをインストールする修正と、その際に指摘されるバージョン違いを修正し、30361dd
ALLOWED_HOSTに設定したドメインを名を加え、1966857
LambdaがWSGIを参照するように振り分けます。1dce3d3

django_sls_helloworld/settings.py

import os
+ import pymysql
+ 
+ pymysql.version_info = (1, 4, 2, "final", 0)
+ pymysql.install_as_MySQLdb()
# Build paths inside the project like this: os.path.join(BASE_DIR, ...)

省略

DATABASES = {
    'default': {
-         'ENGINE': 'django.db.backends.sqlite3',
-         'NAME': os.path.join(BASE_DIR, 'db.sqlite3'),
+         'ENGINE': 'django.db.backends.mysql',
+         'NAME': 'djangodemo',
    }
}

省略

- ALLOWED_HOSTS = []
+ ALLOWED_HOSTS = ["django-sls-helloworld.umihi.co"]

serveless.yml

  endpointType: 'edge'
  securityPolicy: tls_1_2
+ wsgi:
+   app: django_sls_helloworld.wsgi.application
+   packRequirements: false

省略

functions:
  hello:
-     handler: handler.hello
+     handler: wsgi_handler.handler
#    The following are a few example events you can configure

デプロイしてお馴染みの画面がカスタムドメイン先でも現れました。以上です。
ちなみに使い捨てプロジェクトなので、DEBUG=Trueでデプロイし、かつSECRET_KEYもGithubにあげてますが、実運用ではタブーなのでご注意ください。

はじめに

OpenCVで透過png画像を扱い、往年のホビーパソコンのスプライト的なことをやってみよう。
本格的にスプライトを使ったゲームを作りたい人はpygameを使うとよい。私はOpenCVの勉強をしたいだけだ。

基本　RGBA要素について

ここではいらすとやの「決めポーズを取る戦隊もののキャラクターたち（集合）」（を縮小したもの）を使う。背景は透過処理されている。

sentai.png

RGBA画像を取り込むにはcv2.imread()でflags = cv2.IMREAD_UNCHANGEDと指定する。
実際はそんな呪文を覚える必要はなく、2番目の引数として-1を指定すればよい。引数を1にするもしくは省略するとRGBの3チャンネル画像として取り込まれる。

import cv2
filename = "sentai.png"
img4 = cv2.imread(filename, -1)
img3 = cv2.imread(filename)
print (img4.shape)  # 結果：(248, 300, 4)
print (img3.shape)  # 結果：(248, 300, 3)

なお、この画像をcv2.imshow()で表示したとき背景が黒になる。お絵かきソフトで透明キャンバスの上に絵を描くと、透明の部分は色要素がないために黒として扱われるわけだ。RGB成分がすべてゼロ＝(0,0,0)＝黒ということ。

RGBA各要素を取り出す

何度も書くがOpenCV画像はnumpy.ndarray形式でデータ格納されているので、トリミングだけでなく各色要素を取り出すのもスライスでできる。

import cv2
filename = "sentai.png"
img4 = cv2.imread(filename, -1)
b = img4[:, :, 0]
g = img4[:, :, 1]
r = img4[:, :, 2]
a = img4[:, :, 3]

cv2.imshow("img4", img4)
cv2.imshow("b", b)
cv2.imshow("g", g)
cv2.imshow("r", r)
cv2.imshow("a", a)
cv2.waitKey(0)
cv2.destroyAllWindows()

元画像		A要素
B要素	G要素	R要素

各要素はndim=2すなわち(height, width)のシェイプとなっている。だから各要素を画像として表示させるとグレースケールになる。
アカレンジャーはたとえば(G,B,R)=(21,11,213)なので赤の輝度がかなり高い一方で青と緑の輝度は低い。
その一方でキレンジャーは(G,B,R)=(0,171,247)なので赤の輝度はアカレンジャー以上に高く、また緑要素もそれなりに高いことがわかる。
また、アルファ値は0が透明で255が不透明。透明度というより不透明度と覚えたほうがよさそうだ。

では各色要素を各色で表示するにはどうしたらよいかというと、他色成分を0としたRGB画像をあらためて作ってやればよいのだ。

方法その1

import cv2
import numpy as np
filename = "sentai.png"
img3 = cv2.imread(filename)

b = img3[:, :, 0]
g = img3[:, :, 1]
r = img3[:, :, 2]
z = np.full(img3.shape[:2], 0, np.uint8)
imgB = cv2.merge((b,z,z))
imgG = cv2.merge((z,g,z))
imgR = cv2.merge((z,z,r))

cv2.imshow("imgB", imgB)
cv2.imshow("imgG", imgG)
cv2.imshow("imgR", imgR)
cv2.waitKey(0)
cv2.destroyAllWindows()

元のRGB画像で不必要な色の輝度を0にするというやり方もある。

方法その2

import cv2
import numpy as np
filename = "sentai.png"
img3 = cv2.imread(filename)

imgB = img3.copy()
imgB[:, :, (1,2)] = 0  # 3ch(BGR)の1番目(G)と2番目(R)を0にする
imgG = img3.copy()
imgG[:, :, (0,2)] = 0  # 3ch(BGR)の0番目(B)と2番目(R)を0にする
imgR = img3.copy()
imgR[:, :, (0,1)] = 0  # 3ch(BGR)の0番目(B)と1番目(G)を0にする

cv2.imshow("imgB", imgB)
cv2.imshow("imgG", imgG)
cv2.imshow("imgR", imgR)
cv2.waitKey(0)
cv2.destroyAllWindows()

B要素を青で	G要素を緑で	R要素を赤で

画像を合成する

ここからが本番。
背景画像は「宇宙のイラスト（背景素材）」とする。jpeg画像で、アルファ値は持たない。
背景の上に重ねる画像は「宇宙飛行士のイラスト」（を縮小したもの）。

space.jpg
uchuhikoushi.png

事前準備

RGBA画像からRGB画像とマスク画像を作る。先ほど「A要素」として挙げたのは1チャンネルなので背景画像と合成することはできない。B要素を青くR要素を赤くしたのと似た方法で、RGB3チャンネルのマスク画像を作る。

import cv2

filename = "uchuhikoushi.png"
img4 = cv2.imread(filename, -1)

img3 = img4[:, :, :3]  # RGBAのうち最初の3個すなわちRGB
mask1 = img4[:, :, 3]  # RGBAのうち0から数えて3番目すなわちA
mask3 = cv2.merge((mask1, mask1, mask1)) # 3チャンネルのRGB画像とする

元画像（RGBA）	RGB画像	マスク画像

また、背景から前景と同サイズの画像を切り出しておこう。

方法1　透明色を設定する

前景画像の中に「この色は主たる画像の一部ではなく、背景として使われているだけだ」という色がある場合、numpy.where()を使って透明色を設定できる。クロマキーのようなものだ。
最小限の要素のみ書くとこうなる。

# backとfrontは同じシェイプである必要がある
transparence = (0,0,0)
result = np.where(front==transparence, back, front)

back	front	result

容易は容易だが、たとえばこのいらすとやの画像ならば、宇宙飛行士の黒髪に(0,0,0)が使われていないことを事前に確認しておく必要がある。失敗すると透明になったガチャピンのような事態になってしまう。

方法2　マスク処理をする

他サイトを見れば答えはすぐに出てくるが、勉強のために試行錯誤してみよう。
論理演算における恒等式
　　x and 1 = x
　　x and 0 = 0
　　x or 1 = 1
　　x or 0 = x
を、0と1のブール値だけでなく任意の値に対しておこなう。輝度は8ビットで表すから、乱暴に書くと
　　x(任意の色) and 255(白) = x(任意の色)
　　x(任意の色) and 0(黒) = 0(黒)
　　x(任意の色) or 255(白) = 255(白)
　　x(任意の色) or 0(黒) = x(任意の色)
ということ。
下の表は手作業で作ったので、間違っているところがあったらごめんなさい。

No	back	演算	mask	→	tmp
1		OR		→
2		AND		→
3		OR		→
4		AND		→

この段階で使えそうなのは1番と4番だ。それらに前景画像を合成していこう。

No	tmp	演算	front	→	result	評価
1-1		OR		→		×
1-2		AND		→		×
1-3		OR		→		×
1-4		AND		→		○
4-1		OR		→		○
4-2		AND		→		×
4-3		OR		→		×
4-4		AND		→		×

ということで、正解は、1-4および4-1でした。
事前に「背景が黒の前景画像」と「背景が黒で前景が白のマスク画像」を用意しておいたが、それだけでは合成はできなかった。1-4では「背景が白の前景画像」、4-1では「背景が白で前景が黒のマスク画像」が必要だった。まこと人生はままならぬものよ。

画像外への描写への対応

スプライトを名乗るならば背景画像の範囲外にも描写できなければ話にならない。
という解説を書くつもりだったが、すでに前回の記事「OpenCVで日本語フォントを描写する　を関数化する　を汎用的にする」で実装してしまったので説明は略。

方法3　PILを使う

OpenCVの勉強とはいえ、PILに触れないわけにはいかない。

画像に画像を貼り付けする　Image.paste(im, box=None, mask=None)

• im　貼り付けする画像。
• box　左上座標を(x, y)であらわす。ありがたいことに元画像の範囲外でも可。デフォ値はNoneでこのときは左上となる。4要素のタプルで指定する方法もあるがそちらは省略。
• mask　マスク画像。デフォ値はNone。画像は白黒やグレースケールだけでなくRGBA画像も指定可能。RGBAのときはアルファ値がマスクとして扱われるという親切仕様。

画像に透過画像を合成するにはImage.paste(im, box, im)と1番目と3番目に同じ引数を指定するだけでよい。
さすがPILだ、これまでOpenCVでやってきたことは何だったのかと言いたくなってくる。

実行速度比較

以上、3つの方法を示した。また、前回の記事で、画像全体をPIL処理するのでなく必要な部分のみPILするという方法も習得した。
そこで、次の4つの自作関数で実行速度を見てみよう。

• putSprite_npwhere　透明色を設定しnp.whereで画像を合成する。背景画像外への対応あり。
• putSprite_mask　マスク画像を設定し合成する。背景画像外への対応あり。
• putSprite_pil_all　PILで合成する。背景画像全体をPILにする。背景画像外への対応は必要ない。
• putSprite_pil_roi　PILで合成する。PILにするのは合成に必要な部分のみ。ROIを設定する際に背景画像外への対応をおこなっている。

実行する内容はこんな感じ。容量削減のためにアニメGIFのフレームを削っています。
ソースは長いので一番下に。

結果

それぞれ10回実行したときの平均値。

putSprite_npwhere : 0.265903830528259 sec
putSprite_mask    : 0.213901996612548 sec
putSprite_pil_all : 0.973412466049193 sec
putSprite_pil_roi : 0.344804096221923 sec

プログラムが最適化されていないとか私のマシンが遅いとかそもそもPythonは遅いとかは置いといて、PILの遅さが際立っている。そしてPILを使うにしても最小限のROIのみでおこなえば速度が大幅に向上することもわかった。前々回の記事でいただいたコメントは本当にありがたい。

マスク処理とnp.where()はPILよりも速い。np.where()は十分に速いが、内部で判定をおこなっているのでマスク処理よりわずかに遅い。マスク処理はマスク画像を用意する必要があるが、画像を上書きしているだけなので処理的にはもっとも軽いのだろう。

注意事項

マスク処理とnp.where()は半透明を持つ画像には使えない。

マスク処理は0や1だから恒等式が成り立つのであって、半透明すなわち0でも1でもない値で計算したら
　　x(背景の色) and a(中途半端なマスク) = tmp(変な色)
　　tmp(変な色) or y(前景の色) = z(想定外の色)
となってしまうのは当然だ。

np.where()は工夫次第では半透明に対応できるかと思っていろいろ試してみたが、少なくとも私にはできなかった。

次回予告

次は半透明と回転への対応に挑戦したいと思います。

ソース

文字列をPythonコマンドとして使う関数eval()はこの記事をアップする直前に知った。
参考：Python - 関数を文字列から動的に呼び出す

import cv2
import numpy as np
from PIL import Image
import time
import math

# numpy.whereで合成する
#  他関数との関係上RGBA画像を取り込んでいるが
#  使うのはRGB要素のみでアルファ値は使っていない。
#  透明色(0,0,0)を決め打ちしているが良いやり方ではない。
def putSprite_npwhere(back, front4, pos):
    x, y = pos
    fh, fw = front4.shape[:2]
    bh, bw = back.shape[:2]
    x1, y1 = max(x, 0), max(y, 0)
    x2, y2 = min(x+fw, bw), min(y+fh, bh)
    if not ((-fw < x < bw) and (-fh < y < bh)) :
        return back
    front3 = front4[:, :, :3]
    front_roi = front3[y1-y:y2-y, x1-x:x2-x]
    roi = back[y1:y2, x1:x2]
    tmp = np.where(front_roi==(0,0,0), roi, front_roi)
    back[y1:y2, x1:x2] = tmp
    return back

# マスク処理する
#  マスク画像はRGBA画像から都度関数内で作成する。
#  あらかじめマスク画像を作っておいたほうが速いが、
#  こちらのほうが使いやすい。と思う。
def putSprite_mask(back, front4, pos):
    x, y = pos
    fh, fw = front4.shape[:2]
    bh, bw = back.shape[:2]
    x1, y1 = max(x, 0), max(y, 0)
    x2, y2 = min(x+fw, bw), min(y+fh, bh)
    if not ((-fw < x < bw) and (-fh < y < bh)) :
        return back
    front3 = front4[:, :, :3]
    mask1 = front4[:, :, 3]
    mask3 = 255 - cv2.merge((mask1, mask1, mask1))
    mask_roi = mask3[y1-y:y2-y, x1-x:x2-x]
    front_roi = front3[y1-y:y2-y, x1-x:x2-x]
    roi = back[y1:y2, x1:x2]
    tmp = cv2.bitwise_and(roi, mask_roi)
    tmp = cv2.bitwise_or(tmp, front_roi)
    back[y1:y2, x1:x2] = tmp
    return back

# PILで合成する　背景画像全体
def putSprite_pil_all(back, front4, pos):
    back_pil = Image.fromarray(back)
    front_pil = Image.fromarray(front4)
    back_pil.paste(front_pil, pos, front_pil)
    return np.array(back_pil, dtype = np.uint8)

# PILで合成する　背景画像内にある部分のみ
def putSprite_pil_roi(back, front4, pos):
    x, y = pos
    fh, fw = front4.shape[:2]
    bh, bw = back.shape[:2]
    x1, y1 = max(x, 0), max(y, 0)
    x2, y2 = min(x+fw, bw), min(y+fh, bh)
    if not ((-fw < x < bw) and (-fh < y < bh)) :
        return back
    back_roi_pil = Image.fromarray(back[y1:y2, x1:x2])
    front_pil = Image.fromarray(front4[y1-y:y2-y, x1-x:x2-x])
    back_roi_pil.paste(front_pil, (0,0), front_pil)
    back_roi = np.array(back_roi_pil, dtype = np.uint8)
    back[y1:y2, x1:x2] = back_roi
    return back

def main(func):
    filename_back = "space.jpg"
    filename_front = "uchuhikoushi.png"
    img_back = cv2.imread(filename_back)
    img_front = cv2.imread(filename_front, -1)
    bh, bw = img_back.shape[:2]
    xc, yc = bw*0.5, bh*0.5
    rx, ry = bw*0.3, bh*1.2
    cv2.putText(img_back, func, (20,bh-20), cv2.FONT_HERSHEY_SIMPLEX, 1, (255,255,255))

    ### 時間を計るのはここから
    start_time = time.time()

    for angle in range(-180, 180):
        back = img_back.copy()
        x = int(xc + rx * math.cos(math.radians(angle)))
        y = int(yc + ry * math.sin(math.radians(angle)))
        img = eval(func)(back, img_front, (x,y))

        #ここは必要に応じて有効にしたり無効にしたりする
        #cv2.imshow(func, img)
        #cv2.waitKey(1)

    elasped_time = time.time() - start_time
    ### ここまで

    print (f"{func} : {elasped_time} sec")    
    cv2.destroyAllWindows()

if __name__ == "__main__":
    funcs = ["putSprite_npwhere",
             "putSprite_mask",
             "putSprite_pil_all" ,
             "putSprite_pil_roi" ]
    for func in funcs:
        for i in range(10):
            main(func)