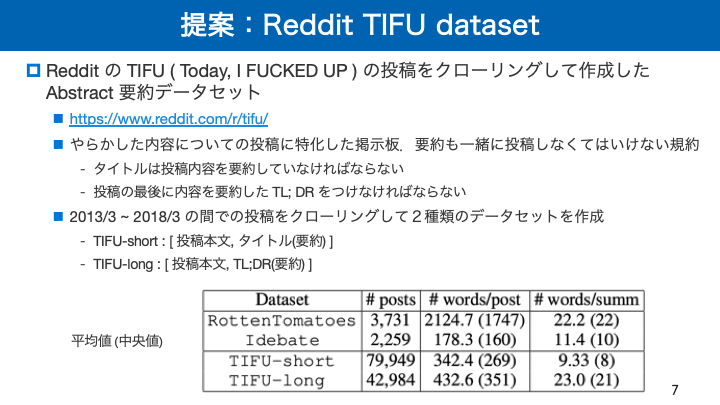
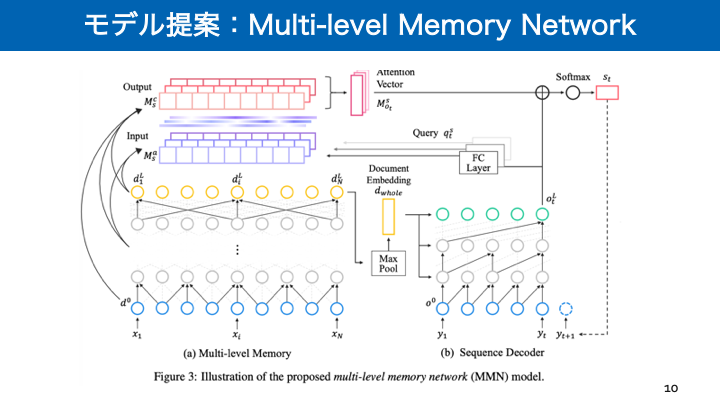
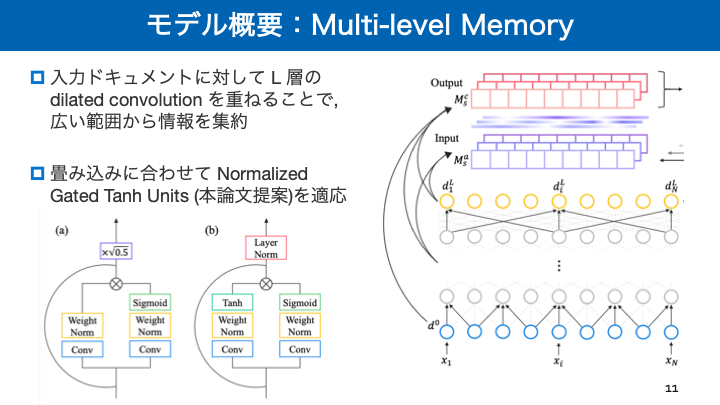
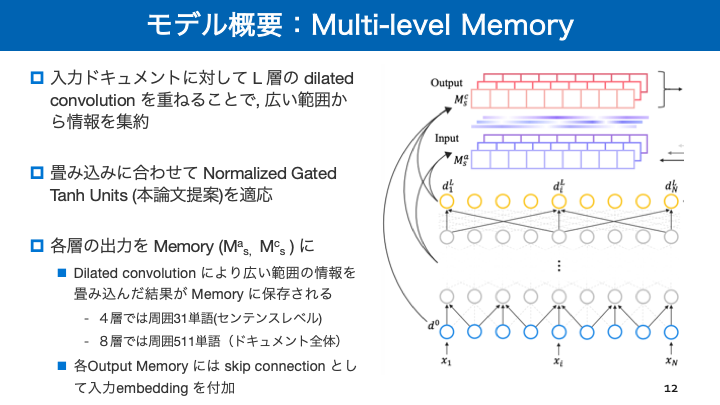
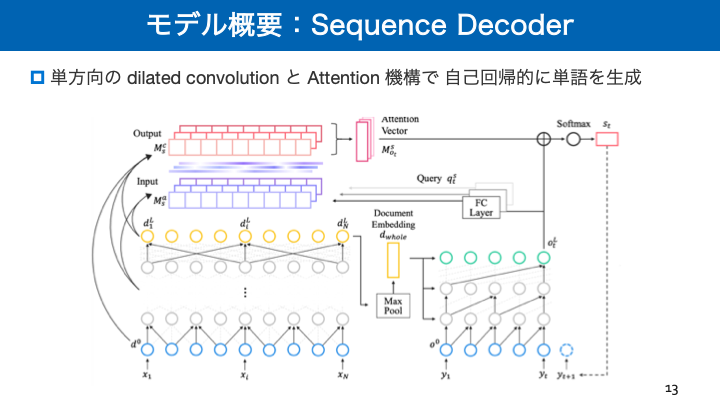
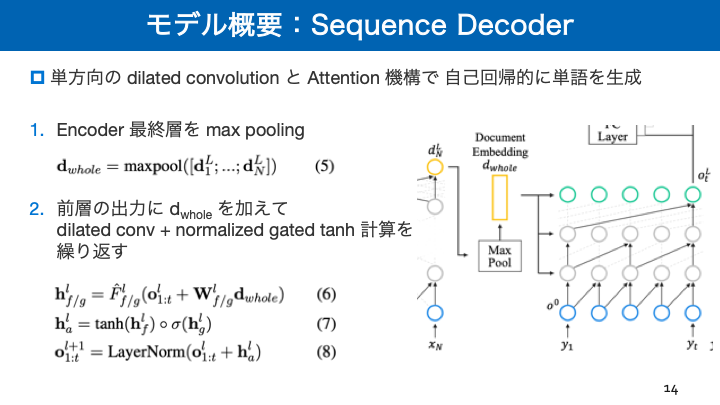
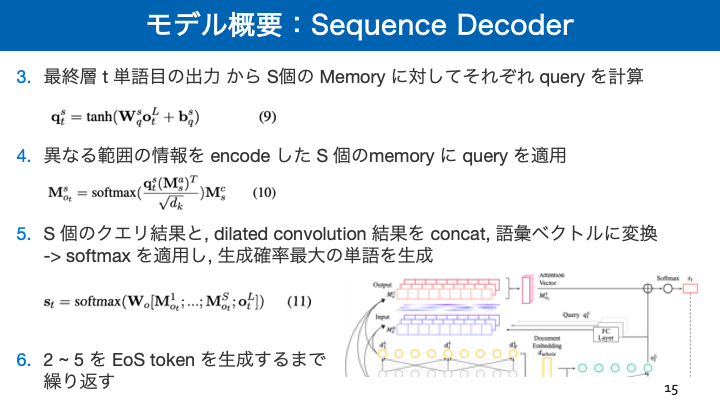
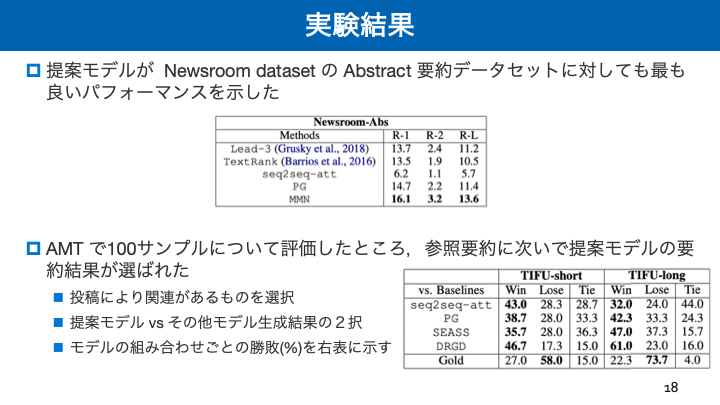
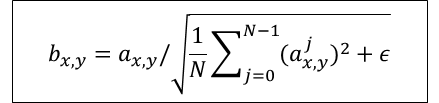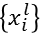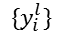- 投稿日:2019-02-18T21:45:42+09:00
Abstractive Summarization of Reddit Posts with Multi-level Memory Networks
- 投稿日:2019-02-18T16:32:40+09:00
【GoogleCloudPlatform】使っているインスタンスにGPUを追加する
東京リージョンでもGPUが使えるようになったけど、新しくインスタンスを立てなおして諸々の設定を最初からやるのは面倒!となったので、既存のインスタンスでGPUを使えるようにどうにか設定しました。
パッケージのバージョンを変更したりなんだかんだあるので、バックアップ推奨です。環境
CentOS 7.6
python 3.5インスタンスのマシン構成を変更する
インスタンスを起動している場合は停止させて、インスタンスの編集画面へ。
編集画面のマシンタイプのところのカスタマイズを選択すると"GPUの数"が選べるようになる。ここで好きなGPU数とタイプを選択し画面一番下の"保存"を選択。
今回はTesla-T4を選択した場合の環境設定手順について書きます。GPUタイプが異なる場合は適宜読み替えてください。
*現在GPUに対応しているリージョンは限られているので注意。もし対応していないリージョンでインスタンスを立てていたら(GPUの選択項目が出てこなければ非対応の可能性高)一旦ディスクイメージを取ってインスタンスを立て直すのが早いかと思います。ここまで設定したら、もう一度 "開始">"起動" でインスタンスを起動。
ドライバダウンロード
まずはOSのバージョンを確認。
$cat /etc/redhat-release念のためcuda-9-0が未インストールなことも確認しておきます。
$rpm -q cuda-9-0NVIDIAのページからCUDAtoolkitをダウンロードしてきます。
$curl -O http://developer.download.nvidia.com/compute/cuda/repos/rhel7/x86_64/cuda-repo-rhel7-9.0.176-1.x86_64.rpmシステムにリポジトリを追加
$sudo rpm -i --force ./cuda-repo-rhel7-9.0.176-1.x86_64.rpmepel-releaseリポジトリをインストール
$sudo yum install epel-releaseYumキャッシュ削除
$sudo yum clean allCUDA9.0のインストール
$sudo yum install cuda-9-0CUDA9.0にドライバが含まれるとの記載もあったが、自身の環境ではうまく動かなかったので手動でNVIDIAドライバをダウンロード。(もしかしたら冗長なのかも。)
$curl -O http://jp.download.nvidia.com/tesla/410.79/NVIDIA-Linux-x86_64-410.79.run
$sudo sh NVIDIA-Linux-x86_64-410.79.run
永続モードを有効にする
$nvidia-smi -pm 1
*ここで以下のようなエラーが出た場合はインスタンスの再起動を試してみるNVIDIA-SMI has failed because it couldn't communicate with the NVIDIA driver. Make sure that the latest NVIDIA driver is installed and running
ここまででインスタンスでGPUを使うための準備完了。
ここからはtensorflow/kerasでGPUを使うための準備をする。cuDNNのダウンロード
以下のサイトでcuDNNをダウンロードする。
今回はlinuxの9.0バージョンを選びました。
https://developer.nvidia.com/rdp/cudnn-downloadインスタンス上にダウンロードしたフォルダを配置したらまずは解凍。
$ tar -xvzf cudnn-9.0-linux-x64-v7.4.2.24.tgz
そんでもってPATHを追加しておきます。
$export CUDA_ROOT="/usr/local/cuda"
$export LIBRARY_PATH=$CUDA_ROOT/lib:$CUDA_ROOT/lib64:$LIBRARY_PATH
$export LD_LIBRARY_PATH=$CUDA_ROOT/lib64/
source ~/.bash_profiletensorflow-gpuの導入
地味にこれが面倒だった。パッケージのバージョンはかなり注意しないとという教訓。
このあたりは各自の環境によってもかなり変わるかと思うので、自身の環境を確認しつつ実行してください。anacondaを使用の場合は以下のコマンドで今の仮想環境のパッケージを確認出来ます。
$ conda listここでtensorflowと表示される場合は注意。tensorflow-gpuとは共存出来ないようなので一旦アンインストールする必要がある。(pip経由でインストールした場合はpipコマンドで削除)
$conda uninstall tensorflowそしてtensorflow-gpuをインストール。最新版のtensorflow-gpuだとエラーになったので、バージョン1.8.0のものを取ってきます。
$conda install tensorflow-gpu==1.8.0
確認
ここまでで準備は全て出来ました。
動作確認したい場合は以下のコードを実行してみてください。keras使ってる人は念のためそちらも確認しておいた方が良さそうです。import tensorflow as tf # Creates a graph. with tf.device('/device:GPU:0'): a = tf.constant([1.0, 2.0, 3.0, 4.0, 5.0, 6.0], shape=[2, 3], name='a') b = tf.constant([1.0, 2.0, 3.0, 4.0, 5.0, 6.0], shape=[3, 2], name='b') c = tf.matmul(a, b) # Creates a session with allow_soft_placement and log_device_placement set # to True. sess = tf.Session(config=tf.ConfigProto( allow_soft_placement=True, log_device_placement=True)) # Runs the op. print(sess.run(c))
- 投稿日:2019-02-18T16:15:57+09:00
ゼロからDLの学習備忘録
- 投稿日:2019-02-18T08:00:06+09:00
PGGAN「段階的な学習により実現した高解像度・安定性・多様性」
論文紹介・画像引用
PROGRESSIVE GROWING OF GANS FOR IMPROVED QUALITY, STABILITY, AND VARIATION
https://arxiv.org/pdf/1710.10196v3.pdf本研究での生成画像
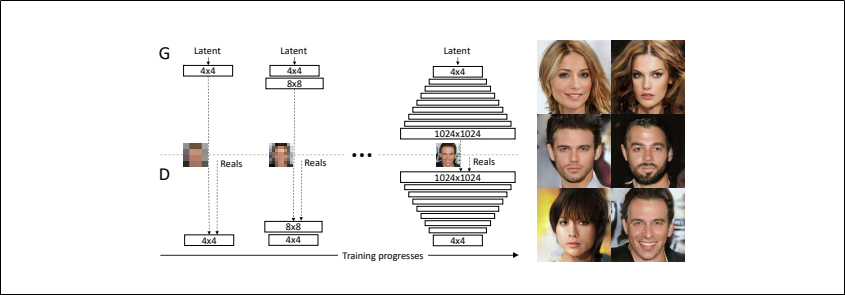
Progressive Growing of GANs
低解像度の画像から始めてネットワークにレイヤーを追加して徐々に解像度を上げていくGAN
従来のGANのように、すべてのスケールについて同時に学習するのではなく
まず初めに大まかな画像構造を捉えてから段階的に細かいところに注意を向けていく
上図のN×Nは解像度がN×Nでのconvolution層を意味する
すべての層は常に訓練可能な状態である
本研究の学習ではGeneratorとDiscriminatorそれぞれが低解像度(4×4)の層だけを組み入れて始める
学習が進むにつれて徐々にGeneratorとDiscriminatorに層を追加していくことで生成画像の解像度を上げるこうすることで高解像度での画像の生成が安定化し、学習時間の短縮ができる
上図右の画像6枚は上述の段階的な学習法(解像度:1024×1024)によって生成された画像である
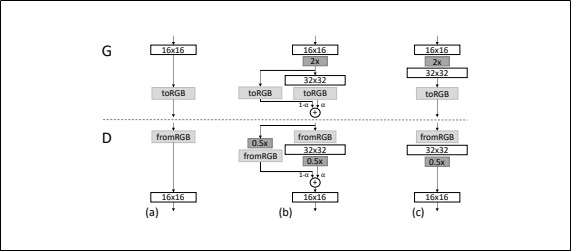
GeneratorとDiscriminatorの解像度を2倍にするとき新しい層を入れる16×16の解像度から32×32の解像度への移り変わりを表している(上図(a)から上図(c))
その移り変わりの間を表したのが上図(b)高解像度の層では残差ブロックのようにしている
$α$は$0$~$1$$2×$と$0.5×$はそれぞれ解像度を2倍、0.5倍にすることを意味する
$to RGB$は特徴ベクトルをRGBに変換する層、$from RGB$はその逆
どちらも$1×1$のconvolution層を使うdiscriminatorを訓練するときは、現在のネットワークの解像度に合わせて縮小された本物の画像を入れる
残差ブロックを使用しているため、Generatorの出力は2つの画像(to RGBされたもの)を足し合わせる
同じようにDiscriminatorでは2つのベクトル(from RGBされたもの)を足し合わせるネットワーク構成
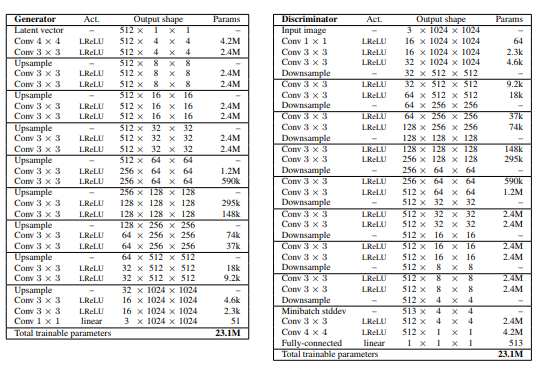
上図左がGeneratorのアーキテクチャ、上図右がDiscriminatorのアーキテクチャ
どちらも3層を1ブロックにしたものを学習の途中で1つずつ追加して積み重ねているGeneratorの最後の1×1のconvolution層は$to RGB$を意味する
DIscriminatorの最初の1×1のconvolution層は$from RGB$を意味するアップサンプリングは2×2で複製、ダウンサンプリングはアベレージプーリング
潜在ベクトルは512次元で本物画像と生成画像は[-1,1]の範囲で表す
leaky ReLU($α=0.2$)を線形変換する最終層を除いて、両ネットワークのすべての層に使う
学習の流れ
4×4の解像度から始めて、Discriminatorに合計800枚の本物画像を見せるまでネットワークの学習をする
その後は次の2つの処理を交互に実行する
新しい3層ブロックを入れる(解像度を上げる)→800枚の本物画像でネットワークを安定化させる→新しい3層ブロックを入れる(解像度を上げる)→・・・工夫点(後述)
batch normalization・layer normalization・weight normalizationはどちらのネットワークにも使わないが
Generatorの3×3のconvolution層の後にpixelwise normalization(後述:Generatorにおけるピクセル特徴ベクトルの正規化)を使うバイアスは0で初期化し、重みは分散1の正規分布に従う
しかし、学習時に各層固有の定数で重みをスケーリングする(後述:学習率の均質化)Descriminatorの最終層には4×4の解像度でミニバッチ全体の標準偏差の特徴マップを追加する(後述:ミニバッチ標準偏差を使った画像多様性の向上)
最適化関数
Adam($α = 0.001, β1 = 0, β2 = 0.99, ε = 10^{−8}$)
ミニバッチサイズ
解像度($4×4~128×128$) :ミニバッチサイズ=$16$
解像度($256×256$) : ミニバッチサイズ=$14$
解像度($512×512$) : ミニバッチサイズ=$6$
解像度($1024×1024$) : ミニバッチサイズ=$3$
ミニバッチサイズを徐々に小さくするのは、メモリに乗るようにするためPGGANの良いところ
学習の安定化
最初は小さい画像のため大幅に安定して生成できる
理由:クラス情報・モード情報が少ない解像度を少しずつ上げていくことによって単純な質問に答えていくだけのような状況で学習できる
従来であれば、潜在表現から1024×1024の画像へのマッピングという難しい最終目標を達成できるように試行錯誤しなくてはならない
複雑である潜在表現から高解像度の画像へのマッピングは段階的に学んだほうが簡単(PGGANの場合)
一層入れて十分に学習する→新しい層(解像度が前回よりも高い層)を入れる→十分に学習する→・・・
一層をちゃんと学習して安定化してから次の層を入れる丁寧なやり方
(従来のGAN)
最初からすべての層を入れて一気にすべての層を学習する
PGGANと比べれば雑なやり方例)数学
(PGGANの場合)
足し算を学習する→引き算を学習する→掛け算を学習する→・・・→・・・・・・・・→センター試験の数学
(従来のGAN)
センター試験の数学(初日)実際には、WGAN-GP損失やLSGAN損失を使用して
メガピクセルスケールの画像を確実に生成するための学習を十分に安定化させる学習時間の短縮
PGGANでは大半のイテレーションが低解像度で行われるため
もちろん最終的な出力解像度にもよるが従来のGANよりも2〜6倍速く学習できるミニバッチ標準偏差を使った画像多様性の向上
GANは訓練データにある一部の画像の特徴やパターンだけを捉える傾向がある
解決策として「ミニバッチ識別」を提案するこれは個々の画像のみならずミニバッチ全体からも特徴統計量を計算することである
最終的には生成画像のミニバッチと訓練画像のミニバッチが同じ統計量を示すことが理想ミニバッチ層はDiscriminatorの最後に追加することで実装できる
ミニバッチ層では入力アクティベーションを統計量に変換するテンソルを学習する
ミニバッチの各サンプルから生成された様々な統計量が層の出力と足し合わせるためDiscriminatorは統計量を使うことができる本研究ではこの処理を大幅に単純化し、画像の多様性も向上させた
シンプルバージョン
本研究で単純化された方法は学習可能なパラメータや新しいハイパーパラメータを使うわけではない
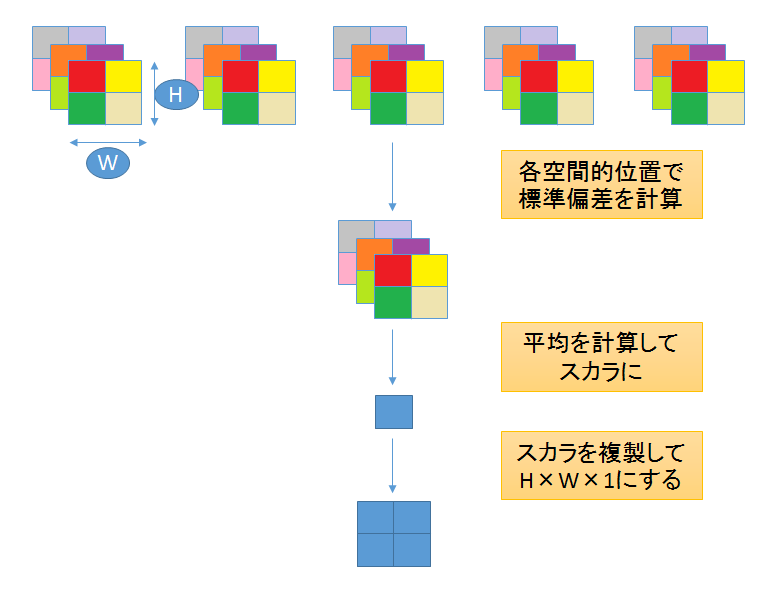
①ミニバッチ上の各空間位置にある各特徴の標準偏差を計算する
②すべての特徴、すべての空間で平均を計算して単一の値を出す
③その値を複製して1枚の特徴マップをつくるこの層はどこにでも入れることはできるが最終層に入れるのが一番良いことがわかった
GeneratorとDiscriminatorの正規化
GANではGeneratorとDiscriminatorの学習によって値の発散が起きやすい
この問題への対策として2つの方法を提案する学習率の均質化
初期値は$N(0,1)$にし、学習時に重みを動的にスケーリングする
重みを動的にスケーリングするとは$\hat{w_i } = w_i / c$をすることである
$w_i$は重み、$c$は各層の正規化定数(Heの初期化を使う)
→スケール不変性が得られる最適化するときにスケールの影響を受けずに
パラメーターの更新ができるようになるため学習速度が上がるスケールを整えているためすべての重みに対して均質の学習速度にすることができる
Generatorにおけるピクセル特徴ベクトルの正規化
Generatorの各convolution層での計算後に各ピクセルの特徴ベクトルを正規化する
正規化は以下のようにする
$ε=10^{-8}$ $N$:特徴マップの数 $a_{x,y}$:ピクセル$(x,y)$の正規化前の特徴ベクトル
$b_{x,y}$:ピクセル$(x,y)$の正規化したの特徴ベクトルGAN評価のためのマルチスケールにおける統計的類似性
上手く学習ができたGeneratorは
局所的な画像構造がすべてのスケールにわたって本物画像と似ている画像を生成する16×16ピクセルのローパス解像度から始めて、
生成画像のラプラシアンピラミッド表現による局所画像の分布と
本物画像のラプラシアンピラミッド表現による局所画像の分布のマルチスケール統計的類似性について考える
短くいうと、マルチスケールで生成画像と本物画像の分布を比較して、分布の距離が近ければ良いGANと考える※ラプラシアンピラミッドについては"laplacian pyramid"で画像検索するとイメージがしやすくなるかもしれない
局所特徴量を得る
これまでの慣例に従って、ピラミッドはフル解像度に達するまで段階的に2倍にする
各レベルは前回のレベルをアップサンプリングしたものとの差をエンコードするラプラシアンピラミッドの各レベルは特定の空間周波数帯に対応する
ランダムに16384枚の画像を選び、各画像のラプラシアンピラミッドの各レベルから128個局所特徴量を抽出する
そうすると各レベルから$2^{21}(2.1M)$個の局所特徴量が得られる($16384×128=2^{21}$)それぞれの局所特徴量は$7×7$のピクセルで$3$チャンネル
$x∈R^{7×7×3}=R^{147}$と表せる訓練データのレベル$l$からの局所特徴量は
と表し、
生成データのレベル$l$からの局所特徴量はと表す
分布距離を測る
①各チャンネルの平均と標準偏差を求めて
訓練データの局所特徴量と生成データの局所特徴量
の正規化を行う
②xとyの統計的な類似度をsliced Wasserstein distance(SWD)で計算する
ワッサースタイン距離は輸送問題に基づいて考えられた分布の距離を測る指標ワッサースタイン距離が小さいということは分布が類似していること、すなわち
この解像度での訓練画像と生成画像は見た目も多様性も同じように見えるということを意味する最低解像度の16×16での分布距離は大まかな画像構造の類似性を表し、
高解像度での分布距離はエッジやノイズの鮮明さといったピクセルレベルでの情報の類似性を表す検証
学習構成を変えたら結果はどう変わるのか?
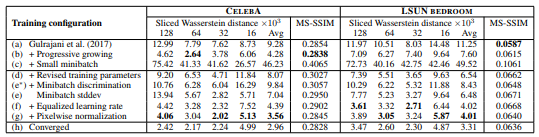
上表は様々な学習構成でのSWD(Sliced Wasserstein distance)とMS-SSIM(multi-scale structural similarity)の数値評価を示している
上表を見る上での注意点
一般的には評価指標の数値が良いことは、色・テクスチャなどの多様性があることを意味するが、
MS-SSIMを見るときは注意が必要だ
上図を見れば(a)よりも(h)の方が明らかにきれいな画像ができているがMS-SSIMの数値はほとんど同じであるこれはMS-SSIMという指標は生成画像の多様性のみを評価するものであり、本物画像との類似性を評価するものではないからである
一方、SVDの数値は大きく改善している結果
最初の学習構成$(a)$はGulrajani et al.(2017)である
これはGeneratorにbatch normalizationを、Discriminatorにlayer normalizationを入れて
ミニバッチサイズを64にしたものである$(b)$は段階的な学習(層を徐々に追加していく学習)のネットワーク
鮮明な画像が生成されている
生成画像の分布と本物画像の分布がより似ていることをSWDの数値が示している高解像度の画像を生成することが目的であるが、そのためにはミニバッチを小さいサイズ(メモリに乗るサイズ)にすることが必要である
このことをしたのが$(c)$である
ミニバッチサイズを64から16に変更している
両指標からもわかるが、生成画像は不鮮明であるbatch normalizationとlayer normalizationを取り除き、ハイパーパラメーターの調整をして学習課程を安定化させたのが$(d)$である
$(e*)$はミニバッチ識別を可能にしたもの(Salimans et al., 2016)だが、生成画像の多様性を評価するMS-SSIMの指標すらも向上しないという結果に終わってしまった
対照的に、本研究でのミニバッチ識別$(e)$ではSWDの平均スコアを改善し鮮明な画像の生成にも成功している
更に本研究で提案した$(f)$と$(g)$を加えるとSWDのスコアと生成画像の質はより良くなっている
最後に$(h)$ではベストネットワークを用いて十分な学習をした結果である
これまでのGANモデルよりも鮮明な画像を生成できている収束と学習時間
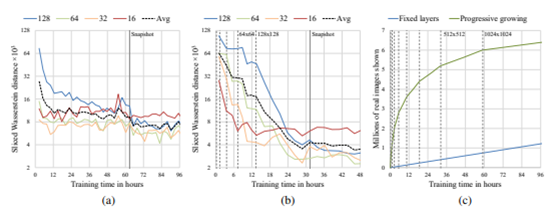
上図$(a)$と$(b)$は訓練時間(横軸)とSWDの数値(縦軸)
上図$(c)$は訓練時間(横軸)とDiscriminatorに見せた本物画像の枚数(縦軸)$(a)$と$(b)$はGulrajani et al. (2017)の学習構成での結果である
ただし$(a)$は段階的な学習(層を徐々に追加していく学習)のネットワークではない(最初からすべての層をネットワークに入れておく)
$(b)$は段階的な学習(層を徐々に追加していく学習)のネットワーク段階的な学習は2つのメリットがあることがわかる
・かなり優れた最適値に収束する
・学習時間を半分にすることができる収束
収束性の向上は徐々にネットワークを大きくしていくという「カリキュラム学習」によるものである
段階的な学習をしない場合はGeneratorとDiscriminatorのすべての層は
大まかな画像構成の多様性と画像の詳細、両方の中間表現を同時に見つけなくてはならないしかし段階的な学習をする場合は、
最初の頃からあった低解像度の層はすでに早い時期に収束しているため
新しい層が加わってきたらネットワークは詳細な表現を学習することのみに専念することができる上図$(b)$の低解像度である$16×16$(赤線)が非常に早く最適値に達し、残りの学習では横ばいになっていることを見るとPGGANの学習法のメリットを実感できる
低解像度の層から順番$(16,32,64,128)$に収束していくこともわかる
学習時間の短縮
縦軸はDiscriminatorに見せた本物画像の枚数である
たくさんDiscriminatorに本物画像を見せたということは、それだけ学習が進んでいることを意味する段階的学習では初期の学習が非常に速いことがわかる
これは初期段階のネットワークは層が少ないため評価が素早くできるからであるフル解像度に達すると、Discriminatorに見せる本物画像の枚数(学習速度)はどちらの方法でも同じになる
上図はPGGANでは96時間で約640万枚の本物画像を見たことを示している
PGGANでなければ同じ枚数を見るためには520時間必要になると推定できるこの場合PGGANは約5.4倍、従来よりも速いことになる
- 投稿日:2019-02-18T08:00:06+09:00
PGGAN 「優しさあふれるカリキュラム学習」
論文紹介・画像引用
PROGRESSIVE GROWING OF GANS FOR IMPROVED QUALITY, STABILITY, AND VARIATION
https://arxiv.org/pdf/1710.10196v3.pdf本研究での生成画像
Progressive Growing of GANs
低解像度の画像から始めてネットワークにレイヤーを追加して徐々に解像度を上げていくGAN
従来のGANのように、すべてのスケールについて同時に学習するのではなく
まず初めに大まかな画像構造を捉えてから段階的に細かいところに注意を向けていく
上図のN×Nは解像度がN×Nでのconvolution層を意味する
すべての層は常に訓練可能な状態である
本研究の学習ではGeneratorとDiscriminatorそれぞれが低解像度(4×4)の層だけを組み入れて始める
学習が進むにつれて徐々にGeneratorとDiscriminatorに層を追加していくことで生成画像の解像度を上げるこうすることで高解像度での画像の生成が安定化し、学習時間の短縮ができる
上図右の画像6枚は上述の段階的な学習法(解像度:1024×1024)によって生成された画像である
GeneratorとDiscriminatorの解像度を2倍にするとき新しい層を入れる16×16の解像度から32×32の解像度への移り変わりを表している(上図(a)から上図(c))
その移り変わりの間を表したのが上図(b)高解像度の層では残差ブロックのようにしている
$α$は$0$~$1$$2×$と$0.5×$はそれぞれ解像度を2倍、0.5倍にすることを意味する
$to RGB$は特徴ベクトルをRGBに変換する層、$from RGB$はその逆
どちらも$1×1$のconvolution層を使うdiscriminatorを訓練するときは、現在のネットワークの解像度に合わせて縮小された本物の画像を入れる
残差ブロックを使用しているため、Generatorの出力は2つの画像(to RGBされたもの)を足し合わせる
同じようにDiscriminatorでは2つのベクトル(from RGBされたもの)を足し合わせるネットワーク構成
上図左がGeneratorのアーキテクチャ、上図右がDiscriminatorのアーキテクチャ
どちらも3層を1ブロックにしたものを学習の途中で1つずつ追加して積み重ねているGeneratorの最後の1×1のconvolution層は$to RGB$を意味する
DIscriminatorの最初の1×1のconvolution層は$from RGB$を意味するアップサンプリングは2×2で複製、ダウンサンプリングはアベレージプーリング
潜在ベクトルは512次元で本物画像と生成画像は[-1,1]の範囲で表す
leaky ReLU($α=0.2$)を線形変換する最終層を除いて、両ネットワークのすべての層に使う
学習の流れ
4×4の解像度から始めて、Discriminatorに合計800枚の本物画像を見せるまでネットワークの学習をする
その後は次の2つの処理を交互に実行する
新しい3層ブロックを入れる(解像度を上げる)→800枚の本物画像でネットワークを安定化させる→新しい3層ブロックを入れる(解像度を上げる)→・・・工夫点(後述)
batch normalization・layer normalization・weight normalizationはどちらのネットワークにも使わないが
Generatorの3×3のconvolution層の後にpixelwise normalization(後述:Generatorにおけるピクセル特徴ベクトルの正規化)を使うバイアスは0で初期化し、重みは分散1の正規分布に従う
しかし、学習時に各層固有の定数で重みをスケーリングする(後述:学習率の均質化)Descriminatorの最終層には4×4の解像度でミニバッチ全体の標準偏差の特徴マップを追加する(後述:ミニバッチ標準偏差を使った画像多様性の向上)
最適化関数
Adam($α = 0.001, β1 = 0, β2 = 0.99, ε = 10^{−8}$)
ミニバッチサイズ
解像度($4×4~128×128$) :ミニバッチサイズ=$16$
解像度($256×256$) : ミニバッチサイズ=$14$
解像度($512×512$) : ミニバッチサイズ=$6$
解像度($1024×1024$) : ミニバッチサイズ=$3$
ミニバッチサイズを徐々に小さくするのは、メモリに乗るようにするためPGGANの良いところ
学習の安定化
最初は小さい画像のため大幅に安定して生成できる
理由:クラス情報・モード情報が少ない解像度を少しずつ上げていくことによって単純な質問に答えていくだけのような状況で学習できる
従来であれば、潜在表現から1024×1024の画像へのマッピングという難しい最終目標を達成できるように試行錯誤しなくてはならない
複雑である潜在表現から高解像度の画像へのマッピングは段階的に学んだほうが簡単(PGGANの場合)
一層入れて十分に学習する→新しい層(解像度が前回よりも高い層)を入れる→十分に学習する→・・・
一層をちゃんと学習して安定化してから次の層を入れる丁寧なやり方
(従来のGAN)
最初からすべての層を入れて一気にすべての層を学習する
PGGANと比べれば雑なやり方例)数学
(PGGANの場合)
足し算を学習する→引き算を学習する→掛け算を学習する→・・・→・・・・・・・・→センター試験の数学
(従来のGAN)
センター試験の数学(初日)実際には、WGAN-GP損失やLSGAN損失を使用して
メガピクセルスケールの画像を確実に生成するための学習を十分に安定化させる学習時間の短縮
PGGANでは大半のイテレーションが低解像度で行われるため
もちろん最終的な出力解像度にもよるが従来のGANよりも2〜6倍速く学習できるミニバッチ標準偏差を使った画像多様性の向上
GANは訓練データにある一部の画像の特徴やパターンだけを捉える傾向がある
解決策として「ミニバッチ識別」を提案するこれは個々の画像のみならずミニバッチ全体からも特徴統計量を計算することである
最終的には生成画像のミニバッチと訓練画像のミニバッチが同じ統計量を示すことが理想ミニバッチ層はDiscriminatorの最後に追加することで実装できる
ミニバッチ層では入力アクティベーションを統計量に変換するテンソルを学習する
ミニバッチの各サンプルから生成された様々な統計量が層の出力と足し合わせるためDiscriminatorは統計量を使うことができる本研究ではこの処理を大幅に単純化し、画像の多様性も向上させた
シンプルバージョン
本研究で単純化された方法は学習可能なパラメータや新しいハイパーパラメータを使うわけではない
①ミニバッチ上の各空間位置にある各特徴の標準偏差を計算する
②すべての特徴、すべての空間で平均を計算して単一の値を出す
③その値を複製して1枚の特徴マップをつくるこの層はどこにでも入れることはできるが最終層に入れるのが一番良いことがわかった
GeneratorとDiscriminatorの正規化
GANではGeneratorとDiscriminatorの学習によって値の発散が起きやすい
この問題への対策として2つの方法を提案する学習率の均質化
初期値は$N(0,1)$にし、学習時に重みを動的にスケーリングする
重みを動的にスケーリングするとは$\hat{w_i } = w_i / c$をすることである
$w_i$は重み、$c$は各層の正規化定数(Heの初期化を使う)
→スケール不変性が得られる最適化するときにスケールの影響を受けずに
パラメーターの更新ができるようになるため学習速度が上がるスケールを整えているためすべての重みに対して均質の学習速度にすることができる
Generatorにおけるピクセル特徴ベクトルの正規化
Generatorの各convolution層での計算後に各ピクセルの特徴ベクトルを正規化する
正規化は以下のようにする
$ε=10^{-8}$ $N$:特徴マップの数 $a_{x,y}$:ピクセル$(x,y)$の正規化前の特徴ベクトル
$b_{x,y}$:ピクセル$(x,y)$の正規化したの特徴ベクトルGAN評価のためのマルチスケールにおける統計的類似性
上手く学習ができたGeneratorは
局所的な画像構造がすべてのスケールにわたって本物画像と似ている画像を生成する16×16ピクセルのローパス解像度から始めて、
生成画像のラプラシアンピラミッド表現による局所画像の分布と
本物画像のラプラシアンピラミッド表現による局所画像の分布のマルチスケール統計的類似性について考える
短くいうと、マルチスケールで生成画像と本物画像の分布を比較して、分布の距離が近ければ良いGANと考える※ラプラシアンピラミッドについては"laplacian pyramid"で画像検索するとイメージがしやすくなるかもしれない
局所特徴量を得る
これまでの慣例に従って、ピラミッドはフル解像度に達するまで段階的に2倍にする
各レベルは前回のレベルをアップサンプリングしたものとの差をエンコードするラプラシアンピラミッドの各レベルは特定の空間周波数帯に対応する
ランダムに16384枚の画像を選び、各画像のラプラシアンピラミッドの各レベルから128個局所特徴量を抽出する
そうすると各レベルから$2^{21}(2.1M)$個の局所特徴量が得られる($16384×128=2^{21}$)それぞれの局所特徴量は$7×7$のピクセルで$3$チャンネル
$x∈R^{7×7×3}=R^{147}$と表せる訓練データのレベル$l$からの局所特徴量は
と表し、
生成データのレベル$l$からの局所特徴量はと表す
分布距離を測る
①各チャンネルの平均と標準偏差を求めて
訓練データの局所特徴量と生成データの局所特徴量
の正規化を行う
②xとyの統計的な類似度をsliced Wasserstein distance(SWD)で計算する
ワッサースタイン距離は輸送問題に基づいて考えられた分布の距離を測る指標ワッサースタイン距離が小さいということは分布が類似していること、すなわち
この解像度での訓練画像と生成画像は見た目も多様性も同じように見えるということを意味する最低解像度の16×16での分布距離は大まかな画像構造の類似性を表し、
高解像度での分布距離はエッジやノイズの鮮明さといったピクセルレベルでの情報の類似性を表す検証
学習構成を変えたら結果はどう変わるのか?
上表は様々な学習構成でのSWD(Sliced Wasserstein distance)とMS-SSIM(multi-scale structural similarity)の数値評価を示している
上表を見る上での注意点
一般的には評価指標の数値が良いことは、色・テクスチャなどの多様性があることを意味するが、
MS-SSIMを見るときは注意が必要だ
上図を見れば(a)よりも(h)の方が明らかにきれいな画像ができているがMS-SSIMの数値はほとんど同じであるこれはMS-SSIMという指標は生成画像の多様性のみを評価するものであり、本物画像との類似性を評価するものではないからである
一方、SVDの数値は大きく改善している結果
最初の学習構成$(a)$はGulrajani et al.(2017)である
これはGeneratorにbatch normalizationを、Discriminatorにlayer normalizationを入れて
ミニバッチサイズを64にしたものである$(b)$は段階的な学習(層を徐々に追加していく学習)のネットワーク
鮮明な画像が生成されている
生成画像の分布と本物画像の分布がより似ていることをSWDの数値が示している高解像度の画像を生成することが目的であるが、そのためにはミニバッチを小さいサイズ(メモリに乗るサイズ)にすることが必要である
このことをしたのが$(c)$である
ミニバッチサイズを64から16に変更している
両指標からもわかるが、生成画像は不鮮明であるbatch normalizationとlayer normalizationを取り除き、ハイパーパラメーターの調整をして学習課程を安定化させたのが$(d)$である
$(e*)$はミニバッチ識別を可能にしたもの(Salimans et al., 2016)だが、生成画像の多様性を評価するMS-SSIMの指標すらも向上しないという結果に終わってしまった
対照的に、本研究でのミニバッチ識別$(e)$ではSWDの平均スコアを改善し鮮明な画像の生成にも成功している
更に本研究で提案した$(f)$と$(g)$を加えるとSWDのスコアと生成画像の質はより良くなっている
最後に$(h)$ではベストネットワークを用いて十分な学習をした結果である
これまでのGANモデルよりも鮮明な画像を生成できている収束と学習時間
上図$(a)$と$(b)$は訓練時間(横軸)とSWDの数値(縦軸)
上図$(c)$は訓練時間(横軸)とDiscriminatorに見せた本物画像の枚数(縦軸)$(a)$と$(b)$はGulrajani et al. (2017)の学習構成での結果である
ただし$(a)$は段階的な学習(層を徐々に追加していく学習)のネットワークではない(最初からすべての層をネットワークに入れておく)
$(b)$は段階的な学習(層を徐々に追加していく学習)のネットワーク段階的な学習は2つのメリットがあることがわかる
・かなり優れた最適値に収束する
・学習時間を半分にすることができる収束
収束性の向上は徐々にネットワークを大きくしていくという「カリキュラム学習」によるものである
段階的な学習をしない場合はGeneratorとDiscriminatorのすべての層は
大まかな画像構成の多様性と画像の詳細、両方の中間表現を同時に見つけなくてはならないしかし段階的な学習をする場合は、
最初の頃からあった低解像度の層はすでに早い時期に収束しているため
新しい層が加わってきたらネットワークは詳細な表現を学習することのみに専念することができる上図$(b)$の低解像度である$16×16$(赤線)が非常に早く最適値に達し、残りの学習では横ばいになっていることを見るとPGGANの学習法のメリットを実感できる
低解像度の層から順番$(16,32,64,128)$に収束していくこともわかる
学習時間の短縮
縦軸はDiscriminatorに見せた本物画像の枚数である
たくさんDiscriminatorに本物画像を見せたということは、それだけ学習が進んでいることを意味する段階的学習では初期の学習が非常に速いことがわかる
これは初期段階のネットワークは層が少ないため評価が素早くできるからであるフル解像度に達すると、Discriminatorに見せる本物画像の枚数(学習速度)はどちらの方法でも同じになる
上図はPGGANでは96時間で約640万枚の本物画像を見たことを示している
PGGANでなければ同じ枚数を見るためには520時間必要になると推定できるこの場合PGGANは約5.4倍、従来よりも速いことになる
- 投稿日:2019-02-18T08:00:06+09:00
PGGAN「優しさあふれるカリキュラム学習」
論文紹介・画像引用
PROGRESSIVE GROWING OF GANS FOR IMPROVED QUALITY, STABILITY, AND VARIATION
https://arxiv.org/pdf/1710.10196v3.pdf本研究での生成画像
Progressive Growing of GANs
低解像度の画像から始めてネットワークにレイヤーを追加して徐々に解像度を上げていくGAN
従来のGANのように、すべてのスケールについて同時に学習するのではなく
まず初めに大まかな画像構造を捉えてから段階的に細かいところに注意を向けていく
上図のN×Nは解像度がN×Nでのconvolution層を意味する
すべての層は常に訓練可能な状態である
本研究の学習ではGeneratorとDiscriminatorそれぞれが低解像度(4×4)の層だけを組み入れて始める
学習が進むにつれて徐々にGeneratorとDiscriminatorに層を追加していくことで生成画像の解像度を上げるこうすることで高解像度での画像の生成が安定化し、学習時間の短縮ができる
上図右の画像6枚は上述の段階的な学習法(解像度:1024×1024)によって生成された画像である
GeneratorとDiscriminatorの解像度を2倍にするとき新しい層を入れる16×16の解像度から32×32の解像度への移り変わりを表している(上図(a)から上図(c))
その移り変わりの間を表したのが上図(b)高解像度の層では残差ブロックのようにしている
$α$は$0$~$1$$2×$と$0.5×$はそれぞれ解像度を2倍、0.5倍にすることを意味する
$to RGB$は特徴ベクトルをRGBに変換する層、$from RGB$はその逆
どちらも$1×1$のconvolution層を使うdiscriminatorを訓練するときは、現在のネットワークの解像度に合わせて縮小された本物の画像を入れる
残差ブロックを使用しているため、Generatorの出力は2つの画像(to RGBされたもの)を足し合わせる
同じようにDiscriminatorでは2つのベクトル(from RGBされたもの)を足し合わせるネットワーク構成
上図左がGeneratorのアーキテクチャ、上図右がDiscriminatorのアーキテクチャ
どちらも3層を1ブロックにしたものを学習の途中で1つずつ追加して積み重ねているGeneratorの最後の1×1のconvolution層は$to RGB$を意味する
DIscriminatorの最初の1×1のconvolution層は$from RGB$を意味するアップサンプリングは2×2で複製、ダウンサンプリングはアベレージプーリング
潜在ベクトルは512次元で本物画像と生成画像は[-1,1]の範囲で表す
leaky ReLU($α=0.2$)を線形変換する最終層を除いて、両ネットワークのすべての層に使う
学習の流れ
4×4の解像度から始めて、Discriminatorに合計800枚の本物画像を見せるまでネットワークの学習をする
その後は次の2つの処理を交互に実行する
新しい3層ブロックを入れる(解像度を上げる)→800枚の本物画像でネットワークを安定化させる→新しい3層ブロックを入れる(解像度を上げる)→・・・工夫点(後述)
batch normalization・layer normalization・weight normalizationはどちらのネットワークにも使わないが
Generatorの3×3のconvolution層の後にpixelwise normalization(後述:Generatorにおけるピクセル特徴ベクトルの正規化)を使うバイアスは0で初期化し、重みは分散1の正規分布に従う
しかし、学習時に各層固有の定数で重みをスケーリングする(後述:学習率の均質化)Descriminatorの最終層には4×4の解像度でミニバッチ全体の標準偏差の特徴マップを追加する(後述:ミニバッチ標準偏差を使った画像多様性の向上)
最適化関数
Adam($α = 0.001, β1 = 0, β2 = 0.99, ε = 10^{−8}$)
ミニバッチサイズ
解像度($4×4~128×128$) :ミニバッチサイズ=$16$
解像度($256×256$) : ミニバッチサイズ=$14$
解像度($512×512$) : ミニバッチサイズ=$6$
解像度($1024×1024$) : ミニバッチサイズ=$3$
ミニバッチサイズを徐々に小さくするのは、メモリに乗るようにするためPGGANの良いところ
学習の安定化
最初は小さい画像のため大幅に安定して生成できる
理由:クラス情報・モード情報が少ない解像度を少しずつ上げていくことによって単純な質問に答えていくだけのような状況で学習できる
従来であれば、潜在表現から1024×1024の画像へのマッピングという難しい最終目標を達成できるように試行錯誤しなくてはならない
複雑である潜在表現から高解像度の画像へのマッピングは段階的に学んだほうが簡単(PGGANの場合)
一層入れて十分に学習する→新しい層(解像度が前回よりも高い層)を入れる→十分に学習する→・・・
一層をちゃんと学習して安定化してから次の層を入れる丁寧なやり方
(従来のGAN)
最初からすべての層を入れて一気にすべての層を学習する
PGGANと比べれば雑なやり方例)数学
(PGGANの場合)
足し算を学習する→引き算を学習する→掛け算を学習する→・・・→・・・・・・・・→センター試験の数学
(従来のGAN)
センター試験の数学(初日)実際には、WGAN-GP損失やLSGAN損失を使用して
メガピクセルスケールの画像を確実に生成するための学習を十分に安定化させる学習時間の短縮
PGGANでは大半のイテレーションが低解像度で行われるため
もちろん最終的な出力解像度にもよるが従来のGANよりも2〜6倍速く学習できるミニバッチ標準偏差を使った画像多様性の向上
GANは訓練データにある一部の画像の特徴やパターンだけを捉える傾向がある
解決策として「ミニバッチ識別」を提案するこれは個々の画像のみならずミニバッチ全体からも特徴統計量を計算することである
最終的には生成画像のミニバッチと訓練画像のミニバッチが同じ統計量を示すことが理想ミニバッチ層はDiscriminatorの最後に追加することで実装できる
ミニバッチ層では入力アクティベーションを統計量に変換するテンソルを学習する
ミニバッチの各サンプルから生成された様々な統計量が層の出力と足し合わせるためDiscriminatorは統計量を使うことができる本研究ではこの処理を大幅に単純化し、画像の多様性も向上させた
シンプルバージョン
本研究で単純化された方法は学習可能なパラメータや新しいハイパーパラメータを使うわけではない
①ミニバッチ上の各空間位置にある各特徴の標準偏差を計算する
②すべての特徴、すべての空間で平均を計算して単一の値を出す
③その値を複製して1枚の特徴マップをつくるこの層はどこにでも入れることはできるが最終層に入れるのが一番良いことがわかった
GeneratorとDiscriminatorの正規化
GANではGeneratorとDiscriminatorの学習によって値の発散が起きやすい
この問題への対策として2つの方法を提案する学習率の均質化
初期値は$N(0,1)$にし、学習時に重みを動的にスケーリングする
重みを動的にスケーリングするとは$\hat{w_i } = w_i / c$をすることである
$w_i$は重み、$c$は各層の正規化定数(Heの初期化を使う)
→スケール不変性が得られる最適化するときにスケールの影響を受けずに
パラメーターの更新ができるようになるため学習速度が上がるスケールを整えているためすべての重みに対して均質の学習速度にすることができる
Generatorにおけるピクセル特徴ベクトルの正規化
Generatorの各convolution層での計算後に各ピクセルの特徴ベクトルを正規化する
正規化は以下のようにする
$ε=10^{-8}$ $N$:特徴マップの数 $a_{x,y}$:ピクセル$(x,y)$の正規化前の特徴ベクトル
$b_{x,y}$:ピクセル$(x,y)$の正規化したの特徴ベクトルGAN評価のためのマルチスケールにおける統計的類似性
上手く学習ができたGeneratorは
局所的な画像構造がすべてのスケールにわたって本物画像と似ている画像を生成する16×16ピクセルのローパス解像度から始めて、
生成画像のラプラシアンピラミッド表現による局所画像の分布と
本物画像のラプラシアンピラミッド表現による局所画像の分布のマルチスケール統計的類似性について考える
短くいうと、マルチスケールで生成画像と本物画像の分布を比較して、分布の距離が近ければ良いGANと考える※ラプラシアンピラミッドについては"laplacian pyramid"で画像検索するとイメージがしやすくなるかもしれない
局所特徴量を得る
これまでの慣例に従って、ピラミッドはフル解像度に達するまで段階的に2倍にする
各レベルは前回のレベルをアップサンプリングしたものとの差をエンコードするラプラシアンピラミッドの各レベルは特定の空間周波数帯に対応する
ランダムに16384枚の画像を選び、各画像のラプラシアンピラミッドの各レベルから128個局所特徴量を抽出する
そうすると各レベルから$2^{21}(2.1M)$個の局所特徴量が得られる($16384×128=2^{21}$)それぞれの局所特徴量は$7×7$のピクセルで$3$チャンネル
$x∈R^{7×7×3}=R^{147}$と表せる訓練データのレベル$l$からの局所特徴量は
と表し、
生成データのレベル$l$からの局所特徴量はと表す
分布距離を測る
①各チャンネルの平均と標準偏差を求めて
訓練データの局所特徴量と生成データの局所特徴量
の正規化を行う
②xとyの統計的な類似度をsliced Wasserstein distance(SWD)で計算する
ワッサースタイン距離は輸送問題に基づいて考えられた分布の距離を測る指標ワッサースタイン距離が小さいということは分布が類似していること、すなわち
この解像度での訓練画像と生成画像は見た目も多様性も同じように見えるということを意味する最低解像度の16×16での分布距離は大まかな画像構造の類似性を表し、
高解像度での分布距離はエッジやノイズの鮮明さといったピクセルレベルでの情報の類似性を表す検証
学習構成を変えたら結果はどう変わるのか?
上表は様々な学習構成でのSWD(Sliced Wasserstein distance)とMS-SSIM(multi-scale structural similarity)の数値評価を示している
上表を見る上での注意点
一般的には評価指標の数値が良いことは、色・テクスチャなどの多様性があることを意味するが、
MS-SSIMを見るときは注意が必要だ
上図を見れば(a)よりも(h)の方が明らかにきれいな画像ができているがMS-SSIMの数値はほとんど同じであるこれはMS-SSIMという指標は生成画像の多様性のみを評価するものであり、本物画像との類似性を評価するものではないからである
一方、SVDの数値は大きく改善している結果
最初の学習構成$(a)$はGulrajani et al.(2017)である
これはGeneratorにbatch normalizationを、Discriminatorにlayer normalizationを入れて
ミニバッチサイズを64にしたものである$(b)$は段階的な学習(層を徐々に追加していく学習)のネットワーク
鮮明な画像が生成されている
生成画像の分布と本物画像の分布がより似ていることをSWDの数値が示している高解像度の画像を生成することが目的であるが、そのためにはミニバッチを小さいサイズ(メモリに乗るサイズ)にすることが必要である
このことをしたのが$(c)$である
ミニバッチサイズを64から16に変更している
両指標からもわかるが、生成画像は不鮮明であるbatch normalizationとlayer normalizationを取り除き、ハイパーパラメーターの調整をして学習課程を安定化させたのが$(d)$である
$(e*)$はミニバッチ識別を可能にしたもの(Salimans et al., 2016)だが、生成画像の多様性を評価するMS-SSIMの指標すらも向上しないという結果に終わってしまった
対照的に、本研究でのミニバッチ識別$(e)$ではSWDの平均スコアを改善し鮮明な画像の生成にも成功している
更に本研究で提案した$(f)$と$(g)$を加えるとSWDのスコアと生成画像の質はより良くなっている
最後に$(h)$ではベストネットワークを用いて十分な学習をした結果である
これまでのGANモデルよりも鮮明な画像を生成できている収束と学習時間
上図$(a)$と$(b)$は訓練時間(横軸)とSWDの数値(縦軸)
上図$(c)$は訓練時間(横軸)とDiscriminatorに見せた本物画像の枚数(縦軸)$(a)$と$(b)$はGulrajani et al. (2017)の学習構成での結果である
ただし$(a)$は段階的な学習(層を徐々に追加していく学習)のネットワークではない(最初からすべての層をネットワークに入れておく)
$(b)$は段階的な学習(層を徐々に追加していく学習)のネットワーク段階的な学習は2つのメリットがあることがわかる
・かなり優れた最適値に収束する
・学習時間を半分にすることができる収束
収束性の向上は徐々にネットワークを大きくしていくという「カリキュラム学習」によるものである
段階的な学習をしない場合はGeneratorとDiscriminatorのすべての層は
大まかな画像構成の多様性と画像の詳細、両方の中間表現を同時に見つけなくてはならないしかし段階的な学習をする場合は、
最初の頃からあった低解像度の層はすでに早い時期に収束しているため
新しい層が加わってきたらネットワークは詳細な表現を学習することのみに専念することができる上図$(b)$の低解像度である$16×16$(赤線)が非常に早く最適値に達し、残りの学習では横ばいになっていることを見るとPGGANの学習法のメリットを実感できる
低解像度の層から順番$(16,32,64,128)$に収束していくこともわかる
学習時間の短縮
縦軸はDiscriminatorに見せた本物画像の枚数である
たくさんDiscriminatorに本物画像を見せたということは、それだけ学習が進んでいることを意味する段階的学習では初期の学習が非常に速いことがわかる
これは初期段階のネットワークは層が少ないため評価が素早くできるからであるフル解像度に達すると、Discriminatorに見せる本物画像の枚数(学習速度)はどちらの方法でも同じになる
上図はPGGANでは96時間で約640万枚の本物画像を見たことを示している
PGGANでなければ同じ枚数を見るためには520時間必要になると推定できるこの場合PGGANは約5.4倍、従来よりも速いことになる