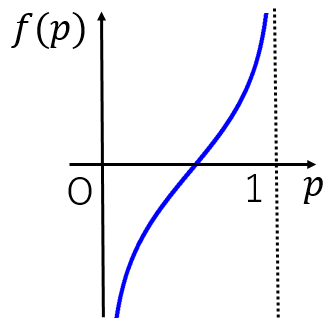- 投稿日:2020-11-15T07:50:53+09:00
[Python]ロジスティック回帰の理論と実装を徹底解説してみた
はじめに
今回の記事では、tensorflowとsckit-learnを用いてロジスティック回帰を実装していきます。
前回の記事で線形回帰についてまとめたので、よろしければ以下の記事もご覧ください。
Pythonでscikit-learnとtensorflowとkeras用いて重回帰分析をしてみる
今回用いるのはirisデータセットです。
iris(アヤメ)データセットについて
irisデータは、アヤメという花の品種のデータです。
アヤメの品種である
Setosa、Virginica、Virginicaの3品種に関するデータが50個ずつ、全部で150個のデータです。実際に中身を見ていきましょう。
from sklearn.datasets import load_iris import pandas as pd iris = load_iris() iris_df = pd.DataFrame(iris.data, columns=iris.feature_names) print(iris_df.head())sepal length (cm) sepal width (cm) petal length (cm) petal width (cm)
0 5.1 3.5 1.4 0.2
1 4.9 3.0 1.4 0.2
2 4.7 3.2 1.3 0.2
3 4.6 3.1 1.5 0.2
4 5.0 3.6 1.4 0.2
iris.feature_namesに各々のカラム名が格納されているので、それをpandasのDataframeの引数に渡すことで上のようなデータを出力できます。
Sepal Lengthはがく弁の長さが、Sepal Widthにはがく弁の幅が、Petal lengthには花びらの長さが、Petal Widthには花びらの幅のデータが格納されています。以下のようにすれ正解ラベルを表示できます。
print(iris.target)[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2]このように、アヤメの品種である
setosa、versicolor、virginicaをそれぞれ0, 1, 2としています。今回はロジスティック回帰によるニ値分類を行うため、
virginicaのデータを削除します。そして、目的変数をもとにそれが
setosa、versicolor、のどちらなのかを識別するモデルを作成します。ロジスティック回帰について
ロジスティック回帰について解説します。
ロジスティック回帰とは、回帰という名前がついていますが、やることは二値分類です。
いくつかの説明変数をもとに、確率を計算して、予測を行います。今回の例では花びらの長さや幅のデータなどをもとにそれが
setosa、versicolorのどちらなのかを識別します。ここで、少し話は飛びますが全てのモデルを線形で近似するときの機械学習のモデルを考えていきます。
今、目的変数を「プールの入場者数」とし、説明変数を「気温」であると仮定し、線形回帰を行います。
$$入場者数 = β_0 + β_1 × 気温$$
この場合、左の入場者数を応答変数と呼び、右の式を線形予測子といいます。
しかし、これは明らかに良くないモデルですよね。なぜなら、右側の式は気温によりマイナスになるかもしれませんが、入場者数はマイナスになることはあり得ません。
そこで、応答変数と線形予測子を対応させるために、以下のように変更します。
$$log(入場者数) = β_0 + β_1 × 気温$$
このように左辺に対数関数を適用することで、両辺を正しく対応させることができました。この場合の対数関数のことをリンク関数といいます。
それでは次に、入試の合格を目的変数にしてみましょう。この場合は当然、合格か不合格なので0か1かになりますよね。
説明変数は勉強時間にしましょう。以下のようなモデルが考えられます。
$$合否(1, 0) = β_0 + β_1 × 勉強時間$$
このモデルも良いモデルではありません。左辺は0か1のみですが、明らかに右辺はそれに対応していません。
それでは次のように目的変数を合格率にしたらどうでしょうか。
$$合格率 = β_0 + β_1 × 勉強時間$$
このモデルも良いモデルではありませんね。左辺の合格率は0から1の範囲をとりますが、右辺はそうではありません。
この応答変数と線形予測子を対応させるために、リンク関数としてロジット関数を用います。ロジット関数は以下の式で表します。
f(p) = ln(\frac{p}{1-p}) \quad (0 < p < 1))ロジット関数についてはこちらの記事を参考にしてください。
確率pで起こる事象Aについて、Aが起こる確率と起こらない確率の比$\frac{p}{1-p}$を
オッズといいますロジット関数は以下の形になります。
リンク関数としてロジット関数を用いると、合格率をpとして以下のモデルを作成できます。
ln(\frac{p}{1-p}) = β_0 + β_1 × 勉強時間このモデルは、左辺と右辺が対応しているため良いモデルといえますね。
しかし、今求めたいのは合格率を予測するモデルなので、pについて解いていきましょう。勉強時間を$x_1$とします。
\begin{align} ln(\frac{p}{1-p}) &= β_0 + β_1 × x_1\\ ln(\frac{p}{1-p}) &= z \quad (z = β_0 + β_1 × x_1)\\ \frac{p}{1-p}&=e^z\\ p& = e^z - e^zp\\ p &= \frac{e^z}{1+e^z}\\ p & = \frac{1}{1+e^{-z}} \end{align}このように、シグモイド関数が導出できました。もう少しzを一般化して
z= β_0 + β_1 × x_1 + β_2 × x_2 ... + β_n × x_nとしましょう。これがロジスティック回帰に用いられる式で、βを最適化することが目標になります。
βの最適化について
以下の式を考えれば、重回帰分析と同じように最小二乗法によりβを最適化することができます。
ln(\frac{p}{1-p}) = β_0 + β_1 × x_1 + β_2 × x_2 ... + β_n × x_n最小二乗法についてはこちらの記事を参考にしてください。
もう一つは最尤法を用いる方法です。
最尤法について
最尤法についてはこちらの記事に分かりやすくまとめられているので、参考にしてください。
最尤法について簡単に解説します。
最尤法を考えるためには、尤度や尤度関数について理解する必要があります。
以下はコトバンクからの引用です。
ゆうど【尤度 likelihood】
確率密度関数において確率変数に観測値を代入したものをいう。つまり,確率密度を観測値で評価した値である。また,これを未知母数の関数とみるとき,とくに尤度関数という。尤度関数の自然対数は対数尤度と呼ぶ。観測値とその確率分布が与えられたとき,尤度あるいは対数尤度を最大にする母数の値は,母数の一つの自然な推定量を与える。これは最尤推定量と呼ばれ,標本サイズが大きくなると母数の真値に漸近的に一致するとか,漸近的に正規分布に従うなど,いろいろ好ましい漸近的性質をもつ。以下はwikipediaからの引用です。
尤度関数(ゆうどかんすう、英: likelihood function)とは統計学において、ある前提条件に従って結果が出現する場合に、逆に観察結果からみて前提条件が「何々であった」と推測する尤もらしさ(もっともらしさ)を表す数値を、「何々」を変数とする関数として捉えたものである。また単に尤度ともいう。
なんだかよく分からないので、数式で確認してみましょう。
N個のデータ$x_1,x_2,x_3,...,x_n$を観測したとき、それぞれの値が生じる確率をp(x)とすると、尤度関数は以下の式で表されます。
$$p(x_1)p(x_2)....p(x_3)$$
ここからは自分の理解なのですが、最尤法とは、
データを観測した時にそのデータが生じる確率を考えることで、元々のデータが従う確率分布を推定する方法だと考えてください。例えば、コインを投げる場合を考えてください。当然コインの裏表はイカサマがない限り同じ確率になります。
統計学でいうところの
ベルヌーイ試行ですね。しかし、現実世界ではコインのように確率分布が感覚的に分かっているものを扱うことは少ないです。なので今回は、コインの裏表がでる確率が等しくないということにします。
このコインが従う確率分布はどのように求めたらよいでしょうか?
感覚的には、コインを沢山投げて記録をとればよさそうですよね。今、コインを3回投げたところ、表、表、裏となりました。
表がでる確率を$p$とすると、裏が出る確率は$1-p$となるので、この事象が起きる確率、すなわち尤度関数は
$$p^2(1-p)$$となりますね。今、この事象が
起きたのです。例えばコインの表が出る確率が$\frac{1}{2}$、裏がでる確率が$\frac{1}{2}$だとするとこの事象が起きる確率は$\frac{1}{8}$になります。コインの表が出る確率が$\frac{2}{3}$、裏がでる確率が$\frac{1}{3}$だとするとこの事象が起きる確率は$\frac{4}{27}$となります。このように考えて、「コインを三回投げて表、表、裏となった」という条件のもとで、コインの表がでる確率$p$と裏がでる確率$1-p$を考えるときに、どのような$p$が尤(もっと)もらしいかを考えるときに用いるのが最尤法です。
今、「コインを3回投げたところ、表、表、裏だった」という事象が
起きたので、尤もらしい$p$とはこの「コインを3回投げたところ、表、表、裏だった」という事象が起きる確率が最大になるような$p$ですよね。つまり、「尤もらしい」$p$を求めるため(最尤法)には、「その事象が起きる確率」である尤度関数が最も大きくなるような$p$を選べば良いことが分かります。
つまり、この例においては$p^2(1-p)$が最大になるような$p$を求めればよいので、両辺の対数をとって微分したり、そのまま微分して最大値$p$を求めれば良さそうですよね。
このように、結果から元のデータが従う確率分布を求める方法が最尤推定やベイズ推定と呼ばれるものです。
今回は初めから裏表のベルヌーイ分布に従うことが分かっていたので簡単に尤度関数を求めることができましたが、実際は元のデータが従う確率分布(正規分布,etc)を求めるところから考えなければならないので、もっと大変になります。
こちらのスライドがとても分かりやすかったので、参考にしてください。
改めてβの最適化について
今回のロジスティック回帰について、尤度関数を考えてみましょう。ロジスティック回帰について、目的変数が(0, 1)で与えられ、あるデータについて説明変数$x_1, x_2, x_3, ..., x_n$が与えられた時、そのデータの目的変数が1である確率$p$は
p = \frac{1}{1+e^{-z}} \quad (z= β_0 + β_1 × x_1 + β_2 × x_2 ... + β_n × x_n)となります。 目的変数が1となる確率が$p$であり、目的変数が0となる確率は$1-p$です。
あるデータに対して、目的変数が(0, 1)のどちらなのか分かった時、つまりそのデータがどちらのデータなのか(今回のirisの例ではSetosa、Virginicaのどちらなのか)が分かった時を考えてください。その
あるデータがその目的変数のデータである確率を$L$とすると上記の$p$(目的変数が1である確率)を用いて、$t_n$を目的変数(0, 1)とするとL = p^{t_n}(1-p)^{1-t_n}と表せます。目的変数が1のとき$L$は$p$となり、目的変数が0のとき$L$は$1-p$となっていることが分かります。
つまり、$L$は目的変数が判明したとき、すなわち結果が分かったときにおける「その事象が起きる確率」であることが分かります。「その事象が起きた」という条件の下で、その事象が起きる確率である$L$を最大にする$p$を求めれば、その$p$は尤もらしい$p$であると考えることができます。
この例はある一つのデータに対してだったので、今度は全てのデータに対して考えていきます。
各々のデータに対して独立となるので、全体の尤度関数は以下のように$n$個のデータの尤度関数の積であると考えることができます。
L(β)= \prod_{n = 1}^{N} p_n^{t_n}(1-p_n)^{1-t_n}この$n$個のデータに対しての尤度関数$L(β)$を最大にする$p$を、つまりは$β$を($p$は$β$の関数であるため)見つけることで、パラメータ$β$を最適化することができそうです。
上記の式を計算しやすくするために、両辺の対数をとり、マイナスをつけると以下の式になります。
E(β) = -logL(β) = - \sum^N_{n = 1} \{t_nlogp_n + (1-t_n)log(1-p_n)\}このようにして導出された$E(β)$を交差エントロピー誤差関数といいます。
sckit-learnで実装
それではsckit-learnで実装していきます。まずはデータセットを準備しましょう。
from sklearn.datasets import load_iris import numpy as np import pandas as pd from pandas import Series, DataFrame import seaborn as sns from sklearn.linear_model import LogisticRegression from sklearn.model_selection import train_test_split from sklearn import metrics import matplotlib.pyplot as plt iris = load_iris() iris_data = iris.data[:100] iris_target_data = pd.DataFrame(iris.target[:100], columns=['Species']) iris_df = pd.DataFrame(iris_data, columns=iris.feature_names) print(iris_df)sepal length (cm) sepal width (cm) petal length (cm) petal width (cm)
0 5.1 3.5 1.4 0.2
1 4.9 3.0 1.4 0.2
2 4.7 3.2 1.3 0.2
3 4.6 3.1 1.5 0.2
4 5.0 3.6 1.4 0.2
.. ... ... ... ...
95 5.7 3.0 4.2 1.2
96 5.7 2.9 4.2 1.3
97 6.2 2.9 4.3 1.3
98 5.1 2.5 3.0 1.1
99 5.7 2.8 4.1 1.3
setosa、versicolorの二つのデータを分類していきます。そのため、最初の100個のデータのみを取り扱います。最初の50個が
setobaについてのデータであり、後の50個がversicolorについてのデータです。
iris_target_dataの中身をみていきましょう。print(iris_target_data)Species
0 0
1 0
2 0
3 0
4 0
.. ...
95 1
96 1
97 1
98 1
99 1このように0と1のデータが格納されたDataframeになっています。
もともとnumpyのarrayだったものをDataframeに返還したのは、以下のようにDataframeのapplyメソッドを使用するためです。
def species(num): if num == 0: return 'setosa' else: return 'versicolor' iris_target_speacies = iris_target_data['Species'].apply(species) print(iris_target_speacies)0 setosa
1 setosa
2 setosa
3 setosa
4 setosa
...
95 versicolor
96 versicolor
97 versicolor
98 versicolor
99 versicolorこのようにDataframeのapplyメソッドを用いれば、指定したカラムに対して引数で指定した関数を実行し、その戻り値を代入したDataframeを受け取ることができます。
axis=1を指定することで横方向に結合できます。次のコードで
iris_dfとiris_target_speaciesを結合します。iris_all_data = pd.concat([iris_df, iris_target_speacies], axis=1) print(iris_all_data)sepal length (cm) sepal width (cm) ... petal width (cm) Species
0 5.1 3.5 ... 0.2 setosa
1 4.9 3.0 ... 0.2 setosa
2 4.7 3.2 ... 0.2 setosa
3 4.6 3.1 ... 0.2 setosa
4 5.0 3.6 ... 0.2 setosa
.. ... ... ... ... ...
95 5.7 3.0 ... 1.2 versicolor
96 5.7 2.9 ... 1.3 versicolor
97 6.2 2.9 ... 1.3 versicolor
98 5.1 2.5 ... 1.1 versicolor
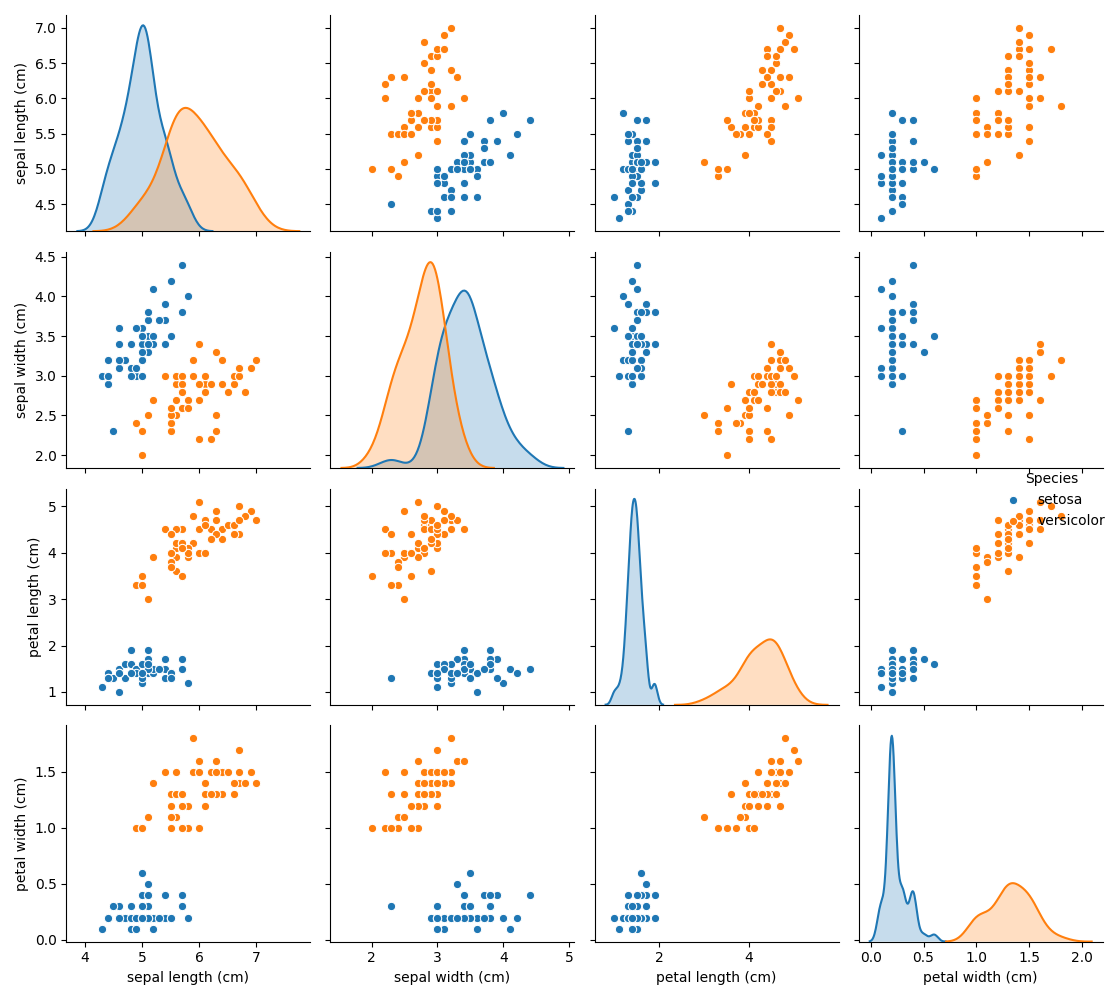
99 5.7 2.8 ... 1.3 versicolor以下のコードでデータを可視化してみましょう。各々のデータに対しての散布図と存在割合を示します。
sns.pairplot(iris_all_data, hue='Species') plt.show()このようなデータなら分類できそうですね。
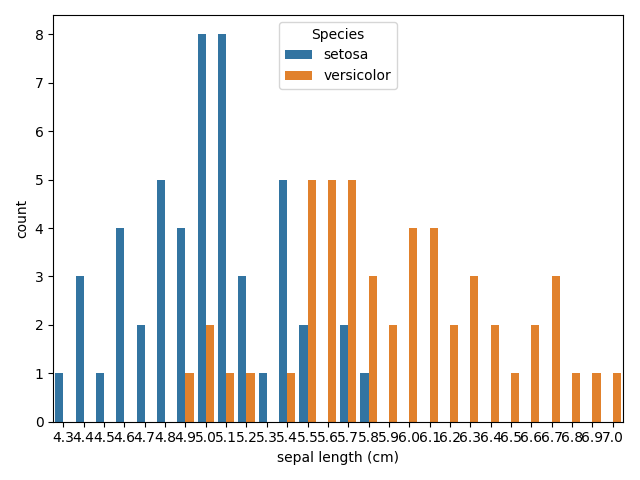
次のコードで
sepal lengthに対しての度数表をみてみましょう。sns.countplot('sepal length (cm)', data=iris_all_data, hue='Species') plt.show()これでデータについてなんとなく理解できたと思います。
そのまま学習
次のコードでモデルを作成しましょう。トレーニング用とテスト用に分けずにそのまま学習します。
logistic_model = LogisticRegression() logistic_model.fit(iris_df, iris_target_data)これでモデルの作成は完了です。
以下のコードで
β_1,β_2,β_3,β_4の値を出力できます。
print(logistic_model.coef_[0])[-0.40247392 -1.46382925 2.23785648 1.00009294]
このままだと分かりにくいので、以下のコードで分かりやすく出力します。
coeff_df = DataFrame([iris_df.columns, logistic_model.coef_[0]]).T print(coeff_df)0 1
0 sepal length (cm) -0.402474
1 sepal width (cm) -1.46383
2 petal length (cm) 2.23786
3 petal width (cm) 1.00009この結果から、
petal lengthやpetal width大きいとversicolorである確率が高く、sepal widthやsepal lengthが大きいとsetosaである確率が大きいことが分かります。この結果はグラフの図示におおよそ一致していることが分かりますね。
次のコードで予測精度を確かめてみましょう。トレーニングしたモデルでそのままテストを行います。
...py
print(logistic_model.score(iris_df, iris_target_data))
```1.0
100パーセントの精度で分類できています。すごいですね。
次のような方法でも精度を確かめることができます。
class_predict = logistic_model.predict(iris_df) print(class_predict)[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1]predictメソッドを用いると、このように与えたデータに対しての予測値をnumpyのarrayの形で得ることができます。
この
class_predictと正解ラベルをmetrics.accuracy_scoreで比較することで予測精度を算出できます。print(metrics.accuracy_score(iris_target_data, class_predict))1.0
こちらの方法でも当然100パーセントです。
テスト用とトレーニング用に分けて学習
次はデータをテスト用とトレー二ング用に分けて学習をしてみましょう。
コードは以下のようになります。
X_train, X_test, Y_train, Y_test = train_test_split(iris_df, iris_target_data) logistic_model2 = LogisticRegression() logistic_model2.fit(X_train, Y_train) coeff_df2 = DataFrame([iris_df.columns, logistic_model2.coef_[0]]).T print(coeff_df2) print(logistic_model2.score(X_test, Y_test))0 1
0 sepal length (cm) -0.381626
1 sepal width (cm) -1.33919
2 petal length (cm) 2.12026
3 petal width (cm) 0.954906
1.0テスト用とトレーニング用にデータを分けても予測精度は100パーセントでした。すごいですね。
tensorflowで実装
tensorflowで実装する場合には、元の数式を理解しておく必要があります。確認しましょう。
p = \frac{1}{1+e^{-z}} \quad (z= β_0 + β_1 × x_1 + β_2 × x_2 ... + β_n × x_n)損失関数には交差エントロピー誤差を使います。尤度関数の対数にマイナスをかけたものです。
E(β) = -logL(β) = - \sum^N_{n = 1} \{t_nlogp_n + (1-t_n)log(1-p_n)\}それでは実装していきます。以下のコードでデータの準備をしましょう。
from sklearn.datasets import load_iris import numpy as np import pandas as pd from pandas import Series, DataFrame import seaborn as sns from sklearn.linear_model import LogisticRegression from sklearn.model_selection import train_test_split from sklearn import metrics import matplotlib.pyplot as plt import tensorflow as tf iris = load_iris() iris_data = iris.data[:100] iris_target_data = pd.DataFrame(iris.target[:100], columns=['Species']) iris_df = pd.DataFrame(iris_data, columns=iris.feature_names) X_train, X_test, Y_train, Y_test = train_test_split(iris_df, iris_target_data) print(X_train.shape) print(X_test.shape) print(Y_train.shape) print(Y_test.shape)(75, 4)
(25, 4)
(75, 1)
(25, 1)次のコードでモデルを作成しましょう。
X = tf.placeholder(dtype=tf.float32, shape=[None, 4]) W = tf.Variable(tf.zeros([4, 1])) b = tf.Variable(tf.zeros([1, 1])) y = tf.nn.sigmoid(tf.matmul(X, W) + b) y = tf.clip_by_value(y, 1e-10, 1.0 - 1e-10) t = tf.placeholder(dtype=tf.float32, shape=[None, 1])Xには説明変数が、tには目的変数が格納されます。 yが上記の数式の$p$にあたります。
yは交差エントロピー誤差関数に代入するときに対数になるため、
y = 0になるとエラーが起きるので、
y = tf.clip_by_value(y, 1e-10, 1.0 - 1e-10)によりyの最小値を1e-10に、yの最大値を
1.0 - 1e-10にしています。以下の式で交差エントロピー誤差関数をAdamで最適化しましょう。
cross_entropy = tf.reduce_sum(t * tf.log(y) + (1 - t) * tf.log(1 - y)) train_step = tf.train.AdamOptimizer(0.001).minimize(cross_entropy)ここまででモデルが完成したので、以下のコードでこのモデルを実行しましょう。
with tf.Session() as sess: sess.run(tf.global_variables_initializer()) for step in range(10000): if step % 10 == 0: loss_val = sess.run(cross_entropy, feed_dict={X: X_train, t: Y_train}) W_val = sess.run(W) b_val = sess.run(b) print('Step: {}, Loss: {} W_val: {} b_val: {}'.format(step, loss_val, W_val, b_val)) sess.run(train_step, feed_dict={X: X_train, t: Y_train}) correct_prediction = sess.run(tf.cast(tf.greater(y, 0.5), tf.int32), feed_dict={X: X_train, t: Y_train}) print('トレーニングデータの評価 : ', metrics.accuracy_score(Y_train, correct_prediction)) test_data = tf.placeholder(dtype=tf.float32, shape=[None, 4]) test_prediction = tf.nn.sigmoid(tf.matmul(test_data, W_val) + b_val) test_correct_prediction = sess.run(tf.cast(tf.greater(test_prediction, 0.5), tf.int32), feed_dict={test_data: X_test}) print('テストデータの評価 : ', metrics.accuracy_score(Y_test, test_correct_prediction))Step: 9990, Loss: 0.10178631544113159 W_val: [[ 0.25520977]
[-3.2158086 ]
[ 3.3751483 ]
[ 3.4625392 ]] b_val: [[-3.2248065]]
トレーニングデータの評価 : 1.0
テストデータの評価 : 1.0
tf.greater(y, 0.5)により、0.5以上のyにはTrueを、0.5より小さいyにはFalseが代入されたブール値が返ってきます。それを
tf.castに代入することで、Trueを1に、Falseを0に変換します。以上でtensorflowによる実装は終了です。
終わりに
ここまでお付き合いいただきありがとうございました。
お疲れさまでした。
- 投稿日:2020-11-15T07:50:53+09:00
ロジスティック回帰の理論と実装を徹底解説してみた
はじめに
今回の記事では、tensorflowとsckit-learnを用いてロジスティック回帰を実装していきます。
前回の記事で線形回帰についてまとめたので、よろしければ以下の記事もご覧ください。
Pythonでscikit-learnとtensorflowとkeras用いて重回帰分析をしてみる
今回用いるのはirisデータセットです。
iris(アヤメ)データセットについて
irisデータは、アヤメという花の品種のデータです。
アヤメの品種である
Setosa、Virginica、Virginicaの3品種に関するデータが50個ずつ、全部で150個のデータです。実際に中身を見ていきましょう。
from sklearn.datasets import load_iris import pandas as pd iris = load_iris() iris_df = pd.DataFrame(iris.data, columns=iris.feature_names) print(iris_df.head())sepal length (cm) sepal width (cm) petal length (cm) petal width (cm)
0 5.1 3.5 1.4 0.2
1 4.9 3.0 1.4 0.2
2 4.7 3.2 1.3 0.2
3 4.6 3.1 1.5 0.2
4 5.0 3.6 1.4 0.2
iris.feature_namesに各々のカラム名が格納されているので、それをpandasのDataframeの引数に渡すことで上のようなデータを出力できます。
Sepal Lengthはがく弁の長さが、Sepal Widthにはがく弁の幅が、Petal lengthには花びらの長さが、Petal Widthには花びらの幅のデータが格納されています。以下のようにすれ正解ラベルを表示できます。
print(iris.target)[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2]このように、アヤメの品種である
setosa、versicolor、virginicaをそれぞれ0, 1, 2としています。今回はロジスティック回帰によるニ値分類を行うため、
virginicaのデータを削除します。そして、目的変数をもとにそれが
setosa、versicolor、のどちらなのかを識別するモデルを作成します。ロジスティック回帰について
ロジスティック回帰について解説します。
ロジスティック回帰とは、回帰という名前がついていますが、やることは二値分類です。
いくつかの説明変数をもとに、確率を計算して、予測を行います。今回の例では花びらの長さや幅のデータなどをもとにそれが
setosa、versicolorのどちらなのかを識別します。ここで、少し話は飛びますが全てのモデルを線形で近似するときの機械学習のモデルを考えていきます。
今、目的変数を「プールの入場者数」とし、説明変数を「気温」であると仮定し、線形回帰を行います。
$$入場者数 = β_0 + β_1 × 気温$$
この場合、左の入場者数を応答変数と呼び、右の式を線形予測子といいます。
しかし、これは明らかに良くないモデルですよね。なぜなら、右側の式は気温によりマイナスになるかもしれませんが、入場者数はマイナスになることはあり得ません。
そこで、応答変数と線形予測子を対応させるために、以下のように変更します。
$$log(入場者数) = β_0 + β_1 × 気温$$
このように左辺に対数関数を適用することで、両辺を正しく対応させることができました。この場合の対数関数のことをリンク関数といいます。
それでは次に、入試の合格を目的変数にしてみましょう。この場合は当然、合格か不合格なので0か1かになりますよね。
説明変数は勉強時間にしましょう。以下のようなモデルが考えられます。
$$合否(1, 0) = β_0 + β_1 × 勉強時間$$
このモデルも良いモデルではありません。左辺は0か1のみですが、明らかに右辺はそれに対応していません。
それでは次のように目的変数を合格率にしたらどうでしょうか。
$$合格率 = β_0 + β_1 × 勉強時間$$
このモデルも良いモデルではありませんね。左辺の合格率は0から1の範囲をとりますが、右辺はそうではありません。
この応答変数と線形予測子を対応させるために、リンク関数としてロジット関数を用います。ロジット関数は以下の式で表します。
f(p) = ln(\frac{p}{1-p}) \quad (0 < p < 1))ロジット関数についてはこちらの記事を参考にしてください。
確率pで起こる事象Aについて、Aが起こる確率と起こらない確率の比$\frac{p}{1-p}$を
オッズといいますロジット関数は以下の形になります。
リンク関数としてロジット関数を用いると、合格率をpとして以下のモデルを作成できます。
ln(\frac{p}{1-p}) = β_0 + β_1 × 勉強時間このモデルは、左辺と右辺が対応しているため良いモデルといえますね。
しかし、今求めたいのは合格率を予測するモデルなので、pについて解いていきましょう。勉強時間を$x_1$とします。
\begin{align} ln(\frac{p}{1-p}) &= β_0 + β_1 × x_1\\ ln(\frac{p}{1-p}) &= z \quad (z = β_0 + β_1 × x_1)\\ \frac{p}{1-p}&=e^z\\ p& = e^z - e^zp\\ p &= \frac{e^z}{1+e^z}\\ p & = \frac{1}{1+e^{-z}} \end{align}このように、シグモイド関数が導出できました。もう少しzを一般化して
z= β_0 + β_1 × x_1 + β_2 × x_2 ... + β_n × x_nとしましょう。これがロジスティック回帰に用いられる式で、βを最適化することが目標になります。
βの最適化について
以下の式を考えれば、重回帰分析と同じように最小二乗法によりβを最適化することができます。
ln(\frac{p}{1-p}) = β_0 + β_1 × x_1 + β_2 × x_2 ... + β_n × x_n最小二乗法についてはこちらの記事を参考にしてください。
もう一つは最尤法を用いる方法です。
最尤法について
最尤法についてはこちらの記事に分かりやすくまとめられているので、参考にしてください。
最尤法について簡単に解説します。
最尤法を考えるためには、尤度や尤度関数について理解する必要があります。
以下はコトバンクからの引用です。
ゆうど【尤度 likelihood】
確率密度関数において確率変数に観測値を代入したものをいう。つまり,確率密度を観測値で評価した値である。また,これを未知母数の関数とみるとき,とくに尤度関数という。尤度関数の自然対数は対数尤度と呼ぶ。観測値とその確率分布が与えられたとき,尤度あるいは対数尤度を最大にする母数の値は,母数の一つの自然な推定量を与える。これは最尤推定量と呼ばれ,標本サイズが大きくなると母数の真値に漸近的に一致するとか,漸近的に正規分布に従うなど,いろいろ好ましい漸近的性質をもつ。以下はwikipediaからの引用です。
尤度関数(ゆうどかんすう、英: likelihood function)とは統計学において、ある前提条件に従って結果が出現する場合に、逆に観察結果からみて前提条件が「何々であった」と推測する尤もらしさ(もっともらしさ)を表す数値を、「何々」を変数とする関数として捉えたものである。また単に尤度ともいう。
なんだかよく分からないので、数式で確認してみましょう。
N個のデータ$x_1,x_2,x_3,...,x_n$を観測したとき、それぞれの値が生じる確率をp(x)とすると、尤度関数は以下の式で表されます。
$$p(x_1)p(x_2)....p(x_3)$$
ここからは自分の理解なのですが、最尤法とは、
データを観測した時にそのデータが生じる確率を考えることで、元々のデータが従う確率分布を推定する方法だと考えてください。例えば、コインを投げる場合を考えてください。当然コインの裏表はイカサマがない限り同じ確率になります。
統計学でいうところの
ベルヌーイ試行ですね。しかし、現実世界ではコインのように確率分布が感覚的に分かっているものを扱うことは少ないです。なので今回は、コインの裏表がでる確率が等しくないということにします。
このコインが従う確率分布はどのように求めたらよいでしょうか?
感覚的には、コインを沢山投げて記録をとればよさそうですよね。今、コインを3回投げたところ、表、表、裏となりました。
表がでる確率を$p$とすると、裏が出る確率は$1-p$となるので、この事象が起きる確率、すなわち尤度関数は
$$p^2(1-p)$$となりますね。今、この事象が
起きたのです。例えばコインの表が出る確率が$\frac{1}{2}$、裏がでる確率が$\frac{1}{2}$だとするとこの事象が起きる確率は$\frac{1}{8}$になります。コインの表が出る確率が$\frac{2}{3}$、裏がでる確率が$\frac{1}{3}$だとするとこの事象が起きる確率は$\frac{4}{27}$となります。このように考えて、「コインを三回投げて表、表、裏となった」という条件のもとで、コインの表がでる確率$p$と裏がでる確率$1-p$を考えるときに、どのような$p$が尤(もっと)もらしいかを考えるときに用いるのが最尤法です。
今、「コインを3回投げたところ、表、表、裏だった」という事象が
起きたので、尤もらしい$p$とはこの「コインを3回投げたところ、表、表、裏だった」という事象が起きる確率が最大になるような$p$ですよね。つまり、「尤もらしい」$p$を求めるため(最尤法)には、「その事象が起きる確率」である尤度関数が最も大きくなるような$p$を選べば良いことが分かります。
つまり、この例においては$p^2(1-p)$が最大になるような$p$を求めればよいので、両辺の対数をとって微分したり、そのまま微分して最大値$p$を求めれば良さそうですよね。
このように、結果から元のデータが従う確率分布を求める方法が最尤推定やベイズ推定と呼ばれるものです。
今回は初めから裏表のベルヌーイ分布に従うことが分かっていたので簡単に尤度関数を求めることができましたが、実際は元のデータが従う確率分布(正規分布,etc)を求めるところから考えなければならないので、もっと大変になります。
こちらのスライドがとても分かりやすかったので、参考にしてください。
改めてβの最適化について
今回のロジスティック回帰について、尤度関数を考えてみましょう。ロジスティック回帰について、目的変数が(0, 1)で与えられ、あるデータについて説明変数$x_1, x_2, x_3, ..., x_n$が与えられた時、そのデータの目的変数が1である確率$p$は
p = \frac{1}{1+e^{-z}} \quad (z= β_0 + β_1 × x_1 + β_2 × x_2 ... + β_n × x_n)となります。 目的変数が1となる確率が$p$であり、目的変数が0となる確率は$1-p$です。
あるデータに対して、目的変数が(0, 1)のどちらなのか分かった時、つまりそのデータがどちらのデータなのか(今回のirisの例ではSetosa、Virginicaのどちらなのか)が分かった時を考えてください。その
あるデータがその目的変数のデータである確率を$L$とすると上記の$p$(目的変数が1である確率)を用いて、$t_n$を目的変数(0, 1)とするとL = p^{t_n}(1-p)^{1-t_n}と表せます。目的変数が1のとき$L$は$p$となり、目的変数が0のとき$L$は$1-p$となっていることが分かります。
つまり、$L$は目的変数が判明したとき、すなわち結果が分かったときにおける「その事象が起きる確率」であることが分かります。「その事象が起きた」という条件の下で、その事象が起きる確率である$L$を最大にする$p$を求めれば、その$p$は尤もらしい$p$であると考えることができます。
この例はある一つのデータに対してだったので、今度は全てのデータに対して考えていきます。
各々のデータに対して独立となるので、全体の尤度関数は以下のように$n$個のデータの尤度関数の積であると考えることができます。
L(β)= \prod_{n = 1}^{N} p_n^{t_n}(1-p_n)^{1-t_n}この$n$個のデータに対しての尤度関数$L(β)$を最大にする$p$を、つまりは$β$を($p$は$β$の関数であるため)見つけることで、パラメータ$β$を最適化することができそうです。
上記の式を計算しやすくするために、両辺の対数をとり、マイナスをつけると以下の式になります。
E(β) = -logL(β) = - \sum^N_{n = 1} \{t_nlogp_n + (1-t_n)log(1-p_n)\}このようにして導出された$E(β)$を交差エントロピー誤差関数といいます。
sckit-learnで実装
それではsckit-learnで実装していきます。まずはデータセットを準備しましょう。
from sklearn.datasets import load_iris import numpy as np import pandas as pd from pandas import Series, DataFrame import seaborn as sns from sklearn.linear_model import LogisticRegression from sklearn.model_selection import train_test_split from sklearn import metrics import matplotlib.pyplot as plt iris = load_iris() iris_data = iris.data[:100] iris_target_data = pd.DataFrame(iris.target[:100], columns=['Species']) iris_df = pd.DataFrame(iris_data, columns=iris.feature_names) print(iris_df)sepal length (cm) sepal width (cm) petal length (cm) petal width (cm)
0 5.1 3.5 1.4 0.2
1 4.9 3.0 1.4 0.2
2 4.7 3.2 1.3 0.2
3 4.6 3.1 1.5 0.2
4 5.0 3.6 1.4 0.2
.. ... ... ... ...
95 5.7 3.0 4.2 1.2
96 5.7 2.9 4.2 1.3
97 6.2 2.9 4.3 1.3
98 5.1 2.5 3.0 1.1
99 5.7 2.8 4.1 1.3
setosa、versicolorの二つのデータを分類していきます。そのため、最初の100個のデータのみを取り扱います。最初の50個が
setobaについてのデータであり、後の50個がversicolorについてのデータです。
iris_target_dataの中身をみていきましょう。print(iris_target_data)Species
0 0
1 0
2 0
3 0
4 0
.. ...
95 1
96 1
97 1
98 1
99 1このように0と1のデータが格納されたDataframeになっています。
もともとnumpyのarrayだったものをDataframeに返還したのは、以下のようにDataframeのapplyメソッドを使用するためです。
def species(num): if num == 0: return 'setosa' else: return 'versicolor' iris_target_speacies = iris_target_data['Species'].apply(species) print(iris_target_speacies)0 setosa
1 setosa
2 setosa
3 setosa
4 setosa
...
95 versicolor
96 versicolor
97 versicolor
98 versicolor
99 versicolorこのようにDataframeのapplyメソッドを用いれば、指定したカラムに対して引数で指定した関数を実行し、その戻り値を代入したDataframeを受け取ることができます。
axis=1を指定することで横方向に結合できます。次のコードで
iris_dfとiris_target_speaciesを結合します。iris_all_data = pd.concat([iris_df, iris_target_speacies], axis=1) print(iris_all_data)sepal length (cm) sepal width (cm) ... petal width (cm) Species
0 5.1 3.5 ... 0.2 setosa
1 4.9 3.0 ... 0.2 setosa
2 4.7 3.2 ... 0.2 setosa
3 4.6 3.1 ... 0.2 setosa
4 5.0 3.6 ... 0.2 setosa
.. ... ... ... ... ...
95 5.7 3.0 ... 1.2 versicolor
96 5.7 2.9 ... 1.3 versicolor
97 6.2 2.9 ... 1.3 versicolor
98 5.1 2.5 ... 1.1 versicolor
99 5.7 2.8 ... 1.3 versicolor以下のコードでデータを可視化してみましょう。各々のデータに対しての散布図と存在割合を示します。
sns.pairplot(iris_all_data, hue='Species') plt.show()このようなデータなら分類できそうですね。
次のコードで
sepal lengthに対しての度数表をみてみましょう。sns.countplot('sepal length (cm)', data=iris_all_data, hue='Species') plt.show()これでデータについてなんとなく理解できたと思います。
そのまま学習
次のコードでモデルを作成しましょう。トレーニング用とテスト用に分けずにそのまま学習します。
logistic_model = LogisticRegression() logistic_model.fit(iris_df, iris_target_data)これでモデルの作成は完了です。
以下のコードで
β_1,β_2,β_3,β_4の値を出力できます。
print(logistic_model.coef_[0])[-0.40247392 -1.46382925 2.23785648 1.00009294]
このままだと分かりにくいので、以下のコードで分かりやすく出力します。
coeff_df = DataFrame([iris_df.columns, logistic_model.coef_[0]]).T print(coeff_df)0 1
0 sepal length (cm) -0.402474
1 sepal width (cm) -1.46383
2 petal length (cm) 2.23786
3 petal width (cm) 1.00009この結果から、
petal lengthやpetal width大きいとversicolorである確率が高く、sepal widthやsepal lengthが大きいとsetosaである確率が大きいことが分かります。この結果はグラフの図示におおよそ一致していることが分かりますね。
次のコードで予測精度を確かめてみましょう。トレーニングしたモデルでそのままテストを行います。
...py
print(logistic_model.score(iris_df, iris_target_data))
```1.0
100パーセントの精度で分類できています。すごいですね。
次のような方法でも精度を確かめることができます。
class_predict = logistic_model.predict(iris_df) print(class_predict)[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1]predictメソッドを用いると、このように与えたデータに対しての予測値をnumpyのarrayの形で得ることができます。
この
class_predictと正解ラベルをmetrics.accuracy_scoreで比較することで予測精度を算出できます。print(metrics.accuracy_score(iris_target_data, class_predict))1.0
こちらの方法でも当然100パーセントです。
テスト用とトレーニング用に分けて学習
次はデータをテスト用とトレー二ング用に分けて学習をしてみましょう。
コードは以下のようになります。
X_train, X_test, Y_train, Y_test = train_test_split(iris_df, iris_target_data) logistic_model2 = LogisticRegression() logistic_model2.fit(X_train, Y_train) coeff_df2 = DataFrame([iris_df.columns, logistic_model2.coef_[0]]).T print(coeff_df2) print(logistic_model2.score(X_test, Y_test))0 1
0 sepal length (cm) -0.381626
1 sepal width (cm) -1.33919
2 petal length (cm) 2.12026
3 petal width (cm) 0.954906
1.0テスト用とトレーニング用にデータを分けても予測精度は100パーセントでした。すごいですね。
tensorflowで実装
tensorflowで実装する場合には、元の数式を理解しておく必要があります。確認しましょう。
p = \frac{1}{1+e^{-z}} \quad (z= β_0 + β_1 × x_1 + β_2 × x_2 ... + β_n × x_n)損失関数には交差エントロピー誤差を使います。尤度関数の対数にマイナスをかけたものです。
E(β) = -logL(β) = - \sum^N_{n = 1} \{t_nlogp_n + (1-t_n)log(1-p_n)\}それでは実装していきます。以下のコードでデータの準備をしましょう。
from sklearn.datasets import load_iris import numpy as np import pandas as pd from pandas import Series, DataFrame import seaborn as sns from sklearn.linear_model import LogisticRegression from sklearn.model_selection import train_test_split from sklearn import metrics import matplotlib.pyplot as plt import tensorflow as tf iris = load_iris() iris_data = iris.data[:100] iris_target_data = pd.DataFrame(iris.target[:100], columns=['Species']) iris_df = pd.DataFrame(iris_data, columns=iris.feature_names) X_train, X_test, Y_train, Y_test = train_test_split(iris_df, iris_target_data) print(X_train.shape) print(X_test.shape) print(Y_train.shape) print(Y_test.shape)(75, 4)
(25, 4)
(75, 1)
(25, 1)次のコードでモデルを作成しましょう。
X = tf.placeholder(dtype=tf.float32, shape=[None, 4]) W = tf.Variable(tf.zeros([4, 1])) b = tf.Variable(tf.zeros([1, 1])) y = tf.nn.sigmoid(tf.matmul(X, W) + b) y = tf.clip_by_value(y, 1e-10, 1.0 - 1e-10) t = tf.placeholder(dtype=tf.float32, shape=[None, 1])Xには説明変数が、tには目的変数が格納されます。 yが上記の数式の$p$にあたります。
yは交差エントロピー誤差関数に代入するときに対数になるため、
y = 0になるとエラーが起きるので、
y = tf.clip_by_value(y, 1e-10, 1.0 - 1e-10)によりyの最小値を1e-10に、yの最大値を
1.0 - 1e-10にしています。以下の式で交差エントロピー誤差関数をAdamで最適化しましょう。
cross_entropy = tf.reduce_sum(t * tf.log(y) + (1 - t) * tf.log(1 - y)) train_step = tf.train.AdamOptimizer(0.001).minimize(cross_entropy)ここまででモデルが完成したので、以下のコードでこのモデルを実行しましょう。
with tf.Session() as sess: sess.run(tf.global_variables_initializer()) for step in range(10000): if step % 10 == 0: loss_val = sess.run(cross_entropy, feed_dict={X: X_train, t: Y_train}) W_val = sess.run(W) b_val = sess.run(b) print('Step: {}, Loss: {} W_val: {} b_val: {}'.format(step, loss_val, W_val, b_val)) sess.run(train_step, feed_dict={X: X_train, t: Y_train}) correct_prediction = sess.run(tf.cast(tf.greater(y, 0.5), tf.int32), feed_dict={X: X_train, t: Y_train}) print('トレーニングデータの評価 : ', metrics.accuracy_score(Y_train, correct_prediction)) test_data = tf.placeholder(dtype=tf.float32, shape=[None, 4]) test_prediction = tf.nn.sigmoid(tf.matmul(test_data, W_val) + b_val) test_correct_prediction = sess.run(tf.cast(tf.greater(test_prediction, 0.5), tf.int32), feed_dict={test_data: X_test}) print('テストデータの評価 : ', metrics.accuracy_score(Y_test, test_correct_prediction))Step: 9990, Loss: 0.10178631544113159 W_val: [[ 0.25520977]
[-3.2158086 ]
[ 3.3751483 ]
[ 3.4625392 ]] b_val: [[-3.2248065]]
トレーニングデータの評価 : 1.0
テストデータの評価 : 1.0
tf.greater(y, 0.5)により、0.5以上のyにはTrueを、0.5より小さいyにはFalseが代入されたブール値が返ってきます。それを
tf.castに代入することで、Trueを1に、Falseを0に変換します。以上でtensorflowによる実装は終了です。
終わりに
ここまでお付き合いいただきありがとうございました。
お疲れさまでした。