20200328のJavaScriptに関する記事は27件です。

投稿日：2020-03-28T23:50:35+09:00

【Ruby on Rails】Ajax通信で特定の要素を変更する

はじめに

RailsのAjax通信使って特定の要素を編集・更新する方法について記載します。
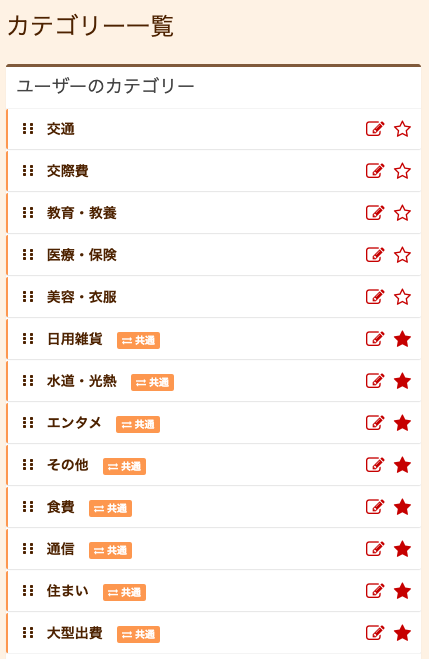
例で簡単なカテゴリー一覧画面の１つのカテゴリーの名前を更新する処理を使います。

バージョン

ruby 2.6.3

rails 5.2.1

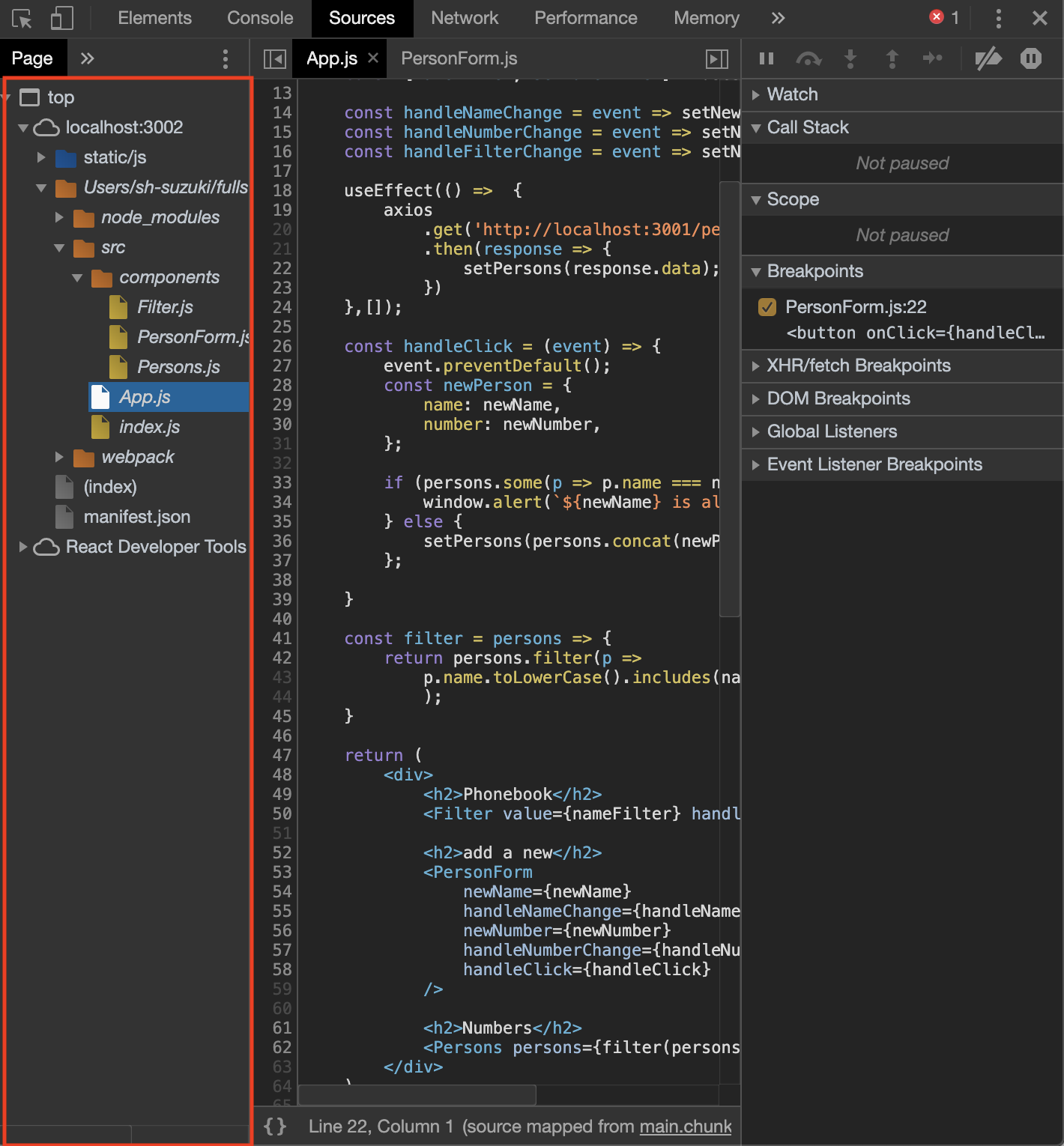
画面概要

以下のような画面です。

この右のほうにある鉛筆マークの編集アイコンボタンを押すと、該当の行のカテゴリー名がフォームに変わります。

カテゴリー名を変更し、「更新」を押すと、

変更後のカテゴリー名にデータが更新され、表示を非同期で変更します。
例では、「交通」→「交通費」に変更します。

処理概要

要素にAjax通信するオプションを追加
link_toにremote: trueオプションをつけます。

Ajax通信するためのルーティングを追加

コントローラやモデルでオブジェクトの取得または更新

追加したアクションのためのJavaScript用のviewファイルを用意し、画面の該当の要素を変更するためのJavaScriptを記載

実装前

実装前の主要なコード部分は以下になります。
app/controllers/categories_controller.rb
def index
  @categories = Category.where(user: current_user).order(:created_at)
end
app/views/categories/index.html.erb
<ul class="todo-list" id="own-categories">
  <% @categories.each do |category| %>
    <li id="category-list-id-<%= category.id %>">
      <%= render 'a_category_list', category: category %>    
    </li>
  <% end  %>
</ul>
app/views/categories/_a_category_list.html.erb
<span class="handle ui-sortable-handle">
  <i class="fa fa-ellipsis-v"></i>
  <i class="fa fa-ellipsis-v"></i>
</span>
<span class="text"><%= category.name %></span>
<%= category.common_mark %>
<div class="tools">
  <%= link_to edit_category_path(category), class: "text-redpepper space-left" do %>
    <i class="fa fa-lg fa-edit"></i>
  <% end %>
  <%= category.common_btn %>
</div>
カテゴリー名を編集するフォームに変更するAjax処理の実装

鉛筆マークの編集アイコンボタンを押下して、カテゴリー名の要素をフォーム要素に変更する処理を記載していきます。
※注意：説明しないclass属性やid属性などがありますが、Ajax通信処理とは関係ありません。

この処理にはgem rails-ujsが必要なので追加してbundle installします。
Gemfile
gem 'rails-ujs'
1. Ajax通信するオプションを追加

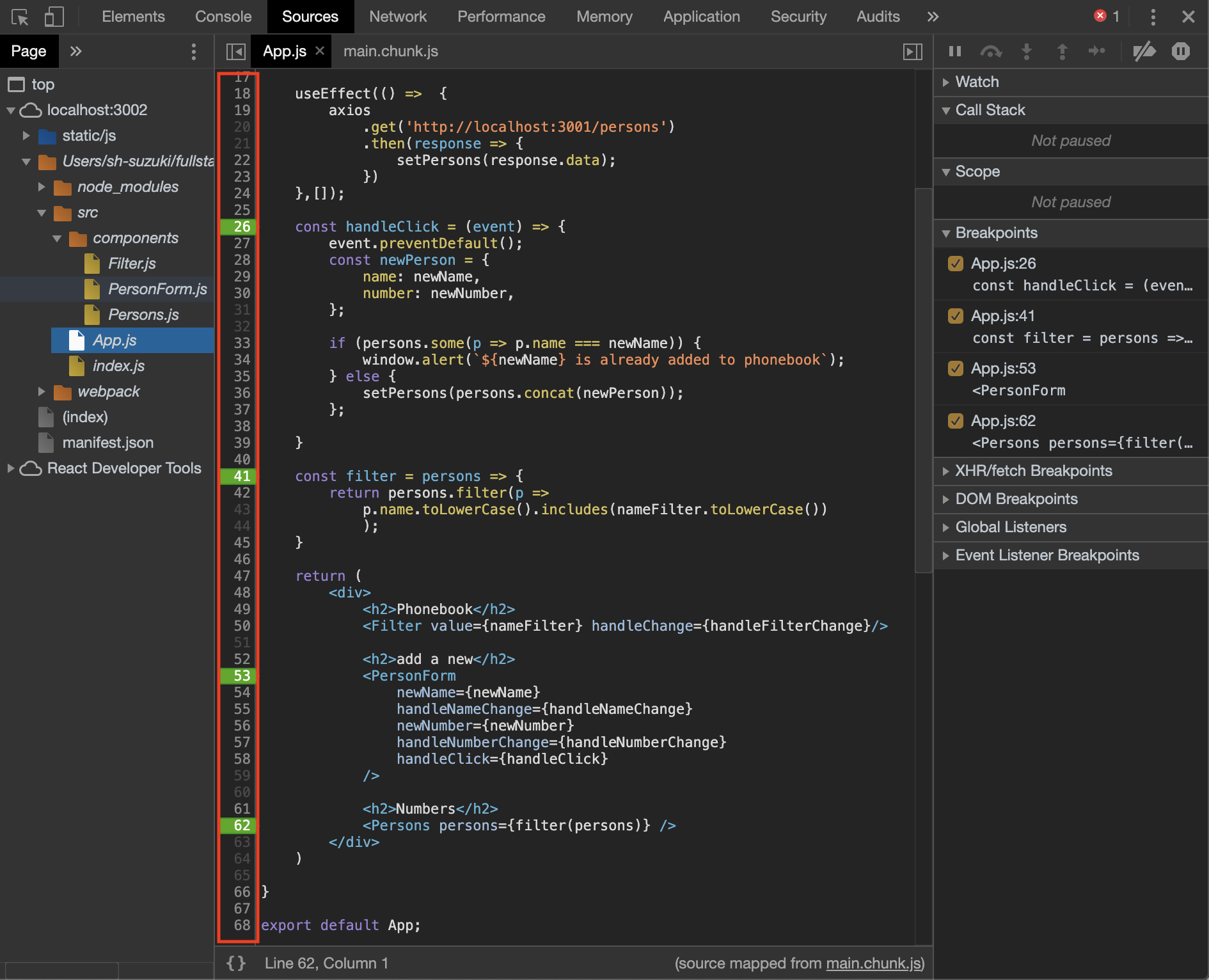
編集アイコンボタンにremote: trueを仕込む。
app/views/categories/_a_category_list.html.erb
<%= link_to edit_category_path(category), remote: true, class: "text-redpepper space-left" do %>
  <i class="fa fa-lg fa-edit"></i>
<% end %>
2. Ajax通信するためのルーティングを追加

Ajax通信するときでも、ルーティングのresourcesメソッドが柔軟に対応してくれます。
ここでは、editアクションを追加します。
config/routes.rb
resources :categories, only: [:index, :edit]
3. コントローラでオブジェクトの取得
app/controllers/categories_controller.rb
def edit
  @category = Category.find(params[:id])
end
4. 追加したアクションのためのJavaScript用のviewファイルを用意し、画面の該当の要素を変更するためのJavaScriptを記載

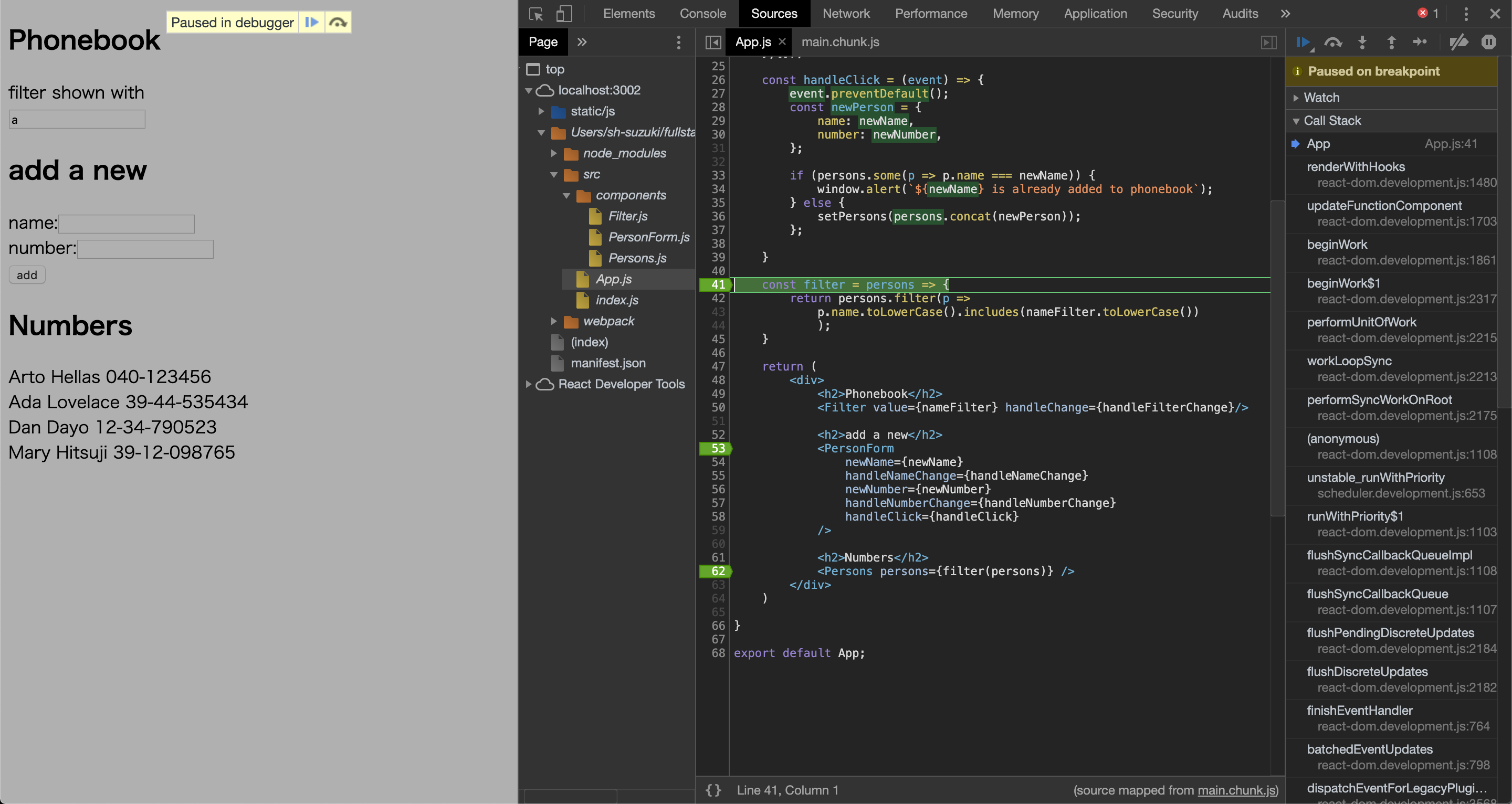
editアクションなので、app/views/categories/edit.js.erbを作成します。
app/views/categories/edit.js.erb
id = "<%= @category.id %>";
target = document.querySelector(`#category-list-id-${id}`);
html = "<%= j(render partial: 'form', locals: { category: @category }) %>";
target.innerHTML = html;
app/views/categories/_form.html.erb
<%= form_with(model: category) do |form| %>
  <div class="row">
    <div class="col-xs-10">
      <div class="input-group input-group-sm">
        <%= form.text_field :name, value: category.name, required: true, class:"form-control", max: 15 %>
        <span class="input-group-btn">
          <%= form.submit submit_btn_letters, class: "btn btn-brown" %>
        </span>
      </div>
    </div>
    <div class="col-xs-1">
      <%= category.cancel_btn %>
    </div>
  </div>
<% end %>
これで、カテゴリー名を編集するためのフォームが表示できます。

カテゴリー名を更新するAjax処理の実装

編集フォームに変更できたので、次に、変更したい文字「交通費」に変更して、
更新ボタンを押下し、更新後のカテゴリー名を表示する処理を記載していきます。

1. Ajax通信するオプションを追加

form_withにremote: trueオプションを追加します。
(明示的に記載しなくてもデフォルトでremote: trueにはなっている。)
app/views/categories/_form.html.erb
<%= form_with(model: category, remote: true) do |form| %>
  
<% end %>
2. Ajax通信するためのルーティングを追加

updateアクションを追加
config/routes.rb
resources :categories, only[:index, :edit, :update]
3. コントローラでオブジェクトの更新

カテゴリー名を「交通費」で更新します。
app/controllers/categories_controller.rb
def update
  @category = Category.find(params[:id])
  @category.update(category_params)
end

private
def category_params
  params.require(:category).permit(:name, :is_common)
end
4. 追加したアクションのためのJavaScript用のviewファイルを用意し、画面の該当の要素を変更するためのJavaScriptを記載

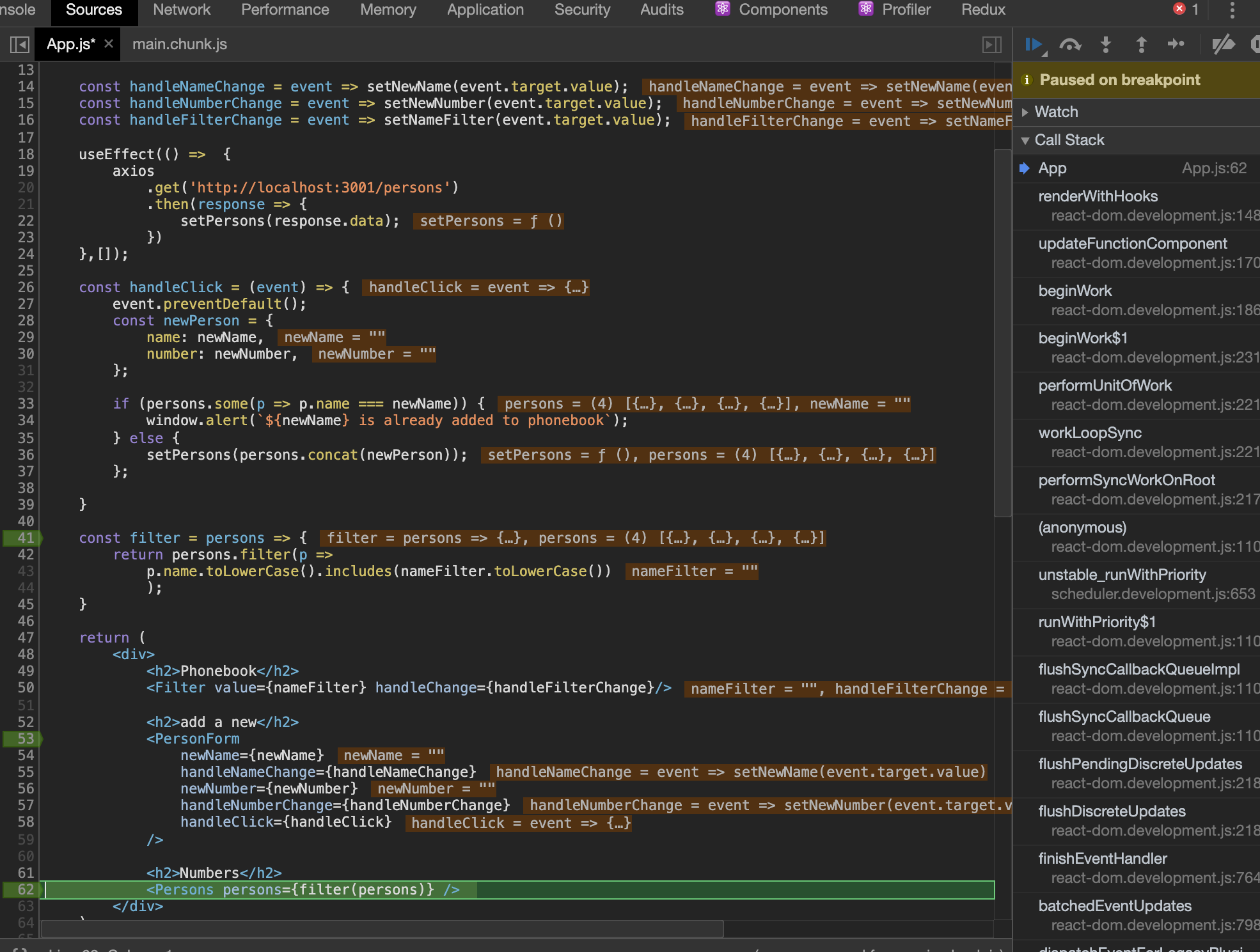
編集フォームを更新したカテゴリー名に変更する処理を行います。
updateアクションなのでapp/views/categories/update.js.erbを作成します。
app/views/categories/update.js.erb
id = "<%= @category.id %>";
target = document.querySelector(`#category-list-id-${id}`);
html = "<%= j(render partial: 'categories/a_category_list', locals: { category: @category }) %>";
target.innerHTML = html;
以上で、カテゴリー名を非同期で更新することができました。

おわりに

JavaScriptでAjax処理を書いてもいいのですが、シンプルなAjax通信はRailsであれば簡単にできます。
ただ、〇〇.js.erbの書き方は癖が強いので要注意です。

　 Tweet
Qiitaで続きを読む

投稿日：2020-03-28T23:34:55+09:00

javascript int変換/キャスト/切り上げ/切り捨て/四捨五入-注意点

はじめに

あれ？javascriptにキャスト演算子てなかったけ？四捨五入てどうやってやるんや？てなった人向けの備忘録てきな記事です。intに変換する際の注意点、例もあわせてどうぞ！

parseInt($hoge, 10)

これがほかの言語でいう (int)的なキャストのメソッドですね。
実数値を持つ変数$hogeに対してparseInt($hoge, 10)のように使います。
ここで第2引数は第1引数の基数(10進数や2進数の10や2のこと)で省略可能ですがデフォルトが10ではなく入力値によって勝手にその基数は判断されるので第2引数まで与えるのが無難です。
parseInt()
parseInt(2.5, 10)
parseInt(2.5)
parseInt("2.5")
parseInt(10, 2)

parseInt(-2.5)
上の例では最初の4つがすべて2を返し、最後の1つは-2を返します。

Number($hoge)

はい、これが僕がずっと勘違いしていたものでこれがいわゆる(int)的なキャストをする関数だと思ってました。javascriptにはこういうキャスト演算子はないんだーってなって一番名前的に近そうなこれがintへのキャストだと皆さん勘違いすると思います。僕だけですかね。はい全く違いました。結論から言えばこれはStringなどの方から数値(小数含む)型への型変換のメソッドでした。

これはそもそも関数ではなくNumberオブジェクトを生成するコンストラクタで、このコンストラクタの引数に値を与えることでその値がNumberオブジェクトになります。基本的にjavascriptではこのNumber型で算術演算を行うためこのコンストラクタが結局キャストのようになるわけです。

これはNumberプリミティブ値(String, boolなどのメソッドを持たない基本のデータ型)を生成する関数でした。従ってこの関数は文字列などから数値への変換を行う型変換の関数でした。単純にNumberオブジェクトを生成したい場合はnew Number($hoge)で初期化する必要がありますね。また上で記したparseInt()もこのNumberオブジェクトのメソッドです。

以下に例を示します。
Number()
Number('123')     // 123
Number('12.3')    // 12.3
Number('123e-1')  // 12.3
Number('')        // 0
Number(null)      // 0
Number('0x11')    // 17
Number('foo')     // NaN
また + 演算子でも number への変換が簡単に行えるようです。
+
+'123'     // 123
+'12.3'    // 12.3
+'123e-1'  // 12.3
+''        // 0
+null      // 0
+'0x11'    // 17
+'foo'     // NaN
Math.floor($hoge)

与えられた数値の切り捨て(与えられた数値と等しい整数、もしくは与えられた数値より小さい最大の整数を返す)を行う関数です。

これも注意が必要で、一瞬、parseInt($hoge)=Math.floor($hoge)と思いませんか？ぼくは思いました。
でも違いますね。上のparseInt()の例と下の例を見比べて貰えばわかりますが、細かい精度の違いは置いておくと

parseInt($hoge) = $hoge >= 0 ? Math.floor($hoge) : Math.ceil($hoge)

となるわけです。Math.floor()などの関数を使う場合は与えられた数値が負の場合もしっかり考慮して関数を選ぶ必要がありますね。
ちなみに正確にMath.floor()はparseInt()に比べて引数にStringをとらない、parseInt()はとても大きい引数や小さい引数にたして予期しない結果を生む可能性があるのでMath.floorの代替としてはつかうべきでない、などの違いがあります。
Math.floor()
Math.floor( 2.5); //  2
Math.floor(-2.5); // -3
Math.ceil($hoge)

与えられた数値の切り上げ(与えられた数値と等しい整数、もしくは与えられた数値より大きい最小の整数を返す)の関数です。
これについての注意点などはMath.floorと同様なので割愛。
Math.ceil()
Math.ceil(.95);    // 1
Math.ceil(4);      // 4
Math.ceil(7.004);  // 8
Math.ceil(-0.95);  // -0
Math.round($hoge)

皆さんお待ちかね、四捨五入の関数ですね。
Math.round()
Math.round( 20.49); //  20
Math.round( 20.5 ); //  21
Math.round( 42   ); //  42
Math.round(-20.5 ); // -20
おわりに

以上業務システムの開発を行っている際によく用いる数値計算の関数などでした。
金銭の計算など値の誤差が許されない状況でこれらの関数の使い分けは非常に重要になってきます。
日頃からそれぞれの関数のポイントを頭に入れて実装をしておくと良いですね！

　 Tweet
Qiitaで続きを読む

投稿日：2020-03-28T23:30:12+09:00

Vue.js私的まとめ

Vue.jsの私的なまとめです。

テンプレート

私的テンプレ
import XxxComponent from './components/XxxComponent'
import xxxMixins from './mixins/xxxMixins'

new Vue({
  el: '#app',
  components: {
    'xxx-component': XxxComponent
  },
  props: {
    item: {
      type: Object,
      required: true,
      default: () => {
        return {
          data: []
        }
      }
    }
  },
  data () {
    return {
      title: 'タイトル',
      item: []
    }
  },
  created () {
    //
  },
  mounted () {
    //
  },
  watch: {
    item (value, oldValue) {
      //
    },
    item: {
      handler (value, oldValue) {
        //
      },
      deep: true
    }
  },
  computed: {
    xxx (param) {
    }
  },
  methods: {
    /**
     * 説明
     * @param {string} param 内容
     * @return {string} return 内容
     */
    xxx (param) {
    }
  },
  mixins: [xxxMixins]
})
el

elはマウントする要素
el: '#app'
el: '#app'としたらHTMLのid="app"の中にVue.jsで使いたいHTMLを書く
<div id="app">
  // 中略
</div>
data

dataはvue.jsで使うデータを定義する
data () {
  return {
    title: 'タイトル',
    list: {
      data: []
    }
  }
}
マスタッシュ構文

HTMLの中に{{ }}でdataやcomputedを表示させる

$dataを付けるとdataやcomputedと区別が付きやすくなる
data () {
  return {
    text: 'タイトル'
  }
}
<h1>{{ $data.text }}</h1>
v-for

v-forで配列からHTMLにループ処理ができる
data() {
  return {
    list: [ 'りんご', 'ばなな', 'すいか' ]
  };
}
<ul>
  <li v-for="item in $data.list">{{ item }}</li>
</ul>
v-model
<input type="text" v-model="$data.text">
v-text
<p v-text="$data.text"></p>
v-if

v-if="!error"

v-if="text !== 'OK'"などの書き方もできる
<div v-if="error">
  <p>エラー</p>
</div>
v-show
<div v-show="error">
  <p>エラー</p>
</div>
v-ifとv-showの違い

v-showはCSSのdisplay要素が変わる

v-ifはHTML要素が変わる

頻繁に変わる場合はv-showを使う

created

createdはelとDOM作成前
created () {
  // 処理
}
mounted

mountedはDOM作成後
mounted () {
  // 処理
}
createdとmountedの違い

createdはelとDOM作成前

mountedはDOM作成後

詳しくはライフサイクルダイアグラムを参照

https://jp.vuejs.org/v2/guide/instance.html#%E3%83%A9%E3%82%A4%E3%83%95%E3%82%B5%E3%82%A4%E3%82%AF%E3%83%AB%E3%83%80%E3%82%A4%E3%82%A2%E3%82%B0%E3%83%A9%E3%83%A0

watch

watchは変更があったら処理される

第1引数が変更後の値

- 第2引数が変更前の値
watch: {
  item (value, oldValue) {
    // 処理
  }
}
配列はhandlerを使う

deepネストされた値もみる
watch: {
  item: {
    handler (value, oldValue) {
      // 処理
    },
    deep: true
  }
}
computed

computedはキャッシュされる
computed: {
  xxx (param) {
    // 処理
  }
}
methods

methodsにはJSDocを入れる
methods: {
  /**
   * 説明
   * @param {string} param 内容
   * @return {string} return 内容
   */
  xxx (param) {
    // 処理
  }
}
mixins

他のファイルからインポートできる

共通部分などに使う
import xxxMixins from './mixins/xxxMixins'

new Vue({
  mixins: [xxxMixins]
})
components
<xxx-component>
import XxxComponent from './components/XxxComponent'

new Vue({
  components: {
    'xxx-component': XxxComponent
  },
})
props

componentsに受け渡す値を定義する

type:型

required:必須かどうか

default:初期値
props: {
  item: {
    type: Object,
    required: true,
    default: () => {
      return {
        data: []
      }
    }
  }
}
template
import template from './templates/XxxTemplate.html'

export default {
  template: `
    <div>
      <p>test</p>
    </div>
  `
}
templateは別ファイルにすることができる

HTMLを分けたほうがHTMLの可読性が良くなる
import template from './templates/XxxTemplate.html'

export default {
  template: template
}
$emit

親コンポーネントにmethodsを動かす
action (param) {
  this.$emit('change-emit', param)
}
<xxx-component  
  @change-emit="action"
></xxx-component>
axios

Ajaxで使う
getData () {
  const action = '/api/'
  const params = {
    params: 'xxx'
  }
  axios.get(action, params)
    .then(response => {
      // 成功時
    }).catch(error => {
      console.error(error)
      // エラー時
    })
}
transition

transitionはアニメーションと使うことができる
<transition name="fade">
  <div v-show="error">
    <p>エラー</p>
  </div>
</transition>
CSSが必要
.fade-enter-active, .fade-leave-active {
  transition: opacity .5s;
}
.fade-enter, .fade-leave-to　{
  opacity: 0;
}

　 Tweet
Qiitaで続きを読む

投稿日：2020-03-28T23:30:11+09:00

アロー関数の解説

アロー関数とは？

アロー関数の()=>{}はfunction (){}.bind(this)と同じ。但し、functionのように関数内部にオブジェクトを指すthisを生成しない。

サンプルプログラム
function outer(ff) {
  setTimeout(ff, 0);
}
class T {
  f() {
    var obj = {
      ff: () => { console.log(this); }
    };
    outer(obj.ff);
  }
}
var t = new T;
t.f();
obj.ffはアロー関数なので関数内部にオブジェクトobjを指すthisを生成しない。
obj.ffはアロー関数なのでfunction(){}.bind(this)と同じ。
関数obj.ffにbindするthisはオブジェクトT。
このプログラムはTを出力する。

obj.ffを外側の関数outerに移動させてもTを出力するのはアロー関数がthisをbindしているから。¹

functionが関数内部にオブジェクトを指すthisを生成するとは？

例１
var obj = {
  f: function () { console.log(this); },
  g: () => { console.log(this); }
}
obj.f();
obj.g();
例２
function Obj() { }
Obj.prototype.f = function () { console.log(this); }
Obj.prototype.g = () => { console.log(this); }
obj = new Obj;
obj.f();
obj.g();
例１も例２も通常関数fは関数内部にオブジェクトobjを指すthisを生成し、thisがobjを指す。
アロー関数gは関数内部にオブジェクトobjを指すthisを生成しないので、thisがWindowを指す。

bindとは？
var f = function () {
  console.log(this);
}.bind({ a: 1 })

setTimeout(f, 0);
bindは関数内部のthisをオブジェクト{a:1}で束縛する。
このプログラムはthisとして{a:1}を出力する。

setTimeoutやaddEventlisterのような非同期関数はthisを書き変えることで有名。 ↩

　 Tweet
Qiitaで続きを読む

投稿日：2020-03-28T21:45:16+09:00

「福井県オープンデータごみ収集日一覧CSVをJSONに変換するツール」README

※この記事は、私がGitHubに公開しているnode.js製ツール「福井県オープンデータごみ収集日一覧CSVをJSONに変換するツール」のREADMEを転載したものです。
解説は「恋に落ちるコード.js」の絵子と樹里です。

福井県オープンデータごみ収集日一覧CSVをJSONに変換するツール

「福井県オープンデータライブラリ」で公開されている、県内17市町の「ごみ収集日一覧」データの形式を、CSV（Shift-JIS）からJSONに変換します。

Description

樹里「というわけで、福井県内自治体のごみ収集日一覧JSONデータを作成するアプリを作ってみた」
絵子「ほう。なんでまた突然」
樹里「それがな、久しぶりに福井県オープンデータに公開されてるデータを使って、アプリでも作ってみようとしたんだがな」
絵子「福井県は昔からオープンデータの公開に熱心だよね」
樹里「で、ごみ収集日一覧のデータを見てみたんだが、なんとShift-JISのCSVなんだよ。この令和の時代に」
絵子「うーん。確かにそのままだと扱いにくいよね」
樹里「Shift-JISのCSVなんだよ。この令和の時代に」
絵子「2回言わなくていいよ。あと太字にしなくてもいいよ」
樹里「これではどうしようもないので、まずはちゃんとしたUTF-8のJSONに変換するツールから作ってみたわけだ」
絵子「なるほど。経緯はよくわかった」

Usage

樹里「使い方は簡単。Node.js製のアプリなので……」
git clone https://github.com/8amjp/fukui-opendata-gomisyusyubi-json.git
cd fukui-opendata-gomisyusyubi-json
npm install
樹里「上記のコマンドでインストールして、」
node index.js
樹里「と実行すれば、distディレクトリにJSONデータが出力される」
絵子「あら本当に簡単」
樹里「じゃあ、アプリがどういう動きをするのか解説しよう」

index.js

樹里「まずは、メインとなるコードだ」
index.js
/*
  「福井県オープンデータライブラリ」の「ごみ収集日一覧」ページで公開されている
  収集日のCSVデータ（Shift-JIS）をJSONに変換します。
*/

const scraper = require('./lib/scraper');
const generator = require('./lib/generator');
const page = 'https://www.pref.fukui.lg.jp/doc/toukei-jouhou/opendata/list_ct_gomisyusyubi.html'; // 「ごみ収集日一覧」ページのURL

(async () => {
    // ページ内の17市町のCSVデータのURLを取得
    const resources = await scraper.scrape(page)
    // すべてのCSVを取得してJSONに変換して出力
    await Promise.all(resources.map(resource => generator.generate(resource)))
    console.log('できたよ！')
})();
絵子「scraperとgeneratorっていうのが、樹里が作ったモジュール？」
樹里「そう。scraperで「ごみ収集日一覧」ページからCSVへのリンクを取得している。で、generatorでCSVを取得してJSONに変換している」
絵子「なるほど」
樹里「では、各モジュールの動きをみてみよう」

lib/scraper.js

樹里「次に、ページをスクレイピングして、CSVへのリンクを取得するscraperモジュールだ」
lib/scraper.js
/*
  指定されたページ内の、CSVへのリンクをを取得します。
*/
const fetch = require('node-fetch');
const cheerio = require('cheerio');
const url = require('url');

module.exports.scrape = async (page) => {
    // 指定されたページのHTMLを取得する
    const response = await fetch(page)
    const body = await response.text()
    // cheerioでページをスクレイピング
    const $ = await cheerio.load(body)
    // 末尾が'.csv'のリンクをすべて取得
    const relativePaths = await $('a[href$=".csv"]').map((i, el) => $(el).attr('href')).get()
    // 絶対パスに変換
    const absolutePaths = await relativePaths.map(path => url.resolve(page, path))
    return absolutePaths
}
樹里「スクレイピングにはcheerioというライブラリを使用している」
絵子「知ってる。jQueryっぽく操作できるやつだよね」
樹里「そう。そのcheerioで、属性セレクターを使って、href属性が ".csv" で終わるa要素、すなわちCSVへのリンクを取得してだな、その配列を返している」
絵子「なるほど」

lib/generator.js

樹里「最後に、データの変換を行うgeneratorモジュールだ」
lib/generator.js
/*
  指定されたURLのCSVを取得し、文字コードをShift-JISからUTF-8にに変換して出力します。
*/
const path = require('path');
const fs = require('fs-extra');
const fetch = require('node-fetch');
const parse = require('csv-parse/lib/sync');

module.exports.generate = async (resource) => {
    // ファイル名を生成
    const file = path.basename(resource, '.csv') + '.json'
    // 指定されたURLのCSVを取得
    const response = await fetch(resource)
    const buffer = await response.arrayBuffer()
    // CSVの文字コードをShift-JISからUTF-8にに変換
    const decoder = new TextDecoder("Shift_JIS")
    const csv = decoder.decode(buffer)
    // CSVをJSONに変換
    const json = await parse(csv, { columns: true, trim: true })
    // JSONを出力
    const result = await fs.outputJson(path.join('dist', file), json, { spaces: 4 })
    return result
};
樹里「まず、node-fetchでCSVを取得して、Shift-JISからUTF-8に変換する」
絵子「へー、TextDecoderっていうので文字コードを変換できるんだね」
樹里「で、csvというライブラリのcsv-parseという機能を使って、CSVをJSONに変換しているわけだ」
絵子「便利なライブラリだねー」

樹里「さて、処理の結果、このようなJSONが出力される」
[
    {
        "行": "あ",
        "音": "あ",
        "町名": "在田町",
        "読み": "あいだ",
        "燃える": "火･金",
        "燃えない": "2･4木",
        "プラスチック製容器包装": "月",
        "カン": "1･3水",
        "ビン": "4水",
        "ペットボトル": "2水",
        "ダンボール": "3水",
        "蛍光灯": "4木",
        "キーワード": "清水",
        "備考": "清水南"
    },
    // 以下略
絵子「これ、キーが日本語になってるけど問題ないの？」
樹里「ああ、仕様に則った正しいJSONだぞ」
絵子「へー、そうなんだ」
樹里「なにより、Shift-JISのCSVよりははるかに扱いやすい」
絵子「よっぽどキライなんだね」

樹里「……さて、無事にShift-JISのCSVをJSONに変換できた」
絵子「めでたしめでたし、だね」
樹里「いやいや、データの形式を変換しただけで、何も出来上がってないぞ。大事なのは、このデータを使ってどんなアプリを作るかだ」
絵子「そりゃそうだ。さ、次はアプリ制作に挑戦だ！」

Author

8amjp

　 Tweet
Qiitaで続きを読む

投稿日：2020-03-28T20:26:59+09:00

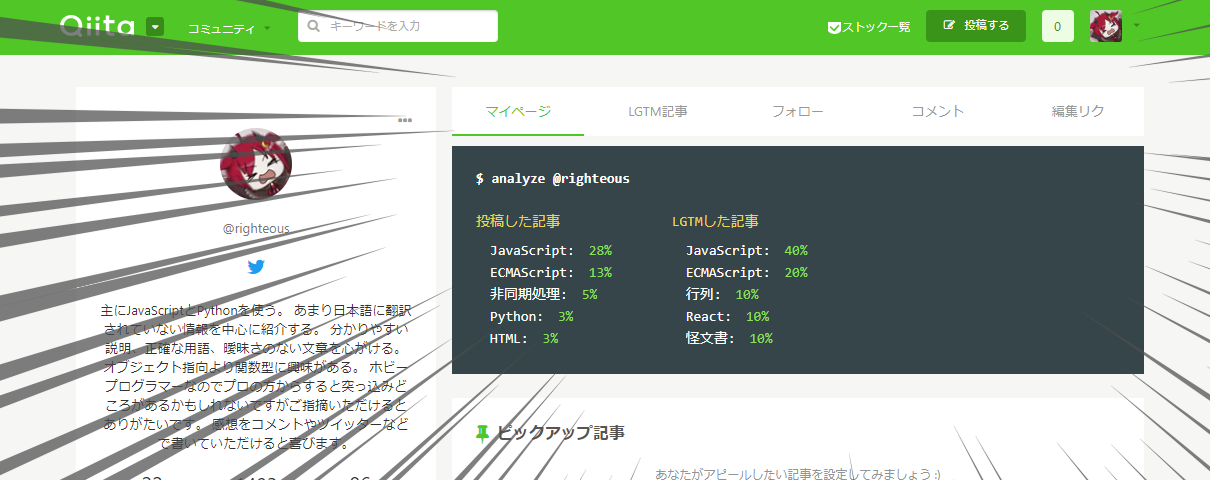
Qiitaのユーザーページにナビゲーションタブを追加するUserScript作った

現状ではユーザーの「LGTMした記事」「フォローしているユーザー」「コメント」「編集リクエスト」を見るためにはいちいち「...」ボタンをクリックしなければいけない。これは面倒なので、より快適に閲覧できるようにナビゲーションタブを追加するUserScriptを作成した。

インストールにはUserScript管理用の拡張機能が必要。

Chrome: Tampermonkey
Firefox: Tampermonkey, Greasemonkey

// ==UserScript==
// @name         Qiita User Page Nav
// @namespace    https://qiita.com/righteous
// @version      0.1
// @description  Adds an navigation tab on user pages
// @author       righteous
// @match        https://qiita.com/*
// @grant        none
// ==/UserScript==

!(function () {
  const targetClassPrefixes = [
    'UserMain__ContentsContainer',
    'UserLgtms__ContentsContainer',
    'UserFollowees__ContentsContainer',
    'UserComments__ContentsContainer',
    'UserEditRequests__ContentsContainer',
  ]

  const selector = targetClassPrefixes.map(c => `[class^="${c}"],[class*=" ${c}"]`).join(',')
  const containerDOM = document.querySelector(selector)
  if (!containerDOM) return

  const [username, curPage = ''] = window.location.pathname.split('/').filter(s => s)
  if (!username) return

  const pages = [
    { path: '', label: 'マイページ' },
    { path: 'lgtms', label: 'LGTM記事' },
    { path: 'following_users', label: 'フォロー' },
    { path: 'comments', label: 'コメント' },
    { path: 'edit_requests', label: '編集リク' },
  ]

  const nav = document.createElement('div')
  nav.classList.add('qiita-user-page-nav')

  for (const page of pages) {
    const linkDOM = document.createElement('a')
    linkDOM.classList.add('ol-ItemList_tabItem')
    if (curPage === page.path) {
      linkDOM.classList.add('is-active')
    }
    linkDOM.textContent = page.label
    linkDOM.href = `/${username}/${page.path}`
    nav.appendChild(linkDOM)
  }
  containerDOM.insertBefore(nav, containerDOM.firstChild)

  const styleDOM = document.createElement('style')
  styleDOM.textContent = `
  .qiita-user-page-nav {
    background-color: white;
    display: flex;
    padding-top: 15px;
    margin-bottom: 10px;
  }

  @media (max-width: 770px) {
    .qiita-user-page-nav .ol-ItemList_tabItem {
      font-size: 8px;
    }
  }
  `
  document.head.appendChild(styleDOM)
})()

　 Tweet
Qiitaで続きを読む

投稿日：2020-03-28T20:17:26+09:00

Google Maps API で近くの目的地までの距離を取得するアプリケーションの作成

はじめに

Google マップで現在位置から目的地までの距離を取得するアプリケーションのつくり方を紹介します。要件は現在位置の取得、現在位置から店舗までの距離の取得やマッピングを行ないます。今回のアプリケーションの作成にあたり、Google Cloud Platform¹（以下、GCP という）を利用できる Google アカウントがあらかじめ必要になります。また、GCP のサービスの中で Google Maps Platform を利用しますので、Google Maps Platform の有効化を事前に行なってください。早速ですが、先述した要件をもとに以下の手順で作成します。

現在位置の取得

現在位置から目的地までの距離の取得

マッピング

また、今回作成するサンプルコードは GitHub にアップロードしています。併せてご活用ください。

現在位置の取得

現在位置の取得には、Geolocation API を利用します。Geolocation API は、ユーザーの同意のもと、現在位置をウェブアプリケーションに通知できます。しかしながら、多くのブラウザで Geolocation API を利用するには、安全なコンテキスト ( HTTPS ) でなければいけません。ローカル開発環境において、常時 SSL 化するには Browsersync² が便利です。以下のコマンドを実行して、Browsersync をインストールしましょう。
$ npm install browser-sync --save-dev
無事にインストールが完了すれば、以下のコマンドを実行してローカルサーバーを立ち上げましょう。
$ npx browser-sync start --server --https
ローカル開発で SSL が有効になっているので、問題なく Geolocation API が利用できます。Local と External が起動したローカルサーバーの URL になります。余談ですが、同じネットワーク環境下にある PC やスマートフォンのブラウザから External URL にアクセスすれば、すべてのブラウザで同期されます。では、Geolocation API の getCurrentPosition() メソッドを呼び出して、現在位置を取得しましょう。こちらのメソッドは非同期通信で情報を取得するため、このあとの処理を async / await 式で非同期処理を書けるように Promise を返しましょう。
main.js
const getCurrentPosition = () => {
  if ('geolocation' in navigator) {
    return new Promise((resolve, reject) => {
      navigator.geolocation.getCurrentPosition(resolve, reject);
    });
  }
};
たとえば、以下のような即時関数を実行すれば現在地の緯度経度を確認できます。
(async () => {
  const currentPosition = await getCurrentPosition();
  const {
    coords: { latitude, longitude }
  } = currentPosition;

  console.log({latitude}, {longitude}); // => {latitude: xx.xxxxxxxx}, {longitude: xxx.xxxxxxxx}
})()
現在位置から目的地までの距離の取得

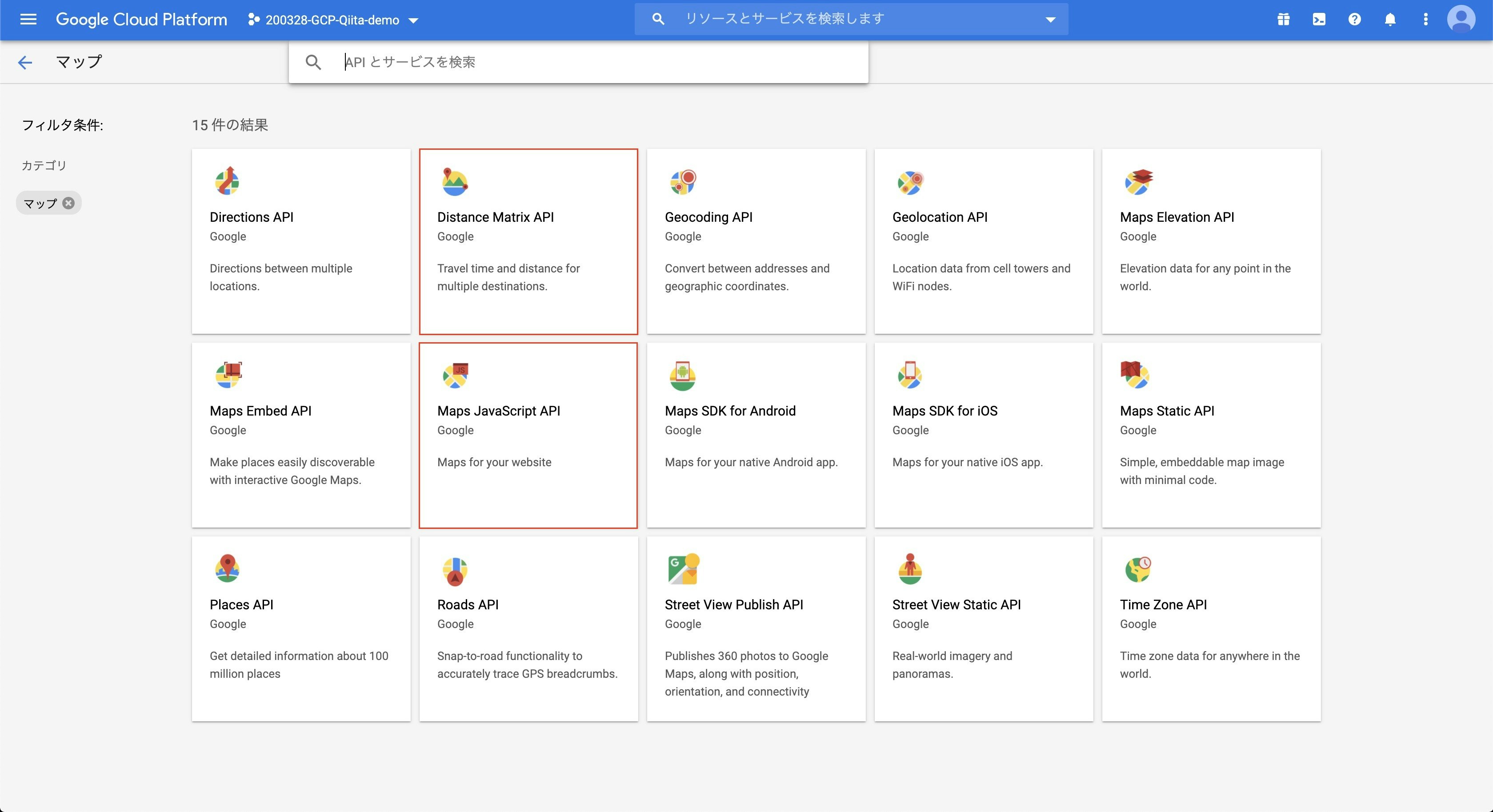
複数の出発地と目的地間の移動距離を取得するには、Maps JavaScript API の Distance Matrix Service を利用します。まずは、Distance Matrix Service を使用できるようにしましょう。Google Cloud Platform の各種画面から新規プロジェクトを作成しましょう。次に API ライブラリ画面から Maps JavaScript API と Distance Matrix Service を有効にしましょう。

認証情報画面から API キーを作成しましょう。本番環境での不正利用を回避するため、かならずキーを制限してください。たとえば、HTTP リファラーでアプリケーションの制限をすれば、指定した Web サイト以外で API キーを利用できません。<script> 要素で Maps JavaScript API を以下のように読み込ませましょう。GOOGLE_MAPS_API_KEY には先ほど作成した API キーを指定します。
index.html
<script src="https://maps.googleapis.com/maps/api/js?key=GOOGLE_MAPS_API_KEY"></script>
これで Maps JavaScript API、および、Distance Matrix Service を利用できます。試しに google.maps.DistanceMatrixService コンストラクタを介してインスタンスを作成してみましょう。無事に作成できたら API が正しく読み込まれています。
main.js
const service = new google.maps.DistanceMatrixService();
console.log({service}); // => インスタンス
それでは、本題の現在位置から目的地までの距離を取得する開発を行ないます。今回のサンプルは『食べログラーメン百名店 WEST 2019』に選ばれたラーメン屋さんの位置情報を用意しました。
ramen_deta.json
[
  {
    "id": "001",
    "name": "燃えよ麺助",
    "latLng": {
      "lat": 34.696335,
      "lng": 135.48689
    }
  },
  {
    "id": "002",
    "name": "人類みな麺類",
    "latLng": {
      "lat": 34.725463,
      "lng": 135.499181
    }
  },
  {
    "id": "003",
    "name": "ラーメン人生JET",
    "latLng": {
      "lat": 34.698637,
      "lng": 135.486647
    }
  },
  {
    "id": "004",
    "name": "総大醤",
    "latLng": {
      "lat": 34.710304,
      "lng": 135.507695
    }
  },
  {
    "id": "005",
    "name": "ラーメン家 みつ葉",
    "latLng": {
      "lat": 34.692421,
      "lng": 135.731966
    }
  }
]
では、現在位置から各店舗の距離を返す fetchDistanceMatrix() メソッドを作成しましょう。少し長くなりますが、一行一行のコードを読めば大してむずかしくないかと思います。travelMode の DRIVING は、時間と距離を計算するときに使う交通手段の指定です。DRIVING は、道路網を使用した標準の運転ルートになります。ほかのオプションの詳しい内容は公式ドキュメントをご参照ください。
main.js
const fetchDistanceMatrix = async () => {
  // 現在位置情報の取得
  const currentPosition = await getCurrentPosition();

  // ラーメンデータの取得
  const ramenData = await fetch('ramen_data.json').then(response =>
    response.json()
  );

  // 緯度経度の取得
  const {
    coords: { latitude: lat, longitude: lng }
  } = currentPosition;

  // インスタンスの作成
  const service = new google.maps.DistanceMatrixService();

  // ラーメン各店舗の緯度経度の取得
  const destinations = ramenData.map(({ latLng }) => latLng);

  // DistanceMatrixService.getDistanceMatrix() メソッドのオプション
  const options = {
    origins: [{lat, lng}], // 出発地
    destinations, // 目的地
    travelMode: 'DRIVING' // 交通手段
  };

  return new Promise((resolve, reject) => {
    service.getDistanceMatrix(options, (response, status) => {
      if (status === 'OK') {
        const { rows } = response;
        const { elements } = rows[0];
        resolve(elements);
      } else {
        reject(status);
      }
    });
  });
};
マッピング

Maps JavaScript API を利用して Google マップ（以下、地図という）を作成します。まずは、地図を埋め込むための HTML 要素の用意、地図をブラウザ全画面に描画するようなスタイルを作成しましょう。
index.html
<style>
  #map {
    height: 100%;
  }
  html, body {
    height: 100%;
    margin: 0;
    padding: 0;
  }
</style>



<div id="map"></div>
HTML の準備が完了したので、現在位置が中央になるように地図を作成しましょう。また、各ラーメン店舗を現在位置から近い順にラベリングしたマーカーを作成しましょう。マーカーの作成には、google.maps.Marker コンストラクタを実行します。
main.js
const initMap = async () => {
  const currentPosition = await getCurrentPosition();
  const ramenData = await fetch('ramen_data.json').then(response =>
    response.json()
  );
  const distanceMatrix = await fetchDistanceMatrix();
  const {
    coords: { latitude: lat, longitude: lng }
  } = currentPosition;
  const embedElement = document.getElementById('map');
  const options = {
    center: { lat, lng },
    zoom: 12
  };

  // ラーメンデータに距離情報の設定します
  ramenData.map((data, i) => {
    data.distanceMatrix = distanceMatrix[i];
  });

  // ラーメンデータを距離の昇べきの順でソートします
  ramenData.sort((a, b) => {
    return a.distanceMatrix.distance.value - b.distanceMatrix.distance.value;
  });

  // 地図の描画
  const map = new google.maps.Map(embedElement, options);

  // マーカーの作成
  ramenData.map(({ latLng }, i) => {
    const label = (i + 1).toString();
    const options = {
      position: latLng,
      label,
      map
    };
    const marker = new google.maps.Marker(options);
  });
};

google.maps.event.addDomListener(window, 'load', initMap);
少し駆け足になりましたが、一通り完成です。現在位置から近い順にラベリングされたマーカーが作成された地図が描画されているかと思います。

さいごに

今回は、現在位置の取得、現在位置から店舗までの距離の取得やマッピングにおける Google Maps API の使い方を中心に解説しました。ここまで習得できれば、あとは、React や Vue.js のような宣言的な View を構築できるライブラリと合わせてアプリケーションを作成できるかと思います。

Google Cloud Platform とは、Google が提供しているクラウドコンピューティングサービスです。 ↩

Browsersync は、ファイル変更の監視やブラウザを自動でリロードするツールです。Web プラットフォーム、ビルドツール（e.g. gulp）、および、その他の Node.js プロジェクトとカンタンに統合できます。 ↩

　 Tweet
Qiitaで続きを読む

投稿日：2020-03-28T19:37:46+09:00

JavaScriptでAdobe Acrobatプラグイン開発

※この記事は文系的冗長性及び反知性的曖昧主義に支配されています¹。

プレ金を、きっかけに！

〜とあるプレミアムフライデー²の深夜〜

わたし「ふぅ、なんとか日付が変わる前に月曜朝の会議資料をPDF化できたぞ！……うん？」

ピロン！ピロン！ピロン！

上司Ａ「議題追加³するからPDFの先頭に加えておいて。他の資料番号とページ番号は振りなおしね。」
上司Ｂ「表紙にはページ番号振らないでって言ったよね？³」
上司Ｃ「資料番号のフォントは統一してって言ったよね？³」
同期達「今日の同期会³楽しかったね！写真を共有します！ウェーイ！」

わたし「ああああああああああああ（あぁあぁあぁああぁあぁああぁ

＿人人人人人人人人人人人人人人人人人人人＿
＞　サタデー・ナイト・フィーバー！！！　＜
￣Y^Y^Y^Y^Y^Y^Y^Y^Y^Y^Y^Y^Y^Y^Y^Y^Y^Y￣

月月火水木金金（プレミアム）

産業革命を経て人類に課せられた十字架、「雑務」「残業」を如何に減らすべきか。ゴルゴダの丘を登りきる前に、こんな社会は滅ぼしてしまいたいところですが、私は一介の文系事務職員です。生まれながらにイチジクの葉を装備しているため、尊大な羞恥心がそれを邪魔します。臆病な自尊心を少しでも満たすべく、可能な限り作業を省力化する方向で頑張るしかありません。

具体的には、JavaScript（Adobe Acrobat SDK）を使ってプラグイン（Folder Level JavaScript File）Watashiwa Kaigi Skiskyを作成し、資料作成に係る一部の作業を自動化しました。この記事は、コードの解説とプラグイン作成のコツを記すものです。ちなみに冒頭の茶番はフィクションです。特定しないで。

軽業師とジャポネズリー

弊社において会議は複数の議題からなり、その資料は以下の要件を満たす必要があります。~~会議資料なんて読めれば何でも良いのでは~~ 日本らしい細やかな気遣いが光りますね。

資料はWordファイル、Excelファイル、PowerPointファイル、PDFを結合して作成する。

ページ番号は議題ごとではなく、全資料を通して右下側に小さく付番する。ただし、表紙には付番せず2枚目を1ページ目とし、書式は「1 / n」とする。

機密性及び共有範囲を資料の左上に小さく表示する。

資料番号は資料の右上に大きく表示し、枠線で囲む。

会議ごとに同じパスワードをかける。

VBAやWindowsバッチで解決することもできますが、せっかくなので未体験のAdobe Acrobat SDKを使うことにしました。具体的には、Adobe Acrobatの標準機能で1.を行ったのち、自作のコードにて2.〜5.の定型作業を自動化します。設定画面の表示と文書の操作、セキュリティの設定ができれば良さそうです。

Super Great Ganbari development Kit

2020年3月プレミアムフライデー現在、最新版であるAdobe Acrobat DC⁴上で作業を自動化する方法として、主に以下が挙げられます。

アクションウィザードでAcrobat上のバッチ処理を行う

デバッガー・コンソールでJavaScriptを実行する

Document Level JavaScriptを書く

Folder Level JavaScript Fileを作成する

C++やC#からAdobe Acrobat SDKを触る

プログラミングしない1.は論外⁵。2.は、デバッガー・コンソールの立ち上げとコードのコピペが面倒なのが単純にして最大の欠点。3.は、個別のExcelファイル内に保存したマクロ（VBA）のようなもので、新規作成した文書だと設定なしには実行できず、後述するセキュリティ設定もできないため却下。4.は、特定の場所に.jsファイルを置くだけでメニューの追加やダイアログの表示が可能なため、他の事務職員が使用する際の敷居を下げることができます。ちなみに5.は、弊社ではコンパイラのインストールが禁止されているため諦めました⁶。

漢は黙ってJavaScript。Windowsのメモ帳で書いたコードをalertデバッグ。古事記にもそう書かかれている。

基本編

※以下の記事は、JavaScripの基礎を習得済みの方を想定して書いています

日本語はもとより、英語の解説記事すら少ないため、命綱は公式ドキュメントです。当該ドキュメントは、ページの構成上、情報が非常に探しづらいです。「JavaScript」→「JavaScript for Acrobat API Reference」→「JavaScript API」と冗長な表示を辿った後は、気合で乗り切りましょう。なお、Windows版のAdobe Acrobatを使用する場合、日本語の文字コードはShift_JIS⁷です。

Adobe社「Acrobat DC SDK Documentation」

開発したFolder Level JavaScript File（.jsファイル）の設置場所は、デバッガーコンソールで下記のコマンドを実行して確認します。
app.getPath("app","javascript");
デバッガー・コンソールの使い方やFolder Level Scriptsに関する詳細な解説は下記の記事をご参照ください。ファイル名は拡張子さえ.jsなら何でも良いのですが、取り急ぎ「config.js」とします。

itaya yuichi氏「Adobe Acrobat proでJavaScriptを使って自動でPDFをExcelに変換した話」（Qiita記事、2018年5月）

「Instructions for Installing Folder Level Scripts (Automation Tools) and Plug-ins」⁸（pdfscripting.com）

なお、Folder Level Scriptsの使用のために特別な設定をする必要はありませんが、以下の手順でJavaScriptを有効化しておかないと警告文が表示されます。使用に差し支えはありませんが、見た目が悪いため、メニューの「編集」→「環境設定」から下記の設定を行いましょう。

Acrobat社「セキュリティリスクとしての PDF の JavaScript」（Adobe Acrobat マニュアル、2017年6月）

Folder Level Scriptsではグローバルオブジェクトとしてapp⁹が利用可能となっているため、例えば以下のコードでデフォルトメニューに自作の項目を追加することができます。
config.js
app.addSubMenu(ParentMenuConfig); //親メニューを追加
app.addMenuItem(RenumPagesMenuConfig); //子メニューを追加

const ParentMenuConfig = { //親メニューの設定
    cName: "Watashiwa Kaigi SkiSky", //親メニュー名（日本語不可）
    cParent: "Edit" //親メニューの表示箇所（日本語だと「編集」メニュー）
}

const RenumPagesMenuConfig = { // 子メニューの設定
    cName: "Renumber Pages", //子メニュー名
    cParent: "Watashiwa Kaigi SkiSky", //親メニュー名
    cExec: "RenumPages()" //メニュークリック時に実行する関数
}
我らが同志、alert()もappのメソッドです。デバッガー・コンソールも使える心の広い方はconsole.println()もオススメです。

また、Folder Level Scriptsのトップレベルスコープのthisは、表示中のPDF文書に関するオブジェクトDoc¹⁰を指します。
const numPages = this.numPages(); //文書のページ数を取得
for (var i = numPages - 1; i >= 0; i--) { //ページを逆順に変更
    this.movePage(i);
}
なお、ファイル選択ダイアログはapp.browseForDoc()またはField.browseForFileToSubmit()で呼び出せますが、前者はPDFのみ、後者は全種類のファイルを選択できます。今回のコードでは使用していませんが、後者は気付きづらいので要注意。

文字追加編

例えばページ番号を追加する場合、以下のようなコードになります。
config.js
const boxWidth = 100;
const rect = doc.getPageBox("Bleed", p); //ページサイズを取得
const pageWidth = rect[2] - rect[0];
var f = doc.addField( //描画範囲を設定
    //第一引数：フィールド名（string）
    //第二引数：フィールドの種類（string）
    //第三引数：フィールドを追加するページ番号（number）
    //第四引数：表示位置（rect）
);
f.value = //略。表示する文字列。
f.fillColor = color.transparent; //背景色（ここでは透明）
f.textSize = 7.1; //文字サイズ
f.alignment = "right"; //表示位置（ここでは右揃え）
f.textFont = "HeiseiKakuGo-W5-UniJIS-UCS2-H"; //フォント（ここでは平成角ゴシック）
f.readonly = true; //読み取り専用
doc.addField()で文字表示用の領域を追加すると同時に描画用オブジェクトField¹¹を得ることができます。Fieldオブジェクトのプロパティを変更することで、その表示内容や様式を設定しています。

表示位置は4つの要素からなる配列rectで設定します。四角形の左下のX座標、Y座標、右上のX座標、Y座標（いずれも左上をゼロとした絶対値）で指定します。単位は"unit size"、デフォルトで”1 unit size = 72 inch”です。悪い文明¹²ですね。バグを生まないよう、下記のような換算関数を準備しておきましょう。
config.js
const unitsize2mm = (us, doc, page) => us * doc.getUserUnitSize(page) / 72 * 25.4;
const mm2unitsize = (mm, doc, page) => mm / 25.4 * 72 / doc.getUserUnitSize(page);
使用できるフォントは非常に限られており、日本語では平成明朝か平成角ゴシックになります。

AFormAut : Field.TextFont プロパティ（個人サイト、2015年5月）

PDFは印刷を前提としたフォーマットなので、一言で「ページサイズ」といっても様々な概念（Box）が存在します。上記では取り急ぎBleed Boxを使っていますが、沼に沈みたい方は他のBoxも調べてみてください。

PDF Page Boxes（ActivePDF Support、2019年4月）

Finding page boundaries（AcrobatUsers.com、2006年9月）

ダイアログ編

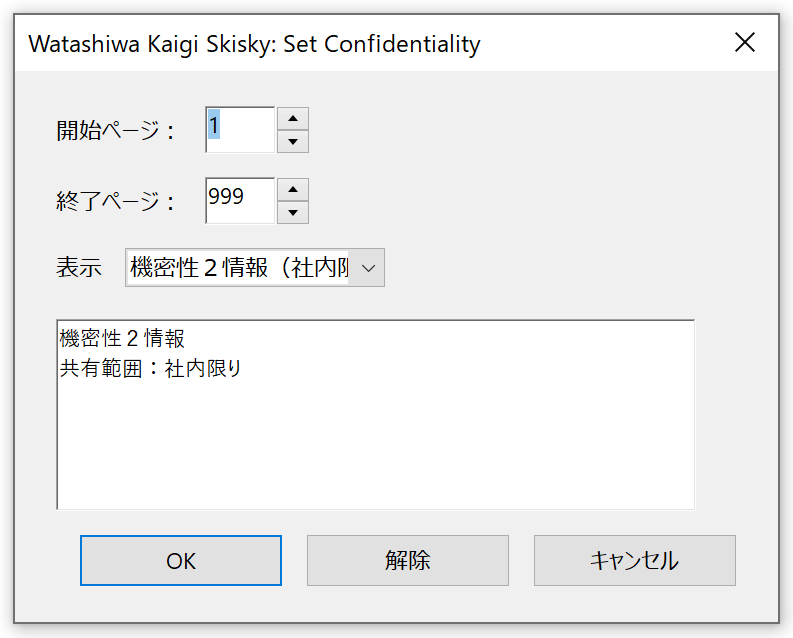
メニューを選択しただけで処理を走らせても良いですが、せっかくなので自動化処理の設定画面がほしいところ。というわけで処理前に設定ダイアログを表示します。
config.js
function RenumPages() {
    renumPagesDialog.doc = this;
    app.execDialog(renumPagesDialog);
}

var renumPagesDialog = {
    doc: null,
    initialize: dialog => {
        //ダイアログ作成時の処理
        dialog.load({
            //略。GUIパーツの初期値をここで指定。
        })
    },
    commit: function (dialog) {
        //略。「OK」を選択した際の動作
    },
    other: function (dialog) {
        //略。「その他」を選択した際の動作
    },
    description: {
        //略。GUIパーツをここに記述。
    }
};
app.execDialog()にDialog box handlersを渡してダイアログを表示します。Dialogオブジェクトのメソッド内でthisは当然Dialogとなるため、DocオブジェクトはDialog box handlersに仕込んでおきましょう。ダイアログ内の各種メソッドの中からでも表示中の文書を示すDocオブジェクトを触れるようになります。

ダイアログに表示するフォームはdescriptionに記載します。配置から文字設定まで独自構文です。幸い、ドキュメントのサンプルが非常に充実しています。レイアウト周りの設定が未だによく分かりませんが、気合で読んで、雰囲気で動かしましょう¹³。

なお、フォームにitem_id（4文字からなる一意の文字列）を設定し、同名のメソッドをDialog box handlersに登録しておけば、フォームに入力や変更があったような場合に毎回呼び出されます。

セキュリティ編

毎回資料に手打ちでパスワードをかけると、タイプミスにより二度と開けないゴミが完成する可能性があります（３敗）。したがって、事前にパスワードに関するセキュリティポリシーを作成しておき、それを適用することにします。
config.js
var setDocSecDialog = {
    doc: null,
    initialize: dialog => getSecPoli(dialog),
    commit: function (dialog) {
        setSecPoli(dialog.store(), this.doc);
    },
    other: dialog => {
        editSecPoli(); //セキュリティポリシー設定画面（Adobe製）を表示
        getSecPoli(dialog);
    },
    description: {
        //略
    }
}

//設定可能なセキュリティポリシー一覧をtrustedFunctionで取得
const getSecPoli = app.trustedFunction(function (dialog) {
    app.beginPriv();
    dialog.load({
        "poli": security.getSecurityPolicies() //登録済みのセキュリティポリシー一覧を取得
            .filter(sp => sp.policyId !== "SP_PKI_default" && sp.policyId !== "SP_STD_default")
            .reduce((map, sp) => {
                map[sp.name] = sp.policyId;
                return map;
            }, {})
    })
    app.endPriv();
});

//セキュリティポリシーをtrustedFunctionでセット
const setSecPoli = app.trustedFunction(function (results, doc) {
    app.beginPriv();
    const aPols = security.getSecurityPolicies();
    const oMyPolicy = aPols
        .filter((aPol, i) => results["poli"][aPol.name] > 0)
        .pop(); //ダイアログで選択したセキュリティポリシーを取得
    if (oMyPolicy) { //セキュリティポリシーを適用
        const rtn = doc.encryptUsingPolicy({ oPolicy: oMyPolicy });
        //略（エラー処理）
    }
    app.endPriv();
});
セキュリティポリシーに関する設定や適用は、文字通りセキュリティ上の問題が生じるため、Folder Level Scriptsのトップレベルスコープから呼び出されたapp.trustedFunction()内でなければ動作させることができません。開始時にapp.beginPriv()を、終了時にapp.endPriv()を忘れないようにしましょう。

Using Trusted Functions（pdfscripting.com）

余談

null安全教の信者である私はTypeScriptの採用も検討しましたが、型定義ファイルの作成に痺れて断念。ちなみに、私のTypeScriptのイメージに最も近いのは以下のツイート。

先生「お型付けしましょうね～」
園児「はーい！」
「any」
「AnyRef」
「Object」
— ザ・世界草原ニュース (@shikamiya) December 6, 2019

Programmierung macht frei

穴を掘っては埋めるだけのような無味乾燥な毎日に潤いを与えるのは、ほんの少しのスパイスです。死んだ魚のような目で単純作業を続けるのではなく、新手一生をスローガンに、これからも知らない言語やSDKに人知れずチャレンジし続けたいと思います。

良い記事を書くためのガイドライン？知らんなぁ……。 ↩

2020年2月頃までは虫の息ながら続いていたプレミアムフライデーですが、昨今の新型コロナウイルス騒ぎにより完全にトドメを刺されたようです。2020年3月28日現在、「次回のプレミアムフライデーは3/27」という表示のままとなっています。 ↩

聞いてない ↩

Adobe Acrobat Reader DCではない点に注意 ↩

それは乙女的にNO! そのような選択肢はNO! 退路は無い!! ↩

弊社さんは……そうやって私が欲しいものを全て奪っていくんですね ↩

この女はやはり…… 何の躊躇いもなくShift_JISに躰を預ける性欲の化身文字コードを食い物としか見ていない下賤の女なんだわ…… ↩

記事で解説されている "user" フォルダはデフォルトでは存在しないようです。 ↩

appのプロパティとメソッドについてはドキュメント参照 ↩

Docのプロパティとメソッドについてはドキュメント参照 ↩

Fieldのプロパティとメソッドについてはドキュメント参照 ↩

「ヤード・ポンド法は悪い文明!! 粉砕する!!」「ヤード・ポンド法を滅ぼそう！」 ↩

「よくわからんが、まぁ動いてるからヨシ!」 ↩

　 Tweet
Qiitaで続きを読む

投稿日：2020-03-28T19:17:40+09:00

転職したいのでReact + Netlify + microCMSを使ってイケてるポートフォリオを作った

本記事でやること

Reactを使ったフロントエンド開発を、今時のサービスを使って簡単に効率よくできる方法を紹介します。
また、ポートフォリオの設計に関してや実装から得られたナレッジ、知っておいたほうがいい実装方法を紹介します。
私のポートフォリオはNetlifyのサーバーに上げているので、実際の挙動などは https://ykonishi.tokyo から確認できます。

ちなみにポートフォリオのソースコードはGitHubにも上げているので、こちらも見ていただけたらと思います。
Yuichi Konishiポートフォリオサイトのソースコード

Reactとは

最近はよくSPA（Single Page Application）という言葉をよく耳にしますが、そのSPAの一つがReactです。
特徴としては、データバインディング、仮想DOM、Componentの3つがあります。
詳細については各リンクを参照してください。

Netlifyとは

Netlifyは静的サイトのホスティングサービスです。
GitHubやGitLabとも簡単に連携ができるので自動デプロイやJSやAPIを必要としないフォームの作成ができるほか、Netlify Functionsで最近流行りのサーバーレス開発もできるなどフロントエンド開発には十分な機能が揃っています。
ちょっとしたサイトを公開する程度であれば無料枠で使えるので、いろいろなサイトで利用されているのをよく目にします。

microCMSとは

microCMSはウォンタ株式会社が提供するヘッドレスCMSです。
ウォンタ株式会社は過去に話題になったOsushiという投げ銭サービスを運営していた会社ですね
microCMSは管理画面から入稿したデータをAPI経由で取得できるので、開発者はフロントエンドに専念することができます。
スキーマの定義はユーザーが自由に登録でき、テキストフィールドやテキストエリアはもちろん、リッチエディタや他コンテンツを参照しに行くようなフィールド定義もできます。
こちらのサービスも無料プランがあるのでちょっとしたことを始めるのには十分いいかもしれません。

設計

ページ構成

ページはHome、Profile、Works、Secret Works（鍵をかけたページ）Contactの5つです。

基本的には名前のとおりのコンテンツが入っていますが、各ページの役割はこのような感じです。

HOME：ホーム
Profile：プロフィールページ
Works：実績ページ
Secret Works：パスワード必須の実績ページ
Contact：お問い合わせページ

コンテンツ

profileやworksなどのコンテンツはmicroCMSで管理し、API経由でデータを取得・表示させます。

デプロイ

デプロイはGitHubとNetlifyを連携することで特定のブランチがアップデートされたら実行されるようにします。
また、環境変数も同時に追加されるように設定します。

フォーム

フォームはNetlify FormsというNetlifyの優れたフォーム機能があるので、こちらを使います。
Netlify FormsはSlackとの連携や登録したメールへの通知機能もあるので非常に便利です。

クラス名とCSS

クラス名にはBEM記法を用いることにしました。
ReactにBEMは時代遅れな気もしますが、ページの量が少ないのと手短に実装したかったのでBEMを採用し、CSSで実装しました。

ちなみにReactでCSSを使うときはカプセル化するかモジュール化するかの2通りから選ぶのがベターです。

これからのReactのスタイリングにはStyled Componentsが最高かもしれない
 CSSモジュール ― 明るい未来へようこそ

デザイン

カラー

ベースカラーを黒にし、アクセントカラーにロイヤルブルーを入れることでクールで落ち着いた印象に仕上げました。

フォント

フォントは筑紫ゴシックをを用いることでモダンかつシャープな印象を与え、クールに加え美しさを表現しました。

巨大なタイポグラフィ

2020年は巨大なフォントのテキスト配置がトレンドになるそうなので入れてみました。

出処はこちらです
2020年に流行するWebデザインの最新トレンド14個まとめ

参考
https://ykonishi.tokyo/works/xgCARmagX

React実装のナレッジ

React実装にはCreate React Appを使いました。
Reactを使い始めるときのデファクトスタンダードですね。

環境変数

Create React Appには環境変数を提供するためのパイプラインが存在します。
使い方は、React環境が入っているディレクトリ直下に.envファイルを作成し、下記のように設定を書き込んできます。
.env
REACT_APP_API_KEY="xxxxxxxxxxxx"
必ずREACT_APP_を頭に付けてください。

呼び出すときは下記のようになります。
process.env.REACT_APP_API_KEY
React環境をgitで管理する際は、必ず.gitignoreに.envを追記しておくことを忘れないでください。
.envファイルには公にしたくない情報も含まれるので、ホスティングに上げないようにしておきたいからです。

クリーンアップ処理

ReactでAPI処理を走らせるとき、APIが走っているのにもかかわらずページが変わってしまい下記のような警告がでる場合があります。
Warning: Can't perform a React state update on an unmounted component. This is a no-op, but it indicates a memory leak in your application. To fix, cancel all subscriptions and asynchronous tasks in a useEffect cleanup function.
こういった警告が出るときはクリーンアップという処理が必要で、実装はこのようになります。
useEffect(() => {
  let cleanedUp = false;
  const url = new URL('https://xxxxx.com);
  url.pathname = '/api/v1/profile'
  fetch(url)
  .then(res => res.json())
  .then(res => {
    if (!cleanedUp) setProfile(res)
  })
  .catch(error => {
    console.log(error)
  })

  const cleanUp = () => {
    cleanedUp = true;
  };
  return cleanUp;
}, []);
クリーンアップはuseEffect内で使用します。
useEffectはアンマウントされるタイミングでreturn処理が走るので、return cleanUpとすることでアンマウント時にcleanedUp変数がtrueになりprofileが更新されずに済みます。

HTMLコードの有効化

HTMLコードをAPIで取得してそのまま表示するとき、そのままではHTMLタグごと表示されてしまうのでdangerouslySetInnerHTMLというのを使ってHTMLに変換させる必要があります。

実装はこのようになります。
<div
  dangerouslySetInnerHTML={{
    __html: profile.biography
  }}
/>
名前にdangerousとあるように、XSS（クロスサイトスクリプティング）の引き金にもなる可能性があるので使わなくて済む場合は使わないことが推奨されています。

遷移時のページ位置

ReactのようなSPAはページが一から読み込まれるのではなく、一部のDOMが更新されるだけなので遷移時にページ位置が変わることがありません。
ですので、ページが変わったら位置をTOPに戻してやる必要があります。
ScrollToTop.jsx
const ScrollToTop = () => {
  window.scrollTo(0, 0);
  return null;
};
export default ScrollToTop;
このコンポーネントはルーティングの箇所に入れておくことで位置の切り替えができます。
Router.jsx
const Router = () => {
  return (
    <BrowserRouter>
      <Route component={ScrollToTop} />
      <Switch>
        <Route exact path="/" component={Home} />
        <Route exact path="/profile" component={Profile} />
      </Switch>
    </BrowserRouter>
  );
};
NotFoundページ

NotFoundページの表示は、ルーティングをひと工夫することで実現させることができます。
Router.jsx
const Router = () => {
  return (
    <BrowserRouter>
      <Route component={ScrollToTop} />
      <Switch>
        <Route exact path="/" component={Home} />
        <Route exact path="/profile" component={Profile} />
        <Route path="*" component={NotFoundPage} />
      </Switch>
    </BrowserRouter>
  );
};
NotFoundPageコンポーネントはどのパスにも当てはまらなかった場合に表示するように一番下に設置し、path="*"とします。
また、必ず一つのコンポーネントが表示されるようにしておかないとNotFoundPageも一緒に表示されてしまうのでSwitchで囲っておきます。

ローディング

ローディングはreact-spinnersというバリエーション豊富で便利なプラグインがあるので、そちらを使いました。
導入も簡単なのでおすすめです。

参考
React Spinners

フォーム作成

フォームはNetlify Formsというのを使うことで簡単に実装できます。

通常のHTMLでは下記のようなコードを入れるだけでいいのですが、Reactの場合はpublic/index.htmlなどにもう一つ別のフォームを入れる必要があります。
Netlifyボットがhtml拡張子以外のファイル内にある、フォームの設定を見に行けないためです。
contact.jsx
<form className="contact-form" name="contact" method="post">
  <input type="hidden" name="form-name" value="contact" />
  <label>
    お名前<span className="required-attention">(必須)</span>
    <input className="contact-form__input" type="text" name="username" required/>
  </label>
  <label>
    Email<span className="required-attention">(必須)</span>
    <input className="contact-form__input" type="email" name="email" required/>
  </label>
  <label>
    会社名
   <input className="contact-form__input" type="text" name="company"/>
  </label>
  <label>
   本文<span className="required-attention">(必須)</span>
   <textarea className="contact-form__textarea field__textarea" name="message" required></textarea>
  </label>
  <button className="contact-form__submit" type="submit">送信</button>
</form>
追加する別のフォームは下記のようになります。
contact.jsxで入れたフィールドはこちらにも必ず追加してください。属性はtypeとnameだけで十分です。
public/index.html

<form name="contact" netlify netlify-honeypot="bot-field" hidden>
  <input type="text" name="name" />
  <input type="email" name="email" />
  <input type="text" name="company" />
  <textarea name="message"></textarea>
</form>
詳しくはこちらを見ていただければと思います。
https://www.netlify.com/blog/2017/07/20/how-to-integrate-netlifys-form-handling-in-a-react-app/

メニュー

メニューはreact-springを使って実装しました。

独自仕様が多いので使いこなすのには少し時間がかかります。
react-springはReactでアニメーションを表現するためのプラグインで、Hooks用のプラグインでスポンサーやコントリビューターも充実しているのでHooks時代のデファクトスタンダードになるかもしれません。(もうすでにそうなっているかも )

参考
React Spring

最後に

React + Netlify + microCMSを試しに使ってポートフォリオを作ってみた結果、データ管理やサーバーのことをほとんど考えずにフロントエンドに専念できました。

microCMSについては今回初めて使ってみましたが、スキーマを自分で定義してカスタマイズできるほか、RDBのようにほかのコンテンツ（テーブルのようなもの）を参照しに行く定義もできるので非常に使い勝手が良かったです。
メンバーの権限管理機能やほかサービスとのデータ連携機能もあるので、仕事で使うのにもいいかもしれません。

Web制作で頭を悩ましがちなお問い合わせページでは、Netlifyにある便利なフォーム機能があったおかげで一瞬で片付きました。
Webhooks連携や登録したメールアドレスへの通知機能があるのは嬉しいポイントです。

デザイン周りではなるべくシンプルにし、行間、テキストの両端揃え、フォントにも気を配りました。
また、質素な見た目にちょっとした動きを与えているので、飽きさせない工夫も取り入れました。

フロント面でもバックエンド面でもなかなかイケてるポートフォリオサイトが出来上がったのではないでしょうか。

私自身フロントエンド開発に疎いので、ご意見やアドバイスなどあれば大歓迎です！

Yuichi Konishiポートフォリオサイト

参考

Netlify
microCMS

　 Tweet
Qiitaで続きを読む

投稿日：2020-03-28T19:17:40+09:00

転職活動始めるのでReact + Netlify + microCMSを使ってイケてるポートフォリオを作った

本記事でやること

Reactを使ったフロントエンド開発を、今時のサービスを使って簡単に効率よくできる方法を紹介します。
また、ポートフォリオの設計に関してや実装から得られたナレッジ、知っておいたほうがいい実装方法を紹介します。
私のポートフォリオはNetlifyのサーバーに上げているので、実際の挙動などは https://ykonishi.tokyo から確認できます。

ちなみにポートフォリオのソースコードはGitHubにも上げているので、こちらも見ていただけたらと思います。
Yuichi Konishiポートフォリオサイトのソースコード

Reactとは

最近はよくSPA（Single Page Application）という言葉をよく耳にしますが、そのSPAの一つがReactです。
特徴としては、データバインディング、仮想DOM、Componentの3つがあります。
詳細については各リンクを参照してください。

Netlifyとは

Netlifyは静的サイトのホスティングサービスです。
GitHubやGitLabとも簡単に連携ができるので自動デプロイやJSやAPIを必要としないフォームの作成ができるほか、Netlify Functionsで最近流行りのサーバーレス開発もできるなどフロントエンド開発には十分な機能が揃っています。
ちょっとしたサイトを公開する程度であれば無料枠で使えるので、いろいろなサイトで利用されているのをよく目にします。

microCMSとは

microCMSはウォンタ株式会社が提供するヘッドレスCMSです。
ウォンタ株式会社は過去に話題になったOsushiという投げ銭サービスを運営していた会社ですね
microCMSは管理画面から入稿したデータをAPI経由で取得できるので、開発者はフロントエンドに専念することができます。
スキーマの定義はユーザーが自由に登録でき、テキストフィールドやテキストエリアはもちろん、リッチエディタや他コンテンツを参照しに行くようなフィールド定義もできます。
こちらのサービスも無料プランがあるのでちょっとしたことを始めるのには十分いいかもしれません。

設計

ページ構成

ページはHome、Profile、Works、Secret Works（鍵をかけたページ）Contactの5つです。

基本的には名前のとおりのコンテンツが入っていますが、各ページの役割はこのような感じです。

HOME：ホーム
Profile：プロフィールページ
Works：実績ページ
Secret Works：パスワード必須の実績ページ
Contact：お問い合わせページ

コンテンツ

profileやworksなどのコンテンツはmicroCMSで管理し、API経由でデータを取得・表示させます。

デプロイ

デプロイはGitHubとNetlifyを連携することで特定のブランチがアップデートされたら実行されるようにします。
また、環境変数も同時に追加されるように設定します。

フォーム

フォームはNetlify FormsというNetlifyの優れたフォーム機能があるので、こちらを使います。
Netlify FormsはSlackとの連携や登録したメールへの通知機能もあるので非常に便利です。

クラス名とCSS

クラス名にはBEM記法を用いることにしました。
ReactにBEMは時代遅れな気もしますが、ページの量が少ないのと手短に実装したかったのでBEMを採用し、CSSで実装しました。

ちなみにReactでCSSを使うときはカプセル化するかモジュール化するかの2通りから選ぶのがベターです。

これからのReactのスタイリングにはStyled Componentsが最高かもしれない
 CSSモジュール ― 明るい未来へようこそ

デザイン

カラー

ベースカラーを黒にし、アクセントカラーにロイヤルブルーを入れることでクールで落ち着いた印象に仕上げました。

フォント

フォントは筑紫ゴシックをを用いることでモダンかつシャープな印象を与え、クールに加え美しさを表現しました。

巨大なタイポグラフィ

2020年は巨大なフォントのテキスト配置がトレンドになるそうなので入れてみました。

出処はこちらです
2020年に流行するWebデザインの最新トレンド14個まとめ

参考
https://ykonishi.tokyo/works/xgCARmagX

React実装のナレッジ

React実装にはCreate React Appを使いました。
Reactを使い始めるときのデファクトスタンダードですね。

環境変数

Create React Appには環境変数を提供するためのパイプラインが存在します。
使い方は、React環境が入っているディレクトリ直下に.envファイルを作成し、下記のように設定を書き込んできます。
.env
REACT_APP_API_KEY="xxxxxxxxxxxx"
必ずREACT_APP_を頭に付けてください。

呼び出すときは下記のようになります。
process.env.REACT_APP_API_KEY
React環境をgitで管理する際は、必ず.gitignoreに.envを追記しておくことを忘れないでください。
.envファイルには公にしたくない情報も含まれるので、ホスティングに上げないようにしておきたいからです。

クリーンアップ処理

ReactでAPI処理を走らせるとき、APIが走っているのにもかかわらずページが変わってしまい下記のような警告がでる場合があります。
Warning: Can't perform a React state update on an unmounted component. This is a no-op, but it indicates a memory leak in your application. To fix, cancel all subscriptions and asynchronous tasks in a useEffect cleanup function.
こういった警告が出るときはクリーンアップという処理が必要で、実装はこのようになります。
useEffect(() => {
  let cleanedUp = false;
  const url = new URL('https://xxxxx.com);
  url.pathname = '/api/v1/profile'
  fetch(url)
  .then(res => res.json())
  .then(res => {
    if (!cleanedUp) setProfile(res)
  })
  .catch(error => {
    console.log(error)
  })

  const cleanUp = () => {
    cleanedUp = true;
  };
  return cleanUp;
}, []);
クリーンアップはuseEffect内で使用します。
useEffectはアンマウントされるタイミングでreturn処理が走るので、return cleanUpとすることでアンマウント時にcleanedUp変数がtrueになりprofileが更新されずに済みます。

HTMLコードの有効化

HTMLコードをAPIで取得してそのまま表示するとき、そのままではHTMLタグごと表示されてしまうのでdangerouslySetInnerHTMLというのを使ってHTMLに変換させる必要があります。

実装はこのようになります。
<div
  dangerouslySetInnerHTML={{
    __html: profile.biography
  }}
/>
名前にdangerousとあるように、XSS（クロスサイトスクリプティング）の引き金にもなる可能性があるので使わなくて済む場合は使わないことが推奨されています。

遷移時のページ位置

ReactのようなSPAはページが一から読み込まれるのではなく、一部のDOMが更新されるだけなので遷移時にページ位置が変わることがありません。
ですので、ページが変わったら位置をTOPに戻してやる必要があります。
ScrollToTop.jsx
const ScrollToTop = () => {
  window.scrollTo(0, 0);
  return null;
};
export default ScrollToTop;
このコンポーネントはルーティングの箇所に入れておくことで位置の切り替えができます。
Router.jsx
const Router = () => {
  return (
    <BrowserRouter>
      <Route component={ScrollToTop} />
      <Switch>
        <Route exact path="/" component={Home} />
        <Route exact path="/profile" component={Profile} />
      </Switch>
    </BrowserRouter>
  );
};
NotFoundページ

NotFoundページの表示は、ルーティングをひと工夫することで実現させることができます。
Router.jsx
const Router = () => {
  return (
    <BrowserRouter>
      <Route component={ScrollToTop} />
      <Switch>
        <Route exact path="/" component={Home} />
        <Route exact path="/profile" component={Profile} />
        <Route path="*" component={NotFoundPage} />
      </Switch>
    </BrowserRouter>
  );
};
NotFoundPageコンポーネントはどのパスにも当てはまらなかった場合に表示するように一番下に設置し、path="*"とします。
また、必ず一つのコンポーネントが表示されるようにしておかないとNotFoundPageも一緒に表示されてしまうのでSwitchで囲っておきます。

ローディング

ローディングはreact-spinnersというバリエーション豊富で便利なプラグインがあるので、そちらを使いました。
導入も簡単なのでおすすめです。

参考
React Spinners

フォーム作成

フォームはNetlify Formsというのを使うことで簡単に実装できます。

通常のHTMLでは下記のようなコードを入れるだけでいいのですが、Reactの場合はpublic/index.htmlなどにもう一つ別のフォームを入れる必要があります。
Netlifyボットがhtml拡張子以外のファイル内にある、フォームの設定を見に行けないためです。
contact.jsx
<form className="contact-form" name="contact" method="post">
  <input type="hidden" name="form-name" value="contact" />
  <label>
    お名前<span className="required-attention">(必須)</span>
    <input className="contact-form__input" type="text" name="username" required/>
  </label>
  <label>
    Email<span className="required-attention">(必須)</span>
    <input className="contact-form__input" type="email" name="email" required/>
  </label>
  <label>
    会社名
   <input className="contact-form__input" type="text" name="company"/>
  </label>
  <label>
   本文<span className="required-attention">(必須)</span>
   <textarea className="contact-form__textarea field__textarea" name="message" required></textarea>
  </label>
  <button className="contact-form__submit" type="submit">送信</button>
</form>
追加する別のフォームは下記のようになります。
contact.jsxで入れたフィールドはこちらにも必ず追加してください。属性はtypeとnameだけで十分です。
public/index.html

<form name="contact" netlify netlify-honeypot="bot-field" hidden>
  <input type="text" name="name" />
  <input type="email" name="email" />
  <input type="text" name="company" />
  <textarea name="message"></textarea>
</form>
詳しくはこちらを見ていただければと思います。
https://www.netlify.com/blog/2017/07/20/how-to-integrate-netlifys-form-handling-in-a-react-app/

メニュー

メニューはreact-springを使って実装しました。

独自仕様が多いので使いこなすのには少し時間がかかります。
react-springはReactでアニメーションを表現するためのプラグインで、Hooks用のプラグインでスポンサーやコントリビューターも充実しているのでHooks時代のデファクトスタンダードになるかもしれません。(もうすでにそうなっているかも )

参考
React Spring

最後に

React + Netlify + microCMSを試しに使ってポートフォリオを作ってみた結果、データ管理やサーバーのことをほとんど考えずにフロントエンドに専念できました。

microCMSについては今回初めて使ってみましたが、スキーマを自分で定義してカスタマイズできるほか、RDBのようにほかのコンテンツ（テーブルのようなもの）を参照しに行く定義もできるので非常に使い勝手が良かったです。
メンバーの権限管理機能やほかサービスとのデータ連携機能もあるので、仕事で使うのにもいいかもしれません。

Web制作で頭を悩ましがちなお問い合わせページでは、Netlifyにある便利なフォーム機能があったおかげで一瞬で片付きました。
Webhooks連携や登録したメールアドレスへの通知機能があるのは嬉しいポイントです。

デザイン周りではなるべくシンプルにし、行間、テキストの両端揃え、フォントにも気を配りました。
また、質素な見た目にちょっとした動きを与えているので、飽きさせない工夫も取り入れました。

フロント面でもバックエンド面でもなかなかイケてるポートフォリオサイトが出来上がったのではないでしょうか。

私自身フロントエンド開発に疎いので、ご意見やアドバイスなどあれば大歓迎です！

Yuichi Konishiポートフォリオサイト

参考

Netlify
microCMS

　 Tweet
Qiitaで続きを読む

投稿日：2020-03-28T19:01:30+09:00

Javascript基本集(4)~DOM操作~

Javascript基本集(4)~DOM操作~

DOMとはDocument Object Model(ドキュメントオブジェクトモデル)の略称で、
HTMLを解析し、データを作成する仕組みのこと。

HTMLは階層構造になっており、DOMによって解析されたHTMLは、階層構造のあるデータとなる。
このことを、DOMツリーやドキュメントツリーと呼び、JavaScriptを使うとDOMツリーを操作してCSSを変更したり、要素を増やしたり、消したりすることが可能。
DOMツリーの一部のことを、ノードオブジェクトと呼ぶ。

ノードの取得

①document.getElementById("id名");

引数に渡したidを持つ要素を取得出来る。

②document.getElementsByClassName("class名");

同じclassを持つ要素を全て取得することが可能。

③document.querySelector("セレクタ名");

引数で指定したセレクタに合致するもののうち一番最初に見つかった要素1つを取得する。

イベント

HTMLの要素に対して行われた処理要求のこと。
「ノードオブジェクト」に「イベント」が起きた時、「関数」を実行出来る。
一つのイベントと一つの関数を紐付ける仕組みのことをイベントリスナと呼ぶ。

①addEventListener
(ノードオブジェクト).addEventListener("イベント名", 関数);
addEventListenerは、あるノードオブジェクトに対して、イベントリスナを追加するメソッド。

②window.onload

ブラウザは上から順に実行をするため、document.getElementById("id名")等のJavaScriptのコードを読み込む際、まだhtmlファイルのheadタグ内までしか読み込まれておらず、bodyタグ内にあるコードは読み込まれないので、ノードオブジェクトは取得できない。
ページの読み込みが終わったらjsの中身を実行するようにできるのが、window.onload。

例は２つ
window.onload = function() { 

  (ノードオブジェクト).addEventListener("イベント名", 関数); 

};
window.addEventListener('load', function() { 

  (ノードオブジェクト).addEventListener("イベント名", 関数);

 });
③innerHTML

innerHTMLを使用するとHTML要素の中身を書き換えることが出来る。
window.addEventListener("load", function() {

  // テキストの要素を取得し、変数で定義
  let btn = document.querySelector("#Button");
  let changeText = document.querySelector("p");
  // ボタンをクリックしたらテキストが置換される
  btn.addEventListener("click", function() {
    changeText.innerHTML = '変更されました';
  });

});
④classList.add

あらかじめ用意されているクラスを追加することが出来る。
// Buttonを取得して、変数で定義
let btn = document.querySelector("#Button");

// クラス追加を押したらクラスが追加される
btn.addEventListener("click", function() {
  changeText.classList.add("クラス名");
});
⑤classList.remove

指定したクラスを削除することが出来る。
　　
他にもありますが、今回はここまで

　 Tweet
Qiitaで続きを読む

投稿日：2020-03-28T18:19:55+09:00

【Vue.js】猫本を参考に基本的なところをまとめてみた。

はじめに

2か月程前、Vue.jsに関して以下の本を用いて学習を始めました。

https://www.amazon.co.jp/%E5%9F%BA%E7%A4%8E%E3%81%8B%E3%82%89%E5%AD%A6%E3%81%B6-Vue-js-mio/dp/4863542453/ref=asc_df_4863542453/?tag=jpgo-22&linkCode=df0&hvadid=295706574430&hvpos=&hvnetw=g&hvrand=10968923051787403043&hvpone=&hvptwo=&hvqmt=&hvdev=c&hvdvcmdl=&hvlocint=&hvlocphy=1028851&hvtargid=pla-524581061219&psc=1&th=1&psc=1

2週間ほど勉強して、少しだけアレンジして作成したToDoリストが以下になります。(Bootstrapでデザインして、状態ボタンを1つ追加しただけだけど)

https://chobimusic.com/vue_nekotodo_arrange/

その後、Laravelと組み合わせたポートフォリオ作成を目指して、Laravelの勉強に専念。

やっとこさ最近LaravelとVueの連携について理解できてきたので、とりあえずVue.jsで新しいポートフォリオのフロントサイドを作り始めようと思ったのですが。。。

手が一切動かない。全然覚えてない。悲しい。。。泣　

2週間程度勉強したのですが、1か月経ち、気づけば頭からすっぽり抜けてしまっていました。。。~~(記憶力なんてこんなもん)~~

ってことで改めて復習がてらVue.jsの基本を記事にまとめてみました。(今後の備忘録も兼ねて)

※WordPressで体裁を整えたものをコピペしたところ、テーブルの形が崩れてしまいました。。。もし当記事が気になりましたら、以下よりご覧いただけますと幸いです。。。

https://chobimusic.com/vuejs_nekobook_summary/

Vue.jsの表示

まずはVue.jsでHello worldしてみる。

index.html
<div id="app">
  <p>{{ message }}</p>
</div>

<script src="https://cdn.jsdelivr.net/npm/vue@2.5.16/dist/vue.js"></script>
<script src="main.js"></script>
appの内側にテンプレートを書き込んでいく。

インターネットに接続できる環境であれば、Vue.jsのインストールにCDNが利用可能。

マスタッシュ記法を用いて{{}}内にプロパティ名を記述するとその値が描画される。

main.js
var app = new Vue({
  el: '#app',
  data: {
    message: 'Hello world'
  }
})
コンストラクタ(クラスのインスタンス生成時に実行されるメソッド)関数Vueを使ってルートとなるVueインスタンスを作成。
data内のデータをテンプレート側に送っている。変数化するとコンソールからもアクセスできるが必須ではない。

実際の描画
<p>hello</p>
基本機能(ディレクティブ/組み込みコンポーネント)

v-bind

クラス、スタイル、属性などタグ内のバインドに使用。※Mustache{{}}はテキストコンテンツ特有の記法のため、タグ内で使用することができない。
<input type="text" v-bind:value="message">
省略パターン
<input type="text" :value="message">
v-for

リストデータを用いて要素を繰り返し描画する際に、繰り返したいタグに対して使用。

v-on

「クリックしたとき」「要素が変わったとき」などDOMイベントのハンドリング(イベント)を受け取り、処理を行う際に使用。
※猫本では、イベントに紐づける処理の内容を「イベントハンドラ」、イベントハンドラをイベントと紐づけることを「ハンドル」と呼んでます。
<button v-on:click="handleClick">クリック</button> 
省略形「@」
<button @click="handleClick">クリック</button>
v-model

データとフォームの入力項目をバインド(同期)する際に使用(双方向データバインディング)。
下記でフォームの文字を編集すると、同期して画面のメッセージも更新される。
<div id="app">
  <input v-model="message">
  <p>{{ message }}</p>
</div>
var app = new Vue({
  el: '#app',
  data: {
    message: 'hello'
  }
})
v-if

プロパティがTrueの時だけ条件分岐でテンプレートを描画したい際に使用。条件を満たさなかった際はコメント化。似たディレクティブにv-showがあり、こちらはstyle="display: none;"のスタイルが付与されて描画。
<templete>タグを使うと複数の要素をグループ化できる。
<templete v-if="ok">
  <h1>タイトル</h1>
  <p>コンテンツ</p>
</templete>
また、v-else-if、v-elseを組み合わせることで複数の条件を指定できる。

<transition>タグ

組み込みコンポーネント。CSSトランジションやアニメーションを容易に適用できる。

基本的なオプションの構成

Vueクラスのインスタンスの生成テンプレート
//main.js

vue = Vue.new({
  el: '#app',
  data: {
    message: "Hello Vue.js"
  },
  computed: {
    computedMessage: function(){ 
      return this.message + "!"
    },
  },
  created: {
  // アクションフック
  },
  methods: {
    myMethod: function(){
    },
  },
})
el: mountする要素

アプリケーションを紐づけるセレクタ。

data:

アプリケーションで使用するデータの登録。

computed:

算出プロパティ。関数によって算出されたデータ。
メソッド内ではthis(Vueインスタンスを指す)を付ける。
テンプレートの可読性を保つためにここに記述。

created:

ライフサイクルハック。特定のタイミングで自動的に呼び出す。呼び出したいタイミングによってメソッドは変える。
処理を割り込ませる仕組みのことを「フック」と呼ぶ

methods:

アプリケーションで使用するメソッド。
コードを管理しやすくするために処理を分けたり、イベントハンドラなど細かな実装を担当する。
コンポーネント

機能をもつUI部品ごとにテンプレートとJavaScriptを1つのセットにして、ほかのUI部品とは切り離した開発、管理をできるようにする仕組み。設計図。再利用が容易になる。
※UI(User Interface)とは、ユーザーがPCとやり取りをする際の入力や表示方法などの仕組み。

index.html
<h1>Vue.js</h1>
<div id="app">
  <hello />
</div>
<script src="https://unpkg.com/vue"></script>
<script>
Vue.component('hello',
{
  template: '<p>Hello!</p>'
})
var app = new Vue({
  el: '#app',
});
</script>
コンポーネントの定義

Vue.component(名前,{設定情報});

コンポーネントの出力

<コンポーネント名 />
<h1>Vue.js</h1>
<div id="app">
  <mycomponent />
</div>
<script src="https://unpkg.com/vue"></script>
<script>
var component = {
  template:'<p>localcomponent</p>'
}
new Vue({
  el: '#app',
  components: {
    'mycomponent':component
  }
});
</script>
ローカルコンポーネントの登録

Vueオブジェクトの「components」プロパティに登録すると、そのコンポーネントのスコープ内だけで使用するように制限できる。
components:{'コンポーネントタグ':コンポーネント名}

※Vue.componentsはグローバルコンポーネント

親子間のコンポーネントデータフローは、「props(親から子)」と「カスタムイベント$emit(子から親)」を使用する。
拡張フレームワークには「Nuxt.js」や「VuePress」がある。

「Vuex」や「Vue Router」といった拡張ライブラリを導入することで効率よく目的に応じたスケールアップも可能。

また、UIコンポーネントサイトとしては「Element」や「Onsen UI」がある。

用語

ディレクティブ

テンプレートとロジックを関連付ける機能。テンプレート内で「v-if」など独自の属性で記述する。オプションで引数や修飾子を扱うことも可能。

マウント(mount)

配置する要素とアプリケーションを紐づけること。

データバインディング

データと描画を同期させる仕組みのこと(JavaScriptのデータとそれを使用する場所を紐づけ、データに変化があれば自動的にDOMを更新する)。リアクティブシステムによって実現している機能の1つ。

DOM(Document Object Model)

JavaScriptでhtmlの要素を操作するための仕組みのこと。(ファイルの特定の部分に目印を付けて「この部分」に「こういう事をしたい」という処理を可能にするための取り決め。)

オプション

Vueインスタンスの中で使用するデータやメソッドを定義する場所。

今回まとめで割愛したこと

テンプレート制御ディレクティブ(v-preやv-htmlなど)
各ディレクティブの修飾子

スクロールイベントの取得(スムーススクロール)　P114

算出プロパティ詳細(ゲッターとセッター、キャッシュ機能、watchオプション)

コンポーネントの親子間のデータフロー　P154

トランジション　P194

Vue CLI P216

Vuex P252

Vue Router P282

予備知識

jQueryとの併用

Vue.jsを使用すると、jQuery(DOM操作系ライブラリ)を併用する機会は減る。マウントした要素内のDOMを直接操作しても仮想DOMは更新されず、データが変わらないため。
DOMを直接参照したい際は、$elや$refsなどカスタムディレクティブを使用する。

所感

復習してみて、今回割愛した各ディレクティブの修飾子がかなり重要な役割を果たす上に、数が多いので把握するのが大変だなと感じた。まずはポートフォリオにトランジションを用いたテキストアニメーションを実装しながら学んでいこうかな。
Vue RouterでSPAも憧れるけどVue CLIの導入が必須っぽいので、まずはVue CLI導入せずにできるところからポートフォリオ制作に活かしつつ、勉強していこうと思います。

参考サイト

猫本公式サポートページ
猫本ソースコードgithub

JavaScript初心者でもすぐわかる！DOMとは何か？

Vue.js童貞がネコ本読んで得たもの①

今後活用したいチュートリアルなど

Vue.js/Vuexを使ってTrello風アプリを作成しよう！
Vue CLI活用

Vue.js & FirebaseでTwitterライクなSNSアプリを作ってみよう！

Vue CLI活用 (Vue Routerアリ、Vuexは使用しない)

Nuxt.js & Contentfulでハイスペックなポートフォリオサイトを超簡単に公開しよう！【JAMstack】

　 Tweet
Qiitaで続きを読む

投稿日：2020-03-28T17:34:10+09:00

フロントエンド開発超初学者が贈る、0から始めるReactハンズオン

始めに

レガシー言語しか触ったことのなかった私が2019年12月中旬に初めて世間で一般的に使用されているプログラミング言語に触れて衝撃と感動を覚えてから早3カ月、、、(その時の記事)
あれからも昼休みや休日を利用して様々なイベントへの参加や自己啓発を行い、知識レベルが浦島太郎状態な現状を脱却すべく研鑽を積んできました。
Lambda関数を使用したサーバーレスなシステム作りに携わったり、Spring bootを使った開発技術を学んだり、HTML5プロフェッショナル認定試験の勉強をやったり...(インプットに夢中になってアウトプットさぼってましたすみません)
その一環でReactを使ったハンズオン学習をする機会があり、その時学んだ内容を自分の中に定着させる意味も込めて記事にしようと思ったので、お時間がある方はお付き合いください。

タイトルにもありますが、自分は超初学者ですので、その認識間違ってるよ！ってところなどありましたら優しくコメントくださると嬉しいです！

そもそもReactってなんぞ

Reactとは、webアプリ開発で使用されるJavaScriptのライブラリです。
webアプリのアーキテクチャの話でよく出てくるMVCモデルのView部分の実装に使われることが多いみたいです。

本記事ではこのReactを使って、
① Hello Worldの表示
② ①+αの表示
を作っていきます。

ハンズオンを実施する前に...

本当にCOBOLのようなレガシー言語しか知らなかった私のこの3カ月の経験からですが、私のような本当にまっさらな知識状態でweb開発の勉強がしたい！と思っている方はReactに触れる前にHTML,CSS,JavaScriptの学習をちょろっとでもいいので実施するのをオススメします。
私も昨年の12月Dev fest Tokyoというイベントに行った際angularというJavaScriptのフレームワークでハンズオン体験をする機会があったのですが、よーわからんけどコピペしてたらなんかいい感じのショッピングサイトが出来上がったという感じでした。

というのも、やはりReactの学習と言ってもその中にはHTMLやJavaScriptの概念がふんだんに出てきて、それらは知っている前提で進んでいくのでそもそもの基礎知識がないとただソースをコピペして成果物を作るだけになってしまいます。

とはいっても、コピペだろうと普段自分が使っているwebサービスに似たものが自分の手によって形となって出来上がるのは、それはそれで感動するのでお試しで実施するのはいいかもしれません。
(かくいう私もこのangularのチュートリアルでwebアプリ開発の楽しさに目覚めて今もこうしてモチベーション高く学習しております。)

それでは早速始めていきたいと思います！！

1-1)Reactを使う環境を設定する

Reactの環境導入は自PCにNode.jsというJavaScriptを使う環境をインストールするだけです。
私はMacbookを使用しているので、こちらの方の記事を参考に導入しました。
基本的にはこの通りに実施すれば問題なくReactの環境を導入できるはずです。
この時npmというパッケージ管理ツールが一緒にインストールされるのですが、これを使ってプロジェクト生成をしたりアプリを起動させたりします。

MacにNode.jsをインストール

1-2)成果物のひな形を作る

今回は私のような初心者でもReactを使ったアプリ開発を体系的に理解しやすいように、公式が提供している"create-react-app"というジェネレータを使ってアプリ全体の枠を最初に作ります。
家だけ先に作って、中に入れる家具や家電は後から追加していくイメージですね。
// ひな形の生成
npx create-react-app react-handson

// 生成したプロジェクトへ移動
cd react-handson
ここでひな形生成時にしれっとnpmではなくnpxを使っていますが、npxはnpmパッケージを簡単に実行できるコマンドで、これもnpmをインストールすれば勝手に使えるようになっています。
ここではグローバルインストールせずに1度だけ実行するために使っています。
要は自分のPCにインストールしなくても一瞬だけ借りて使い終わったら速攻で消してくれる便利なコマンドです。

ここで一度以下コマンドでアプリを起動してみましょう。
npm start

するとしばらくしてブラウザが勝手に開くので、以下のような画面がでればOKです。

2-1)Hello Worldを表示させる

今回は理解しやすくするためにジェネレータによって生成されたコードのうち使わないものは削除します。
rm public/manifest.json 
rm src/*
その後、以下のような最小構成のファイルを作成します。
src/index.js
import React from 'react';
import ReactDOM from 'react-dom';
import App from './App';

ReactDOM.render(<App />, document.getElementById('root'));
src/App.js
import React from 'react';

function App() {
  return <h1>Hello World</h1>;
}

export default App;
htmlファイル内の不要な記述も削除して、以下のようにします。
public/index.html
<!DOCTYPE html>
<html lang="en">
  <head>
    <meta charset="utf-8">
    <meta name="viewport" content="width=device-width, initial-scale=1, shrink-to-fit=no">
    <link rel="shortcut icon" href="%PUBLIC_URL%/favicon.ico">
    <title>React App</title>
  </head>
  <body>
    <div id="root"></div>
  </body>
</html>
この状態でnpm startすると以下のようにHello Worldが出ると思います。

2-2)構成と解説

ここまでの時点でディレクトリ構成は以下のようになっているかと思います。
.
├── node_modules    // 外部ライブラリ
├── README.md       // プロジェクトの説明などを記載するファイル
├── package.json    // 依存するライブラリなどを記載するファイル
├── public          // Web上に公開するディレクトリ
│   ├── favicon.ico // ブラウザのタブに出るアイコン
│   └── index.html  // エントリーポイントとなるhtml
└── src             // 開発者が書くコードを置くディレクトリ
    ├── App.js      // ルートコンポーネント
    └── index.js    // Reactのコードのエントリーポイント
ここでHello Worldの描画に直接関わっている人たちは以下の3人
・index.html
・App.js
・index.js

まずindex.htmlですが、ここに記載する内容が実際に画面に表示されます。
今回のソースで言うと、画面に表示される所はここ↓
index.html
<body>
    <div id="root"></div>
</body>
これだけだと、画面には"root"というid属性を持った空のdivタグが表示されるだけです。
ではなぜ画面にHello Worldが表示されたかというと、誰かが"root"というid属性をキーにdivタグの中にHello Worldを入れたのです。
そのHello Worldという中身を持っているのがApp.jsです。
src/App.js
import React from 'react';

function App() {
  return <h1>Hello World</h1>;
}

export default App;
App.jsの中には<h1>Hello World</h1>というhtmlタグを戻す関数があり、この戻り値がdivタグに入っている形になります。
そして、このhtmlタグをdivタグの中にぶち込んでくれるのがindex.jsです。
index.jsの中身の内、上3行はただのimportなので実質の中身はこの1行。
src/index.js
ReactDOM.render(<App />, document.getElementById('root'));
ぱっと見よくわからないことをやっているように見えますがこれを日本語にすると、App関数の戻り値をindex.html内にあるid属性が"root"のタグの中にレンダリングするということです。
このレンダリングというのがreactの特徴の一つであり、reactの開発はこのように別々で作ったパーツ(コンポーネント)をレンダリング処理によって別のコンポーネントと組み合わせ、出来上がったものを画面に表示するという流れになります。
機能を追加して行く場合、このコンポーネントやコンポーネントを統合するコードを増やしていく事になります。

3-1)コンポーネントを増やしてみる

コンポーネントの使い方を理解するために、複数のコンポーネントを作成しそれらを組み合わせてみましょう。

新しくsrcディレクトリ配下にcomponentsディレクトリを作成し、そこに以下のようなHello.jsを作成します。
src/components/Hello.js
import React from 'react';

function Hello() {
  return (
    <div>
      <h1>Hello World</h1>
      <p>konnitiwa sekai</p>
    </div>
  );
}

export default Hello;
作成したHelloコンポーネントを画面に表示させるためにApp.jsを修正します。
src/App.js
import React from 'react';
import Hello from './components/Hello'; // Helloコンポーネントをimportする

function App() {
  return <Hello />; // importしたHelloコンポーネントを返すように変更する
}

export default App;
importしたコンポーネントはhtmlタグのようにして使うことができます。

ここまでで、アプリを起動させると以下のようになるはずです。

次に、引数を渡してそれをコンポーネントに埋め込んだ関数も追加してみます。

作成したcomponentsディレクトリに以下のようなGreet.jsを作成します。
src/components/Greet.js
import React from 'react';

function Greet({ name }) {
  return <p>Hello {name}さん！</p>; // {}で囲うと変数を埋め込むことができる
}

export default Greet;
最後にGreetコンポーネントを呼び出すロジックをApp.jsに追加します。
src/App.js
import React from 'react';
import Hello from './components/Hello';
import Greet from './components/Greet'; // importを追加

function App() {
  return (
    <div>
      <Hello />
      {/* 引数は属性として渡す */}
      <Greet name="Qiita" />
    </div>
  );
}

export default App;
引数の受け渡し方法ですが、属性に値を設定することで渡すことができます。
この時、引数を渡す時の属性名と受け取る時の変数名は同一でないといけないのでご注意ください。
・function Greet({ name }) {
・<Greet name="Qiita" />

上記の修正が反映した状態でアプリを起動させて、以下が表示されたら成功です。

最後に

webアプリ開発の'ウェ'の字も知らなかった３ヶ月半前からどっぷりと開発知識の習得に邁進していますが、レガシー業界の住人である私にとってこの業界の技術を学ぶのは本当に刺激的です。
今後も記事にしてアウトプットすることでどんどん知識を自分に落とし込んでいこうと思います。
ちなみに、本当はuseStateを用いた状態管理やらページ遷移やらReduxを用いた状態管理やらも書きたかったのですが、量がすごい事になるのでまた別で書こうと思います。

ここまで読んでくださりありがとうございました！

　 Tweet
Qiitaで続きを読む

投稿日：2020-03-28T15:41:04+09:00

【Google MapsAPI】GeoCoding API ~郵便番号で住所を検索する~

GeoCoding API ~郵便番号で住所を検索する~

GeoCoding APIとは

GeoCoding APIは主に、住所を渡すと地理座標を返してくれるようなAPIです。
ショップリストで地図上にお店の場所となるマーカーを配置したり、そのお店の位置を地図で表示したりできるのも　これでしょう。

スタートガイド
 開発者向けドキュメント

GeoCoding APIを始めてみる

Geocoding APIを使用して開発を開始するにあたり、下記を設定する必要があります。

請求先アカウントを作成（プロジェクトで請求を有効にする必要があります）

プロジェクトの作成＆Geocoding APIの有効化

認証要件（APIキー生成が必要です）

※下記の参考ページから「Get Stated」ボタンで設定を進めます。

【参考】Get Started with Google Maps Platform

GeoCoding APIを使ってみる

APIの使用法を確認します。

リクエストの形式は下記のフォーマットで行います。

レスポンスで受け取る形式をJSONかXMLで指定できます。
https://maps.googleapis.com/maps/api/geocode/{outputFormat(json or xml)}?{parameters}
Request(parameters)

今回は日本の郵便番号でリクエストを送り、住所を取得してみましょう。
下記のパラメータを指定してリクエストを送ります。
また、リクエストを送る際、レスポンス結果をフィルタリングすることもできます。

key Value

address 郵便番号

language 日本語

components レスポンス結果をフィルタリングする条件（詳細はこちら）

key APIKey

※リクエストパラメータの詳細はこちら
https://maps.googleapis.com/maps/api/geocode/json?address=1008111&language=ja&components=country:JP&key={YOUR_API_KEY}
Response

レスポンスは下記のようにaddress_components配列の中で分類されて返ってきます。
{
   "results" : [
      {
         "address_components" : [
            {
               "long_name" : "100-8111",
               "short_name" : "100-8111",
               "types" : [ "postal_code" ]
            },
            {
               "long_name" : "１",
               "short_name" : "１",
               "types" : [ "political", "sublocality", "sublocality_level_4" ]
            },
            {
               "long_name" : "千代田",
               "short_name" : "千代田",
               "types" : [ "political", "sublocality", "sublocality_level_2" ]
            },
            {
               "long_name" : "千代田区",
               "short_name" : "千代田区",
               "types" : [ "locality", "political" ]
            },
            {
               "long_name" : "東京都",
               "short_name" : "東京都",
               "types" : [ "administrative_area_level_1", "political" ]
            },
            {
               "long_name" : "日本",
               "short_name" : "JP",
               "types" : [ "country", "political" ]
            }
         ],
         "formatted_address" : "日本 〒100-8111",
         "geometry" : {
            "location" : {
               "lat" : 35.6835978,
               "lng" : 139.7541838
            },
            "location_type" : "ROOFTOP",
            "viewport" : {
               "northeast" : {
                  "lat" : 35.6926604,
                  "lng" : 139.7701912
               },
               "southwest" : {
                  "lat" : 35.6745342,
                  "lng" : 139.7381764
               }
            }
         },
         "place_id" : "ChIJaWqAGwuMGGARe50QFyCjp78",
         "types" : [ "postal_code" ]
      }
   ],
   "status" : "OK"
}
※レスポンスの詳細はこちら

日本の住所の場合、毎度同じ形式ではないことに注意です！！

下記4パターンを比較すると。。。
※他にもパターンがあるかもしれません。

例1) 千葉県千葉市中央区春日　の場合

key Value

administrative_area_level_1 千葉県

locality 千葉市

sublocality 中央区

sublocality 春日

例2) 東京都千代田区千代田１　の場合

key Value

administrative_area_level_1 東京都

locality 千代田区

sublocality 千代田

sublocality 1

例3) 北海道松前郡松前町　の場合

key Value

administrative_area_level_1 北海道

administrative_area_level_2 松前郡

locality 松前町

例4) 東京都利島村　の場合

key Value

administrative_area_level_1 東京都

administrative_area_level_2 利島村

分類の大きさ順に下記のような感じでしょうか。

key Value

administrative_area_level_1 都道府県

administrative_area_level_2 郡、村

locality 市区町

sublocality(sublocality_level_1, sublocality_level_2) 地名等

レスポンスのパターンを理解して、郵便番号で住所自動入力のフォームを実装できそうですね

key	Value
address	郵便番号
language	日本語
components	レスポンス結果をフィルタリングする条件（詳細はこちら）
key	APIKey

key	Value
administrative_area_level_1	千葉県
locality	千葉市
sublocality	中央区
sublocality	春日

key	Value
administrative_area_level_1	東京都
locality	千代田区
sublocality	千代田
sublocality	1

key	Value
administrative_area_level_1	北海道
administrative_area_level_2	松前郡
locality	松前町

key	Value
administrative_area_level_1	東京都
administrative_area_level_2	利島村

key	Value
administrative_area_level_1	都道府県
administrative_area_level_2	郡、村
locality	市区町
sublocality(sublocality_level_1, sublocality_level_2)	地名等

　 Tweet
Qiitaで続きを読む

投稿日：2020-03-28T14:29:21+09:00

有限体のプログラミング後編: リードソロモン符号のしくみ

前編内容

素数べき要素数の有限体のための基礎知識

素数べき要素数の有限体とその作り方

素数べき要素数の有限体の例

素数べき要素数の有限体のガロア群

中編内容

JavaScriptで実装する素数べき要素数有限体

2べき要素数の有限体に特化した実装

後編内容

有限体の応用: リードソロモン符号とBCH符号

注: 記事内のJavaScriptコードについて

この記事内のコードで用いるJavaScriptの仕様は、Array.flatMap()のあるECMAScript2019仕様までを用います。JSファイルは、すべて拡張子は.jsのES moduleです。

非ECMAScriptな要素として、console.logとconsole.assertのみを用います。その他のWeb APIやnode.jsビルトイン等は一切使用していません。

この記事内のコードは、以下のgistに置いています。

https://gist.github.com/bellbind/ba4b307fea8251f7f40aeb7e9349814b

多項式や有限体等の要素は、数値とArrayにマッピングし、それらのデータ処理をfunction式の中で記述します。体や多項式等は、このfunction実装をメンバーに持つObjectとして提供します。たとえば、有理数体Qでの加算は以下のようになります。

$c = \frac{1}{2} \times -\frac{3}{4}$ : const c = Q.mul([1, 2], [-3, 4]);

リードソロモン符号とは

有限体の応用として、エラー検出だけでなくエラー訂正も可能なリードソロモン符号があります。

このリードソロモン符号はCDやMPEG2、ORコードなどでも使われている機能です。

リードソロモン符号のエンコード: バイト列データを入力とし、パリティデータを付与する符号化バイト列を出力

リードソロモン符号のデコード: (エラー混入した)符号化バイト列を入力とし、エラー補正したバイト列データを出力

リードソロモン符号では、有限体GFおよび、符号化バイト列長をN、データバイト列長をK、非負整数値bというパラメータがあります(bの意味は後述)。エンコード側とデコード側双方で同じパラメータを共有することが前提です。
また、パラメータの有限体では、同じ原始元を用いることが必須となります。つまり、PF(p)の場合は原始元となる整数値aを、GF($p^n$)の場合は多項式aを解とする既約多項式fを、pやnとともに指定する必要があります。

ただし、リードソロモン符号で用いる有限体GFは、多くのケースで、1バイト8ビットのビット列に対応するGF($2^8$)を用いています。

パリティデータのバイト長dは、N-Kとなります。パリティデータは素データの直後似付与されます。
リードソロモン符号で訂正可能なエラー数は、dの1/2以下までです。これは素データとパリティデータをあわせた、全符号化データ内でのエラー出現数であり、どこにエラーが出てもデコードでの扱いの差はありません。

リードソロモン符号の実装

リードソロモン符号の内部では、入出力のバイト列は、有限体GF係数の多項式である、として扱います。

リードソロモン符号実装rscode.jsでは、中編で実装したコードを使用します。
多項式としてPolynomialを用い、パラメータとしてGFやPF、GF2nを受け付けます。また、デコード実装では、連立方程式を解くためのFieldUtilsを使用します。
rscode.jsコード全体
rscode.js
// Reed-Solomon code
import {range, FieldUtils} from "./field-utils.js";
import {Polynomial, PolynomialUtils} from "./polynomial.js";

export const RSCode = (FF, N, K, b, debug = false) => {
  const d = N - K, t = d >>> 1;
  const poly = Polynomial(FF), futils = FieldUtils(FF);
  // explict conversion between FF-element array and FF-polynomial
  const a2p = poly.fromArray, rev2p = a => a2p([...a].reverse());
  const p2a = poly.toArray, p2rev = (e, len) => [...p2a(e, len)].reverse();

  // gen = (x-a^b)*(x-a^(b+1)*...*(x-a^(b+d-1)) as extracted poly
  const rsGenerator = () => poly.prod(range(d).map(k => poly.add(
    poly.monomial(FF.one(), 1),
    poly.monomial(FF.neg(FF.alpha(b + k)), 0))));
  const gen = rsGenerator();
  if (debug) console.log("gen", gen);

  const encode = msg => {
    const base = poly.carry(rev2p(msg.map(FF.fromNum)), d);
    const coded = poly.sub(base, poly.mod(base, gen));
    if (debug) console.assert(poly.mod(coded, gen).every(FF.isZero));
    return p2rev(coded, N).map(FF.toNum);
  };

  const rsSyndromes = cx => range(d).map(
    k => poly.apply(cx, FF.alpha(b + k)));
  const hasError = synds => !synds.every(si => FF.isZero(si));

  const rsLx = (synds) => {
    const leqs0 = range(t).map(i => range(t + 1).map(j => synds[i + j]));
    const v = futils.rank(leqs0);
    const leqs = v === t ? leqs0 :
          range(v).map(i => range(v + 1).map(j => synds[i + j]));
    const rlx = futils.solve(leqs);
    return a2p([FF.one(), ...rlx.reverse()]);
  };
  const rsPositions = lx => range(N).filter(
    k => FF.isZero(poly.apply(lx, FF.alpha(-k))));

  const rsOx = (sx, lx) =>
        poly.mod(poly.mul(sx, lx), poly.carry(poly.one(), d));
  const rsDLx = lx => poly.diff(lx);
  const rsErrors = (positions, ox, dlx) => positions.map(k => {
    const akinv = FF.alpha(-k);
    const oAkinv = poly.apply(ox, akinv);
    const dlAkinv = poly.apply(dlx, akinv);
    const ak1b = FF.alpha(k * (1 - b));
    return FF.neg(FF.mul(ak1b, FF.div(oAkinv, dlAkinv)));
  });

  const rsEx = (positions, errors) =>
        poly.sum(positions.map((k, i) => poly.monomial(errors[i], k)));

  const decode = code => {
    const rx = rev2p(code.map(FF.fromNum));
    const synds = rsSyndromes(rx);
    if (debug) console.log("sx", synds);
    if (!hasError(synds)) return code.slice(0, K);

    const lx = rsLx(synds);
    //const lx = PolynomialUtils(poly).findLinearRecurrence(synds);
    if (debug) console.log("lx", lx);
    const positions = rsPositions(lx);
    if (debug) console.log("positions", positions);
    if (positions.length === 0) {
      throw Error(`Cannot recover: error count > ${t}`);
    }

    const sx = a2p(synds);
    const ox = rsOx(sx, lx);
    const dlx = rsDLx(lx);
    const errors = rsErrors(positions, ox, dlx);
    if (debug) console.log("errors", errors);
    const ex = rsEx(positions, errors);
    const cx = poly.sub(rx, ex);
    return p2rev(cx, N).slice(0, K).map(FF.toNum);
  };
  return {encode, decode};
};
rscode.js利用例と結果
QRコードでのリードソロモン符号の例として、

https://kouyama.sci.u-toyama.ac.jp/main/education/2007/infomath/pdf/text/text09.pdf

の73ページの例を利用しました。

コード
rscode-example.js
import {GF2n} from "./gf2n.js";
import {RSCode} from "./rscode.js";

{
  console.log("[Reed-Solomon error detective code]: N=26,K=7,b=0 on GF(2^8)");
  // GF(2^8) System for QR Code
  const n = 8, f = 0b100011101; //a^8+a^4+a^3+a^2+1=0
  // example from https://kouyama.sci.u-toyama.ac.jp/main/education/2007/infomath/pdf/text/text09.pdf
  const N = 26, K = 19, b = 0;
  const {encode, decode} = RSCode(GF2n(n, f), N, K, b);
  const msg = [
    0b10000000, 0b01000100, 0b10000101, 0b10100111, 0b01001001, 0b10100111,
    0b10001011, 0b01101100, 0b00000000, 0b11101100, 0b00010001, 0b11101100,
    0b00010001, 0b11101100, 0b00010001, 0b11101100, 0b00010001, 0b11101100,
    0b00010001,
  ];
  console.log("msg", msg);

  const coded = encode(msg);
  console.log("coded", coded);

  // error injection
  coded[24] ^= 0xff;
  //coded[16] ^= 0x02;
  coded[11] ^= 0xac;
  console.log("error coded", coded);

  const fixed = decode(coded);
  console.log("fixed", fixed);

  console.log("Same as original", fixed.every((c, i) => c === msg[i]));
}
結果
[Reed-Solomon error detective code]: N=26,K=7,b=0 on GF(2^8)
msg [
  128,  68, 133, 167, 73, 167,
  139, 108,   0, 236, 17, 236,
   17, 236,  17, 236, 17, 236,
   17
]
coded [
  128,  68, 133, 167,  73, 167, 139,
  108,   0, 236,  17, 236,  17, 236,
   17, 236,  17, 236,  17, 249, 187,
   11, 161,  75,  69, 244
]
error coded [
  128,  68, 133, 167,  73, 167, 139,
  108,   0, 236,  17,  64,  17, 236,
   17, 236,  17, 236,  17, 249, 187,
   11, 161,  75, 186, 244
]
fixed [
  128,  68, 133, 167, 73, 167,
  139, 108,   0, 236, 17, 236,
   17, 236,  17, 236, 17, 236,
   17
]
Same as original true
このRSCode()は、GF2n(n, f)だけでなく、PF(p)やGF(p, n, f)でも同様に機能します。GF.toNum()、GF.fromNum()により、GFであっても数値配列が入出力となります(GFの既約多項式fは配列表現です)。
以下、このrscode.jsのコードの順をおって説明していきます。

リードソロモン符号のパラメータ
export const RSCode = (FF, N, K, b, debug = false) => {
  const d = N - K, t = d >>> 1;
  const poly = Polynomial(FF), futils = FieldUtils(FF);
RSCode(FF, N, K, b)のパラメータFFは多項式の係数にする有限体です。
このFFとしては、先に実装したGF2n(n, f)、PF(p)、GF(p, n, f)が使えます。

リードソロモン符号では、入力データとパリティデータをあわせた符号データのバイト数をN、入力データのバイト数をKとして用いています。そして、符号データバイト数Nは、有限体FFの要素数-1(つまり$p^n-1$)以下である必要があります。

パリティデータ配列の長さdは、N-Kです。
そして、最大訂正可能エラー数tは、d/2を超えない整数値となります。

最後のパラメータbは整数値で、0や1などを使います。bを変えるとパリティデータ値は変化します。このbの意味は後の説明の中で行います。

実装によっては、後述の生成多項式g(x)もパラメータ扱いになります。
ただし、この多項式値g(x)は、他のパラメータFF、N、K、bで算出できる値です。

入出力データとしての有限体係数の多項式
  const a2p = poly.fromArray, rev2p = a => a2p([...a].reverse());
  const p2a = poly.toArray, p2rev = (e, len) => [...p2a(e, len)].reverse();
リードソロモン符号の入出力バイト列は、有限体GF($2^8$)を係数とする多項式として扱います。

ただし、これまのインデックスを指数値とする多項式の表現とは逆で、リードソロモン符号のデータでは、バイト列の先頭バイトが多項式での最上位桁になります。

この実装では、多項式計算での簡便性のためバイト列の配列を入出力時にreverse()することで、Polynomial(FF)として使う想定にしています。

この逆順配列aと多項式eの相互変換のためにrev2p(a)とp2rev(e)を用意します。

また、コード上でデータ配列と有限体係数多項式を使い分けるために、ArrayとPolynomialの相互変換を示すa2pやp2aも用意しています。

リードソロモン符号の生成多項式
  const rsGenerator = () => poly.prod(range(d).map(k => poly.add(
    poly.monomial(FF.one(), 1),
    poly.monomial(FF.neg(FF.alpha(b + k)), 0))));
  const gen = rsGenerator();
リードソロモン符号でのエンコードでは、パリティデータ長dに応じた「生成多項式(generator polynomial)」という多項式を用意します。

リードソロモン符号での生成多項式g(x)は、有限体の原始元aの指数表現で連続する値$a^0$、$a^1$、$a^2$、$a^3$、...$a^{d-1}$`を解に持つ多項式です。つまり、

$g(x) = \prod_{i=0}^{d-1}(x-a^{i})$

を展開した多項式 $x^d-(a^0+a^1+a^2+...+a^{d-1})x^{d-1}+...+a^{0+1+2+...+d-1}$ をrsGenerator()で作成しています。

前出のRSCode(FF, N, K, b)の最後のパラメータbは、この生成多項式の始点を$a^0=1$以外から始めるためのものであり、生成多項式は

$g(x) = \prod_{i=0}^{d-1}(x-a^{b+i})$

を展開したものになります。上記のコードはこの右辺に相当します。

このパラメータbはエラー値算出のときに影響し、b=1のとき計算がすこし少なくなる効果がありますが、CD, MPEG2, QR codeなどの仕様ではb=0であるようです。

そして、リードソロモン符号での生成多項式g(x)が持つ意味とは、i=b, ..., b+d-1のどれかのときは、$g(a^i)=0$となる多項式である、ということです。

リードソロモン符号のエンコード
  const encode = msg => {
    const base = poly.carry(rev2p(msg.map(FF.fromNum)), d);
    const coded = poly.sub(base, poly.mod(base, gen));
    if (debug) console.assert(poly.mod(coded, gen).every(FF.isZero));
    return p2rev(coded, N).map(FF.toNum);
  };
リードソロモン符号でのエンコードは、

入力メッセージを、多項式として、パリティデータの分だけ桁上げする

桁上げした多項式を、生成多項式でモジュロをとり、その余りの多項式を出す

桁上げしたメッセージから、余りの多項式を引く

を行うだけです。

最後に生成多項式g(x)での余りの多項式を引いているため、エンコードした結果の符号化データ多項式c(x)は、生成多項式g(x)で割り切れる多項式となっています。

c(x) = d(x) * g(x)

つまり、エンコード後の符号化データc(x)はg(x)で割り切れることから、代入するとg(x)が0になる値$a^b$,...$a^{b+d-1}$を代入すると0になる多項式となっています。

つまり、多項式にこれらを代入してすべてが(有限体での)0になればエラーはない、ということになります。

逆に、エラーが一つでもあれば、0にならない値が出てくる、ということになります。

エンコードしたデータと混入したエラーの関係

上記のエンコードした結果の、生成多項式g(x)で割り切れる、(エラーなし)符号化データの多項式をc(x)とします。

c(x)にエラーが混入したエラー混入後データの多項式をr(x)とし、c(x)との差分であるエラーも多項式e(x)で表現します。

r(x) = c(x) + e(x)

この和は、多項式としての各項の係数ごとの和です。

そして、e(x)の0でない各係数を「エラー値(error value)」とよび、各エラー値ごとのe(x)の指数を「エラー位置(error position)」と呼びます。
このエラー位置は、多項式としての指数値であり、バイト列でのインデックス値ではありません(逆順であるため)。

リードソロモン符号で訂正可能なエラー数はt個まであるため、

$e(x) = e_0x^{i_0} + e_1x^{i_1} + ... + e_{t-1}x^{i_{t-1}}$

となります。たとえば混入したエラーの個数が3個なら

$e(x) = e_0x^{i_0} + e_1x^{i_1} + e_{2}x^{i_{2}}$

となります。この$e_0$、$e_1$、$e_2$が各エラー値、$i_0$、$i_1$、$i_2$が各エラー位置になります。

エラーなしデータ多項式c(x)は生成多項式g(x)で割り切れるため、g(x)=0となるxを代入すれば、c(x)も0になります。
たとえば、$c(a^b)=0$です。

よって、このc(x)が0となる$a^b$等を、エラー混入データ多項式r(x)に代入すると、

$r(a^b) = c(a^b) + e(a^b) = e(a^b) = e_0a^{i_0 b} + e_1a^{i_1 b} + e_2a^{i_2 b}$

となって、エラー多項式e(x)だけに関する(有限体の)値になる性質があります。

そして、符号データ長Nが$p^n-1$以下である必要があるのは、この代入結果の値で、エラー位置$i_k$ごとの$a^{i_k}$が区別できる必要があるためです。もし$i_k$として$p^n-1$より大きいものがあるばあい、$i_k$と$i_{k_2} = i_k - (p^n-1)$との区別ができず、エラー位置の特定が不可能になります。

デコード

リードソロモン符号のデコードは少し複雑で、以下の手順に分けられます:

シンドローム値の算出

エラー位置の導出

エラー値の導出

エラー値の補正

シンドローム値の算出
  const rsSyndromes = cx => range(d).map(
    k => poly.apply(cx, FF.alpha(b + k)));
  const hasError = synds => !synds.every(si => FF.isZero(si));
リードソロモン符号の「シンドローム」とは、デコード入力r(x)にg(x)が0になる$a^b$、$a^{b+1}$、$a^{b+d-1}$それぞれを代入した、d個の有限体の値(の配列)のことです。

$s_k = r(a^{b+k}) = e(a^{b+k}) = \sum_{j=0}^{v-1}e_ja^{(b+k)i_j}$

先に示したように、このシンドロームの値がすべて(有限体での)0であればエラーはない、ということになります。

具体的には、b=０でエラーが3個あるとき、$s_k$は以下のようになっています。

$s_0 = e_0 + e_1 + e_2$

$s_1 = e_0a^{i_0} + e_1a^{i_1} + e_2a^{i_2}$

$s_2 = e_0a^{2i_0} + e_1a^{2i_1} + e_2a^{2i_2}$

$s_3 = e_0a^{3i_0} + e_1a^{3i_1} + e_2a^{3i_2}$

...

$s_{d-1} = e_0a^{(d-1)i_0} + e_1a^{(d-1)i_1} + e_2a^{(d-1)i_2}$

エラー値算出のときは、このシンドロームの配列を、d-1次多項式s(x)として利用します。

$s(x) = s_0 + s_1x + ... + s_{d-1}x^{d-1}$

エラー位置の算出
  const rsLx = (synds) => {
    const leqs0 = range(t).map(i => range(t + 1).map(j => synds[i + j]));
    const v = futils.rank(leqs0);
    const leqs = v === t ? leqs0 :
          range(v).map(i => range(v + 1).map(j => synds[i + j]));
    const rlx = futils.solve(leqs);
    return a2p([FF.one(), ...rlx.reverse()]);
  };
  const rsPositions = lx => range(N).filter(
    k => FF.isZero(poly.apply(lx, FF.alpha(-k))));
まず、検出可能エラー個数t以下となる、実際のエラーの個数をvとします。

k=0 ... v-1でのエラー位置$i_k$を求めるための、エラー位置多項式l(x)として、以下の式について考えます。

$l(x) = \prod_{k=0}^{v-1}(1-a^{i_k}x) $

この多項式は、$l(a^{-i_k})=0$となるv次多項式になります(代入値は、指数が負である、つまり逆数であることに注意)。

v=3のときは、
\begin{align}
l(x) &= (1-a^{i_0})(1-a^{i_1})(1-a^{i_2}) \\
  &= 1 - (a^{i_0}+a^{i_1}+a^{i_2})x + (a^{i_0+i_1}+a^{i_0+i_2}+a^{i_1+i_2})x^2-a^{i_0+i_1+i_2}x^3
\end{align}
です。

このl(x)が得られたなら、$a^{-0}$、$a^{-1}$、...、$a^{-N+1}$を、このl(x)へ総当りで代入し、結果が0になるかどうかを判定することで、エラー位置が見つけられます。これがrsPositions(lx)でやっていることです。

この展開した$l(x) = 1 + l_1x + l_2x^2 + ... + l_v x^v$の係数$l_k$を算出しl(x)を作る関数が、rsLx(synds)です。

たとえば、v=3のときは、l(x)の各係数は以下の値に相当します。

$l_1 = -(a^{i_0}+a^{i_1}+a^{i_2})$

$l_2 = a^{i_0+i_1}+a^{i_1+i_2}+a^{i_2+i_0}$

$l_3 = -a^{i_0+i_1+i_2}$

この時点では、l(x)で求める具体的な$i_k$は不明なので、$a^{i_k}$を含んでいるシンドローム値を用いることで、各$l_k$を求めます。

この$l_k$の算出では、以下のシンドローム値を係数としたv個の方程式でなる連立方程式を解くことで行います(各項でかけるsとlのインデックスが逆順関係である点に注意)。

$s_0 l_v + s_1 l_{v-1} + ... + s_{v-1} l_1 + s_v = 0$

$s_1 l_v + s_2 l_{v-1} + ... + s_{v} l_1 + s_{v+1} = 0$

...

$s_{v-1} l_v + s_v l_{v-1} + ... + s_{2v-2} l_1 + s_{2v-1} = 0$

導出時はまず、v=tと仮定して、この連立方程式を作ります。すると、この結果得られた連立方程式の係数行列のランクはvになります。
得られたランクをvとして、改めて連立方程式を作り、解くことでl(x)の係数が求まります。

v=3なら以下になります。

$s_0 l_3 + s_1 l_2 + s_2 l_1 + s_3 = 0$

$s_1 l_3 + s_2 l_2 + s_3 l_1 + s_4 = 0$

$s_2 l_3 + s_3 l_2 + s_4 l_1 + s_5 = 0$

参考: この連立方程式の意味

v=3の例で、一番上の等式について分析します。

$e_0$の項だけにフォーカスすると、$s_0 = e_0a^{0i_0}$、$s_1 = e_0a^{1i_0}$、$s_2 = e_0a^{2i_0}$、$s_3 = e_0a^{3i_0}$です。

そして、$e_0$のエラー位置$i_0$にフォーカスして、つぎに$l_k$を考えます。

$l_2$に$a^{i_0}$をかけると、項の一つが$l_3=a^{i_0+i_1+i_2}$になります。
その余りの$a^{2i_0+i1} + a^{2_i0+i2}$は、$l_1$に$a^{2i_0}$をかけたものの中に含まれます。
最後に余るのが、$a^{3i_0}$になり、$s_3$と同じになります。

このため、$e_0$でくくると、その中は0になります。$e_1$、$e_2$でも同様にくるると中は0になり、等式が成立します。

他の等式はs側で$a^{i_0}$を書ける数が一つづつ増えただけの関係であり、同様にすべて0になります。

そして、この関係は、一般のvについても同様に成立します。

参考: エラー個数とこの連立方程式のランクの関係

各方程式を$e_k$ごとにまとめると、b=0、t=3で実際のエラー数v=2なら

$e_0(l_3+a^{i_0}l2+a^{2i_0}l_1) + e_1(l_3+a^{i_1}l2+a^{2i_1}l_1) + s_3 = 0$

$e_0a^{i_0}(l_3+a^{i_0}l2+a^{2i_0}l_1) + e_1a^{i_1}(l_3+a^{i_1}l2+a^{2i_1}l_1) + s_3 = 0$

$e_0a^{2i_0}(l_3+a^{i_0}l2+a^{2i_0}l_1) + e_1a^{2i_1}(l_3+a^{i_1}l2+a^{2i_1}l_1) + s_3 = 0$

となり、実質

$L_0 = l_3+a^{i_0}l2+a^{2i_0}l_1$

$L_1 = l_3+a^{i_1}l2+a^{2i_1}l_1$

の2変数での連立方程式となるため、連立方程式のランクは2になります。

この連立方程式による計算方法は、"Peterson–Gorenstein–Zierler algorithm"(PGZアルゴリズム)といいます。

ちなみに、ハードウェア実装の場合は連立方程式を解くのに、クラメルの公式で、行列式を用いて解く実装が選ばれます。数あるPGZアルゴリズムの説明記事の中で、$l_k$をシンドローム値だけの式でいきなり表現しているものは、だいたいは行列式を展開したたものです。

参考: Berlekamp-Masseyアルゴリズムによるl(x)の算出

PGZアルゴリズムでの$l_k$を求める連立方程式の方程式はすべて、

$s_k + s_{k-1}l_1 + s_{k-2}l_{2} + \dots + s_{k-v}l_v = 0$

という１つの漸化式を満たすものです。
つまり、シンドローム$s_k$全体は、この漸化式を満たす数列であるとみなせます。

このため、中編にてPolynomialUtilsで実装した、数列sからその線形漸化式を求めるfindLinearRecurrence(s)を用いることでも、l(x)を作ることが可能です。

findLinearRecurrence(s)は、

$s_n + s_{n-1}c_1 - s_{n-2}c_{2} + \dots + s_{n-n}c_n = 0$

が成立する多項式$c(x) = 1 + \sum_{k=1}^n c_k x^k$として返すため、findLinearRecurrence(synds)の結果は、l(x)そのものとなります。

注意する点は、もし実際のエラー個数vがtより多い場合、デコード結果は不定である点です。エラーを加えた結果が、別の符号データからの訂正可能エラーとなりうる場合も起こるからです。

ただし、どの符号データからも訂正可能でなければ、求めたl(x)は、どの$a^{-0}$, ..., $a^{-N+1}$を入れても0にならない式となり、この場合のみ、エラーが多すぎることが検知可能です。

つまり、

発生したエラーの個数が多いと、$エラー訂正できたとしても、もともとのデータに訂正されるとは限らない$

です。リードソロモン符号に限らない話ではありますが、うまく利用するには、用いる状況に応じた、検出可能エラー数を増やす、エラーの比率を下げる、などの設定が必要です。

エラー値の算出
  const rsOx = (sx, lx) =>
        poly.mod(poly.mul(sx, lx), poly.carry(poly.one(), d));
  const rsDLx = lx => poly.diff(lx);
  const rsErrors = (positions, ox, dlx) => positions.map(k => {
    const akinv = FF.alpha(-k);
    const oAkinv = poly.apply(ox, akinv);
    const dlAkinv = poly.apply(dlx, akinv);
    const ak1b = FF.alpha(k * (1 - b));
    return FF.neg(FF.mul(ak1b, FF.div(oAkinv, dlAkinv)));
  });
シンドローム多項式s(x)とエラー位置多項式l(x)の積のd未満の項でなす多項式o(x)、l(x)を微分した多項式dl(x)とします。

$o(x) = s(x)l(x) \mod x^{d}$

$dl(x) = \frac{d}{dx}l(x) = \sum_{k=0}^{v-1}{(-a^{i_k}\prod_{j\ne k}{(1-a^{i_j}x)})}$

これらの多項式を使った以下の式で、エラー位置$i_k$からエラー値$e_k$が求まります。

$e_k = \frac{-a^{i_k(1-b)}o(a^{-i_k})}{dl(a^{-i_k})}$

パラメータb = 1のときは、oをdlで割って負にするだけになります。

$e_k = \frac{-o(a^{-i_k})}{dl(a^{-i_k})}$

参考: エラー値の等式の意味

前提知識として、$x^4-1 = (x-1)(x^3+x^2+x+1)$より、$1+x+x^2+x^3 = \frac{x^4-1}{x-1}$となります。
これは一般的に、$\sum_{i=0}^{n-1}x^i = 1+x+...+x^{n-1} = \frac{x^n - 1}{x - 1}$ の等式であり、有限体係数であっても成立する関係です。

まず単純化のため、パラメータb=0で考えます。

シンドローム$s_k = e_0a^{ki_0} + e_1a^{ki_1} + e_{v-1}a^{ki_v}$で、kは0からd-1までのd個あります。
そして、前述のシンドローム関数s(x)は、エラー値$e_k$ごとにまとめると、以下のようになります。

$s(x) = e_0(1+a^{i_0}x+(a^{i_0}x)^2 + \dots + (a^{i_0}x)^{d-1}) + e_1(1+a^{i_1}x+(a^{i_1}x)^2 + \dots + (a^{i_1}x)^{d-1}) + \dots + e_{v-1}(1+a^{i_{v-1}}x + \dots + (a^{i_{v-1}}x)^{d-1})$

これに、上述の等式を適用することで、

$s(x) = e_0\frac{(a^{i_0}x)^d-1}{a^{i_0}x-1} + e_1\frac{(a^{i_1}x)^d-1}{a^{i_1}x-1} + \dots + e_{v-1}\frac{(a^{i_{v-1}}x)^d-1}{a^{i_{v-1}}x-1}$

となります。この結果の式に、$l(x) = \prod_{k=0}^{v-1}(1-a^{i_k}x)$をかけると、各項にある分母が消え-1になり、

$s(x)l(x) = -e_0 \left( ((a^{i_0}x)^d-1)\prod_{k \ne 0}(1-a^{i_k}x) \right) - e_1\left( ((a^{i_1}x)^d-1)\prod_{k \ne 1}(1-a^{i_k}x)\right) - \dots - e_{v-1}\left( ((a^{i_{v-1}}x)^d-1)\prod_{k \ne {v-1}}(1-a^{i_k}x)\right) $

となります。

ここで、$(a^{i_k}x)^d-1 \mod x^d = -1$となることを利用します。

$o(x) = s(x)l(x) \mod x^d$より、

$o(x) = e_0\prod_{k \ne 0}(1-a^{i_k}x) + e_1\prod_{k \ne 1}(1-a^{i_k}x) + \dots + e_{v-1}\prod_{k \ne {v-1}}(1-a^{i_k}x) = \sum_{j=0}^{v-1}(e_j\prod{k\ne j}(1-a^{i_k}x))$

となります(参考: 結果のo(x)は$v - 1$次多項式になるため、$\mod x^d$でなくても、$\mod x^v$でもよい)。

このo(x)は、たとえばエラー位置$i_0$に対応する$a^{-i_0}$を代入すると、$(1-a^{i_0}x)$を含む$e_0$以外の項が0になります。

$o(a^{-i_0}) = e_0 \prod_{k \ne 0}(1-a^{i_k - i_0})$

となります。一般のb != 0の場合は、

$o(a^{-i_0}) = e_0a^{bi_0} \prod_{k \ne 0}(1-a^{i_k - i_0})$

です。

そして、$a^{-i_0}$を代入すると、$(1-a^{i_0}x)$を含む項が0になるのは、l(x)の微分多項式dl(x)でも同様です。

$dl(a^{-i_0}) = -a^{i_0}\prod_{k \ne 0}(1-a^{i_k-i_0}) $

よって、

$\frac{o(a^{-i_0})}{dl(a^{-i_0})} = -e_0a^{i_0(b-1)} $

$i_0$、$e_0$を一般化すると、

$\frac{o(a^{-i_k})}{dl(a^{-i_k})} = -e_ka^{i_k(b-1)} $

となります。

この右辺の$e_k$以外の部分を打ち消すために、$-a^{i_k(1-b)}$をかけることで、$e_k$が得られることになります。

$-a^{i_k(1-b)}\frac{o(a^{-i_k})}{dl(a^{-i_k})} = e_k $

このアルゴリズムは "Forney algorithm"(もしくはForney's formula)といいます。

このForneyアルゴリズムを使わなくても、エラー位置からすべての$a^{i_k}$がわあkっているので、エラー個数と同じv個のシンドロームの等式で、$e_k$を解くための連立方程式を作って、解くことでもエラー値を求めることができます。

エラー値の多項式
  const rsEx = (positions, errors) =>
        poly.sum(positions.map((k, i) => poly.monomial(errors[i], k)));
rsEx(positions, erros)は、エラー位置とそれに対応するエラー値のリストから、エラーの多項式e(x)を復元する関数です。

このe(x)を入力多項式r(x)から引くことで、補正された多項式c(x)が求まります。

デコード関数本体
  const decode = code => {
    const rx = rev2p(code.map(FF.fromNum));
    const synds = rsSyndromes(rx);
    if (!hasError(synds)) return code.slice(0, K);

    const lx = rsLx(synds);
    //const lx = PolynomialUtils(poly).findLinearRecurrence(synds);
    const positions = rsPositions(lx);
    if (positions.length === 0) {
      throw Error(`Cannot recover: error count > ${t}`);
    }

    const sx = a2p(synds);
    const ox = rsOx(sx, lx);
    const dlx = rsDLx(lx);
    const errors = rsErrors(positions, ox, dlx);
    const ex = rsEx(positions, errors);
    const cx = poly.sub(rx, ex);
    return p2rev(cx, N).slice(0, K).map(FF.toNum);
  };
decode(code)は、ここまで実装してきた

シンドローム算出

エラー位置算出

エラー値算出

エラー多項式で補正

を順に行い、その結果の補正済み多項式c(x)から、メッセージ部分だけを切り出して返す関数です。

BCH符号

リードソロモン符号と似たエラー訂正符号として、BCH符号があります。

リードソロモン符号からみたBCH符号の仕組み

BCH符号も、生成多項式で割り切れるようにするエンコード、シンドロームを計算し、エラー位置とエラー値を求めるデコードといった、大枠はリードソロモン符号と一緒です。

しかし、BCH符号では、デコードでのシンドロームやエラー位置の計算はGF($p^n$)係数の多項式を用いるに対し、入出力データは、その部分体GF(p)係数の多項式として扱うものとなっています。
つまり、GF($2^n$)なBCH符号の場合では、入出力データはバイト列ではなく、ビット列(の多項式)を扱うものとなります。

BCH符号の符号化データのビット数N: $p^n-1$までの整数

BCH符号のエラー個数: t (BCH符号ではtを指定する)

BCH符号の生成多項式: GF($p^n$)の原始元aの$a^1$,...,$a^{2t}$を解にもつ、既約多項式(GF(p)係数の多項式)の最公倍多項式

BCH符号のエンコード: 生成多項式で割り切れるためのGF(p)係数多項式でパリティデータ列を付加

BCH符号のシンドローム: GF(p)係数値をGF($p^n$)係数値として解釈した符号化データ多項式に、生成多項式を0にするそれぞれ値を代入した結果のGF($p^n$)値

BCH符号のエラー位置多項式: PGZアルゴリズムの連立方程式で求めるG($p^n$)係数の多項式

BCH符号のエラー多項式: GF($p^n$)のForneyアルゴリズムで部分体GF(p)値となる係数値を得るG(p)の多項式(ただし、GF(2)係数ならエラー値は1なので自明)

ポイントは、BCH符号の生成多項式g(x)が、GF($p^n$)の値を係数にする多項式ではなく、GF($p^n$)の値を解に持つGF(p)を係数とする既約多項式の積で構築する点です。
この結果、g(x)のモジュロ算を行うエンコードではGF(p)係数の多項式として扱う一方、デコードではGF(p)の値はGF($p^n$)の部分体GF(p)の値であるとし、入力データをG($p^n$)の多項式として扱うことで、リードソロモン符号と同様に行います。

ただし、求めるエラー位置はビット列のインデックスになり、エラー値はビットインデックスでのビット値になります。そしてGF(2)の多項式であれば、エラー値は1のみになり、Forneyアルゴリズム等を用いる必要がなくなります。

一方で、リードソロモン符号より係数値のバリエーションが少ないので、混入したエラー個数が指定のエラー個数を超えるとき、別の符号データの訂正可能データとなる可能性は高くなるでしょう。

BCH符号の実装

BCH符号の共有パラメータは、素数べき有限体GF(2,n,f)、符号化データビット長N、エラー訂正数t、非負整数値cで構成します。パラメータcは、リードソロモン符号におけるbと同じものですがc=1が普通のようです。

与えられたエラー訂正数tから、生成多項式の次数、つまりパリティビット長Dが求まるため、素データビット数はNとtから算出されます。
bchcode.jsコード全体
注: このコードは、有限体係数多項式での計算によるアルゴリズムの実装です。よりビット列に特化させた実装は可能です。
bchcode.js
import {range, uniq, FieldUtils} from "./field-utils.js";
import {Polynomial, PolynomialUtils} from "./polynomial.js";
import {GFUtils} from "./gf.js";

export const BCHCode = (gf, N, t, c) => {
  const gfutils = GFUtils(gf), gfPoly = Polynomial(gf);
  const futils = FieldUtils(gf);
  const pfPoly = gf.poly;

  const pfPoly2gfPoly = (pfp, n) =>
        gfPoly.fromArray(pfPoly.toArray(pfp, n).map(gf.fromSF));
  const gfPoly2pfPoly = (gfp, n) =>
        pfPoly.fromArray(gfPoly.toArray(gfp, n).map(gf.toSF));

  // encode
  const bchGenerator = () => {
    const polys = uniq(range(2 * t).map(
      k => gfutils.findIrreducible(gf.alpha(c + k))), pfPoly.eql);
    return pfPoly.prod(polys);
  };
  const gen = bchGenerator();
  const d = pfPoly.order(gen), K = N - d;

  const encode = msg => {
    const m = pfPoly.carry(msg, d);
    const r = pfPoly.mod(m, gen);
    return pfPoly.sub(m, r);
  };

  // decode
  const bchSyndromes = rx =>
        range(2 * t).map(k => gfPoly.apply(rx, gf.alpha(c + k)));
  const hasError = synds => !synds.every(gf.isZero);

  const bchLx = synds => {
    const leqs0 = range(t).map(i => range(t + 1).map(j => synds[i + j]));
    const v = futils.rank(leqs0);
    const leqs = v === t ? leqs0 :
          range(v).map(i => range(v + 1).map(j => synds[i + j]));
    const rlx = futils.solve(leqs);
    return [gf.one(), ...rlx.reverse()];
  };
  const bchPositions = lx => range(N).filter(
    k => gf.isZero(gfPoly.apply(lx, gf.alpha(-k))));

  const bchOx = (sx, lx) =>
        gfPoly.mod(gfPoly.mul(sx, lx), gfPoly.carry(gfPoly.one(), t));
  const bchDLx = lx => gfPoly.diff(lx);

  const bchErrors = (positions, ox, dlx) => positions.map(k => {
    const akinv = gf.alpha(-k);
    const oAkinv = gfPoly.apply(ox, akinv);
    const dlAkinv = gfPoly.apply(dlx, akinv);
    const ak1b = gf.alpha(k * (1 - c));
    return gf.neg(gf.mul(ak1b, gf.div(oAkinv, dlAkinv)));
  });

  const bchErrorsPF2 = positions => gfPoly.sum(positions.map(
    k => gfPoly.carry(gfPoly.one(), k)));

  const bchEx = (positions, errors) =>
        gfPoly.sum(positions.map((k, i) => gfPoly.monomial(errors[i], k)));

  const decode = code => {
    const rx = pfPoly2gfPoly(code, N);
    const synds = bchSyndromes(rx);
    if (!hasError(synds)) return gfPoly2pfPoly(rx.slice(d), K);

    //const lx = bchLx(synds);
    const lx = PolynomialUtils(gfPoly).findLinearRecurrence(synds);
    const positions = bchPositions(lx);
    if (positions.length === 0) {
      throw Error(`Cannot recover: error count > ${t}`);
    }

    if (pfPoly.K.size() === 2) {
      const ex = bchErrorsPF2(positions);
      const cx = gfPoly.sub(rx, ex);
      return gfPoly2pfPoly(cx.slice(d), K);
    } else {
      const sx = synds;
      const ox = bchOx(sx, lx);
      const dlx = bchDLx(lx);
      const errors = bchErrors(positions, ox, dlx);

      const ex = bchEx(positions, errors);
      const cx = gfPoly.sub(rx, ex);
      return gfPoly2pfPoly(cx.slice(d), K);
    }
  };

  return {K, d, gen, encode, decode};
};
デコードでは、Berlekamp-Masseyアルゴリズムでlxを求める実装を用いるようにしていますが、PGZアルゴリズムのコードbchLx()も載せてあります。
bchcode.js利用コード例
bchcode-example.js
{
  console.log("[BCHCode with GF2n]");
  const gf = GF2n(4, 0b10011);
  const N = 15, t = 2, c = 1;
  const bch = BCHCode(gf, N, t, c);

  const msg = 0b0000101;
  console.log("msg", msg.toString(2).padStart(bch.K, "0"));
  let coded = bch.encode(msg);
  console.log("coded", coded.toString(2).padStart(N, "0"));
  coded = coded ^ (1 << 14);
  coded = coded ^ (1 << 12);
  //coded = coded ^ (1 << 1);
  console.log("error coded", coded.toString(2).padStart(N, "0"));

  const fixed = bch.decode(coded);
  console.log("fixed", fixed.toString(2).padStart(bch.K, "0"));
  console.log();
}
実行結果
[BCHCode with GF2n]
msg 0000101
coded 000010100110111
error coded 101010100110111
fixed 0000101
BCHCode'では、素数べき要素数の有限体としてGF2n'だけでなく、GF'も利用可能ですが、入出力データはGF内の要素の表現形式と同じものになります。つまり、GF2nであればビット列のPF2Polynomialであり、GFなら先頭を下位とする整数配列のPolynomial(PF(p))`になります。
一般化されたBCH符号とリードソロモン符号

BCH符号では、GF(p)係数の入出力データと、その拡大体であるGF($p^n$)係数でのエラー補正計算を行うものでした。

前編では、GF($(p^n)^m$)を、GF($p^n$)係数の多項式を用いて構築しました。
BCH符号の仕組みでは、GF($p^n$)係数の入出力データと、その拡大体であるGF($(p^n)^m$)係数でのエラー補正計算を行うことも可能です。

この、素数要素数に限らない有限体GF(q)とその拡大体GF($q^m$)とで、エンコードとデコードを構成するよう一般化したものが、「一般化されたBCH符号」となります。
一般化されたBCH符号でのn=1、m>1のケースが、ビット列を扱う狭義のBCH符号になります。

そして、この「一般化されたBHC符号」の上で、m=1のケースが、リードソロモン符号相当になります。
GF(q)の値sを解とする一次多項式x-sは、GF(q)係数での既約多項式であり、その総乗は最小公倍多項式です。

参考: 巡回符号

リードソロモン符号やBCH符号は巡回符号の一種です。

巡回符号とは、符号データを、循環シフトさせたデータも必ず符号データになるタイプの符号システムのことです。

前編の最後で、GF($p^n$)では、$x^{p^n-1}-1 = \prod_{k=0}^{p^n-2}(x-a^k)$が成立する、ことを示しました。

これはいくつかの$(x-a^k)$の積であるリードソロモン符号やBCH符号の生成多項式g(x)はともに、$x^{p^n-1}-1$を割り切ることを意味します。

$x^{p^n-1}-1 = b(x)g(x)$

ある符号データ$c(x)=d(x)g(x)$とし、その最上位係数を$v$とすると、1つ巡回したデータは

$c'(x) = xc(x)+V - vx^{p^n-1} = xc(x) - v(x^{p^n-1}-1)$

であり、c(x)、$x^{p^n1-}-1$のg(x)での式を代入すれば、

$c'(x) = xd(x)g(x)-vb(x)g(x) = (xd(x)-vb(x))g(x)$

となり、必ずg(x)で割り切れることが示されました。

一般化すると、$x^{N}-1$を割り切るg(x)で割り切れる、任意のN-1次データc(x)は、巡回させたc'(x)も、必ずg(x)で割り切れるデータになる、という性質を持ちます。

そして、符号化データがこのタイプのデータとなる符号システムのことを、巡回符号と呼びます。

チェックサムのCRCも、巡回符号の一種となります。

巡回符号な符号化システムでは、桁上げ(シフト)と(多項式での)モジュロ算で、符号化(エンコード)が実装できる、とのことです。

　 Tweet
Qiitaで続きを読む

投稿日：2020-03-28T14:28:45+09:00

有限体のプログラミング中編: JavaScriptで実装する有限体

前編内容

素数べき要素数の有限体のための基礎知識

素数べき要素数の有限体とその作り方

素数べき要素数の有限体の例

素数べき要素数の有限体のガロア群

中編内容

JavaScriptで実装する素数べき要素数有限体

2べき要素数の有限体に特化した実装

後編内容

有限体の応用: リードソロモン符号とBCH符号

注: 記事内のJavaScriptコードについて

この記事内のコードで用いるJavaScriptの仕様は、Array.flatMap()のあるECMAScript2019仕様までを用います。JSファイルは、すべて拡張子は.jsのES moduleです。

非ECMAScriptな要素として、console.logとconsole.assertのみを用います。その他のWeb APIやnode.jsビルトイン等は一切使用していません。

この記事内のコードは、以下のgistに置いています。

https://gist.github.com/bellbind/ba4b307fea8251f7f40aeb7e9349814b

多項式や有限体等の要素は、数値とArrayにマッピングし、それらのデータ処理をfunction式の中で記述します。体や多項式等は、このfunction実装をメンバーに持つObjectとして提供します。たとえば、有理数体Qでの加算は以下のようになります。

$c = \frac{1}{2} \times -\frac{3}{4}$ : const c = Q.mul([1, 2], [-3, 4]);

JavaScriptで素数べき要素数有限体

ここから、プログラム上で素数べき要素数の有限体GF($p^n$)の扱い方についての内容となります。

GF($p^n$)のプログラムは、

ユーティリティ

素数要素数の有限体(Prime Field): PF(p)

体Kを係数に持つ多項式: Polynomial(K)

素数べき要素数の有限体 GF($p^n$)

の順に実装します。そのあとで、多項式表現としてビット列を用いるp=2に特化したGF($2^n$)実装について触れます。

この有限体実装を使う応用として、前編の加算表や乗算表のmarkdownテーブルを出すコードを、そして、後編でエラー訂正可能なリードソロモン符号の実装を行います。

ユーティリティ: field-utils.js
コード全体
field-utils.js
// Array utils
export const range = n => [...Array(n).keys()];
export const uniq = (a, eql = (e1, e2) => e1 === e2) =>
      a.filter((e1, i) => a.findIndex(e2 => eql(e1, e2)) === i);
export const transpose = a => range(a[0].length).map(k => a.map(e => e[k]));

// Field suppliment: generate isZero, sub, div, sum, prod
export const Field = K => {
  const {eql, zero, one, add, mul, neg, inv} = K;
  const sub = (a, b) => add(a, neg(b));
  const div = (a, b) => mul(a, inv(b));
  const sum = es => es.reduce((r, e) => add(r, e), zero());
  const prod = es => es.reduce((r, e) => mul(r, e), one());
  const isZero = e => eql(e, zero());
  return {sub, div, sum, prod, isZero, ...K};
};

// Example Field Q: Rational number
export const Q = () => {
  const gcd = (a, b) => a === 0 ? b : gcd(b % a, a);
  const normalize = ([e0, e1]) => {
    const f = gcd(e1, e0);
    return [e0 / f, e1 / f];
  };

  const eql = (a, b) => a[0] * b[1] === a[1] * b[0];
  const zero = () => [0, 1];
  const one = () => [1, 1];
  const neg = e => [-e[0], e[1]];
  const inv = e => normalize([e[1], e[0]]);
  const add = (a, b) => normalize([a[0] * b[1] + b[0] * a[1], a[1] * b[1]]);
  const mul = (a, b) => normalize([a[0] * b[0], a[1] * b[1]]);

  const times = (e, k) => normalize([e[0] * k, e[1]]);
  const pow = (e, k) => normalize([e[0] ** k, e[1] ** k]);
  const toStr = e => e[1] === 1 ? `${e[0]}` : `${e[0]}/${e[1]}`;
  const toNum = e => Math.round(e[0] / e[1]);
  const fromNum = n => [n, 1];

  return Field({
    eql, zero, one, neg, inv, add, mul, times, pow, toStr, toNum, fromNum});
};

// Field utilities
export const FieldUtils = K => {
  const {isZero, zero, one, neg, inv, sub, mul, div} = K;
  // linear equations solver on the field f
  const pivoting = (r, u, i) => {
    for (let v = u + 1; v < r.length; v++) {
      if (!isZero(r[v][i])) {
        [r[u], r[v]] = [r[v], r[u]];
        break;
      }
    }
  };

  const upperTriangle = r => {
    const n = r[0].length - 1, m = r.length;
    for (let i = 0, u = 0; i < n && u < m; i++) {
      if (isZero(r[u][i])) pivoting(r, u, i);
      if (isZero(r[u][i])) continue;
      for (let v = u + 1; v < m; v++) {
        const c = div(r[v][i], r[u][i]);
        for (let j = i; j < n + 1; j++) {
          r[v][j] = sub(r[v][j], mul(c, r[u][j]));
        }
      }
      u++;
    }
  };

  const rank = lineqs => {
    const r = lineqs.map(lineq => lineq.slice());
    upperTriangle(r);
    return r.filter(eq => !eq.slice(0, -1).every(isZero)).length;
  };

  const solve = lineqs => {
    const r = lineqs.map(lineq => lineq.slice());
    upperTriangle(r);
    const n = r[0].length - 1, m = r.length;
    for (let i = n - 1, u = m - 1; i >= 0 && u >= 0; i--) {
      while (u > 0 && isZero(r[u][i])) u--;
      if (isZero(r[u][i])) continue;
      r[u][n] = div(r[u][n], r[u][i]);
      r[u][i] = one();
      for (let v = u - 1; v >= 0; v--) {
        r[v][n] = sub(r[v][n], mul(r[v][i], r[u][n]));
        r[v][i] = zero();
      }
    }
    return r.slice(0, n).map(l => neg(l[n]));
  };
  return {rank, solve};
};
JavaScript配列用ユーティリティ関数群
field-utils.js[1]
export const range = n => [...Array(n).keys()];
export const uniq = (a, eql = (e1, e2) => e1 === e2) =>
      a.filter((e1, i) => a.findIndex(e2 => eql(e1, e2)) === i);
export const transpose = a => range(a[0].length).map(k => a.map(e => e[k]));
range(n): 0からn-1までの数の列挙配列を返す

uniq(a, eql): aのうちの重複要素を除いた配列を返す

transpose(m): 二階配列mの転置配列を返す

二階配列aの転置配列tというのは、a[i][j]の値がt[j][i]に入っている二階配列tのことです。
たとえば、transpose([[1,2,3], ["a","b","c"]])の結果は、[[1,"a"], [2,"b"], [3,"c"]]です。

体の機能補完
field-utils.js[2]
export const Field = K => {
  const {eql, zero, one, add, mul, neg, inv} = K;

  const sub = (a, b) => add(a, neg(b));
  const div = (a, b) => mul(a, inv(b));
  const sum = es => es.reduce((r, e) => add(r, e), zero());
  const prod = es => es.reduce((r, e) => mul(r, e), one());
  const isZero = e => eql(e, zero());

  return {sub, div, sum, prod, isZero, ...K};
};
Field(K)は、基本となる関数群eql(a,b)、zero()、one()、add(a,b)、mul(a,b)、neg(e)、inv(e)を備える体Kをもとに、以下の関数実装を補完します。

sub(a,b): 減算: $a - b$

div(a,b): 除算: $a / b$

sum(es): 体の要素の配列esの総和: $\sum_{i}{e_i}$

prod(es): 体の要素の配列esの総乗: $\prod_{i}{e_i}$

isZero(e): ゼロ判定: $e = 0$

これらの関数の実装に必要な、上述の関数群については、次の有限体Qで説明します。

ちなみに、この記事のプログラミング上での体は、多項式の係数など、積が可換であることを前提とした利用をします。たとえば、積が非可換になる4元数体(quaternion)は対象外です。

有限体Q実装
field-utils.js[3]
export const Q = () => {
  const gcd = (a, b) => a === 0 ? b : gcd(b % a, a);
  const normalize = ([e0, e1]) => {
    const f = gcd(e1, e0);
    return [e0 / f, e1 / f];
  };

  const eql = (a, b) => a[0] * b[1] === a[1] * b[0];
  const zero = () => [0, 1];
  const one = () => [1, 1];
  const neg = e => [-e[0], e[1]];
  const inv = e => normalize([e[1], e[0]]);
  const add = (a, b) => normalize([a[0] * b[1] + b[0] * a[1], a[1] * b[1]]);
  const mul = (a, b) => normalize([a[0] * b[0], a[1] * b[1]]);

  const times = (e, k) => normalize([e[0] * k, e[1]]);
  const pow = (e, k) => normalize([e[0] ** k, e[1] ** k]);
  const toStr = e => e[1] === 1 ? `${e[0]}` : `${e[0]}/${e[1]}`;
  const toNum = e => Math.round(e[0] / e[1]);
  const fromNum = n => [n, 1];

  return Field({
    eql, zero, one, neg, inv, add, mul, times, pow, toStr, toNum, fromNum});
};
体の実装例としての有理数体Qです。

体の要素: ２要素の整数配列 [分子, 分母]

実装した体の演算

eql(a, b): 同値関係 $a = b$

zero(): $0$

one(): $1$

`neg(e): 負数 $-e$

`inv(e): 逆数 $1/e$

add(a, b): 加算 $a + b$

mul(a, b): 乗算 $a * b$

`times(e, k): 整数倍 $ke$

pow(e, k): べき乗 $e^k$

toStr(e): $e$の文字列表現

toNum(e): $e$の数値表現

fromNum(n): 数値表現に対応するQの要素(2要素配列)

引数のa、b、eは体の要素の値で、kは整数値です。

timesとpowのkは、Qの整数[e0, 1]ではない点に注意です。このkは、addやmulで演算の要素の数です。たとえば、$e + e + e$を$3e$、$e * e * e$を$a^3$と表現したものです。

toStr、toNum、fromNumはJavaScriptの値との相互変換機能になります。

これにFieldで追加されるisZero(e)、sub(a, b)、div(a, b)、sum(es)、prod(es)を持ちます。

体のユーティリティFieldUtils(K)
field-utils.js[4]
export const FieldUtils = K => {
  const {isZero, zero, one, neg, inv, sub, mul, div} = K;
  // linear equations solver on the field f
  const pivoting = (r, u, i) => {
    for (let v = u + 1; v < r.length; v++) {
      if (!isZero(r[v][i])) {
        [r[u], r[v]] = [r[v], r[u]];
        break;
      }
    }
  };

  const upperTriangle = r => {
    const n = r[0].length - 1, m = r.length;
    for (let i = 0, u = 0; i < n && u < m; i++) {
      if (isZero(r[u][i])) pivoting(r, u, i);
      if (isZero(r[u][i])) continue;
      for (let v = u + 1; v < m; v++) {
        const c = div(r[v][i], r[u][i]);
        for (let j = i; j < n + 1; j++) {
          r[v][j] = sub(r[v][j], mul(c, r[u][j]));
        }
      }
      u++;
    }
  };

  const rank = lineqs => {
    const r = lineqs.map(lineq => lineq.slice());
    upperTriangle(r);
    return r.filter(eq => !eq.slice(0, -1).every(isZero)).length;
  };

  const solve = lineqs => {
    const r = lineqs.map(lineq => lineq.slice());
    upperTriangle(r);
    const n = r[0].length - 1, m = r.length;
    for (let i = n - 1, u = m - 1; i >= 0 && u >= 0; i--) {
      while (u > 0 && isZero(r[u][i])) u--;
      if (isZero(r[u][i])) continue;
      r[u][n] = div(r[u][n], r[u][i]);
      r[u][i] = one();
      for (let v = u - 1; v >= 0; v--) {
        r[v][n] = sub(r[v][n], mul(r[v][i], r[u][n]));
        r[v][i] = zero();
      }
    }
    return r.slice(0, n).map(l => neg(l[n]));
  };
  return {rank, solve};
};
体Kをパラメータに取るFieldUtils(K)は、指定した体Kの演算を用いて実装する汎用計算を提供します。
ここでは、後の応用で使用する連立方程式用の機能を提供します。

rank(lineqs): 体Kを係数とする連立方程式の係数行列のランク

lineqs: 1次方程式E[0]x0 + E[1]x1 + ... + E[N]xn + E[N+1] = 0を表す配列Eを要素とする連立方程式を表す配列

戻り値: 係数行列のランク

solve(lineqs): 体Kを係数とする連立方程式を解くガウス除去ソルバ

lineqs: 1次方程式E[0]x0 + E[1]x1 + ... + E[N]xn + E[N+1] = 0を表す配列Eを要素とする連立方程式を表す配列

戻り値: 解[x0, x1, ..., xn]の配列

rank(lineqs)での、連立方程式の係数行列とは、方程式a*x+b*y = fとc*x+d*y = gの、変数xとyの連立方程式では、その係数でつくる[[a, b], [c, d]]に相当する行列のことです。

ノート: 係数行列のランク、連立方程式ソルバー実装

係数行列のランクは、変数の実質の次元のことです。3つの方程式がx、y、zと３変数で構成されていても、係数行列のランクが2であれば、2変数で残りの1変数が表現できる係数構成になっていることを意味し、連立方程式として単一の3変数の解を求めることができなくなります。つまり、ランクと変数の数を比較することで、連立方程式が単一の解を持つかどうかの判定ができます。つまり、解ける連立方程式は、変数の数とランクが一致する、ということです。

solve(lineqs)は、連立方程式を満たす解を計算し、配列で出力します。
実装は、ガウス消去法です。
ただし、係数の数と方程式の数が一致しない、冗長な連立方程式でも解けるようにするために、行と列のためのループの変数を分離したため、対角行列特化の実装と比べて、若干複雑になっています。

ランクの計算は、ガウス消去法の前半の結果として得られる上三角行列で明らかになります。
この上三角行列の中の、すべて0でない行の数がランクとなります。
連立方程式ソルバ利用例
solve-example.js
import {Q, FieldUtils} from "./field-utils.js";

{
  const K = Q(), futils = FieldUtils(K);
  const lineqs = [
    [1, 2, -5], // x+2y-5=0
    [2, 3, -8], // 2x+3y-8=0
  ].map(eq => eq.map(K.fromNum));

  console.log("rank =", futils.rank(lineqs));
  console.log("[x, y] =", futils.solve(lineqs).map(K.toStr));
}
実行結果
rank = 2
[x, y] = [ '1', '2' ]
素数要素数の有限体PF(p): pf.js
コード全体
pf.js
import {range, uniq, Field} from "./field-utils.js";

// number utils
const egcd = (a, b) => {
  if (a === 0) return [b, 0, 1];    // b = 0*0 + b*1
  const r = b % a, q = (b - r) / a; // r = b - a*q
  const [g, s, t] = egcd(r, a);     // g = r*s + a*t;
  return [g, t - q * s, s];         // g = (b-a*q)*s + a*t = a*(t-q*s) + b*t
};
const primes = max => {
  const ps = [];
  let ns = range(max).slice(2);
  while (ns.length > 0) {
    const p = ns[0];
    ps.push(p);
    ns = ns.filter(n => n % p);
  }
  return ps;
};
const primeFactors = n => {
  const ps = [];
  for (const p of primes(n)) {
    if (n % p === 0) ps.push(p);
  }
  return ps;
};


// GF(p)
export const PF = (p, pe) => {
  const p1 = p - 1;
  const modp = n => (p + n % p) % p;
  const modp1 = n => (p1 + n % p1) % p1;

  const eql = (a, b) => modp(a) === modp(b);
  const zero = () => 0;
  const one = () => 1;
  const add = (a, b) => modp(a + b);
  const mul = (a, b) => modp(a * b);
  const neg = e => modp(-e);
  const inv = e => modp(egcd(e, p)[1]);

  const times = (e, k) => modp(e * k);
  const pow = (e, k) => {
    k = modp1(k);
    return k === 0 ? one() : k === 1 ? e : mul(e, pow(e, k - 1));
  };
  const toStr = e => `${e}`;
  const toNum = e => e;
  const fromNum = n => n;

  // find primitive element for GF(p)
  const isPrimitiveElement = (e, pfs = primeFactors(p1)) => {
    for (const pf of pfs) if (pow(e, p1 / pf) === 1) return false;
    return true;
  };
  const primitiveElement = p => {
    const pfs = primeFactors(p1);
    for (let e = 2; e < p1; e++) if (isPrimitiveElement(e, pfs)) return e;
    throw Error("never reached");
  };
  const a = pe ? pe : p === 2 ? 1 : p === 3 ? 2 : primitiveElement(p);
  const alpha = (k = 1) => pow(a, k);

  const size = () => p;
  const isPrimitive = () => isPrimitiveElement(a);
  const elems = () => range(p);

  return Field({
    p, eql, zero, alpha, one, add, mul, neg, inv, times, pow,
    toStr, toNum, fromNum, size, elems});
};
整数ユーティリティ関数
pf.js[1]
const egcd = (a, b) => {
  if (a === 0) return [b, 0, 1];    // b = 0*0 + b*1
  const r = b % a, q = (b - r) / a; // r = b - a*q
  const [g, s, t] = egcd(r, a);     // g = r*s + a*t;
  return [g, t - q * s, s];         // g = (b-a*q)*s + a*t = a*(t-q*s) + b*t
};
const primes = max => {
  const ps = [];
  let ns = range(max).slice(2);
  while (ns.length > 0) {
    const p = ns[0];
    ps.push(p);
    ns = ns.filter(n => n % p);
  }
  return ps;
};
const primeFactors = n => {
  const ps = [];
  for (const p of primes(n)) {
    if (n % p === 0) ps.push(p);
  }
  return ps;
};
egcd(a, b): a*s + b*t = g となる[g, s, t]の配列を返す拡張ユークリッド互除法

primes(max): max未満の素数の配列を返す

primeFactors(n): nの素因数の配列を返す

egcdはPF(p)での逆数inv(a)実装で使用します。
また、primeFactorsは、PF(p)での原始元を見つけるために使用します。

素数要素数の有限体PF(q)実装
pf.js[2]
export const PF = (p, pe) => {
  const p1 = p - 1;
  const modp = n => (p + n % p) % p;
  const modp1 = n => (p1 + n % p1) % p1;

  const eql = (a, b) => modp(a) === modp(b);
  const zero = () => 0;
  const one = () => 1;
  const add = (a, b) => modp(a + b);
  const mul = (a, b) => modp(a * b);
  const neg = e => modp(-e);
  const inv = e => modp(egcd(e, p)[1]);

  const times = (e, k) => modp(e * k);
  const pow = (e, k) => {
    k = modp1(k);
    return k === 0 ? one() : k === 1 ? e : mul(e, pow(e, k - 1));
  };
  const toStr = e => `${e}`;
  const toNum = e => e;
  const fromNum = n => n;

  // find primitive element for GF(p)
  const isPrimitiveElement = (e, pfs = primeFactors(p1)) => {
    for (const pf of pfs) if (pow(e, p1 / pf) === 1) return false;
    return true;
  };
  const primitiveElement = p => {
    const pfs = primeFactors(p1);
    for (let e = 2; e < p1; e++) if (isPrimitiveElement(e, pfs)) return e;
    throw Error("never reached");
  };
  const a = pe ? pe : p === 2 ? 1 : p === 3 ? 2 : primitiveElement(p);
  const alpha = (k = 1) => pow(a, k);

  const size = () => p;
  const isPrimitive = () => isPrimitiveElement(a);
  const elems = () => range(p);

  return Field({
    p, eql, zero, alpha, one, add, mul, neg, inv, times, pow,
    toStr, toNum, fromNum, size, elems});
};
PF(p)はパラメータとして素数値pを受け取り、モジュロ演算を用いた、素数要素数の有限体GF(p)を作ります。

PF(p)の要素: 非負整数値(JavaScriptのnumber)

PF(p)の演算実装(Qと同じ関数群を実装)

eql(a, b): a % q === b % q

zero(): 0

one(): 1

add(a, b): a + b % q

mul(a, b): a * b % q

neg(e): q - e

inv(e): [1, s, t] = egcd(e, q)のs % qがeの逆数

times(e, k): l * e % q

pow(e, k): 1にeをk回上記のmulでかける

toStr(e), toNum(e)、fromNum(n): 略

また、有限体として以下の関数を備えます:

alpha(k=1): PF(p)の原始元(のk乗)を返す

isPrimitive(): (パラメータpeで設定可能な)aが原始元かどうか

size(): 要素数を返す

elems(): 全要素の配列を返す

これらに、前述のField()によるisZero(a), sub(a, b)、div(a, b)、sum(es)、prod(es)が追加されたオブジェクトを返します。

ノート: 素数要素数の有限体PF(p)の原始元

PF(q)にも、べき乗していくことで、すべての数になる原始元(Primitive Element)が(複数)存在します。

ただし、有限体GF($p^n$)が原始元aを基準にして、その多項式を要素とするのと違い、要素は整数値を用いるため、数値の中から原始元aになるものを発見しなくてはいけません。

この発見方法は、2からp-1までの数の中から、$p-1$乗までべき乗することで初めて1になる数であるかをチェックすることです。

GF($p^n$)と同様、数eが原始元でなければ、eの指数表現$a^k$としたときの指数kはp-1と互いに素ではない数になります。そして、kとp-1の公約数をdとすると、どの公約数でも、$a^k$は(p-1)/d乗したときにも1になります。 k(p-1)/d mod p-1が0になり、$a^0=1$だからです。

ただし原始元が決まらなければこの公約数dもわかりません。
そこでdになりうる候補としてp-1の素因数を総当りし、どの(p-1)/d乗でも1にならなければ、それは原始元である、として実装することができます。

暗号技術のDH鍵交換などでは、PF(p)の原始元のことを、乗算の巡回群関係だけに注目して、(巡回群としての)生成元(generator)とよんでいます。同時にどの数も$g^0=1$になる、べき乗の指数p-1のことも(巡回群としての)位数(order)と呼びます。

また、暗号化技術では、原始元(生成元)は、解析を難しくするため、大きめ値のものを指定して用います。暗号技術の仕組みの理解するために、小さい値の原始元を用いて手計算で行っても、同様の結果が得られます。

体Kを係数とする多項式Polynomial(K): polynomial.js
コード全体
polynomial.js
import {range, uniq} from "./field-utils.js";

// Polynomial[F]
export const Polynomial = K => {
  const zeros = n => Array(n).fill(K.zero());

  const eql = (a, b) => {
    if (a.length <  b.length) [a, b] = [b, a];
    return a.every((c, k) => k < b.length ? K.eql(c, b[k]) : K.isZero(c));
  };
  const zero = () => [K.zero()];
  const one = () => [K.one()];
  const add = (a, b) => {
    if (a.length < b.length) [a, b] = [b, a];
    return a.map((c, k) => k < b.length ? K.add(c, b[k]) : c);
  };
  const neg = e => e.map(c => K.neg(c));
  const sub = (a, b) => add(a, neg(b));
  const sum = es => es.reduce((r, e) => add(r, e), zero());
  const scale = (e, c) => e.map(ci => K.mul(ci, c));
  const carry = (e, k) => [...zeros(k), ...e];
  const mul = (a, b) => sum(b.map((bk, k) => carry(scale(a, bk), k)));

  const order = e => {
    for (let i = e.length - 1; i > 0; i--) if (!K.isZero(e[i])) return i;
    return 0;
  };
  const mod = (a, b) => {
    const an = order(a), bn = order(b);
    console.assert(bn > 0, "poly.mod");
    if (an < bn) return a.slice(0, bn);
    const f = K.div(a[an], b[bn]);
    return mod(sub(a, carry(scale(b, f), an - bn)).slice(0, an), b);
  };
  const prod = es => es.reduce((r, e) => mul(r, e), one());
  const times = (e, k) => e.map(c => K.times(c, k));
  const diff = e => e.map((c, k) => K.times(c, k)).slice(1);

  const coef = (e, k) => e[k] || K.zero();
  const monomial = (c, k) => carry(scale(one(), c), k);
  const apply = (e, v) => K.sum(e.map((c, k) => K.mul(c, K.pow(v, k))));

  const toStr = (e, name = "x") => {
    const s1 = e.map((c, k) => {
      if (k === 0) {
        const coef = K.toStr(c);
        return coef.includes("+") ? `(${coef})` : coef;
      }
      if (K.isZero(c)) return "";
      const coef = K.eql(c, K.one()) ? "" : K.toStr(c);
      const cstr = coef.includes("+") ? `(${coef})` : coef;
      const pow = k === 1 ? "" : `^{${k}}`;
      return `${cstr}${name}${pow}`;
    }).filter(e => e);
    const s2 = s1.length > 1 && s1[0] === K.toStr(K.zero()) ? s1.slice(1) : s1;
    return s2.reverse().join("+");
  };
  const toArray = (e, len) =>
        e.length < len ? [...e, ...zeros(len - e.length)] : e.slice(0, len);
  const fromArray = cs => cs;
  const R = {
    K, eql, zero, one, add, scale, carry, neg, sub, sum, mul, mod, prod, times,
    order, diff, coef, monomial, apply, toStr, toArray, fromArray,
  };

  if (K.size && K.elems) {
    const toNum = e => e.reduceRight((r, c) => r * K.size() + K.toNum(c), 0);
    const fromNum = n => {
      const e = [];
      while (n > 0) {
        const r = n % K.size();
        e.push(K.fromNum(r));
        n = (n - r) / K.size();
      }
      return e;
    };
    const elems = k => {
      if (k < 0) return [[]];
      const base = elems(k - 1);
      return K.elems().flatMap(c => base.map(b => [...b, c]));
    };
    return {...R, toNum, fromNum, elems};
  } else return R;
};

// Polynomial utilities
export const PolynomialUtils = poly => {
  const {K, eql, one, add, sub, scale, carry, mul, coef, elems} = poly;
  // listing irreducible polynomials
  const kPolynoms = k => elems(k - 1).map(e => add(e, carry(one(), k)));
  const reducibles = n => {
    const rs = [];
    for (let i = 1, nh = n >> 1; i <= nh; i++) {
      const l = kPolynoms(i), r = kPolynoms(n - i);
      for (const lp of l) for (const rp of r) rs.push(mul(lp, rp));
    }
    return uniq(rs, eql);
  };
  const irreducibles = n => {
    const reds = reducibles(n);
    return kPolynoms(n).filter(f => !reds.find(r => eql(f, r)));
  };

  const findLinearRecurrence = s => {
    // Berlekamp-Massey algorithm
    let cx = one(), cl = 1, bx = one(), bl = 1, b = K.one(), m = 0;
    for (let i = 0; i < s.length; i++) {
      const d = K.sum(range(cl).map(k => K.mul(coef(cx, k), s[i - k])));
      m++;
      if (K.isZero(d)) continue;
      const tx = cx, tl = cl;
      cx = sub(cx, scale(carry(bx, m), K.div(d, b)));
      cl = Math.max(cl, bl + m);
      if (cl > tl) [bx, bl, b, m] = [tx, tl, d, 0];
    }
    return cx;
  };

  return {irreducibles, findLinearRecurrence};
};
多項式Polynomial(K)

多項式実装は、代数系としての演算以外にも、多項式固有の操作も提供するため、大きくなります。
いくつかに、分割しながら、説明していきます。
polynomial.js[1]
export const Polynomial = K => {
  const zeros = n => Array(n).fill(K.zero());

  const eql = (a, b) => {
    if (a.length <  b.length) [a, b] = [b, a];
    return a.every((c, k) => k < b.length ? K.eql(c, b[k]) : K.isZero(c));
  };
  const zero = () => [K.zero()];
  const one = () => [K.one()];
  const add = (a, b) => {
    if (a.length < b.length) [a, b] = [b, a];
    return a.map((c, k) => k < b.length ? K.add(c, b[k]) : c);
  };
多項式Polynomial(K)は、パラメータとして体Kを係数とする多項式です。

要素としての多項式: 変数の指数を配列インデックスとする、係数値のJavaScript配列

例 PF(5)係数の多項式 $x^{3}+2x$: [0,2,0,1]

多項式の配列要素数は任意長とし、eqlやaddでの実装のように、配列サイズを超えたインデックスの係数は(体Kでの)0とみなすように各演算を実装します。
polynomial.js[2]
  const neg = e => e.map(c => K.neg(c));
  const sub = (a, b) => add(a, neg(b));
  const sum = es => es.reduce((r, e) => add(r, e), zero());
  const scale = (e, c) => e.map(ci => K.mul(ci, c));
  const carry = (e, k) => [...zeros(k), ...e];
  const mul = (a, b) => sum(b.map((bk, k) => carry(scale(a, bk), k)));

  const order = e => {
    for (let i = e.length - 1; i > 0; i--) if (!K.isZero(e[i])) return i;
    return 0;
  };
  const mod = (a, b) => {
    const an = order(a), bn = order(b);
    console.assert(bn > 0, "poly.mod");
    if (an < bn) return a.slice(0, bn);
    const f = K.div(a[an], b[bn]);
    return mod(sub(a, carry(scale(b, f), an - bn)).slice(0, an), b);
  };
  const prod = es => es.reduce((r, e) => mul(r, e), one());
  const times = (e, k) => e.map(c => K.times(c, k));
次は乗算の実装ですが、まず多項式でのneg(e)、sub(a, b)、sum(es)、scale(e, c)、carry(e, k)、order(e)を実装し、それらを用いてmul(a, b)とmod(a, b)を実装します。

neg(e): 負多項式。e(x)の各係数を(Kでの)負数にした多項式

sub(a, b): 多項式の減算。a(x)からb(x)を係数ごとに引いた多項式

sum(es): 多項式の総和。各項ごとの係数での総和

scale(e, c): e(x)のc倍。e(x)の各係数へｃを(体K)で乗算した多項式。

carry(e, k): e(x)のk桁上げ。e(x)を$x^k$倍した多項式。e(x)配列の頭にk個の0を追加した配列を作る

order(e): e(x)の次数。e(x)配列の0でない最上位要素のインデックスが多項式の次数

多項式の乗算mul(a, b)の実装では、b(x)の各k次の項ごとに、$b_k * a(x) * x^k$し(carry(scale(a, bk), k))、それらの総和を取ります。

多項式のモジュロ算mod(a, b)は、b(x)の次数以下になるまで、a(x)の最上位項が0になるよう引き算で取り除くことを(再帰呼び出しで)繰り返すことで剰余を割り出します。
モジュロ算が配列としての桁を抑える実用効果として、結果の配列の要素数をbの要素数引く1に切り詰めています。

prod(es): esの多項式の総乗の実装

times(e, k): k個のe(x)の総和の実装

これらは応用時に使用するため、用意しました。
polynomial.js[3]
  const diff = e => e.map((c, k) => K.times(c, k)).slice(1);

  const coef = (e, k) => e[k] || K.zero();
  const monomial = (c, k) => carry(scale(one(), c), k);
  const apply = (e, v) => K.sum(e.map((c, k) => K.mul(c, K.pow(v, k))));

  const toStr = (e, name = "x") => {
    const s1 = e.map((c, k) => {
      if (k === 0) {
        const coef = K.toStr(c);
        return coef.includes("+") ? `(${coef})` : coef;
      }
      if (K.isZero(c)) return "";
      const coef = K.eql(c, K.one()) ? "" : K.toStr(c);
      const cstr = coef.includes("+") ? `(${coef})` : coef;
      const pow = k === 1 ? "" : `^{${k}}`;
      return `${cstr}${name}${pow}`;
    }).filter(e => e);
    const s2 = s1.length > 1 && s1[0] === K.toStr(K.zero()) ? s1.slice(1) : s1;
    return s2.reverse().join("+");
  };
  const toArray = (e, len) =>
        e.length < len ? [...e, ...zeros(len - e.length)] : e.slice(0, len);
  const fromArray = cs => cs;
  const R = {
    K, eql, zero, one, add, scale, carry, neg, sub, sum, mul, mod, prod, times,
    order, diff, coef, monomial, apply, toStr, toArray, fromArray,
  };
多項式固有の機能

diff(e): e(x)の微分

coef(e, k): e(x)のk次項の係数(Coefficient)

monimial(c, k): 単項式$cx^k$

apply(e, v): 体Kの値vをe(x)に代入した体Kの値e(x=v)

JavaScriptデータとの相互変換

toStr(e, name="x"): e(a)の文字列表現(LaTeX数式形式)

toArray(e, len): 係数配列化(len要素固定)

fromArray(cs): 係数配列から多項式値の復元

多項式文字列の変数名のデフォルト名は"x"にしています。

例 $a^3+2a$: [0,2,0,1] => "a^{3}+2a"
polynomial.js[4]
  if (K.size && K.elems) {
    const toNum = e => e.reduceRight((r, c) => r * K.size() + K.toNum(c), 0);
    const fromNum = n => {
      const e = [];
      while (n > 0) {
        const r = n % K.size();
        e.push(K.fromNum(r));
        n = (n - r) / K.size();
      }
      return e;
    };
    const elems = k => {
      if (k < 0) return [[]];
      const base = elems(k - 1);
      return K.elems().flatMap(c => base.map(b => [...b, c]));
    };
    return {...R, toNum, fromNum, elems};
  } else return R;
};
Kが有限体の場合(K.size()とK.elems()が存在する)には、以下の関数群を追加します。

toNum(e): e(x)のJavaScript整数表現

fromNum(n): JavaScript整数から多項式を復元

elems(k): k次未満の多項式の列挙

係数が有限体の場合、係数の有限体Kは要素数n未満の整数値にマッピングでき、整数化した係数をn進数の各桁の数とすることで、有限体係数の多項式も単一の整数値にマッピングできます。

多項式ユーティリティPolynomialUtils(poly)
polynomial.js[1]
export const PolynomialUtils = poly => {
  const {K, eql, one, add, sub, scale, carry, mul, coef, elems} = poly;
  // listing irreducible polynomials
  const kPolynoms = k => elems(k - 1).map(e => add(e, carry(one(), k)));
  const reducibles = n => {
    const rs = [];
    for (let i = 1, nh = n >> 1; i <= nh; i++) {
      const l = kPolynoms(i), r = kPolynoms(n - i);
      for (const lp of l) for (const rp of r) rs.push(mul(lp, rp));
    }
    return uniq(rs, eql);
  };
  const irreducibles = n => {
    const reds = reducibles(n);
    return kPolynoms(n).filter(f => !reds.find(r => eql(f, r)));
  };

  const findLinearRecurrence = s => {
    // Berlekamp-Massey algorithm
    let cx = one(), cl = 1, bx = one(), bl = 1, b = K.one(), m = 0;
    for (let i = 0; i < s.length; i++) {
      const d = K.sum(range(cl).map(k => K.mul(coef(cx, k), s[i - k])));
      m++;
      if (K.isZero(d)) continue;
      const tx = cx, tl = cl;
      cx = sub(cx, scale(carry(bx, m), K.div(d, b)));
      cl = Math.max(cl, bl + m);
      if (cl > tl) [bx, bl, b, m] = [tx, tl, d, 0];
    }
    return cx;
  };

  return {irreducibles, findLinearRecurrence};
};
多項式ユーティリティPolynomialUtils(poly)は、パラメータpolyの多項式演算を利用した汎用機能を提供します。

irreducible(n): 有限体係数のn次既約多項式(irreducible polynomial)を全列挙した配列を返す関数

findLinearRecurrence(s): 数列s[k]から、任意階数の線形漸化式(linear recurrence equation)の係数を見つける関数

irreducibles(n)による有限体係数のn次既約多項式の全列挙は、全n次多項式から、n次の可約多項式(reducible polynomial)を取り除いたものです。n次の可約多項式は、n未満次の全多項式同士を掛け合わせることで導出します。

線形漸化式は、任意個の前項の線形和として構成する数列のことです。
たとえばフィボナッチ数の漸化式$s_n = s_{n-1}+s_{n-2}$は２つ前までの項の線形和であり、線形漸化式の一種となります。このフィボナッチ数の漸化式の係数列は、1, 1です。ちなみに、等比aの等比数列は$s_n = as_{n-1}$の線形漸化式であり、等差数列の等比はどのk項でも同じ値の$s_{k} - s_{k-1}$になるため、等比数列はすべて、$s_n = s_{n-1} + (s_{n-1}-s_{n-2}) = 2s_{n_1} - s_{n-1}$の線形漸化式になります。

ただし、findLinearRecurrence(s)では、数列sが線形漸化式によるものである場合、漸化式表現を$s_n + c_1s_{n-1} + c_2s_{n-2} + ... = 0$と表現したときの係数列[1, $c_1$, $c_2$, ...]を(多項式扱いで)返します。

たとえば、フィボナッチ数s = [1, 1, 2, 3, 5, 8]を渡した結果は、配列として[1, -1, -1]、つまり$s_n - s_{n-1} - s_{n-2} = 0$が得られます。
この結果は、sのうちの3つ目以降の項2,3,5,8すべてに対して成立する関係となっています。
参考: Berlekamp-Masseyアルゴリズム
このfindLinearRecurrenceの実装のアルゴリズムは、Berlekamp-Masseyアルゴリズムというものです。

このアルゴリズムは、本来は後述する応用のBCH符号でのエラー位置方程式を、有限体数列から算出するための手法でした。この有限体の演算を切り替えることで、そのまま有理数体Qなどの無限体でも適用可能なものとなり、漸化式を発見する手法として解釈されるものとなりました。

以下は、このアルゴリズムの内容です。

注: wikipediaのコードでのLやその判定条件は直観的ではないので、より素直な多項式の長さを用いるよう、置き換えています

まず、変数cxは漸化式係数(の多項式c(x))であり、数列sをたどるループ内で更新していきます。変数clはこのcxの長さです。

ループ内のdは、s[i]に対し、漸化式cxを適用した結果です。

$d = \sum_{k=0}^{{cl}-1}{c(x)}_k s[i-k]$

dが0であれば、cxの漸化式がそのiの時点では成立していることを意味します。

もし、dが0でなければ、以下の式でcxを更新します。

$c(x) - \frac{d}{b}b(x)x^m$

変数bxは、cxを更新してclが伸びたときの、その直前のcxになります。blはbxの長さです。
bは、bxを更新したときのdです。

mは、cx更新時に使うbxの桁上げ値です。ループで増やし続け、bx更新時にリセットします。
よってi-mはbxを更新した時点のiであり、bとmとbxの関係は、常に以下になります。

$b = \sum_{k=0}^{{bl}-1}{b(x)}_k s[i-m-k]$

このため、cxを更新した時点のiで、この新しいcxを用い、再びdを計算すれば必ず0になります。
\begin{align}
\sum_{k=0}^{{cl}-1}{(c(x) - \frac{d}{b}b(x)x^m)}_{k} s[i-k] &= \sum_{k=0}^{{cl}-1}{c(x)}_k s[i-k] - \frac{d}{b}\sum_{k=0}^{{bl}-1}{b(x)}_k s[i-m-k] \\
&= d - \frac{d}{b}{b} \\
&= 0
\end{align}
よって、ループが数列sの最後まで到達したあとのcxによる漸化式は、そのs全体で成立するものとなっています。

$\sum_{k=0}^{{cl}-1}{c(x)}_k s[i-k] = 0$ (ただしcx.length <= i < s.length)
素数べき要素数の有限体GF(p^n): gf.js
コード全体
gf.js
import {range, uniq, transpose, Field, FieldUtils} from "./field-utils.js";
import {PF} from "./pf.js";
import {Polynomial} from "./polynomial.js";

// GF(p^n)
export const GF = (K, n, f, name="a") => {
  const pn = K.size() ** n, pn1 = pn - 1;
  const poly = Polynomial(K);
  const p2gf = pe => poly.toArray(pe, n);
  const modpn1 = k => (pn1 + k % pn1) % pn1;

  const {eql, add, times, neg, toNum} = poly;
  const zero = () => p2gf(poly.zero());
  const one = () => p2gf(poly.one());
  const a = p2gf(poly.carry(poly.one(), 1));
  const isZero = e => eql(zero(), e);

  const mul0 = (a, b) => poly.mod(poly.mul(a, b), f);
  const pow0 = (e, k) => k === 0 ? one() : mul0(e, pow0(e, k - 1));

  const powList = Object.freeze(
    range(pn1).map(k => Object.freeze(pow0(a, k))));
  const exponent = e => powList.findIndex(pe => eql(e, pe));
  const mul = (a, b) => isZero(a) || isZero(b) ? zero() :
        powList[modpn1(exponent(a) + exponent(b))];
  const pow = (e, k) => isZero(e) ? zero() : k == 1 ? e :
        powList[modpn1(exponent(e) * k)];
  const alpha = (k = 1) => pow(a, k);
  const inv = e => powList[modpn1(-exponent(e))];
  const pows = () => powList;

  const size = () => pn;
  const toStr = e => poly.toStr(e, name);
  const fromNum = num => p2gf(poly.fromNum(num));
  const elems = () => poly.elems(n - 1);
  const isPrimitive = () => uniq(powList, eql).length === powList.length;
  const fromSF = e => p2gf(poly.monomial(e, 0));
  const toSF = e => e[0];

  return Field({
    K, poly, n, f, eql, zero, one, alpha, isZero,
    add, times, neg, exponent, mul, pow, inv,
    pows, toStr, size, toNum, fromNum, elems, isPrimitive, fromSF, toSF,
  });
};

// GF Utilities: judge primitive polynomial, irreducible formula of a GF elem
export const GFUtils = gf => {
  const {poly, n, eql, pow, exponent, elems} = gf;
  const futils = FieldUtils(poly.K);
  const p = gf.K.size(), pn1 = gf.size() - 1;

  const cyclicOrder = e => {
    const k = exponent(e);
    for (let i = 1; i <= n; i++) {
      if (k * (p ** i) % pn1 === k) return i;
    }
    throw Error("never reached");
  };

  const findIrreducible = e => {
    const d = cyclicOrder(e);
    // gfeq: [1, e, e^2, ..., e^d] for c0 + c1e +...+ c(d-1)e^(d-1) + e^d = 0
    const gfeq = range(d + 1).map(k => poly.toArray(pow(e, k), n));
    // coefEqs: split gfeq with each coeddicients in e^0,e^1,...,e^d
    const coefEqs = transpose(gfeq);
    // modDim: [c0, c1, ...c(d-1)] satisfied above equation
    console.assert(futils.rank(coefEqs) === d, "findIrreducible");
    const cs = futils.solve(coefEqs);
    const modDim = poly.fromArray(cs);
    return poly.add(modDim, poly.carry(poly.one(), d));
  };

  const exponentGroups = () => {
    const used = new Set();
    const gs = [];
    for (const expo of range(pn1)) {
      if (used.has(expo)) continue;
      const g = uniq(range(n).map(k => (expo * (p ** k)) % pn1));
      g.forEach(expo => used.add(expo));
      gs.push(g);
    }
    return gs;
  };

  const generatorAutomorphism = () => elems().map(e => pow(e, p));

  return {findIrreducible, exponentGroups, generatorAutomorphism};
};
素数べき要素数の有限体GF(p, n, f)実装
gf.js[1]
export const GF = (K, n, f, name="a") => {
  const pn = K.size() ** n, pn1 = pn - 1;
  const poly = Polynomial(K);
  const p2gf = pe => poly.toArray(pe, n);
  const modpn1 = k => (pn1 + k % pn1) % pn1;

  const {eql, add, times, neg, toNum} = poly;
  const zero = () => p2gf(poly.zero());
  const one = () => p2gf(poly.one());
  const a = p2gf(poly.carry(poly.one(), 1));
  const isZero = e => eql(zero(), e);

  const mul0 = (a, b) => poly.mod(poly.mul(a, b), f);
  const pow0 = (e, k) => k === 0 ? one() : mul0(e, pow0(e, k - 1));

  const powList = Object.freeze(
    range(pn1).map(k => Object.freeze(pow0(a, k))));
  const exponent = e => powList.findIndex(pe => eql(e, pe));
  const mul = (a, b) => isZero(a) || isZero(b) ? zero() :
        powList[modpn1(exponent(a) + exponent(b))];
  const pow = (e, k) => isZero(e) ? zero() : k == 1 ? e :
        powList[modpn1(exponent(e) * k)];
  const alpha = (k = 1) => pow(a, k);
  const inv = e => powList[modpn1(-exponent(e))];
  const pows = () => powList;

  const size = () => pn;
  const toStr = e => poly.toStr(e, name);
  const fromNum = num => p2gf(poly.fromNum(num));
  const elems = () => poly.elems(n - 1);
  const isPrimitive = () => uniq(powList, eql).length === powList.length;
  const fromSF = e => p2gf(poly.monomial(e, 0));
  const toSF = e => e[0];

  return Field({
    K, poly, n, f, eql, zero, one, alpha, isZero,
    add, times, neg, exponent, mul, pow, inv,
    pows, toStr, size, toNum, fromNum, elems, isPrimitive, fromSF, toSF,
  });
};
GF($p^n$)の関数群を作る関数がGF(K, n, f)です。各パラメータは、

K: 有限体の要素の多項式の係数体

n: 2以上の整数値

f: 多項式aが原始元としての解となるn次既約多項式Polynomial(PF(p))

オプションname = "a": 有限体の値の多項式の変数名

となります。GF(PF(p),n,f)の内部では、Polynomial(PF(p))を使用します。

GF($p^n$)の要素は、Polynomial(PF(p))によるn-1次多項式となるJavaScript配列で表しています。
ここではGF($p^n$)の要素である確認がしやすいよう、p2gfにより、要素数をn個固定になるようにしています。

例: GF($2^3$)の$a+1$: [1, 1, 0]

GF($p^n$)が提供する関数群は、有限体としてPF(p)の関数群と同じラインナップになります。

eql(a, b)、add(a, b)、neg(e)、times(e, k)、toStr(e)、toNum(e):Polynomial(PF(p))`の実装そのもの

zero()、one()、fromNum(n): Polynomialのzero()とone()、fromNum(n)をn要素配列化した実装

size(): $p^n$固定

elems(): Polynomialのelems(n - 1)`の全多項式値の配列n要素配列化した実装

乗算やべき乗の実装は、原始元の指数表を作り、指数の加算演算で行う実装にします。

mul0(a, b): Polynomialのmulとmodを使用した有限体要素用の乗算実装

pow0(e, k): mul0を使用したべき乗実装

このpow0を用い、指数値から多項式値をひける原始元の指数表powListを作ります。
そして、このpowListを用い、以下の関数群を実装します。

exponent(e): 0以外の要素の原始元の指数値を返す関数

mul(a, b): 指数値の和で実装した有限体の乗算

pow(e, k): 指数値の乗算で実装した有限体のべき乗

alpha(k=1): 原始元のべき乗$a^k$の多項式値

inv(e): 指数値の負数で実装した有限体の逆数

isPrimitime(): パラメータの既約多項式fが、原始元を解とする多項式かどうか

上記の関数群がaの指数表が成立することに基づいているため、isPrimitive()がfalseなら、このGF｀のインスタンスは機能しないものになります。これらの関数群は、どれもmul0やpow0`を直接使う実装が可能です。ただし、GFの応用は、多項式aが原始元であることに依存しているものが普通であるため、有用ではありません。

PolynomialUtilsのirreducibles()で得た既約多項式が、原始元の多項式になるかどうかを調べるためにも使えます。

最後に、要素の多項式の係数である部分体(sub-field)との間の変換機能をもたせています。

fromSF(e): 部分体Kの要素eを定数項とするGFでの多項式要素に変換する関数

toSF(e): GFの多項式要素eの定数項を返す関数

指数べき要素数の有限体ユーティリティ
gf.js[2]
export const GFUtils = gf => {
  const {poly, n, eql, pow, exponent, elems} = gf;
  const futils = FieldUtils(poly.K);
  const p = gf.K.size(), pn1 = gf.size() - 1;

  const cyclicOrder = e => {
    const k = exponent(e);
    for (let i = 1; i <= n; i++) {
      if (k * (p ** i) % pn1 === k) return i;
    }
    throw Error("never reached");
  };

  const findIrreducible = e => {
    const d = cyclicOrder(e);
    // gfeq: [1, e, e^2, ..., e^d] for c0 + c1e +...+ c(d-1)e^(d-1) + e^d = 0
    const gfeq = range(d + 1).map(k => poly.toArray(pow(e, k), n));
    // coefEqs: split gfeq with each coeddicients in e^0,e^1,...,e^d
    const coefEqs = transpose(gfeq);
    // modDim: [c0, c1, ...c(d-1)] satisfied above equation
    console.assert(futils.rank(coefEqs) === d, "findIrreducible");
    const cs = futils.solve(coefEqs);
    const modDim = poly.fromArray(cs);
    return poly.add(modDim, poly.carry(poly.one(), d));
  };

  const exponentGroups = () => {
    const used = new Set();
    const gs = [];
    for (const expo of range(pn1)) {
      if (used.has(expo)) continue;
      const g = uniq(range(n).map(k => (expo * (p ** k)) % pn1));
      g.forEach(expo => used.add(expo));
      gs.push(g);
    }
    return gs;
  };

  const generatorAutomorphism = () => elems().map(e => pow(e, p));

  return {findIrreducible, exponentGroups, generatorAutomorphism};
};
GFUtils(gf)は、指数べき要素数の有限体GFを用い、以下の関数を実装したものです。

findIrreducible(e): 要素eを解に持つ既約多項式を返す関数

expoentGroups(): 同一既約多項式を満たすGFの元のグルーピング(原始元の指数の配列の配列)

generatorAutonorphism(): GF.elems()への(自己同型群の生成元となる)自己同型変換

findIrreducible(e)は、eを解に持つ既約多項式を見つける関数です。
内部で既約多項式の係数を求める(冗長な)連立方程式を解くため、前述のFieldUtilsを使用します。

exponentGroups()は、たとえばGF(PF(2), 2)であれば、[[0], [1, 2]]を返します。
この結果は、$a^0$で一つの1次既約多項式の解、$a^1$と$a^2$とで同じ2次既約多項式の解であることを示したものです。
findIrreduciblesとexponentGroupsの利用コード例
find-irreducible-example.js
import {PF} from "./pf.js";
import {GF, GFUtils} from "./gf.js";

const p = 2, n = 2, f0 = [1, 1, 1];
const gf = GF(PF(p), n, f0), gfutils = GFUtils(gf);

const eg = gfutils.exponentGroups()[1]; //=> [1, 2]
const f = gfutils.findIrreducible(gf.alpha(eg[0]));
console.log(gf.poly.toStr(f)); //=> "x^{2}+x+1"
GFの応用: GF(p^n)のマークダウン形式の演算表等を作る

以下のコードは、Qiitaに埋め込めるMathJax&Markdown table形式の有限体の加算と乗算の演算表を作る、gf.js実装の応用例です。
calc-table-example.js
import {PF} from "./pf.js";
import {GF} from "./gf.js";

const calcTable = (elems, op) => elems.map(e1 => elems.map(e2 => op(e1, e2)));

const mdTable = (heads, elements) => {
  const maxes = heads.map(
    (h, i) => Math.max(h.length, ...elements.map(l => l[i].length)));
  const top = `| ${heads.map((h, i) => h.padEnd(maxes[i])).join(" | ")} |`;
  const guide = `|-${heads.map((_, i) => "-".repeat(maxes[i])).join("-|-")}-|`;
  const lines = elements.map(
    l => `| ${l.map((e, i) => e.padEnd(maxes[i])).join(" | ")} |`);
  return [top, guide, ...lines].join("\n");
};

const mdCalcTable = (f, table, mark) => {
  const elems = f.elems().map(e => f.toStr(e));
  const len = Math.max(...elems.map(e => e.length));
  const strList = elems.map(e => `$${e.padEnd(len)}$`);
  const strTable = table.map(
    l => l.map(e => `$${f.toStr(e).padEnd(len)}$`));
  const heads = [mark, ...strList];
  const elements = strList.map((e, i) => [`**${e}**`, ...strTable[i]]);
  return mdTable(heads, elements);
};

const outputCalcTables = (gf) => {
  const elems = gf.elems();
  console.log(mdCalcTable(gf, calcTable(elems, gf.add), "+"));
  console.log();
  console.log(mdCalcTable(gf, calcTable(elems, gf.mul), "*"));
  console.log();
};

// example
{
  const p = 2, n = 3, f = [1, 1, 0, 1];
  outputCalcTables(GF(PF(p), n, f));
}
実行結果
| +               | $0        $ | $1        $ | $a        $ | $a+1      $ | $a^{2}    $ | $a^{2}+1  $ | $a^{2}+a  $ | $a^{2}+a+1$ |
|-----------------|-------------|-------------|-------------|-------------|-------------|-------------|-------------|-------------|
| **$0        $** | $0        $ | $1        $ | $a        $ | $a+1      $ | $a^{2}    $ | $a^{2}+1  $ | $a^{2}+a  $ | $a^{2}+a+1$ |
| **$1        $** | $1        $ | $0        $ | $a+1      $ | $a        $ | $a^{2}+1  $ | $a^{2}    $ | $a^{2}+a+1$ | $a^{2}+a  $ |
| **$a        $** | $a        $ | $a+1      $ | $0        $ | $1        $ | $a^{2}+a  $ | $a^{2}+a+1$ | $a^{2}    $ | $a^{2}+1  $ |
| **$a+1      $** | $a+1      $ | $a        $ | $1        $ | $0        $ | $a^{2}+a+1$ | $a^{2}+a  $ | $a^{2}+1  $ | $a^{2}    $ |
| **$a^{2}    $** | $a^{2}    $ | $a^{2}+1  $ | $a^{2}+a  $ | $a^{2}+a+1$ | $0        $ | $1        $ | $a        $ | $a+1      $ |
| **$a^{2}+1  $** | $a^{2}+1  $ | $a^{2}    $ | $a^{2}+a+1$ | $a^{2}+a  $ | $1        $ | $0        $ | $a+1      $ | $a        $ |
| **$a^{2}+a  $** | $a^{2}+a  $ | $a^{2}+a+1$ | $a^{2}    $ | $a^{2}+1  $ | $a        $ | $a+1      $ | $0        $ | $1        $ |
| **$a^{2}+a+1$** | $a^{2}+a+1$ | $a^{2}+a  $ | $a^{2}+1  $ | $a^{2}    $ | $a+1      $ | $a        $ | $1        $ | $0        $ |

| *               | $0        $ | $1        $ | $a        $ | $a+1      $ | $a^{2}    $ | $a^{2}+1  $ | $a^{2}+a  $ | $a^{2}+a+1$ |
|-----------------|-------------|-------------|-------------|-------------|-------------|-------------|-------------|-------------|
| **$0        $** | $0        $ | $0        $ | $0        $ | $0        $ | $0        $ | $0        $ | $0        $ | $0        $ |
| **$1        $** | $0        $ | $1        $ | $a        $ | $a+1      $ | $a^{2}    $ | $a^{2}+1  $ | $a^{2}+a  $ | $a^{2}+a+1$ |
| **$a        $** | $0        $ | $a        $ | $a^{2}    $ | $a^{2}+a  $ | $a+1      $ | $1        $ | $a^{2}+a+1$ | $a^{2}+1  $ |
| **$a+1      $** | $0        $ | $a+1      $ | $a^{2}+a  $ | $a^{2}+1  $ | $a^{2}+a+1$ | $a^{2}    $ | $1        $ | $a        $ |
| **$a^{2}    $** | $0        $ | $a^{2}    $ | $a+1      $ | $a^{2}+a+1$ | $a^{2}+a  $ | $a        $ | $a^{2}+1  $ | $1        $ |
| **$a^{2}+1  $** | $0        $ | $a^{2}+1  $ | $1        $ | $a^{2}    $ | $a        $ | $a^{2}+a+1$ | $a+1      $ | $a^{2}+a  $ |
| **$a^{2}+a  $** | $0        $ | $a^{2}+a  $ | $a^{2}+a+1$ | $1        $ | $a^{2}+1  $ | $a+1      $ | $a        $ | $a^{2}    $ |
| **$a^{2}+a+1$** | $0        $ | $a^{2}+a+1$ | $a^{2}+1  $ | $a        $ | $1        $ | $a^{2}+a  $ | $a^{2}    $ | $a+1      $ |
前半の表もこの実装で生成したものを使用しています。

2べき要素数の有限体に特化したプログラム実装

2要素有限体PF(2)の多項式値として(数値配列ではなく)ビット列を割り当てることで、多項式の演算(addやcarryなど)のために、CPUレベルで実装されるビット演算が適用できるようになります。

以下のgf2n.jsは、ビット列で実装するPF(2)特化のPolynomialを実装したPF2Polynomail、および、このPF2Polynomialを使用して実装したGF2n(p, f)のコードとなります。
コード: gf2n.js
gf2n.js
import {Field, range, uniq} from "./field-utils.js";
import {PF} from "./pf.js";

const msb32 = n => 31 - Math.clz32(n);
const popcnt32 = n => {
  n = (n & 0x55555555) + ((n >>> 1) & 0x55555555);
  n = (n & 0x33333333) + ((n >>> 2) & 0x33333333);
  n = (n & 0x0f0f0f0f) + ((n >>> 4) & 0x0f0f0f0f);
  n = (n & 0x00ff00ff) + ((n >>> 8) & 0x00ff00ff);
  return (n & 0x0000ffff) + ((n >>> 16) & 0x0000ffff);
};

//GF(2) coefficient Polynomial as bits
export const PF2Polynomial = () => {
  const K = PF(2);
  const eql = (a, b) => a === b;
  const zero = () => 0;
  const one = () => 1;
  const add = (a, b) => a ^ b;
  const neg = e => e;
  const sub = (a, b) => add(a, b);
  const sum = es => es.reduce((r, e) => add(r, e), 0);
  const scale = (e, c) => (c & 1) ? e : 0;
  const times = (e, k) => (k & 1) ? e : 0;
  const carry = (e, k) => e << k;
  const mul = (a, b) => {
    let r = 0;
    for (; b > 0; b >>>= 1, a <<= 1) {
      if (b & 1) r ^= a;
    }
    return r;
  };
  const order = e => Math.max(msb32(e), 0);
  const mod = (a, b) => {
    const mb = msb32(b);
    for (let i = msb32(a); i >= mb; i--) {
      if (a & (1 << i)) a ^= b << (i - mb);
    }
    return a;
  };
  const prod = es => es.reduce((r, e) => mul(r, e), one());
  const diff = e => (e & 0xaaaaaaaa) >>> 1;
  const coef = (e, k) => e & (1 << k);
  const monomial = (c, k) => carry(scale(one(), c), k);
  const apply = (e, v) => (v & 1) ? popcnt32(e) & 1 : 0;
  const toStr = (e, name = "x") => {
    const s1 = [...e.toString(2).split("")].reverse().map((v, i) => {
      if (i === 0) return v;
      if (v === "0") return "";
      const pow = i === 1 ? "" : `^{${i}}`;
      return `${name}${pow}`;
    }).filter(e => e);
    const s2 = s1.length > 1 && s1[0] === "0" ? s1.slice(1) : s1;
    return s2.reverse().join("+");
  };
  const toArray = (e, len) => {
    const r = Array(len).fill(0);
    for (let i = 0; i < len; i++) r[i] = (e >>> i) & 1;
    return r;
  };
  const fromArray = bs => {
    let e = 0;
    for (let i = 0; i < bs.length; i++) e |= (bs[i] & 1) << i;
    return e;
  };
  const toNum = e => e;
  const fromNum = e => e;
  const elems = k => range(2 ** (k + 1));
  return {
    K, eql, zero, one, add, scale, neg, sub, sum, times, carry, mul, mod, prod,
    order, diff, coef, monomial, apply,
    toStr, toArray, fromArray, toNum, fromNum, elems,
  };
};

// GF(2^n) as bits
export const GF2n = (n, f, name="a") => {
  const poly = PF2Polynomial();
  const {K, eql, zero, one, add, times, neg, toNum, fromNum} = poly;
  const pn = 2 ** n, pn1 = pn - 1;
  const modpn1 = n => (pn1 + n % pn1) % pn1;

  const isZero = e => e === 0;
  const mul0 = (a, b) => poly.mod(poly.mul(a, b), f);
  const pow0 = (e, k) => k === 0 ? one() : mul0(e, pow0(e, k - 1));

  const powList = Object.freeze(range(pn1).map(k => pow0(2, k)));
  const expoList = range(pn).map(k => k === 0 ? NaN : powList.indexOf(k));
  const exponent = e => expoList[e];
  const mul = (a, b) => isZero(a) || isZero(b) ? zero() :
        powList[modpn1(exponent(a) + exponent(b))];
  const pow = (e, k) => isZero(e) ? zero() : k === 1 ? e :
        powList[modpn1(exponent(e) * k)];
  const alpha = (k = 1) => pow(2, k);
  const inv = e => powList[modpn1(-exponent(e))];
  const pows = () => powList;

  const size = () => pn;
  const elems = () => poly.elems(n - 1);
  const isPrimitive = () => uniq(powList, eql).length === powList.length;
  const toStr = e => poly.toStr(e, name);
  const fromSF = e => e % 2;
  const toSF = e => e % 2;

  return Field({
    K, poly, n, f, eql, zero, one, alpha, add, times, neg,
    exponent, mul, pow, inv,
    pows, toStr, size, toNum, fromNum, elems, isPrimitive, fromSF, toSF,
  });
};
詳細は省きますが、PF2Polynomialが扱うPF(2)係数の多項式はビット列として扱う整数値です。同様にGF2n(n, f)の要素もビット列の整数値です。既約多項式fもビット列の整数値で表現します。

要素 $a^2+a$ : 0b110

既約多項式 $x^3 + x + 1$: 0b1011

多項式の加減算addとaubはどちらもXOR演算(a ^ b)で実装できます。
桁上げcarry(e, k)は、左シフト演算(e << k)になります。

多項式の係数は0か1のみであり、加算と減算の区別がないことなどから、乗算mulやモジュロ残mod等で、ビット列であることに特化させた実装ができます。

Polynomialと同じ関数群を実装しているため、PF2Polynomialは、polynomial.jsで実装したPolynomialUtilsで利用可能となっています。
同様に、GF2nも、gf.jsのGFUtilsで利用可能となっています。

　 Tweet
Qiitaで続きを読む

投稿日：2020-03-28T14:28:21+09:00

有限体のプログラミング前編: 素数べき要素数の有限体

前編内容

素数べき要素数の有限体のための基礎知識

素数べき要素数の有限体とその作り方

素数べき要素数の有限体の例

素数べき要素数の有限体のガロア群

中編内容

JavaScriptで実装する素数べき要素数有限体

2べき要素数の有限体に特化した実装

後編内容

有限体の応用: リードソロモン符号とBCH符号

素数べき要素数の有限体のための基礎知識

素数べき要素数の有限体に取り組むにな、以下の前提知識が必要です。

素数要素数の有限体

多項式

体

四則演算と分配則を備えた数の集合(Set)のことを、「体(Field)」と呼びます。

体の例: 有理数(Rational number, Q)、実数(Real number, R)、複素数(Complex number, C)

四則演算は、加算(Add, +)、減算(Subtract, -)、乗算(Multiply, *)、除算(Divide, /)のことです。

ただし、減算a-bは、bと足すと0になる負数-bを足すこと(a-b = a+(-b))であり、除算a/bは、bと掛けると1になる逆数1/bを掛けること(a/b = a*(1/b))のことです。このため、体は、

加算(a+b)と乗算(a*b)を持つ数の集合

任意の数aについて、a+0=a, a*1=aとなる数0と1が存在する

すべての数aに、a+(-a)=0となる負数-aに相当する数が存在する

0以外のすべての数aに、a*(1/a)=1となる逆数1/aが存在する

数a,b,cについて、a*(b+c) = a*b + a*cが成立する(分配則)

を満たす代数構造(algebraic system)となります。

この条件のうち、逆数の存在を要求しない代数構造は環(Ring)と呼ばれます。
整数(Integer, Z)は、環ですが、体ではありません。

体にならない環との区別として、0以外のすべての数に逆数が存在するかどうかが、体であるかどうかのポイントとなります。

素数要素数の有限体

体の要素である数が有限個であるものを有限体と呼びます。

要素数が素数p個の有限体は、非負整数へのモジュロ演算(剰余演算、a mod p もしくは a % p)での関係として、簡単に構成できます。

p個の数: 0, 1, ..., p-1

加算: a + b mod p

乗算: a * b mod p

数aの負数: p - a mod p

ただし、aに掛けると1となる、aの逆数(inverse)については、単純計算ではなく、全ての数の中から対応する数を見つける必要があります。

素数個要素数の有限体の逆数と拡張ユークリッド互除法

素数要素数の有限体での逆数を得るために、よく行われる手段が、pとaを使った(整数の)拡張ユークリッド互除法(Extended GCD, EGCD)です。

EGCDとは、通常のユークリッドの互除法でaとbの最大公約数(GCD)gを得るだけでなく、a*s + b*t = gとなるsとtも同時に返す計算を行う関数です。

pは素数なので、0以外の有限体の数aとの最大公約数gは必ず1となります。
aとpでEGCDを行った結果のg=1とsとtについての先の等式でmod pをとると、a*s + p*t = 1 mod p、つまり、a * (s mod p) = 1となります。

よって、このEGCDで得られるs mod pが、aにかけることで1になる、有限体での逆数(inverse)となります。

EGCD、および、aの逆元を求める関数は、JavaScriptでは以下のコードとなります。
invp.js
const egcd = (a, b) => {
  if (a === 0) return [b, 0, 1];    // b = a*0 + b*1
  const r = b % a, d = (b - r) / a; // r = b - a*d;
  const [gcd, s, t] = egcd(r, a);   // gcd = r*s + a*t
  return [gcd, t - d * s, s];       // gcd = (b-a*d)*s + a*t = a*(t-d*s) + b*s
}
// example
{
  const a = 5, b = 13;
  const [gcd, s, t] = egcd(a, b); // gcd=1, s=-5, t=2
  console.assert(a * s + b * t == gcd);
}

const modp = p => a => (p + a % p) % p;
const invp = (a, p) => modp(p)(egcd(a, p)[1]);
// example
{
  console.assert(invp(5, 13) === 8);
  console.assert(5 * invp(5, 13) % 13 === 1);
}
素数要素数の有限体の例

ここでは、有限体を表現するのに、全2数の間での加算表と乗算表を用います。
これらの表の中で、全ての数、加算関係と負数(相当する数)、乗算関係と逆数の存在が確認できるでしょう。

以下は、一番単純な要素数が2個の有限体の加算表と乗算表です。

+ 0 1

0 0 1

1 1 0

* 0 1

0 0 0

1 0 1

次に、要素数が3個の有限体の加算表と乗算表です。

+ 0 1 2

0 0 1 2

1 1 2 0

2 2 0 1

* 0 1 2

0 0 0 0

1 0 1 2

2 0 2 1

そして、要素数が5個の有限体の加算表と乗算表です。

+ 0 1 2 3 4

0 0 1 2 3 4

1 1 2 3 4 0

2 2 3 4 0 1

3 3 4 0 1 2

4 4 0 1 2 3

* 0 1 2 3 4

0 0 0 0 0 0

1 0 1 2 3 4

2 0 2 4 1 3

3 0 3 1 4 2

4 0 4 3 2 1

たとえば、3の負数-3に相当する数は、加算表で3の行で0のセルのあるのが2の列であることから、2となります。
また、3の逆数1/3に相当する数は、乗算表で3の行で1のセルのあるのが2の列であることから、2となります。

これらの乗算表の各行の値が全て違う数であることは、体としての性質の一つです。
0以外での乗算a * bでは、aに対して、bごとに0以外のそれぞれ違う値になります。

多項式

もう一つの予備知識として、(1変数の)多項式(polynomial)が必要です。

多項式は、パラメータのべき乗の項の線形和で構成する要素です。以下はすべて多項式です。

$x^3$

$x^3+2x+2$

$3$

普通の数も、変数xの0乗の項$x^0$のみの定数多項式となります。$3 = 3x^0$

0乗も含め、変数xへの指数kごとに、係数$C_K$のついたk次の項$C_kx^k$があって、それらを足し合わせたものが多項式です。項1つの多項式は、単項式(monomial)と呼びます。

以降の説明では、多項式での定数多項式と、係数の数とを識別するために、以下のように多項式は()でくくることにします。

$(x^3)$

$(x^3+2x+2)$

$(3)$

数と同様、多項式も演算が定義された集合の要素です。
数がそうであるように、多項式も、変数に割り当てたり、足したり引いたりする対象(オブジェクト)として扱うものです。

多項式変数

変数xの多項式を割り当てる変数は、a(x),b(x),f(x),g(x)等で表現します。

このxは、係数と同じ種の数です。a(x)に数vを入れることは、a(v)もしくは、a(x=v)として記述します。
このa(v)は、(多項式ではなく)係数と同じ種の数となります。

多項式の次数

多項式中の変数xの指数の最大値は、次数(orderもしくはdegree)と呼びます。
次数がnである多項式のことを、n次多項式と呼びます。$x^3+x+1$は3次多項式です。

変数に付く数を係数(coefficient)と呼びます。係数はn次多項式なら0次の定数項も含めてn+1個あります。

多項式の演算

多項式の加減算は、項ごとの係数の加減算を行います。

例: $(x^3+x+1) + (x^2+1) = (x^3+x^2+2x+2)$

多項式の定数倍n*a(x)も、係数ごとの定数倍となります。

例: $2 * (x^3+x+1) = (2x^3+2x+2)$

多項式の変数倍は、すべての項の指数に1足すことに相当します。

例: $x * (x^3+x+1) = (x^4+x^2+x)$

よって多項式の変数のべき乗倍では、すべての項の指数にその指数を足すことになります。

例: $x^2 * (x^3+x+1) = (x^5+x^3+x^2)$

そして、乗算a(x)*b(x)は、多項式a(x)をb(x)の各項ごとに係数倍と変数倍をし、すべて足し合わすことで行います。

例: $(x^3+x+1) * (x^2+2) = (x^5+x^3+x^2) + (2x^3+2x+2) = (x^5+3x^3+x^2+2x+2)$

この各項ごとに掛け、すべて足し込む計算のことは、一般的に「畳み込み(convolution)」と呼ばれます。

多項式のモジュロ算

一般的に、多項式f(x)とg(x)の間では、f(x) = d(x)*g(x) + r(x)という関係が成立します。
ただし、r(x)の次数は、g(x)の次数未満です。

この場合、r(x)は、f(x)をg(x)で割った余りであり、多項式の剰余と呼びます。

注意点は、剰余となる多項式の条件は、その次数がg(x)の次数より小さいことであり、多項式の係数が正であることではありません。

例: $(x^3+1) \mod (x^3+x+1) = (-x)$

多項式の加減乗算の結果として、その結果の多項式の剰余多項式を得ることを多項式のモジュロ算(剰余演算)といいます。
数でのモジュロ算と同様に、a(x) mod g(x)のように記述します。

数でのモジュロ算と同様に

a(x) + b(x) mod g(x) = (a(x) mod g(x)) + (b(x) mod g(x))

a(x) * b(x) mod g(x) = (a(x) mod g(x)) * (b(x) mod g(x)) mod g(x)

という、演算の途中でモジュロ算を行っても同じ結果となる性質があります。

この性質から、多項式のモジュロ算をするために、分解して足したり掛けたりすることを繰り返すことで行うことも可能です。

例: $(x^5+1) \mod (x^2+x+1)$

まず、$(x^2) \mod (x^2+x+1) = (-x-1)$

$(x^5) \mod (x^2+x+1) = (x^2) * (x^2) * (x) = (-x-1) * (-x-1) * (x) = (x^2+2x+1) * (x) = ((-x-1)+(2x+1)) * (x) = (x^2) = (-x-1)$

よって、$(x^5+1) \mod (x^2+x+1) = (-x)$

有限体係数の多項式

多項式の係数には、有限体も用いる事ができます。

この場合、係数への加減算と乗算で、有限体での加減算と乗算を適用します。
また、係数が有限体であっても、多項式のモジュロ算も成立します。

要素数2の有限体係数の多項式の演算例

$(x^2+x+1) + (x+1) = (x^2+2x+2) = (x^2)$

$(x^2+x+1) * (x+1) = (x^3+2x^2+2x+1) = (x^3+1)$

$(x^2+x+1) \mod (x+1) = (x)(x+1)+(1) \mod (x+1) = (1)$

多項式を数として扱うこと

多項式も加減乗算ができることで、多項式自体を数そのものとしても扱います。

はじめは多項式f(x)の変数xが何なのか気になるかもしれませんが、むしろ多項式内の変数そのものは無視することです。
見るべきは、変数の指数値と係数値です。

プログラミングではn次多項式は、n+1要素の係数値の配列データで表現します。こうなると変数名は消えます。

$x^3+x+2$ => [2,1,0,1]

数式や変数の意味に惑わされるなら、係数値の配列のことだと思うとよいです。f(x)は、f[]のことです。

そして、多項式の演算は、数値配列同士のための演算系だと考えることが可能です。

多項式の加算は、配列の要素ごとの加算

多項式の乗算は、配列同士のconvolution処理

多項式のモジュロ算は、要素数を一定以下に制限する計算

素数べき要素数の有限体とその作り方

素数べき(単一素数のべき乗数)要素数の有限体は、要素数が素数ではなくなるため、要素数でのモジュロ算では体が構成できません。

このため、素数べき要素数の有限体では、多項式を数として、多項式のモジュロ算によって有限体を構成します。

素数べき要素数の有限体の要素

まず、$p^n$要素数の有限体では、(整数ではなく)、p要素数の有限体を係数とするn-1次までの多項式を、要素である数として用います。

たとえば、$8=2^3$要素数の有限体の要素である数は、2次までの全多項式

$(0)$、$(1)$、$(a)$、$(a+1)$、$(a^2)$、$(a^2+1)$、$(a^2+a)$、$(a^2+a+1)$

の8個になります。

有限体要素の多項式で使う変数名は、aやα(アルファ)を使うことが多いです。

素数べき要素数の有限体の加算

この数同士での加算は、多項式での加算となります。つまり、係数同士のpモジュロ算での加算です。

8要素数の有限体の加算の例: $(a^2+a+1) + (a^2+1) = (a)$

素数べき要素数の有限体の乗算

要素数が$p^n$個の有限体での乗算は、n次多項式のモジュロ算での乗算を用います。

たとえば、$8=2^3$個要素の有限体では、3次方程式でモジュロ算をします。その結果、2次多項式のどれかになります。

$(0)$、$(1)$、$(a)$、$(a+1)$、$(a^2)$、$(a^2+1)$、$(a^2+a)$、$(a^2+a+1)$

ただし、結果が有限体となるためには、そのモジュロ算で用いる多項式には、(係数はp要素数の有限体の)n次既約多項式を用います。

既約多項式

n次既約多項式とは、n次多項式のうち、n次未満の多項式をかけ合わせて構築できるn次可約多項式ではないn次多項式のことです。
また、理由は後述しますが、この既約多項式では、最大次数の係数は1に限定してよいです。

係数が有限体の場合、n次多項式を全て列挙することが可能です。このため、可約多項式も既約多項式も全列挙可能です。

8要素数の有限体のための3次既約多項式は以下のようにして求めまります。

全1次多項式: $(x)$、$(x+1)$

全2次多項式: $(x^2)$、$(x^2+1)$、$x^2+x+1$

全3次可約多項式(6個): $(x^3)$、$(x^3+x^2)$、$(x^3+x)$、$(x^3+x^2+x+1)$、$(x^3+x^2+x)$、$(x^3+1)$

全3次既約多項式(2個): $(x^3+x+1)$、$(x^3+x^2+1)$

そして、有限体の多項式要素$(a)$を、この中から選んだ既約多項式の方程式を満たす解となる数に割り当てます。

つまり、既約多項式として$(x^3+x+1)$を選んだら、多項式の演算のもと、$(a)$は$(a)^3+(a)+(1)=(0)$となる値とする、という意味をもたせるということです。

既約多項式は方程式として扱うため、最高次の係数は1に限定できます。
方程式としては、最高次の係数で、その全ての項の係数を割った多項式による方程式と同等だからです。

たとえば、$2x^2+4x+4 = 0$と$x^2+2x+2 = 0$は方程式として同じ

既約多項式による乗算関係

選んだ2要素有限体係数のn次規約方程式に(a)を代入すると、$(a)^3+(a)+(1)=(0)$となります。
この式を変形すると、

$(a)^3 = -(a)-(1) = (a)+(1) = (a+1)$

となり、これは、多項式$(a)$は、3乗することで多項式(a+1)になる、と解釈します。

多項式$(a^3)$を規約多項式$(a^3+a+1)$でモジュロ算をしたことと同等です。

係数は要素数2の有限体なので、$(a^3) \mod (a^3+a+1) = (-a-1) = (a+1)$

n次だけではなく、n次以上の多項式は、選んだn次既約多項式でモジュロ算を行うことで、必ず有限体の多項式の数のどれかになります。

有限体の要素$(a)$に$(a)$を掛け続け、$(a)$のべき乗を計算することで、以下の関係がもたらされます。

$(a^0) = (1)$

$(a^1) = (a)$

$(a^2) = (a^2)$

$(a^3) = (a+1)$

$(a^4) = (a^2+a)$

$(a^5) = (a^2+a+1)$

$(a^6) = (a^2+1)$

$(a^7) = (1)$

ここでは、$(0)$以外の多項式の数すべてが、$(a)$のべき乗数として算出できました。

べき乗を取ることで、すべての要素になる$(a)$のような数を、その有限体の原始元(primitive element)と呼びます。
原始元が解となる既約多項式を、原始多項式と呼びます。

要素数$p^n$によっては、解が原始元とならない既約多項式も存在することがあります。
そういった既約多項式の解を(a)とすると、$(a)$のべき乗では出てこない数が存在します。
この場合でも$(a+1)$等の別の多項式が原始元になります。

しかし、以下の指数表現を用いた乗算の簡略化のために、普通は$(a)$が原始元となるよう、既約多項式を選び直します。

この原始元$(a)$の指数表現を用いることで、簡易に乗算を行うことが可能です。
多項式を一度指数表現にし、指数同士を$p^n-1$のモジュロ算で足した結果の指数表現を多項式表現に戻すことです。

例: $(a^2+a) * (a^2+1)$

指数のモジュロ和: $(a^2+a) * (a^2+1) = (a^4) * (a^6) = (a^{4+6 \mod 7}) = (a^3) = (a+1)$

モジュロ乗算: $(a^2+a) * (a^2+1) = a^4+a^2+a^3+a = (a^3)*a + (a^3) + (a^2+a) = (a+1) * a + (a+1) + (a^2+a) = (a+1)$

まとめ: 素数べき要素数の有限体の作り方

要素数が$p^n$な有限体は、

要素: pモジュロ係数のn次多項式すべて

加算: pモジュロ係数のn次多項式の加算(係数ごとのpモジュロ加算)

n次既約多項式の算出

n未満次多項式を列挙

足してn次になる多項式同士をすべて掛け、n次可約多項式を列挙

n次可約多項式でない、n次多項式を既約多項式として列挙

多項式要素$(a)$を解とするものとして既約多項式を1つ選び、$(a)$について0から$p^n -1$乗までの指数表現を作る

$(a)$が、$(0)$以外の要素がすべて列挙される原始元にならない場合、別の既約多項式を用いる

乗算: $(a)$の指数表現での指数の和で計算(もしくは既約多項式のモジュロ乗算をする)

で構成できます。

有限体の多項式要素と既約多項式の関係

有限体の多項式要素$(a)$は、選んだn次既約多項式の方程式の解です。
つまり、n次方程式として、$(a)$以外のn-1個の解が、別の多項式要素として存在します。

8要素の有限体の3次既約方程式$x^3+x+1=0$を満たすのは、$(a)$、$(a^2)$、$(a^2+a)$です。

また、選ばなかったn次既約多項式の方程式の解となる数も、それぞれn個づつ多項式要素のどれかになっています。

8要素の有限体の3次既約方程式$x^3+x^2+1=0$を満たすのは、$(a+1)$、$(a^2+1)$、$(a^2+a+1)$です。

すべてのn次既約多項式のそれぞれn個の解すべてがこの有限体の要素になります。($(0)$や$(1)$のように、"n次"既約多項式の解にならない要素はあります)。

乗算のとき作った指数表現にすると、同一の方程式の解である関係が見えます。

$x^3+x+1=0$の解: $(a^1)$、$(a^2)$、$(a^4)$

$x^3+x^2+1=0$の解: $(a^3)$、$(a^6)$、$(a^5)=(a^{12})$

さらに言えば、4 * 2 mod 7 = 1であり、5 * 2 mod 7 = 3です。
一般的には、同一方程式の解は、互いに指数をp倍していった関係(つまりp乗した関係)があります。

このため、どのn次既約多項式を選んでも、要素表示として$(a)$にあたるものが入れ替わっただけになります。

結果として、素数べき要素数の有限体は要素数ごとにただ一つの演算関係を持ちます。

有限体は、要素数で唯一の構造が決まるので、有限体の別名であるガロア体(Galois Field)にちなみ、GF($p^n$)と名付けられています。

GF(2), GF(3), GF(5), GF(4)もしくはGF($2^2$),GF(9)もしくは、GF($3^2$)、GF(8)もしくはGF($2^3$), ...

素数べき要素数の有限体の例

以降からは、上述の説明のために用いた、多項式要素である表現のための()は外します。

ここでは実際に例として、要素数の少ない(p,n)=(2,2)、(p,n)=(3,2)、(p,n)=(2,3)の有限体GF($p^n$)を、前述の手順によって構築します。

GF(4)

要素数4の有限体GF(4)は、p=2、n=2の有限体です。

体の要素(1次以下の多項式): $0$, $1$, $a$, $a+1$

加算表(係数ごとの2モジュロ和)

+ $0 $ $1 $ $a $ $a+1$

$0 $ $0 $ $1 $ $a $ $a+1$

$1 $ $1 $ $0 $ $a+1$ $a $

$a $ $a $ $a+1$ $0 $ $1 $

$a+1$ $a+1$ $a $ $1 $ $0 $

(乗算関係をつくるための多項式の列挙)

1次多項式: $x$, $x+1$

2次可約多項式: $x^2$, $x^2+x$, $x^2+1$

2次既約多項式: $x^2+x+1$

選んだ既約方程式から、$a^2+a+1=0$とすると、$a^2$=$a+1$です。よって

$a^0$ = $1$

$a^1$ = $a$

$a^2$ = $a^2$ = $a+1$

$a^3$ = $(a+1)*a$ = $a^2+a$ = $a+1+a$ = $1$

乗算表

* $0 $ $1 $ $a $ $a+1$

$0 $ $0 $ $0 $ $0 $ $0 $

$1 $ $0 $ $1 $ $a $ $a+1$

$a $ $0 $ $a $ $a+1$ $1 $

$a+1$ $0 $ $a+1$ $1 $ $a $

GF(9)

要素数9の有限体GF(9)は、p=3、n=2の有限体です。

体の要素(1次以下の多項式): $0$, $1$, $2$, $a$, $a+1$, $a+2$, $2a$, $2a+1$, $2a+2$

加算表

+ $0 $ $1 $ $2 $ $a $ $a+1 $ $a+2 $ $2a $ $2a+1$ $2a+2$

$0 $ $0 $ $1 $ $2 $ $a $ $a+1 $ $a+2 $ $2a $ $2a+1$ $2a+2$

$1 $ $1 $ $2 $ $0 $ $a+1 $ $a+2 $ $a $ $2a+1$ $2a+2$ $2a $

$2 $ $2 $ $0 $ $1 $ $a+2 $ $a $ $a+1 $ $2a+2$ $2a $ $2a+1$

$a $ $a $ $a+1 $ $a+2 $ $2a $ $2a+1$ $2a+2$ $0 $ $1 $ $2 $

$a+1 $ $a+1 $ $a+2 $ $a $ $2a+1$ $2a+2$ $2a $ $1 $ $2 $ $0 $

$a+2 $ $a+2 $ $a $ $a+1 $ $2a+2$ $2a $ $2a+1$ $2 $ $0 $ $1 $

$2a $ $2a $ $2a+1$ $2a+2$ $0 $ $1 $ $2 $ $a $ $a+1 $ $a+2 $

$2a+1$ $2a+1$ $2a+2$ $2a $ $1 $ $2 $ $0 $ $a+1 $ $a+2 $ $a $

$2a+2$ $2a+2$ $2a $ $2a+1$ $2 $ $0 $ $1 $ $a+2 $ $a $ $a+1 $

1次多項式: $x$, $x+1$, $x+2$

2次可約多項式: $x^2$, $x^2+x$, $x^2+2x$, $x^2+2x+1$, $x^2+2$, $x^2+x+1$

2次既約多項式: $x^2+1$, $x^2+x+2$, $x^2+2x+2$

既約方程式を$a^2+2a+2=0$とすると、$a^2=a+1$です。よって

$a^0$ = $1$

$a^1$ = $a$

$a^2$ = $a+1$

$a^3$ = $(a+1)*a$ = $a^2+a$ = $a+1+a$ = $2a+1$

$a^4$ = $(2a+1)*a$ = $2a^2+a$ = $2(a+1)+a$ = $2$

$a^5$ = $2a$

$a^6$ = $2a^2$ = $2(a+1)$ = $2a+2$

$a^7$ = $(2a+2)*a$ = $2a^2+2a$ = $2(a+1)+2a$ = $a+2$

$a^8$ = $(a+2)*a$ = $a^2*2a$ = $(a+1)+2a$ = $1$

乗算表

* $0 $ $1 $ $2 $ $a $ $a+1 $ $a+2 $ $2a $ $2a+1$ $2a+2$

$0 $ $0 $ $0 $ $0 $ $0 $ $0 $ $0 $ $0 $ $0 $ $0 $

$1 $ $0 $ $1 $ $2 $ $a $ $a+1 $ $a+2 $ $2a $ $2a+1$ $2a+2$

$2 $ $0 $ $2 $ $1 $ $2a $ $2a+2$ $2a+1$ $a $ $a+2 $ $a+1 $

$a $ $0 $ $a $ $2a $ $a+1 $ $2a+1$ $1 $ $2a+2$ $2 $ $a+2 $

$a+1 $ $0 $ $a+1 $ $2a+2$ $2a+1$ $2 $ $a $ $a+2 $ $2a $ $1 $

$a+2 $ $0 $ $a+2 $ $2a+1$ $1 $ $a $ $2a+2$ $2 $ $a+1 $ $2a $

$2a $ $0 $ $2a $ $a $ $2a+2$ $a+2 $ $2 $ $a+1 $ $1 $ $2a+1$

$2a+1$ $0 $ $2a+1$ $a+2 $ $2 $ $2a $ $a+1 $ $1 $ $2a+2$ $a $

$2a+2$ $0 $ $2a+2$ $a+1 $ $a+2 $ $1 $ $2a $ $2a+1$ $a $ $2 $

ちなみに、既約方程式は3つありますが、有限体の多項式な要素は、それぞれそのうちのどれかの解の一つです。よって、その既約多項式に要素をいれると0になります。

$a$は、$x^2+2x+2=0$の解です。

$(a+1)^2$ = $2$なので、2+1=0から、$a+1$は$x^2+1=0$を満たす解になります。

$(a+2)^2$ = $2a+2$なので、(2a+2)+(a+2)+2=0から、$a+2$は$x^2+x+2=0$を満たす解になります。

$2a+1$は、$x^2+2x+2=0$の解です。

$2a+2$は、$x^2+1=0$の解です。

$2a$は、$x^2+x+2=0$の解です。

同一既約方程式の解同士は、べき乗表現から以下の関係になります。

既約方程式 $1 = 3^0 = 3^2$ $3 = 3^1$

$x^2+2x+2=0$ $a = a^9$ $2a+1 = a^3$

$x^2+1=0$ $a+1 = a^2 = (a^2)^9$ $2a+2 = a^6 = (a^2)^3$

$x^2+x+2=0$ $a+2 = a^7 = (a^7)^9$ $2a = a^5 = (a^7)^3$

GF(8)

要素数8の有限体GF(8)は、p=2、n=3の有限体です。

体の要素(2次以下の多項式): $0$, $1$, $a$, $a+1$, $a^2$, $a^2+1$, $a^2+a$, $a^2+a+1$

加算表

+ $0 $ $1 $ $a $ $a+1 $ $a^2 $ $a^2+1 $ $a^2+a $ $a^2+a+1$

$0 $ $0 $ $1 $ $a $ $a+1 $ $a^2 $ $a^2+1 $ $a^2+a $ $a^2+a+1$

$1 $ $1 $ $0 $ $a+1 $ $a $ $a^2+1 $ $a^2 $ $a^2+a+1$ $a^2+a $

$a $ $a $ $a+1 $ $0 $ $1 $ $a^2+a $ $a^2+a+1$ $a^2 $ $a^2+1 $

$a+1 $ $a+1 $ $a $ $1 $ $0 $ $a^2+a+1$ $a^2+a $ $a^2+1 $ $a^2 $

$a^2 $ $a^2 $ $a^2+1 $ $a^2+a $ $a^2+a+1$ $0 $ $1 $ $a $ $a+1 $

$a^2+1 $ $a^2+1 $ $a^2 $ $a^2+a+1$ $a^2+a $ $1 $ $0 $ $a+1 $ $a $

$a^2+a $ $a^2+a $ $a^2+a+1$ $a^2 $ $a^2+1 $ $a $ $a+1 $ $0 $ $1 $

$a^2+a+1$ $a^2+a+1$ $a^2+a $ $a^2+1 $ $a^2 $ $a+1 $ $a $ $1 $ $0 $

1次多項式: $x$, $x+1$

2次多項式: $x^2$, $x^2+1$, $x^2+x$, $x^2+x+1$

3次可約多項式: $x^3$, $x^3+x$, $x^3+x^2$, $x^3+x^2+x$, $x^3+x^2+x+1$, $x^3+1$

3次既約多項式: $x^3+x+1$, $x^3+x^2+1$

既約方程式を$a^3+a+1=0$とすると、$a^3=a+1$です。よって、

$a^0$ = $1$

$a^1$ = $a$

$a^2$ = $a^2$

$a^3$ = $a+1$

$a^4$ = $(a+1)*a$ = $a^2+a$

$a^5$ = $(a^2+a)*a$ = $a^3+a^2$ = $a^2+a+1$

$a^6$ = $(a^2+a+1)*a$ = $a^3+a^2+a$ = $(a+1)+a^2+a$ = $a^2+1$

$a^7$ = $(a^2+1)*a$ = $a^3+a$ = $(a+1)+a$ = $1$

乗算表

* $0 $ $1 $ $a $ $a+1 $ $a^2 $ $a^2+1 $ $a^2+a $ $a^2+a+1$

$0 $ $0 $ $0 $ $0 $ $0 $ $0 $ $0 $ $0 $ $0 $

$1 $ $0 $ $1 $ $a $ $a+1 $ $a^2 $ $a^2+1 $ $a^2+a $ $a^2+a+1$

$a $ $0 $ $a $ $a^2 $ $a^2+a $ $a+1 $ $1 $ $a^2+a+1$ $a^2+1 $

$a+1 $ $0 $ $a+1 $ $a^2+a $ $a^2+1 $ $a^2+a+1$ $a^2 $ $1 $ $a $

$a^2 $ $0 $ $a^2 $ $a+1 $ $a^2+a+1$ $a^2+a $ $a $ $a^2+1 $ $1 $

$a^2+1 $ $0 $ $a^2+1 $ $1 $ $a^2 $ $a $ $a^2+a+1$ $a+1 $ $a^2+a $

$a^2+a $ $0 $ $a^2+a $ $a^2+a+1$ $1 $ $a^2+1 $ $a+1 $ $a $ $a^2 $

$a^2+a+1$ $0 $ $a^2+a+1$ $a^2+1 $ $a $ $1 $ $a^2+a $ $a^2 $ $a+1 $

ちなみに、$a$、$a^2$, $a^2+a$が$x^3+x+1=0$の解であり、$a+1$、$a^2+1$、$a^2+a+1$が$x^3+x^2+1=0$の解です。

同一既約方程式の解同士は、べき乗表現から以下の関係になります。

既約方程式 $1 = 2^0 = 2^3$ $2 = 2^1$ $4 = 2^2$

$x^3+x+1=0$ $a = a^8$ $a^2$ $a^2+a = a^4$

$x^3+x^2+1=0$ $a+1 = a^3 = (a^3)^8$ $a^2+1 = a^6 = (a^3)^2$ $a^2+a+1 = a^5 = (a^3)^4$

素数べき要素数の有限体のガロア群

置換と群

集合の要素同士を入れ替える変換を置換(Permutation)といいます。
入れ替えなので、置換は、変換元に対して、変換先の要素に過不足のない、1対1の変換(全単射, bijection)になります。

置換を行った結果にさらに置換を行う、といった繰り返しの適用が可能で、置換を繰り返し適用することも置換となります。
全要素を入れ替えない恒等置換e(x)も置換とします。

恒等置換を含む、同一対象への置換同士の繰り返し適用関係がとる構造が群(Group)です。
群構造を持つ置換の集合のことを、置換群と呼びます。

演算関係の維持など、対象への入れ替えに制約をつけると、集合要素に対して取りうる全置換の一部分だけが適用可能になります。
このような、大きな群の一部だけで群が構成できる部分集合のことを部分群といいます。

対象の持つ性質や制約と、その性質や制約を維持する置換のなす群の構造は、対応関係を持ちます。
これが群に注目する理由となります。

対象の置換群にどのような部分群構造を持つかを調べることで、その対象が持つ性質や制約が判明します。

体の自己同型

つぎに、体のように要素に演算関係を持つ集合(代数構造)について考えます。

集合についた演算関係を維持する置換のことを自己同型(Automorphism)といいます。

体の場合は、加算と乗算の関係を維持することです。
置換をf(x)とすると、f(x)が自己同型であるには、体の任意の要素a,bに対し、

$f(a) + f(b) = f(a + b)$

$f(a) * f(b) = f(a * b)$

が成立することが条件となります。

恒等置換は、自明な自己同型になります。

また、どんな体のどんな自己同型f(x)も、0と1は入れ替えません。

$f(a) + f(0) = f(a+0) = f(a) = f(a) + 0$ より、$f(0) = 0$

$f(a) * f(1) = f(a*1) = f(a) = f(a) * 1$ より、$f(1) = 1$

そして、0と1が入れ替え不可能なことから、1を足し続けることで得られる整数値(とその負数と逆数)で構成する、有理数体Qの自己同型は、恒等置換e(x)のみです。

部分体と拡大体

例示した加算表と乗算表を見れば、GF(4)やGF(8)は、左上の0と1だけの部分で完結する、要素数2の有限体GF(2)となっています。GF(9)も、左上の0,1,2だけで完結する、要素数3の有限体GF(3)となります。

これはGF(4)やGF(8)はGF(2)を部分体としてもつ構造である、といいます。
同様のことを、GF(4)やGF(8)は、GF(2)の拡大体である、ともいいます。

一般的に、有限体GF($p^n$)は、必ずGF(p)を部分体として持ちます。

体のガロア群

自己同型の変換がなす群のことを、ガロア群といいます。

そして、体のガロア群の部分群の存在が、その体が(何らかの体の)拡大体であるという性質に対応しています。

ある自己同型変換について、変換の前後で変化しない要素をすべてとりだすと、それらは部分体の関係を持っている

このことから、たとえば、

拡大体でなければ、自己同型が成立する置換は、恒等置換のみになる

恒等置換以外の自己同型があれば、部分体が存在する

ことになります。

ちなみに、有理数体と同様の理由で、素数要素数の有限体GF(p)の自己同型は恒等置換のみであり、どんな素数pであっても部分体は存在しません。

素数べき要素数の有限体の自己同型

結論から言うと、有限体GF($p^n$)の自己同型となる変換は、指数表現での指数をp倍($\mod p^n-1)する変換です。この指数のp倍の繰り返しが、その有限体の置換群をなします。

つまり、自己同型は、同一方程式の解同士での入れ替え関係になります。

具体的には、

GF(4): $a$と$a+1$を入れ替える

GF(9): ($a$, $a+1$, $a+2$)の組を($2a+1$、$2a+2$, $2a$)の組とで同時に入れ替える

GF(8): ($a$, $a+1$)の組を($a^2$, $a^2+1$)へ、($a^2$, $a^2+1$)の組を($a^2+a$, $a^2+a+1$)へ、($a^2+a$, $a^2+a+1$)の組を($a$, $a+1$)へ同時に入れ替える

が自己同型変換になっています。

素数べき要素数の有限体のガロア群

既約方程式の解はn個なので、解同士の入れ替えである自己同型、指数のp倍は、n回くりかえせば元に戻る性質があります。

変換をn回繰り返すともとに戻る(恒等置換になる)群のことは、n次巡回群(Cyclic group)といいます。
ちなみに、1次巡回群は恒等置換のことです。

よって、GF(p^n)のガロア群は、n次巡回群である、ということになります。

n次巡回群の部分群は、nの約数次の巡回群すべてです。

たとえば、6回でもとに戻る変換を2回繰り返した変換は、3回行えばもとにもどります。
また、6回でもとに戻る変換を3回繰り返した変換は、2回行えばもとにもどります。

このため6次巡回群は、部分群に、2次巡回群と3次巡回群の双方を持つことになります。

ここで、6次巡回群をガロア群とするGF($64=2^6$)について、群の視点から、その構造を観察していきます。

GF($4=2^2$)のガロア群が2次巡回群、GF($8=2^3$)のガロア群が3次巡回群であることから、GF($64=2^6$)が、GF(4)とGF(8)をそれぞれ部分体もっていることが示唆されます。

これはすなわち、GF(64)の多項式要素には、(GF(4)の)2次既約方程式1つを満たす要素2つと、(GF(8)の)3次既約方定式2つをそれぞれ満たす要素6つが、ともに含まれていることを意味します。

ここから、GF(2)の(1次既約方程式の解でもある)0と1の2つを除く、54(=64-2-2-6)個の要素が6次既約方程式の解であることになります。
さらに、それぞれの6次既約方程式の解は6個づつあるので、(2モジュロ係数の)6次既約方定式の総数は9個あることが得られます。

6次既約多項式が9個あることは、原始元aの指数の2倍(のmod 63)を繰り返すことでできる指数のグルーピングでも確認できます。

0

1,2,4,8,16,32,

3,6,12,24,48,33

5,10,20,40,17,34

7,14,28,56,49,35

9,18,36

11,22,44,25,50,37

13,26,52,41,19,38

15,30,60,57,51,39

21,42

23,46,29,58,53,43

27,54,45

31,62,61,59,55,47

グループ内の要素数に注目することで、$a^21$と$a^42$は部分体GF(4)の要素であり、$a^9$、$a^{18}$、$a^{36}$と$a^{27}$、$a^{54}$、$a^{45}$が部分対GF(8)の要素であることが決まります。

ただし、どの指数のグループが、複数あるどの既約多項式を満たすかは、$a$を解とする原始多項式の選択できまることです。

指定した要素が解となる既約方程式の求め方

ある多項式要素がどの既約方程式を満たすものかを見つけるためには、その多項式要素が解となる既約多項式の係数をとくための連立方程式を作って行います。

たとえば、$a^3+a+1=0$なGF(8)で$a+1$が満たす既約多項式の係数の連立方程式を作ってみます。

$a+1$を解に持つ3次既約方程式を$x^3+s*x^2+t*x+u=0$とし、このs,t,uを求めることです。

ちなみに、$(a+1)^2=a^2+1$、$a^3=a+1$より$(a+1)^3=a^9=a^2$です。
よって、x=a+1を代入すると、$(a^2) +s*(a^2+1) + t*(a+1) + u = 0$となります。

aの多項式として各項を展開し、aの指数ごとに分離して、連立方程式にします。

$(1+s)a^2 + ta + (s+t+u) = 0$

ここから

$a^2$: $1+s=0$

$a^1$: $t=0$

$a^0$: $s+t+u=0$

これを解くと、s=1, t=0, u=1が得られます。
よって、$a+1$を解とする既約方程式は、$x^3+x+1=0$だったのでした。

GF(64)における2次既約多項式や3次既約多項式も、同様に求められます。

ただし、有効な変数に対して連立式が多くなり、得られる連立方程式が一次独立ではなくなるので、機械的に解く場合などでは注意が必要です。有限体での冗長な連立方程式が解ける必要があります。

その他

有限体の平方根

数eの平方根は、2乗するとeになる数のことです。

0以外の有限体の数は原始元aのべき乗でも表現できるので、$a^k$の二乗である$a^{2k \mod p^n-1}$の平方根が$a^k$になります。これは$p^n-1$が偶数か奇数かで違いが出ます。つまり、pが2のときと、それ以外の奇素数とで違いがあります。

p=2のとき: すべての数に平方根が1つづつある

$a^{2m}$の平方根の指数: $m$

$a^{2m+1}$の平方根の指数: $\frac{(2m+1) + (2^n-1)}{2}$

p>2のとき: 数$a^k$の指数kが偶数のとき平方根となる数が2つあり、kが奇数のときは平方根は存在しない

$a^{2m}$の平方根の指数 $m$、$m + \frac{p^n-1}{2}$

また、有限体GF($p^n$)の$p-1$は$1=a^0=a^{p^n-1}$の平方根の一つです(もう一つは1)。$(p-1)^2 = p^2-2p+1 \mod p = 1$だからです。これは当然GF(p)にも当てはまります。

$(p-1)^2 = 1$

逆に考えるとp >= 3のときの、$p-1$は、任意の原始元aで$a^{\frac{p^n-1}{2}}$になります。

$p-1 = a^{\frac{p^n-1}{2}}$

また、p>=5なGF(p)では、$p-1$は2乗するだけで1になるため、原始元にはなりません。

この結果、有限体の0以外の全要素を一つづつかけ合わせたものは$p-1$になることが判明します。

$\prod_{k=0}^{p^n-2}a^k = p - 1$

なぜなら、$a^0$から$a^{p^n-2}$までをかけるので、結果の原始元aの指数は総和$\frac{(p^n-2)(p^n-1)}{2}$になります。
p>2のときは、偶数になるのは$(p^n-1)$側なので、$p^n-1$でmodをとると、$-\frac{p^n-1}{2}$です。これに$p^n-1$を足すと、$\frac{p^n-1}{2}$であり、この結果、総乗したものは$a^{\frac{p^n-1}{2}}$になります。よって、0以外の全要素を相乗すると$p-1$となります。
p=2ならば、偶数になるのは$(p^n-2)$側です。よって$\mod p^n-1$をとると0になり、$a^0=1$で、p=2のときも結果的にp-1になります。

全既約多項式の積

GF($p^n$)の要素は、いずれかの既約方程式を解に持つ多項式でした。

たとえば、GF(4)の$a$と$a+1$は、既約方程式$x^2+x+1=0$解でした。

解であることから、$(x-a)(x-(a+1))$は、$x^2+x+1$と等しくなります。
なぜなら、方程式として$x^2+x+1=0$の解である以上、$x^2+x+1$は$x-a$で割り切れ、また$x-(a+1)$でも割り切れなくてはなりません。そして方程式の次数が2である以上、条件を満たす2次の式は、$(x-a)(x-(a+1))$のみだからです。
これは、展開した各係数$(a)+(a+1)=1$、$(a) * (a+1) = 1$であることでも確認可能です。

また、有限体の0以外の値は、$どれもp^n-1$乗すると1になります。つまり、有限体の0以外の値は

$x^{p^n-1}-1=0$

の解になります。そして、0以外の数である$a^k$は$x^{p^n-1}-1=0$の解であることから、$x^{p^n-1}-1$はどの$x-a^k$で割り切れる式になります。$a^k$は0から$a^{pn-2}$の{p^n-1}種類あり、$x^{p^n-1}-1$の次数も$p^n-1$であるため、

$x^{p^n-1}-1 = \prod_{k=0}^{p^n-2}(x-a^k)$

が成立します。この$x^{p^n-1}-1$は、$a^k$を解に持つ既約多項式すべてをかけ合わせたものでもあります。
言い換えると、$x^{p^n-1}-1$は、GF($p^n$)の要素を解に持つどの既約多項式でも割り切れる多項式である、といえます。

そして、要素0の既約方程式は$x=0$とすると、GF($p^n$)の要素を解に持つ既約多項式を全て掛け合わせると

$x^{p^n}-x=0$

となります。

そして、有限体GF($p^n$)のの要素xはすべて、$x^{p^n}=x$つまり、要素数と同じ$p^n$するともとの値に戻ることも証明されます。

これはn=1であるGF(p)のケースでも同様に成立します。

また、$x^{p^n-1}-1 = \prod_{k=0}^{p^n-2}(x-a^k)$より、右辺を展開したときの$p^n-2$次の係数は、0以外の要素をすべて足した$-\sum_{k=0}^{p^n-2}a^k$であり、これは0になります。よって、

$-\sum_{k=0}^{p^n-2}a^k=0$

です。これは0も含めて、有限体の全要素をすべて足すと0になる、とも言えます。
これは他の係数についても言えます。

$\sum_{k=0}^{p^n-3}a^k\sum_{j=k+1}^{p^n-2}a^j = 0$

$\sum_{k=0}^{p^n-4}a^k\sum_{j=k+1}^{p^n-3}a^j\sum_{i=j+1}^{p^n-2}a^i = 0$

...

GF(p^n)をもとに作る素数べき要素数の有限体GF((p^n)^m)

素数要素数のGF(p)だけでなく、素数べき要素数のGF($p^n$)を係数にした多項式でも、GF($(p^n)^m$)を構築することが可能です。
前述の手法のGF(p)係数とそのモジュロ演算の代わりに、GF($p^n$)係数とその演算系を用いるだけです。

例としてGF(4)を用い、GF($16=4^2$)を構築してみます。

GF(4): $0$、$1$、$a$、$a+1$

$a^2 = a + 1$、$a * (a+1) = 1$

GF(16)の要素16個(原始元はb)

$0$、$1$、$a$、$a+1$

$b$、$b+1$、$b+a$、$b+(a+1)$

$ab$、$ab+1$、$ab+a$、$ab+(a+1)$

$(a+1)b$、$(a+1)b+1$、$(a+1)b+a$、$(a+1)b+(a+1)$

(加算は略)

乗算関係の定義

GF(4)係数の1次多項式(4個): $x$、$x+1$、$x+a$、$x+(a+1)$

GF(4)係数の2次可約多項式(10個): $x^2$、$x^2+x$、 $x^2+ax$、 $x^2+(a+x)x$、 $x^2+1$、 $x^2+(a+1)x+a$、 $x^2+ax+(a+1)$、$x^2+a+1$、 $x^2+x+1$、 $x^2+a$

GF(4)係数の2次既約多項式(6個): $x^2+x+a$、$x^2+x+(a+1)$、$x^2+ax+1$、$x^2+ax+a$、$x^2+(a+1)x+1$、$x^2+(a+1)x+(a+1)$

ここでは、$b^2+b+a=0$を選択します。つまり、$b^2=b+a$

指数表現

$b^0=1$

$b^1=b$

$b^2=b+a$

$b^3=(a+1)b+a$

$b^4=ab+(a+1)(b+a)=ab+ab+b+a+1+1=b+1$

$b^5=b+b+a=a$

$b^6=ab$

$b^7=ab+(a+1)$

$b^8=(a+1)b+a(b+a)=b+(a+1)$

$b^9=(a+1)b+b+a=ab+a$

$b^{10}=ab+a(b+a)=a+1$

$b^{11}=(a+1)b$

$b^{12}=(a+1)(b+a)=(a+1)b+1$

$b^{13}=b+(a+1)(b+a)=ab+1$

$b^{14}=b+a(b+a)=(a+1)b+(a+1)$

$b^{15}=(a+1)b+(a+1)(b+a)=1$

と、bは原始元になり、乗算の関係が構築できます。

２の4乗として作るとき、4次既約多項式3個になりますが、4の2乗で構築するときは、2次既約多項式が6個になります。

この2次既約多項式は、指数を4倍する自己同型によって、同一既約方程式の解としての分類ができます。

また指数の2倍での自己同型では、$b$と$b^2$は同じ4次既約多項式の解に分類されます。
$b^2=b+a$を解に持つ既約多項式は、$x^2+x+(a+1)$です。$b^8$はこの多項式のもう一つのになります。

$x^2+x+a$と$x^2+x+(a+1)$をかけると、$x^4+x+1$となり、これはGF(4)の部分体である2モジュロ係数の4次既約多項式でもあります。
自己同型で分類関係のある要素の既約多項式をかけあわせれば、係数が部分体の要素だけで構成され、その部分体での既約多項式になります。

ここから、2モジュロ係数での要素との対応が得られます。

$x^4+x+1$の解のAと、$x^2+x+a$の解のbを対応させることができます。
同様に、$x^4+x+1$の解のAと、$x^2+x+a$の解のbも対応させることもできます。
この違いは、$A^2$に対応するのが$b+a$か$b+a+1$かの違いとして現れます。

+	0	1
0	0	1
1	1	0

*	0	1
0	0	0
1	0	1

+	0	1	2
0	0	1	2
1	1	2	0
2	2	0	1

*	1	2
0	0	0
1	1	2
2	2	1

+	0	1	2	3	4
0	0	1	2	3	4
1	1	2	3	4	0
2	2	3	4	0	1
3	3	4	0	1	2
4	4	0	1	2	3

*	1	2	3	4
0	0	0	0	0
1	1	2	3	4
2	2	4	1	3
3	3	1	4	2
4	4	3	2	1

+	$0 $	$1 $	$a $	$a+1$
$0 $	$0 $	$1 $	$a $	$a+1$
$1 $	$1 $	$0 $	$a+1$	$a $
$a $	$a $	$a+1$	$0 $	$1 $
$a+1$	$a+1$	$a $	$1 $	$0 $

*	$0 $	$1 $	$a $	$a+1$
$0 $	$0 $	$0 $	$0 $	$0 $
$1 $	$0 $	$1 $	$a $	$a+1$
$a $	$0 $	$a $	$a+1$	$1 $
$a+1$	$0 $	$a+1$	$1 $	$a $

+	$0 $	$1 $	$2 $	$a $	$a+1 $	$a+2 $	$2a $	$2a+1$	$2a+2$
$0 $	$0 $	$1 $	$2 $	$a $	$a+1 $	$a+2 $	$2a $	$2a+1$	$2a+2$
$1 $	$1 $	$2 $	$0 $	$a+1 $	$a+2 $	$a $	$2a+1$	$2a+2$	$2a $
$2 $	$2 $	$0 $	$1 $	$a+2 $	$a $	$a+1 $	$2a+2$	$2a $	$2a+1$
$a $	$a $	$a+1 $	$a+2 $	$2a $	$2a+1$	$2a+2$	$0 $	$1 $	$2 $
$a+1 $	$a+1 $	$a+2 $	$a $	$2a+1$	$2a+2$	$2a $	$1 $	$2 $	$0 $
$a+2 $	$a+2 $	$a $	$a+1 $	$2a+2$	$2a $	$2a+1$	$2 $	$0 $	$1 $
$2a $	$2a $	$2a+1$	$2a+2$	$0 $	$1 $	$2 $	$a $	$a+1 $	$a+2 $
$2a+1$	$2a+1$	$2a+2$	$2a $	$1 $	$2 $	$0 $	$a+1 $	$a+2 $	$a $
$2a+2$	$2a+2$	$2a $	$2a+1$	$2 $	$0 $	$1 $	$a+2 $	$a $	$a+1 $

*	$0 $	$1 $	$2 $	$a $	$a+1 $	$a+2 $	$2a $	$2a+1$	$2a+2$
$0 $	$0 $	$0 $	$0 $	$0 $	$0 $	$0 $	$0 $	$0 $	$0 $
$1 $	$0 $	$1 $	$2 $	$a $	$a+1 $	$a+2 $	$2a $	$2a+1$	$2a+2$
$2 $	$0 $	$2 $	$1 $	$2a $	$2a+2$	$2a+1$	$a $	$a+2 $	$a+1 $
$a $	$0 $	$a $	$2a $	$a+1 $	$2a+1$	$1 $	$2a+2$	$2 $	$a+2 $
$a+1 $	$0 $	$a+1 $	$2a+2$	$2a+1$	$2 $	$a $	$a+2 $	$2a $	$1 $
$a+2 $	$0 $	$a+2 $	$2a+1$	$1 $	$a $	$2a+2$	$2 $	$a+1 $	$2a $
$2a $	$0 $	$2a $	$a $	$2a+2$	$a+2 $	$2 $	$a+1 $	$1 $	$2a+1$
$2a+1$	$0 $	$2a+1$	$a+2 $	$2 $	$2a $	$a+1 $	$1 $	$2a+2$	$a $
$2a+2$	$0 $	$2a+2$	$a+1 $	$a+2 $	$1 $	$2a $	$2a+1$	$a $	$2 $

既約方程式	$1 = 3^0 = 3^2$	$3 = 3^1$
$x^2+2x+2=0$	$a = a^9$	$2a+1 = a^3$
$x^2+1=0$	$a+1 = a^2 = (a^2)^9$	$2a+2 = a^6 = (a^2)^3$
$x^2+x+2=0$	$a+2 = a^7 = (a^7)^9$	$2a = a^5 = (a^7)^3$

+	$0 $	$1 $	$a $	$a+1 $	$a^2 $	$a^2+1 $	$a^2+a $	$a^2+a+1$
$0 $	$0 $	$1 $	$a $	$a+1 $	$a^2 $	$a^2+1 $	$a^2+a $	$a^2+a+1$
$1 $	$1 $	$0 $	$a+1 $	$a $	$a^2+1 $	$a^2 $	$a^2+a+1$	$a^2+a $
$a $	$a $	$a+1 $	$0 $	$1 $	$a^2+a $	$a^2+a+1$	$a^2 $	$a^2+1 $
$a+1 $	$a+1 $	$a $	$1 $	$0 $	$a^2+a+1$	$a^2+a $	$a^2+1 $	$a^2 $
$a^2 $	$a^2 $	$a^2+1 $	$a^2+a $	$a^2+a+1$	$0 $	$1 $	$a $	$a+1 $
$a^2+1 $	$a^2+1 $	$a^2 $	$a^2+a+1$	$a^2+a $	$1 $	$0 $	$a+1 $	$a $
$a^2+a $	$a^2+a $	$a^2+a+1$	$a^2 $	$a^2+1 $	$a $	$a+1 $	$0 $	$1 $
$a^2+a+1$	$a^2+a+1$	$a^2+a $	$a^2+1 $	$a^2 $	$a+1 $	$a $	$1 $	$0 $

*	$0 $	$1 $	$a $	$a+1 $	$a^2 $	$a^2+1 $	$a^2+a $	$a^2+a+1$
$0 $	$0 $	$0 $	$0 $	$0 $	$0 $	$0 $	$0 $	$0 $
$1 $	$0 $	$1 $	$a $	$a+1 $	$a^2 $	$a^2+1 $	$a^2+a $	$a^2+a+1$
$a $	$0 $	$a $	$a^2 $	$a^2+a $	$a+1 $	$1 $	$a^2+a+1$	$a^2+1 $
$a+1 $	$0 $	$a+1 $	$a^2+a $	$a^2+1 $	$a^2+a+1$	$a^2 $	$1 $	$a $
$a^2 $	$0 $	$a^2 $	$a+1 $	$a^2+a+1$	$a^2+a $	$a $	$a^2+1 $	$1 $
$a^2+1 $	$0 $	$a^2+1 $	$1 $	$a^2 $	$a $	$a^2+a+1$	$a+1 $	$a^2+a $
$a^2+a $	$0 $	$a^2+a $	$a^2+a+1$	$1 $	$a^2+1 $	$a+1 $	$a $	$a^2 $
$a^2+a+1$	$0 $	$a^2+a+1$	$a^2+1 $	$a $	$1 $	$a^2+a $	$a^2 $	$a+1 $

既約方程式	$1 = 2^0 = 2^3$	$2 = 2^1$	$4 = 2^2$
$x^3+x+1=0$	$a = a^8$	$a^2$	$a^2+a = a^4$
$x^3+x^2+1=0$	$a+1 = a^3 = (a^3)^8$	$a^2+1 = a^6 = (a^3)^2$	$a^2+a+1 = a^5 = (a^3)^4$

　 Tweet
Qiitaで続きを読む

投稿日：2020-03-28T14:25:02+09:00

正規表現についてjQuery

アプリ開発の中でuser登録の際バリデーションに合わせviewで使用したjQueryの正規表現をメモします。
今回、　!　.match　を使い正規表現で無い場合は使いerrorを返し、
errorの場合ブロックを表示したり非表示したり枠の色変えたりというものです。

例）メールアドレス
$(function(){
  $('.email').on('blur',function(){
    let error;
    let value = $('.email').val();
   //valueがhoge@hoge.hogeの型でない場合error
    if(!value.match(/.+@.+\..+/g)){
      error = true;}
   //もしerrorなら下記ブロックを表示もしくは非表示したり枠の色変えたり
    if(error){
      $('.email-error').show();
      $('.email').css({'border':'1px solid #ea352d'});
    }
    else{
      $('.email-error').hide();
      $('.email').css({'border':'1px solid #ccc'});
    }
  });
});
今回使用した正規表現たち

メールアドレス　hoge@hoge.hogeの型
value.match(/.+@.+\..+/g))
パスワード　７文字以上半角英数含む
value.match(/^(?=.*?[a-z])(?=.*?\d)[a-z\d]{7,}$/i)
名前　全角ひらがな漢字
value.match(/^[あ-けー-龥　]+$/)
名前　全角カタカナ
value.match(/^[ァ-ンヴー]*$/)

使用頻度の多そうな正規表現たち

半角数字が含まれる
value.match(/\d/);
半角数字のみ
value.match(/^\d+$/);
英字が含まれる
value.match(/[a-zA-Z]/);
英字のみ
value.match(/^[a-zA-Z]+$/);
ひらがなのみ
value.match(/^[\u3040-\u309f]+$/);
カタカナのみ
value.match(/^[\u30a0-\u30ff]+$/);
半角カタカナのみ
value.match(/^[\uff65-\uff9f]+$/);
全角のみ
value.match(/^[\u3040-\u30ff]+$/);
URLかどうか(半角英数字)
value.match(/^(https?|ftp)(:\/\/[-_.!~*\'()a-zA-Z0-9;\/?:\@&=+\$,%#]+)$/)

他にも調べる色々あると思いますし、言語によって？正規表現が違ったりすると思いますので、
ちらっと参考程度にお手柔らかに見て頂ければと思います。

　 Tweet
Qiitaで続きを読む

投稿日：2020-03-28T13:44:38+09:00

JavaScriptの主要な組み込みオブジェクトまとめ

組み込みオブジェクトとは

Javascriptに標準で組み込まれているクラスを、組み込みオブジェクトと言います。

オブジェクトの種類

Number

数値を扱うラッパーオブジェクト

String

文字列を扱うラッパーオブジェクト

Boolean

審議値を扱うラッパーオブジェクト

Array

配列を扱うオブジェクト

Function

関数を扱うオブジェクト

Object

全てのオブジェクトのベースとなるオブジェクト

Date

日付や時刻を扱うオブジェクト

RegExp

正規表現を扱うオブジェクト

Error

例外情報を扱うオブジェクト

Math

数学的な定数と関数を提供するオブジェクト

JSON

JSON形式のデータを操作する機能を提供するオブジェクト

チュートリアル

https://developer.mozilla.org/ja/

　 Tweet
Qiitaで続きを読む

投稿日：2020-03-28T13:12:43+09:00

Vue.jsでTO DOアプリを作る

はじめに

Vue.jsの基本的な使い方まとめの続きです。

チュートリアルの鉄板であるTO DOアプリを作成していきます。

テンプレートを用意する

雛形となるHTMLとJSを作成します。

todoディレクトリを作成して、その中にindex.htmlとindex.jsを作成します。
todo/index.html
<!DOCTYPE html>
<html>
    <head>
        <meta charset="UTF-8" />
        <title>TO DOアプリ</title>
    </head>
    <body>
        <div id="app">
          
        </div>
        <script src="https://cdnjs.cloudflare.com/ajax/libs/vue/2.6.10/vue.js"></script>
        <script src="./index.js"></script>
    </body>
</html>
続いてVueインスタンスを作成する。
todo/index.js
var app = new Vue({
  el: '#app'
})
入力フォームとメソッドの追加

form要素の中に入力フォームとボタンを追加する。
<div id="app">
    <h2>TODO List</h2>
    <form>
        <input type="text">
        <button>
          追加
        </button>
    </form>
</div>
続いてbutton要素にv-on:clickを設定する。

buttonがクリックされたらaddItemメソッドを呼び出す。
<button v-on:click="addItem">
VueインスタンスにaddItemメソッドを記述する。

一旦、正常に動いているか確認するため、アラートを表示させてみる。
var app = new Vue({
  el: '#app',
  // メソッド定義
  methods: {
    addItem: function(event) {
      alert()
    }
  }
})
次にbuttonをクリックした時にsubmitイベントが発動して、ページがリロードされるのを防ぐ処理をformに記述する。

preventはデフォルトの動作を停止させる。
<form v-on:submit.prevent>
TO DOリストにタスクを登録

input要素にv-modelを記述して双方向データバインディング出来るようにする。

これで、inputに入力した値がdataオプションで定義するプロパティと同期する。

<input type="text" v-model="newItem">
dataオプションにnewItemと、入力した値(todoのタスク)を保存する配列todoを定義する。
var app = new Vue({
  el: '#app',
  data: {
    newItem: '', // 入力フォームと双方向データバインディング
    todos: [] // 入力したtodoを保存する配列
  },
  methods: {
    addItem: function(event) {
      alert()
    }
  }
})
さらに、入力フォームで入力した値を配列に保存できるようにaddItemメソッドを書き換える。

プロパティにはthis.プロパティ名でアクセスできる。

このthisはVueインスタンスを指す。
var app = new Vue({
  el: '#app',
  data: {
    newItem: '',
    todos: []
  },
  methods: {
    addItem: function(event) {
      var todo = {
        item: this.newItem // todoオブジェクトに入力した値を保存
      }
      this.todos.push(todo) // todoを配列に追加
    }
  }
})
TO DOリストの改善

buttonをクリックしてタスクを追加した後に、inputに文字列が残ってしまうため、文字列をクリアにする記述をする。

さらに、空の文字列を保存するのを防ぐための処理を記述する。
methods: {
    addItem: function(event) {
      // 追加
      if (this.newItem === '') return // 空の文字列の場合はここで処理を終える
      var todo = {
        item: this.newItem
      }
      this.todos.push(todo)
      // 追加
      this.newItem = '' // 入力フォームの文字列をクリア
    }
TO DOリストの表示

HTML側でリスト表示させる記述をする。

v-forディレクィブを使って繰り返し処理をする。
<div id="app">
    <h2>TODO List</h2>
    <form v-on:submit.prevent>
        <input type="text" v-model="newItem">
        <button v-on:click="addItem">
          追加
        </button>
    </form>
    
    <ul>
        <li v-for="todo in todos">
            {{ todo.item }}
        </li>
    </ul>
    
</div>
タスクの完了と未完了の実装

タスクの完了と未完了を管理するチェックボックスを設定する。

addItmeメソッドの変数todoを編集する。

チェック済みかどうか判定するisDoneを追加し、初期値をfalseに設定する。
var todo = {
  item: this.newItem,
  isDone: false // 追加
  }
次に、HTMlにチェックボックスを追加し、v-modelディレクティブにtodo.isDoneを双方向データバインディングさせる。

これで、チェックされるとisDoneがtrueになる。
<ul>
    <li v-for="todo in todos">
        <input type="checkbox" v-model="todo.isDone">
        <span>{{ todo.item }}</span>
    </li>
</ul>
タスクの削除を実装

登録したタスクを個別に削除するため、配列のindexを取得する。

v-for="(値, index) in 配列"で配列のindexが取れる。

続いて削除ボタンを追加し、タスクを削除するメソッドdeleteItemを定義する。

deleteItemメソッドの引数には配列のindexを持たせる。
<ul>
    <li v-for="(todo, index) in todos"> 
        <input type="checkbox" v-model="todo.isDone">
        <span>{{ todo.item }}</span>
        
        <button v-on:click="deleteItem(index)">Delete</button> 
    </li>
</ul>
続いてdeleteItemメソッドを定義する。

配列から要素を削除するJavaScriptのspliceメソッドを使用して、登録されたタスクを削除する。
methods: {
    addItem: function(event) {
    // 〜省略〜
    },
    //追加
    deleteItem(index) {
      this.todos.splice(index, 1) // sprice(削除を始めるindex, 削除する長さ)
    }
  }
まとめ

DOMの取得やデータの更新を意識することなく書けるので、コードの見通しがスッキリする。

そして、データバインディング楽しい

　 Tweet
Qiitaで続きを読む

投稿日：2020-03-28T11:28:35+09:00

Chrome Dev ToolsでJavaScript/TypeScriptデバッグ ~さようならconsole.log~

はじめに

業務でJavascript/TypeScriptを用いて開発をしていて、
毎日のようにデバッグするのですが
そんな中でChrome Dev Tools(DevTools)を使用したお気に入りのデバッグ方法があり、まとめてみました。

以前React Dev ToolsでのReactのデバッグ方法も紹介していますので、興味があれば読んでください。
React Developer Toolsのすすめ

既にご存知の方には当たり前の方法で
記事にするほどのことでもない！と思われるかと思いますが、
知らなかった方が効率よくデバッグできるようになれば幸いです。

対象読者

Javascript/TypeScriptで開発しているが、デバッグ方法がいまいち分からない方

console.logを多用してデバッグをしている方

デバッグを効率化したい方

JavaScript/TypeScripのデバッグ

console.logでのデバッグ
多くの方が行うJavaScript/TypeScripのデバッグとして、
console.logを随所に記述してDevToolsのconsoleから値を見たり、どの処理を通っているかを確認する方法があります。
私自身もよく使いますが、console.logを記述して削除するのが手間だったり、消し忘れでレビューで指摘されたり、コードを汚してしまうことがあるので、面倒だなと感じる部分がありました。

ReactでのJSのコードの抜粋ですが、API通信時の挙動を見たい時など、こんな感じでconsole.logを使いますよね。
...

const countriesApi = "https://restcountries.eu/rest/v2/all";
  useEffect(() => {
    console.log('useEffect');
    const getData = async () => {
      setIsLoading(true);
      const response = await axios.get(countriesApi);
      console.log(`response:${response}`);
      setAllCountries(response.data);
      console.log(`data:${response.data}`);
      setIsLoading(false);
    };
    getData();
  },[]);

...
そしてDevToolsのconsoleで確認。
デバッグ対象のアプリをChromeで開いて、
DevToolsを開いて（Macはcommand + option + iでショートカット）、Consoleのタブに移動します。
少し分かりにくいし、見にくいです。たくさんconsole.logするとどれか分かるように記述しないと読み取りにくい...。

このようなデバッグをDevToolsのSourceを使用することで、
より便利に効率的にデバッグが可能になります！

Chrome Dev ToolsのSourceを利用したデバッグ

まず、デバッグ対象のアプリをChromeで開きます。
DevToolsを開きます（Macはcommand + option + iでショートカット）。
Sourceのタブに移動します。

左側のディレクトリツリーからデバッグしたい対象のファイルを選択します。
そうするとソースコードがDevTools上に表示されます。

デバッグしたい箇所を選択します。
コード表示の行数の左をクリックすることで緑色になり、ブレークポイントを貼ることができます。
これがconsole.logと同じような役割となります。

この状態でアプリを動かします。
今回は簡易的な電話帳アプリを動かします。
人名検索が可能なので、テキストボックスに文字を入力します。

文字を入力した瞬間に、ブレークポイントを貼った人名をフィルターする処理で止まってデバッガが動作しました！！

アプリ側に「Paused in debugger」が出てくるので、それの赤枠の右三角を押します。
次のブレークポイントの処理まで実行させることができます

デバッガを進めていくと、右側に実行結果などのログが出ます。
見たい値や変数のところにマウスオーバーすると、パラメータが見れます。
この方法だとコードにconsole.logを記述する必要がありません。
見れるパラメータもより詳細です。
実際に動かしながら確認するので、直感的にデバッグが可能です。

確認したいパラメータもマウスオーバーすることで簡単に、詳細な情報が得られます。
personsの中身

console.logだと指定した情報しか表示できませんが、
この方法だとブレークポイントを貼った以外の部分の実行された処理のパラメータの確認ができます。
ブレークポイントを貼っていないhandleFilterChangeのeventのパラメータ。

下記のマークを押していくことで、コードを１行ずつステップ実行することも可能です。
別の関数にジャンプしたり、処理を１つずつ実行してくれます。
(フレームワーク使用していると、フレームワーク自体の処理に入り込んでしまうことが多いので、コードのデバッグだと向いてないかもしれません。)

まとめ

Chrome Dev ToolsのSourceのデバッガを使うことで、

console.logを記述しなくて済む

動作した処理全てのパラメータを簡単に確認できる

アプリを動かしながら直感的にデバッグができる

といった効率的なデバッグをすることが可能となります。

私もこの方法でデバッグを始めてから、作業が格段に速くなりました。
undefinedで値が取れていない部分も、どこで処理が失敗しているのかも、すぐに見つけることができます。
かつ、コードがどのように動いているのかを把握できるようになったので言語やフレームワークの理解が深まりました。

知らなかった！という方は是非試してみてください。
どなたかの参考になれば幸いです。

最後まで読んで頂き、ありがとうございました。

　 Tweet
Qiitaで続きを読む

投稿日：2020-03-28T11:09:43+09:00

div要素を横並びにしたいがdisplay: flexが効かない原因

ドットインストールで学習中です。
div要素を横並びにするために
display: flex;
を記述しましたが、効いていないようです。

div要素が横並びにならない原因が分かる方いましたら指摘して頂けるとありがたいです。
よろしくお願いします。

以下が全体のコードです。

<!DOCTYPE html>

JaveScript Practice
<script>
  'use strict';

  const target1 =  document.getElementById('target1');
  const target2 =  document.getElementById('target2');
  const target3 =  document.getElementById('target3');

  target1.addEventListener('click', () => {
    target1.classList.toggle('circle');
  });
  target2.addEventListener('click', () => {
    target2.classList.toggle('circle');
  });
  target3.addEventListener('click', () => {
    target3.classList.toggle('circle');
  });
</script>

　 Tweet
Qiitaで続きを読む

投稿日：2020-03-28T06:35:25+09:00

属性を与えるだけで画像をモーダル化できるコード【コピペ】

概要

imgタグに属性を添えるだけで、画像をモーダル表示できるコードを作成した。

仕様

イベントが発生して初めてDOM生成する。そのせいでちょっと重い。

使い方

モーダル化させたいimgタグに

属性　modal-image="hoge.jpeg"

を追加する。

例

<img src="thumbnail.jpeg" modal-image="original.jpeg">

値

modal-image=" モーダル時に表示させたい画像のパス"
表示している画像(サムネ画像)とモーダル時の画像が同じであれば値は空でOK。

コピペコード

あとは下記コードをはりつける。

JavaScript

/**モーダルのDOM生成 */
const img_modal = document.querySelectorAll('[modal-image]');
/*activeクラスを付与*/
img_modal.forEach(function(index) {
  index.addEventListener('click', openModal);
});

/**
 * DOM生成の後、activeクラスを追加
 */
function openModal() {
  this.parentElement.appendChild(makeModal(this));
  window.setTimeout(() => {
    this.parentElement.getElementsByClassName('gm-modal')[0].classList.add('active');
  }, 10);
  const el_modal = document.querySelectorAll('.js_close');
  el_modal.forEach(function(index) {
    index.addEventListener('click', closeModal);
  });
}

/**
 * activeクラスの削除の後、DOM削除
 */
function closeModal() {
  let gmModal = document.getElementsByClassName('gm-modal')[0];
  gmModal.classList.remove('active');
  window.setTimeout(() => {
    gmModal.parentNode.removeChild(gmModal);
  }, 500);
}

/**
 * モダールのDOMを生成する
 * @param el_img modal-image属性をもった要素
 */
function makeModal(el_img) {
  let DOM = {
    modal : document.createElement('article'),
    overlay : document.createElement('div'),
    content : document.createElement('div'),
    close : document.createElement('button'),
    divImg : document.createElement('div'),
    img : document.createElement('img'),
  }
  const cl_name = 'gm-modal';
  //.modal
  DOM.modal.classList.add(cl_name);
  //&__overlay
  DOM.overlay.classList.add(cl_name + '__overlay', 'js_close');
  //&__content
  DOM.content.classList.add(cl_name + '__content');
  DOM.divImg .classList.add(cl_name + '__img');
  DOM.close.setAttribute('aria-label', 'Close modal');
  DOM.close.classList.add(cl_name + '__close', 'js_close');
  DOM.close.innerHTML = '&times;';
  //altに値があるなら引き継ぐ
  const altValue = el_img.getAttribute('alt');
  if (altValue!='') {
    DOM.img.alt = altValue;
  }
  let modalImage = el_img.getAttribute('modal-image');
  //属性値が空ならsrcと同じ画像を表示
  DOM.img.setAttribute('src', (modalImage=='')? el_img.getAttribute('src') : modalImage);
  DOM.divImg.appendChild(DOM.img);
  DOM.content.appendChild(DOM.close);
  DOM.content.appendChild(DOM.divImg);
  DOM.modal.append(DOM.overlay);
  DOM.modal.append(DOM.content);

  return DOM.modal;
}

CSS

img[modal-image] {
  cursor: pointer;
}

.gm-modal {
  display: flex;
  position: fixed;
  justify-content: space-around;
  align-items: center;
  top: 0;
  left: 0;
  bottom: 0;
  right: 0;
  box-sizing: border-box;
  padding: 2rem;
  background: rgba(0, 0, 0, 0.7);
  backdrop-filter: blur(4px);
  opacity: 0;
  visibility: hidden;
  transition: visibility 0.2s, opacity 0.2s;
}

.gm-modal.active {
  opacity: 1;
  visibility: visible;
}

.gm-modal__overlay {
  position: absolute;
  top: 0;
  right: 0;
  bottom: 0;
  left: 0;
  cursor: default;
}

.gm-modal__content {
  position: relative;
}

.gm-modal__close {
  position: absolute;
  display: inline-block;
  right: 0;
  top: -4rem;
  border: 0px solid transparent;
  outline: 0;
  padding: 1rem;
  line-height: 1.6rem;
  color: #fff;
  background-color: transparent;
  font-size: 2rem;
  cursor: pointer;
}

.gm-modal__img img {
  width: auto;
  height: auto;
  max-width: calc(100vw - 2rem);
  max-height: calc(100vh - 8rem);
}

最後に

cssは細かくプロパティを設定できていないので、タグ名に直接スタイルを当ててると競合してしまうかもしれない。
フィードバックありがとうございます。

　 Tweet
Qiitaで続きを読む

投稿日：2020-03-28T05:19:36+09:00

ブログをはじめるならGitHub Pagesがおすすめ

ブログをやるならGitHub PagesかGitLab Pagesがおすすめです。

私は、少し前にGitLabでブログをやっていましたが、その後、GitHubに移行したというか、戻りました。経緯としてはGitHub -> GitLab -> GitHubという流れです。

syui.github.io

割と長くGitHub PagesやGitLab Pagesでブログをやってきたので、今回は、両者の違いをまとめてみます。

GitLabはプライベートリポジトリが無制限で、HTMLソースを公開しなくていい

Web Serverは、GitHubのほうが安定していて速い

GitLabのほうがドキュメントが充実しており、公式テンプレートがわかりやすい

どちらもCIを回せるけど、GitLabはGitLab CIを回して、public/にビルドするという形態と採用するため、CIが成功しないとページが公開、更新されない。ユーザーが.gitlab-ci.ymlを書く必要がある

GitHub PagesはデフォルトでJekyll Buildを実行しページが公開される仕組み。ただし、リポジトリルートに.nojekyllを置くことでJekyll Buildを実行しないオプションも存在する。よって、HTMLを直に置いてページを作ることもできる

GitHubは、${USER}.github.ioというリポジトリ名を作成することで、当該ドメインが与えられる。branch:masterにHTMLをpushすると更新される。複数のページを用意したい場合は、リポジトリを作ったうえでbranch:gh-pagesにjekyll buildが通るHTMLを置くことでページを公開する

GitLabも同じく${USER}.gitlab.ioというリポジトリ名を作る。ただし、ブランチは基本的にはmasterを使用する。なお、.gitlab-ci.ymlでソースを置くブランチは制御、変更できる

現在、GitHub Pagesには、GitLab CIに相当するGitHub Actionsがあるのでページの自動ビルド、デプロイに関しての不便はない

GitLab Pagesは複数のドメインを登録できる。GitHubは無理。なので必要なときはGitLab Pagesのドメイン設定を使ってGitHub Pagesにリダイレクトさせるなどのハックに利用させてもらってる

GitLabからGitHubに移行した経緯

私は、GitLab Pagesを2年くらい使っていましたし、特に不満もなかったのですが(たまに不安定で遅かったというのはある)、あるとき突然にページが非公開になってしまうことがありました。

で、運営に連絡してみたのですが、返事がなかったので、GitHub Pagesに同じソースでデプロイしました。つまり、ここで移行という形になります。

その後、GitLabの方で非公開が解除されたのですが、なんだったのかよくわからなかったので、その後、GitLabに戻ることはありませんでした。そのような経緯で、それ以降は、GitHub Pagesを使っています。

ただ、GitHubはCI連携がデフォルトではなかったため、通常は、ビルドしたものをリポジトリにpushしなければ更新できません。したがって、Travis CIを回してページのビルド、デプロイを自動化してましたが、GitHub Actionsが登場したので、今はそちらに移行しています。

GitLab Pagesを使った複数ドメインを利用するハック

例えば、blog.syui.cfとlog.syui.cfというドメインをsyui.github.io/blogに飛ばしたいとしましょう。この場合、GitHub Pagesは一つのページに一つしかドメインを指定することができないので難しい。

そこで、GitLab Pagesで２つのドメインを登録した上で、CloudFlareなどのリダイレクトをGitHub Pagesへ走らせることで、blog.syui.cfとlog.syui.cfを目的の場所に飛ばすことができます。
CNAME : gitlab pages

↓

リダイレクト : github pages
とはいえ、これはあくまでリダイレクトという形なので、アクセスは、トップドメインにとどまります。このような形を実現したい場合のみ利用できるハックです。

簡単にブログを立ててみる手順

GitLab Pages

https://gitlab.com/pages

まず、リポジトリを作りましょう。リポジトリ名は${user}.gitlab.ioです。例えば、私の場合、syui.gitlab.ioですね。

そして、以下のリポジトリをpushしましょう。
$ git clone https://gitlab.com/pages/jekyll

$ cd jekyll

# ${USER}に注意
$ git remote add origin git@gitlab.com:${USER}/${USER}.gitlab.io.git

$ git push -u origin master
GitLab CIが通ったのを確認したら、ページが表示されているはずです。(GitLabの場合、成功しても公開まで少し時間がかかります)

ビルド出力はpublicディレクトリでないといけません。このへんは注意です。それぞれのジェネレーター(静的サイトジェネレーターなど)の実行にオプションから指定しないといけない場合があるかもしれません。publicがデフォルトでない場合はそうですね。

複数のページを作りたい場合は、同じような手順に加えて、.gitlab-ci.ymlを調整しましょう。

GitHub Pages

まず、リポジトリを作りましょう。リポジトリ名は${user}.github.ioです。例えば、私の場合、syui.github.ioです。
$ git clone https://gitlab.com/pages/jekyll

$ cd jekyll

# ${USER}に注意
$ git remote add origin git@github.com:${USER}/${USER}.github.io.git

$ git push -u origin master
複数のページを作りたい場合は、同じような手順に加えて、ブランチをgh-pagesにしてpushしましょう。アクセスは、https://${USER}.github.io/リポジトリ名となります。
# リポジトリを作った上で
$ git remote add origin git@github.com:${リポジトリ名}.git
$ git branch -b gh-pages
$ git push -u origin gh-pages

　 Tweet
Qiitaで続きを読む

投稿日：2020-03-28T01:29:06+09:00

【React】export default しか無いコンポーネントの記述の仕方

こっちの方がカッコいいよねと思った

import React from 'react';

export default () => <h1>Hello World!!</h1>;

こっちでも勿論OK

import React from 'react';

const Hello = () => <h1>Hello World!!</h1>;

export default Hello;

　 Tweet
Qiitaで続きを読む

投稿日：2020-03-28T00:58:10+09:00

reCAPTCHAのチェックボックスを送信ボタンにする

概要

reCAPTCHAのチェックボックス、わざわざクリックしたのにフォームの送信ボタンをわざわざもう一回押さなきゃいけないのって面倒くさいと思ったんですよ。

いや、それくらいやれよって思う人も居ると思うんですよ。わかってますよ。

でも僕みたいに最小限の操作だけで物事を行いたいって人も居ると思うんです。

まぁ今回はそんな面倒くさがりの僕みたいなユーザーばっかりのサービスを作るあなたにぴったりなお話です。

※注意

今回はサーバーサイド側のコードは一切ありません。
全てJavaScriptだけで完結しています。

サーバー側はこっちのコードの使いまわしです。
もし宜しかったらこっちの方も見てやってくだしあ！！

まず普通に動くHTMLコードを用意します

無い人はこっちから引っ張って来ましょう。
<!doctype html>
<html lang="ja">
    <head>
        <meta charset="utf-8">
        <title>reCAPTCHAのサンプル</title>
        <script src="https://www.google.com/recaptcha/api.js" async defer></script>
    </head>
    <body>
        <form action="login" method="post">
            ID:<input type="text" name="id"><br>
            パスワード:<input type="password" name="current-password">
            <div class="g-recaptcha" data-sitekey="[あなたのサイトキー]"></div>
            <input type="submit" value="ログイン">
        </form>
    </body>
</html>
引っ張ってきました。

送信ボタンを消します

この記事では送信ボタンはいらない子です。

g-recaptchaの要素にdata-callbackを追加

チェックボックスが押された時にreCAPTCHAに実行してもらう関数名を決めます。
ここでは「formSubmit」と決めています。
<div class="g-recaptcha" data-sitekey="[あなたのサイトキー]"></div>
    
<div class="g-recaptcha" data-sitekey="[あなたのサイトキー]" data-callback="formSubmit"></div>
送信するフォームをJavaScriptから手に取れるようにする

formに名前を付けましょう。
ここでは「loginForm」と決めています。
~~今からお前の名前はloginFormだ！いいかい、loginFormだよ。分かったら返事をするんだ、loginForm！！~~
<form action="login" method="post">
    
<form action="login" method="post" name="loginForm">
ここが肝心！JavaScriptを書く！

それではチェックボックスにチェックが入ったら叩かれる関数を書きましょう。
function formSubmit(){
    document.loginForm.submit();
}
実行されたら指定したformのsubmit()を実行するだけです。
簡単ですねぇ～～～

テスト

完成したら試しに実行してみましょう

以下のGIFのようになれば成功です。

おまけ

やっぱちゃんとチェックボックスが入るアニメーションがみたいですよね？

JavaScriptのsetTimeoutを使って送信を遅らせましょう。
function formSubmit(){
    setTimeout(function() {
        document.loginForm.submit();
    },1000);
}

　 Tweet
Qiitaで続きを読む

投稿日：2020-03-28T00:23:32+09:00

for in文,for of文について

for in文とは

記述方法についてみていきましょう↓↓
for ( 変数 of 配列 ) {

   // 繰り返しの処理を書く

}
上記の通りになります
「配列」の値を1つずつ「変数」へ代入します
通常の「for文」と違い、繰り返す回数やカウンタ変数などを
意識せずに扱えます。

簡単な例を見ていきましょう↓↓
var Giants = ['吉川', '坂本', '丸', '岡本'];

for(var item of Giants) {

    console.log( item );

}　//吉川,坂本,丸,岡本
上記では、
配列「Giants」の値が、
変数「item」に1つずつ代入されていきます。
なので、そのままコンソールログへ「item」を出力するだけなので、
分かりやすいです。
とてもシンプルで、記述しやすいです。

注意点

for of文は、
反復可能なオブジェクトに対してのみ利用することができます。

反復可能なオブジェクトとは...

「イテレータ」というものを
作成するインターフェイスを整えたオブジェクトのことです。
配列 Array や Map 等が該当します。

本日はここまでに致します。

明日は、反復可能なオブジェクトについて説明します。

　 Tweet
Qiitaで続きを読む

20200328のJavaScriptに関する記事は27件です。

【Ruby on Rails】Ajax通信で特定の要素を変更する

はじめに

バージョン

画面概要

処理概要

実装前

カテゴリー名を編集するフォームに変更するAjax処理の実装

1. Ajax通信するオプションを追加

2. Ajax通信するためのルーティングを追加

3. コントローラでオブジェクトの取得

4. 追加したアクションのためのJavaScript用のviewファイルを用意し、画面の該当の要素を変更するためのJavaScriptを記載

カテゴリー名を更新するAjax処理の実装

1. Ajax通信するオプションを追加

2. Ajax通信するためのルーティングを追加

3. コントローラでオブジェクトの更新

4. 追加したアクションのためのJavaScript用のviewファイルを用意し、画面の該当の要素を変更するためのJavaScriptを記載

おわりに

javascript int変換/キャスト/切り上げ/切り捨て/四捨五入-注意点

はじめに

parseInt($hoge, 10)

Number($hoge)

Math.floor($hoge)

Math.ceil($hoge)

Math.round($hoge)

おわりに

Vue.js私的まとめ

テンプレート

el

data

マスタッシュ構文

v-for

v-model

v-text

v-if

v-show

v-ifとv-showの違い

created

mounted

createdとmountedの違い

watch

- 第2引数が変更前の値

computed

methods

mixins

components

props

template

$emit

axios

transition

アロー関数の解説

アロー関数とは？

サンプルプログラム

functionが関数内部にオブジェクトを指すthisを生成するとは？

bindとは？

「福井県オープンデータ ごみ収集日一覧CSVをJSONに変換するツール」README

福井県オープンデータ ごみ収集日一覧CSVをJSONに変換するツール

Description

Usage

index.js

lib/scraper.js

lib/generator.js

Author

Qiitaのユーザーページにナビゲーションタブを追加するUserScript作った

Google Maps API で近くの目的地までの距離を取得するアプリケーションの作成

はじめに

現在位置の取得

現在位置から目的地までの距離の取得

マッピング

さいごに

JavaScriptでAdobe Acrobatプラグイン開発

プレ金を、きっかけに！

月月火水木金金（プレミアム）

軽業師とジャポネズリー

Super Great Ganbari development Kit

基本編

文字追加編

ダイアログ編

セキュリティ編

「福井県オープンデータごみ収集日一覧CSVをJSONに変換するツール」README

福井県オープンデータごみ収集日一覧CSVをJSONに変換するツール