- 投稿日:2020-03-14T14:14:46+09:00
実践NISQハイブリッド量子コンピュータVQE、QAOA、機械学習6周目
0.はじめに
量子コンピュータを始める人に向け、実践的な量子古典ハイブリッド計算の勉強会をしていますが、シリーズで少しずつ内容を変更しながら6周目となりました。過去の動画は、youtubeチャンネルから探せます。
https://www.youtube.com/channel/UCyUL1fQAwwpJMyEK1lyfyHA
0-1.インストール
今回はblueqat, obaq, tensorflow, tensorflow-quantumを利用します。
https://github.com/Blueqat/Blueqat
https://github.com/Blueqat/Obaqpip3 install blueqat obaq0-2.概要
量子アルゴリズムには将来的な誤り訂正が搭載されたときに利用される「汎用アルゴリズム」と、誤り訂正なしで利用される「変分アルゴリズム」があります。
・汎用アルゴリズム(グローバー、ショア、位相推定、量子フーリエ変換、HHL、QSVMなど)
・変分アルゴリズム(VQE,QAOAなどの量子古典ハイブリッドアルゴリズム)ここでは実用性を重視して、量子古典ハイブリッドアルゴリズムを学びたいと思います。量子古典ハイブリッドアルゴリズムの代表格VQE(Variational Quantum Eigensolver)は、「位相推定」アルゴリズムの代替として2013年に当時ハーバード大学(現在はトロント大学)のアラン・アスプル・グジック教授のチームによって開発されました。
現在の量子コンピュータはエラーが多く、汎用アルゴリズムの多くがそうであるように、長い量子回路を組むとエラーが蓄積し正しい答えを得ることができません。それに対して、短い量子回路をたくさん計算し、それを集計し、最適化をかけることで同様な機能を実現するVQEアルゴリズムが現在の主流となっています。
引用:https://arxiv.org/pdf/1304.3061.pdf
1.理論編
最初に理論を確認します。最終的にはどんどんツール化されていますが、内容を確認します。
1-1.固有値・固有ベクトル問題
ある行列に対する固有値と固有ベクトルを見つけることができれば様々な問題を解くことができます。与えられた行列$H$(ハミルトニアンと呼ばれます)に対して、固有値を$E_0$、固有ベクトルを$\mid \psi \rangle$としたときに、
H \mid \psi \rangle = E_0 \mid \psi \rangleを満たすような、$E_0$と$\mid \psi \rangle$を見つけるのが目的です。$\mid \psi \rangle$は状態ベクトル(波動関数)と呼ばれます。
1-2.量子状態と状態ベクトル
量子コンピュータで利用される量子ビットは|0>状態と|1>状態を持っていてベクトルで表現できます。
\mid 0 \rangle = \begin{bmatrix} 1 \\ 0 \end{bmatrix}, \mid 1 \rangle = \begin{bmatrix} 0 \\ 1 \end{bmatrix}また、任意の量子ビットは重ね合わせて量子状態を表現できます。
\mid \psi \rangle = \alpha \mid 0 \rangle + \beta \mid 1 \rangle = \alpha \begin{bmatrix} 1 \\ 0 \end{bmatrix} + \beta \begin{bmatrix} 0 \\ 1 \end{bmatrix} = \begin{bmatrix} \alpha \\ \beta \end{bmatrix}また、下記条件を満たします。
|\alpha|^2+|\beta|^2 = 1$\mid \psi \rangle$は状態ベクトル(波動関数)と呼ばれ量子ビットの量子状態を表します。$\alpha$と$\beta$は複素数で「確率振幅」と呼ばれ、二乗するとその対応する計算基底の出現確率になり、$|\alpha|^2$や$|\beta|^2$は「測定」をすることで取得できます。
1-3.量子状態の極座標表示
ブロッホ球は二つの直交する純粋状態の重ね合わせで表現できる量子状態を単位球面上に表す表記法。
https://ja.wikipedia.org/wiki/%E3%83%96%E3%83%AD%E3%83%83%E3%83%9B%E7%90%83\mid \psi \rangle = \begin{bmatrix} cos\theta & -sin\theta e^{-i\phi}\\ sin\theta e^{i\phi} & cos\theta \end{bmatrix} \begin{bmatrix} 1\\0 \end{bmatrix} = \begin{bmatrix} cos\theta \\ sin\theta e^{i\phi} \end{bmatrix}のように角度を利用したパラメータ表記もできます。
1-4.状態ベクトルの操作と量子ゲート
状態ベクトルを操作するには、量子ゲートを利用します。変分アルゴリズムでは基本のパウリゲート、任意回転ゲート、アダマールゲートを主に利用します。
パウリゲートはXYZの3種類があり、それぞれブロッホ球でのXYZ軸周りでの180度の回転を意味し、対応する行列は、
X= \begin{bmatrix} 0&1 \\ 1&0 \end{bmatrix}, Y= \begin{bmatrix} 0&-i \\ i&0 \end{bmatrix}, Z= \begin{bmatrix} 1&0 \\ 0&-1 \end{bmatrix}となります。また、XYZ軸周りに任意回転にしたのが、RX,RY,RZゲートで、
Rx(\theta) = \begin{bmatrix} \cos\left(\frac{\theta}{2}\right) & -i\sin\left(\frac{\theta}{2}\right)\\ -i\sin\left(\frac{\theta}{2}\right) & \cos\left(\frac{\theta}{2}\right) \end{bmatrix}, Ry(\theta) = \begin{bmatrix} \cos\left(\frac{\theta}{2}\right) & -\sin\left(\frac{\theta}{2}\right)\\ \sin\left(\frac{\theta}{2}\right) & \cos\left(\frac{\theta}{2}\right) \end{bmatrix}, Rz(\theta) = \begin{bmatrix} e^{-i\frac{\theta}{2}} & 0\\ 0 & e^{i\frac{\theta}{2}} \end{bmatrix}となります。状態ベクトルにこれらの量子ゲートを作用させることで量子状態を変化させることができます。
X \begin{bmatrix} 1 \\ 0 \end{bmatrix} = \begin{bmatrix} 0&1 \\ 1&0 \end{bmatrix} \begin{bmatrix} 1 \\ 0 \end{bmatrix} = \begin{bmatrix} 0 \\ 1 \end{bmatrix}1-5.複数量子ビットの状態ベクトルとテンソル積
上記の状態ベクトルは1量子ビットの時のものです。2量子ビット以上の状態ベクトルはテンソル積を使って表現します。
\begin{bmatrix} a \\ b \end{bmatrix} \otimes \begin{bmatrix} c \\ d \end{bmatrix} = \begin{bmatrix} a* \begin{bmatrix} c\\ d \end{bmatrix} \\ b* \begin{bmatrix} c\\ d \end{bmatrix} \end{bmatrix} = \begin{bmatrix} ac \\ ad \\ bc \\ bd \end{bmatrix}3量子ビット以上の場合も同様です。
\begin{bmatrix} a \\ b \end{bmatrix} \otimes \begin{bmatrix} c \\ d \end{bmatrix} \otimes \begin{bmatrix} e \\ f \end{bmatrix} = \begin{bmatrix} ac * \begin{bmatrix} e \\ f \end{bmatrix} \\ ad* \begin{bmatrix} e \\ f \end{bmatrix} \\ bc* \begin{bmatrix} e \\ f \end{bmatrix} \\ bd* \begin{bmatrix} e \\ f \end{bmatrix} \end{bmatrix} = \begin{bmatrix} ace\\ acf\\ ade\\ adf\\ bce\\ bcf\\ bde\\ bdf \end{bmatrix}量子ゲートもテンソル積をとれます。ハミルトニアンの計算の際に利用します。ゲートがない場合には単位行列Iを組み込みます。
\begin{bmatrix} a&b \\ c&d \end{bmatrix} \otimes \begin{bmatrix} e&f \\ g&h \end{bmatrix} \\ = \begin{bmatrix} a* \begin{bmatrix} e&f \\ g&h \end{bmatrix} &b* \begin{bmatrix} e&f \\ g&h \end{bmatrix} \\ c* \begin{bmatrix} e&f \\ g&h \end{bmatrix} &d* \begin{bmatrix} e&f \\ g&h \end{bmatrix} \end{bmatrix} = \begin{bmatrix} ae&af&be&bf\\ ag&ah&bg&bh\\ ce&cf&de&df\\ cg&ch&dg&dh \end{bmatrix}1-6.ハミルトニアンとその期待値
ハミルトニアン$H$はパウリゲートXYZと単位行列Iから構成されるエルミート行列です。ある量子状態$\mid \psi\rangle$が与えられた場合の、ハミルトニアン$H$の期待値$E$は、上記の式の両方に$\langle \psi \mid$を左からかけてみると、
\langle \psi \mid H \mid \psi \rangle = \langle \psi \mid E \mid \psi \rangle\\ \langle \psi \mid H \mid \psi \rangle = E \langle \psi \mid \psi \rangle\\ \langle \psi \mid H \mid \psi \rangle = Eのように計算できます。1量子ビットの例として、任意の量子状態$\mid \psi \rangle$と任意のハミルトニアン$H$から、
\langle \psi \mid H \mid \psi \rangle = \begin{bmatrix} \alpha^* & \beta^* \end{bmatrix} \begin{bmatrix} a&b\\ c&d \end{bmatrix} \begin{bmatrix} \alpha\\ \beta \end{bmatrix}のように計算できます。
1-7.1量子ビットのansatzを使ってハミルトニアンZの期待値を求める
ansatzを使った任意の状態ベクトルにおけるハミルトニアンが$H = Z$の場合の期待値は、
\langle \psi \mid H \mid \psi \rangle = \begin{bmatrix} \alpha^* & \beta^* \end{bmatrix} \begin{bmatrix} 1&0\\ 0&-1 \end{bmatrix} \begin{bmatrix} \alpha\\ \beta \end{bmatrix} = |\alpha|^2 - |\beta|^2となります。$|\alpha|^2$は0がでる確率、$|\beta|^2$は1が出る確率に対応します。確かめてみましょう。
numpyを導入して、状態ベクトルを設定します。
import numpy as np v_a = np.array([0.9387913 +0.j, -0.23971277+0.j, 0. +0.06120872j, 0. -0.23971277j]) v_a複素共役を取ります。
v_b = np.conjugate(v_a) v_barray([ 0.9387913 -0.j , -0.23971277-0.j , 0. -0.06120872j, 0. +0.23971277j])求めたいのは、v_b@Z@v_aになりますので、素直に計算します。ZとIを準備して、
Z = np.array([[1,0],[0,-1]]) I = np.eye(2)ZとIのテンソル積をとった行列をbとaで挟んで計算します。
v_b@np.kron(Z,I)@v_a (0.8775825505048687+0j)1-8.1量子ビットのansatzを使ってハミルトニアンXの期待値を求める
ハミルトニアンが$H = X$の場合のハミルトニアン$H$の期待値は、
\langle \psi \mid H \mid \psi \rangle = \begin{bmatrix} \alpha^* & \beta^* \end{bmatrix} \begin{bmatrix} 0&1\\ 1&0 \end{bmatrix} \begin{bmatrix} \alpha\\ \beta \end{bmatrix} = \alpha^* \beta + \alpha \beta^*となりますが、通常の測定ではこの値を求めることができませんので、ハミルトニアンの変形を通じて解を得ます。
1-9.ハミルトニアンの変形
ハミルトニアン$H$が$Z$の場合には、期待値の計算ができますが、XやYの場合には求めることができません。そこでハミルトニアンの変形を利用します。
X = HZHより、
\langle \psi \mid X \mid \psi \rangle \\ = \langle \psi \mid HZH \mid \psi \rangle\\ = \langle \psi' \mid Z \mid \psi' \rangleのように状態ベクトルを変形することで対応できます。Yの場合は、
Y = RX(-\pi/2) Z RX(\pi/2)と、なり同様に、
\langle \psi \mid Y \mid \psi \rangle \\ = \langle \psi \mid RX(-\pi/2) Z RX(\pi/2) \mid \psi \rangle\\ = \langle \psi'' \mid Z \mid \psi'' \rangleとすることができます。これらは、量子回路の測定の直前に上記のHやRXゲートを入れて測定を行うことで期待値を計算することができます。
1-10.線形結合
実際にはハミルトニアン$H$はエルミート行列で与えられ、ユニタリ行列の和の形で与えられ、下記のように分解できます。
\langle \psi \mid aH_1 + bH_2 \mid \psi \rangle \\ = \langle \psi \mid aH_1 \mid \psi \rangle + \langle \psi \mid bH_2 \mid \psi \rangle \\ = a\langle \psi \mid H_1 \mid \psi \rangle + b\langle \psi \mid H_2 \mid \psi \rangleこれを使えば、複雑なハミルトニアンの場合でも、
H = 1.2 X_0 Z_2 + 2.5 Z_0 X_1 Y_2 - 3.4 Z_2 X_1期待値は、
\langle \psi \mid 1.2 X_0 Z_2 + 2.5 Z_0 X_1 Y_2 - 3.4 Z_2 X_1 \mid \psi \rangle\\ = 1.2\langle \psi \mid X_0 Z_2 \mid \psi \rangle + 2.5 \langle \psi \mid Z_0 X_1 Y_2\mid \psi \rangle - 3.4 \langle \psi \mid Z_2 X_1 \mid \psi \rangleのように個別に計算をして和を求めることで計算できます。
1-11.量子変分原理
次にハミルトニアンの期待値の計算がわかったところで、今度は計算手法を確認します。量子変分原理より、任意の状態ベクトルにおけるハミルトニアンの期待値は基底状態を上回るというのがあります。
\langle \psi (\theta) \mid H \mid \psi (\theta) \rangle \geq E_0固有値を直接求めるのは厳しいので、間接的に固有値の期待値にできるだけ近づける最適化計算に落とし込みます。ハミルトニアン$H$は与えられた式なので、私たちにできるのは状態ベクトル$\mid \psi (\theta) \rangle$をできるだけ固有状態に近づける状態ベクトルを角度の最適化計算として探していくのが今回の目的です。状態ベクトルの探索はansatz(アンザッツ)と呼ばれる回路を作ることで実現します。
1-12.ansatz(アンザッツ)
上記の$\mid \psi \rangle$は量子回路によって作ることができます。その回路のことをansatz(アンザッツ)といいます。ansatzは通常極座標で量子状態を表現する角度パラメータを持った回路です。
ハミルトニアン$H$に対して対応したansatzを使わないと太平洋から一円玉を見つけるような作業になってしまいますが、ここでは例題として1量子ビットのハミルトニアン$H$の固有値を求めてみます。求めたいハミルトニアン$H$は、
from blueqat.pauli import X, Y, Z, I h = 1.23 * I - 4.56 * X(0) + 2.45 * Y(0) + 2.34 * Z(0)のように作ってみました。読み込まれたのはパウリゲートで行列が対応します。パウリゲートの後ろの数字はそれぞれを適用する量子ビットの通し番号です。上記のハミルトニアン$H$は参考として行列表記は、
[[ 3.57, -4.56-2.45j] [-4.56+2.45j, -1.11 ]]となります。そして、ansatzはこれから探しますが探し方はパラメータを割り振ってそれを探します。1量子ビットの任意の状態ベクトルは極座標で2つの角度があれば表現できます。
Circuit().rx(a)[0].rz(b)[0]としてみます。上記は0番目の量子ビットに、Rxゲートを角度aで、Rzゲートを角度bで適用します。aとbでいい値が見つかれば、上記のansatzはハミルトニアンの期待値に対していい答えを返します。
1-13.変分アルゴリズムの計算手順
変分アルゴリズムの計算手順は、
1、パラメータ$\theta$を導入した量子回路(ansatz)を準備(量子計算)
2、量子ビットの測定値からハミルトニアン$H$の期待値$\langle \psi (\theta) \mid H \mid \psi (\theta) \rangle$を計算(古典計算)
3、古典最適化計算により、ハミルトニアン$H$の期待値を最小にするパラメータ$\theta$を探索(古典計算)のように、量子計算と古典計算のハイブリッドで成り立っています。
引用:https://arxiv.org/pdf/1304.3061.pdf
全体の実装は、
import numpy as np from blueqat import Circuit from blueqat.pauli import X, Y, Z, I from blueqat.vqe import AnsatzBase, Vqe import obaq class OneQubitAnsatz(AnsatzBase): def __init__(self, hamiltonian): super().__init__(hamiltonian.to_expr(), 2) self.step = 1 def get_circuit(self, params): a, b = params return Circuit().rx(a)[0].rz(b)[0] # ハミルトニアン h = 1.23 * I - 4.56 * X(0) + 2.45 * Y(0) + 2.34 * Z(0) runner = Vqe(OneQubitAnsatz(h)) result = runner.run() result.circuit.run(backend="obaq", returns="draw") print('Result by VQE') print(runner.ansatz.get_energy(result.circuit, runner.sampler)) # これ以降は確認のために mat = h.to_matrix() print('Result by numpy') print(np.linalg.eigh(mat)[0][0])Result by VQE -4.450591481563331 Result by numpy -4.450818602983201となり、ほぼ近い値が固有値として求まっているのがわかります。実際には、上記のように任意でハミルトニアン$H$を書くことは多くないので定式化にルールを定めます。今後は全てblueqatで自動でやってくれますので、理解だけすれば簡単に実装できます。
2.VQEの実問題
これ以降はansatzとハミルトニアンの関連に触れながら実問題を見ていきます。実問題でこれからみるのは、
1、量子化学計算
2、組合せ最適化問題になります。
2-1.VQEで量子化学計算
量子化学計算はハミルトニアンの作成をパウリ行列を使って行い、VQEを利用して解を得ることができます。量子化学計算はハミルトニアンに対応するansatzの研究が進んでおり、課題として見通しが他の問題よりもよくなっています。
追加のインストール
追加でツールのインストールが必要です。
今回は、blueqatに追加で、openfermionblueqatとopenfermionを追加します。pip install blueqat openfermionblueqat openfermion準備OKです。
2-2.コードをざっくり
今回はopenfermionに準備されたコードを使います。
#ツールの読み込み from blueqat import * from openfermion import * from openfermionblueqat import* import numpy as np #水素分子の原子間の結合の距離を指定し、OpenFermionに入っているデータを読み込み、返します def get_molecule(bond_len): geometry = [('H',(0.,0.,0.)),('H',(0.,0.,bond_len))] description = format(bond_len) molecule = MolecularData(geometry, "sto-3g",1,description=description) molecule.load() return molecule #結果格納用の配列準備 x = [];e=[];fullci=[] #0.2から2.5まで0.1刻みで原子間距離を入れる for bond_len in np.arange(0.2,2.5,0.1): #分子の情報を得る m = get_molecule("{:.2}".format(bond_len)) #ハミルトニアンを得て、第二量子化し、最後にbravi-kitaev変換でパウリ行列に変換 h = bravyi_kitaev(get_fermion_operator(m.get_molecular_hamiltonian())) #あらかじめ用意したUCCAnsatzに入れて実行 runner = vqe.Vqe(UCCAnsatz(h,6,Circuit().x[0])) result = runner.run() x.append(bond_len) e.append(runner.ansatz.get_energy(result.circuit,runner.sampler)) fullci.append(m.fci_energy) #グラフを書く %matplotlib inline import matplotlib.pyplot as plt plt.plot(x,fullci) plt.plot(x,e,"o")こちらが正しく実行されると下記のような画像が出力されます。
今回は水素分子の原子の結合間の距離に応じて、各状態の安定エネルギーをVQEを用いて求めています。
2-3.中身確認
例題として、原子間距離が0.4のものを読み込んで、ハミルトニアンと呼ばれる基本の式が取得できます。
m = get_molecule(0.4) m.get_molecular_hamiltonian()こちら
() 1.322943021475 ((0, 1), (0, 0)) -1.4820918858979102 ((1, 1), (1, 0)) -1.4820918858979102 ((2, 1), (2, 0)) -0.1187350527865787 ((3, 1), (3, 0)) -0.1187350527865787 ((0, 1), (0, 1), (0, 0), (0, 0)) 0.36843967630348756 ((0, 1), (0, 1), (2, 0), (2, 0)) 0.08225771204699692 ((0, 1), (1, 1), (1, 0), (0, 0)) 0.36843967630348756 ((0, 1), (1, 1), (3, 0), (2, 0)) 0.08225771204699692 ((0, 1), (2, 1), (0, 0), (2, 0)) 0.082257712046997 ((0, 1), (2, 1), (2, 0), (0, 0)) 0.3626667179796745 ((0, 1), (3, 1), (1, 0), (2, 0)) 0.082257712046997 ((0, 1), (3, 1), (3, 0), (0, 0)) 0.3626667179796745 ((1, 1), (0, 1), (0, 0), (1, 0)) 0.36843967630348756 ((1, 1), (0, 1), (2, 0), (3, 0)) 0.08225771204699692 ((1, 1), (1, 1), (1, 0), (1, 0)) 0.36843967630348756 ((1, 1), (1, 1), (3, 0), (3, 0)) 0.08225771204699692 ((1, 1), (2, 1), (0, 0), (3, 0)) 0.082257712046997 ((1, 1), (2, 1), (2, 0), (1, 0)) 0.3626667179796745 ((1, 1), (3, 1), (1, 0), (3, 0)) 0.082257712046997 ((1, 1), (3, 1), (3, 0), (1, 0)) 0.3626667179796745 ((2, 1), (0, 1), (0, 0), (2, 0)) 0.36266671797967454 ((2, 1), (0, 1), (2, 0), (0, 0)) 0.08225771204699726 ((2, 1), (1, 1), (1, 0), (2, 0)) 0.36266671797967454 ((2, 1), (1, 1), (3, 0), (0, 0)) 0.08225771204699726 ((2, 1), (2, 1), (0, 0), (0, 0)) 0.08225771204699728 ((2, 1), (2, 1), (2, 0), (2, 0)) 0.38272169831413727 ((2, 1), (3, 1), (1, 0), (0, 0)) 0.08225771204699728 ((2, 1), (3, 1), (3, 0), (2, 0)) 0.38272169831413727 ((3, 1), (0, 1), (0, 0), (3, 0)) 0.36266671797967454 ((3, 1), (0, 1), (2, 0), (1, 0)) 0.08225771204699726 ((3, 1), (1, 1), (1, 0), (3, 0)) 0.36266671797967454 ((3, 1), (1, 1), (3, 0), (1, 0)) 0.08225771204699726 ((3, 1), (2, 1), (0, 0), (1, 0)) 0.08225771204699728 ((3, 1), (2, 1), (2, 0), (3, 0)) 0.38272169831413727 ((3, 1), (3, 1), (1, 0), (1, 0)) 0.08225771204699728 ((3, 1), (3, 1), (3, 0), (3, 0)) 0.38272169831413727こちらはパウリ行列の表現ではないので、今回VQEで計算できるように変換をします。Bravi-Kitaev(ブラビキタエフ)変換やJordan–Wigner(ジョルダンウィグナー)変換がありますが、今回は前者のBK変換をしてみると、
h = bravyi_kitaev(get_fermion_operator(m.get_molecular_hamiltonian()))確認してみると、
print(h) (0.7407724940116754+0j)*I + (0.23528824284103544+0j)*Z[0] + (0.23528824284103542+0j)*Z[0]*Z[1] + (-0.45353118471995524+0j)*Z[2] + (-0.45353118471995524+0j)*Z[1]*Z[2]*Z[3] + (0.18421983815174378+0j)*Z[1] + (0.041128856023498556+0j)*Y[0]*Z[1]*Y[2]*Z[3] + (0.041128856023498556+0j)*X[0]*Z[1]*X[2] + (0.041128856023498556+0j)*X[0]*Z[1]*X[2]*Z[3] + (0.041128856023498556+0j)*Y[0]*Z[1]*Y[2] + (0.14020450296633868+0j)*Z[0]*Z[2] + (0.18133335898983727+0j)*Z[0]*Z[1]*Z[2]*Z[3] + (0.18133335898983727+0j)*Z[0]*Z[1]*Z[2] + (0.14020450296633868+0j)*Z[0]*Z[2]*Z[3] + (0.19136084915706864+0j)*Z[1]*Z[3]このようにきちんと変換されました。ちょっと複雑な形をしていますが、これこそがこれまで学んできたパウリ行列の和で書かれたハミルトニアンです。これをVQEにかけますが、今回はUCC理論と呼ばれる上記のハミルトニアンに対応するansatzがあるため効率的に計算ができます。
runner = vqe.Vqe(UCCAnsatz(h,2,Circuit().x[0])) result = runner.run(verbose = True)そうすると、最適化計算が進み、
params: [0.00803084 0.88310007] val: -0.3685674394653079 params: [0.00803084 0.88310007] val: -0.3685674394653079 (中略) params: [-0.0024937 -0.00256402] val: -0.9043519838381495 params: [-0.0024937 -0.16023561] val: -0.885812805585636最適化のプロセスが出てきました。パラメータが最適化されながら最小基底状態が探索されています。今回は量子化学の理論に基づいて電子の配置をするUCCansatzと呼ばれるものが利用されました。通常ansatzの構成は難しいので、理論的な探究が求まれます。最小エネルギーは、
runner.ansatz.get_energy(result.circuit,runner.sampler) -0.9043519838381495原子間距離0.4の場合の最小値の期待値が求まりました。これを全体でやったのが最初のコードです。
2-4.VQEで組合せ最適化問題
応用として組合せ最適化問題があります。多くの人に馴染みのある問題なので、量子コンピュータは正直どっから手をつけていいかわからんと思うひとおすすめです。組合せ最適化問題は、多くの選択肢からベストな答えを選ぶ問題で、社会問題をうまく定式化し、最小値問題を解くことで最適な組合せを得ることができます。
今回は通常VQEを組合せ最適化問題としてはあまり利用しませんが、例題のハミルトニアンを実行してみます。
2-5.VQEで組合せ最適化問題の定式化
定式化は、答えはわからないが、条件はわかると言う状況に対して、最小値が出れば答えになるように、問題の条件を式の形に落としこみます。
・Z演算子を使う
・最終的にはZ演算子の代わりにQUBOを使うです。まずは例題で、下記を行ってみましょう。定式化は、
h = -Z(0) - Z(0)*Z(1)Zの後ろの数字は、量子ビットの通し番号を表します。0番目と1番目の量子ビットの2つを使っています。また、問題設定で大事なのは、Zの前の係数です。
Z(0)の前は-1のバイアス
Z(0)*Z(1)の前は-1のウェイトが設定されています。Zは期待値として<ψ|Z|ψ>=-1か<ψ|Z|ψ>1のどちらかをとります。hはより小さい値を取ると正解になります。Zの組合せで最終的な答えを判断できます。最終的な答えは、Z(0),Z(1)の値で場合わけすると、
Z(0) Z(1) h -1 -1 0 -1 1 2 1 -1 0 1 1 -2 VQEは上記の表で最小となるZ(0)=1,Z(1)=1の時-2となるものを計算で求めてくれます。今回ansatzはa,bの2パラメータを利用した極座標表記のものを使ってみます。ansatzを含む全体のコードは、
import numpy as np from blueqat import Circuit from blueqat.pauli import X, Y, Z, I from blueqat.vqe import AnsatzBase, Vqe import obaq class OneQubitAnsatz(AnsatzBase): def __init__(self, hamiltonian): super().__init__(hamiltonian.to_expr(), 2) self.step = 1 def get_circuit(self, params): a, b = params return Circuit().ry(a)[0].rz(b)[1].cx[0,1] # この定式化が大事 h = -Z(0) - Z(0)*Z(1) runner = Vqe(OneQubitAnsatz(h)) result = runner.run() result.circuit.run(backend="obaq", returns="draw") print('Result by VQE') print(runner.ansatz.get_energy(result.circuit, runner.sampler))Result by VQE -1.9999943170511056約-2が答えとして出てきましたので正解です。上記問題は役にたたなさそうですが、
・Z(0)をAさん、Z(1)をBさんに見立てる
・Aさんはグループ1に属する(バイアスの設定)
・BさんはAさんと同じグループに属する(ウェイトの設定)という条件をつけた(max-cut)分類問題と同じです。ただ、このままでは毎回問題を解くのが大変なので様々な工夫が必要です、それをみていきましょう。
2-6.定式化は0と1のバイナリ値で
定式化は+1と-1の値の組合せで定式化しました。ただ、産業では0と1を計算として利用します。そこで、01で定式化をするのをQUBOと呼びます。-1と+1でかかれた定式化を0と1で書かれたQUBO式に変換するには、Z演算子を下記のように変換するだけでできます。
q = \frac{Z + 1}{2}これで、-1の時が0に、1の時は1のままで変換されます。定式化は社会問題をQUBO形式で、ハミルトニアンを作ることで実現でき、バイアスとウェイトを設定することで実現できます。この手法は量子コンピュータに限ったことではないので普通の計算に慣れている人でも受け入れられやすいでしょう。
QUBOで便利なルールとして、$0^2=0$そして$1^2=1$のように変形して字数を落とすことができます。
2-7.QUBO式のプログラミング
QUBOへの変換はZを代入して書き換えればいいのですが、毎回行うのは大変なのでblueqatで自動変換してくれます。今回のときたいコスト関数は、
h = -Z(0) - Z(0)*Z(1)に$Z = 2q-1$を代入すると定式化は、
h = -(2*q(0)-1)-(2*q(0)-1)*(2*q(1)-1) = 2*q(1)-4*q(0)*q(1)となりました。上記のコスト関数は以前のように-1と+1ではなく、0と1で考えることができるので簡単です。これをVQEで解くことで、最小値が得られます。
import numpy as np from blueqat import Circuit from blueqat.pauli import X, Y, Z, I from blueqat.pauli import qubo_bit as q from blueqat.vqe import AnsatzBase, Vqe import obaq class QubitAnsatz(AnsatzBase): def __init__(self, hamiltonian): super().__init__(hamiltonian, 2) self.step = 1 def get_circuit(self, params): a, b = params return Circuit().ry(a)[0].rz(b)[1].cx[0,1] h = 2*q(1)-4*q(0)*q(1) runner = Vqe(QubitAnsatz(h.to_expr().simplify())) result = runner.run() result.circuit.run(backend="obaq", returns="draw") print('Result by VQE') print(runner.ansatz.get_energy(result.circuit, runner.sampler))結果は、
Result by VQE -1.9684060830160348上記は定式化を変更しただけですので、量子回路自体は変更されていません。正しく得られていますが実際にはansatzを作るのが難しかったり、その他定式化に有利な回路を作るためにQAOAを利用するのが無難です。
3.QAOA
VQEはansatzを高度化することで問題特化型のアルゴリズムとして発展をさせることができます。ここでは、VQEの変分法をベースに、ansatzを組合せ最適化問題に特化した形で発展をしたQAOA(Quantum Approximate Opitmization Alogirthm)をみてみます。
3-1.量子断熱計算
量子断熱計算は、状態ベクトルを断続的に変化させることで基底状態をキープしたまま時間発展を行うことができる理論です。
初期状態のハミルトニアンを$H_{start}$として、最終的に求めたい問題のハミルトニアンを$H_{final}$としたときに、時間$t$と全体のスケジュール$T$から、
H_{temp} = (1-\frac{t}{T})H_{start} + \frac{t}{T}H_{final}としたときに$T\rightarrow\infty$とすれば、時間発展で変化させた状態ベクトルが、その瞬間瞬間のハミルトニアンに追従し、固有状態をとり固有値$\lambda$を持つようにすることができます。
H_{temp}\mid \psi \rangle = E_{0temp}\mid \psi \rangle時間発展計算は、
\mid \psi_{t+1} \rangle = U \mid \psi_t \rangle = e^{-iHt} \mid \psi_t \rangleとなります。課題は基底状態と第一励起状態が最接近する部分ですが、$E_1(t)-E_0(t)$のエネルギー差に注意して計算することによって、基底状態をキープできます。
3-2.QAOA回路
QAOAは上記の量子断熱計算の時間発展計算をansatzとして変分アルゴリズムに適用したものです。
全体構成を大きく分けて、
1.mixerを選ぶと、初期状態が決まる
2.定式化をQUBOもしくはZで作るです。2番目の定式化は自動的に時間発展されます。
一番左は初期固有状態|+>を作っています。これに対応するハミルトニアンXは時間発展の形でRxで出てきます。通常はmixerはデフォルトではXを選び、初期状態はそれに対応する|+>を作るために、$H^{\otimes N}$ が利用されることが多いです。
また、CX-Rz-CXは問題設定のハミルトニアンのウェイトに対応し、次のRzはハミルトニアンのバイアスに対応しています。
blueqatのQaoaAnsatzはハミルトニアンとステップ分割数を決めれば、自動的にこの時間発展のansatzを構成してくれます。ライブラリ側で適切な計算をしてくれているので、私たちがするのはハミルトニアンの定式化とmixerの選択です。簡単な定式化を解いてみましょう。
h = 2*q(1)-4*q(0)*q(1)を行います。
from blueqat import vqe from blueqat.pauli import qubo_bit as q import obaq h = 2*q(1)-4*q(0)*q(1) step = 2 result = vqe.Vqe(vqe.QaoaAnsatz(h, step)).run() result.circuit.run(backend="obaq", returns="draw") print(result.most_common(12))これを解くことで、量子ビットが共に1の時に最小値が得られます。
(((1, 1), 0.8625473182532257), ((0, 0), 0.08788282214543966), ((1, 0), 0.046340126746094716), ((0, 1), 0.0032297328552398723))最初の数字が答えの候補で、次の数字はそれが現れる確率です。回路もちょっと複雑そうです。ツールに任せて定式化を頑張りましょう!
3-3.交通最適化
交通最適化は度々出てくるテーマです。下記を参考を確認します。
「Quantum Computing at Volkswagen:
Traffic Flow Optimization using the D-Wave Quantum Annealer」
引用:https://www.dwavesys.com/sites/default/files/VW.pdf例題を改造してみます。
1、1台の車に2つのルート選択を許容する(古典)
2、現在の選択ルートから混雑状況を計算(古典)
3、混雑度を最小にするようにルート選択を最小化(QAOA)スタートAからゴールBまで12の道路が通し番号0から11まで付けられています。自動車1と自動車2があり、それぞれ指定されたルートを取ります。ルートはそれぞれ2つずつ提案されており、そのうちの一つを取ります。今回は一番混雑度が低くなるようなルートを選択します。
car1
route1-1(q0):s0,s3,s6,s9
route1–2 (q1):s0,s3,s8,s11
car2
route2–1(q2):s0,s3,s8,s11
route2–2(q3):s2,s7,s10,s113-4.制約条件を満たすmixerを選択する
しかしここでは、ルート選択は1つだけを選ぶわけですから、$q_0$か$q_1$の片方は1で、もう片方は0となるのが条件としてついてきます。また、$q_2$と$q_3$も同様です。
ここで、量子回路でまず量子もつれを作ります。量子もつれは多くのパターンから限られた組み合わせだけが出るように調整できるのでした。簡単な例として、
from blueqat import Circuit Circuit().h[0].cx[0,1].m[:].run(shots=100)こうすると、本来4種類出るところから00と11のみ答えが出ます。
Counter({'00': 51, '11': 49})ちょっと形を変えることで、01と10のもつれに変更できます。
from blueqat import Circuit Circuit().h[0].cx[0,1].x[0].m[:].run(shots=100) #=>Counter({'01': 41, '10': 59})これを使います。つまり、自動車1と自動車2にそれぞれもつれを活用して、01と10に制限をかけるように初期状態を設定します。
今回4量子ビットの回路では、
from blueqat import Circuit Circuit().h[0].cx[0,1].x[0].h[2].cx[2,3].x[2].m[:].run(shots=100) #=>Counter({'0101': 27, '0110': 16, '1001': 29, '1010': 28})この4通りに絞ります。
3-5.混雑度をハミルトニアンで設定
下記が提案されたルートでした。それぞれの道の混雑を量子ビットを使って表現します。
car1
route1-1(q0):s0,s3,s6,s9
route1–2 (q1):s0,s3,s8,s11
car2
route2–1(q2):s0,s3,s8,s11
route2–2(q3):s2,s7,s10,s11道s0から順番にコストを足し合わせていきます。コストはその道の登場する量子ビットを足し合わせて2乗します。途中$0^2=0$または、$1^2=1$より次数を下げています。
h=(q_0+q_1+q_2)^2+(q_0+q_1+q_2)^2+q_0^2+q_0^2+(q_1+q_2)^2+(q_1+q_2+q_3)^2+q_3^2+q_3^2+q_3^2\\ =4q_0+4q_1+4q_2+4q_3+4q_0q_1+4q_0q_2+8q_1q_2+2q_1q_3+2q_2q_3これがそのままハミルトニアンになります。
3-6.具体的コード
具体的な実行コードはこちらです。元々のQAOAのAnsatzを改造しています。
import numpy as np from blueqat import Circuit from blueqat.pauli import X, Y, Z, I from blueqat.pauli import qubo_bit as q from blueqat.vqe import AnsatzBase, Vqe def an(index): return 0.5 * X[index] + 0.5j * Y[index] def cr(index): return 0.5 * X[index] - 0.5j * Y[index] op1 = (cr(1) * an(0) + cr(0) * an(1)).to_expr().simplify() op2 = (cr(3) * an(2) + cr(2) * an(3)).to_expr().simplify() class QaoaQaoaAnsatz(AnsatzBase): def __init__(self, hamiltonian, step=1, init_circuit=None): super().__init__(hamiltonian, step * 2) self.hamiltonian = hamiltonian.to_expr().simplify() if not self.check_hamiltonian(): raise ValueError("Hamiltonian terms are not commutable") self.step = step self.n_qubits = self.hamiltonian.max_n() + 1 if init_circuit: self.init_circuit = init_circuit if init_circuit.n_qubits > self.n_qubits: self.n_qubits = init_circuit.n_qubits else: self.init_circuit = Circuit(self.n_qubits).h[:] self.init_circuit.make_cache() self.time_evolutions = [term.get_time_evolution() for term in self.hamiltonian] self.time_evolutions1 = [term.get_time_evolution() for term in op1] self.time_evolutions2 = [term.get_time_evolution() for term in op2] def check_hamiltonian(self): """Check hamiltonian is commutable. This condition is required for QaoaAnsatz""" return self.hamiltonian.is_all_terms_commutable() def get_circuit(self, params): c = self.init_circuit.copy() betas = params[:self.step] gammas = params[self.step:] for beta, gamma in zip(betas, gammas): beta *= np.pi gamma *= 2 * np.pi for evo in self.time_evolutions: evo(c, gamma) for evo1 in self.time_evolutions1: evo1(c, beta) for evo2 in self.time_evolutions2: evo2(c, beta) return c h = 4*q(0)+4*q(1)+4*q(2)+4*q(3)+4*q(0)*q(1)+4*q(0)*q(2)+8*q(1)*q(2)+2*q(1)*q(3)+2*q(2)*q(3) runner = Vqe(QaoaQaoaAnsatz(h.to_expr().simplify(),4,Circuit().h[0].cx[0,1].x[0].h[2].cx[2,3].x[2])) result = runner.run() # get probability print(result.most_common(12))これを実行すると、
(((1, 0, 0, 1), 0.9285092517501069), ((0, 1, 0, 1), 0.03727452567612003), ((1, 0, 1, 0), 0.019828254090636977), ((0, 1, 1, 0), 0.01438796848312899), ((1, 0, 0, 0), 4.949639957075196e-32), ((1, 1, 1, 0), 4.1497989458064e-32), ((1, 0, 1, 1), 3.9481563859938324e-32), ((0, 0, 1, 0), 2.7174584187380976e-32), ((1, 1, 0, 1), 9.7798953112461e-33), ((0, 0, 0, 1), 6.384745093566593e-33), ((0, 1, 0, 0), 6.162975822039154e-33), ((0, 1, 1, 1), 4.240055143190024e-33))制約条件を満たしながら混雑の最も少ないルートが選択されています。制約条件の決め方はまだまだ改良の余地があり、研究開発が進んでいます。
4-1.古典最適化
変分アルゴリズムの次のパラメータの提案を渡すのは最適化アルゴリズムですが、それは古典で実行されます。
minimizer=vqe.get_scipy_minimizer(method="COBYLA",options={"tol":5.0e-4}) runner = Vqe(QubitAnsatz(cost),minimizer=minimizer) result = runner.run()上記では古典最適化のアルゴリズムを指定できています。主にscipyから選べます。
https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.minimize.html
'Nelder-Mead', 'Powell', 'CG', 'BFGS', 'L-BFGS-B', 'TNC', 'COBYLA', 'SLSQP'
自分の好きなソルバーを組み込むこともできます。
4-2.自作最適化ソルバー
ベイズ最適化のhyperoptを組み込んでみます。
!pip install hyperopt関数を作って、
def hyperopt_minimizer(objective, n_params): from hyperopt import fmin, Trials, tpe, hp trials = Trials() best = fmin(objective, [hp.uniform(f'p{i}', 0., 2 * np.pi) for i in range(n_params)], algo=tpe.suggest, max_evals=100, trials=trials, verbose=1) return list(best.values())設定をすることで使えます。
h = 2*q(1)-4*q(0)*q(1) runner = Vqe(QubitAnsatz(h),minimizer=hyperopt_minimizer) result = runner.run() print('Result by VQE') print(runner.ansatz.get_energy(result.circuit, runner.sampler))100%|██████████| 100/100 [00:00<00:00, 184.33it/s, best loss: -1.9999826942162187] Result by VQE -1.99998269421621875.ansatzを機械学習で学習させる
ハミルトニアンとansatzの間には関連性がありました。ただ、応用を広げるには、任意のハミルトニアンに任意のansatzを作りたいと言う要望があります。機械学習を利用して試してみましょう。
5-1.量子状態の最適化
とりあえず量子ビットの最適化を行い、状態ベクトルを所望の物に近づけます。ここでは、pauliZの固有状態にする例をとりあげます。ある行列と状態ベクトルがあり、状態ベクトルが固有状態の場合には、固有値$\lambda$を使って、
H\mid \psi \rangle = \lambda \mid \psi \rangleが成り立ちます。今回はH=Zとして、その固有値-1に量子状態を最適化してみます。
\begin{bmatrix} 1&0\\ 0&-1 \end{bmatrix} \mid \psi \rangle = -1 \mid \psi \rangle5-2.1量子ビットの状態
1量子ビットの状態は三次元の球上で表現でき、極座標表示で2つの角度で表現できることを以前確認しました。
ということで、今回はrxとryゲートを使って、量子状態を表現します。角度パラメータa,bを作ります。適当なaとbを入れてみます。from blueqat import Circuit a = 0.5 b = 0.5 c = Circuit().rx(a)[0].ry(b)[0].run() cこの時点では適当な量子状態になっています。aとbを最適化してみます。
array([0.94078455+0.j , 0.22360884-0.25480092j])今回ターゲットにするのは、pauliZの期待値ですが、計算は、
\langle \psi \mid Z \mid \psi \rangle = |\alpha|^2 -|\beta|^2となります。$\alpha$と$\beta$は確率振幅です。上記の例でのZの期待値は、
import numpy as np eval = np.square(np.abs(c[0]))-np.square(np.abs(c[1])) eval0.7701511529340693となります。こちらのターゲットはZ=-1に設定して、損失関数を設定します。
loss = (eval - (-1))^2 = (eval+1)^2今回は、
loss = np.square(eval+1) loss3.1334351042338144求めたい量子状態を間接的にハミルトニアンの期待値に設定し、それを損失関数を用いて評価をしています。損失関数を0にするためがんります。
5-3.hyperoptで最適化する
hyperoptで設定します。インストールします。
pip install -q blueqat hyperopt次に実行をします。
from blueqat import Circuit import numpy as np from hyperopt import hp, tpe, fmin #欲しい状態ベクトルを実現する量子回路 def circ(para): return Circuit().rx(para['a'])[0].rz(para['b'])[0].run() #pauliZの期待値の計算 #expectation value def eval(sv): return np.square(np.abs(sv[0]))-np.square(np.abs(sv[1])) #欲しい状態ベクトルの誤差をターゲットから計算します def f(para): svector = circ(para) return np.square(eval(svector) + 1) #TPEでベイズ最適化 best = fmin(f, space={'a': hp.uniform('a', 0, np.pi*2), 'b': hp.uniform('b', 0, np.pi*2)}, algo=tpe.suggest, max_evals=100, verbose=1) print(best) print(eval(circ(best)))これにより、
100%|██████████| 100/100 [00:00<00:00, 199.84it/s, best loss: 1.2342345769234112e-08] {'a': 3.1564989051389323, 'b': 4.45029935472825} -0.9998889038894955これにより、ターゲットに近づきました。実際にサンプルを取ってみると、
Circuit().rx(best['a'])[0].rz(best['b'])[0].m[:].run(shots=1000)Counter({'1': 1000})いい感じでできました。所望の量子状態に持っていくことができました。
5-4.古典NNでの最適化
次にニューラルネットワークでの最適化チュートリアルをやってみます。
1量子ビットの量子回路を使って最適化計算をしてみます。
tfq.layers.ControlledPQCでパラメータ化された量子回路を使ってやってみます。
チュートリアルの実装で、全体のアーキテクチャは3つの部分に分かれます。
1、最初の3つのゲートでデータの入力
2、次の3つのゲートで量子状態の操作
3、古典のニューラルネットワークでパラメータの調整をします。
インストール
google colabの場合には、ちょっと調整をします。
try: %tensorflow_version 2.x except Exception: pass #=>TensorFlow 2.x selected.pip install tensorflow-quantumこれでスタートできます。
ツールの読み込み
下記で読み込んでおきます。
import tensorflow as tf import tensorflow_quantum as tfq import cirq import sympy import numpy as np # 表示用 %matplotlib inline import matplotlib.pyplot as plt from cirq.contrib.svg import SVGCircuitまずは回路の実装
上記の回路の準備をします。
# 古典ニューラルネットで操作する角度パラメータを準備します。3つあります。 control_params = sympy.symbols('theta_1 theta_2 theta_3') # そして、1量子ビットを準備し、上記のパラメータをrz,ry,rx回路に当てはめます。 qubit = cirq.GridQubit(0, 0) model_circuit = cirq.Circuit( cirq.rz(control_params[0])(qubit), cirq.ry(control_params[1])(qubit), cirq.rx(control_params[2])(qubit)) SVGCircuit(model_circuit)古典コントローラの設定
次にコントローラネットワークを実装します。
# こちらは古典の通常のネットワークです controller = tf.keras.Sequential([ tf.keras.layers.Dense(10, activation='elu'), tf.keras.layers.Dense(3) ])初期状態では値はランダムなので役には立ちません。
controller(tf.constant([[0.0],[1.0]])).numpy()array([[ 0. , 0. , 0. ], [-0.36744112, 0.13772306, -0.4180936 ]], dtype=float32)古典コントローラを量子回路に接続
今回はkerasのモデルとして古典NNのコントローラを量子回路に接続します。
入力は2種類あり、古典コントローラに入れる入力値と量子回路に最初に入れるランダム回路です。 このランダム回路の入力を古典NNが学び、調整をしてZの期待値を学びます。
入力2つを準備します。
前者の入力は量子回路が入力されますが、テンソル化されて、tf.stringで入ってくることに注意します。# 量子回路に準備する古典NNが修正する量子状態の入力 circuits_input = tf.keras.Input(shape=(), # The circuit-tensor has dtype `tf.string` dtype=tf.string, name='circuits_input') #古典NNに入力する0か1の数値。 commands_input = tf.keras.Input(shape=(1,), dtype=tf.dtypes.float32, name='commands_input')ハミルトニアンZの期待値を求める処理を記述します。
dense_2 = controller(commands_input) # Zの期待値を量子回路から求めます expectation_layer = tfq.layers.ControlledPQC(model_circuit, # Observe Z operators = cirq.Z(qubit)) expectation = expectation_layer([circuits_input, dense_2])あとは、これを全て tf.keras.Model としてまとめます
# The full Keras model is built from our layers. model = tf.keras.Model(inputs=[circuits_input, commands_input], outputs=expectation)アーキテクチャを確認します。 graphviz package が必要になります。
tf.keras.utils.plot_model(model, show_shapes=True, dpi=70)入力は古典NNへのコマンド入力が0か1になり、入力1つに対して、出力が3つの角度パラメータに。一方量子回路も入力があります。
データセット
このモデルでは、古典への入力値0か1によって、pauliZの期待値+1か-1が出力されます。
# 古典のニューラルネットに対する入力は0か1 commands = np.array([[0], [1]], dtype=np.float32) # 量子回路から出力されるハミルトニアンZの期待値は1か-1 expected_outputs = np.array([[1], [-1]], dtype=np.float32)このほかに量子回路としての入力があります。
入力回路の準備
入力回路は今回ランダムで準備され、この入力回路を補正するようにpauliZの期待値を求めます。
random_rotations = np.random.uniform(0, 2 * np.pi, 3) datapoint_circuits = tfq.convert_to_tensor([ cirq.Circuit( cirq.rx(random_rotations[0])(qubit), cirq.ry(random_rotations[1])(qubit), cirq.rz(random_rotations[2])(qubit)) ] * 2) # Make two copied of this circuitdatapoint_circuits.shapeTensorShape([2])トレーニング
それぞれのコマンドに対してのデータポイントの値を確認できます。
model([datapoint_circuits, commands]).numpy()array([[-0.3738031 ], [ 0.32185417]], dtype=float32)早速これをトレーニングしてみます。
optimizer = tf.keras.optimizers.Adam(learning_rate=0.05) loss = tf.keras.losses.MeanSquaredError() model.compile(optimizer=optimizer, loss=loss) history = model.fit(x=[datapoint_circuits, commands], y=expected_outputs, epochs=30, verbose=0)plt.plot(history.history['loss']) plt.title("Learning to Control a Qubit") plt.xlabel("Iterations") plt.ylabel("Error in Control") plt.show()これによって、NNが量子ビットの状態の制御をできていることがわかります。
- 投稿日:2020-03-14T11:13:59+09:00
tf.keras で作成したモデルのパラメータの量子化 Part1
概要
tf.kerasを使って構築されたネットワークのパラメータを量子化してみました。
パラメータを量子化するメリットは、大雑把に次の2つです。
1. 保存するパラメータのサイズが小さくなる
32bit float を例えば 8bit float に量子化できればメモリ使用量が1/4になります
2. 演算を高速化可能
専用のハードウェアを用意すれば、演算が高速化される(はず)
入力及びパラメータを1bitまで量子化できれば、掛け算がビット演算になるのですんごい速い(AlexNetで58倍高速化できたそうです ※1)デメリットはもちろん、本来のパラメータが量子化されることによって誤差が大きくなり、出力の精度が落ちることです。
後々専用のハードウェアを作成して速度も検証してみたいですが、今回は精度だけ比較してみます。
環境
OS: ubuntu 16.04 LTS
Python: 3.5.2
TensorFlow: 1.13.1量子化とは
量子化とは、アナログ信号などの連続量を整数などの離散値で近似的に表現すること。 自然界の信号などをコンピュータで処理・保存できるようデジタルデータに置き換える際などによく行われる。(Wikipedia, 2019/12/17)
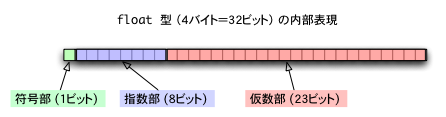
普通、tensorflowを用いてネットワークを構築した場合、重みやしきい値などのパラメータは float32、つまり4Byte で宣言されるのではないかと思います。それらの各ビットは符号部、指数部、仮数部にわけられ、それぞれの役目を果たします。
それらのビットより、float型の数値は、
float の表す値 = (-1)^符号部 × 2^(指数部-127) × 1.仮数部
として計算されます。
(参考:http://www.cc.kyoto-su.ac.jp/~yamada/programming/float.html)これで大きな数から小さな数、整数から小数点以下が細かいものまでfloat型で表現できますね!しかし、実際そんなに細かい数値が必要なのでしょうか。
例えばある重みの値が0.123456789とすれば、
00111101111111001101011011101010
と表現されます。
では、23bit存在した仮数部を10bitに減らしてみるとどうでしょうか。(わかりやすくするために減らした分を0で埋めています)
00111101111111001100000000000000
となりますね。これは0.12182617187という値を指します。元々の数との相対誤差は98.68%です。これはほとんど変わらないと言っていいのではないでしょうか。
この場合だと、仮数部の下13bitが省略されたので、実質19bitで表現されていることになります。これを、32bitだった数値が19bitに量子化された といいます。
なお、今の例では仮数部のみを減らしましたが、指数部なども減らすことでより小さく量子化することが可能です。計測
量子化なし
前回作成したネットワークをそのまま使ってみました。
学習のエポックは10で、このモデルのパラメータを保存しておきます。> model.summary() __________________________________________________________________________________________________ Layer (type) Output Shape Param # Connected to ================================================================================================== input_1 (InputLayer) (None, 480, 640, 3) 0 __________________________________________________________________________________________________ conv2d (Conv2D) (None, 240, 320, 32) 2432 input_1[0][0] __________________________________________________________________________________________________ max_pooling2d (MaxPooling2D) (None, 119, 159, 32) 0 conv2d[0][0] __________________________________________________________________________________________________ batch_normalization_v1 (BatchNo (None, 119, 159, 32) 128 max_pooling2d[0][0] __________________________________________________________________________________________________ activation (Activation) (None, 119, 159, 32) 0 batch_normalization_v1[0][0] __________________________________________________________________________________________________ conv2d_1 (Conv2D) (None, 60, 80, 32) 9248 activation[0][0] __________________________________________________________________________________________________ batch_normalization_v1_1 (Batch (None, 60, 80, 32) 128 conv2d_1[0][0] __________________________________________________________________________________________________ activation_1 (Activation) (None, 60, 80, 32) 0 batch_normalization_v1_1[0][0] __________________________________________________________________________________________________ conv2d_3 (Conv2D) (None, 60, 80, 32) 1056 max_pooling2d[0][0] __________________________________________________________________________________________________ conv2d_2 (Conv2D) (None, 60, 80, 32) 9248 activation_1[0][0] __________________________________________________________________________________________________ add (Add) (None, 60, 80, 32) 0 conv2d_3[0][0] conv2d_2[0][0] __________________________________________________________________________________________________ batch_normalization_v1_2 (Batch (None, 60, 80, 32) 128 add[0][0] __________________________________________________________________________________________________ activation_2 (Activation) (None, 60, 80, 32) 0 batch_normalization_v1_2[0][0] __________________________________________________________________________________________________ conv2d_4 (Conv2D) (None, 30, 40, 64) 18496 activation_2[0][0] __________________________________________________________________________________________________ batch_normalization_v1_3 (Batch (None, 30, 40, 64) 256 conv2d_4[0][0] __________________________________________________________________________________________________ activation_3 (Activation) (None, 30, 40, 64) 0 batch_normalization_v1_3[0][0] __________________________________________________________________________________________________ conv2d_6 (Conv2D) (None, 30, 40, 64) 2112 add[0][0] __________________________________________________________________________________________________ conv2d_5 (Conv2D) (None, 30, 40, 64) 36928 activation_3[0][0] __________________________________________________________________________________________________ add_1 (Add) (None, 30, 40, 64) 0 conv2d_6[0][0] conv2d_5[0][0] __________________________________________________________________________________________________ batch_normalization_v1_4 (Batch (None, 30, 40, 64) 256 add_1[0][0] __________________________________________________________________________________________________ activation_4 (Activation) (None, 30, 40, 64) 0 batch_normalization_v1_4[0][0] __________________________________________________________________________________________________ conv2d_7 (Conv2D) (None, 15, 20, 128) 73856 activation_4[0][0] __________________________________________________________________________________________________ batch_normalization_v1_5 (Batch (None, 15, 20, 128) 512 conv2d_7[0][0] __________________________________________________________________________________________________ activation_5 (Activation) (None, 15, 20, 128) 0 batch_normalization_v1_5[0][0] __________________________________________________________________________________________________ conv2d_9 (Conv2D) (None, 15, 20, 128) 8320 add_1[0][0] __________________________________________________________________________________________________ conv2d_8 (Conv2D) (None, 15, 20, 128) 147584 activation_5[0][0] __________________________________________________________________________________________________ add_2 (Add) (None, 15, 20, 128) 0 conv2d_9[0][0] conv2d_8[0][0] __________________________________________________________________________________________________ flatten (Flatten) (None, 38400) 0 add_2[0][0] __________________________________________________________________________________________________ activation_6 (Activation) (None, 38400) 0 flatten[0][0] __________________________________________________________________________________________________ dropout (Dropout) (None, 38400) 0 activation_6[0][0] __________________________________________________________________________________________________ dense (Dense) (None, 3) 115203 dropout[0][0] __________________________________________________________________________________________________ activation_7 (Activation) (None, 3) 0 dense[0][0] ================================================================================================== Total params: 425,891 Trainable params: 425,187 Non-trainable params: 704 __________________________________________________________________________________________________10エポック学習させて、1000枚のテストデータでの精度が、こんな感じ
Accuracy: 0.815 Calc : [[244. 0. 21.] [ 55. 0. 56.] [ 53. 0. 571.]] Labels : [[265. 0. 0.] [ 0. 111. 0.] [ 0. 0. 624.]] Average_accuracy : [0.92075472 0. 0.9150641 ]やっぱり2つ目のラベルの精度が低いのはおいておきます。
それぞれのレイヤーの学習可能なパラメータを確認してみましょう。> [x.name for x in model.trainable_variables] ['conv2d/kernel:0', 'conv2d/bias:0', 'batch_normalization_v1/gamma:0', 'batch_normalization_v1/beta:0', 'conv2d_1/kernel:0', 'conv2d_1/bias:0', 'batch_normalization_v1_1/gamma:0', 'batch_normalization_v1_1/beta:0', 'conv2d_3/kernel:0', 'conv2d_3/bias:0', 'conv2d_2/kernel:0', 'conv2d_2/bias:0', 'batch_normalization_v1_2/gamma:0', 'batch_normalization_v1_2/beta:0', 'conv2d_4/kernel:0', 'conv2d_4/bias:0', 'batch_normalization_v1_3/gamma:0', 'batch_normalization_v1_3/beta:0', 'conv2d_6/kernel:0', 'conv2d_6/bias:0', 'conv2d_5/kernel:0', 'conv2d_5/bias:0', 'batch_normalization_v1_4/gamma:0', 'batch_normalization_v1_4/beta:0', 'conv2d_7/kernel:0', 'conv2d_7/bias:0', 'batch_normalization_v1_5/gamma:0', 'batch_normalization_v1_5/beta:0', 'conv2d_9/kernel:0', 'conv2d_9/bias:0', 'conv2d_8/kernel:0', 'conv2d_8/bias:0', 'dense/kernel:0', 'dense/bias:0']どうやら、畳み込み層と全結合層は kernel bias の2種類のパラメータをもち、バッチ正規化層は gamma beta の2種類のパラメータを持っているようです。一応中身を確認しておきましょう。どちらも一番後ろのレイヤーのパラメータのみのせておきます。
<tensorflow.python.keras.layers.core.Dense object at 0x7ffa40497128> [<tf.Variable 'dense/kernel:0' shape=(38400, 3) dtype=float32, numpy= array([[-0.01491976, 0.01396543, 0.00093346], [ 0.01540731, 0.00241674, 0.01131605], [ 0.0119241 , -0.01668087, -0.00719858], ..., [-0.00296943, 0.01103336, 0.00349635], [ 0.00204816, -0.00147773, 0.00720838], [-0.00207304, 0.00621508, -0.01145099]], dtype=float32)>, <tf.Variable 'dense/bias:0' shape=(3,) dtype=float32, numpy=array([ 4.8551615e-03, -5.9992936e-03, -4.9170827e-05], dtype=float32)>]<tensorflow.python.keras.layers.normalization.BatchNormalizationV1 object at 0x7f0dc86d2898> [<tf.Variable 'batch_normalization_v1_5/gamma:0' shape=(128,) dtype=float32, numpy= array([1.0053827 , 1.0023135 , 1.0041403 , 0.9895478 , 1.0039909 , 0.98955464, 1.0088704 , 0.9910637 , 0.9913659 , 0.99780196, 1.000202 , 1.0014107 , 1.0005019 , 0.9903944 , 0.9944405 , 0.9973047 , 1.0017028 , 0.9907751 , 0.99735796, 1.0081666 , 0.99636775, 1.0030036 , 0.99932915, 1.004627 , 0.99306023, 1.0017363 , 0.98416674, 0.99064416, 1.0082388 , 1.0035444 , 0.99265665, 0.99718237, 1.0001222 , 0.99854386, 1.0034426 , 0.9999184 , 0.9963349 , 0.9844031 , 1.0056257 , 0.9994289 , 0.99500334, 0.9923768 , 0.99127066, 0.9832162 , 1.0021056 , 1.0047147 , 0.99886245, 1.0052888 , 0.99249786, 1.0065212 , 0.99161077, 0.9932604 , 1.0078368 , 1.003879 , 0.9882739 , 1.0010694 , 0.99350995, 0.99350333, 0.99219364, 0.99605584, 0.9823839 , 0.99674433, 1.0070174 , 1.00066 , 0.99863935, 0.99942183, 1.000792 , 1.0028559 , 0.9946366 , 0.99531853, 1.0003756 , 0.99510074, 0.9922438 , 1.005276 , 1.0053014 , 0.9929603 , 0.99317366, 1.0056378 , 1.003331 , 1.0047318 , 0.99011916, 1.0086612 , 0.99564356, 0.97692627, 0.9968611 , 1.0015146 , 1.0121565 , 0.9942222 , 0.9938692 , 0.98945427, 1.0070571 , 0.99605334, 1.00008 , 1.0103743 , 0.991692 , 0.98665 , 0.9992022 , 0.98171806, 0.99035376, 0.99664146, 1.0095577 , 1.0159916 , 1.0002235 , 0.9792612 , 1.0048499 , 1.0002121 , 1.0031438 , 0.9905956 , 1.0046396 , 0.99771607, 0.99895054, 1.0037303 , 1.0038016 , 1.0067954 , 0.9906669 , 0.9937981 , 0.9853775 , 0.99674666, 0.9853735 , 0.9933321 , 0.9874309 , 1.0152614 , 1.0054263 , 0.99592394, 1.005618 , 0.9954677 , 0.98061544, 1.0030056 ], dtype=float32)>, <tf.Variable 'batch_normalization_v1_5/beta:0' shape=(128,) dtype=float32, numpy= array([ 0.00262505, -0.01182571, 0.00543317, 0.00769176, -0.00662231, -0.01436215, -0.01028995, -0.00620002, -0.00588665, -0.00019779, 0.004008 , -0.00465797, -0.0097509 , -0.00081195, -0.0140775 , -0.0078128 , 0.00924537, -0.0057598 , -0.0017888 , 0.00137905, -0.01389314, 0.00725058, -0.01442415, -0.00770982, -0.01115939, 0.00144741, -0.00496186, -0.00233451, -0.00604108, -0.00561837, 0.00053209, 0.00626049, -0.00196816, 0.00111859, 0.00413055, -0.00590881, -0.00492901, -0.01062248, -0.00155396, -0.00236207, 0.00136854, -0.00125252, -0.01765665, -0.01969386, -0.01379174, -0.00236314, -0.00634788, -0.00099529, -0.00986335, 0.00195062, -0.00986179, -0.00456762, 0.00789357, 0.00510846, -0.00891418, -0.00093365, -0.00342024, -0.01001325, 0.00412015, -0.01361436, -0.01547966, -0.00597356, -0.00561096, 0.00430186, 0.00629607, -0.0032707 , -0.01115292, -0.01054228, -0.00661343, -0.0068517 , 0.00250201, -0.0119157 , 0.00174254, -0.00736857, 0.00990474, -0.01210231, -0.00133941, 0.00786918, -0.01437676, 0.00021543, -0.01157008, 0.00787573, -0.01417518, -0.01176108, 0.01217426, 0.00777597, 0.00527618, 0.00068975, -0.01436776, -0.00979709, 0.00090197, -0.00535901, -0.00172908, 0.00525916, -0.00055489, -0.01297212, -0.00279675, -0.0019424 , -0.01119416, -0.00220624, 0.01222709, 0.01195927, -0.00557467, -0.01582625, -0.00113147, 0.00383603, -0.0025774 , -0.00764492, -0.0054293 , -0.00483815, 0.00011727, 0.00274837, 0.0107253 , 0.00365951, 0.0037286 , -0.0052775 , -0.01400672, -0.01110312, -0.01492126, -0.00020007, -0.02051772, 0.00057484, 0.00417511, -0.01659194, 0.0063057 , -0.00042243, -0.01960172, 0.00553354], dtype=float32)>]kernel, biasは平均値が0に近く見えますね。
gamma, betaはそれぞれ1, 0が平均になっているように見えます。
これってつまり平均が0になるならば、正の値ならば1に、負の値なら-1へ
平均が1になるのであれば1以上の値であれば1に、それ未満であれば-1へ置き換えてやってもうまくいくのではないだろうか。やってみましょう。なお、これらのパラメータの数値が見えない場合は、コードの最初のあたりでeager executionを有効にすると、print()で中身が見えるようになります。その結果学習時間が3倍程度に長くなりますが。これはtensorFlow 2.x からはデフォルトで有効になるみたいですね。実行速度が落ちないといいのですが。
tf.enable_eager_execution()量子化あり(1bit ※2)
それでは、先ほど保存したモデルを読み込んで、パラメータを量子化してみましょう。今回は最も単純な、1bit量子化(バイナリ化)します。
畳み込み層、全結合層のパラメーターの量子化
まずは、畳み込み層及び全結合層のパラメーター、kernelとbiasをバイナリ化してみましょう。ここでのバイナリ化の式は単純で、こんな感じです
if parameter >= 0, then parameter ← 1
otherwise, parameter ← -1main.pyの一部layers = list() i = 0 while True: try: l = model.get_layer(index = i) layers.append(l) i += 1 except Exception as e: print(e, "No more layers.\n") break for num in range(i): try: bias = layers[num].bias kernel = layers[num].kernel except Exception as e: #print(e) continue print(bias) print(kernel) #print(np.shape(bias), np.shape(kernel)) k_shape = np.shape(kernel) b_shape = np.shape(bias) k = tf.reshape(kernel, [-1]) b = tf.reshape( bias, [-1]) new_kernel = np.zeros(len(k)) new_bias = np.zeros(len(b)) for l in range(len(k)): if k[l] >= 0: new_kernel[l] = 1 else: new_kernel[l] = -1 for l in range(len(b)): if b[l] >= 0: new_bias[l] = 1 else: new_bias[l] = -1 new_kernel = np.reshape(new_kernel, k_shape) new_bias = np.reshape(new_bias , b_shape) tf.assign(layers[num].bias , new_bias) tf.assign(layers[num].kernel, new_kernel) print(model.get_layer(index=num).bias) print(model.get_layer(index=num).kernel) print()さて出力は、、
<tf.Variable 'dense/bias:0' shape=(3,) dtype=float32, numpy=array([ 4.8551615e-03, -5.9992936e-03, -4.9170827e-05], dtype=float32)> <tf.Variable 'dense/kernel:0' shape=(38400, 3) dtype=float32, numpy= array([[-0.01491976, 0.01396543, 0.00093346], [ 0.01540731, 0.00241674, 0.01131605], [ 0.0119241 , -0.01668087, -0.00719858], ..., [-0.00296943, 0.01103336, 0.00349635], [ 0.00204816, -0.00147773, 0.00720838], [-0.00207304, 0.00621508, -0.01145099]], dtype=float32)> <tf.Variable 'dense/bias:0' shape=(3,) dtype=float32, numpy=array([ 1., -1., -1.], dtype=float32)> <tf.Variable 'dense/kernel:0' shape=(38400, 3) dtype=float32, numpy= array([[-1., 1., 1.], [ 1., 1., 1.], [ 1., -1., -1.], ..., [-1., 1., 1.], [ 1., -1., 1.], [-1., 1., -1.]], dtype=float32)>上側が元々のkernel及びbiasの値、下側がバイナリ化した結果の値です。無事パラメータを置き換えることができていますね!ただ代入しただけなので型はもちろんfloat32のままです。なので実際はバイナリ化できていませんが、今回は精度だけに着目しているので、とりあえず今はこれでいいでしょう。さて気になる精度は、、
畳み込み層、全結合層のパラメーターのバイナリ化後Accuracy: 0.823 Calc : [[234. 0. 31.] [ 52. 0. 59.] [ 35. 0. 589.]] Labels : [[265. 0. 0.] [ 0. 111. 0.] [ 0. 0. 624.]] Average_accuracy : [0.88301887 0. 0.94391026]あれ、、バイナリ化前より微妙に良くなってる、、もう一度バイナリ化前の結果を見てみよう
バイナリ化前Accuracy: 0.815 Calc : [[244. 0. 21.] [ 55. 0. 56.] [ 53. 0. 571.]] Labels : [[265. 0. 0.] [ 0. 111. 0.] [ 0. 0. 624.]] Average_accuracy : [0.92075472 0. 0.9150641 ]うーん、、誤差レベルでしょうが、わずかに精度が上がっていますね。相変わらず2つ目のラベルの精度が0ですが。
この程度の小さいモデルであれば、kernelとbiasを2値化してもほとんど精度は変わらないようです。バッチ正規化層のパラメーターの量子化
では次は、バッチ正規化層のパラメーター gammaとbeta を量子化してみましょう。
量子化方法は先程の同じですが、gammaは平均値が1になっているっぽいので、1以上なら2、それ未満なら0でやってみましょうか。1bitじゃなくなりますけど笑<tf.Variable 'batch_normalization_v1_5/gamma:0' shape=(128,) dtype=float32, numpy= array([1.0053827 , 1.0023135 , 1.0041403 , 0.9895478 , 1.0039909 , 0.98955464, 1.0088704 , 0.9910637 , 0.9913659 , 0.99780196, 1.000202 , 1.0014107 , 1.0005019 , 0.9903944 , 0.9944405 , 0.9973047 , 1.0017028 , 0.9907751 , 0.99735796, 1.0081666 , 0.99636775, 1.0030036 , 0.99932915, 1.004627 , 0.99306023, 1.0017363 , 0.98416674, 0.99064416, 1.0082388 , 1.0035444 , 0.99265665, 0.99718237, 1.0001222 , 0.99854386, 1.0034426 , 0.9999184 , 0.9963349 , 0.9844031 , 1.0056257 , 0.9994289 , 0.99500334, 0.9923768 , 0.99127066, 0.9832162 , 1.0021056 , 1.0047147 , 0.99886245, 1.0052888 , 0.99249786, 1.0065212 , 0.99161077, 0.9932604 , 1.0078368 , 1.003879 , 0.9882739 , 1.0010694 , 0.99350995, 0.99350333, 0.99219364, 0.99605584, 0.9823839 , 0.99674433, 1.0070174 , 1.00066 , 0.99863935, 0.99942183, 1.000792 , 1.0028559 , 0.9946366 , 0.99531853, 1.0003756 , 0.99510074, 0.9922438 , 1.005276 , 1.0053014 , 0.9929603 , 0.99317366, 1.0056378 , 1.003331 , 1.0047318 , 0.99011916, 1.0086612 , 0.99564356, 0.97692627, 0.9968611 , 1.0015146 , 1.0121565 , 0.9942222 , 0.9938692 , 0.98945427, 1.0070571 , 0.99605334, 1.00008 , 1.0103743 , 0.991692 , 0.98665 , 0.9992022 , 0.98171806, 0.99035376, 0.99664146, 1.0095577 , 1.0159916 , 1.0002235 , 0.9792612 , 1.0048499 , 1.0002121 , 1.0031438 , 0.9905956 , 1.0046396 , 0.99771607, 0.99895054, 1.0037303 , 1.0038016 , 1.0067954 , 0.9906669 , 0.9937981 , 0.9853775 , 0.99674666, 0.9853735 , 0.9933321 , 0.9874309 , 1.0152614 , 1.0054263 , 0.99592394, 1.005618 , 0.9954677 , 0.98061544, 1.0030056 ], dtype=float32)> <tf.Variable 'batch_normalization_v1_5/beta:0' shape=(128,) dtype=float32, numpy= array([ 0.00262505, -0.01182571, 0.00543317, 0.00769176, -0.00662231, -0.01436215, -0.01028995, -0.00620002, -0.00588665, -0.00019779, 0.004008 , -0.00465797, -0.0097509 , -0.00081195, -0.0140775 , -0.0078128 , 0.00924537, -0.0057598 , -0.0017888 , 0.00137905, -0.01389314, 0.00725058, -0.01442415, -0.00770982, -0.01115939, 0.00144741, -0.00496186, -0.00233451, -0.00604108, -0.00561837, 0.00053209, 0.00626049, -0.00196816, 0.00111859, 0.00413055, -0.00590881, -0.00492901, -0.01062248, -0.00155396, -0.00236207, 0.00136854, -0.00125252, -0.01765665, -0.01969386, -0.01379174, -0.00236314, -0.00634788, -0.00099529, -0.00986335, 0.00195062, -0.00986179, -0.00456762, 0.00789357, 0.00510846, -0.00891418, -0.00093365, -0.00342024, -0.01001325, 0.00412015, -0.01361436, -0.01547966, -0.00597356, -0.00561096, 0.00430186, 0.00629607, -0.0032707 , -0.01115292, -0.01054228, -0.00661343, -0.0068517 , 0.00250201, -0.0119157 , 0.00174254, -0.00736857, 0.00990474, -0.01210231, -0.00133941, 0.00786918, -0.01437676, 0.00021543, -0.01157008, 0.00787573, -0.01417518, -0.01176108, 0.01217426, 0.00777597, 0.00527618, 0.00068975, -0.01436776, -0.00979709, 0.00090197, -0.00535901, -0.00172908, 0.00525916, -0.00055489, -0.01297212, -0.00279675, -0.0019424 , -0.01119416, -0.00220624, 0.01222709, 0.01195927, -0.00557467, -0.01582625, -0.00113147, 0.00383603, -0.0025774 , -0.00764492, -0.0054293 , -0.00483815, 0.00011727, 0.00274837, 0.0107253 , 0.00365951, 0.0037286 , -0.0052775 , -0.01400672, -0.01110312, -0.01492126, -0.00020007, -0.02051772, 0.00057484, 0.00417511, -0.01659194, 0.0063057 , -0.00042243, -0.01960172, 0.00553354], dtype=float32)> <tf.Variable 'batch_normalization_v1_5/beta:0' shape=(128,) dtype=float32, numpy= array([ 1., -1., 1., 1., -1., -1., -1., -1., -1., -1., 1., -1., -1., -1., -1., -1., 1., -1., -1., 1., -1., 1., -1., -1., -1., 1., -1., -1., -1., -1., 1., 1., -1., 1., 1., -1., -1., -1., -1., -1., 1., -1., -1., -1., -1., -1., -1., -1., -1., 1., -1., -1., 1., 1., -1., -1., -1., -1., 1., -1., -1., -1., -1., 1., 1., -1., -1., -1., -1., -1., 1., -1., 1., -1., 1., -1., -1., 1., -1., 1., -1., 1., -1., -1., 1., 1., 1., 1., -1., -1., 1., -1., -1., 1., -1., -1., -1., -1., -1., -1., 1., 1., -1., -1., -1., 1., -1., -1., -1., -1., 1., 1., 1., 1., 1., -1., -1., -1., -1., -1., -1., 1., 1., -1., 1., -1., -1., 1.], dtype=float32)> <tf.Variable 'batch_normalization_v1_5/gamma:0' shape=(128,) dtype=float32, numpy= array([2., 2., 2., 0., 2., 0., 2., 0., 0., 0., 2., 2., 2., 0., 0., 0., 2., 0., 0., 2., 0., 2., 0., 2., 0., 2., 0., 0., 2., 2., 0., 0., 2., 0., 2., 0., 0., 0., 2., 0., 0., 0., 0., 0., 2., 2., 0., 2., 0., 2., 0., 0., 2., 2., 0., 2., 0., 0., 0., 0., 0., 0., 2., 2., 0., 0., 2., 2., 0., 0., 2., 0., 0., 2., 2., 0., 0., 2., 2., 2., 0., 2., 0., 0., 0., 2., 2., 0., 0., 0., 2., 0., 2., 2., 0., 0., 0., 0., 0., 0., 2., 2., 2., 0., 2., 2., 2., 0., 2., 0., 0., 2., 2., 2., 0., 0., 0., 0., 0., 0., 0., 2., 2., 0., 2., 0., 0., 2.], dtype=float32)>バッチ正規化層のパラメータ量子化後Accuracy: 0.818 Calc : [[243. 0. 22.] [ 55. 0. 56.] [ 49. 0. 575.]] Labels : [[265. 0. 0.] [ 0. 111. 0.] [ 0. 0. 624.]] Average_accuracy : [0.91698113 0. 0.92147436]こちらも結果は誤差レベルですかね。精度が著しく落ちると思っていたのでこれは予想外の結果です。
なお、gammaは平均が0になるようにしたり、全て1で揃えてしまっても精度は80%程度とそこまで結果は悪くなりませんでした。全てのパラメーターを量子化した結果を最後にのせておきます。
Accuracy: 0.822 Calc : [[230. 0. 35.] [ 51. 0. 60.] [ 32. 0. 592.]] Labels : [[265. 0. 0.] [ 0. 111. 0.] [ 0. 0. 624.]] Average_accuracy : [0.86792453 0. 0.94871795]まとめ
今回は学習済みのモデルのパラメーターを量子化しました。結果は、これくらいの小さなモデルであれば最終的な精度の差はあまりないように見えました。ですが、混合行列を観察してみると、案外結果に変動があるので、ラベルの数が増えたり(今回は実質ラベル2つですが笑)すると大きく精度に差が出る可能性もありますね。
今回はPart1ということで、次回の候補は、
・学習用のデータを増やすことで、元々のモデルでの精度を上げた後に再び試してみる
・今回は学習済みモデルのパラメーターを量子化したが、学習中に少しずつ量子化していく
・入力データ(活性)も量子化してみるのどれかになりそうです。
参考、注釈
※1 Rastegari, M., et al. "Xnor-net: Imagenet classification using binary convolutional neural networks." European conference on computer vision. Springer, Cham, 2016.
※2 本来1bitに量子化すると 0, 1のどちらかの値になる必要があるが、2通りの値しかとらないので、ここでは1bit量子化と書いています
追記
量子化の際に結構な量のパラメータをループで、さらにif文で正負を判定しているので、上に書いたコードだとどうしてもそれなりに時間がかかってしまいます。
旧)重み更新の部分for l in range(len(k)): if k[l] >= 0: new_kernel[l] = 1 else: new_kernel[l] = -1これを高速化できそうな式を発見したのでそれに置き換えてみます。
新1)重み更新の部分for l in range(len(k)): new_kernel[l] = np.float32(2.*np.greater_equal(k[l],0)-1.)これはスマートでかっこいいですね。こんなコードをさっとかけるようになりたいものです、、
追追記
上の追記では、if文を減らすことで計算時間が短縮できました。しかし、実はどうやらforループのほうが時間がかかっているようです。tensorをnumpy配列に変換することで、容易に値を操作できるので、ループを使わずパラメータの値を操作してみましょう。
新2)重み更新の部分new_kernel = kernel.numpy() new_kernel = np.greater_equal(new_kernel, 0) new_kernel = new_kernel * 2. - 1.旧コード、if文を無くした新1コード、ループも消した新2コードで実行時間を比較してみましょう。
旧コード 新1コード 新2コード 実行時間 (sec) 116.17 92.05 0.160 いやぁ、これはすごい違いですね。pythonはやはりループが遅いので、行列やベクトルはなるべくnp.whereやtf.whereなどで一般化したほうがいいですね。なお、実行中にパラメータを標準出力したりしているので、計算だけならもっと高速にできそうですね。
学習後のパラメータを量子化しているのでそこまで重要じゃないかもしれませんが、学習中に更新する場合はこの差が積み重なってとんでもないほど遅くなりそうですね、、、
ループ、if文を避け、numpyやtensorFlow等のライブラリで計算するということは覚えておいたほうが良さそうです!
計測マシン:
Tesla V100-PCIE-32GB
- 投稿日:2020-03-14T00:51:52+09:00
行列の固有ベクトルを微分するときに気を付けること
まとめ
行列の固有値を微分するとき、固有値が縮退していると発散します。適宜対処しましょう。
きっかけ
前回の記事
https://qiita.com/sage-git/items/1afa0bb8b3a7ee36600d
を書いて、固有値が微分できて最適化できるなら、固有ベクトルも同様にできて、欲しい固有ベクトルが得られる行列が得られるんじゃないかと思い、やってみました。
実際得られたのですが、ちょっとした問題があったので、対処しました。数学
導出はこちらのフォーラムを参考に。
https://mathoverflow.net/questions/229425/derivative-of-eigenvectors-of-a-matrix-with-respect-to-its-componentsある行列 $A$ に対し、固有値 $\lambda_i$ があって、それに対応する固有ベクトル $\vec{n}_i$ を考えて、これを微分することを考えます。
固有値の微分
\frac{\partial \lambda_i}{\partial A_{kl}} = \left(\frac{\partial A}{\partial A_{kl}}\vec{n}_i\right)\cdot\vec{n}_iここで $\frac{\partial A}{\partial A_{kl}}\vec{n}_i$ は射影演算子のような感じになりますね。$\vec{n}_i$ の $k$ 番目の成分を $l$ 番目に持ってきて、あとは0というベクトルになります。するとこの微分は $\vec{n}_i$ の $k$ 番目と $l$ 番目を掛け算した値になりますね。思いのほか素直です。
固有ベクトルの微分
$i$ 番目の固有ベクトル $\vec{n}_i$ について、
\frac{\partial \vec{n}_i}{\partial A_{kl}} = \sum_{j\neq i}\left[\frac{1}{\lambda_i - \lambda_j}\left(\frac{\partial A}{\partial A_{kl}}\vec{n}_i\right)\cdot\vec{n}_j\right]\vec{n}_jと書けます。要は、他の固有ベクトルに適当な重みを付けて足し合わせていく感じです。
ここで注意したいのは、$\frac{1}{\lambda_i - \lambda_j}$ という項です。これにより、 同じ固有値が複数あるとき(物理的には縮退に対応)、この微分は発散します。検算
準備
適当な行列
Xを決めて、固有値と固有ベクトルを確認します。import tensorflow as tf X = tf.Variable(initial_value=[[1.0, 0.0, 0.12975], [0.0, 1.0, 0.0], [0.12975, 0.0, 1.1373545]]) eigval, eigvec = tf.linalg.eigh(X) print(eigval) print(eigvec)eigval(固有値)tf.Tensor([0.9218725 1. 1.2154819], shape=(3,), dtype=float32)eigvec(固有ベクトル)tf.Tensor( [[-0.8566836 0. 0.51584214] [-0. -1. 0. ] [ 0.51584214 0. 0.8566836 ]], shape=(3, 3), dtype=float32)固有値を微分
GradientTapeを使って、最小の固有値を計算してみます。with tf.GradientTape() as g: g.watch(X) eigval, eigvec = tf.linalg.eigh(X) Y = eigval[0] dYdX = g.gradient(Y, X) print(dYdX)固有値0の微分tf.Tensor( [[ 0.7339068 0. 0. ] [ 0. 0. 0. ] [-0.88382703 0. 0.2660931 ]], shape=(3, 3), dtype=float32)
- $0.7339068 \approx 0.8566836^2$
- $0.2660931 \approx 0.51584214^2$
- $0.88382703 \approx 2 \times 0.8566836 \times 0.51584214$
ということから、まあ妥当な結果ですね。$2\times$ となっているのは対称行列で下半分しか使っていないためと思われます。
固有ベクトルを微分
eigvec[i, j]は $j$ 番目の固有値に対する固有ベクトルの $i$ 番目の成分です。with tf.GradientTape() as g: g.watch(X) eigval, eigvec = tf.linalg.eigh(X) Y = eigvec[0, 1] dYdX = g.gradient(Y, X) print(dYdX)固有ベクトル1の1番目の成分tf.Tensor( [[ 0. 0. 0. ] [-8.158832 0. 0. ] [ 0. 7.707127 0. ]], shape=(3, 3), dtype=float32)こっちはめんどくさいので検算はさぼります。
ここまでは普通です。
縮退させる
以下のように
Xの値を変更すると、2つの固有値が1になります。X = tf.Variable(initial_value=[[1.1225665, 0.0, 0.12975], [0.0, 1.0, 0.0], [0.12975, 0.0, 1.1373545]])なお、前回の記事のコードを使って求めました。
eigvaltf.Tensor([1. 1. 1.2599211], shape=(3,), dtype=float32)eigvectf.Tensor( [[-0.7269436 0. 0.6866972] [-0. -1. 0. ] [ 0.6866972 0. 0.7269436]], shape=(3, 3), dtype=float32)これを微分すると、両方とも
dYdXtf.Tensor( [[nan 0. 0.] [nan nan 0.] [nan nan nan]], shape=(3, 3), dtype=float32)となりました。
固有値の方がnanになるのは解せませんが、固有ベクトルの微分の方は理論式通りnanになりました。なお、微分する固有ベクトルを3番目にして、つまり $\lambda_i - \lambda_j = 0$となるような $j$ が存在しない $i$ での固有ベクトルの微分も
nanになりました。つまりTensorflowの実装では縮退があるような行列では容赦なくすべての微分がnanになるようです。対策
いくつか回避策が考えられます。
- 問題における同値の範囲で行列を変形させる
- 多少値が変わることを覚悟で値を動かす
- そもそも固有値・固有ベクトルの微分を使わない方向でアルゴリズムを書き直す
ここではランダムに摂動を与えてみます。というのも、この微分は勾配法のために使いますので、一種のアニーリングのような感じで摂動させるだけで、最終的な結果には影響しないとできるからです。
当然、最終的な結果で固有値が縮退している場合は特別に考えなければなりません。縮退を見つける
ともあれ、微分する前に同じ固有値があるかどうかを見つけることを考えます。
eigval[1:] - eigval[:-1]これで一つ隣同士の固有値の差が格納された配列が得られます。
tf.linalg.eighが返す固有値はすでに昇順で並べられていることを利用すれば、絶対値を使わずとも $0$ 以上であることが分かります。そしてこれのうち1つでもほとんど0の成分があると縮退しているとします。tf.math.reduce_any((eigval[1:] - eigval[:-1]) < 1e-20)あとはこれを条件にして、満たさなくなるまでループさせます。
AはN行N列の行列とします。eigval, eigvec = tf.linalg.eigh(A) while tf.math.reduce_any((eigval[1:] - eigval[:-1]) < 1e-20): Ap = A + tf.linalg.diag(tf.random.uniform(shape=[N])*0.001) eigval, eigvec = tf.linalg.eigh(Ap)判定基準の
1e-20や摂動の大きさの0.001は問題によって変わってくると思います。
ひとまず僕が今やりたかったことはこれで解決しました。おまけ
1次元の量子井戸を計算してみます。物理的な説明は
https://qiita.com/sage-git/items/e5ced4c0f555e2b4d77b
など、他のページに譲ります。
$x\in \left[-\pi, \pi\right]$ の範囲が有限のポテンシャル、それ以外は $+\infty$ であるようなポテンシャル $U(x)$ を考えたとき、どのような $U(x)$ を設定すれば基底状態の波動関数が
\psi(x) = A\exp\left(-2x^2\right)となるかを数値的に求めます。やり方としては、ハミルトニアン $H$ を行列で書き、この固有値・固有ベクトルを求め、最小の固有値に対する固有ベクトルがこの $\psi(x)$ になるように勾配法で近づけていきます。 ただ数値計算において、関数を関数として扱えないので、範囲 $\left[-\pi, \pi\right]$ を $N$ 個の点で分割します。 $i$ 番目の点の座標を $x_i$ とすると、波動関数は $\vec{\psi}$ の$i$番目の成分 $ = \psi(x_i)$ というベクトル $\vec{\psi}$ で書けます。
気を付けるところとして、固有ベクトルの符号の自由度がありますので、損失関数は
L_+ = \sum_i^N(n_i - \psi(x_i))^2L_- = \sum_i^N(n_i + \psi(x_i))^2の両方が考えられることが挙げられます。イテレーションを回していると反転するということも普通にあります。今回はこのうち最小の方
L = \min(L_+, L_-)としたらうまくいきました。
これらを踏まえ、以下のようなコードを書きました。
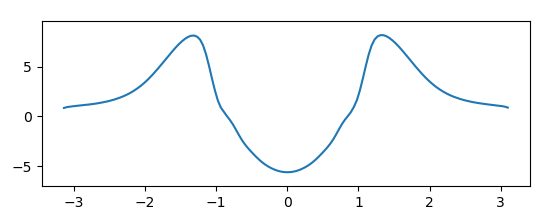
import tensorflow as tf import matplotlib.pyplot as plt import numpy as np def main(): max_x = np.pi N = 150 + 1 dx = max_x*2/N x = np.arange(-max_x, max_x, dx) D = np.eye(N, k=1) D += -1 * np.eye(N) D += D.T D = D/(dx**2) m = 1.0 D_tf = tf.constant(D/(2.0*m), dtype=tf.float32) V0_np = np.exp( - x**2/0.5) V0_np = V0_np/np.linalg.norm(V0_np) V0_target = tf.constant(V0_np, dtype=tf.float32) U0 = np.zeros(shape=[N]) U = tf.Variable(initial_value=U0, dtype=tf.float32) def calc_V(n): H = - D_tf + tf.linalg.diag(U) eigval, eigvec = tf.linalg.eigh(H) while tf.math.reduce_any((eigval[1:] - eigval[:-1]) < 1e-20): H = - D_tf + tf.linalg.diag(U) + tf.linalg.diag(tf.random.uniform(shape=[N])*0.001) eigval, eigvec = tf.linalg.eigh(H) print("found lambda_i+1 - lambda_i = 0") v_raw = eigvec[:, n] return v_raw def calc_loss(): v0 = calc_V(0) dplus = tf.reduce_sum((v0 - V0_target)**2) dminus = tf.reduce_sum((v0 + V0_target)**2) return tf.minimum(dplus, dminus) opt = tf.keras.optimizers.Adam(learning_rate=0.001) L = calc_loss() v0_current = calc_V(0) print(L) while L > 1e-11: opt.minimize(calc_loss, var_list=[U]) v0_current = calc_V(0) L = (tf.abs(tf.reduce_sum(v0_current*V0_target)) - 1)**2 print(L) plt.plot(x, U.numpy()) plt.show() if __name__ == "__main__": main()これを実行し、 Ryzen 5とGTX 1060 を積んだマシンで数十分放置すると、下図のようなグラフが得られました。
つまりこのようなポテンシャルを設定すると、量子井戸中の基底状態の波動関数がGaussian波束になるだろうと分かりました。
残念ながらこれは数値解ですので、解析的に確認ができません。なにかよい関数でフィットして解いてみたいところ。人間にできるかどうかわかりませんが。