- 投稿日:2019-08-19T23:20:39+09:00
Pythonのクラスやインスタンスをおさらいしよう
はじめに
未来電子テクノロジーでインターンをしている宮﨑です。
Pythonの基礎であるクラスとメソッドを再確認するためにまとめたいと思います。
もし誤りがあれば修正するのでどんどん指摘してください。語句説明
クラス・・・設計図や型のようなもの。カテゴリー(動物、フルーツなど)のように実体はない。
インスタンス・・・設計図をもとに作られる「もの」。一つのクラスから複数のインスタンスを作れる。
メソッド・・・クラスの中で定義した関数(処理のまとまり)のこと。書き方の流れ
クラスを用意する
クラス名をclassの後に書く。
class クラス名:メソッドをクラスに追加する
メソッド名をdefの後に書く。
メソッドの第一引数には、それぞれのインスタンス自身を示すselfを追加する。#(例) def info(self): print(self.name)(補足)コンストラクタ
インスタンスを生成した時に、自動的に呼び出すメソッドのことをコンストラクタといい、そのうちインスタンスを初期化するメソッドとして
__init__を使う。
__init__の他には、インスタンスを作るときに呼ばれるメソッド__new__もある。クラスからインスタンスを作成
クラス名()でインスタンスを生成でき、インスタンスを変数に代入する。変数名=クラス名()メソッドを呼び出す
どのインスタンスに対してメソッドを呼び出すのかを明らかにするために、メソッド名の前にインスタンス名をつける。
インタンス名.メソッド名()具体例
#クラスの生成 class Fruit: #コンストラクタの生成 def __init__(self,name): self.name = name #メソッドの生成 def info(self): print(self.name + "です。") #インスタンスの生成 apple = Fruit("リンゴ") #メソッドの呼び出し apple.info() #「リンゴです」と出力されるまとめ
今回は、Pythonのクラスやインスタンスについてまとめました。
何気なく使っているものも、再確認してみるとより使いやすくなるのではないでしょうか。
- 投稿日:2019-08-19T23:08:12+09:00
Yolov3+ROS+Jetsonnanoで作るじゃんけんゲーム
モチベーション
とある家族見学会のイベントで、子供も楽しめるゲームを作ろうと思い立ちました。
子供も楽しめるものといえばじゃんけん…という安易な発想から、カメラ1台でじゃんけんの出し手を認識して勝ったらお菓子を進呈する装置を作ってみました。
今回は、物体検出アルゴリズムとしてYolov3を、動作させる環境としてJetsonNano+ROSの組み合わせで実装しました。
(じゃんけん画像認識自体はすでに色々な方が試行されていますが、ここではYolo・Jetson・ROSという色々と応用が効きそうな方法のお試しも兼ねてやっています。)この記事の中で触れること
- データセットの作成
- Yolov3の学習
- JetsonNanoへの実装
すべての手順について詳細に触れられるわけではありませんが、ポイントになりそうなところを掻い摘んで説明できればと思います。誰かのお役に立てれば。
データセットの作成
一般的にはDeeplearningベースの物体認識では数千枚オーダーのデータセットが必要になってきます。
精度の良い物体検出モデルを作るためには、いろいろな姿勢・背景の手を含む写真を集めてアノテーション(どこにどのポーズの手が写っているかマークする作業)を行う必要があります。画像収集やアノテーションの作業をゼロからやるのはとても大変です。
なんとか手抜きをする方法がないかWebを探して見たところ、じゃんけんを画像認識で実装しているドンピシャな記事を見つけました。
こちらの記事では、画像に写っている手のポーズを推定する(Classification)タスクを扱っていますが、今回は手のポーズに加えてその位置も推定する(Detection)タスクで実装します。上でご紹介した記事では、トルコの高校生の方々が作ったデータセットを使っていますが、ここでもそのデータセットを活用します。
Sign-Language-Digits-Datasetは、0〜9を表す手のポーズをそれぞれおよそ200枚ずつ保持しています。今回は、グー・チョキ・パーがわかればよいので0・2・5の三クラス分のデータを利用します。
このデータセットはそれぞれの写真とそのクラス番号の情報しかありませんが、物体検出の学習を行えるようにするために、どうにかして手の領域をアノテーションしてあげる必要があります。また、白背景だけではなく色々な種類の背景を生成して、よりロバストなモデルを作りたいと思います。
今回のデータセット生成の流れは下記の通りです。
- 手の領域を切り抜いた画像を生成する
- データオーグメンテーション
- 結合された画像に対応するアノテーションデータを自動生成する
手の領域切り抜き
手の領域の切り抜き方法として、安易ではありますがOpenCVの色域抽出機能を使いました。
Sign-Language-Digits-Datasetでは背景が白であるため、下記のように切り抜き自体は比較的うまくいきました。左から元画像、色域抽出によるマスク領域、元画像からマスク領域のみを切り抜いた画像です。元画像には、マスク領域をもとに外接矩形を描画しています。色域抽出に使ったコードはこちら。
def colorRange(hsvImg): HSV_MIN = np.array([0, 20, 40]) HSV_MAX = np.array([20, 220, 255]) hsv_mask = cv2.inRange(hsvImg, HSV_MIN, HSV_MAX) kernel = np.ones((2,2),np.uint8) ksize=5 hsv_mask = cv2.medianBlur(hsv_mask,ksize) hsv_mask = cv2.morphologyEx(hsv_mask, cv2.MORPH_CLOSE, kernel) hsv_mask = cv2.dilate(hsv_mask,kernel,iterations = 1) return hsv_maskデータオーグメンテーション
前項で切り抜かれた手の画像に、色々と手を加えてデータオーグメンテーションをしていきます。
目的は、色々な条件下の画像に反応できるようにするためです。
今回は色々な背景に対応できるようなモデルを作る必要があるため、データセットにも色々な背景を含めてあげる必要があります。
とはいえ、背景の画像を収集するのが面倒だったのでまずはガウシアンノイズを使って背景を埋めてみることにしました。ついでに、元画像を3方向に回転させて合成します。禍々しいね。ガウシアンノイズを加えるために使ったコードはこちら。
def addGaussianNoise(src): row,col,ch= src.shape mean = 0 var = 0.5 sigma = 50 gauss = np.random.normal(mean,sigma,(row,col,ch)) gauss = gauss.reshape(row,col,ch) a=1 noisy = a*src + (4-a)*gauss return noisyちなみに、画像は下記のようにして回転させて合成しています。
def augmentedImage(img): orgH, orgW = img.shape[:2] aImg = np.zeros((orgH*2, orgW*2, 3), np.uint8) aImg[0:orgH,0:orgW] = img #90度 transpose_img = img.transpose(1,0,2) clockwise = transpose_img[:,::-1] aImg[orgH:orgH*2,0:orgW] = clockwise #-90度 counter_clockwise = transpose_img[::-1] aImg[0:orgH,orgW:orgW*2] = counter_clockwise #180度 xAxis = cv2.flip(img, 0) yAxis = cv2.flip(img, 1) xyAxis = cv2.flip(img, -1) aImg[orgH:orgH*2,orgW:orgW*2] = xyAxis return aImg結論から言うと、ガウシアンノイズだけでは背景のオーグメンテーションとして不十分だったので下記のようにWeb上の画像を追加で合成しています。禍々しいね(2回目)。
背景の画像は、こちらのサイトのものをお借りしました。
処理を抜粋するとこんな感じです。backgroundDirの中に背景画像を入れておいて、ランダムに選択・切り抜きした上で100×100のサイズにリサイズしています。backgroundFiles = [r for r in glob.glob(backgroundDir)] bgImg = cv2.imread(random.choice(backgroundFiles)) n = int(random.randint(-10, 10)*15) bgImg = bgImg[300+n:500+n, 200+n:400+n] bgImg = cv2.resize(bgImg, (100, 100))更に、学習と推論を試して見ると子供の手にうまく反応できないことがわかってきました。
どうも、大人と子供の手の大きさや指長さが影響しているようです。
手前味噌ではありますが、アフィン変換で画像を圧縮(つぶして)画像生成しました。縦の長さの30%くらいを圧縮しています。禍(以下略)処理は下記のような感じで。
def pressImage(img, ratio): ratio = 1.0 - ratio orgH, orgW = img.shape[:2] src_pts = np.array([[0, 0], [int(orgW/2), 0], [orgW, orgH]], dtype=np.float32) dst_pts = np.array([[0, int(orgH*ratio)], [int(orgW/2),int(orgH*ratio)], [orgW, orgH]], dtype=np.float32) mat = cv2.getAffineTransform(src_pts, dst_pts) #print(mat) affine_img = cv2.warpAffine(img, mat, (orgW, orgH)) return affine_imgアノテーションデータの生成
前の章で説明したマスク画像を生成した時点で手の領域の座標がわかるので、その情報を使ってアノテーションデータを生成します。下記のようにマスク画像(maskImg)をもとに、外接矩形を検索します。
ここでは、元画像に手が一つしか写っていない前提で最も大きな矩形を選び出しています。dst, contours, hierarchy = cv2.findContours(maskImg, cv2.RETR_TREE, cv2.CHAIN_APPROX_SIMPLE) for i, contour in enumerate(contours): area = cv2.contourArea(contour) if area < size_min: continue if image_size * 0.99 < area: continue x,y,w,h = cv2.boundingRect(contour) if w*h > size_max: size_max = w*h maxX,maxY,maxW,maxH = x,y,w,h各画像ごとにグー、チョキ、パーが写っている座標をアノテーションファイルとして出力すれば学習の準備は完了。
YOLOv3の学習
ここまでで作成したデータセットをもとに、YOLOv3(darknet)を使って学習を進めます。
詳細な手順は各所で紹介されていますので省略しますが、今回は推論速度を優先してtiny-yoloを使っています。
学習時、標準出力にログが表示されます。
バッチサイズを128で設定しているため、128枚の画像を学習するごとにlossやlearning rateなどの情報が出力されます。Region 23 Avg IOU: -nan, Class: -nan, Obj: -nan, No Obj: 0.538939, .5R: -nan, .75R: -nan, count: 0 Region 16 Avg IOU: 0.276084, Class: 0.366372, Obj: 0.541348, No Obj: 0.476522, .5R: 0.218750, .75R: 0.000000, count: 32 Region 23 Avg IOU: -nan, Class: -nan, Obj: -nan, No Obj: 0.539579, .5R: -nan, .75R: -nan, count: 0 1: 485.622101, 485.622101 avg, 0.000000 rate, 3.699675 seconds, 128 imagesavgで表示されているloss、rateで表示されている学習率を縦軸に、イテレーション数を横軸にグラフを書くと下のような感じになります。学習率はデフォルトで0.001を目指すように設定されていますが、今回は1000イテレーション付近ですでにサチっています。
出来上がったモデルとしては、100000イテレーション付近のものがうまく手に反応できていたのでそれを使いましたが、各種ハイパーパラメータはチューニングの余地ありかと思います。
Jetson Nanoへの実装
出来上がったモデルを動作させる環境として、流行りのJetson Nanoを使って見ました。
1万円ちょっと出して強力かつ小型のGPUマシンが手に入るとは、良い時代になりましたね。ケースには、Thingiverseで配布されているものを出力して利用しました。
セットアップについてはからあげさんの記事で詳細に説明されておりますので、そちらを参考にしています。
構成はこちらの通り。
- Jetson Nano(Jetpack4.2.1)
- Logicool C270(USB-Webカメラ)
- IODATA WN-G300UA(USB Wi-FIモジュール)
- ROS melodic
- darknet_ros(darknetのROS向けラッパー)
- usb_cam(UVCカメラドライバ)
ハードウェア類は、特にドライバインストールせずに動作しました。
またGPUをフルに活用するため、ここではPower Mode: MAXNで動作させます。
microUSBでは電力が不足するため、DCジャックから給電できるようにします。また、ファンも取り付けておきました。ちなみに、現在のPower Modeは”nvpmodel -q”で確認できます。
darknet_rosは公式のGitから、usb_camについてはaptでインストールすることができます。
Jetpack4.2.1では、公式の手順から特に変えることなくインストールできました。sudo apt install ros-melodic-usb-cam続いて、darknet_rosを使った推論実行について説明します。
darknet_rosをオリジナルの学習済みモデルにて使う際に作成、変更が必要な設定ファイルは下記の通りです。(ROSのワークスペースを”~/catkin_ws”に作成していると仮定)
- ~/catkin_ws/src/darknet_ros/darknet_ros/config/ros.yaml
- Subscribeするカメラ画像トピックの名前などを指定
- ~/catkin_ws/src/darknet_ros/darknet_ros/config/janken-yolov3-tiny.yaml
- 学習済みモデルと設定ファイル(weights,cfg)や表示時の閾値、クラス名を定義
- ~/catkin_ws/src/darknet_ros/darknet_ros/yolo_network_config/cfg/janken-yolov3-tiny-train-3classes.cfg
- 学習済みモデルに対応する設定ファイル。入力画像サイズもここで変えることができる
- そのほか、学習済みモデルは~/catkin_ws/src/darknet_ros/darknet_ros/yolo_network_config/weightsに格納する
ros.yamlについて、usb_camからの出力トピックを受けられるようにするため、subscriberを下記のように記載します。
subscribers: camera_reading: topic: /usb_cam/image_raw queue_size: 1janken-yolov3-tiny.yamlはこんな感じ。
yolo_model: config_file: name: janken-yolov3-tiny-train-3classes.cfg weight_file: name: janken-yolov3-tiny-train-3classes_100000.weights threshold: value: 0.3 detection_classes: names: - gu - tyoki - pajanken-yolov3-tiny-train-3classes.cfgについては、画像の入力サイズを下げて処理速度を向上させます。width,height部分の設定によって、ネットワークへの入力画像サイズを変更できます。最初だけ抜粋するとこんな感じ。
[net] # Testing batch=1 subdivisions=1 # Training #batch=64 #subdivisions=16 width=288 height=288 channels=3 momentum=0.9 decay=0.0005 angle=0 saturation = 1.5 exposure = 1.5 hue=.1推論用にbatch,subdivisionsを1にするのを忘れずに。
usb_camノードとdarknet_rosを同時に起動させるためのlaunchファイル(janken-yolov3-tiny.launch)を用意しました。
<?xml version="1.0" encoding="utf-8"?> <launch> <node name="usb_cam" pkg="usb_cam" type="usb_cam_node" output="screen" > <param name="video_device" value="/dev/video0" /> <param name="image_width" value="640" /> <param name="image_height" value="480" /> <param name="pixel_format" value="yuyv" /> <param name="camera_frame_id" value="usb_cam" /> <param name="io_method" value="mmap"/> </node> <node name="image_view" pkg="image_view" type="image_view" respawn="false" output="screen"> <remap from="image" to="/usb_cam/image_raw"/> <param name="autosize" value="true" /> </node> <!-- Console launch prefix --> <arg name="launch_prefix" default=""/> <!-- Config and weights folder. --> <arg name="yolo_weights_path" default="$(find darknet_ros)/yolo_network_config/weights"/> <arg name="yolo_config_path" default="$(find darknet_ros)/yolo_network_config/cfg"/> <!-- ROS and network parameter files --> <arg name="ros_param_file" default="$(find darknet_ros)/config/ros.yaml"/> <arg name="network_param_file" default="$(find darknet_ros)/config/janken-yolov3-tiny.yaml"/> <!-- Load parameters --> <rosparam command="load" ns="darknet_ros" file="$(arg ros_param_file)"/> <rosparam command="load" ns="darknet_ros" file="$(arg network_param_file)"/> <!-- Start darknet and ros wrapper --> <node pkg="darknet_ros" type="darknet_ros" name="darknet_ros" output="screen" launch-prefix="$(arg launch_prefix)"> <param name="weights_path" value="$(arg yolo_weights_path)" /> <param name="config_path" value="$(arg yolo_config_path)" /> </node> </launch>システムの起動は、下記の通り。シンプルですね。
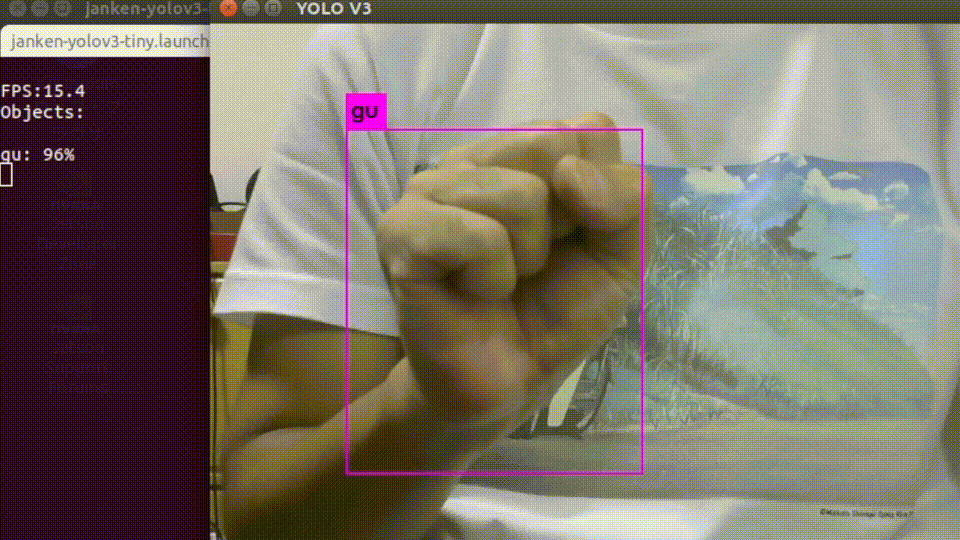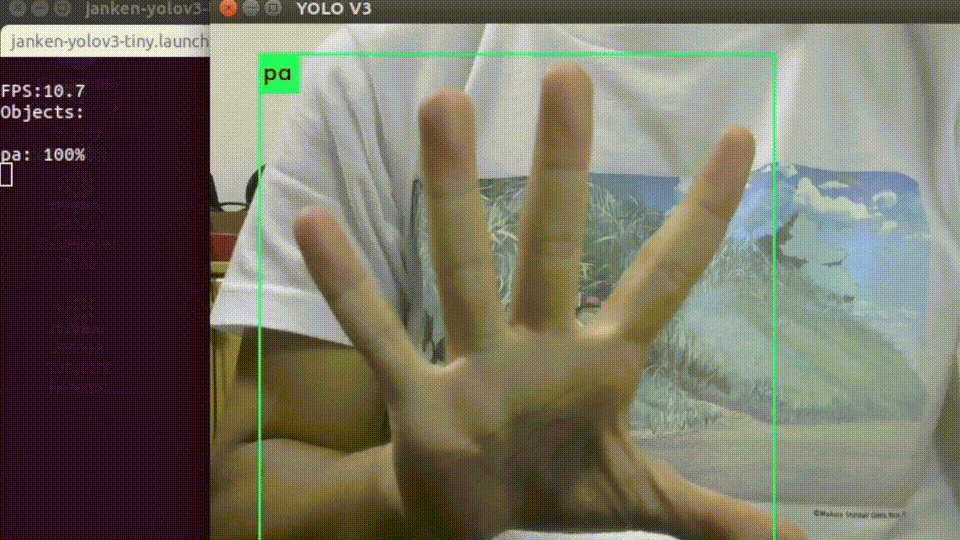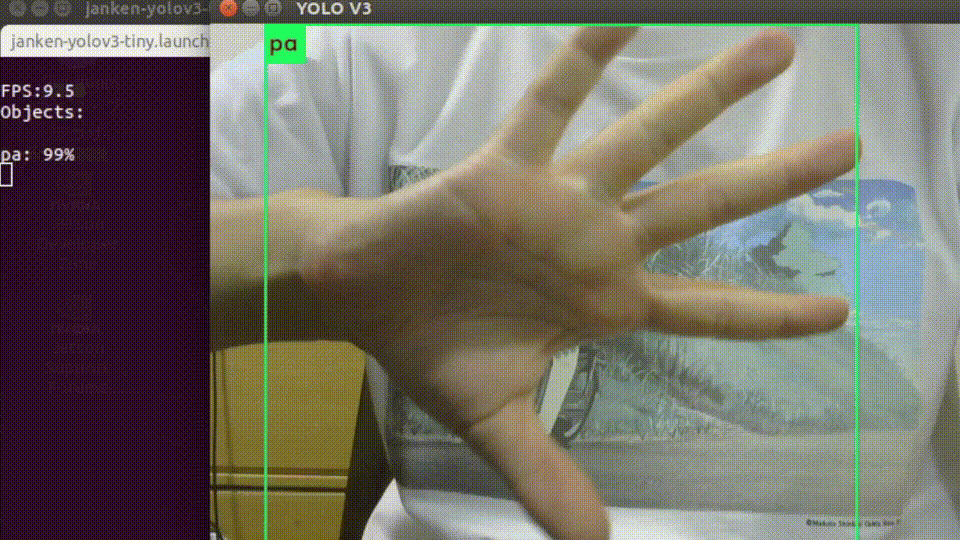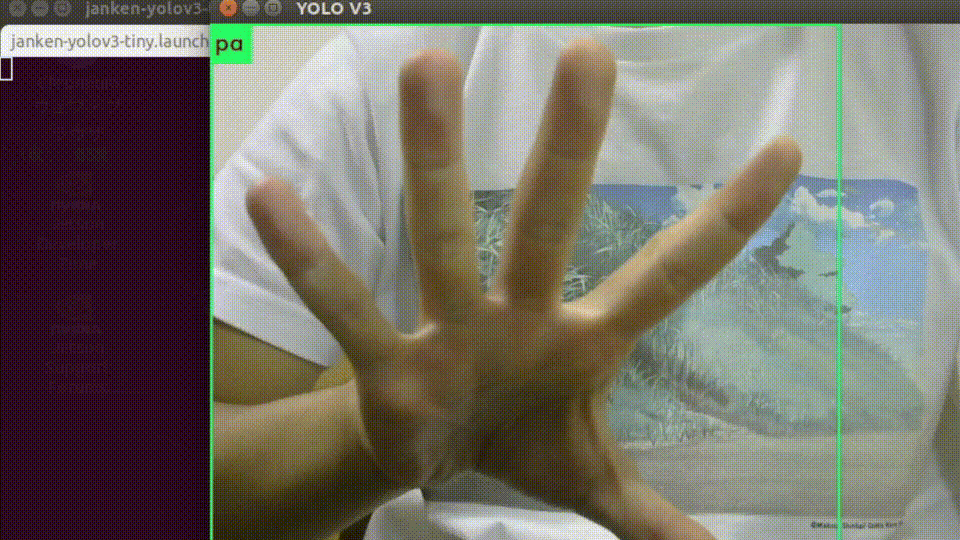
roslaunch darknet_ros janken-yolov3-tiny.launch起動すると、USBカメラの画像と推論結果を重畳されたものが表示されます。
入力画像サイズを縮小していることもあって、平均して10-12fpsくらいの速度で処理できています。
オーギュメンテーションを頑張った甲斐もあり、背景や手の向きに強くなっています。終わりに…
大変に長くなりましたが、ここまで読んでくださってありがとうございます。
単純な推論だけだったらdarknetを単体で使えばよいのですが、今回はじゃんけんの結果に応じてお菓子(うまい棒)が飛び出てくるマシーンを作ったため、ROSを使った実装にしました。
(rosserialを使ってArduinoを制御し、サーボモーターを動かしてうまい棒を飛ばす)何か皆様の参考になる部分があれば幸いです。
- 投稿日:2019-08-19T22:32:57+09:00
連続ウェーブレット変換を使ってみたかったので離散化して実装した
信号の時間-周波数解析の代表的な手法の1つである、連続ウェーブレット変換を勉強していたのですが、実際にプログラミングで実装するためには離散化しなければなりません1。
ググると離散化した後の数式も見つかったのですが、イマイチよく分からなかったので自分で導出して、さらに実装してみました。主に参考としたのは、I. Daubechies著の「ウェーブレット10講」(丸善出版)です。
かなりしっかりした理論の本ですが、ざっと読んだだけだと途中から訳わかめだったので、時間を取ってじっくり読み直したいです。連続ウェーブレット変換の定義
連続ウェーブレット変換の背景やらは色んなところに載っているのでここでは割愛します。時間信号$x(t)$の連続ウェーブレット変換の式は以下の通り。
X(a, b) = \int_{-\infty}^{\infty} x(t)\,\overline{\psi}_{a, b}(t)\,dt \tag{1.1}\psi_{a, b}(t) = \frac{1}{\sqrt{a}}\,\psi\Bigl(\frac{t - b}{a}\Bigr) \tag{1.2}ここで、$\psi(t)$はマザーウェーブレット、$a$はスケール、$b$は時間シフトです。$\overline{\psi}$は$\psi$の複素共役を表します。
スケール$a$は周波数$f$の逆数に相当し、補正係数$\lambda$を用いて以下のように表せます。a = \frac{\lambda}{f}\tag{1.3}一方で、連続ウェーブレット変換の逆変換は以下の通り。
x(t) = \frac{1}{C_{\psi}}\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} X(a, b) \,\psi_{a, b}(t)\,db\,\frac{da}{a^2} \tag{1.4}$C_{\psi}$はadmissible constantと呼ばれる数で、この値が有限であることが逆変換の存在条件になっています。
C_{\psi} = 2\pi\int_{-\infty}^{\infty}\frac{|\hat{\psi}(\omega)|^2}{|\omega|}d\omega<\infty \tag{1.5}ここで、$\hat{\psi}(\omega)$はマザーウェーブレット$\psi(t)$のフーリエ変換です。
実用上、時間信号$x(t)$は実数である場合がほとんどで、この場合は(1.4)式を以下のように変形できるようです。
x(t) = \frac{2}{C_{\psi}}\int_{0}^{\infty} \int_{-\infty}^{\infty} X(a, b) \,\psi_{a, b}(t)\,db\,\frac{da}{a^2} \tag{1.6}文献によって、(1.5)式の係数の$2\pi$が無かったり2、(1.6)式の係数に$2$が出てこなかったり、記述がバラバラですごく混乱しました…
今回は(1.1)式と(1.6)式を離散化していきます。連続ウェーブレット変換の離散化
時間の離散化
連続ウェーブレット変換を離散信号に適用するためには、時間$t$に関する積分が邪魔なので、時間$t$を離散化していきます。
サンプリング周波数を$f_{s}$として、次式を満たす実数$n$を定めます。\begin{align} t &= \frac{n}{f_{s}}\\ &= n\Delta t\tag{2.1.1} \end{align}積分変数の置換のために微分しときます。
\frac{dt}{dn} = \Delta t \tag{2.1.2}この時、時間信号$x(t)$をサンプリングした信号$x[n]$は以下のように表せます。
x[n] = x\Bigl(\lfloor\frac{t}{\Delta t}\rfloor \Delta t \Bigr) \tag{2.1.3}ここでウェーブレットも離散化しておきます。
\psi_{a, b}[n] = \psi_{a, b}(n\Delta t) = \psi_{a, b}\Bigl(\lfloor\frac{t}{\Delta t}\rfloor \Delta t \Bigr) \tag{2.1.4}(2.1.1)-(2.1.4)式より、(1.1)式は以下のように近似できます。
\begin{align} X(a, b) &= \int_{-\infty}^{\infty} x[n]\,\overline{\psi}_{a, b}[n]\,\Delta t\,dn\\ &= \Delta t\sum_{n=-\infty}^{\infty} x[n]\,\overline{\psi}_{a, b}[n]\tag{2.1.5} \end{align}これで離散信号に対応させることができました。丁寧に書きましたがこれくらいは簡単ですね。
連続ウェーブレット逆変換の離散化
次に逆変換を離散化していきます。こっちが曲者でした。
とりあえず逆変換の式を再掲。x(t) = \frac{2}{C_{\psi}}\int_{0}^{\infty} \int_{-\infty}^{\infty} X(a, b) \,\psi_{a, b}(t)\,db\,\frac{da}{a^2} \tag{1.6}(2.1.3)(2.1.4)式を適用すると以下のようになります。
x[n] = \frac{2}{C_{\psi}}\int_{0}^{\infty} \int_{-\infty}^{\infty} X(a, b) \,\psi_{a, b}[n]\,db\,\frac{da}{a^2} \tag{3.1}時間シフトの離散化
まずは時間シフト$b$の離散化です。
後々の計算のしやすさ等を考えて、時間$t$の離散化と同様に、サンプリング周期$\Delta t$を使って離散化します。具体的には以下の式を満たす実数$m$で表します。b = m \Delta t \tag{3.1.1}同じように微分しときます。
\frac{db}{dm} = \Delta t \tag{3.1.2}(3.1.1)(3.1.2)式を(3.1)式に適用してみましょう。
\begin{align} x[n] &= \frac{2}{C_{\psi}}\int_{0}^{\infty} \int_{-\infty}^{\infty} X(a, m\Delta t) \,\psi_{a, m\Delta t}[n]\,\Delta t\,dm\,\frac{da}{a^2}\\ &= \frac{2\Delta t}{C_{\psi}}\int_{0}^{\infty} \sum_{m=-\infty}^{\infty} X(a, m\Delta t) \,\psi_{a, m\Delta t}[n]\,\frac{da}{a^2} \tag{3.1.3} \end{align}とりあえずこれで時間シフト$b$の離散化は終わりです。
スケールの離散化
次はスケール$a$の離散化です。
時間$t$や時間シフト$b$の離散化は、信号自体をサンプリングしたものと考えればすんなりと出せるのですが、スケール$a$は特に決まりがないので、取り方によってはかなり粗い近似になってしまいます。その辺の妥当性については長くなりそうなので別記事へ。離散化の考え方ですが、(1.3)式の周波数$f$に対して、以下のように実数$l$を定めると逆変換の式が綺麗になって嬉しいです。
f = f_{0}\cdot2^{\frac{l}{l_{0}}} \tag{3.2.1}周波数をオクターブ単位で表現しただけです。ここで$f_{0}$は基準周波数で、$l_{0}$はオクターブ分解能です。
例えば、$f_{0}$を440Hz、$l_{0}$を12とすれば、整数$l$に対し、周波数$f$はピアノの各鍵盤の音の高さ(12平均律)を表します。楽曲の解析にちょうど良い。(1.3)式より、スケール$a$は以下のように表せます。
a = a_{l} = \frac{\lambda}{f_{0}} \cdot 2^{-\frac{l}{l_{0}}} \tag{3.2.2}またまた微分しときます。
\begin{align} \frac{da}{dl} &= \frac{\lambda}{f_{0}} \cdot 2^{-\frac{l}{l_{0}}} \cdot \Bigl(-\frac{\ln 2}{l_{0}}\Bigr)\\ &= -\frac{a\ln 2}{l_{0}} \tag{3.2.3} \end{align}(3.2.2)(3.2.3)式より、(3.1.3)式は以下のように変形できます。
\begin{align} x[n] &= \frac{2\Delta t}{C_{\psi}}\int_{\infty}^{-\infty} \sum_{m=-\infty}^{\infty} X(a_{l}, m\Delta t) \,\psi_{a_{l}, m\Delta t}[n]\, \Bigl(-\frac{a_{l}\ln 2}{l_{0}}\Bigr) \frac{dl}{a_{l}^2}\\ &= \frac{2\ln 2 \cdot \Delta t}{C_{\psi}l_{0}}\int_{-\infty}^{\infty} \frac{1}{a_{l}} \sum_{m=-\infty}^{\infty} X(a_{l}, m\Delta t) \,\psi_{a_{l}, m\Delta t}[n]\,dl\\ &\approx \frac{2\ln 2 \cdot \Delta t}{C_{\psi}l_{0}}\sum_{l=-\infty}^{\infty} \frac{1}{a_{l}} \sum_{m=-\infty}^{\infty} X[l, m] \,\psi_{l, m}[n] \tag{3.2.5} \end{align}最後の行で$X(a_{l}, m\Delta t)$を$X[l, m]$、$\psi_{a_{l}, m\Delta t}[n]$を$\psi_{l, m}[n]$と書き直しました。これでスケール$a$の離散化終わりです。
周波数$f$を対数で取ってあげると綺麗になりますね。音声に適用すれば実用性も兼ね備えて良い感じです。
周波数$f$を線形に取る場合でも、同じように積分変数の置換をしてあげればできるはず3。導出のまとめ
整数$l, m, n$を用いて、周波数$f$、スケール$a$、時間シフト$b$、時間$t$を以下のように離散化しました。
f = f_{0}\cdot2^{\frac{l}{l_{0}}}a = \frac{\lambda}{f}b = m \Delta tt = n\Delta tこの時、連続ウェーブレット変換および逆変換は以下のように離散化できます。
X[l, m] = \Delta t\sum_{n=-\infty}^{\infty} x[n]\,\overline{\psi}_{l, m}[n] \tag{4.1}x[n] = \frac{2\ln 2 \cdot \Delta t}{C_{\psi}l_{0}}\sum_{l=-\infty}^{\infty} \frac{1}{a_{l}} \sum_{m=-\infty}^{\infty} X[l, m] \,\psi_{l, m}[n] \tag{4.2}Pythonで実装
数式を導出できたので実装していきましょう。言語はpython3です。
そもそも、Pythonで連続ウェーブレット変換と逆変換を手軽に扱えるモジュールが見つからなくて、それなら自作してやる!ってのがこの記事の始まりだったりします。
コード全文はGitHubに上げています。マザーウェーブレットの実装
マザーウェーブレットは色んな関数がありますが、今回は以下の式で表されるMorletウェーブレットと呼ばれる関数を使います。
\psi(t) = \frac{C_{\omega_{0}}}{\pi^{1/4}}e^{-\frac{1}{2}t^2}\,(e^{j\omega_{0}t} - e^{-\frac{1}{2}\omega_{0}^2}) \tag{5.1.1}ここで$C_{\omega_{0}}$は以下の式で表されます。
C_{\omega_{0}} = \Bigl(1 + e^{-\omega_{0}^2} - 2e^{-\frac{3}{4}\omega_{0}^2}\Bigr)^{-\frac{1}{2}} \tag{5.1.2}それでは
Morletクラスを実装していきましょう。__init__メソッドはこんな感じ。Morlet.pyimport numpy as np class Morlet(object): def __init__(self, w0=6.0): self.w0 = w0 self.Cw = (1 + np.exp(-self.w0 ** 2) - 2 * np.exp(-0.75 * self.w0 ** 2)) ** (-0.5) self.C = self._get_C() # admissible constantadmissible constantの計算
admissible constantの計算部分のコードは以下の通り。
Morlet.pydef _get_C(self): # calc admissible constant wmax = 1000 dw = 0.01 w = np.arange(-wmax, wmax + 1, dw) Wf = self._get_W_fourier(w) C = 2 * np.pi * dw * np.sum(np.abs(Wf) ** 2 / np.abs(w)) return C def _get_W_fourier(self, w): # calc fourier transform of wavelet k = np.exp(-0.5 * self.w0 ** 2) Wf = self.Cw / np.pi ** 0.25 *\ (np.exp(-0.5 * (w - self.w0) ** 2) - k * np.exp(-0.5 * w ** 2)) return Wfadmissible constantは(1.5)式で表されます。
C_{\psi} = 2\pi\int_{-\infty}^{\infty}\frac{|\hat{\psi}(\omega)|^2}{|\omega|}d\omega<\infty \tag{1.5}解析解を求めることが難しいので、近似解を求めます。
Morletウェーブレットのフーリエ変換は以下のように表せます。\hat{\psi}(\omega) = \frac{C_{\omega_{0}}}{\pi^{1/4}} \bigl(e^{-\frac{1}{2}(\omega - \omega_{0})^2} - e^{-\frac{1}{2}(\omega^2 + \omega_{0}^2)} \bigr) \tag{5.1.3}(1.5)式の被積分関数をプロットしてみると下図のようになります。
今回は積分範囲を$-1000\leqq\omega\leqq1000$としましたが、もっと狭くても大丈夫そうですね。スケールの計算
周波数からスケールへの変換は(1.3)式で求められます。
a = \frac{\lambda}{f}\tag{1.3}スケール$a$に対し、ウェーブレット$\psi(\frac{t}{a})$のフーリエ変換は$a\,\hat{\psi}(a\omega)$となります。このピークを取る角周波数$\omega_{c}$がスケール$a$に対応する角周波数と見なせます。よって、スケール$a$に対応する各周波数$\omega$は以下の式を満たします。
a\omega = \omega_{c} \tag{5.1.4}ここで、$\omega_{c}$は以下の式の解となります4。
\omega_{c} = \frac{\omega_{0}}{1 - e^{-\omega_{0}\omega_{c}}} \tag{5.1.5}逆に周波数$f$に対応するスケール$a$は(5.1.4)式を変形することで求められます。
a = \frac{\omega_{c}}{\omega} = \frac{\omega_{c}}{2\pi f} \tag{5.1.6}よって、(1.3)式の補正係数$\lambda$は次式で表せます。
\lambda = \frac{\omega_{c}}{2\pi}コードに起こすとこんな感じ。
Morlet.pydef freq2scale(self, freq): # calc scales from frequencies. # center freq wf is given by the solution of below: # wf = w0 / (1 - exp(-wf * w0)) # if w0 > 5, wf is nearly equal to w0. w_center = self.w0 for i in range(100): w = w_center w_center = self.w0 / (1 - np.exp(-w * self.w0)) if np.abs(w_center - w) < 1.0e-8: break return w_center / (2 * np.pi * freq)$\omega_{c}$の解析解はやっぱり難しいので、近似解を求めています。これがfor文のところですね。
$\omega_{c}$は$\omega_{0}$に近い値になるので、初期値を$\omega_{0}$としておくといいです。ウェーブレットの計算
ウェーブレットの計算はほぼ数式通りです。
Morlet.pydef _get_W(self, t): # calc wavelet k = np.exp(-0.5 * self.w0 ** 2) W = self.Cw / np.pi ** 0.25 *\ np.exp(-0.5 * t ** 2) * (np.exp(1j * self.w0 * t) - k) # [n, s] return W def get_W(self, t, scale): # calc wavelet at scale s tt = t.reshape([1, -1]) / scale.reshape([-1, 1]) W = self._get_W(tt) / scale.reshape([-1, 1]) ** 0.5 return W連続ウェーブレット変換と逆変換の実装
Morletクラスが少し長くなってしまいましたが、ようやく本番です。
連続ウェーブレット変換と逆変換を行うCWaveletクラスを実装していきましょう。
__init__メソッドはこんな感じ。CWavelet.pyimport numpy as np from .Morlet import Morlet class CWavelet(object): def __init__(self, fs, wavelet='morlet', w0=6.0, window_len=None, freq_range=None): self.fs = fs # sampling frequency self.dt = 1 / self.fs # sampling interval self.n_per_octave = 12 self.window_len = window_len self.n = None self.W = None if wavelet == 'morlet': self.wavelet = Morlet(w0=w0) # Wavelet class else: raise ValueError('Unexpected wavelet: ' + str(wavelet)) if freq_range is None: freq_range = (13.75, self.fs // 2) else: freq_range = (max(0, freq_range[0]), min(self.fs // 2, freq_range[1])) self.freq_period = self.get_freq_period(freq_range) self.scale = self.wavelet.freq2scale(self.freq_period)対数スケールで等分された周波数の計算は
get_freq_periodメソッドで取得しています。CWavelet.pydef _get_freq_log(self, freq_range): # get frequencies spaced at epual intervals on log2 scale. # frequencies on log2 scale are calculated from music keys based on 440Hz. k0 = int(self.n_per_octave * np.log2(freq_range[0] / 440)) # minimum key kn = int(self.n_per_octave * np.log2(freq_range[1] / 440)) # maximum key k = np.arange(k0, kn + 1, dtype=np.float64) freq_period = 440 * 2 ** (k / self.n_per_octave) # frequencies return freq_period def get_freq_period(self, freq_range): freq_period = self._get_freq_log(freq_range) return freq_period連続ウェーブレット変換の実装
(4.1)(4.2)式に従って連続ウェーブレット変換を実装していくわけですが、式の通りに素直に実装してしまうと、スケールの数を$M$、時間長を$N$とした時に、計算量が$O(MN^2)$となってしまいます。
しかし、フーリエ変換を利用した畳み込みを行うことで、この計算量を$O(MN\log N)$に減らすことができます5。
フーリエ変換の畳み込み定理から以下の式が成り立ちます。\int_{-\infty}^{\infty} f(\tau)g(t - \tau)\,d\tau = F^{-1}[\hat{f}(\omega)\hat{g}(\omega)] \tag{5.2.1}ここで、$\hat{f}(\omega)$と$\hat{g}(\omega)$はそれぞれ$f(t)$と$g(t)$のフーリエ変換を表し、$F^{-1}[\cdot]$はフーリエ逆変換を表します。信号処理をやっているとお馴染みの式ですね。連続系で表しましたが、離散系でも成り立ちます。
(5.2.1)式を使うと(4.1)式は以下のように表せます。\begin{align} X_{l} &= \Delta t\sum_{n=-\infty}^{\infty} x[n]\,\overline{\psi}_{l, 0}[n - m]\\ &= \Delta t\sum_{n=-\infty}^{\infty} x[n]\,\overline{\psi'}_{l, 0}[m - n]\\ &= \Delta t \cdot F^{-1}[\hat{x}(\omega) \hat{\overline{\psi'}}_{a, 0}(\omega)] \tag{5.2.2} \end{align}ここで$\psi'[n]$は以下で表されます。
\psi'[n] = \psi[-n] \tag{5.2.3}実際には高速フーリエ変換(FFT)を使うので、適切にパディングしてあげないと巡回畳み込みという別の計算になってしまうことに注意です。
FFTで畳み込みを計算する部分を関数にするとこんな感じ。
fft_convolvedef fft_convolve(x1, x2): if x1.shape[-1] < x2.shape[-1]: x1, x2 = x2, x1 x1_len = x1.shape[-1] x2_len = x2.shape[-1] s1 = np.fft.fft(x1, x1_len) s2 = np.fft.fft(x2, x1_len) y = np.fft.ifft(s1 * s2, x1_len) return y[..., x2_len - 1:]この関数を使って
CWaveletクラスに連続ウェーブレット変換を計算するメソッドを実装します。CWavelet.pydef _transform_via_fft(self, x, strides=1): y = fft_convolve(x[..., np.newaxis, :], self.W[..., ::-1].conj()) return y[..., ::strides] def _transform(self, x, strides=1): y = self._transform_via_fft(x, strides) #y = self._transform_directly(x, strides) # too late return y def _update_W(self, N): # if precomputed wavelet is not available, update wavelet. if self.window_len is None: window_len = 2 * N - 1 else: window_len = self.window_len if self.W is None or self.n is None or window_len != self.n.shape[-1]: self.n = np.arange(-(window_len // 2), (window_len + 1) // 2) self.W = self.wavelet.get_W(self.n * self.dt, self.scale) def transform(self, x, strides=1): self._update_W(x.shape[-1]) y = self.dt * self._transform(x, strides) return y何度もウェーブレット変換を行う場合に毎回ウェーブレットを計算し直すのは無駄なので、
_update_Wメソッドで再利用するか計算し直すか判断するようにしています。逆変換の実装
逆変換の場合にもフーリエ変換による計算量削減が可能で、(4.2)式も(5.2.2)式と同じように変形できます。
\begin{align} x[n] &= \frac{2\ln 2 \cdot \Delta t}{C_{\psi}l_{0}}\sum_{l=-\infty}^{\infty} \frac{1}{a_{l}} \sum_{m=-\infty}^{\infty} X[l, m] \,\psi_{l, 0}[n - m]\\ &= \frac{2\ln 2 \cdot \Delta t}{C_{\psi}l_{0}}\sum_{l=-\infty}^{\infty} \frac{1}{a_{l}} \sum_{m=-\infty}^{\infty} X[l, m] \,\psi'_{l, 0}[m - n]\\ &= \frac{2\ln 2 \cdot \Delta t}{C_{\psi}l_{0}}\sum_{l=-\infty}^{\infty} \frac{1}{a_{l}} F^{-1}[\hat{X_{l}}(\omega) \,\hat{\psi'}_{l, 0}(\omega)] \tag{5.2.4} \end{align}逆変換も
CWaveletクラスに実装するとこんな感じになります。CWavelet.pydef transform_inverse(self, y): self._update_W(y.shape[-1]) xs = fft_convolve(y, self.W) / self.scale.reshape([-1, 1]) coefficient = 2 * np.log(2) * self.dt / self.n_per_octave / self.wavelet.C x = coefficient * np.sum(xs.real, axis=-2) return x使ってみる
実装した
CWaveletクラスを使って実際に連続ウェーブレット変換を計算してみます。
今回はサンプリング周波数を44.1KHzとし、0.5~1.0秒で440Hzのsin波、1.5~2.0秒で880Hz、2.5~3.0秒でで1760Hzのsin波を含む3.0秒の信号を解析します。
テストコードは以下。test.pyimport time import numpy as np import matplotlib.pyplot as plt from wavelet.CWavelet import CWavelet fs = 44100 f = 440 t = np.arange(fs // 2) x = np.zeros(3 * fs, dtype=np.float64) x[fs//2:fs] = np.sin(2 * np.pi * f * t / fs) x[fs + fs // 2:2 * fs] = np.sin(2 * np.pi * 2 * f * t / fs) x[2 * fs + fs // 2:3 * fs] = np.sin(2 * np.pi * 4 * f * t / fs) wavelet = CWavelet(fs) start = time.time() y = wavelet.transform(x, strides=1) end = time.time() print(end - start) fig = plt.figure() ax = fig.add_subplot(111) im = ax.imshow(np.abs(y) ** 2, aspect='auto', origin='lower') ax.set_xticks(np.arange(0, y.shape[1], fs // 2)) ax.set_xticklabels(map(str, np.arange(0, 3, 0.5))) ax.set_yticks(np.arange(0, y.shape[0], 12)) ax.set_yticklabels(map(str, wavelet.freq_period[::12])) ax.set_xlabel('Time [s]') ax.set_ylabel('Frequency [Hz]') plt.colorbar(im) fig.tight_layout() plt.show() start = time.time() x2 = wavelet.transform_inverse(y) end = time.time() print(end - start) fig = plt.figure() ax = fig.add_subplot(211) ax.plot(np.arange(x.shape[-1]) / fs, x) ax.set_title('original') ax = fig.add_subplot(212) ax.plot(np.arange(x.shape[-1]) / fs, x2) ax.set_title('recovered') fig.tight_layout() fig = plt.figure() ax = fig.add_subplot(111) ax.plot(x[fs // 2:fs // 2 + 500], label='original') ax.plot(x2[fs // 2:fs // 2 + 500], label='recovered') ax.legend(loc='upper right') plt.show()連続ウェーブレット変換によるスペクトログラムはこんな感じです。
信号の振幅はどの周波数でも1ですが、スペクトログラムでは同じ値になっていませんね。ただし、これはバグではなく連続ウェーブレット変換の仕様のようです。
スペクトログラムの周波数毎のスケールを揃える方法は別記事に書こうと思います。逆変換の結果も見ておきましょう。
振幅が揃っているので(4.2)式の係数は合ってそう。0.5秒から500ポイント描画したものが以下です。
ピッタリ重なっていますね。大丈夫そうです。まとめ
連続ウェーブレット変換を離散化した式を導出し、それをPython3で実装しました。
逆変換の近似の妥当性について詳しい検証が必要ですが、テストコードではうまく復元できていることが確認できました。現在では、英語ができれば専門的な内容であってもネット上で情報を見つけることができます。しかし、そのようなページの中でも信憑性は微妙なページが少なからずあるという良い教訓になりました。
お盆休みを消し飛ばさないためにも、キチンとした文献を読んで学ぶことが大事ですね。実装したコード全文はGitHubに上げています。
参考文献
- I. Daubechies著, 山田道夫, 佐々木文夫訳, 「ウェーブレット10講」, 丸善出版, 2003年.
- C. Torrence and G. P. Compo, "A Practical Guide to Wavelet Analysis", Bulletin of the American Meteorological Society, Vol.79, No.1, p.61-78, 1998.
今回の離散化は離散ウェーブレット変換と異なります。今回はあくまで連続ウェーブレット変換を使ってみようってことを目的としています。 ↩
英語版wikipediaのContinuous wavelet transformのページでは$2\pi$がありません。また、Matlab開発元のMathWorksの逆連続ウェーブレット変換のページでも$2\pi$がありません。 ↩
$a = \frac{\lambda}{l\Delta f}$とおけば、$\frac{da}{dl} = -\frac{\lambda}{l^{2} \Delta f} = -\frac{a}{l}$となるので、これを適用してあげれば導出できます。 ↩
$\frac{d}{d\omega}\hat{\psi}(\omega) = 0$とおいて計算していけば求められます。 ↩
厳密には$N$が2のべき乗の時に成り立ち、それ以外ではもう少し遅くなります。 ↩
- 投稿日:2019-08-19T22:17:40+09:00
鍵盤画像からの輪郭検出の練習PGM
鍵盤画像からの輪郭検出の練習PGM
openCVを用いた輪郭検出の練習PGMです
今回作成したPGMのgithubURL: https://github.com/NanjoMiyako/RinkakuKensyutuTest1
処理手順
1. makeOriginPicture.pyで元画像から鍵盤領域だけを抜き出した
画像を取得
2.RinkakuKensyutu.pyから1で作成した画像から輪郭領域を取得
各輪郭の矩形範囲を描画参考URL
Pythonを用いた画像処理(openCV,skimage) - Qiita
Python, OpenCVで画像ファイルの読み込み、保存(imread, imwrite) | note.nkmk.me
[OpenCV][Python3]検出した輪郭を描画し、輪郭線を近似して滑らかにする - Qiita
- 投稿日:2019-08-19T22:13:04+09:00
ijsonでjsonを少しずつ読み込む
はじめに
大容量のjsonをpythonのjsonライブラリで解析しようとしてメモリがすごく食われてメモリエラーになる事態になってしまいました。
そこでストリーム形式のパーサーを探してijsonを見つけましたが、資料が少ないためまとめます。
※簡単に使えるのでそもそも資料が不要かもしれません。環境
- python:3.6.5
- ijson:2.4
インストール
インストールは普通にpipでインストールします。
>pip install ijson Collecting ijson ... Successfully installed ijson-2.4使用方法
jsonの値の取得
ijsonのitems関数にjsonのファイルオブジェクトと取得したいキーを与えるとジェネレータが返却されます。
そのジェネレータからnextやループでjsonの値をとることができます。import ijson with open(jsonファイル, "r") as file_obj: ijson_generator = ijson.items(file_obj, "キー1.キー2") key2_value = next(ijson_generator)jsonのリストの取得
ほとんど値の取得と同様です。
リストの場合は取得したいキーの後にitemを追加してあげる必要があります。
返却されたジェネレータからループでjsonの値をとることができます。import ijson with open(jsonファイル, "r") as file_obj: ijson_generator = ijson.items(file_obj, "キー1.キー2.item") for value in ijson_generator: valuejson全体の解析
例えば、キーが可変のjsonを受け取る際などにキーを指定せずにjsonの解析をすることもできます。
prefixにはキーがeventには型、valueには値が格納されます。
以下の点が特殊なので気を付けてください。
- jsonのルート階層の情報を解析したときのprefixは空
- dictの始まりのeventはstart_map, valueはNone
- dictの終わりのeventはend_map, valueはNone
- dictのキーのeventはmap_key
- listの始まりのeventはstart_array, valueはNone
- listの終わりのeventはend_array, valueはNone
- listの要素のキーはキー.item
import ijson with open(jsonファイル, "r") as file_obj: pet_parse = ijson.parse(file_obj) for prefix, event, value in pet_parse: print("prefix:{}, event:{}, value:{}".format(prefix, event, value))文字列の解析
今まではjsonファイルを開いて解析していましたが、WEBアプリケーションなどでは送信された文字列を解析したい場面があると思います。
そのような場合でも、ストリーム形式にしてあげることでijsonで解析ができます。import ijson import io json_str = '{"pets": {"type": "dog","age": 5,"like": ["walking","eating","hamster"]},"dog": "bow"}' pet_parser = ijson.parse(io.StringIO(json_str)) for prefix, event, value in pet_parser: print("prefix:{}, event:{}, value:{}".format(prefix, event, value))小ネタ
jsonの階層を無視してすべてのkeyを取りたい場合は、eventを利用して楽にできる
イコールの値を変えれば階層を無視して同じ型の情報を楽に集められるwith open(ファイル名, "r") as file: pet_parser = ijson.parse(file) map_keys = [value for pet_parse, event, value in pet_parser if event == 'map_key'] print('map_keys:{}'.format(map_keys))実例
使用するjson
animal.json{ "pets": { "type": "dog", "age": 5, "like": [ "walking", "eating", "hamster" ] }, "dog": "bow" }使用するpython
pyMod.pyimport ijson import io print('------ get value ---------') with open('animal.json', 'r') as file: pet_type = ijson.items(file, 'pets.type') print(next(pet_type)) print('------ get list ---------') with open('animal.json', 'r') as file: pet_like = ijson.items(file, 'pets.like.item') for value in pet_like: print(value) print('------ get all ---------') with open('animal.json', 'r') as file: pet_parse = ijson.parse(file) for prefix, event, value in pet_parse: print('prefix:{}, event:{}, value:{}'.format(prefix, event, value)) print('------ get all str ---------') json_str = '{"pets": {"type": "dog","age": 5,"like": ["walking","eating","hamster"]},"dog": "bow"}' pet_parser = ijson.parse(io.StringIO(json_str)) for prefix, event, value in pet_parser: print('prefix:{}, event:{}, value:{}'.format(prefix, event, value)) print('------ get keys ---------') with open('animal.json', 'r') as file: pet_parser = ijson.parse(file) map_keys = [value for pet_parse, event, value in pet_parser if event == 'map_key'] print('map_keys:{}'.format(map_keys))結果
------ get value --------- dog ------ get list --------- walking eating hamster ------ get all --------- prefix:, event:start_map, value:None prefix:, event:map_key, value:pets prefix:pets, event:start_map, value:None prefix:pets, event:map_key, value:type prefix:pets.type, event:string, value:dog prefix:pets, event:map_key, value:age prefix:pets.age, event:number, value:5 prefix:pets, event:map_key, value:like prefix:pets.like, event:start_array, value:None prefix:pets.like.item, event:string, value:walking prefix:pets.like.item, event:string, value:eating prefix:pets.like.item, event:string, value:hamster prefix:pets.like, event:end_array, value:None prefix:pets, event:end_map, value:None prefix:, event:map_key, value:dog prefix:dog, event:string, value:bow prefix:, event:end_map, value:None ------ get all str --------- prefix:, event:start_map, value:None prefix:, event:map_key, value:pets prefix:pets, event:start_map, value:None prefix:pets, event:map_key, value:type prefix:pets.type, event:string, value:dog prefix:pets, event:map_key, value:age prefix:pets.age, event:number, value:5 prefix:pets, event:map_key, value:like prefix:pets.like, event:start_array, value:None prefix:pets.like.item, event:string, value:walking prefix:pets.like.item, event:string, value:eating prefix:pets.like.item, event:string, value:hamster prefix:pets.like, event:end_array, value:None prefix:pets, event:end_map, value:None prefix:, event:map_key, value:dog prefix:dog, event:string, value:bow prefix:, event:end_map, value:None ------ get keys --------- map_keys:['pets', 'type', 'age', 'like', 'dog']おわりに
jsonをストリーム形式で解析する方法を記載しましたが、キーの位置次第で一括で変換するよりも遅くなる場合があると思います。
そもそも論を言うとそこまで大きなjsonにするべきではない。少なくともdictの中にdictやlistを持たせるような複雑な構造にしてはいけないと思います。
慣れの問題もあるかもしれませんが、csvは情報が足りないと感じ、xmlは情報が過剰な気がしてjsonが程よい気がして、なんでもかんでもjsonにしたい気持ちもすごくわかります。
ならばせめてjsonの構造を簡単にして大容量にならないように工夫するのが一番かなと思っています。
- 投稿日:2019-08-19T22:12:08+09:00
Serverless Frameworkでboto3をモックしてテストする
Serverless FrameworkやSAMなどのサーバーレスアプリを開発するためのフレームワークでは、Lambda関数をテストする手法として、LocalStackやDynamoDB localを用いてローカルでテストを実行することができます。しかし今回は、それよりも単体テストに近い様なテストをPythonのライブラリであるmotoを用いてboto3をモックし、lambdaのテストを簡単に行う方法を書いていこうと思います。
環境
- Python 3.6
- Serverless Framework 1.39.0
- boto3 1.9.208
- moto 1.3.13
使用例
lambda関数
ここではDynamoDBからアイテムを取得して、レスポンスする簡単なlambdaを作成しました。
import json import boto3 from decimal_encoder import DecimalEncoder def get_article(event, context): dynamodb = boto3.resource('dynamodb') table = dynamodb.Table('article') article_id = event['pathParameters']['article_id'] res = table.get_item( Key={ "article_id": article_id } ) article = res.get('Item') response = { "statusCode": 200, "body": json.dumps(article, cls=DecimalEncoder) } return responseテストコード
@mock_dynamodb2を書くことによってその関数内のboto3のDynamoDB関係のライブラリをモックしてくれる様になります。GETメソッドをテストするときなどはあらかじめテーブルにデータが入っていてほしい場合があるかと思います。そういう時も、テストコード内で通常と同様にput_itemをすることでデータを入れることができます。import unittest import boto3 from moto import mock_dynamodb2 from handler import get_article from test.utility import init_dynamodb class TestEvent(unittest.TestCase): @mock_dynamodb2 def test_get_article(self): # articleテーブルを作成 init_dynamodb() # テストのためのarticleを一つ追加 dynamodb = boto3.resource('dynamodb') table = dynamodb.Table('article') item = { 'article_id': 1, 'title': 'test_title', 'body': 'test_article_body', } table.put_item(Item=item) # lambdaに渡すパラメーターを設定 event = { 'pathParameters': { 'article_id': 1 } } # 関数を実行 response = get_article(event, []) print(response) # {'statusCode': 200, 'body': '{"article_id": 1, "title": "test_title", "body": "test_article_body"}'} # テスト self.assertEqual(200, response['statusCode'])ちなみに、init_dynamodb()の内容は以下の様になっていて、articleというテーブルを事前に作成しています。この様な形で必要なテーブルを全て事前に作成することで、簡潔で綺麗なテストコードにすることができます。
import boto3 from moto import mock_dynamodb2 @mock_dynamodb2 def init_dynamodb(): dynamodb = boto3.resource('dynamodb') dynamodb.create_table(**{ 'TableName': 'article', 'AttributeDefinitions': [ { 'AttributeName': 'article_id', 'AttributeType': 'N' } ], 'KeySchema': [ { 'AttributeName': 'article_id', 'KeyType': 'HASH' } ], 'ProvisionedThroughput': { 'ReadCapacityUnits': 1, 'WriteCapacityUnits': 1 } })まとめ
今回はDynamoDBの機能だけしか使いませんでしたがmotoでは、同様にして様々なAWSのサービスをモック化することができます。対応しているサービスはmotoのgithubに詳しく書いてあるので興味のある人は読んでみてください。サーバーレスアプリのテスト手法の一つとして非常に便利そうなので、ぜひ活用してみてください。
- 投稿日:2019-08-19T22:11:03+09:00
Pythonのproxy回避
はじめに
会社内でmnist.load_data()などで外部のdatasetを利用しようとした場合に、社内のproxyに阻まれてしまいました。さらに、proxyに認証が必要な場合の記事が見つからなかったので、情報共有のために記事にしました。
回避方法
import urllib proxy_support = urllib.request.ProxyHandler({'https':'http:userName:password@proxy_adress:portNumber'}) opener = urllib.request.build_opener(proxy_support) urllib.request.install_opener(opener)こちらの2行目のuserNameとpasswordに自分の社内の認証IDとPASSを記入してください。
そして、@の後に自分の会社のプロキシサーバのアドレスとポート番号を各々当てはめてくれれば通過できると思います。
- 投稿日:2019-08-19T21:50:01+09:00
初心者がdjangoで作ったアプリをサーバーへデプロイしてみたいので環境整えるところまで
環境と背景
MacOS Mojave / CentOS7 / VirtualBox / iterm2
学習の中でせっかくwebアプリを作ったのでデプロイしたい。
VPSなど自分で管理するサーバーへデプロイする方法をMemo
セキュリティ関連の知識は別で蓄える必要があるようなので、ここではデプロイまでのプロセスとして。
必要物を集める
VirtualBox
https://www.virtualbox.org/にアクセスしてダウンロード。間違えようがないくらいデカいボタンがあるけど一応スクショ。
急に文字文字し出すので、「VirtualBox 6.0.10 platform packages」の欄を見て該当の利用OSを選択。Macなので「OS X hosts」。
完了したら、そのままインストールでOKかと。
ちなみにVirtualBoxを一言で解説すると
PCに仮想環境を構築して、他のOSをインストールすることができる仮想化ソフトのこと。(仮想の)パソコンをもう一個持つようなイメージかな。
CentOS
https://www.centos.org/にアクセスしてダウンロード。こちらも大きなボタンがあるので問題なし。
DVD ISOだとフルパッケージだけどまぁ重い。。。ひとまずMinimalで様子をみる。
Oh!激しい文字文字感が。。。
上部のブロックは住んでる地域に近いところで提供してくれているものらしい。ということは下部は遠いってこと。
たしかに、上部のブロックのアドレスを見てみると tsukuba とか yamagata って書いてある。
こういう分散して同じものなのに、あっちこっちからダウンロードできるようになっているものを「ミラーサイト」と呼んでいて、一箇所に集中することで高負荷になってしまうことを避けるための仕組みになっている。
多少、免疫がつくまでは違和感しかなかった。
その他
vagrantという素晴らしいツールがあるそうだが一旦ここでは使わない方向で。
VirtualBoxにCentOSをインストール準備
VirtualBoxを立ち上げて「新規」のボタンを押すと「名前」の入力を求められるので「CentOS 7」などと入力。下のプルダウンも勝手に変わってくれた。
基本は次への連打で良いと思うけど流石に最後の8GBは悩んだが一応そのままで。
終わったら「設定」アイコンを押して、ストレージを選択。
光学ドライブと書いてある場所の右側、おそらくCDと思われる青いアイコンを押して、ファイルを選択を押す。
先ほどダウンロードしておいたCentOS(拡張子ISO)を選んで「OK」
次にネットワークのアイコンを選んで
「アダプター2」のネットワークアダプターを有効にして、「ブリッジアダプター」を選んで「OK」。
起動してOSインストール
起動のアイコンを押して起動。
「Install CentOS 7」 を選択。
この時、ポップアップが出てくるので「capture」を選択しておく。
これで「PC本体画面」と「VirtualBox内の画面」のマウスがそれぞれ選択できるようになる。
左側の⌘キーでどちらのマウスを動かすか、変更が可能。
まずは言語選択で日本語を選択。
ここで「インストール先」を選択して、特に設定は変更しなくて良いので、完了ボタンを押すと、さっきまであった「!マーク」が消える。
「ソフトウェアの選択」を選ぶと、上記のOSインストール時に「Minimal」なら選択できないが、「DVD」を選んだ場合には「開発ツール」というソフトもチェックできるようになる。
ちなみに。
Minimalを選んだ場合にも「開発ツール」はインストール可能。(後ほど)インストールをしている間にROOTパスワードと、ユーザーの作成が可能になるので登録しておく。
インストールが完了すると「再起動ボタン」が出るので再起動する。
インストール後の初期設定
再起動するとユーザー名とパスワードを求められるので、先ほど設定したもの入力して起動。
シャットダウンとかは管理者権限がないとできないので、
$ SUとしてパスワードを入力。コマンドの前の「$」が「#」になる。
「#」になっていればrootユーザーということ。元のユーザーに戻るには
# exit終了するには
# shutdown -h nowしばらくかかってVirtualBoxのTOP画面に戻る。
事前の環境構築
ターミナルからIPアドレスでSSH接続
先ほどシャットダウンしているので、再度、起動アイコンを押して立ち上げる。登録userでログインしておく。
$ ip addrこれで接続されているIPアドレスを確認しておく。
いくつかそれっぽいのが見えるけど、一番下段の方のIPが示しているもの。
ターミナルを立ち上げて
$ ssh user@xxx.xxx.xx.xuserはユーザー名
xxxはIPアドレスを入力。接続後にPythonのバージョンを確認してみると
$ python -Vなんと2系。。。
ここからは
・3系をインストールする準備物
・python3系のインストール
・pipのインストール
・venvのインストール
・venvで環境設定ということで「IUS」というRedHatやCentOSなど向けに新しいRPM(ソフトウェアパッケージ管理ツール)を提供しているリポジトリがあるので追加。
$ suでスーパーユーザーに切り替えて
3系をインストールする準備物# yum install -y https://centos7.iuscommunity.org/ius-release.rpm# yum install epel-releasepython3系のインストール
# yum install python36upipのインストール
# sudo yum install python2-pip更新メッセージが出ていたら最新にしておく。
# pip install --upgrade pipvenvのインストール
# pip install virtualenvおまけ
Cent OS のところで「開発者ツール」を入れたいと思ったら# yum groupinstall "Development Tools"いくつか不足しているらしいのでさらに。
# yum -y install openssl openssl-devel readline-devel zlib-devel curl-devel libyaml-devel flex libxml2-devel zlib-devel libpng-devel libjpeg-devel libXpm-devel freetype freetype-devel
デプロイ前の準備
デプロイするディレクトリを作る。
# mkdir -p /opt/django # cd /opt/django # virtualenv -p python3.6 sns「opt」や「django」は任意の名前。「sns」は任意のプロジェクト名。
ここで作った「sns」ディレクトリに移動すると「bin」ディレクトリもできているので
# source bin/activateでvenv環境に入ることができる。(以前の記事はこちら)
Gitもインストール
(sns)# yum install gitクローン:Gitのリポジトリの内容をそのまま持ってくること
(sns)# git clone https://xxx.xxxxxxは自身のものに合わせて。Bitbucketならリポジトリに入った上部に記載してあるURL。
Djangoもインストールしておく
(sns)# pip install django長くなりそうなので、ひとまずここまで。
- 投稿日:2019-08-19T20:24:25+09:00
2次元のセルラー・オートマトン(ライフゲーム)をPythonで試す
TL;DR
- 2次元環境でのセルラー・オートマトンを復習しつつPythonで動かします。
- 以下のようなアニメーションのものを作ります。
主な参考文献
また、上記書籍のgithubのリポジトリのコードもMITライセンスなので参照・利用させていただきますmm
※本記事では割愛した説明なども山ほどあるので、ALife関係の詳細は書籍をお買い求めください。
前提
以前書いた1次元のセルラー・オートマトンの記事をベースとしています(用語の説明なども含め、重複している箇所の説明は省きます)。
ライフゲームとは
ライフゲーム (Conway's Game of Life[1]) は1970年にイギリスの数学者ジョン・ホートン・コンウェイ (John Horton Conway) が考案した生命の誕生、進化、淘汰などのプロセスを簡易的なモデルで再現したシミュレーションゲームである。単純なルールでその模様の変化を楽しめるため、パズルの要素を持っている。
生物集団においては、過疎でも過密でも個体の生存に適さないという個体群生態学的な側面を背景に持つ。セル・オートマトンのもっともよく知られた例でもある。
ライフゲーム - Wikipediaより。3x3のグリッドで、中央のグリッドが次の時間で0になるのか1になるのかを、周囲のグリッドの現在の条件に応じて決められたルールに応じて変化させる計算となります。
1次元のときは左右の2つのセルに応じて次の時間の中央のセルの状態が決定する、というものでしたが、今度は上下と斜めのセルが増えるので、8個のセルに依存します。
それぞれ1が生きている、0が死んでいると表現され、結果として生まれるアニメーションがまるで生命のように振舞ったりすることから名前にライフと付いています。1次元のときは、例えばウルフラムさんのルール0~ルール255のように、様々なルールが存在しました。
2次元のライフゲームでは、固定で以下のようなルールが存在するようです(それぞれ誕生・生存・過疎・過密と呼ばれます)。ライフゲームのルール
誕生・もしくは再生
中央のセルが死んでいる(0)状態で、且つ周りのセルで生きているセル(1)が3つある場合に、次の時間で中央のセルは誕生(もしくは再生と呼ばれます)します(1になります)。
生存・もしくは均衡状態
中央のセルが生きている(1)状態で、且つ周りに生きている(1)セルが2つもしくは3つある場合は、そのセルはそのまま次の時間も生存(1のまま)します(均衡状態とも呼ばれます)。
過疎・もしくは人口過疎
中央のセルが生きている(1)状態で、且つ周りに生きている(1)セルが1つ以下の場合、次の時間に死にます(0になります)。
過剰・もしくは人口過剰
中央のセルが生きている(1)状態で、且つ周りに生きている(1)セルが3つ以上ある場合、次の時間に死にます(0になります)。
生きている状態が多くても少なくても死んでしまい、死んでいる状態で周りに生きている状態が増えたら生き返り、バランスが良い状態の場合はそのまま生き続けるといった感じです。
人口が多すぎると快適に生活ができなかったり、食料が足りなくて死んでしまい、人口が少なすぎても生活で困ってしまう。何も無い状況から突然生物が生まれたりはせず、親が居てはじめて次の世代が誕生する、といったように現実と照らし合わせると面白いルールですね。
Pythonでの実装
使う環境
- Windows
- Python 3.6.8
- NumPy==1.14.5
- Vispy==0.5.3
- Jupyter notebook
- 前述の書籍のgithubのコード
- ※事前にcloneしてimportできるようにしておきます。可視化でalifebook_lib以下のモジュールを利用します。
初期化処理
まずは必要なモジュールのimportや可視化用のウインドウなど含め初期化処理を進めていきます。
import numpy as np from alifebook_lib.visualizers import MatrixVisualizer visualizer = MatrixVisualizer()縦横でいくつずつセルを設けるかを
WIDTHとHEIGHTという名前で定義します。今回は50個ずつ扱います。WIDTH = 50 HEIGHT = 50続いて行列を初期化します。1次元のセルラー・オートマトンの時と同様、次の時間を扱うために、
stateの他にもnext_stateという名前で行列を用意します。stateの方の行列は、ランダムに0もしくは1の値が設定されるように設定しておきます。
state = np.random.randint(low=0, high=2, size=(HEIGHT, WIDTH)) next_state = np.zeros(shape=(HEIGHT, WIDTH), dtype=np.int8) statearray([[1, 1, 1, ..., 1, 0, 1], [0, 0, 0, ..., 0, 1, 1], [1, 1, 1, ..., 1, 0, 1], ..., [0, 0, 0, ..., 0, 1, 0], [1, 0, 0, ..., 1, 1, 0], [0, 0, 0, ..., 1, 0, 1]])続いて、状態を更新するためのループを実装します。
行列全体に処理をする必要があるので、ネストしたfor文で対応します。while True: for row in range(HEIGHT): for column in range(WIDTH): # ...今回は、更新対象のセル(row, columnの位置のセル)の周囲を含めて、9個のセルの現在の値を参照する必要があります。
それぞれ、以下の図のように東西南北で変数名を設定します。行もしくはカラムのインデックスを加算する箇所(
north_east,east,south_west,south,south_eastの位置)に関しては、インデックスが行列範囲外にならないように、剰余で計算しています(範囲を超えた場合に0に戻るように)。upper_row_idx = row - 1 lower_row_idx = (row + 1) % HEIGHT left_column_idx = column - 1 right_column_idx = (column + 1) % WIDTH north_west = state[upper_row_idx, left_column_idx] north = state[upper_row_idx, column] north_east = state[upper_row_idx, right_column_idx] west = state[row, left_column_idx] center = state[row, column] east = state[row, right_column_idx] south_west = state[lower_row_idx, left_column_idx] south = state[lower_row_idx, column] south_east = state[lower_row_idx, right_column_idx]周りのセルがいくつ生きているか(1なのか)をカウントします。
0か1かの値なので、そのままcenter以外を加算していけば実現できます。neighbor_cell_sum = (north_west + north + north_east, + west + east + south_west + south + south_east)続いて、誕生(もしくは再生)の条件を書きます。中央が生きていて(1)、且つ回りに生きているセルが3つ存在する、という条件になります。
if center == 0 and neighbor_cell_sum == 3: next_state[row, column] = 1生存(もしくは均衡状態)の条件を書きます。中央が生きている(1)で且つ周りに生きているセルが2つもしくは3つの場合はそのまま生きたままになります。
elif center == 1 and neighbor_cell_sum in (2, 3): next_state[row, column] = 1そのほかの過剰や過疎の条件は死ぬように条件を設定しておきます。
else: next_state[row, column] = 0最後に、for文の外で次の時間の状態の行列(
next_state)の値を現在の状態の行列に反映し、可視化のオブジェクトに行列を渡して完成です。state[:] = next_state[:] visualizer.update(1 - state)ループのコードは最終的に以下のようになりました。
while True: for row in range(HEIGHT): for column in range(WIDTH): upper_row_idx = row - 1 lower_row_idx = (row + 1) % HEIGHT left_column_idx = column - 1 right_column_idx = (column + 1) % WIDTH north_west = state[upper_row_idx, left_column_idx] north = state[upper_row_idx, column] north_east = state[upper_row_idx, right_column_idx] west = state[row, left_column_idx] center = state[row, column] east = state[row, right_column_idx] south_west = state[lower_row_idx, left_column_idx] south = state[lower_row_idx, column] south_east = state[lower_row_idx, right_column_idx] neighbor_cell_sum = (north_west + north + north_east + west + east + south_west + south + south_east) if center == 0 and neighbor_cell_sum == 3: next_state[row, column] = 1 elif center == 1 and neighbor_cell_sum in (2, 3): next_state[row, column] = 1 else: next_state[row, column] = 0 state[:] = next_state[:] visualizer.update(1 - state)動かしてみると、以下のようなアニメーションをします。
ランダムな行列(実質ノイズ的な値)から、なんだかセル同士で近寄ったり、その結果消えて無くなったり・・・と、まるで生きているように、顕微鏡で微生物を見ている時みたく、意志を持っているかのような独特な動きになりました。
他のパターンを試す
1次元のセルラー・オートマトンでは各ルールを変えることで生成される模様が変わります。
今回の2次元のライフゲームでは、最初に与える状態の行列を調整することで色々なパターンに切り替わります。サンプルとして本記事では、グライダーとグライダーガンと呼ばれるパターンを動かしてみます。
グライダーパターン
まず、ランダムな初期状態を設定している箇所をコメントアウトします。
# state = np.random.randint(low=0, high=2, size=(HEIGHT, WIDTH))続いて、状態の行列を0で初期化し、グライダーパターンを生成するパターンを行列に与えます(行列の一部だけを更新します)。
pattern = np.array( [[0, 0, 0, 0], [0, 0, 1, 0], [0, 0, 0, 1], [0, 1, 1, 1]]) state[2:2 + pattern.shape[0], 2:2 + pattern.shape[1]] = pattern他のコードはそのままです。この時点で可視化してみると以下のようになります。
visualizer.update(1 - state)左上にのみ、黒い領域が設定されています。この形がなんとなくレトロゲームのグライダーっぽい・・・感じがします。
また、実際に動かしてみると、グライダーのように形をある程度保ったまま移動していくさまを確認できます。興味を惹かれる点として、行列計算のコードはまったく変わっておらず、与える行列の初期値を変えるだけでアニメーションの傾向が変わることです。
グライダー銃(グライダーガン)パターン
グライダーパターンをさらに発展させたものとして、グライダー銃という、周期的にグライダーを生成するようなパターンも存在します。まるでレトロゲームで攻撃のエフェクトを打ち出しているような挙動になります。
コンウェイは「生きたセルの数が無限に増えつづけるパターンはありうるか」という問題に50ドルの懸賞金をかけた。コンウェイ自身は、そのようなパターンとして「周期的だが次々にグライダーを打ち出すもの」や「移動しながら通過した後に破片を残すもの」の存在を予想し、前者を「グライダー銃」、後者を「シュシュポッポ列車」と呼んだ。1970年11月、ビル・ゴスパー(英語版)らは、初めてグライダー銃の具体例を挙げて賞金を獲得した。
ライフゲーム - Wikipediaグライダーパターンと同様に最初に特定の行列の初期値を与えるだけで実現できます。ただし、グライダーパターンと比べて与える行列は大きく複雑です。グライダーパターンが結構発生しやすい(パターンが多い)のに対して、こちらは大分パターンが限られ、しっかり初期値を調整しないと発生してくれないそうです。
以下のように大きな行列の初期値を与えます。
pattern = np.array( [[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1], [1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]])可視化してみると、以下のようになっています。
動かしてみると以下のようなアニメーションになります。
確かに、グライダーパターンが定期的に生成されています。行列の設定だけでこういったアニメーションが生まれるというのはなんだか不思議ですね・・・。
参考文献まとめ
- 投稿日:2019-08-19T18:37:54+09:00
BitDPについて
ある条件を満たす順列の数え上げに関して、n!では間に合わないけど2**nなら間に合いそうという時に使えるテクニックです。
全要素の集合をU、その部分集合をSとしてSに関して条件を満たす並び方の総数をf(S)とします。右(左)端に何を置くかで場合分けを行うと、要素数のひとつ少ないSの部分集合S'の話に帰着するので、帰納的に解くことができます。さらに、dpを効率よく行う方法として、集合をbitで管理するという発想があります。つまり、0110={1, 2}のように対応づけをすると、集合に整数でラベルを貼ることができます。このラベルをn(S)で表すことにすると、S⊇S'ならばn(S)≧n(S')が成立するので、nの小さい方から順に求めていくことで簡単に実装できます。例題:ABC041D
def main(): N, M = map(int, input().split()) edge = [0]*N for i in range(M): x, y = map(int, input().split()) edge[x-1]|=1<<(y-1) dp = [0]*(1<<N) dp[0] = 1 for s in range(1, 1<<N):#集合を添字の小さい順に試す for i in range(N):#全ての要素を考える if ((s>>i)&1) and (not(edge[i]&s)):#i in sかつedge[i]とsが共通部分を持たない dp[s]+=dp[s^(1<<i)] return dp[-1] print(main())(関係ないですがmain()に埋め込むと100msくらい速くなりました。すごい。)
上では色々なbit演算を用いています。いい機会なので、bit演算についてまとめておきます。
|: orのこと。
&: andのこと。
^: xorのこと。実質、繰り上がりのない引き算、足し算
>>: 左シフト。右に0をn個付け加える
<<: 右シフト。右からn桁を削除する
よく使うのは以下のような奴らです。
1<<N: 2**Nのこと
n>>k&1: nのk+1桁目が1かどうか(0-indexedなら右からk番目)
S&T: 集合の積
- 投稿日:2019-08-19T18:35:57+09:00
Python機械学習プログラミングという書籍で間違いを指摘したが認められなかった話
はじめに
[第2版]Python機械学習プログラミングの89ページで間違いと思われる箇所を見つけましたが,認められなかったのでここに書きます.
技術に関する内容ではなく,どちらかといえば日本語に関する内容です.
本文
間違いだと思われる箇所を引用します.(間違いだと思われる箇所は太字にしてあります)
決定木学習の情報利得の文脈でエントロピーに関する話です.
$p(i \mid t)$ は,特定のノード $t$ においてクラス $i$ に属するサンプルの割合を表す.したがって,ノードのサンプルがすべて同じクラスに属している場合,エントロピーは0である.たとえば二値分類においてエントロピーが0になるのは,$p(i=1 \mid t)=1$ または $\mathbf{p(i=0 \mid t)=0}$ の場合である.エントロピーが最大になるのは,各クラスが一様に分布している場合である.二値分類でエントロピーが1になるのは,クラスが$p(i=1 \mid t)=0.5$ および $p(i=0 \mid t)=0.5$で一様に分布している場合である.
間違っていると思った理由を説明します.
二値分類において,エントロピーが0になる場合は2通りあります.
- $p(i=1 \mid t)=1$ および $p(i=0 \mid t)=0$
- $p(i=1 \mid t)=0$ および $p(i=0 \mid t)=1$
二値分類において,エントロピーが1になる場合は1通りあります.
- $p(i=1 \mid t)=0.5$ および $p(i=0 \mid t)=0.5$
以上のことを踏まえると,著者は「 $p(i=1 \mid t)=1$ および $p(i=0 \mid t)=0$ または $p(i=1 \mid t)=0$ および $p(i=0 \mid t)=1$ 」を省略して,「 $p(i=1 \mid t)=1$ または $p(i=1\mid t)=0$ 」と書きたかったのではないかと思いました.
ですので,この文章の,$p(i=0 \mid t)=0$ は $p(i=1 \mid t)=0$ の間違いだとサポートにメールを送ったのですが,認められませんでした.
返信メールの回答部分を抜粋します.
p.89におきまして、式3.6.3下の本文に下記の記述があります。
------------------
したがって、ノードのサンプルがすべて同じクラスに属している場合、エントロピーは 0 である。たとえば二値分類においてエントロピーが 0になるのは、p( i = 1 | t ) = 1 または p( i = 0 | t ) = 0 の場合である。
------------------
「たとえば」からはじまる上の2文目では、「エントロピーが 0 になる」ケースを取り上げたものかと思います。監注35でも「p( i =1 | t)=1 のときは p( i =0 | t)=0 となり」と記載しており、これは上の2文目と同じケースであると考えられます。
また、監注35では、別のケースとして「p( i =1 | t)=0 のときは p( i =0 | t)=1となり」も取り上げています。最初に引用した部分にあるように,回答の引用文の前文でエントロピーが0になるという話をしているのだから,この「たとえば」は明らかに「二値分類」にかかっていると思われます.ですのでこの回答に納得がいかず,再度問い合わせをしたのですが,返信はありませんでした.
最後に
私の理解が間違ってるなどありましたらコメント欄におねがいします.精進いたします.
- 投稿日:2019-08-19T18:18:38+09:00
AC-GANでアニメの顔画像を生成してみた
クラスを条件とした画像生成モデルであるAC-GANを使って、アニメ顔の画像生成してみました。
AC-GANとは
理論的な解説はこちらの記事で書いたので省略。一言でいうと、Dに真偽判定だけではなく、多クラス分類の機能をもたせたものです。
画像はhttps://github.com/gitlimlab/ACGAN-PyTorchより
CIFAR-10でやってみる
手始めとして論文の通りの設定でCIFAR-10を生成してみました。CIFAR-10の訓練データ5万枚を使っているため、1クラスあたりのデータ数は5000枚となります。
サンプリング
クラスラベルも潜在空間の変数も乱数から出力したものです。そこそこ綺麗に出ているのがわかります。潜在空間の補間
AC-GANの論文によると、GANが上手くいっているかどうかを確認する一つの方法として、「潜在空間の補間を行うこと」とありました。これを実行してみます。
行方向でクラスラベルを固定し(0、1、2……)て任意の2つの画像を乱数で生成し、その2つの画像に対応する潜在空間を線形に補間し、対応する画像を生成します(列方向)。出力画像がきれいかどうかはさておいて、このようにクラス単位で滑らかな補間ができれば上手くいっているということになります。
コード
https://gist.github.com/koshian2/d044981c732df855ed25ee4a7372a53e
AnimeFace Character Dataset(全種+論文と同じ)
こちらのAnimeFace Character Datasetを使い、論文と同じ設定で生成してみます。ただし、AnimeFace Character Datasetは176クラスで14490枚の画像があるため、1クラス平均82.3枚とCIFAR-10よりはかなり少ないデータセットになります。
サンプリング
ちょっと出力画像が粗い? ただしこれはネットワーク構造を見直すことで改善します(後述)。潜在空間の補間
潜在空間の補間は上手く言っているように見えますが、実はクラス単位で同一の画像しか生成していないのではないかということに気づきます。これは論文にかかれていたことなのですが、論文のImageNetによる実験では、大量のクラスを同一のネットワーク(AC-GAN)で訓練すると、出力画像の多様性が落ちてしまうという現象が確認されたそうです。ImageNetは1000個のクラスからなりますが、論文では10個のクラスを1つのネットワークとして訓練していました。これも後で試してみます。
コード
https://gist.github.com/koshian2/c067149d97de37a9917237e7c469da51
AnimeFace Character Dataset(全種+ResNetベース)
先程の全種のケースを、ネットワーク構造を変更して実験してみます。
変更点
- GのネットワークをResNetベースに変更する(詳細はコード参照)
- アップサンプリングのレイヤーをConvTransposeからPixelShufflerに変更する
- 損失関数をHinge関数に変更(GauGANの実装を参考にしました)
サンプリング
ネットワークをResNetベースにしたら明らかに綺麗になりました。ただし、多様性の面からは疑問があります(同じ画像を出力しているだけではないか)。
潜在空間の補間
このケースでは、潜在空間の補間がうまくいきませんでした。クラスのラベル(行方向)が効いていなく、それ以外のノイズ(横方向)で説明できてしまいます。データが少なすぎたのか、もしかしたら実装のどこかが良くなかったのかもしれません。
コード
https://gist.github.com/koshian2/9be6d617ba26452a51a9fc2e34477e14
AnimeFace Character Dataset(10種+論文と同じ)
オリジナルの設定に戻し、訓練するクラス数を10に減らします。具体的にはデータの多いクラス上位10個1を採用しました。
サンプリング
全種のクラスと比べて画質が若干良くなりました。論文に書いてあるとおり、AC-GANでは一度に訓練するクラス数が多すぎるのはよくないです。潜在空間の補間
潜在空間の補間は少なくともクラス別の変数はうまく効いているというのがわかります。そこそこ形になっているのが5行目で、潜在空間の乱数によって背景のスタイルをコントロールできているのがわかります。コード
https://gist.github.com/koshian2/7c75e449bf86ba0262a933fed42c7dca
AnimeFace Character Dataset(10種+ResNetベース)
最後にResNetベースで、クラス数10の場合を試してみました。
サンプリング
一部目の位置が怖い感じになっていますが、ぱっと見綺麗に言っているように見えます。ただ多様性の面が厳しそうですね。潜在空間の補間
10種の場合よりかは、クラスの変数が効いているように見えます。しかし、キャラごとの違いが潜在空間の乱数で決まってしまい、class coditionalな生成は上手く行かなかったです。やはり1クラスあたりのデータ数が問題なのかもしれません。コード
https://gist.github.com/koshian2/024e2c247a94c050165942e96a886d27
感想/まとめ
- CIFAR-10(1クラス5000)やImageNet(1クラス1300)のように、1クラスあたりのデータ数が多ければ、AC-GANでもかなりいい感じに生成できそう。AC-GAN自体は若干古い(2016年)モデルなので、最新形を使えばまだ伸びしろはある。
- AnimeFace Character Datasetでは1クラスあたりのデータ数が平均82.3枚で、画像そのものを綺麗に生成することはできたが、生成画像の多様性が課題。データ数が多いほど有利になるのはGANでも変わらない。
- そもそもクラス別にアノテーションされたアニメ絵の画像で、クラス数あたりそこそこの枚数があるデータセットというのを聞いたことがない(存在しない?)
- ResNetが生成画像の高画質化に非常に効いているので、WGANのようにGANの安定性を損失関数でカバーし、ネットワークやデータによる成功可否の依存性を打ち消せれば、GANはかなり有望だと思われる
木之本桜(カードキャプターさくら)、ララ・サタリン・デビルーク(ToLOVEる)、月村真由(ご愁傷さま二ノ宮くん)、向坂環(ToHeart2)、西連寺春菜(ToLOVEる)、天海春香(アイドルマスター)、宮村みやこ(ef)、めろんちゃん(メロンブックス)、スバル・ナカジマ(魔法少女リリカルなのはStrikerS)、日奈森あむ(しゅごキャラ!) ↩
- 投稿日:2019-08-19T18:03:57+09:00
与えられた重みに従ってランダムに値を返す「Weighted Random Selection」をGoで実装する!
Goで 「Weighted Random Selection」 をしたくなる時があります。しかし、Goでは Pythonの
numpyのように便利な関数が提供されていないので自分で作るしかありません。今回は Go で 「Weighted Random Selection」 の実装方法を紹介します。Weighted Random Selection とは
とある重み(確率分布)を元に要素をランダムに選択するやつです。numpyで言うと
numpy.random.choiceに当たります。下記は第一引数 5([0,1,2,3,4]) から3つを確率分布pでランダムに選択する関数です。>>> np.random.choice(5, 3, p=[0.1, 0, 0.3, 0.6, 0]) array([3, 3, 0])ランダムな選択に重複を許可しない場合は引数に
replace=Falseを指定します。>>> np.random.choice(5, 3, replace=False, p=[0.1, 0, 0.3, 0.6, 0]) array([2, 3, 0])今回はGoでこの処理を行う際の実装を紹介します。
Go による Weighted Random Selection
今回は最もシンプルな Linear Scan アルゴリズムで実装します。やることは[0~weightの合計値]の間でランダムに基準となる値を選び、基準からweightを順に引いていき、0以下になったらそれが選択されます。
早速実装していきます。下記はvの中からwの確率分布に従って1つだけ値を取得する関数です。
// 0 ~ max までの範囲でランダムに値を返す var randGenerator = func(max float64) float64 { rand.Seed(time.Now().UnixNano()) r := rand.Float64() * max return r } func weightedChoiceOne(v int, w []float64) float64 { // v を slice に変換 // ex) 5 -> [0, 1, 2, 3, 4] vs := make([]int, 0, v) for i := 0; i < v; i++ { vs = append(vs, i) } // weightの合計値を計算 var sum float64 for _, v := range w { sum += v } // weightの合計から基準値をランダムに選ぶ r := randGenerator(sum) // weightを基準値から順に引いていき、0以下になったらそれを選ぶ for j, v := range vs { r -= w[j] if r < 0 { return v } } // should return error... return 0 }最後の
return 0はたまたま1つも選ばれなかった(基準がweightの合計と丁度一致した時など)場合に到達します。確率的にほとんどありませんが、ここはこの関数を使う状況によってエラーハンドリングや空で返すなどの対策が考えられます。上記のコードを少し変更すれば選ぶ数の指定 & 重複排除も実装できます。ポイントは選ばれた物をスライスから排除しておくことです。
func weightedChoice(v, size int, w []float64) ([]float64, error) { // v を slice に変換 // ex) 5 -> [0, 1, 2, 3, 4] vs := make([]int, 0, v) for i := 0; i < v; i++ { vs = append(vs, i) } // weightの合計値を計算 var sum float64 for _, v := range w { sum += v } result := make([]float64, 0, size) for i := 0; i < size; i++ { r := randGenerator(sum) for j, v := range vs { r -= w[j] if r < 0 { result = append(result, float64(v)) // weightの合計値から選ばれたアイテムのweightを引く sum -= w[j] // 選択されたアイテムと重みを排除 w = append(w[:j], w[j+1:]...) vs = append(vs[:j], vs[j+1:]...) break } } } return result, nil }選択されたアイテムと重みの削除のコードが少し特殊に見えますが、下記の公式Wikiを参考に実装しています。
https://github.com/golang/go/wiki/SliceTricks#deleteこれを使えば与えられたweightにしtがってランダムに値を返します。
func main() { r1 := weightedChoiceOne(5, []float64{0.1, 0.1, 0.2, 0.9, 0.1}) r2, _ := weightedChoice(5, 4, []float64{0.1, 0.9, 0.2, 0.3, 0.1}) fmt.Println(r1) // 3 fmt.Println(r2) // [1 3 2 0] }これで Weighted Random Selection が実装できました! 今回は最もシンプルな Linear Scan での実装を紹介しましたが、そのほかのアルゴリズムはこのサイトが勉強になります。https://blog.bruce-hill.com/a-faster-weighted-random-choice
コードは Go Playground にあげておきます。
https://play.golang.org/p/-vqQEvwCi44
- 投稿日:2019-08-19T17:59:05+09:00
Macにpyenv + AnacondaでPython環境作成の備忘録
はじめに
- Pythonをお勉強するため、Mac上にPython開発環境を整えてみたので、自分用の備忘録としてまとめました。
- ゴールは、Anaconda(Python3系)をインストールしてJupyter Notebookで作業できるまでとしました。
動作環境
- macOS Mojave 10.14.6
1. Homebrewのインストール
1-1. Homebrewとは
wikipedia
Mac OS X オペレーティングシステム上でソフトウェアの導入を単純化するパッケージ管理システムのひとつ。
- パッケージをインストール、アンインストールできる管理システムのこと。
1-2. インストール方法
- Homebrewにアクセス。
- スクリプトをコピーし、ターミナルで実行。
- インストール確認。
bash# スクリプト実行 $ /usr/bin/ruby -e "$(curl -fsSL https://raw.githubusercontent.com/Homebrew/install/master/install)" # ログ ==> This script will install: /usr/local/bin/brew /usr/local/share/doc/homebrew ︙ ==> The Xcode Command Line Tools will be installed. # Xcode Command Line Toolsをインストールする場合は、RETURNを押下。 Press RETURN to continue or any other key to abort ==> /usr/bin/sudo /bin/chmod u+rwx /usr/local/bin # ログイン時のPasswordを入力 Password: ==> /usr/bin/sudo /bin/chmod g+rwx /usr/local/bin ︙ Already up-to-date. ==> Installation successful! # インストール確認 $ brew --version # ログ Homebrew 2.1.92. pyenvのインストール
2-1. pyenvとは
- Pythonのバージョンを管理できるコマンドラインツールのこと。
2-2. インストール方法
Homebrewでpyenvをインストール。- インストール確認。
pyenvにPathを通す。- 設定(Path)の適用。
bash# pyenvをインストール $ brew install pyenv # インストール確認 $ pyenv --version # ログ pyenv 1.2.13 # pyenvにPathを通す $ echo 'export PYENV_ROOT="$HOME/.pyenv"' >> ~/.bash_profile $ echo 'export PATH="$PYENV_ROOT/bin:$PATH"' >> ~/.bash_profile $ echo 'eval "$(pyenv init -)"' >> ~/.bash_profile # 設定の適用 $ source .bash_profile3. Anacondaのインストール
3-1. Anacondaとは
wikipedia
データサイエンスおよび機械学習関連アプリケーション(大規模データ処理、予測分析(英語版)、科学計算)のためのPythonおよびRプログラミング言語のフリーでオープンソースのディストリビューションであり、パッケージ管理および展開の単純化を目指したものである。
- 「Python」 + 「各種ライブラリ」をまとめて含んだパッケージのこと。
3-2. インストール方法
pyenvでインストール可能なAnacondaを検索。- Anacondaをインストール。
bash# インストール可能なAnacondaを検索 $ pyenv install -l | grep anaconda # ログ anaconda-1.4.0 ︙ anaconda2-5.0.0 ︙ anaconda3-5.3.1 # インストール $ pyenv install anaconda3-5.3.14. Anacondaで仮想環境を作成
作成方法
condaで仮想環境を作成。- 作成した仮想環境を作業ディレクトリで有効化(
pyenv local)。activateで仮想環境を起動。- Jupyter Notebookを起動。起動できればゴール。
bash# Anacondaをglobalに切り替え $ pyenv global anaconda3-5.3.1 # 仮想環境を作成 $ conda create --name anaconda_py3.6 python=3.6 anaconda # 作成した仮想環境を作業用ディレクトリで有効化 $ mkdir Workspace $ cd Workspace $ pyenv local anaconda3-5.3.1/envs/anaconda_py3.6 # globalをsystemへ戻す $ pyenv global system # 作成した仮想環境をActivateで起動(フルパスで指定) $ source $PYENV_ROOT/versions/anaconda3-5.3.1/bin/activate anaconda_py3.6 # 作業ディレクトリでjupyter Notebookを起動 $ cd Workspace $ jupyter notebook5. Jupyter Notebookで仮想環境を指定する
- 作成したAnacondaの仮想環境をJupyter Notebook上で指定できるようにする。
5-1. 設定方法
- Anacondaのデフォルト環境:base(root)でJupyter Notebookに対するパッケージ追加とその設定を行う。
bash# パッケージの追加 $ pip install environment_kernels # 設定ファイルの生成 $ jupyter notebook --generate-config # 設定を追加 $ echo "c.NotebookApp.kernel_spec_manager_class = 'environment_kernels.EnvironmentKernelSpecManager'" >> ~/.jupyter/jupyter_notebook_config.py $ echo "c.EnvironmentKernelSpecManager.conda_env_dirs=['/Users/toyoizumi/.pyenv/versions/anaconda3-5.3.1/envs/']" >> ~/.jupyter/jupyter_notebook_config.py6. 仮想環境の切り替え方法
- 環境の切り替えは、
activateとpyenv localを併用。bash# Activateで指定環境を起動できる(フルパスで指定) $ source $PYENV_ROOT/versions/anaconda3-5.3.1/bin/activate anaconda_py3.6 # 作業ディレクトリごとに仮想環境を指定できる $ mkdir Workesapce $ cd Workuspace $ pyenv local anaconda3-5.3.1/envs/anaconda_py3.6 # Deactivateで環境を解除できる(フルパスで指定) $ source $PYENV_ROOT/versions/anaconda3-5.3.1/bin/deactivate anaconda_py3.7
activateをフルパスで実行するのは煩わしいので、aliasを設定。bash# .bashrcにaliasを追加 $ echo 'alias activate="source $PYENV_ROOT/versions/anaconda3-5.3.1/bin/activate"' >> ~/.bashrc # 設定の適用 $ source ~/.bashrc # 「activate + 仮想環境名」で指定環境を起動出来る $ activate anaconda_py3.6 # 指定環境でJupyter Notebookを起動出来る $ jupyter notebook
- 投稿日:2019-08-19T17:12:02+09:00
python のコーディングにVisual studio 2019 Community Bottole Template
pythonのコーディングに何を使っていますか。Pycarmもいいけど私は、Visual Studio 2017/2019を使っています。
多彩なツールを自由に組み込むことができます。今回は、素早くRasipberry pi 用にweb serverを立ち上げるためにBoostrap4用bottle Templateをご紹介します。Visual studio に添付されているbottleWebテンプレートをベースに作成しました。
Boostrap4にこだわる理由は、スマートフォン用のUIを簡単に作ることができるからです。
例えば、スマートフォンやタブレット用ボタンスイッチAPPを作るには、
routes.py に追加
routes.py@route('/btn') @view('btn') def btn(): return dict( year=datetime.now().year )btn.tpl テンプレートをを作成% rebase('layout.tpl', title='Home Page', year=year) <main role="main"> <div class="container" style="margin:2em;"> % ix=0 % for j in range(4): <div class="row" style="margin:1em;"> % for i in range(4): <div class="col-md-3"> <button data-i={{ix}} class='btn btn-outline-primary btn-lg btn-block'style='height:100px;'><h1>ボタン{{ix}}</h1></button> %ix=ix+1 </div> % end </div> % end <hr> </div> <!-- /container --> </main> <script> $(function(){ $('#flipclock').FlipClock({clockFace: 'TwentyFourHourClock'}); var on=0; $('.btn').click(function(){ if($(this).hasClass('btn-primary')) { //off $(this).removeClass("btn-primary"); $(this).addClass("btn-outline-primary"); on=0; } else { //on $(this).removeClass("btn-outline-primary"); $(this).addClass("btn-primary"); on=1; } $.ajax({ type: "POST", url: "/relay", data: { "id":$(this).attr('data-i'), "cmd": on, "relay":$(this).attr('data-i')}, success: function(data){} }); }); }); </script>ファイルをgithubに置いておきます。
https://github.com/yutakahirata/Bottle4Template/tree/master/bottle4/bottle4
tree.txtbottle4 │ app.py │ bottle4.pyproj │ bottle4.pyproj.user │ requirements.txt │ routes.py ├─static │ ├─content #その他必要なスタイルシートを追加します。 │ │ bootstrap-grid.css │ │ bootstrap-grid.css.map │ │ bootstrap-grid.min.css │ │ bootstrap-grid.min.css.map │ │ bootstrap-reboot.css │ │ bootstrap-reboot.css.map │ │ bootstrap-reboot.min.css │ │ bootstrap-reboot.min.css.map │ │ bootstrap.css │ │ bootstrap.css.map │ │ bootstrap.min.css │ │ bootstrap.min.css.map │ │ jumbotron.css │ │ site.css │ │ │ ├─fonts #boostrap4では、不必要 │ │ glyphicons-halflings-regular.eot │ │ glyphicons-halflings-regular.svg │ │ glyphicons-halflings-regular.ttf │ │ glyphicons-halflings-regular.woff │ │ │ └─scripts その他のスクリプト(java scriptをここに配置) │ bootstrap.bundle.js │ bootstrap.bundle.js.map │ bootstrap.bundle.min.js │ bootstrap.bundle.min.js.map │ bootstrap.js │ bootstrap.js.map │ bootstrap.min.js │ bootstrap.min.js.map │ jquery-1.10.2.intellisense.js │ jquery-1.10.2.js │ jquery-1.10.2.min.js │ jquery-1.10.2.min.map │ jquery.validate-vsdoc.js │ jquery.validate.js │ jquery.validate.min.js │ jquery.validate.unobtrusive.js │ jquery.validate.unobtrusive.min.js │ modernizr-2.6.2.js │ respond.js │ respond.min.js │ _references.js │ ├─views │ about.tpl │ contact.tpl │ index.tpl │ layout.tpl<<使い方>>
gitからチェックアウトします。
https://github.com/yutakahirata/Bottle4Template.gitbottle4を選択します。
ソリューションを開きます。bottle4.sln
プロジェクト->テンプレートのエクスポートを行います。
新しいプロジェクトを作成します。検索エリアにbottle4と入力するとテンプレートが現れます。
Visual studio 2019 communityを用いサクサクプログラムが書けます。
「いいね!」してね!
- 投稿日:2019-08-19T16:57:52+09:00
pythonのnp.array配列に格納した2次元座標から、入力した座標に最も近い座標を取得した際の備忘録です
目的
pythonのnp.array配列に格納した2次元座標から、入力した座標に最も近い座標を取得した際の備忘録です
コード
sample.py#!/usr/bin/env python3 # -*- coding: utf-8 -*- import numpy as np PI = 3.1415 coordinate = np.array([ # x, y, th [0.5, 0, PI], [0.9, 0, PI], [0.9, -0.5, PI], [0.9, 0.5, PI], [0.9, 0, PI], [0, 0.5, -1*PI/2], [0, 0.5, 0], [0, 0.5, PI], [-0.5, 0, 0], [-0.9, 0, 0], [-0.9, 0.5, 0], [-0.9, -0.5, 0], [-0.9, 0, 0], [0, -0.5, PI/2], [0, -0.5, 0], [0, -0.5, PI], [0, -0.5, PI/4] ]) # 点p0に一番近い点を取得 def func_search_neighbourhood(p0, ps): L = np.array([]) for i in range(ps.shape[0]): norm = np.sqrt( (ps[i][0] - p0[0])*(ps[i][0] - p0[0]) + (ps[i][1] - p0[1])*(ps[i][1] - p0[1]) ) L = np.append(L, norm) return np.argmin(L) ,ps[np.argmin(L)] def main(): # target coordinate _x = 0 _y = -0.7 target_coor = np.array([_x, _y]) idx, nearrest_coor = func_search_neighbourhood(target_coor, coordinate) print( len( coordinate ) ) print( idx, nearrest_coor[0], nearrest_coor[1], nearrest_coor[2] ) # idx, (x, y, th) if __name__ == '__main__': main()実行結果
$ python sample.py 17 13 0.0 -0.5 1.57075参考
Python/NumPyで2点間の距離を計算
辞書内のPythonの最も近い座標
Python/Numpyで最も近い点を探索
Finding the closest point to a list of points
- 投稿日:2019-08-19T16:47:56+09:00
M5StickVの起動音がうるさいので黙らせた話
概要
M5StickV 買っちゃいました。
で、とりあえず色々遊ぼうと思ったんですけど、こいつ、、
起動したら「ピコーン!」
充電しようと思ってケーブル挿したら「ピコーン!」
再起動したら「ピコーン!」
って、ピコーン!ピコーン!うるさいんですよ。
というわけで、まずは静かにさせることにしました。WAV ファイルを鳴らさなければいい
結論としてはこれだけ。flash に書かれている boot.py の WAV ファイル鳴らしているところを消せばいいんですけど、なかなかいうことを聞いてくれない。
uPyLoader を使ってみた → 不安定
本体フラッシュの boot.py を書き換えるのに uPyLoader をお勧めしている記事が何個か見つかったので試してみたのですが、どうにも不安定。書き込みが成功したり失敗したり、というか、一度だけ書き込みが成功して、それ以降失敗続きです。書き込み成功した1回はいったい何だったのだろう、、?
ampy も使ってみた → GETできない
ampy も使ってみたのだけど、あまり状況変わらず。
> ampy ls /flashとかでファイル一覧は取得できるのだけど、> ampy get /flash/boot.pyだとエラーを吐いて止まる。使い方が違うのかな?(よく分かってない)シリアル接続して pye コマンド【成功】
TeraTerm でシリアル接続してコマンドラインから
>>> pye('/flash/boot.py')で書き換えるのが結局安定してて一番早かった。
書き換えに成功するなら後は簡単。boot.pytry: player = audio.Audio(path = "/flash/ding.wav") #player.volume(100) player.volume(10) wav_info = player.play_process(wav_dev) wav_dev.channel_config(wav_dev.CHANNEL_1, I2S.TRANSMITTER,resolution = I2S.RESOLUTION_16_BIT, align_mode = I2S.STANDARD_MODE) wav_dev.set_sample_rate(wav_info[1]) while True: ret = player.play() if ret == None: break elif ret==0: break player.finish() except: pass30行目くらいから起動音の再生処理が書いてあるので、この辺を消せばいいんだけど、簡単に音量を 100 → 10 に変更してみた。このくらいの音量にすると全然聞こえない。もう少し大きくてもいいかもしれない。
まとめ
boot.py の簡単な修正なら pye コマンドが簡単だった。
uPyLoader や ampy での書き換えがうまくいかないのがイマイチ納得いかないのでもうちょっと試してみようと思う。今後必要になるだろうし、、(上手くいかない理由をご存知の方いらっしゃいましたら教えてください m(_ _)m
- 投稿日:2019-08-19T16:30:01+09:00
重み付き線形回帰を題材に双対表現を堪能しよう
はじめに
ぶっちゃけ回帰における基底関数表現の式とカーネル関数表現の式を毎回忘れるので、どこかにメモを残しておこうってことで記事を書こうと思った次第です。ただまぁ単に覚書にするのは勿体無い気がしたので、簡単な解説記事にしてみました。
覚書用
簡潔にまとめたバージョン。忙しい人もしくは私と同様に思い出したい人用
目的関数
\begin{align*} F &= \frac{1}{2} \left( \mathbf{y} - X \mathbf{w} \right)^T G \left( \mathbf{y} - X \mathbf{w} \right) + \frac{1}{2} \mathbf{w} ^T H \mathbf{w} \\ \end{align*}$\mathbf{y} = (y_1, \dots, y_N)^T \in \mathbb{R} ^N$:出力データ($y_n \in \mathbb{R}$)
$X = (\mathbf{x}_1, \dots, \mathbf{x}_N)^T \in \mathbb{R} ^{N \times D}$:入力データ($\mathbf{x}_n \in \mathbb{R}^D$)
$\mathbf{w} \in \mathbb{R} ^D$:パラメータ
$G \in \mathbb{R} ^{N \times N}$:データの重み(対角行列)
$H \in \mathbb{R} ^{D \times D}$:正則化項の重み(対角行列)最適化
パラメータ
・基底関数表現\begin{align*} \hat{\mathbf{w}} = \left( X^T G X + H\right)^{-1}X^T G \mathbf{y} \\ \tag{1} \end{align*}・カーネル表現
\begin{align*} \hat{\mathbf{w}} = H^{-1} X^T \left( X H^{-1} X^T + G^{-1} \right)^{-1} \mathbf{y} \\ \tag{2} \end{align*}推定値
・基底関数表現\begin{align*} \hat{\mathbf{y}} &= X \hat{\mathbf{w}} \\ &= X \left( X^T G X + H\right)^{-1}X^T G \mathbf{y} \\ &= X X^{\dagger} \mathbf{y} \\ \end{align*}ただし$X^{\dagger} \triangleq \left( X^T G X + H\right)^{-1}X^T G$
・カーネル関数表現
\begin{align*} \hat{\mathbf{y}} &= X \hat{\mathbf{w}} \\ &= X H^{-1} X^T \left( X H^{-1} X^T + G^{-1} \right)^{-1} \mathbf{y} \\ &= K \left( K + G \right)^{-1} \mathbf{y} \end{align*}ただし$K \triangleq X H^{-1} X^T$
解説
重み付き線形回帰の背景
本題は双対表現を得ることなので、重み付き線形回帰自体の説明はさらっとします。
まず重み付き線形回帰を一言で言うと「重み付き線形回帰はデータの信頼度がわかってる場合や特定のデータだけは誤差を小さくしたい場合とかに使える回帰手法」です。
通常の回帰では入力$\mathbf{x}_n$と出力$y_n$のペアが$N$組み与えられた時、以下のような目的関数$F$を\begin{align*} F = \sum_{n=1}^{N} \left( y_n - f( \mathbf{x}_n )\right)^2\\ \end{align*}最小とする関数$f$のパラメータを求めます。つまり全てのデータに対して均等に誤差が小さくなるようにパラメータを求めます。
対して重み付き回帰では、以下のような目的関数になり\begin{align*} F = \sum_{n=1}^{N} g _n \left( y_n - f( \mathbf{x}_n) \right)^2\\ \end{align*}各データに対して解析者が重み$g _n$を与えることで、どのデータについて誤差を小さくしたいかを各データごとに任意で決めることができます。つまり重み付き回帰では重み付きの誤差が小さくなるように関数$f$のパラメータを求めます。もちろん全ての重みが一定$g _n = {\rm constant}$のとき通常の回帰と一致します。
このような各データに対して重みをつけたいという状況はままあります。
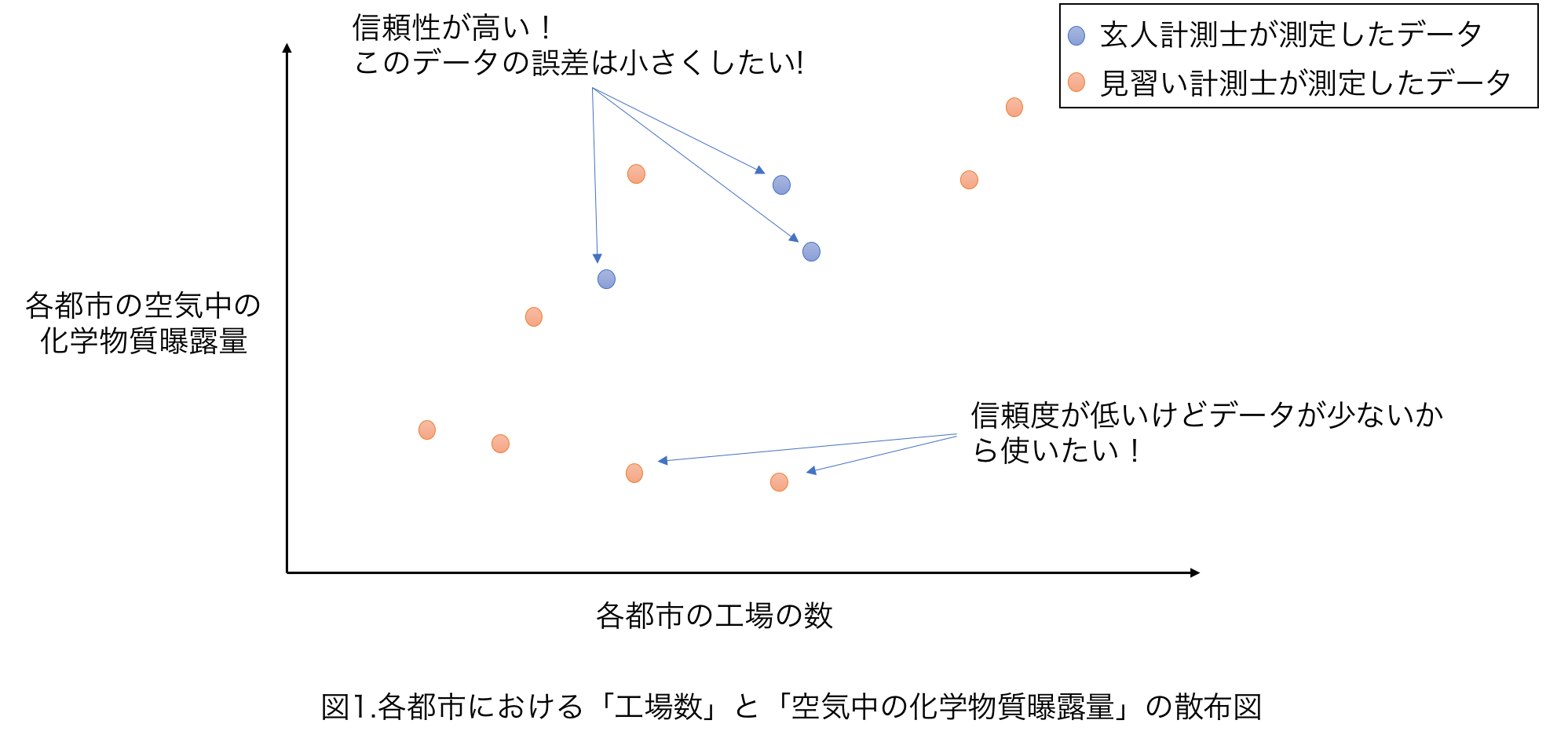
例えば各都市にある工場の数から空気中の化学物質暴露量を予想したい状況を考えてみましょう。
空気中の化学物質暴露量の測定には技術が必要で、玄人計測士はかなりよい精度で測定することができますが、忙しく何箇所も測定することが難しいとしましょう。逆に見習い測定士は測定精度は低いですが、手が空いており多くの都市を測定できるとします(図11)。
このような玄人計測士が測定したデータは信頼できるため、誤差をなるべく小さく(重み$g$を大きく)したいといった状況の時、重み付き回帰がなかなか使えます。重み付き線形回帰の問題設定
それでは本題の双対表現を得るために、ちゃっちゃか式変形をしていきます。
重み付き線形回帰のタスクは$N$個の入力$\mathbf{x}_n \in \mathbb{R}^D$と出力$y_n \in \mathbb{R}$のペアと、各データに対する重み$G = {\rm diag}(g _1, \dots, g _N)$が与えられた時に、以下の目的関数を最小とするようなパラメータ$\mathbf{w}$を求めることになります。\begin{align*} F = \frac{1}{2} \left( \mathbf{y} - X \mathbf{w} \right)^T G \left( \mathbf{y} - X \mathbf{w} \right) + \frac{\beta}{2} \mathbf{w}^T \mathbf{w} \\ \tag{3} \end{align*}ここで$X$は入力$\mathbf{x} _n$を並べた行列$X = (\mathbf{x}_1, \dots, \mathbf{x} _N)\in \mathbb{R} ^{D \times N}$で、$\mathbf{y}$は出力$y _n$を並べたベクトル$(y _1, \dots, y _N) \in \mathbb{R} ^N$です。
解いてみた
最小二乗法でおなじみの式(3)を$\mathbf{w}$で偏微分して$0$とおくことで、最適なパラメータを求めましょう。
\begin{align*} \frac{\partial F}{\partial \mathbf{w}} &= \frac{\partial }{\partial \mathbf{w}} \left\{ \frac{1}{2} \left( \mathbf{y} - X \mathbf{w} \right)^T G \left( \mathbf{y} - X \mathbf{w} \right) + \frac{\beta}{2} \mathbf{w}^T \mathbf{w} \right\} \\ &= \frac{\partial }{\partial \mathbf{w}} \left\{ \frac{1}{2} \left( \mathbf{y}^T G \mathbf{y} - 2 \mathbf{w}^T X^T G \mathbf{y} + \mathbf{w}^T X^T G X\mathbf{w} \right) + \frac{\beta}{2} \mathbf{w}^T \mathbf{w} \right\} \\ &= - X^T G \mathbf{y} + X^T G X \mathbf{w} + \beta \mathbf{w} \\ &= - X^T G \mathbf{y} + \left( X^T G X + \beta I \right) \mathbf{w} \\ &= 0 \end{align*}より
\begin{align*} \left( X^T G X + \beta I \right) \hat{\mathbf{w}} = X^T G \mathbf{y} \\ \hat{\mathbf{w}} = \left( X^T G X + \beta I \right)^{-1} X^T G \mathbf{y} \tag{4} \end{align*}となり、パラメータが推定できました!
次はメインディッシュの双対表現を求めていきましょう!
通常は$\mathbf{w} = \alpha X$とおいて、$\alpha$について解いていき双対表現を求めていきますが、
今回は逆行列の補助定理(Sherman–Morrison–Woodburyの公式)1を使って求めていきます。
まず、$H \triangleq \beta I$とおき式(4)を\begin{align*} \hat{\mathbf{w}} &= \left( X^T G X + H \right)^{-1} X^T G \mathbf{y} \\ &= \left( H + X^T G X \right)^{-1} X^T G \mathbf{y} \tag{5} \end{align*}と書きなおします。
ここでpush through identity(証明)\begin{align*} \left( A + BCD \right)^{-1} B = A^{-1}B \left( DA^{-1}B + C^{-1} \right)^{-1} C^{-1} \\ \end{align*}を使って式変形をしていきます。$A = H、B = X^T,C = G, D = X$とみなすと式(5)は
\begin{align*} \hat{\mathbf{w}} &= \left( H + X^T G X \right)^{-1} X^T G \mathbf{y} \\ &= H^{-1}X^T \left( XH^{-1}X^T + G^{-1} \right)^{-1} G^{-1} G \mathbf{y} \\ &= H^{-1}X^T \left( XH^{-1}X^T + G^{-1} \right)^{-1} \mathbf{y} \tag{6} \end{align*}となり、双対表現が得られました!!
ちなみに式(6)の結果を使って新規入力に対する出力の予測値$\hat{\mathbf{y}}$を求めて見ると\begin{align*} \hat{\mathbf{y}} &= X \hat{\mathbf{w}} \\ &= X H^{-1}X^T \left( XH^{-1}X^T + G^{-1} \right)^{-1} \mathbf{y} \\ \end{align*}となります。またここで$K \triangleq X H^{-1}X^T$とおくと
\begin{align*} \hat{\mathbf{y}} = K \left( K + G^{-1} \right)^{-1} \mathbf{y} \\ \end{align*}となり、みなさんがよく目にする式になります。
実装編
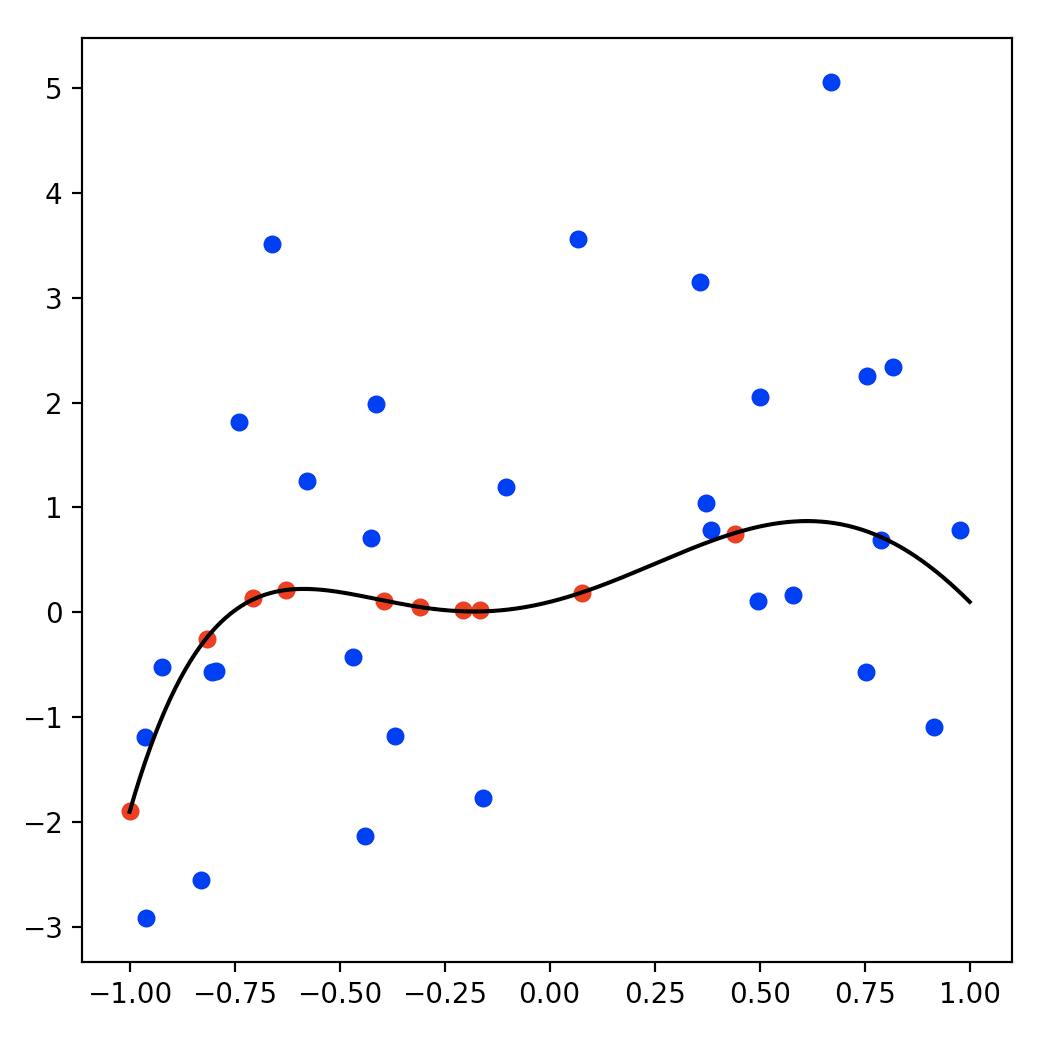
いま、信頼性が高いデータが10点(赤点)と信頼性が低いデータが30点(青点)与えられた時の回帰をやってみましょう。
データは以下のようになります。横軸が入力で縦軸が出力です。
黒線が真の関数を表してます。
このデータに対して、重み付き回帰を行ってみましょう!
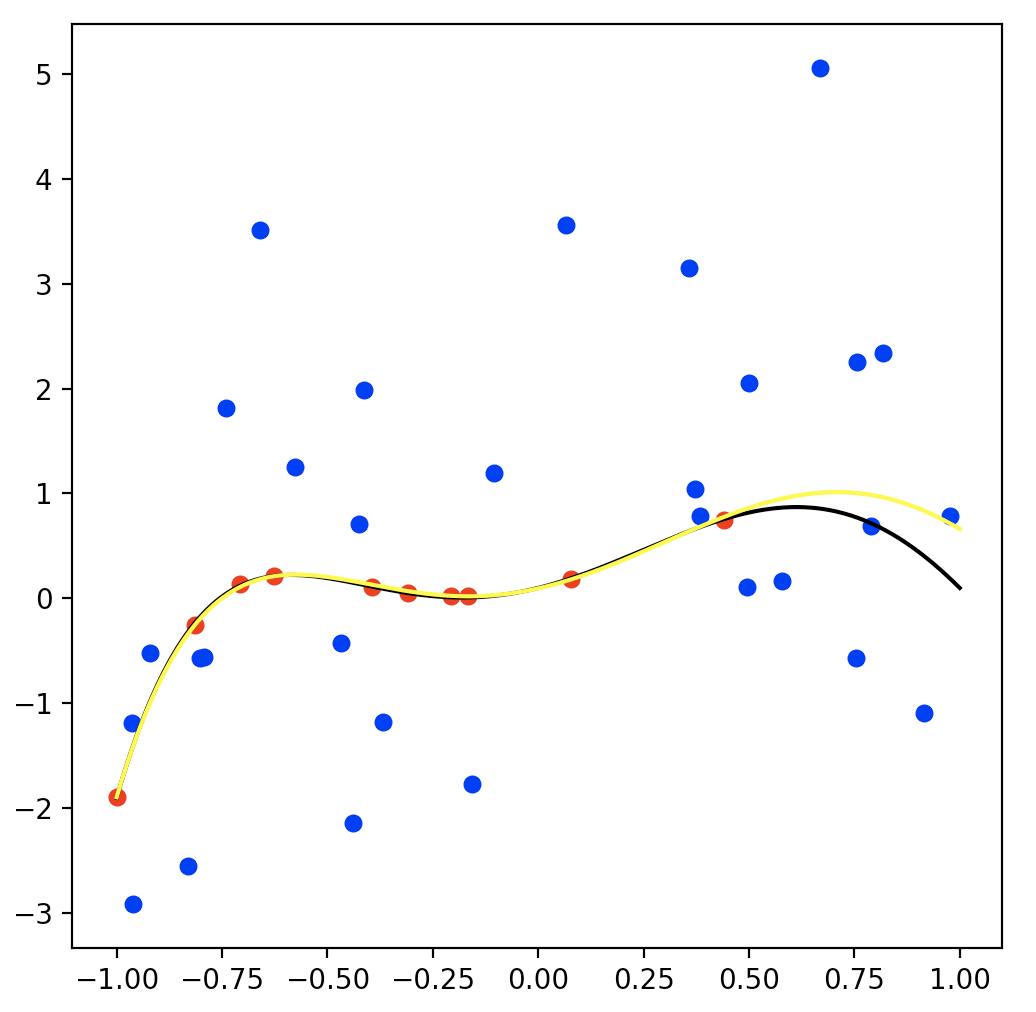
コードは以下のようになります。import numpy as np import matplotlib.pyplot as plt np.random.seed(1) # ---------- データ生成 ---------- # M = 5 w = np.array([0.1, 1.0, 2.5, -2.0, -3.5, 2.0]) # 真の関数のパラメータ power = np.arange(M+1) # 信頼性が高いデータ(ノイズの分散0.01) N1 = 10 x1 = (np.random.rand(N1) * 2 - 1)[:, np.newaxis] y1 = x1**power @ w + np.random.normal(0, 0.01, N1) # 信頼性が低いデータ(ノイズの分散2.0) N2 = 30 x2 = (np.random.rand(N2) * 2 - 1)[:, np.newaxis] y2 = x2**power @ w + np.random.normal(0, 2.0, N2) # 連結 N = N1 + N2 x = np.concatenate([x1, x2]) y = np.concatenate([y1, y2]) # 真の関数 x_all = (np.linspace(-1, 1, 500))[:, np.newaxis] true_y = x_all**power @ w # ---------- データの重みと正則化項 ---------- # g1 = np.ones(N1) * 100.0 # 重みはノイズの分散の逆数が良き g2 = np.ones(N2) * 0.5 beta = 0.1 G = np.diag(np.concatenate([g1, g2])) H = np.eye(M+1) * beta # ---------- パラメータ推定 ---------- # # 基底関数の準備(M次多項式) Phi = x**power # 通常のリッジ回帰 w = np.linalg.pinv(Phi.T @ Phi + H) @ Phi.T @ y f = x_all**power @ w # 重み付き回帰 w_weight_regression = np.linalg.pinv(Phi.T @ G @ Phi + H) @ Phi.T @ G @ y f_weight_regression = x_all**power @ w_weight_regression # 信頼度の高いデータだけ使った場合 Phi_x1_only = x1**power w_x1_only = np.linalg.pinv(Phi_x1_only.T @ Phi_x1_only + H) @ Phi_x1_only.T @ y1 f_x1_only = x_all**power @ w_x1_only # ---------- 描画 ---------- # fig = plt.figure(figsize=(6, 6)) ax = fig.add_subplot(1, 1, 1) ax.scatter(x1, y1, s=30, c='red') ax.scatter(x2, y2, s=30, c='blue') ax.plot(x_all, true_y, c='black') # 真の関数 ax.plot(x_all, f, c='green') # 普通のリッジ回帰 ax.plot(x_all, f_weight_regression, c='yellow') # 重み付き回帰 ax.plot(x_all, f_x1_only, c='pink') # 信頼性の高いデータだけ使ったリッジ回帰 plt.show()結果がこちらになります。黄色の曲線が重み付き回帰で求めたパラメータを使った関数です。
まぁまぁ真の関数を表現できてますね。やった。
ちなみに比較対象として、「普通のリッジ回帰(緑)」と「信頼性の高いデータだけ使ったリッジ回帰(ピンク)」を一緒に実行した結果がこちらです。
普通のリッジ回帰の結果(緑)は信頼性の低いデータ(青点)に引っ張られている感じで、重み付き回帰より真の関数がうまく推定できてないですね。
信頼性の高いデータだけ使ったリッジ回帰の結果(ピンク)はデータ点があるところは真の関数と近いですが、右の方のデータ点が存在しないところは少し真の関数からずれてますね。
こんな感じで、データの信頼度(ノイズの大きさ)がわかっている場合では重み付き回帰が効果的なのがわかりますね。おまけ1:GとHの解釈について
結論から言うと実は$G = {\rm diag}(g _1, \dots, g _N)$の$g _n$は$n$番目のデータに乗っているガウスノイズの精度パラメータと解釈することができます。また$H = \beta I$の$\beta$は関数パラメータ$\mathbf w$の事前分布(ガウス分布)の精度パラメータと解釈できます。
つまり、$G$はデータのノイズの大きさを表現しており$H$は関数(パラメータ)の取りうる範囲を表現しているといった風になります。
なぜこのように解釈できるかはベイズ回帰(MAP推定)を考えてみるとわかりやすいので、簡単にですがみていきましょう。
まず、観測データ$\left( \mathbf{x} _n, y _n \right) _{n=1}^{N}$に対して以下のような確率モデルを考えます。\begin{align*} & y_n = \mathbf{w}^T \mathbf{x}_n + \epsilon_n \\ & \epsilon \sim N(0, \alpha^{-1}) \tag{7}\\ & \mathbf{w} \sim N(0, \beta^{-1}I) \tag{8}\\ \end{align*}ここで推定したいパラメータ$\mathbf{w}$の対数事後分布はベイズの公式より
\begin{align*} \ln p(\mathbf{w}|\mathbf{y}, X) &= \ln \frac{p(\mathbf{y}|\mathbf{w}, X)p(\mathbf{w})}{p(\mathbf{y}|X)} \\ &= \ln p(\mathbf{y}|\mathbf{w}, X) + \ln p(\mathbf{w}) - \ln p(\mathbf{y}|X) \tag{9} \end{align*}となります。また
\begin{align*} & p(\mathbf{y}|\mathbf{w}, X) = \prod _n p(\mathbf{y}_n|\mathbf{w}, \mathbf{x}_n) = \prod _n N(\mathbf{w}^T \mathbf{x}_n, \alpha^{-1}) \\ & p(\mathbf{w}) = N(0, \beta^{-1}I) \end{align*}であるから、式(9)は
\begin{align*} \ln p(\mathbf{w}|\mathbf{y}, X) &= \ln N(\mathbf{w}^T \mathbf{x}_n, \alpha^{-1}) + \ln N(0, \beta^{-1}I) - \ln p(\mathbf{y}|X) \\ &= -\frac{\alpha}{2} \| \mathbf{y} - X \mathbf{w} \|^2 - \frac{\beta}{2}\| \mathbf{w} \| + C \end{align*}となります。2ただし$C$は$\mathbf{w}$について定数となるものをまとめた係数です。
さらに$G = \alpha I$とおき$H = \beta I$とおくと、\begin{align*} \ln p(\mathbf{w}|\mathbf{y}, X) = - \left( \mathbf{y} - X \mathbf{w} \right)^T G \left( \mathbf{y} - X \mathbf{w} \right) - \mathbf{w}^T H \mathbf{w} + C \end{align*}といった、重み付き線形回帰の目的関数とよく似たものがでてきます。
$G=\alpha I$は式(7)からわかるようにノイズの精度パラメータであり、$H=\beta I$は式(8)からわかるようにパラメータ$\mathbf{w}$に関する事前分布のパラメータです。おまけ2:定理とかの証明
push through identityの証明
まず$B + BCDA^{-1}B$っていう天から落ちて来た式を左から$BC$でくくると
\begin{align*} B + BCDA^{-1}B = BC \left( C^{-1} + DA^{-1}B \right) \end{align*}となります。また同じものを右から$A^{-1}B$でくくると
\begin{align*} B + BCDA^{-1}B = \left( A + BCD \right) A^{-1}B \end{align*}となり、
\begin{align*} BC \left( C^{-1} + DA^{-1}B \right) = \left( A + BCD \right) A^{-1}B \end{align*}という等式が得られます。そして両辺に対して右から$\left( C^{-1} + DA^{-1}B \right)^{-1}$と左から$\left( A + BCD \right)^{-1}$をそれぞれ掛けると
\begin{align*} \left( A + BCD \right)^{-1} BC \left( C^{-1} + DA^{-1}B \right) \left( C^{-1} + DA^{-1}B \right)^{-1} &= \left( A + BCD \right)^{-1} \left( A + BCD \right) A^{-1}B \left( C^{-1} + DA^{-1}B \right)^{-1}\\ \left( A + BCD \right)^{-1} BC &= A^{-1}B \left( C^{-1} + DA^{-1}B \right)^{-1} \end{align*}となります。
さらにこれに右から$C^{-1}$を掛けてあげると\begin{align*} \left( A + BCD \right)^{-1} B = A^{-1}B \left( C^{-1} + DA^{-1}B \right)^{-1} C^{-1} \end{align*}となって、証明終了
ちなみにpush through identityは逆行列の補助定理(証明)\begin{align*} \left( A + BCD \right)^{-1} = A^{-1} - A^{-1}B \left( DA^{-1}B + C^{-1} \right)^{-1} DA^{-1} \\ \end{align*}と、push through rule(証明)
\begin{align*} A \left( I + BA \right)^{-1} = \left( I + AB \right)^{-1} A \\ \end{align*}を組み合わせたもので、証明の手順はpush through ruleにならってます。
逆行列の補助定理の証明
実際に積をとって単位行列になるか確認します。
途中、ごちゃごちゃしてるようにみえるけど単に分配法則を適用してるだけです。\begin{align*} \left( A + BCD \right) \left[ A^{-1} - A^{-1}B \left( DA^{-1}B + C^{-1} \right)^{-1} DA^{-1} \right] &= \left\{ I - B \left( DA^{-1}B + C^{-1} \right)^{-1} DA^{-1}\right\} \\ & + \left\{ BCDA^{-1} - BCD A^{-1}B \left( DA^{-1}B + C^{-1} \right)^{-1} DA^{-1} \right\} \\ &= \left\{ I + BCDA^{-1} \right\} \\ & - \left\{ B \left( DA^{-1}B + C^{-1} \right)^{-1} DA^{-1} + BCD A^{-1}B \left( DA^{-1}B + C^{-1} \right)^{-1} DA^{-1} \right\} \\ &= I + BCDA^{-1} - \left( B + BCD A^{-1}B \right) \left( DA^{-1}B + C^{-1} \right)^{-1} DA^{-1} \\ &= I + BCDA^{-1} - BC \left(C^{-1} + D A^{-1}B \right) \left( DA^{-1}B + C^{-1} \right)^{-1} DA^{-1} \\ &= I + BCDA^{-1} - BCDA^{-1} \\ &= I \\ \end{align*}証明終了
push through ruleの証明
まず、$A + ABA$を$A$でくくると
\begin{align*} A + ABA = A \left( I + BA \right) \\ A + ABA = \left( I + AB \right) A \\ \end{align*}となるので、
\begin{align*} A \left( I + BA \right) = \left( I + AB \right) A \\ \end{align*}の等式が得られます。次にそれらに右から$\left( I + AB \right)^{-1}$を掛けると
\begin{align*} A = \left( I + AB \right) A \left( I + BA \right)^{-1} \\ \end{align*}となり、さらに両辺に左から$\left( I + BA \right)^{-1}$を掛けると
\begin{align*} \left( I + BA \right)^{-1} A = A \left( I + BA \right)^{-1} \\ \end{align*}となって証明終了
おまけ3:基底関数のバージョン
目的関数
\begin{align*} F = \frac{1}{2} \left( \mathbf{y} - \Phi \theta \right)^T G \left( \mathbf{y} - \Phi \theta \right) + \frac{1}{2} \theta^T H \theta\\ \end{align*}$\mathbf{y} \in \mathbb{R} ^N$:出力($N$個のデータ)
$\Phi \in \mathbb{R} ^{N \times M}$:計画行列($M$個の基底関数)
$\theta \in \mathbb{R} ^M$:パラメータ
$G \in \mathbb{R} ^{N \times N}$:データの重み(対称行列)
$H \in \mathbb{R} ^{M \times M}$:正則化項の重み(対称行列)推定したパラメータ
・基底関数表現\begin{align*} \hat{\theta} = \left( \Phi^T G \Phi + H\right)^{-1}\Phi^T G \mathbf{y} \\ \end{align*}・カーネル表現
\begin{align*} \hat{\theta} = H^{-1} \Phi^T \left( \Phi H^{-1} \Phi^T + G^{-1} \right)^{-1} \mathbf{y} \\ \end{align*}
- 投稿日:2019-08-19T14:03:01+09:00
Pythonの強化学習ライブラリKeras-RLのパラメータ設定
はじめに
PythonライブラリKeras-RLは強化学習のことがあまりわかっていなくても使えてしまうのですが、
細かいチューニングをしようと思うとパラメータの意味を理解していないといけません。そうすると強化学習の数式レベルの理解がある程度必要になります
(行動価値関数などの最終的な式の意図や動作が把握できている程度でよい)。よくわかっていないという人は個人的には以下の連載記事が一番わかりやすかったのでおすすめです。
今さら聞けない強化学習(1):状態価値関数とBellman方程式
本記事では、Keras-RLの各パラメータがどのような意味を持つのかを説明しながら、
実際の設定値などを紹介していきたいと思います。(私も完全に理解している訳ではないので誤りがありましたらコメントいただければと思います)
想定読者
- 強化学習の思想やKeras-RLの使い方の流れはわかったけど、細かいパラメータを適当に設定している人
Keras-RLのパラメータ
Keras-RL Documentationの Available Agentsには以下のAgentが利用可能であると記載されています。
- DQN
- DDPG
- NAF
- CEM
- SARSA
また、DDQN(DoubleDQN)とDuelingDQNはDQNのパラメータで設定できます。
数が多いので、ここでは最もメジャーなDQNに絞ってパラメータを見ていきます。
環境、DNNモデル
まずはgymの環境とDNNモデルを作成しておきます。
環境は例としてCartPole-v0とします。from keras.models import Sequential from keras.layers import Dense, Activation, Flatten, Dropout import gym env = gym.make('CartPole-v0') nb_actions = env.action_space.n model = Sequential() model.add(Flatten(input_shape=(1,) + env.observation_space.shape)) model.add(Dense(16)) model.add(Activation('relu')) model.add(Dropout(0.5)) model.add(Dense(16)) model.add(Activation('relu')) model.add(Dense(nb_actions)) model.add(Activation('linear'))DNNの入力層と出力層はニューロン数が固定されます。
DQNのDNNは「環境の観測値に応じた行動価値関数の近似」をするために用いられるので、
「環境で観測される値の次元=env.observation_space.shape」が入力となり、
「行動空間の次元=nb_actions」が出力となります。その間の層は全結合(Dense)やDropout、活性化関数(Activation)を自由に積み重ねてください。
Experience Replay用のメモリ
Experience ReplayとはDNNの学習を安定させるために用いられる仕組みです。
DNNは時系列に相関があるデータをその順番のまま使うとうまく学習できないらしいので、
メモリにaction、reward、observationsなどのデータを経験(Experience)として保管しておいて、後でランダムにデータを再生(Replay)して学習を行います。from rl.memory import SequentialMemory memory = SequentialMemory(limit=50000, window_length=1, ignore_episode_boundaries=False)
パラメータ 必須 意味 limit ○ メモリ(collections.deque)の上限サイズ。action(行動)、reward(報酬)、observations(観測)のそれぞれにdequeが用意される。上限を超えると古いデータが書き換えられていく window_length ○ 観測を何個連結して処理するか。例えば時系列の複数の観測をまとめて1つの状態とする場合に利用。 ignore_episode_boundaries エピソードの境界を無視するかどうか(別のエピソードの経験を利用する場合はTrue)。 なお、もうひとつ
rl.memoryにあるEpisodeParameterMemoryクラスはCEMで利用可能なメモリとのことです。行動ポリシー
from rl.policy import LinearAnnealedPolicy from rl.policy import SoftmaxPolicy from rl.policy import EpsGreedyQPolicy from rl.policy import GreedyQPolicy from rl.policy import BoltzmannQPolicy from rl.policy import MaxBoltzmannQPolicy from rl.policy import BoltzmannGumbelQPolicy # どれか選択 policy = LinearAnnealedPolicy(EpsGreedyQPolicy(), attr='eps', value_max=1., value_min=.1, value_test=.05, nb_steps=1000) policy = SoftmaxPolicy() policy = EpsGreedyQPolicy(eps=0.1) policy = GreedyQPolicy() policy = BoltzmannQPolicy(tau=1., clip=(-500., 500.)) policy = MaxBoltzmannQPolicy(eps=.1, tau=1., clip=(-500., 500.)) policy = BoltzmannGumbelQPolicy(C=1.0)行動ポリシーとは、環境において行動を選択する基準となるものです。
上記以外にも、Policyクラスを継承して自作してもいいとのことです。
LinearAnnealedPolicyは引数に指定したポリシーについて、attrに指定したパラメータをvalue_maxからvalue_minまでnb_steps回目までに線形に変化させるというものです。
value_testについてはテスト時の固定的なパラメータ値となります。
BoltzmannGumbelQPolicyについてはトレーニング時のみに利用できるポリシーとのことです。
パラメータ 必須 意味 eps ランダムな行動を選択する確率(イプシロン)。値が大きいほど探索に重きを置いて行動を決定する。 tau ボルツマン分布を利用したソフトマックス手法のQ値を割る値。 clip Q値を tauで割った後にクリップする範囲。C ガンベル分布の乗数 betaの計算式beta = C/np.sqrt(action_counts)で利用。エージェント
from rl.agents.dqn import DQNAgent agent = DQNAgent(nb_actions=nb_actions, memory=memory, gamma=.99, batch_size=32, nb_steps_warmup=1000, train_interval=1, memory_interval=1, target_model_update=10000, delta_range=None, delta_clip=np.inf, custom_model_objects={}, model=model, policy=None, test_policy=None, enable_double_dqn=False, enable_dueling_network=False, dueling_type='avg')大量にパラメータがありますが、必須のものはごく一部です。
パラメータ 必須 意味 nb_actions ○ 行動空間の次元数。環境により決まるためこの段階で変更することはない。 memory ○ 事前に作ったExperience Replay用のメモリ。 gamma 行動価値関数の式に出てくる割引率。将来の価値をどれくらい考慮するかを決める(値が大きいほど将来の価値を大きく反映する)。1未満の値を設定する。 batch_size 学習のバッチサイズ nb_steps_warmup ウォームアップステップ数。学習の初期は安定しないため、学習率を徐々に上げていく期間。 train_interval トレーニングのインターバル。 train_intervalステップ毎に学習が実行される。memory_interval Experience Replay用のメモリにデータを貯めるインターバル。 memory_intervalステップ毎にメモリに経験が保存される。target_model_update 0以上の値。1未満の値の場合はSoft updateと呼ばれ、 (1 - target_model_update) * old + target_model_update * newの式で重みが更新される。1以上の値の場合はHard updateと呼ばれ、int(target_model_update)ステップごとに重みが完全に更新される。delta_range 非推奨のパラメータ。delta_clipを代わりに使ってくれとのこと。もし値が設定された場合は delta_clip = delta_range[1]となる。delta_clip Huber損失のデルタ値。 custom_model_objects ターゲットモデルを生成する際のオプション。詳細はこちらを参照。 model ○ 事前に作ったDNNのモデル。 policy 行動ポリシー。設定しない場合はEpsGreedyQPolicyが適用される。 test_policy テスト時の行動ポリシー。設定しない場合はGreedyQPolicyが適用される。 enable_double_dqn DoubleDQN(DDQN)を適用するかどうか。 enable_dueling_network DuelingDQNを適用するかどうか。Trueにすると出力層の前の層にDueling Networkを挿入してくれる。 dueling_type Duelingネットワークのタイプ(enable_dueling_networkがTrueのときに使用)。行動価値関数 Q(s,a)を状態価値関数V(s)とアドバンテージA(s,a)から計算する際の計算方法を決める。avg、max、naiveが選択できるが、avgが推奨されているとのこと。具体的な式は以下を参照。 avg:
Q(s,a;theta) = V(s;theta) + (A(s,a;theta)-Avg_a(A(s,a;theta)))
max:Q(s,a;theta) = V(s;theta) + (A(s,a;theta)-max_a(A(s,a;theta)))
naive:Q(s,a;theta) = V(s;theta) + A(s,a;theta)エージェントのコンパイル
from keras.optimizers import Adam agent.compile(optimizer=Adam(lr=1e-3), metrics=['mse'])
パラメータ 必須 意味 optimizer ○ DNN重み更新の最適化手法。利用可能な手法はKerasのoptimizers。更新式はこの記事に整理されている。Adamであれば学習率(Learning rate: lr)は1e-3が論文で推奨されているらしい metrics 評価関数のリストで、Kerasの評価関数が使える。または自作の lambda y_true, y_pred: metricの形式で指定できる。指定の有無にかかわらずmean_qという評価関数が追加される。エージェントの学習
agent.fit(env=env, nb_steps=nb_steps, action_repetition=1, callbacks=None, verbose=1, visualize=False, nb_max_start_steps=0, start_step_policy=None, log_interval=10000, nb_max_episode_steps=None)
パラメータ 必須 意味 env ○ 事前に作った強化学習環境。 nb_steps ○ シミュレーションのステップ数。1ステップは、1回の観測、行動、報酬の獲得。 action_repetition 行動の繰り返し回数。2以上にすると、観測なしに同じ行動を action_repetition回繰り返す。callbacks コールバックのリスト。 rl.callbacks.Callbackを継承したコールバックが使える。ステップの開始・終了、エピソードの開始・終了、アクションの開始・終了がイベントとなる。verbose ロギングのモード。0でロギングなし、1で log_intervalステップ毎にロギング、2でエピソード毎にロギング。具体的にはrl.callbacks.TrainIntervalLoggerが呼ばれる。visualize 可視化のEnable。具体的には rl.callbacks.Visualizerが呼ばれる。環境でrender(mode='human'))が実装されていないと例外が起きる。nb_max_start_steps この値を最大値とする乱数値回目からステップを開始する。シミュレーションの開始位置を変動させたい場合に利用。この間はExperience Replayに記録されない。 start_step_policy nb_max_start_stepsが0でない場合に有効。nb_max_start_stepsまでの間にどのような行動ポリシーとするかをlambda observation: actionの形式で指定。Noneの場合はランダムに行動が選択される。log_interval ロギングするステップ間隔。 nb_max_episode_steps 1エピソードにおける最大のステップ数。 このパラメータを見ればわかるように、Keras-RLではエピソード数を決めるのではなく、
ステップ数と1エピソードにおける最大のステップ数で「最小のエピソード数」が決まります。
つまり、nb_steps / nb_max_episode_stepsが最小エピソード数となります。例えば
nb_steps=3000、nb_maxepisode_steps=300の場合は、最低3000/300=10回のエピソードが繰り返されます。
ただし、nb_max_episode_stepsよりも少ないステップ数でエピソードが終了することもあるので、
エピソード数は最大でnb_steps回となります(ほぼありえませんが、毎回1ステップ目でシミュレーションが終了する場合)。おわりに
今回はDQNのパラメータを見てきましたが、他のAgentでも共通する部分もあればそうでない部分もあります。
(異なる部分は例えば、SARSAはExperience Replayをしないのでメモリが不要、など)公式ドキュメントがそれほど充実しているわけではないので、
もし他のAgentのパラメータ設定について知りたい場合はソースコードを見るのが手っ取り早いと思います。
- 投稿日:2019-08-19T13:26:59+09:00
xarrayによるnetCDF読込と便利な内挿処理
はじめに
Python環境でのnetCDFファイルの処理に関し,かつてよりnetCDF4というパッケージが用いられてきた.その後,機能性や応用性を増強したarray処理用パッケージxarrayが開発され,シェアが広がりつつある(たぶん).
今回は,ひとつの有用な機能である内挿処理を用いるコードの例を紹介する.Pythonのバージョンは3.7系.使用モジュール
import numpy as np import xarray as xr import multiprocessing as mp準備:Look Up Tableの作成
準備段階として,まず,サンプルとなる配列をnetCDF形式で保存する.
本記事では,内挿補間により一つの値を取得するための土台として,この配列をLook up table (LUT)と名付ける.# 各次元のサイズ sz_1 = 10 sz_2 = 9 sz_3 = 8 # 各次元の配列(今回は0-1間で等間隔に値をとった配列を使用) ax_1 = np.linspace(0,1,sz_1) ax_2 = np.linspace(0,1,sz_2) ax_3 = np.linspace(0,1,sz_3) # 3種類の3次元データ(適当に作成) data1 = np.arange(sz_1*sz_2*sz_3 ).reshape(sz_1,sz_2,sz_3) data2 = np.linspace(0,10,sz_1*sz_2*sz_3 ).reshape(ln_0,ln_1,ln_2) data3 = np.linspace(-1,1,sz_1*sz_2*sz_3 ).reshape(sz_1,sz_2,sz_3) # xarray配列の生成 LUT = xr.Dataset({'data1': (['dim_1', 'dim_2', 'dim_3'], data1), 'data2': (['dim_1', 'dim_2', 'dim_3'], data2), 'data3': (['dim_1', 'dim_2', 'dim_3'], data3),}, coords={'dim_1': ax_1, 'dim_2': ax_2, 'dim_3': ax_3,}) # netCDFで保存 LUT.to_netcdf('sample_interp_3d.nc')内挿処理用クラスの定義
クラスを定義する.役割は2つで,
sample_lut()が呼ばれた直後(__init__)に自動でLUTが読み込まれる.- 各次元の値を指定することで内挿保管した値を返す(
Extract()).xarrayには,
interp()というメソッドが備わっており,次元の値を指定した配列値の取得がとても簡単かつ直感的な形でできる(scipyの関数を用いているらしい.詳細はこちら→公式).class sample_lut(object): def __init__(self): self.LUT = self.Open() def Open(self): ''' Open LUT as xarray dataset. ''' return xr.open_dataset('sample_interp_3d.nc').load() def Extract(self,dict_items): ''' Extract result. ''' extracted = self.LUT.interp(dim_1=dict_items['v_1'], dim_2=dict_items['v_2'], dim_3=dict_items['v_3'],) r_1 = extracted.data1.data r_2 = extracted.data2.data r_3 = extracted.data3.data return [r_1, r_2, r_3]上記コードですこし補足を加える.
open_dataset()でnetCDFファイルの読込が可能.詳細はこちら→公式load()メソッドは,デフォルトでは部分的にのみにしか読み込まない配列を,一度すべてメモリに書き出すために含めている.公式ドキュメントには下記のような記述がある.実際,このあと行う並列処理の際にload()なしだと予期せぬ挙動を示したため,今回は含めている.xarray’s lazy loading of remote or on-disk datasets is often but not always desirable. Before performing computationally intense operations, it is often a good idea to load a Dataset (or DataArray) entirely into memory by invoking the load() method.
(Google翻訳)xarrayのリモートデータセットまたはディスク上のデータセットの遅延読み込みは、常に望ましいとは限りません。計算量の多い操作を実行する前に、load()メソッドを呼び出してDataset(またはDataArray)を完全にメモリにロードすることをお勧めします。内挿処理の実行
# テーブル読込 LUT = sample_lut() # 入力(各次元の値を指定) items = dict(v_1 = 0.1, v_2 = 0.2, v_3 = 0.3) # 内挿補間 outp = LUT.Extract(items) print(outp) # [79.7 1.10848401 -0.7783032 ]multiprocessingを用いた並列処理
内挿処理の速度はそこまで早くないため,入力の組み合わせが大量にある場合,コードを並列化するのがよい.
# 各次元の値を適当に100個作成 ar_v1, ar_v2, ar_v3 = np.random.rand(3,100) # 先にLUTを読み込んでおく LUT = sample_lut() # 内挿処理を関数化 def process(v1, v2, v3): items = dict(v_1 = v1, v_2 = v2, v_3 = v3) # 関数外部で読み込んだLUTを用いて内挿 outp = LUT.Extract(items) return outp # 並列処理(3変数を入力に使用するためにstarmap関数を使用) num_proc = 4 p = mp.Pool(processes=num_proc) ar_out = p.starmap(process, zip(ar_v1, ar_v2, ar_v3)) p.close() print(ar_out)注意点:読み込み時に
load()を含めなかった際の挙動クラス定義のところで
load()に関する補足説明を加えたが,これを使用しなかった(xr.open_dataset('sample_interp_3d.nc')だけにした)場合,次のような挙動が発生する.# 先にLUTを読み込んでおく LUT = sample_lut() def process(n): # 入力を1組だけに固定 items = dict(v_1 = 0.1, v_2 = 0.2, v_3 = 0.3) # 関数外部で読み込んだLUTを用いて内挿 outp = LUT.Extract(items) return outp # 並列処理(テストとして,同じ入力での計算を100回行う) num_proc = 4 p = mp.Pool(processes=num_proc) ar_out = p.map(process, range(100)) p.close() print(ar_out) ''' 出力が一致しない [[ 2.62198422e+017 6.41668327e-309 -7.78303199e-001] [ 2.62198422e+017 6.41668327e-309 -7.78303199e-001] : : : [ 2.62198422e+017 6.41668327e-309 -7.78303199e-001] [ 7.97000000e+001 6.41668327e-309 0.00000000e+000] [ 7.97000000e+001 6.41668327e-309 0.00000000e+000] : : : [ 7.97000000e+001 6.41668327e-309 0.00000000e+000] [ 7.97000000e+001 1.10848401e+000 -7.78303199e-001] : : : '''挙動発生の仕組みは不明だが,
load()を含めることによってこのようなエラーは解消される.おわりに
ものすごく便利そうなパッケージxarrayの記事がもう少し増えてくれることを祈る.
- 投稿日:2019-08-19T13:26:00+09:00
【備忘録】PythonでSQLite3を使う
環境
Windows 10
Python 3.6.8(Anaconda3)SQLite3のダウンロード
①https://www.sqlite.orgにアクセス
②「Download」をクリック
④展開したフォルダ内のファイルをAnacondaのパス(※)が通っているフォルダにコピーし、ターミナルから
sqlite3コマンドで呼び出せるようにする
※ C:\Users{ユーザー名}\Anaconda3\Scripts などSQLite3の使い方
概要
sqlite3をインポートしたうえで、conn = sqlite3.connect('DB名')でデータベースと接続し、curs = conn.cursor()でカーソルオブジェクトを生成し、curs.execute('SQL文')でSQL文を実行し、conn.commit()でコミット(実行を確定)する。
最後に、curs.close()とconn.close()でカーソルとDB接続を終了する。コード例
import sqlite3 conn = sqlite3.connect('test.db') # カーソル(こいつにどうして欲しいか指示をしていく) curs = conn.cursor() # テーブル作成を指示する(コミットしないとDBに登録されないので要注意) curs.execute( 'CREATE TABLE persons(id INTEGER PRIMARY KEY AUTOINCREMENT, name String)' ) conn.commit() # テーブルに値を挿入する curs.execute( 'INSERT INTO persons(name) values("Taro")' ) conn.commit() # 値を更新する curs.execute('UPDATE persons SET name = "Jiro" WHERE name = "Taro"') conn.commit() # 検索してコンソールに表示する curs.execute( 'SELECT * FROM persons;' ) print(curs.fetchall()) # カーソルとDB接続を終了する curs.close() conn.close()
- 投稿日:2019-08-19T13:22:10+09:00
ABC138参戦記
はじめに
ABC138に参加しました。結果は以下の通りです。
結果:5完 60分+2WA
順位:742
パフォーマンス:1490
レート変動:1506→1502
結果はちょっと良くなかったですね...来週の第一回日本最強プログラマー学生選手権の予選に向けて頑張りたいと思います。
以下問題を振り返っていきます。言語はPython3(Pypy3)です。A
time: 1:30
はいa = int(input()) s = input() print('red' if a<3200 else s)(ちょっと短く書き直してみました)
B
time: 1:30
はいN = int(input()) A = list(map(int, input().split())) res = 0 for ai in A: res+=1/ai print(1/res)C
time: 18:00
ソートして小さい方からかなぁと思ったのですが確信が持てず、一回飛ばしてDを先に解きました。戻ってきてからも証明がよくわからなかったのでぐだぐだ考えてしまいました...冷静に考えればそれはそうだし、C問題なのでそんなに深く考えるべきではなさそうだし、目をつぶって提出すべきでしたね。完全に戦略ミスです。反省。N = int(input()) v = list(map(int, input().split())) v.sort() for i in range(N-1): v = [(v[0]+v[1])/2]+v[2:] print(v[0])D 8:00+1WA
time: 10:00+1WA
ちょっと前にオイラーツアーとかを学んでたので、それかなぁとか思ったんですが、冷静にDに出るようなものではなさそうなので、もう少し考えると、まず頂点pのカウンターにxを加えておき、それを最後に下に累積和的な感じで伝えていけば良いことがわかりました。どうやって下に伝えるかですが、DFSでもBFSでも良さそうだったので、dequeを使うと簡単に実装できるBFSを用いました。ちょっといもす法っぽいなぁと思いながらpypyで提出しましたが、結果はなんと1948ms! 心臓に悪いですね... あと一回リストをprintするものを提出するという大失態を犯し1WA。反省。from collections import deque N, Q = map(int, input().split()) G = [[] for _ in range(N)] count = [0]*N for i in range(N-1): a, b = map(int, input().split()) G[a-1].append(b-1) G[b-1].append(a-1) for i in range(Q): p, x = map(int, input().split()) count[p-1]+=x q = deque([0]) flag = [False]*N while q: v = q.pop() flag[v] = True for e in G[v]: if flag[e]: continue count[e]+=count[v] q.append(e) print(*count)本番ではリストを空白区切で出力するのに' '.join(list(map(str, count)))を使ったのですが冗長すぎました。*countの方が簡潔で速いです。
E
time: 27:00+1WA
まず、文字列tの前方から貪欲にsの出来るだけ長い部分列を取り除いていく問題であることがわかります。ただそれをナイーブに実装していてはとても間に合わないので、下処理を施しておくことで、どうにか高速に処理できないかなぁと考えます。ここでよくあるテクニックが各要素についてそれが出現するインデックスをはじめにメモしておくことです(インデックスの逆写像的なやつです)。
こうすれば任意の要素についてその出現箇所がすぐにわかるようになります。そうすると部分列というのはインデックスの増加列と対応しているので(実は今日、こういう話を数学のゼミでちょっと触れました)、tの前方から、tの要素に対応するインデックスの中から適当に一つ選ぶことによって出来るだけ長い増加列を作るという問題にすり替わります。これは貪欲に実現できます。つまり、「直前のインデックスより大きい最小のインデックスを選ぶ」とすれば良いです。これは二分探索によりO(logn)で実現できるので全体としてはO(nlogn)くらいで解けました。
ところで、これは本質ではないですが、pythonのbisectライブラリにはbisect_leftとbisect_rightという二つの関数が存在します。どちらもxよりも大きい最小の要素のインデックスを返しますが、xが要素に含まれる際の挙動が異なります。例えばbisect_left([0, 1, 2, 3, 4], 1) = 1ですが, bisect_right([[0, 1, 2, 3, 4], 1) = 2となります。より正確に言えば、bisect_leftはx以上要素のうち最小のインデックスを返し、bisect_rightはxより真に大きい要素のうち最小のインデックスを返します。今回は狭義の増加列を求めたいのでbisect_rightを使うべきですが、僕は最初bisect_leftを使ってしまいWAになってしまいました。反省。import sys from bisect import bisect_right s = input() t = input() n = len(t) index = [[] for i in range(26)] for i in range(len(s)): j = ord(s[i])-97 index[j].append(i) tmp = -1 ans = 0 for i in range(n): j = ord(t[i])-97 if len(index[j])==0: print(-1) sys.exit() k = bisect_right(index[j], tmp) if k<len(index[j]): tmp = index[j][k] else: ans+=1 tmp = index[j][0] print(ans*len(s)+tmp+1)97はord('a')です。
F
制約が10**18と無茶苦茶大きいので$log$がかかる感じにならないと間に合いそうにないです。そこで二進表示の桁ごとに考えるという方針が立ちます。ごちゃごりゃ考えていると、$x\rm xory$がxで割った余りであることから、$x \rm xor y < x$であることがわかります。もしxとyの二進数での桁が異なるとすると例えばx=1010, y = 10001などを考えればわかるようにx xor yはyと同じ桁数になってしまうので$x<x \rm xor y$となり矛盾します。よってxとyの桁数は等しいことがわかります。そうすると必然的に$y%x=y-x$となるので、結局問題の条件は$x \rm xor y = y-xと$言い換えることができます。これは桁ごとに考えることができるので、x,yの各桁ごとの組は(0, 0), (0, 1), (1, 1)のみであることもわかります。問題は端っこの処理です。こういうのは桁dpだろうなぁと思ったのですが、うまくまとめきれずコンテスト中には解けませんでした。
以下は解説を参考にして書きました。
問題を整理すると以下のようにまとめられます。L<x, y<R、x, yの最上位ビットが同じであるという三つの条件を満たす(0, 0), (0, 1), (1, 1)の列 の個数を求める。
そこで以下のようなdpを考えます。
dp[i][flag_L][flag_R][flag_M](i:確定している桁, flag_L:L<xがすでに満たされているか, flag_R:flag_Lと同様, flag_M:最上位ビットが等しいという条件がすでに満たされているか)普通の桁dpと比べて条件が2つ増えており、なかなかに煩雑ですが、気合いを入れて実装すると以下のようになります。
L, R = map(int, input().split()) mod = 10 ** 9 +7 l = '{:060b}'.format(L) r = '{:060b}'.format(R) memo = [[[[-1]*2 for i in range(2)] for j in range(2)] for k in range(60)] def f(pos, flagL, flagR, flagM): if pos == 60: return 1 if memo[pos][flagL][flagR][flagM] != -1: return memo[pos][flagL][flagR][flagM] ret = 0 #(0, 0) if flagL or l[pos] == '0': ret+=f(pos+1, flagL, 1 if r[pos]=='1' else flagR, flagM) #(0, 1) if flagM and (flagL or l[pos]=='0') and (flagR or r[pos]=='1'): ret += f(pos+1, flagL, flagR, flagM) #(1, 1) if flagR or r[pos]=='1': ret += f(pos+1, 1 if l[pos]=='0' else flagL, flagR, 1) memo[pos][flagL][flagR][flagM] = ret%mod return ret%mod print(f(0, 0, 0, 0)%mod)二進表示の文字列を取得する'{:060b}'.format()は覚えておきたいですね。あと条件分岐も3つのif文の線型結合的に書くと、結構楽に実装できるのはうまいなぁと思いました。今回は再帰関数の方が楽っぽいですね。
メモ
ord: alphabet→num
bisect_rightとbisect_leftの違い
インデックスの逆写像
桁DP
'{:060b}'.format()
- 投稿日:2019-08-19T13:17:14+09:00
WaveNetの解説とkeras実装
はじめに
今更WaveNetの解説?と思われる方もいると思いますが、個人的に得られる知見が多かったディープラーニングのモデルだったので、実装した当時のメモや記憶を頼りにアウトプットしていきたいと思います。
ソースコードはgithubで公開しています。
https://github.com/kshina76/keras_wavenet環境
python3.7.3
Anaconda3
keras2.2.4
tensorflow1.13.1WaveNetとは
CNN(畳み込みニューラルネットワーク)を何層にもわたって構築されたネットワーク。論文が発表された当初、とても流暢な英語や日本語を発声させることができるとして話題になった技術でした。論文が発表される以前の音声合成では、機械に発声させるとロボットのような声でとても人間とは程遠い発声でしたが、WaveNetの登場により、人間の声なのか機械が作り出した声なのか判別できなくなるほどのものを作り上げることができるようになりました。
音声の研究者も「このような音声合成技術ができるのに10年はかかると思った」といわれるほど、衝撃的な技術だったそうです。
また、WaveNetはGoogle assistantに音声合成技術として搭載されているようです。詳しいモデル構成を説明するにあたって、まずはデータの取り扱いや前処理について説明する必要があるので、そのことを説明したのちにモデル構成の説明に入っていこうと思います。
データの前処理
今回は、音声データとしてvctk corpusを使用しました。
無音区間の除去
WaveNetでは、切り出した音声区間がすべて無音だと、無音を学習してしまうことにより生成する音声が無音になってしまうという不具合があるそうです。なので、まずは無音区間の除去を行うことにします。
※指定した音声区間とは、receptive field(受容野)という区間のことで、説明は後述するので、ここではWaveNetの学習の際に入力するサンプル長だと思ってください。
音声データ取得
まずは、音声ファイルのパスを一覧取得するメソッドを実装します。directoryには、複数の音声ファイルが置かれているディレクトリを指定してください。
def get_files(self, directory): files = [] for dir_path,dir_name,file_name in os.walk(directory): for file_name in file_name: files.append(os.path.join(dir_path,file_name)) return files音声ファイルのパスから音声を取り込むメソッドを実装します。サンプリングレートは16000とします。
def get_audio(self, files, sample_rate): for file in files: audio, _ = librosa.load(file, sr=sample_rate) yield audio除去と正規化
それでは、実際に無音区間の除去を実行しましょう。今回thresholdは、20に設定しています。ついでに正規化も行っておきます。
for audio in get_audio(files, sample_rate): audio, _ = librosa.effects.trim(audio, top_db=threshold) audio /= np.abs(audio).max()μ-law量子化
人間の聴覚に合わせた量子化方法。音が大きくなればなるほど粗い量子化幅になり、小さければ小さいほど細かい量子化幅になる特殊な量子化。この量子化方法により、少ない量子化ビット数でも量子化誤差の低減を可能にする。
WaveNetでは8bit量子化をしてからモデルに入力として渡すので、'mu'は256とするdef transform(x): x = x.astype(float_type) y = np.sign(x) * np.log(1 + mu * np.abs(x)) / np.log(1 + mu) y = np.digitize(y, 2 * np.arange(mu) / mu - 1) - 1 return y.astype(int_type) def itransform(y): y = y.astype(float_type) y = 2 * y / mu - 1 x = np.sign(y) / self.mu * ((1 + self.mu) ** np.abs(y) - 1) return x.astype(float_type)paddingとtrimming
今回は、WaveNetの入力として7680サンプルとるので、7680サンプルに満たない音声が入力されたら足りない分をゼロで埋める処理(ゼロパディング)をします。
逆に7680を超えている音声が入力されたら7680サンプルに合わせるようにトリミングをします。
また、切り取る区間はランダムで指定するようになっています。if self.threshold is not None: if len(audio) <= self.receptive_field: # padding pad = self.receptive_field - len(audio) audio = np.concatenate((audio, np.zeros(pad, dtype=np.float32))) # padding with middle of quantized audio quantized = np.concatenate((quantized, self.quantize // 2 * np.ones(pad))) quantized = quantized.astype(np.int64) else: # trimming audio into receptive_field (trimming) start = random.randint(0, len(audio) - self.receptive_field - 1) audio = audio[start:start + self.receptive_field] quantized = quantized[start:start + self.receptive_field]以上で前処理は終了しますが、実用的なWaveNetとしては、メルスペクトログラムを計算して話者の特定をすることで、自由自在なモデルを構築できるようになります。その処理をglobal conditioningといいます。githubで公開しているのでそちらを見てください。
WaveNetモデルの構築
WaveNetの全体像
上記のWaveNetモデルを3つのセクションに分けて実装していきます。
Residual Block
def ResidualBlock(self, block_in, dilation_index): res = block_in tanh_out = Conv2D(self.d_channels, (self.filter_size, 1),padding='same', dilation_rate=(dilation_index, 1), activation='tanh')(block_in) sigm_out = Conv2D(self.d_channels, (self.filter_size, 1), padding='same', dilation_rate=(dilation_index, 1), activation='sigmoid')(block_in) marged = Multiply()([tanh_out, sigm_out]) res_out = Conv2D(self.r_channels, (1,1), padding='same')(marged) skip_out = Conv2D(self.s_channels, (1,1), padding='same')(marged) res_out = Add()([res_out,res]) return res_out, skip_outResidualNet
さっき作ったResidualBlockを重ねることでResidualNetを構築していきます。
def ResidualNet(self, block_in): skip_out_list = [] for dilation_index in self.dilation: res_out, skip_out = self.ResidualBlock(block_in, dilation_index) skip_out_list.append(skip_out) block_in = res_out return skip_out_listWaveNet
ResidualNetとその他のactivationをつなげることでWaveNetの完成です。
def wavenet(self): inputs = Input(shape=(self.img_rows, self.img_columns, self.a_channel)) causal_conv = Conv2D(self.r_channels, (self.filter_size, 1), padding='same')(inputs) skip_out_list = self.ResidualNet(causal_conv) skip_out = Add()(skip_out_list) skip_out = Activation('relu')(skip_out) skip_out = Conv2D(self.a_channel, (1,1), padding='same', activation='relu')(skip_out) prediction = Conv2D(self.a_channel, (1,1), padding='same')(skip_out) prediction = Flatten()(prediction) prediction = Dense(self.a_channel, activation='softmax')(prediction) model_wavenet = Model(input=inputs,output=prediction) optimizer = Adam() model_wavenet.compile(optimizer=optimizer,loss='categorical_crossentropy',metrics=['accuracy']) model_wavenet.summary() return model_wavenet
- 投稿日:2019-08-19T13:14:36+09:00
UWSC を Python で置換しよう(1)環境構築編
はじめに
Windowsの自動化には、昔からUWSCという超便利なツールがあったのですが、開発者がいなくなってしまい、今後バージョンアップや、新しいOSへの対応が期待できない状態になってしまいました。そこで、今後も開発が継続されていくであろうPythonにその機能を移植していきたいと思います
※構築には2時間ほどかかります
環境構築
ここでは、UWSCに合わせて、Windowsでの実行環境を用意していこうと思います
UWSCが持っていた機能に合わせてモジュールを追加します
- OS : Windows 10 64bit
- MW : Python 3.7.4 64bit
- -- : PyAutoGUI (画像判定 / マウス・キーボード操作)
- -- : OpenCV (画像処理)
- -- : PyWin32 (Win32Api/Win32COM OLE/COMオブジェクト操作)
- -- : PyAudio (オーディオ操作)
- -- : SpeechRecognition (音声認識)
- -- : eSpeak (音声合成)
- -- : Selenium (ブラウザ操作)
- -- : BeautifulSoup (html/xmlパーサー)
- -- : xlrd , xlwt (Excel 読み書き)
- -- : ReportLab (PDF 読み書き)
- -- : PyInstaller (EXE 形式単一実行ファイル生成)
- -- : ConfigParser (cfg/ini 形式の読み込み)
- -- : Math (三角関数の利用[デフォルトモジュール])
- -- : Time (時間関数 時間取得/計測など[デフォルトモジュール])
- -- : Os , Sys (環境 [デフォルトモジュール])
- -- : re (正規表現 [デフォルトモジュール])
UWSCのマニュアルを読む限り追加、無料版UWSCと有償版UWSC Proが持っていた機能は網羅できるはず
まず、モジュールの中にMicrosoft Visual C++ Build Toolsが必要なものがあるのでインストールする
※Visual Studio 2019のBuild Tools ではPyAudioがコンパイルできなかった
# 以下URLよりVisual C++ Build Toolsをダウンロードしてインストール https://go.microsoft.com/fwlink/?LinkId=691126 #(インストールが終わったら一度ここで再起動)ではPythonのセットアップ開始、PowerShellを開いて実行します
powershell#Windows x86-64 executable installer Invoke-WebRequest -Uri "https://www.python.org/ftp/python/3.7.4/python-3.7.4-amd64.exe" -OutFile "python-3.7.4-amd64.exe" python-3.7.4-amd64.exe #インストール先は C:¥Python37 とする、インストール時にPATHを設定するにCheckを忘れない #(インストールが終わったら一度ここで再起動)再起動したら、PowerShellを開いてモジュールを追加していきます
cd C:¥Python37 pip install --upgrade pip --user pip install pyautogui pip install opencv_python pip install pywin32PyAudioはちょっと問題が多いので、以下からパッケージをダウンロードする。ここでは、Win10 64bit & Python 3.7.x 64Bitな環境なので
PyAudio‑0.2.11‑cp37‑cp37m‑win_amd64.whlをダウンロードhttps://www.lfd.uci.edu/~gohlke/pythonlibs/#pyaudioダウンロードしたファイルをpipでインストール
pip install .¥PyAudio‑0.2.11‑cp37‑cp37m‑win_amd64.whlさらにモジュールを追加していきます
pip install speechrecognition pip install speake3 pip install selenium pip install beautifulsoup4 pip install xlrd xlwt pip install reportlab pip install pyinstaller pip install configparser導入したモジュールは以下の通りです
pip freeze altgraph==0.16.1 beautifulsoup4==4.8.0 configparser==3.8.1 future==0.17.1 MouseInfo==0.0.4 numpy==1.17.0 opencv-python==4.1.0.25 pefile==2019.4.18 Pillow==6.1.0 PyAudio==0.2.11 PyAutoGUI==0.9.47 PyGetWindow==0.0.7 PyInstaller==3.5 PyMsgBox==1.0.7 pyperclip==1.7.0 PyRect==0.1.4 PyScreeze==0.1.22 PyTweening==1.0.3 pywin32==224 pywin32-ctypes==0.2.0 reportlab==3.5.23 selenium==3.141.0 soupsieve==1.9.3 speake3==0.3 SpeechRecognition==3.8.1 urllib3==1.25.3 xlrd==1.2.0 xlwt==1.3.0あとはブラウザの制御を行うためにWeb Driverを各種導入します
導入しているブラウザのバージョンに合わせたものをダウンロードして、Pythonのインストール先に解凍(ここではC:¥Python37)
- Chrome (ChromeDriver)
https://chromedriver.storage.googleapis.com/index.html
- FireFox (Gekko Driver)
https://github.com/mozilla/geckodriver/releasesさいごに
ここまでセットアップして、環境構築は完了です。
次回は
UWSC を Python で置換しよう(2)関数置き換え
ということで、UWSCで書いたスクリプトを構築した環境を使ってPythonスクリプトに置き換えてみる予定です。
- 投稿日:2019-08-19T12:58:00+09:00
筋肉空間の提案とボディービルの掛け声生成への応用
本文書について
本文書では、筋肉トレーニングメニューを含むテキストを入力としてボディービル大会等で用いられる掛け声を生成・出力する手法について述べる。
提案する手法は、入力された筋トレメニューを主要な筋肉部位を基底として定義した筋肉空間上のベクトルに変換し、当該筋肉ベクトルを用いて適切なボディービルの掛け声を推定・出力する。
本文書ではさらに、当該手法を用いて実装した筋トレメニューをつぶやくとボディービルの掛け声をreplyするslack botについて、その出力結果と使用感について共有する。ボディービルの掛け声生成
概要
より具体的に書くと筋トレメニュー空間から掛け声空間への写像である。
例えば
腕立て伏せを大胸筋が歩いているに紐付ける、などの組み合わせによるルールを用いることで当該写像を実現することは出来るが、筋トレメニューや掛け声は両者とも日々増えていく性質を持つため、すべての組み合わせを網羅したルールを記述することは現実的ではない。一つの方法として、固定次元を持つ何らかの中間的な空間へ一時的に写像しベクトル間の類似度を参照して変換する方法が考えられる。
筋トレメニューからの中間空間への変換と中間空間からの掛け声への変換を独立に考えることが出来るため、両者間のすべての組み合わせを検討することなく筋トレメニューからボディービルの掛け声への変換が実現できる。本文書では、中間的な空間として主要な筋肉部位を基底として定義する 筋肉空間 の利用を提案する。
筋肉空間
ここでは、人体における主要な筋肉をいくつか選択し各筋肉に対応する基底ベクトルによって筋肉空間を定義する。
主要筋肉は各筋トレメニューが鍛える対象となる筋肉や掛け声に紐付けられる筋肉との関連性が求めやすいため、筋トレメニュー空間及び掛け声空間からの筋肉空間への写像が比較的容易と考えられるためである。本文書では、下記の11筋肉を主要筋肉として定義し各主要筋肉に対応する基底を持つ11次元の空間を筋肉空間として定義した。
各筋トレメニュー及び掛け声は後述する処理により筋肉空間上の11次元のベクトルとして表現することが出来る。
- 三角筋
- 僧帽筋
- 上腕二頭筋
- 上腕三頭筋
- 広背筋
- 大胸筋
- 腹直筋
- 大臀筋
- 大腿四頭筋
- 大腿二頭筋
- 腓腹筋
筋トレメニュー/掛け声からの筋肉ベクトルへの変換方法について
筋トレメニュー空間の各元はメニュー名に紐づく筋肉であるターゲット筋肉の情報を持つ。
メニュー名 ターゲット筋肉 腕立て伏せ 大胸筋,上腕三頭筋 プランク 大腰筋,腹横筋,脊柱起立筋 ツイストドラゴンフラッグ 外腹斜筋,内腹斜筋 また同様に掛け声空間の各元も掛け声に紐づくターゲット筋肉情報を持つ。
掛け声名 ターゲット筋肉 大胸筋が歩いている 大胸筋 お尻にバタフライ 大臀筋,中臀筋 筋トレメニュー空間及び掛け声空間を筋肉空間に写像する上で主要筋肉とターゲット筋肉間の類似度を利用する。
本文書では、筋トレメニューまたは掛け声に紐づく各ターゲット筋肉を主要筋肉の類似度に基づく筋肉ベクトル$\vec{t}$に変換し、その和を筋トレメニューまたは掛け声の筋肉ベクトル$\vec{m}$とした。
ここで、ターゲット筋肉と主要筋肉の類似度は各筋肉の定義文をそれぞれ用意し、文間の類似度をCOTOHAのsimilarity APIを用いて算出した。
例えば、腓腹筋とヒラメ筋であれば、予め用意したそれぞれの定義文脚のふくらはぎを構成する筋肉、腓腹筋とともに下腿三頭筋を構成する筋肉間の類似度を計算する。筋肉ベクトル$\vec{m}$は下記の式で表現することが出来る。
\vec{m} = \sum \vec{t}ただし、
t_i = \left\{ \begin{array}{ll} 1 & (t^{def} = m_i^{def}) \\ 0.8 & (\arg \max_i similarity(t^{def}, m_i^{def})) \\ 0 & (other) \end{array} \right. \\ここでt_iは筋肉ベクトル$\vec{t}$のi次元目の値を、$t^{def}$はターゲット筋肉の定義文を、$m_i^{def}$はi番目の主要筋肉の定義文を、$similarity(X,Y)$はX,Y間の類似度を示す。
参考スクリプト(muscle_space.py)
# -*- coding: utf-8 -*- import sys import os import pickle import json import requests import time CLIENT_ID = 'XXX' CLIENT_SECRET = 'XXX' API_BASE_URL = 'https://api.ce-cotoha.com/api/dev/nlp/' ACCESS_TOKEN_PUBLISH_URL = 'https://api.ce-cotoha.com/v1/oauth/accesstokens' def get_access_token(): headers = {'Content-Type': 'application/json', 'charset': 'UTF-8',} data = {'grantType':'client_credentials', 'clientId':CLIENT_ID, 'clientSecret':CLIENT_SECRET} data = json.dumps(data) response = requests.post(ACCESS_TOKEN_PUBLISH_URL, headers=headers, data=data) response = json.loads(response.text) return response['access_token'] if not os.path.isfile('./ACCESS_TOKEN.pickle'): ACCESS_TOKEN = get_access_token() with open('ACCESS_TOKEN.pickle', mode='wb') as f: pickle.dump(ACCESS_TOKEN, f) with open('ACCESS_TOKEN.pickle', mode='rb') as f: ACCESS_TOKEN = pickle.load(f) def similarity(s1,s2): global ACCESS_TOKEN headers = {'Content-Type': 'application/json', 'charset': 'UTF-8', 'Authorization': 'Bearer '+ACCESS_TOKEN} data = {'s1':s1, 's2':s2} data= json.dumps(data) response = requests.post(API_BASE_URL+'v1/similarity', headers=headers, data=data) response = json.loads(response.text) if response['status'] == 99998: ACCESS_TOKEN = get_access_token() with open('ACCESS_TOKEN.pickle', mode='wb') as f: pickle.dump(ACCESS_TOKEN, f) return similarity(s1,s2) try: score = response['result']['score'] except: print(response['message']) time.sleep(1) return similarity(s1,s2) return score class MuscleSpace: def __init__(self, basis_path, other_path, vec_path): self.basis_muscles = dict() self.other_muscles = dict() self.muscle2vector = dict() with open(basis_path) as fin: for line in fin: line = line.strip() m,d = line.split(',') self.basis_muscles[m] = d with open(other_path) as fin: for line in fin: line = line.strip() m,d = line.split(',') self.other_muscles[m] = d if os.path.isfile(vec_path): with open(vec_path, mode='rb') as f: self.muscle2vector = pickle.load(f) else: self._compute_muscle_vector() def _compute_muscle_vector(self): idx = list(self.basis_muscles.keys()) for m in self.basis_muscles.keys(): vec = [0.] * len(idx) vec[idx.index(m)] = 1. self.muscle2vector[m] = vec for m,d in self.other_muscles.items(): vec = [0.] * len(idx) for basis_m in idx: sim = similarity(d, self.basis_muscles[basis_m]) vec[idx.index(basis_m)] = sim self.muscle2vector[m] = vec with open(vec_path, mode='wb') as f: pickle.dump(self.muscle2vector, f) def muscles2vec(self, muscles): vec =[0.]*len(self.basis_muscles) for m in muscles: m_vec = self.muscle2vector[m] if max(m_vec)==1.: vec[m_vec.index(1.)] += 1. else: vec[m_vec.index(max(m_vec))] += 0.8 return vec if __name__ == "__main__": ''' 【basis_definition.txt 例】 三角筋,肩を覆う大きな筋肉 僧帽筋,背中の中央から上部の表層に広がる大きな筋 ... 【other_definition.txt 例】 肩甲下筋,腕を内向きにひねる肩関節内旋の主働筋 小胸筋,胸部の筋肉のうち、胸郭外側面にある胸腕筋のうちの一つ ... ''' ms = MuscleSpace('../data/basis_definition.txt', '../data/other_definition.txt', '../data/m_vec.pickle') vec = ms.muscles2vec(['大胸筋', 'ヒラメ筋']) print(vec)掛け声生成
上述した筋肉ベクトルへの変換手法を用いて筋トレメニューからの掛け声生成を行う。
まず、入力された文章に含まれる筋トレメニューをすべて抽出する。
抽出された筋トレメニューに対して筋肉ベクトル変換を行うことで入力文に対する筋肉ベクトルを得ることが出来る。得られた筋肉ベクトルと予め計算した掛け声に対する筋肉ベクトルについて筋肉空間上のcos類似度を計算することで類似している掛け声を推定する。
ここでは多様な掛け声が生成されることを期待して類似度が高い掛け声10個までをランダムに選択し、また予め用意した文字列をランダムに追加する実装とした。
参考スクリプト(muscle_shout.py)
# -*- coding: utf-8 -*- import sys import random import numpy as np from collections import defaultdict from muscle_space import MuscleSpace class MuscleShout: def __init__(self, muscle_space, shouts_path, menu_path): self.muscle_space = muscle_space self.shout2vector = dict() with open(shouts_path,'r') as fin: for line in fin: line = line.strip() items = line.split(',') shout = items[0] if len(items)>1: muscles = items[1:] self.shout2vector[shout] = self.muscle_space.muscles2vec(muscles) else: self.shout2vector[shout] = list() self.menu2muscles = defaultdict(set) with open(menu_path,'r') as fin: for line in fin: line = line.strip() items = line.split(',') menu = items[0] muscles = items[1:] self.menu2muscles[menu] |= set(muscles) def _sentence2muscle_vec(self, sentence): muscles = list() for menu in self.menu2muscles.keys(): if menu in sentence: for m in self.menu2muscles[menu]: muscles.append(m) return self.muscle_space.muscles2vec(muscles) def _cos_sim(self, v1, v2): v1 = np.array(v1) v2 = np.array(v2) return np.dot(v1, v2) / (np.linalg.norm(v1) * np.linalg.norm(v2)) def _select_shout(self, muscle_vector): candidate = list() others = list() for shout,svec in self.shout2vector.items(): if svec: cos_sim = self._cos_sim(svec, muscle_vector) if cos_sim > 0: candidate.append(shout) else: others.append(shout) while( len(candidate)< 10): candidate.append(random.choice(others)) return random.choice(candidate) def _shout2muscle(self,shout): mvec = self.shout2vector[shout] if not mvec: return '筋肉' muscles = list(self.muscle_space.basis_muscles.keys()) return muscles[mvec.index(max(mvec))] def reply(self, sentence): m_vec = self._sentence2muscle_vec(sentence) chosen_shout = self._select_shout(m_vec) chosen_muscle = self._shout2muscle(chosen_shout) reply_text = '' reply_text += random.choice([chosen_muscle+'が! ', chosen_muscle+'!! ', chosen_muscle+'を見てよ! ', '今日も', '出た!', 'いいね!', 'ハロー!マッソー!' ]) reply_text += chosen_shout reply_text += random.choice(['!', '!!', 'ー!!', '!マッソー!', '!'+chosen_shout+'!!', '!'+chosen_muscle+'が!!', ]) return reply_text if __name__ == "__main__": ''' 【shout.txt 例】 僧帽筋が並じゃないよ,僧帽筋 二頭がチョモランマ,上腕二頭筋 ... 【menu.txt 例】 腕立て伏せ,大胸筋,上腕三頭筋 クランチ,腹直筋 ... ''' muscle_space = MuscleSpace('../data/basis_definition.txt', '../data/other_definition.txt', '../data/m_vec.pickle') muscle_shout = MuscleShout(muscle_space, '../data/shout.txt', '../data/menu.txt') reply_text = muscle_shout.reply('バイシクルクランチ20回×3セット') print(reply_text)slackbotとしての実装
下記記事を参考にslackbotとして実装を行い、所属している開発チームslackの筋トレ用チャンネル(
muscleチャンネル)で公開した。muscleチャンネルでは、開発チームの有志が日々自身が実施した筋肉トレーニング内容を書き込んだり、筋トレにおける知識を共有する場となっている。
本チャンネルにおいて、筋トレ内容に対してボディービルの掛け声をreplyするbotが存在すれば、日々の筋トレに対するモチベーション向上に寄与することは想像に難くない。実装において、用意した筋トレメニュー、掛け声、筋肉定義文の種類数は下記のとおりである。
種類数 筋トレメニュー 118 掛け声 72 筋肉定義文 32 入出力例
まとめ
本文書では筋トレメニューを入力としてボディービル大会等で用いられる掛け声を生成する手法を提案した。
また当該手法を用いてslack botを実装することで同僚の筋トレへのモチベーション維持に貢献し、ひいては開発環境の向上に繋げることが出来た。今回の実装では筋トレメニュー名のみを対象としていたが、実際のテキストではその回数・セット数も同時に述べられることが多い(例:バイシクルクランチ20回×3セット)。
今後はテキスト中の回数やセット数に応じて出力される掛け声が変化するような改良を行うことで、さらなる開発環境の向上に寄与していきたい。
また、ぜひ読者の皆様も、お持ちであろう筋トレ用のコミュニケーションツールにおいて実装を試みて欲しい。参考文献
- 公益社団法人 日本ボディビル・フィットネス連盟 (監修)「ボディビルのかけ声辞典」、スモール出版
- 荒川 裕志「筋肉の使い方・鍛え方パーフェクト事典」、ナツメ社
- 投稿日:2019-08-19T08:23:41+09:00
Vue.js & Django を Docker と組み合わせてSPA+APIサーバー環境をつくる
はじめに
今回は、Django REST Frameworkを使った、
Vue.jsをSPAとして運用できる環境の作り方をシェアできればと思います。Docker Composeを使うので、本番で使うときはGKEなどの
モダンなコンテナ型オーケストレーションツールを選択可能かつ、開発でも
メンバーの増員などに柔軟に対応できる環境を作れたらと思います。今回は抜粋で書いているので、
不足等ございましたら、ご連絡よろしくお願いいたします。構成
構成は下記のような形にします。
本来だと下記に+DBもあるような構成が基本ですが、
コンテナ上で動かす場合と、クラウドのDBサービスを使用する場合など
多岐の選択があるため、今回はなしとします。サーバー構成
サーバー名 名称 ポート番号 開発サーバー(Vue.js) front 8080 APIサーバー(Django) back 8001 Webサーバー(Nginx) web 8000 Docker Compose ファイルで骨組みを作る
最初にdocker-compose.ymlファイルと各種サーバーのDockerfileを作成して、
骨組みを形作っていきます。1. docker-compose.ymlを作成
注意点としては、バックエンド側のstaticファイルをnginxに置いて
配信可能とする点です。
今回はAPIサーバーとしての使用のため、不要と思われますが、
djangoのデバッグ画面(管理画面など)を表示する際に使用できるので、
volumesにて、同期します。
基本的に起動は、拡張していくことも考えて、
Shellファイルに落とし込んでいきます。
(直で記載でも良いとは思います。)docker-compose.ymlversion: '3' services: web: build: context: ./ dockerfile: ./web/Dockerfile environment: TZ: 'Asia/Tokyo' ports: - 8000:8000 volumes: - ./web/logs/nginx/:/var/log/nginx/ - ./web/uwsgi_params:/etc/nginx/uwsgi_params - ./back/static:/var/www/static/ depends_on: - back back: build: context: ./back dockerfile: Dockerfile command: 'sh /server/start.sh' expose: - "8001" volumes: - ./back:/server/ front: build: context: ./front command: 'sh /app/start.sh' volumes: - ./front:/app/:cached - ./front/node_modules:/app/node_modules ports: - "8080:8080"2. DockerFile フロントエンド側を作成
npmを使用するために、nodeイメージを入れます。
後ほど立ち上げるためにコメントアウトなども挟むので、
一旦スキップしても構いません。Dockerfile(フロントエンド)FROM node:10.7.0 WORKDIR /app RUN npm install -g @vue/cli ADD ./package.json /app/package.json RUN npm install ADD ./start.sh /app/start.sh3. DockerFile バックエンド側を作成
バックエンド側をゴリゴリ書いていきます。
ライブラリのインストールも都度できるように
requirements.txt経由でインストールします。Dockerfile(バックエンド)FROM python:3.7 ENV PYTHONUNBUFFERED 1 WORKDIR /server ADD . /server/ RUN pip install --upgrade pip RUN pip install -r requirements.txt4. DockerFile Webサーバー側を作成
設定ファイル、Vue.jsで作成しビルドしたものを格納します。
バージョンはお好みのものをご使用ください。Dockerfile(Webサーバー)FROM nginx:1.11.7 # 設定ファイル ADD ./web/nginx.conf /etc/nginx/nginx.conf ADD ./web/default.conf /etc/nginx/sites-available/default ADD ./web/default.conf /etc/nginx/sites-enabled/default ADD ./web/uwsgi_params /etc/nginx/uwsgi_params RUN mkdir /var/www RUN mkdir /var/www/front RUN mkdir /var/www/staticここまで作成するとある程度骨組み部分は出来上がった状態になります。
ここから、実際にサーバーとして使用できるように
各サーバー内に手を加えて初期構築をしていきます。フロントエンド側を作成
Vue.jsを使えるようにVue CLIを導入して、
使用できる状態にしていきます。
エラーを防ぐために一旦Dockerfileで書いた下記をコメントアウトしますFROM node:10.7.0 WORKDIR /app RUN npm install -g @vue/cli # ADD ./package.json /app/package.json # RUN npm install # ADD ./start.sh /app/start.shVue CLIを入れることで、Vueの開発環境を簡単に作成することができます。
早速Terminalからプロジェクトを作成し、開発サーバーとして立ち上げてみましょう。
各種設定方法を聞かれますが、enterで進んでいくとデフォルトのものがインストールされます。ターミナル// hoge-projectにはプロジェクト名を入力してください。 $ docker-compose run front vue create hoge-project先ほどDockerfileに入力したコメントアウトを外して、
start.shを軽く記載した後、立ち上げてみましょう。
(プロジェクト先に向き先を当てるため、ファイルの向き先も変更するか、
プロジェクトフォルダを移動して、動くか確認してみてください。)start.shnpm run serveターミナル$ docker-compose build front $ docker-compose up -d frontローカルホストで確認すると無事立ち上がっているかと思います。
バックエンド側を作成
次にDjango側を作成していきます。
ターミナルからDjangoアプリの初期作成コマンドを打ちます。ターミナル$ docker-compose exec back django-admin startproject mysite次にアプリケーションを作成します。
最後の確認の際に使います。ターミナル$ docker-compose exec back python mysite/manage.py startapp testapi起動用のシェルも書いておきます。
start.sh#!/bin/bash sleep 5 python manage.py makemigrations python manage.py migrate python manage.py collectstatic --noinput uwsgi --socket :8001 --module mysite.wsgiDjango REST Frameworkを使用するので
インストールする設定ファイルに記載します。requirements.txtdjango>=2.1.10 uwsgi==2.0.17.1 djangorestframework==3.8.2一旦ここまでで、最後に疎通確認するので、
次に進みます。Webサーバーを立てる
nginx.conf, default.conf, uwsgi_paramsなどの
設定ファイルを作成していきます。1. nginx.conf
nginx.confuser www-data; worker_processes auto; pid /run/nginx.pid; daemon off; events { worker_connections 65535; multi_accept on; use epoll; } http { sendfile on; tcp_nopush on; tcp_nodelay on; types_hash_max_size 2048; client_max_body_size 20M; keepalive_timeout 3600; proxy_connect_timeout 3600; proxy_send_timeout 3600; proxy_read_timeout 3600; send_timeout 3600; client_body_timeout 300; include /etc/nginx/mime.types; default_type application/octet-stream; log_format with_time '$remote_addr - $remote_user [$time_local] ' '"$request" $status $body_bytes_sent ' '"$http_referer" "$http_user_agent" $request_time'; access_log /dev/stdout with_time; error_log stderr; gzip on; gzip_disable "msie6"; include /etc/nginx/conf.d/*.conf; include /etc/nginx/sites-enabled/*; limit_req_zone $binary_remote_addr zone=perip:10m rate=5r/s; limit_req_status 429; }2. default.conf
default.conf# development upstream webserver { ip_hash; server back:8001; } map $http_upgrade $connection_upgrade { default upgrade; '' close; } server { listen 8000; server_name 127.0.0.1; client_header_buffer_size 1k; large_client_header_buffers 8 32k; add_header Strict-Transport-Security 'max-age=31536000'; add_header X-Frame-Options DENY; add_header X-XSS-Protection "1; mode=block"; error_page 500 502 503 504 /50x.html; # フロントエンド location / { root /var/www/front; try_files $uri $uri/ /index.html; } # バックエンドサーバー 静的ファイル群 location /static { alias /var/www/static; } # バックエンドサーバー location /back/ { include /etc/nginx/uwsgi_params; uwsgi_pass webserver; proxy_redirect off; proxy_set_header Host $host; proxy_set_header X-Real-IP $remote_addr; proxy_set_header X-Forwarded-For $proxy_add_x_forwarded_for; proxy_set_header X-Forwarded-Host $server_name; proxy_read_timeout 86400s; proxy_send_timeout 86400s; } # バックエンド adminサーバー location /admin/ { include /etc/nginx/uwsgi_params; uwsgi_pass webserver; proxy_redirect off; proxy_set_header Host $host; proxy_set_header X-Real-IP $remote_addr; proxy_set_header X-Forwarded-For $proxy_add_x_forwarded_for; proxy_set_header X-Forwarded-Host $server_name; } location = /50x.html { root /usr/share/nginx/html; } }3. uwsgi_params
uwsgi_paramsuwsgi_param QUERY_STRING $query_string; uwsgi_param REQUEST_METHOD $request_method; uwsgi_param CONTENT_TYPE $content_type; uwsgi_param CONTENT_LENGTH $content_length; uwsgi_param REQUEST_URI $request_uri; uwsgi_param PATH_INFO $document_uri; uwsgi_param DOCUMENT_ROOT $document_root; uwsgi_param SERVER_PROTOCOL $server_protocol; uwsgi_param REQUEST_SCHEME $scheme; uwsgi_param HTTPS $https if_not_empty; uwsgi_param REMOTE_ADDR $remote_addr; uwsgi_param REMOTE_PORT $remote_port; uwsgi_param SERVER_PORT $server_port; uwsgi_param SERVER_NAME $server_name;問題ないかテスト
試しにVue.js側でAxiosを導入して、
リクエストを送ってみて、きちんとAPIサーバーから値が帰ってくるか、
確認してみます。1. Vue.js側のAxios通信の作成
試しにボタンからAPIサーバーへリクエストを送る処理を書いていきます。
戻り値を表示する部分も用意します。ターミナル$ docker-compose run front npm install -S axiosインストールしたAxiosをmain.jsにセッティングします。
main.jsimport Vue from 'vue' import App from './App.vue' import axios from 'axios' Vue.config.productionTip = false Vue.prototype.$axios = axios new Vue({ render: h => h(App), }).$mount('#app')初期作成されたHelloWorld.vueに追記していきます。
HelloWorld.vue<template> <div class="hello"> <h1>{{ msg }}</h1> <!-- 下記記載 --> <h2>ここに結果が表示されます → {{ result }}</h2> <button @click="getAPI()">クリック!</button> <p> For a guide and recipes on how to configure / customize this project,<br> check out the <a href="https://cli.vuejs.org" target="_blank" rel="noopener">vue-cli documentation</a>. </p> <!-- ~~~ 割愛 ~~~ --> </template> <script> export default { name: 'HelloWorld', props: { msg: String }, // 下記記載 data () { return { result: 'No Result', url: 'http://localhost:8000/back/testapi/get/' } }, methods: { getAPI () { this.$axios.get(this.url) .then(response => { this.result = response.data.message }) } } } </script>2. Django側のレスポンス処理の作成
URLConfへの記載、Views.pyにてレスポンス処理を書いていきます。
今回はhello worldを返すようにします。root側のurls.pyfrom django.contrib import admin from django.urls import path urlpatterns = [ path('admin/', admin.site.urls), path('back/testapi', include('testapi.urls', namespace='testapi')), ]App側のurls.pyfrom django.urls import include, path from .views import * app_name = 'testapi' urlpatterns = [ path('get/', GetTestAPI.as_view()), ]views.pyfrom django.shortcuts import render from rest_framework import status, viewsets, filters from rest_framework import permissions from rest_framework.response import Response class GetTestAPI(APIView): permission_classes = (permissions.AllowAny,) def get(self, request, format=None): return Response(data={'status': 'Hello World!'}, status=status.HTTP_200_OK)settings.py# ~~ 省略 ~~ # Application definition INSTALLED_APPS = [ 'django.contrib.admin', 'django.contrib.auth', 'django.contrib.contenttypes', 'django.contrib.sessions', 'django.contrib.messages', 'django.contrib.staticfiles', 'rest_framework', 'testapi' ] # ~~ 省略 ~~3. 疎通
サーバーを立ち上げてブラウザ上から確認してみます。
$ docker-compose up -dまとめ
現在SPA+APIサーバー環境をDocker上で構築することで、
短い時間で、簡単に構築することができます。現在弊社では、HRモンスターと呼ばれる
採用の新しいスタイルを提供するサービスをローンチいたしました。ローンチ後のさらなる機能追加、改善などのPDCAサイクルを回すべく、
エンジニアを募集しております。
https://www.wantedly.com/projects/341182Kubernetes、Vue.js(Javascript)、Django(Python)といったモダンな技術を使って、
開発しておりますので、もしご興味がある方はぜひ、ご応募お待ちしております。
- 投稿日:2019-08-19T08:04:41+09:00
1次元のセルラー・オートマトンをPythonで試す
TL;DR
- セルラーオートマトンの計算モデルの説明について触れます。
- 1次元のセルラーオートマトンの実装をPythonで進めて動かしてみます。
- 過程で必要になる知識なども、忘れているものなどがあるので調べつつまとめます。
主な参考文献
また、上記書籍のgithubのリポジトリのコードもMITライセンスなので参照・利用させていただきますmm
※本記事では割愛した説明なども山ほどあるので、ALife関係の詳細は書籍をお買い求めください。
セルラー・オートマトンとは
格子状のセルと単純な規則による、離散的計算モデルである。計算可能性理論、数学、物理学、複雑適応系、数理生物学、微小構造モデリングなどの研究で利用される。非常に単純化されたモデルであるが、生命現象、結晶の成長、乱流といった複雑な自然現象を模した、驚くほどに豊かな結果を与えてくれる。
セル・オートマトン - Wikipedia
- セル・オートマトンとも呼ばれます。
- 自然界の模様(e.g., : 貝殻の模様)などで見られるような模様を生成します。
- グリッド上でのデータを参照して、次の段階のデータが決まります(その連続で、結果として模様が生成される)。
- セルラー・オートマトンにはいくつも種類や条件がありますが、共通して以下のような条件を満たしています。
- グリッドの空間がある : 線としての1次元、面としての2次元、立体としての3次元のそれぞれのセルラー・オートマトンがあります。各次元とも、グリッドを参照して計算が実行されます。
- 時間が絡んでくる : 現在の状態を加味して、次の状態を生み出して・・・といったように、時間的な要因が絡んできます。
- グリッドの各セルが状態を持つ : 次の時間の結果を左右するパラメーターを、各セルが持ちます。
- 状態を加味して次の時間にどうなるか、の条件を持つ : 現在の各セルが○○の条件なので、次のセルは××になる、といったような条件を持ちます。
※普通色だと0が黒、1が白なイメージが強いですが、本記事の図なとではgithubのコードに合わせて1を黒、0を白として設定していきます。
今回の実装は、参考文献に合わせて以下のように対応します。
- グリッド空間 : 1次元のセルラーオートマトンを対象とします。
- 状態 : 0か1かの2値で扱います。
- 条件 : 両隣と自身のセルの状態を参照して、次のセルの状態を決定します。
2値で3つのセルを参照するので、8つの組み合わせができる
0か1の2値で、左右と中央の3つのセルを参照して次の時間のセルの状態を決定するので、8つのパターンが存在します($2^3$件のパターン)。
8個のパターンで、次の時間にそれぞれ黒か白(1か0)のどちらになるので、256パターンある
前述の8つのパターンで、それぞれ次の時間が黒になるのか白になるのかのパターン数を調べると、$2^8 = 256$パターン存在します。
1次元のセルラー・オートマトンを体系的に研究したスティーブン・ウルフラムさん(1980年ごろ)によると、この256パターンを、0~255の範囲で「ルール0」~「ルール255」と呼ぶそうです。(30番目のルールであれば「ルール29」といった具合に)
この各ルールで、生成される模様が異なったり、傾向によってクラスターが分けられたりしています。
Pythonで動かしてみる
以下のようなものをPythonで書いて作ってみます。
- 1行ずつ更新がされる。
- 最初は全て0で初期化し、その後に1番上の行の真ん中のみ1にする(その1の部分をトリガーにその後の反応が起きるようにする)。
- 各行で、現在の値に応じて次の時間が0か1かに変化するようにします。
使う環境
- Windows
- Python 3.6.8
- NumPy==1.14.5
- Vispy==0.5.3
- Jupyter notebook
- 前述の書籍のgithubのコード
ビットシフトを思い出す&調べる
別の言語ではビットシフトなどを昔使っていた時期もありますが、長いこと使わない生活をしていたのと、Pythonでは使ったことがないため、調べつつ復習しておきます(今回、各ルールを反映するために使用します)。
参考 : Python ビット演算 超入門
今回使うのは、前述の8パターンでそれぞれが0になるのか1になるのかという値です。
たとえば、00001111といったような値になります。
どうやらPythonでは先頭に0bと付けることで、2進数で表現することができるようです。先ほどの00001111を例に挙げると、15になります。
0b0000111115これがウルフラムさんの研究で言うところのルール15になります。
※2進数で、1111と表現しても同様に15になりますが、今回は8パターンに合わせて8つの数値で00001111といったように表現します。
0b11111500000000で0、00000001で1、0b00000010で2、0b00000011で3...と増えていきます。
0b0000000000b0000000110b0000001020b000000113最後となるルール255は、8つの数字が全て1のケースとなります。
0b11111111255また、10進数などを2進数にしたい場合には、binでキャストすると変換してくれます。
bin(15)'0b1111'2進数の数値を左にずらす(ビットシフトの左シフト)処理は、Pythonでは
元の数字 << ずらす桁数と書くと表現できます。
以下のように1 << 0とすると、1が左に0動く(0なので値そのまま)となります。bin(1 << 0)'0b1'
1 << 1とすると、1が左に1桁分移動するので、0b10になります。 同様に、1 << 2とすれば2桁分移動して0b100となります。bin(1 << 1)'0b10'bin(1 << 2)'0b100'右方向に移動させる右シフトは、逆に
>>の記号を使って表現します。bin(15 >> 0)'0b1111'bin(15 >> 1)'0b111'ルール番号に応じた、次の時間の値を求めるには?
現在の3つの値(左・中央・右)の値(0か1か)と、算出したいルール(例えばルール15であれば00001111)を求めるにはどうすればいいのでしょうか?
まずは3つの値から、0~7までの番号を算出するコードを考えます。
left、center、rightという三つの変数を用意し、それぞれが0か1を取るようにします。left = 0 center = 0 right = 0これらの変数を、8パターンを表現するには$2^3$が必要なので、
2 ** 2 * left + 2 ** 1 * center + 2 ** 0 * rightという計算をすると、0~7までの8パターンが表現できます(2進数で表すと0b000~0b111までが表現できます)。left = 0 center = 0 right = 02 ** 2 * left + 2 ** 1 * center + 2 ** 0 * right0left = 0 center = 0 right = 12 ** 2 * left + 2 ** 1 * center + 2 ** 0 * right1left = 0 center = 1 right = 02 ** 2 * left + 2 ** 1 * center + 2 ** 0 * right2...
left = 1 center = 1 right = 12 ** 2 * left + 2 ** 1 * center + 2 ** 0 * right7ルール1であれば0b00000001となり、ルール15であれば0b00001111、ルール16であれば0b00010000となります。算出するにはこれらの値を右端(1桁目)から見ていって、対象の値が0なのか1なのかを確認すればいいことが分かります。
つまり、前述の0~7までの値分を右シフトして、残った値の1桁目が0なのか1なのかで判定すれば求めることができます。
ルール1であれば0で右シフトすれば1、1~7で右シフトすれば0となり、ルール15であれば0~3で右シフトすれば1、4~7で右シフトすれば0となり、ルール16であれば4で右シフトした時のみ1、それ以外は0となるといった具合です。1桁目の値が0なのか1なのかの算出に、論理積を使います。右辺の値を1桁の1で設定すれば、左辺も1桁目の値が参照されて0か1かの算出がされます。
1桁目のみで計算されるので、掛け算と同じような挙動になります。左辺と右辺が両方1になるなる時のみ結果が1となり、それ以外のバターンは全て0になります。両辺とも0のケース :
0b0 & 0b00左辺のみ1のケース :
0b1 & 0b00右辺のみ1のケース :
0b0 & 0b10両辺とも1のケース :
0b1 & 0b11左辺の1桁目が0の場合(10) :
0b10 & 0b10左辺の1桁目が1の場合(11) :
0b11 & 0b11前述の左中央右の0と1の値から8パターンを算出する計算と、論理積で期待していた結果が得られます。
たとえば、ルール15(0b00001111)であれば、0~3が1、4~7が0となる結果が得られます。(15 >> 0) & 11(15 >> 1) & 11(15 >> 2) & 11(15 >> 3) & 1(15 >> 4) & 10...
(15 >> 7) & 10他の、たとえばルール16(0b00010000)でも試してみましょう。4桁分右シフトした時のみ1となり、他は0になります。
(16 >> 4) & 11(16 >> 0) & 10(16 >> 7) & 10この辺りは、(書籍のコードを初見で見た時に)非理系出身の身からすると少し頭が混乱しますね・・・
(自分で整理すると理解できる・・)これで必要なビットシフトの復習や調査ができたので、コードの内容に本格的に入っていきます。
実装を進める
一部、可視化用に利用するため、githubのリポジトリをクローンしておきます。alifebook_libパッケージ以下を利用します。
まずは必要なモジュールのimportと可視化用のオブジェクトを用意しておきます。
import numpy as np from alifebook_lib.visualizers import ArrayVisualizer visualizer = ArrayVisualizer()可視化用のウインドウが立ち上がります。
続いて可視化領域のサイズを指定します。今回は600x600ピクセルの領域に描画していきます。
SPACE_SIZE = 600試すルール番号を定義します。今回はルール30を使います。
RULE = 30セルラー・オートマトンの状態のベクトルを初期化します。現在の状態と、次の状態を保持する必要があるので、それぞれ
stateとnext_stateという名前で扱います。
サイズは、可視化領域の1行分を扱うので、SPACE_SIZEの600のベクトルとなります。state = np.zeros(shape=SPACE_SIZE, dtype=np.int8) next_state = np.zeros(shape=SPACE_SIZE, dtype=np.int8)このままだと全て値が0ですが、初期値として最初の状態の真ん中のみ1に調整します。こうすることで、一番上の真ん中部分から反応が生まれてきます。
state[len(state) // 2] = 1続いて、現在の状態が次の時間にどのような状態になるのかの計算をループで実行します。
ビットシフト関係の節で触れたように、左・中央・右の値を取得します。while True: for i in range(SPACE_SIZE): left = state[i - 1] center = state[i] right = state[(i + 1) % SPACE_SIZE]中央のインデックスが0の時、左のインデックスは-1となりますが、-1のインデックスは最後のインデックスが参照される(今回はベクトルの右端の数値が参照される)ため問題ありません。
右の方は、中央のインデックスが右端の場合(599)にそのままだと600でインデックスを超えてしまうので、剰余を求めることで、そういったケースには左端になるようにしてあります。
続いて、前述のビットシフトなどの節の計算を使って、0~7のパターンのインデックスを算出する計算と、右シフトと論理積で次の時間の状態を算出・設定する処理を追加します。
pattern_index = 2 ** 2 * left + 2 ** 1 * center + 2 ** 0 * right next_state[i] = RULE >> pattern_index & 1そして、1行分の計算(SPACE_SIZE件数分のループ)が1回終わったら、次の時間の状態の計算結果を現在の状態のベクトルに持ってきて、可視化の状態を更新して終わりです。
state[:] = next_state[:] visualizer.update(1 - state)色は0が黒、1が白ですが、今回は逆(1が黒)で扱うので、
1 - stateとして0が1、1が0になるようにしてあります。コード全体
import numpy as np from alifebook_lib.visualizers import ArrayVisualizer visualizer = ArrayVisualizer() SPACE_SIZE = 600 RULE = 30 state = np.zeros(shape=SPACE_SIZE, dtype=np.int8) next_state = np.zeros(shape=SPACE_SIZE, dtype=np.int8) state[len(state) // 2] = 1 while True: for i in range(SPACE_SIZE): left = state[i - 1] center = state[i] right = state[(i + 1) % SPACE_SIZE] pattern_index = 2 ** 2 * left + 2 ** 1 * center + 2 ** 0 * right next_state[i] = RULE >> pattern_index & 1 state[:] = next_state[:] visualizer.update(1 - state)完成です!
実行してみると、wikipediaのページのサンプルにあるような、以下のような模様が生成されます。アニメーションで見てみると、初期値の真っ黒な状態から、while文のループで次の状態が更新され続け、且つ可視化のモジュールで1回更新するたびに更新箇所が1行下がるので、段々上から模様が生成されていることが分かります(縮小したので小さくて潰れていますが・・・)。
参考文献まとめ
- 投稿日:2019-08-19T07:55:24+09:00
AtCoder Beginner Contest 138 D - Ki のテストケースがコンテスト後に増えている件について
AtCoder Beginner Contest 138 D - Ki のテストケースがコンテスト後に増えている件について
追記: 1≤ai<bi≤N の条件があるので、以下の想像は誤りです!!
AtCoder Beginner Contest 138 の終了後も D 問題を解説を見て試行錯誤していたら、AC だったコードが WA になって、after_contest_15, after_contest_16, after_contest_17 が増えていることに気づいた. 解説 PDF にも修正が入っていた.
問題文には 「この木の根は頂点 1 で、i 番目の辺 (1≤i≤N−1) は頂点 ai と頂点 bi を結びます。」とだけ書かれていて、頂点 ai と頂点 bi のどちらが根に近いかは不明なのだが、テストケースが追加される前は頂点 ai のほうが根に近いという決めつけをしていても通るテストケースになっていたと思われます. 追加されたテストケースはこの決めつけをしていると通らないように思われます. (だから解説 PDF に「根に近い頂点から順に行えば」という追記が入ったと思われる).
なので、追加されたテストケースの入力例としては、「入力例 1」の4行目をひっくり返した以下で行えそうである.
4 3 1 2 2 3 4 2 2 10 1 100 3 1出力例は、「出力例 1」と同じ
100 110 111 110となる.
- 投稿日:2019-08-19T07:22:49+09:00
ペイントソフトを作って、ついでに手書き数字認識もする
Python で手書き文字認識をするチュートリアルはよくあるんですが、既存のデータセットを使って「はい予測精度90%でました」ばかりで、「僕の数字も認識してくれよ!」ってなります。せっかくなので数字を自分で手書きして、 AI(えーあい) に認識してもらうアプリケーションを作ります。(ウィンドウの描画に使用したゲームエンジン
pyxelについては記事末尾に参考リンクをまとめておきます。)文字を書いて
sを押すと、その数字を予測します。コード全体はこちら(pyxelDigitRecognition)注意:機械学習を使いますが、遊びの記事なので全然厳密ではありません。
この記事の対象読者
ペイントソフトを作りたい人
手書き文字認識をしてみたい人
(適当な実装を許してくれる人)
環境
scikit-learn 0.21.3
pyxel 1.2.4
Windows 10
記事の流れ
- Pyxel でペイントソフトをつくる
- digit データセットで学習
- 予測してみる
1. Pyxel でペイントソフトをつくる
まず単純なお絵描きソフトを作ります。
作り方はかなり簡単で以下のようにします。画面の各ピクセルを表す二次元配列を作る(今回は64x64) WHILE True: # 各フレームで if マウスをドラッグ中: マウスの座標の色を変える 二次元配列をもとに画面を描画実装の際はマウスの座標の周りも同時に色を変えて、太い線を描画しています(下図)。
ペイントソフト(クリックで展開)
# constants WINDOW_SIZE = 64 # 0 white, -1 black ウィンドウの色情報 windowData = [[0]*WINDOW_SIZE for _ in range(WINDOW_SIZE)] pyxel.init(WINDOW_SIZE, WINDOW_SIZE) # window 初期化 pyxel.mouse(visible=True) def update(): if pyxel.btnp(pyxel.MOUSE_LEFT_BUTTON, hold=2, period=1): # マウスの座標の色を変える x, y = pyxel.mouse_x, pyxel.mouse_y if 0 <= x < pyxel.width and 0 <= y < pyxel.height: windowData[y][x] = -1 def draw(): pyxel.cls(pyxel.COLOR_WHITE) for y in range(pyxel.height): for x in range(pyxel.width): if windowData[y][x]==-1: pyxel.pix(x, y, pyxel.COLOR_BLACK) pyxel.run(update, draw)できたのはこれ。
2. digit データセットで学習
データを集めるのはめんどくさいので、sklearn の digit データセットを使用します。
これは手書き数字認識でよく使用される MNIST を小さくした?感じのデータセットで、
- 8x8 ピクセル
- 16段階グレースケール
- 10 クラス(0~9)
- データ数:1797
です。公式ドキュメントによればこんな画像が入っています。
分類は k近傍法を使用してみました。k近傍法は先人が説明し尽くしているので、リンクだけ貼ります。
●アルゴリズム
OpenCV documentation●irisデータへの使用例
K近傍法(多クラス分類)
学習するコード(クリックで展開)
def train(): digits = load_digits() X = digits.data y = digits.target X_train,X_test,y_train,y_test = train_test_split(X, y) knn = KNeighborsClassifier() knn.fit(X_train, y_train) print(knn.score(X_test, y_test)) # 0.98 # save model with open('knn_digit.pkl', 'wb') as f: pickle.dump(knn, f)交差検証も何もしていませんが、遊びなのでこれでよしとします。(せいど98%!)
3. 予測してみる
学習できた()ので実際に予測してみます。
お絵描きの画面は 64x64, RGB なので、予測する前に 8x8, 16段階グレースケールに変換することに気を付けます。今回はウィンドウを 8x8 の画像で保存し、それを読みだして数字認識をします。
予測するコード(クリックで展開)
def predict() -> int: with open('knn_digit.pkl', 'rb') as f: loaded_model = pickle.load(f) img = Image.open("images/screen_shot.png") # ウィンドウの画像 img = img.convert('L') # convet (r,g,b) to 0-255 img = (255 - np.array(img))//16 + 1 # convert to 0-15 img = img.reshape(1, 64) pred = loaded_model.predict(img)[0] # np.array to int return predこれで数字認識ができるようになりました。大きく丁寧に書くと結構認識できます!
ただ 8x8 に圧縮してるので、小さい数字や細い文字は予測できないのであしからず。
上のgifの「8」は小さく書きすぎて、 8x8 ピクセルにすると潰れてしまうのが原因です(画像ちっさい…)。
最後に
簡単にまとめましたが、
pickleで学習モデルを読み込むとPyxelのウィンドウが落ちてしまうのが治せず結構困ったりしました。(モデルの読み込みを別のpythonファイルで実行するとなぜかうまく行きました…)今回のアルゴリズムもデータセットも全く実用に耐えるものではありませんが、アプリケーションにすると中々面白かったです!
お気づきの点がありましたら、ご意見お待ちしております。
参考リンク
- 投稿日:2019-08-19T07:19:03+09:00
【Python】オブジェクト指向プログラミング基礎vol.6~ポリモーフィズム~
ポリモーフィズム
同名のメソッドが、インスタンスによって振る舞いを適切に変えること
以下のプログラムを見ると、
Soccerクラス、Baseballクラス、Basketballクラスすべてが
get_score()メソッドを持つ。class Soccer: def get_score(self): print('kick') class Baseball: def get_score(self): print('swing') class Basketball: def get_score(self): print('throw') def motion(sports): sports.get_score() soccer = Soccer() baseball = Baseball() basketball = Basketball() motion(soccer) motion(baseball) motion(basketball)実行結果
kick swing throwこのように異なるクラスに共通の名前のメソッドを定義することで、どのクラスのオブジェクトかを気にせずget_score()メソッドを使用できるようになっている。
しかし、ポリモーフィズムを使わないで実装を行う余地が残ってしまっている
ポリモーフィズムを使わないで実装を強制する方法として、抽象クラス・抽象メソッドを利用する方法がある
抽象(基底)くらすとは
継承されることを前提としたクラス、インスタンスを生成できない
抽象メソッドとは
実装をもたない、インターフェースを規定するためのメソッド、抽象クラスに定義できる
抽象メソッドはサブクラスの中のオーバーライドによって実装されなければいけない
Pythonで抽象クラス・抽象メソッドを利用するには、ABC (Abstract Base Class)モジュールを使う
抽象クラスを定義するにはABCクラスを継承し、抽象メソッドを定義するには
@abstractmethodデコレータを使用するfrom abc import ABC, abstractmethod class Sports(ABC): @abstractmethod def get_score(self): pass class Soccer: def get_score(self): print('kick') class Baseball: def get_score(self): print('swing') class Basketball: def get_score(self): print('throw') soccer = Soccer() baseball = Baseball() basketball = Basketball() soccer.get_score() baseball.get_score() basketball.get_score()実行結果
kick swing throw