- 投稿日:2020-08-02T23:49:34+09:00
マルウェア自衛のためのちょっとしたスクリプト
皆様、在宅ワーク万歳な日々を過ごしでしょうか?
先週は久々に現場に駆り出されましたが、
電車内はコロナ禍なんて嘘のような様子でしたコロナとは…
セキュリティ需要の高まり
それはさておき、在宅の増えた昨今では端末のセキュリティについて
考えることも増えたのではないかと思います。最近だとEMOTETなどのようなマルウェアなどのニュースを見聞きして
怖いなと警戒心が一時的に高まったりすることもあるかとおもいます。でも日時が立つとそんな警戒心なども薄れて、変なサイトにアクセスしてしまったり、
行きつけのサイトに変なものを埋め込まれたりする可能性も
無きにしも非ずです。そんなマルウェアが私たちの端末で悪さをするには
自動起動登録する必要があります。
なので、日々自動起動されるプログラムを確認することで、
うちに忍び込む不審な輩に気づくきっかけになったら…!というわけで「autorunsc.exe」という便利なツールを使用して、
自動起動プログラムの際をログ収集するスクリプトを書いてみました。import部分
import subprocess import zipfile import os import sys import urllib.request as req import pandas as pd from glob import glob from plyer import notification from alittleuseful import loglotate # pip install pandas # pip install plyer # pip install git+https://github.com/ardnico/mainalittleusefulは私が個人的にgithubで公開してる、
ログを書き込むライブラリです
他にも変な機能を公開していますが、よければ使ってくれたら
嬉しいかなって。。。命名定義
csv_file = f'{os.getcwd()}\\out.csv' rcsv_file = f'{os.getcwd()}\\out_old.csv' enc = "utf-16" URL = "https://download.sysinternals.com/files/Autoruns.zip" zip_file = "A.zip" path='.' logger = loglotate( logname = "StartUpSec", outputdir = [os.getcwd()], lsize = 100000, num = 20, timestanp = 1 # 1:on other:off )静的命名や関数の呼び出し部分です
関数:autorunsc.exeのダウンロード
def download_tool(tf:bool): # file download if tf == False: logger.write('[INFO]Because the tool has not existed, the one will download') req.urlretrieve(URL,zip_file) with zipfile.ZipFile(zip_file, 'r') as z_file: try: z_file.extractall(path=path) logger.write("[SUCCESS]Tool download succeeded") except Exception as e: logger.write('[ERROR]Failed to download or unzip autorunsc.exe') logger.write(f'[ERROR]{e}') sys.exit(0)「autorunsc.exe」が存在しなかった場合、requestを使用して
ツールをダウンロードします。
ダウンロードがZIP解凍まで行います。関数:「autorunsc.exe」の実行から自動起動プログラムの比較まで
def get_log(): if os.path.exists(rcsv_file) == True: try: os.remove(rcsv_file) except Exception as e: logger.write('[ERROR]Failed to remove oldcsvfile') logger.write(f'[ERROR]{e}') sys.exit(0) if os.path.exists(csv_file) == True: try: os.rename(csv_file,rcsv_file) df_old = pd.read_csv(rcsv_file,encoding=enc) except Exception as e: logger.write('[ERROR]Failed to rename oldcsvfile') logger.write(f'[ERROR]{e}') sys.exit(0) else: df_old = '' with open(csv_file, mode='w', encoding=enc) as fp: cp = subprocess.run([f'{os.getcwd()}\\autorunsc.exe','-nobanner','-c','-a','*'], encoding=enc, stdout=fp) try: if df_old == '': flag = 0 else: flag = 2 except: if len(df_old.index) <= 0: flag = 0 else: flag = 1 if flag==0 or flag==2: logger.write("[INFO]StartUp Program's log has created") else: with open(csv_file,encoding=enc) as f: data = f.read().split('\n') with open(rcsv_file,encoding=enc) as f: data2 = f.read().split('\n') l_diff = list(set(data)^set(data2)) if len(l_diff) > 0: logger.write("[DIFF INFO]The difference of the startup program has existed") for i in l_diff: logger.write(f"[DIFF]{i}") notification.notify( title='The difference of startup program has existed', message=i, app_name='Diff notify' ) else: logger.write("[INFO]The difference did not exsist")CSVファイルの扱いで少々長くなってしまいましたが、
動きとしては以下の通りです。
- CSVファイルをローテーション
- 最新のCSVと一世代前のCSVファイルの内容を比較
- 差異が存在する場合ログに書き込み+ポップ通知
実行部分
if __name__ == "__main__": os.chdir(r"C:\python\notebooks\StartUpProgramSec") tooltf = os.path.exists(f"{os.getcwd()}\\autorunsc.exe") download_tool(tooltf) get_log() logger.write("[INFO]The process completed")以上です。
- 投稿日:2020-08-02T23:14:52+09:00
AtCoder Beginner Contest 174 参戦記
AtCoder Beginner Contest 174 参戦記
9ペナの大爆死. 終了1分半前にギリギリE問題を通したおかげで、レーティングが小ダウンで済んだ.
ABC174A - Air Conditioner
1分で突破. 書くだけ.
X = int(input()) if X >= 30: print('Yes') else: print('No')ABC174B - Distance
2分半で突破. 書くだけ.
N, D = map(int, input().split()) result = 0 for _ in range(N): X, Y = map(int, input().split()) if X * X + Y * Y <= D * D: result += 1 print(result)ABC174D - Alter Altar
20分くらい?で突破. RE×1, WA×4. 一番左にある白い石を一番右にある赤い石とスワップするを繰り返して、白い石の右側に赤い石がない状態にすれば良い. 言うのは簡単なのに、実装でハマりました…….
N = int(input()) c = input() d = list(c) i = 0 j = N - 1 result = 0 while True: while i < N and d[i] != 'W': i += 1 while j > 0 and d[j] != 'R': j -= 1 if i == N or j == -1 or i >= j: break d[i] = 'R' d[j] = 'W' result += 1 print(result)ABC174C - Repsept
28分くらい?で突破. C問題だからナイーブに書いても行けるかと思ったら、入力例3で TLE 食らって真っ青. 多分最大値は K - 1 だろうとヤマを張って出したら通った…….
K = int(input()) t = 7 for i in range(K): if t % K == 0: print(i + 1) break t = (t * 10 + 7) % K else: print(-1)追記: K で割った余りの0以外は K - 1 種類なので、最大値は K - 1 に決まっていた. 途中で同じ値がでてくるとループなので0になることはない.
ABC174E - Logs
47分で突破. TLE×1、RE×3. heapq で正答が出るコードを書いて提出してから K≤109 に気づくチョンボ. 24分間 heapq のまま高速化の努力をした後に、これは駄目だとなった瞬間ににぶたんを閃いて、13分でコードを書いたらもう終了1分半前. 通った、助かった. しかし、
abs(ng - ok) > 1でよく通ったな.from math import ceil N, K, *A = map(int, open(0).read().split()) def is_ok(n): t = 0 for a in A: if a <= n: continue t += ceil(a / n) - 1 return t <= K ok = 1000000000 ng = 0.0000000001 while abs(ng - ok) > 1: m = (ok + ng) // 2 if is_ok(m): ok = m else: ng = m print(ceil(ok))
- 投稿日:2020-08-02T23:06:24+09:00
バイバイ Python。 ハロー Julia!
こちらの記事は、Rhea Moutafis 氏により2020年5月に公開された『 Bye-bye Python. Hello Julia! 』の和訳です。
本記事は原著者から許可を得た上で記事を公開しています。バイバイ Python。 ハロー Julia!
Pythonの勢いに歯止めがかかると同時に新しい競争相手の登場だ
Juliaがまだあなたにとって未知であっても、心配しないでほしい。 Photo by Julia Caesar on Unsplash
誤解しないでほしい。 Pythonの人気は、コンピュータ科学者、データサイエンティスト、AIスペシャリストといった堅固なコミュニティによって支えられている。
しかし、これらの人々と一緒に夕食をともにしたことがあれば、彼らがPythonの弱点についてどれほどわめき散らしているのかも知っているだろう。 速度が遅いことに始まり過度のテストが必要になること、以前のテストにもかかわらずランタイムエラーが発生することまで、うんざりすることはたくさんある。
そのため、ますます多くのプログラマーが他の言語を使うようになってきている。トッププレイヤーはJulia、Go、Rustだ。 Juliaは数学的・技術的なタスクに最適である一方、Goはモジュラープログラムに最適であり、Rustはシステムプログラミングの最高の選択肢だ。
データサイエンティストとAIスペシャリストは多くの数学的問題を扱っているため、彼らにとってJuliaはその中の勝者だ。 そして、厳しく見てみても、JuliaにはPythonが勝つことのできない利点が存在する。
Pythonの禅 vs. Juliaの貪欲
人々が新しいプログラミング言語を作り出すのは古い言語の優れた機能を維持し、悪い部分を修正したいという理由があるときだ。
このような理由から、Guido van Rossumは1980年代後半にABCを改善するためにPythonを生み出した。 ABCはプログラミング言語としてはあまりに完璧すぎた。その柔軟性のない構造のため教えやすかったが、現実的な使用には適していなかったのだ。
対照的に、Pythonは非常に実用的だ。 作者たちの意図を反映した Zen of Python 1の中に、それを見ることができる。
醜いより美しいほうがいい。
暗示するより明示するほうがいい。
複雑であるよりは平易であるほうがいい。
それでも、込み入っているよりは複雑であるほうがまし。
ネストは浅いほうがいい。
密集しているよりは隙間があるほうがいい。
読みやすいことは善である。
特殊であることはルールを破る理由にならない。
しかし、実用性を求めると純粋さが失われることがある。
...それでも、PythonはABCの優れた点を引き継いでいる。例えば、読みやすさ、シンプルさ、初心者にとって優しい点などだ。 しかし、PythonはABCに比べてはるかに堅牢で、現実的な使用に適している。
ABCは、Pythonへの道を切り開き、PythonはJuliaへの道を切り開いた Photo by David Ballew on Unsplash
同様に、Juliaの作者たちは他の言語の良い部分を引き継いで、悪い部分を捨てたいと考えている。 しかし、Juliaの方がはるかに野心的だ。1つの言語を置き換えるのではなく、すべての言語を打ち負かしたいと考えているのだ。
Juliaの作者たちが言うにはこうだ:
つまり僕たちは欲張りなんだ。それじゃ物足りないんだ。
僕たちが欲しい言語はこんな感じだ。まず、ゆるいライセンスをもったオープン ソース言語。 そこに、Cの速さとRubyの動的さが欲しい。 Lispのような同図像性があって真のマクロを使えるけど、Matlabのように分かりやすくて自然な数学的記述もできる言語だ。 そのうえ、Python並みに汎用プログラミングに使えて、R並みに簡単に統計分析ができて、Perl並みに文字列処理を自然にできて、Matlab並みに線形代数計算に強くて、シェル並みにうまくプログラムをつなぎ合わせることができる。 さらに、すっごい簡単に覚えられるけど、凄腕ハッカーも満足させられるものだ。 インタラクティブに使えて、かつコンパイルもできる。
Juliaは、現在存在するすべての利点をブレンドしつつも、それを他の言語に存在する欠点と引き換えにしようとしない。 Juliaは若い言語であるものの、作者たちが設定した目標の多くはすでに達成している。
Julia開発者たちがJuliaを好んで使う理由
汎用性
Juliaは、単純な機械学習アプリケーションから巨大なスーパーコンピュータシミュレーションまで、あらゆる用途に使用可能だ。 ある程度はPythonでも実現可能だ。ところが、Pythonは何とかしてこれをお得意のものにした。
それとは対照に、Juliaはまさにこのために作られた。 1からだ。
速度
Juliaの作者たちはCと同じくらい高速な言語を作成したいと考えていたが、できたものはさらに高速だった 。 近年、Pythonの高速化は容易になってきたが、そのパフォーマンスはJuliaができることとはかけ離れている。
2017年にJuliaは Petaflop Club にまで加わった。それはピークパフォーマンスで毎秒1ペタフロップの速度を超えることができる言語の小さなクラブだ。 Juliaを除くと現在そのクラブにいるのはC、C++、Fortranだけだ。
コミュニティ
Pythonには30年以上の歴史があり、巨大で協力的なコミュニティがある。 1回のGoogle検索では回答を得られないPython関連の質問はほとんどない。
対照的に、Juliaコミュニティは非常に小さい。 これは、答えを見つけるためにより調べるのに時間がかかることを意味する一方で、同じ人と何度も関わるかもしれないということだ。 そして、これはかけがいのないプログラマー関係になる可能性があるということだ。
コード変換
Juliaでコーディングするために、Juliaコマンドを1つも知る必要さえない。 Julia内でPythonおよびCコードを使うことができるのみならず、 Python内でJulia を使うことさえもできてしまう!
言うまでもなく、これにより、Pythonコードの弱点を極めて簡単に修正することができる。 言いかえれば、Juliaを学びながら生産性を維持することもできるということだ。
ライブラリ
これは、Pythonの最も優れた点の1つだ。膨大な数のよくメンテナンスされたライブラリ群を抱えているということだ。 Juliaには多くのライブラリがなく、ユーザーはそれらが(まだ)驚くほどメンテナンスされていないと不満を述べている。
しかし、Juliaが限られたリソースを持つ非常に若い言語であることを考慮すると、既に存在するライブラリの数はかなり印象的だ。 Juliaのライブラリの量が増加しているという事実は別としても、Juliaはプロットを処理するためにCおよびFortranのライブラリとインターフェースを持つこともできる。
動的かつ静的な型
Pythonは100%の動的型付け言語だ。 これは、例をあげるとプログラムは実行時に変数が浮動小数点か整数かを決定しているということを意味する。
これは初心者に非常にやさしい一方で、多くのバグをもらしうる。 つまり、考えられるすべてのシナリオでPythonコードをテストする必要があるということだ。これは、多くの時間を要する非常にばかげたタスクだ。
Juliaの作者たちもJuliaを簡単に学習できるようにしたかったため、Juliaは動的型付けを完全にサポートしている。 しかし、Pythonとは対照的に、必要に応じて静的な型を導入することができる。たとえば、CやFortranでの静的な型と同じようにだ。
これにより、時間を大幅に節約できる。コードをテストしない言い訳を見つける代わりに、可能なところであればどこででも型を指定することができる。
データ:小さなときに投資する
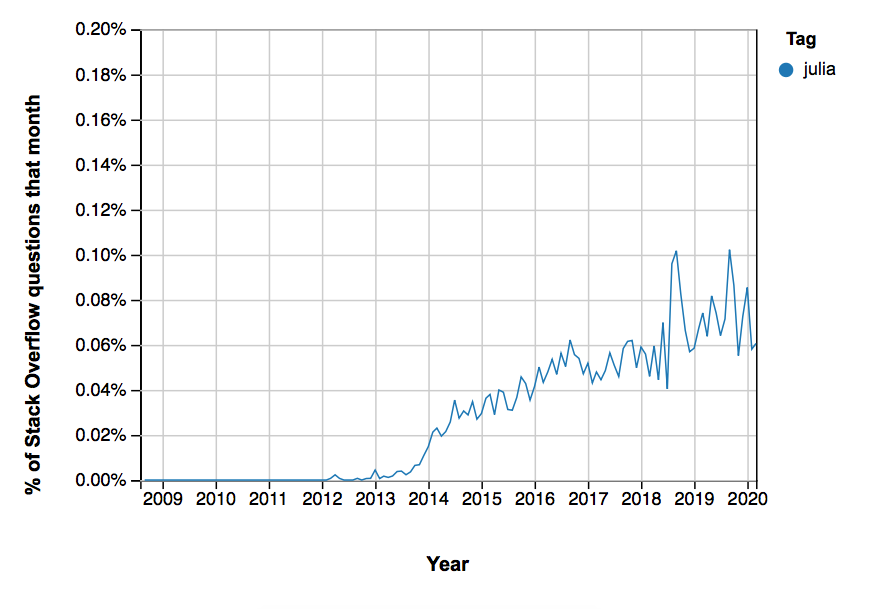
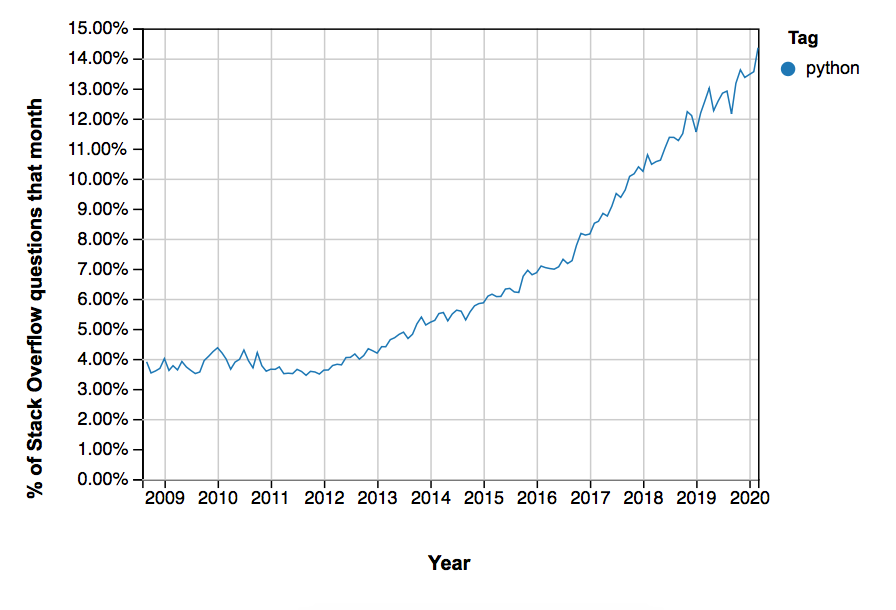
StackOverflow でJulia(上)およびPython(下)のタグが付けられた質問の数。
これらすべてはかなり素晴らしいように聞こえるが、次のことを忘れないことが大切だ。JuliaはPythonに比べてまだ小さいということだ。
StackOverflowでの質問の数は、かなり良い指標の1つだ。現時点で、Pythonのタグ付けは、Juliaよりも約20倍多くなっている。
これは、Juliaが不人気であることを意味しているのではない。むしろ、多くのプログラマーに新しい言語が使われるようになるまでに時間がかかるのは当然のことだ。
次のことを考えてみてみよう。コード全体を別の言語で本当に書きたいだろうか? いいや、そうではなくあなたは将来のプロジェクトで新しい言語を試してみたいと考えているのではないだろうか。 これがすべてのプログラミング言語でリリースから使われるようになるまでの間にタイムラグが生じる理由だ。
しかし、今すぐに使うことにした場合はどうだろうか。Juliaでは非常に多くの言語変換が可能なのでそれは難しくはない。そう、あなたは将来に投資しているのだ。 ますます多くの人々がJuliaを採用するときには、あなたはすでに彼らの質問に答えるのに十分な経験を積んでいることだろう。 また、より多くのPythonコードをJuliaに置き換えるほど、あなたのコードの耐久性は向上していくだろう。
Juliaに愛を示す時がきた Photo by Alexander Sinn on Unsplash
最後に伝えたいこと:Juliaを学び、あなたの強みにしよう
40年前、人工知能はニッチな現象にすぎなかった。 業界と投資家はそれを信じていなかった、そして多くの技術は洗練されたものではなく実用に耐えなかった。 しかし、当時それを学んだ者は今日の巨人となっている。需要が非常に高く、給与は NFLプレーヤーに相当する。
同様に、Juliaはまだ非常にニッチだ。 しかし、Juliaが大きくなったとき、勝者はJuliaを早期に採用した人だろう。
私はあなたが今Juliaを採用すれば、10年以内にうんとお金を稼ぐことが保証されると言っているわけではない。 しかし、チャンスの数は増えるだろう。
考えてみてほしい。たいていの巷のプログラマーは、職務経歴書にPythonを載せている。 そして今後数年で、さらに多くのPythonプログラマーが求人市場に出てくるだろう。 しかし、企業のPythonに対する需要が鈍化した場合、Pythonプログラマーの将来性は低下するだろう。 それは最初はゆっくりだが、必然的なものだ。
一方、Juliaを職務経歴書に載せることができれば、あなたは本当の優位性を持つことができる。 正直言って、他のPythonistaとの違いはどれほどあるだろうか。 大きな差ではないだろう。 しかし、3年後であっても、それほど多くのJuliaプログラマーは存在しないだろう。
Juliaスキルがあれば、仕事の要件を超えて興味があることを示すだけでなく、 学習意欲のある人間であり、プログラマーであることの意味をより広く理解していることも示していることになる。 言いかえれば、あなたはその仕事に適任だ。
あなたと他のジュリアプログラマーは未来のロックスターで、あなたはそれを知っている。 そういえば、 Juliaの作者たちは2012年にこのように言っている:
僕たちは言い訳できないほど欲張りだと認識しているけど、それでも全てが欲しいんだ。2年半ほど前に、この欲張りな言語を生み出すための仕事に取りかかった。 完璧ではないけど、バージョン1.0リリースまでもう少しだ。出来上がった言語は Juliaと名付けた。 すでに僕たちの無理な要求の90%を実現してくれてるけど、より完成度の高いものにするには他の人からの無理な要求も聞かないといけない。 だから、もし君が欲張りで理不尽で要求の厳しいプログラマーでもあるなら、Juliaを試してもらいたいんだ。
Pythonは今でも異常なほど人気がある。 しかし、あなたが今ジュリアを学ぶなら、それは将来もしかするとゴールデンチケットになるかもしれない。 そういう意味で、『バイバイ Python。 ハロー Julia!』
翻訳協力
Original Author: Rhea Moutafis
Original Article: Bye-bye Python. Hello Julia!
Thank you for letting us share your knowledge!この記事は以下の方々のご協力により公開する事が出来ました。
改めて感謝致します。
選定担当: @_masa_u
翻訳担当: @_masa_u
監査担当: @r_pg10
公開担当: @_masa_uご意見・ご感想をお待ちしております
今回の記事は、いかがだったでしょうか?
・こうしたら良かった、もっとこうして欲しい、こうした方が良いのではないか
・こういったところが良かった
などなど、率直なご意見を募集しております。
いただいたお声は、今後の記事の質向上に役立たせていただきますので、お気軽にコメント欄にてご投稿ください。Twitterでもご意見を受け付けております。
みなさまのメッセージをお待ちしております。
日本語訳はこちらから引用させていただきました: プログラマが持つべき心構え (The Zen of Python) ↩
- 投稿日:2020-08-02T23:05:55+09:00
【Python】データサイエンス100本ノック(構造化データ加工編) 019 解説
Youtube
動画解説もしています。
問題
P-019: レシート明細データフレーム(df_receipt)に対し、1件あたりの売上金額(amount)が高い順にランクを付与し、先頭10件を抽出せよ。項目は顧客ID(customer_id)、売上金額(amount)、付与したランクを表示させること。なお、売上金額(amount)が等しい場合は同一順位を付与するものとする。
解答
コードdf_amount_rank = pd.concat([df_receipt[['customer_id', 'amount']] \ ,df_receipt['amount'].rank(method='min', ascending=False)], axis=1) df_amount_rank.columns = ['customer_id', 'amount', 'amount_ranking'] df_amount_rank.sort_values('amount_ranking', ascending=True).head(10)出力customer_id amount amount_ranking 1202 CS011415000006 10925 1.0 62317 ZZ000000000000 6800 2.0 54095 CS028605000002 5780 3.0 4632 CS015515000034 5480 4.0 72747 ZZ000000000000 5480 4.0 10320 ZZ000000000000 5480 4.0 97294 CS021515000089 5440 7.0 28304 ZZ000000000000 5440 7.0 92246 CS009415000038 5280 9.0 68553 CS040415000200 5280 9.0解説
・PandasのDataFrame/Seriesにて、ランク列を新たに作成し、列を連結して、データを順位付けする方法です。
・数字情報をランキング形式で見たい時に使用します。
・'concat('<列名A>','<列名B>','<列名C>')'は、指定した列を連結する関数です。concatenate(=連結する)という動詞が元です。
・'rank(method(average/min/max/first),'ascending=True/False')'は、指定した列のランキングを表示する関数です。
・今回の場合、amount のランキングを rank で表示し、指定された列と連結するために concat を使用しています。
・'columns('<列名A>','<列名B>','<列名C>')'は、列名を再指定する関数です。
・P-017,018で使用した sort_values を用いて、ランキング順に並び直して表示しています。※rankの参考記事はこちら
- 投稿日:2020-08-02T23:02:11+09:00
プログラミング未経験者にPython教えてみた
心がけたこと
- 型とか変数とか宣言とか、お作法の話は後回し
- とにかくプログラムを実行してもらってエラーに遭遇してもらう
- 一度にたくさん詰め込まない
前提
職場
- 製造業
- 色々あって僕も初心者も違う会社だけど同じチーム
ぼく(ざっくりいうと技術サイド)
- プログラミング経験は学生時代7年、業務で5年
- Python経験は学生時代2年、業務で1年
- 社内研修でプログラミング講師を2ヶ月経験済み
初心者(ざっくりいうと営業サイド)
- プログラミング経験なし(そもそも異業種)
- Pythonは自身では書かないが、業務で実行する機会はたまにある。
- 元会社からプログラミングを学ぶように言われているものの手も足も出ない。
- 投稿日:2020-08-02T22:48:26+09:00
Fusion 360 を Pythonで動かそう その11 パスに沿った点がAPIにないので代替案を考えた
はじめに
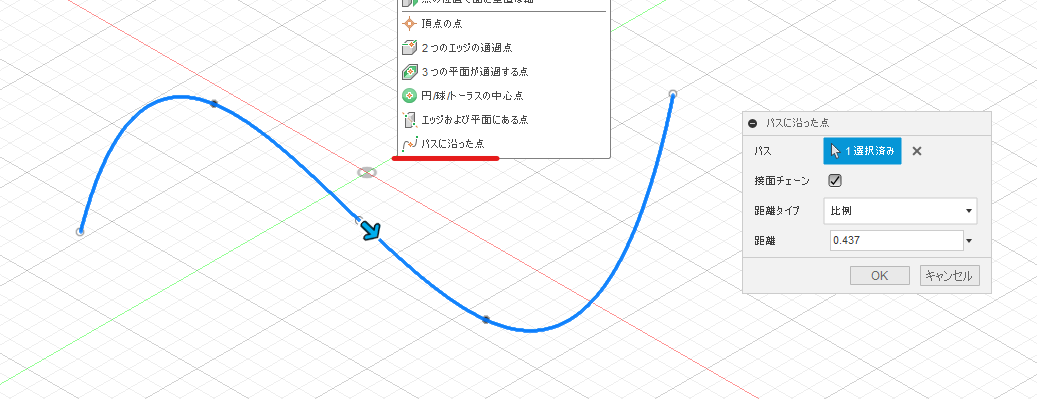
Fusion 360 に パスに沿った点 というコマンドがあります。これを Fusion 360 API で実現しようと紆余曲折した記録です
リファレンスマニュアルを調べてみる
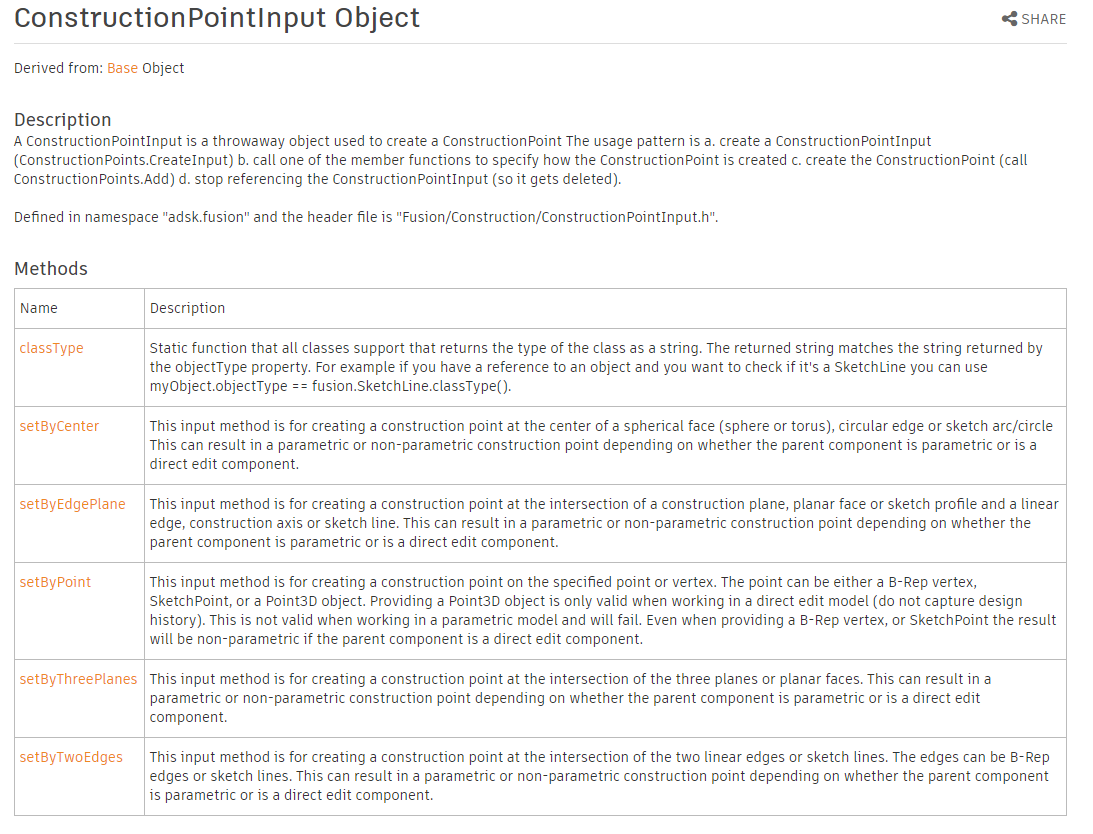
Fusion 360 API で構築の点を作成する方法の指定は ConstructionPointInput Object を使います。リファレンスマニュアルのメソッドの中にある setBy で始まるものが UI での各コマンドに対応しているのでこの中から「パスに沿った点」を探します
setByCenter > 円/球/トーラスの中心点
setByEdgePlane > エッジおよび平面にある点
setByPoint > 頂点の点
setByThreePlanes > 3つの平面が通過する点
setByTwoEdges > 2つのエッジの通過点
あれ・・・???パスに沿った線に対応するメソッドがない???「パスに沿った点」はないけど「パスに沿った平面」はあった!
パスに沿った点によく似たコマンドで パスに沿った平面 というのがあります。
なぜかこちらはちゃんと ConstructionPlaneInput.setByDistanceOnPath メソッドがあるようです。平面は有るのに点は無いのはなぜだー!といっても無いものは無いので開き直って代替案を考えることにしました。パスに沿った平面をつくる > その平面とパスとの交点をつくる という手順を Fusion 360 API でやってみます
手順
最初と最後のおまじないから途中まで
import adsk.core, adsk.fusion, traceback def run(context): ui = None try: app = adsk.core.Application.get() ui = app.userInterface design = app.activeProduct # Get the root component of the active design. rootComp = design.rootComponent # # ここにコードを追加していく # except: if ui: ui.messageBox('Failed:\n{}'.format(traceback.format_exc()))スケッチの中のスプラインを取得する
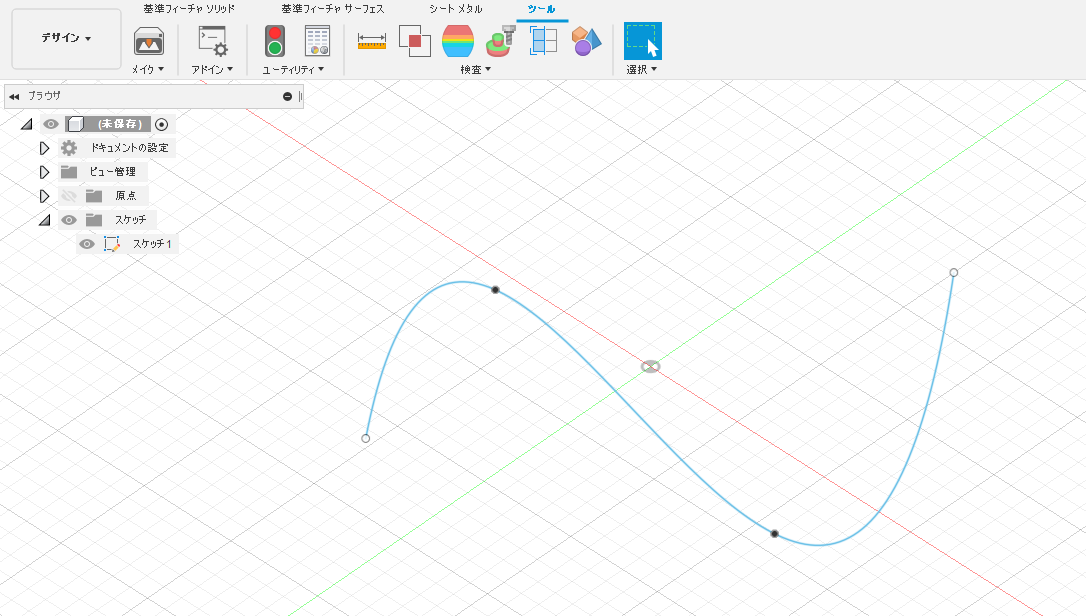
スケッチ1のなかのスプラインを取得して crvPath に代入しています
# スケッチの中のスケッチ1を取得 > スケッチ1の中のスプラインカーブを取得 sketch1 = rootComp.sketches.item(0) crvPath = sketch1.sketchCurves.sketchFittedSplines.item(0)パスに沿った平面を作成する
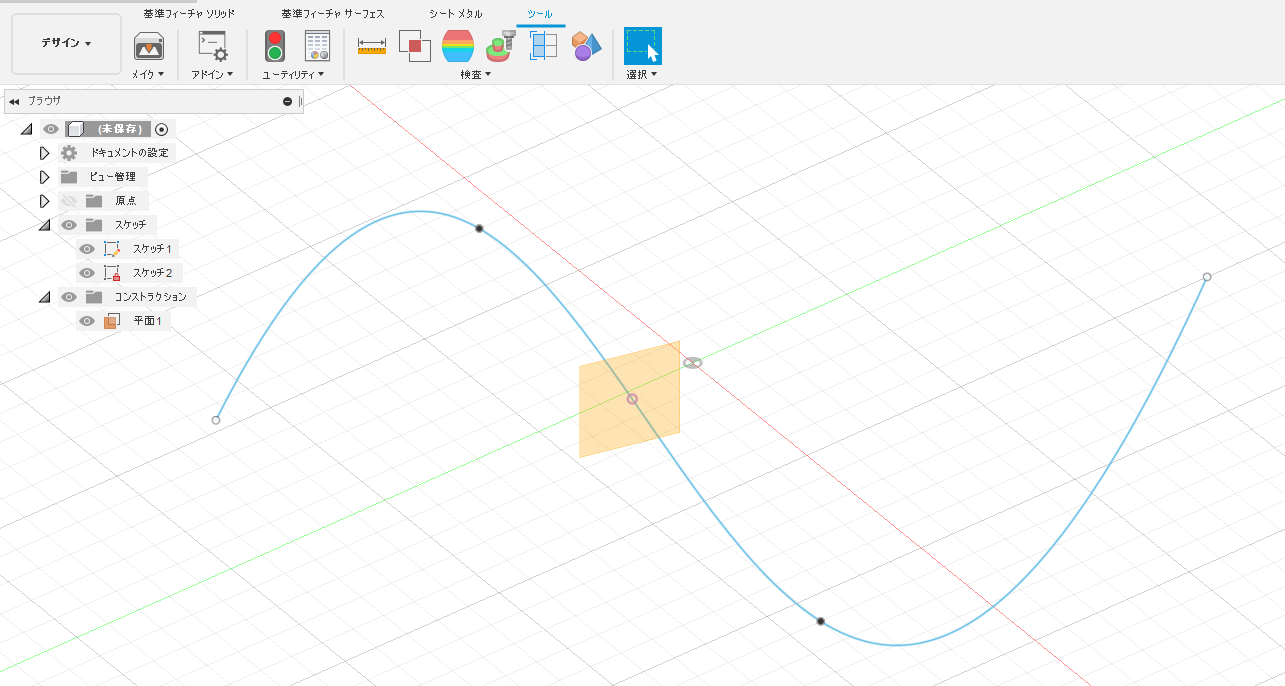
setByDistanceOnPath を使ってパスに沿った面を作成します。始点を0、終点を1として0~1の値を指定するのですが、直接数値を入力するのではなく、ValueInput オブジェクトで指定する必要があります。
# constructionPlanes オブジェクトを取得 planes = rootComp.constructionPlanes # ConstructionPlaneInput オブジェクトを取得 planeInput = planes.createInput() # パスに沿った平面を作成 distance = adsk.core.ValueInput.createByReal(0.4) planeInput.setByDistanceOnPath(crvPath, distance) plane = planes.add(planeInput)平面とパスの交点を作る
Fusion 360 には平面とパスとの交点を作るコマンドはありませんが、Sketch.intersectWithSketchPlane メソッド でスケッチ平面と曲線との交点を作ることができます。指定するパスは曲線一本だとしても配列にしないといけないようです。ここでは
entitiesという配列にcrvPathを追加して intersectWithSketchPlane メソッドの引数に入れています。# 新しいスケッチを追加 sketch2 = rootComp.sketches.add(plane) # スケッチ平面とパスとの交点を作成 entities = [] entities.append(crvPath) skPoints = sketch2.intersectWithSketchPlane(entities)まとめ
できたのはいいけど手数が多くて結構面倒でしたね。 pointInput.setByDistanceOnPath はリファレンスに載っていないだけで実は使えるのではと淡い期待を抱いてこんなコードを描いて実行してみた・・・けどエラーが出てしまってだめでした!
# Get construction points points = rootComp.constructionPoints # Create construction point input pointInput = points.createInput() # Add construction point by distance on path distance = adsk.core.ValueInput.createByReal(0.4) pointInput.setByDistanceOnPath(crvPath, distance) point = points.add(pointInput)早く API に実装されてほしいー!
- 投稿日:2020-08-02T21:06:32+09:00
[メモ]PCAとt-SNE
importする
import scipy as sp import sklearn.base from sklearn.manifold import TSNE import matplotlib.pyplot as plt import pandas as pddataの読み込み
data = 'table_rdf.csv' df = pd.read_csv(data,index_col=0).dropna(axis=1)t-SNEの実行
X_reduced = TSNE(n_components=2, random_state=0).fit_transform(df)色分けの設定
dataの読み込みdata_2 = 'y_rdf.csv' df_2 = pd.read_csv(data_2,index_col=0).dropna(axis=1)列方向(縦方向)にソート
df2_s = df_2.sort_index() df2_s.head()mergeする
df_merge = pd.merge(df, df_2, how='left',right_index=True,left_index=True) df_merge.head()プリントする
plt.scatter(X_reduced[:, 0], X_reduced[:, 1], c=df_merge['target']) plt.colorbar()PCAをする
from sklearn.decomposition import PCA pca = PCA(n_components=2).fit(df) values = pca.transform(df) fig = plt.figure() plt.scatter(values[:,0], values[:,1], c=df_merge['target']) plt.xlabel("value1") plt.ylabel("value2") plt.colorbar() plt.show()
- 投稿日:2020-08-02T21:04:55+09:00
【ラビットチャレンジ(E資格)】深層学習(day4)
はじめに
2021/2/19・20に実施される日本ディープラーニング協会(JDLA)E資格合格を目指して、ラビットチャレンジを受講した際の学習記録です。
ラビットチャレンジは「現場で潰しが効くディープラーニング講座」の通学講座録画ビデオを編集した教材を活用したコースです。
質問等のサポートはありませんが、E資格受験のための格安(2020年6月時点での最安値)の講座です。科目一覧
応用数学
機械学習
深層学習(day1)
深層学習(day2)
深層学習(day3)
深層学習(day4)Section1:実装演習
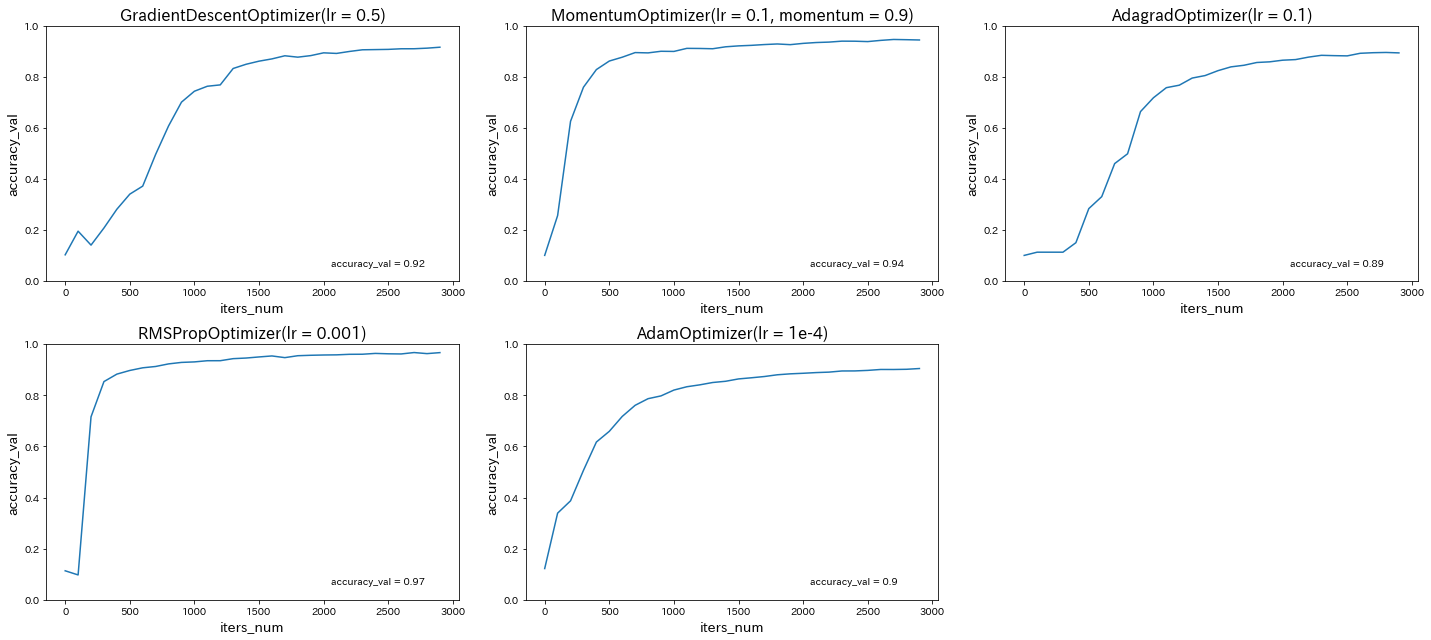
Tensorflow
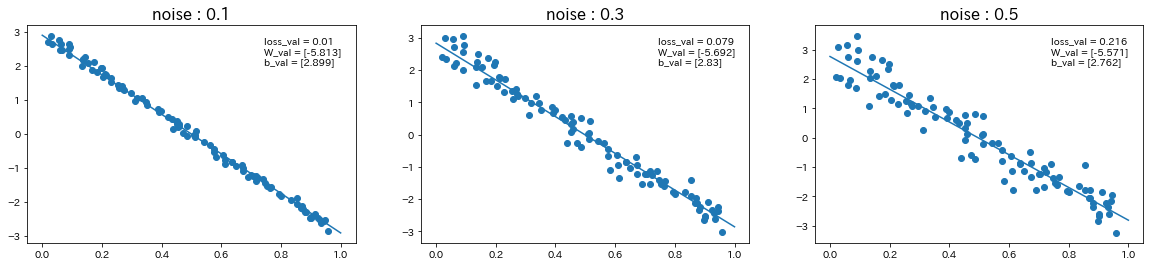
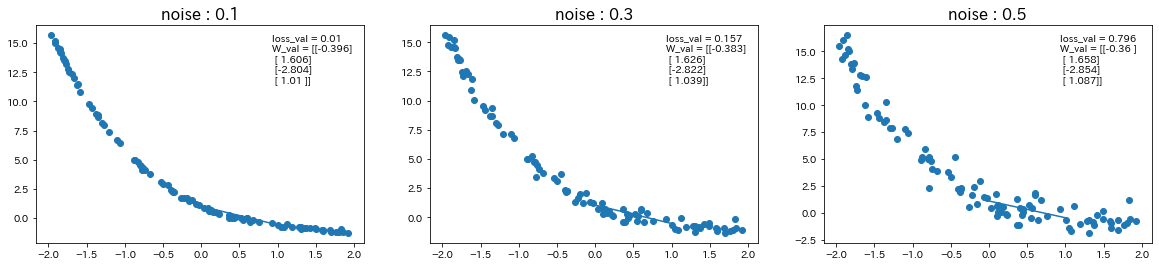
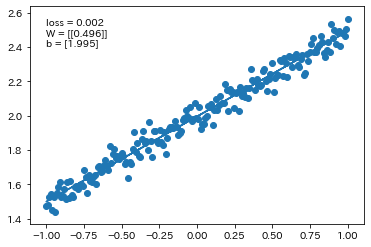
線形回帰
→ ノイズの値が大きいほど、誤差が大きくなり、予測精度が下がることが確認された。
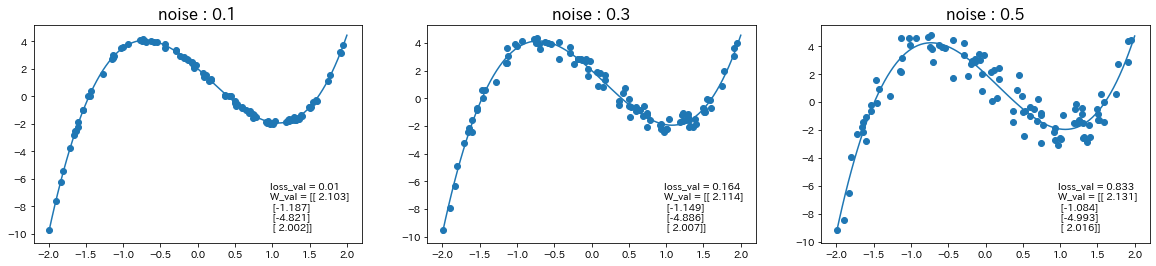
非線形回帰
→ ノイズの値が大きいほど、誤差が大きくなり、予測精度が下がることが確認された。
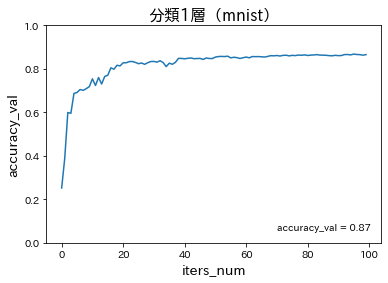
分類1層(mnist)
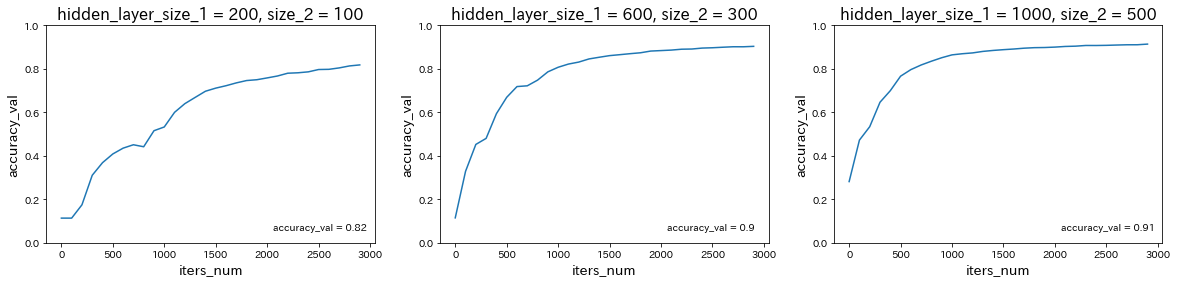
分類3層(mnist)
分類CNN(mnist)
keras
線形回帰
単純パーセプトロン
Simple_perceptron# モジュール読み込み import numpy as np from keras.models import Sequential from keras.layers import Dense, Activation from keras.optimizers import SGD # 乱数を固定値で初期化 np.random.seed(0) # シグモイドの単純パーセプトロン作成 model = Sequential() model.add(Dense(input_dim=2, units=1)) model.add(Activation('sigmoid')) model.summary() model.compile(loss='binary_crossentropy', optimizer=SGD(lr=0.1)) # トレーニング用入力 X と正解データ T X = np.array( [[0,0], [0,1], [1,0], [1,1]] ) T = np.array( [[0], [1], [1], [1]] ) # トレーニング model.fit(X, T, epochs=30, batch_size=1) # トレーニングの入力を流用して実際に分類 Y = model.predict_classes(X, batch_size=1) print("TEST") print(Y == T)
- np.random.seed(0)をnp.random.seed(1)に変更
発生する乱数が下記のような異なる値で固定されることになるので、学習結果も変わる。
np.random.seed()import numpy as np # 乱数を固定値で初期化 np.random.seed(0) print(np.random.randn()) -> 1.764052345967664 # 乱数を固定値で初期化 np.random.seed(1) print(np.random.randn()) -> 1.6243453636632417
- エポック数を100に変更
エポック数を増加させると、lossは減少することが確認された。
- AND回路, XOR回路に変更
OR回路、AND回路は線形分離可能だが、XORは線形分離不可能なので学習できないことが確認された。
- OR回路にしてバッチサイズを10に変更
バッチサイズを増加させると、lossは増加することが確認された。
- エポック数を300に変更
エポック数を増加させると、lossは減少することが確認された。
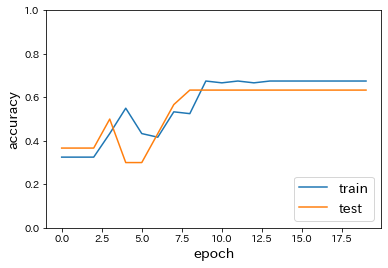
分類(iris)
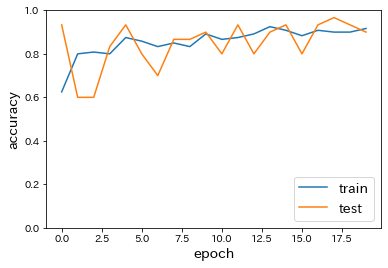
classifiy_irisimport matplotlib.pyplot as plt from sklearn import datasets iris = datasets.load_iris() x = iris.data d = iris.target from sklearn.model_selection import train_test_split x_train, x_test, d_train, d_test = train_test_split(x, d, test_size=0.2) from keras.models import Sequential from keras.layers import Dense, Activation # from keras.optimizers import SGD #モデルの設定 model = Sequential() model.add(Dense(12, input_dim=4)) model.add(Activation('relu')) # model.add(Activation('sigmoid')) model.add(Dense(3, input_dim=12)) model.add(Activation('softmax')) model.summary() model.compile(optimizer='sgd', loss='sparse_categorical_crossentropy', metrics=['accuracy']) history = model.fit(x_train, d_train, batch_size=5, epochs=20, verbose=1, validation_data=(x_test, d_test)) loss = model.evaluate(x_test, d_test, verbose=0) #Accuracy plt.plot(history.history['accuracy']) plt.plot(history.history['val_accuracy']) plt.ylabel('accuracy', fontsize=14) plt.xlabel('epoch', fontsize=14) plt.legend(['train', 'test'], loc='lower right', fontsize=14) plt.ylim(0, 1.0) plt.show()
- 中間層の活性関数をsigmoidに変更
→ accuracyの減少が確認された。
- SGDをimportし、optimizerをSGD(lr=0.1)に変更
→ epochごとのaccuracyのばらつきが増加したように思われる。
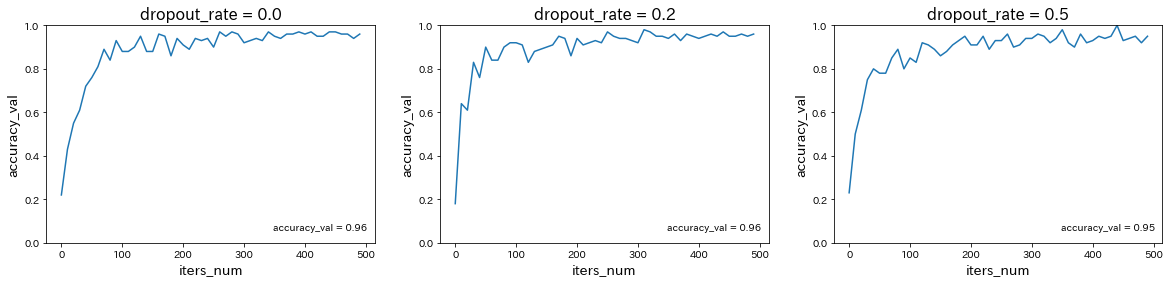
分類(mnist)
classify_mnist# 必要なライブラリのインポート import sys, os sys.path.append(os.pardir) # 親ディレクトリのファイルをインポートするための設定 import keras import matplotlib.pyplot as plt from data.mnist import load_mnist (x_train, d_train), (x_test, d_test) = load_mnist(normalize=True, one_hot_label=True) # 必要なライブラリのインポート、最適化手法はAdamを使う from keras.models import Sequential from keras.layers import Dense, Dropout from keras.optimizers import Adam # モデル作成 model = Sequential() model.add(Dense(512, activation='relu', input_shape=(784,))) model.add(Dropout(0.2)) model.add(Dense(512, activation='relu')) model.add(Dropout(0.2)) model.add(Dense(10, activation='softmax')) model.summary() # バッチサイズ、エポック数 batch_size = 128 epochs = 20 model.compile(loss='categorical_crossentropy', optimizer=Adam(lr=0.001, beta_1=0.9, beta_2=0.999, epsilon=None, decay=0.0, amsgrad=False), metrics=['accuracy']) history = model.fit(x_train, d_train, batch_size=batch_size, epochs=epochs, verbose=1, validation_data=(x_test, d_test)) loss = model.evaluate(x_test, d_test, verbose=0) print('Test loss:', loss[0]) print('Test accuracy:', loss[1]) # Accuracy plt.plot(history.history['accuracy']) plt.plot(history.history['val_accuracy']) plt.ylabel('accuracy') plt.xlabel('epoch') plt.legend(['train', 'test'], loc='upper left') # plt.ylim(0, 1.0) plt.show()
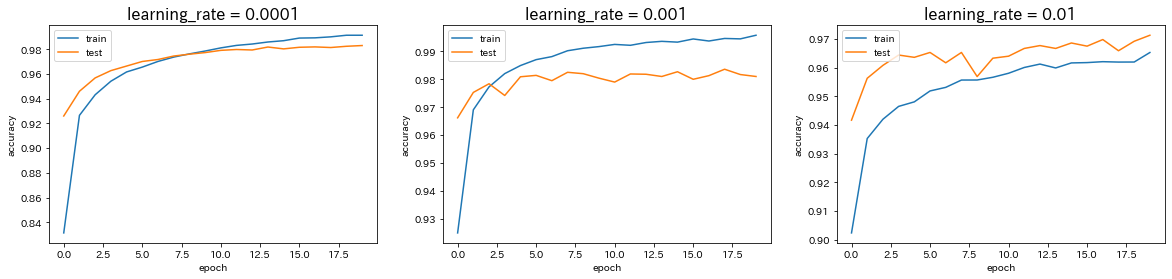
load_mnistのone_hot_labelをFalseに変更、または誤差関数をsparse_categorical_crossentropyに変更
→ 誤差関数として'categorical_crossentropy'を使う場合はデータの形式をone_hot_label形式に、'sparse_categorical_crossentropy'を使う場合はone_hot_labelではない形式にする必要がある。Adamの引数の値を変更
→ 学習率を0.0001から0.001に変更すると、予測精度はほぼ変わらないが、学習の早さは向上した。しかし、学習率を0.001からさらに0.01に変更すると、予測精度が低下した。CNN分類(mnist)
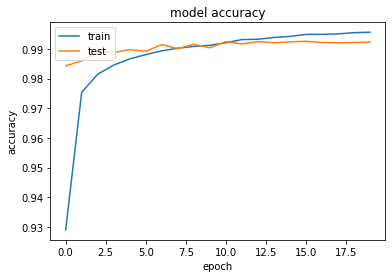
classify_mnist_with_CNN# 必要なライブラリのインポート import sys, os sys.path.append(os.pardir) # 親ディレクトリのファイルをインポートするための設定 import keras import matplotlib.pyplot as plt from data.mnist import load_mnist (x_train, d_train), (x_test, d_test) = load_mnist(normalize=True, one_hot_label=True) # 行列として入力するための加工 batch_size = 128 num_classes = 10 epochs = 20 img_rows, img_cols = 28, 28 x_train = x_train.reshape(x_train.shape[0], img_rows, img_cols, 1) x_test = x_test.reshape(x_test.shape[0], img_rows, img_cols, 1) input_shape = (img_rows, img_cols, 1) # 必要なライブラリのインポート、最適化手法はAdamを使う from keras.models import Sequential from keras.layers import Dense, Dropout, Flatten from keras.layers import Conv2D, MaxPooling2D from keras.optimizers import Adam model = Sequential() model.add(Conv2D(32, kernel_size=(3, 3), activation='relu', input_shape=input_shape)) model.add(Conv2D(64, (3, 3), activation='relu')) model.add(MaxPooling2D(pool_size=(2, 2))) model.add(Dropout(0.25)) model.add(Flatten()) model.add(Dense(128, activation='relu')) model.add(Dropout(0.5)) model.add(Dense(num_classes, activation='softmax')) model.summary() # バッチサイズ、エポック数 batch_size = 128 epochs = 20 model.compile(loss='categorical_crossentropy', optimizer=Adam(), metrics=['accuracy']) history = model.fit(x_train, d_train, batch_size=batch_size, epochs=epochs, verbose=1, validation_data=(x_test, d_test)) # Accuracy plt.plot(history.history['accuracy']) plt.plot(history.history['val_accuracy']) plt.title('model accuracy') plt.ylabel('accuracy') plt.xlabel('epoch') plt.legend(['train', 'test'], loc='upper left') # plt.ylim(0, 1.0) plt.show()→ CNNにより、99%以上という非常に高い予測精度が得られることが確認された。
CIFAR-10
classify_cifar10#CIFAR-10のデータセットのインポート from keras.datasets import cifar10 (x_train, d_train), (x_test, d_test) = cifar10.load_data() #CIFAR-10の正規化 from keras.utils import to_categorical # 特徴量の正規化 x_train = x_train/255. x_test = x_test/255. # クラスラベルの1-hotベクトル化 d_train = to_categorical(d_train, 10) d_test = to_categorical(d_test, 10) # CNNの構築 import keras from keras.models import Sequential from keras.layers.convolutional import Conv2D, MaxPooling2D from keras.layers.core import Dense, Dropout, Activation, Flatten import numpy as np model = Sequential() model.add(Conv2D(32, (3, 3), padding='same',input_shape=x_train.shape[1:])) model.add(Activation('relu')) model.add(Conv2D(32, (3, 3))) model.add(Activation('relu')) model.add(MaxPooling2D(pool_size=(2, 2))) model.add(Dropout(0.25)) model.add(Conv2D(64, (3, 3), padding='same')) model.add(Activation('relu')) model.add(Conv2D(64, (3, 3))) model.add(Activation('relu')) model.add(MaxPooling2D(pool_size=(2, 2))) model.add(Dropout(0.25)) model.add(Flatten()) model.add(Dense(512)) model.add(Activation('relu')) model.add(Dropout(0.5)) model.add(Dense(10)) model.add(Activation('softmax')) # コンパイル model.compile(loss='categorical_crossentropy',optimizer='adam',metrics=['accuracy']) #訓練 history = model.fit(x_train, d_train, epochs=20) tf.executing_eagerly() #評価 & 評価結果出力 print(model.evaluate(x_test, d_test)) # Accuracy plt.plot(history.history['accuracy']) plt.title('model accuracy') plt.ylabel('accuracy') plt.xlabel('epoch') plt.show() # モデルの保存 # model.save('./CIFAR-10.h5')RNN(2進数足し算の予測)
RNN(2進数足し算の予測)# import tensorflow as tf import tensorflow.compat.v1 as tf tf.disable_v2_behavior() # logging levelを変更 tf.logging.set_verbosity(tf.logging.ERROR) import numpy as np import matplotlib.pyplot as plt import keras from keras.models import Sequential from keras.layers.core import Dense, Dropout,Activation from keras.layers.wrappers import TimeDistributed from keras.optimizers import SGD from keras.layers.recurrent import SimpleRNN, LSTM, GRU # データを用意 # 2進数の桁数 binary_dim = 8 # 最大値 + 1 largest_number = pow(2, binary_dim) # largest_numberまで2進数を用意 binary = np.unpackbits(np.array([range(largest_number)], dtype=np.uint8).T,axis=1)[:, ::-1] # A, B初期化 (a + b = d) a_int = np.random.randint(largest_number/2, size=20000) a_bin = binary[a_int] # binary encoding b_int = np.random.randint(largest_number/2, size=20000) b_bin = binary[b_int] # binary encoding x_int = [] x_bin = [] for i in range(10000): x_int.append(np.array([a_int[i], b_int[i]]).T) x_bin.append(np.array([a_bin[i], b_bin[i]]).T) x_int_test = [] x_bin_test = [] for i in range(10001, 20000): x_int_test.append(np.array([a_int[i], b_int[i]]).T) x_bin_test.append(np.array([a_bin[i], b_bin[i]]).T) x_int = np.array(x_int) x_bin = np.array(x_bin) x_int_test = np.array(x_int_test) x_bin_test = np.array(x_bin_test) # 正解データ d_int = a_int + b_int d_bin = binary[d_int][0:10000] d_bin_test = binary[d_int][10001:20000] model = Sequential() model.add(SimpleRNN(units=16, return_sequences=True, input_shape=[8, 2], go_backwards=False, activation='relu', # dropout=0.5, # recurrent_dropout=0.3, # unroll = True, )) # 出力層 model.add(Dense(1, activation='sigmoid', input_shape=(-1,2))) model.summary() model.compile(loss='mean_squared_error', optimizer=SGD(lr=0.1), metrics=['accuracy']) # model.compile(loss='mse', optimizer='adam', metrics=['accuracy']) history = model.fit(x_bin, d_bin.reshape(-1, 8, 1), epochs=5, batch_size=2) # テスト結果出力 score = model.evaluate(x_bin_test, d_bin_test.reshape(-1,8,1), verbose=0) print('Test loss:', score[0]) print('Test accuracy:', score[1])Epoch 1/5
10000/10000 [==============================] - 28s 3ms/step - loss: 0.0810 - accuracy: 0.9156
Epoch 2/5
10000/10000 [==============================] - 28s 3ms/step - loss: 0.0029 - accuracy: 1.0000
Epoch 3/5
10000/10000 [==============================] - 28s 3ms/step - loss: 9.7898e-04 - accuracy: 1.0000
Epoch 4/5
10000/10000 [==============================] - 28s 3ms/step - loss: 4.8765e-04 - accuracy: 1.0000
Epoch 5/5
10000/10000 [==============================] - 28s 3ms/step - loss: 3.3379e-04 - accuracy: 1.0000
Test loss: 0.0002865186012966387
Test accuracy: 1.0
RNNの出力ノード数を128に変更
Epoch 1/5
10000/10000 [==============================] - 29s 3ms/step - loss: 0.0741 - accuracy: 0.9194
Epoch 2/5
10000/10000 [==============================] - 29s 3ms/step - loss: 0.0020 - accuracy: 1.0000
Epoch 3/5
10000/10000 [==============================] - 29s 3ms/step - loss: 6.9808e-04 - accuracy: 1.0000
Epoch 4/5
10000/10000 [==============================] - 28s 3ms/step - loss: 4.0773e-04 - accuracy: 1.0000
Epoch 5/5
10000/10000 [==============================] - 28s 3ms/step - loss: 2.8269e-04 - accuracy: 1.0000
Test loss: 0.0002439875359702302
Test accuracy: 1.0
→ 出力ノード数を16から128に変更した場合、予測精度が向上した。RNNの出力活性化関数をsigmoidに変更
Epoch 1/5
10000/10000 [==============================] - 28s 3ms/step - loss: 0.2498 - accuracy: 0.5131
Epoch 2/5
10000/10000 [==============================] - 28s 3ms/step - loss: 0.2487 - accuracy: 0.5302
Epoch 3/5
10000/10000 [==============================] - 28s 3ms/step - loss: 0.2469 - accuracy: 0.5481
Epoch 4/5
10000/10000 [==============================] - 28s 3ms/step - loss: 0.2416 - accuracy: 0.6096
Epoch 5/5
10000/10000 [==============================] - 27s 3ms/step - loss: 0.2166 - accuracy: 0.7125
Test loss: 0.18766544096552618
Test accuracy: 0.7449744939804077
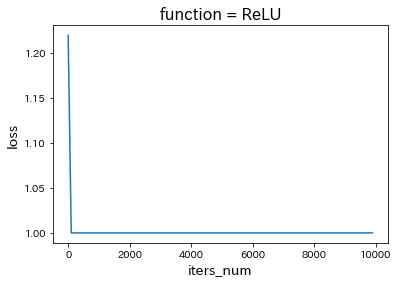
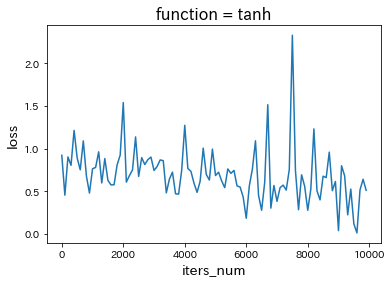
→ 出力活性化関数をReLUからsigmoidに変更した場合、予測精度が低下した。RNNの出力活性化関数をtanhに変更
Epoch 1/5
10000/10000 [==============================] - 28s 3ms/step - loss: 0.1289 - accuracy: 0.8170
Epoch 2/5
10000/10000 [==============================] - 28s 3ms/step - loss: 0.0022 - accuracy: 1.0000
Epoch 3/5
10000/10000 [==============================] - 28s 3ms/step - loss: 7.1403e-04 - accuracy: 1.0000
Epoch 4/5
10000/10000 [==============================] - 27s 3ms/step - loss: 4.1603e-04 - accuracy: 1.0000
Epoch 5/5
10000/10000 [==============================] - 28s 3ms/step - loss: 2.8925e-04 - accuracy: 1.0000
Test loss: 0.00024679134038564263
Test accuracy: 1.0
→ 出力活性化関数をReLUからTanhに変更すると、予測精度が向上した。最適化方法をadamに変更
Epoch 1/5
10000/10000 [==============================] - 31s 3ms/step - loss: 0.0694 - accuracy: 0.9385
Epoch 2/5
10000/10000 [==============================] - 32s 3ms/step - loss: 0.0012 - accuracy: 1.0000
Epoch 3/5
10000/10000 [==============================] - 31s 3ms/step - loss: 5.4037e-05 - accuracy: 1.0000
Epoch 4/5
10000/10000 [==============================] - 31s 3ms/step - loss: 3.3823e-06 - accuracy: 1.0000
Epoch 5/5
10000/10000 [==============================] - 31s 3ms/step - loss: 2.4213e-07 - accuracy: 1.0000
Test loss: 5.572893907904208e-08
Test accuracy: 1.0
→ 最適化方法をsgdからadamに変更すると、予測精度が向上した。RNNの入力Dropoutを0.5に設定
Epoch 1/5
10000/10000 [==============================] - 30s 3ms/step - loss: 0.2324 - accuracy: 0.5875
Epoch 2/5
10000/10000 [==============================] - 31s 3ms/step - loss: 0.2106 - accuracy: 0.6230
Epoch 3/5
10000/10000 [==============================] - 31s 3ms/step - loss: 0.2046 - accuracy: 0.6264
Epoch 4/5
10000/10000 [==============================] - 31s 3ms/step - loss: 0.2032 - accuracy: 0.6244
Epoch 5/5
10000/10000 [==============================] - 30s 3ms/step - loss: 0.1995 - accuracy: 0.6350
Test loss: 0.15461890560702712
Test accuracy: 0.8619986772537231
→ 入力Dropoutを0.5に設定すると、学習が進まなくなった。RNNの再帰Dropoutを0.3に設定
Epoch 1/5
10000/10000 [==============================] - 32s 3ms/step - loss: 0.1459 - accuracy: 0.8306
Epoch 2/5
10000/10000 [==============================] - 32s 3ms/step - loss: 0.0947 - accuracy: 0.9058
Epoch 3/5
10000/10000 [==============================] - 32s 3ms/step - loss: 0.0895 - accuracy: 0.9099
Epoch 4/5
10000/10000 [==============================] - 31s 3ms/step - loss: 0.0881 - accuracy: 0.9112
Epoch 5/5
10000/10000 [==============================] - 31s 3ms/step - loss: 0.0871 - accuracy: 0.9120
Test loss: 0.09418297858566198
Test accuracy: 0.9016276597976685
→ 再帰Dropoutを0.3に設定すると、予測精度が低下した。RNNのunrollをTrueに設定
Epoch 1/5
10000/10000 [==============================] - 20s 2ms/step - loss: 0.0938 - accuracy: 0.8871
Epoch 2/5
10000/10000 [==============================] - 20s 2ms/step - loss: 0.0032 - accuracy: 0.9999
Epoch 3/5
10000/10000 [==============================] - 20s 2ms/step - loss: 9.4733e-04 - accuracy: 1.0000
Epoch 4/5
10000/10000 [==============================] - 21s 2ms/step - loss: 5.3410e-04 - accuracy: 1.0000
Epoch 5/5
10000/10000 [==============================] - 20s 2ms/step - loss: 3.6424e-04 - accuracy: 1.0000
Test loss: 0.0003125413816745379
Test accuracy: 1.0
→ unrollをTrueに設定(ループせずに計算を行う)した場合、予測精度がわずかに低下した。メモリが集約されたため、計算時間は早くなった。Section2:強化学習
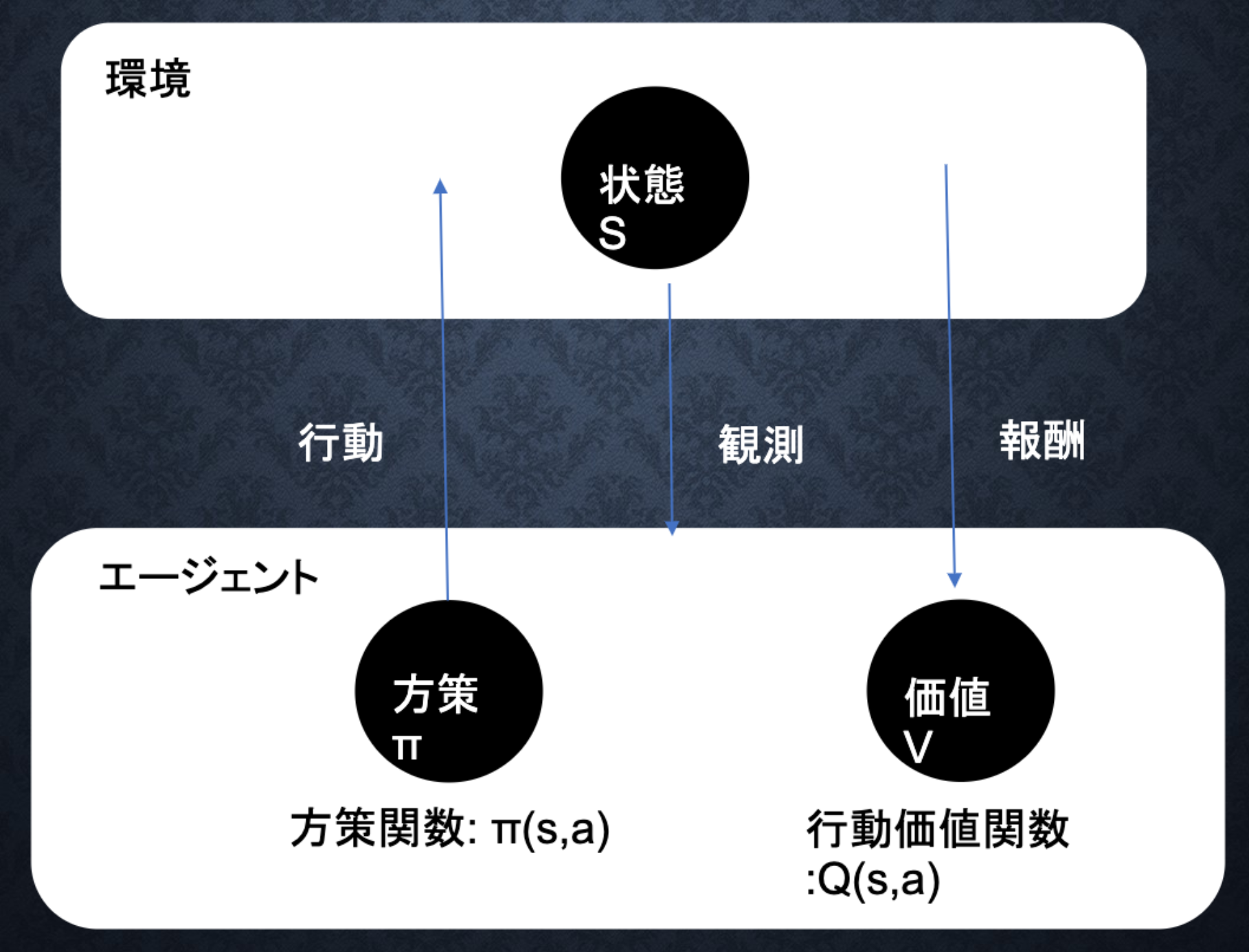
強化学習とは
長期的に報酬を最大化できるように環境の中で行動を選択できるエージェントを作ることを目標とする機械学習の一分野。
→ 行動の結果として与えられる利益(報酬)を基に、行動を決定する原理を改善していく仕組み。教師あり学習および教師なし学習では、データから予測すること、データに含まれるパターンを見つけ出すのがそれぞれの目標である。
一方、強化学習では、優れた方策を見つけることが目標。
環境について事前に完璧な知識があれば、最適な行動を予測し決定することは可能であるが、強化学習では不完全な知識を基に行動しながら、データを収集し最適な行動を見つけていく。
Q学習
行動する毎に行動価値関数を更新することにより学習を進める手法。関数近似法
価値関数や方策関数を関数近似する手法。探索と利用のトレードオフ
過去のデータでベストとされる行動のみを常にとり続ければ、他のさらにベストな行動を見つけることはできない。(探索が足りない状態)
$\longleftrightarrow$ 未知の行動のみを常にとり続ければ、過去の経験が活かせない、(利用が足りない状態)強化学習のイメージ
行動価値関数
価値を表す関数として、状態価値関数(ある状態に注目する場合)と行動価値関数(状態と価値を組み合わせた価値に注目する場合)の2種類がある。
方策関数
方策関数とは、方策ベースの強化学習手法において、ある状態でどのような行動をとるのかの確率を与える関数のこと。
方策勾配法
$$ \theta^{(t+1)} = \theta^{(t)}+\epsilon \nabla J(\theta) $$
- 投稿日:2020-08-02T21:04:23+09:00
【ラビットチャレンジ(E資格)】深層学習(day3)
はじめに
2021/2/19・20に実施される日本ディープラーニング協会(JDLA)E資格合格を目指して、ラビットチャレンジを受講した際の学習記録です。
ラビットチャレンジは「現場で潰しが効くディープラーニング講座」の通学講座録画ビデオを編集した教材を活用したコースです。
質問等のサポートはありませんが、E資格受験のための格安(2020年6月時点での最安値)の講座です。科目一覧
応用数学
機械学習
深層学習(day1)
深層学習(day2)
深層学習(day3)
深層学習(day4)Section1:再帰型ニューラルネットワークの概念
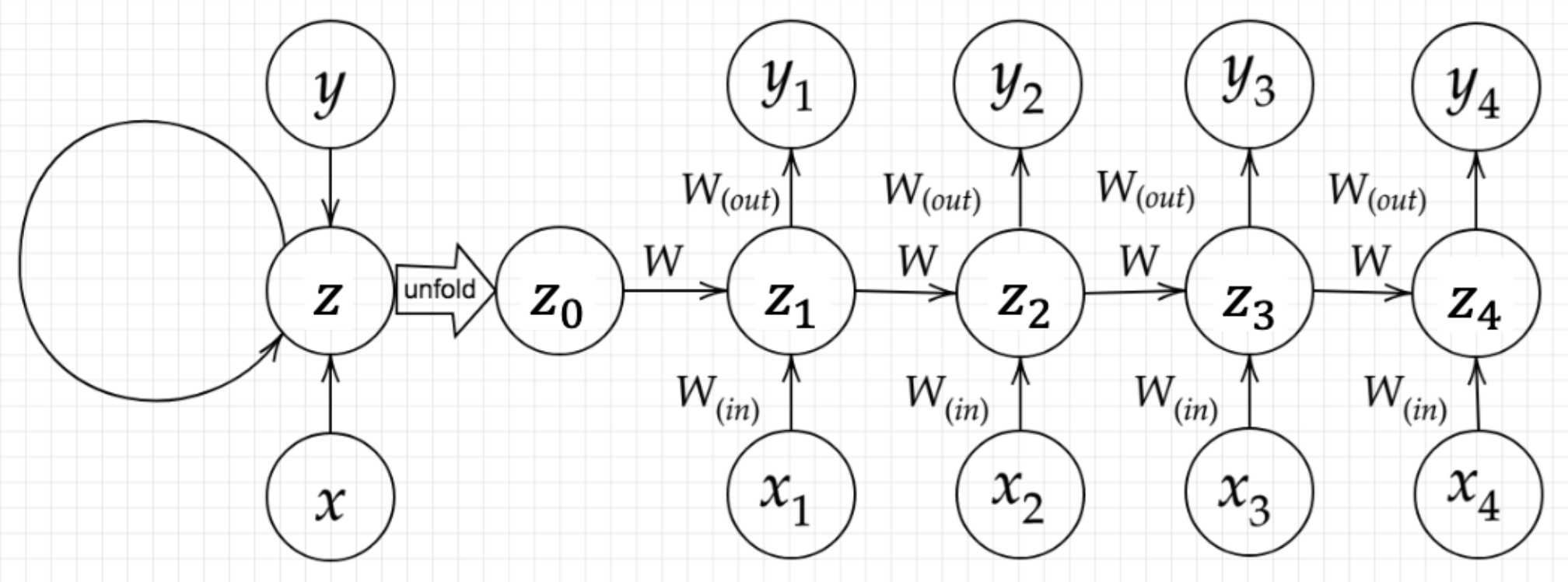
Recurrent Neural Network(RNN)とは、時系列データに対応可能なニューラルネットワークのことである。
時系列データは時間的順序を追って一定間隔ごとに観察され、しかも相互に統計的依存関係が認められるようなデータの系列のことであり、音声データやテキストデータがある。RNNは時系列データを扱うため、初期の状態と過去の時間 $t-1$ の状態を保持し、次の時間 $t$ の状態を求める再帰的構造が必要になる。
$$ u^t = W_{(in)}x^t+Wz^{(t-1)}+b $$
$$ z^t = f(W_{(in)}x^t+Wz^{(t-1)}+b) $$
$$ v^t = W_{(out)}z^t+c $$
$$ y^t = g(W_{(out)}z^t+c) $$RNNにおいてのパラメータ調整方法として、誤差逆伝播の一種であるBPTTがある。
【パラメータの更新式】
$$ W_{(in)}^{t+1} = W_{(in)}^{t}-\epsilon\frac{\partial E}{\partial W_{(in)}} = W_{(in)}^{t}-\epsilon \sum_{z=0}^{T_t}\delta^{t-z}[x^{t-z}]^T $$
$$ W_{(out)}^{t+1} = W_{(out)}^{t}-\epsilon\frac{\partial E}{\partial W_{(out)}} = W_{(out)}^{t}-\epsilon \delta^{out,t}[z^{t}]^T $$
$$ W^{t+1} = W^{t}-\epsilon\frac{\partial E}{\partial W} = W_{(in)}^{t}-\epsilon \sum_{z=0}^{T_t}\delta^{t-z}[x^{t-z-1}]^T $$
$$ b^{t+1} = b^t-\epsilon\frac{\partial E}{\partial b} = b^t-\epsilon \sum_{z=0}^{T_t}\delta^{t-z} $$
$$ c^{t+1} = c^t-\epsilon\frac{\partial E}{\partial c} = c^t-\epsilon \delta^{out,t} $$simple_RNN(バイナリ加算)import sys, os sys.path.append(os.pardir) # 親ディレクトリのファイルをインポートするための設定 import numpy as np from common import functions import matplotlib.pyplot as plt def d_tanh(x): return 1/(np.cosh(x) ** 2) # データを用意 # 2進数の桁数 binary_dim = 8 # 最大値 + 1 largest_number = pow(2, binary_dim) # largest_numberまで2進数を用意 binary = np.unpackbits(np.array([range(largest_number)],dtype=np.uint8).T,axis=1) input_layer_size = 2 hidden_layer_size = 16 output_layer_size = 1 weight_init_std = 1 learning_rate = 0.1 iters_num = 10000 plot_interval = 100 # ウェイト初期化 (バイアスは簡単のため省略) W_in = weight_init_std * np.random.randn(input_layer_size, hidden_layer_size) W_out = weight_init_std * np.random.randn(hidden_layer_size, output_layer_size) W = weight_init_std * np.random.randn(hidden_layer_size, hidden_layer_size) # Xavier # W_in = np.random.randn(input_layer_size, hidden_layer_size) / (np.sqrt(input_layer_size)) # W_out = np.random.randn(hidden_layer_size, output_layer_size) / (np.sqrt(hidden_layer_size)) # W = np.random.randn(hidden_layer_size, hidden_layer_size) / (np.sqrt(hidden_layer_size)) # He # W_in = np.random.randn(input_layer_size, hidden_layer_size) / (np.sqrt(input_layer_size)) * np.sqrt(2) # W_out = np.random.randn(hidden_layer_size, output_layer_size) / (np.sqrt(hidden_layer_size)) * np.sqrt(2) # W = np.random.randn(hidden_layer_size, hidden_layer_size) / (np.sqrt(hidden_layer_size)) * np.sqrt(2) # 勾配 W_in_grad = np.zeros_like(W_in) W_out_grad = np.zeros_like(W_out) W_grad = np.zeros_like(W) u = np.zeros((hidden_layer_size, binary_dim + 1)) z = np.zeros((hidden_layer_size, binary_dim + 1)) y = np.zeros((output_layer_size, binary_dim)) delta_out = np.zeros((output_layer_size, binary_dim)) delta = np.zeros((hidden_layer_size, binary_dim + 1)) all_losses = [] for i in range(iters_num): # A, B初期化 (a + b = d) a_int = np.random.randint(largest_number/2) a_bin = binary[a_int] # binary encoding b_int = np.random.randint(largest_number/2) b_bin = binary[b_int] # binary encoding # 正解データ d_int = a_int + b_int d_bin = binary[d_int] # 出力バイナリ out_bin = np.zeros_like(d_bin) # 時系列全体の誤差 all_loss = 0 # 時系列ループ for t in range(binary_dim): # 入力値 X = np.array([a_bin[ - t - 1], b_bin[ - t - 1]]).reshape(1, -1) # 時刻tにおける正解データ dd = np.array([d_bin[binary_dim - t - 1]]) u[:,t+1] = np.dot(X, W_in) + np.dot(z[:,t].reshape(1, -1), W) z[:,t+1] = functions.sigmoid(u[:,t+1]) # z[:,t+1] = functions.relu(u[:,t+1]) # z[:,t+1] = np.tanh(u[:,t+1]) y[:,t] = functions.sigmoid(np.dot(z[:,t+1].reshape(1, -1), W_out)) #誤差 loss = functions.mean_squared_error(dd, y[:,t]) delta_out[:,t] = functions.d_mean_squared_error(dd, y[:,t]) * functions.d_sigmoid(y[:,t]) all_loss += loss out_bin[binary_dim - t - 1] = np.round(y[:,t]) for t in range(binary_dim)[::-1]: X = np.array([a_bin[-t-1],b_bin[-t-1]]).reshape(1, -1) delta[:,t] = (np.dot(delta[:,t+1].T, W.T) + np.dot(delta_out[:,t].T, W_out.T)) * functions.d_sigmoid(u[:,t+1]) # delta[:,t] = (np.dot(delta[:,t+1].T, W.T) + np.dot(delta_out[:,t].T, W_out.T)) * functions.d_relu(u[:,t+1]) # delta[:,t] = (np.dot(delta[:,t+1].T, W.T) + np.dot(delta_out[:,t].T, W_out.T)) * d_tanh(u[:,t+1]) # 勾配更新 W_out_grad += np.dot(z[:,t+1].reshape(-1,1), delta_out[:,t].reshape(-1,1)) W_grad += np.dot(z[:,t].reshape(-1,1), delta[:,t].reshape(1,-1)) W_in_grad += np.dot(X.T, delta[:,t].reshape(1,-1)) # 勾配適用 W_in -= learning_rate * W_in_grad W_out -= learning_rate * W_out_grad W -= learning_rate * W_grad W_in_grad *= 0 W_out_grad *= 0 W_grad *= 0 if(i % plot_interval == 0): all_losses.append(all_loss) print("iters:" + str(i)) print("Loss:" + str(all_loss)) print("Pred:" + str(out_bin)) print("True:" + str(d_bin)) out_int = 0 for index,x in enumerate(reversed(out_bin)): out_int += x * pow(2, index) print(str(a_int) + " + " + str(b_int) + " = " + str(out_int)) print("------------") lists = range(0, iters_num, plot_interval) plt.plot(lists, all_losses, label="loss") plt.xlabel("iters_num", fontsize=14) plt.ylabel("loss", fontsize=14) plt.show()
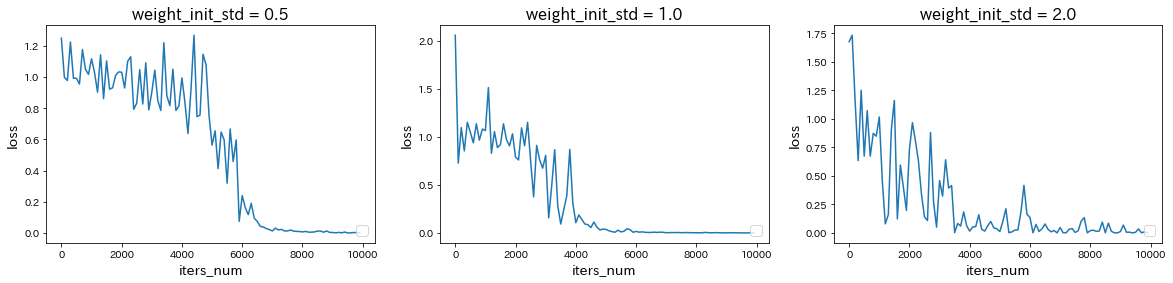
weight_init_stdを変更
→ weight_init_stdを1.0から0.5に減少または2.0に増加させると、どちらも収束が遅くなった。learning_rateを変更
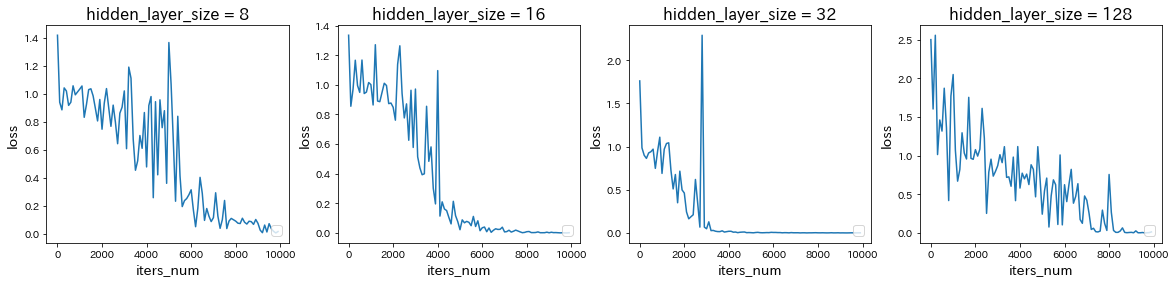
→ learning_rateを0.1から0.01に減少させると学習が遅くなったが、1.0に増加させると学習が早くなり、さらに3.0に増加させると学習が進まなかった。hidden_layer_sizeを変更
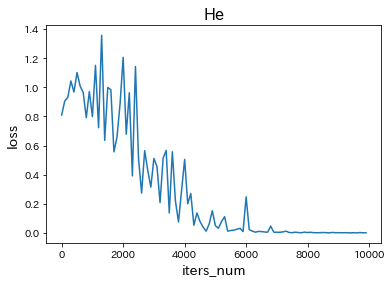
→ hidden_layer_sizeを16から8に減少させると学習が遅くなったが、32に増加させると学習が早くなり、さらに128に増加させると学習が遅くなった。中間層の活性化関数を変更
Section2:LSTM(Long Short-Term Memory)
単純なRNNでは、誤差逆伝播を行う際の勾配消失のため、長距離依存関係を上手く学習することができない。
LSTMはその問題点を解消する手法として用いられている。
- Input gate:$ i_t = \sigma(W^{(i)}x_t + U^{(i)}h_{t-1} + b^{(i)} ) $
- Forget gate:$ f_t = \sigma(W^{(f)}x_t + U^{(f)}h_{t-1} + b^{(f)} ) $
- output gate:$ o_t = \sigma(W^{(o)}x_t + U^{(o)}h_{t-1} + b^{(o)} ) $
- メモリーセル:$ \tilde c_t = tanh(W^{(\tilde c)}x_t+U^{(\tilde c)}h_{t-1}+b^{(\tilde c)}, \quad c_t = i_t \circ \tilde c_t+ f_t \circ c_{t-1} $
- 状態の更新:$ h_t = o_t \circ tanh(c_t) $
CEC(Constant Error Carousel)
勾配消失および勾配爆発の解決方法として、勾配が1であれば解決できる。
課題:入力データについて、時間依存度に関係なく重みが一律である。
→ ニューラルネットワークの学習特性がないということ。入力ゲートと出力ゲート
入力ゲートと出力ゲートを追加し、それぞれのゲートへの入力値の重みを重み行列W、Uで可変可能とすることにより、CECの課題を解決。忘却ゲート
CECは過去の情報がすべて保管されているが、過去の情報が不要になった場合、削除することはできず保管され続ける。
そこで、過去の情報が不要になった場合、そのタイミングで情報を忘却する昨日として、忘却ゲートが誕生した。覗き穴結合
CECの保存されている過去の情報を任意のタイミングで他のノードに伝播させたり、忘却させたい。
CEC自身の値は、ゲート制御に影響を与えていない。
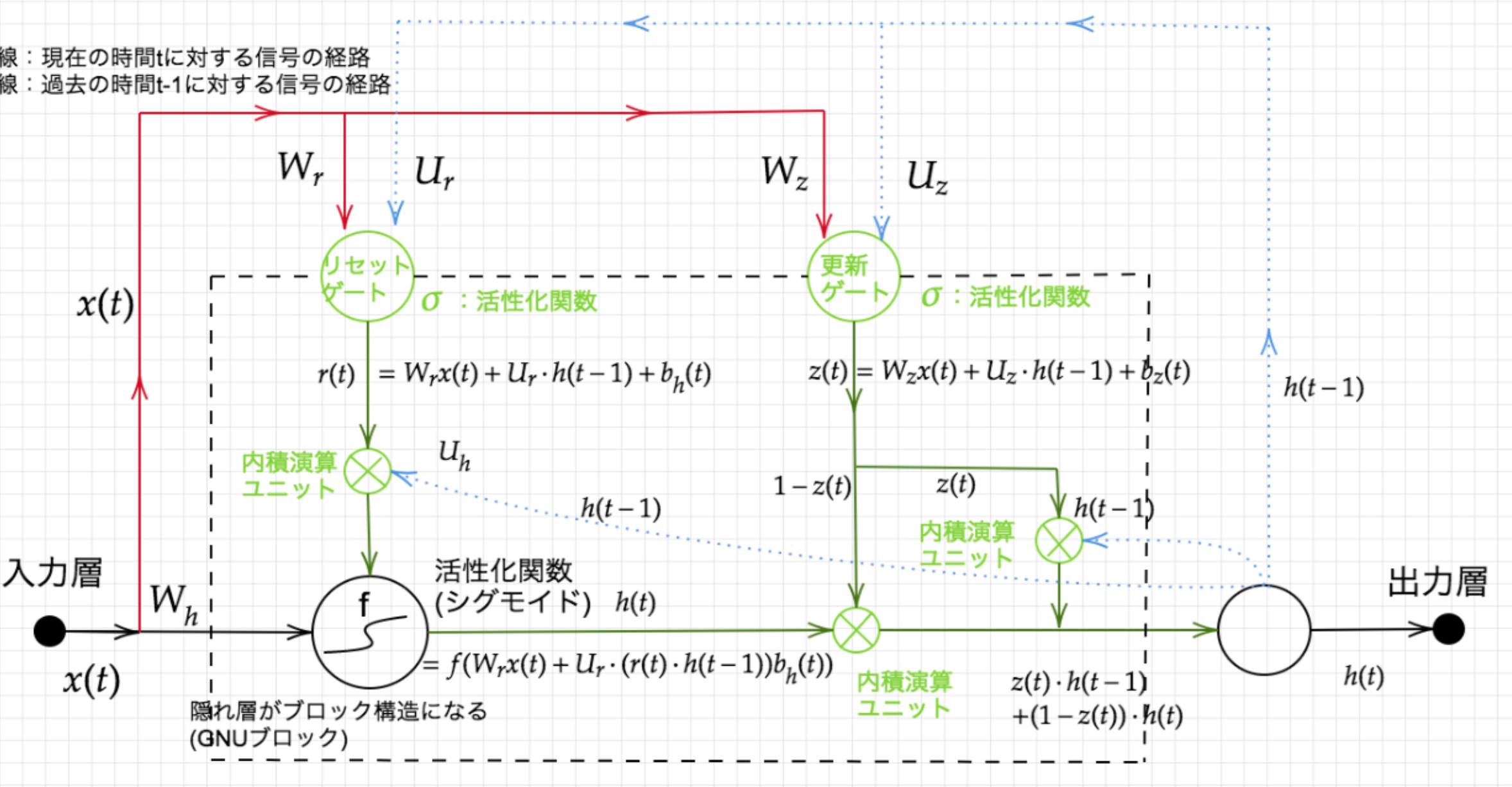
→ CEC自身の値に重み行列を介して伝播可能にした構造として覗き穴結合。Section3:GRU(Gated Recurrent Unit)
従来のLSTMでは、パラメータが多数存在していたため、計算付加が大きかった。
そこで、GRUではそのパラメータを大幅に削減し、精度は同等またはそれ以上が望めるようになった構造をしている。
- Update gate:$ z_t = \sigma(W^{(z)}x_t + U^{(z)}h_{t-1}) $
- Reset gate:$ r_t = \sigma(W^{(r)}x_t + U^{(r)}h_{t-1}) $
- 状態の更新:$ \tilde h_t = tanh(Wx_t+r_t \circ Uh_{t-1}), \quad h_t = z_t \circ h_{t-1}) + (1-z_t) \circ \tilde h_t $
Reset gateの値が0の場合、前の状態を無視。
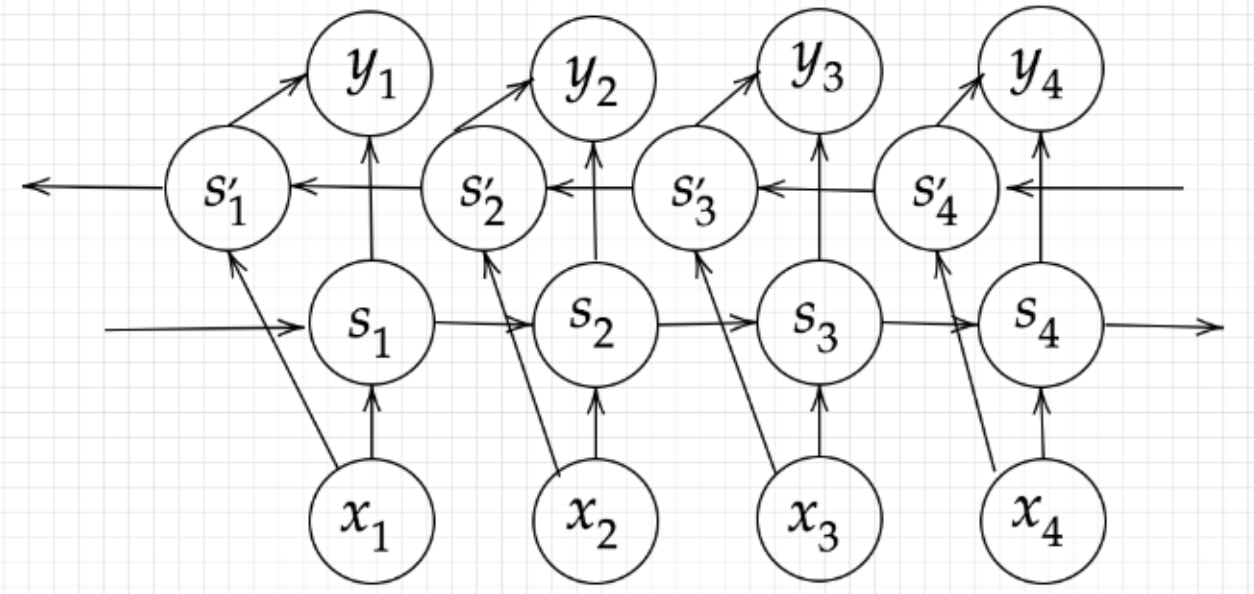
Update gateの値が1の場合、前の状態をそのままコピー。Section4:双方向RNN(Bidirectional RNN)
過去の情報だけでなく、未来の情報を加味することで、精度を向上させるためのモデル。
文章の推敲や機械翻訳に使用される。Section5:Seq2Seq
通常のRNNは入力と出力の長さや順序が同じでなければならない。
一方、Seq2SeqはEncoder-Decoderモデルの一種で、入力側と出力側で別々のRNNを使う。
機械対話や機械翻訳に使用される。
Encoder RNN
ユーザーがインプットしたテキストデータを単語等のトークンに区切って渡す構造。
vec1をRNNに入力し、hidden stateを出力。
このhidden stateと次の入力vec2をまたRNNに入力してきたhidden state
最後のvecを入れたときのhidden stateをfinal stateをしてとっておく。
このfinal stateがthought vectorと呼ばれ、入力した文の意味を表すベクトルとなる。Decoder RNN
システムがアウトプットデータを単語等のトークンごとに生成する構造。【Decoder RNNの処理手順】
1. Decoder RNN:Encoder RNNのfinal state(thought vector)から、各tokenの生成確率を出力していく。final stateをDecoder RNNのinitial stateとして設定し、Embeddingを入力。
2. Sampling:生成確率に基いてtokenをランダムに選ぶ。
3. Embedding:2で選ばれたtokenをEmbeddingしてDecoder RNNへの次の入力とする。
4. Detokenize:1-3を繰り返し、2で得られたtokenを文字列に直す。
HRED
過去n-1個の発話から次の発話を生成する。
Seq2seqでは会話の文脈無視で応答がなされたが、HREDでは前の単語の流れに即して応答されるため、より人間らしい文章が生成される。
Seq2seqとContext RNN(Encoderのまとめた各文章の系列をまとめて、これまでの会話コンテキスト全体を表すベクトルに変換する構造)を組み合わせた構造により、過去の発話の履歴を加味した応答を生成している。
課題1:確率的な多様性が字面にしかなく、会話の「流れ」のような多様性がない。
→ 同じコンテキスト(発話リスト)を与えられても、答えの内容が会話の流れとしては毎回同じものしか出せない。
課題2:短く情報量に乏しい答えをしがちである。
→ 短いよくある答えを学ぶ傾向がある。VHRED
HREDにVAEの潜在変数の概念を追加することにより、HREDの課題を解決した構造。VAE
潜在変数zに確率分布を仮定したもの。Section6:Word2vec
RNNでは、単語のような可変長の文字列をNNに与えることはできない。
word2vecでは学習データからボキャブラリを作成し、「ボキャブラリ数×任意の単語ベクトルの次元数」の重み行列により、大規模データの分散表現の学習を現実的な計算速度とメモリ量で実現可能にした。
結果の数値ベクトルは、生のテキストをデータの視覚化、機械学習、および深層学習に適した数値表現に変換するために使用できる。Section7:Attention Mechanism
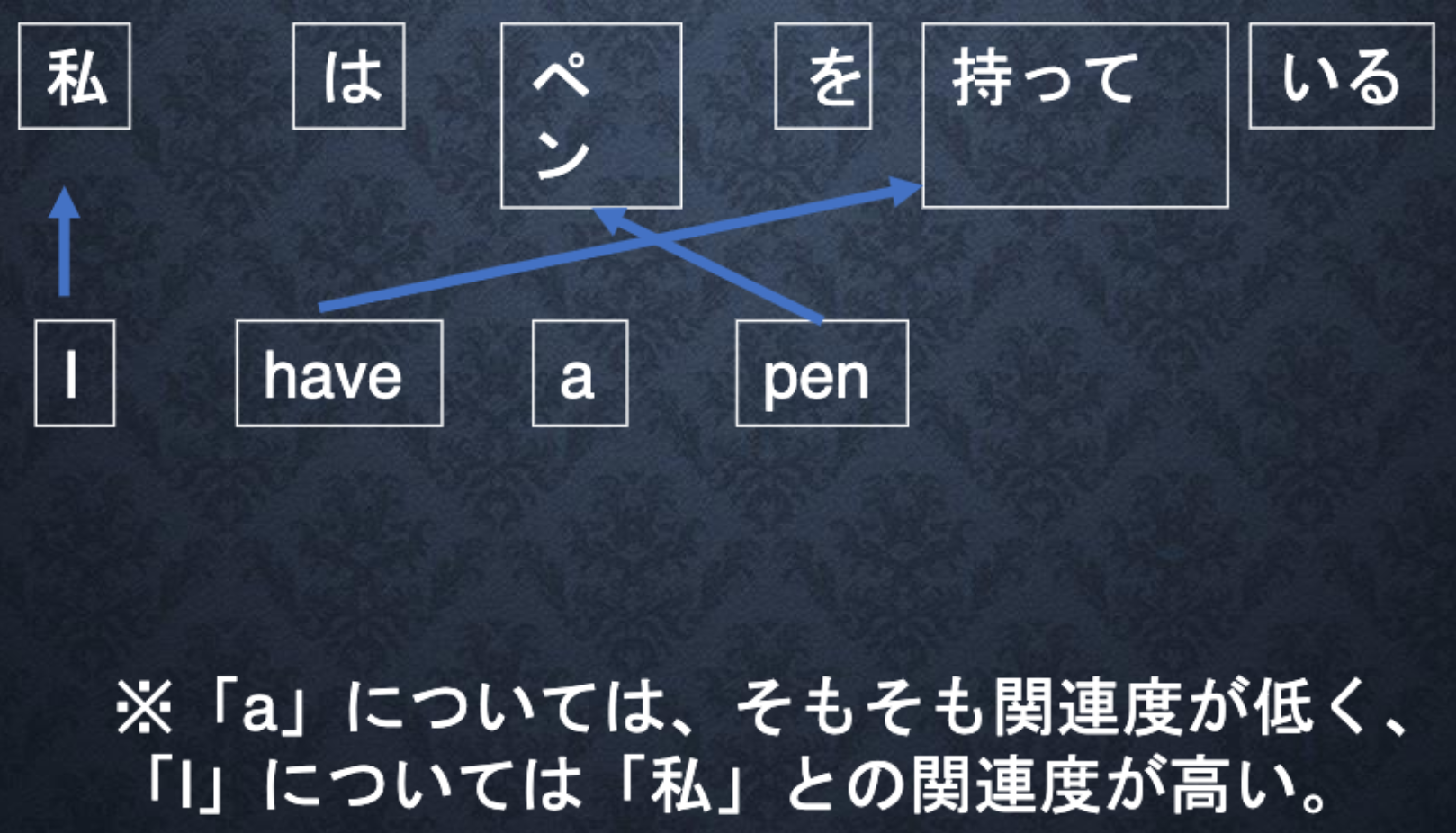
「入力と出力のどの単語が関連しているか」の関連度を学習する仕組み。
Decoderが各単語を出力する際の情報として、Encoderにおける各単語の隠れ状態の重み付き平均を入力として用いるという方法で、翻訳元の文の文脈情報をより詳細に捉えることができるようになる。
Attentionの機構が導入されたことによって、ニューラル機械翻訳の精度は大きく向上し、従来の統計的機械翻訳モデルの性能を凌駕することとなった。
- 投稿日:2020-08-02T19:22:13+09:00
Featherフォーマットを使ってPython・R・Julia間で簡単にデータをやり取りする
Python、R、Juliaそれぞれの強みがあるので組み合わせて使いたい場面がしばしばあるかと思います。コードを直接呼び出す機能もありますが、データ解析の場面ではそこまで密に結合させなくても別々のスクリプトで違うステップを担当すれば十分なことも多いでしょう。たとえばPythonでデータのスクレイピングをして、Juliaでマルチスレッドに解析を回し、Rで統計解析や可視化を行うといったケースは想像しやすいかと思います。
Why Feather?
そんなとき、Pythonでpickleで保存するともちろん他のプログラミング言語にデータを持っていくことができない、いっぽうでCSVでの保存は遅かったり読み込み時にパースし直すのが面倒、など微妙にやりづらさを覚えることがあります。今回はそんなワークフロー構築での悩みを解決してくれる Featherフォーマット とその使い方を簡単に紹介します。Featherはデータ保存用の軽量なフォーマットで、シンプルなAPIで使え、プログラミング言語間での行き来が自由で、かつ読み書きが高速なことを特徴とします。
こちらの比較記事 によるとFeatherは速度、メモリ消費の両面で優れたパフォーマンスを示すようです。実際の性能はどのようなデータを格納するかによって異なるでしょうが、ともかく簡単に使えるので試してみる価値は十分にあるのではないでしょうか。
注意
Featherフォーマットは行ラベルに対応していません。そのためpandasで行ラベルを与えている場合はあらかじめ
df.reset_index()してやる必要があります。 Rはぜんぜん行ラベルは使わない気がしますし、 推奨できないという話もあります 。Feather形式読み書きのコード
Python
python.pyimport pandas as pd import feather # read df = feather.read_dataframe("foobar.feather") # write feather.write_dataframe(df, "foobar.feather")R
r.rlibrary(feather) # read df <- read_feather("foobar.feather") # write write_feather(df, "foobar.feather")Julia
julia.jlusing DataFrames using Feather # read df = Feather.read("foobar.feather") # write Feather.write("foobar.feather", df)これだけです。いずれの言語でも型やヘッダなど気にすることなく読み書きができるためCSVより楽だと思います。
追記:最近 Feather V2 がリリースされました。まだJuliaでの対応パッケージが出揃っていないのでここでは扱いません。本記事の内容はFeather V1を対象としたものとなります。
- 投稿日:2020-08-02T19:11:27+09:00
yukicoder contest 259 復習
結果
感想
A問題を難しいと感じて逃げてしまいました。基本に従えば難しくないので反省しています。
B問題も定数を間違えてしまって時間をロスしてしまいました。勿体ないです…。
C問題はあまりやったことのない類の問題でしたが解けました。粘れてよかったです。A問題
①$t$の範囲は$D$に依存し$D$は極めて大きくその$t$の最小値$T$を求める必要がある②$tT$では成り立つという単調性がある、これらの二つの条件があることから$T$は二分探索により求めることがあります。また、ある$t$におけるそれぞれのスライムの合計の走った距離を$O(N)$で求められれば、計算量が$O(N \log{D})$となるので間に合うプログラムを書けると考えました。
ここで、$t$における全てのスライムの合計の進んだ距離を考えますが、二つのスライム(速さは$v_1$,$v_2$)が合体すると一つのスライムになり、残ったスライムの速さは$v_1+v_2$になります。したがって、合計の進む距離に注目すればそれぞれのスライムが合体しないものとしても変わらないので、全てのスライムが(合体しない時に)$t$まででどれだけ進むかを考えれば$O(N)$で求めることができます。
また、二分探索についてはこの記事を参照してください。さらに、この問題は$O(N \log{D})$ではなく$O(N)$でも解くことができます(本解)。
A.pyn,d=map(int,input().split()) x=list(map(int,input().split())) v=list(map(int,input().split())) s=sum(v) def f(k): return s*k #lは偽,rは真 l,r=0,1000000000000 while l+1<r: k=l+(r-l)//2 if f(k)>=d: r=k else: l=k print(r)B問題
まず、素数判定をクエリで行うのでエラトステネスの篩によって判定する可能性のある素数を全てチェックします(これによりクエリの素数判定が$O(1)$になります)。ここで$p$が素数ではないと判定されれば$-1$を出力すれば良いので、以下では$p$を素数と仮定して議論をすすめます。
この元で$A^{P!}\ (mod \ P)$を単純に$((A^1)^2)^3…$と求めていくと$mod \ P$の条件下でも間に合いません。ここで思い出すべきはフェルマーの小定理です。$剰余$の累乗に関わる問題では常識なので覚えておくべきだと思います。この定理では、素数$p$に対して$p$の倍数でない$A$について$A^{p-1}=1 \ (mod \ p)$が成り立ちます。ここで、$A^{p!}=(A^{p-1})^x \ (x=1,2,…,p-2,p)$が成り立つので($\because \ p$は素数より$2$以上)、$A$が$p$の倍数の場合は$A^{p!}=0\ (mod \ P)$、そうでない場合は$A^{p!}=1\ (mod \ P)$となります。
以上をまとめれば、$p$が素数でない時は$-1$、$p$が素数で$A\%p=0$の時は$0$、$p$が素数で$A\%p \neq 0$の時は$1$を出力すれば良いです。
コード中の
MAXRRの範囲を変え忘れてWAを出しました。辛かったです。このせいでだいぶ時間を食いました。B.cc//コンパイラ最適化 #pragma GCC optimize("Ofast") //インクルードなど #include<bits/stdc++.h> using namespace std; typedef long long ll; //マクロ //forループ //引数は、(ループ内変数,動く範囲)か(ループ内変数,始めの数,終わりの数)、のどちらか //Dがついてないものはループ変数は1ずつインクリメントされ、Dがついてるものはループ変数は1ずつデクリメントされる //FORAは範囲for文(使いにくかったら消す) #define REP(i,n) for(ll i=0;i<ll(n);i++) #define REPD(i,n) for(ll i=n-1;i>=0;i--) #define FOR(i,a,b) for(ll i=a;i<=ll(b);i++) #define FORD(i,a,b) for(ll i=a;i>=ll(b);i--) #define FORA(i,I) for(const auto& i:I) //xにはvectorなどのコンテナ #define ALL(x) x.begin(),x.end() #define SIZE(x) ll(x.size()) //定数 #define INF 1000000000000 //10^12:∞ #define MOD 1000000007 //10^9+7:合同式の法 #define MAXR 6000000 //10^5:配列の最大のrange //略記 #define PB push_back //挿入 #define MP make_pair //pairのコンストラクタ #define F first //pairの一つ目の要素 #define S second //pairの二つ目の要素 #define PN true //素数 #define NPN false //素数ではない //非本質 #define MAXRR 3000 //√MAXR以上の数を設定する //MAXRまでの整数は素数であると仮定する(ここから削る) vector<bool> PN_chk(MAXR+1,PN);//0indexでi番目が整数iに対応(0~MAXR) //素数を格納する配列を用意しておく vector<ll> PNs; void se(){ //0と1は素数ではない PN_chk[0]=NPN;PN_chk[1]=NPN; FOR(i,2,MAXRR){ //たどり着いた時に素数と仮定されているなら素数 if(PN_chk[i]) FOR(j,i,ll(MAXR/i)){PN_chk[j*i]=NPN;} } FOR(i,2,MAXR){ if(PN_chk[i]) PNs.PB(i); } } ll modpow(ll a,ll n,ll p){ if(n==0)return 1; ll t=modpow(a,n/2,p); t=t*t%p; if(n&1)t=t*a%p; return t; } signed main(){ //入力の高速化用のコード ios::sync_with_stdio(false); cin.tie(nullptr); se(); ll t;cin>>t; REP(_,t){ ll a,p;cin>>a>>p; if(!PN_chk[p]){ cout<<-1<<endl; continue; } if(a%p==0){ cout<<0<<endl; continue; } cout<<1<<endl; } }C問題
類題を知っていればあとは実装を頑張れば良いので、精進の力を感じました。
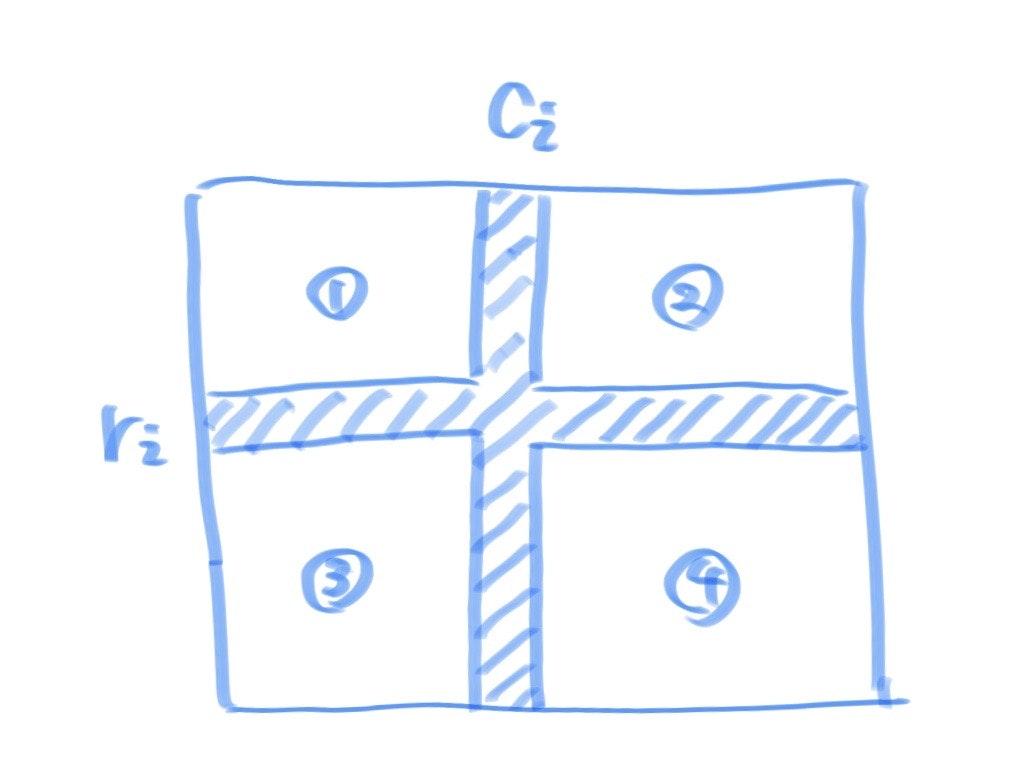
まず、以下のように$r_i,c_i$をおけば下図の四つの部分に分けることができます。
この元で、求める答えは①,②,③,④のそれぞれの長方形に含まれる数の積の積を求めれば良いことがわかります。このような長方形に含まれる部分については二次元累積で事前計算をすることによりクエリ処理を$O(1)$で行うことができます。
事前計算による表の作成において、二次元累積和の場合は以下のようになります。また、それぞれのマス目を$a[x][y]$とし、以下は全て0-indexedです。
$s[x][y] := [0, x) × [0, y)$ の長方形区間の和
$s[x+1][y+1] = s[x][y+1] + s[x+1][y] - s[x][y] + a[x][y]$したがって、二次元累積積の場合も同様にすれば以下のようになります。
$s[x][y] := [0, x) × [0, y)$ の長方形区間の積
$s[x+1][y+1] = s[x][y+1] \times s[x+1][y] \div s[x][y] \times a[x][y]$よって、この二次元累積積を四方向に定義すればよく残りの三つの長方形区間については以下のようになります。区間の表現は数学の定義と違うのですが、雰囲気を理解してもらえればと思います。(以下を記述せずに雰囲気でやろうとしていました。方針を記述することを徹底します。)
$s[x][y] := [w-1, x) × [0, y)$ の長方形区間の積
$s[x-1][y+1] = s[x][y+1] \times s[x-1][y] \div s[x][y] \times a[x][y]$$s[x][y] := [0, x) × [h-1, y)$ の長方形区間の積
$s[x+1][y-1] = s[x][y-1] \times s[x+1][y] \div s[x][y] \times a[x][y]$$s[x][y] := [w-1, x) × [h-1, y)$ の長方形区間の積
$s[x+1][y+1] = s[x][y+1] \times s[x+1][y] \div s[x][y] \times a[x][y]$これを実装することができれば、あとは開区間であることに注意すればプログラムを書くことができます。また、$10^9+7$で割った余りを求めれば良いので、自分のmodintライブラリを用いました。
追記(8/2)
全体から塗り潰した部分を割るとすると0除算が面倒なので、複数の数の積を求める問題はできるだけ積のみで表現することを意識した方が良さそうです。
C.cc//コンパイラ最適化 #pragma GCC optimize("Ofast") //インクルードなど #include<bits/stdc++.h> using namespace std; typedef long long ll; //マクロ //forループ //引数は、(ループ内変数,動く範囲)か(ループ内変数,始めの数,終わりの数)、のどちらか //Dがついてないものはループ変数は1ずつインクリメントされ、Dがついてるものはループ変数は1ずつデクリメントされる //FORAは範囲for文(使いにくかったら消す) #define REP(i,n) for(ll i=0;i<ll(n);i++) #define REPD(i,n) for(ll i=n-1;i>=0;i--) #define FOR(i,a,b) for(ll i=a;i<=ll(b);i++) #define FORD(i,a,b) for(ll i=a;i>=ll(b);i--) #define FORA(i,I) for(const auto& i:I) //xにはvectorなどのコンテナ #define ALL(x) x.begin(),x.end() #define SIZE(x) ll(x.size()) //定数 #define INF 1000000000000 //10^12:∞ #define MOD 1000000007 //10^9+7:合同式の法 #define MAXR 100000 //10^5:配列の最大のrange //略記 #define PB push_back //挿入 #define MP make_pair //pairのコンストラクタ #define F first //pairの一つ目の要素 #define S second //pairの二つ目の要素 template<ll mod> class modint{ public: ll val=0; //コンストラクタ modint(ll x=0){while(x<0)x+=mod;val=x%mod;} //コピーコンストラクタ modint(const modint &r){val=r.val;} //算術演算子 modint operator -(){return modint(-val);} //単項 modint operator +(const modint &r){return modint(*this)+=r;} modint operator -(const modint &r){return modint(*this)-=r;} modint operator *(const modint &r){return modint(*this)*=r;} modint operator /(const modint &r){return modint(*this)/=r;} //代入演算子 modint &operator +=(const modint &r){ val+=r.val; if(val>=mod)val-=mod; return *this; } modint &operator -=(const modint &r){ if(val<r.val)val+=mod; val-=r.val; return *this; } modint &operator *=(const modint &r){ val=val*r.val%mod; return *this; } modint &operator /=(const modint &r){ ll a=r.val,b=mod,u=1,v=0; while(b){ ll t=a/b; a-=t*b;swap(a,b); u-=t*v;swap(u,v); } val=val*u%mod; if(val<0)val+=mod; return *this; } //等価比較演算子 bool operator ==(const modint& r){return this->val==r.val;} bool operator <(const modint& r){return this->val<r.val;} bool operator !=(const modint& r){return this->val!=r.val;} }; using mint = modint<MOD>; //入出力ストリーム istream &operator >>(istream &is,mint& x){//xにconst付けない ll t;is >> t; x=t; return (is); } ostream &operator <<(ostream &os,const mint& x){ return os<<x.val; } //累乗 mint modpow(const mint &a,ll n){ if(n==0)return 1; mint t=modpow(a,n/2); t=t*t; if(n&1)t=t*a; return t; } signed main(){ //入力の高速化用のコード //ios::sync_with_stdio(false); //cin.tie(nullptr); ll h,w;cin>>h>>w; vector<vector<ll>> A(h,vector<ll>(w,0)); REP(i,h)REP(j,w)cin>>A[i][j]; vector<vector<vector<mint>>> s(4,vector<vector<mint>>(h+1,vector<mint>(w+1,1))); REP(j,h){ REP(k,w){ ll x,y; x=j;y=k; s[0][x+1][y+1]=s[0][x+1][y]*s[0][x][y+1]/s[0][x][y]*A[x][y]; } } REP(j,h){ REP(k,w-1){ ll x,y; x=j;y=w-1-k; s[1][x+1][y-1]=s[1][x+1][y]*s[1][x][y-1]/s[1][x][y]*A[x][y]; } } REP(j,h-1){ REP(k,w){ ll x,y; x=h-1-j;y=k; s[2][x-1][y+1]=s[2][x-1][y]*s[2][x][y+1]/s[2][x][y]*A[x][y]; } } REP(j,h-1){ REP(k,w-1){ ll x,y; x=h-1-j;y=w-1-k; s[3][x-1][y-1]=s[3][x-1][y]*s[3][x][y-1]/s[3][x][y]*A[x][y]; } } #if 0 REP(i,4){ REP(j,h){ REP(k,w){ cout<<s[i][j][k]<<" "; } cout<<endl; } cout<<endl; } #endif ll q;cin>>q; REP(_,q){ ll r,c;cin>>r>>c; mint ans=1; ll x,y; x=r-1;y=c-1; ans*=s[0][x][y]; //x=r;y=w-c; ans*=s[1][x][y]; //x=h-r;y=c; ans*=s[2][x][y]; //x=h-r;y=w-c; ans*=s[3][x][y]; cout<<ans<<endl; } }
- 投稿日:2020-08-02T18:48:10+09:00
Mac でPython の開発環境を構築する
バージョン、パッケージ管理
brew install pyenv brew install pipenv設定
.bash_profile または .zshrc に追記
export PYENV_ROOT="$HOME/.pyenv" export PATH="$PYENV_ROOT/bin:$PATH" eval "$(pyenv init -)"
source ~/.bash_profile
source ~/.zshrc
のいずれかを実行Python
pyenv install -l pyenv install 3.8.5 pyenv global 3.8.5ターミナルを終了させて、もう一度起動する
python --versionで 3.8.5 になっていることを確認する
- 投稿日:2020-08-02T18:34:28+09:00
PythonでNumPy配列「ndarray」をliltに変換する【tolist()】
Pythonでcsvから値を抽出して、for文で回そうと思ったら抽出したデータがndarrayという、カンマ(,)がないバージョンの配列になっていたので苦戦。 => 解決したのでメモ
抽出先のcsv
sample.csvsample_name,sample_colomn aaaaaaaaaaa,bbbbbbbbbbbbb ccccccccccc,ddddddddddddd抽出するためのロジック
sample.pyimport pandas as pd import numpy as np sample_data = pd.read_csv('sample.csv',index_col='sample_colomn') sample_colomn = sample_data.index.values print(sample_colomn) # ['bbbbbbbbbbbbb' 'ddddddddddddd']
['bbbbbbbbbbbbb' 'ddddddddddddd']をfor文で回そうとしたらTypeError: only integer scalar arrays can be converted to a scalar indexと怒られました。対策
tolist()を使用して、カンマ(,)がないバージョンの配列を、普通の配列(list)に変換する
sample.pyimport pandas as pd import numpy as np sample_data = pd.read_csv('sample.csv',index_col='sample_colomn') sample_colomn = sample_data.index.values print(sample_colomn.tolist()) # ['bbbbbbbbbbbbb', 'ddddddddddddd']以上です!
- 投稿日:2020-08-02T16:11:49+09:00
『統計検定準1級対応統計学実践ワークブック』をR, Pythonで解く~第18章質的回帰~
日本統計学会公式認定 統計検定準1級対応 統計学実践ワークブック
が統計検定の準備だけでなく統計学の整理に役立つので、R, Pythonでの実装も試みた。問18.1
データ
- 手打ちで転記した下記
- 18.1.csv
L1,患者,寛解 8,2,0 10,2,0 12,3,0 14,3,0 16,3,0 18,1,1 20,3,2 22,2,1 24,1,0 26,1,1 28,1,1 32,1,0 34,1,1 38,3,2R
df<-read.csv('19.1.csv') head(df)A data.frame: 6 × 3 L1 患者 寛解 <int> <int> <int> 1 8 2 0 2 10 2 0 3 12 3 0 4 14 3 0 5 16 3 0 6 18 1 1
- 1行1患者のデータに展開
df2<-data.frame() for (i in (1:nrow(df))) { yo<-df[i, 3] for (j in (1:df[i, 2])) { rem = rem - 1 if (rem >= 0) { remission = 1 } else { remission = 0 } tmp.df<-data.frame(L1 = df[i, 1], REM = remission) df2<-rbind(df2, tmp.df) } } df2$REM = as.factor(df2$REM) head(df2)A data.frame: 6 × 2 L1 REM <int> <fct> 1 8 0 2 8 0 3 10 0 4 10 0 5 12 0 6 12 0
- ロジスティック回帰
model<-glm(REM ~ L1, df2, family = binomial("logit")) summary(model)Call: glm(formula = REM ~ L1, family = binomial("logit"), data = df2) Deviance Residuals: Min 1Q Median 3Q Max -1.9448 -0.6465 -0.4947 0.6571 1.6971 Coefficients: Estimate Std. Error z value Pr(>|z|) (Intercept) -3.77714 1.37862 -2.740 0.00615 ** L1 0.14486 0.05934 2.441 0.01464 * --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 (Dispersion parameter for binomial family taken to be 1) Null deviance: 34.372 on 26 degrees of freedom Residual deviance: 26.073 on 25 degrees of freedom AIC: 30.073 Number of Fisher Scoring iterations: 4Python
import pandas as pd import statsmodels.api as sm df = pd.read_csv('18.1.csv') df.head()L1 患者 寛解 0 8 2 0 1 10 2 0 2 12 3 0 3 14 3 0 4 16 3 0df2 = pd.DataFrame(columns = ['L1', 'REM']) for i in range(len(df)): rem = df.iloc[i, 2] for j in range(df.iloc[i, 1]): rem -= 1 if rem >= 0: remission = 1 else: remission = 0 df2 = df2.append({'L1': df.iloc[i, 0], 'REM': remission}, ignore_index=True) df2.head()L1 REM 0 8 0 1 8 0 2 10 0 3 10 0 4 12 0df_x = pd.DataFrame(df2['L1']) df_x = sm.add_constant(df_x) logit_mod = sm.Logit(np.asarray(df2['REM'].astype('float')), np.asarray(df_x.astype('float'))) logit_res = logit_mod.fit(disp=0) print(logit_res.summary())Logit Regression Results ============================================================================== Dep. Variable: y No. Observations: 27 Model: Logit Df Residuals: 25 Method: MLE Df Model: 1 Date: Sun, 02 Aug 2020 Pseudo R-squ.: 0.2414 Time: 06:58:18 Log-Likelihood: -13.036 converged: True LL-Null: -17.186 Covariance Type: nonrobust LLR p-value: 0.003967 ============================================================================== coef std err z P>|z| [0.025 0.975] ------------------------------------------------------------------------------ const -3.7771 1.379 -2.740 0.006 -6.479 -1.075 x1 0.1449 0.059 2.441 0.015 0.029 0.261 ==============================================================================問18.2, 18.3
データ
- 手打ちで転記
- 18.2.csv
smoking,obesity,snoring,cases,hypertension 0,0,0,60,5 1,0,0,17,2 0,1,0,8,1 1,1,0,2,0 0,0,1,187,35 1,0,1,85,13 0,1,1,51,15 1,1,1,23,8R
df<-read.csv('18.2.csv') head(df)A data.frame: 6 × 5 smoking obesity snoring cases hypertension <int> <int> <int> <int> <int> 1 0 0 0 60 5 2 1 0 0 17 2 3 0 1 0 8 1 4 1 1 0 2 0 5 0 0 1 187 35 6 1 0 1 85 13
- 1行1患者に展開
df2<-data.frame() for (i in (1:nrow(df))) { ht<-df[i, 5] for (j in (1:df[i, 4])) { ht = ht - 1 if (ht >= 0) { hypertension = 1 } else { hypertension = 0 } tmp.df<-data.frame(df[i, 1:3], HT = hypertension) df2<-rbind(df2, tmp.df) } } df2$HT = as.factor(df2$HT) head(df2)A data.frame: 6 × 4 smoking obesity snoring HT <int> <int> <int> <fct> 1 0 0 0 1 2 0 0 0 1 3 0 0 0 1 4 0 0 0 1 5 0 0 0 1 6 0 0 0 0
- 18.2 ロジスティック回帰
model.logit<-glm(HT ~ smoking + obesity + snoring, df2, family = binomial("logit")) summary(model.logit)Call: glm(formula = HT ~ smoking + obesity + snoring, family = binomial("logit"), data = df2) Deviance Residuals: Min 1Q Median 3Q Max -0.8578 -0.6330 -0.6138 -0.4212 2.2488 Coefficients: Estimate Std. Error z value Pr(>|z|) (Intercept) -2.37766 0.38010 -6.255 3.97e-10 *** smoking -0.06777 0.27812 -0.244 0.8075 obesity 0.69531 0.28508 2.439 0.0147 * snoring 0.87194 0.39749 2.194 0.0283 * --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 (Dispersion parameter for binomial family taken to be 1) Null deviance: 411.42 on 432 degrees of freedom Residual deviance: 398.92 on 429 degrees of freedom AIC: 406.92 Number of Fisher Scoring iterations: 4
InterceptのPrが少し違うのが?だがほかはテキスト通り
18.3 プロビットモデル
model.probit<-glm(HT ~ smoking + obesity + snoring, df2, family = binomial("probit")) summary(model.probit)Call: glm(formula = HT ~ smoking + obesity + snoring, family = binomial("probit"), data = df2) Deviance Residuals: Min 1Q Median 3Q Max -0.8542 -0.6337 -0.6142 -0.4211 2.2531 Coefficients: Estimate Std. Error z value Pr(>|z|) (Intercept) -1.37312 0.19308 -7.112 1.15e-12 *** smoking -0.03865 0.15682 -0.246 0.8053 obesity 0.39996 0.16748 2.388 0.0169 * snoring 0.46507 0.20464 2.273 0.0230 * --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 (Dispersion parameter for binomial family taken to be 1) Null deviance: 411.42 on 432 degrees of freedom Residual deviance: 399.00 on 429 degrees of freedom AIC: 407 Number of Fisher Scoring iterations: 4Python
- 18.2
import pandas as pd import statsmodels.api as sm df = pd.read_csv('18.2.csv') df.head()smoking obesity snoring cases hypertension 0 0 0 0 60 5 1 1 0 0 17 2 2 0 1 0 8 1 3 1 1 0 2 0 4 0 0 1 187 35df2 = pd.DataFrame(columns = ['smoking', 'obesity', 'snoring', 'hypertension']) for i in range(len(df)): ht = df.iloc[i, 4] for j in range(df.iloc[i, 3]): ht -= 1 if ht >= 0: hypertension = 1 else: hypertension = 0 df2 = df2.append({'smoking': df.iloc[i, 0], 'obesity': df.iloc[i, 1], 'snoring': df.iloc[i, 2], 'hypertension': hypertension}, ignore_index=True) df2.head()smoking obesity snoring hypertension 0 0 0 0 1 1 0 0 0 1 2 0 0 0 1 3 0 0 0 1 4 0 0 0 1
- 18.2 ロジスティック回帰
df_x = pd.DataFrame(df2.iloc[:, 0:3]) df_x = sm.add_constant(df_x) logit_mod = sm.Logit(np.asarray(df2['hypertension'].astype('float')), np.asarray(df_x.astype('float'))) logit_res = logit_mod.fit(disp=0) print(logit_res.summary())Logit Regression Results ============================================================================== Dep. Variable: y No. Observations: 433 Model: Logit Df Residuals: 429 Method: MLE Df Model: 3 Date: Sun, 02 Aug 2020 Pseudo R-squ.: 0.03040 Time: 07:05:53 Log-Likelihood: -199.46 converged: True LL-Null: -205.71 Covariance Type: nonrobust LLR p-value: 0.005832 ============================================================================== coef std err z P>|z| [0.025 0.975] ------------------------------------------------------------------------------ const -2.3777 0.380 -6.254 0.000 -3.123 -1.633 x1 -0.0678 0.278 -0.244 0.807 -0.613 0.477 x2 0.6953 0.285 2.439 0.015 0.137 1.254 x3 0.8719 0.398 2.193 0.028 0.093 1.651 ==============================================================================
- 18.3 プロビットモデル
df_x = pd.DataFrame(df2.iloc[:, 0:3]) df_x = sm.add_constant(df_x) probit_mod = sm.Probit(np.asarray(df2['hypertension'].astype('float')), np.asarray(df_x.astype('float'))) probit_res = probit_mod.fit(disp=0) print(probit_res.summary())Probit Regression Results ============================================================================== Dep. Variable: y No. Observations: 433 Model: Probit Df Residuals: 429 Method: MLE Df Model: 3 Date: Sun, 02 Aug 2020 Pseudo R-squ.: 0.03019 Time: 07:07:14 Log-Likelihood: -199.50 converged: True LL-Null: -205.71 Covariance Type: nonrobust LLR p-value: 0.006077 ============================================================================== coef std err z P>|z| [0.025 0.975] ------------------------------------------------------------------------------ const -1.3731 0.193 -7.120 0.000 -1.751 -0.995 x1 -0.0387 0.157 -0.246 0.805 -0.346 0.269 x2 0.4000 0.168 2.384 0.017 0.071 0.729 x3 0.4651 0.204 2.274 0.023 0.064 0.866 ==============================================================================
- 投稿日:2020-08-02T15:24:07+09:00
はじめてのPython3 ~はじめての比較編~
はじめに
注意点などはこちらを参照してください。
If文による条件分岐
import random x = random.randint(1, 3) # 1から3のランダムな数値を代入 if x == 1: print("これは1です") # 条件式が成立した場合 elif x == 2: print(“これは2です”) #条件式2が成立したときの処理 else: print("これは1や2ではありません") # 条件式が成立しなかった場合・if文では:(コロン)を忘れずに
エラーになる。(筆者はよく忘れてしまう)
・elsifではない
elsifが使われる言語があるため混同しやすい。インデント
コードの行頭を字下げすることを「インデント」という。
Pythonでは、1段のインデントに、tab1回か半角スペース4つを入力。# 省略 if x == 2000: print("2000ポイント")Pythonでは、条件式のあとの「:」(コロン)やelseのあとの「:」(コロン)から始まって、
インデント行が終わるまでを、ひとかたまりのブロックとして扱う。インデントは、Python では、条件式が成立した時に実行する処理を表すと同時に、
プログラマーにとって、条件式に応じて実行する処理を見分けやすくする。比較演算子
一覧
例 意味 真になる例 a < b a が b よりも小さい 10 < 15 a > b a が b よりも大きい 10 > 7 a <= b a が b 以下である 10 <= 15 a >= b a が b 以上である 10 >= 7 a != b a と b が等しくない 10 != 1 例文
飲酒可能かどうかを比較する
import random age = random.randint(18, 22) # ageに、何才かを18~22の範囲でランダムに代入 text = "" if age < 20: text = "飲酒不可" else: text = "飲酒可能" print(str(age) + "才は" + text)
- 投稿日:2020-08-02T14:37:20+09:00
時系列の解析 SARIMAモデルにて売上予測してみた
Pythonで時系列解析・分析を行っていくうえでの基礎知識として、SARIMAモデルにて車の売上予測をしてみます。平均・分散、正規分布などの統計学の初歩知識を前提とした学習の自身の振り返りの為の記事です。
実践!PythonによるSARIMAモデルの推定
①SARIMAを用いた時系列データの分析手順
1.データの読み込み
2.データの整理
3.データの可視化
4.データの周期の把握 (パラメーターsの決定)
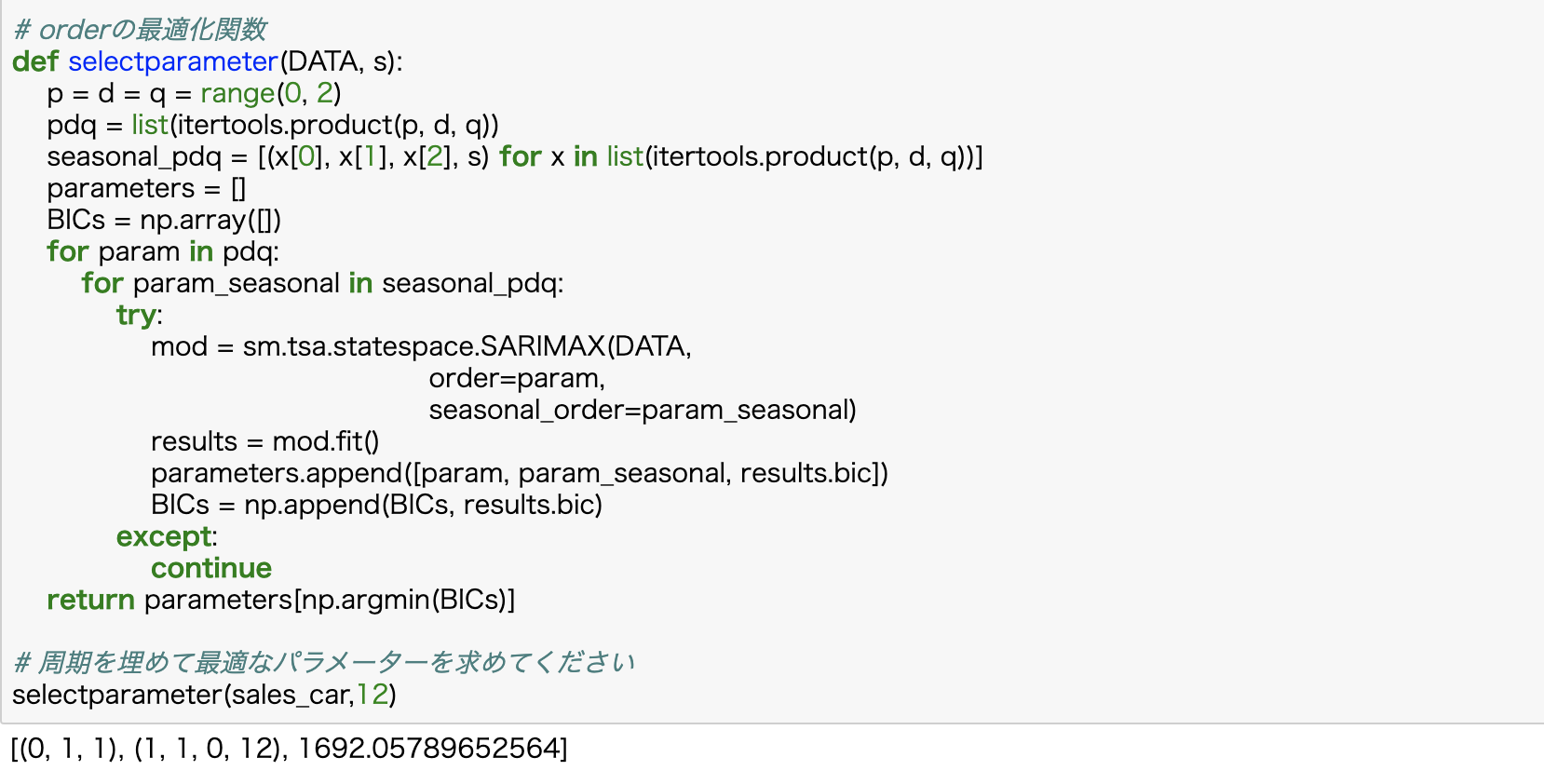
5.s以外のパラメーターの決定 6.モデルの構築
7.データとの予測とその可視化②実践!PythonによるSARIMAモデルの推定
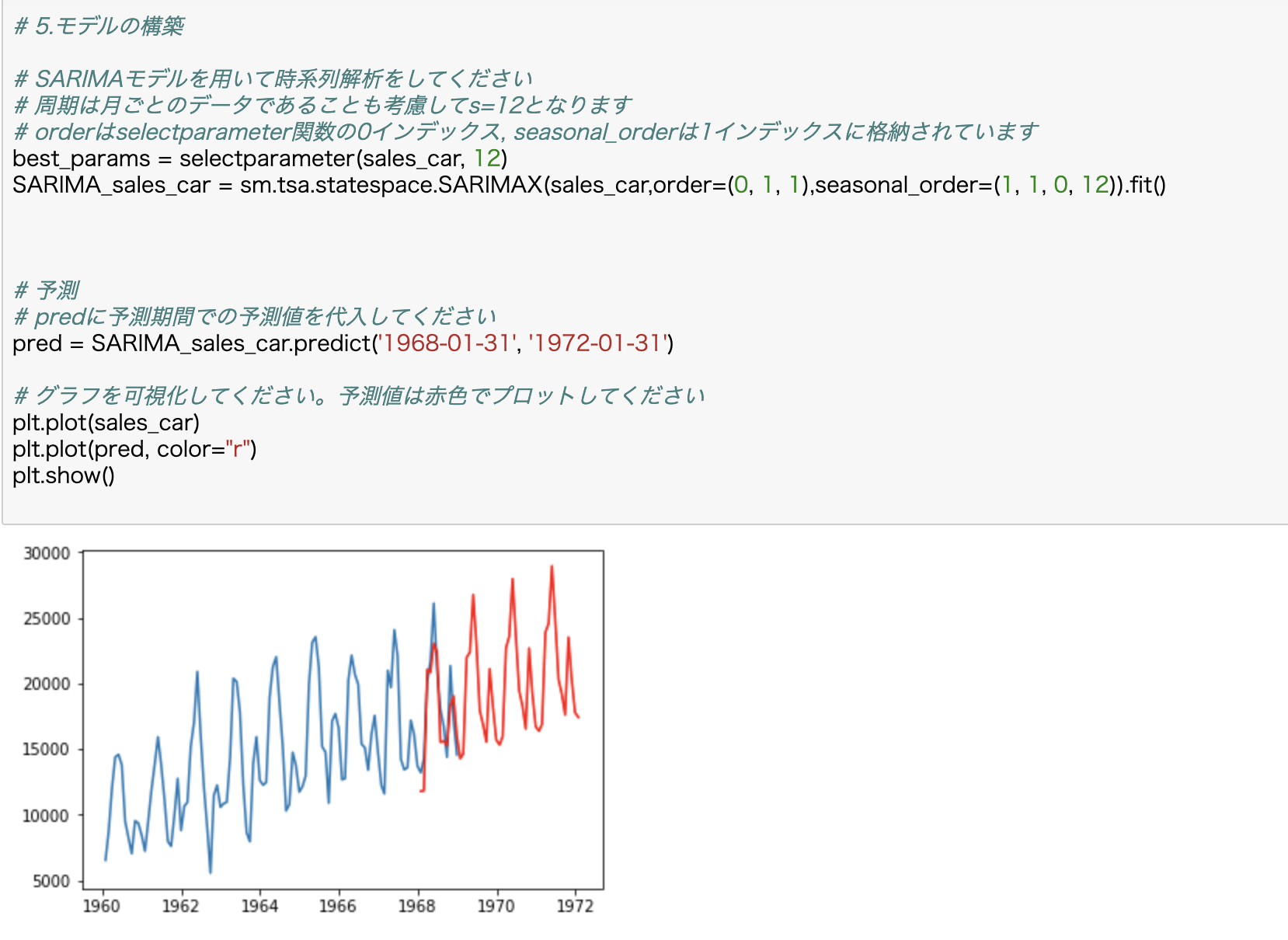
③1968-01-31から1972-01-31のある会社の車の売上データの予測と可視化
④SARIMAモデル (Seasonal ARIMA model)とは
ARIMAモデルに周期成分を取り入れたモデルをSARIMAモデルといいます。<<ARMAモデルとは定常な時系列のモデルであり、非定常な時系列は定常な時系列に変換した後にARMAモデルに当てはめる必要がモデルの事。 ? 階差分をとった系列に対してARMA( ?,? )を考えるモデルをARIMA( ?,?,? )モデルといいます。 時系列が ( ? 次式のトレンド) + (定常部分) といえる場合に有効なモデルです。>>
SARIMAモデルは、時系列方向の説明にARIMA( ?,?,? ) モデルを使うだけでなく、周期方向の説明にもARIMA( ?,?,? )モデルを使おう、というものです。
SARIMAモデルでは合計7個のパラメータがあります。 時系列方向のARIMA( ?,?,? )に加え季節差分方向のARIMA( ?,?,? )、さらには周期 ? があるためです。
- 投稿日:2020-08-02T14:32:59+09:00
新しいMacを買ってからpyenv + poetryでPythonの環境構築手順書
前提
MacOS Catalinaでの手順です。
zsh対応しています。pyenvとは?
Pythonのバージョンを簡単に切り替えるためのツールとなります。
最近はPython2は使うことないと思いますが、Python3内でのバージョン切り替えが簡単にできるようになるのは便利です。poetryとは?
Pythonのパッケージ管理するツールとなります。
.zshrcの設定
echo 'export PIPENV_VENV_IN_PROJECT=1' >> ~/.zshrc . ~/.zshrcecho $PIPENV_VENV_IN_PROJECT > 1pyenvのインストール
git clone git://github.com/yyuu/pyenv.git ~/.pyenv git clone git://github.com/yyuu/pyenv-update.git ~/.pyenv/plugins/pyenv-update~/.zshrcにパスを追加
vim ~/.zshrc.zshrcexport PYENV_ROOT="$HOME/.pyenv" export PATH="$PYENV_ROOT/bin:$PATH" if command -v pyenv 1>/dev/null 2>&1; then eval "$(pyenv init -)" fiターミナルを再起動
pyenv update pyenv --version > pyenv 1.2.20pyenvで使うPythonのバージョンを設定
今回は3.7.4にしてますが、お好きなバージョンを指定してください
pyenv install 3.7.4 pyenv global 3.7.4 pyenv versions > * 3.7.4 (set by /Users/***/.pyenv/version)ターミナルの再起動
バージョンの確認python --version > Python 3.7.4 pip --version > pip 19.0.3 from /Users/***/.pyenv/versions/3.7.4/lib/python3.7/site-packages/pip (python 3.7)pipの設定
pip install --upgrade pip pip --version > pip 20.2 from /Users/***/.pyenv/versions/3.7.4/lib/python3.7/site-packages/pip (python 3.7)poetryのインストール
curl -sSL https://raw.githubusercontent.com/sdispater/poetry/master/get-poetry.py | python~/.zshrcにパスを追記
vim ~/.zshrcexport PATH="$HOME/.poetry/bin:$PATH"ターミナルを再起動
poetry --version > Poetry version 1.0.10 poetry self update > You are using the latest versionローカルのPythonに必要なパッケージを追加する
ここ必要に応じてパッケージを追加してください
飛ばしても大丈夫ですpip install pipenv pip install awscli pip install awslogsインストールしたパッケージの確認
バージョンは異なる可能性が高いですpip freeze > awscli==1.16.254 > awslogs==0.11.0 > boto3==1.9.244 > botocore==1.12.244 > certifi==2019.9.11 > colorama==0.4.1 > docutils==0.15.2 > jmespath==0.9.4 > pipenv==2018.11.26 > pyasn1==0.4.7 > python-dateutil==2.8.0 > PyYAML==5.1.2 > rsa==3.4.2 > s3transfer==0.2.1 > six==1.12.0 > termcolor==1.1.0 > urllib3==1.25.6 > virtualenv==16.7.5 > virtualenv-clone==0.5.3Poetryでプロジェクトの作成
新規でプロジェクトを作成する場合
poetry new my-package既存のプロジェクトをpoetryで管理する場合
(色々聞かれますが、そのままEnterで大丈夫です)poetry initパッケージを追加する
poetry add [パッケージ名]pyproject.tomlからパッケージをインストール
poetry installpyproject.tomlからパッケージを更新
poetry update以上となります。
お疲れ様でした。
- 投稿日:2020-08-02T14:32:37+09:00
初めてのPython スクスタのMVを連続再生させる -曲リストのスクロール-
始めに
Pythonを自学するための題材にスクスタのMV連続再生機能を選んでは見たものの、出来上がったプログラムはMVのループ再生こそ出来るが、実際は一曲のみしか再生できず連続再生機能と言うにはお粗末すぎる物だった。
今回は再生終了後に曲リストを下に送る動作の実装をしてみます。
前回の記事:初めてのPython スクスタのMVを連続再生させる
設計
上記画像の赤枠の内側をクリックすれば曲送りができますが曲一覧を見ればわかるように、曲ごとに全く異なる上共通部分として使えそうな範囲も他の曲と被っているため一意な部分を選ぶのは難しそうです。
ここは先に画面内で確実に一意となる部分の座標を取得しそこからOffset分を加算した座標をクリックさせます。上記画像の青枠で囲まれた部分を対象としました。
ソースコード
pydef.py# coding:utf-8 MAIN_PATH:str=".\\MVPlay\\" FILE_TYPE:str="*.png" #引数用定数 FILES:int=0 FILEEVENTS:int=1 WAITTIME:int=2 #X,Y座標取得用定数 X:int=0 Y:int=1 #イベント定義用定数 CLICK:int=0 SWIPE:int=1 RECURE:int=2 EXIT:int=3 #ファイルイベント用定数 FILE:int=0 EVENT:int=1 ARG1:int=2 ARG2:int=3 ARG3:int=4 #ファイルイベントを定義 FILEEVENTS_MAIN:list=[ #ファイル名とマッチした画像の時、座標が指定された値分Offsetされた位置をクリックする [".\\MVPlay\\03scroll.png",CLICK,[220,630],None,None] ]pyfunc.py# coding:utf-8 from pydef import* #ファイルイベントを取得 def getFileEvent(fn:str,fev): for tmpl in fev: if tmpl[FILE]==fn: return tmpl return None #画像認識が成功する度増え続け、全てのファイルが終わったら最初に戻る def sequentialCount(i:int,maxcount:int): if i>=maxcount: return 0 else: return i+1main.py# coding:utf-8 import pyautogui import glob import time from pydef import* from pyfunc import* #イベントに対応した処理を実行 #main関数を再帰的に呼び出すのでpyfuncではなくmainに記述 def fileEvent(arg:list,loc:list): #何もないときはクリック if arg==None: pyautogui.click(loc[X],loc[Y]) #クリックイベント elif arg[EVENT]==CLICK: loc=[x+y for (x,y) in zip(loc,arg[ARG1])] pyautogui.click(loc[X],loc[Y]) #スワイプイベント elif arg[EVENT]==SWIPE: _n=None #未実装 #再帰処理イベント elif arg[EVENT]==RECURE: flist=glob.glob(arg[ARG1]+FILE_TYPE) main([flist,arg[ARG2],arg[ARG3]]) #終了イベント elif arg[EVENT]==EXIT: exit() #受け取ったファイルリストとファイルイベントリストを元に #イベントを実行し続ける def main(arg:list): i:int=0 while True: #画像認識チェック loc=pyautogui.locateCenterOnScreen(arg[FILES][i]) if not(loc==None): time.sleep(arg[WAITTIME]) #ファイルイベント実行 fileEvent(getFileEvent(arg[FILES][i],arg[FILEEVENTS]),loc) i=sequentialCount(i,len(arg[FILES])-1) time.sleep(arg[WAITTIME]) flist=glob.glob(MAIN_PATH+FILE_TYPE) main([flist,FILEEVENTS_MAIN,0.5])前回に比べると一気に長くなりましたが殆どは定数の宣言ですね。
簡単な説明
pydef.py[".\\MVPlay\\03scroll.png",CLICK,[220,630],None,None]この定義はパスを含め".\MVPlay\03scroll.png"と同じ名前のファイルが読み込まれた時、画像認識でマッチしたX座標とY座標にそれぞれ220,620を加算してクリックするという意味です。
main.py#イベントに対応した処理を実行 #main関数を再帰的に呼び出すのでpyfuncではなくmainに記述 def fileEvent(arg:list,loc:list): #何もないときはクリック if arg==None: pyautogui.click(loc[X],loc[Y]) #クリックイベント elif arg[EVENT]==CLICK: loc=[x+y for (x,y) in zip(loc,arg[ARG1])] pyautogui.click(loc[X],loc[Y]) #スワイプイベント elif arg[EVENT]==SWIPE: _n=None #未実装 #再帰処理イベント elif arg[EVENT]==RECURE: flist=glob.glob(arg[ARG1]+FILE_TYPE) main([flist,arg[ARG2],arg[ARG3]]) #終了イベント elif arg[EVENT]==EXIT: exit()ファイルに定義されたイベントは今回新たに追加されたfileEvent関数で処理されます。
CLICK以外のイベントは必要になるかもしれない程度なので今の所特に意味はないです。総評
これでMVボタンを押す→再生ボタンを押す→MV再生が終わって曲リスト画面に戻ったら次の曲に移動するという一連の作業が自動化されました。
今回組んでて思ったのはlistが便利すぎるということに尽きます、話に聞いてもいまいちピンときてなかったですが触ってみると実感できますね、ファイルイベント定義してるところでコールバック関数呼び出しさせる設計も楽しいかもしれません。最後に
曲リスト移動機能もついたので、大分自分の理想とする連続再生に近づいてきた感はありますが、未クリアの曲及びMVが未実装の曲の所で止まってしまうという問題は依然残っています。
次はこの問題点の解消を行っていきたいと思います。
- 投稿日:2020-08-02T14:27:02+09:00
Pythonで米国取引所上場銘柄のTicker Symbolを取得する
はじめに
ニューヨーク証券取引所(NYSE)とNASDAQの株価のデータを取得しようと思ったら、銘柄のTicker Symbolを知る必要があったため、その方法を記します。上場している銘柄すべてがリストアップされているかを確認していませんので、参考まで。
環境
Windows 10 home
Anaconda(Python 3.7.6)
Pandas 0.24.2
Ticker Symbolを取得する
NASDAQのftpからリストを取得して、成型します。
import pandas as pd others_list = 'ftp://ftp.nasdaqtrader.com/symboldirectory/otherlisted.txt' nasdaq_list = 'ftp://ftp.nasdaqtrader.com/symboldirectory/nasdaqlisted.txt' def symbols_nyse(): other = pd.read_csv(others_list, sep='|') #NYSEのものを取得する company_nyse = other[other['Exchange']=='N'][['ACT Symbol', 'Security Name']] #ETFはMYSE MKT、NYSE ARCA、MATSがある。 etf_other = other[other['ETF'] == 'Y'][['ACT Symbol', 'Security Name', 'Exchange']] #indexはリセットする company_nyse = company_nyse.reset_index(drop=True) etf_other = etf_other.reset_index(drop=True) #ACT Symbol -> Symbol company_nyse = company_nyse.rename(columns={'ACT Symbol':'Symbol'}) etf_other = eft_other.rename(columns={'ACT Symbol':'Symbol'}) return company_nyse, etf_other def symbols_nasdaq(): nasdaq = pd.read_csv(nasdaq_list, sep='|') #StatusがNormalのものだけを取得する nasdaq_normal = nasdaq[nasdaq['Financial Status']=='N'] #Test issueでないものを選択する nasdaq_normal = nasdaq_normal[nasdaq_normal['Test Issue']=='N'] #ETFかどうかで判別 company_nasdaq = nasdaq_normal[nasdaq_normal['ETF']=='N'][['Symbol', 'Security Name']] etf_nasdaq = nasdaq_normal[nasdaq_normal['ETF']=='Y'][['Symbol', 'Security Name']] #indexはリセットする company_nasdaq = company_nasdaq.reset_index(drop=True) etf_nasdaq = etf_nasdaq.reset_index(drop=True) return company_nasdaq, etf_nasdaq def symbols_all(): company_nyse, etf_other = symbols_nyse() company_nasdaq, etf_nasdaq = symbols_nasdaq() #NYSEとNASDAQは区別する company_nyse['Market'] = 'NYSE' company_nasdaq['Market'] = 'NASDAQ' #NASDAQのETFも区別しておく etf_nasdaq['Exchange'] = 'NASDAQ'#etf_otherのcolum名に合わせる return (pd.concat([company_nyse, company_nasdaq], ignore_index=True, sort=False), pd.concat([etf_other, etf_nasdaq], ignore_index=True, sort=False))Ticker Symbolを表示
'Symbol'列を見れば、上場している企業のTicker Symbolがわかります。
company, etf = symbols_all() company参考
- 投稿日:2020-08-02T14:19:54+09:00
きゃぷちゃん(CAPTCHA)にHIWAIな言葉を言わせたい
CAPTCHAってあるやん?あれってなんか可愛いよね、可愛いよねぇぇぇ!?!?(錯乱)
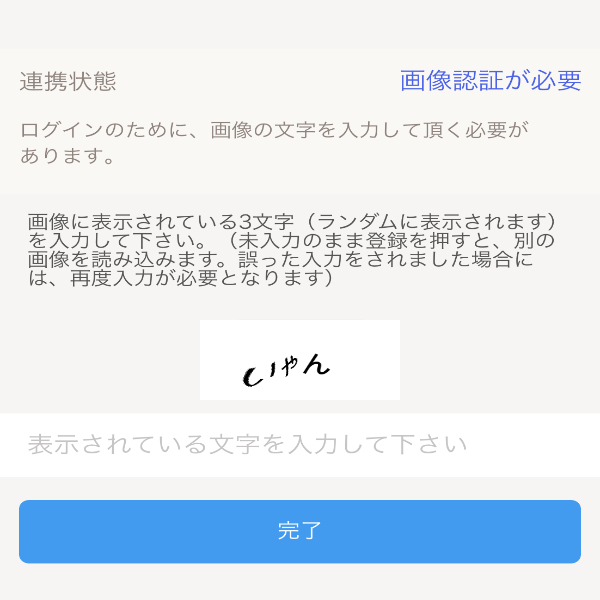
きゃわわ
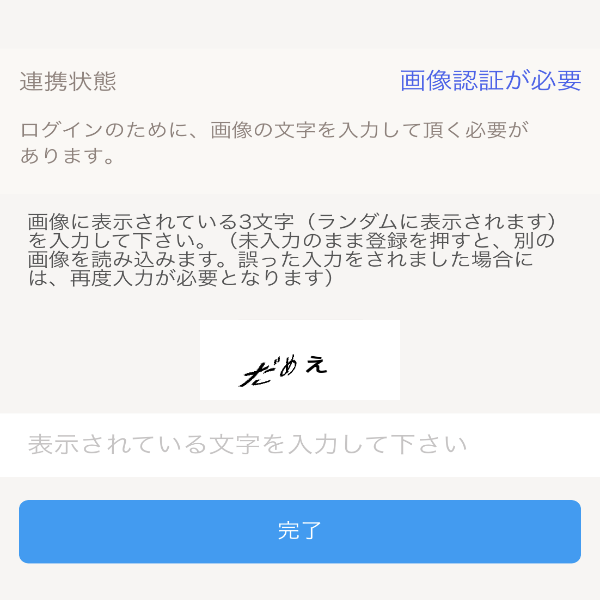
OPPAIも是非
Pythonで最も美しいOPPAIを描いた人が優勝結果
コード
テキストの作成
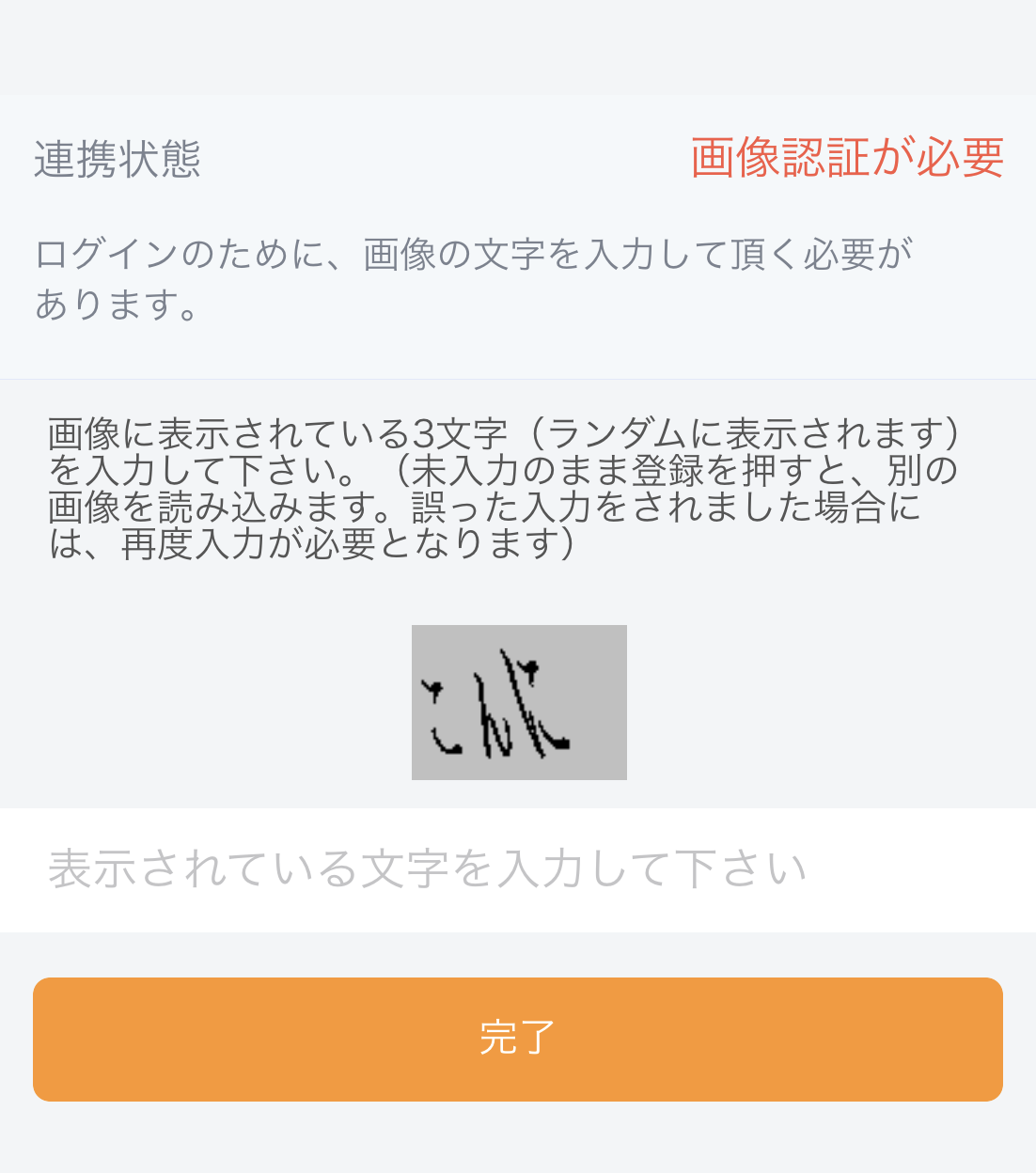
py.pyimport PIL.Image import PIL.ImageDraw import PIL.ImageFont import cv2 import numpy as np import matplotlib.pyplot as plt # 使うフォント,サイズ,描くテキストの設定 ttfontname = "/System/Library/Fonts/Supplemental/Arial Unicode.ttf" fontsize = 36 text = "ぽーくぴっつ" # 画像サイズ,背景色,フォントの色を設定 canvasSize = (300, 150) backgroundRGB = (255, 255, 255) textRGB = (0, 0, 0) # 文字を描く画像の作成 img = PIL.Image.new('RGB', canvasSize, backgroundRGB) draw = PIL.ImageDraw.Draw(img) # 用意した画像に文字列を描く font = PIL.ImageFont.truetype(ttfontname, fontsize) textWidth, textHeight = draw.textsize(text,font=font) textTopLeft = (canvasSize[0]//6, canvasSize[1]//2-textHeight//2) # 前から1/6,上下中央に配置 draw.text(textTopLeft, text, fill=textRGB, font=font) img.save(text + ".png")画像を歪める
py.pyimg_BGR = cv2.imread("ぽーくぴっつ.png") img_RGB = cv2.cvtColor(img_BGR, cv2.COLOR_BGR2RGB) height = np.shape(img_RGB)[0] width = np.shape(img_RGB)[1] img_RGB_2 = img_RGB.copy() #中心と半径の指定 center = np.array((50,50)) r = 100 #ピクセルの座標を変換 for x in range(width): for y in range(height): #中心からの距離 d = np.linalg.norm(center - np.array((y,x))) #半径より小さければ座標を変換する処理をする if d < r: #vectorは変換ベクトル。説明はコード外で。 vector = (d / r)**1.4 * (np.array((y,x)) - center) #変換後の座標を整数に変換 p = (center + vector).astype(np.int32) #色のデータの置き換え img_RGB_2[y,x,:]=img_RGB[p[0],p[1],:]画像を重ねる
py.pyimg1 = cv2.imread('CHAPCHA.png') img2 = img_RGB_2 img1 = cv2.cvtColor(img1, cv2.COLOR_BGR2RGB) img1 =cv2.resize(img1,(600,600)) img2 =cv2.resize(img2,(200,80)) #画像を重ねる位置の基準としてオフセットの位置を指定 x_img=200 y_img=320 img1[y_img:y_img+img2.shape[0], x_img:x_img+img2.shape[1]]=img2 cv2.imwrite(text + "2.png",img1)まとめ
CAPTCHAは可愛い
罵倒パターンも作れるのでそうゆう性癖の人は是非きゃぷちゃんにHIWAIな言葉を言わせたいって人はLGTMを、いやいや、きゃぷちゃんに罵られる方が興奮するやろ!って人はコメントにリクエストしてくだせぇ
どっちも好きに決まってんだろ常考って人はLGTMとフォローしてくだせぇ参考
・実際これ
OpenCVによる画像処理入門 改訂第2版 (KS情報科学専門書)
- 投稿日:2020-08-02T14:17:22+09:00
動的計画法アルゴリズム問題の解き方(初学者から見た)
動的計画法(Dynamic Programing, DP)
LeetCode, AtCoder等のプログラミングコンテストでよく出題される問題の1種で、総当たり(ブルートフォース)でコーディングを行うと指数関数的な計算量(例えば$O(2^n)$)になってしまうコードの計算量を大幅に抑える(例えば$O(n^2)$等)ことができます。
そのため、プログラミングコンテストだけではなく、普段のコーディングの際にも役に立つことがある考え方だと思います。
注意)
- 本記事では、初学者が動的計画法を使い、限られた解答時間でアルゴリズム問題を解く手順について説明します。そのため短時間で理解できる分かり易さを重視し、数学的に厳密な説明は行いません。
- 疑似コードはPythonで記述します。また、関連用語はwikipediaの記載を用いています。
- 体系的に知りたい方はこちらや、wikipediaで説明されているので、参照されたし。
- また、この記事はMITの講義も参考にしています。非常に分かり易くお勧めです。
動的計画法が初見には解り難い理由
- 動的計画法は、一般的に次のように説明されます。
例えばwikipediaの場合:定義
細かくアルゴリズムが定義されているわけではなく、下記2条件を満たすアルゴリズムの総称である。
定義1. 帰納的な関係の利用:より小さな問題例(部分問題)の解や計算結果を帰納的な関係を利用してより大きな問題例を解くのに使用する。
定義2. 計算結果の記録:小さな問題例、計算結果から記録し、同じ計算を何度も行うことを避ける。帰納的な関係での参照を効率よく行うために、計算結果は整数、文字やその組みなどを見出しにして管理される。
- 定義2.計算結果の記録について、直感的には計算結果をキャッシュしておく、と理解できると思います。メモを取ると言うと直感的かと思うので、「メモ化」と呼ぶことにします。
- 問題は定義1.ですが、初学者には理解に苦しむところがあります。
- より小さな問題例(部分問題,Subproblem)って何?
- 何で部分問題を使って帰納的な関係を利用してより大きな問題(問題自体)を解けるの?
- どうして動的計画法が使えそうかわかるの?
- そもそも動的計画法(Dynamic Programming)という単語の意味が解らん!
- Dynamic Programmingという言葉を考えたベルマンさんは、中長期的な研究を憎悪していた国防長官から数学の研究をしていることを隠すためにこの様な名前にした1…との事なので解り難くて当然

これらの事を説明しながら、動的計画法の問題を解く手順を見ていきます。
動的計画法問題解答の手順
例題:ナップザック問題
例題として、有名なナップザック問題を取り上げます。
問題:
あなたは泥棒です。時計を盗むため、時計店に忍び込みました。時計の配列を$S$で表すと、そこには様々な価格の高価な時計が$S[0],...S[i],...,S[n-1]$まで大量にありますが、あなたが持ち帰ることの出来る重さ$W$は決まっています。制約条件の制限重量$W$以内で、最も高い合計価格を求めるにはどうすればよいでしょうか?例えば時計が1000個($n=1000$)あった場合、時計の組み合わせ全て試すと、各時計を含める、含めないの2通りを全ての時計に対して考えるため、$2^{n}=2^{1000}≒10^{301}$となり、指数関数的に膨大な計算量となります。
1.動的計画法が使える可能性があるか判断する
限られた解答時間内で問題に挑む際には、無駄な検討を避けるため、最初に動的計画法を適用できそうか否かの見当を付ける必要があると思います。
従って、ここでは動的計画法が適用できるかを証明するのではなく、短時間でこの問題に対して動的計画法を適用できそうか、という見当をつけることが目的です。さて、動的計画法が適用できるかは、定義に書かれている事が適用できるか否かという事です。それはどうすれば確認できるでしょうか?
それは、以下の条件I.、条件II.が最初の数分で見当つきそうだ、となれば動的計画法を適用する候補となります。条件I. 部分問題が解ける事
定義1.によると大きな問題例を分解した、部分問題が解ける事が必須になります。この「部分問題が解ける」とはどのような場合のことを言うのでしょうか?
それは、$S$を入力データの配列とすると、$S$の一部に対して、全体の解と同じ条件で解が求められることを言います。具体的には、ナップザック問題では時計店にある数多の時計(=$S$)の中から、例えば$i$以降の時計(=$S[i:]$)だけを考えたときに、制限重量$w$の制約条件下で、ナップザックに入る最大の合計価格を求めることができる、という事です。この様に求めたい最大化や最小化する対象の値を$V[i:,w]$と書くことにします。ナップザック問題の場合、$V[i:,w]$はナップザックに入る残りの制限重量が$w$の時、時計番号$i$以降($i~n$)の合計価格の事です。
計算量は膨大になりますが、$V[i:,w]$は例題の説明で述べた通りの総当たりアプローチ(ブルートフォース)で、制限重量$w$以下になる時計の組み合わせを全て考えれば、その中で最も合計価格が大きい値として求めることが可能です。
従って、この条件は満たしているという見当がつけられそうです。なお、配列の一部分とは、以下の3種類の部分配列のことです。
- $S[:i]$ - 配列の接頭辞(prefix)
- $S[i:]$ - 配列の接尾辞(suffix)
- $S[i:j]$ - 部分配列(subarray)
今回は例として$S[i:]$ - 配列の接尾辞(suffix)の場合を取り上げています。
条件II. 再帰的に問題が解ける事
2つ目に、条件I.で解くことの出来た部分問題は、再帰的に解けそうか、という事を確認する必要があります。これは定義1.で「帰納的な関係」と言われているものです。
再帰的に解けるという事は、一例として、$S[i:]$までの求める最大の合計価格を$V[i:]$で表すと、次のような漸化式で表せる関係が有るという事です。$V[i:] = V[i+1:] + v_{i+1}$ ($v_{i+1}$は定数) ・・・①
つまり、$V[i:]$は$V[i+1:]$を使うことで、計算量$O(1)$で求められそうだ、という見当が付けばこの段階では良しとします。
ナップザック問題の場合ですが、この段階では制限重量を考慮すると少し複雑になるため無視して、$v_{i}$を時計$i$の価格だと考えると①により$V[i:]$の最大値を求めることができます。とは言うものの、制限重量を無視しているため単純に全時計の合計価格になりますが、制限重量は後程考慮するとして、再帰的な関係が確認できたことで、この段階では条件IIに見当がついた、とします。
2.再帰関数(又は漸化式)を考える
ここまで、上記条件I.、条件II.を短時間で検討することで、この問題は動的計画法で解ける可能性が高い、という見当をつけました。
そこで、いよいよ動的計画法を用いたアルゴリズムを考えます。以下説明のために式を先に、後でコードを書きますが、実際問題を解く際にはコードから考えても構いません。私の場合は式よりコードの方が考えやすく、結局問題を解くのに必要なのはコードであるため、最初からコードで考えています。条件II.について、重量制限を考慮した定式化を行ってみます。例えば、今回は部分配列=接尾辞として考えているため、各時計$S[i]$を$i=n-1$から$i=0$に降順で考えていくとします。先述の通り、最初に$i=n-1$の時計をナップザックに入れる場合、入れない場合それぞれについて考える必要があります。式にすると、①を拡張して次のように表せます。
ナップザックに$i=n-1$の時計を入れる場合:
$V[n-2:,w] = V[n-1:,w-weight_{n-1}] + value_{n-1}$ ・・・③
ナップザックに$S[n-1]$を入れない場合:
$V[n-2:,w] = V[n-1:,w]$ ・・・④
ここで、$weight_{n-1}$は時計$n-1$の重さ、$value_{n-1}$は価格を表します。上式により$V[n-2:,w]$が求まったら次は、③式、④式それぞれの場合に対して、i=n-2をナップザックに入れる場合、入れない場合を考えます。
従って、この関係を$i=0,...,n-1$すべてに渡り適用するため、③、④式を$n-2=i、n-1=i+1$で置き換えて一般化すると、次のように書けます。
ナップザックに$S[i+1]$を入れる場合:
$V[i:,w] = V[i+1:,w-weight_{i+1}] + value_{i+1}$ ・・・⑤
ナップザックに$S[i+1]$を入れない場合:
$V[i:,w] = V[i+1:,w]$ ・・・⑥ここで、重量制限$w$は時計をナップザックに入れた場合、その重量分だけ減っていく事に注意してください。
これをpythonのコードとして書いた場合、次のようになります。
(※ここでは、分かり易さのため直接式をコードに変換したもので、実際は境界条件等を考慮する必要があります。)# weight:各時計の重量: # 例)weight = [10, 20, 30, 35] # value:各時計の価格= # 例)value = [5,12,17,20] def V(i, w): #時計iを含む場合: if w >= weight[i]: V1 = V(i+1, w-weight[i]) + value[i] #時計iを含まない場合: V2 = V(i+1, w)漸化式が2つ出来ましたが、条件I.について考察することで、2つの漸化式を1つにまとめることが出来ます。
3.部分問題を解く再帰関数(漸化式)にする
条件I.では総当たり(ブルートフォース)により、時計番号$i$までで、制限重量$w$以下における最大合計価格を求めることが出来ることを考えました。そしてそれは、漸化式を用いても同様に求めることが出来るはずです。
⑤、⑥式の様に、合計価格$V[i:,w]$の値が2つあった時、制限重量$w$が同じであれば、合計価格が小さい方は最大値になり得ないため、直ちに不要だと判断できます。従って、⑤、⑥2つの漸化式は次の式にまとめることが出来ます。
$V[i:,w] = max(V[i+1:,w-weight_{i+1}] + value_{i+1}$, $V[i+1:,w]$) ・・・⑦これで、部分問題の最大値を求める式が出来ました。
pythonで書くと以下のようになります。# weight:各時計の重量: # 例)weight = [10, 20, 30, 35] # value:各時計の価格= # 例)value = [5,12,17,20] def V(i, w): #時計iを含む場合: V1 = 0 if w >= weight[i]: V1 = V(i+1, w-weight[i]) + value[i] #時計iを含まない場合: V2 = V(i+1, w) return max(V1, V2)$V(i, w)$は呼ばれるたびに、時計$i$を含む場合、含まない場合の両方を検討しますが、同じ制限重量$w$以下で合計価格が小さい方は全体の最大価格になることはないため、$max()$により合計価格が大きい方のみ返り値に設定します。
これにより、最大値になり得ない組み合わせを$i$の時点で判断できることが解ると思います。具体例として、制限重量$W=5$のナップザックと、次のような時計があるとします。
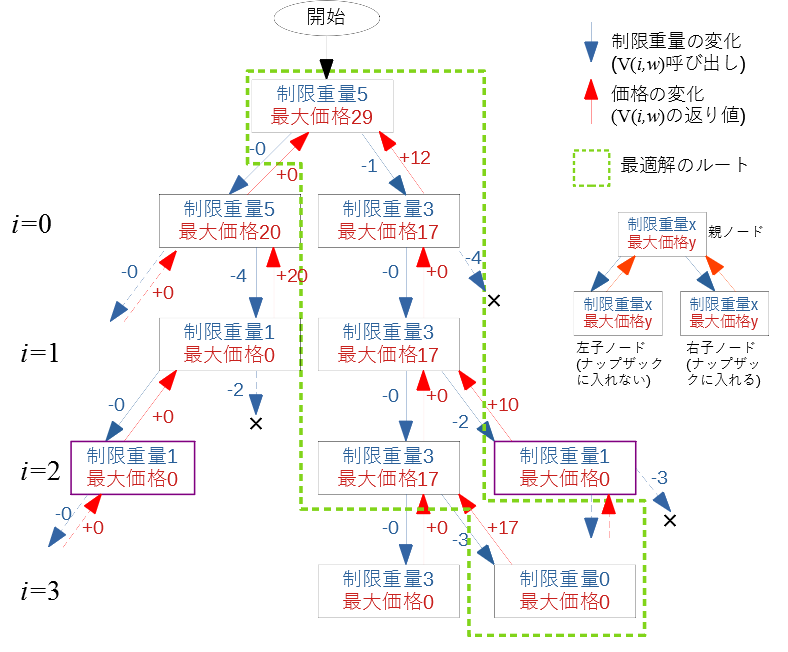
時計 0 1 2 3 重量 2 4 2 3 価格 12 20 10 17 この再帰関数呼び出しの具体例をツリーで書くと下図のようになります。
再帰関数の関数呼び出しは上から下ですが、返り値は最も深い呼び出し先から返すことになります。
それにより、制限重量は青い矢印の通り上から下に計算しますが、最大価格の算出は、赤い矢印の通り下から上に辿ることになります。各ノードには下方にある2つの子ノードからそれぞれ赤い矢印が入っていますが、右側の子ノードは$i$の時計をナップザックに入れる場合、左側の子ノードが入れない場合それぞれの$V[i:,w]$の戻り値を表します。子ノードから戻ってきた最大価格が大きい方のみが採用されて上のノードにもどされていく事で、最終的に最大価格29が得られます。さて、ここまでで漸化式(再帰関数)を使うことで、総当たりせずに最大価格を得られる方法が解りましたが、定義2.のメモ化を使うことで、メモリ使用量を犠牲にする代わり、より計算量を削減することが出来ます。
4.メモ化する
図 2 再帰呼び出しツリーの$i=2$の行に、紫で囲ったノードがあります。これらのノードは、現在の時計$i$と重量制限$w$が同じ$V[i:,w]$を2回呼びだしています。即ち、このノードより子ノードの計算は全て同じであるため、最初呼び出した際にメモに記録しておけば以降の計算を省略できます。
メモのサイズはいくつ必要でしょうか? すべての時計の重さが整数だとすると、$w$の取りうる値の範囲は$0 \leq w \leq W$であるため、メモはW+1個分必要です。$i$の取りうる値の範囲は$0 \leq i \leq n-1$であるため、$n$個分必要になります。
従って、メモのサイズは$W×(n-1)$になります。今までは配列の境界条件を考慮していなかったのですが、ここでは配列の境界条件も考慮して、
Pythonで書けば次のようになります。# weight:各時計の重量: weight = [2, 4, 2, 3] # value:各時計の価格: value = [12,20,10,17] n = len(value) # ナップザックの制限容量: W = 5 #メモを確保 memo = [[0] * (W+1) for _ in range(n)] def V(i, w): if i >= n: # 配列の最後を過ぎた場合 return 0 if memo[i][w]: # メモにある場合 return memo[i][w] #時計iを含む場合: V1 = 0 if w >= weight[i]: V1 = V(i+1, w-weight[i]) + value[i] #時計iを含まない場合: V2 = V(i+1, w) memo[i][w] = max(V1, V2) return memo[i][w] V(0, W)5.計算量の確認
既にメモにある場合、計算はしなくてよいので、メモの数だけ再帰関数を計算すればよい事になります。従って、計算量は$O(nW)$となります。
よく横軸配列のインデックス、縦軸重さのグラフ又はテーブルで説明されることが多いのですが、私にとっては再帰関数を軸に説明した方が直感的に感じたため、このような記事を認めてみました。
- 投稿日:2020-08-02T14:12:17+09:00
google-images-download フォルダーはできるけどダウンロードされない
不具合
googleimagesdownload を使って、学習用画像をダウンロードしようとしたけどエラーになった
Unfortunately all 10 could not be downloaded because some images were not downloadable. 0 is all we got for this search filter!
対処方法
パッチを含んだgoogle-images-downloadをダウンロードしてinstall
$ git clone https://github.com/Joeclinton1/google-images-download.git gid-joeclinton
$ pip install -e gid-joeclinton
- 投稿日:2020-08-02T13:13:56+09:00
PythonでEDINETコードリストを取得する
金融界隈で定量的な分析やデータサイエンスをやっている9uantです.
twitterもやってるので,興味ある方はぜひフォローしていただけると!証券コードとEDINETコードを対応させる表データの取得が面倒だったため,共有したい.
EDINETコードと証券コード
証券コードは,上場企業の株価情報を取得する際に使用する4桁の数字である.実際には末尾に0を加えて5桁とする.
EDINETコードは,決算情報のデータベースであるEDINET上で企業情報を取得する際に使用するアルファベット+数字である.4桁の証券コードをEDINETコードに変換する方法を紹介する.
EDINETコードリストを取得する
EDINETタクソミノ及びコードリストの下部に,「EDINETコードリスト」がある.今回はPythonを使ってこのcsvデータを取得する.
chromedriverを事前にダウンロードする必要がある.
chromedriverのダウンロードサイトから,ご自身のchromeのバージョンに合わせてダウンロードされたい.get_edinet_code_csv.pyimport glob import os import shutil import time from selenium import webdriver import zipfile def get_edinet_code_csv(edinetcode_dir): ''' EDINETコードリストのcsvファイルを指定したディレクトリにダウンロードする Prameter: edinetcode_dir: str EDINETコードリストのcsvファイルをダウンロードするディレクトリ Return: edinet_code_list_path: str EDINETコードリストのcsvファイルが存在するパス ''' ''' # ディレクトリが既に存在する場合は,ディレクトリを削除する if os.path.exists(edinetcode_dir): shutil.rmtree(edinetcode_dir) ''' # seleniumでchromeからzipファイルをダウンロード chromeOptions = webdriver.ChromeOptions() prefs = {"download.default_directory" : edinetcode_dir} # 保存先のディレクトリの指定 chromeOptions.add_experimental_option("prefs",prefs) chromeOptions.add_argument('--headless') # ブラウザ非表示 driver = webdriver.Chrome('chromedriverのパス', chrome_options=chromeOptions) # EDINETのEDINETコードリストにアクセス driver.get('https://disclosure.edinet-fsa.go.jp/E01EW/BLMainController.jsp?uji.bean=ee.bean.W1E62071.EEW1E62071Bean&uji.verb=W1E62071InitDisplay&TID=W1E62071&PID=W0EZ0001&SESSIONKEY=&lgKbn=2&dflg=0&iflg=0') driver.execute_script("EEW1E62071EdinetCodeListDownloadAction('lgKbn=2&dflg=0&iflg=0&dispKbn=1');") time.sleep(5) driver.quit() # ダウンロードしたzipファイルのパスを取得 list_of_files = glob.glob(edinetcode_dir+r'/*') # ワイルドカードを追加 latest_file = max(list_of_files, key=os.path.getctime) #作成日時が最新のファイルパスを取得 # zipファイルを同じディレクトリに展開 zip_f = zipfile.ZipFile(latest_file) zip_f.extractall(edinetcode_dir) zip_f.close() # zipファイルを削除 os.remove(latest_file) list_of_files = glob.glob(edinetcode_dir+r'/*') # ワイルドカードを追加 return max(list_of_files, key=os.path.getctime) # 展開したcsvファイルのパスを返す証券コード→EDINETコード
証券コードの配列を,EDINETコードの配列に変換する.
stockcode_to_edinetcode.pyimport numpy as np import pandas as pd edinet_code_path=get_edinet_code_csv(r"EDINETコードリストのcsvのダウンロード先ディレクトリのパス") edinet_code_df=pd.read_csv(edinet_code_path,encoding="cp932",header=1,usecols=['EDINETコード', '提出者名', '証券コード']) def stockcode_to_edinetcode(codes): ''' 証券コード(の配列)に対応するEDINETコードの配列を取得する Parameter: codes: int or float or str or list 証券コード,またはその配列 Return: edinet_codes: list 引数の順番に対応したEDINETコードの配列 ''' # 全ての引数を配列に変換 if type(codes) in (str, int, float): codes = [int(codes)] edinet_codes = [] for code in codes: # 4桁の証券コードを5桁に変換 if len(str(int(code)))==4: code = str(int(code))+'0' tmp = edinet_code_df[edinet_code_df['証券コード']==int(code)]['EDINETコード'] if len(tmp)==0: # 対応するEDINETコードが存在しない場合np.nanを返す edinet_codes.append(np.nan) else: edinet_codes.append(tmp.to_list()[0]) return edinet_codes
- 投稿日:2020-08-02T13:05:52+09:00
【感染症モデル入門】4月の流行と今回の流行の違いとは...‼
いよいよ、毎日、世界標準な新規感染数になりました。
2020年7月31日現在(厚生労働省より)
総感染数;35233
重症者;80
死亡数;1010
新規感染数;1574しかし、政府は依然注視するということで、非常事態宣言を発する段階ではないという説明をしています。
理由
①重体な患者が少ない
②医療施設はひっ迫していない
...
以下は宣言出さない直接の理由とはなりませんが、
③経済を回す必要があるあたりを揚げていますが、今一つ一般人には理解できない状況です。
そこで、上記の理由をデータ推移からみようと思います。
※他国の状況と比較するのは一つの方法ですが、今回はデータ処理で国内の状況をみようと思います4月の流行と今回の流行
まず、一枚の絵の比較は以下のとおりです。
4月の流行
4月の流行では、以下の順番に訪れています
①新規感染数(青い棒グラフ)の増加
②現存感染数(cases;赤いプロット)の増加
③遅れて累計治癒数(緑の小さな点プロット)と日々治癒数(緑の大きなプロット)の増加
④累計死亡数(青いプロット)の増加
と続きました。そして、治癒の遅れは24日-26日程度と見積もられ、退院するとみられます。死亡数の遅れはグラフの形状は似ており上下(死亡率を見て)を合わせ、(横軸ずらして完全にフィットさせて見積もる必要がありますが)、おおざっぱに目間でフィットさせて約10日程度(死亡率3-4%)のようです。
※精査する必要がありますが、ここでは遅れと死亡率がその程度あるという認識が大切です
今回の流行
今回の流行で同じような絵を描いて見ると様相は一変します。
①新規感染数の上昇は20(6/20)辺りから指数関数的に増加
②それに伴って現存感染数(赤いプロット)が増加しています。20日より手前は第一波の余波が残っているようです
③そして治癒数です。今回の流行では累計治癒数(緑の小さいプロット)及び日々治癒数(緑のプロット)はすぐ立ち上がって、ほぼ現存感染数と同じ曲線を描いています。なお、この累計治癒数は今回の流行だけを見たいので一度5/31時点で0クリアしています。
④死亡数は立ち上がりから30日以上たっていますが、ほぼフラットで10日前からほんのちょっと立ち上がりかけていますが、傾きは非常に小さい状況です。定常状態になると赤いプロットと平行になってきますがまだまだ先なようです
(この時点で、死亡率1%以下なようで、4月と比較して下がっていると言えます)
⑤現存重症数(黒いプロット)が現存感染数(赤いプロット)と同形状で増加に転じてきた。これは先日取り上げた通りの性質です
治癒数曲線をよく見ると
ということで、今回の流行の新規感染数と日々治癒数を重ねてみることとしました。
結果は以下のとおりです。
以下の絵は、日々治癒数を左に6日ずらすと得られました。
これ以上ずらすと日々治癒数が新規感染数を上回ってしまいます。
また、もう少し右にずらすと、新規感染数より大きくずれて下回ってしまいます。つまりこの程度の遅れで多くの人が治癒(退院)していると考えるのが妥当なようです。
この点を称して
①若者感染が中心
②無症状・軽症が多い
という表現で表されているようです。
そして、この部分が4月の感染とは大きく異なるという主張となるのだと思います。
とはいえ、現存感染数(要入院・要監視対象者)は感染が拡大する限り、減少せず、医療や保健所の作業は増大していきます。すなわち、緑のプロットの右側部分の人は現存感染数として、入院や自宅待機など監視対象総数になると考えれば拡大は明白です。
今後の感染数拡大の予測
そして、何より地域の広がりや感染年齢の広がりは注意が必要で、こういう広がりはおおざっぱに云えば、感染拡大が広がればそういう地域や層に自然に広がると考えるのが自然です。
※本来なら、こういう地域や年齢層の広がりの時系列分析をしたいと思いますが、この記事では取り上げません
ということで、ここでは新規感染数の現状を示したいと思います。
新規感染数の広がりはこの記事を書いている現在、以下のとおりです。
トレンドについての分析結果を示します。全国
順調に増加しています。
2000人/日は目前で、5000人/日も視野に入ってきました。
増加率は、約10倍/30日程度です。
月末には10000人/日以上になるという予測が成り立ちます。
東京
一方、東京は7/31に463人の新規感染数が出たので、一度マイナスになりそうでしたが、増加傾向に転じています。
しかし、増加率は小さく、このままの推移で抑えられる可能性があるという予測が立ちます。
最も、上記のマイナス傾向は単に検査数が少なかった影響のようでもあるので予断は許さない状況です。
東京以外
全国と東京の状況から予測できますが、実際計算してみると、急激な増加となっています。
増加率は約10倍/25日であり、単純計算では10000人/日は25日辺りと予測できます。その前にお盆明けには5000人/日程度に拡大しているものと想定されます。
つまり、地方で流行拡大しており、ここでは示しませんが、地域拡大もして、年齢層拡大(若年層から高齢者)も発生しているのは容易に想像されることで、今後危険な展開を危惧します。
まとめ
・4月の流行と今回の流行を比較してみた
・今回の流行では治癒数曲線が4月の流行や通常の予測とは大きく異なることが分かった
・感染数予測は今後も地方で大幅に拡大する予測であり、お盆明け5000人/日、月末10000人/日の新規感染数が発生すると予測でき、危惧される・本記事のスコープ外だが、6日程度で治癒というのは、無症状・軽症者への監視期間がその程度に設定されているものと考えられ、議論の必要がある
・地域拡大や年齢層拡大の評価をデータ分析でやってみようと思うコードは以下に置きました
データ作成用
COVID-19_Japan/test_pd.py
厚労省公開の日々pdfから、csv作成し、それらを加工するプログラムです。東京以外のデータはエクセル上で手動処理して作成しています。全体のグラフ作成用
COVID-19_Japan/simple_draw_Japan.py
感染予測グラフ作成用
作成済data(7/31現在)
以下に置いてあります
upload日付で最新版と4月流行分の判断をしてください
COVID-19_Japan/data
- 投稿日:2020-08-02T11:56:48+09:00
ImportError: cannot import name '_check_sample_weight'
内容
from tslearn.clustering import TimeSeriesKMeans
で、
ImportError: cannot import name '_check_sample_weight'
が出てしまい行き詰まったのでメモ。
どうやらscikit-learnのバージョンが古かったらしい。環境
- MacOS
- Anaconda環境
scikit-learn 0.21.3tslearn 0.4.1
解決策
参考より
pip install -U scikit-learn
で無事動いた。
↓ アップデート後のバージョン
scikit-learn 0.23.1
- 投稿日:2020-08-02T11:26:20+09:00
ITエンジニアにおすすめの20年7月書籍(私の今月のtwitterから書籍関連まとめ)
本記事では、私が20年7月に読んでTwitterに投稿した書籍紹介をまとめ、解説します。
はじめに
私のtwitter投稿から、20年7月に読んだ投稿に関する内容のまとめです。
小川雄太郎@ISID_AI_team
https://twitter.com/ISID_AI_team書籍紹介以外にもたくさんつぶやいているので、興味がある方はぜひフォローしてください。
本のジャンル
ITやデータサイエンティストのスキルセットとして、
・ビジネス
・ITインフラ
・データサイエンスアルゴリズム
の3分野が挙げられますが、読む本は、ビジネス系が多いです。
IT関連はネットで調べたり、一気にがっつり調べることが多いので。20年7月に読んだ書籍
ビジネス関連
【おすすめ・第1位】
書籍感想【アマゾンで私が学んだ 新しいビジネスの作り方】
— 小川雄太郎 (@ISID_AI_team) July 28, 2020
2003年から2015年までアマゾン・ジャパンに在籍し今の日本のアマゾン、まさに新しいビジネス立ち上げを繰り返されてきた太田さんの書籍。
新規事業を創り上げるノウハウとマインドが非常に丁寧に書かれた書籍です。https://t.co/U8poiSQJAl・イノベーション気質の組織作りの手法
・HowではなくWhyからはじめる新規事業立案
・顧客から得るデータを活用し新規事業を継続的改善
・インプットKPI、アウトプットKPI
・大きく深いビジョン
・新規ビジネスに必要な3タイプの人材と当事者意識
など、一見知っている概念が多いのですが、それらが非常に深く丁寧に書かれています。
また、データ活用が自然と当たり前のように新規事業のカイゼンに活用される様が描かれています。
数年に1冊レベルのビジネス書籍でとても感銘を受けました。良い本でした。【おすすめ・第2位】
「ワークマンは商品を変えずに売り方を変えただけでなぜ2倍売れたのか 」
— 小川雄太郎 (@ISID_AI_team) July 9, 2020
三井物産デジタルなど率いた土屋さんがCIOとしてワークマンに着任し、ワークマンプラスなどの成功までの話。
現場社員のデータ分析現場経営などを惜しみなく公開。DXを謳う前に、是非この本をhttps://t.co/aT4D9tJSzG・ただ、AIの活用を否定しているわけではなく、AIにしかできない画像判定系はAIに任せる姿勢(AI接客)
・ワークマンのデータ分析用の研修体系を公開
・その他、データサイエンス系以外にも広報系などワークマン躍進の内側を公開元USJの森岡さんの書籍を読んでいるような興奮を覚える、良い本だった
【おすすめ・第3位】
書籍感想【アフターデジタル2 UXと自由】
— 小川雄太郎 (@ISID_AI_team) July 23, 2020
前著はDXされた中国の現状紹介であり、
本書は日本でどうDXを進めていくかが解説でした。
DXとはアナログのデジタル化や新技術導入ではなく、顧客のUX向上を目的とし、データとAIを活用し進めていくという旨が解説されていますhttps://t.co/n5n58xtj4cアフターデジタル2の対となる「UXインテリジェンス」資料が以下よりダウンロードできるようになっており、
以下PDFのp. 19のデータからのUX改善に、データサイエンスやAIが活用されることになります。
アフターデジタル2と対で以下のスライドを見るのもおススメです。https://www.bebit.co.jp/news/article/ad2-download
【その他】
「シン・ニホン AI×データ時代における日本の再生と人材育成」2月発刊。
— 小川雄太郎 (@ISID_AI_team) July 9, 2020
コンパクトにAIを解説し、その後、AI×データの今後の社会が描かれています。
そして、その社会での予想課題と対策として、日本の政策の現状と筆者なりの政策提言が解説された良い本です。https://t.co/b6HPebZcvh#シンニホン今月読んだおすすめ本シリーズ(20年7月)。
— 小川雄太郎 (@ISID_AI_team) July 5, 2020
「ネットビジネス進化論」
書籍アフターデジタルの共著者である小原さんの最新作。
デジタルビジネスの6つの特徴を解説し、それぞれのビジネス事例を解説しています。
DX時代、デジタルビジネスを学ぶのに非常に良い書籍です。https://t.co/5P3jse06X2惜しいなと思ったのはタイトル。
なぜ「ネットビジネス」にしたのだろう?
私には、eコマースやアフィリエイトっぽく感じてしまう。
「デジタルビジネス進化論」というタイトルにしていれば、書籍内容ともマッチしていたし、DXの流れで、もっとたくさんの人に手に取ってもらいやすかったかもと思ったIT関連
【おすすめ・第1位】
今月読んだ書籍紹介「AWSではじめるデータレイク」
— 小川雄太郎 (@ISID_AI_team) July 15, 2020
データレイクが必要となるまでの歴史、データウェアハウス、データマートとの違い、ETLなどの詳細な解説。
そして、実際に、AWSのS3、Redshift、Glue、AthenaやQuickSightで模擬データのデータ分析基盤を構築する実践編。https://t.co/pHoXXjTeLDまだAmazonレビューついていないが、神本だと私は思う。データレイクやデータ分析基盤としてのセキュリティに1章割かれているのも素晴らしい。
この本のあとには、「図解即戦力 ビッグデータ分析のシステムと開発がこれ1冊でしっかりわかる教科書」
がおすすめです。こちらレビュー記事です
https://dev.classmethod.jp/articles/book-review-of-data-lake-starting-with-aws/【おすすめ・第2位】
こちらは読んだのが6月末ですが。。。
今月読んだ本で好きだったシリーズ(20年6月)。
— 小川雄太郎 (@ISID_AI_team) June 30, 2020
「オブジェクト指向UIデザイン」ユーザーがする事ではなく、ユーザーが得るものを先に考えるのがオブジェクト指向UIだそうです。動詞ではなく名詞に着目。フロントエンドでのドメイン駆動開発的なイメージを受けました。https://t.co/75EAxkS2vU【おすすめ・第3位】
今月読んだおすすめ本シリーズ(20年7月)。
— 小川雄太郎 (@ISID_AI_team) July 5, 2020
「More Effective Agile」
読んだのは先月ですが、アジャイルでもスクラムの書籍です。スクラムの解説入門レベルではなく、実際スクラムを実践していくなかで悩むであろう事象とその解決例が記載された「スクラム実践書籍」です。https://t.co/X5EQ7NaTiy本書も引用しつつ、今月Machine Learning 15minutesで発表したスライドはこちらです。
【イベント発表】第 46 回 Machine Learning 15minutes! Broadcast、
「SIer で自然言語処理 AI 製品をアジャイル開発した際の試行錯誤」(20 年 8 月)
発表スライド
https://drive.google.com/file/d/1xT_o7YbfLWfSBrjSw4l3-h2uAolS9jPe/view?fbclid=IwAR3SlNzvg1kCVYZpD7IFOiBkoy9kz9RmDIkIbFGyCPw43ZpuNCCnuuaJMLMその他、本書のレビュー記事です
https://iwashi.co/2020/07/10/More-Effective-Agile【その他】
書籍「DataRobotではじめるビジネスAI入門」
— 小川雄太郎 (@ISID_AI_team) July 20, 2020
DataRobotを使いながら、ビジネスでのAI活用を学ぶ本です。ただ読むのではなく、きちんとツールを動かしながら読めば、ビジネスAI基礎が身につくと感じました。そしてツールを動かす経験の後、他の本も読むと良いと思いますhttps://t.co/2kDWo23qDr
備考
【情報発信】
最近私は、自分が面白いと思った記事やサイト、読んだ本の感想などのAIやビジネス、経営系の情報をTwitterで発信しています。小川雄太郎@ISID_AI_team
https://twitter.com/ISID_AI_team私が見ている情報、面白い、重要だ!と思った内容を共有しています。
【その他】私がリードする、AIテクノロジー部開発チームではメンバを募集中です。興味がある方はこちらからお願い致します
【免責】本記事の内容そのものは著者の意見/発信であり、著者が属する企業等の公式見解ではございません
- 投稿日:2020-08-02T10:47:01+09:00
複数のヒストグラムを重ねて表示する時に、bin幅を統一する方法(matplotlib)
背景
forループを使って複数のヒストグラムを重ね合わせて表示する場合、bin幅を指定しないとデータごとに幅が異なり比較しづらかったので、bin幅を統一して表示する方法を調べました。
※自分用のメモなので読みづらかったらすみませんimport・使ったデータセット
import numpy as np import pandas as pd import matplotlib.pyplot as plt from sklearn.datasets import load_wine wine = load_wine() df_wine = pd.DataFrame(data=wine.data, columns=wine.feature_names) df_wine['target'] = wine.targetscikit-learnのワインデータセットを使います。
targetという列にはワインの種類を表すラベルを入れました。方法
plt.hist()の引数のbinsにリストを渡すと、リストで指定された値を区間の区切りとしたヒストグラムが描出される。
(bins=[0,1,2,3,4]とすると、0~1, 1~2, 2~3, 3~4の4つの区間の棒が描出される)これを利用して、
np.linspace(最小値, 最大値, 区切りたい数)でリストを作り、各ラベル用のplt.hist()の引数として渡すことで、共通のbinを指定する。↓bin幅調整なし
feature_name = 'hue' target_names = df_wine['target'].unique() for target in target_names: plt.hist(df_wine[df_wine.target == target][feature_name], alpha=0.6, label=target) plt.title(feature_name) plt.legend()↓bin幅調整あり
feature_name = 'hue' target_names = df_wine['target'].unique() # 最大値と最小値の間をn_bin等分した幅でヒストグラムの棒を表示するように設定(各targetのbin幅を統一する) n_bin = 15 x_max = df_wine[feature_name].max() x_min = df_wine[feature_name].min() bins = np.linspace(x_min, x_max, n_bin) for target in target_names: plt.hist(df_wine[df_wine.target == target][feature_name], bins=bins, alpha=0.6, label=target) plt.title(feature_name) plt.legend()参考にした記事
- 投稿日:2020-08-02T09:33:55+09:00
2. Pythonで綴る多変量解析 6-3. リッジ回帰・ラッソ回帰(scikit-learn)[正則化の効き方]
- リッジ回帰・ラッソ回帰それぞれの正則化の効き方の違いを、もう少し詳しく見ていきたいと思います。
- 正則化パラメータ$λ$を50通り生成して、それぞれの回帰モデルについて$λ$を入れ替えながら推定を50回くり返します。
- その過程で、変数ごとに推定される係数がどのように変化していくかを観察します。
⑴ ライブラリのインポート
# データ加工・計算・分析ライブラリ import numpy as np import pandas as pd # グラフ描画ライブラリ import matplotlib.pyplot as plt %matplotlib inline # 機械学習ライブラリ import sklearn from sklearn.linear_model import Ridge, Lasso # 回帰モデル生成のためのクラス# matplotlibを日本語表示に対応させるモジュール !pip install japanize-matplotlib import japanize_matplotlib⑵ データの取得と読み込み
# データを取得 url = 'https://raw.githubusercontent.com/yumi-ito/sample_data/master/ridge_lasso_50variables.csv' # 取得したデータをDataFrameオブジェクトとして読み込み df = pd.read_csv(url) print(df)
- このダミーデータは、列の0番目が目的変数y、列の1番目以降の説明変数は全部で50あります。標本数は150です。
- すでに標準化をしてあるので、各変数はいずれも平均0、標準偏差1となっています。
- また、目的変数yですが、これは意図的に作成されています。1番目の変数x_1の正しい係数を「5」とし、これに正規分布に従うノイズを加算して算出されたものです。その正解「5」を推定できるかどうかも一つの関心となります。
# 「y」列を削除して説明変数xを作成 x = df.drop('y', axis=1) # 「y」列を抽出して目的変数yを作成 y = df['y']⑶ 正則化パラメータλの生成
# λ(alpha)を50通り生成 num_alphas = 50 alphas = np.logspace(-2, 0.7, num_alphas) print(alphas)
numpy.logspace()は、底を10とする対数をとると等差数列になるという、ひとひねりのある関数です。- 引数に
(開始値, 終了値, 生成する数)を指定しますが、実際に対数をとってみると次のようになります。np.log10(alphas)
- 開始値-2、終了値0.7、全50個の等差数列になっています。
- 等差数列なら
numpy.arange()でも良さそうなところを、あとで可視化する際に対数目盛をつかう必要からこのようにしています。対数目盛
対数目盛は、目盛ごとに値が倍々に増えていきます。x軸かy軸のいずれか、もしくは両方の軸につかったものを対数グラフといいます。
普通の目盛のことを線形目盛と呼びますが、それを対数目盛に変換すると・・・
数直線上でギュッと軸目盛を圧縮したような感じになるので、桁数のかけ離れたデータなどを視覚的に比較しやすくしてくれます。
⑷ リッジ回帰による推定
# 回帰係数を格納する変数 ridge_coefs = [] # alphaを入れ替えながらリッジ回帰の推定をくりかえす for a in alphas: ridge = Ridge(alpha = a, fit_intercept = False) ridge.fit(x, y) ridge_coefs.append(ridge.coef_)
alphaを入れ替えながらリッジ回帰の推定をくりかえし、回帰係数をridge_coefsに追加していきます。- モデルのひな型を生成する
Ridge()の引数fit_intercept = Falseは、切片を計算するかどうかという指定で、Falseにすると切片を計算しない、すなわち切片0で必ず原点を通ることになります。# 集積された回帰係数をnumpyのarrayに変換 ridge_coefs = np.array(ridge_coefs) print("配列の形状:", ridge_coefs.shape) print(ridge_coefs)
- 50×50の配列で、パラメータ毎に50通り、係数50個の組が得られています。
- これを可視化します。x軸にパラメータを置きますが、
alphasを対数変換してマイナスをかけたlog_alphasをつかいます。- グラフ内にテキスト表示をする
plt.text()関数は、引数は(x, y, "str")で座標と文字列を指定します。# alphasを対数変換(-log10) log_alphas = -np.log10(alphas) # グラフ領域のサイズ指定 plt.figure(figsize = (8,6)) # x軸にλ、y軸に係数を置いた折れ線グラフ plt.plot(log_alphas, ridge_coefs) # 説明変数x_1を表示 plt.text(max(log_alphas) + 0.1, np.array(ridge_coefs)[0,0], "x_1", fontsize=13) # x軸の範囲を指定 plt.xlim([min(log_alphas) - 0.1, max(log_alphas) + 0.3]) # 軸ラベル plt.xlabel("正則化パラメータλ(-log10)", fontsize=13) plt.ylabel("回帰係数", fontsize=13) # 目盛線 plt.grid()
- x軸が$-log_{10}$なので、左へ行くほど正則化パラメータ$λ$の値は大きく、ペナルティの強度は強くなります。
- 説明変数x_1をもとに目的変数yを生成しているので、変数x_1だけは独り線形を示しています。
- 左側に行くほど係数の絶対値は小さく、右側へ行くほどペナルティの縛りが緩くなるので絶対値の大きい係数が推定されやすいという傾向が見てとれます。
⑸ ラッソ回帰による推定
- リッジ回帰と同じ正則化パラメータ(alphas)をつかって、ラッソ回帰の推定を50回くり返します。
# 回帰係数を格納する変数 lasso_coefs = [] # alphaを入れ替えながらラッソ回帰の推定をくりかえす for a in alphas: lasso = Lasso(alpha = a, fit_intercept = False) lasso.fit(x, y) lasso_coefs.append(lasso.coef_)# 集積された回帰係数をnumpyのarrayに変換 lasso_coefs = np.array(lasso_coefs) print("配列の形状:", lasso_coefs.shape) print(lasso_coefs)
- 同じくx軸が$-log_{10}$の片対数グラフを描画します。
# グラフ領域のサイズ指定 plt.figure(figsize = (8,6)) # x軸にλ、y軸に係数を置いた折れ線グラフ plt.plot(log_alphas, lasso_coefs) # 説明変数x_1を表示 plt.text(max(log_alphas) + 0.1, np.array(lasso_coefs)[0,0], "x_1", fontsize=13) # x軸の範囲を指定 plt.xlim([min(log_alphas) - 0.1, max(log_alphas) + 0.3]) # 軸ラベル plt.xlabel("正則化パラメータλ(-log10)", fontsize=13) plt.ylabel("回帰係数", fontsize=13) # 目盛線 plt.grid()
- 変数x_1以外は、係数がほぼ0となっています。
- それ以外の変数で、0ではない係数は、右端の方のパラメータの強度がもっとも緩いあたりにわずかに見られます。
まとめ
- リッジ回帰は、数ある変数に対して`全体的に絶対値の小さい係数が推定される傾向があります。
- ラッソ回帰は、部分的に少数の変数は0ではない係数となり、それ以外の係数はすべて0になるという傾向があります。
- ラッソ回帰では係数のほとんどが0になることから、回帰係数を求めながら同時に次元削減をしているに等しいともいえましょう。
- 投稿日:2020-08-02T09:24:49+09:00
愛犬に「あたしをYoutubeでスターにして!」と言われたので、YoutubeAPIで分析してみた
はじめまして。
IT業界初心者なので言葉の定義が間違っている可能性があります。お気づきの点があればアドバイスいただけると助かります。今年の5月に我が家に犬を迎え、撮影した動画の整理も兼ねてYoutubeをはじめてみました。
はじめるにあたりいろいろな動画をチェックしたのですが、個人の気づきとしては、、、
- 「Youtubeで生計立てられるんじゃないの?」と思うくらい人気の動物系Youtuberがいる
- 再生回数と動画のクオリティには、大きな関係はなさそう
(当たり前かもしれませんが、再生回数100万回超えの動画が、再生回数1万回の動画にくらべて、クオリティが極端に高いわけではない)という感じで興味深かったので、YoutubeAPIを使って分析することにしました。
分析対象
我が家ではウェルシュ・コーギーという犬種を飼い始めました。
※ かわいいかわいい愛犬のYoutubeはこちら!
自分のYoutubeに関連した分析を行いたいので、コーギーに関連する動画ならびにYoutuberを分析対象とします。
今回の記事の対象
今回の記事は以下の人を対象に書いています。
- 単にコーギーに関する動画の再生回数に興味がある人
- Pythonにさわったことがあり、YoutubeAPIで何ができるか気になる人
簡単な結論
残念ながら、YoutubeAPIはあまり万能ではなく、分析できる内容が非常に限られてしまいました。まずは「できたこと」を一通り解説します。
できたこと
できたこと 1
Search functionを用いて人気の動画・チャンネルの情報を検索できます。
詳細・コードはYoutubeAPIのリファレンスとYoutube Data APIを使ってPythonでYoutubeデータを取得するを参考にしてください。今回はq='コーギー'、order='viewCount' と指定したので、検索語句コーギーにヒットする動画を再生回数の多い順に取得することに成功しました。
なお、1000件の動画情報を取得しようと試みましたが、Youtube APIの仕様によりできませんでした。
(950件は取得できました。)
また、おおむね再生回数が多い動画が表示されますが、検索するたびに結果が変わります。私が調査した際には、900番目から950番目には再生回数100回以下の動画が多く存在していました。私も再生回数100回以上の動画を投稿しているのですが表示されなかったので、残念ながら検索結果を過度に信頼することはできません。できたこと 2
videos functionを用いて、videoIdを指定して動画の情報を取得することができます。
詳細はこちらのYoutube Data APIのリファレンスを確認ください。Youtube Data APIを使ってPythonでYoutubeデータを取得するでは、「できたこと 1」の手法で多くの動画の基本情報を取得し、ここで取得したvideoIdを用いて再生回数やいいねの数を取得しています。
なお、videos functionでチャンネルIDを指定することはできません。
あるチャンネル(たとえばHIKAKINとか)のすべての動画の情報を取得したいと考えたとしても、取得する方法がありません。
ただの実力不足かもしれませんが。。できたこと 3
channels functionを用いて、Idを指定してチャンネルの情報を検索することができます。
詳細はこちらのYoutube Data APIのリファレンスを確認ください。また、チャンネルIdを指定することでチャンネルの総再生回数・総いいねの数 等を取得できる関数(以下)を作成しました。
#channelIdを入力することで、そのチャンネルの再生回数やいいね数を取得する関数を作成 def channel_statistics(id): statistics = youtube.channels().list(part = 'statistics', id = id).execute()['items'][0]['statistics'] return statistics df_static = pd.DataFrame(list(df_channel['channelId'].apply(lambda x : channel_statistics(x)))) df_channel_output = pd.concat([df_channel,df_static], axis = 1)分析結果
上述した通り分析内容は限られ、結果も頑健ではありませんが、
せっかく調べたので、分析結果も公表します。コーギー市場は、もはや「コーギー犬ノエさん」の一人勝ち
再生回数が多い動画の情報を950件取得し、よく再生されている上位10チャンネルを動画のアップロード年ごとに比較してみました。
結果、2018年までは群雄割拠の状況でしたが、2019年にすい星のごとく「コーギー犬ノエさん」が現れ、2019年・2020年は2位に圧倒的大差をつけていることがわかります。動画をたくさん上げるだけでは、総再生回数はあまり伸びない
「2位に圧倒的大差をつけたノエさんが、動画をもっとも投稿しているのでは?」と考え、上位10チャンネルの総再生回数と総動画投稿数を比較しました。
結果、総再生回数は「コーギー犬ノエさん」がトップでしたが、総動画投稿数は別のチャンネルがトップでした。再生回数といいねの数には相関があるが、よくないねの数にも同様に相関がある
皆さんの推測通り、動画の再生回数が増えるといいねの数が増えます。相関係数は0.87です。
少々意外だったのは、動画の再生回数が増えるとよくないねの数も増えてしまい、相関係数も0.82と、いいねの数と再生関数の相関係数と近いです。
おわりに
コーギー犬ノエさんのYoutubeは、北海道&子供&コーギー2匹でとても面白い!
ちなみにほぼ毎日動画を投稿されてます。動物系Youtuber、厳しい世界なんですね。。。
※ うちの愛犬も、「しょうがないわん。そんなに頑張りたくないわん。」と、人気Youtuberになることを諦めてくれました!
- 投稿日:2020-08-02T08:02:59+09:00
Pythonでマージソートをなるべく少ない行数で実装してみた
友人がときどきアルゴリズムの実装の勉強していて、マージソートの実装に取り組んでいると聞いて俺もやるか〜ってなるのは多分きっと自然な流れ。
せっかくだからなんか勝負しようぜってことでなるべく少ない行数で実装したほうが勝ちみたいな謎勝負が行われました。
言語は友人がPythonでやろうと思ってたとのことだったのでPythonでやることになりました。負けないぞぉルール
- データ配列は1〜10までの数字がランダムに並んだものを使う
- データ配列の生成、出力部分のコードは共通として、いじらないようにする
- とにかく
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]が出力されれば良い共通部分のコードは以下の通り
from data import generate_data data = generate_data() # 1〜10の数値がバラバラに並んでる print(data) # この下に実装別ファイルに
data.pyがあり、そこのgenerate_data関数でデータを生成します。
データは[5, 1, 3, 9, 2, 8, 7, 4, 10, 6]みたいなのが生成されます。
data.pyの中身は適当になんとなく作っただけだし、ここでは省略します。実装結果
上記のルールに則ってゴリゴリに書いたらこんな感じになりました。
from data import generate_data data = generate_data() # 1〜10の数値がバラバラに並んでる print(data) # この下に実装 divide = lambda data: data if len(data) == 1 else [min(data), max(data)] if len(data) <= 2 else [divide([data[i] for i in range(len(data) // 2)]), divide([data[i] for i in range(len(data) // 2, len(data))])] merge = lambda left, right: [right.pop(0) if len(left) == 0 else left.pop(0) if len(right) == 0 else left.pop(0) if left[0] < right[0] else right.pop(0) for i in range(len(left) + len(right))] if type(left[0]) is int and type(right[0]) is int else merge(left, merge(right[0], right[1])) if type(left[0]) is int else (merge(merge(left[0], left[1]), right) if type(right[0]) is int else merge(merge(left[0], left[1]), merge(right[0], right[1]))) print(merge(divide(data)[0], divide(data)[1]))出力[5, 1, 3, 9, 2, 8, 7, 4, 10, 6] [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]「長い。三行で」と言われても問題ない出来になりました。とりあえず解説していきます。
おおまかな流れ
マージソートは「分割統治法」というやつに基づいているらしく、一旦データ配列を最小単位まで分割し、分割した各データから適切にデータを選んで結合しながら元に戻して並び替えするらしいです。考えた人すげー
アルゴリズムの詳細については数多の先人たちが色んな解説をしているのでここでは省きます。というわけで、上記の3行の実装結果は
1行目: 分割
2行目: 結合
3行目: 出力
といった感じに役割分担されてます。まずは「分割」から見ていきます。
「分割」の実装
目的
該当のコードはこれですね。
「分割」のコードdivide = lambda data: data if len(data) == 1 else [min(data), max(data)] if len(data) <= 2 else [divide([data[i] for i in range(len(data) // 2)]), divide([data[i] for i in range(len(data) // 2, len(data))])]データ配列を
[7, 6, 3, 2, 4, 5, 1, 8]とすると「分割」の目的はこの配列から[ [ [6, 7], [2, 3] ], [ [4, 5], [1, 8] ], ]のような階層構造を持つ多重配列を生成するということになります。
最小単位を要素数が2以下になるように半分ずつに分割していき、最小単位の要素数が2以下だったら小さい順にしておく
みたいなことをやってます。小さい順にするやつは本来「結合」の役目ですが、ここでやっておくと都合が良いのでこの時点でやっちゃいます。書き換え
「分割」の関数は本来こんな感じになってます。
本来の形def divide(data): if (len(data) <= 2): return data if len(data) == 1 else [min(data), max[data]] else: half_count = len(data) // 2 left = [data[i] for i in range(half_count)] right = [data[i] for i in range(half_count, len(data))] return [divide(left), divide(right)]要素数が2以下のときは小さい順にした配列を返し、それ以外のときは
leftとrightに半分ずつ分けて再帰することで上記の階層構造を実現することができます。
else以降、half_countの変数使っているところは直接len(data) // 2に置き換えれば変数を使わずに済みます。あ、leftとrightも一回しか使ってないじゃん!そのまま返り値内にぶちこんじゃえ〜ってやると返り値にぶちこんじゃえ〜def divide(data): if (len(data) <= 2): return data if len(data) == 1 else [min(data), max[data]] else: return [divide([data[i] for i in range(len(data) // 2)]), divide([data[i] for i in range(len(data) // 2, len(data))])]になります。
あ、ifとelseのどっちもreturn1文だけじゃん。それ三項演算子で1行じゃんってことで三項演算子で1行じゃんdef divide(data): return data if len(data) == 1 else [min(data), max(data)] if len(data) <= 2 else [divide([data[i] for i in range(len(data) // 2)]), divide([data[i] for i in range(len(data) // 2, len(data))])]といって感じに落ち着きます。関数内に
returnが1文しかないならラムダ式使ってラムダ式にしちゃえdivide = lambda data: data if len(data) == 1 else [min(data), max(data)] if len(data) <= 2 else [divide([data[i] for i in range(len(data) // 2)]), divide([data[i] for i in range(len(data) // 2, len(data))])]見事1行に収まりました。ラムダ式でも再帰が使えるのはいいですね。
「結合」の実装
目的
該当のコードはこれですね。
「結合」のコードmerge = lambda left, right: [right.pop(0) if len(left) == 0 else left.pop(0) if len(right) == 0 else left.pop(0) if left[0] < right[0] else right.pop(0) for i in range(len(left) + len(right))] if type(left[0]) is int and type(right[0]) is int else merge(left, merge(right[0], right[1])) if type(left[0]) is int else (merge(merge(left[0], left[1]), right) if type(right[0]) is int else merge(merge(left[0], left[1]), merge(right[0], right[1])))ぐへぇ、なげぇよ...
「結合」の目的は分割後のデータ[ [ [6, 7], [2, 3] ], [ [4, 5], [1, 8] ], ]の分割後のデータを下の階層から順に結合していき、最終的に全て結合して階層1つの元の形に戻すことです。
流れとしては流れ1[ [2, 3, 6, 7], [1, 4, 5, 8] ]流れ2[1, 2, 3, 4, 5, 6, 7, 8]といった具合です。この流れを実現するために、
merge関数では
- 引数の左右の要素が両方ともその子要素が数値のときに結合する
- 結合は左右の最初の要素の小さいほうを
popし、新しい配列の子要素として加えて行う- それ以外のときは左右の要素の子要素で再帰し、左右の要素の子要素が数値になるようにする
といったことをやります。言葉で説明しても理解しにくいのでコードを見ましょう。
書き換え
「結合」の関数は本来こんな感じになってます。
本来の形def merge(left, right): if type(left[0]) is int and type(right[0]) is int: # 両方とも子要素が数値のとき result = [] # 新しい配列を用意する for i in range(len(left) + len(right)): # left, rightの要素が無くなったらまだあるほうをpopしていく if len(left) == 0: result.append(right.pop(0)) elif len(right) == 0: result.append(left.pop(0)) # どっちもまだ残ってたら小さいほうをpopする elif left[0] < right[0]: result.append(left.pop(0)) else: result.append(right.pop(0)) return result else: """ 階層によっては同じレベルでも子要素が数値だったり配列だったりするので 子要素が数値のやつはそのままにして再帰する """ if type(left[0]) is int: return merge(left, merge(right[0], right[1])) elif type(right[0]) is int: return merge(merge(left[0], left[1]), right) else: return merge(merge(left[0], left[1]), merge(right[0], right[1]))実装の詳細はコメントにて。
わざとif-elif-elseで完結するようにしました。ということは「分割」のときと同様に、三項演算子で返り値を1行にすることができて、さらにラムダ式で関数を1行で記述することができますね!
resultをリスト内包表記で表そうとしたとき、popでちゃんと要素減ってくれんのかなと心配していましたが、実際にやってみたらちゃんと減っててくれたのでリスト内包表記と三項演算子を使ってforの部分を1行で表すことができました。「出力」の実装
「出力」のコードprint(merge(divide(data)[0], divide(data)[1]))ここ本来は
data = divide(data) print(merge(data[0], data[1]))にして
divideの実行は1回に留めるべきですが、ご覧のように変数の確保で1行使ってしまって行数の無駄になるので無理やり二度実行してます。まあ要素数10個程度じゃ誤差だよ誤差おわり
間違いなく俺の中のクソコード・オブ・ザ・イヤー大賞の受賞コードになると思われます。ありがとうございました。
![bouhan_camera_dorobou[1].png](https://qiita-user-contents.imgix.net/https%3A%2F%2Fqiita-image-store.s3.ap-northeast-1.amazonaws.com%2F0%2F260656%2F62eb22dc-8430-29bd-9053-4744c9521b6c.png?ixlib=rb-1.2.2&auto=format&gif-q=60&q=75&s=5dfcf79475a7ff6fb8bef0b8c5be408c)