- 投稿日:2020-01-01T23:53:11+09:00
TensorFlow2 + Keras による画像分類に挑戦7 ~層タイプ・活性化関数について理解する~
はじめに
TensorFlow2 + Keras を利用した画像分類(Google Colaboratory 環境)についての勉強メモ(第7弾)です。題材は、ド定番である手書き数字画像(MNIST)の分類です。
- TensorFlow2 + Keras による画像分類に挑戦 シリーズ
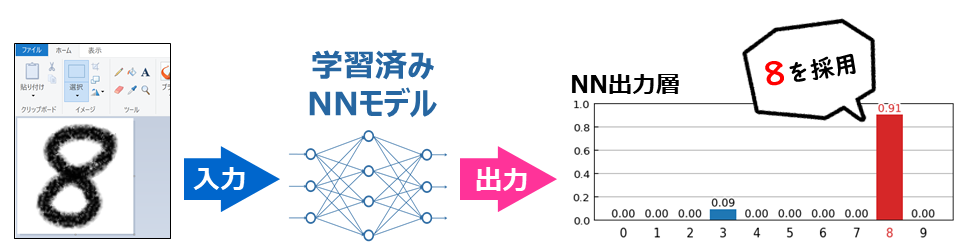
前回は、自分で用意した画像について、TF公式HPの「初心者のための TensorFlow 2.0 入門」で紹介されていたモデルで予測(分類)を行ないました。
今回は、そのチュートリアルで取り上げられているニューラルネットワークモデルについて、それを構成してる層のタイプ(
Dense、Dropout、Flatten)と、活性化関数について勉強してみました。モデルの記述方法
以下のコードは「初心者のための TensorFlow 2.0 入門」からのコピペです。
NNモデルの構築(記述1)model = tf.keras.models.Sequential([ tf.keras.layers.Flatten(input_shape=(28, 28)), tf.keras.layers.Dense(128, activation='relu'), tf.keras.layers.Dropout(0.2), tf.keras.layers.Dense(10, activation='softmax') ])上記のコードでは活性化関数を指定するキーワード引数の
activationを文字列で指定していますが、次のように直接的に関数を与えて指定することもできます。NNモデルの構築(記述2)model = tf.keras.models.Sequential([ tf.keras.layers.Flatten(input_shape=(28, 28)), tf.keras.layers.Dense(128, activation=tf.nn.relu), # 変更 tf.keras.layers.Dropout(0.2), tf.keras.layers.Dense(10, activation=tf.nn.softmax) # 変更 ])また、ここでは、ニューラルネットの層構成情報を
Sequential(...)の引数としてリスト型で与えていますが、次のようにadd(...)を使って層をひとつずつ追加していくこともできます。NNモデルの構築(記述3)model = tf.keras.models.Sequential() # (0) model.add( tf.keras.layers.Flatten(input_shape=(28, 28)) ) # (1) model.add( tf.keras.layers.Dense(128, activation=tf.nn.relu) ) # (2) model.add( tf.keras.layers.Dropout(0.2) ) # (3) model.add( tf.keras.layers.Dense(10, activation=tf.nn.softmax) ) # (4)モデルの概要を表示
上記のように層を設定したNNモデルは
summary()で、その概要を確認することができます。モデルの概要確認model.summary()実行結果Model: "sequential" _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= flatten (Flatten) (None, 784) 0 _________________________________________________________________ dense (Dense) (None, 128) 100480 _________________________________________________________________ dropout (Dropout) (None, 128) 0 _________________________________________________________________ dense_1 (Dense) (None, 10) 1290 ================================================================= Total params: 101,770 Trainable params: 101,770 Non-trainable params: 0 _________________________________________________________________表は上から下に向かって、入力層、中間層(隠れ層)、・・・、出力層となります。
表内の左端の値は「層の名前」になります。
add()の際にname=を省略していると自動的に付与されるもので、モデルを構築するたびにflatten_1、flatten_2のように番号がついていきます。左から2番目の
( )の値は「層のタイプ」になります。ここではFlatten、Dense、Dropoutの3タイプが登場します。この解説は次のセクションで。項目「Output Shape」のタプルの2個目の数値は、当該層のニューロン数(=当該層からの出力数)になります。
(None, 128)であれば、その層には 128個のニューロン(ノード)が存在するということです。つづいて、項目「Param」は、パラメータ(当該層の入力に係る重みとバイアス)の総数になります。
例えば、第2層「dense (Dense) 」の $100480$ は、第1層の出力数 $784$ と 第2層のノード数 $128$ を掛けた数だけの重みのパラメータ、第2層ノード数 $128$ 個のバイアス をあわせた全パラメータ数にになります。つまり、 $784\times 128 + 128=100480$ です。これらパラメータの最適値を求めるための操作がトレーニング(訓練・学習)になります。
表の最後には、Total params(総パラメータ数)、Trainable params(トレーニングにより求められるパラメータ)、Non-trainable params(トレーニングでは求めないパラメータ)の数が記載されています。
各層の役割・動作・意味
Flatten層
手書き数字文字の1枚のイメージは 28 $\times$28 pixel であり、大きさが (28,28) の numpy.ndarray 型、つまり2次元配列です。Flatten層では、これを平坦化して 1次元配列的に直しています。よって、その出力数は、
model.summary()で確認したように $28\times 28=784$ となります。プログラムでは、次のようにしてモデルにFlatten層を追加しています。
model.add( tf.keras.layers.Flatten(input_shape=(28, 28)) ) # (1)
input_shape引数には、x_train[*].shapeと一致させて(28, 28)を指定しています。もし、32 $\times$32 pixel の画像を入力とするならばinput_shape=(32, 32)のようにします。リファレンスはこちら。Dense層
前層と当該層のあいだを全結合(密結合)した全結合層を意味します。ニューラルネットワークを構成する標準的な層となります。
プログラムでは、次のようにしてモデルにDense層を追加しています。
中間層としての全結合層model.add( tf.keras.layers.Dense(128, activation=tf.nn.relu) ) # (2)出力層としての全結合層model.add( tf.keras.layers.Dense(10, activation=tf.nn.softmax) ) # (4)1個目の引数には、その層を構成するノード数(ニューロン数)を与えます。上記の (2) のように中間層として設定する全結合層のノード数をいくつにするか?はモデルの性能を左右する要素になります(ユーザが勘なり試行錯誤で設定するハイパーパラメータになります)。なお、ノード数が多ければ高性能なモデルになるというわけではないです(少なくともノードが増えると、それだけパラメータ数が増えるので計算量が大きくなり学習に時間がかかります)。
一方で、多クラス分類問題を扱っている場合、出力層として設定する全結合層のノード数は、分類したいクラス数と一致させる必要があります。MNISTの場合は、0~9までの数字の分類、つまり 10クラス分類問題なので、ここでは
10を設定する必要があります。また、
activation引数には、活性化関数を与えます。ここでは、ReLU関数(tf.nn.relu)とSoftMax関数(tf.nn.softmax)が使われていますが、その詳細は次のセクションで解説します。なお、activation=を省略した場合は、活性化関数は適用されず、計算された値がそのまま出力される仕様です)。リファレンスはこちら。Dropout層
モデルをトレーニングする際に(ノード単位で)指定された確率に応じて前層から次層への出力を遮断する働きをします(前層の対応ノードを確率に応じて不活性/ドロップさせるとも表現されます)。この層を設けることで過学習という状況になりづらくなるようです。
これについては、「【ニューラルネットワーク】Dropout(ドロップアウト)についてまとめる」の解説が、とても分かりやすかったです。
プログラムでは、次のようにしてモデルにDropout層を追加しています。
model.add( tf.keras.layers.Dropout(0.2) ) # (3)引数には、不活性させたいノード割合を 0.0 から 1.0 の範囲で指定します。これを 0.0 に設定すると、実質的にDropout層が存在しないのと同じになります。また、1.0 に設定するとネットワークが Dropout層で完全遮断されるので、一切の学習が機能しません(実際には、
ValueError: rate must be a scalar tensor or a float in the range [0, 1), got 1というエラーが発生します)。なお、不活性されるノードは、指定した確率に応じてランダムに選択されます。よって、このDropout層をもうけていると、トレーニング毎に学習済みモデルが(わずかに)変化します。そのため、Dense層のノード数と正解率の関係など、他のハイパーパラメータの影響を調べるときなどは、
seed=1のように引数を与え、ランダムシードを固定します(ただし、トレーニングのほうでランダム要素があると、ここを固定しても実行毎に生成される学習済みモデルが変化します)。リファレンスはこちら。
過学習に対するDropout層の有効性を評価
Dropout層のパラメータ(不活性させるノード割合 rate )を、0.0 から 0.8 まで、0.2 刻みで変化させたモデルを用意します。これについて、Epochs数=100 でトレーニングと評価を行なって、Dropout層を入れることが過学習に対して有効であるのか?を観察しました。
トレーニングのEpoch毎に、トレーニングデータ
x_trainに対する正答率(accuracy)と損失関数値(loss)、テストデータx_testに対する正答率(val_accuracy)と損失関数値(val_loss)を取得してプロットしました。mport numpy as np import tensorflow as tf # (1) 手書き数字画像のデータセットをダウンロード mnist = tf.keras.datasets.mnist (x_train, y_train), (x_test, y_test) = mnist.load_data() # (2) データの正規化 x_train, x_test = x_train / 255.0, x_test / 255.0 # (3) NNモデルを構築 # ■■ Dropout rate を 0.0 から 0.8 まで変化させる ■■ epochs = 100 results = list() for p in np.arange(0.0, 1.0, 0.2) : print(f'■ Dropout p={p:.1f}') tf.keras.backend.clear_session() model = tf.keras.models.Sequential() model.add( tf.keras.layers.Flatten(input_shape=(28, 28)) ) model.add( tf.keras.layers.Dense(128, activation=tf.nn.relu) ) model.add( tf.keras.layers.Dropout(p) ) # ここのパラメータpの影響をみる model.add( tf.keras.layers.Dense(10, activation=tf.nn.softmax) ) # (4) モデルのコンパイル model.compile(optimizer='adam',loss='sparse_categorical_crossentropy',metrics=['accuracy']) # (5) モデルのトレーニング(学習・訓練) r = model.fit(x_train, y_train, validation_data=(x_test,y_test), epochs=epochs) print(r.history) results.append( dict( rate=p, hist=r.history ) ) # ■■ グラフ出力 ■■ import numpy as np import matplotlib.pyplot as plt import matplotlib.ticker as tk ylim = dict( ) ylim['accuracy'] = (0.90, 1.00) ylim['val_accuracy'] = (0.95, 1.00) ylim['loss'] = (0.00, 0.20) ylim['val_loss'] = (0.05, 0.30) xt_style = lambda x, pos=None : f'{x:.0f}' for v in ['accuracy','loss','val_accuracy','val_loss'] : plt.figure(dpi=96) for r in results : plt.plot( range(1,epochs+1),r['hist'][v],label=f"rate={r['rate']:.1f}") plt.xlim(1,epochs) plt.ylim( *(ylim[v]) ) plt.gca().xaxis.set_major_formatter(tk.FuncFormatter(xt_style)) plt.tick_params(direction='in') plt.legend(bbox_to_anchor=(1.02, 1), loc='upper left', borderaxespad=0) plt.xlabel('epoch') plt.ylabel(v) plt.show()実験結果
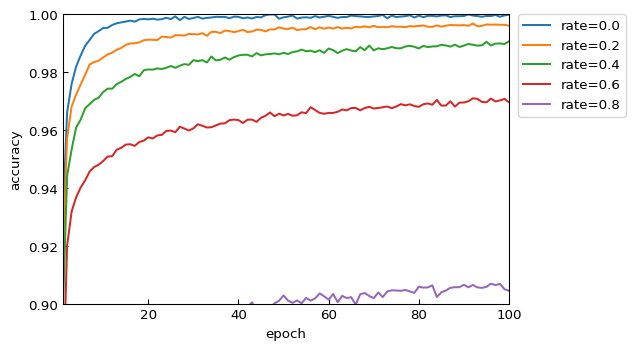
トレーニングデータに対する正答率 accuracy
いずれのモデルでも学習を進めれば進めるほど良い値となっていきます。特に、実質的なDropout層ナシと等価である rate=0.0 では、最高スコア 1.0 に到達しています。基本的に、不活性化割合(rate)が小さいほど、学習が速く進み、最終的な正答率も良くなっています。
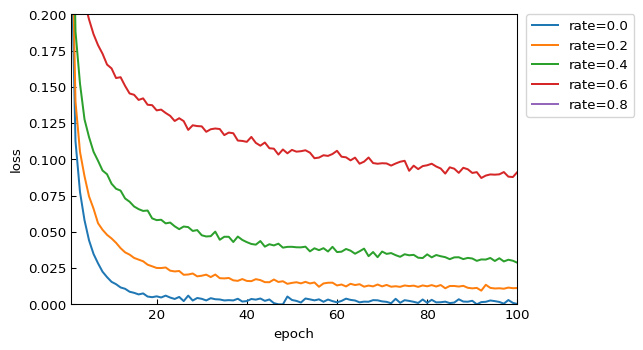
トレーニングデータに対する損失関数値 loss
基本的に、正答率(accuracy)と同様の傾向です。
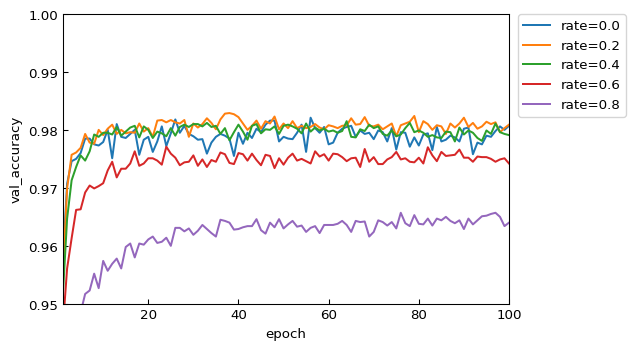
テストデータに対する正答率 val_accuracy
ここからが、汎化性能を含めた真の評価指標になります。
rate=0.2 と 0.4 は収束も早く、最終的な値も良好です。一方で、0.6 は、0.2 や 0.4 と比較すると明らかに性能が劣っています。0.0 は、他と比較して値がやや安定しません。
正答率だけを見ている限りでは、過学習を起しているような傾向は読み取れません。
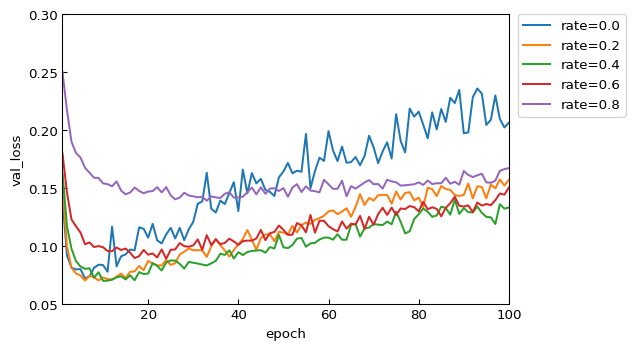
テストデータに対する損失関数値 val_loss
rate=0.0(Dropout層なしと等価)では、Epoch=8 ぐらいを境にして徐々に値が悪くなっています。明確に過学習の傾向が読み取れます。
Epoch=20 以降の各データの傾きを観察すると、不活性割合(rate)が大きいほど過学習しずらいモデルになっていることが分かります。Dropout層の有効性を確認することができました。
総合して評価すると、チュートリアルで設定されていた rate=0.2、Epochs=5 という値は、十分にチューニングされた良いパラメータであったことが確認できました。
活性化関数
活性化関数を適用しない場合、第2層の1個目のノード出力 $y_1$ は次のように計算されます($x_i$は前層の $i$ 番目ノードの出力、$w_{i1}$ は重み、$b_{1}$ はバイアス)。
$$ y_1 = b_1 + \sum_{i=1}^{784} x_{i}w_{i1} $$
一方、活性化関数 $f$ を適用すると、その $y_1$ は次のようになります。
$$ y_1 = f ( b_1 + \sum_{i=1}^{784} x_{i}w_{i1} ) $$
ニューラルネットで使用される活性化関数は、様々なものがありますが、大きくは中間層でよく使われるもの、問題タイプに応じて出力層で使われるものに分けられます。
中間層では、ReLU関数やシグモイド関数が利用されます。また、多クラス分類問題の出力層では、その性質からSoftnMax関数が、2クラス分類問題ではシグモイド関数が使用されます。
ReLU関数
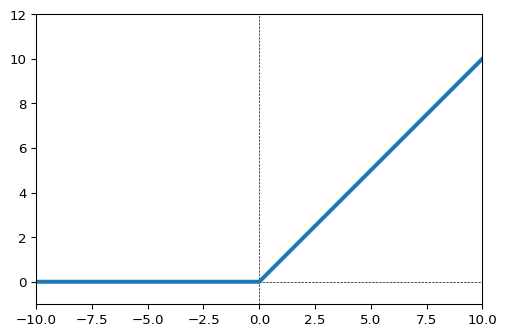
中間層において最も一般に用いられる活性化関数らしいです。入力が0未満の場合は出力は0、入力が0以上のときは、入力をそのまま出力します。
tf.nn.relu()。リファレンスはこちら。ReLU関数import numpy as np import matplotlib.pyplot as plt import tensorflow as tf xmin, xmax = -10,10 x = np.linspace(xmin, xmax,1000) y = tf.nn.relu(x) # ReLU関数 # グラフで形状を確認 plt.figure(dpi=96) plt.plot(x,y,lw=3) plt.xlim(xmin, xmax) plt.ylim(-1, 12) plt.hlines([0],*(plt.xlim()),ls='--',lw=0.5) plt.vlines([0],*(plt.ylim()),ls='--',lw=0.5)ReLU関数の亜種に「Leaky Relu関数」「Parametric ReLU関数」などがあるようです。
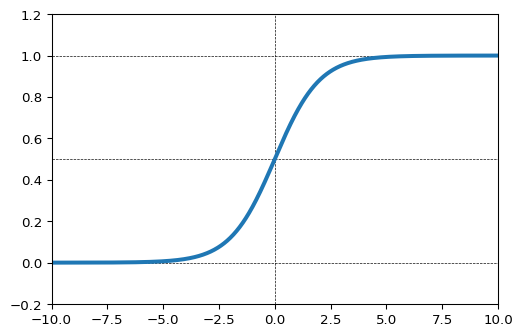
シグモイド関数
中間層において、よく用いられる活性化関数のひとつ。ただし、層数が多いNNモデルでシグモイド関数を活性化関数として使用すると、勾配消失問題が起きるために、ReLU関数に人気を奪われ気味だそうです。
tf.math.sigmoid()。リファレンスはこちら。import numpy as np import matplotlib.pyplot as plt import tensorflow as tf xmin, xmax = -10,10 x = np.linspace(xmin, xmax,1000) y = tf.math.sigmoid(x) # シグモイド関数 # グラフで形状を確認 plt.figure(dpi=96) plt.plot(x,y,lw=3) plt.xlim(xmin, xmax) plt.ylim(-0.2, 1.2) plt.hlines([0,0.5,1],*(plt.xlim()),ls='--',lw=0.5) plt.vlines([0],*(plt.ylim()),ls='--',lw=0.5)SoftMax関数
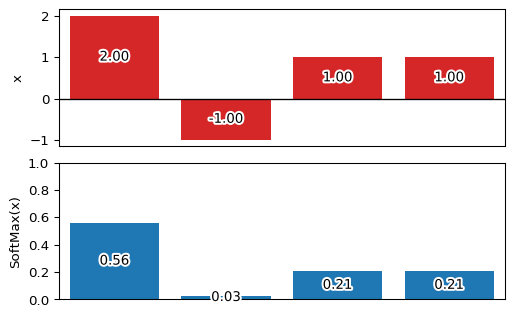
一般に、多クラス分類問題の出力層で使用されます。入力に関わらず出力は 0.0 ~ 1.0 の範囲をとり、出力の総和が 1.0 となるのが特徴です。
tf.nn.softmax()。リファレンスはこちら。例えば、次のように
[2, -1, 1, 1]という入力に対してSoftMax関数を適用すると、[0.56, 0.03, 0.21, 0.21]といった出力(要素の総和は 1.0)を得ることができます。ReLU関数import numpy as np import matplotlib.pyplot as plt import matplotlib.patheffects as pe import tensorflow as tf x = np.array( [2, -1, 1, 1], dtype=np.float64 ) fx = tf.nn.softmax(x) fx = fx.numpy() # 'numpy.ndarray'で内容取得 np.set_printoptions(precision=2) print(f'fx = {fx}') print(f'fx.sum() = {fx.sum():.2f}') fig, ax = plt.subplots(nrows=2, ncols=1, dpi=96) plt.subplots_adjust(hspace=0.12) ep = (pe.Stroke(linewidth=3, foreground='white'),pe.Normal()) tp = dict(horizontalalignment='center',verticalalignment='center') ax[0].bar( np.arange(0,len(x)), x, fc='tab:red' ) ax[1].bar( np.arange(0,len(fx)), fx ) ax[1].set_ylim(0,1) for i, p in enumerate([x,fx]) : ax[i].tick_params(axis='x', which='both', bottom=False, labelbottom=False) ax[i].set_xlim(-0.5,len(p)-0.5) for j, v in enumerate(p): t = ax[i].text(j, v/2, f'{v:.2f}',**tp) t.set_path_effects(ep) ax[0].hlines([0],*(plt.xlim()),lw=1) ax[0].set_ylabel('x') ax[1].set_ylabel('SoftMax(x)')次回
未定
- 投稿日:2020-01-01T00:35:06+09:00
TensorFlow2 + Keras による画像分類に挑戦6 ~自分で用意した画像の前処理・分類をしてみる~
はじめに
TensorFlow2 + Keras を利用した画像分類(Google Colaboratory 環境)についての勉強メモ(第6弾)です。題材は、ド定番である手書き数字画像(MNIST)の分類です。
- TensorFlow2 + Keras による画像分類に挑戦 シリーズ
前回は、あらかじめ MNIST で用意されている手書き数字イメージを使って予測(分類)を行ないました。今回は、自分で用意した画像を使って、学習済みにモデルに分類をさせてみたいと思います。また、その際に要求されるリサイズやトリミングなどの前処理に関するPythonプログラム(Pillowライブラリを利用)なども解説していきたいと思います。
手書き数字画像の作成
ペイントで 100 $\times$100 pixel のサイズで「8」の手書き文字を作成して、カラー(RGB)の PNGファイルとして保存しました。名前は
test-8.pngとしました。Google Colab. に画像ファイルをアップロード
次のように、Google Colab. のサイドメニューのファイルタブをアクティブにして、デスクトップからドラッグ&ドロップすればアップロードすることができます。アップロードしたファイルは一定時間で削除されます。
また、次のようにコードセルを書いて実行すれば、ファイル選択ダイアログを使って同様にアップロードすることができます。
アップロードされたファイル(
test-8.png)の絶対パスは/content/test-8.pngとなります。また、カレントディレクトリは/contentなので、単にtest-8.pngだけでもアクセスすることができます。なお、GoogleDriveをマウントして、それを参照することもできます。詳しくは、Google Colaboratory(初利用からファイルの読込みまで)@Qiita を参照してください。
画像ファイルの読込み・内容の確認
アップロードした画像ファイルを読み込んで、内容確認のために表示します。なお、画像は Pillow(PIL Fork)を利用して扱います。わずか3行です。
import PIL.Image as Image img = Image.open('test-8.png') display(img)学習済みモデルに入力可能な形式に変換
学習済みモデルに入力するためには、次の前処理が必要になります。
- グレースケール画像にする。
- 28 $\times$28 pixel にリサイズする。
- numpy.ndarray 型の2次元配列にする。
- 白が「0.0」、黒が「1.0」になるようにする。
次のようなコードで上記の前処理ができます。注意すべき点は、通常の256段階グレースケール画像は、白が「255」、黒が「0」なので、それを反転させる必要があるということです。
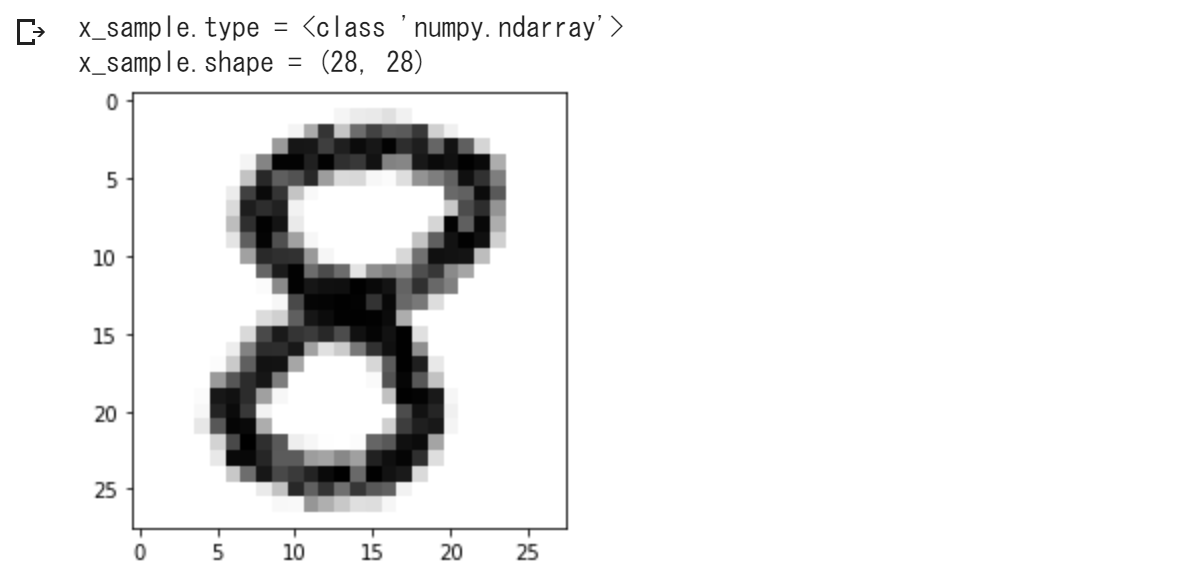
import numpy as np import PIL.Image as Image import matplotlib.pyplot as plt img = Image.open('test-8.png') img = img.convert('L') # 1. グレースケールに変換 img = img.resize((28,28)) # 2. 28x28にリサイズ x_sample = np.array(img) # 3. numpy.ndarray型に変換 x_sample = 1.0 - x_sample / 255.0 # 4. 反転・正規化 y_sample = 8 # 正解データ # 確認出力 print(f'x_sample.type = {type(x_sample)}') print(f'x_sample.shape = {x_sample.shape}') plt.figure() plt.imshow(x_sample,vmin=0.,vmax=1.,cmap='Greys') plt.show()この
x_sampleについて、学習済みモデルで予測を行なって、第4回 で示したプログラムで予測結果レポートを作成してあげると、次のようになります。いい感じに予測(分類)を行なうことができました。
再掲:予測結果レポート作成のプログラム
基本的には、第4回 で示したプログラムと同じですが、
x_sampleに単体の入力データ、y_sampleに正解データ、modelに学習済みモデルが格納されている前提に書き換えています。matplotlib_日本語出力準備処理!pip install japanize-matplotlib import japanize_matplotlibimport numpy as np import matplotlib.pyplot as plt import matplotlib.patheffects as pe import matplotlib.transforms as ts s_sample = model.predict(np.array([x_sample]))[0] # 予測(分類) fig, ax = plt.subplots(nrows=2,figsize=(3,4.2), dpi=120, gridspec_kw={'height_ratios': [3, 1]}) plt.subplots_adjust(hspace=0.05) # 上側に手書き数字のイメージを表示 ax[0].imshow(x_sample,interpolation='nearest',vmin=0.,vmax=1.,cmap='Greys') ax[0].tick_params(axis='both', which='both', left=False, labelleft=False, bottom=False, labelbottom=False) # 正解値と予測値を左上に表示 t = ax[0].text(0.5, 0.5, f'正解:{y_sample}', verticalalignment='top', fontsize=9, color='tab:red') t.set_path_effects([pe.Stroke(linewidth=2, foreground='white'), pe.Normal()]) t = ax[0].text(0.5, 2.5, f'予測:{s_sample.argmax()}', verticalalignment='top', fontsize=9, color='tab:red') t.set_path_effects([pe.Stroke(linewidth=2, foreground='white'), pe.Normal()]) # 下側にNN予測出力を表示 b = ax[1].bar(np.arange(0,10),s_sample,width=0.95) b[s_sample.argmax()].set_facecolor('tab:red') # 最大項目を赤色に # X軸設定 ax[1].tick_params(axis='x',bottom=False) ax[1].set_xticks(np.arange(0,10)) t = ax[1].set_xticklabels(np.arange(0,10),fontsize=11) t[s_sample.argmax()].set_color('tab:red') # 最大項目を赤色に offset = ts.ScaledTranslation(0, 0.03, plt.gcf().dpi_scale_trans) for label in ax[1].xaxis.get_majorticklabels() : label.set_transform(label.get_transform() + offset) # Y軸設定 ax[1].tick_params(axis='y',direction='in') ax[1].set_ylim(0,1) ax[1].set_yticks(np.linspace(0,1,5)) ax[1].set_axisbelow(True) ax[1].grid(axis='y')前処理:画像中央に数字がない場合、汚れがある場合に対応
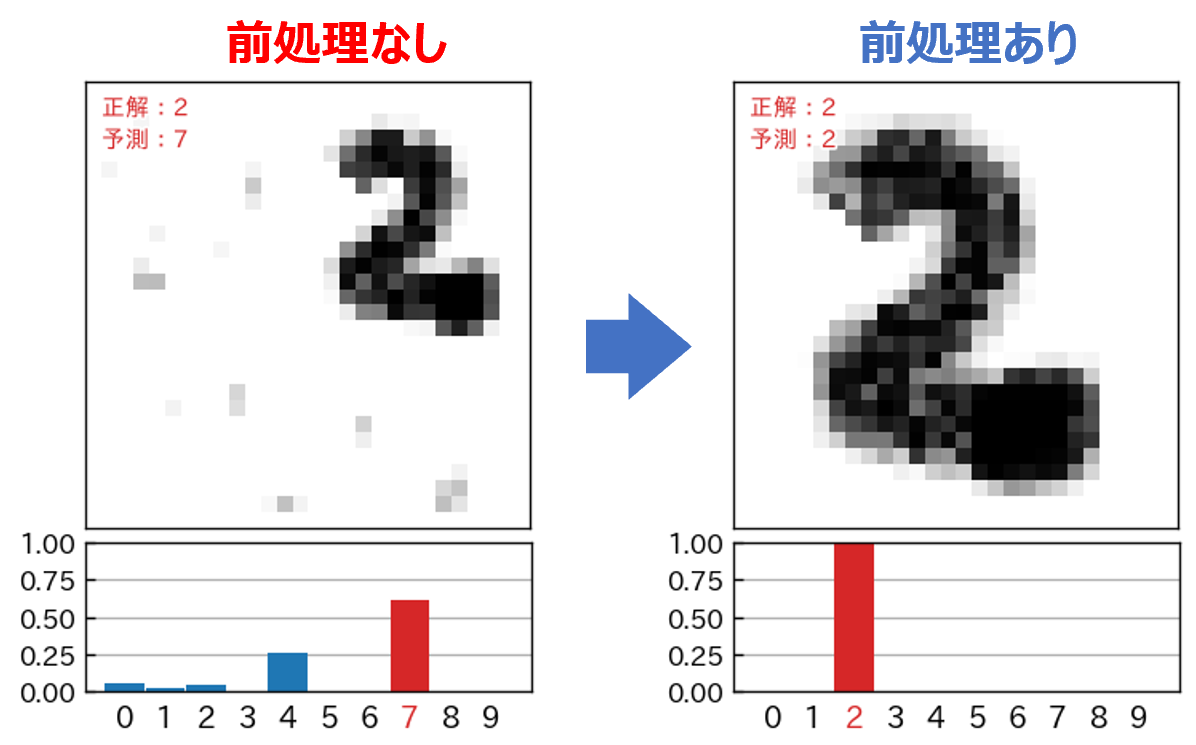
自分で手書き数字の画像を用意すると、次のように数字が画像の中央に位置していない場合があります。
このような画像に対して、そのまま予測(分類)をかけると、次のように酷い結果となってしまいます。
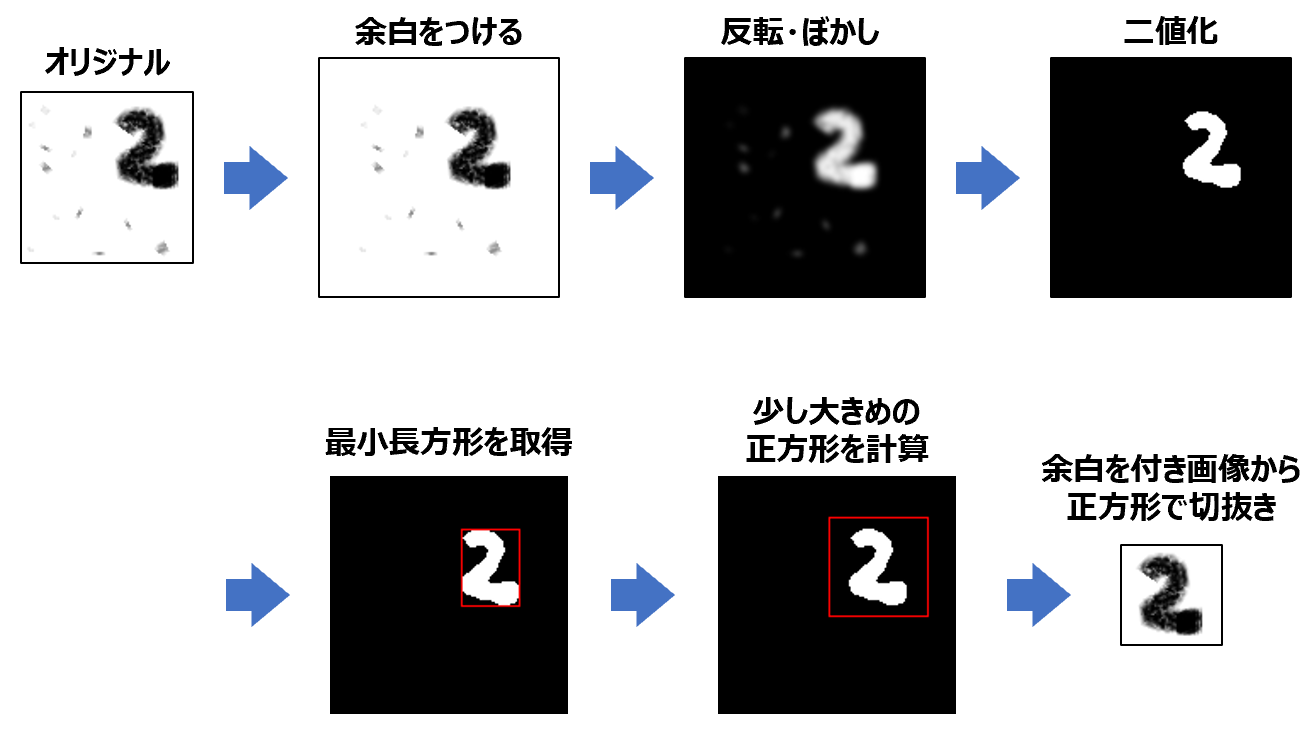
このようなことから、予測を行なう前に、文字部分を中央に移動して、さらに図の大きさに対して、正味の文字部が 90% ぐらいの大きさになるような前処理をする必要があります。また、文字以外の汚れやゴミなどを取り除く処理が必要になります。
ここでは、次のような(自動化された)前処理をしたいと思います。
前処理import numpy as np from PIL import Image, ImageChops,ImageFilter, ImageOps, ImageDraw import matplotlib.pyplot as plt # 図の上下左右に指定幅の余白(白色)を付加 def add_margin(img, margin): w, h = img.size w2 = w + 2 * margin h2 = h + 2 * margin result = Image.new('L', (w2, h2), 255) result.paste(img, (margin, margin)) return result # 引数で与えられた長方形の長辺にあわせたサイズの # 正方形(ただし、ちょっと大きくした)の正方形を計算 def to_square( rect ): x1, y1, x2, y2 = rect # (x1,y1)は左上、(x2,y2)は右下の座標 s = max( x2-x1, y2-y1 ) # 長辺の長さを取得 s = int(s*1.3) # 少しだけ大きく nx1 = (x1+x2)/2 - s/2 nx2 = (x1+x2)/2 + s/2 ny1 = (y1+y2)/2 - s/2 ny2 = (y1+y2)/2 + s/2 return (nx1,ny1,nx2,ny2) img = Image.open('test-2x.png') img = img.convert('L') #display(img) # 画像の上下左右に白色の余白を付ける img = add_margin(img,int(max(img.size)*0.2)) #display(img) # 反転画像を作成 img2 = ImageOps.invert(img) # ぼかしをかける img2 = img2.filter(ImageFilter.GaussianBlur(1.5)) #display(img2) # 二値化 img2 = img2.point(lambda p: p > 150 and 255) #display(img2) # 黒色以外の最小領域(長方形)を取得 rect = img2.getbbox() # tmp = img2.convert('RGB') # ImageDraw.Draw(tmp).rectangle(rect, fill=None, outline='red') # display(tmp) # 長方形を長辺にあわせた正方形に変換 sqr = to_square(rect) # tmp = img2.convert('RGB') # ImageDraw.Draw(tmp).rectangle(sqr, fill=None, outline='red') # display(tmp) # 正方形でトリミング img = img.crop(sqr) #display(img) # 以降は前と同じ img = img.convert('L') # 1. グレースケールに変換 img = img.resize((28,28)) # 2. 28x28にリサイズ x_sample = np.array(img) # 3. numpy.ndarray型に変換 x_sample = 1.0 - x_sample / 255.0 # 4. 反転・正規化 y_sample = 2 # 正解データ # 確認出力 print(f'x_sample.type = {type(x_sample)}') print(f'x_sample.shape = {x_sample.shape}') plt.figure() plt.imshow(x_sample,vmin=0.,vmax=1.,cmap='Greys') plt.show()前処理せずに予測分類した場合と、前処理してから予測分類した場合についての結果の比較です。予測モデルについてあれこれ試行錯誤する以前に前処理が重要であることを改めて実感します。
次回
- だいぶ外堀は埋めたので、いよいよニューラルネットワークのモデル構築について勉強していきたいと思います。