MYJLab Advent Calendar 2019 18日目の記事です。

推しメン堀未央奈のブログで遊んでみました。テキストマイニング編です。

スクレイピング

乃木坂46 堀未央奈 公式ブログをスクレイピングします。

scraiping.py

from time import sleep
from bs4 import BeautifulSoup
from selenium import webdriver
from selenium.webdriver.chrome.options import Options
from selenium.webdriver.common.keys import Keys

def main():
    options = Options()
    driver = webdriver.Chrome(executable_path="ドライバのパスをここに", chrome_options=options)
    url = "http://blog.nogizaka46.com/miona.hori/"  
    driver.get(url) 
    lines=[]
    #     １枚目取り出す
    get(driver,lines)
    click_tag = driver.find_elements_by_css_selector('#sheet > div:nth-child(1) > a:nth-child(12)')
    click_tag[0].click()

    #     2枚目以降取り出す
    for i in range(10):
        sleep(2)
        click_tag = driver.find_elements_by_css_selector('#sheet > div:nth-child(1) > a:nth-child(13)')
        click_tag[0].click()
        get(driver,lines)

    with open('miona.txt', 'w') as f:
        for i in range(len(lines)):
            f.write(lines[i])
    driver.quit()

# ブログ内容の取得
def get(driver,lines):
    sleep(1)
    soup = BeautifulSoup(driver.page_source, "html.parser")
    for element in soup.select('.entrybody'):
        lines.append(element.text)
    return lines

if __name__ == '__main__':
    main()

単純な構造でスクレイピングしやすいです！わーい

前処理

クレンジング処理

def cleansing

以下のいらない情報たちを削除

• URLテキスト
• 絵文字
• 句読点
• ハッシュタグ ( 堀氏は文章にハッシュタグ入れがちなのですが、今回はカット )
• 空白の行
• スペース
• インスタとTwitterのアカウントID

単語の分割処理

def wakti
形態素解析器はJanomeを使用します。複合名詞化も可能にしたかったので、Analayzerのを用いました。

ストップワードの除去

def stop_word
ストップワードを指定して除去します。

preprocessing.py

from janome.analyzer import Analyzer
from janome.tokenfilter import *

import re
import neologdn
import emoji

import collections
import unicodedata
import string

def stop_word(text):

    stop_words = [ u'てる', u'いる', u'なる', u'れる', u'する', u'ある', u'こと', u'これ', u'さん', u'して', \
             u'くれる', u'やる', u'くださる', u'そう', u'せる', u'した',  u'思う',  \
             u'それ', u'ここ', u'ちゃん', u'くん', u'', u'て',u'に',u'を',u'は',u'の', u'が', u'と', u'た', u'し', u'で', \
             u'ない', u'も', u'な', u'い', u'か', u'ので', u'よう', u'ん', u'みたい',u'の',u'私',u'自分',u'たくさん',\
             u'ん',u'もの',u'こと']

    list=[]
    for i in range(len(text)):
        if text[i] not in stop_words:
            list.append(text[i])
    return list

def wakati(text,list):
    a = Analyzer(token_filters=[CompoundNounFilter()])
    for token in a.analyze(text):
#        名詞のみで分かち書きする場合
#        if token.part_of_speech.split(',')[0] in ['名詞']:
        if token.part_of_speech.split(',')[0] in ['名詞','形容詞','形容動詞']:
            list.append(token.base_form)
    return " ".join(list)


def cleansing(text):  
    text = re.sub(r'https?://[\w/:%#\$&\?\(\)~\.=\+\-]+', '', text)
    text = re.sub(r'#', '', text)
    text = re.sub(r'\n', '', text)
    text = re.sub(r'@horimiona_2nd', '', text)
    text = re.sub(r'@horimiona2nd', '', text)
    text = neologdn.normalize(text)
    text = ''.join(c for c in text if c not in emoji.UNICODE_EMOJI)
    text = unicodedata.normalize("NFKC", text) 
    table = str.maketrans("", "", string.punctuation  + "「」、。・")
    text = text.translate(table)
    return text

def main():
    text_file = 'miona.txt'
    with open(text_file) as f:
        s = f.read()
    s_after_cleansing = cleansing(s)
    word_list=[]
    wakati(s_after_cleansing,word_list)
    s_after_wakati = " ".join(word_list)
    s_after_rmstop = stop_word(word_list)
#     ベクトル化用にテキストファイルで保存
    with open('miona_wakati_file.txt', 'w', encoding='utf-8') as f:
        f.write(s_after_wakati)


if __name__ == '__main__':
    main()

ベクトル化

def generate_vectors

モデルの作成

gensimのWord2Vecを使いました。

from gensim.models import word2vec

def generate_vectors():
    model = word2vec.Word2Vec(word2vec.LineSentence('miona_wakati_file.txt'),
                     size=70, window=5, min_count=1,iter=5)
    model.save('miona_w2v.model')

テスト

from gensim.models import word2vec

model = word2vec.Word2Vec.load('miona_w2v.model')

words = ['日奈子','写真','乃木坂']
for word in words:
    similar_words = model.most_similar(positive=[word])
    print(word,':',[w[0] for w in similar_words])

いろんな可視化

テキストデータを可視化します。フォントはマメロン使用します。

理想

AIテキストマイニング by ユーザーローカルで出てくる感じ

ワードクラウド

スコアが高い単語を複数選び出し、その値に応じた大きさで図示してる。

from wordcloud import WordCloud
import matplotlib.pyplot as plt 
from matplotlib.font_manager import FontProperties

def create_wordcloud(text):
    fpath = "mamelon/Mamelon.otf"
    wordcloud = WordCloud(background_color="white",font_path=fpath, width=900, height=500).generate(text)

    plt.figure(figsize=(15,12))
    plt.imshow(wordcloud)
    plt.axis("off")
    plt.show()
    wordcloud.to_file("miona.png")

ファンの人なら未央奈っぽいっていうのはわかるはず！

(追記 12/19)

研究室の先輩まるたくさんの助言により、形容詞、形容動詞も含めてみました！

単語出現頻度

文章中に出現する単語の頻出を棒グラフで表示する。

import matplotlib.pyplot as plt 
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.font_manager import FontProperties

def count(text):
    c = collections.Counter(text)
    mc = c.most_common()
    value=[]
    count=[]
    for i in range(10):
        value.append(mc[i][0])
        count.append(mc[i][1])

    fp = FontProperties(fname=r'mamelon/Mamelon.otf')
    plt.figure(figsize=(16, 8), dpi=50)
    plt.title("堀未央奈ブログ頻出単語TOP10", fontproperties=fp, fontsize=24)
    plt.xlabel('出現頻度が多い10単語', fontproperties=fp,fontsize=22)
    plt.ylabel('出現頻度数', fontproperties=fp, fontsize=22)

    x = np.arange(len(value))
    plt.xticks(x,value,fontproperties=fp,fontsize=18)
    plt.yticks(fontsize=18)
    y = np.array(count)
    plt.bar(x,y)
    plt.savefig('bar_word.png')
    plt.show()

以下も土曜以降に追加するのでしばしお待ちを?‍♂️

共起キーワード

2次元マップ

係り受け解析

階層的クラスタリング

感情分析

日本語評価極性辞書を利用したライブラリのosetiを使って感情分析します。ポジティブ/ネガティブ表現の個数を表示することが可能です。

import oseti
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.font_manager import FontProperties

def negapozi(text):
    analyzer = oseti.Analyzer()
    n = analyzer.count_polarity(text)
    posi = 0
    nega = 0
    for i in range(len(n)):
        posi += n[i]['positive']
        nega += n[i]['negative']

    x = np.array([posi,nega])
    fp = FontProperties(fname=r'mamelon/Mamelon.otf')
    label = ["positive","negative"]
    colors = ["lightcoral","lightblue"]
    plt.figure(figsize=(11, 8), dpi=50)
    plt.title("堀未央奈ブログネガポジ判定",fontproperties=fp,fontsize = 24)
    plt.rcParams['font.size'] = 20
    plt.pie(x,counterclock=False,startangle=90,colors=colors,autopct="%1.1f%%")
    plt.legend(label, fontsize=20,bbox_to_anchor=(0.9, 0.7))
    plt.savefig('negaposi.png')
    plt.show()

(追記 12/19)

研究室の先輩まるたくさんの助言により、形容詞、形容動詞、動詞も含めてみました！
名詞で分かち書きしたテキストのみで、ネガポジを判断するとかいうダメダメなことをしてましたorz

若干ポジティブが多い

感想

辞書微妙ぁあ眠い！

記事完成までのTODO

以下のまるたくさんのアドバイスを実行

• 形態素解析器をjanomeからMecabに変更する
• 辞書は新語対応したものを

随時更新していきます。今月末までを目安に完成させたいです。(アドベントカレンダーあと2記事書かなきゃいけないやばい)
記事完成したら、Qiitaの変更通知送ってツイートします！
途中ですいません?‍♂️
ちょっと無理矢理感あるコードかもなので、何かご指摘あればよろしくお願いします?‍♂️

参考文献

• pythonで絵文字を駆逐する
• Pythonで全角・半角記号をまとめて消し去る

次次回に乃木坂46 堀未央奈のブログで遊んでみた(2) 〜チャットボット開発編〜します！(軽く)(がっつりしない)(あくまでも予定)

この記事は、ハンズラボ Advent Calendar 2019 の20日目の記事です

---

自己紹介

今年の10月に中途で入社いたしました@jxxpsameです。
日々ユニケージという謎テクノロジーに触れております。

こうやってブログのような形式で何かをアウトプットするのは中学生の頃のyahoo!ブログ以来なのでガチガチに緊張してます。

---

概要

Face++のDetect APIを使って某球団の女装コンテストを採点してみました。

---

動機

• 所属するチームでpythonを学んでいこうという風潮があり勉強していたから
• 某球団のファンだから
• API使って何かやってみたかった
• 身内だけでもいいからウケたらいいなという下心

---

環境

• OS
  • MacOS Catalina
• 言語
  • Python 3.8
• 使用したAPI
  • Face++のDetect API

---

Face++って何

北京のMegviiが開発している顔認証プラットフォームの名称です。
Face++のDetect APIは顔を認証して様々な属性を取得できます。
今回はその属性の中からBeauty Scoreという属性を利用して採点します。

また、Face++の利用方法は以下の記事を参考にさせていただきました。
Pairsをpythonで分析してみた〜顔写真編〜
写真を送ると顔を検出して、顔面偏差値まで教えてくれるFace++APIのご紹介

---

採点対象

某球団の女装コンテスト参加者7名
（今村 石川 高橋 山下 戸郷 直江 横川）
画像は以下にアップされているものを利用しました。
Instagram

---

ソース

import requests
import json
import pprint

# API
# key:人物名 value:画像のURLを辞書型で宣言
url_dict = {'人物名:画像のURL'}

# 対象の人の数ループ
for img_data in url_dict.items():
    response = requests.post(
        'https://api-us.faceplusplus.com/facepp/v3/detect',
        {
            'api_key': "[Face++から取得したAPIKey]",
            'api_secret': "[Face++から取得したAPISeacret]",
            'image_url': img_data[1], # 画像のURL
            'return_attributes': 'beauty' # 取得したい属性
        }
    )

    # json整形
    json_dict = json.loads(response.text)
    print(img_data[0]) # 人物名出力
    pprint.pprint(json_dict['faces'][0]['attributes']['beauty'])

---

結果

各選手の名前にinstagramの投稿ページのリンクを貼りましたので合わせてご覧ください。
今村
{'female_score': 77.524, 'male_score': 78.338}
石川
{'female_score': 88.169, 'male_score': 84.546}
高橋
{'female_score': 79.26, 'male_score': 76.487}
山下
{'female_score': 76.926, 'male_score': 78.077}
戸郷
{'female_score': 82.532, 'male_score': 81.738}
直江
{'female_score': 78.401, 'male_score': 79.444}
横川
{'female_score': 71.818, 'male_score': 69.508}

今回は女装コンテストということでfemele_scoreの方を採用いたします。
優勝は石川選手でした！

---

ちなみに

実際の順位と比べてみると以下のようになりました。

	実際の順位	Face++で出した順位
石川	1位	1位
今村	2位	5位
高橋	3位	3位
直江	4位	4位
山下	5位	6位
戸郷	6位	2位
横川	7位	7位

参考
巨人７選手が美しき女装姿！１位石川慎吾ら大変身

戸郷と今村以外はほぼ実際の順位と同じ結果になりました。
Face++恐るべし。

---

おまけ

他人の顔だけをサンプルデータに使うのは気が引けたので自分（25歳・男性）の顔でもbeauty scoreを測定してみました。

'beauty': {'female_score': 67.239, 'male_score': 62.417},

クッソ低い...
femele_scoreの方が高かったのでもしかしてと思って取得する属性にgender(性別)とついでにage(年齢)を追加してもう一度測定しました。
{'age': {'value': 34},
'beauty': {'female_score': 67.253, 'male_score': 62.442},
'gender': {'value': 'Female'}}

ハンズラボの皆様。
34歳・女性となった私をこれからよろしくお願いいたします。

---

ハンズラボ Advent Calendar 2019 21日目は @jnuank さんです

まずあるSQL結果の値配列をリスト型への値入れ替えていく

サンプルクエリー

users_id_query = '''
SELECT CAST(user_id as char) as user_id FROM users_table;
'''

※前提として user_id がint であるという点が重要。リスト型にしたかったらこれを変換しないとエラーになってしまう。

Python で上記のクエリー実行すておく。

users_ids = execute_query('my_database', users_id_query)

結果は「111,222,333」みたいにしたいわけ：

users_result = [str(x['user_id']) for x in users_ids['rows']]
users_ids_string = ','.join(users_result)

users_ids_string にはほしいような、カンマ区切りの値が見事に入ってくれる。

用意したリストを別のクエリーの IN で使う

サンプルSQL

users_login_query = '''
SELECT count(0) FROM login_log_table where user_id in (user_ids_string)
'''

「user_ids_string」は次で実際の値と置き換えるパラメータ。

entry_users_ids = execute_query('my_database', users_login_query.replace('user_ids_string', entry_users_ids_string))    

実行先を指定しながら値も同時にリプレイス。

はじめに

フューチャー Advent Calendar 2019（2）の19日目です。
18日目は、noko_qiiさんの「SageMakerとpapermillでサクッと始めるJupyterNotebookベースな機械学習案件向け開発環境構築・利用ガイドライン」でした。
Advent Calendarって、社内の人が様々なトピックで記事を投稿していて面白いですね。

無事に新人研修が終わり、需要予測のチームに配属されました。
今日は、最近学んだことの中から、回帰分析の１つである単回帰分析についてまとめました。

回帰分析って何？

回帰分析とは、結果となる数値と要因となる数値の関係を数式(回帰式)で表す統計的手法です。
具体例を交えながら説明します。
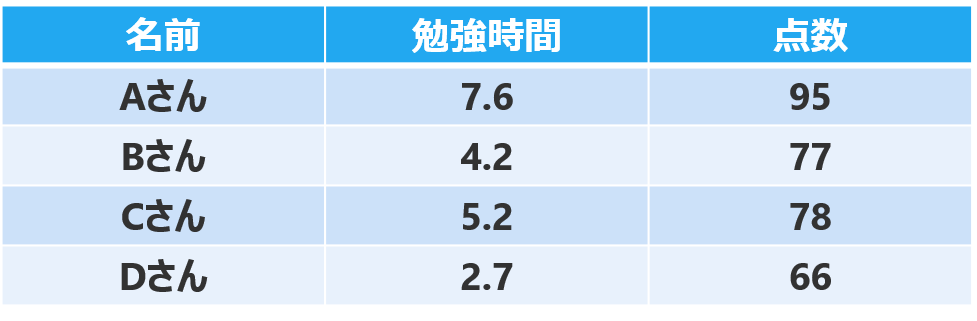
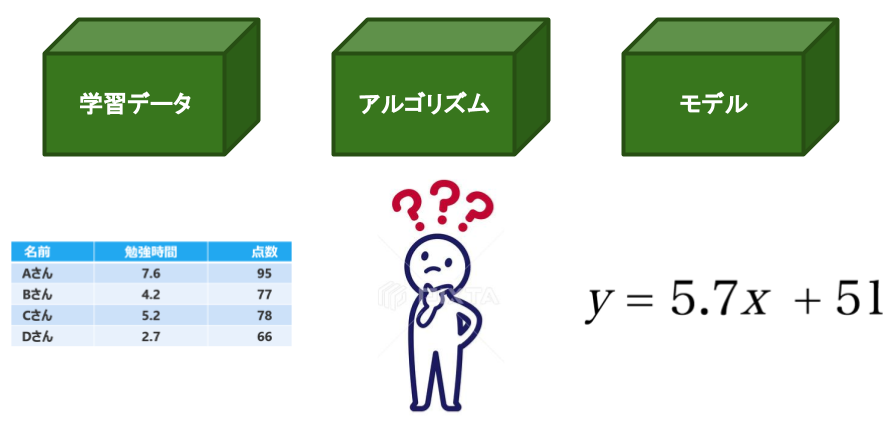
例えば、あるクラスのAさん〜Dさんの「勉強時間」と「テストの点数」のデータがあります。
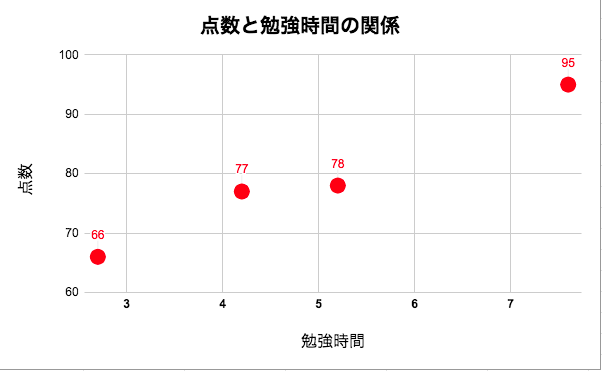
回帰分析は、「勉強時間」と「テストの点数」の関係を数式で表現します。

このデータを視覚化すると、下のようなグラフになります。
横軸が勉強時間、縦軸がテストの点数を表しています。
勉強時間が長くなるほど、テストの点数が上がっている傾向がわかります。

4人のデータを用いて、「勉強時間」と「テストの点数」の関係を数式で表します。
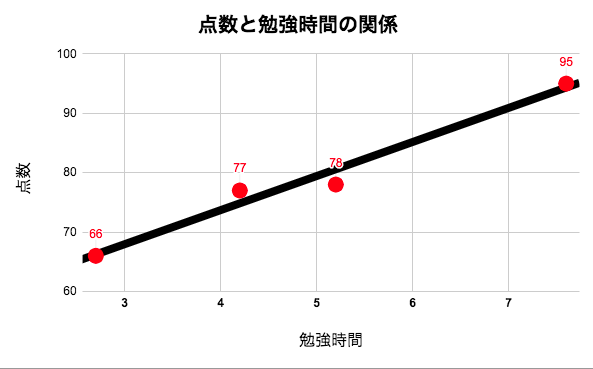
「勉強時間」と「テストの点数」の関係が線形であると仮定して、データに当てはまる直線を下記のように引きます。

黒の直線は下の式(回帰式)で表せます。

y = 5.7x + 51 

この式（回帰式）の意味は、

(点数)= 5.7 × (学習時間) + 51

となります。
学習時間が0のとき、51点となり、１時間勉強するごとに5.7点ずつ点数が上がっていることを意味しています。
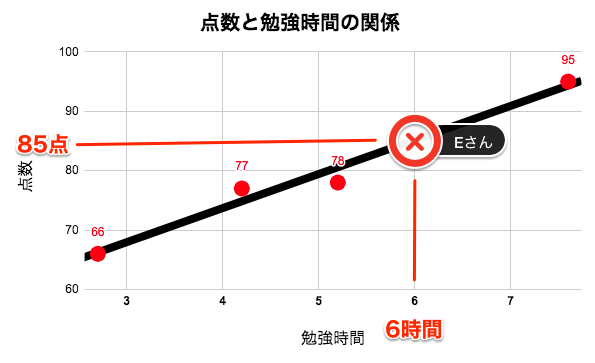
この式（回帰式）を利用することで、勉強時間から、他の生徒がどの程度の点数を獲得できるかが予測できるようになります。
例えば、勉強時間が6時間のEさんの点数は、

\begin{align}
(Eさんの点数) &= 5.7× (学習時間) + 51 \\
&= 5.7 × 6 + 51 \\
&= 85(点)
\end{align}

と求めることができます。

このように、回帰分析は、結果となる数値と要因となる数値の関係を回帰式で表します。
また、要因となる数値を説明変数、結果となる数値を目的変数といいます。
今回の例でいうと、「勉強時間」から「点数」を予測したので、「勉強時間」が説明変数で、「点数」が目的変数となります。

回帰分析のうち、1つの目的変数を1つの説明変数で予測するものを単回帰分析と言います。
そして、1つの目的変数を２つ以上の説明変数で予測するものを重回帰分析と言います。

単回帰分析

y = a + b_1x_1 \\

重回帰分析

y = a + b_1x_1 + b_2x_2 + ・・・ + b_nx_n \\
y:目的変数 \\
a:切片 \\
b:回帰係数 \\
x:説明変数 

重回帰分析では、天気や気温、宣伝費用や暦などの説明変数と、商品の売上数という目的変数の関係を回帰式として表現します。
では、どのようにしてインプットしたデータから、回帰式を算出しているのか。

まずは単回帰分析について、Pythonで実装していきたいと思います。
また、仕組みの理解を目的とするため、scikit-learnやStatsModelsのような機械学習のライブラリを利用しないで実装します。

単回帰分析

単回帰分析は、1つの目的変数を1つの説明変数で予測する分析手法でした。
また、目的変数と説明変数は線形の関係があるという仮定があります。
つまり、目的変数と説明変数は、下記の回帰式で表現できるという仮定があります。

\begin{align}
y &= w_1x + w_0 \\
(目的変数) &= w_1×(説明変数) + w_0
\end{align}

先ほどの例では、

(点数)= 5.7 × (学習時間) + 51

でした。

どのようなアルゴリズムで、5.7という傾きや、51という切片を算出したのか。
勉強時間と点数のデータ(49人分)の学習データを使いながら実装していきます。

まずは、必要なライブラリのimportと、学習データを読み込みます。

今回使用する学習データはこちらをクリック

TestScores_StudyHours_Liner.csv

https://drive.google.com/open?id=1z80g4kKGMMBbnCaAz_iUAYTLkEvz4cZI

Hours	Scores
5.2	78
4.2	77
7.6	95
2.7	66
9.1	91
1.3	59
3.6	72
9.4	100
6.8	88
8.5	89
8.4	98
2.6	71
2.8	66
4	73
6.9	88
5.2	83
7.9	96
4.6	76
5.4	85
5.4	79
5.2	83
4.4	80
2.2	68
2.1	64
3.4	69
1.2	57
0.2	58
2	63
4.7	77
4.5	78
5.5	84
8.3	97
4.3	75
0.9	62
5.8	82
8.2	100
6.1	87
3.3	73
6.3	88
6.6	89
4.5	78
3.8	74
3.8	73
4.7	80
1.5	60
5	81
9.1	91
4.3	74
1.3	58

ちなみに、この記事で書いてあるコードはGoogle colaboratoryで実装しています。
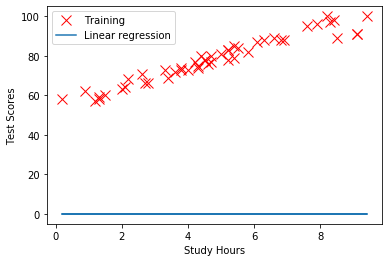
Google colaboratoryは、googleアカウントがあれば、誰でもクラウド上でPythonを実行できるサービスです。説明は要らないから、コードを見たいって人は、下記画像からcolaboratoryに飛べるので、見てください。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

data= np.loadtxt("./TestScores_StudyHours_Liner.csv",delimiter=",",skiprows=1)

どのようなデータが入っているのか、プロットして確認します。

plt.plot(data[:,0],data[:,1],'rx',markersize=10,label='Training')
plt.xlabel('Study Hours')
plt.ylabel('Test Score')
plt.grid(True)
plt.show()

横軸が勉強時間、縦軸がテストの点数を表していて、49人分のデータがプロットされています。
これらのデータを入力して、直線の傾き(w₁)や切片(w₀)を算出していきます。

y = w_1x + w_0

直線の傾き(w₁)や切片(w₀)を算出するのに、コスト関数(平均二乗誤差)と最急降下法を用います。

コスト関数(平均二乗誤差)

コスト関数(平均二乗誤差)は、ある回帰式が学習データとどれだけフィットしているかを定量的に評価します。
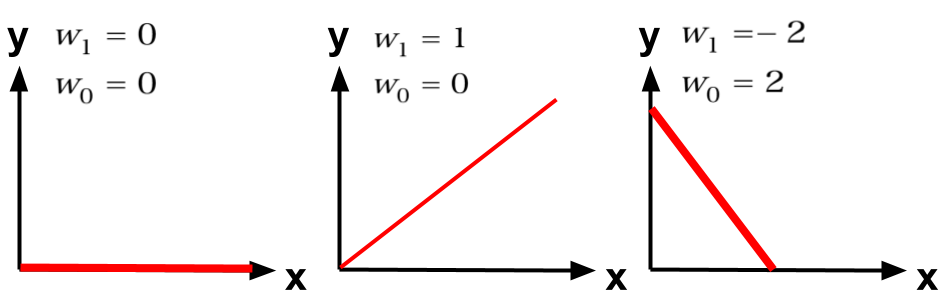
もう少し具体的にいうと、コスト関数はモデルが算出した予測値と学習データの実際値の差(残差)を計算します。

例えば、(w₀,w₁) = (0,0)　のときの、回帰式は下記のようになります。

\begin{align}
y &= w_1x + w_0 \\
y &= 0 
\end{align}

このときの、回帰式と学習データの関係を視覚化すると、下のグラフになります。

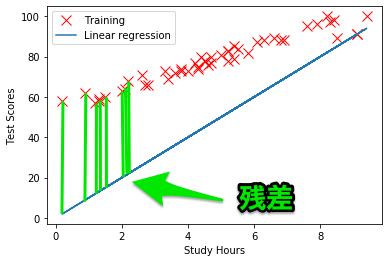
w0,w1 = 0,0
plt.plot(data[:,0],data[:,1],'rx',markersize=10,label='Training')
plt.xlabel('Study Hours')
plt.ylabel('Test Scores')

plt.plot(data[:,0],data[:,0]*w1 + w0,'-',label='Linear regression')
plt.legend()
plt.show()

青い線が、(w₀,w₁) = (0,0)　のときの回帰式、赤×が学習データです。

【補足】係数と直線の関係

補足ですが、(w₀,w₁)=(0,0)(0,1)(2,-2)のときの直線は下のようになります。

y = w_1x + w_0 \\

コスト関数は、残差{(予測した値)-(実際の値)}を、それぞれのデータで計算し、全ての残差の和を計算します。

(w₀,w₁) = (0,10)のときは、こちらが残差になります。

コスト関数は、平均二乗誤差を計算します。
学習データそれぞれの残差の二乗を計算し、その総和を、2×テータ数で割った値がコストとなります。
式で表現すると、

\begin{align}
J(w_0,w_1) &= \frac{1}{2m}\sum_{i=1}^{m}(\hat{y}-y)^2 \\
 &= \frac{1}{2m}\sum_{i=1}^{m}(w_1x + w_0-y)^2
\end{align}

\begin{align}
m &: データ数 (m=49) \\
\hat{y} &: 予測値 (\hat{y}=w_1x + w_0) \\
y &: 実測値
\end{align}

では、(w₀,w₁) = (0,0)　のときのコストを計算して見ます。
まずは、コスト関数を定義します。

# コスト関数
def cost_function(w0,w1,data):
    cost = 0
    m = len(data)
    for i in range(m):
        x = data[i,0]
        y = data[i,1]
        cost += ((w1 * x +w0) -y)**2
    cost = cost / (2*m)
    return cost

(w₀,w₁) = (0,0)　のときのコストは、

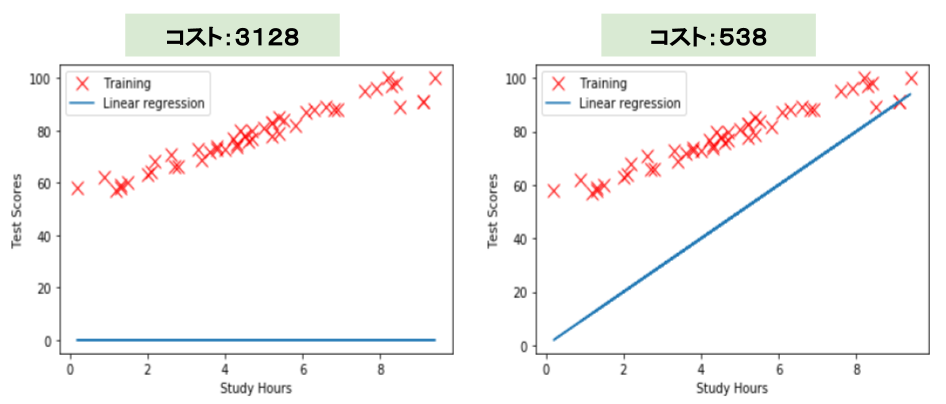
w0,w1 = 0,0
cost_0_0 =cost_function(w0,w1,data)
print(cost_0_0)
#3128.3979591836733

3128と求めることができました。

w₀,w₁ = 0,10のときのコストも求めます。

w0,w1 = 0,10
cost_0_10 =cost_function(w0,w1,data)
print(cost_0_10)
#538.9285714285714

コストは、538と求められました。

左の画像と右の画像の直線を見比べると、右のw₀,w₁ = 0,10のときの回帰式のほうが学習データに近いことが、視覚的にわかります。
また、コスト関数を比べても、左のコストが3128に対して、右のコストが538と、コストが大幅に減少していることがわかります。
このように、回帰式が学習データとフィットしているかは、コスト関数を用いることで、定量的に評価できます。
単回帰分析においてのモデルの学習とは、コストが最小となる回帰係数を算出することです。

そして、コストが最小となる回帰係数を算出するのに、ポイントとなるのが、最急降下法です。

最急降下法

最急降下法は、関数を最小にするようなパラメーターを求めるためのアルゴリズムです。
今回はコスト関数から得られるコストを最小にするような回帰係数（w₀,w₁)を求めたいです。

コスト関数は下記の式でした。

\begin{align}
J(w_0,w_1) &= \frac{1}{2m}\sum_{i=1}^{m}(\hat{y}-y)^2 \\
 &= \frac{1}{2m}\sum_{i=1}^{m}(w_1x + w_0-y)^2
\end{align}

\begin{align}
m &: データ数  \\
\hat{y} &: 予測値 (\hat{y}=w_1x + w_0) \\
y &: 実測値
\end{align}

コスト関数をw₀で偏微分すると、

\begin{align}
\frac{\partial }{\partial w_0}J(w_0,w_1) &= \frac{\partial }{\partial w_0}\frac{1}{2m}\sum_{i=1}^{m}(w_1x + w_0-y)^2 \\
&= \frac{1}{m}(w_1x + w_0-y)
\end{align}

コスト関数をw₁で偏微分すると、

\begin{align}
\frac{\partial }{\partial w_1}J(w_0,w_1) &= \frac{\partial }{\partial w_1}\frac{1}{2m}\sum_{i=1}^{m}(w_1x + w_0-y)^2 \\
&= \frac{1}{m}(w_1x + w_0-y)x
\end{align}

と求めることができます。
偏微分をすると、コスト関数の傾きがわかります。
コストが小さくなるように、w₀,w₁を更新したいので、元々の回帰係数から偏微分で得られた値を引きます。

\begin{align}
w_0 &:= w_0 - \alpha\frac{1}{m}(w_1x + w_0-y) \\
w_1 &:= w_1 - \alpha\frac{1}{m}(w_1x + w_0-y)x
\end{align}

\begin{align}
\alpha &:学習率 \\
m &:データ数 \\
x &:説明変数 \\
y &:目的変数 \\
\end{align}

αは学習率と呼ばれ、回帰係数を更新する値の大きさを調整します。
学習率は、大きすぎると回帰係数が収束しない可能性があり、また、小さすぎると、回帰係数の収束に時間がかかってしまいます。
今回は学習率=0.01でと決めて、進めていきます。

では、最急降下法を実装していきます。

# 最急降下法(Gradient Descent)
def gradientDescent(w0_in,w1_in,data,alpha):
    w0_gradient,w1_gradient = 0,0  #初期値
    m = float(len(data))           #データ数
    for i in range(len(data)):
        x,y = data[i,0], data[i,1]
        w0_gradient += (1/m) * (((w1_in * x) + w0_in) -y)
        w1_gradient += (1/m) * ((((w1_in * x) + w0_in) -y) * x)
    w0_out = w0_in - (alpha * w0_gradient) #回帰係数の更新
    w1_out = w1_in - (alpha * w1_gradient) #回帰係数の更新
    return [w0_out, w1_out]

w0_gradient、w1_gradientは、初期値0を設定しています。
また、α、w₀、w₁、学習回数の初期値を設定します。

alpha = 0.01
init_w0,init_w1 = 0,0
iterations = 1000 #学習回数

それではコスト関数と最急降下法を用いて、単回帰分析のモデルの学習を定義していきます。
今回は、1000回の回帰係数の更新する中で、コストがどのように推移するかを可視化するために、J_historyを追加します。

def run(data,init_w0,init_w1,alpha,iterations):
    w0,w1 = init_w0,init_w1
    J_history = [] #コストの履歴を格納用
    for i in range(iterations):
        w0,w1 = gradientDescent(w0,w1,np.array(data),alpha)
        J_history.append(cost_function(w0,w1,data)) #コストの履歴をJ_historyに追加
    return [w0,w1, J_history]

それでは、モデルの学習（コストが最小となる回帰係数の算出）をします。

[w0,w1, J_history] = run(data,init_w0,init_w1,alpha,iterations)
print("w0 = {} /w1 = {}".format(w0,w1))
#w0 = 47.325313552065204 /w1 = 6.135761014127023

回帰係数を求めることができました。

\begin{align}
y &= w_1x + w_0 \\
  &= 6.13x + 47.3 \\
\end{align}

この式とつまり、

(テストの点数)= 6.13×(勉強時間) + 47.3 

ということを意味しています。
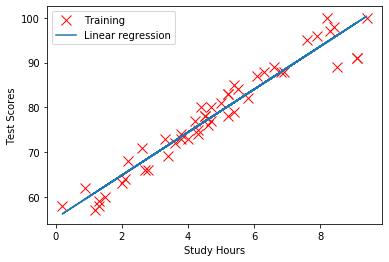
また、回帰式と学習データを視覚化すると、

plt.plot(data[:,0],data[:,1],'rx',markersize=10,label='Training')
plt.xlabel('Study Hours')
plt.ylabel('Test Scores')

plt.plot(data[:,0],data[:,0]*w1 + w0,'-',label='Linear regression')
plt.legend()
plt.show()

このように、学習データにフィットした直線を描くことができました。

また、コストの推移も確認してみましょう。

# コストと学習回数のグラフ
plt.plot(range(len(J_history)),J_history,"-b",linewidth=1)
plt.xlabel("Number of Iterations")
plt.ylabel("Cost J")
plt.grid(True)
plt.show()

縦軸がコストで、横軸が学習回数を表しています。
学習を繰り返すごとに、コストが下がっているのがわかります。

学習回数を1000回と決めてしまいましたが、学習回数が1回、10回、100回、1000回のときに算出される回帰式を比較してみました。

iterations_ = [1,10,100,1000]

plt.plot(data[:,0],data[:,1],'rx',markersize=10,label='Training')
plt.xlabel('Study Hours')
plt.ylabel('Test Scores')

for iteration in iterations_:
    [w0,w1, J_history]  = run(data,init_w0,init_w1,alpha,iteration)
    plt.plot(data[:,0],data[:,0]*w1 + w0,'-',label='Linear regression_{}'.format(iteration))

plt.legend()
plt.show()

学習を繰り返すごとに、回帰式が学習データを捉えられるようになっていることがわかります。

まとめ

単回帰分析は、目的変数と説明変数が線形の回帰式で表現できるという仮説がある。

y = w_1x + w_0 

ある回帰係数（w₀、w₁）のときの回帰式が、学習データにどれだけフィットしているかはコスト関数を用いて評価する。
最急降下法を用いて、コストが小さくなるような回帰係数を算出する。

あとがき

今日は単回帰分析についてのまとめを書きました。
本当は重回帰分析について書きたかったのですが、単回帰分析だけで結構長くなってしまったので、別記事にします。
最後まで読んでいただきありがとうございました。

引用元

https://github.com/nficano/pytube/issues/497

こちらの内容を元に作成しております。

変更内容

＿main＿.py のソースコード修正
length(self)
の戻り値修正

変更前
return self.player_config_args['length_seconds']

変更後
return self.player_config_args['player_response']['videoDetails']['lengthSeconds']

変更前

__main__.py

    @property
    def length(self):
        """Get the video length in seconds.
        :rtype: str
        """
        return self.player_config_args['length_seconds']

変更後

__main__.py

  @property
    def length(self):
        """Get the video length in seconds.
        :rtype: str
        """
        return self.player_config_args["player_response"]["videoDetails"]['lengthSeconds']

この記事は、Fusic Advent Calendar 2019 18日目の記事です。

昨日は @tutida による「Lambda Destinations を SAM で試してみた」でした。Lambdaの新機能、良さそうですね！

本記事は、lightGBMでのハイパラ探索のやってみた記事です。とりあえず動かし方を知る、初心者向けの内容となります。

本記事の対象者

• lightGBM（回帰）でBayesian Optimizationをやってみたい人・やり方忘れた人

ベイズ最適化によるハイパーパラメータ探索について

本記事では説明を割愛させていただきます。（私自体がまだ勉強できてません?）
こちらの動画やこちらの記事がわかりやすそうです。

環境

• Google Colab（CPU）: Python3

データセット

• House Sales in King County, USAを使います。
• 「このデータセットには、シアトルを含むキング郡の住宅販売価格が含まれています。2014年5月から2015年5月の間に販売された住宅が含まれます。」とのことです。
• レコード数は21,613件です。
• 説明変数は18個ありますが、今回は以下の10個のみを使用します。

'sqft_living','grade', 'sqft_above', 'sqft_living15',
'bathrooms','view','sqft_basement','lat','waterfront'

• 目的変数はpriceです。

内容

探索前・後で比較してみます。

探索前

データセットのアップロードとデータの前処理を行った後、学習させます。

参考までにデータの前処理までのコードはこちら

import gc
import lightgbm as lgb
import math
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import urllib.request

from google.colab import files
from sklearn.metrics import mean_absolute_error
from sklearn.model_selection import train_test_split, KFold


seed = 12345
num_round = 1000
n_folds = 3

# 手元からデータをColabにアップロードする
uploaded = files.upload()

org_df = pd.read_csv('kc_house_data.csv')
df = org_df[['price', 'sqft_living','grade', 'sqft_above', 'sqft_living15','bathrooms','view','sqft_basement','lat','waterfront']]

train_df, test_df = train_test_split(df, test_size=0.2, shuffle=True, random_state=seed)

train_df = train_df.reset_index(drop=True)
test_df = test_df.reset_index(drop=True)
y_train = train_df.pop('price')
y_test = test_df.pop('price')

以下、学習部分のコードです。

categorical_features = ["grade", "view", "waterfront"]
params = {
    "application": "regression_l1",
    'learning_rate': 0.1,
    "metric": "mae",
}

shuffle = False

kf = KFold(n_splits=n_folds, shuffle=shuffle, random_state=seed)

models = []
for train_index, test_index in kf.split(train_df):
    train_features = train_df.loc[train_index]
    train_target = y_train.loc[train_index]

    test_features = train_df.loc[test_index]
    test_target = y_train.loc[test_index]

    d_training = lgb.Dataset(train_features, label=train_target, categorical_feature=categorical_features, free_raw_data=False)
    d_test = lgb.Dataset(test_features, label=test_target,categorical_feature=categorical_features, free_raw_data=False)

    model = lgb.train(params,
                      train_set=d_training,
                      num_boost_round=num_round,
                      valid_sets=[d_training,d_test],
                      verbose_eval=50,
                      early_stopping_rounds=50)

    models.append(model)
    del train_features, train_target, test_features, test_target, d_training, d_test
    gc.collect()

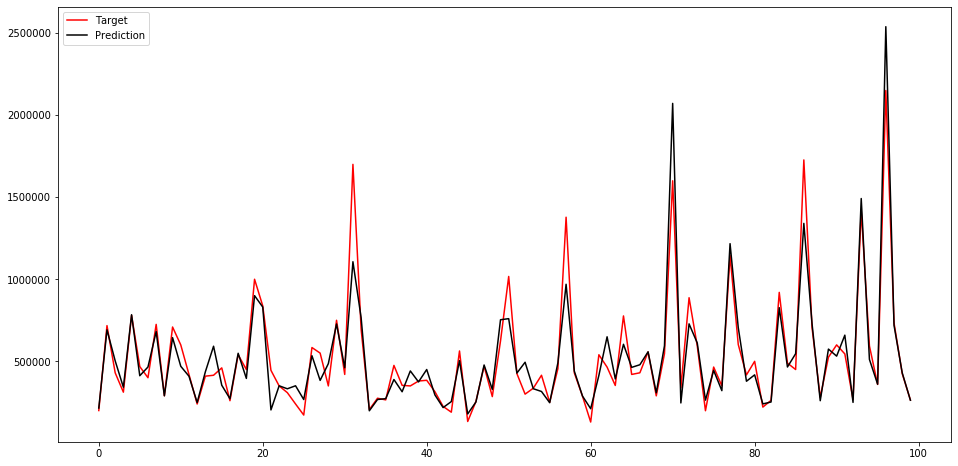
学習前に分割して残しておいたテストデータに対して評価を実行すると、mean_absolute_errorが 82482.93 となりました。
先頭から100個目までのテストデータのラベル値・予測値をプロットすると以下のようなになりました。

参考までに評価のコードはこちら

def pred(X_test, models, batch_size=1000):
    iterations = (X_test.shape[0] + batch_size -1) // batch_size
    print('iterations', iterations)

    y_test_pred_total = np.zeros(X_test.shape[0])
    for i, model in enumerate(models):
        print(f'predicting {i}-th model')
        for k in range(iterations):
            y_pred_test = model.predict(X_test[k*batch_size:(k+1)*batch_size], num_iteration=model.best_iteration)
            y_test_pred_total[k*batch_size:(k+1)*batch_size] += y_pred_test

    y_test_pred_total /= len(models)
    return y_test_pred_total

preds = pred(test_df, models)

mean_absolute_error(y_test, preds)

xs = list(range(100))
fig = plt.figure(figsize=(16, 8))
plt.plot(xs, y_test.values[:100], color = 'r')
plt.plot(xs, preds[:100], color = 'k');
plt.legend(['Target', 'Prediction'], loc = 'upper left');
plt.show()

ハイパラ探索

BayesianOptimizationを使用しました。
以下のコードです。

! pip install bayesian-optimization

from bayes_opt import BayesianOptimization

def lgb_eval(num_leaves, feature_fraction, bagging_fraction, max_depth, lambda_l1, lambda_l2):
    train_data = lgb.Dataset(train_df, label=y_train, categorical_feature=categorical_features, free_raw_data=False)
    params = {
        'application': 'regression_l1',
        'num_iterations': num_round,
        'learning_rate': 0.1,
        'early_stopping_round': 50,
        'metric':'mae'
    }

    params["num_leaves"] = math.ceil(num_leaves)
    params['feature_fraction'] = max(min(feature_fraction, 1), 0)
    params['bagging_fraction'] = max(min(bagging_fraction, 1), 0)
    params['max_depth'] = math.ceil(max_depth)
    params['lambda_l1'] = max(lambda_l1, 0)
    params['lambda_l2'] = max(lambda_l2, 0)

    cv_result = lgb.cv(params, train_data, num_boost_round=num_round, nfold=n_folds, seed=seed, verbose_eval=50)

    return max(cv_result['l1-mean'])

lgbBO = BayesianOptimization(lgb_eval, {'num_leaves': (31, 100),
                                        'feature_fraction': (0.6, 1),
                                        'bagging_fraction': (0.8, 1),
                                        'max_depth': (5, 15),
                                        'lambda_l1': (0, 1),
                                        'lambda_l2': (0, 1)}, random_state=seed)

init_round=10
opt_round=15

lgbBO.maximize(init_points=init_round, n_iter=opt_round)

ちなみに上記のmaximizeを計測した結果は以下でした。

CPU times: user 6.6 s, sys: 366 ms, total: 6.97 s
Wall time: 3.7 s

この処理により、以下のパラメータが得られました。

lgbBO.max['params']

{'bagging_fraction': 0.9192732020838761,
 'feature_fraction': 0.6207830180410134,
 'lambda_l1': 0.8950895280539212,
 'lambda_l2': 0.7282661803271173,
 'max_depth': 13.183500113899145,
 'num_leaves': 65.51536994557694}

探索後

上記のパラメータを使って再度学習させてみます。

categorical_features = ["grade", "view", "waterfront"]
params = {
    "application": "regression_l1",
    "learning_rate": 0.1,
    "metric": "mae",
}

params.update(lgbBO.max['params'])
params['num_leaves'] = math.ceil(params['num_leaves'])
params['max_depth'] = math.ceil(params['max_depth'])

shuffle = False

kf = KFold(n_splits=n_folds, shuffle=shuffle, random_state=seed)

turned_models = []
for train_index, test_index in kf.split(train_df):
    train_features = train_df.loc[train_index]
    train_target = y_train.loc[train_index]

    test_features = train_df.loc[test_index]
    test_target = y_train.loc[test_index]

    d_training = lgb.Dataset(train_features, label=train_target, categorical_feature=categorical_features, free_raw_data=False)
    d_test = lgb.Dataset(test_features, label=test_target,categorical_feature=categorical_features, free_raw_data=False)

    model = lgb.train(params,
                      train_set=d_training,
                      num_boost_round=num_round,
                      valid_sets=[d_training,d_test],
                      verbose_eval=25,
                      early_stopping_rounds=50)

    turned_models.append(model)
    del train_features, train_target, test_features, test_target, d_training, d_test
    gc.collect()

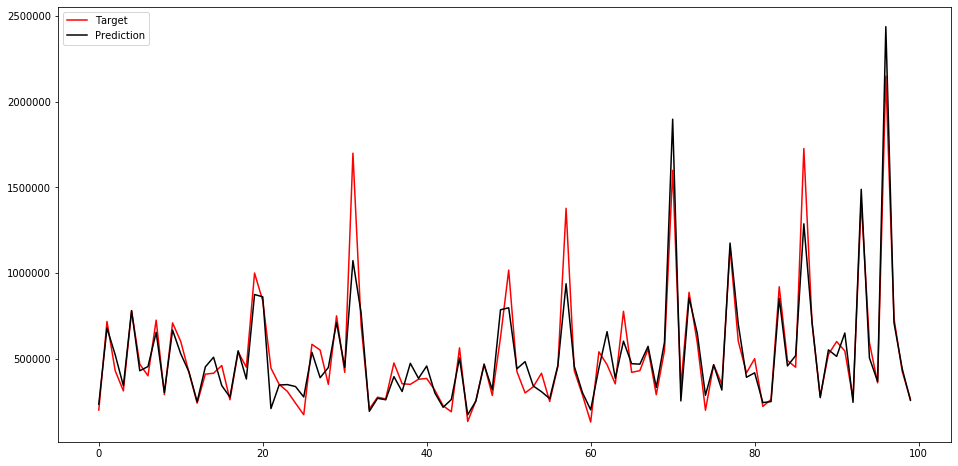
学習したモデルで評価すると、mean_absolute_errorが83192.65となりました。
探索前より悪くなってしまっていますね…。
ちなみにグラフは以下のようになりました。

まとめ・感想

• ベイズ最適化によるハイパーパラメータ探索をやってみました。
• 実装自体は様々な記事を上げてくださっているので、簡単にできました。
• 一方で、結果としては探索後のほうが探索前より悪くなってしまいました。いくつか理由を考えみました。
  • maximize()のイテレーションが少なく局所解に陥っている or 探索が足りていない？
  • 探索範囲の指定が効果的なものに出来ていない？
• いずれにしろ、「BayesianOptimization使っておけば素人でも誰でもチューニングできる」というわけでは無さそうだと感じました。
• 現在、Kaggleで表データコンペに参加しているので、そちらでも同じようなことをやろうと思っています。もし効果が出たら別記事で報告させていただきます。

参考にした記事

• scikit-optimize の BayesSearchCV を用いたベイズ最適化によるハイパーパラメータ探索
• Predicting King County House Prices
• google Colaboratoryでファイルを読み込む方法
• Hyperparameters Optimization for LightGBM, CatBoost and XGBoost Regressors using Bayesian Optimization.

以上です！

機械学習では多様なデータを組み合わせて使うことがおおく、様々な前処理が必要になってきます。学習・推論プロセスの再現性を高めるためには、手動でのコマンド実行や単純なシェルスクリプトのみで管理するのは相当に厳しくなってきます、、、というのは、この記事をお読みの皆さまの多くが実感されていることと思います。

そこで世の中にはタスクランナーと呼ばれるツールが開発されており、元祖である GNU make から Luigi, Airflow など様々なツールがあります。A curated list of awesome pipeline toolkits には、そのようなツールのリストが作られていて、2019年12月現在、168 もの(!!)ツールが並んでいます。

そんなよくいえば百花繚乱、悪く言えば決定打に欠けるタスクランナーですが、この記事では、私が最近気に入って使っている Snakemake の魅力を伝えたいと思います。

Snakemake の魅力?

一言にまとめるなら、 Python のパワフルさと make のシンプルさを兼ね備えている 点が大きな特徴です。

（一番右が Snakemake のアイコンです）

make のシンプルさ

Snakemake は比較的シンプルな記述が可能 です。タスク記述は YAML風(?) で、わりと Makefile に近い、シンプルな書き味に仕上がっています。例えば、こんな感じです。

ruleA:
    input: "httpd_access.log"
    output: "analyzed_log.txt"
    shell: "analysis_command {input} > {output}"

けっこう Makefile に似ています、よね！？

同じく Python ベースのタスクランナーである Luigi, AirFlow といったタスクランナーでは、各タスクをクラスとして定義します。入力などをメソッドとして記述するため、少々記述が煩雑になります。

Snakemake のセットアップは Python 環境があれば conda install snakemake, pip install snakemake といったコマンド1つで終わりで、こちらもシンプルです。AirFlow のようにサーバを立てたりといった面倒はありません。make のように「最初からシステムに入っている」にはさすがに及びませんが。

Python のパワフルさ

Snakemake は Python ベースのツールで、タスク記述も Python スクリプトに変換して実行しています。つまり、

　　いざとなったら Python コードでやりたい放題

です。このあたりは最近よくある Python ベースのタスクランナーに共通する利点です。

さきほどの記述にあった shell: のところを script: とすると、Python コードを書くこともできます。またルール記述以外の部分は通常の Python コードとして実行されるので、適当な関数を定義して、ルールのなかでそれらの関数を使うこともできます。当然、Python と同じく # でコメントを書くこともできます。

Python ベースで動作するおかげで make のように謎の記号がでてくることがありません。また、特殊変数にも名前がついていることは、個人的にとてもありがたいです。記号は覚えにくいのと、ネットで検索するのがけっこう難しいんですよね。

特徴的な機能

色々と特徴的な機能がありますが、ここでは下記 2 点を取り上げます。

• ワイルドカード
• リモートファイルのサポート

ワイルドカード

冒頭に挙げた例は httpd_access.log を入力して analyzed_log.txt を出力するという単純極まる例でしたが、多くのタスクランナーと同じく Snakemake にも一つのタスク記述で複数ファイルの変換を指定できる書き方があります。それが「ワイルドカード」です。

ruleA:
    input: "img_{img_num}.jpg"
    output: "annot_{img_num}.txt"
    shell: "analysis_command {input} > {output}"

この記述の {img_num} の部分がワイルドカードです。中の文字列は任意のものを指定可能です。このように書いておくと、annot_001.txt, annot_002.txt,... の生成には、それぞれ img_001.jpg, img_002.jpg,... が必要、ということが指定できます。

また、ワイルドカードは複数書いても構いません。例えば {date}/img_{img_num}.jpg といったような書き方も OK です。

make のパターンルールに相当する機能ですが、謎の記号みがなくていい感じかなと思うところです。

リモートファイルのサポート

機械学習でもクラウドのストレージを使うことも多くなってきてると思います。Snakemake はそのようなリモートファイルのサポートもあります。

書き方は非常に単純で input: S3.remote('input.txt') などと書くと、処理の開始前にダウンロードしてくれます。また、output: S3.remote('output.txt') とすると、処理成功時にアップロードしてくれます。前述のワイルドカードも（たいていは）サポートされているので、ローカルにファイルがある場合とあまり変わらずにタスクを書くことができます。

どんな用途に向いている？

小規模チームや初期実験・探索フェーズでの利用 にフィットするかと思います。

セットアップは非常に容易ですし、学習コストも高くありません。記述がシンプルなので、色々と試行錯誤もやりやすいと思います。開発者の方はバイオインフォマティクスの研究者の方なこともあってか、研究寄りの状況で使いやすいツールになっているように感じます。

また make を使っているけど、変数が覚えられない という方や、 もう少し柔軟にタスクを書きたい という方にはピッタリだと思います。これは私自身がそのパターンですね Python と親和性の高い、今ドキの使い方に合わせやすい make という感覚で使えると思います。

一方、タスク実行状況の可視化などは強くないので、大規模な ML チームの開発基盤としては若干、力不足かもしれません。可視化ツールも出てきているようですが、Airflow や Luigi と比較できるほど成熟してないかな、という印象です。

実際のつかいこなし

私自身は Snakemake と make の両方を使っています。

make で済むところは make で済ませ、 $@ とか変数を使いたくなるようなときには Snakemake を使うことが多いです。だいたいの場合、

• make は 「1 ファイルで複数のスクリプトがおいておける置き場」として利用
• Snakemake で主要な分析処理を実行

という役割分担ですね。

# Makefile - さまざまなコマンドの寄せ集め場所として。
analyze:
    snakemake analyze  # 分析の中身は Snakemake で管理

clean:
    rm -rf work/*

deploy-model:
    # デプロイ用コマンドを適当に

Snakemake の改善希望な点

Snakemake のタスク記述はけっこうシンプルですが、make と比べるとちょっと煩雑です。基本的に Snakemake ではファイル間の依存関係を記述する前提になっているため、タスク同士をつなぐ依存関係を書きたいときは output: touch(some-file) 等と、タスク完了を示す空ファイルを touch する形になります。make とくらべるとちょっと冗長ですね。

あと同じ記述の繰り返しが増えがちです。このあたりは、タスクがちゃんとした Python クラスになってる Luigi や AirFlow だと、似て非なるタスクをループでバンバン生成したりと、よりやりたい放題できるので、YAML 風記述を採用したことのデメリットですね¹。ワイルドカードで色々と対応できるっちゃできるのですが、ファイル名に制約があったり、ワイルドカードでどう書くといいか知恵を絞るという少々不毛な作業になることもあったりなかったり。

・・・このあたりを改善できるようなコードをこの年末年始に書きたい、なぁ。

まとめ

以上、Snakemake の紹介でした。凝ったツールに手を出すのは気が重いけど、make を使い続けるのもしんどいなぁ、と思ってるような方はぜひ一度、 Snakemake を試してもらえればと思います。使ってみての疑問点など、コメントに書いてもらえば分かる範囲でお答えできればと思います。

なお、Snakefile の書き方やコマンドラインオプションなどをまとめた Snakemake チートシートという記事も書いているので、興味のある方は参照してもらえればうれしいです。

---

1. Snakemake は、タスク定義を Python オブジェクトに内部で置き換えてから、実行します。逆に言えばタスク定義の時点では Python オブジェクトではないため、自由に生成したりはできない、ということですね。 ↩

はじめに

AWS-Bacthをmotoを使用してmockし、ジョブを登録するところまでできたので備忘録として残しておく。

mock対象リソース

• IAM Role
• AWS-Bacth コンピューティング環境
• AWS-Bacth ジョブキュー
• AWS-Bacth ジョブ定義

コード

test_aws_batch.py

#!/usr/bin/env python
# -*- coding: utf-8 -*-
import unittest
import boto3
from moto import mock_batch, mock_iam


class MyTestCase(unittest.TestCase):
    @mock_iam
    @mock_batch
    def test_aws_batch(self):
        client = boto3.client('batch')
        iam = boto3.client('iam')

        # iam roleをmock
        iams = iam.create_role(
            RoleName='test_matsu_iam',
            AssumeRolePolicyDocument='string',

        )
        iam_arn = iams.get('Role').get('Arn')
        print("iamRoleArn: " + iam_arn)

        # aws-batch コンピューティング環境をmock
        batch = client.create_compute_environment(
            computeEnvironmentName='test_matsu_batch',
            type='UNMANAGED',
            serviceRole=iam_arn
        )
        compute_environment_arn = batch.get('computeEnvironmentArn')
        print("computeEnvironmentArn: " + compute_environment_arn)

        # aws-batch ジョブキューをmock
        job_qs = client.create_job_queue(
            jobQueueName='test_matsu_job_q',
            state='ENABLED',
            priority=1,
            computeEnvironmentOrder=[
                {
                    'order': 1,
                    'computeEnvironment': compute_environment_arn
                },
            ]
        )
        job_q_arn = job_qs.get('jobQueueArn')
        print("jobQueueArn: " + job_q_arn)

        # aws-batch ジョブ定義をmock
        job_definition = client.register_job_definition(
            jobDefinitionName='test_matsu_job_definition',
            type='container',
            containerProperties={
                'image': 'string',
                'vcpus': 123,
                'memory': 123
            },
        )
        job_definition_arn = job_definition.get('jobDefinitionArn')
        print("jobDefinitionArn: " + job_definition_arn)

        # ジョブを追加
        client.submit_job(
            jobName='string',
            jobQueue=job_q_arn,
            jobDefinition=job_definition_arn
        )

        # ジョブ一覧を取得
        jobs = client.list_jobs(
            jobQueue=job_q_arn
        )

        # ジョブ一覧を出力
        print("jobSummaryList: " + str(jobs.get('jobSummaryList')))


if __name__ == '__main__':
    unittest.main()

実行結果

$ python -m unittest test.test_aws_batch -v
test_aws_batch (test.test_aws_batch.MyTestCase) ... iamRoleArn: arn:aws:iam::123456789012:role/test_matsu_iam
computeEnvironmentArn: arn:aws:batch:ap-northeast-1:123456789012:compute-environment/test_matsu_batch
jobQueueArn: arn:aws:batch:ap-northeast-1:123456789012:job-queue/test_matsu_job_q
jobDefinitionArn: arn:aws:batch:ap-northeast-1:123456789012:job-definition/test_matsu_job_definition:1
jobSummaryList: [{'jobId': 'ee3a3206-fdfe-404f-a1c1-9c444b41b546', 'jobName': 'string'}]
ok

----------------------------------------------------------------------
Ran 1 test in 0.167s

OK

各種リソースがモックされ、ジョブを投入することに成功。

終わりに

このmockでAWSの実リソースを使わずにAWS-Batchにジョブを投入するテストが可能になった。
ただ残念なのは、投入したジョブの内容がjobId,jobNameしかないこと。
ジョブの作成時間やステータスに関連するテストには利用できそうにない。
投入したジョブを使用するテストにはunittestのmockを使用するのが良さそうというのが結論。

はじめに

AWS-Batchをmotoを使用してmockし、ジョブを登録するところまでできたので備忘録として残しておく。

mock対象リソース

• IAM Role
• AWS-Batch コンピューティング環境
• AWS-Batch ジョブキュー
• AWS-Batch ジョブ定義

コード

test_aws_batch.py

#!/usr/bin/env python
# -*- coding: utf-8 -*-
import unittest
import boto3
from moto import mock_batch, mock_iam


class MyTestCase(unittest.TestCase):
    @mock_iam
    @mock_batch
    def test_aws_batch(self):
        client = boto3.client('batch')
        iam = boto3.client('iam')

        # iam roleをmock
        iams = iam.create_role(
            RoleName='test_matsu_iam',
            AssumeRolePolicyDocument='string',

        )
        iam_arn = iams.get('Role').get('Arn')
        print("iamRoleArn: " + iam_arn)

        # aws-batch コンピューティング環境をmock
        batch = client.create_compute_environment(
            computeEnvironmentName='test_matsu_batch',
            type='UNMANAGED',
            serviceRole=iam_arn
        )
        compute_environment_arn = batch.get('computeEnvironmentArn')
        print("computeEnvironmentArn: " + compute_environment_arn)

        # aws-batch ジョブキューをmock
        job_qs = client.create_job_queue(
            jobQueueName='test_matsu_job_q',
            state='ENABLED',
            priority=1,
            computeEnvironmentOrder=[
                {
                    'order': 1,
                    'computeEnvironment': compute_environment_arn
                },
            ]
        )
        job_q_arn = job_qs.get('jobQueueArn')
        print("jobQueueArn: " + job_q_arn)

        # aws-batch ジョブ定義をmock
        job_definition = client.register_job_definition(
            jobDefinitionName='test_matsu_job_definition',
            type='container',
            containerProperties={
                'image': 'string',
                'vcpus': 123,
                'memory': 123
            },
        )
        job_definition_arn = job_definition.get('jobDefinitionArn')
        print("jobDefinitionArn: " + job_definition_arn)

        # ジョブを追加
        client.submit_job(
            jobName='string',
            jobQueue=job_q_arn,
            jobDefinition=job_definition_arn
        )

        # ジョブ一覧を取得
        jobs = client.list_jobs(
            jobQueue=job_q_arn
        )

        # ジョブ一覧を出力
        print("jobSummaryList: " + str(jobs.get('jobSummaryList')))


if __name__ == '__main__':
    unittest.main()

実行結果

$ python -m unittest test.test_aws_batch -v
test_aws_batch (test.test_aws_batch.MyTestCase) ... iamRoleArn: arn:aws:iam::123456789012:role/test_matsu_iam
computeEnvironmentArn: arn:aws:batch:ap-northeast-1:123456789012:compute-environment/test_matsu_batch
jobQueueArn: arn:aws:batch:ap-northeast-1:123456789012:job-queue/test_matsu_job_q
jobDefinitionArn: arn:aws:batch:ap-northeast-1:123456789012:job-definition/test_matsu_job_definition:1
jobSummaryList: [{'jobId': 'ee3a3206-fdfe-404f-a1c1-9c444b41b546', 'jobName': 'string'}]
ok

----------------------------------------------------------------------
Ran 1 test in 0.167s

OK

各種リソースがモックされ、ジョブを投入することに成功。

終わりに

このmockでAWSの実リソースを使わずにAWS-Batchにジョブを投入するテストが可能になった。
ただ残念なのは、投入したジョブの内容がjobId,jobNameしかないこと。
ジョブの作成時間やステータスに関連するテストには利用できそうにない。
投入したジョブを使用するテストにはunittestのmockを使用するのが良さそうというのが結論。

はじめに

pyenvでpythonのバージョンを変えようと思い別バージョンをインストールした矢先エラーが置きたので対処した手順をメモ
環境: MacOS Mojave バージョン 10.14.6

起こったエラー

$pyenv install 3.6.4

python-build: use openssl from homebrew
python-build: use readline from homebrew
Downloading Python-3.6.4.tar.xz...
-> https://www.python.org/ftp/python/3.6.4/Python-3.6.4.tar.xz
Installing Python-3.6.4...
python-build: use readline from homebrew

BUILD FAILED (OS X 10.14.6 using python-build 20160602)

Inspect or clean up the working tree at /var/folders/_4/hss19f1x2b12ys793gz8lsd00000gn/T/python-build.20191218170128.37056
Results logged to /var/folders/_4/hss19f1x2b12ys793gz8lsd00000gn/T/python-build.20191218170128.37056.log

Last 10 log lines:
  File "/private/var/folders/_4/hss19f1x2b12ys793gz8lsd00000gn/T/python-build.20191218170128.37056/Python-3.6.4/Lib/ensurepip/__main__.py", line 5, in <module>
    sys.exit(ensurepip._main())
  File "/private/var/folders/_4/hss19f1x2b12ys793gz8lsd00000gn/T/python-build.20191218170128.37056/Python-3.6.4/Lib/ensurepip/__init__.py", line 204, in _main
    default_pip=args.default_pip,
  File "/private/var/folders/_4/hss19f1x2b12ys793gz8lsd00000gn/T/python-build.20191218170128.37056/Python-3.6.4/Lib/ensurepip/__init__.py", line 117, in _bootstrap
    return _run_pip(args + [p[0] for p in _PROJECTS], additional_paths)
  File "/private/var/folders/_4/hss19f1x2b12ys793gz8lsd00000gn/T/python-build.20191218170128.37056/Python-3.6.4/Lib/ensurepip/__init__.py", line 27, in _run_pip
    import pip
zipimport.ZipImportError: can't decompress data; zlib not available
make: *** [install] Error 1

やったこと

$ brew install zlib
$ brew install sqlite
$ export LDFLAGS="${LDFLAGS} -L/usr/local/opt/zlib/lib"
$ export CPPFLAGS="${CPPFLAGS} -I/usr/local/opt/zlib/include"
$ export LDFLAGS="${LDFLAGS} -L/usr/local/opt/sqlite/lib"
$ export CPPFLAGS="${CPPFLAGS} -I/usr/local/opt/sqlite/include"
$ export PKG_CONFIG_PATH="${PKG_CONFIG_PATH} /usr/local/opt/zlib/lib/pkgconfig"
$ export PKG_CONFIG_PATH="${PKG_CONFIG_PATH} /usr/local/opt/sqlite/lib/pkgconfig"

結果

$ python --version
Python 2.7.13 :: Anaconda custom (x86_64)

$ pyenv install 3.6.4

$ pyenv global 3.6.4

$ python --version
Python 3.6.4

メモ

環境： Mac OSX 10.15.1（19B88）

pyenvで新しいpythonバージョンをインストールしようとすると、以下のエラーが出ることがある。

terminal

$ pyenv install python3.6.2

python-build: definition not found: python3.6.2

See all available versions with `pyenv install --list'.

If the version you need is missing, try upgrading pyenv:


$ pyenv install 3.6.2

python-build: use openssl from homebrew
python-build: use readline from homebrew
Downloading Python-3.6.2.tar.xz...
-> https://www.python.org/ftp/python/3.6.2/Python-3.6.2.tar.xz
Installing Python-3.6.2...
python-build: use readline from homebrew

BUILD FAILED (OS X 10.15.1 using python-build 1.2.8)

Inspect or clean up the working tree at /var/folders/3k/g2s6z15s20q8bzy_5btxg29r0000gn/T/python-build.20191218194948.78102
Results logged to /var/folders/3k/g2s6z15s20q8bzy_5btxg29r0000gn/T/python-build.20191218194948.78102.log

Last 10 log lines:
  File "/private/var/folders/3k/g2s6z15s20q8bzy_5btxg29r0000gn/T/python-build.20191218194948.78102/Python-3.6.2/Lib/ensurepip/__main__.py", line 4, in <module>
    ensurepip._main()
  File "/private/var/folders/3k/g2s6z15s20q8bzy_5btxg29r0000gn/T/python-build.20191218194948.78102/Python-3.6.2/Lib/ensurepip/__init__.py", line 189, in _main
    default_pip=args.default_pip,
  File "/private/var/folders/3k/g2s6z15s20q8bzy_5btxg29r0000gn/T/python-build.20191218194948.78102/Python-3.6.2/Lib/ensurepip/__init__.py", line 102, in bootstrap
    _run_pip(args + [p[0] for p in _PROJECTS], additional_paths)
  File "/private/var/folders/3k/g2s6z15s20q8bzy_5btxg29r0000gn/T/python-build.20191218194948.78102/Python-3.6.2/Lib/ensurepip/__init__.py", line 27, in _run_pip
    import pip
zipimport.ZipImportError: can't decompress data; zlib not available
make: *** [install] Error 1

と表示が出る場合は、以下で回避できる。

CFLAGS="-I$(xcrun --show-sdk-path)/usr/include" pyenv install 3.6.2

はじめに

私がPythonを勉強して一通り基本となる構文を学んだところで作った、「入力された整数nが素数なのか合成数なのか判定するプログラム」です。自分の日記的な意味合いも兼ねて書いています。
まだまだ至らない点が多いと思いますが、アドバイスなどが有りましたらよろしくおねがいします。

プログラムの原理

今回の素数の判定方法は「入力された n に対して、n の約数が√nまでの素数に無ければ素数である。」という事実に基づいて行いました。
詳しい証明は以下をご覧ください。
自然数nが√n以下のすべての素数で割り切れなければ，nは素数であることの証明

実際のプログラム

import math
from sympy import primerange
n = int(input("素数か確かめたい数を入力してください。>> "))
num = int(math.sqrt(n)) + 1
primlist = list(primerange(2,num)) #1

for i in primlist: #2
    if n % i == 0: #3
        print("合成数です。")
        break
    elif i == primlist[-1] :
        print("素数です。")

大まかな流れ

1. 素数リストを√nまでの数字で作成する。
2. nを素数リストで割ってみる。
3. 割り切れたら「合成数です。」と表示する。素数リストの最後まで行ったら「素数です。」と表示する。

実際やっていること

1.は#1で、SymPyのprimerangeを用いることにより、素数リストを作成しました。
2.は#2で、for構文を用いて素数リストから文字を取り出しています。
3.は#3で、if構文を用いて「n を素数で割った余りが0か否か」で判定しています。

反省点

初めて素数判定を作りましたが、動くものができて個人的に満足しています。
しかし、n が大きくなると(7桁を超える)と途端に計算速度が遅くなってしまうので、なんとか改善したいです。
また、よく考えたらmathを使う必要がなかったので修正したいと思います。初めての自作プログラムなので今回は記念に残しています。
このプログラムを用いれば素因数分解もできそうな気がしてきたので手を加えてみたいとおもいます。
最後まで読んでくださいまして有難うございました。

この記事は、NTTコミュニケーションズ Advent Calendar 2019の18日目の記事です。
昨日は @yusuke84 さんの記事、Hoge Fuge でした。

はじめに

会社のAdvent Calendarということで、当初はある程度流れに忖度して技術的なTipsを書こう！
とか考えて、Neural Networkについてネタ探ししてたのですが、結局自分が興味のある話、それも実装よりも理論一辺倒な話に落ち着いてしまった、本記事はそんな成れの果てです。
（まあ１人くらい暴走しても良いですよね、きっと）

というわけで、Neural Networkを用いた物理系の表現について、少し前から気になってる話をツラツラと書いていきます。そのうちに、この辺の話を端緒に新規性のある手法を論文化するから、それ相応の評価を会社から頂戴したい、そんなことを妄想しております。（チラッ

おまえ誰やねん！？

普段は技術開発部でデータサイエンス＆AIに資する基礎技術を研究開発している入社２年目社員です。
本垢（ほぼROM専）の方が汚染されているため、こちらの垢@BootCamp_2019からの投稿です。

こちらの垢名から察するに、弊社の社内研修である「BootCamp」の、本年度データサイエンス＆AIコースの講師をしていました。

あとはコトあるごとに「統計検定１級」「数学検定１級」とか、研究業界では差して役に立たない資格を見せびらかしてるアイツです。

会社では多変量時系列解析、スパース推定、要因分析などをメインに研究開発していますが、個人的には非線形力学、縮約理論、情報統計力学とかが好きです。

本記事も結果的に個人の趣味に立脚したものになってしまいました。（てへぺろ

モチベ

最近、いえ少し前から、様々な分野でDeep Learningの応用が議論されるようになってきました。
これは大変喜ばしいコトで、元々数理科学の理論系にいた自分にとってはDeep Learningに本腰を入れる素晴らしいモチベーションになります。
異分野で大切にされている理論やスキームをDeep Learningに取り込むことは、一部で幻滅期に入ったと噂？されるDeep Learningに新しい風を取り込むことと同義であり、多くの視点で次の進化を模索することは素敵なことだと思います。

本記事は、その辺を少し共感して欲しくて書いたものです。

できるだけ平易なモデルと説明でまとめたつもりなので、雰囲気面白いと思ってもらえればありがたいです。
（よく知ってる方は、ぜひ多体位相振動子モデルのHamilton力学を教えてください。今一番気になっています。）

Neural Networkを使った力学系表現

Neural Networkと微分方程式

世界は微分方程式でできている。

例えば、高校物理で学ぶバネ単振動の運動方程式は以下のように記述されます。
（$m$は質量、$a$は加速度、$k$はバネ定数、$x$は物体の位置で、釣り合いの位置は原点の、シンプルな１次元運動を考えるとします。）
$$
ma = -kx
$$
¹
この先、実はもう少し深く掘り下げて学習すると、物体の速度$v$は位置$x$の１階時間微分であり、また加速度$a$は速度$v$の１階時間微分を意味することを学びます。すなわち、加速度$a$は位置$x$の２階時間微分を意味します。
これを位置が時間の関数$x(t)$であることを明示し丁寧に記述すると、先ほどの運動方程式は以下のように書き直すことができます。
$$
m\frac{d^2x(t)}{dt^2} = -kx(t)
$$

微分方程式（Differential Equation）とは、未知関数とその導関数の関係式として記述される関数方程式のことです。バネ単振動の運動方程式もまさに微分方程式です。

より良い物理現象の理論的解釈には、より良い数学モデルが必要不可欠です。
微分方程式を用いることで、現実世界の現象を（何らかの仮定と近似に基づいて）数学の問題として定式化することができ、その問題の解の意味を解釈することで、元の現象それ自体に理論的な解釈を与えうるものです。

例えば、先ほどのバネ単振動を表現する微分方程式を数学的に解くと、以下のような解を得ます。
（ただし、$A$は振幅、$\alpha$は初期位相で、いずれも初期位置$x(0)$と初期速度$v(0)$から決定されます。）
$$
x(t)=A\sin\left(\sqrt{\frac{k}{m}} t +\alpha\right)
$$
そしてこの解は、下図のように時間$t$と位置$x$の平面でプロットすると、実際の単振動の挙動と見事に一致することが見て取れます。

²

実は微分方程式を用いた数学モデルへの定式化は、何も物理現象のみが対象というわけではなく、生物、化学、政治、経済、社会といった多岐に渡る現象に有用です。
言い換えれば、世の中的な現象は意外すぎるほど微分方程式で表現でき、逆に妥当な微分方程式の発見は現象の理論的解釈と等価な問題と言うことができます。（夢を持って言い切って良いはず！）

とは言え、残念なことに日本の高等教育では、微分方程式の解き方は教えても、微分方程式の作り方はあまり教えられません。解くのは適当なツールを使えば誰でも簡単にできる一方、作るのは難しくよっぽど重要です。
微分方程式作りに興味のある方は、こちらの書籍³がおすすめです。応用例が非常に多く掲載され、モデル・ビルディングの訓練にも最適な良書です。

微分方程式とResNet

言い忘れましたが本記事で取り扱う微分方程式は、厳密には常微分方程式と呼ばれるグループです。しかし、常微分方程式が何たるか？は長くなるので他所に譲り、メンドくさいので以降も常微分方程式を微分方程式と連呼することとします。

さて、基本の１階微分方程式は一般に以下の形式で与えられます。
$$
\frac{dx(t)}{dt}=f(x(t))
$$
ところで微分は、その定義より以下の極限で求めることができます。
$$
\frac{dx(t)}{dt}=\lim_{\Delta t\to0}\frac{x(t+\Delta t)-x(t)}{\Delta t}
$$
なので微分方程式の挙動を計算機でシミュレーションしたい場合、最も単純には以下のように時間を$\Delta t$間隔で離散化して、離散時刻$t_n=n\Delta t$に基づいて数値計算を行います。
$$
\frac{x(t_{n+1})-x(t_n)}{\Delta t}=f(x(t_n))
$$
これを少し式変形します。
$$
x(t_{n+1})=x(t_n)+f(x(t_n))\Delta t
$$
そして少々天下り的ですが$g(x(t_n))=f(x(t_n))\Delta t$と新しく置き直せば、最終的に以下のように表現することができます。
$$
x(t_{n+1})=x(t_n)+g(x(t_n))
$$
この形式、勘の良いディープラーニング術者はどこかで見たことありませんか？
実はこれ、じっと睨めば画像認識タスクで一世を風靡したResNet⁴と同じ形式の方程式と見ることができます。

逆にニューラルネットワーク側から、順を追ってこの方程式に辿り着いてみます。

以下はResNet⁴のFigure 2.から引用した図です。

任意のアーキテクチャの各層では、結局のところ何某かの入力$x$に対して、線形変換（Afiine変換など）と非線形変換（活性化関数など）を適当に組み合わせて構成されている、柔軟な非線形変換$\mathcal{F}(x)$を出力とし、次の層へ伝播しています。
図の中央鉛直矢印の伝播経路は、まさにこれを模式的に示しています。（図はReluとありますが、一般にはRelu以外も可です。）

ResNetの肝は右側の「$x$ identity」と記載された伝播経路（迂回路）にあります。
詳細は原論文⁴に譲りますが、この伝播経路（迂回路）は恒等写像で、入力をそのまま出力に合流させます。
それにより、非常に層数の多いネットワークでも効率的に学習を進むことが知られており、その理由は誤差逆伝播が効率的に進むからではないかと考えられています。

ここで、$n$番目ResNetブロックについて入力を$x_n$、出力を$x_{n+1}$とすると、先ほどの図は以下のように書き直すこともできます。

$$
x_{n+1}=x_n+\mathcal{F}^{(n)}(x_n)
$$

これはまさに、先ほど示した離散化された微分方程式そのものと同じ形式の方程式だと言えます。
より明示的に示せば微分方程式内の$x(t_n)$とResNetブロックの$x_n$を対応させれば、わかりやすいと思います。

さらにResNetの一般化として知られるRevNet⁵では、各ブロックは以下のような対称的な構造をしています。

$$
\begin{eqnarray}
x_{n+1}&=&x_n+\mathcal{F}(y_n)\\
y_{n+1}&=&y_n+\mathcal{G}(x_n)
\end{eqnarray}
$$
先ほどまでと同様の議論で考えれば、これは次の連立微分方程式を離散化したものとなっていることがわかります。
$$
\begin{eqnarray}
\frac{dx(t)}{dt}&=&f(y(t))\\
\frac{dy(t)}{dt}&=&g(x(t))
\end{eqnarray}
$$

ここまでの議論から察するに、ResNet（あるいはRevNet）で全ての微分方程式を記述できるわけではないことに注意が必要です。
この辺の詳細は、最近巷を賑わせているこちらの書籍⁶が詳しいです。この書籍は非常に良書なので、ディープラーニングと物理学の深淵なる関係を探求したい方は、ぜひ手に取ってもらえたら嬉しいです。
特に本記事では議論の簡単化のために、ユニット数などについての考察を端折ったので、こちらの書籍などで詳細は確認してください。

ODENet (Neural Ordinary Differential Equations)

NeurIPS 2018⁷のベストペーパーに選ばれたこちらの論文⁸は、まさに微分方程式で駆動される時間発展方程式とニューラルネットワークを結びつける画期的な手法を提案しています。なお著者実装がGithub⁹で公開されています。

ODENetでは、ResNetやRNNの隠れ層などの層毎の処理を、時間方向に連続極限を取った時間発展方程式と考え、それを（常）微分方程式として陽に解くことでニューラルネットワークを構築するお話です。
連続化することで、深層学習の層という概念がなくなり、メモリや計算量の効率が良く、またBack Propagationに相当する最適化として、（常）微分方程式のソルバーが使えるなど、様々な革新的な手法を提案しています。

こちらはODENet⁸のFigure 1.から引用した図です。左図は通常のResNetで離散的な時間発展を記述している一方で、右図のODENetでは連続的な時間発展を表現できている。もはや離散的な層の概念がなく、雰囲気矢印（ベクトル場）多いなあ、と感じていただけると完璧です。

他にも、 Normalizing Flow¹⁰（NF）を拡張した手法Continuous Normalizing Flow（CNF）で効率的に確率密度が学習できたり、潜在変数の時間発展を連続化することで時系列データを効率的に学習する手法が提案されています。

ODENetについての細かい理論説明はこちらのサイト¹¹¹²¹³がわかりやすいので、ぜひ参照してください。

余談ですが、このNormalizing Flow、同じ著者の別のレポジトリ¹⁴でコードが公開されています。実際にヘンテコな確率密度を構成してみると楽しいです。

例えば、我々をいつも暖かく見守ってくれるアイツの確率密度も、こんな風にわりときれいに求めることができます。

Neural NetworkとHamilton力学

Hamilton力学ってなんぞ

Hamilton力学とはHamiltonianという不思議な特性関数を用いて、現象を解析する解析力学の一形式です。
Hamiltonianは物理学におけるエネルギーに相当する物理量であり、物理系の持つ多くの性質をHamiltonianで記述することができます。
（Hamiltonianは必ずしも物理現象のみに限定される概念ではないですが、物理現象を題材にした方が以降の議論がイメージしやすいので、ここではエネルギーだとか言ってます。）

まあ難しい話は棚上げして、高校物理の全エネルギーと等価な物理量だと思うことにします。
すなわち、Hamiltonianと運動エネルギー＆ポテンシャルエネルギーをそれぞれ$\mathcal{H}, \mathcal{K}, \mathcal{U}$と表記すると、以下のように関係性にあります。

$$
\mathcal{H}=\mathcal{K}+\mathcal{U}
$$

もうひとつ重要な概念として、Hamilton力学では一般化座標と一般化運動量が登場します。
とは言え、ここでは簡単に一般化座標は通常の座標、一般化運動量は通常の運動量（質量と速度の積）と考えれば十分です。これらをそれぞれ、$q,p$と表記すると、通常の物理量とは以下の関係で表記できます。

$$
\begin{eqnarray}
q(t)&=&x(t)\\
p(t)&=&mv(t)
\end{eqnarray}
$$

とても天下り的ですが、そんな酔狂な表記もあるんだなくらいに思っていただいて、実際にバネ単振動の微分方程式についてのHamiltonianを求めてみます。

これはとても簡単で、運動エネルギーとポテンシャルエネルギーをそれぞれ一般化座標と一般化運動量を用いて、以下のように書き直すだけで十分です。
$$
\begin{eqnarray}
\mathcal{K}&=&\frac{1}{2}mv^2(t)=\frac{1}{2m}p^2(t)\\
\mathcal{U}&=&\frac{1}{2}kx^2(t)=\frac{1}{2}kq^2(t)
\end{eqnarray}
$$
すなわち、バネ単振動のHamiltonianは以下のような感じです。
$$
\mathcal{H}=\frac{1}{2m}p^2(t)+\frac{1}{2}kq^2(t)
$$

ではなぜ、Hamiltonianなどという量を導入するのかというと、正準変換や正準方程式という対称性が美しく、然れども便利な関係性があるからです。
もどかしいですが、こちらも詳細は他に譲り、ここでは以下のような関係があると信じることとします。
$$
\begin{eqnarray}
\frac{dq(t)}{dt}&=&\frac{\partial \mathcal{H}}{\partial p}\\
\frac{dp(t)}{dt}&=&-\frac{\partial \mathcal{H}}{\partial q}
\end{eqnarray}
$$

そして例として、ひとまずバネ単振動のHamiltonianを適用してみます。
$$
\begin{eqnarray}
\frac{dq(t)}{dt}&=&\frac{\partial \mathcal{H}}{\partial p}=\frac{p(t)}{m}\\
\frac{dp(t)}{dt}&=&-\frac{\partial \mathcal{H}}{\partial q}=-kq(t)
\end{eqnarray}
$$

このままでは少しわかりにくいので、一般化座標及び一般化運動量を元の物理量に戻します。
$$
\begin{eqnarray}
\frac{dx(t)}{dt}&=&\frac{mv(t)}{m}=v(t)\\
m\frac{dv(t)}{dt}&=&-kx(t)
\end{eqnarray}
$$

最初の関係式は速度が位置の時間微分であることが表現されています。
問題は２つめの関係式ですが、これは実は元のバネ単振動の運動方程式そのものとなっています。
実際に速度が位置の時間微分（最初の関係式）であることを代入してみると、本記事で冒頭に取り上げたバネ単振動の運動方程式と一致することが詳かになります。
$$
m\frac{dv(t)}{dt}=m\frac{d^2x(t)}{dt^2}=-kx(t)
$$

実はHamiltonianには現象を記述する重要な情報が過分に含まれており、（若干の語弊を許せば）Hamiltonianの視点で現象を解析するのがHamilton力学です。
ここではバネ単振動の単体運動を取り扱ったのでありがたみが伝わりにくいですが、多体運動や相互結合など複雑な現象になると本領が発揮されてきます。

Hamiltonian（及びLagrangian）については、まずはこの辺¹⁵を読んでみるのが良いかもしれません。
ちなみに、それ以前の高校物理みたいな話はNewton力学と呼んだりします。

Hamilton Neural Network

ここでは現象を表現するNeural Networkのうち、先ほど紹介したODENetとはまた異なるアプローチを紹介します。
こちらの手法もNeurIPS 2019⁷に採択されており、こちらの原論文¹⁶と著者実装¹⁷で、すぐにお試ししてみることができます。

こちらの手法は直感的には非常にシンプルで分かりやすいです。
Hamilton力学の肝となる正準方程式をそのまま損失関数とすることで、一般化座標と一般化運動量の入力からHamiltonianをうまく表現するようなNeural Networkを学習しています。

ここでポイントとなるのは、良いか悪いかは別として必ずしもHamiltonianそのものを学習しているわけではなく、Hamiltonianに類する何かを学習している点が重要です。
そのため、現象の具体的なHamiltonianが未知の場合でも、その時間発展を上手く表現できるNeural Networkを構成できるものと期待できるのです。

Hamilton Neural Networkの学習の大まかな流れは以下のような感じです。

(1) 時間方向に離散化された一般化座標と一般化運動量を入力データとする。

(2) Neural Networkはパラメタ$ \theta $で特徴付けられているものとする

(3) 順伝播でスカラー値$\mathcal{H}_{\theta}$を出力する（この出力の段階でHamiltonianという要請は特に入れていないことに注意）。

(4) 自動微分を用いた逆伝播で以下の値を算出する。
$$
\frac{\partial \mathcal{H}_\theta}{\partial p},\:\frac{\partial \mathcal{H}_\theta}{\partial q}
$$

(5) 一つ先の時刻の情報を使って一般化座標と一般化運動量の時間微分を求める（これが教師データに相当）。
$$
\frac{dq(t)}{dt},\:\frac{dp(t)}{dt}
$$

(6) 正準方程式に基づいて、以下の損失関数を最小化するように学習する。
$$
L_{HNN}=\left(\frac{\partial \mathcal{H}_\theta}{\partial p}-\frac{dq(t)}{dt}\right)^2+\left(\frac{\partial \mathcal{H}_\theta}{\partial q}+\frac{dp(t)}{dt}\right)^2
$$

以下はHamiltonian Network¹⁶のFigure 1.から引用した図です。

BaselineとされているシンプルなNeural Networkと比較して、提案手法は元の物理現象の挙動をうまく表現できていることがわかります。

面白い応用としては以下のFigure 4.のように、物理現象の画像データのみを入力としても、現象を上手く再現できているあたりでしょうか。

ただ問題としては、単体運動は比較的実測値と等価なものを表現できている一方で、相互作用の働く多体運動に対してはあまり上手く学習できていません。

以下のFigure B.3.を見ると明らかなように、３体運動ではわりと初期の段階から挙動が崩壊しており、お互いの引力で衝突しそうですね。
もっともBaselineと比較すれば、円軌道を保とうとしてる雰囲気を感じられるので比較的よろしいかと思いますが。

とは言え、とても直感的でシンプルなNeural Networkであるにも関わらず、特に単体運動を具体的に表現できているのは大変興味深いです。まだまだ発展の余地があると思うので、研究開発が捗りますね。

こちらの論文についてはこの辺のサイト¹⁸¹⁹の解説がわかりやすいので適宜参照してください。

まとめ

そんな感じで刺さる人には刺さる内容をまとめた記事でした。
徳の高いまとめを書こうと思ったのですが、今ちょうど会社の開発合宿で南紀白浜に来ており、しかも夕飯食べに行く集合時間まで残り10分を切ってるので、また今度、覚えていたらにしようと思います！お腹空きました。。。

弊チームの神も大浴場から戻られたようなので、一旦ここまでで。

明日は同じチーム＆同じ大学の偉大な先輩@kirikeiさんの大変徳の高い記事です！！！
正座してお待ちしております！！！勉強します！！！

---

1. わからない物理 運動方程式の解法【単振動】から一部引用。単振動を例に、テイラー展開、指数関数、保存量といった多角的な解法を示し比較している。 ↩

2. 受験メモ 力学の最難関！単振動とは？東大院生が徹底解説！【高校物理】から一部引用。単振動の理論を満遍なく網羅し、図もわかりやすい。 ↩

3. 微分方程式で数学モデルを作ろう, 日本評論社 (1990/4/9). ↩

4. Deep Residual Learning for Image Recognition, Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun, 2015. ↩

5. The Reversible Residual Network: Backpropagation Without Storing Activations, Aidan N. Gomez, Mengye Ren, Raquel Urtasun, and Roger B. Grosse, 2017. ↩

6. ディープラーニングと物理学 原理がわかる、応用ができる, 講談社 (2019/6/22). ↩

7. Neural Information Processing Systems、略してNeurIPS。未だに旧略称NIPSの方がしっくりくる今日この頃。 ↩

8. Neural Ordinary Differential Equations, Ricky T. Q. Chen, Yulia Rubanova, Jesse Bettencourt, and David Duvenaud, 2018. ↩

9. Github rtqichen/torchdiffeq PyTorch Implementation of Differentiable ODE Solvers、論文⁸の著者実装。 ↩

10. Eric Jang Normalizing Flows Tutorial, Part 1: Distributions and Determinantsがわかりやすい。 ↩

11. SlideShare [DL輪読会]Neural Ordinary Differential Equations、論文⁸の内容が体系的にまとめられている。 ↩

12. Github yoheikikuta/paper-reading [2018] Neural Ordinary Differential Equations、論文⁸の内容についてこちらもわかりやすい。 ↩

13. AINOW 【NIPS 2018最優秀賞論文】トロント大学発 ： 中間層を微分可能な連続空間で連結させる、まったく新しいNeural Networkモデル、論文⁸の内容をとても噛み砕いてイメージさせてくれる。 ↩

14. Github rtqichen/ffjord code for "FFJORD: Free-form Continuous Dynamics for Scalable Reversible Generative Models".。こちらはFFJORD: Free-form Continuous Dynamics for Scalable Reversible Generative Modelsの著者実装である。 ↩

15. 宇宙に入ったカマキリ 解析力学 ラグランジュ形式とハミルトン形式を適宜参照。特にラグランジュ形式との比較がわかりやすい。 ↩

16. Hamiltonian Neural Networks, Sam Greydanus, Misko Dzamba, and Jason Yosinski, 2019. ↩

17. Github greydanus/hamiltonian-nn Hamiltonian Neural Networks、論文¹⁶の著者実装である。 ↩

18. AI-SCHOLAR エネルギー保存則を満足する物体運動の予測を可能とする Hamiltonian Neural Networks、いつもお世話になっております。 ↩

19. Github yoheikikuta/paper-reading [2019] Hamiltonian Neural Networks、相変わらずわかりやすいです。 ↩

Djangoハンズオン

• 目標
  • ごくごく簡単なTodoアプリを作成し、Djangoの処理の流れを理解する。
• 前提知識
  • 簡単なHTMLの理解
  • httpメソッドの理解(GET,POST)
• このハンズオンではやらないこと
  • アプリケーションの見た目をきれいにすること(CSS,bootstrap)

環境

OS: Ubuntu 18.04
Python: 3.6.8
Django: 2.2.5　-> 2.2.8

Windowsについては後々から追加していきます。Macは手元にないですがLinuxと一緒でしょう（？）。可能であれば追加します。

前回の記事を参照し、ディレクトリ構成が以下の状態になっていることが前提です。
もしまだ設定できていない場合は、先に環境の作成をお願いします。

Todoアプリの作成

ここからアプリを作成していきます。
django-admin startapp mytodoとコンソール上に入力します。
python manage.py startapp mytodoでも構いません。

作成後は以下のように、mytodoというアプリのディレクトリ＋ファイルが作成されます。

.
|-- config
|   |-- __init__.py
|   |-- __pycache__
|   |-- settings.py
|   |-- urls.py
|   `-- wsgi.py
|-- db.sqlite3
|-- manage.py
|-- myenv
|   |-- bin
|   |-- include
|   `-- lib
`-- mytodo
    |-- __init__.py
    |-- admin.py
    |-- apps.py
    |-- migrations
    |-- models.py
    |-- tests.py
    `-- views.py

Djangoのタイムゾーンと言語の設定を最初に行います。

settings.py

#デフォルト'EN-en'
LANGUAGE_CODE = 'ja'
#デフォルト'UTC'
TIME_ZONE = 'Asia/Tokyo'

現在は作成されたTodoアプリがDjangoからはわからない状態です。Djangoがアプリケーションを認識するためには、config/settings.pyの中の設定に、作成したアプリケーションを追加することが必要です。

settings.py

INSTALLED_APPS = [
    'django.contrib.admin',
    'django.contrib.auth',
    'django.contrib.contenttypes',
    'django.contrib.sessions',
    'django.contrib.messages',
    'django.contrib.staticfiles',
    'mytodo', 　　　　　　　　　　　　　　　　#追加
]

これでアプリの登録までが終わり、いよいよアプリを作り込んで行きます。

モデルの作成

Todoなら作成日や終了日などを入れたほうがより実践的ですが、今回はとことん簡単にします。
今回定義するモデルは下記のとおりです。

models.py

from django.db import models


class Task(models.Model):
    doing = 0
    done = 1
    TASK_STATUS_CHOICES = [
        (doing,'進行中'),
        (done,'完了'),
    ]
    title = models.CharField(max_length=50)
    body = models.models.TextField()
    status =models.IntegerField(default=0,choices=TASK_STATUS_CHOICES)

モデルのコーディングが終わったら、manage.pyのある階層で、コンソール上でpython manage.py makemigrationsを実行します。
このコマンドによって、モデルからDBを作成するのに必要なファイルが作成されます。
エラーなく作成されると下記のように表示されます。

(myenv)~/Projects/python/django_handson$ python manage.py makemigrations
Migrations for 'mytodo':
  mytodo/migrations/0001_initial.py
    - Create model Task

この時点ではDBに対して変更は入っていません。次のpython manage.py migrateコマンドをうつことで、DBに対して先程のマイグレーションファイルが実行されます。

(myenv)~/Projects/python/django_handson$ python manage.py migrate
Operations to perform:
  Apply all migrations: admin, auth, contenttypes, mytodo, sessions
Running migrations:
  Applying contenttypes.0001_initial... OK
  Applying auth.0001_initial... OK
  Applying admin.0001_initial... OK
  Applying admin.0002_logentry_remove_auto_add... OK
  Applying admin.0003_logentry_add_action_flag_choices... OK
  Applying contenttypes.0002_remove_content_type_name... OK
  Applying auth.0002_alter_permission_name_max_length... OK
  Applying auth.0003_alter_user_email_max_length... OK
  Applying auth.0004_alter_user_username_opts... OK
  Applying auth.0005_alter_user_last_login_null... OK
  Applying auth.0006_require_contenttypes_0002... OK
  Applying auth.0007_alter_validators_add_error_messages... OK
  Applying auth.0008_alter_user_username_max_length... OK
  Applying auth.0009_alter_user_last_name_max_length... OK
  Applying auth.0010_alter_group_name_max_length... OK
  Applying auth.0011_update_proxy_permissions... OK
  Applying mytodo.0001_initial... OK
  Applying sessions.0001_initial... OK

TODO以外にもuserという文字が表示されています。
余談ですが、Djnagoがデフォルトで用意しているUserモデルがDBに反映されています。

ここまでできればモデルの作成は完了です。

ルーティング・ビュー・テンプレートの作成

先程作成したモデルをベースにCRUDを実装していきます。
個人で開発の際は、私はビュー→テンプレート→ルーティングの順番で書いていきますが、個人差があるところだと思いますので慣れてくれば自分の順番で書いてください。

まず、Todoをリストですべて表示するページを作成していきます。
１つのモデルを1欄で表示する際は、Djangoのクラスベースビューを使用するとコード量がぐっと減らせて楽です。

ビューの作成

ビューの役割は受け取ったリクエストからDBからデータを取得し、テンプレートに埋め込みレスポンスとして返すことです。

ビューには2種類の書き方があり、関数ベースのビューとクラスベースのビューが存在します。
どちらでもかけますが、今回はクラスベースビューで書きます。

クラスベースビューには、参照をするためのListView(一覧),DetailView(詳細)、
更新のためのCreateView(作成),UpdateView(更新),DeleteView(削除)などが用意されています。
これらを使用することで、単純な処理であれば一瞬でビューを用意できるようになっています。

今回は一覧を作成しますが、必要な記述は以下のとおりです。

mytodo/views.py

from django.views.generic import ListView

from mytodo.models import Task

class TaskListView(ListView):
    model = Task
    template = 'mytodo/list.html'

modelには表示したいモデルを指定します。先程作成したモデルをインポートし使用します。
テンプレートはHTMLにpythonの制御文を埋め込んだようなファイルで拡張子は.htmlです。

テンプレートの作成

日本語に訳すと鋳型とか型とか言われるものですが、ビューがDBなどから取ってきた値を埋め込むための型です。ビューがテンプレートとDBから取得してきた値などを埋め込むことをレンダリングといいます。ビューでDjangoがテンプレートファイルに書かれた制御分をもとにデータを埋め込んだhtmlファイルを吐き出します。

{{}}はデータの表示、{% %}はPythonライクな制御分の埋め込みに使用します。

まずはtemplateフォルダの場所をsettings.pyに以下のように記述します。

config/settings.py

TEMPLATES = [
    {
        'BACKEND': 'django.template.backends.django.DjangoTemplates',
        'DIRS': [os.path.join(BASE_DIR,'templates')], #変更
        'APP_DIRS': True,
        'OPTIONS': {
            'context_processors': [
                'django.template.context_processors.debug',
                'django.template.context_processors.request',
                'django.contrib.auth.context_processors.auth',
                'django.contrib.messages.context_processors.messages',
            ],
        },
    },
]

templatesフォルダをmanage.pyと同じ階層に作成し、その中に、mytodoというフォルダを作成します。

その中にlist.htmlというファイルを作成します。
今回、全く見た目についてはカバーしませんので、適当なhtmlファイルを作成します

templates/mytodo/list.html

<h1>リスト</h1>

<ul>
  {% for task in object_list %}
  <li><a href="#">{{ task.title }}</a> {{ task.get_status_display }}</li>
  {% endfor %}
</ul>

ルーティングの設定

requestのurlから適切なビューを呼ぶための設定を行います。
urls.pyファイル内で設定します。

configフォルダの中のurls.pyにすべて書いても構わないのですが、複数のアプリを作成した際には大量のコードで溢れてしまい著しく保守性を損ないます。アプリの移植性も損ないます。
そこで、mytodoアプリの中にもurls.pyを作成し、config側でそれをインクルードするという手法がよく取られます。

まずmytodo/urls.pyを作成し、編集していきます。

urls.py

from django.urls import path

from .views import TaskListView

app_name = 'mytodo'

urlpatterns = [
    path('',TaskListView.as_view(), name='task-list'),
]

urls.pyで、リクエストされたURLとビューの対応付けを行います。
これをconfig側で追加します。

config/urls.py

from django.contrib import admin
from django.urls import path, include


urlpatterns = [
    path('admin/', admin.site.urls),
    path('mytodo/', include('mytodo.urls',namespace='mytodo')),#追加
]

path関数は、第一引数にurlの'/'以降に登録する文字列、第二引数にviewや他のURLConfを登録することができます。

ここまで作成することでルーティングが完了します。
早速確認しましょうpython manage.py runserverでサーバーを起動し、確認します。

ルートには何もルーティングしていないため、Page not foundが表示されます。
登録されているurlは少し下にリストが表示されています。

urlにmytodoを追加してhttp://127.0.0.1:8000/mytodoとしてアクセスします。
現状は何もデータが登録されていないため、見出しのみしか表示されていません。真っ白です。

Createの実装

同じような手順でCRUDのCREATEを実装していきます。

ビュー

Createも同様にクラスベースビューを使って実装していきます。
先程のviews.pyに追記していきます。

mytodo/views.py

import django.views.generic import ListView,CreateView # 追記

(中略)

class TaskCreateView(CreateView):
    model = Task
    fields = '__all__'
    initial = {'status':0}
    template_name = 'mytodo/create.html'
    success_url = reverse_lazy('mytodo:task-list')

実装方法はListView同様にmodelとtemplateを登録します。
initialはTaskモデルのChoiceフィールドの初期状態を設定することができます。
fieldsは、サーバ側で受け取るデータを指定することができます。
今回はすべてのデータを受け取るとしていますが、Taskモデルの中のtitleのみ受け取るということも可能です。

テンプレート

次はテンプレートを作成します。

templates/mytodo/create.html

<form action="" method="post">
  {% csrf_token %}
  {{ form.as_p }}
  <input type="submit" value="登録">
</form>

{{form.as_p}}にはCreateViewのmodelとfieldsに対応したフォームのhtmlが生成されます。
生成したフォームにcssに当てるのは少し工夫が必要ですが、今回は味のあるhtml独特の見た目を楽しみましょう。

{% csrf_token %}については気にしないでください。

ルーティング

urls.pyにviewを登録します。

mytodo/urls.py

from django.urls import path

from .views import TaskListView, TaskCreateView #追記

app_name = 'mytodo'

urlpatterns = [
    path('',TaskListView.as_view(), name='task-list'),
    path('create',TaskCreateView.as_view(), name='task-create'),#追記
]

path関数の最後のnameとはurlに名前をつけることができます。
先程のviews.pyに出てきたreverse_lazyなどの関数の引数として使うことができます。

以上でCreateの実装が完了です。
サーバーを起動し、このURLhttp://127.0.0.1:8000/mytodo/createにアクセスします。
以下のような味のあるフォームが表示されれば成功です。

試しに何個か登録させてみましょう。

詳細画面の作成

残りはCRUDのうちUPDATEとDELETEが残っていますが、先にDetailViewを作成します。
現在はタスクの一覧(ListView)だけですが、よりタスクの詳細な情報を表示するページ(DetailView)を作成します。

先程同様ビューから作成していきます。
実装は以下の通り、とてもシンプルです

mytodo/views.py

from django.views.generic import ListView,CreateView,DetailView

(中略)

class TaskDetailView(DetailView):
    model = Task
    template_name = 'mytodo/detail.html'

templateの実装は以下のとおりです。
また同じようにtemplates/mytodoフォルダにdetail.htmlというファイルを作成します。

templates/mytodo/detail.html

<h1>詳細</h1>
<div>タイトル:{{object.title}}</div>
<div>status:{{object.get_status_display}}</div>
<div>内容:{{object.body}}</div>
<p><a href="#">編集</a></p>

最後にURLを登録します。
urlpatternsのリストにpath('detail',TaskDetailView.as_view(), name='task-detail')
]を追加します。

これでDetailViewの実装は完了です。

一覧ページからのDetailViewへの遷移を実装します。
list.htmlのaタグのリンクを編集します。

templates/mytodo/detail.html

<h1>詳細</h1>
<div>タイトル:{{object.title}}</div>
<div>status:{{object.get_status_display}}</div>
<div>内容:{{object.body}}</div>
<p><a href="{% url 'mytodo:task-update' object.pk%}">編集</a></p>　#変更

object.pkでテンプレートに受け渡されたオブジェクトの主キーを取得することができます。

更新機能の実装

これも同様にViewから実装していきます。

mytodo/views.py

from django.views.generic import ListView,CreateView,DetailView, UpdateView
from django.urls import reverse_lazy

from mytodo.models import Task

(中略)

class TaskUpdateView(UpdateView):
    model = Task
    fields = '__all__'
    template_name = 'mytodo/update.html'
    success_url = reverse_lazy('mytodo:task-list')

CreateViewとほぼ同じですね。
もし、アップデートを許すフィールドを限定したい場合はfieldsをいじるといいでしょう。

ほぼ同じ作業なので一気にルーティングとテンプレートの実装を行います。

テンプレートはCreateとまるっきり一緒です。

templates/mytodo/update.html

<form action="" method="post">
  {% csrf_token %}
  {{ form.as_p }}
  <input type="submit" value="登録">
</form>

ルーティングに新たにUpdateViewを追記します。
detailと同じく、主キーによって更新をかけるべきデータを判別します。。

mytodo/urls.py

urlpatterns = [
    path('',TaskListView.as_view(), name='task-list'),
    path('detail/<int:pk>/',TaskDetailView.as_view(), name='task-detail'),
    path('create/', TaskCreateView.as_view(), name='task-create'),
    path('update/<int:pk>/', TaskUpdateView.as_view(), name='task-update'),                 #追加
]

この編集画面への遷移を詳細画面から行えるように若干変更しておきます。

templates/mytodo/detail.html

<h1>詳細</h1>
<div>タイトル:{{object.title}}</div>
<div>status:{{object.get_status_display}}</div>
<div>内容:{{object.body}}</div>
<p><a href="{% url 'mytodo:task-update' object.pk%}">編集</a></p>

削除機能の追加

いよいよ最後です。
削除ビューを実装します。
例のごとく、ビューから実装していきます。

ビューの実装。

mytodo/views.py

from django.views.generic import ListView,CreateView,DetailView, UpdateView
from django.urls import reverse_lazy

from mytodo.models import Task

(中略)

class TaskDeleteView(DeleteView):
    model = Task
    template_name = 'mytodo/delete.html'
    success_url = reverse_lazy('mytodo:task-list')

テンプレートの実装。
削除するよっていうのを遅れればいいのでとても簡素

templates/mytodo/delete.html

<form action="" method="post">
  {% csrf_token %}
  <p>本当に削除しますか？</p>
  <p><input type="submit" value="Yes"></p>
  <p><a href="{% url 'mytodo:task-list' %}">戻る</a></p>
</form>

ルーティングの実装。
最終型が以下のとおりです。

mytodo/urls.py

from django.urls import path

from .views import TaskListView, TaskCreateView, TaskDetailView, TaskUpdateView, TaskDeleteView

app_name = 'mytodo'

urlpatterns = [
    path('',TaskListView.as_view(), name='task-list'),
    path('detail/<int:pk>/',TaskDetailView.as_view(), name='task-detail'),
    path('create/', TaskCreateView.as_view(), name='task-create'),
    path('update/<int:pk>/', TaskUpdateView.as_view(), name='task-update'),
    path('delete/<int:pk>/', TaskDeleteView.as_view(), name='task-delete'),            #追加
]

最後にこの削除ビューに遷移するurlを追記しておしまいです。
ついでにlist.htmlをテンプレートの制御文を使って申し訳程度の処理を行っておきます。

templates/mytodo/list.html

<h1>リスト</h1>

<a href="create/"><p>新規追加</p></a>
<ul>
  {% for task in object_list %}
  {% if task.status != 0 %}
    <li><del><a href="detail/{{ task.id }}">{{ task.title }}</a>  </del>{{ task.get_status_display }} <a href="{% url 'mytodo:task-delete' task.pk %}">削除</a></li>
  {% else %}
    <li><a href="detail/{{ task.id }}">{{ task.title }}</a>  {{ task.get_status_display }} <a href="{% url 'mytodo:task-delete' task.pk %}">削除</a></li>
  {% endif %}

  {% empty %}
    <li>No tasks</li>
  {% endfor %}
</ul>

おわりに

アマチュアDjango使いの記事に最後までお付き合い頂きありがとうございました。
何か間違い等があれば遠慮なくツッコミお待ちしております。

概要

このサイトにあるFXのデータを、ローソク足表示させます。

環境

• Python 3.6 on Anaconda
• Jupiter notebook

とりあえず株価データを表示するサンプルを動かす

表示に関してはこの投稿がより詳しく書いてあります。
ここのサイトのサンプルそのままに表示させます。

fig.py

import plotly.graph_objects as go

import pandas as pd
from datetime import datetime

df = pd.read_csv('https://raw.githubusercontent.com/plotly/datasets/master/finance-charts-apple.csv')

fig = go.Figure(data=[go.Candlestick(x=df['Date'],
                open=df['AAPL.Open'],
                high=df['AAPL.High'],
                low=df['AAPL.Low'],
                close=df['AAPL.Close'])])

fig.show()

以下のように表示されました。

FXのデータを表示

このサイトのHISTDATA_COM_ASCII_EURJPY_M1_201911.zipを表示させてみたいと思います。
そのためにまず、zipファイルの中身をpd.DataFrameに変換します。

import pandas as pd
from zipfile import ZipFile
ascii_minute_names = ["datetime_str", "Open", "High", "Low", "Close", "Volume"]
ascii_minute_datetime_format = "%Y%m%d %H%M%S"

with ZipFile("HISTDATA_COM_ASCII_EURJPY_M1201911.zip", 'r') as z:
    with z.open("DAT_ASCII_EURJPY_M1_201911.csv") as f:
        df = pd.read_csv(f, names=ascii_minute_names, sep=";")
        df["datetime"] = pd.to_datetime(df.datetime_str, format=ascii_minute_datetime_format)
        df = df.set_index("datetime")
        del df["datetime_str"]

print(df.head())

"""
output:
                        Open     High      Low    Close  Volume
datetime                                                       
2019-11-01 00:00:00  120.599  120.601  120.595  120.598       0
2019-11-01 00:01:00  120.597  120.598  120.592  120.595       0
2019-11-01 00:02:00  120.597  120.603  120.597  120.601       0
2019-11-01 00:03:00  120.600  120.600  120.592  120.598       0
2019-11-01 00:04:00  120.597  120.603  120.593  120.597       0
"""

表示ぃ！　※データが大きいので実行時間かかります。

import plotly.graph_objects as go

import pandas as pd
from datetime import datetime

fig = go.Figure(data=[
    go.Candlestick(
        x=df.index,
        open=df.Open,
        high=df.High,
        low=df.Low,
        close=df.Close
    )
])

fig.show()

以下のように表示されました。

以上！

背景

iタウンページの特定の情報を網羅的に取得するために、賢早くんというExcelマクロが配布されていたのですが、2019年11月のiタウンページ側の仕様変更により使用できなくなってしまいました。
そこで、スクレイピングの練習も兼ねて、Python初心者（大学の講義で少し触れた程度）が青息吐息でプログラミングに挑戦しました。
最終目標は「特定の小カテゴリーから店舗名・住所・カテゴリを取得する」です。

規約の確認

タウンページの規約ですが、以下の二点が禁止されています。
・ｉタウンページのサービスに多大な影響を与える行為
・自動的にアクセスするプログラムを使用してｉタウンページに繰り返しアクセスする行為
https://itp.ne.jp/guide/web/notice/
今回は、ページの続きを読み込むためのボタンを最下まで押すだけというクソコードなので、繰り返しのアクセスではなく通常の利用の範疇ではないかと想定しています（これが不可なら通常利用でも最下までたどり着けない仕様……）。

環境

• Windows10
• Spyder3.3.6(Python3.7)
• Selenium
• Google Chrome 79

コード

Seleniumのインストール

Anaconda Prompt上で

pip install selenium

ドライバの指定・Chromeの起動

driver = webdriver.Chrome(executable_path='/Users/*****/*****/Selenium/chromedriver/chromedriver.exe')
driver.get('https://itp.ne.jp/genre/?area=13&genre=13&subgenre=177&sort=01&sbmap=false')

ドライバを指定した後，ブラウザで指定したURLを立ち上げます。
今回はパチンコ店を調べたので，エリア「東京都」，カテゴリ「屋内遊戯」で検索した場合のURLです。

最下行まで表示

while True:
    try:
        driver.find_element_by_class_name('m-read-more__text').click()
    except:
        print('☆「更に表示」連打終了☆')
        break

エラーを吐くまで（＝最下行まで）「さらに表示」ボタンを連打します。
これでHTML上に，ヒットしたすべての店舗情報を表示します。

カテゴリー名を回収

elist = []
elems = driver.find_elements_by_class_name("m-article-card__header__category")
for e in elems:
     elist.append(e.text)
print(elist)

str_ = '\n'.join(elist)
print(str_)
with open("str_.txt",'w')as f:
    f.write(str_)

空のリストを作成して，Class名がm-article-card_header_categoryの要素のinnerTextをそこに放り込みます。
そののち，リストを1要素ずつ改行した文章にして，テキストで出力します。

終わり

flist = []
elems2 = driver.find_elementｓ_by_class_name("m-article-card__header__title__link")
for f in elems2:
     flist.append(f.text)
print(flist)

str2_ = '\n'.join(flist)
print(str2_)
with open("str2_.txt",'w')as f:
    f.write(str2_)


glist = []
elems3 = elems2 = driver.find_elementｓ_by_class_name("m-article-card__lead__caption")
for g in elems3:
     glist.append(g.text)
print(glist)

str3_ = '\n'.join(glist)
print(str3_)
with open("str3_.txt",'w')as f:
    f.write(str3_)


print('成功')
driver.quit()

タイトルとキャプション（住所・電話番号・最寄駅）についても，同じように出力します。
※キャプションはタイトルやカテゴリーと行数が違うので，Excelで整形しました。

詰まったところ

解決したところ

・forの後に:（コロン）を付け忘れる
・無限回繰り返す方法がわからない
→While True:でした。Trueが大文字始まりというところでも詰まりました
・ファイルに書き出す方法がわからない
→ファイル名を””で囲んでいなかったのが原因でした
・chromeDriverの場所の指定の仕方がわからない
→Chromedriverの入っているフォルダーまでしか指定していませんでした。当然Chromedriver.exeまで指定
・コマンドプロンプトでpip install seleniumを実行しても、Spyder上で実行できない
→Anaconda Prompt側で実行しないといけない
……他多数

未解決問題

・pipが何かわかっていない
・htmlの構造がわからない
→結局わからなかったのでSeleniumでブラウザを動かす形に
・【住所】の他に【電話番号】【最寄駅】がついてくる
→これが結構致命的で、おそらく本当は店舗１件をひとまとまりとして書き出した方がいいのでしょう（今回はExcelで処理しました）。本格的に必要になれば書き換える予定です

その他

・全国すべての店舗を表示するURLはhttps://itp.ne.jp/genre/
・東京都の店舗を表示するURLはhttps://itp.ne.jp/genre/?area=13

こんにちは。
meshgridって混乱しませんか？
今日はmeshgridを中心に書いていきます。
そしてそれを利用した等高線を書く為のメソッドであるcontourで遊ぼうと思います。

meshgridとは

meshgridは格子点を作るために使われます。

格子点とは

座標平面上にある点で、x座標、y座標とも整数である点を格子点という。

つまり、この画像の点全てのことですね。

さぁ、コードを書きます。

import numpy as np
x = [0, 1, 2, 3]
y = [0, 1, 2, 3]

X, Y = np.meshgrid(x, y)

XとYは以下のようになります。

何これ〜〜〜〜〜〜〜〜~~?!?!?!?!?!?!?!と思う人も多いかもしれませんが、もう少し頑張ってください。
これが何を表しているのかを整理しましょう。
最初の座標平面とこの行列がどう関係しているか見ていきます。
下記の画像を見てください。

どうですか？
少しはピンと来ましたか？
そう。XとYの行列の位置は平面上の座標と一致しているんです！（上下は転置されている）
つまり、行列の左上は座標では左下。
行列の右下に行くにつれて、座標では右上に行くのです。

この一致しているという事実を知っていれば、XとYの大きさは(len(y), len(x))となりますよね。
そしてlen(x) * len(y) = 格子点の数になります。
なぜかって？
まず紙に書いて、ゆっくり考えてみてください。

では大きさの違うx、yを考えてみようと思います。

Xについて考えると、Xは必ず０か１しか要素として持ちません。
なぜなら、xという配列の中には0,1しかありませんからね。
そして０から１までを一つの棒と考えれば、y = 0, 100, 200に3本重ねれますよね。
これは、[0, 1]が３行必要ってことです。だからXの行列は3 * 2 = len(y) * len(x)なんですね。

Yも同じですよね。

結構まどろっこしい説明をしましたが、一言で言うと
行列の大きさは格子点の縦×横に等しいです
こうみるととても簡単だし、混乱も防げますよね。
それにしても美しい。

meshgridを利用して等高線を書く。

import numpy as np
import matplotlib.pyplot as plt

# z = 2(x + y)
def f(x, y):
    return 2 * (x + y)

x = [-1, 0, 1, 2, 3]
y = [-1, 0, 1, 2, 3]

X, Y = np.meshgrid(x, y)

fig, ax = plt.subplots()
cont = ax.contour(X, Y, f(X, Y), levels=[0, 2, 4]) # ここだけ説明。
cont.clabel(fmt='%1.1f', fontsize=14)
plt.show()

結果はこうなります。
実際 x = 2, y = -1 であれば、z = 2(2 - 1) = 2 * 1 = 2ですよね。

contourだけ説明しますね。
contour(X, Y, Z=f(X,Y), levels=[0, 2, 4])
まずcontourは等高線を求める為のツールです。
等高線とはx,yから導き出されるZの同じ値を結んだものです。
X,Yは格子点で、f(X,Y)でそれぞれの格子点でのZを求めています。
そのZにそって線を結んでいくんですね。それぞれの位置のZを知るために、格子点が必要となるわけです。
最後のlevelsは任意ですが、ここに指定されたものが線として表示されます。

まとめ

今日はmeshgridを中心に書きました。
そしてmeshgridを使う等高線を書く為のツールであるcontourで遊んでみました。
meshgridはいろんな所で使います。
しっかり理解しておくことはマストでしょう。
ありがとうございました。

参照文献

格子点とは？

はじめに

一般にPythonは遅いと言われているが、実際に他言語と比べてどれだけ遅いのかを調べてみた。

測定方法

PythonとJAVAの2言語間で、円周率を近似するプログラムを走らせる。
それぞれの差から実行速度が何倍異なるかを調べた。

結論

JAVAのほうが、Pythonより約60倍速いと思われる。
ただし、円周率の近似の結果値をうまく出力できなかったため、本記事だけではJAVAのほうが速いと主張できない。

やったこと

近似式

ライプニッツの公式から円周率を近似した。

π = 4{(1-1/3)+(1/5-1/7)+...(1/[4n+1] - 1/[4n+3] ) }

で求まるらしい。

実行時間の測定方法

JAVA、Pythonともに、

(計算の実行終了時刻 - 計算の実行開始時刻)

を用いて実行時間を求めた。

Pythonのコード

import time

num = 100000000  # 計算の繰り返し回数
pi = 0  # 円周率の近似値


if __name__ == '__main__':
    start = time.time()

pi = 0
for i in range(num):
    pi += (1 / (i * 4 + 1) - 1 / (i * 4 + 3))
print(pi4)    # 3.141592153589902

elapsed_time = time.time() - start
print("elapsed_time:% .2f" % elapsed_time + "[sec]")

JAVAのコード

public class SpeedTest{
   public static void main(String[] args){
       long startTime = System.currentTimeMillis();

       //以下に計測する処理を記述

       int num = 100000000;  // 計算の繰り返し回数
       float pi = 0;  // 円周率の近似値を4で割ったもの
       float pi4 = 0;  // 円周率の近似値

       for(int i = 0;i<num; i++){
         pi += (1 / (i * 4 + 1) - 1 / (i * 4 + 3));
       }
       pi4 = pi * 4;
       //以上、計測する処理内容

       long endTime = System.currentTimeMillis();

       System.out.println(pi4);

       System.out.println("time:" + (endTime - startTime)+"[msec]");
   }

}

結果

Python、JAVAともに1億回の処理をそれぞれ2回行ったところ、

Pythonでは33.88 sec, 31.55 sec
平均32.72 secが得られた。

JAVAでは528 msec, 568 msec
平均548 msecが得られた。
　　--> 平均0.548 sec

以上のことから、PythonとJAVAでは59.71倍の実行速度差が存在する。

一方で、円周率の近似値の出力では、
Pythonでは3.1415926445762157が得られ、
JAVAでは4.0が得られた。

π = 3.1415926535...
であるため、
Pythonでは8桁の精度で求められたのに対して、
JAVAでは精度としては1桁も合っていない。

これはfloat型などでは計算結果が勝手に丸まってしまうことに由来するようだ。
JAVAで計算が正しく行われたかどうかが明らかでないため、この結果からJAVAのほうが速い！と言い張るのは難しい。

環境

Python... Python3.6.8, PyCharm 2019.1.2
JAVA... JAVA10.0.2, Eclips Photon Release (4.8.0)

参考URL

【Python】処理にかかる時間を計測して表示
https://qiita.com/fantm21/items/3dc7fbf4e935311488bc

【Java入門】処理時間をナノ秒・マイクロ秒で計測する方法
https://www.sejuku.net/blog/44904