- 投稿日:2019-03-18T23:59:01+09:00
ラズパイのボタンをプッシュしたら写真撮ってS3へ上げる
モチベーション
部品が揃ってきたので、ラズパイとAWSを連携。
ラズパイのボタンをプッシュしたら写真撮ってS3へ上げる。環境
- RaspberryPi3B+
- Raspbian 9.8
- RPi.GPIO
- picamera
- amazon S3
- boto3
- python
準備
以下の2記事の複合技なので準備はこちらにお任せします。
Raspberry Pi カメラ画像をS3へアッロード
Raspberryでボタン押下をGPIOの割り込みで検出pythonコード
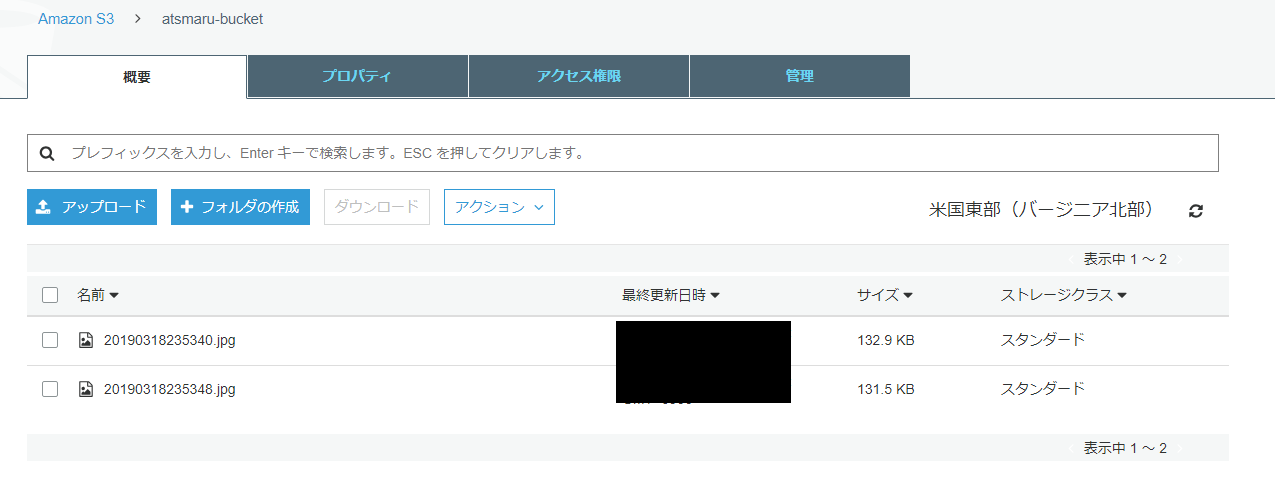
takePicToS3.py# coding: utf-8 import picamera import boto3 import time from datetime import datetime def take_pic_from_picamera(filename): print("take_pic_from_picamera:"+filename) with picamera.PiCamera() as camera: # camera.resolution = (1024, 768) camera.resolution = (500, 500) camera.start_preview() camera.led = False #camera warm-up time time.sleep(2) camera.capture(filename) print("done") def upload_to_S3(filename): print("upload_to_S3:"+filename) bucket_name = "atsmaru-bucket" s3 = boto3.resource('s3') s3.Bucket(bucket_name).upload_file('/home/pi/'+filename, filename) print("done") # main #timestr = datetime.now().strftime('%Y%m%d%H%M%S') #filename=timestr+'.jpg' #take_pic_from_picamera(filename) #upload_to_S3(filename)button_to_S3.py# coding: utf-8 import RPi.GPIO as GPIO import time import datetime from datetime import datetime import takePicToS3 BUTTON_PIN = 21 def main(): setup_gio() try: while(True): time.sleep(1) # Keyboard入力があれば終わり except KeyboardInterrupt: print("break") teardown_gio() def setup_gio(): GPIO.setwarnings(False) # Set the layout for the pin declaration GPIO.setmode(GPIO.BCM) # BCMの21番ピンを入力に設定 GPIO.setup(BUTTON_PIN,GPIO.IN) # callback登録(GIO.FALLING:立下りエッジ検出、bouncetime:300ms) GPIO.add_event_detect(BUTTON_PIN, GPIO.FALLING, callback=callback, bouncetime=300) def teardown_gio(): GPIO.cleanup() def callback(channel): print("button pushed %s"%channel) timestr = datetime.now().strftime('%Y%m%d%H%M%S') filename=timestr+'.jpg' takePicToS3.take_pic_from_picamera(filename) takePicToS3.upload_to_S3(filename) if __name__ == "__main__": main()実行
pi@raspberrypi:~ $ python button_to_s3.py button pushed 21 take_pic_from_picamera:20190318235340.jpg done upload_to_S3:20190318235340.jpg done button pushed 21 take_pic_from_picamera:20190318235348.jpg done upload_to_S3:20190318235348.jpg done done ^Cbreak
- 投稿日:2019-03-18T23:24:02+09:00
Raspberryでpython GPIOの割り込み検出
モチベーション
ラズパイからなんらしかのセンサーの値を元にAWSに通知を上げ、なんらかしら(なんらかしらばっかり 笑)の動作をしたい。まず簡単なところでボタンのプッシュを検出する。GPIOの値をポーリングはできるので、割り込みで実現してみた。
環境
- RaspberryPi3B+
- Raspbian 9.8
- RPi.GPIO
参考
https://sourceforge.net/p/raspberry-gpio-python/wiki/Inputs/
配線
3.3V R│10K GND ── Button ──┴─── BCM21(GPIO.29)pythonプログラム
gio_int.py# coding: utf-8 import RPi.GPIO as GPIO import time BUTTON_PIN = 21 def main(): GPIO.setwarnings(False) # Set the layout for the pin declaration GPIO.setmode(GPIO.BCM) # BCMの21番ピンを入力に設定 GPIO.setup(BUTTON_PIN,GPIO.IN) # callback登録(GIO.FALLING:立下りエッジ検出、bouncetime:300ms) GPIO.add_event_detect(BUTTON_PIN, GPIO.FALLING, callback=callback, bouncetime=300) try: while(True): time.sleep(1) # Keyboard入力があれば終わり except KeyboardInterrupt: print("break") GPIO.cleanup() def callback(channel): print("button pushed %s"%channel) if __name__ == "__main__": main()実行
ポチポチとボタンを2回押すと検出できました。
Ctrl-Cで終わりです。pi@raspberrypi:~ $ python gio_int.py button pushed 21 button pushed 21 ^Cbreak pi@raspberrypi:~ $ちなみに、bouncetime=1にして動かしてみると、チャタリングのためにボタン1回を2回と検出することがありました。
- 投稿日:2019-03-18T23:24:02+09:00
Raspberryでボタン押下をGPIOの割り込みで検出
モチベーション
ラズパイからなんらしかのセンサーの値を元にAWSに通知を上げ、なんらかしら(なんらかしらばっかり 笑)の動作をしたい。まず簡単なところでボタンのプッシュを検出する。GPIOの値をポーリングはできるので、割り込みで実現してみた。
環境
- RaspberryPi3B+
- Raspbian 9.8
- RPi.GPIO
参考
https://sourceforge.net/p/raspberry-gpio-python/wiki/Inputs/
配線
3.3V R│10K GND ── Button ──┴─── BCM21(GPIO.29)pythonプログラム
gio_int.py# coding: utf-8 import RPi.GPIO as GPIO import time BUTTON_PIN = 21 def main(): GPIO.setwarnings(False) # Set the layout for the pin declaration GPIO.setmode(GPIO.BCM) # BCMの21番ピンを入力に設定 GPIO.setup(BUTTON_PIN,GPIO.IN) # callback登録(GIO.FALLING:立下りエッジ検出、bouncetime:300ms) GPIO.add_event_detect(BUTTON_PIN, GPIO.FALLING, callback=callback, bouncetime=300) try: while(True): time.sleep(1) # Keyboard入力があれば終わり except KeyboardInterrupt: print("break") GPIO.cleanup() def callback(channel): print("button pushed %s"%channel) if __name__ == "__main__": main()実行
ポチポチとボタンを2回押すと検出できました。
Ctrl-Cで終わりです。pi@raspberrypi:~ $ python gio_int.py button pushed 21 button pushed 21 ^Cbreak pi@raspberrypi:~ $ちなみに、bouncetime=1にして動かしてみると、チャタリングのためにボタン1回を2回と検出することがありました。
- 投稿日:2019-03-18T23:08:19+09:00
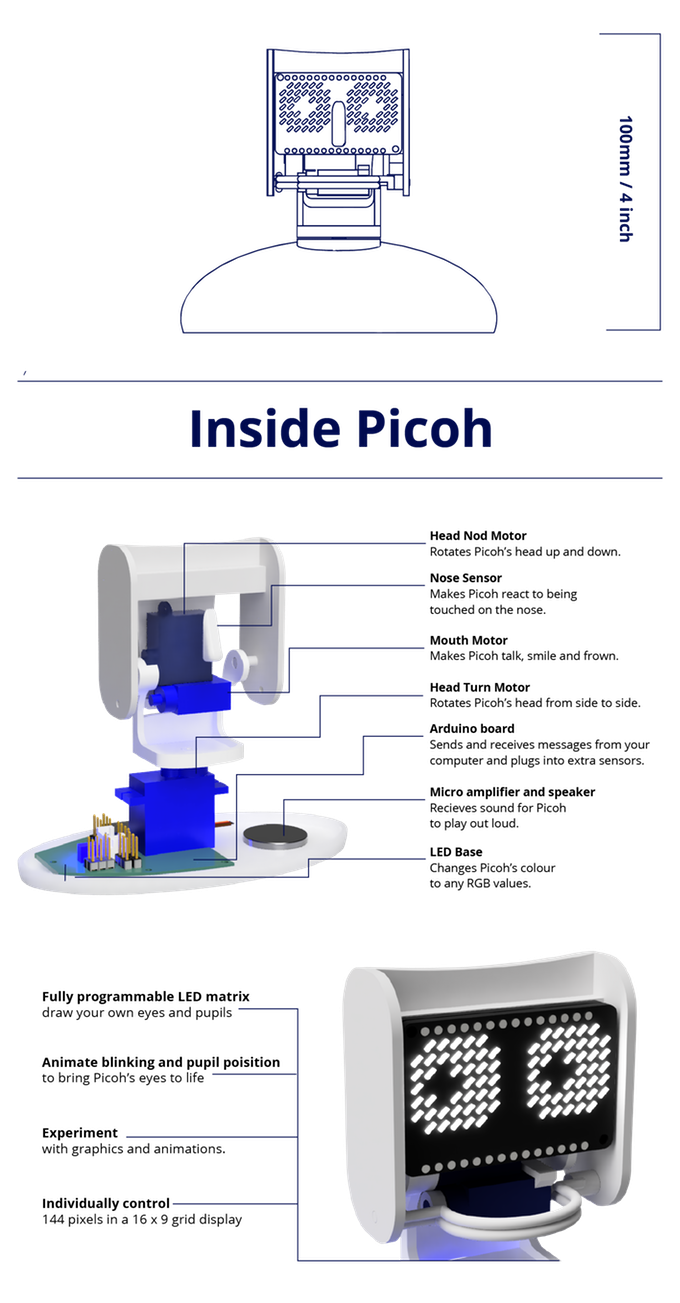
プログラミングできてキューティーなロボット「Picoh」
Kickstarterで行われているクラウドファンディング
https://www.kickstarter.com/projects/ohbot2/picoh-an-expressive-little-robot-head
約¥14,683(配送料含む?) £88以上のプレッジ £1=147.52円(2019/3/18)
2019年3月24日(日) 2時7分まで(日本時間)Picohってなに?
Picoh(ピコ)とは学校教育向けのロボットです
(←ちょうどこんな頭だけのやつ
様々なセンサーが搭載されており、プログラミングすることによってカスタマイズができますPicoh開発ツール
Platform OS 説明 Ohbot App Windows Windows App Python 3 Windows, Raspberry Pi, macOS Scratch 3 Chromebook 対応予定 Youtubeへのリンク
https://youtu.be/FsYLbatz844
https://www.kickstarter.com/projects/ohbot2/picoh-an-expressive-little-robot-head より
搭載機能(センサー) 説明 ヘッドノッドモーター ピコの頭を上下に回転させる 鼻センサー 鼻に触れてピコーを反応させる 口のモーター ピコトーク、笑顔としかめ面 ヘッドターンモーター ピコの頭を左右に回転させる アルデュイーノボード コンピュータとメッセージを送受信し、追加のセンサーに接続する マイクロアンプとスピーカー ピコが大音量で演奏するためのもの LEDベース ピコの色を任意のRGB値に変更する プログラム可能なLEDマトリックス 自分の目と瞳孔を描く 点滅と瞳孔位置をアニメート ピコの目を生き返らせるために 実験 グラフィックスとアニメーション 個別制御 16×9グリッド表示で144ピクセル Google翻訳より
できること
・LEDの点灯や口のモーター部分を制御することで顔の表情を変える
・人の顔を認識し、その人の名前で挨拶する
・要求に応じて時間や日付を教えてくれたり、歌を歌う、音楽に合わせて踊ることも可能そのほかにもカスタマイズ次第でたくさんのことができます!!(今思いつかない...
最後に
教育向けということで子供向けかと思いきや、大人でも楽しめそうですね
日本人で紹介している人をあまり見かけなかったので、一人でも多くの人に知ってもらえれば嬉しいです
興味を持った方はページトップのリンク先に詳細が書かれています(英語ですが・・・)
最後まで読んでくれてしゃーした
- 投稿日:2019-03-18T23:01:11+09:00
[Docker]アラフォーがDockerに挑んでみた(黎明編)
はじめに
業務でDockerが絡むシステムを担当することになってしまい、「現場入ってから追々理解してもらえばだいじょうぶっすー」という言葉を信じていたのだけど、「追々じゃなく今理解せんとこれ開発出来んやん」ということに気付いたので今更ながらDockerの扉を叩くことにしました。
アラフォーの日々少なくなってゆく脳細胞で理解出来るでしょうか。なぜ今Dockerなのか(私の場合)
現場の方からは「アプリ単位のVMみたいなもんやと思ってもらえればー」と聞いていた。ふーん、そっかぁ。そういうもんがあるんやな、ぐらい知っとけばいいんかな。と思ってました。
ところが、いざ実作業に入ると確かにDockerをよく知らなくても、既存のAPIなりを呼んでいけば仕様を満たす実装は出来る。
けどテストクラス書くときに
「これってbeforeでDockerの状態をまずお膳立てしてやらんとテストしようがないけどどうなってるのが正しいのか・・・Dockerの何をどう見てassertTrueとかするの・・・」
というところで唸ることになってしまった。これはマズい。Dockerってなんやのん、ということを知る必要が出てきてしまいました。
つまり、使いたくなった!とかそういうわけではなく、業務上困り始めたし、そんならやってみるかーって流れです。あしたっていまさッ!
ジョジョの奇妙な冒険のポコという登場人物が「あしたっていまさッ!」という名言を残しています。
私がDockerを勉強するのも今なんでしょう。先延ばしにしてたけど。幸い酒飲んでアニメ見てソシャゲする時間の余裕はあります。やろうではないですか。Dockerってなんやのん
いきなり小難しいサイトや本を読んでもきっと頭に入らないので、まずはやんわり気味に情報を入手していくことにしました。
Dockerのすべてが5分でわかるまとめ!(コマンド一覧付き)うーん、でVMと何が変わらないんだ?
アプリ単位でのイメージを切り出せるから、開発環境が作りやすいというのは何となくわかる。
とりあえず使ってみますか。Dockerをインストールしてみる
必要なもの
- PC
- ネット環境
- メールアドレス
以上であります。因みに今回使用したマシンのスペックは下記。- macOS Sierra 10.12.6
- MacBook (Retina, 12-inch, Early 2015)
- プロセッサ 1.3 GHz Intel Core M
- メモリ 8G
説明するまでもない手順
Dockerのサイトの、「Download from Docker Hub」と書いてるいかにもなボタンを押下。
https://docs.docker.com/docker-for-mac/install/
ポチッとするとSign Inせよと言われるので、アカウントがない場合はCreate Accountのリンクからアカウントを作成。私はアカウントなかったので作りました。
上のメニューのとこからSign Inすると、Get Dockerボタン押下でdmgファイルダウンロード出来ます。やったね。
これでインストール出来たのか不安になったので、
docker versionをターミナルで叩いてみる。$ docker version Client: Docker Engine - Community Version: 18.09.2 API version: 1.39 Go version: go1.10.8 Git commit: 6247962 Built: Sun Feb 10 04:12:39 2019 OS/Arch: darwin/amd64 Experimental: false Server: Docker Engine - Community Engine: Version: 18.09.2 API version: 1.39 (minimum version 1.12) Go version: go1.10.6 Git commit: 6247962 Built: Sun Feb 10 04:13:06 2019 OS/Arch: linux/amd64 Experimental: false何やらインストールは出来てるみたいですね!
ついでなのでPythonもインストールしてみよう
Dockerのウリとして、アプリケーションなどの実行環境や設定方法をまとめて1つのパッケージにし、それを「Dockerイメージ」として保存・配布しているそうです。
なるほど、それが現場の方の「アプリ単位のVMみたいなもんやと思ってもらえればー」ってとこに繋がるのかな。
今現場で使っているPythonが3.6なので、自宅学習用にもせっかくなのでそれをインストールしてみます。
ちなみに素のMacBookにはPython2.7.10がインストールされている状態ですので、Docker上にPython3.6をインストール出来るなら、MacBookの環境を汚さない、ってことになるハズ。やってみましょう。
インストール前の状態がこちら。$ python --version Python 2.7.10Python3.6のDockerイメージインストール
おもむろに
sudo docker pull python:3.6をターミナルから実行します。自分しか使わないマシンなのに、sudoにパスワードかけてらっしゃる!?$ sudo docker pull python:3.6 Password: 3.6: Pulling from library/python 22dbe790f715: Pull complete 0250231711a0: Pull complete 6fba9447437b: Pull complete c2b4d327b352: Pull complete 270e1baa5299: Pull complete 400bad26d6c0: Pull complete 1d360410c080: Pull complete 1224d2c3c8d9: Pull complete 5d7d0629cdba: Pull complete Digest: sha256:dfd0b1fcad1f056d853631413b1e1a3afff81105a27e5ae7839a6b87389f5db8 Status: Downloaded newer image for python:3.6終わったようなので
docker image lsで見てみましょう。lsコマンド感覚で何インストールしてるのか見られるみたい。$ docker image ls REPOSITORY TAG IMAGE ID CREATED SIZE python 3.6 d6b15f660ce8 13 days ago 924MBうん、Python3.6はインストール出来てる・・・みたい。
Dockerイメージの起動
docker run -it python:3.6でPythonを起動してみます。docker run -it python:3.6 Python 3.6.8 (default, Mar 5 2019, 06:26:06) [GCC 6.3.0 20170516] on linux Type "help", "copyright", "credits" or "license" for more information.無事Python3.6が起動してるみたいですね。
exitでDockerを停止した後、改めてpython --versionでバージョンを見てやるとpython --version Python 2.7.10おー、元々のバージョンは何も変わってない。
これで「本体のMacBookに入ってるPython2.7.10」を汚すことなく、Python3.6(正確には3.6.8だけど)がDockerという仮想環境にインストール出来て、実行も出来る環境が出来たってことですね。
まとめを書きながら進めていたので時間はかかりましたが、単純にお手持ちのPCに導入するだけならここまででしたら1時間もかからないと思います。ここから更にいじって遊んでみたいので、後日色々試していきます。
- 投稿日:2019-03-18T22:54:51+09:00
FlappyBird で強化学習の練習 その1: DQN
— ᴉɥsᴉuɐʞɐu oɹɐʇuǝʞ (@cfiken) 2019年3月18日この記事は何
せっかく Pythonで学ぶ強化学習 をざっと読んだので、手を動かしてみる大作戦です。
FlappyBird という数年前に話題になったゲームがあり、それを強化学習を用いて学習していきたいと思います。
のんびり動かしてみつつ、色々やったことを記録していこうと考えています
前: FlappyBird で強化学習の練習 その0: 環境編
次: 来週本記事はひとまずベースラインとなるシンプルな DQN で学習をさせたものを紹介します。
以降の更新で、まずは Rainbow のそれぞれのアイディアを試しつつ、ベースラインからの改良度合いを見ていけたらと考えています。
勉強しつつ書いてるので、何か誤りなどあればコメントいただけると助かります
実装は jupyter notebook 上で行っており、 今回のコードはこちらです。
リポジトリはこちら: cfiken/flappybird-try目次
- DQN とは
- FlappyBird における問題設定
- DQN による学習結果
- 実装の紹介
- まとめ
DQN とは
DQN は Deep Q-Network の略で、強化学習における Q-Learning を、ディープラーニングを使って実現する手法のことを言います。
ここでは詳解はしません(詳しい記事は既に死ぬほどあります)。
発表論文は nature に掲載されています。
Deep Mind による記事Q-Learning では、ある状態と行動の価値(Q値)をTD誤差を用いて反復的に更新し、それが最大となるような行動を取りました。
\begin{align} Q\left(s_{t}, a_{t}\right) &= Q\left(s_{t}, a_{t}\right)+\eta *\left(R_{t+1}+\gamma \max _{a} Q\left(s_{t+1}, a\right)-Q\left(s_{t}, a_{t}\right)\right) \\ \pi(a|s_t) &= \mathrm{arg}\max_a Q(s_t, a) \end{align}DQN では Q-Learning に対して、TD誤差を用いて反復的にQ値を推定するのではなく、状態を入力として入れるとそれぞれの行動をとった際の価値を出力するようなニューラルネットワークに置き換えて価値を推定するモデルとなっています。
\begin{align} Q\left(s_{t}, a \right) &= f(s_t; \boldsymbol{\theta}) \,\,\,\, (f\mathrm{: neural \, network \, model})\\ \pi(a|s_t) &= \mathrm{arg}\max_a Q(s_t, a) \end{align}特に DQN の発表論文である では、ゲーム画面という画像から CNN を使って直接価値を推定し、それを使って人間並みの能力を持つエージェントが作成できたという点でとても話題になった手法とのことでした。
また、DQN では、学習の難しい強化学習で学習を安定化させるためのノウハウがいくつか入っています。本記事の実装では Experience Replay と Fixed Target Q-Network, reward clipping などを取り入れています。
FlappyBird における問題設定
強化学習には、状態、行動、報酬のセットが必要です。FlappyBird というタスクを解くにあたって、どのようにそれぞれを定義するかについて説明します。
状態 (state)
単に状態といっても次の2通りがあります。
- gym のインターフェースから得られる生の状態
- 学習に使うために前処理を適用した後の状態
前者は、FlappyBird の gym 上のインスタンスを
envからenv.step(action)やenv.reset()で得られる状態です。
FlappyBird の場合は、(height, width, channel) = (288, 512, 3)で、それぞれ0-255の値を取る画像データが得られます。ここから、学習をしやすくするために前処理を行ったものが後者にあたります。
今回は、まずそれぞれのデータをまずグレースケールに変換し、全体を255.0で割って 0~1 の値に変換します。
それを時系列で 4 frame 並べ、 shape を(width, height, frames)としたものを学習に使用する状態としています。
コードとしては、Observerクラスのtransformメソッドにあたります。class Observer: # ... def transform(self, state): grayed = Image.fromarray(state).convert('L') # h, w, c -> h, w resized = grayed.resize((self.width, self.height)) resized = np.array(resized).astype(np.float32) resized = np.transpose(resized, (1, 0)) # h, w -> w, h normalized = resized / 255.0 if len(self._frames) == 0: for i in range(self.frame_count): self._frames.append(normalized) else: self._frames.append(normalized) feature = np.array(self._frames) feature = np.transpose(feature, (1, 2, 0)) # [f, w, h] -> [w, h, f] return feature行動 (action)
FlappyBird における行動は、何もしない (=0) か飛ぶ (=1) の二種類です。
今回の実装では、学習をしやすくするために「同じ行動を4回繰り返す」という制約を入れています。
すなわち行動は、「4step の間何もしない」か「4step の間飛び続ける」のどちらかとしました。
あくまで今回の実装ではそうしたというだけで、生の行動をそのまま扱っても問題ないかと思います。報酬 (reward)
FlappyBird のデフォルトの実装では、
- ドカンの間を一つ抜けるたびに +1
- ぶつかってしまうと -5
- それ以外は 0
という報酬が与えられます。今回は学習をしやすくするため、次のような reward shaping を加えました。
def reward_shaping(self, reward): if 0.1 > reward > -0.1: return 0.01 elif reward <= -0.1: return -1.0 else: return 1.0全体の学習を安定化させるために報酬をクリップしつつ、長生きする方が良いということを学習させる意図で、前に進むだけで少しの報酬が与えられるようにしています。
ここまでの定義は、あくまで私が識者に聞いたりしつつ現在それで試しているというだけのもので、工夫の余地があると思います。
DQN による学習結果
学習後のモデルで50回ゲームをプレイし、スコア(超えたドカンの数)の平均値を最終スコアとします。
50回実行した上での平均スコアは
42.2600でした。平均約42本のドカンを超えているようです。
とはいえまだスコアはブレが大きく、1本で死んでるプレイもあり、安定して攻略できているとは言えません。
が、人間がプレイしても40を超えるのは結構難しいので(私は結構やって人力スコア20ちょいでした...)、人間レベルに達したと言っても良さそうです。下記は、冒頭に上げたものと同じで、 episode 45 で89回成功したときの動画です。
— ᴉɥsᴉuɐʞɐu oɹɐʇuǝʞ (@cfiken) 2019年3月18日下記は50プレイ分の結果です。
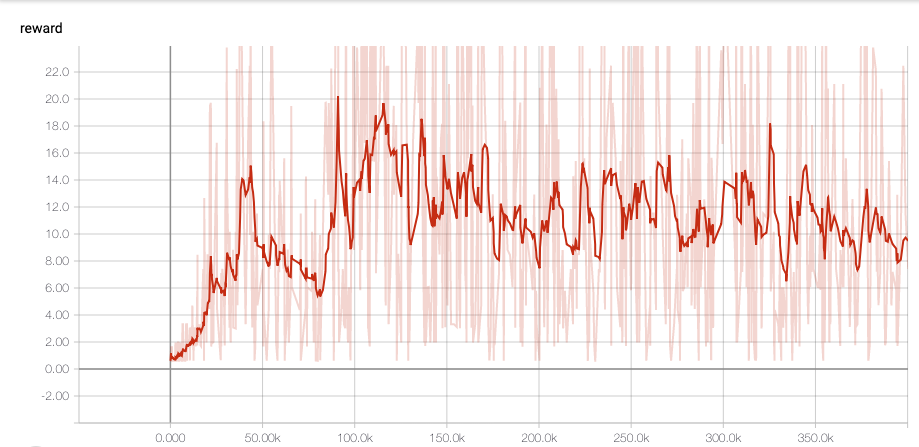
episode 0, total reward: 21.0000 episode 1, total reward: 44.0000 episode 2, total reward: 12.0000 episode 3, total reward: 29.0000 episode 4, total reward: 32.0000 episode 5, total reward: 68.0000 episode 6, total reward: 264.0000 episode 7, total reward: 50.0000 episode 8, total reward: 22.0000 episode 9, total reward: 10.0000 episode 10, total reward: 14.0000 episode 11, total reward: 1.0000 episode 12, total reward: 32.0000 episode 13, total reward: 150.0000 episode 14, total reward: 12.0000 episode 15, total reward: 16.0000 episode 16, total reward: 7.0000 episode 17, total reward: 44.0000 episode 18, total reward: 36.0000 episode 19, total reward: 58.0000 episode 20, total reward: 40.0000 episode 21, total reward: 81.0000 episode 22, total reward: 11.0000 episode 23, total reward: 32.0000 episode 24, total reward: 26.0000 episode 25, total reward: 35.0000 episode 26, total reward: 45.0000 episode 27, total reward: 1.0000 episode 28, total reward: 100.0000 episode 29, total reward: 79.0000 episode 30, total reward: 38.0000 episode 31, total reward: 23.0000 episode 32, total reward: 57.0000 episode 33, total reward: 88.0000 episode 34, total reward: 31.0000 episode 35, total reward: 5.0000 episode 36, total reward: 55.0000 episode 37, total reward: 75.0000 episode 38, total reward: 3.0000 episode 39, total reward: 7.0000 episode 40, total reward: 14.0000 episode 41, total reward: 93.0000 episode 42, total reward: 31.0000 episode 43, total reward: 22.0000 episode 44, total reward: 13.0000 episode 45, total reward: 89.0000 episode 46, total reward: 28.0000 episode 47, total reward: 35.0000 episode 48, total reward: 10.0000 episode 49, total reward: 24.0000 average reward by 50: 42.2600また、学習中の TensorBoard での reward の様子です。
100k step ほどで学習は終わっていそうですね。
実装の紹介
実行時の notebook はこちらです。
主要なところを紹介していきます。Experience クラス
まずは次のように
NamedTupleを使って Experience クラスを定義します。
学習のため、エージェントに行動をさせた結果を学習データとして Experience Reply に積みますが、その1データ分を格納するクラスを作っておきます。class Experience(NamedTuple): state: gym.spaces.Box action: int reward: float next_state: gym.spaces.Box done: boolここでの state や reward は上記で定義したもの(変換済みのもの)です。
モデル
次に、ニューラルネットによるモデルを定義します。入力を状態、出力を各行動 (0 or 1) 毎の価値を出力するようなモデルです。
今回はtf.keras.Modelのサブクラスとして作成し、後にこれを用いて keras の Functional API を使えるようなモデルに変換しました。
(keras, サブクラスでも Functional API 使えるようになってほしい)class AgentModel(tf.keras.Model): def __init__(self, is_training: bool, num_outputs: int): super(AgentModel, self).__init__() self.is_training = is_training self.num_outputs = num_outputs k_init = tf.keras.initializers.glorot_normal() relu = tf.nn.relu self.conv_01 = tf.keras.layers.Conv2D(16, kernel_size=8, strides=4, padding='same', kernel_initializer=k_init, activation=relu) self.conv_02 = tf.keras.layers.Conv2D(32, kernel_size=4, strides=4, padding='same', kernel_initializer=k_init, activation=relu) self.conv_03 = tf.keras.layers.Conv2D(64, kernel_size=3, strides=2, padding='same', kernel_initializer=k_init, activation=relu) self.flatten = tf.keras.layers.Flatten() self.dense = tf.keras.layers.Dense(256, kernel_initializer=k_init, activation=relu) self.output_layer = tf.keras.layers.Dense(num_outputs, kernel_initializer=k_init) def call(self, inputs): outputs = inputs outputs = self.conv_01(outputs) outputs = self.conv_02(outputs) outputs = self.conv_03(outputs) outputs = self.flatten(outputs) outputs = self.dense(outputs) outputs = self.output_layer(outputs) return outputsモデルの構成としては、特に工夫せずに書籍などを参考にしました。
3層の convolution レイヤのあと、flat なベクトルに変形し、dense レイヤを通して2つの値を出力します。
このように定義したモデルを、後ほど定義する Agent クラスで次のように使っています。
このようにしないと、 Keras API を使えなかったためです。tf.keras.Modelsのサブクラスでも Keras API を使う方法を知ってる方いれば教えてください inputs = tf.keras.Input(shape=self.input_shape) model = AgentModel(is_training=True, num_outputs=len(self.actions)) outputs = model(inputs) self.model = tf.keras.Model(inputs=inputs, outputs=outputs)
inputs = tf.keras.Input(shape=self.input_shape) model = AgentModel(is_training=True, num_outputs=len(self.actions)) outputs = model(inputs) self.model = tf.keras.Model(inputs=inputs, outputs=outputs)Agent クラス
Agent クラスでは、次のことを行います。
- ニューラルネットによるモデルを準備する
- 状態を入力として行動を返す
- データをもとにモデルを学習する
class Agent: def __init__(self, actions, epsilon, input_shape, learning_rate=0.0001): self.actions = actions self.epsilon = epsilon self.input_shape = input_shape self.learning_rate = learning_rate self.model = None self._teacher_model = None self.initialize() def initialize(self): self.build() optimizer = tf.train.RMSPropOptimizer(self.learning_rate) self.model.compile(optimizer, loss='mse') def save(self, model_path): self.model.save_weights(model_path, overwrite=True) @classmethod def load(cls, env, model_path, epsilon=0.0001): actions = list(range(env.action_space.n)) input_shape = (env.width, env.height, env.frame_count) agent = cls(actions, epsilon, input_shape) agent.initialize() agent.model.load_weights(model_path) return agent def build(self): inputs = tf.keras.Input(shape=self.input_shape) model = AgentModel(is_training=True, num_outputs=len(self.actions)) outputs = model(inputs) self.model = tf.keras.Model(inputs=inputs, outputs=outputs) # teacher_model を更新するため、両方のモデルで一度計算し重みを取得する self._teacher_model = AgentModel(is_training=True, num_outputs=len(self.actions)) dummy = np.random.randn(1, *self.input_shape).astype(np.float32) dummy = tf.convert_to_tensor(dummy) _ = self.model.call(dummy) _ = self._teacher_model.call(dummy) self.update_teacher() def policy(self, state) -> int: ''' epsilon greedy で受け取った state をもとに行動を決定する ''' # epsilon greedy if np.random.random() < self.epsilon: return np.random.randint(len(self.actions)) else: estimates = self.estimate(state) return np.argmax(estimates) def estimate(self, state): ''' ある state の状態価値を推定する ''' state_as_batch = np.array([state]) return self.model.predict(state_as_batch)[0] def update(self, experiences, gamma): ''' 与えられた experiences をもとに学習 ''' states = np.array([e.state for e in experiences]) next_states = np.array([e.next_state for e in experiences]) estimated_values = self.model.predict(states) next_state_values = self._teacher_model.predict(next_states) # train for i, e in enumerate(experiences): reward = e.reward if not e.done: reward += gamma * np.max(next_state_values[i]) estimated_values[i][e.action] = reward loss = self.model.train_on_batch(states, estimated_values) return loss def update_teacher(self): self._teacher_model.set_weights(self.model.get_weights()) def play(self, env, episode_count: int = 2, render: bool = True): total_rewards = [] for e in range(episode_count): state = env.reset() done = False episode_reward = 0 while not done: if render: env.render() action = self.policy(state) step_reward = 0 for _ in range(4): next_state, reward, done = env.step_with_raw_reward(action) if done: break step_reward += reward episode_reward += reward state = next_state print('episode {}, total reward: {:.4f}'.format(e, episode_reward)) total_rewards.append(episode_reward) env.reset() print('average reward by {}: {:.4f}'.format(episode_count, np.mean(total_rewards)))
def policyでは、epsilon greedy によって、ランダムに選んだ行動か、与えられた状態をもとに最も価値が高くなる行動を返しています。
def updateでは、experiences (データの batch)からモデルの学習を行っています。また、ここでは Fixed Target Q-Network というテクニックを使用しています。
次のように、update内で、遷移先の状態価値の計算にはself.modelではなくself._teacher_modelを使用し、それを正解ラベルとして学習を行っています。estimated_values = self.model.predict(states) next_state_values = self._teacher_model.predict(next_states)
self.modelは各 minibatch 毎にパラメータが更新されているため、遷移先状態もself.modelを用いて推定を行ってしまうと、TD誤差も不安定になってしまいます。
これを避けるために、self._teacher_modelを用意し、定期的に更新しつつも各 minibatch では同じモデルを使えるようにしています。Trainer クラス
Trainer クラスは、名前の通りモデルの学習を行うクラスです。
agent を初期化し、行動させながらデータを溜め、そのデータを使って agent を学習させます。また、学習状況の可視化や、モデルの保存、前述したteacher_modelの更新などの処理も含まれています。
細かい実装はソースを見ていただくとして、メインの学習部分を下記に貼ります。class Trainer: # ... 略 ... def train_loop(self, env, agent, episode_count, initial_count): for episode in range(episode_count): state = env.reset() done = False step_count = 0 episode_reward = 0 while not done: action = agent.policy(state) step_reward = 0 for _ in range(4): next_state, reward, done = env.step(action) if done: break step_reward += reward e = Experience(state, action, step_reward, next_state, done) self.experiences.append(e) episode_reward += step_reward loss = self.step(episode, agent) state = next_state if not self.training and (len(self.experiences) >= self.buffer_size or episode >= initial_count): self.begin_training(agent) self.training = True self.end_episode(episode, episode_reward, loss, agent)エピソードカウント分、下記のループを回します。
- 環境を初期化する
- Agent モデルに状態を渡して行動を受け取る
- 環境に対して行動し、遷移先状態と報酬、ゲームが終わったかどうかのフラグを得る
- 得られた状態、行動、遷移先状態、報酬を experiences に追加する
- (ある程度データが溜まっていれば)モデルを1ステップ学習させる
行動選択後に少し注意点があります。
action = agent.policy(state) step_reward = 0 for _ in range(4): next_state, reward, done = env.step(action) if done: break step_reward += reward現在の状態から行動を受け取ったあと、4回連続でそれを実行しています。
これは、問題設定で書いた「同じ行動を4回繰り返す」をコードに落としたものです。
通常ではこのような処理は必要なく、得られた行動を1度だけ環境に対して実行してやれば良いと思います。まとめ
FlappyBird を強化学習で攻略する第一歩として、ベースラインとなる DQN を実装しました。
学習させた結果、人間レベルのプレイが既に出来てきました。
とはいえ、学習が難しいと言われる強化学習を取り扱うためには、問題設定や前処理がかなり重要になってくることも分かりました。
報酬や行動をどのように定義すればうまくいくかなどについても、実問題への適用の際には熟考する必要がありそうです。
- 投稿日:2019-03-18T22:42:44+09:00
FXの一分足データから五分後の上昇下落を予想する
ディープラーニングを初めて実装した
今回はディープを使ってFXの株価予想をしていきたいと思う。理由は僕がお金稼ぎに興味があるから。今まで勉強してきて金を稼ぐよりも強い動機は今までにない。
開発環境はGoogleColaboratory
言語はpython3
実装にはtensorflow/kerasを使用した使用するデータはFXの一分足データを処理して特徴量を11用意した。期間は2018/1/1~2018/10/8
期間が中途半端なのはデータを習得した日付である。許して。
時系列データなので本当はバックプロパゲーションではなくリカレントのほうがいいのだとは思うが習作なのでとりあえずはこれでいく。
上がるか下がるかのニクラス分類問題にする。
実装
from google.colab import files import pandas as pd import io dataM1 = pd.read_csv('/content/drive/My Drive/out_2018usdjpy.csv', sep = ",") import random import numpy as np import pandas as pd import tensorflow as tf from sklearn.model_selection import train_test_split from sklearn.feature_extraction import DictVectorizer from sklearn import preprocessing import time import keras #csvデータの読み取り time1 = time.time() dataM2 = dataM1.dropna() #欠損値がある行の削除 data1 = dataM2.values#numpy配列に変更 print(data1.shape) col = 11 #特徴量の数 X = data1[col:, 1:col]#特徴量行列の設定 y = data1[col:, col:]#ターゲットデータの設定 print(X.shape) hl = y#numpy配列に変更 print(hl.shape) time2= time.time() time3 = time2-time1 print(time3) sc=preprocessing.StandardScaler() sc.fit(X) X_std=sc.transform(X) #データの正規化 X_train, X_test, y_train, y_test=train_test_split(X_std,hl.reshape(-1,), test_size=0.3,random_state = 1) #テストデータとトレーニングデータを分割 print(X_train.shape[0]) print(X_train.shape[1]) print(X_train.shape) print(y_train.shape) np.random.seed(123) tf.set_random_seed(123) time4 = time.time() y_train_onehot = keras.utils.to_categorical(y_train) model = keras.models.Sequential() model.add(keras.layers.Dense(units = 300, input_dim = X_train.shape[1], kernel_initializer ="glorot_uniform", bias_initializer ='zeros', activation = "tanh" )) model.add(keras.layers.Dense(units = 300, input_dim = 300, kernel_initializer ="glorot_uniform", bias_initializer ='zeros', activation = "tanh" )) model.add(keras.layers.Dense(units = 300, input_dim = 300, kernel_initializer ="glorot_uniform", bias_initializer ='zeros', activation = "tanh" )) model.add(keras.layers.Dense(units = 300, input_dim = 300, kernel_initializer ="glorot_uniform", bias_initializer ='zeros', activation = "tanh" )) model.add(keras.layers.Dense(units = 300, input_dim = 300, kernel_initializer ="glorot_uniform", bias_initializer ='zeros', activation = "tanh" )) model.add(keras.layers.Dense(units = y_train_onehot.shape[1], input_dim = 300, kernel_initializer ="glorot_uniform", bias_initializer ='zeros', activation = "softmax" )) sgd_optimizer = keras.optimizers.SGD(lr=0.01,decay = 1e-7,momentum= .9) model.compile(optimizer= sgd_optimizer,loss='categorical_crossentropy') history = model.fit(X_train, y_train_onehot, batch_size = 64, epochs = 0, verbose= 1, validation_split = 0.1 ) y_train_pred = model.predict_classes(X_train,verbose =0) print("first 3 predictions: ",y_train_pred[:3]) correct_preds = np.sum(y_train == y_train_pred,axis = 0) time5 = time.time() print(time5-time4) train_acc = correct_preds / y_train.shape[0] print("training accuracy: %.2f%%" % (train_acc * 100)) y_test_pred = model.predict_classes(X_test,verbose =0) correct_preds2 = np.sum(y_test == y_test_pred,axis = 0) test_acc = correct_preds2 / y_test.shape[0] print("test accuracy: %.2f%%" % (test_acc * 100))結果
training accuracy: 50.15%
test accuracy: 50.09%感想
まあ儲からないよなっていう印象。流石はランダムウォークというべきか。結果を見ての通りにクラス分類で50%ってことはそういうことなんだろうと思う。
今回はとりあえず学習させてみて挙動を見たかったのでこれで良い。改善したいことはこちらの記事にまとめた。
- 投稿日:2019-03-18T22:30:29+09:00
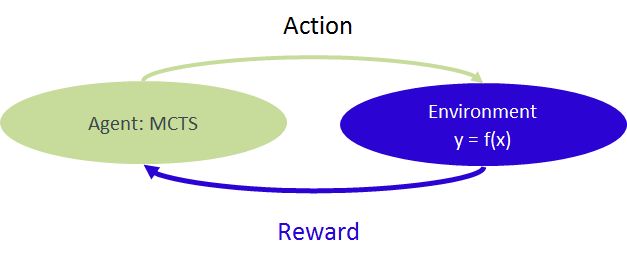
Monte Carlo Tree Search for finding a minimum of a multi-variable equation
Introduction
In this my first post on Qiita, I describe Monte Carlo tree search (MCTS) for solving a simple math problem. The purpose is to show how MCTS can be utilized for a general math problem other than Chess, Go, Shogi, etc.
Monte-Carlo Tree Search (MCTS)
MCTS is known as an efficient tree search algorithm for computational Go programs. In this post, we see how MCTS can be applied for solving a simple multi-variable equation.
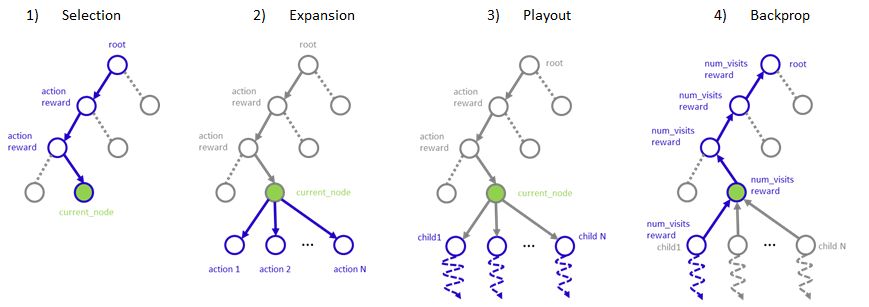
MCTS starts from a root node and repeats a procedure below until it reaches terminal conditions:
1) Selection: selects one terminal node using a rule
2) Expansion: add additional nodes represents possible actions to a selected node.
3) Playout: take random actions from expanded nodes and score values of these nodes based on the outcome of random actions.
4) Backpropergation: reflect playout result to all parent nodes up to a rootExample problem
Let's assume a multi-variable equation in the following form and find a minimum using MCTS:
y = f(x) = (x_1 - a)^2 + (x_2 - b)^2 + (x_3 - c)^2 + (x_4 -d)^2Generally, the form of f(x) is unknown in a type of problems that MCTS would be employed. In this simple example, we already know f(x) take a minimum value at (x1, x2, x3, x4) = (a, b, c, d). We would like MCTS to find a series of actions to reach this minimum. To apply this problem to MCTS, we define discrete actions for x:
- Add x1 to +1
- Add x1 to -1
- Add x2 to +1
- Add x2 to -1
...
etc.Starting from arbitrary initial values of x and repeating actions, it results in a sequence of actions: (x1:+1, x2:-1, ....). MCTS tries to find an action sequence that maximizes a cumulative reward.
Reinforcement learning
A process to solve the problem can be seen as a reinforcement learning, where the relationship y=f(x) can be seen as "environment" receiving actions from MCTS agent and returning "reward" to MCTS agent.
Pseudo code
Main part of the code has structure below. Since MCTS is probabilistic, it may or may not reach the actual minimum. Thus, a tree is generated multiple times and a best result is returned.
Software versions
- Python 3.5.2
- Numpy 1.14.2+mkl
Code
from math import * from copy import copy import numpy as np import random class environment: def __init__(self): self.a = 0. self.b = 2. self.c = 1. self.d = 2. self.x1 = -12. self.x2 = 14. self.x3 = -13. self.x4 = 9. self.f = self.func() def func(self): return (self.x1 - self.a)**2+(self.x2 - self.b)**2+(self.x3 - self.c)**2+(self.x4 - self.d)**2 def step(self, action): f_before = self.func() if action == 1: self.x1 += 1. elif action == -1: self.x1 -= 1. elif action == 2: self.x2 += 1. elif action == -2: self.x2 -= 1. elif action == 3: self.x3 += 1. elif action == -3: self.x3 -= 1. elif action == 4: self.x4 += 1. elif action == -4: self.x4 -= 1. f_after = self.func() if f_after == 0: reward = 100 terminal = True else: reward = 1 if abs(f_before) - abs(f_after) > 0 else -1 terminal = False return f_after, reward, terminal, [self.x1, self.x2, self.x3, self.x4] def action_space(self): return [-4, -3, -2, -1, 0, 1, 2, 3, 4] def sample(self): return np.random.choice([-4, -3, -2, -1, 0, 1, 2, 3, 4]) class Node(): def __init__(self, parent, action): self.num_visits = 1 self.reward = 0. self.children = [] self.parent = parent self.action = action def update(self, reward): self.reward += reward self.visits += 1 def __repr__(self): s="Reward/Visits = %.1f/%.1f (Child %d)"%(self.reward, self.num_visits, len(self.children)) return s def ucb(node): return node.reward / node.num_visits + sqrt(log(node.parent.num_visits)/node.num_visits) def reward_rate(node): return node.reward / node.num_visits SHOW_INTERMEDIATE_RESULTS = False env = environment() num_mainloops = 20 max_playout_depth = 5 num_tree_search = 180 best_sum_reward = -inf best_acdtion_sequence = [] best_f = 0 best_x = [] for _ in range(num_mainloops): root = Node(None, None) for run_no in range(num_tree_search): env_copy = copy(env) terminal = False sum_reward = 0 # 1) Selection current_node = root while len(current_node.children) != 0: current_node = max(current_node.children, key = ucb) _, reward, terminal, _ = env_copy.step(current_node.action) sum_reward += reward # 2) Expansion if not terminal: possible_actions = env_copy.action_space() current_node.children = [Node(current_node, action) for action in possible_actions] # Routine for each children hereafter for c in current_node.children: # 3) Playout env_playout = copy(env_copy) sum_reward_playout = 0 action_sequence = [] _, reward, terminal, _ = env_playout.step(c.action) sum_reward_playout += reward action_sequence.append(c.action) while not terminal: action = env_copy.sample() _, reward, terminal, _ = env_playout.step(action) sum_reward_playout += reward action_sequence.append(action) if len(action_sequence) > max_playout_depth: break if terminal: print("Terminal reached during a playout. #########") # 4) Backpropagate c_ = c while c_: c_.num_visits +=1 c_.reward += sum_reward + sum_reward_playout c_ = c_.parent #Decision current_node = root action_sequence = [] sum_reward = 0 env_copy = copy(env) while len(current_node.children) != 0: current_node = max(current_node.children, key = reward_rate) action_sequence.append(current_node.action) for action in action_sequence: _, reward, terminal, _ = env_copy.step(action) sum_reward += reward if terminal: break f, _, _, x = env_copy.step(0) if SHOW_INTERMEDIATE_RESULTS == True: print("Action sequence: ", str(action_sequence)) print("Sum_reward: ", str(sum_reward)) print("f, x (original): ", env.f , str([env.x1, env.x2])) print("f, x (after MCT): ", str(f), str(x) ) print("----------") if sum_reward > best_sum_reward: best_sum_reward = sum_reward best_action_sequence = action_sequence best_f = f best_x = x print("Best Action sequence: ", str(best_action_sequence)) print("Action sequence length: ", str(len(best_action_sequence))) print("Best Sum_reward: ", str(best_sum_reward)) print("f, x (original): ", env.f , str([env.x1, env.x2, env.x3, env.x4])) print("f, x (after MCTS): ", str(best_f), str(best_x) )Result
Running the code above, it prints the best action sequence found by MCTS.
f, x (original) -- corresponds initial state, and
f, x (after MCTS) --- shows final x take all actions and falue of f(x).Terminal reached during a playout. ######### Terminal reached during a playout. ######### ... Terminal reached during a playout. ######### Best Action sequence: [3, -4, -4, 3, 3, 3, -4, -4, 3, 3, 3, -4, -2, -2, -4, -2, -2, -4, 0, 3, 1, -3, -2, 1, -4, -4, -3, 3, -1, -2, 3, 1, 1, 4, 1, 4, 2, -2, 1, -2, 3, -3, 1, 2, -2, -3, 1, 3, -4, -4, -1, -2, -4, 1, 3, -2, 4, 3, 3, 1, -3, -2, 1, -2, 1, 1, 4, -1, 1, 4, -4, -2, -4, 3, 3, 1, 2, -2, -4, -4, 4, -2, -3, 3, 4, 2, -1, -2, -1, -3, 4, 0, 3, -4, -3, -3, 3, -2, 3, 2, 2, -4, -2, -4, 1, -4, 4, -3 , 1, 3, -1, -2, 4, 3, -4, -1, 2, 4, 2, 1, 4, -4, 4, -3, 1, -1, 4, 0, -3, 2, 1, 4 , 1, -1, 3, 3, -3, -2, 3, 3] Action sequence length: 140 Best Sum_reward: 141 f, x (original): 533.0 [-12.0, 14.0, -13.0, 9.0] f, x (after MCTS): 0.0 [0.0, 2.0, 1.0, 2.0]References
- https://www.youtube.com/watch?v=Fbs4lnGLS8M
- https://jeffbradberry.com/posts/2015/09/intro-to-monte-carlo-tree-search/
- https://en.wikipedia.org/wiki/Monte_Carlo_tree_search
Note
This code can be freely copied, modified, and used. Please cite if this post is useful.
- 投稿日:2019-03-18T22:01:25+09:00
GoogleColaboratory でGoogleDriveのをマウントするときのディレクトリの位置がわからなかった話
ディレクトリの名前がわからなかった
GoogleColaboratory でGoogleDriveのをマウントする方法についてはこちらの記事がわかりやすい。
https://qiita.com/k_uekado/items/45b76f9a6f920bf0f786
こんなに簡単になっていたとは驚きだ。
ところでここで、マウントはできたもののディレクトリの指定がうまく行かず何度もNot existになった。
公式のここを参考にしてもうまくいかない。
https://colab.research.google.com/notebooks/io.ipynb
解決方法
なんと公式のディレクトリ名が間違っている。
公式で挙げられているドライブのルートディレクトリはこうなっている。
/content/gdrive/My Drive/
実際には下記が正しい。
/content/drive/My Drive/
gdriveではなくdriveであるので注意されたし。あとはGoogle Colaboratory を使っていればgoogle colabというファイルがあるといった具合だ。
- 投稿日:2019-03-18T21:40:50+09:00
最近のColaboratory
いくつか古い項目も在るが過去のColaboratoryから更新されて気づいた部分についてまとめてみる。
- ChainerとPytorchがデフォルトインストールされるようになっていてpipしなくていい
- OpenAIGymもデフォルトインストールされるようになった
- 右上に現在のランタイムのRAMとディスクの使用量が表示されるようになった
- Googleドライブのマウント2行になった
google_drive_mount.pyfrom google.colab import drive drive.mount('/content/drive')
- 投稿日:2019-03-18T21:34:05+09:00
【Python】自前の大規模コーパスでWord2vecのモデルを訓練して既存のモデルと性能比較を行う!!
はじめに
最初からネットにあがってるモデルをそのまま使うのが一般的と思えるWord2vec
ある特定の分野における単語の分散表現は,そのある特定の分野のコーパスでモデルを訓練させた方が,精度が上がりかつ元のモデルには存在しなかった単語の分散表現が新規に作成されるのでは
という仮説の元,自前で用意した大規模文書コーパスを使ってWord2vecの訓練を行う
準備
形態素解析済みの大規模コーパス
1.クエリ・フォーカスを入力に,クエリに関する検索エンジン・サジェストを収集
2.その後,Google Custom Search API使って各「クエリ AND サジェスト」の検索結果(URL群)を取得
3.取得したURL群を入力に,スクレイピングによってウェブページの文書集合作成
4.文書集合をMecabで形態素解析形態素解析済みのWikipediaの大規模コーパス
1.wikipediaのほうで既に分かち書き(形態素解析済)の文書コーパスをダウンロード
用意した2つのコーパスをマージする
・2つのファイルを1つにマージし訓練コーパスとする
・コマンドラインまたはプログラムでマージする(ここは省略)
・一文で一行としている
・訓練コーパスを「wiki_and_webpage_appended.txt」とするモデルの訓練
#coding:utf-8 from gensim.models import word2vec import logging logging.basicConfig(format='%(asctime)s : %(levelname)s : %(message)s', level=logging.INFO) sentences = word2vec.Text8Corpus('./wiki_and_webpage_appended.txt') model = word2vec.Word2Vec(sentences, size=20, min_count=2, window=20) model.save("./text.model")今回は
・クエリ:「花粉症」
・次元数:20
・単語の必要最低限の出現回数:2回
・ウィンドウサイズ:20
とした
Word2vecのパラメータ設定はコチラ出来上がったモデルはtext.modelとしてカレントディレクトリ内に保存される
今回の場合,訓練には1時間ほどかかった
次回,既存モデル(Wikipedia文章で作成されたモデル)と今回作ったモデルの比較検証を行う
- 投稿日:2019-03-18T21:34:05+09:00
【Python】Gensim使ってWord2vecのモデル訓練 - Neural Network -
はじめに
最初からネットにあがってるモデルをそのまま使うのが一般的と思えるWord2vec
ある特定の分野における単語の分散表現は,そのある特定の分野のコーパスでモデルを訓練させた方が,精度が上がりかつ元のモデルには存在しなかった単語の分散表現が新規に作成されるのでは
という仮説の元,自前で用意した大規模文書コーパスを使ってWord2vecの訓練を行う
準備
形態素解析済みの大規模コーパス
1.クエリ・フォーカスを入力に,クエリに関する検索エンジン・サジェストを収集
2.その後,Google Custom Search API使って各「クエリ AND サジェスト」の検索結果(URL群)を取得
3.取得したURL群を入力に,スクレイピングによってウェブページの文書集合作成
4.文書集合をMecabで形態素解析形態素解析済みのWikipediaの大規模コーパス
1.Wikipediaではスクレイピングを禁止している代わりに,Wikipediaの大規模コーパスを公開しているのでそれをダウンロード
2.ダウンロードしたWikipediaの大規模コーパスに対してMecabを適用し形態素解析実行
- 投稿日:2019-03-18T21:34:05+09:00
【Python】GensimでWord2vecのモデル訓練 - Neural Network -
はじめに
最初からネットにあがってるモデルをそのまま使うのが一般的と思えるWord2vec
ある特定の分野における単語の分散表現は,そのある特定の分野のコーパスでモデルを訓練させた方が,精度が上がりかつ元のモデルには存在しなかった単語の分散表現が新規に作成されるのでは
という仮説の元,自前で用意した大規模文書コーパスを使ってWord2vecの訓練を行う
準備
形態素解析済みの大規模コーパス
1.クエリ・フォーカスを入力に,クエリに関する検索エンジン・サジェストを収集
2.その後,Google Custom Search API使って各「クエリ AND サジェスト」の検索結果(URL群)を取得
3.取得したURL群を入力に,スクレイピングによってウェブページの文書集合作成
4.文書集合をMecabで形態素解析形態素解析済みのWikipediaの大規模コーパス
1.wikipediaのほうで既に分かち書き(形態素解析済)の文書コーパスをダウンロード
用意した2つのコーパスをマージする
・2つのファイルを1つにマージし訓練コーパスとする
・コマンドラインまたはプログラムでマージする(ここは省略)
・一文で一行としている
・訓練コーパスを「wiki_and_webpage_appended.txt」とする実行
#coding:utf-8 from gensim.models import word2vec import logging logging.basicConfig(format='%(asctime)s : %(levelname)s : %(message)s', level=logging.INFO) sentences = word2vec.Text8Corpus('./wiki_and_webpage_appended.txt') model = word2vec.Word2Vec(sentences, size=20, min_count=2, window=20) model.save("./text.model")今回は
・クエリ:「就活」
・次元数:20
・単語の必要最低限の出現回数:2回
・ウィンドウサイズ:20
とした
Word2vecのパラメータ設定はコチラ出来上がったモデルはtext.modelとしてカレントディレクトリ内に保存される
今回の場合,訓練には1時間ほどかかった
次回,既存モデル(Wikipedia文章で作成されたモデル)と今回作ったモデルの比較検証を行う
- 投稿日:2019-03-18T21:34:05+09:00
【Python】自前の大規模コーパスでWord2vecのモデル訓練と性能比較!!
はじめに
最初からネットにあがってるモデルをそのまま使うのが一般的と思えるWord2vec
ある特定の分野における単語の分散表現は,そのある特定の分野のコーパスでモデルを訓練させた方が,精度が上がりかつ元のモデルには存在しなかった単語の分散表現が新規に作成されるのでは
という仮説の元,自前で用意した大規模文書コーパスを使ってWord2vecの訓練を行う
準備
形態素解析済みの大規模コーパス
1.クエリ・フォーカスを入力に,クエリに関する検索エンジン・サジェストを収集
2.その後,Google Custom Search API使って各「クエリ AND サジェスト」の検索結果(URL群)を取得
3.取得したURL群を入力に,スクレイピングによってウェブページの文書集合作成
4.文書集合をMecabで形態素解析形態素解析済みのWikipediaの大規模コーパス
1.wikipediaのほうで既に分かち書き(形態素解析済)の文書コーパスをダウンロード
用意した2つのコーパスをマージする
・2つのファイルを1つにマージし訓練コーパスとする
・コマンドラインまたはプログラムでマージする(ここは省略)
・一文で一行としている
・訓練コーパスを「wiki_and_webpage_appended.txt」とする実行
#coding:utf-8 from gensim.models import word2vec import logging logging.basicConfig(format='%(asctime)s : %(levelname)s : %(message)s', level=logging.INFO) sentences = word2vec.Text8Corpus('./wiki_and_webpage_appended.txt') model = word2vec.Word2Vec(sentences, size=20, min_count=2, window=20) model.save("./text.model")今回は
・クエリ:「就活」
・次元数:20
・単語の必要最低限の出現回数:2回
・ウィンドウサイズ:20
とした
Word2vecのパラメータ設定はコチラ出来上がったモデルはtext.modelとしてカレントディレクトリ内に保存される
今回の場合,訓練には1時間ほどかかった
次回,既存モデル(Wikipedia文章で作成されたモデル)と今回作ったモデルの比較検証を行う
- 投稿日:2019-03-18T20:44:48+09:00
python、djangoのurls.pyで設定するnameってなんやねん??
python、djangoのurls.pyで設定するnameってなんやねん??
ということをdjangoをやりはじめた当初はよく分かっていませんでした。
いまでも怪しいのでまとめてみましょう。djangoをにはurls.py(djangoはurls.pyが2つ存在するのですが、アプリケーションの中にあるurls.pyのことです)にnameと書くことがあります。
from django.urls import path from . import views app_name = 'board' urlpatterns = [ path('', views.ListView.as_view(), name='board'), path('good/<int:pk>', views.good, name='good'), ]こんな風になっています。ひとつひとつ解体していくと・・・。
path('good/<int:pk>',これはURLの設定。
views.goodこれはそのURLに使う関数の設定。
この設定が無いとviews.pyで関数を作ってもそのページで使用できません。name='good'なんだこいつ??
このname='good'。html部分によく使われます。
以下はフォームを送信するとurls.pyで設定したpath('good/int:pk', に飛びます。<form action="{% url 'board:good' post.pk %}" method="post"> {% csrf_token %} <input type="submit" name="good" value="いいね" id="test">({{ post.good }} いいね)<p style="color:red"><font size="1"><strong>押すと1ページ目まで戻ってしまいます!(いつか直す!)</strong></font></p> </form>
飛ぶのはいいのですがメンテナンス部分には問題があって、これって例えば
<form action="/board/good/" method="post">と書いてしまうと設定しているurlが変更になると該当箇所は全部書き換えですよね?
なのでurlにname='good'のように名前を設定しておいてpath('good/<int:pk>', views.good, name='good'),formのurlも名前であるgoodに書き換えます。
<form action="{% url 'board:good' post.pk %}" method="post">'board:good'と書き換えればurlが変更してもnameは変更になっていないのでform部分は変更する必要が無いんですね。
多分これは逆引きという方法だと思います。普通にURL書くのは正引き?間違ってたら教えてください。
他にもメリットがあるような気がしているのですが今のところよく分かっていませんw
ちなみに'board:good'のboardはurls.pyの
app_name = 'board'です。
boardアプリケーションのgoodと名前のついたurlを指定しているんですね。
djangoプロジェクト内には複数のアプリケーションを作ることが可能なので、app_nameを重複させないように気を付けてくださいね。
重複させたらどうなるのか試したことはないけれど。
- 投稿日:2019-03-18T20:37:35+09:00
アルゴリズム(DFS/BFSを1ステップずつ追いかけてみる)
DFS / BFSとは
- Wikipedia - 深さ優先探索(Depth-First Search、DFS、バックトラック法)
- Wikipedia - 幅優先探索(Breadth-First Search、BFS)
Wikipediaにはなんだか難しそうな事が書いてありますが、「経路を順にたどってゴールに到達するような問題」「ルールに基づいて一定範囲を塗りつぶすような問題」を実装する際に役に立つアルゴリズムです。迷路を解くとか一定エリアの広さを考えるといった問題が出てきたらまずはこの DFS / BFS が適用可能かどうか考えてみると良い 1 と思います。
「知らないと詰む」系のアルゴリズムですし、知ってると気持ちよく解ける 2 のでぜひ DP(動的計画法)の前にこちらを使い倒せるようにしてください。
迷路のような典型的な問題であればすぐに DFS / BFS を思いつくのですが、塗りつぶしや領域判定でこれが使えることは慣れないと思いつきにくいです。
実装イメージ
実装にあたって用意するものは下記の2点です。
- 探索候補地点を格納する「探索候補スタック」
- 探索済み地点を格納する「探索済みリスト」
これらを使って、DFS を組む時の具体的なロジックイメージは下記の通りです。※BFS を組む場合は「候補探索スタック」を「候補探索キュー」に、
popをpop(0)もしくはpopleft(collections.deque の場合)に読み替えてください探索スタート地点を「探索候補スタック」に積む while スタックが空っぽになるまで スタックから次の探索地点を1つ取り出す(pop) 「探索済みリスト」に取り出した地点を格納(ここが現在地点) 現在地点から、次に行こうと思えば行けるポイントを全部探し出す for 地点 in 次に行こうと思えば行けるポイント if その地点は既に「探索済みリスト」にある? 探索済みなので「探索候補スタック」には入れない(continue) if その地点は既に「探索候補スタック」にある?(閉路があるなら可能性あり、木なら可能性なし) 探索予定なので「探索候補スタック」には入れない(continue) 未探索かつ候補にも入っていない地点なので「探索候補スタック」に追加する(append) print 探索済み地点これをブン回せば、最後に出てくる「探索済みリスト」が探索の足跡を全部記録してくれています。
塗りつぶし面積などを求めたい場合はこうやってDFSすると探索の足跡サイズ(配列の大きさ)がそのまま面積になりますし、迷路の最短経路を求めたい場合は上記をキューに変更してBFSするとゴールまでの最短距離が分かります(ゴールに到着した瞬間に break)
DFS は再帰で実装する例もよく紹介されますが、個人的には DFS だろうと BFS だろうと同じロジックで実装できる、上記の「空っぽになるまで while でブン回す」方がシンプルでオススメです。
【重要】なんでこれでできるの?
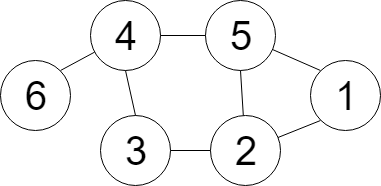
DFS / BFS の手法によってなぜ経路探索が無駄なく実現できるのか、なぜスタックだと深さ優先でキューだと幅優先が実現されるのかについては、ぜひ頭の中できちんと理解をしておいてください。特に「探索済みリスト」と「探索候補スタック」がどのように変化していくのかを 1 ステップ 1 ステップ理解することが重要です。
というわけで、上記のような地図を、1 から 6 まで DFS で辿る動きを追ってみましょう。ロジックイメージと地図を横に置いて、下記を読み進めてみてください。
while 1 ループ目(終了地点)
- 現在位置:1
- 探索済みリスト:( 1 )
- 探索候補スタック:( 2, 5 )
スタート地点として「探索候補スタック」に積まれていた 1 が pop され、探索済みリストに格納されます。あわせて 1 から移動する先の候補として 2 と 5 が「探索候補スタック」に積まれます。
while 2 ループ目(終了地点)
- 現在位置:5
- 探索済みリスト:( 1, 5 )
- 探索候補スタック:( 2, 4 )
「探索候補スタック」の一番後ろから 5 が pop され、探索済みリストに格納されます。5 から移動する先の候補は 1 と 2 と 4 ですが、1 は既に「探索済みリスト」に、2 は既に「探索候補スタック」に存在することから探索候補の対象外となり、4 だけが「探索候補スタック」に積まれます。
while 3 ループ目(終了地点)
- 現在位置:4
- 探索済みリスト:( 1, 5, 4 )
- 探索候補スタック:( 2, 3, 6 )
「探索候補スタック」の一番後ろから 4 が pop され、探索済みリストに格納されます。4 から移動する先の候補は 3 と 5 と 6 ですが、5 は既に「探索済みリスト」に存在することから探索候補の対象外となり、3 と 6 が「探索候補スタック」に積まれます。
while 4 ループ目(終了地点)
- 現在位置:6
- 探索済みリスト:( 1, 5, 4, 6 )
- 探索候補スタック:( 2, 3 )
「探索候補スタック」の一番後ろから 6 が pop され、探索済みリストに格納されます。6 から移動する先の候補は 4 ですが、4 は既に「探索済みリスト」に存在することから探索候補の対象外となり、「探索候補スタック」には何も積まれません。
while 5 ループ目(終了地点)
- 現在位置:3
- 探索済みリスト:( 1, 5, 4, 6, 3 )
- 探索候補スタック:( 2 )
「探索候補スタック」の一番後ろから 3 が pop され、探索済みリストに格納されます。3 から移動する先の候補は 2 と 4 ですが、4 は既に「探索済みリスト」に、2 は既に「探索候補スタック」に存在することから探索候補の対象外となり、「探索候補スタック」には何も積まれません。
while 6 ループ目(終了地点)
- 現在位置:2
- 探索済みリスト:( 1, 5, 4, 6, 3, 2 )
- 探索候補スタック:( )
「探索候補スタック」の一番後ろから 2 が pop され、探索済みリストに格納されます。2 から移動する先の候補は 1 と 3 と 5 ですが、全て「探索済みリスト」に存在することから探索候補の対象外となり、「探索候補スタック」には何も積まれません。
ここで探索候補スタックが空っぽになりますので while ループは終了します。
- 投稿日:2019-03-18T20:34:58+09:00
PythonからDLLを使う(classを使ってみる)
はじめに
前回のPythonからDLLを使うの続き
クラスはどうやって使うのかなって思ったので、調べながら進めました。C++でDLLの準備
VS2017で、前回のようにDLLのプロジェクトを作る。今回のプロジェクト名は「DLLTestClass」としました。
DLLTestClass.h#pragma once #ifdef DLLTESTCLASS_EXPORTS #define DLLTESTCLASS_API extern "C" __declspec(dllexport) #else #define DLLTESTCLASS_API extern "C" __declspec(dllimport) #endif // DLLTEST_EXPORTS class Hoge { private: int m_count; public: Hoge(); const wchar_t* showMessage(const wchar_t* message); void count(); void showCount(); }; DLLTESTCLASS_API const wchar_t* showMsg(const wchar_t* mes); DLLTESTCLASS_API void countData(); DLLTESTCLASS_API void showCount();DLLTestClass.cpp// DLLTestClass.cpp : DLL アプリケーション用にエクスポートされる関数を定義します。 // #include "stdafx.h" #include "DLLTestClass.h" #include <iostream> #include <string> Hoge::Hoge() { m_count = 0; } const wchar_t* Hoge::showMessage(const wchar_t* message) { return message; } void Hoge::count() { m_count = m_count + 1; } void Hoge::showCount() { std::cout << m_count << std::endl; } /* ラッパー */ Hoge hoge; const wchar_t* showMsg(const wchar_t* mes) { return hoge.showMessage(mes); } void countData() { hoge.count(); } void showCount() { hoge.showCount(); }stdafx.h// stdafx.h : 標準のシステム インクルード ファイルのインクルード ファイル、 // または、参照回数が多く、かつあまり変更されない、プロジェクト専用のインクルード ファイル // を記述します。 // #pragma once #include "targetver.h" #define WIN32_LEAN_AND_MEAN // Windows ヘッダーからほとんど使用されていない部分を除外する // Windows ヘッダー ファイル #include <windows.h> // プログラムに必要な追加ヘッダーをここで参照してください #include "DLLTestClass.h"C++側の実装はこんな感じ。そのままビルド通ると思います。
よくわかってない中進めていたのですが、ラッパー関数を作ってあげないと、うまく使えないっぽい??(こういうもんなんですかね?)
何か別のライブラリを加えれば、python側でスマートに呼べるみたいなのだけど、、、、ちょっと何を言ってるのかわからないです。とりあえず、python側でcountData()を呼べばカウントがガシガシ行われるようにしてみました。(恐る恐る)
Python側を作る
VSでビルドしたDLLをPython側の環境に持ってきます。(DLLTestClass.dll)
test.py# coding: utf-8 from ctypes import * dll2 = cdll.LoadLibrary("DLLTestClass.dll") # 文字列セット txt = u"あいうえ" dll2.showMsg.argtypes = [c_wchar_p] dll2.showMsg.restype = c_wchar_p print(dll2.showMsg(txt)) # 加算 dll2.countData() dll2.countData() dll2.countData() dll2.countData() # 表示 dll2.showCount()実行結果
> py test.py あいうえ 4テキスト入力して、返ってきて、ちゃんとカウントが4回行われて、表示されました。
ほんと、c_wchar_pの書き方とかググるだけでは本当によくわからなくて時間かかりました。
文字列を受け取って、返す流れとか文字化けとかの戦いでした。検索ワードがよくなかったのかなあ。。クラスを実行するのよりマルチバイト文字列のところが時間かかりました。
何が正しくて何が正しくないのか謎でしたが、今回ひとまず動いたのでヨシとしようと思います。
- 投稿日:2019-03-18T19:24:04+09:00
SVD (singular value decomposition) に入門する
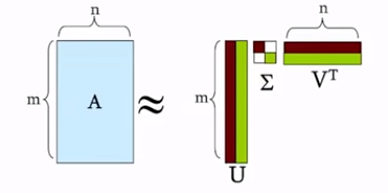
0. 概要
SVD (singular value decomposition)は次元削減(Dimensionality Reduction)分野で用いられる技術である。
例えば、患者のあらゆる生体データから癌など特定の病気と結びつきの強い生体データのみを抽出したりすることにも活用できる。
機械学習で扱うデータ量が多い場合や、感度解析をしたい場合等に用いる。以下のスタンフォード大学のレクチャーが非常に分かりやすい。彼もSVDは次元削減テクニックの内の1つといっている。
https://www.youtube.com/watch?v=P5mlg91as1c1. 理論
SVDとは、任意$i×j$の実数行列$A$を幾何的に解釈可能な3つの行列の積へと分解することに他ならない。
基本の定理は次式である。A_{m×n}=U_{m×r}\Sigma_{r×r} V^{T}_{n×r}各変数の説明は以下である。
$\Sigma$: 正数$\sigma$からなる$r×r$の対角行列で、特異値であり寄与度が高い順にソートされている。固有値からルートを取るだけである。
$U$: $m×r$の直行行列(すなわち、逆行列を計算できる)
また、$A$の左特異ベクトルといい、$m$次元空間における$A$の列の正規直交基底となっている。$V$: $n×r$の直行行列(すなわち、$U^{T}U=V^{T}V=E$)
また、$A$の右特異ベクトルといい、$n$次元空間における$A$の行の正規直交基底となっている。求めた固有値から固有ベクトルを計算して単位ベクトル化するだけである。である。
さらに展開すると、次式のように表現できる。
A =U_{m×r}\Sigma_{r×r} V^{T}_{n×r}\\ =\Sigma _{i}\sigma _{i}u_{i}\circ v^{T}_{i}\\ =\left\{ u_{1},u_{2},\ldots ,u_{i}\right\} \begin{bmatrix} \sigma_{1} & & \\ & \sigma _{2} & \\ & & \ddots \\ & & & \sigma _{i} \end{bmatrix} \begin{bmatrix} v^{T}_1 \\ v^{T}_2 \\ \vdots \\ v^{T}_i \end{bmatrix}この時、$\Sigma$はソートされているため、$\sigma _{1}\geq \sigma _{2}\geq \dots \geq \sigma _{n}$となっている。
$\Sigma$は対角行列のため、$\Sigma \Sigma^{T}=\Sigma^{2}$となり、各特異値$\sigma$は$AA^{T}$の固有値から平方根を取ったものとなる。
すなわち、$AA^{T}=U \Sigma V^{T}V \Sigma^{T} U^{T} = U\Sigma\Sigma^TU^T$となる。イメージ的な話:
$\Sigma$は固有値、$V$は固有ベクトル、じゃあ$U$は・・?
ある行列$A$と積をとっても同じ向きになるベクトルが$V$。$V\Sigma$で$A$と同じ方向のある大きさのベクトルになる。
いわゆる、$A$のデータに見られる共通的な特徴。そして、$U$が主成分(固有値)。もっと単純に言うと
$U$は列の類似度
$V^T$は行の類似度
$\Sigma$は各類似度の強調度2. 計算する
SVDで分解する$A$を次のように定義する
A=\begin{bmatrix} 4 & 0 \\ 3 & -5 \end{bmatrix}Step. 1: $\Sigma$を求める。
まず$A^{T}A$を求める。
A^{T}A=\begin{bmatrix} 4 & 3 \\ 0 & -5 \end{bmatrix} \begin{bmatrix} 4 & 0 \\ 3 & -5 \end{bmatrix} =\begin{bmatrix} 25 & -15 \\ -15 & 25 \end{bmatrix}次に$A^{T}A$から固有値を求める。
(A-\lambda E)=\begin{bmatrix} 25 - \lambda & -15 \\ -15 & 25 - \lambda \end{bmatrix}\\ =(25-\lambda)^{2}-(-15)^2=625-25\lambda-25\lambda+\lambda^{2} - 225\\ = \lambda^{2}-50\lambda+400次式で$\lambda^{2}-50\lambda+400 = 0$を解き、固有値$\lambda$を解く
\lambda^{2}-50\lambda+400 = 0 \\ =(\lambda^{2}-50\lambda+25^{2}-25^{2})+400 :おもむろに平方完成\\ =(\lambda-10)(\lambda-40) -400 +400\\ =(\lambda-10)(\lambda-40) \\よって$\lambda=10$、$\lambda=40$が出てきた。
次にこれを固有値から特異値(Singular values)$\sigma_i$に変換する。といっても、ただ固有値のルートを取るだけである。
\sigma_1=\sqrt{40}=6.32456, \sigma_2=\sqrt{10}=3.1623次に、これを対角行列として配置するが、その際に数値をソートする。今回は$40$の方が大きいのでこちらが上位である。
※ どのようにソートしたか覚えておけば、各要素の寄与率が分かる。\Sigma=\begin{bmatrix} 6.32456 & 0 \\ 0 & 3.1623 \end{bmatrix}, \Sigma^{-1}=\frac{1}{6.32456 * 3.1623 - 0 * 0}\begin{bmatrix} 3.1623 & 0 \\ 0 & 6.32456 \end{bmatrix} =\begin{bmatrix} 0.15812 & 0 \\ 0 & 0.31623 \end{bmatrix}Step. 2: $V$を求める。
固有値が求まったので、次に$V$、これすなわち固有ベクトルを求める。$\lambda=40$の場合:
次式の固有方程式に従って計算を進めていく。
(A^{T}A - \lambda E)\overrightarrow {x} = 0求めた$\lambda$を代入して
(A^{T}A - \lambda E)\overrightarrow {x} =\begin{bmatrix} 25 - 40 & -15 \\ -15 & 25 - 40 \end{bmatrix} \begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix} =\begin{bmatrix} -15 & -15 \\ -15 & -15 \end{bmatrix}\begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix}$\overrightarrow {x}$を求める。
\begin{bmatrix} -15 & -15 \\ -15 & -15 \end{bmatrix}\begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix} =\begin{bmatrix} 0 \\ 0 \end{bmatrix}よって、以下の固有ベクトルが求まった。
\begin{bmatrix} -15 & -15 \\ -15 & -15 \end{bmatrix}\begin{bmatrix} 1 \\ -1 \end{bmatrix} =\begin{bmatrix} 0 \\ 0 \end{bmatrix}固有ベクトルを扱いやすいよう単位ベクトル化する。
v_1=\frac{1}{L}\begin{bmatrix} 1 \\ -1 \end{bmatrix} =\frac{1}{\sqrt{(1)^{2}+(-1)^{2}}}\begin{bmatrix} 1 \\ -1 \end{bmatrix} =\begin{bmatrix} \frac{1}{\sqrt{2}} \\ -\frac{1}{\sqrt{2}} \end{bmatrix} =\begin{bmatrix} 0.707106 \\ -0.707106 \end{bmatrix}これで単位ベクトルとなった。
$\lambda=10$の場合:
同様にもう一方の固有ベクトルも求めていく。求めた$\lambda$を代入して
(A^{T}A - \lambda E)\overrightarrow {x} =\begin{bmatrix} 25 - 10 & -15 \\ -15 & 25 - 10 \end{bmatrix} \begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix} =\begin{bmatrix} 15 & -15 \\ -15 & 15 \end{bmatrix}\begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix}$\overrightarrow {x}$を求める。
\begin{bmatrix} 15 & -15 \\ -15 & 15 \end{bmatrix}\begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix} =\begin{bmatrix} 0 \\ 0 \end{bmatrix}よって、以下の固有ベクトルが求まった。
\begin{bmatrix} 15 & -15 \\ -15 & 15 \end{bmatrix}\begin{bmatrix} 1 \\ 1 \end{bmatrix} =\begin{bmatrix} 0 \\ 0 \end{bmatrix}固有ベクトルを扱いやすいよう単位ベクトル化する。
v_2=\frac{1}{L}\begin{bmatrix} 1 \\ 1 \end{bmatrix} =\frac{1}{\sqrt{(1)^{2}+(1)^{2}}}\begin{bmatrix} 1 \\ 1 \end{bmatrix} =\begin{bmatrix} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \end{bmatrix} =\begin{bmatrix} 0.707106 \\ 0.707106 \end{bmatrix}最後に合わせて、$V$とする。
V = \begin{bmatrix} v_1 & v_2 \end{bmatrix} =\begin{bmatrix} 0.707106 & 0.707106 \\ -0.707106 & 0.707106 \end{bmatrix}$V^T$は以下である。
V^T =\begin{bmatrix} 0.707106 & -0.707106 \\ 0.707106 & 0.707106 \end{bmatrix}Step. 3: $U$を求める。
残すは$U$だけである。まずは次式を変形して、A_{m×n}=U_{m×r}\Sigma_{r×r} V^{T}_{n×r}$U=$の形にする。移項すると逆行列になる。直行行列のため、$^T=^{-1}$の関係のであり、移項すると転置が消える/転置になる。
U_{m×r}=A_{m×n}V_{n×r}\Sigma^{―1}_{r×r}$U$を求める。
U =\begin{bmatrix} 4 & 0 \\ 3 & -5 \end{bmatrix} \begin{bmatrix} 0.707106 & 0.707106 \\ -0.707106 & 0.707106 \end{bmatrix} \begin{bmatrix} 0.15812 & 0 \\ 0 & 0.31623 \end{bmatrix}\\ =\begin{bmatrix} 4 & 0 \\ 3 & -5 \end{bmatrix} \begin{bmatrix} 0.707106 * 0.15812 + 0 & 0 + 0.707106 * 0.31623 \\ -0.707106 * 0.15812 + 0 & 0 + 0.707106 * 0.31623 \end{bmatrix}\\ =\begin{bmatrix} 4 & 0 \\ 3 & -5 \end{bmatrix} \begin{bmatrix} 0.11181 & 0.2236 \\ -0.11181 & 0.2236 \end{bmatrix}\\ =\begin{bmatrix} 0.44724 & 0.89448 \\ 0.89448 & -0.44724 \end{bmatrix}よって、ここに$U$、$V$、$\Sigma$が以下のようにそろった。
U=\begin{bmatrix} 0.44724 & 0.89448 \\ 0.89448 & -0.44724 \end{bmatrix}, V = \begin{bmatrix} 0.707106 & 0.707106 \\ -0.707106 & 0.707106 \end{bmatrix}, \Sigma=\begin{bmatrix} 6.32456 & 0 \\ 0 & 3.1623 \end{bmatrix}最後に分解した$U$、$V$、$\Sigma$を用いて、次式から$A$を求めて検算する。
A_{m×n}=U_{m×r}\Sigma_{r×r} V^{T}_{n×r}値を代入して、
A =\begin{bmatrix} 0.44724 & 0.89448 \\ 0.89448 & -0.44724 \end{bmatrix} \begin{bmatrix} 6.32456 & 0 \\ 0 & 3.1623 \end{bmatrix} \begin{bmatrix} 0.707106 & -0.707106 \\ 0.707106 & 0.707106 \end{bmatrix}\\ =\begin{bmatrix} 0.44724 & 0.89448 \\ 0.89448 & -0.44724 \end{bmatrix} \begin{bmatrix} 4.4721 & -4.4721 \\ 2.2361 & 2.2361 \end{bmatrix} =\begin{bmatrix} 4 & 0 \\ 3 & 5 \end{bmatrix}元の$A$に戻った!
3. コード
numpyを使うと、$V$は$V^T$として帰ってくるので注意
import numpy as np A = np.array([ [4, 0], [3, -5] ]) U, s, V = np.linalg.svd(A, full_matrices=True) print(U) print(np.diag(s)) print(V) print("---") # a = usv print( np.dot( U, np.dot(np.diag(s), V)) )
- 投稿日:2019-03-18T17:59:39+09:00
Astropyで宇宙論的な計算を行う
Introduction
このページは、内容としてはAstropyのCosmological Calculationsのページを和訳したものですが、ところどころで私なりのアレンジを加えています。
Astropyモジュールを使って、宇宙論的な計算を行う方法をご紹介します。Installation
PyPIに登録されているので
pip install astropyでインストールするか、Anacondaがインストールされていれば
conda install -c astropy sphix-astropyでインストールすることができます(Anacondaの場合は、すでにインストールされている場合もあります)。
初めてのastropy.cosmology
ハッブル定数
以下のようにすることで、WMAP9yrから推定された、redshift z=0でのハッブル定数を求めることができます。
>>> from astropy.cosmology import WMAP9 >>> WMAP9.H(0) <Quantity 69.32 km / (Mpc s)>固有距離
z=3における、1ミリ秒角の固有距離を、kpc単位で算出します。
>>> WMAP9.kpc_proper_per_arcmin(3) <Quantity 472.97709236 kpc / arcmin>共動距離
リストなどのシーケンスを渡すことで、一気に共動距離を求めることができます。以下はz=0, 1, ..., 9までの共動距離を求めています。
>>> WMAP9.comoving_distance(range(10)) <Quantity [ 0. , 3363.0706321 , 5291.73040581, 6503.90188771, 7344.44470431, 7968.80246409, 8455.45279875, 8848.30522052, 9173.9669946 , 9449.58596714] Mpc>Flat Lambda CDM modelとニュートリノ種の実効数
平坦なΛ-CDMモデルでのニュートリノ種の実効数を求めることができます。ここではハッブル定数 H_0, オメガマター Ω_m0, CMB温度 T_cmb0を指定しています。
>>> from astropy.cosmology import FlatLambdaCDM >>> cosmo = FlatLambdaCDM(H0=70, Om0=0.3, Tcmb0=2.725) >>> cosmo.Neff 3.04今後も時間があれば追記していく予定です。
- 投稿日:2019-03-18T17:58:34+09:00
pythonフレームワークのdjangoとbottleでHello World!するまでの流れをまとめてみよう
少し今まで学んだことの復習をしたいです。 今回はdjangoとbottleでのHello World!までの流れを復習します。
pythonフレームワークのdjangoでHello World!するまでの流れをまとめてみよう ]
djangoはコマンドプロンプトからテンプレートを作成することができます。
コマンドはpy -m django startproject 任意の名前これでテンプレートをダウンロードできます。
tree ディレクトリ名 /fコマンドでディレクトリ構成を確認。
│ manage.py │ └─djangotest settings.py urls.py wsgi.py __init__.pyこれがdjangoの基本的なテンプレートになります。
まずsettings.pyを開きます。
LANGUAGE_CODEはデフォルトは英語なので’ja’に変更しておきましょう。
TIME_ZONEはAsia/Tokyoに! ここまできたら実際にハローワールドをさせるためのアプリケーションを作成しましょう。
ディレクトリのmanage.pyのある部分で└─djangotest │ manage.py
py manage.py startapp 任意のアプリ名
これでhelloworldを出力するdjangoアプリケーションのテンプレートが作成されます。
再びディレクトリ構成を確認してみると・・・。└─djangotest │ manage.py │ ├─djangotest │ │ settings.py │ │ urls.py │ │ wsgi.py │ │ __init__.py │ │ │ └─__pycache__ │ settings.cpython-37.pyc │ __init__.cpython-37.pyc │ └─helloworld │ admin.py │ apps.py │ models.py │ tests.py │ views.py │ __init__.py │ └─migrations __init__.pyhelloworld以下が追加されていますね。(今回はアプリ名をhelloworldにしました。)
アプリケーションを作ったらsettings.pyに認識させなくてはいけません。
settings.pyの以下の部分にINSTALLED_APPS = [ 'django.contrib.admin', 'django.contrib.auth', 'django.contrib.contenttypes', 'django.contrib.sessions', 'django.contrib.messages', 'django.contrib.staticfiles', ]
'helloworld.apps.HelloworldConfig',
と加えてください。helloworldのところはあなたが作成したアプリケーション名ですよ。
僕はhelloworldとしたのでhelloworldとなっているだけです。
大文字小文字間違えないでね。
次はアプリケーションにアクセスするURLを作ります。
urls.pyというfrom django.contrib import admin from django.urls import path urlpatterns = [ path('admin/', admin.site.urls), ]
こんなことが書いてある場所にfrom django.urls import path, include←includeを追加 path('アプリをアクセスさせたいURL名', include('作成したアプリケーション名).urls')),
と書いてください。
僕の場合こうなります。path('helloworld', include('helloworld.urls')),
しかし実はアプリケーションの方にもurls.pyを作らないといけません。└─djangotest │ manage.py │ ├─djangotest │ │ settings.py │ │ urls.py │ │ wsgi.py │ │ __init__.py │ │ │ └─__pycache__ │ settings.cpython-37.pyc │ __init__.cpython-37.pyc │ └─helloworld │ admin.py │ apps.py │ models.py │ tests.py │ views.py │ __init__.py │ └─migrations __init__.pyhelloworldディレクトリの中にurls.pyというファイルを追加しましょう。
urls.pyにはまずこう記載します。from django.urls import path from . import viewsfrom django.urls import pathと書かないとurlにパスが通りません。
またfrom . import viewsは後ほどこのurlsの中身をviews.pyに記載するので参照できるようにするためにこのように書いておきます。
さらにこの下にapp_name = 'アプリケーション名' urlpatterns = [ path('', viewsで作成する関数名.html, name='任意の名前'),
というように記載します。
ではviews.pyにhelloworldするための関数を書いていきましょう。from django.http import HttpResponse def 先ほど指定した関数(request): return HttpResponse("Hello World!")
そうしたらコマンドプロンプトでpy manage.py のあるディレクトリに移動をして、py manage.py runserver
こんな感じで出てくるのでYou have 14 unapplied migration(s). Your project may not work properly until you apply the migrations for app(s): admin, auth, contenttypes, sessions. Run 'python manage.py migrate' to apply them. March 18, 2019 - 16:25:27 Django version 2.0.2, using settings 'djangotest.settings' Starting development server at http://127.0.0.1:8000/ Quit the server with CTRL-BREAK.
http://127.0.0.1:8000/
このURLを開きます。
・・・がpage not foundになるはずなので。
urlsで指定した・・・。from django.urls import path, include←includeを追加 path('アプリをアクセスさせたいURL名', include('作成したアプリケーション名).urls')),
アプリをアクセスさせたいURL名!!http://127.0.0.1:8000/ の後ろに追加しましょう。
このURLにアクセスするとHello World!と表示されますよ。
・・・ちなみに。app_name = 'アプリケーション名' urlpatterns = [ path('', viewsで作成する関数名.html, name='任意の名前'),
アプリケーション側に記載したURL。path('/hogeee/', viewsで作成する関数名.html, name='任意の名前'),
とかにするとURLが
http://127.0.0.1:8000/任意のURL名/hogeee/
とかになるので試してみてね。pythonフレームワークのbottleでHello World!するまでの流れをまとめてみよう
続いてはbottle編。
bottleはdjangoみたいにコマンドプロンプトでテンプレート作ってくれる機能はあるんですかね?
僕はそれ習ったことないので普通にファイルを作成します。
任意のディレクトリを作成してそこにパイソンファイルを作ってください。
僕はこんな感じにしました。└─helloworld helloworld.py
すくなっ!!!!!!!!!
bottleは最軽量のpythonフレーワークなのです。
helloworld.pyにはこのように書きました。from bottle import route, run @route('/helloworld') def helloworld(): return 'Hello World!' run(host='localhost', port=8080, debug=True)
bottleからroute, runをimportします。from bottle import route, run
@route('/helloworld')
routeは先ほどのurls.pyの機能を果たしています。urlを構築しているのです。
その下に関数def helloworld(): return 'Hello World!'
ここがdjangoでいうviews.pyの関数部分です。一番最後に
run(host='localhost', port=8080, debug=True)
この部分がdjangoでいうmanage.pyの部分ですね。
ローカルサーバーがhelloworld.py内に格納されているので、コマンドプロンプトでpy helloworld.py
とするとサーバーが起動、http://localhost:8080/(routeで指定したurl)
とURLに打ち込むとHello Worldコマンドが出力されます。
bottleは1つのファイルでアプリケーションが作れるのでお手軽ですが、その分拡張性はdjangoに劣るので自分の開発したいものに合わせて使い分けるといいですね。
- 投稿日:2019-03-18T17:33:14+09:00
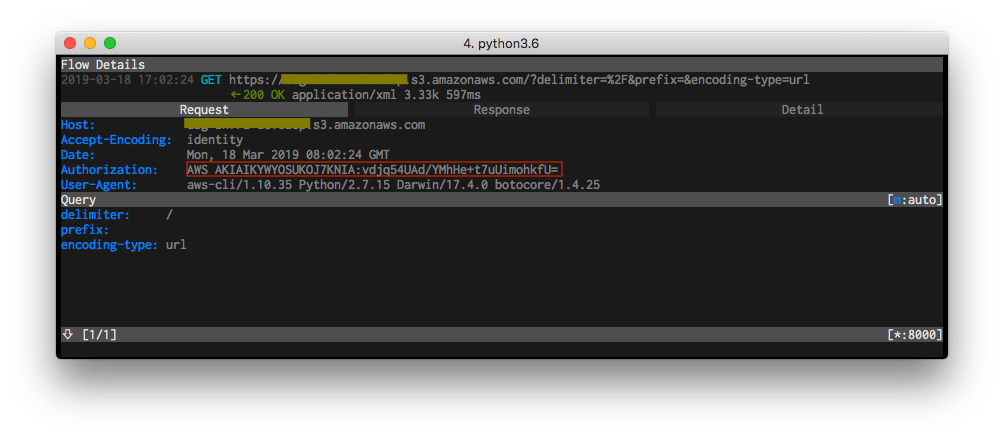
botocore の通信の中身を mitmproxy で確認
Overview
ちょっと前にこんな記事が出てたので、s3 アクセス時の署名のバージョンを確認したい話。
https://dev.classmethod.jp/cloud/aws/s3-sigv2-abolition/tcpdump だと ssl の中身見れないので、Man-in-The-Middle proxy 使います。
準備
以下とりあえずサンプルで
aws s3で試してますが、
aws ec2 describe-instancesとかでも使えます。mitmproxy
インストールとpemの設定は済ませておいてください。
mac の人は homebrew じゃなくてもpip install mitmproxyで普通に入ります。export MITMPROXY_CA=mitmproxy-ca-cert.pem起動
mitmproxy -p 8000
localhost:8000で起動します(ポートはお好みで
あとでプロキシ経由でアクセスすると、ここに通信の中身が出ます。botocore
awscliもbotoも中身botocoreを使用していて、AWS_CA_BUNDLEでオレオレ証明書をバンドルできるので、
https://boto3.amazonaws.com/v1/documentation/api/latest/guide/configuration.htmlmitmproxy の証明書をバンドルしておきます。
export AWS_CA_BUNDLE=$MITMPROXY_CAこれを忘れると
[SSL: CERTIFICATE_VERIFY_FAILED] certificate verify failedになるので注意。挙動確認
awscli の設定は済ませておいてください。
$ python -V Python 2.7.15 $ virtualenv .venv (..snip..) $ . .venv/bin/activate署名v2(古いバージョン)
あかんやつ$ pip install awscli==1.10.35 (..snip..) $ aws --version aws-cli/1.10.35 Python/2.7.15 Darwin/17.4.0 botocore/1.4.25$ export HTTPS_PROXY=http://localhost:8000 $ export YOUR_BUCKET=your_bucket $ aws s3 ls s3://$YOUR_BUCKET署名v4
OKなやつ$ unset HTTPS_PROXY $ pip install -U awscli (..snip..) $ aws --version aws-cli/1.16.125 Python/2.7.15 Darwin/17.4.0 botocore/1.12.115$ export HTTPS_PROXY=http://localhost:8000 $ export YOUR_BUCKET=your_bucket $ aws s3 ls s3://$YOUR_BUCKETという話。
おまけ
まぁ署名のバージョン知りたいだけなら
--debugオプションで見れるんですけどね。$ aws s3 --debug ls s3://${YOUR_BUCKET} 2>&1 | grep -A 1 -i 'signature' 2019-03-18 17:07:00,252 - MainThread - botocore.auth - DEBUG - Calculating signature using v4 auth. 2019-03-18 17:07:00,252 - MainThread - botocore.auth - DEBUG - CanonicalRequest: -- 2019-03-18 17:07:00,252 - MainThread - botocore.auth - DEBUG - Signature: 466b9a9d3febd9940d5948b285b41516307c618ad024df36be331490350eb05e
- 投稿日:2019-03-18T16:57:23+09:00
Prometheusのすすめ - Grafanaでアラート発生時にジョブ実行 Python+Flaskでwebhook recieve-
Prometheusのすすめとか書いてますが、本記事はPrometheusについて一切触れていません。
Grafanaのアラート時のwebhookを受信してアラート内容に沿った処理をするwebhook recieveを作りました。Postされるjson内容
私の設定している環境ではGrafanaでアラート発生時にPOSTされるjsonの内容は以下になります。
※環境によってはtagsの箇所が違ったりするので、jsonの内容を見ながらpythonコードを書いた方がいいです。{ 'ruleName': 'CPU使用率アラートグラフ alert', 'ruleUrl': 'http://XXX.XXX.XXX.XXX:XXXX/d/lCE6nYDmz/all-servers-alert?fullscreen=true&edit=true&tab=alert&panelId=4&orgId=1', 'imageUrl': 'https://s3.ap-northeast-1.amazonaws.com/XXXXXX/69Ima6QI5KACp3NL3Grs.png', 'title': '[Alerting] CPU使用率アラートグラフ alert', 'ruleId': 6, 'state': 'alerting', 'message': '【障害通知】CPU使用率', 'evalMatches': [ { 'value': 96.23523011138367, 'tags': { 'instance': 'XXX-XXXXX-web01' }, 'metric': 'XXX-XXXXX-web01' } ] }python実行環境(nginx+uwsgi)を用意する。
探せばいくらでも出てくるのでこの記事では割愛します。
ここが参考になります。私の環境ではPrometheusと同じサーバに同居させていて
「http://IPアドレス/dev」にアクセスするとpythonにwsgiプロトコル経由で実行されるように設定しています。コード
app.py#!/usr/bin/env python3 # -*- coding: utf-8 -*- from flask import Flask, render_template, request, redirect, session , make_response app = Flask(__name__) import subprocess import re @app.route("/dev/webhook", methods = ["POST"]) def webhook(): ''' Grafanaのアラートからスクリプトを実行する為のWebHookRecive ''' postjson = request.json if not request.remote_addr == '127.0.0.1': print("## not local request") return elif postjson['state'] == 'alerting': print("## state: Alerting") print(postjson) text = postjson['message'] rulename = postjson['ruleName'] if not postjson['evalMatches'][0]['tags'] == None: instance = postjson['evalMatches'][0]['tags']['instance'] alert = re.match('ICMP',rulename) cmd = "sh /usr/script/grafana/"+instance+"_"+alert+".sh" #/usr/script/grafana/配下にインスタンス名(NameTag)_アラート名.shでスクリプトを配置する。 #内容は再起動なり、SSHでリモートコマンドするなりのスクリプト subprocess.call(cmd.split()) print(text) elif: print("## State: without Alert") print(postjson) return 'OK'
- 投稿日:2019-03-18T16:52:35+09:00
seleniumでtryとifを合わせる【python】
やりたかったことの最終型を先に書く。
test.pydef test(huga) try: hoge_1 = driver.find_element_by_xpath("//*[@class='hoge class']").text piyo_1 = driver.find_element_by_xpath("//*[@id='root']/div/div/span").text driver.find_element_by_xpath("//*[@id='root']/div").click hoge_2 = driver.find_element_by_xpath("//*[@class='hoge class']").text piyo_2 = driver.find_element_by_xpath("//*[@id='root']/div/div/span").text if hoge_1 == hoge_2: result = "NG(要素1失敗)" elif piyo_1 == piyo_2: result = "NG(要素2失敗)" else: result = "OK" except: result = "要素取得失敗" return result暫定。後で編集。
- 投稿日:2019-03-18T16:51:30+09:00
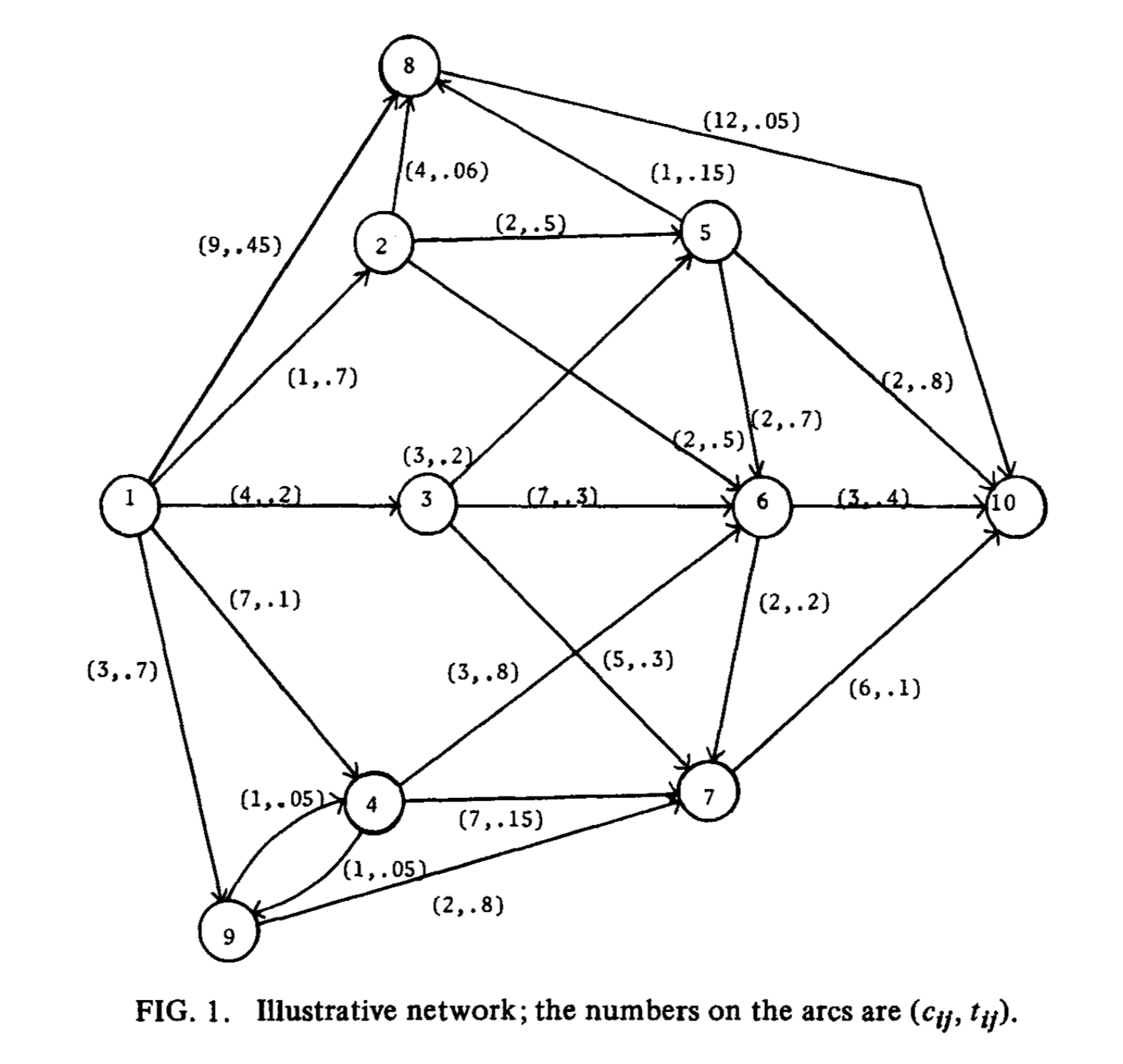
Hander-Zang Algorithm 制約付き最短路
制約付き最短路とは
グラフ$G=(V, A)$が与えられているとします.
$V$: 点集合, $A \subset V \times V$: 枝集合$(i ,j) \in A$ で始点が$i$, 終点が$j$である枝を表します.
各枝$(i, j)$には二種類の重みがあり, それを$c_{ij}$, ${t_{ij}} \in \mathbb{R}$とします.制約付き最短路問題とは, 始点$s$, 終点$e$があって, $s$と$e$を結ぶパスの中で
- 枝の$t_{ij}$の総和が$\lambda$以下で
- 枝の$c_{ij}$の総和が最小のもの
を見つける問題です. 特に1. の形の制約はナップサック型制約と呼ばれるため,
上の形の問題はナップサック型制約付き最短路問題と呼ばれます.始点$s$と終点$e$を結ぶパスの集合を$\bar{X} \subset 2^{A}$($A$の冪集合)とすると, 下記のように問題を記述できます.
\begin{align} \min_{X \in \bar{X}} &\sum_{(i, j) \in X}c_{ij}\\ {\rm s.t.} &\sum_{(i, j) \in X}t_{ij} \leq \lambda \end{align}さらに簡略化のために
f(X) := \sum_{(i, j) \in X}c_{ij}\\ g(X) := \sum_{(i, j) \in X}t_{ij}とおいて, 上記の問題を
\begin{align*} \min_{X \in \bar{X}} & ~~ f(X)\\ {\rm s.t.} ~~& g(X)\leq \lambda \end{align*}と書くことにします. この問題を今後CSPと呼びます.
下記ではCSPの最適値を
\displaystyle f^* \left(=f(X^*) = \min_{X \in \bar{X}; g(X) \leq \lambda} ~~ f(X)\right)と書きます.
Hander-Zang Algorithm([1])の流れ
- CSPの下限値を与えるようなDCSPを定義する
- DCSPを解きながら, CSPの良い下限値と同時に実行可能解を求める
- 最適解の保証が行われるまで第k最短路問題をとく
DCSP
$u \in \mathbb{R}$に対して, 以下を定義します.
\displaystyle L(u, X) := f(X) + u(g(X) - \lambda)\\ L(u) := \min_{X \in \bar{X}}L(u, X)$L(u)$はCSPに対するラグランジュ緩和での目的関数です.
ここで, よく知られている弱双対性から
$$
L(u) \leq f^* (=CSPの最適値) ~~ (\forall u \geq 0)
$$
が成立します.(証明) $X^*$をCSPの最適解とすると, $X^*$はCSPの実行可能解なので
$X^* \in \bar{X}, g(X^*) \leq \lambda$を満たしている. $u \geq 0$に留意すると,
$\displaystyle L(u) = \min_{X \in \bar{X}} L(u, X) \leq L(u, X^*) = f(X^*) + u\left(g(X^*)-\lambda\right) \leq f(X^*) = f^*$ (終)$\forall u \geq 0$について, $L(u)$はCSPの最適値の下限を与えるので, その中で最大のものに興味があります. そこでDCSPを次のような問題として定義します.
$$
L^* = L(u^*) = \max_{u \geq 0}L(u)
$$もし, CSPに凸性があれば, 強双対性である$L^* = f^*$が成立しますが,
今回の場合は一般には成立しません.$L(u)$を計算するのは簡単で, $(i, j)$の枝の重みを$c_{ij} + u t_{ij}$としたグラフ上での$s-e$最短路長が$L(u)$になることは, すぐに確認できます.
CSPの上限と下限の更新
DCSP $\displaystyle \max_{u \geq 0}L(u)$の最適解を求めるのは容易ではありません. なので, 次のような手続きでDCSPの近似解(=CSPの下限)を見つけるのと同時に, CSPの上限も更新していきます.
簡単に例を見ていきます.
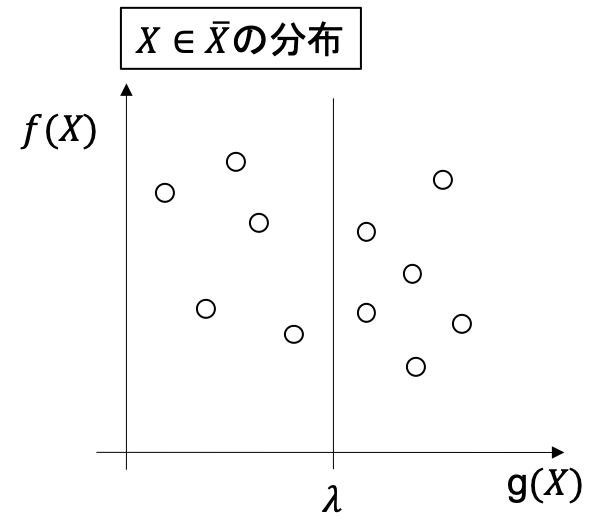
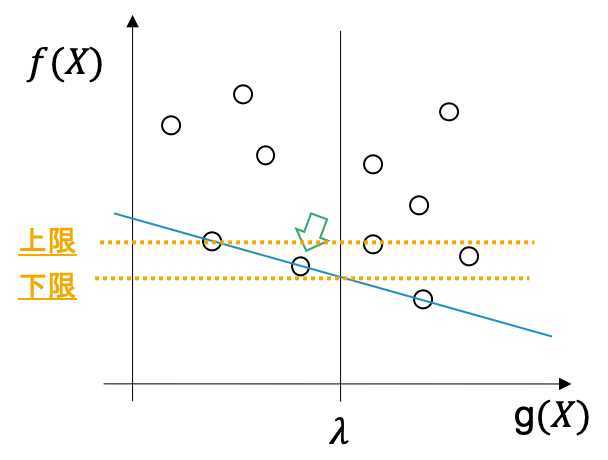
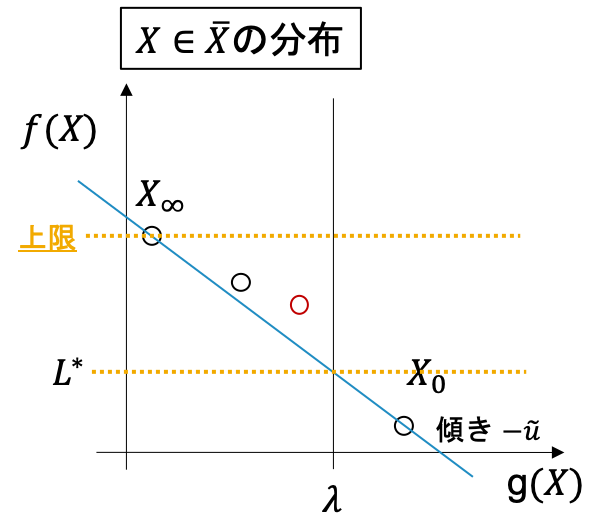
1 まず, $L(0)$と$L(+\infty)$を求めて, その最適解をそれぞれ$X_0, X_{\infty}$とします(下図).
ここで, もし$X_0$が$g(X_0) \leq \lambda$ を満たしているならば, $X_0$を最適解として出力して終了します. もし$g(X_\infty) > \lambda$であれば, 実行可能解なし(制約を満たすパスが存在しない)となり, 終了します. そうでないならば$f(X_\infty)$がCSPの最適値の上限になることは図より明らかですね. さらに$X_0$と$X_\infty$を結ぶ直線の傾きに$-1$をかけたものを$u$とします.
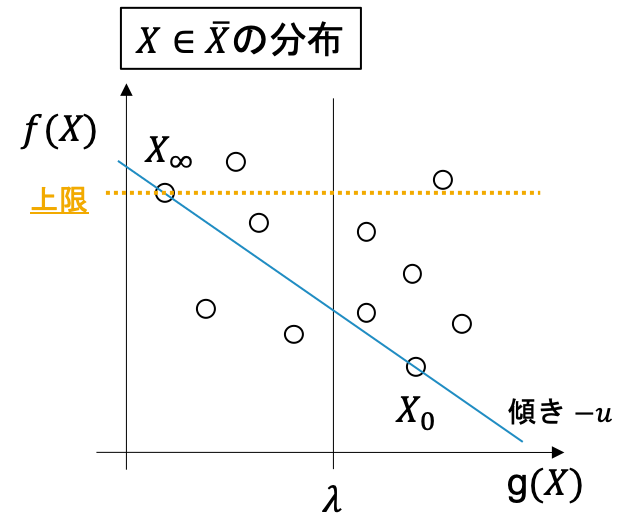
2 $L(u)$を解きます. これは上図でいうと, $g(X) = \lambda$上での切片が最小となるような, 傾き$-u$の直線を通る$\tilde{X} \in \bar{X}$を求めることに相当し, $L(u)$にはそのときの切片の値が入ります (下図).
上の議論より, このときの$L(u)$がCSPの下限としてとれます.
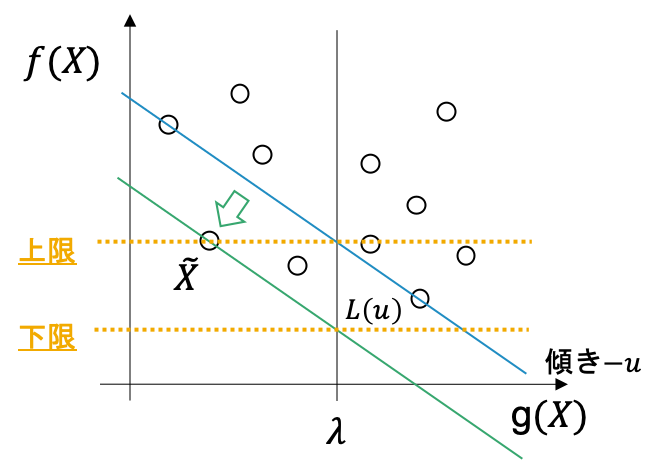
また, もし$g(\tilde{X}) \leq \lambda$であれば, 上限値も$f(\tilde{X})$で更新できます.3 実行可能領域$R = {X; X \in \bar{X}, g(X) \leq \lambda}$, 非実行可能領域$C={X; X\in \bar{X} g(X) > \lambda}$について, 上記の手続きで$R$上で$f(X)$が最小の点を$p_{r_{min}}$, $C$上で最小の点を$p_{c_{min}}$とします. (図の場合, $p_{r_{min}} = \tilde{X}, p_{c_{min}} = X_0$)
$p_{r_{min}}$と$p_{c_{min}}$を結ぶ直線の傾きに$-1$をかけたものを$u$として, $L(u)$を解き, $p_{r_{min}}$, $p_{c_{min}}$のどちらかをそのとき得られた解に更新します.
さらに, それによって可能であれば上限と下限と更新します.これを$u$が更新されなくなるまで繰り返します.
もし, そのとき上限 = 下限であれば, $p_{r_{min}}$が最適解として出力されます.第k最短路による最適性の保証
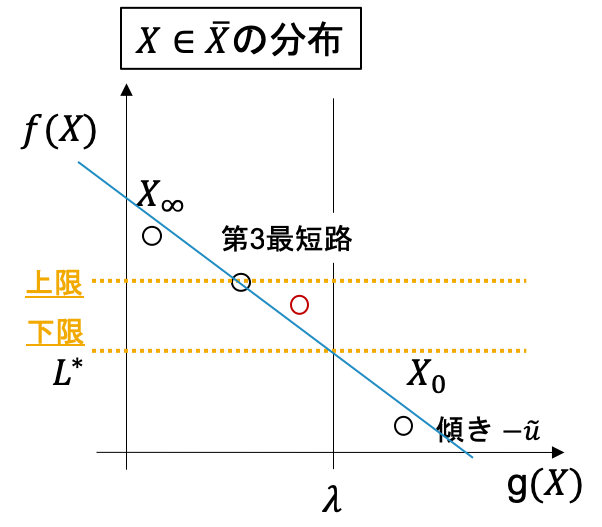
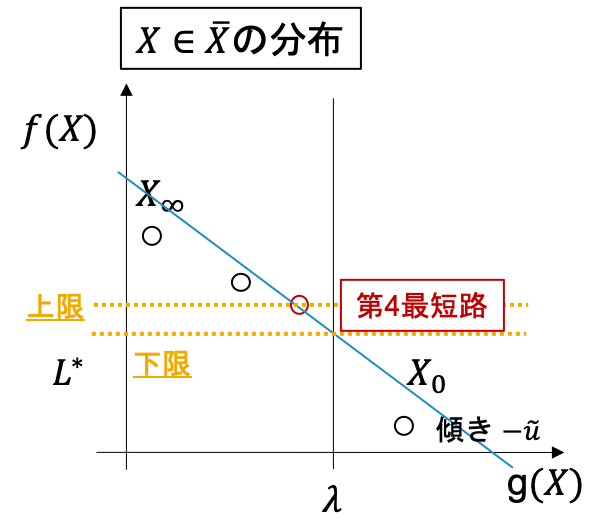
そうではない場合(例えば下図; 赤丸が最適解)は, 最適解をさらに第$k$最短路により求めます.
前のステップの最後の$u$を$\tilde{u}$として,$L(\tilde{u})$の第3最適解以降を求めていきます(下図). 前述しているように$L(u)$自体はグラフの枝の重みを変更したグラフの最短路問題に帰着できるため, これはグラフ上での第$k$最短路を求めることに相当します.
見つかった解に従って, 上限下限と$p_{r_{min}}$を更新していきます.
第$k$最短路がなくなったり, 上限と下限のギャップがなくなれば(もしくは逆転する) そのときの$p_{r_{min}}$を最適解として出力します.
Pythonでの実装
このHander-Zangアルゴリズムをpythonで実装しました.
最短路計算にはDijkstra(もしくは負の枝が含まれる場合は)Bellman-Ford法
第1-K最短路を求めるのはEppstein法([3])$O(|A|+|V|\log|V|+K)$を用いています.
(Yen法([2])も実装しましたが, Eppstein法の方が圧倒的に速いです)例
論文([1])中の例です(グラフデータ). このとき1から10へのパスでコスト$t$の総和が1以下のパスで最小のものを求めると, 次のようになります.
python dual_algorithm.py fig1_graph.csv 1 10 1 Build Date: Mar 07 2019 Main Algorithm : Hander-Zang algorithm Shortest Path Algorithm : Dijkstra or Bellman-Ford algorithm K Shortest Path Algorithm : Yen algorithm the number of nodes: 10 the number of edges: 22 We obtain shortest path on weight (#STEP1) f = 5.000, g = 1.000 We obtain shortest path on cost (#STEP2) f = 20.000, g = 0.350 Best Solution: 20.000 ------------------------------------------------------------ Iter Step Update Best LB UB Gap Time ------------------------------------------------------------ 1 #1 LB - 5.00 - -% 0s 2 #2 UB 20.00 5.00 20.00 78.95% 0s 3 #3 20.00 5.00 20.00 78.95% 0s 4 #3 UB 15.00 5.00 15.00 71.43% 0s 5 #3 LB 15.00 11.00 15.00 28.57% 0s 6 #4 LB 15.00 12.00 15.00 21.43% 0s 7 #4 LB UB 14.00 13.00 14.00 7.69% 0s 8 #4 LB 14.00 13.50 14.00 3.85% 0s 9 #4 LB 14.00 15.00 14.00 -7.69% 0s *Optimal Solution: 14.00 path [('1', '3', 0), ('3', '6', 0), ('6', '10', 0)] f = 14.000, g = 0.900step#1#2が$L(0), L(+\infty)$を求めることで, step#3がCSPの上限と下限の更新, step#4が第k最短路に対応しています.
参考文献
[1] Handler, Gabriel Y., and Israel Zang. "A dual algorithm for the constrained shortest path problem." Networks 10.4 (1980): 293-309.
[2] Yen, Jin Y. "Finding the k shortest loopless paths in a network." management Science 17.11 (1971): 712-716.
[3] Eppstein, David. "Finding the k shortest paths." SIAM Journal on computing 28.2 (1998): 652-673.
- 投稿日:2019-03-18T16:42:30+09:00
python: 配列の結合
pythonで配列を結合する方法
以下のように,ndarrayの場合はnp.r_[配列A, 配列B]で結合可能.
listの場合は + を用いることで結合可能.In [1]: import numpy as np In [2]: a = np.array([1,2,3]) In [3]: b = np.array([4,5,6]) In [4]: np.r_[a, b] Out[4]: array([1, 2, 3, 4, 5, 6]) In [5]: a = [1,2,3] In [6]: b = [4,5,6] In [7]: a + b Out[7]: [1, 2, 3, 4, 5, 6]
- 投稿日:2019-03-18T16:38:30+09:00
機械学習で用いる行列の単語を整理した② (分散共分散行列、相関行列)
分散共分散行列
言葉の通り、分散+共分散の意味を持つ。複数の分散がどのような相関を持つのかを求められる。
分散とは、与えられたデータに対して、どれくらいばらつきがあるかを示す指標である。標準偏差等と非常に似ている。
数式で表すと偏差(各値―平均値)を2乗し足し足し合わせて、平均を取る。
分散:
s^{2}=\dfrac {1}{n}\sum ^{n}_{n=1}\left( x_{i}-\overline {x}\right) ^{2}誤差が2乗の積和のため、感覚的に直値との差が分からない。
標準偏差:
s=\sqrt{\dfrac {1}{n}\sum ^{n}_{n=1}\left( x_{i}-\overline {x}\right) ^{2}}誤差の平方根を取るため、感覚的に直値との差が分かる。
分散は1つのデータ群からばらつきを示す指標である。例えば、1学年の数学の点数が沢山与えられて、どれくらい点数にばらつきがあるかを見たいとき等に使う。
ここで、標本(データ)が2つの群から形成され、その関係性を見たい場合に共分散を用いる。
例えば、生徒の「数学」と「理科」の点数がそれぞれ与えられたとする。その時に共分散を求めることで、数学が出来る人は理科もできる(正値になる)。もしくは数学が出来る人は理科が出来ない(不値になる)といった関係性を求められる。
計算的には「数学の点数―数学の平均値」と「理科の点数―理科の平均値」を掛け合わせればよい。
共分散(標本共分散行列):
cov=\dfrac {1}{n}\sum ^{n}_{i=1}\left( x_{i}-\overline {x}\right) \left( y_{i}-\overline {y}\right) ^{T}共分散(不変共分散行列):
cov=\dfrac {1}{n-1}\sum ^{n}_{i=1}\left( x_{i}-\overline {x}\right) \left( y_{i}-\overline {y}\right) ^{T}※一般的には標本共分散行列を用いる。
次に、共分散行列の「行列」を考える。
共分散行列は以下のように定義され、実対象行列である。\Sigma=\begin{bmatrix} cov_{xx} & cov_{xy} \\ cov_{yx} & cov_{yy} \end{bmatrix} =\begin{bmatrix} s^{2}_{xx} & cov_{xy} \\ cov_{yx} & s^{2}_{yy} \end{bmatrix}ここで、$\Sigma$は共分散行列を示す。$s^2_{xx}$は$x$の分散を示す。$cov_{xy}$は$x$と$y$の共分散を示す。
共分散$cov_{xx}$は$x$の分散を計算しているのと同じ処理になる。なお、例は2次元であるが、3次元も$x, y, z$の組が増えていくだけである。
計算
ここで生徒3人の国語、数学、理科の得点が次のように与えられたとする
math: x = \begin{bmatrix} 80 & 20 & 50 \end{bmatrix}science: y =\begin{bmatrix} 100 & 30 & 80 \end{bmatrix}lang: z =\begin{bmatrix} 50 & 50 & 50 \end{bmatrix}次式の行列式を解き、共分散行列を求める。
\Sigma=\begin{bmatrix} cov_{xx} & cov_{xy} & cov_{xz} \\ cov_{yx} & cov_{yy} & cov_{yz} \\ cov_{zx} & cov_{zy} & cov_{zz} \end{bmatrix} =\begin{bmatrix} s^{2}_{xx} & cov_{xy} & cov_{xz} \\ cov_{yx} & s^{2}_{yy} & cov_{yz} \\ cov_{zx} & cov_{zy} & s^{2}_{zz} \end{bmatrix}まずは対角成分を求める。
$xx$の分散について求める
mean_{math} = \frac{1}{3}(80 + 20 + 50) = 50cov_{xx} = s^{2}_{xx} = \frac{1}{3} \left\{ (80-50)^{2} + (20-50)^{2} + (50-50)^{2} \right\} = \frac{1800}{3} = 600同様に、$yy$と$zz$を求める
cov_{yy} = s^{2}_{yy} = 866.667cov_{zz} = s^{2}_{zz} = 0次に共分散の$xy$成分を求める。
cov_{xy} = \dfrac {1}{n} \sum ^{n}_{i=1} \left( x_{i}-\overline {x}\right) \left( y_{i}-\overline {y}\right) ^{T} =\dfrac {1}{3} \left\{ (80 - 50), (20 - 50), (50 - 50) \right\} \left\{ (100 - 70), (30 - 70), (80 - 70) \right\} ^{T} \\ =\dfrac {1}{3}det\left\{ \left[ 30, -30, 0 \right] \begin{bmatrix} 30 \\ -40 \\ 10 \end{bmatrix} \right\} = \dfrac {1}{3} * 2100 = 700同様に$xz$~$zy$までを求める
cov_{xz} = 0 \\ cov_{yx} = 700 \\ cov_{yz} = 0 \\ cov_{zx} = 0 \\ cov_{zy} = 0 \\よって、以下の行列が得られた。
\Sigma=\begin{bmatrix} 600 & 700 & 0 \\ 700 & 866.667 & 0 \\ 0 & 0 & 0 \end{bmatrix}これから、数学と理科の相関は700と大きな値を示し、国語と数学/理科の相関は少ないということが分かった。
コード
import numpy as np A = np.array([ [80, 20, 50], # math [100, 30, 80], # science [50, 50, 50] # lang ]) print(np.var(A[0])) # xx print(np.var(A[1])) # yy print(np.var(A[2])) # zz # xy = yx a = A[0] - np.mean(A[0]) b = A[1] - np.mean(A[1]) print("---------") print( 1/3 * np.dot(a, b.T)) print(np.cov(A, bias=True))相関行列 (基準化)
標本(データ)が2つ以上の群から形成され、その関係性を見たい場合に相関係数を用いる。
共分散行列と殆ど使い勝手は同じであるが、こちらは$-1~+1$の範囲で正規化(基準化)されている。
$1$が最も相関があり、$-1$が最も相関がない。共分散行列で求めた値を基準化するため標準偏差で割るだけである。
割り算が発生するため、標準偏差が$0$になる計算には使えない。共分散は誤差を2乗及び平方根を取らないため、符号が残る。標準偏差は誤差を2乗して平方根を取るため、符号が残る。
すなわち、$xx$の共分散と標準偏差は同じ値を示すため、$1$になる。よって、対角成分は全て$1$である。数式は以下である。
corr = \dfrac{\dfrac {1}{n-1}\sum ^{n}_{i=1}=\left( x_{i}-\overline {x}\right) \left( y_{i}-\overline {y}\right) ^{T}}{\sqrt {\dfrac {1}{n}\sum ^{n}_{i=0}\left( x_{i}-\overline {x}\right) ^{2}} \sqrt {\dfrac {1}{n}\sum ^{n}_{i=0}\left( y_{i}-\overline {y}\right) ^{2}}}相関行列は以下で計算する。
corr_{mat}=\begin{bmatrix} corr_{xx} & corr_{xy} & corr_{xz} \\ corr_{yx} & corr_{yy} & corr_{yz} \\ corr_{zx} & corr_{zy} & corr_{zz} \end{bmatrix}計算
ここで生徒3人の国語、数学、理科の得点が次のように与えられたとする
math: x = \begin{bmatrix} 80 & 20 & 50 \end{bmatrix}science: y =\begin{bmatrix} 100 & 30 & 80 \end{bmatrix}lang: z =\begin{bmatrix} 40 & 50 & 40 \end{bmatrix}相関係数$xx$を求める
Error_x = \left\{ (80-50) + (20-50) + (50-50) \right\} \\ cov_{xx} = \frac{1}{3} Error_x * Error_x^{T}=600 \\ std_{xx} = \sqrt{ \frac{1}{3} \left\{ (80-50)^{2} + (20-50)^{2} + (50-50)^{2} \right\}} = 24.495 \\ corr_{xx} = \frac{cov_{xx}}{std_{xx} * std_{xx}} = \frac{600}{24.495 * 24.495} = 1同様に$xy$~$zz$まで求める。
corr_{xy} = 0.971 corr_{xz} = -0.866 corr_{yz} = -0.961よって、以下の行列が得られた。
corr_{mat}=\begin{bmatrix} 1 & 0.971 & -0.866 \\ 0.971 & 1 & -0.961 \\ -0.866 & -0.961 & 1 \end{bmatrix}コード
import numpy as np A = np.array([ [80, 20, 50], # math [100, 30, 80], # science [40, 50, 40] # lang ]) print(np.corrcoef(A)) print("---------") idx = 0 idy = 0 num = 3 a_v = np.sqrt( 1/num * np.sum(np.power( (A[idx] - np.mean(A[idx])), 2 ) ) ) b_v = np.sqrt( 1/num * np.sum(np.power( (A[idy] - np.mean(A[idy])), 2 ) ) ) a = (A[idx] - np.mean(A[idx])) b = (A[idy] - np.mean(A[idy])) cor = 1/num * (np.dot(a, b.T)) print(cor / (a_v * b_v))
- 投稿日:2019-03-18T16:20:45+09:00
openpyxlでセルの値を中央揃えにする
Introduction
以下のようなデータファイルtest.xlsxがあります。
この一行目を中央揃えにしてレポートとして提出してほしいと依頼がありました。今回はこの作業を自動化したいと思います。
スクリプトとその実行結果
以下にこの自動化を行うためのスクリプトを紹介します。
sheet_align.py''' sheet_numberformat.py purpose: read xlsx and set number format automatically ''' import openpyxl as xl from openpyxl.styles.alignment import Alignment # set input file name inputfile = 'test.xlsx' # read input xlsx wb1 = xl.load_workbook(filename=inputfile) ws1 = wb1.worksheets[0] # write in sheet for row in ws1: for cell in row: if cell.row == 1: cell.alignment = Alignment(horizontal = 'center', vertical = 'center', wrap_text = False) # save xlsx file wb1.save(inputfile)結果は以下のようになります。
スクリプト詳細
from openpyxl.styles.alignment import Alignment
from openpyxl.styles.alignment import AlignmentここでインポートしているAlignment関数は、セルを何揃えにするかを指定するオブジェクトを返します。
何揃えかを指定
# write in sheet for row in ws1: for cell in row: if cell.row == 1: cell.alignment = Alignment(horizontal = 'center', vertical = 'center')この部分で、もしセルが一行目なら水平方向・垂直方向ともに中央揃え、を指定しています。
horizontalで水平方向を、verticalで垂直方向を何揃えにするかを指定します。horizontal, verticalでは以下の定数を指定することができます。'left' 'center' 'distributed' 'general' 'justify' 'centerContinuous' 'fill' 'right'そのほかにも
textRotationで文字を回転させることができます。何度回転するかは0-180の整数で指定します。試しにif文の中を次の行に変えてみます。cell.alignment = Alignment(horizontal = 'center', vertical = 'center', textRotation = 90)実行結果は以下のように、一行目が90度回転したものとなります。
- 投稿日:2019-03-18T16:17:31+09:00
PythonからDLLを使う
はじめに
あることから、PythonでC++で作られたDLLを読み込みたいので調べる必要が出てきました。
私自身PythonもC++もさわり程度しか知らないため、少しハマりました。
様々な記事が既に世の中に存在していますが、自分のために書き残そうと思います。まずDLLを準備
VS2017 使用しています。
ダイナミックリンクライブラリのプロジェクトを作成。名前は何でもいいと思います。
今回はDLLTestという名前で作っています。
DLLプログラムを作っていきます
DLLTest.h#pragma once #ifdef DLLTEST_EXPORTS #define DLLTEST_API extern "C" __declspec(dllexport) #else #define DLLTEST_API extern "C" __declspec(dllimport) #endif // DLLTEST_EXPORTS DLLTEST_API int GetData(int, int);DLLTest.cpp// DLLTest.cpp : DLL アプリケーション用にエクスポートされる関数を定義します。 // #include "stdafx.h" #include "DLLTest.h" int GetData(int a, int b) { return a + b; }stdafx.h// stdafx.h : 標準のシステム インクルード ファイルのインクルード ファイル、 // または、参照回数が多く、かつあまり変更されない、プロジェクト専用のインクルード ファイル // を記述します。 // #pragma once #include "targetver.h" #define WIN32_LEAN_AND_MEAN // Windows ヘッダーからほとんど使用されていない部分を除外する // Windows ヘッダー ファイル #include <windows.h> #include <string> // プログラムに必要な追加ヘッダーをここで参照してください #include "DLLTest.h"はい、以上です。ハマりどころは後述します。先に成功パターンで。
Debugビルドを行ってDLLを作成します。DLLはプロジェクトの中のDebugフォルダの中にあります。次にPython側で呼び出し
PCにはPython 3.7と2.7がインストールされていますが、3.7を今回利用しています。
VS2017で作ったDLLをpythonのソースの場所へコピーしてきます。
そして、LoadLibraryにDLL名をセットします。test.py# coding: utf-8 from ctypes import * dll = cdll.LoadLibrary("DLLTest.dll") print(dll.GetData(100, 101))これで、Pythonを実行すると。DLLで結果を出すことができました。
> py test.py 201ハマったところ
「OSError: [WinError 193] %1 は有効な Win32 アプリケーションではありません。」と出た。
解決
DLLのビルドがx64ではなかった。Pythonを64ビットでインストールしてたため。気づくのに少し時間かかりました。。
「AttributeError: function 'GetData' not found」と出た。
解決
extern "C"が抜けていた。DLLTest.h#define DLLTEST_API extern "C" __declspec(dllexport)いろいろ勉強になりました。
- 投稿日:2019-03-18T15:54:14+09:00
Pythonで処理中に棒をぐるぐる回して作業が終わったらdone
環境
- PC:windows10
- 言語 :python 3.6.7
概要
ただし,表示をするだけではなく,別スレッドの処理が完了したらdone表示,という内容にします.
コード
import threading import time import sys class TestClass: def __init__(self): self.work_ended = False def guruguru(self): while not self.work_ended: sys.stdout.write('\b' + '|') sys.stdout.flush() time.sleep(0.12) sys.stdout.write('\b' + '/') sys.stdout.flush() time.sleep(0.12) sys.stdout.write('\b' + '-') sys.stdout.flush() time.sleep(0.12) sys.stdout.write('\b' + '\\') sys.stdout.flush() time.sleep(0.12) sys.stdout.write('\b' + ' ') # 最後に末尾1文字を空白で書き換える sys.stdout.flush() def work(self): time.sleep(3) self.work_ended = True def multithread_processing(self): print("Collecting package metadata: ", end="") t1 = threading.Thread(target=self.guruguru) t2 = threading.Thread(target=self.work) t1.start() t2.start() t2.join() t1.join() sys.stdout.write("\b" + "done") sys.stdout.flush() if __name__ == '__main__': tc = TestClass() tc.multithread_processing() print() # 改行して終了解説
multithread_processing()
最初に
Collecting package metadata:をコンソールに表示して,次に2つのスレッドを立てて,両方が完了したらdoneを表示しています.guruguru()
名前通り,ぐるぐる棒を回します.
sys.stdout.write+sys.stdout.flushの組み合わせで,コンソールに即時表示しています.また,
\bでカーソルを1つ戻した後に文字を追加することで,コンソールに表示された既存の文字列の末尾だけを上書きしています.work()
実用上はここに任意の作業を書きます.
上のコードでは3秒間スリープするだけの処理です.あとがき
スレッドをデーモン化すれば,上のコードの
work_endedのような条件を使わなくてもいいのではないかと思ったのですが,デーモンスレッドが終了するタイミングが調整しづらかったため,上のような書き方になりました.