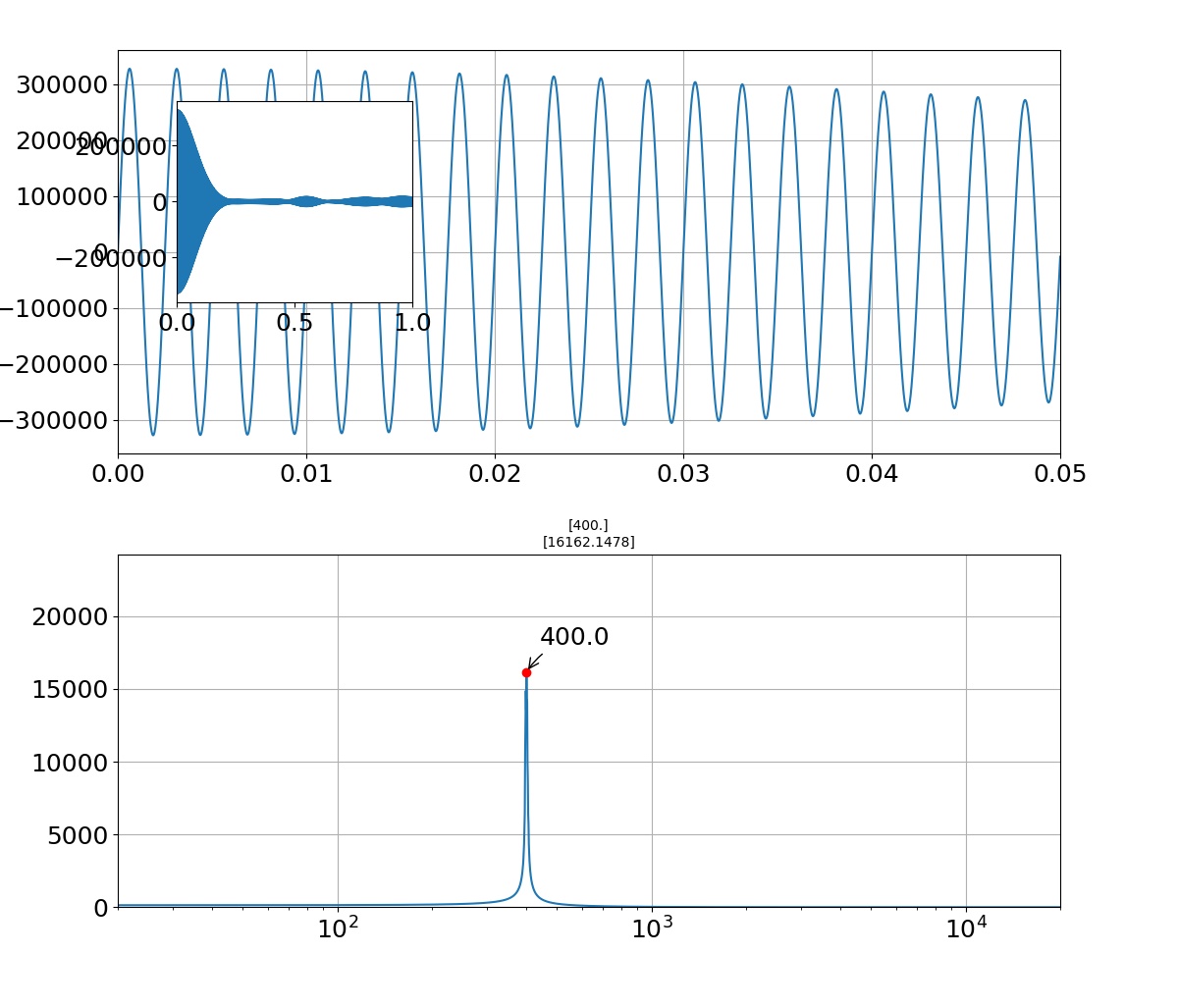
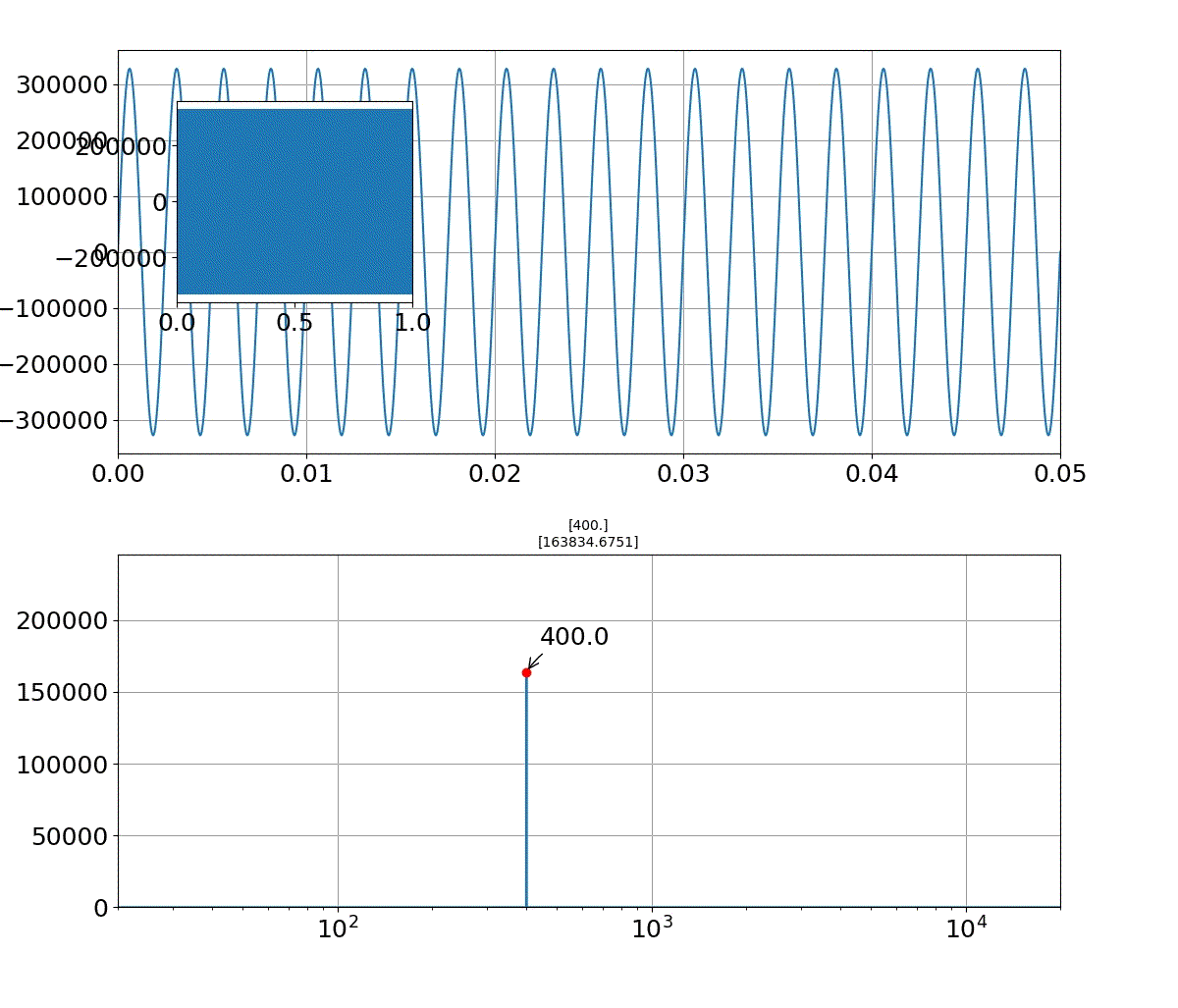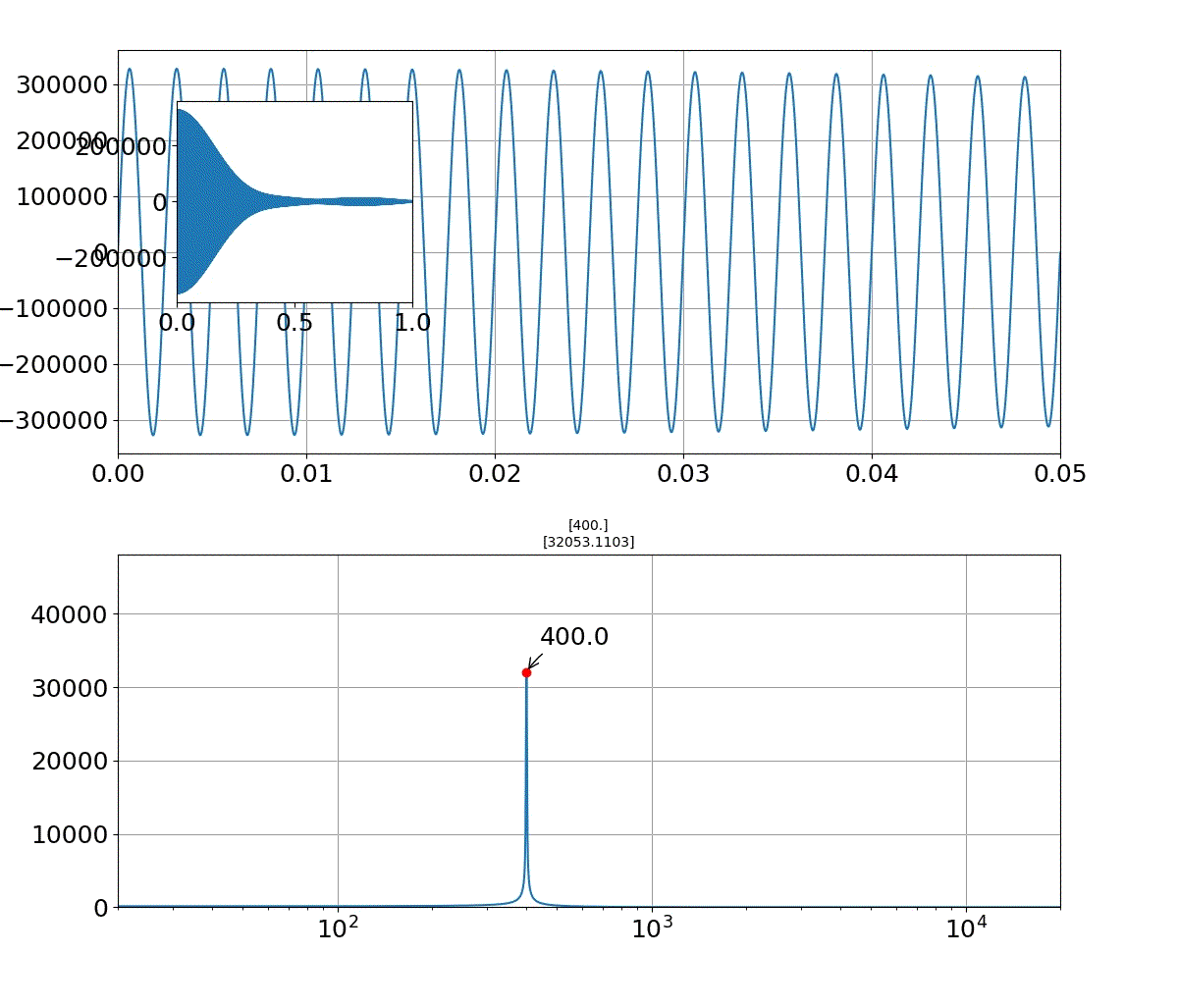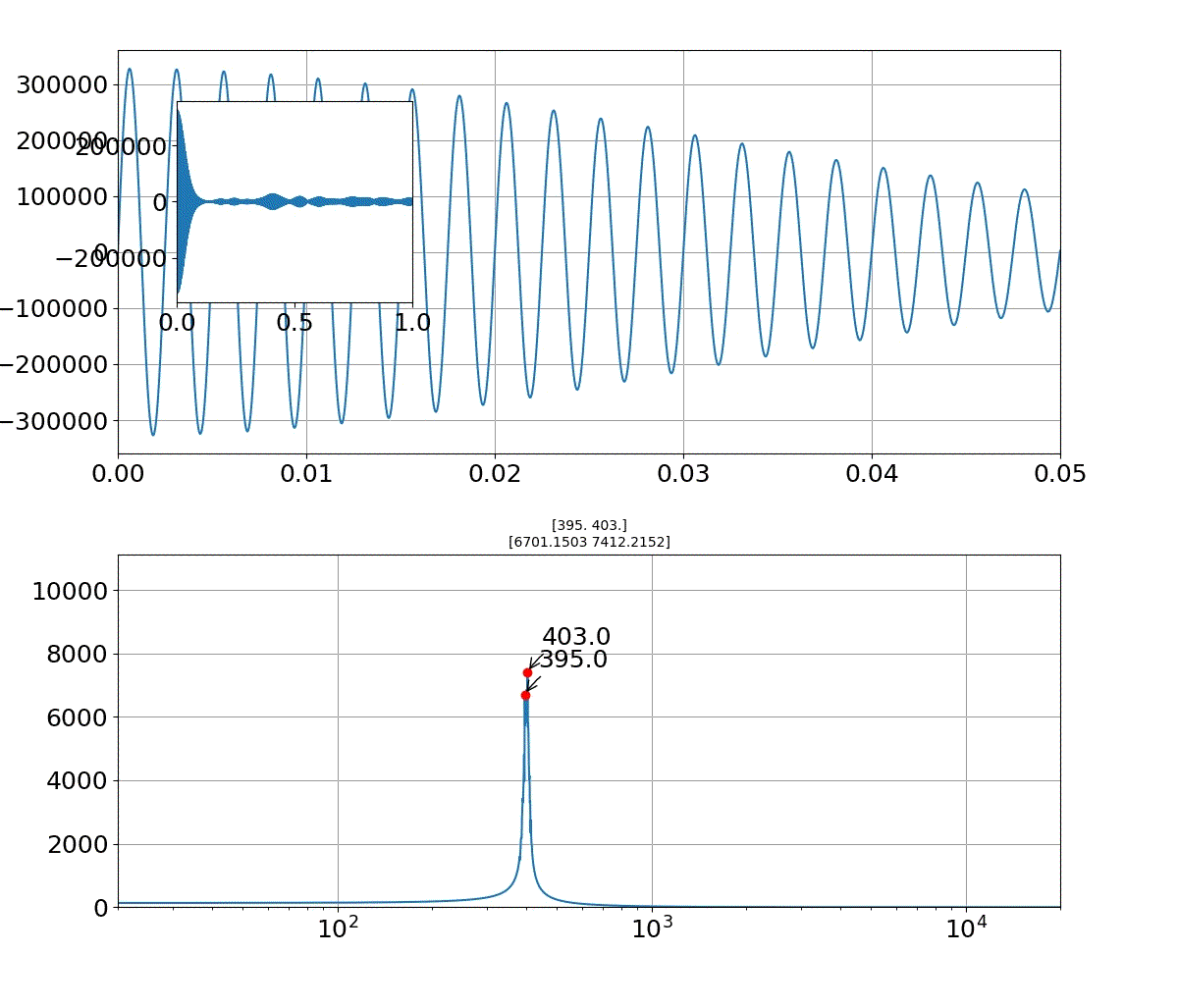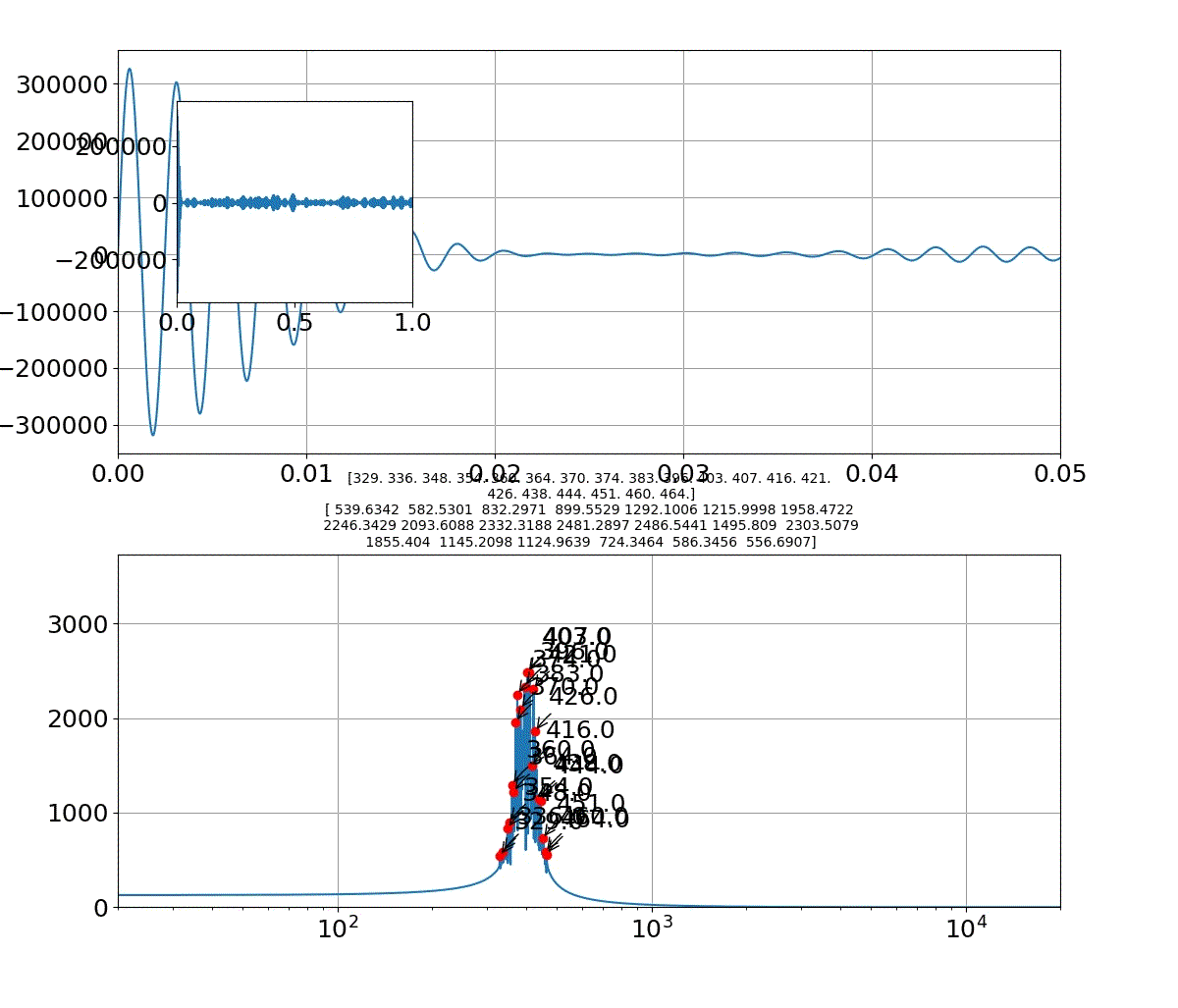
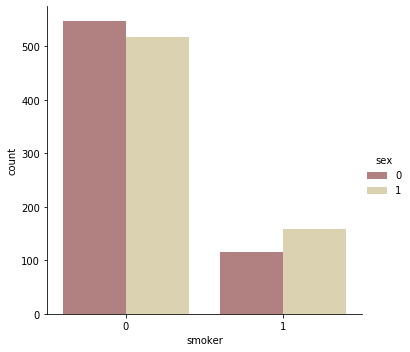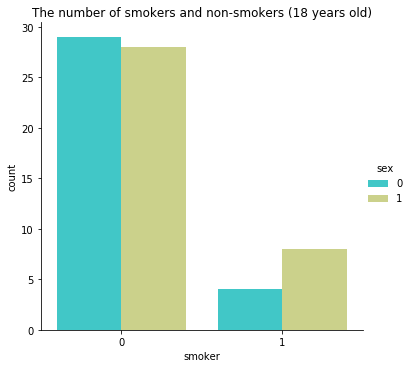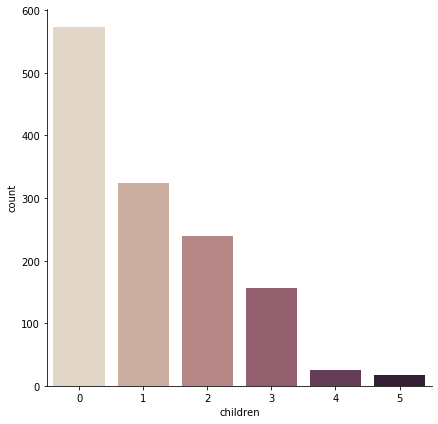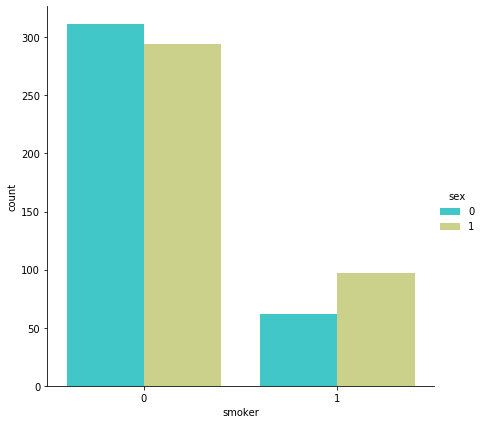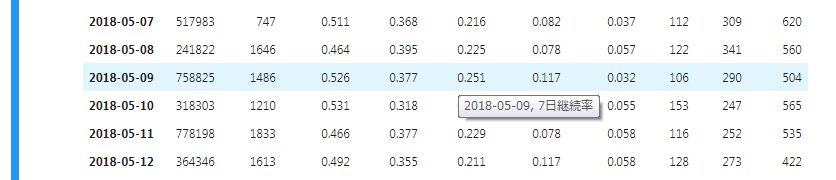- 投稿日:2019-07-27T23:17:07+09:00
LINEbotのログインURLを出してみる
LINEbotのログインURLを出す
今回はみんな大好きPythonを用いてLINEのログインURLを出してみたいと思います
必要なもの
・Python3.6実行環境
準備
ログインURLを出すために、まず「linepy」というモジュールをインストールします。
pipが使える方は[pip install linepy]でインストールできます。https://github.com/fadhiilrachman/li
実行してみる
モジュールをインストールし終わったら実行をしてみましょう
test.pyfrom linepy import* cl = LINE()実行結果
ログインについて
LINEbotは自己責任でやりましょう。
アカウントが規制になっても自己責任です。著者について
著者は学生です。ぜひTwitterフォローしてくださいね。
- 投稿日:2019-07-27T22:27:41+09:00
Qiitaコーパスを作る会 2️⃣前処理をする
はじめに
前回の記事でQiitaの全記事を取得したので、次は以下の記事を参考に前処理を行っていきます。
前処理をする
記事の抜き出し
Qiita APIで取得できる記事データには、
rendered_bodyにHTML形式、bodyにマークダウン形式の記事情報が含まれています。今回は、パースのしやすいHTML形式の方を使用します。
json_to_text.py# -------------------------------------------------- # Qiita APIから取得したデータの記事部分を抜き出しファイル出力 # -------------------------------------------------- import json from datetime import datetime, timedelta from bs4 import BeautifulSoup import os start = datetime.strptime(os.getenv('START_DATE'), '%Y-%m-%d') # 開始日を設定 end = datetime.strptime(os.getenv('END_DATE'), '%Y-%m-%d') # 終了日を設定 for i in range((end - start).days): today = (start + timedelta(i)).strftime('%Y-%m-%d') print(today) # データ読み込み with open('data/qiita_' + today + '.json') as json_data: articles = json.load(json_data) # 記事の集約 for article in articles: soup = BeautifulSoup(article['rendered_body'], 'html.parser') # 本文の抜き出し sentences = soup.find_all('p') for sentence in sentences: text = sentence.text + '\n' # ファイル書き込み with open('data/qiita.txt', 'a') as f: f.write(text)このプログラムを実行すると、
dataフォルダの中に、HTMLからpタグ(段落)部分のみを抽出したqiita.txtが生成されます。形態素解析
次に形態素解析を行います。日本語は英語のように単語同士が分かれていないので、単語ごとに分割する必要があるためです。
形態素解析器にはMeCabを使用しています。
注)MeCabは別途インストールが必要です。NEologd辞書と一緒に入れてしまうのが楽でオススメです。text_to_wakati.py# -------------------------------------------------- # テキストファイルを分かち書き # -------------------------------------------------- import os import MeCab # データ読み込み with open('data/qiita.txt') as text_data: tagger = MeCab.Tagger( '-Owakati -b ' + os.getenv('MECAB_BUFFER') + ' -d ' + os.getenv('MECAB_DIC_PATH')) line = text_data.readline() while line: # 分かち書き result = tagger.parse(line) line = text_data.readline() if result != None: # ファイル書き込み with open('data/qiita_wakati.txt', 'a') as f: f.write(result)単語の正規化
最後に単語の正規化を行います。
今回は、以下の処理のみ行いました。
- 英字大文字を全て小文字に
- 日本語の半角を全角に
- 一部の記号を統一
- 数字を全て0に
数字を全て0にしてしまうのは、今回に限ってはやめた方が良いかもしれません。なぜなら、技術用語における数字は結構重要なケースも多いと考えられるからです(バージョンなど)。
preprocessing.py# -------------------------------------------------- # 分かち書きされたテキストの前処理 # -------------------------------------------------- import os import re import jaconv # データ読み込み with open('data/qiita_wakati.txt') as wakati_data: data = wakati_data.read() # 大文字→小文字 data = data.lower() # 半角→全角 data = jaconv.h2z(data) # 記号(-など)の正規化 data = jaconv.normalize(data) # 数字の置き換え data = re.sub(r'[0-9]+', '0', data) # ファイル書き込み with open('data/qiita_corpus.txt', 'w') as f: f.write(data)おわりに
次回→Qiitaコーパスで単語埋め込みの様子をみてみる
- 投稿日:2019-07-27T20:17:53+09:00
最尤推定を用いた回帰
この記事は古川研究室 Workout_calendar 12日目の記事です.
本記事は古川研究室の学生が学習の一環として書いたものです.内容が曖昧であったり表現が多少異なったりする場合があります.
概要
はじめに,私は今回のイベントで3本記事を出します.一貫して回帰がテーマになっていますが,それぞれ違うパラメータ推定方法でアプローチしているのが特徴です.具体的に,第1回では最尤推定,第2回ではMAP推定,第3回ではベイズ推定を用いて回帰を行います.もし,興味があれば本記事だけでなく第2回や第3回も見て頂けると嬉しいです.
本記事の内容をざっくり言うと,最尤推定を使用して回帰モデルのパラメータ$\mathbf w,\beta$を推定し,新規入力に対する出力の予測分布を求めたり,最尤推定で得られる結果が最小二乗法と等価になっていることを確認します.
この記事で行ったことをリスト化すると以下のようになっています.
「記事内で行ったこと」
- (理論)最尤推定を用いたモデルのパラメータと予測分布の導出
- (実装)最尤推定を用いた回帰のスクラッチ実装
まずは,簡単に用語などの説明を行いたいと思います
最尤推定,MAP推定,ベイズ推定について
データセット$X$が与えられている状況で,モデルのパラメータ$\mathbf{w}$を推定する統計的な手法に最尤推定,MAP推定,ベイズ推定があります.これらの手法は,最尤推定とMAP推定がモデルのパラメータ$\mathbf{w}$に関して,最も「良い」答えをただ一つ求める点推定(それ以外の他の可能性は全て切り捨てる)なのに対して,ベイズ推定はパラメータ$\mathbf{w}$に関して「良い」だけでなく,「まあまあ良い」答えなどあらゆる答え(可能性)を含んだ分布を推定できることが大きな違いです.ここで,ベイズの定理は次のような式になっています.
\begin{eqnarray} p(\mathbf{w}|X)=\frac{p(X|\mathbf{w})p(\mathbf{w})}{p(X)} \end{eqnarray}以下は,この定理を使ったパラメータ推定方法です.
①最尤推定(事前知識なしで尤度$p(X|\mathbf{w})$を最大にするパラメータを選ぶ)
\begin{eqnarray} \mathbf{w}_{ML}=\underset{w}{\arg \max \,}p(X|\mathbf{w}) \end{eqnarray}②MAP推定(事前知識ありで事後分布$p(\mathbf{w}|X)$を最大にするパラメータを選ぶ)
\begin{eqnarray} \mathbf{w}_{MAP}=\underset{w}{\arg \max \,}p(X|\mathbf{w})p(\mathbf{w}) \end{eqnarray}③ベイズ推定(パラメータ$\mathbf{w}$の分布を推定する)
\begin{eqnarray} p(\mathbf{w}|X)=\frac{p(X|\mathbf{w})p(\mathbf{w})}{p(X)} \end{eqnarray}尤度とは
本記事では,データセット$X$が与えられているとき,ベイズの定理から次の式が得られます.
\begin{eqnarray} p(\mathbf{w}|X,\beta)=\frac{p(X|\mathbf{w},\beta)p(\mathbf{w})}{p(X)} \end{eqnarray}$\mathbf w$と$\mathbf \beta$はそれぞれパラメータです(詳細は後で出てきます).このとき,$p(X|\mathbf w,\beta)$を尤度,$p(\mathbf w)$を事前分布,$p(X)$をエビデンス,$p(\mathbf w|X,\beta)$を事後分布といいます.ここで,$X$は与えられているので確率変数ではなく,$\mathbf w,\beta$は確率変数です.
尤度$p(X|\mathbf w,\beta)$は,既に手に入ったデータセット$X$からパラメータ$\mathbf w,\beta$を見て,$\mathbf w,\beta$が何か一意に決まったときの$X$に対する尤もらしさを表します.ここで,尤度は分布全てを足しても1にはならないため,確率ではありません.そのため尤度は,尤度関数とも呼ばれます.
もし文章で分からなければこちらの記事をご覧ください.視覚的に説明されていて,文章でイメージするよりも分かりやすいのでとてもおすすめです.
最尤推定による回帰のタスク設定
与えられているもの
入力$\mathbf x=(x_1,...,x_N), x\in\mathbf R$と出力$\mathbf y=(y_1,...,y_N), y\in\mathbf R$のデータセット仮定
・$\mathbf x$と$\mathbf y$のデータセットは,独立同分布(i.i.d.)に従うとします.・$y_i,f,\epsilon$を次のように仮定します($\beta$はガウスノイズの精度です).
\begin{eqnarray} y_i&=&f(x_i;\mathbf w)+\epsilon_i \end{eqnarray}\begin{eqnarray} f(x_i;\mathbf w)=\mathbf{w}^T\boldsymbol{\phi}(x_i) \end{eqnarray}\begin{eqnarray} \epsilon_i&\sim& N(0,\beta^{-1}) \end{eqnarray}$\;\;\;$ここで,基底関数$\boldsymbol{\phi}(x)$とパラメータ$\mathbf{w}$は$D$個あるので次のようになります.
\begin{eqnarray} \boldsymbol{\phi}(x_i)&=&(\phi_1(x_i),...,\phi_{D}(x_i))^T \end{eqnarray}\begin{eqnarray} \mathbf{w}&=&(w_1,...,w_{D})^T \end{eqnarray}タスク
尤度が最大となるパラメータ$\mathbf w_{ML},\beta_{ML}$を推定する.
\begin{eqnarray} \mathbf w_{ML},\;\beta_{ML} &=&\underset{\mathbf{w},\;\beta}{\arg \max\,}\left(p(\mathbf y|\mathbf x,\mathbf{w},\beta)\right)\\\ &=&\underset{\mathbf{w},\;\beta}{\arg \max\,}\left(\prod_{i=1}^{N}p(y_i|x_i,\mathbf{w},\beta)\right)\ \end{eqnarray}推定した$\mathbf w_{ML},\beta_{ML}$から,新規入力$x^*$に対する出力$y^{*}$の予測分布$p(y^*|x^*,\mathbf
w_{ML},\beta_{ML})$を求めることができます.解析解の導出
対数尤度関数を最大化するパラメータ$\mathbf w_{ML},\mathbf{\beta}_{ML}$を求める
1-1 尤度の式を変形して対数尤度関数を求める
1-2 対数尤度関数を偏微分して,極値を求める推定したパラメータ$\mathbf w_{ML},\mathbf \beta_{ML}$から,新規入力$x^*$に対する出力$y^*$の予測分布を求める
1. 対数尤度関数を最大化するパラメータを求める
1-1 尤度の式を変形して対数尤度関数を求める
はじめに,観測データが$(x_i,y_i)$,出力が$y_i=f(x_i;\mathbf w)+\epsilon_i$とすると,尤度$p\left(y_i|x_i,\mathbf w,\beta\right)$を次のように仮定します.
\begin{eqnarray} p\left(y_i|x_i,\mathbf{w},\beta\right) &=&N\left(y_i|f(x_i;\mathbf w),\beta^{^-1}\right)\\ &=&\sqrt\frac{\beta}{{2\pi}}\exp\left(-\frac{\beta}{2}(y_i-f(x_i;\mathbf w))^{2}\right)\\ &=&\sqrt\frac{\beta}{{2\pi}}\exp\left(-\frac{\beta}{2}\left(y_i-\mathbf{w}^{T}\boldsymbol{\phi}\left(x_i\right)\right)^{2}\right) \end{eqnarray}次に,データセット全体の尤度を求めると,独立同分布(i.i.d.)に従うと仮定しているので次のようになります.
\begin{eqnarray} \prod_{i=1}^{N} p\left(y_i|x_i,\mathbf{w},\beta\right)=p(y_1|x_1,\mathbf{w},\beta)\times \cdots \times p(y_N|x_N,\mathbf{w},\beta) \end{eqnarray}更に,対数尤度は次のように求められます.
\begin{eqnarray} \ln \left(\prod_{i=1}^{N} p\left(y_i|x_i,\mathbf{w},\beta\right)\right) &=&\sum_{i=1}^{N}\ln p(y_i|x_i,\mathbf{w},\beta)\\ &=&\sum_{i=1}^{N} \{ \frac{1}{2}\ln \frac{\beta}{2\pi}-\frac{\beta}{2}(y_i-\mathbf{w}^{T}\boldsymbol{\phi}(x_i))^{2} \} \\ &=&-\frac{\beta}{2}\sum_{i=1}^{N}(y_i-\mathbf{w}^{T}\boldsymbol{\phi}(x_i))^{2}+\frac{N}{2}\ln \beta-\frac{N}{2}\ln {2\pi}\\ &=&-\frac{\beta}{2}\|\mathbf{y}-\Phi\mathbf{w}\|^{2}+\frac{N}{2}\ln \beta-\frac{N}{2}\ln {2\pi} \end{eqnarray}ここで,$N$,$D$はデータ数と基底関数の数を表しており,$\mathbf{y},\mathbf{w},\Phi$はそれぞれ次のようになっています.
\begin{eqnarray} \mathbf{y}&=&\left(y_1,...,y_N\right)^{T}\\ \mathbf{w}&=&(w_1,...,w_D)^{T}\\ \Phi &=& \left( \begin{array}{cccc} \phi_{1}(x_1) & \cdots & \phi_{D}(x_1)\\ \vdots & \ddots & \vdots\\ \phi_{1}(x_N) & \cdots & \phi_{D}(x_N)\\ \end{array} \right)\\ \end{eqnarray}求めた対数尤度はパラメータ$\mathbf{w},\beta$による関数とみなせるので,対数尤度関数$L(\mathbf{w},\beta)$とおくと次のようになります.
\begin{eqnarray} L(\mathbf{w},\beta)&=&-\frac{\beta}{2}\|\mathbf{y}-\Phi\mathbf{w}\|^{2}+\frac{N}{2}\ln \beta-\frac{N}{2}\ln {2\pi}\\ &=&-\beta\frac{1}{2}\|\mathbf{y}-\Phi\mathbf{w}\|^{2}+\frac{N}{2}\ln \beta-\frac{N}{2}\ln {2\pi}\\ &=&-\beta E(\mathbf{w})+\frac{N}{2}\ln \beta-\frac{N}{2}\ln {2\pi} \end{eqnarray}ここで,$E(\mathbf{w})=\frac{1}{2}\|\mathbf{y}-\Phi\mathbf{w}\|^{2}$です.
この式のパラメータ$\mathbf{w}$について注目すると,第二項と第三項は定数であり,第一項は$\beta$(スカラー)倍された目的変数とモデルの出力の二乗誤差$E(\mathbf{w})$になっていることが分かります.つまり,パラメータ$\mathbf{w}$に関して尤度関数を最大化するということは二乗誤差を最小にするという問題と等価であることを示しています.このことから,回帰における最小二乗法を解くという行為は最尤推定という統計的手法によって妥当性が裏付けられた解き方であるということが分かります.ただし,ガウスノイズの仮定の下でのみ成り立つことに注意しなければいけません.
1-2 対数尤度関数を偏微分して,極値を求める
① $\mathbf{w}$で偏微分して,極値を求める
次に,先ほど導出した対数尤度関数$L(\mathbf{w},\beta)$を$\mathbf{w}$で偏微分し,$0$となる極値$\mathbf{w}_{ML}$を求めます.ここで,パラメータ$\mathbf{w}$に関係ないとみなせる定数項は全て$const$にまとめています.\begin{eqnarray} \frac{\partial L(\mathbf{w},\beta)}{\partial \mathbf{w}} &=&\frac{\partial}{\partial \mathbf{w}}\{-\frac{\beta}{2}\|\mathbf{y}-\Phi\mathbf{w}\|^{2}+const\}\\ &=&\frac{\partial}{\partial \mathbf{w}}\{-\frac{\beta}{2}(\mathbf{y}-\Phi\mathbf{w})^{T}(\mathbf{y}-\Phi\mathbf{w})+const\}\\ &=&\frac{\partial}{\partial \mathbf{w}}\left\{-\frac{\beta}{2}\left(\mathbf{y}^T\mathbf{y}-\mathbf{y}^T\Phi\mathbf{w}-\mathbf{w}^T\Phi^T\mathbf{y}+\mathbf{w}^T\Phi^T\Phi\mathbf{w}\right)+const\right\}\\ &=&\frac{\partial}{\partial \mathbf{w}}\left\{-\frac{\beta}{2}\left(\mathbf{y}^T\mathbf{y}-\mathbf{w}^T(\mathbf{y}^T\Phi)^T-\mathbf{w}^T\Phi^T\mathbf{y}+\mathbf{w}^T\Phi^T\Phi\mathbf{w}\right)+const\right\}\\ &=&\frac{\partial}{\partial \mathbf{w}}\left\{-\frac{\beta}{2}\left(\mathbf{y}^T\mathbf{y}-2\mathbf{w}^T\Phi^T\mathbf{y}+\mathbf{w}^T\Phi^T\Phi\mathbf{w}\right)+const\right\}\\ &=&-\frac{\beta}{2}(0-2\Phi^T\mathbf{y}+2\Phi^T\Phi\mathbf{w})+0\\ &=&0 \end{eqnarray}ここで,上から3行目第2項に出てくる$\mathbf{y}^T\Phi\mathbf{w}$は,$\mathbf{a},\mathbf{b}$がベクトルの時に成り立つ$\mathbf{a}^T\mathbf{b}=\mathbf{b}^T\mathbf{a}$の関係を利用して,$\mathbf{a}^T=\mathbf{y}^T\Phi$,$\mathbf{b}=\mathbf{w}$と置いて式変形を行いました.
従って,式を整理すると次の式が得られます.
\begin{eqnarray} \Phi^{T}\Phi\mathbf{w}=\Phi^{T}\mathbf{y} \end{eqnarray}よって,最尤推定で求められた$\mathbf{w}_{ML}$は,
\begin{eqnarray} \mathbf{w}_{ML} &=&(\Phi^{T}\Phi)^{-1}\Phi^T\mathbf{y}\\ &=&\Phi^{\dagger}\mathbf{y} \end{eqnarray}となります.この式は,最小二乗法の正規方程式として知られています.また,$N×D$行列$\Phi^{\dagger}$はムーア=ペンローズの一般化逆行列もしくは疑似逆行列と呼ばれ,長方行列に対しての逆行列みたいなものと考えることができます.余談ですが,もし仮に$N=D$で$\Phi$が正則であるとすると,$(AB)^{-1}=B^{-1}A^{-1}$より,
\begin{eqnarray} \Phi^{\dagger} &=&(\Phi^{T}\Phi)^{-1}\Phi^T\\ &=&\Phi^{-1}(\Phi^T)^{-1}\Phi^T\\ &=&\Phi^{-1} \end{eqnarray}となって,$\Phi^{\dagger}=\Phi^{-1}$が成り立つことが分かります.
② $\beta$で偏微分して,極値を求める
次に,$\beta_{ML}$を求めます.ここで,対数尤度関数$L(\mathbf{w},\beta)$は以下の式となっており,
\begin{eqnarray} L(\mathbf{w},\beta) =-\frac{\beta}{2}\|\mathbf{y}-\Phi\mathbf{w}\|^{2}+\frac{N}{2}\ln \beta-\frac{N}{2}\ln {2\pi} \end{eqnarray}この式を$\beta$について偏微分し,$0$となる極値を求めます.
\begin{eqnarray} \frac{\partial L\left(\mathbf{w},\beta\right)}{\partial \beta} &=&-\frac{1}{2}\|\mathbf{y}-\Phi\mathbf{w}\|^{2}+\frac{N}{2\beta_{ML}}+0 &=&0 \end{eqnarray}得られた式を$\beta_{ML}$について整理すると次のようになります.
\begin{eqnarray} \frac{1}{\beta_{ML}} =\frac{1}{N}\sum_{i=1}^{N}(y_i-\mathbf{w}^{T}\boldsymbol{\phi}(x_i))^{2} \end{eqnarray}この式は,最尤推定で求めたガウスノイズの分散($\beta_{ML}^{-1}$)は平均二乗誤差の値と等しくなるということを示しています.
2. 推定したパラメータから,新規入力に対する出力の予測分布を求める
推定した$\mathbf w_{ML},\beta_{ML}$から,予測分布$p(y^{*}|x^{*},\mathbf w_{ML},\beta_{ML})$は次のようになります.
\begin{eqnarray} p(y^{*}|x^{*},\mathbf{w}_{ML},\beta_{ML}) &=&N\left(y^{*}|f(x^{*};\mathbf w_{ML}),\beta_{ML}^{-1}\right)\\ &=&N\left(y^{*}|\mathbf{w}_{ML}^{T}\boldsymbol{\phi}(x^{*}),\beta_{ML}^{-1}\right) \end{eqnarray}最尤推定を用いた回帰の実装
導出した式から,スクラッチで実装を行いました
# 最尤推定 %matplotlib inline import numpy as np import matplotlib.pyplot as plt np.set_printoptions(precision=3) def Phi(X): # X : [[x0],[x1],...] # phi : e.g. [1, x, x**2] # return : [[phi_1(X),...,phi_n(X)]] result = np.array([[1, x[0], x[0]**2, x[0]**3] for x in X]) return result N = 10 beta = 0.3 np.random.seed(1111) x = np.linspace(-1,1,N) t = np.sin(np.pi*np.linspace(-1.5,1.5,100)) y = np.sin(np.pi*x) + np.random.normal(0,beta,N) x_test = np.linspace(-1.5,1.5,100) y_test = np.sin(np.pi*x_test) + np.random.normal(0,beta,len(x_test)) # 学習 x = np.array([[i] for i in x]) x_test = np.array([[i] for i in x_test]) y = np.array([[i] for i in y]) w_ML = np.dot(np.dot(np.linalg.inv(np.dot(Phi(x).T, Phi(x))), Phi(x).T), y.ravel()) w_ML = np.array([[w] for w in w_ML]) # テスト predict = np.dot(w_ML.T, Phi(x_test).T).ravel() variance_ML = np.sum(np.square(y-np.dot(Phi(x), w_ML))) / N sigma = np.sqrt(variance_ML) fig, ax = plt.subplots(1,2,figsize=(12,4)) ax[0].plot(np.linspace(-1.5,1.5,len(t)),t,label='sin',color='b') ax[0].plot(x_test.ravel(), predict.ravel(),label='predict curve',color='r') ax[0].scatter(x.ravel(), y, label='train_data',color='b') ax[1].fill_between(x_test.ravel(), predict+sigma*3, predict-sigma*3, alpha=0.1, label='3sigma') ax[1].fill_between(x_test.ravel(), predict+sigma, predict-sigma, alpha=0.1, label='sigma') ax[1].plot(x_test.ravel(), predict.ravel(),label='predict curve',color='r') ax[1].scatter(x_test.ravel()[::5],y_test[::5], label='test_data',color='0.1') ax[0].set_title('train') ax[1].set_title('test') ax[0].set_xlim(-1.5,1.5) ax[0].set_ylim(-1.5,1.5) ax[1].set_xlim(-1.5,1.5) ax[1].set_ylim(-1.5,1.5) ax[0].legend(loc='upper right',fontsize=9) ax[1].legend(loc='upper right',fontsize=9) plt.show() for i, w in enumerate(w_ML.ravel()): print('w{}: {:.2f}'.format(i,w),end=' ')実験結果 3次多項式のとき
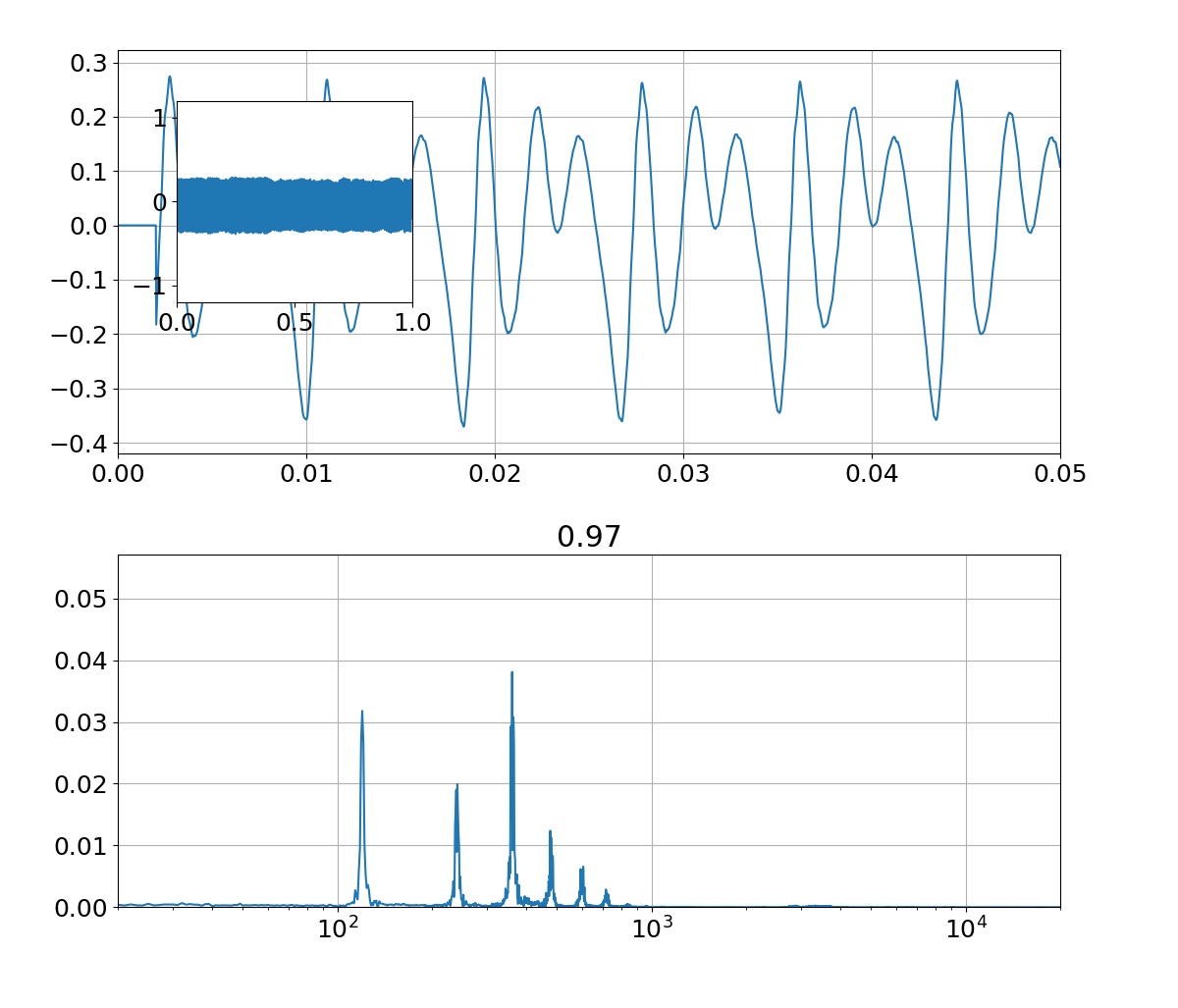
sin関数からサンプリングした10点の学習データに対して,3次多項式のモデルを使って回帰を行った結果がこれです.$x$の定義域が-1.5から1.5付近までは,学習データもテストデータもある程度上手くできてることが分かります.また,パラメータ$\mathbf{w}$は,あまり大きな値になっていない(過学習していない)ことが分かります.分散(sigma)については,ある程度広がりを持っていることが右図から分かります.
実験結果 9次多項式のとき
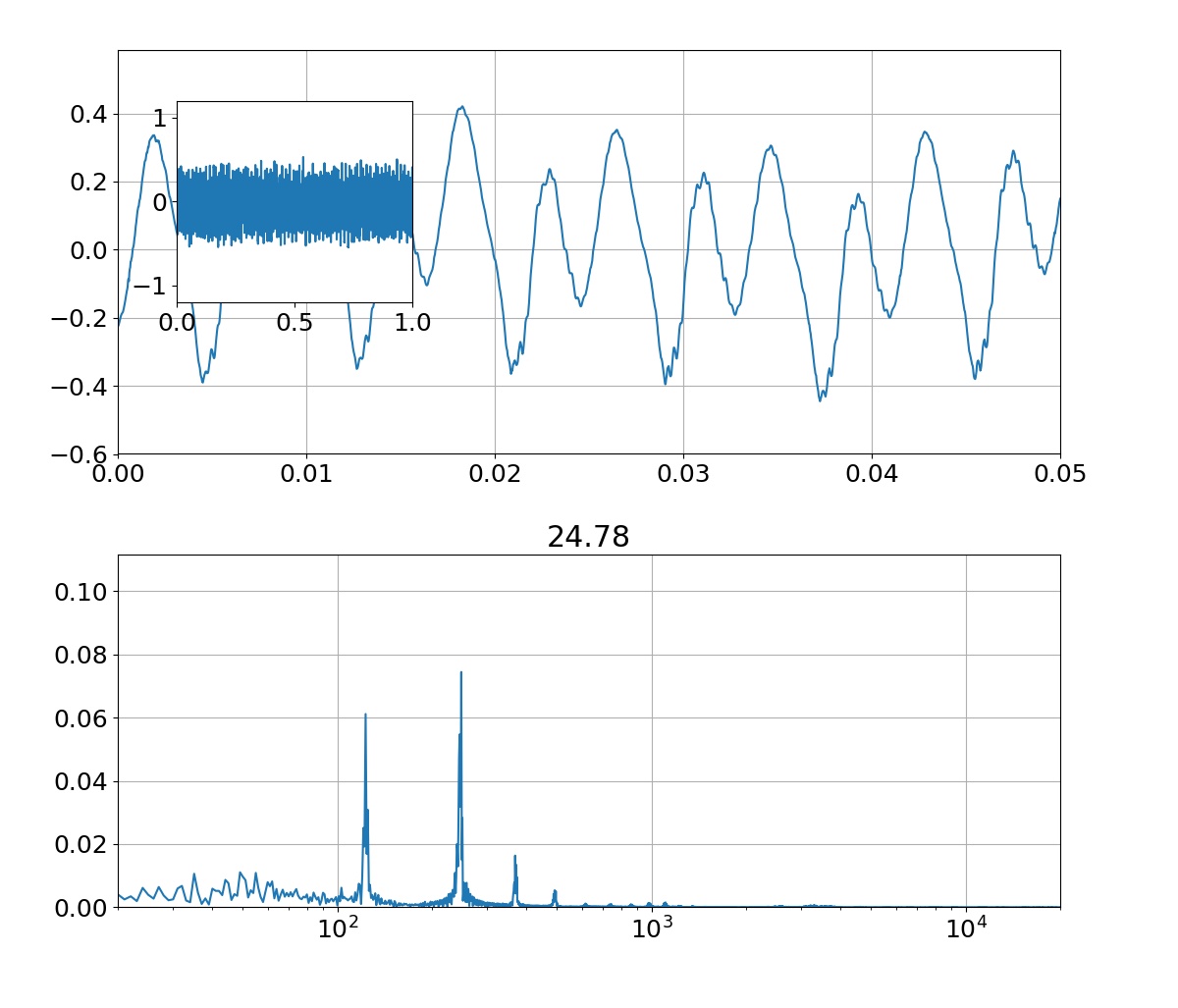
同じ条件で,9次多項式のモデルで回帰を行った結果がこれです.左図を見ると全ての学習データを通る曲線になっていることが分かりますが,一方で右図のテストデータには全然上手くいっていないことが分かります.パラメータ$\mathbf{w}$の値を見てみると3次多項式の結果と比べてかなり大きな値になっていることが分かり,このことから学習データに対して過学習していると考えられます.また,全ての学習データを通る曲線になっているので平均二乗誤差が$0$となり,分散(sigma)がないことが右図から分かります.
感想
数式の導出とスクラッチによる実装を行ったことで,最尤推定を使った回帰のイメージがつかめたと思います.
参考文献
- 投稿日:2019-07-27T19:46:54+09:00
pythonを使ったデータ探索と回帰【kaggle, EDA,randomforest】
今回はコレを紹介しながら写経します。
データについて
試用するデータは保険料のデータ(と思われる)。
データには住所や年齢、喫煙、子供の数などと、保険料が入っている。
このデータをEDAで色々な角度から見ていってモデルの変数選択をして、
最終的に回帰で保険料を算出しようという試み。早速はじめます
import numpy as np import pandas as pd import os import matplotlib.pyplot as pl import seaborn as sns import warnings warnings.filterwarnings('ignore') data = pd.read_csv('C:/・・・/insurance.csv')いつもの
data.head() data.isnull().sum()age sex bmi children smoker region charges 0 19 female 27.900 0 yes southwest 16884.92400 1 18 male 33.770 1 no southeast 1725.55230 2 28 male 33.000 3 no southeast 4449.46200 3 33 male 22.705 0 no northwest 21984.47061 4 32 male 28.880 0 no northwest 3866.85520age 0 sex 0 bmi 0 children 0 smoker 0 region 0 charges 0 dtype: int64データにNaNが含まれてない日はついている日です。
カテゴリカルデータをエンコードして、変数の相関を計算します。from sklearn.preprocessing import LabelEncoder #sex le = LabelEncoder() le.fit(data.sex.drop_duplicates()) data.sex = le.transform(data.sex) # smoker or not le.fit(data.smoker.drop_duplicates()) data.smoker = le.transform(data.smoker) #region le.fit(data.region.drop_duplicates()) data.region = le.transform(data.region)カテゴリカルデータにフィルターをかけて重複しているものをファクターに変換しています。
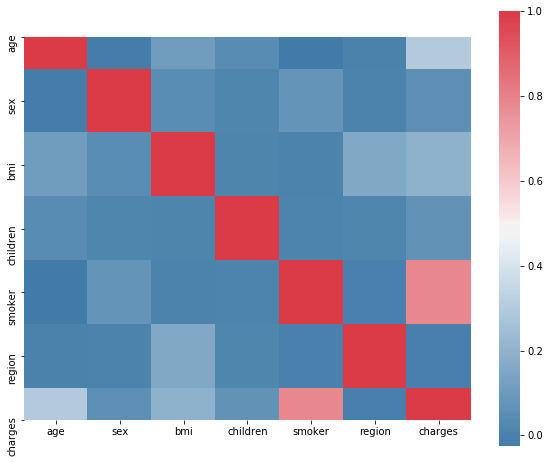
regionのような変数にはonehotencorderなどを使用すべきなのでしょうが今回は怠慢にもlabelencorderで行くようです。data.corr()['charges'].sort_values()region -0.006208 sex 0.057292 children 0.067998 bmi 0.198341 age 0.299008 smoker 0.787251 charges 1.000000f, ax = pl.subplots(figsize=(10, 8)) corr = data.corr() sns.heatmap(corr, mask=np.zeros_like(corr, dtype=np.bool), cmap=sns.diverging_palette(240,10,as_cmap=True), square=True, ax=ax)相関を計算した結果、喫煙者であることと、保険料に正の相関がありそうです。
筆者はbmiと相関があると想定していたようです。費用の分布を確認します。
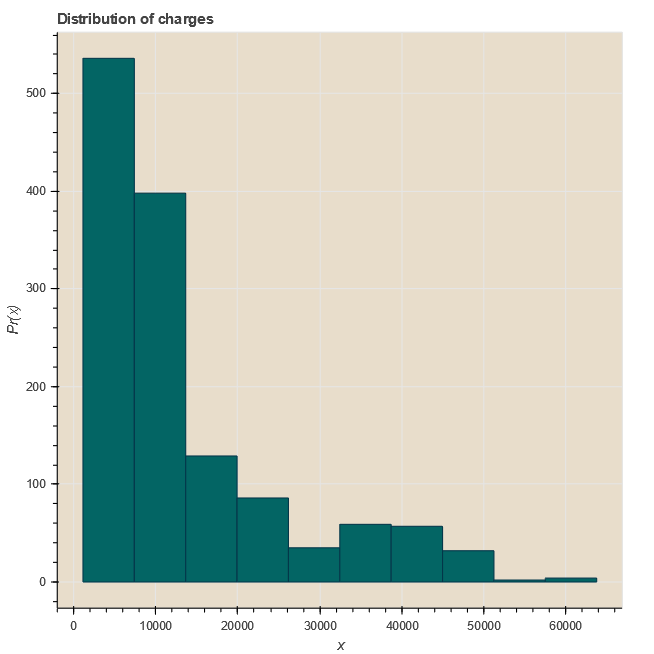
from bokeh.io import output_notebook, show from bokeh.plotting import figure output_notebook() import scipy.special from bokeh.layouts import gridplot from bokeh.plotting import figure, show, output_file p = figure(title="Distribution of charges",tools="save",background_fill_color="#E8DDCB") hist, edges = np.histogram(data.charges) p.quad(top=hist, bottom=0, left=edges[:-1], right=edges[1:],fill_color="#036564", line_color="#033649") p.xaxis.axis_label = 'x' p.yaxis.axis_label = 'Pr(x)'元のソースコードでは
show(gridplot(p,ncols = 2, plot_width=400, plot_height=400, toolbar_location=None))なのですが、動かなかったので
show(p)費用の分布をみるとべらぼうに高い値は少ないようです。
大体10000くらい。f= pl.figure(figsize=(12,5)) ax=f.add_subplot(121) sns.distplot(data[(data.smoker == 1)]["charges"],color='c',ax=ax) ax.set_title('Distribution of charges for smokers') ax=f.add_subplot(122) sns.distplot(data[(data.smoker == 0)]['charges'],color='b',ax=ax) ax.set_title('Distribution of charges for non-smokers')喫煙者と非喫煙者での費用分布の違いを見ると、
喫煙者はふたこぶの分布で、さらに費用は高い傾向にある。
喫煙していなければ10000くらいで大体のデータが収まっています。sns.catplot(x="smoker", kind="count",hue = 'sex', palette="pink", data=data)女性は1,男性は0に相当します
喫煙者を確認してみると、男性のほうが喫煙者でありそうです。
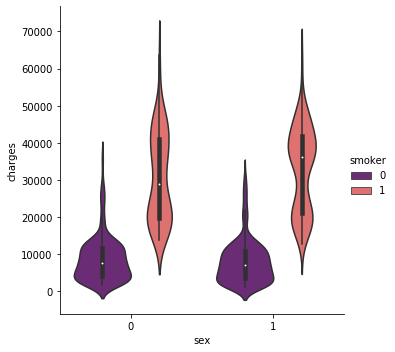
この関係から、男性全体の治療費は女性よりも多くなりそうですね。sns.catplot(x="sex", y="charges", hue="smoker", kind="violin", data=data, palette = 'magma')バイオリンplotで治療費と人数の密度を見てみましょう
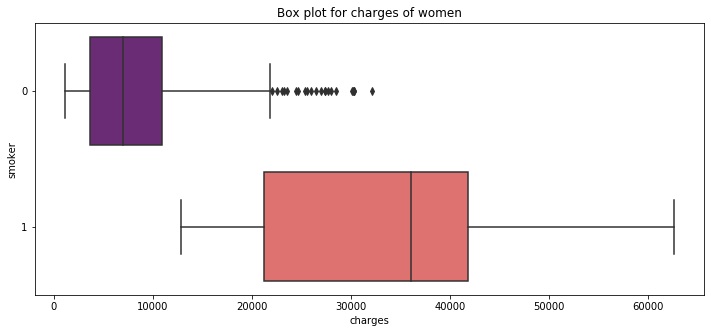
こっちのほうが分かりやすい視覚化ですよねpl.figure(figsize=(12,5)) pl.title("Box plot for charges of women") sns.boxplot(y="smoker", x="charges", data = data[(data.sex == 1)] , orient="h", palette = 'magma')喫煙者のboxplot 女性から
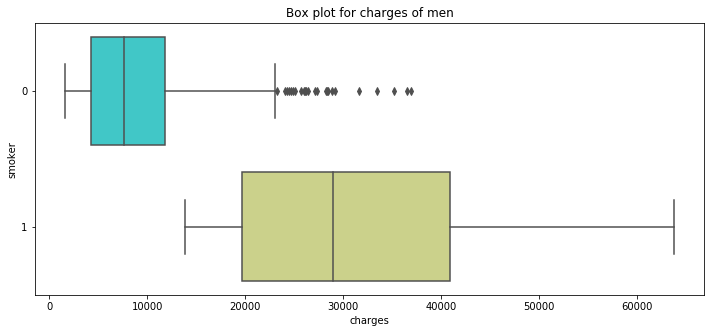
pl.figure(figsize=(12,5)) pl.title("Box plot for charges of men") sns.boxplot(y="smoker", x="charges", data = data[(data.sex == 0)] , orient="h", palette = 'rainbow')男性も。
年齢との関係を見てみましょう。
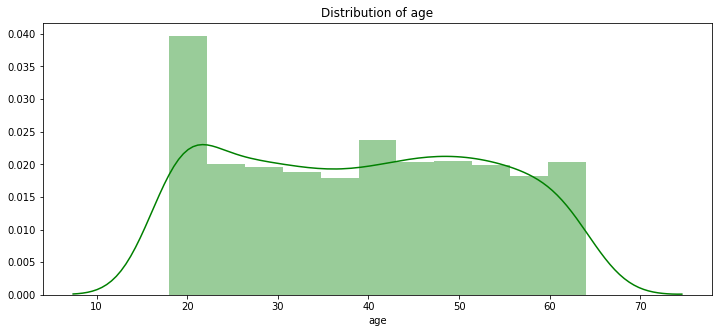
pl.figure(figsize=(12,5)) pl.title("Distribution of age") ax = sns.distplot(data["age"], color = 'g')患者の最もヤングな年齢が18
シニアは64です
18歳で吸ってる人はいるのでしょうか??sns.catplot(x="smoker", kind="count",hue = 'sex', palette="rainbow", data=data[(data.age == 18)]) pl.title("The number of smokers and non-smokers (18 years old)")あらま
18歳でも吸ってる人がいるんですね。
やはり18歳でも治療費は高くなるのでしょうか。pl.figure(figsize=(12,5)) pl.title("Box plot for charges 18 years old smokers") sns.boxplot(y="smoker", x="charges", data = data[(data.age == 18)] , orient="h", palette = 'pink')18歳の金額分布。
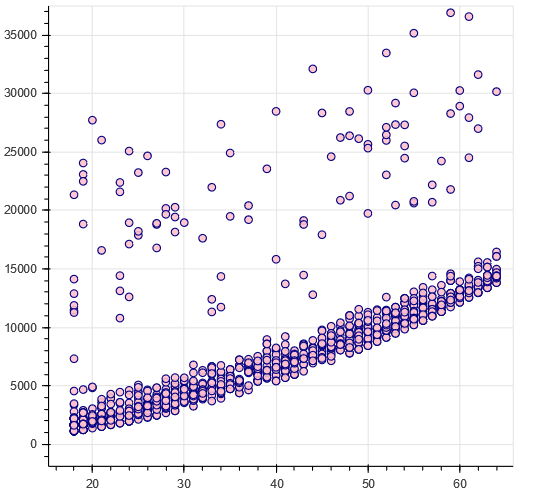
18歳でも喫煙者は治療費が高くなっているようですね。g = sns.jointplot(x="age", y="charges", data = data[(data.smoker == 0)],kind="kde", color="m") g.plot_joint(pl.scatter, c="w", s=30, linewidth=1, marker="+") g.ax_joint.collections[0].set_alpha(0) g.set_axis_labels("$X$", "$Y$") ax.set_title('Distribution of charges and age for non-smokers')喫煙している人の金額分布
(若い人ほど単純にやすい)g = sns.jointplot(x="age", y="charges", data = data[(data.smoker == 1)],kind="kde", color="c") g.plot_joint(pl.scatter, c="w", s=30, linewidth=1, marker="+") g.ax_joint.collections[0].set_alpha(0) g.set_axis_labels("$X$", "$Y$") ax.set_title('Distribution of charges and age for smokers')喫煙者の金額分布
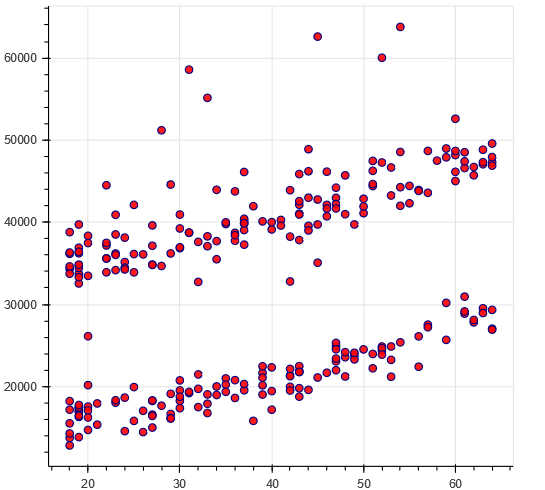
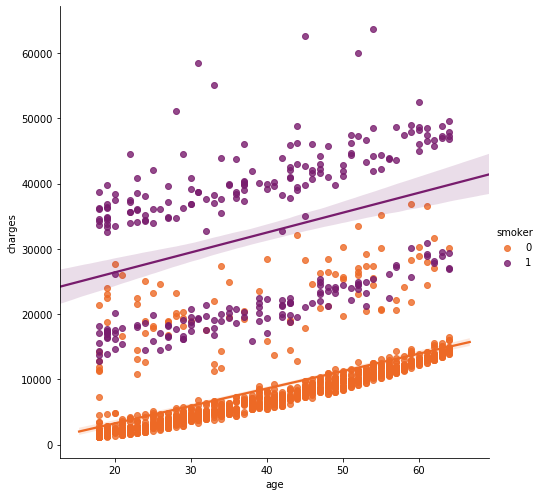
年齢と金額をみると金額は二こぶになっている。#non - smokers p = figure(plot_width=500, plot_height=450) p.circle(x=data[(data.smoker == 0)].age,y=data[(data.smoker == 0)].charges, size=7, line_color="navy", fill_color="pink", fill_alpha=0.9) show(p)#smokers p = figure(plot_width=500, plot_height=450) p.circle(x=data[(data.smoker == 1)].age,y=data[(data.smoker == 1)].charges, size=7, line_color="navy", fill_color="red", fill_alpha=0.9) show(p)sns.lmplot(x="age", y="charges", hue="smoker", data=data, palette = 'inferno_r', size = 7) ax.set_title('Smokers and non-smokers')重ね合わせてplotみるとこんな感じ
喫煙者の2グループについて、それぞれのグループに分けて回帰をしている。
非喫煙者は直線が年齢と比例して増加していっている。
自然の摂理ですよね。健康第一!喫煙者ではばらつきが大変大きく、単純に年齢を重ねたら高くなるのか?と聞かれると説明できない部分が多いデータになっている。
Bmiと比べてみましょう
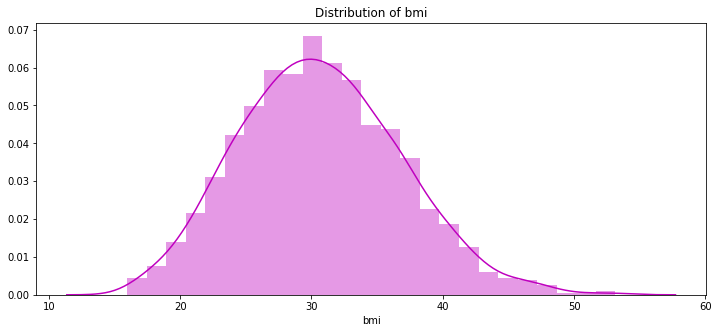
治療費とbmiは関係があるのでしょうか?pl.figure(figsize=(12,5)) pl.title("Distribution of bmi") ax = sns.distplot(data["bmi"], color = 'm')Bmiの分布は平均30のきれいな分布です。
30ってどんなもんなのかグーグルに聞いてみましょう
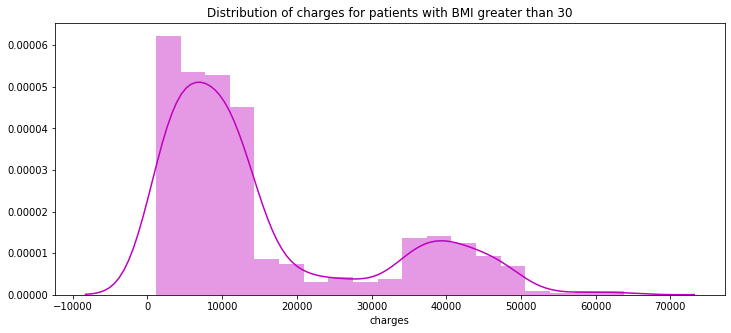
30は肥満の始まりらしいです。Bmiを30で切り分け、30以上以下で費用分布を見ましょうpl.figure(figsize=(12,5)) pl.title("Distribution of charges for patients with BMI greater than 30") ax = sns.distplot(data[(data.bmi >= 30)]['charges'], color = 'm')30以上の分布
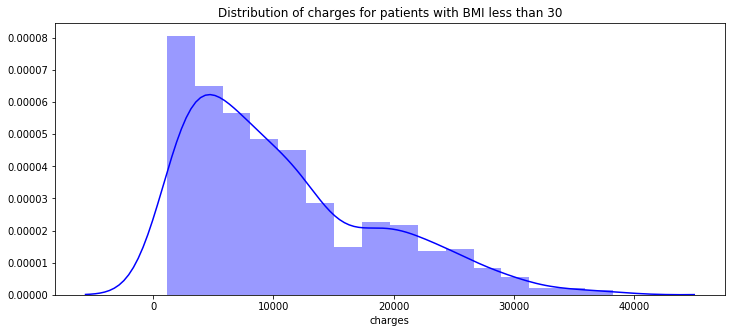
pl.figure(figsize=(12,5)) pl.title("Distribution of charges for patients with BMI less than 30") ax = sns.distplot(data[(data.bmi < 30)]['charges'], color = 'b')30以下の分布
Bmiが30を超えるほど高額を支払っています
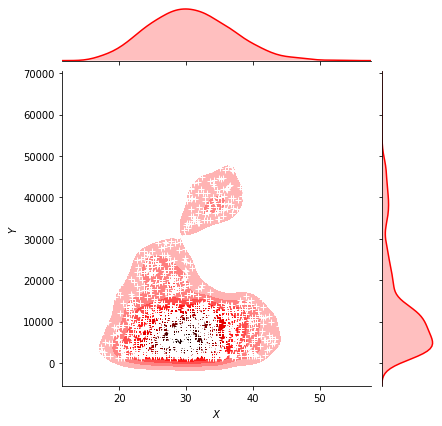
g = sns.jointplot(x="bmi", y="charges", data = data,kind="kde", color="r") g.plot_joint(pl.scatter, c="w", s=30, linewidth=1, marker="+") g.ax_joint.collections[0].set_alpha(0) g.set_axis_labels("$X$", "$Y$") ax.set_title('Distribution of bmi and charges')Bmiに関して治療費と合わせてみてみましょ
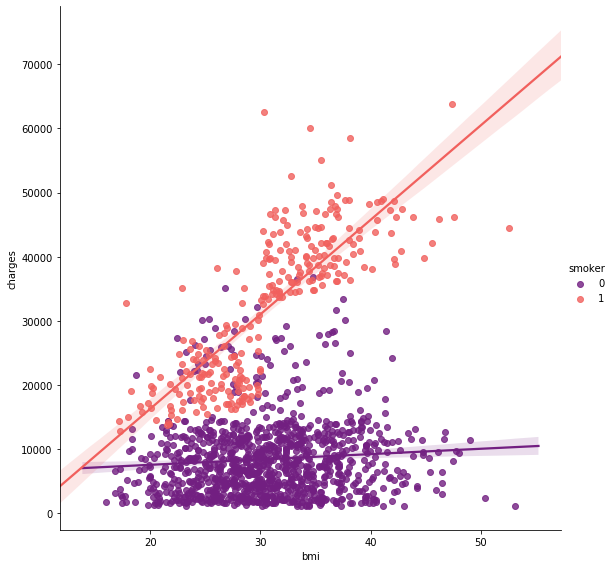
さらに喫煙者とbmiではどうなるでしょうか
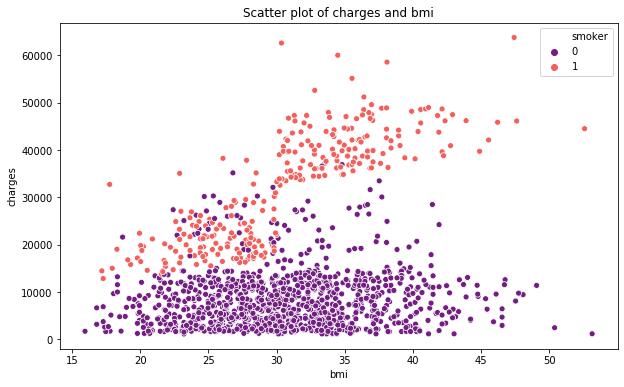
pl.figure(figsize=(10,6)) ax = sns.scatterplot(x='bmi',y='charges',data=data,palette='magma',hue='smoker') ax.set_title('Scatter plot of charges and bmi') sns.lmplot(x="bmi", y="charges", hue="smoker", data=data, palette = 'magma', size = 8)喫煙者であればbmiと治療費に関する直線の傾きが上がっていますね。
子供を持っていたら何か特徴はみられるのでしょうか?
sns.catplot(x="children", kind="count", palette="ch:.25", data=data, size = 6)ほとんど子供を持っていないようです
子供を抱えていたら喫煙したりするのでしょうか?sns.catplot(x="smoker", kind="count", palette="rainbow",hue = "sex", data=data[(data.children > 0)], size = 6) ax.set_title('Smokers and non-smokers who have childrens')子持ちに喫煙者がいますね。
でも喫煙してない親のほうがかなり多いことがわかりますそれぞれの変数から回帰
from sklearn.linear_model import LinearRegression from sklearn.model_selection import train_test_split from sklearn.preprocessing import PolynomialFeatures from sklearn.metrics import r2_score,mean_squared_error from sklearn.ensemble import RandomForestRegressorx = data.drop(['charges'], axis = 1) y = data.charges x_train,x_test,y_train,y_test = train_test_split(x,y, random_state = 0) lr = LinearRegression().fit(x_train,y_train) y_train_pred = lr.predict(x_train) y_test_pred = lr.predict(x_test) print(lr.score(x_test,y_test))0.7962732059725786線形回帰してみました
予測値と実際の値を比較して精度を測定すると0.79でした
データが必ずしも綺麗とは限らないので参考程度にしましょうX = data.drop(['charges','region'], axis = 1) Y = data.charges quad = PolynomialFeatures (degree = 2) x_quad = quad.fit_transform(X) X_train,X_test,Y_train,Y_test = train_test_split(x_quad,Y, random_state = 0) plr = LinearRegression().fit(X_train,Y_train) Y_train_pred = plr.predict(X_train) Y_test_pred = plr.predict(X_test) print(plr.score(X_test,Y_test))0.8849197344147237変数を減らしてシンプルにしています。
Regionを消すと、予測の精度は0.88まで上がりました。ランダムフォレストを使ってみます
forest = RandomForestRegressor(n_estimators = 100, criterion = 'mse', random_state = 1, n_jobs = -1) forest.fit(x_train,y_train) forest_train_pred = forest.predict(x_train) forest_test_pred = forest.predict(x_test) print('MSE train data: %.3f, MSE test data: %.3f' % ( mean_squared_error(y_train,forest_train_pred), mean_squared_error(y_test,forest_test_pred))) print('R2 train data: %.3f, R2 test data: %.3f' % ( r2_score(y_train,forest_train_pred), r2_score(y_test,forest_test_pred)))MSE train data: 3729086.094, MSE test data: 19933823.142 R2 train data: 0.974, R2 test data: 0.873ランダムフォレストといえばclassifierをよく見る気がしますが、
こんかいはregressorを使用していきます。二条平均平方根MSEとR二乗値を確認します
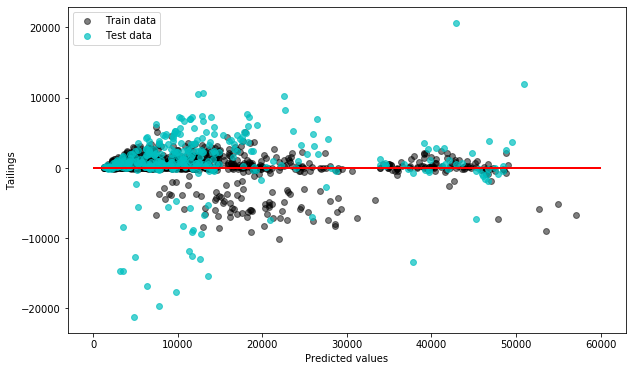
pl.figure(figsize=(10,6)) pl.scatter(forest_train_pred,forest_train_pred - y_train, c = 'black', marker = 'o', s = 35, alpha = 0.5, label = 'Train data') pl.scatter(forest_test_pred,forest_test_pred - y_test, c = 'c', marker = 'o', s = 35, alpha = 0.7, label = 'Test data') pl.xlabel('Predicted values') pl.ylabel('Tailings') pl.legend(loc = 'upper left') pl.hlines(y = 0, xmin = 0, xmax = 60000, lw = 2, color = 'red') pl.show()X軸に予測値
Y軸に予測値と実際の値との差をplotしている
Trainとtestどちらもplotしている以上
seabornやbokehはplotがとても分かりやすくなって素敵な資料が作成できそうです。
そこに時間を割くかは置いといても、見やすいplotは見にくいplotよりは理解を深めてくれるのでマスターしていきたいです。個人的にはlabelencorderの使用例が見られたのがうれしかった。
こんな感じでランダムフォレストで回帰がうごくのかって勉強になりました。
- 投稿日:2019-07-27T19:34:05+09:00
Evernoteのサードパーティ用アクセストークンをOAuth認証で取得する
はじめに
ノートテイキングアプリEvernoteのサードパーティアプリを開発するにあたり、アプリで利用するアクセストークンをOAuth認証により取得する方法を確立させたのでメモ。
まず、Evernoteのサードパーティアプリ利用時のユーザー認可の方法には以下の二通りの方法がある。1
- EvernoteとサードパーティアプリのOAuth認証により取得したCookieをクライアント側で保存し、以降サードパーティアプリ利用時の認可に利用
- EvernoteとサードパーティアプリのOAuth認証により取得したアクセストークンをサーバー側で保存し、以降サードパーティアプリ利用時の認可に利用
1は不特定多数のユーザーが各ユーザー自身のEvernoteアカウント上のリソースをサードパーティアプリから利用することを想定した方法である。
2は管理者や特定の少数のユーザーが特定のEvernoteアカウント上のリソースをサードパーティアプリから利用することを想定した方法である。本記事では2の利用方法を実現させるために、OAuth認証によりアクセストークンを取得する方法を紹介する。
手順
API Key取得
Evernoteのサードパーティアプリごとに必要となるAPI KeyをEvernote開発者用サイトを通じて取得する。
API Keyリクエスト
http://dev.evernote.com/doc/ にアクセスし、画面内の「GET AN API KEY」をクリック。
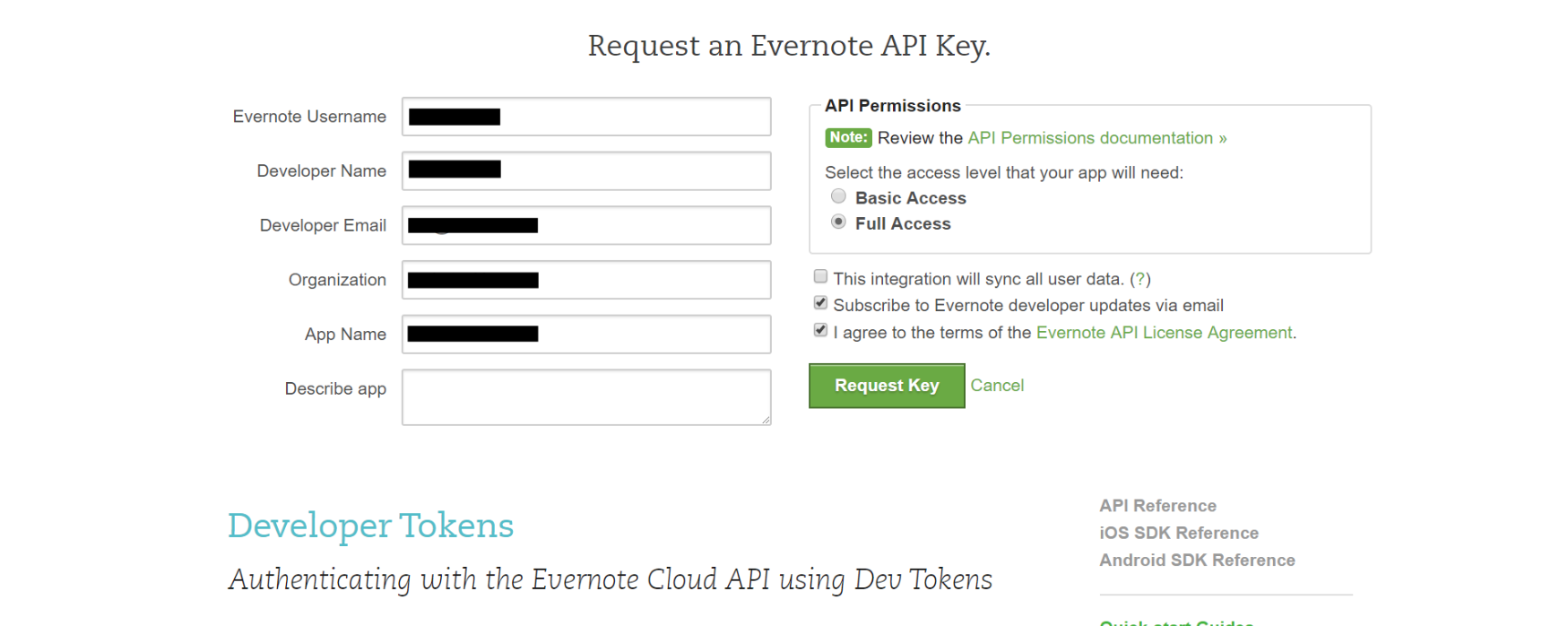
画面上部に下記フォームが表示されるので、入力欄に適当に入力して、「Full Access」を選択し、「I agree 〜」にチェックを入れて、「Request Key」をクリック。
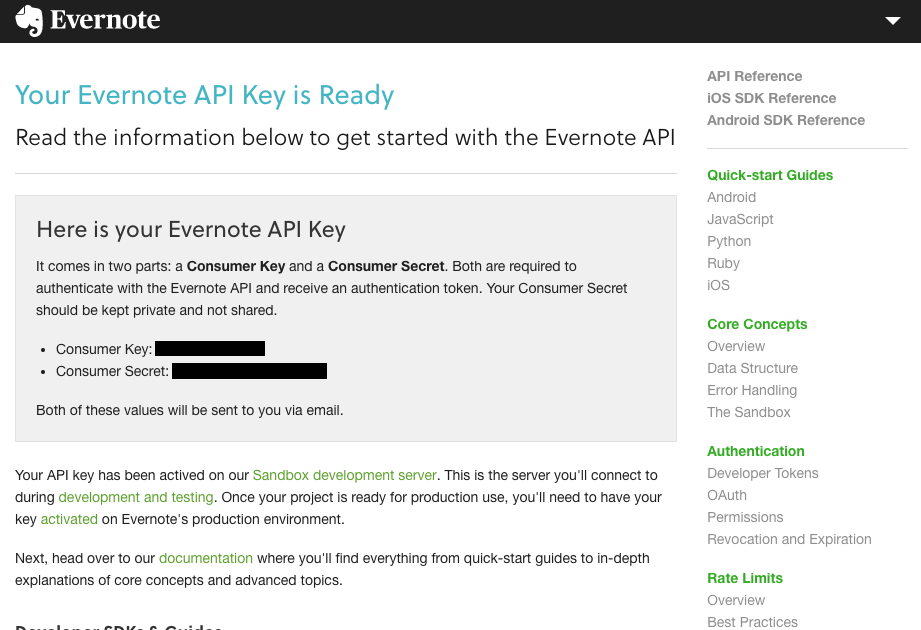
画面が遷移し「Consumer Key」と「Consumer Secret」が表示されるので控えておく。
ここまでで取得したAPIキーはEvernoteのサンドボックス環境(Sandbox development server)では利用できるが、実際にコンシューマーが利用するEvernoteのプロダクション環境(production servers)で利用するためには次手順のAPI Keyアクティベートを行う必要がある。
API Keyアクティベート
http://dev.evernote.com/support/glossary.php#k にアクセスし、「this form」をクリック。
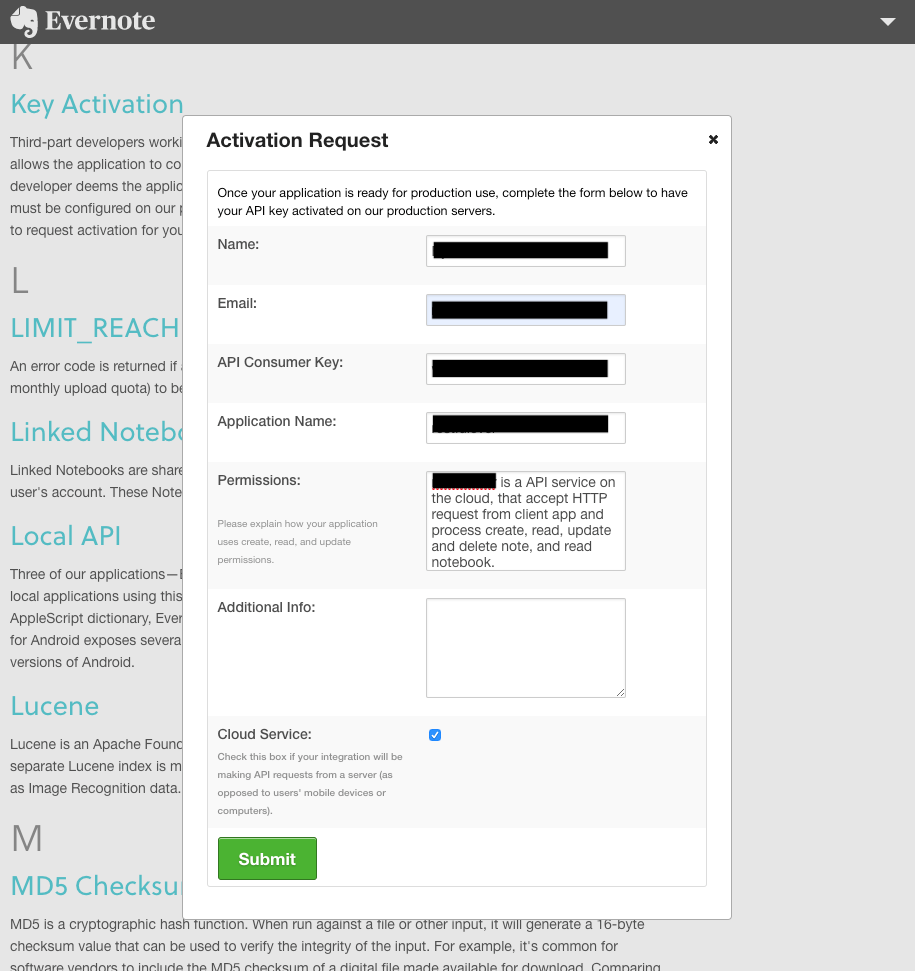
画面内に下記フォームが表示されるので先程控えた情報と合わせて入力し、「Submit」をクリック。
Evernote開発者サポートから下記のようなメールが届いたらサードパーティアプリのAPI Keyのアクティベートは完了(アクティベートをリクエストしてから完了するまでには数日要する)。
差出人: devsupport@evernote.com 送信日時: 2018年7月21日 2:37:03 (UTC+09:00) 大阪、札幌、東京 宛先: XXXXXXXX 件名: Re: xxxxxxxx ##- Please type your reply above this line -## xxxxxxxx (Evernote Developer Relations) Jul 20, 10:37 AM PDT Hello xxxxxxxx, We have activated your API key (xxxxxxx) on our production service. If you have questions, please proceed to Stack Overflow and join the community discussion there: http://stackoverflow.com/questions/tagged/evernote Thank you for building with our API, Evernote Developer Relations xxxxxxxx Jul 19, 1:10 AM PDT xxxxxxxx [XXXXXX-XXXX]アクセストークン取得
Evernote開発者用ドキュメントでは各開発言語向けのSDKが取り揃えられている。今回はそのうちのPython2向けのSDKを利用してアクセストークン取得を行う。2
また、Python2向けSDKではサンプルとして「client」、「django」、「pyramid」を利用した3種類のOAuth実装用のコードが含まれているが、今回はDjangoを利用した方法をもとにしたアクセストークン取得の手順を記載する。
前提
$ python -V Python 2.7.10SDKをローカル環境にgit clone
$ git clone https://github.com/evernote/evernote-sdk-python.git各種モジュールをpip install
$ cd evernote-sdk-python/sample/django $ pip install -r requirements.txtviews.py編集
evernote-sdk-python/sample/django/oauth内のviews.pyを下記のように編集する。(コード内①②③の箇所)views.pyfrom evernote.api.client import EvernoteClient from django.core.urlresolvers import reverse from django.shortcuts import render_to_response from django.shortcuts import redirect # rename config.py.template to config.py and paste your credentials. from config import EN_CONSUMER_KEY, EN_CONSUMER_SECRET def get_evernote_client(token=None): if token: return EvernoteClient(token=token, sandbox=True) else: return EvernoteClient( consumer_key=EN_CONSUMER_KEY, consumer_secret=EN_CONSUMER_SECRET, sandbox=False #・・・① True => False ) def index(request): return render_to_response('oauth/index.html') def auth(request): client = get_evernote_client() callbackUrl = 'http://%s%s' % ( request.get_host(), reverse('evernote_callback')) request_token = client.get_request_token(callbackUrl) # Save the request token information for later request.session['oauth_token'] = request_token['oauth_token'] request.session['oauth_token_secret'] = request_token['oauth_token_secret'] # Redirect the user to the Evernote authorization URL return redirect(client.get_authorize_url(request_token)) def callback(request): try: client = get_evernote_client() access_token = client.get_access_token( #・・・② client.get_access_token( => access_token = client.get_access_token( request.session['oauth_token'], request.session['oauth_token_secret'], request.GET.get('oauth_verifier', '') ) except KeyError: return redirect('/') print('\n--*-- Access Token --*--\n' + access_token + '\n') #・・・③ note_store = client.get_note_store() notebooks = note_store.listNotebooks() return render_to_response('oauth/callback.html', {'notebooks': notebooks}) def reset(request): return redirect('/')config.py作成
evernote-sdk-python/sample/django/oauth内のconfig.py.templateをconfig.pyにリネームして、API Key取得手順で取得した「consumer key」と「consumer secret」を記載する。config.pyEN_CONSUMER_KEY = 'your consumer key' EN_CONSUMER_SECRET = 'your consumer secret'OAuth認証実施、アクセストークン取得
evernote-sdk-python/sample/django/内のmanage.pyを実行してローカルでサーバーを起動。$ python manage.py runserverブラウザから
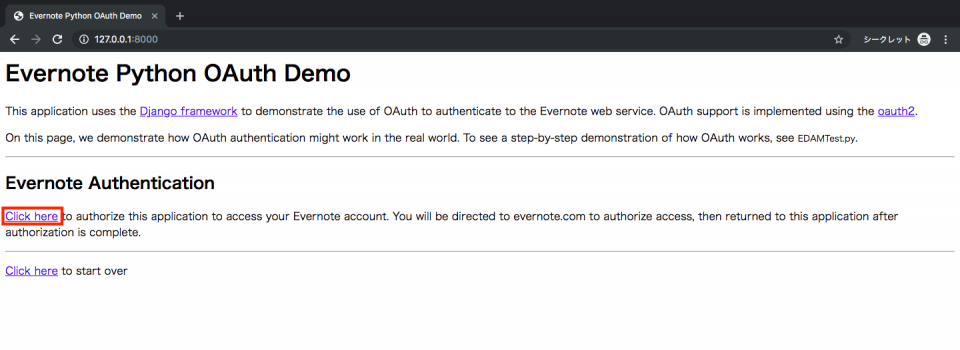
http://127.0.0.1:8000/にアクセス。
表示される画面内の「Click here」をクリック。
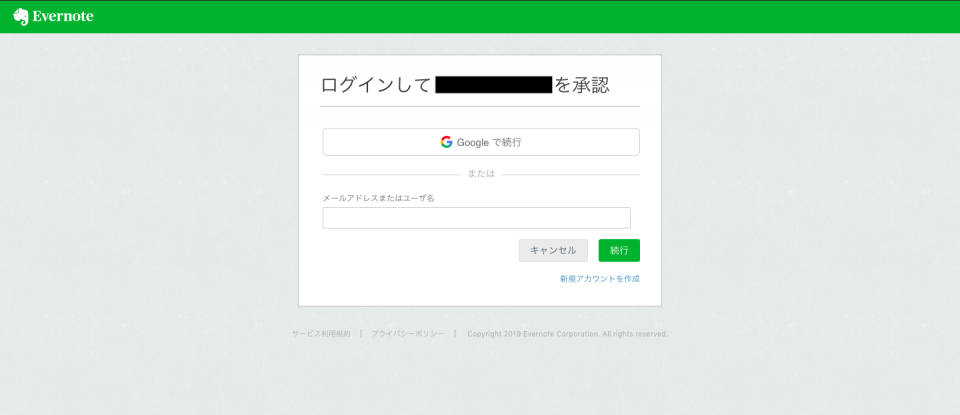
Evernoteのログイン画面が表示されるので、サードパーティアプリにアクセスさせたいEvernoteアカウントでログイン。
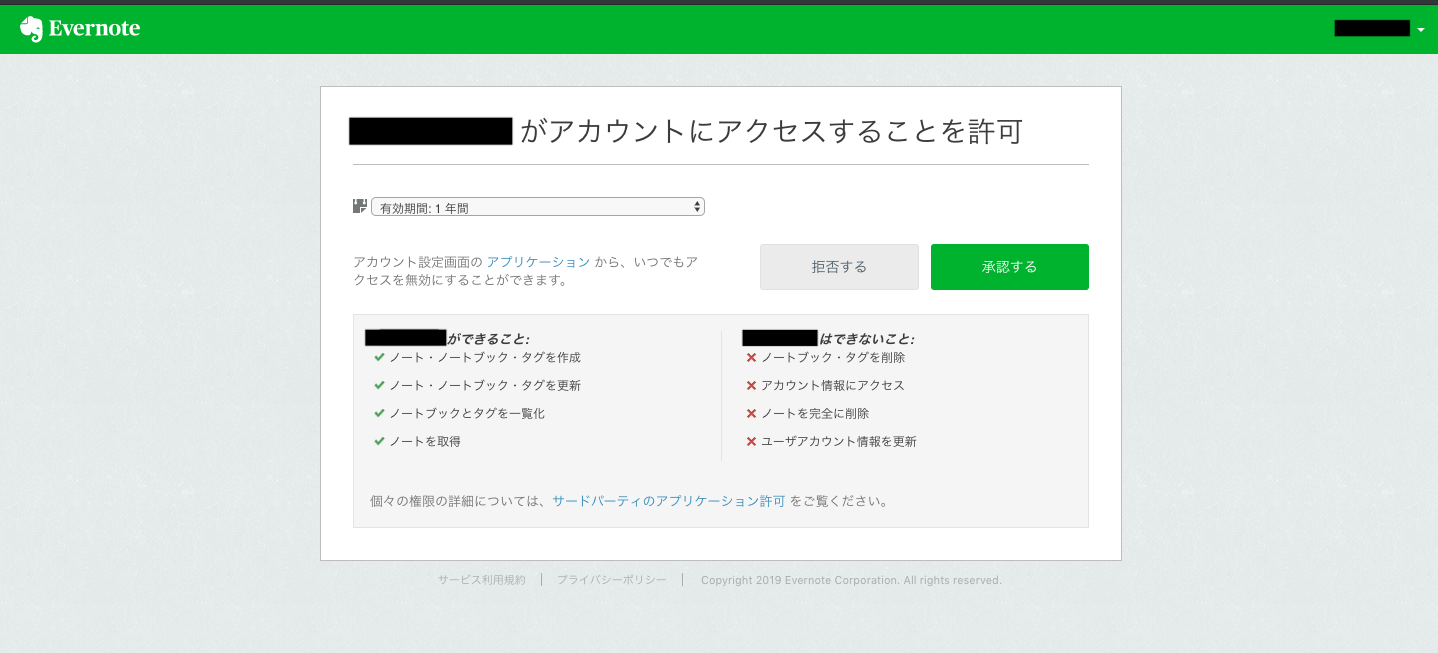
ログインをすると下記の承認画面に遷移するので、承認の有効期間を1日間、1週間、30日間、1年間から選択し、「承認する」をクリック。
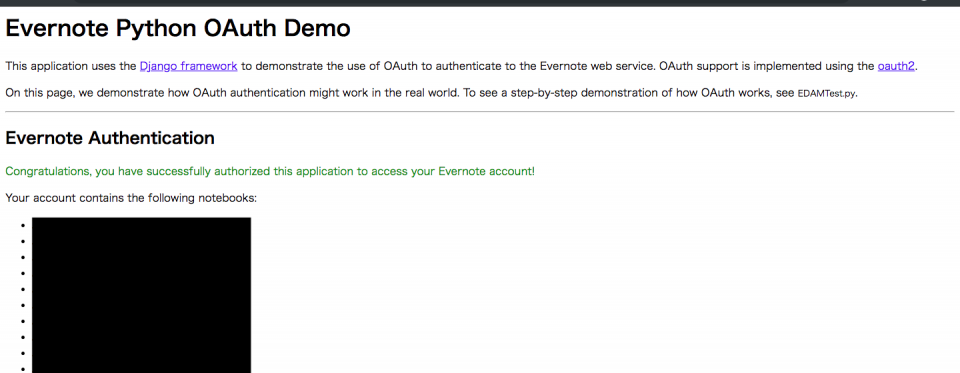
ログインしたEvernoteアカウント内のノートブック一覧が画面に表示されたらサードパーティアプリのOAuth認証完了である。
manage.pyを実行したターミナル上で--*-- Access Token --*--の下にアクセストークンが表示される。
これでEvernoteのサードパーティ用のアクセストークンを取得することができた。--*-- Access Token --*-- <S=xxx:U=xxxxxxx:E=xxxxxxxxxxx:C=xxxxxxxxxxx:P=xxx:A=xxxxx:V=x:H=xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx>次回、今回の手順で取得したアクセストークンを利用したサードパーティアプリの実装の一例を投稿予定。
補足
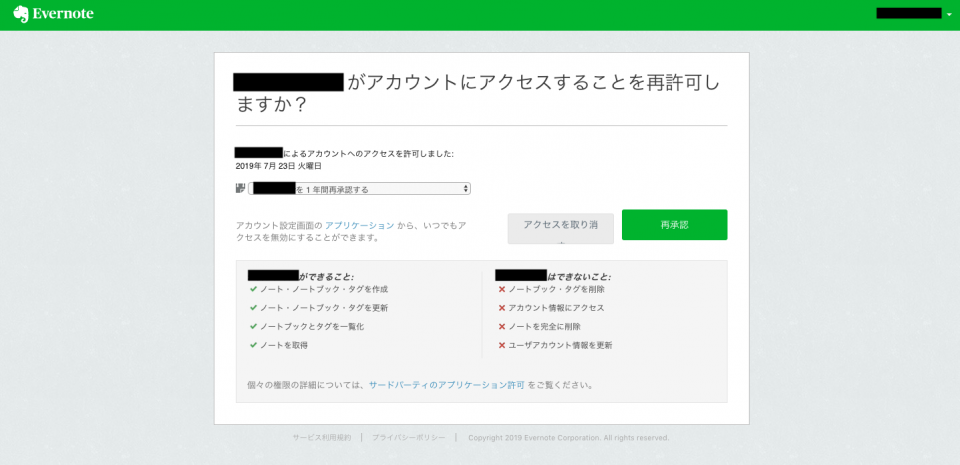
すでに同じEvernoteアカウント、同じサードパーティアプリ(=API Key)で承認済みの場合は下記ような承認画面が表示されて再承認を求められる。再承認をすると新しいアクセストークンが取得でき、再承認前のアクセストークンと同様に利用することができる。
また、Evernoteのサードパーティ製アプリケーションにある通り、自分のEvernoteアカウントのサードパーティアプリごとの承認状況はアプリケーションページで管理できる。承認の取り消しを行うと、その承認時に取得したアクセストークンは無効となり利用できなくなる。
参考
https://myenigma.hatenablog.com/entry/2016/01/23/090212
https://stackoverflow.com/questions/46260328/evernote-sdk-how-can-i-get-the-permission-to-access-all-notebooks-metadata
以前まではわざわざOAuth認証を利用しなくてもDeveloper Tokensにある通り開発者用トークンというアクセストークンを利用する方法もあったようだが、現在はサンドボックス環境向けのみ取得可能で、プロダクション環境向けは取得できなくなっている。 ↩
残念なことに公式のPython向けSDKはPython2のみでPython3は未提供の様子(Python3向けSDKのページもあるにはあるが、作成中の様子で2017年9月から更新がされていないので公式は多分やる気なし)。ただしPython3向けのpypiパッケージevernote3は利用可能。 ↩
- 投稿日:2019-07-27T18:46:35+09:00
from csv to json with Python
csv形式からjson形式へ
知り合いのおじさんが経営する学習塾で使用する英単語テスト作成システムの新調のため,csv形式で保存されていた単語のデータをjson形式に変換する必要がありました.
備忘録として初投稿しようと思います.
Pythonで変換
探せばフリーソフトなど見つかりそうでしたが,最近利用しているPandasの復習も兼ねてPythonで変換しました.
利用したモジュール
- json
- pandas
- argparse
csv形式のファイルの仕様
1行目に乱数,2行目に単語,3行目に意味が入力されています.
乱数はテスト作成でランダムに出題できるよう,マクロで並び替えを行う際に使用します.新しい環境では利用しないため削除します.
word_db.csvrandom num, name, mean 0.93837248,apple,りんご ... ...json形式のファイルの仕様
システム自体を製作したのは別の方なので,実際の仕様ではありませんが以下のようにします.
word_db.json[ { "name": "単語", "mean": "単語の意味", "id": "一意に設定する文字列", "rank": "習熟度を表す数値(int)", }, ]ソースコード
あれこれ書く前に結果だけ載せておきます.
細かい部分は変更しておりますが,おおまかな雰囲気はこんな感じです.
csv_to_json.pyimport json import argparse import pandas as pd def csv_to_json(src_file, dst_file): if dst_file: dst_file = dst_file else: dst_file = 'tmp.json' df = pd.read_csv(src_file) df['id'] = [None for _ in range(len(df.index))] df['rank'] = [0 for _ in range(len(df.index))] df.to_json(dst_file, force_ascii=False, orient='records') with open(dst_file, 'r', encoding='utf-8') as f: json_out = json.load(f) with open(dst_file, 'w', encoding='utf-8') as f: json.dump(json_out, f, ensure_ascii = False, indent = 4, separators = (',', ': ')) if __name__ == '__main__': parser = argparse.ArgumentParser() # add argument: csv file name parser.add_argument('src', help='source csv file name') parser.add_argument('--dst', help='destination json file name') # analysis arguments args = parser.parse_args() csv_to_json(args.src, args.dst)利用する際はこんな感じ.
$ python3 csv_to_json.py word_db.csvこの場合
tmp.jsonというjson形式のファイルが作成されます.
ファイル名を指定したい場合は以下の通り.$ python3 csv_to_json.py word_db.csv --dst (指定したいファイル名).json2度も書き込んでいる理由
最初はリストを用いて適当に変換してしまおうと思っていましたが,列の追加・削除やデータの形式を保った状態での書き込みが面倒だったので,pandasを用いることにしました.
その際データの整形がうまくいかず1行で出力されてしまったので,なんとなく見栄えがいいと思い2回目に整形してDumpしています.
以上.
今後複数の単語データを変換する可能性があったため,コンソールによるファイル名の設定を行えるようにできたのは嬉しい!
Pythonペーペーですが楽しくて時間を忘れますね〜
初投稿で至らない部分も多くあると思いますので,改善点やご指摘お待ちしています.
- 投稿日:2019-07-27T17:59:08+09:00
Pythonでメソッドのオーバーライドの抑制
継承時のメソッドのオーバーライドの禁止は,JavaやC++では
finalキーワードで実現できますが,Pythonの標準機能としてはありません.
ということで,Python(勿論3系)においてどうやってやればよいかを調べたり,考えたりしました.環境
- Ubuntu 18.04
- Python 3.6
- mypy: 0.720
mypy
Python 3.5から型ヒントが導入されましたが,その型ヒントを使って静的に型チェックを行うためのツールです.
そんなmypyですが,@finalというデコレータを用いて,オーバーライドをしてはいけないメソッドであることを表明することができます.使い方としては以下の通りです.
@finalを使って,helloというfinalメソッドだと表明しています.final.pyfrom typing_extensions import final class Base: @final def hello(self) -> None: print("hello") class Derived(Base): def hello(self) -> None: print("こんにちは") Base().hello() Derived().hello()このファイルに対してmypyを使うと警告を出してくれます.
$ mypy final.py final.py:9: error: Cannot override final attribute "hello" (previously declared in base class "Base")ただ,Type Hintsと同様に実行時に影響は無いのでその点注意が必要です.
$ python3 final.py hello こんにちはPros
pip install mypyするだけなので導入が楽.Cons
- 実行時にエラーにならないし,警告も出ない.
参考
Metaclassの利用
mypyによる静的解析もよいのですが,実行時にチェックして例外が上がる方が自分としては嬉しいものです.
イメージとしては,標準ライブラリの抽象基底クラスモジュールであるabc(https://docs.python.org/ja/3/library/abc.html) のような感じでしょうか.ということで,https://github.com/python/cpython/blob/3.7/Lib/abc.py を参考に実装してみたのがこれです(参考と言っても
__isfinalmethod__くらいしか残っていない気がしますが).
全てのメソッドを基底クラスと突き合わせているだけの単純な実装です.import inspect def final(funcobj): funcobj.__isfinalmethod__ = True return funcobj class FinalMeta(type): def __new__(mcls, name, bases, namespace, **kwargs): cls = super().__new__(mcls, name, bases, namespace, **kwargs) # メンバ関数と@staticmethod for funcname, func in inspect.getmembers(cls, inspect.isfunction): for base in bases: base_func = getattr(base, funcname, None) if base_func and getattr(base_func, '__isfinalfunction__', False) and \ func != base_func: raise TypeError("Overriding @final function: {}()".format(funcname)) # @classmethod for funcname, func in inspect.getmembers(cls, inspect.ismethod): for base in bases: base_func = getattr(base, funcname, None) if base_func and getattr(base_func, '__isfinalfunction__', False) and \ func.__func__ != getattr(base_func, '__func__', None): raise TypeError("Overriding @final method: {}()".format(funcname)) return cls自分は初めて知ったのですが,classmethodだけは,関数の実体が
__func__にいるみたいです.第一引数のクラスは固定なので,引数を一つ減らす形でラップしているといったところでしょうか.使用例
以下のような基底クラスを準備します.
class A(metaclass=FinalMeta): @final def final_member(self): pass @classmethod @final def final_class(cls): pass @staticmethod @final def final_static(): pass def overridable(self): print("from A")メンバ関数のオーバーライド
try: class B(A): def final_member(self): pass except TypeError as e: print(e) print("prohibit overriding final member function") #=> Overriding @final function: final_member() #=> prohibit overriding final member functionclassmethodのオーバーライド
try: class C(A): @classmethod def final_class(cls): pass except TypeError as e: print(e) print("prohibit overriding final class method") #=> Overriding @final function: final_class() #=> prohibit overriding final class methodstaticmethodのオーバーライド
try: class E(A): @staticmethod def final_static(): pass except TypeError as e: print(e) print("prohibit overriding final static method") #=> Overriding @final function: final_static() #=> prohibit overriding final static method正常
class F(A): def overridable(self): print("from F") F().overridable() #=> from Fぱっと見ちゃんと動いていそうです.
Pros
- 実行時にオーバーライドを検出して例外を起こせる.
Cons
- 実行時のオーバーヘッドは多分ある.
- 個人的な興味外なので,計測はしていません.
- かなり実装がナイーブなので,dict等使って管理すれば少しは速くなりそう.
- まともな実装であれば,継承もメソッドの数も大したことにはならないので,多分誤差.
この程度が気になるならそもそもPythonを使わない方がよさそう.補足
abcの場合はインスタンス化時に例外が上がるが,これはクラス定義時に例外を上げるようにすると,抽象クラスを継承した抽象クラスの定義ができなくなる等の都合だと思います.
今回のfinalには関係のない都合なので,こちらはクラス定義時に例外が上がるようにしました.まとめ
オーバーライドを抑制するための手段を二つ紹介しました.
抑制と書いているのは,結局 https://qiita.com/eduidl/items/99f856c9710ef10bfec0 と同じように,setattrを使ったりすれば,結局のところいくらでも抜け道があるからです.結局それがPython的ということなのでしょうか.関連リンク
- 自分と同じようなことを考える人はいるようで先例がいくつかありました.(実装がどれも気に入らないまたは,ぱっと理解できなかったかで結局あまり参考にはしていません.)
3つ目のリンク先のこれが一番好き.
# We'll fire you if you override this method.
- 投稿日:2019-07-27T17:17:54+09:00
LeetCode / Symmetric Tree
(ブログ記事からの転載)
[https://leetcode.com/problems/symmetric-tree/]
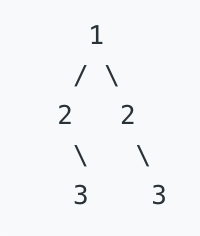
Given a binary tree, check whether it is a mirror of itself (ie, symmetric around its center).
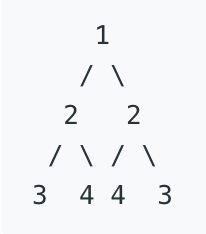
For example, this binary tree [1,2,2,3,4,4,3] is symmetric:
But the following [1,2,2,null,3,null,3] is not:
Note:
Bonus points if you could solve it both recursively and iteratively.前回記事のSame Treeに続き、バイナリツリーを扱った問題。
今度はSymmetric、つまり左右対照の図形かどうかを判定します。
ボーナスポイントをくれるとのことですし、recursiveな解法とiterativeな解法の両方を探してみましょう。解答・解説
解法1
recursiveな解法。
# Definition for a binary tree node. # class TreeNode: # def __init__(self, x): # self.val = x # self.left = None # self.right = None class Solution: def isSymmetric(self, root): if not root: return True else: return self.isMirror(root.left, root.right) def isMirror(self, left, right): if not left and not right: return True if not left or not right: return False if left.val == right.val: outPair = self.isMirror(left.left, right.right) inPiar = self.isMirror(left.right, right.left) return outPair and inPiar else: return False2つ関数を定義していますが、前回のSame Treeと異なりバイナリツリー1つしかないので、もしツリーがない場合Trueを返す処理を挟んでいるだけです。
isMirror関数の処理はSame Treeに似ていますが、
(左側のツリーの左側と右側のツリーの右側)、(右側のツリーの左側と右側のツリーの左側)の各々が同一かどうかを判定するようにします。解法2
Iterativeな解法。
せっかくなので前回記事でも取り扱った、deque型を使って書いてみます。from collections import deque class Solution: def isSymmetric(self, root): if not root: return True deq = deque([(root.left, root.right),]) while deq: t1, t2 = deq.popleft() if not t1 and not t2: continue elif (not t1 or not t2) or (t1.val != t2.val): return False deq.append((t1.left, t2.right)) deq.append((t1.right, t2.left)) return True以下にSame Treeの時のコードを再掲します。微妙な差異しかないのが分かるかと思います。
from collections import deque class Solution: def isSameTree(self, p, q): def check(p, q): if not p and not q: return True if not q or not p: return False if p.val != q.val: return False return True deq = deque([(p, q),]) while deq: p, q = deq.popleft() if not check(p, q): return False if p: deq.append((p.left, q.left)) deq.append((p.right, q.right)) return True
- 投稿日:2019-07-27T16:12:55+09:00
[コード解説] RRT : Rapidly-exploring random tree
■Rapidly-exploring random tree(PythonRobotics)
*コード参考サイト
!!!PythonRobotics!!!
https://github.com/AtsushiSakai/PythonRobotics/tree/master/PathPlanning/RRT
?こちらのGitHub参考にしております。ものすごく良いコードがたくさんあるので、ぜひ覗いてみては、、、?RRTのアルゴリズムの説明。
私のサイト:RRTアルゴリズム
https://meerobots.blogspot.com/2019/07/rapidly-exploring-random-treerrt.html【Pythonコード説明】
説明の流れ
1.全体コード
2.メイン文
3.RRTのコード
ざっくり書いてます。少しでも参考になれば、、、また何かご指摘があれば宜しくお願い致します。
■注意
現在コード修正中なようです!!!!お気を付けください。A1.コード全体
rrt.py""" Path planning Sample Code with Randomized Rapidly-Exploring Random Trees (RRT) author: AtsushiSakai(@Atsushi_twi) """ import math import random import matplotlib.pyplot as plt show_animation = True class RRT: """ Class for RRT planning """ class Node(): """ RRT Node """ def __init__(self, x, y): self.x = x self.y = y self.parent = None def __init__(self, start, goal, obstacle_list, rand_area, expand_dis=1.0, goal_sample_rate=5, max_iter=500): """ Setting Parameter start:Start Position [x,y] goal:Goal Position [x,y] obstacleList:obstacle Positions [[x,y,size],...] randArea:Ramdom Samping Area [min,max] """ self.start = self.Node(start[0], start[1]) self.end = self.Node(goal[0], goal[1]) self.min_rand = rand_area[0] self.max_rand = rand_area[1] self.expand_dis = expand_dis self.goal_sample_rate = goal_sample_rate self.max_iter = max_iter self.obstacleList = obstacle_list self.node_list = [] def planning(self, animation=True): """ rrt path planning animation: flag for animation on or off """ self.node_list = [self.start] for i in range(self.max_iter): rnd = self.get_random_point() nearest_ind = self.get_nearest_list_index(self.node_list, rnd) nearest_node = self.node_list[nearest_ind] new_node = self.steer(rnd, nearest_node) new_node.parent = nearest_node if not self.check_collision(new_node, self.obstacleList): continue self.node_list.append(new_node) print("nNodelist:", len(self.node_list)) # check goal if self.calc_dist_to_goal(new_node.x, new_node.y) <= self.expand_dis: print("Goal!!") return self.generate_final_course(len(self.node_list) - 1) if animation and i % 5: self.draw_graph(rnd) return None # cannot find path def steer(self, rnd, nearest_node): new_node = self.Node(rnd[0], rnd[1]) d, theta = self.calc_distance_and_angle(nearest_node, new_node) if d > self.expand_dis: new_node.x = nearest_node.x + self.expand_dis * math.cos(theta) new_node.y = nearest_node.y + self.expand_dis * math.sin(theta) return new_node def generate_final_course(self, goal_ind): path = [[self.end.x, self.end.y]] node = self.node_list[goal_ind] while node.parent is not None: path.append([node.x, node.y]) node = node.parent path.append([node.x, node.y]) return path def calc_dist_to_goal(self, x, y): dx = x - self.end.x dy = y - self.end.y return math.sqrt(dx ** 2 + dy ** 2) def get_random_point(self): if random.randint(0, 100) > self.goal_sample_rate: rnd = [random.uniform(self.min_rand, self.max_rand), random.uniform(self.min_rand, self.max_rand)] else: # goal point sampling rnd = [self.end.x, self.end.y] return rnd def draw_graph(self, rnd=None): plt.clf() if rnd is not None: plt.plot(rnd[0], rnd[1], "^k") for node in self.node_list: if node.parent: plt.plot([node.x, node.parent.x], [node.y, node.parent.y], "-g") for (ox, oy, size) in self.obstacleList: plt.plot(ox, oy, "ok", ms=30 * size) plt.plot(self.start.x, self.start.y, "xr") plt.plot(self.end.x, self.end.y, "xr") plt.axis([-2, 15, -2, 15]) plt.grid(True) plt.pause(0.01) @staticmethod def get_nearest_list_index(node_list, rnd): dlist = [(node.x - rnd[0]) ** 2 + (node.y - rnd[1]) ** 2 for node in node_list] minind = dlist.index(min(dlist)) return minind @staticmethod def check_collision(node, obstacleList): for (ox, oy, size) in obstacleList: dx = ox - node.x dy = oy - node.y d = dx * dx + dy * dy if d <= size ** 2: return False # collision return True # safe @staticmethod def calc_distance_and_angle(from_node, to_node): dx = to_node.x - from_node.x dy = to_node.y - from_node.y d = math.sqrt(dx ** 2 + dy ** 2) theta = math.atan2(dy, dx) return d, theta def main(gx=5.0, gy=10.0): print("start " + __file__) # ====Search Path with RRT==== obstacleList = [ (5, 5, 1), (3, 6, 2), (3, 8, 2), (3, 10, 2), (7, 5, 2), (9, 5, 2) ] # [x,y,size] # Set Initial parameters rrt = RRT(start=[0, 0], goal=[gx, gy], rand_area=[-2, 15], obstacle_list=obstacleList) path = rrt.planning(animation=show_animation) if path is None: print("Cannot find path") else: print("found path!!") # Draw final path if show_animation: rrt.draw_graph() plt.plot([x for (x, y) in path], [y for (x, y) in path], '-r') plt.grid(True) plt.pause(0.01) # Need for Mac plt.show() if __name__ == '__main__': main()B1. メイン文
1 : スタート、ゴール、障害物の位置、設定
2 : RRT実行rrt.pydef main(gx=5.0, gy=10.0): print("start " + __file__) # ====Search Path with RRT==== obstacleList = [ (5, 5, 1), (3, 6, 2), (3, 8, 2), (3, 10, 2), (7, 5, 2), (9, 5, 2) ] # [x,y,size] # Set Initial parameters rrt = RRT(start=[0, 0], goal=[gx, gy], rand_area=[-2, 15], obstacle_list=obstacleList) path = rrt.planning(animation=show_animation) if path is None: print("Cannot find path") else: print("found path!!") # Draw final path if show_animation: rrt.draw_graph() plt.plot([x for (x, y) in path], [y for (x, y) in path], '-r') plt.grid(True) plt.pause(0.01) # Need for Mac plt.show() if __name__ == '__main__': main()C1.変数定義:位置XY
rrt.pyclass RRT: """ Class for RRT planning """ class Node(): """ RRT Node """ def __init__(self, x, y): self.x = x self.y = y self.parent = NoneC2.定義:スタート、ゴール、障害物(位置とサイズ)、ゴール選ぶ割合、ノードのバス距離、
rrt.pydef __init__(self, start, goal, obstacle_list, rand_area, expand_dis=1.0, goal_sample_rate=5, max_iter=500): """ Setting Parameter start:Start Position [x,y] goal:Goal Position [x,y] obstacleList:obstacle Positions [[x,y,size],...] randArea:Ramdom Samping Area [min,max] """ self.start = self.Node(start[0], start[1]) self.end = self.Node(goal[0], goal[1]) self.min_rand = rand_area[0] self.max_rand = rand_area[1] self.expand_dis = expand_dis self.goal_sample_rate = goal_sample_rate self.max_iter = max_iter self.obstacleList = obstacle_list self.node_list = []C3.アニメーション用データ
rrt.pydef planning(self, animation=True): """ rrt path planning animation: flag for animation on or off """ self.node_list = [self.start] for i in range(self.max_iter): rnd = self.get_random_point() nearest_ind = self.get_nearest_list_index(self.node_list, rnd) nearest_node = self.node_list[nearest_ind] new_node = self.steer(rnd, nearest_node) new_node.parent = nearest_node if not self.check_collision(new_node, self.obstacleList): continue self.node_list.append(new_node) print("nNodelist:", len(self.node_list)) # check goal if self.calc_dist_to_goal(new_node.x, new_node.y) <= self.expand_dis: print("Goal!!") return self.generate_final_course(len(self.node_list) - 1) if animation and i % 5: self.draw_graph(rnd) return None # cannot find pathC4.現在の位置とランダム位置との関係から新しい位置を計算
rrt.pydef steer(self, rnd, nearest_node): new_node = self.Node(rnd[0], rnd[1]) d, theta = self.calc_distance_and_angle(nearest_node, new_node) if d > self.expand_dis: new_node.x = nearest_node.x + self.expand_dis * math.cos(theta) new_node.y = nearest_node.y + self.expand_dis * math.sin(theta) return new_nodeC5.コース結果?
rrt.pydef generate_final_course(self, goal_ind): path = [[self.end.x, self.end.y]] node = self.node_list[goal_ind] while node.parent is not None: path.append([node.x, node.y]) node = node.parent path.append([node.x, node.y]) return pathC6.ゴールまでの距離計算
rrt.pydef calc_dist_to_goal(self, x, y): dx = x - self.end.x dy = y - self.end.y return math.sqrt(dx ** 2 + dy ** 2)C7.ランダム位置生成 任意の回数後ゴール地点選ぶ
rrt.pydef get_random_point(self): if random.randint(0, 100) > self.goal_sample_rate: rnd = [random.uniform(self.min_rand, self.max_rand), random.uniform(self.min_rand, self.max_rand)] else: # goal point sampling rnd = [self.end.x, self.end.y] return rndC8.グラフ生成
rrt.pydef draw_graph(self, rnd=None): plt.clf() if rnd is not None: plt.plot(rnd[0], rnd[1], "^k") for node in self.node_list: if node.parent: plt.plot([node.x, node.parent.x], [node.y, node.parent.y], "-g") for (ox, oy, size) in self.obstacleList: plt.plot(ox, oy, "ok", ms=30 * size) plt.plot(self.start.x, self.start.y, "xr") plt.plot(self.end.x, self.end.y, "xr") plt.axis([-2, 15, -2, 15]) plt.grid(True) plt.pause(0.01)C9.ランダム点から近い点を探索
rrt.py@staticmethod def get_nearest_list_index(node_list, rnd): dlist = [(node.x - rnd[0]) ** 2 + (node.y - rnd[1]) ** 2 for node in node_list] minind = dlist.index(min(dlist)) return minindC10.衝突判定:この方法では点で見ている。
・障害物の位置と次の位置のから距離d算出
・障害物を円として定義し、距離dが半径より小さいと衝突rrt.py@staticmethod def check_collision(node, obstacleList): for (ox, oy, size) in obstacleList: dx = ox - node.x dy = oy - node.y d = dx * dx + dy * dy if d <= size ** 2: return False # collision return True # safeC11.今の位置からランダム位置の距離と角度を算出
次の位置を計算するためrrt.py@staticmethod def calc_distance_and_angle(from_node, to_node): dx = to_node.x - from_node.x dy = to_node.y - from_node.y d = math.sqrt(dx ** 2 + dy ** 2) theta = math.atan2(dy, dx) return d, thetaこれにて終了!
最適性は担保してないけど、簡単に実装できそう。。。
- 投稿日:2019-07-27T15:53:53+09:00
Pythonの抽象基底クラスの抜け道
Pythonの標準ライブラリには抽象基底クラス用のabcというモジュールがあります.もしかしてと思ってやってみたら,やはり抜け道があったので誰得だと思いますが投稿します.
TL;DR
delattrを使ってoverrideを取り消します.環境
- Ubuntu 18.04
- Python 3.6, 3.7
通常の使い方
抽象クラス(
Base)を継承したクラス(Derived)が@abstractmethodでデコレートされた関数(抽象関数)をoverrideしていないときは,以下のように例外になります.from abc import ABC, abstractmethod class Base(ABC): @abstractmethod def method(self): print("from Base") class Derived(Base): pass Derived()Traceback (most recent call last): File "abc.py", line 13, in <module> Derived() TypeError: Can't instantiate abstract class Derived with abstract methods methodoverrideすると,ちゃんと実行できます.
# 上は同じ class Derived(Base): def method(self): print("from Derived") Derived() Derived().method()from Derived抜け道
Pythonにはメタプログラミングに便利な組み込み関数がいくつかあります.
hasattrやsetattrです.
そして今回使うのは,delattrです.その名の通り,attrをdelします.
ということで,一旦overrideした上でそのメソッドを消すことを考えてみます.from abc import ABC, abstractmethod class Base(ABC): @abstractmethod def method(self): print("from Base") class Derived(Base): def method(self): print("from Derived") delattr(Derived, 'method') # del Derived.method でも可 Derived() Derived().method()from Baseということで,抽象関数を呼び出すことに成功?しました.(実際には抽象関数は空か例外を上げるかのどちらかだと思うので何の意味も無いと思います.)
原理としては,
ABCはMetaclassを使っているので,class定義時でのみチェックされているということだと思います.感想
プライベート関数等の例もあるので,わざと抜け道を残している気もします 1 .
setattrやdelattrは用法用量を守って正しく使いましょう(使わないのがベストだと思いますが).参考
- https://docs.python.org/ja/3/library/abc.html
- https://docs.python.org/ja/3/library/functions.html#delattr
Rubyにも
sendとかあるし,そういうことができてこその動的型付け言語みたいなところはある. ↩
- 投稿日:2019-07-27T15:23:54+09:00
AtCoder Beginners Contest 過去問チャレンジ1
AtCoder Beginners Contest 過去問チャレンジ1
AtCoder Beginners Selection(以下 abs) を解いたので、AtCoder Beginners Contest (以下 abc)の準備は万端かと思いきや、abs には難易度 ABC 問題しかなく、abc には難易度 DEF の問題が出るようなので、過去問のD以上の問題にチャレンジ.
あと abs を解くときに input() が動かなくてひどい目にあって raw_input() に差し替えたが、Python 3 は input() で大丈夫らしいので、Python 2 から 3 に切り替えた. print に括弧を付けるのがめんどくさいなと思っていたが、map や range が list じゃないことのほうがめんどくさいかもしれない.
ABC133D - Rain Flows into Dams
山iに降った水の量をRiとすると
(R1+R2) / 2 = A1 (R2+R3) / 2 = A2 (R3+R4) / 2 = A3 (R4+R5) / 2 = A3 ... (RN+R1) / 2 = ANになることが分かる.
この時 R1 を求めるのは中学で習う連立一次方程式が分かっていれば特に何も難しいことはない.((R1+R2) / 2) - ((R2+R3) / 2) + ((R3+R4) / 2) - ((R4+R5) / 2) + ... + ((RN+R1) / 2) = A1 - A2 + A3 - A4 + ... + AN R1 = A1 - A2 + A3 - A4 + ... + AN
(Ri+Ri+1) / 2 = AiからRi+1 = 2 * Ai - Riなので、R1 一つ分かりさえすれば残りはドミノ倒し的に分かるので、後はこれを Python のコードに落とすだけ.n = int(input()) a = [int(e) for e in input().split()] result = [sum(a[::2])-sum(a[1::2])] for i in range(len(a) - 1): result.append(2*a[i]-result[i]) print(' '.join(map(str, result)))ABC132D - Blue and Red Balls
再帰的に定式化は出来たものの遅い. 再帰関数の切り札 memoize や、小さい数字の部分は一発で返るようにして高速化したものの、TLE は一つも減らずに敗退.
n, k = [int(e) for e in input().split()] divisor = 10 ** 9 + 7 cache = {} def memoize(f): global cache def _(*args): if not args in cache: cache[args] = f(*args) return cache[args] return _ @memoize def f(n, x): if n == 0: return 1 elif n == 1: return x elif x == 1: return 1 elif x == 2: return n + 1 elif x == 3: return (n + 1) * (n + 2) // 2 else: return sum(f(i, x - 1) for i in range(n + 1)) % divisor for i in range(1, k + 1): print(f(k - i, i) * f(n - k - i + 1, i + 1) % divisor)ABC131D - Megalomania
締め切り時間でソートして、順番に制限時間を超過しないか確認していくだけ. かんたんすぎる感じで、D 問題って難易度に波があるなあという感想.
import sys from functools import cmp_to_key n = int(input()) data = [[int(j) for j in input().split()] for i in range(n)] t = 0 data.sort(key = cmp_to_key(lambda x, y: x[1] - y[1])) for d in data: t += d[0] if t > d[1]: print('No') sys.exit() print('Yes')ABC130D - Enough Array
素直に書き下ろしてみたが、予想通り TLE が出た. ウインドウをずらしながら計算するのって20年近く前に大学で習ったよなあと書き直したら通った. 要するに A[i..j] で初めて K を越えたなら A[i+1...j-1] は絶対 K 未満なので、この区間をチェックするだけ無駄なのだ. なので ai+1 を先頭とする部分列は、A[i+1..j] からチェックを開始すれば良い.
n, k = [int(e) for e in input().split()] data = [int(e) for e in input().split()] result = 0 i = 0 j = 0 v = 0 while True: v += data[j] if v < k: j += 1 else: result += len(data) - j v -= data[i] if j > i: v -= data[j] i += 1 if j < i: j += 1 if j == len(data): print(result) break
- 投稿日:2019-07-27T14:16:16+09:00
Pythonでファイル名の末尾が.jpgかどうかをチェックするサンプル
Pythonで正規表現を使ってファイル名の末尾が.jpgかどうかをチェックするスクリプトを書いてみました。
Pythonでは正規表現中のエスケープシーケンスは[]を使います。サンプル
script.pyimport re # ファイル名の末尾が.jpgもしくは.JPGとなっているかチェック def is_jpg(file_name): result = re.match(r'.*[.]jpg', file_name, flags=re.IGNORECASE) print(result) if result is not None: print('matched') else: print('None. unmatched') t1 = 'aaaa.jpg' t2 = 'bbb.JPG' t3 = 'ccc.jpg.' t4 = 'ddd.JPG.' t5 = 'aaaajpg' t6 = 'JPGbbbb' print('----') print(t1) is_jpg(t1) print('----') print(t2) is_jpg(t2) print('----') print(t3) is_jpg(t3) print('----') print(t4) is_jpg(t4) print('----') print(t5) is_jpg(t5) print('----') print(t6) is_jpg(t6)実行結果
$ python3 script.py ---- aaaa.jpg <re.Match object; span=(0, 8), match='aaaa.jpg'> matched ---- bbb.JPG <re.Match object; span=(0, 7), match='bbb.JPG'> matched ---- ccc.jpg. <re.Match object; span=(0, 7), match='ccc.jpg'> matched ---- ddd.JPG. <re.Match object; span=(0, 7), match='ddd.JPG'> matched ---- aaaajpg None None. unmatched ---- JPGbbbb None None. unmatched
- 投稿日:2019-07-27T13:36:57+09:00
Pandasで長いテーブルを表示する際にカラムとかを分かりやすくするライブラリを作った
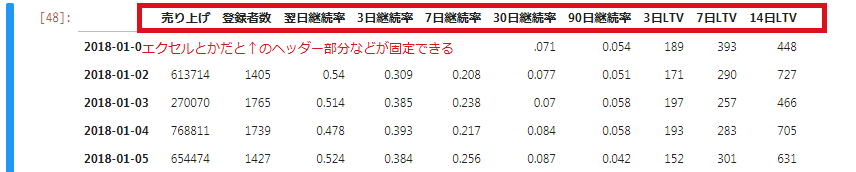
個人的に、共有用のJupyterで出力したHTMLとか含め、Pandasで長いテーブルを表示する時があります。
そういった場合に、エクセルなどのようにカラム名のヘッダー部分を固定表示して、スクロールしてもどのカラムなのかが分かりやすいようにしたり・・・といったことがJupyterだとやり方がよく分かりません(Pandas関係とJupyter関係を軽く調べたくらいなのでもしかしたらもっと調べればあるのかもしれませんが・・・)。
そのため、2時間くらいあればPyPI登録まで含め終わるでしょ・・・という印象だったため、自分でライトなライブラリを書いてみました(Github)。
データフレームから生成されたテーブルの、対象のセルにマウスオーバーするとインデックスとカラムの情報をツールチップで表示してくれます。
これで縦横に長いデータフレームでも安心
インストール方法
pipでインストールができます。
$ pip install pandastabletooltip使い方
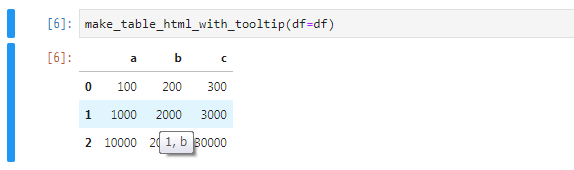
インターフェイスは1つの関数だけで、データフレームを放り込むだけです。
from pandastabletooltip import make_table_html_with_tooltip import pandas as pd df = pd.DataFrame(data=[{ 'a': 100, 'b': 200, 'c': 300, }, { 'a': 1000, 'b': 2000, 'c': 3000, }, { 'a': 10000, 'b': 20000, 'c': 30000, }]) make_table_html_with_tooltip(df=df)息抜きにこういったライトなプログラミングもいいですね
- 投稿日:2019-07-27T13:02:43+09:00
セサミ スマートロック のWebAPIを使ってみる サンプルプログラム(python)
Sesameとは
2018年末時点で世界5万台を売り上げているスマートロックのIotデバイスでCANDY HOUSEが開発、販売をしているプロダクト。
CANDY HOUSEについて: https://jp.candyhouse.co/
このプロダクトのすごいところは、他のスマートロックとは異なりWebAPIを提供しているので、自作プログラムからSesameを動かすことができる。SesameのWebAPIを使ってみる
まず、SesamiのWebAPIを使う条件 参考(https://ameblo.jp/candyhouse-inc/entry-12352517694.html)
①自身がオーナーであるSesame本体
②SesamiがペアリングされているWiFiアクセスポイント
③インターネット接続のあるPC
※①の補足
Sesameへの登録は、
・オーナー
・マネージャー
・ゲスト
の3種類あり、オーナーにならないとAPIキーの発行が出来ない。また、オーナー登録は1人のユーザーしか出来ない。
(WiFIアクセスポイントも同様に1人しか登録出来ないようなので注意)プログラムからSesameを動かすまでの流れ(今回はpython)
①Sesameのスマホアプリで、Sesameスマートロックの登録とWiFiアクセスポイントの登録(それぞれ別で設定して、最後のこの2つをペアリングする)
Sesameスマートロック の登録 参考(https://ameblo.jp/candyhouse-inc/entry-12343105491.html)
WiFiアクセスポイントの設定 参考(https://ameblo.jp/candyhouse-inc/entry-12332339299.html)②Sesamiスマホアプリでの、ドアの解錠ボタンがある画面左下の'管理'ボタンから画面遷移し、「セサミの管理」に移動。そして、連携-クラウドの部分をアクティブにする。これをしないと、エラーが返ってくる。
③APIキーの発行
開発者用のWebページから行う。
サイト(https://my.candyhouse.co/#/distribution/0)
'Sesame List'に自分がオーナー権限を持っているSesameがあるかを確認し、APISettingsの画面で、APIKeyを発行。
④Sesame WebAPIのリファレンスを参考にAPIキーの認証状態を確認するcurl -H "Authorization: YOUR_AUTH_TOKEN" \ https://api.candyhouse.co/public/sesames→https通信を許可するSSL照明の期限が切れているとSSLエラーが返ってくるので注意
その場合はこっちのコマンドで対応(本来は、証明書の再発行が必要)curl --insecure -H "Authorization: YOUR_AUTH_TOKEN" https://api.candyhouse.co/public/sesamesAPIキーの使用承認が降りていると、登録しているSesameの情報が返ってくる。
ここまできたら下準備完了⑤pythonのデモプログラムを起動
https://github.com/yagami-cerberus/pysesame2
基本的にpysesami2のライブラリを使えば、同期、非同期の任意の方法でSesameを動かせるようになる。サンプルその1
鍵が閉まっていたら開けて、開いていたら閉じる
from uuid import UUID import time from pysesame2 import Sesame def main(): device_id = UUID('DEVICEID') sesame = Sesame(device_id, 'APIKEY') if sesame.get_status()['responsive'] == True: if sesame.get_status()['locked'] == True: task = sesame.async_unlock() else: task = sesame.async_lock() while task.pooling() is False: print('SesameProcessing...') time.sleep(1) print('SesameResult: {}'.format(task.is_successful)) else: print('Sesame can not be found') if __name__=='__main__': main()サンプルその2
__鍵が閉じていたら開けて、3秒たったら閉める。
from uuid import UUID import time from pysesame2 import Sesame def sesameOpen(): device_id = UUID('DEVICEID') sesame = Sesame(device_id, 'APIKEY') if sesame.get_status()['responsive'] is True: if sesame.get_status()['locked'] is True: task = sesame.async_unlock() while task.pooling() is False: print("\033[32m{}\033[0m".format('SesameProcessing...')) time.sleep(1) print("\033[32mSesameResult: {}\033[0m".format(task.is_successful)) ssm_cls=threading.Timer(3, sesameClose, args=[sesame]) ssm_cls.start() else: print('Sesame is unlocked') else: print('Sesame can not be found') def sesameClose(sesame): task = sesame.async_lock() print("\033[35m{}\033[0m".format('Called Sesame locked')) if __name__=='__main__': sesameOpen()その他参考サイト
Qiita: https://qiita.com/kt-sz/items/e8ccec02605584e62b53
APIリファレンス: https://docs.candyhouse.co/#introduction
- 投稿日:2019-07-27T12:24:09+09:00
JavaとC++は学ぶな!!初心者が学ぶべき言語【さらに厳選】
注意事項
この記事には以下の要素が含まれます。苦手な方はご注意くださいね。
- Pythonへの熱いdisり
- C言語なんてなかった
- JDK問題について深く知らないので怖がっている
- いわゆる関数型言語に言及しないスタイル(
F#とかScalaとか?)はじめに
という記事が出ているのですが、C++erとしては遺憾の意を示さざるを得ません。そのうえでこれからプログラミングを始める人におすすめする言語を紹介します。え、C++?初心者にはおすすめできません。
初心者におすすめする言語が満たすべき要件
- 人口がそこそこいる
- Windowsでも容易に開発環境が構築できる
- 動作結果が目で見てわかる
- コンパイルしなくていい
- 言語規格が少なくとも5年以内に更新されている
- 言語規格が後方互換性を備えていること
- 日本語資料が豊富にあること
- 非力なPCでも開発できる
人口がそこそこいる
プログラミング言語を作っている人もたくさんいるので無限にプログラミング言語は存在し得るわけですが、さすがにある程度ユーザー数がいない言語を薦めるわけにはいきません。
Windowsでも容易に開発環境が構築できる
例えばPythonはなぜかWindowsだと動かないという事態によく遭遇します(私だけ・・・?)。初心者にエラー文を読んで原因を切り分けさせるのは無理です。
他の言語でもWindowsで完璧に動くぜ!って言うのは以外と少ないです。Rubyはだいぶ頑張っていると思いますがそれでも特に音声やグラフィックが絡むと
cannot load such fileと言われがちです(なぜかmsys2 mingw64 rubyでruby2dが使えない、チャットで問い合わせ中)。動作結果が目で見てわかる
初心者はコンソールなんてまともに扱えませんし、"Hello world!"っていう文字を見せられても感動できません。
なんか図形が動くとかそういう視覚に容易に訴えられるのが望ましいです。
C++はGUIを作るのが極めて難しいのでこういうのは無理です(2D graphics標準化は頓挫したしな)。
言語標準ライブラリに2D描画ライブラリがあるか、十分メンテされてユーザーが居る2Dライブラリがあることが望ましいですね。
コンパイルしなくていい
コンパイルはなれている人でもやっぱり面倒だと思います。もちろんいろいろ自動化することは出来ますが、自動化を組むのが今度は面倒です。
ちなみに面倒くさがれない人は多分プログラミングにあまり向いていません。
言語規格が少なくとも5年以内に更新されている
プログラミング言語も切磋琢磨し日々様々な改善がなされているべきです。ある程度保守的なC++ですら3年おきに更新しているんですから5年経っても更新されない言語は死んでます。え?C言語?2017年末にC11と全く同じ内容をリネームして出してたけどあれはないでしょ。
言語規格が後方互換性を備えていること
初心者が頑張ってググって出てきた情報どおりに書いて動かそうとしたら動かないとなるとモチベーションが吹き飛びます。初心者じゃなくても心が折れます。セキュリティ上の懸念などからdeprecatedになる機能が出るのは仕方ないとしても、Pythonみたいに巨大なbreaking changeを噛ましてくる言語はおすすめできません。
日本語資料が豊富にあること
ただでさえわからないプログラミング言語を学ぶのに、自分の母国語じゃない資料で勉強するとか脳みそがパンクしてしまいます。
非力なPCでも開発できる
プログラミングするのに15万超えるようなPC買えと言われても多くの人は困ってしまいます。Unityとかは結構メモリー持っていくのでつらそうです。一般に出回っているPCはメモリーが4GBのものが多いです。
おすすめしたい言語
これらを満たす言語を残念ながら私の狭い知識では一つしか上げることが出来ませんでした。
JavaScriptブラウザ上で動くのがやっぱり大きいです。Canvas APIを叩くことで図形が描画できます。実行環境をブラウザにすることで、ChromeかFirefoxを入れてもらえば(運が良ければすでに入っている)ほぼセットアップが終わります。
そのままのJavaScriptを使ったブロックくずしゲーム - ゲーム開発 | MDN
というStep-by-StepでCanvas APIを使う資料がなんとMDNにありますし実に良いです。言語の人口も計算不能なレベルで大きく、開発も盛んです。
おすすめしたかった言語
RubyRuby自体はかなりいい言語で、日本語資料も開発者が日本人ですからたくさんあります。グラフィックではRuby2dが結構良さそうなライブラリなんですよね、動けば。うごけー。
おすすめできない言語の例
C++C++erが言うんだから間違いない(確信)。Visual Studioはコンソールアプリケーションを作る分には手順を簡単にしてくれますが、外部ライブラリを使うには不向きです。外部ライブラリをまともに使うにはCMakeという別の言語の助けが必要になります。ものすごく難しいってわけではないですが、他の言語より難しいのは確かです。
C++自体もC++17以降を使う分には極端に難しいということはないと思うのですが(C++er基準)、何分古い情報が多いのとまともな入門書がないのが辛い気がします。
グラフィックライブラリ自体はopennframeworksとかDXライブラリとかがあります。
C#Unityはゲーム業界でもっとも使われているライブラリです。これはC#で書くことが出来ますが、Unityで使えるC#のバージョンがものすごく古いという問題がありました。ようやく新しいC#への追従の動きが一昨年くらいからあるわけですが果たしてC#の進化に追いつけるのか・・・?
C#自体はC#7.0とかC#8.0で書く分には悪くないと思いますが古い情報に出くわしやすい印象です。
Java広く使われている言語で進化を続けています。が!Oracle JDK vs OpenJDK問題を経て(Oracle) JDK8で止まる勢とOpenJDKに移る勢で分裂している気がします。おなじくJVMで動く言語
ScalaのドキュメントにはJDK8をいれろって書いてあります。C++erとしては言語そのものよりJVMレベルのゴタゴタが気になってしまいます。ちなみにOpenJDKは自分でPATH通さないといけない問題はchocolatey使えやって思ってます。
2Dグラフィックは言語標準ライブラリにある気がします。
- 投稿日:2019-07-27T11:22:36+09:00
Effective Python 2章メモ
項目14. Noneを返すよりは例外を選ぶ
・戻り値としてNoneを返すより例外を返すほうが良い
戻り値としてNoneを返す処理はバグの原因となる可能性があるので
Noneを返すより例外を返してあげるほうが良い。16. リストを返さずにジェネレータを返すことを考える
・ジェネレータを返す処理の方がメモリ効率が良い場合が多い。
"""0〜100間の偶数値を取得する""" # リストを使う場合は、全ての偶数値を格納したリストを生成する必要がある。 def even_list(): even_list = [] for i in range(0, 100): if i % 2 == 0: even_list.append(i) # 0〜98まで格納する return even_list # ジェネレータの場合は値を1つずつ返すだけ def even_generator(): for i in range(0, 100): if i % 2 == 0: yield i # 0〜98まで一つずつ返す項目18. 可変長位置引数を使って、見た目をすっきりさせる
・可変長位置引数(*args)を使いコードをすっきりさせる
可変長引数を使用しない場合
def log(message, values): if not values: print(message) else: values_str = ','.join(str(x) for x in values) print('%s: %s' % (message, values_str)) log('My number are', [1, 2]) log('Hi there', []) # いちいち空リストを渡さないといけない >>> My numbers are: 1, 2 Hi there可変長引数を使用した場合
def log(message, *values): if not values: print(message) else: values_str = ','.join(str(x) for x in values) print('%s: %s' % (message, values_str)) log('My numbers are', 1, 2) log('Hi there') # 可変長引数なので、何も渡さなくて良い # 可変長引数にリストを渡す場合 nums = [1, 2] log('My numbers are', *nums) >>> My numbers are: 1, 2 Hi there My numbers are: 1, 2■注意点
可変長引数はタプルに変換されて関数に渡されるため
関数呼び出し元がジェネレータをわたしている場合は
全てのジェネレータの値がタプルに格納される。
(ジェネレータのメリットが消されてしまう)def my_generator(): for i in rante(10): yield i def my_func(*args): print(args) it = my_generator() my_func(*it) >>>> (0, 1, 2, 3, 4, 5, 6, 7, 8, 9)21. 動的なデフォルト引数を指定するときにはNoneとドキュメンテーション文字列を使う
・参照型の引数(リストや辞書)を使う場合はデフォルト値をNoneにする
デフォルト引数の値は関数が定義されたときの1度しか評価されないため、
test関数が定義された時の1回だけlistが宣言される。
そのため、全てのtest関数の呼び出しで、listが共有される。def test(num, list=[]): list.append(num) return list test1 = test(1) print('test1:', test1) test2 = test(2) print('test2:', test2) # 「2」だけが格納されたリストが表示されると思いきや >>> test1: [1] test2: [1, 2]・リストや辞書をデフォルト引数として使用する場合はデフォルト値にNoneを指定する
listがNoneであれば、初期化するよう処理を追加すれば問題なく動作する。def test(num, list=None): if list is None: list = [] list.append(num) return list test1 = test(1) print('test1:', test1) test2 = test(2) print('test2', test2) >>> test1: [1] test2: [2]感想
第一章より語訳がキツい!
- 投稿日:2019-07-27T10:57:22+09:00
VGG16で画像認識してみた
はじめに
せっかくPythonを始めたのだから機械学習で画像認識をしてみようと思った。
今回は、画像を集めてCNN(畳み込みニューラルネットワーク)で学習して~という手法は取らずに、VGG16という学習済みのモデルを使って画像認識を行います。VGG16とは
全16層の畳み込みニューラルネットワークで、1000クラスを学習したモデルです。
認識できるのは学習した1000クラスに限られます。
1000クラス(犬,猫,...など)以外の、たとえば人間の画像を認識させるとガスマスクと認識したりします(人間だと認識できていない)使ったもの
・Python 3.6
・numpy 1.16.4
・tensorflow 1.3.0
・keras 2.2.4
・OpenCV 4.1.0やったこと
手順としては以下のようになります。
入力画像の前処理 → 学習済みモデルの読み込み → 画像の判定 → 結果の出力入力画像の前処理
以下は入力画像のpathを受け取って前処理を行う関数。
import numpy as np import cv2 from keras.applications.vgg16 import preprocess_input def img_preprocess(img_path): img = cv2.imread(img_path) #読み込み size = (224,224) img = cv2.resize(img, size) #サイズ変更 img = np.array(img) #np.arrayにする img = np.expand_dims(img, axis=0) #入力用に次元を一つ追加する img = preprocess_input(img) #VGG16に入力するための前処理を行う return img画像の読み込みはOpenCV(cv2)のimreadで行う。(入力された画像は配列で受け取られる)
VGG16への入力画像サイズは224×224なのでcv2.resizeでサイズを変更。(ここで、imgは(224, 224, 3)の配列となる。最後の3はカラーで入力しているのでRGBの3層あることを示している。)
入力はnp.arrayで行うので変換。preprocess_input()を用いてVGG16に入力するための前処理を行う。学習済みモデルの読み込み
VGG16は簡単に呼び出すことができる。
model = VGG16()全結合層を外すか、重みの種類はどうするかなどを選べるが、重みは1種類しか提供されていないし今回はモデルをそのまま使うので全結合層もそのままにする。
最初に実行するときはデータをダウンロードするので時間がかかる。学習済みモデルを出力するには
pickleを使う。
import pickle #モデルの保存 model_filename = 'model.sav' pickle.dump(model, open(model_filename, 'wb') #モデルの読み込み loaded_model = pickle.load(open(model_filename, 'rb'))画像の判定
1行でできる!便利!
pred = model.predict(img)predに対してdecode_prediction()を適応する。
decode_predictionしたpredは[(class1, description1, probability1), (class2, description2, probability2), ...]のタプルで与えられる。
top=nと指定すると、probability(確率)が最も高いものからn個のデータを取得できる。result = decode_predictions(pred, top=1)[0]コード
main.pyと同じディレクトリにあるimgファイルから入力画像を取得する。認識結果の出力を整える&翻訳するといった細かいところまで含んだものを下に示す。
main.pyimport utils import pickle import numpy as np from keras.applications.vgg16 import preprocess_input, decode_predictions #画像のpathを取得 img_path = utils.get_img_path() #入力画像の前処理 img = utils.img_preprocess(img_path) #学習済みモデルの読み込み model_filename = 'model.sav' model = pickle.load(open(model_filename, 'rb')) #画像の判定 pred = model.predict(img) #最もスコアの高いものを取得 result = decode_predictions(pred, top=1)[0] name_en = result[0][1] score = round(result[0][2]*100, 1) #翻訳 name_ja = utils.name_trans(name_en) print("この画像に映っているのは: {0}({1}) {2}%" .format(name_ja, name_en, score)) print(result)utils.pyimport os, glob import numpy as np import cv2 from keras.applications.vgg16 import preprocess_input from requests import get #入力画像のpathを取得する def get_img_path(): path = './img/' img_name_arr = os.listdir(path) img_name = img_name_arr[0] return path + img_name #入力画像の前処理を行う def img_preprocess(img_path): img = cv2.imread(img_path) #読み込み size = (224,224) img = cv2.resize(img, size) #サイズ変更 img = np.array(img) #np.arrayにする img = np.expand_dims(img, axis=0) #入力用に次元を一つ追加する img = preprocess_input(img) #VGG16に入力するための前処理を行う return img #predictから得られた名前が_(アンダースコア)付きの英単語なので翻訳する def name_trans(name): #'_'を取り除く if '_' in name: name_arr = name.split('_') name = '' for i in range(len(name_arr)): if i == (len(name_arr) - 1): name += name_arr[i] else: name += (name_arr[i] + " ") #GASで作ったAPIで翻訳 trans_from = 'en' trans_to = 'ja' trans_url = ( 'https://script.google.com/macros/s/AKfycbzPH7k0wm5QqP78MtGXt2cOZ_dR0X0G-jMxJODwZvQM3hG89Cct/exec' + '?text=' + name + '&source=' + trans_from + '&target=' + trans_to ) res = get(trans_url) name_ja = res.text return name_ja翻訳については前回の記事を参照してください。
Google Apps Scriptで作った無料翻訳APIを使う実行してみる
結果
この画像に映っているのは: 旅客機(airliner) 84.8%正解!
おわりに
学習済みモデルを使った画像認識は画像データの用意、データの整理、ラベル付けといっためんどくさい作業がないので非常に楽。
しかもVGG16に関してはkerasが色々やってくれる。
次はVGG16の全結合層を外してFine-Tuningを試してみようと思う。参考
Applications - Keras
Python scikit-learnで機械学習モデルを保存&ロードする
KerasでVGG16を使う - 人工知能に関する断創録
- 投稿日:2019-07-27T09:44:06+09:00
python ビッグデータを取り扱ったときのメモ
こちらは個人メモレベルです。調べたことを箇条書き的に記載しています。
■目的
数10GBのファイルを読み込みデータ解析する。
(1)(再)読み込み速度を早くする。
(2)メモリ消費量を抑える。
(3)解析性能を向上させる。■メモリ消費量調査方法
import memory_profiler #メモリ消費を見たいメソッドの上に@profileを記述 #以下はクラスメソッドに記述した例 @classmethod @memory_profiler.profile def main_process(cls, f_filter,...):出力例Line# Mem usage Increment Line Contents 314 29.8 MiB 0.0 MiB @classmethod 315 @memory_profiler.profile 316 def main_process(cls, 329 29.8 MiB 0.0 MiB cls.section = section 330 29.8 MiB 0.0 MiB cls.section_map.clear()※ループの中で何回も呼び出される行のメモリ消費量は最大値が出力される模様
■オブジェクトサイズ調査方法
from pympler import asizeof print('size of 10 = %d' % asizeof(10)) #バイトサイズが返ってくる24■要素の集合を定義する方法
tuple('abc_1234561', datetime.datetime(2019, 1, 20, 10, 20), 12345, 67890, 1234.5678) #書き込み不可 #要素名で参照不可named_tuplent = namedtuple("REPORT","name count value1 value2 va1ue3") nt('abc_123456', datetime.datetime(2019, 1, 20, 10, 20), 12345, 67890, 1234.5678) #書き込み不可 #要素名で参照不可array.arrayimport array array.array('I',[123, 456, day]) #全ての要素が同一の型であることnumpy.arrayimport numpy numpy.array([1,2, 3]) #要素がすべて数値であることlistls=[abc_1234561, datetime.datetime(2019, 1, 20, 10, 20), 12345, 67890, 1234.5678] #要素名でアクセス不可classclass Report_slot: __slots__ = ('name', 'count','value1','value2','va1ue3') def __init__(self, name, count, value1, va1ue2, value3): self.name = name self.count = count self.value1 = value1 self.va1ue2 = va1ue2 self.va1ue3 = value3 #要素名でアクセス可能 #__slots__でプロパティを限定することでオブジェクトサイズを減らす。■要素の集合の容量、アクセス性能
要素数は5とし、以下の型で定義した場合のオブジェクトサイズ、アクセス速度(sec/100000回)を調査。
'abc_123456', datetime.datetime(2019, 1, 20, 10, 20), 12345, 67890, 1234.5678
種類 オブジェクトサイズ 生成 参照 tuple 168 0.048 0.026 named_tuple 80 0.159 0.064 list 176 0.080 0.026 class 424 0.176 0.034 class(slot) 224 0.146 0.038 ■クラスについて
Javaのstaticメソッド、abstractメソッド相当の定義方法
class DataAnalysis: @classmethod @abstractmethod def master_map(cls, file, target_filter): pass■オブジェクトのシリアライズ
同一のファイルを何度も読み込む必要がある場合、読み込んだ結果を
バイナリファイルとして書き出すことで性能を向上させることができる。(1)生成
書き込み単位を分けることでchunkを指定することができる。
import pickle # chunk1 with open('pickle_file', 'wb') as f: pickle.dump([[1, 2], [3, 4], [5, 6]]), f) # chunk2 with open('pickle_file', 'wb') as f: pickle.dump([[7, 8], [9, 10], [11, 12]]), f)(2)読み込み
書き出したオブジェクトの合成が不要なケース。
f = open(f_xx, 'rb') while 1: try: unpickler = pickle.Unpickler(f) list_items = unpickler.load() # 合成が必要な場合ここでlistを結合(extend)する。 print(list_items) except EOFError: breakprint 1回目: [[1, 2], [3, 4], [5, 6]] print 2回目: [[7, 8], [9, 10], [11, 12]]■pythonファイルのパッケージ化
複数のpythonファイルをパッケージ化する。
(1)フォルダ構成
init.pyを定義すること。
Pycharm project/ hoge(ルート)/ __init__.py hogesum.py submodule/ __init__.py hogesum_a.py hogesum_b.py hogesum_c.py(2)明示的な相対import
Pycharmではimport文を絶対参照で記述する場合、プロジェクト直下にパッケージを配置しなければならない。
また配置を変更したりパッケージ名を変更した場合、importのパスが通らなくなる。
このため、パッケージがどこに配置されても良いように、パッケージ内のモジュールは相対importする。(a)hogesum.pyでsubmodule下のhogesum_cをimportする。
from submodule import hogesum_c as panalysis※Pycharmで「Unresolved reference」の警告が表示される場合、
hogeフォルダを右クリックして「Mark Directory As」→ 「Source Root」を選択すると警告が消える。(b)hogesum_c.pyでhogesum_a.pyで定義されたクラスをimportする
from .hogesum_a import DataAnalysis from .hogesum_a import Filter
- 投稿日:2019-07-27T09:25:24+09:00
Dataset を使った TensorFlow のモデルを SavedModel を使用して保存・復元する
Dataset を使った TensorFlow のモデルを SavedModel を使用して保存・復元する
はじめに
TensorFlow の tf.data.Dataset を使用したモデルを SavedModel 保存・復元する方法について説明したいと思います。
保存したモデルを C++ で復元・利用する方法についてはこちらで説明しています。本記事で説明しているソースコードは こちら に載せてあります。
実行環境
- Windows
- Python 3.6
- tensorflow 1.10.0
モデルの学習から保存まで
はじめに学習用データとその正解ラベル、検証用のデータを作成します。
今回はy = 2 * xを学習してみることにします。train.py# 学習用データ train = np.array(np.random.sample((100, 1)) * 10, dtype='float32') train_label = 2 * train # 検証用データ test_data = np.array([[1.0], [2.0], [3.0]], dtype='float32') test_label = test_data実行時に指定されるデータのための placeholder を作成します。
後で利用しやすいように、各々にnameも付けておきます。train.pybatch_size = tf.placeholder(tf.int64, name='batch_size') x = tf.placeholder(tf.float32, shape=[None, 1], name='input') y = tf.placeholder(tf.float32, shape=[None, 1], name='target')上記の placeholder を用いて Dataset と Iterator を生成します。
Iterator が返すデータ自体は改めて指定するので、ここではtf.data.Iterator.from_structureを使用して形だけを作成しておきます。train.pydataset = tf.data.Dataset.from_tensor_slices((x, y)).batch(batch_size).repeat() iter = tf.data.Iterator.from_structure(dataset.output_types, dataset.output_shapes) dataset_init_op = iter.make_initializer(dataset, name='dataset_init')上記の Iterator からモデルへの入力となるデータ(tensor)を取得します。
train.pyx_, y_ = iter.get_next()上記のデータを使用してモデルを作成します。
train.py# make a simple model prediction = tf.identity(tf.layers.dense(x_, 1), name='output') # Optimize loss loss = tf.reduce_mean(tf.square(prediction - y_), name='loss') optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.01) train_op = optimizer.minimize(loss, name='train')ここから学習を開始していきます。初めに
dataset_init_opを実行して、学習に使用するデータを指定します。train.pywith tf.Session() as sess: sess.run(tf.global_variables_initializer()) sess.run(dataset_init_op, feed_dict={ x: train, y: train_label, batch_size: BATCH_SIZE })次に、実際の学習を進めていきます。学習量データは入力済みのため、ここでは学習の実行(
train_op)と loss の取得(loss)のみrunの引数で指定しています。train.pyfor i in range(EPOCHS): _, loss_value = sess.run([train_op, loss]) print("Iter: {}, Loss: {:.4f}".format(i, loss_value))学習が完了したら
dataset_init_opを再度実行して、検証用のデータを指定します。
更にpredictionを実行して検証結果を取得・表示します。train.pysess.run(dataset_init_op, feed_dict={ x: test_data, y: test_label, batch_size: test_data.shape[0] }) results = sess.run(prediction) for i in range(len(results)): print("{} {}".format(test_data[i], results[i]))最後に
tf.saved_model.simple_saveを使用してmodelというフォルダにモデルを保存します。train.pyinputs_dict = { "x": x, "y": y, "batch_size": batch_size } outputs_dict = { "output": prediction } tf.saved_model.simple_save(sess, './model', inputs_dict, outputs_dict)上記を実行すると以下のような結果が得られます。
Iter: 0, Loss: 81.2936 Iter: 1, Loss: 11.0675 Iter: 2, Loss: 0.0215 Iter: 3, Loss: 0.0091 Iter: 4, Loss: 0.0231 Iter: 5, Loss: 0.0119 Iter: 6, Loss: 0.0125 Iter: 7, Loss: 0.0121 Iter: 8, Loss: 0.0144 Iter: 9, Loss: 0.0160 [1.] [2.1919134] [2.] [4.1599956] [3.] [6.1280775]モデルの復元と推論
学習時と同様に入力データを生成します。
test.pytest_data = np.array([[2.0], [3.0], [4.0]], dtype='float32') test_label = test_datamodel フォルダからモデルのデータを復元します。
test.pygraph = tf.Graph() with graph.as_default(): with tf.Session(graph=graph) as sess: tf.saved_model.loader.load( sess, [tag_constants.SERVING], './model' )次に、iterator を初期化する
dataset_initをグラフから取得します。test.pydataset_init_op = graph.get_operation_by_name('dataset_init')この
dataset_initと上記の入力データを使用して iterator の初期化を行います。test.pysess.run(dataset_init_op, feed_dict={ 'input:0': test_data, 'target:0': test_label, 'batch_size:0': test_data.shape[0] } )最後に推論を行い、結果を取得します。
test.pyresults = sess.run('output:0') for i in range(len(results)): print("{} {}".format(test_data[i], results[i]))実行すると以下のような結果が得られます。
[2.] [4.1599956] [3.] [6.1280775] [4.] [8.09616]ハマりどころ1
上記の結論に達するまでに、下記の例外が発生する問題がなかなか解決できずに苦労しました。
FailedPreconditionError (see above for traceback): GetNext() failed because the iterator has not been initialized以下のようなコードを書いていたところ
test_data = np.array([[1.0], [2.0], [3.0]], dtype='float32') test_label = test_data dataset = tf.data.Dataset.from_tensor_slices((test_data, test_label)) iter = dataset.make_initializable_iterator() x_, y_ = iterator.get_next() graph = tf.Graph() with graph.as_default(): with tf.Session(graph=graph) as sess: tf.saved_model.loader.load( sess, [tag_constants.SERVING], './model' ) sess.run(iter.initializer, feed_dict={ 'input:0': test_data, 'target:0': test_label, 'batch_size:0': test_data.shape[0] } ) results = sess.run('output:0')
sess.run('output:0')の実行時に下記の例外が発生してしまいました。FailedPreconditionError (see above for traceback): GetNext() failed because the iterator has not been initializedこれは、上記のコード内で
iter.initializerを実行した場合でも、モデルの中に保存されている Iterator を初期化することにはならない為のようです。ハマりどころ2
初めは SavedModel ではなく、freeze した .pb 形式のモデルを保存・復元しようとしていたのですがこのやり方だと Iterator の保存・復元が上手くできませんでした。(やり方はあるかも知れませんが、できるという情報もできないという情報も見つけられなかったため、途中で諦めてしまいました)
- 投稿日:2019-07-27T05:25:44+09:00
(Twitter)Pythonでリプライにいいねして返信するbotを作る(怪しい日本語ジェネレーターbot)
とりあえず動かす
初心者が書いたものなのでなぜか認証が2つあったりスマートではないです。とりあえず動けばいいや!って方に...(寝ぼけてたまま書いてるので後で再チェックします..)
reply.py# -*- coding: utf-8 -*- import requests import linecache import tweepy import json from requests_oauthlib import OAuth1Session Twitter_ID = "自分のID(@はいりません)" SCREEN_NAME = '自分のアカウントの名前' CK="取得したやつ" CS="取得したやつ" AT="取得したやつ" AS="取得したやつ" api = OAuth1Session(CK, CS, AT, AS) auth = tweepy.OAuthHandler(CK, CS) auth.set_access_token(AT, AS) api2 = tweepy.API(auth) timeline=api2.mentions_timeline(count=1) for status in timeline: status_id=status.id screen_name=status.author.screen_name.encode("UTF-8") scrn = screen_name.replace(' ', '') scr = scrn.rstrip('\n') print("@" + scr) print(status.text) inp = status.text inp = inp.lstrip("自分のID(@つける)") print(inp) #ここから好きな処理 #この場合は怪しい日本語に変換してます response = requests.get('https://correctjp.work/api/index.php?text='+inp+'&json=no&type=normal') #ここまで好きな処理 #response.textに返信するテキストが入るようにすればOK reply_text="@"+screen_name+" "+response.text api2.create_favorite(status.id) if str(status.in_reply_to_screen_name)==Twitter_ID and str(status.user.screen_name)!=Twitter_ID: api2.update_status(status=reply_text,in_reply_to_status_id=status_id) else: print("エラー")これを保存して
crontab -eを実行して
* * * * * python /var/reply.py > /var/log/cron.log 2>&1 * * * * * sleep 10; PYTHONIOENCODING=utf-8 python /var/reply.py > /var/log/cron.log 2>&1 * * * * * sleep 20; PYTHONIOENCODING=utf-8 python /var/reply.py > /var/log/cron.log 2>&1 * * * * * sleep 30; PYTHONIOENCODING=utf-8 python /var/reply.py > /var/log/cron.log 2>&1 * * * * * sleep 40; PYTHONIOENCODING=utf-8 python /var/reply.py > /var/log/cron.log 2>&1 * * * * * sleep 50; PYTHONIOENCODING=utf-8 python /var/reply.py > /var/log/cron.log 2>&1一番下にこれを追記します。
sudo service cron restartで動きます!
解説
ここから先は独り言みたいなものなので見てもメリットはありません。有限の人生の時間を無駄にしないためにブラウザバック推奨です。
CK,CS,AT,AS
- CK=consumer key
- CS=consumer secret
- AT=access token
- AS=access token secret
です。APIの申請、アプリの作成、APIキーの取得については他の人の記事を参照してください。
api = OAuth1Sess..から..weepy.API(auth)
api = OAuth1Session(CK, CS, AT, AS)APIとの接続をして、apiに...ん?これ必要?(寝ぼけてるのであとで確認します...zzz...)
auth = tweepy.OAuthHandler(CK, CS) auth.set_access_token(AT, AS) api2 = tweepy.API(auth)ここでAPIと接続してTwitterAPIが使えるようにします。
timeline=api2.mentions_timeline(count=1)
最新のリプライを取得します。countを変えると前のリプライにも返信します。
for status in timeline:..から..print(inp)
正直自分でも分からないです。status_id=status.id screen_name=status.author.screen_name.encode("UTF-8")status_idにstatus.idに突っ込んでるのと名前で日本語が使えるようにUTF-8にしてます。
scrn = screen_name.replace(' ', '') scr = scrn.rstrip('\n') print("@" + scr) print(status.text) inp = status.text inp = inp.lstrip("自分のID(@つける)") print(inp)文字列の処理です。
返信するユーザー名に@をつけたり改行を削除したりです。inp = inp.lstrip("自分のID(@つける)")ここに自分のIDを@付きで書きます。(返信時に自分のユーザー名を含めないため)
余計な処理は適当に削除してください...
response = requests.get('https://correctjp.work/api/index.php?text='+inp+'&json=no&type=normal')
response = requests.get('https://correctjp.work/api/index.php?text='+inp+'&json=no&type=normal')ここには好きな処理を入れてください。response.textとしてリプしたいテキストが出力されればOKです。inpにはリプされた文字列が入ります。(@や空白などは先ほどの処理で削除済み)
reply_text="@"..から..tatus_id)
reply_text="@"+screen_name+" "+response.text api2.create_favorite(status.id) if str(status.in_reply_to_screen_name)==Twitter_ID and str(status.user.screen_name)!=Twitter_ID: api2.update_status(status=reply_text,in_reply_to_status_id=status_id)reply_text="@"+screen_name+" "+response.textリプライを用意します。
api2.create_favorite(status.id)リプをファボります。
if str(status.in_reply_to_screen_name)==Twitter_ID and str(status.user.screen_name)!=Twitter_ID:無限ループを起こさないように、返信先が自分の場合は返信しません。(自分が含まれてる場合に変更する必要があるかも、)
api2.update_status(status=reply_text,in_reply_to_status_id=status_id)リプライを送信します。
else: print("エラー")
そのままです。できなかった時にエラーと表示します。
お疲れ様でした!
(適当なので鵜呑みにしないでください...)
- 投稿日:2019-07-27T02:23:16+09:00
django-restframework-social-oauth2 で writable-nested-serializers と ListField を両立させる
writable-nested-serializers は 子serializerがListFiledを使用している場合、うまく動かない
https://www.django-rest-framework.org/api-guide/relations/#writable-nested-serializers
この問題のソリューションは、ListFieldをちょこっとだけいじれば良い
いつもながら、メモ程度なので最低限しか書かない親serializer
class PrivateCommentSerializer(serializers.ModelSerializer): class Meta: model = PrivateComment fields = ( 'id', 'user', 'text', 'file', 'set_file', ) set_file = WrapListField(source='files', child=serializers.FileField(), write_only=True, allow_empty=True, required=False)子serializer
class PrivateCommentFilesSerializer(serializers.ModelSerializer): class Meta: model = PrivateCommentFiles fields = ( 'id', 'comment', 'file', )ListFieldのオーバーライド
class WrapListField(serializers.ListField): """ Writable nested representations と ListField を両立させる為に作成 """ def to_representation(self, data): return [self.child.to_representation(item) if item is not None else None for item in data.all()]ぶっちゃけ data を data.all() に変更しただけ
もしかしたらドキュメントを隅々まで見れば解決方法があったかもしれないけど
ソース見た方が早かった
- 投稿日:2019-07-27T02:23:16+09:00
django-restframework で writable-nested-serializers と ListField を両立させる
writable-nested-serializers は 子serializerがListFiledを使用している場合、うまく動かない
https://www.django-rest-framework.org/api-guide/relations/#writable-nested-serializers
この問題のソリューションは、ListFieldをちょこっとだけいじれば良い
いつもながら、メモ程度なので最低限しか書かない親serializer
class PrivateCommentSerializer(serializers.ModelSerializer): class Meta: model = PrivateComment fields = ( 'id', 'user', 'text', 'file', 'set_file', ) set_file = WrapListField(source='files', child=serializers.FileField(), write_only=True, allow_empty=True, required=False)子serializer
class PrivateCommentFilesSerializer(serializers.ModelSerializer): class Meta: model = PrivateCommentFiles fields = ( 'id', 'comment', 'file', )ListFieldのオーバーライド
class WrapListField(serializers.ListField): """ Writable nested representations と ListField を両立させる為に作成 """ def to_representation(self, data): return [self.child.to_representation(item) if item is not None else None for item in data.all()]ぶっちゃけ data を data.all() に変更しただけ
もしかしたらドキュメントを隅々まで見れば解決方法があったかもしれないけど
ソース見た方が早かった
- 投稿日:2019-07-27T02:21:23+09:00
【音声発生】本物はどっちだ??
ついに出来たのかもしれない。。。ということでフォルマント合成ですが、リアルな音声の再現ができたようです。
本物はどっちだ??
1 2 やったこと
・本物の音声をよく見ると
・音声と似たフォルマントを作る
・リアル音声のFFTとフォルマント合成音声のFFT図・本物の音声をよく見ると
本物がどっちかは別にして、上記のフォルマント(振幅の大きなピーク)を見ると、
①基準振動の整数倍のピーク以外に、小さな高周波ピークが集団で発生している
②ピークは裾が広がっている
という二つの特徴がある。
①については、先日の記事でorder=1や適当にピーク抽出の制約を工夫すれば行けるめどがあった。これだけでも一応音声っぽい音は発生できていたが、それだけでは、あの金属的な音になってしまっていた。
ということで、ここでは本物の音声を再現するために、この裾を本物っぽく作ることとした。・音声と似たフォルマントを作る
普通こういう単一ピークに裾を作るには、サブピークを追加するのだが、このサブピークは綺麗な裾状になっている。つまり、ある連続的な周波数のピーク、すなわち一定の基準振動の周りに分布する一連のピークであると想像できる。すなわち一番簡単な解釈は適当に正規分布する振動数で発する音の重ね合わせで構成されていると考察するのが素直である。
参考から、正規分布する関数は以下のように作成できる。
【参考】
・Numpyによる乱数生成まとめR=[] for i in range(10000): r = 100+randn() # 標準正規分布で乱数を1万個生成 R.append(r) plt.hist(R, bins=100) # 100本のヒストグラムを作成 plt.pause(1) plt.savefig('./fft_sound/figure_histgram.jpg')
この乱数を使って、周波数が正規分布するサイン波は以下のように作成できる。def sin_wav(A,f1,fr,sec): point = np.arange(0,fr*sec) f0=f1 #+2*randn() sin_wav =0.01*A* (np.sin(2*np.pi*f0*point/fr)) return sin_wav,f0 fr=44100 sec=1 fn= fr*sec t = np.linspace(0,sec, fn) f0=400 sin_wave=0 f=[] for i in range(0,1000,1): f1=f0+2*randn() sw,f2=sin_wav(A,f1,fr,sec) sin_wave += sw f.append(f2) sin_wave = [int(x * 32767.0) for x in sin_wave] plt.plot(t,sin_wave) plt.xlim(0,0.1*sec) plt.savefig('./fft_sound/create_sin'+str(sec)+'.jpg') plt.pause(1) plt.close()
1 2 そして、以下のコードでFFTする
def FFT(sig,fn,fr): freq =fft(sig,fn) Pyy = np.sqrt(freq*freq.conj())/fn f = np.arange(0,fr,fr/fn) ld = signal.argrelmax(Pyy, order=3) #相対強度の最大な番号をorder=10で求める ssk=0 fsk=[] Psk=[] maxPyy=max(np.abs(Pyy)) for i in range(len(ld[0])): #ピークの中で以下の条件に合うピークの周波数fと強度Pyyを求める if np.abs(Pyy[ld[0][i]])>0.005*maxPyy and f[ld[0][i]]<20000 and f[ld[0][i]]>20: fssk=f[ld[0][i]] Pssk=np.abs(Pyy[ld[0][i]]) fsk.append(fssk) Psk.append(Pssk) ssk += 1 return freq,Pyy,fsk,Psk,f start_time=time.time() def draw_pic(freq,Pyy,fsk,Psk,f,sk,sig,sec): matplotlib.rcParams.update({'font.size': 18, 'font.family': 'sans', 'text.usetex': False}) fig = plt.figure(figsize=(12,12)) #(width,height) axes1 = fig.add_axes([0.1, 0.55, 0.8, 0.4]) # main axes axes2 = fig.add_axes([0.15, 0.7, 0.2, 0.2]) # insert axes axes3 = fig.add_axes([0.1, 0.1, 0.8, 0.35]) # main axes axes1.plot(t, sig) axes1.grid(True) axes1.set_xlim([0, 0.05]) axes2.set_xlim(0,sec) axes2.plot(t,sig) Pyy_abs=np.abs(Pyy) axes3.plot(f,Pyy_abs) #axes3.axis([min(fsk)*0.9, max(fsk)*1.1, 0,max(Pyy_abs)*1.5]) #0.5, 2 axes3.grid(True) axes3.set_xscale('log') axes3.set_ylim(0,max(Pyy_abs)*1.5) axes3.set_xlim(20,20000) axes3.set_title('{0:3.2f}'.format(time.time()-start_time)) axes3.set_title('{}'.format(np.round(fsk[:len(fsk)],decimals=1))+'\n'+'{}'.format(np.round(Psk[:len(fsk)],decimals=4)),size=10) #グラフのタイトルにピーク周波数とピーク強度を出力する axes3.plot(fsk[:len(fsk)],Psk[:len(fsk)],'ro') #ピーク周波数、ピーク強度の位置に〇をつける # グラフにピークの周波数をテキストで表示 for i in range(len(fsk)): axes3.annotate('{0:.1f}'.format(fsk[i]), xy=(fsk[i], Psk[i]), xytext=(10, 20), textcoords='offset points', arrowprops=dict(arrowstyle="->",connectionstyle="arc3,rad=.2") ) plt.pause(1) wavfile=str(sec)+'_'+str(sk) plt.savefig('./fft_sound/figure_'+wavfile+'_.jpg') plt.clf() freq,Pyy,fsk,Psk,f=FFT(sin_wave,fn,fr) draw_pic(freq,Pyy,fsk,Psk,f,1,sin_wave,sec)FFT図に以下のピークが表れる
ピークの絶対値はちょっと大きいですが、一応綺麗な裾を持ったピークが現れました。
これは、上記のとおり1000回乱数を振った結果です。
そして、このサイン波を重畳したピークの特徴は、減衰が大きいということです。ただし、減衰した後は持続することもわかります。
また、減衰率は重畳する周波数の分布幅に依存することが分かりました。すなわち、分布幅を0,0.1,0.5,1,2,3,5,7,10,20と変化させたとき以下のように変化します。
・リアル音声のFFTとフォルマント合成音声のFFT図
コードは以下のおまけのとおりです。
今回はマイク入力の振動をFFTしてそのピークと周波数を利用して、サイン波を計算します。
したがって、流れはほとんと変わりません。
この結果として以下のような母音が発生できます。
※f0=f0+3*randn()としています
母音 音声 合成 あ え い お う ここで、上記の単一ピーク作成ではサイン波の合成を1000回実施したが、実際の音声ではピーク数回数とした。これで一応ピークの裾を再現できている。これを多数回実施した場合もやってみたが、何が適正かを考えると結局裾のテールを再現すればよく、以下のコードで十分だという結論に到達した。
※ピークの数次第では、もっと多数回回した方がいい場合もあると思われるが、今回は以下のようにパラメータで再現している
※一応、以下に10回回す場合のコードを掲載しておくdef sin_wav(A,f0,fr,t): point = np.arange(1000,fr*t+1000) f0=f0 #+1*randn() sin_wav =30*A* (np.sin(2*np.pi*f0*point/fr)) return sin_wav def create_wave(A,f0,fr,t,wsk):#A:振幅,f0:基本周波数,fr:サンプリング周波数,再生時間[s] sin_wave=0 for i in range(0,len(A),1): for j in range(10): f1=f0[i]+0.5*randn() sw=sin_wav(A[i],f1,fr,t) sin_wave += sw/10 ...※上記コードでpointの範囲の最初の点を1000ずらしているのは減衰項を考慮してサイン波の合成信号が減衰した後のものを採用している。このようにすることにより、0-0.05secの部分でも減衰が見えないこととなっている
まとめ
・フォルマント合成においてピークの裾状形状を基準周波数が正規分布したサイン波を取り入れることにより、より現実的な音声が再現できた
・連続するセンテンスに対しても応用できたので確立したいと思う
おまけ
import numpy as np from matplotlib import pyplot as plt import wave import struct import pyaudio from scipy.fftpack import fft, ifft import cv2 from scipy import signal import matplotlib import time from numpy.random import * #パラメータ RATE=44100 sec =1 #秒 CHUNK=int(RATE*sec) p=pyaudio.PyAudio() sa= 'u' #'u' #'o' #'i' #'e' #'a' stream=p.open(format = pyaudio.paInt16, channels = 1, rate = RATE, frames_per_buffer = CHUNK, input = True, output = True) # inputとoutputを同時にTrueにする fr = RATE #サンプリング周波数 fn=fr*sec def sin_wav(A,f0,fr,t): point = np.arange(1000,fr*t+1000) f0=f0+3*randn() sin_wav =30*A* (np.sin(2*np.pi*f0*point/fr)) return sin_wav def create_wave(A,f0,fr,t,wsk):#A:振幅,f0:基本周波数,fr:サンプリング周波数,再生時間[s] sin_wave=0 for i in range(0,len(A),1): f1=f0[i] sw=sin_wav(A[i],f1,fr,t) sin_wave += sw sin_wave = [int(x * 32767.0) for x in sin_wave] binwave = struct.pack("h" * len(sin_wave), *sin_wave) w = wave.Wave_write('./fft_sound/out_sin_'+str(sec)+'_'+str(wsk)+'.wav') p = (1, 2, fr, len(binwave), 'NONE', 'not compressed') w.setparams(p) w.writeframes(binwave) w.close() def sound_wave(wsk): wavfile = './fft_sound/out_sin_'+str(sec)+'_'+str(wsk)+'.wav' wr = wave.open(wavfile, "rb") input = wr.readframes(wr.getnframes()) output = stream.write(input) sig =[] sig = np.frombuffer(input, dtype="int16") /32768.0 return sig t = np.linspace(0,sec, fn) def FFT(sig,fn,fr): freq =fft(sig,fn) Pyy = np.sqrt(freq*freq.conj())/fn f = np.arange(0,fr,fr/fn) ld = signal.argrelmax(Pyy, order=3) #相対強度の最大な番号をorder=10で求める ssk=0 fsk=[] Psk=[] maxPyy=max(np.abs(Pyy)) for i in range(len(ld[0])): #ピークの中で以下の条件に合うピークの周波数fと強度Pyyを求める if np.abs(Pyy[ld[0][i]])>0.005*maxPyy and f[ld[0][i]]<20000 and f[ld[0][i]]>20: fssk=f[ld[0][i]] Pssk=np.abs(Pyy[ld[0][i]]) fsk.append(fssk) Psk.append(Pssk) ssk += 1 return freq,Pyy,fsk,Psk,f matplotlib.rcParams.update({'font.size': 18, 'font.family': 'sans', 'text.usetex': False}) fig = plt.figure(figsize=(12,12)) #(width,height) start_time=time.time() def draw_pic(freq,Pyy,fsk,Psk,f,sk,sig,wsk): axes1 = fig.add_axes([0.1, 0.55, 0.8, 0.4]) # main axes axes2 = fig.add_axes([0.15, 0.7, 0.2, 0.2]) # insert axes axes3 = fig.add_axes([0.1, 0.1, 0.8, 0.35]) # main axes axes1.plot(t, sig) axes1.grid(True) axes1.set_xlim([0, 0.05]) axes2.set_ylim(-1.2,1.2) axes2.set_xlim(0,sec) axes2.plot(t,sig) Pyy_abs=np.abs(Pyy) axes3.plot(f,Pyy_abs) #axes3.axis([min(fsk)*0.9, max(fsk)*1.1, 0,max(Pyy_abs)*1.5]) #0.5, 2 axes3.grid(True) axes3.set_xscale('log') axes3.set_ylim(0,max(Pyy_abs)*1.5) axes3.set_xlim(20,20000) axes3.set_title('{0:3.2f}'.format(time.time()-start_time)) plt.pause(0.001) wavfile=str(sec)+'_'+sa+str(sk) plt.savefig('./fft_sound/figure_'+wavfile+'_'+str(wsk)+'.jpg') plt.clf() wsk=0 while True: input = stream.read(CHUNK) sig =[] sig = np.frombuffer(input, dtype="int16") /32768.0 #サイン波を-32768から32767の整数値に変換(signed 16bit pcmへ) swav = [int(x * 32767.0) for x in sig] #バイナリ化 binwave = struct.pack("h" * len(swav), *swav) w = wave.Wave_write("./fft_sound/out_"+str(sec)+"_"+str(wsk)+".wav") params = (1, 2, fr, len(binwave), 'NONE', 'not compressed') w.setparams(params) w.writeframes(binwave) w.close() #入力音声をFFTして描画する freq,Pyy,fsk,Psk,f=FFT(sig,fn,fr) draw_pic(freq,Pyy,fsk,Psk,f,1,sig,wsk) #マイク入力を出力 input = binwave output = stream.write(input) #FFTで得られた周波数Pskと振幅fsk A=Psk/max(Psk)/len(fsk) f=fsk #上記のAとfを使ってサイン波でフォルマント合成 sigs =[] create_wave(A, f, fr, sec,wsk) sigs = sound_wave(wsk) #フォルマント合成音声をFFTして描画する freqs,Pyys,fsks,Psks,fss=FFT(sigs,fn,fr) draw_pic(freqs,Pyys,fsks,Psks,fss,2,sigs,wsk) wsk += 1
- 投稿日:2019-07-27T02:18:32+09:00
TouchDesignerから外部ライブラリを参照したい、、、
初投稿です!
TouchDesignerを使い倒したい!
TouchDesignerはソフト一つで3Dも、pythonも、その他ソフトの連携も可能で便利なソフトですが、表現が割と同じようなものになりがちだと感じます。
Keras使いたい、、、
唐突ですが、自分の今年の目標は「Kerasを用いたインタラクション作品」の制作です。これをTouchDesignerで実現するためにはKerasをimportしなくては始まりません、、、前置きが長くてすみません。これから外部ライブラリ参照の方法を記します。
外部ライブラリ参照方法
TextDATとTextportを開く
Textportを見ながらPythonをTextDATで実行することで、現在参照しているファイルの場所などを逐一確認できるのでおすすめです!現在のPathを確認
text1
import os,sys
path = os.path
print(path)
見てわかるように、TouchDeignerのPythonは、TouchDesignerの中にあるデフォルトのフレームワークを参照しています。実はもうこの時点でこれから行うPathの参照を行なっているのですが、Pathの参照をPreferenceから行なっただけではPathを変更できないみたいなのです。知っとくと便利なコマンド
実行したいDATを選んで、、、
- cmd + e = TextDATを外部エディタで編集
- cmd + r = TextDATを実行
PreferenceからPathを変更
- Preferenceを開きます、
- Add External Python to Search Pathに参照したいPathを設定します。自分であれば、
/Users/username/anaconda3/envs/TouchDesigner/lib/python3.5/site-packages これは、anacondaでTouchDesigner専用の環境を作ったので、上記のようになっています。 TouchDesignerのデフォルトのバージョンは3.5系なので、指定するPathは3.5系のPythonでないといけません。- TouchDesignerを再起動
- import keras !!!
しかしここではおそらくエラーが出ると思います。ここではまだデフォルトのPathのままなのです。(正直なんでかわかってない)TextDATからPathを設定
先人の知恵に頼る(自分の場合これでもダメだった)
import sys, os path = '/Users/username/anaconda3/envs/TouchDesigner/lib/python3.5/site-packages' if not path in sys.path: sys.path.append(path) print('Append new module search path:', path)もろ以下を参考にしています。
他の方法で参照
text1
import sys, os os.chdir('/Users/username/anaconda3/envs/TouchDesigner/lib/python3.5/site-packages') import keras print(keras)これでPathは通りました。まだKerasを使って何かしたわけでもないので、この参照の仕方でこれから別のエラーとか出る可能性はあるかもしれませんが、一応参照できました!!!
anacondaでPython専用の環境を作る(おまけ)
Touchdesignerのためだけに色々とPythonの環境をいじるのは面倒だと思ったので、anacondaで専用の環境を作りました。
1. まずはPython3.5系を選択
2.好きなライブラリをインポート!
3. 実行
これでバージョン管理などが楽にできそう今の現状(記事に全く関係ない)
自分はクラシックギターのレッスンやワークショップを受けにしばしば福岡に来ます。今日はせっかくPathが通ったので、今すぐQiitaに投稿したいと思い、あるwi-fiが使えるBarに駆け込んで、そこで書いております。初めはためらってましたが、外国人の店長の方がとてもフレンドリーでいい人で、快く使わせてもらっています。とにかく福岡は人がいいです。クラシックギターの会社の方も自分が山口から来ているので、アパートの空き部屋を宿泊に使っていいよと言ってくださり、そこにレッスンの日はお世話になっています。よく行っている福岡の勉強会もハンズオン形式で、とてもわかりやすく、無料で、優しくて、申し訳ない気持ちになります。本当に自分は人に恵まれているのです。なので、今回拙い文章ではありますが、できるだけ丁寧にまとめてみました。
- 投稿日:2019-07-27T02:07:48+09:00
django-restframework-social-oauth2 で twitter login ができる様にする
django-restframework-social-oauth2 は
現在生の状態だとTwitterログイン機能が使用できない。
仕方がないのでチョロっといじくり回して認証が通る様にしたので書き残しておく。
ぶっちゃけただのメモレベルなので、参考程度に見て欲しい。問題
Twitter API は、リソースにアクセスする際、アクセストークンが2つ必要になる
その為、公式ドキュメントに記載のある以下の方法では、トークンが一つしか送れない為、勿論エラーになるcurl -X POST -d "grant_type=convert_token&client_id=<client_id>&client_secret=<client_secret>&backend=<backend>&token=<backend_token>" http://localhost:8000/auth/convert-token解決
token のキーに無理やりアクセストークンを2つ載せ、Twitter oauth のメソッドを一つだけオーバーライドし、トークンを書き換えればいい
書き換えるのは 同モジュール内の backends にある TwitterOAuthfrom social_core.backends.twitter import TwitterOAuth class TwitterOAuthModifyToken(TwitterOAuth): """Twitter OAuth authentication backend""" def user_data(self, access_token, *args, **kwargs): oauth_token = access_token.get('oauth_token').split('&')[0] oauth_token_secret = access_token.get('oauth_token').split('&')[1].split('=')[1] access_token['oauth_token'] = oauth_token access_token['oauth_token_secret'] = oauth_token_secret return super(TwitterOAuthModifyToken, self).user_data(access_token, *args, **kwargs)POSTする json の書き方はこういう感じ、%26はパーセンテージエンコーディングしたアンパサンド
"token": "oauth_token=<oauth_token>%26oauth_token_secret=<oauth_token_secret>"あとは、今作ったコイツを setting.py のバックエンドに指定すれば
AUTHENTICATION_BACKENDS = ( # Twitter 'okero.backends.TwitterOAuthModifyToken', )コレで認証が通る
モジュールの中身を漁る時間がない人はお試しあれ