- 投稿日:2019-02-15T23:48:22+09:00
matplotlibのよく使う記法まとめ
すぐ忘れるので、matplotlibのよく使う記法をまとめておく
公式:https://matplotlib.org/gallery.html普段は散布図とかplotとかしか使わないけど、こうして見るといろんなグラフがかけるみたい
matplotlib,pyplot,pylabの違い
matplotlibがパッケージ全体
pyplotはそのモジュール、スクリプトで作図するときに使う
pylabのimportは推奨されてない模様、インタラクティブな作図にはこっちを使うらしい基本的には、
import matplotlib.pyplot as pltのように使う参考:
https://matplotlib.org/faq/usage_faq.html#matplotlib-pyplot-and-pylab-how-are-they-related
https://stackoverflow.com/questions/11469336/what-is-the-difference-between-pylab-and-pyplotグラフを描く
シンプルな例は以下
import matplotlib.pyplot as plt import numpy as np x = np.arange(0,10,0.2) y = np.sin(x) plt.plot(x,y) plt.show()macでmatplotlibを呼ぶと
ValueError: unknown locale: UTF-8で怒られることがある。
locale周りの設定がおかしいため。以下を参考に直す。
Mac で ValueError: unknown locale: UTF-8 のエラーを解決したい
https://www.lifewithpython.com/2016/09/python-ValueError-unknown-locale-UTF-8.htmlインスタンス化する
plt.figure()でインスタンス化し、axesに対してプロットしていく
多分この使い方が多いと思うimport matplotlib.pyplot as plt import numpy as np x = np.arange(0,10,0.2) y = np.sin(x) fig = plt.figure() ax = fig.add_subplot(111) ax.plot(x,y) plt.show()以下のように描いても同じ
fig, ax = plt.subplots(1, 1) ax.plot(x,y) plt.show()複数のグラフを描く
複数のウィンドウに分けて描画
fig = plt.figure()の引数に適当にユニークな数字を入れておく。
figureに引数を与えることで、新たな図が生成される。
参考: https://matplotlib.org/api/_as_gen/matplotlib.pyplot.figure.htmlimport matplotlib.pyplot as plt import numpy as np x = np.arange(0,10,0.2) y = np.sin(x) fig = plt.figure(1) ax = fig.add_subplot(111) ax.plot(x,y) fig = plt.figure(2) ax = fig.add_subplot(111) ax.plot(x,y) plt.show()1つのウィンドウに複数のグラフを描画
1つのウィンドウに複数のグラフを描く場合は以下のようにする。
fig = plt.figure() ax1 = fig.add_subplot(211) ax1.plot(x,y) ax2 = fig.add_subplot(212) ax2.plot(x,y) plt.show()以下のように描いても同じ、axesをタプルで受け取るのがちょっと気持ち悪い
fig, (ax1, ax2) = plt.subplots(1, 2) ax1.plot(x,y) ax2.plot(x,y) plt.show()グラフの保存
savefigでグラフの保存が可能
import matplotlib.pyplot as plt import numpy as np x = np.arange(0,10,0.2) y = np.sin(x) fig = plt.figure() ax = fig.add_subplot(111) ax.plot(x,y) plt.savefig("./test2")複数のグラフを描画した場合には、figureインスタンスに対してもsavefigが使える。
import matplotlib.pyplot as plt import numpy as np x = np.arange(0,10,0.2) y = np.sin(x) fig = plt.figure(1) ax = fig.add_subplot(111) ax.plot(x,y) fig.savefig("./test1") fig = plt.figure(2) ax = fig.add_subplot(111) ax.plot(x,y) fig.savefig("./test2")グラフを整形する
グラフの線の色、太さ、線の種類などはよく使う。
それぞれ、color,linewidth,linestyleの引数を与えることで設定できる。import matplotlib.pyplot as plt import numpy as np x = np.arange(0,10,0.2) y = np.sin(x) fig = plt.figure() ax = fig.add_subplot(111) ax.plot(x,y,color="red",linewidth=2,linestyle="dashed") plt.show()引数の詳細は公式の以下のページから確認できる。
https://matplotlib.org/api/_as_gen/matplotlib.pyplot.plot.htmlタイトルや軸名をつける
シンプルな例は以下
import matplotlib.pyplot as plt import numpy as np x = np.arange(0,10,0.2) y = np.sin(x) plt.plot(x,y) plt.title("test") plt.xlabel("x") plt.ylabel("y") plt.show()インスタンス化した場合は次のようにする。
import matplotlib.pyplot as plt import numpy as np x = np.arange(0,10,0.2) y = np.sin(x) fig = plt.figure() ax = fig.add_subplot(111) ax.plot(x,y) ax.set_title("test") ax.set_xlabel("x") ax.set_ylabel("y") plt.show()グラフの余白、幅を調整する
plt.subplots_adjustで調整可能import matplotlib.pyplot as plt import numpy as np x = np.arange(0,10,0.2) y = np.sin(x) plt.plot(x,y) plt.subplots_adjust(left=0.1, right=0.95, bottom=0.1, top=0.95) plt.show()わかりづらいが調整できてる。
デフォルト値は以下
left = 0.125 # the left side of the subplots of the figure right = 0.9 # the right side of the subplots of the figure bottom = 0.1 # the bottom of the subplots of the figure top = 0.9 # the top of the subplots of the figure wspace = 0.2 # the amount of width reserved for space between subplots, # expressed as a fraction of the average axis width hspace = 0.2 # the amount of height reserved for space between subplots, # expressed as a fraction of the average axis height1つのウィンドウに複数のグラフを描画し軸名など入れた場合、グラフが重なることがある。
その場合は、plt.subplots_adjust(hspace=0.4)のように調整できる。
横幅は、wspaceで調整可能。fig = plt.figure() plt.subplots_adjust(hspace=0.6) ax1 = fig.add_subplot(211) ax1.plot(x,y) ax2 = fig.add_subplot(212) ax2.plot(x,y) plt.show()参考:https://www.haya-programming.com/entry/2018/10/11/030103
軸を設定し直す
ちょっとめんどくさい
import matplotlib.pyplot as plt import numpy as np x = np.arange(0,10,0.2) y = np.sin(x) fig = plt.figure() ax = fig.add_subplot(111) ax.plot(x,y) ticks = "abcdefghijklmnopqrstuvwxyz" plt.xticks(x,list(ticks)) plt.show()設定し直したい次元と、元の軸の次元が合ってなくても設定できる模様。
x軸に時刻を設定、フォーマット
datetimeをそのままx軸に利用できる。
import matplotlib.pyplot as plt import pandas as pd x = [ '2018/08/08T12:15:45.000', '2018/08/08T12:15:45.200', '2018/08/08T12:17:45.600' ] x = pd.to_datetime(x,format='%Y/%m/%dT%H:%M:%S.%f') y = [1,2,3] fig = plt.figure() ax = fig.add_subplot(111) ax.plot(x,y) plt.show()フォーマットは、
ax.xaxis.set_major_formatter(mdates.DateFormatter('%m/%d\n%H:%M'))を使って行う。import matplotlib.pyplot as plt import pandas as pd import matplotlib.dates as mdates x = [ '2018/08/08T12:15:45.000', '2018/08/08T12:15:45.200', '2018/08/08T12:17:45.600' ] x = pd.to_datetime(x,format='%Y/%m/%dT%H:%M:%S.%f') y = [1,2,3] fig = plt.figure() ax = fig.add_subplot(111) ax.plot(x,y) ax.xaxis.set_major_formatter(mdates.DateFormatter('%m/%d\n%H:%M')) plt.show()
- 投稿日:2019-02-15T23:17:33+09:00
競技プログラミングで Python を使う時は関数にしよう
すごいシンプルなんですが競技プログラミングで Python を使う時は関数を定義してその中で問題を解こうという話です。
Global 変数はアクセスに時間がかかる
理由はすごいシンプルで関数内の変数は実行時(解釈された時)に固定の配列に格納され、インデックスでアクセスされます。一方で Global 変数は実行時にはインデックスでアクセスされない(実行時に数が固定できないから)ため、ローカル変数と比べてアクセスに時間がかかります。
どのくらい違うの?
問題とコード、もちろん実行環境にもよりますが、AtCoder の問題を解いていた時に、全く同じコードで、
・グローバル変数を定義して解いた時にはTLE
・関数内にローカル変数として解いた時にはACというケースがありました(見てみたら400-500msec違うテストケースも)。
というわけで競技プログラミングで Python を使う時は関数内に解法を書く習慣をつけるとよさそうです。
参考
https://stackoverflow.com/questions/11241523/why-does-python-code-run-faster-in-a-function
- 投稿日:2019-02-15T22:16:45+09:00
cpulimitで同一プロセス名の複数のpidのプロセスを捕捉するスクリプトを書いた
どうも、haniokasaiです
cpulimitはプロセス名でプロセスを捕捉できますが、同一名で複数のプロセスは捕捉はされずまったくランダムにpidを決定して捕捉します。
それだと少なくとも私は結構困りますから、pythonスクリプトですべてのプロセスを捕捉するスクリプトを書きました。
https://github.com/haniokasai/cpulimit-multiple
コメントでconfigと書いているらへんを修正して、
python3 cpumultilimit.pyで実行できます。
- 投稿日:2019-02-15T22:13:02+09:00
決定木ベースの機械学習モデル(Random Forests, XGBboost)からdefragTreesを利用して一目でわかるルールの抽出を試みる。
はじめに
背景
近年の機械学習モデルは年々その複雑さを増しています。特にビジネスで機械学習モデルから何かを説明する際に、人間の目にとってはブラックボックス化した機械学習モデルを解釈することが困難です。そこで、そのブラックボックス化した機械学習モデルから人間の目にも一目でわかる単純なルールを取り出すことが望まれていました。
内容
本ページでは次のような決定木ベースの機械学習モデルを構築します。
- Random Forests
- XGBboost
その単純化されたルールの抽出を試みるために、defragTreesを利用する。
LightGBMはほぼ同じなの元のページを参考にしてください。学銃的な背景
本ページは、Making Tree Ensembles Interpretable: A Bayesian Model Selection Approachを参考にしています。この論文のソースコードはdefragTreesを参考にしています。
また日本語でスライドを読みたい方はアンサンブル木モデル解釈のためのモデル簡略化法を参考にしてください。インストール
defragTreesは pip コマンドや git+URLに対応していません。そのため、ここからdefragTrees.pyをダウンロードしてください。ダウンロードしたdefragTrees.pyはソースファイルと同一なフォルダに入れて「from defragTrees import DefragModel」とすれば実行することができます。
import numpy as np from sklearn.datasets import make_classification from imblearn.ensemble import BalancedRandomForestClassifier from sklearn.model_selection import StratifiedKFold, cross_validate from sklearn.metrics import accuracy_score, cohen_kappa_score, balanced_accuracy_score, make_scorer, f1_score, recall_score from sklearn.ensemble import RandomForestClassifier import lightgbm as lgb import xgboost as xgb from defragTrees import DefragModel from sklearn.externals.joblib import dump from sklearn.externals.joblib import load実験
テスト用のデータ作成
パラメータの値
- n_samples: サンプルの数
- アンケート調査であれば回答者数に該当
- n_features: 特徴量の数
- 分類対象(クラス)を識別するために利用する特徴量の数
- 例えば、アンケート調査であれば質問と回答のペア
- n_informative:分類対象と関係のある特徴量の数
- この数が多ければ多いほど予測が簡単になる
- n_classes: 分類対象が何種類あるか
- 2値分類問題にするならば 2 をセット
- random_state: ランダムシードの設定
data = make_classification(n_samples=1000, #生成するサンプル数 n_features=110, n_informative=100, weights=[0.7,0.3], n_classes=2, random_state=43) data_set = data[0] # 特徴量 target_set = data[1] # クラスラベル #from sklearn.datasets import load_iris #iris = load_iris() #data_set = iris.data #target_set =iris.targetRandom Forests
モデルの構築
model = BalancedRandomForestClassifier(random_state = 43, n_jobs = 1, n_estimators = 500, max_features = "log2", class_weight = 'balanced', sampling_strategy = 'all', max_depth = None, oob_score=False) scoring = {'accuracy': make_scorer(accuracy_score), 'kappa': make_scorer(cohen_kappa_score), 'blanced_accuracy': make_scorer(balanced_accuracy_score) } skf = StratifiedKFold(n_splits=5,shuffle=True,random_state=0) scores = cross_validate(model, data_set, target_set,n_jobs = 1, cv=skf, return_train_score=True,scoring=scoring) print(scores["test_accuracy"]) print(scores["test_kappa"]) print(scores["test_blanced_accuracy"]) model.fit(data_set, target_set)[0.735 0.765 0.795 0.765 0.815] [0.46356275 0.49570815 0.56008584 0.5 0.59606987] [0.77261905 0.775 0.81071429 0.7797619 0.825 ] BalancedRandomForestClassifier(bootstrap=True, class_weight='balanced', criterion='gini', max_depth=None, max_features='log2', max_leaf_nodes=None, min_impurity_decrease=0.0, min_samples_leaf=2, min_samples_split=2, min_weight_fraction_leaf=0.0, n_estimators=500, n_jobs=1, oob_score=False, random_state=43, replacement=False, sampling_strategy='all', verbose=0, warm_start=False)Random Forests から単純なルールを抽出する
splitter = DefragModel.parseSLtrees(model) # parse sklearn tree ensembles into the array of (feature index, threshold) mdl = DefragModel(modeltype='classification', maxitr=100, qitr=0, tol=1e-6, restart=20, verbose=0) mdl.fit(data_set, target_set, splitter, 10, fittype='FAB') # results score, cover, coll = mdl.evaluate(data_set, target_set) print() print('<< defragTrees >>') print('----- Evaluated Results -----') print('Test Error = %f' % (score,)) print('Test Coverage = %f' % (cover,)) print('Overlap = %f' % (coll,)) print() print('----- Found Rules -----') print(mdl)[Seed 0] TrainingError = 0.30, K = 2 [Seed 1] TrainingError = 0.30, K = 3 [Seed 2] TrainingError = 0.30, K = 2 [Seed 3] TrainingError = 0.30, K = 3 [Seed 4] TrainingError = 0.30, K = 2 [Seed 5] TrainingError = 0.30, K = 2 [Seed 6] TrainingError = 0.30, K = 2 [Seed 7] TrainingError = 0.30, K = 2 [Seed 8] TrainingError = 0.30, K = 3 [Seed 9] TrainingError = 0.30, K = 2 [Seed 10] TrainingError = 0.30, K = 3 [Seed 11] TrainingError = 0.30, K = 2 [Seed 12] TrainingError = 0.30, K = 1 [Seed 13] TrainingError = 0.30, K = 2 [Seed 14] TrainingError = 0.30, K = 1 [Seed 15] TrainingError = 0.30, K = 2 [Seed 16] TrainingError = 0.30, K = 2 [Seed 17] TrainingError = 0.30, K = 2 [Seed 18] TrainingError = 0.30, K = 2 [Seed 19] TrainingError = 0.30, K = 3 Optimal Model >> Seed 0, TrainingError = 0.30, K = 2 << defragTrees >> ----- Evaluated Results ----- Test Error = 0.300000 Test Coverage = 1.000000 Overlap = 0.942000 ----- Found Rules ----- [Rule 1] y = 0 when x_31 < 14.781519 [Rule 2] y = 0 when x_13 >= -13.205372 x_28 < 13.061854 x_96 < 12.163099 [Otherwise] y = 0結果の解釈
本データを分類するために二つのルールが抽出された。
- Rule 1
- y = 0 when
- x_31 < 14.781519
- 解釈:31番目の特徴量(x_31)の値が14.781519未満のとき、クラスラベル(y)は0と分類される
- Rule 2
- y = 0 when
- x_13 >= -13.205372
- x_28 < 13.061854
- x_96 < 12.163099
- 13番目の特徴量(x_13)の値が-13.205372以上、28番目の特徴量(x_28)の値が13.061854未満、96番目の特徴量(x_96)の値が12.163099未満のとき、クラスラベル(y)は0と分類される
- それ以外は クラスラベルは0となる
XGBoost
モデルの構築
model = xgb.XGBClassifier(max_depth = 50, learning_rate = 0.16, min_child_weight = 1, n_estimators = 200) scoring = {'accuracy': make_scorer(accuracy_score), 'kappa': make_scorer(cohen_kappa_score), 'blanced_accuracy': make_scorer(balanced_accuracy_score) } skf = StratifiedKFold(n_splits=5,shuffle=True,random_state=0) scores = cross_validate(model, data_set, target_set,n_jobs = 1, cv=skf, return_train_score=True,scoring=scoring) print(scores["test_accuracy"]) print(scores["test_kappa"]) print(scores["test_blanced_accuracy"]) num_round = 50 dtrain = xgb.DMatrix(data_set, label=target_set) param = {'max_depth':50, 'learning_rate':0.16, 'min_child_weight':1, 'n_estimators':200} bst = xgb.train(param, dtrain, num_round) # output xgb model as text bst.dump_model('xgbmodel.txt')[0.8 0.825 0.88 0.8 0.86 ] [0.46236559 0.54188482 0.67741935 0.44444444 0.62365591] [0.7047619 0.74642857 0.8 0.69047619 0.77619048] [19:39:56] src/tree/updater_prune.cc:74: tree pruning end, 1 roots, 194 extra nodes, 0 pruned nodes, max_depth=14 [19:39:56] src/tree/updater_prune.cc:74: tree pruning end, 1 roots, 212 extra nodes, 0 pruned nodes, max_depth=14 [19:39:56] src/tree/updater_prune.cc:74: tree pruning end, 1 roots, 210 extra nodes, 0 pruned nodes, max_depth=18 [19:39:56] src/tree/updater_prune.cc:74: tree pruning end, 1 roots, 208 extra nodes, 0 pruned nodes, max_depth=18 [19:39:56] src/tree/updater_prune.cc:74: tree pruning end, 1 roots, 226 extra nodes, 0 pruned nodes, max_depth=23 [19:39:56] src/tree/updater_prune.cc:74: tree pruning end, 1 roots, 208 extra nodes, 0 pruned nodes, max_depth=18 [19:39:56] src/tree/updater_prune.cc:74: tree pruning end, 1 roots, 208 extra nodes, 0 pruned nodes, max_depth=18 [19:39:56] src/tree/updater_prune.cc:74: tree pruning end, 1 roots, 200 extra nodes, 0 pruned nodes, max_depth=14 [19:39:56] src/tree/updater_prune.cc:74: tree pruning end, 1 roots, 216 extra nodes, 0 pruned nodes, max_depth=12 [19:39:56] src/tree/updater_prune.cc:74: tree pruning end, 1 roots, 222 extra nodes, 0 pruned nodes, max_depth=15 [19:39:56] src/tree/updater_prune.cc:74: tree pruning end, 1 roots, 202 extra nodes, 0 pruned nodes, max_depth=12 [19:39:56] src/tree/updater_prune.cc:74: tree pruning end, 1 roots, 206 extra nodes, 0 pruned nodes, max_depth=17 [19:39:56] src/tree/updater_prune.cc:74: tree pruning end, 1 roots, 222 extra nodes, 0 pruned nodes, max_depth=20 [19:39:56] src/tree/updater_prune.cc:74: tree pruning end, 1 roots, 242 extra nodes, 0 pruned nodes, max_depth=18 [19:39:56] src/tree/updater_prune.cc:74: tree pruning end, 1 roots, 246 extra nodes, 0 pruned nodes, max_depth=15 [19:39:56] src/tree/updater_prune.cc:74: tree pruning end, 1 roots, 284 extra nodes, 0 pruned nodes, max_depth=22 [19:39:56] src/tree/updater_prune.cc:74: tree pruning end, 1 roots, 312 extra nodes, 0 pruned nodes, max_depth=17 [19:39:56] src/tree/updater_prune.cc:74: tree pruning end, 1 roots, 348 extra nodes, 0 pruned nodes, max_depth=23 [19:39:56] src/tree/updater_prune.cc:74: tree pruning end, 1 roots, 336 extra nodes, 0 pruned nodes, max_depth=16 [19:39:56] src/tree/updater_prune.cc:74: tree pruning end, 1 roots, 354 extra nodes, 0 pruned nodes, max_depth=23 [19:39:56] src/tree/updater_prune.cc:74: tree pruning end, 1 roots, 378 extra nodes, 0 pruned nodes, max_depth=18 [19:39:56] src/tree/updater_prune.cc:74: tree pruning end, 1 roots, 390 extra nodes, 0 pruned nodes, max_depth=19 [19:39:56] src/tree/updater_prune.cc:74: tree pruning end, 1 roots, 394 extra nodes, 0 pruned nodes, max_depth=19 [19:39:56] src/tree/updater_prune.cc:74: tree pruning end, 1 roots, 412 extra nodes, 0 pruned nodes, max_depth=20 [19:39:56] src/tree/updater_prune.cc:74: tree pruning end, 1 roots, 414 extra nodes, 0 pruned nodes, max_depth=18 [19:39:56] src/tree/updater_prune.cc:74: tree pruning end, 1 roots, 414 extra nodes, 0 pruned nodes, max_depth=25 [19:39:56] src/tree/updater_prune.cc:74: tree pruning end, 1 roots, 452 extra nodes, 0 pruned nodes, max_depth=21 [19:39:56] src/tree/updater_prune.cc:74: tree pruning end, 1 roots, 444 extra nodes, 0 pruned nodes, max_depth=27 [19:39:56] src/tree/updater_prune.cc:74: tree pruning end, 1 roots, 444 extra nodes, 0 pruned nodes, max_depth=21 [19:39:56] src/tree/updater_prune.cc:74: tree pruning end, 1 roots, 450 extra nodes, 0 pruned nodes, max_depth=22 [19:39:56] src/tree/updater_prune.cc:74: tree pruning end, 1 roots, 470 extra nodes, 0 pruned nodes, max_depth=25 [19:39:56] src/tree/updater_prune.cc:74: tree pruning end, 1 roots, 464 extra nodes, 0 pruned nodes, max_depth=23 [19:39:56] src/tree/updater_prune.cc:74: tree pruning end, 1 roots, 464 extra nodes, 0 pruned nodes, max_depth=19 [19:39:57] src/tree/updater_prune.cc:74: tree pruning end, 1 roots, 460 extra nodes, 0 pruned nodes, max_depth=21 [19:39:57] src/tree/updater_prune.cc:74: tree pruning end, 1 roots, 444 extra nodes, 0 pruned nodes, max_depth=21 [19:39:57] src/tree/updater_prune.cc:74: tree pruning end, 1 roots, 456 extra nodes, 0 pruned nodes, max_depth=24 [19:39:57] src/tree/updater_prune.cc:74: tree pruning end, 1 roots, 448 extra nodes, 0 pruned nodes, max_depth=25 [19:39:57] src/tree/updater_prune.cc:74: tree pruning end, 1 roots, 416 extra nodes, 0 pruned nodes, max_depth=26 [19:39:57] src/tree/updater_prune.cc:74: tree pruning end, 1 roots, 406 extra nodes, 0 pruned nodes, max_depth=33 [19:39:57] src/tree/updater_prune.cc:74: tree pruning end, 1 roots, 400 extra nodes, 0 pruned nodes, max_depth=29 [19:39:57] src/tree/updater_prune.cc:74: tree pruning end, 1 roots, 368 extra nodes, 0 pruned nodes, max_depth=24 [19:39:57] src/tree/updater_prune.cc:74: tree pruning end, 1 roots, 348 extra nodes, 0 pruned nodes, max_depth=24 [19:39:57] src/tree/updater_prune.cc:74: tree pruning end, 1 roots, 320 extra nodes, 0 pruned nodes, max_depth=26 [19:39:57] src/tree/updater_prune.cc:74: tree pruning end, 1 roots, 300 extra nodes, 0 pruned nodes, max_depth=27 [19:39:57] src/tree/updater_prune.cc:74: tree pruning end, 1 roots, 282 extra nodes, 0 pruned nodes, max_depth=29 [19:39:57] src/tree/updater_prune.cc:74: tree pruning end, 1 roots, 258 extra nodes, 0 pruned nodes, max_depth=24 [19:39:57] src/tree/updater_prune.cc:74: tree pruning end, 1 roots, 240 extra nodes, 0 pruned nodes, max_depth=24 [19:39:57] src/tree/updater_prune.cc:74: tree pruning end, 1 roots, 238 extra nodes, 0 pruned nodes, max_depth=32 [19:39:57] src/tree/updater_prune.cc:74: tree pruning end, 1 roots, 182 extra nodes, 0 pruned nodes, max_depth=22 [19:39:57] src/tree/updater_prune.cc:74: tree pruning end, 1 roots, 176 extra nodes, 0 pruned nodes, max_depth=25XGBoost から単純なルールを抽出する
splitter = DefragModel.parseXGBtrees('xgbmodel.txt') # parse sklearn tree ensembles into the array of (feature index, threshold) mdl = DefragModel(modeltype='classification', maxitr=100, qitr=0, tol=1e-6, restart=20, verbose=0) mdl.fit(data_set, target_set, splitter, 10, fittype='FAB') # results score, cover, coll = mdl.evaluate(data_set, target_set) print() print('<< defragTrees >>') print('----- Evaluated Results -----') print('Test Error = %f' % (score,)) print('Test Coverage = %f' % (cover,)) print('Overlap = %f' % (coll,)) print() print('----- Found Rules -----') print(mdl)[Seed 0] TrainingError = 0.30, K = 3 [Seed 1] TrainingError = 0.30, K = 3 [Seed 2] TrainingError = 0.30, K = 2 [Seed 3] TrainingError = 0.30, K = 4 [Seed 4] TrainingError = 0.30, K = 2 [Seed 5] TrainingError = 0.30, K = 3 [Seed 6] TrainingError = 0.30, K = 3 [Seed 7] TrainingError = 0.30, K = 1 [Seed 8] TrainingError = 0.30, K = 3 [Seed 9] TrainingError = 0.30, K = 3 [Seed 10] TrainingError = 0.30, K = 2 [Seed 11] TrainingError = 0.30, K = 3 [Seed 12] TrainingError = 0.30, K = 3 [Seed 13] TrainingError = 0.30, K = 3 [Seed 14] TrainingError = 0.30, K = 4 [Seed 15] TrainingError = 0.30, K = 2 [Seed 16] TrainingError = 0.30, K = 2 [Seed 17] TrainingError = 0.30, K = 3 [Seed 18] TrainingError = 0.30, K = 3 [Seed 19] TrainingError = 0.30, K = 4 Optimal Model >> Seed 0, TrainingError = 0.30, K = 3 << defragTrees >> ----- Evaluated Results ----- Test Error = 0.300000 Test Coverage = 1.000000 Overlap = 0.122000 ----- Found Rules ----- [Rule 1] y = 0 when x_1 < 0.389858 x_3 >= -1.891694 x_4 < 13.444655 x_10 >= -15.387629 x_12 >= -11.851440 x_14 >= -16.041128 x_18 >= -14.103243 x_45 < 13.571693 x_68 >= -11.976764 x_89 < 16.081133 [Rule 2] y = 0 when x_1 < 0.389858 x_3 < 0.876493 x_9 < 2.240515 x_20 < 12.560732 x_26 < 15.807751 x_41 < 14.043766 x_78 >= -15.805157 x_81 < 14.394110 [Rule 3] y = 0 when x_1 >= -0.301440 [Otherwise] y = 0結果の解釈
本データを分類するために3つのルールが抽出された。ルールの解釈の仕方はRandomForestsと同様に行えばよいので一つでだけ例をあげる。
- ルール3
- y = 0 when x_1 >= -0.301440
- 特徴量 1 が -0.301440 以下のとき、クラスラベルは 0 と分類される
まとめ
決定木ベースの複雑な機械学習モデルを構築し、もし 特徴量が *** だったら、クラスラベルは *** に分類されるというルールを抽出できた。どれほどの効果があるかはわからないが、defragTreesを動かすことができた。
- 投稿日:2019-02-15T21:58:29+09:00
Python の基本構造
今日はPythonの基本構造についてまとめてみました。
構造
- パッケージ ... 初期化モジュール(__init__.py)とその他モジュール群(.py)で構成されたフォルダ
- モジュール ... .pyの拡張子を持つファイル
- クラス ... classで定義され、初期化関数(__init__)とその他関数群で構成される
- 関数 ... defで定義されるもの
特徴
パッケージ
モジュール群(.pyファイル)で構成されたフォルダ。初期化モジュールは必ず必要であるが、不要の場合は中身を空(passを記入)にしておくとよい。インポートの方法は
from パッケージ import モジュールが一番シンプルである。また、パッケージは多層化が可能である。モジュール
クラスや関数などで構成されたファイル。一つのライブラリに相当する。パッケージ化されていない場合、インポートの方法は
import モジュールとなる。クラス
関数群で構成されたもの。初期化関数は必ず必要であるが、不要の場合は中身を空(passを記入)にしておくとよい。
関数
最小単位の定義。クラスとしてではなく、単体としても定義することができる。
今日はここまで。質問等があればぜひおしらせください!
- 投稿日:2019-02-15T20:58:39+09:00
文字遷移確率でポケモンの名前をランダム作成
文字の遷移確率で遊ぶ
特定の文章サンプル内の文字遷移確率をもとめてランダム単語を作ります。
文字の遷移確率とは
「大和」「大井」「大淀」というサンプルで考えて「大」は「和」「井」「淀」それぞれに33%の確率で遷移する文字だと計算できます。以上のような計算をサンプル中に登場する文字全てで行います。
ポケモンの名前で実験
実験結果です、コードは後述。
2 Z ♀ ♂ ァイクタ アージュラ ィアンリルー イノムーリス ウマスバナ ェリンパ エルガーナン ォレジャ オムーンZ カシェリダ ガスピジー キーホールキ ギラース クトリルガー グノームナト ケニンド ゲピウマナ コモン♂ ゴングマ サクース ザルルピ シャタスブ ジロットーチ スリムス ズレアズ セルトノク ゼルゲボ ソハナクラ ゾウマンガ ターリオコ ダールロウカ チルナイルト ッタスル ツブビゴ ティナマケ デンメイン トンタング ドキブネ ナノクイ ニングラ ヌギラティ ネーププス ノードキモメ ハストドゴー バックヌギ パルフライ ヒポタマ ビワンカメノ ピィオニド フカルトライ ブイホーラー プスカルゲ ヘラセクラ ベトドーン ペリトリア ホータツベイ ボミルドシェ ポチャンZ マオウオン ミライク ムパルリア メノムッグカ モネッス ャモリッスタ ヤミラール ューランテイ ユキンブ ョンリン ヨーナクー ラピンデプク リリアリ ルシギア レジョッツ ロスバスタマ ワルビィ ングート ーノオングノコモン♂ とか ポチャンZ とか ゾウマンガ とかそれっぽいなにかができました。「2」とか1文字で終わっているのはサンプル中でその後に続く文字が存在しない文字です。ちなみに自分はポケモンをやったことがありません、見た目にわかりやすく数が多いという理由でポケモンを選びました。
ソースコード
import csv import io import numpy as np import os import sys TsvData = """1 フシギダネ 2 フシギソウ 3 フシギバナ 4 ヒトカゲ 5 リザード 6 リザードン 7 ゼニガメ 8 カメール 9 カメックス 10 キャタピー 11 トランセル 12 バタフリー 13 ビードル 14 コクーン 15 スピアー 16 ポッポ 17 ピジョン 18 ピジョット 19 コラッタ 20 ラッタ 21 オニスズメ 22 オニドリル 23 アーボ 24 アーボック 25 ピカチュウ 26 ライチュウ 27 サンド 28 サンドパン 29 ニドラン♀ 30 ニドリーナ 31 ニドクイン 32 ニドラン♂ 33 ニドリーノ 34 ニドキング 35 ピッピ 36 ピクシー 37 ロコン 38 キュウコン 39 プリン 40 プクリン 41 ズバット 42 ゴルバット 43 ナゾノクサ 44 クサイハナ 45 ラフレシア 46 パラス 47 パラセクト 48 コンパン 49 モルフォン 50 ディグダ 51 ダグトリオ 52 ニャース 53 ペルシアン 54 コダック 55 ゴルダック 56 マンキー 57 オコリザル 58 ガーディ 59 ウインディ 60 ニョロモ 61 ニョロゾ 62 ニョロボン 63 ケーシィ 64 ユンゲラー 65 フーディン 66 ワンリキー 67 ゴーリキー 68 カイリキー 69 マダツボミ 70 ウツドン 71 ウツボット 72 メノクラゲ 73 ドククラゲ 74 イシツブテ 75 ゴローン 76 ゴローニャ 77 ポニータ 78 ギャロップ 79 ヤドン 80 ヤドラン 81 コイル 82 レアコイル 83 カモネギ 84 ドードー 85 ドードリオ 86 パウワウ 87 ジュゴン 88 ベトベター 89 ベトベトン 90 シェルダー 91 パルシェン 92 ゴース 93 ゴースト 94 ゲンガー 95 イワーク 96 スリープ 97 スリーパー 98 クラブ 99 キングラー 100 ビリリダマ 101 マルマイン 102 タマタマ 103 ナッシー 104 カラカラ 105 ガラガラ 106 サワムラー 107 エビワラー 108 ベロリンガ 109 ドガース 110 マタドガス 111 サイホーン 112 サイドン 113 ラッキー 114 モンジャラ 115 ガルーラ 116 タッツー 117 シードラ 118 トサキント 119 アズマオウ 120 ヒトデマン 121 スターミー 122 バリヤード 123 ストライク 124 ルージュラ 125 エレブー 126 ブーバー 127 カイロス 128 ケンタロス 129 コイキング 130 ギャラドス 131 ラプラス 132 メタモン 133 イーブイ 134 シャワーズ 135 サンダース 136 ブースター 137 ポリゴン 138 オムナイト 139 オムスター 140 カブト 141 カブトプス 142 プテラ 143 カビゴン 144 フリーザー 145 サンダー 146 ファイヤー 147 ミニリュウ 148 ハクリュー 149 カイリュー 150 ミュウツー 151 ミュウ 152 チコリータ 153 ベイリーフ 154 メガニウム 155 ヒノアラシ 156 マグマラシ 157 バクフーン 158 ワニノコ 159 アリゲイツ 160 オーダイル 161 オタチ 162 オオタチ 163 ホーホー 164 ヨルノズク 165 レディバ 166 レディアン 167 イトマル 168 アリアドス 169 クロバット 170 チョンチー 171 ランターン 172 ピチュー 173 ピィ 174 ププリン 175 トゲピー 176 トゲチック 177 ネイティ 178 ネイティオ 179 メリープ 180 モココ 181 デンリュウ 182 キレイハナ 183 マリル 184 マリルリ 185 ウソッキー 186 ニョロトノ 187 ハネッコ 188 ポポッコ 189 ワタッコ 190 エイパム 191 ヒマナッツ 192 キマワリ 193 ヤンヤンマ 194 ウパー 195 ヌオー 196 エーフィ 197 ブラッキー 198 ヤミカラス 199 ヤドキング 200 ムウマ 201 アンノーン 202 ソーナンス 203 キリンリキ 204 クヌギダマ 205 フォレトス 206 ノコッチ 207 グライガー 208 ハガネール 209 ブルー 210 グランブル 211 ハリーセン 212 ハッサム 213 ツボツボ 214 ヘラクロス 215 ニューラ 216 ヒメグマ 217 リングマ 218 マグマッグ 219 マグカルゴ 220 ウリムー 221 イノムー 222 サニーゴ 223 テッポウオ 224 オクタン 225 デリバード 226 マンタイン 227 エアームド 228 デルビル 229 ヘルガー 230 キングドラ 231 ゴマゾウ 232 ドンファン 233 ポリゴン2 234 オドシシ 235 ドーブル 236 バルキー 237 カポエラー 238 ムチュール 239 エレキッド 240 ブビィ 241 ミルタンク 242 ハピナス 243 ライコウ 244 エンテイ 245 スイクン 246 ヨーギラス 247 サナギラス 248 バンギラス 249 ルギア 250 ホウオウ 251 セレビィ 252 キモリ 253 ジュプトル 254 ジュカイン 255 アチャモ 256 ワカシャモ 257 バシャーモ 258 ミズゴロウ 259 ヌマクロー 260 ラグラージ 261 ポチエナ 262 グラエナ 263 ジグザグマ 264 マッスグマ 265 ケムッソ 266 カラサリス 267 アゲハント 268 マユルド 269 ドクケイル 270 ハスボー 271 ハスブレロ 272 ルンパッパ 273 タネボー 274 コノハナ 275 ダーテング 276 スバメ 277 オオスバメ 278 キャモメ 279 ペリッパー 280 ラルトス 281 キルリア 282 サーナイト 283 アメタマ 284 アメモース 285 キノココ 286 キノガッサ 287 ナマケロ 288 ヤルキモノ 289 ケッキング 290 ツチニン 291 テッカニン 292 ヌケニン 293 ゴニョニョ 294 ドゴーム 295 バクオング 296 マクノシタ 297 ハリテヤマ 298 ルリリ 299 ノズパス 300 エネコ 301 エネコロロ 302 ヤミラミ 303 クチート 304 ココドラ 305 コドラ 306 ボスゴドラ 307 アサナン 308 チャーレム 309 ラクライ 310 ライボルト 311 プラスル 312 マイナン 313 バルビート 314 イルミーゼ 315 ロゼリア 316 ゴクリン 317 マルノーム 318 キバニア 319 サメハダー 320 ホエルコ 321 ホエルオー 322 ドンメル 323 バクーダ 324 コータス 325 バネブー 326 ブーピッグ 327 パッチール 328 ナックラー 329 ビブラーバ 330 フライゴン 331 サボネア 332 ノクタス 333 チルット 334 チルタリス 335 ザングース 336 ハブネーク 337 ルナトーン 338 ソルロック 339 ドジョッチ 340 ナマズン 341 ヘイガニ 342 シザリガー 343 ヤジロン 344 ネンドール 345 リリーラ 346 ユレイドル 347 アノプス 348 アーマルド 349 ヒンバス 350 ミロカロス 351 ポワルン 352 カクレオン 353 カゲボウズ 354 ジュペッタ 355 ヨマワル 356 サマヨール 357 トロピウス 358 チリーン 359 アブソル 360 ソーナノ 361 ユキワラシ 362 オニゴーリ 363 タマザラシ 364 トドグラー 365 トドゼルガ 366 パールル 367 ハンテール 368 サクラビス 369 ジーランス 370 ラブカス 371 タツベイ 372 コモルー 373 ボーマンダ 374 ダンバル 375 メタング 376 メタグロス 377 レジロック 378 レジアイス 379 レジスチル 380 ラティアス 381 ラティオス 382 カイオーガ 383 グラードン 384 レックウザ 385 ジラーチ 386 デオキシス 387 ナエトル 388 ハヤシガメ 389 ドタイトス 390 ヒコザル 391 モウカザル 392 ゴウカザル 393 ポッチャマ 394 ポッタイシ 395 エンペルト 396 ムックル 397 ムクバード 398 ムクホーク 399 ビッパ 400 ビーダル 401 コロボーシ 402 コロトック 403 コリンク 404 ルクシオ 405 レントラー 406 スボミー 407 ロズレイド 408 ズガイドス 409 ラムパルド 410 タテトプス 411 トリデプス 412 ミノムッチ 413 ミノマダム 414 ガーメイル 415 ミツハニー 416 ビークイン 417 パチリス 418 ブイゼル 419 フローゼル 420 チェリンボ 421 チェリム 422 カラナクシ 423 トリトドン 424 エテボース 425 フワンテ 426 フワライド 427 ミミロル 428 ミミロップ 429 ムウマージ 430 ドンカラス 431 ニャルマー 432 ブニャット 433 リーシャン 434 スカンプー 435 スカタンク 436 ドーミラー 437 ドータクン 438 ウソハチ 439 マネネ 440 ピンプク 441 ペラップ 442 ミカルゲ 443 フカマル 444 ガバイト 445 ガブリアス 446 ゴンベ 447 リオル 448 ルカリオ 449 ヒポポタス 450 カバルドン 451 スコルピ 452 ドラピオン 453 グレッグル 454 ドクロッグ 455 マスキッパ 456 ケイコウオ 457 ネオラント 458 タマンタ 459 ユキカブリ 460 ユキノオー 461 マニューラ 462 ジバコイル 463 ベロベルト 464 ドサイドン 465 モジャンボ 466 エレキブル 467 ブーバーン 468 トゲキッス 469 メガヤンマ 470 リーフィア 471 グレイシア 472 グライオン 473 マンムー 474 ポリゴンZ 475 エルレイド 476 ダイノーズ 477 ヨノワール 478 ユキメノコ 479 ロトム 480 ユクシー 481 エムリット 482 アグノム 483 ディアルガ 484 パルキア 485 ヒードラン 486 レジギガス 487 ギラティナ 488 クレセリア 489 フィオネ 490 マナフィ 491 ダークライ 492 シェイミ 493 アルセウス """ def run(): # 名前を変数に読み込む name = [] nameLength = [] for l in io.StringIO(TsvData): iname = l.strip().split("\t")[1] name.append(iname) nameLength.append(len(iname)) # 文字の集計 allChar = [] for c in list("".join(name)): allChar.append(c) uniqueChar = np.unique(allChar).tolist() # 遷移確率を求める dim = len(uniqueChar) x = np.zeros((dim, dim)) for iname in name: ilen = len(iname) for i in range(ilen): curIdx = uniqueChar.index(iname[i]) #if i > 0: # preIdx = uniqueChar.index(iname[i - 1]) # x[curIdx][preIdx] += 1 if i < (ilen - 1): nextIdx = uniqueChar.index(iname[i + 1]) x[curIdx][nextIdx] += 1 # 遷移確率からランダムに名前を作る x = x / np.sum(x, axis=1).reshape(-1, 1) x[np.isnan(x)] = 0 for i in range(len(uniqueChar)): newName = uniqueChar[i] rrange = np.random.randint(np.min(nameLength), np.max(nameLength)) for n in range(rrange + 1): prob = x[uniqueChar.index(newName[-1])] if np.max(prob) == 0: break newChar = np.random.choice(uniqueChar, 1, p=prob) newName += newChar[0] print(str(newName)) if __name__ == "__main__": run() """ python main.py """動機とか
文書特徴抽出時に分かち書き処理をしたくないので自力で学習型分かち書きを作り、その工程でできたランダム単語作成がおもしろかったのでそこのお話だけ共有しました。自作に至った経緯はRNNを調べていて確率遷移を求めている事が分かったのでその程度で済む簡単な物であればディープラーニング使うまでもなく実装できそうだと思ったためです。
- 投稿日:2019-02-15T20:58:36+09:00
Azure FunctionsのHTTPトリガーでBlob Storageにある画像を表示する(Azure Functions v1、Python 3.6.1)
Azure FunctionsのHTTPトリガーでBlob Storageにある画像を表示してみましょう。
※Chrome上のAzure Portalの表示がなんか調子悪いのでEdgeでやってます。Function Appの作成
Azure Portalにログインします。
リソースの作成からFunction Appを作成します。
できたら、リソースに移動します。
Pythonでやりたいので、ランタイムバージョンを~1に変更します。
Azure FunctionsでPython3を使うを参考にPythonの設定をします。
https://{your-app-name}.scm.azurewebsites.net/DebugConsoleを開きます。
{your-app-name}にはFunction Appの名前を入れてください。(例:gachimoto-blob)下記コマンドでPython3をインストールします。
> cd D:\home\site\tools > nuget.exe install -Source https://www.siteextensions.net/api/v2/ -OutputDirectory D:\home\site\tools python361x64 > mv /d/home/site/tools/python361x64.3.6.1.3/content/python361x64/* /d/home/site/tools/pipでazure-storageライブラリをインストールしましょう。
> D:\home\site\tools\python.exe -m pip install azure-storageストレージアカウントの作成
デプロイが完了したら、リソースへ移動します。
ストレージアカウント名とkey1をメモります。
コンテナの作成
コンテナを作成します。testという名前のコンテナを作成しました。Blobはアクセスできるようにしています。
画像のアップロード
testコンテナへ、
lena.jpgをアップロードしてみました。
Blobのアクセスを可能にしているので、URLから見れてしまいます。
例:https://{your-storage-account}.blob.core.windows.net/test/lena.jpg
Function Appの関数作成
画像のアップロードができたら、Function Appに戻ります。
HttpTriggerPython31の内容を次のようにします。
import os import json from azure.storage.blob import BlockBlobService account_name='{your-storage-account}' account_key='{your-storage-account-key}' container_name='test' service = BlockBlobService(account_name=account_name,account_key=account_key) blobs = service.list_blobs(container_name) files = [] for blob in blobs: files.append(blob.name) def write_http_response(status, body): return_dict = { "status": status, "body": body, "headers": { "Content-Type": "text/html" } } output = open(os.environ['res'], 'w') output.write(json.dumps(return_dict)) write_http_response(200, "<html><h1>" + files[0] + "</h1><img src=" + "\"" + "https://{your-storage-account}.blob.core.windows.net/test/" + files[0] + "\"" + ">" + "</html>")
account_nameとaccount_keyには、メモったストレージアカウント名とkey1を入れます。testコンテナの中にあるBlobのリストを取得し、リストの一番最初のファイルのURLをHTMLタグに入れて返しています。
保存および実行をクリックし、出力が進捗状況200 OKになれば成功です。<html><h1>lena.jpg</h1><img src="https://{your-storage-account}.blob.core.windows.net/test/lena.jpg"></html>まとめ
- Azure Functionsを用いて、Blob Storageの画像を表示しました
- GETでHTMLを返すやつができました
- 次はクエリ文字列つけたり、見れる人制限したり、SAS使ったりしたいですよね?
参考文献
- 投稿日:2019-02-15T20:22:51+09:00
No.034【Python】文字列の置換について①
今回は、「文字列の置換」について書いていきます。
I'll write about the replacement of strings in python" on this page.
■ 文字列指定による置換 : replace
The replacement of strings
>>> # string型 replace()を利用する >>> >>> w = "one two three four five" >>> >>> print(w.replace(" ", "-")) one-two-three-four-five >>> >>> >>> # 上記処理の削除方法:空文字列""にする >>> >>> print(w.replace(" ", "")) onetwothreefourfive>>> w = "one two three four five" >>> >>> print(w.replace("one", "egg")) egg two three four five >>> >>> print(w.replace("three", "mayonnaise")) one two mayonnaise four five>>> # 複数の文字列置換 >>> >>> # replace()を適用することで置換が可能 >>> >>> print(w.replace("two", "egg").replace("four", "salt")) one egg three salt five >>> >>> W = "one two one two one" >>> >>> print(W.replace("one", "XtwoY").replace("two", "YYY")) XYYYY YYY XYYYY YYY XYYYY >>> >>> print(W.replace("two", "ZZZ").replace("one","XtwoY")) XtwoY ZZZ XtwoY ZZZ XtwoY >>> # ↑上記の様に、順番には注意すること>>> # 改行文字による置換 >>> >>> w_lines = "one\ntwo\nthree" >>> >>> print(w_lines) one two three >>> >>> print(w_lines.replace("\n", "-")) one-two-three >>> # Unix系OS:\n Windows系:\r\n>>> w_lines_multi = "one\ntwo\r\nthree" >>> >>> print(w_lines_multi) one two three >>> >>> print(w_lines_multi.replace("\r\n", "-").replace("\n", "-")) one-two-three >>> >>> >>> print(w_lines_multi.replace("\n", "-").replace("\r\n", "-")) one-two -three >>> # ↑順番によっては求める結果が得られないことがある■ 複数文字指定による置換: translate
Replacement of multiple string assignments: translate
>>> # str型のtranslate()を利用する >>> # translate()に指定する変換テーブル:str.maketrans()にて作成 >>> >>> w = "one two one two one two" >>> >>> print(w.translate(str.maketrans({"o":"O", "t":"T", "e":"E"}))) OnE TwO OnE TwO OnE TwO >>> >>> >>> print(w.translate(str.maketrans({"o":"ZZZ", "t": None}))) ZZZne wZZZ ZZZne wZZZ ZZZne wZZZ>>> # 辞書ではなく、3つの文字列を引数として指定することも可能 >>> >>> print(w.translate(str.maketrans('ow', 'ZW', 'n'))) Ze tWZ Ze tWZ Ze tWZ>>> # 以下の場合、第一・第二引数の文字列の長さは一致が必要 >>> # 置換先文字列に長さ2つ以上文字列は指定不可 >>> >>> print(w.translate(str.maketrans('ow', 'ZZW', 'n'))) Traceback (most recent call last): File "<pyshell#88>", line 1, in <module> print(w.translate(str.maketrans('ow', 'ZZW', 'n'))) ValueError: the first two maketrans arguments must have equal length随時に更新していきますので、
定期的な購読をよろしくお願いします。
I'll update my articles at all times.
So, please subscribe my articles from now on.本記事について、
何か要望等ありましたら、気軽にメッセージをください!
If you have some requests, please leave some messages! by You-Tarinまた、「Qiita」へ投稿した内容は、随時ブログへ移動して行きたいと思いますので、よろしくお願いします。
- 投稿日:2019-02-15T18:28:17+09:00
pythonでgRPC とりあえずインストール
goでgRPCはやったことあったけどpythonではどうやるんだろうーと思ったので、チュートリアルにチャレンジ
マシンはmacです
間違いあったら指摘いただけると助かりますインストール
# grpcのインストール pip install --upgrade pip sudo python -m pip install grpcio sudo python -m pip install grpcio-tools# サンプルコードのインストール git clone -b v1.18.0 https://github.com/grpc/grpc動くことを確認
cd grpc/examples/python/helloworld python greeter_server.py # 別ターミナルで python greeter_client.py Greeter client received: Hello, you! # 出たねprotoファイルからスクリプトを生成
protoファイルを作る
// vim my_if.proto // なにかをするservice(xx_pb2_proto.pyのコメントとして使用される) service MyGrpc { // なにかを受け取るRPC(xx_pb2_proto.pyのコメントとして使用される) rpc GetSomething (MyReq) returns (MyResp) {} } message MyReq { int32 int_param = 1; string str_param = 2; } message MyResp { int32 status = 1; string message = 2; }コマンドで生成
python -m grpc_tools.protoc -I./ --python_out=. --grpc_python_out=. ./my_if.proto(いちいちコマンド打つのは面倒いのでこちらの記事を参考に設定ファイルで作成するようにしました)
my_if_pb2.pyとmy_if_pb2_grpc.pyが生成される。(pb2の2はProtocol Buffers Python APIのバージョンを示していて1と互換性がない)
内容は以下:
- classes for the messages defined in route_guide.proto
- classes for the service defined in route_guide.proto
- RouteGuideStub, which can be used by clients to invoke RouteGuide RPCs
- RouteGuideServicer, which defines the interface for implementations of the RouteGuide service
- a function for the service defined in route_guide.proto
- add_RouteGuideServicer_to_server, which adds a RouteGuideServicer to a grpc.Server
自分用に読み換えると以下のような雰囲気(たぶん)
- messages用クラス
- service用クラス
MyGrpcStubはMyGrpcを呼び出すのに使用するクライアントMyGrpcServicerはserviceを実装する用のインターフェース- service用のfunc
add_MyGrpcServicer_to_serverはgrpcサーバにMyGrpcServicerを追加するとりあえずインストールからスクリプト生成まで完了
- 投稿日:2019-02-15T18:27:35+09:00
酒が飲めるワンライン
perl (5.18.2 で確認)
perl -E 'say"$_月は横浜で酒が飲めるぞ"for(1..12)'ruby
ruby -e '12.times{|i|puts"#{i+1}月は横浜で酒が飲めるぞ"}'bash
for i in {1..12};do;echo $i月は横浜で酒が飲めるぞ;donepython3 (3.7.2 で確認)
python3 -c `[print("%d月は横浜で酒が飲めるぞ" % n) for n in range(1, 13)]`emacs-lisp (GNU Emacs 26.1 で確認)
(require 'cl)(let ((x 0))(while (< x 12) (cl-incf x)(insert (format "%d月は横浜で酒が飲めるぞ\n" x))))
- 投稿日:2019-02-15T18:21:51+09:00
Codewars で複数のプログラミング言語で全ての問題を解いていきたい時に便利な操作
# 今回は画像(スクショ)だけで手抜き~!
# Codewars についてご存じない方は、先に『【Codewars】ブラウザでコーディングの基礎からトレーニングできるサイト (ブラウザでvimが使えて32種類のプログラミング言語に対応。4000個以上の問題が投稿されています!)』 をお読み頂くようお願い致します。
このような感じで、View Profile メニューから Kata タブを選択することで、他の言語で解き忘れがないか確認できます。すでにやった問題を自分の学習中の言語全てで解いてみたい方におススメです。
- 投稿日:2019-02-15T17:55:11+09:00
広色域で24ビットカラーは割とアウト
結論
24ビットカラーで広色域(DCI-P3)は無理があるので、iPhoneのカメラの写真がHEIF(拡張子heic)になったのは必然だった。
総天然ショック
良い子のみんな! PC-9801の4096色パレットの色域がどれだけ狭かったか、よく覚えているよね!
量子ドットや4K8K(BT.2020)やiPhone(DCI-P3)でいよいよsRGBがオワコンになりつつある(ただしWebを除く)。来るべきニューメディア時代に、24ビットカラーは対応できるのか?
そんな問題意識のもと、値が1変わったときに、sRGBとAdobeRGBの色がどれだけ変わるのか調べてみた。
pip install colormathが必要。import numpy as np from colormath.color_diff import delta_e_cie2000 from colormath.color_objects import sRGBColor, AdobeRGBColor, LabColor from colormath.color_conversions import convert_color TEST_COLOR = None def to_lab(srgb): return convert_color(TEST_COLOR(*(srgb / 255)), LabColor, target_illuminant='d65') def srgb_to_lab(srgb): if len(srgb.shape) == 1: lab = to_lab(srgb) return lab else: labs = np.apply_along_axis(to_lab, 1, srgb) return labs ciede2000 = np.vectorize(delta_e_cie2000) STEP = np.eye(3) def cd(c): return ciede2000(srgb_to_lab(c), srgb_to_lab(c - STEP)) def calc_maxcd_by_one(): r = np.arange(1, 255, 16) grid = np.array(np.meshgrid(r, r, r)).T.reshape(-1,3) cds = np.apply_along_axis(cd, 1, grid) a = grid[int(cds.argmax() / 3)] b = a - STEP[cds.argmax() % 3] return cds.max(), a, b def main(): global TEST_COLOR TEST_COLOR = sRGBColor maxcd, color_from, color_to = calc_maxcd_by_one() print('sRGB:') print(f'Max Color Difference of 1-step: {maxcd} color: {color_from} -> {color_to}') TEST_COLOR = AdobeRGBColor maxcd, color_from, color_to = calc_maxcd_by_one() print('Adobe RGB:') print(f'Max Color Difference of 1-step: {maxcd} color: {color_from} -> {color_to}') if __name__=='__main__': main()結果:
sRGB: Max Color Difference of 1-step: 1.1805655454210477 color: [33 33 33] -> [33. 32. 33.] Adobe RGB: Max Color Difference of 1-step: 1.6538699060386761 color: [33 33 33] -> [33. 32. 33.]この色差(color difference)の単位はCIE DE2000(ΔE00)。古い色差(ΔE76)では、
- 無彩色付近
- 近い色同士
で人間の知覚よりもずっと小さな値が出てしまっていた問題を解消している。
そもそも色差は人間の感覚を数値化したもので、だいたい以下のような感覚に対応している(ことになっている)。
ΔE 感覚 <= 1.0 人間の目には違いがわからない 1-2 よく見ると違いがわかる > 2 一目で違いがわかる もちろん現実には色差3がわからなかったり、プロが1以下の色差を見分けたりする。とはいえ、見比べても10の差がわからなかったり、0.1を見分けられたりすることはない。
さて、sRGBで1.18、AdobeRGBで1.65の色差をどう考えればいいのか。「よく見ると違いがわかる」ということになっている。実際に私のディスプレイでsRGBで見ると、かなり苦戦するものの、見える。
見える!
24ビットカラーが落とし所として絶好すぎて抜け出せない分野はたくさんある。帯域不足でエセ8bit時代みたいな絵になってる状態(JPEG 2000でありがち)では、こんな話に意味はない。
高品質な画像を求めるなら、広色域で24ビットカラーは無理がある。iPhoneがHEIF(拡張子heic)の30ビットカラーに移行したのも当然だった。
ちなみに
ProPhoto RGB(ROMM RGB)では2を超えてくる。48ビットカラーのリニアワークフローがお勧め。
- 投稿日:2019-02-15T17:15:15+09:00
Pythonのサンプル集
Logger
# -*- coding:utf-8 -*- import logging from logging import getLogger, FileHandler, StreamHandler, Formatter import datetime def my_logger(modname, log_filename=None, dry_run=False, log_format='%(asctime)s - %(name)s - %(levelname)s - %(message)s'): ''' ログ出力フォーマット設定 ''' handler_format = Formatter(log_format) logger = getLogger(modname) ''' loggerのログレベル設定(ハンドラに渡すエラーメッセージのレベル) ''' logger.parent.setLevel(logging.DEBUG) ''' ファイル出力 dry_run = Trueのときにはファイル出力しないようにする ''' if log_filename and not dry_run: file_handler = FileHandler(log_filename) file_handler.setLevel(logging.DEBUG) file_handler.setFormatter(handler_format) logger.addHandler(file_handler) ''' 標準出力 ''' stream_handler = StreamHandler() stream_handler.setLevel(logging.DEBUG) stream_handler.setFormatter(handler_format) logger.addHandler(stream_handler) return logger if __name__ == '__main__': my_logger = my_logger('main', '/var/log/sample.log') my_logger.debug('This is a debug log') my_logger.info('This is a info log') my_logger.warn('This is a warn log') my_logger.error('This is a error log') my_logger.critical('This is a critical log') ''' 2019-02-15 17:04:13,673 - main - DEBUG - This is a debug log 2019-02-15 17:04:13,674 - main - INFO - This is a info log 2019-02-15 17:04:13,674 - main - WARNING - This is a warn log 2019-02-15 17:04:13,674 - main - ERROR - This is a error log 2019-02-15 17:04:13,674 - main - CRITICAL - This is a critical log '''requestsでタイムアウト処理
import requests from requests.packages.urllib3.util.retry import Retry from requests.adapters import HTTPAdapter s = requests.Session() ''' totalで5回リトライをする backoff_factor=1の場合、リトライ間隔は、1回目は1秒、2回目は2秒、3回目は3秒・・・ status_forcelistで定義されたstatusのときのみリトライする ''' retries = Retry(total=5, backoff_factor=1, status_forcelist=[ 500, 502, 503, 504 ]) s.mount('http://', HTTPAdapter(max_retries=retries)) s.mount('https://', HTTPAdapter(max_retries=retries)) ''' connection timeoutが10秒、read timeoutが30秒 ''' r = s.get('https://example.com/', timeout=(10.0, 30.0)) r.raise_for_status() ''' response bodyを表示 ''' print(r.text) ''' status codeを表示 ''' print(r.status_code)
- 投稿日:2019-02-15T16:55:23+09:00
ブル・ベアファンド自動裁定 〜はじめの一歩〜
導入
お前だれ
都内某T大学部4年、機械学習・統計手法でバイオインフォマ、ケモインフォマでケモケモしたりFinTechしようとしている株式会社Smart Tradeインターンの小林(Twitterアカウント)です。
神田のランチリポーターもやってます。
今回何やるの?
当社インターン5ヶ月目ということでいつまでも初心者とは言って居られなくなったので販売できそうなアルゴの実装を本気で目指して行きたいと思います。
その"はじめの一歩"として今回は以下を達成目標とします。
- ブル・ベアファンドの仕組みを理解する
- QuantX Factoryでブル・ベアファンドをの自動裁定を実装する
QuantX Factoryって何?
株式会社Smart Tradeが
" 金融の民主化 "
を理念に、これまで一部の有識者だけの物であったトレードアルゴリズムをより簡易にコード上で開発するためのプラットフォームです。
何が強いの?
- Web上のプラットフォームのため開発環境構築が不要であること
- 各銘柄の終値や高値などの各種データが用意されておりデータセットの用意不要 (公式ドキュメント参考)
- 開発したトレードアルゴリズムは審査を通過すればQuantX Storeで販売可能
- 上級者の方にはQuantX Labといった開発環境も
本題
ブル・ベアファンドの仕組みを理解する
ブル・ベアファンドとは
日経平均株価などの対応する株価指数の短期の値上がり・値下がりを利用して利益を出すことを狙いとした投資信託のことです。
上手くブル・ベアファンドの売買を行えば上昇相場でも下落相場でも利益を出すことができます。
ブル、ベアと二つの投資信託はそれぞれ対応する株価指数に対して特有の"動き方"と"倍率"を持っています。
それぞれの動き方
まず、それぞれの"動き方"について見て行きましょう。
ブル型ファンド (Bull fund) の動き
その名からもわかる通り(レバレッジ型とも呼ばれます)
株価指数の値上がりに対し "牛の角が突き上げる" ように値上がりする投資信託のことで基本的には株価指数の値動きに対応するものと考えます。上の図は黒線が対応する株価指数の動きであり赤線がブルファンドの値動きです。(イメージ)
この図からも
"対応する株価指数が上昇する時はブルファンドを買う"
という結論に至るかと思います。
ベア型ファンドの (Bear Fund) の動き
これまたその名からわかる通り(インバース型とも呼ばれます)
株価指数の値上がりに対し "熊が爪を振り下ろす" ように値下がりする投資信託のことで基本的には株価指数の値動きに対して逆転するものと考えます。上の図は黒線が対応する株価指数の動きであり青線がベアファンドの値動きです。(イメージ)
この図からも
"対応する株価指数が下落する時はベアファンドを買う"
という結論に至るかと思います。
倍率について
ブル・ベアファンドは対応する株価指標に対応して値動きすると説明しましたが、単純に等倍で値動きしている用では短期で大きな利益を出すことはできません。
そこで登場するのが値動きの倍率です。
少し例を見てみましょう
銘柄コード 銘柄名 概要 1367 ダイワ上場投信 TOPIXレバレッジ TOPIXの動きの2倍の値動きをする 1350 日経平均レバレッジ・インデックス連動型上場投信 日経平均の動きの2倍の値動きをする 1356 TOPIXベア2倍上場投信 TOPIXの動きの2倍の逆転した値動きをする 1357 日経ダブルインバース上場投信 日経平均の動きの2倍の逆転した値動きをする 大体2倍の銘柄が多いですがトリプルと言った3倍などもあります。
高い倍率のブルベアファンドのメリットとして短期の株価指数の少しの動きで大きな利益を得ることができることが挙げられますが、裏を返せばリスクも倍になるという事なので注意が必要です。より詳細に値動きと損益に関して知りたいかたはコチラをご覧ください。
ブル・ベアファンドをの自動裁定を実装する
選択銘柄
- 1321 : 日経225連動型上場投資信託
- これを今回のブルベアの対応する株価指標とします。
- 1570 : 日経平均レバレッジ上場投信 (ブル型)
- 1357 : 日経ダブルインバース上場投信 (ベア型)
以下各銘柄はそれぞれ株価指標・ブル・ベアと呼称します。
指標
今回は特に選定せず実装が容易い二つを選ぶました。
ここではブルベアの実装をメインとするので各指標の実装と理論についてはリンクの方を参照してください。
RCIに関してはインターン生の佐々木さん(@akihirosasaki)の実装を借りさせていただきました。アルゴリズム
とりあえずははじめの一歩なのでアルゴリズムは単純にしました。
- 上記の各指標を株価指標のみで計算し株価指標が上昇するか下落するかを予測
- 予測結果の元
- 上昇する場合ブルを買い、ベアを売る
- 下落する場合ブルを売り、ベアを買う
実装
今回ははじめの一歩ですのでQuantX Factoryの使い方も含めて説明していきます、既に理解されている方は読み飛ばしつつでお願いします。
コードはここをスタートとして書いていきましょう。
cloneボタンを押して好きな名前をつけてコピーを作成して下さい。
ここからも直接コピーできます
#必要なライブラリの読み込み import numpy as np import pandas as pd import talib as ta #RCIを計算する関数 def get_rci(close, period): rank_period = np.arange(period, 0, -1) length = len(close) rci = np.zeros(length) for i in range(length): if i < period - 1: rci[i] = 0 else : rank_price = close[i - period + 1: i + 1].rank(method='min', ascending = False).values rci[i] = (1 - (6 * sum((rank_period - rank_price)**2)) / (period**3 - period)) * 100 return rci def initialize(ctx): # 設定 ctx.logger.debug("initialize() called") ctx.configure( channels={ # 利用チャンネル "jp.stock": { "columns": [ ], "symbols": [ ] } } ) def _my_signal(data): buy_sig = sell_sig = return { "buy:sig":buy_sig, "sell:sig":sell_sig, } # シグナル登録 ctx.regist_signal("my_signal", _my_signal) def handle_signals(ctx, date, current): ''' current: pd.DataFrame ''' # ctx.logger.debug(df) # ctx.logger.debug(df["buy:sig"]) # ctx.logger.debug(df["sell:sig"]) # 買いシグナル # 売りシグナル銘柄と終値などの読み込み
まずは今回使う銘柄と終値などのデータを読み込めるようにしましょう。
24行目から
"jp.stock": { "symbols": [ ], "columns": [ ] }の様なコードがあると思います、このコードを以下のコードにしましょう。(コピペを推奨します)
"jp.stock": { "symbols": [ "jp.stock.1321", #日経225連動型上場投資信託 "jp.stock.1357", #日経ダブルインバース上場投信 bear "jp.stock.1570", #日経平均レバレッジ上場投信 bull ], "columns": [ "close_price_adj" ] }このコードは
-"jp.stock": 日本株
-"symbols": 銘柄は指定した三つの銘柄コードのもの
-"columns": 値は今回終値の調整値だけを用いるので"close_price_adj"
となります。指標の計算とシグナル出し
次はRCI、RSIを用いた指標計算に移ります。
38行目あたりの
def _my_signal(data)から、ここは買い売りシグナル(今回は日経平均の上昇下落シグナル)を生成する部分となります。def _my_signal(data): buy_sig = sell_sig = return { "buy:sig":buy_sig, "sell:sig":sell_sig, }このコードを以下の様に書き換えましょう
def _my_signal(data): cp = data["close_price_adj"].fillna(method='ffill') # ctx.logger.debug(cp) rci9 = pd.DataFrame(0, index=cp.index, columns=cp.columns) rsi7 = pd.DataFrame(0,index=cp.index, columns=cp.columns) for (sym,val) in cp.items(): rci9[sym]=get_rci(cp[sym], 9) for (sym,val) in cp.items(): rsi7[sym] = ta.RSI(cp[sym].values.astype(np.double), timeperiod=7) # ctx.logger.debug(rci9) # ctx.logger.debug(rsi7) buy_sig= (rci9 < -80) | (rsi7 < 30) sell_sig= (rci9 > 80) | (rsi7 > 70) return { "buy:sig":buy_sig, "sell:sig":sell_sig, "rci9:g2":rci9, "rsi7:g2":rsi7, }順を追って説明すると
cp = data["close_price_adj"].fillna(method='ffill') # データ"close_price_adj"の欠損を無くし使えるデータに整形 # ctx.logger.debug(cp) #データの中身が気になる方はこの行の先頭の#を外して実行してみて下さい。 rci9 = pd.DataFrame(0, index=cp.index, columns=cp.columns) # 指標RCIの計算結果を保存するための容れ物を用意します、容れ物の形状はcpと同じにしています。 rsi7 = pd.DataFrame(0,index=cp.index, columns=cp.columns) # 指標RSIの計算結果を保存するための容れ物を用意します、容れ物の形状はcpと同じにしています。となり...
for (sym,val) in cp.items(): rci9[sym]=get_rci(cp[sym], 9) for (sym,val) in cp.items(): rsi7[sym] = ta.RSI(cp[sym].values.astype(np.double), timeperiod=7) #指標RCI,RSIを計算する関数get_rci(),ta.RSI()を呼び出し各銘柄においてfor分により計算しています。 # ctx.logger.debug(rci9) # ctx.logger.debug(rsi7) #各指標RSI, RCIがどの様な値になっているか確認したい場合先頭の#を外して実行してみて下さい。今回は株価指標の銘柄においてのみ格指標を計算すれば良いのですが今後拡張することを考え計算しておきます。ちなみにここではRCI, RSIそれぞれ9日、7日の期間で計算しています。
各指標の値で計算したのち...
buy_sig= (rci9 < -80) | (rsi7 < 30) # rci9が-80より小さい、もしくはrsi7が30より小さい時買いシグナルを出す(上昇すると予測) sell_sig= (rci9 > 80) | (rsi7 > 70) # rci9が80より大きい、もしくはrsi7が70より大きい時売りシグナルを出す(下落すると予測) return { "buy:sig":buy_sig, "sell:sig":sell_sig, "rci9:g2":rci9, "rsi7:g2":rsi7, } #デバッグや結果に描画などでも使える様にreturnで返すここまでで株価指標の上昇と下落の予測シグナルを出すことができる様になりました。
ちなみに61行目の
ctx.regist_signal("my_signal", _my_signal)でこのシグナルを登録しています。これをしなければ後で使えないのでしっかり登録しましょう。シグナルの処理
ここからが本題です、63行目から
def handle_signals(ctx, date, current):以降を書いていきます。ここはデータ構造が少し複雑になるので順を追ってコードを書いていきます。まず、
''' current: pd.DataFrame '''「 current: pd.DataFrame...? 」
となる方もいるかと思いますので説明いたします、先ほども41行目あたりで出てきましたpd.DataFrameですがこれは"容れ物"です、が、ここの"容れ物"少し41行目のものとは訳が違います。
というと、この
currentという容れ物には既に中に色々入っています。
試しにctx.logger.debug(current)を追加、以下のコードで実行しcurrent中身を確認しましょう。def handle_signals(ctx, date, current): ''' current: pd.DataFrame ''' ctx.logger.debug(current)以下の様なログが出てきたと思います。
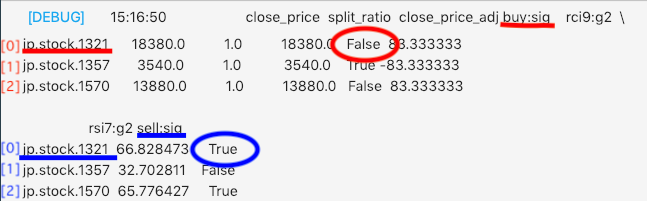
ここでは上昇予測である買いシグナル(buy:sig)と下降予測である売りシグナル(sell:sig)
を用いたいのでcurrent["buy:sig"],current["sell:sig"]で指定します。ただし今回は株価指標である
"jp.stock.1321"の各シグナルのみ用いるので
current["buy:sig"][0],current["sell:sig"][0]という指定になります。
ちなみにここでの[0]とは以下のDataFrameの0行目(株価指標のシグナル)を指定していることになります。これを踏まえてコードを以下の様に書きます。
def handle_signals(ctx, date, current): ''' current: pd.DataFrame ''' # ctx.logger.debug(current) bear = ctx.getSecurity("jp.stock.1357") bull = ctx.getSecurity("jp.stock.1570") # 買いシグナル df_buy = current["buy:sig"][0] if df_buy: bull.order_target_percent(0.10, comment="BULL BUY") bear.order_target_percent(0, comment="BEAR SELL") # 売りシグナル df_sell = current["sell:sig"][0] if df_sell: bear.order_target_percent(0.10, comment="BEAR BUY") bull.order_target_percent(0, comment="BULL SELL")それぞれ説明すると、
bear = ctx.getSecurity("jp.stock.1357") #指定したベアの銘柄のオブジェクトをbearとして保存します、あとで注文に用います。 bull = ctx.getSecurity("jp.stock.1570") #指定したブルの銘柄のオブジェクトをbullとして保存します、あとで注文に用います。こうして取引する銘柄を指定した後
# 買いシグナル df_buy = current["buy:sig"][0] if df_buy: bull.order_target_percent(0.10, comment="BULL BUY") bear.order_target_percent(0, comment="BEAR SELL")
df_buyがTrueの時、つまりブルベアが対応する株式指標の銘柄が値上がりと予測
bull: 2倍値上がりするであろうブル銘柄の総保有額が総資産の10%となる様に買いbear: 2倍値下がりするであろうベア銘柄を総保有額が総資産の0%となる様に売る(全売り)# 売りシグナル df_sell = current["sell:sig"][0] if df_sell: bear.order_target_percent(0.10, comment="BEAR BUY") bull.order_target_percent(0, comment="BULL SELL")
df_buyがTrueの時、つまりブルベアが対応する株式指標の銘柄が値下がりと予測
bull: 2倍値下がりするであろうブル銘柄を総保有額が総資産の0%となる様に売る(全売り)bear: 2倍値上がりするであろうベア銘柄の総保有額が総資産の10%となる様に買いそのほかの注文方法は公式ドキュメント参考にしてください
やっと完成です!
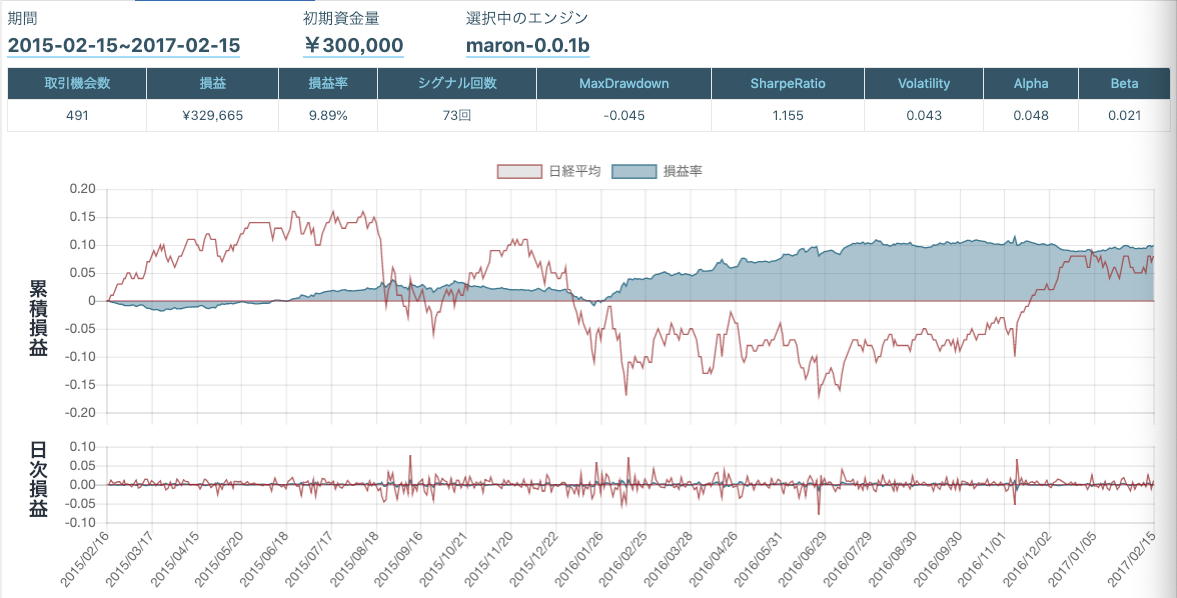
一応完成コードはコチラ結果
評価・考察
- 結果からわかる様に下落が連続的に続く場面に関して一定の利益を上げている
- 日経平均が細かく上下を繰り返すと振り回されて損出を出すことが多くなる
- 各種指標RSI・RCIの計算期間が短すぎると日経平均に過敏に反応してしまう?
今後の展望
- ブルベアの特徴である短期トレードに強い指標を選別する。
- 利確・損切り機能をつけて安定性をつける。
終わりに
今回は販売可能なレベルを目指しブルベアアルゴリズムの実装を目指しました。
今後開発の進捗を報告する予定ですのでよろしくお願いいたします。宣伝
もくもく会もやってるよ
日時:毎週水曜日18時〜
場所:神田 千代田共同ビル4階 SmartTrade社オフィス
内容:基本黙々と自習しながら猛者の方に質問して強くなっていく会
備考:お菓子と終わりにお酒が出るよ詳細はこちらだよ
Pythonアルゴリズム勉強会HP:https://python-algo.connpass.com/
(conpassって言うイベントサイトに飛びます)免責注意事項
このコード・知識を使った実際の取引で生じた損益に関しては一切の責任を負いかねますので御了承下さい。
materials
bull-bear:Designed by Rawpixel.com
- 投稿日:2019-02-15T16:45:35+09:00
【Discord】発言したユーザのユーザIDを取得する方法【Python】
特定のユーザのときだけ別の処理をしたいというときに。
@client.event async def on_message(message): print (message.author.id)おそらく上のような形でmessageオブジェクトを受け取っていると思うので、
message.author.idでそのメッセージは発言したユーザのIDを取得することができます。
特定のユーザに意地悪したいときとかに使えますね。
最後に
message.authorではユーザ名が取得できるのですが、これだとその人が名前変えたときとかに動かなくなるという問題があって、同じ悩みを抱えた人もいるんじゃないかと思って書いてみました。
ちなみにdiscordアプリからは普通にそのユーザを右クリックすることでIDを拾えます。(画像の一番下)
もしかしたら権限とかで表示されない可能性もあります。(デベロッパモードじゃないと見れないとか)
- 投稿日:2019-02-15T16:17:03+09:00
対数の底変換(算数)
対数の底変換.証明も概念も非常に簡単だが,なぜだかいつも底変換の方法を忘れてしまうので,備忘として.
python では $\ln x $ をよく使うので,自然対数を用いて,その他の底を取るときの対数を記す.
例えば,底が $a(>0)$ とする.
$\log _ab$ を $f(x) = \ln x$ を用いて表す.$b = a^{\log _ab} = (e^{\ln a})^{\log _ab} = e^{\ln b}$
ということで,第3,4項に対して自然対数を取って,
$\ln a \times \log _ab = \ln b$
変形して,
$\log _ab = \frac{\ln b}{\ln a}$まあ,自明ですね.
import numpy as np x = np.array([...]) # convert the base of log into 0.1 np.log(x) / np.log(0.1)
- 投稿日:2019-02-15T15:53:21+09:00
きっかけは「指ぱっちん」
きっかけは「指ぱっちん」
指ぱっちんでITらしいことをしてみようということで、
指ぱっちん をきっかけに ブラウザ を制御して Youtube動画 を開いてみようという話になりました。指ぱっちんをしてブラウザを制御する方法には、Python 。
Youtube動画のブラウザ上の制御には、React を使ってみることにしました。
Python について
音声認識が簡単にできる言語はあるか、ライブラリはあるかをチームで話し合った結果
Pythonで使用できるPyAudioというライブラリを使うことになりました。環境構築
PyAudioを利用するためPythonの実行環境が必要です。
そこで、PCにLinuxOS(ubuntu)を入れてLinux上で環境構築することにしました。
ubuntuのバージョンは16.04
pythonのバージョンは3.5です。
pythonはubuntuにプリインストールされているものです。以下のコマンドでPyAudioがインストールされます。
$sudo apt install python-pyaudioまた、以下のプログラムでdataに音データが格納されます。
録音サンプル.py#インポート import pyaudio #puaudioオブジェクトの生成 p = pyaudio.PyAudio() #一定時間録音して結果をstreamに格納 #引数は他ウェブサイトを参照 #ストリームの準備 stream = p.open(format=pyaudio.paInt16, channels=1, rate=44100, input=True, frames_per_buffer=1024) #録音 data = stream.read(CHUNK) #録音結果はバイトコードなので変換をかけて-1~1の数値の配列に #numpyが入ってなければインストールして import numpy as np data=np.frombuffer(data, dtype="int16")/32768
React について
Reactとは、インタラクティブなユーザーインタフェースを作成できるJavaScript library
環境構築
1.WindowsマシンにNode.js の最新バージョンインストール。
2.Reactをインストール>npm install react --save3.以下のコマンドでプロジェクト作成
>npx create-react-app my-app4.ReactPlayerをインストール
>npm install react-player --save
実装について(React編)
React側は、表示されるページを生成します。
1.インストールされた領域のsrcフォルダ配下でスクリプトを書く
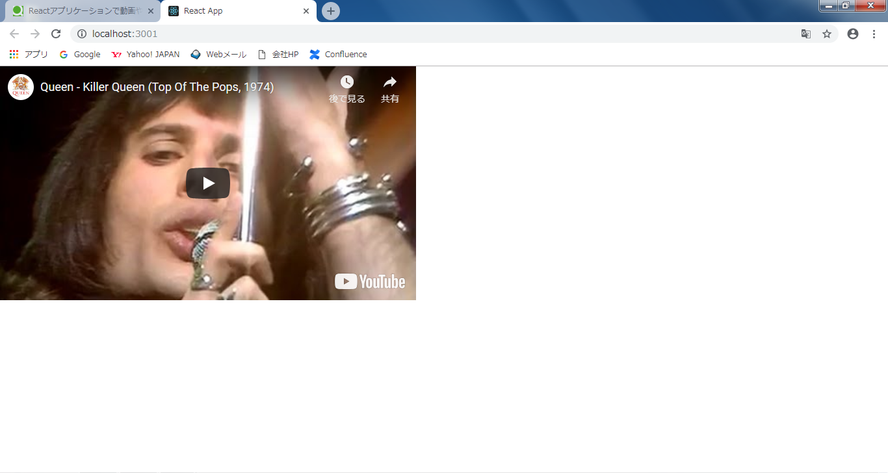
App.jsimport React, { Component } from "react"; import "./App.css"; import ReactPlayer from "react-player" class App extends Component { render() { // 動画のIDはランダムで出るようにしてみる var list = [ "HgzGwKwLmgM", "2ZBtPf7FOoM", "vNhhAEupU4g", "fJ9rUzIMcZQ", "GugsCdLHm-Q", "-tJYN-eG1zk", "04854XqcfCY", "rY0WxgSXdEE", "kijpcUv-b8M", "a01QQZyl-_I", "rdvabdyZ7vU" ]; var random = Math.floor(Math.random() * 10); console.log(list[random]); // 動画を表示する return <ReactPlayer url={"https://youtu.be/" + list[random]} playing /> } } export default App;2.スクリプト実行
>npm run start3.実行結果
D:\temp\指パッチン >npm run start > hello-world@0.1.0 start D:\temp\指パッチン > react-scripts start Compiled successfully! You can now view hello-world in the browser. Local: http://localhost:3000/ On Your Network: http://172.20.7.51:3000/ Note that the development build is not optimized. To create a production build, use npm run build.やったぜ
youtubeを画面に埋め込んだWEBページを起動させることができました。
ブラウザを開き、localhost:3000にアクセスしています。
また、youtubeのビデオID部分はjsにてランダムで変えることができるようになっています。
実装について(Python編)
Python側では、音を反応してブラウザを立ち上げるよう実装します。
実装にあたり使用したライブラリは以下です。
- PyAudio マイクで周囲の音を拾い、ストリームデータを作成。
- NumPy PyAudioで作成したストリームデータを数値データに変換。
- Selenium ブラウザを起動し、htmlファイルを起動。
- geckodriver FireFoxをseleniumで操作する。
下記のソースコードを作成しました。app.pyimport pyaudio import numpy as np from selenium import webdriver from selenium.webdriver.firefox.firefox_binary import FirefoxBinary CHUNK = 1024 FORMAT = pyaudio.paInt16 CHANNELS = 1 RATE = 44100 RECORD_SECONDS = 5 threshold = 0.8 path = "{ここに表示したいページのURL}" binary = FirefoxBinary('/usr/bin/firefox') binary.add_command_line_options('-headless') driver = "" isOpen = 0 def open_web(path): global driver global isOpen if isOpen == 0: driver = webdriver.Firefox(firefox_binary=binary) driver.get(path) isOpen = 1 else: driver.quit() isOpen = 0 p = pyaudio.PyAudio() stream = p.open(format=FORMAT, channels=CHANNELS, rate=RATE, input=True, frames_per_buffer=CHUNK) print("* recording") while True: data = stream.read(CHUNK) data=np.frombuffer(data, dtype="int16")/32768 # 入力された音の大きさがthresholdで指定したしきい値を超えた場合、ブラウザを開くようにする。 if data.max() > threshold: open_web(path)しきい値を低くしすぎると常に反応してしまうため、
ある程度大きい音に反応するように調整する必要があります。しくみ
PCのマイクである程度大きな音を認識すれば、
selenium経由でfirefoxが立ち上がる仕組みです。
また、フラグ管理しているため、指ぱっちんをするたびに
ブラウザを立ち上げ/終了を繰り返すことができます。React側で作成したページを呼び出せば、
指ぱっちんだけでyoutube起動が実現できます。
やったね感想
やってみたいアイデアから、どのように実現するかを考えての実装だったため
動くものになるか不安がありました。
しかし、なんとか実行環境を整えて実現できたという点は、良かったとおもいます。Python実行環境について、最初はWindowsPCで環境構築をしていましたが、VisualStudioのインストールが必要であるなど
環境構築が困難だったため、PCにLinuxOS(ubuntu)を入れて実現することにしました。実現できていない点として、現在のソースではマイクで拾った音の大きさで、
によって周囲で指パッチンされたかを判定しています。指パッチンだけで、自在にブラウザが立ち上がるのは、なかなか愉快。
参考情報のリンク
以下のサイトの情報やサンプルソースを参考にさせていただきました。
Pythonの参考サイト
PyAudioの基本メモ2 音声入出力 - たけし備忘録 http://takeshid.hatenadiary.jp/entry/2016/01/10/153503
Pythonで音を監視して一定以上の音量を録音する - Qiita https://qiita.com/mix_dvd/items/dc53926b83a9529876f7
PyAudio Document(英語) https://people.csail.mit.edu/hubert/pyaudio/docs/
Reactの参考サイト
出来る限り短く説明するReact.js入門 - Qiita https://qiita.com/rgbkids/items/8ec309d1bf5e203d2b19
Reactアプリケーションで動画や音楽ファイルを扱うために「react-player」を使用する - Qiita https://qiita.com/reiji1020/items/a65d84980b67f13449e1
React本体ダウンロード https://react-cn.github.io/react/downloads.html
- 投稿日:2019-02-15T15:42:35+09:00
Airflow を単体の docker container で立ち上げる
目的
- Airflow の最小構成を構築することにより airflow.cfg などの設定方法の理解を深める
- puckel/docker-airflow を参考にする
結論
- puckel/docker-airflow に以下の patch を当てる
diff --git a/script/entrypoint.sh b/script/entrypoint.sh index fb3f9ad..62d4198 100755 --- a/script/entrypoint.sh +++ b/script/entrypoint.sh @@ -70,8 +70,8 @@ fi case "$1" in webserver) airflow initdb - if [ "$AIRFLOW__CORE__EXECUTOR" = "LocalExecutor" ]; then - # With the "Local" executor it should all run in one container. + if [ "$AIRFLOW__CORE__EXECUTOR" != "CeleryExecutor" ]; then + # With the "Sequential" or "Local" executor it should all run in one container. airflow scheduler & fi exec airflow webserver※ PR 送りましたが author はもうメンテしてないようで merge される可能性は低いです。。
あと、数時間前に別の人が同じような PR してたので確認不足でした。。
https://github.com/puckel/docker-airflow/pull/316以下のコマンドで build して起動
docker build --rm -t puckel/docker-airflow . # -e LOAD_EX=y で example_dags を有効にする docker run -d -p 8080:8080 -e LOAD_EX=y puckel/docker-airflow webserverairflow.cfg について
airflow/config_templates にある default_airflow.cfg などを参考にするとよい
また puckel/docker-airflow や、Google Cloud Composer などの設定と見比べるとより理解が深まると思われるSequentialExecutor と LocalExecutor
puckel/docker-airflow でも docker container 単体で動作させる際の Executor としては SequentialExecutor が選択されています
By default, docker-airflow runs Airflow with SequentialExecutor :
docker run -d -p 8080:8080 puckel/docker-airflow webserverしかし前述の通り patch を当てないとこれは動作しません
今まではここで疑問を持たずに docker-compose-LocalExecutor.yml を利用してきました
おそらく SequentialEecutor にも airflow scheduler は必要なのだと思われますairflow/executors/local_executor.py には以下のようなコメントがあります
LocalExecutor runs tasks by spawning processes in a controlled fashion in different
modes. Given that BaseExecutor has the option to receive aparallelismparameter to
limit the number of process spawned, when this parameter is0the number of processes
that LocalExecutor can spawn is unlimited.
The following strategies are implemented:
1. Unlimited Parallelism (self.parallelism == 0): In this strategy, LocalExecutor will
spawn a process every timeexecute_asyncis called, that is, every task submitted to the
LocalExecutor will be executed in its own process. Once the task is executed and the
result stored in theresult_queue, the process terminates. There is no need for a
task_queuein this approach, since as soon as a task is received a new process will be
allocated to the task. Processes used in this strategy are of class LocalWorker.
2. Limited Parallelism (self.parallelism > 0): In this strategy, the LocalExecutor spawns
the number of processes equal to the value ofself.parallelismatstarttime,
using atask_queueto coordinate the ingestion of tasks and the work distribution among
the workers, which will take a task as soon as they are ready. During the lifecycle of
the LocalExecutor, the worker processes are running waiting for tasks, once the
LocalExecutor receives the call to shutdown the executor a poison token is sent to the
workers to terminate them. Processes used in this strategy are of class QueuedLocalWorker.
Arguably,SequentialExecutorcould be thought as a LocalExecutor with limited
parallelism of just 1 worker, i.e.self.parallelism = 1.
This option could lead to the unification of the executor implementations, running
locally, into just oneLocalExecutorwith multiple modes.SequentialExecutor は parallelism を 1 に限定した LocalExecutor と考えることもできます
docker-compose-LocalExecutor.yml も postgresql と webserver しか service はありません
ちなみに SequentialExecutor 以外では sqlite が利用できないことから postgresql が利用されていますhttps://github.com/apache/airflow/blob/1.10.2/airflow/configuration.py#L163-L169
SequentialExecutor 側にもこんなコメントがあります
This executor will only run one task instance at a time, can be used
for debugging. It is also the only executor that can be used with sqlite
since sqlite doesn't support multiple connections.
Since we want airflow to work out of the box, it defaults to this
SequentialExecutor alongside sqlite as you first install it.デバッグ用、初期インストール時のデフォルト
https://github.com/apache/airflow/blob/1.10.2/airflow/executors/sequential_executor.py#L29-L34
- 投稿日:2019-02-15T15:39:08+09:00
Airflow を単体の docker container で立ち上げる
目的
- Airflow の最小構成を構築することにより airflow.cfg などの設定方法の理解を深める
- puckel/docker-airflow を参考にする
結論
- puckel/docker-airflow に以下の patch を当てる
diff --git a/script/entrypoint.sh b/script/entrypoint.sh index fb3f9ad..62d4198 100755 --- a/script/entrypoint.sh +++ b/script/entrypoint.sh @@ -70,8 +70,8 @@ fi case "$1" in webserver) airflow initdb - if [ "$AIRFLOW__CORE__EXECUTOR" = "LocalExecutor" ]; then - # With the "Local" executor it should all run in one container. + if [ "$AIRFLOW__CORE__EXECUTOR" != "CeleryExecutor" ]; then + # With the "Sequential" or "Local" executor it should all run in one container. airflow scheduler & fi exec airflow webserver※ PR 送りましたが author はもうメンテしてないようで merge される可能性は低いです。。
あと、数時間前に別の人が同じような PR してたので確認不足でした。。
https://github.com/puckel/docker-airflow/pull/316以下のコマンドで build して起動
docker build --rm -t puckel/docker-airflow . # -e LOAD_EX=y で example_dags を有効にする docker run -d -p 8080:8080 -e LOAD_EX=y puckel/docker-airflow webserverairflow.cfg について
airflow/config_templates にある default_airflow.cfg などを参考にするとよい
また puckel/docker-airflow や、Google Cloud Composer などの設定と見比べるとより理解が深まると思われるSequentialExecutor と LocalExecutor
puckel/docker-airflow でも docker container 単体で動作させる際の Executor としては SequentialExecutor が選択されています
By default, docker-airflow runs Airflow with SequentialExecutor :
docker run -d -p 8080:8080 puckel/docker-airflow webserverしかし前述の通り patch を当てないとこれは動作しません
今まではここで疑問を持たずに docker-compose-LocalExecutor.yml を利用してきました
おそらく SequentialEecutor にも airflow scheduler は必要なのだと思われますairflow/executors/local_executor.py には以下のようなコメントがあります
LocalExecutor runs tasks by spawning processes in a controlled fashion in different
modes. Given that BaseExecutor has the option to receive aparallelismparameter to
limit the number of process spawned, when this parameter is0the number of processes
that LocalExecutor can spawn is unlimited.
The following strategies are implemented:
1. Unlimited Parallelism (self.parallelism == 0): In this strategy, LocalExecutor will
spawn a process every timeexecute_asyncis called, that is, every task submitted to the
LocalExecutor will be executed in its own process. Once the task is executed and the
result stored in theresult_queue, the process terminates. There is no need for a
task_queuein this approach, since as soon as a task is received a new process will be
allocated to the task. Processes used in this strategy are of class LocalWorker.
2. Limited Parallelism (self.parallelism > 0): In this strategy, the LocalExecutor spawns
the number of processes equal to the value ofself.parallelismatstarttime,
using atask_queueto coordinate the ingestion of tasks and the work distribution among
the workers, which will take a task as soon as they are ready. During the lifecycle of
the LocalExecutor, the worker processes are running waiting for tasks, once the
LocalExecutor receives the call to shutdown the executor a poison token is sent to the
workers to terminate them. Processes used in this strategy are of class QueuedLocalWorker.
Arguably,SequentialExecutorcould be thought as a LocalExecutor with limited
parallelism of just 1 worker, i.e.self.parallelism = 1.
This option could lead to the unification of the executor implementations, running
locally, into just oneLocalExecutorwith multiple modes.SequentialExecutor は parallelism を 1 に限定した LocalExecutor と考えることもできます
docker-compose-LocalExecutor.yml も postgresql と webserver しか service はありません
ちなみに SequentialExecutor 以外では sqlite が利用できないことから postgresql が利用されていますhttps://github.com/apache/airflow/blob/1.10.2/airflow/configuration.py#L163-L169
SequentialExecutor 側にもこんなコメントがあります
This executor will only run one task instance at a time, can be used
for debugging. It is also the only executor that can be used with sqlite
since sqlite doesn't support multiple connections.
Since we want airflow to work out of the box, it defaults to this
SequentialExecutor alongside sqlite as you first install it.デバッグ用、初期インストール時のデフォルト
https://github.com/apache/airflow/blob/1.10.2/airflow/executors/sequential_executor.py#L29-L34
- 投稿日:2019-02-15T14:59:34+09:00
不均衡データに対する損失関数の工夫
はじめに
研究の用途においては、データセットによる精度への影響を避けるため、各クラスのデータ数が同じくらいの均衡なデータセットがよく利用されています。しかし、いざ実サービスで学習用のデータを集めようとしても、全てのクラスで同じ数のデータを集めるのは難しい場合があります。そのような不均衡なデータセットに対して、2019/01/16にarxivで発表があった Class-Balanced Loss や Focal Lossなど、損失関数の工夫だけでどこまで精度を上げられるのか検証してみました。
データ不均衡による精度の劣化
CIFAR-10データセットを使って学習および検証を行いました。学習データはCIFAR-10の訓練用画像 50,000枚(各class 5,000枚)からautomobileとdeerとfrogのデータを250枚に減らして、意図的に不均衡にしたものを使用しています。検証にはCIFAR-10の検証用画像 10,000枚(各class 1,000枚)を使います。学習時のデータ数に基づいて、automobileとdeerとfrogの minorityグループ、それ以外の majorityグループ、10,000枚全てを使ったallグループの3つに分け、それぞれのグループ毎に検証して、正解率(Accuracy)を計測しました。学習データと検証データの内訳は下記の表のとおりになります。
class 学習データ 検証データ(minority) 検証データ(majority) 検証データ(all) 0 airplane 5,000 0 1,000 1,000 1 automobile 250 1,000 0 1,000 2 bird 5,000 0 1,000 1,000 3 cat 5,000 0 1,000 1,000 4 deer 250 1,000 0 1,000 5 dog 5,000 0 1,000 1,000 6 frog 250 1,000 0 1,000 7 horse 5,000 0 1,000 1,000 8 ship 5,000 0 1,000 1,000 9 truck 5,000 0 1,000 1,000 ネットワークの構造はResNet18で、全ての検証は下記の要件に従って学習を行います。
Epoch BatchSize Optimizer LearningRate 25 128 SGD Momentum
Momentum=0.9
WeightDecay=0.00050.1(1〜15 epoch)
0.01(16〜20 epoch)
0.001(21〜25 epoch)ちなみに、不均衡ではない普通のCIFAR-10に対し、一般的な損失関数 SoftmaxCrossEntropy で学習した結果は次のようになりました。全てのグループでAccuracyが90%を超えています。
MajorityのAccuracy MinorityのAccuracy AllのAccuracy 90.23 % 94.4 % 91.4 % 次は、これを不均衡データにした場合の結果になります。
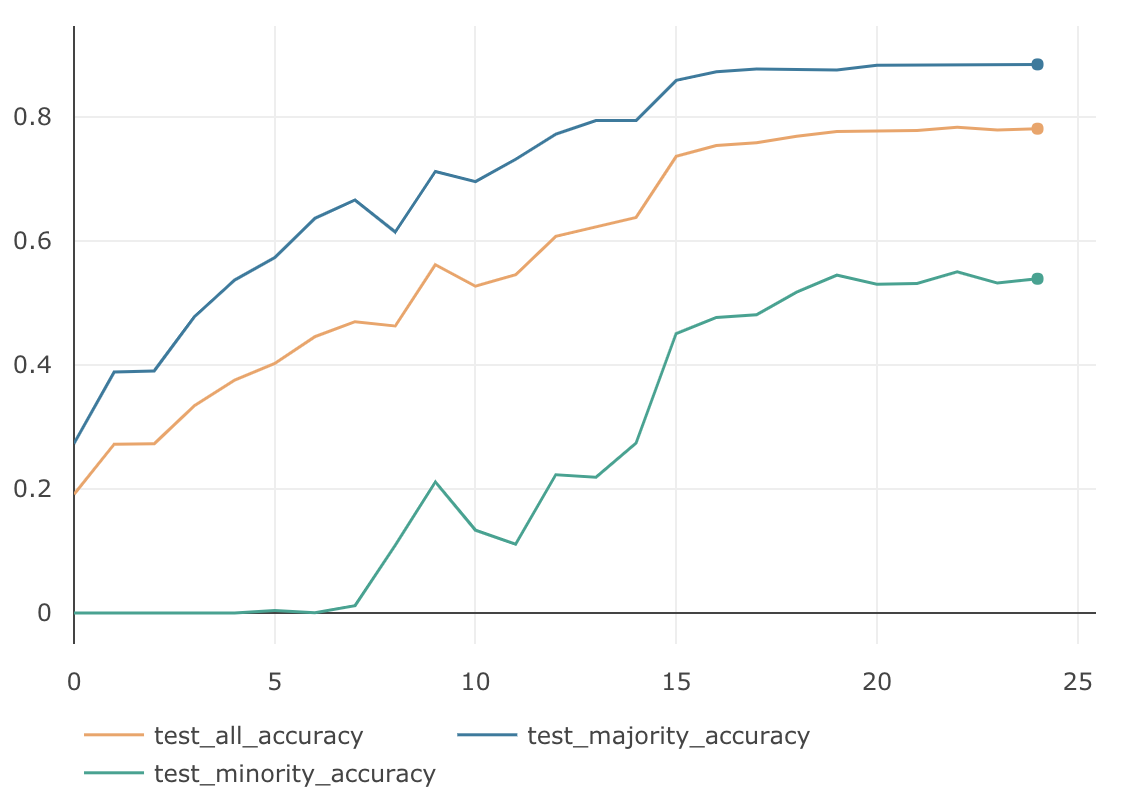
MajorityのAccuracy MinorityのAccuracy AllのAccuracy 87.93 % 50.4 % 76.5 % 均衡なデータの場合に比べて、Minorityグループの精度が極端に悪く、それにひきずられる形でAllグループの精度も76.5%と悪くなりました。
データ数の逆数でバランシング
損失関数の工夫として、クラスのデータ数の逆数を重みとして掛けて、Lossへの寄与率をクラスのデータ数に反比例するように調節する手法がよく使われています。クラス数が$C$で、各クラスのラベルが $y\in \{1, 2,...,C\}$であるデータセットについて考えてみます。モデルが出力するSoftmaxの値を$ \boldsymbol{p} =[p_1, p_2,..., p_C]^T$, ただし $p_i \in [0,1] \hspace{3pt} \forall \hspace{3pt} i$ 。学習時のミニバッチ数を$B$ 。ミニバッチ内の正解ラベルを$ \boldsymbol{m} =[m_1, m_2,..., m_B]^T$,ただし $m_i \in \{1, 2,...,C\} $ 。 その場合、通常のSoftmaxCrossEntropyLossは下記のようになります。
\textbf{CE}(\hspace{2pt}\boldsymbol{p}, \boldsymbol{m}) = -\sum_{i=1}^{B}log(p_{m_i}) \tag{1}クラス$y$の学習データの数を$n_y$とすると、クラス数の逆数でバランシングした損失関数InverseClassFrequencyLossは下記のように書けます。
\textbf{ICF}(\hspace{2pt}\boldsymbol{p}, \boldsymbol{m}) = -\sum_{i=1}^{B} \frac{1}{n_{m_i}} log(p_{m_i}) \tag{2}InverseClassFrequencyLossの検証結果は次のようになりました。(実際の検証では、ミニバッチ単位のLossの出力の大きさを通常のSoftmaxCrossEntropyLossと揃えるために、加重平均をとっています。加重平均をとっても、各クラスの全体に対する寄与率は変わりません。)
MajorityのAccuracy MinorityのAccuracy AllのAccuracy 74.1 % 74.67 % 73.58 % 通常のSoftmaxCrossEntropyLossに比べてMinorityグループの精度がだいぶ高くなりました。ただMajorityグループの精度は落ちてしまったため、Allグループの精度は悪くなっています。
Focal Loss
OneStageのObject Detectionの学習において、背景(EasyNegative)がほとんどであり、クラスが不均衡状態になっているという仮説のもと、それを自動的にコスト調節してくれる損失関数として、Facebook AI Researchが提案した手法1です。ICCV2017で発表されStudent Best Paperに選ばれています。
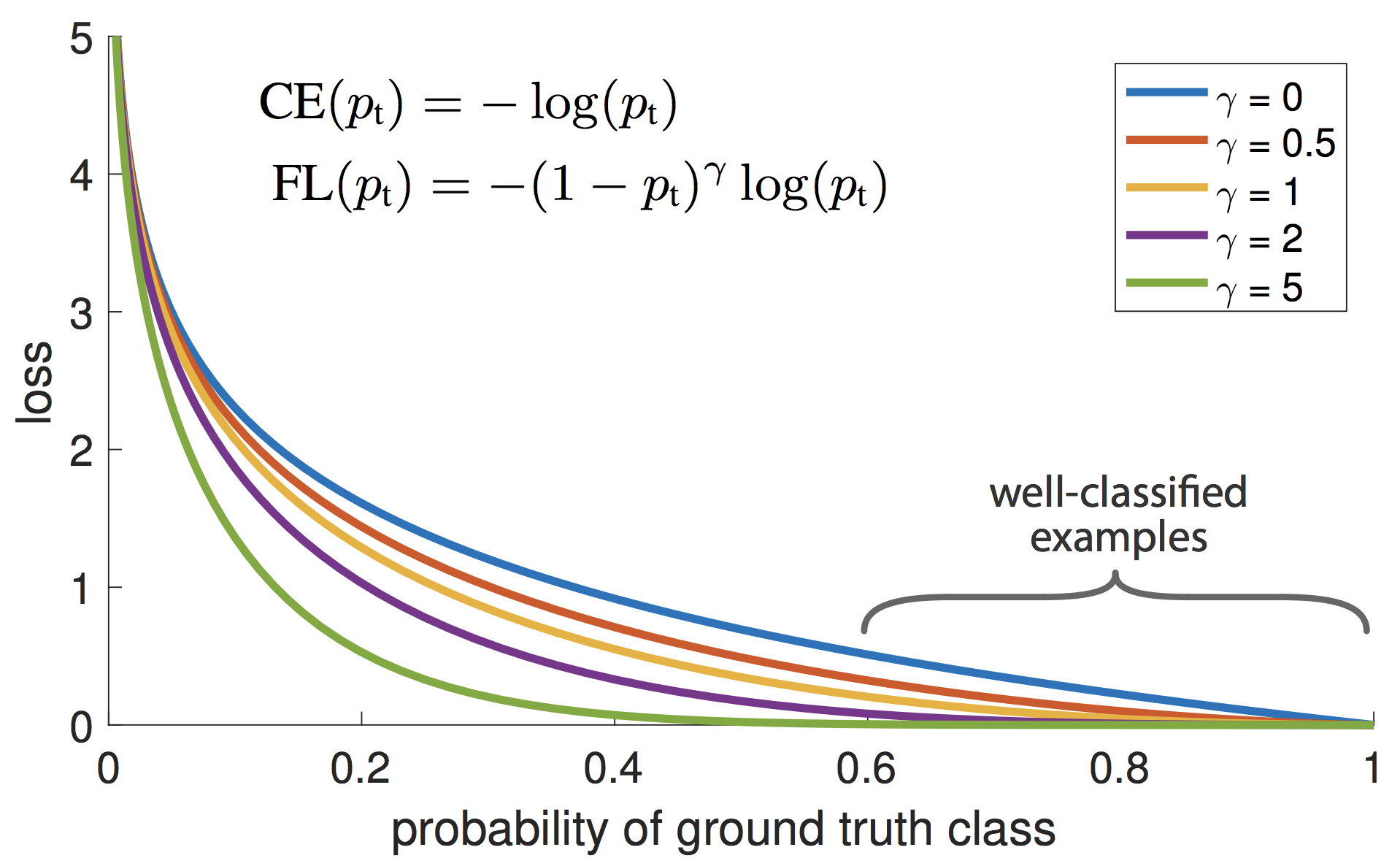
上の図が示すように、$p_t$が小さく0に近い場合(大きく間違っている場合)は、係数は1に近いためあまり影響を受けません。逆に$p_t$が大きく1に近い場合(ほとんど間違っていない場合)は、係数は0に近いためLossとしてほとんど計上されなくなります。このように損失関数の係数部分が自動的にEasyNegativeExampleをDownWeightし、結果としてHardNegativeに比重が置かれるように機能します。
このFocalLossを多クラス分類のSoftmaxCrossEntropyに適応すると下記のように書けます。
\textbf{FL}(\hspace{2pt}\boldsymbol{p}, \boldsymbol{m}) = -\sum_{i=1}^{B} (1-p_{m_i})^\gamma log(p_{m_i}) \tag{3}$\gamma\in \{1.0, 1.5, 2.0\}$ の3パターンで検証してみました。
$\gamma$ MajorityのAccuracy MinorityのAccuracy AllのAccuracy 1.0 88.47 % 55.03 % 78.33 % 1.5 87.91 % 53.56 % 77.61 % 2.0 86.37 % 49.53 % 75.32 % InverseClassFrequencyLossに比べると、Minorityグループの精度は全体的に落ちていますが、Majorityグループの精度は全て高くなっています。$\gamma=1.0$のAllグループの精度は、これまでの不均衡データ検証の中では最も良い結果となりました。下図は $\gamma=1.0$のグラフになります。
本質的なクラスのデータ数でバランシング
先述した InverseClassFrequencyLossの検証結果からもわかる通り、クラスのデータ数の逆数を重みとして掛ける事で、不均衡データに対するバランシングの効果が期待できます。この考え方をさらに深掘りした Class-Balanced Loss Based on Effective Number of Samples2 という興味深い論文がarxivに上がっていたので紹介します。この論文では、InverseClassFrequencyLossで利用しているクラスのデータ数というのは、実は本質的なデータ数ではないという考え方を元に理論が構築されています。どういうことかと言うと、例えば、class0のデータが800枚、class1のデータが500枚からなるデータセットがあるとします。それぞれのclassをData Augmentationして、class0もclass1も1,000枚に増やした場合、表面上のデータ数はどちらも1,000枚と同じになりますが、本質的なデータ数という意味ではこの2つは違います。このように実データ数と本質的なデータ数には差があるという事です。
もう一つ。ある画像から特徴ベクトルを抽出し、その特徴ベクトルを分類器にかける事で、画像のクラス分類するといったケースを考えてみます。この場合、分類に利用している特徴ベクトルは、ベクトルの次元数が固定です。したがって、そのベクトルの表現パターン数以上のデータ表現はできません。つまり、どんなに多くの画像を集めたとしても、この分類器にとってのデータ数は、ベクトルの表現量を超える事はないという事です。これもまた、実データ数と本質的なデータ数には差があるという例となります。
この差は、タスクの種類やデータセットの特性、およびその周辺情報によっても変わってくるため、拡大や回転したものを同じデータ扱いにするのか、同じオブジェクトが写っていれば同じデータ扱いにするのか、これらは一概には決められません。しかし、ここで重要なのは、どのようなデータセットにおいても、少なからず実データ数と本質的なデータ数には差があるという事です。
したがって、データセットのデータを、全てユニークなデータとしてカウントした値を不均衡データのバランシングに使うのではなく、本質的なデータ数に配慮した値を用いてデータバランシングを行うべき、というのが本論文の主張になります。理論
本質的なデータ数が具体的にどのような値になるのか説明します。本質的なデータ数の最大値を$N$とおきます。例えば、車の画像が無限にあったとして、全ての車の画像を本質的なデータ空間に写像した場合、$N$パターンとなります。実データ数を$n$、その本質的なデータ数を$E_n$とすると、下記のように書けます。
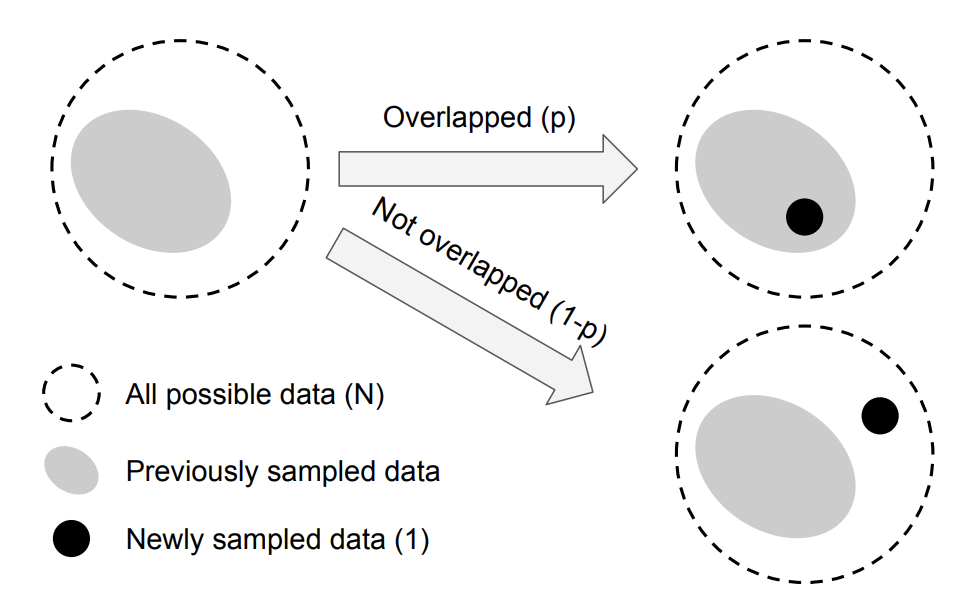
E_n = (1 - \beta^n)/(1 - \beta) \tag{4} \\ ただし、 \beta = (N - 1)/Nと、いきなり式が出てきましたが、数学的帰納法を使ってこれを証明します。
まず、$E_1$は重なりようがないので、$E_1 = 1$となります。次に、$E_{n-1}$で成立する場合に$E_n$でも成立するかを考える必要がありますが、その前に下の図を見てください。これは、$n$個目のデータをサンプリングした際の、本質的なデータ空間の変化の様子を示した概念図になります。破線の領域は本質的なデータ空間を表しています。したがって、この領域のデータ数は$N$です。灰色の領域は$n-1$個の実データが写像された本質的なデータ空間の領域になります。したがって、この領域のデータ数は$E_{n-1}$です。次に、$n$個目のデータを本質的なデータ空間に写像しようとした場合、$E_{n-1}/N$の確率で灰色の領域に入ります。
したがって、p = \frac{E_{n-1}}{N}とすると、$E_n$の期待値は下記のようになります。
E_n = pE_{n-1} + (1-p)(E_{n-1} + 1) = 1 + \frac{N - 1}{N}E_{n-1} \tag{5}ここで、式$(4)$が$E_{n-1}$では成立すると仮定すると、
E_{n-1} =(1 - \beta^{n-1})/(1 - \beta) \tag{6}と書け、式$(5)$の$E_{n-1}$に代入すると、
E_{n} =1 + \frac{N - 1}{N}E_{n-1} = 1 + \beta \frac{1 - \beta^{n-1}}{1 - \beta} = \frac{1 - \beta + \beta - \beta^{n}}{1 - \beta} = \frac{1 - \beta^{n}}{1 - \beta} \tag{7}となります。$E_n$の場合も式$(4)$を満たすことがわかったので、証明はこれで完了となります。
式$(4)$にあるように、$\beta = (N - 1)/N$とおいており、$N\geqq1$なので、$\beta$の取り得る値の範囲は$0 \leqq \beta < 1$です。したがって、$n \rightarrow \infty$ の場合 $\beta^{n} \rightarrow 0$ となるので、
\lim_{n \to \infty}E_n = \lim_{n \to \infty}\frac{1 - \beta^{n}}{1 - \beta} = \frac{1}{1 - \beta} = Nとなります。これは無限のデータを本質的なデータ空間に写像した場合、そのデータ数は$N$に収束する事を表しています。
次に、$\beta = 0$ $(N = 1)$の場合をみてみると、
E_{n} = (1 - 0^n) / (1 - 0) = 1となり、$\beta = 0$では、全てのデータは本質的には全て同じものである事がわかります。
また、$\beta \rightarrow 1$ $(N \rightarrow \infty)$の場合は、
f(\beta) = 1 - \beta^n, \quad g(\beta) = 1 - \betaとすると、
f'(\beta) = -n \beta^{n-1}, \quad g'(\beta) = -1ロピタルの定理より、
\lim_{\beta \to 1} E_n = \lim_{\beta \to 1} \frac{f(\beta)}{g(\beta)} = \lim_{\beta \to 1} \frac{f'(\beta)}{g'(\beta)} = \lim_{\beta \to 1} \frac{(-n \beta^{n-1})}{(-1)} = nとなります。したがって $\beta \rightarrow 1$では、全てのデータは本質的にもユニークであり、重複がない状態である事がわかります。
実際のデータセットの場合
クラス$y$の学習データの実データ数を$n_y$とすると、クラス$y$の本質的なデータ数 $E_{n_y}$は、
E_{n_y} = (1 - \beta_y^{n_y})/(1 - \beta_y) \\ ただし、 \beta_y = (N_y - 1)/N_yとなります。しかし、クラス$y$についての周辺情報がないため、$N_y$(クラスyを本質的に表現できるデータ数の最大値)を正確に求めるのは極めて難しい作業です。そこで、各クラスの$N_y$は、データセットの画素数や学習するネットワーク構造など、すべてのクラスに共通するもののみに依存すると仮定し、$N_y = N$, $\beta_y = \beta$として、全クラスで同じ値を使います。すると、$E_{n_y}$は下記のようになります。
E_{n_y} = (1 - \beta^{n_y})/(1 - \beta) \\ ただし、 \beta = (N - 1)/N
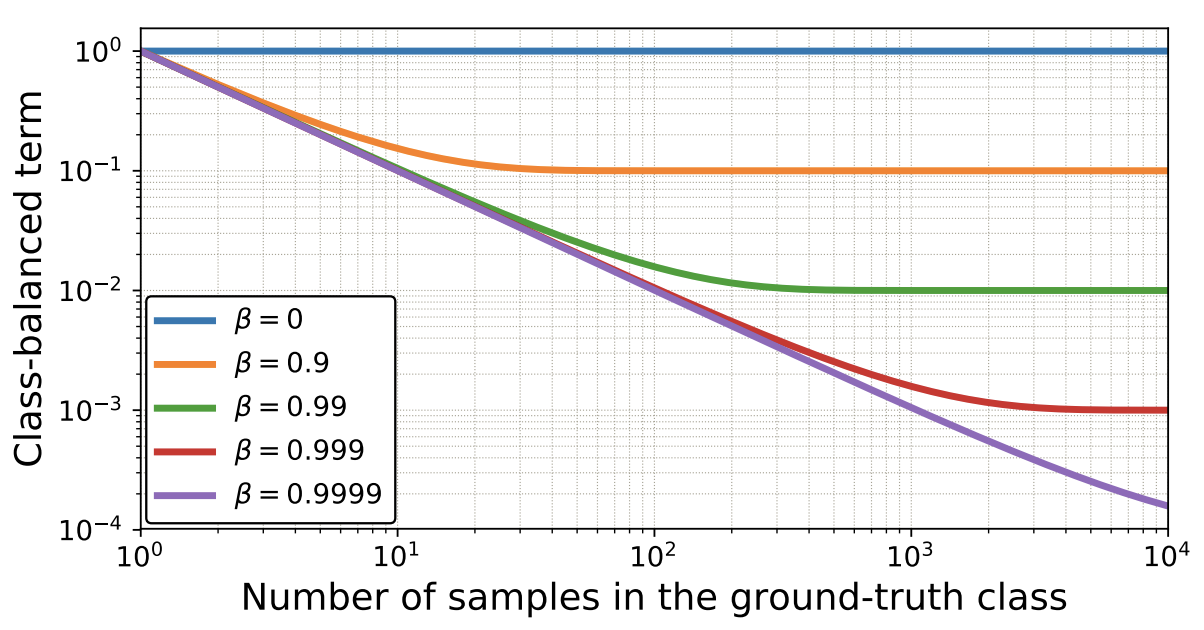
下図は $\beta$の値によって、$n_y$と$E_{n_y}$の関係がどのように変化するのかを可視化したグラフになります。横軸が$n_y$で縦軸が$E_{n_y}$です。
Class Balanced Loss
InverseClassFrequencyLossでは、クラスのデータ数の逆数を重みとしてバランシングしていましたが、このクラスのデータ数の部分を本質的なクラスのデータ数 $E_{n_y}$に置き換える事で、ClassBalancedLoss になります。
SoftmaxCrossEntropyLoss を ClassBalanced 化すると下記のようになります。
\textbf{CB}_{softmax}(\hspace{2pt}\boldsymbol{p}, \boldsymbol{m}) = -\sum_{i=1}^{B} \frac{1}{E_{n_{m_i}}} log(p_{m_i}) = -\sum_{i=1}^{B} \frac{1 - \beta}{1 - \beta^{n_{m_i}}} log(p_{m_i})FocalLoss を ClassBalanced 化すると下記のようになります。
\textbf{CB}_{focal}(\hspace{2pt}\boldsymbol{p}, \boldsymbol{m}) = -\frac{1}{E_{n_{m_i}}} \sum_{i=1}^{B} (1-p_{m_i})^\gamma log(p_{m_i}) = -\frac{1 - \beta}{1 - \beta^{n_{m_i}}} \sum_{i=1}^{B} (1-p_{m_i})^\gamma log(p_{m_i})$\beta$はハイパーパラメータで、値の範囲は$0 \leqq \beta < 1$になります。$\beta = 0$は重みを全く掛けていない状態に相当し、$\beta \rightarrow 1$はInverseClassFrequencyLossと同じ状態に相当します。
検証
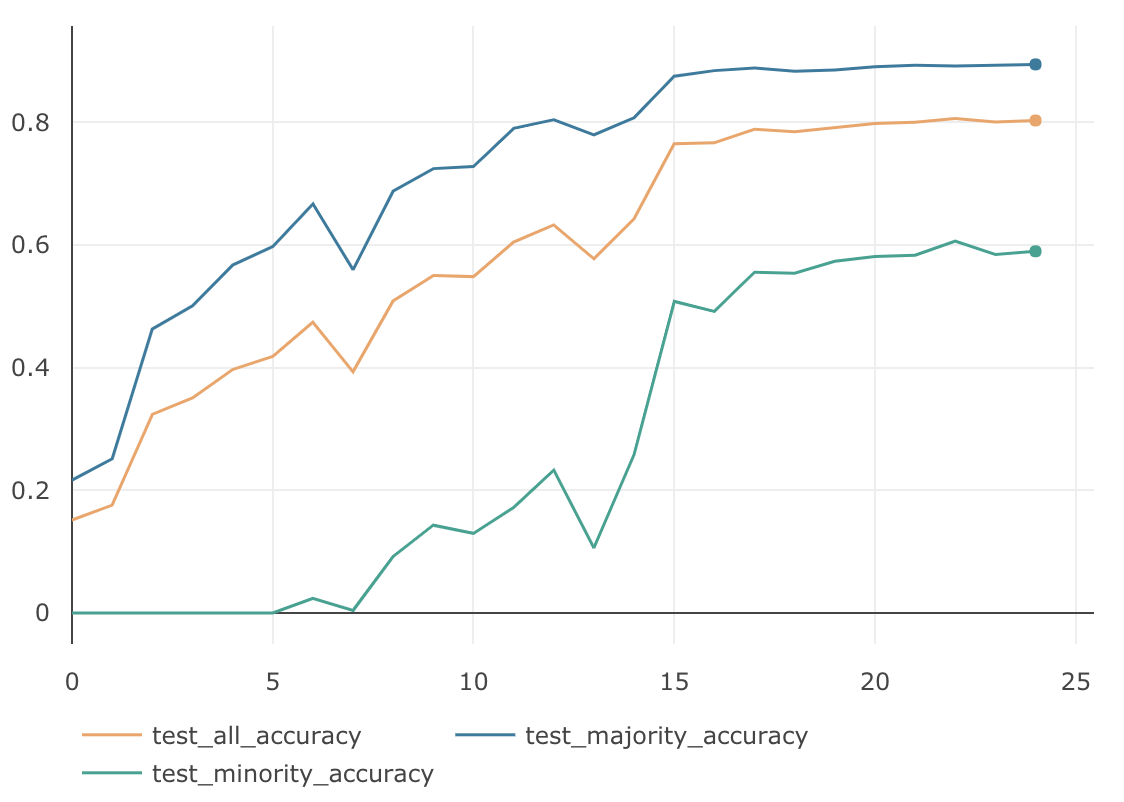
ClassBalancedSoftmaxは、$\beta\in \{0.9, 0.99, 0.999, 0.9999\}$ の4パターンで検証してみました。
$\beta$ MajorityのAccuracy MinorityのAccuracy AllのAccuracy 0.9 88.66 % 49.23 % 76.83 % 0.99 89.45 % 58.67 % 80.22 % 0.999 86.76 % 66.37 % 80.64 % 0.9999 80.94 % 75.23 % 79.23 % $\beta=0.999$の時に、AllのAccuracyは $80.64$% となり、今までのどの検証よりも良い結果となっています。下記がそのグラフです。
ClassBalancedFocalLossは、$\gamma=1.0$固定として、$\beta\in \{0.9, 0.99, 0.999, 0.9999\}$ の4パターンで検証してみました。
$\beta$ $\gamma$ MajorityのAccuracy MinorityのAccuracy AllのAccuracy 0.9 1.0 88.67 % 53.70 % 78.18 % 0.99 1.0 89.42 % 60.63 % 80.60 % 0.999 1.0 85.11 % 64.70 % 78.99 % 0.9999 1.0 72.40 % 62.67 % 69.48 % $\beta=0.99$の時に、AllのAccuracyは $80.60$% となり、ClassBalancedSoftmaxの最高値とほぼ同等の精度となりました。下記がグラフになります。
まとめ
ClassBalancedな損失関数を使えば、SoftmaxCrossEntropyやFocalLoss、どちらの場合も精度が向上する事が確認できました。また、理論部分に関しても証明付きで綺麗にまとまっており、とても読みやすい論文となっています。ただ、本質的なデータ空間という、独特な抽象概念を土台に理論が組み立てられているため、$\beta$ の値をあらかじめ正確に決めることは、原理的に不可能です。したがって、実際のデータに対してこの損失関数を適用する場合は、いくらか学習を試しながら、ハイパーパラメータ$\beta$の値を探査し、最適な値を決める必要があります。
- 投稿日:2019-02-15T14:59:34+09:00
不均衡データを損失関数で攻略してみる
はじめに
研究の用途においては、データセットによる精度への影響を避けるため、各クラスのデータ数が同じくらいの均衡なデータセットがよく利用されています。しかし、いざ実サービスで学習用のデータを集めようとしても、全てのクラスで同じ数のデータを集めるのは難しい場合があります。そのような不均衡なデータセットに対して、2019/01/16にarxivで発表があった Class-Balanced Loss や Focal Lossなど、損失関数の工夫だけでどこまで精度を上げられるのか検証してみました。
データ不均衡による精度の劣化
CIFAR-10データセットを使って学習および検証を行いました。学習データはCIFAR-10の訓練用画像 50,000枚(各class 5,000枚)からautomobileとdeerとfrogのデータを250枚に減らして、意図的に不均衡にしたものを使用しています。検証にはCIFAR-10の検証用画像 10,000枚(各class 1,000枚)を使います。学習時のデータ数に基づいて、automobileとdeerとfrogの minorityグループ、それ以外の majorityグループ、10,000枚全てを使ったallグループの3つに分け、それぞれのグループ毎に検証して、正解率(Accuracy)を計測しました。学習データと検証データの内訳は下記の表のとおりになります。
class 学習データ 検証データ(minority) 検証データ(majority) 検証データ(all) 0 airplane 5,000 0 1,000 1,000 1 automobile 250 1,000 0 1,000 2 bird 5,000 0 1,000 1,000 3 cat 5,000 0 1,000 1,000 4 deer 250 1,000 0 1,000 5 dog 5,000 0 1,000 1,000 6 frog 250 1,000 0 1,000 7 horse 5,000 0 1,000 1,000 8 ship 5,000 0 1,000 1,000 9 truck 5,000 0 1,000 1,000 ネットワークの構造はResNet18で、全ての検証は下記の要件に従って学習を行います。
Epoch BatchSize Optimizer LearningRate 25 128 SGD Momentum
Momentum=0.9
WeightDecay=0.00050.1(1〜15 epoch)
0.01(16〜20 epoch)
0.001(21〜25 epoch)ちなみに、不均衡ではない普通のCIFAR-10に対し、一般的な損失関数 SoftmaxCrossEntropy で学習した結果は次のようになりました。全てのグループでAccuracyが90%を超えています。
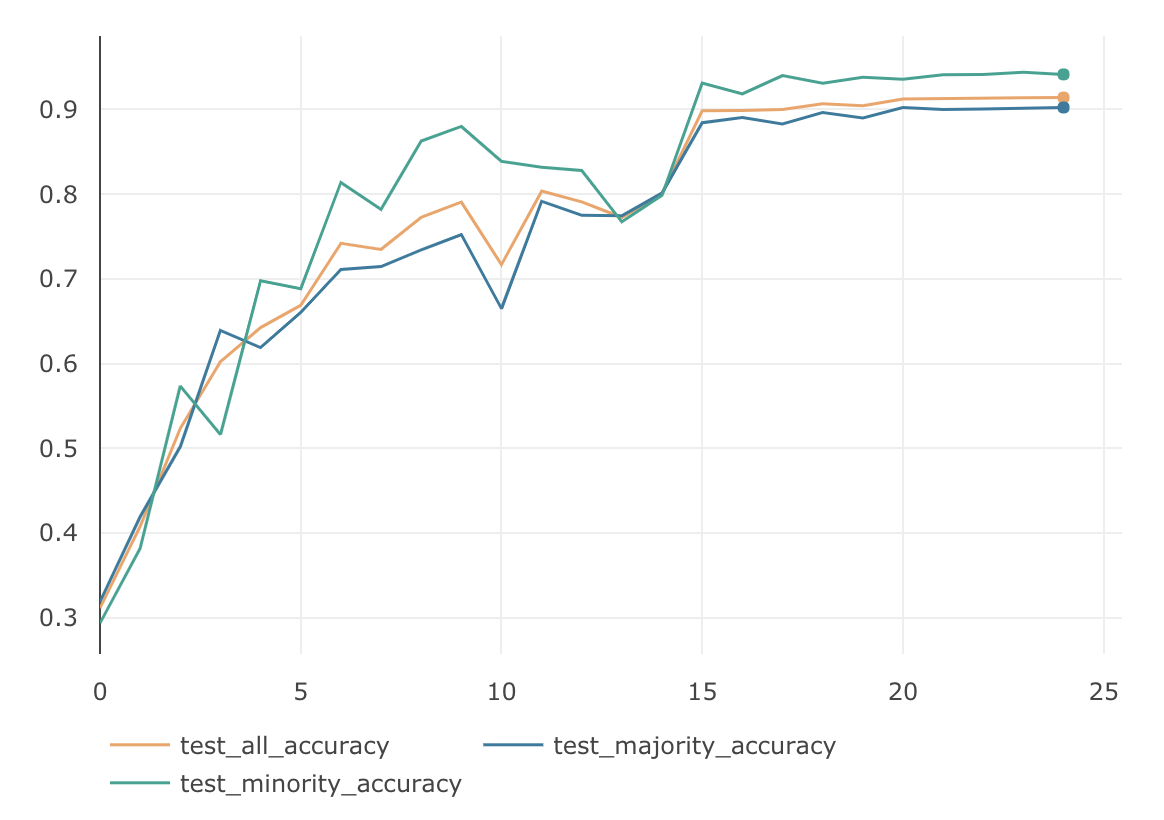
MajorityのAccuracy MinorityのAccuracy AllのAccuracy 90.23 % 94.4 % 91.4 % 次は、これを不均衡データにした場合の結果になります。
MajorityのAccuracy MinorityのAccuracy AllのAccuracy 87.93 % 50.4 % 76.5 % 均衡なデータの場合に比べて、Minorityグループの精度が極端に悪く、それにひきずられる形でAllグループの精度も76.5%と悪くなりました。
データ数の逆数でバランシング
損失関数の工夫として、クラスのデータ数の逆数を重みとして掛けて、Lossへの寄与率をクラスのデータ数に反比例するように調節する手法がよく使われています。クラス数が$C$で、各クラスのラベルが $y\in \{1, 2,...,C\}$であるデータセットについて考えてみます。モデルが出力するSoftmaxの値を$ \boldsymbol{p} =[p_1, p_2,..., p_C]^T$, ただし $p_i \in [0,1] \hspace{3pt} \forall \hspace{3pt} i$ 。学習時のミニバッチ数を$B$ 。ミニバッチ内の正解ラベルを$ \boldsymbol{m} =[m_1, m_2,..., m_B]^T$,ただし $m_i \in \{1, 2,...,C\} $ 。 その場合、通常のSoftmaxCrossEntropyLossは下記のようになります。
\textbf{CE}(\hspace{2pt}\boldsymbol{p}, \boldsymbol{m}) = -\sum_{i=1}^{B}log(p_{m_i}) \tag{1}クラス$y$の学習データの数を$n_y$とすると、クラス数の逆数でバランシングした損失関数InverseClassFrequencyLossは下記のように書けます。
\textbf{ICF}(\hspace{2pt}\boldsymbol{p}, \boldsymbol{m}) = -\sum_{i=1}^{B} \frac{1}{n_{m_i}} log(p_{m_i}) \tag{2}InverseClassFrequencyLossの検証結果は次のようになりました。(実際の検証では、ミニバッチ単位のLossの出力の大きさを通常のSoftmaxCrossEntropyLossと揃えるために、加重平均をとっています。加重平均をとっても、各クラスの全体に対する寄与率は変わりません。)
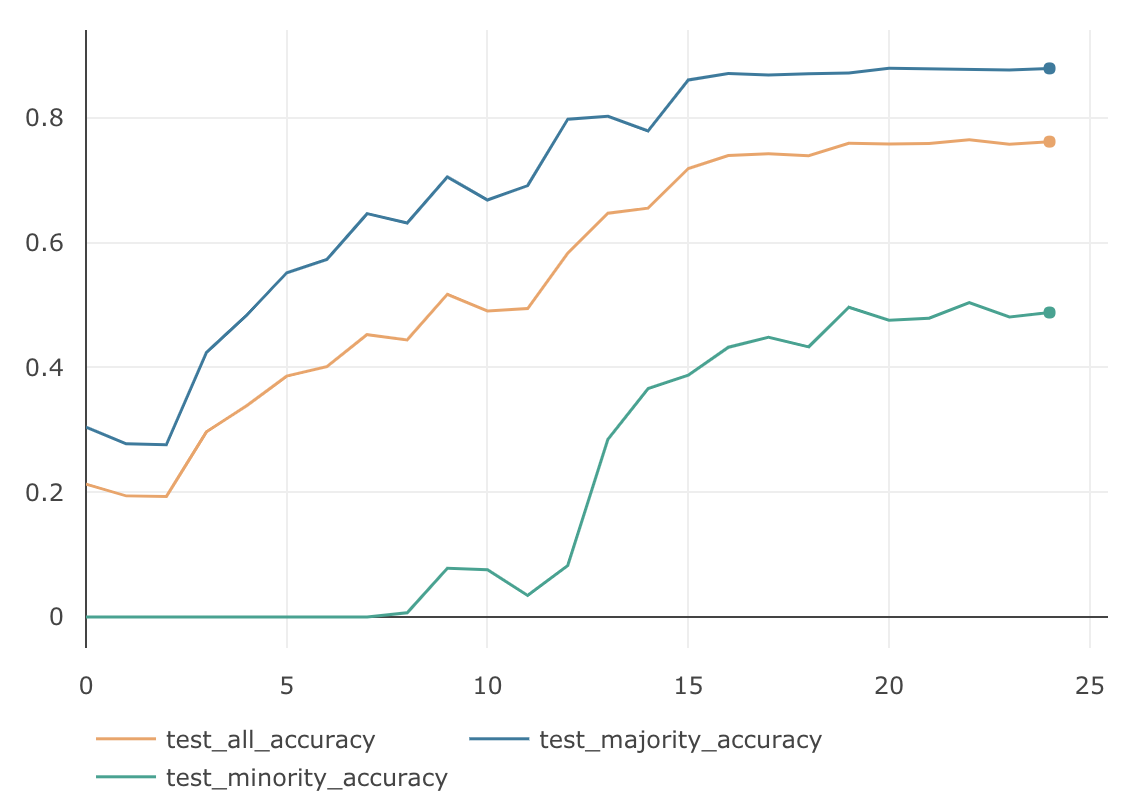
MajorityのAccuracy MinorityのAccuracy AllのAccuracy 74.1 % 74.67 % 73.58 % 通常のSoftmaxCrossEntropyLossに比べてMinorityグループの精度がだいぶ高くなりました。ただMajorityグループの精度は落ちてしまったため、Allグループの精度は悪くなっています。
Focal Loss
OneStageのObject Detectionの学習において、背景(EasyNegative)がほとんどであり、クラスが不均衡状態になっているという仮説のもと、それを自動的にコスト調節してくれる損失関数として、Facebook AI Researchが提案した手法1です。ICCV2017で発表されStudent Best Paperに選ばれています。
上の図が示すように、$p_t$が小さく0に近い場合(大きく間違っている場合)は、係数は1に近いためあまり影響を受けません。逆に$p_t$が大きく1に近い場合(ほとんど間違っていない場合)は、係数は0に近いためLossとしてほとんど計上されなくなります。このように損失関数の係数部分が自動的にEasyNegativeExampleをDownWeightし、結果としてHardNegativeに比重が置かれるように機能します。
このFocalLossを多クラス分類のSoftmaxCrossEntropyに適応すると下記のように書けます。
\textbf{FL}(\hspace{2pt}\boldsymbol{p}, \boldsymbol{m}) = -\sum_{i=1}^{B} (1-p_{m_i})^\gamma log(p_{m_i}) \tag{3}$\gamma\in \{1.0, 1.5, 2.0\}$ の3パターンで検証してみました。
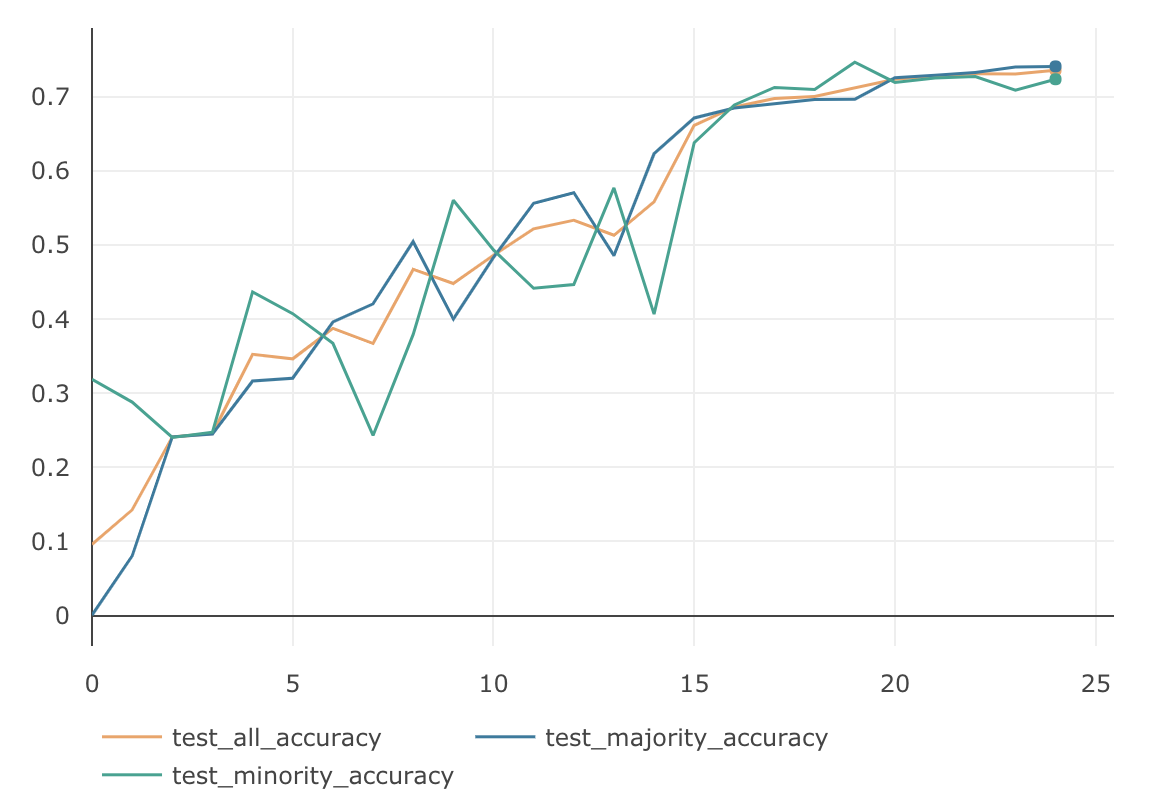
$\gamma$ MajorityのAccuracy MinorityのAccuracy AllのAccuracy 1.0 88.47 % 55.03 % 78.33 % 1.5 87.91 % 53.56 % 77.61 % 2.0 86.37 % 49.53 % 75.32 % InverseClassFrequencyLossに比べると、Minorityグループの精度は全体的に落ちていますが、Majorityグループの精度は全て高くなっています。$\gamma=1.0$のAllグループの精度は、これまでの不均衡データ検証の中では最も良い結果となりました。下図は $\gamma=1.0$のグラフになります。
本質的なクラスのデータ数でバランシング
先述した InverseClassFrequencyLossの検証結果からもわかる通り、クラスのデータ数の逆数を重みとして掛ける事で、不均衡データに対するバランシングの効果が期待できます。この考え方をさらに深掘りした Class-Balanced Loss Based on Effective Number of Samples2 という興味深い論文がarxivに上がっていたので紹介します。この論文では、InverseClassFrequencyLossで利用しているクラスのデータ数というのは、実は本質的なデータ数ではないという考え方を元に理論が構築されています。どういうことかと言うと、例えば、class0のデータが800枚、class1のデータが500枚からなるデータセットがあるとします。それぞれのclassをData Augmentationして、class0もclass1も1,000枚に増やした場合、表面上のデータ数はどちらも1,000枚と同じになりますが、本質的なデータ数という意味ではこの2つは違います。このように実データ数と本質的なデータ数には差があるという事です。
もう一つ。ある画像から特徴ベクトルを抽出し、その特徴ベクトルを分類器にかける事で、画像のクラス分類するといったケースを考えてみます。この場合、分類に利用している特徴ベクトルは、ベクトルの次元数が固定です。したがって、そのベクトルの表現パターン数以上のデータ表現はできません。つまり、どんなに多くの画像を集めたとしても、この分類器にとってのデータ数は、ベクトルの表現量を超える事はないという事です。これもまた、実データ数と本質的なデータ数には差があるという例となります。
この差は、タスクの種類やデータセットの特性、およびその周辺情報によっても変わってくるため、拡大や回転したものを同じデータ扱いにするのか、同じオブジェクトが写っていれば同じデータ扱いにするのか、これらは一概には決められません。しかし、ここで重要なのは、どのようなデータセットにおいても、少なからず実データ数と本質的なデータ数には差があるという事です。
したがって、データセットのデータを、全てユニークなデータとしてカウントした値を不均衡データのバランシングに使うのではなく、本質的なデータ数に配慮した値を用いてデータバランシングを行うべき、というのが本論文の主張になります。理論
本質的なデータ数が具体的にどのような値になるのか説明します。本質的なデータ数の最大値を$N$とおきます。例えば、車の画像が無限にあったとして、全ての車の画像を本質的なデータ空間に写像した場合、$N$パターンとなります。実データ数を$n$、その本質的なデータ数を$E_n$とすると、下記のように書けます。
E_n = (1 - \beta^n)/(1 - \beta) \tag{4} \\ ただし、 \beta = (N - 1)/Nと、いきなり式が出てきましたが、数学的帰納法を使ってこれを証明します。
まず、$E_1$は重なりようがないので、$E_1 = 1$となります。次に、$E_{n-1}$で成立する場合に$E_n$でも成立するかを考える必要がありますが、その前に下の図を見てください。これは、$n$個目のデータをサンプリングした際の、本質的なデータ空間の変化の様子を示した概念図になります。破線の領域は本質的なデータ空間を表しています。したがって、この領域のデータ数は$N$です。灰色の領域は$n-1$個の実データが写像された本質的なデータ空間の領域になります。したがって、この領域のデータ数は$E_{n-1}$です。次に、$n$個目のデータを本質的なデータ空間に写像しようとした場合、$E_{n-1}/N$の確率で灰色の領域に入ります。
したがって、p = \frac{E_{n-1}}{N}とすると、$E_n$の期待値は下記のようになります。
E_n = pE_{n-1} + (1-p)(E_{n-1} + 1) = 1 + \frac{N - 1}{N}E_{n-1} \tag{5}ここで、式$(4)$が$E_{n-1}$では成立すると仮定すると、
E_{n-1} =(1 - \beta^{n-1})/(1 - \beta) \tag{6}と書け、式$(5)$の$E_{n-1}$に代入すると、
E_{n} =1 + \frac{N - 1}{N}E_{n-1} = 1 + \beta \frac{1 - \beta^{n-1}}{1 - \beta} = \frac{1 - \beta + \beta - \beta^{n}}{1 - \beta} = \frac{1 - \beta^{n}}{1 - \beta} \tag{7}となります。$E_n$の場合も式$(4)$を満たすことがわかったので、証明はこれで完了となります。
式$(4)$にあるように、$\beta = (N - 1)/N$とおいており、$N\geqq1$なので、$\beta$の取り得る値の範囲は$0 \leqq \beta < 1$です。したがって、$n \rightarrow \infty$ の場合 $\beta^{n} \rightarrow 0$ となるので、
\lim_{n \to \infty}E_n = \lim_{n \to \infty}\frac{1 - \beta^{n}}{1 - \beta} = \frac{1}{1 - \beta} = Nとなります。これは無限のデータを本質的なデータ空間に写像した場合、そのデータ数は$N$に収束する事を表しています。
次に、$\beta = 0$ $(N = 1)$の場合をみてみると、
E_{n} = (1 - 0^n) / (1 - 0) = 1となり、$\beta = 0$では、全てのデータは本質的には全て同じものである事がわかります。
また、$\beta \rightarrow 1$ $(N \rightarrow \infty)$の場合は、
f(\beta) = 1 - \beta^n, \quad g(\beta) = 1 - \betaとすると、
f'(\beta) = -n \beta^{n-1}, \quad g'(\beta) = -1ロピタルの定理より、
\lim_{\beta \to 1} E_n = \lim_{\beta \to 1} \frac{f(\beta)}{g(\beta)} = \lim_{\beta \to 1} \frac{f'(\beta)}{g'(\beta)} = \lim_{\beta \to 1} \frac{(-n \beta^{n-1})}{(-1)} = nとなります。したがって $\beta \rightarrow 1$では、全てのデータは本質的にもユニークであり、重複がない状態である事がわかります。
実際のデータセットの場合
クラス$y$の学習データの実データ数を$n_y$とすると、クラス$y$の本質的なデータ数 $E_{n_y}$は、
E_{n_y} = (1 - \beta_y^{n_y})/(1 - \beta_y) \\ ただし、 \beta_y = (N_y - 1)/N_yとなります。しかし、クラス$y$についての周辺情報がないため、$N_y$(クラスyを本質的に表現できるデータ数の最大値)を正確に求めるのは極めて難しい作業です。そこで、各クラスの$N_y$は、データセットの画素数や学習するネットワーク構造など、すべてのクラスに共通するもののみに依存すると仮定し、$N_y = N$, $\beta_y = \beta$として、全クラスで同じ値を使います。すると、$E_{n_y}$は下記のようになります。
E_{n_y} = (1 - \beta^{n_y})/(1 - \beta) \\ ただし、 \beta = (N - 1)/N
下図は $\beta$の値によって、$n_y$と$E_{n_y}$の関係がどのように変化するのかを可視化したグラフになります。横軸が$n_y$で縦軸が$E_{n_y}$です。
Class Balanced Loss
InverseClassFrequencyLossでは、クラスのデータ数の逆数を重みとしてバランシングしていましたが、このクラスのデータ数の部分を本質的なクラスのデータ数 $E_{n_y}$に置き換える事で、ClassBalancedLoss になります。
SoftmaxCrossEntropyLoss を ClassBalanced 化すると下記のようになります。
\textbf{CB}_{softmax}(\hspace{2pt}\boldsymbol{p}, \boldsymbol{m}) = -\sum_{i=1}^{B} \frac{1}{E_{n_{m_i}}} log(p_{m_i}) = -\sum_{i=1}^{B} \frac{1 - \beta}{1 - \beta^{n_{m_i}}} log(p_{m_i})FocalLoss を ClassBalanced 化すると下記のようになります。
\textbf{CB}_{focal}(\hspace{2pt}\boldsymbol{p}, \boldsymbol{m}) = -\frac{1}{E_{n_{m_i}}} \sum_{i=1}^{B} (1-p_{m_i})^\gamma log(p_{m_i}) = -\frac{1 - \beta}{1 - \beta^{n_{m_i}}} \sum_{i=1}^{B} (1-p_{m_i})^\gamma log(p_{m_i})$\beta$はハイパーパラメータで、値の範囲は$0 \leqq \beta < 1$になります。$\beta = 0$は重みを全く掛けていない状態に相当し、$\beta \rightarrow 1$はInverseClassFrequencyLossと同じ状態に相当します。
検証
ClassBalancedSoftmaxは、$\beta\in \{0.9, 0.99, 0.999, 0.9999\}$ の4パターンで検証してみました。
$\beta$ MajorityのAccuracy MinorityのAccuracy AllのAccuracy 0.9 88.66 % 49.23 % 76.83 % 0.99 89.45 % 58.67 % 80.22 % 0.999 86.76 % 66.37 % 80.64 % 0.9999 80.94 % 75.23 % 79.23 % $\beta=0.999$の時に、AllのAccuracyは $80.64$% となり、今までのどの検証よりも良い結果となっています。下記がそのグラフです。
ClassBalancedFocalLossは、$\gamma=1.0$固定として、$\beta\in \{0.9, 0.99, 0.999, 0.9999\}$ の4パターンで検証してみました。
$\beta$ $\gamma$ MajorityのAccuracy MinorityのAccuracy AllのAccuracy 0.9 1.0 88.67 % 53.70 % 78.18 % 0.99 1.0 89.42 % 60.63 % 80.60 % 0.999 1.0 85.11 % 64.70 % 78.99 % 0.9999 1.0 72.40 % 62.67 % 69.48 % $\beta=0.99$の時に、AllのAccuracyは $80.60$% となり、ClassBalancedSoftmaxの最高値とほぼ同等の精度となりました。下記がグラフになります。
まとめ
ClassBalancedな損失関数を使えば、SoftmaxCrossEntropyやFocalLoss、どちらの場合も精度が向上する事が確認できました。また、理論部分に関しても証明付きで綺麗にまとまっており、とても読みやすい論文となっています。ただ、本質的なデータ空間という、独特な抽象概念を土台に理論が組み立てられているため、$\beta$ の値をあらかじめ正確に決めることは、原理的に不可能です。したがって、実際のデータに対してこの損失関数を適用する場合は、いくらか学習を試しながら、ハイパーパラメータ$\beta$の値を探査し、最適な値を決める必要があります。
- 投稿日:2019-02-15T14:16:53+09:00
CodinGame の TRON BATTLE で FloodFill アルゴリズムを実装してみた
# この記事は、『CodinGame はBOT(AIプログラム)でバトルするのが正しい楽しみ方かもしれません』 の続きです。
以下のようなデバッグ出力ができるように CodinGame の TRON BATTLE プログラムを改造してみた。
P=0という出力から、自機のプレイヤー番号は0であることが分かる。Input{X0:2, Y0:2, X1:10, Y1:0}という出力からプレイヤー0のスタート位置(tail)は、(2, 2) であることと、現在位置(head)の座標が (10, 0) であることが分かる。 *自機のプレイヤー(プレイヤー0)のヘッドから見て現時点で到達可能であるマスが+記号で表示されている。ちなみにマイナス記号は何もない印である。P=0 Input{X0:2, Y0:2, X1:10, Y1:0} + + + + + + + + + + 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -1. 出来たソース
- コメントは全部削除しました。(読めるでしょ?w)
- 自己流でFloodFillアルゴリズムを実装してみました。
- FloodFillで到達可能範囲を計算しながら「一切」その結果を使ってないので「強くない」です。『CodinGame はBOT(AIプログラム)でバトルするのが正しい楽しみ方かもしれません』 で紹介したソースと強さは全く変わってませんw(誰か助けてw)
using System; using System.Linq; using System.IO; using System.Text; using System.Collections; using System.Collections.Generic; class Player { static void Main(string[] args) { Player control = new Player(); string[] numbers; Input[] inputs; // game loop while (true) { numbers = Console.ReadLine().Split(' '); int N = int.Parse(numbers[0]); int P = int.Parse(numbers[1]); Console.Error.WriteLine("P={0}", P); inputs = new Input[N]; for (int i = 0; i < N; i++) { numbers = Console.ReadLine().Split(' '); int X0 = int.Parse(numbers[0]); int Y0 = int.Parse(numbers[1]); int X1 = int.Parse(numbers[2]); int Y1 = int.Parse(numbers[3]); inputs[i] = new Input(i, X0, Y0, X1, Y1); } Input me = inputs[P]; string dir = control.HandleInputs(me, inputs); control.DumpMap(); Console.WriteLine(dir); } } Cell[,] map = new Cell[30, 20]; Queue<Cell> ffQueue = new Queue<Cell>(); private Player() { for(int y=0; y<20; y++) { for(int x=0; x<30; x++) { map[x, y] = new Cell(x, y, -1); } } } private string HandleInputs(Input me, Input[] inputs) { Console.Error.WriteLine(me); foreach(var input in inputs) { if (input.X1 < 0) DeleteIdsFromMap(input.Id); else AddInputToMap(input); } ExecuteFloodfill(me); if (CanMoveTo(me, -1, 0)) return "LEFT"; if (CanMoveTo(me, 1, 0)) return "RIGHT"; if (CanMoveTo(me, 0, -1)) return "UP"; if (CanMoveTo(me, 0, 1)) return "DOWN"; return "?"; } void AddInputToMap(Input input) { this.map[input.X1, input.Y1].V = input.Id; } void DeleteIdsFromMap(int id) { for(int y=0; y<20; y++) { for(int x=0; x<30; x++) { if (map[x, y].V == id) map[x, y].V = -1; } } } bool CanMoveTo(Input me, int xOffset, int yOffset) { int x = me.X1+xOffset; int y = me.Y1+yOffset; if (x < 0) return false; if (x > 29) return false; if (y < 0) return false; if (y > 19) return false; return map[x, y].V == -1 || map[x, y].V == 9; } bool IsEmptyCell(Cell center, int xOffset, int yOffset) { int x = center.X+xOffset; int y = center.Y+yOffset; if (x < 0) return false; if (x > 29) return false; if (y < 0) return false; if (y > 19) return false; return map[x, y].V == -1; } void DumpMap() { for(int y=0; y<20; y++) { for(int x=0; x<30; x++) { if (map[x, y].V == -1) Console.Error.Write("-"); else if (map[x, y].V == 9) Console.Error.Write("+"); else Console.Error.Write(map[x, y].V); Console.Error.Write(" "); } Console.Error.WriteLine(); } } void ExecuteFloodfill(Input me) { for(int y=0; y<20; y++) { for(int x=0; x<30; x++) { if (map[x, y].V == 9) map[x, y].V = -1; } } Cell c = map[me.X1, me.Y1]; if (IsEmptyCell(c, -1, 0)) ffQueue.Enqueue(map[c.X-1, c.Y]); if (IsEmptyCell(c, 1, 0)) ffQueue.Enqueue(map[c.X+1, c.Y]); if (IsEmptyCell(c, 0, -1)) ffQueue.Enqueue(map[c.X, c.Y-1]); if (IsEmptyCell(c, 0, 1)) ffQueue.Enqueue(map[c.X, c.Y+1]); FloodfillLoop(); } void FloodfillLoop() { while(ffQueue.Count > 0) { Cell c = ffQueue.Dequeue(); if(map[c.X, c.Y].V != -1) continue; c.V = 9; if (IsEmptyCell(c, -1, 0)) ffQueue.Enqueue(map[c.X-1, c.Y]); if (IsEmptyCell(c, 1, 0)) ffQueue.Enqueue(map[c.X+1, c.Y]); if (IsEmptyCell(c, 0, -1)) ffQueue.Enqueue(map[c.X, c.Y-1]); if (IsEmptyCell(c, 0, 1)) ffQueue.Enqueue(map[c.X, c.Y+1]); } } } class Input { public int Id; public int X0; public int Y0; public int X1; public int Y1; public Input(int id, int x0, int y0, int x1, int y1) { this.Id = id; this.X0 = x0; this.Y0 = y0; this.X1 = x1; this.Y1 = y1; } public override string ToString() { return String.Format("Input{{X0:{0}, Y0:{1}, X1:{2}, Y1:{3}}}", X0, Y0, X1, Y1); } } class Cell { public int X; public int Y; public int V; public Cell(int x, int y, int v) { this.X = x; this.Y = y; this.V = v; } public override string ToString() { return String.Format("Cell{{X:{0}, Y:{1}, V:{2}}}", X, Y, V); } }2. 最後に
TRON BATTLE については書く記事としてはこれで終わりになるかもしれません。
C# で挑戦される方の「手始め」の参考にでもなればと思い投稿してみました。# Wood 1 League を抜け出したいのだが…
- 投稿日:2019-02-15T14:13:45+09:00
pythonでcsv dictを読み書きする方法
備忘録です.
辞書型配列の読込と書込です.
参考はこちらCSVファイル読込の際には全ての値の型が保持されていないため,毎回データの型を指定する必要があることに注意.
import csv # moduledef read_dict(file): with open(file, newline = "") as f: read_dict = csv.DictReader(f, delimiter=",", quotechar='"') ks = read_dict.fieldnames return_dict = {} for k in ks: return_dict[k] = [] for row in read_dict: for k, v in row.items(): return_dict[k].append(v) # notice the type of the value is always string. return return_dictdef write_csv(file, save_dict): save_row = {} with open(file,'w') as f: writer = csv.DictWriter(f, fieldnames=save_dict.keys(),delimiter=",",quotechar='"') writer.writeheader() k1 = list(save_dict.keys())[0] length = len(save_dict[k1]) for i in range(length): for k, vs in save_dict.items(): save_row[k] = vs[i] writer.writerow(save_row)
- 投稿日:2019-02-15T12:38:22+09:00
pythonで配列を値渡しする方法
備忘録です.
関数に配列を渡すときに参照渡しになっていると困るときがあったので.
配列のあとに[:]をつけると値渡しになります.def hoge(arr): arr[0] += 1 arr_ref = [0, 1] arr_val = [0, 1] hoge(arr_ref) hoge(arr_val[:]) print(arr_ref) print(arr_val)出力結果
[1, 1] [0, 1]確かに2つ目の配列が値渡しになっています.
- 投稿日:2019-02-15T12:38:22+09:00
pythonで配列のコピーを渡す方法
備忘録です.
追記
コメントをいただきました.
深い構造の配列でこのタイプの渡し方をすると下層にある値は変化してしまうため,copy.deepcopy()という関数を使うべきだというコメントをいただきました.
関数に配列を渡すときに参照渡しになっていると困るときがあったので.
配列のあとに[:]をつけると値渡しになります.def hoge(arr): arr[0] += 1 arr_ref = [0, 1] arr_val = [0, 1] hoge(arr_ref) hoge(arr_val[:]) print(arr_ref) print(arr_val)出力結果
[1, 1] [0, 1]確かに2つ目の配列が値渡しになっています.
- 投稿日:2019-02-15T12:36:17+09:00
Numpyと画像とガンマと速度
TL;DR
ファイルに保存された画像データには、ほとんどの場合、ガンマがかかっている。印刷系なら1.8。動画系なら2.2。sRGBならガンマっぽいけれど実はガンマではない、ガンマ2.2に近い処理がされている。
これを元に戻す処理がデガンマ。デガンマしないと、cv2.blurとかで色がおかしくなる。
ガンマのかかったデータがチャンネル当たり8ビットなら、デガンマ後は16ビットで扱う。でないと元のデータが失われ、露骨なトーンジャンプが発生する。
デガンマしたままでデータを引き回すのがリニアワークフロー。データ量は2倍になるが、ガンマ・デガンマは重い処理の上に、ガンマがかかっているかどうか&ガンマはいくつなのかを間違えることがある。「入り口でデガンマ、出口でガンマ」と決め打ちするメリットは大きい。昔はメモリが足りなかったので、データ量2倍はきつかったのだ。
ガンマの発祥はCRTの特性云々という話があるが、ガンマは人間の知覚に沿った圧縮手法と考えたほうがいい。物理現象(混色)はリニア、知覚はガンマなのだ。
リニアワークフローを貫徹できればいいのだが、時として、16ビットでは困る場合に出くわす。ライブラリが8ビット&ガンマ前提だったり、速度が欲しかったり。
そのときに愚直に1.8や2.2でガンマする必要があるかどうか考えると、速度がかなり違ってくるかもしれない。
np.powerはnp.sqrtの6倍くらい遅い
%timeit a = np.sqrt(np.arange(1,1000).astype(np.float)) 5.89 µs ± 17.1 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each) %timeit a = np.power(np.arange(1,1000).astype(np.float), 0.5) 33.1 µs ± 16.9 ns per loop (mean ± std. dev. of 7 runs, 10000 loops each)2でガンマすることにして、np.power(x, 0.5)をnp.sqrtに置き換えると、だいぶ速くなる。
- 投稿日:2019-02-15T12:29:56+09:00
現在のパスとその中のファイル一覧の取得方法
備忘録です.
pythonで現在のパスとそのパス内にあるファイルの取得方法です.
import os print(getcwd()) # can see the path to the current working directory. print(os.listdir(os.getcwd())) # can see the list of the files in the current working directory.
- 投稿日:2019-02-15T12:29:56+09:00
pythonで現在のパスとその中のファイル一覧の取得方法
備忘録です.
pythonで現在のパスとそのパス内にあるファイルの取得方法です.
import os print(os.getcwd()) # can see the path to the current working directory. print(os.listdir(os.getcwd())) # can see the list of the files in the current working directory.
- 投稿日:2019-02-15T11:34:13+09:00
気分を認識するための計算モデル
感情や気分の心理学的な定義は、感情を使ったアプリの開発に役立てられると考えています。ここでは、感情の構成要素と、それを気分へ変換する方法を論文1をもとに書きます。
概要
感情は、ArousalとValenceという構成要素から成ります。Arousalは感情の覚醒度合いで、高ければ覚醒、低ければ鎮静を表します。Valenceはポジ・ネガです。感情クラスとArousal,Valenceの対応2を示した図は以下です。
Table 2
Emotion ratings for arousal, valence, CF-self, CF-other, and CF-overall in alphabetical order.
Emotion Arousal Valence CF-self CF-other CF-overall Affectionate 2.9 2.57 6.41 5.8 6.105 Aggressive 8.12 7.67 4.26 5.9 5.08 Aggrieved 5.91 5.65 4.85 5.05 4.95 Aghast 7.2 6.47 3.71 4.43 4.07 Agonized 6.99 7.52 2.42 3.21 2.815 Amused 3.45 2.47 6.4 6.09 6.245 Angry 8.06 7.5 4.58 5.38 4.98 Anxious 7.04 6.59 4.07 5.2 4.635 Apologetic 4.73 4.84 4.43 4.33 4.38 Ashamed 5.88 6.01 3.56 3.8 3.68 Bored 4.04 5.83 3.74 5.35 4.545 Carefree 3.4 2.34 6.62 6.34 6.48 Caring 3.65 3.06 6.53 5.48 6.005 Compassionate 4.95 5.47 4.56 4.34 4.45 Concerned 6.27 5.6 5.58 5.51 5.545 Confident 2.7 2.61 6.55 5.52 6.035 Confused 6.29 6.14 3.55 4.4 3.975 Contemptuous 6.46 7.53 2.63 3.62 3.125 Content 2.05 2.28 6.35 5.56 5.955 Cross 6.97 6.68 5.22 6.11 5.665 Curious 5.01 3.34 6.95 6.03 6.49 Desperate 7.48 7.53 3.54 4.16 3.85 Disappointed 5.95 6.73 4.72 5.26 4.99 Disgusted 6.87 7.42 3.34 3.89 3.615 Doubtful 6.05 6.25 4.85 5.45 5.15 Embarrassed 4.96 5.04 4.19 4.73 4.46 Enthusiastic 5.73 2.66 5.2 4.76 4.98 Envious 7.54 6.75 3.89 5.09 4.49 Expectant 5.37 3.57 5.49 5.88 5.685 Frantic 8.41 7.41 3.27 3.5 3.385 Frustrated 6.9 7.46 4.21 5.4 4.805 Grateful 3 2.52 6.46 5.29 5.875 Grievous 6.26 6.82 3.98 4.6 4.29 Guilty 6.59 7.03 3.4 3.49 3.445 Hateful 8.16 8.27 2.42 3.45 2.935 Humble 4.96 5.9 3.48 3.25 3.365 Hurt 6.26 6.64 3.88 4.76 4.32 In love 6.27 1.72 5.48 5.52 5.5 Interested 3.96 2.54 7.36 6.19 6.775 Jaunty 5.98 3.98 4.35 4.9 4.625 Jealous 6.14 6.92 3.26 5.2 4.23 Joyful 4.55 2 6.58 6.2 6.39 Jubilant 5.08 1.77 5.17 4.62 4.895 Jumpy 7.22 6.37 3.54 4.41 3.975 Lonely 5.78 7.17 3.85 5.14 4.495 Lyrical 5.08 3.18 5.03 5.2 5.115 Melancholic 4.42 5.76 4.16 4.23 4.195 Offended 6.04 6.49 3.92 5.27 4.595 Panic 8.26 7.78 2.8 3.36 3.08 Pardoning 3.56 3.36 5.17 4.13 4.65 Passionate 5.69 2.21 6.11 4.78 5.445 Proud 4.12 2.8 5.38 5.44 5.41 Relaxed 1.72 2.37 6.07 5.08 5.575 Relieved 2.68 2.45 5.38 5.02 5.2 Remorseful 5.29 5.53 3.33 3.35 3.34 Sad 5.91 6.6 4.51 5.48 4.995 Shocked 7.56 6.86 3.26 3.89 3.575 Sick 6.71 7.6 3.65 4.23 3.94 Surprised 5.74 4.09 4.73 5.14 4.935 Triumphant 5.5 3.48 3.77 4.09 3.93 Troubled 6.43 5.77 4.89 5.39 5.14 Wistful 5.47 6.03 3.52 3.74 3.63 The German translations were used in the actual questionnaire.
提案手法では、この感情を気分へ変換するために、フレームを用いています。気分は、ある期間(フレーム)内の感情の系列から、何らかの写像Fを対応させることで数値的に変換し、この数値を量子化することで気分を分類します。
写像関数Fは以下のようなものが考えられます:
- 平均
- 最大値
- 最も継続した値
- 最初に経験した値
- 最後に経験した値
この中で最も精度の高いのは、移動平均のようです。
jupyterで実行
感情の乱数を生成します。
from random import random size = 100 rate = 0.3 es_tmp = [(2*(random()-0.5), 2*(random()-0.5)) for _ in range(size)] es = [] for e in es_tmp: if random() < rate: es.append(e) else: es.append((0,0))移動平均関数を作成します。
import numpy as np def mean(es, n=10): out1 = [] out2 = [] out3 = [] for i,_ in enumerate(es): s = i-n if s < 0: s = 0 target = es[s:i+1] tmp_v = [x[0] for x in target] tmp_a = [x[1] for x in target] x = sum(tmp_v)/n y = sum(tmp_a)/n out1.append(x) out2.append(y) z = np.dot(x,y) if z > 0: out3.append(2-np.sign(x)) elif z < 0: out3.append(3+np.sign(x)) else: out3.append(0) return out1, out2, out3 V, A, Q = mean(es, 10)気分の減衰をシミュレートします。
os = [[],[],[],[]] r = 0.9 for i, (x,y,c) in enumerate(zip(V,A,Q)): try: for j in range(len(os)): os[j].append(os[j][i-1]*r) except: for j in range(len(os)): os[j].append(0) os[int(c-1)][i] = abs(x*y)プロットします。
%matplotlib inline import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D plt.figure(num=None, figsize=(9, 9), dpi=80, facecolor='w', edgecolor='k') plt.subplot(411) plt.scatter(x=V, y=A, c=Q) plt.subplot(412) for o in os: plt.plot(o) plt.legend(["amusement","anxiety","distress","calmness"], loc=1) plt.subplot(413) plt.plot([x[0] for x in es]) plt.legend(["valence"], loc=1) plt.subplot(414) plt.plot([x[1] for x in es], "y") plt.legend(["arousal"], loc=1)出力
- 投稿日:2019-02-15T11:02:53+09:00
python インデント 質問 emacs
はじめに
今回はpythonのインデントに関する質問をさせてください。
ubuntu18.03
emacs25-2利用規約によると・・・
Use 4 spaces per indentation level.
半角スペース4つとあります。
結構のライブラリがこれに従ってるらしいです。本題
私は基本的にインデントはTABを使用していて、そのTABをわかりやすくするためにelispを書いています。
int main() { > for(int i = 0; i < 1; i++) { > > print("test"); > } }c++であれば、上のようにTABのはじめに”>”のような記号が表記されます。
ここで一つ目の質問です。
pythonでインデントをスペースにしている状況でも、上のように">"を表示させることは可能ですか?
(何かしらインデントを表す表記がほしいです。)次に二つ目の質問です。
一つ目の質問が不可能であるとき、pythonのインデントをTABにしてもよいのでしょうか。よろしくお願いします。








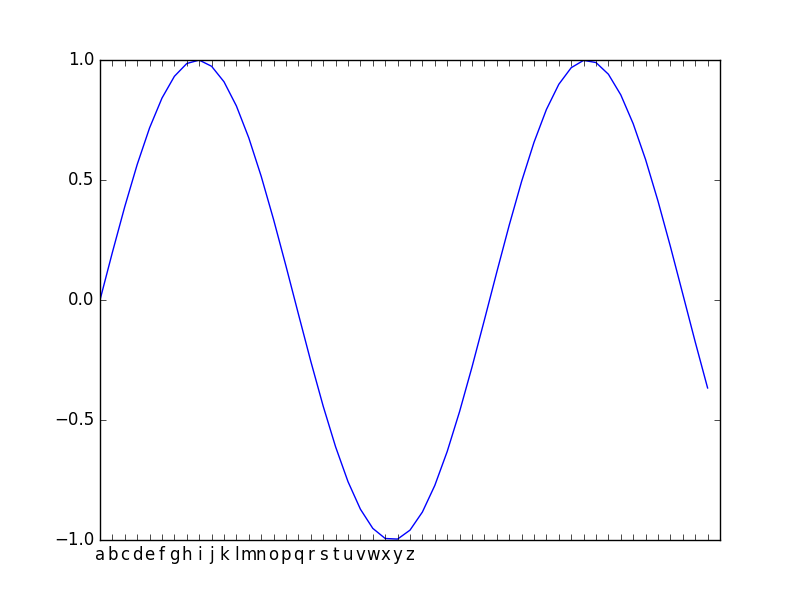
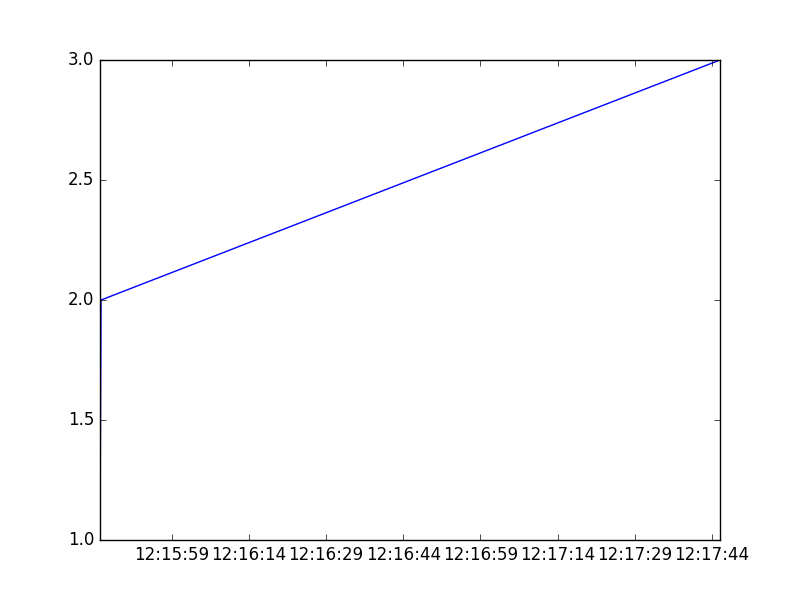



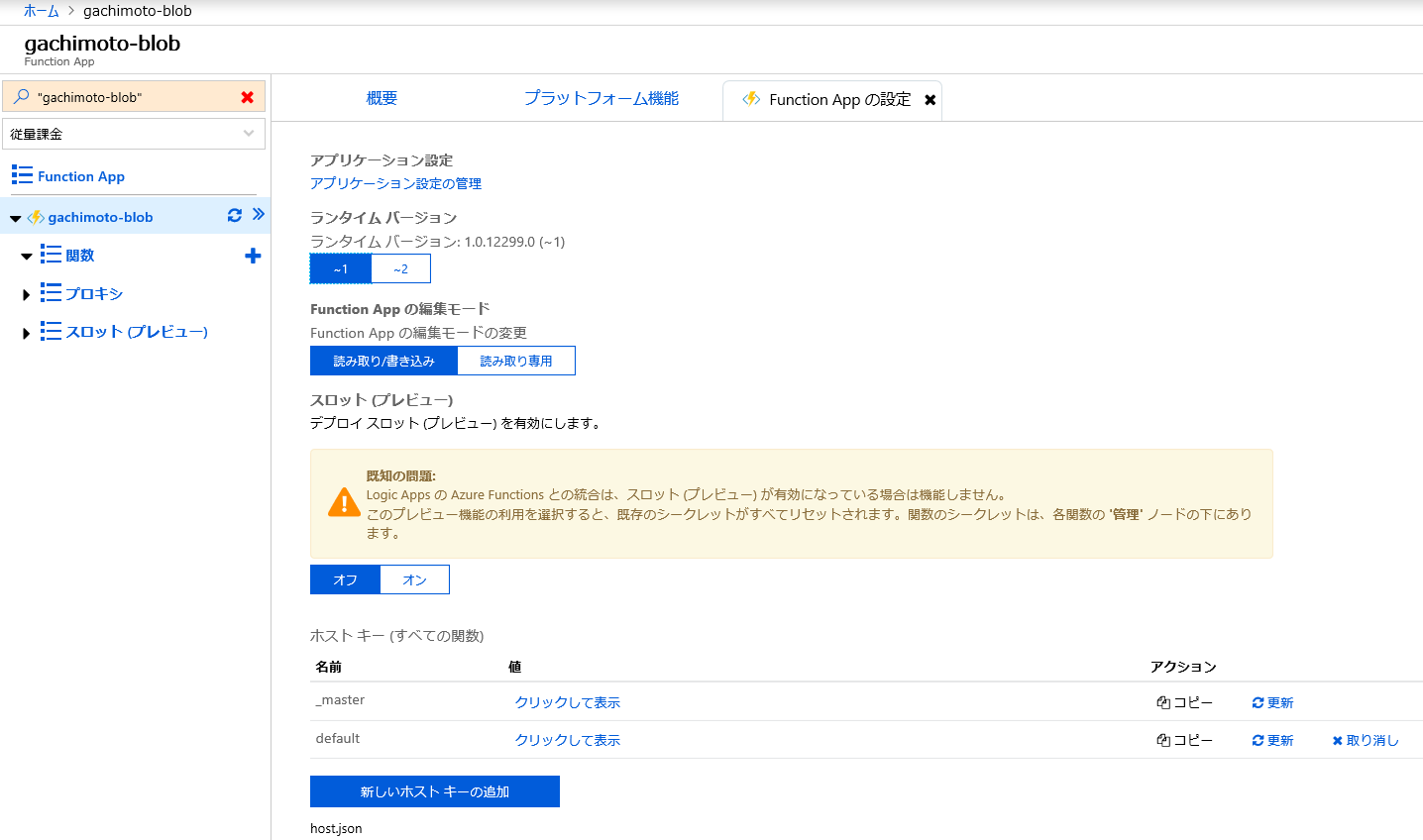
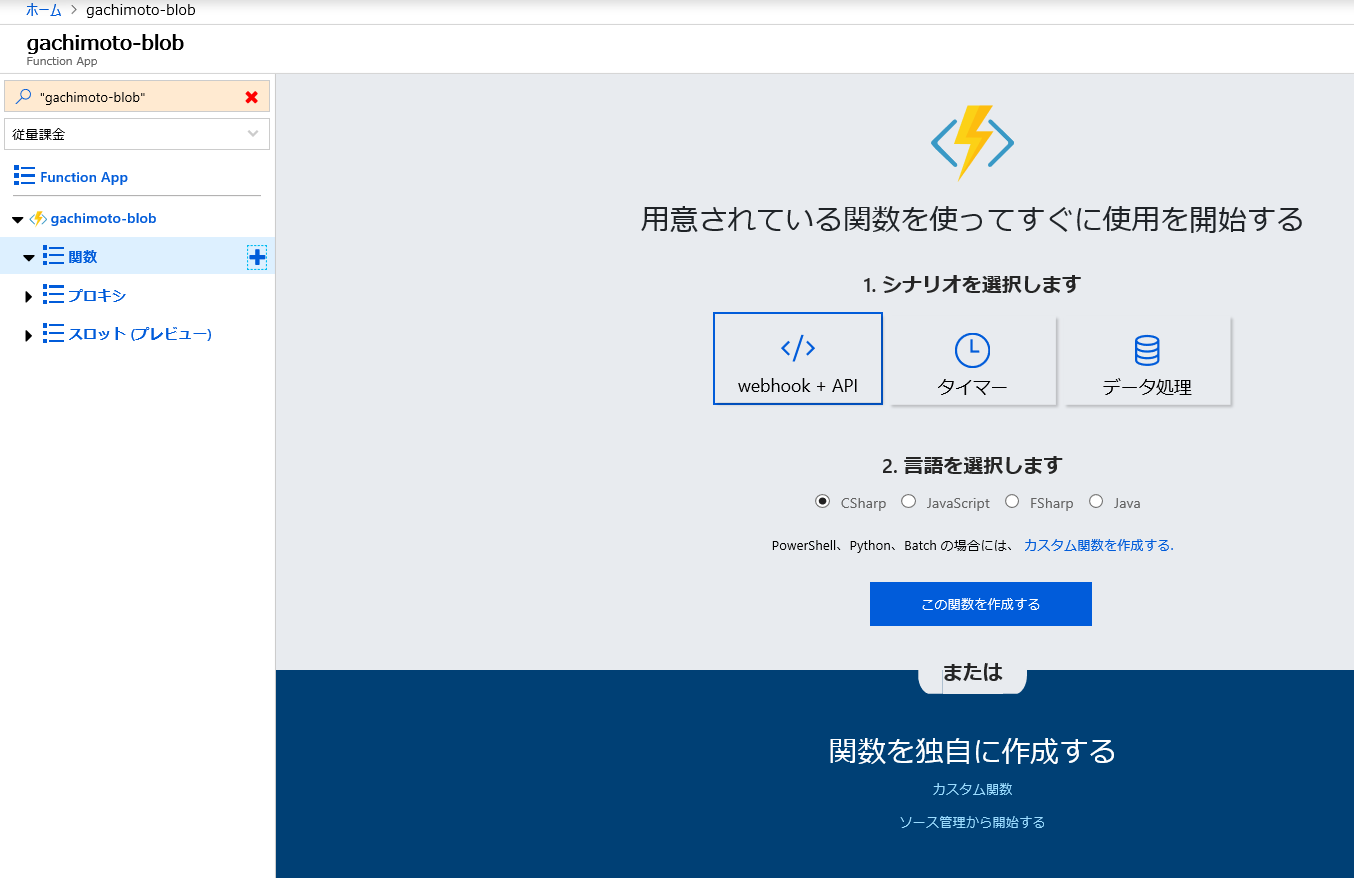
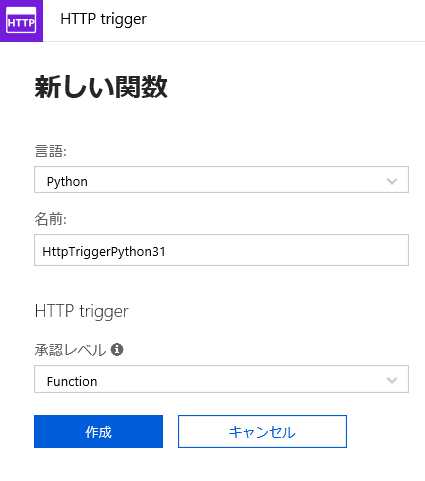
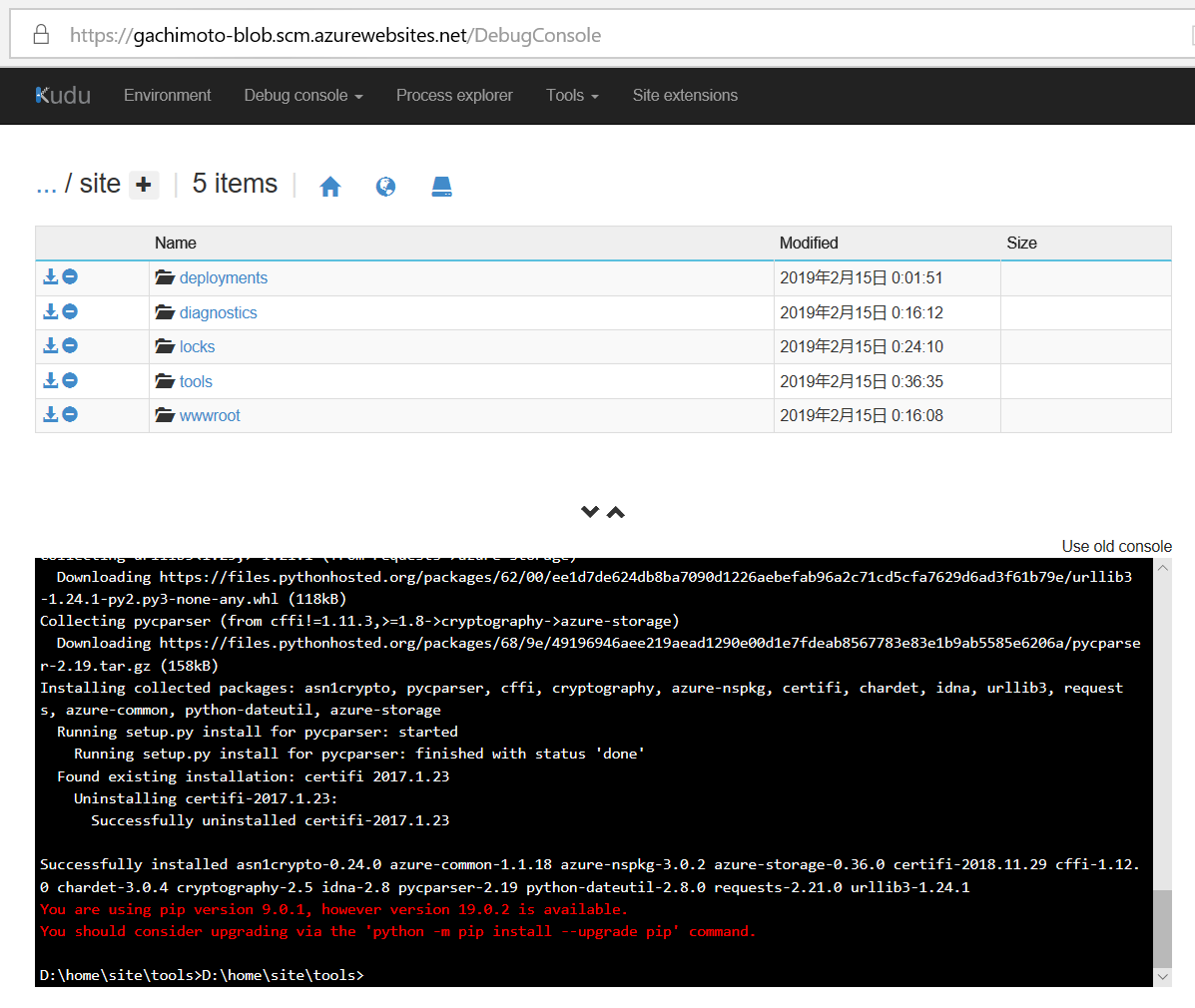
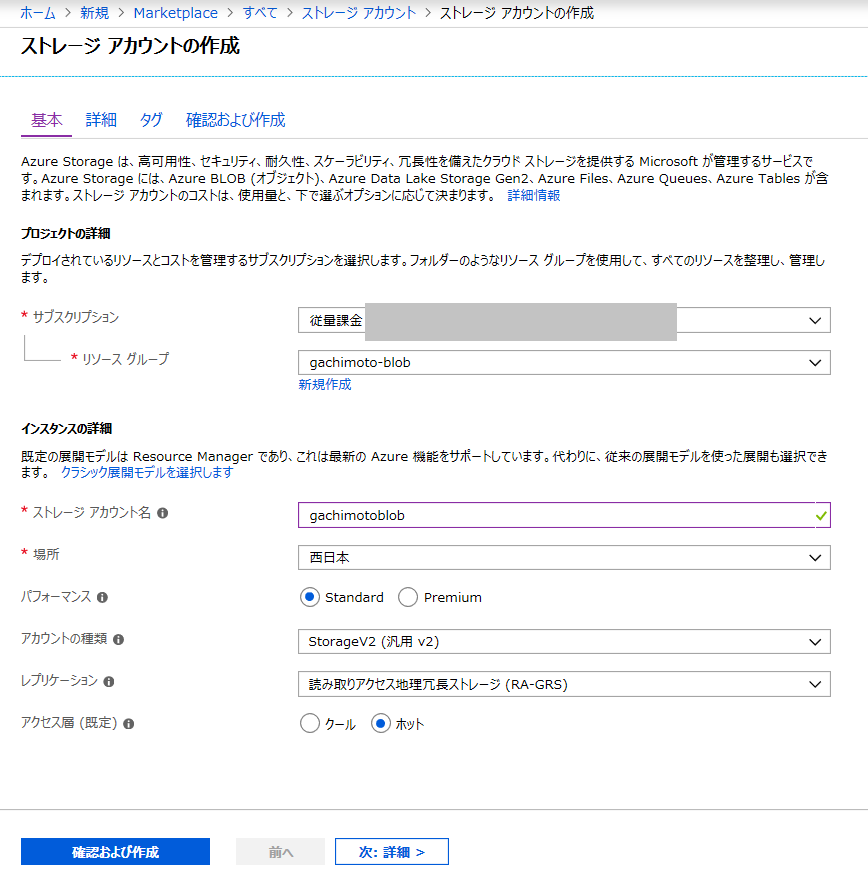
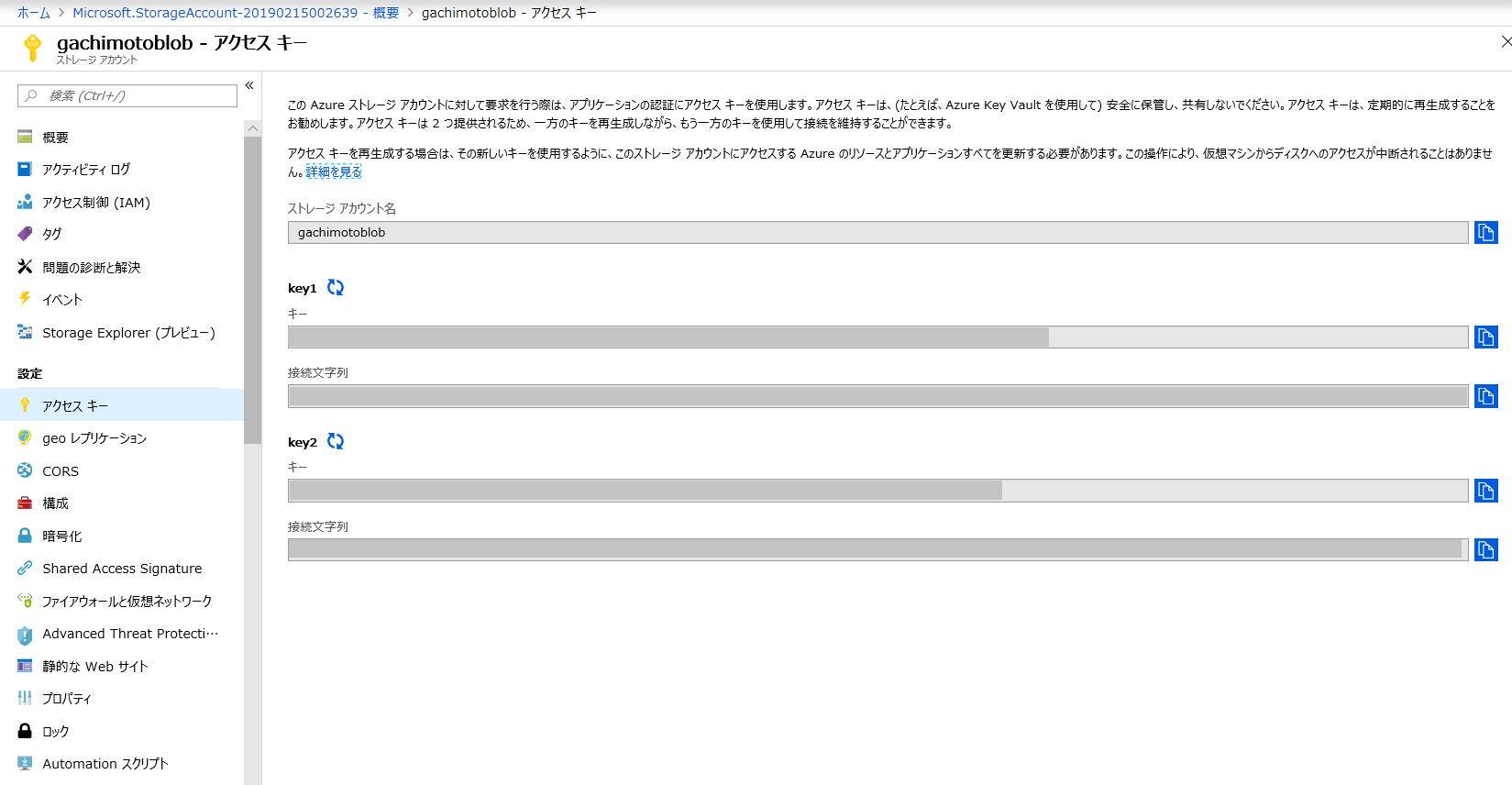
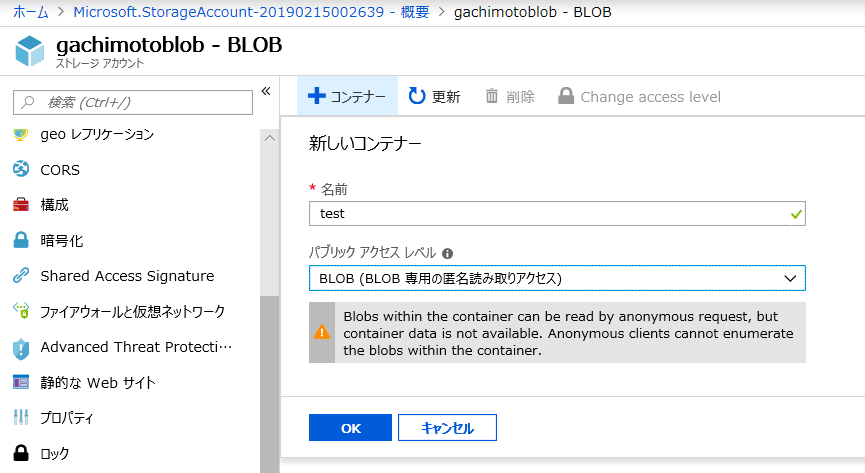
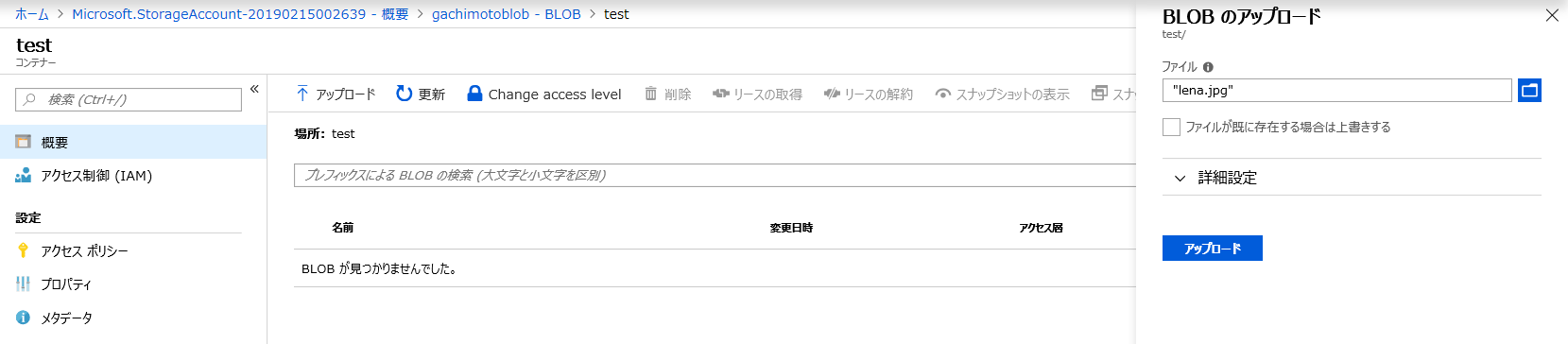
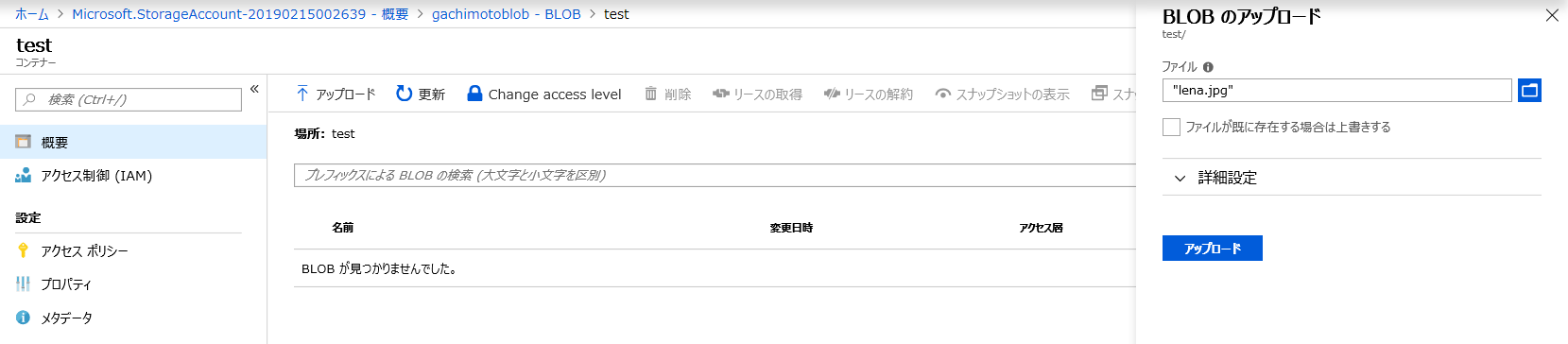
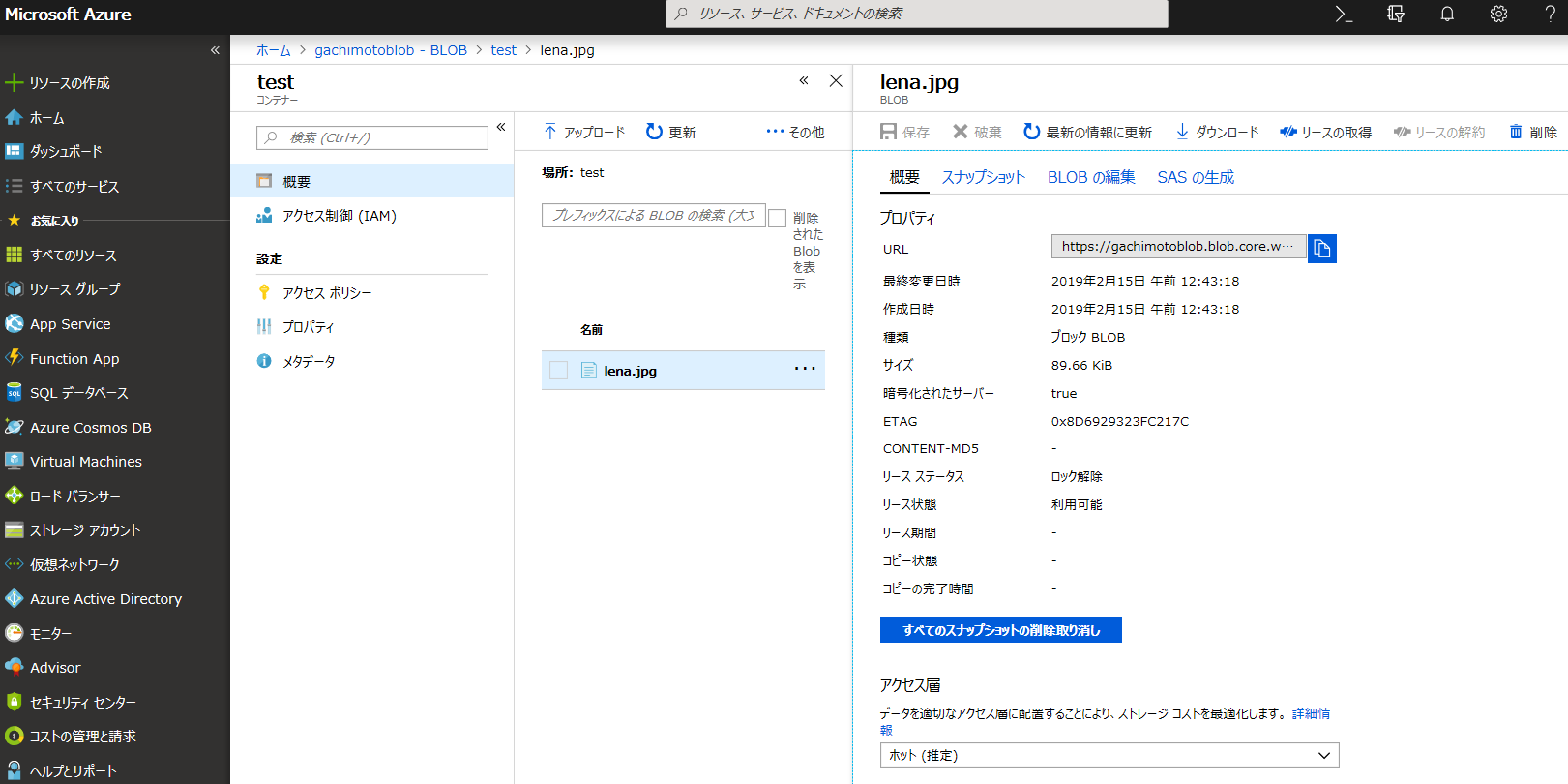
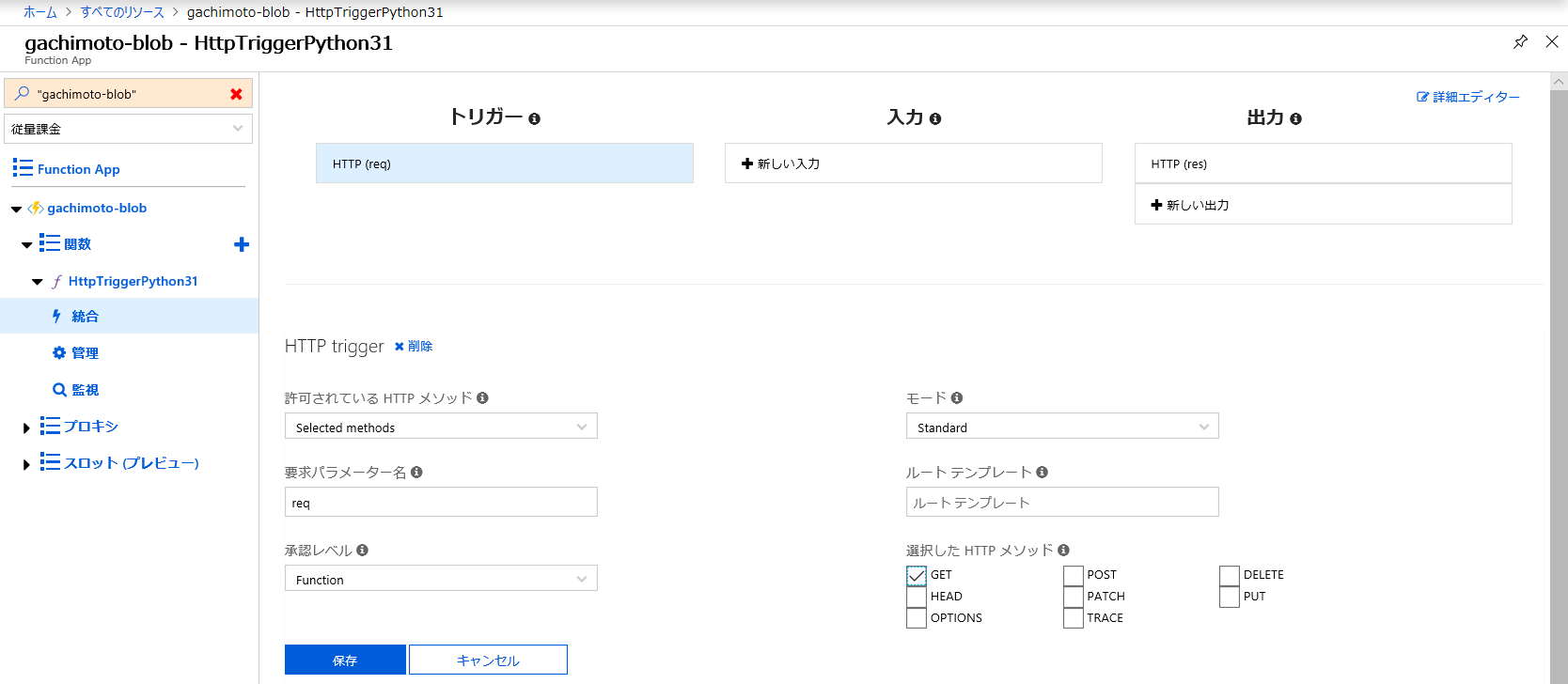
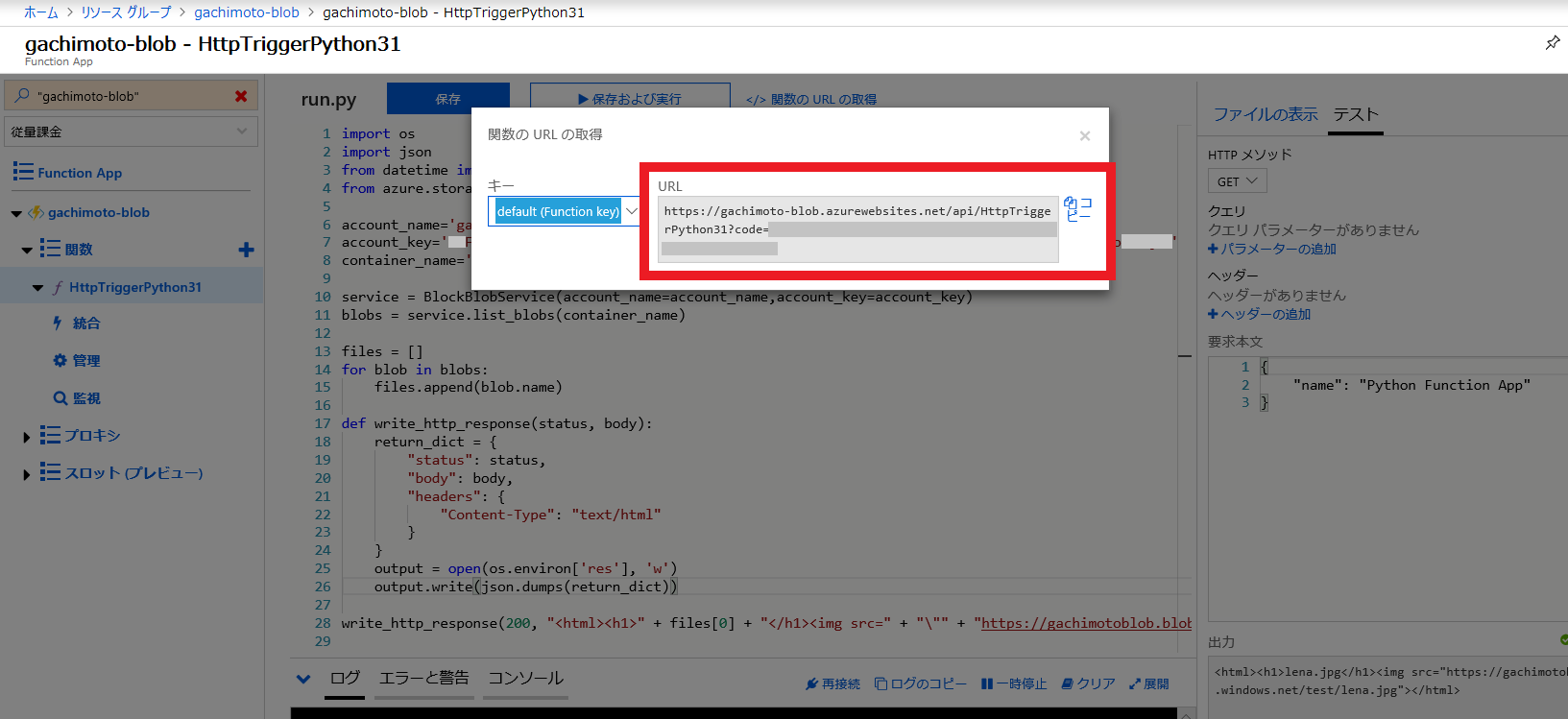






![115 [更新済み]-01.jpg](https://qiita-image-store.s3.amazonaws.com/0/318424/2ddff4af-d160-958b-bdc1-f2930bb9a7c3.jpeg)