- 投稿日:2019-02-15T14:59:34+09:00
不均衡データに対する損失関数の工夫
はじめに
研究の用途においては、データセットによる精度への影響を避けるため、各クラスのデータ数が同じくらいの均衡なデータセットがよく利用されています。しかし、いざ実サービスで学習用のデータを集めようとしても、全てのクラスで同じ数のデータを集めるのは難しい場合があります。そのような不均衡なデータセットに対して、2019/01/16にarxivで発表があった Class-Balanced Loss や Focal Lossなど、損失関数の工夫だけでどこまで精度を上げられるのか検証してみました。
データ不均衡による精度の劣化
CIFAR-10データセットを使って学習および検証を行いました。学習データはCIFAR-10の訓練用画像 50,000枚(各class 5,000枚)からautomobileとdeerとfrogのデータを250枚に減らして、意図的に不均衡にしたものを使用しています。検証にはCIFAR-10の検証用画像 10,000枚(各class 1,000枚)を使います。学習時のデータ数に基づいて、automobileとdeerとfrogの minorityグループ、それ以外の majorityグループ、10,000枚全てを使ったallグループの3つに分け、それぞれのグループ毎に検証して、正解率(Accuracy)を計測しました。学習データと検証データの内訳は下記の表のとおりになります。
class 学習データ 検証データ(minority) 検証データ(majority) 検証データ(all) 0 airplane 5,000 0 1,000 1,000 1 automobile 250 1,000 0 1,000 2 bird 5,000 0 1,000 1,000 3 cat 5,000 0 1,000 1,000 4 deer 250 1,000 0 1,000 5 dog 5,000 0 1,000 1,000 6 frog 250 1,000 0 1,000 7 horse 5,000 0 1,000 1,000 8 ship 5,000 0 1,000 1,000 9 truck 5,000 0 1,000 1,000 ネットワークの構造はResNet18で、全ての検証は下記の要件に従って学習を行います。
Epoch BatchSize Optimizer LearningRate 25 128 SGD Momentum
Momentum=0.9
WeightDecay=0.00050.1(1〜15 epoch)
0.01(16〜20 epoch)
0.001(21〜25 epoch)ちなみに、不均衡ではない普通のCIFAR-10に対し、一般的な損失関数 SoftmaxCrossEntropy で学習した結果は次のようになりました。全てのグループでAccuracyが90%を超えています。
MajorityのAccuracy MinorityのAccuracy AllのAccuracy 90.23 % 94.4 % 91.4 % 次は、これを不均衡データにした場合の結果になります。
MajorityのAccuracy MinorityのAccuracy AllのAccuracy 87.93 % 50.4 % 76.5 % 均衡なデータの場合に比べて、Minorityグループの精度が極端に悪く、それにひきずられる形でAllグループの精度も76.5%と悪くなりました。
データ数の逆数でバランシング
損失関数の工夫として、クラスのデータ数の逆数を重みとして掛けて、Lossへの寄与率をクラスのデータ数に反比例するように調節する手法がよく使われています。クラス数が$C$で、各クラスのラベルが $y\in \{1, 2,...,C\}$であるデータセットについて考えてみます。モデルが出力するSoftmaxの値を$ \boldsymbol{p} =[p_1, p_2,..., p_C]^T$, ただし $p_i \in [0,1] \hspace{3pt} \forall \hspace{3pt} i$ 。学習時のミニバッチ数を$B$ 。ミニバッチ内の正解ラベルを$ \boldsymbol{m} =[m_1, m_2,..., m_B]^T$,ただし $m_i \in \{1, 2,...,C\} $ 。 その場合、通常のSoftmaxCrossEntropyLossは下記のようになります。
\textbf{CE}(\hspace{2pt}\boldsymbol{p}, \boldsymbol{m}) = -\sum_{i=1}^{B}log(p_{m_i}) \tag{1}クラス$y$の学習データの数を$n_y$とすると、クラス数の逆数でバランシングした損失関数InverseClassFrequencyLossは下記のように書けます。
\textbf{ICF}(\hspace{2pt}\boldsymbol{p}, \boldsymbol{m}) = -\sum_{i=1}^{B} \frac{1}{n_{m_i}} log(p_{m_i}) \tag{2}InverseClassFrequencyLossの検証結果は次のようになりました。(実際の検証では、ミニバッチ単位のLossの出力の大きさを通常のSoftmaxCrossEntropyLossと揃えるために、加重平均をとっています。加重平均をとっても、各クラスの全体に対する寄与率は変わりません。)
MajorityのAccuracy MinorityのAccuracy AllのAccuracy 74.1 % 74.67 % 73.58 % 通常のSoftmaxCrossEntropyLossに比べてMinorityグループの精度がだいぶ高くなりました。ただMajorityグループの精度は落ちてしまったため、Allグループの精度は悪くなっています。
Focal Loss
OneStageのObject Detectionの学習において、背景(EasyNegative)がほとんどであり、クラスが不均衡状態になっているという仮説のもと、それを自動的にコスト調節してくれる損失関数として、Facebook AI Researchが提案した手法1です。ICCV2017で発表されStudent Best Paperに選ばれています。
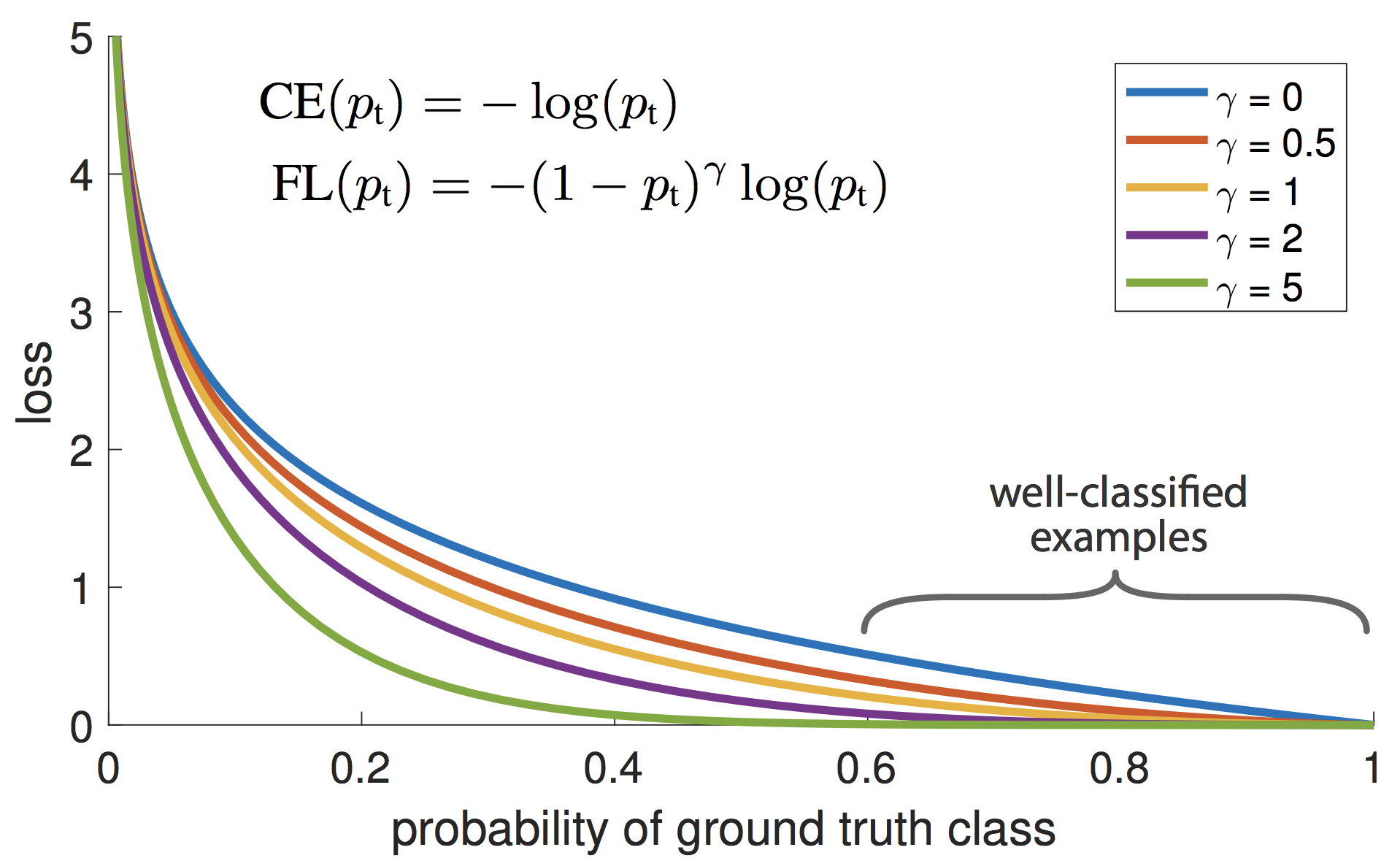
上の図が示すように、$p_t$が小さく0に近い場合(大きく間違っている場合)は、係数は1に近いためあまり影響を受けません。逆に$p_t$が大きく1に近い場合(ほとんど間違っていない場合)は、係数は0に近いためLossとしてほとんど計上されなくなります。このように損失関数の係数部分が自動的にEasyNegativeExampleをDownWeightし、結果としてHardNegativeに比重が置かれるように機能します。
このFocalLossを多クラス分類のSoftmaxCrossEntropyに適応すると下記のように書けます。
\textbf{FL}(\hspace{2pt}\boldsymbol{p}, \boldsymbol{m}) = -\sum_{i=1}^{B} (1-p_{m_i})^\gamma log(p_{m_i}) \tag{3}$\gamma\in \{1.0, 1.5, 2.0\}$ の3パターンで検証してみました。
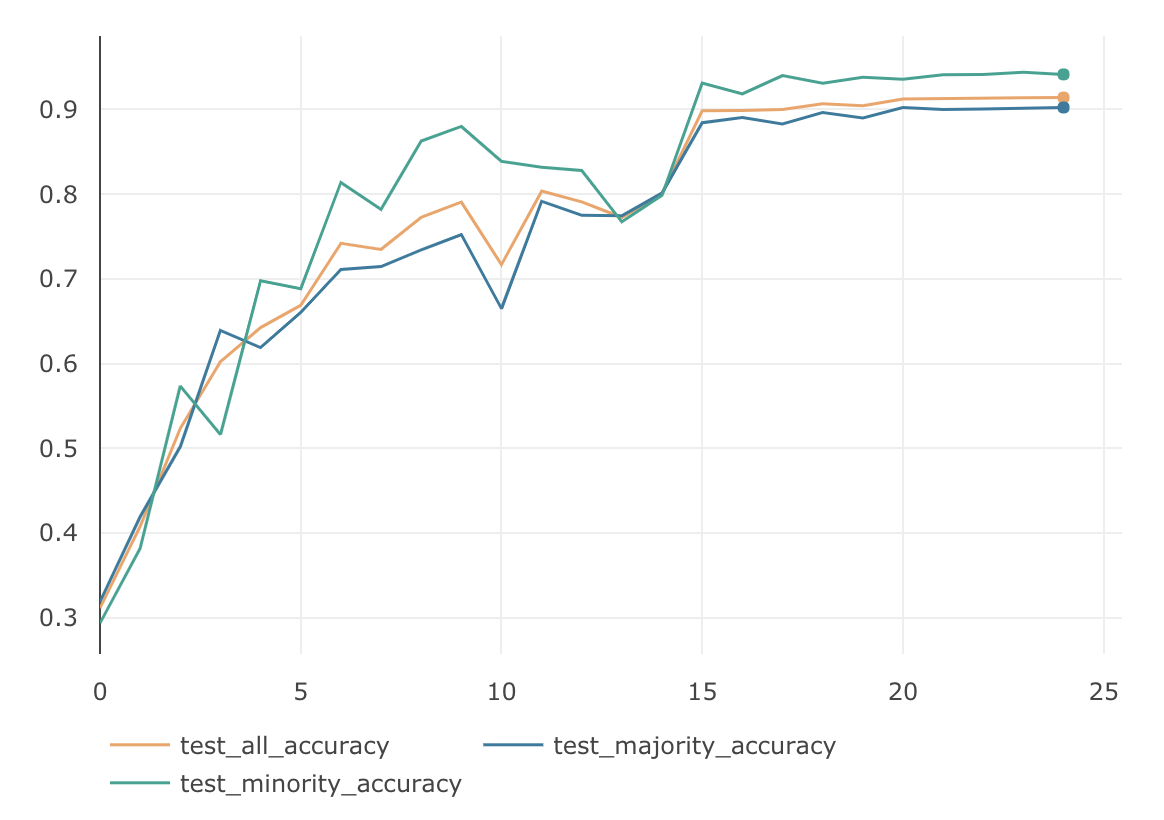
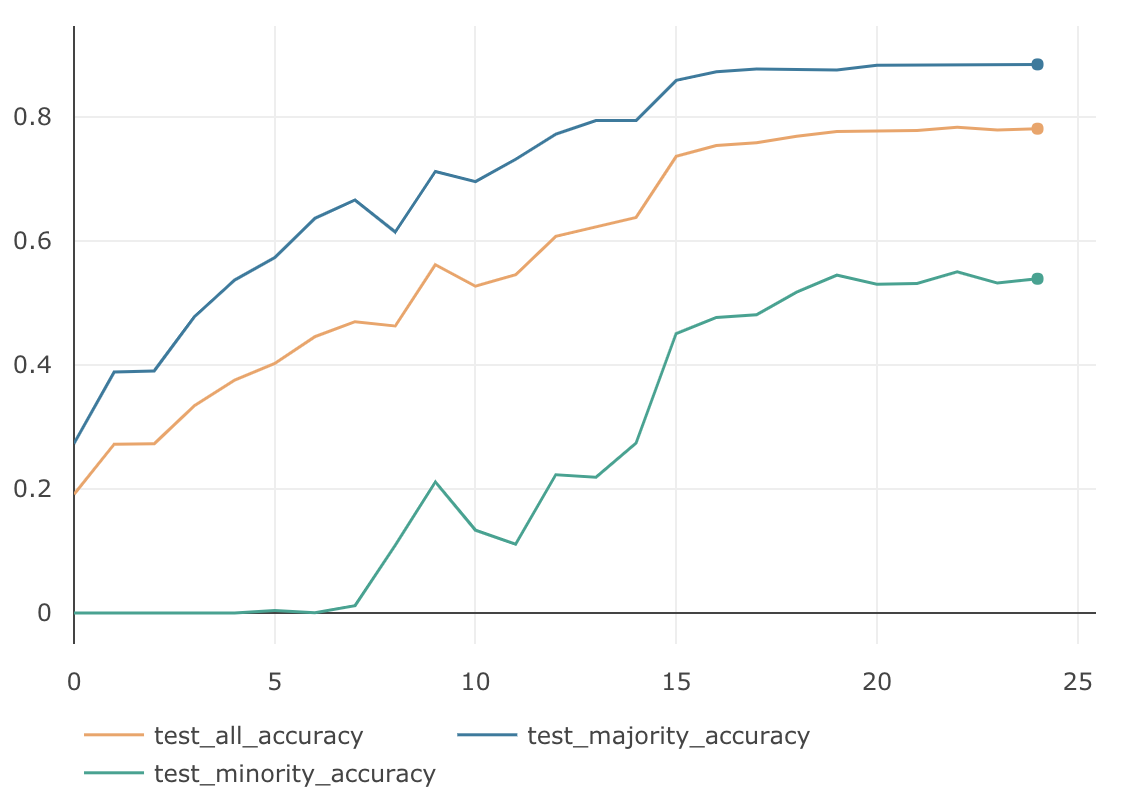
$\gamma$ MajorityのAccuracy MinorityのAccuracy AllのAccuracy 1.0 88.47 % 55.03 % 78.33 % 1.5 87.91 % 53.56 % 77.61 % 2.0 86.37 % 49.53 % 75.32 % InverseClassFrequencyLossに比べると、Minorityグループの精度は全体的に落ちていますが、Majorityグループの精度は全て高くなっています。$\gamma=1.0$のAllグループの精度は、これまでの不均衡データ検証の中では最も良い結果となりました。下図は $\gamma=1.0$のグラフになります。
本質的なクラスのデータ数でバランシング
先述した InverseClassFrequencyLossの検証結果からもわかる通り、クラスのデータ数の逆数を重みとして掛ける事で、不均衡データに対するバランシングの効果が期待できます。この考え方をさらに深掘りした Class-Balanced Loss Based on Effective Number of Samples2 という興味深い論文がarxivに上がっていたので紹介します。この論文では、InverseClassFrequencyLossで利用しているクラスのデータ数というのは、実は本質的なデータ数ではないという考え方を元に理論が構築されています。どういうことかと言うと、例えば、class0のデータが800枚、class1のデータが500枚からなるデータセットがあるとします。それぞれのclassをData Augmentationして、class0もclass1も1,000枚に増やした場合、表面上のデータ数はどちらも1,000枚と同じになりますが、本質的なデータ数という意味ではこの2つは違います。このように実データ数と本質的なデータ数には差があるという事です。
もう一つ。ある画像から特徴ベクトルを抽出し、その特徴ベクトルを分類器にかける事で、画像のクラス分類するといったケースを考えてみます。この場合、分類に利用している特徴ベクトルは、ベクトルの次元数が固定です。したがって、そのベクトルの表現パターン数以上のデータ表現はできません。つまり、どんなに多くの画像を集めたとしても、この分類器にとってのデータ数は、ベクトルの表現量を超える事はないという事です。これもまた、実データ数と本質的なデータ数には差があるという例となります。
この差は、タスクの種類やデータセットの特性、およびその周辺情報によっても変わってくるため、拡大や回転したものを同じデータ扱いにするのか、同じオブジェクトが写っていれば同じデータ扱いにするのか、これらは一概には決められません。しかし、ここで重要なのは、どのようなデータセットにおいても、少なからず実データ数と本質的なデータ数には差があるという事です。
したがって、データセットのデータを、全てユニークなデータとしてカウントした値を不均衡データのバランシングに使うのではなく、本質的なデータ数に配慮した値を用いてデータバランシングを行うべき、というのが本論文の主張になります。理論
本質的なデータ数が具体的にどのような値になるのか説明します。本質的なデータ数の最大値を$N$とおきます。例えば、車の画像が無限にあったとして、全ての車の画像を本質的なデータ空間に写像した場合、$N$パターンとなります。実データ数を$n$、その本質的なデータ数を$E_n$とすると、下記のように書けます。
E_n = (1 - \beta^n)/(1 - \beta) \tag{4} \\ ただし、 \beta = (N - 1)/Nと、いきなり式が出てきましたが、数学的帰納法を使ってこれを証明します。
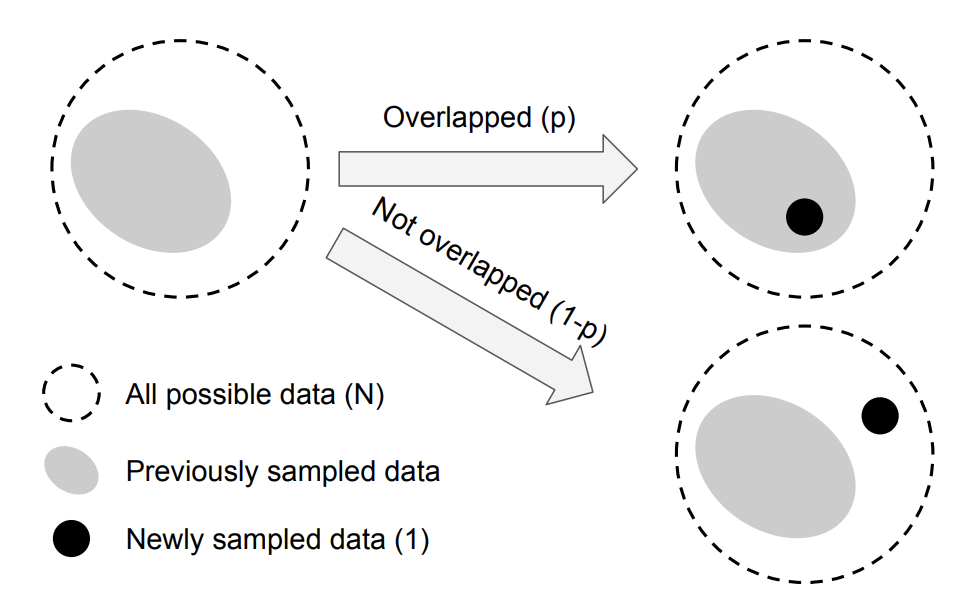
まず、$E_1$は重なりようがないので、$E_1 = 1$となります。次に、$E_{n-1}$で成立する場合に$E_n$でも成立するかを考える必要がありますが、その前に下の図を見てください。これは、$n$個目のデータをサンプリングした際の、本質的なデータ空間の変化の様子を示した概念図になります。破線の領域は本質的なデータ空間を表しています。したがって、この領域のデータ数は$N$です。灰色の領域は$n-1$個の実データが写像された本質的なデータ空間の領域になります。したがって、この領域のデータ数は$E_{n-1}$です。次に、$n$個目のデータを本質的なデータ空間に写像しようとした場合、$E_{n-1}/N$の確率で灰色の領域に入ります。
したがって、p = \frac{E_{n-1}}{N}とすると、$E_n$の期待値は下記のようになります。
E_n = pE_{n-1} + (1-p)(E_{n-1} + 1) = 1 + \frac{N - 1}{N}E_{n-1} \tag{5}ここで、式$(4)$が$E_{n-1}$では成立すると仮定すると、
E_{n-1} =(1 - \beta^{n-1})/(1 - \beta) \tag{6}と書け、式$(5)$の$E_{n-1}$に代入すると、
E_{n} =1 + \frac{N - 1}{N}E_{n-1} = 1 + \beta \frac{1 - \beta^{n-1}}{1 - \beta} = \frac{1 - \beta + \beta - \beta^{n}}{1 - \beta} = \frac{1 - \beta^{n}}{1 - \beta} \tag{7}となります。$E_n$の場合も式$(4)$を満たすことがわかったので、証明はこれで完了となります。
式$(4)$にあるように、$\beta = (N - 1)/N$とおいており、$N\geqq1$なので、$\beta$の取り得る値の範囲は$0 \leqq \beta < 1$です。したがって、$n \rightarrow \infty$ の場合 $\beta^{n} \rightarrow 0$ となるので、
\lim_{n \to \infty}E_n = \lim_{n \to \infty}\frac{1 - \beta^{n}}{1 - \beta} = \frac{1}{1 - \beta} = Nとなります。これは無限のデータを本質的なデータ空間に写像した場合、そのデータ数は$N$に収束する事を表しています。
次に、$\beta = 0$ $(N = 1)$の場合をみてみると、
E_{n} = (1 - 0^n) / (1 - 0) = 1となり、$\beta = 0$では、全てのデータは本質的には全て同じものである事がわかります。
また、$\beta \rightarrow 1$ $(N \rightarrow \infty)$の場合は、
f(\beta) = 1 - \beta^n, \quad g(\beta) = 1 - \betaとすると、
f'(\beta) = -n \beta^{n-1}, \quad g'(\beta) = -1ロピタルの定理より、
\lim_{\beta \to 1} E_n = \lim_{\beta \to 1} \frac{f(\beta)}{g(\beta)} = \lim_{\beta \to 1} \frac{f'(\beta)}{g'(\beta)} = \lim_{\beta \to 1} \frac{(-n \beta^{n-1})}{(-1)} = nとなります。したがって $\beta \rightarrow 1$では、全てのデータは本質的にもユニークであり、重複がない状態である事がわかります。
実際のデータセットの場合
クラス$y$の学習データの実データ数を$n_y$とすると、クラス$y$の本質的なデータ数 $E_{n_y}$は、
E_{n_y} = (1 - \beta_y^{n_y})/(1 - \beta_y) \\ ただし、 \beta_y = (N_y - 1)/N_yとなります。しかし、クラス$y$についての周辺情報がないため、$N_y$(クラスyを本質的に表現できるデータ数の最大値)を正確に求めるのは極めて難しい作業です。そこで、各クラスの$N_y$は、データセットの画素数や学習するネットワーク構造など、すべてのクラスに共通するもののみに依存すると仮定し、$N_y = N$, $\beta_y = \beta$として、全クラスで同じ値を使います。すると、$E_{n_y}$は下記のようになります。
E_{n_y} = (1 - \beta^{n_y})/(1 - \beta) \\ ただし、 \beta = (N - 1)/N
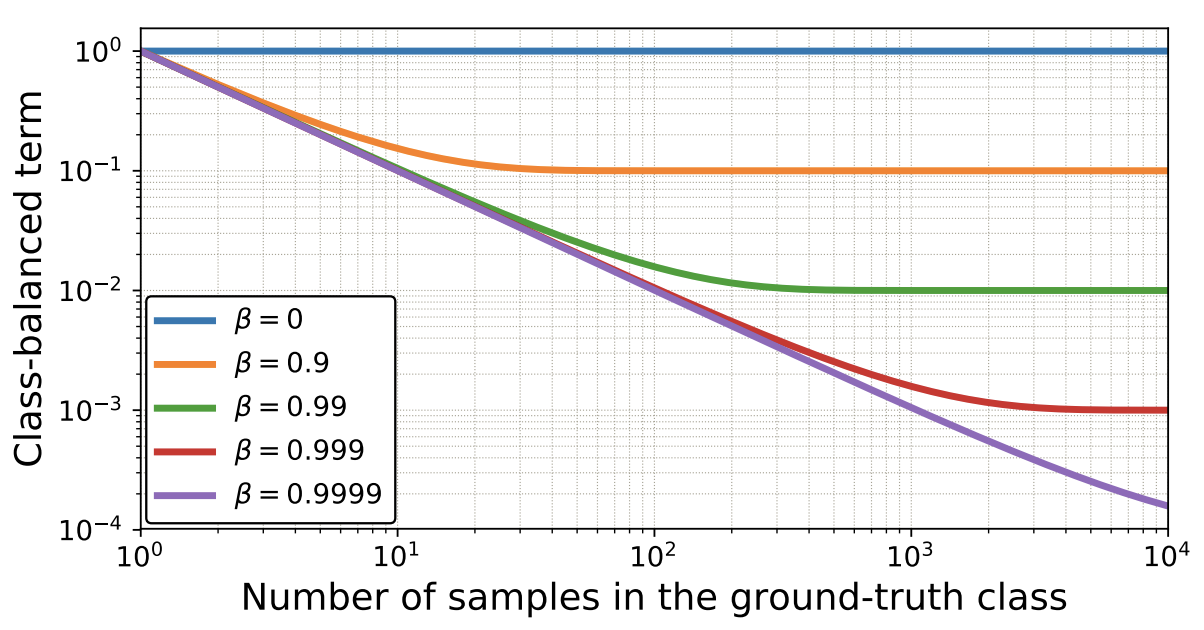
下図は $\beta$の値によって、$n_y$と$E_{n_y}$の関係がどのように変化するのかを可視化したグラフになります。横軸が$n_y$で縦軸が$E_{n_y}$です。
Class Balanced Loss
InverseClassFrequencyLossでは、クラスのデータ数の逆数を重みとしてバランシングしていましたが、このクラスのデータ数の部分を本質的なクラスのデータ数 $E_{n_y}$に置き換える事で、ClassBalancedLoss になります。
SoftmaxCrossEntropyLoss を ClassBalanced 化すると下記のようになります。
\textbf{CB}_{softmax}(\hspace{2pt}\boldsymbol{p}, \boldsymbol{m}) = -\sum_{i=1}^{B} \frac{1}{E_{n_{m_i}}} log(p_{m_i}) = -\sum_{i=1}^{B} \frac{1 - \beta}{1 - \beta^{n_{m_i}}} log(p_{m_i})FocalLoss を ClassBalanced 化すると下記のようになります。
\textbf{CB}_{focal}(\hspace{2pt}\boldsymbol{p}, \boldsymbol{m}) = -\frac{1}{E_{n_{m_i}}} \sum_{i=1}^{B} (1-p_{m_i})^\gamma log(p_{m_i}) = -\frac{1 - \beta}{1 - \beta^{n_{m_i}}} \sum_{i=1}^{B} (1-p_{m_i})^\gamma log(p_{m_i})$\beta$はハイパーパラメータで、値の範囲は$0 \leqq \beta < 1$になります。$\beta = 0$は重みを全く掛けていない状態に相当し、$\beta \rightarrow 1$はInverseClassFrequencyLossと同じ状態に相当します。
検証
ClassBalancedSoftmaxは、$\beta\in \{0.9, 0.99, 0.999, 0.9999\}$ の4パターンで検証してみました。
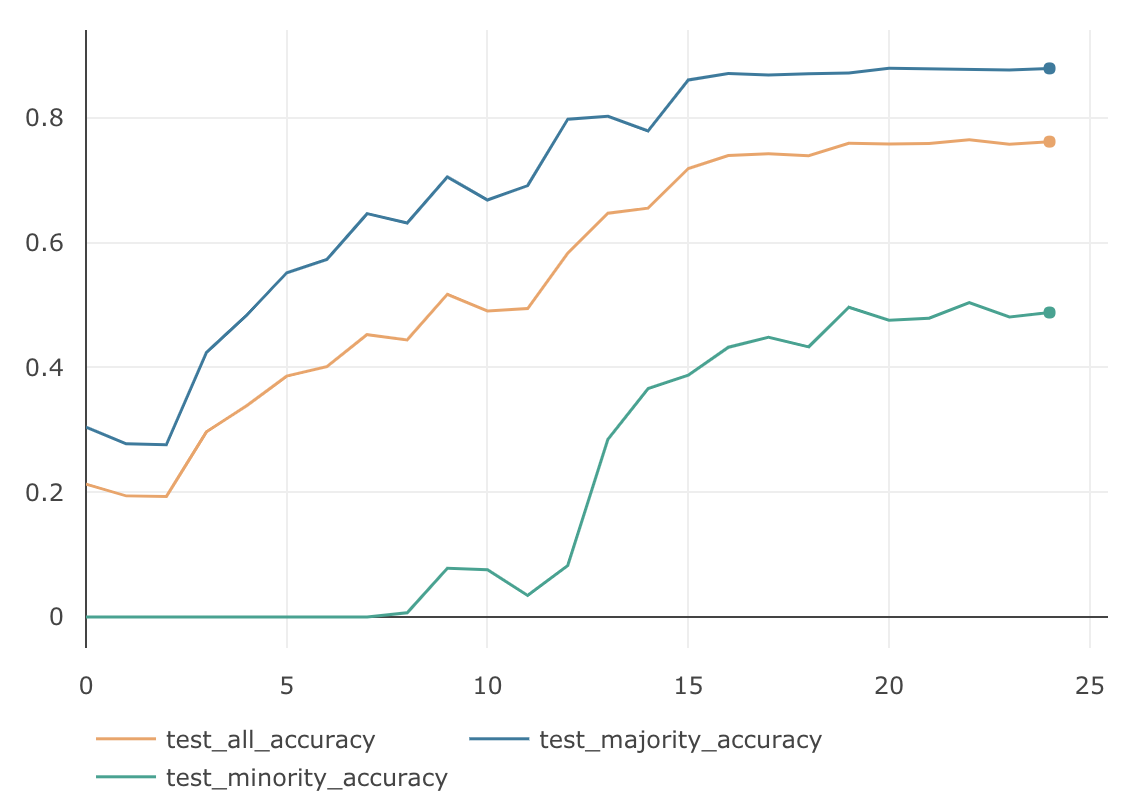
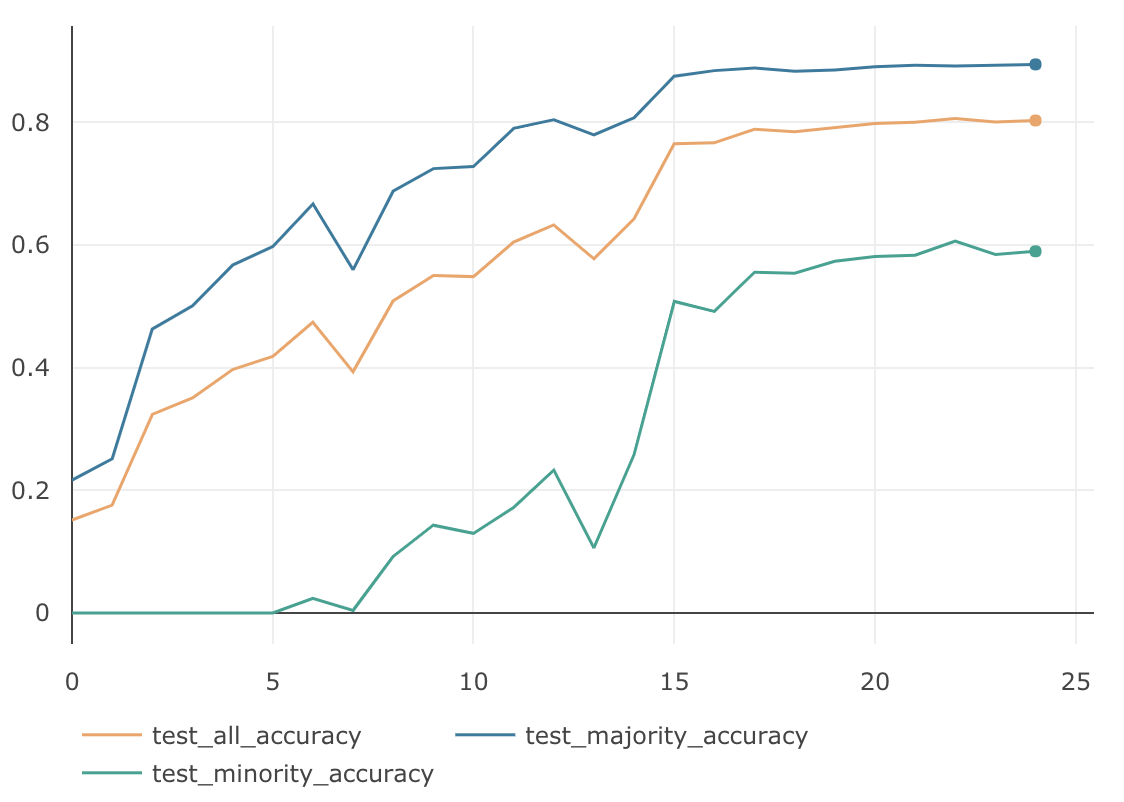
$\beta$ MajorityのAccuracy MinorityのAccuracy AllのAccuracy 0.9 88.66 % 49.23 % 76.83 % 0.99 89.45 % 58.67 % 80.22 % 0.999 86.76 % 66.37 % 80.64 % 0.9999 80.94 % 75.23 % 79.23 % $\beta=0.999$の時に、AllのAccuracyは $80.64$% となり、今までのどの検証よりも良い結果となっています。下記がそのグラフです。
ClassBalancedFocalLossは、$\gamma=1.0$固定として、$\beta\in \{0.9, 0.99, 0.999, 0.9999\}$ の4パターンで検証してみました。
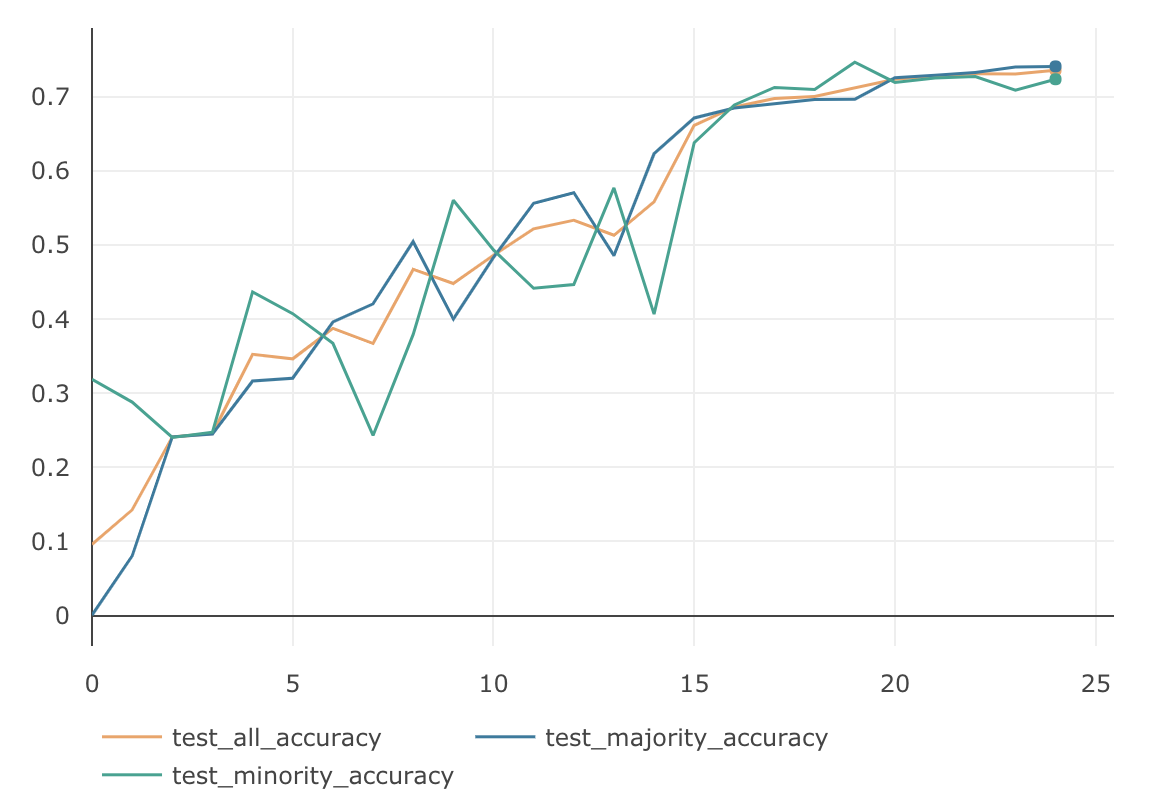
$\beta$ $\gamma$ MajorityのAccuracy MinorityのAccuracy AllのAccuracy 0.9 1.0 88.67 % 53.70 % 78.18 % 0.99 1.0 89.42 % 60.63 % 80.60 % 0.999 1.0 85.11 % 64.70 % 78.99 % 0.9999 1.0 72.40 % 62.67 % 69.48 % $\beta=0.99$の時に、AllのAccuracyは $80.60$% となり、ClassBalancedSoftmaxの最高値とほぼ同等の精度となりました。下記がグラフになります。
まとめ
ClassBalancedな損失関数を使えば、SoftmaxCrossEntropyやFocalLoss、どちらの場合も精度が向上する事が確認できました。また、理論部分に関しても証明付きで綺麗にまとまっており、とても読みやすい論文となっています。ただ、本質的なデータ空間という、独特な抽象概念を土台に理論が組み立てられているため、$\beta$ の値をあらかじめ正確に決めることは、原理的に不可能です。したがって、実際のデータに対してこの損失関数を適用する場合は、いくらか学習を試しながら、ハイパーパラメータ$\beta$の値を探査し、最適な値を決める必要があります。
- 投稿日:2019-02-15T14:59:34+09:00
不均衡データを損失関数で攻略してみる
はじめに
研究の用途においては、データセットによる精度への影響を避けるため、各クラスのデータ数が同じくらいの均衡なデータセットがよく利用されています。しかし、いざ実サービスで学習用のデータを集めようとしても、全てのクラスで同じ数のデータを集めるのは難しい場合があります。そのような不均衡なデータセットに対して、2019/01/16にarxivで発表があった Class-Balanced Loss や Focal Lossなど、損失関数の工夫だけでどこまで精度を上げられるのか検証してみました。
データ不均衡による精度の劣化
CIFAR-10データセットを使って学習および検証を行いました。学習データはCIFAR-10の訓練用画像 50,000枚(各class 5,000枚)からautomobileとdeerとfrogのデータを250枚に減らして、意図的に不均衡にしたものを使用しています。検証にはCIFAR-10の検証用画像 10,000枚(各class 1,000枚)を使います。学習時のデータ数に基づいて、automobileとdeerとfrogの minorityグループ、それ以外の majorityグループ、10,000枚全てを使ったallグループの3つに分け、それぞれのグループ毎に検証して、正解率(Accuracy)を計測しました。学習データと検証データの内訳は下記の表のとおりになります。
class 学習データ 検証データ(minority) 検証データ(majority) 検証データ(all) 0 airplane 5,000 0 1,000 1,000 1 automobile 250 1,000 0 1,000 2 bird 5,000 0 1,000 1,000 3 cat 5,000 0 1,000 1,000 4 deer 250 1,000 0 1,000 5 dog 5,000 0 1,000 1,000 6 frog 250 1,000 0 1,000 7 horse 5,000 0 1,000 1,000 8 ship 5,000 0 1,000 1,000 9 truck 5,000 0 1,000 1,000 ネットワークの構造はResNet18で、全ての検証は下記の要件に従って学習を行います。
Epoch BatchSize Optimizer LearningRate 25 128 SGD Momentum
Momentum=0.9
WeightDecay=0.00050.1(1〜15 epoch)
0.01(16〜20 epoch)
0.001(21〜25 epoch)ちなみに、不均衡ではない普通のCIFAR-10に対し、一般的な損失関数 SoftmaxCrossEntropy で学習した結果は次のようになりました。全てのグループでAccuracyが90%を超えています。
MajorityのAccuracy MinorityのAccuracy AllのAccuracy 90.23 % 94.4 % 91.4 % 次は、これを不均衡データにした場合の結果になります。
MajorityのAccuracy MinorityのAccuracy AllのAccuracy 87.93 % 50.4 % 76.5 % 均衡なデータの場合に比べて、Minorityグループの精度が極端に悪く、それにひきずられる形でAllグループの精度も76.5%と悪くなりました。
データ数の逆数でバランシング
損失関数の工夫として、クラスのデータ数の逆数を重みとして掛けて、Lossへの寄与率をクラスのデータ数に反比例するように調節する手法がよく使われています。クラス数が$C$で、各クラスのラベルが $y\in \{1, 2,...,C\}$であるデータセットについて考えてみます。モデルが出力するSoftmaxの値を$ \boldsymbol{p} =[p_1, p_2,..., p_C]^T$, ただし $p_i \in [0,1] \hspace{3pt} \forall \hspace{3pt} i$ 。学習時のミニバッチ数を$B$ 。ミニバッチ内の正解ラベルを$ \boldsymbol{m} =[m_1, m_2,..., m_B]^T$,ただし $m_i \in \{1, 2,...,C\} $ 。 その場合、通常のSoftmaxCrossEntropyLossは下記のようになります。
\textbf{CE}(\hspace{2pt}\boldsymbol{p}, \boldsymbol{m}) = -\sum_{i=1}^{B}log(p_{m_i}) \tag{1}クラス$y$の学習データの数を$n_y$とすると、クラス数の逆数でバランシングした損失関数InverseClassFrequencyLossは下記のように書けます。
\textbf{ICF}(\hspace{2pt}\boldsymbol{p}, \boldsymbol{m}) = -\sum_{i=1}^{B} \frac{1}{n_{m_i}} log(p_{m_i}) \tag{2}InverseClassFrequencyLossの検証結果は次のようになりました。(実際の検証では、ミニバッチ単位のLossの出力の大きさを通常のSoftmaxCrossEntropyLossと揃えるために、加重平均をとっています。加重平均をとっても、各クラスの全体に対する寄与率は変わりません。)
MajorityのAccuracy MinorityのAccuracy AllのAccuracy 74.1 % 74.67 % 73.58 % 通常のSoftmaxCrossEntropyLossに比べてMinorityグループの精度がだいぶ高くなりました。ただMajorityグループの精度は落ちてしまったため、Allグループの精度は悪くなっています。
Focal Loss
OneStageのObject Detectionの学習において、背景(EasyNegative)がほとんどであり、クラスが不均衡状態になっているという仮説のもと、それを自動的にコスト調節してくれる損失関数として、Facebook AI Researchが提案した手法1です。ICCV2017で発表されStudent Best Paperに選ばれています。
上の図が示すように、通常の損失関数に$(1-p_t)^\gamma$が係数として乗じられています。したがって、$p_t$が小さく0に近い場合(大きく間違っている場合)は、この係数は1に近いため通常の損失関数の値に近くなります。逆に$p_t$が大きく1に近い場合(ほとんど間違っていない場合)は、係数は0に近いため損失関数の値はLossとしてほとんど計上されなくなります。このように損失関数の係数部分が自動的にEasyNegativeExampleをDownWeightし、結果としてHardNegativeに比重が置かれるように機能します。
このFocalLossを多クラス分類のSoftmaxCrossEntropyに適応すると下記のように書けます。
\textbf{FL}(\hspace{2pt}\boldsymbol{p}, \boldsymbol{m}) = -\sum_{i=1}^{B} (1-p_{m_i})^\gamma log(p_{m_i}) \tag{3}$\gamma\in \{1.0, 1.5, 2.0\}$ の3パターンで検証してみました。
$\gamma$ MajorityのAccuracy MinorityのAccuracy AllのAccuracy 1.0 88.47 % 55.03 % 78.33 % 1.5 87.91 % 53.56 % 77.61 % 2.0 86.37 % 49.53 % 75.32 % InverseClassFrequencyLossに比べると、Minorityグループの精度は全体的に落ちていますが、Majorityグループの精度は全て高くなっています。$\gamma=1.0$のAllグループの精度は、これまでの不均衡データ検証の中では最も良い結果となりました。下図は $\gamma=1.0$のグラフになります。
本質的なクラスのデータ数でバランシング
先述した InverseClassFrequencyLossの検証結果からもわかる通り、クラスのデータ数の逆数を重みとして掛ける事で、不均衡データに対するバランシングの効果が期待できます。この考え方をさらに深掘りした Class-Balanced Loss Based on Effective Number of Samples2 という興味深い論文がarxivに上がっていたので紹介します。この論文では、InverseClassFrequencyLossで利用しているクラスのデータ数というのは、実は本質的なデータ数ではないという考え方を元に理論が構築されています。どういうことかと言うと、例えば、class0のデータが800枚、class1のデータが500枚からなるデータセットがあるとします。それぞれのclassをData Augmentationして、class0もclass1も1,000枚に増やした場合、表面上のデータ数はどちらも1,000枚と同じになりますが、本質的なデータ数という意味ではこの2つは違います。このように実データ数と本質的なデータ数には差があるという事です。
もう一つ。ある画像から特徴ベクトルを抽出し、その特徴ベクトルを分類器にかける事で、画像のクラス分類するといったケースを考えてみます。この場合、分類に利用している特徴ベクトルは、ベクトルの次元数が固定です。したがって、そのベクトルの表現パターン数以上のデータ表現はできません。つまり、どんなに多くの画像を集めたとしても、この分類器にとってのデータ数は、ベクトルの表現量を超える事はないという事です。これもまた、実データ数と本質的なデータ数には差があるという例となります。
この差は、タスクの種類やデータセットの特性、およびその周辺情報によっても変わってくるため、拡大や回転したものを同じデータ扱いにするのか、同じオブジェクトが写っていれば同じデータ扱いにするのか、これらは一概には決められません。しかし、ここで重要なのは、どのようなデータセットにおいても、少なからず実データ数と本質的なデータ数には差があるという事です。
したがって、データセットのデータを、全てユニークなデータとしてカウントした値を不均衡データのバランシングに使うのではなく、本質的なデータ数に配慮した値を用いてデータバランシングを行うべき、というのが本論文の主張になります。理論
本質的なデータ数が具体的にどのような値になるのか説明します。本質的なデータ数の最大値を$N$とおきます。例えば、車の画像が無限にあったとして、全ての車の画像を本質的なデータ空間に写像した場合、$N$パターンとなります。実データ数を$n$、その本質的なデータ数を$E_n$とすると、下記のように書けます。
E_n = (1 - \beta^n)/(1 - \beta) \tag{4} \\ ただし、 \beta = (N - 1)/Nと、いきなり式が出てきましたが、数学的帰納法を使ってこれを証明します。
まず、$E_1$は重なりようがないので、$E_1 = 1$となります。次に、$E_{n-1}$で成立する場合に$E_n$でも成立するかを考える必要がありますが、その前に下の図を見てください。これは、$n$個目のデータをサンプリングした際の、本質的なデータ空間の変化の様子を示した概念図になります。破線の領域は本質的なデータ空間を表しています。したがって、この領域のデータ数は$N$です。灰色の領域は$n-1$個の実データが写像された本質的なデータ空間の領域になります。したがって、この領域のデータ数は$E_{n-1}$です。次に、$n$個目のデータを本質的なデータ空間に写像しようとした場合、$E_{n-1}/N$の確率で灰色の領域に入ります。
したがって、p = \frac{E_{n-1}}{N}とすると、$E_n$の期待値は下記のようになります。
E_n = pE_{n-1} + (1-p)(E_{n-1} + 1) = 1 + \frac{N - 1}{N}E_{n-1} \tag{5}ここで、式$(4)$が$E_{n-1}$では成立すると仮定すると、
E_{n-1} =(1 - \beta^{n-1})/(1 - \beta) \tag{6}と書け、式$(5)$の$E_{n-1}$に代入すると、
E_{n} =1 + \frac{N - 1}{N}E_{n-1} = 1 + \beta \frac{1 - \beta^{n-1}}{1 - \beta} = \frac{1 - \beta + \beta - \beta^{n}}{1 - \beta} = \frac{1 - \beta^{n}}{1 - \beta} \tag{7}となります。$E_n$の場合も式$(4)$を満たすことがわかったので、証明はこれで完了となります。
式$(4)$にあるように、$\beta = (N - 1)/N$とおいており、$N\geqq1$なので、$\beta$の取り得る値の範囲は$0 \leqq \beta < 1$です。したがって、$n \rightarrow \infty$ の場合 $\beta^{n} \rightarrow 0$ となるので、
\lim_{n \to \infty}E_n = \lim_{n \to \infty}\frac{1 - \beta^{n}}{1 - \beta} = \frac{1}{1 - \beta} = Nとなります。これは無限のデータを本質的なデータ空間に写像した場合、そのデータ数は$N$に収束する事を表しています。
次に、$\beta = 0$ $(N = 1)$の場合をみてみると、
E_{n} = (1 - 0^n) / (1 - 0) = 1となり、$\beta = 0$では、全てのデータは本質的には全て同じものである事がわかります。
また、$\beta \rightarrow 1$ $(N \rightarrow \infty)$の場合は、
f(\beta) = 1 - \beta^n, \quad g(\beta) = 1 - \betaとすると、
f'(\beta) = -n \beta^{n-1}, \quad g'(\beta) = -1ロピタルの定理より、
\lim_{\beta \to 1} E_n = \lim_{\beta \to 1} \frac{f(\beta)}{g(\beta)} = \lim_{\beta \to 1} \frac{f'(\beta)}{g'(\beta)} = \lim_{\beta \to 1} \frac{(-n \beta^{n-1})}{(-1)} = nとなります。したがって $\beta \rightarrow 1$では、全てのデータは本質的にもユニークであり、重複がない状態である事がわかります。
実際のデータセットの場合
クラス$y$の学習データの実データ数を$n_y$とすると、クラス$y$の本質的なデータ数 $E_{n_y}$は、
E_{n_y} = (1 - \beta_y^{n_y})/(1 - \beta_y) \\ ただし、 \beta_y = (N_y - 1)/N_yとなります。しかし、クラス$y$についての周辺情報がないため、$N_y$(クラスyを本質的に表現できるデータ数の最大値)を正確に求めるのは極めて難しい作業です。そこで、各クラスの$N_y$は、データセットの画素数や学習するネットワーク構造など、すべてのクラスに共通するもののみに依存すると仮定し、$N_y = N$, $\beta_y = \beta$として、全クラスで同じ値を使います。すると、$E_{n_y}$は下記のようになります。
E_{n_y} = (1 - \beta^{n_y})/(1 - \beta) \\ ただし、 \beta = (N - 1)/N
下図は $\beta$の値によって、$n_y$と$E_{n_y}$の関係がどのように変化するのかを可視化したグラフになります。横軸が$n_y$で縦軸が$E_{n_y}$です。
Class Balanced Loss
InverseClassFrequencyLossでは、クラスのデータ数の逆数を重みとしてバランシングしていましたが、このクラスのデータ数の部分を本質的なクラスのデータ数 $E_{n_y}$に置き換える事で、ClassBalancedLoss になります。
SoftmaxCrossEntropyLoss を ClassBalanced 化すると下記のようになります。
\textbf{CB}_{softmax}(\hspace{2pt}\boldsymbol{p}, \boldsymbol{m}) = -\sum_{i=1}^{B} \frac{1}{E_{n_{m_i}}} log(p_{m_i}) = -\sum_{i=1}^{B} \frac{1 - \beta}{1 - \beta^{n_{m_i}}} log(p_{m_i})FocalLoss を ClassBalanced 化すると下記のようになります。
\textbf{CB}_{focal}(\hspace{2pt}\boldsymbol{p}, \boldsymbol{m}) = -\frac{1}{E_{n_{m_i}}} \sum_{i=1}^{B} (1-p_{m_i})^\gamma log(p_{m_i}) = -\frac{1 - \beta}{1 - \beta^{n_{m_i}}} \sum_{i=1}^{B} (1-p_{m_i})^\gamma log(p_{m_i})$\beta$はハイパーパラメータで、値の範囲は$0 \leqq \beta < 1$になります。$\beta = 0$は重みを全く掛けていない状態に相当し、$\beta \rightarrow 1$はInverseClassFrequencyLossと同じ状態に相当します。
検証
ClassBalancedSoftmaxは、$\beta\in \{0.9, 0.99, 0.999, 0.9999\}$ の4パターンで検証してみました。
$\beta$ MajorityのAccuracy MinorityのAccuracy AllのAccuracy 0.9 88.66 % 49.23 % 76.83 % 0.99 89.45 % 58.67 % 80.22 % 0.999 86.76 % 66.37 % 80.64 % 0.9999 80.94 % 75.23 % 79.23 % $\beta=0.999$の時に、AllのAccuracyは $80.64$% となり、今までのどの検証よりも良い結果となっています。下記がそのグラフです。
ClassBalancedFocalLossは、$\gamma=1.0$固定として、$\beta\in \{0.9, 0.99, 0.999, 0.9999\}$ の4パターンで検証してみました。
$\beta$ $\gamma$ MajorityのAccuracy MinorityのAccuracy AllのAccuracy 0.9 1.0 88.67 % 53.70 % 78.18 % 0.99 1.0 89.42 % 60.63 % 80.60 % 0.999 1.0 85.11 % 64.70 % 78.99 % 0.9999 1.0 72.40 % 62.67 % 69.48 % $\beta=0.99$の時に、AllのAccuracyは $80.60$% となり、ClassBalancedSoftmaxの最高値とほぼ同等の精度となりました。下記がグラフになります。
まとめ
ClassBalancedな損失関数を使えば、SoftmaxCrossEntropyやFocalLoss、どちらの場合も精度が向上する事が確認できました。また、理論部分に関しても証明付きで綺麗にまとまっており、とても読みやすい論文となっています。ただ、本質的なデータ空間という、独特な抽象概念を土台に理論が組み立てられているため、$\beta$ の値をあらかじめ正確に決めることは、原理的に不可能です。したがって、実際のデータに対してこの損失関数を適用する場合は、いくらか学習を試しながら、ハイパーパラメータ$\beta$の値を探査し、最適な値を決める必要があります。
- 投稿日:2019-02-15T14:06:37+09:00
RealNVPの論文を読んだので要約とメモ
Density estimation using Real NVP(Laurent Dinh, Jascha Sohl-Dickstein, Samy Bengio. 2016)を読んだので要約とメモ。筆者の理解と疑問を青色でメモしている。
一言で言うと、画像生成用に拡張したNICE。
カップリングレイヤがアフィンになり、内部で2種類のマスクとCNNを使用。評価はbits/dimensionでVAE,DRAWの変種と互角。PixelRNNには及ばない。NICEより生成画像がきれい。先にNICE: Non-linear Independent Components Estimation(Laurent Dinh, David Krueger, Yoshua Bengio. 2014)を読んだほうが理解しやすい。
本文
概要
機械学習において確率的モデルの教師なし学習は中心的だがチャレンジングな問題である。特に、学習、サンプリング、推定、評価が容易なモデル設計することはこの問題を解く上で重要である。本論文では実数値非体積保存(real-valued non-volume preserving (real NVP))変換と呼ぶ、強力な、安定的で可逆な、学習可能変換を用いてそのようなモデル(学習等が容易な確率的モデル)を拡張する。これは対数尤度を直接計算でき、サンプリング、潜在変数の推定が効率的に直接でき、潜在空間が解釈可能である。4つのデータセットを使って、サンプリングにより自然な画像をモデリングする能力、対数尤度の評価、潜在変数の操作を示す。
1. イントロ
表現学習のドメインは教師あり学習の進歩によって非常に発達した。しかし教師なし学習は巨大なラベルなしデータを利用し、これらの進歩を、そうでないならば非効率または不可能な形式に拡張できるポテンシャルを持っている。教師ありの進歩を使って教師なしも進歩できる
教師なし学習の原理的な手法の一つに確率的生成モデリングがある。それらは新しいコンテンツを作る能力だけでなく、幅広い再構成の能力があり、その応用は画像修復[61,46,59]、ノイズ除去[3]、彩色[71]、超解像[9]などがある。
関心のあるデータは一般に高次元で構造化されており、このドメインのチャレンジはその複雑性を捉えるだけ強力で、なお訓練可能なモデルを作ることである。本論文では表現力が強く、かつ扱いやすい高次元データのモデリング手法であるreal-valued non-volume preserving (real NVP) transformationsを導入してこの問題に取り組む。
本モデルは効率的な直接の推定、サンプリング、データ点の対数密度推定ができる。さらに、本アーキテクチャはモデルが抽出した階層構造の特徴から、直接・効率的な入力画像の再構成ができる。
2. 関連研究
確率的生成モデルの多くの研究が対数尤度での訓練にフォーカスしている。
[無向グラフモデル]
- 最大対数尤度モデルの一種はRestricted Boltzmann Machines [58]やDeep Boltzmann Machines [53]といった、確率的無向グラフと呼ばれるものである。これらのモデルは、潜在変数での効率的な直接または近似の事後確率推定のために、彼ら自体の2部構造が持つ条件付き独立の性質を利用して訓練する。しかし、潜在変数上での、関連する周辺分布が計算できないために、評価、サンプリングでMean Field inferenceやMarkov Chain Monte Carloのような近似を使わざるをえない。これらはそのような複雑なモデルでは収束時間が確定せず、相関の高いサンプルを生成する結果になる事が多い。似たようなサンプルになる? さらに、これらの近似はモデルのパフォーマンスを妨げることもある[7]。
[有向グラフモデル(VAE)]
- これに対して有向グラフモデルは伝承サンプリングの観点から定義されており、概念的にも計算の簡単さでも魅力がある。しかし無向グラフモデルの持つ条件付き独立の構造が欠けており、潜在変数上の直接および近似事後確率推定が面倒になる[56]。近年のstochastic variational inference[27]とamortized inference[13, 43, 35, 49]の進歩により対数尤度の変分下限を最大化することでディープな有向グラフモデルの学習と近似推定が効率的になった[45]。特に、variational autoencoder algorithm [35, 49]はガウス分布の潜在変数zをサンプルxにマップする生成ネットワークと、それに対応した、サンプルxを意味のある潜在空間zにマップする近似推定ネットワークをreparametrization trick [68]を利用して同時に学習する。それらの近年のディープニューラルネットにおけるbackpropagation [51, 39]の進歩を利用した成功はスピーチ合成[12]から言語モデリング[8]までいくつかの応用に適用されている。しかし、推定処理における近似は高次元のディープな表現を学習する能力を制限しており、近似推定を改善する近年の研究の動機となっている[42, 48, 55, 63, 10, 59, 34]。
[自己回帰モデル]
- そのような近似は潜在変数を捨てれば全く回避できる。自己回帰モデル(Autoregressive models[18, 6, 37, 20])は訓練の柔軟性を保持しながらこの戦略を実装できる。この種のアルゴリズムは、次元上での固定の順番によって確率論のチェインルールを使うことで、結合分布を条件付き分布に分解してモデリングできる。これにより対数尤度評価とサンプリングが簡単になる。この辺よくわからないこの分野の最近の研究はstate-of-the-artな画像生成モデル[61, 46]や言語モデル[32]を学習するため、リカレントネットワーク[51]、とくにLSTM[26]の近年の進歩とresidual networks [25, 24]を利用している。次元の順番は、任意なこともあるが、モデルの訓練で重要になりうる[66]。この種のモデルは時系列になるため、計算効率は制限される。たとえば、サンプリング処理が並列化できないため、スピーチ・音楽合成やリアルタイムレンダリングといった応用では面倒が起きる。加えて、自己回帰モデルには自然な潜在表現がなく、また半教師あり学習に利用可能かどうかは示されていない。
[GAN]
- 一方、Generative Adversarial Networks (GANs) [21]は最大尤度の原理を全く回避して微分可能な生成ネットワークを訓練できる。代わりに生成ネットワークには本物のデータとサンプルとを識別するディスクリミネータネットワークが関係してくる。計算が難しい対数尤度ではなく、ディスクリミネータは生成ネットに敵対する形で訓練シグナルを送る。訓練が成功したGAN[21, 15, 47]はくっきりしたリアルなサンプルを生成できる[38]。しかし、生成サンプルの多様性を測る尺度は現在のところ扱いづらい[62, 22, 30]。加えて、訓練が不安定[47]であり、発散を防ぐために慎重なハイパラのチューニングが必要となる。
潜在変数$z \sim p_Z$をサンプル$x \sim p_X$にマップする生成ネットワークgを訓練するには、理論的にはGANのディスクリミネータやVAEの近似推定は必要ない。実際、gが全単射なら、次の変数変換の式を使って最大尤度で訓練できる。
p_X(x) = p_Z(z) \left| det \bigl( \frac{\partial{g(z)}}{\partial{z^{T}}} \bigr)\right|^{-1} \tag{1}この式は独立成分分析(ICA) [4, 28], gaussianization [14, 11],deep density models[5, 50, 17, 3]などのいくつかの論文で議論されている。nonlinear ICA solutions [29]の証明によれば、自己回帰モデルは最大尤度非線形ICAの計算可能なインスタンスだとみなすことができ、残り(residual)は独立要素に対応する。residualが何を意味するのかわからない。独立成分分析いずれ調べる。
しかし、変数変換のナイーブな応用は計算コストが高く、条件が悪いため、この種のラージスケールモデルは一般的な使用はできない。3. モデルの定義
本論文では、高次元連続空間で最大尤度を使って高度に非線形なモデルを学習する問題に取り組む。対数尤度を最適化するため、変数変換を使って、連続データ上で対数尤度計算を可能にするもっと柔軟なアーキテクチャを導入する。本論文の先行研究である[17](Nice: non-linear independent components estimation)に基づき、扱いやすい直接の密度評価と推定を可能にする強力な全単射な関数を定義する。さらに、導かれたコスト関数は固定形式の二乗誤差[38,47]のような再構成誤差に依存せず、結果としてサンプルがシャープになる。二乗誤差を使うと画像がぼやけることが知られている。
また、この柔軟性はマルチレベルの抽象化で非常に深いマルチスケール構造を定義するためにbatch normalization [31]とresidual networks [24, 25]における最近の進歩を利用できるようする。3.1. 変数変換の式
観測されたデータ変数$x \in X$、潜在変数$z \in Z$上のシンプルな事前確率分布$p_Z$、全単射な$f:X \rightarrow Z$($g=f^{-1}$とする)があり、変数変換の式はXにおけるモデル分布を次のように定義する。
\begin{align} p_X(x)&=p_Z(f(x))\left| det \bigl( \frac{\partial{f(x)}}{\partial{x^T}} \bigr) \right| \tag{2} \\ log(p_X(x))&=log(p_Z(f(x))) + log \Bigl( \left| det \bigl( \frac{\partial{f(x)}}{\partial{x^T}} \bigr) \right| \Bigr) \tag{3} \end{align}ここで$\frac{\partial{f(x)}}{\partial{x^T}} $はxにおけるfのヤコビ行列。
(3)は(2)の両辺にlogをつけたもの結果の分布からサンプルそのものは逆変換サンプリング[16]を使って生成できる。(逆変換サンプリングは$f^{-1}$を使って潜在変数を逆変換してサンプルに戻すやつ。[16]は未読。
サンプル$z\sim p_Z$は潜在空間から得られ、その逆の画像$x=f^{-1}(z)=g(z)$は元の空間でサンプルを生成する。点xにおける確率密度の計算はその像であるf(x)の確率密度を計算し、関連するヤコビ行列の行列式$\frac{\partial{f(x)}}{\partial{x^T}}$を掛けることで実現できる。(2)式のことを言っている。
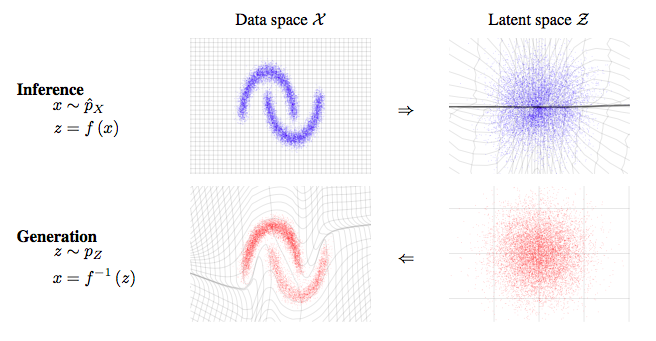
図1も参照。直接的で効率的な推定は正確で高速なモデルの評価を可能にする。
図1:RealNVPはデータ分布$\hat{p_X}$と潜在分布$p_Z$(一般的にはガウス分布)の間の可逆で、安定なマッピングを学習する。2次元のトイデータセットで学習されたマッピングを示す。関数$f(x)$は左上のデータ分布からサンプルxを右上の潜在分布からの近似サンプルzへ写像する。これはデータを受け取って潜在状態の推定を直接行うことに相当する。逆関数$f^{-1}(z)$はサンプルzを右下の潜在分布から左下のデータ分布からの近似サンプルxへ写像する。これはモデルからサンプルを生成することに対応する。$f(x), f^{-1}(x)$両方について$X$と$Z$の空間のグリッド線の変換も示されている。3.2. カップリングレイヤ
定義域と終域が高次元な関数のヤコビ行列の計算と、巨大な行列の行列式計算は計算コストが非常に高い。この事実は全単射な関数という制約と合わせて、(2)式で任意の分布をモデリングするのを非現実的にする。
[17]で示したように、関数$f$を慎重に設計すると、非常に柔軟で扱いやすい全単射なモデルを学習できる。変換のヤコビ行列の行列式の計算はこの原理を使って効率よく訓練するのに重要なので、本論文では三角行列の行列式はその対角要素の積として効率的に計算できるというシンプルな事実を利用する。
本論文ではシンプルな全単射の系列をスタックすることで、柔軟で扱いやすい全単射な関数を作る。各シンプルな全単射において、入力ベクトルの一部は逆が計算しやすい関数を使って更新される。しかしそれは入力ベクトルの残りと複雑な依存関係にある。各シンプルな全単射をアフィンカップリングレイヤと呼ぶ。D次元の入力xと、$d \lt D$があるとして、アフィンカップリングレイヤの出力yは次式。
\begin{align} y_{1:d}&=x_{1:d} \tag{4} \\ y_{d+1:D}&=x_{d+1:D} \odot exp(s(x_{1:d})) + t(x_{1:d}) \tag{5} \\ \end{align}入力ベクトルxの要素を[1:d]と[d+1:D]に分けて使っている
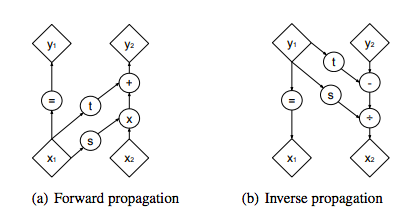
ここで$s$と$t$はスケールと平行移動を表す$R^{d} \mapsto R^{D-d}$の関数であり、$\odot$はアダマール積または要素ごとの積である(図2(a)参照)。
図2:順方向・逆方向伝播の計算グラフ。カップリングレイヤは入力ベクトルの一片である$x_1$に条件付けられた、スケーリング後に定数オフセットを加算するというシンプルで可逆な変換を、入力ベクトルのもう一つの部分$x_2$に対して適用する。性質がシンプルなので、この変換は簡単に逆を計算でき、行列式も簡単である。しかし、条件付きの性質があるので、関数sとtによってキャプチャされ、そうでなければ弱い関数が非常に増強される。sとtがあるから、シンプルだが表現力が強い関数になった。
順方向・逆方向操作の計算コストは等しい。3.3. 性質
この変換のヤコビ行列は
\frac{\partial{y}}{\partial{x^T}}= \begin{bmatrix} \mathbb{I}_d & 0 \\ \frac{\partial{y_{d+1:D}}}{\partial{x^T_{1:d}}} & diag(exp[s(x_{1:d})]) \end{bmatrix} \tag{6}$diag(exp[s(x_{1:d})])$は対角要素がベクトル$exp[s(x_{1:d})]$に対応する対角行列である。このヤコビ行列が三角行列であるという事実により、その行列式は効率的に$exp \left[ \sum_j s(x_{1:d}) \right]_j$として計算できる。カップリングレイヤのヤコビ行列の行列式計算はsやtのヤコビ行列の計算を含まないので、これらは好きなだけ複雑でよい。本論文ではディープCNNを使う。sとtの隠れ層はその入力や出力よりも要素数が多い。
確率モデルを定義する観点で、カップリングレイヤのその他の面白い性質として、その可逆性がある。実際、逆方向の計算が順方向の伝播より複雑になることはなく(図2(b)参照)、
\left\{ \begin{array}{ll} y_{1:d} &= x_{1:d} \\ y_{d+1:D} &= x_{d+1:D} \odot exp(s(x_{1:d}))+ t(x_{1:d}) \end{array} \right. \tag{7} \\\Leftrightarrow \left\{ \begin{array}{ll} x_{1:d} &= y_{1:d} \\ x_{d+1:D} &= (y_{d+1:D}-t(y_{1:d})) \odot exp(-s(y_{1:d})) \end{array} \right. \tag{8} \\(7)->(8)は$exp(s)$の逆が$exp(-s)$であることを使う
であり、このモデルではサンプリングが推定と同じくらい効率的であることを示している。カップリングレイヤの逆の計算はs,tの逆の計算を含まず、これらの関数は任意でよいことが確認できる。3.4. Masked convolution
任意の二値マスクbを使って分割が計算でき、yに関する関数形を使って次のように書ける。
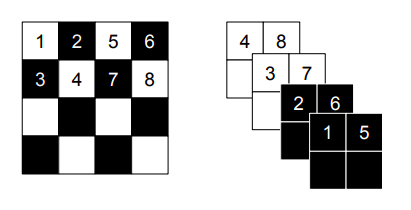
y=b \odot x +(1-b) \odot \bigl( x\odot exp(s(b\odot x)) + t(b\odot x) \bigr) \tag{9}画像の局所的な相関構造を利用するために2つの分割を使用する。空間的なチェッカーボードパターンと、チャネルごとのマスキングである(図3参照)。
空間的チェッカーボードのマスクは空間的な座標の和が奇数なら1、そうでなければ0である。x座標とy座標のインデックスの和が奇数の箇所は1。
チャネルごとマスクbは画像をチャネル次元で半分に分け、最初の半分は1、後は0。
ここで示したモデルでは、$s(\cdot),t(\cdot)$ともにrectifiedな畳み込みネットワークである。
図3:アフィンカップリングレイヤのマスキング手法。左は空間的チェッカーボードパターンマスク。右はチャネルごとマスク。絞り(squeezing)操作は4x4x1テンソル(左)を2x2x4テンソル(右)に縮める。絞り操作の前にチェッカーボードパターンはカップリングレイヤのために使用され、チャネルごとパターンはその後使用される。黒が1,白が。squeezingってなんだ?処理のどこかにsqueezeが入っていて、マスクはその前後で2種類とも利用される(マスク$\neq$squeeze)ということかな3.5. カップリングレイヤを結合する
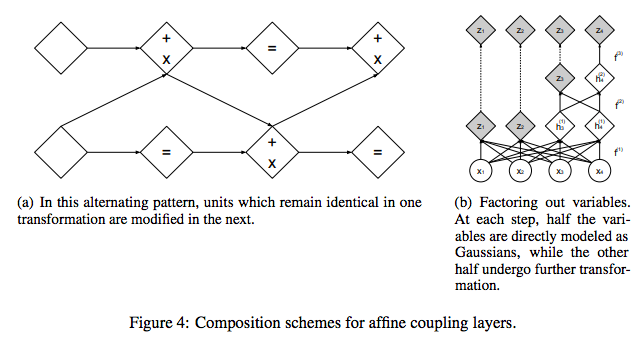
カップリングレイヤは強力だが、その順方向変換はいくつかの要素を不変のままにする。この困難はカップリングレイヤをかわりばんこに合成することで克服できる。つまり一つのカップリングレイヤで変更されなかった要素は次のレイヤで変更されるようにする(図4(a)参照)。
結果の関数のヤコビ行列の行列式は次の事実から計算可能である。\begin{align} \frac{\partial{(f_b \circ f_a)}}{\partial{x_a^T}}(x_a) &=\frac{\partial{f_a}}{\partial{x_a^T}}(x_a) \cdot \frac{\partial{f_b}}{\partial{x_a^T}}(x_b=f_a(x_a)) \tag{10}\\ det(A \cdot B)&=det(A)det(B) \tag{11} \end{align}(10)がわからない。$x_b$って何
同様に、逆も簡単に計算できる。
(f_b \circ f_a)^{-1} = f_a^{-1} \circ f_b^{-1} \tag{12}
図4:アフィンカップリングレイヤの合成方法
(a)かわりばんこのパターンにより、一つの変換では不変だったユニットが次で修正される。
(b)変数を除外する。各ステップで、変数の半分は直接ガウス分布としてモデリングされる。一方でもう半分は更に変換される。3.6. マルチスケールアーキテクチャ
squeezing操作を使ってマルチスケールアーキテクチャを実装する。この操作は各チャネルごとに、画像を2x2xcの部分正方形に分割し、その後それらを1x1x4cの部分正方形にreshapeする。squeezingはs x s x cのテンソルを$\frac{s}{2} \times \frac{s}{2} \times 4c$ のテンソルに変換する(図3参照)。
各スケールで、いくつかの操作を組み合わせて系列にする。最初に3つのカップリングレイヤとチェッカーボードマスクを交互に適用する。次にsqueezingする。最後にまた3つのカップリングレイヤとチャネルごとのマスキングを交互に適用する。チャネルごとのマスキングは結果の分割が前のチェッカーボードマスクと重複しないように選ばれる。チェッカーボードだと混ざらないのだろうか。マスクの目的は何?
最後のスケールでは、4つのカップリングレイヤとチェッカーボードマスクだけを交互に適用する。D次元のベクトルをすべてのカップリングレイヤを通して伝播させるのは、計算コスト・メモリコストにおいても、訓練が必要なパラメータ数においても厄介である。そこで[57]の設計に従い、一定間隔で次元の半分を除外(factor out)する((14)式を見よ)。(14)式から読みづらいが、左辺の(z,h)のうちzは除外することを言っている。この操作は再帰的に定義できる(図4(b)参照)。
\begin{align} h^{(0)}&=x \tag{13} \\ (z^{(i+1)}, h^{(i+1)}) &=f^{(i+1)}(h^{(i)}) \tag{14} \\ z^{L} &= f^{(L)}(h^{(L-1)}) \tag{15} \\ z&=(z^{(1)},...,z^{(L)}) \tag{16} \end{align}実験では、$i \leq L$についてこの操作を使用した。上記のカップリング-squeeze-カップリングの操作は$f^{(i)}$を計算するときにレイヤごとに実行される((14)式)。($f^{(i)}$の内部にカップリング〜が入っているという意味。)各レイヤで、空間解像度が減少するごとに、sとtの隠れ層の特徴数が2倍になる。s,tはCNNだから、チャネル方向に2倍にすることを言ってる。異なるスケールで除外された全ての変数は最後の変換の出力を得るために結合される((16)式)。
結果として、モデルは除外されるユニットを、より細かいスケール(前のレイヤ)でガウス分布化(Gaussianize)する必要がある。粗いスケール(後のレイヤ)で除外されるより前に。一般には粗いほうが前になる気がするが、スケールが細かい=低レベルな表現を見ている、という意味で細かいものが前と書いてあるんじゃないか。
図4(b)を見ると、次のレイヤでzになって除外されるユニットを、今のレイヤにおいて(今はまだhだが)gaussianizeするという意味だろう
これはより局所的で、精選された特徴に対応する、中間レベルの表現の定義になる[53,49]。付録D参照。さらに、前方のレイヤでGaussianizingとユニットの除外を行うことは誤差関数をネットワーク中に分散するという実践的なメリットがあり、中間分類器を使って中間レイヤをガイドする[40]ことと似た哲学に従っている。さらにモデルの計算量とメモリ使用を大きく減らすこともでき、より大きいモデルを訓練できる。
3.7. Batch normalization
訓練シグナルの伝播を更に改善するため、deep residual networks [24, 25], batch normalization [31], weight normalization [2, 54]をsとtで使う。付録Eで説明するが、最近のミニバッチの移動平均に基づく新しいbatch normalizationの変種を使用する。これは非常に小さいミニバッチで訓練すると、よりロバストになる。
batch normalizationをカップリングレイヤ全体の出力にも適用する。batch normalizationの効果は、各次元における線形のリスケーリングとして動作するので、ヤコビ行列の計算にも容易に取り込まれる。すなわち、推定されたバッチ統計量$\tilde{\mu}$と$\tilde{\sigma}^2$があって、リスケーリング関数
x \mapsto \frac{x-\tilde{\mu}}{\sqrt{\tilde{\sigma}^2+\epsilon}} \tag{17}はヤコビ行列の行列式
\bigl(\prod_i (\tilde{\sigma_i}^2+\epsilon) \bigr)^{-\frac{1}{2}} \tag{18}を持つ。
このbatch normalizationの形式は深層強化学習のreward normalization[44,65]に似たものである。4. 実験
4.1. 手順
(2)式のアルゴリズムは制限のない空間で分布を学習する方法を示している。一般的にはデータは大きさが限られている。例えば画像のピクセルは推奨されるjittering procedure[64,62](?)をの適用後、$[0,255]^{D}$の範囲に収まる。境界値の影響をへらすために、代わりにロジット(logit)($\alpha + (1-\alpha)\odot \frac{x}{256}$)の密度をモデリングする。$\alpha$はここでは0.5を使用した。対数尤度とbits per dimensionを計算するときはこの変換を考慮にいれた。CIFAR-10, CelebA, LSUNは訓練中に水平フリップでデータ拡張した。
モデルは4つの自然画像データセットで訓練した。CIFAR-10 [36], Imagenet [52], Large-scale Scene Understanding (LSUN) [70], CelebFaces Attributes (CelebA) [41]である。具体的には、Imagenetは32x32と64x64のダウンサンプル版[46]で訓練した。LSUNはbedroom, tower, church outdoorのカテゴリで訓練した。LSUNの手順は[47]同様で、短い辺が96pxになるように画像をダウンサンプルし、64x64のランダムクロップを適用した。CelebAでは[38]と同じ手順で、ほぼ中央の148x148のクロップを取り、それを64x64にリサイズした。
3.6節で説明したマルチスケールアーキテクチャを使用する。カップリングレイヤで、[46]で提案されたようにReLU活性化関数とスキップコネクションありのディープ畳み込みresidualネットワークを使用する。スケーリング関数sを計算するため、hyperbolic tangent関数を学習されたスケールに掛けて使用する。一方、平行移動関数tはaffine outputを持つ。(?)マルチスケールアーキテクチャは最後の入力が4x4xcテンソルになるまで再帰的に繰り返される。32x32の画像データセットについては、4個のresidual blockを使い、最初のカップリングレイヤについては隠れフィーチャマップが32個、チェッカーボードマスクを使用した。64x64画像ではresidual blockは2個だけ使用した。バッチサイズは64を使用。CIFAR-10は8個のresidual block, フィーチャマップは64, ダウンスケールは1回のみ。デフォルトパラメータのADAM[33]で最適化し、$5\cdot10^{-5}$の重みスケールパラメータで$L_2$正則化を使用した。
事前分布$p_Z$を等方性単位ノルムガウス分布(isotropic unit norm Gaussian)に設定した。しかし自己回帰モデルや、(目的関数に多少変更を加えた)VAEのように、訓練中に学習される分布を含めて$p_Z$にはどんな分布でも使用できる。
4.2. 結果
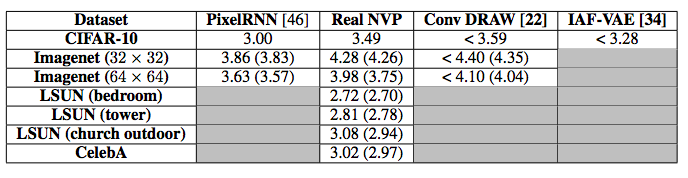
bits per dimensionの値を表1に示した。ベースラインのPixel RNN [46]より優れているとは言えないが、他の生成モデルとは互角である。パラメータ数の増加につれて性能が上がっていることがわかるため、より大きいモデルでは更に性能が上がると予想される。CelebAとLSUNでは、バリデーションセットのbits per dimensionは訓練中いたるところで減少しており、少し過学習があるとみられる。bits per dimension
表1: CIFAR-10, Imagenet, LSUN, CelebAのBits/dimの結果。CIFAR-10はテスト、それ以外はバリデーション(括弧内は訓練での結果)。比較のため、図5にモデルが生成したサンプルとデータセットからのサンプルを示す。[62, 22]が述べているように、最大尤度はキャパシティが限られているセッティングでは、クオリティよりも多様性に価値を置く基準である。結果として、本モデルはたまに全然ありそうになりサンプルを出力しており、特にCelebAではよく分かる。VAEとは対照的に、本モデルで生成されたサンプルは全体的に一貫しているだけでなくくっきりしている。本論文の想定は、これらのVAEのようなモデルとは対照的にrealNVPは頻度が多い要素より少ない要素を捉えることを推奨させる$L_2$ノルムのような固定形式の再構成誤差に依存しないというものであった。自己回帰モデルとは異なり、本モデルのサンプリングは入力の次元で並列化できるので非常に効率的に行われる。ImagenetとLSUNでは、背景・前景の概念をよく捉えており、明るさや、反射と影に関して一貫した光源方向といったライティングの作用も捉えているようである。
図5: 左の列はデータセットのサンプル。右の列はそのデータセットで訓練されたモデルのからのサンプル。この図にあるデータセットは次の順。CIFAR-10, Imagenet (32 × 32), Imagenet (64 × 64), CelebA, LSUN (bedroom)また、潜在変数のなめらかな一貫した意味づけについても示す。本論文では潜在空間で、4つのバリデーションサンプル$z_{(1)},z_{(2)},z_{(3)},z_{(4)}$に関して多様体を定義し、2つのパラメータ$\phi$および$\phi'$について次のようにパラメータ表示した。
z= cos(\phi)(cos(\phi')z_{(1)}+ sin(\phi')z_{(2)}) +sin(\phi)(cos(\phi')z_{(3)} + sin(\phi')z_{(4)}) \tag{19}右辺の第1項目がz1とz2、2項目がz3とz4の間の補間になっている。さらに、第1項目と2項目自体が別のパラメータ$\phi$によって補間される。
結果の多様体は$g(z)$を計算してデータ空間に戻した。結果は図6。モデルはピクセル空間の補完がうまくいくような意味の概念を持って潜在空間を構成しているようである。さらなる可視化は付録。潜在空間が意味的に一貫した補完ができることをテストするために、CelebAでクラス条件付きモデルを訓練し、学習された表現がクラスラベルに渡って意味的に一貫していることがわかった(付録F)。5. 議論と結論
本論文では、直接の対数尤度評価、推定、サンプリングを可能にする、ヤコビ行列の行列式が扱いやすい可逆な関数を定義した。この種の生成モデルの性能がサンプルクオリティと対数尤度両面で競争力があることを示した。変換の関数形には例えばdilated convolutions [69]とresidual networksの構造[60]における最近の進歩を利用してさらなる改善の余地がある。
本論文は自己回帰モデル、VAE、GANの間のギャップを橋渡しする技術を示した。これは自己回帰モデルのように、訓練において扱いやすい直接の対数尤度評価を可能にし、また、VAEの生成モデルに似たもっと柔軟な関数形を可能にする。これはモデルの分布から高速な直接のサンプリングを可能にする。VAEとは異なり、またGANのように、本技術は固定形式の再構成誤差を必要とせず、高レベルの特徴に関してコストを定義し、シャープな画像を生成する。
最後に、VAE・GAN両方と異なり、本技術は入力空間と同じだけ高次元の意味のある潜在空間を学習できる。このことはアルゴリズムを特に半教師あり学習に適したものにする可能性がある。これについては更に研究したい。出力が構造化されたアルゴリズムを作るために、RealNVP生成モデルは追加の変数(例えばクラスラベル)で条件付けることもできる。それ以上に、可逆な変換は確率分布モジュールとして扱うことができるので、自己回帰モデルやVAEなど他の確率モデルを改善するためにも使用できる。VAEについては、この変換は柔軟な再構成誤差[38]と柔軟な確率的推定分布(stochastic inference distribution)[48]両方に使用できる。本論文で示したように、確率モデルは一般にbatch normalizationで恩恵を受ける。
強力な訓練可能な可逆関数の定義は生成的教師なし学習以外のドメインでも有用である。例えば、強化学習では、可逆関数は連続Qlearning [23]でargmax操作が扱いやすいように関数を拡張したり、また局所線形ガウス近似(local linear Gaussian approximations [67])がより適切な表現を見つける(?)等に役立つ。
References
- [1] Martın Abadi, Ashish Agarwal, Paul Barham, Eugene Brevdo, Zhifeng Chen, Craig Citro, Greg S Corrado, Andy Davis, Jeffrey Dean, Matthieu Devin, et al. Tensorflow: Large-scale machine learning on heterogeneous distributed systems. arXiv preprint arXiv:1603.04467, 2016.
- [2] Vijay Badrinarayanan, Bamdev Mishra, and Roberto Cipolla. Understanding symmetries in deep networks. arXiv preprint arXiv:1511.01029, 2015.
- [3] Johannes Ballé, Valero Laparra, and Eero P Simoncelli. Density modeling of images using a generalized normalization transformation. arXiv preprint arXiv:1511.06281, 2015.
- [4] Anthony J Bell and Terrence J Sejnowski. An information-maximization approach to blind separation and blind deconvolution. Neural computation, 7(6):1129–1159, 1995.
- [5] Yoshua Bengio. Artificial neural networks and their application to sequence recognition. 1991.
- [6] Yoshua Bengio and Samy Bengio. Modeling high-dimensional discrete data with multi-layer neural networks. In NIPS, volume 99, pages 400–406, 1999.
- [7] Mathias Berglund and Tapani Raiko. Stochastic gradient estimate variance in contrastive divergence and persistent contrastive divergence. arXiv preprint arXiv:1312.6002, 2013.
- [8] Samuel R Bowman, Luke Vilnis, Oriol Vinyals, Andrew M Dai, Rafal Jozefowicz, and Samy Bengio. Generating sentences from a continuous space. arXiv preprint arXiv:1511.06349, 2015.
- [9] Joan Bruna, Pablo Sprechmann, and Yann LeCun. Super-resolution with deep convolutional sufficient statistics. arXiv preprint arXiv:1511.05666, 2015.
- [10] Yuri Burda, Roger Grosse, and Ruslan Salakhutdinov. Importance weighted autoencoders. arXiv preprint arXiv:1509.00519, 2015.
- [11] Scott Shaobing Chen and Ramesh A Gopinath. Gaussianization. In Advances in Neural Information Processing Systems, 2000.
- [12] Junyoung Chung, Kyle Kastner, Laurent Dinh, Kratarth Goel, Aaron C Courville, and Yoshua Bengio. A recurrent latent variable model for sequential data. In Advances in neural information processing systems, pages 2962–2970, 2015.
- [13] Peter Dayan, Geoffrey E Hinton, Radford M Neal, and Richard S Zemel. The helmholtz machine. Neural computation, 7(5):889–904, 1995.
- [14] Gustavo Deco and Wilfried Brauer. Higher order statistical decorrelation without information loss. In G. Tesauro, D. S. Touretzky, and T. K. Leen, editors, Advances in Neural Information Processing Systems 7, pages 247–254. MIT Press, 1995.
- [15] Emily L. Denton, Soumith Chintala, Arthur Szlam, and Rob Fergus. Deep generative image models using a laplacian pyramid of adversarial networks. In Advances in Neural Information Processing Systems 28: 10 Published as a conference paper at ICLR 2017 Annual Conference on Neural Information Processing Systems 2015, December 7-12, 2015, Montreal, Quebec, Canada, pages 1486–1494, 2015.
- [16] Luc Devroye. Sample-based non-uniform random variate generation. In Proceedings of the 18th conference on Winter simulation, pages 260–265. ACM, 1986.
- [17] Laurent Dinh, David Krueger, and Yoshua Bengio. Nice: non-linear independent components estimation. arXiv preprint arXiv:1410.8516, 2014.
- [18] Brendan J Frey. Graphical models for machine learning and digital communication. MIT press, 1998.
- [19] Leon A. Gatys, Alexander S. Ecker, and Matthias Bethge. Texture synthesis using convolutional neural networks. In Advances in Neural Information Processing Systems 28: Annual Conference on Neural Information Processing Systems 2015, December 7-12, 2015, Montreal, Quebec, Canada, pages 262–270, 2015.
- [20] Mathieu Ger Published as a conference paper at ICLR 2017
- [46] Aaron van den Oord, Nal Kalchbrenner, and Koray Kavukcuoglu. Pixel recurrent neural networks. arXiv preprint arXiv:1601.06759, 2016.
- [47] Alec Radford, Luke Metz, and Soumith Chintala. Unsupervised representation learning with deep convolutional generative adversarial networks. CoRR, abs/1511.06434, 2015.
- [48] Danilo Jimenez Rezende and Shakir Mohamed. Variational inference with normalizing flows. arXiv preprint arXiv:1505.05770, 2015.
- [49] Danilo Jimenez Rezende, Shakir Mohamed, and Daan Wierstra. Stochastic backpropagation and approximate inference in deep generative models. arXiv preprint arXiv:1401.4082, 2014.
- [50] Oren Rippel and Ryan Prescott Adams. High-dimensional probability estimation with deep density models. arXiv preprint arXiv:1302.5125, 2013.
- [51] David E Rumelhart, Geoffrey E Hinton, and Ronald J Williams. Learning representations by backpropagating errors. Cognitive modeling, 5(3):1, 1988.
- [52] Olga Russakovsky, Jia Deng, Hao Su, Jonathan Krause, Sanjeev Satheesh, Sean Ma, Zhiheng Huang, Andrej Karpathy, Aditya Khosla, Michael Bernstein, et al. Imagenet large scale visual recognition challenge. International Journal of Computer Vision, 115(3):211–252, 2015.
- [53] Ruslan Salakhutdinov and Geoffrey E Hinton. Deep boltzmann machines. In International conference on artificial intelligence and statistics, pages 448–455, 2009.
- [54] Tim Salimans and Diederik P Kingma. Weight normalization: A simple reparameterization to accelerate training of deep neural networks. arXiv preprint arXiv:1602.07868, 2016.
- [55] Tim Salimans, Diederik P Kingma, and Max Welling. Markov chain monte carlo and variational inference: Bridging the gap. arXiv preprint arXiv:1410.6460, 2014.
- [56] Lawrence K Saul, Tommi Jaakkola, and Michael I Jordan. Mean field theory for sigmoid belief networks. Journal of artificial intelligence research, 4(1):61–76, 1996.
- [57] Karen Simonyan and Andrew Zisserman. Very deep convolutional networks for large-scale image recognition. arXiv preprint arXiv:1409.1556, 2014.
- [58] Paul Smolensky. Information processing in dynamical systems: Foundations of harmony theory. Technical report, DTIC Document, 1986.
- [59] Jascha Sohl-Dickstein, Eric A. Weiss, Niru Maheswaranathan, and Surya Ganguli. Deep unsupervised learning using nonequilibrium thermodynamics. In Proceedings of the 32nd International Conference on Machine Learning, ICML 2015, Lille, France, 6-11 July 2015, pages 2256–2265, 2015.
- [60] Sasha Targ, Diogo Almeida, and Kevin Lyman. Resnet in resnet: Generalizing residual architectures. CoRR, abs/1603.08029, 2016.
- [61] Lucas Theis and Matthias Bethge. Generative image modeling using spatial lstms. In Advances in Neural Information Processing Systems, pages 1918–1926, 2015.
- [62] Lucas Theis, Aäron Van Den Oord, and Matthias Bethge. A note on the evaluation of generative models. CoRR, abs/1511.01844, 2015.
- [63] Dustin Tran, Rajesh Ranganath, and David M Blei. Variational gaussian process. arXiv preprint arXiv:1511.06499, 2015.
- [64] Benigno Uria, Iain Murray, and Hugo Larochelle. Rnade: The real-valued neural autoregressive densityestimator. In Advances in Neural Information Processing Systems, pages 2175–2183, 2013.
- [65] Hado van Hasselt, Arthur Guez, Matteo Hessel, and David Silver. Learning functions across many orders of magnitudes. arXiv preprint arXiv:1602.07714, 2016.
- [66] Oriol Vinyals, Samy Bengio, and Manjunath Kudlur. Order matters: Sequence to sequence for sets. arXiv preprint arXiv:1511.06391, 2015.
- [67] Manuel Watter, Jost Springenberg, Joschka Boedecker, and Martin Riedmiller. Embed to control: A locally linear latent dynamics model for control from raw images. In Advances in Neural Information Processing Systems, pages 2728–2736, 2015.
- [68] Ronald J Williams. Simple statistical gradient-following algorithms for connectionist reinforcement learning. Machine learning, 8(3-4):229–256, 1992.
- [69] Fisher Yu and Vladlen Koltun. Multi-scale context aggregation by dilated convolutions. arXiv preprint arXiv:1511.07122, 2015.
- [70] Fisher Yu, Yinda Zhang, Shuran Song, Ari Seff, and Jianxiong Xiao. Construction of a large-scale image dataset using deep learning with humans in the loop. arXiv preprint arXiv:1506.03365, 2015.
- [71] Richard Zhang, Phillip Isola, and Alexei A Efros. Colorful image colorization. arXiv preprint arXiv:1603.08511, 2016
この記事のまとめ
- NICE同様、対数尤度の直接最適化でデータをモデリングする可逆な関数を設計した
- NICEでは加法的カップリングレイヤだったが、2種類(s,t)のCNNからなるアフィンカップリングレイヤに変更した
- 画像生成の性能自体はNICEより進化したが、それほどではない
- CNNにマスクが導入されているが、これの目的がよくわからない
展望
- 評価指標であるbits/dimensionを理解したい。