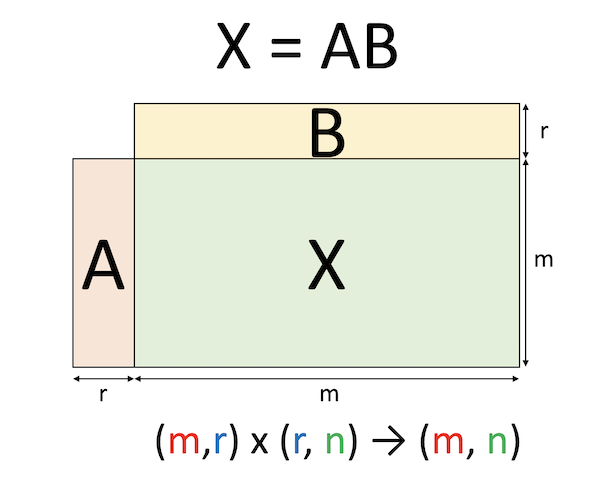
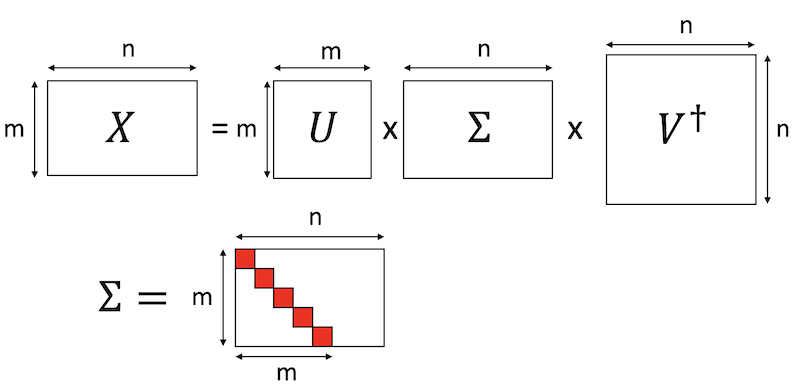
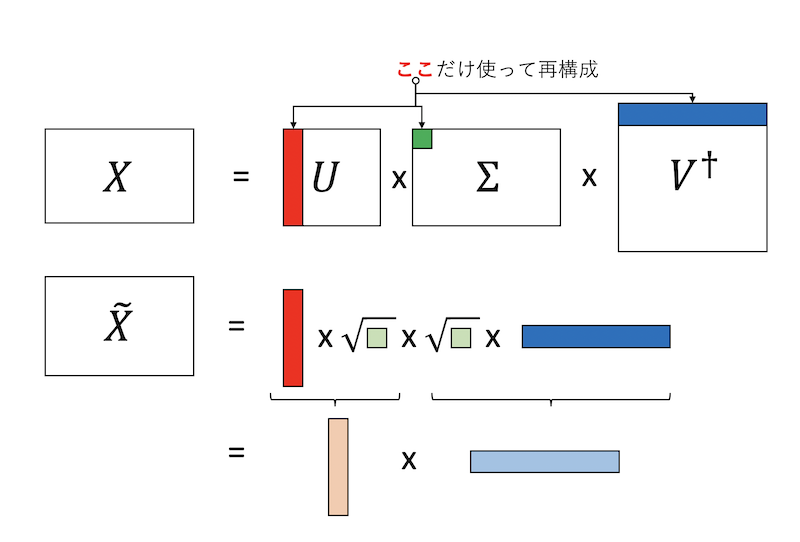
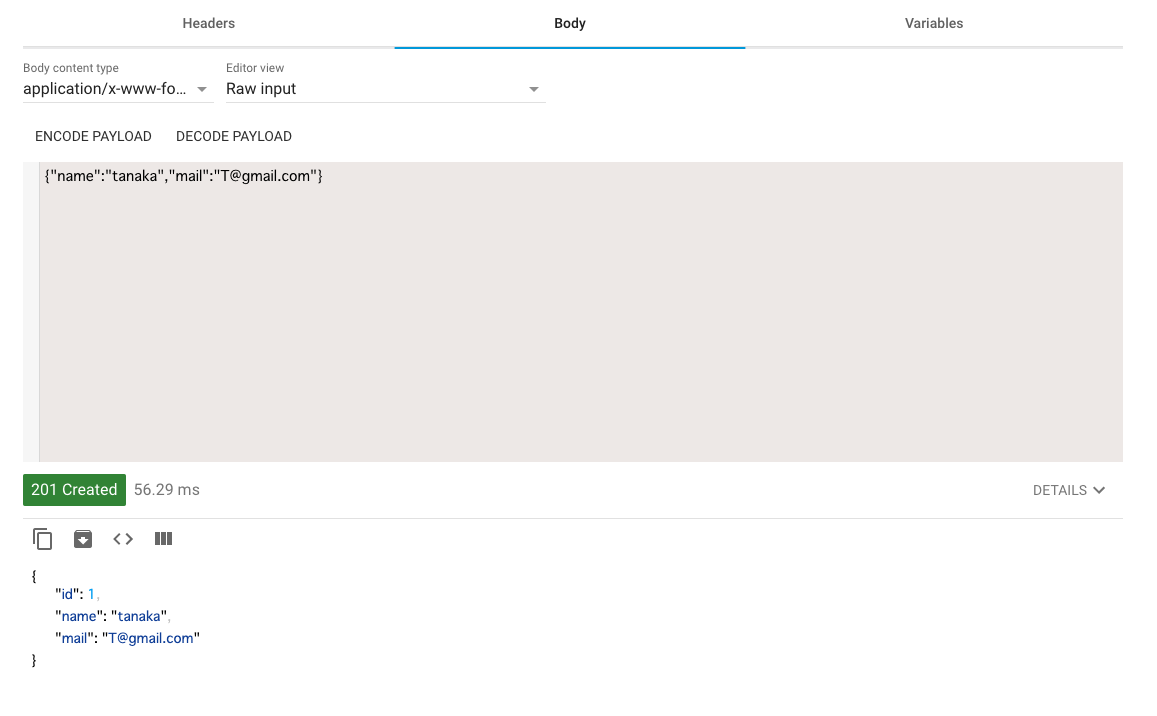
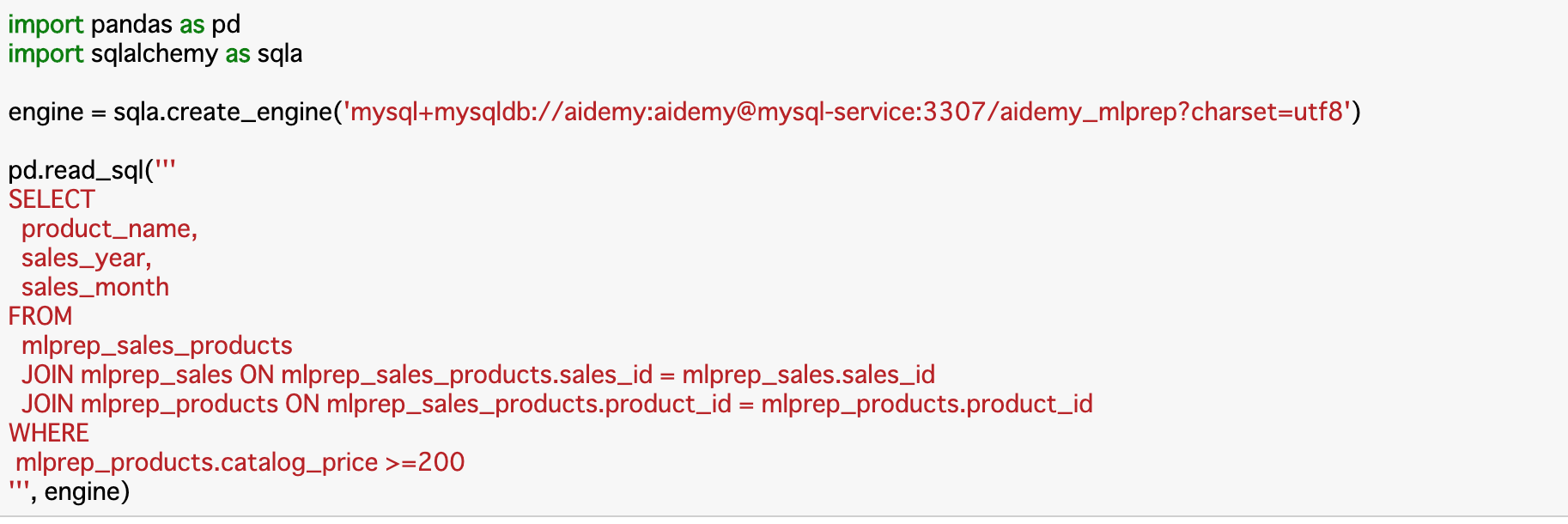
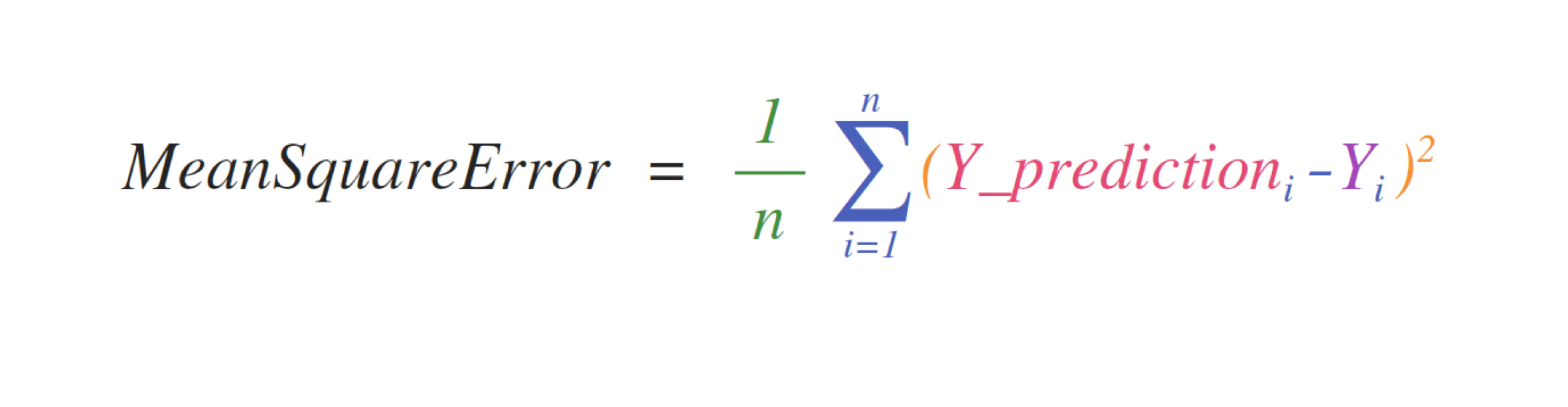20201021のPythonに関する記事は30件です。

投稿日：2020-10-21T23:32:20+09:00

Pythonってどんなプログラミング言語？

はじめに

どうも現在44歳の最近スケボーを始めたジジイです。
世間一般的には、まぁーいい歳、いいジジイです。

興味を持ったものは実際に自分で経験してやってみる。行動する！！
という信念を掲げまして、
去年の終わり頃からプログラミングに興味を持ち、仕事をしながら現在某プログラミングスクールに通っています。こちらはもう終盤に入っている状況。
こちらではRubyやらjQueryやらRailsなどを学びWebアプリケーションをいくつか作ってきました。
また現在進行形で個人アプリを制作中でもあります。

と、ここまでいろいろと勉強してきたんですが、無性にPythonというプログラミング言語が気になってしょうがない今日この頃！！
なぜか惹かれるこのPython...
Pythonってなんなんだ...
パ・イ・ソ・ン......？

どうでもいい前置きが長くなりましたが、
こちらではプログラミング言語 Pythonについて学習した内容を備忘録として記載していきたいと思います。

Pythonに興味を持った方々の参考になれば幸いでございます。
また、記載内容に間違いなどございましたら遠慮なくご指摘願います。
宜しくお願い致します。

Pythonの特徴

Pythonは1990年にグイド・ヴァンロッサムというオランダ人に開発されたプログラミング言語

文法がシンプルでわかりやすい、可読性が高い

汎用性の高いプログラミング言語なのでさまざまな開発が可能

オブジェクト指向言語である

専門的なライブラリが豊富にある

Pythonのライブラリは、数万個以上のライブラリが公開されています。
大きく分けると以下の様なライブラリがあるとのこと。　

数値計算・信号処理・統計処理

画像処理・音声処理・動画処理

ウェブ開発・サーバー・フレームワーク

ネットワーク

データベース

ドライバ

自然言語処理

この様に多くのライブラリがありますので、効率的な開発をすることができる。

そして一例として、下記の様なサービスの構築に使われている模様。

Youtube

Instagram

DropBox

Reddit

Blender

どんなことが出来るのか？

分別の自動化

ルート最適化の自動化

自動応答

支払いの自動化

データ収集の自動化

データ記録の自動化

株の自動売買

仮想通貨の自動売買

支払いの自動化

Webアプリケーション

デスクトップアプリの開発

人工知能/機械学習の開発

植物やペットの監視システム

おもちゃのAI戦車

ドローンの自動操縦

と、詳しい内容は今回は省きますが、いろいろな事が出来るようですね。

そして、最後に、

『既存のパターン化された仕事は、これからどんどんロボットや人工知能搭載のソフトウェアに置き換わっていき、代わりに人工知能分野の開発者が必要とされています。

その結果、人工知能開発によく使われるPythonに人々が集まっているという状況があります。その他にも、増え続けるビッグデータの経営資源化、スマホやウェアラブルによってより複雑になる個人の消費行動、セキュリティや自動運転のための画像解析技術、このようなことから今まさに時代はPythonを求めているのですね。』

とのことです。

これからどの様な時代が来るのか楽しみでありますね。
時代に乗り遅れない様に常に好奇心を持って新しいことにチャレンジして行こうと思います。

まとめ

検索していろいろ調べて見ましたが、まだまだ浅い部分しか触れてないので、これからいろいろと学習していきます。
だが、どうやって学習して行こうか考察中。
何かおすすめあればご教授のほど、よろしくお願い致します！！

参考記事

最近話題の言語【Python】でできる15のこと(2020年版)
【初心者向け】Pythonの特徴8選
 Pythonとは？特徴やメリット・勉強法を解説【初心者向け】

上記サイトを参考に書かせていただきました。ありがとうございましたm(_ _)m

　 Tweet
Qiitaで続きを読む

投稿日：2020-10-21T23:28:24+09:00

行列から探して、編集してみよう

こんばんは(*´ω｀)

昨日の延長です。
もう少し難易度を上げてみます。

取りあえず、ランダムで整数 0 ~ 4 を
無作為に選んで8行8列の行列を作ってみます。
test.py
import numpy as np
arr = np.random.randint(0,4,(8,8))
print(arr)
実行結果.py
[[2 2 3 2 2 3 2 2]
 [3 1 0 2 1 2 3 1]
 [3 0 1 3 3 1 2 1]
 [1 2 1 1 1 2 2 2]
 [1 2 3 2 3 0 3 0]
 [0 2 0 0 0 1 0 3]
 [0 2 3 0 0 2 2 1]
 [3 3 2 3 3 2 2 0]]
取りあえず、ランダムに構成した行列から 0 を探します。
@LouiS0616さんに教わった記述は 1 つだけ見つけるやり方みたいで、
他にやり方があると思うのですが、すいません、上手くいきませんでした m(_ _)m。
取りあえず、正攻法で行きます。
test.py
arr_pt=[]# カラのリストを作ります。

for i in range(8):
    for j in range(8):
        if arr[i,j] == 0:
            arr_pt.append([i,j])#カラのリストに、arr[i,j] == 0 となる座標を入れていきます。
実行結果.py
[[2 0 2 1 1 0 3 3]
 [3 0 3 3 2 0 2 3]
 [2 2 0 3 0 2 0 2]
 [3 0 2 2 2 2 0 2]
 [3 0 3 0 1 0 1 0]
 [2 2 1 2 1 0 2 3]
 [1 3 2 1 2 0 0 1]
 [3 0 3 2 2 3 3 2]]
#以下のリストは見やすくするために、一旦、改行入れました m(_ _)m
#尚、座標は 0 行、0 列からのカウントになっています。
[[0, 1], [0, 5], [1, 1], [1, 5], [2, 2], [2, 4], [2, 6], [3, 1], 
[3, 6], [4, 1], [4, 3], [4, 5], [4, 7], [5, 5], [6, 5], [6, 6], [7, 1]]
python のリストは上限が無いので、
ランダムに生成した行列でも 0 の数が異なるのですが、
一通り、座標を格納してくれます、有難う( ｀ー´)ノ

後は、格納したリストから、座標情報を取り出してみます。
今回は0 が見つかった行と列、全てを 0 に編集します。
取りあえず、さらっと載せますが、説明は後でします。
test.py
for k in range(len(arr_pt)):
    for l in range(8):
        arr[arr_pt[k][0],l] = 0
    for m in range(8):
        arr[m,arr_pt[k][1]] = 0

print(arr)
実行結果.py
#before
[[3 2 3 2 2 1 2 2]
 [3 2 3 2 0 3 0 0]
 [3 3 3 0 2 2 0 1]
 [1 3 1 1 3 0 0 1]
 [2 0 1 3 2 0 3 3]
 [0 1 0 0 1 0 3 1]
 [2 0 3 0 1 3 2 2]
 [0 0 3 2 1 3 2 0]]
#after
[[0 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 0]]
全部 0 になっちゃいました(笑)
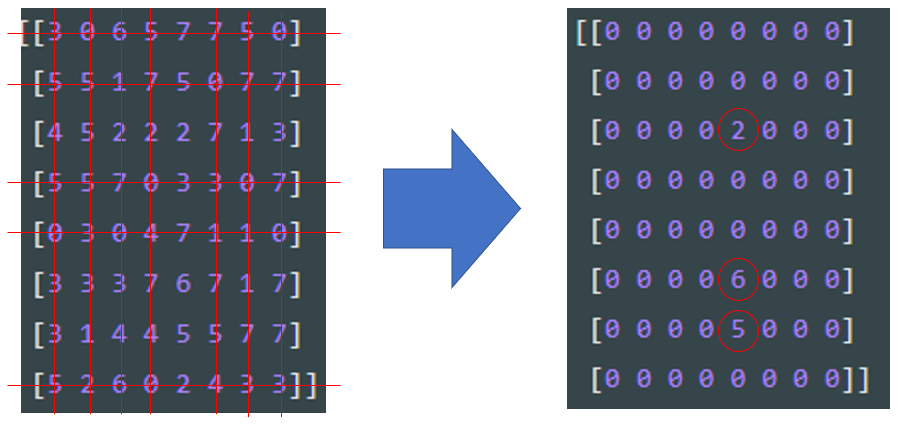
ちょっとバランスを調整しつつ、
全体像を再掲します。
test.py
import numpy as np

arr = np.random.randint(0,8,(8,8))# 8x8 の行列なので、0 - 8 をランダムに選ぶ事にしました。 
print(arr)

arr_pt=[]

for i in range(8):
    for j in range(8):
        if arr[i,j] == 0:
            arr_pt.append([i,j])

print(arr_pt)

#arr_pt[0][0] は arr_pt[0] = X としてしまえば、X[0] って事です
#これをヒントにしたの記述を読んでみてください
for k in range(len(arr_pt)):
    for l in range(8):
        arr[arr_pt[k][0],l] = 0 # arr_pt[k] を X とすると arr[X[0],l] になります/特定の行の値を all 0
    for m in range(8):
        arr[m,arr_pt[k][1]] = 0 # arr_pt[k] を X とすると arr[m,X[1]] になります/特定の列の値を all 0

print(arr)
実行結果.py
#before
[[3 0 6 5 7 7 5 0]
 [5 5 1 7 5 0 7 7]
 [4 5 2 2 2 7 1 3]
 [5 5 7 0 3 3 0 7]
 [0 3 0 4 7 1 1 0]
 [3 3 3 7 6 7 1 7]
 [3 1 4 4 5 5 7 7]
 [5 2 6 0 2 4 3 3]]

# 0 address (= arry_pt)
[[0, 1], [0, 7], [1, 5], [3, 3], [3, 6], [4, 0], [4, 2], [4, 7], [7, 3]]

#after
[[0 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 0]
 [0 0 0 0 2 0 0 0]
 [0 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 0]
 [0 0 0 0 6 0 0 0]
 [0 0 0 0 5 0 0 0]
 [0 0 0 0 0 0 0 0]]
実行結果のイメージはこんな感じです。

個人的には、0 の座標を見つけてリストに取り込んだ後が悩みました。
例えば以下の実行結果から、例えば arr_pt[0] とすると。。
実行結果.py
[[0, 1], [0, 7], [1, 5], [3, 3], [3, 6], [4, 0], [4, 2], [4, 7], [7, 3]] # arr_pt
[0, 1]# arr_pt[0]
っとなります。座標を取り出すのは良いけど、
どうやって、8 x 8 の行列の要素に反映すればいいのか分かりませんでした。
さらっと書いていますが、arr_pt[0][0] とすれば [0,1] から 0 を取り出してくれます。
逆に arr_pt[0][1] とすれば [0,1] から 1 を取り出してくれます。

面白いですね。

あとは、ここまで for を使い込まなくても良い気がしますが
すいません、good idea が思い浮かばず。。

有識者の方、アドバイスがあれば宜しくお願い致します。m(_ _)m

　 Tweet
Qiitaで続きを読む

投稿日：2020-10-21T23:11:13+09:00

[翻訳]NumPy公式チュートリアル "NumPy: the absolute basics for beginners"

訳者による紹介

本記事は、NumPy v.1.19 公式Documentation内の "NumPy: the absolute basics for beginners" の翻訳です。このドキュメントが開発版から本リリース扱いに変わったことをきっかけに、公開しました。

近年Pythonの人気は高止まりしています。その理由の一つは、AIブームとPythonの機械学習ライブラリの充実でしょう。Pythonが機械学習など科学技術計算分野でのライブラリが豊富であることが、さらなるライブラリの拡充や、初心者に限らない支持を引き起こしているようです。

NumPyはこれら科学技術計算ライブラリの基盤となるシステムです。NumPyが採用される理由に、Pythonの速度の問題があります。Pythonは言語の特性上、一部の操作は非常に低速であることで知られています。そのため多くのライブラリは、Pythonの速度が処理のボトルネックになることを回避するために、C言語で実装されたNumPyなどを使うことで大量のデータ処理にも耐えうる速度を実現しているのです。

NumPyはとても便利かつ高速に作動する魅力がありますが、Python自身と比べるとすこしとっつきにくいかもしれません。本記事では、NumPyの基礎を、画像をまじえつつ明快に説明していています。解説の範囲は"Quickstart tutorial"の半分以上をカバーしているので、あの無味乾燥なチュートリアルを読まずとも、ある程度のことができるようになるはずです。

また、【初心者向け】図解でわかるNumPyとデータ表現にも目を通すと参考になるかもしれません。執筆者は本記事の画像の作成者です。
誤訳等の指摘をいただけると大変助かります。

以下翻訳

NumPy完全初心者へのガイドへようこそ！もしコメントや提案があれば、遠慮なく連絡してください！

Welcome to NumPy!

NumPy (Numerical Python)は科学と工学(engineering)のほとんどすべての領域で用いられているオープンソースPythonライブラリです。Numpyは数値データを扱うための世界標準であり、ScientificPythonとPydata系の中核です[Pydata ecosystems: Numpyの開発元Pydataの製品群]。NUmpyユーザーには始めたてのプログラマーから、最先端の科学・工学研究と開発を行うベテラン研究者までいます。Numpy APIはPandas, SciPy, Matplotlib, scikit-learn, scikit-imageや他のほとんどのデータサイエンス用や科学用Pythonパッケージに広く用いられています。
Numpyライブラリは多次元の配列と行列データ構造を持ちます（これに関しては後の節でより詳しく説明します）。Numpyは、同種[同じデータ型]のn次元の配列オブジェクトであるndarrayを、配列を効率的に処理するためのメソッドと併せて提供します。Numpyは配列についての多様な数学的操作を行うために用いることができます。Numpyは配列と行列の効率的な計算を保証する力強いデータ構造をPythonに付け足し、これら配列と行列で働く高度の数学的機能を持った巨大なライブラリを提供します。
Learn more about NumPy here!

NumPyをインストールする

NumPyをインストールするには、科学用Pythonディストリビューションを利用することを強く勧めます。もし
お使いのOSにNumPyをインストールするための完全な手引きが必要なら、ここですべての詳細を見つけることができます。

もしすでにPythonを使っているなら、以下のコードでNumPyをインストールできます。
conda install numpy
あるいは
pip install numpy
もしまだPythonを持っていないのであれば、Anacondaの使用を検討するのがよいでしょう。AnacondaはPythonを一番簡単に始められる方法です。このディストリビューションを使う利点は、NumPyやデータ解析に使われる主要なパッケージ、pandas、Scikit-Learnなどを個々にインストールすることをそこまで心配する必要がないことです。

You can find all of the installation details in the Installation section at SciPy.

NumPyをインポートする方法

パッケージやライブラリを使いたい時はいつでも、最初に使いたいものをアクセス可能にする必要があります。
NumPyとそれに備わるすべての機能を使いはじめるには、NumPyをインポートしなければなりせん。これは次のインポート文[statement]によって簡単にできます。
import numpy as np
(我々はNumPyをnpと省略します。それは時間を節約するためであり、またコードを標準化しておくことで、そのコードを使って働く誰もが簡単に理解でき実行できるようにするためです。)

コード例の読み方

もしコードがたくさんのチュートリアルを読むのにまだ慣れていないなら、どのように次のようなコードブロックを理解すればよいかわからないかもしれません。
>>> a = np.arange(6)
>>> a2 = a[np.newaxis, :]
>>> a2.shape
(1, 6)
もしこのやり方をよく知らなくても、この表記法はとても理解しやすいです。もし>>>があれば、入力、つまりあなたが入力するだろうコードを指しています。コードの前に>>>がないものはすべて出力、つまりコードを実行した結果です。これはPythonをコマンドラインで実行するときのスタイルですが、IPythonを使うときは、異なるスタイルが表示されるかもしれません。

Python list と NumPy arrayの違いは何ですか?

NumPyは、配列を作り数値データを操作するための高速かつ効率的な方法を非常に多く備えています。Pyhonリストは一つのリストに異なったデータ型を持つことが可能ですが、NumPy配列で配列上のすべての要素は同種でなければなりません。もし配列に他のデータ型が混ざっていれば、配列上で働くはずの数学的操作はひどく非効率になるでしょう。

NumPyはなぜ使われているのですか?

NumPy配列はPythonリストよりも高速で簡潔です。[Pythonの]配列はメモリーをあまり使わず、使用するのに便利です。それと比べてもNumPyがデータをためるためにメモリーを使う量ははるかに少なく、データタイプを識別するメカニズムも備えています。このことはコードをさらに最適化することを可能にします。

配列とはなんですか?

配列とはNumPyライブラリの主要なデータ構造のひとつです。配列は値たちのグリッドであり配列は生のデータについての情報、要素をどのように配置するかについての情報、要素をどのように理解(interpret)するかについての情報を持ちます。NumPyが持つ諸要素からなるgridは、様々な方法でインデックスすることができます。要素はすべて同種であり、配列のdtypeとして表されます。

配列は正の整数のタプル、ブール値(booleans)、別の配列や整数によってインデックス可能です。配列のrankは次元の数です。配列のshapeは各次元に沿った配列のサイズを表す整数のタプルです。
NumPy配列を初期化する一つの方法は、Pythonリストから初期化することです。二次元以上のデータにはネストしたリストを用います。

例:
>>> a = np.array([1, 2, 3, 4, 5, 6])
あるいは
>>> a = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])
配列の要素にアクセスするには鍵括弧を使います。配列の要素にアクセスするとき、NumPyのインデックスは0から始まることを忘れないでください。これはあなたが配列の最初の要素にアクセスしたいならば、配列”0”にアクセスすることになるだろうという意味です。
>>> print(a[0])
[1 2 3 4]
配列についてさらに詳しく

この節では 1D array, 2D array, ndarray, vector, matrix を扱います

「ndarray」と表記される配列を時折目にしたことがあるかもしれません。これは「N次元配列」の略記です。N次元配列は簡単に言うと任意の次元数をもつ配列です。「1-D」ないし一次元配列、「2-D」ないし二次元配列、etc...、もまた目にしたことがあるかもしれません。NumPyのndarrayクラスは行列とベクトルのどちらを表すのにも使われます。ベクトルは一次元配列（行ベクトルと列ベクトルの違いはありません）であり、行列は二次元の配列を参照します。 3D（三次元）以上の配列では、テンソルという用語もよく使われます。

配列の属性とはなんですか？

配列は通常、同じ種類かつ同じサイズの項目の固定サイズのコンテナです。配列の次元数と項目は配列の形から定義されます。配列の形は各次元のサイズを規定する自然数のタプルです。
NumPyでは、次元はaxesと呼ばれます。すなわち、もし次のような配列があるなら
[[0., 0., 0.],
 [1., 1., 1.]]
この配列は二つの軸を持ちます。一つ目の軸の長さは2で、二つ目の長さは3です。
他のPythonコンテナと同様に、インデックスやスライシングで配列の内容にアクセスしたり修正したりすることができます。ですが典型的なコンテナオブジェクトと違って、同じデータを異なる配列で共有できるので、ある配列で行われた変更が、別の配列で現れるかもしれません。

配列の属性は配列固有の情報を反映します。もし新たに配列を作らずに配列のプロパティを得る、あるいは設定する必要があるなら、配列の属性を通して配列にアクセスすることが多いです。

Read more about array attributes here and learn about array objects here.

簡単な配列をつくる方法

この節では np.array(), np.zeros(), np.ones(), np.empty(), np.arange(), np.linspace(), dtypeを扱います

NumPy配列を作るには、関数np.array()を使います。
簡単な配列を作るのに必要なことは、リストを渡すことです。必要に応じてリストのデータ型を指定することもできます。 You can find more information about data types here.
>>> import numpy as np
>>> a = np.array([1, 2, 3])
次のように配列を視覚化することができます。
これらの視覚化は概念をわかりやすくし、NumPyの発想と仕組みの基礎的な理解を与えるためのものであることに注意してください。配列と配列操作はここで表現されたものよりはるかに複雑です。
要素の連続から作る配列以外にも、0で埋め尽くされた配列を簡単に作成することができます。
>>> np.zeros(2)
array([0., 0.])
他にも1で埋め尽くされた配列を作ることができます。
>>> np.ones(2)
array([1., 1.])
あるいは空の配列だってすら！empty関数は、初期内容がランダムかつメモリの状態に依存する配列を作成します。empty関数をzero関数(やそれに似たもの)に優先して使う理由はスピードです。後ですべての要素を埋めるのを忘れないようにしてください！
>>> # Create an empty array with 2 elements
>>> np.empty(2)
array([ 3.14, 42.  ])  # may vary
連続した要素の配列を作成できます：
>>> np.arange(4)
array([0, 1, 2, 3])
そして均等に間隔をあけた列からなる配列も作成できます。そのためには、最初の数・最後の数・ステップ数を指定します。
>>> np.arange(2, 9, 2)
array([2, 4, 6, 8])
np.linspace()を使用して、指定した間隔で線形に間を空けた値を持つ配列を作成することができます。
>>> np.linspace(0, 10, num=5)
array([ 0. ,  2.5,  5. ,  7.5, 10. ])
データタイプを指定する

デフォルトのデータ型は浮動小数点(np.float64)ですが、使いたいデータ型をdtypeキーワードで明示的に指定できます。
>>> x = np.ones(2, dtype=np.int64)
>>> x
array([1, 1])
Learn more about creating arrays here

要素を追加・削除・ソートする

この節は np.sort(), np.concatenate()を扱います

要素をソートするとき、np.sort()を使うと簡単です。この関数を呼ぶ際には、軸、種類、順序を指定できます。

この配列を例にとると、
>>> arr = np.array([2, 1, 5, 3, 7, 4, 6, 8])
こうして昇順に素早く並び替えることができます。
>>> np.sort(arr)
array([1, 2, 3, 4, 5, 6, 7, 8])
sortは配列にソートされたコピーをかえしますが、その外にも以下を利用できます
・argsort: 指定された軸による間接ソート
・lexsort: 複数のキーによる間接的な静的ソート[indirect stable sort on multiple keys]
・searchsorted: ソートされた配列から要素を発見する
・partition: 部分ソート

これらの配列を例にしましょう:
>>> a = np.array([1, 2, 3, 4])
>>> b = np.array([5, 6, 7, 8])
np.concatenate()でこれらの配列を連結することができます。
>>> np.concatenate((a, b))
array([1, 2, 3, 4, 5, 6, 7, 8])
また、この配列を例にとると、:
>>> x = np.array([[1, 2], [3, 4]])
>>> y = np.array([[5, 6]])
こうすることで連結できます:
>>> np.concatenate((x, y), axis=0)
array([[1, 2],
       [3, 4],
       [5, 6]])
配列から要素を削除するには、インデックスを使用して残したい要素を選択するのが簡単です。
連結についてさらに知りたい場合は、右を参照してください: concatenate.

配列の形とサイズをどうやって知るか?

このセクションは ndarray.ndim, ndarray.size, ndarray.shapeを扱います

ndarray.ndim は配列の軸の数、すなわち次元の数を示します。

ndarray.sizeは配列の要素の総数を示します。これは配列のサイズの要素を掛けたものです。

ndarray.shapeは配列の次元ごとに格納されている要素の数を示す整数のタプルを表示します。たとえば、2行3列の2次元配列がある場合、配列の形状は(2,3)です。

たとえば、次の配列を作成するとします。
>>> array_example = np.array([[[0, 1, 2, 3],
...                           [4, 5, 6, 7]],
...                          [[0, 1, 2, 3],
...                           [4, 5, 6, 7]],
...                          [[0 ,1 ,2, 3],
...                           [4, 5, 6, 7]]])
配列の次元数を調べるには、次を実行します:
>>> array_example.ndim
3
配列の要素の総数を調べるには、次を実行します:
>>> array_example.size
24
そして配列の形状を調べるには、次を実行します:
>>> array_example.shape
(3, 2, 4)
配列を変形できますか？

この節では arr.reshape()を扱います

もちろん!
arr.reshape()を使えば、データを変更せずに配列に新しい形を与えることができます。この変形メソッドを使うときは、作りたい配列は元の配列と同じ要素数の必要があることを忘れないでください。12個の要素の配列を変形するなら、新たな配列もまた合計で12個の要素を持つことを確かめる必要があります。
この配列を用いるなら:
>>> a = np.arange(6)
>>> print(a)
[0 1 2 3 4 5]
配列を変形するためにreshape()を使えます。たとえば、この配列を3行2列の配列に変形することができます:
>>> b = a.reshape(3, 2)
>>> print(b)
[[0 1]
 [2 3]
 [4 5]]
np.shape()とともに、いくつかのパラメーターを指定することが可能です。:
>>> numpy.reshape(a, newshape=(1, 6), order='C')]
array([[0, 1, 2, 3, 4, 5]])
aは形状を変更する配列です。
newshape は新しい配列の形です。整数か整数のタプルを指定することができます。整数を指定した場合、その整数の長さの配列が生まれます。形状は元の形状と互換性をもつ必要があります。
order: C はCに似たインデックス順序で読み書きすることを表し、FはFortranに似たインデックス順序で読み書きすることを表します。Aは要素がメモリ上でFortran連続であれば、Fortranに似たインデックス順序を使い、そうでなければCに似たインデックスを使うことを意味します(これは任意のパラメーターであり、必ず指定する必要はありません)。
If you want to learn more about C and Fortran order, you can read more about the internal organization of NumPy arrays here. Essentially, C and Fortran orders have to do with how indices correspond to the order the array is stored in memory. In Fortran, when moving through the elements of a two-dimensional array as it is stored in memory, the first index is the most rapidly varying index. As the first index moves to the next row as it changes, the matrix is stored one column at a time. This is why Fortran is thought of as a Column-major language. In C on the other hand, the last index changes the most rapidly. The matrix is stored by rows, making it a Row-major language. What you do for C or Fortran depends on whether it’s more important to preserve the indexing convention or not reorder the data.
Learn more about shape manipulation here.

1D配列を2D配列に変換する方法（配列に新しいaxisを加える方法）

この節では np.newaxis, np.expand_dimsを扱います

np.newaxis と np.expand_dims を使えば、既存の配列の次元を増やすことが可能です。

np.newaxisを使用すると、一度だけ使用した場合には、配列の次元が一次元増加します。つまり、1D配列は2D配列に、2D配列は3D配列に、となります。

例えば、次の配列では、
>>> a = np.array([1, 2, 3, 4, 5, 6])
>>> a.shape
(6,)
np.newaxis を使って新たな軸を追加できます。:
>>> a2 = a[np.newaxis, :]
>>> a2.shape
(1, 6)
np.newaxis を使うことで、行ベクトルか列ベクトルのどちからの1D配列を明示的に変形することができます。たとえば、第1次元上の軸を挿入することで、1D配列を行ベクトルに変換することができます。
>>> row_vector = a[np.newaxis, :]
>>> row_vector.shape
(1, 6)
また、列ベクトルには、第2次元上の軸を挿入できます:
>>> col_vector = a[:, np.newaxis]
>>> col_vector.shape
(6, 1)
np.expand_dims で指定した軸を挿入して、配列を拡張することも可能です。
たとえば、この配列では、:
>>> a = np.array([1, 2, 3, 4, 5, 6])
>>> a.shape
(6,)
インデックス位置1に軸を追加するにはnp.expand_dimsを使用できます。:
>>> b = np.expand_dims(a, axis=1)
>>> b.shape
(6, 1)
インデックス位置0に軸を追加するためには次のようにします。:
>>> c = np.expand_dims(a, axis=0)
>>> c.shape
(1, 6)
添え字アクセスとスライス(Indexing and slicing)

Numpy配列の添え字アクセスとスライスはPythonリストをスライスするのと同じ方法で行えます。
>>> data = np.array([1, 2, 3])

>>> data[1]
2
>>> data[0:2]
array([1, 2])
>>> data[1:]
array([2, 3])
>>> data[-2:]
array([2, 3])
これは次のように視覚化できます:

さらなる分析や操作に使うために、配列の一部や配列の特定の要素を取り出す必要があるかもしれません。そのためには、配列をサブセット、スライス、そして/もしくはインデクスしなければならないでしょう。

配列から特定の条件を満たす値を抜き出したいなら、NumPyを使うと簡単です。

たとえば、次の配列を例にします。
>>> a = np.array([[1 , 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])
配列にある5未満の数値を簡単に表示できます.
>>> print(a[a < 5])
[1 2 3 4]
また、例えば5以上の数値を選択して、その条件を用いて配列のインデックスを作成することもできます。
>>> five_up = (a >= 5)
>>> print(a[five_up])
[ 5  6  7  8  9 10 11 12]
2で割れる要素たちを取り出すこともできます。:
>>> divisible_by_2 = a[a%2==0]
>>> print(divisible_by_2)
[ 2  4  6  8 10 12]
& と | 演算子を使い、二つの条件を満たす要素をとりだすこともできます:
>>> c = a[(a > 2) & (a < 11)]
>>> print(c)
[ 3  4  5  6  7  8  9 10]
また、論理演算子& と | を使って、配列の値がある条件を満たすか否かを示すブール値を返すこともできます。これは名前や別カテゴリーの値を持つ配列のときに便利です。
>>> five_up = (a > 5) | (a == 5)
>>> print(five_up)
[[False False False False]
 [ True  True  True  True]
 [ True  True  True True]]
np.nonzero() を使い配列から要素の要素やインデクスを選択することも可能です。
次の配列を起点にしましょう:
>>> a = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])
np.nonzero() を使って、この場合では5未満の、要素のインデクスを表示することができます:
>>> b = np.nonzero(a < 5)
>>> print(b)
(array([0, 0, 0, 0]), array([0, 1, 2, 3]))
この例では配列のタプルが返されます。返されるタプルはそれぞれの次元に一つずつです。第一の配列は条件を満たす値がある行インデクスを表し、第二の配列は条件を満たす値がある列インデクスを示します。

要素がある座標のリストを生成したい場合、この配列をzipし、座標のリストを反復処理して、表示することができます。たとえば、:
>>> list_of_coordinates= list(zip(b[0], b[1]))

>>> for coord in list_of_coordinates:
...    print(coord)
(0, 0)
(0, 1)
(0, 2)
(0, 3)
np.nonzero()を使って配列中で5未満の要素を表示することもまたできます:
>>> print(a[b])
[1 2 3 4]
 ```shell

探している要素が配列に存在しない場合、戻り値のインデクスの配列は空になります。たとえば、以下のようになります。

```shell
>>> not_there = np.nonzero(a == 42)
>>> print(not_there)
(array([], dtype=int64), array([], dtype=int64))
既存のデータから配列をつくる方法

この節では slicing and indexing, np.vstack(), np.hstack() ,np.hsplit(), .view(), copy()を扱います

既存の配列の部分からたやすく配列を作ることができます。
次の配列があるとしましょう。
>>> a = np.array([1,  2,  3,  4,  5,  6,  7,  8,  9, 10])
配列のスライスしたい部分を指定することで、配列の部分からいつでも新しい配列を作ることができます。
>>> arr1 = a[3:8]
>>> arr1
array([4, 5, 6, 7, 8])
ここで、インデクス位置3からインデクス位置8までの範囲を指定しています。

既存の配列二つを連結するのは縦横どちらにもできます。次の二つの配列、a1,a2があるとします。
>>> a1 = np.array([[1, 1],
...               [2, 2]])

>>> a2 = np.array([[3, 3],
...               [4, 4]])
vstackを使って、これらを縦に積み重ねることができます。
>>> np.vstack((a1, a2))
array([[1, 1],
       [2, 2],
       [3, 3],
       [4, 4]])
そしてhstackで横に積み重ねることができます。
>>> np.hstack((a1, a2))
array([[1, 1, 3, 3],
       [2, 2, 4, 4]])
hsplitで配列をいくつかの小さな配列に分割することができます。配列を同形配列何個に分割するかや、分割後の列の数を指定することができます。

この配列があるとしましょう:
>>> x = np.arange(1, 25).reshape(2, 12)
>>> x
array([[ 1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12],
       [13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24]])
もしあなたがこの配列を3つの同じ形の配列へと分割したいなら、次のコードを実行しましょう。
>>> np.hsplit(x, 3)
[array([[1,  2,  3,  4],
        [13, 14, 15, 16]]), array([[ 5,  6,  7,  8],
        [17, 18, 19, 20]]), array([[ 9, 10, 11, 12],
        [21, 22, 23, 24]])]
もし3列目と4列目の後ろで配列を分割したいなら、次のコードを実行しましょう。
>>> np.hsplit(x, (3, 4))
[array([[1, 2, 3],
        [13, 14, 15]]), array([[ 4],
        [16]]), array([[ 5, 6, 7, 8, 9, 10, 11, 12],
        [17, 18, 19, 20, 21, 22, 23, 24]])]
Learn more about stacking and splitting arrays here.

viewメソッドを使って、元の配列と同じデータを参照する新たな配列を作ることができます(浅いコピー:shallow copy)。

ビューはNumPyの重要な概念の一つです。NumPyの関数は、添字アクセスやスライスなどの操作と同様に、可能な限りビューを返します。これはメモリの節約になり、高速です（データのコピーを作成する必要がありません）。しかし注意しなければならないことがあります––ビュー内のデータを変更すると、元の配列も変更されてしまいます。

次のような配列を作成したとしましょう。
>>> a = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])
ここでaをスライスしてb1をつくり、b1の最初の要素を変更します。この操作はaの対応する要素をも変更します。
>>> b1 = a[0, :]
>>> b1
array([1, 2, 3, 4])
>>> b1[0] = 99
>>> b1
array([99,  2,  3,  4])
>>> a
array([[99,  2,  3,  4],
       [ 5,  6,  7,  8],
       [ 9, 10, 11, 12]])
copyメソッドを使用すると、配列とそのデータの完全なコピーを作成します（ディープコピー）。これを配列に使用するには、次のコードを実行します。
>>> b2 = a.copy()
配列の基本的演算(operation)

この節では加算、減算、乗算、除算などを扱います

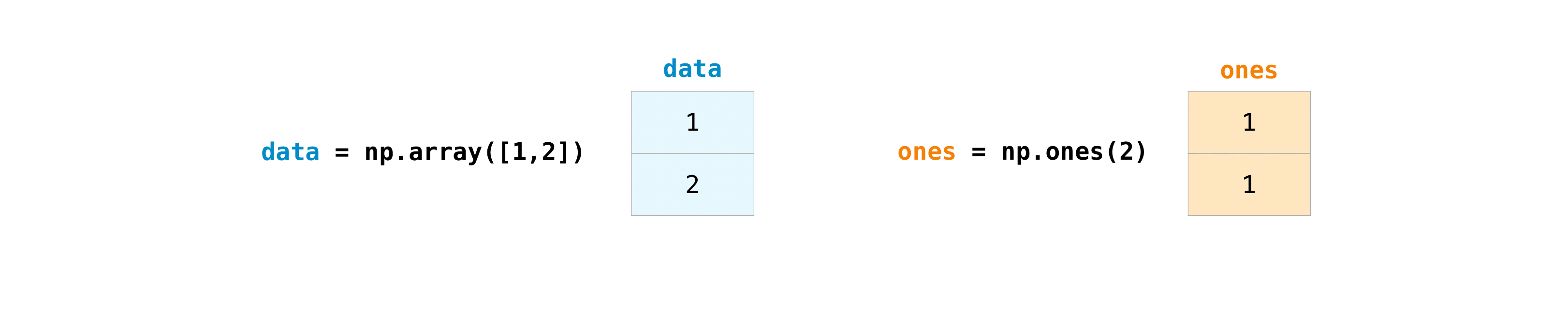
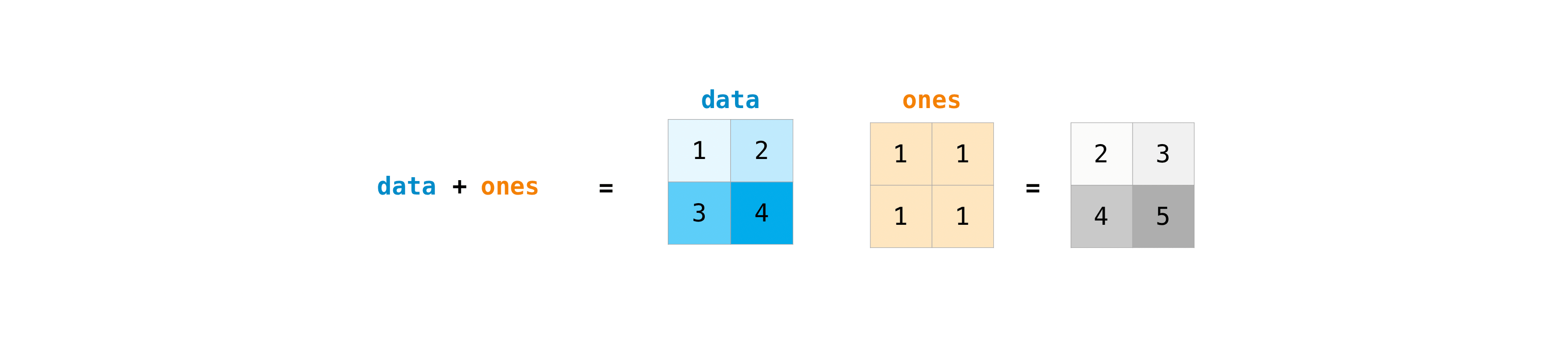
配列を作成したら、その配列で作業を始めることができます。例えば、”data”と”ones”と呼ばれる二つの配列を作成したとしましょう。

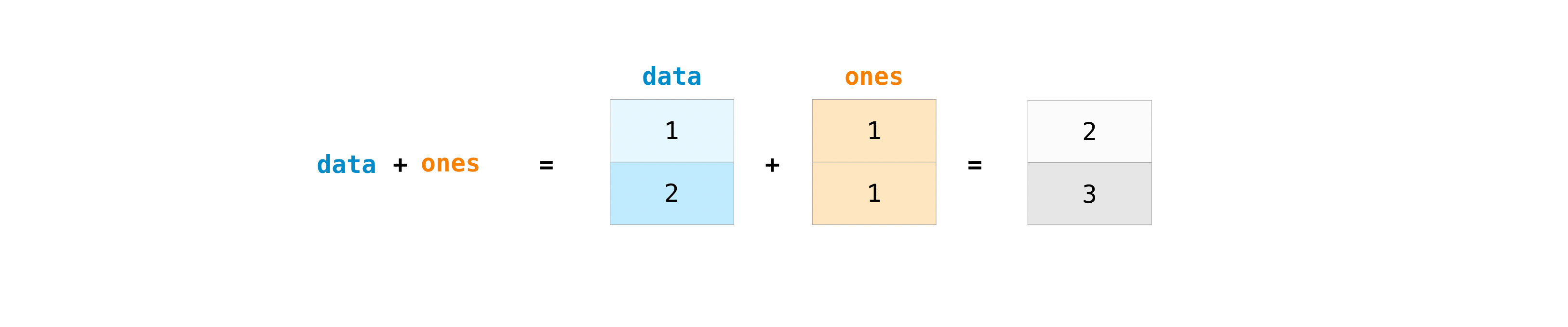
プラス記号を使って配列を足し合わせることができます。
>>> data = np.array([1, 2])
>>> ones = np.ones(2, dtype=int)
>>> data + ones
array([2, 3])
もちろん、できることは加算だけに留まりません!
>>> data - ones
array([0, 1])
>>> data * data
array([1, 4])
>>> data / data
array([1., 1.])
NumPyでは基本的操作は簡単です。もし配列の合計を知りたいなら、sum()を使いましょう。これは1D, 2Dやそれ以上の配列で動きます。
>>> a = np.array([1, 2, 3, 4])

>>> a.sum()
10
二次元配列で列や行を加算したいなら(To add the rows or the columns in a 2D array)、軸を指定します。
この配列から始める場合、:
>>> b = np.array([[1, 1], [2, 2]])
行は次のように合計できます:
>>> b.sum(axis=0)
array([3, 3])
列は次のように合計できます。:
>>> b.sum(axis=1)
array([2, 4])
Broadcasting

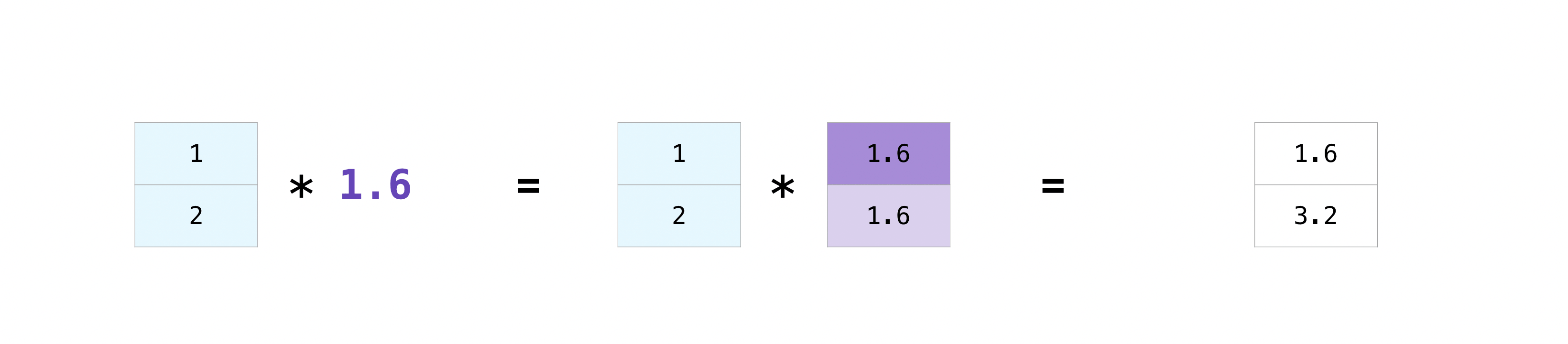
配列とひとつの数とで、あるいは異なるサイズの配列間で、演算したい時があります（前者はベクトルとスカラー間の演算とも呼ばれます）。たとえば、ある配列（”data”と呼びます）は何マイル離れているかの情報を持っており、あなたはそれをキロメートルに変換したいものとします。この操作を次のように行うことができます。
>>> data = np.array([1.0, 2.0])
>>> data * 1.6
array([1.6, 3.2])
NumPyは掛け算が一つ一つのセルで行われなければならないことを了解しています。このコンセプトはブロードキャストと呼ばれます。ブロードキャステトはNumPyが相異なる形の配列の演算を行うための仕組みです。配列の次元は互換性がなければなりません。例えば、両方の配列の次元が同じか、片方が1次元の場合にそうです。もしそうでなければ、ValueErrorが発生します。

より便利な配列操作

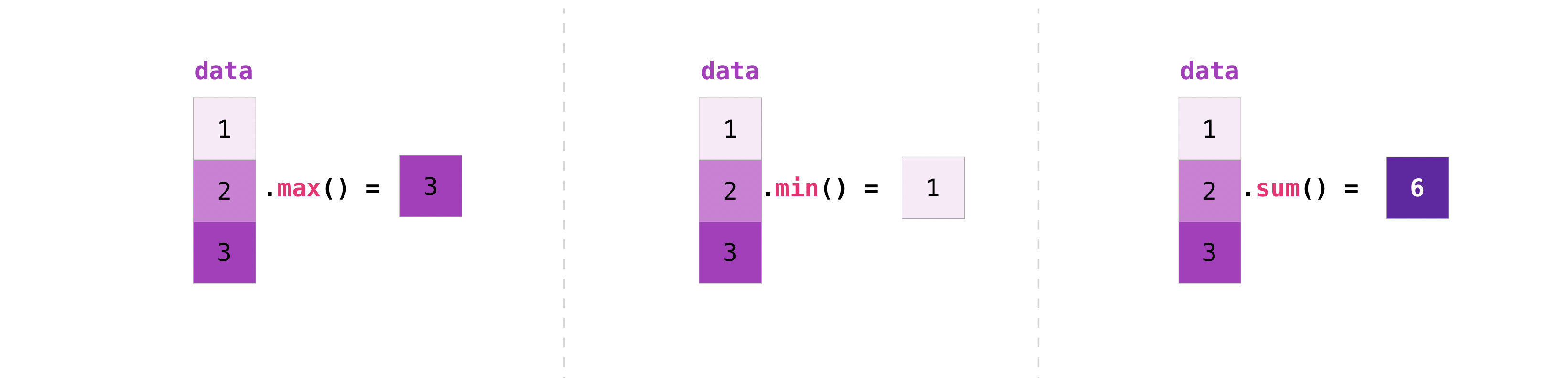
This section covers maximum, minimum, sum, mean, product, standard deviation, and more

NumPyは集合関数も実行する。min, max, sumに加えて、平均を得るためのmean, 要素をかけ合わせた結果を得るためのprod, 標準偏差を得るためのstdなどを簡単に実行できます。
>>> data.max()
2.0
>>> data.min()
1.0
>>> data.sum()
3.0
まずこの配列、“a”から始めましょう
>>> a = np.array([[0.45053314, 0.17296777, 0.34376245, 0.5510652],
...              [0.54627315, 0.05093587, 0.40067661, 0.55645993],
...              [0.12697628, 0.82485143, 0.26590556, 0.56917101]])
行や列に沿って集計したいというのは非常によくあることです。デフォルトでは、NumPy集計関数はすべて、配列全体の総和を返します。配列の要素の合計や最小値を知りたいときは、次のコードを用います。
>>> a.sum()
4.8595784
あるいは:
>>> a.min()
0.05093587
どの軸で集計関数をさせたいのか指定することができます。たとえば、axis=0とすることで、各列内の最小値を見つけることができます。
>>> a.min(axis=0)
array([0.12697628, 0.05093587, 0.26590556, 0.5510652 ])
上記の4つの数値は元の配列の行の数値と一致しています。4行の配列では、結果として、4つの値を得ることができます。

行列を作る

Pythonリストを渡して、NumPyでその配列を表す2D配列（または「行列」）を作ることができます。
>>> data = np.array([[1, 2], [3, 4]])
>>> data
array([[1, 2],
       [3, 4]])
添え字アクセスとスライス操作は、行列を扱う際に便利です。
>>> data[0, 1]
2
>>> data[1:3]
array([[3, 4]])
>>> data[0:2, 0]
array([1, 3])
行列の操作はベクトルの操作と同じ方法でできます。
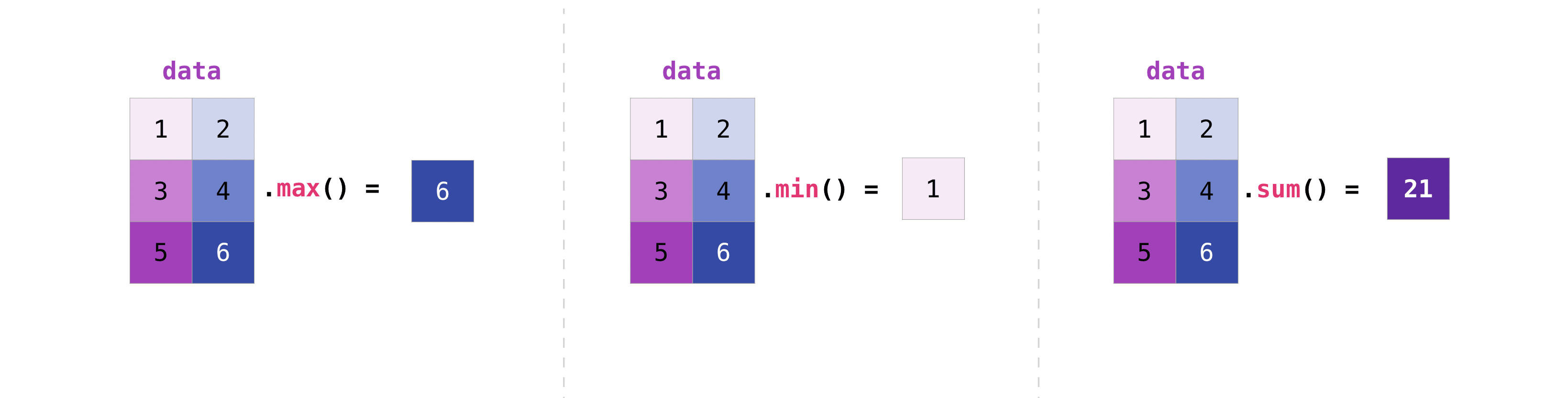
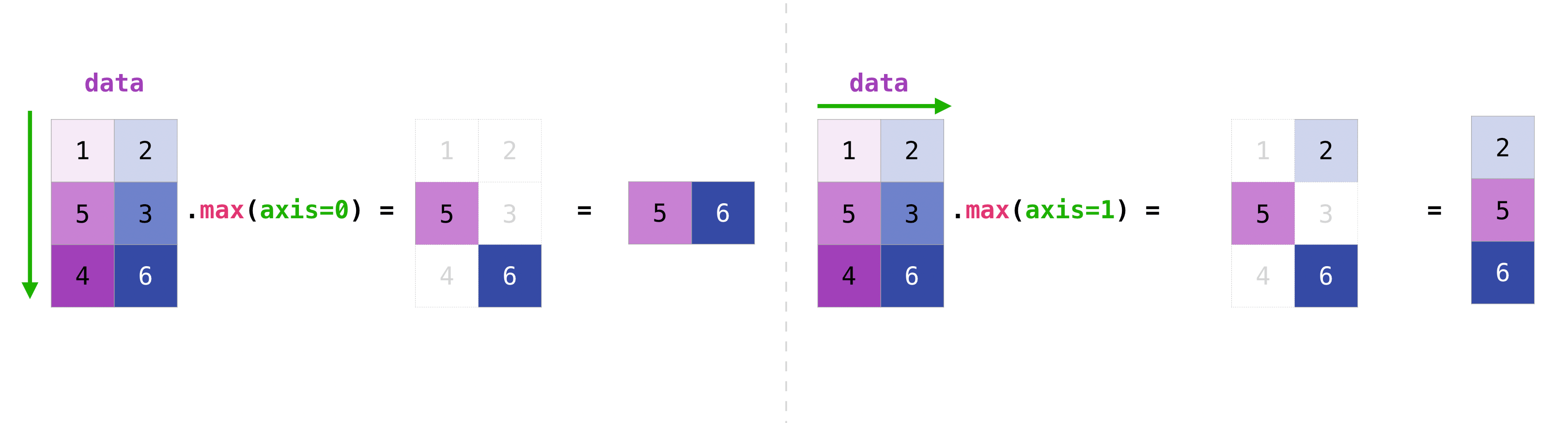
>>> data.max()
4
>>> data.min()
1
>>> data.sum()
10
行列内のすべての値を集計することも、軸パラメータを使って列か行をまたいで[across columns or rows]集計することができます。
>>> data.max(axis=0)
array([3, 4])
>>> data.max(axis=1)
array([2, 4])
行列を作成したら、同じサイズの行列が二つあれば、算術演算子を使って足し算や掛け算を行えます。
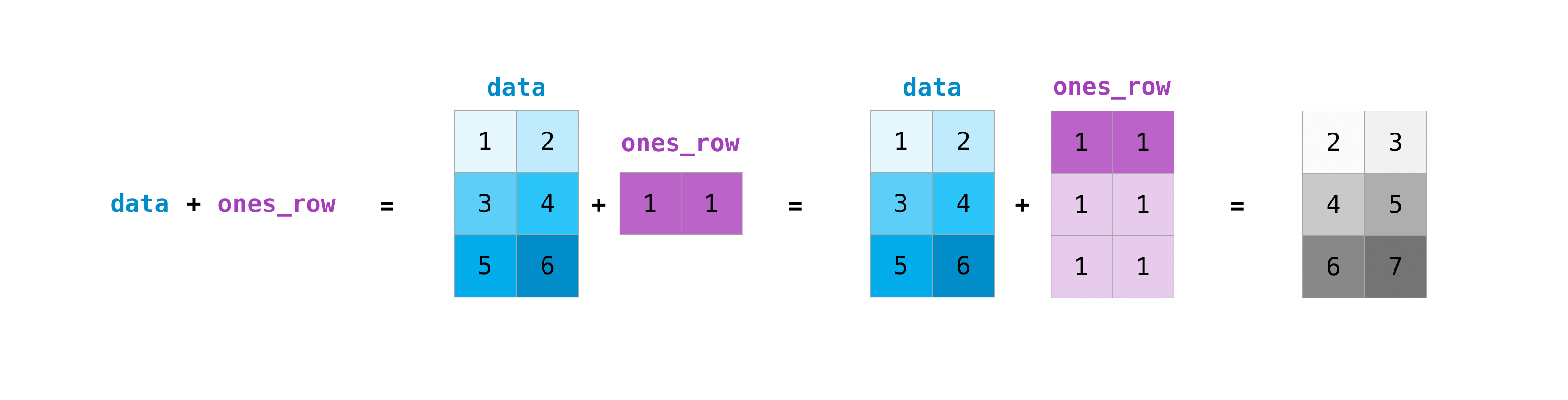
>>> data = np.array([[1, 2], [3, 4]])
>>> ones = np.array([[1, 1], [1, 1]])
>>> data + ones
array([[2, 3],
       [4, 5]])
異なるサイズの行列に対してもこれらの算術演算をすることができますが、一方の行列が一行か一列しかない場合に限ります。この場合、NumPyは演算のためにブロードキャスト規則を使います。
>>> data = np.array([[1, 2], [3, 4], [5, 6]])
>>> ones_row = np.array([[1, 1]])
>>> data + ones_row
array([[2, 3],
       [4, 5],
       [6, 7]])
NumPyがN次元の配列を表示するとき、最後の軸は最もループし、対して最初の軸は緩やかにループすることに注意してください[次の例では最後の軸である列に関しては12回のループが、最初の軸については4回のループがある]。
たとえば、
>>> np.ones((4, 3, 2))
array([[[1., 1.],
        [1., 1.],
        [1., 1.]],

       [[1., 1.],
        [1., 1.],
        [1., 1.]],

       [[1., 1.],
        [1., 1.],
        [1., 1.]],

       [[1., 1.],
        [1., 1.],
        [1., 1.]]])
NumPyで配列を初期化したい場合がよくあります。NumPyはones()やzeros()といった関数や、乱数生成のためのrandom.Generatorクラスを提供しています。初期化に必要なのは、ただ生成してほしい要素数を渡すことだけです。
>>>np.ones(3)
array([1., 1., 1.])
>>> np.zeros(3)
array([0., 0., 0.])
# the simplest way to generate random numbers
>>> rng = np.random.default_rng(0)
>>> rng.random(3)
array([0.63696169, 0.26978671, 0.04097352])
この関数やメソッドに二次元の行列を表すタプルを与えれば、ones()、zeros() と random() を使って二次元配列も生成可能です。
>>> np.ones((3, 2))
array([[1., 1.],
       [1., 1.],
       [1., 1.]])
>>> np.zeros((3, 2))
array([[0., 0.],
       [0., 0.],
       [0., 0.]])
>>> rng.random((3, 2))
array([[0.01652764, 0.81327024],
       [0.91275558, 0.60663578],
       [0.72949656, 0.54362499]])  # may vary
乱数を生成する

乱数生成の使用は多くの数学的あるいは機械学習アルゴリズムの配置や評価の重要なパートです。人工神経ネットワークの重さのランダムな初期化、ランダムなセットへの分割、あるいはデータセットのランダムシャッフル、どれにせよ、乱数（実際には、再現可能な擬似乱数の数）の生成をできることは欠かせません。Generator.integersを使って、最小値から最大値までのランダムな整数を出力できます（Numpyでは最小値は含まれ、最大値は含まれない事に注意してください）。endpoint=Trueを設定して、最高値を含む乱数を生成することができます。

0から4までのランダムな整数から成る2×4行列を生成することができます:
>>> rng.integers(5, size=(2, 4))
array([[2, 1, 1, 0],
       [0, 0, 0, 4]])  # may vary
重複しない要素を取り出し数える方法

この節では np.unique()を扱います

Np.uniqueで配列の要素を重複なしに一つずつ取り出すことができます。
たとえば、この配列を例にします。
>>> a = np.array([11, 11, 12, 13, 14, 15, 16, 17, 12, 13, 11, 14, 18, 19, 20])
Np.uniqueを使って配列中のユニークな値を知ることができます。
>>>
>>> unique_values = np.unique(a)
>>> print(unique_values)
[11 12 13 14 15 16 17 18 19 20]
Numpy配列のユニークな値のインデクス（配列のユニークな値それぞれの最初のインデックス）を得るためには、np.unique()に配列とともにreturn_index引数を渡してください。
>>> unique_values, indices_list = np.unique(a, return_index=True)
>>> print(indices_list)
[ 0  2  3  4  5  6  7 12 13 14]
Numpy配列のユニークな値がそれぞれいくつあるかをしるために、np.unique()に配列とともにreturn_counts引数をわたすことができます。
>>> unique_values, occurrence_count = np.unique(a, return_counts=True)
>>> print(occurrence_count)
[3 2 2 2 1 1 1 1 1 1]
これは二次元配列でも作用します! この配列を用いた場合、
>>> a_2d = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12], [1, 2, 3, 4]])
こうしてユニークな値を見つけることができます。
>>> unique_values = np.unique(a_2d)
>>> print(unique_values)
[ 1  2  3  4  5  6  7  8  9 10 11 12]
軸引数が渡されなかった場合、二次元配列は一次元に平坦化されます。
もしユニークな行や列を知りたい場合、必ずaxis引数をわたすようにしてください。ユニークな行をしるためにはaxis=0を指定し、列にはaxis=1を指定してください。
>>> unique_rows = np.unique(a_2d, axis=0)
>>> print(unique_rows)
[[ 1  2  3  4]
 [ 5  6  7  8]
 [ 9 10 11 12]]
ユニークな列やインデックス位置や出現数を得るためには、以下のようにします:
>>> unique_rows, indices, occurrence_count = np.unique(
...     a_2d, axis=0, return_counts=True, return_index=True)
>>> print(unique_rows)
[[ 1  2  3  4]
 [ 5  6  7  8]
 [ 9 10 11 12]]
>>> print(indices)
[0 1 2]
>>> print(occurrence_count)
[2 1 1]
行列の転置と変形

この節では arr.reshape(), arr.transpose(), arr.T()を扱います
行列の転置を必要とすることはしばしばあります。Numpy配列は行列を転置させるプロパティTを持ちます。

また、配列の次元を入れ替える必要があるかもしれません。これはたとえば、データセットと異なる入力の配列形を想定したモデルがある場合などに起こります。このような場合にreshapeメソッドが役に立ちます。必要なのは、行列に必要な新しい寸法[dimensions]を渡すだけです。
>>> data.reshape(2, 3)
array([[1, 2, 3],
       [4, 5, 6]])
>>> data.reshape(3, 2)
array([[1, 2],
       [3, 4],
       [5, 6]])
.transposeを使って、指定した値に従い、配列の軸を反転させたり変更したりすることもできます。

この配列を例にとりましょう：
>>> arr = np.arange(6).reshape((2, 3))
>>> arr
array([[0, 1, 2],
       [3, 4, 5]])
arr.transpose()を使って配列を転置できます。
>>> arr.transpose()
array([[0, 3],
       [1, 4],
       [2, 5]])
配列を反転させる方法

この節は np.flip を扱います

NumPyのnp.flip()はaxisを基準に、配列の軸を反転させることができます。np.flip()を使うときは反転させたい配列と軸を指定してください。軸を指定しない場合、NumPyは与えられた配列をすべての軸に関して反転させます。

1D配列を反転させる

次のような一次元配列を例にとりましょう：
>>> arr = np.array([1, 2, 3, 4, 5, 6, 7, 8])
こうやって配列を反転できます：
>>> reversed_arr = np.flip(arr)
反転された配列を表示したいなら、このコードを実行しましょう:
>>> print('Reversed Array: ', reversed_arr)
Reversed Array:  [8 7 6 5 4 3 2 1]
2D配列を反転させる

2D配列も、ほぼ同じやり方で反転します。

この配列を例にとりましょう：
>>> arr_2d = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])
すべての列と行で内容を反転させることができます。
>>> reversed_arr = np.flip(arr_2d)
>>> print(reversed_arr)
[[12 11 10  9]
 [ 8  7  6  5]
 [ 4  3  2  1]]
行だけを反転するのはこうするだけです:
>>> reversed_arr_rows = np.flip(arr_2d, axis=0)
>>> print(reversed_arr_rows)
[[ 9 10 11 12]
 [ 5  6  7  8]
 [ 1  2  3  4]]
列だけを反転するには:
>>> reversed_arr_columns = np.flip(arr_2d, axis=1)
>>> print(reversed_arr_columns)
[[ 4  3  2  1]
 [ 8  7  6  5]
 [12 11 10  9]]
一つの行や列だけを反転させることもできます。たとえば、インデックスが1の行（2行目）を反転させることできます:
>>> arr_2d[1] = np.flip(arr_2d[1])
>>> print(arr_2d)
[[ 1  2  3  4]
 [ 8  7  6  5]
 [ 9 10 11 12]]
インデックスが1の列（2列目）を反転させることもできます:
>>> arr_2d[:,1] = np.flip(arr_2d[:,1])
>>> print(arr_2d)
[[ 1 10  3  4]
 [ 8  7  6  5]
 [ 9  2 11 12]]
多次元配列を再整形・平坦化させる方法

この節では .flatten(), ravel()を扱います

配列をフラットにする一般的な方法は二つあります。.flatten() と .ravel()です。この二つの主要な違いは、.ravel()を使って作られた配列は、実は親配列への参照（つまり「ビュー」）なのです。したがって、新しい配列を何か変更すると、親配列もまた同様に変更されるということになります。ravelはコピーを作らないので、メモリ効率が良いです。
>>> x = np.array([[1 , 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])
You can use flatten to flatten your array into a 1D array.

flattenを使って、配列を1D配列にすることができます。
>>> x.flatten()
array([ 1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12])
When you use flatten, changes to your new array won’t change the parent array.
For example:

flatten‘を使うと、配列への変更は親配列に適用されません。

たとえば：
>>> a1 = x.flatten()
>>> a1[0] = 99
>>> print(x)  # Original array
[[ 1  2  3  4]
 [ 5  6  7  8]
 [ 9 10 11 12]]
>>> print(a1)  # New array
[99  2  3  4  5  6  7  8  9 10 11 12]
But when you use ravel, the changes you make to the new array will affect the parent array.
For example:

しかしravelを使うと、配列への変更は親配列に適用されません。
>>> a2 = x.ravel()
>>> a2[0] = 98
>>> print(x)  # Original array
[[98  2  3  4]
 [ 5  6  7  8]
 [ 9 10 11 12]]
>>> print(a2)  # New array
[98  2  3  4  5  6  7  8  9 10 11 12]
docstringにアクセスして詳細を知る

この節では help(), ?, ??を扱います。

データサイエンスエコシステムに関しては[when it comes to]、PythonとNumPyはユーザーのことを念頭に置いて作られています。このことの良い例の一つが、ドキュメンテーションへのアクセスが備え付けられていることです。すべてのオブジェクトは文字列への参照があり、その文字列はdocstringとして知ら得ています。たいていの場合、このdocstringは手短かつ簡潔なオブジェクトの概要と使い方を含みます。Pythonは組み込みのhelp関数を持ち、これはdocstringにアクセスするのを手助けします。つまり、より情報が必要なときはたいてい、help()を使って必要な情報をすぐに見つけることができます。

たとえば、
>>> help(max)
Help on built-in function max in module builtins:

max(...)
    max(iterable, *[, default=obj, key=func]) -> value
    max(arg1, arg2, *args, *[, key=func]) -> value

    With a single iterable argument, return its biggest item. The
    default keyword-only argument specifies an object to return if
    the provided iterable is empty.
    With two or more arguments, return the largest argument.
更なる情報へのアクセスはなかなか役立つので、IPythonは？をドキュメンテーションと関連した他の情報にアクセスするための略号として用います。IPythonは複数の言語で使える、インタラクティブな計算を行うためのコマンドシェルです。IPythonについてのさらなる情報はこちら。

たとえば、
In [0]: max?
max(iterable, *[, default=obj, key=func]) -> value
max(arg1, arg2, *args, *[, key=func]) -> value

With a single iterable argument, return its biggest item. The
default keyword-only argument specifies an object to return if
the provided iterable is empty.
With two or more arguments, return the largest argument.
Type:      builtin_function_or_method
この表記法を、オブジェクトメソッドやオブジェクトそのものにさえ使うことができます。

次の配列を作ったとしましょう。
>>> a = np.array([1, 2, 3, 4, 5, 6])
すると、たくさんの役立つ情報を得ることができます（最初にオブジェクトそのものの詳細、次にaがインスタンスであるndarrayのdocstringが続きます）。
In [1]: a?
Type:            ndarray
String form:     [1 2 3 4 5 6]
Length:          6
File:            ~/anaconda3/lib/python3.7/site-packages/numpy/__init__.py
Docstring:       <no docstring>
Class docstring:
ndarray(shape, dtype=float, buffer=None, offset=0,
        strides=None, order=None)

An array object represents a multidimensional, homogeneous array
of fixed-size items.  An associated data-type object describes the
format of each element in the array (its byte-order, how many bytes it
occupies in memory, whether it is an integer, a floating point number,
or something else, etc.)

Arrays should be constructed using `array`, `zeros` or `empty` (refer
to the See Also section below).  The parameters given here refer to
a low-level method (`ndarray(...)`) for instantiating an array.

For more information, refer to the `numpy` module and examine the
methods and attributes of an array.

Parameters
----------
(for the __new__ method; see Notes below)

shape : tuple of ints
        Shape of created array.
...
これはあなたが作成した関数や他のオブジェクトにも作用します。ただ。関数内に文字リテラルを使ってdocstringを入れるのを忘れないで下さい（""" """ か ''' ''' でドキュメンテーションを囲む）。

たとえば、次の関数を作った場合、
>>> def double(a):
...  '''Return a * 2'''
...  return a * 2
この関数について情報を得るには、次のようにします。
 In [2]: double?
Signature: double(a)
Docstring: Return a * 2
File:      ~/Desktop/<ipython-input-23-b5adf20be596>
Type:      function
関心あるオブジェクトのソースコードを読むことで、また違った水準の情報に触れることができます。二重疑問符(??)を使うことで、ソースコードにアクセスできます。

たとえば、
In [3]: double??
Signature: double(a)
Source:
def double(a):
    '''Return a * 2'''
    return a * 2
File:      ~/Desktop/<ipython-input-23-b5adf20be596>
Type:      function
当該のオブジェクトがPython以外の言語でコンパイルされている場合、??を使うと?と同じ情報が返ってきます。このことは、たくさんの組み込みオブジェクトやタイプで見ることができます。たとえば、
In [4]: len?
Signature: len(obj, /)
Docstring: Return the number of items in a container.
Type:      builtin_function_or_method
そして :
In [5]: len??
Signature: len(obj, /)
Docstring: Return the number of items in a container.
Type:      builtin_function_or_method
これらが同一の出力なのは、これらがPythonではない言語でコンパイルされているからです。

数式を扱う

NumPyが科学のPythonコミュニティでここまで広く使われている理由の一つに、配列上で作用する数式を簡単に実装できることがあります。

たとえば、これが平均二乗誤差（回帰を扱う教師付き機械学習モデルで使われる中心的な公式）です。

この式の実装はNumPyではシンプルで式そのままです：
error  = (1/n) * np.sum(np.square(predictions - labels))
これが非常にうまく機能するのは、予測値とラベルが1個でも1000個の値でも含むことができるからです。必要なのは、予測値とラベルが同じサイズであることだけです。

これは次のように可視化することができます。

この例では、予測とラベルは3つの値をもつベルトルであり、それゆえnは3という値をとります。引き算を行った後、ベクトルの値は二乗されます。そしてNumPyが値を合計し、その結果が予測値の誤差とモデルの品質のスコアとなります。

NumPyをセーブ・ロードする方法

この節は np.save, np.savez, np.savetxt, np.load, np.loadtxtを扱います

いつか、配列をディスクに保存して、コードをもう一度実行することなくロードしたいと思うことがあるでしょう。さいわい、NumPyではオブジェクトを保存したりロードしたりする方法がいくつかあります。ndarrayオブジェクトは、loadtxt と savetxt関数で通常のテキストファイルをロード・セーブし、load and save関数で.npz拡張子のNumPyバイナリファイルを扱うことができます。そして、savez関数で.npz拡張子のNumpyファイルを扱うことができます。

.npyと .npzファイルは、ファイルが異なるアーキテクチャ上でも正しく復旧できるように、データ、形状、dtypeやその他の、ndarrayを再構築するために必要な情報を格納しています。

1つのndarrayオブジェクトを保存したい場合、np.saveを使って.npyファイルとして保存してください。複数のndarrayを配列に保存したい場合、np.savezを使って.npzとして保存してください。また、savez_compressedを用いて圧縮されたnpz形式で保存することで、複数の配列を1つのファイルに保存することもできます。

np.save()でセーブ・ロード・配列するのは簡単です（It’s easy to save and load and array with np.save().）。保存したい配列とファイルネームを指定することを忘れないでください。たとえば、この配列をつくった場合、
>>> a = np.array([1, 2, 3, 4, 5, 6])
"filename.npy"として保存できます。
>>> np.save('filename', a)
np.load()で配列を復元できます。
>>> b = np.load('filename.npy')
もし配列を確かめたいなら、このコードを実行すればよいです。
>>> print(b)
[1 2 3 4 5 6]
np.savetxtを使えば、.csvや.txtファイルのようなプレーンテキストとしてNumPyファイルを保存できます。

たとえば、次の配列を作った場合、
>>> csv_arr = np.array([1, 2, 3, 4, 5, 6, 7, 8])
```shell

You can easily save it as a .csv file with the name “new_file.csv” like this:

```shell
>>> np.savetxt('new_file.csv', csv_arr)
loadtxt()を使って、簡単に保存したテキストファイルを読み込めます。
>>> np.loadtxt('new_file.csv')
array([1., 2., 3., 4., 5., 6., 7., 8.])
savetxt()とloadtxt()関数はヘッダー、フッター、区切り文字といった追加パラメーターを受け付けます。テキストファイルは共有に便利な一方で、.npyと.npzファイルは小さく、読み書きが高速です。もしテキストファイルのもっと洗練された取り扱いが必要なら(たとえば欠損値を含む行列[lines]を扱う場合)、genfromtxt 関数を使う必要があるでしょう。

savetxtを使うとき、ヘッダー、フッター、コメントなどを指定することができます。

Learn more about input and output routines here.

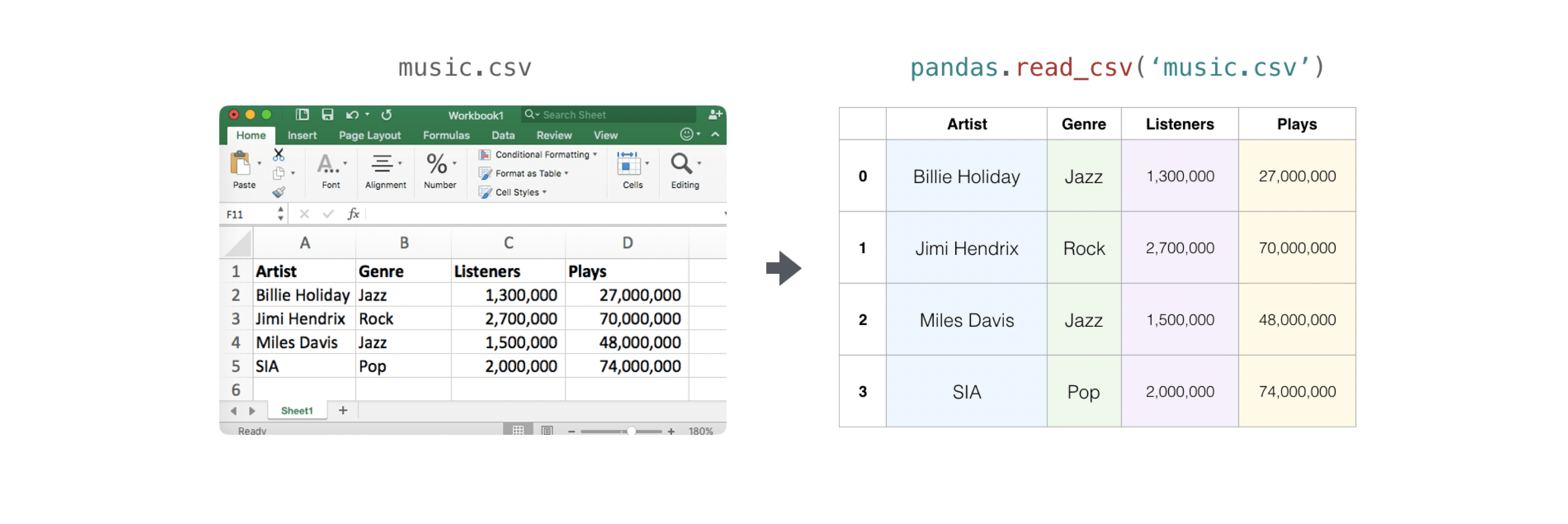
CSVをインポート・エクスポートする方法

既存の情報が入っているCSVファイルを読み込むのは簡単です。最も簡単な方法はPandasを使うことです。
>>> import pandas as pd

>>> # If all of your columns are the same type:
>>> x = pd.read_csv('music.csv', header=0).values
>>> print(x)
[['Billie Holiday' 'Jazz' 1300000 27000000]
 ['Jimmie Hendrix' 'Rock' 2700000 70000000]
 ['Miles Davis' 'Jazz' 1500000 48000000]
 ['SIA' 'Pop' 2000000 74000000]]

>>> # You can also simply select the columns you need:
>>> x = pd.read_csv('music.csv', usecols=['Artist', 'Plays']).values
>>> print(x)
[['Billie Holiday' 27000000]
 ['Jimmie Hendrix' 70000000]
 ['Miles Davis' 48000000]
 ['SIA' 74000000]]
配列のエクスポートもPandasを使えば簡単です。NumPyに慣れていない方は、配列の値からPandasデータフレームを作り、そのデータフレームをPandasでCSVファイルに書き出すのが良いでしょう。

配列"a"を作ったとしましょう。
>>> a = np.array([[-2.58289208,  0.43014843, -1.24082018, 1.59572603],
...              [ 0.99027828, 1.17150989,  0.94125714, -0.14692469],
...              [ 0.76989341,  0.81299683, -0.95068423, 0.11769564],
...              [ 0.20484034,  0.34784527,  1.96979195, 0.51992837]])
Pandasデータフレームを次のように作成できます。
>>> df = pd.DataFrame(a)
>>> print(df)
          0         1         2         3
0 -2.582892  0.430148 -1.240820  1.595726
1  0.990278  1.171510  0.941257 -0.146925
2  0.769893  0.812997 -0.950684  0.117696
3  0.204840  0.347845  1.969792  0.519928
次のようにしてデータフレームを保存できます。
>>> df.to_csv('pd.csv')
CSVはこう
>>> data = pd.read_csv('pd.csv')
NumPyのsavetxtメソッドを使って保存することもできます。
>>> np.savetxt('np.csv', a, fmt='%.2f', delimiter=',', header='1,  2,  3,  4')
コマンドラインを使っているなら、次のようなコマンドで保存したCSVをいつでも読み込むことができます。
$ cat np.csv
#  1,  2,  3,  4
-2.58,0.43,-1.24,1.60
0.99,1.17,0.94,-0.15
0.77,0.81,-0.95,0.12
0.20,0.35,1.97,0.52
または、テキストエディタでいつでも開くことができます。

Pandasについてもっと詳しく知りたい方は、official Pandas documentationを見てみてください。Pandasをインストールする方法については、official Pandas installation informationを参照してください。

Matplotlibで配列をプロットする

値のプロットを作成する必要がある場合、Matplotlibを使用すると非常に簡単です。

たとえば、このような配列があるかもしれません。
>>> a = np.array([2, 1, 5, 7, 4, 6, 8, 14, 10, 9, 18, 20, 22])
Matplotlibをすでにインストールしているなら、このようにインポートできます。
>>> import matplotlib.pyplot as plt

# If you're using Jupyter Notebook, you may also want to run the following
# line of code to display your code in the notebook:

%matplotlib inline
値をプロットするには、面倒な操作はいりません。
>>> plt.plot(a)

# If you are running from a command line, you may need to do this:
# >>> plt.show()
たとえば、1D配列を次のようにプロットできます。
‘>>> x = np.linspace(0, 5, 20)
>>> y = np.linspace(0, 10, 20)
>>> plt.plot(x, y, 'purple') # line
>>> plt.plot(x, y, 'o')      # dots
Matplotlibでは、膨大な数の可視化オプションを使うことができます。
>>> from mpl_toolkits.mplot3d import Axes3D
>>> fig = plt.figure()
>>> ax = Axes3D(fig)
>>> X = np.arange(-5, 5, 0.15)
>>> Y = np.arange(-5, 5, 0.15)
>>> X, Y = np.meshgrid(X, Y)
>>> R = np.sqrt(X**2 + Y**2)
>>> Z = np.sin(R)

>>> ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap='viridis')
To read more about Matplotlib and what it can do, take a look at the official documentation. For directions regarding installing Matplotlib, see the official installation section.

mage credits: Jay Alammar http://jalammar.github.io/

　 Tweet
Qiitaで続きを読む

投稿日：2020-10-21T23:05:32+09:00

How to install richzhang/colorization on Windows 10

What is this?

This document shows you how to install Colorful Image Colorization on Windows 10 and Python 3.x (3.8.6).

Steps

Step 1. Install Python on Windows

Version 3.8 of Windows x86-64 executable installer seems better:
https://www.python.org/downloads/windows/

Step 2. Install richzhang/colorization

Clone the repository

git clone https://github.com/richzhang/colorization.git

CUDA

Download and install CUDA 10.2:
https://developer.nvidia.com/cuda-downloads

PyTorch (torch)

pip install torch===1.6.0 torchvision===0.7.0 -f https://download.pytorch.org/whl/torch_stable.html

# For more details see below
# https://stackoverflow.com/questions/56859803/modulenotfounderror-no-module-named-tools-nnwrap

Others

Please note that I chose scikit-image instead of skimage.

pip install wheel scikit-image matplotlib argparse
pip install ipython

Step 3. Run

cd colorization
python demo_release.py -i imgs/ansel_adams3.jpg

Congratulations!

Logs

PyTorch (torch)

Click here to see command-line logs

C:\Users\AAA>pip install torch===1.6.0 torchvision===0.7.0 -f https://download.pytorch.org/whl/torch_stable.html
Looking in links: https://download.pytorch.org/whl/torch_stable.html
Collecting torch===1.6.0
  Downloading https://download.pytorch.org/whl/cu102/torch-1.6.0-cp38-cp38-win_amd64.whl (1077.4 MB)
     |████████████████████████████████| 1077.4 MB 833 bytes/s
Collecting torchvision===0.7.0
  Downloading https://download.pytorch.org/whl/cu102/torchvision-0.7.0-cp38-cp38-win_amd64.whl (1.1 MB)
     |████████████████████████████████| 1.1 MB 6.8 MB/s
Collecting future
  Downloading future-0.18.2.tar.gz (829 kB)
     |████████████████████████████████| 829 kB 3.2 MB/s
Collecting numpy
  Downloading numpy-1.19.2-cp38-cp38-win_amd64.whl (13.0 MB)
     |████████████████████████████████| 13.0 MB 6.8 MB/s
Collecting pillow>=4.1.1
  Downloading Pillow-8.0.0-cp38-cp38-win_amd64.whl (2.1 MB)
     |████████████████████████████████| 2.1 MB 6.4 MB/s
Using legacy 'setup.py install' for future, since package 'wheel' is not installed.
Installing collected packages: future, numpy, torch, pillow, torchvision
    Running setup.py install for future ... done
Successfully installed future-0.18.2 numpy-1.19.2 pillow-8.0.0 torch-1.6.0 torchvision-0.7.0

PIL seems to be the name used in Python 2.x, and pillow seems to be the name used in Python 3.x.

Others

Click here to see command-line logs

C:\Users\AAA>pip install wheel scikit-image matplotlib argparse
Collecting wheel
  Using cached wheel-0.35.1-py2.py3-none-any.whl (33 kB)
Collecting scikit-image
  Downloading scikit_image-0.17.2-cp38-cp38-win_amd64.whl (11.7 MB)
     |████████████████████████████████| 11.7 MB 3.3 MB/s
Collecting matplotlib
  Downloading matplotlib-3.3.2-cp38-cp38-win_amd64.whl (8.5 MB)
     |████████████████████████████████| 8.5 MB 6.4 MB/s
Collecting argparse
  Using cached argparse-1.4.0-py2.py3-none-any.whl (23 kB)
Collecting scipy>=1.0.1
  Downloading scipy-1.5.3-cp38-cp38-win_amd64.whl (31.4 MB)
     |████████████████████████████████| 31.4 MB 6.4 MB/s
Collecting imageio>=2.3.0
  Downloading imageio-2.9.0-py3-none-any.whl (3.3 MB)
     |████████████████████████████████| 3.3 MB ...
Requirement already satisfied: pillow!=7.1.0,!=7.1.1,>=4.3.0 in c:\home\sdk\python38\lib\site-packages (from scikit-image) (8.0.0)
Collecting tifffile>=2019.7.26
  Downloading tifffile-2020.10.1-py3-none-any.whl (152 kB)
     |████████████████████████████████| 152 kB 6.8 MB/s
Collecting PyWavelets>=1.1.1
  Downloading PyWavelets-1.1.1-cp38-cp38-win_amd64.whl (4.3 MB)
     |████████████████████████████████| 4.3 MB 6.8 MB/s
Requirement already satisfied: numpy>=1.15.1 in c:\home\sdk\python38\lib\site-packages (from scikit-image) (1.19.2)
Collecting networkx>=2.0
  Downloading networkx-2.5-py3-none-any.whl (1.6 MB)
     |████████████████████████████████| 1.6 MB ...
Collecting pyparsing!=2.0.4,!=2.1.2,!=2.1.6,>=2.0.3
  Using cached pyparsing-2.4.7-py2.py3-none-any.whl (67 kB)
Collecting certifi>=2020.06.20
  Using cached certifi-2020.6.20-py2.py3-none-any.whl (156 kB)
Collecting python-dateutil>=2.1
  Using cached python_dateutil-2.8.1-py2.py3-none-any.whl (227 kB)
Collecting cycler>=0.10
  Using cached cycler-0.10.0-py2.py3-none-any.whl (6.5 kB)
Collecting kiwisolver>=1.0.1
  Downloading kiwisolver-1.2.0-cp38-none-win_amd64.whl (58 kB)
     |████████████████████████████████| 58 kB ...
Collecting decorator>=4.3.0
  Downloading decorator-4.4.2-py2.py3-none-any.whl (9.2 kB)
Collecting six>=1.5
  Using cached six-1.15.0-py2.py3-none-any.whl (10 kB)
Installing collected packages: wheel, scipy, imageio, tifffile, PyWavelets, pyparsing, certifi, six, python-dateutil, cycler, kiwisolver, matplotlib, decorator, networkx, scikit-image, argparse
Successfully installed PyWavelets-1.1.1 argparse-1.4.0 certifi-2020.6.20 cycler-0.10.0 decorator-4.4.2 imageio-2.9.0 kiwisolver-1.2.0 matplotlib-3.3.2 networkx-2.5 pyparsing-2.4.7 python-dateutil-2.8.1 scikit-image-0.17.2 scipy-1.5.3 six-1.15.0 tifffile-2020.10.1 wheel-0.35.1

c:\home\sdk\python38 is a directory name that is unique to my environment.

First run

Click here to see command-line logs

C:\home\src\colorization>python demo_release.py -i imgs/ansel_adams3.jpg
Downloading: "https://colorizers.s3.us-east-2.amazonaws.com/colorization_release_v2-9b330a0b.pth" to C:\Users\AAA/.cache\torch\hub\checkpoints\colorization_release_v2-9b330a0b.pth
100.0%
Downloading: "https://colorizers.s3.us-east-2.amazonaws.com/siggraph17-df00044c.pth" to C:\Users\AAA/.cache\torch\hub\checkpoints\siggraph17-df00044c.pth
100.0%
C:\home\sdk\python38\lib\site-packages\torch\nn\functional.py:3118: UserWarning: Default upsampling behavior when mode=bilinear is changed to align_corners=False since 0.4.0. Please specify align_corners=True if the old behavior is desired. See the documentation of nn.Upsample for details.
  warnings.warn("Default upsampling behavior when mode={} is changed "
C:\home\sdk\python38\lib\site-packages\skimage\color\colorconv.py:1128: UserWarning: Color data out of range: Z < 0 in 367 pixels
  return xyz2rgb(lab2xyz(lab, illuminant, observer))
C:\home\sdk\python38\lib\site-packages\skimage\color\colorconv.py:1128: UserWarning: Color data out of range: Z < 0 in 33 pixels
  return xyz2rgb(lab2xyz(lab, illuminant, observer))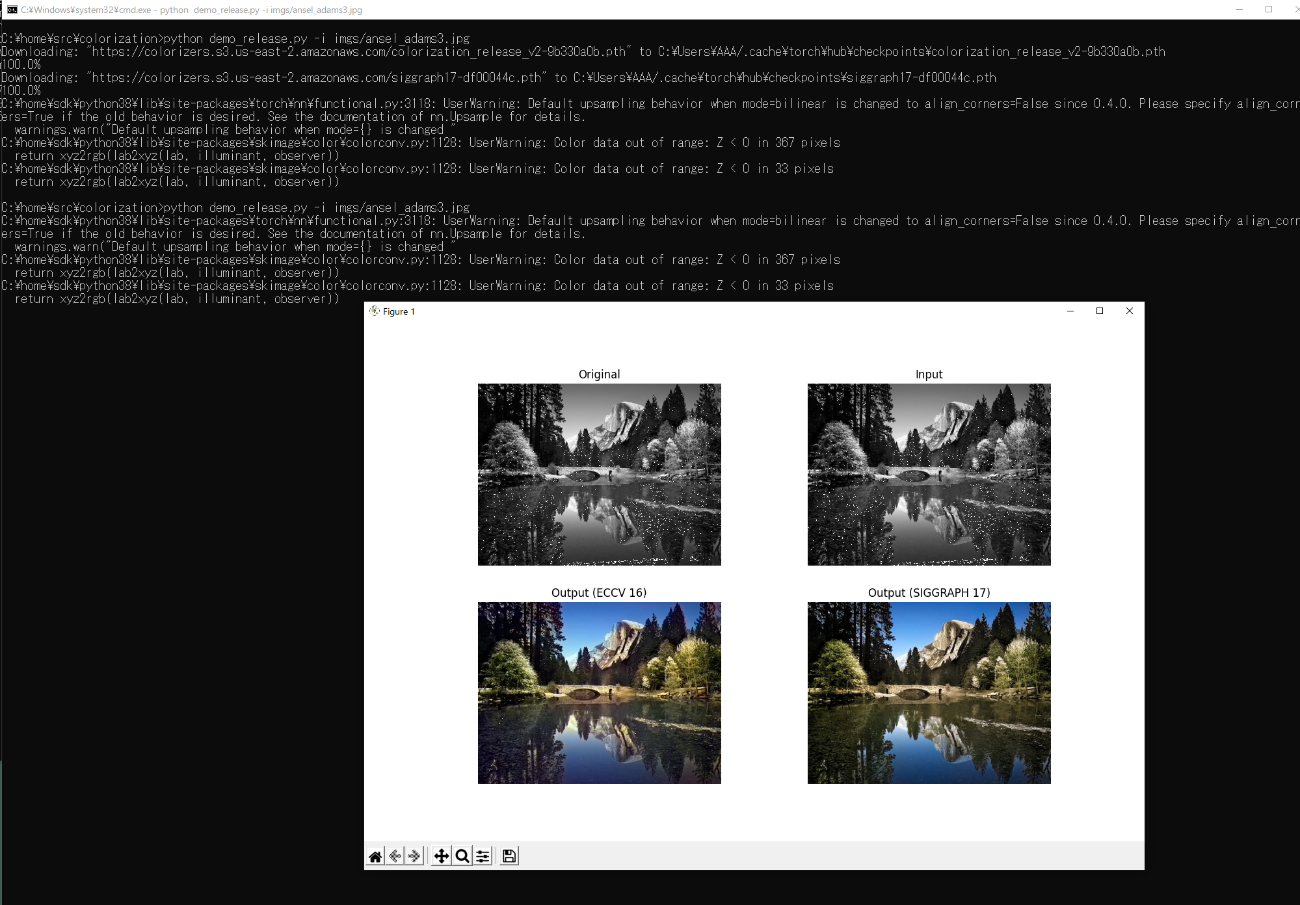![](https://storage.googleapis.com/zenn-user-upload/owfupao294w6w9z4j0wr2w813agg)

Note

This page is a clone of the Zenn article.

　 Tweet
Qiitaで続きを読む

投稿日：2020-10-21T22:48:13+09:00

フレーム数を見ながら動画再生する方法(Mac)

動画をコマ送りしながらチェックして気になる場面のフレーム数を知りたいケースが多い。
割とありそうな需要にもかかわらず最近の動画プレーヤーは秒表示しかできなくて調べても全然方法が出てこない。
なんとかならないかと必死で調べて苦肉の策としての対応を見つけたのでメモ。
他にいい方法あれば是非教えてください。
なんでこんな基本的なことができるプレーヤーがないんだろうか。（QuictimePlayer7はできたらしいけれど32bitアプリは今は動かせない。）

方法

mpvというプレーヤーを少しだけ書き換えてコンパイルします。
まずGitからソースコードをダウンロード。

書き換えるのはplayer/osd.cのget_term_status_msg関数の中に一行追加するだけ。（今のバージョンだと200行目くらい）
// Playback position
sadd_hhmmssff(&line, get_playback_time(mpctx), opts->osd_fractions);
saddf(&line, " / ");
sadd_hhmmssff(&line, get_time_length(mpctx), opts->osd_fractions);
sadd_percentage(&line, get_percent_pos(mpctx));
///////////　追加　////////////////
line = talloc_asprintf_append(line, " (%d frame)", (int)(mpctx->video_pts * mpctx->tracks[0]->stream->codec->fps+0.5));
///////////　ここまで　////////////
あとはREADMEにしたがってコンパイルしてインストールする。
するとターミナルの再生時刻の表示の末尾にフレーム数が表示されるようになります。
(Paused) V: 00:00:00 / 00:00:03 (21%) (19 frame)

　 Tweet
Qiitaで続きを読む

投稿日：2020-10-21T22:23:47+09:00

pythonでシーザー暗号を作成、復号する

# substitute PLAIN the letter
PLAIN = "EBG KVVV vf n fvzcyr yrggre fhofgvghgvba pvcure gung ercynprf n yrggre jvgu gur yrggre KVVV yrggref nsgre vg va gur nycunorg. EBG KVVV vf na rknzcyr bs gur Pnrfne pvcure, qrirybcrq va napvrag Ebzr. Synt vf SYNTFjmtkOWFNZdjkkNH. Vafreg na haqrefpber vzzrqvngryl nsgre SYNT."

for i in range(26):
    KEY = i
    enc = ""

    for char in list(PLAIN):
        ASCII = ord(char)
        if (ASCII == 32):                   # if ASCII is SPC, make space.
            enc += " "
            continue
        if (122 >= ASCII and ASCII >= 97):  # if ASCII is lower
            num = ASCII - 97
            num = (num + KEY) % 26
            ASCII = num + 97
            enc += chr(ASCII)
        elif (90 >= ASCII and ASCII >= 65): # if ASCII is upper
            num = ASCII - 65
            num = (num + KEY) % 26
            ASCII = num + 65
            enc += chr(ASCII)
        else :                              # if ASCII is symbol
            enc += chr(ASCII)

    print(f"--------- Shifted {i} character ---------")
    print(enc)
    print("")

使いたい方はこのコードをコピーし、適当な名前を付けて保存してください。拡張子を「.py」にするのをお忘れなく（例、test.py）

そのあと、コードの一番上にあるPLAIN変数の中身を暗号にしたい文字や解読したい文字にしてください。（例、PLAIN = "hogehoge"）

その状態で保存し、実行しします。

# python test.py

そうすると、１～２５文字ずらした文字列を表示されます。（アルファベットは全部で２６文字です。）

　 Tweet
Qiitaで続きを読む

投稿日：2020-10-21T21:52:31+09:00

django-filterの使い方を理解する

django-filterとは

検索条件を短いコードで書くことができます!!!
僕的にはこれを知った時には革命的だと思いました。

django-filter 公式ドキュメント

※この記事では、Django Rest Frameworkの使用と初期設定は終わっている想定です!!!!!!!

modelとseiralizerを定義

サンプルになりますが、このようなモデルとシリアライザを定義しておきます。
models.py
class Book(models.Model):
    id = models.UUIDField(primary_key=True, default=uuid.uuid4, editable=False)
    is_deleted = models.CharField(max_length=1, default='0')
    created_at = models.DateTimeField(auto_now_add=True)
    updated_at = models.DateTimeField(auto_now=True)
    title = models.CharField(max_length=128)
    sub_title = models.CharField(max_length=128)
    price = models.DecimalField(max_digits=8, decimal_places=2, blank=True, null=True)
    author = models.ForeignKey(Author, on_delete=models.PROTECT, blank=True, null=True)
    publisher = models.ForeignKey(Publisher, on_delete=models.PROTECT)
serializer.py
class BookSerializer(serializers.ModelSerializer):
    class Meta:
        model = Book
        fields = '__all__'
基本的な書き方

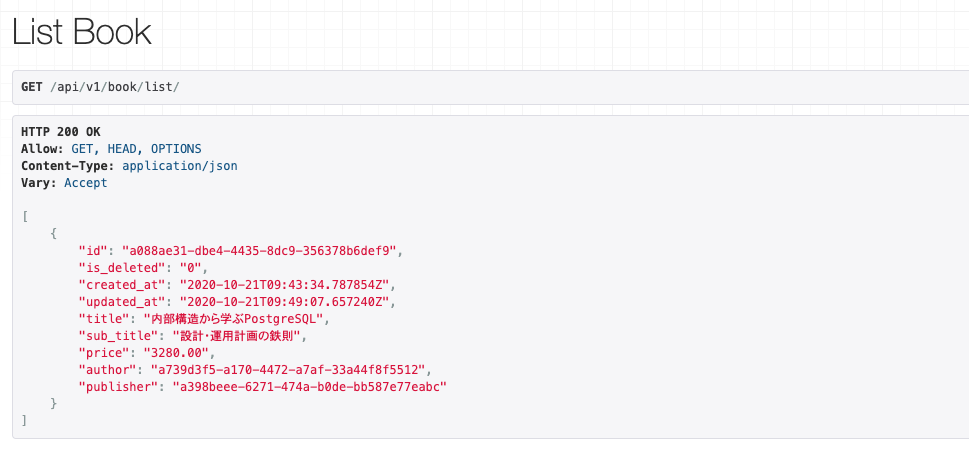
まずは手始めにdjango-filterで
検索条件などで絞り込まずに一覧の取得を行ってみます。
view.py
from django_filters import rest_framework as filters

class FilterBook(filters.FilterSet):
    class Meta:
        model = Book
        fields = '__all__'

class ListBook(APIView):

    def get(self, request):
        filterset = FilterBook(request.query_params, queryset=Book.objects.all())
        serializer = BookSerializer(instance=filterset.qs, many=True)
        return Response(serializer.data)
FilterSetを継承したクラスを作成して、そこでモデルを指定します。
DjangoのFormやSerializerに似ていますね。

そしてこの作成したListBookAPIのURL
/api/v1/book/list/(省いています。)
にブラウザからリクエストすると、このようなデータがレスポンスされます。
もちろんデータはサンプルです笑

検索条件を指定する

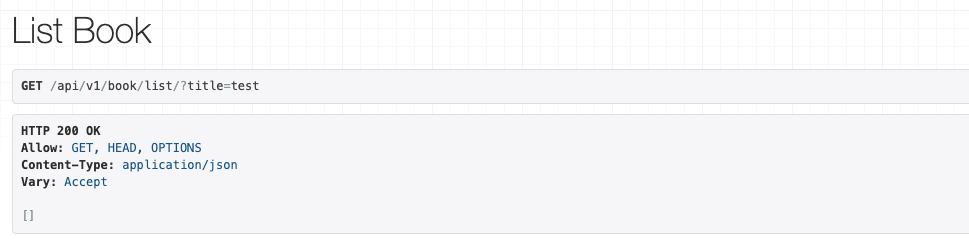
それでは検索条件を指定してリクエストする。
先ほどリクエストしたURLは/api/v1/book/list/でしたが、そこのクエリパラメータを指定します。
/api/v1/book/list/?title=testに変更してリクエストするとレスポンスが変わります。

今回のレスポンスは何も返却されませんでした。
このtitle=testというのは、Bookモデルのtitleがtestに一致するオブジェクトを返します。
その他にもtitleをsub_titleに変更して、/api/v1/book/list/?sub_title=testに
リクエストをしてもレスポンスは何にも返ってきません。

ただし、クエリパラメータをBookモデルに存在しないフィールドを指定すると
絞り込みができず、レスポンスにデータが返ってきます。

検索条件を変更する

先ほどは、titleやsub_titleで絞り込んで
データを抽出しました。

ただ今回は、titleは検索条件でいいけど、sub_titleは検索条件として要らない！
なんてことがあるかと思います。
そんな時は、Filterクラスのfieldsで、該当のみに指定することができます。
views.py
class FilterBook(filters.FilterSet):
    class Meta:
        model = Book
        fields = ['title']
このようにすることで、先ほどはsub_titleで絞り込みできていましたが、titleでしか絞り込みができなくなりました。

検索方法をカスタマイズする

先ほどfieldsを__all__で指定した場合だと、デフォルトの検索方法になってしまい
数値の検索や、部分一致などの検索方法が使えませんでした。
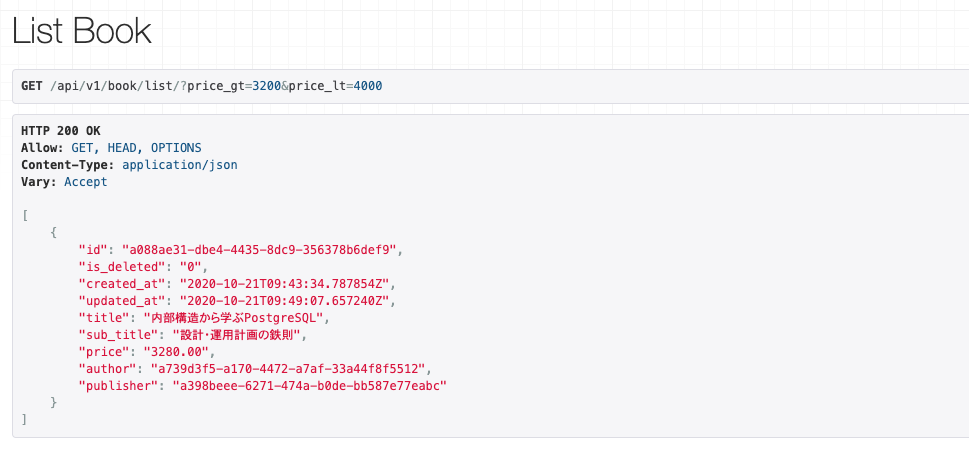
(例えば、/api/v1/book/list/?price=testにリクエストしても、絞り込みはされません。)

そこで、検索方法をカスタマイズしていきます。
views.py
class FilterBook(filters.FilterSet):
    # UUID
    id = filters.UUIDFilter()

    # 部分一致
    title = filters.CharFilter(lookup_expr='icontains')

    # 金額を調べる
    price = filters.NumberFilter()
    price__gt = filters.NumberFilter(field_name='price', lookup_expr='gt')
    price__lt = filters.NumberFilter(field_name='price', lookup_expr='lt')

    class Meta:
        model = Book
        fields = []
カスタマイズの内容です。
filters.UUIDFilter()は、UUIDへの対応です。IDで検索かけても引っかかるようになりました。
filters.CharFilter(lookup_expr='icontains')で
部分一致にしました。このlookup_exprの引数は、Djangoのfield lookups
と同じ指定ができます。
filters.NumberFilter(field_name='price', lookup_expr='gt')
は数値の対応と範囲を指定しています。
field_nameは、モデルの対象フィールドを指定します。
通常はフィルターのフィールド名とモデルのフィールド名で一致していれば、指定しなくても問題ありません。

それではカスタマイズ後にリクエストをします。
api/v1/book/list/?title=sqlや
api/v1/book/list/?price_gt=3200&price_lt=4000
にリクエストしても、データがレスポンスされるようになりました。

リレーションにも対応する

ForeignKeyで結びついたモデルも検索条件にしたい場合は、
field_nameに指定します。
指定方法はdjangoのlookup式で対応できます。
views.py
class FilterBook(filters.FilterSet):
    author_last_name = filters.CharFilter(field_name='author__last_name',lookup_expr='icontains')
デフォルトのフィルターをカスタマイズする

デフォルトのフィルターでは、CharFilterが完全一致だったりでフィールドごとにカスタマイズする必要がありました。
フィールドごとにカスタマイズするのではなく、CharFilterのデフォルトをカスタマイズしようということです。
views.py
class FilterBook(filters.FilterSet):

    class Meta:
        model = Book
        fields = ['title']
        filter_overrides = {
            models.CharField: {
                'filter_class': filters.CharFilter,
                'extra': lambda f: {
                    'lookup_expr': 'icontains',
                },
            },
        }
class Meta:にfilter_overrridesとデフォルトの設定にしたい内容を記載します。
今回これで、モデルにCharFiledを使っているフィールドは、デフォルトで全て部分一致になりました。

独自のカスタマイズをする

絞りこむ際に独自の検索を行うことができます。
ハイフンを取り除き、部分一致にする例を作成しました。
views.py
class FilterBook(filters.FilterSet):
    title = filters.CharFilter(method='title_custom_filter')

    class Meta:
        model = Book
        fields = []

    @staticmethod
    def title_custom_filter(queryset, name, value):
        # nameはフィールド名前
        # valueはクエリパラメータ
        # name__icontains
        lookup = '__'.join([name, 'icontains'])
        # ハイフンを消す
        replaced_value = value.replace('-', '')
        return queryset.filter(**{
            lookup: replaced_value,
        })
CharFilterの引数にメソッドの名前を文字列で渡すと、そのメソッドが検索時に実行されます。
nameにフィールド名、value検索のパラメータが渡されます。
なのでそこを変更すれば、自由に検索条件が作成できる分けです。

今回では、例えば
/api/v1/book/list/?title=gと同じように
/api/v1/book/list/?title=g---
にリクエストを送信してもレスポンスがくるようになりました。

この他の詳しい情報は、
ぜひ公式ドキュメントを
ご確認いただければとおもいます!!!!!!!!!!!!!!!!!

　 Tweet
Qiitaで続きを読む

投稿日：2020-10-21T21:35:28+09:00

pytest-mockのよく使う実装方法をまとめてみた

pytest-mockの使い方を調べたのでメモ
今後も使いそうなユースケースを都度調べるのが面倒なのでまとめてみました。
pytestを調べてから1日で書いた記事なので色々過不足があると思いますが、もっと良い方法が見つかったら随時アップデートしていきたいと思います。

pytest、pytest-mockについて

pythonのテストコードを実装するときに使うライブラリの1つです。
詳細は公式ホームページを参照してください。

pytest

https://docs.pytest.org/en/latest/index.html

pytest-mock

https://pypi.org/project/pytest-mock/

説明に使うメソッド

下記のhogeメソッドをテスト対象とします。

from mailer import Mailer

# messagesの例
# ['1通目の本文', '2通目の本文']
def hoge(messages):
    try:
        # messagesの数だけメール送信
        for message in messages:
          has_error = Mailer.send(message)
          if has_error:
            # エラー発生時は1を返却
            return 1

        # 正常終了時は0を返却
        return 0
    except Exception as e:
        # 例外発生時は2を返却
        return 2

この記事を書いたときに使ったバージョンは下記の通りです。

python 3.8.5
pytest 6.1.1
pytest-mock 3.3.1

`Mailer.send`をモックに差し替える

test_hoge.py

from hoge import hoge
from mailer import Mailer
from unittest.mock import call

def test_hoge(mocker):
    # Mailer.sendをモックに差し替える
    mailer_mock = mocker.patch.object(Mailer, 'send')

    messages = ['1通目の本文', '2通目の本文']

    # 上記でMailer.sendをモックにしているのでhogeを実行しても本物のMailer.sendは実行されません
    assert hoge(messages) == 0

呼び出し回数を検証したい

test_hoge.py

from hoge import hoge
from mailer import Mailer
from unittest.mock import call

def test_hoge(mocker):
    # Mailer.sendをモックに差し替える
    mailer_mock = mocker.patch.object(Mailer, 'send')

    messages = ['1通目の本文', '2通目の本文']
    assert hoge(messages) == 0

    # Mailer.sendが2回呼ばれることを確認できます
    assert mailer_mock.call_count == 2

呼び出されないことを検証したい

test_hoge.py

from hoge import hoge
from mailer import Mailer
from unittest.mock import call

def test_hoge(mocker):
    # Mailer.sendをモックに差し替える
    mailer_mock = mocker.patch.object(Mailer, 'send')

    # messagesが空なのでMailer．sendは呼ばれないようにする
    messages = []
    assert hoge(messages) == 0

    # Mailer.sendが呼ばれないことを検証
    mailer_mock.assert_not_called()

パラメーターを検証したい

test_hoge.py

from hoge import hoge
from mailer import Mailer
from unittest.mock import call

def test_hoge(mocker):
    # Mailer.sendをモックに差し替える
    mailer_mock = mocker.patch.object(Mailer, 'send')

    messages = ['1通目の本文', '2通目の本文']
    assert hoge(messages) == 0

    # 1回目は'1通目の本文'、2回目は'2通目の本文'がパラメーターで渡されて呼び出されていることが検証できます
    mailer_mock.assert_has_calls([call('1通目の本文'), call('2通目の本文')])

戻り値を制御したい

test_hoge.py

from hoge import hoge
from mailer import Mailer
from unittest.mock import call

def test_hoge(mocker):
    # side_effectに配列で戻り値のリストを渡します
    # 呼び出されるごとに配列の先頭から順番に返却されます
    # この例の場合、1回目はFalse、2回目はTrueが返却されます
    mailer_mock = mocker.patch.object(Mailer, 'send', side_effect = [False, True])

    messages = ['1通目の本文', '2通目の本文']

    # 2回めのMailer.sendがTrueを返却するので戻り値1の検証ができます
    assert hoge(messages) == 1

例外を発生させたい

test_hoge.py

from hoge import hoge
from mailer import Mailer
from unittest.mock import call

def test_hoge(mocker):
    # side_effectに例外を指定します
    # この例の場合、1回目はFalse、2回目は例外が発生します
    mailer_mock = mocker.patch.object(Mailer, 'send', side_effect = [False, Exception('error')])

    messages = ['1通目の本文', '2通目の本文']

    # 2回めのMailer.sendが例外が発生するので戻り値2の検証ができます
    assert hoge(messages) == 2

　 Tweet
Qiitaで続きを読む

投稿日：2020-10-21T21:24:01+09:00

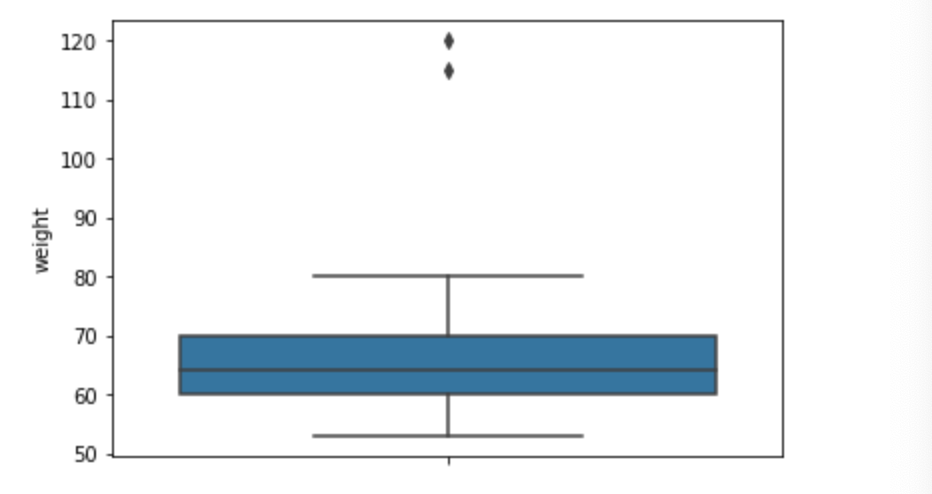
区間推定を行ってみた。

区間推定

今回は前回に引き続き推定を行っていきたいと思います。
前回は点推定を行いましたので気になる方は見てみてください。

データに関して

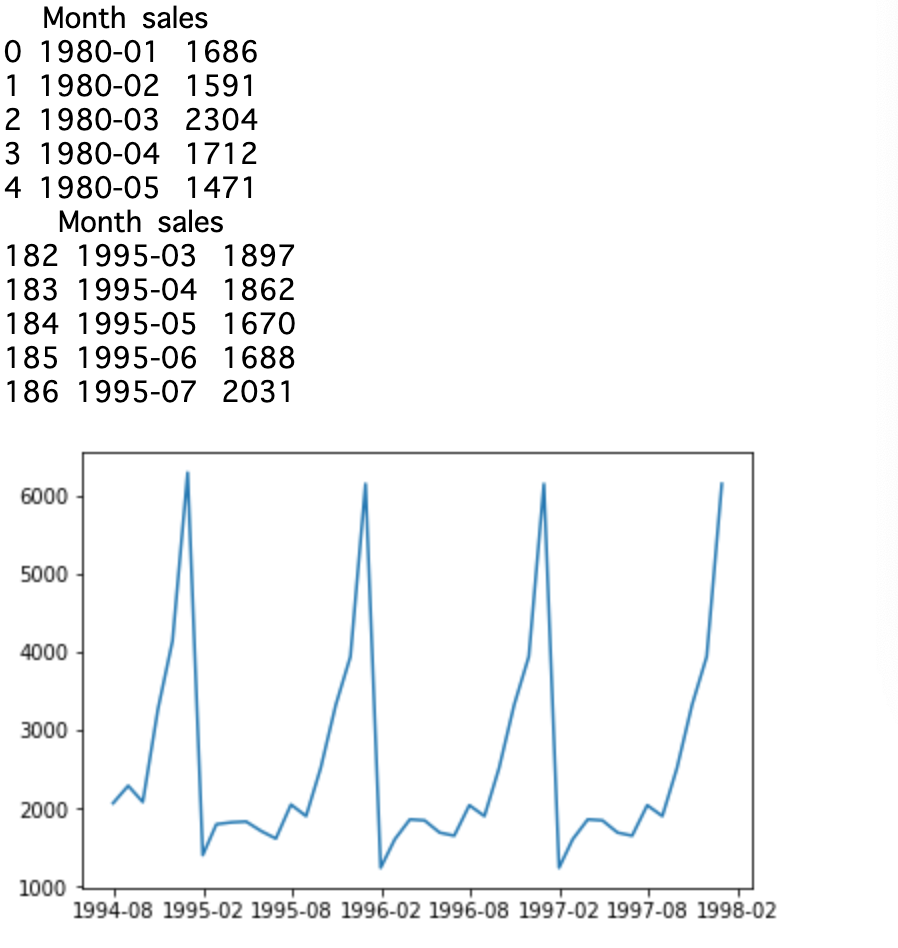
今回もPokemonのデータセットを使用して区間推定を行ってみました。
データは下のようになっています。
今回もこのデータのHPのデータをを母集団として区間推定を行っていきたいと思います。

まずHPの平均と分散を求めてみたいと思います。
score = np.array(df['HP'])
mean = np.mean(score)
var = np.var(score)
print("HP　平均: {} , 分散: {} ".format(mean , var))
HP　平均: 69.25875 , 分散: 651.2042984374999
これらを母平均・母分散として分析を行っていきたいと思います。

　正規分布の母平均の区間推定（母分散が分かっている場合）

今回先ほどのHPデータを母集団とし、それが正規分布に従っていると仮定したうえでさらに母分散も分かっている場合を考えていきます。

母集団に正規分布を仮定しているため、標本平均$\bar{X}$は$N(μ,σ^2/n)$に従います。
つまり、標本平均という推定量は期待値は母平均μであるものの、標準偏差$\sqrt{σ^2/n}$でばらついている。このような推定量の標準偏差のことを「標準誤差」といいます。

また標本平均$\bar{X}$は$N(μ,σ^2/n)$に従っていることから、$Z = (\bar{X}-μ)/\sqrt{σ^2/n}$と標準化を行うことができ、Zは標準正規分布に従います。この標準化を行うことで何がいいのかというと信頼区間を
計算することが容易に出来るようになるということです。

まず母平均・母分散と標本データの標本平均・標本分散を計算します。
今回の標本のサンプルサイズは20にしています。
np.random.seed(0)
n = 20
sample = np.random.choice(score , n)

p_mean = np.mean(score)
p_var = np.var(score)

s_mean = np.mean(sample)
s_var = np.var(sample , ddof = 1)
母平均: 69.25875 , 母分散: 651.2042984374999
標本平均: 68.8 , 標本分散(不偏分散): 451.26000000000005

今回はこの標本平均を使用して母平均の信頼区間を算出してみたいと思います。(母分散はわかっているとします。)
標本平均から母平均の95%の信頼区間を求めることを考えます。まず標本平均$\bar{X}$を標準化すると$Z = (\bar{X}-μ)/\sqrt{σ^2/n}$となります。そのためまずは$Z$の95%信頼区間を考えてみます。
すると
$P(z_{0.975}≦(\bar{X}-μ)/\sqrt{σ^2/n} ≦z_{0.025})=0.95…①$
という不等式を立てることが出来ます。
この式は確率変数$Z = (\bar{X}-μ)/\sqrt{σ^2/n}$が区間$[z_{0.975},z_{0.025}]$に入る確率が95%であることを表しています。
この$①$の式を母平均のμについての不等式になるように変形すると
$P( \bar{X}-z_{0.025}*\sqrt{σ^2/n}≦μ≦\bar{X}-z_{0.095} * \sqrt{σ^2/n})=0.95$
となります。

よって、母分散が分かっているときの95%の信頼区間を求めるには、
$[\bar{X}-z_{0.025}*\sqrt{σ^2/n} , \bar{X}-z_{0.095} * \sqrt{σ^2/n}]$
を求めればよいということになります。

実装してみました。
rv = stats.norm()
#rv.isf(0.025)には標準正規分布の確率が0.025の点を表している。それに標準誤差を掛ける。
lcl = s_mean - rv.isf(0.025) * np.sqrt(p_var/n)
ucl = s_mean - rv.isf(0.975) * np.sqrt(p_var/n)
lcl , ucl
(57.616, 79.984)

以上より、母平均の95%信頼区間は(57.616, 79.984)であると分かりました。
先程求めた母平均は69.25875でしたので信頼区間内に母平均が含まれていることが分かります。

この信頼区間は同じように何回も標本抽出を行い、区間推定を行うとそのうち95%の区間推定には母平均が含まれるということになります。かみ砕いた形で言ってみると、100回区間推定を行った場合、そのうちの95回は母平均を含む信頼区間が求まるけど、5回は求めた信頼区間に母平均が含まないといったことです。

母分散の区間推定

母分散の区間推定を行っていきます。ここでは母集団に正規分布を仮定し母平均も分かっていない場合を考えてみます。

先程、母平均の信頼区間を算出する際に標準化を行い、標準正規分布に従う確率変数に変換したように、不偏分散$s^2$も何らかの変換を行い代表的な確率分布に従う確率変数を作成する必要があります。
この時に使用される確率分布がカイ二乗分布になります。
不偏分散$s^2$に対して$Y=(n-1)s^2/σ^2$へ変換することでこの変数Yは自由度n-1のカイ二乗分布に従うことが知られています。

では母分散の信頼区間を求めていきたいと思います。まず$\chi{}^2(n-1) $の95%信頼区間を求めていきます。

$P(\chi{}^2_{0.975}(n-1) ≦ (n-1)s^2/σ^2 ≦\chi{}^2_{0.025}(n-1)) = 0.95$

これを今回母分散の信頼区間を求めたいので$σ^2$が真ん中に来るようにします。

$P((n-1)s^2/\chi{}^2_{0.025}(n-1) ≦ σ^2 ≦(n-1)s^2/\chi{}^2_{0.975}(n-1)) = 0.95$

これより、母分散$σ^2$の95%信頼区間は

$[(n-1)s^2/\chi{}^2_{0.025}(n-1) , (n-1)s^2/\chi{}^2_{0.975}(n-1)]$

になります。
rv = stats.chi2(df=n-1)
lcl = (n-1) * s_var / rv.isf(0.025)
hcl = (n-1) * s_var / rv.isf(0.975)

lcl , hcl
(260.984, 962.659)

母分散の信頼区間は(260.984, 962.659)となりました。母分散は651.204であったので区間内に含まれていることが分かります。

母平均の区間推定（母分散が分かっていない場合）

先程母平均の信頼区間を求める際に母分散が分かっているという状況で分析を進めました。しかしながら実際母平均が分からず、母分散が分かっているという状況はあまりありません。
そのため、今回は母分散が分からないときの母平均の信頼区間の推定を行っていきたいと思います。

母分散が分かっているときは、標本平均$\bar{X}$の標準誤差$\sqrt{σ^2/n}$によって区間推定を行いました。今回はこの母分散$σ^2$が分からないため、その代わりに推定量である不偏分散$s^2$を使用した$\sqrt{s^2/n}$を標準誤差として代用します。

まず、母分散が分かっているときと同じように標本平均$\bar{X}$を$\sqrt{s^2/n}$を使用して変換を行います。

$t = (\bar{X} - μ) / \sqrt{s^2/n}$

この$t$は

$Y=(n-1)s^2/σ^2$
$Z = (\bar{X}-μ)/\sqrt{σ^2/n}$

この二つを使用して変換を行うと、

$t = Z / \sqrt{Y/(n-1)}$

で表すことが出来ます。
よってこの$t$は自由度n-1のt分布に従うことが分かります。

今$t = (\bar{X} - μ) / \sqrt{s^2/n}$は自由度n-1のt分布に従うことが分かったので、ここから母平均の95%信頼区間を求めていきます。

$P(t_{0.975}(n-1)≦ (\bar{X} - μ) / \sqrt{s^2/n}　≦ t_{0.025}(n-1)) = 0.95$

この式を母平均のμが真ん中になるように変形します。

$P(\bar{X} - t_{0.025}(n-1) * \sqrt{s^2/n}≦ μ ≦ \bar{X} - t_{0.975}(n-1)*\sqrt{s^2/n}) = 0.95$

これにより、母平均の95%信頼区間は

$[ \bar{X} - t_{0.025}(n-1) * \sqrt{s^2/n} , \bar{X} - t_{0.975}(n-1)*\sqrt{s^2/n} ]$

となります。
rv = stats.t(df=n-1)
lcl = s_mean - rv.isf(0.025) * np.sqrt(s_var/n)
ucl = s_mean - rv.isf(0.975) * np.sqrt(s_var/n)

lcl , ucl
(58.858, 78.742)

母平均の95%信頼区間は(57.616, 79.984)であると分かりました。
先程求めた母平均は69.25875でしたので信頼区間内に母平均が含まれていることが分かります。

まとめ

今回は区間推定を行ってみました。
実際に手を動かして実装を行うことによって理解が深まったりするので手を動かしてアウトプットするのはいいなと記事を書いてて思いました！

＜参考資料＞
pythonで理解する統計解析の基礎

　 Tweet
Qiitaで続きを読む

投稿日：2020-10-21T20:43:58+09:00

DockerでSparkを動かしたらlocalhost:4040にアクセスできない件について

SparkのSpark Web UI (localhost:4040)だけが何故か接続できなかったので、色々調べていたのですが解決策が乗っておらず、慣れていない人であれば同じ悩みを抱えている人がいると思ったので、初投稿します。また業務中に起きたエラーのため、コードなどは一切載せていませんのでご理解のほどよろしくお願いいたします。

環境

DockerでPythonのコンテナとSparkのコンテナ(wokerを接続している)をBridgeしている
どちらの環境にもPyspark、javaの環境がインストールされている。

環境構築の参考

SparkのMaster1つとWorker1つをdocker-composeで上げてpysparkを動かすまで
https://qiita.com/hrkt/items/fe9b1162f7a08a07e812

ゴール

PythonのDockerの中に入って(docker exec...) spark-submitを行い、処理を行っている間にlocalhost:4040に接続してWebUIを確認したい。

問題について

起動してからlocalhost:8080はつながるのになぜか4040は接続ができない

解決策

Sparkが処理中時にのみlocalhost:4040にアクセスできる

docker-compose.ymlのSparkのコンテナにport 4040:4040と書いていたが、Job管理をするPython側にport 4040:4040を書く必要があった。(今回はこれが該当)

まとめ

StackOverFlowなどを読んでも全く分からなかったが、先輩に聞いたら一発で解決した。インフラにもっと強くなりたいです。

おまけ

sparkの中でサンプルコードを動かしていたが、df.show()すると
initial job has not accepted any resources; check your cluster ui to ensure that workers are registered and have sufficient resourcesと出て止まってしまう。リソースが足りないとのことで、メモリ設定などを変えたが解決しなかった。

サンプルコードはこちらから借りてきました。

PySpark のスクリプトファイルで引数を扱う
https://blog.amedama.jp/entry/2018/03/17/113516

参考にしたサンプルコード
from pyspark import SparkConf
from pyspark import SparkContext
from pyspark.sql import SparkSession
def main():
    conf = SparkConf()
    conf.setAppName('example')
    sc = SparkContext(conf=conf)
    spark = SparkSession(sc)
    df = spark.sql('SELECT "Hello, World!" AS message')
    df.show()
解決策
conf = SparkConf().setMaster('local')

　 Tweet
Qiitaで続きを読む

投稿日：2020-10-21T20:38:07+09:00

MySQL初心者の私がよく書き込みでハマるポイント

pythonからMySQLに書き込みを行う時、いつもハマる。
今回こそハマりどころメモしておく。

実施内容のイメージ

Pythonを使ってローカルのcsvをローカルにたてたMySQLやGoogle Cloud PLatformのMySQLにデータを書き込む。

環境

Python3
mysql-connector
GCPのCloud SQL(MySQL)(今回は)
接続方法やSSL化については今回は省略。純粋にSQL文のハマりどころについてです。

書き込む際のコード

main.py

# -*- coding: utf-8 -*-
import os
import sys
import time
import glob
import shutil
import datetime
import logging
import traceback
import pandas as pd
import mysql.connector
import ssl
ssl.match_hostname = lambda cert, hostname: True

def insert_sql():
    schema = 'hogehoge2'#db名のこと
    connection = mysql.connector.connect(
                        port="3306",#基本はこのポートを使うことが多い
                        host='**.**.**.**',#gcpのIP
                        user='hogehoge',
                        password='fugafuda',
                        db=schema,
                        charset='utf8',
                        ssl_ca="./cloudstorage_cert/server-ca.pem",#証明書を使いたいので今回はこのフォルダにおいて指定
                        ssl_cert="./cloudstorage_cert/client-cert.pem",
                        ssl_key="./cloudstorage_cert/client-key.pem"
    )

    df = pd.read_csv(filename,engine="python")
    for r in range(df.shape[0]):
        cur = connection.cursor()
        sql = "insert into schema.table (col1,col2,col3,col4) values ('%s','%s',%s,%s);"%(
                    datetime.datetime.now(),
                    str(datetime.datetime.now()),
                    100,
                    1.5
                )
        print(sql)
        cur.execute(sql)
        cur.close()
        connection.commit()
    connection.close()
    print("done")

if __name__ == '__main__':
    insert_sql()

注意ポイント

1.テーブルを指定するとき、ちゃんとスキーマ（db）を記載する

my.sql

ダメな例
insert into mytable (datetime,col2,col3,col4) values ('2020-10-20 10:39:13.252105','2020-10-20 10:39:13.252105',100,1.5);
いい例
insert into myshema.mytable (datetime,col2,col3,col4) values ('2020-10-20 10:39:13.252105','2020-10-20 10:39:13.252105',100,1.5);

2. 文字列や時間など数字ではないものは、SQL文の中でシングルクオートで囲む

example.py

#ダメな例
sql = "insert into myshema.mytable (datetime,col2,col3,col4) values (%s,%s,%s,%s);"%(
                    temp.loc[r,"DateTime"],
                    str(temp.loc[r,"DateTime"]),
                    100,
                    1.5
                    )
#いい例
sql = "insert into myshema.mytable (datetime,col2,col3,col4) values ('%s','%s',%s,%s);"%(
                    temp.loc[r,"DateTime"],
                    str(temp.loc[r,"DateTime"]),
                    100,
                    1.5
                    )

3. connectionに対してcommit()しないとデータが反映されない

connection.close()は忘れないのだが、connection.commit()を忘れてデータが更新されないことがある。cur.commit()はしない。connectionでcommit()することに注意。

以上のあたりでよくハマる。sql文の最後の;はあってもなくても動作した

　 Tweet
Qiitaで続きを読む

投稿日：2020-10-21T20:18:30+09:00

全プログラミング言語の用語整理

言語自体の整理

1. 動的型付けのプログラミング言語

プログラムでは様々な「型」を扱います。例えば、文字列値と整数値と少数値は異なる型です。この他にも様々な型があり、プログラムにミスがあって異なった型を指定しまう事でエラーを発生させることがあります。

動的型付けのプログラミング言語の場合はプログラムを実行時に型検査を行います。厳格なエラーを対処しなくてもプログラムは動作するので初心者には学びやすい言語が多くなっています。しかしその反面、非常に分かりにくい不具合を作り込んでしまう可能性もあります。

言語名 F-S Initial release 起源

JavaScript FS HTML と合わせて使用して動きのある WEB ページを開発するために使用 1995

Ruby FS 日本人により開発された。可読性を重視した構文 1995

Python FS 最近ではAI やデータ解析処理の場面において利用されおり注目度の高い言語 1990

PHP S 動的な WEB サイトを実装する為の言語であるため、ライブラリを用いなくても WEB アプリケーション向けの処理が実装 1995

2. 静的型付けのプログラミング言語

動的型付けのプログラミング言語の場合、「コンパイル」を行う事でプログラミング時に型チェックを行います。静的型付けのプログラミング言語に比べて型チェックが厳格になっているので実装する処理も多くなります。

静的型付けのプログラミング言語に比べて難易度は高いと言えます。

言語名 F-S Initial release 起源

C - 高速に動作。システムの共通言語として様々なplatformで使用。garbage collection等、最近の機能は実装されてなく習得難易度はとても高い 1972

C++ - C を元にオブジェクト指向や例外処理等の概念を取り入れた言語 1993-2

C# - Microsoft が開発した .Net Framework と言うプラットフォーム上で動作させるためのプログラム 2000

Objective-C / Swift - Apple 社の MacOS や iOS 用のアプリケーションを開発するためのプログラム言語 1984/2014-6

SQL - データベースから情報の取得、追加、更新、削除と言った処理を行う為の言語 1974

各言語詳細

1. フロントエンド
Js
（npmやYarn　パッケージ管理）
ーVue　　Initial release February 2014;
ーーnuxt　VueのFramework　　Initial release   October 26, 2016;
ーーーVuexなどのライブラリ


ーReact　　Initial release   May 29, 2013;
ーーNext　ReactのFramework
ーーーReduxなどのライブラリ
ーーーMaterial UI Reactのcomponents、Vuetifyみたいな感じか

react native Initial-March 26, 2015

angular Initial release 2.0 / 14 September 2016; 
Python　　First appeared  1990;
(pip　パッケージ管理)
ーDjango　Python-web-framework 　　Initial releas21 July 2005
Ruby　1995
（gem　パッケージ管理）
ーーrails　　August 2004;
2. サーバーエンド
PHP
（composer　パッケージ管理）
ーLaravel PHPのFramework　　Initial release June 2011
JavaScript
Node Initial release    May 27, 2009;
Node express November 16, 2010;

言語名	F-S		Initial release
JavaScript	FS	HTML と合わせて使用して動きのある WEB ページを開発するために使用	1995
Ruby	FS	日本人により開発された。可読性を重視した構文	1995
Python	FS	最近ではAI やデータ解析処理の場面において利用されおり注目度の高い言語	1990
PHP	S	動的な WEB サイトを実装する為の言語であるため、ライブラリを用いなくても WEB アプリケーション向けの処理が実装	1995

言語名	F-S		Initial release
C	-	高速に動作。システムの共通言語として様々なplatformで使用。garbage collection等、最近の機能は実装されてなく習得難易度はとても高い	1972
C++	-	C を元にオブジェクト指向や例外処理等の概念を取り入れた言語	1993-2
C#	-	Microsoft が開発した .Net Framework と言うプラットフォーム上で動作させるためのプログラム	2000
Objective-C / Swift	-	Apple 社の MacOS や iOS 用のアプリケーションを開発するためのプログラム言語	1984/2014-6
SQL	-	データベースから情報の取得、追加、更新、削除と言った処理を行う為の言語	1974

　 Tweet
Qiitaで続きを読む

投稿日：2020-10-21T19:49:25+09:00

Dlibを使って顔の輪郭をとる（１）

顔の輪郭とか口の動き抽出するやつを今すぐパッと試したい。

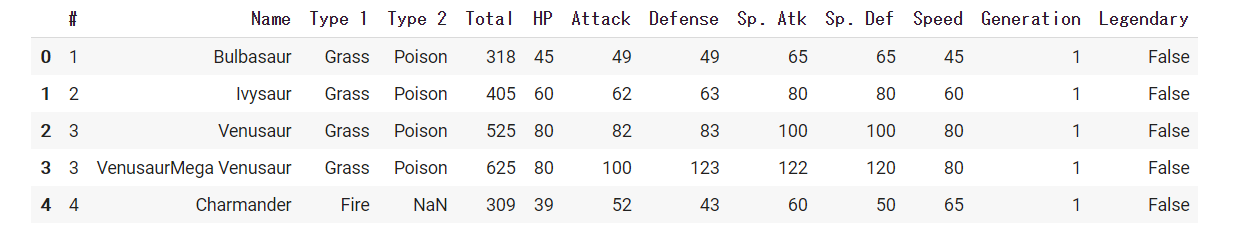
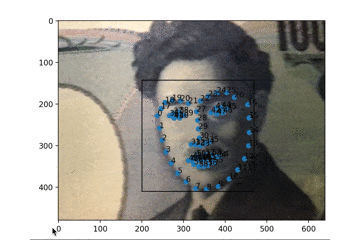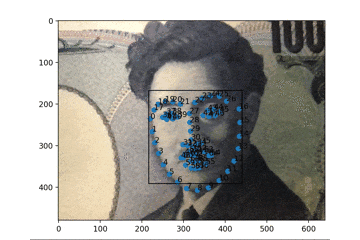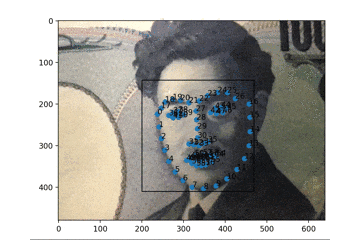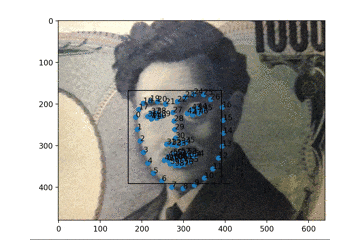
やること

DlibとPythonを使って、顔の輪郭や口の動きをとるフェイストラッキングを実行します。
PC（ここではMac）のWEBカメラで取得したものに即座に反映、表示します。
この記事は2017年に公開いただいているのQiita記事を今トレースする場合の備忘メモです。

過去のQiita記事に答えがあるので参考にします

Qiita記事：dlibの顔ランドマーク認識の結果をリアルタイムにmatplotlibで表示する

基本は上記に沿ってありがたく実行させていただくだけですが、ちょっとだけ変更があります。

変更箇所

データファイルの参照先URLが変更になっているので、別途DLして実行します。

https://www.kkaneko.jp/dblab/dlib/dlibface.html
こちらを参考に、

http://dlib.net/files/
こちらを開いて、「shape_predictor_68_face_landmarks.dat.bz2」をDLし展開します。

前述のプログラムの中の
python
predictor_path = "hoge" 
のhogeのところにさきほどのファイルを絶対パスで指定すれば安心です。

実行結果

PCのカメラにお札を見せているところです。もちろん実写の顔もちゃんととれます。

次回

もうちょっと早く認識＆表示できてなおかつ勘弁な方法があれば試したいです。
表情判定もやっておきたいです。

　 Tweet
Qiitaで続きを読む

投稿日：2020-10-21T19:43:41+09:00

PyMuPDFで「exception stack overflow!」

はじめに

備忘録としてのメモ。
ググっても答えに辿り着けなかったので、念のため残しておく。

問題点

PyMuPDF を使って PDF のコピーをするときに、まれに exception stack overflow! が発生することがある。

コード
new_doc = fitz.open()
new_doc.insertPDF(docsrc=old_doc, from_page=1, to_page=1)
エラー
mupdf: exception stack overflow!
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
   ・
   ・
   ・　
  File "/Users/ijufumi/workspaces/python_sample/.venv/lib/python3.6/site-packages/fitz/fitz.py", line 3581, in insertPDF
    val = _fitz.Document_insertPDF(self, docsrc, from_page, to_page, start_at, rotate, links, annots)
RuntimeError: exception stack overflow!
対応策

insertPDFを実行する時に、 annots=False を指定する。

コード（修正後）
new_doc = fitz.open()
new_doc.insertPDF(docsrc=old_doc, from_page=1, to_page=1, annots=False)
原因

公式ドキュメントでは見つけられなかったけど、いくつかのアノテーションがあるとこの例外が発生する。

お願い

もし、公式ドキュメントなどで見つけた人がいましたら、コメント頂けると幸いです。

　 Tweet
Qiitaで続きを読む

投稿日：2020-10-21T18:36:49+09:00

Scikit-learn の impute で欠損値を埋める

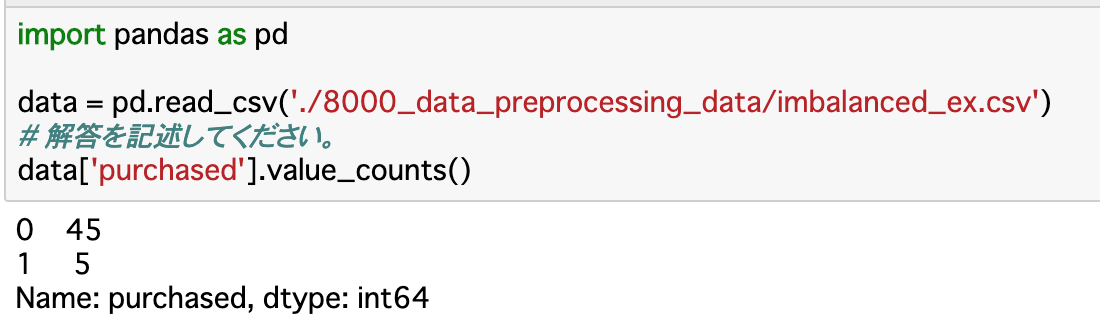
Scikit-learn の impute は、機械学習の前処理として欠損データを埋めるのに使われます。簡単なデータを利用して挙動を確認してみました。

テスト用データ作成
data = {
    'A': [a for a in range(10)],
    'B': [a * 2 for a in range(10)],
    'C': [a * 3 for a in range(10)],
    'D': [a * 4 for a in range(10)],
        }
import pandas as pd

data = pd.DataFrame(data)
data
A B C D

0 0 0 0 0

1 1 2 3 4

2 2 4 6 8

3 3 6 9 12

4 4 8 12 16

5 5 10 15 20

6 6 12 18 24

7 7 14 21 28

8 8 16 24 32

9 9 18 27 36
import numpy as nan
data2 = pd.DataFrame(data)
#data2['B'][3] = np.nan
data2.loc.__setitem__(((2), ("B")), np.nan)
data2.loc.__setitem__(((3), ("C")), np.nan)
data2.loc.__setitem__(((5), ("C")), np.nan)
data2.loc.__setitem__(((6), ("D")), np.nan)
data2.loc.__setitem__(((7), ("D")), np.nan)
data2
A B C D

0 0 0.0 0.0 0.0

1 1 2.0 3.0 4.0

2 2 NaN 6.0 8.0

3 3 6.0 NaN 12.0

4 4 8.0 12.0 16.0

5 5 10.0 NaN 20.0

6 6 12.0 18.0 NaN

7 7 14.0 21.0 NaN

8 8 16.0 24.0 32.0

9 9 18.0 27.0 36.0
%matplotlib inline
import matplotlib.pyplot as plt
plt.plot(data2)
[<matplotlib.lines.Line2D at 0x7fdb46668c18>,
 <matplotlib.lines.Line2D at 0x7fdb46668d30>,
 <matplotlib.lines.Line2D at 0x7fdb46668e80>,
 <matplotlib.lines.Line2D at 0x7fdb46668fd0>]
以上のようにして、欠損値を１つ含むB列、２つ含むC列、連続した欠損値を含むD列を作成しました。

SimpleImputer

SimpleImputerクラスは、欠損値を入力するための基本的な計算法を提供します。欠損値は、指定された定数値を用いて、あるいは欠損値が存在する各列の統計量（平均値、中央値、または最も頻繁に発生する値）を用いて計算することができます。

default(mean)

デフォルトは平均値で埋めます。
from sklearn.impute import SimpleImputer

imp = SimpleImputer() #missing_values=np.nan, strategy='mean')
data3 = pd.DataFrame(imp.fit_transform(data2))
data3
0 1 2 3

0 0.0 0.000000 0.000 0.0

1 1.0 2.000000 3.000 4.0

2 2.0 9.555556 6.000 8.0

3 3.0 6.000000 13.875 12.0

4 4.0 8.000000 12.000 16.0

5 5.0 10.000000 13.875 20.0

6 6.0 12.000000 18.000 16.0

7 7.0 14.000000 21.000 16.0

8 8.0 16.000000 24.000 32.0

9 9.0 18.000000 27.000 36.0
%matplotlib inline
import matplotlib.pyplot as plt
plt.plot(data3)
[<matplotlib.lines.Line2D at 0x7fdb465dd2b0>,
 <matplotlib.lines.Line2D at 0x7fdb465dd3c8>,
 <matplotlib.lines.Line2D at 0x7fdb465dd518>,
 <matplotlib.lines.Line2D at 0x7fdb465dd668>]
以上のように、データの種類によっては、平均値で埋めるのは不自然になったりしますね。

median

欠損値を中央値で埋めることもできます。
from sklearn.impute import SimpleImputer

imp = SimpleImputer(missing_values=np.nan, strategy='median')
data4 = pd.DataFrame(imp.fit_transform(data2))
data4
0 1 2 3

0 0.0 0.0 0.0 0.0

1 1.0 2.0 3.0 4.0

2 2.0 10.0 6.0 8.0

3 3.0 6.0 15.0 12.0

4 4.0 8.0 12.0 16.0

5 5.0 10.0 15.0 20.0

6 6.0 12.0 18.0 14.0

7 7.0 14.0 21.0 14.0

8 8.0 16.0 24.0 32.0

9 9.0 18.0 27.0 36.0
%matplotlib inline
import matplotlib.pyplot as plt
plt.plot(data4)
[<matplotlib.lines.Line2D at 0x7fdb465310b8>,
 <matplotlib.lines.Line2D at 0x7fdb465311d0>,
 <matplotlib.lines.Line2D at 0x7fdb46531320>,
 <matplotlib.lines.Line2D at 0x7fdb46531470>]
平均値と同様、中央値で埋める場合も、データの内容によっては不自然な埋め型になってしまうことがありますね。

most_frequent

最頻値で埋めることもできます。
from sklearn.impute import SimpleImputer

imp = SimpleImputer(missing_values=np.nan, strategy='most_frequent')
data5 = pd.DataFrame(imp.fit_transform(data2))
data5
0 1 2 3

0 0.0 0.0 0.0 0.0

1 1.0 2.0 3.0 4.0

2 2.0 0.0 6.0 8.0

3 3.0 6.0 0.0 12.0

4 4.0 8.0 12.0 16.0

5 5.0 10.0 0.0 20.0

6 6.0 12.0 18.0 0.0

7 7.0 14.0 21.0 0.0

8 8.0 16.0 24.0 32.0

9 9.0 18.0 27.0 36.0
%matplotlib inline
import matplotlib.pyplot as plt
plt.plot(data5)
[<matplotlib.lines.Line2D at 0x7fdb46495898>,
 <matplotlib.lines.Line2D at 0x7fdb464959b0>,
 <matplotlib.lines.Line2D at 0x7fdb46495b00>,
 <matplotlib.lines.Line2D at 0x7fdb46495c50>]
最頻値がない場合は最初の値で埋めるようですね。

constant

あらかじめ決まった数値を設定してそれで埋めることもできます。
from sklearn.impute import SimpleImputer

imp = SimpleImputer(missing_values=np.nan, strategy='constant', fill_value=99)
data6 = pd.DataFrame(imp.fit_transform(data2))
data6
0 1 2 3

0 0.0 0.0 0.0 0.0

1 1.0 2.0 3.0 4.0

2 2.0 99.0 6.0 8.0

3 3.0 6.0 99.0 12.0

4 4.0 8.0 12.0 16.0

5 5.0 10.0 99.0 20.0

6 6.0 12.0 18.0 99.0

7 7.0 14.0 21.0 99.0

8 8.0 16.0 24.0 32.0

9 9.0 18.0 27.0 36.0
%matplotlib inline
import matplotlib.pyplot as plt
plt.plot(data6)
[<matplotlib.lines.Line2D at 0x7fdb464890b8>,
 <matplotlib.lines.Line2D at 0x7fdb464891d0>,
 <matplotlib.lines.Line2D at 0x7fdb46489320>,
 <matplotlib.lines.Line2D at 0x7fdb46489470>]
まあ、なんて不自然なんでしょ。

KNNImputer

KNNImputerクラスは、k-Nearest Neighborsアプローチを使用して欠損値を埋めます。デフォルトでは、欠落値をサポートするユークリッド距離メトリックであるnan_euclidean_distancesが、最近傍を見つけるために使用されます。隣人の特徴は，一様に平均化されるか，各隣人までの距離によって重み付けされます．サンプルに1つ以上の特徴が欠落している場合，そのサンプルの隣人は，入力される特定の特徴に応じて異なることがあります．利用可能な隣人の数がn_neighborsよりも少なく、訓練セットへの定義された距離がない場合、その特徴の訓練セット平均が入力中に使用されます。定義された距離を持つ隣人が少なくとも1つある場合、残りの隣人の加重平均または非加重平均が入力時に使用されます。

n_neighbors=2

考慮に入れる隣人の数を明示的に n_neighbors=2 にしてみましょう。
from sklearn.impute import KNNImputer
imputer = KNNImputer(n_neighbors=2)
data7 = pd.DataFrame(imputer.fit_transform(data2))
data7
0 1 2 3

0 0.0 0.0 0.0 0.0

1 1.0 2.0 3.0 4.0

2 2.0 4.0 6.0 8.0

3 3.0 6.0 9.0 12.0

4 4.0 8.0 12.0 16.0

5 5.0 10.0 15.0 20.0

6 6.0 12.0 18.0 18.0

7 7.0 14.0 21.0 26.0

8 8.0 16.0 24.0 32.0

9 9.0 18.0 27.0 36.0
%matplotlib inline
import matplotlib.pyplot as plt
plt.plot(data7)
[<matplotlib.lines.Line2D at 0x7fdb46246ef0>,
 <matplotlib.lines.Line2D at 0x7fdb461d3048>,
 <matplotlib.lines.Line2D at 0x7fdb461d3198>,
 <matplotlib.lines.Line2D at 0x7fdb461d32e8>]
２連続で欠損しているような場合、うまく埋められないようですね。

default(n_neighbors=5)

デフォルトでは隣人を５人まで考慮するようです。
from sklearn.impute import KNNImputer
imputer = KNNImputer()
data8 = pd.DataFrame(imputer.fit_transform(data2))
data8
0 1 2 3

0 0.0 0.0 0.0 0.0

1 1.0 2.0 3.0 4.0

2 2.0 5.2 6.0 8.0

3 3.0 6.0 12.0 12.0

4 4.0 8.0 12.0 16.0

5 5.0 10.0 16.2 20.0

6 6.0 12.0 18.0 23.2

7 7.0 14.0 21.0 23.2

8 8.0 16.0 24.0 32.0

9 9.0 18.0 27.0 36.0
%matplotlib inline
import matplotlib.pyplot as plt
plt.plot(data8)
[<matplotlib.lines.Line2D at 0x7fdb461b86a0>,
 <matplotlib.lines.Line2D at 0x7fdb461b87b8>,
 <matplotlib.lines.Line2D at 0x7fdb461b8908>,
 <matplotlib.lines.Line2D at 0x7fdb461b8a58>]
D列の埋め方は比較的マシになりましたが、その代わりB列C列の埋め方に少し悪影響が出ましたね。

まとめ

欠損値の埋め方に完璧な方法はたぶん存在しないので、データの特徴をよく考えながら、準最適な方法を選びましょう！

	A	B	C	D
0	0	0	0	0
1	1	2	3	4
2	2	4	6	8
3	3	6	9	12
4	4	8	12	16
5	5	10	15	20
6	6	12	18	24
7	7	14	21	28
8	8	16	24	32
9	9	18	27	36

	A	B	C	D
0	0	0.0	0.0	0.0
1	1	2.0	3.0	4.0
2	2	NaN	6.0	8.0
3	3	6.0	NaN	12.0
4	4	8.0	12.0	16.0
5	5	10.0	NaN	20.0
6	6	12.0	18.0	NaN
7	7	14.0	21.0	NaN
8	8	16.0	24.0	32.0
9	9	18.0	27.0	36.0

	0	1	2	3
0	0.0	0.000000	0.000	0.0
1	1.0	2.000000	3.000	4.0
2	2.0	9.555556	6.000	8.0
3	3.0	6.000000	13.875	12.0
4	4.0	8.000000	12.000	16.0
5	5.0	10.000000	13.875	20.0
6	6.0	12.000000	18.000	16.0
7	7.0	14.000000	21.000	16.0
8	8.0	16.000000	24.000	32.0
9	9.0	18.000000	27.000	36.0

	0	1	2	3
0	0.0	0.0	0.0	0.0
1	1.0	2.0	3.0	4.0
2	2.0	10.0	6.0	8.0
3	3.0	6.0	15.0	12.0
4	4.0	8.0	12.0	16.0
5	5.0	10.0	15.0	20.0
6	6.0	12.0	18.0	14.0
7	7.0	14.0	21.0	14.0
8	8.0	16.0	24.0	32.0
9	9.0	18.0	27.0	36.0

	0	1	2	3
0	0.0	0.0	0.0	0.0
1	1.0	2.0	3.0	4.0
2	2.0	0.0	6.0	8.0
3	3.0	6.0	0.0	12.0
4	4.0	8.0	12.0	16.0
5	5.0	10.0	0.0	20.0
6	6.0	12.0	18.0	0.0
7	7.0	14.0	21.0	0.0
8	8.0	16.0	24.0	32.0
9	9.0	18.0	27.0	36.0

	0	1	2	3
0	0.0	0.0	0.0	0.0
1	1.0	2.0	3.0	4.0
2	2.0	99.0	6.0	8.0
3	3.0	6.0	99.0	12.0
4	4.0	8.0	12.0	16.0
5	5.0	10.0	99.0	20.0
6	6.0	12.0	18.0	99.0
7	7.0	14.0	21.0	99.0
8	8.0	16.0	24.0	32.0
9	9.0	18.0	27.0	36.0

	0	1	2	3
0	0.0	0.0	0.0	0.0
1	1.0	2.0	3.0	4.0
2	2.0	4.0	6.0	8.0
3	3.0	6.0	9.0	12.0
4	4.0	8.0	12.0	16.0
5	5.0	10.0	15.0	20.0
6	6.0	12.0	18.0	18.0
7	7.0	14.0	21.0	26.0
8	8.0	16.0	24.0	32.0
9	9.0	18.0	27.0	36.0

	0	1	2	3
0	0.0	0.0	0.0	0.0
1	1.0	2.0	3.0	4.0
2	2.0	5.2	6.0	8.0
3	3.0	6.0	12.0	12.0
4	4.0	8.0	12.0	16.0
5	5.0	10.0	16.2	20.0
6	6.0	12.0	18.0	23.2
7	7.0	14.0	21.0	23.2
8	8.0	16.0	24.0	32.0
9	9.0	18.0	27.0	36.0

　 Tweet
Qiitaで続きを読む

投稿日：2020-10-21T17:46:07+09:00

Django ForeignKeyのon_deleteの引数

参考

Django 公式
 stackoverflow

ForeignKeyのon_deleteについて
models.py
# サンプルのモデル
class Book(AbstractModel):
    publisher = models.ForeignKey(Publisher, on_delete=models.CASCADE)
models.CASCADE

参照しているオブジェクト(例: Publisher)が削除されたら
一緒にオブジェクト(例: Book)を削除する
例: ブログの記事を消したらそこに寄せられたコメントも必要ないから消す

models.PROTECT

参照しているオブジェクト(例: Publisher)が削除されても
オブジェクト(例: Book)は削除しない
全てのオブジェクトを削除したいなら全部手動でやらなきゃならない。

models.SET_NULL

参照しているオブジェクト(例: Publisher)が削除されたら
オブジェクト(例: Book)にはNULL(例: establishmentにNULL)がセットされる
例: ユーザを削除するとき、ブログにユーザが寄せたコメントだけは匿名で残したいときなんかはこれが使える。
※null=Trueにする必要あり。

models.SET_DEFAULT

参照しているオブジェクト(例: Publisher)が削除されたら
オブジェクト(例: Book)にはdefaultで設定した値(例: establishmentにdefault)がセットされる
models.py
publisher = models.ForeignKey(Publisher, on_delete=models.SET_DEFAULT, default='不明')
models.SET

独自で設定した値を代入する。
callableを渡す。
models.py
def get_publisher():
    # とりあえず一つ目返す
    return Publisher.objects.all().first()

class Book(AbstractModel):

    publisher = models.ForeignKey(Publisher, on_delete=models.SET(get_publisher))
models.RESTRICT

※これはDjango3.1の機能です。
オブジェクトを削除する際に
参照しているオブジェクトが存在すると、削除せずにRestrictedErrorとする。
models.py
class Artist(models.Model):
    name = models.CharField(max_length=10)

class Album(models.Model):
    artist = models.ForeignKey(Artist, on_delete=models.CASCADE)

class Song(models.Model):
    artist = models.ForeignKey(Artist, on_delete=models.CASCADE)
    album = models.ForeignKey(Album, on_delete=models.RESTRICT)
console
artist_one = Artist.objects.create(name='artist one')
album_one = Album.objects.create(artist=artist_one)
song_one = Song.objects.create(artist=artist_one, album=album_one)
album_one.delete()
# Raises RestrictedError.
# 参照しているsongが存在するためエラー


artist_two = Artist.objects.create(name='artist two')
album_two = Album.objects.create(artist=artist_two)
song_two = Song.objects.create(artist=artist_one, album=album_two)
# artist_oneを使っていることに注意
artist_two.delete()
# Raises RestrictedError.
# artist_twoを削除するとCASCADEしているalbumも削除されるため、
# 参照しているSongでエラーが発生する

　 Tweet
Qiitaで続きを読む

投稿日：2020-10-21T16:40:13+09:00

Tonelli-Shanks アルゴリズムの理解と実装(2)

はじめに

前回の記事はこちらです。

実装

まず、今回仮定する条件をもう一度しておきます。

Input:

$p$ : 奇素数

$n$ : 整数, ただし$n$は$p$の倍数ではない

Output:

$x$ : $x^2 \equiv n\ {\rm mod}\ p$, かつ $0 < x < n$を満たす¹

$n$が$p$の倍数なら、$n \equiv 0\ {\rm mod}\ p$で剰余とは言いづらいので今回は除外します(例外としてコード中に組み込みます)。

Legendre記号

$$\left(\begin{array}
nn\\
p
\end{array}\right) := n^{\frac{p-1}{2}} \equiv \begin{cases}
1\ {\rm mod}\ p\Leftrightarrow n は平方剰余\\
-1\ {\rm mod}\ p \Leftrightarrow n は平方非剰余
\end{cases}$$

でした。ここで、$n$が$p$の倍数なら当然
$$\left(\begin{array}
nn\\
p
\end{array}\right) = 0$$
となるので、ここで例外処理をしておきます。

なお、pow(a, b, c)は$a^b \ {\rm mod}\ c$を表します²。
def legendre_symbol(n, p):
    ls = pow(n, (p - 1) // 2, p)
    if ls == 1:
        return 1
    # pow関数は0 ~ p-1の範囲で値を返します
    elif ls == p - 1:
        return -1
    else:
        # ls == 0、つまりnがpの倍数の場合
        raise Exception('n:{} = 0 mod p:{}'.format(n, p))
pが4で割って3余る素数の場合

$$x = \pm n^{\frac{p+1}{4}}$$

が答えでした。一応答えが正しいことを確認するcheck_sqrt関数も定義しておきます。
# 基本的にここでassertionエラーは出ないはず
def check_sqrt(x, n, p):
    assert(pow(x, 2, p) == n % p)

def modular_sqrt(n, p):
    if p % 4 == 3:
        x = pow(n, (p + 1) // 4, p)
        check_sqrt(x, n, p)
        return [x, p - x]
    else:
        # これから説明
        pass
pが4で割って1余る素数の場合

ここからTonelli-Shanksのアルゴリズムの実装です。

Step 1.

$$p-1 = Q \cdot 2^S$$

という形に変形します($Q$は奇数で、$S$は正の整数です)。

Pythonでは多くの場合、大文字は定数を意味するので小文字のq, sを使います。
def modular_sqrt(n, p):
    ...
    else:
        # Step 1.
        q, s = p - 1, 0
        while q % 2 == 0:
            q //= 2
            s += 1
    ...
Step 2.

平方非剰余である$z$をランダムに選美ます。

前回も述べたように、半数は平方非剰余なので$2$から総当たりしています。

なぜ$1$から始めないのかというと、$x^2 \equiv 1\ {\rm mod} p$なる$x$は自明に存在($x=1$)して、任意の$p$に対して$1$は平方剰余だからです。
def modular_sqrt(n, p):
    ...
    else:
        # Step 1.
        q, s = p - 1, 0
        while q % 2 == 0:
            q //= 2
            s += 1

        # Step 2.
        z = 2
        while legendre_symbol(z, p) != -1:
            z += 1
    ...
Step 3.

$$\begin{cases}
M_0 = S\\
c_0 = z^Q\\
t_0 = n^Q\\
R_0 = n^{\frac{Q+1}{2}}
\end{cases}$$

これはそのままです。先ほどと同様、すべて小文字で定義します。
def modular_sqrt(n, p):
    ...
    else:
        ...
        # Step 2.
        z = 2
        while legendre_symbol(z, p) != -1:
            z += 1

        # Step 3.
        m, c, t, r = s, pow(z, q, p), pow(n, q, p), pow(n, (q + 1) // 2, p)
    ...
Step 4.

もし$t_i \equiv 1$なら、$\pm R_i$が$n$の平方根であり、ループ文を抜けて終了。

そうでない場合は、以下のように値を更新する。

$$\begin{cases}
M_{i+1} = \left(\left(t_i\right)^{2^{j}}\equiv 1 を満たす最小のj, ただし0 < j < M_i\right)\\
\\
c_{i+1} = \left(c_i\right)^{2^{M_i - M_{i+1}}}\\
\\
t_{i+1} = t_i \cdot \left(c_i\right)^{2^{M_i - M_{i+1}}}\\
\\
R_{i+1} = R_i \cdot \left(c_i\right)^{2^{M_i - M_{i+1}-1}}
\end{cases}$$

さて、これを実装する上で、2つ補足説明をしておきます。

1つ目。

$M_{i+1}$を求める上で、$j = 1, 2, \cdots$と順に代入していく分けですが、「$t_i$を$2$回掛けて$(t_i)^2$を計算し、1になるか調べる。ならなければ$t_i$を$4$回掛けて$(t_i)^4$を計算し、1になるか調べる。…」とする以下のコードは少し無駄が多いと思いませんか？(m_updateが$M_{i+1}$に相当します)
for j in range(1, m):
    if pow(t, pow(2, j), p) == 1:
        m_update = j
        break
せっかく$(t_i)^2$を計算しているなら、それを2乗することで$(t_i)^4$が求められるので再利用しましょう³。
pow_t = pow(t, 2, p)
for j in range(1, m):
    if pow_t == 1:
        m_update = j
        break
    pow_t = pow(pow_t, 2, p)
2つ目。

$$b_i = \left(c_i\right)^{2^{M_i - M_{i+1}-1}}$$

と定義すると、値の更新は以下のようにすっきりと書けます。この記号はWikipediaにも記載されています。

$$\begin{cases}
M_{i+1} = \left(\left(t_i\right)^{2^{j}}\equiv 1 を満たす最小のj, ただし0 < j < M_i\right)\\
\\
c_{i+1} = b_i^2\\
\\
t_{i+1} = t_i \cdot b_i^2\\
\\
R_{i+1} = R_i \cdot b_i
\end{cases}$$

前回はこれ以上変数を導入するとややこしいかなと思ったので割愛していました。

以上2点を踏まえて、以下のようにコードが書けます。
def modular_sqrt(n, p):
    ...
    else:
        ...
        # Step 3.
        m, c, t, r = s, pow(z, q, p), pow(n, q, p), pow(n, (q + 1) // 2, p)

        # Step 4.
        while t != 1:
            pow_t = pow(t, 2, p)
            for j in range(1, m):
                if pow_t == 1:
                    m_update = j
                    break
                pow_t = pow(pow_t, 2, p)
            b = pow(c, int(pow(2, m - m_update - 1)), p)
            m, c, t, r = m_update, pow(b, 2, p), t * pow(b, 2, p) % p, r * b % p

        # 答えの確認
        check_sqrt(r, n, p)
        return [r, p - r]
実装上の注意としては、$c_{i+1}, t_{i+1}, R_{i+1}$に更新する際に$M_i$と$M_{i+1}$の両方を用いるので、一旦m_update = jとおいてmをすぐに更新しないことです。

その他

$p$が素数であるかどうかの確認は実は多項式時間で可能です⁴。
from gmpy2 import is_prime

is_prime(p)
あるいは
from Crypto.Util.number import isPrime

isPrime(p)
で高速な素数判定が可能です。

どちらも標準では入っていないモジュールだと思うので、pip3でインストールする必要があります。

全体のソースコード
#!/usr/bin/env python3

from Crypto.Util.number import isPrime
# from gmpy2 import is_prime

def legendre_symbol(n, p):
    ls = pow(n, (p - 1) // 2, p)
    if ls == 1:
        return 1
    elif ls == p - 1:
        return -1
    else:
        # in case ls == 0
        raise Exception('n:{} = 0 mod p:{}'.format(n, p))

def check_sqrt(x, n, p):
    assert(pow(x, 2, p) == n % p)

def modular_sqrt(n:int, p:int) -> list:
    if type(n) != int or type(p) != int:
        raise TypeError('n and p must be integers')

    if p < 3:
        raise Exception('p must be equal to or more than 3')

    if not isPrime(p):
        raise Exception('p must be a prime number. {} is a composite number'.format(p))

    if legendre_symbol(n, p) == -1:
        raise Exception('n={} is Quadratic Nonresidue modulo p={}'.format(n, p))

    if p % 4 == 3:
        x = pow(n, (p + 1) // 4, p)
        check_sqrt(x, n, p)
        return [x, p - x]

    # Tonelli-Shanks
    q, s = p - 1, 0
    while q % 2 == 0:
        q //= 2
        s += 1
    z = 2
    while legendre_symbol(z, p) != -1:
        z += 1
    m, c, t, r = s, pow(z, q, p), pow(n, q, p), pow(n, (q + 1) // 2, p)
    while t != 1:
        pow_t = pow(t, 2, p)
        for j in range(1, m):
            if pow_t == 1:
                m_update = j
                break
            pow_t = pow(pow_t, 2, p)
        b = pow(c, int(pow(2, m - m_update - 1)), p)
        m, c, t, r = m_update, pow(b, 2, p), t * pow(b, 2, p) % p, r * b % p
    check_sqrt(r, n, p)
    return [r, p - r]

print(modular_sqrt(5, 41))
# => [28, 13]
$0 < x < p$で解が見つかれば、その$x$に対して$p$を順々に足して(あるいは引いて)いったものも当然解になるので、今回は$0 < x < p$の範囲に限定しました。 ↩

Pythonであればa ** b % cという書き方もできますが、pow関数を使った方がより高速に動作します。 ↩

例えば、$0 < j < 10$なら、前者はpow関数の呼び出しは最大18回ですが、後者は9回で済みます。すごくアバウトな計算量評価ですが、こういった観点から後者の方を今回採用しました。ただ、実際はどちらを使っても元々のアルゴリズムが高速なのでほぼ差は出ません。 ↩

「$p$が素数でない(=合成数である)」と「$p$の素因数分解の結果が分かる」は別です。今回は前者について触れています。後者が多項式時間でできてしまうと、いわゆるRSA暗号などの安全性に対する理論が瓦解してしまいます。(かといって、多項式時間ではできないだろうと言われているだけで、まだ未解決の問題のままです。) ↩

　 Tweet
Qiitaで続きを読む

投稿日：2020-10-21T16:39:44+09:00

Tonelli-Shanks アルゴリズムの理解と実装(1)

はじめに

奇素数$p$と$0$でない整数$n$が与えられた際に

$$ x^2 \equiv n\ {\rm mod}\ p$$

なる$x\not \equiv 0$が存在するならば、$n$は$p$を法として平方剰余(Quadratic Residue)であると言い、そのような$x$が存在しないならば$n$は平方非剰余(Quadratic Nonresidue)であると言います。

例えば、$n=2$は$p=7$を法として平方剰余($x=3$などが解)ですが、$n=3$は平方非剰余です。

さて、平方剰余かどうかの判定はそれほど難しくありません。

まずは、Legendre(ルジャンドル)記号を以下で定義します。

$$\left(\begin{array}
nn\\
p
\end{array}\right) := n^{\frac{p-1}{2}}$$

この時、以下が成立します(証明は少し難しいのでここでは省略します)。

$$\left(\begin{array}
nn\\
p
\end{array}\right) \equiv \begin{cases}
1\ {\rm mod}\ p\Leftrightarrow n は平方剰余\\
-1\ {\rm mod}\ p \Leftrightarrow n は平方非剰余
\end{cases}$$

実際、$n = 2, p = 7$なら

$$\left(\begin{array}
nn\\
p
\end{array}\right) = 2^{\frac{7-1}{2}} = 8 \equiv 1\ {\rm mod}\ 7$$

であり、$n = 3, p = 7$なら

$$\left(\begin{array}
nn\\
p
\end{array}\right) = 3^{\frac{7-1}{2}} = 27 \equiv -1\ {\rm mod}\ 7$$

です。

この記事では、$n$が平方剰余であると分かった場合に、その平方根$x$を求める方法について書いていきます。以下、特に断りがなければ$\equiv$は全て${\rm mod}\ p$です。

pが4で割って3余る素数の場合

この場合は実は簡単で、

$$x = \pm n^{\frac{p+1}{4}}$$

が答えです。実際、$n$は平方剰余であるという前提なので

$$\left(\begin{array}
nn\\
p
\end{array}\right) = n^{\frac{p-1}{2}} \equiv 1$$

が成立し、

$$x^2 = n^{\frac{p+1}{2}} = n^{\frac{p-1}{2}} \cdot n \equiv n$$

となります。例えば、$n = 2, p = 7$なら

$$x = \pm 2^{\frac{7+1}{4}} = \pm 4 \equiv 3, 4\ {\rm mod}\ 7$$

となります。

pが4で割って1余る素数の場合

ここが今回取り上げるTonelli-Shanksのアルゴリズムになります。

記号の命名は基本的にWikipediaに準拠しています。

Step 1.

$p-1$を$2$で割れるまで割り算し、

$$p-1 = Q \cdot 2^S$$

という形に変形します($Q$は奇数で、$S$は正の整数です)。

Step 2.

$p$を法として平方非剰余である数をランダムに選び、それを$z$とします。

「ランダムに」と言っていますが、$1$から$p-1$までの間に平方剰余と平方非剰余の個数は半分ずつなので¹、$z = 1, 2, …$と小さい順に総当たりしても計算量的には問題ありません。

なお、平方非剰余かどうかは上記のLegendre記号を使えば確かめられますし、当然その定義上、

$$z^{\frac{p-1}{2}} \equiv -1$$

です。

Step 3.

まず4つの数$M_0, c_0, t_0, R_0$を以下のように定義します。

$$\begin{cases}
M_0 = S\\
c_0 = z^Q\\
t_0 = n^Q\\
R_0 = n^{\frac{Q+1}{2}}
\end{cases}$$

Step 4.

以下のようにループ文および漸化式を立てます。

もし$t_i \equiv 1$なら、$\pm R_i$が$n$の平方根であり、ループ文を抜けて終了。

そうでない場合は、以下のように値を更新する。

$$\begin{cases}
M_{i+1} = \left(\left(t_i\right)^{2^{j}}\equiv 1 を満たす最小のj, ただし0 < j < M_i\right)\\
\\
c_{i+1} = \left(c_i\right)^{2^{M_i - M_{i+1}}}\\
\\
t_{i+1} = t_i \cdot \left(c_i\right)^{2^{M_i - M_{i+1}}}\\
\\
R_{i+1} = R_i \cdot \left(c_i\right)^{2^{M_i - M_{i+1}-1}}
\end{cases}$$

…一気に見にくくなりました。

「もし$t_i \equiv 1$なら、$\pm R_i$が$n$の平方根であり」とはどういう事か？

無限ループになることはないのか？

実際にコーディングして動かしたい / 例を見せてくれ

などなどあると思いますが、順番に解説していきます。

準備

漸化式をいくつも立てていますが、実は$i$の値によらず以下が成立します。

$$\begin{cases}
\left(c_i\right)^{2^{M_i -1}} \equiv -1\\
\\
\left(t_i\right)^{2^{M_i -1}} \equiv 1\\
\\
\left(R_i\right)^2 \equiv t_i \cdot n
\end{cases}$$

順番に数学的帰納法を使って確認していきます。

1つ目の式

$$\left(c_i\right)^{2^{M_i -1}} \equiv -1$$

を示します。まず、$i = 0$ならば、

$$\left(c_0\right)^{2^{M_0 -1}} = \left(z^Q\right)^{2^{S -1}} = z^{Q \cdot 2^{S -1}}$$

ここで、Step 1.より$\frac{p-1}{2} = Q \cdot 2^{S-1}$なので、

$$z^{Q \cdot 2^{S -1}} = z^\frac{p-1}{2}$$

これはStep 2.で定義したので$-1$に等しくなります。

つぎに、$i$で成立するとして$i+1$で成立することを示します。

$$\left(c_{i+1}\right)^{2^{M_{i+1} -1}} = \left(\left(c_i\right)^{2^{M_i - M_{i+1}}}\right)^{2^{M_{i+1} -1}} = \left(c_i\right)^{2^{M_i - 1}}$$

となり、$i$で成立すると仮定しているのでこれも$-1$になります。

2つ目の式

$$\left(t_i\right)^{2^{M_i -1}} \equiv 1$$

を示します。$i = 0$ですが、1つ目の時と同様にして

$$\left(t_0\right)^{2^{M_0 -1}} = \left(n^Q\right)^{2^{S-1}} = n^{Q \cdot 2^{S-1}} = n^\frac{p-1}{2}$$

$n$は平方剰余であるという仮定なので、これはLegendre記号の定義から$1$に等しくなります。

次に、$i+1$についてですが、これは少し込み入った証明となります。

$$\left(t_{i+1}\right)^{2^{M_{i+1} -1}} = \left(t_i \cdot \left(c_i\right)^{2^{M_i - M_{i+1}}}\right)^{2^{M_{i+1} -1}} = \left(t_{i}\right)^{2^{M_{i+1} -1}} \cdot \left(c_{i}\right)^{2^{M_i -1}}$$

ここで、$\left(t_{i}\right)^{2^{M_{i+1} -1}}$に注目します。

これを二乗すると、$\left(t_{i}\right)^{2^{M_{i+1}}}$になり、Step 4.の$M_{i+1}$の定義から$1$に等しくなります。

では、二乗すると$1$になる数は？と言われれば、もちろん$1, -1$の$2$つだけです²。

しかし、今回$\left(t_{i}\right)^{2^{M_{i+1} -1}} \equiv 1$…($\ast$)とはなりません。なぜなら、もしこれが成立してしまうと、「Step 4.で

$$\left(t_i\right)^{2^{j}}\equiv 1 を満たす最小のj$$

を$M_{i+1}$と定義したにもかかわらず、$j = M_{i+1}-1$でも上の式($\ast$)が成立してしまっている」という矛盾が生じてしまうためです。

よって、$\left(t_{i}\right)^{2^{M_{i+1} -1}} \equiv -1$となります。

また、$\left(c_{i}\right)^{2^{M_i -1}}$は$1$つ目の式から$-1$と証明したばかりなので、結果として、

$$\left(t_{i}\right)^{2^{M_{i+1} -1}} \cdot \left(c_{i}\right)^{2^{M_i -1}} \equiv (-1) \cdot (-1) = 1$$

となります。

3つ目の式

$$\left(R_i\right)^2 \equiv t_i \cdot n$$

を示します。$i = 0$ならば、

$$\left(R_0\right)^2 = \left(n^{\frac{Q+1}{2}}\right)^2 = n^{Q+1} = n^Q\cdot n = t_0 \cdot n$$

また、$i+1$の場合は

$$\left(R_{i+1}\right)^2 = \left(R_i \cdot \left(c_i\right)^{2^{M_i - M_{i+1}-1}}\right)^2 = \left(R_i\right)^2 \cdot \left(c_i\right)^{2^{M_i - M_{i+1}}}$$

$i$で成立、つまり$\left(R_i\right)^2 \equiv t_i \cdot n$を仮定しているので

$$\left(R_i\right)^2 \cdot \left(c_i\right)^{2^{M_i - M_{i+1}}} \equiv t_i \cdot n \cdot \left(c_i\right)^{2^{M_i - M_{i+1}}}$$

定義より$t_{i+1} = t_i \cdot \left(c_i\right)^{2^{M_i - M_{i+1}}}$であるので

$$t_i \cdot n \cdot \left(c_i\right)^{2^{M_i - M_{i+1}}} = t_{i+1} \cdot n$$

以上で$3$つの式全てを証明できました。

各疑問点の解消

まず

「もし$t_i \equiv 1$なら、$\pm R_i$が$n$の平方根であり」とはどういう事か？

から説明します。とは言っても、上で示してきた式の$3$つ目

$$\left(R_i\right)^2 \equiv t_i \cdot n$$

を見れば明らかです。つまり、$t_i$を更新していき、どこかのタイミングで$t_i\equiv 1$になれば、その時点で上の式は

$$\left(R_i\right)^2 \equiv n$$

と同じ意味になります。

次に、

無限ループになることはないのか？

です。つまり、$t_i = 1$になるような$i$はないのではないか、ということです。

それにはまず、$M_i$の単調減少性について説明する必要があります。$M_{i+1}$を

$\left(t_i\right)^{2^{j}}\equiv 1 を満たす最小のj, ただし0 < j < M_i$

と定義していましたが、そもそも本当に$0 < j < M_i$にそのような$j$が存在するのでしょうか？

実は、その点については、上で示してきた式のうち$2$つ目

$$\left(t_i\right)^{2^{M_i -1}} \equiv 1$$

が保証してくれています。つまり、$j = 1, 2, …$と調べていき、運が悪くてずっと$\left(t_i\right)^{2^{j}}\not \equiv 1$だったとしても、$j = M_i -1$の時には$\left(t_i\right)^{2^{j}}\equiv 1$になり$M_{i+1}$としての条件を満たします。

よって、$M_{i+1}$は必ず$M_i -1$以下となり(添え字があるのでわかりにくいですね…)、

$$M_{i+1} \leq M_i -1 < M_i$$

これで、$M_i$の単調減少性が言え、いつかは$M_{end} = 1$となる時が来ます。

この時、上で示してきた式のうち$2$つ目

$$\left(t_i\right)^{2^{M_i -1}} \equiv 1$$

を用いると、

$$\left(t_{end}\right)^{2^{M_{end} -1}} \equiv 1 \Rightarrow t_{end} \equiv 1$$

$t$の値が$1$になったので、これで無限ループすることはなくなりました。

例

Wikipediaの例をそのまま引用します。

$x^2 \equiv 5 \ {\rm mod}\ 41$

なる$x$を求めます($n = 5, p = 41$)。まず、Legendre記号を使って

$$\left(\begin{array}
55\\
41
\end{array}\right) = 5^{\frac{41-1}{2}} = 5^{20} \equiv 1\ {\rm mod}\ 41$$

と、$5$が平方剰余であることを念のため確認しておきましょう。

Step 1.

$p-1 = Q \cdot 2^S$、つまり$41-1 = 5 \cdot 2^3$とします。$Q = 5, S = 3$です。

Step 2.

平方非剰余である数$z$を選ぶ。Legendre記号を使うと、$1, 2$は平方剰余であるが、$3$は

$$\left(\begin{array}
33\\
41
\end{array}\right) = 3^{\frac{41-1}{2}} = 3^{20} \equiv -1\ {\rm mod}\ 41$$

と、平方非剰余であるので$z=3$とする。

Step 3.

$$\begin{cases}
M_0 = S\\
c_0 = z^Q\\
t_0 = n^Q\\
R_0 = n^{\frac{Q+1}{2}}
\end{cases}$$

つまり、

$$\begin{cases}
M_0 = 3\\
c_0 = 3^5 \equiv 38\\
t_0 = 5^5 \equiv 9\\
R_0 = 5^{\frac{5+1}{2}} \equiv 2
\end{cases}$$

Step 4.

ここから、$t_i=1$になるまでループに入ります。

$$\begin{cases}
M_{i+1} = \left(\left(t_i\right)^{2^{j}}\equiv 1 を満たす最小のj, ただし0 < j < M_i\right)\\
\\
c_{i+1} = \left(c_i\right)^{2^{M_i - M_{i+1}}}\\
\\
t_{i+1} = t_i \cdot \left(c_i\right)^{2^{M_i - M_{i+1}}}\\
\\
R_{i+1} = R_i \cdot \left(c_i\right)^{2^{M_i - M_{i+1}-1}}
\end{cases}$$

$i=0$の時

$$\begin{cases}
M_{1} = \left(\left(9\right)^{2^{j}}\equiv 1 を満たす最小のj\right) = 2\\
\\
c_{1} = \left(38\right)^{2^{3 - 2}} \equiv 9\\
\\
t_{1} = 9 \cdot \left(38\right)^{2^{3 - 2}} \equiv 40\\
\\
R_{1} = 2 \cdot \left(38\right)^{2^{3 - 2-1}} \equiv 35
\end{cases}$$

$i=1$の時

$$\begin{cases}
M_{2} = \left(\left(40\right)^{2^{j}}\equiv 1 を満たす最小のj\right) = 1\\
\\
c_{2} = \left(9\right)^{2^{2 - 1}} \equiv 40\\
\\
t_{2} = 40 \cdot \left(9\right)^{2^{2 - 1}} \equiv 1\\
\\
R_{2} = 35 \cdot \left(9\right)^{2^{2 - 1-1}} \equiv 28
\end{cases}$$

$t_2 = 1$なので、答えは$\pm R_2 = 28, 13$となります。

実際、確かに$13^2 \equiv 28^2 \equiv 5 \ {\rm mod} \ 41$は成立します。

実装

長くなってしまったので、こちらに回します。

簡単な証明を載せておくと、$i^2 \equiv (p-i)^2$なので、$1$から$p-1$までの数を二乗した平方数のバリエーションとしては多くても$\frac{p-1}{2}$個です。しかし、「多くても」と言っていますがこれ以外に重複はありません。これは$i^2 \equiv (i+k)^2$を仮定して背理法で示せます。 ↩

素数$p$でしか成立しません。合成数なら、$x^2 \equiv 1\ {\rm mod}\ 24$なる$x$として、$x = 1$と$x = -1 \equiv 23$以外にも$x=5$などが考えられます。素数$p$で$x = \pm 1$しか解をもたない理由は、$x^2-1$を因数分解すると容易に証明できます。 ↩

　 Tweet
Qiitaで続きを読む

投稿日：2020-10-21T15:47:04+09:00

大名行列を特異値分解してみる

はじめに

線形代数には、特異値分解という操作があります。行列を特異値と、それをくくりだす行列に分解する処理です。この分解は可逆処理ですが、特異値の大きいところだけを取り、小さいところを無視することで元の行列を近似することができます。近年、この性質を利用した情報圧縮が様々な場所で積極的に利用されています。筆者の身近なところでは、量子状態をテンソルネットワークで近似する際、特異値分解が中心的な役割を果たします。

本稿では、特異値分解がどういう処理なのか、実際に簡単な行列で試してみて、「なるほど情報圧縮だなぁ」というのを実感することを目的とします。

コードは以下においておきます。

https://github.com/kaityo256/daimyo_svd

Google ColabでJupyter Notebookを開きたい場合はこちらをクリックしてください。

特異値分解してみる

まず細かいことはさておき、特異値分解により情報圧縮ができることを確認してみましょう。以下、Google Colabでの実行を想定しています。他の環境で実行する場合は、フォントへのパスの指定の方法など、適宜読み替えてください。

対象となる行列の準備

まずは必要なものをimportしましょう。
from PIL import Image, ImageDraw, ImageFont
import numpy as np
from scipy import linalg
次に、日本語フォントをインストールします。
!apt-get -y install fonts-ipafont-gothic
インストールに成功したら、ImageFontのフォントオブジェクトを作っておきましょう。
fpath='/usr/share/fonts/opentype/ipafont-gothic/ipagp.ttf'
fontsize = 50
font = ImageFont.truetype(fpath, fontsize)
白地に黒で「大名行列」と書きましょう。
LX = 200
LY = fontsize
img  = Image.new('L', (LX,LY),color=255)
draw = ImageDraw.Draw(img)
draw.text((0,0), "大名行列", fill=0, font=font)
img
こんな感じで「大名行列」が表示された成功です。

さて、描画したイメージから、NumPy配列の形で行列を受け取りましょう。単にnp.arrayにimg.getdata()を食わすだけですが、それだと一次元配列になってしまうので、reshapeで行列にします。
data = np.array(img.getdata()).reshape((LY,LX))
このdataがもとの行列となります。行列要素は、0から255までの値を持ち、ピクセルの輝度を表現します。

逆に、行列をイメージとして表示してみましょう。
Image.fromarray(np.uint8(data))
以下のような表示がされたら成功です。

ここで、この行列のランクも確認しておきましょう。np.linalg.matrix_rankで確認できます。
np.linalg.matrix_rank(data) # => 47
行列のランクは、最大でmin(行, 列)となります。dataは50行200列の行列なので、ランクは最大で50ですが、「大名行列」の上下に余白があるために少しランクが落ちて、47になっています。これを、より低ランクな行列で近似しましょう、というのが特異値分解による圧縮です。

特異値分解と圧縮

では、行列dataを特異値分解しましょう。scipy.linalg.svdで一発です。
u, s, v = linalg.svd(data)
それぞれの形状も確認しておきましょう。
print(f"u: {u.shape}")
print(f"s: {s.shape}")
print(f"v: {v.shape}")
結果はこんな感じです。
u: (50, 50)
s: (50,)
v: (200, 200)
uは50x50、vは200x200の正方行列です。sは数学的には50行200列の対角行列ですが、どうせ対角成分しかないのでscipy.linalg.svdは一次元配列を返すことに注意しましょう。このsが特異値であり、全て非負の実数で、scipy.linalg.svdは降順に並べてくれます。uとvも特異値に対応した順番に並んでいます。

特異値分解ができたので、もとの行列を低ランク近似しましょう。特異値を大きい方からr個だけ残すことにします。対応して、uの左から列ベクトルをr個とったものをur、
vの上から行ベクトルをr個取った行列をvrとします。それぞれ50行r列、r行200列の行列になります。特異値については、r行r列の対角行列にしましょう。非負の実数なので、平方根を取ることができます。これをsrとし、ur*srをA、sr*vrをBという行列にします。

以上の操作をそのまま実装したのが以下のコードです。ここではr=10としています。
rank = 10
ur = u[:, :rank]
ss = np.sqrt(s)
sr = np.matrix(linalg.diagsvd(ss[:rank], rank,rank))
vr = v[:rank, :]
A = ur*sr
B = sr*vr
Aは50行r列、Bはr行200列の行列ですから、その積はもとの行列であるdataと同じ、50行200列になります。
print(f"A: {A.shape}")
print(f"B: {B.shape}")
print(f"AB: {(A*B).shape}")
実行結果↓
A: (50, 10)
B: (10, 200)
AB: (50, 200)
しかし、dataのランクが47だったのに対し、A*Bは特異値を10個しか残していないため、ランクが10の行列になります。
np.linalg.matrix_rank(A*B) # => 10
確かにランクが10になっていますね。これが低ランク近似と呼ばれる所以です。

さて、dataという行列が、AとBという二つの行列で近似されました。どれくらいデータが圧縮されたか見てみましょう。行列の要素数はsizeで取れます。
print((A.size + B.size)/data.size) # => 0.25
特異値を10個残した場合は、データは25%に圧縮されたことがわかります。

データの復元

さて、低ランク近似のより、どれくらい情報が失われたか、イメージになおして見てみましょう。A*Bにより近似されたデータを画像に復元してみます。ただし、もともとピクセルデータが0から255までの値だったのが、近似によりはみ出してしまって画像がおかしくなるのでnumpy.clipにより0から255までに押し込めています。
b = np.asarray(A*B)
b = np.clip(b, 0, 255)
Image.fromarray(np.uint8(b))
こんな感じに復元されました。

まとめ

特異値分解がどのように情報圧縮に使われるかを確認するため、「大名行列」と書かれた画像を行列だと思って、特異値分解し、低ランク近似した行列を作り、情報圧縮率を確認し、データを復元してみました。このコードを試してみて、「なるほど低ランク近似だなぁ」と思ってもらえれば幸いです。

補足資料

上記の操作の数学的な側面について補足しておきます。

特異値とは

正方行列$A$について、以下のような分解を考えます。

$$
A = P^{-1} D P
$$

ただし、$P$は正則行列、$D$は対角行列です。このような分解ができる時、$A$は対角化可能といい、$D$は対角要素に$A$の固有値を並べたもの、$P$は$A$の固有ベクトルを列ベクトルとして並べたものになります。

行列の固有値と固有ベクトルは大事だ、というのは線形代数を学ぶ理由でも書きました。行列の性質は、固有値と固有ベクトルで決まります。そして固有ベクトルは、固有値の絶対値が大きい順番に元の行列の性質の責任を担います。例えば、絶対値最大の固有値を持つ固有ベクトルは、行列が時間発展演算子の場合には平衡状態に、行列が量子力学の時間非依存ハミルトニアンを表すならば基底状態を表現します。また、行列がマルコフ遷移行列の場合には絶対値最大の固有値絶対値が1となり、二番目に大きい固有値が定常状態への緩和速度を決めます¹。

さて、行列の固有値、固有ベクトルは、正方行列にしか定義できません。しかし、一般の長方形の行列に対して似たようなことがしたい場合があります。そんな時に使うのが特異値分解です。

$m$行$n$列($m<n$) の行列$X$を考えます。特異値分解とは、行列$X$を以下のように分解することです。

$$
X = U \Sigma V^\dagger
$$

ただし、$U$はm行m列の正方行列、$V$はn行n列の正方行列で、どちらもユニタリ行列です。$V^\dagger$は$V$の随伴行列です。$\Sigma$は$m$行$n$列の対角行列で、対角に並んだ要素を$X$の特異値と呼びます。特異値は非負の実数で、要素数は$X$の行と列の少ない方、$m<n$の場合は$m$個となります。便利のために、$\Sigma$は上から特異値の大きい順に並べておきます。

ランクとは

行列のランク(階数)とは、行列を「行ベクトルが並んだものとみなしたときの線形独立なベクトルの数」もしくは「列ベクトルが並んだものとみなしたときの線形独立なベクトルの数」です。両者の定義は一致します。$m$行$n$列($mn$の場合も同様です。以上から、$m$行$n$列の行列のランクは、最大で$\min(m,n)$となります。直感的に、行列が線形従属なベクトルを多数含めば含むほど、行列が持つ「本質的な情報量」が減るのはわかると思います。

低ランク近似

さて、行列積の定義により、$m$行$r$列の行列と、$r$行$n$列の行列をかけると、真ん中の$r$個の足がつぶれて$m$行$n$列の行列になります。ここから$r$を小さくとることで、$m$行$n$列の行列を、$m$行$r$列の行列と$r$行$n$列の行列二つで近似することができます。

行列のランクは、行と列の小さい方で決まります。したがって、$r < m < n$ならば、$m$行$r$列の行列も、$r$行$n$列も、ランクは最大で$r$です。ランク$r$同士の行列をかけてもランクは増えないので、$AB$という$m$行$n$列の行列のランクも$r$となります。

このように、ある行列を別の小さい行列の積で近似する際、もとの行列より低いランクの行列で近似する、低ランク近似になっています。このような小さい行列の作り方にはいろんな方法がありますが、フロベニウスノルムの意味で最良近似になっているのが特異値分解を用いた近似です。

いま、$m$行$n$列の行列$X$の特異値分解

$$
X = U \Sigma V^\dagger
$$

が得られているとしましょう。$U$と$V$はそれぞれ$m$行$m$列、$n$行$n$列の正方行列で、どちらもユニタリ行列です。$V^\dagger$は$V$の随伴行列(転置して複素共役をとったもの)です。$\Sigma$は$m$行$n$列の対角行列で、対角要素に特異値が並んでいます。この際、上から大きい順に並べておきます($U$と$V$も対応するように決めます)。

さて、特異値を$r$個だけ使った低ランク近似をすることにしましょう。これは、$\Sigma$の左上から$r$行$列$の正方行列部分だけ使い、$U$の列ベクトルを左から$r$個、$V^\dagger$の行ベクトルを上から$r$個とってもとの行列を近似する形になります。さて、特異値は非負の実数で、$\Sigma$は対角行列なので、$\Sigma = \sqrt{\Sigma} \sqrt{\Sigma}$と分けることができます。これを$U$由来の行列と$V^\dagger$由来行列とまとめましょう。図解するとこんな感じです。

以上から、

$$
\tilde{X} = A B
$$

を得ます。こうして、$m$行$n$列の行列$X$が、特異値分解を通じて$m$行$r$列の行列$A$と、$r$行$n$列の行列$B$の積として近似できました。もとの行列のランクは最大で$\min(m,n)$ですが、こうして近似された行列のランクは最大で$r$になります。もともと$m*n$個あった行列要素は、$r*(m+n)$になりました。$r$が小さいときには情報が圧縮されたことがわかります。

マルコフ遷移行列と線形代数の関係は、いつか書きたいと思いつつ数年書けてません。「書いて！」という強い要望があれば頑張れるかも。 ↩

　 Tweet
Qiitaで続きを読む

投稿日：2020-10-21T15:18:27+09:00

Python標準 ConfigParser でキー名の大文字/小文字を維持する

Python標準のライブラリ configparser でINIファイルの読み書きを行えます。
https://docs.python.org/ja/3/library/configparser.html

INIファイルとは、セクション・キー・値の構成からなる、設定ファイルなどに使われることがあるファイル形式です。
https://ja.wikipedia.org/wiki/INI%E3%83%95%E3%82%A1%E3%82%A4%E3%83%AB

configparserでは、デフォルトでキーの大文字/小文字を区別しない仕様になっています。
import configparser


ini_filename = "sample.ini"
"""INIファイルのなかみ
[General]
Name = hogehoge
"""

parser = configparser.ConfigParser()
parser.read(ini_filename)

""" 大文字/小文字/混在 どうであっても読み込める """
assert parser["General"]["Name"] == "hogehoge", "混在"
assert parser["General"]["name"] == "hogehoge", "小文字"
assert parser["General"]["NAME"] == "hogehoge", "大文字"
これはINIファイルの読み込み/書き込みのどちらにも作用します。

RawTherapeeというソフトで使われるサイドカーファイルがINIファイル風の中身になっており、
これを一括編集しようと思ったのですが、RawTherapeeのサイドカーファイルはキー名の大文字/小文字を区別しています。
そのため、ConfigParserクラスでそのまま編集/保存までしてしまうと、キー名がすべて小文字になってしまい、
RawTherapeeでちゃんと読み込めなくなる問題がありました。

これは ConfigParserインスタンスの .optionxform に適宜関数をセットしてやることで解決します。
読み書き時のキー名は、optionxform 関数で変換した結果が使われます。

したがって、つぎのように optionxform を設定してやると、キー名を維持したまま、INIファイルを保存できます。
parser = configparser.ConfigParser()
parser.optionxform = str
parser.read(ini_filename)

parser["General"]["Name"] = "test"

with open(ini_filename, "w") as fp:
    parser.write(fp)

　 Tweet
Qiitaで続きを読む

投稿日：2020-10-21T14:43:57+09:00

Python jnjaテンプレート内でのデータの文字列変換の仕方

最初に

　DjangoまたはFlaskフレームワーク内でjinjaテンプレートを使ってフロントエンドのHTMLを生成する際の覚書です。しばらくするとすぐに忘れてしまうのでここに書かせていただきます

やりたい事

以下の２つを同時に行いたいです

Panda?s dataframeのデータを文字列に変換します

文字列の最後が「計」の字であるかどうかを判断します

「計」のある行は空白セルも含めて全て背景色を変えます

結論

Panda?s dataframeのデータを文字列に変換するには

{% for 行 in df請求一覧[ 開始行NO : 終了行NO ].itertuples() %} で順にデータを取り出し行に入れます

行の２列目のデータを 行[ 1 ] | string で文字列に変換します

これ以外の方法では私は文字列に変換出来ませんでした?

エラーを吐いちゃうんですよね〜?

前提条件

データは df請求一覧：Panda?s dataframe 形式

計の字は各行の２列目

このdf請求一覧 がjinjaテンプレートを組み込んだHTML list.html に渡されます

データ形式

システム名開発所属名開発工数請求金額

ほげシステム風開発部 100.0 10000000

ほげシステム水開発部 200.0 20000000

ほげシステム土開発部 300.0 30000000

計 600.0 60000000

風システム風開発部 100.0 10000000

風システム水開発部 200.0 20000000

風システム土開発部 300.0 30000000

計 600.0 60000000

ソースコード
list.html
  {% if df請求一覧.empty == None %}
    <div>請求一覧は表示できません</div>
  {% else %}
    <table class="small tablelock2">
      <thead>
        <tr>
          <th>NO</th>
          {% for 列名 in df請求一覧 %}
            <th>{{ 列名 }}</th>
          {% endfor %}
        </tr>
      </thead>
      <tbody>
        {% for 行 in df請求一覧[ 開始行NO : 終了行NO ].itertuples() %}
          <tr>
            {% for データ in 行 %}
              {% if ( データ == None ) %}
                {% if ( 行[ 1 ]|string ).endswith( '計' ) %}
                  <td class="littlesum"></td>
                {% else %}
                  <td class="data"></td>
                {% endif %}
              {% else %}
                {% if ( 行[ 1 ]|string ).endswith( '計' ) %}
                  <td class="littlesum">{{ データ }}</td>
                {% else %}
                  <td class="data">{{ データ }}</td>
                {% endif %}
              {% endif %}
            {% endfor %}
          </tr>
        {% endfor %}
      </tbody>
    </table>
  {% endif %}

システム名	開発所属名	開発工数	請求金額
ほげシステム	風開発部	100.0	10000000
ほげシステム	水開発部	200.0	20000000
ほげシステム	土開発部	300.0	30000000
	計	600.0	60000000
風システム	風開発部	100.0	10000000
風システム	水開発部	200.0	20000000
風システム	土開発部	300.0	30000000
	計	600.0	60000000

　 Tweet
Qiitaで続きを読む

投稿日：2020-10-21T14:41:40+09:00

webAPIを作ってみた！ EC2でDjangoRestFramework 1から環境構築

はじめに

この記事ではDjangoでwebAPIを作成しよう！という記事です。

RDSのMySQLを使用しています。

前回の記事の続きですのでわからなくなったら参考にしてください
[AWS]EC2,RDS,Djangoを使ってみた。1から環境構築

$             <- 自分のPCターミナルでのコマンド
[ec2-user] $  <- EC2にログイン中でのコマンド
MySQL >       <- MySQLにログイン中でのコマンド
#             <- 私のコメント
>>>           <- 実行結果(出力値)

前提条件

EC2,RDS,Djangoの接続完了済

Djangoのプロジェクト作成

前回の記事でも書きましたが、もう一度書いておきます。

プロジェクトを作成しましょう

#testDjangoというプロジェクトを作成する
[ec2-user] $ django-admin startproject testDjango

[ec2-user] $ cd
[ec2-user] $ cd testDjango

#pollsと言う名前のアプリを作成する
[ec2-user] $ python manage.py startapp polls

前回の記事[2.2],[2.5]参照

FileZillaを使ってsettings.pyを編集

testDjango/settings.py

#IPアドレスをグーグルなどで検索した時エラー内容を返してくれる
DEBUG = True

#変更
ALLOWED_HOSTS = ['(EC2のオープンIPアドレス)','localhost']

#変更
INSTALLED_APPS = [
    'django.contrib.admin',
    'django.contrib.auth',
    'django.contrib.contenttypes',
    'django.contrib.sessions',
    'django.contrib.messages',
    'django.contrib.staticfiles',
    'rest_framework',
    'polls.apps.PollsConfig',
]
#(アプリ名).apps.(先頭大文字アプリ名)Config

...
(略)
...

#デフォルトの設定をリマーク
# DATABASES = {
#     'default': {
#         'ENGINE': 'django.db.backends.sqlite3',
#         'NAME': BASE_DIR / 'db.sqlite3',
#     }
# }

#新しく記入
#[NAME]はRDS内のテーブル名、後に作成します。
#[USER,PASSWORD,HOST]はそれぞれ入力
DATABASES = {
    'default': {
        'ENGINE': 'django.db.backends.mysql',
        'NAME': 'dbtest',
        'USER': '(DBマスターユーザー)',
        'PASSWORD': '(DBマスターユーザーパスワード)',
        'HOST': '(DBエンドポイント)',
        'PORT': '3306',
    }
}

...
(略)
...

#日本語に変更
#LANGUAGE_CODE = 'en-us'
LANGUAGE_CODE = 'ja'

#日本時間に変更
# TIME_ZONE = 'UTC'
TIME_ZONE = 'Asia/Tokyo'

USE_I18N = True

USE_L10N = True

USE_TZ = True


# Static files (CSS, JavaScript, Images)
# https://docs.djangoproject.com/en/3.1/howto/static-files/

STATIC_URL = '/static/'

RDSのMySQLにログイン

[ec2-user] $ mysql -h (DBエンドポイント) -u (DBマスターユーザー名) -p
# パスワードを要求されるので入力(文字は表示されないが打ち込めています)（コピペ可）

>>> Welcome to the MariaDB monitor.
# が表示されればRDSのMySQLに接続ができた

#データベース内一覧を表示(小文字でも可 show database;)
MySQL > SHOW databases;

#「dbtest」という名前のテーブルを作成
MySQL > CREATE DATABASE dbtest;

#終了
MySQL > exit

Djangoの設定

モデルの作成

polls/models.py

from django.db import models

class User(models.Model):
    #作成時刻を記録
    created = models.DateTimeField(auto_now_add=True)
    #Userの名前を記録
    name = models.CharField(max_length=100, blank=True, default='')
    #Userのemail
    mail = models.TextField()

    class Meta:
        ordering = ('created',)

データベースのマイグレーションを行う

[ec2-user] $ python manage.py makemigrations polls
[ec2-user] $ python manage.py migrate

確認してみます

MySQL > show databases;
MySQL > use dbtest;
MySQL > show tables;
>>>
+----------------------------+
| Tables_in_dbtest           |
+----------------------------+
| auth_group                 |
| auth_group_permissions     |
| auth_permission            |
| auth_user                  |
| auth_user_groups           |
| auth_user_user_permissions |
| django_admin_log           |
| django_content_type        |
| django_migrations          |
| django_session             |
| example_table              |
| polls_user                 | <--生成されている
+----------------------------+   (アプリ名)_user

MySQL > exit

以下の記事が参考になります
【学習メモ】MakemigrationsとMigrateについて

serializers.pyの作成

デフォルトでは生成されていないため、メモ帳か何かで作成しFileZillaで転送してください

シリアライズとは、ソフトウェア内部で扱っているデータをそのまま、保存したり送受信することができるように変換することです。

polls/serializers.py

from rest_framework import serializers
from polls.models import User


class UserSerializer(serializers.ModelSerializer):
    class Meta:
        model = User
        fields = ('id', 'name', 'mail')

views.pyを実装

polls/views.py

from django.http import HttpResponse, JsonResponse
from django.views.decorators.csrf import csrf_exempt
from rest_framework.parsers import JSONParser
from polls.models import User
from polls.serializers import UserSerializer


@csrf_exempt
def user_list(request):

    if request.method == 'GET':
        #UserをMySQLから全件取得
        polls = User.objects.all()
        serializer = UserSerializer(polls, many=True)
        #Jsonで返してくる
        return JsonResponse(serializer.data, safe=False)

    elif request.method == 'POST':
        data = JSONParser().parse(request)
        serializer = UserSerializer(data=data)
        if serializer.is_valid():
            serializer.save()
            #登録成功するとJsonデータが帰ってくる  ##status 200番台は処理が成功した
            return JsonResponse(serializer.data, status=201)
        return JsonResponse(serializer.errors, status=400)

polls/urls.pyを作成する

これも新規作成してください

polls/urls.py

from django.urls import path
from polls import views

urlpatterns = [
    path('user/', views.user_list),
]

大元のurls.pyに接続します

testDjango/urls.py

from django.contrib import admin
from django.urls import path, include

urlpatterns = [
    path('admin/', admin.site.urls),
    path('', include('polls.urls')),
]

これで設定は終了です。

テストする

ローカルのサーバーを立てます
ローカルとはなんぞ？と言う方は以下の記事がわかりやすかったです
djangoは誰が動かしているのか？（デプロイのための俯瞰）

[ec2-user] $ cd
[ec2-user] $ cd testDjango

[ec2-user] $ python manage.py runserver

このあとGoogleChromeなどで

http://(EC2のオープンIPアドレス)/user/

と検索すると

[]

と空の括弧が返ってきたと思います。

データを入れる

このままだと不便なので
GoogleChromeの拡張機能のARCをダウンロードしましょう

Advanced REST clientダウンロード

GETで通信してみると空の括弧が返ってきます

POSTで通信してみます。その際に

{"name":"tanaka","mail":"T@gmail.com"}

この情報を追加します。

SENDを押すとレスポンスが返ってきます

またGETできちんと登録できたか確認してみるといいでしょう。

またデータベースは

MySQL > use dbtest;
MySQL > SELECT * FROM polls_user;
>>>
+----+----------------------------+--------+-------------+
| id | created                    | name   | mail        |
+----+----------------------------+--------+-------------+
|  1 | 2020-10-21 05:10:23.730602 | tanaka | T@gmail.com |
+----+----------------------------+--------+-------------+

これで登録に成功しました。

おわりに

この記事で誰かの役に立っていただければ幸いです。

次回は　NginX,Gunicorn　を使って本番環境(初心者の私が作る)を作ってみようかと思います。

それではでは

参考サイト

以下と本記事の途中に非常に参考にさせていただいたサイトを紹介しています。
ありがとうございました。

[1].Django REST frameworkチュートリアルその１
[2].djangoは誰が動かしているのか？（デプロイのための俯瞰）
[3].【学習メモ】MakemigrationsとMigrateについて

[4].よく使うMySQLコマンド集

　 Tweet
Qiitaで続きを読む

投稿日：2020-10-21T14:25:27+09:00

超解像手法/ESPCNを組んでみた

概要

今回は、超解像手法の1つであるESPCN(efficient sub-pixel convolutional neural network)を組みましたので、そのまとめとして投稿します。
元論文はこちらから→Real-Time Single Image and Video Super-Resolution Using an Efficient Sub-Pixel Convolutional Neural Network

1.はじめに

超解像とは、解像度が低い画像や動画像に対して解像度を向上させる技術のことであり、ESPCNは2016年に提案された手法のことです。(ちなみに初のDeeplearningの手法として挙げられるSRCNNは2014年)
SRCNNはバイキュービック法など、既存の拡大手法に組み合わせて解像度の向上を図る手法でしたが、このESPCNではDeeplearningのモデルの中に拡大フェーズが導入されており、任意の倍率で拡大することができます。
今回は、この手法をpythonで組みましたので、コード紹介をしたいと思います。
コードの全容はGitHubにも投稿しているのでそちらをご確認ください。
https://github.com/nekononekomori/espcn_keras

2.ESPCNとは

ESPCNとは、DeeplearningのモデルにSubpixel Convolution(Pixel shuffle)を導入して解像度の向上を図った手法のことです。コードを載せるのがメインなので、詳細の説明は省きますが、ESPCNについて説明しているサイトを載せておきます。
https://buildersbox.corp-sansan.com/entry/2019/03/20/110000
https://qiita.com/oki_uta_aiota/items/74c056718e69627859c0
https://qiita.com/jiny2001/items/e2175b52013bf655d617

3.PC環境

cpu : intel corei7 8th Gen
gpu : NVIDIA GeForce RTX 1080ti
os : ubuntu 20.04

4.コード説明

GitHubを見ていただくと分かるのですが、主に3つのコードからなっています。
・datacreate.py →　データセット生成プログラム
・model.py →　ESPCNのプログラム
・main.py →　実行プログラム
datacreate.pyとmodel.pyで関数を作成し、main.pyで実行しています。

datacreate.pyの説明

datacreate.py

import cv2
import os
import random
import glob
import numpy as np
import tensorflow as tf

#任意のフレーム数を切り出すプログラム
def save_frame(path,        #データが入っているファイルのパス
               data_number, #1枚の画像から切り取る写真の数
               cut_height,  #保存サイズ(縦)(低画質)
               cut_width,   #保存サイズ(横)(低画質)
               mag,         #拡大倍率
               ext='jpg'):

    #データセットのリストを生成
    low_data_list = []
    high_data_list = []

    path = path + "/*"
    files = glob.glob(path)

    for img in files:
        img = cv2.imread(img, cv2.IMREAD_GRAYSCALE)
        H, W = img.shape

        cut_height_mag = cut_height * mag
        cut_width_mag = cut_width * mag

        if cut_height_mag > H or cut_width_mag > W:
            return

        for q in range(data_number):
            ram_h = random.randint(0, H - cut_height_mag)
            ram_w = random.randint(0, W - cut_width_mag)

            cut_img = img[ram_h : ram_h + cut_height_mag, ram_w: ram_w + cut_width_mag]

            #がウシアンフィルタでぼかしを入れた後に縮小
            img1 = cv2.GaussianBlur(img, (5, 5), 0)
            img2 = img1[ram_h : ram_h + cut_height_mag, ram_w: ram_w + cut_width_mag]
            img3 = cv2.resize(img2, (cut_height, cut_width))

            high_data_list.append(cut_img)
            low_data_list.append(img3)

    #numpy → tensor　+ 正規化
    low_data_list = tf.convert_to_tensor(low_data_list, np.float32)
    high_data_list = tf.convert_to_tensor(high_data_list, np.float32)
    low_data_list /= 255
    high_data_list /= 255

    return low_data_list, high_data_list

これは、データセットを生成するプログラムになります。

def save_frame(path,        #データが入っているファイルのパス
               data_number, #1枚の画像から切り取る写真の数
               cut_height,  #保存サイズ(縦)(低解像度)
               cut_width,   #保存サイズ(横)(低解像度)
               mag,         #拡大倍率
               ext='jpg'):

ここは関数の定義です。コメントアウトで書いている通りですが、
pathはフォルダのパスです。(例えば、fileという名前のフォルダに写真が入っているなら、"./file"と入力です。)
data_numberは1枚の写真を複数枚切り取ってデータのかさましをします。
cut_heightとcut_wedthは低解像度の画像サイズです。最終的な出力結果は倍率magをかけた値になります。
(cut_height = 300, cut_width = 300, mag = 300なら、
結果は900 * 900のサイズの画像となります。)

    path = path + "/*"
    files = glob.glob(path)

ここは、ファイルにある全ての写真をリストにして返しています。

for img in files:
        img = cv2.imread(img, cv2.IMREAD_GRAYSCALE)
        H, W = img.shape

        cut_height_mag = cut_height * mag
        cut_width_mag = cut_width * mag

        if cut_height_mag > H or cut_width_mag > W:
            return

        for q in range(data_number):
            ram_h = random.randint(0, H - cut_height_mag)
            ram_w = random.randint(0, W - cut_width_mag)

            cut_img = img[ram_h : ram_h + cut_height_mag, ram_w: ram_w + cut_width_mag]

            #ガウシアンフィルタでぼかしを入れた後に縮小
            img1 = cv2.GaussianBlur(img, (5, 5), 0)
            img2 = img1[ram_h : ram_h + cut_height_mag, ram_w: ram_w + cut_width_mag]
            img3 = cv2.resize(img2, (cut_height, cut_width))

            high_data_list.append(cut_img)
            low_data_list.append(img3)

ここは先ほどリストにした写真を1枚ずつ取り出して、data_numberの数だけ切り取っています。
切り取る場所をランダムにしたいのでrandom.randintを使用しています。
そして、ガウシアンフィルタでぼかして低解像度画像を生成しています。
最後にリストにappendで追加しています。

    #numpy → tensor　+ 正規化
    low_data_list = tf.convert_to_tensor(low_data_list, np.float32)
    high_data_list = tf.convert_to_tensor(high_data_list, np.float32)
    low_data_list /= 255
    high_data_list /= 255

    return low_data_list, high_data_list

ここは、keras, tensorflowではnumpy配列ではなくtensorに変換する必要があるため、変換を行っています。同時に正規化もここでしておきます。

最後に、低解像度の画像を格納したリストと高解像度の画像を格納したリストを返して関数は終了です。

model.pyの説明

model.py

import tensorflow as tf
from tensorflow.python.keras.models import Model
from tensorflow.python.keras.layers import Conv2D, Input, Lambda

def ESPCN(upsampling_scale):
    input_shape = Input((None, None, 1))

    conv2d_0 = Conv2D(filters = 64,
                        kernel_size = (5, 5),
                        padding = "same",
                        activation = "relu",
                        )(input_shape)
    conv2d_1 = Conv2D(filters = 32,
                        kernel_size = (3, 3),
                        padding = "same",
                        activation = "relu",
                        )(conv2d_0)
    conv2d_2 = Conv2D(filters = upsampling_scale ** 2,
                        kernel_size = (3, 3),
                        padding = "same",
                        )(conv2d_1)

    pixel_shuffle = Lambda(lambda z: tf.nn.depth_to_space(z, upsampling_scale))(conv2d_2)

    model = Model(inputs = input_shape, outputs = [pixel_shuffle])

    model.summary()

    return model

さすがと言いますか、短いですね。

さて、ESPCNの論文をみていると、このような構造をしていると書いています。

Convolution層の詳細はこちらを→kerasのドキュメント
pixel_shuffleはkerasには標準搭載されていないので、lambdaで代用しました。
lambbdaは任意の式をモデルに組み込めるので、拡大を表しています。
lambdaのドキュメント→https://keras.io/ja/layers/core/#lambda
tensorflowのドキュメント→https://www.tensorflow.org/api_docs/python/tf/nn/depth_to_space

ここのpixel shuffleに関しては色々なやり方があるみたいです。

model.pyの説明

model.py

import model
import data_create
import argparse
import os
import cv2

import numpy as np
import tensorflow as tf

if __name__ == "__main__":

    def psnr(y_true, y_pred):
        return tf.image.psnr(y_true, y_pred, 1, name=None)

    train_height = 17
    train_width = 17
    test_height = 200
    test_width = 200

    mag = 3.0
    cut_traindata_num = 10
    cut_testdata_num = 1

    train_file_path = "../photo_data/DIV2K_train_HR" #写真が入ったフォルダ
    test_file_path = "../photo_data/DIV2K_valid_HR" #写真が入ったフォルダ

    BATSH_SIZE = 256
    EPOCHS = 1000
    opt = tf.keras.optimizers.Adam(learning_rate=0.0001)

    parser = argparse.ArgumentParser()
    parser.add_argument('--mode', type=str, default='espcn', help='espcn, evaluate')

    args = parser.parse_args()

    if args.mode == "espcn":
        train_x, train_y = data_create.save_frame(train_file_path,   #切り取る画像のpath
                                                cut_traindata_num,  #データセットの生成数
                                                train_height, #保存サイズ
                                                train_width,
                                                mag)   #倍率

        model = model.ESPCN(mag) 
        model.compile(loss = "mean_squared_error",
                        optimizer = opt,
                        metrics = [psnr])
#https://keras.io/ja/getting-started/faq/
        model.fit(train_x,
                    train_y,
                    epochs = EPOCHS)

        model.save("espcn_model.h5")

    elif args.mode == "evaluate":
        path = "espcn_model"
        exp = ".h5"
        new_model = tf.keras.models.load_model(path + exp, custom_objects={'psnr':psnr})

        new_model.summary()

        test_x, test_y = data_create.save_frame(test_file_path,   #切り取る画像のpath
                                                cut_testdata_num,  #データセットの生成数
                                                test_height, #保存サイズ
                                                test_width,
                                                mag)   #倍率
        print(len(test_x))
        pred = new_model.predict(test_x)
        path = "resurt_" + path
        os.makedirs(path, exist_ok = True)
        path = path + "/"

        for i in range(10):
            ps = psnr(tf.reshape(test_y[i], [test_height, test_width, 1]), pred[i])
            print("psnr:{}".format(ps))

            before_res = tf.keras.preprocessing.image.array_to_img(tf.reshape(test_x[i], [int(test_height / mag), int(test_width / mag), 1]))
            change_res = tf.keras.preprocessing.image.array_to_img(tf.reshape(test_y[i], [test_height, test_width, 1]))
            y_pred = tf.keras.preprocessing.image.array_to_img(pred[i])

            before_res.save(path + "low_" + str(i) + ".jpg")
            change_res.save(path + "high_" + str(i) + ".jpg")
            y_pred.save(path + "pred_" + str(i) + ".jpg")

    else:
        raise Exception("Unknow --mode")

メインは結構長いのですが、短くできるならもっとできるかなぁというのが感想です。
以下で、中身の説明をしていこうと思います。

import model
import data_create
import argparse
import os
import cv2

import numpy as np
import tensorflow as tf

ここでは、関数や同じディレクトリにある別のファイルを読み込んでいます。
datacreate.pyとmodel.pyとmain.pyは同じディレクトリにおいてください。

    def psnr(y_true, y_pred):
        return tf.image.psnr(y_true, y_pred, 1, name=None)

今回は、生成画像の良し悪しの判断基準にpsnrを使用しましたので、そこの定義です。
psnrはピーク信号対雑音比という名前で、簡単に言うと比較したい画像の画素値の差分を計算するって感じです。ここでは詳細の説明を省きますが、この記事とかは割と詳しく、複数の評価法が記載されています。

    train_height = 17
    train_width = 17
    test_height = 200
    test_width = 200

    mag = 3.0
    cut_traindata_num = 10
    cut_testdata_num = 1

    train_file_path = "../photo_data/DIV2K_train_HR" #写真が入ったフォルダ
    test_file_path = "../photo_data/DIV2K_valid_HR" #写真が入ったフォルダ

    BATSH_SIZE = 256
    EPOCHS = 1000
    opt = tf.keras.optimizers.Adam(learning_rate=0.0001)

ここは、今回使用する値を設定しています。config.pyとして別にしている方もgithubを見ていたら結構いますが、大規模プログラムではないため、まとめています。

学習データのサイズは、trainデータは論文が51*51と書いてあったのでそのmagで割った値の17*17を採用しました。testは見やすいように大きめにしているだけです。結果はこれの３倍の大きさになります。
データの数はファイルに含まれている画像の数の10倍です。(800枚であればデータ数は8,000)

今回、データに使用したのはよく超解像で使われているDIV2K Datasetです。データの質がいいので、少ないデータである程度の精度が出ると言われています。

    parser = argparse.ArgumentParser()
    parser.add_argument('--mode', type=str, default='espcn', help='espcn, evaluate')

    args = parser.parse_args()

ここは、モデルの学習と評価を分けたかったのでこのような形にして、--modeで選択できるようにしました。
詳細の説明はしないので、python公式のドキュメントを載せておきます。
https://docs.python.org/ja/3/library/argparse.html

  if args.mode == "espcn":
        train_x, train_y = data_create.save_frame(train_file_path,   #切り取る画像のpath
                                                cut_traindata_num,  #データセットの生成数
                                                train_height, #保存サイズ
                                                train_width,
                                                mag)   #倍率

        model = model.ESPCN(mag) 
        model.compile(loss = "mean_squared_error",
                        optimizer = opt,
                        metrics = [psnr])
#https://keras.io/ja/getting-started/faq/
        model.fit(train_x,
                    train_y,
                    epochs = EPOCHS)

        model.save("espcn_model.h5")

ここで、学習させています。srcnnと選択(後ほどやり方は記載)するとこのプログラムが動きます。

data_create.save_frameで、data_create.pyのsave_frameという関数を読み込んで、使えるようにしています。ここで、train_xとtrain_yにデータが入ったので、モデルを同様に読み込んで、compile, fitを行います。

compileなどの詳細の説明はkerasのドキュメントをご覧ください。割と論文と同じものを採用して行っています。

最後にモデルを保存してお終いです。

    elif args.mode == "evaluate":
        path = "espcn_model"
        exp = ".h5"
        new_model = tf.keras.models.load_model(path + exp, custom_objects={'psnr':psnr})

        new_model.summary()

        test_x, test_y = data_create.save_frame(test_file_path,   #切り取る画像のpath
                                                cut_testdata_num,  #データセットの生成数
                                                test_height, #保存サイズ
                                                test_width,
                                                mag)   #倍率
        print(len(test_x))
        pred = new_model.predict(test_x)
        path = "resurt_" + path
        os.makedirs(path, exist_ok = True)
        path = path + "/"

        for i in range(10):
            ps = psnr(tf.reshape(test_y[i], [test_height, test_width, 1]), pred[i])
            print("psnr:{}".format(ps))

            before_res = tf.keras.preprocessing.image.array_to_img(tf.reshape(test_x[i], [int(test_height / mag), int(test_width / mag), 1]))
            change_res = tf.keras.preprocessing.image.array_to_img(tf.reshape(test_y[i], [test_height, test_width, 1]))
            y_pred = tf.keras.preprocessing.image.array_to_img(pred[i])

            before_res.save(path + "low_" + str(i) + ".jpg")
            change_res.save(path + "high_" + str(i) + ".jpg")
            y_pred.save(path + "pred_" + str(i) + ".jpg")

    else:
        raise Exception("Unknow --mode")

いよいよラストの説明です。
まずは、psnrが使えるように先ほど保存したモデルを読み込みます。
次に、test用のデータセットを生成し、predictで画像を生成します。

psnr値をその場で知りたかったので、計算してます。
画像を保存したかったので、tensorからnumpy配列に変換して、保存してついに終わりです！

こんな感じでしっかり高解像度化できています。

5.終わりに

今回はESPCNを組んでみました。次はどの論文を実装してみようか悩みどころですね。
要望・質問などいつでもお待ちしております。読んでいただきありがとうございました。

　 Tweet
Qiitaで続きを読む

投稿日：2020-10-21T13:41:39+09:00

時系列分析4　SARIMAモデルの構築

Aidemy　2020/10/29

はじめに

　こんにちは、んがょぺです！バリバリの文系ですが、AIの可能性に興味を持ったのがきっかけで、AI特化型スクール「Aidemy」に通い、勉強しています。ここで得られた知識を皆さんと共有したいと思い、Qiitaでまとめています。以前のまとめ記事も多くの方に読んでいただけてとても嬉しいです。ありがとうございます！
　今回は、次系列分析の4つ目の投稿になります。どうぞよろしくお願いします。

＊本記事は「Aidemy」での学習内容を「自分の言葉で」まとめたものになります。表現の間違いや勘違いを含む可能性があります。ご了承ください。

今回学ぶこと
・SARIMAモデルの構築

SARIMAモデルについて

・SARIMAモデルとは、データを階差系列に変換するARIMA(p,d,q)を、更に季節周期を持つ時系列にも対応できるようにしたモデルのことである。
・SARIMAモデルでは、SARIMA(sp,sd,sq,s)というパラメータを持つ。

sp,sd,sq

・sp,sd,sqはそれぞれ「季節性自己相関」「季節性導出」「季節性移動平均」といい、ARIMAのp,d,qと基本的には変わらない。
・sp,sd,sqのデータは過去の季節期間を経たデータに影響されるということが加わった。
・SARIMAのもう一つのパラメータである「s」は季節周期を表す。12ヶ月周期なら、s=12とすれば良い。
・sqに関しては、影響される「過去の季節期間」が何周期前のものかを表す。

パラメータの決定

・以上のようなパラメータについて、適切な値を調べる必要がある。
・このときに使われるのが、情報量基準というものである。今回はその中でも「BIC」というものを使う。ただし、今回は詳しくは扱わない。
・BICの値が低ければ低いほどパラメータの値は適切であると言える。

自己相関係数/偏自己相関係数の可視化

・偏自己相関とは、自己相関を行う二つの値の間のデータの影響を取り除いたものである。
・例えば、y1とy7の偏自己相関は、その間のy2〜y6の影響を除去したものになる。
・この偏自己相関を可視化することによって、パラメータ「s」の最適な値を設定する。
・可視化したとき、周期の部分で偏自己相関の値が高くなるので、ここをsの値にすれば良い。

・偏自己相関の可視化（グラフ化）は以下のように行う。
sm.graphics.tsa.plot_pacf(データ)

・コード（ワインの売り上げデータの相関の可視化）

・結果

SARIMAモデルの構築

・構築の手順
　①データ読み込み:pd.read_csv()
　②データ整理:pd.date_range()
　③データ可視化:sm.graphics.tsa.plot_pacf()
　④データ周期（s）把握:④から。
　⑤s以外のパラメータ設定:BICで把握
--ここから新しい部分--
　⑥モデル構築:sm.tsa.statespace.SARIMAX().fit()
　⑦データ予測/可視化:predict() / plt.show()

・⑥モデル構築のSARIMAX()の引数については以下のようになる。
SARIMAX(データ,order=(p,d,q),seasonal_order=(sp,sd,sq,s))

・⑦データ予測のpredict()は以下のようになる。予測開始時だけは時系列データにある時間である必要がある。
モデル.predict("予測開始時","予測終了時")

・一連のコード実行（⑤は行っていない）

・結果

まとめ

・SARIMAモデルとは、データを階差系列に変換するARIMA(p,d,q)を、更に季節周期を持つ時系列にも対応できるようにしたモデルのことである。
・SARIMAモデルにはパラメータ(sp,sd,sq,s)がある。
・sp,sd,sqはBICという情報量基準を用いて適切な値を調べる。
・sは偏自己相関を図式化して調べる。
・これらのパラメータをsm.tsa.statespace.SARIMAX().fit()に渡してモデルを構築し、predict()で予測を行う。

今回は以上です。最後まで読んでいただき、ありがとうございました。

　 Tweet
Qiitaで続きを読む

投稿日：2020-10-21T13:41:07+09:00

機械学習における前処理4　データの変換

Aidemy　2020/10/29

はじめに

　こんにちは、んがょぺです！バリバリの文系ですが、AIの可能性に興味を持ったのがきっかけで、AI特化型スクール「Aidemy」に通い、勉強しています。ここで得られた知識を皆さんと共有したいと思い、Qiitaでまとめています。以前のまとめ記事も多くの方に読んでいただけてとても嬉しいです。ありがとうございます！
　今回は機械学習の前処理の4つ目の投稿になります。どうぞよろしくお願いします。

＊本記事は「Aidemy」での学習内容を「自分の言葉で」まとめたものになります。表現の間違いや勘違いを含む可能性があります。ご了承ください。

今回学ぶこと
・連続値について
・カテゴリ形データの変換
・スケール調整について
・縦持ちデータと横持ちデータについて

連続値について

連続値のカテゴリ化

・データの前処理時に、連続値を分割してカテゴリ化したい場合がある。
・具体的には、年齢のデータ[10,15,18,20,27,32]があり、これを「10代、20代、30代」に分けたい（連続値のカテゴリ化）と考える。

・実行は、pandasのcut(x,bins=[],labels=[],right=)関数で行う。
・各引数について
　・「x」は渡すデータを表す。
　・「bins」には区切りになる数値を配列で渡す。
　・「labels」にはカテゴリごとの名前を配列で渡す。
　・「right」には区間の分け方を「Aより大きくB以下」にするならTrueを、「A以上B未満」にするならFalseにする。（Default=Trueだが、日本人的思考ならFalseで「A以上B未満」の形にした方が直感的に分かりやすい）
x = [10,15,18,20,27,32]
bins = [10,20,30,40] #10~20,20~30,30~40という意味
labels = ['10代','20代','30代']
#カテゴリ化
pd.cut(x,bins=bins,labels=labels,right=False)
#[10代,10代,10代,20代,20代,30代]
カテゴリ型データをone-hotエンコーディングする

・前項でカテゴリ化したデータを、そのカテゴリに属していれば「1」、属していなければ「0」というように変換する。
・例えば、「10代」のカテゴリなら[1,1,1,0,0,0]といった出力になるようにする。
・このような変換を「one-hotエンコーディング」という。
・例えば{'age':[10代,10代,10代,20代,20代,30代]}というデータがDataFrame（変数df）で与えられていた場合
pd.get_dummies(df['age'])で変換できる。
・また、'age'以外にも列があり、その全てを変換したいときは引数は「df」のみで良い。
・変換後の列に元の列の名前を残したい時は、第二引数にprefix='age'のように列名を渡せば良い。
result = pd.cut(x,bins=bins,labels=labels,right=False)
df = pd.DataFrame({'age':result})
#one-hotエンコーディングの実行
pd.get_dummies(df['age'],prefix='age')
'''
age_10代   age_20代   age_30代
0   1   0   0
1   1   0   0
2   1   0   0
3   0   1   0
4   0   1   0
5   0   0   1
'''
スケール調整について

・モデルに渡す数値型のデータ項目の中に、相対的に値が大きなデータが入っていると、学習の効率を下げてしまう恐れがある。
・このようなときに、全ての数値型のデータ項目を一定の基準に収まるように値を調整することを「スケール調整」という。
・一般的な基準は「平均0、分散1」である。この場合、scikit-learnのpreprocessingモジュールのscale()関数を使うと良い。

・コード（平均50分散10の正規乱数をスケール調整）

Box-Cox変換

・データが「正規分布」に近づくように変換するとき、Box-Cox変換というものを行う。
・正規分布とは、データの個数が中央に行くほど多く、端に行くほど少なくなる分布のことである。
・Box-cox変換を行うとき、scipyのstatsモジュールのboxcox()関数を使う。

・boxcox関数に対しては変数を二つ渡すが、一つ目には変換後の配列が、二つ目には、変換のときに使われるパラメータ「λ」が格納される。

・コード（自由度3のx^2をBox-Cox変換）

・結果

縦持ちデータと横持ちデータ

縦持ちデータと横持ちデータとは

・縦持ちデータは、データの情報が増えたときに「縦に」データを増やす（行の追加）ような構造であり、横持ちデータは「横に」データを増やす（列の追加）ような構造であるものを指す。
・例えば、会計報告として、「購入者」と「購入物」、「値段」のデータがあるとする。データが増えたとき、単純に3つの列を持つデータに縦方向にデータを追加するのが縦持ちデータ、購入物を横方向に展開してそこにデータを追加するのが横持ちデータである。
・縦持ちデータは、列を追加する必要がないため、データ構造の変更やロジックの変更に対応しやすいというメリットがある。
・一方横持ちデータは確認の際に直感的に理解しやすいというメリットがある。
・モデルにデータを渡すときには、このどちらかの形式に変換する必要がある。

縦持ちデータを横持ちデータに変換

・pandasのpivot(index,columns,values)関数を使う。
・各引数について、「index」は同じ要素を一行にまとめる元のDataFrameの列、「columns」は新しい列にするための元の列、「values」は列の値にする元の列を渡す。

・先ほどの例で言えば、「購入者」は同じ人が多く続くので「index」に、「購入物」は横方向に展開させたいので「columns」に、「値段」は列の値になるので「values」に格納する。
・さらに、変換後のdfのインデックスはこのとき渡したindexになっているので、これを普通のインデックス番号に戻したい時は、pivot()に「.reset_index()」をつける。また、この時、列のname属性が残ってしまうので、変換後のdfのcolumnsに.columns.set_names(None)をつける。
df = pd.DataFrame({
      '購入者': ['佐藤','田中','加藤','田中','加藤'],
      '購入物': ['ペン','紙','飲料','ハサミ','のり']
      '値段': [500, 250, 250, 600, 200]
})
##縦持ちデータを横持ちデータに変換
pivoted_df = df.pivot(index='購入者',columns='購入物',values='値段').reset_index()
pivoted_df.columns = pivoted_df.columns.set_names(None)
'''
    購入者   ペン  紙 飲料  ハサミ   のり
0   佐藤  500             
1   田中      250     600 
2  加藤          250     200
'''
横持ちデータを縦持ちデータに変換

・pandasのmelt(frame,id_vars,value_vars,var_name,value_name)で変換できる。
・各引数について
　・frame:変換元のdf
　・id_vars:キーになる列(配列で渡す)
　・value_vars:変換後の値になる列(配列で渡す)
　・var_name:横方向に展開されている列をまとめる列の名前
　・value_name:変換後の値になる列の名前

・前項で作った横持ちデータなら、以下のようになる。
pd.melt(pivoted_df,id_vars=['購入者'],value_vars=['ペン','紙','飲料','ハサミ','のり'],var_name='購入物',value_name='値段')

まとめ

・連続値をカテゴリ化したい時は、pandasのcut(x,bins=[],labels=[],right=)で行う。
・カテゴリ化したデータを、そのカテゴリに属していれば「1」、属していなければ「0」というように変換することを「one-hotエンコーディング」と言い、pd.get_dummies()で行う。
・数値型データの値を相対的に揃えることを「スケール調整」といい、preprocessing.scale()
で行う。
・データを正規分布に近づけるように変換することを「Box-Cox変換」と言い、stats.boxcox()で行う。
・縦持ちデータから横持ちデータに変換する時はpivot(index,columns,values)を使い、その逆を行う時はmelt(frame,id_vars,value_vars,var_name,value_name)を使う。

今回は以上です。最後まで読んでいただき、ありがとうございました。

　 Tweet
Qiitaで続きを読む

投稿日：2020-10-21T13:40:34+09:00

機械学習における前処理3　欠損値・外れ値・不均衡データ

Aidemy　2020/10/29

はじめに

　こんにちは、んがょぺです！バリバリの文系ですが、AIの可能性に興味を持ったのがきっかけで、AI特化型スクール「Aidemy」に通い、勉強しています。ここで得られた知識を皆さんと共有したいと思い、Qiitaでまとめています。以前のまとめ記事も多くの方に読んでいただけてとても嬉しいです。ありがとうございます！
　今回は、機械学習の前処理の3つめの投稿になります。どうぞよろしくお願いします。

＊本記事は「Aidemy」での学習内容を「自分の言葉で」まとめたものになります。表現の間違いや勘違いを含む可能性があります。ご了承ください。

今回学ぶこと
・欠損値の取り扱い
・外れ値の取り扱い
・不均衡データの取り扱い

欠損値の扱い

欠損値について

・欠損値は「NaN」で表される中身のないデータのことである。
・NaNがデータに存在する場合、全体の平均や標準偏差を計算することができない。
・欠損値を1つでも含むデータを全て削除してしまうとデータに無駄や偏りが生じる。

欠損値発生のメカニズム

・前項で見たように、欠損値を含むデータは適切に処理しなければデータ分析が行えない。よって欠損値に対して適切な前処理を行う必要があるが、その方法は欠損値発生のメカニズムごとに異なる。

・欠損値発生のメカニズムには、以下の3種類がある。
1.MCAR:データの欠損する（NaNになる）確率が、データそのものと無関係である（無作為に生じている）時
　　　　ex)コンピュータの不具合でデータの一部が消失した。
2.MAR:データの欠損する確率が、その項目以外の項目から影響があると推測できる時
　　　　ex)男女を対象にしたアンケートで「性別」の項目が女性であると「年齢」の項目の欠損確率が高くなる。
3.NMAR:データの欠損する確率が、その項目から影響があると推測できる時
　　　　ex)男女を対象にしたアンケートで実際の年齢が高い人ほど「年齢」の項目の欠損確率が高くなる。

欠損値の対処

・欠損値発生のメカニズムごとに適切な対処法は異なる。

・MCARの場合、欠損値を含むデータを全て削除する「リストワイズ削除」を行うことも可能。これによりデータ数が少なくなりすぎる時は「代入法」（後述）も使える。
・MARの場合は「代入法」を使う。リストワイズ削除が不適切なのは、例で言えば、女性のデータが多く削除されてしまいデータに偏りが生じるからである。
・NMARの場合は適切に対処することが困難であるため、基本的にはデータを再収集する。

代入法

・欠損値の代入法は大きく分けて2種類ある。詳しくは後述。
　1.単一代入法:欠損値を補完して完全なデータセットを一つ作り、それを使ってモデルを作る方法。
　2.多重代入法:欠損値を補完した完全なデータセットを複数作り、そのそれぞれについてモデルを作り、最後にモデルを一つに統合する方法。

欠損値の可視化

・データを可視化することで、どこにNaNがあるかを調べる。
・NaNがどの列に何件あるかを簡易的に知りたい時は、pandasの「データ.isnull().sum()」を使えば良い。
・欠損値全体の状況を可視化したい時は、missingnoパッケージのmatrix関数を使うと良い。

・コード

・結果（白い部分が欠損値）

単一代入法

・単一代入法において欠損値を補完する際には、その用途に合わせて三種類の方法がある。

・平均値代入法:欠損値NaNに、その項目の平均値を代入する。平均値が増える分全体の分散は小さくなるので、分散や誤差を考慮すべきときには使えない。
・確率的回帰代入法:詳しくは扱わないが、分散や誤差を考慮することができる。
・ホットデック法:欠損値を含むデータ行（レシピエント）とデータが近いデータ行（ドナー）から値をもらうことで補完する。
・データの近さは、「最近傍法」という方法を用いて判定する。

ホットデック法

・ホットデック法は以下のように記述して実行する。
knnimpute.knn_impute_few_observed(matrix, missing_mask, k)

・引数について、「matrix」にはnp.matrixに変換したデータを渡す。「missing_mask」には、matrixのどこに欠損値が含まれるかをnp.isnan(matrix)で行列化したデータを渡す。「k」は、「最近傍法」のKNNで考慮に入れる近くの点の個数を指定する。

・KNNは「教師あり学習（分類）」で学んだ手法で、特定のデータ点を分類するときに、その近くのk個の点を考慮に入れる手法である。

・また、データをnp.matrixに変換しているので、必要に応じて元のデータ形式に戻す必要がある。

・コード

多重代入法について

・単一代入法の場合、補完した値はあくまで予測値であるため、これを使ったモデルの分析結果が必ずしも正確とは言い切れない欠点がある。
・これに対し、多重代入法はデータの補完を複数回行ってデータセットを複数作り、それらの分析結果を一つに統合して最終結果を出すため、確実性の上がった予測を行うことが可能である。

・多重代入法で使うモデルはstatsmodelsのmiceを使って以下のように表せる。
mice.MICE(formula, optimizer, imp_data)

・各引数について、「formula」には、モデルで予測する変数の式を渡す。例えば、「distance」という変数について、「time」と「speed」で予測する線形重回帰モデルの場合、以下のように表す。
'distance ~ time + speed'
・「optimizer」では分析モデルを指定し、「imp_data」には、dataをMICEで扱えるようにするために作成する「mice.MICEData(data)関数」を渡す。

・これで作成したMICEモデルに対してfit()メソッドを使うことで補完した分析結果を取得できる。（多重代入法の実行）
・fit()の第一引数には、一度の補完のための試行回数を指定し、第二引数にはデータセットの作成数を渡す。

・この分析結果に対して、summary()メソッドを使うことで結果を確認できる。

・コード

外れ値について

外れ値によって起こる問題

・外れ値とは、他のデータと著しく離れたデータのことを指す。
・外れ値が混在すると、「分析結果が正確でなくなる」「モデルの学習が遅くなる」といった問題が生じる。
・よって、外れ値についても前処理の段階で検知し、除外する必要がある。

外れ値の可視化

・外れ値が存在するかどうかは可視化するとわかりやすい。
・可視化にはseabornのboxplot(x,y,whis)を使う。描画されるのは「箱ひげ図」であり、外れ値を「♦︎」で示してくれる。
・引数「x」「y」はx軸y軸のデータ、「whis」は外れ値とみなす基準を指定する。

・データが二次元の時はjoinplot(x,y,data)も使うことができる。散布図のように点がプロットされるので、外れ値を目視で検知する。
・引数「data」にはDataFrameを渡せば良い。

・コード（縦軸の離れ具合がわかれば良いので、y軸のみ指定する）

・結果

外れ値の検知 [LOF]

・外れ値が存在することがわかったら、実際に外れ値を検知する。
・検知には「どのような値を外れ値とするか」といった基準が必要になる。今回は、その基準が予め定められた上で検知を行う、scikit-learnの「LOF」という方法を扱う。
・LOFの外れ値判定は以下のように行われる。
　①近くにデータ点が少ない点を外れ値と考える。
　②「近く」の判定はk個の近傍点を使って行われる。
　③この判定（データの密度）が周囲と相対的に低い点を外れ値と判定する。

・LOFはLocalOutlierFactor(n_neighbors=k)で使うことができる。
・n_neighborsには近傍点の数kの個数を指定する。

・あとは普通のモデルのようなfit_predict(data)メソッドでデータを学習させて、外れ値を検出する。
・dataにはDataFrameをそのまま渡すことができる。
・戻り値としてはarray([1,1,-1,1,...])のような配列が返される。このうち「-1」の部分が外れ値とみなされた部分になる。
・これに対してdata[戻り値を格納した変数 == -1]のように指定すると、外れ値とみなされた行を抽出できる。

・コード

・結果（外れ値の出力）

外れ値の検知 [isolationForest]

・LOFとは別の外れ値検知の方法として、「isolationForest」というものがある。
・isolationForestでは、ランダムにデータを分割し、その深さに値を設定していくということを繰り返して外れ値を検知する。
・isolationForestは距離や密度に依存しないため、計算が複雑でなく省メモリである。また、大規模データであっても計算をスケールしやすいといった特徴もある。

・isolationForestもLOFと同様「IsolationForest()関数」を使うことで外れ値を予測できる。

分類モデルの作成はIsolationForest()で行い、これにfit()メソッドを使って学習を行わせ、predict()で予測を行う。この戻り値はLOFと同様「-1」が外れ値となるので、 data[predictions == -1]のようにして取得する。

・コード

・結果

不均衡データについて

不均衡データによって起こる問題

・データ値のうち特定の値が極端に多かったり少なかったりするデータを「不均衡データ」という。
・例えば、二値分類のように「0」か「1」の値を持つ場合に、1000件のデータのうち999件が「1」で1件が「0」のデータであったとする。このデータで予測する場合、「1」を予測するなら99.9%的中するが、「0」はほぼ予測できない。
・よって、不均衡データについても、データの前処理段階で適切に調整する必要がある。

・調整の方法には以下の3つがある。
　・オーバーサンプリング:頻度が少ないデータを増やして均衡を取る方法。
　・アンダーサンプリング:頻度が多いデータを減らして均衡を取る方法。
　・SMOTE-ENN:少ない方を増やし(SMOTE)、多い方を減らし(ENN)て均衡を取る。

・不均衡データを調整するにあたり、はじめに行うのは「不均衡データがあるか」の確認、すなわち、それぞれの値の個数（頻度）を可視化することである。
・個数の可視化は以下のように行う。
データ['列'].value_counts()

・コード（ある人が自動車を購入したかどうかのデータ）

オーバーサンプリング

・オーバーサンプリングは、頻度の少ないデータを増やして多いデータとの均衡を取る方法である。
・データの増やし方は何種類かあるが、簡単なのは「既存のデータをランダムに水増しする」手法である。
・水増しには、不均衡データを調整する際に使われるimbalanced-learnのRandomOverSampler(ratio='minority')が使われる。
・RandomOverSamplerを定義したら、実際に　.fit_sample(X,y)で実行する。
・これには目的変数Xと説明変数yをわたし、水増ししたものを格納する変数としても、2つ用意する。

・コード

アンダーサンプリング

・アンダーサンプリングは、頻度が多いデータを減らして均衡を取る方法である。
・データの減らし方は、RandomUnderSampler()で行える。この時引数で指定するratioについて、今回は頻度の多い方を扱うので、'majority'とする。

・コード

SMOTE-ENN

・SMOTEはオーバーサンプリング（データの水増し）に使われ、ENNはアンダーサンプリング（データの削除）に使われる。
・また、SMOTEでは最近傍法（kNN）を使って、増やすべきデータを推測して水増しを行い、ENNでも、kNNと同じように減らすべきデータを推測して削除を行う。
・SMOTEとENNの使い方はSMOTEENN(smote=,enn=)で行う。基本的にはROSやRUSと同様であるが、引数ではkNNで使う近傍点の個数(k_neighbors,n_neighbors)を指定する必要がある。

・コード

まとめ

・欠損値は「NaN」で表される中身のないデータのことである。
・外れ値は他のデータと著しく離れたデータのことである。
・不均衡データは特定の値が極端に多かったり少なかったりするデータのことである。
・これらのデータは機械学習の妨げになるものなので、前処理をしなければならない。

・欠損値は「代入法」でNaNに数値を代入することで補完する。
・外れ値は「LOF」「isolationForest」で取得し、除外する。
・不均衡データは「オーバーサンプリング」「アンダーサンプリング」あるいはその両方を行うことでデータの均衡を取る。

今回は以上です。最後まで読んでいただき、ありがとうございました。

　 Tweet
Qiitaで続きを読む

投稿日：2020-10-21T13:40:05+09:00

機械学習における前処理2　データの取得

Aidemy　2020/10/29

はじめに

　こんにちは、んがょぺです！バリバリの文系ですが、AIの可能性に興味を持ったのがきっかけで、AI特化型スクール「Aidemy」に通い、勉強しています。ここで得られた知識を皆さんと共有したいと思い、Qiitaでまとめています。以前のまとめ記事も多くの方に読んでいただけてとても嬉しいです。ありがとうございます！
　今回は、機械学習の前処理の2つ目の投稿になります。どうぞよろしくお願いします。

＊本記事は「Aidemy」での学習内容を「自分の言葉で」まとめたものになります。表現の間違いや勘違いを含む可能性があります。ご了承ください。

今回学ぶこと
・Excelからのデータ取得
・データベースからのデータ取得

Excelからのデータ取得

データ読み込み

・データ前処理の一番最初に行うことは「データの読み込み」である。
・データの読み込み元であるデータソースには「ファイル」「データベース」「Webサイト」などがあり、今回はその中でも読み込むことが多いExcelファイルとデータベースからのデータ取得について扱う。

・Excelからのデータ読み込みはpandasで行う。
・「データハンドリング2」で学んだように、Excelファイルの読み込みにはpd.read_excel()を使う。
・この引数には「ファイルのリンク」と「Excel内のシート名」を指定できる。
・また、第一引数には個別に設定したpd.ExcelFile("ファイル名")を渡すこともできる。

Excelデータの結合

・複数のシートに整理されているデータを一つのデータとして扱いたい時は、前処理として、データの結合を行う必要がある。
・例としては、商品データのシートAと販売データのシートBを横方向に結合させるといったことが考えられる。
・この結合にはpd.merge(left,right,on=)を使う。
・引数「left」「right」は左側/右側に結合するシートの指定、「on」は結合に使う列の名前を指定する。

・コード

・結果

Excelデータの絞り込み

・読み込んだり結合したりしたExcelデータ（シート）から、特定の文字列を持つデータ（行）を絞り込みたい時は、DataFlame.query('指定する文字列のある列 > 文字列')とする。
・この文字列について、複数指定したい時はリストで渡し、上記コードの「>」の部分は「==」または「in」にする。

・例えば、pandasで読み込んだデータ「df」のproduct_idが1と3の行を抽出したい時は以下のようにする。
df.query('product_id == [1,3]')
データの集約（グループ化）

・読み込んだ商品シート「df」に「type」という列があり、そこではデータが、食品を表す「food」、飲料を表す「drink」、お菓子を表す「sweet」のどれかに属しているとする。
・このうち「food」に属するデータの個数を知りたい時などは、「food」に属するデータを集約してグループ化する必要がある。
・グループ化には、df.groupby('グループ化する列の名前')を使う。
・この時複数の列でグループ化する時は('列1','列2'])というふうにすれば良い。
・このgroupbyメソッドで返されるデータの形は「GroupByオブジェクト」であり、これに対してcount(),mean(),sum(),max()などのメソッドを使うことで、グループ化したデータの個数などを求めることができる。（Pandasコースでも学習済み）

・今回の例ならば、以下のようにすれば良い。
gb = df.groupby('type')
gb['food'].count()
データベースからのデータ取得

データベースからのデータ読み込み

・データベースからの読み込みはpd.read_sql()で行うが、引数で渡す値が特殊なものになる。
・第一引数には、読み込むデータベースのテーブルと列を以下のように指定する。

'''
SELECT
列1,
列2　　(最後の列には「,」はいらない)
FROM テーブル
'''

・第二引数には、接続するデータベースの情報を以下のようにまとめて渡す。

sqla.create_engine('接続データベース+ドライバー名://接続ユーザー名:パスワード@ホスト名:ポート番号/データベース名?charset=文字コード')

・データ読み込みの一連の流れを以下に記述する。(データベースの情報は架空のもの)
import sqalchemy as sqla
#データベースの情報をまとめる
engine = sqla.create_engine('mysql+mysqldb://ngayope:ngayope@mysql-service:3307/database1?charset=utf8')
#データベース「database1」の「products」テーブルから「product_id」と「product_name」を取得
pd.read_sql('''
SELECT
 product_id,
 product_name
FROM products
''',engine)
テーブルの結合

・データベースのテーブルの結合も、Excelの時と同じように、pd.merge(left,right,on=)でも行うことができるが、データベースの場合はより簡単に結合させることができる。
・結合の場合、SQLのJOINを使う。
・以下に結合の方法を記載(列1をキーとして、テーブルAにテーブルBを結合する時)

'''
SELECT
テーブルA.列1，
テーブルB.列1
FROM
テーブルA
JOIN テーブルB ON テーブルA.列1 = テーブルB.列1　（追加することを記述）
'''

データの絞り込み

・データの絞り込みは、WHERE句を使って行う。使う時はSELECT、FROMと同列で行う。
・複数の条件で絞り込みをしたい時は「OR」「AND」を使う。「AND」は条件全てを満たす物を抽出する。

'''
WHERE
テーブル名.列名 = 抽出したい値1 OR
テーブル名.列名 = 抽出したい値2
'''

・ここまでのコード（データは商品の販売年月や定価を表している）

・上記コードの解説：
「SELECT」で今回出力する3つのデータを指定している。
「FROM」で「どの商品を販売したか」のテーブルであるmlprep_sales_productsを指定し、「JOIN ON」で、これとmlprep_sales,mlprep_productsを結合している。
最後に「WHERE」でmlprep_productsテーブルの定価を示す列「catalog_price」が200以上であるもののみ抽出している。

データの集約

・pandasのGroupByを使った方法を説明したが、SQLにも同じ働きを持つGROUP BY句があり、これを使ってデータを集約できる。
・データを集約する時は、必要に応じてデータを結合してから、そのデータを一つのテーブルに集約する。

'''
JOIN テーブルB ON テーブルA.列1 = テーブルB.列1
GROUP BY 集約する列
'''

まとめ

・Excelのデータ読み込みはpd.read_excel()、データ結合はpd.merge()、データ絞り込みはdf.query()、データ集約（グループ化）はdf.groupby()で行う。
・データベースのデータ読み込みはpd.read_sql()で行う。
・第一引数には、「SELECT 列 FROM テーブル」で読み込むテーブルと列を指定する。
・同様に、データ結合には「JOIN」、絞り込みには「WHERE」、集約には「GROUP BY」を使う。
・第二引数には、sqla.create_engine()__でまとめたデータベースの情報を指定する。

今回は以上です。最後まで読んでいただき、ありがとうございました。

　 Tweet
Qiitaで続きを読む

投稿日：2020-10-21T13:39:41+09:00

機械学習における前処理1　データ分析のプロセス

Aidemy　2020/10/29

はじめに

　こんにちは、んがょぺです！バリバリの文系ですが、AIの可能性に興味を持ったのがきっかけで、AI特化型スクール「Aidemy」に通い、勉強しています。ここで得られた知識を皆さんと共有したいと思い、Qiitaでまとめています。以前のまとめ記事も多くの方に読んでいただけてとても嬉しいです。ありがとうございます！
　今回は、機械学習の前処理の1つ目の投稿になります。どうぞよろしくお願いします。

＊本記事は「Aidemy」での学習内容を「自分の言葉で」まとめたものになります。表現の間違いや勘違いを含む可能性があります。ご了承ください。

今回学ぶこと
・データ分析の流れ

データ分析の流れ

・データ分析の流れ（プロセス）として、CRISP-DMやKDDといったものが提唱されている。

CRISP-DM

・CRISP-DMは、以下のようなプロセスになっている。
　①ビジネス理解:課題は何か、データ分析を使ってどうするかを明確にする。
　②データ理解:データの取得、データが分析に使える形かを理解する。
　③データ準備:データを④モデリングで使える形に整形する。
　④モデリング:データにモデルを適用し、分析する。
　⑤評価:分析結果が十分であるかを評価する。
　⑥適用:実際に課題や業務に分析結果を適用する。

・ただし、これらのプロセスは必ずしも一方通行のものではなく、必要に応じて戻ることもある。
・今回学ぶデータの前処理は、このプロセスの②③にあたる。

・図

KDD

・KDDは以下のようなプロセスになっている。
　①データ取得:課題や目標を定めてデータを取得する。
　②データ選択:取得したデータのうち、分析（データマイニング）に使うデータを選択する。
　③データクレンジング:欠損値や外れ値の削除などのデータクレンジングを行う。
　④データ変換:クレンジング済みデータの形式をデータマイニングに使える形式に変換する。
　⑤データマイニング:変換したデータに対して回帰や分類などを行って分析、学習を行う。
　⑥解釈・評価:データマイニングで得られた結果からパターンを解釈し、評価する。

・図

今回は以上です。最後まで読んでいただき、ありがとうございました。

　 Tweet
Qiitaで続きを読む

投稿日：2020-10-21T13:09:28+09:00

Pythonで(決定性有限)直積オートマトンを求める

概要

直積オートマトンを求めます。
pythonで決定性有限オートマトンを扱うのにはautomata-libを使用します。

pip install automata-lib

以下の記事を参考にしました。
Pythonで決定性有限オートマトンを実装して、3の倍数を判定する

環境

python 3.8
windows 10

恐らく3系ならなんでも動く、、と思う。

コード

directproduct.py

from automata.fa.dfa import DFA

SYMBOL_FORMAT = lambda s0, s1 : f'({s0}, {s1})'

def directproduct(dfa0:DFA, dfa1:DFA) -> DFA:
    new_input_symbols : set = dfa0.input_symbols | dfa1.input_symbols
    new_initial_state : str = SYMBOL_FORMAT(dfa0.initial_state, dfa1.initial_state)
    new_final_state : set = set([SYMBOL_FORMAT(f0, f1) for f0 in list(dfa0.final_states) for f1 in list(dfa1.final_states)])

    new_states : set = set()
    new_trans : dict = {}
    for s0 in list(dfa0.states):
        for s1 in list(dfa1.states):
            state = SYMBOL_FORMAT(s0, s1)
            new_states.add(state)
            new_trans[state] = {
                s : SYMBOL_FORMAT(dfa0.transitions[s0][s], dfa1.transitions[s1][s]) for s in list(new_input_symbols)
            }

    return DFA(
        states = new_states,
        input_symbols = new_input_symbols,
        transitions = new_trans,
        initial_state = new_initial_state,
        final_states = new_final_state
    )

def main():
    # 3の倍数を受理するオートマトン
    modulo_three = DFA(
        states = {'a', 'b', 'c'},
        input_symbols = {'0', '1'},
        transitions = {
            'a': {'0': 'a', '1': 'b'},
            'b': {'0': 'c', '1': 'a'},
            'c': {'0': 'b', '1': 'c'}
        },
        initial_state = 'a',
        final_states = {'a'}
    )
    # 2の倍数を受理するオートマトン
    modulo_two = DFA(
        states = {'d', 'e'},
        input_symbols = {'0', '1'},
        transitions = {
            'd' : {'0' : 'd', '1' : 'e'},
            'e' : {'0' : 'd', '1' : 'e'}
        },
        initial_state = 'd',
        final_states = {'d'}
    )
    # 2の倍数かつ3の倍数を受理する = 6の倍数を受理するオートマトン
    modulo_six = directproduct(modulo_three, modulo_two)

    print('Input number > ', end='')
    num : int = int(input())
    entry : str = format(num, 'b')
    if modulo_six.accepts_input(entry):
        print("Result: Accepted")
    else:
        print("Result: Rejected")

if __name__ == '__main__':
    main()

ちょこっと解説

SYMBOL_FORMAT関数は、状態の命名規則を定義しています。
directproduct関数が本記事の主役です。
定義に従って、各パラメータを計算するシンプルなものです。最速のアルゴリズムがあったら知りたいな。

main関数は、「3の倍数を受理するオートマトン」と「2の倍数を受理するオートマトン」から直積オートマトンである「6の倍数を受理するオートマトン」を求めて実行しています。

実行例

Input number > 18
Result: Accepted

18は6の倍数なので受理されます。

Input number > 15
Result: Rejected

15は6の倍数ではないので受理されません。

　 Tweet
Qiitaで続きを読む

投稿日：2020-10-21T13:02:34+09:00

PythonとRedisを使ってAlibabaクラウド上にゲームリーダーボードを構築

このガイドでは、PythonとRedisを使ってAlibaba Cloud上にゲームリーダーボードを構築していきます。

本ブログは英語版からの翻訳です。オリジナルはこちらからご確認いただけます。一部機械翻訳を使用しております。翻訳の間違いがありましたら、ご指摘いただけると幸いです。

目的

このデモの主なアイデアは、ゲームアプリケーションでリーダーボードを生成するためにデータベースを叩くのではなく、キャッシュ層（Redis）を使用することです。このアプローチは、リアルタイムの応答を必要とする大規模なデータベースに適しています。

前提条件

必須ではありませんが、Pythonの基本的な理解があることはプラスになります（サンプルコードはPythonです）。今回はRedisを活用しているので、Redisがどんなものなのかを知るためにも読んでおくと良いでしょう。

Alibaba CloudでのRedisクラスタの作成については、このガイドで別途ステップバイステップのコマンドを読んで、それに沿って進めていけばいいので、ここでは割愛します。設定は簡単でわかりやすいです。

実施の様子

1、Elastic Compute Service(ECS)とApsaraDB for Redisのセットアップを行います。このチュートリアルでは、OSとしてUbuntu 16.04を使用していますが、ソリューション自体はどのOSでも可能です。選択したOSによってコードが若干異なる場合があります。
2、ECSサーバにログインします。
ssh -i  root@
3、環境をインストールするための手順を実行します。
rm /usr/bin/python # Change python into version 3
ln -s /usr/bin/python3 /usr/bin/python
apt-get update # Update Ubuntu
export LC_ALL=C # Set Locale
apt-get install python3-pip # Install pip
pip install redis # Install python-redis
apt-get install apache2 # Install apache
mkdir /var/www/python # Set Environment
a2dismod mpm_event
a2enmod mpm_prefork cgi
4、etc/apache2/sites-enabled/000-default.conf を置き換えます。
-----
<VirtualHost *:80>
        DocumentRoot /var/www/python
        <Directory /var/www/python>
                Options +ExecCGI
                DirectoryIndex leaderboards.py
        </Directory>
        AddHandler cgi-script .py
        ErrorLog ${APACHE_LOG_DIR}/error.log
        CustomLog ${APACHE_LOG_DIR}/access.log combined
</VirtualHost>
-----
5、そのファイルを/var/www/leaderboards.pyに置き、8行目の設定を編集します（以下のソースコード）。
6、ファイル内のパーミッションを編集します。
chmod 755 /var/www/python/leaderboards.py
7、Apache を再起動します。
service apache2 restart
8、ウェブブラウザにアクセスして、パブリックIPアドレスを入力してください。それが動作しているかを見る必要があります。

コード説明

以下はPythonでのコードサンプルですが、これについてはさらに説明します。

コードの説明:
1、Redisに接続します（8行目）：
r = redis.StrictRedis(host='', port=6379, db=0, password='') 
これを正しく動作させるためには、ホスト名とパスワードを更新する必要があります。ApsaraDB for Redisの作成時に「接続アドレス」から取得できます。作成時に設定したパスワードでもあります。

2、リーダーボードにスコアを追加します(16行目)
r.zincrby(leaderboardName, gamer, random.randint(1,1000000)) 
LeaderboardName はリーダーボードの名前に設定するキー、gamer はゲーマーのユーザー名または ID、最後のパラメータはスコアを入れる場所です (この場合は乱数です)。

3、最高スコアのトップ10を取得します（19行目）。
r.zrange(leaderboardName, 0, 9, desc=True, withscores=True)
LeaderboardNameはリーダーボードの名前を設定するキーで、2番目のパラメータはどのランクから開始するか(0が開始)、3番目のパラメータはどこで停止するか(-1で最後まで表示する)です。値desc=Trueは、リーダーボードを降順にソートします(デフォルトではFalse)。

4、現在のプレイヤーの順位を取得します (30行目)。
r.zrevrank(leaderboardName, gamer)+1
LeaderboardNameはリーダーボードの名前に設定するキーで、gamerはゲーマーのユーザー名またはIDです。データベースではランクは1ではなく0から始まるので、1つ(+1)を追加する必要があります。
5、現在のプレイヤー（または誰でも）のスコアを取得します（34行目）。
r.zscore(leaderboardName, gamer) 
LeaderboardNameはリーダーボードの名前に設定するキーで、gamerはゲーマーのユーザー名またはIDです。

コードを実行する

以下は、ウェブサーバ上でコードを実行したときの期待されるレスポンスです。

結論

Redisはデータをインメモリで保存し、製品の成熟度によって毎秒数百万リクエストのパフォーマンスに達することができます。このため、このユースケースやその他のキャッシングニーズに最適なデータベースとなっています。

Alibaba Cloud上のRedisの詳細については、ApsaraDB for Redisのページを参照してください。

アリババクラウドは日本に２つのデータセンターを有し、世界で60を超えるアベラビリティーゾーンを有するアジア太平洋地域No.1(2019ガートナー)のクラウドインフラ事業者です。
アリババクラウドの詳細は、こちらからご覧ください。
アリババクラウドジャパン公式ページ

　 Tweet
Qiitaで続きを読む

	A	B	C	D
0	0	0	0	0
1	1	2	3	4
2	2	4	6	8
3	3	6	9	12
4	4	8	12	16
5	5	10	15	20
6	6	12	18	24
7	7	14	21	28
8	8	16	24	32
9	9	18	27	36

	A	B	C	D
0	0	0	0	0
1	1	2	3	4
2	2	4	6	8
3	3	6	9	12
4	4	8	12	16
5	5	10	15	20
6	6	12	18	24
7	7	14	21	28
8	8	16	24	32
9	9	18	27	36

	A	B	C	D
0	0	0	0	0
1	1	2	3	4
2	2	4	6	8
3	3	6	9	12
4	4	8	12	16
5	5	10	15	20
6	6	12	18	24
7	7	14	21	28
8	8	16	24	32
9	9	18	27	36