自分メモです。

AWSにはまった

sudo netstat -nap | grep 8888

sudo kill -9 [PID]

ssl つくり

sudo openssl req -x509 -nodes -days 365 -newkey rsa:1024 -keyout "cert.key" -out "cert.pe
m" -batch

sudo systemstl status

Jupyter Notebook Config

sudo vi /home/ubuntu/.jupyter/jupyter_notebook_config.py

Jupyter Notebook

sudo jupyter-notebook --allow-root

apache

sudo apt-get install apache2

2

df -h

sudo apt update

sudo apt install apt-transport-https
sudo apt install ca-certificates
sudo apt install software-properties-common
sudo apt install curl

$$
\def\bra#1{\mathinner{\left\langle{#1}\right|}}
\def\ket#1{\mathinner{\left|{#1}\right\rangle}}
\def\braket#1#2{\mathinner{\left\langle{#1}\middle|#2\right\rangle}}
$$

自作の量子計算シミュレータを使って、量子テレポーテーション、やってみたよ。

• 量子計算シミュレータ、つくってみた
• qlazy - Quantum Computer Simulator

はじめに

「量子テレポーテーション」のお勉強です。以下を参考にさせていただきました。

• 量子テレポーテーション - Wikipedia
• EMANの物理学:量子力学:量子テレポーテーション
• 吾輩は量子プログラミング言語である。名前はまだ無い。 Microsoftで生れ量子テレポーテーションした事だけは記憶している。
• 量子テレポーテーションを実際にやってみた話

量子テレポーテーションというのは、量子もつれを利用して、ある量子状態をそのまま他方に転送することを言います。「テレポーテーション」といっても物体が瞬間移動するわけではありませんし、光速を超えて情報伝達がなされるわけでもありません。

いま、送信者をAlice、受信者をBobと呼ぶことにします。まず、２つの「量子（例えば、光子）」をもつれさせて、一方をAlice、他方をBobに渡します。光子は電子スピンと同様、２つの状態の重ね合わせで表現できる「量子」なので、スピンのように、もつれさせることができます（と思ってください）。

Aliceは、もう一つ別の「量子」をもっていて、これを適当な重ね合わせ状態にします。この量子状態をBobに転送（テレポート）することを考えます。どうやるかというと、、、

Aliceは転送したい「量子」ともつれている片割れの「量子」の２つを合わせて「ベル測定」という特別な測定を行います。ベル測定というのは、２つの量子状態を一度に測定するもので、結果は４つの状態のいずれかになります。

AliceはBobに、この測定結果を通常の通信路で伝達します。Bobはそれ受け取り、その測定結果に応じて、自分がもっている、もつれている片割れの「量子」に、ある操作（量子ゲート）を適用します。そうすると、あーら不思議、Bobがもっている「量子」が、Aliceが転送したかった量子状態そのものにすり替わっているではありませんか！驚き！となります。

ざっくり、文書で書くと以上のようなことなのですが、なぜこんなことになるのか、次に、数式で確認してみましょう。

原理

３つの量子ビットを用意します。０番目をAliceがBobに送信したい量子ビットとします。１番目と２番目はもつれさせて、１番目をAliceに渡し、２番目をBobに渡すものとします。

０番目（AliceがBobに送信したいもの）を、とりあえず、

\ket{\psi} = \alpha \ket{0} + \beta \ket{1}

と書いておきます（後述するシミュレータではX軸周りとZ軸周りの回転ゲートで、適当な量子状態を作成して、$\alpha$と$\beta$を決めています）。

１番目と２番目は、以下のようにアダマールゲートと制御NOTゲートを通して、もつれさせます。

q1 |0> ----H--*---
q2 |0> -------CX--

そうすると、１番目と２番目の量子ビットに関して、以下の量子状態ができます。

\frac{1}{\sqrt{2}} (\ket{0}_{1}\ket{0}_{2} + \ket{1}_{1}\ket{1}_{2})

先程の０番目と合わせると、トータルで以下のような状態になります。

\frac{1}{\sqrt{2}} \ket{\psi}_{0} (\ket{0}_{1}\ket{0}_{2} + \ket{1}_{1}\ket{1}_{2}) \tag{1}

ここで、Aliceが「ベル測定」を行うのですが、その説明をします。いま、２量子系を考えているので、その測定は、数学的には４つの基底への射影演算をやることに相当します。ベル測定とは、以下の４つの基底への射影演算として定義されます。

\ket{\Phi^{+}} = \frac{1}{\sqrt{2}} (\ket{00} + \ket{11}) \\
\ket{\Phi^{-}} = \frac{1}{\sqrt{2}} (\ket{00} - \ket{11}) \\
\ket{\Psi^{+}} = \frac{1}{\sqrt{2}} (\ket{01} + \ket{10}) \\
\ket{\Psi^{-}} = \frac{1}{\sqrt{2}} (\ket{01} - \ket{10})

定義がわかったので、(1)式の０番目と１番目の量子ビットに対してベル測定をやってみます。射影演算は４つあります。各々、測定後の結果を列挙します。

• $\ket{\Phi^{+}}$への射影

\begin{align}
&\frac{1}{\sqrt{2}} \ket{\Phi^{+}}_{01} \bra{\Phi^{+}}_{01} \ket{\psi}_{0} (\ket{0}_{1}\ket{0}_{2} + \ket{1}_{1}\ket{1}_{2}) \\
&= \frac{1}{\sqrt{2}} \ket{\Phi^{+}}_{01} (\alpha \bra{0}_{1} + \beta\bra{1}_{1}) (\ket{0}_{1} \ket{0}_{2} + \ket{1}_{1} \ket{1}_{2}) \\
&= \frac{1}{\sqrt{2}} \ket{\Phi^{+}}_{12} (\alpha \ket{0}_{2} + \beta \ket{1}_{2}) \tag{2}
\end{align}\\

同様にして、他の３つも計算できます。

• $\ket{\Phi^{-}}$への射影

\begin{align}
&\frac{1}{\sqrt{2}} \ket{\Phi^{-}}_{01} \bra{\Phi^{-}}_{01} \ket{\psi}_{0} (\ket{0}_{1}\ket{0}_{2} + \ket{1}_{1}\ket{1}_{2}) \\
&= \frac{1}{\sqrt{2}} \ket{\Phi^{-}}_{01} (\alpha \ket{0}_{2} - \beta \ket{1}_{2}) \tag{3}
\end{align}

• $\ket{\Psi^{+}}$への射影

\begin{align}
&\frac{1}{\sqrt{2}} \ket{\Psi^{+}}_{01} \bra{\Psi^{+}}_{01} \ket{\psi}_{0} (\ket{0}_{1}\ket{0}_{2} + \ket{1}_{1}\ket{1}_{2}) \\
&= \frac{1}{\sqrt{2}} \ket{\Psi^{+}}_{01} (\beta \ket{0}_{2} + \alpha \ket{1}_{2}) \tag{4}
\end{align}

• $\ket{\Psi^{-}}$への射影

\begin{align}
&\frac{1}{\sqrt{2}} \ket{\Psi^{-}}_{01} \bra{\Psi^{-}}_{01} \ket{\psi}_{0} (\ket{0}_{1}\ket{0}_{2} + \ket{1}_{1}\ket{1}_{2}) \\
&= \frac{1}{\sqrt{2}} \ket{\psi^{-}}_{01} (-\beta \ket{0}_{2} + \alpha \ket{1}_{2}) \tag{5}
\end{align}

上の４つの式を眺めてみると、どうでしょう。なんとなく２番目の量子ビットの状態が、もともとAliceが設定した状態に似ていることがわかると思います（(2)式はそのものです）。２番目の量子ビットは、Bobに渡してあったものなのですが、Aliceが測定することで、遠隔地にいるBobが持っている量子に影響を及ぼすことができる、というのが量子もつれの不思議なところであり、量子テレポーテーションの肝でもあります。

さて、あとはBobがもっている２番目の量子ビットを操作して、Aliceの最初の０番目の状態に完全に一致させることを考えます。これは、Aliceからベル測定の結果が何だったかを教えてもらえれば、簡単で、

• $\ket{\Phi^{+}}$の場合

q2 --I-- # 何もしない

• $\ket{\Phi^{-}}$の場合

q2 --Z--

• $\ket{\Psi^{+}}$の場合

q2 --X--

• $\ket{\Psi^{-}}$の場合

q2 --X--Z--

という量子ゲートに通してあげれば、Aliceが転送したかった状態を２番目の量子ビットに完全再現することができる、というわけです。

シミュレータで実行（その１）

では、シミュレータで、以上のことが本当にできるか確認してみましょう。が、ちょっと待ってください。ベル測定ってシミュレータでどうやるんでしたっけ？という疑問がわいてきますよね。

実は、普通の測定（Z方向の測定）でベル測定できるようにするために、ちょっとした工夫が必要になります。具体的には、以下の回路を通してあげます。

q0 --*---H--M  -> b0
q1 --CX-----M  -> b1

この制御NOTゲートとアダマールゲートの組み合わせで、通常の基底からベル基底に変換することができるのです（ここで、b0,b1は最後の測定結果に応じて0/1の値が格納される古典レジスタです）。

ベル基底の４つの状態を上の回路に（頭の中で！？）通してみれば、すぐにわかります（以下、正規化の係数はいちいち書くのが面倒なので省略しました）。

\begin{align}
\ket{\Phi^{+}} &= \ket{00} + \ket{11} \\
&\rightarrow (\ket{0} + \ket{1}) \ket{0} + (\ket{0} - \ket{1}) \ket{0} = \ket{00} \\
\ket{\Phi^{-}} &= \ket{00} - \ket{11} \\
&\rightarrow (\ket{0} + \ket{1}) \ket{0} - (\ket{0} - \ket{1}) \ket{0} = \ket{10} \\
\ket{\Psi^{+}} &= \ket{01} + \ket{10} \\
&\rightarrow (\ket{0} + \ket{1}) \ket{1} + (\ket{0} - \ket{1}) \ket{1} = \ket{01} \\
\ket{\Psi^{-}} &= \ket{01} - \ket{10} \\
&\rightarrow (\ket{0} + \ket{1}) \ket{1} - (\ket{0} - \ket{1}) \ket{1} = \ket{11} \\
\end{align}

となって、ベル基底とb0,b1の値のセットとが対応づけられるようになります。つまり、b0,b1の観測をすることが、すなわちベル測定したことになる、という寸法です。

さて、ようやくシミュレーションの準備が整いました。
qlazyで実行します。測定結果に応じて、適用する量子回路を変えないといけないので、Linuxコマンドではちょっとやりにくいです。なので、Pythonでやってみます。コードは、以下の通りです。

from qlazypy import QState

qs = QState(3)

# prepare qubit (id=0) that Alice want to send to Bob by rotating around X,Z
qs.ry(0,phase=0.3).rz(0,phase=0.4)

# make entangled 2 qubits (id=1 for Alice, id=2 for Bob)
qs.h(1).cx(1,2)

# initial state (before teleportation)
print("== Alice (initial) ==")
qs.show(id=[0])
print("== Bob (initial) ==")
qs.show(id=[2])

# Alice execute Bell-measurement to her qubits 0,1
qs.cx(0,1).h(0)
b0 = qs.m(id=[0],shots=1).lst
b1 = qs.m(id=[1],shots=1).lst
print("== Bell measurement ==")
print("b0,b1 = ", b0,b1)

# Bob operate his qubit (id=2) according to the result
if b0 == 0 and b1 == 0:  # phi+
    pass
elif b0 == 0 and b1 == 1:  # psi+
    qs.x(2)
elif b0 == 1 and b1 == 0:  # psi-
    qs.z(2)
elif b0 == 1 and b1 == 1:  # phi-
    qs.x(2).z(2)

# final state (before teleportation)
print("== Alice (final) ==")
qs.show(id=[0])
print("== Bob (final) ==")
qs.show(id=[2])

qs.free()

これを実行すると、

== Alice (initial) ==
c[0] = +0.8910+0.0000*i : 0.7939 |+++++++++
c[1] = +0.1403+0.4318*i : 0.2061 |+++
== Bob (initial) ==
c[0] = +0.0000+0.0000*i : 0.0000 |
c[1] = +1.0000+0.0000*i : 1.0000 |+++++++++++
== Bell measurement ==
b0,b1 =  1 0
== Alice (final) ==
c[0] = +0.0000+0.0000*i : 0.0000 |
c[1] = +1.0000+0.0000*i : 1.0000 |+++++++++++
== Bob (final) ==
c[0] = +0.8910+0.0000*i : 0.7939 |+++++++++
c[1] = +0.1403+0.4318*i : 0.2061 |+++

となり、確かに、最初Aliceが持っていた量子状態が、きちんとBobの量子ビットに乗り移っていることがわかります。めでたしめでたし！

シミュレータで実行（その２）

ここで、説明を終了しても良いのですが、もうひとつの実行例を掲載しておきます。実は、ベル測定そのものを実装したので、その動作も確認してみました。mb()というメソッドでベル測定を実行できます。コードは以下の通りです。

from qlazypy import QState

BELL_PHI_PLUS  = 0
BELL_PHI_MINUS = 3
BELL_PSI_PLUS  = 1
BELL_PSI_MINUS = 2

qs = QState(3)

# prepare qubit (id=0) that Alice want to send to Bob by rotating around X,Z
qs.ry(0,phase=0.3).rz(0,phase=0.4)

# make entangled 2 qubits (id=1 for Alice, id=2 for Bob)
qs.h(1).cx(1,2)

# initial state (before teleportation)
print("== Alice (initial) ==")
qs.show(id=[0])
print("== Bob (initial) ==")
qs.show(id=[2])

# Alice execute Bell-measurement to her qubits 0,1
print("== Bell measurement ==")
result = qs.mb(id=[0,1],shots=1).lst

# Bob operate his qubit (id=2) according to the result
if result == BELL_PHI_PLUS:
    print("result: phi+")
elif result == BELL_PSI_PLUS:
    print("result: psi+")
    qs.x(2)
elif result == BELL_PSI_MINUS:
    print("result: psi-")
    qs.x(2).z(2)
elif result == BELL_PHI_MINUS:
    print("result: phi-")
    qs.z(2)

# final state (before teleportation)
print("== Alice (final) ==")
qs.show(id=[0])
print("== Bob (final) ==")
qs.show(id=[2])

qs.free()

これを実行すると、

== Alice (initial) ==
c[0] = +0.8910+0.0000*i : 0.7939 |+++++++++
c[1] = +0.1403+0.4318*i : 0.2061 |+++
== Bob (initial) ==
c[0] = +1.0000+0.0000*i : 1.0000 |+++++++++++
c[1] = +0.0000+0.0000*i : 0.0000 |
== Bell measurement ==
result: psi-
== Alice (final) ==
c[0] = +1.0000+0.0000*i : 1.0000 |+++++++++++
c[1] = +0.0000+0.0000*i : 0.0000 |
== Bob (final) ==
c[0] = +0.8910+0.0000*i : 0.7939 |+++++++++
c[1] = +0.1403+0.4318*i : 0.2061 |+++

となり、こちらも無事テレポーテーション成功です！

補足（2019.4.20追記）

qlazyには特定の量子ビットを指定してshowメソッドで量子状態を表示する機能があり、上の例ではそれを使っています。もちろんシミュレータならではの機能なのですが、だとしても、重ね合わさって、場合によってはもつれているトータルな状態に対して、そんなことできるの、とか、どうやってんの、という疑問があるかもしれないので、ちょっと説明しておきます。

内部的には、表示したい特定の量子ビット以外のビットを仮に測定し無理やり波束を収縮させます。結果得られた確率振幅の係数たちの中から、表示したい量子ビットの組み合わせに相当するノンゼロの係数をピックアップして表示します。ノンゼロの係数がなかったらゼロとします。最後に、測定前の状態に戻します。以上がやっている内容です。

表示したい量子ビットとそれ以外の量子ビットの世界がきっぱりとテンソル積で分解できる形になっていれば、こんな実装でいいのかなと。問題はもつれていてテンソル積の形になっていない場合です。この実装だとshowで表示するたびに結果が変わりますね。まー、これはこれで面白いし（もつれていたということがわかる）、こんな適当実装でも結構使える場合も多いかなと思っています。

ちなみに上の量子テレポーテーションの例で言うと、Aliceがベル測定した段階で、Bobの量子ビットのもつれはほどけるので、何回showしても結果は同じです（のはずです）。

以上

結論

• ext4のdir_indexのhashの衝突が原因のようである。
• 解決方法はいくつか見つかったが、良い解決法は見つからなかった。
• ディレクトリを分けることで対応することにした。

状況

同じフォルダに大量にファイルを生成している途中で(1505406ファイル目で発生)No space left on deviceのエラーが出ました。
調べたところ、ストレージの容量不足でもinode数の枯渇でもなさそうです。

環境

OS：Ubuntu 16.04.6 LTS
ファイルシステム：ext4

ストレージの残量とinode数の確認

まずはNo space left on deviceの原因の多くであるストレージの容量不足かどうか、inode数が枯渇しているかどうかを調べました。

ストレージの残量はdf、inodeはdf -iで調べられます。
結果はどちらも該当していませんでした。

原因はdir_indexのhashの衝突か？

よく調べるとext4: Mysterious “No space left on device”-errorsというサイトに行き着きました。

曰く、ext4はdir_indexのハッシュのメカニズムとしてhalf_md4を使っているが、half_md4はアルゴリズムはmd4を使うものの32ビット分しか使用しないため、十分なファイル数があった時は衝突する可能性が高いとのこと。

dir_indexはext3から導入され、その名の通りインデックスで検索を高速化させるためのものですが、上記サイトによると、インデックスに使うハッシュの衝突が原因の可能性がありそうです。

dir_indexの調査

まず、dir_indexが有効化されてるかを調べます。
dfを打ち、Filesystemの行にある調べたいファイルシステム名をメモします。
次に以下を打ち込みます。YOUR_FILE_SYSTEM_NAMEは先ほど調べたファイルシステム名を入力します。

dir_indexが有効かの確認

sudo tune2fs -l YOUR_FILE_SYSTEM_NAME| grep -o dir_index

実行後にdir_indexと出てくればdir_indexが有効化されていることになります。

対策

対策としては以下の三通りを思いつきました。
1. ハッシュのアルゴリズムを変更する
2. dir_indexを無効化する
3. ディレクトリを分ける

1はtune2fsのマニュアルを見るとhalf_md4の他にteaが選べるようです。
以下でhash_algを変更できますが、先程のext4: Mysterious “No space left on device”-errorsにはteaに変更してもハッシュの衝突は発生したと書いてあるのであまり期待しないほうが良さそうです。

hash_algの変更

sudo tune2fs -E "hash_alg=tea" YOUR_FILE_SYSTEM_NAME

そもそもパフォーマンスの面でhash_md4が選択されておりteaに変更するとパフォーマンスに影響が出るとも書いてあるので、その面でもしないほうが良さそうです。

2は以下でdir_indexの無効化ができますがインデックスを無効化するとパフォーマンスに大きく影響が出るのでこれもしないほうが良さそうです。

dir_indexの無効化

sudo tune2fs -O "^dir_index"

3はインデックスはディレクトリ毎に作成されるのでディレクトリを分ければ衝突は回避できますが、分けたディレクトリでまた衝突する可能性はあります。

1,2,3番の対策を考えた結果、迂闊にファイルシステムを変更してパフォーマンスに影響が出ては困るので今回は3のディレクトリを分けて対応することにしました。

何か良い解決方法はないものか...

調べてもこれ以上の解決方法は見つかりませんでした。
どなたか良い解決方法をご存知の方いらっしゃいましたらご教授いただけると幸いです。

使いたいときにいつも混乱するので、ここにまとめておく。
図の左側はインターネットに接続できるクライアント環境（Windowsパソコンなど）、右側はインターネット接続のないサーバセグメントを想定している。

共通オプション

• -f: バックグラウンドで動作
• -N: リモートでコマンドを実行しない
• -g: ポートフォワードで作ったトンネルを他の端末が使うことを許可する（本記事では利用していません）

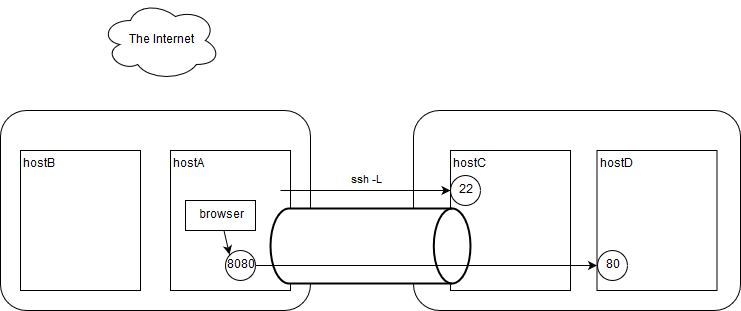
ローカルポートフォワード

用途

• sshクライアント端末から、sshサーバ側ネットワークにある特定サーバ特定ポートにアクセスしたい

コマンド

hostA$ ssh -fN -L 8080:hostD:80 userC@hostC

リモートポートフォワード

用途

• sshサーバ端末から、sshクライアント側ネットワークにある特定サーバ特定ポートにアクセスさせたい

コマンド

hostA$ ssh -fN -R 8080:hostB:80 userC@hostC

ダイナミックポートフォワード

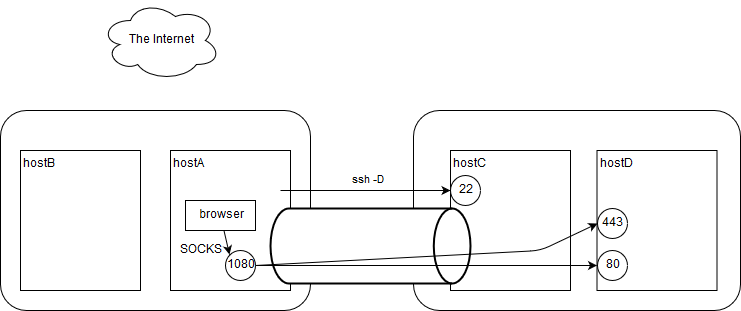
用途

• sshクライアント端末から、sshサーバ側ネットワークにある、あらゆるサーバにアクセスしたい

コマンド

hostA$ ssh -fN -D 1080 userC@hostC

# hostAのブラウザにlocalhost:1080をSOCKSプロキシとする設定を投入する

リバースダイナミックポートフォワード

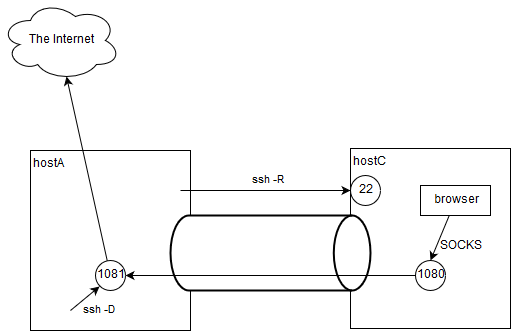
用途

• sshサーバ端末から、sshクライアント側ネットワークにある、あらゆるサーバにアクセスさせたい（特にインターネット）

コマンド(パターン1)

hostA$ ssh -fN -D 1081 userA@localhost  # hostAの中にSOCKSプロキシを準備
hostA$ ssh -fN -R 1080:localhost:1081 userC@hostC

# hostCのブラウザにlocalhost:1080をSOCKSプロキシとする設定を投入する

コマンド(パターン2)

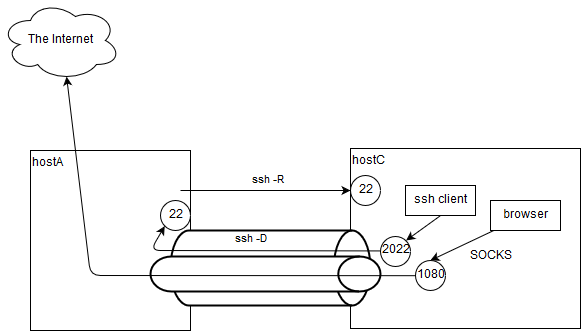
hostA$ ssh -fN -R 2022:localhost:22 userC@hostC
hostC$ ssh -fN -D 1080 -p 2022 userA@localhost   # hostCでの実行に注意

番外編

SOCKSプロキシの設定ができないツールでもSOCKSを使いたい

ダイナミックポートフォワードやリバースダイナミックポートフォワードを利用する際、
ブラウザであればSOCKSプロキシ設定が簡単に可能だが、apt,yumコマンド、自作ツールなどでの対応は難しかったりする。

しかし、proxychains を使うことで、通信を横取りしてSOCKSプロキシを通すことができる。（LD_PRELOADを使い、通信関連APIを上書きしているようだ）

$(HOME)/.proxychains/proxychains.conf

[ProxyList]
# SSH reverse proxy
socks5  127.0.0.1 1080

hostC$ proxychains telnet google.com 80
hostC# proxychains yum update
hostC# proxychains apt-get update

はじめに

Windowsユーザの場合、IPアドレスから同じLAN内のPCの名前(NetBIOS名)を取得することができました、ではMacOSやLinuxから同じことはできないのでしょうか。
というのが発端です

比較してみよう

• WindowsでIPからホスト名(NetBIOS名)を引く場合

nbtstat -A "IPアドレス"

例 : Desktop-Main001 というPCが見つかりました

>nbtstat -A 192.168.1.15

ローカル エリア接続:
ノード IP アドレス: [127.0.0.1] スコープ ID: []

           NetBIOS リモート コンピューター ネーム テーブル

       名前               種類         状態
    ---------------------------------------------
    Desktop-Main001      <00>  一意        登録済
    MAC アドレス = 00-00-00-00-00-00

• MacOSX/LinuxでIPからホスト名(NetBIOS名)を引く場合

実はSambaUtilsで調べることができます

smbutil -v status -ae "IPアドレス"

例 : Desktop-Main001 というPCが見つかりました

$ smbutil -v status -ae 192.168.1.15
Using IP address of 192.168.1.15: 192.168.1.15
NetBIOS Name                     Number  Type    Description
Desktop-Main001        　　　     0x00    UNIQUE  [Workstation Service]

最後に

これで、特定のIPを使ってる機材の名前がわからなくなった時に調べることができますね
参考までに

はじめに

LinuxのCGIでフォアグラウンドジョブとバックグランドジョブと、ジョブを切り替えて作業をする方法についてまとめてみました。

環境

Ubuntu 16.04.6 LTS

内容

まずは、Rubyで作成してプログラム（ジョブ）を普通にフォアグランドで実行します。

./test.rb

実行中のプログラム（ジョブ）を停止する場合は、Ctrl + z

ジョブが停止している事の確認を行います。

jobs
[1]+  停止                  ./test.rb

ジョブ番号と一緒にプロセス番号も表示したい場合は、オプションを指定します。21407がプロセスIDになります。

jobs -l
[1]+ 21407 停止                  ./test.rb

ちなみにだが、プロセスIDのみを表示する場合。

ps -a
  PID TTY          TIME CMD
22625 pts/8    00:00:28 ruby
22858 pts/8    00:00:00 ps

停止中のジョブをフォアグランドで再開する場合は、ジョブ番号を指定して再開します。[1]がジョブ番号になります。ちなみに、fg 1だけでも動きます。

fg %1

実行中のジョブを強制的に終了する場合はCtrl + c。ただし、余程の事情がない限り、あまりしない方がいいと思われる。

停止中のジョブをバックグラウンドで再開する場合。

bg %1

バックグラウンドでジョブが動いている状態で、jobsを打つと、確かに実行中である事が確認できます。ジョブの後ろに&がついている事が、バックグラウンドで動いている事の印になります。

jobs
[1]+  実行中               ./test.rb &

&をつけて、最初からバックグラウンドで動かす事もできます。

./test.rb &

バックグラウンドで動いているジョブを一時停止したい場合は、fg %1でフォアグランドにもってきた後に、Ctrl + zする事になります。

バックグラウンドで動いていようと、フォアグランドで動いていようと関係なく、実行中のジョブを強制終了する場合、Ctrl + c以外に、ジョブ番号を指定して終了する事もできます。

kill %1

この後、jobsを打つと、終了した事が表示されます。

jobs
[1]+  Terminated              ./test.rb

killで強制終了する場合は、ジョブ番号を指定する以外に、プロセスIDを指定して強制終了させる事もできます。ジョブ番号の時は%を指定したが、プロセスIDの場合は付けない事になります。21407はプロセスIDです。

kill 21407

ちなみにですが、バックグランドで動いているジョブに対し、フォアグランドでコマンドを打ちたい場合は、Enterを押すと、コマンドプロンプトが表示されます。

最後にだが、今、画面で動いているジョブが、フォアグランドなのか、バックグランドなのか確認したい場合は、Enterを押す事になる（と思われます）。Enterを押して、コマンドプロンプトが表示されたら、バックだし、何も反応がなければ、フォアという判断しかしようがないと（思われる）。

はじめに

レンタルサーバーや会社が管理しているサーバーでは、自分のアカウントにsudo権限が与えられておらず、apt-getやyumなどで自由にアプリケーションをインストールできない場合が多い。

とはいっても、必須なアプリケーションはシステム自体にインストールされているため実際に困ることは多くないが、「gccのバージョンが古い」などの致命的な問題があったりなかったりラジバンダリ・・・（zshとか、Pythonの一部のライブラリとかね）

そこで、「ローカル環境に無理やり最新版のgccをインストールしてしまおう！」と思い立ち、いろいろ調べてやってみた結果をまとめました。

gccをインストールする際の注意点

gccはかなり容量の大きいアプリケーションです（確か４Gくらい）。そのため以下のことに気を付けましょう

• インストール先の空き容量
  • 容量を検討してディスクを決めましょう
• インストール時間（makeにじかんがかかるがかかる）
  • tmuxとかを使っておくと安心

gccのインストール方法

以下が実際に実行したコマンドになります。なお、各種ソースは2019年4月現在での最新のものになります。

# 適当なディレクトリへ移っておく（ご自由に）
cd ~/TMP

# gccソースのDLと解凍
wget http://ftp.tsukuba.wide.ad.jp/software/gcc/releases/gcc-8.3.0/gcc-8.3.0.tar.gz
tar -zxvf gcc-8.3.0.tar.gz
# gccディレクトリへ移動
cd gcc-8.3.0


#依存関係のあるパッケージをgccのディレクトリへ入れておく
# gmp
wget https://gmplib.org/download/gmp/gmp-6.1.2.tar.bz2
tar xjf ./gmp-6.1.2.tar.bz2
mv gmp-6.1.2 gmp

# mpfr
wget https://www.mpfr.org/mpfr-current/mpfr-4.0.2.tar.bz2
tar xjf ./mpfr-4.0.2.tar.bz2
mv mpfr-4.0.2 mpfr

# mpc
wget http://ftp.gnu.org/gnu/mpc/mpc-1.1.0.tar.gz
tar -zxvf mpc-1.1.0.tar.gz
mv mpc-1.1.0 mpc


# buildとinstall
mkdir build
cd build

# configureやmakeをするディレクトリへLIBRARY_PATHを通しておく
unset LIBRARY_PATH

# 環境によってオプションは適宜変更すること（私の環境では以下の通り）
../configure --prefix=$HOME/local --enable-languages=c,c++ --disable-multilib
make
makefile

これでOKです。エラーが出た場合は、まずconfigureのオプションから確認するとよいでしょう。

また、インストールしたディレクトリにパスを通すのを忘れないようにしましょう。

参考

GCC 4.8.2をビルドしてホームディレクトリにインストール