- 投稿日:2019-03-30T23:52:36+09:00
SageMaker を ローカルPC に構築する
あまり見かけないのですが、SageMakerのライブラリは GitHub に公開されているので、ローカルに構築可能です。
SageMaker は無料枠が無いので、お金をかけたくない個人ユーザーは活用すると良いと思います。
リポジトリ
The SageMaker Python SDK is built to PyPI and can be installed with pip as follows:
pip install sagemaker
You can install from source by cloning this repository >and running a pip install command in the root directory of the repository:
git clone https://github.com/aws/sagemaker-python-sdk.git
cd sagemaker-python-sdk
pip install .Amazon SageMaker Examples - SageMakerのサンプルソース集
使い方
Anaconda をインストールして、Jupyter Notebook や Jupyter lab と一緒に使いましょう。
ただ、conda skeleton でビルドしようとして上手くいかなかったので、公式の手順の通りに pip コマンドで入れてしまいました。。。
併せて、awscli もインストールすると使い方が広がります。
- 投稿日:2019-03-30T23:35:15+09:00
脳死で覚えるDjango入門
前書き
全てのプログラマーは写経から始まる。 by俺
良質な写経元を提供するためにあります。
無駄のないコードと無駄のない説明を用意したつもりです。
Djangoを忘れかけた時に立ち返られる原点となれば幸いです。
実行環境
- python (3.6.8)
- Django (2.1.7)
すること
Webアプリ制作練習の王道、Todoアプリを作ります。(データベースにはMySQLを使います。)
(1) install
pipとか意味わかんないって人は知りません。
・django
$ pip install django・MySQL
mac以外の人は自分で調べてください。(ごめん)$ brew install mysql $ pip install pymysql(2) プロジェクトの生成
自分で名前を決めるところは<>で表記します。
$ django-admin startproject <project_name>今回では、
$ django-admin startproject todo_projectとした。
(注)
<project_name>にハイフンは使えません。(3) 確認
$ python manage.py runserverロケットが出てきましたか?
(4) アプリの作成
Djangoでは、プロジェクトの中にアプリを作るという考え方を採用している。
python manage.py startapp <app_name>今回では、
python manage.py startapp todoとした。
(5) アプリの登録
Djangoでは、アプリをプロジェクトに登録する必要がある。
<project_name>/<project_name>/settings.pyにINSTALLED_APPSというリストがある。そこに
todo.apps.TodoConfigを追加する。settings.pyINSTALLED_APPS = [ 'todo.apps.TodoConfig', 'django.contrib.admin', 'django.contrib.auth', 'django.contrib.contenttypes', 'django.contrib.sessions', 'django.contrib.messages', 'django.contrib.staticfiles', ](6) index.htmlを表示する。
ローカルホスト名というURLを叩くとindex.htmlが表示されるようにする。(
ローカルホスト名ってのはhttp://127.0.0.1:8000/みたいなやつです。サーバーを立ち上げたときにターミナルに記述されているはずです。)そのためには以下の手順を踏む。
1. index.htmlを作る
2. viewsを設定
2. アプリのルーティングを設定
3. プロジェクトのルーティングを設定1. index.htmlを作る
<project_name>/<app_name>/にtemplatesというフォルダを作り、その中に'todo'というフォルダを作り、その中にindex.htmlというファイルを作る。今回では、
- todo_project
- todo_project
- db.sqlite3
- manage.py
- todo
- 色々
- temlates / todo / index.html ←こいつ
こんな感じになる。
中には適当に
index.htmlHelloとか書いておいてください。
2. viewsを設定
railsでいうcontrollerの部分。
ルーティングで呼び出すための関数を定義しておく。
<project_name>/<app_name>/views.pyを下のように編集する。views.pyfrom django.shortcuts import render # Create your views here. def index(request): return render(request, 'todo/index.html')3. アプリのルーティングを設定
<project_name>/<app_name>の中にurls.pyを作成する。今回では、
- todo_project
- todo_project
- db.sqlite3
- manage.py
- todo
- 色々
- urls.py ←こいつ
それを下のように編集する。
todo/urls.pyfrom django.urls import path from . import views urlpatterns = [ path('', views.index, name='index') ]一見、これで
ローカルホスト名のURLを叩けばviewsの中のindex関数を実行し、index.htmlを表示してくれそう...でも、Djangoではプロジェクトのルーティングを設定する必要がある。
3.プロジェクトのルーティングを設定
<project_name>/<project_name>の中にurls.pyが既に存在している。今回では、
- todo_project
- todo_project
- 色々
- urls.py ←こいつ
- db.sqlite3
- manage.py
- todo
それを下のように編集する。
todo_project/urls.py"""todo_project URL Configuration The `urlpatterns` list routes URLs to views. For more information please see: https://docs.djangoproject.com/en/2.1/topics/http/urls/ Examples: Function views 1. Add an import: from my_app import views 2. Add a URL to urlpatterns: path('', views.home, name='home') Class-based views 1. Add an import: from other_app.views import Home 2. Add a URL to urlpatterns: path('', Home.as_view(), name='home') Including another URLconf 1. Import the include() function: from django.urls import include, path 2. Add a URL to urlpatterns: path('blog/', include('blog.urls')) """ from django.contrib import admin from django.urls import path, include urlpatterns = [ path('admin/', admin.site.urls), path('', include('todo.urls')) ]これで、サーバーを立ち上げるとHelloと出力されるはずです。
(7) データベースの設定
mysqlを立ち上げる。
$ mysql -u rootデータベースを作る。
create database <database_name>;今回は、
create database mydb;とした。
次にDjangoに設定をする必要がある。
<project_name>/<project_name>/settings.pyのDATABASESの部分を下のように編集する。settings.py# Database # https://docs.djangoproject.com/en/2.1/ref/settings/#databases import pymysql pymysql.install_as_MySQLdb() DATABASES = { 'default': { 'ENGINE': 'django.db.backends.mysql', 'NAME': 'mydb', 'USER': 'root', 'PASSWORD': '', 'HOST': '', 'PORT': '' } }(8) モデルの作成
ここからはTodoアプリの制作に入りますので、ディレクトリの説明の時、
<project_name>という抽象的な言い方はせず、todo_projectと書いていきます。
todo_project/todo/models.pyを下のように編集する。models.pyfrom django.db import models # Create your models here. class Post(models.Model): body = models.CharField(max_length=200)(9) マイグレーションファイルの作成
$ python manage.py makemigrations <app_name>今回では、
<app_name>はtodoなので、$ python manage.py makemigrations todoとなる。
すると、
todo_project/todo/migrationsに0001_initial.pyが作成される。そのファイルには先ほど定義したPostモデルをデータベースに作成するコードが書かれている。(10) マーグレーションファイルの実行
$ python manage.py migrate(11) 管理ページ
Djangoには超絶便利な管理ページが用意されている。
管理画面から先ほど作成したデータベースを確認します。
$ python manage.py createsuperuserこのコマンドを実行すると、いくつかの質問が与えられる。
usernameやpasswordを自分で登録しましょう。ローカルサーバーを立ち上げ、
$ python manage.py runserver
ローカルホスト名/adminというURLを打ち込みましょう。すると、
このように、管理ページが表示されます。
先ほど入力した
usernameとpasswordを入力しましょう。すると、
このような管理画面が表示されます。
この画面からデータベースのデータを見たり、追加したりすることができます。
まだ今の状態では、管理画面から先ほどのPostモデルを見ることができません。
見られるようにするために、
todo_project/todo/admin.pyを下のように編集します。admin.pyfrom django.contrib import admin from .models import Post # Register your models here. admin.site.register(Post)これでPostモデルも見られるようになったはずです。
(12) ルーティングの実装
下表のようなルーティングを実装します。
メソッド パス名 説明 GET / Todoリスト一覧表示 POST /create Todo追加 POST / <int:id>/deleteTodos削除
todo_project/todo/urls.pyを下のように編集する。urls.pyfrom django.urls import path from . import views urlpatterns = [ path('', views.index, name='index') path('create', views.create, name='create'), path('<int:id>/delete', views.delete, name='delete') ]
views.pyにcreate関数やdelete関数はまだ未定義ですので、お使いのエディタさんがおこおこするかもしれません。(13) Formクラスを実装
todo_project/todoにforms.pyを作成し、下のように編集しましょう。forms.pyfrom django import forms from .models import Post class PostForm(forms.ModelForm): class Meta: model = Post fields = ('body', )(14) viewsを実装
todo_project/todo/views.pyを下のように編集しましょう。views.pyfrom django.shortcuts import render, get_object_or_404 from django.http import HttpResponse, HttpResponseRedirect from django.urls import reverse from .models import Post from .forms import PostForm # Create your views here. def index(request): posts = Post.objects.all() form = PostForm() context = {'posts': posts, 'form': form} return render(request, 'todo/index.html', context) def create(request): form = PostForm(request.POST) form.save(commit=True) return HttpResponseRedirect(reverse('index')) def delete(request, id=None): post = get_object_or_404(Post, pk=id) post.delete() return HttpResponseRedirect(reverse('index'))これで、ルーティングで呼び出される関数の実装が完了しました。また、index.htmlの中で、テンプレートシステムを使うことで、
contextなどの変数を扱うことができます。(15) base.htmlの作成と実装
index.htmlと同じディレクトリにbase.htmlを用意します。(
todo_project/todo/templates/todoの中です。)
base.htmlを下のように編集します。base.html{% load staticfiles %} <!DOCTYPE html> <html> <head> <title>Todo list</title> </head> <body> <div class="container"> {% block content %} {% endblock %} </div> </body> </html>(16) index.htmlの実装
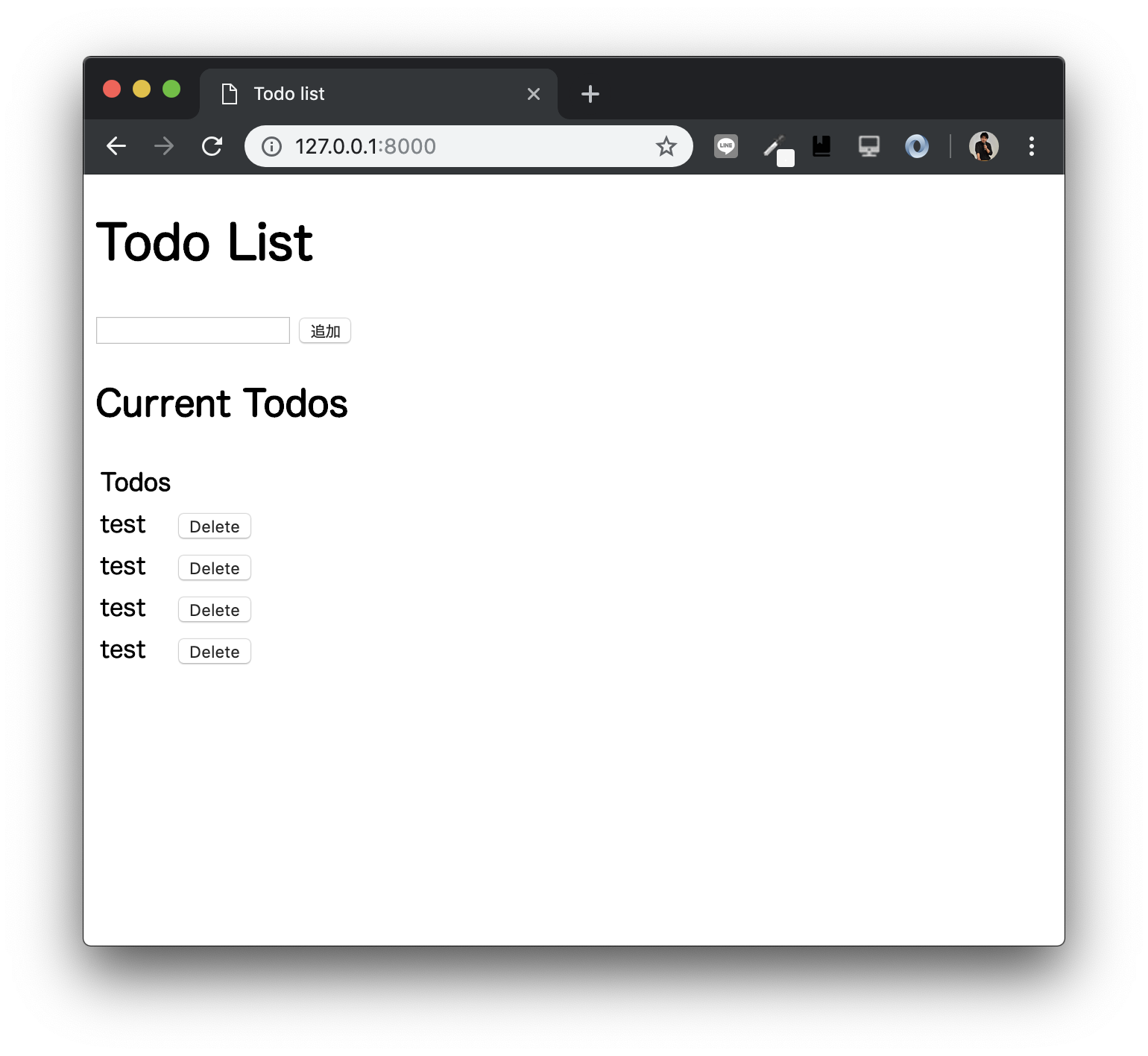
index.htmlを下のように編集する。index.html{% extends 'todo/base.html' %} {% block content %} <h1>Todo List</h1> <form action="{% url 'create' %}" method="POST"> {{ form.body }} <input type="submit" value="追加"> {% csrf_token %} </form> <h2>Current Todos</h2> <table> <thead> <th>Todos</th><th> </th> </thead> <tbody> {% for post in posts %} <tr> <td> <div> {{ post.body }} </div> </td> <td> <form action="{% url 'delete' post.id %}" method="post"> {% csrf_token %} <button>Delete</button> </form> </td> </tr> {% endfor %} </tbody> </table> {% endblock %}すると、
めでたくTodoリストアプリが完成します。
自己紹介
冒頭に書くと邪魔になるので最後にひっそりと自己紹介させてください。
名前 綿岡晃輝 職業 大学院生 (2019年4月から) 分野 機械学習, 深層学習, 音声処理 @Wataoka_Koki Twitterフォローしてね!
- 投稿日:2019-03-30T23:14:15+09:00
TensorFlowで嵐の顔を判別
はじめに
今回 TensorFlow を初めて使いました。TensorFlow で画像認識をやりたいのですが、公式のサンプルはあまりピンと来ず、よさそうな記事を見つけたので参考にしました。
参考にした記事
keras(tensorflow)で花の画像から名前を特定 - Qiita過去のiPhoneを使った機械学習の投稿
iPhoneで顔認識 - Qiita
機械学習でストリートファイター - Qiita
iPhoneと機械学習でフライドチキンの部位を分類する - QiitaTensorflowの準備
TensorFlowって何
(ウィキペディアより)
TensorFlow(テンソルフロー)とは、Googleが開発しオープンソースで公開している、機械学習に用いるためのソフトウェアライブラリである。具体的には、Python環境で下記を実行するとインストールできます。
pip install tensorflow画像判別に必要なもの
1. 訓練画像を集めます。
2. 訓練画像から学習モデルを作ります。
3. 入力画像を学習モデルに与えると判別されます。訓練画像の準備
imagesフォルダ以下に画像を集めます。フォルダー名がカテゴリー名(分類名)となります。150枚以上が望ましいのですが、私は50枚程で心が折れました。
今回は、相葉、松本、二宮、大野、櫻井の5人です。入力画像から「強いて言えば誰か」を判別します。使い方
- images フォルダ内に学習モデル用の訓練画像を用意します。
- inputs フォルダ内に予測したい入力画像を用意します。
- python model.py → mymodel.hdf5 が作成されます。
- python main.py → print で結果が出力されます。
ソースコード
以下を実行します。足りないものは pip install 行ってください。
model.py# -*- coding: utf-8 -*- import sys import os import gc import glob import numpy as np import pandas as pd import random, math import traceback from PIL import Image from keras.models import Sequential from keras.layers import Convolution2D, MaxPooling2D from keras.layers import Activation, Dropout, Flatten, Dense from keras.utils import np_utils class MyModel: def __init__(self): self.images_dir = './images' self.hdf5_file = './mymodel.hdf5' self.sub_dir = [name for name in os.listdir(self.images_dir) if name != ".DS_Store"] #------------------------------------ # 学習モデルの作成と保存 #------------------------------------ def save_model(self): try: # 画像読み込み train_data = [] for i, sdir in enumerate(self.sub_dir): print("->", sdir) files = [name for name in os.listdir(self.images_dir + "/" + sdir) if name != ".DS_Store"] for f in files: data = self.create_data_from_image(self.images_dir + '/' + sdir + '/' + f) train_data.append([data,i]) # シャッフル random.shuffle(train_data) X, Y = [],[] for data in train_data: X.append(data[0]) Y.append(data[1]) test_idx = math.floor(len(X) * 0.8) xy = (np.array(X[0:test_idx]), np.array(X[test_idx:]), np.array(Y[0:test_idx]), np.array(Y[test_idx:])) x_train, x_test, y_train, y_test = xy # 正規化 self.x_train = x_train.astype("float") / 256 self.x_test = x_test.astype("float") / 256 self.y_train = np_utils.to_categorical(y_train, len(self.sub_dir)) self.y_test = np_utils.to_categorical(y_test, len(self.sub_dir)) # 学習モデルの保存 model = self.create_model_from_shape(self.x_train.shape[1:]) model.fit(self.x_train, self.y_train, batch_size=32, nb_epoch=10) model.save_weights(self.hdf5_file) # テスト score = model.evaluate(self.x_test, self.y_test) print('loss=', score[0]) print('accuracy=', score[1]) except Exception as e: print('Exception:', traceback.format_exc(), e.args) #------------------------------------ # 入力画像の予測 #------------------------------------ def predict_from_dir(self, dir): X = [] files = [name for name in os.listdir(dir) if name != ".DS_Store"] for f in files: data = self.create_data_from_image(os.path.join(dir,f)) X.append(data) X = np.array(X) model = self.create_model_from_shape(X.shape[1:]) model.load_weights(self.hdf5_file) predictions = model.predict(X) return predictions # 画像ファイルからデータを作成 def create_data_from_image(self, file): img = Image.open(file) img = img.convert("RGB") img = img.resize((50,50)) data = np.asarray(img) return data # Shape から Model の作成 def create_model_from_shape(self, shape): # K=32, M=3, H=3 model = Sequential() model.add(Convolution2D(32, 3, 3, border_mode='same', input_shape=shape)) # K=64, M=3, H=3 調整 model.add(Activation('relu')) model.add(MaxPooling2D(pool_size=(2, 2))) model.add(Dropout(0.25)) model.add(Convolution2D(64, 3, 3, border_mode='same')) model.add(Activation('relu')) # K=64, M=3, H=3 調整 model.add(Convolution2D(64, 3, 3)) model.add(MaxPooling2D(pool_size=(2, 2))) model.add(Dropout(0.25)) model.add(Flatten()) model.add(Dense(512)) # biases model.add(Activation('relu')) model.add(Dropout(0.5)) model.add(Dense(len(self.sub_dir))) model.add(Activation('softmax')) model.compile(loss='categorical_crossentropy', optimizer='rmsprop', metrics=['accuracy']) return model if __name__ == "__main__": m = MyModel() m.save_model() gc.collect()main.py# -*- coding: utf-8 -*- import sys, os import numpy as np import pandas as pd from PIL import Image from model import MyModel images_dir = './images' inputs_dir = './inputs' categories = [name for name in os.listdir(images_dir) if name != ".DS_Store"] inputs = [name for name in os.listdir(inputs_dir) if name != ".DS_Store"] # 入力画像の予測値 predictions = MyModel().predict_from_dir(inputs_dir) # 結果出力 strcat = '' for cat in categories: strcat += cat.ljust(10,' ') print(" ", strcat) for i,input in enumerate(inputs): strpre = input.ljust(14, ' ') for pre in predictions[i]: strpre += str(round(pre,3)).ljust(10,' ') print(strpre)結果
Aiba Matsumoto Ninomiya Ohno Sakurai aiba.png 1.0 0.0 0.0 0.0 0.0 ninomiya.png 0.0 0.0 1.0 0.0 0.0 sakurai.png 0.0 0.0 0.0 0.0 1.0 koji1.png 0.0 0.0 0.0 1.0 0.0 koji2.png 0.0 0.0 0.0 1.0 0.0 koji3.png 0.0 0.0 0.0 1.0 0.0
入力画像 予測結果 Aiba Ninomiya Sakurai koji1.png
koji3.png
koji3.pngOhno う~ん、0と1しか出ないのですね。要勉強です。
まとめ
私(Koji4104)は大野くんに似ているという結果が出ました。私も違う景色を見てみたいです。
- 投稿日:2019-03-30T23:11:58+09:00
PyPIパッケージをCondaコマンドでインストールする方法
Conda を使っていてよく困ります。しかも以外とググっても出てこない。。。
こちらで紹介するのは、その解決方法の1つとして使える方法です。
PyPIのPythonモジュールからcondaパッケージを構築する
パッケージ作成$ conda skeleton pypi <PACKAGE> $ conda build <PACKAGE>この後にインストールします。
インストールconda install --use-local <PACKAGE>参考
Building conda packages with conda skeleton — conda build 3.17.8+139.g395ee91c.dirty documentation
(conda skeleton を使った condaパッケージの構築方法)
- 投稿日:2019-03-30T23:03:51+09:00
Windows に Python 開発環境を構築して簡単なスクレイピングツールをつくった話
概要
前々から、とあるサイトをスクレイピングをして、自分用データとして出力したいなぁという思いがあったのですが、いつもどおりニュースサイトを眺めていると、オライリーから「Python による Web スクレイピング」という本の第2版が発売されるという記事が目に入り、「特に言語は決めていなかったけど、こういう本が出るくらいだから Python はスクレイピングに向いているんだろうなぁ」と思って調べてみると、確かにライブラリが豊富なもようで、しかも「Python は何らかのかたちで触れてみたいなぁ」という気持ちもずっと持っていたので、これは好機とばかりに、Python で簡単なスクレイピングツールをつくろう、と思い立ったのがこの記事の話のきっかけです。(長い)
ちなみに、とあるサイトというのは「沼津まちあるきスタンプ」で、自分用に出力したいというのは「スタンプ設置店舗」の一覧です。このスタンプもいまやかなりの設置店舗数にのぼっており、計画的に行かないとロスが大きいということで、これまではスプレッドシートを使って手動で管理していたのですが、定期的に設置店舗が追加されるため、そのたびにメンテするのが億劫に感じたことで、スクレイピングツールをつくりたいと思っていました。
本記事では、スタンプ設置店舗一覧を CSV ファイルとして出力するのがゴールです。
環境
OS : Windows 10 Pro
Terminal : Windows PowerShell(管理者権限で起動)
Editor : Visual Studio Code準備
Python インストール
Chocolatey を使ってインストールしました。
chocolateychoco install pythonが、Python 日本語コミュニティが充実しており、インストーラを使った方法が丁寧に書かれています。通常はこちらを参照しながらの方が良いでしょう。
Python ライブラリをインストール
Python 用パッケージ管理用コマンドの pip を使ってインストールします。
PowerShell で Chocolatey を使って Python をインストールした場合、PowerShell を再起動しておかないと失敗するかもしれません。requests
HTTP クライアントです。
本記事では、沼津まちあるきスタンプの HTML を取得するために使います。pippip install requestsBeautifulSoup4
HTML 解析ライブラリです。
本記事では、取得した HTML の中から、スタンプ設置店舗情報の部分を抽出するために使います。pippip install beautifulsoup4公式ドキュメントを日本語に翻訳されている方がいらっしゃるようです。
VSCode 拡張機能をインストール
Python
VSCode で Python を扱うならたぶん必須。
Excel Viewer
CSV をカラムごとに整形して表示してくれます。
出力した CSV が意図した通りになっているかを見るために使います。スクレイピングツールをつくる
HTML の抽出
ライブラリ「requests」を使用して、沼津まちあるきスタンプの HTML を取得し、取得したデータからライブラリ「Beautifulsoup4」を使用して、スタンプ設置箇所の HTML を抽出します。
main.pyimport re import requests from bs4 import BeautifulSoup r = requests.get('https://www.llsunshine-numazu.jp/') html = r.content soup = BeautifulSoup(html, 'html.parser') shop_list = soup.find_all('dl', class_=re.compile('^shop_'))これで
shop_listにスタンプ設置箇所の HTML が入りました。とても簡単ですね。CSV に出力するための加工
設置店舗ごとの HTML はこのようになっています。
html<dl class="shop_yoshiko"> <dt class="shop1">ゲーマーズ沼津店</dt> <dd><strong>メンバー/津島善子</strong> 住所/沼津市添地町72青秀ビル1階<br> 営業時間/平日 11:00~20:00<br> 土日祝 10:00~20:00<br> 定休日/なし <a href="https://www.gamers.co.jp/shop/37445/" target="_blank" class="link_shop">店舗のホームページを見る</a></dd> </dl>この中から、
dtタグの値を「店名」、ddタグの値を「情報」、aタグの値を「リンク」として抽出します。(実際に自分用に使っているものはddタグの中をさらに細かく抽出していますが、コードが読みづらいので、この記事では理解の容易さのため、タグごとにしておきます)main.pyoutput_list = [] output_list.append(['店名', '情報', 'リンク']) # ヘッダ # スタンプ設置箇所ごとに処理 for shop in shop_list: name = shop.dt.text info = shop.dd.text.replace('\n', ' ').replace('\r', ' ') link = '' if shop.find('a') is not None: # a タグがない場合の対策 link = shop.find('a').get('href') output_list.append([name, info, link])CSV に出力
ここまでくれば、あとは出力するのみです。
main.pyimport csv # これは先頭に記述してください with open('shop_list.csv', 'w', encoding='UTF-8') as f: writer = csv.writer(f, lineterminator='\n') writer.writerows(output_list)これで、実行したディレクトリに
shop_list.csvが出力されているはずです。
Visual Studio Code の Excel Viewer で見てみましょう。まとめ
実際に Python を書いてみると、ライブラリの優秀さもあって拍子抜けするほど簡単でした。
また、Python 関連のドキュメントがことごとく日本語化されているのにも驚きました。
Python というと機械学習が取り沙汰されることが多いですが、簡単なスクリプトを組むのにも良さそうですね。
いろいろとハードルが低いので、これからプログラミングを始める人にもおすすめされる理由がわかりました。
次はもう少し高度なものに挑戦してみたいと思います。
- 投稿日:2019-03-30T22:32:10+09:00
最小作用の原理をTensorflowで確認
解いた式
ラグランジアン
$$
L = K - U
$$を時間積分した
$$
S = \int L \mathrm{d}t
$$を馬鹿正直に数値的に最小化したら、それっぽい軌跡が得られました。
2次元平面での重力ポテンシャルの公転運動です。お断り
今回も機械学習の話ではありません。
もうちょいくやしく
数値的に解くので、位置 $\vec{r}(t)$ は時間について離散的な関数となります。$N$ ステップの軌跡だと思うと、軌跡はベクトルみたいに書けます。
$$
x = \Bigl(\vec{r}(0), \vec{r}(\Delta t), \cdots, \vec{r}(N\Delta t) \Bigr)^\mathrm{T}
$$速度は単純な差分で書けます。
ある時間ステップ $i$ では、その前後の成分の差分で速度が計算できます。テイラー展開の1次までとる発想です。\vec{p}(i\Delta t) = \frac{1}{2\Delta t}\Bigl(\vec{r}\left((i + 1)\Delta t\right) - \vec{r}\left((i - 1)\Delta t\right)\Bigr)$p$は普通は運動量に使う記号ですが、速度に使っています。これを行列表記にしますと
v = \frac{1}{2\Delta t}\left( \begin{matrix} -2 & 2 & 0 & 0 & \cdots \\ -1 & 0 & 1 & 0 & \cdots \\ 0 & -1 & 0 & 1 & \cdots \\ & & \vdots & & \\ 0 & \cdots & -1 & 0 & 1 \\ 0 & \cdots & 0 & -2 & 2 \\ \end{matrix} \right) \left( \begin{matrix} \vec{r}(0) \\ \vec{r}(\Delta t) \\ \vec{r}(2\Delta t) \\ \vdots \\ \vec{r}((N-1)\Delta t) \\ \vec{r}(N\Delta t) \\ \end{matrix} \right)1番目と$N$ 番目の成分(つまり端、最初と最後)はとなりの成分との差とします。
差分を取る行列を $D = \frac{1}{2\Delta t}(\cdots) $としますと、v = Dxになります。
以降、$x$, $v$の$i$ステップ目の成分は添え字で表記することにします。
x_i = \vec{r}(i\Delta t)\\ v_i = \vec{p}(i\Delta t)また運動の途中で質量 $m$ は一定だとします。
位置と速度が定義されたので、各時間ステップでの運動エネルギーK_i = \frac{1}{2}mv_i^2とポテンシャル
U_i = G\frac{mM}{\left(x_i - \vec{R}\right)^2}が書けます。
ここで$G$は重力定数、$M$は公転中心の質量、$\vec{R}$は公転中心の座標とします。今回は$G=1$、$M=1$、$\vec{R}=0$としてしまいます。最後に、各時間ステップごとのラグランジアン
L_i = K_i - U_iを求めた後、それを全ステップにわたって合計した作用
S = \sum_i \Delta t L_iが計算できます。
さて、最初の位置 $x_1$ と最後の位置 $x_N$ を固定し、その間の $x_i$ をいろいろ動かして、$S$を最小化させてみることを考えます。
最小作用の原理
変分的に書くと、
\delta S = 0となり、自然界はこれを満たすような位相空間中の軌跡を取るというのが、解析力学の教えるところです。
ここから運動方程式などのハミルトン力学が派生していきます。つまりこの原理は普通は理論の礎になるもので、そのまま解く対象にはならないなという印象です。$S$ は普通は位置と共役運動量 $r$, $p$の関数なのでこのように変分的に書きますが、
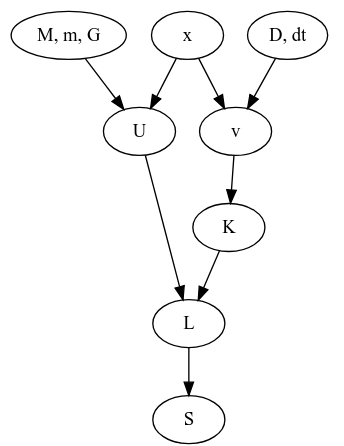
今回の話の依存関係を追ってみますと、というグラフになっています。ここで$M, m, G, D$は系が決まれば定数となるものです。となれば独立に変更できそうなのは$x$だけですね。そして$x$は2次元中の$N$個の点列だと思うと、$2(N-2)$ 個のパラメータがあるように見えます。すると、
x(軌跡) = \mathop{\rm arg~min}\limits_x \left[S\right]として、なんかオプティマイザがつかえそうですね。
Tensorflowの
trainerの出番です。実装開始
ライブラリ
import tensorflow as tf import numpy as np import matplotlib.pyplot as plt注意
ここでの
tensorflowのバージョンは1.xです。Eagerモードがデフォルトになる2.xでは実装を変えなければなりません。定数
G = 1.0 m = 1.0 Mc = 1.0 Mm = Mc*m fp = tf.float64 Nstep = 500 Ndim = 2 Time_all = 6.4 dt = Time_all/Nstep
Time_allは軌跡の始点と終点の間にかかった時間で、dtはそれを総ステップ数Nstepで割ったものになります。位置
r_init = tf.get_variable("position_init", shape=[1, Ndim], dtype=fp, trainable=False) r_fin = tf.get_variable("position_final", shape=[1, Ndim], dtype=fp, trainable=False) r_path = tf.get_variable("position_path", shape=[Nstep - 2, Ndim], dtype=fp) r = tf.concat([r_init, r_path, r_fin], 0)微分用行列
d_mat = np.eye(Nstep, k=1) d_mat = d_mat - d_mat.T d_mat[0, 0] = -1 d_mat[-1, -1] = 1 d_mat = tf.constant(d_mat/2)/dt上で出てきた式を頑張ってnumpy行列にし、最後に
tf.constantに渡しています。速度
dr = tf.matmul(d_mat, r)ここで、
rの形状は(N, 2)で、d_matは(N, N)なので、drは(N, 2)の形状のtf.Tensorです。運動エネルギー
vr_i = tf.reduce_sum(dr**2, axis=1) K_i = 0.5*vr_i*m各成分を2乗して足したらベクトルの長さの2乗ですね。
reduce_sumにaxisを渡しているので、dr**2の形状(N, 2)のうちの2のほうが総和の対象となります。そのためvr_iの形状は(N, )です。位置エネルギー
rr_i = tf.rsqrt(tf.reduce_sum(r**2, axis=1)) U_i = - G*Mm*rr_iラグランジアン
L_i = K_i - U_i作用
S = tf.reduce_sum(L_i)*dt
dtはなくてもいいんじゃないかな。最小化
optimizer = tf.train.AdamOptimizer(0.05) minimize = optimizer.minimize(S)困った時のAdam。結果のところにありますが、一応
GradientDescentも試しています。初期座標
代入演算
r_path_0 = tf.placeholder(fp, shape=[Nstep - 2, Ndim]) r_init_0 = tf.placeholder(fp, shape=[1, Ndim]) r_fin_0 = tf.placeholder(fp, shape=[1, Ndim]) init_assign = [tf.assign(r_path, r_path_0), tf.assign(r_init, r_init_0), tf.assign(r_fin, r_fin_0)] initializer = tf.global_variables_initializer()
rは最小化の対象化でtf.Variableです。これに所定の初期値を与える方法として、
tf.get_variablesのinitializerオプションにて、tf.constant(value=hogehoge)とする。- 受け皿の
tf.placeholderを用意し、tf.assignで上書きが考えられます。今回は
r_pathの定義が初期値を決める処理より先に来てしまったので前者が使いにくく、後者としました。実際の値
r1 = np.array([1.0, 0.0]) r2 = np.array([0.0, 1.0]) r3 = np.array([-1.0, 0.0]) r4 = np.array([0.0, -1.0]) r5 = np.array([1.0, 0.0]) rs = np.c_[r1, r2, r3, r4, r5].T ts = np.arange(5)/4 ts_interp = np.arange(Nstep)/(Nstep - 1) x_interp = np.interp(ts_interp, ts, rs[:, 0]) y_interp = np.interp(ts_interp, ts, rs[:, 1]) r0_np = np.c_[x_interp, y_interp].reshape(Nstep, Ndim)$(1,0), (0, 1), (-1, 0), (0, -1), (1, 0)$ の順に原点周りを1周し、その間を適当に補間した感じです。つまり原点周りに菱型に回る軌跡を初期状態としました。
rsがその通って欲しいチェックポイント5点を並べたもので、tsがその時刻です。ここでは開始を$t=0$, 終点を$t=1$にしました。注意:ここでの$t$はMD中での$t$とは異なり、ただのnp.interp用の横軸です。実行
可視化のmatplotlibとその初期化
fig = plt.figure() ax1 = fig.add_subplot(121) ax2 = fig.add_subplot(122) lines1, = ax1.plot(x_interp, y_interp) lines2, = ax2.plot(x_interp, y_interp) ax2.set_xlim((-1.5, 1.5)) ax2.set_ylim((-1.5, 1.5)) ax1.set_xlim((-1.5, 1.5)) ax1.set_ylim((-1.5, 1.5))
ax1は左半分で座標を、ax2は右半分で速度をプロットします。
が、ここでは速度の計算がまだなされていないので、座標をプロットしてお茶を濁します。セッション
with tf.Session() as sess: sess.run(initializer)初期値代入
sess.run(init_assign, feed_dict={r_path_0: r0_np[1:-1, :], r_init_0: r0_np[0:1, :], r_fin_0: r0_np[-1:, :]})最小化実行
step = 0 while True: sess.run(minimize) step += 1可視化
if step%2 == 0: r_t = sess.run(r) lines1.set_data(r_t[:, 0], r_t[:, 1]) v_t = sess.run(dr) lines2.set_data(v_t[:, 0], v_t[:, 1]) plt.pause(0.001)2イテレーションごとに、matplotlibの
ax2にセットされた値をset_dataで更新していきます。
たまに初期ウィンドウから大きく外れるので、set_xlimset_ylimで適宜調整します。
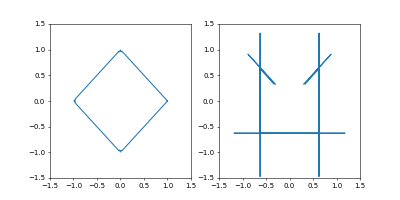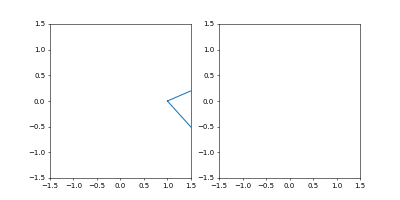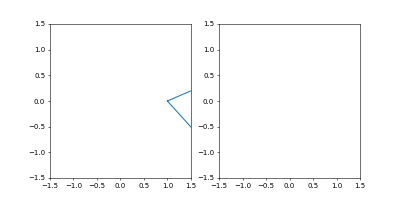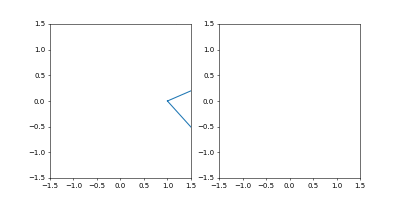
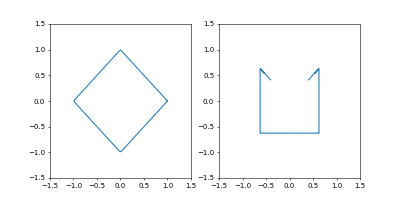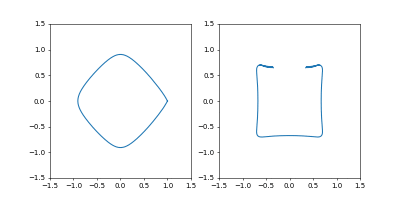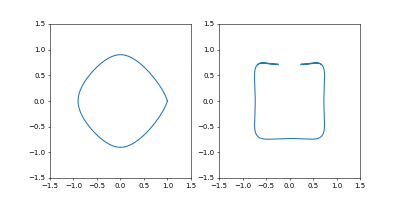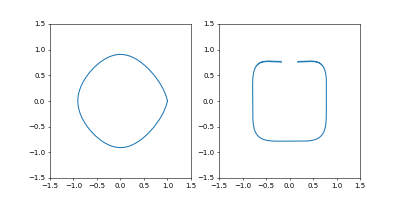
終わるときは、端末をアクティブにしてCtrl+Cです。結果
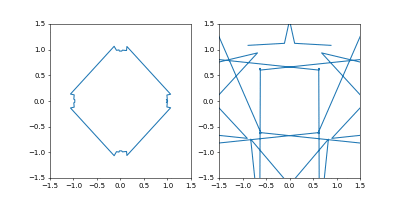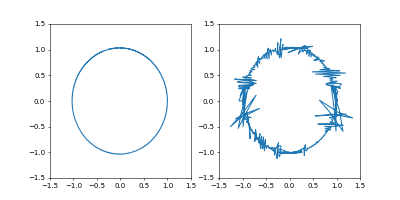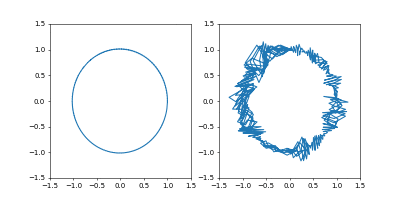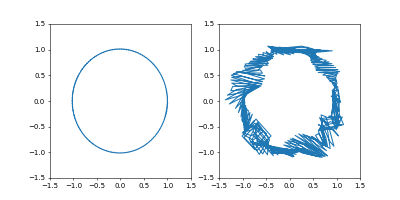
左が位置、右が速度の図です。
- Adam
学習率は $0.05$ です。
GIF動画1周が1000イテレーションです。
収束が近づいた時に暴れるのが難点ですね。真剣にやるなら、収束が進んだ段階で学習率を変えたり、オプティマイザを変えるなどの工夫がいることでしょう。
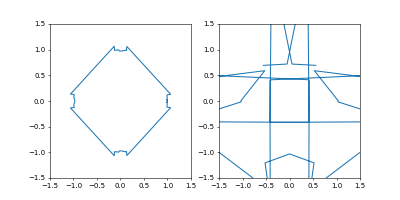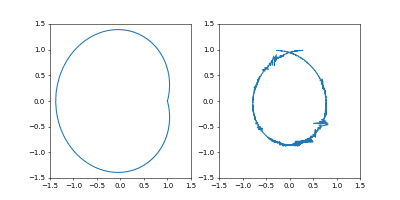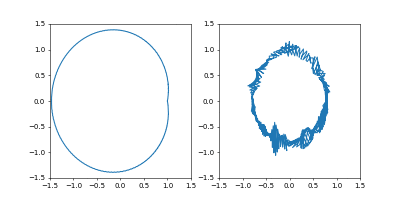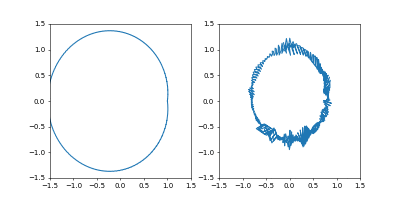
- GradientDecent
まず、Adamの時と同じ学習率 $0.05$ にすると発散しました。
動画1周が250イテレーションくらい。
学習率を $0.01$にすると発散はしませんでしたが、非常に収束が遅くなりました。
動画一周で1000イテレーション。フレームレートはAdamのものと同じです。
- おまけ
Adamで
Time_all = 10.0としてみました。1000イテレーションでは若干収束には届きませんでしたが、1周にかかる時間を増やしたのに合わせて先ほどの軌跡よりも原点から遠くに行って、速度も小さくなっているのがわかると思います。
余談
今回は経路の最初と最後を固定しました。
もしここも動くようにすると、運動エネルギーを小さく、位置エネルギーを大きくすれば作用も小さくなりますが、これは今回の系では無限遠で静止というのになってしまいそうですね。まあ動かないまでもある程度の束縛(一周する=最初と最後の位置が一緒である)とかを課したもとでの最小化とかも考えられますが、今回はこの辺にしておきます。
野望
経路積分
- 投稿日:2019-03-30T21:50:47+09:00
ウェブページURLのリダイレクト有無を一括確認するためのPythonスクリプト
リンク先ウェブページがいつの間にか無くなり、トップページなどにリダイレクトされていないかを一括チェックするためのPythonスクリプトを書きました。
はじめに
外部公開されているウェブページを一括確認したいだけであれば、「Bulk URL HTTP Status Code, Header & Redirect Checker | httpstatus.io」で一括チェックをして、結果をCSVダウンロードするだけで十分だと思います。アクセス元制限がされているイントラウェブページのリンク切れ確認や、cronなどで定期的に実行しておきたい場合はスクリプトで対応する意味があるかもしれません。
Pythonスクリプト
Python3でスクリプト作成しています。第一引数を渡したCSVファイルの1列目のURLを、requestsライブラリを利用したHTTP GETを行い、HTTP Status Codeと最終的なURLを取得し、ターミナルとCSVファイルに出力しています。DoSにならないように1件処理ごとに5秒間のsleepを入れています。
check.pyimport sys, requests, csv, time input_file = sys.argv[1] #リンク切れチェック関数 def missing_link_check(input_csv): with open(input_csv, 'r', newline='') as input_file: csv_reader = csv.reader(input_file, delimiter=',', quotechar='"') #アウトプットファイルはインプットファイル名の.csv直前に_outputを追加したものとする file_index = input_csv.find('.csv') output_csv = input_csv[:file_index] + '_output' + input_csv[file_index:] with open(output_csv, 'w', newline='') as output_file: csv_writer = csv.writer(output_file, delimiter=',', quotechar='"', quoting=csv.QUOTE_ALL) for row in csv_reader: check_url = row[0] try: r = requests.get(check_url) except Exception as e: print(e) else: #リダイレクト履歴がある場合は、HTTP Status Codeは一番最初のものを使用する if len(r.history) == 0: print(check_url + ',' + str(r.status_code) + ',' + r.url) csv_writer.writerow([check_url, r.status_code, r.url]) else: print(check_url + ',' + str(r.history[0].status_code) + ',' + r.url) csv_writer.writerow([check_url, r.history[0].status_code, r.url]) time.sleep(5) missing_link_check(input_file)インプットファイルは以下のような形式です。CSVファイルを想定していますが、1列目の値しか使わないので、URLだけ記述してカンマで区切って2列目以降を入れる必要はありません。今回はHTTP Status Codeごとの挙動がわかりやすいように、httpstat.usのURLを利用させていただきました。
input_file.csvhttps://httpstat.us/200 https://httpstat.us/201 https://httpstat.us/202 https://httpstat.us/203 https://httpstat.us/204 https://httpstat.us/205 https://httpstat.us/206 https://httpstat.us/300 https://httpstat.us/301 https://httpstat.us/302 〜以下略〜スクリプトを実行すると、以下のように「リクエストURL」「HTTP Status Code」「最終的に表示されたURL」が表示されます。HTTP Status Codeが300番台はPermanentとTemporaryの違いはありますが、リダイレクトされた結果「リクエストURL」と「最終的に表示されたURL」が異なることが分かります。「HTTP Status Code」も出力していますので、404でページが無くなったものも探すことができます。
なお、requestsライブラリをインストールしていない場合はインストールしておいてください(例「$ pip3 install requests」)。
スクリプトの実行$ python3 check.py input.csv https://httpstat.us/200,200,https://httpstat.us/200 https://httpstat.us/201,201,https://httpstat.us/201 https://httpstat.us/202,202,https://httpstat.us/202 https://httpstat.us/203,203,https://httpstat.us/203 https://httpstat.us/204,204,https://httpstat.us/204 https://httpstat.us/205,205,https://httpstat.us/205 https://httpstat.us/206,206,https://httpstat.us/206 https://httpstat.us/300,300,https://httpstat.us/300 https://httpstat.us/301,301,https://httpstat.us https://httpstat.us/302,302,https://httpstat.us 〜以下略〜結果は第一引数のファイル名の「.csv」の前に「_output」を付けたファイル名でCSV出力します。入力ファイル名が(hogehoge.csv)であることを決め打ちしていますので、他の拡張子を使いたい場合はスクリプト自体を修正してください。
input_output.csv$ cat input_output.csv "https://httpstat.us/200","200","https://httpstat.us/200" "https://httpstat.us/201","201","https://httpstat.us/201" "https://httpstat.us/202","202","https://httpstat.us/202" "https://httpstat.us/203","203","https://httpstat.us/203" "https://httpstat.us/204","204","https://httpstat.us/204" "https://httpstat.us/205","205","https://httpstat.us/205" "https://httpstat.us/206","206","https://httpstat.us/206" "https://httpstat.us/300","300","https://httpstat.us/300" "https://httpstat.us/301","301","https://httpstat.us" "https://httpstat.us/302","302","https://httpstat.us"参考ページ
- 投稿日:2019-03-30T19:06:38+09:00
t値とp値について
Qiita初投稿
- 投稿テストも兼ねて統計学の基礎中の基礎であるt値とp値についてまとめてみました。
- 自分は統計初心者で、まだまだ理解が及んでないとこも多々あります!もし認識違いあればコメント頂けると幸いです。
- 途中、説明を飛ばしてて雑な部分が多々ありますが、ご容赦ください。
- Pythonコードに関しても多少冗長なとこあるかもですがお許しください。
t分布について
t値、p値の意味について考える前にまず前提知識としてt分布の便利な使い方を統計初心者の自分の理解で簡潔にまとめるとズバリ
正規分布する母集団の母平均と母分散が未知である時、母平均を推定する問題に利用される。
だと認識しています。(あくまでも母集団の分布は正規分布である事が条件です。)なので、母平均の推定は勿論ですが、その検定にもt分布(t値)は使われます。
因みに、母分散未知の場合、母平均の推定を行う場合、代わりにサンプルの不偏分散を使って推定を行います。
t分布の例
ある正規母集団からサンプルサイズ $n$ を抽出した時の確率変数 $X$ の平均 $\overline{X}$ は自由度 $n-1$ のt分布に従う。
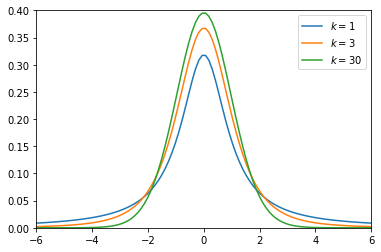
と書いても良く分からないと思うので、実際にt分布をプロットしてみようと思います。因みにt分布はその自由度によって、分布の様子が変わってきます。Pythonで確認してみます。
import numpy as np import matplotlib.pyplot as plt from scipy import stats %matplotlib inline # -6 から 6 の区間で100列の一次元配列を作成 x = np.linspace(-6, 6, 100) # 縦横1.0の図(箱)を用意 fig, ax = plt.subplots(1, 1) # 自由度(1, 3, 30)の3つのt分布をプロット deg_of_freedom = [1, 3, 30] for k in deg_of_freedom: ax.plot(x, stats.t.pdf(x, k), label=r'$k=%i$' % k) plt.xlim(-6, 6) plt.ylim(0, 0.4) plt.legend() plt.show()上記を見てわかる通り、自由度が大きくなるに連れて、分布がシャープになっています。
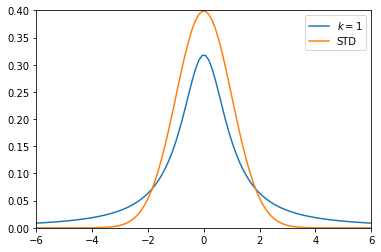
これはつまり、サンプルサイズ $n$ が大きいほど、サンプル平均の分布は元の母集団の平均値に寄ったシャープな分布をすると言えることが分かります。つまり、データ数が大きいほどより平均値の予測にブレが出なくなってくるとも言え、なんとなく直感的に分かりやすい結果になるかと思います。(統計検定では自由度が30以上のt分布は近似的に標準正規分布とみなす。って感じで解く問題が多いです。)ここで、自由度1のt分布と正規分布を重ねてみます。
# 縦横1.0の図(箱)を用意 fig, ax = plt.subplots(1, 1) # 自由度1のt分布をプロット ax.plot(x, stats.t.pdf(x, 1), label='$k=1$') # 平均0 標準偏差1の正規分布(標準正規分布)をプロット ax.plot(x, stats.norm.pdf(x, loc=0, scale=1), label='STD') plt.xlim(-6, 6) plt.ylim(0, 0.4) plt.legend() plt.show()上記の結果から、t分布は標準正規分布よりも、分布が広がっていることが分かります。
感覚的に考えても、母分散が既知の場合に、母平均推定に使われる標準正規分布より、母分散未知の場合に、母平均推定に使われるt分布の方が、その予測精度が落ちてしますのは合点がいくかと思います。t値について
ここで再び先ほどの例ですが
ある正規母集団からサンプルサイズ $n$ を抽出した時の確率変数 $X$ の平均 $\overline{X}$ は自由度 $n-1$ のt分布に従う。
と言った場合、その時の不偏分散を $s^2$ とすると、その分布のt値は以下の式で与えられます。
$$t = \frac{\overline{X} - \mu}{\frac{s}{\sqrt{n}}} ・・・①$$上の式をみてわかる通り、tの信頼区間を設定して、更に$\mu$ についてまとめると以下の良く見る式になって、母平均の区間推定ができます。
$$ \overline{X} - t\frac{s}{\sqrt{n}} \leq \mu \leq \overline{X} + t\frac{s}{\sqrt{n}} ・・・②$$
こんな簡単な計算で母平均を推測出来てしまうなんて、統計学おそるべしです。。。
この時の $t$ の値は自由度や、信頼区間に寄って大きく異なるため、求める精度との相談で決めていくことになります。p値について
上の推定では $\mu$ の値を予測することが目的でしたが、今度は逆に $\mu$ の値をある値と仮定して、その仮定が最もらしいか調べてみると言った処理を行います。これがいわゆる検定です。(厳密な表現ではないかも知れませんので悪しからず)
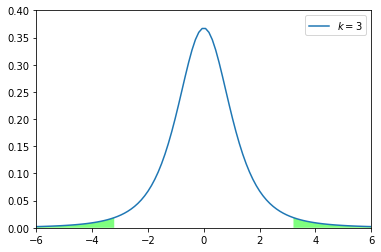
今、式①より、サンプル平均 $\overline{X}$、母平均 $\mu$(仮定した値)、サンプル数 $n$、不偏分散 $s^2$、自由度 $n-1$が定まっているので、後は信頼区間さえ決めてあげれば、自ずとt値は定まります。ここで、先ほどPythonで記述した自由度3のt分布をみた時に、以下の緑色部分が5%部分(滅多に起こらない)になります。
# 縦横1.0の図(箱)を用意 fig, ax = plt.subplots(1, 1) # y=0の関数を作成(後で範囲の塗り潰しに使う) y = 0 # 自由度1のt分布の両側95%点 t = stats.t.ppf(1-(1-0.95)/2, 3) # 自由度3のt分布をプロット ax.plot(x, stats.t.pdf(x, 3), label='$k=3$') # 範囲の塗り潰し ax.fill_between(x, stats.t.pdf(x, 3), y, where=x < -t, facecolor='lime', alpha=0.5) ax.fill_between(x, stats.t.pdf(x, 3), y, where=x > t, facecolor='lime', alpha=0.5) plt.xlim(-6, 6) plt.ylim(0, 0.4) plt.legend() plt.show()つまり、母平均をある値に仮定した時、取りうるt値は95%の確率で上図の白抜き部分 $-3.18\leq t \leq3.18$ に収まっていることが分かります。逆に出てきたサンプルサイズが予想より大きかったり、小さかったりするとそのt値は緑色の範囲内に入ってしまい、前提の仮定が崩れる(帰無仮説が棄却される)ことになります。
尚、この時に取りうる確率のことをp値と言います。
つまり上の例のように有意水準を5%とした際に、p値が5%以上であれば帰無仮説を棄却せず、逆に5%未満であれば帰無仮説を棄却し、対立仮説を採用することになります。
今回のブログで学んだこと
- t検定のおさらい
- matplotlibで指定したグラフの範囲を塗り潰せるようになった
- 投稿日:2019-03-30T18:51:50+09:00
株式会社いい生活のインターンを退職しました
株式会社いい生活の長期インターンを退職したので、退職ポエムを書きます。
期間
長期インターンの期間は12月末から3月いっぱいの3ヵ月くらい。1Weekサマーインターンにも参加してた。
参加経緯
Wantedlyでお金がもらえるサマーインターンを探してたら見つけた。
いい金額がもらえそうだったので飛びついたら通っちゃいました。
サマーインターン終了後に連絡したら、快く長期インターンも受け入れてもらえました。もちろん有給です。
本当にありがとうございます。作業内容
3ヵ月ほどいましたが、1月半くらいづつ2か所の部署で作業してました。
作業内容はこちらの要望に沿った形で用意してくれました。
- ダッシュボードの構築
- Redmineからのチケット収集プログラム
- Redashの環境構築
を行って部署のダッシュボードをつくって、データを可視化したりしてました。- 物件の売値推定
実際の物件データをもらえたので、それを使って物件がいくらで売れるか機械学習してました。感想
- おいしいご飯をごちそうになれる
- コードレビューは勉強になった
- インターン内容の自由度が高い
- Slackに社員の顔スタンプがある
- 家が遠かったのでリモートで参加できた
- 本当に助かりました
三か月ほどでしたが、とてもためになったインターンでした。早川さんがごはんおごってくれるらしいので、時々伺えたらと思っています。
- 投稿日:2019-03-30T17:36:49+09:00
Pythonで学ぶあたらしい統計学の教科書 - 統計学用語の理解 & 記述統計と推測統計
※こちらの記事は"Pythonで学ぶあたらしい統計学の教科書"に基づいて、統計学初学者が頭の整理とアウトプットを目的に掲載している記事です。本の内容のみならず、自分で調べた内容、自分のイメージにマッチした内容を追記している場合もあります。
※今回はまだまだPythonを使用しません。
そもそも統計学とは
データの適切な取り扱い方を探る方法論を体系化した学問であると言えます。
統計学の中でもジャンルとして、2つに大きく分別されます。
- 記述統計 ・・・ 既知の手持ちデータの整理・要約する
- 推測統計 ・・・ 未知のデータを推測する記述統計と推測統計の関係について、イメージ図がめちゃくちゃ分かりやすいのがあったので、下記画像見ればOK。
統計学の基礎用語
- 標本 ・・・ 手持ちの既知データ
- 母集団 ・・・ 未知のデータを含んだ、すべてのデータ
標本という母集団のごく一部のデータを用いて、母集団という全体について議論するということが推測統計の目的ということがこの段階でわかれば問題なし。
抽象化された標本を得るプロセス
用語
- 確率変数 ・・・ ある確率分布に従って変化する値
- 実現値 ・・・ 確率変数における具体的な値
- サンプリング ・・・ 母集団から標本を得ること、サンプリング = 標本抽出
- 単純ランダムサンプリング ・・・ 母集団から各要素がランダムでサンプリングする方法
- 確率分布 ・・・ 確率変数とそれに付与された確率との対応を表したもの
- 母集団分布 ・・・ 母集団が従う確率分布のこと
例 「小さな湖の中にいる魚を釣る」
話を簡潔にするために、下記の3つの前提条件を設定します。
- 母集団は、5匹の魚ですべて同じ種である。
- 5匹それぞれの大きさが2, 3, 4, 5, 6cmである。(小数点第1位を四捨五入)
- 釣った魚はすぐに湖の中にリリースする。この湖の中で魚を1匹釣り、3cmの魚を釣ったと仮定します。5匹の中から3cmの魚1匹を釣っているので、確率としては、1/5となります。
このときの確率をP(2.5≦体長<3.4)=1/5という表記をします。この式の意味は、体長が3cmの魚を釣れる確率は1/5であるという意味です。
体長は四捨五入するので、3cmの魚の場合は2.5cm以上、3.4cm以下の魚になります。
Pは、Probability(確率)の頭文字を表します。このときの3cmの魚は実現値です。
また、次の釣りで釣る魚の大きさはどの大きさか分かりませんが、変数xという大きさの魚になります。この変数xを確率変数です。この確率は、3cmの魚のみならず、他の魚を釣る場合も同じ確率となるので、下記のような確率分布となります。
P(1.5≦体長<2.4)=1/5
P(2.5≦体長<3.4)=1/5
P(3.5≦体長<4.4)=1/5
P(4.5≦体長<5.4)=1/5
P(5.5≦体長<6.4)=1/5あるデータが、ある確率分布と対応している時、「確率分布に従う」という表現をします。
上記の例では、「釣れる魚の体長は、{1/5, 1/5, 1/5, 1/5, 1/5}の確率分布に従う」という表現になります。母集団分布を通して、標本を得るプロセスを見直してみます。
① 以下の母集団から、単純ランダムサンプリングにより標本を1つ得る
1.5≦体長<2.4 : 1匹
2.5≦体長<3.4 : 1匹
3.5≦体長<4.4 : 1匹
4.5≦体長<5.4 : 1匹
5.5≦体長<6.4 : 1匹② 以下の確率分布に従う確率変数を1つ取得する
P(1.5≦体長<2.4)=1/5
P(2.5≦体長<3.4)=1/5
P(3.5≦体長<4.4)=1/5
P(4.5≦体長<5.4)=1/5
P(5.5≦体長<6.4)=1/5①と②を同じプロセスだとみなします。
①と②を同じだと見なすプロセスは、単純ランダムサンプリングで得たデータを基に、未知の母集団を推測する、ということです。
つまり、既知データから未知のデータを推測するという統計学のプロセスがここに詰まっているという私の理解です。これまでのプロセスをすべてまとめると下記のように表現できます。
母集団分布に従う確率変数として、3cmの魚というデータが実現値として得られたその他参考サイト
確率変数とは - 統計WEB
サンプリング方法の種類~データの取り方~ - Knowledge Makersコメント
今回用いた魚を釣るという例は、箱の中にある球を取り出すという事象で表現することも可能ですね。
私は球を取り出すモデルは、中学・高校でも確率の問題でよく題材にされるので、イメージは行いやすい印象でした。
- 投稿日:2019-03-30T17:36:49+09:00
統計学1 - 統計学用語の理解 & 記述統計と推測統計
※こちらの記事は"Pythonで学ぶあたらしい統計学の教科書"に基づいて、統計学初学者が頭の整理とアウトプットを目的に掲載している記事です。本の内容のみならず、自分で調べた内容、自分のイメージにマッチした内容を追記している場合もあります。
※今回はまだまだPythonを使用しません。
そもそも統計学とは
データの適切な取り扱い方を探る方法論を体系化した学問であると言えます。
統計学の中でもジャンルとして、2つに大きく分別されます。
- 記述統計 ・・・ 既知の手持ちデータの整理・要約する
- 推測統計 ・・・ 未知のデータを推測する記述統計と推測統計の関係について、イメージ図がめちゃくちゃ分かりやすいのがあったので、下記画像見ればOK。
統計学の基礎用語
- 標本 ・・・ 手持ちの既知データ
- 母集団 ・・・ 未知のデータを含んだ、すべてのデータ
標本という母集団のごく一部のデータを用いて、母集団という全体について議論するということが推測統計の目的ということがこの段階でわかれば問題なし。
抽象化された標本を得るプロセス
用語
- 確率変数 ・・・ ある確率分布に従って変化する値
- 実現値 ・・・ 確率変数における具体的な値
- サンプリング ・・・ 母集団から標本を得ること、サンプリング = 標本抽出
- 単純ランダムサンプリング ・・・ 母集団から各要素がランダムでサンプリングする方法
- 確率分布 ・・・ 確率変数とそれに付与された確率との対応を表したもの
- 母集団分布 ・・・ 母集団が従う確率分布のこと
例 「小さな湖の中にいる魚を釣る」
話を簡潔にするために、下記の3つの前提条件を設定します。
- 母集団は、5匹の魚ですべて同じ種である。
- 5匹それぞれの大きさが2, 3, 4, 5, 6cmである。(小数点第1位を四捨五入)
- 釣った魚はすぐに湖の中にリリースする。この湖の中で魚を1匹釣り、3cmの魚を釣ったと仮定します。5匹の中から3cmの魚1匹を釣っているので、確率としては、1/5となります。
このときの確率をP(2.5≦体長<3.4)=1/5という表記をします。この式の意味は、体長が3cmの魚を釣れる確率は1/5であるという意味です。
体長は四捨五入するので、3cmの魚の場合は2.5cm以上、3.4cm以下の魚になります。
Pは、Probability(確率)の頭文字を表します。このときの3cmの魚は実現値です。
また、次の釣りで釣る魚の大きさはどの大きさか分かりませんが、変数xという大きさの魚になります。この変数xを確率変数です。この確率は、3cmの魚のみならず、他の魚を釣る場合も同じ確率となるので、下記のような確率分布となります。
P(1.5≦体長<2.4)=1/5
P(2.5≦体長<3.4)=1/5
P(3.5≦体長<4.4)=1/5
P(4.5≦体長<5.4)=1/5
P(5.5≦体長<6.4)=1/5あるデータが、ある確率分布と対応している時、「確率分布に従う」という表現をします。
上記の例では、「釣れる魚の体長は、{1/5, 1/5, 1/5, 1/5, 1/5}の確率分布に従う」という表現になります。母集団分布を通して、標本を得るプロセスを見直してみます。
① 以下の母集団から、単純ランダムサンプリングにより標本を1つ得る
1.5≦体長<2.4 : 1匹
2.5≦体長<3.4 : 1匹
3.5≦体長<4.4 : 1匹
4.5≦体長<5.4 : 1匹
5.5≦体長<6.4 : 1匹② 以下の確率分布に従う確率変数を1つ取得する
P(1.5≦体長<2.4)=1/5
P(2.5≦体長<3.4)=1/5
P(3.5≦体長<4.4)=1/5
P(4.5≦体長<5.4)=1/5
P(5.5≦体長<6.4)=1/5①と②を同じプロセスだとみなします。
①と②を同じだと見なすプロセスは、単純ランダムサンプリングで得たデータを基に、未知の母集団を推測する、ということです。
つまり、既知データから未知のデータを推測するという統計学のプロセスがここに詰まっているという私の理解です。これまでのプロセスをすべてまとめると下記のように表現できます。
母集団分布に従う確率変数として、3cmの魚というデータが実現値として得られたその他参考サイト
確率変数とは - 統計WEB
サンプリング方法の種類~データの取り方~ - Knowledge Makersコメント
今回用いた魚を釣るという例は、箱の中にある球を取り出すという事象で表現することも可能ですね。
私は球を取り出すモデルは、中学・高校でも確率の問題でよく題材にされるので、イメージは行いやすい印象でした。
- 投稿日:2019-03-30T16:53:46+09:00
#python で #Github #API を叩いて1個の Issue 情報を取得するスクリプト例
公開のレポジトリであれば特に認証も必要ない
#!/usr/bin/env python3 import requests, os, json owner = os.environ.get('OWNER') repository = os.environ.get('REPOSITORY') issue_number = os.environ.get('NUMBER') api_url = 'https://api.github.com/repos/' + owner + '/' + repository + '/issues/' + issue_number res = requests.get(api_url) result = res.json() print(json.dumps(result))example
$ OWNER=YumaInaura REPOSITORY=YumaInaura NUMBER=22 python3 single-issue.py | jq . { "url": "https://api.github.com/repos/YumaInaura/YumaInaura/issues/22", "repository_url": "https://api.github.com/repos/YumaInaura/YumaInaura", "labels_url": "https://api.github.com/repos/YumaInaura/YumaInaura/issues/22/labels{/name}", "comments_url": "https://api.github.com/repos/YumaInaura/YumaInaura/issues/22/comments", "events_url": "https://api.github.com/repos/YumaInaura/YumaInaura/issues/22/events", "html_url": "https://github.com/YumaInaura/YumaInaura/issues/22", "id": 394759299, "node_id": "MDU6SXNzdWUzOTQ3NTkyOTk=", "number": 22, "title": "「私はロボットではありません」失敗!皆大嫌いなあいつは「ReCAPCHA」というらしい。@yumainara @qiita #認証 #google", "user": { "login": "YumaInaura", "id": 13635059, "node_id": "MDQ6VXNlcjEzNjM1MDU5", "avatar_url": "https://avatars2.githubusercontent.com/u/13635059?v=4", "gravatar_id": "", "url": "https://api.github.com/users/YumaInaura", "html_url": "https://github.com/YumaInaura", "followers_url": "https://api.github.com/users/YumaInaura/followers", "following_url": "https://api.github.com/users/YumaInaura/following{/other_user}", "gists_url": "https://api.github.com/users/YumaInaura/gists{/gist_id}", "starred_url": "https://api.github.com/users/YumaInaura/starred{/owner}{/repo}", "subscriptions_url": "https://api.github.com/users/YumaInaura/subscriptions", "organizations_url": "https://api.github.com/users/YumaInaura/orgs", "repos_url": "https://api.github.com/users/YumaInaura/repos", "events_url": "https://api.github.com/users/YumaInaura/events{/privacy}", "received_events_url": "https://api.github.com/users/YumaInaura/received_events", "type": "User", "site_admin": false }, "labels": [], "state": "open", "locked": false, "assignee": null, "assignees": [], "milestone": null, "comments": 0, "created_at": "2018-12-29T04:13:31Z", "updated_at": "2018-12-29T04:13:31Z", "closed_at": null, "author_association": "OWNER", "body": "# バスはどれ?\r\n\r\nわからないぜ。\r\n\r\n\r\n\r\n\r\n\r\n\r\n\r\n\r\n#ReCaptcha Qiita\r\n\r\nhttps://qiita.com/amagasu1234/items/9760c2c410776fd02e12\r\n\r\n# reCAPTCHA: Easy on Humans, Hard on Bots - Google\r\n\r\n人間に優しくボットに厳しく。\r\n\r\n\r\n\r\n\r\n# 僕らは人間じゃなかったらしいな?\r\n\r\n# V3らしい\r\n\r\n\r\n\r\n\r\n# スコア制らしい\r\n\r\n\r\n\r\n\r\n#フロントエンドはこれだけ!\r\n\r\n```js\r\n <script src=\"https://www.google.com/recaptcha/api.js?render=reCAPTCHA_site_key\"></script>\r\n <script>\r\n grecaptcha.ready(function() {\r\n grecaptcha.execute('reCAPTCHA_site_key', {action: 'homepage'}).then(function(token) {\r\n ...\r\n });\r\n });\r\n </script>\r\n```\r\n\r\nすごすぎ。\r\n\r\nこれは採用したくなる。\r\n\r\nおそるべしGoogle\r\n\r\n#で、なぜ嫌いなの?\r\n\r\nローカライズ全然出来てない。\r\n日本人が理解する「バス」が分からない。\r\n画像のローカライズって大変そう。\r\nでも現状一番の選択肢なんだろうな、コスパ考えると。\r\n\r\n# 以上。\r\n\r\n誰かバスの見つけ方おしえてください。\r\n\r\n", "closed_by": null }Original by Github issue
- 投稿日:2019-03-30T16:04:39+09:00
pandas DataFrameの複数条件による行抽出のメモ
結論
or,andではなく、|(or),&(and)を使うべし。or、andの場合のエラー
誤りdf3.loc[(df3["品目"] == "パッケージ") or (df3["品目"] == "パッケージ")]ValueError: The truth value of a Series is ambiguous. Use a.empty, a.bool(), a.item(), a.any() or a.all().
下記にてエラー回避
正df3.loc[(df3["品目"] == "パッケージ") | (df3["品目"] == "パッケージ")]補足追記 => 括弧忘れがち注意!!!
各条件は括弧で囲わないとエラーになる。
SyntaxError: invalid syntax
参考にさせていただきました。
詳細は下記に詳しく紹介されています。
- 投稿日:2019-03-30T15:33:43+09:00
Online Computer Science Homework Help
Have you difficulties in doing programming in computer science. Our full support through Computer science assignment help will overcome your difficulties. To acquire proper grip over computer science visit our webpage domyhomework.co now. You will surely score well after that. Our highly qualified experts provide depth explanation to make each concept understandable. for more info visit my website:https://www.domyhomework.co/computer-science-assignment-help.html
- 投稿日:2019-03-30T15:09:56+09:00
Django入門01(設定編)
以下を参考に進めながら引っかかったところを追記する
Qiita:Django入門にはDjango Girls Tutorialがおすすめ
Djangoのチュートリアルをいろいろ探してみた結果、「Django Girls Tutorial」がとても良心的に感じました。Web開発の経験がない人でも一人で進められるのではと思うほどの丁寧さでした。
環境作成
Anacondaを使うのであれば
Environments -> Create
で環境作成して、必要なものをpipでインストールすれば良い。以降ターミナル(というかコマンドプロンプト)を起動する際は、Djangoの環境の「▶」から
open terminal
をクリックすればターミナルが開く。DB設定
migrateでテーブル作成されるので、アプリ用のユーザーを作成し、アプリが使うスキーマに対して権限を与え、参照するだけのスキーマにはselect権限のみ付与する。
MySQL Workbenchを使う場合は
Navigator(左サイドバー)-> Users and Privileges
でユーザー作成画面を開き、
add account
でユーザー作成。
Schema Privileges
から権限設定。settings
Djangoのプロジェクトを作成後、MySQLを利用する為にsettings.pyを編集する。
まずデフォルトは以下のようにsqlite3を使う設定になっている。
DATABASES = {
'default': {
'ENGINE': 'django.db.backends.sqlite3',
'NAME': os.path.join(BASE_DIR, 'db.sqlite3'),
}
}
これを以下のように修正する。
DATABASES = {
'default': {
'ENGINE': 'django.db.backends.mysql',
'NAME': '(接続するスキーマ名)',
'USER': '(接続するユーザー名)',
'PASSWORD': '(接続するユーザーのパスワード',
'HOST': '(DBのホスト。IPアドレスかドメイン)',
'PORT': '',
'OPTIONS': {
'init_command': "SET sql_mode='STRICT_TRANS_TABLES'",
}
}
}
MySQL clientの設定
そのまま
python manage.py migrate
を実行すると
django.core.exceptions.ImproperlyConfigured: Error loading MySQLdb module.
Did you install mysqlclient?
のエラーが出てしまう。MySQL clientが必要なので
pip install PyMySQL
でPyMySQLをインストールする。
さらにmanage.pyに以下を追記することでMySQLdb moduleを有効化する。
import pymysql
pymysql.install_as_MySQLdb()
- 投稿日:2019-03-30T15:00:03+09:00
マンデルブロ集合の3次元への拡張が見たい!
はじめに
マンデルブロ集合は、2次元で画像表現したときに拡大しても同じパターンが現れる(フラクタル)図形として有名です。
数学者ブノワ・マンデルブロの名前を取って数学者エイドリアン・ドゥアディが命名しました。
How to use the OpenCV parallel_for_ to parallelize your codeより画像を引用。白い縁取りの内側にある黒い領域がマンデルブロ集合に該当する領域。とても美しい図形だと筆者は思います。
マンデルブロ集合に興味を持たれた方は@ryunryunryunさんの愛おしすぎるMandelbrot集合をProcessingで描くをご覧ください。わかりやすい解説とコードがあります。描画方法を理解した上で画像を見るとマンデルブロ集合の魅力が増加すると思います。
本記事は上記@ryunryunryunさんの記事とコード、およびOpenCVのparallel_for_()関数のチュートリアルを要約した拙作OpenCV(C++)チュートリアル:parallel_for_でコードを並列化する(マンデルブロ集合)をもとにして執筆しています。本記事の概要
本記事のテーマは、通常2次元画像として表現されるマンデルブロ集合を、3次元の立体として表現できないかということです。
後述のようにマンデルブロ集合は複素数を用いて定義され、実軸と虚軸をx, y座標にマッピングすることで2次元画像の表現を得ます。3次元(3軸)で定義可能なマンデルブロ集合は複素数による定義にならないと予想されるため、おそらくもうマンデルブロ集合とは呼べませんが、3次元立体としてマンデルブロ集合っぽいもので、かつ数学的にも納得いくような表現を見たい!というのが筆者のモチベーションです。
こんなかんじかな?当然ですが、先行研究が存在します。
中でも著しいのはDaniel Whiteらによるマンデルバルブと呼ばれるもので、10年ほど前に発表されています。
先行研究については後述します。マンデルブロ集合の定義
定義式をwikipediaの記事から引用すると
次の漸化式
\left\{ \begin{array}{ll} Z_{n+1} = Z_n^2 + c \\ Z_0 = 0 \end{array} \right.で定義される複素数列{$Z_n$} $n\in N \cup$ {$0$}が $n\rightarrow \infty$の極限で無限大に発散しないという条件を満たす複素数 $c$ 全体が作る集合がマンデルブロ集合である。
となります。
つまり、はじめに複素数cを選び、それとは別の複素数$z_0=0$から開始して、上記の漸化式の計算を繰り返し、どんなにnが大きくなっても$z_n$の絶対値が発散しなければ、その複素数cはマンデルブロ集合に含まれる、というものです。
この漸化式は後で式(*)として使います。定義の使い方
上記のどんなにnが大きくなっても$z_n$の絶対値が発散しなければという条件は、次の式で表現されます。
\limsup_{n\to\infty} |z_{n+1}| \leq 2 \tag{1}左辺の$|\cdot|$は絶対値で、一般に複素数$z=a+bi$の絶対値は
|z|=\sqrt{a^2+b^2} \tag{2}で定義されます。
マンデルブロ集合を定義する漸化式
\left\{ \begin{array}{ll} Z_{n+1} = Z_n^2 + c \\ Z_0 = 0 \end{array} \right. \tag{*}において、cは複素数ですので実部と虚部の2要素を持ちます。つまり
c=x+yi \tag{3}と表せます。
このxとyには適切なスケールに変換された画像の座標が入ります。漸化式(*)の展開
式(*)において、n=0の時$Z_0$=0ですので、
\begin{align} Z_{0+1} &= 0^2 + c \\ &=c \\ &=x+yi \end{align}となります。
1行目から2行目へは式(3)$c=x+yi$を使いました。
次のn=1では、\begin{align} Z_{1+1} &= (x+yi)^2 + c \\ &= x^2 + 2xyi - y^2 + c \\ &=x^2 + x - y^2 + 2xyi + yi \\ &=x^2 + x - y^2 + (2xy + y)i \tag{4} \end{align}となります。
この時、右辺の実部は$x^2 + x - y^2$, 虚部は$2xy + y$です。この値を式(2)に代入して、計算に使用した複素数$c$がマンデルブロ集合に属するかどうかを式(1)で判断します。実用的にはn=無限大まで計算せずに、適当な大きい整数を上限に計算し、上限まで式(1)を満たし続けたピクセルc(x,y)はマンデルブロ集合に属するものとします。escape time algorithmと呼ばれるマンデルブロ集合の判定方法です。
3次元への拡張
次のように考えました。
- 従来の定義では複素数がx軸、y軸と対応付けられる。
- 描画対象の空間に3番目の軸としてz軸(高さ方向)を付け加える
- 実部、虚部、?部の3つ組で一つの数を表す数を用意して、同様の計算をすれば良い
従来のアルゴリズムから変更の必要がある箇所は次の通りです。
- 画像はx,yの2次元なので、高さ方向の変数を作ってイテレートする
- 式(1)の判定で3軸目の項を考慮する
- 式(4)が示すように、変数の更新時に3軸目の項を考慮する(例えば虚数は2乗すると実数として計算できるが、3軸目の数でも類似の処理が必要かもしれない。)
以降では説明のために3軸目の数をzとして、式(*)の複素数$Z_n$に対応するものを$W_n$と呼びます。Wは実部、虚部、?部を持つ数です。つまり,
W=x+yi+zjです。
ただし$j$は3軸目の要素であることを表します。四元数
複素数の拡張として四元数quaternion(クォターニオン)が知られています。
四元数は1843年にハミルトンにより劇的な発見をされたことで有名です。興味がある方はwikipediaの記事や、書籍1等をご覧ください。カッコいいです。四元数は次のように表されます。wikipediaの記事から引用します。
a + bi + cj + dkここで、 a, b, c, d は実数であり、i, j, k は基本的な「四元数の単位」である。
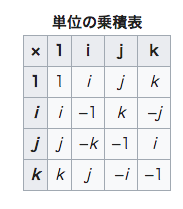
四元数の単位i, j, k については次式が成り立ちます。
i^2=j^2=k^2=ijk=-1単位i, j, k同士の積は下表のように定義されます。
wikipediaの記事から引用します。これらは掛ける順番が異なると結果が変わり、例えば$ij=k$ですが、順番を逆にした場合$ji=-k$となります。
試したこと
改変が必要な箇所を再掲します。
- 画像はx,yの2次元なので、高さ方向の変数を作ってイテレートする
- 式(1)の判定で3軸目の項を考慮する
- 式(4)が示すように、変数の更新時に3軸目の項を考慮する(例えば虚数は2乗すると実数として計算できるが、3軸目の数でも類似の処理が必要かもしれない。)
1は簡単です。
forで回すだけです。2については、複素数の絶対値が2を超えないことがマンデルブロ集合の判定式でした。
判定式(1)を再掲すると、\limsup_{n\to\infty} |z_{n+1}| \leq 2 \tag{1}です。
なぜ2なのでしょうか?まだ調べていませんが、今回使用した数$W=x+yi+zj$は絶対値が$|W|=\sqrt{x^2 + y^2 + z^2}$となるよう定義することにしました。したがって、z=0の時、つまり高さがない平面上では従来のマンデルブロ集合と同様の図形が描かれます。3については、四元数の単位i, j, k同士の積の定義を利用しました。
式(*)を再掲すると、\left\{ \begin{array}{ll} Z_{n+1} = Z_n^2 + c \\ Z_0 = 0 \tag{*} \end{array} \right.であり、従来のアルゴリズムでは複素数$Z_n$の2乗を計算する必要があります。拡張アルゴリズムでは数$W_n$の2乗を計算することにします。この計算は四元数の単位同士の積の定義を用いて、
\begin{align} W_n^2 &=(x+yi+zj)^2 \\ &=x^2 + y^2ii +z^2jj + 2xyi + 2yzij + 2zxj \\ &=x^2 - y^2 -z^2 + 2xyi + 2yzk + 2zxj \end{align}と展開できます。
最右辺の6個の項を分類すると、実数 : $x^2 - y^2 -z^2$
虚数(i): $2xyi$
?数(j) : $2zxj$
四元数でkに対応する数: $2yzk$となります。ただし、最後の四元数でkに対応する数は使用しません。理由は3次元空間には第4の軸がないからです。
漸化式の更新は今計算した$W_n^2$(従来は$Z_n^2$)に数$c$(複素数$c$)を足すことで完了します。つまり拡張された$c$を$c=a+bi+dj$とすると、式(*)より、更新された$W_{n+1}$は実部: $x^2 - y^2 -z^2 +a$
虚部(i): $2xyi +bi$
?部(j) : $2zxj +dj$を持つことになります。
実装
@ryunryunryunさんの記事愛おしすぎるMandelbrot集合をProcessingで描くのコード(processing)を元に、pythonに移植実装しました。
と言っても先述の3つ以外はほぼ変更していません。import numpy as np import cv2 w = 800 // 2 h = 700 // 2 depth = 200 // 2 #z軸方向。これは書き出す画像の枚数になる img = np.ones([h, w, 1]) * 255 iteration = 1000 #画像のピクセルを適切なスケールに変換する #real re_min = -2 re_max = 0.7 #imagi im_min = (re_min - re_max) * h / w / 2.0 im_max = -im_min #quart q_min = int(im_min * 1.6) q_max = int(im_max * 1.6) print(im_min, im_max) #マンデルブロ集合に属するか判定する def is_in_mandelbrot(a, b, d): x = 0 y = 0 z = 0 prev_x = x prev_y = y prev_z = z for i in range(iteration): cond = x ** 2 + y ** 2 + z ** 2 if cond >= 4: return -i else: prev_x = x prev_y = y prev_z = z x = next_x(prev_x, prev_y, prev_z, a) y = next_y(prev_x, prev_y, prev_z, b) z = next_z(prev_x, prev_y, prev_z, d) return 1 #数Wの更新用 def next_x(x, y, z, a): ret = x ** 2 - y ** 2 - z ** 2 + a return ret def next_y(x, y, z, b): ret = 2 * x * y + b return ret def next_z(x, y, z, d): ret = 2 * z * x + d return ret #範囲を変換する関数 def _map(a,b,c,d,e): # map a from b-c to d-e b_c = abs(b - c) d_e = abs(d - e) prop = a / b_c x = prop * d_e + d return x #描画開始 for z in range(depth): for i in range(h): for j in range(w): a = _map(j, 0, w, re_min, re_max) b = _map(i, 0, h, im_min, im_max) d = _map(z, 0, depth, q_min, q_max) ret = is_in_mandelbrot(a, b, d) if ret == 1: color = 0 else: color = _map(-ret, 0, iteration * 0.1, 255, 0) img[i, j] = color font = cv2.FONT_HERSHEY_SIMPLEX cv2.putText(img, str(d), (w-100, h-20), font, 0.75, (150, 150, 150), 1, cv2.LINE_AA) name = "{0:04d}".format(z) cv2.imwrite("out/{}.png".format(name), img)実行
google colab(python3)で実行しました。
実行する前に出力先ディレクトリを作ります。
!mkdir out実行すると
out以下に0000.pngのような画像がたくさんできます。これらの画像は3次元の集合を高さ方向でスライスした断面画像となります。
番号が若いほうが3次元空間の下側です。結果
右下の数値は空間内の高さ(コードではforの変数z)を示し、スライスは3次元空間の下から上方向に上昇しています。
ちょうど真ん中の画像(高さ=0に対応する)が、見慣れたマンデルブロ集合になっています。いかがでしょうか。割とそれっぽいオブジェクトになっている気がします。
しかし、筆者の想像(はじめの方にあるスケッチ参照)と異なるのは、周囲の小さい突起たちが高さの変化と共になめらかにスライドしていくところです。なめらかに収縮ではなく、なめらかにスライドするということは、中心部分の大きな円(球)に沿って同じ形が高さ方向に続いているということです。例えるならばなるとです。中心の球体の周囲に、高さ方向に長い、小突起型の断面をしたなると状の物体が巻き付いているようなイメージとなります。もっとボツボツとくっついているものだと想像していました。
もう一つ気になるのが、集合の周囲に見える微細な黒点(本体と連結していない)です。特に右下の数値近くの黒点はだいたいどの高さの画像でも示されています。高さ=0でも。これはおかしいので、どこかにミスがあるかもしれません。
拡大したときにフラクタル構造を持っているかなど、確認しなければならないことがたくさんありそうです。先行研究
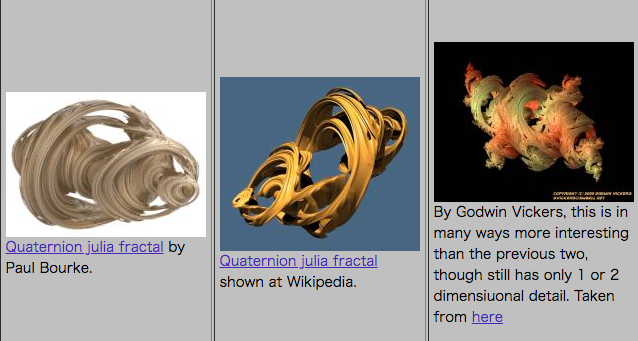
おそらく3次元のマンデルブロ集合として最も有力なのは、マンデルバルブと呼ばれるものだと思います。
The Mandelbulb: first 'true' 3D image of famous fractalによると、イギリスのアマチュアフラクタル画像作家Daniel Whiteにより2007年に発表されました。彼とFractal Forumsは研究を続け、その後2009年にメンバーの一人Paul Nylanderにより改良版が示されています。
マンデルバルブ(改良版:次数8)
Paul Nylanderによる。Daniel WhiteのウェブサイトSkytopia内、The Unravelling of the Real 3D Mandelbulbより引用。マンデルバルブのギャラリーで詳細な画像が見られます。
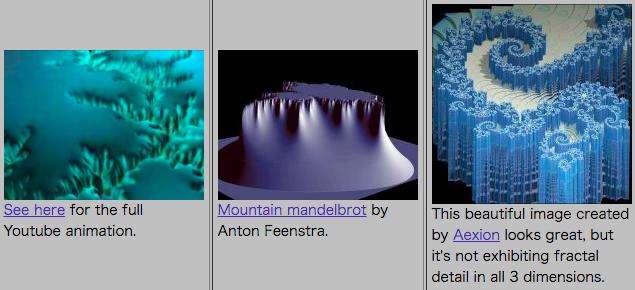
マンデルブロ集合を3次元に拡張する試みはこれ以前から行われており、Daniel WhiteによりThe Mystery of the REAL, 3D Mandelbrot Fractalにまとめられています。これによると、彼以前の多くの(全ての)先行研究は次の4タイプに分類できます。
タイプ1:
回転体
タイプ2:
頂上が2次元である山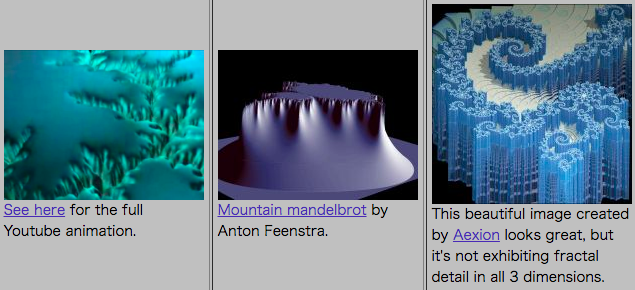
タイプ3:
フーセンガムっぽいホイップクリーム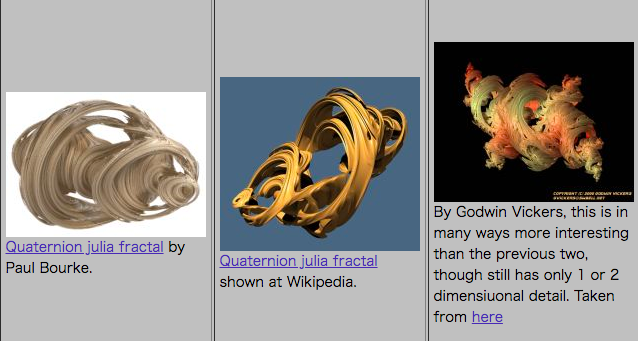
タイプ4:
ジャングルジムの狂気本記事のコードで描画できる図形は、おそらくタイプ1:回転体です。このタイプは四元数の利用を含む複数の方法で描画できるそうです。表の1行目左端にある画像を引用します。
Jules Ruisによる3次元マンデルブロ集合技術的なこと
Daniel Whiteのウェブサイト内の、Further exploration of the 3D Mandelbulbに示されています。
マンデルバルブの定義
従来のマンデルブロ集合同様、次式で定義されます。
Z_{t+1} = Z_{t}^n +cただし、Zとcはデカルト座標系のx, y, zを表すことができるhypercomplex ('triplex') numbers(超複素数、多元数)です。超複素数は複素数や四元数等の一般化です。
この超複素数のべき乗は次のように定義されます:(x,y,z)^n = r^n \bigl( sin(\theta n) cos(\phi n) , sin(\theta n) sin(\phi n) , cos(\theta n) \bigr)ただし、
\begin{align} r &= \sqrt{x^2 + y^2 + z^2} \\ \theta &= atan2( \sqrt{x^2+y^2}, z ) \\ \phi &= atan2(y,x) \end{align}超複素数同士の和($Z_n +c $)は複素数と同様、各部同士で加算を行います。
それ以外は従来のマンデルブロ集合と同様のアルゴリズムです。
nは3Dマンデルバルブの次数で、求めているものに最も近いのはn=8のときとされています。マンデルバルブの見た目からマンデルブロ集合を連想しづらいかもしれませんが、比較すると似ている事がわかります。
まだ先があるかも
先述のThe Mandelbulb: first 'true' 3D image of famous fractalの中で、Daniel Whiteはマンデルバルブが完全に本物の3Dマンデルブロ集合ではないとして、次のように述べています。
“There are still ‘whipped cream’ sections, where there isn’t detail,”
“If the real thing does exist – and I’m not saying 100 per cent that it does – one would expect even more variety than we are currently seeing.”「まだ詳細にならない”ホイップクリーム状の”場所があるんだ。」
「もし本物が存在するなら、 ―100%あるとは言わないけど、― 今見ているものよりもっとバラエティに富んでいるはずだよ。」まとめ
- マンデルブロ集合の定義をおさらいし、従来2次元画像として表現される同集合を3次元空間に拡張できるのではないかという仮説を立てた
- 四元数の定義と積を利用してマンデルブロ集合の定義式を拡張した
- 拡張した集合の、高さ方向のスライス画像を生成するスクリプトをpythonで書いた
- マンデルバルブ
これを端緒に、数学に対する理解を深めていきたい。
数学をつくった人びと〈2〉 (ハヤカワ文庫NF―数理を愉しむシリーズ), pp299-300. *ハミルトン以前にはガウスによる発見(1817)があり、それ以前にも四元数に関する研究は存在したものとされている。 ↩
- 投稿日:2019-03-30T12:19:44+09:00
Jupyterは紙
ポエム
Jupyter1はまっさらな紙だ. テキストはもちろんグラフやマルチメディアなファイルの描画までもでき, 聡明なデータ解析界隈の方々はここにかたちあるものを, 時には未来までも描いているのだろう.
私にはできなかった. 数学的教養とテキストエディタがなかったからだ23.
Jupyterは真っ白な紙だ. 真っ白な紙の上では, 字は汚いし漢字は書けないしspellだってまともに書けない4.
シームレスさを求めた結果, plainファイルをインターフェースとすることで, 任意のエディタからpythonを実行できるREPL wrapperができた.
簡単に美味しいREPLのレパートリーを増やしませんか?
お客様ぁ〜、REPLをもっとシームレス簡単にエディタから実行できるoctaltree/wreplのご紹介です!これ、見ての通りWatch-Read-Eval-Print Loop!だから使い勝手がとってもいいんです!
使い方は簡単ですっ。例えば
foo.pyを持ってくる、ご注目!
いきますよ、よく見といてください。
これ、上下に編集するだけ!ただただひたすらに、上下に上下にしこしこ しこしこ。foo.pyimport numpy as np a = np.arange(6).reshape((2, 3)) print(a) # ここまで書いて一度保存 b = a * 2 print(b)実行結果が千切りになって出てくるんです!さぁご覧ください!はいっ!これで千切りのかぁ〜んせぇい!
$ wrepl foo.py # 実行後にfoo.pyをエディタで編集する > import numpy as np > a = np.arange(6).reshape((2, 3)) > print(a) > # ここまで書いて一度保存 # start 2019-03-30T02:34:27Z [[0 1 2] [3 4 5]] # finish 2019-03-30T02:34:27Z > b = a * 2 > print(b) # start 2019-03-30T02:34:33Z [[ 0 2 4] [ 6 8 10]] # finish 2019-03-30T02:34:33Zでも、よく切れるでしょう?
再現方法はというと、このまんま保存されていて、じゃぶじゃぶじゃぶとログファイルを実行するだけ!とっても簡単で、便利なんです。
executedimport numpy as np a = np.arange(6).reshape((2, 3)) print(a) # ここまで書いて一度保存 # start 2019-03-30T02:34:27Z #1 [[0 1 2] #1 [3 4 5]] # finish 2019-03-30T02:34:27Z b = a * 2 print(b) # start 2019-03-30T02:34:33Z #1 [[ 0 2 4] #1 [ 6 8 10]] # finish 2019-03-30T02:34:33Zちなみにお客様ぁ、これ、実行ごとにグローバル変数を保存していて、実はこれ以前の変数を使うことができるんですね。変数を保存してるので、差分だけを実行できて使いやすいんですっ。
いきましょう!同じfoo.pyをもってきます。今度は、しこしこ しこしこfoo.pyimport numpy as np a = np.arange(6).reshape((2, 3)) print(a) # ここまで書いて一度保存 b = a * 2 print(b) # ここでwrepl foo.pyをC-cで終了し再度実行した import matplotlib.pyplot as plt print(a + b)$ wrepl foo.py` > # ここでwrepl foo.pyをC-cで終了し再度実行した > import matplotlib.pyplot as plt > print(a + b) # start 2019-03-29T15:48:49Z [[ 0 3] [ 6 9] [12 15]] # finish 2019-03-29T15:48:49Zわかりますよねぇ。この結果は一目瞭然でぇ〜す。さあ、ご覧ください!
a,bが保存されていた変数、print(a + b)が新たに実行されたスニペット、この結果は皆さまお好みでお召し上がりになってください、でもね、この
pltってなんか気になりません?思い出しました?そう、あれ!あの視覚化で有名なmatplotlibが、なんとご家庭で、このoctaltree/wreplがあれば、簡単に再現することができちゃうんです。これ、実際関数にくるんで保存してください。ほんっとに美味しいから、オススメなんです。def f(): plt.plot(range(len(a)), a[:, 0]) plt.show() f() # fが保存されるためaが変更されていなければ同じグラフを見ることができるa = np.arange(6) def draw(a): def view(a): plt.plot(a, a * 2) plt.show() return lambda: view(a) f = draw(a) f() a = -a f() # これだけくるんであげるとfはaを内部に持つ関数であるため # グローバル変数aが変更されても同じグラフを見ることが出来るさあお客様ぁ、このoctaltree/wrepl見ていただけました?任意のpythonが実行できるし、お手入れも簡単だし、データを美味しく、たっぷり解析してくださいね。
いろんなファイルが簡単REPLに!octaltree/wrepl、今ならMITがついて、お値段0円でのご提供です。スゥーッ
こんなもの!(ガシャーン) こんな!wreplなんて!
こんなぁぁぁッ!参考文献
- Joel Grus (@joelgrus). "I Don't Like Notebooks - Joel Grus - #JupyterCon 2018". Google スライド. https://docs.google.com/presentation/d/1n2RlMdmv1p25Xy5thJUhkKGvjtV-dkAIsUXP-AL4ffI/preview#slide=id.g362da58057_0_1, (参照 2019-03-30)
- atouda. "【クッソー☆】霊夢と魔理沙のチョコ咀嚼☆口移しチャレンジ". ニコニコ動画. https://www.nicovideo.jp/watch/sm28108413, (参照 2019-03-30).
- 谷口です。 (id:taniguchideath). "【書き起こし】 RRM姉貴 るりま サラダおろし". 谷口です。のブログ. http://taniguchidesu.hatenablog.com/entry/2016/04/18/003416, (参照 2019-03-30).
- 投稿日:2019-03-30T11:30:38+09:00
argparserとnamedtupleを用いてコマンドライン引数の受け渡し
0.はじめに
コマンドライン引数を用いて,変数を受け渡す必要があったので今回はargparserを利用しました.
また,今回は受け渡す変数に対して以下の制約を設けたかったのでNamedTupleとの併用を試みた.・変数が定義域外に出ていた場合はclip
・変数を静的に
・変数の型が異なっている場合はエラー上の3点を満足するために今回の方法を考案した.
1.argparser
簡単な使用法.
以下のように,変数名,型,デフォルト値,コマンドラインで取る引数の個数を指定.その他にも
choicesによって,取るべき値の選択肢を配列として渡したり,actionによって,引数があった場合に関数を呼び出すことができる.また,引数名に-がついている場合はコマンドライン引数がなくてもエラーは起きず,数値の前に引数名をコマンドラインに示していればしっかりと代入される.注意したいのは,ここで渡した変数はimmutableではないこと.つまり,動的であるため,代入すると値が変わる.一方で,引数に取られた型が間違っている場合はエラーを吐き出すことができる.
import sys from argparse import ArgumentParser as ArgPar argp = ArgPar() argp.add_argument( "-test", type = int, default = 10, nargs = 1 # コマンドライン引数を何個取るか ) args = argp.parse_args([1:]) print(args.test) # 実行結果(コマンドライン引数なしのとき) -> 102.NamedTuple
辞書をクラス化したようなもので,変数が静的になる.
簡単な実行方法は以下のような形.注意したいのは以下のようにNamedTupleに対して,代入すべき型名を明示的に渡すことはできても実際には強制力を持たず,簡単に違う型の値を代入できることである.from typing import Callable from typing import List from typing import Optional from typing import NamedTuple from typing import Tuple class Parameters( NamedTuple( "_Parameters", [("batch_size", int), ("epochs", int), ("lr", float), ("momentum", float), # between 0 and 1 ("weight_decay", float), ("width_coef", Callable[[int], ndarray]), ("n_blocks", Callable[[int], ndarray]), # how many convolutional blocks we have in one group of blocks ("drop_rates", Callable[[float], ndarray]), # dropout rate in each groups: between 0 and 1 ("lr_step", Callable[[float], ndarray]), # when we reduce the learning rate ("lr_decay", float) ])): pass ParametersDict = { "batch_size": 128, "epochs": 200, "lr": 0.1, "momentum": 0.9, "weight_decay": 5.0e-04, "width_coef": [10, 10, 10], "n_blocks": [4, 4, 4], "drop_rates": [0.2, 0.2, 0.2], "lr_step": [0.3, 0.6, 0.8], "lr_decay": 0.5 } HyperParameters = Parameters(**ParametersDict) print(HyperParameter.batch_size) # 実行結果 -> 1283.組み合わせてArpParse × NamedTupleを作成
import numpy as np import sys from numpy import ndarray from typing import Callable from typing import List from typing import Optional from typing import NamedTuple from typing import Tuple from argparse import ArgumentParser as ArgPar # NamedTupleのクラス class Parameters( NamedTuple( "_Parameters", [("batch_size", int), ("epochs", int), ("lr", float), ("momentum", float), # between 0 and 1 ("weight_decay", float), ("width_coef", Callable[[int], ndarray]), ("n_blocks", Callable[[int], ndarray]), # how many convolutional blocks we have in one group of blocks ("drop_rates", Callable[[float], ndarray]), # dropout rate in each groups: between 0 and 1 ("lr_step", Callable[[float], ndarray]), # when we reduce the learning rate ("lr_decay", float) ])): pass # パラメータの範囲をデフォルト指定.範囲を動的に変化させたい場合は向かない. ParametersRange = { "batch_size": (2 ** 4, 2 ** 10), "epochs": (100, 300), "lr": (1.0e-4, 1.0e-1), "momentum": (1 - 5.0e-1, 1 - 1.0e-4), # between 0 and 1 "weight_decay": (1.0e-6, 1.0e-1), "width_coef": (5, 15), "n_blocks": (2 ** 1, 2 ** 3), # how many convolutional blocks we have in one group of blocks "drop_rates": (0, 0.5), # dropout rate in each groups: between 0 and 1 "lr_step": (0., 1.), # when we reduce the learning rate "lr_decay": (0.01, 0.5) } # ArgParserを使う. argp = ArgPar() # 引数名や値,型の設定 argp.add_argument("-batch_size", type = int, default = [128], nargs = 1, help = "batch size: type = int, range = (2 ** 4, 2 ** 10)") argp.add_argument("-epochs", type = int, default = [200], nargs = 1, help = "epochs: type = int, range = (100, 300)") argp.add_argument("-lr", type = float, default = [0.1], nargs = 1, help = "lr: type = float, range = (1.0e-4, 1.0e-1)") argp.add_argument("-momentum", type = float, default = [0.9], nargs = 1, help = "momentum: type = float, range = (1 - 5.0e-1, 1 - 1.0e-4)") argp.add_argument("-weight_decay", type = float, default = [5.0e-4], nargs = 1, help = "weight_decay: type = float, range = (1.0e-6, 1.0e-1)") argp.add_argument("-width_coef", type = int, default = [10, 10, 10], nargs = 3, help = "width_coef: type = int, range = (5, 15)") argp.add_argument("-n_blocks", type = int, default = [4, 4, 4], nargs = 3, help = "n_blocks: type = int, range = (2 ** 1, 2 ** 3)") argp.add_argument("-drop_rates", type = float, default = [0.2, 0.2, 0.2], nargs = 3, help = "drop_rates: type = float, range = (0, 0.5)") argp.add_argument("-lr_step", type = float, default = [ 3 / 10, 3 / 5, 4 / 5], nargs = 3, help = "lr_step: type = float, range = (0, 1)") argp.add_argument("-lr_decay", type = float, default = [0.5], nargs = 1, help = "lr_decay: type = float, range = (0.01, 0.5)") # コマンドライン引数を実際に引いてくる ArgParameters = argp.parse_args() # Parserが引いてきた値をチェックし,NamedTupleに格納するための配列 ParametersInput = {} for param_name, param_range in ParametersRange.items(): # parserに入っているparam_nameと同じ名前の値を取る. params = getattr(ArgParameters, param_name) # 現状,argparserにはすべての変数が配列として格納されているため,長さ1なら変数単体に直す. n_params = len(params) # 辞書に一旦配列を用意 ParametersInput[param_name] = [] for param in params: # clipする変数の型が間違っているかもしれないので念のために型を変換するためのクラスを持ってくる param_type = type(param) # clipし,最終的に代入スべき型に変換 ParametersInput[param_name].append(param_type(np.clip(param, param_range[0], param_range[1]))) if n_params == 1: # 長さ1なら中身のみに切り替え.例えば,[128]なら128として代入 ParametersInput[param_name] = ParametersInput[param_name][0] # 上の操作で得られたParserを変換したものを静的にするためにNamedTupleに代入 HyperParameters = Parameters(**ParametersInput)
- 投稿日:2019-03-30T09:09:55+09:00
python 基本ライブラリの使い方メモ
numpyの基本
配列作成 np.array([数字])
0〜nまでの配列を作成 np.arange(n)
データの型チェック sample.dtype
次元数確認 sample.ndim
要素数確認 sampe.size
2行3列, int型で全てが0の行列を作成 np.zeros((2,3), dtype='i')
2行3列,float型で全てを任意の値にした行列を作成 np.full((2,3), dtype='f')
昇順にソート sample.sort() 降順にソート sample[::-1].sort()
配列の合計 sample.sum()
配列の積み上げ sample.cumsum()
行列の形を変える sample.reshape
1行目,すべての行を抜き出し sample[0,:]
行列の掛け算 np.dot(sample1, sample2) ※ *を使うと要素を掛け算してしまう乱数作成
乱数作成import numpy.random as random 以降はrandomを先につける前提
random.seed(0) #乱数を固定 rand(100) #0〜1の乱数を100個生成rand(10,10) #0〜1の乱数で10×10の行列を生成rand(100)*40+30 #30〜70の乱数を100個生成 randn(10) #標準正規分布(平均0、分散1)の乱数を10個発生randn(2,100) #標準正規分布による2×100の行列normal(50,10) #平均50,標準偏差10の正規分布 binormal(n=100,p=0.5) #二項分布。成功率0.5を100回試行 poisson(lam=10) #ポアソン分布。λ=10のポアソン分布 beta(a=3, b=5) #ベータ分布 randint(0,100,20) #0〜99の整数を20個生成randint(0,100,(5,5)) #0〜99の整数で5×5の行列を生成 random() #0.0〜1.0範囲のfloat型の値を生成uniform(2.0,5.0) #2.0以上5.0未満のfloat型の、一様分布の値を生成 array=["りんご","バナナ","かき","もも","オレンジ","さくらんぼ"]choice(array,3) #arrayから3つ選出。replace=Falseで重複なしScipyの基礎
Scipyのモジュール import scipy as sp# 線形代数用のモジュール import scipy.linalg as linalg
サンプルデータ sample= np.array([[1,-1,-1],[-1,1,-1],[-1,-1,1]])とします。
行列式 linalg.det(sample) 逆行列 linalg.inv(sample)
固有値, 固有ベクトル eig_value, eigvector = linalg.eig(sample)
ニュートン法による二次方程式の解def function(x): return (x**2+2*x+1)from scipy.optimize import newtonprint(newton(function,0)二次方程式の最小値をBrent法により求める
from scipy.optimize import minimize_scalarprint(minimize_scalar(function,method="Brent")Pandasの基礎
データの作成
テーブルを読み込む pd.read_csv('データ名')
1列のデータテーブルを作る→Seriesを使う。
0〜9までの配列に対して、インデックスを特定の文字(a〜j)にする場合df = pd.Series([0,1,2,3,4,5,6,7,8,9],index['a','b','c','d','e','f','g','h','i','j'])
- データが複数列のテーブルを作る→DataFrame
sample1 = {'ID':['100','101','102','103','104'],'city':['Tokyo','Osaka','Kyoto','Hokkaidao','Tokyo'],'birth_year':[1990,1989,1992,1997,1982],'name':['Hiroshi','Akiko','Yuki','Satoru','Steeve']} df1 = pd.DataFrame(sample1)データを観察する
- データサイズの確認 df.shape
- 要約統計量 df.describe(include='all') ※データタイプはSeriesの形式
- データの型を見る df1.dtypes
- 降順にソートする df.sort_values('カラム名',ascending= False)
- ユニークな値の個数をカウントする df.nunique()
- 欠損値の個数をカウントする df.isnull().sum()
データを取捨選択する
- 欠損値のある行を排除する df1.dropna()
- 特定のcolumn(tempやdepth)に欠損値がある場合,その行を削除する df.dropna(subset=['temp','depth'])
- 欠損値を0で埋める df1.fillna(0)
- カラムmembersが100以下の行を全て削除 df1[df1['members'] > 100]
- データ行を削除 .drop(['指定行名'], axis=0)
- データ列を削除 .drop(['指定列名'], axis=1)
- 列を抜き出す。df["カラム名1", "カラム名2"] ※列が一つの場合はドットを使っても良い df.カラム名
- 0行目から3行目まで取得 df.[:3] ←この場合0,1,2行目が抽出される
- loc属性を使用して特定の行を抽出 df1.loc[2]
- 0~2行目のcityとnameのみ抽出 df1.loc[0:2,["city","name"]]
- loc属性はカラム名で取り出すが、行・列の"番目"で取り出すにはiloc属性を用いる。
- 単一のデータのみ取り出す場合は、at属性・iat属性を用いる
- 条件を満たしている行を取り出す df1[df1.birth_year>1990] df1[df1["birth_year"]==1990]
- cityカラムがTokyoまたはOsakaであるデータを取り出す .isindf1[df1['city'].isin(['Tokyo','Osaka'])]
データを編集する
- 転置(行と列を入れ替える) df.T
- データタイプをcategoryに変換する df1.city.astype('category')
- カラム名を変更する df.rename(columns={'変更前':'変更後'})
- カラムを追加してデータを入れる df['追加するカラム名']=データ値
- データのグループ集計 .groupby("グループするカラム名")["集計するカラム名"]df2.groupby("sex")["math"].mean()
データテーブルを結合
※df1=[index,名前と年齢]、df2=[index,名前と出身地]というデータフレームがあったとする。
- インデックスで結合する場合はmergeでもconcatでも可
pd.concat([df1, df2], axis=1) pd.merge(df1, df2, right_index=True, left_index=True)
- データ列で結合する場合はmergeを使う。名前をもとにしてテーブルをつなげる
pd.merge(df1,df2, on='名前')Matplotlibの基礎
準備import matplotlib.pyplot as pltimport matplotlib as mplimport seaborn as sns
散布図 plt.plot(x,y,"o") またはplt.scatter(x,y)
連続曲線plt.plot(x,y,label="Label")plt.legend()
ヒストグラム plt.hist(data) plt.grid(True)
箱ひげ図 plt.boxplot(data) plt.grid(True)
- 投稿日:2019-03-30T09:09:55+09:00
python 配列・行列・科学技術計算ライブラリの使い方メモ
numpyの基本
配列作成 np.array([数字])
0〜nまでの配列を作成 np.arange(n)
データの型チェック sample.dtype
次元数確認 sample.ndim
要素数確認 sampe.size
2行3列, int型で全てが0の行列を作成 np.zeros((2,3), dtype='i')
2行3列,float型で全てを任意の値にした行列を作成 np.full((2,3), dtype='f')
昇順にソート sample.sort() 降順にソート sample[::-1].sort()
配列の合計 sample.sum()
配列の積み上げ sample.cumsum()
行列の形を変える sample.reshape
1行目,すべての行を抜き出し sample[0,:]
行列の掛け算 np.dot(sample1, sample2) ※ *を使うと要素を掛け算してしまう乱数作成
乱数作成import numpy.random as random 以降はrandomを先につける前提
random.seed(0) #乱数を固定 rand(100) #0〜1の乱数を100個生成rand(10,10) #0〜1の乱数で10×10の行列を生成rand(100)*40+30 #30〜70の乱数を100個生成 randn(10) #標準正規分布(平均0、分散1)の乱数を10個発生randn(2,100) #標準正規分布による2×100の行列normal(50,10) #平均50,標準偏差10の正規分布 binormal(n=100,p=0.5) #二項分布。成功率0.5を100回試行 poisson(lam=10) #ポアソン分布。λ=10のポアソン分布 beta(a=3, b=5) #ベータ分布 randint(0,100,20) #0〜99の整数を20個生成randint(0,100,(5,5)) #0〜99の整数で5×5の行列を生成 random() #0.0〜1.0範囲のfloat型の値を生成uniform(2.0,5.0) #2.0以上5.0未満のfloat型の、一様分布の値を生成 array=["りんご","バナナ","かき","もも","オレンジ","さくらんぼ"]choice(array,3) #arrayから3つ選出。replace=Falseで重複なしScipyの基礎
Scipyのモジュール import scipy as sp# 線形代数用のモジュール import scipy.linalg as linalg
サンプルデータ sample= np.array([[1,-1,-1],[-1,1,-1],[-1,-1,1]])とします。
行列式 linalg.det(sample) 逆行列 linalg.inv(sample)
固有値, 固有ベクトル eig_value, eigvector = linalg.eig(sample)
ニュートン法による二次方程式の解def function(x): return (x**2+2*x+1)from scipy.optimize import newtonprint(newton(function,0)二次方程式の最小値をBrent法により求める
from scipy.optimize import minimize_scalarprint(minimize_scalar(function,method="Brent")Pandasの基礎
データの作成
テーブルを読み込む pd.read_csv('データ名')
1列のデータテーブルを作る→Seriesを使う。
0〜9までの配列に対して、インデックスを特定の文字(a〜j)にする場合df = pd.Series([0,1,2,3,4,5,6,7,8,9],index['a','b','c','d','e','f','g','h','i','j'])
- データが複数列のテーブルを作る→DataFrame
sample1 = {'ID':['100','101','102','103','104'],'city':['Tokyo','Osaka','Kyoto','Hokkaidao','Tokyo'],'birth_year':[1990,1989,1992,1997,1982],'name':['Hiroshi','Akiko','Yuki','Satoru','Steeve']} df1 = pd.DataFrame(sample1)データを観察する
- データサイズの確認 df.shape
- 要約統計量 df.describe(include='all') ※データタイプはSeriesの形式
- データの型を見る df1.dtypes
- 降順にソートする df.sort_values('カラム名',ascending= False)
- ユニークな値の個数をカウントする df.nunique()
- 欠損値の個数をカウントする df.isnull().sum()
- ヒストグラムを書く df.hist(bins=10)
データを取捨選択する
- 欠損値のある行を排除する df1.dropna()
- 特定のcolumn(tempやdepth)に欠損値がある場合,その行を削除する df.dropna(subset=['temp','depth'])
- 欠損値を0で埋める df1.fillna(0)
- カラムmembersが100以下の行を全て削除 df1[df1['members'] > 100]
- データ行を削除 .drop(['指定行名'], axis=0)
- データ列を削除 .drop(['指定列名'], axis=1)
- 列を抜き出す。df["カラム名1", "カラム名2"] ※列が一つの場合はドットを使っても良い df.カラム名
- 0行目から3行目まで取得 df.[:3] ←この場合0,1,2行目が抽出される
- 条件を満たしている行を取り出す df1[df1.birth_year>1990] df1[df1["birth_year"]==1990]
- loc属性はloc["インデックスラベル","カラムラベル"]で指定できる。 ※単一要素の指定ではat属性も使える
#0~1行目のcityとnameのみ抽出 df1.loc[0:2,["city","name"]]
- cityカラムがTokyoまたはOsakaであるデータを取り出す df1[df1['city'].isin(['Tokyo','Osaka'])]
データを編集する
- 転置(行と列を入れ替える) df.T
- データタイプをcategoryに変換する df1.city.astype('category')
- カラム名を変更する df.rename(columns={'変更前':'変更後'})
- カラムを追加してデータを入れる df['追加するカラム名']=データ値
- データのグループ集計 .groupby("グループするカラム名")["集計するカラム名"]
#男女別に数学の成績をグループ集計する。 df2.groupby("sex")["math"].mean()データテーブルを結合
※df1=[index,名前と年齢]、df2=[index,名前と出身地]というデータフレームがあったとする。
- インデックスで結合する場合はmergeでもconcatでも可
pd.concat([df1, df2], axis=1) pd.merge(df1, df2, right_index=True, left_index=True)
- データ列で結合する場合はmergeを使う。名前をもとにしてテーブルをつなげる
pd.merge(df1,df2, on='名前')Matplotlibの基礎
準備import matplotlib.pyplot as pltimport matplotlib as mplimport seaborn as sns
散布図 plt.plot(x,y,"o") またはplt.scatter(x,y)
連続曲線plt.plot(x,y,label="Label")plt.legend()
ヒストグラム plt.hist(data) plt.grid(True)
箱ひげ図 plt.boxplot(data) plt.grid(True)
- 投稿日:2019-03-30T09:05:43+09:00
日章旗で円周率を求めてみた
Pythonを使って円周率を出すプログラムを作ってみました。
数学に興味を持ってもらうためのツールとしてPythonを活用しました。pi.py#平成も終わりそうなので日章旗で円周率を求めてみた %matplotlib inline #玉手箱3つ(matplotlib、random、math)を使う import matplotlib.pyplot as plt import random import math #dot(点)を0とする dot = 0 #1万個点を打つ for i in range(10000): #点のx座標は1~100 x = random.randint(1, 100) #点のy座標は1~100 y = random.randint(1, 100) #中心から点までの距離(三平方の定理) d = math.sqrt((x-50)**2 + (y-50)**2) #もしdが50以下なら if (d <= 50): #dotに1を足す cnt += 1 #赤色で点を打つ plt.scatter(x, y, marker='.', c='r') #その他の場合 else: #白色で点を打つ plt.scatter(x,y,marker='.', c='w') plt.axis('equal') plt.show() #円周率を求める p = dot / 10000 pi = p * 4 print(pi)
- 投稿日:2019-03-30T03:08:22+09:00
Kaggleに登録したら次にやること ~ これだけやれば十分闘える!Titanicの先へ行く入門 10 Kernel ~
事業会社でデータアナリストをしているu++です。
普段ははてなブログでKaggleや競技プログラミングの記事を定期的に書いていて、「Kaggle Tokyo Meetup」というイベントで登壇した経験もあります。本記事では「Kaggleに登録したら次にやること」と題して、Kaggleに入門したい方に向けて次のようなコンテンツを掲載します。
- Kaggleの概要
- 環境構築不要な「Kernel」の使い方
- 入門 10 Kernel
- 1. まずはsubmit! 順位表に載ってみよう
- 2. 全体像を把握! submitまでの処理の流れを見てみよう
- 3. ここで差がつく! 仮説に基づいて新しい特徴量を作ってみよう
- 4. 勾配ブースティングが最強?! いろいろな機械学習アルゴリズムを使ってみよう
- 5. 機械学習アルゴリズムのお気持ち?! ハイパーパラメータを調整してみよう
- 6. submitのその前に! 「Cross Validation」の大切さを知ろう
- 7. 三人寄れば文殊の知恵! アンサンブルを体験しよう
- 8. Titanicの先へ行く①! 複数テーブルを結合してみよう
- 9. Titanicの先へ行く②! 画像データに触れてみよう
- 10. Titanicの先へ行く③! テキストデータに触れてみよう
- メダルが獲得できる開催中のコンペティションに参加しよう
- さらなる学びのために
Kaggleの入門というと、チュートリアルとして用意されている「Titanic : Machine Learning from Disaster」が有名です。今回も最初はTitanicを題材に話を進めます。しかし個人的には、メダルが獲得できる開催中のコンペティションに参加してこそ、歴戦の猛者たちと切磋琢磨することができ、学びや楽しみも大きいのではないかと感じています。
本記事を経て、少しでも多くの方が開催中のコンテストに参加してくださったら嬉しいです。なお本記事執筆の背景はポエム要素を含むので、はてなブログに掲載予定です。
Kaggleの概要
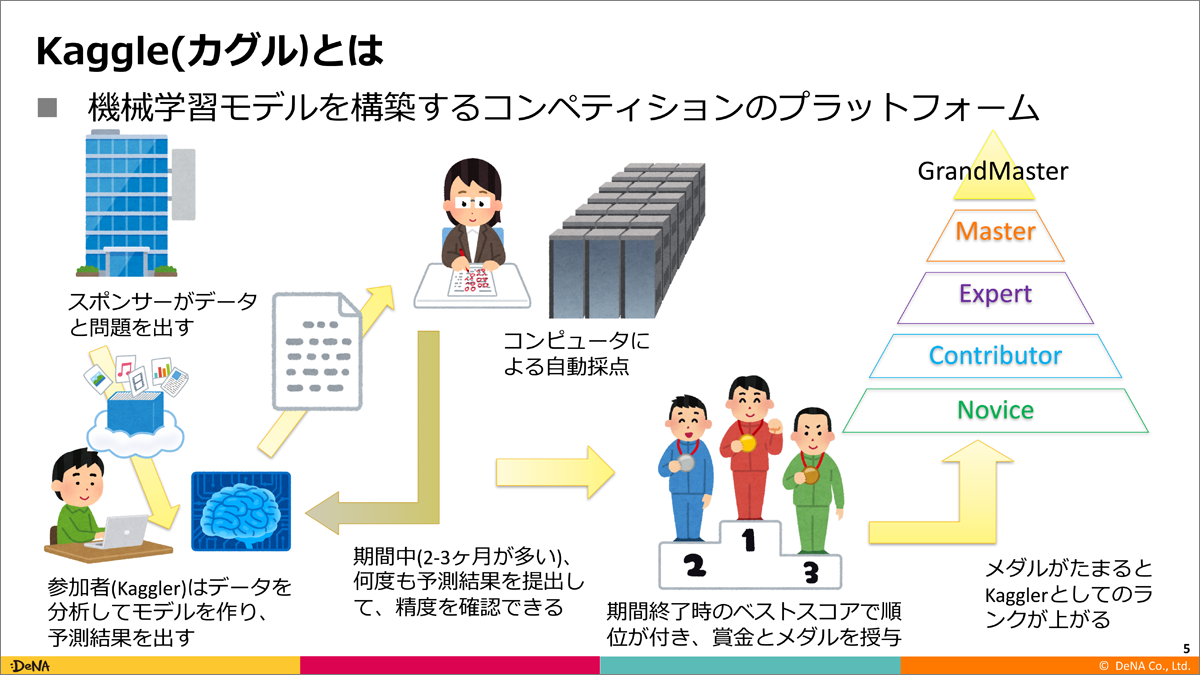
Kaggleとは、主に機械学習モデルを構築するコンペティションのプラットフォームです。
(DeNAでデータサイエンスチーム(通称Kaggle枠)のマネージャを務める原田さんの資料より引用)キスモ取締役の大越さんの資料も、Kaggleとは何かが簡潔にまとめられています。原田さんの資料と合わせて、最初にご覧いただくのがオススメです。
環境構築不要な「Kernel」の使い方
Kernelとは?
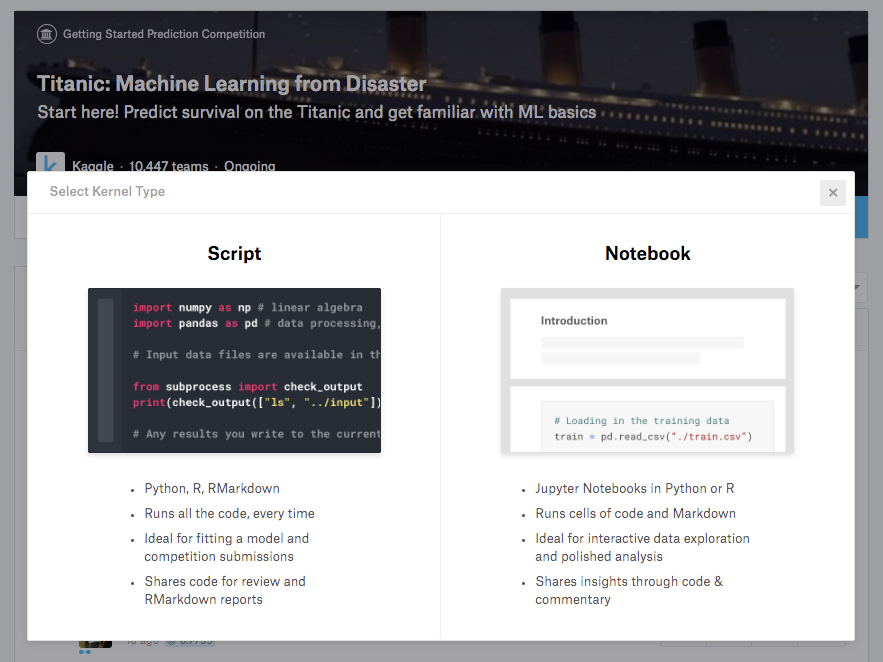
Kaggleには、Kernelと呼ばれるブラウザ上の実行環境が用意されています。言語としては現在、Python3とRが対応しています。それぞれScript形式かNotebook形式を選択可能です。
Kernelには、機械学習モデルの構築に必要なさまざまなパッケージがあらかじめインストールされており、初心者がつまづきやすい環境構築が必要ありません。RAMは16Gあり、GPUも使用可能です。一般的なノートパソコン以上の性能が自由に使える環境が整っています。
本記事では、このKernelを用いたKaggle入門コンテンツを提供します。
自分で手を動かしながらKaggleのエッセンスを学べるような10つのKernelを用意しました。
言語としてはPython3、形式はNotebookを選択します。Kernelの使い方
ここでは、Kernelの具体的な使い方を解説します。
次の章にある「1. まずはsubmit! 順位表に載ってみよう」のリンクをクリックして、作業してみてください。リンクを開くと、次のようなKernelのページが開きます。まずは右上の「Fork」をクリックしてください。
すると、自分で編集できる画面に遷移します。ForkしたKernelは元のKernelとは別物なので、自分の好き勝手に編集して問題ありません。
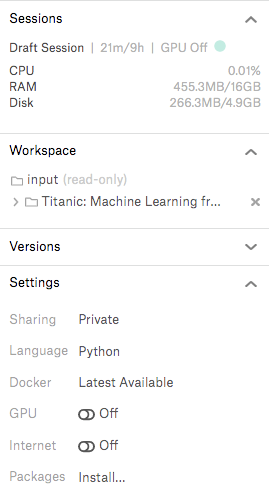
Kernelは「Public」「Private」という公開設定があります。現在の状況は右のサイドバー>Settings>Sharingから確認できます。例えば、私のKennelは皆さんに使ってもらうために「Public」になっています。デフォルトは「Private」なので、意図的に操作しない限りは「Public」にはなりません。安心して自由に記述することが可能です。
Kernelはいくつものセルに分割されています。セルには2種類あり、1つは説明文などを記述する「Markdown」、もう1つはPythonのコードを記述する「Code」です。次の写真で言うと、上のセルがMarkdown、下のセルがCodeです。
セルは自由に追加・削除ができます。新規追加は上の画像で出ている「+Code」「+Markdown」から可能で、移動・削除はセルを選択した状態でメニューバーの「Edit」「Insert」から操作できます。
Codeセル内でSHIFT+ENTERすると、個々の単位でプログラムを実行できます。段階的にプログラムを処理できるので、個々のセルで何が起きているかが理解しやすいかと思います。
Kernelの操作方法やショートカットなどは、Jupyter Notebookとほぼ同様です。さらなる便利な使い方の詳細が知りたい場合は「Jupyter Notebook 使い方」などで調べると良いでしょう。
入門 10 Kernel
ここでは、自分で手を動かしながらKaggleのエッセンスを学べるような10つのKernelを掲載します。
本記事内では理論的な面を解説し、各テーマに対応するKernelで実践していただく構成になっています。本記事を読むだけでも理解できるような構成にしていますが、ぜひKernelをForkしてご自身で操作してみてください。
現在、最初の2つのKernelを公開しています。今後、随時更新予定です。
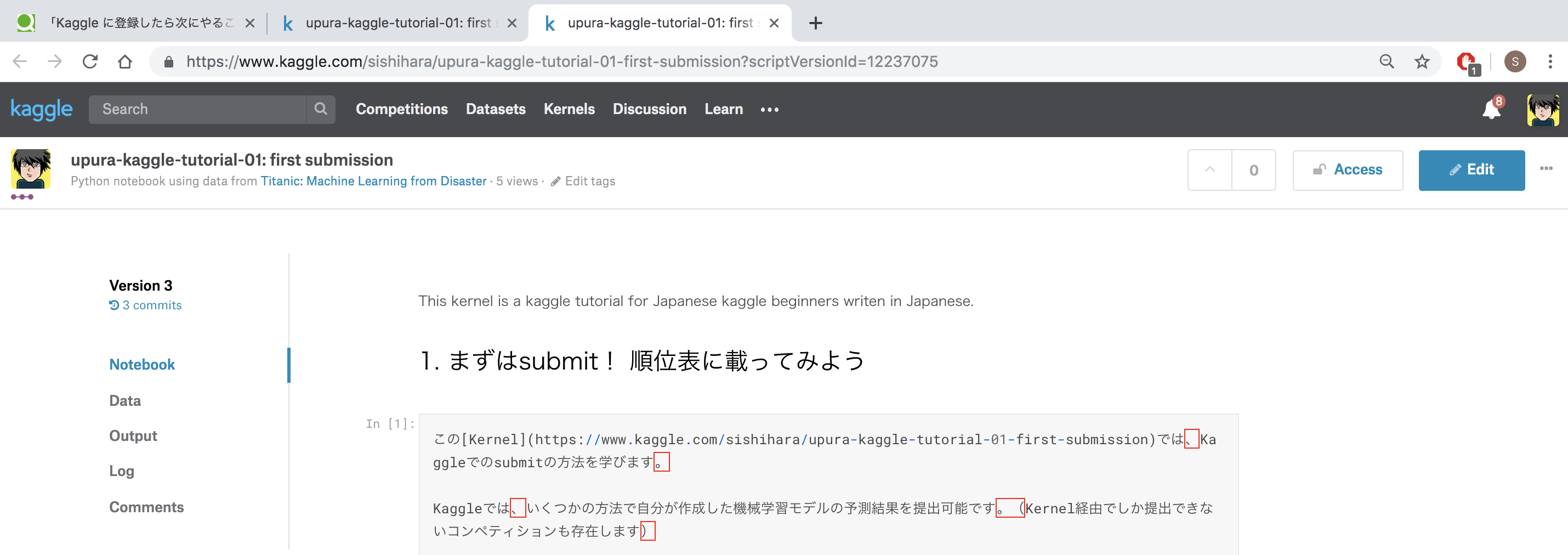
1. まずはsubmit! 順位表に載ってみよう
このKernelでは、Kaggleでのsubmitの方法を学びます。
Kaggleでは、いくつかの方法で自分が作成した機械学習モデルの予測結果をsubmit可能です。(Kernel経由でしかsubmitできないコンペティションも存在します)
- Kernel経由
- csvファイルを直接アップロード
- Kaggle APIを利用
今回は、Kernel経由でsubmitしてみましょう。
このKernelにはいろいろなセルが含まれていますが、一旦は何も考えずに右上の「COMMIT」をクリックしてみてください。
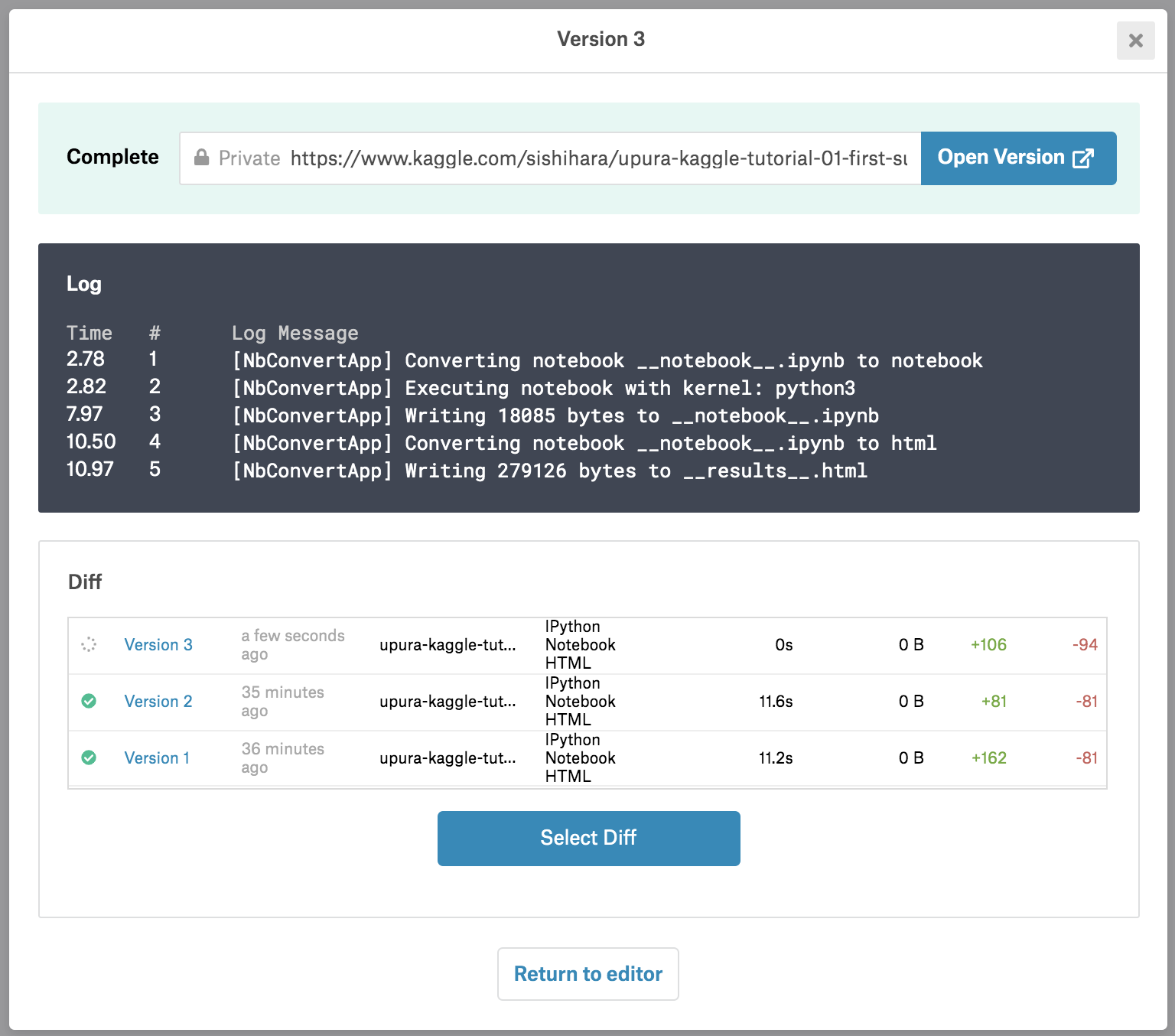
次のような画面が立ち上がり、Kernel全体が実行されます。
実行が終わったら「Open Version」をクリックしましょう。
実行されたKernelの情報が表示されています。KernelはCOMMITするごとに、自動的にバージョンが管理されます。
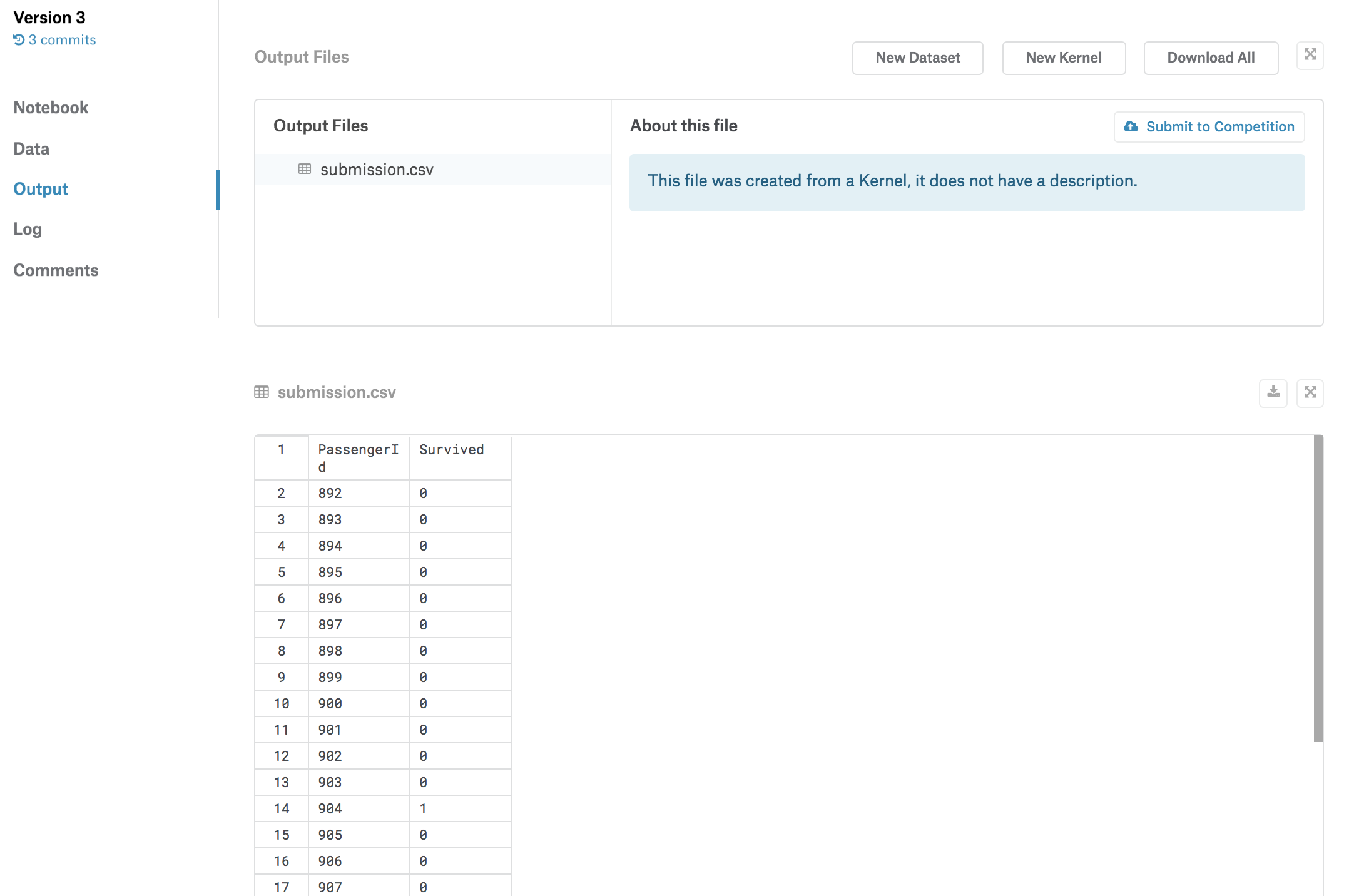
左の「Output」タブを押すと、このバージョンのKernelでの予測結果が「submission.csv」というファイルで保存されています。
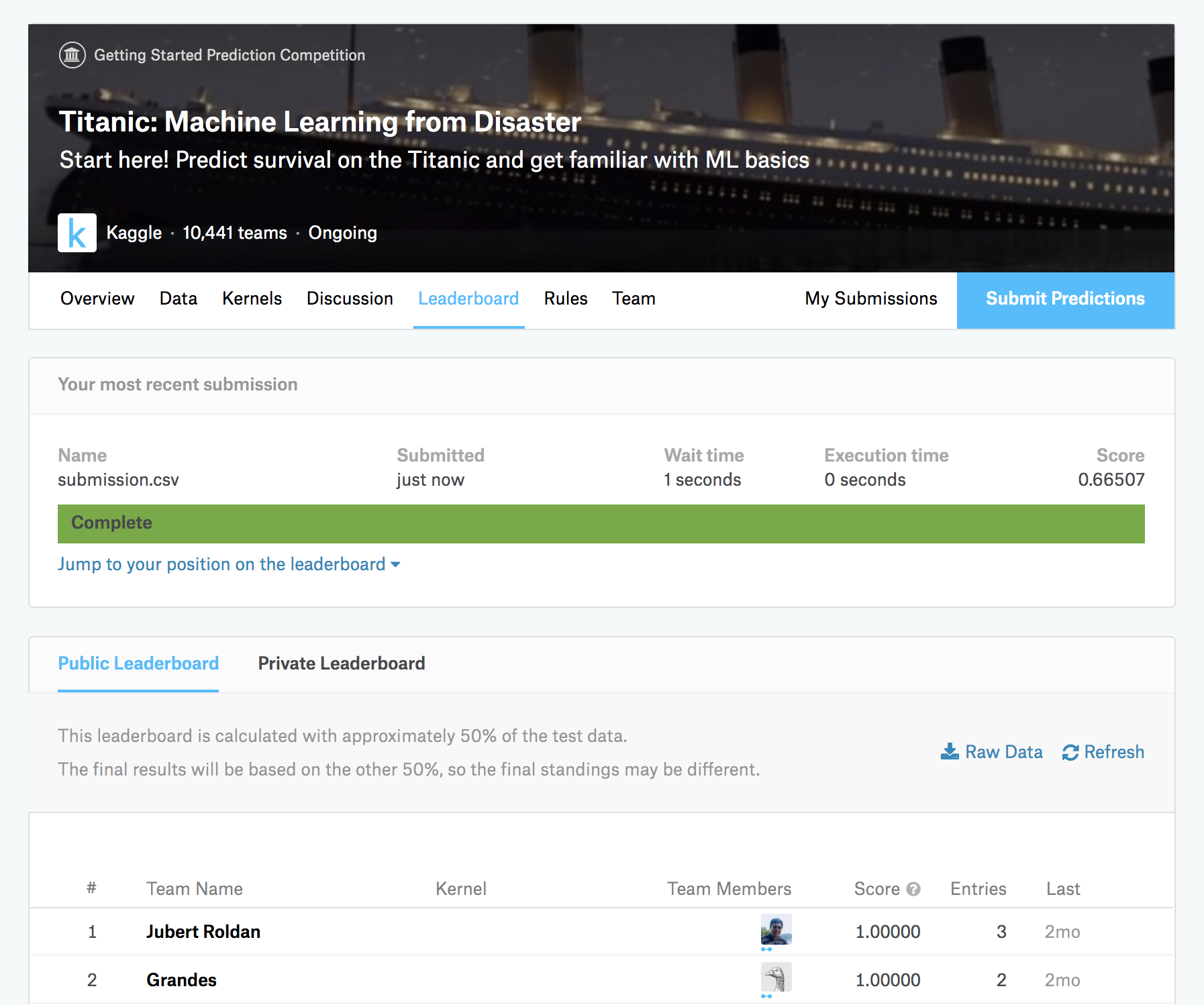
「Submit to Competition」を押すと、このファイルがsubmitされます。スコアが計算され、今回の場合は「0.66507」という値が算出されています。
無事にスコアが付いたので、順位表にも自分のアカウントが登場しました。
このKernelでは、Kernel経由でsubmitする方法を学びました。「Output」タブから「submission.csv」をダウンロードすることも可能なので、csvファイルを直接アップロードする方法も試してみてください。
なおKaggle APIを利用してsubmitする方法に興味があれば、こちらのブログなどをご覧ください。
2. 全体像を把握! submitまでの処理の流れを見てみよう
このKernelでは、前回は一旦無視したKernelの処理の流れを具体的に見ていきます。ぜひ、実際に一番上からセルを実行しながら読み進めてみてください。
具体的な処理の流れは、次のようになっています。
- パッケージの読み込み
- データの読み込み
- 特徴量エンジニアリング
- 機械学習アルゴリズムの学習・予測
- submit(提出)
パッケージの読み込み
import numpy as np import pandas as pdまずは、以降の処理で利用する「パッケージ」をimportします。 パッケージをimportすることで、標準では搭載されていない便利な機能を拡張して利用できます。
例えば次のセルでimportするnumpyは数値計算に秀でたパッケージで、pandasはTitanicのようなテーブル形式のデータを扱いやすいパッケージです。
ここでは、最初に必要な2つのパッケージをimportしています。importはどこで実施しても構いません。(特にScript形式の場合は、冒頭でのimportが望ましいです)
データの読み込み
ここでは、Kaggleから提供されたデータを読み込みます。
まずはどういうデータが用意されているかを確認しましょう。詳細はKaggleのコンペティションのページの「Data」タブに記載されています。
train = pd.read_csv("../input/train.csv") test = pd.read_csv("../input/test.csv") gender_submission = pd.read_csv("../input/gender_submission.csv")
- 「gender_submission.csv」は、submitのサンプルです。このファイルで提出ファイルの形式を確認できます。仮の予測として、女性のみが生存する(Survivedが1)という値が設定されています。
- 「train.csv」は機械学習の訓練用のデータです。これらのデータについてはTitanic号の乗客の性別・年齢などの属性情報と、その乗客に対応する生存したか否かの情報(Survived)が格納されています。
- 「test.csv」は、予測を実施するデータです。これらのデータについてはTitanic号の乗客の性別・年齢などの属性情報のみが格納されており、訓練用データの情報を基に予測値を算出することになります。
- 「train.csv」と比較すると、Survivedという列が存在しないと分かります。(この列があったら全て正解できてしまうので当然ですね)
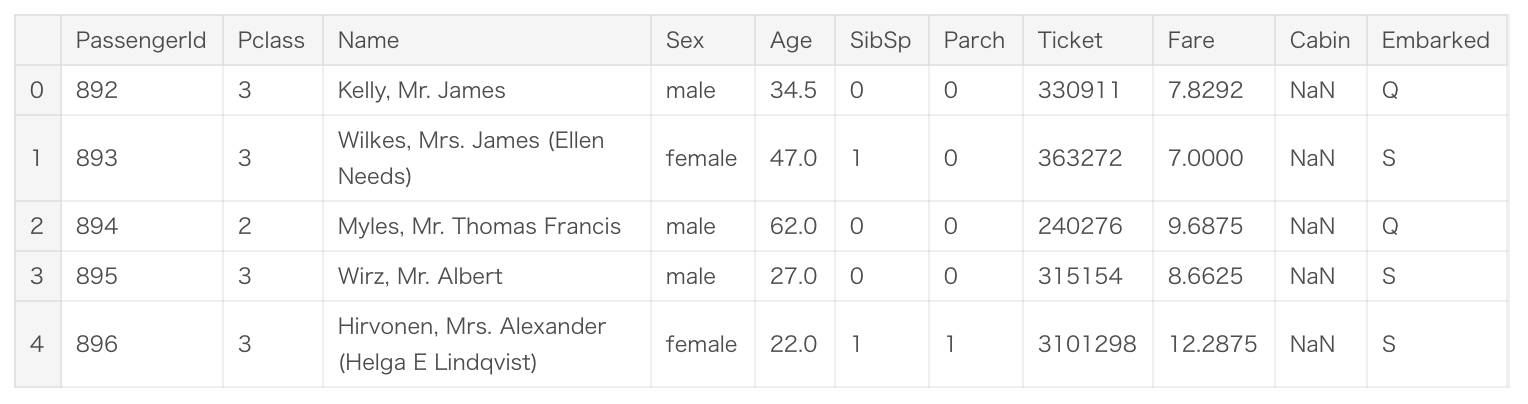
これらは、Kaggleから提供された大元のデータです。
例えばName, Sexなどは文字列で格納されており、そのままでは機械学習アルゴリズムの入力にすることはできません。 機械学習アルゴリズムが扱える数値の形式に変換していく必要があります。
Nanというのは、データの欠損です。こうした欠損値は、一部の機械学習アルゴリズムではそのまま扱うこともできますが、平均値など代表的な値で穴埋めする場合も多いです。
特徴量エンジニアリング
次のような処理を「特徴量エンジニアリング」と呼びます。
- 読み込んだデータを機械学習アルゴリズムが扱える形に変換
- 既存のデータから、機械学習アルゴリズムが予測する上で有用な新しい特徴量を作成
前者について、例えばSexの'male', 'female'をそれぞれ0, 1に変換します。また欠損を平均値などで穴埋めする処理も行います。具体的な処理内容については、Kernelを参照ください。
後者については、次のKernel「3. ここで差がつく! 仮説に基づいて新しい特徴量を作ってみよう」で詳しく掘り下げていきます。
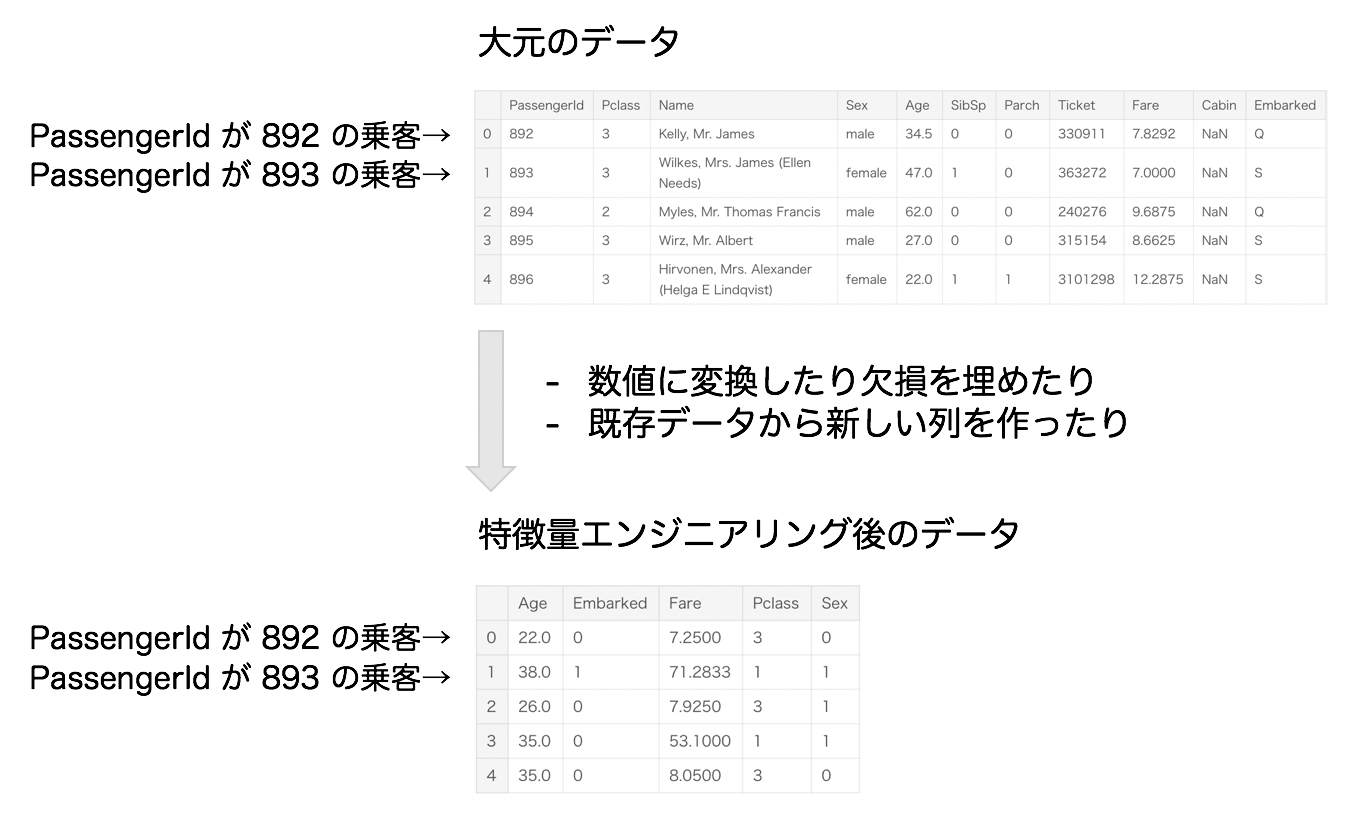
大元のデータから次のようなデータを作成するイメージになっています。
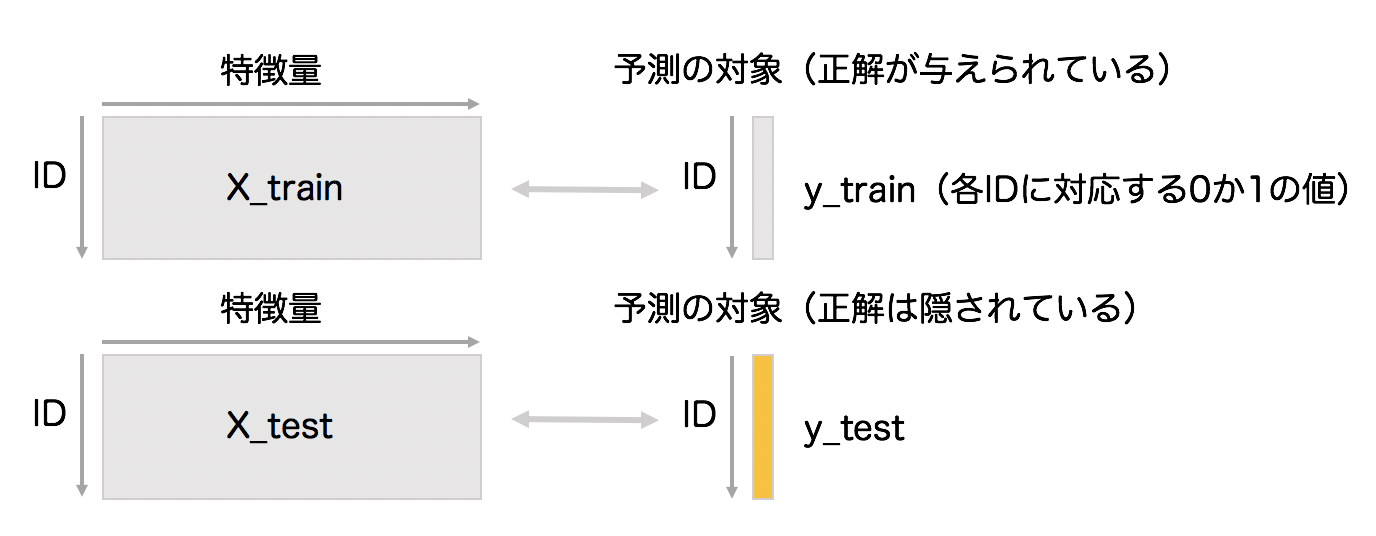
特徴量エンジニアリング後のデータを、より一般化して表現したのが、次の図です。
大元のデータから特徴量エンジニアリングを経て、X_train, y_train, X_testというデータの塊を作ります。大雑把に表現すると機械学習は、X_train, y_trainの対応関係を学習し、X_testに対応する(隠された)y_testの値を当てるという枠組みになっています。
機械学習アルゴリズムの学習・予測
用意した特徴量と予測の対象のペアから、機械学習アルゴリズムを用いて予測器を学習させましょう。
from sklearn.linear_model import LogisticRegression clf = LogisticRegression(penalty='l2', solver="sag", random_state=0) clf.fit(X_train, y_train)ここではロジスティック回帰という機械学習アルゴリズムを利用します。
機械学習アルゴリズムの振る舞いはハイパーパラメータという値で制御されます。
LogisticRegression()の括弧内の値が該当します。ハイパーパラメータの調整方法については「5. 機械学習アルゴリズムのお気持ち?! ハイパーパラメータを調整してみよう」で詳しくみていきます。学習を終えると、予測値が未知の特徴量(X_test)を与えて予測させることができます。
y_pred = clf.predict(X_test)y_predには0か1の予測値が格納されています。
submit(提出)
最後に、Kernel経由でsubmitするために予測値を提出ファイルの形式に整えます。
sub = pd.DataFrame(pd.read_csv("../input/test.csv")['PassengerId']) sub['Survived'] = list(map(int, y_pred)) sub.to_csv("submission.csv", index = False)Kaggleの運営側はy_testの中身を把握しているので、y_testとy_predが比較され、自分の提出した予測値の性能がスコアとして返ってくる仕組みになっています。
このKernelでは、submitに向けたKaggleでの処理の流れを追いました。
3. ここで差がつく! 仮説に基づいて新しい特徴量を作ってみよう
1つ目のKernelでは、Kernelを用いてKaggleのコンペティションに提出して順位表に載る方法、2つ目のKernelでは全体の処理の流れを解説しました。
3〜7つ目のKernelでは、既存のKernelに手を加えていきながら、スコアを上げていく方法を学んでいきます。ここで紹介する方法は、メダルが獲得できる開催中のコンペティションにも汎用的に使えるものだと思っています。「このような方法でスコアを上げているんだな〜」と知り、自分でコンペティションに参加していく際の道標になればと考えています。
ここでは、特徴量エンジニアリングの部分で、スコアの向上を体験してみましょう。
さっそく特徴量エンジニアリングの解説を始めようかと思いますが、その前に前提的な話として、Kaggleに取り組む上で欠かせない「再現性」の話をします。
再現性の大切さ
「再現性がある」とは、何度実行しても同じ結果が得られることです。Kaggleで言うと、同一のスコアが得られると言い換えても良いでしょう。
再現性がないと、実行ごとに異なるスコアが得られてしまいます。今後、特徴量エンジニアリングなどでスコアの向上を試みても、予測モデルが改善されたか否かを正しく判断できなくなる問題が生じます。
実は、2つ目のKernelには再現性がありません。その原因は、Ageという特徴量の欠損値を埋める際の乱数です。ここでは標準偏差を考慮した乱数で欠損値を穴埋めしているのですが、この乱数は実行ごとに値が変わるようになってしまっています。
age_avg = data['Age'].mean() age_std = data['Age'].std() data['Age'].fillna(np.random.randint(age_avg - age_std, age_avg + age_std), inplace=True)何度実行しても同じ値を発生させるためには、seedというものを固定すれば良いです。
np.random.seed(seed=777)機械学習アルゴリズムの大半は乱数を利用するので、再現性を担保するためにはseedを設定しておかなければなりません。2つ目のKernelを振り返ると、機械学習アルゴリズムのロジスティック回帰のハイパーパラメータとして
random_state=0を与え、seedを固定していました。clf = LogisticRegression(penalty='l2', solver="sag", random_state=0)このようにKaggleを進めていく際には、きちんと再現性が取れていることを随時確認していきましょう。(なお、GPUを利用する場合など、どうしても再現性が担保できない場合もあります)
仮説から新しい特徴量を作る
「仮説と可視化から新しい特徴量を作る Kaggleのタイタニックを例に」に書いたような内容を掲載予定です。
特徴量エンジニアリングの技法を学ぶ
- 日本語の書籍としては『機械学習のための特徴量エンジニアリング』があります。
- スライドでは「最近のKaggleに学ぶテーブルデータの特徴量エンジニアリング」が詳しいです。
4. 勾配ブースティングが最強?! いろいろな機械学習アルゴリズムを使ってみよう
これまでは機械学習アルゴリズムとして、ロジスティック回帰を採用していました。
ここでは、いろいろな機械学習アルゴリズムを紹介します。
現在のKaggleでよく使われているのは、勾配ブースティングという機械学習アルゴリズムの「LightGBM」というパッケージです。実際にKernelでLightGBMを使って学習・予測を実行し、スコアの変化を確認してみたいと思います。
5. 機械学習アルゴリズムのお気持ち?! ハイパーパラメータを調整してみよう
先にも説明したように、機械学習アルゴリズムの振る舞いはハイパーパラメータという値で制御されます。もちろん、ハイパーパラメータの値次第で予測結果は変わり得ます。
ハイパーパラメータの調整は、主に2種類の方法があると思います。
- チューニングツールを使う
- 手動で調整
前者としては、Grid search, Bayesian Optimization,Hyperopt, Optunaなど、いくつかのツールがあります。Kernelでは、これらの使い方を解説予定です。
ただし最近のKaggleのコンペティションでは、データサイズが大きいため上記のツールでのハイパーパラメータ調整が現実的な時間で終わらない問題もあります。また一般に、ハイパーパラメータでのスコアの上がり幅は特徴量エンジニアリングで良い特徴量を見つけた場合に劣るので、あまり時間をかけずに手動で微調整をする場合も多いように感じます。
チューニングツールを使うにせよ、手動で調整するにせよ、機械学習アルゴリズムをブラックボックス的に利用するのではなく、ハイパーパラメータを正しく理解することが非常に大切です。
LightGBMを利用する場合は、英語ですが公式のdocumentationの一読をオススメします。なお日本語の記事だと、例えばこちらにLightGBMなどの勾配ブースティングの主要なハイパーパラメータ解説がありました。
6. submitのその前に! 「Cross Validation」の大切さを知ろう
3〜5つ目のKernelでは、特徴量エンジニアリング・機械学習アルゴリズム・ハイパーパラメータの面で、スコアを上げていく方法を学びました。
これまでスコアの上昇は、実際にKaggleに提出することで確認していました。しかし実際には、Kaggleのコンペティションには1日のsubmit回数に制限があり、スコアが上がる保証もないのに気軽に提出するのは得策ではありません。
またメダルが獲得できるコンペティションでは、y_testの一部データのみがpublic LBに利用されておりスコアを随時確認できますが、最終順位は残りのprivate LBのデータに対する性能で決定します。
public LBで良いスコアが出ても、public LBのデータのみに過学習した結果の可能性があり、必ずしもprivate LBでの性能に寄与するかは分からないということです。
ここでは以上のKaggleのコンペティションに参加していく上での問題を踏まえて、訓練用データを用いて予測モデルの性能を測る「Cross Validation」という手法を解説します。
「Cross Validationはなぜ重要なのか【kaggle Advent Calendar 3日目】」に書いたような内容を掲載予定です。
7. 三人寄れば文殊の知恵! アンサンブルを体験しよう
ここでは、機械学習における「アンサンブル」について解説します。アンサンブルとは、複数のモデル(学習器)を組み合わせることで精度の高いモデルを獲得する手法です。
「『Kaggle Ensembling Guide』はいいぞ【kaggle Advent Calendar 7日目】」に書いたような内容を掲載予定です。
8. Titanicの先へ行く①! 複数テーブルを結合してみよう
Titanicでは訓練用データが「train.csv」という1つのcsvファイルにまとまっていますが、複数ファイルが用意されている場合も多いです。
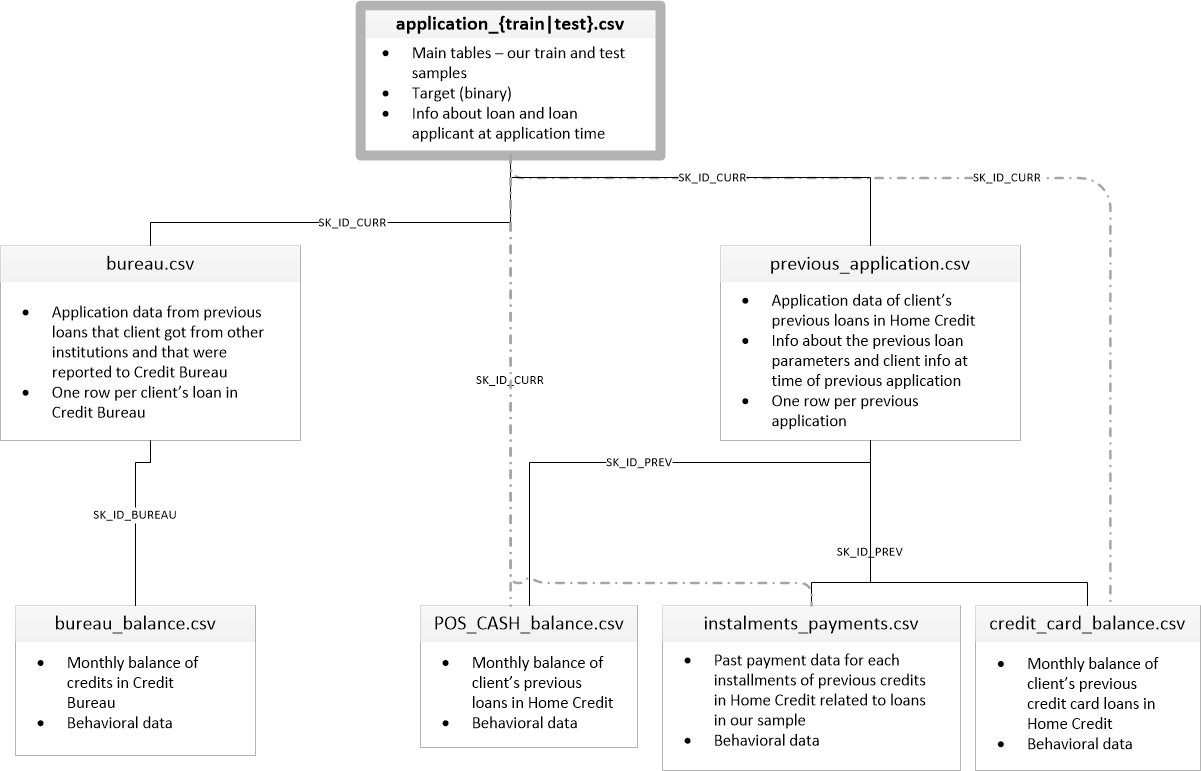
例えば「Home Credit Default Risk」というコンペティションでは、次の図のような関係を持つ複数のファイルが提供されました。
(画像はHome Credit Default Riskの「Data」タブから引用)個人的には、こういったコンペティションに直面した際のデータの扱い方が分からず、Titanicの次へ行く障壁の1つになっているのではないかと考えています。
ここでは、複数のファイルを結合して機械学習アルゴリズムに入力するためのデータを用意する方法を掲載予定です。
9. Titanicの先へ行く②! 画像データに触れてみよう
Kaggleのコンペティションで扱うデータは、大きく分けて次の3種類があります。
- テーブルデータ
- 画像データ
- テキストデータ
Titanicのデータはテーブルデータに該当しますが、他のコンペティションでは画像データやテキストデータを扱う場合も多いです。
「PetFinder.my Adoption Prediction」のように、3種類全てのデータを扱うコンペティションも存在します。テーブルデータとしてはペットの犬種や年齢、画像データとしてはペットの写真、テキストデータとしてはペットの説明文といった情報が提供されました。
9〜10つ目のKernelでは、それぞれ画像とテキストデータを扱う方法を解説予定です。
10. Titanicの先へ行く③! テキストデータに触れてみよう
ここでは、テキストデータを扱う方法を解説します。
メダルが獲得できる開催中のコンペティションに参加しよう
入門 10 Kernelで学んだこと
- 1つ目のKernelでは、Kernelを用いてKaggleのコンペティションに提出して順位表に載る方法、2つ目のKernelでは全体の処理の流れを解説しました。
- 3〜7つ目のKernelでは、既存のKernelに手を加えていきながら、スコアを上げていく方法を学びました。
- 8〜10つ目のKernelでは、Titanicでは扱わない複数テーブルを結合する方法、画像・テキストデータを扱う方法を紹介しました。
(3つ目以降はKernelはまだ無いですが、Kernelで取り扱う内容には触れました。私のKernel準備が整う前に、ご自身で検索するなどして勉強することもできそうです)
タイトルにもある通り「これだけやれば十分戦える!」と言える内容になっているかと思います。ぜひ次は、メダルが獲得できる開催中のコンペティションに参加してみてください。
開催中のコンペティションを確認する
開催中のコンペティションの一覧は、KaggleのCompetitionsというページの「Active Competitions」で確認できます。それぞれのページでは具体的なコンペティションの内容が記載されています。
ただし、Titanicと同様のチュートリアル的なコンペティションなど、開催中でもメダルが獲得できないコンペティションもあるので注意が必要です。Kaggleでメダルが獲得できるコンペティションか否かは、トップページの「Tiers」部分の表記で確認できます。
例えば、メダルが獲得できるコンペティションでは、次のような表記です。
一方で、メダルが付与されないコンペティションでは、次のような表記になっています。
なお、Kaggleのコンペティションには、いくつかの分類があります。一概には言えませんが、ある程度この分類でもメダル獲得の可否が判断できます。
- Common Competition Types
- Featured
- Research
- Getting Started
- Playground
- Other Competition Types
- Recruitment
- Annual
- Limited Participation
こちらの分類の日本語訳は、こちらで解説されています。
初心者にオススメの戦い方
ここでは参加するコンペティションが決まった後、初心者にオススメの戦い方を書いておきます。tkm2261さん流のKaggle入門方法にも、似たような内容が記載されています。
- ベースラインとなるKernelを探す
- 本記事の内容を参考に、ベースラインを改善する
ベースラインとなるKernelを探す
今回は「Santander Customer Transaction Prediction」を例に解説します。
まず「Kernels」タブに行き、右のプルダウンで「Most Votes」を選びましょう。
すると、参加者に多く「いいね」された順にKernelが表示されます。
0.9,0.901など数字の数字は、そのKernel経由でsubmitされスコアが付いていることを意味します。稀に、csvファイルでのアンサンブルのみを実施しているKernelが上位に来ているのは注意が必要です。きちんと、Kaggleから提供された大元のデータからsubmitまでの一連の流れを実行しているKernelをベースラインとすると良いでしょう。最上位のKernelはタイトルに「EDA」と入っています。これは「Explanatory Data Analysis」、日本語だと「探索的データ分析」を意味します。これらのKernelは、提供されたデータの特徴などを解説してくれており、ベースラインとして適していると思います。
本記事の内容を参考に、ベースラインを改善する
ベースラインのKernelが決まったら、本記事の入門 10 Kernelと同様に、KernelをForkして自分で手を動かしてみてください。
例えば特徴量エンジニアリングで新しい特徴量を追加したり、機械学習アルゴリズムを差し替えたり、ハイパーパラメータを調整したり、アンサンブルをしてみたり、いろいろな手数があるかと思います。自分のアイディアでスコアが増減する経験を楽しんでみてください。
できれば、自分が取り組んだコンペティションには終了日まで継続して取り組んでみてほしいです。Twitterのタイムラインなどで一喜一憂したり、終了後に共有される上位者の解法から多くのことを学んだり、Kaggleの醍醐味が味わえるかと思っています。
その意味では、締切2週間前くらいのコンペティションに参加するのも1つの手だと思います。(コンペティションの参加は締切1週間前に締め切られる点には注意してください)
さらなる学びのために
最後に、さらなる学びに向けたリンクをいくつか掲載します。
kagger-ja slack
主に日本人のKagglerが集まっているSlackのワークスペースです。質問が飛び交うチャンネルやコンペティションの解法を共有するチャンネルなどが活発で、参加して閲覧しているだけでも多くの知見が得られると思います。メールアドレスをフォームに入力するだけで、誰でも参加可能です。
過去ログはこちらで公開されています。
kaggler-ja wiki
kagger-ja slackで話題になった内容などを体系的にまとめたページです。次のようなコンテンツがまとめられています。
- kaggle初心者ガイド
- なんでもkaggle関連リンク
- よくある質問
- 過去コンペ情報
Kaggle Tokyo Meetupの動画・資料
Kaggle Tokyo Meetupは、Kagglerが一堂に会すイベントです。上位に入賞した方が解法をプレゼンしたり、多種多様なLTがあったり、学びの多いイベントです。
過去5回開催されており、特に第4回は動画も公開されているのでオススメです。
tkm2261さんのKaggle入門動画
次のコンテンツが動画で用意されています。
- Kaggleについて
- Porto Seguroコンペについて
- GCP立ち上げ(アカウント作ると付いてくる$300クーポン使用)
- Bitbucketでgitリポジトリ作成
- GCPの使い方
- Ubuntuセットアップ
- Anacondaセットアップ
- Pythonコーディング (Pandas, scikit-learn, xgboost)
- Gitの使い方
- loggerの使い方
- ロジスティック回帰
- Cross Validation解説
- Grid Search解説
- xgboost解説
- on hot encoding解説
- Kaggleの提出方法
- おまけ: 私の過去コンペのコードの解説
twitter Kaggle リスト
私が日々見ているKagglerを集めたtwitterのリストです。Kaggleに取り組む方々の日常から、さまざまな刺激を受けています。
おわりに
本記事では「Kaggleに登録したら次にやること」と題して、Kaggleに入門したい方に向けた情報を掲載しました。少しでも多くの方のお役に立てていれば幸いです。
Kaggle入門者に向けたより良いコンテンツになるよう、随時更新を重ねていきたいと思います。
- 投稿日:2019-03-30T02:18:13+09:00
ConoHa VPS(CentOS7)+Flask+Nginx+uWSGIでWEBアプリを作ってみる(2)
ConoHa VPS(CentOS7)+Flask+Nginx+uWSGIでWEBアプリを作ってみる(1)
の続き。Nginx+uWSGIを使って本番環境で動かしてみます。
以下を参考にしました。
- Flask + uWSGI + Nginx でハローワールドするまで @ さくらのVPS (CentOS 6.6)
- Flask+Nginx+uWSGI+CentOS7でアプリケーションを作る際にやったこと+日記::12/9
- 便利で超強力なWSGIサーバー uWSGI を使ってみよう
1. ドメイン取得
とりあえずドメインを取得します。
お名前.comとかGoogle Domainsからドメインは取れます。
無料だったらFreenomというサービスがあるようです。参考
- freenomでドメインの取得
- 無料のドメインを取得する
- freenom で取得した無料ドメインを ConoHa の VPS に登録する2. uWSGIとは
まず,WSGI(Web Server Gateway Interface; ウィズギーと読むらしい)とは,Pythonで実装されたWebアプリケーションとWebサーバ間のインターフェースを規定した仕様(PEP333)です。uWSGIは,既存のWebサーバ(Nginxなど)にWSGI仕様を付加し,WSGIに対応したWebサーバを作成します。つまり,
[WSGIに対応したWebサーバ] = Nginx + uWSGIといった関係になっている(と思われます)。
3. uWSGIの設定
uWSGIの設定ファイルを作成します。設定ファイル名は何でもよいですがuwsgi.iniとしておきます。
なお,デーモン化するためにdaemonizeを指定しています。uwsgi.ini[uwsgi] module = app socket = /home/{ユーザ名}/app/uwsgi.sock chmod-socket = 666 callable = app uid = {ユーザ名} gid = {ユーザ名} daemonize = /home/{ユーザ名}/uwsgi/uwsgi.log pidfile = /home/{ユーザ名}/uwsgi/app.pidsocket, daemonize, pidfileのパスはpermissionが問題なければどこでも良いと思います。
4. Nginxの設定
Nginxの設定ファイルは/etc/nginx/conf.d/に拡張子confで置けば勝手に読み込まれるので,名前をapp.confとして次のように作成します。
app.confserver { listen 80; server_name {取得したドメイン}; charset utf-8; client_max_body_size 75M; location / { try_files $uri @myapp; } location @myapp { include uwsgi_params; uwsgi_pass unix:///home/{ユーザ名}/app/uwsgi.sock; } }これで,Nginxを再起動すればいけるはずですが,permissionエラーになってしまいました。どうやら,Nginxがユーザnginxで実行されていることが原因のようだったので,以下のように5行目をコメントアウトして{ユーザ名}で実行するように設定を変更しました。
/etc/nginx/nginx.conf# For more information on configuration, see: # * Official English Documentation: http://nginx.org/en/docs/ # * Official Russian Documentation: http://nginx.org/ru/docs/ #user nginx; user {ユーザ名}; worker_processes auto; error_log /var/log/nginx/error.log; pid /run/nginx.pid;5. サーバの起動
ここまでくれば,以下の手順でサーバを起動できるはずです。
$ cd /home/{ユーザ名}/app $ systemctl restart nginx $ source env/bin/activate (env) $ uwsgi --ini uwsgi.inihttp://{取得したドメイン}にアクセスできれば成功です。
停止する場合は以下のようにします。$ cd /home/{ユーザ名}/app $ source env/bin/activate (env) $ uwsgi --stop /home/{ユーザ名}/uwsgi/app.pid (env) $ deactivate $ systemctl stop nginxおわり。
- 投稿日:2019-03-30T00:21:35+09:00
Responder + Vue.jsプロジェクト作成手順
TL;DR
最近
responderというPython製の非同期処理が売りのWebフレームワークを知ったので、Vue.jsと組み合わせてプロジェクトを作成した手順を紹介します。プロジェクト作成
Responder側
まずはディレクトリを作成して
pipenvで環境を作っていきます。$ mkdir responder-vue-sample $ cd responder-vue-sample $ pipenv --python 3.7
Pipfileを以下のように編集[[source]] name = "pypi" url = "https://pypi.org/simple" verify_ssl = true [dev-packages] [packages] asgiref = "==2.3.2" responder = "*" [requires] python_version = "3.7"
responder以外にasgirefをPipfileにバージョンを固定して記述しています。
asgirefはresponderの依存パッケージでresponderをインストールすれば自動的にインストールされるのですが、記事投稿時そのままでは3.0.0が入ってしまいVue.jsのビルド済みファイルが入るstaticディレクトリ配下のファイルを正しく読み込めないため2.3.2で固定しています。以下のコマンドでライブラリをインストールします。
$ pipenv installサーバープログラム
プロジェクト直下に
app.pyを作成してstatic/index.htmlを表示するだけのコードを記述します。app.pyjimport responder api = responder.API() if __name__ == '__main__': api.add_route('/', static=True) api.run()Vue.js側
まず
vue-cliをグローバルにインストールします。$ npm install -g @vue/cliインストール後、先程作ったプロジェクト直下にVue.jsのプロジェクトを作っていきます。
カレントディレクトリの指定以外はお好みで大丈夫です。$ vue create . Vue CLI v3.5.1 ? Generate project in current directory? (Y/n) Y ? Please pick a preset: (Use arrow keys) ❯ default (babel, eslint) Manually select featuresVue.jsのプロジェクトの作成ができたら、ビルドしたファイルを
staticに吐くようにpackage.jsonを編集します。package.json{ "name": "responder-vue-sample", "version": "0.1.0", "private": true, "scripts": { "serve": "vue-cli-service serve", - "build": "vue-cli-service build", + "build": "vue-cli-service build --dest static", "lint": "vue-cli-service lint" }, "dependencies": { "vue": "^2.6.6" }, "devDependencies": { "@vue/cli-plugin-babel": "^3.5.0", "@vue/cli-plugin-eslint": "^3.5.0", "@vue/cli-service": "^3.5.0", "babel-eslint": "^10.0.1", "eslint": "^5.8.0", "eslint-plugin-vue": "^5.0.0", "vue-template-compiler": "^2.5.21" }, "eslintConfig": { "root": true, "env": { "node": true }, "extends": [ "plugin:vue/essential", "eslint:recommended" ], "rules": {}, "parserOptions": { "parser": "babel-eslint" } }, "postcss": { "plugins": { "autoprefixer": {} } }, "browserslist": [ "> 1%", "last 2 versions", "not ie <= 8" ] }次にベースURLを
/からstaticに変更するためにvue.config.jsを作成してpublicPathを変更します。vue.config.jsmodule.exports = { publicPath: "static" }最終的に以下のようなファイル構成になるかと思います。
$ tree -L 1 tree -L 1 . ├── Pipfile ├── Pipfile.lock ├── README.md ├── app.py ├── babel.config.js ├── node_modules ├── package.json ├── public ├── src ├── static ├── templates ├── vue.config.js └── yarn.lockビルドと実行
では実際にビルドしてからサーバープログラムを起動して
responderからVue.jsが呼べているか確認していきます。$ pipenv run responder build # or yarn build $ pipenv run python app.pyこれで
localhost:5042にアクセスして以下のようにVue.jsのホーム画面が出たら終了です。お疲れ様でした。完成したものはこちら
https://github.com/KeisukeToyota/responder-vue-sample