• 環境
  • CentOS Linux release 7.8.2003 (Core)
  • Eclipse IDE for Enterprise Java Developers.Version: 2020-03 (4.15.0)
  • openjdk version "11.0.7" 2020-04-14 LTS
  • JSF 2.3.9

事象 : ajaxの処理を追加してページを表示しようとしたらHTTPSステータス500になった

EclipseのConsoleのエラー

javax.faces.view.facelets.TagException: /base.xhtml @18,103 <f:ajax> Unable to attach <f:ajax> to non-ClientBehaviorHolder parent
    at com.sun.faces.facelets.tag.jsf.core.AjaxHandler.applyNested(AjaxHandler.java:276)
    at com.sun.faces.facelets.tag.jsf.core.AjaxHandler.apply(AjaxHandler.java:148)
    at javax.faces.view.facelets.DelegatingMetaTagHandler.applyNextHandler(DelegatingMetaTagHandler.java:137)
    at com.sun.faces.facelets.tag.jsf.ComponentTagHandlerDelegateImpl.apply(ComponentTagHandlerDelegateImpl.java:179)
...省略...

base.xhtml

...省略...
<h:inputHidden id="file">
  <f:ajax event="change" execute="@form" render="@form" listener="#{uploadBean.uploadFile}" />
</h:inputHidden>
...省略...

原因 : f:ajaxはClientBehaviorHolderインタフェースを実装したタグ内でないと使えないから

Register an AjaxBehavior instance on one or more UIComponents implementing the ClientBehaviorHolder interface.
ajax(JSF 2.2 View Declaration Language: Facelets Variant)

(ざっくり訳)ClientBehaviorHolderインタフェースを実装する1つまたは複数のUIComponentsにAjaxBehaviorインスタンスを登録します。
今回の場合は、h:inputHiddenがClientBehaviorHolderインタフェースを実装しているかが問題だが、ClientBehaviorHolderのJavaDocを見たら対象外だった・・・

All Known Implementing Classes:
HtmlBody, HtmlCommandButton, HtmlCommandLink, HtmlDataTable, HtmlForm, HtmlGraphicImage, HtmlInputFile, HtmlInputSecret, HtmlInputText, HtmlInputTextarea, HtmlOutcomeTargetButton, HtmlOutcomeTargetLink, HtmlOutputLabel, HtmlOutputLink, HtmlPanelGrid, HtmlPanelGroup, HtmlSelectBooleanCheckbox, HtmlSelectManyCheckbox, HtmlSelectManyListbox, HtmlSelectManyMenu, HtmlSelectOneListbox, HtmlSelectOneMenu, HtmlSelectOneRadio
ClientBehaviorHolder (JavaServer Faces API (2.2))

対応 : タグをh:inputTextに変更する

...省略...
<h:inputText id="file" style="display:none;">
  <f:ajax event="change" execute="@form" render="@form" listener="#{uploadBean.uploadFile}" />
</h:inputText>
...省略...

SpringToolSuite4にLombokをインストールする。
MACのSTSでLombokを利用するにあたり、メモしたいと思います。

①公式サイトからダウンロード
https://projectlombok.org/download

②ダウンロードファイル（lombok.jar）をSpringToolSuite4のインストール場所に設置
/Applications/SpringToolSuite4.app/Contents/MacOS/ここに配置

③lombok.jarを起動しインストール（一覧にインストール先がない場合[Specifylocation]ボタンを押して、対象を選択）
インストール先:/Applications/SpringToolSuite4.app/Contents/Eclipse/eclipse.ini
選択後:Quit Installerクリック

インストールが完了すると、stsのフォルダ内にlombokが入ります。
以上でインストール完了です。

JavaのStream APIとSQLの対比に関するメモ。

Streamの公式ドキュメント

Java8の公式ドキュメントの内容を抜粋。
https://docs.oracle.com/javase/jp/8/docs/api/java/util/stream/Stream.html

順次および並列の集約操作をサポートする要素のシーケンスです。
（中略）
コレクションとストリームは、表面上似た点があるものの、異なる目的を持っています。コレクションは主に、要素の効率的な管理やアクセスに注力しています。これに対し、ストリームは要素の直接アクセスや操作の手段を持たず、代わりにソースやそのソースに対して集約的に実行される計算操作を宣言的に記述することに注力しています。
（中略）
ストリーム・パイプラインは順次、並列のいずれかで実行できます。この実行モードは、ストリームのプロパティの1つです。ストリームの作成時には、順次実行または並列実行の初期選択が行われます。

僕の理解が足りなくてドキュメント読んでも分かりにくいですが、ざっくり書くとこんなもの。

• コレクションと似ている
• 集約操作を行う
• 要素の直接アクセスや操作（get, remove）をするものではない
• 処理を順次・並列で選択できる

集約操作はSQLをイメージしてもらえれば理解は速くなります。

Stream APIとSQLの対比一覧

Stream API	対応するSQL	説明
Stream#map	SELECT	Stream内の要素を別の値やオブジェクトに変換する操作
Stream#filter	WHERE	条件に一致したデータのみにフィルタリングする操作。引数にはbooleanが戻り値となる式を書くことが必要。
Stream#max	MAX	最大値の取得
Stream#min	MIN	最小値の取得
IntStream#sum Collectors#summingInt	SUM	合計の取得

サンプルコード

前提条件

• lombok プラグインが導入されている前提
• スコープは適当

人物データとクラス

人物データを格納するテーブルとそのデータを保持するクラスを以下のように定義する。

■Personテーブル

id	name	age	job
1	yamada	25	---:
2	suzuki	28	---:
3	sato	30	---:
4	nakamura	41	---:
5	yamamoto	38	---:
6	akiyama	22	---:
7	tanabe	43	---:
8	ito	24	---:

■Personクラス

Persion.java

@Data
@AllArgsConstructor
public class Person {
    private int id;
    private String name;
    private int age;
}

更にPersonテーブルの全データを格納したリストをList<Person>として定義する。
List<Person>は以下と同義である。

List<Person> personList = Arrays.asList(
    new Person(1, "yamada", 25),
    new Person(2, "suzuki", 28),
    new Person(3, "sato", 30))
    new Person(4, "nakamura", 41))
    new Person(5, "yamamoto", 38))
    new Person(6, "akiyama", 22))
    new Person(7, "tanabe", 43))
    new Person(8, "ito", 24))
);

Stream#map

Java

List<String> nameList = personList.stream()
        .map(Person::getName)
      .collect(Collectors.toList()); 

SQL

SELECT
  p.name
FROM
  Person p

＜結果＞
["yamada", "suzuki", "sato", "nakamura, "yamamoto", "akiyama", "tanabe", ito]

Stream#filter

Java

List<String> nameList = personList.stream()
        .filter(p -> p.getAge() >= 40)
        .map(Person::getName)
        .collect(Collectors.toList()); 

SQL

SELECT
  p.name
FROM
  Person p
WHERE
  p.age >= 40 

＜結果＞
["nakamura", "tanabe"]

Stream#max

Java

Integer max = personList.stream()
        .map(Person::getAge)
        .max(Comparator.comparingInt(x -> x))
        .orElse(null);

SQL

SELECT
  max(p.age) max_age
FROM
  Person p

＜結果＞
43

Stream#min

Java

Integer max = personList.stream()
        .map(Person::getAge)
        .min(Comparator.comparingInt(x -> x))
        .orElse(null);

SQL

SELECT
  min(p.age) min_age
FROM
  Person p

＜結果＞
22

IntStream#sum／Collectors#summingInt

Java

int sum = personList.stream()
        .mapToInt(Persion::getAge)
        .sum();

int sum2 = personList.stream()
        .collect(Collectors.summingInt(Persion::getAge));

SQL

SELECT
  sum(p.age) sum_age
FROM
  Person p

＜結果＞
251

今回の記事では、ソ連の革命家、医師、哲学者、小説作家であったアレクサンダーボグダノフが提唱したテクトロジーと呼ばれる実践的組織構造学について紹介する。
テクトロジーでは組織が安定、成長、破綻する環境、条件について詳細に解説し、安定した組織を生成する手法について解説している。
テクトロジーの概念を拝借し、創造的な組織創造の手法を紹介したいと思う。

テクトロジーにおける組織の定義

テクトロジーでは、組織をオープンクローズ型の成長する有機体システムと定義している。
組織とは以下の要素で構成されている。
ビジョン・・・組織の目指すべき方向性。
経済・・・組織のボディ。巨大であるほど収容できる人の人数が増加する
金融・・・組織を循環する血液。
生産・・・もの、サービスを生産し、組織の経済を巨大化する手段。

これらの有機的な要素が相互作用し、成長することで組織という有機体が構成されていると考える。

テクトロジーにおける成長する有機体システムとは

テクトロジーでは、組織をオープンクローズ型の成長する有機体システムと定義している。
テクトロジーにおける組織の定義を中国の陰陽論によって説明することができる。
陰陽論とは、原初は混沌（カオス）の状態であると考え、この混沌の中から光に満ちた明るい澄んだ気、すなわち陽の気が上昇して天となり、重く濁った暗黒の気、すなわち陰の気が下降して地となった。この二気の働きによって万物の事象を理解し、また将来までも予測しようというのが陰陽思想である。
組織が外部からエネルギーを取り入れ、出力するインプット、アウトプットの運動を陰陽論における陽の気と捉えることができる。
逆に組織内部に沈殿し、成長し、ヒエラルキーを形成する秩序生成を担う運動を陰陽論における陰の気と捉えることができる。

テクトロジーにおける生産の定義

テクトロジーでは、組織における生産活動は以下の3つに分類されている。
人の生産・・・人に教育を施し、組織活動に従事する生産者を作成する
モノ、サービスの生産・・・外部から取得した資材を用いて、モノ、サービスの生産を行う。
アイデア・・モノ、サービスを生成するための知識、アイディアを作成する。
組織における生産活動を高めることで、組織の経済を成長させることができる。

テクトロジーにおける組織が不安定化する条件

テクトロジーにおける組織が不安定化する条件として以下の2点が挙げられる。
・外部からのエネルギー取得の減少・・外部から人、モノ、金の循環が減少することで組織のサイズ、経済を維持することできなくなる。
・ヒエラルキーシステムの固定化・・・ヒエラルキーシステムが巨大化し、組織が硬直化してしまう。
組織不安定化を回避する手法として以下の手段が有効とされている。
生産手段を研究、開発、更新を行い、組織の経済成長のスピードを増加させる。
組織が硬直化の原因になっているヒエラルキーシステムを解体し、適切なサイズに組み替える。

まとめ

アレクサンダーボグダノフがテクトロジーに関するアイディアを発表した時期は1920年代である。
独学で組織が破綻する条件、環境を発見し、持続可能な成長のコンセプトを提唱したアレクサンダーボグダノフの先見性は恐るべきものである。
ソ連は軍事、IT、経済においてアメリカと張り合うことができた超大国だった。
ソ連時代に考えられたアイディア、思想などは現代においても見直されるべきものだと思われる。

AtCoder Beginner Contest 169 B問題「Multiplication 2」の解説を行います。

問題URL :
https://atcoder.jp/contests/abc169/tasks/abc169_b

問題概要

$N$個の整数で構成された数列 ($A_1,...,A_N$)が与えられる。
$A_1×...×A_N$, つまり

\prod_{i=1}^{N} A_i

を求めよ。ただし、この値が$10^{18}$を超える場合は-1と出力せよ。

制約

・$2 \leq N \leq 10^5$
・$0 \leq A_i \leq 10^{18}$
・入力は全て整数

解説

この問題ですが多倍長整数の知識が必要な問題でした。これらの数列の値を、int型で入力しかけ算をするとオーバーフローが発生してしまいます。また、制約が$10^{18}$までであることから、long int型で入力しかけ算をしてもオーバーフローが発生してしまいます。

従って、何かしらの対策をしないといけません。

対策1 (数列を降順にソートする)

降順にソートすると、数列を、数字の大きい順に並び替えることが出来ます。数列をソートしても総積は同じなので、これは有効な手です。
その後、数列の値を掛け合わせて$10^{18}$を超えた時に-1と出力し処理を終了すればよいです。
計算量は ソートに$O(logN)$, かけ算に$O(N)$かかるので$O(NlogN)$です。

また、処理を終了しないと、一部言語ではTLEになります。理由は単純で、多倍長整数のかけ算に計算時間がかかってしまうからです。
例えば、Python3,C++,Javaで、$100×100$, $10^5×10^5$, $10^9×10^9$のかけ算、また$10^{18}$の複数回のかけ算をそれぞれ実行して、計算時間を比較してみます
(AtCoderのコードテストを利用しました)
(Python3ではint,C++ではlong long int, Javaではdouble型として値を入力して実行しました。)
(オーバーフローが発生する前提で計算をしています)

計算	Python3	C++	Java
$100×100$	18ms	6ms	122ms
$10^5×10^5$	21ms	10ms	106ms
$10^9×10^9$	18ms	7ms	122ms
$10^{18}×10^{18}$	19ms	8ms	122ms
${10^{18}}^{100}$	18ms	6ms	118ms
${10^{18}}^{10000}$	585ms	8ms	113ms
${10^{18}}^{100000}$	10500ms	9ms	118ms

ご覧の通り、C++やJavaでは計算時間にさほど差はみられませんが、Python3だと、計算回数が多くなることで実行時間制限である2sec(2000ms)より多くの計算時間がかかっていることが分かります。

対策2 (0に注意する)

数列の中に$0$が1つでも存在していると、総積は当然$0$になりますが、対策1と同様のことをすると、実は$0$を含んだ数列でも-1が出力されてしまいます。
理由は簡単です。ソートすることで$0$でない、値が大きい項により、総積が$10^{18}$を超えたと判定され、-1と出力されてしまうからです。
これが、コーナーケースであるzero_01.txtなどでWA判定が出てしまう原因になります。
なので、数列を読み込むとき、$0$の項が存在していたら1にするフラグ関数を作ってしまいましょう。そうすると、かけ算をする前に総積が$0$であるかを判定することが出来ます!
Python3では　A.count(0)で$0$の項が存在しているかを確かめることができます。

まとめ・解答例

つまり、この問題に対する各言語のポイントは以下のようになります。

・Python3
多倍長整数同士のかけ算は計算時間が多くかかるので避けた方がよい
・C++,Java
オーバーフローによる計算の誤りを避けた方が良い

以下、Python3,C++,Javaでの解答例を示します。

Python3での解答例

ABC169.py

N = int(input())
A = list(map(int,input().split()))
A.sort()
A.reverse()
if A.count(0) > 0:
  print(0)
else:
  f = 0
  ans = 1
  for i in range(N):
    ans *= A[i]
    if ans > 10**18:
      f += 1
      print(-1)
      break
  if f == 0:
    print(ans)

C++での解答例

ABC169.cpp

#include<bits/stdc++.h>
using namespace std;
int main(){
  int n;
  cin >> n;
  vector<long int> vec(n);
  for (int i = 0; i < n; i++){
    long int a;
    cin >> a;
    vec.at(i) = a;
    if(vec.at(i) == 0){
      cout << 0 << endl;
      return 0;
    }
  }
  sort(vec.begin(),vec.end());
  reverse(vec.begin(),vec.end());
  long int ans = 1;
  for (int i = 0; i < n; i++){
    if (vec.at(i) > 1000000000000000000/ans){
      cout << -1 << endl;
      return 0;
    }else{
      ans *= vec.at(i);
    }
  }
  cout << ans << endl;
}

Javaでの解答例

ABC169.java

import java.util.Scanner;
import java.util.Arrays;
public class Main{
  public static void main(String[] args){
    Scanner scan = new Scanner(System.in);
    int n = scan.nextInt();
    long [] a = new long[n];
    for (int i = 0; i < n; i++){
      a[i] = scan.nextLong();
      if (a[i] == 0){
        System.out.println(0);
        return;
      }
    }

    Arrays.sort(a);

    long ans = 1;

    for (int i = n-1; i >= 0; i--){
      if (a[i] > 1000000000000000000L/ans){
        System.out.println(-1);
        return;
      }else{
        ans *= a[i];
      }
    }
    System.out.println(ans);
  }
}

今回、ソフト開発の過程でJavaからのデータベースアクセスを勉強していて、データベースの読み出しに成功したので記事にしてみました。
JDBCを使ってのデータベースアクセスはほぼ初めての経験なので、SQLite3の復習も兼ねて順を追ってやっていきたいと思います。

SQLite3の使い方については、Qiita:SQLite3操作コマンド関連まとめの記事でまとめてありますのでご参照ください。

環境

今回の開発環境については以下のとおりです。

• Ubuntu 18.04.5LTS
• OpenJDK 11.0.8
• SQLite3 3.22.0

---

データベースを作っておく

既存のデータベースから要素を読み出すために、予めデータベースを作っておきます。

データベースを作成

sqlite3 test.db

table1を定義

CREATE TABLE table1(id INTEGER PRIMARY KEY, name TEXT NOT NULL);

この時点で、ディレクトリにデータベースファイルが作成されます。

INSERT文でいくつかのデータの入れておいたので、SELECT文で見てみます。

SELECT * FROM table1;
id          name      
----------  ----------
1           satou     
2           suzuki    
3           tanaka    
4           katou     
5           takahashi 

データベースの確認が取れました。

---

JDBCのダウンロード

JavaからSQLite3にアクセスするには、JDBCドライバーが必要になります。
JDBCのリポジトリからJDBCをダウンロードしましょう。
バージョンは、任意のものでいいと思いますが、今回は執筆時点で最新のsqlite-jdbc-3.30.1.jarをダウンロードします。

JDBCがダウンロードできたら、先程作成したデータベースを格納してあるディレクトリにコピーしておきましょう。

---

Javaプログラミング作成

今回は参考にさせていただいたサイトのコードを元に適宜変更を加えて、javaファイルを作成しました。

TestDAtabaseDriver.java

import java.sql.*;

public class TestDatabaseDriver {
    public static void main(String[] args) {

        Connection connection = null;
        Statement statement = null;

        try {
            Class.forName("org.sqlite.JDBC");

            // データベースのPATHを指定。相対パスでも絶対パスでも行けるようです
            connection = DriverManager.getConnection("jdbc:sqlite:test.db");
            statement = connection.createStatement();
            String sql = "select * from table1";
            ResultSet rs = statement.executeQuery(sql);
            while (rs.next()) {
                System.out.println(rs.getString(1));
            }
        } catch (ClassNotFoundException e) {
          e.printStackTrace();
        } catch (SQLException e) {
          e.printStackTrace();
        } finally {
            try {
                if (statement != null) {
                    statement.close();
                }
            } catch (SQLException e) {
                e.printStackTrace();
            }
            try {
                if (connection != null) {
                    connection.close();
                }
            } catch (SQLException e) {
                e.printStackTrace();
            }
        }
    }
}

コンパイルして実行

javac *.java && java -classpath .:sqlite-jdbc-3.30.1.jar TestDatabaseDriver

実行結果

1
2
3
4
5

この結果から、TestDAtabaseDriver.javaのSystem.out.println(rs.getString(1));の部分で読み出す部分が決まるようなので、少し変更を加えてみましょう。

変更前

System.out.println(rs.getString(1));

変更後

System.out.println(rs.getString(1) + "|" + rs.getString(2));

実行してみます。

コンパイルして実行

javac *.java && java -classpath .:sqlite-jdbc-3.30.1.jar TestDatabaseDriver

実行結果

1|satou
2|suzuki
3|tanaka
4|katou
5|takahashi

まとめ

無事にデータベースを読み出すことができました。
今回は初めてのJDBCに挑戦ということで、ほとんどがコピペで終始してしまいましたが、これを元に幅を広げて、再利用性の高いものにしていきたいと思います。

---

参考サイト

• TECHSCORE BROG/3分で構築！SQLiteを色々な環境で動かしてみる

AtCoder Beginner Contest 169 A問題「Multiplication 1」の解説を行います。

問題URL :
https://atcoder.jp/contests/abc169/tasks/abc169_a

問題概要

整数$A$,$B$が与えられる。
$A×B$を求めよ。

制約

・$1 \leq A \leq 100$
・$1 \leq B \leq 100$
・入力は全て整数

解説

問題文通りに実装すれば良いです。
以下、Python3,C++,Javaでの解答例を示します。

Python3での解答例

A169.py

x,y = map(int,input().split())
print(x*y)

C++での解答例

A169.cpp

#include<bits/stdc++.h>
using namespace std;
int main(){
  int x,y;
  cin >> x >> y;
  cout << x * y << endl;
}

Javaでの解答例

A169.java

import java.util.Scanner;
public class Main{
  public static void main(String[] args){
    Scanner scan = new Scanner (System.in);
    int x = scan.nextInt();
    int y = scan.nextInt();
    System.out.println(x*y);
  }
}

類題(オーバーフローに注意しましょう)

今回は制約が両方とも100以内なので大丈夫なのですが、このような場合はどうでしょう？

$X×Y$を求めよ。
ただし制約は以下の通りである。
・$1 \leq X \leq 10^5$
・$1 \leq Y \leq 10^5$

Python3の場合はint型で扱える値は無限なので大丈夫なのですが、

C++の解答例のコードでこの問題の最大制約の場合で実行してみます。

入力

input.txt

100000 100000

出力

output.text

1410065408

本来、$10^5 × 10^5 = 10^{10}$なので、このような表記にはならない...と思った方も多いと思います。

これはオーバーフローという、C++やJava等、int型で表現できる値で制限がかかっている言語で発生する現象です。

$10^{10}$ を $2^{31}$で割ると余りが$1410065408$となります。

C++やJavaのint型で表現できるのは $-2^{31}$から$2^{31}-1$までの値です。
よってint型とint型の積がint型であることから、このようなオーバーフローが発生してしまうのです。

C++では、例えば long long intを使うことで表現できる値が増えます。
long long intで表現できる値は$-2^{63}$から$2^{63}-1$です。
よって、以下のコードを書けば先ほどのような問題を回避できます。

overflow対策.cpp

#include<bits/stdc++.h>
using namespace std;
int main(){
  long long int x,y;
  cin >> x >> y;
  cout << x * y << endl;
}

output.text

10000000000

AtCoderの問題文やサンプルには　たまにオーバーフローに注意して下さいや32bit 整数に収まらない場合もある.などの表記がある場合があります。
そのような場合は、変数の型がlong long intであるかどうかを疑ってから提出するようにしましょう。
余計なWA(不正解)ができてしまいペナルティ5分が発生してしまうので....

AtCoder Beginner Contest 170 B問題「 Crane and Turtle 」の解説を行います。

問題URL :
https://atcoder.jp/contests/abc170/tasks/abc170_b

問題概要

庭に何匹かの動物がいる。
情報として、
・庭の動物の総数$X$,
・足の総数$Y$
が与えられる。
鶴の足の本数は$2$本、亀の足の本数は$4$本である。

$X$,$Y$の情報にあてはまるような鶴と亀の数の組み合わせが存在するかを判定せよ。
出力：
・存在する "Yes"と出力
・存在しない "No"と出力

制約

・ $1 \leq X \leq 100$
・ $1 \leq Y \leq 100$
・入力の全ての値は整数

解説

解法1(全探索)

幸い、$X$と$Y$の制約が小さいので、以下のような処理を行えばよいです。

・$X,Y$を入力
・フラグ関数$flag$を宣言し0で初期化する
・亀の匹数を$i$として、$i$を$(0,X)$の区間でとり　以下の繰返し処理を行う
　　・もし $Y - 2i $が$4$で割り切れ、かつその商が$X-i$であれ
　　　ば"Yes"と出力し、以降のループを終了する
　　　これにより組み合わせのフラグが立ったので$flag$に1を加算する
・もし$flag = 0$ならば組み合わせはないので"No"と出力する

Python3での解答例は以下のようになります。
(C++,Javaでも同様の解法で解くことができます)

Python3での解答例(解法1)

B.py

x,y = map(int,input().split())
flag = 0
for i in range(x+1):
  if (y - 2*i)%4 == 0 and (y -  2 * i)//4 == x - i:
    flag += 1
    print("Yes")
    break
if flag == 0:
  print("No")

※for i in range(x+1)としているのは、iの値を$(0,x)$の区間で取っているためです。 for i in range(x)とすると、iの値を$(0,x-1)$の区間でとることになります。

解法2

鶴の匹数を$a$,亀の匹数を$b$とおくと、以下のような連立方程式が成り立つことになります。

  \begin{cases}
    a+b = X \\
    2a+4b = Y
  \end{cases}

これを解くと

  \begin{cases}
    a = \frac{4x-Y}{2}　\\
    b = \frac{-2x+Y}{2} \\
  \end{cases}

という2つの解が得られます。
この両方が整数解でかつ0より大きいかどうかを判定すればよいです。
(制約が小さいので、今回は解法1
でも余裕で実行時間制限に間に合います)

Python3での解答例(解法2)

B2.Py

x,y = map(int,input().split())
a = (4*x-y)/2
b = (-2*x+y)/2
if a%1 == 0 and 0 <= a and b%1 == 0 and 0 <=b:
  print("Yes")
else:
  print("No")

一般的には解法2ではなく解法1で解かれる方が多いので、ここでは解法1で解いたC++,Javaの解答例を以下に示します。

C++での解答例(解法1)

B1.cpp

#include<bits/stdc++.h>
using namespace std;
int main(){
  int x,y;
  cin >> x >> y;
  int flag = 0;
  for (int i = 0; i <= x; i++){
    if ((y-2*i)%4 == 0 && (y - 2 * i)/4 == x-i){
      flag++;
      cout << "Yes" << endl;
      break;
      }
    }
  if (flag == 0){
    cout << "No" << endl;
  }
}

Javaでの解答例(解法1)

B1.cpp

import java.util.Scanner;
public class Main{
  public static void main(String[] args){
    Scanner scan = new Scanner(System.in);
    int x = scan.nextInt();
    int y = scan.nextInt();
    int flag = 0;
    for (int i = 0; i <= x; i++){
      if ((y-2*i)%4 == 0 && (y - 2 * i)/4 == x-i){
        flag++;
        System.out.println("Yes");
        break;
      }
    }
    if  (flag == 0){
      System.out.println("No");
    }
  }
}

Java(Spring Boot)を使ってWebアプリ開発を進める際のテンプレートです。
下記にサンプルプロジェクトを作りました。
https://github.com/hrk-okd/spring-sample

ソースコードの説明

作成環境

• Windows 10
• jdk-12.0.1
• IntelliJ IDEA Community Edition 2019.1.3 x64

ソース作成の思想

サンプルなので思想というほどのものではありませんが、一点だけ意識して書いたのは「コンストラクタインジェクション」でDIする方法を採用していることです。

サンプルプロジェクトのライブラリ構成

サンプルプロジェクトのライブラリは以下の通りです。

＜引用元＞
https://github.com/hrk-okd/spring-sample/blob/0710e4585767eb3dc260054b57d7607a9543bb60/spring-mvc/build.gradle#L18-L44

dependencies {
    // https://mvnrepository.com/artifact/org.springframework.boot/spring-boot
    compile group: 'org.springframework.boot', name: 'spring-boot', version: '2.1.6.RELEASE'
    // https://mvnrepository.com/artifact/org.springframework.boot/spring-boot-starter
    compile group: 'org.springframework.boot', name: 'spring-boot-starter', version: '2.1.6.RELEASE'
    // https://mvnrepository.com/artifact/org.springframework.boot/spring-boot-starter-web
    compile group: 'org.springframework.boot', name: 'spring-boot-starter-web', version: '2.1.6.RELEASE'

    // https://mvnrepository.com/artifact/org.projectlombok/lombok
    compileOnly group: 'org.projectlombok', name: 'lombok', version: '1.18.8'

    // junit 5
    // https://mvnrepository.com/artifact/org.junit.jupiter/junit-jupiter-engine
    testCompile group: 'org.junit.jupiter', name: 'junit-jupiter-engine', version: '5.5.1'

    // mockito 全般
    // https://mvnrepository.com/artifact/org.mockito/mockito-core
    testCompile group: 'org.mockito', name: 'mockito-core', version: '3.0.0'

    // mockito ExtendWith
    // https://mvnrepository.com/artifact/org.mockito/mockito-junit-jupiter
    testCompile group: 'org.mockito', name: 'mockito-junit-jupiter', version: '3.0.0'

    // mockito assertThat().isEqualTo
    // https://mvnrepository.com/artifact/org.assertj/assertj-core
    testCompile group: 'org.assertj', name: 'assertj-core', version: '3.13.0'
}

spring-boot/spring-boot-starter/spring-boot-starter-web

基本のライブラリです。
Spring Bootを使用するなら、深く考えずに入れておきましょう。
Webアプリケーションを作らない場合、spring-boot-starter-webは除外しても問題ないでしょう。|

lombok

クラスやメソッドに @Getter や @Setter のアノテーションを付けることによって、getterやsetterを書く必要がなくなります。これは本当に便利です。

現場によっては余計なプラグインはインストールするなというところもあるでしょう。
でも、僕個人としては、開発効率UPのために全現場で導入必須と考えています。

junit-jupiter

こちらはJUnit5に対応するためのライブラリです。JUnit4で使いにくかった点が改善されているので、可能ならばこちらに対応しておくのが良いでしょう。

mockito-core/mockito-junit-jupiter

mockitoはユニットテストで使用するライブラリで、モックを使用することが可能です。モックのライブラリもいくつかありますが、僕が現場で知って良いと思ったので、こちらを取り込んでいます。

mockito-junit-jupiterは入れなくてもモックを使用することは可能です。ただし、このライブラリで使用できる @ExtendWith アノテーションを使用すると、フィールドにアノテーションを付けることでモックを作ることが可能。
テストコードの手間も削減できます。

assertj-core

こちらもユニットテストで使用するライブラリで、検証用のメソッドassertとそれに関するメソッドが豊富に揃えられています。
通常のJUnitでは書きにくい内容も楽に検証することが可能です。

まとめ

Spring Bootで開発を行うためのサンプルプロジェクトを用意しました。

実際に開発を行う上ではもっと多くのライブラリが必要になると思いますが、ミニマムから構成して徐々に機能を追加していくには、こういったサンプルを用意しておいた方が良いでしょう。

近年はgithubの台頭もあり、個人でも多くのリポジトリを持てるし公開することも可能。
会社でリポジトリが用意されると思いますが、個人のリポジトリもあらかじめ用意して、必要な情報を素早く取り出せるようにしておくのが良いですね。

客先常駐型のエンジニアは、自分のPCは持ち込めない現場が多いですが、githubのソース取得を制限されることは稀です。
自分が気持ち良く仕事ができるようにしておく上でも、情報をまとめたソースをアップしておきましょう。

JUnitのテスト起動的なものを試してみる

Junitで使用される@Testアノテーション について
このアノテーション を実装したメソッドはテストメソッドとして起動するが、
どのような原理で動いているか気になったので
その実装内容に関して考察してみる

Junitのテストメソッド起動

そもそもJunitで起動するJavaファイルは特定のディレクトリの配下で指定されたJavaファイルのみである？
例えば「src/test」のような設定フォルダの配下にJavaファイルを置くと
そのsrc/testを起点としてテスト起動する。

つまりsrc/testの配下をエントリーポイントとして設定していると考えられるため、
そのディレクトリ配下のJavaファイル(クラスファイル)をトラバースして
@Testアノテーション が設定されているメソッドのみを実行していると考えている
(Junitの実装を見たわけではないので断言できない)

このようにある特定のフォルダ以下をエントリーポイントとして設定しているのは
クラスパスの設定によってクラスローダーのrootパスから順番にJavaファイルを読み込んで
@Testアノテーション が設定されているメソッドを探して、
もしアノテーション が付与されているなら、対象のクラスをインスタンス化して
メソッドを実行しているのではないかと思った。

このような考察のもと、リフレクションを使用して同じような実装ができないか試してみた。

　
　

アノテーション の作成

@Testアノテーション のようにメソッドに付与するアノテーション を作成する

package anno;

import java.lang.annotation.ElementType;
import java.lang.annotation.Retention;
import java.lang.annotation.RetentionPolicy;
import java.lang.annotation.Target;

@Retention(RetentionPolicy.RUNTIME)
@Target(ElementType.METHOD)
public @interface TestAnno {
  boolean testFlg() default false;
}

今回はtestFlgでtrue設定されたメソッドのみ
メソッド起動の対象となるように実装した
　
　

起動のエントリーポイントの作成

@TestAnnoが付与されているクラスとメソッドを探しだし、invokeされるようなクラスの作成を行った

import java.lang.reflect.InvocationTargetException;
import java.lang.reflect.Method;
import java.net.URL;
import java.nio.file.Files;
import java.nio.file.Path;
import java.nio.file.Paths;
import java.util.stream.Stream;

import anno.TestAnno;


public class Entry {

  public static void main(String[] args) throws Exception {

    // *1
    final String resourceName = "test";
    final ClassLoader classLoader = Thread.currentThread().getContextClassLoader();
    final URL testRoot = classLoader.getResource(resourceName);
    final String appRootStr = classLoader.getResource(".").getFile().toString();



　　// *2
    try (Stream<Path> paths = Files.walk(Paths.get(testRoot.toURI()))) {

      paths.filter(Files::isRegularFile).forEach(path -> {


        // *3
        String targertAbsolutePath = path.normalize().toFile().getAbsolutePath().toString();
        String targetClassName = targertAbsolutePath.substring(appRootStr.length(), targertAbsolutePath.length()).replace(".class", "").replace("/", ".");

        // 4
        Class<?> testClass;
        Object testClassInstance;
        try {
          testClass = Class.forName(targetClassName);
          testClassInstance = testClass.newInstance();
        } catch (Exception e) {
          throw new RuntimeException(e);
        }

　　　　　// *5
        for( Method method : testClass.getMethods() ) {

          TestAnno testAnnotation = method.getAnnotation(TestAnno.class);
          if ( testAnnotation == null ) continue;

          try {
            if ( testAnnotation.testFlg() )
              method.invoke(testClassInstance);
          } catch (IllegalAccessException | IllegalArgumentException | InvocationTargetException e) {
            e.printStackTrace();
          }

        }


      });


      System.out.println("Test End");
    }



  }

}

＊1
　ここの処理では、test駆動するパッケージの指定を行っている
　今回はパッケージ名[test]配下のjavaファイルを対象とする。
　→ testRootとする

＊2
　testRoot配下のjavaファイルを抽出するためにwalk関数を使って
　ディレクトリトラバースをする。
　通常ファイルであれば(つまりクラスファイルであれば)処理対象とするようにフィルタリングして
　クラスファイルのみStream処理の対象としている

＊3
　ここでは、抽出するクラスファイルをパッケージ名込みで文字列として取得し
　*4のClass.forNameでリフレクションを取得できるようにしている

＊4
　テスト対象のクラスをリフレクションとして取得し、
　インスタンスを取得しておく

＊5
　取得したクラスオブジェクトからメソッドオブジェクトを抽出して、
　testAnnotationが付与されている、かつ、testFlgがtrueのものを
　invokeする。

このような手順で、@testAnnotationが付与されているメソッドを抽出することができた。

テスト起動されるメソッドの実装

ここでは、実際にテスト起動されるメソッドをもつクラスを定義する。

package test;

import anno.TestAnno;

public class Test {

  @TestAnno(testFlg=true)
  public void testMethod() {


    String className = this.getClass().getName();
    String methodName = Thread.currentThread().getStackTrace()[1].getMethodName();
    System.out.println("invoked " + className + ":" + methodName);

  }

  @TestAnno(testFlg=false)
  public void testMethod2() {


    String className = this.getClass().getName();
    String methodName = Thread.currentThread().getStackTrace()[1].getMethodName();
    System.out.println("invoked " + className + ":" + methodName);

  }

  @TestAnno(testFlg=true)
  public void testMethod3() {


    String className = this.getClass().getName();
    String methodName = Thread.currentThread().getStackTrace()[1].getMethodName();
    System.out.println("invoked " + className + ":" + methodName);

  }

}

@TestAnno(testFlg=true)のように設定を行い、
testFlgがtrueのメソッドのみinvokeされるか確認すると
正常に動作しました。

　
　
以上になりますが、
コンテキストクラスローダーの設定や内容などが理解できていないので、
また暇なときに調べてみようと思います。

今回実装していて難しかった点は、パッケージ名を取得するところでした。
あまり参考できるサイトがなかったので、こういった実装は需要がないのかもしれません。

今回はJunitの動きで疑問に思った点の実装内容の考察でしたが、
アノテーション の設定によって起動するクラスやメソッドについては
同じような実装がなされているのかと思います。

例えば、スプリングフレームワークのオートワイヤリングやコンポーネントスキャンなども
同じような考え方ではないのかなと思っています。

また機会があれば、リフレクションの詳細についても調べてみようかと

今回の実装で、クラスローダやリフレクションの動きについて
全然わかってないことに気づいたので
Javaを記事を書く際は、その辺の詳細を調べていこうかと思います。

上記の記載したコードは一部切り取っているものが多いので
興味がある方はGithubを参考ください。
https://github.com/ktkt11122334/qiita/tree/master/test

AtCoder Beginner Contest 170 A問題「 Five Variables 」の解説を行います。

問題URL :
https://atcoder.jp/contests/abc170/tasks/abc170_a

問題概要

5つの変数$x_1,x_2,x_3,x_4,x_5$が与えられる。
もとの変数は$x_i = i$であったが、1つのみ$0$が代入された。では、$0$が代入された変数がどれであったかを答えよ。

制約

・入力の$x_1,x_2,x_3,x_4,x_5$は、代入された後のものとしてありえる組み合わせである。

解説

解法1

全ての値に対して$0$であるかどうかの条件分岐を行う方法です。
これにより、$0$が代入された変数がどれであるかを求めることが出来ます。

解法2

$x_1,x_2,x_3,x_4,x_5$の数列を数列$(X)$とおきます。
実は、最初の5つの変数の総和が$15$であることを利用すると、
15から$X$の総和を引いたもの
が$0$が代入された変数の値であることが分かります。よってこれを計算して出力すればよいでしょう。

以下、Python3,C++,Javaでの解答例を示します。(解法2の解法を利用しました)

各言語解答例

Python3での解答例

A.py

x = list(map(int,input().split()))
print(15 - sum(x))

C++での解答例

A.cpp

#include<bits/stdc++.h>
using namespace std;
int main(){
  int ans = 15;
  for (int i = 0; i < 5; i++){
    int x;
    cin >> x;
    ans = ans - x;
  }
  cout << ans << endl;
}

(改行を忘れないこと!!)

Javaでの解答例

A.java

import java.util.Scanner;
public class Main{
  public static void main(String[] args){
    Scanner scan = new Scanner(System.in);
    int ans = 15;
    for (int i = 0; i < 5; i++){
      int x = scan.nextInt();
      ans = ans - x;
    }
    System.out.println(ans);
  }
}

AtCoder Beginner Contest 174 B問題「Distance」の解説を行います。

問題URL : https://atcoder.jp/contests/abc174/tasks/abc174_b

問題概要

2次元平面上に$N$個の点があり、$i$個目の点の座標は$(X_i , Y_i)$である。
これらのうち、原点からの距離が$D$以下であるような点は何個あるかを求めよ。
ただし、座標$(p,q)$にある点と原点との距離は$\sqrt{p^2+q^2}$である。

制約

・$1\leq N \leq 2×10^5$
・$0\leq D \leq 2×10^5$
・$|X_i|,|Y_i| \leq 2×10^5$
・入力は全て整数

解法

この問題ですが、以下のようなことを実行するコードを書けばACできます。

・$N,D$を入力する
・変数$ans$をカウンターとして宣言し、0で初期化する
・$N$回以下のことを繰り返す

・$(X_i,Y_i)$の情報を受け取り、$\sqrt{{X_i}^2+{Y_i}^2}$を求める。もしそれが$D$以下であれば$ans$に1を加算する

・$ans$が、$D$以下である点の個数なのでこれを出力すればよい

(以下のコードはPythonでの解答例です)

B.py

N,D = map(int,input().split())
ans = 0
for i in range(N):
  x,y = map(int,input().split())
  if (x**2+y**2)**0.5 <= D:
    ans += 1
print(ans)

このコードでもACは出来るのですが、"誤差を気にする"という方は以下のように書き換えた方が良いかも知れません。

B2.py

N,D = map(int,input().split())
ans = 0
for i in range(N):
  x,y = map(int,input().split())
  #ここを書き換える!!
  if (x**2+y**2) <= D**2:
    ans += 1
print(ans)

$\sqrt{{x_i}^2+{y_i}^2} \leq D$ではなく
${x_i}^2+{y_i}^2 \leq D^2$で$D$以下かどうかを判定しています。
制約より、$0 \leq D$なので、このように不等式の条件を言い換えることができます。
また、${x_i}^2+{y_i}^2$で単純に比較すると, $\sqrt{{x_i}^2+{y_i}^2}$で比較するよりも誤差があまり出ない(整数の2乗同士を足すので)ので、誤差を気にせず条件分岐することが出来ます。

以下、C++,Javaでの解答例を示します。
※($x_i^2+y_i^2 \leq D$)で解いたコードです

C++での解答例

B.cpp

include<bits/stdc++.h>
using namespace std;
int main(){
    int n;
    long long int d;
    cin >> n >> d;
    int ans = 0;
    for (int i = 0; i < n; i++){
        long long int x,y;
        cin >> x >> y;
        if (x*x+y*y <= d*d){
            ans++;
        }
    }
    cout << ans << endl;
}

Javaでの解答例

B.java

import java.util.Scanner;
public class Main {
    public static void main(String[] args){
        Scanner scan = new Scanner(System.in);
        int n;
        long d;
        n = scan.nextInt();
        d = scan.nextLong();
        int ans = 0;
        for (int i = 0; i < n; i++) {
            long x,y;
            x = scan.nextLong();
            y = scan.nextLong();
            if (x*x+y*y <= d*d) {
                ans++;
            }
        }
        System.out.println(ans);
    }
}

ちなみに、C++では計算時間が101msだったのに対し、Javaは634msであったので、C++の計算速度が速いのが一目瞭然ですね。

springのチュートリアルでの学習をまとめる

やったこと

タスクのスケジュール

【環境】

• Spring Tool Suite 4 :Version: 4.4.1.RELEASE
• ProductName:Mac OS X
• ProductVersion:10.14.6

【作るアプリ】

Spring の @Scheduledアノテーションを使用し、5秒ごとに現在時刻を出力するアプリを作成する

• 適当なディレクトリに移動

$ git clone https://github.com/spring-guides/gs-scheduling-tasks.git
$ cd gs-scheduling-tasks

• 編集：pom.xml

  • awaitility 依存関係の追加(cheduledTasksTest.java のテストのため)

• スケジュールされたタスクを作成

  • 作成：新規ファイル (src/main/java/.../schedulingtasks/ScheduledTasks.java)

• スケジューリングを有効にする

  • 編集：(src/main/.../schedulingtasks/SchedulingTasksApplication.java)

import org.springframework.scheduling.annotation.EnableScheduling;

• 実行可能 JAR を構築する
  • 移動：mavenディレクトリに移動する
  • 実行1:「./mvnw spring-boot:run」 を使用してアプリケーションを実行する
  • 実行2:「./mvnw clean package」のあとログに表示されるパスをコピペして貼る。

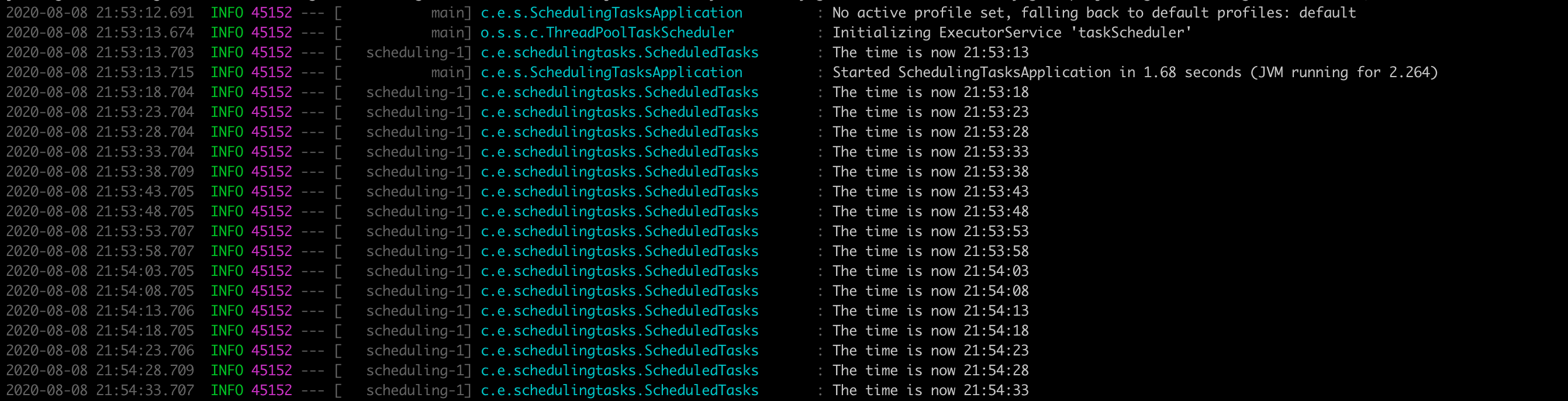
[INFO]
[INFO] Results:
[INFO]
[INFO] Tests run: 1, Failures: 0, Errors: 0, Skipped: 0
[INFO]
[INFO]
[INFO] --- maven-jar-plugin:3.2.0:jar (default-jar) @ scheduling-tasks ---
[INFO] Building jar: /Users/#{myname}/projects/gs-scheduling-tasks/initial/target/scheduling-tasks-0.0.1-SNAPSHOT.jar
[INFO]
[INFO] --- spring-boot-maven-plugin:2.3.2.RELEASE:repackage (repackage) @ scheduling-tasks ---
[INFO] Replacing main artifact with repackaged archive
[INFO] ------------------------------------------------------------------------
[INFO] BUILD SUCCESS
[INFO] ------------------------------------------------------------------------
[INFO] Total time:  9.307 s
[INFO] Finished at: 2020-08-08T21:52:43+09:00
[INFO] ------------------------------------------------------------------------

#実行、アプリ起動
$ /Users/#{myname}/projects/gs-scheduling-tasks/initial/target/scheduling-tasks-0.0.1-SNAPSHOT.jar

• アプリ起動
  • $ /Users/#{myname}/projects/gs-scheduling-tasks/initial/target/scheduling-tasks-0.0.1-SNAPSHOT.jar

参考記事(いつもありがとうございます)

タスクのスケジュール
Spring Bootでtaskを定期実行する方法