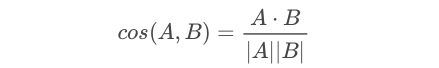20201019のPythonに関する記事は30件です。

投稿日：2020-10-19T23:58:08+09:00

【CRUD】【Django】PythonフレームワークDjangoを使ってCRUDサイトを作成する～2～

シリーズ一覧(全記事完成したら更新していきます)

モデルを作成する

DjangoにはORM(オブジェクト関係マッピング)があります。
ORMとは、プログラムのソースコードとデータベースのデータを相互に変換する機能を指します。
Djangoの場合はmodele.pyにPythnで記述します。

では、Post（投稿機能の）モデルを書いていきます。

/crud/blog/models.py

from django.db import models
from django.contrib.auth.models import User
from django.utils import timezone


class Post(models.Model):
    # タイトル CHAR 最大100文字
    title = models.CharField(max_length=100)
    # 内容 テキスト
    content = models.TextField()
    # 著者 外部キー制約(1対多リレーション) ユーザ 親データと共に子データも削除
    author = models.ForeignKey(User, on_delete=models.CASCADE)
    # 投稿日 日付型 現在時刻
    date_posted = models.DateTimeField(default=timezone.now)

    # 管理画面の表示設定 タイトルを表示
    def __str__(self):
        return self.title

マイグレーション

(crud-_w5mSGH2) C:\django\crud>python manage.py makemigrations
Migrations for 'blog':
  blog\migrations\0001_initial.py
    - Create model Post

(crud-_w5mSGH2) C:\django\crud>

以下のファイルが自動で生成されます。
編集する必要はありませんよ。

/crud/blog/migrations/0001_initial.py

# Generated by Django 3.1.1 on 2020-10-12 12:32

from django.conf import settings
from django.db import migrations, models
import django.db.models.deletion
import django.utils.timezone


class Migration(migrations.Migration):

    initial = True

    dependencies = [
        migrations.swappable_dependency(settings.AUTH_USER_MODEL),
    ]

    operations = [
        migrations.CreateModel(
            name='Post',
            fields=[
                ('id', models.AutoField(auto_created=True, primary_key=True, serialize=False, verbose_name='ID')),
                ('title', models.CharField(max_length=100)),
                ('content', models.TextField()),
                ('date_posted', models.DateTimeField(default=django.utils.timezone.now)),
                ('author', models.ForeignKey(on_delete=django.db.models.deletion.CASCADE, to=settings.AUTH_USER_MODEL)),
            ],
        ),
    ]

マイグレート

(crud-_w5mSGH2) C:\django\crud>python manage.py migrate
Operations to perform:
  Apply all migrations: admin, auth, blog, contenttypes, sessions
Running migrations:
  Applying contenttypes.0001_initial... OK
  Applying auth.0001_initial... OK
  Applying admin.0001_initial... OK
  Applying admin.0002_logentry_remove_auto_add... OK
  Applying admin.0003_logentry_add_action_flag_choices... OK
  Applying contenttypes.0002_remove_content_type_name... OK
  Applying auth.0002_alter_permission_name_max_length... OK
  Applying auth.0003_alter_user_email_max_length... OK
  Applying auth.0004_alter_user_username_opts... OK
  Applying auth.0005_alter_user_last_login_null... OK
  Applying auth.0006_require_contenttypes_0002... OK
  Applying auth.0007_alter_validators_add_error_messages... OK
  Applying auth.0008_alter_user_username_max_length... OK
  Applying auth.0009_alter_user_last_name_max_length... OK
  Applying auth.0010_alter_group_name_max_length... OK
  Applying auth.0011_update_proxy_permissions... OK
  Applying auth.0012_alter_user_first_name_max_length... OK
  Applying blog.0001_initial... OK
  Applying sessions.0001_initial... OK

(crud-_w5mSGH2) C:\django\crud>

データを登録する

本来のブログであれば投稿画面から記事を投稿するのですが、まだ実装していません。
Djngoには管理画面があり、そこからデータの登録ができます。
ですので一旦管理画面から記事データを登録しようと思います。

管理画面にPostを表示させる

管理画面に表示させる内容をDjangoに伝えなくてはいけません。以下ファイルを修正しましょう。

crud/blog/admin.py

from django.contrib import admin
from .models import Post

admin.site.register(Post)

管理ユーザを作成する

管理画面にログインするための管理者ユーザを作成します。
ユーザ：admin
パスワード：pass

(crud-_w5mSGH2) C:\django\crud>python manage.py createsuperuser
ユーザー名 (leave blank to use 'wmgoz'): admin
メールアドレス: ***@***.com　#←自分のメアドを使用してください
Password:
Password (again):
このパスワードは短すぎます。最低 8 文字以上必要です。
このパスワードは一般的すぎます。
Bypass password validation and create user anyway? [y/N]: y
Superuser created successfully.

(crud-_w5mSGH2) C:\django\crud>

管理画面にログインする

開発サーバを起動させて管理画面にログインしましょう。

python manage.py runserver

次に管理画面「http://127.0.0.1:8000/admin/」にアクセスしましょう。

以下のような管理画面が表示されました。

データを登録してみる！

管理画面の「Posts」横の「+追加」をクリックし、データ入力に進みます。

データ①の登録：

データ②の登録：

2つの記事の投稿が完了しました。

本日はここまでにします。ありがとうございました。

　 Tweet
Qiitaで続きを読む

投稿日：2020-10-19T23:51:33+09:00

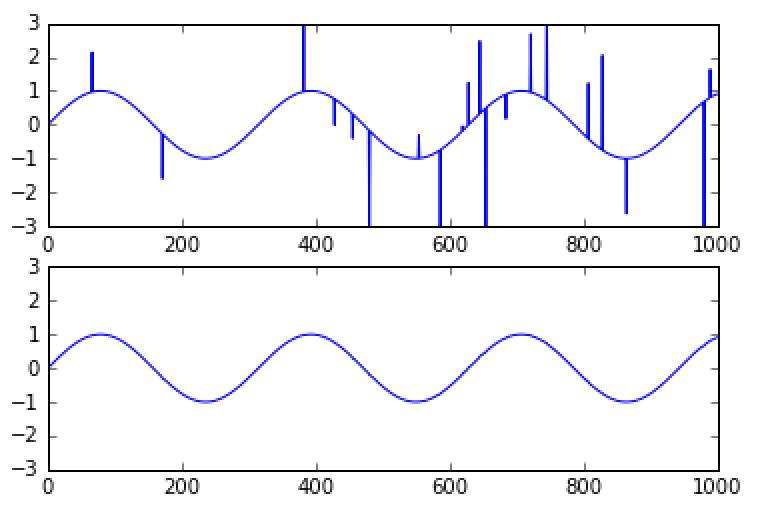
1次元のメディアンフィルター（中央値フィルター）

画像処理ではよく使われるメディアンフィルター。
OpenCVを使えば画像の２次元配列に対して
median = cv2.medianBlur(img,5)
とするだけで処理できる。

時系列データなどの１次元データにおいても外れ値がある場合，
メディアンフィルターで取り除くことができる。
１次元用のメディアンフィルターというのはnumpyにもopencvにも関数が見当たらず，
すこし工夫したのでメモ。
インデックスで各点ごとに中央値を選ぶ領域を抽出して２次元配列にしてから，
np.medianを行方向に適用している。
median.py
import numpy as np
import matplotlib.pyplot as plt

# 1次元配列に対するメディアンフィルター
# kはフィルターの大きさで奇数
def median1d(arr, k):
    w = len(arr)
    idx = np.fromfunction(lambda i, j: i + j, (k, w), dtype=np.int) - k // 2
    idx[idx < 0] = 0
    idx[idx > w - 1] = w - 1
    return np.median(arr[idx], axis=0)

# 外れ値を含む正弦波
x = np.sin(np.arange(1000) / 50)
x[np.random.randint(0, len(x), 20)] += np.random.randn(20) * 3

# フィルタリング
y = median1d(x, 5)

plt.figure(1)
plt.clf()
plt.subplot(2, 1, 1)
plt.plot(x)
plt.ylim([-3, 3])
plt.subplot(2, 1, 2)
plt.plot(y)
plt.ylim([-3, 3])

　 Tweet
Qiitaで続きを読む

投稿日：2020-10-19T23:23:47+09:00

【python】enumerateの動作

enumerateの動作が面白かったので記載する。

動作

enumerateは辞書をfor文に入れる時に非常に役に立つ。
d = {5:1, 6:2, 7:3}
上のような辞書をfor文に入れる。
for i, x in enumerate(d):
     print(i,x)
#0 5
1 6
2 7
上記からenumerateを実行すると
iには数列の番号が
xにはキーが
入る。

　 Tweet
Qiitaで続きを読む

投稿日：2020-10-19T23:11:11+09:00

Djangoチュートリアル（ブログアプリ作成）⑤ - 記事作成機能編

前回、Djangoチュートリアル（ブログアプリ作成）④ - ユニットテスト編ではユニットテストの実装方法を学んでいきました。

本来であれば、せっかくなので期待するテストを先に書くテスト駆動開発スタイルで実装していきたいところですが
このチュートリアルでは Django ではどんなことが出来るかを学びながらなので、先に実装してからユニットテストを書いていきます。

これから、何回かに分けて今回は以下の機能を追加していきます。

1.記事の作成 (Create)
2.記事の詳細 (Read)
3.記事の編集 (Update)
4.記事の削除 (Delete)

これら機能の頭文字をとって「CRUD」とここでは呼ぶことにします。
(厳密にいえば既に blog_list で Read は出来るので違うかもしれませんが）

さて、今回はベースともいえる記事の作成機能を追加していきましょう。
これまでは管理サイトを使って superuser　権限で記事を追加していましたが、アプリ内で記事を作成出来たほうが便利ですよね。

form の準備

アプリからデータを追加するときは form という仕組みを使います。
form がユーザから入力データを受け付け、view を通して model へデータを渡してデータベースへ登録することができるようになります。

まずは blog アプリ配下に forms.py というファイルを作成します。
.
├── blog
│   ├── __init__.py
│   ├── admin.py
│   ├── apps.py
│   ├── forms.py # 追加
│   ├── migrations
│   │   ├── 0001_initial.py
│   │   └── __init__.py
│   ├── models.py
│   ├── tests
│   │   ├── __init__.py
│   │   ├── test_forms.py
│   │   ├── test_models.py
│   │   ├── test_urls.py
│   │   └── test_views.py
│   ├── urls.py
│   └── views.py
├── db.sqlite3
├── manage.py
├── mysite
│   ├── __init__.py
│   ├── settings.py
│   ├── urls.py
│   └── wsgi.py
└── templates
    └── blog
        ├── index.html
        └── post_list.html
作成した forms.py の中身はこのようになります。
forms.py
from django import forms
from .models import Post

class PostCreateForm(forms.ModelForm): # DjangoのModelFormでは強力なValidationを使える

    class Meta:
        model = Post # Post モデルと接続し、Post モデルの内容に応じてformを作ってくれる
        fields = ('title', 'text') # 入力するカラムを指定
説明文も入れているのである程度わかるかと思います。
データを投入したい model を指定すると form が対応する入力フォームを用意してくれるようになります。

なお、最終行でデータを入力するカラムをフィールドとして指定していますが、
fields = 'all' と定義することで全てのカラムを手入力するように指定することもできます。

urls.py の修正

新たに view に追加するクラスは **PostCreateView と名前を予め決めておき、
urls.py では次のようにルーティングを追加しておきましょう。
urls.py
from django.urls import path
from . import views

app_name = 'blog'

urlpatterns = [
    path('', views.IndexView.as_view(), name='index'),
    path('post_list', views.PostListView.as_view(), name='post_list'),
    path('post_create', views.PostCreateView.as_view(), name='post_create'), # 追加
]
success_url では、データベースの変更に成功した場合にリダイレクトさせるページを指定しています。
「アプリ名：逆引きURL名」の形で指定し、結果的に urls.py で指定した 'post_list' にリダイレクトされることになります。
※reverse_lazy は、view に対応した「URLの文字列」を返す。今回であれば /blog/post_list を返してくれます

views.py の修正

先ほど追加するクラス名は PostCreateView と決めましたね。
また、form で入力フォーム用のクラスも作成しました。

次は views.py の中で、またまた汎用クラスビューを使ってクラスを作成します。
views.py
from django.views import generic
from django.urls import reverse_lazy
from .forms import PostCreateForm # forms.py で作ったクラスをimport
from .models import Post

class IndexView(generic.TemplateView):
    template_name = 'blog/index.html'

class PostListView(generic.ListView):
    model = Post

class PostCreateView(generic.CreateView): # 追加
    model = Post # 作成したい model を指定
    form_class = PostCreateForm # 作成した form クラスを指定
    success_url = reverse_lazy('blog:post_list') # 記事作成に成功した時のリダイレクト先を指定
Django の強力なクラスベース汎用ビューのおかげで、これだけのコードで済みます。
作成したい model、作成した form クラス、そして記事作成が成功した時のリダイレクト先を指定してあげるだけです。

template の準備

まだ記事作成（投稿）用の html は作成していなかったので、templates/blog 配下に作成してあげましょう。
名前は post_form.html とします。
※クラスベース汎用ビューの命名規則に沿うことで template 名を指定しなくても OK になります
└── templates
    └── blog
        ├── index.html
        ├── post_form.html # 追加
        └── post_list.html
post_create.html
<form action="" method="POST">
  <table class="table">
      <tr>
        <th>タイトル</th>
        <td>{{ form.title }}</td>
      </tr>
      <tr>
        <th>本文</th>
        <td>{{ form.text }}</td>
      </tr>
  </table>
  <button type="submit" class="btn btn-primary">送信</button>
  {% csrf_token %}
</form>
forms.py の fields で指定した入力フィールドを form という変数で受け取ることができるので、
template 側では form.title と form.text という形で取り出すことができます。

また CSRF (クロスサイトリクエストフォージェリ) という、入力フォームを利用した攻撃を防ぐためのものです。
入力フォームを html に表示させる時は、必ず入れておきましょう。

この状態で runserver コマンドでサーバを起動すると、見た目はひどいものですが入力フォームが表示されます。
（度々ですが、まずは Django の基本をおさえてから見た目を整えます）

では試しに値を入力し、送信してみましょう。

送信を押すと、post_list にリダイレクトされます。
そして、先ほど投稿した記事が追加されていることが分かるかと思います。

これで無事に記事投稿機能を追加することができました。

test_views.py の修正

最後に今回の機能のテストを実装しましょう。

test_views.py に下記のテストクラスを作成します。
test_views.py
...
class PostCreateTests(TestCase):
    """PostCreateビューのテストクラス."""

    def test_get(self):
        """GET メソッドでアクセスしてステータスコード200を返されることを確認"""
        response = self.client.get(reverse('blog:post_create'))
        self.assertEqual(response.status_code, 200)

    def test_post_with_data(self):
        """適当なデータで　POST すると、成功してリダイレクトされることを確認"""
        data = {
            'title': 'test_title',
            'text': 'test_text',
        }
        response = self.client.post(reverse('blog:post_create'), data=data)
        self.assertEqual(response.status_code, 302)

    def test_post_null(self):
        """空のデータで POST を行うとリダイレクトも無く 200 だけ返されることを確認"""
        data = {}
        response = self.client.post(reverse('blog:post_create'), data=data)
        self.assertEqual(response.status_code, 200)
基本となる GET の確認、適当なデータの投入とリダイレクトの確認、そして空データ投入時のレスポンスを見ています。

最後にテストを実行しましょう。

無事に通りましたね。

次回は一気に記事の詳細画面を作成していきます。

　 Tweet
Qiitaで続きを読む

投稿日：2020-10-19T22:41:58+09:00

【情報圧縮ノート003 】ダルかった大学の電磁気学の教授の講談と板書をJpeg１枚に圧縮してまえ計画。

情報圧縮ノート計画というものをはじめました。
あの、かったるかった大学の先生の板書。
チンタラしているのに早口でまくし立てるからついていけない。
しかもその90分授業が年に30講近くある。
だいたい最初に全体像を教えてくれと思うのに勿体ぶる。
木を見せて森を最後に見せる。
定食の一番好きなオカズは最後にとるタイプの教授ばっかり。
そこで、そんな教授たちの性癖の裏をかいて全体像を一気に把握したい。
そういう企みのもとで情報を一気に圧縮していきます。
電磁気学全体をビル・建築物にみたて、
1)前提・仮定を基礎工事
2)結論を最上階とか屋上
にして全体を見通します。

これはまだ下書き、というか大学のときのノートですが、
AdobeIllustratorとかで清書します。

https://www.instagram.com/1jpeg1knowledge/

　 Tweet
Qiitaで続きを読む

投稿日：2020-10-19T22:37:15+09:00

ルービックキューブロボットのソフトウェアをアップデートした 6. 機械操作(Arduino)

この記事はなに？

私は現在2x2x2ルービックキューブを解くロボットを開発中です。これはそのロボットのプログラムの解説記事集です。

かつてこちらの記事に代表される記事集を書きましたが、この時からソフトウェアが大幅にアップデートされたので新しいプログラムについて紹介しようと思います。

該当するコードはこちらで公開しています。

関連する記事集

「ルービックキューブを解くロボットを作ろう！」
1. 概要編
2. アルゴリズム編
3. ソフトウェア編
4. ハードウェア編

ルービックキューブロボットのソフトウェアをアップデートした
1. 基本関数
2. 事前計算
3. 解法探索
4. 状態認識
5. 機械操作(Python)
6. 機械操作(Arduino)(本記事)
7. 主要処理

今回は機械操作(Arduino)編として、soltvvo3_arduino.inoを紹介します。

定数と変数

グローバルに置いた定数と変数です。
const int magnet_threshold = 50;
const long turn_steps = 400;
const int step_dir[2] = {11, 9};
const int step_pul[2] = {12, 10};
const int sensor[2] = {14, 15};
const int grab_deg[2] = {74, 74};
const int release_deg[2] = {96, 96};
const int offset = 3;

char buf[30];
int idx = 0;
long data[3];
定数はポート番号だったりサーボモーターの角度だったりです。変数はスペース区切りで値が与えられるのを分割する時に使います。

サーボライブラリ周り

サーボモーターを使う関係でサーボライブラリをインクルードしてservo0, servo1を定義しておきます。
#include <Servo.h>

Servo servo0;
Servo servo1;
セットアップ

セットアップです。
void setup() {
  Serial.begin(115200);
  for (int i = 0; i < 2; i++) {
    pinMode(step_dir[i], OUTPUT);
    pinMode(step_pul[i], OUTPUT);
    pinMode(sensor[i], INPUT);
  }
  servo0.attach(7);
  servo1.attach(8);
  servo0.write(release_deg[0] + 5);
  servo1.write(release_deg[1] + 5);
  delay(70);
  servo0.write(release_deg[0]);
  servo1.write(release_deg[1]);
}
ピンのインプット、アウトプットの定義と、サーボモーターを動かしてアームを外側に移動させます。

アームを回転させる

ステッピングモーターを回す関数です。台形駆動を実装しましたが、その関係でタイマーなどを使わずdelayを使う、少しカッコ悪い実装です。
void move_motor(long num, long deg, long spd) {
  bool hl = true;
  if (deg < 0) hl = false;
  digitalWrite(step_dir[num], hl);
  long steps = abs(deg) * turn_steps / 360;
  long avg_time = 1000000 * 60 / turn_steps / spd;
  long max_time = 1500;
  long slope = 50;
  bool motor_hl = false;
  long accel = min(steps / 2, max(0, (max_time - avg_time) / slope));
  int num1 = (num + 1) % 2;
  // 加速
  for (int i = 0; i < accel; i++) {
    motor_hl = !motor_hl;
    digitalWrite(step_pul[num], motor_hl);
    delayMicroseconds(max_time - slope * i);
  }
  // 平常運転
  for (int i = 0; i < steps * 2 - accel * 2; i++) {
    motor_hl = !motor_hl;
    digitalWrite(step_pul[num], motor_hl);
    delayMicroseconds(avg_time);
  }
  // 減速
  for (int i = 0; i < accel; i++) {
    motor_hl = !motor_hl;
    digitalWrite(step_pul[num], motor_hl);
    delayMicroseconds(max_time - slope * accel + accel * (i + 1));
  }
}
基本的には以下の流れで処理しています。

角度から回すべきステップ数を計算

回転数からパルスの幅を計算

加速、減速に使うステップ数を計算

アームのキャリブレーション

アームのステッピングモーターを使っている部分は適宜ちゃんとした角度になるようにキャリブレーションします。このとき、アーム側につけた磁石とステッピングモーター側につけたホールセンサ(磁気センサ)を使います。
void motor_adjust(long num, long spd) {
  int max_step = 150;
  int delay_time = 800;
  bool motor_hl = false;
  digitalWrite(step_dir[num], LOW);
  while (analogRead(sensor[num]) <= magnet_threshold) {
    motor_hl = !motor_hl;
    digitalWrite(step_pul[num], motor_hl);
    delayMicroseconds(delay_time);
  }
  while (analogRead(sensor[num]) > magnet_threshold) {
    motor_hl = !motor_hl;
    digitalWrite(step_pul[num], motor_hl);
    delayMicroseconds(delay_time);
  }
}
1つ目のwhile文がトリッキーですが、すでにアームが正しい位置にあると判定される場合でも、少しアームの角度がずれていることがあるので一回アームをずらしています。

2つ目のwhile文で磁石がホールセンサの前に来るまでステッピングモーターを回転させます。

パズルを離す

アームを外側に移動させ、パズルを離す関数です。
void release_arm(int num) {
  if (num == 0)servo0.write(release_deg[num] + offset);
  else servo1.write(release_deg[num] + offset);
}
あまり綺麗な書き方ではありません。綺麗な書き方をご存知の方はぜひ教えてください。offsetについては速くモーターを動かすためのオーバーシュートを実装したのですが、オーバーシュートしたまま目標値に戻さなくても良いことがわかりoffsetを足したままになっています。

パズルを掴む

アームを中心に移動させ、パズルを掴む関数です。
void grab_arm(int num) {
  if (num == 0)servo0.write(grab_deg[num] - offset);
  else servo1.write(grab_deg[num] - offset);
  delay(70);
  if (num == 0)servo0.write(grab_deg[num]);
  else servo1.write(grab_deg[num]);
}
ここではoffsetで作ったオーバーシュートが役に立ちます。これによってより速くパズルを掴むことを期待しています(実際どれくらい効果があるのかはわかりません)

メインループ

メインループはコマンドを受け取って該当の関数を呼び出します。
void loop() {
  while (1) {
    if (Serial.available()) {
      buf[idx] = Serial.read();
      if (buf[idx] == '\n') {
        buf[idx] = '\0';
        data[0] = atoi(strtok(buf, " "));
        data[1] = atoi(strtok(NULL, " "));
        data[2] = atoi(strtok(NULL, " "));
        if (data[1] == 1000) grab_arm(data[0]);
        else if (data[1] == 2000) release_arm(data[0]);
        else if (data[1] == 0) motor_adjust(data[0], data[2]);
        else move_motor(data[0], data[1], data[2]);
        idx = 0;
      }
      else {
        idx++;
      }
    }
  }
}
コマンドの種類によって呼び出す関数が違います。

まとめ

今回は実際にアクチュエータを動かすArduinoのプログラムを紹介しました。私の言語に対する知識不足によるところなのか、一部綺麗でない書き方をしていると思います。ぜひコメントで良い書き方を教えてください。

次回はPythonのメイン処理を解説します。

　 Tweet
Qiitaで続きを読む

投稿日：2020-10-19T22:25:37+09:00

うんち?でも足し算がしたい！～絵文字で四則演算～

はじまり

実家に帰ったら甥(6)にこんな質問をされた。

「?+6はなーんだ？」

「カレーライス！」と適当に答えると、甥は満足そうに「正解！100点！」と言って去っていった。このとき私はまだ齢6才の甥がUnicodeを知っていることに気づいていなかった…。

?の足し算を考えてみる

甥曰く

「先生に”数字以外で足し算はできません。"って言われた」

らしい。だがそんなことはない、Word2Vecで
「王様」- 「男」+ 「女」= 「女王」
の演算ができたように、?にも四則演算を導入してあげればいいのだ！（適当）

「うんこ」という文字列に対して6を足すのは難しそうなので、絵文字「?」に6を足すことを考える。絵文字に限らず文字は内部的にはUnicodeで表現されているらしい。（2020/06現在ではUnicode 13.0 が最新）

例えばフルーツと野菜は以下のような種類がある。参考

Unicode 表示名称

1F345 ? TOMATO

1F346 ? AUBERGINE

1F347 ? GRAPES

1F348 ? MELON

1F349 ? WATERMELON

1F34A ? TANGERINE

1F34B ? LEMON

1F34C ? BANANA

1F34D ? PINEAPPLE

1F34E ? RED APPLE

1F34F ? GREEN APPLE

1F350 ? PEAR

1F351 ? PEACH

1F352 ? CHERRIES

1F353 ? STRAWBERRY

ここで足し算を
? + 1 = (?のUnicode値 + 1 の絵文字) = ?と決めよう。

その他演算も同様に

引き算：
? - 1 = (?のUnicode値 - 1 の絵文字) = ?

わり算：
? / 2 = (?のUnicode値 / 2 の絵文字) = 簾

かけ算：
? * 2 = (?のUnicode値 * 2 の絵文字) = U3E698

また絵文字同士の四則演算も同様にできることにする。

※わり算は見たことがない漢字が出てきがちで、かけ算はUnicodeの範囲から外れてしまうのが残念…。でもとりあえず足し算ができるのでヨシ！としよう。

Pythonでいじる

Unicodeの表を眺めて探すのは人間のやることではない。Pythonにやらせよう。

Unicodeの値はPythonでは組み込み関数ordで取得できる．
>>> ord('?')
128169

# 16進表示で`U+1F4A9`と書くのが普通なので一応
>>> hex(ord("?"))
'0x1f4a9'
そしてchrでUnicode値を文字に変換する。
>>> chr(128169)
'?'
このUnicode値で足し算をしてみる。
>>> chr(ord('?') + 6)
'?'
なるほど．?+ 6 = ? ！！　確かに「うんこ + 6 = 100点」、甥っ子すげえな！

Unicode物語

どうでもいいけど、?の絵文字の近くは物語を感じる配置になってる。

Unicode 表示名称物語

1F4A1 ? ELECTRIC LIGHT BULB バグを解決する方法をひらめいた?

1F4A2 ? ANGER SYMBOL と思ったが、ダメダメでおこ?

1F4A3 ? BOMB 勢いでＰＣを爆破?

1F4A4 ? SLEEPING SYMBOL 家に帰って寝るぜ?

1F4A5 ? COLLISION SYMBOL たたき起こされた?

1F4A6 ? SPLASHING SWEAT SYMBOL 急いで職場へ向かう?

1F4A7 ? DROPLET 泣いて謝る?

1F4A8 ? DASH SYMBOL 謝ったらスッキリして屁が出た?

1F4A9 ? PILE OF POO ついでに?

1F4AA ? FLEXED BICEPS ?<力こそパワー。筋肉は裏切らない。

（※これで何かがわかることは決してないし、Unicodeを定めた人はこんなアホなことを考えていないと思う。）

個人的におもしろかった数式

一位： ? / 6 = 危

→ 排泄物の16.6%は危ない

おわり。

最後に

単純にUnicodeの値で四則演算をすると演算が閉じていないのが残念だけど、とりあえずうんこでも足し算ができることがわかりました！！

参考文献

図書館員のコンピュータ基礎講座
：Unicodeの表を参考にした

Let’s EMOJI
：絵文字の一覧表や検索が便利

Unicode	表示	名称
1F345	?	TOMATO
1F346	?	AUBERGINE
1F347	?	GRAPES
1F348	?	MELON
1F349	?	WATERMELON
1F34A	?	TANGERINE
1F34B	?	LEMON
1F34C	?	BANANA
1F34D	?	PINEAPPLE
1F34E	?	RED APPLE
1F34F	?	GREEN APPLE
1F350	?	PEAR
1F351	?	PEACH
1F352	?	CHERRIES
1F353	?	STRAWBERRY

Unicode	表示	名称	物語
1F4A1	?	ELECTRIC LIGHT BULB	バグを解決する方法をひらめいた?
1F4A2	?	ANGER SYMBOL	と思ったが、ダメダメでおこ?
1F4A3	?	BOMB	勢いでＰＣを爆破?
1F4A4	?	SLEEPING SYMBOL	家に帰って寝るぜ?
1F4A5	?	COLLISION SYMBOL	たたき起こされた?
1F4A6	?	SPLASHING SWEAT SYMBOL	急いで職場へ向かう?
1F4A7	?	DROPLET	泣いて謝る?
1F4A8	?	DASH SYMBOL	謝ったらスッキリして屁が出た?
1F4A9	?	PILE OF POO	ついでに?
1F4AA	?	FLEXED BICEPS	?<力こそパワー。筋肉は裏切らない。

　 Tweet
Qiitaで続きを読む

投稿日：2020-10-19T22:23:35+09:00

PythonのFlaskで画像データをreturnし、HTMLのcanvas要素へ描写する

PythonのFlaskで取得した画像データをHTMLのcanvas要素へ描写します。

やりたいこと

Google Cloud Storageに保存した画像データをCloud functionsで読み出して、手元のHTMLのcanvas要素に描写します。Cloud functionsでは画像イメージがまずはblob形式で読み出されます。これをpngやjpgに変換してflaskでreturnして、canvas要素で描写します。

Cloud functionsでStorageのファイルを読み込んでダウンロードする

ここは公式ドキュメントが充実しているので迷いませんでした。

https://cloud.google.com/storage/docs/downloading-objects#code-samples
main.py
from google.cloud import storage

def download_blob(bucket_name, source_blob_name, destination_file_name):
    """Downloads a blob from the bucket."""
    # bucket_name = "your-bucket-name"
    # source_blob_name = "storage-object-name"
    # destination_file_name = "local/path/to/file"

    storage_client = storage.Client()

    bucket = storage_client.bucket(bucket_name)
    #bucket_nameとは、Storageに作った格納先の名前。手動で設定したもの

    blob = bucket.blob(source_blob_name)#要するにファイル名
    blob.download_to_filename(destination_file_name)

    print(
        "Blob {} downloaded to {}.".format(
            source_blob_name, destination_file_name
        )
    )
実行するとローカルにファイルがダウンロードされます。

単体ファイルとしてダウンロードさせるのではなく、flaskでjpgとしてreturnしてダウンロードする

この辺で詰まり始めた。要するに、blobをbytesで読んで、それにheaderなどをつけて画像としてreturnする。その際、Flaskのsend_fileというモジュールを使う。いや、これわからんでしょ。

なお、今回はホスティングはGCPのCloud functionsでやっているので、app.run()などはありません。ただこれをホスティングすると、あるURLを叩いたらdownload_blob(）の関数が動きます。
main.py
from google.cloud import storage
import io
from flask import send_file

def download_blob(request):
    """Downloads a blob from the bucket."""
    bucket_name = "your-bucket-name"
    source_blob_name = "storage-object-name"

    storage_client = storage.Client()

    bucket = storage_client.bucket(bucket_name)
    #bucket_nameとは、Storageに作った格納先の名前。手動で設定したもの

    blob = bucket.blob(source_blob_name)#要するにファイル名
    image_binary= blob.download_as_bytes()
    return send_file(
            io.BytesIO(image_binary),
            mimetype='image/jpeg',
            as_attachment=True,
            attachment_filename='%s.jpg' % source_blob_name)
Cloud functionsでのデプロイは下記を参考に。
https://qiita.com/NP_Systems/items/f0f6de899a84431685ff

ライブラリなどインストールしていたら下記を打つだけで、ローカルでエミュレートします。
teriminal.
functions-framework --target=hello  --port=8081
ホスティングしたURLを叩いたら、画像がダウンロードされます。でも単体ファイルとは違って、returnしています。これを使って、あとは受け取ったものをcanvasへ描写します

canvas要素への描写

ここもかなり詰まりました。こんなシンプルなことなのに。
このサイト本当に助かりました。
https://stackoverflow.com/questions/57014217/putting-an-image-from-flask-to-an-html5-canvas

phpですがhtmlでも同じようなものです。
index.php
<?php get_header(); ?>
<main>
<article>
  <section>
       <input type="button" value="Start" onclick="main();"/>
        <canvas></canvas>
  </section>
</article>
</main>

<script language="javascript" type="text/javascript">

    function main(){
      var canvas = document.getElementsByTagName('canvas');
      var ctx = canvas[0].getContext('2d');

      var img = new Image();
      img.src = 'http://0.0.0.0:8081';//FlaskでホスティングしたURL

      img.onload = function() {
        img.style.display = 'none'; // ようわからん
        console.log('WxH: ' + img.width + 'x' + img.height)

        ctx.drawImage(img, 0, 0);
        var imageData = ctx.getImageData(0, 0, img.width*2, img.height*2)

        for(x = 0 ; x < 100 ; x += 10) {
          for(y = 0 ; y < 100 ; y += 10) {
             ctx.putImageData(imageData, x, y);
          }
        }
      };    }
</script>
<?php get_footer(); ?>
感想

いや、こんなシンプルなことなのに詰まりまくった。blobやpngへの理解が浅い気がする。

　 Tweet
Qiitaで続きを読む

投稿日：2020-10-19T22:19:15+09:00

SONYのNNCチャレンジ（音声データを用いてAudioStockに役立つものを作れ）に応募する。

0. 私は誰？

　数学科博士課程の院生です。専門は解析であり計算機代数やまして機械学習の知識はほとんどありませんが研究のために計算機を使うことはあり、Pythonだけはなんとか使うことができます。第一回のNNCチャレンジ（画像分類）にも参加しましたが明確な目的意識がなく、知識不足もあってめぼしい成果物は得られませんでした（提出だけはしました）。
　

1. SONY NNCチャレンジとは

　SONYが運営する機械学習の統合開発環境「Neural Network Console (NNC)」を使った機械学習のコンテストです。
コンテストの運営はSONYと株式会社ledgeさんらしいです。概要は以下のURLにあります。
https://nnc-challenge.com/

2. 今回のテーマ

　今回の公募で扱うのは音声データということで、自分の中でやりたいことがはっきり決まりました。私はいわゆる"音ゲー"が趣味で、普段から聞いているのはほとんどゲーム楽曲です。その中でも特に大好きな作曲家であるt+pazolite("とぱぞらいと"と読みます。)さんは非常に独特な音楽を作ります。その独特な世界観は機械にも判別できるのではないか、というのが今回のテーマです。つまり「機械はt+pazolite曲を判別できるか」ということです。コンテストテーマに即した言い方をすれば、「お気に入りの楽曲を学習してユーザーに新しい曲をレコメンドする機能を作る」でしょうか。すでにAmazon Prime Musicなどではユーザーに楽曲をお勧めする機能は実装されています。"チャレンジ"としては独自性がないかもしれませんが自分の実力とコンテストの期限を鑑みるとあまりテーマ選択に時間をかけられません。何より自分が興味のあるテーマの方がチャレンジにも気合が入ります。今回はこちらのテーマでいきます。

3. 何が必要か

　私の今回のテーマは入力された楽曲がt+pazoliteさん(以下"とぱぞ")によるものかどうか判定する"識別器"を作ることです。つまり何らかの楽曲データを入力したとき、"0"("とぱぞ曲"ではない)または"1"("とぱぞ曲"である)を返すプログラムを（機械が自ら学習して）作ることになります。どんな曲が"0"でどんな曲が”1”かを"0"または"1"のラベル付きの大量の楽曲たちで学習させ、未知の曲に対してこの判定ができるプログラムを作るのです。NNCでは入力は配列なので楽曲データを何らかの形で配列にする必要があります。wav形式の音楽ファイルが配列形式なので楽曲をこの形式に変換します。
（NNC公式ドキュメント、https://support.dl.sony.com/wp-content/uploads/sites/2/2017/11/19120828/starter_guide_sound_classification.pdf）
また、入力データの配列はすべて同じ形の配列であることが必要です。今回はNNC公式から一万曲以上の楽曲データが同じサイズのwav形式で配布されたので(学習用データ提供：Audiostock)こちらに合わせて"とぱぞ曲"を整形します。

4. 楽曲データの整形

　"1"判定のデータとしてとぱぞ曲を整形します。手持ちのとぱぞ曲はm4a形式だったのでwav形式に変換する必要があります。こちらの投稿を参考にPythonでプログラミングしました。
（M4AをWAVに変換する(その逆も)
https://wave.hatenablog.com/entry/2017/01/29/160000）
　楽曲がwav形式に変換できたら、次はサイズを提供された学習用データと同じサイズに揃えます。楽曲の配列サイズは1.ステレオかモノラルか、2.サンプリングレート、3.楽曲の長さ（秒数）
によって決まります（NNC公式ドキュメント参照）。ステレオモノラルに関しては提供データと手持ちデータが両方ともモノラルだったので変える必要はありませんでした。サンプリングレートに関しては公式配布のものが8kHz、手持ちの楽曲が48kHzだったのでダウンサンプリングする必要があります。ただし、単純にサンプリングレートを6分の１にすると間延びした（遅くなった）楽曲データが生成されるので方法は選ぶ必要があります。こちらの記事の方法で簡単に目当てのサンプリングレート変換を達成できました。
（Downsampling wav audio file
https://stackoverflow.com/questions/30619740/downsampling-wav-audio-file）
最後に楽曲の長さを揃えます。提供データはすべて24秒に整形されていたので手持ち楽曲も24秒に"切りそろえ"ます。こちらの記事を参考に出力ファイルの名前を元楽曲の名前に通し番号を振ったものに変え、フォルダ内のすべての楽曲に対して同様の操作を繰り返すプログラムを書きました。
（【Python】WAVファイルを等間隔に分割するプログラム【サウンドプログラミング】
http://tacky0612.hatenablog.com/entry/2017/11/21/164409）

5. アノテーションCSVファイルの作成

　NNCにデータを入力するために、最後にアノテーション作業を行います。アノテーションとは各楽曲に対してそれが"1"であるか"0"であるかのラベルをつけることです。NNCではこの入力を楽曲のパスとその曲に対応する"0"または"1"を書き込んだCSVファイルとしてアップロードすることで行います。楽曲データはCSVに書き込んだパスから自動的にアップロードされます（NNC公式ドキュメント参照）。Pythonで楽曲の入ったフォルダからパスを取得し、CSVに書き出すプログラムを書きました。"とぱぞ曲"と"そうでない曲"を別々のフォルダに配置して、とぱぞ曲のパスに”1”を、そうでない曲に"0"を対応させました。
私はCSVを作った時点で楽曲の順番をシャッフルしましたがNNC上で上がってきたデータをシャッフルする機能があるので特に必要なかったです。

6. 学習

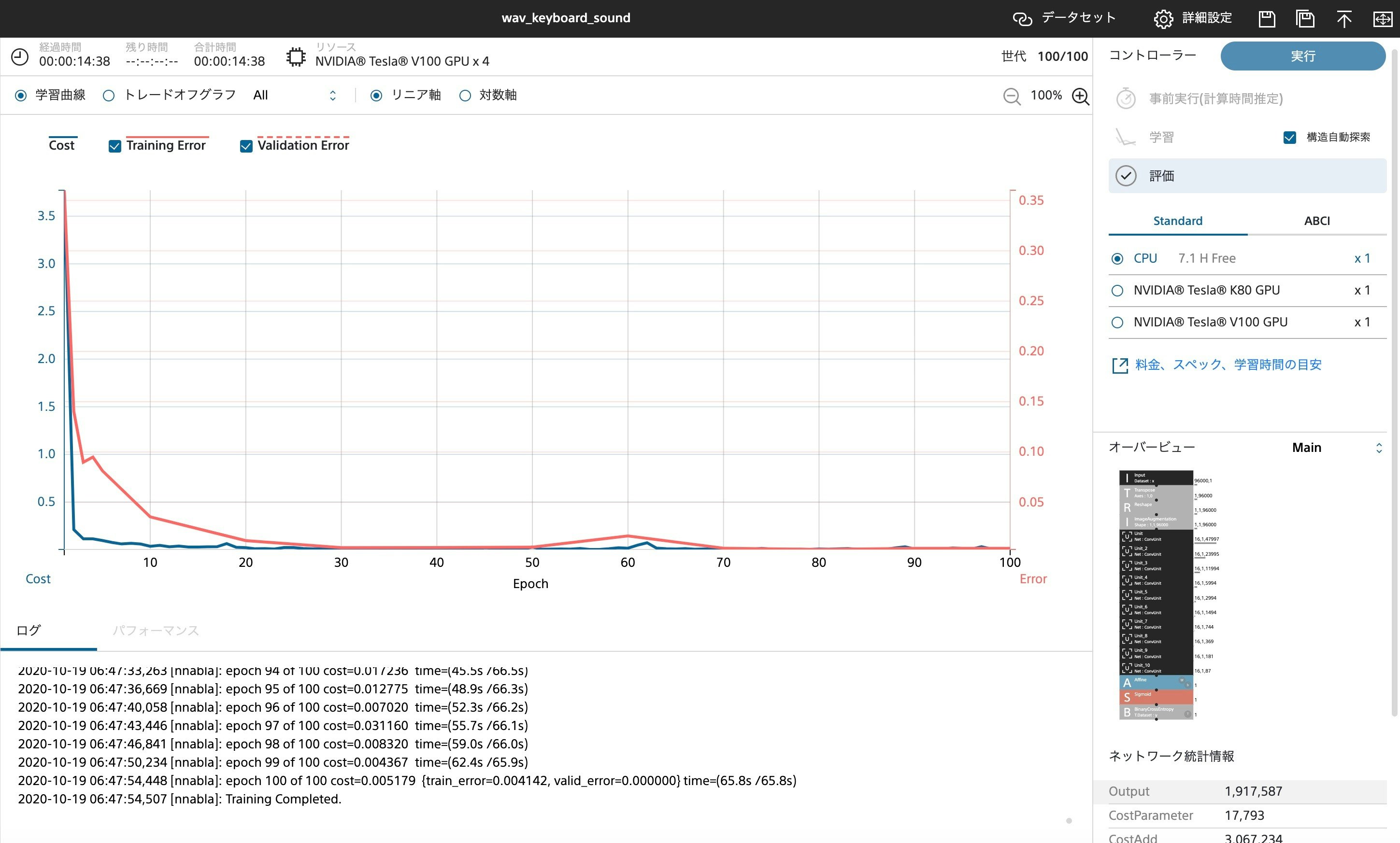
　データが揃ったのでいよいよ学習です。なのですがこの時点で締め切り当日の午後2時になっていました。学習にもそれなりの時間がかかることはわかっていたのでNNCのサンプルプロジェクトから音声データ用のものを借りて、入出力を今回のテーマに合わせたものを使うことにしました。具体的にはwav_keyboard_soundというプロジェクトの入力を(96000, 1)、出力前の処理をAffine -> Sigmoid -> Binarycrossentropyに変えたものを使いました。時間配分がうまくいかなかったのは悔しい限りです。

結果

　

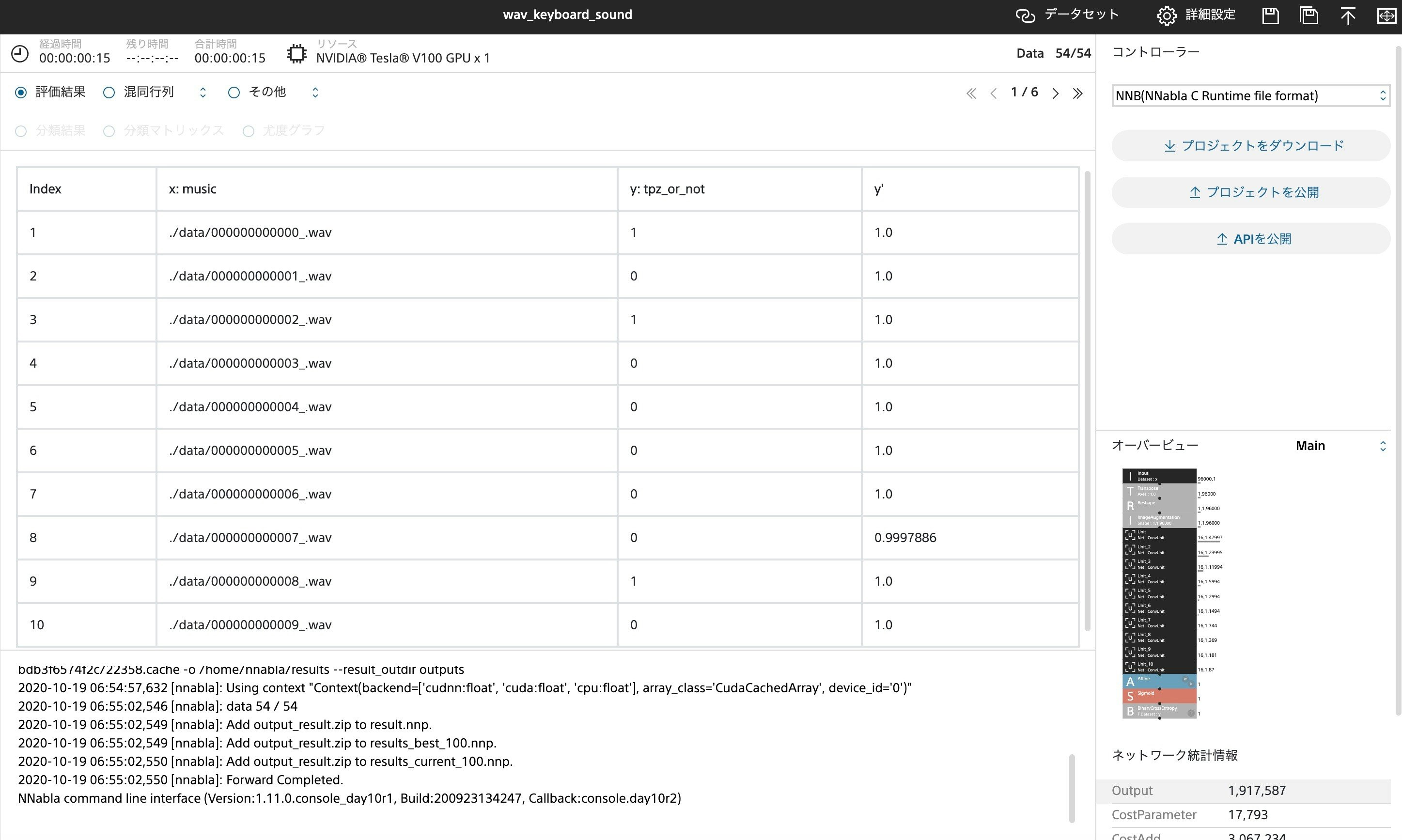
　結果はまさに圧倒的で、機械に対しても"とぱぞ曲"が圧倒的な認識率を誇っていることがわかります。写真は楽曲データを12秒に切りそろえたもの5450個を学習に使っています。TESLA V100 4機を用いた学習でこれらの処理に14分でした。CPUでの学習も試みたのですが2時間以上学習にかかり結果を出すことを断念しました。返す返すも時間配分のまずさが悔やまれます。次回があれば与えられた時間をうまく使ってデータの前処理、効率の良い学習等の比較も試せるようにしたいです。

　 Tweet
Qiitaで続きを読む

投稿日：2020-10-19T22:07:26+09:00

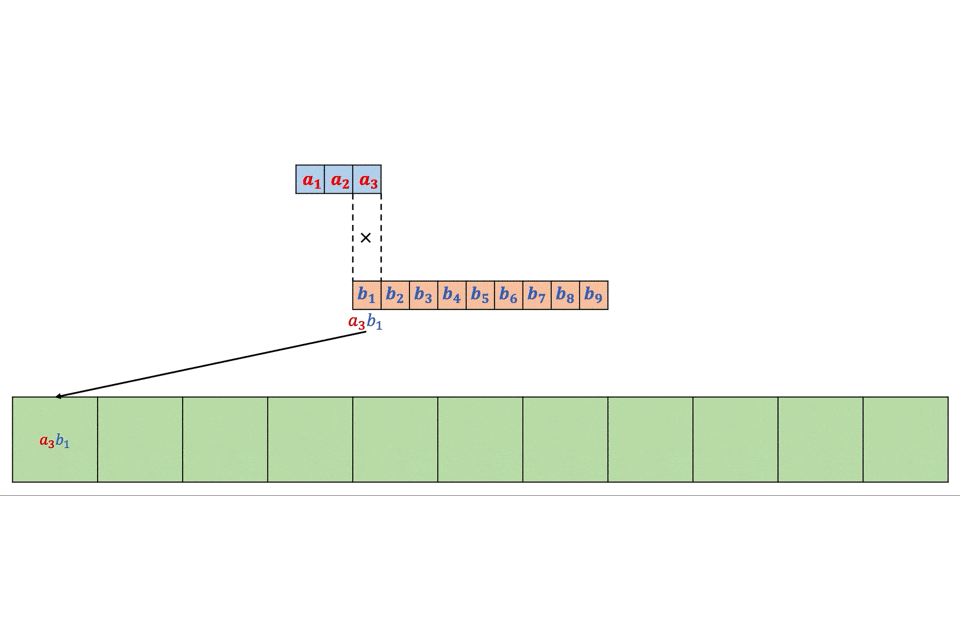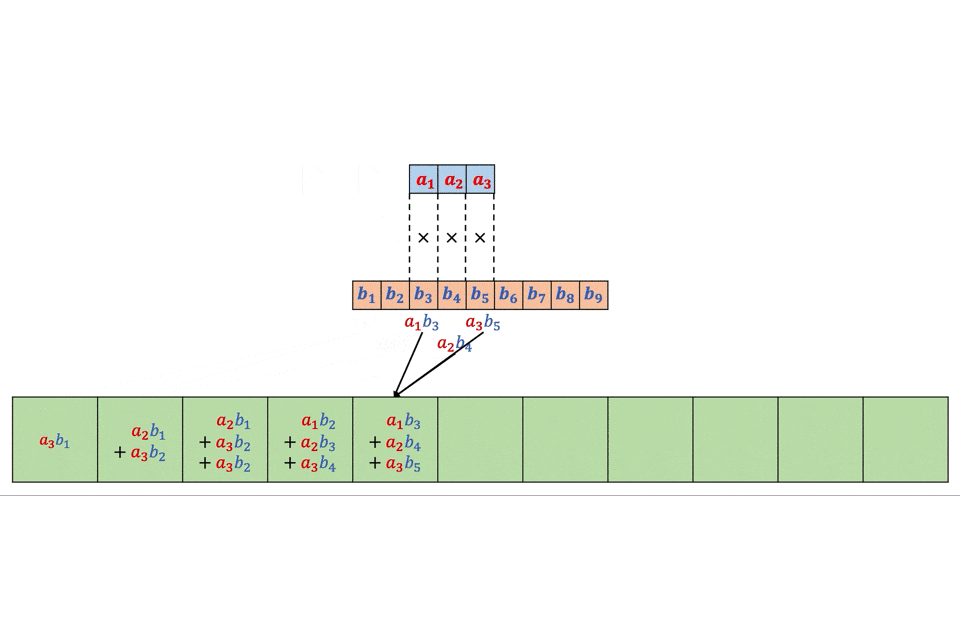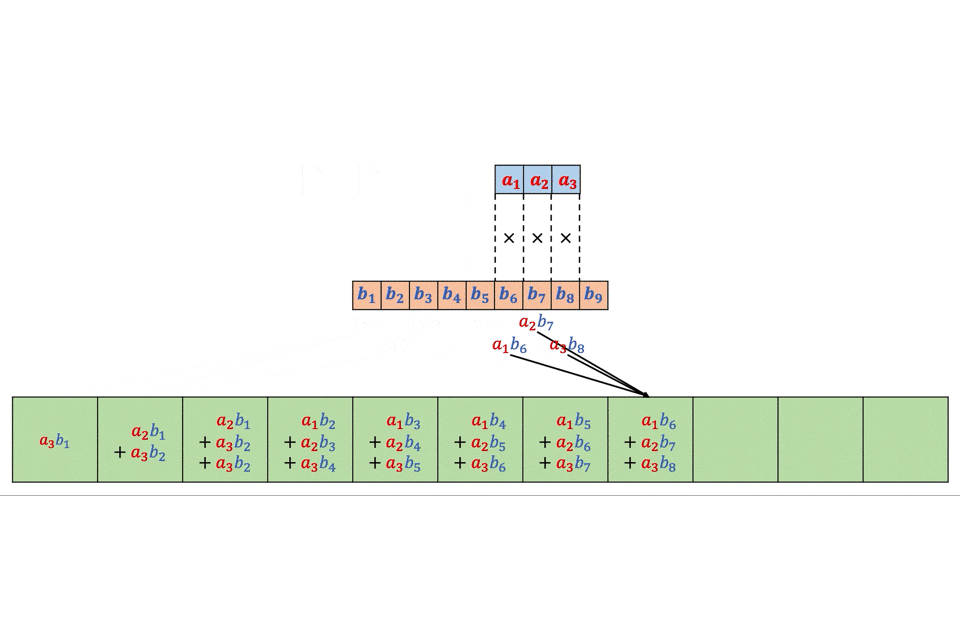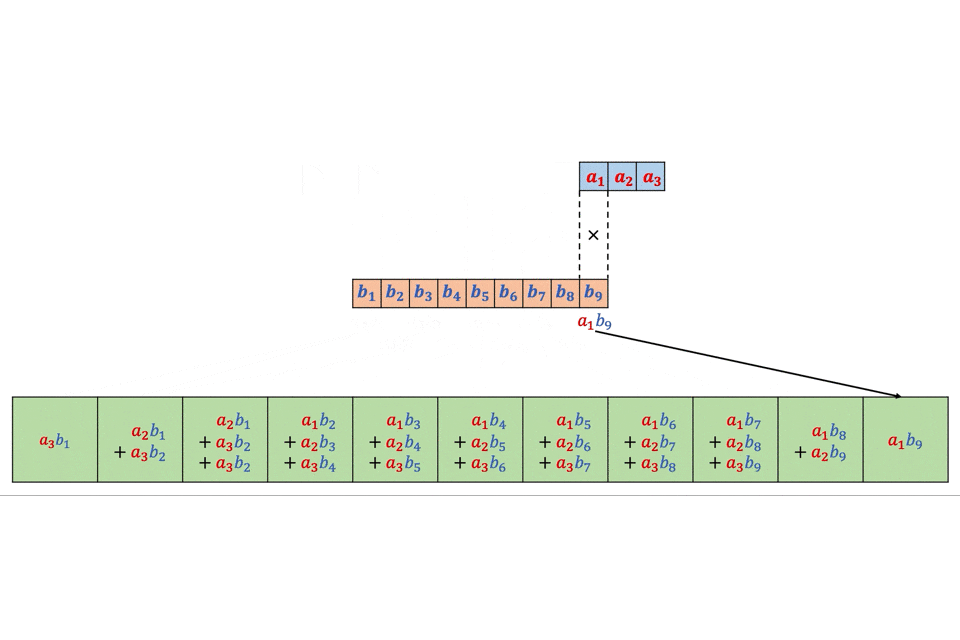
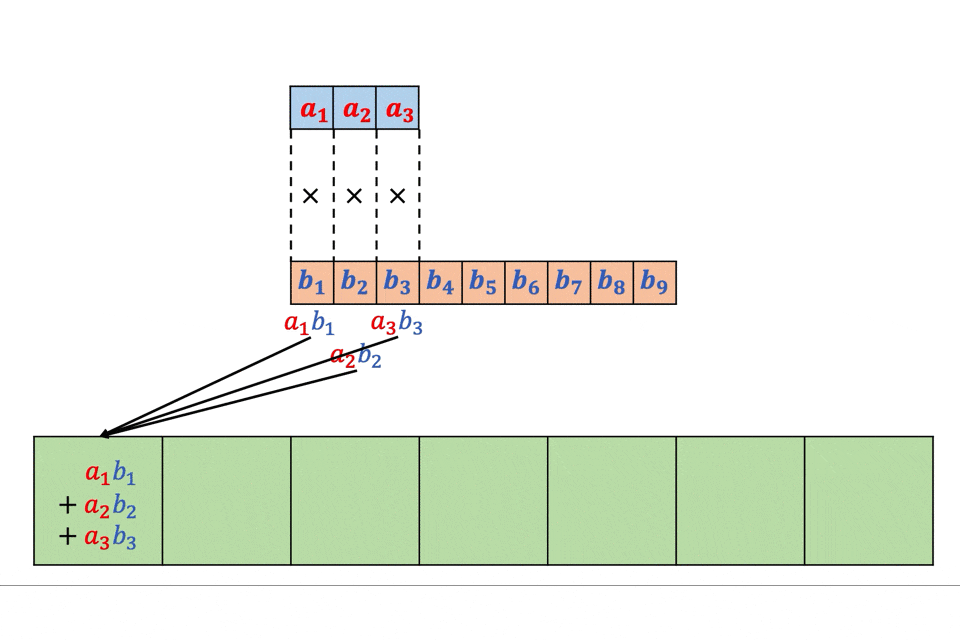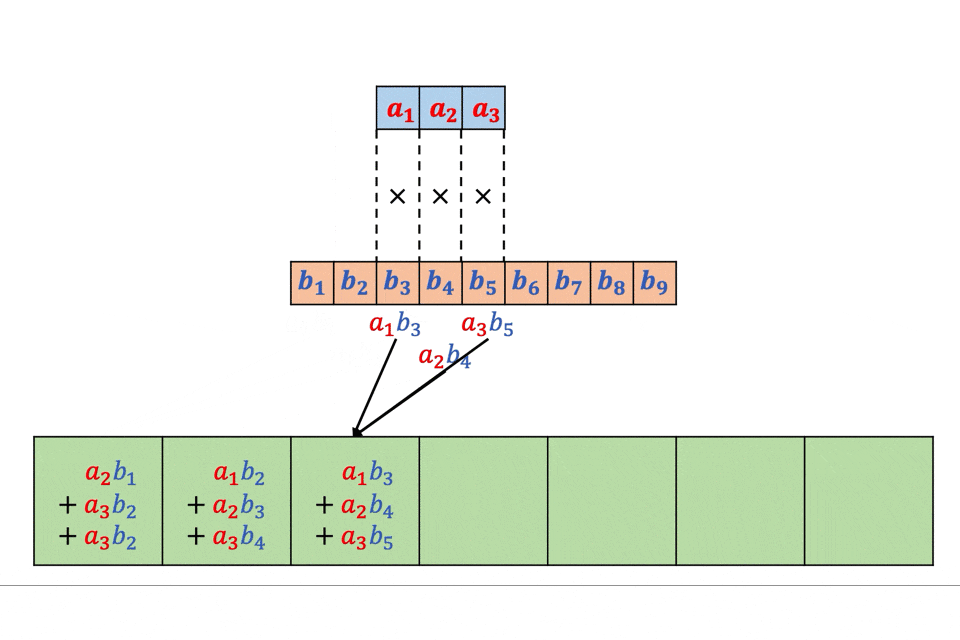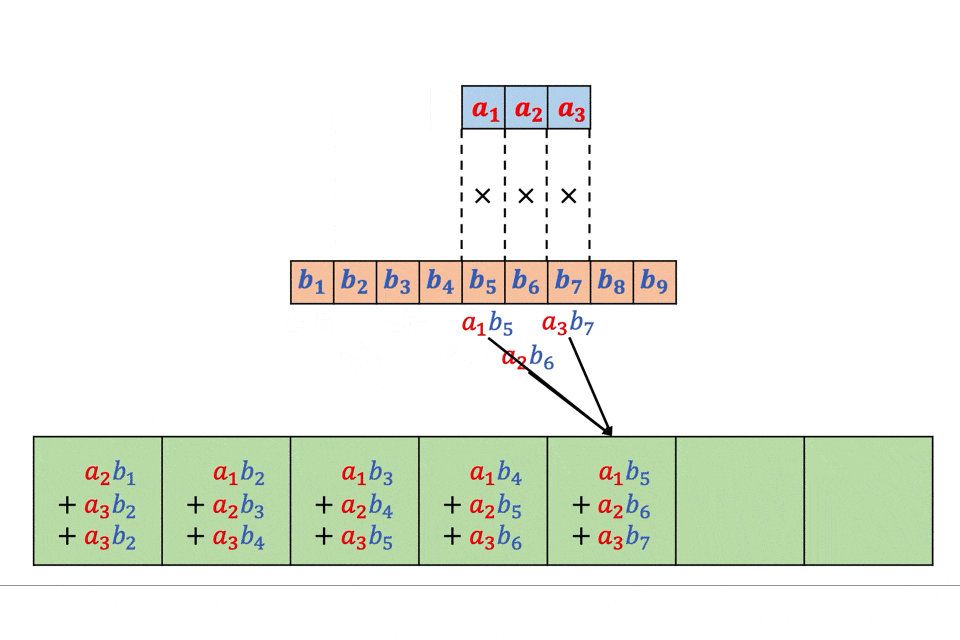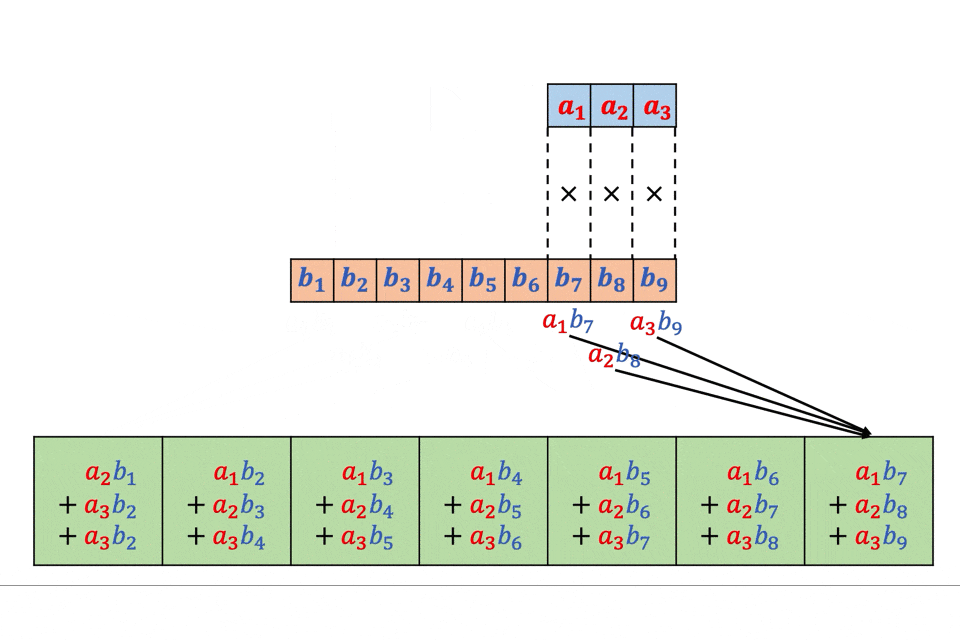
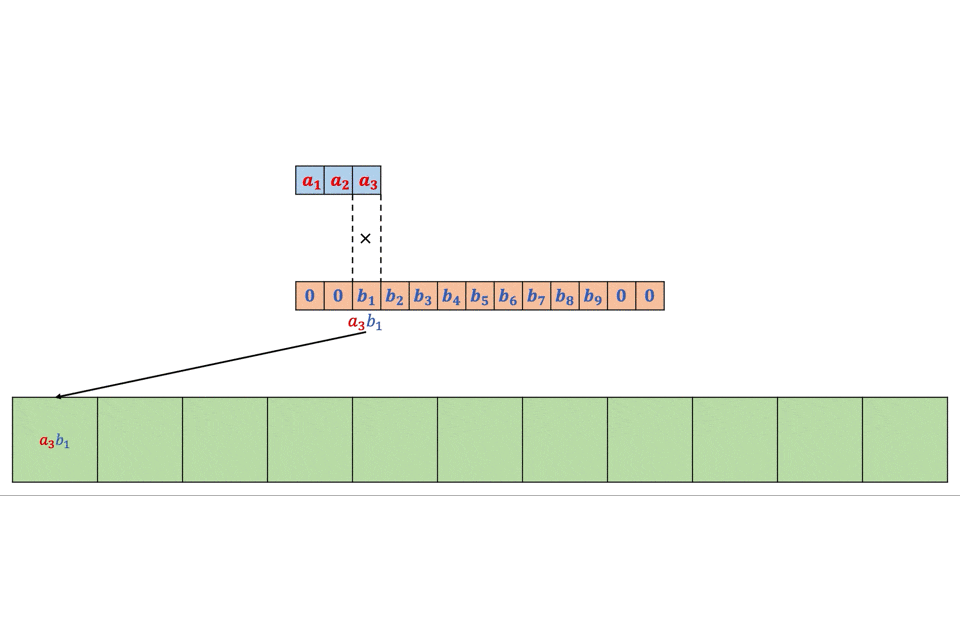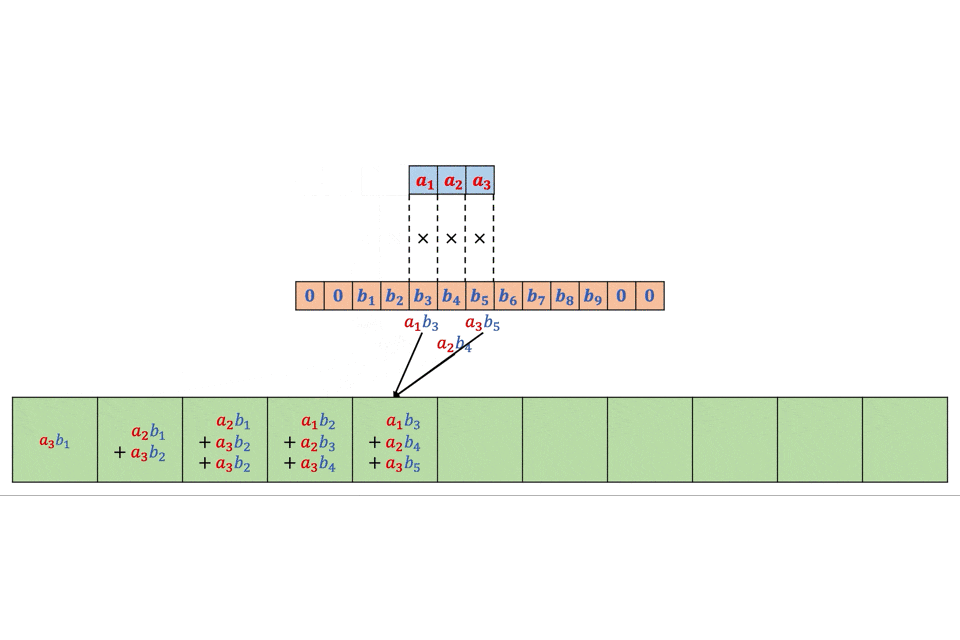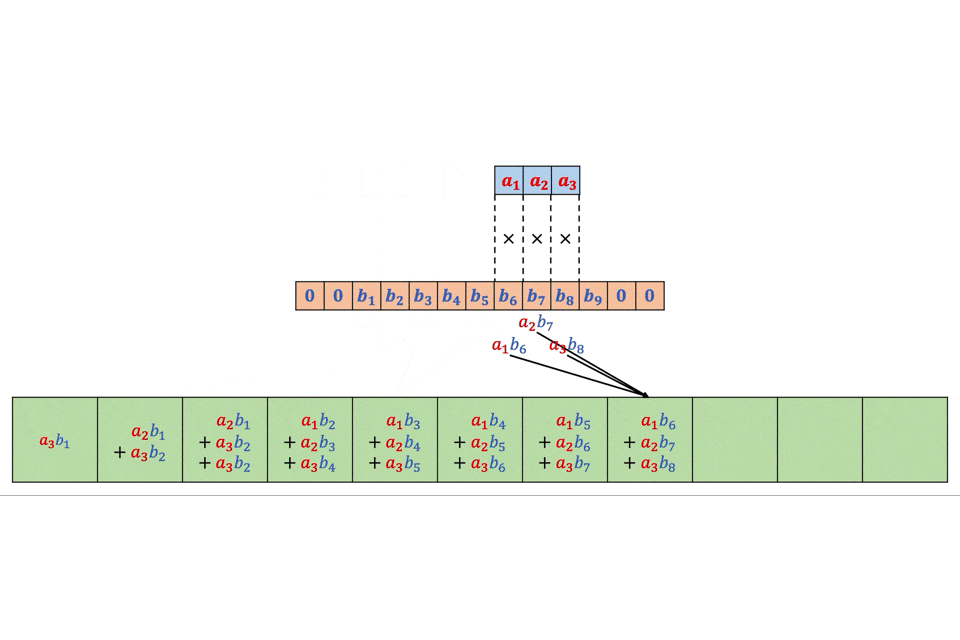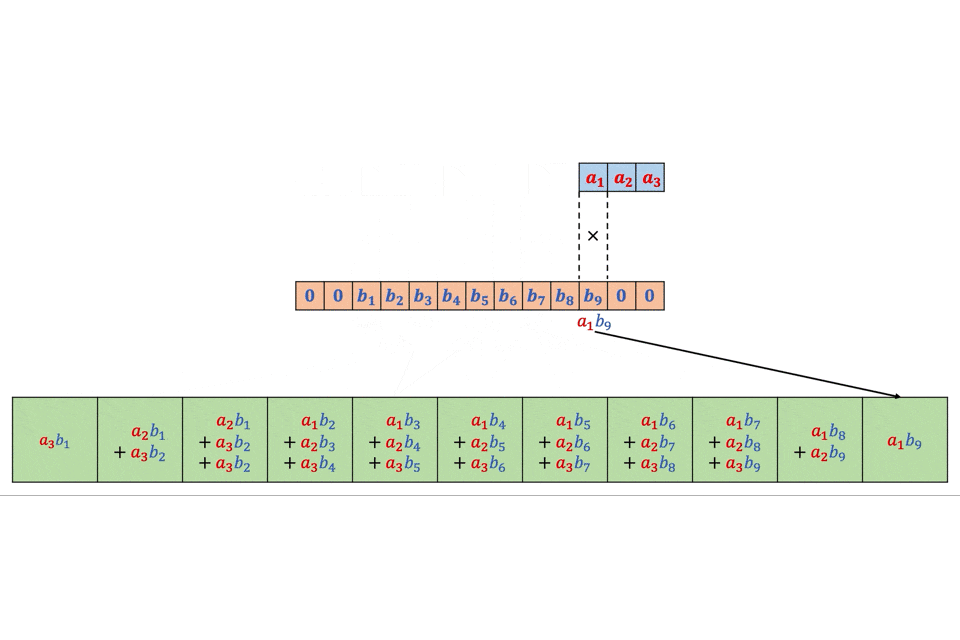
スライディングウィングを創造で書いた。

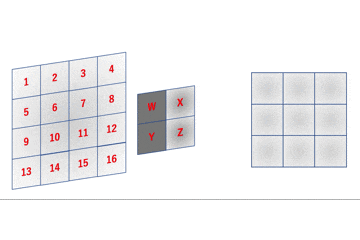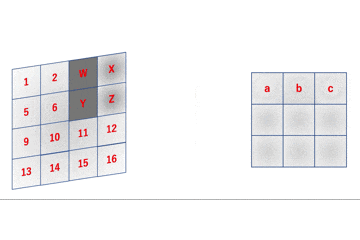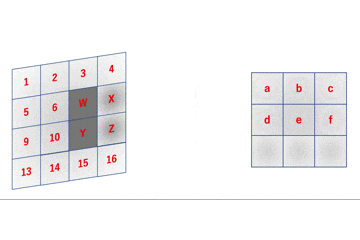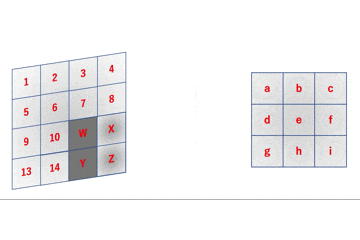
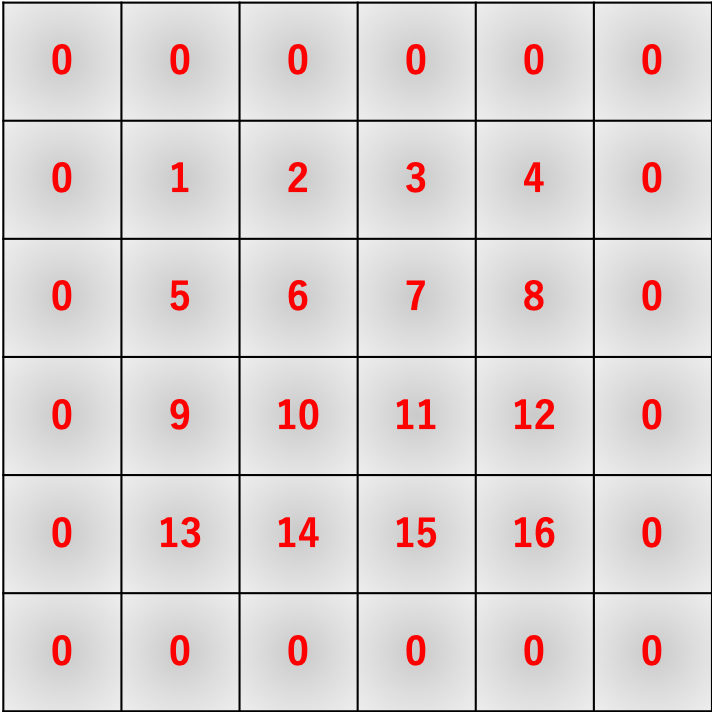
img = np.array(range(100)).reshape([10,10])
img = np.zeros([100,100])
img[0:50,0:50] = 1

win_size = 2
def SlidingWindow(win_size,img):
  split_img = []
  yx = []
  for i in range(img.shape[0]-win_size+1):
    for j in range(img.shape[1]-win_size+1):
      split_img.append(img[i:i+win_size,j:j+win_size])
      yx.append([i,j])
  all = []
  for img_,yx_ in zip(split_img,yx):
    all = all + [(i+yx_[0],j+yx_[1]) for (i,j) in list(zip(*np.where(img_ == 1)))]
  return Counter(all)
SlidingWindow(4,img)

　 Tweet
Qiitaで続きを読む

投稿日：2020-10-19T21:10:20+09:00

【情報圧縮ノート002 】$PATHを通さないと $conda で Anacondaが使えない

なぜか英語を使ってますが、理由は、まぁその、早い話が自分のインスタグラムの使い回しの画像だからです。
＊情報圧縮ノートは、今まで文章で説明されたいた概念(Knowledge)を１枚のjpegで表現するものです。

　 Tweet
Qiitaで続きを読む

投稿日：2020-10-19T21:05:04+09:00

Pythonでスクレイピング(データ取得)

今回はwikipediaから映画の興行収入を取得しようと思う。
scrapingの準備編はこちら

とりあえず、ソースコードと結果は下記となる。

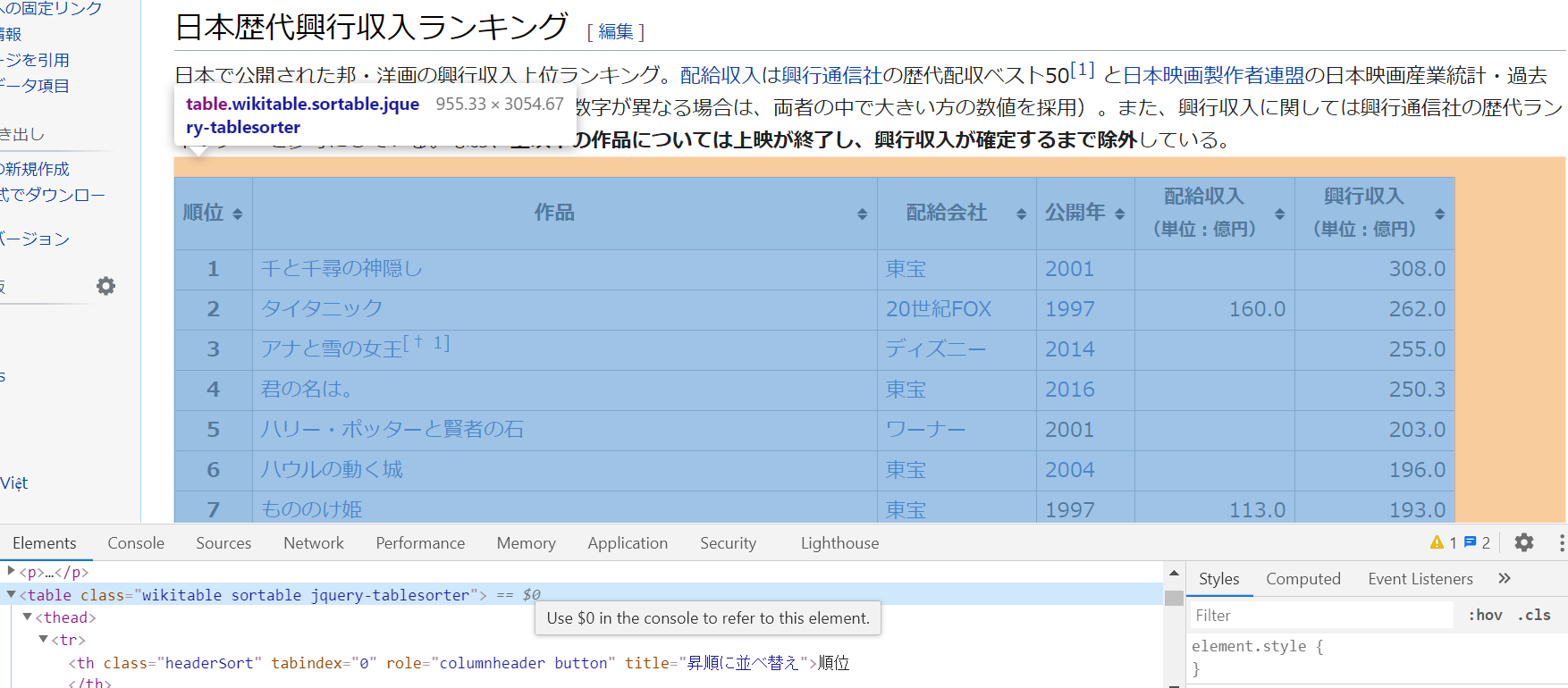
from urllib.request import urlopen
from bs4 import BeautifulSoup

# 取得するページ
html = urlopen('https://ja.wikipedia.org/wiki/%E6%97%A5%E6%9C%AC%E6%AD%B4%E4%BB%A3%E8%88%88%E8%A1%8C%E5%8F%8E%E5%85%A5%E4%B8%8A%E4%BD%8D%E3%81%AE%E6%98%A0%E7%94%BB%E4%B8%80%E8%A6%A7')
bs = BeautifulSoup(html)

get_info = bs.select('table.wikitable tbody tr')
movies = []

for index, info in enumerate(get_info):
    for info_td in info.select('td'):
        if index <= 100:
            movies.append(info_td.text)
        else:
            break

print(movies)

結果

['千と千尋の神隠し\n', '東宝\n', '2001\n', '\n', '308.0\n', 'タイタニック\n', '20世紀FOX\n', '1997\n', '160.0\n', '262.0\n', 'アナと雪の女王[† 1]\n', 'ディズニー\n', '2014\n', '\n', '255.0\n', '君の名 は。\n', '東宝\n', '2016\n', '\n', '250.3\n', 'ハリー・ポッターと賢者の石\n', 'ワーナー\n', '2001\n', '\n', '203.0\n', 'ハウルの動く城\n', '東宝\n', '2004\n', '\n', '196.0\n', 'もののけ姫\n', '東宝\n', '1997\n', '113.0\n', '193.0\n', '踊る大捜査線 THE MOVIE 2 レインボーブリッジを封鎖せよ![† 2]\n', '東宝\n', '2003\n', '\n', '173.5\n', 'ハリー・ポッターと秘密の部屋[† 3]\n', 'ワーナー\n', '2002\n', '\n', '173.0\n', 'アバター\n', '20世紀FOX\n', '2009\n', '\n', '156.0\n', '崖の上のポニョ\n', '東宝\n', '2008\n', '\n', '155.0\n', 'ラスト サムライ\n', 'ワーナー\n', '2003\n', '\n', '137.0\n', 'E.T.[† 4][ † 5]\n', 'CIC\n', '1982\n', '96.2\n', '135.0\n', 'アルマゲドン\n', 'ディズニー\n', '1998\n', '83.5\n', '135.0\n', 'ハリー・ポッターとアズカバンの囚人\n', 'ワーナー\n', '2004\n', '\n', '135.0\n', 'アナ と雪の女王2\n', 'ディズニー\n', '2019\n', '\n', '133.5\n', 'ボヘミアン・ラプソディ\n', '20世紀FOX\n', '2018\n', '\n', '131.0\n', 'ジュラシック・パーク[† 6]\n', 'UIP\n', '1993\n', '83.0\n', '128.5\n', 'スター・ウォーズ エピソード1/ファントム・メナス\n', '20世紀FOX\n', '1999\n', '78.0\n', '127.0\n', '美女と野獣\n', 'ディズニー\n', '2017\n', '\n', '124.0\n', 'アラジン\n', 'ディズニー\n', '2019\n', '\n', '121.6\n', '風立ちぬ\n', '東宝\n', '2013\n', '\n', '120.2\n', 'アリス・イン・ワンダーランド\n', 'デ ィズニー\n', '2010\n', '\n', '118.0\n', 'スター・ウォーズ/フォースの覚醒\n', 'ディズニー\n', '2015\n', '\n', '116.3\n', '南極物語\n', 'ヘラルド・東宝\n', '1983\n', '59.0\n', '110.0\n', 'マトリックス・リローデッド\n', 'ワーナー\n', '2003\n', '\n', '110.0\n', 'ファインディング・ニモ\n', 'ディズニー\n', '2003\n', '\n', '110.0\n', 'ハリー・ポッターと炎のゴブレット\n', 'ワーナー\n', '2005\n', '\n', '110.0\n', 'パイレーツ・オブ・カリビアン/ワールド・エンド\n', 'ディズニー\n', '2007\n', '\n', '109.0\n', 'トイ・ストーリー3\n', 'ディズニー\n', '2010\n', '\n', '108.0\n', 'インデペンデンス・デイ\n', '20世紀FOX\n', '1996\n', '66.5\n', '106.5\n', 'ロード・オブ・ザ・リング/王の帰還\n', 'ヘラルド・松竹\n', '2004\n', '\n', '103.2\n', '踊る大捜査線 THE MOVIE\n', '東宝\n', '1998\n', '53.0\n', '101.0\n', 'トイ・ストーリー4\n', 'ディズニー\n', '2019\n', '\n', '100.9\n', 'パイレーツ・オブ・カリビアン/デッドマンズ・チェスト\n', 'ディズニー\n', '2006\n', '\n', '100.2\n', '子猫物語\n', '東宝\n', '1986\n', '54.0\n', '98.0\n', 'ミッション:インポッシブル2\n', 'UIP\n', '2000\n', '\n', '97.0\n', 'ハリー・ポッターと死の秘宝 PART2\n', 'ワーナー\n', '2011\n', '\n', '96.7\n', 'A.I.[† 7]\n', 'ワーナー\n', '2001\n', '\n', '96.6\n', 'ジュラシック・ワールド\n', '東宝東和\n', '2015\n', '\n', '95.3\n', 'バック・トゥ・ザ・フューチャー PART2\n', 'UIP\n', '1989\n', '55.3\n', '95.0\n', 'ロスト・ワールド/ジュラシック・パーク\n', 'UIP\n', '1997\n', '58.0\n', '95.0\n', 'ハリー・ポッターと不死鳥の騎士団\n', 'ワーナー\n', '2007\n', '\n', '94.0\n', 'モンスターズ・インク\n', 'ディズニー\n', '2002\n', '\n', '93.7\n', '名探偵コナン 紺青の 拳\n', '東宝\n', '2019\n', '\n', '93.7\n', 'スター・ウォーズ エピソード2/クローンの攻撃\n', '20世紀FOX\n', '2002\n', '\n', '93.5\n', '劇場版 コード・ブルー -ドクターヘリ緊急救命-\n', '東宝\n', '2018\n', '\n', '93.2\n', '借りぐらしのアリエッティ\n', '東宝\n', '2010\n', '\n', '92.5\n', '天と地と[† 8]\n', '東映\n', '1990\n', '50.5\n', '92.0\n', 'ベイマックス\n', 'ディズニー\n', '2014\n', '\n', '91.8\n', '名探偵コナン ゼロの執行人\n', '東宝\n', '2018\n', '\n', '91.8\n', 'スター・ウォーズ エピソード3/シ スの復讐\n', '20世紀FOX\n', '2005\n', '\n', '91.7\n', 'ロード・オブ・ザ・リング\n', 'ヘラルド・松竹\n', '2002\n', '\n', '90.7\n', 'ダ・ヴィンチ・コード\n', 'ソニーPE\n', '2006\n', '\n', '90.5\n', 'ジョ ーズ[† 9]\n', 'CIC\n', '1975\n', '50.2\n', '90.0\n', 'モンスターズ・ユニバーシティ\n', 'ディズニー\n', '2013\n', '\n', '89.6\n', 'パイレーツ・オブ・カリビアン/生命の泉\n', 'ディズニー\n', '2011\n', '\n', '88.7\n', 'ターミネーター2\n', '東宝東和\n', '1991\n', '57.5\n', '87.9\n', '永遠の0\n', '東宝\n', '2013\n', '\n', '87.6\n', 'マトリックス\n', 'ワーナー\n', '1999\n', '50.0\n', '87.0\n', 'ROOKIES -卒 業-\n', '東宝\n', '2009\n', '\n', '85.5\n', '世界の中心で、愛をさけぶ\n', '東宝\n', '2004\n', '\n', '85.0\n', 'STAND BY ME ドラえもん\n', '東宝\n', '2014\n', '\n', '83.8\n', 'シン・ゴジラ\n', '東宝\n', '2016\n', '\n', '82.5\n', '敦煌\n', '東宝\n', '1988\n', '45.0\n', '82.0\n', 'バック・トゥ・ザ・フューチャー PART3\n', 'UIP\n', '1990\n', '47.5\n', '82.0\n', 'ターミネーター3\n', '東宝東和\n', '2003\n', '\n', '82.0\n', 'HERO\n', '東宝\n', '2007\n', '\n', '81.5\n', 'ディープ・インパクト\n', 'UIP\n', '1998\n', '47.2\n', '81.0\n', 'ジュラシック・ワールド/炎の王国\n', '東宝東和\n', '2018\n', '\n', '80.6\n', 'THE LAST MESSAGE 海猿\n', '東宝\n', '2010\n', '\n', '80.4\n', 'ハリー・ポッターと謎のプリンス\n', 'ワーナー\n', '2009\n', '\n', '80.0\n', 'ロード・オブ・ザ・リング/二つの塔\n', 'ヘラルド・松竹\n', '2003\n', '\n', '79.0\n', '映画 妖怪ウォッチ 誕生の秘密だニャン!\n', '東宝\n', '2014\n', '\n', '78.0\n', '花より男子F\n', '東宝\n', '2008\n', '\n', '77.5\n', 'ゲド戦記[† 10]\n', '東宝\n', '2006\n', '\n', '76.9\n', 'シックス・センス\n', '東宝東和\n', '1999\n', '45.0\n', '76.8\n', 'ズートピア\n', 'ディズ ニー\n', '2016\n', '\n', '76.3\n', 'スパイダーマン\n', 'ソニーPE\n', '2002\n', '\n', '75.0\n', 'スタ ー・ウォーズ/最後のジェダイ\n', 'ディズニー\n', '2017\n', '\n', '75.0\n', 'インディ・ジョーンズ/最後 の聖戦\n', 'UIP\n', '1989\n', '44.0\n', '74.0\n', 'BRAVE HEARTS 海猿\n', '東宝\n', '2012\n', '\n', '73.3\n', '踊る大捜査線 THE MOVIE3 ヤツらを解放せよ!\n', '東宝\n', '2010\n', '\n', '73.1\n', 'ファンタ スティック・ビーストと魔法使いの旅[† 11]\n', 'ワーナー\n', '2016\n', '\n', '73.1\n', '怪盗グルーのミニオン大脱走\n', '東宝東和\n', '2017\n', '\n', '73.1\n', 'スター・ウォーズ/スカイウォーカーの夜明け\n', 'ディズニー\n', '2019\n', '\n', '72.7\n', 'ポケットモンスター ミュウツーの逆襲\n', '東宝\n', '1998\n', '41.5\n', '72.4\n', 'ダイ・ハード3\n', '20世紀FOX\n', '1995\n', '48.0\n', '72.0\n', 'スパイダー マン3\n', 'ソニーPE\n', '2007\n', '\n', '71.2\n', 'LIMIT OF LOVE 海猿\n', '東宝\n', '2006\n', '\n', '71.0\n', 'スピード\n', '20世紀FOX\n', '1994\n', '45.0\n', '70.3\n', 'ゴーストバスターズ\n', 'コロンビア\n', '1984\n', '41.0\n', '70.0\n', 'オーシャンズ11\n', 'ワーナー\n', '2002\n', '\n', '69.0\n', '名 探偵コナン から紅の恋歌\n', '東宝\n', '2017\n', '\n', '68.9\n', 'パール・ハーバー\n', 'ディズニー\n', '2001\n', '\n', '68.8\n', 'ONE PIECE FILM Z\n', '東映\n', '2012\n', '\n', '68.7\n', 'ナルニア国物語/第1章:ライオンと魔女\n', 'ディズニー\n', '2006\n', '\n', '68.6\n', 'ハリー・ポッターと死の秘宝 PART1\n', 'ワーナー\n', '2010\n', '\n', '68.6\n', 'ファインディング・ドリー\n', 'ディズニー\n', '2016\n', '\n', '68.3\n', 'パイレーツ・オブ・カリビアン/呪われた海賊たち\n', 'ディズニー\n', '2003\n', '\n', '68.0\n']

解説

html = urlopen('https://ja.wikipedia.org/wiki/%E6%97%A5%E6%9C%AC%E6%AD%B4%E4%BB%A3%E8%88%88%E8%A1%8C%E5%8F%8E%E5%85%A5%E4%B8%8A%E4%BD%8D%E3%81%AE%E6%98%A0%E7%94%BB%E4%B8%80%E8%A6%A7')

上記コードでデータを取得するページを指定する。
今回はwikipediaを使用する。

get_info = bs.select('table.wikitable tbody tr')

ここで、属性を持つtableのtrの内容を取得する。
今回指定したのはwikipediaの下記の箇所

for index, info in enumerate(get_info):
    for info_td in info.select('td'):
        if index <= 100:
            movies.append(info_td.text)
        else:
            break

取得したtrの内容を回してtdの内容の文字だけを配列に追加
最後にprintで表示すると結果が取得できる。

次回は取得したデータからグラフ作成します。
多分d3.js使用かな

　 Tweet
Qiitaで続きを読む

投稿日：2020-10-19T20:34:29+09:00

VSCodeでPythonが動かなくなった話(Windows10)

起きたこと

変数のマウスオーバーで型が出てこないことに困った

そもそも実行できない

「Python入ってないからインストールしなさいよ。拡張機能のPython(※)より。」と英語で通知

python is not installedとかって書いてあったんだと思う

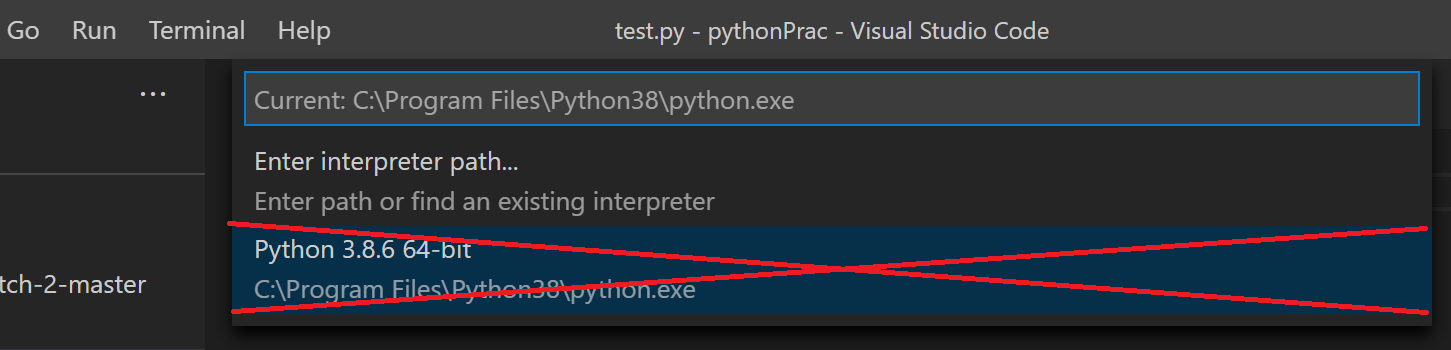
下の画像の赤枠に「パイソンのインタプリタが選択されてないから選択しなさいよ」と英語で言われる

select python interpreterって書いてあったと思う

※Microsoftが出してるPythonの拡張機能。VSCodeでPython書くときに必ず入れるやつ

ダメだった対策

コマンドプロンプトから"python"と打って起動することの確認。インストールは勿論パスが通っていることも確認できた。

「インタプリタを選択しろ」と言われているところをクリック

バツを付けているものが出ていれば選択して解決だったが、何も出ず。

python.exeの場所を確認しパスを書き込んでも動かず

設定(ctrl+,)から"python.pythonpath"と検索しパスを入力

一つ上の項目ができない時にやってみる対策らしいが意味なし

最終的な解決

Pythonの拡張機能のフォルダを消して、当該拡張機能を再度インストール

"C:\Users\username.vscode\extensions"に拡張機能のフォルダがあって、その中の"ms-python..."ってフォルダ

お気持ち

半日溶かした。英語の記事読むのは疲れるけど3つくらいは全部ちゃんと読み込んでみた方が良い。誰かの役に立ってほしいというよりも単純に、140字以内に愚痴をまとめられなかった。

　 Tweet
Qiitaで続きを読む

投稿日：2020-10-19T19:54:07+09:00

CheckboxTreeviewを使ったチェックリスト→テキスト作成

コード作成の経緯

youtubeの動画の使用機材リストを説明欄に書きたいと思ったけど、
曲ごとに違うじゃない？

それをGUIで選べたら楽じゃー！
こうしたいわけよ。

と思っていざコード書いたらゴリゴリに時間がかかったので、共有するよ。

言い訳をすると

tkinterがあんまりわかってない

classが使いこなせない

という感じなので、classで書かれたのをいじったりするのが全くできなかったわけ。
頑張ろうっと。
もっときれいに書けるかもしれないですが、、、目をつぶってください。

概要

csv読みに行く→GUI表示→チェック項目をクリップボードに

という流れ。

コード
import tkinter as tk
from ttkwidgets import CheckboxTreeview
import pandas as pd
import pyperclip

def list_to_txt(lis_checked_item):
    '''
    「listを改行ありでクリップボードに格納したい！」
    引数：list
    '''
    inst_txt = '\n'.join(lis_checked_item)
    pyperclip.copy(inst_txt)

ttk = tk.ttk
window = tk.Tk()
ct = CheckboxTreeview(window, show='tree') # hide tree headings
ct.pack()

#copy button 
tk.Button(window, text="copy", command=lambda: list_to_txt(ct.get_checked())).pack()

style = ttk.Style(window)

# remove the indicator in the treeview 
style.layout('Checkbox.Treeview.Item', 
             [('Treeitem.padding',
               {'sticky': 'nswe',
                'children': [('Treeitem.image', {'side': 'left', 'sticky': ''}),
                             ('Treeitem.focus', {'side': 'left', 'sticky': '',
                                                 'children': [('Treeitem.text', 
                                                               {'side': 'left', 'sticky': ''})]})]})])

# make it look more like a listbox                                                               
style.configure('Checkbox.Treeview', borderwidth=1, relief='sunken')

# get data
path = "./inst.csv"
inst_data = pd.read_csv(path, sep=',', encoding='shift_jis',header=0)

inst_list = list(inst_data["型番"].values + " / " + inst_data["メーカ"] )

# add items in treeview
for value in inst_list: 
    ct.insert('', 'end', iid = value, text=value)

window.mainloop()
出力結果

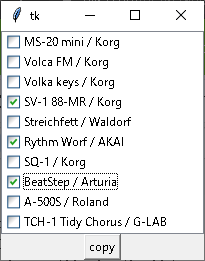
チェックした項目だけがクリップボードに。
下記みたくなります。
SV-1 88-MR / Korg
Rythm Worf / AKAI 
BeatStep / Arturia
いやあ、むずかしむずかし。

機材リストのcsv

列名は型番、メーカは入れるようにしてください。読みに行ってます。
コピペする場合、場所は実行ファイルと同じ階層にしてね！

引用

下記の記事で本当に助かった。ありがとうございます。
ttkwidgets Documentation Release 0.11.0
Documentation » ttkwidgets » CheckboxTreeview
Python Tkinter Tk support checklist box?
How to create selected checkbox list item using Tkinter

以上。

　 Tweet
Qiitaで続きを読む

投稿日：2020-10-19T19:09:28+09:00

[Unity]超絶初心者でもML-Agents Release8を動かす方法[Windows]

免責

この記事を見てる人は超絶初心者なので問題が起こったとしても私は責任を負わないこととします。また記事を見て進めた時点で同意したとみなします。またWindows以外のユーザーは今回扱いません。

バージョン確認

結構な速度で更新されてるML-Agentsですが2020/10/19時点の最新版であるML-Agents Release 8の環境構築とテストをしていきたいと思います。

実行環境

わかりやすく言うとインストールするものリストです。

バージョンインストール

ML-Agents Release 8 未

Unity 2019.4.1f1 済

Anaconda3 2020.7 未

Python 3.7.9 未

Unityは2018.4以降が対応してますが、
今回はUnity2019.4.1f1で進めていきます。
同様にPython3.6.1以降が対応してますが、
今回は仮想化とは？？？の人のためにAnacondaで仮想環境を作っていこうと思います。
Anacondaは後述で3.7環境を作るので、3.8対応の一番新しい2020.7(2020/10/19時点)を使います。
またUnityとUnity Hubはすでにインストールが済んでいる前提で進めます。
当然ですがネット環境も必要です。
今回GPUでの学習に関しては動かすことが目的なので含んでいません、予めご了承ください。

ANACONDA3インストール手順

既にインストール済みの方は飛ばしてください。
ダウンロード場所はAnaconda3のサイトをスクロールしたところにあります。

とりあえずNEXTで読み進めていってください。

今回はディレクトリを合わせるためJust Meで

インストール先のフォルダを聞かれますが今回はC:\Users\ ユーザー名\anaconda3に素直にインストールしましょう。
最後の項目ですが下の画像のようにチェックします。赤くなっていますが気にしないでOKです。

上の項目は面倒なパスを通すために必要で、下の項目はあまり関係がないのですが今回Python3.7をメインに使う都合上外します。
チェックでき次第インストールしましょう。
インストールが済んだらコマンドプロンプトを開いてcondaと打ち確認しましょう。
コマンドプロンプトがわからない方はWindowsの検索バーにcmdと打ちアプリを開きましょう。

開くと黒地に、
C:\Users\ ユーザー名>
と表示されているので
condaと入力してエンター、以下のようにヘルプが出力されればインストール完了です。

今後このようにコマンドプロンプトからコマンドを実行する際は、
$ conda
のように表記するので覚えておいて下さい。（$は、続くコマンドを実行するの意味）

ML-Agentsダウンロード手順

すでにダウンロードしている方はディレクトリ階層だけ合わせてください。
ML-Agents Release 8のサイトをスクロールしてSource code(zip)をダウンロード、
C:\Users\ ユーザー名\　直下に解凍しましょう。

ディレクトリはC:\Users\ ユーザー名\ml-agents-release_8 となるはずです。
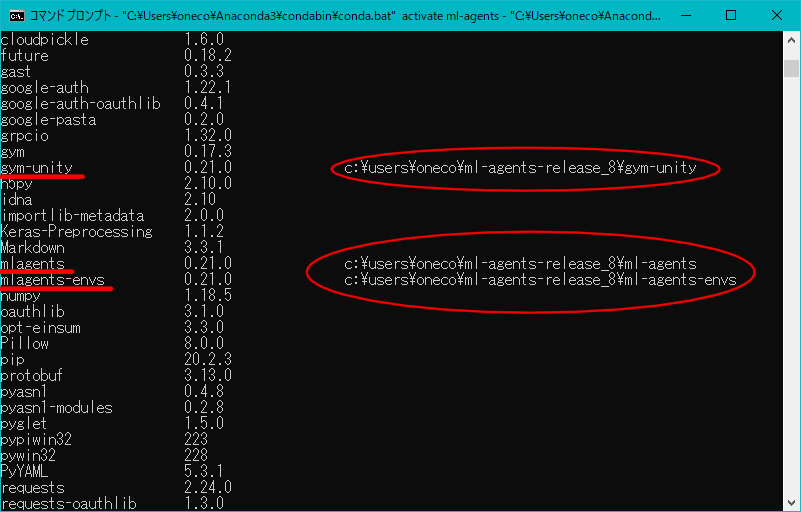
フォルダ内のcom.unity.ml-agentsファイルはUnityで使います。

mlagents

mlagents_envs

gym_unity

のファイルは次のPythonのインストールの時に使います。
それぞれの働きについて詳しくはここを見てください。

Python3.7インストール手順

コマンドを実行します。
$ conda create -n ml-agents python=3.7
実行したら仮想環境の構築が終わるまでしばらく待ちましょう。
途中y/n？ときかれるので yを押してエンター
動作が終わると、再び
C:\Users\ ユーザー名>　
と表示されるのでそれから次のステップに移ります。
以降も同様に一つのコマンドの処理が終わるまで待ってから行ってください。
$ conda activate ml-agents
コマンドプロンプトが、(ml-agents)C:\Users\ ユーザー名>　のように変化します。
これで仮想環境にライブラリを追加できます。
$ pip install -e ./ml-agents-release_8/ml-agents-envs
$ pip install -e ./ml-agents-release_8/ml-agents
$ pip install -e ./ml-agents-release_8/gym-unity
上から順に入れていきます。ちゃんとディレクトリ階層があっていればインストールが始まります。
時間がかかるので焦らずお茶を飲みましょう。
$ pip list
最後に追加したライブラリがあるか確認します。

Unityのテスト環境構築

Unity Hubを開いてプロジェクト>リストに追加をクリック。

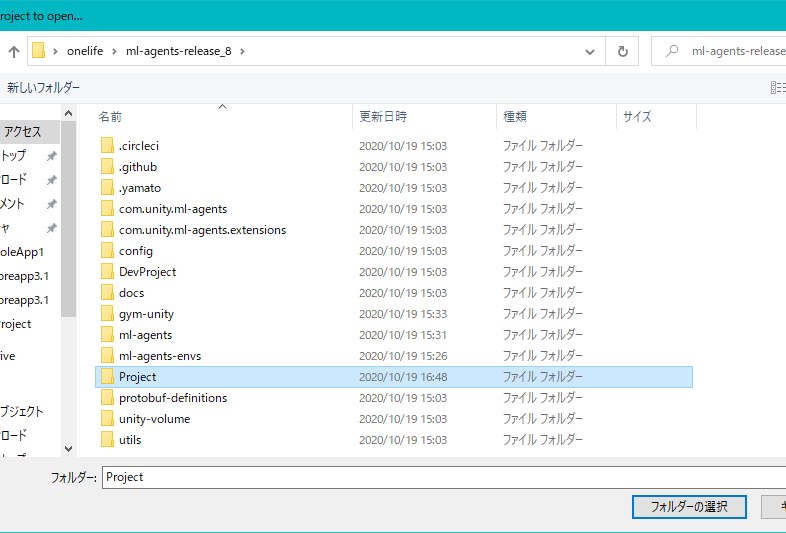
C:\Users\ ユーザー名\ml-agents-release_8 内のProjectフォルダを選んで、フォルダーの選択。

Unityバージョンを2019.4.1f1に変更後、プロジェクト名をクリックして起動。

プロジェクトのアップグレードの確認をする。次に出てくるポップアップもYesを選択。

インポートが終わるまでお茶でも飲みましょう。
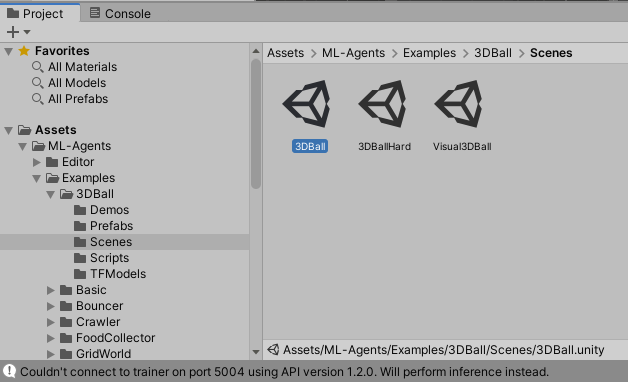
次に、Assets>ML-Agents>Examples>3DBall>Scenesフォルダから3DBall.unityをダブルクリックで実行します。

シーンが読み込まれたらUnity上部のPlayボタンを押して、シーンを実行してみます。
(少し読み込みがあるので待ちましょう）

可愛いシーンが再生されましたね！
このシーンには頭の上に乗ったボールを落とさないように学習済みのデータが設定されています。
ではPlayをもう一度押しシーンを終了して、1から学習してみましょう。
(ml-agents) C:\Users\ ユーザー名> の状態で
$ mlagents-learn ./ml-agents-release_8\config\ppo\3DBall.yaml --run-id=3DBall-1 --train
色々出てきた最後に、Start training by pressing the Play button in the Unity Editor.
と表示されたらUnityのPlayボタンを押してください。
そうするとボックス君たちが微振動を始めるかと思います。~~それが世界のおわｒ~~　学習の始まりです。
人によってはパソコンがブオーンと唸るかもしれませんが我慢です。（古いパソコンでさすがにヤバそうだったらPlayを停止するか、コマンドプロンプトでCtrl+Cを押して終了してください。）
しばらくはコマンドプロンプトとUnityを眺めててください。学習が終われば自動的に止まります。
コマンドプロンプトに表示されてくるMean Rewardが平均的な報酬ですので、これが高くなっていくようなら学習が順調に進んでます。

学習が終わると色々コマンドプロンプトに表示されたあと、(ml-agents) C:\Users\ ユーザー名>　の状態に戻りますので、
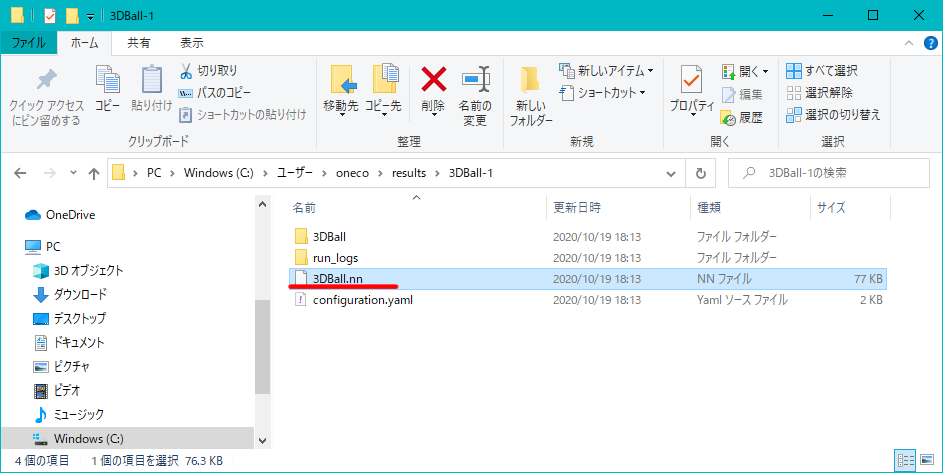
C:\Users\ ユーザー名\results\3DBall-1ファイルを開きます。

3DBall.nnというNN形式のファイルが先ほどの学習で手に入った学習済みデータです。(NNはニューラルネットワークの意(Neural Network))
UnityのProject内にドラッグアンドドロップで移して、右クリックRenameで3DBall-NNと間違わないよう名前を変更します。
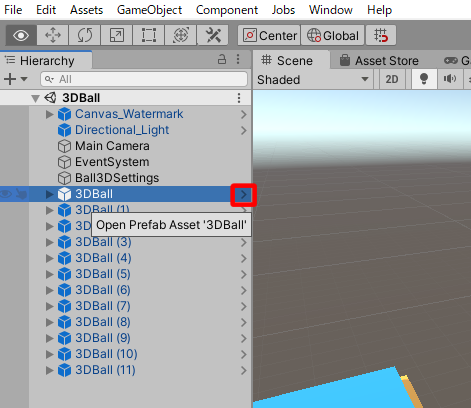
次にHierarchyから3DBallの右の矢印>をクリックして、3DBallのPrefabを開きます。

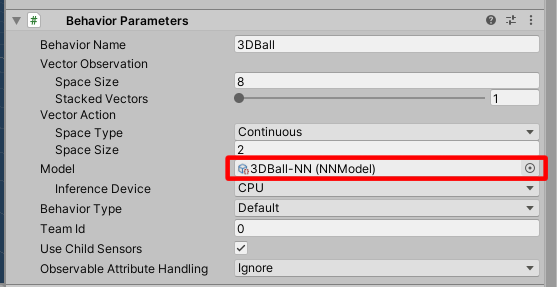
するとPrefabの設定画面に移るのでSceneの背景が青色に代わるのを確認した後、HierarchyからAgentを選択状態にすると、InspectorにBehavior Parametersというコンポーネントがあります。

そこのModelに先ほど追加した学習済みのNNファイルをドラッグアンドドロップ等で設定してください。
設定後Hierarchyの左上の小さな左矢印<でPrefabの設定画面から抜けます。
Unity上部のPlayを押してシーンを再生すると、Hierarchy内の3DBallが割り当てた学習済みファイルになってるのが確認できるかと思います。（見た目上大きな変化はないかもしれませんが、先ほど学習したデータです）

以上で学習のテストは終了です。
他にもデモシーンが用意されてるので学習時のシーンと.yamlの名前を変えながら試してみるとよいかと思います。

まっさらなUnityのプロジェクト構築

番外編ですが、デモシーン無しのまっさらなML-Agents用の新規プロジェクトの作り方です。
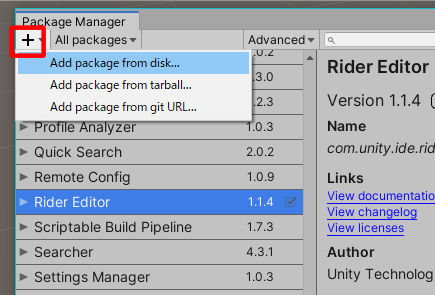
メニューからWindow>Package Managerを開きます。
左上の+ボタンを押してAdd package from diskを選びます。

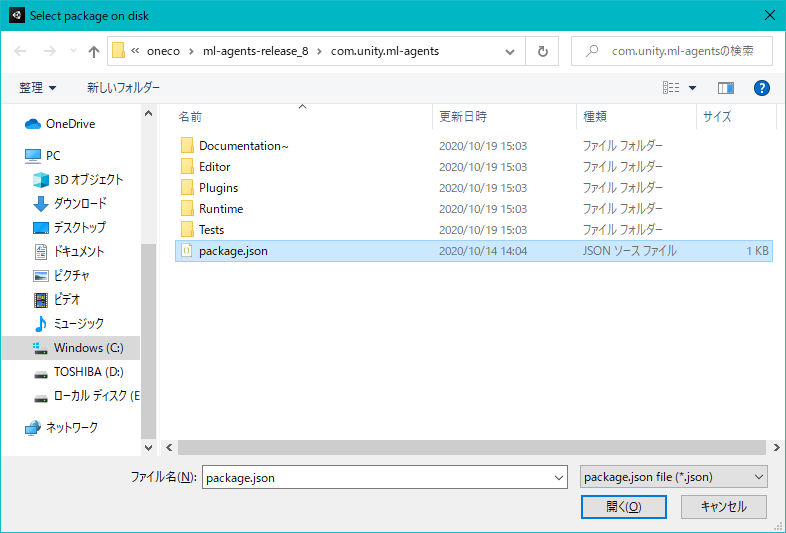
C:\Users\ ユーザー名\ml-agents-release_8 に移動してcom.unity.ml-agentsフォルダ内のpackage.jsonを開きます。

インポートが終われば完了です。

	バージョン	インストール
ML-Agents	Release 8	未
Unity	2019.4.1f1	済
Anaconda3	2020.7	未
Python	3.7.9	未

　 Tweet
Qiitaで続きを読む

投稿日：2020-10-19T18:56:38+09:00

[基本情報技術者試験]うるう年の判定のアルゴリズムをPythonで書いてみた。

概要

基本情報技術者試験の午後の試験でアルゴリズムがあります。過去問を解いても理解ができません…。実際にアルゴリズムをPythonで書いて、理解を深めていきたいと思います。

前回はユークリッドの互除法のアルゴリズムを書きました。

今回はうるう年の判定のアルゴリズムから書いてみます。

うるう年の判定

アルゴリズム

西暦が4で割り切れ、かつ、100で割り切れなければ、うるう年である。ただし、西暦が400で割り切れれば、うるう年である。どちらにも該当しないなら、うるう年ではない。

コード
# うるう年の判定を行うIsLeapYear関数
def IsLeapYear(Year):
    # 外側の分岐処理
    if Year % 4 == 0 and Year % 100 != 0: # この条件が真なら
        Ans = True # うるう年である
    else:
        # 内側の分岐処理
        if Year % 400 == 0: # この条件が真なら
            Ans = True # うるう年である
        else:
            Ans = False # うるう年ではない
    return Ans

print("実行結果：",IsLeapYear(2104))
print("実行結果：",IsLeapYear(2105))
print("実行結果：",IsLeapYear(2200))
print("実行結果：",IsLeapYear(2400))
実行結果
実行結果： True
実行結果： False
実行結果： False
実行結果： True
まとめ

うるう年の判定って意外とややこしいんだなー

次回は配列の最大値をのアルゴリズムを書こうかな

参考

こちらの本のCHAPTER3 02うるう年の判定を引用または参考にしました。情報処理教科書基本情報技術者試験のアルゴリズム問題がちゃんと解ける本第2版

　 Tweet
Qiitaで続きを読む

投稿日：2020-10-19T18:08:14+09:00

Twitterのデータをプログラミング不要で収集する方法

ご挨拶

こんにちは、マンボウです。
初投稿として、コロナ関連tweet分析シリーズをやってみました。
Pythonに疲れたのでnehanでデータ分析してみた（コロナ関連、あのワードは今？）
Pythonに疲れたのでnehanでデータ分析してみた（コロナ禍でもライブに行きたい - 後編）
Pythonに疲れたのでnehanでデータ分析してみた（コロナ禍でもライブに行きたい - 前編）

今回は、その締めくくりとして、そもそもTwitterのデータをどう集めるのか、をご紹介したいと思います。もちろん、分析ツールnehanを使って。

Amazon S3を蓄積用のストレージとして使います。

API利用申請をする

まず、Twitter API利用申請をしないといけません。
これはGoogleで検索すればたくさんやり方が出てきますので、割愛します。
ただの申請作業なのですが、色々書いたり、そもそも英語だったり、と若干面倒だったりします。

Twitter APIを叩く

nehanは、外部データを取り込むためのコネクタをたくさん用意しています。

Cdata社のドライバを採用しているので、Webサービスのデータも取り込み可能です。

Twitterを選び、取得したAPI情報を入れると、SQLクエリでtweetデータを取得することができます。

取得したtweetデータを蓄積する

取得したデータに一手間加え、AmazonS3に蓄積します。
いつ取得したデータかがわかるように、1列追加して処理時間を入れておきます。

このとき、変数機能が役立ちます。実行時間、実行日を動的に定義しています。

で、最後にS3にエクスポートすれば、蓄積は完成。エクスポートするファイル名に変数を入れ、処理日がわかるようにしています。

毎日データを処理・蓄積する

上記の処理を毎日手で実行するわけにもいかないので、自動更新設定を行います。
tweetデータを更新、S3に格納するフローを、毎日0時0分に自動実行するように設定しています。

Twitter APIが反応せず、データが取れないこともあり、たまに失敗しています。。。

蓄積したデータを再度取得し、分析する

Amazon S3に蓄積された日別のデータを一括で取得し、nehanに取り込みます。

こうして取り込んだデータを、これまで分析していました。

まとめ

外部データを収集し自社データと掛け合わせて見る、ことがやりたくなる一方で、その収集はとても面倒だったりします。
nehanを使えば収集はもちろん、分析にダイレクトにつなげることができます。
もちろんプログラミング不要で。
データの収集やPythonを書くのに疲れた分析者の皆様、nehanで快適な分析生活を送ってみてはいかがでしょうか？

※分析ツールnehanのご紹介はこちらから。

　 Tweet
Qiitaで続きを読む

投稿日：2020-10-19T17:24:57+09:00

Python で parameter store を使う

はじめに

以前、仕事で使った Parameter Store（AWS Systems Manager）をまた使うことになったので思い出しました。

今回もPoetry + Dockerを開発環境にしています。
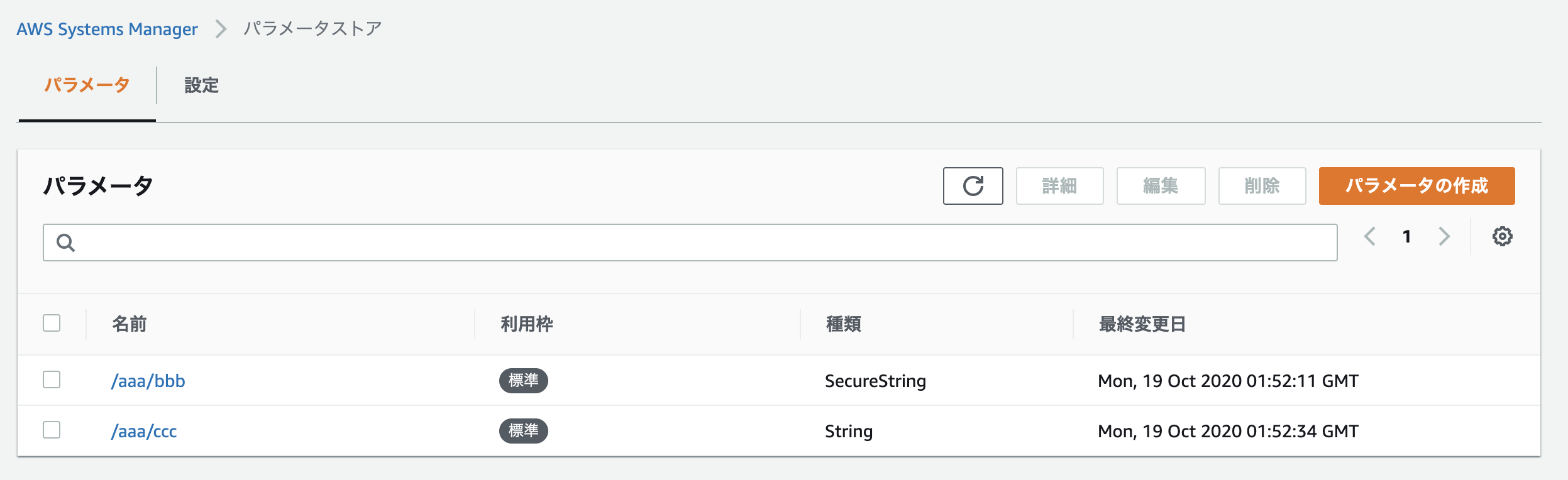
ソースは Github にあげてあります。

Parameter Store を設定する

/aaa で始まるように作成

ファイル

mainとライブラリとしてファイルを分けています。

main.py

from src.ssm_manager import SsmManager

print("start")

ssm_manager = SsmManager(region_name="ap-northeast-1")
ssm_manager.load_parameter(base_ssm_path="/aaa")
print(ssm_manager.parameters)

ssm_manager.py

from typing import List, Dict

import boto3


class SsmManager:
    def __init__(self, region_name: str):
        self.__ssm = boto3.client('ssm', region_name=region_name)
        self.__parameters = []
        self.__base_ssm_path = None

    @property
    def parameters(self) -> List[Dict[str, any]]:
        return [{
            'name': item['Name'].replace(f'{self.__base_ssm_path}/', ''),
            'value': item['Value']
        } for item in self.__parameters]

    def load_parameter(self, base_ssm_path: str) -> None:
        self.__base_ssm_path = base_ssm_path
        result = []
        next_token = None
        while True:
            dict_parameter = {
                'Path': base_ssm_path,
                'Recursive': True,
                'WithDecryption': True,
            }
            if next_token is not None:
                dict_parameter['NextToken'] = next_token
            response = self.__ssm.get_parameters_by_path(**dict_parameter)
            parameters = response['Parameters']
            result.extend(parameters)
            if 'NextToken' not in response:
                break
            next_token = response['NextToken']
        self.__parameters = result

終わりに

これで、環境変数などに入れていたRDSのパスワードなどを保存できます。

　 Tweet
Qiitaで続きを読む

投稿日：2020-10-19T17:15:16+09:00

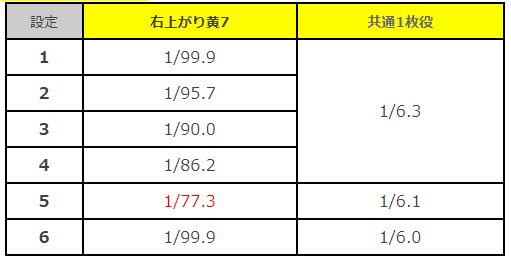
【パチスロ】アナターのオット!?はーですの「右上がり黄７」による設定判別

はじめに

6号機の「はーです」でましたね！
私はAT中が好きでちょいちょい打っています。
で、この台は「右上がり黄七」の出現に設定差がかなりあるのですが、
何回転ぐらいで、判別できるかプログラムで試してみたいと思います。

なお、設定が偶数か奇数かは、他の要素で何となく推測できているものとして、奇遇に分けて調査してみました。

プロット

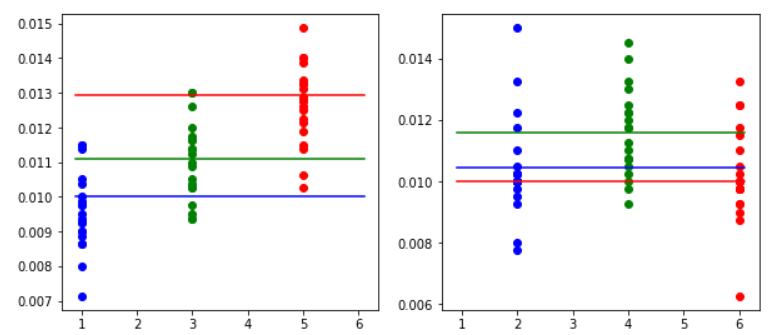
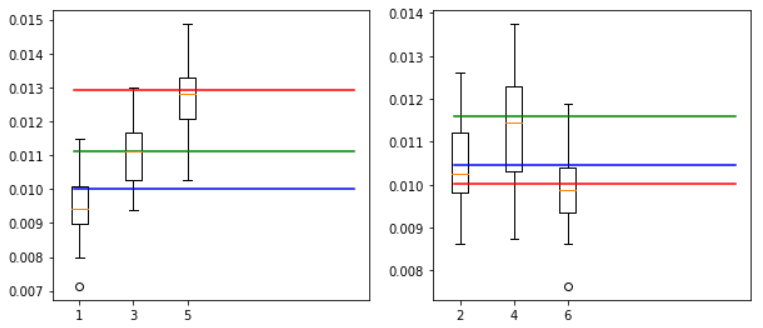
設定1,3,5と2,4,6に分けて2000, 4000, 6000, 8000回転を20回ずつ実行してみました。
奇数は(1,3) or 5なら2000回転で判別できそうな感じがします。
偶数は(2,6) or 4なら4000回転で判別できそうな感じがします。

2000回転(左奇数、右偶数)

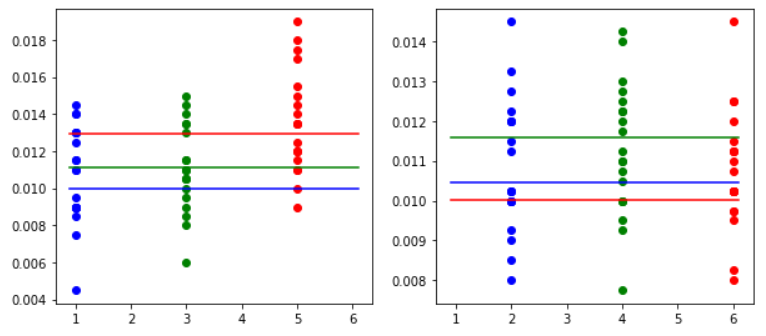
4000回転(左奇数、右偶数)

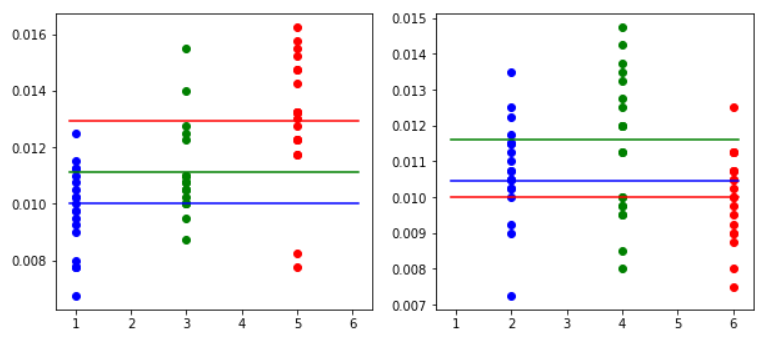
6000回転(左奇数、右偶数)

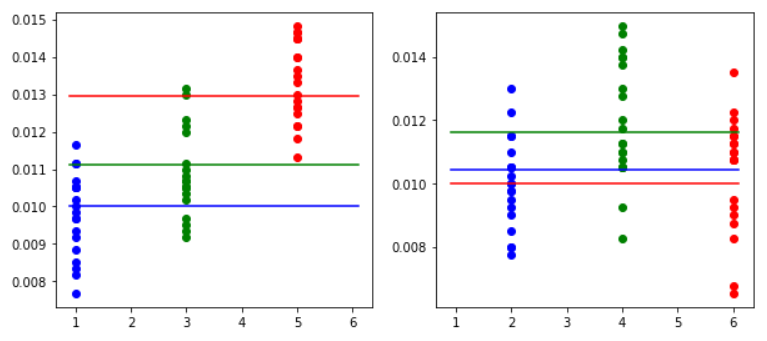
8000回転(左奇数、右偶数)

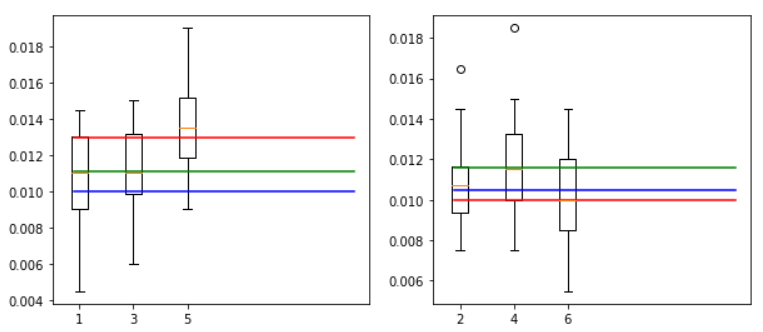
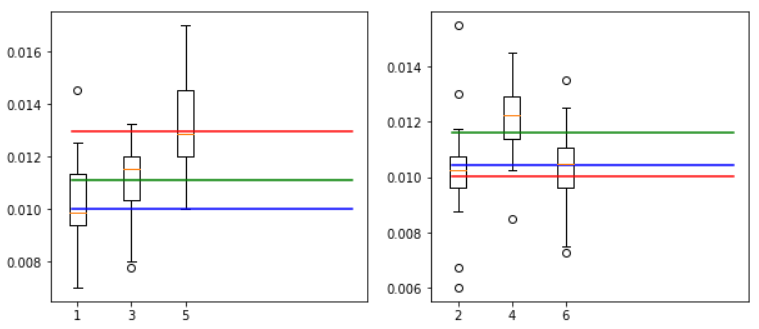
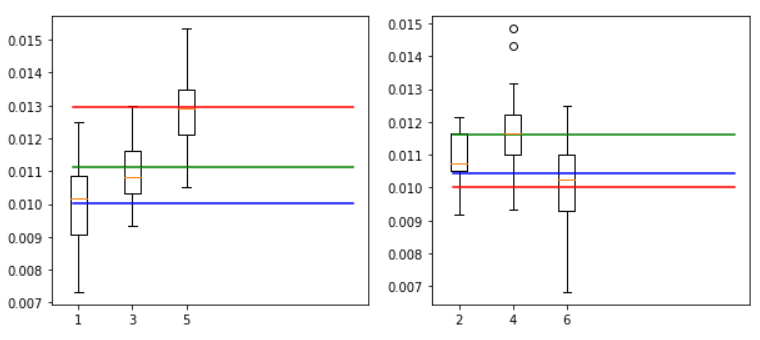
箱ひげ図

2000回転(左奇数、右偶数)

4000回転(左奇数、右偶数)

6000回転(左奇数、右偶数)

8000回転(左奇数、右偶数)

ソース

すいません、python勉強中なので、へたくそです。orz
# 必要なものをインポート
import numpy as np
import matplotlib.pyplot as plt
import math

# 乱数を固定
np.random.seed(10)

# 試行回数
T = 20 

# 回数数
N = 4000

# 設定別「右上がり黄7発生確率」 
PROP = np.array([ 1 / 99.9, 1 / 95.7, 1/ 90.0, 1 / 86.2, 1 / 77.3, 1 / 99.9 ])
COLORS = ['blue', 'green', 'red']

odds = [0, 2, 4]
evens = [1, 3, 5]

fig, axes = plt.subplots(nrows=8, ncols=2, figsize=(10,40), sharex=False)

for i, n in enumerate([2000, 4000, 6000, 8000]):
    for even in [0, 1]:
        if even == 0:
            temp = odds
        else:
            temp = evens
        # plot
        yarray = []
        for j, s in enumerate(temp):
            x = np.full(T, s + 1)
            y = done(n, T, PROP[s])
            yarray.append(y)
            axes[i,even].scatter(x, y, color=COLORS[j])
            x = np.array([0.9, 6.1])
            y = np.full(2, PROP[s])
            axes[i,even].plot(x, y, color=COLORS[j])

        # 箱ひげ図
        axes[i + 4,even].boxplot(yarray)
        if even == 0:
            axes[i + 4,even].set_xticklabels(['1', '3', '5'])
        else: 
            axes[i + 4,even].set_xticklabels(['2', '4', '6'])

        for j, s in enumerate(temp):
            x = np.array([0.9, 6.1])
            y = np.full(2, PROP[s])
            axes[i + 4,even].plot(x, y, color=COLORS[j])


def done(N, t, p):
    ret = np.array([])
    for n in range(t): # t回試行
        a = np.random.rand(N)  # N回転する
        ret = np.append(ret, len(np.where(a < p)[0]) / N)
    return ret
最後に

個人的には、「右上がり黄7」で判別するより、「チャンスゾーンからのゴッドラッシュ当選確率」を見たほうが良いように思う。

　 Tweet
Qiitaで続きを読む

投稿日：2020-10-19T16:16:42+09:00

gensimを用いたTF-IDFの実装

前回は文春オンラインの記事をスクレイピングして、ネガポジ分析を行いました。
今回は文春オンラインの記事の内容に対してgensimを使ってTF-IDFを行い、重要単語を抽出してみようと思います！

流れ

参考記事
TF-IDFとは
形態素解析
DF-IDFを実行する前の準備
TF-IDFの実装
TF-IDFで上位の単語を出力

参考記事

TF-IDFについて　　　　　　https://mieruca-ai.com/ai/tf-idf_okapi-bm25/
gensimのtfidfについて　　　https://qiita.com/tatsuya-miyamoto/items/f1539d86ad4980624111

TF-IDFとは

TF-IDFが高い場合は、その文章を特徴付けるような単語となり、
それほど重要ではない単語と言うことができると思います。

例えば、スポーツ新聞をみており、一つの記事に注目してその記事の文章に「ホームラン」と言う単語があれば、
この記事の内容は野球についてである、とすぐに分かります。
このような場合は野球と言う単語のTF-IDFは高い値を示す可能性が高いと思います。
一方、ある記事の文章に選手と言う単語が入っていたとしましょう。
スポーツ新聞なので、おそらくどの記事にも多く使われていることでしょう。
このような場合、選手と言う単語のTF-IDFは低いと思います。

詳しくはこちらを参考にしてください。

今回はTF-IDFを使って記事ごとの重要な単語を抽出してみます。
それでは早速作業してみましょう。
まずは必要なライプラリーを読み込みます。

from gensim import corpora
from gensim import models
from janome.tokenizer import Tokenizer
from pprint import pprint
import pandas as pd
import logging

前回の記事で作成した文春オンラインをCSVファイルとして保存していたので、そちらを利用します。

df = pd.read_csv('/work/data/BunshuOnline/news.csv')
doc_list = list(df.news_page_list)

記事の内容を確認してみましょう。

for i in range(10):
    print('%s.' % i, '〜%s〜' % df['title'][i])
    print(df['news_page_list'][i][:200], end='\n\n')

0. 〜波乱はルーキーたちの走り次第？ “怪物世代”の初陣に注目 第97回箱根駅伝予選会を読む〜
「例年なら『駅伝はトラックとは別物だから、1年生は戦力としてあまり期待しすぎないほうがいい』という話が出るんです。でも、今年はちょっと雰囲気が違いますね」 そんな風に今季の驚きを語るのは、スポーツ紙の駅伝担当記者だ。 春先から続くコロナ禍の中で、今年はここまでスポーツ界も大きな影響を受けてきた。それは学生長距離界においても同様で、春から夏にかけて大会の中止はもちろん、記録会や各校の練習にも大きな支

1. 〜スマホやタブレットじゃやっぱり不十分？ 「オンライン授業」に最適のPCとは〜
 2020年は、まさにデジタル教育の歴史にとって特記されるべき重要な年となった。まずは、小学校においてプログラミング教育が必修化された。そして、予期せぬコロナ禍の到来によって、デジタル機器を使っての学習は不可避のものとなった。 コロナで家族そろって自宅に籠っていた間、親はリモートワーク、子どもはオンライン学習に励むため、家に1台しかないPCを親子で取り合うことになった経験を持つ読者は多いだろう。 

2. 〜幼児教育「ヨコミネ式」創設者・横峯吉文氏のDVを元妻と子供が告白《法廷闘争“全面対決”へ》〜
 保育園児が跳び箱10段を跳び、倒立歩行。さらに九九算も覚え、漢字を読み書きし、3年間で平均2000冊の本を読破する――。「すべての子供が天才である」をモットーに、鹿児島から全国に広がった独創的な教育方法がある。子供の向上心や競争心に火を付け、強制することなく自分で学ぶ力を伸ばすこの教育法は「ヨコミネ式」と呼ばれている。いまでは、全国で約400もの保育園・幼稚園が、このヨコミネ式カリキュラムを導入

3. 〜BTS会社社長、韓国8位の株式富豪に…「共通点はオタクなこと」J.Y.Parkが語った素顔〜
 上場前から大騒ぎだった。 10月15日、「防弾少年団（BTS）」の所属事務所「Big Hit Entertainment（BHエンタテインメント、以下BH社）」がKOSPI（韓国取引所）に上場した。初値は公募価格の2.6倍をつけ、時価総額は8兆8169億ウォン（約8800億円同日15時時点）。韓国の3大音楽事務所の時価総額を合わせたものをはるかに超え、韓国最大手の音楽事務所に躍り出た。 創業者、

4. 〜「レジ袋はいりません」からの流れでびっくりするほど挙動不審になった話〜
 漫画家の山本さほさんが、厄介な人たちを引き寄せるトラブル続きな日々をつづります。今回は、薬局とスーパーで買い物をしたときのお話です。毎週木曜日更新。 最近更新が遅れ気味ですが、次回は10月22日（木）公開予定です（たぶん）。『きょうも厄日です』の単行本が好評発売中です。山本さんのハプニングが詰まった第1巻は、大炎上したあの区役所との“闘い”を大幅描きおろし!!きょうも厄日です 1山本 さほ 文藝

5. 〜三浦春馬さん、竹内結子さん、木村花さん…芸能人「自殺の連鎖」はなぜ起きるのか？〜
 三浦春馬さんが亡くなってから3カ月が経とうとしているが、いまだに彼の自死をめぐる報道は止まない。 三浦さんだけではない。リアリティー番組「テラスハウス」に出演していた木村花さん、芦名星さん、藤木孝さん、竹内結子さんなど、芸能人の死をめぐる報道が「次なる死」を招きかねないと警鐘を鳴らすのが、筑波大学教授の斎藤環氏だ。「大変言いにくいことですが、精神科で患者が自死すると、同じように死を選ぶ患者が続発

6. 〜内部資料入手「GoToトラベル事務局」大手出向社員に日当4万円〜
 10月1日から東京発着の旅行も対象に加わった政府の観光支援策「GoToトラベル事業」。その運営を担う「GoToトラベル事務局」に出向している大手旅行代理店社員に、国から高額な日当が支払われていることが、「週刊文春」の取材でわかった。 GoToトラベル事務局を構成するのは、全国旅行業協会（ANTA）などを除けば、業界最大手のJTBを筆頭に、近畿日本ツーリストを傘下に置くKNT－CTホールディングス

7. 〜「お前は何アゲだ？ 何で俺だけ“たたき上げ”なんだ！」“最後の怪物幹事長”二階俊博がキレた瞬間〜
 自民党幹事長の通算在職記録を更新中の二階俊博は寝業師、すなわち「政治技術の巧者」という報道のされ方をすることが多い。政策というと親中派であること、運輸や土地改良事業の族議員であることぐらいは知られるが、政治思想は意外と知られていない。メディアで多くを語る姿を見ない二階が今回、インタビューで「政治の原点」を語った。 与えられた時間は30分間、限られた時間の中で、私は二階にいくつもの質問を矢継ぎ早に

8. 〜「バラバラにした遺体を鍋で……」白石隆浩被告が証言した、おぞましい犯行の一部始終〜
「背後に回って、首を左腕で絞めた」 2017年10月に神奈川県座間市のアパートで男女9人の遺体が見つかった事件で、強盗・強制性交殺人の罪に問われている白石隆浩被告（30）の裁判員裁判が、東京地裁立川支部（矢野直邦裁判長）で10月14日にあった。この日は、3人目に殺害したCさん（当時20、男性）の事件に関しての被告人質問が行われた。白石被告は、Cさんは殺害されることに承諾していなかったといい、殺害時

9. 〜「長さ」ではなく…美容師が教える、髪を切るときに言うといい「意外な言葉」〜
 掛け布団がだんだん心地よくなってきた、今日この頃。朝夜の急激な気温差に、薄めの上着を羽織ったり、そろそろヘアスタイルも秋冬仕様に変えようかな、と思っている貴方へ。 いざ予約をして実際に美容師さんと顔を合わせたところで、希望をどう伝えればいいのかわからなくなっちゃう、そんなことはありませんか？ 今回は、どうすれば美容師さんに伝わるのか？ のお話です。 よくあるお客様のオーダーの例をあげていきます。

形態素解析

形態素解析を行います。
gensimのTokenizer()を用いることで簡単に実装することができます。
記号は必要ないので、part_of_speechを用いて除外します。

t = Tokenizer()
wakati_list = []
for doc in doc_list:
    tokens = t.tokenize(doc)
    wakati = []
    for token in tokens:
        if token.part_of_speech.split(',')[0] not in ['記号']:
            wakati.append(token.base_form)
    wakati_list.append(wakati)

分かち書きと記号の除去がうまくできたか確認してみましょう。

for wakati in wakati_list:
    print(wakati[:10])

['例年', 'だ', '駅伝', 'は', 'トラック', 'と', 'は', '別物', 'だ', 'から']
['2020', '年', 'は', 'まさに', 'デジタル', '教育', 'の', '歴史', 'にとって', '特記']
['保育園', '児', 'が', '跳び箱', '10', '段', 'を', '跳ぶ', '倒立', '歩行']
['上場', '前', 'から', '大騒ぎ', 'だ', 'た', '10', '月', '15', '日']
['漫画', '家', 'の', '山本', 'さ', 'ほす', 'ん', 'が', '厄介', 'だ']
['三浦', '春', '馬', 'さん', 'が', '亡くなる', 'て', 'から', '3', 'カ月']
['10', '月', '1', '日', 'から', '東京', '発着', 'の', '旅行', 'も']
['自民党', '幹事', '長', 'の', '通算', '在職', '記録', 'を', '更新', '中']
['背後', 'に', '回る', 'て', '首', 'を', '左腕', 'で', '絞める', 'た']
['掛け布団', 'が', 'だんだん', '心地よい', 'なる', 'て', 'くる', 'た', '今日', 'この']

DF-IDFを実行する前の準備

次にgensimのcorporaを使って単語にIDを添付していきます。

dictionary = corpora.Dictionary(wakati_list)
print('==={単語: ID}===')
pprint(dictionary.token2id)

2020-10-19 06:49:28,202 : INFO : adding document #0 to Dictionary(0 unique tokens: [])
2020-10-19 06:49:28,228 : INFO : built Dictionary(2877 unique tokens: ['1', '10', '11', '12', '17']...) from 10 documents (total 13512 corpus positions)


==={単語: ID}===
{'!': 1021,
 '!!': 1822,
 ',': 2023,
 '-': 568,
 '.': 569,
 ~~~~<省略>~~~~~
 'なんて': 1084,
 'なんで': 1085,
 'なんとなく': 2693,
 'なー': 2694,
 'に': 104,
 ~~~~<省略>~~~~~
 'メモアプリ': 2497,
 'メンタル': 1890,
 'メンバー': 174,
 'メーカー': 742,
 'モダン': 743}

次に単語ごとの記事ごとの出現回数をカウントします。

corpus = list(map(dictionary.doc2bow, wakati_list))
print('===(単語ID, 出現回数)===')
pprint(corpus)

===(単語ID, 出現回数)===
[[(0, 10),
  (1, 5),
  (2, 1),
  (3, 1),
  (4, 1),
  ~~~~<省略>~~~~~
  (2872, 1),
  (2873, 1),
  (2874, 2),
  (2875, 1),
  (2876, 1)]]

TF-IDFの実装

次に出現回数のデータを用いていよいよTF-IDFを算出します。
gensimのmodelsを利用します。
gensimは本当にたくさんの機能がありますね。
計算結果の一部を表示させます。

test_model = models.TfidfModel(corpus)
corpus_tfidf = test_model[corpus]
print('===(単語ID, TF-IDF)===')
for doc in corpus_tfidf:
    print(doc[:4])

===(単語ID, TF-IDF)===
[(0, 0.010270560215244124), (1, 0.010876034850944512), (2, 0.011736346492935309), (3, 0.006756809998052433)]
[(0, 0.0042816896254018535), (3, 0.005633687484063879), (5, 0.008303667688079712), (7, 0.005633687484063879)]
[(0, 0.001569848428761509), (1, 0.006649579327355055), (3, 0.005163870001530652), (5, 0.00761118904775017)]
[(0, 0.004119674666568976), (1, 0.006543809340846026), (3, 0.006775642806339103), (5, 0.02496707813315839)]
[(0, 0.01276831026581211), (1, 0.013521033373868814), (7, 0.04200016584013773), (13, 0.04200016584013773)]
[(1, 0.007831949836845296), (2, 0.0422573475812842), (7, 0.024328258270175436), (11, 0.00625933452375299)]
[(0, 0.00115918318434994), (1, 0.004910079468851687), (9, 0.013246186396066643), (11, 0.0039241607229361)]
[(0, 0.0014966665107978136), (1, 0.006339594643539755), (2, 0.06841066655360874), (3, 0.009846289814745559)]
[(0, 0.0026696482016164125), (1, 0.003769373987012683), (5, 0.004314471125835394), (6, 0.007739059517798651)]
[(0, 0.0011200718719816475), (25, 0.020161293695669654), (26, 0.06631869535917725), (27, 0.0037917579432113335)]

単語IDでは分かりにくいので、単語を表示します。

texts_tfidf = []
for doc in corpus_tfidf:
    text_tfidf = []
    for word in doc:
        text_tfidf.append([dictionary[word[0]], word[1]])
    texts_tfidf.append(text_tfidf)
print('===[単語, TF-IDF]===')
for i in texts_tfidf:
    print(i[20:24])

===[単語, TF-IDF]===
[['U', 0.022445636964346205], ['m', 0.11222818482173101], ['あくまで', 0.022445636964346205], ['あそこ', 0.022445636964346205]]
[['しっかり', 0.02616203449412644], ['しまう', 0.002898944443406048], ['じゃ', 0.004151833844039856], ['せる', 0.005797888886812096]]
[['これ', 0.0026571889707680363], ['さらに', 0.013652529666738833], ['しまう', 0.010628755883072145], ['じゃ', 0.003805594523875085]]
[['ここ', 0.006775642806339103], ['こと', 0.008239349333137951], ['これ', 0.0034865640168190394], ['さて', 0.015732555392960215]]
[['記事', 0.006384155132906055], ['家', 0.04200016584013773], ['最近', 0.07295284301359403], ['あの', 0.09752136505414427]]
[['て', 0.053620572470353435], ['できる', 0.01792908931110876], ['です', 0.03132779934738118], ['でも', 0.0018489852575983943]]
[['その', 0.0034775495530498207], ['そもそも', 0.010081089692211678], ['て', 0.020865297318298923], ['です', 0.019640317875406748]]
[['じゃ', 0.007256376823656625], ['すぎる', 0.017102666638402184], ['せる', 0.005066636590574954], ['そう', 0.01451275364731325]]
[['しまう', 0.009037509134257363], ['じゃ', 0.004314471125835394], ['せる', 0.018075018268514726], ['そう', 0.012943413377506183]]
[['そう', 0.005430510747744854], ['その', 0.006720431231889886], ['そもそも', 0.00974094962350806], ['そんな', 0.01948189924701612]]

TF-IDFで上位の単語を出力

それではいよいよTF-IDFで上位の単語を記事ごとに表示してみましょう！
今回はTF-IDFが0.1以上の単語のみ表示させてみます！

for i in range(len(texts_tfidf)):
    print('')
    print('%s.' % i, '〜%s〜' % df['title'][i])
    for text in texts_tfidf[i]:
        if text[1] > 0.13:
            print(text)

0. 〜波乱はルーキーたちの走り次第？ “怪物世代”の初陣に注目 第97回箱根駅伝予選会を読む〜
['ルーキー', 0.29179328053650067]
['予選', 0.26934764357215446]
['会', 0.2353324044944065]
['年生', 0.13467382178607723]
['校', 0.17956509571476964]
['監督', 0.13467382178607723]
['練習', 0.15711945875042344]
['走り', 0.15711945875042344]
['駅伝', 0.3591301914295393]
['高校', 0.14119944269664392]

1. 〜スマホやタブレットじゃやっぱり不十分？ 「オンライン授業」に最適のPCとは〜
['.', 0.17005322421182187]
['/', 0.2807205709669065]
['LAVIE', 0.1684323425801439]
['Office', 0.1310029331178897]
['PC', 0.561441141933813]
['子ども', 0.2092962759530115]
['学習', 0.14971763784901682]
['搭載', 0.1684323425801439]
['機能', 0.1684323425801439]

2. 〜幼児教育「ヨコミネ式」創設者・横峯吉文氏のDVを元妻と子供が告白《法廷闘争“全面対決”へ》〜
['教育', 0.15248089693189756]
['A', 0.1435114324064918]
['ミネ', 0.1715400483643072]
['ヨコ', 0.1715400483643072]
['保育園', 0.37738810640147585]
['吉文', 0.3259260918921837]
['子', 0.2744640773828915]
['子供', 0.2573100725464608]
['暴力', 0.2230020628735994]
['氏', 0.17938929050811475]
['祖母', 0.13723203869144576]
['鹿児島', 0.13723203869144576]

3. 〜BTS会社社長、韓国8位の株式富豪に…「共通点はオタクなこと」J.Y.Parkが語った素顔〜
['.', 0.14159299853664192]
['BH', 0.20257378379369387]
['BoA', 0.13504918919579592]
['JYP', 0.13504918919579592]
['SM', 0.13504918919579592]
['アーティスト', 0.13504918919579592]
['事務所', 0.27009837839159184]
['億', 0.13504918919579592]
['社', 0.28318599707328385]
['韓国', 0.40514756758738774]

4. 〜「レジ袋はいりません」からの流れでびっくりするほど挙動不審になった話〜
['更新', 0.14590568602718806]
['!!', 0.13952153089428201]
['22', 0.13952153089428201]
['おろす', 0.13952153089428201]
['きょう', 0.27904306178856403]
['たぶん', 0.13952153089428201]
['つづる', 0.13952153089428201]
['ほす', 0.13952153089428201]
['ほる', 0.13952153089428201]
['トラブル', 0.13952153089428201]
['ハプニング', 0.13952153089428201]
['区役所', 0.13952153089428201]
['単行本', 0.13952153089428201]
['厄介', 0.13952153089428201]
['厄日', 0.27904306178856403]
['大幅', 0.13952153089428201]
['好評', 0.13952153089428201]
['山本', 0.41856459268284607]
['巻', 0.13952153089428201]
['引き寄せる', 0.13952153089428201]
['木曜日', 0.13952153089428201]
['次回', 0.13952153089428201]
['毎週', 0.13952153089428201]
['漫画', 0.13952153089428201]
['炎上', 0.13952153089428201]
['薬局', 0.13952153089428201]
['詰まる', 0.13952153089428201]
['買い物', 0.13952153089428201]
['闘い', 0.13952153089428201]

5. 〜三浦春馬さん、竹内結子さん、木村花さん…芸能人「自殺の連鎖」はなぜ起きるのか？〜
['さん', 0.14596954962105263]
['投影', 0.16163344929474321]
['木村', 0.16163344929474321]
['死', 0.4849003478842297]
['自殺', 0.14790071653449471]
['芸能人', 0.25419809869738275]

6. 〜内部資料入手「GoToトラベル事務局」大手出向社員に日当4万円〜
['旅行', 0.1593642568499776]
[',', 0.20266551686226678]
['GoTo', 0.32933146490118353]
['トラベル', 0.20266551686226678]
['事務', 0.3546646545089669]
['出向', 0.1519991376467001]
['大手', 0.17733232725448345]
['局', 0.3546646545089669]
['技師', 0.17733232725448345]
['技術', 0.17707139649997508]
['日当', 0.25333189607783346]
['社員', 0.17733232725448345]

7. 〜「お前は何アゲだ？ 何で俺だけ“たたき上げ”なんだ！」“最後の怪物幹事長”二階俊博がキレた瞬間〜
['二', 0.25653999957603274]
['階', 0.3200732773176539]
['国土', 0.13717426170756597]
['俊博', 0.13083466706402622]
['原点', 0.13083466706402622]
['均衡', 0.16354333383003275]
['政治', 0.26166933412805243]
['発展', 0.22896066736204587]
['県議', 0.13083466706402622]
['秘書', 0.16354333383003275]
['道路', 0.22896066736204587]

8. 〜「バラバラにした遺体を鍋で……」白石隆浩被告が証言した、おぞましい犯行の一部始終〜
['さん', 0.2575923910688616]
['C', 0.5029569855573655]
['殺害', 0.3889560913276654]
['白石', 0.3695082867612821]
['被告', 0.3889560913276654]

9. 〜「長さ」ではなく…美容師が教える、髪を切るときに言うといい「意外な言葉」〜
['師', 0.23953570973227745]
['お客様', 0.19582749984882405]
['ヘア', 0.14687062488661806]
['ヘアスタイル', 0.44061187465985413]
['美容', 0.44061187465985413]

gensimに便りっきりの簡単な実装でしたが、ある程度重要そうな単語のみを抽出できているのではないでしょうか？
gensimは非常に便利であることが分かりました。

次回はTF-IDFとword2vecを用いて、テーマを決めてクラスタリングを実装してみようかと思います！

　 Tweet
Qiitaで続きを読む

投稿日：2020-10-19T15:49:47+09:00

ラズパイを使って、【ある作業】を自動化してみた

はじめに

みなさんの会社では、始業・終業はどういった感じでしょうか？
社内放送で知らせる・時間になったら各々勝手に仕事を始める（終わる）・時間になったら朝会（終礼）を始めるなどなどあるかと思います。

自分が以前勤めていた会社では、
1. ipodで始業時間にアラーム（小音）が鳴る
2. そのアラームを担当の人が止める
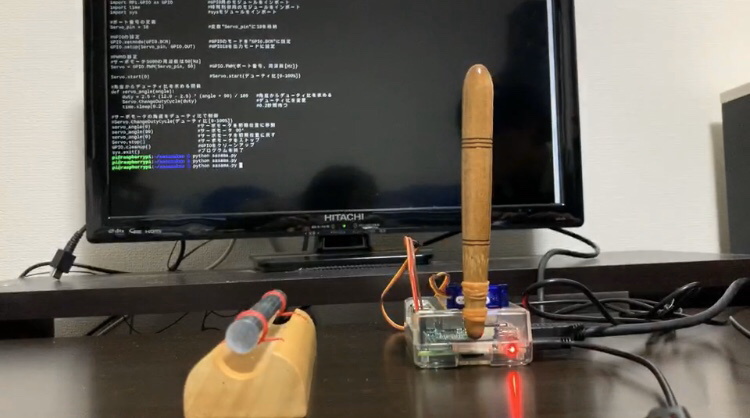
3. 以下のようなチャイム（？）を手動で鳴らして社内の人に伝える

↑これを棒で叩いて鳴らす

という流れでやっていました。

~~正直、毎日アラームを止めて叩くのは手間がかかると。~~シンプルにアラームを定刻に鳴らせばいいのではないかと。

しかし、それだと面白みがないのでどうせならこのチャイムを叩く動作を自動化してしまおう！ということでラズパイ（とPython）を使って自動化しました（勉強がてら）。
ちょうど同期がラズパイを持っていたこともあり同期と二人でネタ半分で作ることにしました。

準備

自動化するにあたって、何が必要がをまず調べました。とはいっても幸いラズパイは同期が持っていたので追加で準備するモノはあまりなかったです。購入物は以下の通りです。

サーボモーター

ジャンパーワイヤ

どちらもAmazonで購入！サーボモーターは、デジタルマイクロサーボSG90（770円）を買いました。

自動化の仕組みとしてはシンプルで、モーターの角度をプログラムで制御してチャイムを叩くだけ。自動化と言うとかっこいいですがやっていることはたいしたことありません（笑）

開発

今回書いたコードはこんな感じです。
# -*- coding: utf-8 -*-             #エンコードの指定
import RPi.GPIO as GPIO             #GPIO用のモジュールをインポート
import time                         #時間制御用のモジュールをインポート
import sys                          #sysモジュールをインポート

#ポート番号の定義
Servo_pin = 18                      #変数"Servo_pin"に18を格納

#GPIOの設定
GPIO.setmode(GPIO.BCM)              #GPIOのモードを"GPIO.BCM"に設定　GPIOをポート番号で扱う方法に設定
GPIO.setup(Servo_pin, GPIO.OUT)     #GPIO18を出力モードに設定

#PWMの設定
#サーボモータSG90の周波数は50[Hz]
Servo = GPIO.PWM(Servo_pin, 50)     #GPIO.PWM(ポート番号, 周波数[Hz])

Servo.start(0)                      #Servo.start(デューティ比[0-100%])

#角度からデューティ比を求める関数
def servo_angle(angle):
    duty = 2.5 + (12.0 - 2.5) * (angle + 90) / 180   #角度からデューティ比を求める
    Servo.ChangeDutyCycle(duty)                      #デューティ比を変更
    time.sleep(0.2)                                  #0.2秒間待つ

#サーボモータの角度をデューティ比で制御
#Servo.ChangeDutyCycle(デューティ比[0-100%])
servo_angle(0)                 #サーボモータを初期位置に移動
servo_angle(90)                #サーボモータ 90°
servo_angle(0)                 #サーボモータを初期位置に戻す
Servo.stop()                   #サーボモータをストップ
GPIO.cleanup()                 #GPIOをクリーンアップ
sys.exit()                     #プログラムを終了
コード自体は、ただサーボモーターの角度を制御するだけなので難しくなくネットにも沢山情報があったのでスムーズにできました。

自分は機械科卒ですが電子工作的なことはあまり経験がなかった（大学では旋盤、溶接、製図等を主に学んでいた）こともありジャンパーワイヤーをつなげる際はビビリつつも調べながらやりました。

自動化するということで、始業・終業時間にプログラムが作動するようクーロンで設定しました。
自分はクーロンの存在を知らず、同期から教えてもらいました（勉強になった）

cronとは、多くのUNIX系OSで標準的に利用される常駐プログラム（デーモン）の一種で、利用者の設定したスケジュールに従って指定されたプログラムを定期的に起動してくれるもの。
参照元：IT用語辞典 e-Words

できあがったもの

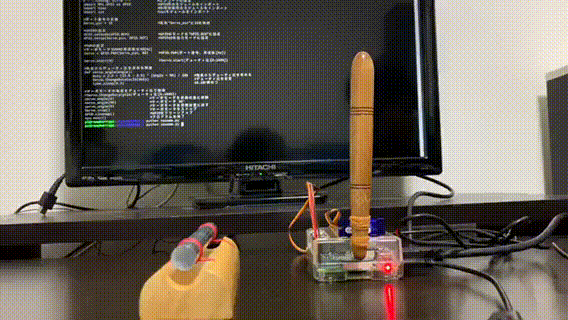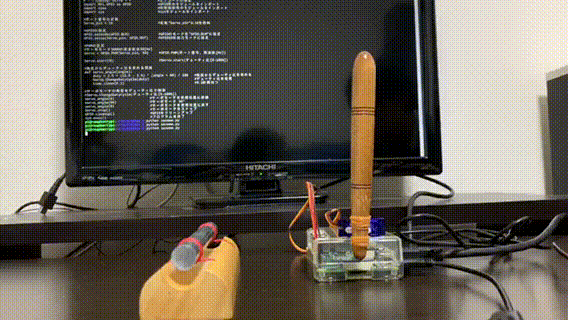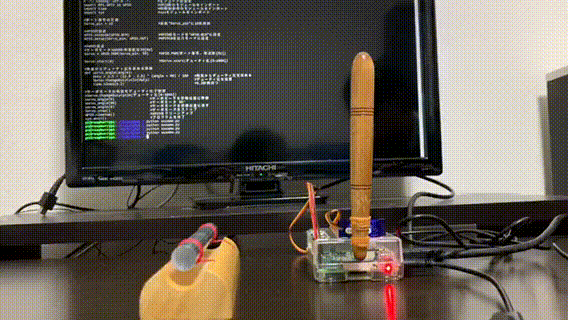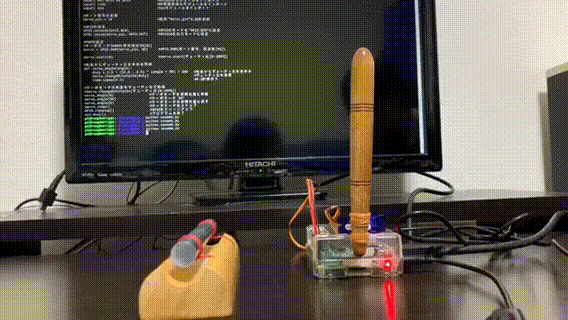
かなーりシンプルです！

こちらが、デモ動画になります。（音は想像で！）

どうでしょうか？かなりシュールな仕上がりになりました（笑）
実際に使用する際は、１度しか叩かないようにしております。
これでもうわざわざ手動で叩く必要も無く、かつチャイムの味（？）だけ残すことができました。

まとめ

今回は、始業・終業のチャイムをラズパイで自動化してみました。

こうやって、生活していて感じたチョットした不便なこと・非効率的なことを解決することが出来るのがプログラミングの面白さなのかなと思います。
実際にやってみて面白かったし、知らなかったことも学べてとてもいい経験となりました。

みなさんもこんな感じで簡単なモノでいいので作ってみてはいかがでしょうか？

　 Tweet
Qiitaで続きを読む

投稿日：2020-10-19T14:57:45+09:00

ファイルコピーしてセル値書き換え@python

やりたいこと

テンプレートとなるExcelをコピーして、
ファイル名を変更。
ついでに表紙扱いのシートの一部の値だけ書き換えたい。

背景

仕事上、とあるテンプレートを元に
似たようなファイルをいくつか用意しないといけないのだが、
一部のセル値だけ値の変更が必要。

ファイル複製だけならbatとかでよいが、
値の変更をわざわざExcel開いて書き換えるのも面倒なので。
VBAでも可だがあんまり使いたくない。できればPythonの練習も兼ねたい。

ファイル名とか変更値とかはcsvに定義しておけば
変更楽だし使いまわしできるしいいよね。

流したスクリプト
cpFileCopyNameByCSVlist.py
import os
import sys
import pandas as pd
import shutil
import openpyxl


csvname = './cpfilelist.csv'
resultFolder = './cpResult/'
templatefilename = './template.xlsx'

shutil.rmtree(resultFolder)
os.mkdir(resultFolder)

#read list from csv
data = pd.read_csv(csvname).values.tolist()
wsname = 'header'

for row in data:
    #copy template file　renamed by list.csv
    print(row[0] +":"+row[1])
    newFileName = resultFolder + row[0] +'.xlsx'
    newTitleName = row[1]
    shutil.copyfile(templatefilename,newFileName)

    # change cell.value from csv valye

    wb = openpyxl.load_workbook(newFileName)
    ws=wb[wsname]
    ws['B5'] = newTitleName
    wb.save(newFileName)
    wb.close()

sys.exit(0)
メモ

pandasって便利だなー。

　 Tweet
Qiitaで続きを読む

投稿日：2020-10-19T14:22:32+09:00

第2回 Neural Network Console Challenge 類似曲検索を実現する

1.はじめに

　Neural Network Console Challenge ( NNC Challenge )とは、SONYさんが開発したAI開発ツールNeural Network Consoleを使い、協賛企業が提供するデータを用いてディープラーニングに挑戦するAI開発コンテストで、今回が第2回目です。

　今回の協賛企業は、映像制作・イベント・音効業務用のBGM・効果音などを販売しているAudiostockさんです。提供されるデータは、10,000点を超えるBGMデータで、2020.09.16 ~ 2020.10.19 の期間で開催されました。

　そして今回のテーマは、A）AudiostockのBGM検索の自動分類アルゴリズムを作り出す、B）自由な発想で音声データを解析する（自由テーマ）、の2つの中から選ぶというもので、私も参加しましたのでチャレンジ内容を記します。

＊学習用データ提供：Audiostock

2.Audiostockは何をやっている会社？

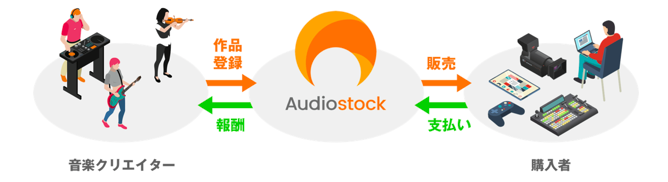
　Audiostockは、音楽クリエイターからBGMや効果音などの作品を登録して貰いオンラインで著作権フリーの音楽として販売します。購入者は映像制作・イベント・音効業務などを行っている方です。販売が成立するとAudiostockは購入者から支払いを受け、作品を制作した音楽クリエイターに報酬を支払うというサービスを行っています。
　

　購入者にとっては、自分の必要とする音楽を著作権法を気にすることなく手軽に買えますし、音楽クリエイターにとっては、自分の作品を効率的に販売する機会が得られるというわけです。

　現在、契約している音楽クリエイターは16千人、販売している音源は60万点で毎月1万点づつ増えているとのことです。

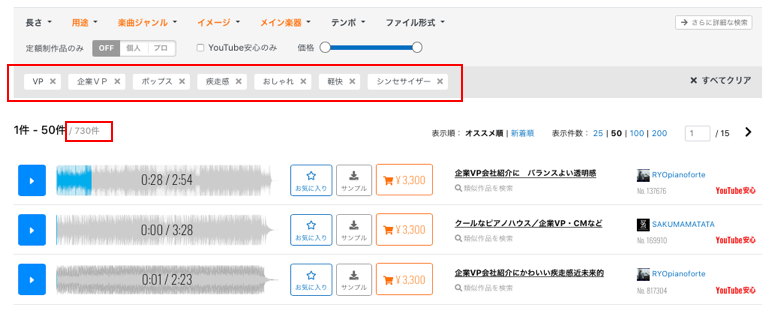
　では、実際のオンライン販売のWebページを見てみましょう。どうやって自分の好みの曲を探すかと言うと、「長さ」,「用途」,「楽曲ジャンル」,「イメージ」,「メイン楽器」,「テンポ」,「ファイル形式」という各カテゴリでタグを指定をして、自分の探したい曲を絞り込んで探します。これ以外の方法もありますが、メインはこの方法の様です。

　カテゴリをクリックするとタグの一覧（楽曲ジャンルだと「ポップス」〜「クラシック」まで21個のタグがあります）が表示されますので、好みのタグにチェックを入れて適用ボタンを押すと絞り込みが掛かります。

　タグで絞り込んだ後は、1つ1つ曲を聞いて選ぶことになります。曲を聞くプロセスは上手く出来ていて、矢印上下キーを押すだけで次から次へとスムーズに曲が聞けますし、マウスで曲の任意の位置から再生できます。

　※タグによる絞り込み検索の他に、タグと1行コメントを対象としてキーワード検索で曲を絞り込む方法もありますが、タグで選ぶのと本質的な違いは小さいです。

3.今回提供されたデータ

　今回、Audiostockさんから提供されたデータは、以下の3つです。

　02_rawdataは、BGMのフルサイズデータで10,802個（サンプルレート44.1KHz)あります。音質が良く聞いていて楽しいのですが、曲の長さはまちまちで全体の容量も200GB超えとそのままでは扱い難いです。

　01_加工済みデータは、02_rawdataをコンパクトにしたもので、同じく10,802個あります。曲の長さを曲頭から24secで切り揃え、サンプルレートを8kHzにダウンサンプルすることで、全体の容量を3GB程度に抑えています。音質はあまり良くありませんが、ディープラーニングで使うには、こちらが良いでしょう。

　BGMデータ一覧は、BGMの1行コメントやタグをまとめたもので、こんなイメージです。

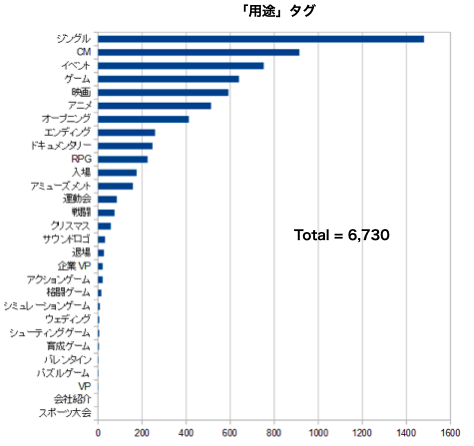
　音楽は画像と違いゼロからアノテーションするには相当時間が掛かるため、BGMデータ一覧は非常に貴重なデータです。そのため、主要カテゴリのタグ付け状況を見てみます。まず「用途」タグです。

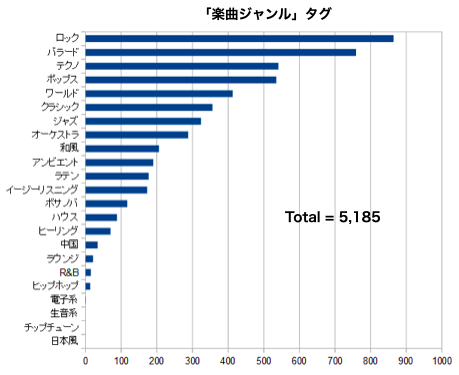
　1位はジングルで、CM、イベント、ゲーム、映画と続きます。1位のジングルは、番組の節目に挿入される短い音楽ですので、ジングルを探している場合は効果的な絞り込みが出来そうです。しかし、それ以外は曖昧な絞り込みになってしまいそうです。例えば映画と言っても様々なものがあるわけで、このタグで探している曲を効率的に絞り込めるかどうかはちょっと疑問です。タグ使用数は6,730件(重複使用なしで使用率62％)と思ったほど多くありません。

　次に、「楽曲ジャンル」タグです。

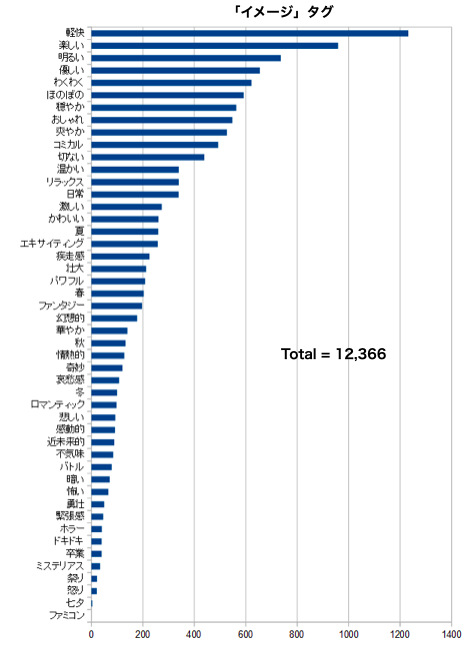
　1位はロックで、バラード、テクノ、ポップス、ワールドと続きます。5位のワールドは、世界の各地域の民族音楽の総称です。曲のジャンルだけの絞り込みなので、特殊なジャンルの絞り込みは別として、あくまでもサブ的なものだと思います。タグ使用数は5,185件(重複使用なしで使用率48％)と少な目です。

そして、「イメージ」タグです。

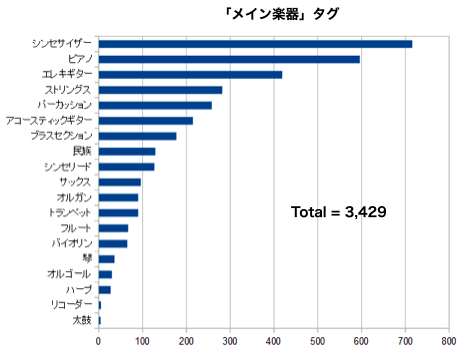
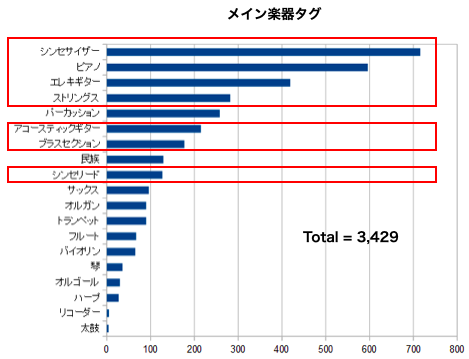
　1位は軽快で、楽しい、明るい、優しい、わくわくと続きます。探している曲のイメージを自分なりの言葉にするのは簡単なので上手くハマれば効果的かもしれません。しかし、イメージは主観的なもので、例えば楽しいと思うか明るいと思うかは人それぞれと言う気がします。

　最後に、「メイン楽器」タグです。

　1位はシンセサーザーで、ピアノ、エレキギター、ストリング、パーカッションと続きます。このカテゴリのタグは使っている楽器を明示するものなので客観的なものだと思います。タグの使用合計は3,429件(重複使用なしで使用率32％)と一番少ないです。

　タグについてまとめると、「用途」タグ・「楽曲」タグは絞り込み効果が薄く、「イメージ」タグは主観的なバラツキが多いように思います。「メイン楽器」は客観的なタグだと思います。

　そして、的確なタグが付いていないと絞り込みの時にリストから外れてしまうにも関わらず、全体的にタグの使用率は低いです。重複使用がないとしても使用率は、「用途」タグで62％、「楽曲ジャンル」タグで48％、「メイン楽器」タグで32％です。

　※全体的にタグの使用率が低い理由は、タグ付けはAidiostock事務局で行うのではなく原則音楽クリエイターに任されているので、クリエイターの方々のタグ付けのバラツキが影響しているかもしれません。但し、これは無理からぬことで、毎月1万点の新曲が追加される中では、事務局でのタグ編集は補助的なものにならざるを得ないと思います。
　

4.テーマ選定

　自分が購入者だとしてAudiostockに会員登録（会員登録は無料です）し、実際に曲を選んでみることにしました。想定は、企業のプロモーションビデオを作成するとして、そのBGMを選ぶというものです。
　
　「用途」タグはVP,企業VP、「楽曲ジャンル」タグはポップス、「イメージ」タグは疾走感,おしゃれ,軽快、「メイン楽器」タグはシンセサイザーでタグ付けして曲を絞り込むと、全部で730曲リストアップされます。

　ここから1曲づつ曲を聞くわけですが、730曲を全部聞くのは現実的ではありません。なぜなら、選曲に1曲あたり平均10秒しか掛けなかったとしても2時間掛かるからです。曲を聞くのは画像を選ぶよりはるかに時間が掛かります。

　そう考えると、タグで絞り込んで1曲づつ聞いて自分のイメージに大体合うような曲に出会ったら、絞り込んだ曲の中からその曲の類似曲検索が出来ると良いと思いました。

　また、先程のBGMデータ一覧の分析から分かった、全体的にタグの使用率が低いことを考えると、タグの絞り込みで外れてしまった曲の中にも好みの曲がある可能性があります。その場合、リストから外れた曲の中から自分のイメージに大体合うような曲の類似曲検索をするのは効果的な手法だと思います。

　そこで、今回のテーマは「類似曲検索」にすることにしました。

5.ラフスケッチを作る

　テーマが決まったので、類似曲検索を実現するためのラフスケッチを作成します

1) 波形データを画像に変換する
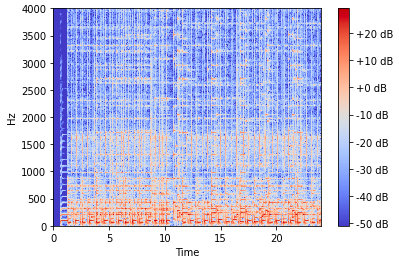
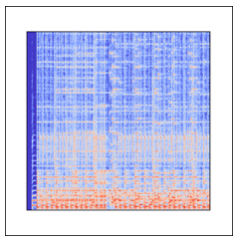
　BGMの波形データをディープラーンングそのまま扱うこともできますが、波形の様な時系列データは処理に時間が掛かりやすいので、波形データの特徴を画像データに変換して扱うことにします。そのために、BGMの波形データをメル周波数スペクトログラムに変換することにします。

　これがメル周波数スペクトログラムの例です。縦軸は周波数(Hz)、横軸は経過時間(sec)で、色は音圧レベル(db)を表します。メル周波数と言うのは、人間の聴覚特性に合うように周波数を調整したものです。つまり、サウンドの時系列変化を表す画像と言えます。

2) BGM分類器を作成する
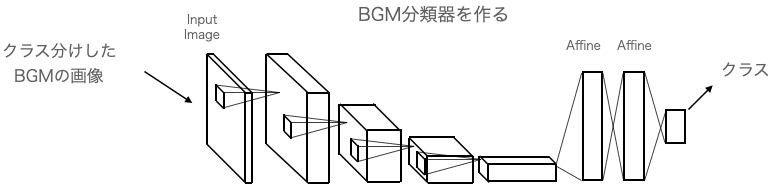
　クラス分けしたBGMの画像を入力し、CNNで重みを学習させます。最初はデタラメなクラスを出力しますが誤差逆伝播によって次第に正しいクラスを出力するようなネットワークの重みを学習します。

　この結果、BGMを適切にクラス分けできるBGM分類器が出来ます。

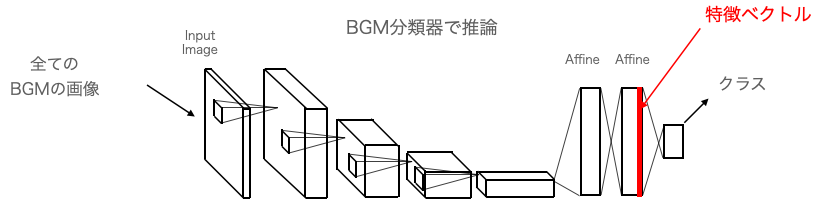
3) BGMの特徴ベクトルを取得する
　BGMの画像をBGM分類器に入力するとクラスが出力されますが、クラスは様々な処理を行った上での最終結果なので情報量が少ないです。それよりも、その前の全結合層(Affine)の方が圧倒的に情報量が豊富なので、ここから特徴ベクトルを取り出すことにします。

　これによって、全てのBGMの画像を入力すると、全てのBGMの特徴ベクトルを取得出来るわけです。

4) 特徴ベクトルから類似曲を探す
　2つのベクトルがどのくらい同じ方向を向いているかは、下記の式を使ってcos類似度を計算すれば求めることが出来ます。cos類似度は−１〜＋１で表され、全く同じ方向を向いているとき＋１になります。

　従って、類似曲を探したい曲の特徴ベクトルと他の曲の特徴ベクトルのCOS類似度を全て計算して結果をソートすれば、類似度が大きい順に曲が検索できるわけです。

　これでラフスケッチが出来ましたので、後はこれに沿って具体的に進めて行きます。

6.波形データを画像に変換する

　Pythonで音楽や音の分析に使用するパッケージlbrosaを使って、BGMの波形データをメル周波数スペクトログラムに変換します。
import sys
import numpy as np
import librosa
import matplotlib.pyplot as plt
import scipy.io.wavfile
import librosa.display
import os

def save_png(filename,soundpath,savepath):

    #音声ファイル読み込み
    wav_filename = soundpath+filename
    rate, data = scipy.io.wavfile.read(wav_filename)

    #16bitの音声ファイルのデータを-1から1に正規化
    data = data / 32768
    # フレーム長
    fft_size = 1024                 
    # フレームシフト長 
    hop_length = int(fft_size / 4)  

    # 短時間フーリエ変換実行
    amplitude = np.abs(librosa.core.stft(data, n_fft=fft_size, hop_length=hop_length))

    # 振幅をデシベル単位に変換
    log_power = librosa.core.amplitude_to_db(amplitude)

    # グラフ表示
    plt.figure(figsize=(4, 4)) 
    librosa.display.specshow(log_power, sr=rate, hop_length=hop_length)
    plt.savefig(savepath+filename + '.png',dpi=200)    

soundpath = './input/'
savepath = './output/'
cnt = 0

for filename in os.listdir(soundpath):
    cnt += 1
    print(cnt,'件を処理しました', filename)
    save_png(filename,soundpath,savepath)
    plt.close() 
　コードを実行すると、800×800ピクセルのpng画像が得られます。周辺に余白が出来るので、センターから600×600でクロップして224×224にリサイズします。

7.BGM分類器を作成する

　どうやってデータセットを作るかですが、ゼロからBGMを分類するのは大変過ぎるので、BGMデータ一覧表にあるタグをなんとか利用したいわけです。タグを頼りにする場合、「用途」や「楽曲ジャンル」は曖昧だし、「イメージ」は主観的です。客観的なのは「メイン楽器」だと思い、「メイン楽器」のタグを元に分類してみることにしました。

　使用頻度が多いタグにフォーカスし、「パーカッション」の様にサウンドの主体にはならないものや「民族」の様にサウンドが多様なものは除外して、赤枠のタグが付いている曲だけを抽出します。その結果、シンセサイザー716曲、ピアノ596曲、エレキギター419曲、ストリングス282曲、アコースティックギター215曲、ブラスセクション177曲、シンセリード127曲をピックアップしました。後は、ひたすらピックアップした曲を聞いて分類を行いました。。

　例えば、シンセサイザーのタグが付いていても、あくまでもバッキングで使用しているだけでメインで使っているのはサックスだとか、確かに使っているが短時間しか使っていないとかいう様なものを省いて行きました（こういうのがかなり多いです）。最終的に、タグの統廃合も含めて「アコースティックギター」,「エレキギター」,「ピアノ」,「シンセサイザー」の4種類に分け各75曲づつ計300曲を選びました。

　そして、先程説明した方法で、300曲の波形データを画像に変換します。そして、NNCでデータセットを作成します。

　300個のデータは学習：評価＝7:3で分割し、学習データ210個、テストデータ90個を作成しました。

　ニューラルネットワークの設計については、コンテスト参加者の特典として事務局からNNCのcloud版のGPUを10,000円分使える権利を付与して頂いたので、心おきなくトライが出来ました。GPUだとCPUの20倍くらいのスピードで学習が出来るのでほとんどストレスなしで色々試せるのは、非常にありがたかったです。

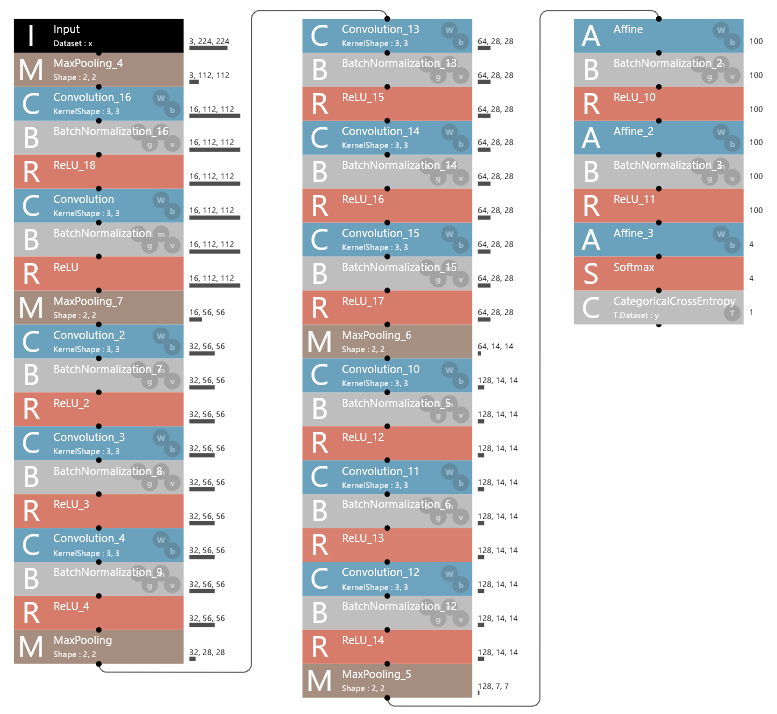
　色々トライした結果、学習データが210個と少ないせいでしょうか、コストパラメータは比較的小さなモデルの方が良い結果が出ました。

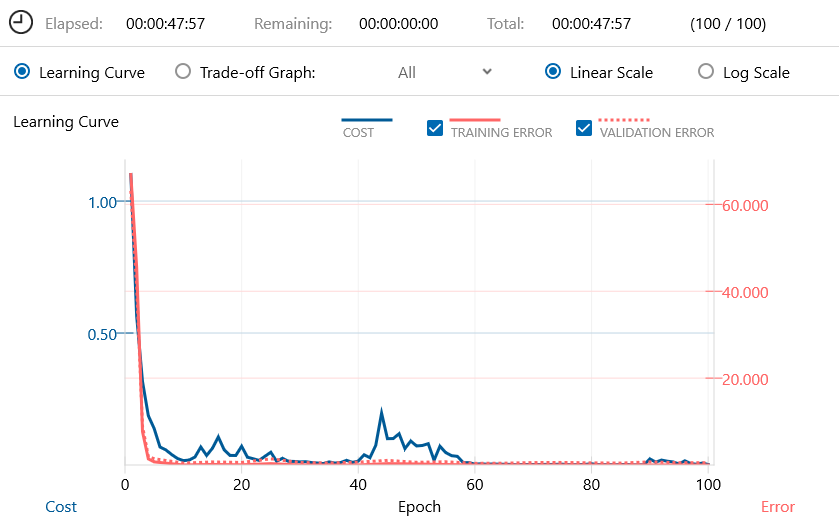
　このモデルのコストパラメータは1,128,700で、CPUでも実用的に動くレベルです。

　学習曲線(Learning Curve)です。

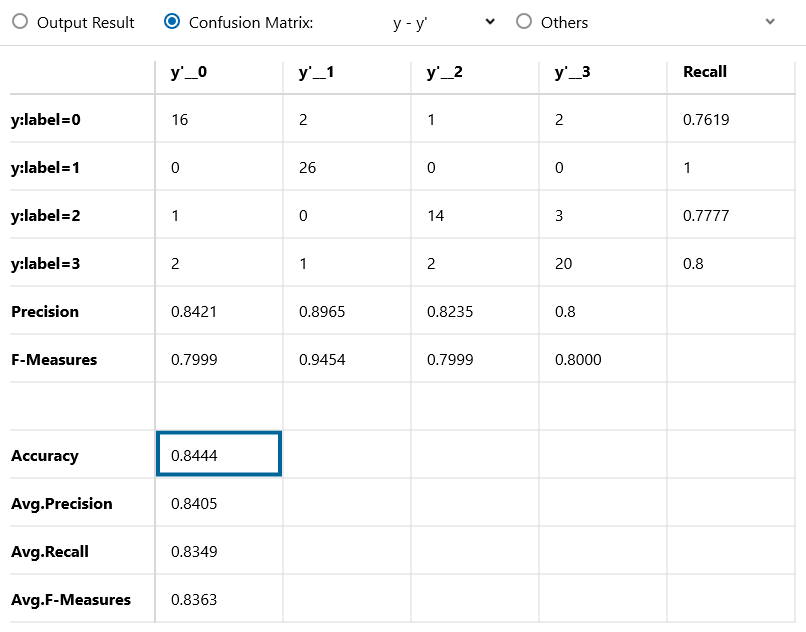
　学習は、この後の処理を考えて、あえてNNC Windows版(CPU)を使って行い、100epochが48分で完了しました。検証エラー(VALIDATION ERROR)のbestは、60epoch時に0.530326です。

　混同行列(Confusion Matrix)と精度です。

　精度(Accuracy)は84.44％で、label毎のRecallも大きなバラツキはなく、まずまずの分類精度です。

8.BGMの特徴ベクトルを取得する

　BGM分類器が出来ましたので、それを使って全てのBGMの特徴ベクトルを求めます。最初、結構複雑なことをしなければいけないのかなと思っていましたが、Neural Network Console (Windows版) は上手く作られています、「学習されたニューラルネットワークの途中出力を分析する」という機能があるのです。

　まず、全てのBGMの波形を画像に変換してテストデータ（正解データはなんでも良い）を作成し、先程学習した時のテストデータと入れ替えておきます。

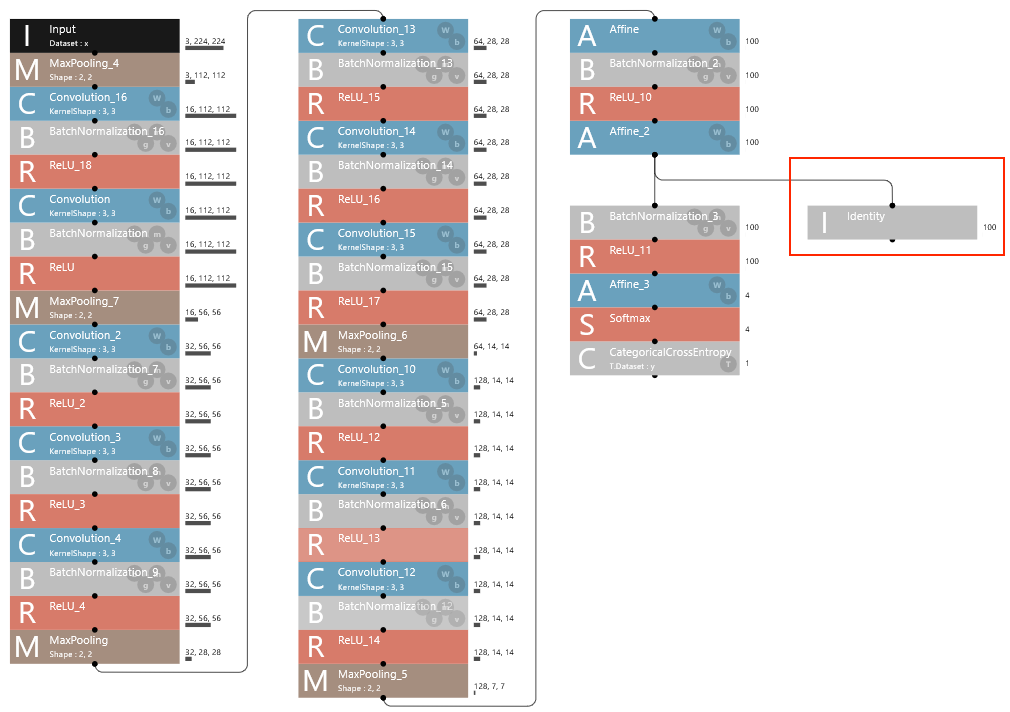
　次に、途中結果出力用のネットワークを作成します。

　基本的に学習用ネットワークのコピーですが、2つ目のAffineからIdentifyへの分岐接続を追加し、特徴ベクトルが取り出せるようにしています。

　このネットワークを、EDITタブにActivationMonitorという名前で追加登録して、CONFIGのExecutorの指定もこのActivationMonitorに変更し、Global ConfigのMax Epochを0にします。

　Open in EDIT Tab with Weight で学習済みニューラルネットワークを重み付きで読み込み学習を開始すると、Max Epochが0なので何もせず学習が完了します。そして評価を開始すれば、テストデータに登録された各画像の特徴ベクトルを、CSVファイル(output_result.csv)で出力してくれるんです。こんな風に小回りを効かせることが出来るなんて凄いです！

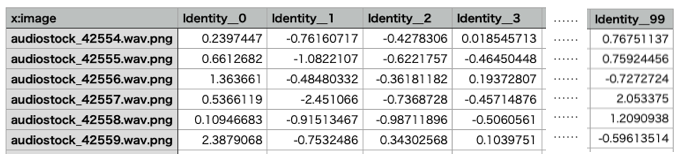
　これが、CSVファイルのイメージです。Affineが100次元なので、特徴ベクトルも100次元になっています。

＊エディター等で、y:labelとCategoricalCrossEntropyの列は削除し、x:imageの名称は簡略化したものを表示しています。

9.特徴ベクトルから類似曲を検索する

　各BGMの特徴ベクトルをまとめたCSVファイルができましたので、Pythonを使って類似度TOP５の曲を検索します。
import csv
import numpy as np

# 初期設定
N = 500  # 類似度を計算するindex (audiostock_43054を指定)

# cos類似度計算関数
def cos_sim(v1, v2):
    return np.dot(v1, v2) / (np.linalg.norm(v1) * np.linalg.norm(v2))

# 特徴ベクトルをarrayに読み込む
with open('./output_result.csv', 'r') as f:
     reader = csv.reader(f)

     h = next(reader)  # ヘッダーをスキップ
     for i, line in enumerate(reader):
        if i == 0:
            array = np.array(line[1:], dtype=float)
            index = [line[0]]
        else:
            array = np.vstack([array,np.array(line[1:], dtype=float)])
            index.append(line[0])
     print('特徴ベクトル読み込み完了', array.shape)
     print('index読み込み完了', len(index))

# cos類似度計算    
for i in range(len(array)):
    x = cos_sim(array[N], array[i])     
    if i == 0:
        score = x
    else:
        score = np.hstack([score,x])
print('cos類似度計算完了', score.shape)

# TOP5のindex検索
for j in range(1,6):
    b = np.where(score==np.sort(score)[-j])
    n = int(b[0])
    print('TOP'+str(j), index[n][:16], 'score = '+str(score[n]))
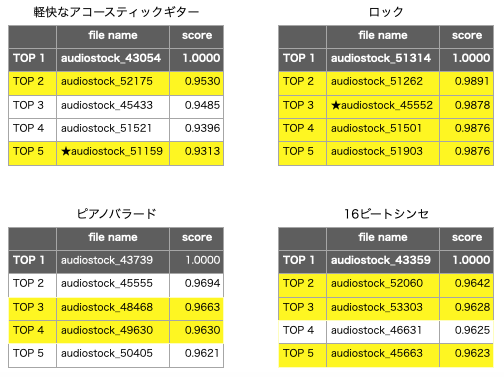
　コードを実行すると、類似度が高い順に曲名が並びます。TOP1のaudiostock_43054は検索対象曲そのものです（なのでcos類似度は最大の1です）。TOP2以降を見ると、一番類似度が高いのは、audiostock_52175で類似度は0.9530となります。

　それでは、色々な曲を対象に類似曲を検索してみます。

　曲を4つピックアップして、TOP2〜TOP5の中にTOP1と類似の曲が含まれているかを実際に聞いて確認し、該当すると思われる曲を黄色でマーキングしてみました。

　その結果16曲の内11曲が類似曲と判定でき、平均約7割くらいの精度で類似曲を検索できることが分かりました。そして、類似曲11曲中9曲はデータセットには無い曲で、類似曲検索が効果的に働いていることも分かりました。

　特に、★印を付けた軽快なアコースティックギターのTOP5とかロックのTOP3は、正に狙い通りの類似曲だなーと思いました。

10.まとめ

　今回のチャレンジで、BGMクラス分類器を使った類似曲検索は結構使えることが分かりました。現在の曲検索の方法に加えて、この手法を追加して使うことで膨大なBGMの中から効率的に自分の好みの曲を見つけることが出来ると思います。

　また、Neural Network Consoleは「学習されたニューラルネットワークの途中出力を分析する」という、小回りが利く機能を持っていることを今回初めて知りました。Neural Network Console は痒いところに手が届く使いやすいAIツールなので、おすすめです。

　
　

　 Tweet
Qiitaで続きを読む

投稿日：2020-10-19T13:33:43+09:00

Heroku入門 - Python DjangoでHello Worldを表示する with Raspberry PI 3

この記事の目的

PaaS(プラットフォーム・アズ・ア・サービス)の一つであるHeroku(ヘロク)に、PythonのWEBサーバのDjangoで作成した最も単純なアプリケーションをリリースし、画面に「Hello World...」を表示する手順を確認します。

※本記事の内容は、執筆時点(2020/10/18)のものです。今後の仕様変更や機能改修により内容がそぐわなくなる場合はご了承下さい。

Herokuとは

Herokuは、セールスフォース・ドットコム社のForce.comやGoogle社のGoogle AppEngineと並び、最も有名なPaaSの一つです。

Heorkuの本サイト
https://jp.heroku.com/

Herokuを利用すると、サーバの調達からセットアップやネットワークの構築、さらにサーバ類の保守・メンテナンスなどのインフラ環境の手間を一切考慮する必要がなく、カスタマイズしたアプリケーションをリリースし運用することができます。

Herokuにデプロイされたアプリケーションは、Dyno(ダイノ)と呼ばれる完全に独立したモジュール単位で実行され、自動的にスケール・イン(Dyno数を減少)、スケール・アウト(Dyno数を増加)することが可能です。

また、Dyno数の増減に応じて負荷分散やルーティング処理が自動的に行われ、利用者はその設定や操作を意識する必要がありません。

Herokuはこれ以外にも様々な機能を備えています。詳細はHeroku本サイトをご参照ください。

無料利用範囲について
Herokuには無料のお試しプランがあります。
・RAMの容量制限：512MBまで
・同時実行Dyno数：最大2個
・30分間アイドル状態でスリープに移行
・一月当たりのDyno利用時間：最大1,000時間

実行環境

今回は、Raspberry PI 3でDjangoアプリを構築し、Herokuにリリースします。
実行環境(WEBアプリケーション構築環境)の詳細は以下です。

WEBアプリケーション構築環境詳細
・Raspberry PI 3 model B (Memory 1GB)
・OSバージョン：Raspbian GNU/Linux 10 (buster)
・Kernelバージョン：Linux raspberrypi 4.19.97-v7+
・Python 3.7.3
・Git Version 2.20.1

WEBアプリケーション環境の構築

Djangoで「Hello World...」を表示するWEBアプリを作成します。
WEBアプリが完成したら、Herokuにリリースします。

1. django-toolbeltのインストール

django-toolbeltをインストールします。
django-toolbeltとはPyPIで提供されるライブラリで、Herokuで実行に必要な機能の一式がまとめられたパッケージです。pip installでインストールします。

django-toolbeltの詳細
https://pypi.org/project/django-toolbelt/

以下のコマンドを実行します。

pip install django-toolbelt

以下のように表示されたらOKです。
インストールされたソフトウェア名が表示されます。

2. Djangoプロジェクトの作成

Djangoプロジェクトを作成します。作成手順は一般的なDjangoの手順と同じです。
今回は以下の手順で進めました。

(1)django-adminコマンドのパスを設定
　export PATH=~/.local/bin:$PATH
(2)django-adminコマンドを実行
　django-admin startproject herokutest
　プロジェクトフォルダ「herokutest」が作成されます。
(3)settings.pyの編集
　settinigs.pyの以下の部分を修正します。
　(ファイルの場所：[プロジェクトフォルダ]/herokutest/settings.py)
settings.py
ALLOWED_HOSTS = ['*']
LANGUAGE_CODE = 'ja'
TIME_ZONE = 'Asia/Tokyo'
(4)helloアプリケーションの作成
　(作成したプロジェクトフォルダheroku内で実行)
　python manage.py startapp hello
(5)views.pyの編集
　views.pyを以下のように設定します。
　(ファイルの場所：作成されたhelloフォルダ内)
views.py
from django.shortcuts import render
from django.http import HttpResponse

def index(request):
    return HttpResponse('Hello World Heroku Test!')
(6)urls.pyの編集
　urls.pyを以下のように設定します。
　(ファイルの場所：[プロジェクトフォルダ]/herokutest/urls.py)
urls.py
from django.contrib import admin
from django.urls import path
import hello.views as hello

urlpatterns = [
    path('admin/', admin.site.urls),
    path('hello/', hello.index),
]
(7)画面表示の確認
　以下のコマンドを実行し、ブラウザでローカル環境にアクセスし、画面の表示を確認します。(コマンドは[プロジェクトフォルダ]直下で実行)
　python manage.py runserver
　ローカル環境：localhost:8000/hello/

　画面表示結果↓

WEBアプリケーション環境の構築は以上です。

Herokuアカウントの登録

Herokuサイトで新規にアカウント登録を行います。
メールアドレスとパスワードを入力し、アカウント登録を行って下さい。
ここでは手順を省略します。

Heroku CLIのインストール

Herokuコマンドを使用するにあたり、Heroku CLIをインストールします。
以下のサイトからダウンロードします。

https://devcenter.heroku.com/articles/heroku-cli

Raspberry PIでは、下図の赤線部のLinux(arm)からダウンロードを行います。

↓

ダウンロード後、解凍しbinフォルダにパスを通しておきます。

Herokuのログイン

以下のコマンドでHerokuへログインを行います。
heroku login
ブラウザが開き、ログインボタンが表示されますので、ログインを行って下さい。
以下の画面となればログイン成功です。

SSH鍵の作成

ここでは、Heroku用に個別に使用する目的で、他の鍵と区別した新たなSSH鍵を作成する手順を確認します。
作成するSSH鍵の場所を~/herokukeys/とします。

以下の手順でSSH鍵を作成します。

(1) SSH鍵を格納するフォルダを作成します。
　mkdir ~/herokukeys
(2) SSH鍵ペアを作成します。
　ssh-keygen -f ~/herokukeys/id_rsa
　herokukeysフォルダ内に秘密鍵(id_rsa)と公開鍵(id_rsa.pub)が作成されます。
(3) SSH鍵作成時にパスフレーズを設定した場合、接続の際に入力を求められますので、これを省略するために以下のコマンドを実行しておきます。
　ssh-add ~/herokukeys/id_rsa
(4) 作成したSSH公開鍵を登録します。
　heroku keys:add ~/herokukeys/id_rsa.pub
(5) Herokuサイトにおいて個別に作成したSSH鍵を使用するように以下の設定を実行しておきます。
　設定対象ファイル：~/.ssh/config
~/.ssh/config
Host heroku
  HostName heroku.com
  User git
  IdentityFile /home/pi/herokukeys/id_rsa
Herokuにデプロイする際の必要な設定

HerokuにWEBアプリケーションをデプロイ(リリース)するためにいくつかの設定が必要となります。

1. Procfileファイルを作成する

HerokuがWeb用のDynoであるWeb Dynoを実行するように、以下のコマンドでProcfileを作成します。
作成する場所は、[プロジェクトフォルダ]直下です。

echo "web: gunicorn herokutest.wsgi --log-file -" > Procfile

2. runtime.txtファイルを作成する

実行するPythonのバージョンを記載します。
以下のようにpythonの文字は小文字で、ハイフンも付加して記載します。
作成する場所は、[プロジェクトフォルダ]直下です。

echo "python-3.7.3" > runtime.txt

3. requirements.txtファイルを作成する

Pythonの実行に必要なライブラリを定義するファイルです。
Herokuはこの内容を見て必要なライブラリのインストールを行います。
作成する場所は、[プロジェクトフォルダ]直下です。

今回は内容を以下としました。
requirements.txt
asgiref==3.2.10
dj-database-url==0.5.0
dj-static==0.0.6
Django==3.1.2
django-toolbelt==0.0.1
gunicorn==20.0.4
psycopg2==2.8.6
pytz==2020.1
sqlparse==0.4.1
static3==0.7.0
requirements.txtの作り方のコツ
requirements.txtファイルは以下のコマンドで作成できます。
pip freeze > requirements.txt
上記ファイルは、このコマンドを実行後、必要なもののみを抽出しました。

WEBアプリケーションのGit化

1. Gitの初期設定

Gitの初期設定を行っておきます。
user.emailはHerokuに登録したメールアドレスとして下さい。
git config --global user.email "メールアドレス"
git config --global user.name "ユーザ名"
2. ソースのコミット

(1) Gitリポジトリを初期化します。
　[プロジェクトフォルダ]直下で実行します。
　git init
(2) ソースのコミットを行います。
　git add .
　git commit -m "(コミットコメントを設定)"
　コミットされたソースの一覧が画面に表示されればOKです。

Herokuへのデプロイ(リリース)

1. アプリケーションの作成

以下のコマンドでHeroku上にアプリケーションを作成します。
[プロジェクトフォルダ]直下で実行します。
heroku create

Herokuでは、アプリケーション名が自動的に付与されます。
リリースが成功した後は、WEBアプリケーションにアクセスするには、付与されたURLにアクセスします(有料版ではさらに独自ドメインを取得しこれに代えることができます)。

上記では、アプリケーション名としてmysterious-citadel-41347が付与されました。

2. デプロイ(リリース)の実行

事前にデプロイにあたり、Djangoソースの調整を行います。
今回はStatic Assets(静的コンテンツファイル)を使用していないことを設定する必要があります。
以下のコマンドを実行します。
heroku config:set DISABLE_COLLECTSTATIC=1

以下のコマンドでデプロイ(リリース)の実行を実行します。
git push heroku master

3. 画面表示の確認

エラーなくデプロイが成功したら、画面確認を行います。

"heroku open"コマンドでWEBアプリケーションを起動することができますが、今回はURL末尾にhello/を付加する必要があるため、ブラウザに直接URLを入力して確認を行います。

URL：https://(アプリケーション名).herokuapp.com/hello/

画面表示結果

ブラウザでは上記のように表示され、無事「Hello World Heroku Test!」の表示確認ができました。

関連情報

django-toolbeltの詳細
https://pypi.org/project/django-toolbelt/

Heorkuの本サイト
https://jp.heroku.com/

ご意見など

ご意見、間違い訂正などございましたらお寄せ下さい。

　 Tweet
Qiitaで続きを読む

投稿日：2020-10-19T13:17:57+09:00

WindowsサーバのIISでDjangoを動作させる方法

以下は本手順は割愛

IISのインストール

IISの基本設定

Pythonのインストール

Djangoの基本設定

仮想環境の作成

対象のディレクトリに移動して以下を実行
python -m venv venv
Djandoとwfastcgiをインストール

まずはvenvを有効化しておく
venv\Scripts\activate.bat
IISでDjangoを使用する場合、wfastcgiが必要なので合わせてインストール。
(venv)> pip install django
(venv)> pip install wfastcgi
wfastcgiの有効化
(venv)> venv\Scripts\wfastcgi-enable.exe
以下のように出ればOK
構成変更を構成コミット パス "MACHINE/WEBROOT/APPHOST" の "MACHINE/WEBROOT/APPHOST" のセクション "system.webServer/fastCgi" に適用しました
"d:\webroot\venv\scripts\python.exe|d:\webroot\venv\lib\site-packages\wfastcgi.py" can now be used as a FastCGI script processor
出力されたは後で使います。
d:\webroot\venv\scripts\python.exe|d:\webroot\venv\lib\site-packages\wfastcgi.py

system.webServer/handlers のアンロック
(venv)> %windir%\system32\inetsrv\appcmd unlock config -section:system.webServer/handlers
以下のように出ればOK
構成パス "MACHINE/WEBROOT/APPHOST" のセクション "system.webServer/handlers" のロックを解除しました。
ハンドラーマッピングでPythonファイルを実行できるようにする。

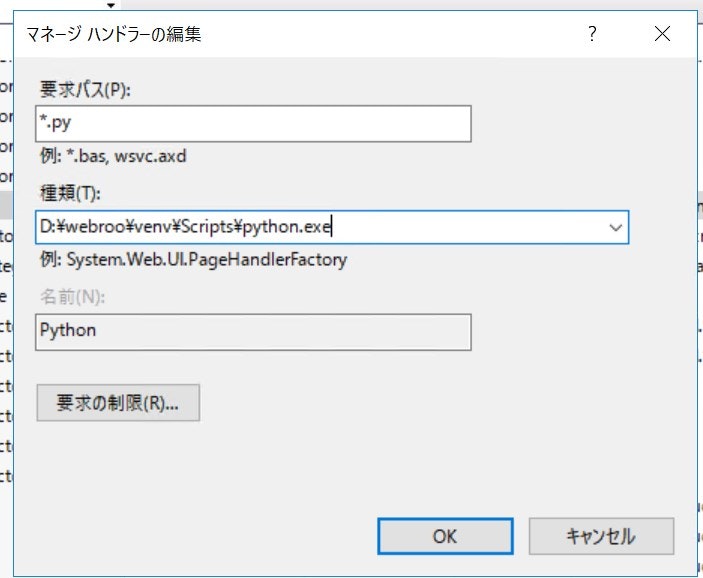
[サイト] -> [ハンドラーマッピング] で以下のように設定

scriptProcessorはwfastcgi-enable.exeで取得した結果を使うこと。

web.configの作成

以下のファイルを作成し、Djangoのルートディレクトリに配置。
web.config
<?xml version="1.0" encoding="UTF-8"?>
<configuration>
    <appSettings>
        <add key="WSGI_HANDLER" value="django.core.wsgi.get_wsgi_application()" />
        <add key="PYTHONPATH" value="D:\webroot" />
        <add key="DJANGO_SETTINGS_MODULE" value="app.settings" />
    </appSettings>
    <system.webServer>
        <handlers>
            <add name="Python FastCGI"
                 path="*"
                 verb="*"
                 modules="FastCgiModule"
                 scriptProcessor="d:\webroot\venv\scripts\python.exe|d:\webroot\venv\lib\site-packages\wfastcgi.py"
                 resourceType="Unspecified" />
        </handlers>
    </system.webServer>
</configuration>
これで準備完了です。

　 Tweet
Qiitaで続きを読む

投稿日：2020-10-19T12:08:13+09:00

Machine Learning : Supervised - Decision Tree

目標

決定木を理解して、scikit-learn で試す。

理論

決定木は、分類に重要な特徴量に閾値を設定して木構造を構築することで分類を行います。

決定木は木構造の可視化により、どの特徴量が分類に重要か、どの程度の閾値を境にどちらに分類されるかを知ることのできる意味解釈性の高い分類モデルであり、多クラス分類や回帰にも使用できます。

決定木による分類

決定木のアルゴリズムにはいくつか種類がありますが、ここでは scikit-learn で採用されている CART アルゴリズムに従います。

決定木の概念

木構造では下図のように木の開始を根ノード、木の終端を葉ノードと呼びます。また各ノードにおいて、1つ上のノードは親ノード、1つ下のノードは子ノードと呼びます。

CART では根ノードから始めて、情報利得が最大となる特徴量で閾値を決めて分割します。これを葉ノードが純粋になる、つまり葉ノードに含まれるカテゴリーがすべて同じになるまで分割していきます。

ただし、葉ノードが純粋になるまで分割すると過学習になってしまうため、剪定を行うことでこれを緩和します。

決定木の学習

決定木の学習は、下の式の情報利得 $IG$ を最大にすることによって行われます。
IG(D_{parent}, f) = I(D_{parent}) - \frac{N_{left}}{N_{parent}} I(D_{left}) - \frac{N_{right}}{N_{parent}} I(D_{right})
ここで、$f$ は分割を行う特徴量、$D_{parent}$ は親ノードに含まれるのデータ、$D_{left}, D_{right}$ は左右の子ノードのデータ、$N_{parent}$ は親ノードのデータ数、$N_{left}, N_{right}$ は左右の子ノードのデータ数、そして $I$ は後述の不純度を表します。

訓練時は各特徴量において左右の子ノードの不純度が小さくなるほど情報利得が大きくなり、その特徴量の設定された閾値に基づいて分割されることになります。

不純度の評価に用いられる指標としては、以下の 3つが代表的です。ここで、$C_i (i=1, 2, .., K)$ は $K$ 個のカテゴリー、$t$ はノード、$P(C_i | t)$ はあるノードにおいてそのカテゴリーのデータが選ばれる確率を表します。

分類誤差 $I_E$ はノードの変化に敏感ではないので、後述の木の剪定に使用されます。
I_E = 1 - \max_i P(C_i | t)
エントロピー $I_H$ はノードに含まれるデータがすべて同じカテゴリーに属しているとき 0 になります。
I_H = -\sum^K_{i=1} P(C_i | t) \ln P(C_i | t)
ジニ $I_G$ は誤分類の確率を最小化する指標と解釈でき、エントロピーと同様にノードに含まれるデータがすべて同じカテゴリーに属しているとき 0 になります。
I_G = 1 - \sum^K_{i=1} P^2 (C_i | t)
それぞれ下図のような関数となっており、scikit-learn では gini がデフォルトになっています。

決定木の剪定

訓練時は葉ノードが純粋になるまで木を深くしていきますが、そのままでは過学習になってしまうので、これを緩和するために剪定を行います。

木の剪定のための評価基準として、訓練データを再度入力した際の再代入誤り率を定義します。あるノード $t$ における再代入誤り率 $R(t)$ は、分類誤差 $I_E$ とノード $t$ の周辺確率 $P(t)$ を用いて以下の式で表されます。
R(t) = \left( 1 - \max_i P(C_i | t) \right) \times P(t) \\
P(t) = \frac{N(t)}{N}
ここで、$N(t)$ はノード $t$ に含まれるデータ数、$N$ は訓練データの総数を表しています。

木の剪定ではこの再代入誤り率に基づいて木の分岐を除去していきます。scikit-learn では引数 max_leaf_nodes で必要なノード数まで剪定・確保することができます。

実装

実行環境

ハードウェア

・CPU Intel(R) Core(TM) i7-6700K 4.00GHz

ソフトウェア

・Windows 10 Pro 1909
・Python 3.6.6
・matplotlib 3.3.1
・numpy 1.19.2
・scikit-learn 0.23.2

実行するプログラム

実装したプログラムは GitHub で公開しています。
decision_tree_clf.py
decision_tree_reg.py
結果

決定木による分類

これまでに使用してきた breast cancer dataset に決定木を適用しました。なお、決定木では特徴量ごとに閾値を決めるので、前処理として特徴量の標準化を行う必要はありません。
Accuracy 97.37%
Precision, Positive predictive value(PPV) 97.06%
Recall, Sensitivity, True positive rate(TPR) 98.51%
Specificity, True negative rate(TNR) 95.74%
Negative predictive value(NPV) 97.83%
F-Score 97.78%
決定木の可視化と解釈性

scikit-learn には決定木を可視化する plot_tree 関数が用意されており、訓練後のモデルの木構造を簡単に見ることができます。

また、以下のように訓練後のモデルの各ノードにおける判断の基準をコマンドラインに表示することもできます。
The binary tree structure has 9 nodes and has the following tree structure:
node=0 test node: go to node 1 if X[:, 27] <= 0.1423499956727028 else to node 2.
    node=1 test node: go to node 3 if X[:, 23] <= 957.4500122070312 else to node 4.
    node=2 test node: go to node 5 if X[:, 23] <= 729.5499877929688 else to node 6.
        node=3 leaf node.
        node=4 leaf node.
        node=5 test node: go to node 7 if X[:, 4] <= 0.10830000042915344 else to node 8.
        node=6 leaf node.
            node=7 leaf node.
            node=8 leaf node.

Rules used to predict sample 0: 
decision id node 0 : (X_test[0, 27] (= 0.2051) > 0.1423499956727028)
decision id node 2 : (X_test[0, 23] (= 844.4) > 729.5499877929688)

The following samples [0, 1] share the node [0] in the tree
It is 11.11%% of all nodes.
下図は、iris dataset に対して多クラス分類を実行した際の識別境界を表しています。

決定木による回帰

回帰問題のデータは正弦波に乱数を加えました。木を深くすることで表現力が向上することが見て取れます。

下図は多出力の回帰問題に適用した例です。

参考

1.10. Decision Tree

平井有三．『はじめてのパターン認識』，森北出版，2012．

　 Tweet
Qiitaで続きを読む

投稿日：2020-10-19T11:55:00+09:00

CNN高速化シリーズ ~FCNN: Fourier Convolutional Neural Networkの導入~

概要

畳み込みニューラルネットワーク(CNN)の登場により画像認識の分野は大きく進展しました。
AlexNetから始まりVGGNetやGoogLeNetなどの様々なネットワークが提案されその効果を示してきました。
そんなCNNですが、畳み込み演算の処理が重いため非常に時間がかかってしまうことが難点として挙げられます。その重さは全結合層を完全に無視できてしまうほどで、畳み込み処理を高速化することができれば学習時間を大幅に削減することが可能となります。
そこで注目されているのが空間領域での畳み込み=周波数空間での要素積という関係です。
本記事では周波数領域で畳み込みを行う上での基礎理論について説明します。
日本語の記事はほとんど見当たらなかったので論文から頑張って読み解いています。間違いや勘違いなど散見されるかもしれませんのでぜひご指摘ください。

本記事で取り扱う論文は

Fast Training of Convolutional Networks through FFTs; Michael Mathieu, Mikael Henaff, Yann LeCun; arXiv:1312.5851v5 [cs.CV] 6 Mar 2014

です。

目次

畳み込みとは

線形畳み込み

循環畳み込み

線形畳み込みと循環畳み込みを等しくする方法

CNNでの畳み込み

周波数領域へ

2.2 アルゴリズム

2.3 実装と空間計算量

3 実験

4 今後について

実装してみる?

付録

厳密な畳み込みとCNN

Cooley-Turkey FFTアルゴリズム

畳み込みとは

周波数領域での畳み込みを正しく理解するためにも、まずは空間領域での畳み込みというものについて改めて考えてみます。
畳み込み処理には2種類あり、それぞれ線形畳み込み(直線畳み込み)と循環畳み込み(巡回畳み込み)と呼ばれています。まずはこの二つについて説明します。

以降使用する変数を先に紹介しておきます。

$I \cdots$入力サイズ

$F \cdots$フィルタサイズ

$O \cdots$出力サイズ

線形畳み込み

線形畳み込みは下図のように表される畳み込み処理のことです。

このように、フィルタの右端と入力の左端とが重なる地点からスタートし、通り抜けたら終了するような感じです。
数学的な式は別に不要なので載せませんが、こういう動作をしていることは理解しておいてください。
そして、この線形畳み込みは入力が周期関数ではないことに注意してください。

また、サイズについては次のような関係式が成り立ちます。
O = I + F - 1
GIFでは$I = 9$及び$F = 3$ですので、出力サイズは$O = 9 + 3 - 1 = 11$となります。

循環畳み込み

循環畳み込みは下図のように表される畳み込み処理のことです。

こちらはフィルタの左端と入力の左端とが重なる地点からスタートし、フィルタの右端と入力の右端が重なったら終了するような感じですね。
線形畳み込みとの違いはまさにこれで、この場合入力は周期関数である必要があります。
線形畳み込みのGIFで表されている両端それぞれ2つ分は入力が周期関数であるから必要ない、みたいな理解で良いと思います(厳密には異なると思いますが厳密さは特に求めていないので)。

また、サイズについては以下の関係式が成り立ちます。
O = I - F + 1
GIFでは$I = 9$及び$F = 3$ですので、出力サイズは$O = 9 - 3 + 1 = 7$となります。

線形畳み込みと循環畳み込みを等しくする方法

線形畳み込みと循環畳み込みを等しくするためには、入力の両端に$O = I + F - 1$になるようにゼロパディングを施す必要があります。

出力結果が線形畳み込みと等しくなっていることが確認できますね。

CNNでの畳み込み

さて、CNNでの畳み込み演算はどちらに当てはまるのでしょうか？入力の観点から考えてみます。

CNNに入力されるデータは通常画像であり、その画像とは写真であることが大多数でしょう。よって、パターン模様の画像認識をするのではない場合画像は周期性を持たないことが予想できます。
ということは、入力が非周期的であるためCNNは線形畳み込みを行う必要がありますね。

しかし、まだこれを結論とするには早いです。下図を御覧ください。

こちらはCNNの畳み込みの様子を表しています。ご覧の通り、フィルタは入力画像を通り過ぎたりしていませんので、この図では循環畳み込みを行っていることになります。これではせっかくの畳み込み演算から正しく情報を得ることができていないことになります。
ただし、入力画像が上下左右に($F - 1$だけ重なって)周期的に配置されていると仮定すればこの畳み込みを正しいと見做すことはできます。

「結局どっちなんだ」と言いたいですがまだ考えることがあります。それはCNNに必須の技術であるパディングです。

この図だと数が足りませんが、必要数だけパディングを施せば循環畳み込みは線形畳み込みに等しくすることができるんでしたね。すると、パディングという処理を入力画像に正しく施せば線形畳み込みをすることができ、畳み込み演算から正しく情報を得ることができるというわけです。
以前書いた記事でパディングの役目を「サイズ維持」と「端の情報を余さず得る」としていますが、これはそういうことです。(執筆当時はそんなこと露ほども考えてませんでしたが笑)

さて、このパディングという処理のせいで一層議論がややこしくなります。CNNでの畳み込み特有のストライドも考慮するとより一層...
このパディング、CNNでの畳み込みによる出力画像のサイズ減衰を防ぐ(あるいは軽減する)ために用いられることが多いです。よって、パディング幅はストライドに依存して増減するので、循環畳み込みを線形畳み込みにしたいとは全く考えていないわけです。
するとパディング幅に過不足が生じます。パディング幅が多い分には問題ないのですが、少ない場合は正しく循環畳み込み$\rightarrow$線形畳み込みへの変換が行われなくなることになります。

結局のところ、結論としては「CNNでの畳み込みは線形/循環畳み込みの中間」といったところでしょうか。
「これだけ引っ張っておいて結論が曖昧かよ」とつっこみたいですが、まあそうとしか言えないので仕方ないでしょう。
理論的に厳密な議論をするとなると、実は前提から異なりますしね。

ここまでが前提になります。ここからいよいよ周波数領域での理論に移ります。
ちなみに「数学的な厳密さは？」と思った方は付録の方をご覧ください。

周波数領域へ

さて、ここまでの話はぼくが論文を読んでいる中で必要かなと感じてあちこちで調べた結果を要約したものです。まだまだ甘いですが、まあこれぐらいの話が頭に入っていれば大丈夫だと思います。
それではいよいよ論文の内容に入ります。論文2.1のBackpropagationは空間領域でのCNNと周波数領域でのCNNとを比較する部分を述べているだけなのでカットして、2.2から読んでいきます。
ちなみに論文の和訳ではなく意訳や追記をしています。なお、この節の図は論文から引用させていただいています。

2.2 アルゴリズム

空間領域での畳み込み演算はフーリエ(周波数)領域での要素積と等価であることはよく知られています。そのため、空間領域での畳み込み演算はフーリエ変換器$\mathcal{F}$とその逆演算$\mathcal{F}^{-1}$を用いて
f * g = \mathcal{F}^{-1}\big(\mathcal{F}_f(k) \odot \mathcal{F}_g(k)\big)
と表すことができます。ただし、記号$ * $は空間領域での畳み込み演算を、記号$\otimes$は行列演算における要素積を表します。
注意しなければならないのは、上式の演算を行うには要素積の性質上$f,g$が近しいサイズ(というより等しいサイズ)である必要があるということです。
しかし一般に入力(サイズ$I_h \times I_w$)とフィルタ(サイズ$F_h \times F_w$)とは全く異なるサイズになっています。そのため、実装する際は入力やフィルタのサイズを揃えるようにパディングが必要になります。(トリミングすることもあるかもしれません)

議論の簡単のために、$I_h = I_w = I$および$F_h = F_w = F$とします。また、出力のサイズは$O_h \times O_w$とし、これも$O_h = O_w = O$と表すことにします。また、入力のチャンネル数を$C$、フィルタの枚数を$M$、ミニバッチのサイズを$B$としておきます。
空間領域での畳み込み演算の計算量はパディングなし、ストライド$1$だと
O^2 F^2 \quad (\because O = I - F + 1)
となります。パディング幅$2p$、ストライド$s$とすると
O^2 F^2 \quad \left(\because O = \left\lceil \cfrac{I - F + 2p}{s} \right\rceil + 1 \right)
ですね。

一方、フーリエ領域での計算量はフーリエ変換を高速フーリエ変換(FFT: Fast Fourier Transformation)で行った場合$$2C_{order}O^2 \log{O}$$で、要素積の計算量は、複素数演算であることに注意すると$$4O^2$$と表されます。$C_{order}$は定数です。
よって、その和の$$2C_{order}O^2 \log{O} + 4O^2$$がフーリエ領域での畳み込み演算の計算量ということになります。
論文では$O = I$としているみたいです。

各入力チャンネルやフィルタは独立しているため、それぞれに1度フーリエ変換を施すだけで済みます。特定の畳み込みに関しては学習効率が低下する可能性はありますが、FFTを効果的に再利用することが可能なため、効率低下によるオーバーヘッドを補う以上の恩恵を得ることができます。

順伝播や逆伝播について計算量を求めると、フーリエ領域での畳み込み演算の優位性がより明白になります。

空間領域フーリエ領域

$\displaystyle\sum_{C}{x_C * F_{CM}}$ $BCMO^2F^2$ $2C_{order}I^2(BM + BC + CM)\log{I} + 4BCMI^2$

$\cfrac{\partial L}{\partial y_M} * w^{\top}_{CM} $ $BCMI^2F^2$ $2C_{order}O^2(BM + BC + CM)\log{O} + 4BCMO^2$

$\cfrac{\partial L}{\partial y_M} * x_C$ $BCMO^2F^2$ $2C_{order}I^2(BM + BC + CM)\log{I} + 4BCMI^2$

注意すべきは、ここでの$O$は空間領域・周波数領域両方とも$$O = I - F + 1$$または$$O = \left\lceil \cfrac{I - F + 2p}{s} \right\rceil + 1 $$で計算されるものである、ということです。特にフーリエ領域においては先の議論と異なっていることに注意してください。
おそらく計算量の比較を正しく行うために揃えたのだと思われます。

この表から読み取れることとして、空間領域での計算量は5つの項の積で表されているのに対してフーリエ領域での計算量は最大4つの項の積で表されている、ということです。
ざっくりいうと空間領域では計算量のオーダが5次(より正確には7次)、フーリエ領域では4次(より正確には5次)である、というわけです。

これがどれくらいの効果を生むのか実際に順伝播について計算して確かめてみましょう。
B = 128 \quad C = 96 \\
M = 256 \quad F = 7
として、$I = 16, 64$の二つを計算してみると、$O = I - F + 1 = 10, 58$であるから、空間領域について
BCMO^2F^2 = 128 \times 96 \times 256 \times 10^2 \times 7^2 = 15,414,067,200 \simeq 154億 \\
BCMO^2F^2 = 128 \times 96 \times 256 \times 58^2 \times 7^2 = 518,529,220,608 \simeq 5185億
フーリエ領域について
2C_{order}I^2(BM + BC + CM)\log{I} + 4BCMI^2 = 2 \times 16 \times 16^2 \times (128 \times 256 + 128 \times 96 + 96 \times 256) \log{16} + 4 \times 128 \times 96 \times 256 \times 16^2 = 1,581,554,875.654148 + 3,221,225,472 = 4,802,780,347.654148 \simeq 48億 \\
2C_{order}I^2(BM + BC + CM)\log{I} + 4BCMI^2 = 2 \times 16 \times 64^2 \times (128 \times 256 + 128 \times 96 + 96 \times 256) \log{64} + 4 \times 128 \times 96 \times 256 \times 64^2 = 37,957,317,015.69955 + 51,539,607,552 = 89,496,924,567.69955 \simeq 895億
※論文中に$C_{order}$をいくらとして計算したかが載っていないので、グラフと概ね一致する$C_{order} = 16$を採用しました。

という感じで、入力のサイズが大きくなるにつれてどんどん差が広がっていきます。

2.3 実装と空間計算量

アルゴリズムとしては非常に単純なフーリエ領域での畳み込み演算ですが、実装に際して大きく2つの問題点が存在します。

現行のGPU、主にNVIDIA製のGPUに対応するCUDAで実装されているFFTは大きな入力で限られた数だけFFTするのに最適化されているため、本アルゴリズムにおいては最適ではない

フーリエ変換されたフィルタを保持するために多量のメモリ領域(空間計算量)が必要となる

それぞれの問題に対しては以下のような最適化・対応策が提案されています。

Cooley-Turkey FFTアルゴリズムを実装

ミニバッチ・チャンネル方向に並列化可能に

もともと2次元FFTは行方向と列方向に並列化可能

以上から本アルゴリズムでの小規模かつ大量の入力を効率的かつ高速にフーリエ変換できる

各畳み込みで使用するメモリを使い回す(上書きする)ことで省メモリ化。また、実数値入力のフーリエ変換が対称行列となることを利用して、下三角行列(または上三角行列)のみ保持する

メモリを使い回すため、逆伝播の計算の際に再FFTが必要になる

三角行列で保持することで保持すべきメモリ量は$X^2 \Rightarrow \frac{X(X + 1)}{2}$に

これで理論面は終了です。あとは実験結果とかですね。
もうちょっと具体的にどういう演算で計算が進んでいるのか載せて欲しかったです...実装しようとした段階でいくつか疑問点も出てきましたし...まあその辺りは通常のCNNと似た動作をするようにすればいいんでしょうが。

3 実験

実験はCUDAConv GPU実装とTorch7機械学習環境を比較対象として、NVIDIA製のGeForce GTX TitanGPUを使用して行われました。
実験で得られた精度は載せられていませんが、許容誤差範囲内の差しかなかったようです。

あるCNNの、入力チャンネル数$C = 96$、出力チャンネル数(つまりフィルタ枚数)$M = 256$である第2層に注目して、そのレイヤのフィルタサイズ・入力サイズ・ミニバッチサイズを変更した実験結果は下図の通りとなっています。

ほとんどの場合でフーリエ領域での畳み込み演算が高速に動作していることが示されています。特に時間計算量が大きい$$\cfrac{\partial L}{\partial y_M} * x_C $$においてより顕著な優位性が認められます。
これは、フィルタサイズが大きいものを利用しているためである可能性が高いと考えられています。
また、FFT適用前にフィルタは入力と同サイズまでパディングされるため、より大きなフィルタを利用しても良いということになります。

※この考察についてですが、現行のCNNの多くが小さなフィルタサイズを利用しているのは省メモリの観点からだったりします。
確かにFCNNの実装がこのままであればどうせ大量のメモリを消費するので、いっそのこと大きなフィルタを使うのはアリかもしれません。
ちなみにこのままの実装が用いられることは多分ありません。しっかり別の省メモリ技術が確立されています。
そちらについてはまた別の記事を書きます。

続いて、先ほどは第2層にのみ注目していたCNNについて、今度は第1層〜第5層までに注目して、ミニバッチサイズ$B$を変更して実験した結果を下図に示します。

なお、入力層の入力への勾配は計算する必要がないためデータが取られていません。
ほとんどの場合で最速か次点くらいの速度を誇っていることが読み取れます。また、トータルで見ると全て最速であるためFCNNがほぼ全ての場合で有効であることが言えます。
また、順伝播がかなり高速となっており、これは学習済みネットワークを用いて推論を行うときなどに最大限その恩恵を得られるということを示唆しています。

最後に、上記のCNNにプーリングレイヤと全結合層を追加した時の実験結果です。この実験はパディングやメモリへのアクセスなどの実装の詳細によってパフォーマンスが変化するかを確認するためのものです。

この実験においてもFCNNはその優位性を証明してみせました。

4 今後について

箇条書きにしておきます。

フーリエ領域内でフィルタを直接学習する方法を探る

フーリエ領域内で非線形関数を使用する方法を探る

これにより逆変換の必要がなくなり、より高速に

現在の実装では入力画像を2の累乗のサイズになるようにパディングする必要があるため、これを改良する

フィルタサイズを大きくしたときの影響を調べる

以上が論文の内容になります。シンプルながら強力なアルゴリズムですね〜
これ以降様々な研究がされているようです。

実装してみる?

実装してみたい...のですが、いくつか疑問があります。

畳み込み演算の前後でFFT・IFFTする必要がある？

論文の模式図では入力チャンネル数と出力チャンネル数が揃っているが、空間領域での畳み込み層の出力チャンネル数はフィルタの枚数に依存しているはず

また、チャンネル数をどちらに合わせるにせよ、どうやってその次元に揃えるかが問題

それぞれ論文の中で明記されてない...はずですが、微妙に読み取れたりもするんですよね〜
例えば4 今後についてで

フーリエ領域内でフィルタを直接学習する方法を探る

フーリエ領域内で非線形関数を使用する方法を探る

これにより逆変換の必要がなくなり、より高速に

みたいなことを言っているので、行列積演算の前後でのみFFT/IFFTしてるっぽいとか、実験の最後の表でチャンネル数がCNNと同じように変化しているとか、直接書いてはいないけど多分そうだと思える記述が見受けられます。

あと、後発論文とかいくつか探して読んでみたりしていますが、そっちではFFTを最初の1回で済ませて、全てフーリエ領域で実行する手段についての記述も見受けられましたので、その辺りも含めてまだまだ勉強不足のため今回は実装を見送ります。フーリエ変換についてもまだ理解不足感が否めませんしね〜

付録

おまけとして数学的なことを載せておきます。

厳密な畳み込みとCNN

次のような入力行列$\boldsymbol{A}$とフィルタ行列$\boldsymbol{W}$の畳み込みを考えます。ただし、パディングなし、ストライド$1$とします。
※以降の行列要素のインデックスとか間違ってたらごめんなさい
\boldsymbol{A} = \left( \begin{array}[ccc]
  aa_{1, 1} & a_{1, 2} & a_{1, 3} & a_{1, 4} \\
  a_{2, 1} & a_{2, 2} & a_{2, 3} & a_{2, 4} \\
  a_{3, 1} & a_{3, 2} & a_{3, 3} & a_{3, 4} \\
  a_{4, 1} & a_{4, 2} & a_{4, 3} & a_{4, 4}
\end{array} \right) \qquad
\boldsymbol{W} = \left( \begin{array}[ccc]
  ww_{1, 1} & w_{1, 2} \\
  w_{2, 1} & w_{2, 2} \\
\end{array} \right)
これの畳み込み結果は次のようになります。
\begin{align}
  \boldsymbol{AW} &= \left( \begin{array}[ccc]
    aa_{1, 1}w_{1, 1} + a_{1, 2}w_{1, 2} + a_{2, 1}w_{2, 1} + a_{2, 2}w_{2, 2}
  & a_{1, 2}w_{1, 1} + a_{1, 3}w_{1, 2} + a_{2, 2}w_{2, 1} + a_{2, 3}w_{2, 2}
  & a_{1, 3}w_{1, 1} + a_{1, 4}w_{1, 2} +   a_{2, 3}w_{2, 1} + a_{2, 4}w_{2, 2} \\
    a_{2, 1}w_{1, 1} + a_{2, 2}w_{1, 2} + a_{3, 1}w_{2, 1} + a_{3, 2}w_{2, 2}
  & a_{2, 2}w_{1, 1} + a_{2, 3}w_{1, 2} + a_{3, 2}w_{2, 1} + a_{2, 3}w_{2, 2}
  & a_{2, 3}w_{1, 1} + a_{2, 4}w_{1, 2} + a_{3, 3}w_{2, 1} + a_{2, 4}w_{2, 2} \\
    a_{3, 1}w_{1, 1} + a_{3, 2}w_{1, 2} + a_{4, 1}w_{2, 1} + a_{4, 2}w_{2, 2}
  & a_{3, 2}w_{1, 1} + a_{3, 3}w_{1, 2} + a_{4, 2}w_{2, 1} + a_{4, 3}w_{2, 2}
  & a_{3, 3}w_{1, 1} + a_{3, 4}w_{1, 2} + a_{4, 3}w_{2, 1} + a_{4, 4}w_{2, 2}
  \end{array} \right) \\
  &= \left( \begin{array}[ccc]
    s\displaystyle\sum_{k=1}^{2}{\displaystyle\sum_{l=1}^{2}{a_{k, l}w_{k, l}}}
  & \displaystyle\sum_{k=1}^{2}{\displaystyle\sum_{l=1}^{2}{a_{k, l+1}w_{k, l}}}
  & \displaystyle\sum_{k=1}^{2}{\displaystyle\sum_{l=1}^{2}{a_{k, l+2}w_{k, l}}} \\
    \displaystyle\sum_{k=1}^{2}{\displaystyle\sum_{l=1}^{2}{a_{k+1, l}w_{k, l}}} 
  & \displaystyle\sum_{k=1}^{2}{\displaystyle\sum_{l=1}^{2}{a_{k+1, l+1}w_{k, l}}}
  & \displaystyle\sum_{k=1}^{2}{\displaystyle\sum_{l=1}^{2}{a_{k+1, l+2}w_{k, l}}} \\
    \displaystyle\sum_{k=1}^{2}{\displaystyle\sum_{l=1}^{2}{a_{k+2, l}w_{k, l}}}
  & \displaystyle\sum_{k=1}^{2}{\displaystyle\sum_{l=1}^{2}{a_{k+2, l+1}w_{k, l}}}
  & \displaystyle\sum_{k=1}^{2}{\displaystyle\sum_{l=1}^{2}{a_{k+2, l+2}w_{k, l}}}
  \end{array} \right)
\end{align}
規則性が見えると思います。では一般化してみましょう。
フィルタサイズを$F_h \times F_w$としたとき、出力の$(i, j)$成分$o_{i, j}$は
o_{i, j} = \displaystyle\sum_{k=1}^{F_h}{\displaystyle\sum_{l=1}^{F_w}{a_{i+k-1, j+l-1}w_{k, l}}}
と書くことができます。後々のために添え字の足し算の順序を変えていますので注意してください。

これがCNNでの畳み込み演算となります。循環畳み込みですね。
ところで、数学的には2次元離散畳み込み演算は次式で表されます。
(g * f)_{i, j} = o_{i, j} = \displaystyle\sum_{k}{\displaystyle\sum_{l}{f_{i-k+1, j-l+1}g_{k, l}}}
なんとなく$f$を入力、$g$をフィルタと見做して、一般的な式とは逆順にしてあります。また、$k, l$はインデックスが有効になる全ての値を取ります。
この時点で「あれ？」と思った方は鋭いです。
これは行列で書くと(サイズはそれぞれCNNの時に揃えます)
\begin{align}
  \boldsymbol{g*f} &=　\left( \begin{array}[ccc]
    s\displaystyle\sum_{k}{\displaystyle\sum_{l}{f_{2-k, 2-l}g_{k, l}}}
  & \displaystyle\sum_{k}{\displaystyle\sum_{l}{f_{2-k, 3-l}g_{k, l}}}
  & \displaystyle\sum_{k}{\displaystyle\sum_{l}{f_{2-k, 4-l}g_{k, l}}} 
  & \displaystyle\sum_{k}{\displaystyle\sum_{l}{f_{2-k, 5-l}g_{k, l}}} 
  & \displaystyle\sum_{k}{\displaystyle\sum_{l}{f_{2-k, 6-l}g_{k, l}}} \\
    \displaystyle\sum_{k}{\displaystyle\sum_{l}{f_{3-k, 2-l}g_{k, l}}}
  & \displaystyle\sum_{k}{\displaystyle\sum_{l}{f_{3-k, 3-l}g_{k, l}}}
  & \displaystyle\sum_{k}{\displaystyle\sum_{l}{f_{3-k, 4-l}g_{k, l}}} 
  & \displaystyle\sum_{k}{\displaystyle\sum_{l}{f_{3-k, 5-l}g_{k, l}}} 
  & \displaystyle\sum_{k}{\displaystyle\sum_{l}{f_{3-k, 6-l}g_{k, l}}} \\
  \displaystyle\sum_{k}{\displaystyle\sum_{l}{f_{4-k, 2-l}g_{k, l}}}
  & \displaystyle\sum_{k}{\displaystyle\sum_{l}{f_{4-k, 3-l}g_{k, l}}}
  & \displaystyle\sum_{k}{\displaystyle\sum_{l}{f_{4-k, 4-l}g_{k, l}}} 
  & \displaystyle\sum_{k}{\displaystyle\sum_{l}{f_{4-k, 5-l}g_{k, l}}} 
  & \displaystyle\sum_{k}{\displaystyle\sum_{l}{f_{4-k, 6-l}g_{k, l}}} \\
  \displaystyle\sum_{k}{\displaystyle\sum_{l}{f_{5-k, 2-l}g_{k, l}}}
  & \displaystyle\sum_{k}{\displaystyle\sum_{l}{f_{5-k, 3-l}g_{k, l}}}
  & \displaystyle\sum_{k}{\displaystyle\sum_{l}{f_{5-k, 4-l}g_{k, l}}} 
  & \displaystyle\sum_{k}{\displaystyle\sum_{l}{f_{5-k, 5-l}g_{k, l}}} 
  & \displaystyle\sum_{k}{\displaystyle\sum_{l}{f_{5-k, 6-l}g_{k, l}}} \\
\displaystyle\sum_{k}{\displaystyle\sum_{l}{f_{6-k, 2-l}g_{k, l}}}
  & \displaystyle\sum_{k}{\displaystyle\sum_{l}{f_{6-k, 3-l}g_{k, l}}}
  & \displaystyle\sum_{k}{\displaystyle\sum_{l}{f_{6-k, 4-l}g_{k, l}}} 
  & \displaystyle\sum_{k}{\displaystyle\sum_{l}{f_{6-k, 5-l}g_{k, l}}} 
  & \displaystyle\sum_{k}{\displaystyle\sum_{l}{f_{6-k, 6-l}g_{k, l}}} \\
  \end{array} \right) \\
  &= \left( \begin{array}[ccccc]
    ff_{1, 1}g_{1, 1}
  & f_{1, 2}g_{1, 1} + f_{1, 1}g_{1, 2}
  & f_{1, 3}g_{1, 1} + f_{1, 2}g_{1, 2}
  & f_{1, 4}g_{1, 1} + f_{1, 3}g_{1, 2}
  & f_{1, 4}g_{1, 2} \\
    f_{2, 1}g_{1, 1} + f_{1, 1}g_{2, 1}
  & f_{2, 2}g_{1, 1} + f_{2, 1}g_{1, 2} + f_{1, 2}g_{2, 1} + f_{1, 1}g_{2, 2}
  & f_{2, 3}g_{1, 1} + f_{2, 2}g_{1, 2} + f_{1, 3}g_{2, 1} + f_{1, 2}g_{2, 2}
  & f_{2, 4}g_{1, 1} + f_{2, 3}g_{1, 2} + f_{1, 4}g_{2, 1} + f_{1, 3}g_{2, 2}
  & f_{2, 4}g_{1, 2} + f_{1, 4}g_{2, 2} \\
    f_{3, 1}g_{1, 1} + f_{2, 1}g_{2, 1}
  & f_{3, 2}g_{1, 1} + f_{3, 1}g_{1, 2} + f_{2, 2}g_{2, 1} + f_{2, 1}g_{2, 2}
  & f_{3, 3}g_{1, 1} + f_{3, 2}g_{1, 2} + f_{2, 3}g_{2, 1} + f_{2, 2}g_{2, 2}
  & f_{3, 4}g_{1, 1} + f_{3, 3}g_{1, 2} + f_{2, 4}g_{2, 1} + f_{2, 3}g_{2, 2}
  & f_{3, 4}g_{1, 2} + f_{2, 4}g_{2, 2} \\
    f_{4, 1}g_{1, 1} + f_{3, 1}g_{2, 1}
  & f_{4, 2}g_{1, 1} + f_{4, 1}g_{1, 2} + f_{3, 2}g_{2, 1} + f_{3, 1}g_{2, 2}
  & f_{4, 3}g_{1, 1} + f_{4, 2}g_{1, 2} + f_{3, 3}g_{2, 1} + f_{3, 2}g_{2, 2}
  & f_{4, 4}g_{1, 1} + f_{4, 3}g_{1, 2} + f_{3, 4}g_{2, 1} + f_{3, 3}g_{2, 2}
  & f_{4, 4}g_{1, 2} + f_{3, 4}g_{2, 2} \\
    f_{4, 1}g_{2, 1}
  & f_{4, 2}g_{2, 1} + f_{4, 1}g_{2, 2}
  & f_{4, 3}g_{2, 1} + f_{4, 2}g_{2, 2}
  & f_{4, 4}g_{2, 1} + f_{4, 3}g_{2, 2}
  & f_{4, 4}g_{2, 2}
  \end{array} \right) \\
\end{align}
となります。

こうしてみると一目瞭然ですが、CNNでの畳み込みと数学で定義されている畳み込みは異なります。この差異は循環畳み込みと線形畳み込みとの違い...と思ったら実は違います。
先に紹介した線形畳み込みと循環畳み込みを等しくする方法のようにパディングを施しても同じにはなりません。
実際に試してみます。
\boldsymbol{A} = \left( \begin{array}[cccccc]
  00 & 0 & 0 & 0 & 0 & 0 \\
  0& a_{1, 1} & a_{1, 2} & a_{1, 3} & a_{1, 4} & 0 \\
  0 & a_{2, 1} & a_{2, 2} & a_{2, 3} & a_{2, 4} & 0 \\
  0 & a_{3, 1} & a_{3, 2} & a_{3, 3} & a_{3, 4} & 0 \\
  0 & a_{4, 1} & a_{4, 2} & a_{4, 3} & a_{4, 4} & 0 \\
  0 & 0 & 0 & 0 & 0 & 0
\end{array} \right)
として、
\boldsymbol{AW} = \left( \begin{array}[ccccc]
    aa_{1, 1}w_{2, 2}
  & a_{1, 1}w_{2, 1} + a_{1, 2}w_{2, 2}
  & a_{1, 2}w_{2, 1} + a_{1, 3}w_{2, 2}
  & a_{1, 3}w_{2, 1} + a_{1, 4}w_{2, 2} 
  & a_{1, 4}w_{2, 1} \\
    a_{1, 1}w_{1, 2} + a_{2, 1}w_{2, 2}
  & a_{1, 1}w_{1, 1} + a_{1, 2}w_{1, 2} + a_{2, 1}w_{2, 1} + a_{2, 2}w_{2, 2}
  & a_{1, 2}w_{1, 1} + a_{1, 3}w_{1, 2} + a_{2, 2}w_{2, 1} + a_{2, 3}w_{2, 2}
  & a_{1, 3}w_{1, 1} + a_{1, 4}w_{1, 2} + a_{2, 3}w_{2, 1} + a_{2, 4}w_{2, 2}
  & a_{1, 4}w_{1, 1} + a_{2, 4}w_{2, 1} \\
    a_{2, 1}w_{1, 2} + a_{3, 1}w_{2, 2}
  & a_{2, 1}w_{1, 1} + a_{2, 2}w_{1, 2} + a_{3, 1}w_{2, 1} + a_{3, 2}w_{2, 2}
  & a_{2, 2}w_{1, 1} + a_{2, 3}w_{1, 2} + a_{3, 2}w_{2, 1} + a_{3, 3}w_{2, 2}
  & a_{2, 3}w_{1, 1} + a_{2, 4}w_{1, 2} + a_{3, 3}w_{2, 1} + a_{3, 4}w_{2, 2}
  & a_{2, 4}w_{1, 1} + a_{3, 4}w_{2, 1} \\
    a_{3, 1}w_{1, 2} + a_{4, 1}w_{2, 2}
  & a_{3, 1}w_{1, 1} + a_{3, 2}w_{1, 2} + a_{4, 1}w_{2, 1} + a_{4, 2}w_{2, 2}
  & a_{3, 2}w_{1, 1} + a_{3, 3}w_{1, 2} + a_{4, 2}w_{2, 1} + a_{4, 3}w_{2, 2}
  & a_{3, 3}w_{1, 1} + a_{3, 4}w_{1, 2} + a_{4, 3}w_{2, 1} + a_{4, 4}w_{2, 2}
  & a_{3, 4}w_{1, 1} + a_{4, 4}w_{2, 1} \\
    a_{4, 1}w_{1, 2}
  & a_{4, 1}w_{1, 1} + a_{4, 2}w_{1, 2}
  & a_{4, 2}w_{1, 1} + a_{4, 3}w_{1, 2}
  & a_{4, 3}w_{1, 1} + a_{4, 4}w_{1, 2}
  & a_{4, 4}w_{1, 1}
\end{array} \right)
となります。形状は一致しますし、各要素の足し算の数も一緒ですがインデックスが異なっていますね。
と、いうことはCNNの畳み込みは数学的に定義されている畳み込みとは別の演算ということになります。

これが本記事の畳み込みにおいてチラッと述べた

理論的に厳密な議論をするとなると、実は前提から異なりますしね。

のことです。そもそも「CNNの畳み込みが数学的な畳み込みである」という前提が間違っていたのです。

「ではCNNの畳み込みは数学的にはどういう定義の処理に当たるのか、というか対応する数学的定義は存在するのか」という疑問があると思いますが、これについてはきちんと対応する数学的定義があります。相互関係です。
(g \star f)_{i, j} = o_{i, j} = \displaystyle\sum_{k}{\displaystyle\sum_{l}{f_{i+k-1, j+l-1}g_{k, l}}}
数学的な畳み込みと同じく、$k, l$は有効なインデックスとなる全ての値を取ります。これだとCNNの畳み込みと同じような定義ですので、同じ結果が得られることが想像できると思います。

この相互相関は二つの信号($f$と$g$)がどのくらい似ているのかを計算しています。あまり関係ないので詳しくは参考サイトに譲りますが、つまりCNNのフィルタは入力の特定パターンと似ている分布関数を学習していることになります。

ここで重要なのは相互相関をなんとか数学的な畳み込みに持っていけるのかどうかです。これまで当たり前のように畳み込み畳み込みと言っていた処理が実は畳み込みではありませんでした、では議論の根底から覆ってしまうことになり、全部考え直す必要が出てきてしまいます。一生懸命フィルタの解釈について考えてきた研究者の方々が泣いてしまいます...

改めてじっくり数学的な畳み込みとパディングを施した時のCNN畳み込みとを見比べてみましょう。
\left( \begin{array}[ccccc]
  ff_{1, 1}g_{1, 1}
& f_{1, 2}g_{1, 1} + f_{1, 1}g_{1, 2}
& f_{1, 3}g_{1, 1} + f_{1, 2}g_{1, 2}
& f_{1, 4}g_{1, 1} + f_{1, 3}g_{1, 2}
& f_{1, 4}g_{1, 2} \\
  f_{2, 1}g_{1, 1} + f_{1, 1}g_{2, 1}
& f_{2, 2}g_{1, 1} + f_{2, 1}g_{1, 2} + f_{1, 2}g_{2, 1} + f_{1, 1}g_{2, 2}
& f_{2, 3}g_{1, 1} + f_{2, 2}g_{1, 2} + f_{1, 3}g_{2, 1} + f_{1, 2}g_{2, 2}
& f_{2, 4}g_{1, 1} + f_{2, 3}g_{1, 2} + f_{1, 4}g_{2, 1} + f_{1, 3}g_{2, 2}
& f_{2, 4}g_{1, 2} + f_{1, 4}g_{2, 2} \\
  f_{3, 1}g_{1, 1} + f_{2, 1}g_{2, 1}
& f_{3, 2}g_{1, 1} + f_{3, 1}g_{1, 2} + f_{2, 2}g_{2, 1} + f_{2, 1}g_{2, 2}
& f_{3, 3}g_{1, 1} + f_{3, 2}g_{1, 2} + f_{2, 3}g_{2, 1} + f_{2, 2}g_{2, 2}
& f_{3, 4}g_{1, 1} + f_{3, 3}g_{1, 2} + f_{2, 4}g_{2, 1} + f_{2, 3}g_{2, 2}
& f_{3, 4}g_{1, 2} + f_{2, 4}g_{2, 2} \\
  f_{4, 1}g_{1, 1} + f_{3, 1}g_{2, 1}
& f_{4, 2}g_{1, 1} + f_{4, 1}g_{1, 2} + f_{3, 2}g_{2, 1} + f_{3, 1}g_{2, 2}
& f_{4, 3}g_{1, 1} + f_{4, 2}g_{1, 2} + f_{3, 3}g_{2, 1} + f_{3, 2}g_{2, 2}
& f_{4, 4}g_{1, 1} + f_{4, 3}g_{1, 2} + f_{3, 4}g_{2, 1} + f_{3, 3}g_{2, 2}
& f_{4, 4}g_{1, 2} + f_{3, 4}g_{2, 2} \\
  f_{4, 1}g_{2, 1}
& f_{4, 2}g_{2, 1} + f_{4, 1}g_{2, 2}
& f_{4, 3}g_{2, 1} + f_{4, 2}g_{2, 2}
& f_{4, 4}g_{2, 1} + f_{4, 3}g_{2, 2}
& f_{4, 4}g_{2, 2}
\end{array} \right) \\
\left( \begin{array}[ccccc]
    aa_{1, 1}w_{2, 2}
  & a_{1, 1}w_{2, 1} + a_{1, 2}w_{2, 2}
  & a_{1, 2}w_{2, 1} + a_{1, 3}w_{2, 2}
  & a_{1, 3}w_{2, 1} + a_{1, 4}w_{2, 2} 
  & a_{1, 4}w_{2, 1} \\
    a_{1, 1}w_{1, 2} + a_{2, 1}w_{2, 2}
  & a_{1, 1}w_{1, 1} + a_{1, 2}w_{1, 2} + a_{2, 1}w_{2, 1} + a_{2, 2}w_{2, 2}
  & a_{1, 2}w_{1, 1} + a_{1, 3}w_{1, 2} + a_{2, 2}w_{2, 1} + a_{2, 3}w_{2, 2}
  & a_{1, 3}w_{1, 1} + a_{1, 4}w_{1, 2} + a_{2, 3}w_{2, 1} + a_{2, 4}w_{2, 2}
  & a_{1, 4}w_{1, 1} + a_{2, 4}w_{2, 1} \\
    a_{2, 1}w_{1, 2} + a_{3, 1}w_{2, 2}
  & a_{2, 1}w_{1, 1} + a_{2, 2}w_{1, 2} + a_{3, 1}w_{2, 1} + a_{3, 2}w_{2, 2}
  & a_{2, 2}w_{1, 1} + a_{2, 3}w_{1, 2} + a_{3, 2}w_{2, 1} + a_{3, 3}w_{2, 2}
  & a_{2, 3}w_{1, 1} + a_{2, 4}w_{1, 2} + a_{3, 3}w_{2, 1} + a_{3, 4}w_{2, 2}
  & a_{2, 4}w_{1, 1} + a_{3, 4}w_{2, 1} \\
    a_{3, 1}w_{1, 2} + a_{4, 1}w_{2, 2}
  & a_{3, 1}w_{1, 1} + a_{3, 2}w_{1, 2} + a_{4, 1}w_{2, 1} + a_{4, 2}w_{2, 2}
  & a_{3, 2}w_{1, 1} + a_{3, 3}w_{1, 2} + a_{4, 2}w_{2, 1} + a_{4, 3}w_{2, 2}
  & a_{3, 3}w_{1, 1} + a_{3, 4}w_{1, 2} + a_{4, 3}w_{2, 1} + a_{4, 4}w_{2, 2}
  & a_{3, 4}w_{1, 1} + a_{4, 4}w_{2, 1} \\
    a_{4, 1}w_{1, 2}
  & a_{4, 1}w_{1, 1} + a_{4, 2}w_{1, 2}
  & a_{4, 2}w_{1, 1} + a_{4, 3}w_{1, 2}
  & a_{4, 3}w_{1, 1} + a_{4, 4}w_{1, 2}
  & a_{4, 4}w_{1, 1}
\end{array} \right)
なんだかイケる気がしてきませんか？
例えば
\left( \begin{array}[ccc]
  gg_{1, 1} & g_{1, 2} \\
  g_{2, 1} & g_{2, 2} \\
\end{array} \right)
= \left( \begin{array}[ccc]
  ww_{2, 2} & w_{2, 1} \\
  w_{1, 2} & w_{1, 1} \\
\end{array} \right)
なんてことをすると、
\left( \begin{array}[ccccc]
  ff_{1, 1}g_{1, 1}
& f_{1, 2}g_{1, 1} + f_{1, 1}g_{1, 2}
& f_{1, 3}g_{1, 1} + f_{1, 2}g_{1, 2}
& f_{1, 4}g_{1, 1} + f_{1, 3}g_{1, 2}
& f_{1, 4}g_{1, 2} \\
  f_{2, 1}g_{1, 1} + f_{1, 1}g_{2, 1}
& f_{2, 2}g_{1, 1} + f_{2, 1}g_{1, 2} + f_{1, 2}g_{2, 1} + f_{1, 1}g_{2, 2}
& f_{2, 3}g_{1, 1} + f_{2, 2}g_{1, 2} + f_{1, 3}g_{2, 1} + f_{1, 2}g_{2, 2}
& f_{2, 4}g_{1, 1} + f_{2, 3}g_{1, 2} + f_{1, 4}g_{2, 1} + f_{1, 3}g_{2, 2}
& f_{2, 4}g_{1, 2} + f_{1, 4}g_{2, 2} \\
  f_{3, 1}g_{1, 1} + f_{2, 1}g_{2, 1}
& f_{3, 2}g_{1, 1} + f_{3, 1}g_{1, 2} + f_{2, 2}g_{2, 1} + f_{2, 1}g_{2, 2}
& f_{3, 3}g_{1, 1} + f_{3, 2}g_{1, 2} + f_{2, 3}g_{2, 1} + f_{2, 2}g_{2, 2}
& f_{3, 4}g_{1, 1} + f_{3, 3}g_{1, 2} + f_{2, 4}g_{2, 1} + f_{2, 3}g_{2, 2}
& f_{3, 4}g_{1, 2} + f_{2, 4}g_{2, 2} \\
  f_{4, 1}g_{1, 1} + f_{3, 1}g_{2, 1}
& f_{4, 2}g_{1, 1} + f_{4, 1}g_{1, 2} + f_{3, 2}g_{2, 1} + f_{3, 1}g_{2, 2}
& f_{4, 3}g_{1, 1} + f_{4, 2}g_{1, 2} + f_{3, 3}g_{2, 1} + f_{3, 2}g_{2, 2}
& f_{4, 4}g_{1, 1} + f_{4, 3}g_{1, 2} + f_{3, 4}g_{2, 1} + f_{3, 3}g_{2, 2}
& f_{4, 4}g_{1, 2} + f_{3, 4}g_{2, 2} \\
  f_{4, 1}g_{2, 1}
& f_{4, 2}g_{2, 1} + f_{4, 1}g_{2, 2}
& f_{4, 3}g_{2, 1} + f_{4, 2}g_{2, 2}
& f_{4, 4}g_{2, 1} + f_{4, 3}g_{2, 2}
& f_{4, 4}g_{2, 2}
\end{array} \right) \\
= \left( \begin{array}[ccccc]
  ff_{1, 1}w_{2, 2}
& f_{1, 2}w_{2, 2} + f_{1, 1}w_{2, 1}
& f_{1, 3}w_{2, 2} + f_{1, 2}w_{2, 1}
& f_{1, 4}w_{2, 2} + f_{1, 3}w_{2, 1}
& f_{1, 4}w_{2, 1} \\
  f_{2, 1}w_{2, 2} + f_{1, 1}w_{1, 2}
& f_{2, 2}w_{2, 2} + f_{2, 1}w_{2, 1} + f_{1, 2}w_{1, 2} + f_{1, 1}w_{1, 1}
& f_{2, 3}w_{2, 2} + f_{2, 2}w_{2, 1} + f_{1, 3}w_{1, 2} + f_{1, 2}w_{1, 1}
& f_{2, 4}w_{2, 2} + f_{2, 3}w_{2, 1} + f_{1, 4}w_{1, 2} + f_{1, 3}w_{1, 1}
& f_{2, 4}w_{2, 1} + f_{1, 4}w_{1, 1} \\
  f_{3, 1}w_{2, 2} + f_{2, 1}w_{1, 2}
& f_{3, 2}w_{2, 2} + f_{3, 1}w_{2, 1} + f_{2, 2}w_{1, 2} + f_{2, 1}w_{1, 1}
& f_{3, 3}w_{2, 2} + f_{3, 2}w_{2, 1} + f_{2, 3}w_{1, 2} + f_{2, 2}w_{1, 1}
& f_{3, 4}w_{2, 2} + f_{3, 3}w_{2, 1} + f_{2, 4}w_{1, 2} + f_{2, 3}w_{1, 1}
& f_{3, 4}w_{2, 1} + f_{2, 4}w_{1, 1} \\
  f_{4, 1}w_{2, 2} + f_{3, 1}w_{1, 2}
& f_{4, 2}w_{2, 2} + f_{4, 1}w_{2, 1} + f_{3, 2}w_{1, 2} + f_{3, 1}w_{1, 1}
& f_{4, 3}w_{2, 2} + f_{4, 2}w_{2, 1} + f_{3, 3}w_{1, 2} + f_{3, 2}w_{1, 1}
& f_{4, 4}w_{2, 2} + f_{4, 3}w_{2, 1} + f_{3, 4}w_{1, 2} + f_{3, 3}w_{1, 1}
& f_{4, 4}w_{2, 1} + f_{3, 4}w_{1, 1} \\
  f_{4, 1}w_{1, 2}
& f_{4, 2}w_{1, 2} + f_{4, 1}w_{1, 1}
& f_{4, 3}w_{1, 2} + f_{4, 2}w_{1, 1}
& f_{4, 4}w_{1, 2} + f_{4, 3}w_{1, 1}
& f_{4, 4}w_{1, 1}
\end{array} \right) \\
\underbrace{=}_{足し算の順番入れ替え}
\left( \begin{array}[ccccc]
    ff_{1, 1}w_{2, 2}
  & f_{1, 1}w_{2, 1} + f_{1, 2}w_{2, 2}
  & f_{1, 2}w_{2, 1} + f_{1, 3}w_{2, 2}
  & f_{1, 3}w_{2, 1} + f_{1, 4}w_{2, 2} 
  & f_{1, 4}w_{2, 1} \\
    f_{1, 1}w_{1, 2} + f_{2, 1}w_{2, 2}
  & f_{1, 1}w_{1, 1} + f_{1, 2}w_{1, 2} + f_{2, 1}w_{2, 1} + f_{2, 2}w_{2, 2}
  & f_{1, 2}w_{1, 1} + f_{1, 3}w_{1, 2} + f_{2, 2}w_{2, 1} + f_{2, 3}w_{2, 2}
  & f_{1, 3}w_{1, 1} + f_{1, 4}w_{1, 2} + f_{2, 3}w_{2, 1} + f_{2, 4}w_{2, 2}
  & f_{1, 4}w_{1, 1} + f_{2, 4}w_{2, 1} \\
    f_{2, 1}w_{1, 2} + f_{3, 1}w_{2, 2}
  & f_{2, 1}w_{1, 1} + f_{2, 2}w_{1, 2} + f_{3, 1}w_{2, 1} + f_{3, 2}w_{2, 2}
  & f_{2, 2}w_{1, 1} + f_{2, 3}w_{1, 2} + f_{3, 2}w_{2, 1} + f_{3, 3}w_{2, 2}
  & f_{2, 3}w_{1, 1} + f_{2, 4}w_{1, 2} + f_{3, 3}w_{2, 1} + f_{3, 4}w_{2, 2}
  & f_{2, 4}w_{1, 1} + f_{3, 4}w_{2, 1} \\
    f_{3, 1}w_{1, 2} + f_{4, 1}w_{2, 2}
  & f_{3, 1}w_{1, 1} + f_{3, 2}w_{1, 2} + f_{4, 1}w_{2, 1} + f_{4, 2}w_{2, 2}
  & f_{3, 2}w_{1, 1} + f_{3, 3}w_{1, 2} + f_{4, 2}w_{2, 1} + f_{4, 3}w_{2, 2}
  & f_{3, 3}w_{1, 1} + f_{3, 4}w_{1, 2} + f_{4, 3}w_{2, 1} + f_{4, 4}w_{2, 2}
  & f_{3, 4}w_{1, 1} + f_{4, 4}w_{2, 1} \\
    f_{4, 1}w_{1, 2}
  & f_{4, 1}w_{1, 1} + f_{4, 2}w_{1, 2}
  & f_{4, 2}w_{1, 1} + f_{4, 3}w_{1, 2}
  & f_{4, 3}w_{1, 1} + f_{4, 4}w_{1, 2}
  & f_{4, 4}w_{1, 1}
\end{array} \right) \\
\Leftrightarrow
\left( \begin{array}[ccccc]
    aa_{1, 1}w_{2, 2}
  & a_{1, 1}w_{2, 1} + a_{1, 2}w_{2, 2}
  & a_{1, 2}w_{2, 1} + a_{1, 3}w_{2, 2}
  & a_{1, 3}w_{2, 1} + a_{1, 4}w_{2, 2} 
  & a_{1, 4}w_{2, 1} \\
    a_{1, 1}w_{1, 2} + a_{2, 1}w_{2, 2}
  & a_{1, 1}w_{1, 1} + a_{1, 2}w_{1, 2} + a_{2, 1}w_{2, 1} + a_{2, 2}w_{2, 2}
  & a_{1, 2}w_{1, 1} + a_{1, 3}w_{1, 2} + a_{2, 2}w_{2, 1} + a_{2, 3}w_{2, 2}
  & a_{1, 3}w_{1, 1} + a_{1, 4}w_{1, 2} + a_{2, 3}w_{2, 1} + a_{2, 4}w_{2, 2}
  & a_{1, 4}w_{1, 1} + a_{2, 4}w_{2, 1} \\
    a_{2, 1}w_{1, 2} + a_{3, 1}w_{2, 2}
  & a_{2, 1}w_{1, 1} + a_{2, 2}w_{1, 2} + a_{3, 1}w_{2, 1} + a_{3, 2}w_{2, 2}
  & a_{2, 2}w_{1, 1} + a_{2, 3}w_{1, 2} + a_{3, 2}w_{2, 1} + a_{3, 3}w_{2, 2}
  & a_{2, 3}w_{1, 1} + a_{2, 4}w_{1, 2} + a_{3, 3}w_{2, 1} + a_{3, 4}w_{2, 2}
  & a_{2, 4}w_{1, 1} + a_{3, 4}w_{2, 1} \\
    a_{3, 1}w_{1, 2} + a_{4, 1}w_{2, 2}
  & a_{3, 1}w_{1, 1} + a_{3, 2}w_{1, 2} + a_{4, 1}w_{2, 1} + a_{4, 2}w_{2, 2}
  & a_{3, 2}w_{1, 1} + a_{3, 3}w_{1, 2} + a_{4, 2}w_{2, 1} + a_{4, 3}w_{2, 2}
  & a_{3, 3}w_{1, 1} + a_{3, 4}w_{1, 2} + a_{4, 3}w_{2, 1} + a_{4, 4}w_{2, 2}
  & a_{3, 4}w_{1, 1} + a_{4, 4}w_{2, 1} \\
    a_{4, 1}w_{1, 2}
  & a_{4, 1}w_{1, 1} + a_{4, 2}w_{1, 2}
  & a_{4, 2}w_{1, 1} + a_{4, 3}w_{1, 2}
  & a_{4, 3}w_{1, 1} + a_{4, 4}w_{1, 2}
  & a_{4, 4}w_{1, 1}
\end{array} \right)
となり、同じになりました！これが意味することは相互相関と数学的な畳み込みとはうまくすれば同じ操作とすることが可能であるということです。この場合の「うまくする」は、離散であればインデックスの反転、連続の場合は原点対称ですね。

ということで、CNNのフィルタは反転した畳み込みフィルタを学習していると見なすことができ、研究者は泣かずに済むということですね笑

Cooley-Turkey FFTアルゴリズム

まずはそもそもの離散フーリエ変換の定義から確認してみます。簡単のため1次元の長さ$N$のベクトル$\boldsymbol{x}$を離散フーリエ変換で考えると
X_k = \mathcal{F}_{\boldsymbol{x}}(k) = \sum_{p=0}^{N-1}{x_p e^{-j\frac{2 \pi}{N}kp}} = \sum_{p=0}^{N-1}{x_p W_N^{kp}} \quad k = 0, 1, \ldots N-1 \\
W_N^{kp} = e^{-j\frac{2 \pi}{N}kp}
となります。ここで虚数記号を$j$としています。また$W_N = e^{-j\frac{2 \pi}{N}}$は回転因子と呼ばれています。理由は後述します。
この計算量は$\mathcal{O}(N^2)$ですが、この計算は$N$が偶数であると仮定すると高速化することができます。そのアルゴリズムはFFT: Fast Fourier Transformation: 高速フーリエ変換と呼ばれており、次のように表すことができます。
\begin{align}
  X_{2k} = \mathcal{F}_{\boldsymbol{x}}(2k) &= \sum_{p=0}^{N-1}{x_p W_N^{2kp}} & \\
  &= \sum_{p=0}^{N-1}{x_p W_{N/2}^{kp}} & (\because W_N^{2kp} = e^{-j\frac{2 \pi}{N}2kp} = e^{-j\frac{2 \pi}{N/2}kp} = W_{N/2}^{kp}) \\
  &= \sum_{p=0}^{N/2-1}{x_p W_{N/2}^{kp}} + \sum_{p=N/2}^{N-1}{x_p W_{N/2}^{kp}} & (\because 前半部分と後半部分に分け、W_{N/2}^{kp}の要素数\frac{N}{2}に合わせる) \\
  &= \sum_{p=0}^{N/2-1}{x_p W_{N/2}^{kp}} + \sum_{p=0}^{N/2-1}{x_{p+N/2} W_{N/2}^{k(p+N/2)}} & (\because 後半の和をp=0スタートにシフト) \\
  &= \sum_{p=0}^{N/2-1}{x_p W_{N/2}^{kp}} + \sum_{p=0}^{N/2-1}{x_{p+N/2} W_{N/2}^{kp}} & (\because W_{N/2}^{k(N/2)} = e^{-j\frac{2 \pi}{N/2}k(N/2)} = e^{-j2k \pi} = 1) \\
  &= \sum_{p=0}^{N/2-1}{(x_p + x_{p+N/2}) W_{N/2}^{kp}} \quad k = 0, 1, \ldots, \cfrac{N}{2} & \\

  X_{2k+1} = \mathcal{F}_{\boldsymbol{x}}(2k+1) &= \sum_{p=0}^{N-1}{x_p W_N^{(2k+1)p}} & \\
  &= \sum_{p=0}^{N-1}{x_p W_{N}^{p}W_{N/2}^{kp}} & \\
  &= \sum_{p=0}^{N/2-1}{x_p W_{N}^{p}W_{N/2}^{kp}} + \sum_{p=N/2}^{N-1}{x_p W_{N}^{p}W_{N/2}^{kp}} & \\
  &= \sum_{p=0}^{N/2-1}{x_p W_{N}^{p}W_{N/2}^{kp}} + \sum_{p=0}^{N/2-1}{x_{p+N/2} W_{N}^{p+N/2}W_{N/2}^{k(p+N/2)}} & \\
  &= \sum_{p=0}^{N/2-1}{x_p W_{N}^{p}W_{N/2}^{kp}} - \sum_{p=0}^{N/2-1}{x_{p+N/2} W_{N}^{p}W_{N/2}^{kp}} & \\
  &= \sum_{p=0}^{N/2-1}{(x_p - x_{p+N/2}) W_{N}^{p} W_{N/2}^{kp}} \quad k = 0, 1, \ldots, \cfrac{N}{2}-1 &
\end{align}
$W$は定義から回転角が時計回りに$\frac{2\pi}{N}$である単位円周上の点を表すことになるため、回転因子と呼ばれています。

このため、以下のような関係式が成立します。
W_{2n}^{kn} = e^{-j\frac{2 \pi}{2n}kn} = e^{-j k \pi} = (-1)^k
この関係式は要するに回転角$k\pi$の時の値ですね。先のFFTの式変形にこの式を随所で用いています。
ナニコレ?という人へ

複素数に馴染みのない方には何をやっているのか分からないかもしれませんので、数学史上最も美しいと言われるオイラーの公式を紹介しておきます。
さらにその前にテイラー展開も必要なのですが...その辺りは掘り出すと無限に話が膨らむので割愛します。
e^{jx} = \cos x + j \sin x
これがオイラーの公式です。これに$x=\pi$を代入して得られる
e^{j \pi} = \cos \pi + j \sin \pi \Leftrightarrow e^{j \pi} = -1 + j0 \\
\therefore e^{j \pi} + 1 = 0
は数学史上最も美しい式とよく評されています。その辺りの感性は残念ながらぼくにはあまりよくわかりませんが...まあすごいということ自体はわかります。
とにかく、このオイラーの公式に$x=-k\pi$を代入すると
\begin{align}
  e^{j(-k \pi)} &= \cos (-k \pi) + j \sin (-k \pi) \\
  &= (-1)^k \\
\end{align}
となり、先ほどの関係式が得られます。
このFFTアルゴリズムにより計算量は半分になります。そしてこの操作を拡張したのがCooley-TurkeyのFFTアルゴリズムです。
Cooley_TurkeyのFFTアルゴリズムでは、ベクトルの長さ$N$を2の累乗であると仮定し、FFTを繰り返し適応することでさらなる高速化を図るものとなります。
分割を繰り返してベクトル長が$1$になるとそのフーリエ変換値を求めることで全てのフーリエ変換値が求まることになります。
具体的に計算してみる

※間違ってたら教えてください！
具体的に計算して確かめてみましょう。まずはFFTから確認します。
入力を$\boldsymbol{x} = (x_0, x_1, \ldots, x_7)$の長さ$N=8$のベクトルであるとします。これのフーリエ変換ベクトルを$\boldsymbol{X} = (X_0, X_1, \ldots, X_7)$とすると、まずは定義通りに
\begin{align}
  \boldsymbol{X}^\top &= \left( \begin{array}[c]
    d\displaystyle\sum_{p=0}^{7}{x_p W_8^{0}} \\
    \displaystyle\sum_{p=0}^{7}{x_p W_8^{p}} \\
    \displaystyle\sum_{p=0}^{7}{x_p W_8^{2p}} \\
    \displaystyle\sum_{p=0}^{7}{x_p W_8^{3p}} \\
    \displaystyle\sum_{p=0}^{7}{x_p W_8^{4p}} \\
    \displaystyle\sum_{p=0}^{7}{x_p W_8^{5p}} \\
    \displaystyle\sum_{p=0}^{7}{x_p W_8^{6p}} \\
    \displaystyle\sum_{p=0}^{7}{x_p W_8^{7p}} \\
  \end{array}\right)
  = \left( \begin{array}[c]
    xx_0W_8^0 + x_1W_8^0 + x_2W_8^0 + x_3W_8^0 + x_4W_8^0 + x_5W_8^0 + x_6W_8^0 + x_7W_8^0 \\
    x_0W_8^0 + x_1W_8^1 + x_2W_8^2 + x_3W_8^3 + x_4W_8^4 + x_5W_8^5 + x_6W_8^6 + x_7W_8^7 \\
    x_0W_8^0 + x_1W_8^2 + x_2W_8^4 + x_3W_8^6 + x_4W_8^8 + x_5W_8^{10} + x_6W_8^{12} + x_7W_8^{14} \\
    x_0W_8^0 + x_1W_8^3 + x_2W_8^6 + x_3W_8^9 + x_4W_8^{12} + x_5W_8^{15} + x_6W_8^{18} + x_7W_8^{21} \\
    x_0W_8^0 + x_1W_8^4 + x_2W_8^8 + x_3W_8^{12} + x_4W_8^{16} + x_5W_8^{20} + x_6W_8^{24} + x_7W_8^{28} \\
    x_0W_8^0 + x_1W_8^5 + x_2W_8^{10} + x_3W_8^{15} + x_4W_8^{20} + x_5W_8^{25} + x_6W_8^{30} + x_7W_8^{35} \\
    x_0W_8^0 + x_1W_8^6 + x_2W_8^{12} + x_3W_8^{18} + x_4W_8^{24} + x_5W_8^{30} + x_6W_8^{36} + x_7W_8^{42} \\
    x_0W_8^0 + x_1W_8^7 + x_2W_8^{14} + x_3W_8^{21} + x_4W_8^{28} + x_5W_8^{35} + x_6W_8^{42} + x_7W_8^{49} \\
  \end{array}\right) \\
  &= \left( \begin{array}[cccccccc]
    WW_8^0 & W_8^0 & W_8^0 & W_8^0 & W_8^0 & W_8^0 & W_8^0 & W_8^0 \\
    W_8^0 & W_8^1 & W_8^2 & W_8^3 & W_8^4 & W_8^5 & W_8^6 & W_8^7 \\
    W_8^0 & W_8^2 & W_8^4 & W_8^6 & W_8^8 & W_8^{10} & W_8^{12} & W_8^{14} \\
    W_8^0 & W_8^3 & W_8^6 & W_8^9 & W_8^{12} & W_8^{15} & W_8^{18} & W_8^{21} \\
    W_8^0 & W_8^4 & W_8^8 & W_8^{12} & W_8^{16} & W_8^{20} & W_8^{24} & W_8^{28} \\
    W_8^0 & W_8^5 & W_8^{10} & W_8^{15} & W_8^{20} & W_8^{25} & W_8^{30} & W_8^{35} \\
    W_8^0 & W_8^6 & W_8^{12} & W_8^{18} & W_8^{24} & W_8^{30} & W_8^{36} & W_8^{42} \\
    W_8^0 & W_8^7 & W_8^{14} & W_8^{21} & W_8^{28} & W_8^{35} & W_8^{42} & W_8^{49} \\
  \end{array}\right)
  \left( \begin{array}[c]
    xx_0 \\
    x_1 \\
    x_2 \\
    x_3 \\
    x_4 \\
    x_5 \\
    x_6 \\
    x_7 \\
  \end{array}\right) \\
  &= \left( \begin{array}[cccccccc]
    11 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\
    1 & e^{-j\frac{\pi}{4}} & -j & e^{-j\frac{3\pi}{4}} & -1 & e^{-j\frac{5\pi}{4}} & j & e^{-j\frac{7\pi}{4}} \\
    1 & -j & -1 & j & 1 & -j & -1 & j \\
    1 & e^{-j\frac{3\pi}{4}} & j & e^{-j\frac{\pi}{4}} & -1 & e^{-j\frac{7\pi}{4}} & -j & e^{-j\frac{5\pi}{4}} \\
    1 & -1 & 1 & -1 & 1 & -1 & 1 & -1 \\
    1 & e^{-j\frac{5\pi}{4}} & -j & e^{-j\frac{7\pi}{4}} & -1 & e^{-j\frac{\pi}{4}} & j & e^{-j\frac{3\pi}{4}} \\
    1 & j & -1 & -j & 1 & j & -1 & -j \\
    1 & e^{-j\frac{7\pi}{4}} & j & e^{-j\frac{5\pi}{4}} & -1 & e^{-j\frac{3\pi}{4}} & -j & e^{-j\frac{\pi}{4}} \\
  \end{array}\right)
  \left( \begin{array}[c]
    xx_0 \\
    x_1 \\
    x_2 \\
    x_3 \\
    x_4 \\
    x_5 \\
    x_6 \\
    x_7 \\
  \end{array}\right)
\end{align}
と書くことができます。これと一致するか確認しながら計算していきます。
\begin{align}
  X_{2k} &= \sum_{p=0}^{3}{(x_p + x_{p+4}) W_{4}^{kp}} \\
  X_{2k+1} &= \sum_{p=0}^{3}{(x_p - x_{p+4})W_{8}^{p} W_{4}^{kp}}
\end{align}
ですから
\begin{align}
  X^{(0)} &= (X_0, X_2, X_4, X_6) \\
  X^{(1)} &= (X_1, X_3, X_5, X_7)
\end{align}
として
\begin{align}
  X^{(0)\top} &= \left( \begin{array}[c]
    XX_0 \\
    X_2 \\
    X_4 \\
    X_6
  \end{array} \right) = \left( \begin{array}[c]
    d\displaystyle\sum_{p=0}^{3}{(x_p + x_{p+4}) W_4^{0}} \\
    \displaystyle\sum_{p=0}^{3}{(x_p + x_{p+4}) W_4^{p}} \\
    \displaystyle\sum_{p=0}^{3}{(x_p + x_{p+4}) W_4^{2p}} \\
    \displaystyle\sum_{p=0}^{3}{(x_p + x_{p+4}) W_4^{3p}}
  \end{array} \right) & \\
  &= \left( \begin{array}[c]
    ((x_0 + x_4) W_4^0 + (x_1 + x_5) W_4^0 + (x_2 + x_6) W_4^0 + (x_3 + x_7) W_4^0 \\
    (x_0 + x_4) W_4^0 + (x_1 + x_5) W_4^1 + (x_2 + x_6) W_4^2 + (x_3 + x_7) W_4^3 \\
    (x_0 + x_4) W_4^0 + (x_1 + x_5) W_4^2 + (x_2 + x_6) W_4^4 + (x_3 + x_7) W_4^6 \\
    (x_0 + x_4) W_4^0 + (x_1 + x_5) W_4^3 + (x_2 + x_6) W_4^6 + (x_3 + x_7) W_4^9 \\
  \end{array} \right) & \\
　&= \left( \begin{array}[c]
    xx_0 W_4^0 + x_1 W_4^0 + x_2 W_4^0 + x_3 W_4^0 + x_4 W_4^0 + x_5 W_4^0 + x_6 W_4^0 + x_7 W_4^0 \\
    x_0 W_4^0 + x_1 W_4^1 + x_2 W_4^2 + x_3 W_4^3 + x_4 W_4^0 + x_5 W_4^1 + x_6 W_4^2 + x_7 W_4^3 \\
    x_0 W_4^0 + x_1 W_4^2 + x_2 W_4^4 + x_3 W_4^6 + x_4 W_4^0 + x_5 W_4^2 + x_6 W_4^4 + x_7 W_4^6 \\
    x_0 W_4^0 + x_1 W_4^3 + x_2 W_4^6 + x_3 W_4^9 + x_4 W_4^0 + x_5 W_4^3 + x_6 W_4^6 + x_7 W_4^9 \\
  \end{array} \right) & \\
  &= \left( \begin{array}[cccccccc]
    WW_4^0 & W_4^0 & W_4^0 & W_4^0 & W_4^0 & W_4^0 & W_4^0 & W_4^0 \\
    W_4^0 & W_4^1 & W_4^2 & W_4^3 & W_4^0 & W_4^1 & W_4^2 & W_4^3 \\
    W_4^0 & W_4^2 & W_4^4 & W_4^6 & W_4^0 & W_4^2 & W_4^4 & W_4^6 \\
    W_4^0 & W_4^3 & W_4^6 & W_4^9 & W_4^0 & W_4^3 & W_4^6 & W_4^9 \\
  \end{array} \right)
  \left( \begin{array}[c]
    xx_0 \\
    x_1 \\
    x_2 \\
    x_3 \\
    x_4 \\
    x_5 \\
    x_6 \\
    x_7
  \end{array} \right) & \\
  &= \left( \begin{array}[cccccccc]
    11 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\
    1 & -j & -1 & j & 1 & -j & -1　& j \\
    1 & -1 & 1 & -1 & 1 & -1 & 1 & -1 \\
    1 & j & -1 & -j & 1 & j & -1 & j \\
  \end{array} \right)
  \left( \begin{array}[c]
    xx_0 \\
    x_1 \\
    x_2 \\
    x_3 \\
    x_4 \\
    x_5 \\
    x_6 \\
    x_7
  \end{array} \right) & \\

  X^{(1)\top} &= \left( \begin{array}[c]
    XX_1 \\
    X_3 \\
    X_5 \\
    X_7
  \end{array} \right) = \left( \begin{array}[c]
    d\displaystyle\sum_{p=0}^{3}{(x_p - x_{p+4})W_8^{p} W_4^{0}} \\
    \displaystyle\sum_{p=0}^{3}{(x_p - x_{p+4})W_8^{p} W_4^{p}} \\
    \displaystyle\sum_{p=0}^{3}{(x_p - x_{p+4})W_8^{p} W_4^{2p}} \\
    \displaystyle\sum_{p=0}^{3}{(x_p - x_{p+4})W_8^{p} W_4^{3p}}
  \end{array} \right) & \\
  &= \left( \begin{array}[c]
    ((x_0 - x_4)W_8^{0} W_4^0 + (x_1 - x_5)W_8^1 W_4^0 + (x_2 - x_6)W_8^2 W_4^0 + (x_3 - x_7)W_8^3 W_4^0 \\
    (x_0 - x_4)W_8^0 W_4^0 + (x_1 - x_5)W_8^1 W_4^1 + (x_2 - x_6)W_8^2 W_4^2 + (x_3 - x_7)W_8^3 W_4^3 \\
    (x_0 - x_4)W_8^0 W_4^0 + (x_1 - x_5)W_8^1 W_4^2 + (x_2 - x_6)W_8^2 W_4^4 + (x_3 - x_7)W_8^3 W_4^6 \\
    (x_0 - x_4)W_8^0 W_4^0 + (x_1 - x_5)W_8^1 W_4^3 + (x_2 - x_6)W_8^2 W_4^6 + (x_3 - x_7)W_8^3 W_4^9 \\
  \end{array} \right) & \\
　&= \left( \begin{array}[c]
    xx_0 W_8^0 W_4^0 + x_1 W_8^1 W_4^0 + x_2 W_8^2 W_4^0 + x_3 W_8^3 W_4^0 - x_4 W_8^0 W_4^0 - x_5 W_8^1 W_4^0 - x_6 W_8^2 W_4^0 - x_7 W_8^3 W_4^0 \\
    x_0 W_8^0 W_4^0 + x_1 W_8^1 W_4^2 + x_2 W_8^2 W_4^4 + x_3 W_8^3 W_4^6 - x_4 W_8^0 W_4^0 - x_5 W_8^1 W_4^2 - x_6 W_8^2 W_4^4 - x_7 W_8^3 W_4^6 \\
    x_0 W_8^0 W_4^0 + x_1 W_8^1 W_4^3 + x_2 W_8^2 W_4^6 + x_3 W_8^3 W_4^9 - x_4 W_8^0 W_4^0 - x_5 W_8^1 W_4^3 - x_6 W_8^2 W_4^6 - x_7 W_8^3 W_4^9 \\
    x_0 W_8^0 W_4^0 + x_1 W_8^1 W_4^4 + x_2 W_8^2 W_4^8 + x_3 W_8^3 W_4^{12} - x_4 W_8^0 W_4^0 - x_5 W_8^1 W_4^4 - x_6 W_8^2 W_4^8 - x_7 W_8^3 W_4^{12}
  \end{array} \right) & \\
  &= \left( \begin{array}[cccccccc]
    WW_8^0 & W_8^1 & W_8^2 & W_8^3 & -W_8^0 & -W_8^1 & -W_8^2 & -W_8^3 \\
    W_8^0 & W_8^5 & W_8^{10} & W_8^{15} & -W_8^0 & -W_8^5 & -W_8^{10} & -W_8^{15} \\
    W_8^0 & W_8^7 & W_8^{14} & W_8^{21} & -W_8^0 & -W_8^7 & -W_8^{14} & -W_8^{21} \\
    W_8^0 & W_8^9 & W_8^{18} & W_8^{27} & -W_8^0 & -W_8^9 & -W_8^{18} & -W_8^{27} \\
  \end{array} \right)
  \left( \begin{array}[c]
    xx_0 \\
    x_1 \\
    x_2 \\
    x_3 \\
    x_4 \\
    x_5 \\
    x_6 \\
    x_7
  \end{array} \right) & (\because W_8^c W_4^d = W_8^{c+2d}) \\
  &= \left( \begin{array}[cccccccc]
    11 & e^{-j\frac{\pi}{4}} & -j & e^{-j\frac{3\pi}{4}} & -1 & e^{-j\frac{5\pi}{4}} & j & e^{-j\frac{7\pi}{4}} \\
    1 & e^{-j\frac{3\pi}{4}} & j & e^{-j\frac{\pi}{4}} & -1 & e^{-j\frac{7\pi}{4}} & -j & e^{-j\frac{5\pi}{4}} \\
    1 & e^{-j\frac{5\pi}{4}} & -j & e^{-j\frac{7\pi}{4}} & -1 & e^{-j\frac{\pi}{4}} & j & e^{-j\frac{3\pi}{4}} \\
    1 & e^{-j\frac{7\pi}{4}} & j & e^{-j\frac{5\pi}{4}} & -1 & e^{-j\frac{3\pi}{4}} & -j & e^{-j\frac{\pi}{4}} \\
  \end{array} \right)
  \left( \begin{array}[c]
    xx_0 \\
    x_1 \\
    x_2 \\
    x_3 \\
    x_4 \\
    x_5 \\
    x_6 \\
    x_7
  \end{array} \right) & (\because -1 = W_8^4)
\end{align}
きっちり偶数列と奇数列の値がそれぞれ計算できていますね！それではさらにCooley-Turekeyアルゴリズムで試していきましょう。まず下準備として
\begin{align}
  \boldsymbol{x}^{(0)} &= (x_0 + x_4, x_1 + x_5, x_2 + x_6, x_3 + x_7) \\ 
  \boldsymbol{x}^{(1)} &= \left((x_0 - x_4)W_8^0, (x_1 - x_5)W_8^1, (x_2 - x_6)W_8^2, (x_3 - x_7)W_8^3 \right)
\end{align}
とおきます。この場合
\left\{ \begin{array}[c]
  b\boldsymbol{X}^{(0)} = \mathcal{F}_{\boldsymbol{x}^{(0)}}(k) \\
  \boldsymbol{X}^{(1)} = \mathcal{F}_{\boldsymbol{x}^{(1)}}(k)
\end{array} \right.
\quad k = 0, 1, \ldots, 3
とすることができますね。このそれぞれに対してFFTを行うと
\begin{align}
  \boldsymbol{X}_{2k}^{(0)} &= \mathcal{F}_{\boldsymbol{x}^{(0)}}(2k) \\
  &= \sum_{p=0}^{1}{\left(x_p^{(0)} + x_{p+2}^{(0)} \right) W_{2}^{kp}} \\
  \boldsymbol{X}_{2k+1}^{(0)} &= \mathcal{F}_{\boldsymbol{x}^{(0)}}(2k+1) \\
  &= \sum_{p=0}^{1}{\left(x_p^{(0)} - x_{p+2}^{(0)} \right)W_4^p W_{2}^{kp}} \\
　　\boldsymbol{X}_{2k}^{(1)} &= \mathcal{F}_{\boldsymbol{x}^{(1)}}(2k) \\
  &= \sum_{p=0}^{1}{\left(x_p^{(1)} + x_{p+2}^{(1)} \right) W_{2}^{kp}} \\
  \boldsymbol{X}_{2k+1}^{(1)} &= \mathcal{F}_{\boldsymbol{x}^{(1)}}(2k+1) \\
  &= \sum_{p=0}^{1}{\left(x_p^{(1)} - x_{p+2}^{(1)}\right)W_4^p W_{2}^{kp}}
\end{align}
となります。一応実際に書き下して正しいか確認しておきます。
\begin{align}
  \boldsymbol{X}_{2k}^{(0)} &= \left( \begin{array}[c]
    XX_{0}^{(0)} \\
    X_{2}^{(0)}
  \end{array} \right) = \left( \begin{array}[c]
    XX_0 \\
    X_4
  \end{array} \right) & \\
  &= \left( \begin{array}[c]
    d\displaystyle\sum_{p=0}^{1}{\left(x_p^{(0)} + x_{p+2}^{(0)} \right) W_2^0} \\
    \displaystyle\sum_{p=0}^{1}{\left(x_p^{(0)} + x_{p+2}^{(0)} \right) W_2^p}
  \end{array} \right) = \left( \begin{array}[c]
    (\left(x_0^{(0)} + x_2^{(0)} \right) W_2^0 + \left(x_1^{(0)} + x_3^{(0)} \right) W_2^0 \\
    \left(x_0^{(0)} + x_2^{(0)} \right) W_2^0 + \left(x_1^{(0)} + x_3^{(0)} \right) W_2^1
  \end{array} \right) & \\
  &= \left( \begin{array}[c]
    (\{(x_0 + x_4) + (x_2 + x_6)\}W_2^0 + \{(x_1 + x_5) + (x_3 + x_7) \} W_2^0 \\
    \{(x_0 + x_4) + (x_2 + x_6)\}W_2^0 + \{(x_1 + x_5) + (x_3 + x_7) \} W_2^1
  \end{array} \right) & \\
  &= \left( \begin{array}[cccccccc]
    WW_2^0 & W_2^0 & W_2^0 & W_2^0 & W_2^0 & W_2^0 & W_2^0 & W_2^0 \\
    W_2^0 & W_2^1 & W_2^0 & W_2^1 & W_2^0 & W_2^1 & W_2^0 & W_2^1
  \end{array} \right) \left( \begin{array}[c]
    xx_0 \\
    x_1 \\
    x_2 \\
    x_3 \\
    x_4 \\
    x_5 \\
    x_6 \\
    x_7
  \end{array} \right) && \\
  &= \left( \begin{array}[cccccccc]
    11 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\
    1 & -1 & 1 & -1 & 1 & -1 & 1 & -1
  \end{array} \right) \left( \begin{array}[c]
    xx_0 \\
    x_1 \\
    x_2 \\
    x_3 \\
    x_4 \\
    x_5 \\
    x_6 \\
    x_7
  \end{array} \right) & \\

  \boldsymbol{X}_{2k+1}^{(0)} &= \left( \begin{array}[c]
    XX_{1}^{(0)} \\
    X_{3}^{(0)}
  \end{array} \right) = \left( \begin{array}[c]
    XX_2 \\
    X_6
  \end{array} \right) & \\
  &= \left( \begin{array}[c]
    d\displaystyle\sum_{p=0}^{1}{\left(x_p^{(0)} - x_{p+2}^{(0)} \right)W_4^p W_2^0} \\
    \displaystyle\sum_{p=0}^{1}{\left(x_p^{(0)} - x_{p+2}^{(0)} \right)W_4^p W_2^p}
  \end{array} \right) = \left( \begin{array}[c]
    (\left(x_0^{(0)} - x_2^{(0)} \right)W_4^0 W_2^0 + \left(x_1^{(0)} - x_3^{(0)} \right)W_4^1 W_2^0 \\
    \left(x_0^{(0)} - x_2^{(0)} \right)W_4^0 W_2^0 + \left(x_1^{(0)} - x_3^{(0)} \right)W_4^1 W_2^1
  \end{array} \right) & \\
  &= \left( \begin{array}[c]
    (\{(x_0 + x_4) - (x_2 + x_6)\}W_4^0 W_2^0 + \{(x_1 + x_5) - (x_3 + x_7)\}W_4^1 W_2^0 \\
    \{(x_0 + x_4) - (x_2 + x_6)\}W_4^0 W_2^0 + \{(x_1 + x_5) - (x_3 + x_7)\}W_4^1 W_2^1
  \end{array} \right) & \\
  &= \left( \begin{array}[cccccccc]
    WW_4^0 & W_4^1 & -W_4^0 & -W_4^1 & W_4^0 & W_4^1 & -W_4^0 & -W_4^1 \\
    W_4^0 & W_4^5 & -W_4^0 & -W_4^5 & W_4^0 & W_4^5 & -W_4^0 & -W_4^5
  \end{array} \right) \left( \begin{array}[c]
    xx_0 \\
    x_1 \\
    x_2 \\
    x_3 \\
    x_4 \\
    x_5 \\
    x_6 \\
    x_7
  \end{array} \right) & \\
  &= \left( \begin{array}[cccccccc]
    11 & -j & -1 & j & 1 & -j & -1 & j \\
    1 & j & -1 & -j & 1 & j & -1 & -j
  \end{array} \right) \left( \begin{array}[c]
    xx_0 \\
    x_1 \\
    x_2 \\
    x_3 \\
    x_4 \\
    x_5 \\
    x_6 \\
    x_7
  \end{array} \right) & (\because W_4^c W_2^d = W_4^{c+2d}, -1 = W_4^2) \\

  \boldsymbol{X}_{2k}^{(1)} &= \left( \begin{array}[c]
    XX_{0}^{(1)} \\
    X_{2}^{(1)}
  \end{array} \right) = \left( \begin{array}[c]
    XX_1 \\
    X_5
  \end{array} \right) & \\
  &= \left( \begin{array}[c]
    d\displaystyle\sum_{p=0}^{1}{\left(x_p^{(1)} + x_{p+2}^{(1)} \right) W_2^0} \\
    \displaystyle\sum_{p=0}^{1}{\left(x_p^{(1)} + x_{p+2}^{(1)} \right) W_2^p}
  \end{array} \right) = \left( \begin{array}[c]
    (\left(x_0^{(1)} + x_2^{(1)} \right) W_2^0 + \left(x_1^{(1)} + x_3^{(1)} \right) W_2^0 \\
    \left(x_0^{(1)} + x_2^{(1)} \right) W_2^0 + \left(x_1^{(1)} + x_3^{(1)} \right) W_2^1
  \end{array} \right) & \\
  &= \left( \begin{array}[c]
    (\left\{(x_0 - x_4)W_8^0 + (x_2 - x_6)W_8^2 \right\}W_2^0 + \left\{(x_1 - x_5)W_8^1 + (x_3 - x_7)W_8^3 \right\}W_2^0 \\
    \left\{(x_0 - x_4)W_8^0 + (x_2 - x_6)W_8^2 \right\}W_2^0 + \left\{(x_1 - x_5)W_8^1 + (x_3 - x_7)W_8^3 \right\}W_2^1
  \end{array} \right) & \\
  &= \left( \begin{array}[cccccccc]
    WW_8^0 & W_8^1 & W_8^2 & W_8^3 & -W_8^0 & -W_8^1 & -W_8^2 & -W_8^3 \\
    W_8^0 & W_8^5 & W_8^2 & W_8^7 & -W_8^0 & -W_8^5 & -W_8^2 & -W_8^7
  \end{array} \right) \left( \begin{array}[c]
    xx_0 \\
    x_1 \\
    x_2 \\
    x_3 \\
    x_4 \\
    x_5 \\
    x_6 \\
    x_7
  \end{array} \right) & \\
  &= \left( \begin{array}[cccccccc]
    11 & e^{-j\frac{\pi}{4}} & -j & e^{-j\frac{3\pi}{4}} & -1 & e^{-j\frac{5\pi}{4}} & j & e^{-j\frac{7\pi}{4}} \\
    1 & e^{-j\frac{5\pi}{4}} & -j & e^{-j\frac{7\pi}{4}} & -1 & e^{-j\frac{\pi}{4}} & j & e^{-j\frac{3\pi}{4}}
  \end{array} \right) \left( \begin{array}[c]
    xx_0 \\
    x_1 \\
    x_2 \\
    x_3 \\
    x_4 \\
    x_5 \\
    x_6 \\
    x_7
  \end{array} \right) & \\

  \boldsymbol{X}_{2k+1}^{(1)} &= \left( \begin{array}[c]
    XX_{1}^{(1)} \\
    X_{3}^{(1)}
  \end{array} \right) = \left( \begin{array}[c]
    XX_3 \\
    X_7
  \end{array} \right) & \\
  &= \left( \begin{array}[c]
    d\displaystyle\sum_{p=0}^{1}{\left(x_p^{(1)} - x_{p+2}^{(1)} \right)W_4^p W_2^0} \\
    \displaystyle\sum_{p=0}^{1}{\left(x_p^{(1)} - x_{p+2}^{(1)} \right)W_4^p W_2^p}
  \end{array} \right) = \left( \begin{array}[c]
    (\left(x_0^{(1)} - x_2^{(1)} \right)W_4^0 W_2^0 + \left(x_1^{(1)} - x_3^{(1)} \right)W_4^1 W_2^0 \\
    \left(x_0^{(1)} - x_2^{(1)} \right)W_4^0 W_2^0 + \left(x_1^{(1)} - x_3^{(1)} \right)W_4^1 W_2^1
  \end{array} \right) & \\
  &= \left( \begin{array}[c]
    (\left\{(x_0 - x_4)W_8^0 - (x_2 - x_6)W_8^2 \right\}W_4^0 W_2^0 + \left\{(x_1 - x_5)W_8^1 - (x_3 - x_7)W_8^3 \right\}W_4^1 W_2^0 \\
    \left\{(x_0 - x_4)W_8^0 - (x_2 - x_6)W_8^2 \right\}W_4^0 W_2^0 + \left\{(x_1 - x_5)W_8^1 - (x_3 - x_7)W_8^3 \right\}W_4^1 W_2^1
  \end{array} \right) \\
  &= \left( \begin{array}[cccccccc]
    WW_8^0 & W_8^3 & -W_8^2 & -W_8^5 & -W_8^0 & -W_8^3 & W_8^2 & W_8^5 \\
    W_8^0 & W_8^7 & -W_8^2 & -W_8^9 & -W_8^0 & -W_8^7 & W_8^2 & W_8^9
  \end{array} \right) \left( \begin{array}[c]
    xx_0 \\
    x_1 \\
    x_2 \\
    x_3 \\
    x_4 \\
    x_5 \\
    x_6 \\
    x_7
  \end{array} \right) & \\
  &= \left( \begin{array}[cccccccc]
    11 & e^{-j\frac{3\pi}{4}} & j & e^{-j\frac{\pi}{4}} & -1 & e^{-j\frac{7\pi}{4}} & -j & e^{-j\frac{5\pi}{4}} \\
    1 & e^{-j\frac{7\pi}{4}} & j & e^{-j\frac{5\pi}{4}} & -1 & e^{-j\frac{3\pi}{4}} & -j & e^{-j\frac{\pi}{4}}
  \end{array} \right) \left( \begin{array}[c]
    xx_0 \\
    x_1 \\
    x_2 \\
    x_3 \\
    x_4 \\
    x_5 \\
    x_6 \\
    x_7
  \end{array} \right) & \left(\because W_8^c W_4^d W_2^e = W_8^{c+2d+4e}, -1 = W_8^4 \right)
\end{align}
正しく計算できていることがわかりますね(遠い目)。ではもう一回FFTを適用しましょう。
\begin{align}
  \boldsymbol{x}^{(00)} &= \left(x_0^{(0)} + x_2^{(0)}, x_1^{(0)} + x_3^{(0)} \right) = \big((x_0 + x_4) + (x_2 + x_6), (x_1 + x_5) + (x_3 + x_7) \big) \\
  \boldsymbol{x}^{(01)} &= \left( \left(x_0^{(0)} - x_2^{(0)} \right)W_4^0, \left(x_1^{(0)} - x_3^{(0)} \right)W_4^1 \right) = \left(\{(x_0 + x_4) - (x_2 + x_6)\}W_4^0, \{(x_1 + x_5) - (x_3 + x_7)\}W_4^1 \right) \\
  \boldsymbol{x}^{(10)} &= \left(x_0^{(1)} + x_2^{(1)}, x_1^{(1)} + x_3^{(1)} \right) = \left((x_0 - x_4)W_8^0 + (x_2 - x_6)W_8^2, (x_1 - x_5)W_8^1 + (x_3 - x_7)W_8^3 \right) \\
  \boldsymbol{x}^{(11)} &= \left( \left(x_0^{(0)} - x_2^{(0)} \right)W_4^0, \left(x_1^{(0)} - x_3^{(0)} \right)W_4^1 \right) = \left( \left\{(x_0 - x_4)W_8^0 - (x_2 - x_6)W_8^2 \right\}W_4^0, \left\{(x_1 - x_5)W_8^1 - (x_3 - x_7)W_8^3 \right\}W_4^1 \right)
\end{align}
とすると
\left\{ \begin{array}[c]
  b\boldsymbol{X}^{(00)} = \mathcal{F}_{\boldsymbol{x}^{(00)}}(k) \\
  \boldsymbol{X}^{(01)} = \mathcal{F}_{\boldsymbol{x}^{(01)}}(k) \\
  \boldsymbol{X}^{(10)} = \mathcal{F}_{\boldsymbol{x}^{(10)}}(k) \\
  \boldsymbol{X}^{(11)} = \mathcal{F}_{\boldsymbol{x}^{(11)}}(k)
\end{array} \right.
\quad k = 0, 1
ですので
\begin{align}
  \boldsymbol{X}_{2k}^{(00)} &= \mathcal{F}_{\boldsymbol{x}^{(00)}}(2k) \\
  &= \sum_{p=0}^{0}{\left(x_p^{(00)} + x_{p+1}^{(00)}\right) W_{1}^{kp}} \\
  \boldsymbol{X}_{2k+1}^{(00)} &= \mathcal{F}_{\boldsymbol{x}^{(00)}}(2k+1) \\
  &= \sum_{p=0}^{0}{\left(x_p^{(00)} - x_{p+1}^{(00)}\right)W_2^{p} W_{1}^{kp}} \\
  \boldsymbol{X}_{2k}^{(01)} &= \mathcal{F}_{\boldsymbol{x}^{(01)}}(2k) \\
  &= \sum_{p=0}^{0}{\left(x_p^{(01)} + x_{p+1}^{(01)}\right) W_{1}^{kp}} \\
  \boldsymbol{X}_{2k+1}^{(01)} &= \mathcal{F}_{\boldsymbol{x}^{(01)}}(2k+1) \\
  &= \sum_{p=0}^{0}{\left(x_p^{(01)} - x_{p+1}^{(01)}\right)W_2^{p} W_{1}^{kp}} \\
  \boldsymbol{X}_{2k}^{(10)} &= \mathcal{F}_{\boldsymbol{x}^{(10)}}(2k) \\
  &= \sum_{p=0}^{0}{\left(x_p^{(10)} + x_{p+1}^{(10)}\right) W_{1}^{kp}} \\
  \boldsymbol{X}_{2k+1}^{(10)} &= \mathcal{F}_{\boldsymbol{x}^{(10)}}(2k+1) \\
  &= \sum_{p=0}^{0}{\left(x_p^{(10)} - x_{p+1}^{(10)}\right)W_2^{p} W_{1}^{kp}} \\
  \boldsymbol{X}_{2k}^{(11)} &= \mathcal{F}_{\boldsymbol{x}^{(11)}}(2k) \\
  &= \sum_{p=0}^{0}{\left(x_p^{(11)} + x_{p+1}^{(11)}\right) W_{1}^{kp}} \\
  \boldsymbol{X}_{2k+1}^{(11)} &= \mathcal{F}_{\boldsymbol{x}^{(11)}}(2k+1) \\
  &= \sum_{p=0}^{0}{\left(x_p^{(11)} - x_{p+1}^{(11)}\right)W_2^{p} W_{1}^{kp}} \\
\end{align}
こ、ここまできたら気合でやってやる...!
\begin{align}
  \boldsymbol{X}_{2k}^{(00)} &= X_0 \\
  &= \sum_{p=0}^{0}{\left(x_p^{(00)} + x_{p+1}^{(00)}\right) W_{1}^{0}} = \left(x_0^{(00)} + x_{1}^{(00)}\right) W_{1}^{0} \\
  &= \left(((x_0 + x_4) + (x_2 + x_6)) + ((x_1 + x_5) + (x_3 + x_7))\right) W_{1}^{0} \\
  &= \left( \begin{array}[cccccccc]
    WW_{1}^{0} & W_{1}^{0} & W_{1}^{0} & W_{1}^{0} & W_{1}^{0} & W_{1}^{0} & W_{1}^{0} & W_{1}^{0}
  \end{array} \right) \left( \begin{array}[c]
    xx_0 \\
    x_1 \\
    x_2 \\
    x_3 \\
    x_4 \\
    x_5 \\
    x_6 \\
    x_7
  \end{array} \right) \\
  &= \left( \begin{array}[cccccccc]
    11 & 1 & 1 & 1 & 1 & 1 & 1 & 1
  \end{array} \right) \left( \begin{array}[c]
    xx_0 \\
    x_1 \\
    x_2 \\
    x_3 \\
    x_4 \\
    x_5 \\
    x_6 \\
    x_7
  \end{array} \right) \\

  \boldsymbol{X}_{2k+1}^{(00)} &= X_4 \\
  &= \sum_{p=0}^{0}{\left(x_p^{(00)} - x_{p+1}^{(00)}\right)W_2^{p} W_{1}^{kp}} = \left(x_0^{(00)} - x_{1}^{(00)}\right)W_2^0 W_{1}^{0} \\
  &= \left(((x_0 + x_4) + (x_2 + x_6)) - ((x_1 + x_5) + (x_3 + x_7))\right) W_2^0 W_{1}^{0} \\
  &= \left( \begin{array}[cccccccc]
    WW_{2}^{0} & -W_{2}^{0} & W_{2}^{0} & -W_{2}^{0} & W_{2}^{0} & -W_{2}^{0} & W_{2}^{0} & -W_{2}^{0}
  \end{array} \right) \left( \begin{array}[c]
    xx_0 \\
    x_1 \\
    x_2 \\
    x_3 \\
    x_4 \\
    x_5 \\
    x_6 \\
    x_7
  \end{array} \right) \\
  &= \left( \begin{array}[cccccccc]
    11 & -1 & 1 & -1 & 1 & -1 & 1 & -1
  \end{array} \right) \left( \begin{array}[c]
    xx_0 \\
    x_1 \\
    x_2 \\
    x_3 \\
    x_4 \\
    x_5 \\
    x_6 \\
    x_7
  \end{array} \right) \\

  \boldsymbol{X}_{2k}^{(01)} &= X_2 \\
  &= \sum_{p=0}^{0}{\left(x_p^{(01)} + x_{p+1}^{(01)}\right) W_{1}^{kp}} = \left(x_0^{(01)} + x_{1}^{(01)}\right) W_{1}^{0} \\
  &= \left(\{(x_0 + x_4) - (x_2 + x_6)\}W_4^0 + \{(x_1 + x_5) - (x_3 + x_7)\}W_4^1 \right) W_{1}^{0} \\
  &= \left( \begin{array}[cccccccc]
    WW_{4}^{0} & W_{4}^{1} & -W_{4}^{0} & -W_{4}^{1} & W_{4}^{0} & W_{4}^{1} & -W_{4}^{0} & -W_{4}^{1}
  \end{array} \right) \left( \begin{array}[c]
    xx_0 \\
    x_1 \\
    x_2 \\
    x_3 \\
    x_4 \\
    x_5 \\
    x_6 \\
    x_7
  \end{array} \right) \\
  &= \left( \begin{array}[cccccccc]
    11 & -j & -1 & j & 1 & -j & -1 & j \\
  \end{array} \right) \left( \begin{array}[c]
    xx_0 \\
    x_1 \\
    x_2 \\
    x_3 \\
    x_4 \\
    x_5 \\
    x_6 \\
    x_7
  \end{array} \right) \\

\boldsymbol{X}_{2k+1}^{(01)} &= X_6 \\
  &= \sum_{p=0}^{0}{\left(x_p^{(01)} - x_{p+1}^{(01)}\right)W_2^{p} W_{1}^{kp}} = \left(x_0^{(01)} - x_{1}^{(01)}\right)W_2^0 W_{1}^{0} \\
  &= \left(\{(x_0 + x_4) - (x_2 + x_6)\}W_4^0 - \{(x_1 + x_5) - (x_3 + x_7)\}W_4^1 \right) W_2^0 W_{1}^{0} \\
  &= \left( \begin{array}[cccccccc]
    WW_{4}^{0} & -W_{4}^{1} & -W_{4}^{0} & W_{4}^{1} & W_{4}^{0} &  -W_{4}^{1} & -W_{4}^{0} & W_{4}^{1}
  \end{array} \right) \left( \begin{array}[c]
    xx_0 \\
    x_1 \\
    x_2 \\
    x_3 \\
    x_4 \\
    x_5 \\
    x_6 \\
    x_7
  \end{array} \right) \\
  &= \left( \begin{array}[cccccccc]
    11 & j & -1 & -j & 1 & j & -1 & -j
  \end{array} \right) \left( \begin{array}[c]
    xx_0 \\
    x_1 \\
    x_2 \\
    x_3 \\
    x_4 \\
    x_5 \\
    x_6 \\
    x_7
  \end{array} \right) \\

  \boldsymbol{X}_{2k}^{(10)} &= X_1 \\
  &= \sum_{p=0}^{0}{\left(x_p^{(10)} + x_{p+1}^{(10)}\right) W_{1}^{0}} = \left(x_0^{(10)} + x_{1}^{(10)}\right) W_{1}^{0} \\
  &= \left(((x_0 - x_4)W_8^0 + (x_2 - x_6)W_8^2) + ((x_1 - x_5)W_8^1 + (x_3 - x_7)W_8^3) \right) W_{1}^{0} \\
  &= \left( \begin{array}[cccccccc]
    WW_{8}^{0} & W_{8}^{1} & W_{8}^{2} & W_{8}^{3} & -W_{8}^{0} & -W_{8}^{1} & -W_{8}^{2} & -W_{8}^{3}
  \end{array} \right) \left( \begin{array}[c]
    xx_0 \\
    x_1 \\
    x_2 \\
    x_3 \\
    x_4 \\
    x_5 \\
    x_6 \\
    x_7
  \end{array} \right) \\
  &= \left( \begin{array}[cccccccc]
    11 & e^{-j\frac{\pi}{4}} & -j & e^{-j\frac{3\pi}{4}} & -1 & e^{-j\frac{5\pi}{4}} & j & e^{-j\frac{7\pi}{4}}
  \end{array} \right) \left( \begin{array}[c]
    xx_0 \\
    x_1 \\
    x_2 \\
    x_3 \\
    x_4 \\
    x_5 \\
    x_6 \\
    x_7
  \end{array} \right) \\

  \boldsymbol{X}_{2k+1}^{(10)} &= X_5 \\
  &= \sum_{p=0}^{0}{\left(x_p^{(10)} - x_{p+1}^{(10)}\right)W_2^{p} W_{1}^{kp}} = \left(x_0^{(10)} - x_{1}^{(10)}\right)W_2^0 W_{1}^{0} \\
  &= \left(\{(x_0 - x_4)W_8^0 + (x_2 - x_6)W_8^2\} - \{(x_1 - x_5)W_8^1 + (x_3 - x_7)W_8^3\}\right) W_2^0 W_{1}^{0} \\
  &= \left( \begin{array}[cccccccc]
    WW_{8}^{0} & -W_{8}^{1} & W_{8}^{2} & -W_{8}^{3} & -W_{8}^{0} & W_{8}^{1} & -W_{8}^{2} & W_{8}^{3}
  \end{array} \right) \left( \begin{array}[c]
    xx_0 \\
    x_1 \\
    x_2 \\
    x_3 \\
    x_4 \\
    x_5 \\
    x_6 \\
    x_7
  \end{array} \right) \\
  &= \left( \begin{array}[cccccccc]
    11 & e^{-j\frac{5\pi}{4}} & -j & e^{-j\frac{7\pi}{4}} & -1 & e^{-j\frac{\pi}{4}} & j & e^{-j\frac{3\pi}{4}}
  \end{array} \right) \left( \begin{array}[c]
    xx_0 \\
    x_1 \\
    x_2 \\
    x_3 \\
    x_4 \\
    x_5 \\
    x_6 \\
    x_7
  \end{array} \right) \\

  \boldsymbol{X}_{2k}^{(11)} &= X_3 \\
  &= \sum_{p=0}^{0}{\left(x_p^{(11)} + x_{p+1}^{(11)}\right) W_{1}^{0}} = \left(x_0^{(11)} + x_{1}^{(11)}\right) W_{1}^{0} \\
  &= \left(\{(x_0 - x_4)W_8^0 - (x_2 - x_6)W_8^2\}W_4^0 + \{(x_1 - x_5)W_8^1 - (x_3 - x_7)W_8^3\}W_4^1 \right) W_{1}^{0} \\
  &= \left( \begin{array}[cccccccc]
    WW_{8}^{0} & W_{8}^{3} & -W_{8}^{2} & -W_{8}^{5} & -W_{8}^{0} & -W_{8}^{3} & W_{8}^{2} & W_{8}^{5}
  \end{array} \right) \left( \begin{array}[c]
    xx_0 \\
    x_1 \\
    x_2 \\
    x_3 \\
    x_4 \\
    x_5 \\
    x_6 \\
    x_7
  \end{array} \right) \\
  &= \left( \begin{array}[cccccccc]
    11 & e^{-j\frac{3\pi}{4}} & j & e^{-j\frac{\pi}{4}} & -1 & e^{-j\frac{7\pi}{4}} & -j & e^{-j\frac{5\pi}{4}}
  \end{array} \right) \left( \begin{array}[c]
    xx_0 \\
    x_1 \\
    x_2 \\
    x_3 \\
    x_4 \\
    x_5 \\
    x_6 \\
    x_7
  \end{array} \right) \\

  \boldsymbol{X}_{2k+1}^{(11)} &= X_7 \\
  &= \sum_{p=0}^{0}{\left(x_p^{(11)} - x_{p+1}^{(11)}\right)W_2^{p} W_{1}^{kp}} = \left(x_0^{(11)} - x_{1}^{(11)}\right)W_2^0 W_{1}^{0} \\
  &= \left(\{(x_0 - x_4)W_8^0 - (x_2 - x_6)W_8^2\}W_4^0 - \{(x_1 - x_5)W_8^1 - (x_3 - x_7)W_8^3\}W_4^1\right) W_2^0 W_{1}^{0} \\
  &= \left( \begin{array}[cccccccc]
    WW_{8}^{0} & -W_{8}^{3} & -W_{8}^{2} & W_{8}^{5} & -W_{8}^{0} & W_{8}^{3} & W_{8}^{2} -& W_{8}^{5}
  \end{array} \right) \left( \begin{array}[c]
    xx_0 \\
    x_1 \\
    x_2 \\
    x_3 \\
    x_4 \\
    x_5 \\
    x_6 \\
    x_7
  \end{array} \right) \\
  &= \left( \begin{array}[cccccccc]
    11 & e^{-j\frac{7\pi}{4}} & j & e^{-j\frac{5\pi}{4}} & -1 & e^{-j\frac{3\pi}{4}} & -j & e^{-j\frac{\pi}{4}}
  \end{array} \right) \left( \begin{array}[c]
    xx_0 \\
    x_1 \\
    x_2 \\
    x_3 \\
    x_4 \\
    x_5 \\
    x_6 \\
    x_7
  \end{array} \right)
\end{align}
という感じですね！しっかり一致しています。
ここまでの書き下しによる計算の確認では$\boldsymbol{x}^{(0)}$などを展開して計算していますが、実際の実装ではそのようなことは行われないことに注意してください。
また、お気づきの方もいらっしゃるかもしれませんが、下記のようにビット反転並び替えが発生しています。
X^{(000)} = X_{2k}^{(00)} = X_0 = X_{(000)_{(2)}} \quad
X^{(001)} = X_{2k+1}^{(00)} = X_4 = X_{(100)_{(2)}} \\
X^{(010)} = X_{2k}^{(01)} = X_2 = X_{(010)_{(2)}} \quad
X^{(011)} = X_{2k+1}^{(01)} = X_6 = X_{(110)_{(2)}} \\
X^{(100)} = X_{2k}^{(10)} = X_1 = X_{(001)_{(2)}} \quad
X^{(101)} = X_{2k+1}^{(10)} = X_5 = X_{(101)_{(2)}} \\
X^{(110)} = X_{2k}^{(11)} = X_3 = X_{(011)_{(2)}} \quad
X^{(111)} = X_{2k+1}^{(11)} = X_7 = X_{(111)_{(2)}}
分解の仕方を考えると当然といえば当然の順番の入れ替えが発生しています。このままだと効率が悪いので、実装の段階でうまくすることで正しい順序で計算できるようにすることができます。
詳しくは参考サイトをご覧ください。
これにより計算量は$\mathcal{O}(N \log_2 N)$まで削減されます。計算量の世界において対数オーダというのは非常に優秀なものであり、$N$の値が余程法外な値を取らなければ現実的な時間内に計算を終えることができるという保証になります。

とまあそんな具合で高速なフーリエ変換が可能となるわけです。ただ、時間計算量のオーダが$\mathcal{O}(N \log_2 N)$となる大変有効な計算手法ではありますが欠点がないわけでなく、仮定から空間計算量の観点では効率が悪くなります。なんせ2の累乗に揃える必要があります。通常はゼロパディングで行いますが、変換対象のサイズが大きくなればなるほど2の累乗から離れやすくなり、余分に無駄なゼロパディングをする必要が出てきます。
そのため、使用する場合はメモリの余裕などをきちんと考慮して時間/空間計算量のトレードオフを加味しましょう。

参考

Fast Training of Convolutional Networks through FFTs; Michael Mathieu, Mikael Henaff, Yann LeCun; arXiv:1312.5851v5 [cs.CV] 6 Mar 2014

深層学習の畳み込み層の処理は「畳み込み」じゃなかった件

自己相関と相互相関

高速フーリエ変換入門 -- Cooley-Tukey のアルゴリズム

おわりに

付録の方が本編の10倍は時間掛かった...誰の役に立つのやら...
今後FCNN関連の論文をこんな感じでまとめつつ情報収集していずれ実装していきたいなぁと思っています。
何か情報をお持ちの方はぜひ教えてください！

	空間領域	フーリエ領域
$\displaystyle\sum_{C}{x_C * F_{CM}}$	$BCMO^2F^2$	$2C_{order}I^2(BM + BC + CM)\log{I} + 4BCMI^2$
$\cfrac{\partial L}{\partial y_M} * w^{\top}_{CM} $	$BCMI^2F^2$	$2C_{order}O^2(BM + BC + CM)\log{O} + 4BCMO^2$
$\cfrac{\partial L}{\partial y_M} * x_C$	$BCMO^2F^2$	$2C_{order}I^2(BM + BC + CM)\log{I} + 4BCMI^2$

　 Tweet
Qiitaで続きを読む

投稿日：2020-10-19T11:52:05+09:00

pytestでライブラリの中身まで入ってデバッグテストする設定

あらすじ

pytestやunittestなどのテストをしているときに、自分のコードだけのステップ実行では問題が解決しないことがあります。
そんな時、インストールしたライブラリの中までデバッグしたい場合があります。
以下の設定をすれば、pipなどでインストールしたライブラリ内にブレークポイントを設定することもできます。

ただし、C言語で実装されたライブラリは本記事の末尾で紹介する参考ページのような方法が必要です。

通常のデバッグの場合

デバッグテストではなく、通常のデバッグのときには、
VSCodeでライブラリの中身まで入ってデバッグする設定をご覧いただくといいと思います。

普段の設定

普段は、vscodeでデバッグしているとき、launch.jsonは以下の設定になっていることが多いと思います。
launch.json
{
    // IntelliSense を使用して利用可能な属性を学べます。
    // 既存の属性の説明をホバーして表示します。
    // 詳細情報は次を確認してください: https://go.microsoft.com/fwlink/?linkid=830387
    "version": "0.2.0",
    "configurations": [
        {
            "name": "Python: Current File",
            "type": "python",
            "request": "launch",
            "program": "${file}",
            "console": "integratedTerminal"
        }
    ]
}
デバッグテストで他者のライブラリに潜る設定

"request"が"test"になっている構成があると、デバッグテストのときに使用されます。

また、この構成は、最初の１つだけが読み込まれます。
以降に同様の構成があると無視されます。

この構成にjustMyCodeがあり、「自分のコードだけ」か切り替えることが出来ます。
launch.json
{
    // IntelliSense を使用して利用可能な属性を学べます。
    // 既存の属性の説明をホバーして表示します。
    // 詳細情報は次を確認してください: https://go.microsoft.com/fwlink/?linkid=830387
    "version": "0.2.0",
    "configurations": [
        {
            "name": "Python: Current File",
            "type": "python",
            "request": "launch",
            "program": "${file}",
            "console": "integratedTerminal"
        },
        {
            "name": "Debug Tests",
            "type": "python",
            "request": "test",
            "console": "integratedTerminal",
            "justMyCode": false
        }
    ]
}
もちろん、元に戻すときには、追加した行を消すだけでOKです。

C言語で実装されたライブラリの場合

混合モードデバッグ機能と言って、Python と C++ を同時にデバッグする方法がVisual Studioで提供されています。
VScodeでも、Python と OpenCV を混合でデバッグ（ステップ実行）する方法を参考にして各種ライブラリをデバッグすることが可能です。

Excelsior!

　 Tweet
Qiitaで続きを読む

投稿日：2020-10-19T11:38:02+09:00

nameについて簡単に

name

実行しているコードでは、__ name __ =' __ main __ 'が入る
import されたファイルの内部では、__ name __ ='ファイル名'が入ってる
これを区別する事で、どのファイルを実行しているかが分かる
従って、mainファイルを他のファイルで呼び出した時に、main()は実行されない仕組みが作れる

具体例

bファイルにif name == 'main':がない場合
b.py
def import_print_name():
  return __name__

print(import_print_name())
main.py
import b

def main():
  print("importしたファイル名になる。今回の場合",b.import_print_name())
  print(__name__)

if __name__ == '__main__':
  main()
実行結果（mainを実行）.
b
importしたファイル名になる。今回の場合 b
__main__
上記bは、import bの時点で呼び出される

bファイルにif name == 'main':がある場合
b.py
def import_print_name():
  return __name__

if __name__=='__main__':
  print(import_print_name())
main.py
import b

def main():
  print("importしたファイル名になる。今回の場合",b.import_print_name())
  print(__name__)

if __name__ == '__main__':
  main()
実行結果（mainを実行）.
importしたファイル名になる。今回の場合 b
__main__

　 Tweet
Qiitaで続きを読む

投稿日：2020-10-19T10:19:33+09:00

Python基礎④

Pythonの基礎知識④です。
引き続き自分の勉強メモです。
過度な期待はしないでください。

過去投稿記事

Python基礎
 Python基礎②
Python基礎③

クラスの定義

　-「もの」を生成する仕組み
　その「もの」を生成するには、まずその「設計図」を用意する必要がある。
　その設計図のことをクラス、
　「もの」のことをインスタンスと呼ぶ。

インスタンスを生成する

1、「クラスを用意する」
　- クラスは「class クラス名:」で定義
例
class Vehicletype: # 行末にコロンは必須
    pass # 何も処理がない事を表す
    # インデントを揃える（半角スペース４つ分）
2、「クラスからインスタンスを生成」
　-「クラス名()」とそのクラスを呼び出すことで、
　クラスを用いて新しくインスタンスを生成することが出来る。
　そして、「変数名 = クラス名()」とすることで、生成したインスタンスを変数に代入することが出来る。
例
class Vehicletype: # 行末にコロンは必須
    pass # 何も処理がない事を表す
    # インデントを揃える（半角スペース４つ分）

vehicle_type1 = Vehicletype()
               # Vehicletypeクラスからインスタンスを生成
3、インスタンスに情報を追加

-「vehicle_type1.name = 'トラック'」とすることで、menu_item1に
　「name」が「トラック」であるという情報を追加することが出来る。
　この時、「name」のことを「インスタンス変数」と呼ぶ。
例
class Vehicletype: # 行末にコロンは必須
    pass # 何も処理がない事を表す
    # インデントを揃える（半角スペース４つ分）

vehicle_type1 = Vehicletype()
               # Vehicletypeクラスからインスタンスを生成
vehicle_type1.name = 'トラック'

print(vehicle_type1.name) 
# 出力結果 →　トラック


vehicle_type2 = Vehicletype()
               # Vehicletypeクラスからインスタンスを生成
vehicle_type2.name = 'バス'

print(vehicle_type2.name) 
# 出力結果 →　バス
クラスの中に処理を追加

　-クラスの中では関数を定義することが出来る。
　クラスの中で定義した関数のことをメソッドと呼ぶ。

　-メソッドの定義の方法
　第1引数にselfを追加する必要がある
例
class Vehicletype: 
    def hello(self): # 第1引数にselfを追加
    # インデントを揃える（半角スペース４つ分）
      print('こんにちは')
　-クラスの中で定義したメソッドを呼び出す
　「インスタンス.メソッド名()」とすることで、そのメソッドを呼び出すことが出来る
例
class Vehicletype: 
    def hello(self): # 第1引数にselfを追加
    # インデントを揃える（半角スペース４つ分）
        print('こんにちは')
        # インデントを揃える（半角スペース４つ分）

vehicle_type1 = Vehicletype()
               # Vehicletypeクラスからインスタンスを生成
vehicle_type1.hello()

# 出力結果 →　こんにちは
インスタンスメソッド

　-インスタンスメソッドの第1引数に指定した「self」には、そのメソッドを呼び出したインスタンス自身が代入されている。
　そのため、「self.name」とすることで、そのメソッドを呼び出している「vehicle_type1」の「name」の値を取得することが出来る。
例
class Vehicletype:
    def info(self): # selfにvehicle_type1が代入されている
        print(self.name)

vehicle_type1 = Vehicletype()
vehicle_type1.name = 'トラック'

vehicle_type1.info 
# 出力結果 →　トラック
　-「return」を使って戻り値として返すことが出来る
例
class Vehicletype:
    def info(self): # selfにvehicle_type1が代入されている
        return self.name

vehicle_type1 = Vehicletype()
vehicle_type1.name = 'トラック'

print(vehicle_type1.info )
# 出力結果 →　トラック
　-インスタンスメソッド（引数）
例
class Vehicletype:
    def info(self, count): # countに「4」が代入される、「self」の分だけ引数の順番がずれる

vehicle_type1 = Vehicletype()
vehicle_type1.name = 'トラック'

vehicle_type1.info(4)
　-__init__メソッド
　__init__メソッドは、「クラス名()」でインスタンスを生成した直後に自動で呼び出されるメソッド。
例
class Vehicletype:
    def __init__(self):
        print('車種をお選びください')

vehicle_type1 = Vehicletype()
                # インスタンスが生成されたので__init__メソッドが自動で呼び出される

# 出力結果 →　車種をお選びください
　-__init__メソッド（値を代入）
　インスタンスを生成すると同時にインスタンス変数に値を代入することが出来る。
例
class Vehicletype:
    def __init__(self):
        self.name = 'トラック'

vehicle_type1 = Vehicletype()
                # インスタンスが生成されたので__init__メソッドが自動で呼び出される

print(vehicle_type1.name)
# 出力結果 →　トラック
-__init__メソッド（引数）
　インスタンスメソッドと同じように、引数を受け取ることも出来る。
例
class Vehicletype:
    def __init__(self, name):
        self.name = name

vehicle_type1 = Vehicletype('トラック')
                # インスタンスが生成されたので__init__メソッドが自動で呼び出される

print(vehicle_type1.name)
# 出力結果 →　トラック

　 Tweet
Qiitaで続きを読む

20201019のPythonに関する記事は30件です。

【CRUD】【Django】PythonフレームワークDjangoを使ってCRUDサイトを作成する～2～

シリーズ一覧(全記事完成したら更新していきます)

モデルを作成する

マイグレーション

マイグレート

データを登録する

管理画面にPostを表示させる

管理ユーザを作成する

管理画面にログインする

データを登録してみる！

1次元のメディアンフィルター（中央値フィルター）

【python】enumerateの動作

動作

Djangoチュートリアル（ブログアプリ作成）⑤ - 記事作成機能編

form の準備

urls.py の修正

views.py の修正

template の準備

test_views.py の修正

【 情報圧縮ノート003 】ダルかった大学の電磁気学の教授の講談と板書をJpeg１枚に圧縮してまえ計画。

ルービックキューブロボットのソフトウェアをアップデートした 6. 機械操作(Arduino)

この記事はなに？

関連する記事集

定数と変数

サーボライブラリ周り

セットアップ

アームを回転させる

アームのキャリブレーション

パズルを離す

パズルを掴む

メインループ

まとめ

うんち?でも足し算がしたい！～絵文字で四則演算～

はじまり

?の足し算を考えてみる

Pythonでいじる

Unicode物語

個人的におもしろかった数式

一位： ? / 6 = 危

最後に

参考文献

PythonのFlaskで画像データをreturnし、HTMLのcanvas要素へ描写する

やりたいこと

Cloud functionsでStorageのファイルを読み込んでダウンロードする

単体ファイルとしてダウンロードさせるのではなく、flaskでjpgとしてreturnしてダウンロードする

canvas要素への描写

感想

SONYのNNCチャレンジ（音声データを用いてAudioStockに役立つものを作れ）に応募する。

0. 私は誰？

1. SONY NNCチャレンジとは

2. 今回のテーマ

3. 何が必要か

4. 楽曲データの整形

5. アノテーションCSVファイルの作成

6. 学習

スライディングウィングを創造で書いた。

【 情報圧縮ノート002 】$PATHを通さないと $conda で Anacondaが使えない

Pythonでスクレイピング(データ取得)

結果

解説

VSCodeでPythonが動かなくなった話(Windows10)

起きたこと

ダメだった対策

最終的な解決

お気持ち

CheckboxTreeviewを使ったチェックリスト→テキスト作成

コード作成の経緯

概要

コード

出力結果

機材リストのcsv

引用

[Unity]超絶初心者でもML-Agents Release8を動かす方法[Windows]

免責

バージョン確認

実行環境

ANACONDA3インストール手順

ML-Agentsダウンロード手順

Python3.7インストール手順

【情報圧縮ノート003 】ダルかった大学の電磁気学の教授の講談と板書をJpeg１枚に圧縮してまえ計画。

【情報圧縮ノート002 】$PATHを通さないと $conda で Anacondaが使えない

【パチスロ】アナターのオット!?はーですの「右上がり黄７」による設定判別