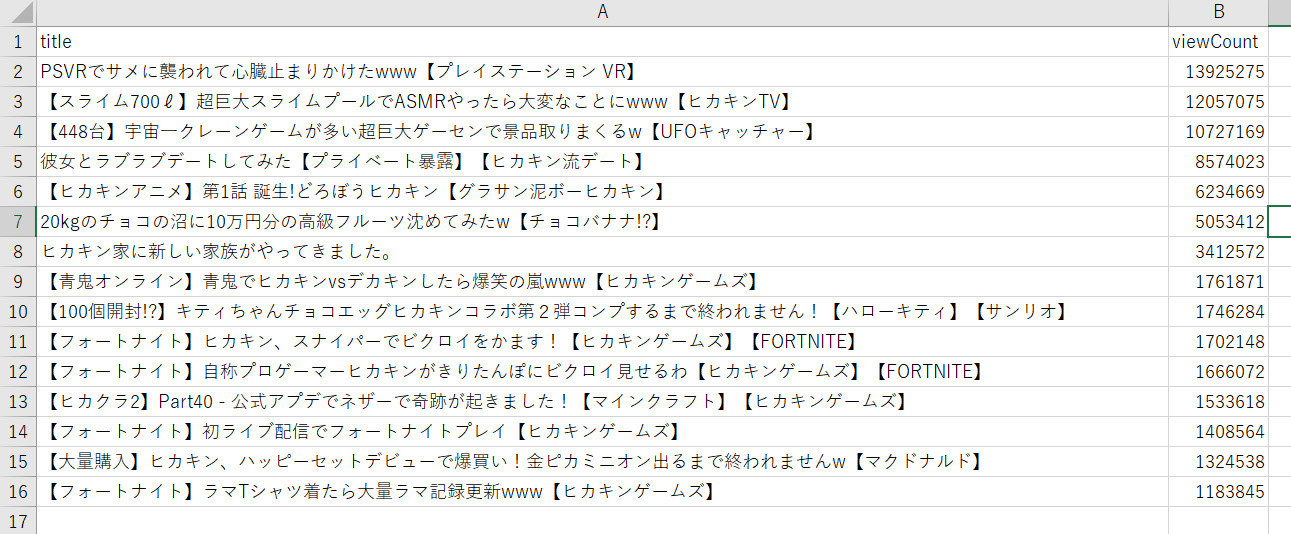
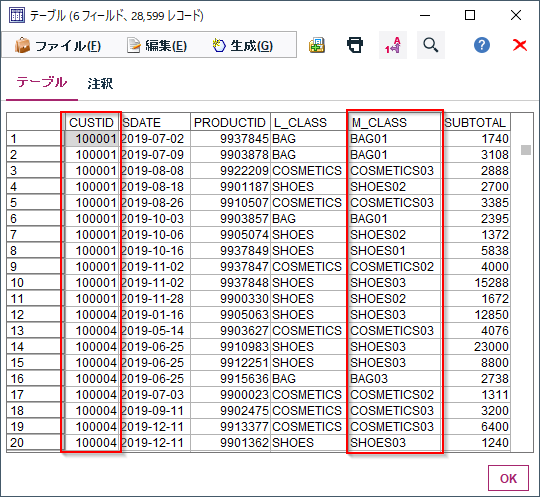
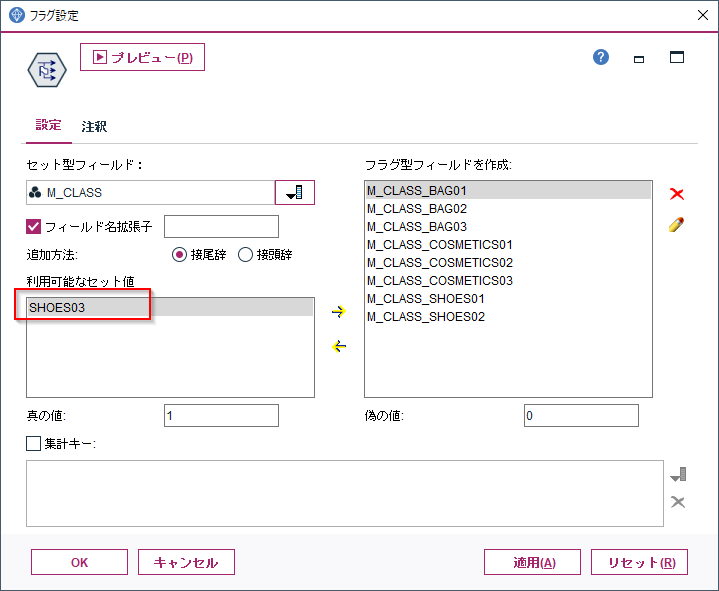
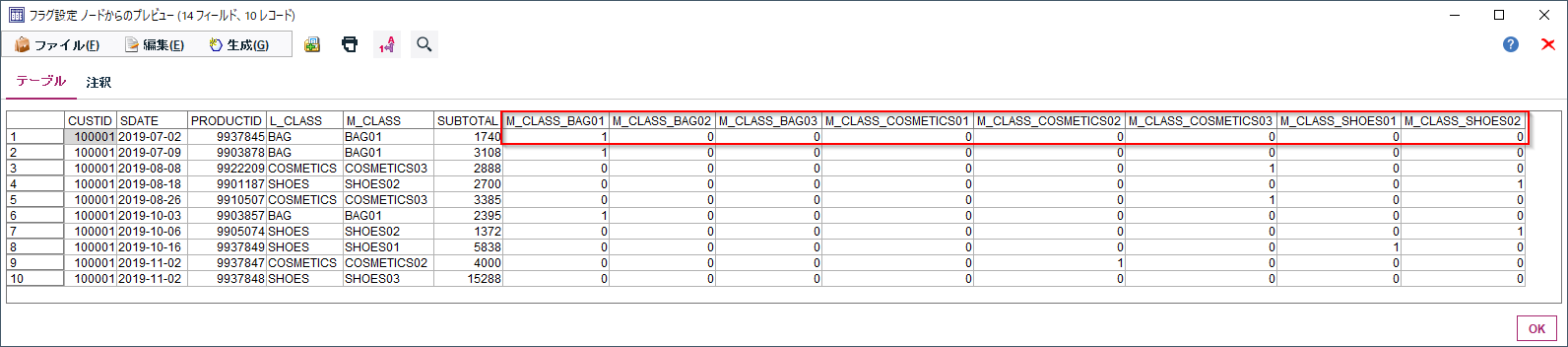
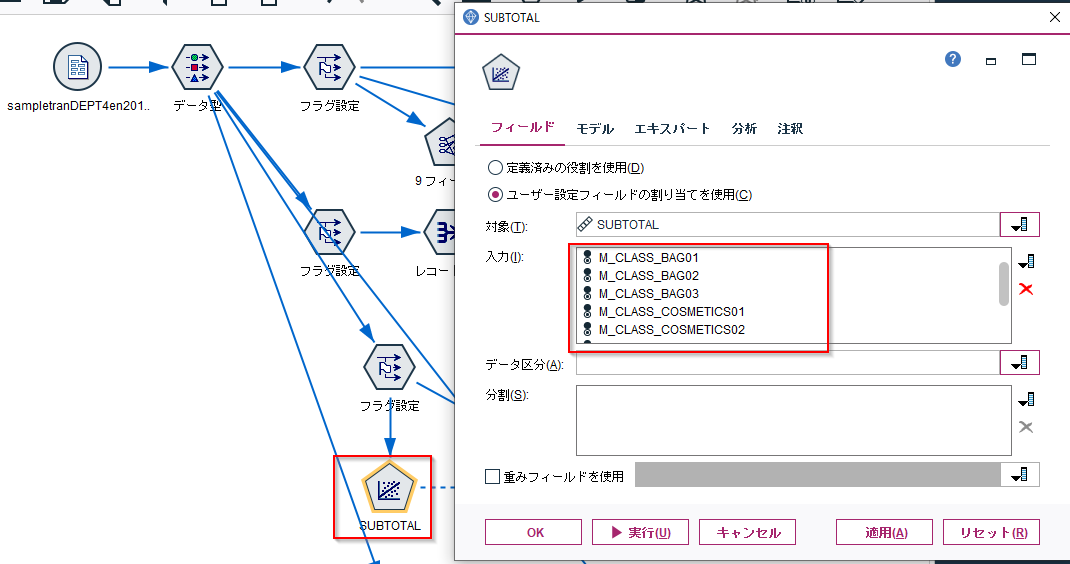
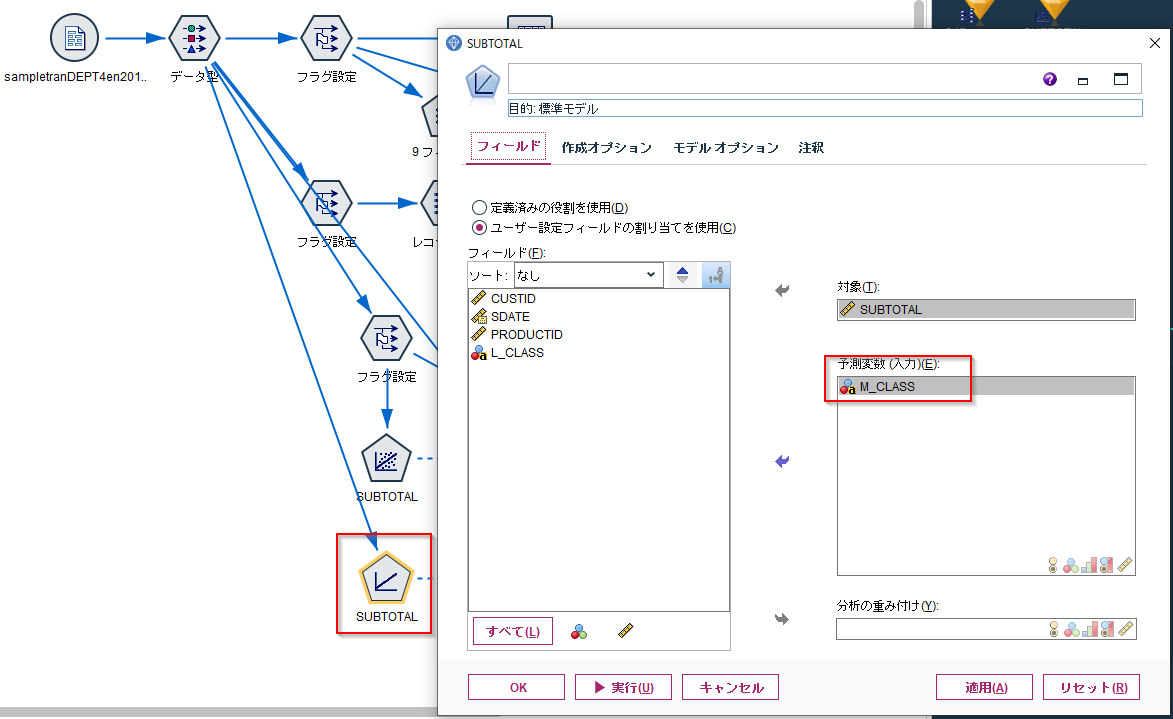
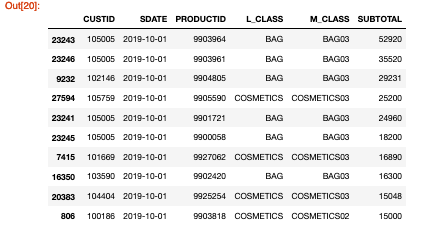
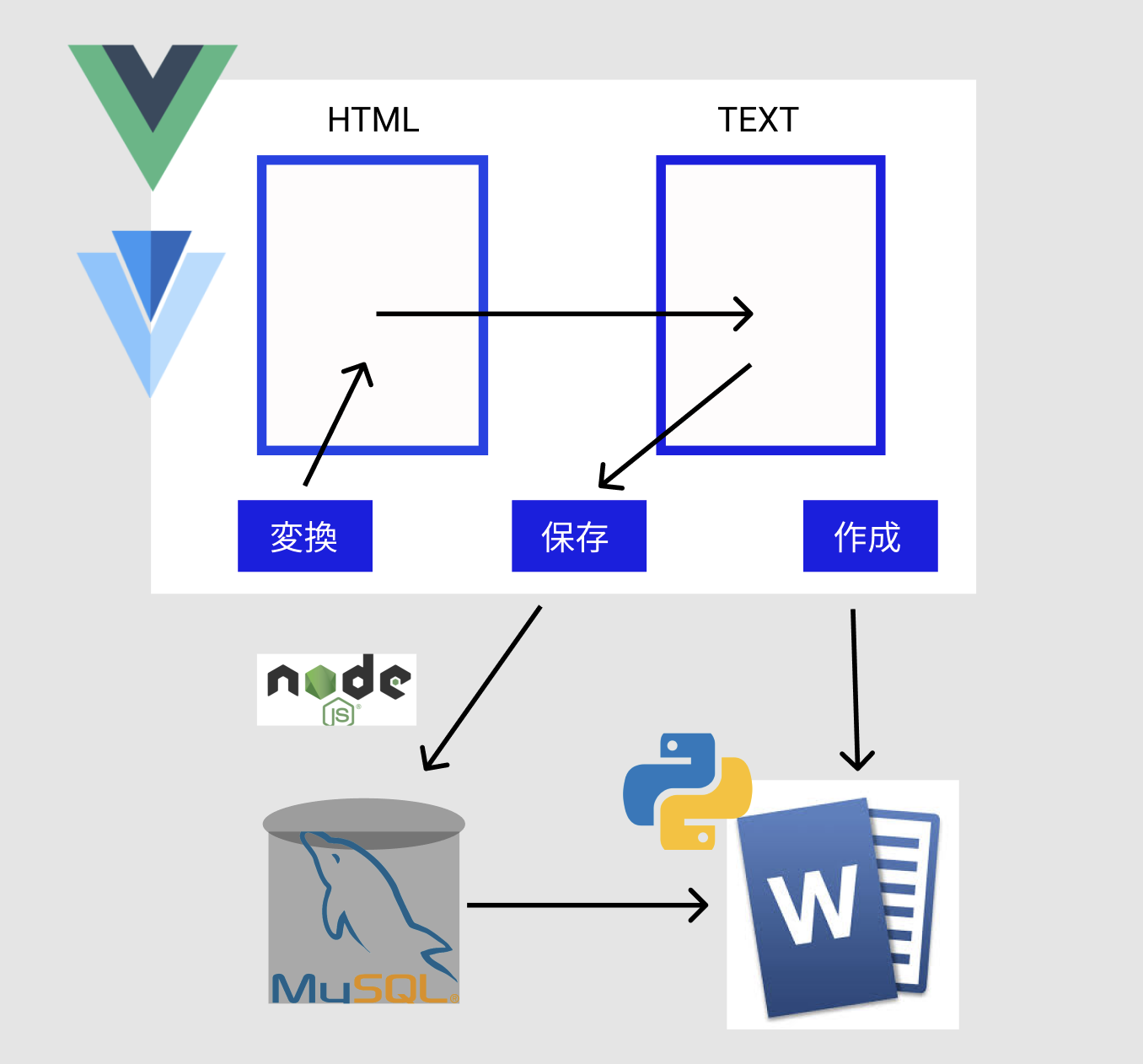
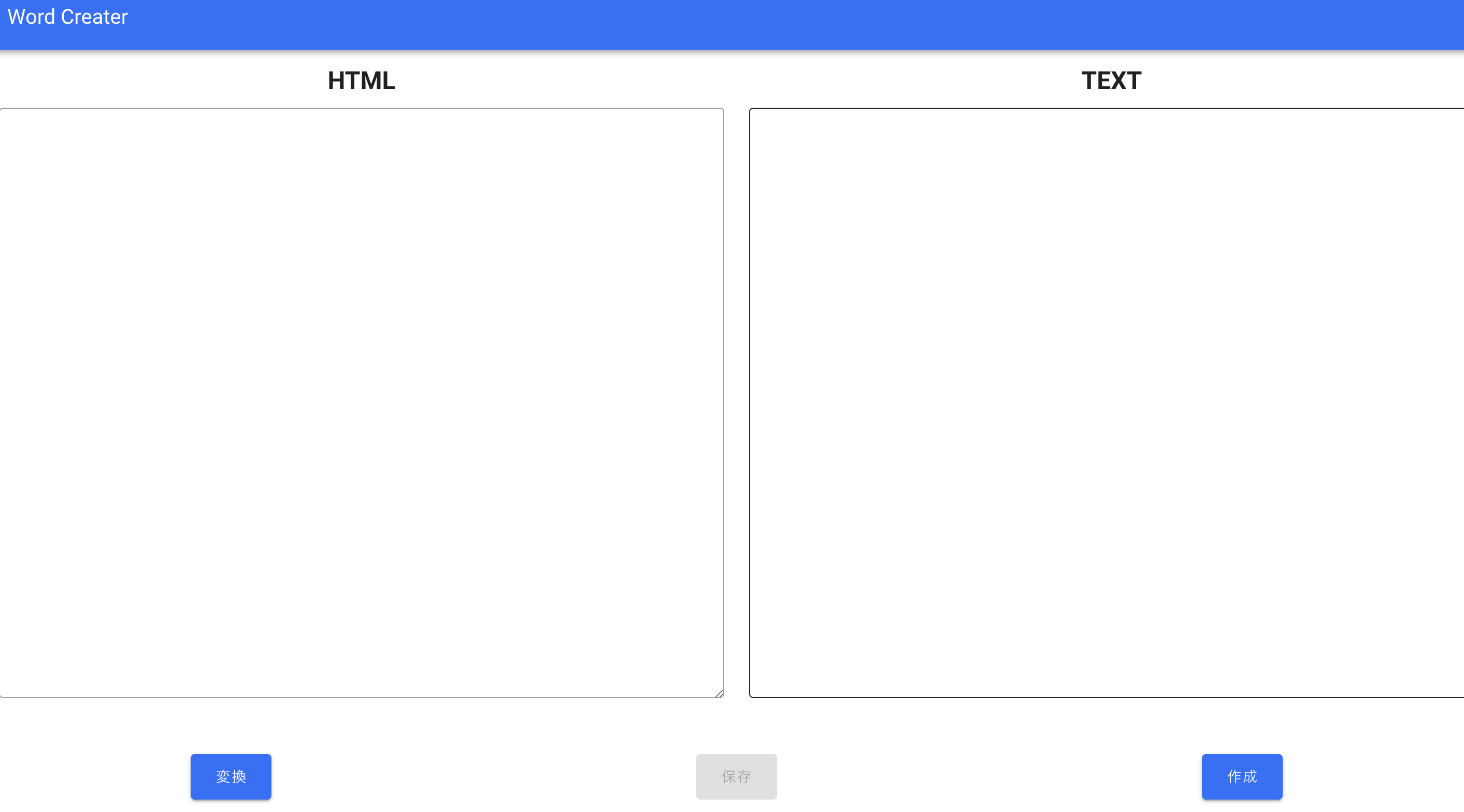
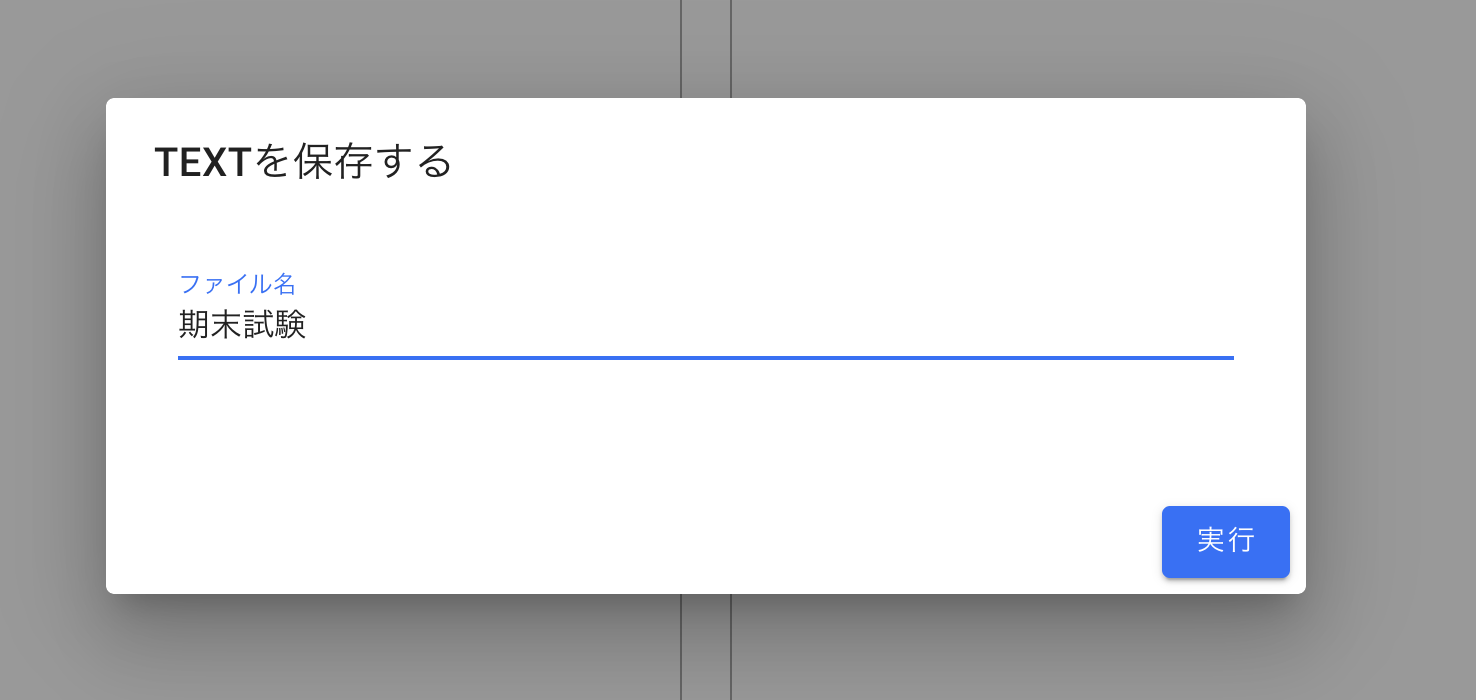
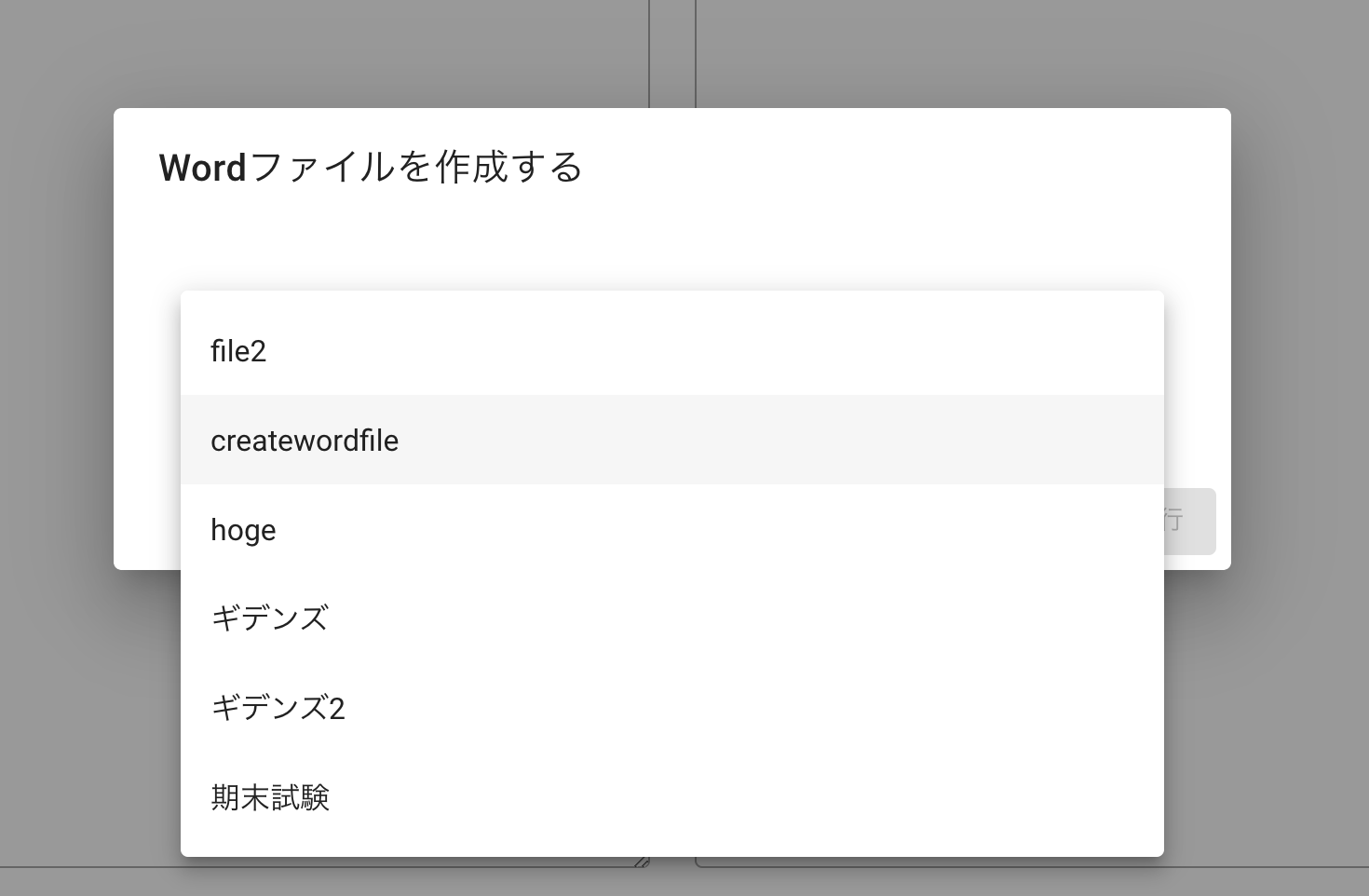
- 投稿日:2020-07-27T23:22:28+09:00
atomからgithubのリモートリポジトリをクローンする方法
はじめに
githubを使用するにあって毎回リモートリポジトリからクローン後ブランチ切ってから作業に入る。
その際に以下の手順で行っていた。
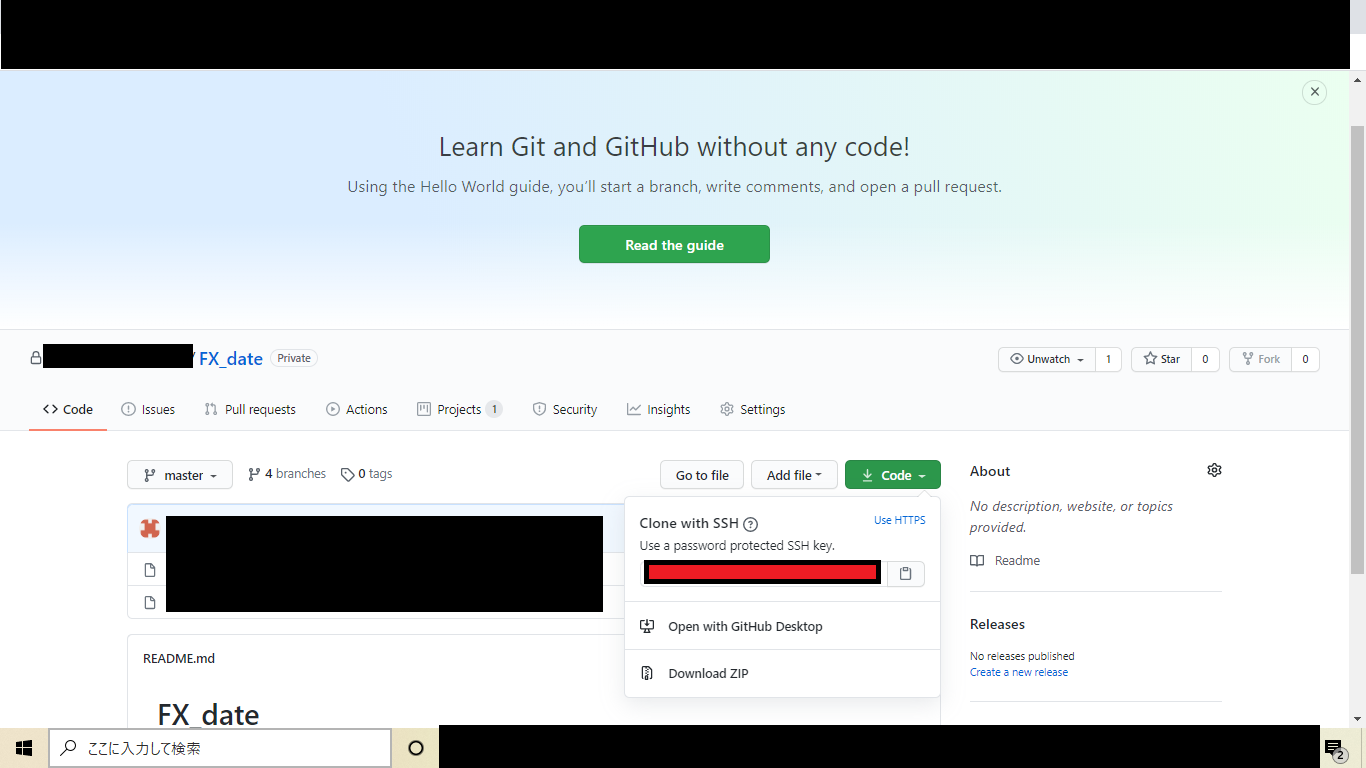
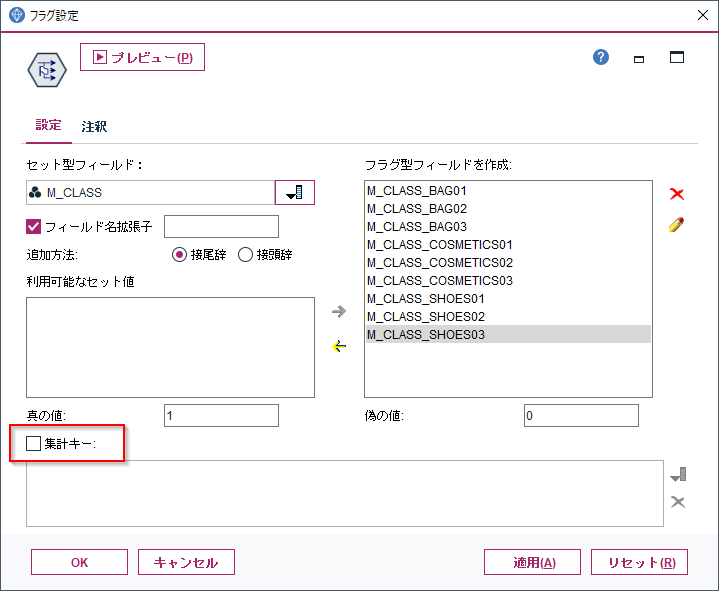
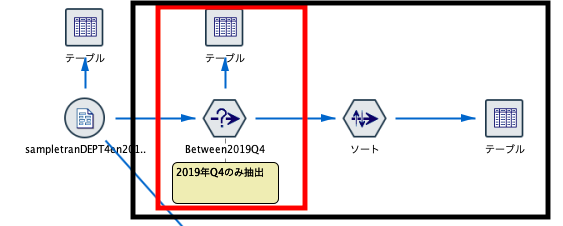
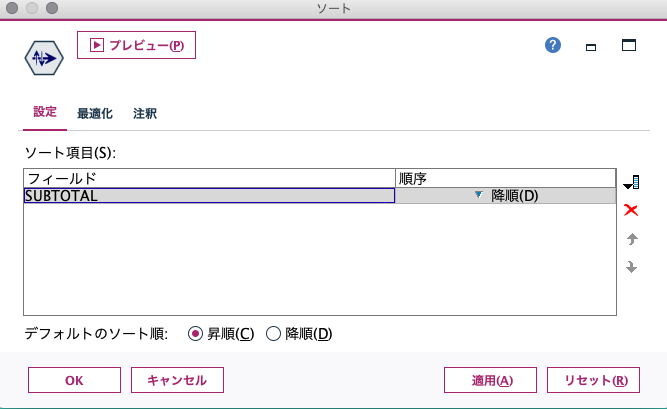
①github上のURLコピー(下画像赤枠)
②前にクローンしたフォルダ削除
③gitbush立ち上げてgit clone URLコマンド実行
正直めんどい。簡単にしたい。と思って調べたらatom上で上記の操作ができる方法があったため簡単にまとめる。対象とする方
・atomからの操作だけでgithubのリモートリポジトリをクローンしたい方
・新しいrepositoryを作成してそれをAtomと連携したい方環境
・Windows10
・Atom 1.48.0※atom,githubアカウント,git,gitbushはインストール済みであることとします。
手順
手順①:github上のクローンしたいリポジトリのURLコピー
これは上記で記載した①と同様
手順②:Atom起動
手順③:コマンドパレットを開く(shift+ctrl+Pで開ける)
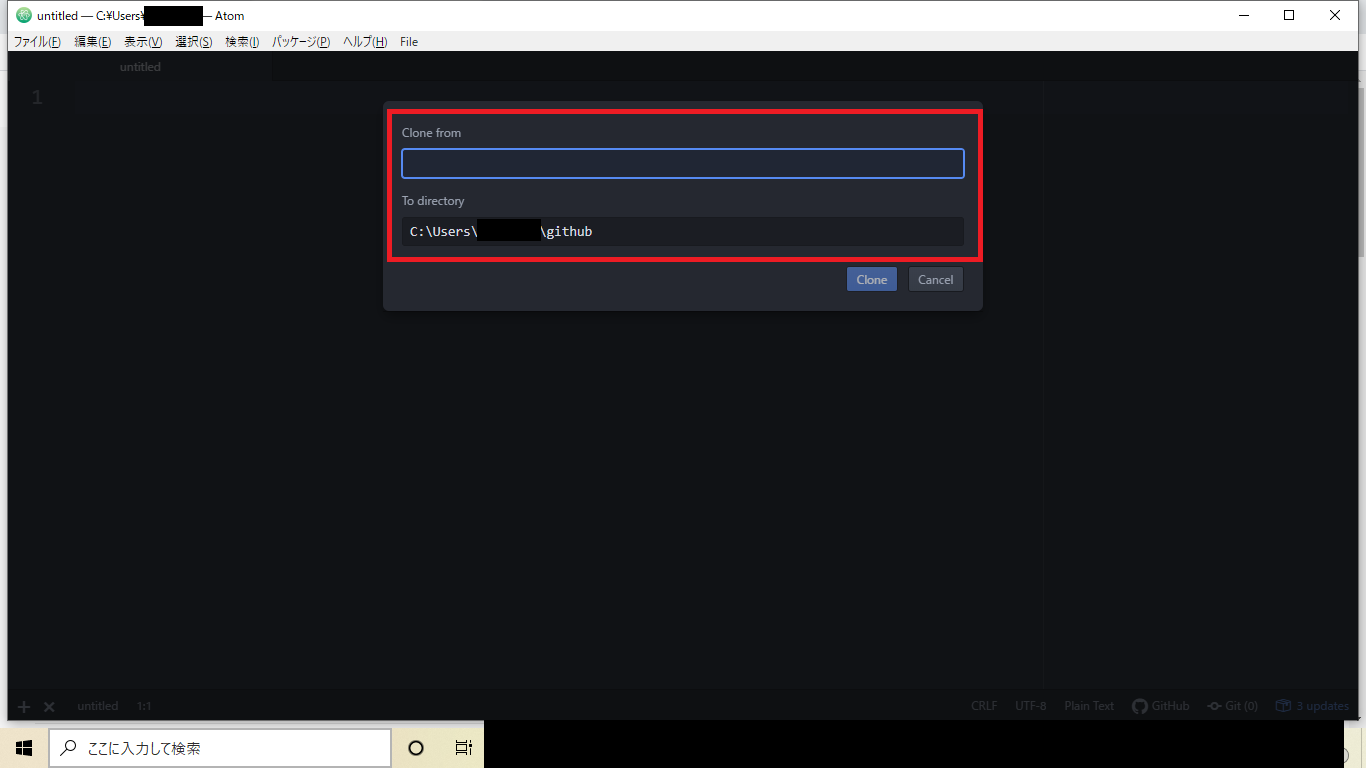
手順④:
github:cloneを実行(alt+Gで実行可)手順⑤:必要事項を入力
手順④を実行すると
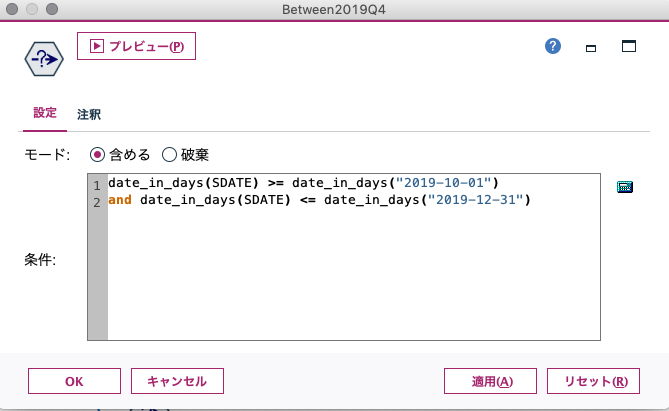
clone fromとTo directoryを入力を促される(下画像赤枠箇所)
clone fromには手順①でコピーしたURLを入力
To directoryにはクローンしたい場所(path)を指定
それぞれ入力後cloneを実行すると指定した場所にリポジトリがクローンされている。
※同じリポジトリ名のフォルダがあるとエラーがでるためあらかじめ削除しておくこと。参照URL
以下の方のHPを参考にしましたので載せておきます。
・ 【GitHub】リポジトリをコピーする「clone」コマンドの紹介
・ 【Qiita】atomと新たに作成したrepositoryを再連携する方法(github)
- 投稿日:2020-07-27T23:10:07+09:00
基本情報のPythonサンプル問題のソースをColaboratoryで動かしてみる
はじめに
基本情報技術者試験(以下FE試験)では,プログラミングの出題がCOBOLからPythonに代わりました。2020年の秋試験からPythonが出題されます(当初の予定では2020春試験からでしたが,コロナの影響で春試験が中止になりました。)
Pythonの特徴の一つは,プログラミング初心者にも学習しやすいことです。ただ,言語としては学習しやすくても,初心者の方には自分一人で「Pythonを動かして試す環境」を準備することは難しいことでしょう。
そこで,この記事では「FE試験受験のためにPythonを試してみたいけど,どうやって動かせばいいのか分からない」方に向けて,Pythonが動作する環境の準備について解説します。さらに,IPA(FE試験の実施機関)が公表しているPythonのサンプル問題を実際に動かしてみます。この記事の対象読者
- プログラミングが初めて。
- FE試験を受験したい。
- Pythonを学びたい。でも,どうやればPythonのプログラムを動かすか分からない。
- FE試験の午前問題の出題キーワードがなんとなく理解できている,または,調べたら理解できる。
準備するもの
- Googleのアカウント(gmailのアカウントがあればOK)
- Chromeなどのブラウザが使える環境(MacでもWindowsでもOK)
Python実行環境
プログラミング言語を動作させるには,エディタやコンパイラ・インタープリタをパソコンにインストールすることが多いです。しかも,必要なライブラリの導入や開発環境(IDE)の操作に慣れる必要があるなど,結構高いハードルを越えなければいけません。
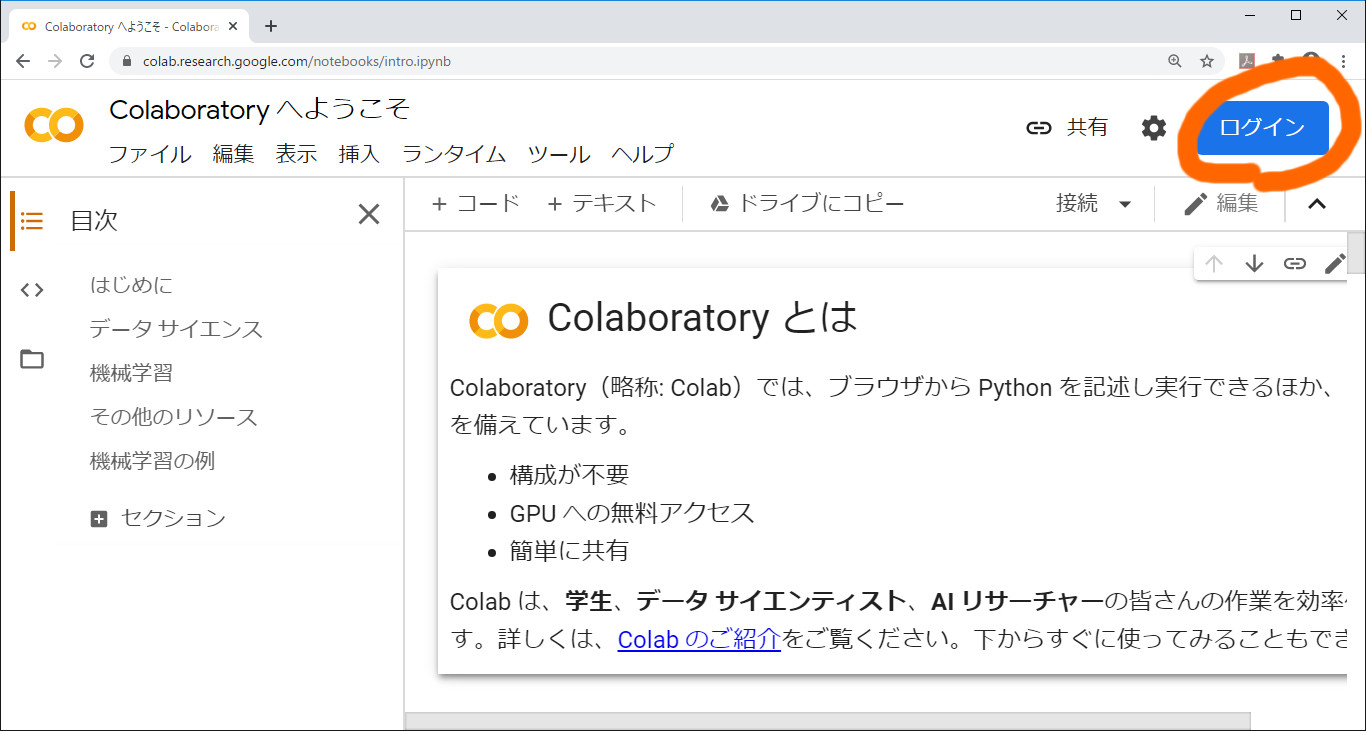
ところがありがたいことに,GoogleサマがWebブラウザだけでPython を実行できる環境を提供しており,無償で利用できます。もともとは機械学習の練習用(とはいえかなり本格的)の環境らしいのですが,FE試験試験のサンプル問題を動かすこともできます。この環境をColaboratoryと呼びます。この記事ではColaboratoryを利用してサンプルプログラムを動かします。Colaboratoryにアクセス
では早速アクセスしてみましょう。ブラウザ(Chrome推奨)でhttps://colab.research.google.com/にアクセスします。Googleアカウントにログインしていない場合,右上のログインのアイコンからログインしてください。
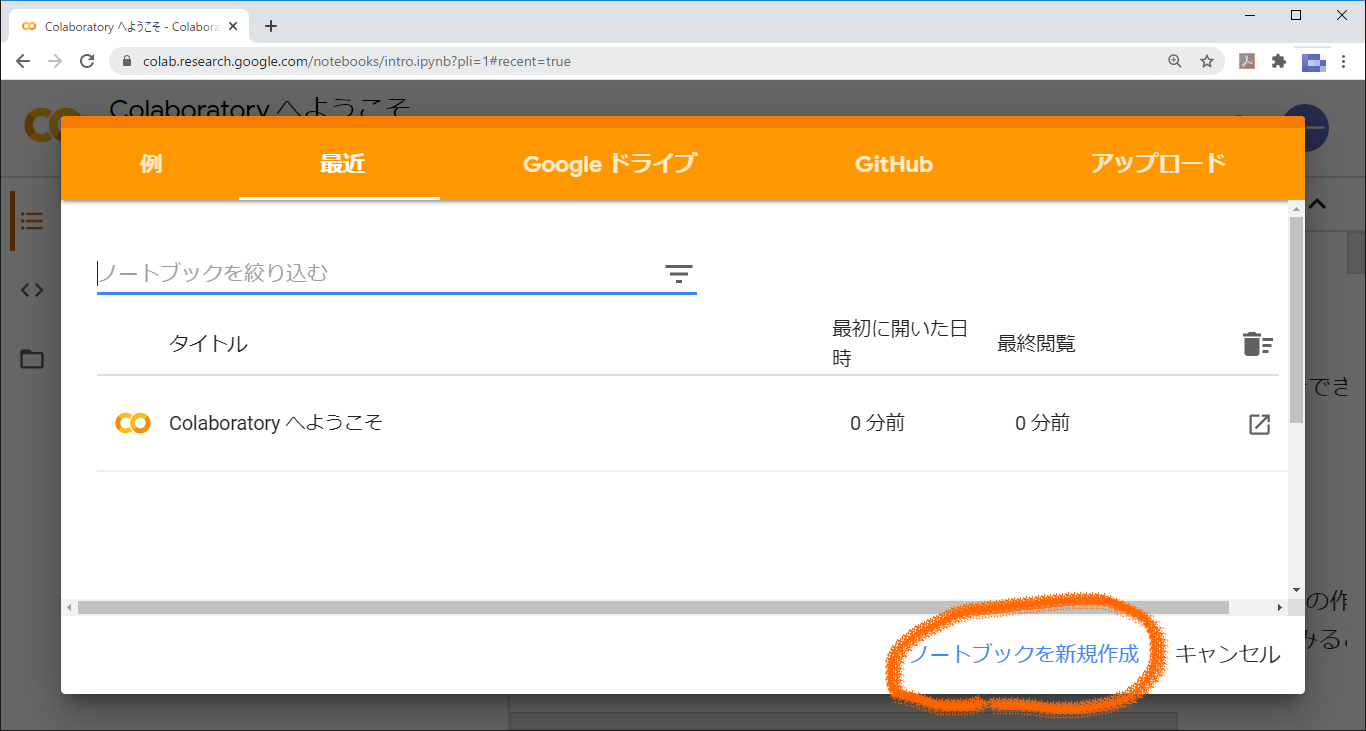
ログインすると,ノートブック一覧画面が出ます。ノートブックとは,関連するファイルをまとめるための,フォルダのようなものです。FE試験の勉強用であれば,1問で1ノートブックに対応させるとよいでしょう。サンプル問題用のノートブックを作るために「ノートブックを新規作成」をクリックします。
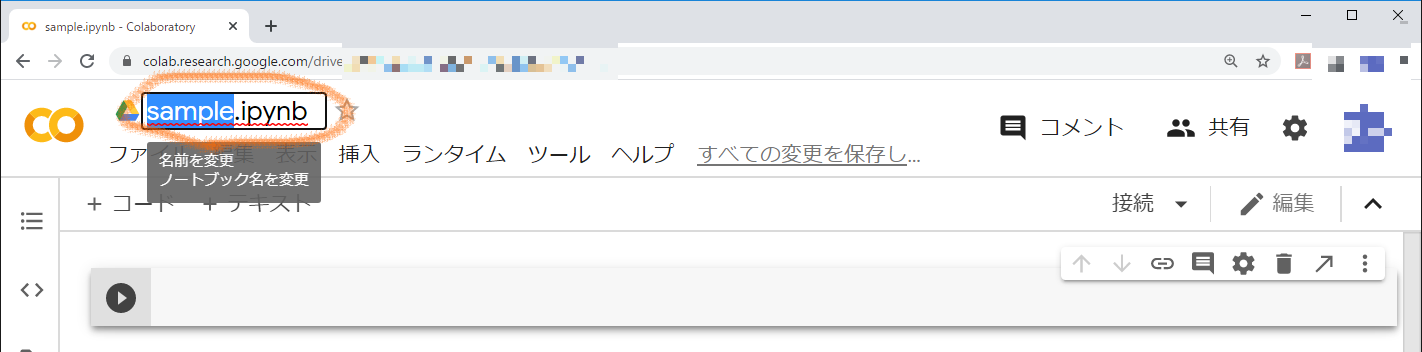
早速コードの入力画面が出てきます。あとでノートブックを開くときにわかりやすくするために,ノートブックの名前を変更しておきましょう。デフォルトの名前である「Untitled0.ipynb」をクリックして,「sample.ipynb」に変更します。
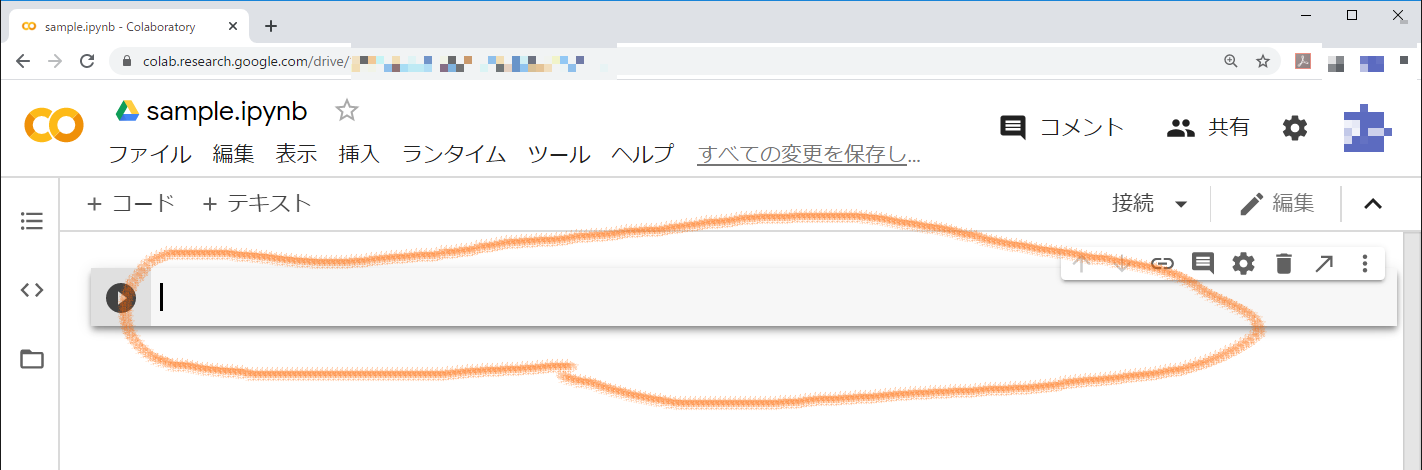
ファイル名を変更したら,コード入力の箇所(線で囲った箇所です。セルと呼びます。)にサンプルプログラムを入力します。
もちろん手入力が一番勉強になります。が,楽したい方のために,サンプルプログラムを掲載しておきます。コピペしてください。
sample.py# 著作権はIPAにあります。 import math import matplotlib.pyplot as plt def parse(s): return [(x[0],int(x[1:])) for x in s.split(';')] class Marker: def __init__(self): self.x, self.y, self.angle = 0, 0, 0 plt.xlim(-320, 320) plt.ylim(-240, 240) def forward(self, val): rad = math.radians(self.angle) dx = val * math.cos(rad) dy = val * math.sin(rad) x1, y1, x2, y2 = self.x, self.y, self.x + dx, self.y + dy plt.plot([x1, x2], [y1, y2], color='black', linewidth=2) self.x, self.y = x2, y2 def turn(self, val): self.angle = (self.angle + val) % 360 def show(self): plt.show() def draw(s): insts = parse(s) marker = Marker() stack = [] opno = 0 while opno < len(insts): print(stack) code, val = insts[opno] if code == 'F': marker.forward( val ) elif code == 'T': marker.turn( val ) elif code == 'R': stack.append({'opno': opno, 'rest': val }) elif code == 'E': if stack[-1]['rest'] > 1 : opno = stack[-1]['opno'] stack[-1]['rest'] -= 1 else: stack.pop() opno += 1 marker.show()コードの入力が終わったら,実行してみましょう。左の実行アイコンをクリックしてください。初回の実行時には少し時間がかかります。
・・・あれ,何も出てきません。それもそのはず,このサンプルプログラムには関数やクラスの定義だけしか書かれておらず,メインルーチンに相当する箇所がありません。それでは,この関数やクラスを呼び出してみましょう。
ページの上の方にある「+コード」をクリックしてください。
すると,サンプルプログラムを入力したセルの下に,もう一つセルが現れます。
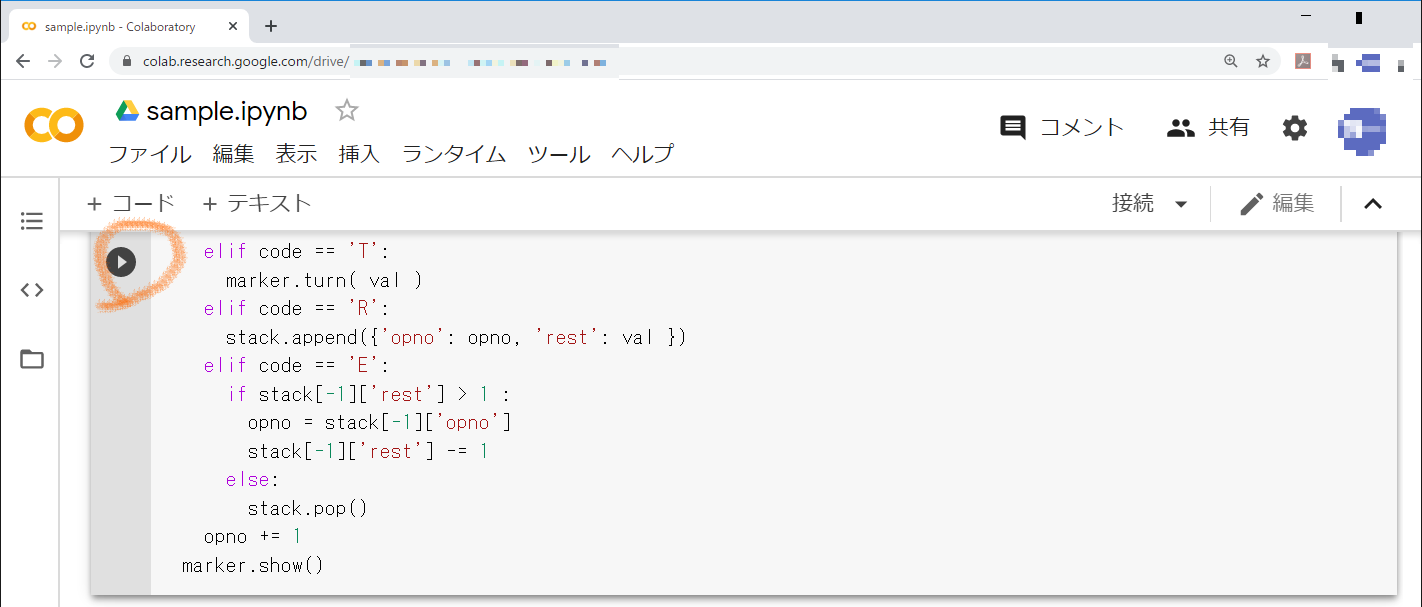
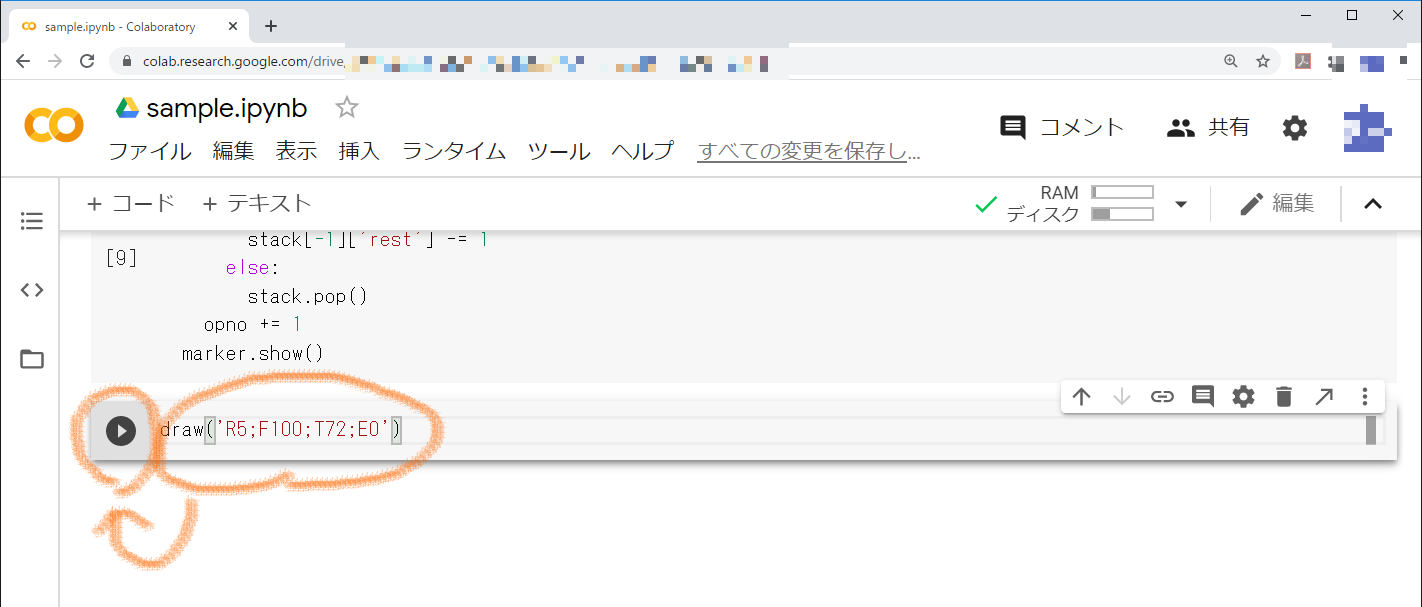
このセルに,サンプル問題で「引数として与えられた命令列の各命令を解釈実行し,描画結果を表示する」と解説されたdraw関数を実行します。引数は,問題文空欄bの回答である選択肢カ(R5;F100;T72;E0)を使い,「draw('R5;F100;T72;E0')」を入力します。入力したら,左の実行アイコンを押します。
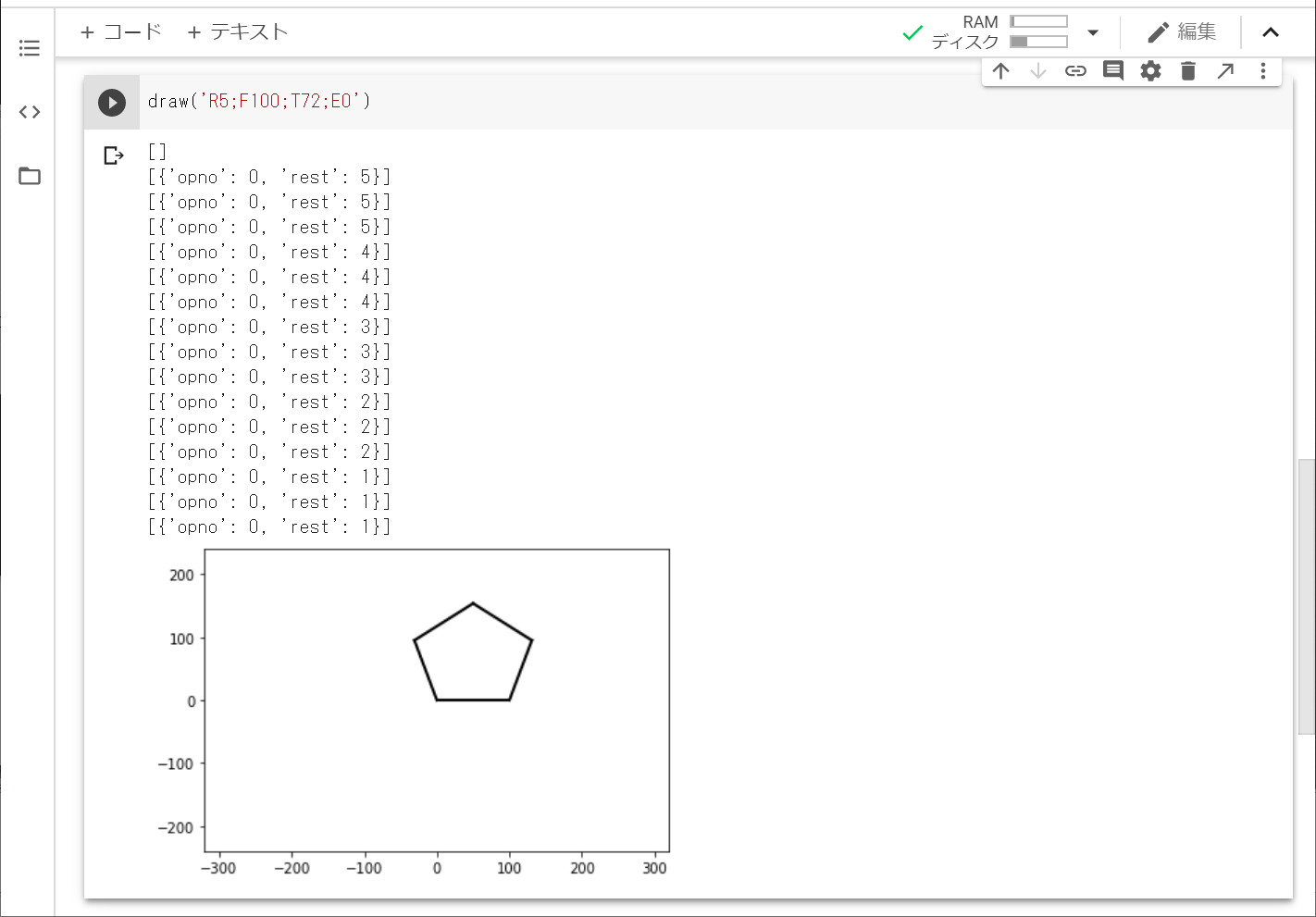
サンプルコードの入力や,入力した文字列が合っていれば,以下のように五角形が表示されるはずです。
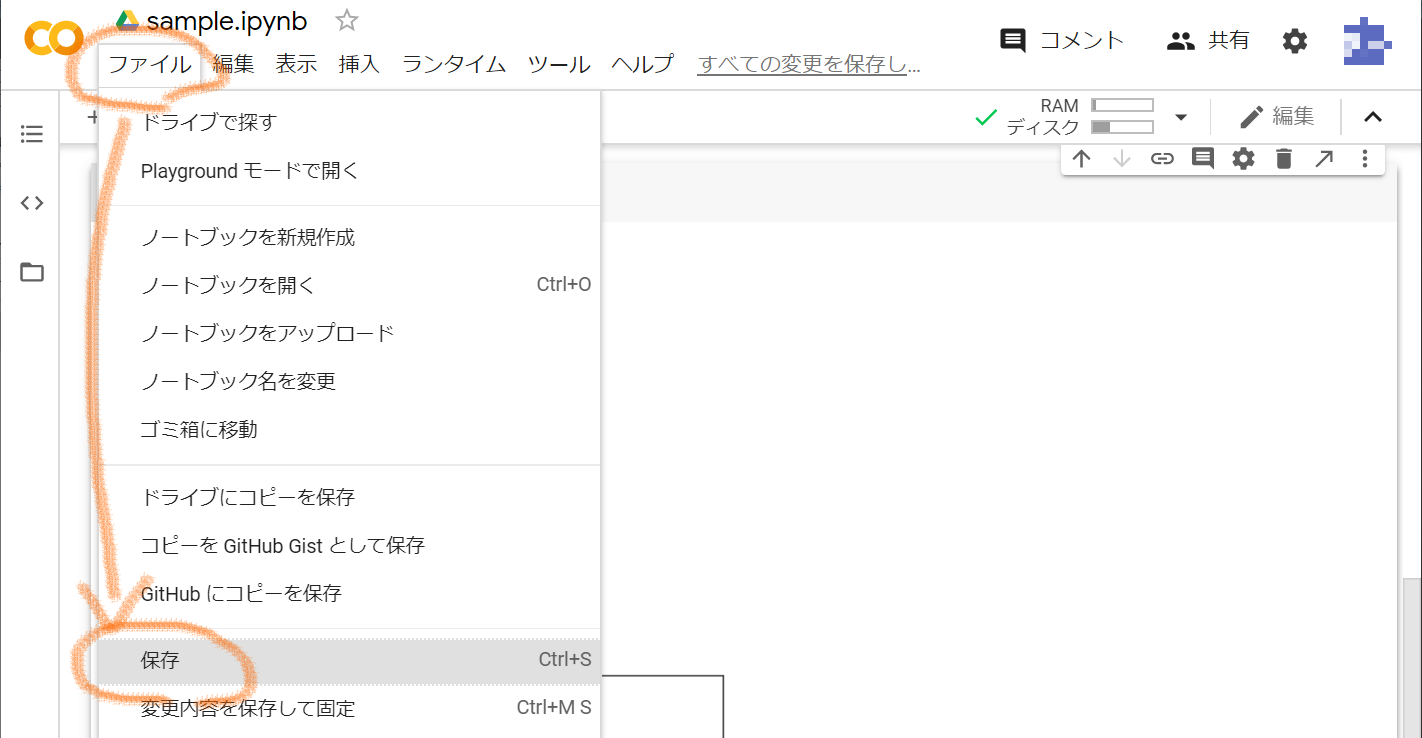
作業が終わったら,ノートブックを保存しておきましょう。保存したノートブックは,次回開くことができます。画面上の方にある「ファイル」から「保存」をクリックします。保存ができたら,ブラウザを閉じても大丈夫です。
お疲れさまでした。
- 投稿日:2020-07-27T23:08:56+09:00
量子情報理論の基本:トポロジカル表面符号
$$
\def\bra#1{\mathinner{\left\langle{#1}\right|}}
\def\ket#1{\mathinner{\left|{#1}\right\rangle}}
\def\braket#1#2{\mathinner{\left\langle{#1}\middle|#2\right\rangle}}
$$はじめに
フォールトトレラント量子計算を実現するためには各部品の誤り率が$10^{-4}=0.01\%$程度以下で、かつ、連結符号という構成によって(Steane符号をベースとした場合)$7$の何乗個もの量子ビットが必要になるという話を前回しました。これで多くの人は絶望的な気分になるのですが、今回説明する「トポロジカル表面符号(topological surface code)」によって、希望の光が見えてくるはずです。
この後の節で何を説明しようとしているか最初に言っておきます。まず、「理論説明」ではトポロジカル表面符号(以下「表面符号」と呼ぶことにします)の符号状態と基本的な論理演算をどのように構成するかを述べ、その上で誤り訂正を上手に実行できることを説明します。「動作確認」では、量子計算シミュレータqlazyを使って、符号状態を作成してノイズを加え誤りを訂正するという一連の流れが正しく動作することを確認します。
参考にさせていただいたのは、以下の文献です。
- 小柴、森前、藤井「観測に基づく量子計算」コロナ社(2017年)
- 慶應義塾大学「量子コンピュータ授業 #14 幾何学符号」
- K.Fujii,"Quantum Computation with Topological Codes - from qubit to topological fault-tolerance",arXiv:1504.01444v1 [quant-ph] 7 Apr 2015
- 量子コンピュータの誤り訂正技術
理論説明
表面符号の定義
面演算子と頂点演算子
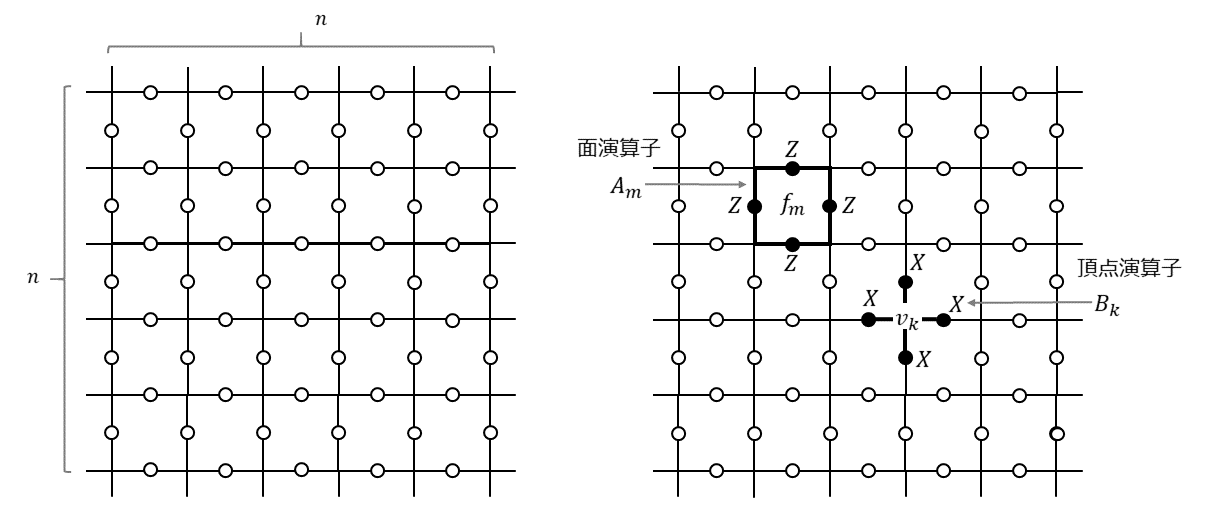
表面符号とは、平面上に量子ビットを規則正しく並べて、その上で規則正しく定義されたスタビライザー群の生成元によって規定される誤り訂正符号のことです。例えば、$n \times n$の2次元格子を考え、その辺の真ん中に量子ビットを配置することを考えます(下図左)。そして、周期的境界条件を満たしているものとします。つまり、一番上と一番下の辺は同じものであり一番左と一番右の辺は同じものだとします。一番上の辺と一番下の辺をくるっと丸めてくっつけて筒状にしてから、筒の両端にできた2つの円をぐるっと回してくっつけるとドーナツ形=トーラスが出来上がりますが、そんなイメージです。3次元のオブジェクトを図示するのは大変なので、以下では平面上に表現された格子を使って説明していきますが、頭の中ではトーラスの展開図だと思っておいてください。
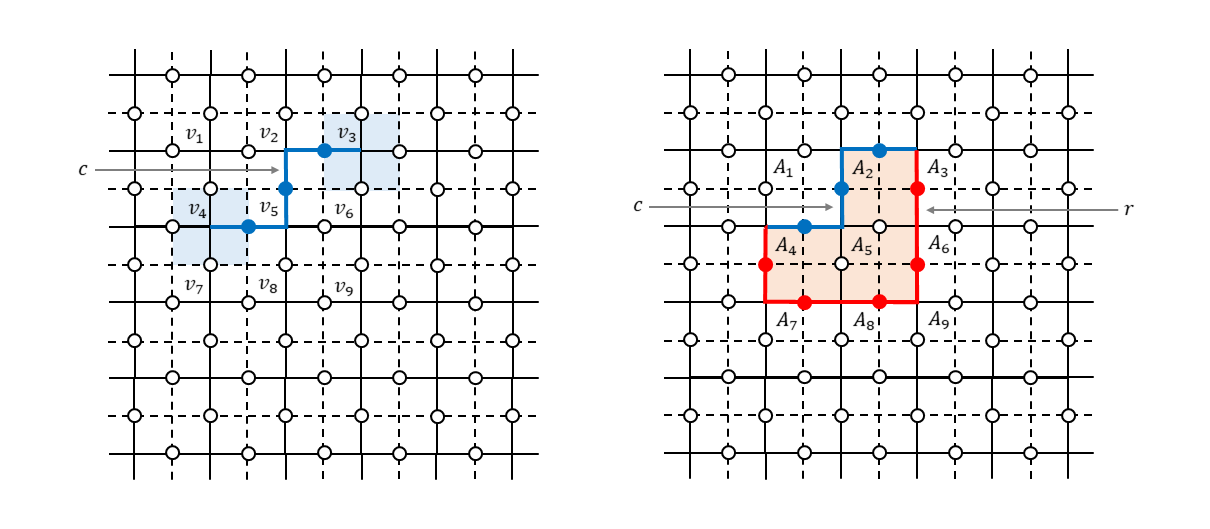
スタビライザー符号を構築するには生成元が必要です。というわけで、この格子上に2種類の生成元を定義します。ひとつは「面演算子(plaquette operator)」というもので、もうひとつは「頂点演算子(star operator)」というものです(上図右)。
面演算子$A_m$は格子の各面$f_m$に対応して以下のように定義されます。
A_m = \prod_{i \in \partial f_m} Z_i \tag{1}ここで、$\partial f_m$は$m$番目の面$f_m$の境界に相当する4つの辺を表し、$Z_i$は$i$番目の辺に配置された量子ビットに対するパウリ$Z$演算子です。上図右に示したように各面を囲む四角形としてイメージしておけば良いです。これが格子全面に敷き詰められています。
一方、頂点演算子は格子の各頂点$v_k$に対応して以下のように定義されます。
B_k = \prod_{j \in \delta v_k} X_j \tag{2}ここで、$\delta v_k$は、$k$番目の頂点$v_k$に接続している4つの辺を表し、$X_j$は$j$番目の辺に配置された量子ビットに対するパウリ$X$演算子です。上図右に示したように各頂点を中心にした十文字としてイメージしておけば良いです。これも先程と同様に格子全面に敷き詰められています。面演算子同士、頂点演算子同士は可換ですし、頂点演算子と面演算子は重なる場合は必ず量子ビット2個を共有する形になるので可換です($X_{i}X_{j}$と$Z_{i}Z_{j}$は可換なので)。したがって、これで可換な生成元が定義できました。
さて、ここで問題です。この$n \times n$の2次元格子に量子ビット(辺)と面演算子と頂点演算子はそれぞれいくつあるでしょうか。周期的な境界条件を考慮すると、量子ビット(辺)の数は$2n^2$個、面演算子(面)の数は$n^2$個、頂点演算子(頂点)の数は$n^2$個であることがわかります。両者合わせて可換な$2n^2$個の生成元があるのですが、全部が独立というわけではありません。面演算子のすべての積は恒等演算子$I$ですし、頂点演算子のすべての積も恒等演算子$I$です1。拘束条件が2個あるので、独立な生成元の個数は$2n^2-2$ということになります。量子ビット(辺)の数は$2n^2$個だったので、この符号空間で記述することができる論理ビット数は$2n^{2}-(2n^{2}-2)=2$個ということになります。
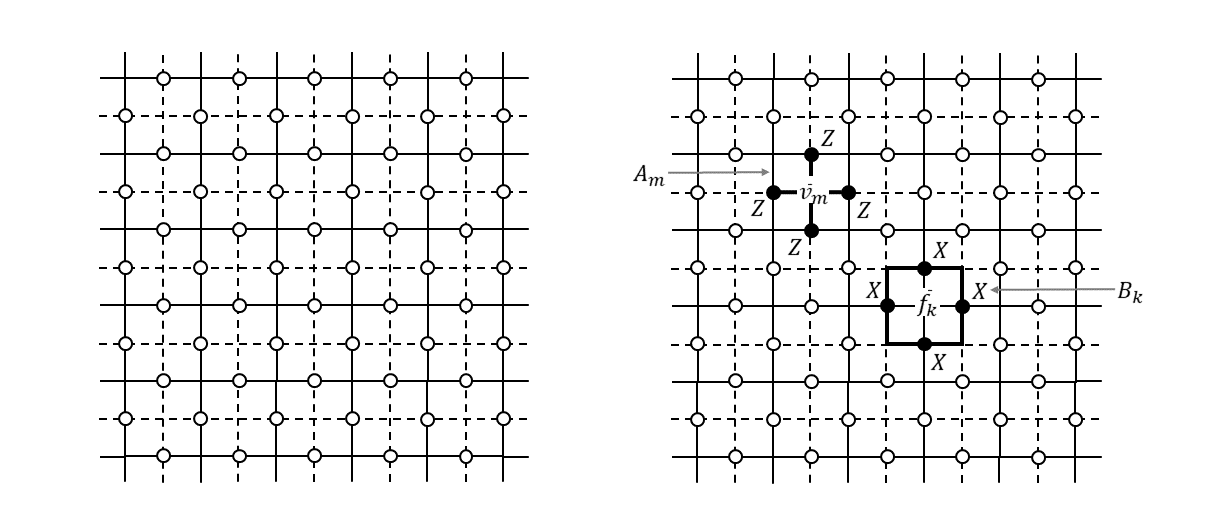
双対格子
上図で示した格子は頂点同士をつないだものを辺としましたが、面同士をつないだものを辺とした別の格子を考えることもできます。つまり、面の中央に頂点をおいてそれらをつないだような格子です(下図左、破線で示されています)。このような格子のことを「双対格子(dual lattice)」と呼びます。
この双対格子を使って面演算子と頂点演算子を表現すると、不思議なことが起きます(というかちょっと考えればすぐわかると思いますが)。面演算子の形が十文字になり、頂点演算子の形が四角形となり、図形のイメージが逆転します(上図右)。
元の格子(primal lattice)の面・辺・頂点は、双対格子においては各々頂点・辺・面となりますので、生成元$A_m,B_k$は以下のように双対格子の言葉で書き直すことができます。
A_m = \prod_{i \in \delta \bar{v}_m} Z_i \tag{3}B_k = \prod_{j \in \partial \bar{f}_k} X_j \tag{4}ここで、$\bar{v}_m$は面$f_m$を双対格子で表したときの頂点、$\bar{f}_k$は頂点$v_k$を双対格子で表したときの面です(以降、双対格子上の実体であることを明示するため記号の上にバーをつけることにします)。なぜこのようなものをここで導入したかについては、この後の説明の中でわかりますので、一応覚えておいてください2。
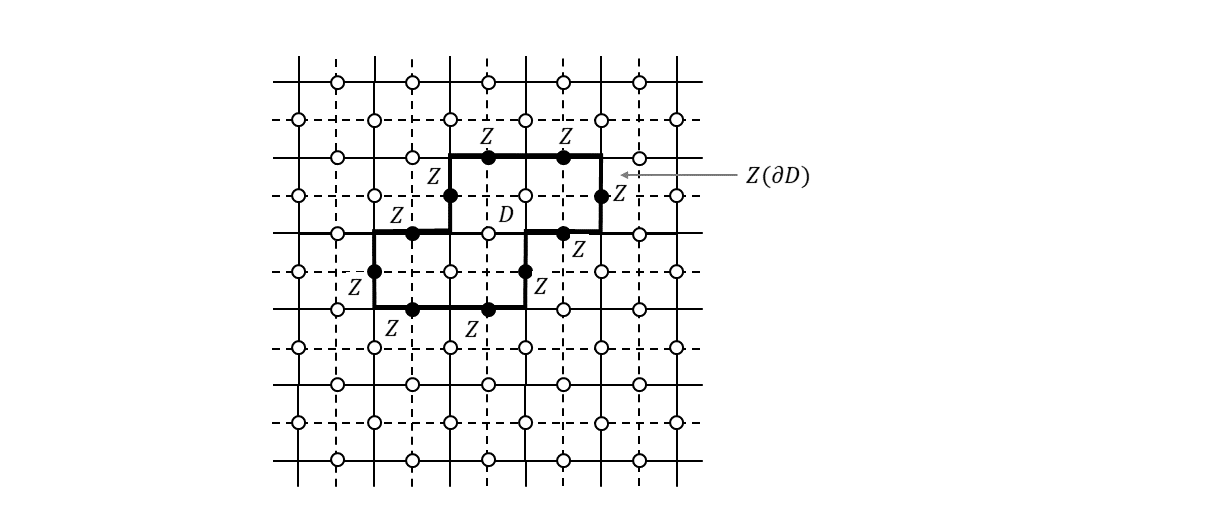
自明なループ
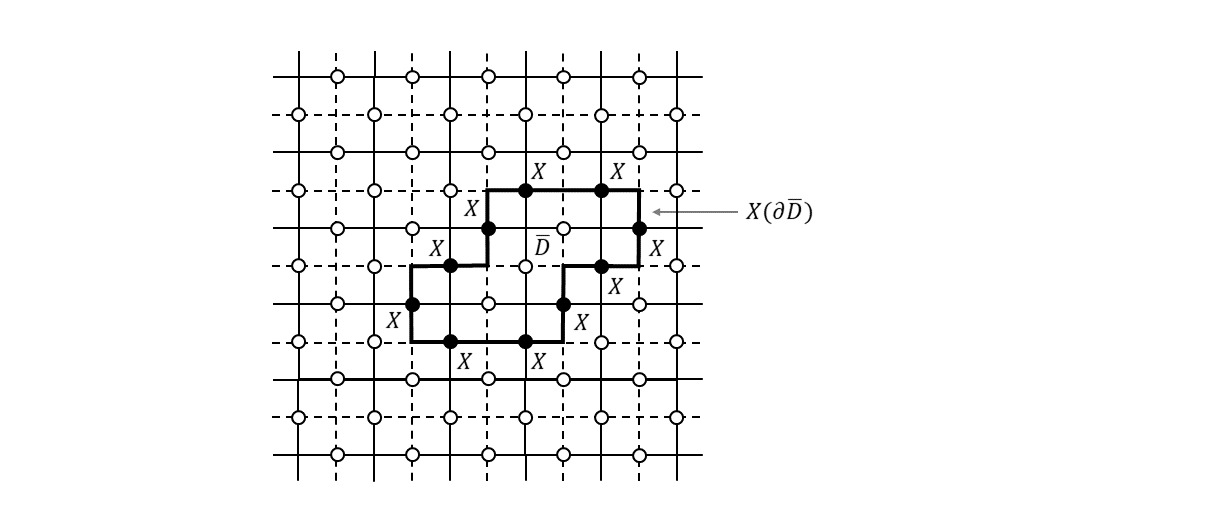
生成元が定義できたところで、格子=トーラス上で定義されるループが演算子的にどんな性質を持っているのかを考えてみます。まず、格子上の面$D$の境界$\partial D$を考えます(下図)。
このようなループのことを「自明なループ」と呼びます3。ループを構成する各辺に置いた$Z$演算子の積を$Z(\partial D)$と書くことにすると、
Z(\partial D) = \prod_{m,f_m \in D} A_{m} \tag{5}が成り立ちます。右辺は面$D$を構成するすべての面演算子の積をとった形になっていますが、これはわかりますでしょうか。隣接した2つの面演算子は1つの$Z$演算子を共有していますので、両者の積をとると共通した辺が$I$となります。$D$に含まれる面演算子すべてで積をとると$D$の境界以外のすべての辺は$I$となり、結局境界$\partial D$の上にある$Z$演算子だけが残ることになります。式(5)から明らかなように、この演算子$Z(\partial D)$は、すべての生成元と可換で、かつ、スタビライザー群の要素になっています($A_{m}$の積なので)。
次に、双対格子上に定義された面$\bar{D}$の境界$\partial \bar{D}$を考えます(下図)。
双対格子上のループを構成する各辺に置いた$X$演算子の積を$X(\partial \bar{D})$と書くことにすると、
X(\partial \bar{D}) = \prod_{k,\bar{f}_k \in \bar{D}} B_{k} \tag{6}が成り立ちます。先ほどと同様に面を構成するすべての面演算子(元の格子においては頂点演算子だったもの)の積をとると境界上の$X$演算子だけが残る形になります。式(6)から明らかなように、この演算子$X(\partial \bar{D}))$も、すべての生成元と可換で、かつ、スタビライザー群の要素です。
というわけで、元の格子の自明なループ上に配置された$Z$演算子の積、および双対格子の自明なループ上に配置された$X$演算子の積はスタビライザー群の要素であり、これを符号状態に適用しても符号状態は不変になります。
非自明なループ
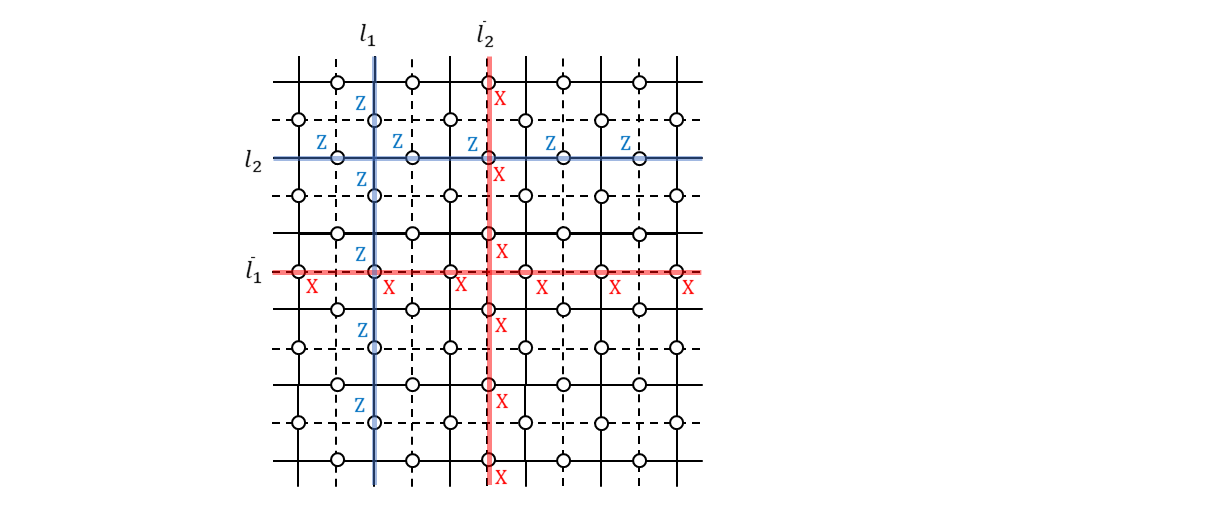
次に、自明でないループ=非自明なループの上に配置された$Z$演算子と$X$演算子がどんな性質を持つのかを見ていきます。
上図に$l_1$と書かれている直線がありますが、これは周期的境界条件を前提とするとトーラスに巻き付くループになります。ループなのですが連続的な変形で一点に収縮させることができないので非自明なループです。この各辺に$Z$演算子を並べて積をとったものを、
\tilde{Z}_1 = Z(l_1) \tag{7}と書くことにします。そうすると、この演算子と生成元たちは可換になります。面演算子に含まれるのは$Z$演算子だけなので当然ですし、頂点演算子の方は$l_1$と重なる辺は必ず2個ですので可換になります4。可換なのですが、これはスタビライザー群の要素ではありません。つまり生成元の積の形で表すことができません。嘘だと思ったら頑張ってやってみてください。例えば、$l_1$上に並んだ$Z$演算子の積をつくりたいため$l_1$に隣接する形に面演算子を並べたとしましょう。でも、これらの積によってできあがるのは$Z(l_1)$ともうひとつ別の非自明なループ上に配置された$Z$演算子です。
すべての生成元と可換でありスタビライザー群の要素ではない演算子というのは一体何でしょうか。答えは論理演算子です。ん?となったかもしれないので、一応説明しておきます。スタビライザー群$S$を独立な生成元を使って、
S = < g_1, g_2, \cdots g_{n-k} > \tag{8}のように書き、スタビライザー状態を$\ket{\psi}$とします。すべての生成元$g_i$と可換な演算子$g \notin S$を持ってくると、
g \ket{\psi} = g g_{i} \ket{\psi} = g_{i} g \ket{\psi} \tag{9}が成り立つので、$g\ket{\psi}$は$g_i$の固有値$+1$に対応した固有空間たちの積空間上の状態(同時固有状態)です。つまり、符号空間上の状態です。が、$g\ket{\psi} = \ket{\psi}$は成り立ちません($g \notin S$なので)。したがって、$g$は符号空間からはみ出すことなく論理状態だけを変える演算子、つまり論理演算子ということになります。
いま、式(7)で定義された$\tilde{Z}_1$を1番目の論理ビットに対する論理$Z$演算子だとします5。
では、1番目の論理ビットに対する$X$演算子はどのように定義すれば良いでしょうか。
\tilde{X}_1 = X(\bar{l}_1) \tag{10}とすれば、すべての生成元と可換で、$\tilde{X}_1 \tilde{Z}_1 \tilde{X}_1 = -\tilde{Z}_1$を満たすようにできるので、これでOKです。
さらに、2番目の論理ビットに対する$Z$演算子は、
\tilde{Z}_2 = Z(l_2) \tag{11}とすれば良いです。$\tilde{Z}_1$を定義する際に縦方向にぐるっと回る非自明ループを使ったので、横方向にぐるっと回る非自明ループを使います6。
2番目の論理ビットに対する$X$演算子は、すべての生成元と可換で、$\tilde{Z}_2$と反可換になるように、
\tilde{X}_2 = X(\bar{l}_2) \tag{12}とすれば良いです。これですべての基本論理演算子が出揃いました。繰り返しますが、上図で示した4つのループはひとつの例です。トポロジー的に別の非自明ループを元の格子と双対格子で各々用意すれば、それによって2つの論理ビットに対する$Z$演算子と$X$演算子を定義できます7。
誤り訂正
符号空間と基本的な論理演算子が定義できたので、この符号を使ってどのように誤り訂正が実現できるかを説明します。
ビット反転エラー
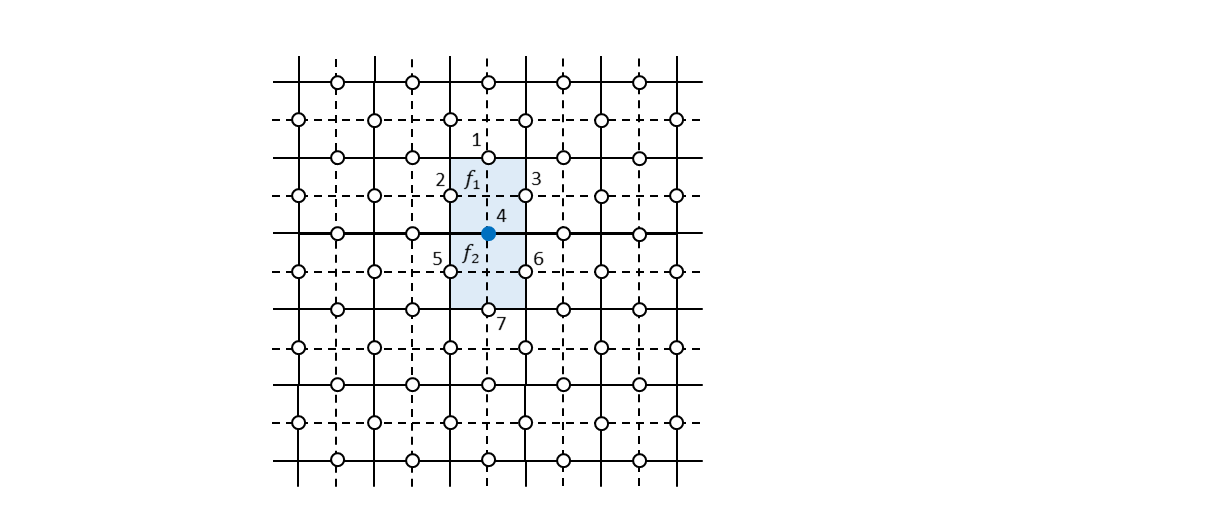
まず、ビット反転エラーがどこか1つのビットに発生した場合にどのように誤りビットを特定できるかについて見ていきます。例えば、下図で番号4のビットにビット反転エラーが発生したとします。
この場合、すべての生成元を測定すると上図の$f_1$と$f_2$に対応した面演算子$Z_{1} Z_{2} Z_{3} Z_{4}$および$Z_{4} Z_{5} Z_{6} Z_{7}$のみが測定値$-1$を出力します。元の論理状態を$\ket{\psi_{L}}$とすると、
\begin{align} Z_{1} Z_{2} Z_{3} Z_{4} (X_{4} \ket{\psi_{L}}) &= - X_{4} (Z_{1} Z_{2} Z_{3} Z_{4} \ket{\psi_{L}}) = -X_{4} \ket{\psi_{L}} \\ Z_{4} Z_{5} Z_{6} Z_{7} (X_{4} \ket{\psi_{L}}) &= - X_{4} (Z_{4} Z_{5} Z_{6} Z_{7} \ket{\psi_{L}}) = -X_{4} \ket{\psi_{L}} \tag{13} \end{align}となることから、測定値は$100\%$の確率で$-1$になることがわかります。したがって、各生成元をシンドローム測定して$-1$を出したものが面演算子だった場合、ビット反転エラーがあったということになり、その場所は面演算子同士が接しているところであると特定することができます。特定されたビットに再度ビット反転を施すことで元の状態に戻すことができます。
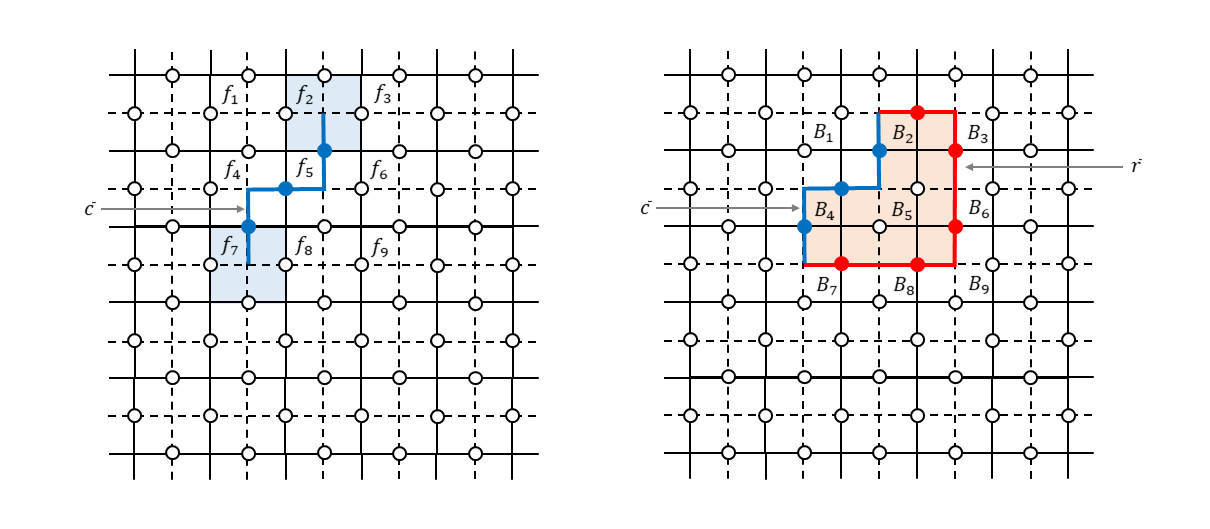
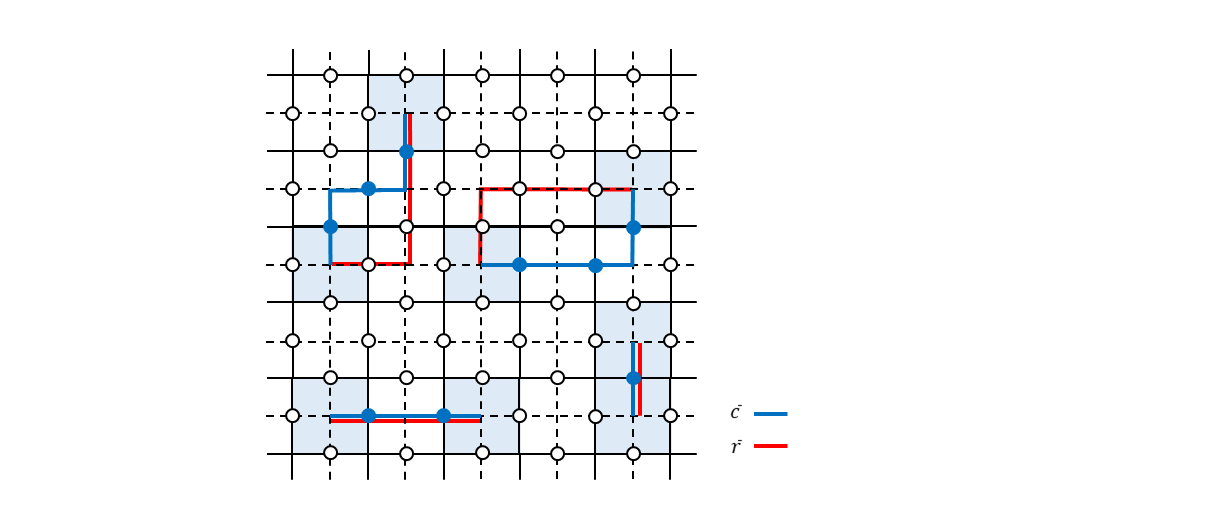
では、2つ以上のビットにビット反転エラーがあったときはどうでしょうか。例えば、下図左のように青で示した3つのビットにエラーがあった場合について考えます。
生成元を測定して$-1$を出力するのは面$f_2$と面$f_7$に対応した面演算子だけです。面$f_4$と面$f_5$を構成するビットにもエラーが発生しているのですが各々2ビット同時にビット反転しているため測定値としては$+1$になってしまいます。このように隣接している面に属するビットにエラーがあった場合、双対格子で見るとつながったチェーンのように見えるので「エラーチェーン」と言ったりしますが(青の線で示しました)、このチェーンの端点に相当する面演算子だけがシンドローム測定で反応します(測定値が$-1$になります。薄い青で塗りつぶした部分です)。この端点の情報から何とか全体のエラーチェーンを復元して誤り訂正しないといけません。いわゆる不良設定問題?というわけで、頑張ったとしても何となく確率的にしか成功しない手法なのね?という雰囲気になったかもしれません。が、ご安心ください。ここが表面符号のとてもエライところだと思うのですが、実はエラーチェーンの推定がある程度外れていても大丈夫なのです。なぜ大丈夫なのかを説明します。
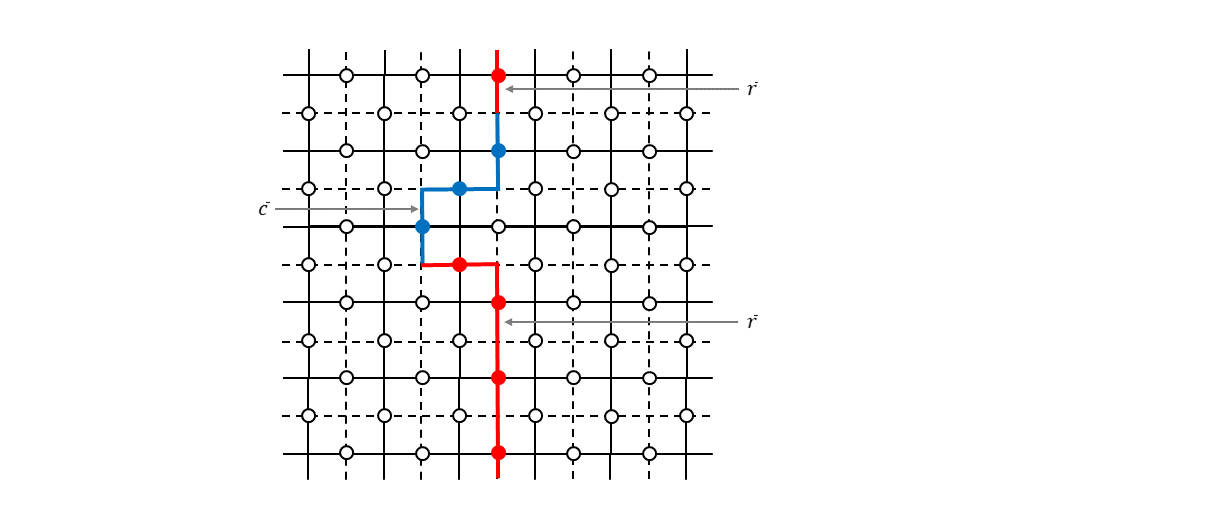
上図右を見てください。本当のエラーチェーンが$\bar{c}$だったとします(青の線で示しました)。それに対して推定したエラーチェーンが$\bar{r}$だったとします(赤の線で示しました)。このとき本当のエラーは$X(\bar{c})$なのですが、推定したエラーは$X(\bar{r})$です。$X(\bar{c})$と$X(\bar{r})$とは図からわかるように頂点演算子$B_2,B_4,B_5$(薄いオレンジ色で塗りつぶした部分です)の積を演算することで互いに移行することができます。つまり、
X(\bar{c}) = B_{2} B_{4} B_{5} X(\bar{r}) \tag{14}です。したがって、エラーが$X(\bar{r})$だと思って回復処理をしたとしても、
\begin{align} X(\bar{r}) X(\bar{c}) \ket{\psi_{L}} &= X(\bar{r}) B_{2} B_{4} B_{5} X(\bar{r}) \ket{\psi_{L}} \\ &= X(\bar{r}) X(\bar{r}) B_{2} B_{4} B_{5} \ket{\psi_{L}} \\ &= B_{2} B_{4} B_{5} \ket{\psi_{L}} = \ket{\psi_{L}} \tag{15} \end{align}となり、結局元の状態に戻ったことになります8。というわけで、上図右のように本当のエラーチェーンと連続変形で移ることができるエラーチェーンが推定できていれば、問題なく元の符号状態を回復することができます。
が、下図のように本当のエラーチェーンと連続変形できないようにエラーチェーンを推定すると回復処理は失敗することになります。
位相反転エラー
次に、位相反転エラーがどこか1つのビットに発生した場合について考えます。下図のように4番目のビットに位相反転エラーが発生したとします。
この場合、すべての生成元を測定すると上図の$v_1$と$v_2$に対応した頂点演算子$X_{1} X_{3} X_{4} X_{6}$および$X_{2} X_{4} X_{5} X_{7}$のみが測定値$-1$を出力します。元の論理状態を$\ket{\psi_{L}}$とすると、
\begin{align} X_{1} X_{3} X_{4} X_{6} (Z_{4} \ket{\psi_{L}}) &= - Z_{4} (X_{1} X_{3} X_{4} X_{6} \ket{\psi_{L}}) = -Z_{4} \ket{\psi_{L}} \\ X_{2} X_{4} X_{5} X_{7} (Z_{4} \ket{\psi_{L}}) &= - Z_{4} (X_{2} X_{4} X_{5} X_{7} \ket{\psi_{L}}) = -Z_{4} \ket{\psi_{L}} \tag{16} \end{align}となることから、測定値は$100\%$の確率で$-1$になることがわかります。したがって、各生成元をシンドローム測定して$-1$を出したものが頂点演算子だった場合、位相反転エラーがあったということになり、その場所は頂点演算子同士が接しているところであると特定することができます。特定されたビットに再度位相反転を施すことで元の状態に戻すことができます。
では、2つ以上のビットに位相反転エラーがあったときはどうでしょうか。例えば、下図左のように青で示した3つのビットにエラーがあった場合について考えます。
生成元を測定して$-1$を出力するのは頂点$v_3$と頂点$v_4$に対応した頂点演算子だけです(薄い青で塗りつぶした部分です)。頂点$v_2$と頂点$v_5$を構成するビットにエラーが発生しているのですが各々2ビット同時に位相反転しているため測定値としては$+1$になってしまいます。この場合、頂点$v_3,v_2,v_5,v_4$をつないだエラーチェーンを推定する必要があります。が、先程と同様に、推定したエラーチェーン$r$が本当のエラーチェーン$c$から連続変形できるものになっていれば、推定したものに基づいて作成した$Z(r)$を適用することで元の論理状態に回復させることができます。回復が失敗するのは推定したチェーンが本当のチェーンから連続変形できない場合です。
エラーチェーンの推定
いま見てきたようにエラーチェーンの推定が多少外れていたとしても回復できるのですが、推定したエラーチェーンが本当のエラーチェーンと連続変形によって移行できないものになっていると誤り訂正は失敗します。なるべく失敗しないようにしたいわけですが、どのように推定するのが一番良いでしょうか、ということについて考えてみます。
いま、エラーチェーン$\bar{c}$上にビット反転エラー$X(\bar{c})$が発生したとします(位相反転エラーの場合も同様の議論が成り立つので、ここではビット反転エラーのみについて考えます)。ここで、エラーチェーン$\bar{c}$はつながった1本のチェーンであるとは限りません。複数のチェーンをひっくるめて$\bar{c}$と表しているのだとイメージしておいてください(下図の青線)。
このようなエラーが発生する確率$p(\bar{c})$は、
p(\bar{c}) = (1-p)^{|E|} \prod_{i \in E} \Bigl(\frac{p}{1-p} \Bigr)^{z_i} \tag{17}と表せます。ここで、$|E|$は辺の総数、$z_i$は$i$番目の辺が$\bar{c}$に含まれる場合$1$、そうでない場合$0$という値をとるバイナリ値とします9。
シンドローム測定の結果$\bar{c}$の境界$\partial \bar{c}$という端点が得られたときに、一番もっともらしいエラーチェーンは、$\partial \bar{c}$を得たという条件のもとで条件付き確率$p(\bar{c}^{\prime}|\partial \bar{c})$が最大になる$\bar{c}^{\prime}$であると考えるのが良さそうです。つまり、
\bar{r} = \arg \max_{\bar{c}^{\prime}} p(\bar{c}^{\prime}|\partial \bar{c}) \tag{18}によってエラーチェーンを推定するのが良さそうです。ここで、$p(\bar{c}^{\prime}|\partial \bar{c})$は、
p(\bar{c}^{\prime}|\partial \bar{c}) \propto (1-p)^{|E|} \prod_{i \in E} \Bigl( \frac{p}{1-p} \Bigr)^{z_{i}^{\prime}} \Bigr|_{\partial \bar{c}^{\prime} = \partial \bar{c}} \tag{19}と表すことができます。このとき、$z_{i}^{\prime}$は$i$番目の辺が$\bar{c}^{\prime}$に含まれる場合$1$、そうでない場合$0$という値をとるバイナリ値であるとしているので、式(19)を最大にするバイナリ系列$\{ z_{i}^{\prime} \}$を求めれば、式(18)の$\bar{r}$がわかったことになります。式(19)をじっと眺めればわかる通り、これを最大にするためにはバイナリ系列$\{ z_{i}^{\prime} \}$の中に含まれる$1$の個数が最小になるようにすれば良いです。言い方を変えると、すべての端点を距離が最小になるようにつなげば良いということになります(下図の赤線)。このようなグラフ最適化アルゴリズムは「最小重み完全マッチングアルゴリズム(minimum weight perfect matching algorithm)」と呼ばれており、多項式ステップで解けるアルゴリズムが知られています(が、よくわかっていないので、説明省略します、汗)。
エラー確率と訂正失敗率
一般に、符号化する際のビット数を大きくして冗長度を上げると、性能の良い(訂正失敗率が低い)誤り訂正が実現できますが、その前提としてビットあたりのエラー確率がある閾値以下になっていることが必要です。
例えば、1ビットを$N$ビットで冗長化する古典反復符号を考えると、$N$ビットのうち半数を越えないエラーであれば多数決をとることで完全復元できます。ざっくり言うと、ビットあたりのエラー確率が閾値$1/2$よりも小さければだいたい復元できます。ここで「だいたい」と言ったのは、伝送したい1つの信号を構成する半数以上のビットにエラーが紛れ込む場合も確率的にあり得るのでその場合復元は失敗します、という意味です。が、$N$の値を十分に大きくとることができれば、この失敗率を限りなくゼロにすることができます。もちろん、このときエラー確率が閾値($1/2$)よりも小さい場合という前提条件は必須になります。エラー確率が閾値よりも大きかった場合は、$N$の値を大きくすると逆効果です。大きくすればするほど確実に復元が失敗する方向に向かいます10。
量子誤り訂正符号の場合も同様で、誤り訂正が効果を発揮するか否かは、ビットあたりのエラー確率がある閾値以下になっていることが必要です。ある閾値以下になっていれば、$N$を十分に大きくすれば訂正失敗率が限りなくゼロに近くなります。が、逆にエラー確率が閾値以上になっていると、$N$を大きくすると訂正失敗率はかえって大きくなります。
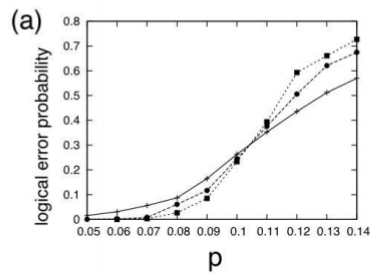
では、表面符号の場合この閾値はどの程度になるでしょうか。数値シミュレーションした結果が参考文献3に掲載されているので、以下に引用します。
ここで、横軸がビットごとのエラー確率、縦軸が訂正失敗率を表していて、実線が$n=10$、破線が$n=20$、点線が$n=30$の訂正失敗率をプロットしたものになります(いま$n \times n$の格子を考えています)。このS字カーブの変曲点からエラー確率の閾値は$10.3\%$程度と求められているそうです。ちなみに、このシミュレーションは「最小重み完全マッチングアルゴリズム」でエラーチェーンの推定をした場合です。
表面符号は、複数のエラーチェーンのパターンに対して同じシンドローム測定の結果が得られる縮退符号なので、実は最小距離が最適とは限りません。同じ訂正結果を与える合計確率が最大になるようにしたものが最適な復号なので、そうした場合この閾値は$10.9\%$程度になるそうです。
また、正方格子ではビット反転エラーも位相反転エラーも同じエラー確率の閾値を持つのですが、蜂の巣形やカゴメ形などに格子形状を変えるとビット反転エラーと位相反転エラーの閾値は非対称になります。実際の物理系においてはビット反転よりも位相反転の方が大きい場合が多いため、そのような想定でのシミュレーションも行われているようです(詳細は参考文献3をご参照ください)。
いま説明した$10\%$程度のエラー閾値というのは表面符号で符号状態が保持・伝送されることに伴って発生するエラーに関するものです。実際の量子計算においては初期状態準備、論理演算、測定に伴うエラーも考慮に入れないといけません。それらすべてを合わせてフォールトトレラントな量子計算を実現するためには、各部品あたりのエラー率はだいたい$1\%$程度必要と見積もられているようです。前回の記事で説明したようにSteane符号のようなCSS符号をベースとした連結符号を想定すると$10^{-4}=0.01\%$程度以下の閾値11が必要ということだったので、これは大きな進展です。「はじめに」で「希望の光」と言っていたのはこのことです。
動作確認
それでは、量子計算シミュレータqlazyを使って、$3 \times 3$の格子上で表面符号を構成し誤り訂正が正しく実行できることを確認してみます。
実装
全体のPythonコードを示します。
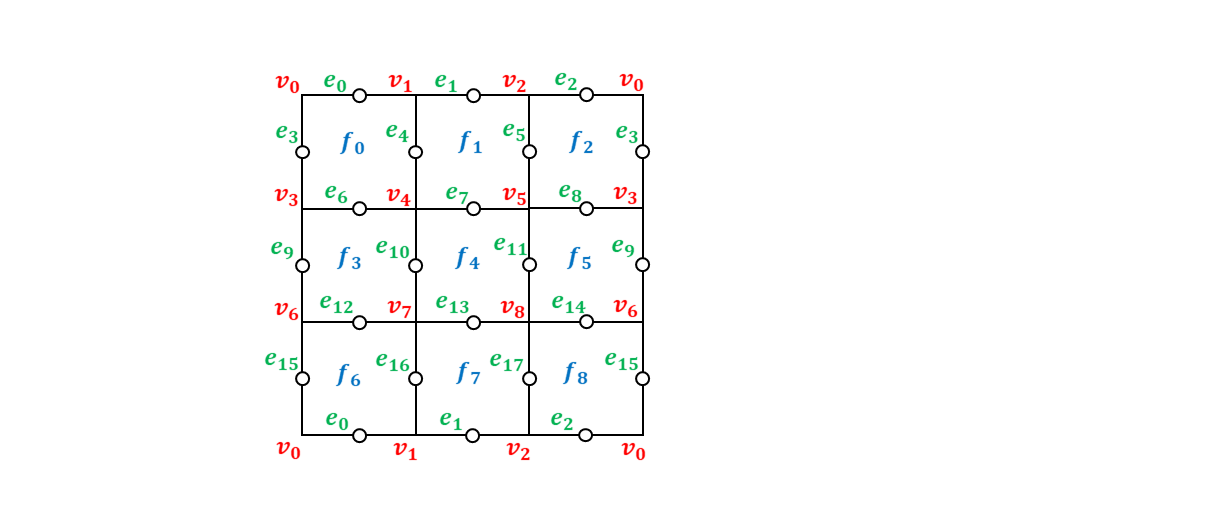
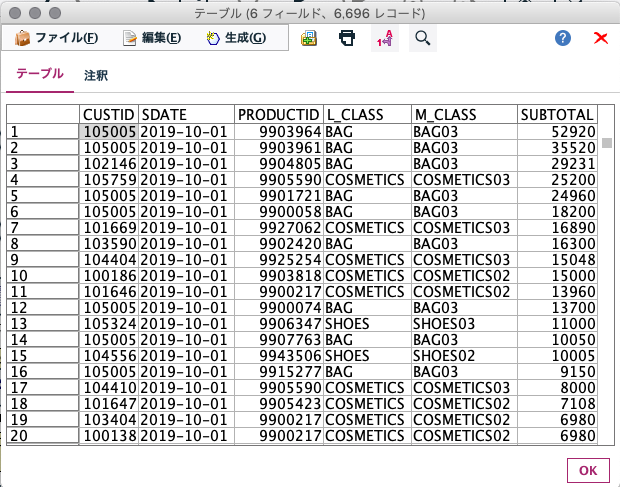
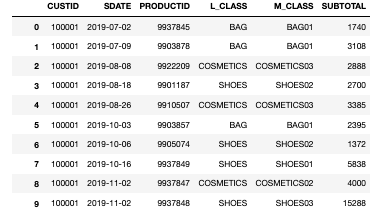
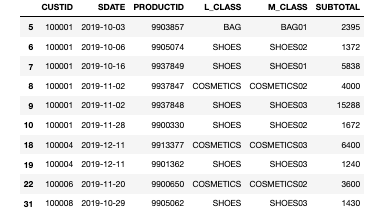
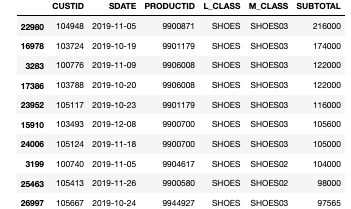
from qlazypy import QState Lattice = [{'edge': 0, 'faces':[0, 6], 'vertices':[0, 1]}, {'edge': 1, 'faces':[1, 7], 'vertices':[1, 2]}, {'edge': 2, 'faces':[2, 8], 'vertices':[0, 2]}, {'edge': 3, 'faces':[0, 2], 'vertices':[0, 3]}, {'edge': 4, 'faces':[0, 1], 'vertices':[1, 4]}, {'edge': 5, 'faces':[1, 2], 'vertices':[2, 5]}, {'edge': 6, 'faces':[0, 3], 'vertices':[3, 4]}, {'edge': 7, 'faces':[1, 4], 'vertices':[4, 5]}, {'edge': 8, 'faces':[2, 5], 'vertices':[3, 5]}, {'edge': 9, 'faces':[3, 5], 'vertices':[3, 6]}, {'edge':10, 'faces':[3, 4], 'vertices':[4, 7]}, {'edge':11, 'faces':[4, 5], 'vertices':[5, 8]}, {'edge':12, 'faces':[3, 6], 'vertices':[6, 7]}, {'edge':13, 'faces':[4, 7], 'vertices':[7, 8]}, {'edge':14, 'faces':[5, 8], 'vertices':[6, 8]}, {'edge':15, 'faces':[6, 8], 'vertices':[0, 6]}, {'edge':16, 'faces':[6, 7], 'vertices':[1, 7]}, {'edge':17, 'faces':[7, 8], 'vertices':[2, 8]}] F_OPERATORS = [{'face':0, 'edges':[ 0, 3, 4, 6]}, {'face':1, 'edges':[ 1, 4, 5, 7]}, {'face':2, 'edges':[ 2, 3, 5, 8]}, {'face':3, 'edges':[ 6, 9, 10, 12]}, {'face':4, 'edges':[ 7, 10, 11, 13]}, {'face':5, 'edges':[ 8, 9, 11, 14]}, {'face':6, 'edges':[ 0, 12, 15, 16]}, {'face':7, 'edges':[ 1, 13, 16, 17]}, {'face':8, 'edges':[ 2, 14, 15, 17]}] V_OPERATORS = [{'vertex':0, 'edges':[ 0, 2, 3, 15]}, {'vertex':1, 'edges':[ 0, 1, 4, 16]}, {'vertex':2, 'edges':[ 1, 2, 5, 17]}, {'vertex':3, 'edges':[ 3, 6, 8, 9]}, {'vertex':4, 'edges':[ 4, 6, 7, 10]}, {'vertex':5, 'edges':[ 5, 7, 8, 11]}, {'vertex':6, 'edges':[ 9, 12, 14, 15]}, {'vertex':7, 'edges':[10, 12, 13, 16]}, {'vertex':8, 'edges':[11, 13, 14, 17]}] LZ_OPERATORS = [{'logical_qid':0, 'edges':[0, 1, 2]}, {'logical_qid':1, 'edges':[3, 9, 15]}] LX_OPERATORS = [{'logical_qid':0, 'edges':[0, 6, 12]}, {'logical_qid':1, 'edges':[3, 4, 5]}] def make_logical_zero(): qs = QState(19) # data:18 + ancilla:1 mvals = [0, 0, 0, 0, 0, 0, 0, 0, 0] # measured values of 9 plaquette operators for vop in V_OPERATORS: # measure and get measured values of 9 star operators qid = vop['edges'] qs.h(18).cx(18,qid[0]).cx(18,qid[1]).cx(18,qid[2]).cx(18,qid[3]).h(18) mvals.append(int(qs.m(qid=[18]).last)) qs.reset(qid=[18]) return qs, mvals def measure_syndrome(qs, mvals): syn = [] for fop in F_OPERATORS: # plaquette operators qid = fop['edges'] qs.h(18).cz(18,qid[0]).cz(18,qid[1]).cz(18,qid[2]).cz(18,qid[3]).h(18) syn.append(int(qs.m(qid=[18]).last)) qs.reset(qid=[18]) for vop in V_OPERATORS: # star operators qid = vop['edges'] qs.h(18).cx(18,qid[0]).cx(18,qid[1]).cx(18,qid[2]).cx(18,qid[3]).h(18) syn.append(int(qs.m(qid=[18]).last)) qs.reset(qid=[18]) for i in range(len(syn)): syn[i] = syn[i]^mvals[i] return syn def get_error_chain(syn): face_id = [i for i,v in enumerate(syn) if i < 9 and v == 1] vertex_id = [i-9 for i,v in enumerate(syn) if i >= 9 and v == 1] e_chn = [] if face_id != []: # chain type: X for lat in Lattice: if lat['faces'][0] == face_id[0] and lat['faces'][1] == face_id[1]: e_chn.append({'type':'X', 'qid':[lat['edge']]}) break if vertex_id != []: # chain type: Z for lat in Lattice: if lat['vertices'][0] == vertex_id[0] and lat['vertices'][1] == vertex_id[1]: e_chn.append({'type':'Z', 'qid':[lat['edge']]}) break return e_chn def error_correction(qs, e_chn): for c in e_chn: if c['type'] == 'X': [qs.x(i) for i in c['qid']] if c['type'] == 'Z': [qs.z(i) for i in c['qid']] def Lz(self, q): [self.z(i) for i in LZ_OPERATORS[q]['edges']] return self def Lx(self, q): [self.x(i) for i in LX_OPERATORS[q]['edges']] return self if __name__ == '__main__': QState.add_methods(Lz, Lx) print("* initial state: logical |11>") qs_ini, mval_list = make_logical_zero() # logical |00> qs_ini.Lx(0).Lx(1) # logical |00> -> |11> qs_fin = qs_ini.clone() # for evaluating later print("* add noise") qs_fin.x(7) # bit flip error at #7 # qs_fin.z(7).x(7) # bit and phase flip error at #7 syndrome = measure_syndrome(qs_fin, mval_list) err_chain = get_error_chain(syndrome) print("* syndrome measurement:", syndrome) print("* error chain:", err_chain) error_correction(qs_fin, err_chain) print("* fidelity after error correction:", qs_fin.fidelity(qs_ini)) QState.free_all(qs_ini, qs_fin)まず、格子上の面と辺と頂点番号を以下のように決めました。ここで、$v_i$が面、$e_i$が辺、$f_i$が頂点を表しています。
プログラム冒頭に記載したグローバル変数Lattice,F_OPERATORS,V_OPERATORS,LZ_OPERATORS,LX_OPERATORSはこの面・辺・頂点を前提にしたときのグラフ構造や生成元や論理演算子を定義するためのデータです。Latticeは各辺に接続している面番号と頂点番号からなる辞書のリストです。これで格子のグラフ構造が漏れなく記述できることになります。F_OPERATORSは各面の境界を構成する辺番号からなる辞書のリストであり、これで$9$個の面演算子を定義します。V_OPERATORSは各頂点に接続する辺番号からなる辞書のリストであり、これで$9$個の頂点演算子を定義します。LZ_OPERATORSは2つの論理$Z$演算子を定義するためのもので、$0$番目の論理$Z$が$Z_{0} Z_{1} Z_{2}$、$1$番目の論理$Z$が$Z_{3} Z_{9} Z_{15}$であることを表しています。LX_OPERATORSは2つの論理$X$演算子を定義するためのもので、$0$番目の論理$X$が$X_{0} X_{6} X_{12}$、$1$番目の論理$X$が$X_{3} X_{4} X_{5}$であることを表しています。
この構成を前提に、main処理部の各部分を順に見ていきます。
qs_ini, mval_list = make_logical_zero() # logical |00>で、論理ゼロ状態を作成します。関数make_logical_zeroの中身は以下です。
def make_logical_zero(): qs = QState(19) # data:18 + ancilla:1 mvals = [0, 0, 0, 0, 0, 0, 0, 0, 0] # measured values of 9 plaquette operators for vop in V_OPERATORS: # measure and get measured values of 9 star operators qid = vop['edges'] qs.h(18).cx(18,qid[0]).cx(18,qid[1]).cx(18,qid[2]).cx(18,qid[3]).h(18) mvals.append(int(qs.m(qid=[18]).last)) qs.reset(qid=[18]) return qs, mvals今回、必要なデータビットは18ビット(0番-17番)ですが、初期状態作成やシンドローム測定のため補助ビットを1ビット追加して(18番)、合計19ビット用意します。補助ビットはもっと沢山必要なのでは?と思われるかもしれませんが、何度もリセットしながら使い回すので大丈夫です。
最初に物理的なゼロ状態をQState(19)で作っておいてforループ内で生成元を間接測定します。頂点演算子の分しか測定していないように見えますが、これはこれで良いのです。最初に用意するのが物理的なゼロ状態、すなわち面演算子の固有値+1に対応した同時固有状態なので面演算子を測定しても状態は変わりません。また面演算子と頂点演算子は可換なのではじめに面演算子を測定しても良いです。という事情があり、ここは頂点演算子の測定だけでOKです。
で、9個ある頂点演算子を順に測定するのですが、測定結果が+1(測定値の指標としては0)だった場合はこのまま次の頂点演算子の測定に移れば良いですが、測定値が-1(測定値の指標としては1)だったときが問題です。固有値をひっくり返す演算子を用意して演算するやり方もありますが、ここではそれを端折ります。つまり、スルーします。が、測定値(の指標)は記録しておきます。すべての生成元の固有値+1に対する同時固有状態は得られませんが、何番目の生成元を測定したら測定値が-1になるべきなのかはわかるので、これでシンドローム測定は可能です。固有値が-1の生成元を測定する場合、シンドローム測定値の解釈を逆にすれば良いだけです。上の関数でmvalsというリスト変数に測定値(の指標)を格納するようにしています。18個の要素があるのですが、面演算子については絶対0なので、有無を言わさず最初に9個の0からなるリストを用意して、頂点演算子を測定するたびにその結果をmvalsにappendしていきます。最後に量子状態qsとmvalsをリターンします。
main処理部に戻ります。
qs_ini.Lx(0).Lx(1) # logical |00> -> |11>で、2つの論理ビットに対して論理$X$を施すことで論理状態$\ket{1_{L} 1_{L}}$を作成します($\ket{0_{L} 0_{L}}$から出発しても良かったのですが、論理$X$演算子を使ってみたかったので出発点を$\ket{1_{L} 1_{L}}$にしてみました)。論理$X$演算子は、
def Lx(self, q): [self.x(i) for i in LX_OPERATORS[q]['edges']] return selfのように定義されています。見ての通りですので、説明省略します。
qs_fin = qs_ini.clone() # for evaluating laterで、最後に誤り訂正結果を評価するための状態複製を行います。これで初期状態が作成できたことになります。
次に、
qs_fin.x(7) # bit flip error at #7で、7番目のビットにビット反転エラーを加えます(何でも良いので、適当に決めました)。
syndrome = measure_syndrome(qs_fin, mval_list)で、シンドローム測定をしてエラービットとエラーの種類を特定します。関数measure_syndromeの中身は以下です。
def measure_syndrome(qs, mvals): syn = [] for fop in F_OPERATORS: # plaquette operators qid = fop['edges'] qs.h(18).cz(18,qid[0]).cz(18,qid[1]).cz(18,qid[2]).cz(18,qid[3]).h(18) syn.append(int(qs.m(qid=[18]).last)) qs.reset(qid=[18]) for vop in V_OPERATORS: # star operators qid = vop['edges'] qs.h(18).cx(18,qid[0]).cx(18,qid[1]).cx(18,qid[2]).cx(18,qid[3]).h(18) syn.append(int(qs.m(qid=[18]).last)) qs.reset(qid=[18]) for i in range(len(syn)): syn[i] = syn[i]^mvals[i] return syn面演算子と頂点演算子を順に測定しながら測定結果をリストに格納していきます。これがシンドローム値になるのですが、先程説明したように固有値-1(測定指標が1)が正常値になっている生成元もありますので、その場合解釈を逆転させる必要があります。初期状態生成時に記録した測定値リストmvalsの値に応じて、
for i in range(len(syn)): syn[i] = syn[i]^mvals[i]のようにシンドローム値を逆転させます。この結果を正しいシンドローム値としてリターンします。
main処理部に戻ります。
err_chain = get_error_chain(syndrome)で、エラーチェーンを推定します。$3 \times 3$の格子では1ビットの誤りしか訂正できないので簡単です。関数get_error_chainの中身は以下です。
def get_error_chain(syn): face_id = [i for i,v in enumerate(syn) if i < 9 and v == 1] vertex_id = [i-9 for i,v in enumerate(syn) if i >= 9 and v == 1] e_chn = [] if face_id != []: # chain type: X for lat in Lattice: if lat['faces'][0] == face_id[0] and lat['faces'][1] == face_id[1]: e_chn.append({'type':'X', 'qid':[lat['edge']]}) break if vertex_id != []: # chain type: Z for lat in Lattice: if lat['vertices'][0] == vertex_id[0] and lat['vertices'][1] == vertex_id[1]: e_chn.append({'type':'Z', 'qid':[lat['edge']]}) break return e_chnシンドロームの値が1になっている場所から面演算子の番号face_idと頂点演算子の番号vertex_idを特定します。特定した面演算子から対応する面の境界を構成する辺の番号がわかるので、その共通する辺の番号がビット反転エラーがあったビット番号になります。また、特定した頂点演算子から対応する頂点に接続する辺の番号がわかるので、その共通する辺の番号が位相反転エラーがあったビット番号になります。このようにして、エラーチェーンを構成するビット番号とエラーの種類がわかります。それを辞書リストe_chnに格納して、リターンします。
main処理部に戻ります。いま得られたエラーチェーンから、
error_correction(qs_fin, err_chain)で、元の状態を復元します。関数error_correctionの中身は以下です。
def error_correction(qs, e_chn): for c in e_chn: if c['type'] == 'X': [qs.x(i) for i in c['qid']] if c['type'] == 'Z': [qs.z(i) for i in c['qid']]見た通りの処理です(説明略)。これで誤り訂正が完了します。main処理部の最後、
print("* fidelity after error correction:", qs_fin.fidelity(qs_ini))で、初期状態と誤り訂正後の最終状態との忠実度を表示します。忠実度が1.0となれば誤り訂正は成功です。
結果
実行結果を以下に示します。
* initial state: logical |11> * add noise * syndrome measurement: [0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0] * error chain: [{'type': 'X', 'qid': [7]}] * fidelity after error correction: 1.0シンドローム測定によって1番目と4番目の面演算子が反応して、7番目のビットにビット反転エラーがあったと特定されました。初期状態との忠実度は1.0となり、正しく復元されることがわかりました。
次に、加えるエラーを以下のようにビット・位相反転エラーとしてみました。
# qs_fin.x(7) # bit flip error at #7 qs_fin.z(7).x(7) # bit and phase flip error at #7実行結果は、
* initial state: logical |11> * add noise (phase and bit flip): X_7 Z_7 * syndrome measurement: [0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0] * error chain: [{'type': 'X', 'qid': [7]}, {'type': 'Z', 'qid': [7]}] * fidelity after error correction: 1.0となり、こちらも正しく誤り訂正できることがわかりました。
おわりに
これで表面符号の基本が理解できました。トポロジーを駆使することで強力な符号が構成できるのはとても新鮮で興味深かったです。また、個人的にはあまり馴染みがなかった代数的トポロジーについても、参考文献を通して勉強できました。
今回は専らトーラス状に構成した表面符号について説明しましたが、物理的にトーラスをどう実現するの?とか、たとえ実現できたとしても2つの論理ビットしか表現できない(穴が1個の場合ですが)という問題があります。これを打破すべく、トーラスではない単なる平面(ただし欠陥付き)を使った表面符号も提案されているようなので、次回はそれについて勉強してみたいと思います。
謝辞:本記事をまとめるに際し、株式会社Nextremer様が主催されている勉強会「第四回トポロジカル量子計算とその周辺」に参加し勉強させていただきました。ポイントになる部分をわかりやすく講義していただき理解が進みました。この場をお借りし感謝致します。
以上
これ大丈夫でしょうか。トーラス上に面演算子が隙間なく敷き詰められています。すべての面演算子を集めると各辺に対応した$Z$演算子は必ず2回登場するのでその積は恒等演算子$I$となります。同様に頂点演算子もトーラス上に隙間なく敷き詰められています。すべての頂点演算子を集めると各辺に対応した$X$演算子は必ず2回登場するのでその積は恒等演算子$I$となります。 ↩
このあたり、参考文献3では、鎖複体(chain complex)を使った代数的トポロジーの言葉で一般的に記述されています。正方格子以外にもいろいろなタイプの格子の上で表面符号が考えられそうで面白いのですが、長くなるので本記事では省略します。 ↩
連続変形によって一点に収縮させることができるループのことを「自明なループ」と言います。 ↩
図では$l_1$を直線で表しましたが、直線ではないループであったとしても頂点演算子と重なる辺は必ず2個になります。図を書いて1分ほど考えればわかると思います。 ↩
ここでは、$l_1$を使って1番目の論理ビットに対する$Z$演算子を定義しましたが、縦方向にぐるっと回る非自明なループ(直線でなくても良い)であれば何を使っても良いです。 ↩
縦方向にぐるっと回る非自明ループを使うと$\tilde{Z}_1$と同じ効果を表す論理演算になってしまうので、トポロジー的に違うループを使う必要があります。 ↩
ちなみに、穴が1個のドーナツ(トーラス)を考えることで2つの論理ビットを表現することができましたが、実は、穴が2個のドーナツを考えると4つの論理ビットを表現することができます。一般に種数$g$の閉曲面を使って$2g$個の論理ビットを表現することができます。種数$g$の閉曲面上に描かれた格子の面、辺、点の数を各々$|F|,|E|,|V|$とすると$|F|+|V|-|E|=2-2g$という関係が成り立つことから証明できます。 ↩
$\bar{r}+\bar{c}$が自明なループになるので$X(\bar{r}+\bar{c})$は符号状態に対して何の影響も及ぼしません、という理解でも良いです。 ↩
式(17)は一見すると難しそうな感じがするかもしれませんが、$\bar{c}$に含まれる辺の数を$M$としてみると、$p(\bar{c})=(1-p)^{|E|-M} p^{M}=(1-p)^{|E|}(\frac{p}{1-p})^{M}$とできることからわかると思います。 ↩
エラー確率を横軸、訂正失敗率を縦軸にとった曲線で誤り訂正符号の特性を表現できますが、それはエラー確率の閾値を変曲点としたS字カーブになります。で、$N$の値を大きくするに従ってS字のカーブがきつくなり、$N$無限大の極限では階段状の特性曲線になります。 ↩
これは結構甘い見積もりらしく、実際には$10^{-5}-10^{-6}$と言われているらしいです。 ↩
- 投稿日:2020-07-27T22:52:53+09:00
【高等学校学習指導要領 情報Ⅰ】教員研修用教材:データの形式と可視化(python)
はじめに
今回は文部科学省のページで公開されている情報Ⅰの教員研修用教材の「第4章情報通信ネットワークとデータの活用・巻末」内の「データの形式と可視化」について、Rのソースコードの個所を、pythonで実装及び若干の補足考察をしていきたいと思います。
教材
高等学校情報科「情報Ⅰ」教員研修用教材(本編):文部科学省
第4章情報通信ネットワークとデータの活用・巻末 (PDF:10284KB)環境
- ipython
- Colaboratory - Google Colab
今回やること
教材の学習24「データの形式と可視化」(p202-)内のRで示されている実装例をpythonに書き換えていきたいと思います。
前提
教材には
総務省統計局の身体測定のサンプルデータから,箱ひげ図とヴァイオリンプロットを作成した。
と書いてあるが、Rで読み込んでいるデータファイルが50m走の男女の結果っぽいので、こちらで適当に用意した以下のデータを使用しました。
high_male_data.csvまた、後半のpython実装版にて使用している"diamonds.csv"はkaggleのサイト上のものを使われていただきました。
Diamonds - Kaggle質的データとその種類
箱ひげ図とヴァイオリンプロット
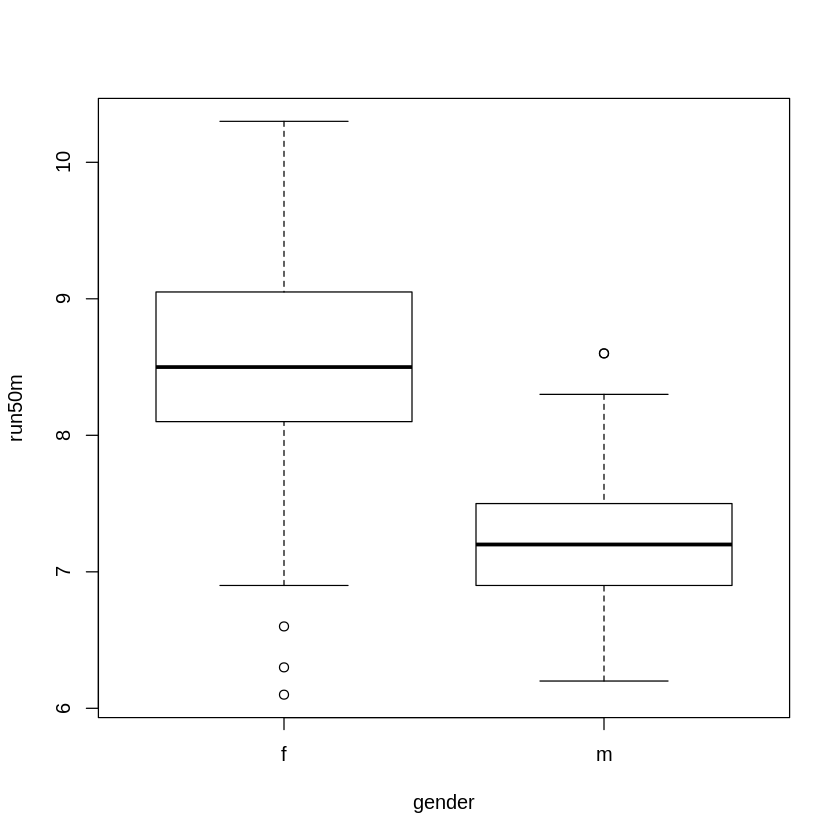
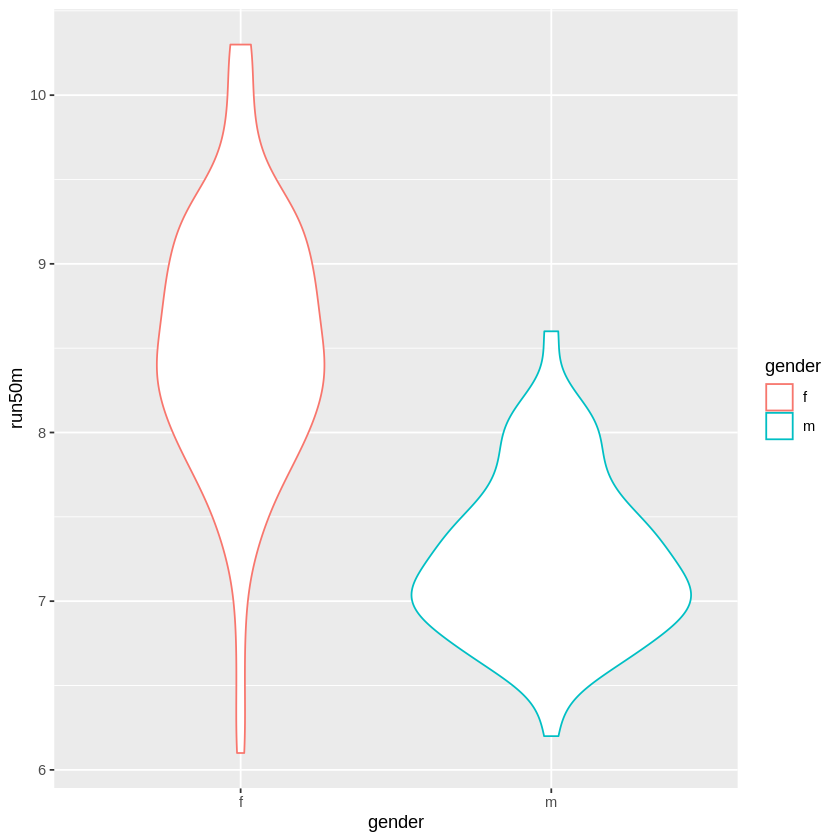
R実装版のソースコード(教材より)
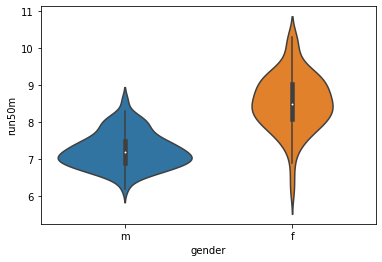
library( ggplot2 ) # データの読み込み gen_50 <- read.csv("gen_50.csv") boxplot(run50m~gender, data=gen_50) ggplot(data=gen_50, aes(x=gender, y=run50m, color=gender)) + geom_violin()ちなみに、実際の教材に書かれているソースコードは以下のようになっております。
ここにバグがあるのでご注意ください。
誤:boxplot(run50m~gender.data=gen_50)
正:boxplot(run50m~gender,data=gen_50)R実装版の出力結果
python実装版のソースコード
import pandas as pd import matplotlib.pyplot as plt import seaborn as sns gen_50 = pd.read_csv('/content/gen_50.csv') plt.subplots_adjust(wspace=0.5) sns.boxplot(x = 'gender', y = 'run50m', data = gen_50) plt.show() sns.violinplot(x = "gender", y = "run50m", data = gen_50) plt.show()ヴァイオリンプロットの描画にseabornモジュールを使ったので、箱ひげ図の描画にもseabornモジュールを使いました。
python実装版の出力結果
ヒストグラムと散布図と箱ひげ図
データの可視化は何のために行うのだろうか。可視化することによって,問題を発見することができ,それに対して詳細な分析や解釈,解決策を考えることができるからである。ここでは,統計解析ソフトウェア R の ggplot2 というパッケージに含まれている diamonds サンプルデータを用いて説明しよう。このデータは,実際に米国で流通したダイアモンドのカラット,カット,透明度,大きさ,価格などを含んだ数万件の大きなデータである。
R実装版のソースコード(教材より)
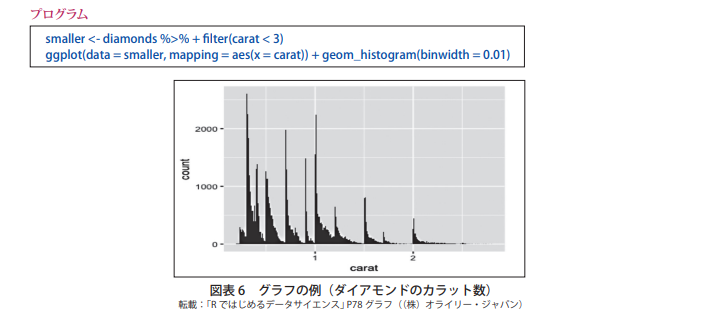
library(ggplot2) diamonds smaller <- diamonds %>% filter(carat < 3) ggplot(data = smaller, mapping = aes(x = carat)) + geom_histogram(binwidth = 0.01) ggplot(data = diamonds) + geom_point(mapping = aes(x = carat, y = price)) ggplot(diamonds, aes(cut, price)) + geom_boxplot()ちなみに、実際の教材に書かれているソースコードは以下のようになっております。
ここにバグがあるのでご注意ください。
誤:smaller <- diamonds %>% + filter(carat < 3)
正:smaller <- diamonds %>% filter(carat < 3)R実装版の出力結果
A tibble: 53940 × 10 carat cut color clarity depth table price x y z <dbl> <ord> <ord> <ord> <dbl> <dbl> <int> <dbl> <dbl> <dbl> 0.23 Ideal E SI2 61.5 55 326 3.95 3.98 2.43 0.21 Premium E SI1 59.8 61 326 3.89 3.84 2.31 ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ (省略) ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0.86 Premium H SI2 61.0 58 2757 6.15 6.12 3.74 0.75 Ideal D SI2 62.2 55 2757 5.83 5.87 3.64python実装版のソースコード
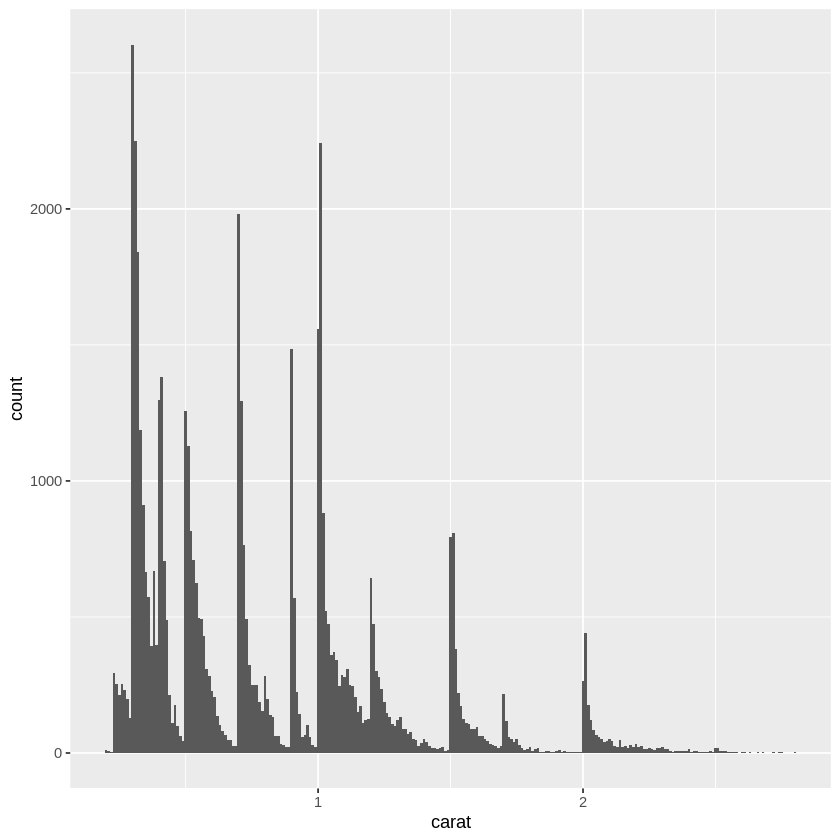
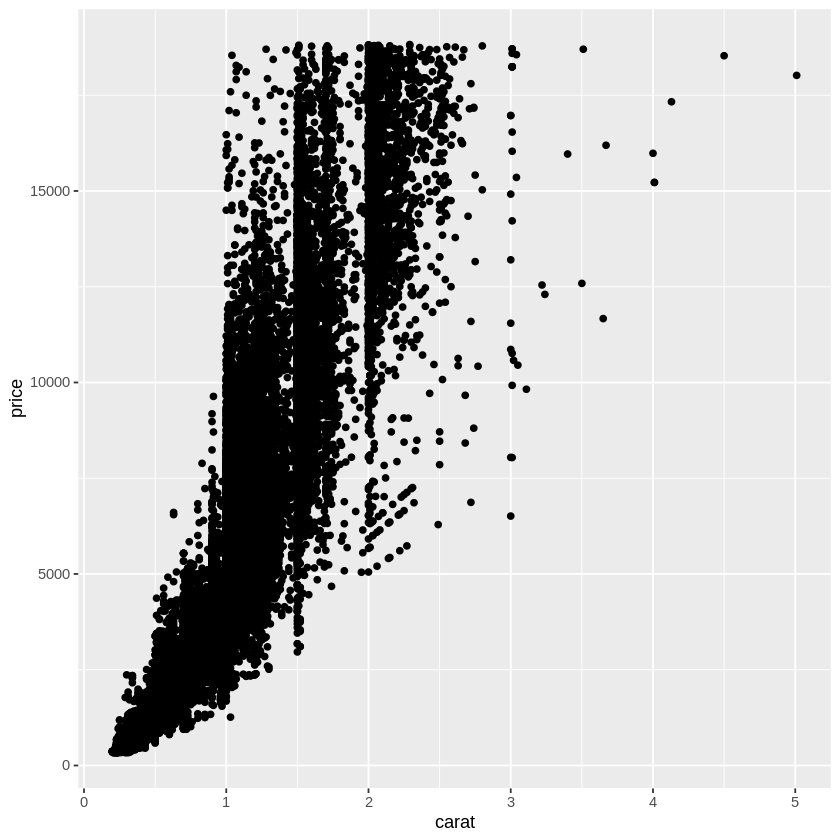
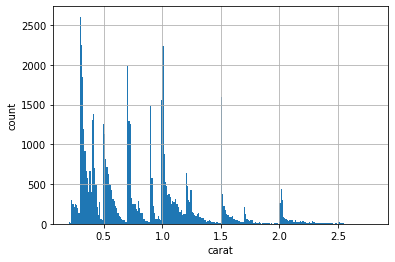
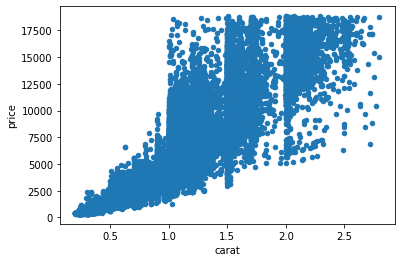
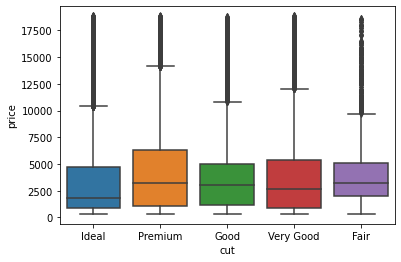
import pandas as pd import matplotlib.pyplot as plt import seaborn as sns df = pd.read_csv('/content/diamonds.csv') df_carat_lt3 = df[df['carat'] < 3] # x軸にcarat、y軸にcount plt.xlabel('carat') plt.ylabel('count') # ヒストグラムを描画する df_carat_lt3['carat'].hist(bins=250) plt.show() # 散布図を描画 df_carat_lt3.plot.scatter(x = 'carat', y = 'price') plt.show() sns.boxplot(x = 'cut', y = 'price', data = df_carat_lt3) plt.show()python実装版の出力結果
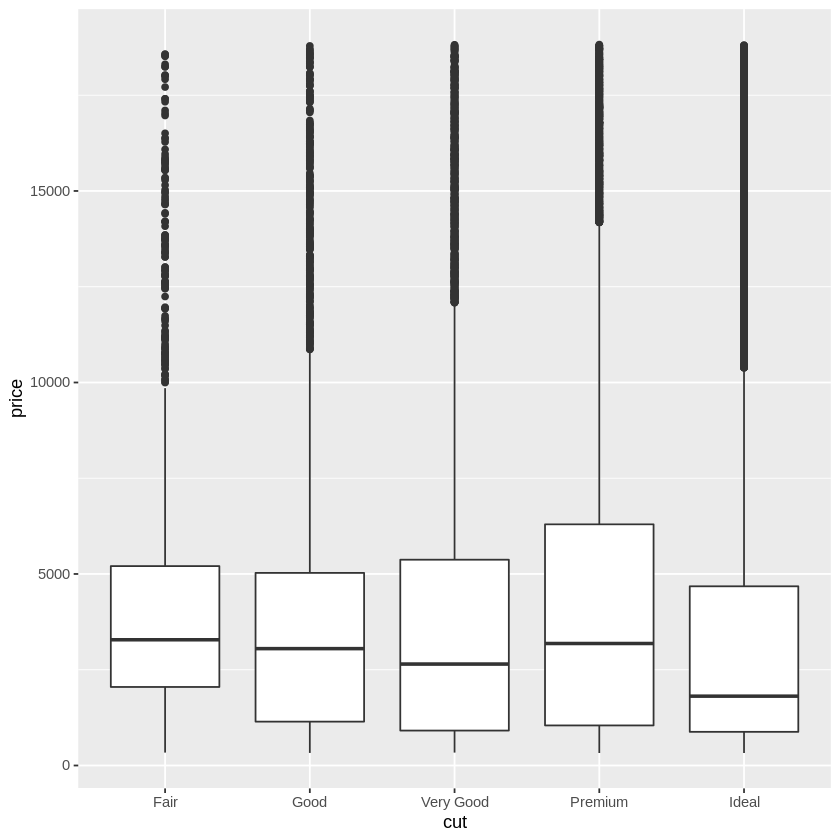
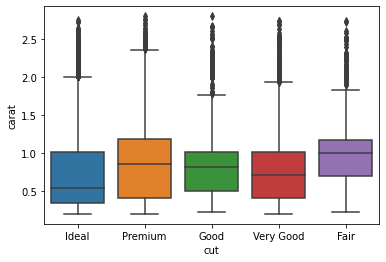
カラット数が大きくなるほど、価格もあがることがわかる。
最後の図のx軸の順番があまり良い形ではないですがカットの質の順番はIdeal>Premium>Very Good>Good>Fairです。
コメント
教材には、以下のように書かれています。
これは不思議な現象に見えるだろう。カットの質が上がるほど,価格が下がっている。色や透明度の高さなどでも同様の逆転現象が起こる。ヒントは「交絡因子」である。交絡因子とは,対象としている 2変数と相互に相関の高い隠れた変数(因子)のことである。
これまでの結果からカラット数が高いほど価格も高いことがわかってます。
ここから考えられるのは、カラット数の大きいダイヤモンドは、カットの質が悪いものが多いということが推測されます。
(すなわちカットの質が上がるほど価格が下がっているのは、交絡因子であるカラット数等による影響があるのではないかということです)python実装版のソースコード(cut vs carat)
sns.boxplot(x = 'cut', y = 'carat', data = df_carat_lt3) plt.show()python実装版の出力結果(cut vs carat)
想定した通りであり、特に中央値をみるとカットの質が一番高いIdealのカラット数は一番低くカットの質が一番低いFairのカラット数は一番低いことがわかりました。
このダイアモンドに関するデータ分析でもっと詳しく分析したものが見たい場合は、以下のサイト等を確認すると良いと思います。
https://www.kaggle.com/fuzzywizard/diamonds-in-depth-analysisダイアモンドのカットの質について(補足)
- カットの質が上がるほど、カラットあたりのコストが増加する。
- カラット数の大きいダイヤモンド原石はより良い対称性とプロポーションを達成するためにより多くの材料が必要となり大きな無駄ができてしまう。
ソースコード
python版
https://gist.github.com/ereyester/03b8424d62159c662b41baaa8337b11cR版
https://gist.github.com/ereyester/b8a7877e06642d47974f43c388d6bd65
- 投稿日:2020-07-27T22:51:49+09:00
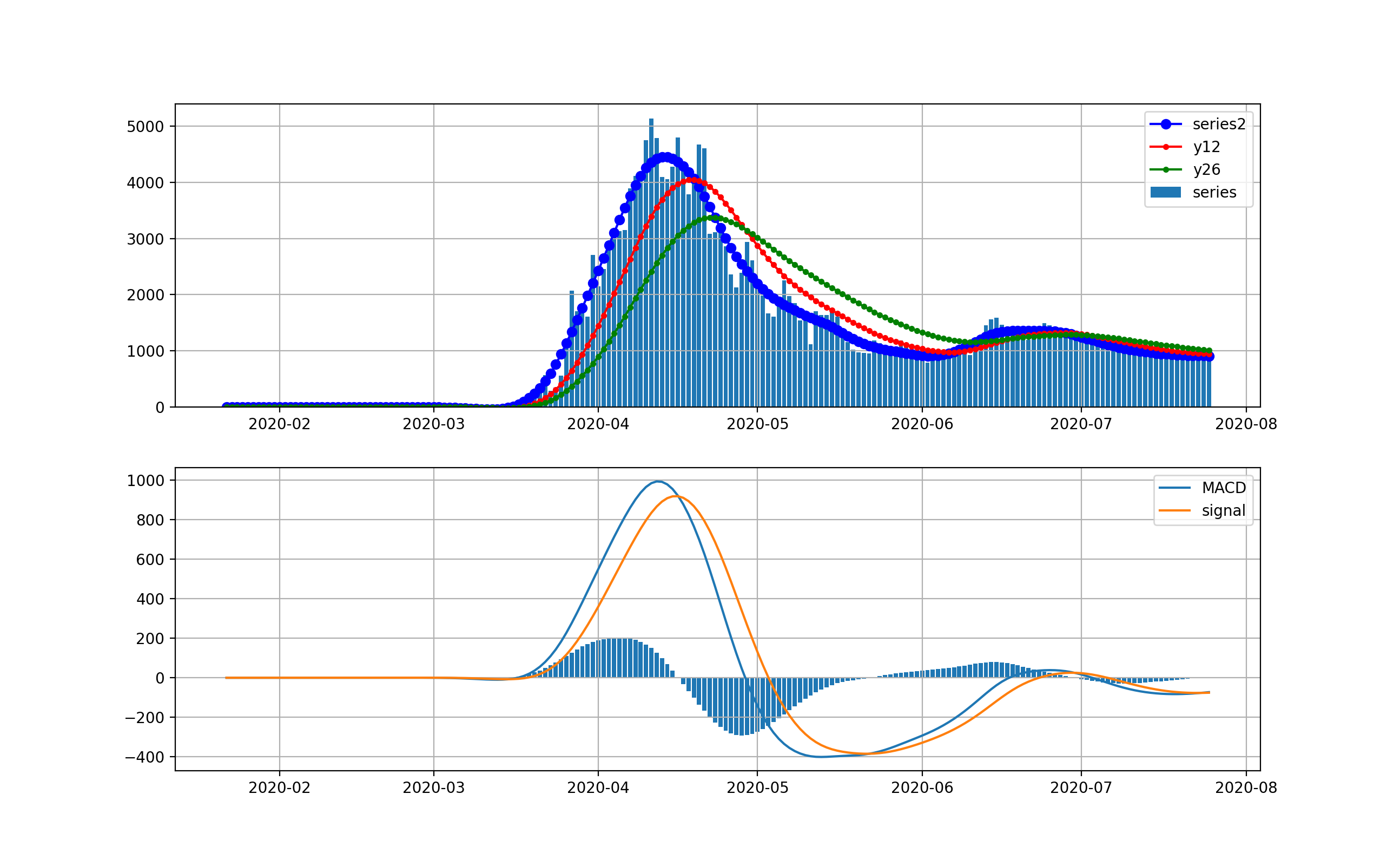
【感染症モデル入門】MACDで見る世界の感染状況♬
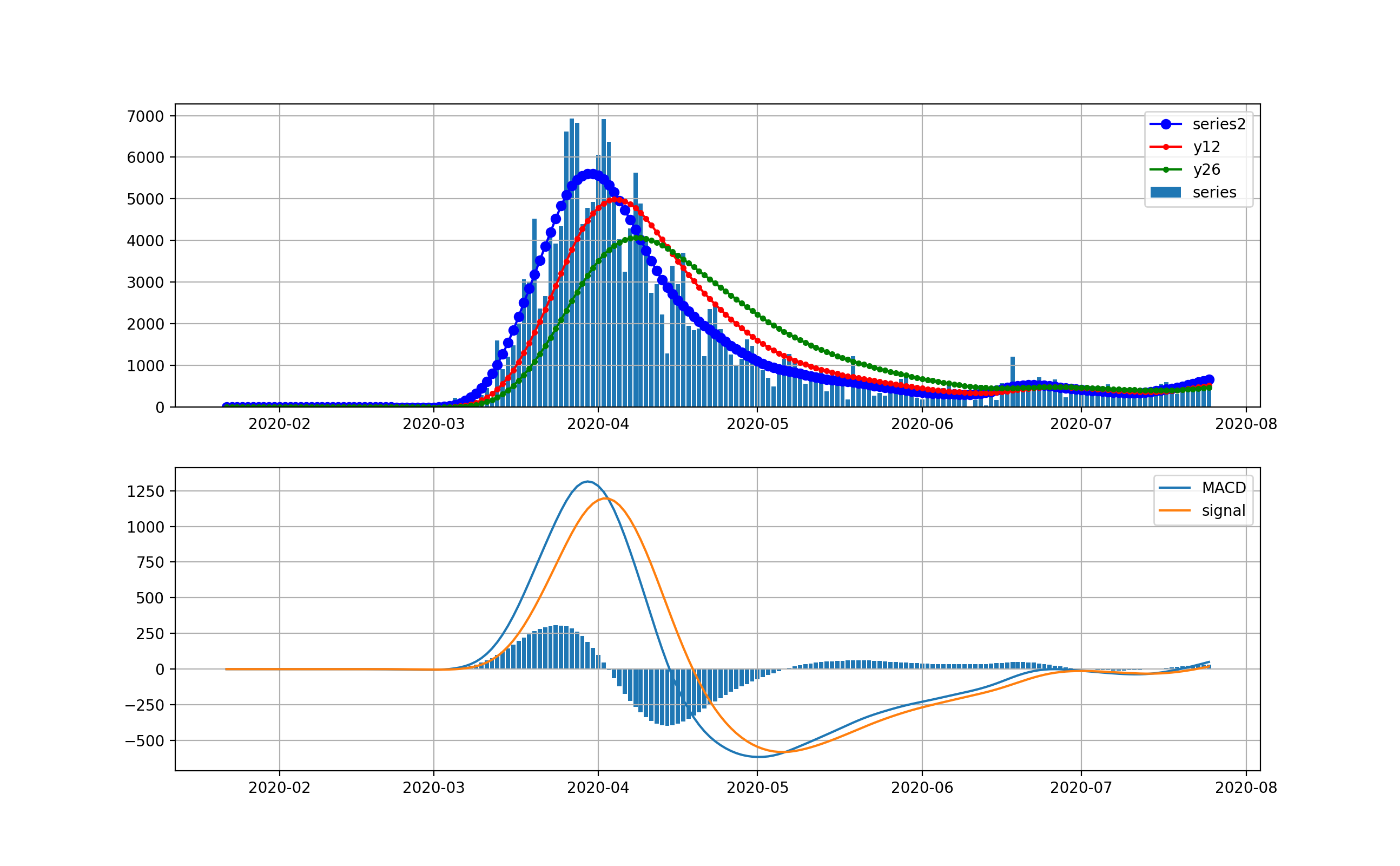
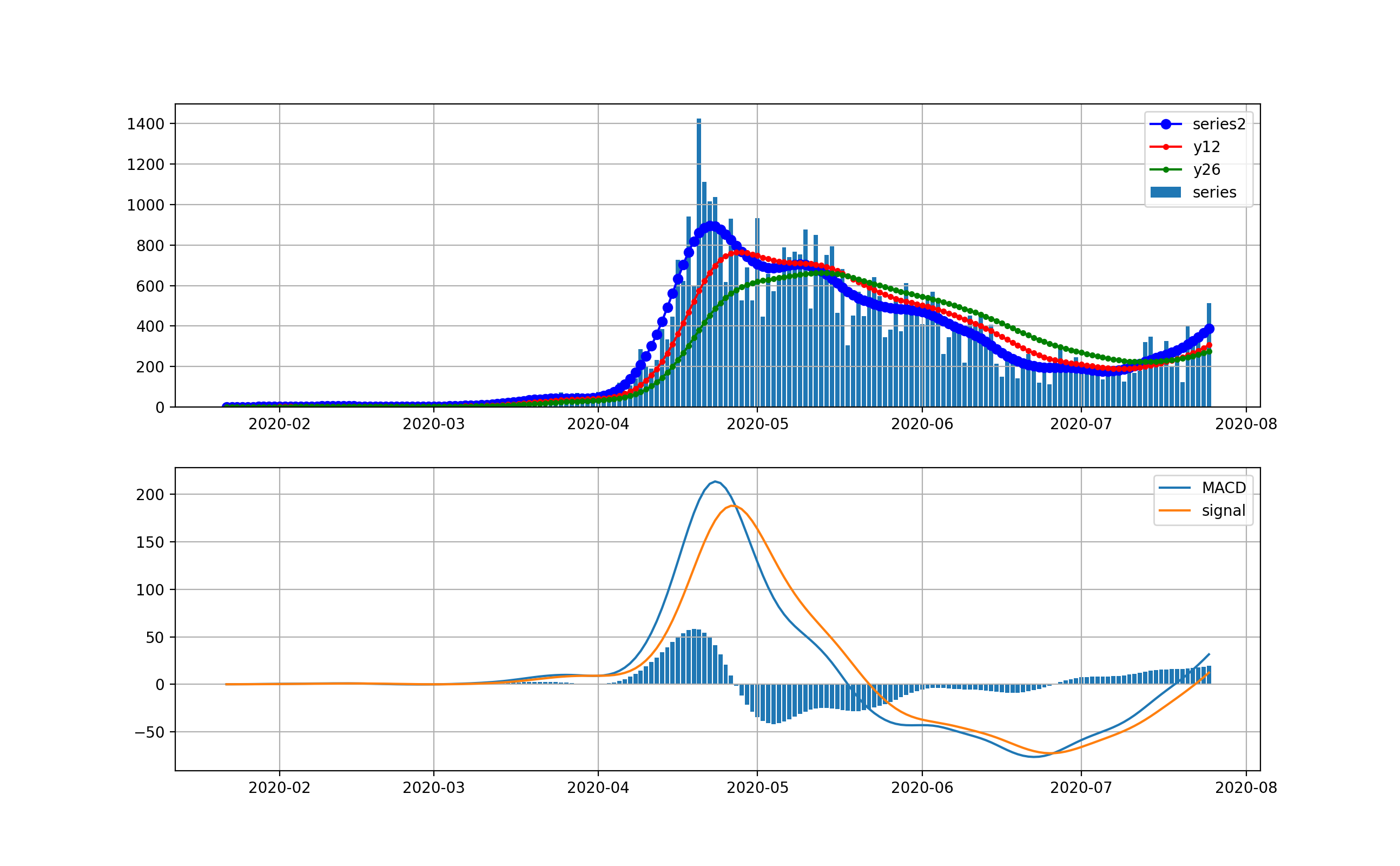
世界の感染状況をMACDしてみようと思う。
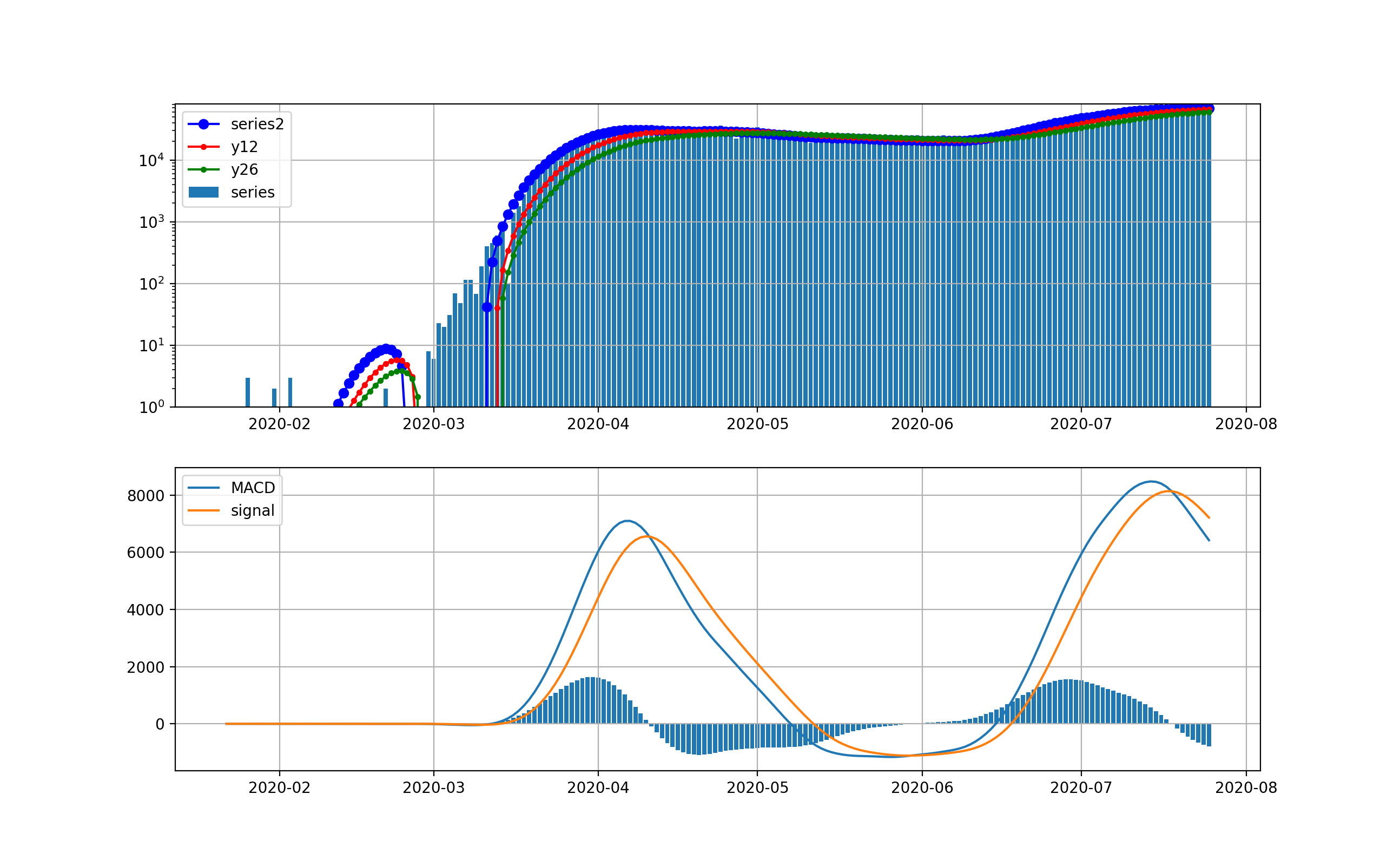
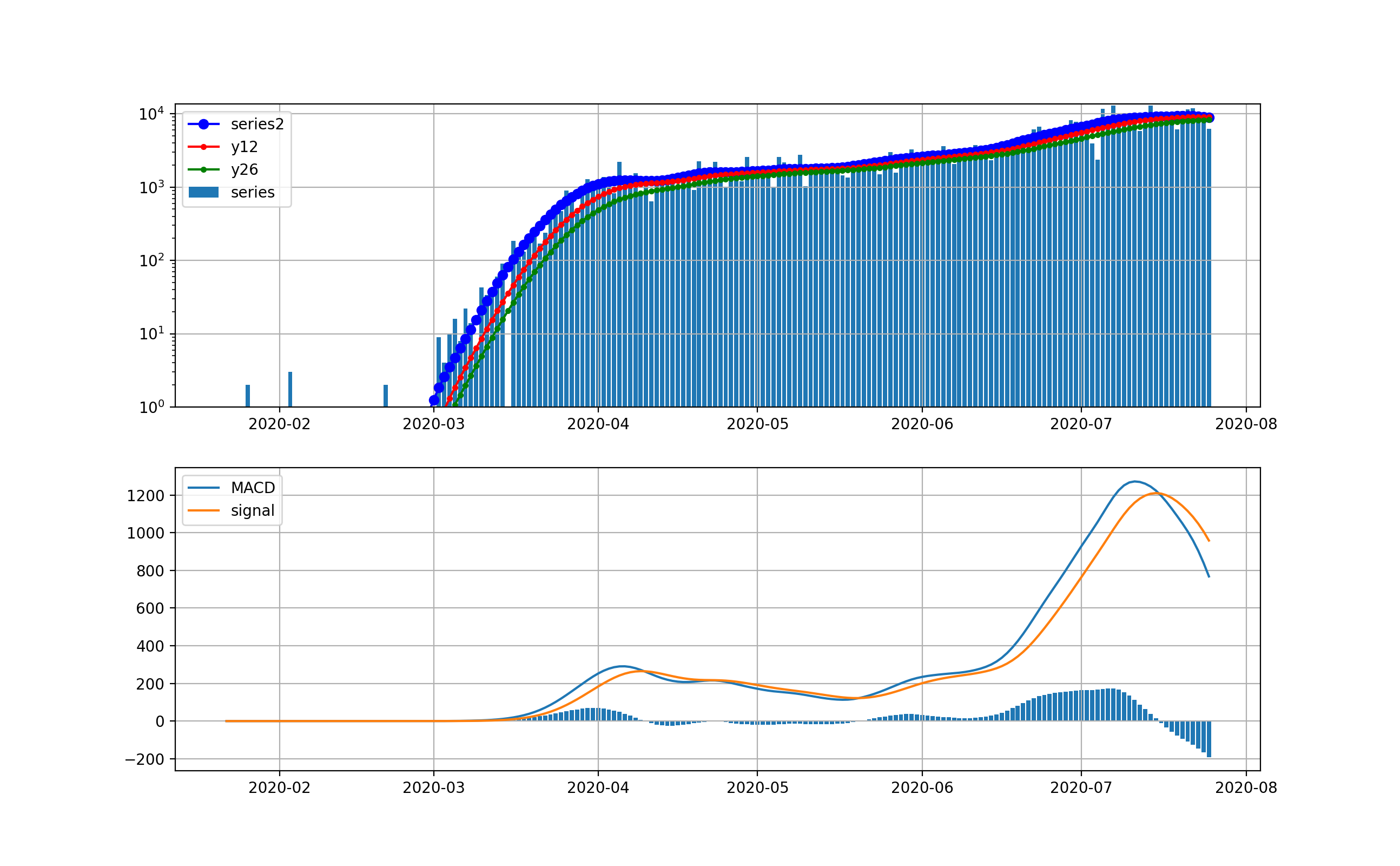
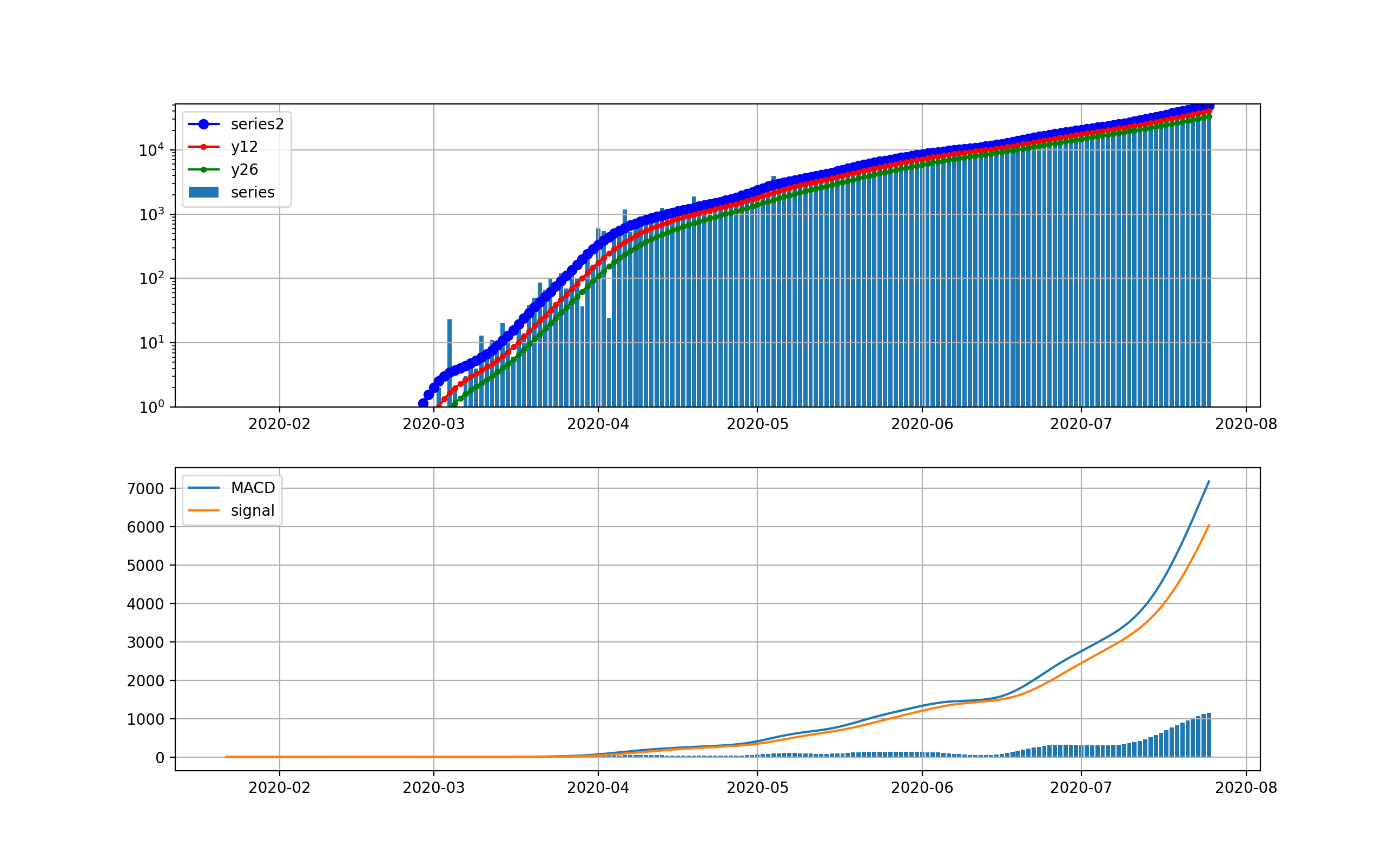
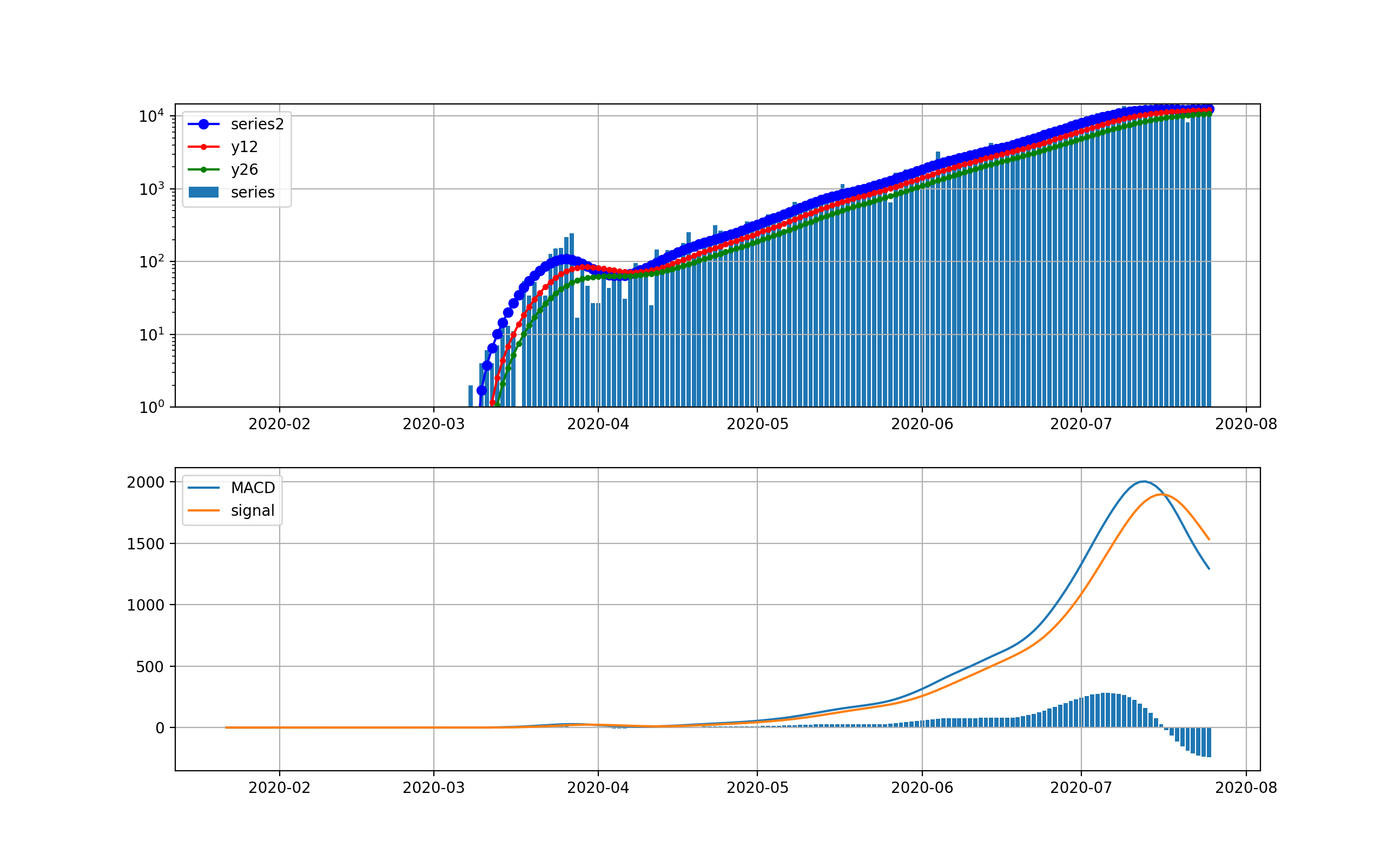
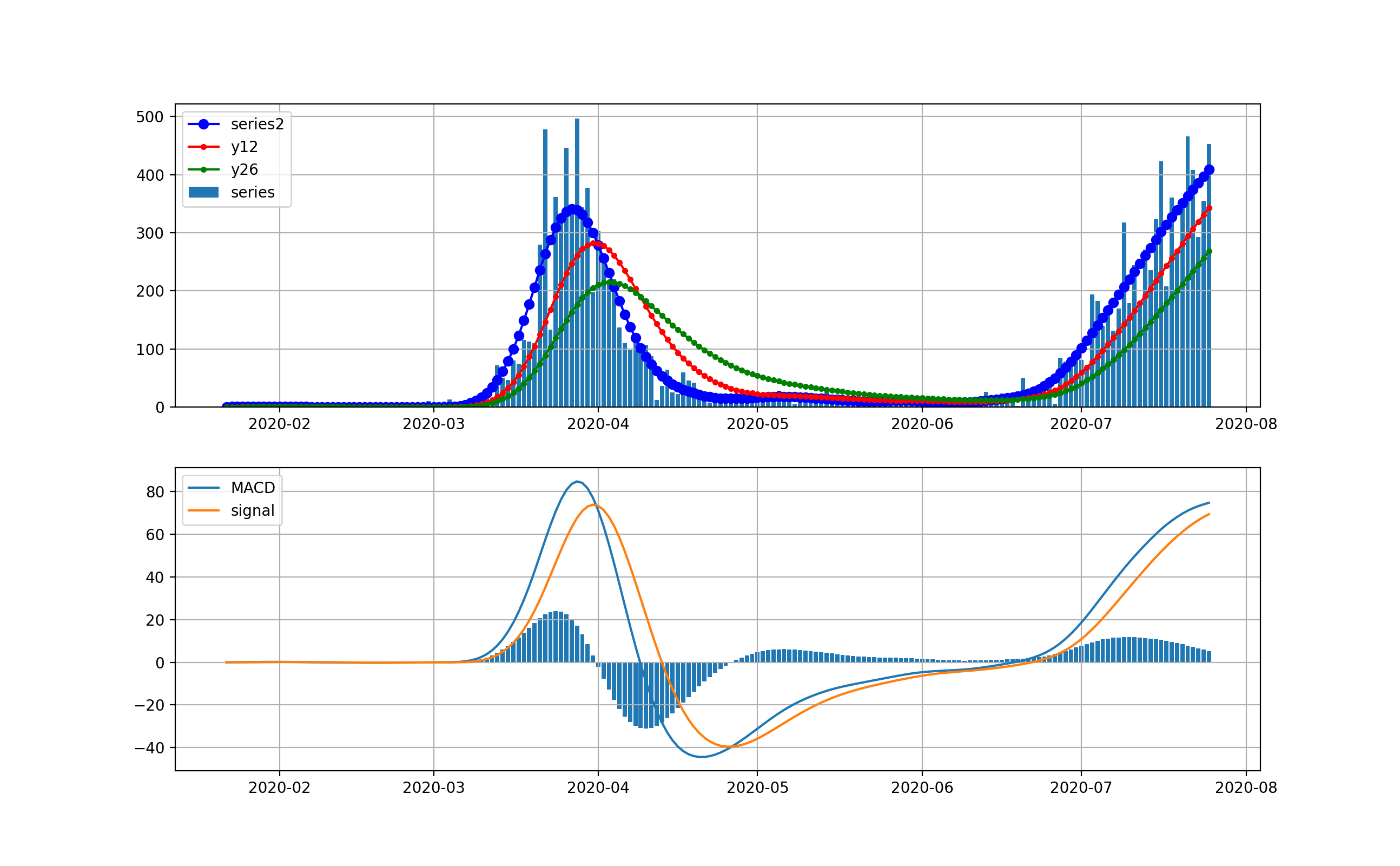
オリパラを一年後に控えて、感染爆発から半年経過時点での感染状況を俯瞰することは有意義だと思う。世界全体の状況
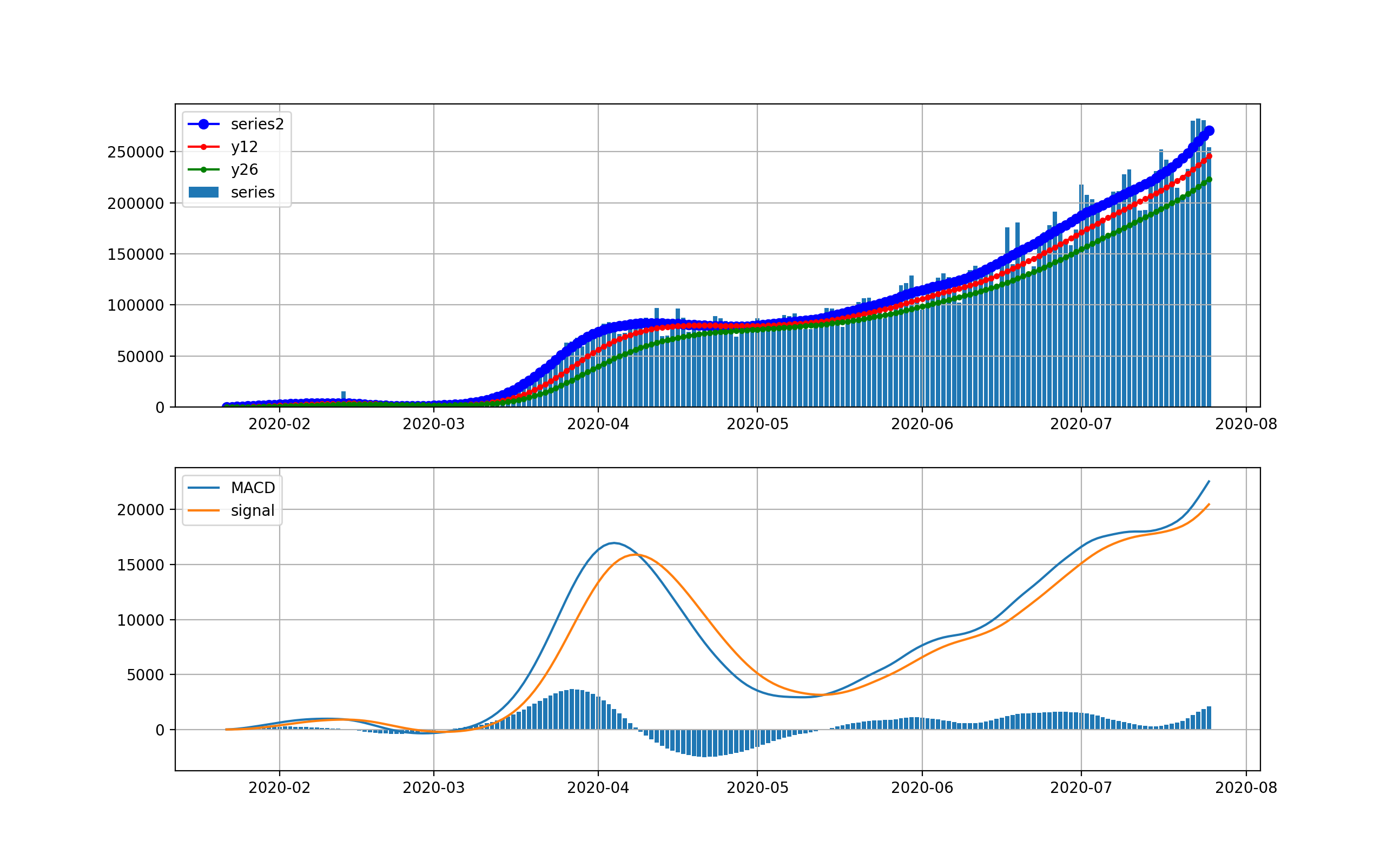
以下のとおりです。上段は、新規感染数seriesの棒グラフとトレンドの青いプロット、12日移動平均、26日移動平均を描画している。下段は、そのMACDとSignal、そしてMACD-Signalの棒グラフを描画しています。上段から世界は6月ごろから加速度的に急激に増加しているのが分かります。その結果、下段のグラフから4月に一度減少傾向になったものの5月上旬から棒グラフがプラス側に触れて、マイナスになっていません。
これが毎日新規感染数が最大だというニュースの実態です。そしてお気づきだと思いますが、武漢や中国の感染ピークはこのグラフでは、ほんの序の口で、小さくほとんど見えません。
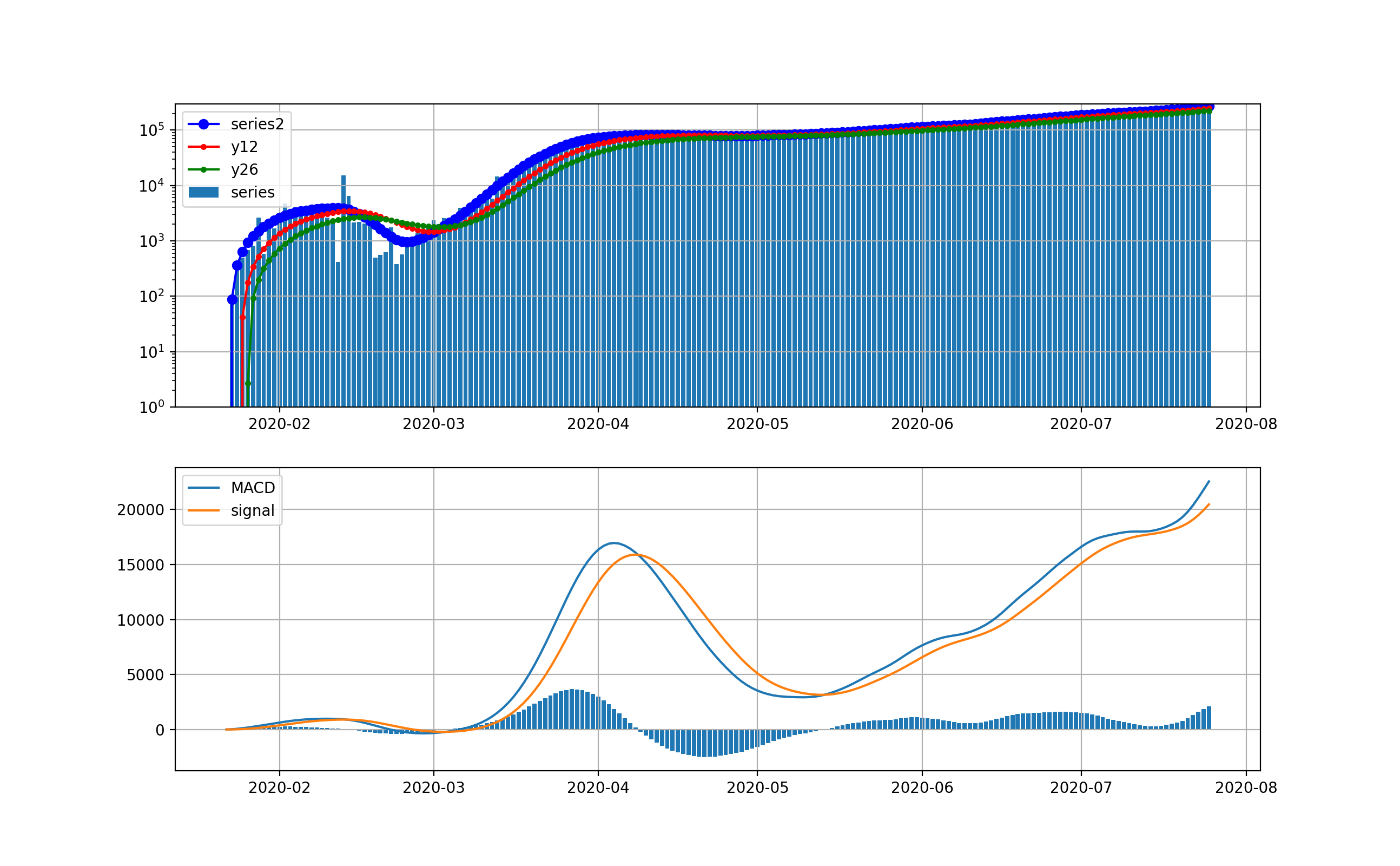
そこで、縦軸を対数グラフで描画します。
このグラフでは2月から3月の第一波が見えています。今の状況と比較すると2桁差があることが分かります。
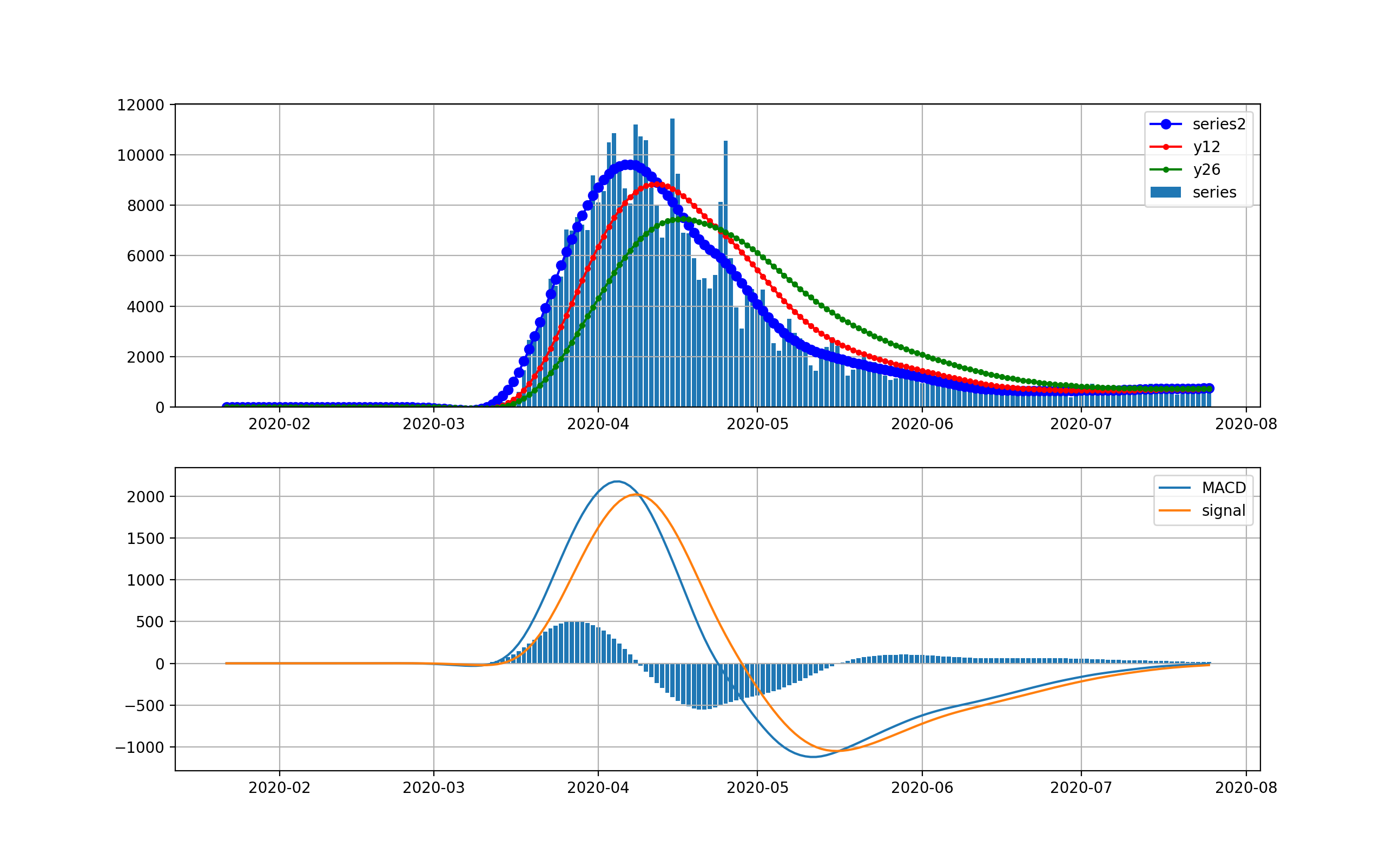
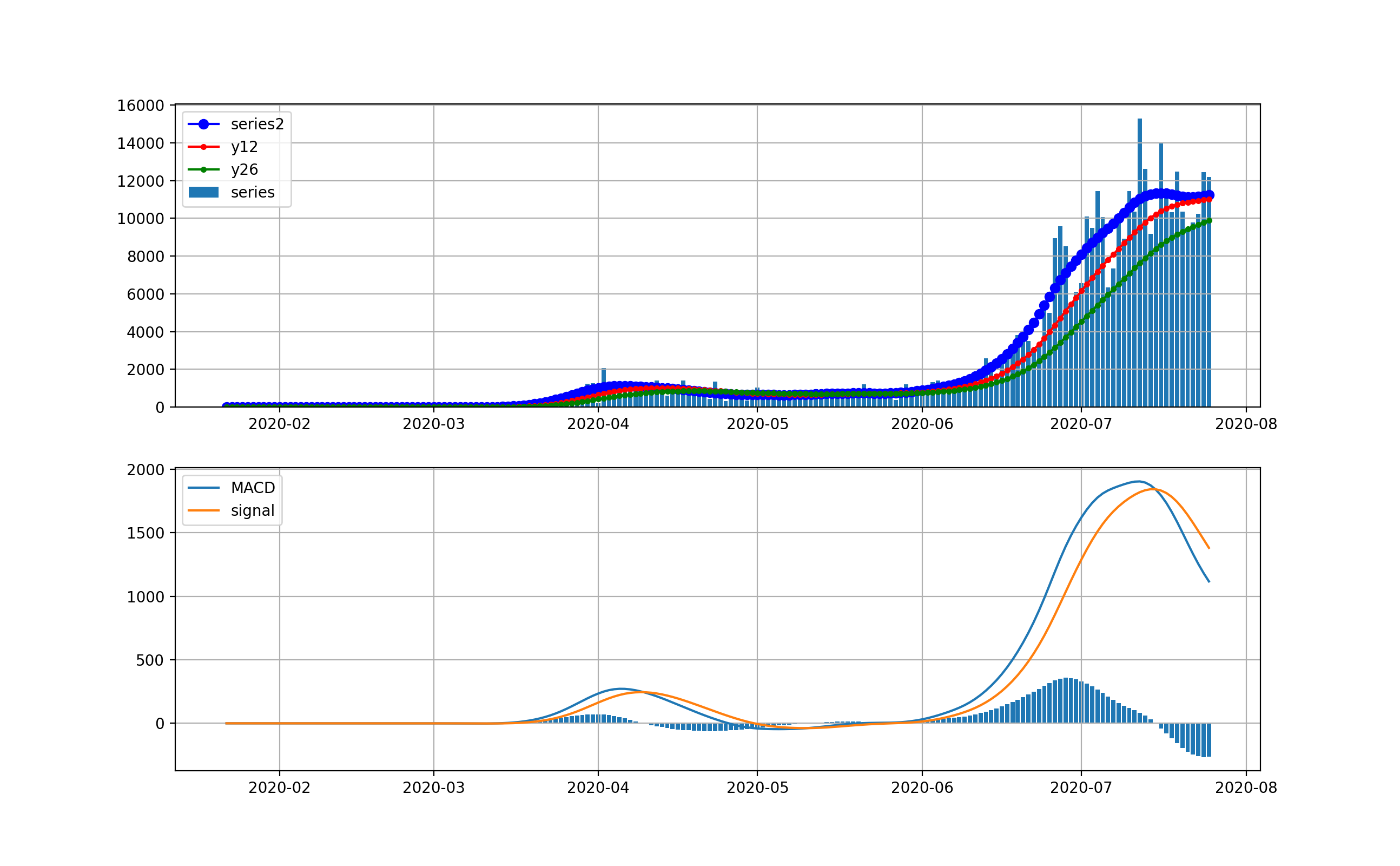
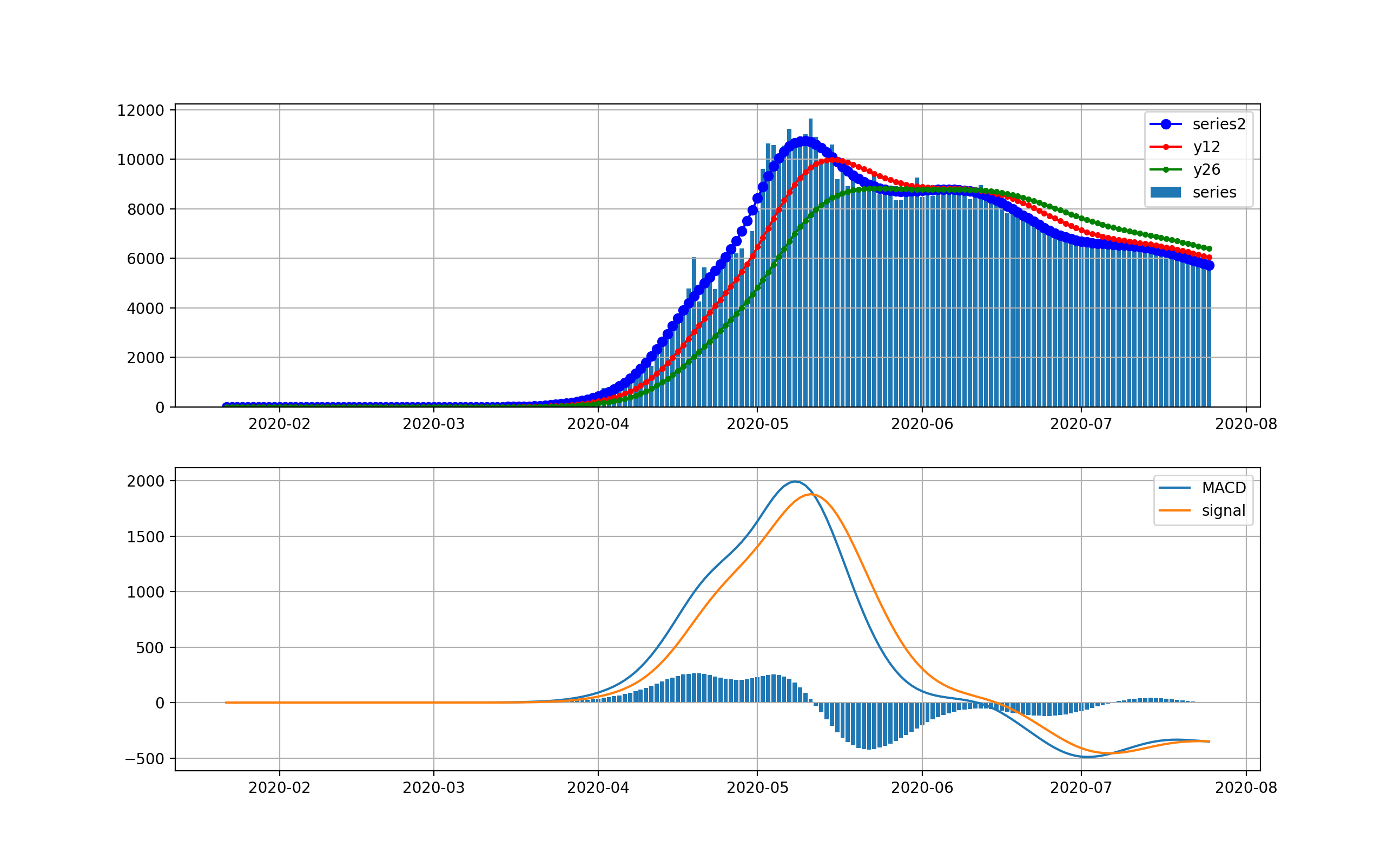
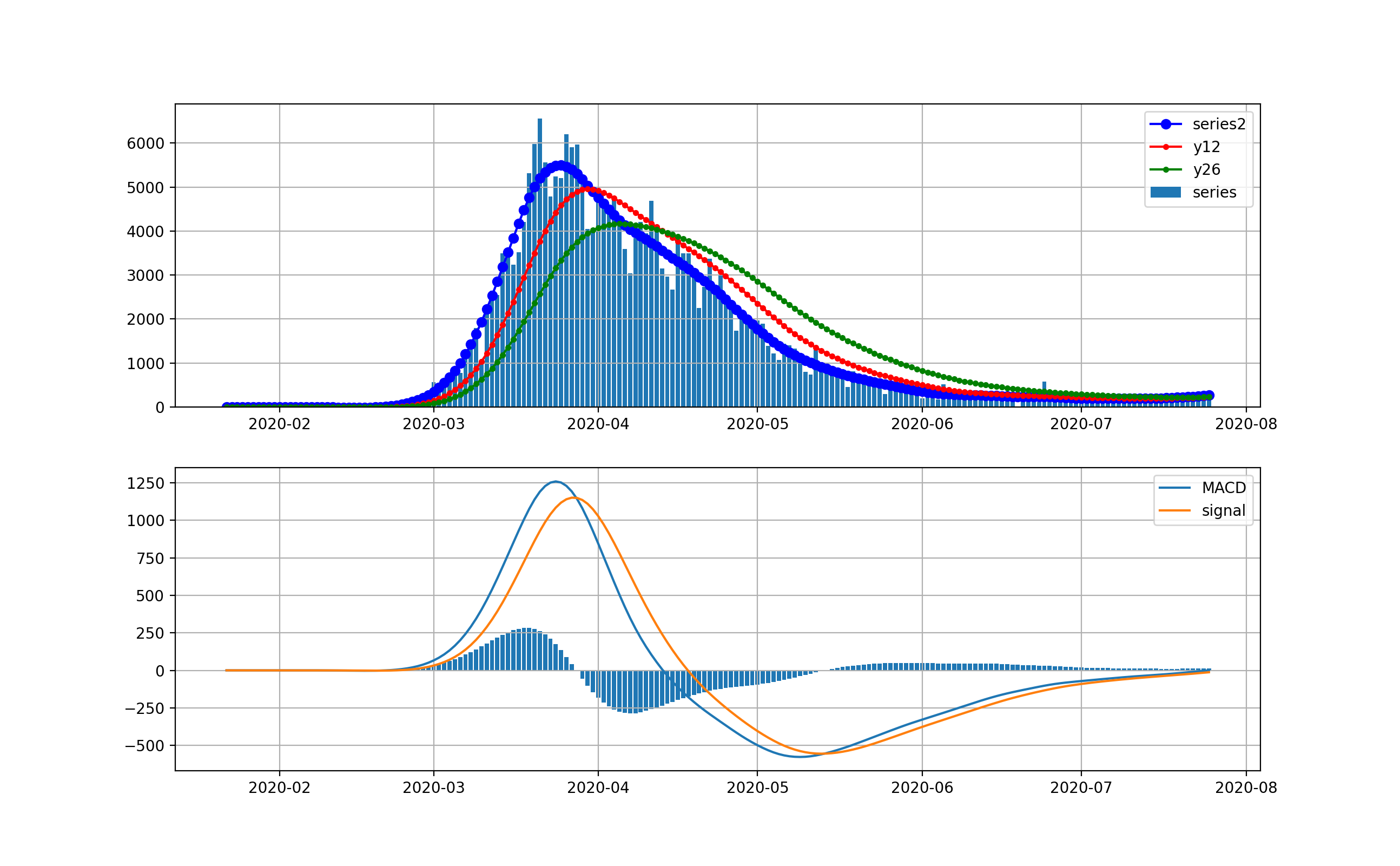
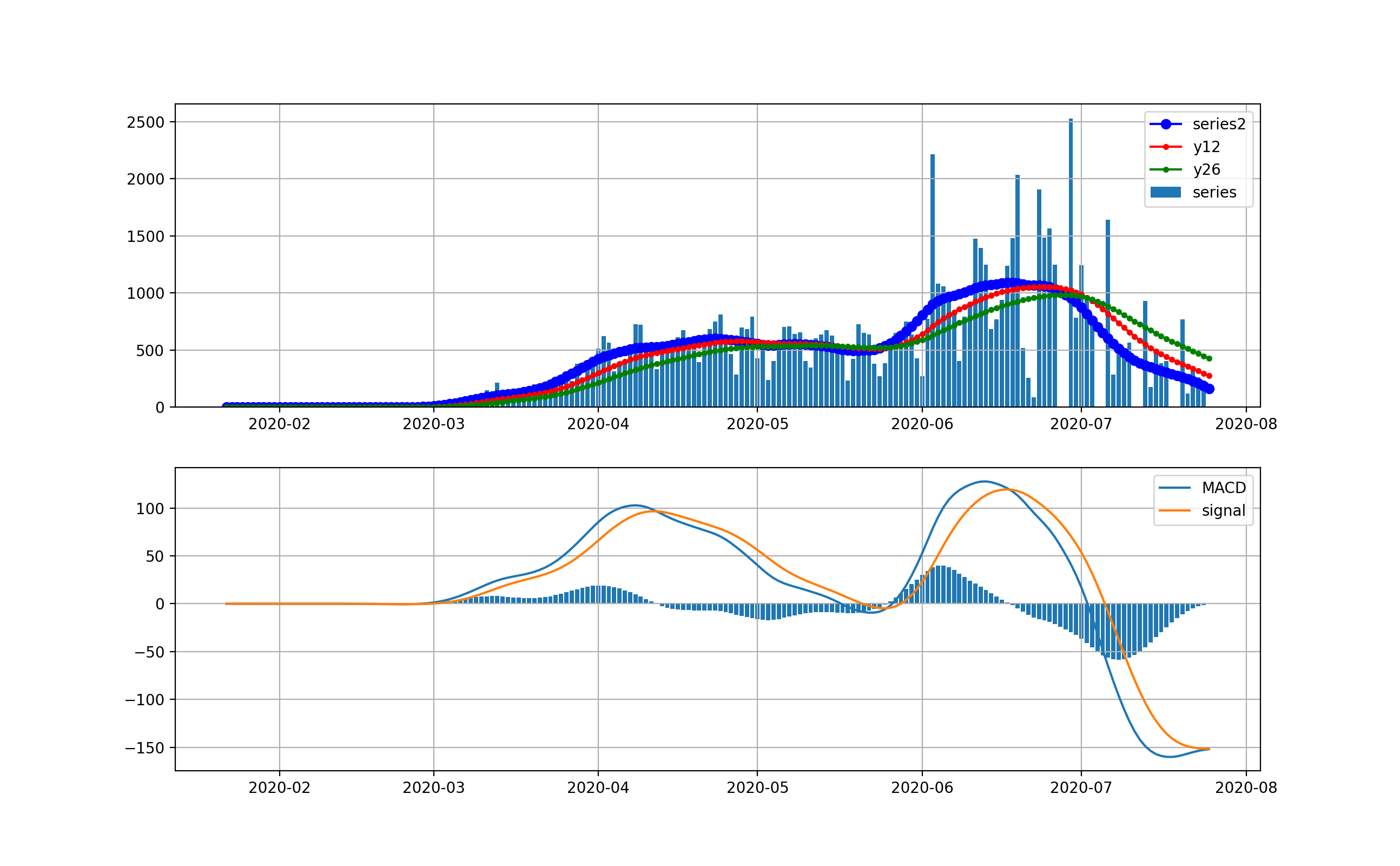
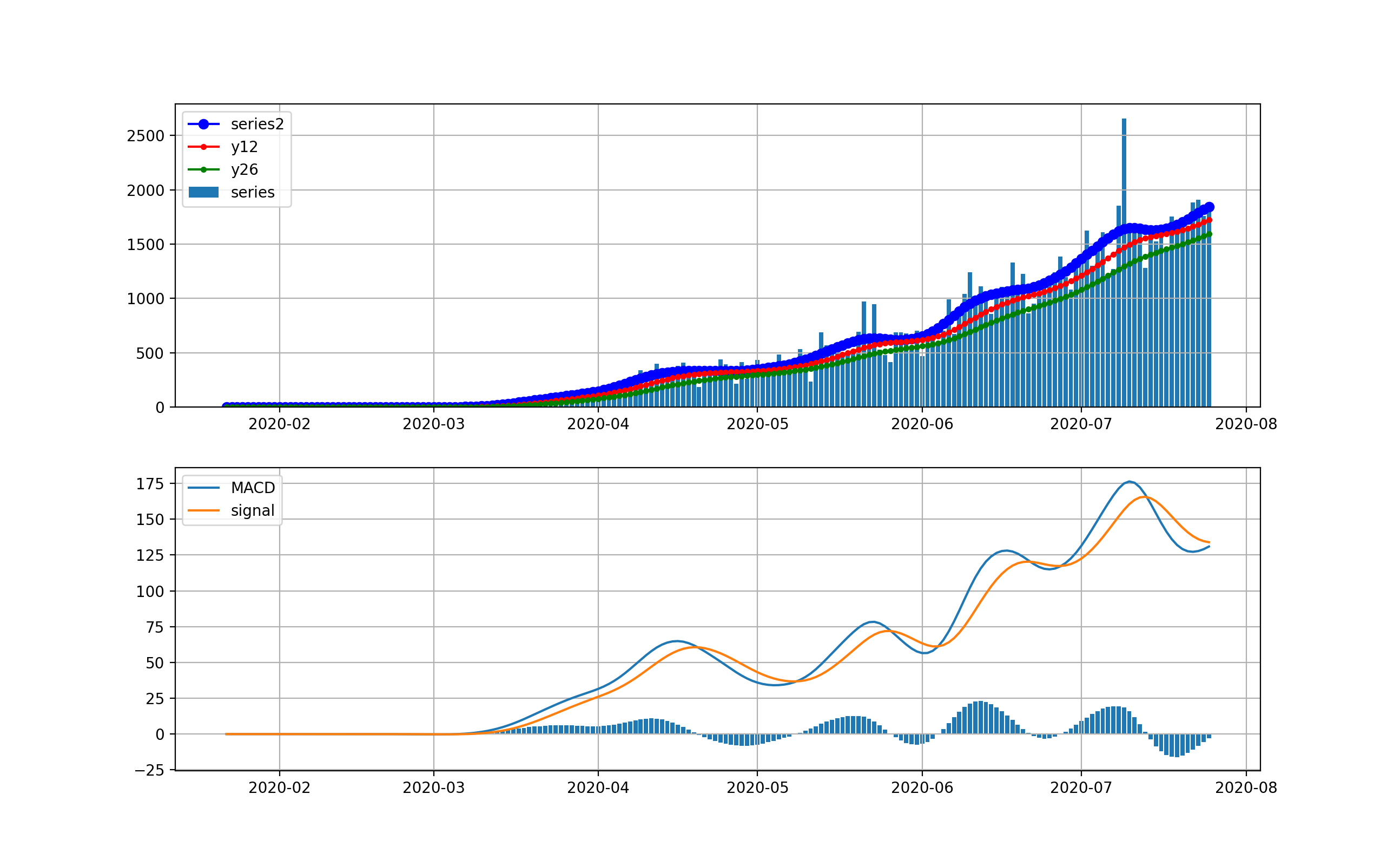
米国の状況
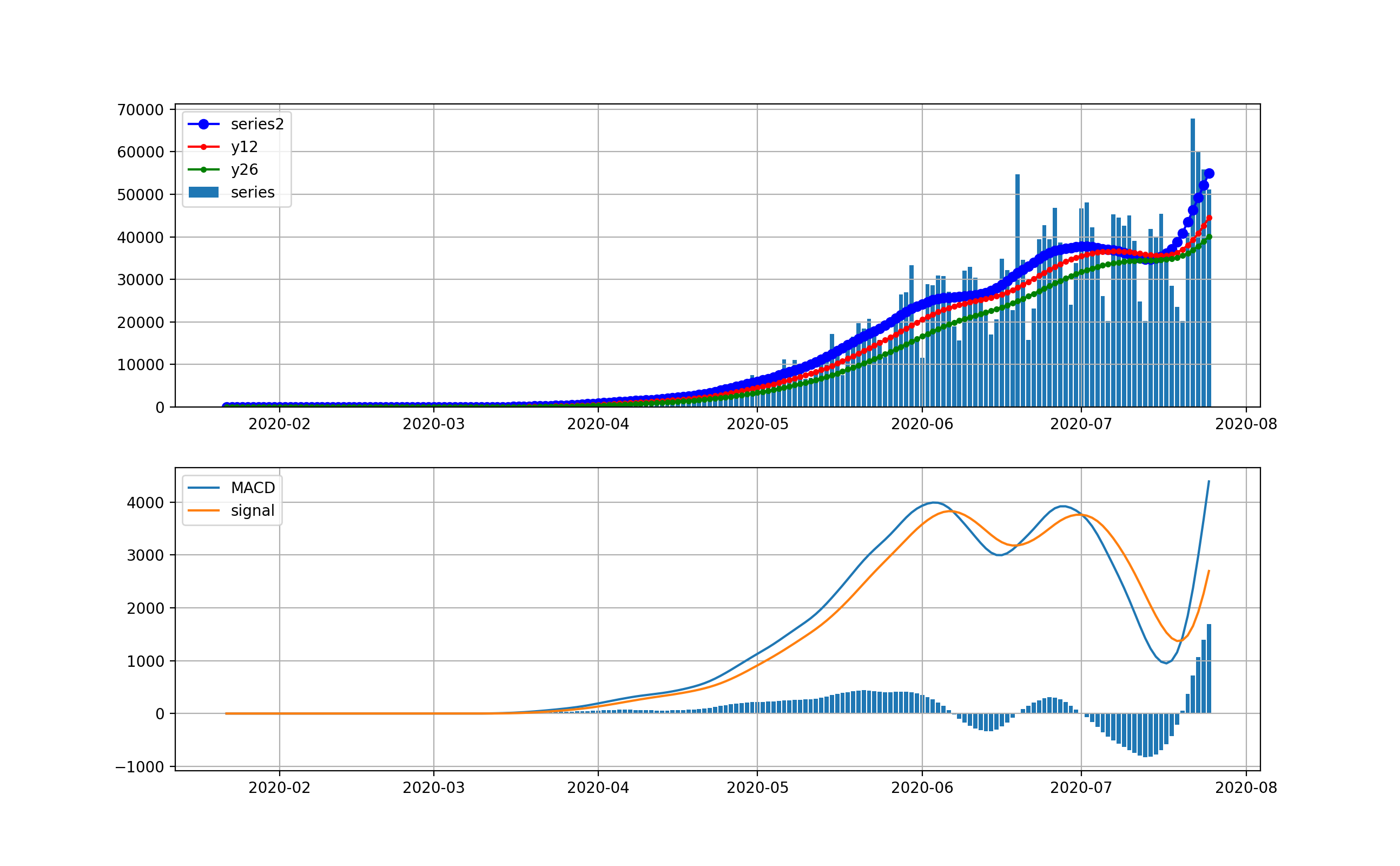
現在、米国が最大の感染数国です。
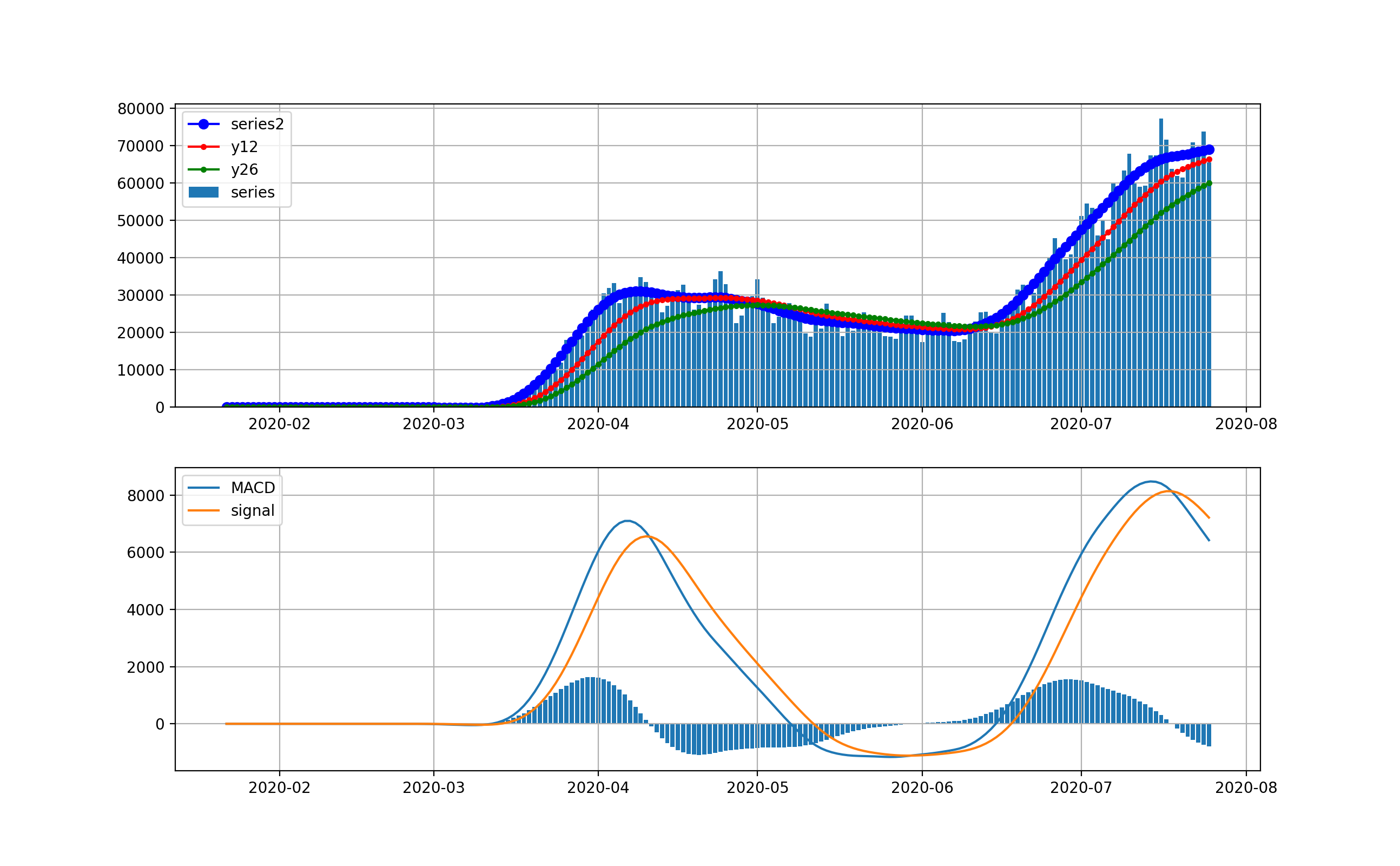
米国は4月から5月にかけて、第一波が来ました。一度、日々の新規感染数は20000人程度まで減少しましたが、6月中旬から大幅に増加して、日々70000程度まで来ました。今後は、下のMACDを見ると減少を示唆するように棒グラフがマイナスに触れています。上段のグラフからは減少するようには見えませんが、今後減少してくるのかもしれません。
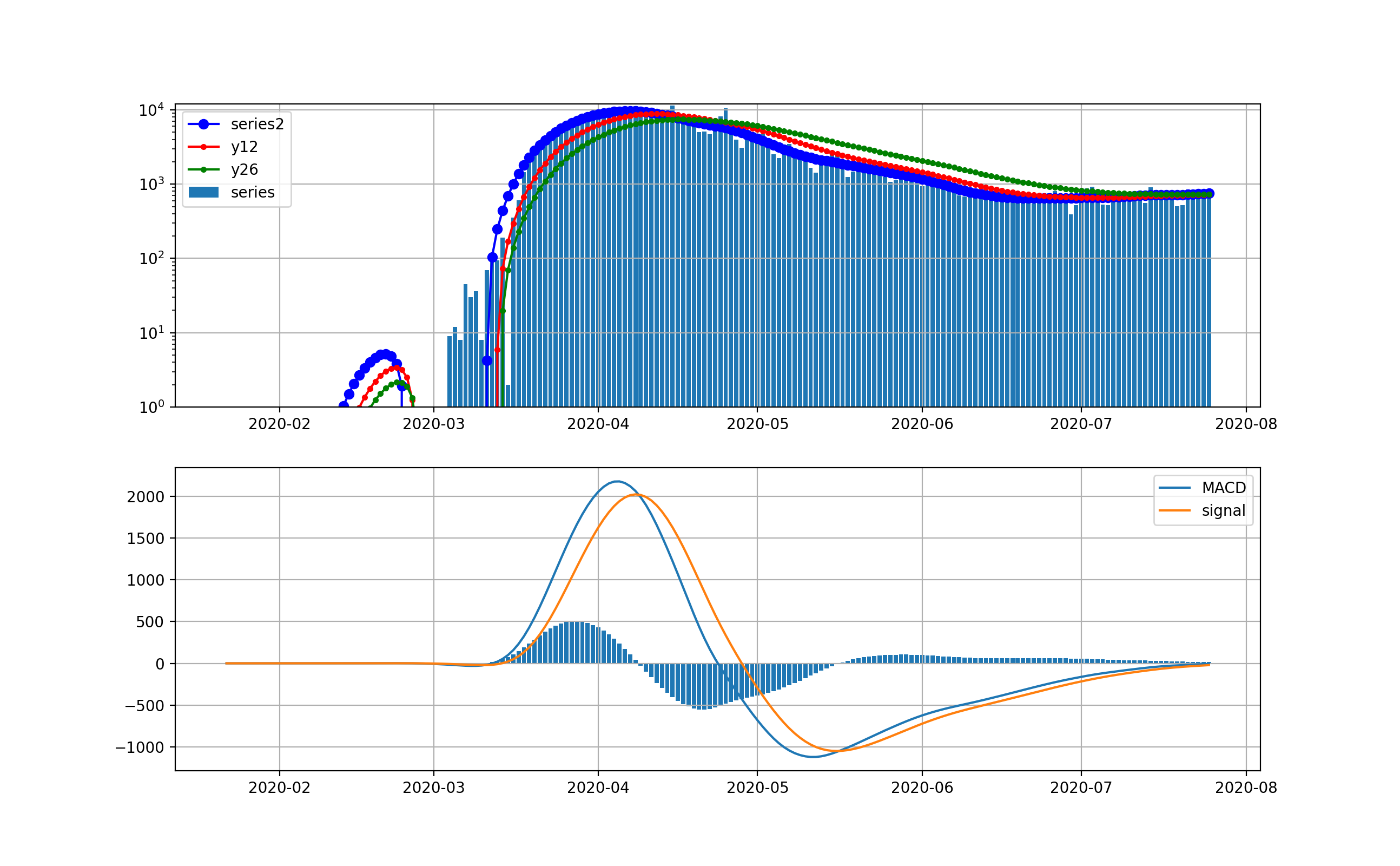
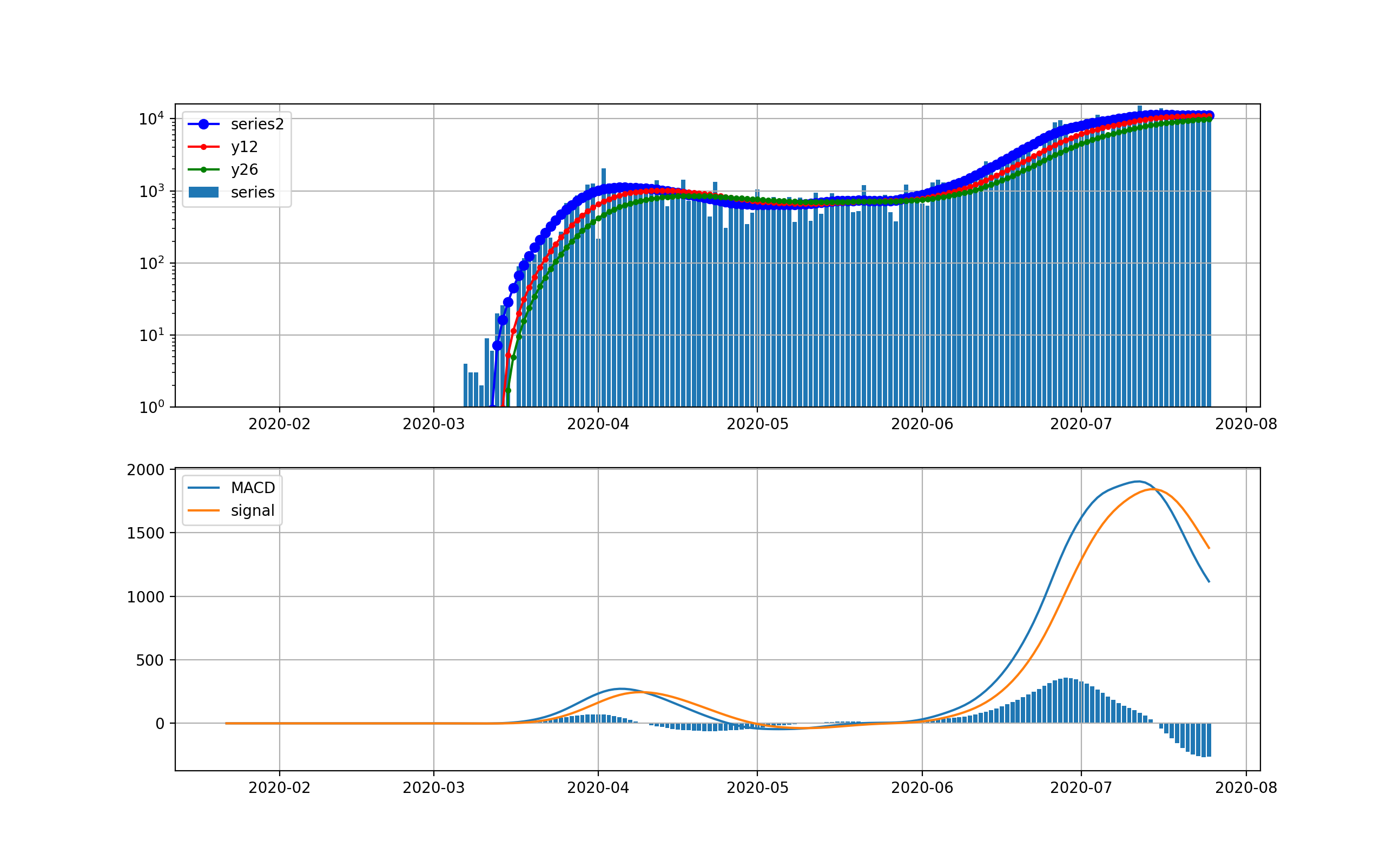
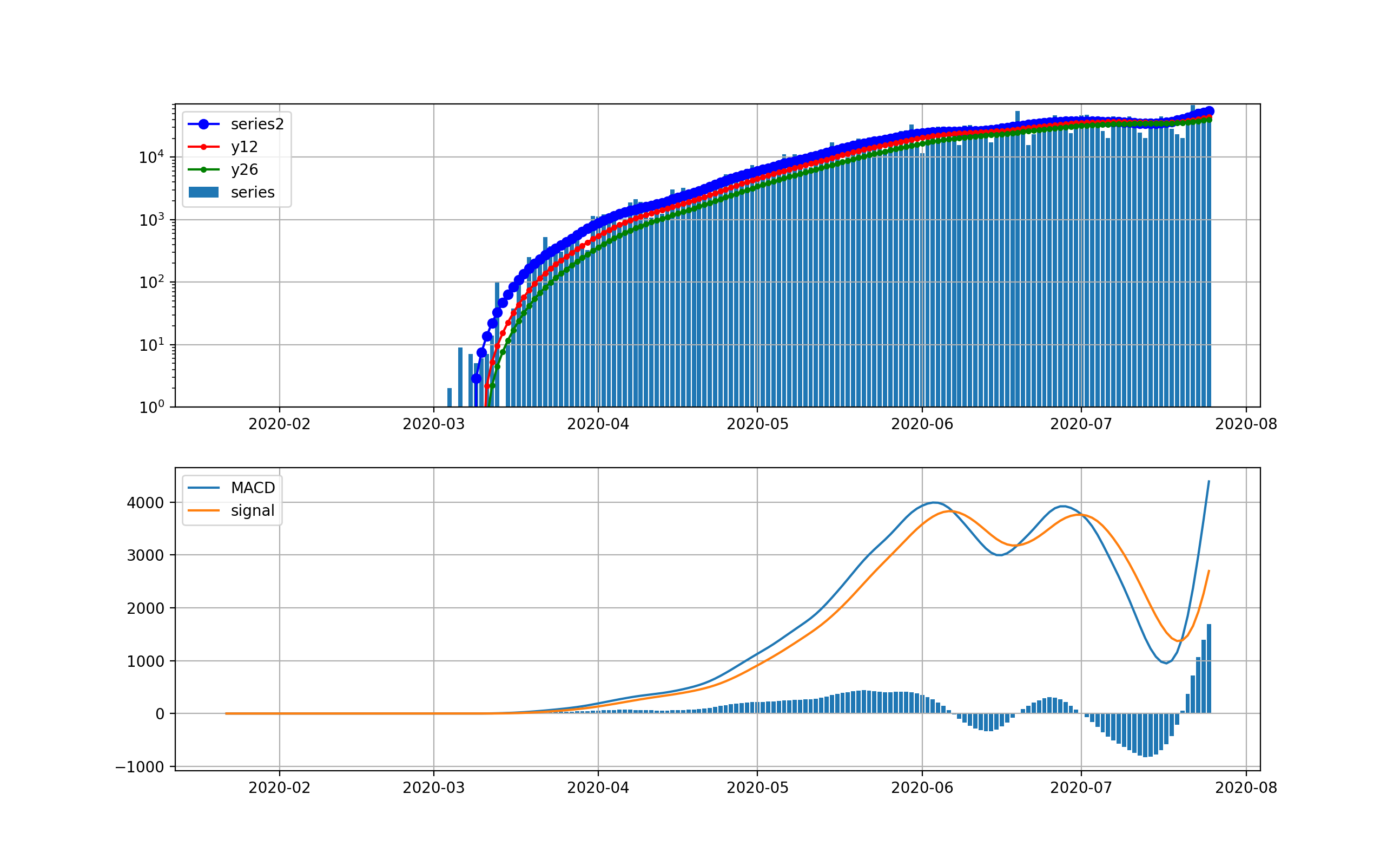
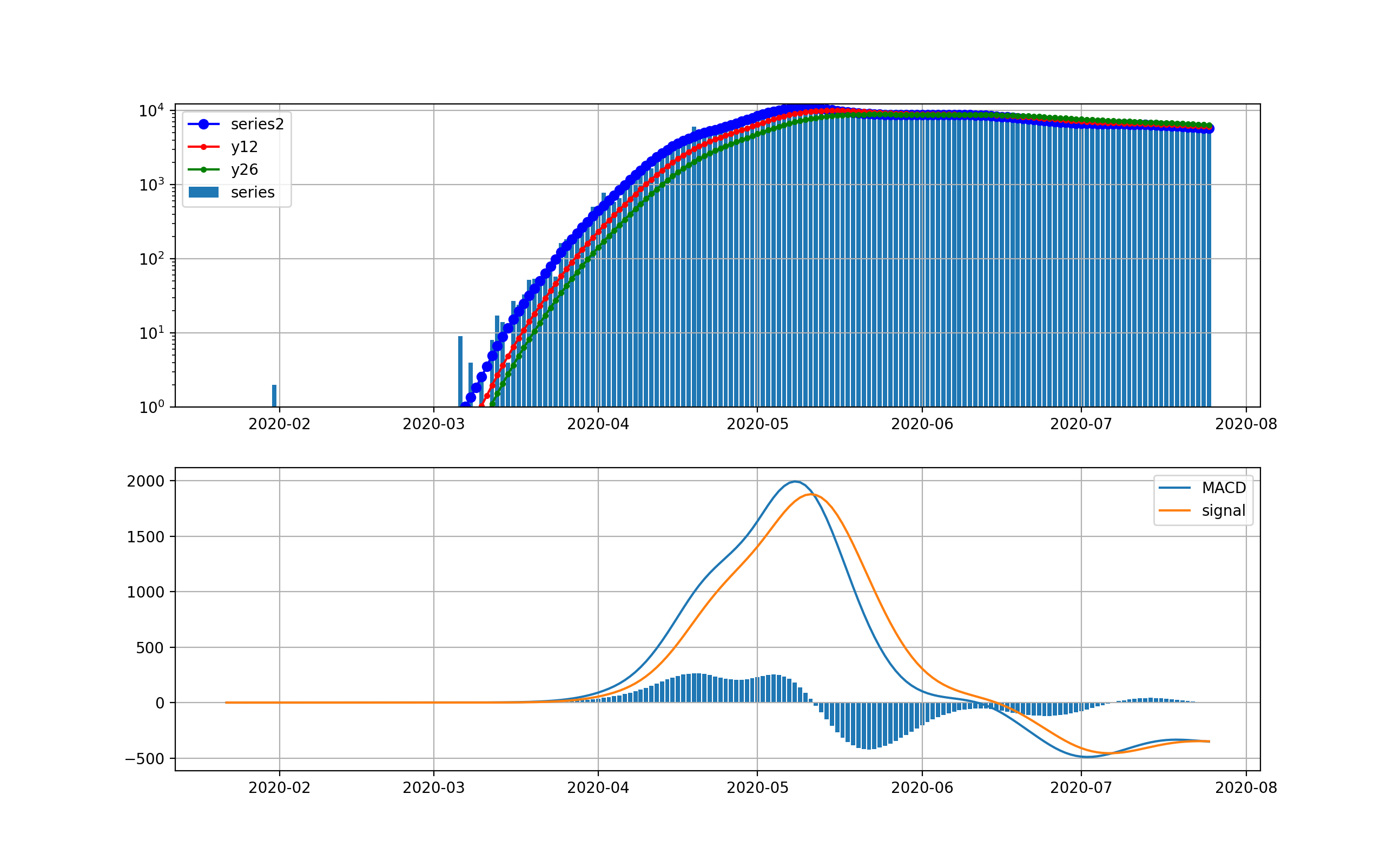
対数グラフは以下のとおりです。2月は検出数ほぼ0だったのが分かります。3月ひと月で今のオーダーまで3.5桁増えたのが分かります。
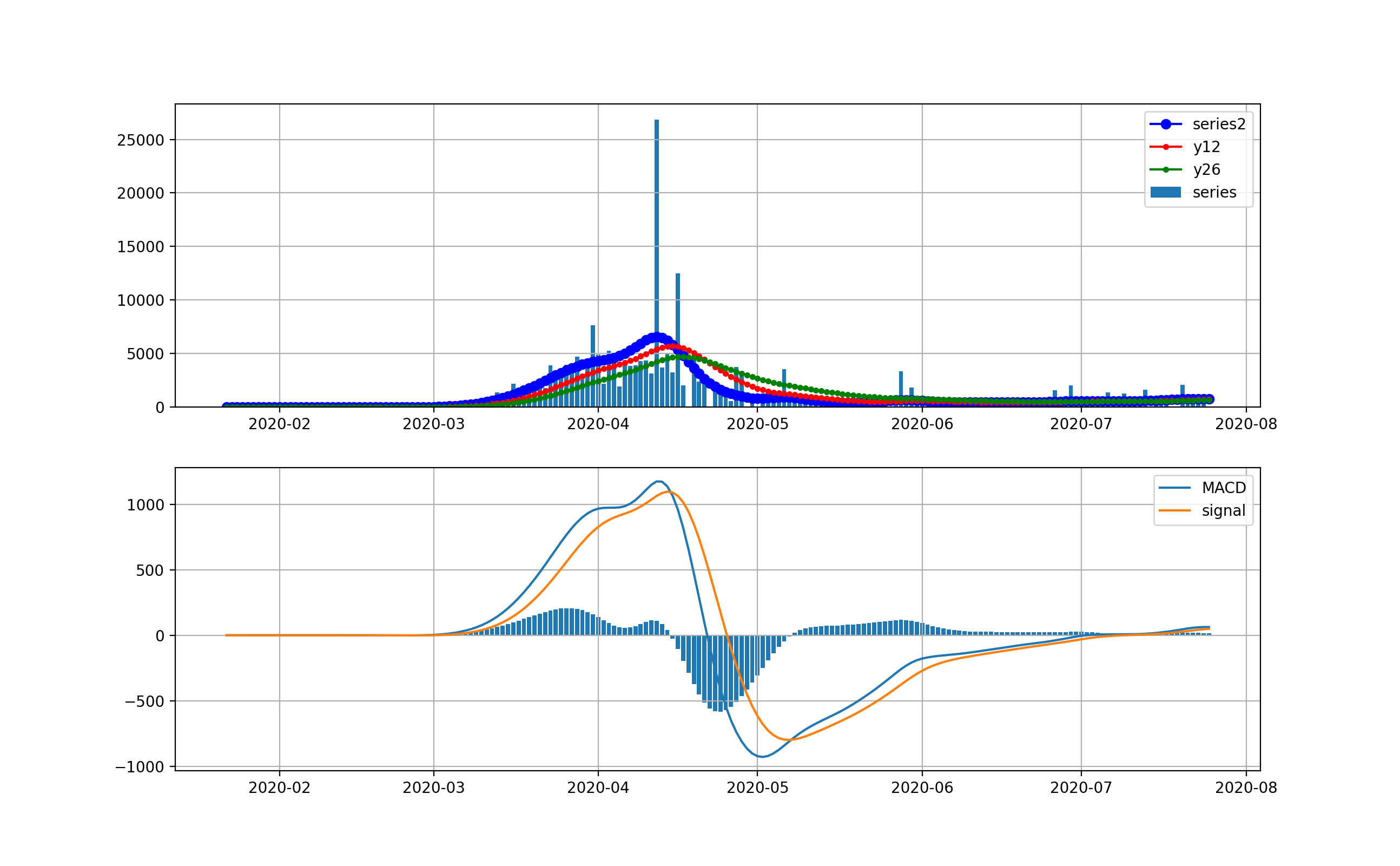
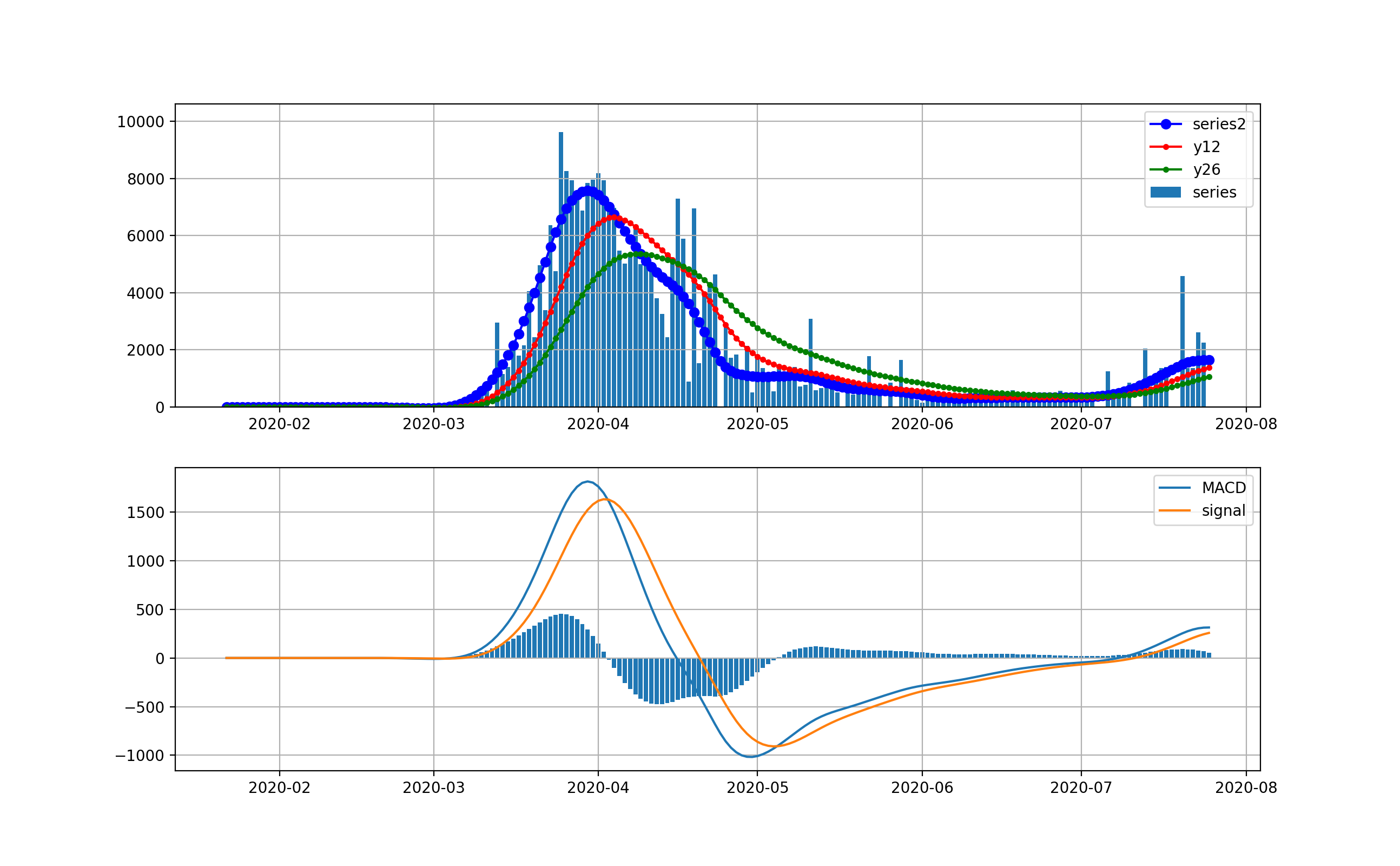
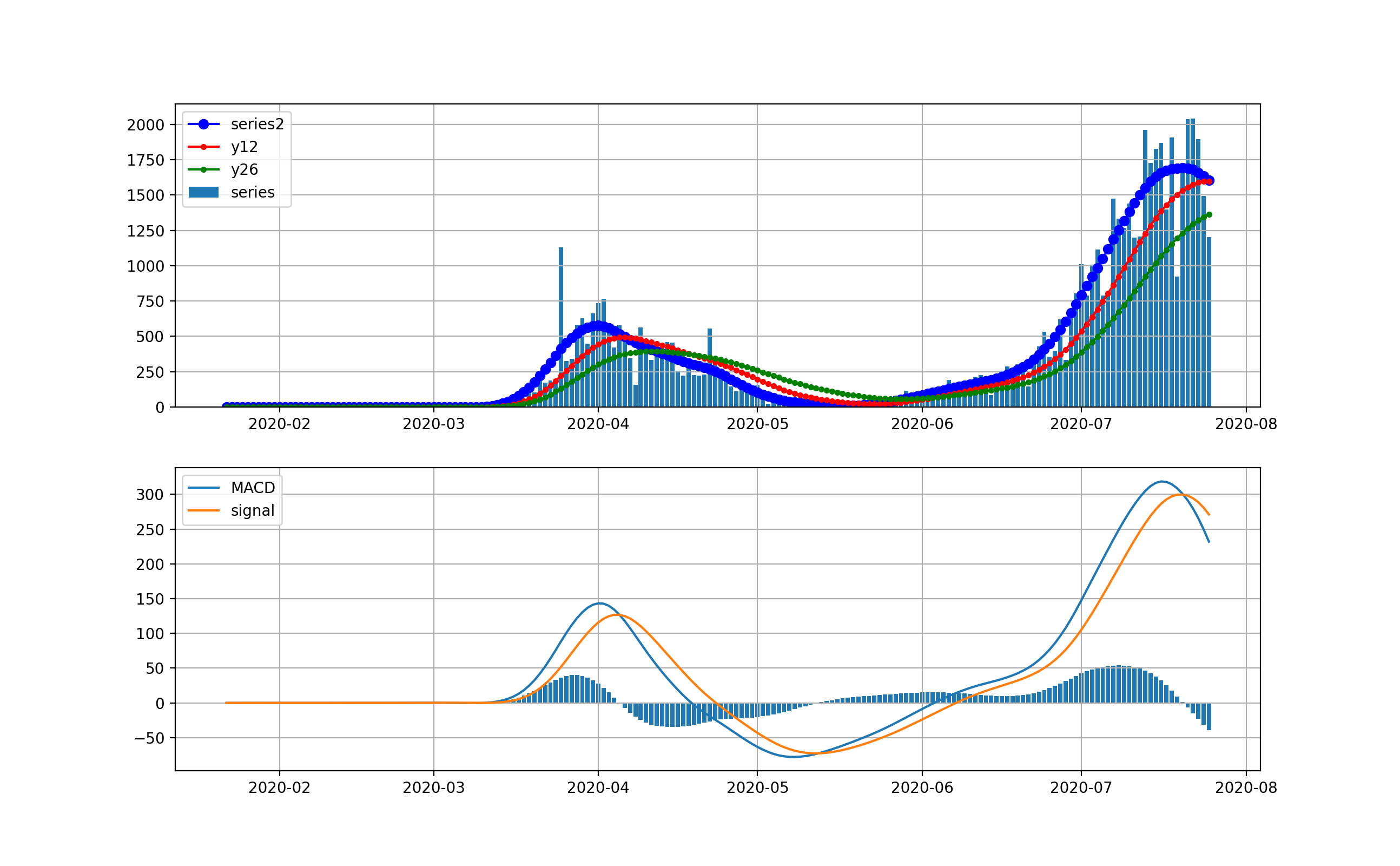
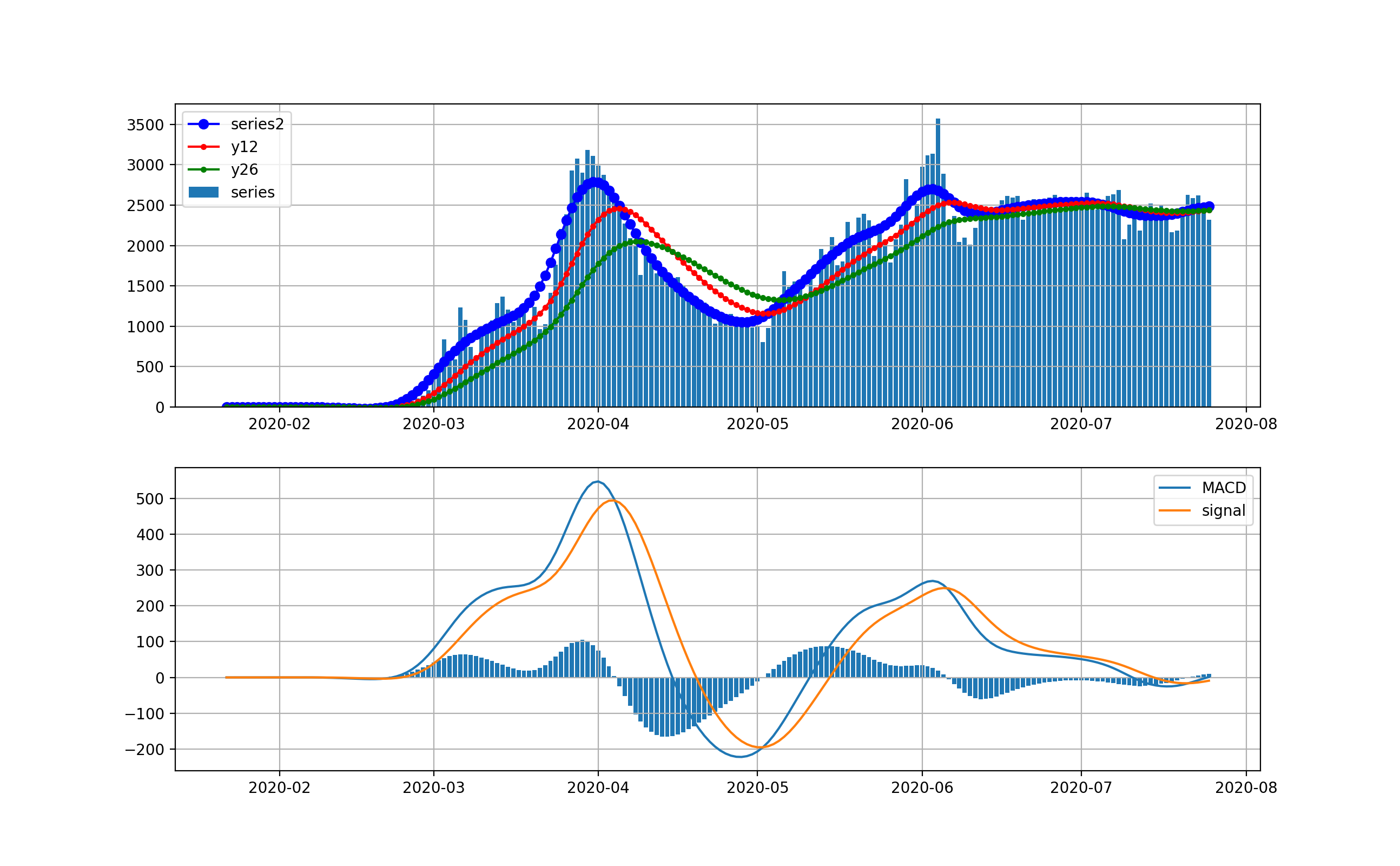
NYの状況
米国で感染数が最初に爆発したのはNYです。以下のグラフを見ると4月上旬の新規感染数が10000人に達した後、終息しつつあると見えます。
対数グラフでは、以下のとおりです。このグラフで見ると、まだまだ1000人弱の新規感染数が発生しているのが分かりまだまだ予断を許さない状況だと見えます。つまりMACDもよく見ると棒グラフが5月中旬からプラスに転じて上昇の傾向が出始めていることを示しています。
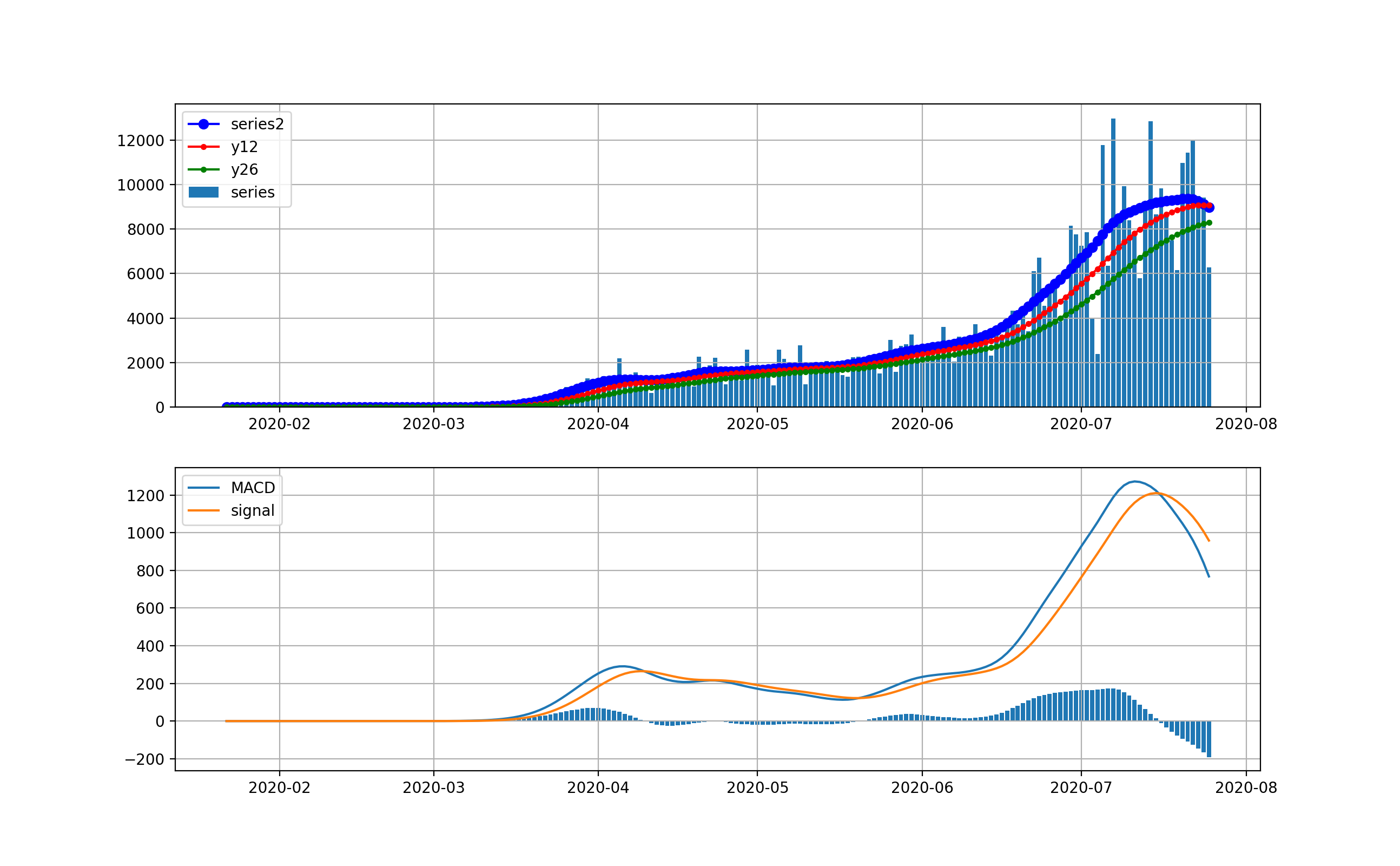
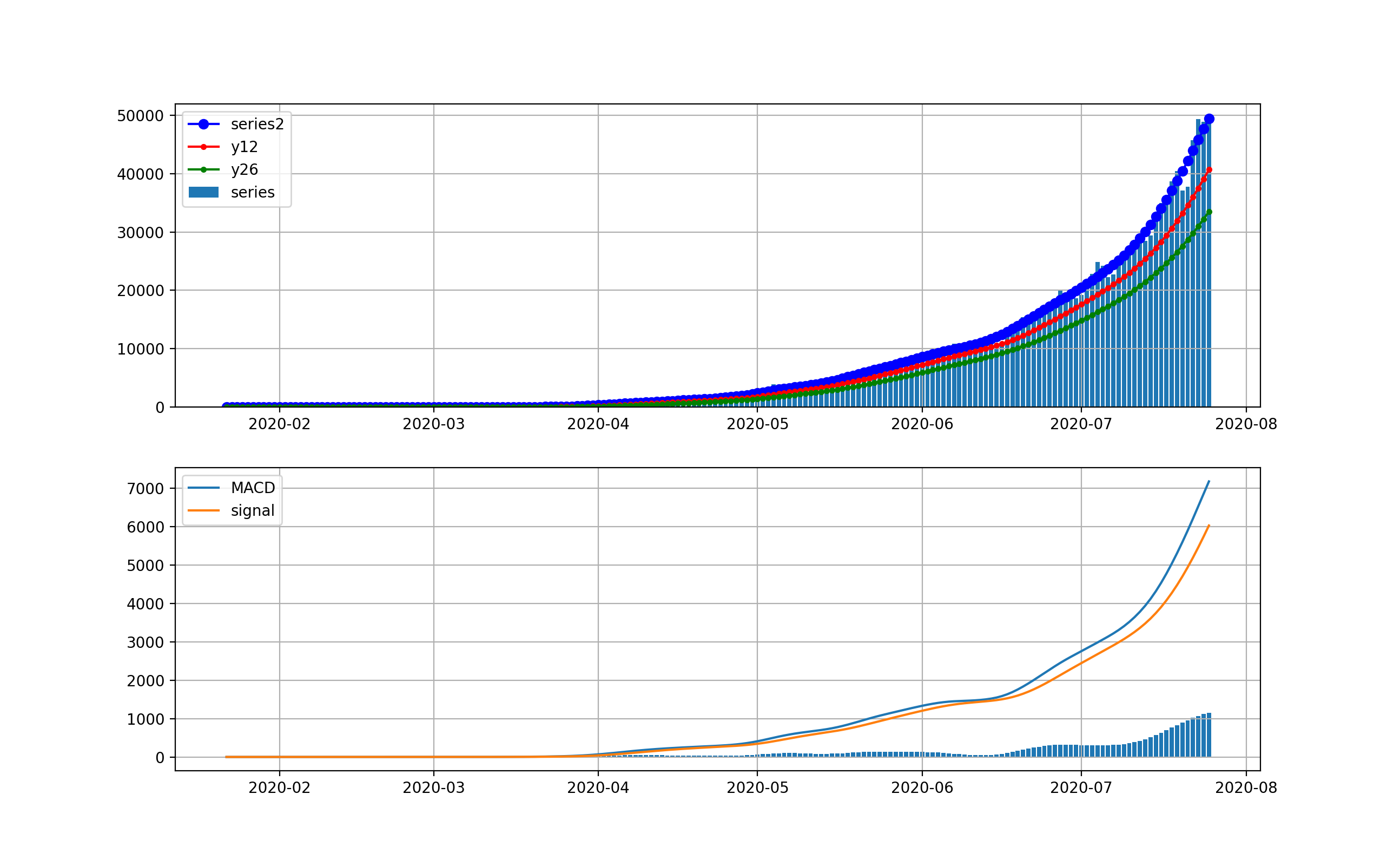
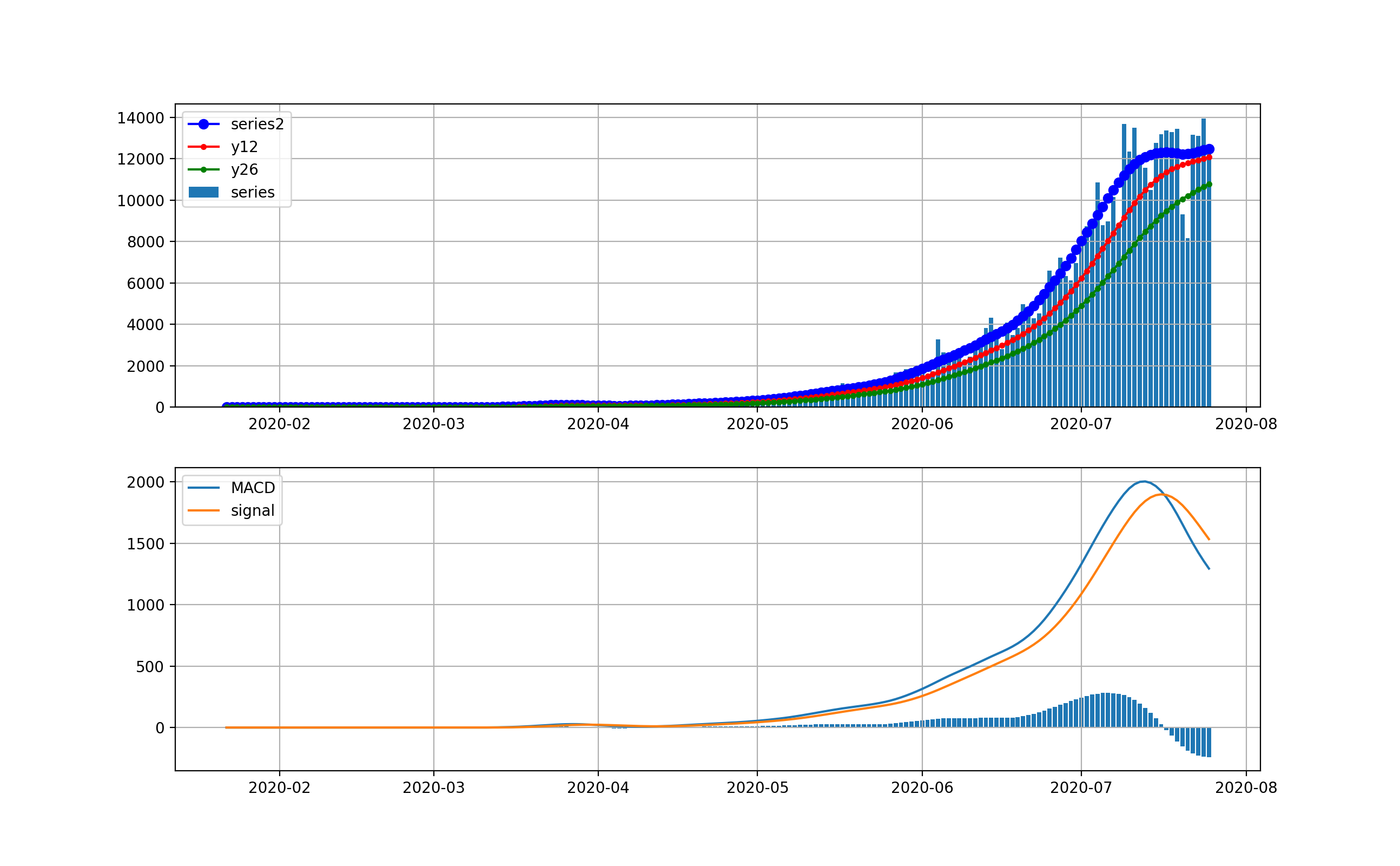
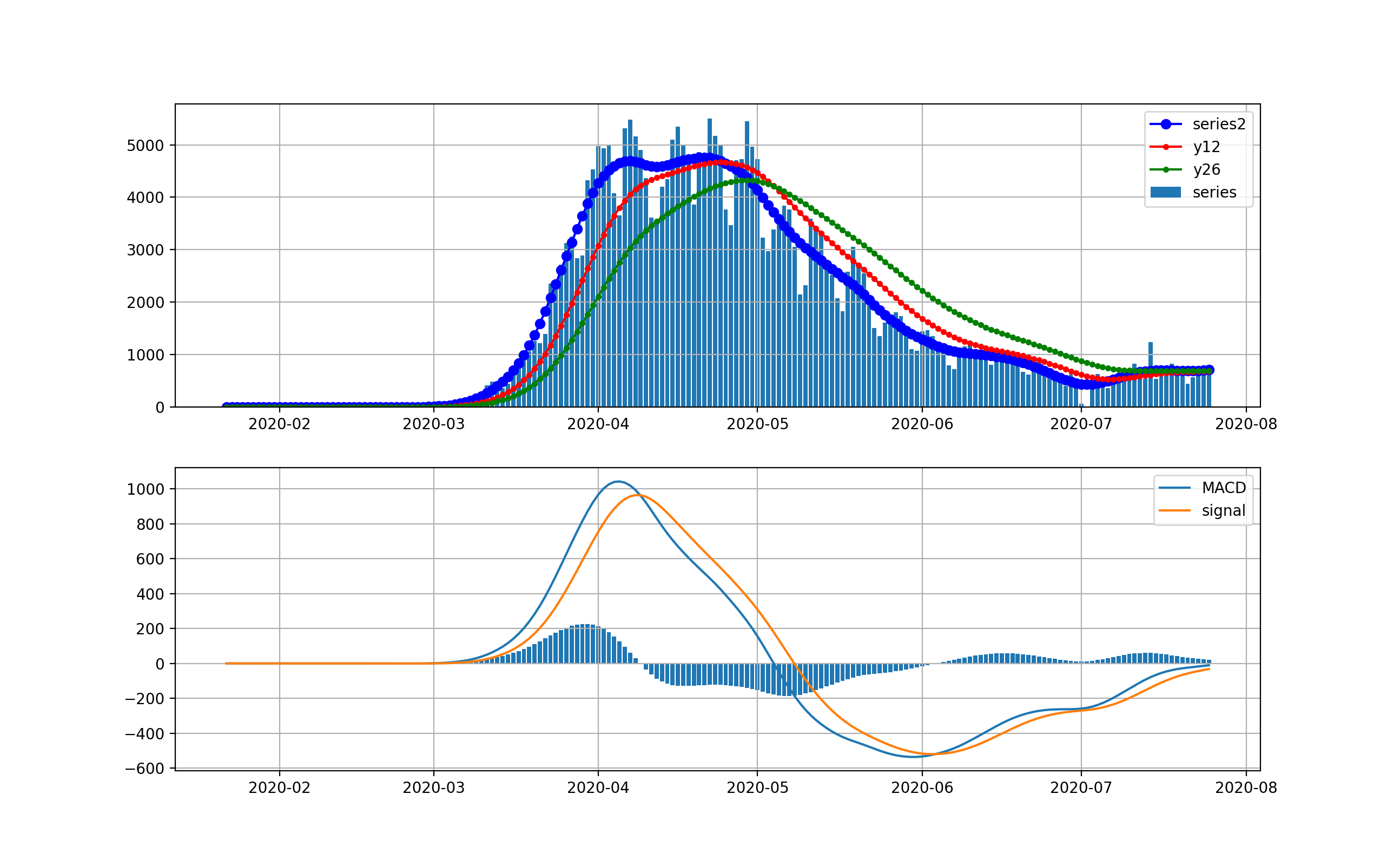
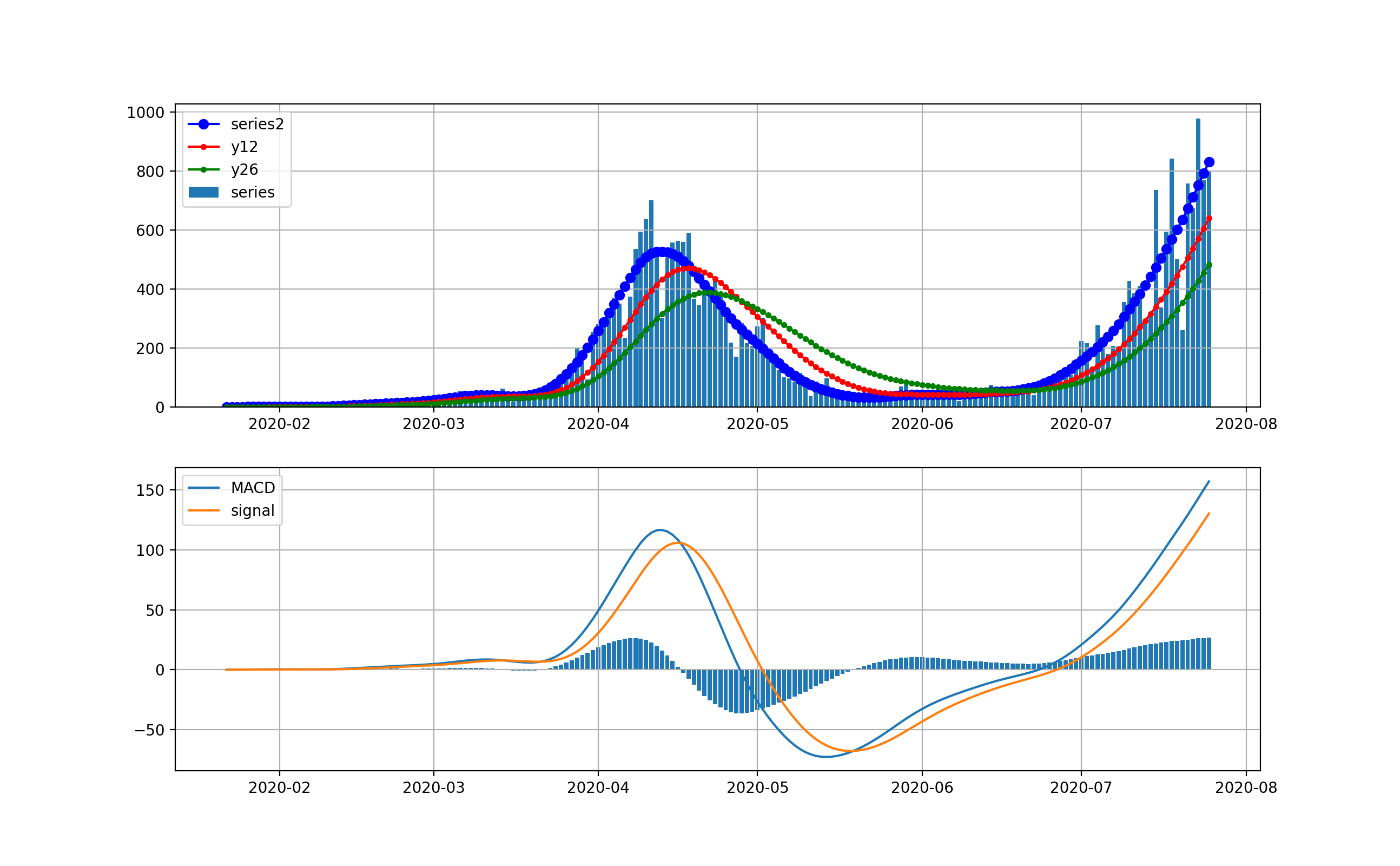
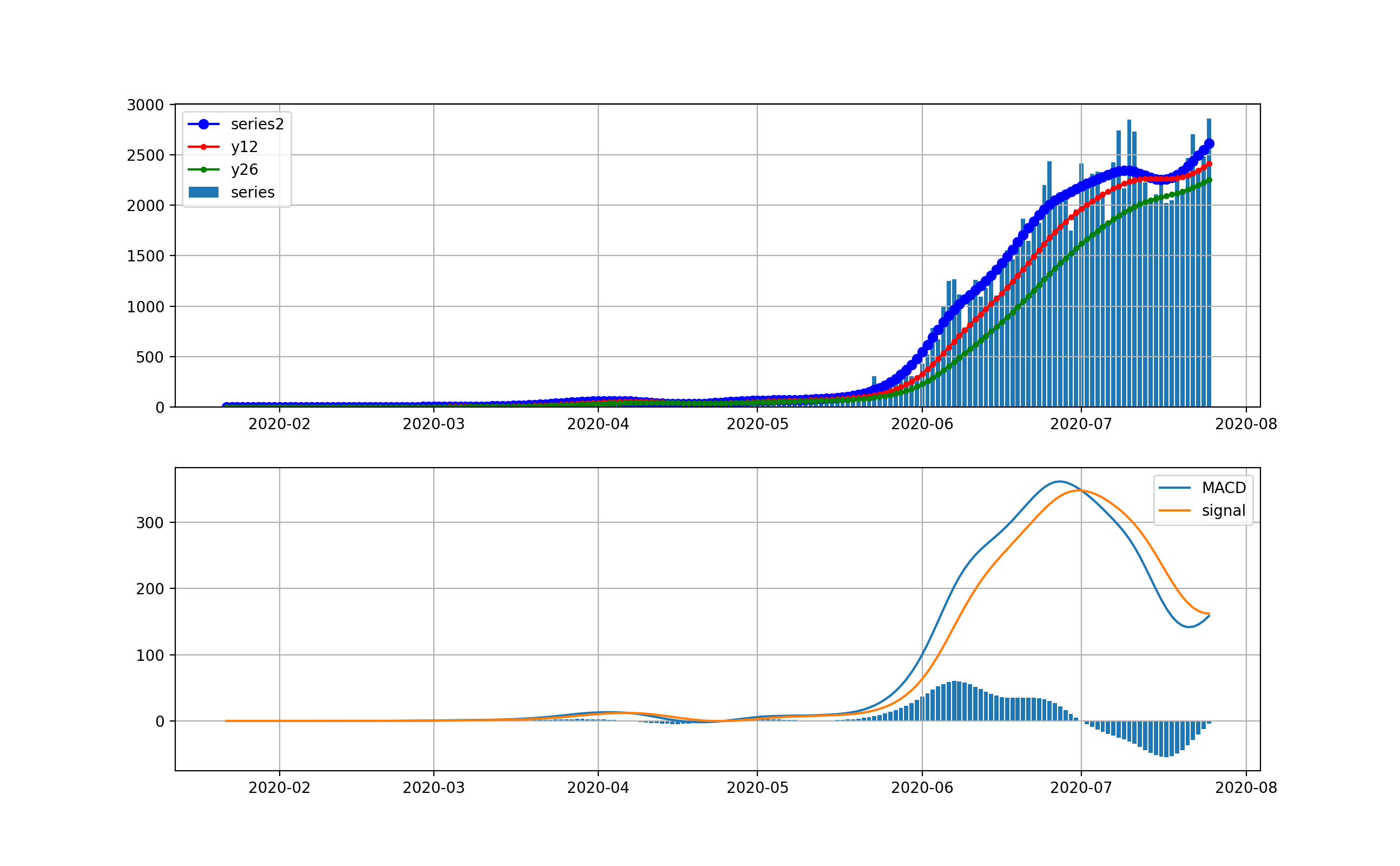
Californiaの状況
ここへ来てNYを超えてきたのがカリフォルニアです。カリフォルニアは4月ごろの立ち上がりから6月までは1000-2000人程度を維持してきました。しかし6月中旬から急に立ち上がって現在10000人を超えるレベルに達しました。しかし、ここでMACDを見ると棒グラフがマイナスに転じて減少傾向が出始める兆候が出ています。
対数グラフは以下のとおりです。1000人から2000人レベルまで、ゆっくりと増加して来たように見えます。そしてこおで一挙に10000人レベルに達しています。
Floridaの状況
もう一つの都市がFloridaです。FloridaはCaliforniaよりさらに顕著で、6月中旬まで1000人以下だったのが、急激に立ち上がり、一挙に12000人レベルに到達しました。
対数グラフだともっと顕著に見えます。つまり4月に急激に1000人レベルに達し、その後は若干減少しましたが、6月上旬から急激な増加をしてひと月あまりで10000人レベルに到達してしまいました。ただし、FloridaもCalifornia同様棒グラフがマイナスになっており、減少予兆となっています。
Indiaの状況
今世界で一番増加していて、まずい状況な国の一つは、インドだと思います。以下のとおり唯々上昇して50000人を超えており、しかもMACDも棒グラフがプラスであり、指数関数的にまだまだ増加と見えます。
対数グラフで見ると以下のとおりです。3月はひと月で3桁ペースでしたが、現在でも2か月で10倍のほぼ直線を描いていて恐怖です。
Brasilの状況
BrasilもIndiaと同様ヤバい状況です。こちらは立ち上がりは小さめですが、5月ごろから感染爆発して10000人、6月30000人、そして7月はもう一段増加して60000人レベルになっています。Brasilは一度棒グラフがマイナスを示しましたが、7月に急激にプラスに転じています。
対数グラフは以下のとおりです。感染拡大は指数関数より弱かったですが、7月は最後の立ち上がり部分は直線的に見えます。今後のさらなる増加が危ぶまれます。
South Africaの状況
South Africaは最近ヤバいと言われています。以下のような状況です。IndiaやBrasil同様最近急激に増加して両国ほどではありませんが、新規感染数が12000人を超えてきたことが原因です。しかし、直近のMACD見ると、棒グラフがマイナスを示し減少の可能性が出てきていると思えます。
対数グラフでは以下のとおりです。
Russiaの状況
Russiaも一時期ヤバい国の一つでした。現在は以下のとおりです。5月上旬に10000人を超えましたが、徐々に減少して来ていて、現在5000人程度の日々新規感染数です。棒グラフもほぼマイナスに落ち着いているようですが、7月は弱くプラスも見えています。予断は許さない状況です。
対数グラフでは以下のとおりです。
ヨーロッパの状況
これらの国は似ています。そこで連続して並べます。ざっくり云うと、これらの国は第一波が終息してましたがまだまだ不十分で、ここへ来て第二波が立ち上がり始め新規感染数が1000人弱-2000人弱程度発生している状況です。
France
Germany
Italy
Spain
United Kingdom
Turkey
Swedenの状況
噂のSwedenは以下のとおりです。4-6月は700人程度でコンスタントでしたが、7月の増加して、今減少傾向にあるようです。何が減少させているかは不明です。
Israelの状況
Israelは第一波より第二波の方が大きく見えます。しかし、第二波が2000人程度をピークに減少に転じるようです。
Japanの状況
Australiaの状況
Indonesiaの状況
IndonesiaはIndia型でまだまだどんどん増加している状況で、2000人弱まで増加してきました。
Iranの状況
Russiaと同様ほぼ終息無く、第二波が発生して日々2500人以上の新規感染者が出ています。
Iraqの状況
IraqはSouthAfricaと同様、6月から感染爆発して現在2500人以上の新規感染者を出しています。そして飽和しそうですがやはり増加に転じたようです。
Singapoleの状況
3月頃はうまくいっていたSingapoleは現在以下のとおりです。ほぼ終息しつつありましたが、日本同様7月上旬から増加に転じています。
まとめ
・噂の各国の感染状況を俯瞰した
・世界の状況は、ますます感染拡大している
・世界で毎日25万人以上が感染している
・6月中旬から増加に転じた国が多いようだ
・7日周期は多いが、Swedenは土日は完全休業だ
- 投稿日:2020-07-27T22:38:08+09:00
pygameを使った手書き文字認識アプリ
初めに
pygameを用いてDNNによる簡単な手書き文字認識アプリを作ってみたので軽く解説していきます。
pygameを使ってpythonだけで簡単にインタラクションのあるアプリを簡単に開発できるので、これからpythonを勉強していく人や初心者の方のモチベーションになれば嬉しいです。
コードは全てgithub上に載せています。勝手に使ってもらって大丈夫です。Github : https://github.com/ozora-ogino/predict-handdrawingNumber_NN
今回の開発では、DNNの構築にTensorflow、ゲーム開発でpygameを使っています。
また、DNNの学習のためにmnistデータセットを使用しています。Pygameとは
Pygameは、Pythonで2Dゲームを制作する際の最も有名なゲームライブラリです。
Pythonで2Dゲームを作るには、ゲームライブラリを使うのが一般的で、簡単なブロック崩しゲームならば160行くらいのソースコードで作成できます。使い方
Githubにも載せていますが、こちらで改めて説明します。
最初に、リポジトリをクローンしていただきます。
git clone https://github.com/ozora-ogino/predict-handdrawingNumber_NN/requirements.txtから必要なパッケージをインストールします。
pip install -r requirements.txtdraw.pyがメインになります。
すでに学習済みのモデルを用意しているので実行していだだければ機能します。python draw.py改めてモデルを学習したい際はcreateModel.pyでモデルを作り直してください。
python createMain.pyモデルの定義はmodel.pyの中の関!
数で行なっているので変更してもらえればお好きなようにNNで実行できます。github に実行結果のスクリーンショットを載せています。
実行していただくと、数字を描くための酢sクリーンが表示されます。
数字を描いていただいて、Enterを押していただくと文字の認識を行い、予測結果をterminal上に表示します。
終了の際にはスクリーン閉じてください。終わりに
今回はpygaemを用いて簡単な手書き文字認識アプリを作ってみました。
この程度のアプリなら簡単に作れますのでぜひアレンジしたりして試してみてください。
今回の記事はpython初学者の方やpygameでどんなことができるのか知りたい方むけに作ってみました。
誰かの手助けになれば幸いです。instagramでpythonやプログラミング、エンジニアとして必要な情報の配信を始めたのでフォローしてもらえると嬉しいです。!
- 投稿日:2020-07-27T22:33:47+09:00
初心者のためのseaborn基礎②ヒストグラム(distplot)
seabornとは
Pythonのグラフ描画のためのライブラリです。。最も有名なライブラであるmatplotlibのラッパー関数(内包プログラム)という位置づけ。簡単に見た目綺麗なグラフの描画が出来る他、一括での処理などの機能もある程度充実しています。細かく指定して描画するならmatplotlib、簡単に綺麗にならseabornのです。
ヒストグラム(distplot)
今回のテーマはヒストグラムです。ヒストグラム作成には
distplotを試用します。見た目やパラメータの違いは「matplotlib」を用いた下記の記事と比較してみて下さい。
★初心者のためのpandas基礎matplotlibでヒストグラム作成準備
まずは、pipで
seabornのライブラリをインストールして下さい。pip?って方はこちら。ライブラリをインポートします。
seabornにsnsという名前をつけてimportします。import seaborn as snsサンプルはタイタニックのデータで試してみます。タイタニックがわからない人は「kaggle タイタニック」で調べて下さい。
pandasでデータフレームを作ります。dataframe = pd.read_csv('train.csv')基本作成
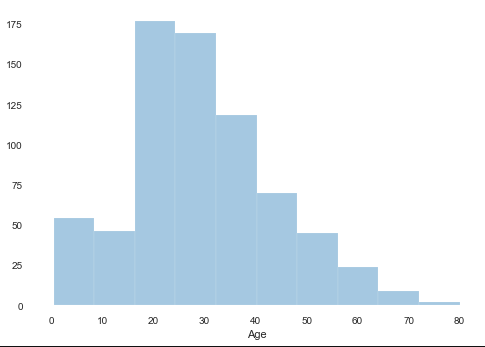
ヒストグラム作成には
distplotを使用します。例としてAge(年齢)別のヒストグラムを作成します。
kdeでは、密度近似関数の描画の有無をしています。難しいので呪文のように設定して下さい。
rugをTrueにするとY軸の総計が1になるように正規化されます。難しいので呪文のように設定して下さい。sns.distplot(dataframe['Age'],kde=False, rug=False)binsの設定
binsを用いて棒の数を設定します。例として10を設定します。sns.distplot(dataframe['Age'],bins = 10,kde=False, rug=False)binsの数はいくつがいいの?って疑問を感じ際は、スタージェスの公式というのを調べて下さい。
(応用)複数を重ねる
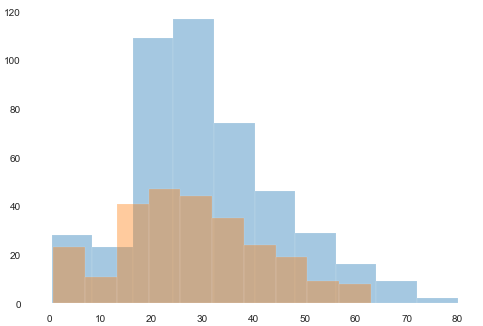
あまり用途はないかも知れませんが、重ねるには、2回構文を書くだけです。Sex(性別)で分けてみましょう。
前準備としてデータを分けます。malelist_m = dataframe['Sex'] == 'male' malelist_f = dataframe['Sex'] == 'female'連続で構文を書きます。
sns.distplot(dataframe[malelist_m]['Age'],bins = 10,kde=False, rug=False ) sns.distplot(dataframe[malelist_f]['Age'],bins = 10,kde=False, rug=False )
ラベル等を使いたい場合は「matplotlib」の機能を使う必要があります。
以上です。最後に
初心者にもわかるように、Pythonで機械学習を実施する際の必要な知識を簡便に記事としてまとめております。
目次はこちらになりますので、他の記事も参考にして頂けると幸いです。
- 投稿日:2020-07-27T22:03:12+09:00
GCP - Cloud Functions with Pythonについて調査した
仕様
ランタイム
- 実行環境:
Python3.7 on Ubuntu 18.04ソースコードの構造
デプロイ時にアップロードされるファイルは構造化された条件に従っている必要がある。
- 例1
. └── main.py
- 例2
. ├── main.py └── requirements.txt
- 例3
. ├── main.py └── requirements.txt └── mylocalpackage/ ├── __init__.py └── myscript.pyCloud Functions の命名
プロイ時に name プロパティが設定される。
関数の名前は識別子として使用されるため、リージョン内で一意でなければならない。依存関係の指定
公開パッケージの利用
requirements.txt内に依存パッケージを記述するとデプロイ時にpip経由でインストールしてくれる。
下記パッケージはデプロイ時に関数と一緒に自動的にインストールされる。
関数のコードでこれらのパッケージのいずれかを使用している場合、次のバージョンを requirements.txt ファイルに含めることをおすすめします。aiohttp==3.6.2 async-timeout==3.0.1 attrs==19.3.0 cachetools==4.1.1 certifi==2020.6.20 chardet==3.0.4 click==6.7 Flask==1.0.2 google-api-core==1.21.0 google-api-python-client==1.9.3 google-auth==1.18.0 google-auth-httplib2==0.0.3 google-cloud-core==0.28.1 google-cloud-trace==0.19.0 googleapis-common-protos==1.52.0 grpcio==1.30.0 httplib2==0.18.1 idna==2.8 itsdangerous==0.24 Jinja2==2.10 MarkupSafe==1.0 multidict==4.7.6 opencensus==0.1.6 pip==18.0 protobuf==3.12.2 pyasn1==0.4.8 pyasn1-modules==0.2.8 pytz==2020.1 PyYAML==5.3.1 requests==2.21.0 rsa==4.6 setuptools==40.2.0 six==1.15.0 uritemplate==3.0.1 urllib3==1.24.3 Werkzeug==0.14.1 wheel==0.31.1 wrapt==1.10.11 yarl==1.4.2Cloud Functions の関数のタイプ
Cloud Functions には、HTTP 関数とバックグラウンド関数の 2 つのタイプがある。
HTTP 関数
標準的な HTTP リクエストから HTTP 関数を実行します。この HTTP リクエストはレスポンスを待ち、GET、PUT、POST、DELETE、OPTIONS など、通常の HTTP リクエスト メソッドを処理します。Cloud Functions を使用する際は、TLS 証明書が自動的にプロビジョニングされるため、すべての HTTP 関数を、セキュアな接続を使用して呼び出すことができます。(HTTP 関数の作成)
sample.pyfrom flask import escape def hello_http(request): """HTTP Cloud Function. Args: request (flask.Request): The request object. <http://flask.pocoo.org/docs/1.0/api/#flask.Request> Returns: The response text, or any set of values that can be turned into a Response object using `make_response` <http://flask.pocoo.org/docs/1.0/api/#flask.Flask.make_response>. """ request_json = request.get_json(silent=True) request_args = request.args if request_json and 'name' in request_json: name = request_json['name'] elif request_args and 'name' in request_args: name = request_args['name'] else: name = 'World' return 'Hello {}!'.format(escape(name))バックグラウンド関数
バックグラウンド関数を使用すると、Pub/Sub トピックのメッセージや Cloud Storage バケットの変更など、Cloud インフラストラクチャのイベントを処理できる。(バックグラウンド関数の作成)
sample.pydef hello_pubsub(event, context): """Background Cloud Function to be triggered by Pub/Sub. Args: event (dict): The dictionary with data specific to this type of event. The `data` field contains the PubsubMessage message. The `attributes` field will contain custom attributes if there are any. context (google.cloud.functions.Context): The Cloud Functions event metadata. The `event_id` field contains the Pub/Sub message ID. The `timestamp` field contains the publish time. """ import base64 print("""This Function was triggered by messageId {} published at {} """.format(context.event_id, context.timestamp)) if 'data' in event: name = base64.b64decode(event['data']).decode('utf-8') else: name = 'World' print('Hello {}!'.format(name))ローカルマシンからのデプロイ
gcloud ツールによるデプロイ
gcloud コマンドライン ツールで gcloud functions deploy コマンドを実行して、関数のコードを含むディレクトリから関数をデプロイする。
引数 説明 NAME デプロイする Cloud Functions の関数の登録名。 --entry-point ENTRY-POINT ソースコード内の関数またはクラスの名前。 --runtime RUNTIME pythonであればpython37またはpython38を指定する。 TRIGGER 関数のトリガーの種類を指定する。 --stage-bucket=STAGE_BUCKET ソースコードを保存するバケット名を指定。 NAMEをソースコード内に含まれないカスタム文字列を指定する場合、実行するソースコードの関数は--entry-point ENTRY-POINTで指定する。
--runtimeは2回目以降のデプロイ時は省略可能。--stage-bucketで保存先を指定する場合は毎回指定する必要がある。また、このフラグを使用する場合はバケットへの書き込み権限が必要になる。
TRIGGERについて
トリガー種別 値 HTTP --trigger-http Google Cloud Pub/Sub --trigger-topic TOPIC_NAME GCSアップロードイベント --trigger-resource YOUR_TRIGGER_BUCKET_NAME \ --trigger-event google.storage.object.finalize デプロイコマンド
gcloud functions deploy NAME --entry-point NAME --runtime RUNTIME TRIGGER [FLAGS...]クイックスタート
Cloud Storage にファイルをアップロードして関数をトリガーする
サンプルシステムの概要
GCSへファイルがアップロードされたら、ファイル情報をログに出力し、さらにBigQueryへデータを挿入するところまで実装してみる。
準備
GCPシステム構成
- GCS バケット名 :
sample-cloudfunctions- BigQuery データセット . テーブル :
samples.testCloud Storage バケットを作成する
構文 :
gsutil mb gs://YOUR_TRIGGER_BUCKET_NAMEgsutil mb gs://sample-cloudfunctions # バケットがバージョニング対応でないことを確認 gsutil versioning set off gs://sample-cloudfunctionsサンプルコード
- ファイル構成
. ├── main.py └── requirements.txtrequirements.txtgoogle-cloud-bigquerymain.py# coding: utf-8 from google.cloud import bigquery def load_bigquery(data, context): """Background Cloud Function to be triggered by Cloud Storage. Load To Bigquery Args: data (dict): The Cloud Functions event payload. context (google.cloud.functions.Context): Metadata of triggering event. Returns: None; the output is written to Stackdriver Logging """ print('Event ID: {}'.format(context.event_id)) print('Event type: {}'.format(context.event_type)) print('Bucket: {}'.format(data['bucket'])) print('File: {}'.format(data['name'])) print('Metageneration: {}'.format(data['metageneration'])) print('Created: {}'.format(data['timeCreated'])) print('Updated: {}'.format(data['updated'])) client = bigquery.Client() # データセットをセット dataset_id = 'samples' dataset_ref = client.dataset(dataset_id) table_name = 'test' job_config = bigquery.LoadJobConfig() # スキーマ定義 job_config.schema = [ bigquery.SchemaField("name", "STRING"), bigquery.SchemaField("age", "INTEGER"), ] # 開始行はスキップ job_config.skip_leading_rows = 1 # フォーマットを指定 job_config.source_format = bigquery.SourceFormat.CSV # GSCのリソースURI uri = "gs://{}/{}".format(data['bucket'], data['name']) # API リクエスト load_job = client.load_table_from_uri( uri, dataset_ref.table(table_name), job_config=job_config ) print("Starting job {}".format(load_job.job_id)) # 結果を表示 load_job.result() # Waits for table load to complete. print("Job finished.") # テーブルからデータを取得 GCSからのデータ取り込み確認 destination_table = client.get_table(dataset_ref.table(table_name)) print("Loaded {} rows.".format(destination_table.num_rows))デプロイ
gcloud functions deploy load_bigquery \ --runtime python38 \ --trigger-resource sample-cloudfunctions \ --trigger-event google.storage.object.finalizeテスト
- 予め用意していたファイルをアップロード
gsutil cp sample.csv gs://cloudfunctions-sample
- ログを確認 構文 :
gcloud functions logs read [FUNCTION_NAME]gcloud functions logs read load_bigquery --limit 15 D load_bigquery g2dfwptfywjx 2020-07-29 05:43:19.105 Function execution started load_bigquery g2dfwptfywjx 2020-07-29 05:43:19.117 Event ID: 1384453759070888 load_bigquery g2dfwptfywjx 2020-07-29 05:43:19.117 Event type: google.storage.object.finalize load_bigquery g2dfwptfywjx 2020-07-29 05:43:19.117 Bucket: sample-cloudfunctions load_bigquery g2dfwptfywjx 2020-07-29 05:43:19.117 File: sample.csv load_bigquery g2dfwptfywjx 2020-07-29 05:43:19.117 Metageneration: 1 load_bigquery g2dfwptfywjx 2020-07-29 05:43:19.117 Created: 2020-07-29T05:43:17.582Z load_bigquery g2dfwptfywjx 2020-07-29 05:43:19.117 Updated: 2020-07-29T05:43:17.582Z load_bigquery g2dfwptfywjx 2020-07-29 05:43:20.537 Starting job 3b748f9e-ae61-42bc-817b-1b2bdb2c3d8a load_bigquery g2dfwptfywjx 2020-07-29 05:43:24.975 Job finished. load_bigquery g2dfwptfywjx 2020-07-29 05:43:25.438 Loaded 3 rows. D load_bigquery g2dfwptfywjx 2020-07-29 05:43:25.441 Function execution took 6337 ms, finished with status: 'ok'ログを確認すると
Loaded 3 rows.と出力されており、予め用意しておいたデータがBigQueryへロードされたことが確認できた。
- 投稿日:2020-07-27T21:45:08+09:00
初心者のためのseaborn基礎①データ件数を集計グラフ化(Countplot)
seabornとは
Pythonのグラフ描画のためのライブラリです。。最も有名なライブラであるmatplotlibのラッパー関数(内包プログラム)という位置づけ。簡単に見た目綺麗なグラフの描画が出来る他、一括での処理などの機能もある程度充実しています。細かく指定して描画するならmatplotlib、簡単に綺麗にならseabornのです。
準備
まずは、pipで
seabornのライブラリをインストールして下さい。pip?って方はこちら。ライブラリをインポートします。
seabornにsnsという名前をつけてimportします。import seaborn as snsサンプルはタイタニックのデータで試してみます。タイタニックがわからない人は「kaggle タイタニック」で調べて下さい。
pandasでデータフレームを作ります。dataframe = pd.read_csv('train.csv')データ件数集計(Countplot)
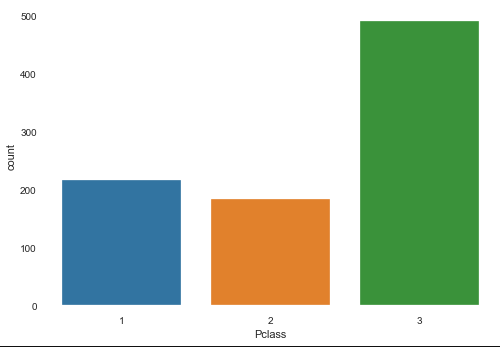
最も基本的なデータの件数の集計可視化です。これには
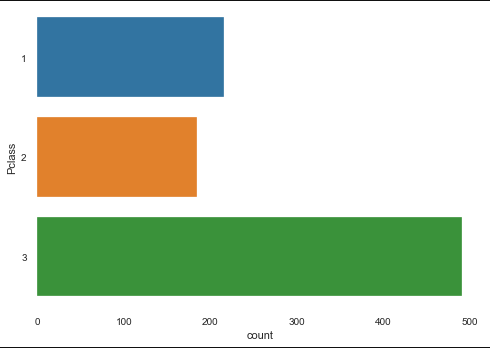
Countplotを使います。基本的にはY軸は件数なので、X軸のみを指定します。
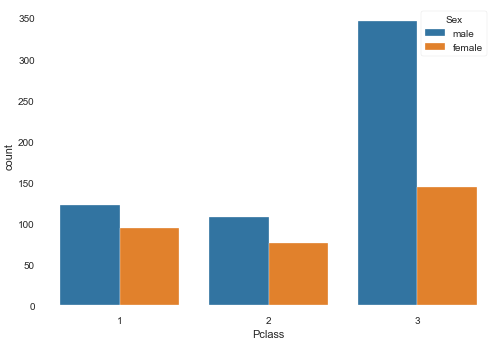
例として、Pclass(部屋の等級)と件数の関係を描画します。X軸xにPclass、元データdataにdataframeを指定します。sns.countplot(x="Pclass", data=dataframe)sns.countplot(y="Pclass", data=dataframe)系列を追加する場合は
hueを追加します。(例としてhueにSex(性別)を追加します。)sns.countplot(y="Pclass", data=dataframe, hue='Sex')その他にも軸の中の順序や色の変更は可能なので、興味があれば調べてみて下さい。
また、ラベルの変更などは、元ラッパー元であるmatplotlibを修正すれば可能ですが、複雑なので省略します。
Countplotだとメリットは感じにくいかもしれません。他のdistplotpairplotjointplot等の方がメリットを感じられると思います。最後に
初心者にもわかるように、Pythonで機械学習を実施する際の必要な知識を簡便に記事としてまとめております。
目次はこちらになりますので、他の記事も参考にして頂けると幸いです。
- 投稿日:2020-07-27T20:53:56+09:00
株価と統計値(平均、標準偏差)
株価+αを取得
Financial Modeling Prepから株価+αを取得する
def get_df_stock_screener(exchange): requests_cache.install_cache("stock-screener") url = f"https://financialmodelingprep.com/api/v3/stock-screener?marketCapMoreThan=100000&volumeMoreThan=100÷ndLowerThan=10&betaLowerThan=10&betaMoreThan=-10&exchange={exchange}&apikey={apikey}" response = requests.get(url) content = response.content.decode() json_content = json.load(StringIO(content)) return pd.DataFrame(json_content).set_index("symbol")requests_cache
pandasでread_jsonするときにキャッシュでアクセスする方法を使ってキャッシュに保存する
Stock Screener
[ { "symbol" : "AAPL", "companyName" : "Apple Inc.", "marketCap" : 1382174560000, "sector" : "Technology", "beta" : 1.2284990000000000076596506914938800036907196044921875, "price" : 318.8899999999999863575794734060764312744140625, "lastAnnualDividend" : 3.0800000000000000710542735760100185871124267578125, "volume" : 51500795, "exchange" : "Nasdaq Global Select", "exchangeShortName" : "NASDAQ" }, { "symbol" : "AMZN", "companyName" : "Amazon.com Inc.", "marketCap" : 1215457260000, "sector" : "Technology", "beta" : 1.5168630000000000723758830645238049328327178955078125, "price" : 2436.8800000000001091393642127513885498046875, "lastAnnualDividend" : 0, "volume" : 6105985, "exchange" : "Nasdaq Global Select", "exchangeShortName" : "NASDAQ" } ]の形で返ってくる
ベータ値
$$ r_a = \alpha + \beta r_b $$
$ r_a $は株のリターン
$ r_b $は市場(例:S&P 500)のリターン
$ \beta $は市場のリターンに対する係数
$ \beta = 2 $の場合、市場のリターンが3%上昇すると株のリターンが6%上昇する
$ \alpha $は市場のリターンの無関係な株のリターンlastAnnualDividend
去年の1年間の1株当たりの配当金
統計値の計算
DataFrame作成
df_stock_screener_nasdaq = get_df_stock_screener("nasdaq") df_stock_screener_nyse = get_df_stock_screener("nyse") df_stock_screener = pd.concat([df_stock_screener_nasdaq, df_stock_screener_nyse]) df_stock_screener["sector"].replace("", np.nan, inplace=True) df_stock_screener.dropna(subset=["sector"], inplace=True) df_stock_screener_target = df_stock_screener[["price","beta","lastAnnualDividend","volume"]]欠損値
sectorは空の場合がある
ETFとかが空になるっぽい
対象からETFは外した方が解釈しやすいので、dropする
dropnaは空文字はdropしないので、空文字をnanにreplaceするdescribe
describeで要約統計量を取得できる
df_stock_screener_target.describe()price beta lastAnnualDividend volume count 6153.000000 6153.000000 6153.000000 6.153000e+03 mean 130.651825 0.940899 0.589505 1.701368e+06 std 5257.505324 0.874763 1.033488 5.608641e+06 min 0.010000 -8.439448 0.000000 1.000000e+02 25% 5.730000 0.301854 0.000000 8.373300e+04 50% 13.770000 0.881456 0.000000 3.761930e+05 75% 34.160000 1.392074 0.840000 1.274612e+06 max 291621.000000 8.949109 9.680000 1.566431e+08price
平均は130ドルで標準偏差は5257ドル、最大は291621ドル
外れ値の存在で、統計値がほとんど意味を成していない
株分割も任意にできるため、株価の大小は意味を成さないbeta
平均は0.94で標準偏差は0.87、最小は-8.43、最大は8.94
betaはその導出法から平均が1に近いのは市場との一致するという意味で正しそう配当、株数
株数が任意である以上、その絶対値の比較はそこまで意味を持たない
- 投稿日:2020-07-27T20:52:51+09:00
Effective Python 第2版 超まとめ
概要
本記事はEffective Python 第2版の内容を自分なりに短くまとめた記事になります。
※ 執筆中ですが、先行で公開しています。理解に必要な説明の部分を大きく省略していますし、全てを網羅しているわけでもありません。また、例示のコードや一部内容は私の解釈も含みます。
未読の方は、本書を手に取り読む事を強くお勧めします。尚、本記事は本書と同様に、Python3(もっというと3.8)を基本とします。
% python3.8 Python 3.8.5 (default, Jul 21 2020, 10:48:26) [Clang 11.0.3 (clang-1103.0.32.62)] on darwinPythonic 思想
The Zen of Python
>>> import thisPythonで書く時だけならず、プログラマとして一読の価値のある考え方となります。
日本語で解説されている方もおられるので、そちらを見ていただくのも良いと思います。ぐぐってください。PEP8に従う
コーディングする環境にはPEP8のLinterを入れましょう。
PEP8のスタイルガイド読むとより理解が深まるので一度は読むことをお勧めします。
Linterで全てがチェックされているとも限りません。以下、Visual Studio Codeでflake8を使ったLintingでチェックされなかった例です。
(2020/08/10時点。Linterも複数あり、それぞれにオプションもあるため、全てにおいてチェックされないことを確認したわけではありません)# Wrong: # operators sit far away from their operands income = (gross_wages + taxable_interest + (dividends - qualified_dividends) - ira_deduction - student_loan_interest)# Correct: # easy to match operators with operands income = (gross_wages + taxable_interest + (dividends - qualified_dividends) - ira_deduction - student_loan_interest)# Correct: if not seq: if seq:# Wrong: if len(seq): if not len(seq):※ コンテナやシーケンスが空値の場合、Falseと評価されることを使います。
Python2は止める
Python2はすでにサポートが終了しています。
2to3もしくはsixの利用を検討してください。文字列のフォーマット
Python3ではいくつかのフォーマット方式がありますが、結論としてf文字列を使ってください。
>>> example = 'pi =' >>> pi = 3.1415 >>> '%s %.2f' % (example, pi) # フォーマットと変数を対応させる必要がある 'pi = 3.14' >>> '{} {:.2f}'.format(example, pi) # 同上 'pi = 3.14' >>> f'{example} {pi:.2f}' # 新しい構文 より簡潔にわかりやすく書ける 'pi = 3.14' >>> places = 3 >>> f'{example} {pi:.{places}f}' # フォーマット指定子のオプションにも変数が使える 'pi = 3.142'代入にアンパックを使う
Indexを使うより、見た目がすっきりします。
>>> signals = [('red', 'danger'), ('yellow', 'warning'), ('green', 'safe')] >>> for signal in signals: ... f'{signal[0]} is {signal[1]}.' # Indexのため、内容が把握しづらい ... 'red is danger.' 'yellow is warning.' 'green is safe.' >>> for color, state in signals: # アンパックによる代入 ... f'{color} is {state}.' # 内容が明確で読みやすい ... 'red is danger.' 'yellow is warning.' 'green is safe.'Indexが使いたい場合は、enumerateを使う
rangeを使うより、見た目がすっきりします。
>>> favorite_colors = ['red', 'yellow', 'green'] >>> for color in favorite_colors: # indexが不要な場合 ... f'favorite color is {color}.' ... 'favorite color is red.' 'favorite color is yellow.' 'favorite color is green.' >>> for i in range(len(favorite_colors)): ... f'No.{i+1} favorite color is {favorite_colors[i]}.' # 全体的に読みづらい ... 'No.1 favorite color is red.' 'No.2 favorite color is yellow.' 'No.3 favorite color is green.' >>> for rank, color in enumerate(favorite_colors, 1): # 第二引数で開始する値を指定できる ... f'No.{rank} favorite color is {color}.' ... 'No.1 favorite color is red.' 'No.2 favorite color is yellow.' 'No.3 favorite color is green.'イテレータを並列に処理するにはzipかzip_longestを使う
rangeやenumerateを使うより、見た目がすっきりします。
並列処理するイテレータの状態により望ましい動作をするzipを使いましょう。>>> colors = ['red', 'yellow', 'green', 'gold'] >>> states = ['danger', 'warning', 'safe'] >>> for color, state in zip(colors, states): # 短いものに合わせる ... f'{color} is {state}.' ... 'red is danger.' 'yellow is warning.' 'green is safe.' >>> import itertools >>> for color, state in itertools.zip_longest(colors, states): # 長いものに合わせる ... f'{color} is {state}.' ... 'red is danger.' 'yellow is warning.' 'green is safe.' 'gold is None.'for elseを使わない
elseブロックの実行条件が直感的ではないので、ヘルパ関数を用意して記述しましょう。
whileでも同様です。>>> n = 5 >>> for i in range(2, n): ... surplus = n % i ... if surplus == 0: ... break # else節は実行されない ... else: # break文が実行されなかった場合に実行される ... f'{n} is prime number.' ... '5 is prime number.' >>> def is_prime(number): ... '''ヘルパ関数''' ... for i in range(2, number): ... surplus = number % i ... if surplus == 0: ... return False ... return True ... >>> if is_prime(n): # ヘルパ関数を使うことで処理が明瞭となる ... f'{n} is prime number.' ... '5 is prime number.'walrus演算子 :=
python3.8から使えるようになった新しい構文「代入式」に利用する演算子です。
a := b は a walrus(ウォルラス) b と発音します。代入と比較が同時に行えるようになることで1行減らすことができ、制御構文のスコープ外に制御のための変数(以下の例ではcount)を持ち出さなくて済みます。
>>> example = '9876543210' >>> count = len(example) # while文だけでcountを使いたいが、外のスコープでの宣言が必要 >>> while count > 1: ... if count == 5: ... f'{example}' ... example = example[1:] ... count = len(example) # 更新用に同じ処理を繰り返し書くケースがある ... '43210' >>> example = '9876543210' >>> while (count := len(example)) > 1: # スコープと行数を抑制できる。演算子の評価順に注意。 ... if count == 5: ... f'{example}' ... example = example[1:] ... '43210'リストと辞書
シーケンスのスライスとストライド
いくつか抑えておくポイントがあります。
>>> a = [1, 2, 3, 4, 5] >>> a[:3] # 先頭から利用する場合は、0は省略する [1, 2, 3] >>> a[3:] # 末尾から利用する場合も同様 [4, 5] >>> a[:-1] # 負のIndexも指定可能 [1, 2, 3, 4] >>> a[:10] # 範囲外のIndexも指定可能 [1, 2, 3, 4, 5] >>> a[10] # 範囲外に直接のアクセスはNG Traceback (most recent call last): File "<stdin>", line 1, in <module> IndexError: list index out of range >>> a[2:4] = ['a', 'b', 'c'] # スライスを使った代入 >>> a # 指定した範囲が代入した値で置き換わり、サイズも変更される [1, 2, 'a', 'b', 'c', 5] >>> a[-1:1:-2] # start、end、strideは一度に使わない。負の値が加わると特に複雑になる。 [5, 'b'] >>> c = a[::-2] # メモリや計算が許容できるなら、strideとsliceを分ける >>> c[:-1] [5, 'b']どうしてもstart、end、strideが必要な場合はitertoolsのisliceの利用も検討してください。
catch-all アンパックを使う
Indexを使うより、わかりやすく安全にシーケンスを分割できます。
>>> a = [1, 2, 3, 4, 5] >>> first, second, *others = a # *をつけることでfirst, second以外をothersでリストとして受け取る >>> first, second, others (1, 2, [3, 4, 5]) >>> first, *others, last = a # 順番はどこでも良い >>> first, others, last (1, [2, 3, 4], 5) >>> first, *others, last = a[:2] # catch-all変数の長さは0が許容される >>> first, others, last (1, [], 2)ただし、アスタリスク付きの式は常にリストを返すので、メモリには注意をしてください。
key引数を使ったソート
pythonのlistはsort関数が使えますが、key引数を使うことで複雑な基準でソートが可能です。
(独自に定義されたクラスのオブジェクトもメソッドを定義し、ソートに対応することはできますが、複数の順序付けをサポートする必要があります。)>>> class Target: ... def __init__(self, text, number): ... self.number = number ... self.text = text ... def __repr__(self): ... return f'{self.text} {self.number}' ... >>> targets = [ ... Target('berry', 4), ... Target('cherry', 2), ... Target('durian', 1), ... Target('apple', 2), ... Target('elderberry', 3) ... ] >>> repr(targets) '[berry 4, cherry 2, durian 1, apple 2, elderberry 3]' >>> targets.sort(key=lambda x:(-x.number, x.text)) # タプルの利用や符号変換ができる >>> repr(targets) '[berry 4, elderberry 3, apple 2, cherry 2, durian 1]' >>> targets.sort(key=lambda x: x.text, reverse=True) # 符号変換ができない場合はreverseで >>> targets.sort(key=lambda x: x.number) # タプルの場合とは、優先順序が逆転する形になる >>> repr(targets) '[durian 1, cherry 2, apple 2, elderberry 3, berry 4]'dictの挿入順序
T.B.D.
- 投稿日:2020-07-27T20:43:57+09:00
matplotlibのTimes New Romanがボールド体になる問題
下記のプログラムを追加すると解決します.
import matplotlib del matplotlib.font_manager.weight_dict['roman'] matplotlib.font_manager._rebuild()
- 投稿日:2020-07-27T20:23:06+09:00
[cx_Oracle入門](第15回) タプル以外の形式で結果セットを作成する
連載目次
検証環境
- Oracle Cloud利用
- Oracle Linux 7.7 (VM.Standard2.1)
- Python 3.8
- cx_Oracle 8.0
- Oracle Database 19.5 (ATP, 1OCPU)
- Oracle Instant Client 18.5
概要
cx_Oracleは結果セットをタプルのリストで戻します。しかし、これをリストや辞書で返したいケースもあるかと思います。その場合の備えがcx_Oracleにはあるので、その方法を解説します。
Cursor.rowfactory
Cursorオブジェクトのrowfactory属性は、レコードを取り出す際に呼ばれるメソッドを定義します。この属性は、デフォルトではタプルを生成します。この動きを上書きすることで、レコードの形式を他の形に変更することが可能になります。
以下のアプリケーションを改定する形で、実際のコーディングを見ていきます。
sample15a.pyimport cx_Oracle USERID = "admin" PASSWORD = "FooBar" DESTINATION = "atp1_low" SQL = """ select object_id, owner, object_name, object_type from all_objects order by object_id fetch first 5 rows only """ with cx_Oracle.connect(USERID, PASSWORD, DESTINATION) as connection: with connection.cursor() as cursor: for row in cursor.execute(SQL): print(row)$ python sample15a.py (2, 'SYS', 'C_OBJ#', 'CLUSTER') (3, 'SYS', 'I_OBJ#', 'INDEX') (4, 'SYS', 'TAB$', 'TABLE') (5, 'SYS', 'CLU$', 'TABLE') (6, 'SYS', 'C_TS#', 'CLUSTER')結果セットをリストで返す
sample15b.py(抜粋)with cx_Oracle.connect(USERID, PASSWORD, DESTINATION) as connection: with connection.cursor() as cursor: cursor.execute(SQL) cursor.rowfactory = lambda *args: list(args) rows = cursor.fetchall() for row in rows: print(row)下から4行目がrowfactoryの実装です。ラムダ式を使用して各レコードをタプルからリストに変換しています。この1行が追加されているだけで、他のコーディングには特段の変更は入っていません。実行結果は以下のとおり、リストになっています。
$ python sample15b.py [2, 'SYS', 'C_OBJ#', 'CLUSTER'] [3, 'SYS', 'I_OBJ#', 'INDEX'] [4, 'SYS', 'TAB$', 'TABLE'] [5, 'SYS', 'CLU$', 'TABLE'] [6, 'SYS', 'C_TS#', 'CLUSTER']結果セットを辞書で返す
列名を要素にした辞書でレコードを戻すことも可能です。
sample15c.py(抜粋)with cx_Oracle.connect(USERID, PASSWORD, DESTINATION) as connection: with connection.cursor() as cursor: cursor.execute(SQL) columns = [col[0] for col in cursor.description] cursor.rowfactory = lambda *args: dict(zip(columns, args)) rows = cursor.fetchall() for row in rows: print(row) for row in rows: print(row["OBJECT_NAME"])列名は上から4行目で取得しています。cursor.descriptionは、各列のメタデータを格納しているタプルのリストの形式の読み取り専用属性になります。この属性の各タプルの要素番号0が列名となります。上から5行目で、ラムダ式を使用して、前の行の情報を利用して辞書を作成しています。実行結果は以下のとおり、辞書になっています。
$ python sample15c.py {'OBJECT_ID': 2, 'OWNER': 'SYS', 'OBJECT_NAME': 'C_OBJ#', 'OBJECT_TYPE': 'CLUSTER'} {'OBJECT_ID': 3, 'OWNER': 'SYS', 'OBJECT_NAME': 'I_OBJ#', 'OBJECT_TYPE': 'INDEX'} {'OBJECT_ID': 4, 'OWNER': 'SYS', 'OBJECT_NAME': 'TAB$', 'OBJECT_TYPE': 'TABLE'} {'OBJECT_ID': 5, 'OWNER': 'SYS', 'OBJECT_NAME': 'CLU$', 'OBJECT_TYPE': 'TABLE'} {'OBJECT_ID': 6, 'OWNER': 'SYS', 'OBJECT_NAME': 'C_TS#', 'OBJECT_TYPE': 'CLUSTER'} C_OBJ# I_OBJ# TAB$ CLU$ C_TS#結果セットをData Classで返す
rowfactoryはPython3.7の新機能であるData Classにも対応可能です。結果セットと同じData Classを作成しておくと、何かと便利そうです。Data Class自体の説明は以下をご参照ください。
Python3.7からは「Data Classes」がクラス定義のスタンダードになるかもしれない
以下、サンプルと実行結果です。
sample15d.pyimport cx_Oracle from dataclasses import dataclass @dataclass class AllObject: object_id: int owner: str object_name: str object_type: str def display(self): return f"{self.owner}.{self.object_name}は{self.object_type}(ID:{self.object_id})です" USERID = "admin" PASSWORD = "FooBar" DESTINATION = "atp1_low" SQL = """ select object_id, owner, object_name, object_type from all_objects order by object_id fetch first 5 rows only """ with cx_Oracle.connect(USERID, PASSWORD, DESTINATION) as connection: with connection.cursor() as cursor: cursor.execute(SQL) cursor.rowfactory = lambda *args: AllObject(*args) rows = cursor.fetchall() [print(r.display()) for r in rows]$ python sample15d.py SYS.C_OBJ#はCLUSTER(ID:2)です SYS.I_OBJ#はINDEX(ID:3)です SYS.TAB$はTABLE(ID:4)です SYS.CLU$はTABLE(ID:5)です SYS.C_TS#はCLUSTER(ID:6)です
- 投稿日:2020-07-27T20:18:11+09:00
Djangoプロジェクト環境構築
自分のローカル環境構築メモです。
環境
- OS: macOS Catalina
- Python 3.7.1
- venv
- Django
pyenv, Python インストール
macOSだとPythonがプリインストールされていますが、
バージョンが2系なので、pyenvから3系をインストールします。
https://github.com/pyenv/pyenv## まず pyenvをインストール $ brew install pyenv.zprofile(bash なら.bash_profile) 編集
以下、追加します
eval "$(pyenv init -)"pvenvコマンドの有効化
編集済の.zprofileをロードし、pvenvコマンドを有効化します。
$ source ~/.zprofilepvenvからPython 3.7.1インストール
- Python 3.7.1インスール
$ pyenv install 3.7.1
- Python 3.7.1をデフォルトバージョンに設定
$ pyenv global 3.7.1Djangoプロジェクト環境を仮想化する
ローカルグローバル環境に余計なパッケージが含まれないよう(プロジェクト単位でのパッケージ管理)
仮想環境の上にDjango関連パッケージをインストールします。仮想環境作成は
venvモジュールを使います。venv仮想環境構築
## プロジェクトディレクトリ作成 $ mkdir hogeproject $ cd hogeproject ## venv 仮想環境作成 $ python -m venv myhogeenv ## 作成されたディレクトリ確認するとこんな感じ $ pwd /xxxx/xxxx/hogeproject $ tree -L 3 . └── myhogeenv ├── bin │ ├── activate │ ├── activate.csh │ ├── activate.fish │ ├── easy_install │ ├── easy_install-3.7 │ ├── pip │ ├── pip3 │ ├── pip3.7 │ ├── python -> /Users/xxxx/.pyenv/versions/3.7.1/bin/python │ └── python3 -> python ├── include ├── lib │ └── python3.7 └── pyvenv.cfg仮想環境起動
## 起動 $ source myhogeenv/bin/activate ## 起動完了したらプロンプトに(myhogeenv)がつく。 (myhogeenv) $Djangoインストール
venv仮想環境が起動されている状態でDjangoをインストールします。
(Djangoはpipでインストール)## Django version記載のrequirements.txtを配置する (myhogeenv) $ echo "Django~=2.2.4" > requirements.txt ## 配置済のrequirements.txt ディレクトリ確認 (myhogeenv) $ pwd /xxxx/xxxx/hogeproject (myhogeenv) $ tree -L 3 . ├── myhogeenv │ ├── bin │ │ ├── activate │ │ ├── activate.csh │ │ ├── activate.fish │ │ ├── easy_install │ │ ├── easy_install-3.7 │ │ ├── pip │ │ ├── pip3 │ │ ├── pip3.7 │ │ ├── python -> /Users/xxxx/.pyenv/versions/3.7.1/bin/python │ │ └── python3 -> python │ ├── include │ ├── lib │ │ └── python3.7 │ └── pyvenv.cfg └── requirements.txt ## Django インストール (myhogeenv) $ pip install -r requirements.txt
- 投稿日:2020-07-27T20:18:02+09:00
matplotlibでTimes New Romanが使えないとき (Ubuntu)
下記のようなエラーが出る場合.
UserWarning: findfont: Font family ['Times New Roman'] not found. Falling back to DejaVu Sans. (prop.get_family(), self.defaultFamily[fontext]))Terminalから以下のコマンドを入力することで解決する.
$ sudo apt install msttcorefonts -qq $ rm ~/.cache/matplotlib -rf
ttf-mscorefonts-installerはTabで選択したい位置にカーソルを合わせてEnterを押す.
- 投稿日:2020-07-27T19:57:21+09:00
初心者のためのpandas基礎⑧桁数処理
pandasとは
Pythonにて、構造化データ(テーブル型のデータ)を扱うためのライブラリです。ファイルの読み込みやその後の加工・抽出処理などを簡単に行うことができ(SQL的な感覚で行うことができ)、機械学習などのデータの前処理で必須となるライブラリです。
他項目への目次はこちらになります。はじめに
本記事では、桁数の処理方法です。はじめに理解して頂きたいこととして、pandasそのもの桁数を調整する方法と個別のデータフレームや変数の桁数を調整する方法があります。また、注意として、pandasの丸めは四捨五入ではなく、偶数への丸めとなります。偶数への丸めを知らない人は調べて下さい。
準備
まずはライブラリをインポートします。pandasにpdという名前をつけてimportします。
import pandas as pdサンプルはタイタニックのデータで試してみます。タイタニックがわからない人は「kaggle タイタニック」で調べて下さい。
dataframe = pd.read_csv('train.csv')pandasの桁数調整
pandasの様々設定は
optionにて管理されます。(他にも様々なオプションがあるので興味がある方は調べて下さい。)全体の桁数はdisplay.float_formatで、小数点以下の桁数はdisplay.precisionで管理されています。
実際に確認してみましょう。Inprint(pd.options.display.float_format) print(pd.options.display.precision)OutNone 6全体の桁数に制約はなく、小数点以下は6桁表示となっています。実際のデータをみてると、例えばFareは小数点以下四桁まで表示されています。これは元々のCSVのデータが4桁までしかないためこのような表示となっていますが、桁数が多ければ6桁までの表示となります。
次にこの値を変更し、小数点以下2桁表示にします。(Fareの表示が2桁になります)
pd.options.display.precision = 2
初期化をしたい場合はreset_optionを使いましょう。pd.reset_option('display.precision')個別に設定する方法
個別の設定は
round()を使います。小数点以下2桁にする場合は、下記になります。(Fareの表示が2桁になります)dataframe.round(2)列毎に設定する場合は下記になります。(例:Ageを1桁、Fareを3桁とする。)
dataframe.round({'Age':1, 'Fare':3})最後に
初心者にもわかるように、Pythonで機械学習を実施する際の必要な知識を簡便に記事としてまとめております。
目次はこちらになりますので、他の記事も参考にして頂けると幸いです。
- 投稿日:2020-07-27T19:28:54+09:00
文書要約のLexRankや、Googleページランクのアルゴリズムではなぜ固有ベクトルが登場するの?
本記事では、文書要約アルゴリズム(および、重要文の抽出手法)であるLexRankの手続き(Googleが初期に採用していた、各サイトの重要度を測るページランク手法を応用した手法)に、なぜ線形代数の固有ベクトルや固有値分解が登場するのかを解説します。
はじめに
2020年8月1日に
「Deep Learning Digital Conference」
が開催されます。https://dllab.connpass.com/event/178714/
上記イベントの【個人セッション】で、
【AI・ディープラーニングを駆使して、「G検定合格者アンケートのフリーコメント欄」を分析してみた】
というLTを、同僚(2月から中途入社してきたメンバの御手洗さん)と発表します。(概要)
2020年5月に実施した「第2回G検定合格者がおススメするAI・DL本アンケート」のフリーコメント欄、「ディープラーニング協会へのご意見・ご要望」に寄せられた意見を、ディープラーニング協会らしく、機械学習とディープラーニングを駆使して分析した結果を紹介します。本発表ではワードクラウド、説明性XAI、クラスタリング、要約、ALBERTなどの自然言語処理技術の概要を解説し、そして実際にこれらの技術を、G合格者のみなさまの「ディープラーニング協会へのご意見・ご要望」データに適用すると、どのような分析結果が出たのか紹介します。私(小川)は日本ディープラーニング協会を運営している委員なので、
アンケートのフリーコメントを解析し、
皆さまの意見を運営陣に報告・カイゼンする必要があるのですが、
フリーコメントの解析を手でやるのがしんどいです。そこで、
ディープラーニングのエンジニアらしく、機械学習を駆使しようじゃないか!
という取り組みを実施しました(ちゃんと手作業での整理もしましたが・・・)。LexRank
フリーコメントの解析の途中で、文書を自動要約する場面があります。
今回要約手法には、簡単な手法であるLexRankアルゴリズムを採用することにしました。
LexRankは「初期のGoogleで各サイトの重要度を測るページランク手法」を応用した、文書要約(および、重要文の抽出)のアルゴリズムです。
以下、LexRankの解説例です。
https://ohke.hateblo.jp/entry/2018/11/17/230000
https://www.ai-shift.co.jp/techblog/938
2月に中途入社してきた御手洗さんと、このコロナの最中のため、ずっと各自、自宅から、ペアプロをしてました。
ペアプロといっても、僕が指示して彼が頑張り、その間私は別の仕事をする、
分からなくなったら私に聞く、
なので、
ペアプロというよりは、ずっといつでも私に質問できる状態という感じでしょうか。。。で、LexRankも実装してくれて、
さて発表スライドを作っているときに、私から彼にした質問が以下の3つです。[A] 各サイトの重要度を測るページランクの手法を応用したLexRankでは、アルゴリズムになぜ固有値分解が登場するの?
[B] ページランクに相当する、各文章の重要度は、固有ベクトルというけど、固有値いくつの固有ベクトルなの?
[C] なんで固有ベクトルがページランクや、LexRankでは各文章での重要度に相当するの?
です。
そして私からの解説が以下になります。
文書要約のLexRankや、Googleページランクのアルゴリズムで固有値分解が登場する理由
これは線形代数の固有値、固有ベクトル、固有値分解のお話になります。
まずは、以下のサイトを読んでみてください。
なぜ線形代数を学ぶ? Googleのページランクに使われている固有値・固有ベクトルの考え方
https://math-fun.net/20180809/1195/そして上記のサイトの情報だけでは、私の[A]-[C]の質問には答えられない(と思いますので)
補足すると、以下の通りです。[1] ページランクとは、ページ間の遷移確率を行列で表した行列Aの、固有値1の固有ベクトルの値です
[2] 固有値1の固有ベクトルなので、そのベクトルをページ間の遷移確率行列Aに再度かけ算しても、また、同じ値のベクトルになります。
つまり、
vec_after = A * eigen_vecここで、vec_afterはeigen_vecと同じ(なぜなら、固有値が1なので固有値倍されても同じ値)
[3] つまり、固有値1の固有ベクトルの各行の値は”各サイトのパワー”を示します。
そして全サイトのパワーの割合がどんなパターンだと(すなわち、どんな固有ベクトルだと)、
遷移確率行列Aで遷移しても、変化しないのか?
サイトパワーが遷移行列Aで遷移しても変化することのない状態が、各サイトの静的なパワー(ページランク)を示します。※サイトのパワーと言われて理解しづらい人は、そのサイトを見ている人の数、だと思ってください。
そのサイトを見ている人の数が、遷移行列で変換したあとでも変化しない、
すなわち、そのサイトの静的な集客人数≒サイトの重要度、という考え方です。[4] この[3]が、固有値1の固有ベクトルがページランクに相当する理由です。
[5] 今回はLexRankなので、
検索におけるページ間の遷移行列(被リンク数の行列)とホームページの強さ(ページランク)は、
それぞれ、各文書と文書の類似度行列と各文書の強さ(重要さ)として扱われます。以上が、LexRankに固有ベクトルがや固有値分解が登場する理由であり、最初の3つの質問、
[A] 各サイトの重要度を測るページランクの手法を応用したLexRankでは、アルゴリズムになぜ固有値分解が登場するの?
[B] ページランクに相当する、各文章の重要度は、固有ベクトルというけど、固有値いくつの固有ベクトルなの?
[C] なんで固有ベクトルがページランクや、LexRankでは各文章での重要度に相当するの?の回答になります。
まとめ
以上、本記事では、「初期のGoogleで各サイトごとの重要度を測るページランク手法」を応用した、文書要約(および、重要文の抽出)のアルゴリズムであるLexRankのアルゴリズムに、なぜ線形代数の固有ベクトルや固有値分解が登場するのかを解説しました。
最近私は、自分が面白いと思った記事やサイト、読んだ本の感想などのAIやビジネス、経営系の情報をTwitterで発信しています。
小川雄太郎@ISID_AI_team
https://twitter.com/ISID_AI_team私が見ている情報を共有しているので、是非こちらアカウントもどうぞよろしくお願い致します。
【備考】私がリードする、AIテクノロジー部開発チームではメンバ募集中です。興味がある方はこちらからお願い致します
【免責】本記事の内容そのものは著者の意見/発信であり、著者が属する企業等の公式見解ではございません
- 投稿日:2020-07-27T18:46:39+09:00
Python FastAPIの入門
はじめに
Tornadoの紹介記事を書いていて、APIServerとしても良いよ的な私感を述べたのですが
APIServerならこの、FastAPIもとても良いので記事にしてみました対象
フルスタックエンジニア、フロントエンジニア、これから勉強しようと思っている人、Pythonが好きな人
python3.6以上がインストールされていることゴール
インストール〜簡易的なJSONを出力できるまで
Swaggerでの表示FastAPIとは
後発なWebFrameworkだけあってモダンな機能、パフォーマンスの高さを意識したものとなっている
以下公式
- 高速:NodeJSやGolangと同等のパフォーマンス
- 開発効率UP
- 簡単:使いやすく学習しやすいように設計されている
(ドキュメントを読む時間が短縮・・・英語ですけどね
- 自動インタラクティブドキュメント(Swagger UI)インストール
FastAPIのインストールはpipのみ
$ pip install fastapi uvicornpipってとても優秀なやつだと、毎回思います(コピペ)
今回はASGI ServerになるuvicornもinstallHello World
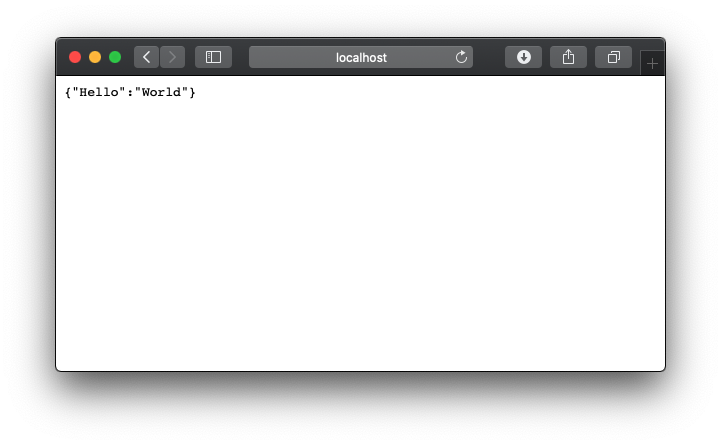
これもまぁ公式なのですが
main.pyfrom fastapi import FastAPI app = FastAPI() @app.get("/") def read_root(): return {"Hello": "World"}起動&閲覧
ターミナルで
$ uvicorn main:app --reload --host 0.0.0.0reloadオプションはソース変更時自動的にreloadしてくれるもの
hostオプションに0.0.0.0を指定してるのはDockerやVMで起動し、PortForwardするおまじない詳しくはここなど
simple JSON
さらに、ちょっとコードを加えることで簡易的なAPIっぽくしてみます
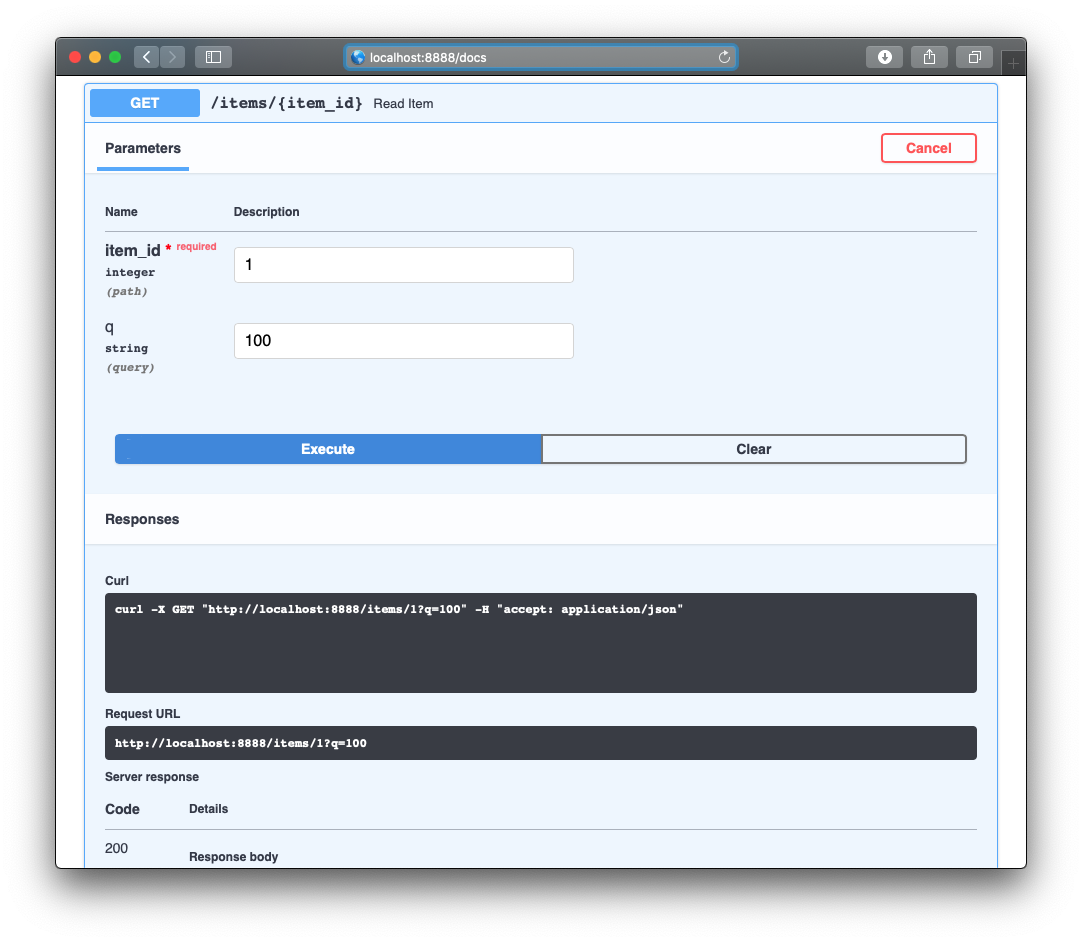
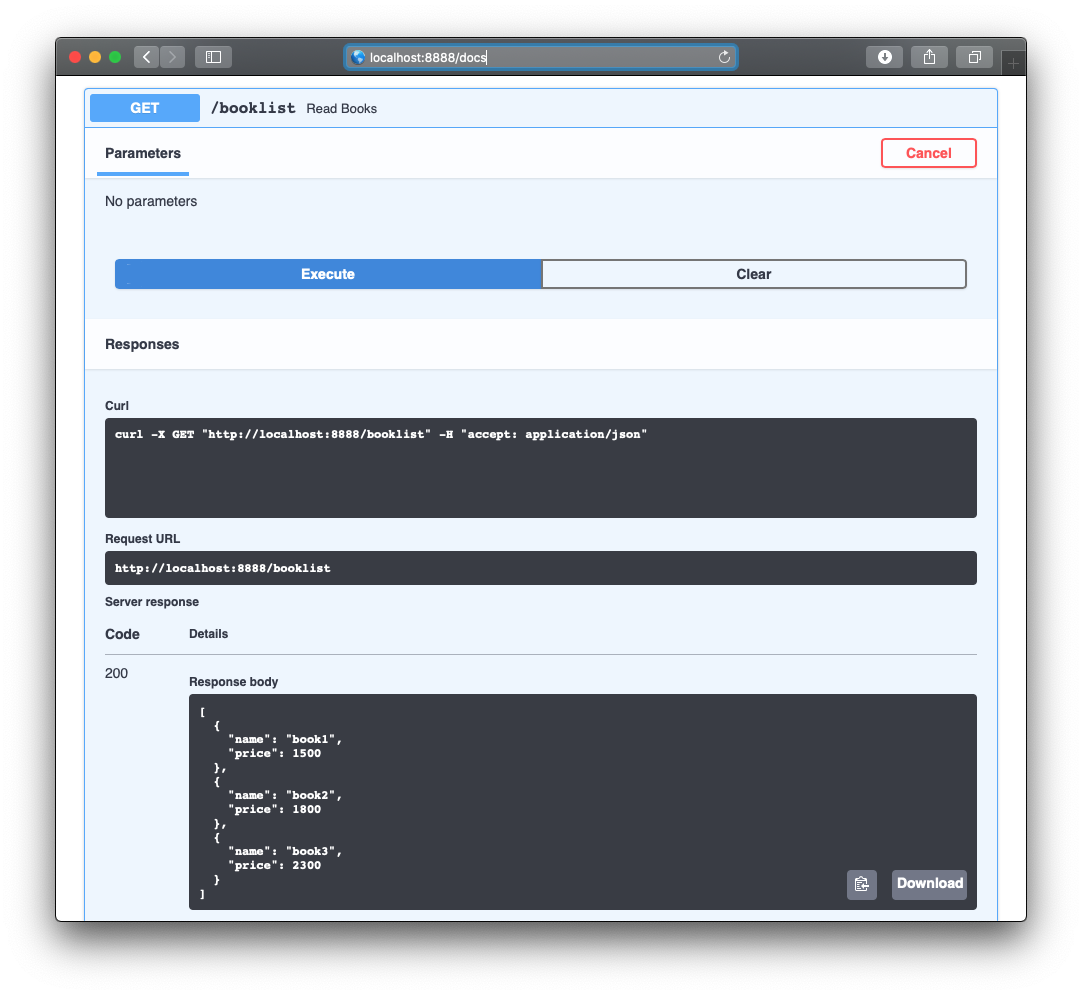
localhost:8000/docs にアクセスするだけでSwaggerがみれてしまうんですねソース
main.pyfrom fastapi import FastAPI from typing import Optional app = FastAPI() @app.get("/") def read_root(): return {"Hello": "World"} @app.get("/items/{item_id}") def read_item(item_id: int, q: Optional[str] = None): return {"item_id": item_id, "q": q} @app.get("/booklist") def read_books(): books = [ {'name': 'book1', 'price': 1500}, {'name': 'book2', 'price': 1800}, {'name': 'book3', 'price': 2300}, ] return books
- 投稿日:2020-07-27T18:36:57+09:00
Web-WF Python Tornado その2
はじめに
webServer APIServerとして、かんたん・すぐれている(と思っている)Tornadoを何回かにわけて紹介したいと思います
Web-WF Python Tornado その1
Web-WF Python Tornado その2 (この記事
Web-WF Python Tornado その3(Openpyexcelの紹介)対象
フルスタックエンジニア、フロントエンジニア、これから勉強しようと思っている人、Pythonが好きな人
Python3.6以上、tornadoがインストールされている
ゴール
今回はベースになるフォルダ構成や各種ファイルの説明、https化 までを説明
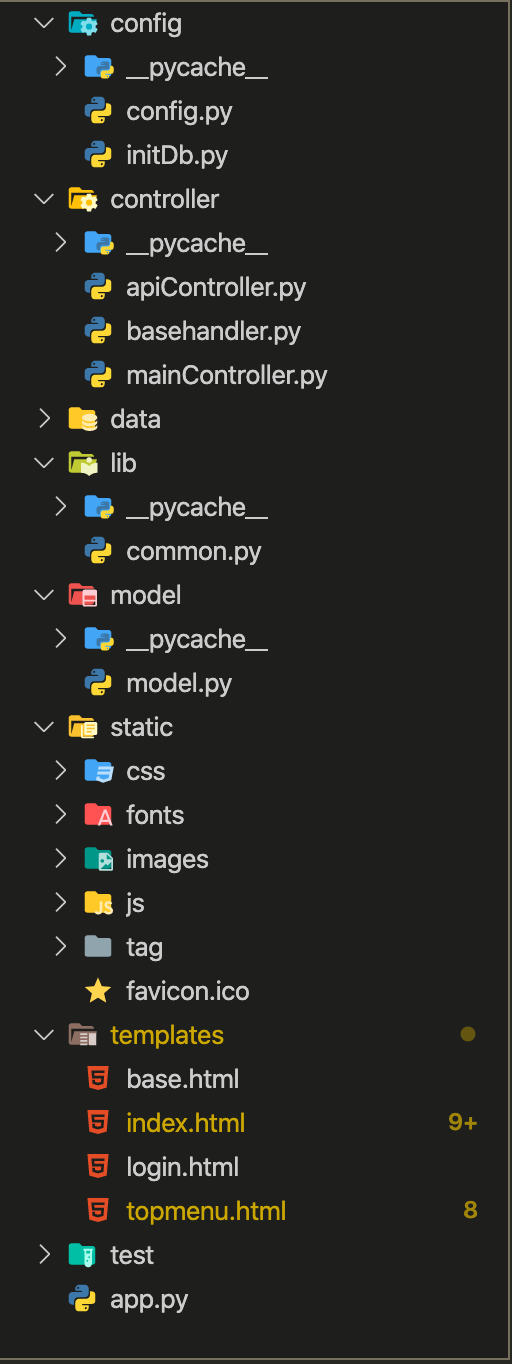
フォルダ構成
config
- ・config.py
- tornadoの起動設定を記述
- ・intDb.py
- DBの設定を記述
controller
- ・apiController.py
- get, postなどに対応する部分を記述
- ・basehandler.py
- authなど全体的に処理したいものを記述
- ・mainController.py
- loginやauthに関わる処理を記述
data
- ・sample.sql
- プロジェクトのDDL
lib
- ・common.py
- 共通的に使うclass, 関数など
model
- ・model.py
- テーブル定義、データモデル(プロジェクトの大きさで更に分割)
static
- ・css/
- css関連
- ・fonts/
- font関連
- ・images/
- 画像関連
- ・js/
- javascriptモジュール関連
- ・tag/
- このsampleではriot.jsを使用していたのでさり気なくアピール
- ・favicon.ico
- favicon
templates
- ・base.html/
- script読み込みなど側部分を記述
- ・index.html
- メインコンテンツを記述
- ・login.html/
- ログイン画面を記述
- ・topmenu.html
- トップメニュー(ヘッダー)を記述
test
- ・test/
- 各種テストファイル
app.py
- ・app.py
- tornado起動部分、対応urlを記述
app.py を以下のように変更して外部ファイルをインポート
app.pyimport tornado.ioloop import tornado.web # 外部ファイルをインポート from controller.mainController import * from controller.apiController import *全体的なイメージとしてはhtml部分をvue.jsだったりnuxt.jsで作成した静的ファイルを置くか、tornadoをapiサーバーのみに使い、nuxt.js等から利用するという使い方が良いのかなと思います
このあたりはプロジェクトの規模だったりメンバーの構成に合わせて選択するしか無いかなと考えているのですが、だれかベストプラクティスありますか?起動&閲覧
ターミナルで
$ python app.pyはい、僕はいつもこんなシンプルな画面をプロジェクトのミニマムとして用意しています
https / options
さらに、sslに対応させ、あると便利なoptionsの設定もしておきます
ソース&閲覧
起動部分の抜粋
cert.pemとprivkey.pemは「オレオレ自己認証」で作成
server側はLet's Encryptを利用して運用することも出来ます
(自動化出来るとはいえ更新が面倒です)app.pyif __name__ == '__main__': options.parse_command_line() if os.path.exists(BASE_DIR + '/config/config.py'): options.parse_config_file(BASE_DIR + '/config/config.py') http_server = tornado.httpserver.HTTPServer(application, ssl_options={ "certfile": "/etc/cert/cert.pem", "keyfile": "/etc/cert/privkey.pem", "ssl_version": ssl.PROTOCOL_TLSv1_2, "ciphers": "EECDH+HIGH+AES!SHA:!ADH:!RC4:!MD5:!aNULL:!eNULL:!SSLv2:!LOW:!EXP:!PSK:!SRP:!DSS:!KRB5", }) http_server.listen(8888) tornado.ioloop.IOLoop.current().start()config.py# logレベルの設定 # logging = "WARNING" logging = "ERROR"
- 投稿日:2020-07-27T18:26:49+09:00
YOTUBE Data API V3を使ってみた
概要
スクレイピング入門書でyoutube Data API V3を使ってみた。
色々と詰まりまくったのでその証跡を残しておく。実装したコード
youtube_api_metadata.pyimport os import logging import csv from apiclient.discovery import build from pymongo import MongoClient, ReplaceOne, DESCENDING from typing import Iterator, List from pymongo.collection import Collection YOUTUBE_API_KEY=os.environ['YOUTUBE_API_KEY'] logging.getLogger('googleapiclient.discovery_cache').setLevel(logging.ERROR) def main(): mongo_client = MongoClient('localhost', 27017) collections = mongo_client.youtube.videos query = input('検索値を指定して下さい。:') for items_per_page in search_videos(query): save_to_momgo(collections, items_per_page) save_to_csv(collections) def search_videos(query: str, max_pages: int=5): youtube = build('youtube', 'v3', developerKey=YOUTUBE_API_KEY) search_request = youtube.search().list( part='id', q=query, type='video', maxResults=15, ) i = 0 while search_request and i < max_pages: search_response = search_request.execute() video_ids = [item['id']['videoId'] for item in search_response['items']] video_response = youtube.videos().list( part='snippet,statistics', id=','.join(video_ids), ).execute() yield video_response['items'] search_requst = youtube.search().list_next(search_request, search_response) i += 1 def save_to_momgo(collection: Collection, items: List[dict]): for item in items: item['_id'] = item['id'] for key, value in item['statistics'].items(): item['statistics'][key] = int(value) operation = [ReplaceOne({'_id': item['_id']}, item, upsert=True) for item in items] result = collection.bulk_write(operation) logging.info(f'Upserted {result.upserted_count} documents.') def save_to_csv(collection: Collection): with open('top_videos_list.csv', 'w',newline='', encoding='utf-8-sig') as f: writer = csv.DictWriter(f, ['title', 'viewCount']) writer.writeheader() for item in collection.find().sort('statistics.viewCount', DESCENDING): writer.writerows([{'title' : item['snippet']['title'], 'viewCount': item['statistics']['viewCount']}]) if __name__ == '__main__': logging.basicConfig(level=logging.INFO) main()詰まり①
コードを実装し、何度か実行していたら以下エラーが発生。
sample.pygoogleapiclient.errors.HttpError: <HttpError 403 when requesting https://www.googleapis.com/youtube/v3/videos?part=snippet%2Cstatistics&id=wXeR58bjCak%2CujxXyCrDnU0%2CQhhUVI0sxCc%2CKZz-7KSMjZA%2CWq-WeVQoE6U%2CG-qWwfG9mBE%2CYqUwEPSZQGQ%2CIuopzT_TWPQ%2CmcFspy1WhL8%2Ck9dcl7F6IFY%2C--Z5cvZ4JEw%2C3hidJgc9Zyw%2CdYSmEkcM_8s%2Ch6Hc4RuK8D8%2CRQfN2re3u4w&key=<YOUTUBE_API_KEY>&alt=json returned "The request cannot be completed because you have exceeded your <a href="/youtube/v3/getting-started#quota">quota</a>.">最初はよくわからず、何が原因かを探しまくった。
結果、原因は単純に"quota"の使用制限がかかったのだと思われる。
GCPから新しいプロジェックトを作成し、認証タブからAPIキーを新規に発行。
キーを以下で環境変数に設定し、再度pythonファイルを実行。set YOUTUBE_API_KEY=<YOUTUBE_API_KEY>結果,問題なく実行されCSVファイルが出力された。
(scraping3.7) C:\Users\user\scraping3.7\files>python save_youtube_videos_matadata.py 検索値を指定して下さい。:ひかきん INFO:root:Upserted 15 documents. INFO:root:Upserted 0 documents. INFO:root:Upserted 0 documents. INFO:root:Upserted 0 documents. INFO:root:Upserted 0 documents.詰まり②
上記コードの内、以下が機能があまりよくわからず。
これが気になってしょうがなくなり開発がストップ。operation = [ReplaceOne({'_id': item['_id']}, item, upsert=True) for item in items]公式で調べまくった結果,以下のフォーマットで引数を受け取る事がわかった。
公式ReplaceOne(filter, replacement, options)以下の場合
ReplaceOne({'city': '東京'}, {'city':'群馬'}, upsert=True)'city':'東京'のデータが存在する場合、city':'群馬'に更新。
'city':'東京'が存在しない場合、新たに'city':'群馬'を挿入。参考書
- 投稿日:2020-07-27T17:35:38+09:00
主成分分析とK-meansクラスタリングを使った協調フィルタリング
レコメンドエンジンのAPI利用を考える
レコメンドエンジンはWEB APIなどで利用する機会が多く、精度を保ったまま素早く結果を返すことを要求されます。
そのため本記事では映画の視聴履歴に基づくレコメンド機能を実装する際に、主成分分析とK-meansクラスタリングを利用して、レコメンド精度をなるべく保ちつつ、APIの利用に耐えるように計算速度とのバランスを取ります。今回利用するレコメンドのロジックは、選択した映画に対する各ユーザーの評価が似た映画を抽出してレコメンドするという単純なアイテムベース協調フィルタリングです。
主成分分析とK-meansクラスタリング
主成分分析(PCA)は高次元や超次元のベクトルの主成分のみを抽出して、ベクトルの次元を下げてデータ量を削減する手法です。
主成分分析後の次元数を予め決められるので、主成分の次元を決めるとデータ量も決まるので、分析する元ベクトルの次元が膨大になっても計算量を一定に保つことができます。さらに、Kmeansクラスタリングである程度クラスタリングをしておくことで評価する対象の映画を限定し、比較回数を減少させて、レスポンスのスピードを向上を狙います。
今回はMovieLensというフリーの映画評価のデータセットを利用します。
https://grouplens.org/datasets/movielens/100k/ざっくりと言うと。。。。
自分が好きな映画に各ユーザーから似たような評価をされている映画はそれも好きなはず!!
でも全員といちいち比較していたら時間がかかっちゃって大変なので、先にざっくりと似てる人たちでグループ作っておいて(クラスタリング)、その中でもさらに重要そうな映画の評価だけ抜き出して(主成分分析)比較しよう!主成分分析についてもう少し
例えば1万本の映画の評価データがあった際に、全員が見ている映画やほとんど誰も見ていないデータがあった場合に、あまりいい情報にならないから比較対象から外しちゃっても良いよね。特徴が出やすい100本くらいに絞っておこう。(厳密に言うと違うのですがだいたいこんな感じです。)
データの取得
https://grouplens.org/datasets/movielens/100k/
からml-100k.zipをダウンロードして展開します。
中にはいくつかのファイルがありますがREADMEに説明があります。
今回主に利用するのは、u1.baseです。プログラム
プログラム内にコメントを記載して一通り下記します。
recommend.pyimport numpy as np import pandas as pd from sklearn.decomposition import PCA from sklearn.cluster import KMeans # TSV形式のデータの読み込み datum = np.loadtxt("u1.base", delimiter="\t", usecols=(0, 1, 2), skiprows=1) # ユーザーIDと映画IDの一覧を用意 user_ids = [] movie_ids = [] for row in datum: user_ids.append( row[0] ) movie_ids.append( row[1] ) user_ids = list(set(user_ids)) movie_ids = list(set(movie_ids)) # 映画IDごとの評価データを整理 vectors = {} for movie_id in sorted(movie_ids): vectors[movie_id] = {} for user_id in user_ids: # 見ていない映画はデフォルト-1評価とする vectors[movie_id][user_id] = -1 # ベクトルにユーザーの各評価を格納 for row in datum: vectors[row[1]][row[0]] = row[2] dataset = [] # データを整形 for movie_id in vectors: temp_data = [] for user_id in sorted(vectors[movie_id]): temp_data.append(vectors[movie_id][user_id]) dataset.append(temp_data) # Kmeansで3つのクラスタに分類 predict = KMeans(n_clusters=3).fit_predict(dataset) # 主成分分析後の次元数 DIMENTION_NUM = 128 # 主成分分析 pca = PCA(n_components=DIMENTION_NUM) dataset = pca.fit_transform(dataset) print('累積寄与率: {0}'.format(sum(pca.explained_variance_ratio_))) # 映画ID1に似た映画を探す MOVIE_ID = 1 # 映画ID1のクラスターIDを取得 CLUSTER_ID = predict[movie_ids.index(MOVIE_ID)] distance_data = {} for index in range(len(predict)): # 同じクラスター内にある場合ベクトルの距離を比較 if predict[index] == CLUSTER_ID: distance = np.linalg.norm( np.array(dataset[index], dtype=float) - np.array(dataset[movie_ids.index(MOVIE_ID)], dtype=float) ) distance_data[movie_ids[index]] = distance # ベクトルの距離順に表示 print(sorted(distance_data.items(), key=lambda x: x[1]))結果
累積寄与率: 0.7248119795849713 [(1.0, 0.0), (121.0, 67.0315681132561), (117.0, 69.90161652852805), (405.0, 71.07049485275981), (151.0, 71.39559068741323), (118.0, 72.04600188124728), (222.0, 72.78595965661094), (181.0, 74.18442192660996), (742.0, 76.10520742268852), (28.0, 76.27732956739469), (237.0, 76.31850794116573), (25.0, 76.82773190547944), (7.0, 76.96541606511116), (125.0, 77.07961442692692), (95.0, 77.42577990621398), (257.0, 77.87452368514414), (50.0, 78.80566867021435), (111.0, 78.9631520879044), (15.0, 78.97825600046046), (69.0, 79.22663656944697), (588.0, 79.64989759225082), (82.0, 80.23718315576053), (71.0, 80.26936193506091), (79.0, 81.02025503780014).....ID=1の映画がトイ・ストーリーで、一番近いとされた映画ID=121がインデペンデンス・デイでした。
寄与率は0.72ということは、主成分だけで元データの72%程度復元できているということです。
なんとなくわかる気もしますね!!!その後の実装
今回は一つのスクリプトでデータ整形からクラスタリングと主成分分析、比較まで通して行ってしまいましたが、
本来は主成分分析までを行ったデータをデータベースに格納しておいて、比較のみ都度行うように実装します。また、映画データや評価データは日々増えていくので適切な期間を決めてクラスタリングや主成分分析をバッチなどでやり直していくようにします。
API化する際には主成分の次元数やクラスタ数、APIキャッシュなどを駆使してレコメンド精度とレスポンススピードを調整していきます。
このレコメンド精度ですが、最初はなんとなく感覚で合っているかどうかで見てもよいですが、CTRやCVRなどと兼ねわせて実際のデータを加味したディープラーニングを駆使していくとさらに今風の機械学習といったふうになります。次回はPythonのflaskなどを用いいてAPIにするところを書こうと思います。
- 投稿日:2020-07-27T17:21:18+09:00
PyAutoGUIでリモートワークサボり隊
本日の困りごと
リモートワーク中、ベッドでゴロゴロしてると会社のパソコンが一定時間でスクリーンセーバーかかってSkypeとかも退席中になるやん?なんか定期的にマウス動かすとかでなんとかできひんのかな(原文ママ)
経緯
元クライアントとLINE(仕事しろ)。
折角のリモートで仕事サボっててもバレないのに、厄介なのが「離席中」表示とスクリーンセーバーだという。
私の困りごとは「まさかLINEで元クライアントからそんな相談受けると思わなかった」コトです。ほんと、LINEのトーク画面貼り付けようか迷いました。ぱ「なんか売ってるじゃないですか」
客「会社PCにそんなの入れられないでしょうが」
ぱ「えー。じゃあ…そのPCってRPA検証用とかでPython入ってませんでした?」
客「おー!よく知ってるね!」…というわけでPythonで解決させた話です(仕事しろ)。
環境
OS:Windows10
Python3.X今回の解決方法
以下のようなサンプルコードをお渡ししました。
ここではsample.pyというファイルとしておきましょう。import pyautogui as pg import time try: while True: time.sleep(180) pg.moveTo(100, 100, 0.5) pg.moveTo(100, 200, 0.5) pg.moveTo(200, 200, 0.5) pg.moveTo(200, 100, 0.5) except KeyboardInterrupt: print('仕事しよ')あとはコマンドプロンプトを起動してPythonを実行するだけ。
python sample.pyさて。簡単にコードの解説をしておきます。
メインの処理はこの5行。time.sleep(180) pg.moveTo(100, 100, 0.5) pg.moveTo(100, 200, 0.5) pg.moveTo(200, 200, 0.5) pg.moveTo(200, 100, 0.5)「180秒おきにマウスをぐるっと一周まわす」ということをさせています。
time.sleepは「○秒処理を停止させる」関数です。
利用している端末のスリープまでの時間に合わせてカッコ内の秒数を調整しましょう。
(スリープまでの時間より少し短めに設定しています)
pg.moveToはマウスを指定した座標へ動かす処理。サンプルでは0.5秒かけて動かしています。このメイン処理を
while True:と書くことで、永久ループさせています。
一度実行した後は、ずっとこの処理を走らせておくという悪の所業です。
…とはいえ、Skypeに応答しないといけない時だったり、「やっぱり仕事しようかなー」と思うこともあるはずですし、何より業務終了後はパソコンをシャットダウンしないといけないことでしょう。
なので、この永久ループを以下のコードで囲っています。try: ## (中略) ## except KeyboardInterrupt:
try/exceptの例外処理を利用し、[Ctrl]+[c]のキーボード入力をキャッチして永久ループを抜けるようにしています。
仕事に戻りたい処理を終了させたい時は[Ctrl]+[c]を押す…というわけです。参考文献
退屈なことはPythonにやらせよう ―ノンプログラマーにもできる自動化処理プログラミング
moveTo周りは以下のオライリー本のサンプルコードを利用しています。18章辺りをご覧ください。
- 投稿日:2020-07-27T15:06:11+09:00
枠など全て消して、背景が透明なグラフを作成
枠など全て消して、背景が透明なグラフを作成
PowerPointとかで、グラフを張り付けるとき枠とか軸が要らない時、
色々表示しないように設定が必要。忘れそうなのでメモ。波形をグラフ化して、PNGファイルで保存する。
透明部分が結構広いのが玉の傷。個々も削れるのだろうか。import soundfile as sf import matplotlib.pyplot as plt # 波形読み込み a1,fs=sf.read("a1.wav") b1,fs=sf.read("b1.wav") c1,fs=sf.read("c1.wav") n1,fs=sf.read("n1.wav") settings = [ """ (a1, "g_a1.png", "#808080"), (b1, "g_b1.png", "#4d4d4d"), (c1, "g_c1.png", "#b2b2b2"), (n1, "g_n1.png", "#dddddd"), """ (a1, "c_a1.png", "#FBBF9C"), (b1, "c_b1.png", "#ff9999"), (c1, "c_c1.png", "#B8B400"), (n1, "c_n1.png", "darkgrey"), ] for value, name, color in settings: fig, ax = plt.subplots() fig.patch.set_alpha(0) ax.patch.set_alpha(0) ax.plot(value, c=color) plt.ylim(-0.8, 0.8) plt.tick_params(labelbottom=False, labelleft=False, labelright=False, labeltop=False, bottom=False, left=False, right=False, top=False) plt.gca().spines['right'].set_visible(False) plt.gca().spines['top'].set_visible(False) plt.gca().spines['left'].set_visible(False) plt.gca().spines['bottom'].set_visible(False) fig.savefig(name, transparent=True)
- 投稿日:2020-07-27T14:55:05+09:00
SPSS ModelerのフラグノードをPythonで書き換える。購入商品カテゴリのフラグ化
SPSS Modelerでカテゴリデータをフラグとして集計して横持ちデータに変換したり、ダミー変数化するフラグノードをPythonのpandasで書き換えてみます。
0.加工のイメージ
以下のID付POSデータから以下の3パターンの加工を行ってみます。
■加工前
誰(CUSTID)がいつ(SDATE)何(PRODUCTID、L_CLASS商品大分類、M_CLASS商品中分類)をいくら(SUBTOTAL)購入したかが記録されたID付POSデータを使います。①各顧客毎に商品カテゴリ(M_CLASS)ごとの購入ありなしのフラグ化
②各顧客毎に商品カテゴリ(M_CLASS)ごとの購回数を集計
③商品カテゴリ(M_CLASS)をつかったモデルを作成するためにダミー変数化1-1.①各顧客毎に商品カテゴリごとの購入ありなしのフラグ化。Modeler版
■加工後イメージ
顧客毎(CUSTID)に商品中分類(M_CLASS)ごとの購入があったかどうかをフラグ化します。一行目をみるとCUSTID=100001はBAG01,COSMETIC02と03,SHOES01と02と03を購入したことがわかります。
フラグノードは、データ型ノードとの組合せで使われます。
まずデータ型ノードで商品中分類(M_CLASS)にどんなカテゴリ値があるかを認識します。データ型ノードで「値の読み込み」を行うと、自動で中分類のすべてのカテゴリが認識されます。
次にフラグノードでフラグ化させたいフィールドの値を選びます。以下の例では商品中分類(M_CLASS)にはBAG01,BAG02,BAG03,COMETICS01,COSMETIC02,COSMETIC03,
SHOES01,SHOES02,SHOES03があり、これらを列として展開して、購入があれば1(真の値)、なければ0(偽の値)を入れます。集計キーにCUSTIDを選ぶことで、CUSTIDで一意のレコードに集約されます。この設定の結果をプレビューすると下のようになります。顧客毎(CUSTID)に商品中分類(M_CLASS)ごとの購入があったかどうかをフラグ化できました。
フラグ化はアソシエーション分析の前処理でよく使われます。
aprioriモデルなどをつかって、以下のようなBAG03、COSMETIC02,COSMETIC03を買っている人はSHOES03も買うといったルールを発見できます。1-2.①各顧客毎に商品カテゴリごとの購入ありなしのフラグ化。pandas版
pandasでフラグ化する場合はget_dummies関数を使います。最初からget_dummiesを使っても、指定したデータに入っているカテゴリ値をすべて自動判定してフラグ化することができて便利なのですが、テストデータやスコアリングデータには学習データに存在するカテゴリが含まれていない可能性があるため、あらかじめカテゴリ値を定義することが推奨されます。
- 参考
- python】機械学習でpandas.get_dummiesを使ってはいけない - 静かなる名辞
https://www.haya-programming.com/entry/2019/08/17/184527以下のようにM_CLASSに含まれるカテゴリのユニーク値でカテゴリを定義します。
M_CLASS_list=df1['M_CLASS'].unique() df1["M_CLASS"] = pd.Categorical(df1["M_CLASS"], categories=M_CLASS_list) df1["M_CLASS"].cat.categoriesBAG01,BAG02,BAG03,COMETICS01,COSMETIC02,COSMETIC03,
SHOES01,SHOES02,SHOES03が定義されます。そして、get_dummiesで0,1のフラグにします。
まず、df1[['CUSTID','M_CLASS']]でCUSTIDとM_CLASSに絞り込んだdataframeを与えます。そうしない場合はSDATE
などの集計に使わない他の列もついてきてしまいますので集計の際に厄介です。
columnsでフラグ化する列であるM_CLASSを指定します。
prefixで列名の接頭辞を指定しています。
.groupby('CUSTID').max()で、CUSTIDで一意にし、maxで0,1フラグ化されたカテゴリ値の最大値を取ります。つまり買っていれば1が立ちます。df_flg1=pd.get_dummies(df1[['CUSTID','M_CLASS']], columns=["M_CLASS"], prefix="M_CLASS").groupby('CUSTID').max()これでフラグ化ができました。
CUSTID=100001はBAG01,COSMETIC02,COSMETIC03,SHOES01,SHOES02,SHOES03を購入したことがわかります。ちなみにdf1["M_CLASS"] = pd.Categorical(df1["M_CLASS"], categories=M_CLASS_list)の設定をしていない場合、対象としたdataframeに存在するカテゴリのみでフラグ化されてしまいます。
以下の例だと、カテゴリ設定していないdfの先頭5行に存在していたBAG01,COSMETIC03,SHOES02しかフラグ化されていません。カテゴリを定義したdataframeのdf1を使うと先頭の5行にはBAG01,COSMETIC03,SHOES02しかなくてもそれ以外のカテゴリもフラグ化されています。
2-1. ②各顧客毎に商品カテゴリ(M_CLASS)ごとの購回数を集計 Modeler版
先ほどは各商品カテゴリで購入の有無をフラグ化しましたが、次は何回購入したかを集計します。
■加工後イメージ
結果は以下のようになります。
一行目をみるとCUSTID=100001はBAG01を3回、,COSMETIC02を1回,COSMETIC03を2回,SHOES01を1回,SHOES02を3回,SHOES03を1回購入したことがわかります。
先ほどのデータ型ノードは流用して、フラグノードと集計ノードを使います。
フラグノードの設定は基本的には先ほどと同じですが、フラグノード内では集計を行っていません。
プレビューをすると、フラグは作られていますが、CUSTIDで集約されていません。
次の集計ノードでCUSTIDで集計しています。
ここで各フラグの列の合計を計算しています。(レコード件数は不要なのでチェックを外しています)。ちなみにここで最大値を選べば先ほどのありなしフラグと同じ結果になります。
結果がでました。先ほどのフラグよりもより顧客の特徴をあらわした変数ができています。
2-2. ②各顧客毎に商品カテゴリ(M_CLASS)ごとの購回数を集計 pandas版
pandas版での先ほどとの違いは.groupby('CUSTID').sum()で、maxdではなくsumを計算しているところです。
df_flg1=pd.get_dummies(df[['CUSTID','M_CLASS']], columns=["M_CLASS"], prefix="M_CLASS").groupby('CUSTID').sum()期待の結果が得られます。
3-1. ③商品カテゴリ(M_CLASS)をつかったモデルを作成するためにダミー変数化 Modeler版
一般的に、カテゴリ変数を機械学習にかけるためには通常はカテゴリ変数から0,1のダミー変数を作ります。しかし、Modelerの場合は多くのモデルでは、自動的にダミー変数化してモデルを作ってくれるので意識することがあまりありません。ただ、線形回帰やロジスティック回帰などのいくつかのモデルではダミー変数化が必要です。
ここではその手順を示します。
データ型ノードは流用し、フラグノードでダミー変数を作ることができます。設定としては先ほどの設定から一つフラグを外します。ここではSHOES03をはずしました。
最後の一つのダミー変数は、他のダミー変数がすべて0であることで表現できます。残してしまうとモデルが不安定になるため外す必要があります。このようにダミー変数化すると、以下のように線形回帰モデルの説明変数として入力が可能になります。
なお、1次線形回帰モデルではダミー変数化しなくても説明変数として入力が可能です。
作成後のモデルの係数を確認すると、内部的にダミー変数が作られたことがわかります。そのため1次線形回帰モデルではフラグノードは不要です。
3-2. ③商品カテゴリ(M_CLASS)をつかったモデルを作成するためにダミー変数化 pandas版
scikitlearnをはじめとしてPythonのモデル作成では原則としてカテゴリ型の変数はダミー変数化する必要があります。もともとget_dummiesはフラグ化というよりはダミー変数をつくるために用意されている関数になるため、名前もそういう名前になっています。
ダミー変数を作る場合は
drop_first=Trueを指定します。このオプションによって、ModelerでSHOES03を作らなかったように、カテゴリ数-1個のダミー変数を作ります。
また、groupbyなどの集計は不要になります。df_dummy=pd.get_dummies(df1,columns=["M_CLASS"],prefix="M_CLASS",drop_first=True)以下のようになります。Modelerとの違いが2点ありますが、ダミー変数作成という意味では気にする必要はありません。
1.DROPされたダミー変数はSHOES03ではなくBAG01になっています。
2.M_CLASSの列自体はなくなっています。4. サンプル
サンプルは以下に置きました。
ストリーム
https://github.com/hkwd/200611Modeler2Python/blob/master/flag/flag.str?raw=true
notebook
https://github.com/hkwd/200611Modeler2Python/blob/master/flag/flag.ipynb
データ
https://raw.githubusercontent.com/hkwd/200611Modeler2Python/master/data/sampletranDEPT4en2019S.csv■テスト環境
Modeler 18.2.1
Windows 10 64bit
Python 3.6.9
pandas 0.24.15. 参考情報
pandas.get_dummies — pandas 1.0.5 documentation
https://pandas.pydata.org/pandas-docs/stable/reference/api/pandas.get_dummies.html
- 投稿日:2020-07-27T14:53:29+09:00
SPSS Modelerの基本ノードをPythonで書き換える。
SPSS Modelerの基本ノードをPythonで書き換えます。
1.はじめに
本稿で扱うノード
- 条件抽出ノード
- ソートノード
使用データ
以下のようなID付きPOSデータを使用します。
- Who: CUSTID
- When: SDATE
- What: PRODUCTID, L_CLASS, M_CLASS
- How much: SUBTOTAL2.SPSS Modelerのストリーム
サンプルデータから2019年4Qのデータのみを抽出します。
2-1.ノードの準備、データの確認
CSVファイルから直接接続されているテーブルノードを実行して、データを確認します。
- 結果
2-2.条件抽出ノード
2-1で確認したデータから、SDATEが2019年4期(2019/10/1-2019/12/31)のデータを抽出します。
ストリーム全体像の該当箇所は赤枠で囲った部分です。
ノードを配置した後、該当のノードを右クリックして編集を選択し、設定タブの条件に抽出条件を記載します。
上記設定後、条件抽出ノードから接続されているテーブルノードを実行します。
- 結果
SDATEに表示される日付が指定の日付の範囲内のものに絞られました。
2-3.ソートノード
2-3-1.単列指定
2-2で抽出した2019年4期のデータをSUBTOTALの大きい順(降順)に並べ替えます。
ソートノードを右クリックして編集を選択し、フィールドを"SUBTOTAL"、順序を"降順"に設定します。
ソートノードの後にあるテーブルノードを実行します。
SUBTOTALが降順に並びました。
上位3データは大きい順に216000,174000,122000です。2-3-2.複数列指定
2-2で抽出した2019年4期のデータをSDATEの小さい順(昇順)にした後、SUBTOTALの大きい順(降順)に並べ替えます。
ソートノードを右クリックして編集を選択し、フィールド選択の画面で"SUBTOTAL"と"SDATE"を選択します。適用したら、"SDATE"は順序を"昇順"、"SUBTOTAL"は順序を"降順"に設定します。
ソートノードの後にあるテーブルノードを実行します。
SDATEの昇順、SUBTOTALの降順にデータが並びました。
2019年10月1日のSUBTOTAL上位3位は52920,35520,29231です。3.pythonでの同処理の記述方法
3-1. データの確認
まずはcsvを取り込んだ状態でデータを見てみます。
- pandasを使用してcsvを読み込むコード
import pandas as pd sample_df = pd.read_csv('sampletranDEPT4en2019S.csv')
- 結果
2019年の1年分の範囲のデータがあることが確認できました。
3-2. 条件抽出
pandasではquery()で文字列として条件を記載することができます。
- 条件抽出コード
sample4q_df = sample_df.query('"2019-10-01" <= SDATE <= "2019-12-31"') sample4q_df.head(10)
- 結果
3-3. ソート
レコードをソートする方法は複数ありますが、ここではpandasのsort_values()を使用したソート方法を記載します。
3-3-1. 単列ソート
- ソートコード
sample4q_top10_df = sample4q_df.sort_values('SUBTOTAL', ascending=False) sample4q_df.head(10)sort_values(ソートしたいカラム名, ascending=[True:昇順, False:降順])というように使用します。
- 結果
SUBTOTALが降順に並び、数値が大きい上位10番目までのレコードが出力できました。
上位3データは大きい順に216000,174000,122000です。
SPSSでの処理とPythonでの処理の結果が一致しました。3-3-2. 複数列ソート
- ソートコード
sample4q_multisort_top10_df = sample4q_df.sort_values(['SDATE', 'SUBTOTAL'], ascending=[True, False]) sample4q_multisort_top10_df.head(10)sort_values([ソートしたいカラム名1, ソートしたいカラム名2], ascending=[カラム1のソート方法, カラム2のソート方法])というように記述します。
SDATEの昇順、SUBTOTALの降順にデータが並びました。
2019年10月1日のSUBTOTAL上位3位は52920,35520,29231です。
SPSSでの処理とPythonでの処理の結果が一致しました。4. まとめ
条件抽出ノードの書き換えはquery() で条件を記載することで簡単にpythonでの書き換えができました。
一方で、sort_values()を利用したソートノードの書き換えは、1つの列を指定してソートする際にはさほど不便を感じませんでしたが、複数列を指定してソートする際はカラムの指定とソート方法の指定を別のリストでカラム順に記載しなければならず、わかりづらいと感じます。5. 本稿で使用したデータ
6. テスト環境
Modeler 18.2.1
MacBook Air 10.14.6
Python3.6.1
- 投稿日:2020-07-27T14:45:30+09:00
【Python初心者】Classの使い方とは?5stepsで理解しよう!(_init_、self)
結論
class クラス名(): #クラス名 def メソッド名(self): #メソッド名 実行したい処理 #実行したい処理 インスタンス名 = クラス名() #呼び出す各論
classの定義
class クラス名():↓
classの使い方
class クラス名(): 実行したい処理classを使うためには、インスタンス化する必要がある。
これにより、classを呼び出すことができる。
(実行したい処理に関しては、「メソッドの定義」で説明する)↓
インスタンス化
class クラス名(): 実行したい処理 インスタンス名 = クラス名() #インスタンス生成実行したい処理には、「メソッド」を使用することができる。
↓
メソッドの定義
class クラス名(): def メソッド名(self): #メソッドの定義 インスタンス名 = クラス名()メソッド名(self)の()の中には、必ず1つ以上の引数を渡す。その際、最初の引数はselfにする。
classの呼び出し方
インスタンス名.メソッド名()結論
class クラス名(): #クラス名 def メソッド名(self): #メソッド名 実行したい処理 #実行したい処理 インスタンス名 = クラス名() #インスタンス名 インスタンス名.メソッド名() #呼び出す具体例
class message(): #クラス名=message def hello (self): #メソッド名=hello print("Hello!") #実行したい処理=「Hello!」を出力 mess = message() #インスタンス名=mess mess.hello() #インスタンス生成
- 投稿日:2020-07-27T14:45:30+09:00
【Python初心者】classの使い方とは?5stepsで理解しよう!(メソッドとインスタンス)
今回目指すアウトプット
結論
・クラス
・メソッド
・インスタンス
の3つを定義する。結論class クラス名(): #クラス名をつける def メソッド名(self): #メソッド名をつける 実行したい処理 #実行したい処理 インスタンス名 = クラス名() #インスタンス名をつける インスタンス名.メソッド名() #呼び出す各論
classの定義(step1)
step1class クラス名(): # <--- これをまず覚える↓
classの使い方(step2)
step2class クラス名(): 実行したい処理 # <--- ここに処理をかくclassを使うためには、インスタンス化する必要がある。
これにより、classを呼び出すことができる。
(実行したい処理に関しては、「メソッドの定義」で説明する)↓
インスタンス化(step3)
step3class クラス名(): 実行したい処理 インスタンス名 = クラス名() # <--- インスタンス化して呼び出せるようにする実行したい処理には、「メソッド」を使用することができる。
↓
メソッドの定義(step4)
step4class クラス名(): def メソッド名(self): #メソッドの定義(実行したい処理を関数化) インスタンス名 = クラス名()メソッド名(self)の()の中には、必ず1つ以上の引数を渡す。その際、最初の引数はselfにする。
classの呼び出し方(step5)
step5インスタンス名.メソッド名()# <--- これで呼び出す結論
結論class クラス名(): #クラス名 def メソッド名(self): #メソッド名 実行したい処理 #実行したい処理 インスタンス名 = クラス名() #インスタンス名 インスタンス名.メソッド名() #呼び出す具体例
例1class message(): #クラス名=message def hello(self): #メソッド名=hello print("Hello!") #実行したい処理=「Hello!」を出力 mess = message() #インスタンス名=mess mess.hello() #呼び出す例2class mypetinfo: # <--- mypetinfoというclassを作成 family = '犬' # <---ここから下は関数 def say(self): print('ワン') def growl(self): print('ウー') PI = mypetinfo() # <---インスタンス化して呼び出せるようにする PI.family # 表示されず print(tora.family) # 犬 PI.say() # ワン PI.growl()# ウーこれができたら、次はinitを理解しよう。
- 投稿日:2020-07-27T14:42:44+09:00
RigNetをWindows10で動かしてみた
はじめに
SIGGRAPH 2020に投稿されたRigNetがGithubに公開されていたので、さっそく自宅のWindowsPCで動かしてみました!
この記事では、環境構築からquick_startをWindows上で実行するところまでの手順を記載します。
最後にオマケとしてPIFuHDで生成された.objファイルで試した結果も記載します。(私の手順が悪かったのかあまり良い感じではないですが、一応載せておきます...)RigNetのプロジェクトページはこちら
PIFuHDのプロジェクトページはこちら
以前書いた「PIFuHDをWindowsでとりあえず動かしてみた」実行環境
- Windows10 64bit Home
- Anaconda3
- RTX2080Ti
- CUDA 10.2
環境構築
基本的には、RigNetのGithubで用意していただいている手順をなぞります。
本家はUbuntuでの環境構築方法なので、少し弄って自分のPCで動くようにしております。コードのクローン
(base)$git clone https://github.com/zhan-xu/RigNet.git (base)$cd RigNet仮想環境の作成
(base)$conda create -n rignet python=3.6 (base)$conda activate rignetライブラリのインストール
自分のPCのCUDAのバージョンが本家とは異なるため、pytorchのバージョンなどを変更してインストールしています。
(rignet)$pip install numpy scipy matplotlib tensorboard opencv-python open3d==0.9.0 (rignet)$pip install trimesh[easy] (rignet)$pip install torch===1.5.1 torchvision===0.6.1 -f https://download.pytorch.org/whl/torch_stable.html (rignet)$pip install --no-cache-dir torch-scatter==latest+cu102 -f https://pytorch-geometric.com/whl/torch-1.5.0.html (rignet)$pip install --no-cache-dir torch-sparse==latest+cu102 -f https://pytorch-geometric.com/whl/torch-1.5.0.html (rignet)$pip install --no-cache-dir torch-cluster==latest+cu102 -f https://pytorch-geometric.com/whl/torch-1.5.0.html (rignet)$pip install --no-cache-dir torch-spline-conv==latest+cu102 -f https://pytorch-geometric.com/whl/torch-1.5.0.html (rignet)$pip install torch-geometricbinvoxのダウンロード
こちらからbinvox.exeをダウンロードし、RigNetディレクトリ配下に格納する。
(Windows 64 bit executable をクリックすればよい。)学習済みモデルのダウンロード
READMEに記載されているリンクからtrained_models.zipをダウンロードし、RigNet配下で解凍する。
ソースコードの修正
binvoxを使うときにエラーが発生するので、quick_start.pyを以下のように修正しました。
[quick_start.py] def create_single_data(mesh_filaname): """ create input data for the network. The data is wrapped by Data structure in pytorch-geometric library :param mesh_filaname: name of the input mesh :return: wrapped data, voxelized mesh, and geodesic distance matrix of all vertices """ mesh = o3d.io.read_triangle_mesh(mesh_filaname) mesh_v = np.asarray(mesh.vertices) mesh_vn = np.asarray(mesh.vertex_normals) mesh_f = np.asarray(mesh.triangles) # vertices v = np.concatenate((mesh_v, mesh_vn), axis=1) v = torch.from_numpy(v).float() # topology edges print(" gathering topological edges.") tpl_e = get_tpl_edges(mesh_v, mesh_f).T tpl_e = torch.from_numpy(tpl_e).long() tpl_e, _ = add_self_loops(tpl_e, num_nodes=v.size(0)) # surface geodesic distance matrix print(" calculating surface geodesic matrix.") surface_geodesic = calc_surface_geodesic(mesh) # geodesic edges print(" gathering geodesic edges.") geo_e = get_geo_edges(surface_geodesic, mesh_v).T geo_e = torch.from_numpy(geo_e).long() geo_e, _ = add_self_loops(geo_e, num_nodes=v.size(0)) # batch batch = np.zeros(len(v)) batch = torch.from_numpy(batch).long() # voxel # ここを修正 # os.system("./binvox -d 88 -pb " + mesh_filaname) os.system("binvox.exe -d 88 -c " + mesh_filaname) with open(mesh_filaname.replace('.obj', '.binvox'), 'rb') as fvox: vox = binvox_rw.read_as_3d_array(fvox) data = Data(x=v[:, 3:6], pos=v[:, 0:3], tpl_edge_index=tpl_e, geo_edge_index=geo_e, batch=batch) return data, vox, surface_geodesic実行
quick_start.pyを実行する
(rignet)$python quick_start.py上記コマンドを実行すると、画面上に以下が表示されるかと思います!
加えて、RigNet/quick_start配下に新しく、17872_ori_rig.txtと17872_remesh_1.binvoxが出力されているかと思います。
ちなみに
本家様が色々サンプルを用意して下さっているので、試すのであればquick_start.pyの以下部分を弄れば他サンプルも確認できます。
# Here we provide 16 examples. For best results, we will need to override the learned bandwidth and its associated threshold # To process other input characters, please first try the learned bandwidth (0.429 in the provided model), and the default threshold 1e-5. # We also use these two default parameters for processing all test models in batch. model_id, bandwidth, threshold = 17872, 0.045, 0.75e-5 #model_id, bandwidth, threshold = 8210, 0.05, 1e-5 #model_id, bandwidth, threshold = 8330, 0.05, 0.8e-5 #model_id, bandwidth, threshold = 9477, 0.043, 2.5e-5 #model_id, bandwidth, threshold = 17364, 0.058, 0.3e-5 #model_id, bandwidth, threshold = 15930, 0.055, 0.4e-5 #model_id, bandwidth, threshold = 8333, 0.04, 2e-5 #model_id, bandwidth, threshold = 8338, 0.052, 0.9e-5 #model_id, bandwidth, threshold = 3318, 0.03, 0.92e-5 #model_id, bandwidth, threshold = 15446, 0.032, 0.58e-5 #model_id, bandwidth, threshold = 1347, 0.062, 3e-5 #model_id, bandwidth, threshold = 11814, 0.06, 0.6e-5 #model_id, bandwidth, threshold = 2982, 0.045, 0.3e-5 #model_id, bandwidth, threshold = 2586, 0.05, 0.6e-5 #model_id, bandwidth, threshold = 8184, 0.05, 0.4e-5 #model_id, bandwidth, threshold = 9000, 0.035, 0.16e-5おわりに
今回は、SIGGRAPH2020に投稿されたRigNetのサンプルをWindows上で動かしてみました。
PIFuHD同様に丁寧にREADMEが書かれているので、簡単に環境構築できて試せるかと思います。性能自体はサンプルを動かしてみるとよい感じにリグが入っていた気がします!
PIFuHDなどの簡単に3Dオブジェクトが作れるものと組み合わせれば、個人的には遊ぶ幅ができてとてもうれしいです!おまけ
以前に遊んでみたPIFuHDで作成された.objファイルでもできないかなぁと少し試してみました。
対象obj
PIFuHDのサンプルで作られる以下のファイルを今回は使いました。
(サンプル実行後の私の環境だと、pifuhd/results/pifuhd_final/recon/result_test_512.obj)
meshの削減
そのまま使おうとするとエラーが出てしまったので、MeshLabを使ってメッシュ量を減らしました。
1.ファイルのインポート
[File] -> [Import Mesh] で、result_test_512.objを読み込みます。
2.メッシュの削減
[Filters] > [Remeshing, Simplification and Reconstruction] -> [Simplification: Quadric Edge Collapse Decimation]
を実行し、今回は Target number of faces に 2000 を設定し、Applyボタンを押しました。
※この 2000 という値は私が適当に設定したものです。(サンプルのファイルサイズが大体これぐらいでした。)3.エクスポート
[File] -> [Export Mesh As...] でファイルをエクスポートします。
今回は 7777_remesh.obj というファイル名で、RigNet/quick_start配下にエクスポートしました。コードの修正
quick_start.pyを以下2か所を修正する。
[quick_start.py] ... # Here we provide 16 examples. For best results, we will need to override the learned bandwidth and its associated threshold # To process other input characters, please first try the learned bandwidth (0.429 in the provided model), and the default threshold 1e-5. # We also use these two default parameters for processing all test models in batch. # ここを修正 model_id, bandwidth, threshold = 7777, 0.066, 2.5e-5 #model_id, bandwidth, threshold = 17872, 0.045, 0.75e-5 #model_id, bandwidth, threshold = 8210, 0.05, 1e-5 #model_id, bandwidth, threshold = 8330, 0.05, 0.8e-5 #model_id, bandwidth, threshold = 9477, 0.043, 2.5e-5 #model_id, bandwidth, threshold = 17364, 0.058, 0.3e-5 #model_id, bandwidth, threshold = 15930, 0.055, 0.4e-5 #model_id, bandwidth, threshold = 8333, 0.04, 2e-5 #model_id, bandwidth, threshold = 8338, 0.052, 0.9e-5 #model_id, bandwidth, threshold = 3318, 0.03, 0.92e-5 #model_id, bandwidth, threshold = 15446, 0.032, 0.58e-5 #model_id, bandwidth, threshold = 1347, 0.062, 3e-5 #model_id, bandwidth, threshold = 11814, 0.06, 0.6e-5 #model_id, bandwidth, threshold = 2982, 0.045, 0.3e-5 #model_id, bandwidth, threshold = 2586, 0.05, 0.6e-5 #model_id, bandwidth, threshold = 8184, 0.05, 0.4e-5 #model_id, bandwidth, threshold = 9000, 0.035, 0.16e-5 # create data used for inferece print("creating data for model ID {:d}".format(model_id)) mesh_filename = os.path.join(input_folder, '{:d}_remesh.obj'.format(model_id)) data, vox, surface_geodesic = create_single_data(mesh_filename) data.to(device) print("predicting joints") data = predict_joints(data, vox, jointNet, threshold, bandwidth=bandwidth, mesh_filename=mesh_filename) data.to(device) print("predicting connectivity") pred_skeleton = predict_skeleton(data, vox, rootNet, boneNet, mesh_filename=mesh_filename) print("predicting skinning") pred_rig = predict_skinning(data, pred_skeleton, skinNet, surface_geodesic, mesh_filename) print("Saving result") # ここを修正 if False: # here we use original mesh tesselation (without remeshing) mesh_filename_ori = os.path.join(input_folder, '{:d}_ori.obj'.format(model_id)) pred_rig = tranfer_to_ori_mesh(mesh_filename_ori, mesh_filename, pred_rig) pred_rig.save(mesh_filename_ori.replace('.obj', '_rig.txt')) else: # here we use remeshed mesh pred_rig.save(mesh_filename.replace('.obj', '_rig.txt')) print("Done!")実行
(rignet)$python quick_start.py加えて、RigNet/quick_start配下に新しく、7777_remesh_rig.txtと7777_remesh_1.binvoxが出力されているかと思います。
感想
コード中にも記載があるように、閾値などのパラメータを変えることが必要だと思います。
今回は良いパラメータを見つけられなかったのと、私の知識不足が原因でどこかの手順で悪いことしてしまったことから、上画像のような結果になったと思われます...。RigNetのサンプルにあるようなポーズの画像からPIFuHDで3Dモデルを作ってやればうまくいくのかしら...
- 投稿日:2020-07-27T14:37:35+09:00
cgitbのHTML出力前にContent-Typeを送信する
環境
- python2.7
- Apache2.4
問題点
cgitbではHTMLの一行目に<!--: spamが出力されるため、Content-Typeを送信していないとApache側でエラーが発生してしまう。AH02429: Response header name '<!--' contains invalid characters, aborting request
方法
cgitbのHTML出力前にContent-typeを出力する。from __future__ import absolute_import, print_function, unicode_literals import sys import cgitb def my_except_hook(exctype, value, traceback): print('Content-Type: text/html') print('') hook = cgitb.Hook() hook(exctype, value, traceback) sys.__excepthook__(exctype, value, traceback) sys.excepthook = my_except_hook
- 投稿日:2020-07-27T14:07:20+09:00
【Vue.js, Express, Python】HTMLからテキストとWordファイルを自動生成する
課題、目的
今まで毎週Wordで書いてきたレポートを、最後に一つのWordファイルにまとめて提出する、という謎の課題が期末に出された。
しかし私は、Wordファイルが増えるのが嫌なので、Wordファイルで作成したレポートを、はてなブログにまとめて保存していた。
はてなブログからWordにコピペしようとしたのだが、Wordファイルの表示がaタグなどがじゃまできれいにならない。
これらを手作業で直すのはあまりに億劫である。
そこで、HTMLファイルをテキストに変換すればうまくいきそう、と思い、変換サイトを見つけたが、せっかくなので自分で作ってみることにした。
ついでに、勉強と経験のために変換されたテキストを元にWordファイルを自動生成することにした。文章が長すぎると404エラーになったり、他にもまだバグがあるかもしれないが、コードの整理をする前に頭の整理をするため、記事を書いていく。
完成形
https://github.com/wafuwafu13/Word-Creater
1 デザイン
2 HTML => TEXT 変換
3 TEXT保存
4 Wordファイル作成
実装
1 デザイン
Vuetifyを用いた。
2 HTML => TEXT 変換
JavaScriptでHTMLタグを削除する正規表現 を実装した。
3 TEXT保存
保存すべきカラムは、名前(name)とテキスト(text)である。
axiosを使ってVueからExpressにクエリパラメータとして両者を送信し、ExpressからMySQLに保存することにした。
Node.jsでMySQLに接続する方法は
Node.jsアプリケーションとMySQLを接続しよう!
を参考にした。
公式はこれ。
https://github.com/mysqljs/mysqlApp.vueclickSaveBtn () { console.log('pushed save button') this.saveDialog = false axios .get('http://localhost:3000/' + this.saveFilename + '/' + this.text) .then(res => console.log(res)) .catch(error => { console.log('error occurs in axios ' + error) }) },server.jsapp.get('/:name/:text', (req, res) => { console.log('from frontend params: name => ' + req.params.name) console.log('from frontend params: text => ' + req.params.text) connection.query({ sql: 'INSERT INTO documents (name, text) values (?, ?)', values: [req.params.name, req.params.text] }, (error, results) => { console.log('↓ results from db') console.log(results) }) })4 Wordファイル作成
まずは、MySQLにある名前(name)のデータを選択肢としてブラウザに表示させる。
この記事が参考になった。
Nuxt.jsとmysqlを連携してデータを表示してみたApp.vueclickCreateBtn () { console.log('pushed create button') axios .get('http://localhost:3000/filenames') .then(res => { console.log('↓response from server') console.log(res.data) for (let i = 0; i < res.data.length; i++) { this.filenames.push(res.data[i].name) } }) .catch(error => { console.log('error occurs in axions ' + error) }) },server.jsapp.get('/filenames', (req, res) => { let filenames = [] connection.query('SELECT name from documents', (error, row, fields) => { if (error) { console.log('error occured in db: '+ error) } let files = [] for (let i = 0; i < row.length; i++) { files.push(row[i]) } filenames = JSON.stringify(files) res.header('Content-Type', 'application/json; charset=utf-8') res.send(filenames) }) })なお、Node.js側でCORSポリシーを無効にしなければならないので注意。
server.jsapp.use(function(req, res, next) { res.header("Access-Control-Allow-Origin", "*"); res.header("Access-Control-Allow-Headers", "Origin, X-Requested-With, Content-Type, Accept"); next(); });最後に、選択された名前のファイルを元に、そのファイル名とテキストをDBから取り出してWordファイルを作成していく。
PythonとMySQLを連携させるのにはmysqlclientを用いた。
この記事が参考になった。
Python3でMySQLを使う – 基本操作からエラー処理まで
公式はこれ。
https://pypi.org/project/mysqlclient/Node.jsとPythonを連携させるのにはPython-shellを用いた。
この記事が参考になった。
Python-shellの使い方
公式はこれ。
https://www.npmjs.com/package/python-shellPythonからWordファイルを作成する方法はこの記事が参考になった。
【python-docx】PythonでWordを操作するApp.vueclickStartCreateBtn () { this.createDialog = false axios .get('http://localhost:3000/word/' + this.createFilename) .then(res => console.log(res)) .catch(error => { console.log('error occurs in axios ' + error) }) }server.jsapp.get('/word/:filename', (req, res) => { let filename = req.params.filename console.log('from frontend params: filename => ' + filename) let { PythonShell } = require('python-shell') let pyshell = new PythonShell('createWord.py') pyshell.send(filename) pyshell.on('message', function (data) { console.log(data); }); })createWord.pyfilename = sys.stdin.readline() print('filename =>', filename.strip()) con = MySQLdb.connect( host = os.environ.get("DB_HOST"), user = os.environ.get("DB_USER"), passwd = os.environ.get("DB_PASSWORD"), db = os.environ.get("DB_NAME"), ) cur = con.cursor() sql = "select text from documents where name = %s" cur.execute(sql, (filename.strip(),)) rows = cur.fetchall() document = Document() print('text =>', rows[0][0]) text = rows[0][0] document.add_paragraph(text) document.save(filename.strip()+'.docx') print('success')まとめ
役に立つものを作りたいわけじゃなかったので、Python-shellに出会えただけで大きな収穫だった。
応用が効きそうなので気が向いたら色々試していきたい。