20210227のPythonに関する記事は30件です。

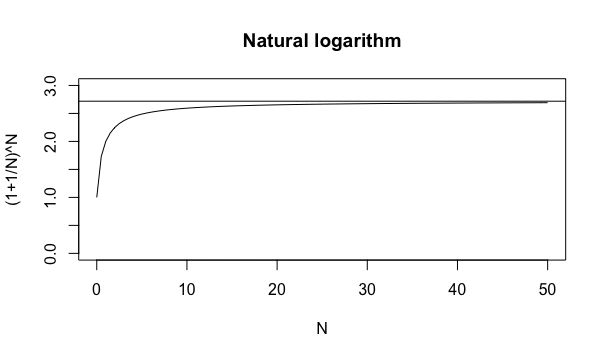
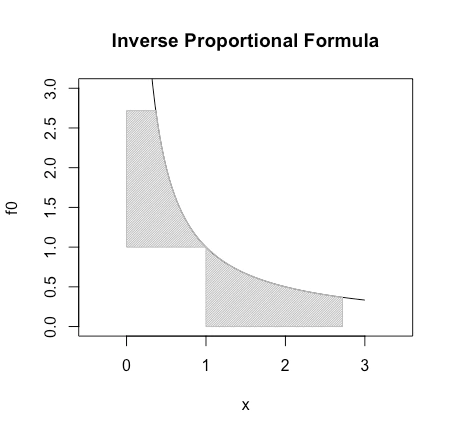
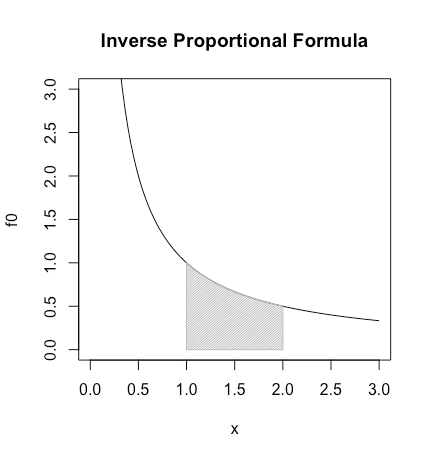
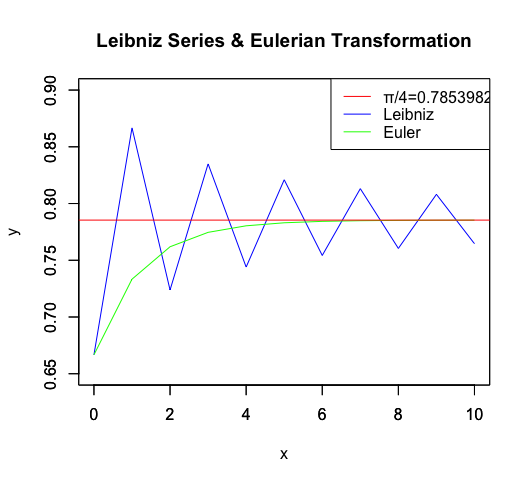
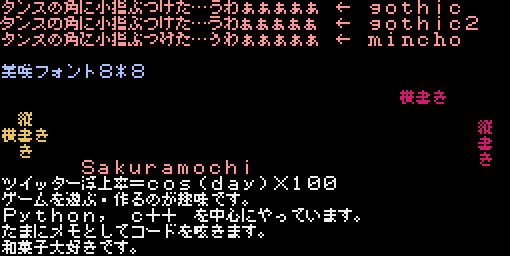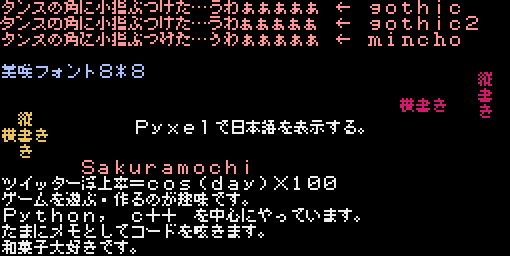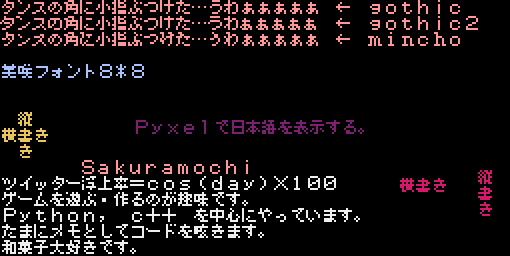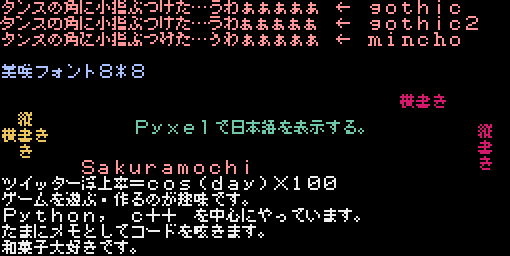
投稿日：2021-02-27T23:53:34+09:00

本番環境などを想定した際のDjangoプロジェクトのTips

pythonのwebフレームワークであるDjango

プロジェクト自体は、django-admin startproject <project-name>で始められる。
プロジェクトをローンチして、書き始めてもいいんですが、本番環境を見据えて予め色々やった方がいいことをまとめて行こうと思います。
現在、Djangoを本番環境に移行している最中で、最初からこうしておけばよかった...と思うのでツラツラと書き連ねて行こうと思います。

プロジェクト全体の構想をある程度練って、それぞれのapplicationを大きくしすぎない（サーバーサイドのコードが増大しすぎてみづらい。）

本番環境用と開発環境用でsettings.pyを切り分ける

.envを最初から作っておく。

docker上で開発する。(デプロイする時に面倒にならないために)

test.pyを有効に使っていく（障害予防）

templatesのBASE_DIRは、applicationごとに管理（プロジェクト全体一つの所に格納すると管理が面倒）

TemplateViewを積極的に活用（サーバーサイドのコードをブサイクにしない）

とりあえず、思いつく限り書きました。今後また思うところがあれば改善していきます。
ぜひ、コメントください。

最終更新日

2021/2/27

　 Tweet
Qiitaで続きを読む

投稿日：2021-02-27T23:29:05+09:00

Abc193参加記録

今回から気が向いたらAbcの記事とか書いてみようかと思います。
Abc193は4完でした。4完でも青パフォがでたのでいつもより難しかった気がします。

Abc193 C - Unexpressed

全探索の問題です。$ a^b $で表せる数の方を探索します。

例えば$ a=2 $のとき$ 1\leq a^b \leq N $となる$ b $の個数は精々$ O(\mathrm{log}N) $です。
また$ a,b $ は$2$以上の整数なので$ 2\leq a \leq \lfloor\sqrt{N}\rfloor $を探索すればよい形になります。
$\sqrt{10^{10}}=10^5$なので十分間に合います。

気を付けるべきは$ a $について全部探索してしまうと$ 2^4=4^2 $みたいなものが重複してしまうことですが、この量であればsetを使って既出かどうかをチェックしても問題ありません。

（反射的にm * m > nチェック入れたけど今回要らなかったかな）
n = int(input())
m = int(n ** 0.5)
if m * m > n:
    m -= 1

diff = 0
s = set()
for a in range(2, m+1):
    x = a * a
    while x <= n:
        if not x in s:
            diff += 1
            s.add(x)
        x *= a
print(n-diff)
Abc193 D - Poker

一見難しそうですが、実は場合分けに注意すれば愚直に全ケースを調べても間に合う問題です。
最後のカードの組み合わせは最悪でも精々9×9通りで、各々について愚直に点数を計算しても9x9x9のループで済んでしまいます。

高橋君に配られた最後のカードが1,2,3,...,9の場合
青木君に配られた最後のカードが1,2,3,...,9の場合
を調べるのだけれども、注意するべき点は

高橋君に i のカードを配れない場合

青木君に i のカードを配れない場合

高橋君に i のカードを配ったせいで青木君に i のカードが配れない場合

高橋君と青木君に異なるカード i, j を配った場合

高橋君と青木君に同じカード i を配った場合

です。
これをチェックするために事前に「全体で各カード何枚配ったか」「高橋君には各カード何枚配ったか」「青木君には各カード何枚配ったか」を記録しておきます。

1～3.の場合は配れないので計算に含めないようにします。
4. の場合の数は単純に$$ (iの残り枚数)\times(jの残り枚数) $$
5. の場合の数は$$ (iの残り枚数)\times(iの残り枚数-1) $$です。

あとは配った結果の点数を計算して高橋君の方が高い場合のみを加算して、伏せられたカードとしてあり得るすべてのカードの組み合わせで割ってあげれば答えが出ます。
k = int(input())
s = input()
t = input()

count = [0] * 10
count_a = [0] * 10
count_b = [0] * 10
for i in range(4):
    x, y = int(s[i]), int(t[i])
    count[x] += 1
    count[y] += 1
    count_a[x] += 1
    count_b[y] += 1

power10 = [1] * 6
for i in range(1, 6):
    power10[i] = power10[i-1] * 10

ans = 0
div = (9 * k - 8) * (9 * k - 9)
for i in range(1, 10):
    if count[i] + 1 > k:
        continue
    num_i = k - count[i]
    for j in range(1, 10):
        num_j = k - count[j]
        if i == j:
            if count[i] + 2 > k:
                continue
            num_j -= 1
        elif count[j] + 1 > k:
            continue
        score_a = 0
        score_b = 0
        for l in range(1, 10):
            score_a += l * power10[count_a[l] + 1] if l == i else l * power10[count_a[l]]
            score_b += l * power10[count_b[l] + 1] if l == j else l * power10[count_b[l]]
        if score_a > score_b:
            ans += num_i * num_j
print(ans / div)
Abc193 E - Oversleeping

$y, q$について走査すれば拡張ユークリッドの互除法で行けそうな気がしましたが、負の値に対応できず解けませんでした。

$ 2n(X+Y)+X≤t<2n(X+Y)+X+Y $

$ m(P+Q)+P≤t<m(P+Q)+P+Q $

が条件なので、求める答えは$ t=2n(X+Y)+X $もしくは$ t=m(P+Q)+P $を満たしているはずです（ピンと来なければ直線の図を書いてみる）

前者の場合は$$ t=2n(X+Y)+X=m(P+Q)+D $$として$D$を$[P, P+Q)$の区間で走査して拡張ユークリッドの互除法。
後者の場合は$$ t=2n(X+Y)+D=m(P+Q)+P $$として$D$を$[X, X+Y)$の区間で走査して拡張ユークリッドの互除法。
ここまで来たものの負の値に対処できず挫折しました。

拡張ユークリッドの互除法とCRTについては復習したいと思います。
走査しないでも行けるらしいです。

　 Tweet
Qiitaで続きを読む

投稿日：2021-02-27T23:27:33+09:00

キャディプログラミングコンテスト2021(AtCoder Beginner Contest 193) 参戦記

ABC193A - Discount

2分で突破. 書くだけ.

A, B = map(int, input().split())

print(100 - (B / A) * 100)

ABC193B - Play Snuke

3分半で突破. 各店舗ごとに売り切れ前にたどり着けるか判定し、売り切れ前にたどり着けた中で一番安いのを出力するだけ.

INF = 10 ** 18

N = int(input())

result = INF
for _ in range(N):
    A, P, X = map(int, input().split())
    if X - A > 0:
        result = min(result, P)
if result == INF:
    print(-1)
else:
    print(result)

ABC193C - Unexpressed

8分で突破. 入出力例2でa^bで表せるものが少ないことが分かるので、全列挙すればいいなと思いました. 最低2乗なので、Nの二乗根まで回せば OK で計算量的にも問題なし.

N = int(input())

s = set()
for i in range(2, int(N ** 0.5) + 1):
    for j in range(2, N + 1):
        t = i ** j
        if t > N:
            break
        s.add(t)
print(N - len(s))

ABC193D - Poker

18分半で突破. 81パターンしかないので、何も難しいことはなく、全部計算すれば OK.

def f(cards):
    c = {}
    for i in range(1, 10):
        c[i] = 0
    for i in cards:
        c[i] += 1
    result = 0
    for k in c:
        result += k * pow(10, c[k])
    return result


K = int(input())
S = input()
T = input()

all = {}
for i in range(1, 10):
    all[i] = K

s = list(map(int, S[:4]))
t = list(map(int, T[:4]))

for i in s:
    all[i] -= 1
for i in t:
    all[i] -= 1

x = 9 * K - 8

result = 0
for i in range(1, 10):
    if all[i] == 0:
        continue
    a = all[i] / x
    all[i] -= 1
    k = f(s + [i])
    for j in range(1, 10):
        if all[j] == 0:
            continue
        b = all[j] / (x - 1)
        l = f(t + [j])
        if k > l:
            result += a * b
    all[i] += 1
print(result)

　 Tweet
Qiitaで続きを読む

投稿日：2021-02-27T23:16:41+09:00

Python+OpenCVでイラスト塗り絵化プログラムの作成

はじめに

塗り絵をやりたくなったが、塗り絵を買いにいくのがめんどくさかったので、自分で作ってみた。
画像処理はopencvを利用した。
色鉛筆は100均に買いに行った。

完成物

元画像

塗り絵化

準備

opencvのインストール

コマンドラインに下記コマンドを入力
pip install opencv-python

塗り絵化アルゴリズム

画像入力

グレースケール化

膨張処理

２と３の差分取得

白黒反転

目的としては、画像のエッジを取得したいだけなので、エッジ抽出フィルタとかを使ってもできるかもしれない。
有名所で言えば、ソーベルフィルタ・ラプラシアンフィルタ・キャニーフィルタなど。
試していないから、気が向いたら今度やってみてもいいかも。

今回は、エッジが強く出過ぎるのを避けるために、エッジフィルタは利用しなかった。
画像を少し膨張させて、元の画像と差分を取ることで、エッジを抽出した。
差分を取ると、エッジが白・ベタ塗りが黒、で出力されるので、最後に白黒反転させて完成。

実際利用したコード
toNurie.py
import numpy as np
import cv2

#1. 画像入力
#2. グレースケール化(グレースケールで入力)
img = cv2.imread('Free.jpg', cv2.IMREAD_GRAYSCALE)

#3. 膨張処理
neiborhood = np.ones((5, 5), dtype=np.uint8)
dilated = cv2.dilate(img, neiborhood24, iterations=1)

#4. ２と３の差分取得
diff = cv2.absdiff(dilated, img)

#5. 白黒反転
result = 255 - diff

#画像出力
cv2.imwrite('output.jpg', result)
終わりに

好きなアニメシーンの塗り絵ができちゃう！

　 Tweet
Qiitaで続きを読む

投稿日：2021-02-27T22:56:48+09:00

PythonからGPUデバイスが使用可能かチェックする

TL;DR

Pythonの処理からデバイス番号を指定して，指定したGPUが使えるかどうかをチェックする方法です．
ここで使えるとは，デバイスが存在することを指します．

GPUデバイスが使用可能かチェックする

NVIDIAからライブラリ等が提供されているわけではないので，nvidia-smiコマンドを叩いた結果から確認します．
（ライブラリがあった場合はご教授お願い致します）

以下のようにします．
"""
GPUデバイスが使用可能か確認する
"""
import subprocess


def check_gpu_device(device: int) -> bool:
    """
    GPUデバイスが使用可能か確認する
    Args:
        device: デバイス番号
    """
    output = subprocess.check_output(["nvidia-smi", "-L"])
    lines = output.decode().split('\n')
    for line in lines:
        if line == "":
            continue
        gpu_device_id = line.split(":")[0]
        if gpu_device_id == f"GPU {device}":
            return True
    return False
-Lオプションを付けることで1行1デバイスで列挙できるので，Pythonから扱いやすくなります．
（--query-gpuでもOKです）

まとめ

PythonからGPUデバイスが使用可能かチェックする処理を紹介しました．
基本的には自分が使っているPCのデバイス番号は把握しているかと思いますが，何かしらのアプリケーションの形で提供している場合には使えるかと思います．
ご参考になれば幸いです．

　 Tweet
Qiitaで続きを読む

投稿日：2021-02-27T22:53:08+09:00

ApexLegendsの戦績をLINEで検索したい

したいこと

大人気のバトルロワイヤルfps、「ApexLegends」の戦績を気軽に検索したいのでLINEで教えてもらえるようにしたい．

できたこと

公式アカウントにコマンドを送るとほしい情報を返信してくれる．
よかったら追加して試してみてください(無料会員なので仮に月1000回送信しちゃったら多分止まります)
https://lin.ee/corhpIr

コマンドの紹介(v1.1.4現在)

基本は "!"から始める．
! [プラットフォーム(origin or psn or xbl)] [プレイヤーネーム] [コマンド]

それぞれの間は半角空白
使えるコマンド

kill :キル数

rank :ランク(ダイヤとか)

rankscore :ランクのスコア

id :ID(ほとんどはそのままだけどsteam とかで変えてるときはoriginのID？)

level :レベル．ゲーム内では500までしか表示されないけどそれ以上でも表示される

実装するために

大まかですが利用したサービス、方法を紹介します．
Heroku:ここにコードをデプロイして自動化させていただいてます．
LINE Developper:公式アカウントの設立やWebhookの設定など

実際の動作

利用者:コマンド送信 ----> えーぺっくすとらっかー:コマンド受信
LINEのWebhook:受け取ったテキストを送信 -----> Heroku:テキストを受信してプログラム実行
Heroku:実行結果をLINEに送信 ----> LINE:受け取ったテキストを利用者に返信

大体のイメージに過ぎないですがこんな感じで動いてると思います．

LINE Developper

これで公式ラインの作成設定をしました．
やり方などは多くの方が記事にしているのでそちらをご覧ください．

Heroku

これも同様に僕よりもっとわかりやすく解説してある記事があるのでそちらをどうぞ

ここで僕なりの注意点ですが、後述するオウム返しするコードだけコピペしてからHerokuにデプロイやアプリ作成をしたほうが無難です．
私はコードができる前にいろいろといじったた何回デプロイしても動かなくなってしまいました．(たぶん余計なファイルもデプロイしてしまった．)

オウム返ししよう

では実際に書いてみましょう．とはいっても僕もすべて理解しているわけではありません．というかほとんど理解してないです．

ここを参考にするのが一番です．僕もそうしました．この記事の最後まで動いたら私の記事に帰ってきてください．

オウム返しから進化しよう

オウム返しできましたかね？
ではここでオウム返し以外もしゃべらせましょう．オウム返しの部分は
line_bot_api.reply_message(event.reply_token,TextSendMessage(text=event.message.text))
というコードの
TextSendMessage(text=event.message.text)
のevent.message.textです．この変数に送信したテキストが格納されているんですね．

これが理解できればあとはこれを利用して作業するだけです．

ApexLegendsの戦績をもってこよう

ここ以降は明日書きます．LGTMして待っててください．

参考にさせていただいた記事(というかまんまパクリ)

https://qiita.com/kaonashikun/items/8004dfc9deea6c25754b
https://qiita.com/hayapo/items/2ade5e149f98ec19afc1

　 Tweet
Qiitaで続きを読む

投稿日：2021-02-27T22:16:10+09:00

都市鉄道の混雑率調査結果（令和元年度実績）のPDFからデータを抽出して混雑率のランキングを作成

から「資料３：最混雑区間における混雑率（2019）（PDF形式）」から混雑率ランキングを作成する
# PDFをダウンロード
wget https://www.mlit.go.jp/report/press/content/001365144.pdf -O data.pdf

# pdfplumberをインストール
pip install pdfplumber
pip install pandas
import pdfplumber
import pandas as pd

with pdfplumber.open("data.pdf") as pdf:

    dfs = []

    for page in pdf.pages:

        table = page.extract_table()

        col = ["".join(i.split()) if i else "線路" for i in table[0]]

        df_tmp = pd.DataFrame(table[1:], columns=col)

        dfs.append(df_tmp)

df = pd.concat(dfs).reset_index(drop=True)

# 空白文字除去、正規化
for col in df.select_dtypes(include=object).columns:
    df[col] = df[col].str.replace("\s", "", regex=True).str.normalize("NFKC")

df

# 結合セルを補完
df["事業者名"].fillna(method="ffill", inplace=True)
df["線名"].fillna(method="ffill", inplace=True)
df["区間"].fillna(method="ffill", inplace=True)

# カンマを除去してintに変換
df["輸送力（人）"] = df["輸送力（人）"].str.replace(",", "").astype(int)
df["輸送人員（人）"] = df["輸送人員（人）"].str.replace(",", "").astype(int)
df["混雑率（％）"] = df["混雑率（％）"].astype(int)

df.dtypes

df["混雑率ランキング"] = df["混雑率（％）"].rank(method="min", ascending=False).astype(int)

df1 = df.set_index("混雑率ランキング").sort_index()

df1["線路"] = df1["線路"].fillna("")

df1.to_csv("rank.csv")
CSV

CSVデータ

※ランキングに並び替える前のデータ

ランキング

混雑率ランキング事業者名線名線路区間時間帯編成・本数（両・本）輸送力（人）輸送人員（人）混雑率（％）

1 東京地下鉄東西木場→門前仲町 7:50~8:50 10×27 38448 76388 199

2 東日本横須賀武蔵小杉→西大井 7:26~8:26 13×11 20504 40060 195

3 東日本総武緩行錦糸町→両国 7:34~8:34 10×26 38480 74820 194

4 東日本東海道川崎→品川 7:39~8:39 13×19 35036 67560 193

5 東京都日暮里・舎人ライナー赤土→西日暮里小学校前 7:20~8:20 5×18 4441 8407 189

6 東日本京浜東北大井町→品川 7:35~8:35 10×26 38480 71350 185

6 東日本埼京板橋→池袋 7:50~8:50 10×19 27960 51850 185

8 東日本中央快速中野→新宿 7:40~8:40 10×30 44400 81550 184

9 東急電鉄田園都市池尻大橋→渋谷 7:50~8:50 10×27 40338 73712 183

10 東日本南武武蔵中原→武蔵小杉 7:30~8:30 6×25 22200 40380 182

11 東日本総武快速新小岩→錦糸町 7:34~8:34 13×19 35416 64100 181

12 東京地下鉄千代田町屋→西日暮里 7:45~8:45 10×29 44022 78927 179

13 東急電鉄目黒不動前→目黒 7:50~8:50 6×24 21264 37766 178

14 東日本京浜東北川口→赤羽 7:20~8:20 10×25 37000 64150 173

15 東急電鉄東横祐天寺→中目黒 7:50~8:50 8.8×24 31650 54311 172

16 首都圏新都市鉄道つくばエクスプレス青井→北千住 7:30~8:30 6×22 18304 31324 171

17 東京地下鉄半蔵門渋谷→表参道 8:00~9:00 10×27 38448 64930 169

18 京王電鉄京王下高井戸→明大前 7:40~8:40 10×27 37800 63089 167

19 東日本武蔵野東浦和→南浦和 7:21~8:21 8×14 16576 27450 166

20 東京地下鉄有楽町東池袋→護国寺 7:45~8:45 10×24 34176 56269 165

21 西武鉄道新宿下落合→高田馬場 7:37~8:37 9.2×25 32020 52446 164

22 横浜市 4号日吉本町→日吉 7:15~8:15 4×19 7220 11747 163

22 東日本横浜小机→新横浜 7:27~8:27 8×19 22496 36670 163

24 東日本京葉葛西臨海公園→新木場 7:29~8:29 9.3×24 32856 53320 162

24 東日本高崎宮原→大宮 6:57~7:57 13×14 25816 41880 162

26 東京都大江戸中井→東中野 7:50~8:50 8×20 15600 25158 161

26 東京都三田西巣鴨→巣鴨 7:40~8:40 6×20 16800 27118 161

28 東京地下鉄銀座赤坂見附→溜池山王 8:00~9:00 6×30 18300 29264 160

29 東京地下鉄丸ノ内新大塚→茗荷谷 8:00~9:00 6×31 24552 39049 159

29 東京都新宿西大島→住吉 7:40~8:40 9.8×17 23240 36968 159

29 東京地下鉄南北駒込→本駒込 8:00~9:00 6×18 15948 25422 159

32 東京地下鉄日比谷三ノ輪→入谷 7:50~8:50 8×27 27216 43068 158

32 西日本鉄道貝塚名島→貝塚 7:30~8:30 2×6 1488 2346 158

32 小田急電鉄小田原世田谷代田→下北沢 7:41~8:41 9.7×36 48858 77126 158

32 西武鉄道池袋椎名町→池袋 7:30~8:30 9×24 30072 47397 158

32 東京地下鉄丸ノ内四ツ谷→赤坂見附 8:10~9:10 6×30 23760 37651 158

37 東急電鉄大井町九品仏→自由が丘 7:30~8:30 5.7×21 17472 27259 156

37 東日本山手内回り新大久保→新宿 7:45~8:45 11×23 37421 58290 156

39 東京地下鉄副都心要町→池袋 7:45~8:45 9×18 23040 35672 155

40 名古屋鉄道常滑豊田本町→神宮前 7:40~8:40 5.6×17 9330 14148 152

41 京王電鉄井の頭池ノ上→駒場東大前 7:45~8:45 5×28 19600 29333 150

41 東武鉄道伊勢崎小菅→北千住 7:30~8:30 8.4×41 45314 67956 150

41 東日本常磐快速松戸→北千住 7:18~8:18 14.2×19 38852 58230 150

44 阪急電鉄神戸本線神崎川→十三 7:34~8:34 8.6×24 26574 39700 149

44 名古屋鉄道本線(東) 神宮前→金山 7:40~8:40 6.2×35 21996 32678 149

44 東日本山手外回り上野→御徒町 7:40~8:40 11×22 35794 53380 149

44 東日本常磐緩行亀有→綾瀬 7:23~8:23 10×24 33600 50060 149

48 京成電鉄押上京成曳舟→押上 7:40~8:40 8×24 23232 34411 148

48 名古屋鉄道犬山下小田井→枇杷島分岐点 7:30~8:30 7.5×11 8690 12899 148

48 大阪市高速電気軌道御堂筋梅田→淀屋橋 8:00~9:00 10×27 36990 54595 148

51 名古屋鉄道本線(西) 栄生→名鉄名古屋 7:30~8:30 7.4×28 22164 32642 147

52 阪急電鉄宝塚本線三国→十三 7:31~8:31 8.3×23 24768 36275 146

52 東日本根岸新杉田→磯子 7:14~8:14 10×13 19240 28080 146

54 福岡市空港・箱崎大濠公園→赤坂 8:00~9:00 6×20 16200 23566 145

55 西日本鉄道天神大牟田平尾→薬院 8:00~9:00 6.4×18 14112 20266 144

56 京浜急行電鉄本線戸部→横浜 7:30~8:30 9.5×27 32000 45889 143

56 仙台市南北北仙台→北四番丁 8:00~9:00 4×17 9792 14000 143

58 横浜市 1・3号三ツ沢下町→横浜 7:30~8:30 6×14 10864 15274 141

58 東日本信越新津→新潟 7:27~8:27 4.2×9 4518 6387 141

58 名古屋鉄道瀬戸矢田→大曽根 7:30~8:30 4×14 7000 9862 141

58 名古屋市東山名古屋→伏見 7:30~8:30 6×29 17954 25351 141

62 大阪市高速電気軌道中央森ノ宮→谷町四丁目 7:50~8:50 6×17 13668 19114 140

63 東武鉄道野田新船橋→船橋 7:00~8:00 6×11 9108 12621 139

63 相模鉄道本線西横浜→平沼橋 7:40~8:40 9.7×26 35280 49022 139

63 東急電鉄多摩川矢口渡→蒲田 7:40~8:40 3×20 7360 10257 139

63 西日本片町鴫野→京橋 7:30~8:30 7×16 17424 24300 139

67 札幌市東西菊水→バスセンター前 8:00~9:00 7×15 13650 18778 138

68 東日本宇都宮土呂→大宮 6:56~7:56 13×14 25816 35440 137

68 近畿日本鉄道名古屋米野→名古屋 7:35~8:35 4.7×18 11560 15870 137

70 名古屋鉄道津島甚目寺→須ヶ口 7:30~8:30 6.7×6 4630 6278 136

70 南海電気鉄道南海本線粉浜→岸里玉出 7:25~8:25 6.4×21 16680 22704 136

72 近畿日本鉄道奈良河内永和→布施 7:35~8:35 8.2×20 22700 30670 135

72 東急電鉄池上大崎広小路→五反田 7:50~8:50 3×24 8832 11943 135

72 名古屋市名城・名港金山→東別院 7:30~8:30 6×21 13031 17633 135

72 東武鉄道東上北池袋→池袋 7:30~8:30 10×24 33120 44728 135

76 近畿日本鉄道大阪俊徳道→布施 7:33~8:33 7×20 19040 25470 134

77 東武鉄道野田初石→流山おおたかの森 7:10~8:10 6×10 8280 10959 132

78 埼玉高速鉄道埼玉高速鉄道川口元郷→赤羽岩淵 7:13~8:13 6×15 13230 17350 131

78 東京都浅草本所吾妻橋→浅草 7:30~8:30 8×24 23040 30128 131

80 大阪市高速電気軌道御堂筋難波→心斎橋 7:50~8:50 10×26 35620 46335 130

80 三岐鉄道北勢西別所→馬道 7:00~8:00 3.7×3 679 884 130

80 東京地下鉄東西高田馬場→早稲田 8:00~9:00 10×24 34176 44302 130

80 東京臨海高速鉄道りんかい大井町→品川シーサイド 8:00~9:00 10×12 18720 24341 130

80 広島高速交通広島新交通1号牛田→白島 7:45~8:45 6×22 6292 8168 130

85 京都市東西山科→御陵 7:30~8:30 6×11 6600 8503 129

86 東日本五日市東秋留→拝島 7:04~8:04 6×6 5328 6830 128

86 小田急電鉄江ノ島南林間→中央林間 7:08~8:08 8.2×13 15052 19299 128

88 名古屋市桜通吹上→今池 7:30~8:30 5×14 9855 12544 127

88 福岡市七隈桜坂→薬院大通 8:00~9:00 4×15 5730 7302 127

88 札幌市東豊北13条東→さっぽろ 8:00~9:00 4×16 8256 10464 127

88 京成電鉄本線大神宮下→京成船橋 7:20~8:20 7×18 15246 19396 127

88 近畿日本鉄道南大阪北田辺→河堀口 7:31~8:31 7×20 19180 24410 127

88 近畿日本鉄道京都向島→桃山御陵前 7:36~8:36 5.9×18 14734 18720 127

94 京王電鉄相模原京王多摩川→調布 7:20~8:20 10×12 16800 21136 126

94 神戸新交通ポートアイランド貿易ポート→センターターミナル 8:00~9:00 6×27 8127 10280 126

96 東日本青梅西立川→立川 7:03~8:03 9.1×17 22792 28465 125

96 南海電気鉄道高野百舌鳥八幡→三国ヶ丘 7:20~8:20 7.2×24 22596 28272 125

96 東日本白新新発田→新潟 7:40~8:40 4.4×5 2688 3368 125

99 大阪市高速電気軌道谷町谷町九丁目→谷町六丁目 7:50~8:50 6×22 18084 22409 124

99 名古屋市上飯田上飯田→平安通 7:30~8:30 4×8 4208 5214 124

99 東武鉄道野田北大宮→大宮 7:30~8:30 6×14 11592 14322 124

102 名古屋鉄道小牧味鋺→上飯田 7:30~8:30 4×8 3712 4557 123

102 神戸市西神・山手妙法寺→板宿 7:15~8:15 6×19 14478 17766 123

102 東海関西八田→名古屋 7:31~8:31 4.1×7 4140 5080 123

105 西日本可部可部→広島 7:30~8:30 4×5 2580 3137 122

105 大阪市高速電気軌道長堀鶴見緑地蒲生四丁目→京橋 7:40~8:40 4×20 7600 9235 122

105 京阪電気鉄道京阪本線野江→京橋 7:50~8:50 7.4×35 31553 38641 122

108 京都市烏丸京都→五条 7:30~8:30 6×15 12540 15180 121

108 北海道函館琴似→桑園 7:31~8:31 6×10 8538 10346 121

108 新京成電鉄新京成前原→新津田沼 7:06~8:06 6×13 9698 11714 121

108 新京成電鉄新京成上本郷→松戸 7:23~8:23 6×14 10444 12629 121

112 横浜シーサイドライン金沢シーサイドライン新杉田→南部市場 7:30~8:30 5×13 3068 3676 120

112 東海中央新守山→大曽根 7:49~8:49 9.7×13 18045 21653 120

114 神戸市海岸ハーバーランド→中央市場前 7:32~8:32 4×10 3620 4300 119

114 北海道札沼八軒→桑園 7:22~8:22 6×6 4734 5647 119

114 阪急電鉄京都本線上新庄→淡路 7:35~8:35 8.2×24 25296 30025 119

114 東日本仙山作並→仙台 7:35~8:35 5.5×4 2970 3540 119

118 阪急電鉄千里下新庄→淡路 7:34~8:34 7.8×12 12276 14450 118

119 泉北高速鉄道泉北高速鉄道深井→中百舌鳥 6:54~7:54 7.7×13 13302 15558 117

120 名古屋市鶴舞塩釜口→八事 7:30~8:30 6×15 12879 14913 116

120 東葉高速鉄道東葉高速東海神→西船橋 7:08~8:08 10×12 18216 21055 116

122 札幌市南北中島公園→すすきの 8:00~9:00 6×15 12420 14183 114

123 大阪市高速電気軌道四つ橋難波→四ツ橋 7:50~8:50 6×21 17262 19507 113

123 西武鉄道西武有楽町新桜台→小竹向原 7:32~8:32 9.8×16 21716 24546 113

123 埼玉新都市交通伊奈鉄道博物館→大宮 7:02~8:02 6×14 3626 4114 113

123 大阪市高速電気軌道千日前鶴橋→谷町九丁目 7:50~8:50 4×14 7560 8565 113

127 東日本東北松島→仙台 7:30~8:30 5.4×7 5090 5690 112

127 北海道千歳白石→苗穂 7:29~8:29 6×7 5781 6474 112

129 東日本東北岩沼→仙台 7:30~8:30 5.3×12 8502 9450 111

129 阪神電気鉄道本線出屋敷→尼崎 7:32~8:32 5.6×25 17364 19353 111

129 西日本山陽(2) 倉敷→岡山 7:30~8:30 6.6×8 6044 6683 111

129 東日本越後吉田→新潟 7:50~8:50 5.2×5 3286 3650 111

133 熊本市水前寺新水前寺駅前→味噌天神前 7:30~8:30 1.2×22 1273 1384 109

133 神戸新交通六甲アイランド魚崎→南魚崎 7:30~8:30 4×21 3717 4043 109

135 西日本大阪環状京橋→桜ノ宮 7:30~8:30 8×17 19862 21375 108

135 西日本東海道塚本→大阪 7:30~8:30 7×12 13068 14100 108

135 西日本東西大阪天満宮→北新地 7:35~8:35 7×16 17424 18840 108

135 西日本大阪環状鶴橋→玉造 7:30~8:30 8×17 19862 21370 108

139 愛知高速交通(リニモ) 東部丘陵杁ヶ池公園→長久手古戦場 8:00~9:00 3×9 2196 2360 107

140 西日本阪和快速堺市→天王寺 7:25~8:25 8×13 14248 15105 106

140 東日本仙石陸前原ノ町→仙台 7:45~8:45 4×10 5560 5920 106

140 九州鹿児島(3) 普通八代→熊本 7:39~8:39 2.8×5 1700 1805 106

140 西日本関西緩行東部市場前→天王寺 7:25~8:25 6×6 5014 5300 106

140 東海東海道(2) 熱田→名古屋 7:46~8:46 6.3×15 13160 13930 106

145 西日本東海道緩行茨木→新大阪 7:40~8:40 7×13 14157 14889 105

145 九州鹿児島(1) 普通香椎→博多 7:16~8:16 8.4×7 6760 7075 105

145 西日本吉備備中高松→岡山 7:20~8:20 3×3 1032 1082 105

145 大阪市高速電気軌道谷町東梅田→南森町 7:50~8:50 6×22 18084 18915 105

149 大阪市高速電気軌道堺筋日本橋→長堀橋 7:50~8:50 8×20 22240 23109 104

149 仙台市東西連坊→宮城野通 8:00~9:00 4×11 4268 4458 104

151 西日本阪和緩行美章園→天王寺 7:30~8:30 5.5×8 6106 6305 103

151 西日本山陽(2) 東岡山→岡山 7:00~8:00 4.8×5 2924 3003 103

151 遠州鉄道鉄道助信→八幡 7:10~8:10 4×5 2760 2830 103

151 ゆりかもめ東京臨海新交通臨海汐留→竹芝 8:00~9:00 6×19 5909 6075 103

151 北海道函館白石→苗穂 7:35~8:35 6×9 7506 7714 103

156 愛知環状鉄道愛知環状鉄道新上挙母→三河豊田 7:35~8:35 3×8 3156 3227 102

156 筑豊電気鉄道筑豊電気鉄道萩原→熊西 7:00~8:00 1.8×10 967 989 102

156 西日本福知山快速伊丹→尼崎 7:30~8:30 7.6×11 11930 12220 102

156 九州鹿児島(1) 快速二日市→博多 8:28~9:28 4×1 440 450 102

160 北大阪急行電鉄南北緑地公園→江坂 7:30~8:30 10×13 17905 18115 101

160 東海東海道(1) 安倍川→静岡 7:31~8:31 6.2×10 8216 8280 101

162 九州豊肥肥後大津→熊本 6:13~7:13 2×3 800 800 100

162 神戸電鉄有馬丸山→長田 7:30~8:30 3.8×19 8176 8182 100

162 東海東海道(2) 枇杷島→名古屋 7:45~8:45 7.5×15 15158 15145 100

165 阪堺電気軌道上町松虫→阿倍野 7:30~8:30 1.2×18 1350 1335 99

165 西日本東海道尼崎→大阪 7:35~8:35 11.8×13 21148 20895 99

165 東日本中央緩行代々木→千駄ヶ谷 8:01~9:01 10×23 34040 33790 99

165 大阪市高速電気軌道南港ポートタウンコスモトレード→スクエアセンター前 8:00~9:00 4×24 4032 3975 99

165 九州鹿児島(1) 快速香椎→博多 7:07~8:07 9×2 2070 2050 99

170 西日本東海道快速茨木→新大阪 7:30~8:30 12×13 21430 20977 98

170 西日本おおさか東久宝寺→放出 7:35~8:35 6.3×6 5538 5400 98

170 江ノ島電鉄江ノ島電鉄石上→藤沢 7:10~8:10 4×5 1500 1468 98

170 西日本宇野茶屋町→岡山 6:50~7:50 5.2×5 3128 3056 98

174 大阪市高速電気軌道堺筋南森町→北浜 7:50~8:50 8×20 22240 21643 97

174 九州鹿児島(1) 普通二日市→博多 7:13~8:13 7.6×8 6950 6772 97

176 山陽電気鉄道本線西新町→明石 7:00~8:00 4.4×15 8052 7736 96

176 九州鹿児島(2) 快速折尾→小倉 7:28~8:28 9×1 990 950 96

176 西日本山陽(1) 岩国→広島 7:30~8:30 6.2×9 7564 7237 96

179 大阪市高速電気軌道四つ橋西梅田→肥後橋 8:00~9:00 6×22 18084 17226 95

179 九州篠栗快速吉塚→博多 6:49~7:49 6×1 740 700 95

179 九州日豊普通行橋→小倉 7:12~8:12 7×3 2310 2190 95

179 大阪市高速電気軌道中央阿波座→本町 7:50~8:50 6×13 10452 9934 95

183 西日本関西快速久宝寺→天王寺 7:30~8:30 7.3×12 12150 11400 94

183 養老鉄道養老北大垣→室 6:50~7:50 3×3 1224 1150 94

183 名古屋ガイドウェイバス志段味守山→砂田橋 7:27~8:27 1×24 1656 1550 94

186 九州日田彦山普通田川後藤寺→城野 6:44~7:44 2×1 220 200 91

187 九州鹿児島(2) 普通折尾→小倉 8:03~9:03 5.5×6 3780 3355 89

187 阪神電気鉄道なんば千鳥橋→西九条 7:32~8:32 6.4×11 8994 8008 89

189 西日本芸備志和口→広島 7:30~8:30 4.5×4 2120 1863 88

190 西日本呉広→広島 7:30~8:30 5.1×7 4896 4265 87

190 四日市あすなろう鉄道内部赤堀→あすなろう四日市 7:00~8:00 3×6 1044 904 87

190 近畿日本鉄道けいはんな荒本→長田 7:26~8:26 6×16 12576 10940 87

190 北総鉄道北総新柴又→京成高砂 7:24~8:24 8×11 12320 10760 87

194 熊本電気鉄道菊池亀井→北熊本 7:30~8:30 2×4 1040 887 85

194 広島電鉄宮島東高須→広電西広島 7:30~8:30 3×18 2700 2287 85

196 九州鹿児島(4) 大牟田→熊本 6:30~7:30 3×2 760 640 84

196 東海東海道(1) 東静岡→静岡 7:35~8:35 5.2×9 6488 5420 84

196 西日本山陽(1) 西条→広島 7:30~8:30 6.4×7 6040 5083 84

196 大阪市高速電気軌道今里筋鴫野→緑橋 7:40~8:40 4×14 5264 4415 84

200 九州篠栗普通吉塚→博多 7:43~8:43 5.8×4 3080 2515 82

200 三岐鉄道三岐平津→暁学園前 7:20~8:20 2.7×3 1270 1040 82

202 京福電気鉄道嵐山本線蚕ノ社→嵐電天神川 7:30~8:30 1.5×12 1655 1343 81

203 大阪市高速電気軌道南港ポートタウン住之江→平林公園 7:40~8:40 4×24 4032 3234 80

204 水間鉄道水間近義の里→貝塚市役所前 7:00~8:00 2×3 750 589 79

204 能勢電鉄妙見絹延橋→川西能勢口 7:00~8:00 5.2×13 8521 6728 79

204 岡山電気軌道東山岡山駅前停留場→東山停留場 7:10~8:10 1×15 1200 942 79

204 神戸市北神谷上→新神戸 7:18~8:18 6×8 6096 4830 79

208 西日本津山福渡→岡山 7:20~8:20 2.3×3 784 593 76

209 西日本大阪環状玉造→鶴橋 7:25~8:25 8×15 17361 13061 75

210 西日本福知山緩行塚口→尼崎 7:30~8:30 7×9 9801 7230 74

211 小田急電鉄多摩五月台→新百合ヶ丘 7:26~8:26 8×12 13632 10018 73

211 大阪市高速電気軌道長堀鶴見緑地森ノ宮→大阪ビジネスパーク 7:40~8:40 4×18 6840 5020 73

211 九州日田彦山快速田川後藤寺→城野 7:33~8:33 2×1 220 160 73

214 京福電気鉄道北野線撮影所前→常盤 7:30~8:30 1×6 552 385 70

215 静岡鉄道静岡清水県立美術館前→県総合運動場 8:00~9:00 2×10 2600 1781 69

215 樽見鉄道樽見東大垣→大垣 6:54~7:54 1×3 350 241 69

215 関東鉄道常総西取手→取手 7:25~8:25 2×9 2520 1732 69

218 名古屋臨海高速鉄道西名古屋港ささしまライブ→名古屋 7:30~8:30 4×6 3492 2349 67

219 大阪市高速電気軌道今里筋鴫野→蒲生四丁目 7:40~8:40 4×12 4512 2964 66

220 流鉄流山小金城趾→幸谷 7:00~8:00 2×5 1415 915 65

220 大阪市高速電気軌道千日前日本橋→谷町九丁目 7:50~8:50 4×13 7020 4544 65

222 九州日豊快速行橋→小倉 7:23~8:23 7×1 770 475 62

223 九州鹿児島(3) 快速八代→熊本 7:40~8:40 1×1 90 55 61

224 天竜浜名湖天竜浜名湖西掛川→掛川市役所前 7:04~8:04 1.3×3 480 250 52

225 叡山電鉄叡山本線元田中→出町柳 7:00~8:00 1.4×12 1605 756 47

226 阪堺電気軌道阪堺今船→今池 7:30~8:30 1×5 375 172 46

227 山万ユーカリが丘地区→ユーカリが丘センター 6:30~7:30 3×8 1120 359 32

227 東海交通事業城北比良→小田井 7:40~8:40 1×3 330 107 32

229 能勢電鉄日生日生中央→山下 6:45~7:45 6.3×7 5515 1611 29

230 長良川鉄道越美南前平公園→美濃太田 7:00~8:00 1.5×2 311 84 27

231 関東鉄道竜ヶ崎竜ヶ崎→佐貫 6:40~7:40 2×3 810 186 23

混雑率ランキング	事業者名	線名	線路	区間	時間帯	編成・本数（両・本）	輸送力（人）	輸送人員（人）	混雑率（％）
1	東京地下鉄	東西		木場→門前仲町	7:50~8:50	10×27	38448	76388	199
2	東日本	横須賀		武蔵小杉→西大井	7:26~8:26	13×11	20504	40060	195
3	東日本	総武	緩行	錦糸町→両国	7:34~8:34	10×26	38480	74820	194
4	東日本	東海道		川崎→品川	7:39~8:39	13×19	35036	67560	193
5	東京都	日暮里・舎人ライナー		赤土→西日暮里小学校前	7:20~8:20	5×18	4441	8407	189
6	東日本	京浜東北		大井町→品川	7:35~8:35	10×26	38480	71350	185
6	東日本	埼京		板橋→池袋	7:50~8:50	10×19	27960	51850	185
8	東日本	中央	快速	中野→新宿	7:40~8:40	10×30	44400	81550	184
9	東急電鉄	田園都市		池尻大橋→渋谷	7:50~8:50	10×27	40338	73712	183
10	東日本	南武		武蔵中原→武蔵小杉	7:30~8:30	6×25	22200	40380	182
11	東日本	総武	快速	新小岩→錦糸町	7:34~8:34	13×19	35416	64100	181
12	東京地下鉄	千代田		町屋→西日暮里	7:45~8:45	10×29	44022	78927	179
13	東急電鉄	目黒		不動前→目黒	7:50~8:50	6×24	21264	37766	178
14	東日本	京浜東北		川口→赤羽	7:20~8:20	10×25	37000	64150	173
15	東急電鉄	東横		祐天寺→中目黒	7:50~8:50	8.8×24	31650	54311	172
16	首都圏新都市鉄道	つくばエクスプレス		青井→北千住	7:30~8:30	6×22	18304	31324	171
17	東京地下鉄	半蔵門		渋谷→表参道	8:00~9:00	10×27	38448	64930	169
18	京王電鉄	京王		下高井戸→明大前	7:40~8:40	10×27	37800	63089	167
19	東日本	武蔵野		東浦和→南浦和	7:21~8:21	8×14	16576	27450	166
20	東京地下鉄	有楽町		東池袋→護国寺	7:45~8:45	10×24	34176	56269	165
21	西武鉄道	新宿		下落合→高田馬場	7:37~8:37	9.2×25	32020	52446	164
22	横浜市	4号		日吉本町→日吉	7:15~8:15	4×19	7220	11747	163
22	東日本	横浜		小机→新横浜	7:27~8:27	8×19	22496	36670	163
24	東日本	京葉		葛西臨海公園→新木場	7:29~8:29	9.3×24	32856	53320	162
24	東日本	高崎		宮原→大宮	6:57~7:57	13×14	25816	41880	162
26	東京都	大江戸		中井→東中野	7:50~8:50	8×20	15600	25158	161
26	東京都	三田		西巣鴨→巣鴨	7:40~8:40	6×20	16800	27118	161
28	東京地下鉄	銀座		赤坂見附→溜池山王	8:00~9:00	6×30	18300	29264	160
29	東京地下鉄	丸ノ内		新大塚→茗荷谷	8:00~9:00	6×31	24552	39049	159
29	東京都	新宿		西大島→住吉	7:40~8:40	9.8×17	23240	36968	159
29	東京地下鉄	南北		駒込→本駒込	8:00~9:00	6×18	15948	25422	159
32	東京地下鉄	日比谷		三ノ輪→入谷	7:50~8:50	8×27	27216	43068	158
32	西日本鉄道	貝塚		名島→貝塚	7:30~8:30	2×6	1488	2346	158
32	小田急電鉄	小田原		世田谷代田→下北沢	7:41~8:41	9.7×36	48858	77126	158
32	西武鉄道	池袋		椎名町→池袋	7:30~8:30	9×24	30072	47397	158
32	東京地下鉄	丸ノ内		四ツ谷→赤坂見附	8:10~9:10	6×30	23760	37651	158
37	東急電鉄	大井町		九品仏→自由が丘	7:30~8:30	5.7×21	17472	27259	156
37	東日本	山手	内回り	新大久保→新宿	7:45~8:45	11×23	37421	58290	156
39	東京地下鉄	副都心		要町→池袋	7:45~8:45	9×18	23040	35672	155
40	名古屋鉄道	常滑		豊田本町→神宮前	7:40~8:40	5.6×17	9330	14148	152
41	京王電鉄	井の頭		池ノ上→駒場東大前	7:45~8:45	5×28	19600	29333	150
41	東武鉄道	伊勢崎		小菅→北千住	7:30~8:30	8.4×41	45314	67956	150
41	東日本	常磐	快速	松戸→北千住	7:18~8:18	14.2×19	38852	58230	150
44	阪急電鉄	神戸本線		神崎川→十三	7:34~8:34	8.6×24	26574	39700	149
44	名古屋鉄道	本線(東)		神宮前→金山	7:40~8:40	6.2×35	21996	32678	149
44	東日本	山手	外回り	上野→御徒町	7:40~8:40	11×22	35794	53380	149
44	東日本	常磐	緩行	亀有→綾瀬	7:23~8:23	10×24	33600	50060	149
48	京成電鉄	押上		京成曳舟→押上	7:40~8:40	8×24	23232	34411	148
48	名古屋鉄道	犬山		下小田井→枇杷島分岐点	7:30~8:30	7.5×11	8690	12899	148
48	大阪市高速電気軌道	御堂筋		梅田→淀屋橋	8:00~9:00	10×27	36990	54595	148
51	名古屋鉄道	本線(西)		栄生→名鉄名古屋	7:30~8:30	7.4×28	22164	32642	147
52	阪急電鉄	宝塚本線		三国→十三	7:31~8:31	8.3×23	24768	36275	146
52	東日本	根岸		新杉田→磯子	7:14~8:14	10×13	19240	28080	146
54	福岡市	空港・箱崎		大濠公園→赤坂	8:00~9:00	6×20	16200	23566	145
55	西日本鉄道	天神大牟田		平尾→薬院	8:00~9:00	6.4×18	14112	20266	144
56	京浜急行電鉄	本線		戸部→横浜	7:30~8:30	9.5×27	32000	45889	143
56	仙台市	南北		北仙台→北四番丁	8:00~9:00	4×17	9792	14000	143
58	横浜市	1・3号		三ツ沢下町→横浜	7:30~8:30	6×14	10864	15274	141
58	東日本	信越		新津→新潟	7:27~8:27	4.2×9	4518	6387	141
58	名古屋鉄道	瀬戸		矢田→大曽根	7:30~8:30	4×14	7000	9862	141
58	名古屋市	東山		名古屋→伏見	7:30~8:30	6×29	17954	25351	141
62	大阪市高速電気軌道	中央		森ノ宮→谷町四丁目	7:50~8:50	6×17	13668	19114	140
63	東武鉄道	野田		新船橋→船橋	7:00~8:00	6×11	9108	12621	139
63	相模鉄道	本線		西横浜→平沼橋	7:40~8:40	9.7×26	35280	49022	139
63	東急電鉄	多摩川		矢口渡→蒲田	7:40~8:40	3×20	7360	10257	139
63	西日本	片町		鴫野→京橋	7:30~8:30	7×16	17424	24300	139
67	札幌市	東西		菊水→バスセンター前	8:00~9:00	7×15	13650	18778	138
68	東日本	宇都宮		土呂→大宮	6:56~7:56	13×14	25816	35440	137
68	近畿日本鉄道	名古屋		米野→名古屋	7:35~8:35	4.7×18	11560	15870	137
70	名古屋鉄道	津島		甚目寺→須ヶ口	7:30~8:30	6.7×6	4630	6278	136
70	南海電気鉄道	南海本線		粉浜→岸里玉出	7:25~8:25	6.4×21	16680	22704	136
72	近畿日本鉄道	奈良		河内永和→布施	7:35~8:35	8.2×20	22700	30670	135
72	東急電鉄	池上		大崎広小路→五反田	7:50~8:50	3×24	8832	11943	135
72	名古屋市	名城・名港		金山→東別院	7:30~8:30	6×21	13031	17633	135
72	東武鉄道	東上		北池袋→池袋	7:30~8:30	10×24	33120	44728	135
76	近畿日本鉄道	大阪		俊徳道→布施	7:33~8:33	7×20	19040	25470	134
77	東武鉄道	野田		初石→流山おおたかの森	7:10~8:10	6×10	8280	10959	132
78	埼玉高速鉄道	埼玉高速鉄道		川口元郷→赤羽岩淵	7:13~8:13	6×15	13230	17350	131
78	東京都	浅草		本所吾妻橋→浅草	7:30~8:30	8×24	23040	30128	131
80	大阪市高速電気軌道	御堂筋		難波→心斎橋	7:50~8:50	10×26	35620	46335	130
80	三岐鉄道	北勢		西別所→馬道	7:00~8:00	3.7×3	679	884	130
80	東京地下鉄	東西		高田馬場→早稲田	8:00~9:00	10×24	34176	44302	130
80	東京臨海高速鉄道	りんかい		大井町→品川シーサイド	8:00~9:00	10×12	18720	24341	130
80	広島高速交通	広島新交通1号		牛田→白島	7:45~8:45	6×22	6292	8168	130
85	京都市	東西		山科→御陵	7:30~8:30	6×11	6600	8503	129
86	東日本	五日市		東秋留→拝島	7:04~8:04	6×6	5328	6830	128
86	小田急電鉄	江ノ島		南林間→中央林間	7:08~8:08	8.2×13	15052	19299	128
88	名古屋市	桜通		吹上→今池	7:30~8:30	5×14	9855	12544	127
88	福岡市	七隈		桜坂→薬院大通	8:00~9:00	4×15	5730	7302	127
88	札幌市	東豊		北13条東→さっぽろ	8:00~9:00	4×16	8256	10464	127
88	京成電鉄	本線		大神宮下→京成船橋	7:20~8:20	7×18	15246	19396	127
88	近畿日本鉄道	南大阪		北田辺→河堀口	7:31~8:31	7×20	19180	24410	127
88	近畿日本鉄道	京都		向島→桃山御陵前	7:36~8:36	5.9×18	14734	18720	127
94	京王電鉄	相模原		京王多摩川→調布	7:20~8:20	10×12	16800	21136	126
94	神戸新交通	ポートアイランド		貿易ポート→センターターミナル	8:00~9:00	6×27	8127	10280	126
96	東日本	青梅		西立川→立川	7:03~8:03	9.1×17	22792	28465	125
96	南海電気鉄道	高野		百舌鳥八幡→三国ヶ丘	7:20~8:20	7.2×24	22596	28272	125
96	東日本	白新		新発田→新潟	7:40~8:40	4.4×5	2688	3368	125
99	大阪市高速電気軌道	谷町		谷町九丁目→谷町六丁目	7:50~8:50	6×22	18084	22409	124
99	名古屋市	上飯田		上飯田→平安通	7:30~8:30	4×8	4208	5214	124
99	東武鉄道	野田		北大宮→大宮	7:30~8:30	6×14	11592	14322	124
102	名古屋鉄道	小牧		味鋺→上飯田	7:30~8:30	4×8	3712	4557	123
102	神戸市	西神・山手		妙法寺→板宿	7:15~8:15	6×19	14478	17766	123
102	東海	関西		八田→名古屋	7:31~8:31	4.1×7	4140	5080	123
105	西日本	可部		可部→広島	7:30~8:30	4×5	2580	3137	122
105	大阪市高速電気軌道	長堀鶴見緑地		蒲生四丁目→京橋	7:40~8:40	4×20	7600	9235	122
105	京阪電気鉄道	京阪本線		野江→京橋	7:50~8:50	7.4×35	31553	38641	122
108	京都市	烏丸		京都→五条	7:30~8:30	6×15	12540	15180	121
108	北海道	函館		琴似→桑園	7:31~8:31	6×10	8538	10346	121
108	新京成電鉄	新京成		前原→新津田沼	7:06~8:06	6×13	9698	11714	121
108	新京成電鉄	新京成		上本郷→松戸	7:23~8:23	6×14	10444	12629	121
112	横浜シーサイドライン	金沢シーサイドライン		新杉田→南部市場	7:30~8:30	5×13	3068	3676	120
112	東海	中央		新守山→大曽根	7:49~8:49	9.7×13	18045	21653	120
114	神戸市	海岸		ハーバーランド→中央市場前	7:32~8:32	4×10	3620	4300	119
114	北海道	札沼		八軒→桑園	7:22~8:22	6×6	4734	5647	119
114	阪急電鉄	京都本線		上新庄→淡路	7:35~8:35	8.2×24	25296	30025	119
114	東日本	仙山		作並→仙台	7:35~8:35	5.5×4	2970	3540	119
118	阪急電鉄	千里		下新庄→淡路	7:34~8:34	7.8×12	12276	14450	118
119	泉北高速鉄道	泉北高速鉄道		深井→中百舌鳥	6:54~7:54	7.7×13	13302	15558	117
120	名古屋市	鶴舞		塩釜口→八事	7:30~8:30	6×15	12879	14913	116
120	東葉高速鉄道	東葉高速		東海神→西船橋	7:08~8:08	10×12	18216	21055	116
122	札幌市	南北		中島公園→すすきの	8:00~9:00	6×15	12420	14183	114
123	大阪市高速電気軌道	四つ橋		難波→四ツ橋	7:50~8:50	6×21	17262	19507	113
123	西武鉄道	西武有楽町		新桜台→小竹向原	7:32~8:32	9.8×16	21716	24546	113
123	埼玉新都市交通	伊奈		鉄道博物館→大宮	7:02~8:02	6×14	3626	4114	113
123	大阪市高速電気軌道	千日前		鶴橋→谷町九丁目	7:50~8:50	4×14	7560	8565	113
127	東日本	東北		松島→仙台	7:30~8:30	5.4×7	5090	5690	112
127	北海道	千歳		白石→苗穂	7:29~8:29	6×7	5781	6474	112
129	東日本	東北		岩沼→仙台	7:30~8:30	5.3×12	8502	9450	111
129	阪神電気鉄道	本線		出屋敷→尼崎	7:32~8:32	5.6×25	17364	19353	111
129	西日本	山陽(2)		倉敷→岡山	7:30~8:30	6.6×8	6044	6683	111
129	東日本	越後		吉田→新潟	7:50~8:50	5.2×5	3286	3650	111
133	熊本市	水前寺		新水前寺駅前→味噌天神前	7:30~8:30	1.2×22	1273	1384	109
133	神戸新交通	六甲アイランド		魚崎→南魚崎	7:30~8:30	4×21	3717	4043	109
135	西日本	大阪環状		京橋→桜ノ宮	7:30~8:30	8×17	19862	21375	108
135	西日本	東海道		塚本→大阪	7:30~8:30	7×12	13068	14100	108
135	西日本	東西		大阪天満宮→北新地	7:35~8:35	7×16	17424	18840	108
135	西日本	大阪環状		鶴橋→玉造	7:30~8:30	8×17	19862	21370	108
139	愛知高速交通(リニモ)	東部丘陵		杁ヶ池公園→長久手古戦場	8:00~9:00	3×9	2196	2360	107
140	西日本	阪和	快速	堺市→天王寺	7:25~8:25	8×13	14248	15105	106
140	東日本	仙石		陸前原ノ町→仙台	7:45~8:45	4×10	5560	5920	106
140	九州	鹿児島(3)	普通	八代→熊本	7:39~8:39	2.8×5	1700	1805	106
140	西日本	関西	緩行	東部市場前→天王寺	7:25~8:25	6×6	5014	5300	106
140	東海	東海道(2)		熱田→名古屋	7:46~8:46	6.3×15	13160	13930	106
145	西日本	東海道	緩行	茨木→新大阪	7:40~8:40	7×13	14157	14889	105
145	九州	鹿児島(1)	普通	香椎→博多	7:16~8:16	8.4×7	6760	7075	105
145	西日本	吉備		備中高松→岡山	7:20~8:20	3×3	1032	1082	105
145	大阪市高速電気軌道	谷町		東梅田→南森町	7:50~8:50	6×22	18084	18915	105
149	大阪市高速電気軌道	堺筋		日本橋→長堀橋	7:50~8:50	8×20	22240	23109	104
149	仙台市	東西		連坊→宮城野通	8:00~9:00	4×11	4268	4458	104
151	西日本	阪和	緩行	美章園→天王寺	7:30~8:30	5.5×8	6106	6305	103
151	西日本	山陽(2)		東岡山→岡山	7:00~8:00	4.8×5	2924	3003	103
151	遠州鉄道	鉄道		助信→八幡	7:10~8:10	4×5	2760	2830	103
151	ゆりかもめ	東京臨海新交通臨海		汐留→竹芝	8:00~9:00	6×19	5909	6075	103
151	北海道	函館		白石→苗穂	7:35~8:35	6×9	7506	7714	103
156	愛知環状鉄道	愛知環状鉄道		新上挙母→三河豊田	7:35~8:35	3×8	3156	3227	102
156	筑豊電気鉄道	筑豊電気鉄道		萩原→熊西	7:00~8:00	1.8×10	967	989	102
156	西日本	福知山	快速	伊丹→尼崎	7:30~8:30	7.6×11	11930	12220	102
156	九州	鹿児島(1)	快速	二日市→博多	8:28~9:28	4×1	440	450	102
160	北大阪急行電鉄	南北		緑地公園→江坂	7:30~8:30	10×13	17905	18115	101
160	東海	東海道(1)		安倍川→静岡	7:31~8:31	6.2×10	8216	8280	101
162	九州	豊肥		肥後大津→熊本	6:13~7:13	2×3	800	800	100
162	神戸電鉄	有馬		丸山→長田	7:30~8:30	3.8×19	8176	8182	100
162	東海	東海道(2)		枇杷島→名古屋	7:45~8:45	7.5×15	15158	15145	100
165	阪堺電気軌道	上町		松虫→阿倍野	7:30~8:30	1.2×18	1350	1335	99
165	西日本	東海道		尼崎→大阪	7:35~8:35	11.8×13	21148	20895	99
165	東日本	中央	緩行	代々木→千駄ヶ谷	8:01~9:01	10×23	34040	33790	99
165	大阪市高速電気軌道	南港ポートタウン		コスモトレード→スクエアセンター前	8:00~9:00	4×24	4032	3975	99
165	九州	鹿児島(1)	快速	香椎→博多	7:07~8:07	9×2	2070	2050	99
170	西日本	東海道	快速	茨木→新大阪	7:30~8:30	12×13	21430	20977	98
170	西日本	おおさか東		久宝寺→放出	7:35~8:35	6.3×6	5538	5400	98
170	江ノ島電鉄	江ノ島電鉄		石上→藤沢	7:10~8:10	4×5	1500	1468	98
170	西日本	宇野		茶屋町→岡山	6:50~7:50	5.2×5	3128	3056	98
174	大阪市高速電気軌道	堺筋		南森町→北浜	7:50~8:50	8×20	22240	21643	97
174	九州	鹿児島(1)	普通	二日市→博多	7:13~8:13	7.6×8	6950	6772	97
176	山陽電気鉄道	本線		西新町→明石	7:00~8:00	4.4×15	8052	7736	96
176	九州	鹿児島(2)	快速	折尾→小倉	7:28~8:28	9×1	990	950	96
176	西日本	山陽(1)		岩国→広島	7:30~8:30	6.2×9	7564	7237	96
179	大阪市高速電気軌道	四つ橋		西梅田→肥後橋	8:00~9:00	6×22	18084	17226	95
179	九州	篠栗	快速	吉塚→博多	6:49~7:49	6×1	740	700	95
179	九州	日豊	普通	行橋→小倉	7:12~8:12	7×3	2310	2190	95
179	大阪市高速電気軌道	中央		阿波座→本町	7:50~8:50	6×13	10452	9934	95
183	西日本	関西	快速	久宝寺→天王寺	7:30~8:30	7.3×12	12150	11400	94
183	養老鉄道	養老		北大垣→室	6:50~7:50	3×3	1224	1150	94
183	名古屋ガイドウェイバス	志段味		守山→砂田橋	7:27~8:27	1×24	1656	1550	94
186	九州	日田彦山	普通	田川後藤寺→城野	6:44~7:44	2×1	220	200	91
187	九州	鹿児島(2)	普通	折尾→小倉	8:03~9:03	5.5×6	3780	3355	89
187	阪神電気鉄道	なんば		千鳥橋→西九条	7:32~8:32	6.4×11	8994	8008	89
189	西日本	芸備		志和口→広島	7:30~8:30	4.5×4	2120	1863	88
190	西日本	呉		広→広島	7:30~8:30	5.1×7	4896	4265	87
190	四日市あすなろう鉄道	内部		赤堀→あすなろう四日市	7:00~8:00	3×6	1044	904	87
190	近畿日本鉄道	けいはんな		荒本→長田	7:26~8:26	6×16	12576	10940	87
190	北総鉄道	北総		新柴又→京成高砂	7:24~8:24	8×11	12320	10760	87
194	熊本電気鉄道	菊池		亀井→北熊本	7:30~8:30	2×4	1040	887	85
194	広島電鉄	宮島		東高須→広電西広島	7:30~8:30	3×18	2700	2287	85
196	九州	鹿児島(4)		大牟田→熊本	6:30~7:30	3×2	760	640	84
196	東海	東海道(1)		東静岡→静岡	7:35~8:35	5.2×9	6488	5420	84
196	西日本	山陽(1)		西条→広島	7:30~8:30	6.4×7	6040	5083	84
196	大阪市高速電気軌道	今里筋		鴫野→緑橋	7:40~8:40	4×14	5264	4415	84
200	九州	篠栗	普通	吉塚→博多	7:43~8:43	5.8×4	3080	2515	82
200	三岐鉄道	三岐		平津→暁学園前	7:20~8:20	2.7×3	1270	1040	82
202	京福電気鉄道	嵐山本線		蚕ノ社→嵐電天神川	7:30~8:30	1.5×12	1655	1343	81
203	大阪市高速電気軌道	南港ポートタウン		住之江→平林公園	7:40~8:40	4×24	4032	3234	80
204	水間鉄道	水間		近義の里→貝塚市役所前	7:00~8:00	2×3	750	589	79
204	能勢電鉄	妙見		絹延橋→川西能勢口	7:00~8:00	5.2×13	8521	6728	79
204	岡山電気軌道	東山		岡山駅前停留場→東山停留場	7:10~8:10	1×15	1200	942	79
204	神戸市	北神		谷上→新神戸	7:18~8:18	6×8	6096	4830	79
208	西日本	津山		福渡→岡山	7:20~8:20	2.3×3	784	593	76
209	西日本	大阪環状		玉造→鶴橋	7:25~8:25	8×15	17361	13061	75
210	西日本	福知山	緩行	塚口→尼崎	7:30~8:30	7×9	9801	7230	74
211	小田急電鉄	多摩		五月台→新百合ヶ丘	7:26~8:26	8×12	13632	10018	73
211	大阪市高速電気軌道	長堀鶴見緑地		森ノ宮→大阪ビジネスパーク	7:40~8:40	4×18	6840	5020	73
211	九州	日田彦山	快速	田川後藤寺→城野	7:33~8:33	2×1	220	160	73
214	京福電気鉄道	北野線		撮影所前→常盤	7:30~8:30	1×6	552	385	70
215	静岡鉄道	静岡清水		県立美術館前→県総合運動場	8:00~9:00	2×10	2600	1781	69
215	樽見鉄道	樽見		東大垣→大垣	6:54~7:54	1×3	350	241	69
215	関東鉄道	常総		西取手→取手	7:25~8:25	2×9	2520	1732	69
218	名古屋臨海高速鉄道	西名古屋港		ささしまライブ→名古屋	7:30~8:30	4×6	3492	2349	67
219	大阪市高速電気軌道	今里筋		鴫野→蒲生四丁目	7:40~8:40	4×12	4512	2964	66
220	流鉄	流山		小金城趾→幸谷	7:00~8:00	2×5	1415	915	65
220	大阪市高速電気軌道	千日前		日本橋→谷町九丁目	7:50~8:50	4×13	7020	4544	65
222	九州	日豊	快速	行橋→小倉	7:23~8:23	7×1	770	475	62
223	九州	鹿児島(3)	快速	八代→熊本	7:40~8:40	1×1	90	55	61
224	天竜浜名湖	天竜浜名湖		西掛川→掛川市役所前	7:04~8:04	1.3×3	480	250	52
225	叡山電鉄	叡山本線		元田中→出町柳	7:00~8:00	1.4×12	1605	756	47
226	阪堺電気軌道	阪堺		今船→今池	7:30~8:30	1×5	375	172	46
227	山万	ユーカリが丘		地区→ユーカリが丘センター	6:30~7:30	3×8	1120	359	32
227	東海交通事業	城北		比良→小田井	7:40~8:40	1×3	330	107	32
229	能勢電鉄	日生		日生中央→山下	6:45~7:45	6.3×7	5515	1611	29
230	長良川鉄道	越美南		前平公園→美濃太田	7:00~8:00	1.5×2	311	84	27
231	関東鉄道	竜ヶ崎		竜ヶ崎→佐貫	6:40~7:40	2×3	810	186	23

　 Tweet
Qiitaで続きを読む

投稿日：2021-02-27T21:42:49+09:00

Python DataFrame

初めに

月の最高気温の平均を使ってpandasのDataFrameで勉強したこと。属性について学んだ。

pandas バージョン
- 1.0.5

データは以下のサイトから取得した。

max_temperature.csv

年,1月,2月,3月,4月,5月,6月,7月,8月,9月,10月,11月,12月,年の値
1876,6.6,8.2,13.6,17.5,21.7,22.8,28.6,31.6,26.8,20.4,15.8,11.0,18.7
1877,8.8,8.8,11.3,19.1,21.5,26.0,31.0,30.5,25.8,21.3,14.4,10.2,19.1
1878,7.2,7.1,12.9,16.2,22.7,24.1,29.8,28.5,26.3,20.2,14.1,10.9,18.3
1879,9.0,10.9,13.0,17.1,21.9,25.2,30.4,31.1,25.4,19.4,15.7,14.0,19.4
1880,8.8,10.1,13.8,16.7,22.6,23.9,28.0,29.5,27.0,21.6,16.8,11.1,19.2
・・・

csvファイル読み込み

import pandas as pd

df = pd.read_csv('max_temperature.csv')
print(df)

        年    1月    2月    3月    4月    5月    6月    7月    8月    9月   10月   11月   12月   年の値
0    1876   6.6   8.2  13.6  17.5  21.7  22.8  28.6  31.6  26.8  20.4  15.8  11.0  18.7
1    1877   8.8   8.8  11.3  19.1  21.5  26.0  31.0  30.5  25.8  21.3  14.4  10.2  19.1
2    1878   7.2   7.1  12.9  16.2  22.7  24.1  29.8  28.5  26.3  20.2  14.1  10.9  18.3
3    1879   9.0  10.9  13.0  17.1  21.9  25.2  30.4  31.1  25.4  19.4  15.7  14.0  19.4
4    1880   8.8  10.1  13.8  16.7  22.6  23.9  28.0  29.5  27.0  21.6  16.8  11.1  19.2
..    ...   ...   ...   ...   ...   ...   ...   ...   ...   ...   ...   ...   ...   ...
140  2016  10.6  12.2  14.9  20.3  25.2  26.3  29.7  31.6  27.7  22.6  15.5  13.8  20.9
141  2017  10.8  12.1  13.4  19.9  25.1  26.4  31.8  30.4  26.8  20.1  16.6  11.1  20.4
142  2018   9.4  10.1  16.9  22.1  24.6  26.6  32.7  32.5  26.6  23.0  17.7  12.1  21.2
143  2019  10.3  11.6  15.4  19.0  25.3  25.8  27.5  32.8  29.4  23.3  17.7  12.6  20.9
144  2020  11.1  13.3  16.0  18.2  24.0  27.5  27.7  34.1  28.1  21.4  18.6  12.3  21.0

[145 rows x 14 columns]

csvファイル読み込み（インデックス指定あり）

df = pd.read_csv('max_temperature.csv', index_col='年')
print(df)

        1月    2月    3月    4月    5月    6月    7月    8月    9月   10月   11月   12月   年の値
年
1876   6.6   8.2  13.6  17.5  21.7  22.8  28.6  31.6  26.8  20.4  15.8  11.0  18.7
1877   8.8   8.8  11.3  19.1  21.5  26.0  31.0  30.5  25.8  21.3  14.4  10.2  19.1
1878   7.2   7.1  12.9  16.2  22.7  24.1  29.8  28.5  26.3  20.2  14.1  10.9  18.3
1879   9.0  10.9  13.0  17.1  21.9  25.2  30.4  31.1  25.4  19.4  15.7  14.0  19.4
1880   8.8  10.1  13.8  16.7  22.6  23.9  28.0  29.5  27.0  21.6  16.8  11.1  19.2
...    ...   ...   ...   ...   ...   ...   ...   ...   ...   ...   ...   ...   ...
2016  10.6  12.2  14.9  20.3  25.2  26.3  29.7  31.6  27.7  22.6  15.5  13.8  20.9
2017  10.8  12.1  13.4  19.9  25.1  26.4  31.8  30.4  26.8  20.1  16.6  11.1  20.4
2018   9.4  10.1  16.9  22.1  24.6  26.6  32.7  32.5  26.6  23.0  17.7  12.1  21.2
2019  10.3  11.6  15.4  19.0  25.3  25.8  27.5  32.8  29.4  23.3  17.7  12.6  20.9
2020  11.1  13.3  16.0  18.2  24.0  27.5  27.7  34.1  28.1  21.4  18.6  12.3  21.0

[145 rows x 13 columns]

属性

at

行/列の名前のペアで単一の値を返します。

print(df.at[1876, '1月'])

6.6

axes

行名と列名を唯一の要素として持っています。これらはこの順番で返されます。

print('axes')
print(df.axes)

[Int64Index([1876, 1877, 1878, 1879, 1880, 1881, 1882, 1883, 1884, 1885,
            ...
            2011, 2012, 2013, 2014, 2015, 2016, 2017, 2018, 2019, 2020],
           dtype='int64', name='年', length=145), Index(['1月', '2月', '3月', '4月', '5月', '6月', '7月', '8月', '9月', '10月', '11月',
       '12月', '年の値'],
      dtype='object')]

columns

DataFrameの列名を返します。

print(df.columns)

Index(['1月', '2月', '3月', '4月', '5月', '6月', '7月', '8月', '9月', '10月', '11月',
       '12月', '年の値'],
      dtype='object')

dtypes

各列のデータ型を持つ Series を返します。

print(df.dtypes)
print('type(df.dtypes): {}'.format(df.dtypes))

1月     float64
2月     float64
3月     float64
4月     float64
5月     float64
6月     float64
7月     float64
8月     float64
9月     float64
10月    float64
11月    float64
12月    float64
年の値    float64
dtype: object
type(df.dtypes): <class 'pandas.core.series.Series'>

empty

DataFrameが空かどうかを示します。

print(df.empty)

False

iat

整数のペアに対応した行/列ペアの単一の値を返します。

print(df.iat[0, 0])
print(df.iat[1, 2])

6.6
11.3

iloc

インデックスで指定された行を返します。

print(df.iloc[0])

1月      6.6
2月      8.2
3月     13.6
4月     17.5
5月     21.7
6月     22.8
7月     28.6
8月     31.6
9月     26.8
10月    20.4
11月    15.8
12月    11.0
年の値    18.7
Name: 1876, dtype: float64

index

行名を返します。

print(df.index)

Int64Index([1876, 1877, 1878, 1879, 1880, 1881, 1882, 1883, 1884, 1885,
            ...
            2011, 2012, 2013, 2014, 2015, 2016, 2017, 2018, 2019, 2020],
           dtype='int64', name='年', length=145)

loc

行/列名または真偽値を要素にもつ配列で指定したグループを返します。

print(df.loc[1876])

1月      6.6
2月      8.2
3月     13.6
4月     17.5
5月     21.7
6月     22.8
7月     28.6
8月     31.6
9月     26.8
10月    20.4
11月    15.8
12月    11.0
年の値    18.7
Name: 1876, dtype: float64

print(df.loc[[1876, 1877]])

       1月   2月    3月    4月    5月    6月    7月    8月    9月   10月   11月   12月   年の値
年
1876  6.6  8.2  13.6  17.5  21.7  22.8  28.6  31.6  26.8  20.4  15.8  11.0  18.7
1877  8.8  8.8  11.3  19.1  21.5  26.0  31.0  30.5  25.8  21.3  14.4  10.2  19.1

print(df.loc[1876, '1月'])

6.6

print(df.loc[df.index < 1880])

       1月    2月    3月    4月    5月    6月    7月    8月    9月   10月   11月   12月   年の値
年
1876  6.6   8.2  13.6  17.5  21.7  22.8  28.6  31.6  26.8  20.4  15.8  11.0  18.7
1877  8.8   8.8  11.3  19.1  21.5  26.0  31.0  30.5  25.8  21.3  14.4  10.2  19.1
1878  7.2   7.1  12.9  16.2  22.7  24.1  29.8  28.5  26.3  20.2  14.1  10.9  18.3
1879  9.0  10.9  13.0  17.1  21.9  25.2  30.4  31.1  25.4  19.4  15.7  14.0  19.4

df.loc[df.index < 1880] = 0
print(df.loc[df.index < 1880])

       1月   2月   3月   4月   5月   6月   7月   8月   9月  10月  11月  12月  年の値
年
1876  0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0
1877  0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0
1878  0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0
1879  0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0

print(df.loc[df.index < 1880, '1月'])

年
1876    6.6
1877    8.8
1878    7.2
1879    9.0
Name: 1月, dtype: float64

ndim

print(df.ndim)

shape

print(df.shape)

(145, 13)

size

145 × 13 = 1885

print(df.size)

values

DataFrameの値のみが返され、軸のラベルは削除されます。

print(df.values)

[[ 6.6  8.2 13.6 ... 15.8 11.  18.7]
 [ 8.8  8.8 11.3 ... 14.4 10.2 19.1]
 [ 7.2  7.1 12.9 ... 14.1 10.9 18.3]
 ...
 [ 9.4 10.1 16.9 ... 17.7 12.1 21.2]
 [10.3 11.6 15.4 ... 17.7 12.6 20.9]
 [11.1 13.3 16.  ... 18.6 12.3 21. ]]

参考記事

　 Tweet
Qiitaで続きを読む

投稿日：2021-02-27T21:42:49+09:00

Python DataFrame 属性について覚え書き

初めに

月の最高気温の平均を使ってpandasのDataFrameで勉強したこと。属性について学んだ。

pandas バージョン
- 1.0.5

データは以下のサイトから取得した。

max_temperature.csv

年,1月,2月,3月,4月,5月,6月,7月,8月,9月,10月,11月,12月,年の値
1876,6.6,8.2,13.6,17.5,21.7,22.8,28.6,31.6,26.8,20.4,15.8,11.0,18.7
1877,8.8,8.8,11.3,19.1,21.5,26.0,31.0,30.5,25.8,21.3,14.4,10.2,19.1
1878,7.2,7.1,12.9,16.2,22.7,24.1,29.8,28.5,26.3,20.2,14.1,10.9,18.3
1879,9.0,10.9,13.0,17.1,21.9,25.2,30.4,31.1,25.4,19.4,15.7,14.0,19.4
1880,8.8,10.1,13.8,16.7,22.6,23.9,28.0,29.5,27.0,21.6,16.8,11.1,19.2
・・・

csvファイル読み込み

import pandas as pd

df = pd.read_csv('max_temperature.csv')
print(df)

        年    1月    2月    3月    4月    5月    6月    7月    8月    9月   10月   11月   12月   年の値
0    1876   6.6   8.2  13.6  17.5  21.7  22.8  28.6  31.6  26.8  20.4  15.8  11.0  18.7
1    1877   8.8   8.8  11.3  19.1  21.5  26.0  31.0  30.5  25.8  21.3  14.4  10.2  19.1
2    1878   7.2   7.1  12.9  16.2  22.7  24.1  29.8  28.5  26.3  20.2  14.1  10.9  18.3
3    1879   9.0  10.9  13.0  17.1  21.9  25.2  30.4  31.1  25.4  19.4  15.7  14.0  19.4
4    1880   8.8  10.1  13.8  16.7  22.6  23.9  28.0  29.5  27.0  21.6  16.8  11.1  19.2
..    ...   ...   ...   ...   ...   ...   ...   ...   ...   ...   ...   ...   ...   ...
140  2016  10.6  12.2  14.9  20.3  25.2  26.3  29.7  31.6  27.7  22.6  15.5  13.8  20.9
141  2017  10.8  12.1  13.4  19.9  25.1  26.4  31.8  30.4  26.8  20.1  16.6  11.1  20.4
142  2018   9.4  10.1  16.9  22.1  24.6  26.6  32.7  32.5  26.6  23.0  17.7  12.1  21.2
143  2019  10.3  11.6  15.4  19.0  25.3  25.8  27.5  32.8  29.4  23.3  17.7  12.6  20.9
144  2020  11.1  13.3  16.0  18.2  24.0  27.5  27.7  34.1  28.1  21.4  18.6  12.3  21.0

[145 rows x 14 columns]

csvファイル読み込み（インデックス指定あり）

df = pd.read_csv('max_temperature.csv', index_col='年')
print(df)

        1月    2月    3月    4月    5月    6月    7月    8月    9月   10月   11月   12月   年の値
年
1876   6.6   8.2  13.6  17.5  21.7  22.8  28.6  31.6  26.8  20.4  15.8  11.0  18.7
1877   8.8   8.8  11.3  19.1  21.5  26.0  31.0  30.5  25.8  21.3  14.4  10.2  19.1
1878   7.2   7.1  12.9  16.2  22.7  24.1  29.8  28.5  26.3  20.2  14.1  10.9  18.3
1879   9.0  10.9  13.0  17.1  21.9  25.2  30.4  31.1  25.4  19.4  15.7  14.0  19.4
1880   8.8  10.1  13.8  16.7  22.6  23.9  28.0  29.5  27.0  21.6  16.8  11.1  19.2
...    ...   ...   ...   ...   ...   ...   ...   ...   ...   ...   ...   ...   ...
2016  10.6  12.2  14.9  20.3  25.2  26.3  29.7  31.6  27.7  22.6  15.5  13.8  20.9
2017  10.8  12.1  13.4  19.9  25.1  26.4  31.8  30.4  26.8  20.1  16.6  11.1  20.4
2018   9.4  10.1  16.9  22.1  24.6  26.6  32.7  32.5  26.6  23.0  17.7  12.1  21.2
2019  10.3  11.6  15.4  19.0  25.3  25.8  27.5  32.8  29.4  23.3  17.7  12.6  20.9
2020  11.1  13.3  16.0  18.2  24.0  27.5  27.7  34.1  28.1  21.4  18.6  12.3  21.0

[145 rows x 13 columns]

属性

at

行/列の名前のペアで単一の値を返します。

print(df.at[1876, '1月'])

6.6

axes

行名と列名を唯一の要素として持っています。これらはこの順番で返されます。

print('axes')
print(df.axes)

[Int64Index([1876, 1877, 1878, 1879, 1880, 1881, 1882, 1883, 1884, 1885,
            ...
            2011, 2012, 2013, 2014, 2015, 2016, 2017, 2018, 2019, 2020],
           dtype='int64', name='年', length=145), Index(['1月', '2月', '3月', '4月', '5月', '6月', '7月', '8月', '9月', '10月', '11月',
       '12月', '年の値'],
      dtype='object')]

columns

DataFrameの列名を返します。

print(df.columns)

Index(['1月', '2月', '3月', '4月', '5月', '6月', '7月', '8月', '9月', '10月', '11月',
       '12月', '年の値'],
      dtype='object')

dtypes

各列のデータ型を持つ Series を返します。

print(df.dtypes)
print('type(df.dtypes): {}'.format(df.dtypes))

1月     float64
2月     float64
3月     float64
4月     float64
5月     float64
6月     float64
7月     float64
8月     float64
9月     float64
10月    float64
11月    float64
12月    float64
年の値    float64
dtype: object
type(df.dtypes): <class 'pandas.core.series.Series'>

empty

DataFrameが空かどうかを示します。

print(df.empty)

False

iat

整数のペアに対応した行/列ペアの単一の値を返します。

print(df.iat[0, 0])
print(df.iat[1, 2])

6.6
11.3

iloc

インデックスで指定された行を返します。

print(df.iloc[0])

1月      6.6
2月      8.2
3月     13.6
4月     17.5
5月     21.7
6月     22.8
7月     28.6
8月     31.6
9月     26.8
10月    20.4
11月    15.8
12月    11.0
年の値    18.7
Name: 1876, dtype: float64

index

行名を返します。

print(df.index)

Int64Index([1876, 1877, 1878, 1879, 1880, 1881, 1882, 1883, 1884, 1885,
            ...
            2011, 2012, 2013, 2014, 2015, 2016, 2017, 2018, 2019, 2020],
           dtype='int64', name='年', length=145)

loc

行/列名または真偽値を要素にもつ配列で指定したグループを返します。

print(df.loc[1876])

1月      6.6
2月      8.2
3月     13.6
4月     17.5
5月     21.7
6月     22.8
7月     28.6
8月     31.6
9月     26.8
10月    20.4
11月    15.8
12月    11.0
年の値    18.7
Name: 1876, dtype: float64

print(df.loc[[1876, 1877]])

       1月   2月    3月    4月    5月    6月    7月    8月    9月   10月   11月   12月   年の値
年
1876  6.6  8.2  13.6  17.5  21.7  22.8  28.6  31.6  26.8  20.4  15.8  11.0  18.7
1877  8.8  8.8  11.3  19.1  21.5  26.0  31.0  30.5  25.8  21.3  14.4  10.2  19.1

print(df.loc[1876, '1月'])

6.6

print(df.loc[df.index < 1880])

       1月    2月    3月    4月    5月    6月    7月    8月    9月   10月   11月   12月   年の値
年
1876  6.6   8.2  13.6  17.5  21.7  22.8  28.6  31.6  26.8  20.4  15.8  11.0  18.7
1877  8.8   8.8  11.3  19.1  21.5  26.0  31.0  30.5  25.8  21.3  14.4  10.2  19.1
1878  7.2   7.1  12.9  16.2  22.7  24.1  29.8  28.5  26.3  20.2  14.1  10.9  18.3
1879  9.0  10.9  13.0  17.1  21.9  25.2  30.4  31.1  25.4  19.4  15.7  14.0  19.4

df.loc[df.index < 1880] = 0
print(df.loc[df.index < 1880])

       1月   2月   3月   4月   5月   6月   7月   8月   9月  10月  11月  12月  年の値
年
1876  0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0
1877  0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0
1878  0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0
1879  0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0

print(df.loc[df.index < 1880, '1月'])

年
1876    6.6
1877    8.8
1878    7.2
1879    9.0
Name: 1月, dtype: float64

ndim

print(df.ndim)

shape

print(df.shape)

(145, 13)

size

145 × 13 = 1885

print(df.size)

values

DataFrameの値のみが返され、軸のラベルは削除されます。

print(df.values)

[[ 6.6  8.2 13.6 ... 15.8 11.  18.7]
 [ 8.8  8.8 11.3 ... 14.4 10.2 19.1]
 [ 7.2  7.1 12.9 ... 14.1 10.9 18.3]
 ...
 [ 9.4 10.1 16.9 ... 17.7 12.1 21.2]
 [10.3 11.6 15.4 ... 17.7 12.6 20.9]
 [11.1 13.3 16.  ... 18.6 12.3 21. ]]

参考記事

　 Tweet
Qiitaで続きを読む

投稿日：2021-02-27T21:33:51+09:00

Pythonで学ぶ制御工学　第9弾：時間応答（2次遅れ系）

#Pythonで学ぶ制御工学< 時間応答（2次遅れ系） >

はじめに

基本的な制御工学をPythonで実装し，復習も兼ねて制御工学への理解をより深めることが目的である．
その第9弾として「時間応答（2次遅れ系）」を扱う．

時間応答（2次遅れ系）

時間応答の2次遅れ系について，図を使っての説明を以下に示す．

続いては，RLC回路を例に1次遅れ系を導出する．

このようにして，2次遅れ系の形にした時に，対応する部分がゲイン，固有角振動数および減衰係数となる．

実装

ここでは，適当なゲイン，固有角振動数および減衰係数を指定し，ステップ応答の図を出力するプログラムを実装する．なお，出力する図は4つあり，ステップ応答・減衰係数を変化させたステップ応答・固有角振動数を変化させたステップ応答・ゲインを変化させたステップ応答である．

ソースコード
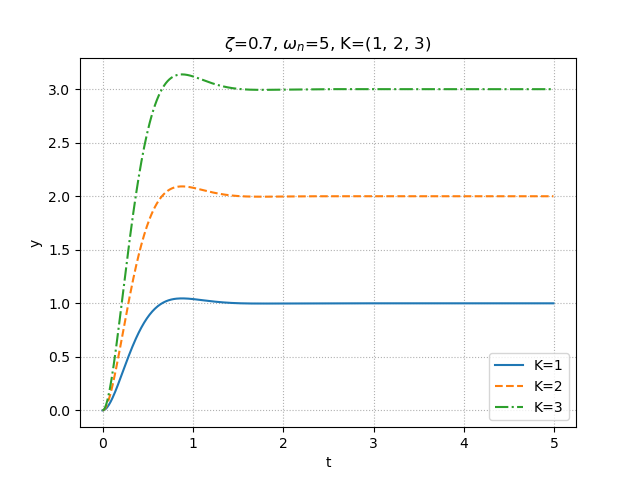
step.py
"""
2021/02/27
@Yuya Shimizu

時間応答（2次遅れ系）
"""

from control.matlab import *
import matplotlib.pyplot as plt
import numpy as np
from for_plot import *    #自分で定義した関数をインポート
#定義した関数について (https://qiita.com/Yuya-Shimizu/items/f811317d733ee3f45623)


##2次遅れ系のステップ応答

zeta, omega_n, K = 0.4, 5, 1   #減衰係数と固有角振動数とゲインの設定
P = tf([0, K*omega_n**2], [1, 2*zeta*omega_n, omega_n**2])  #2次遅れ系
y, t = step(P, np.arange(0, 5, 0.01))   #ステップ応答（0~5秒で，0.01刻み）

fig1, ax1 = plt.subplots()
ax1.plot(t, y)
plot_set(ax1, 't', 'y') #グリッドやラベルを与える関数(自作のfor_plotライブラリより)
plt.title(f"$\zeta$={zeta}, $\omega_n$={omega_n}, K={K}")
plt.show()


##2次遅れ系のステップ応答（減衰係数zetaを変化させる）
zeta = (-0.1, 0, 0.3, 1)   #4種類の減衰係数を用意
omega_n = 5
K = 1

#図示の準備
fig2, ax2 = plt.subplots()
LS = linestyle_generator()  #線種を与える関数(自作のfor_plotライブラリより)

for i in range(len(zeta)):
    P = tf([0, K*omega_n**2], [1, 2*zeta[i]*omega_n, omega_n**2])  #2次遅れ系
    y, t = step(P, np.arange(0, 3, 0.01))   #ステップ応答（0~3秒で，0.01刻み）
    ax2.plot(t, y, ls=next(LS), label=f"$\zeta$={zeta[i]}")

plot_set(ax2, 't', 'y', 'best')
plt.title(f"$\zeta$={zeta}, $\omega_n$={omega_n}, K={K}")
plt.show()


##2次遅れ系のステップ応答（固有角振動数omega_nを変化させる）
zeta = 0.7
omega_n = (1, 5, 10)   #3種類の固有角振動数を用意
K = 1

#図示の準備
fig3, ax3 = plt.subplots()
LS = linestyle_generator()  #線種を与える関数(自作のfor_plotライブラリより)

for i in range(len(omega_n)):
    P = tf([0, K*omega_n[i]**2], [1, 2*zeta*omega_n[i], omega_n[i]**2])  #2次遅れ系
    y, t = step(P, np.arange(0, 5, 0.01))   #ステップ応答（0~5秒で，0.01刻み）
    ax3.plot(t, y, ls=next(LS), label=f"$\omega_n$={omega_n[i]}")

plot_set(ax3, 't', 'y', 'best')
plt.title(f"$\zeta$={zeta}, $\omega_n$={omega_n}, K={K}")
plt.show()


##2次遅れ系のステップ応答（ゲインKを変化させる）
zeta = 0.7
omega_n = 5
K = (1, 2, 3)   #3種類のゲインを用意

#図示の準備
fig3, ax3 = plt.subplots()
LS = linestyle_generator()  #線種を与える関数(自作のfor_plotライブラリより)

for i in range(len(K)):
    P = tf([0, K[i]*omega_n**2], [1, 2*zeta*omega_n, omega_n**2])  #2次遅れ系
    y, t = step(P, np.arange(0, 5, 0.01))   #ステップ応答（0~5秒で，0.01刻み）
    ax3.plot(t, y, ls=next(LS), label=f"K={K[i]}")

plot_set(ax3, 't', 'y', 'best')
plt.title(f"$\zeta$={zeta}, $\omega_n$={omega_n}, K={K}")
plt.show()
出力①：ステップ応答

出力②：減衰係数を変化させたステップ応答

出力③：固有角振動数を変化させたステップ応答

出力④：ゲインを変化させたステップ応答

結果

はじめの説明でもあったように，減衰係数$\zeta$を負値にすると一定値に収束せず発散してしまい，0だと持続振動，0~1ならオーバーシュートが生じる．さらに詳しく述べると，小さな値ほど，そのオーバーシュートは大きくなる．1以上ならば，オーバーシュートは生じない．また，固有角振動数$\omega_n$は1次遅れ系のときの時定数と同様と説明したとおり，変化させることによって応答性が変わっていることが分かる．しかし，1次遅れ系の時定数と違って，固有角振動数は大きくなるほど，応答が速くなる．ゲインKは定常値を変化させる．

感想

前回に引き続き，今回は2次遅れ系ということで，固有角振動数や減衰係数，ゲインの意味と特徴を知り，また固有角振動数や減衰係数，ゲインが制御対象によって中身は変わるということを知った．またPythonでの実装を通して，グラフでの意味のとらえ方にも触れることができた．

参考文献

Pyhtonによる制御工学入門　　南祐樹　著　　オーム社

　 Tweet
Qiitaで続きを読む

投稿日：2021-02-27T20:30:22+09:00

AtCoder Beginner Contest 174 C問題

AtCoderを始めましたが、ABCのA・B問題はほぼ解ける、C問題は運が良ければ解けるというレベルです。
まずはC問題を難なく解けるというの目標に、まずは過去問のC問題までをどんどんやっていってます。

自力では解けなかった問題を、解説を見て、理解した内容の整理とその結果のコードを書いていきたいと思います。

問題

高橋君は K の倍数と 7 が好きです。
7,77,777,… という数列の中に初めて K の倍数が登場するのは何項目ですか？
存在しない場合は代わりに -1 を出力してください。

解けなかった原因

ループで末尾に７を追加して1桁増やしながら、Kで割れたら桁数を出力して終了させればいいかと思ったが、
以下がわからず行き詰まる。

存在しない場合の判定方法がわからない。
どこまで7を追加したらもう割り切れる数値が存在しないと判断できるのか

桁数がどんどん増えていった結果、例えばサンプル3だと10⁹⁹⁹⁹⁸²の桁数の数値をKで割ることになるのは、やめた方がいいのはわかるけど、
じゃあどうすればいいのか

解説を見て理解した内容

7が1桁増えるということ

・数値*10＋7
　7 → 77      = 7 * 10 + 7
　77 → 777  = 77 * 10 + 7
　777→7777 = 777 * 10 + 7

・Kで割った余りも余り*10＋7
　K=9
　　7 % K  = 7
　　77 % K = 5
　　→ (7 * 10 + 7) % K = 5
　　
　　777 % K = 3
　　→ (5 * 10 + 7) % K = 3

・余りの数の法則性
　同じ余りのパターンをぐるぐる回り、1順は最大K回
　K = 6
　7 % K     = 1
　77 % K    = 5
　777 % K   = 3
　7777 % K  = 1
　77777 % K = 5

ACしたコード
K = int(input().strip())

a = 7
for i in range(K) :
    b = a%K
    if b == 0 :
        print(i+1)
        exit()

    a = b*10+7
print(-1)

　 Tweet
Qiitaで続きを読む

投稿日：2021-02-27T20:22:36+09:00

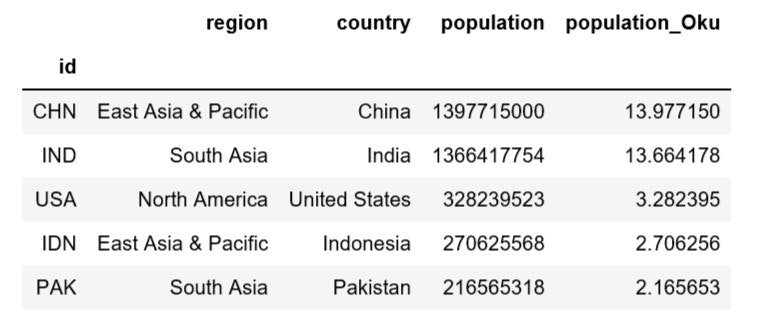
[Python] World Bankのdatasetから世界各国の人口データをdataframeにて入手する

時々、世界各国の人口データを使いたいときがあったのですが、Wikipediaなどからエクセルにコピーして読み込まないといけませんでした。

しかし、最近、World bankより人口を含んだデータセットが提供されていることが分かり、データフレームとして簡単に取り込むことができたので、自分の忘備録として記録に残します。

なお、私はWindows10でJupyterNotebookにてPythonを利用しています。

まず、pipでインストールします。
pip install world_bank_data --upgrade
次に、こちらのコードを実行します。
import pandas as pd
import world_bank_data as wb
pd.set_option('display.max_rows', 20)

# Same data set, indexed with the country code
population = wb.get_series('SP.POP.TOTL', id_or_value='id', simplify_index=True, mrv=1)
countries = wb.get_countries()

# Aggregate region, country and population
df = countries[['region', 'name']].rename(columns={'name': 'country'}).loc[countries.region != 'Aggregates']
df['population'] = population
df['population'] =df['population'].fillna(0).astype(int) #浮動小数点n表示になるのでintに変換
df['population_Oku'] = population/100000000
df.sort_values('population', ascending = False).head(5)
そうすると、このようなに世界の人口Top5を表示できます。

アジアの人口トップ10も出してみました。
df[df['region'].str.contains("East Asia")].sort_values('population', ascending = False).head(10)
こちらの英語のサイトを参考にしています。
ページの一番下のplottyで作ってあるチャートはなかなかいいなと思いました。

　 Tweet
Qiitaで続きを読む

投稿日：2021-02-27T20:12:18+09:00

The Iris Dataset いろいろ

機械学習で Python の練習をしたいなぁと思っていろいろ触りました。

環境

Colaboratory

Colaboratory とは
Colaboratory（略称: Colab）は、ブラウザから Python を記述、実行できるサービスです。次の特長を備えています。
・環境構築が不要
・GPU への無料アクセス
・簡単に共有

以前、機械学習の勉強をしたときは Jupyter Notebook を使ったので、今回は Colaboratory を使ってみることにしました。

教材

The Iris Dataset
3種類のアイリス（Setosa、Versicolour、Virginica）について、花びらやがく片の長さで分類していきます。

そのまま実行してみる
plot_iris_dataset.py
print(__doc__)


# Code source: Gaël Varoquaux
# Modified for documentation by Jaques Grobler
# License: BSD 3 clause

import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from sklearn import datasets
from sklearn.decomposition import PCA

# import some data to play with
iris = datasets.load_iris()
X = iris.data[:, :2]  # we only take the first two features.
y = iris.target

x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5

plt.figure(2, figsize=(8, 6))
plt.clf()

# Plot the training points
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Set1,
            edgecolor='k')
plt.xlabel('Sepal length')
plt.ylabel('Sepal width')

plt.xlim(x_min, x_max)
plt.ylim(y_min, y_max)
plt.xticks(())
plt.yticks(())

# To getter a better understanding of interaction of the dimensions
# plot the first three PCA dimensions
fig = plt.figure(1, figsize=(8, 6))
ax = Axes3D(fig, elev=-150, azim=110)
X_reduced = PCA(n_components=3).fit_transform(iris.data)
ax.scatter(X_reduced[:, 0], X_reduced[:, 1], X_reduced[:, 2], c=y,
           cmap=plt.cm.Set1, edgecolor='k', s=40)
ax.set_title("First three PCA directions")
ax.set_xlabel("1st eigenvector")
ax.w_xaxis.set_ticklabels([])
ax.set_ylabel("2nd eigenvector")
ax.w_yaxis.set_ticklabels([])
ax.set_zlabel("3rd eigenvector")
ax.w_zaxis.set_ticklabels([])

plt.show()
今回は上部分だけ見てみます。
(3Dのやつは、なんかいじっても見づらそうなのでいったん見ない)
plot_iris_dataset.py
print(__doc__)


# Code source: Gaël Varoquaux
# Modified for documentation by Jaques Grobler
# License: BSD 3 clause

import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from sklearn import datasets
from sklearn.decomposition import PCA

# import some data to play with
iris = datasets.load_iris()
X = iris.data[:, :2]  # we only take the first two features.
y = iris.target

x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5

plt.figure(2, figsize=(8, 6))
plt.clf()

# Plot the training points
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Set1,
            edgecolor='k')
plt.xlabel('Sepal length')
plt.ylabel('Sepal width')

plt.xlim(x_min, x_max)
plt.ylim(y_min, y_max)
plt.xticks(())
plt.yticks(())

plt.show()
データセットを変えてみる

まずは中身の確認
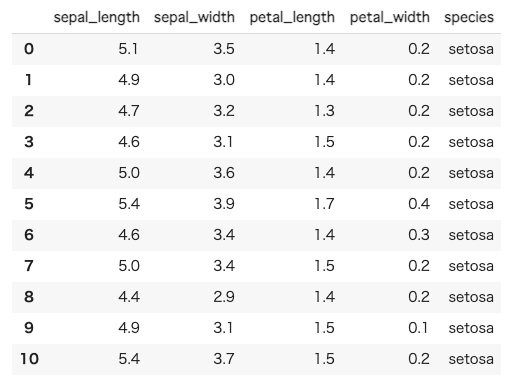
import seaborn as sns
iris = sns.load_dataset("iris") 
# ちなみにこのirisはpandasのdataframeです。
iris.head(20)
X = iris.data[:, :2] の部分を X = iris.data[:, 2:4]に変える。

ラベルも Sepal から Petal へ変える。
# import some data to play with
iris = datasets.load_iris()
X = iris.data[:, 2:4]  # we only take the first two features.
y = iris.target
plt.xlabel('Petal length')
plt.ylabel('Petal width')
iris.data[:, 2:4]

NumPy 入門 #多次元配列の要素を選択する

NumPy 独自の記法

行列があった場合
array([[1, 2, 3],
       [4, 5, 6],
       [7, 8, 9]])
1列目の値 [1, 4, 7] をすべて取得したい場合は
x[:, 0]
2列目から3列目の値をすべて取得したい場合は
x[:, 1:2]
グラフの表示を変えてみる

matplotlib.pyplot.scatter — Matplotlib 3.3.4.post2472+g1ec609a3f documentation
# Plot the training points
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Set1, marker="*",
            edgecolor='')
お星さまになった

感想

Colaboratory が思いのほか良かったです。
とりあえず実行してグラフィックで結果を見たい場合に便利だなぁと思いました。

　 Tweet
Qiitaで続きを読む

投稿日：2021-02-27T17:15:37+09:00

【投資】相場の勢いを表すストキャスティクスをデータ分析して分かったこと

＜あらすじ＞
「買われすぎ」や「売られすぎ」といった相場の勢いを表す過熱感
その過熱感を数値で判断できるストキャスティクスについて検証しました。

TOPIX500銘柄の過去5年分のデータを使って
ストキャスティクスの買いサインの数日後に、株価が上がっているのかを調査します。

＜結論＞
・市場の過熱感を知りたいときはストキャスティクスよりRSIを使うべきである

きっかけ

「買われすぎ」や「売られすぎ」といった相場の勢いを表す過熱感
前回、その過熱感を数値で判断できるRSIについて検証しました。

投資タイミングを判断するときに必ず見てほしい指標RSIをデータ分析

【結論】
・RSIの使い方次第で確実に勝率を上げられる
・投資タイミングの判断材料として有効である

RSIの検証結果が予想以上の成績であったため
同じ過熱感を表す指標として有名なストキャスティクスについても検証してみたいと思います。

※この記事だけでも内容は完結していますが、先にRSIの記事を読んでいただいた方が理解しやすいかもです

ストキャスティクス（stochastics）

ストキャスティクスは一定期間の一番高かった値段と安かった値段の値幅に対して、現在の株価がどのくらいの位置いるのかということを数値化したもので、「売られすぎ」なのか「買われすぎ」なのかを知りたいときに役立ちます。

過熱感を表すテクニカル指標として、RSIと並んで個人投資家に人気があります。

ストキャスティクスの使い方を簡単に紹介します。
「%K」「%D」「slow%D」の3つのラインを組み合わせて使用するテクニカル分析で
それぞれの算出方法は以下の通りです。（$n$は5, 9, 14が使用されることが多い）
▼ストキャスティクの算出方法

ここで重要なことは
・3つのラインは全て一定期間の一番高かった株価と一番安かった株価を使って、現在の株価の過熱感を表す
・3つのラインは全て0～100％の値をとり、一般的に30％以下が売られすぎ、70％以上が買われすぎ
・株価への反応の速さは「%K > %D > slow%D」の順である

これらの3つのラインを個別で使用する場合や、2つを組み合わせて使用する場合があり
%Kと%Dを使用するストキャスティクスを「ファストストキャスティクス」
%Dとslow%Dを使用するストキャスティクスを「スローストキャスティクス」といいます。
「ファスト」は株価の動きに敏感に反応し、「スロー」は反応は遅いがだましは少なくなります。
自分の投資スタイルや銘柄に合わせて使い分ける必要があります。

ストキャスティクスは様々な使い方があるため、少し難易度が高いです。
そこで最も良い使い方を見つけるべく検証したいと思います。

買いサイン

ストキャスティクスの買いサインは、3つのラインのうち1つだけを使う場合と2つを組み合わせて使用する場合で異なります。

1つのライン：基準値を下から上に突き抜けたとき
2つのライン：基準値以下でゴールデンクロスしたとき

▼ストキャスティクスの買いサイン（基準値=30%の場合）

1つだけを使う場合は「%K」「%D」「slow%D」の3種類
2つを組み合わせて使用する場合は「%Kと%D」「%Dとslow%D」の2種類
が、使用されます。

一般的に30％以下が売られすぎと言われるため、今回の検証では基準値に30%,20%,10％を使用します。

検証方法

大まかな流れはTOPIX500銘柄を対象に5年分のデータからストキャスティクスの買いサインを見つけ、その数日後に株価が上がっているのかを調査します。また、買いサインの基準値を変化させて結果を比較します。

買いサインから何％株価が変動したのかを表す、株価の変化率（変動率）の分布も求めました。

一旦、検証パラメータを羅列しますが、後ほど例を使って説明します。
また、検証プログラムは記事の最後に記載します。

【検証期間】
2015年1月1日～2021年2月12日の約5年間

【対象銘柄】
TOPIX500銘柄

【ストキャスティクスの設定期間】
1. 5日
2. 9日（最も使われる）
3. 14日

【株価の上昇を確認する日】
1. 1日後
2. 3日後
3. 5日後
4. 10日後

【基準値】
＜基準値を下から上に突き抜けたとき＞
1. 30％
2. 20％
3. 10％
＜基準値以下でゴールデンクロスしたとき＞
1. 30％
2. 20％
3. 10％

例

ストキャスティクスの買いサインが生じた日から見て、数日後に上昇してるかを確認します。
▼検証方法の概要（基準値：30％を下から上に突き抜けたとき）

▼検証方法の概要（基準値：30％以下でゴールデンクロスしたとき）

上の例では基準値を30%としましたが、基準値を30,20,10％の3通りで検証します。
前回検証したRSIでは基準値を30,25,20％の3通りで検証しましたが、ストキャスティクスは比較的簡単に30%以下になるため基準値を下げました。

実際にトヨタ自動車のデータを使って、買いサインの基準値を20％とした場合を説明します。
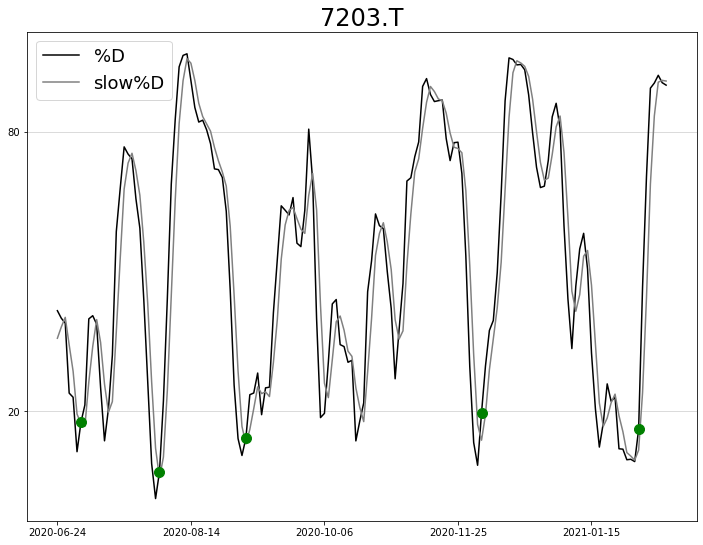
まず、1つのラインを使用した買いサイン「基準値=20%を下から上に突き抜けたとき」の例です。（slow%Dを使用）
見やすさのために2019年1月～2021年2月の約2年分のデータを用いました。
青丸はストキャスティクスのslow%Dが20%を下から上に突き抜けた日を示しています。
この時の株価から1,3,5,10日後に上がっているのかを調べます。
▼ストキャスティクス「slow%D」（設定期間：14日,基準値：20％）の買いサイン

次に、2つのラインを使用した買いサイン「基準値=20%以下でゴールデンクロスしたとき」の例です。（%Dとslow%Dを使用）
見やすさのために2020年6月～2021年2月の約8ヵ月分のデータを用いました。
緑丸はストキャスティクスの%Dとslow%Dが20%以下でゴールデンクロスした日を示しています。
※ ゴールデンクロスの前後で%Dとslow%Dがともに基準値以下のタイミングのみを選択
この時の株価から1,3,5,10日後に上がっているのかを調べます。
▼ストキャスティクス「%Dとslow%D」（設定期間：14日,基準値：20％）の買いサイン

また、それぞれ買いサインから1,3,5,10日後に株価がどれだけ変動したか（変化率）を求め、分布図も作成します。

検証結果

ここでは1,3,5,10日後に上昇している確率を基準値30,10％の2通りと、分布図を一部記載します。
残りの結果は記事の最後にまとめて記載します。
使用するデータは前述の通りTOPIX500銘柄の5年間です。

【ストキャスティクスの設定期間】
1. 5日
2. 9日（最も使われる）
3. 14日

【基準値】
＜基準値を下から上に突き抜けたとき＞
1. 30％
2. 10％
＜基準値以下でゴールデンクロスしたとき＞
1. 30％
2. 10％

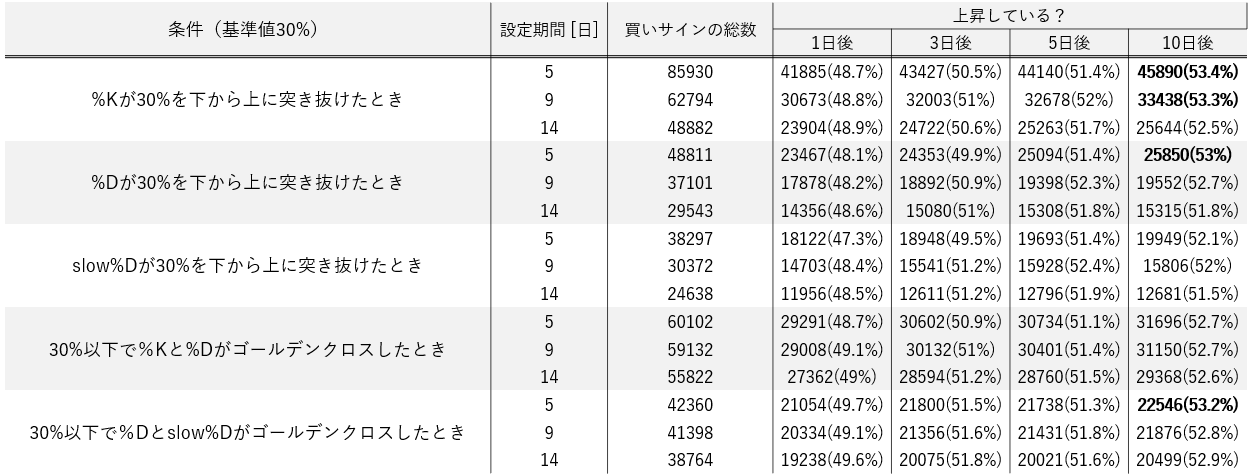
早速ですが結果を表にまとめました。
上昇確率が53％以上の場合に太字となっています。
▼基準値が30%のとき

▼基準値が10%のとき

【表からわかること】
・設定期間によるが買いサインの総数が多い（RSIと比較すると同様の条件で5倍程度）
・上昇確率が50%を下回る場合も多い
・基準値を小さく（条件を厳しく）しても結果が明確に上昇しない
・ラインを1つ使用した場合も2つ使用した場合もどちらの方が良いとは言えない

次に株価の変化率（買いサインから何％株価が変動したか）の分布をいくつか示します。
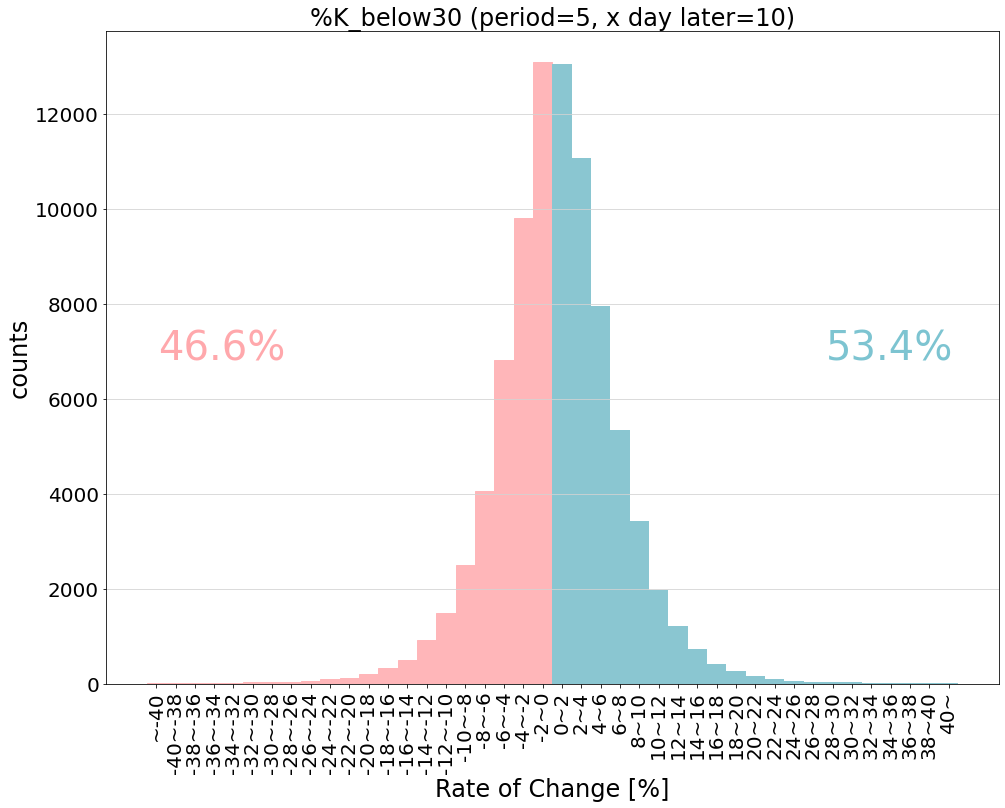
青が上昇，赤が下落を表します。
以下は上昇確率が54%で最も成績が良い条件での変化率分布です。
▼3日後の株価の変化率分布（設定期間：5日, 10%以下で％Dとslow%Dがゴールデンクロスしたとき）

以下は１つのラインを使った場合で最も成績が良い条件での変化率分布です。
▼10日後の株価の変化率分布（設定期間：5日, %Kが30%を下から上に突き抜けたとき）

【表からわかること】
・どちらも少しだけではあるが、山が右にずれている
・「-2~0」と「0~2」の数は同程度だが「-10~-2」よりも「2~10」の数が少しづつ多い
・10%以上の上昇など大きな上昇は見込めない

ストキャスティクスの結果は前回検証したRSIよりも明らかに悪いです。(RSIでは上昇確率55%以上が多数)
同じ過熱感を表す指標ですが、算出方法が異なると勝率も大きく変わります。

まとめ

「買われすぎ」や「売られすぎ」といった相場の勢いを表す過熱感
その過熱感を数値で判断できるストキャスティクスについて検証しました。
ストキャスティクスは一定期間の一番高かった値段と安かった値段の値幅に対して、現在の株価がどのくらいの位置いるのかで数値化します。
株価への反応の速さが異なる3つのラインの買いサインを検証したところ、一部の条件で数日後の上昇確率が53%を超える買いサインが存在しました。しかし、この結果は同じ過熱感を表すRSIと比べると良い結果とは言えません。

＜ストキャスティクスとRSIの算出方法の違い＞
ストキャスティクス：ある期間の株価の最高値と最安値から算出
RSI：ある期間の株価の上がり幅と下がり幅から算出

この算出方法の違いにより、同じ設定期間でも算出に使う株価のデータ数が異なります。
＜例：設定期間が9日＞
ストキャスティクスは9日間の株価のうち最高値，最安値，現在の株価の3日分です。（9分の3）
RSIは9日間の株価のうち全ての日にちの株価から算出した値動き幅を使います。（9分の9）

この違いが検証結果の違いに影響を与えているのではないかと考えます。
RSIでは設定期間を長くすると動きが滑らかになるため、だましの数が減り上昇確率が上がりやすいです。
一方でストキャスティクスは設定期間を長くしても、その傾向が見られません。
これはストキャスティクスの場合、設定期間を長くすると使用する株価の割合が小さくなるためと考えられます。

以上より、「市場の過熱感を知りたいときはストキャスティクスよりRSIを使うべき」と結論付けます。

今回の検証ではストキャスティクスのシンプルな買いサインについて検証しましたが、ひょっとするともっと有効な買いサインの判断方法が存在するのかもしれません。ただ、初心者にはRSIの方が使いやすいとはっきり言えます。

次は

「RSI」「ストキャスティクス」と検証しましたが、過熱感を表す有名な指標として「移動平均線乖離率」があります。
次回はこの移動平均線乖離率について検証したいと思います。
また、いずれは過熱感を表す指標とMACDなどのトレンドを表すテクニカル分析を組み合わせた検証も考えています。

＜Youtube＞
分析動画を投稿しています。
検証結果を多くの方に見てもらえると嬉しいです。
https://www.youtube.com/channel/UCKM_EhOxMfXkcLFOwAdEKcQ
↑チャンネル登録していただけますと励みになります。

＜過去記事＞
・日経225全銘柄の投資効率を検証
・【5年分データ分析】ゴールデンクロスの数日後に株価は上がっているのか
・【5年分データ分析】MACDの買いサインから上がる確率を検証しました
・コロナ・ショック後から株価上昇し続けている１５銘柄

検証結果の追加

数が多く全てを載せきれないため
基準値20%での1,3,5,10日後に上昇している確率と以下の変化率の分布を記載します。

【検証期間】
2015年1月1日～2021年2月12日の約5年間

【対象銘柄】
TOPIX500銘柄

【ストキャスティクスの設定期間】
1. 5日
2. 9日（最も使われる）
3. 14日

【株価の上昇を確認する日】
1. 1日後
2. 3日後
3. 5日後
4. 10日後

【基準値】
＜基準値を下から上に突き抜けたとき＞
1. 30％
＜基準値以下でゴールデンクロスしたとき＞
1. 10％

▼基準値が20%のとき

▼%Kが基準値30%を下から上に突き抜けたとき（設定期間：5，9，14日）

▼%Dとslow%Dが基準値10%以下でゴールデンクロスしたとき（設定期間：5，9，14日）

検証プログラム

プログラム内で使用している自作の関数や株価データの取得方法は以下の記事をご参照ください。（執筆中）
・株分析ツールの使い方（備忘録）
import trade_package as tp # 株価分析用に自作した関数をまとめたもの
import pandas as pd
import matplotlib.pyplot as plt
from math import ceil 

# 銘柄コードの読み込み
stocks = tp.get.topix500()

# 条件と保存ファイル名の設定
point = 10
line = "slowk"
line2 = "slowd"
case = "%D%slowD_below"+str(point)

# resultデータフレーム作成
day = [1,3,5,10]  # 株価を確認する日（〇日後の株価）
col=["buy_sign_count"]
period = [5,9,14]   # 設定期間
for d in day:
    col.append("roc_d"+str(d)+"_plus")
result = pd.DataFrame(data=0,index=range(len(period)),columns=col)
# rocマップのデータフレーム
col=[]
for p in period:
    for d in day:
        col.append("roc_p"+str(p)+"_d"+str(d))
index=[]
# 分布図の設定(-40~40%を2%間隔)
for i in range(-42,42,2):
    if(i==40):
        index.append(str(i)+"~")
    elif(i==-42):
        index.append("~"+str(i+2))
    else:
        index.append(str(i)+"~"+str(i+2))
roc_map = pd.DataFrame(data=0,index=index,columns=col)

for code in stocks.code:
    print(code)
    # 用意した株価データの読み込み
    read_data = tp.get.price(code)

    for p in range(len(period)):
        data = read_data.copy()

        # ファーストストキャスティクス
        tp.tech.stochf(data,K=period[p],D=3)
        # スローストキャスティクス
        tp.tech.stoch(data,fastK=period[p],slowK=3,slowD=3)
        data["buy_sign"] = False

        # タイミングを取得
        for i in range(len(data.index)-1):
            # 下から上へ突破したとき
            # if(data[line].iat[i]<point and data[line].iat[i+1]>=point):
            #     data["buy_sign"].iat[i+1] = True
            # ゴールデンクロス
            if(data[line].iat[i]<point and data[line2].iat[i]<point \
                and data[line].iat[i]<data[line2].iat[i] and data[line].iat[i+1]>data[line2].iat[i+1]):
                data["buy_sign"].iat[i+1] = True

        # 〇日後に上昇しているか確認    
        for bs in data.index[data.buy_sign]:
            for d in day:
                if(len(data.Close[:bs])+d<=len(data.Close)):
                    data.at[bs,"roc_d"+str(d)] = (data.Close[len(data.Close[:bs])+d-1]-data.Close[bs])/data.Close[bs]*100
                else:
                    # 〇日後の株価がない場合は最新の株価
                    data.at[bs,"roc_d"+str(d)] = (data.Close[-1]-data.Close[bs])/data.Close[bs]*100
                # 分布に振り分け
                roc_index = 20+ceil(data.at[bs,"roc_d"+str(d)]/2)
                if(roc_index<0):
                    roc_index=0
                elif(roc_index>41):
                    roc_index=41   
                roc_map.at[index[roc_index],"roc_p"+str(period[p])+"_d"+str(d)] += 1


# 上昇した数をカウント/roc分布を画像出力
for p in range(len(period)):
    result["buy_sign_count"].iat[p] = sum(roc_map.iloc[:,p*len(day)])
    for d in range(len(day)):
            result["roc_d"+str(day[d])+"_plus"].iat[p]=sum(roc_map.iloc[21:,p*len(day)+d])

            # roc分布を画像出力
            fig = plt.figure(figsize=(16, 12))
            ax = fig.add_subplot(111)
            bar_list = ax.bar(roc_map.index,roc_map["roc_p"+str(period[p])+"_d"+str(day[d])], width=1, color="#8ac6d1")
            [bar_list[i].set_color("#ffb6b9") for i in range(21)]
            ax.set_xticklabels(roc_map.index,rotation=90)
            ax.tick_params(labelsize=20)
            ax.grid(axis="y",c="lightgray")
            title = case+" (period="+str(period[p])+", x day later="+str(day[d])+")"
            ax.set_title(title,fontsize=24)
            ax.set_xlabel("Rate of Change [%]", fontsize=24)
            ax.set_ylabel("counts", fontsize=24)
            win = round(result.at[p,"roc_d"+str(day[d])+"_plus"]/result.at[p,"buy_sign_count"]*100,1)
            fig.text(0.75,0.5,"{:}%".format(win),size=40,color="#7dc4d1")
            fig.text(0.17,0.5,"{:}%".format(100-win),size=40,color="#ffa8ac")
            fig.savefig(title+".png", bbox_inches='tight')

print(result)

　 Tweet
Qiitaで続きを読む

投稿日：2021-02-27T17:09:06+09:00

【ワーシャルフロイド法】数学一切できない文系Fラン卒の俺が全点対最短経路問題(APSP)系のコードを解説する

まえがき

皆さん、競技プログラミングをはじめて素数だとか約数だとか基本的な数字を出すためのロジックを勉強された後は、やっぱりいろんなかっこいい名前の付いた手法を勉強したくなりますよね。
そしてやっぱり最短経路問題とか、迷路とか、なんかかっこいい問題やりたいですよね。
でもなんかダイクストラ法とか難しそうだしなぁとか、DPってなんなんだろうなぁ、グラフ理論ってなんなんだよぉということに頭を悩ませてやる気がなくなってしまうこともあるかと思います。

というわけで、今回はアホ糞簡単なロジックで全点対最短経路問題が解けてしまうワーシャルフロイド法について解説していこうと思います。

今回は専門用語や前提知識がめっちゃ多くて難しかったですが、参考資料などは読まなくても理解できるよう勧めていければと思います。

最短経路問題とは

グラフ理論における最短経路問題（さいたんけいろもんだい、英: shortest path problem）とは、重み付きグラフの与えられた2つのノード間を結ぶ経路の中で、重みが最小の経路を求める最適化問題である。

まぁよくわからないですよね。
グラフ理論についてはあとで軽く触れます。（というか軽くしかしらない）

簡単に言うと、いくつかの町とそれを結ぶ道があって、どの道を通ると何分かかるよというコストが与えられているわけです。
場合によっては道を通れる方向に制限があったり、時刻に制限があったり色々する中で、最短の経路を求めましょうという問題の総称がグラフ理論における最短経路問題ということです。

最短経路問題の種類

2頂点対最短経路問題

特定の2つのノード間の最短経路問題。一般的に単一始点最短経路問題のアルゴリズムを使用する。

単一始点最短経路問題 (SSSP：Single Source Shortest Path)

特定の1つのノードから他の全ノードとの間の最短経路問題。この問題を解くアルゴリズムとしては、ダイクストラ法やベルマン-フォード法がよく知られている。

全点対最短経路問題

グラフ内のあらゆる2ノードの組み合わせについての最短経路問題。この問題を解くアルゴリズムとしては、ワーシャル-フロイド法が知られている。

本当はダイクストラ法とワーシャルフロイド法を両方紹介できたらよかったのですが、ワーシャルフロイド法を理解するのに思った以上に時間がかかってしまったので今回はワーシャルフロイド法のみの解説となります。

全点対最短経路問題に対応しているので当然単一始点最短経路問題も解けるのですが、アルゴリズムの実行に時間がかかるのでTLEになったりなんなりと、結局単一始点最短経路問題はそれはそれで勉強する必要があることに注意してください。

グラフ理論とは

グラフ理論

グラフは頂点と辺から構成され、辺は二つの頂点を結ぶものです。
つまり、○をいくつか書いて、それを線で結んだ物を想像してください。
もっと言えば、複数の場所と、それをつなげる道でできた図と考えていただければ問題ありません。

グラフはG=(V,E)として表現されます（まだ全然わからなくてOK）
V = {v, b, x, z, a, y }
E = { (b,y), (b,y), (y,v), (z,a), (x,x), (b,x), (x,v), (a,z) }
G = (V, E)

Vは頂点の集合体であり、有限集合（元の数が有限で0~nまでの数字って感じ）です。
要はすべての行きたい場所の集合で、行きたい場所は無限にあっちゃだめということです。
集合論

EはVの二項関係です。つまり、Vの要素を２つ並べたものです。どの場所からどの場所へ移動できるかということです。
二項関係

つまり、G（グラフ）はすべての頂点Vと、どの頂点からどの頂点へ移動できるかのEで表されるということです。
このとき、Vを頂点（ノード）集合と呼び、Eを辺やエッジと呼びます。

グラフの種類

有向グラフ

経路として移動できる方向が限られているものです。東京から大阪にはいけるが、大阪から東京にはいけないというイメージです。
uからvにしか行けないので、(u,v)だけをEに渡すことで表現できます。

無向グラフ

経路として移動できる方向が限られていないものです。東京と大阪を行き来できることをイメージしてください。
無向グラフでは (u,v)と(v,u)両方をEに渡しておけば表現できます。
もちろん(u,v)だけで表現してもいいですが、有向グラフで実装して両方向をEとして与えるほうが実装を共通化しやすいということですね。

ワーシャルフロイド法とは

全点対最短経路問題において、有向無向グラフどちらでも使える手法です。

事前準備として、ある頂点iから頂点jへ移動するときにかかるコストを事前に用意しておきます。
つまり、グラフのEを事前に用意しておきます。

それをもとにある頂点から移動可能なすべての頂点への移動コストを２次元リストで表現するということを実装していきます。
以下記事の「実際に確かめてみよう」の章にある表を作るイメージですね。
こちらの記事も参考になるかと思いますので良ければご覧ください。
https://qiita.com/okaryo/items/8e6cd73f8a676b7a5d75

つまり、すべてのiから移動可能なすべてのjへのコストを全部出したリストを作るということです。
全探索なので計算量が多いですが、あらゆる最短経路問題に対応できます。（速度が必要な時は、都度最適なアルゴリズムを使う必要があります。）

DP 動的計画法とは

一発で全体最適な答えが出るわけではない問題で、局所的最適解を積み上げて全体最適となる答えを求めに行く手法のこと。
ワーシャルフロイド法もDPの一種。
ナップザック問題や、迷路などでも使われる。

実装解説

以下の問題を例として解説します。
Python3だとTLEして、PyPyだとACしたので注意してください。
遅い言語だと通らないです。
ABC012 D https://atcoder.jp/contests/abc012/tasks/abc012_4
#n = 頂点の数
#m = 経路の数
n,m=map(int,input().split())

#float("inf")は無限を表現できる。
#到達不可能なものはコスト∞として評価する。
ans=float("inf") 

#まず二次元のリストを作り、全辺における移動コストの表を作成する。
#つまりグラフにおけるEの値だけコストを埋めたリストを作る。
#それ以外の移動コスト（頂点の中継が必要なもの）についてはいったん到達不可能=∞とする。
#コストはaからbに移動する時のものなので、インデックスをd[a][b]と表現するため二次元になっている。

#頂点の数nだけ、無限を入れたlistをn個つくる。 n=3なら[inf,infi,inf],[inf,infi,inf],[inf,infi,inf]
#無限になっているのは、コストの最大値が1000なので経路が存在しない場合はそれより大きい数字にしたいが、最大コストを求めてそれ以上にするのが面倒なので∞にしている。
d=[[float("inf") for i in range(n)] for i in range(n)] 


#まず最初に、同じ頂点同士の移動はコストがかからないので0とする。
#aからのa bからのbなど。
for i in range(n):
    d[i][i]=0

#つぎに、Eとして与えられている隣接する頂点の移動コストを入力する。
#移動経路を一つずつ取り出して、コストを入力していく。
for i in range(m):
    #バス停a,bとコストtをうけとり、バス停の数字に対応するインデックスにコストを突っ込んでいく。
    #以後、aからbへの移動コストが欲しい場合はd[a][b]で取り出すことができるようになる。
    #経路が存在しない場合、dを初期化した時点で無限が入っているので、コストは無限となる。
    #このとき、無向グラフであればd[a][b]もd[b][a]も入力するし、有向グラフであれば片方だけでよい。
    #今回は双方向の移動が可能なので、無向グラフとして実装する。
    a,b,t=map(int,input().split())
    d[a-1][b-1]=t
    d[b-1][a-1]=t

#ワーシャルフロイド法により、上で作った「隣接する頂点同士の移動コストの表」から、「全始点から全終点までの経路コストの表」を作成する。
#これもdd[a][b]の形でアクセスしたいので、２次元配列になる 例 [[0, 12, 26, 27, 18], [12, 0, 14, 21, 30], [26, 14, 0, 7, 16], [27, 21, 7, 0, 9], [18, 30, 16, 9, 0]]
#コスト0は同じ頂点同士の移動コスト。
#この関数は解説が長くなるので後述する。
warshall_floyd(d)

#最後に最悪のケースを想定しないといけないので、
#各頂点を始点としたとき最も数字が大きい値（最悪のケース）をすべて取り出し、これが最も小さい値を答えとする。
for i in range(n):
  ans=min(ans,max(d[i]))

print(ans)
以下ワーシャルフロイド関数
引用元　Pythonで競技プログラミング〜基本的なアルゴリズム〜
def warshall_floyd(d):
  for k in range(n):# 中継点
    for i in range(n):# 始点
      for j in range(n):# 終点
        # 繰り返し見ていくので、現時点の i から j へ向かうコスト と 今検証している k を経由して j に向かうコスト の小さい方を i から j へ向かうコストとして登録する
            d[i][j] = min(d[i][j],d[i][k] + d[k][j])
  return d

#この関数がワーシャルフロイド法。
#移動コスト一覧表dと、頂点の数nがあれば動作する。

#iとjが始点と終点で、それをすべてのkを通る形ですべての始点と終点を全検索しているのですべての経路を検証網羅している。
#この時、k（中継点）を使わないなら d[i][j] そのまま、k を使うとd[i][k] + d[k][j] が最短となる。
#（ぜんぜんわからん）

#私はこれだと理解できなかったので、もう少し解説する。

#【i,jを求めるタイミングで中継点って常に最短になるの？】
#疑問をもう少しちゃんと表現します。
# 例えばABCDEの頂点があり、DからしかアクセスできないEがあり、AEを求めたいとします
# 始点A 中継点D 終点E を求めるタイミングで、AD=A→C→Dが最適であるとわかっていない場合、AからDに隣接していないのでたどり着けず中継点= DのときのAE=∞になります。
# 始点A　中継点B　終点Eのときには、ABが隣接しているため移動できますが、BE=B→C→D→Eが最適であるとわかっていない場合Eにたどり着けないので中継点= BのときにAE = ∞になります
# 始点A　中継点C　終点EのときにもACは移動できますが、CE=C→D→Eが最適であるとわかっていない場合にたどり着けないので中継点= CのときにAE = ∞になります
# 当然AやEが中継点でも同様です。
# 上記の検証の後にBEやAD、CEが求められたとしても、もう一度同じ中継点でAEを評価するタイミングが無ければ答えを出すことができません。
# AEのときにはわからなくても一周してEAの時にわかるかもしれないと思うかもしれませんが、有向グラフの場合復路が許容されないので判別することができない可能性があります。
#
#解説　https://www.slideshare.net/chokudai/abc012　スライド44～
#スライドの例にあわせて、AB（最短経路A→C→F→D→E→B）を求めたいとする。
#まず、ワーシャルフロイドはすべての中継点を起点として、すべての始点終点を全探索する実装である
#ABの最短経路を探索する場合、中継点A~Fそれぞれを経由する場合のABを毎回確認している。Aを経由するAB Bを経由するAB Cを経由するAB...
#当然最初は中継点の最短距離がでていないため、AからBにたどり着くことすらできない。
#ただし、ABの最短距離において中継点はCFDEがあるわけなので、
#ABの最短経路を確認するには、一番最後に見る中継点FのABを見るときに、それ以外の経路が最短になっていれば問題ない。
#では、中継点Fを終点として経路を確認してみよう。
#最短経路をABではなくAFの観点から見てみと、ACFとなりACもAFも直接移動できるので、中継点Cを見たタイミングでAFの最短経路が求まっていることがわかる。
#つぎにFBをみてみると、これは複数経由しているので難しく見えるが、AFBと考え方は同じでもう一度分解して直接移動できる範囲を見ていけばいい。
#FDEはDの中継点を見た時点で求まっているし、DEBもEの中継点を見た時点で求まっている。
#これにより、Fの中継点を見るタイミングで、Fより前の最短経路は求まっていることが証明できる。
#つまり、ある経路ABの最短経路を求める場合、ABのなかで一番最後に確認する中継点を検証するタイミングで、
#それ以前にでてくる中継点については最短経路が求まっているといえる。
#これにより、【i,jを求めるタイミングで中継点って常に最短になるの？】で定義した疑問でAEをみる時、
#その中継点BEやAD CEは、中継点Dを見る時点で時点で最短経路が出ているので、ADEを検証する時にAEの最短経路を求めることが可能となっていると証明できる。

#【kijのループ順番を間違えても上手く動くの？】
#例えばikj jikなど
#
#解説 https://qiita.com/tmaehara/items/f56be31bbb7a468a04ed
#うごかないけど最大３回繰り返せば上手く動くらしい。
#とりあえず中継点を全て求める必要があるから、中継点を一番外側のループに置く必要があると覚えておくこと。
　あとがき

ワーシャルフロイド法ってただの３重ループなのに、これが本当に問題ないのかを理解するためにどんだけ知識がいるんや...

今回は理系の知り合い３人くらい動員して数日かかって理解しました。
もはや自分が何をわかっていないのかを言語化するだけでも苦労して、みんなには迷惑をかけたなぁと思います。
いや本当いま学生でじぇんじぇん勉強していない奴がいたら言いたい。

勉強しないならエンジニアにはなるな！！死ぬぞ！！

エンジニアはすごいですね。
アルゴリズムを理解する数学力、ロジックを理解する論理的思考能力、自分の疑問や理解を伝える国語力、グローバルなドキュメントにアクセスするための英語力に読解力...すべてを兼ね備えたスーパーマンなんだなぁと思いました。
僕もスーパーマンでありたいと思ったけど、今の感じじゃサイドキックにしかなれなさそうだ。

あとこれはどうでもいいんですけど、先週勉強して、ちょうどその週のABCに出た問題が最短経路問題だったんで、C問題飛ばしてついつい解こうとしちゃったんだけど、開始即あぁこれ単一始点最短経路問題だからダイクストラ法だってなってすごい悔しかったですね。
知ってて何もできないのが一番無力感味わうので最悪でした。
皆さんはこれをみたらダイクストラ法も勉強しましょうね。
僕は...来週かな...

　 Tweet
Qiitaで続きを読む

投稿日：2021-02-27T17:07:09+09:00

Pytorch Lightningを使用したBERT文書分類モデルの実装

はじめに

PytorchでのBERTの分類モデル実装時に、コードの長さと使いまわしのしにくさを感じていたところ、Pytorch Lightningというフレームワークを知ったので実装してみました。

※Pytorch Lightningとは何か？については下記の記事が分かりやすく、参考にさせて頂きました。
PyTorch 三国志（Ignite・Catalyst・Lightning）

Google Colaboratoryで実行できるnotebookもgitで公開していますので、よろしければ参考にして頂き、間違っている点などあれば是非ご指摘いただけますと幸いです。
pytorch_lightning_text_classification.ipynb

環境

Google Colaboratory

各種インポート

%%capture
!pip install transformers==3.5.1
!pip install fugashi
!pip install ipadic
!pip install pytorch-lightning==1.1.0

import os
import numpy as np
import pandas as pd
import pytorch_lightning as pl
import torch
import torch.optim as optim
from pytorch_lightning.callbacks import EarlyStopping, ModelCheckpoint
from sklearn.model_selection import train_test_split
from torch import nn
from torch.utils.data import DataLoader, Dataset
from transformers import BertModel
from transformers.tokenization_bert_japanese import BertJapaneseTokenizer

モデリング用データセットの前処理

BERTの分類モデルを作成する際には、前処理として文章をtokenizeしてDataLoaderにする必要があります。今回は自作DatasetとLightningDataModuleを継承したクラスを使用して前処理を行い、モデリングできる状態にしていきます。

classの定義

class CreateDataset(Dataset):
    """
    DataFrameを下記のitemを保持するDatasetに変換。
    text(原文)、input_ids(tokenizeされた文章)、attention_mask、labels(ラベル)
    """

    def __init__(self, data, tokenizer, max_token_len):
        self.data = data
        self.tokenizer = tokenizer
        self.max_token_len = max_token_len

    def __len__(self):
        return len(self.data)

    def __getitem__(self, index):
        data_row = self.data.iloc[index]
        text = data_row[TEXT_COLUMN]
        labels = data_row[LABEL_COLUMN]

        encoding = self.tokenizer.encode_plus(
            text,
            add_special_tokens=True,
            max_length=self.max_token_len,
            padding="max_length",
            truncation=True,
            return_attention_mask=True,
            return_tensors='pt',
        )

        return dict(
            text=text,
            input_ids=encoding["input_ids"].flatten(),
            attention_mask=encoding["attention_mask"].flatten(),
            labels=torch.tensor(labels)
        )

class CreateDataModule(pl.LightningDataModule):
    """
    DataFrameからモデリング時に使用するDataModuleを作成
    """
    def __init__(self, train_df, valid_df, test_df, batch_size=16, max_token_len=512, 
                 pretrained_model='cl-tohoku/bert-base-japanese-char-whole-word-masking'):
        super().__init__()
        self.train_df = train_df
        self.valid_df = valid_df
        self.test_df = test_df
        self.batch_size = batch_size
        self.max_token_len = max_token_len
        self.tokenizer = BertJapaneseTokenizer.from_pretrained(pretrained_model)

    def setup(self):
        self.train_dataset = CreateDataset(self.train_df, self.tokenizer, self.max_token_len)
        self.vaild_dataset = CreateDataset(self.valid_df, self.tokenizer, self.max_token_len)
        self.test_dataset = CreateDataset(self.test_df, self.tokenizer, self.max_token_len)

    def train_dataloader(self):
        return DataLoader(self.train_dataset, batch_size=self.batch_size, shuffle=True, num_workers=os.cpu_count())

    def val_dataloader(self):
        return DataLoader(self.vaild_dataset, batch_size=self.batch_size, num_workers=os.cpu_count())

    def test_dataloader(self):
        return DataLoader(self.test_dataset, batch_size=self.batch_size, num_workers=os.cpu_count())

使い方

まずは文章とラベルから成るtrain_df、valid_df、test_df(全てDataFrame)を用意します。今回はcriterionにnn.CrossEntropyLossを使用するので、ラベルは数値型に変換しておきます。

# こんな感じ（データはlivedoorのニュースコーパス）
train_df.head(3)
# > 　　text  category
# > 0   スティーブン・...    1
# > 1   10月末、K-1イ ...   0
>#  2   今日は大みそか...    6

あとはDataFrameをCreateDataModuleに渡してsetup()すれば完成です。

# 用意したDataFrameの文章、ラベルのカラム名
TEXT_COLUMN = "text"
LABEL_COLUMN = "category"

# 作ったDataFrameを渡してsetup
data_module = CreateDataModule(train_df,valid_df,test_df)
data_module.setup()

setup後のdata_moduleの中身は下記のような形になっています。

# datasetへのアクセス
item = data_module.train_dataset[0]
print(item["input_ids"])
# > tensor([   2,   27,   26,   26,   70,   25,    6,  120,  356,  186,  337,    7,
# >         1266,  307,  163,  239,  181,    6,   93,   40,  123,   29,   14,   16,
# >          ・・・
# >         2690,   23,   19,  322,  197,   11, 1266,   87,  550,  181,    6,  466,
# >         1823,  577,  693,   11,  142,  125,   47,    3])

print(item["input_ids"].shape)
# > torch.Size([512])

# dataloaderのバッチの中身を確認
batch = next(iter(data_module.train_dataloader()))
print(batch["input_ids"])
# > tensor([[   2,   55,   28,  ...,   18,   19,    3],
# >         [   2,  569,   67,  ...,  145,  427,    3],
# >         ...,
# >         [   2,   45,   49,  ...,  163, 1143,    3],
# >         [   2,  672,   11,  ...,    8,  451,    3]])

print(batch["input_ids"].shape)
# > torch.Size([16, 512])
#  → batch_size × max_token_lenになっている

モデリングの実行 & 精度検証

クラスの定義

データの準備が整ったら、LightningModuleを継承してモデリング用クラスを作成します。
def xx_stepで、training/validation/testの各フェーズごとにミニバッチの処理を定義することができる点が特徴です。関数名をフックにして各フェーズで必要となる処理、例えばtraining時のmodel.train()やloss.backward()、validation時のmodel.valid()やtorch.no_grad()といった処理は内部的に行ってくれるため、記述は不要です。全フェーズで必要な.to(device)などの処理も内部的にやってくれます。
__init__、forwardを定義するところは普通にpytorchで実装する場合とほぼ変わりません。

class TextClassifier(pl.LightningModule):
    def __init__(self, n_classes: int, n_epochs=None, 
                 pretrained_model='cl-tohoku/bert-base-japanese-char-whole-word-masking'):
        super().__init__()

        # モデルの構造
        self.bert = BertModel.from_pretrained(
            pretrained_model, return_dict=True)
        self.classifier = nn.Linear(self.bert.config.hidden_size, n_classes)
        self.n_epochs = n_epochs
        self.criterion = nn.CrossEntropyLoss()

        # BertLayerモジュールの最後を勾配計算ありに変更
        for param in self.bert.parameters():
            param.requires_grad = False
        for param in self.bert.encoder.layer[-1].parameters():
            param.requires_grad = True

    # 順伝搬
    def forward(self, input_ids, attention_mask, labels=None):
        output = self.bert(input_ids, attention_mask=attention_mask)
        preds = self.classifier(output.pooler_output)
        loss = 0
        if labels is not None:
            loss = self.criterion(preds, labels)
        return loss, preds

    # trainのミニバッチに対して行う処理
    def training_step(self, batch, batch_idx):
        loss, preds = self.forward(input_ids=batch["input_ids"],
                                    attention_mask=batch["attention_mask"],
                                    labels=batch["labels"])
        return {'loss': loss,
                'batch_preds': preds,
                'batch_labels': batch["labels"]}

    # validation、testでもtrain_stepと同じ処理を行う
    def validation_step(self, batch, batch_idx):
        loss, preds = self.forward(input_ids=batch["input_ids"],
                                    attention_mask=batch["attention_mask"],
                                    labels=batch["labels"])
        return {'loss': loss,
                'batch_preds': preds,
                'batch_labels': batch["labels"]}

    def test_step(self, batch, batch_idx):
        loss, preds = self.forward(input_ids=batch["input_ids"],
                                    attention_mask=batch["attention_mask"],
                                    labels=batch["labels"])
        return {'loss': loss,
                'batch_preds': preds,
                'batch_labels': batch["labels"]}

    # epoch終了時にvalidationのlossとaccuracyを記録
    def validation_epoch_end(self, outputs, mode="val"):
        # loss計算
        epoch_preds = torch.cat([x['batch_preds'] for x in outputs])
        epoch_labels = torch.cat([x['batch_labels'] for x in outputs])
        epoch_loss = self.criterion(epoch_preds, epoch_labels)
        self.log(f"{mode}_loss", epoch_loss, logger=True)

        # accuracy計算
        num_correct = (epoch_preds.argmax(dim=1) == epoch_labels).sum().item()
        epoch_accuracy = num_correct / len(epoch_labels)
        self.log(f"{mode}_accuracy", epoch_accuracy, logger=True)

    # testデータのlossとaccuracyを算出（validationの使いまわし）
    def test_epoch_end(self, outputs):
        return self.validation_epoch_end(outputs, "test")

    # optimizerの設定
    def configure_optimizers(self):
        # pretrainされているbert最終層のlrは小さめ、pretrainされていない分類層のlrは大きめに設定
        optimizer = optim.Adam([
            {'params': self.bert.encoder.layer[-1].parameters(), 'lr': 5e-5},
            {'params': self.classifier.parameters(), 'lr': 1e-4}
        ])

        return [optimizer]

使い方

インスタンスの作成、及び各種設定

クラスを使用してインスタンスを作成したら、EarlyStoppingとモデルの保存先の設定を行います。

# epoch数
N_EPOCHS = 10

# モデルインスタンスを作成
model = TextClassifier(n_classes=9,n_epochs=N_EPOCHS)

# EarlyStoppingの設定
# 3epochで'val_loss'が0.05以上減少しなければ学習をストップ
early_stop_callback = EarlyStopping(
    monitor='val_loss', 
    min_delta=0.05, 
    patience=3, 
    mode='min')

# モデルの保存先
# epoch数に応じて、「epoch=0.ckpt」のような形で指定したディレクトリに保存される
checkpoint_callback = ModelCheckpoint(
    dirpath="./checkpoints",
    filename='{epoch}',
    verbose=True,
    monitor='val_loss',
    mode='min'
)

# Trainerに設定
trainer = pl.Trainer(max_epochs=N_EPOCHS,
                     gpus=1,
                     progress_bar_refresh_rate=30,
                     callbacks=[checkpoint_callback, early_stop_callback])

学習の実行

設定が終わったらいよいよ学習です。勝手にループしてくれるので、for文の記述は不要です。

# 学習
trainer.fit(model, data_module)

進捗もいい感じに表示してくれます。

テストの実行

一番lossが少なかった時点のモデルを使用してtestデータへの当てはめを行います。

# テスト
result = trainer.test(ckpt_path=checkpoint_callback.best_model_path)
# > -----------------------------------------------------------
# > DATALOADER:0 TEST RESULTS
# > {'test_accuracy': 0.9170632222977566,
# >  'test_loss': tensor(0.2891, device='cuda:0'),
# >  'val_accuracy': 0.9196378041878891, ← この数値は最後のvalidation epochの結果（≠ 最良モデル）
# >  'val_loss': tensor(0.3031, device='cuda:0')}
# > -----------------------------------------------------------

TensorBoard

モデリング用クラス作成時にself.log()で定義した数値はTensorBoardでも確認可能です。

# Google Colaboratoryの場合
%load_ext tensorboard
%tensorboard --logdir /content/lightning_logs

checkpointからのモデルをロード

下記のような形で、checkpointを指定してモデルをロードすることも可能です。

# 指定したcheckpointのモデルをロード
trained_model = TextClassifier.load_from_checkpoint('./checkpoints/epoch=0.ckpt',n_classes=9)

感想

普通に実装するよりは格段にスッキリするし、使いまわしもしやすくなったと感じます。また、Early Stoppingなどを手軽に実装できるのも嬉しいですね。まだまだ未開拓な部分もたくさんあるので、徐々に開拓していきたいです。

参考

公式ドキュメント
PYTORCH LIGHTNING DOCUMENTATION
Pytorch Lightningとは何か的なところ
PyTorch 三国志（Ignite・Catalyst・Lightning）
実装（記事）
【実装解説】日本語版BERTでlivedoorニュース分類：Google Colaboratoryで（PyTorch）
速習 pytorch-lightning: 今すぐ機械学習の実験をしたいそこのキミへ
 日本語BERTモデルをPyTorch用に変換してfine-tuningする with torchtext & pytorch-lightning
実装（youtube動画、全部英語）
PyTorch Lightning MasterClass←公式、再生リスト
Fine-Tuning BERT with HuggingFace and PyTorch Lightning for Multilabel Text Classification | Dataset
Fine-Tuning BERT with HuggingFace and PyTorch Lightning for Multilabel Text Classification | Train

　 Tweet
Qiitaで続きを読む

投稿日：2021-02-27T16:42:11+09:00

find.elementとfind.elementsの使い分けには気をつけなければいけない

概要

pythonでSelenium BeautifulSoupを使ってスクレイピングの勉強をしています。
タイトルの通り、何度もしくじったのでメモがてらにアウトプット。seleniumとは？
みたいな基本や細かいところはすっ飛ばします。今回はメルカリを対象に書いてます。
soupも若干触れますが、基本はseleniumの記事です。

findの細かい種類や簡単な概要はこちら参考になると思います。
https://kurozumi.github.io/selenium-python/locating-elements.html

初期の設定はこんな感じで。ただメルカリのトップページを開くだけです。
余計なimportも沢山ありますがスルーしてください。
from selenium import webdriver
from time import sleep
import os
from bs4 import BeautifulSoup
import sys
import urllib.request
import chromedriver_binary

options = webdriver.ChromeOptions()
options.add_argument('--no-sandbox') 
options.add_argument('--disable-dev-shm-usage')
browser = webdriver.Chrome('chromedriver',options=options)
url = "https://www.mercari.com/jp/"
browser.get(url)
ITEM = 'ウィスキー山崎'
find.element

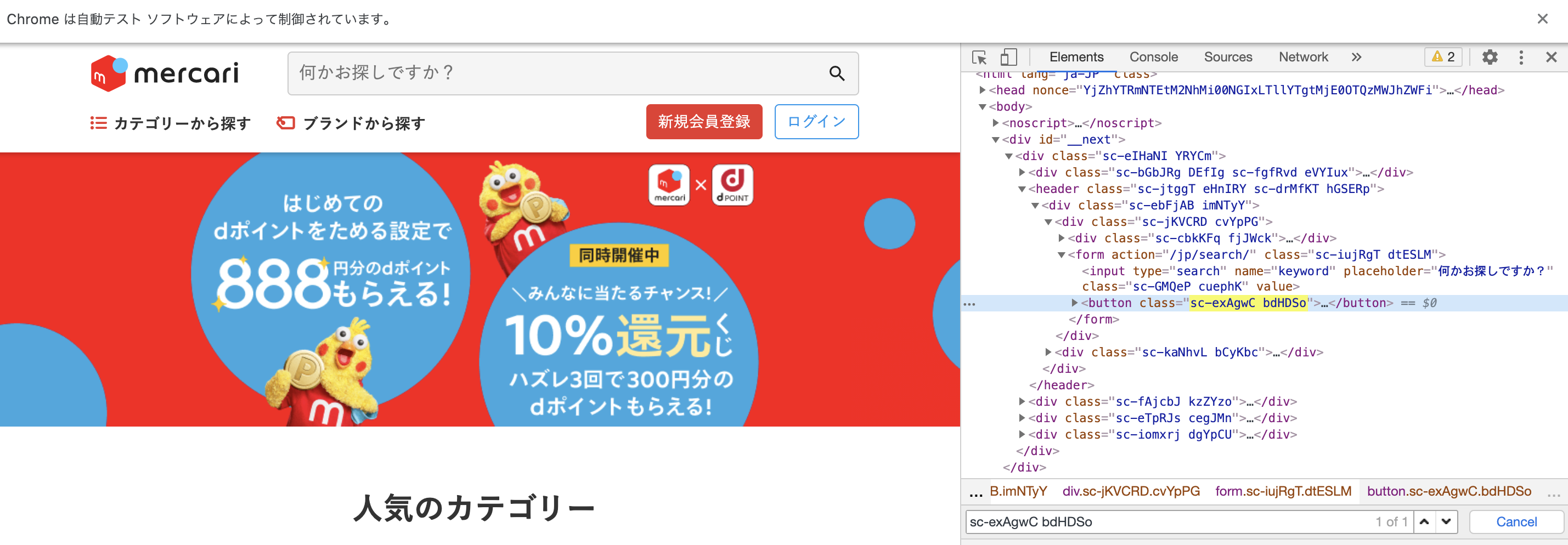
対象の要素を一つだけ取得する。もし参照したいクラス等に重複があれば一番最初に参照するノードが取得される
なので参照する時に、同名のクラス名がないか先に確認しておくべきです（自戒）複数あっても一番最初に参照されるのであれば問題ないですけどね。

とりあえずトップページで検索ワードは何も入れずにただ検索ボタンをクリックしてみました。
browser.find_element_by_css_selector('.sc-exAgwC.bdHDSo').click()
とりあえずなんか表示されてますwww
新しく更新された順ですかね？
ちなみに検索ボタン押す前のトップページを検証ツールで見てみると

同名のクラスは１つしかない事がわかります。
なのでパスさえ間違えなければ、何も問題なく通りますね。
試しにわざとタイポしてみます
browser.find_element_by_css_selector('.sc-exAgwC.bdHDSoaaaaa').click()
↓
selenium.common.exceptions.NoSuchElementException: Message: no such element: Unable to locate element: {"method":"css selector","selector":".sc-exAgwC.bdHDSoaaaaa"}
そんな要素はねーよって言われてます。

余談ですけどsoupにして同様のミスをすると「None」で返ってきます。
この違いは注意した方が良いかも。

find.elements

対象の要素をlist型にして全て取得する。同名クラスが複数あって全て取得したい場合はこちらを使う事になります。例えば対象が3つあった場合は
[対象1,対象2,対象３]
こんな感じのlistで返ってきます。
あくまで個人的にですがseleniumでelementsは使い勝手があまり良くないなぁと感じでいます。対象データをスクレイピングして整形したりしたい時って主にsoupでやってしまうので、ブラウザ操作に使われがちなseleniumで全件取得が活躍した事が今のところあまりありません。

ちなみに今回の記事を執筆しようと思ったのは下記コードで詰まった時なのですが
search_word = browser.find_element_by_xpath("//input[@name='keyword']")
↓
selenium.common.exceptions.ElementNotInteractableException: Message: element not interactable
見て察しがつくと思いますが、商品の検索窓にキーワードを入れるための要素を取得しようとしています。
私は当初これを普通にelementで取得しようとして上手くいきませんでした。
何故ならこの（"//input[@name='keyword']")がまさかの対象が2件あったわけですw

今回欲しいのは2個目の要素なので、elementでやると1個目の要素が返ってきて、想定した場所でクリックができていないわけです。指定の仕方を変えればelementでもいけると思うのですが、今回は強引にこんな感じで指定します。
search_word = browser.find_elements_by_xpath("//input[@name='keyword']")[1]
'keyword'要素はlist型で二つ返ってきているので下記の様になっています。
[keyword0,keyword1]
ので、最後に[1]を書いてどこの要素を使うか指定する必要があります。

無事指定したワードが入力されました。
あとこれまた余談ですがsoupで指定を間違えると空リストで返ってきます。

selenium.common.exceptions.ElementNotInteractableException: Message: element not interactableがウザい

elementでミスっている時、このエラーで色々と探っていて、原因を気づくのにだいぶ時間がかかりました。
画面上に要素が表示されていないから、画面をデカくしろだの、chromedriverのバージョンが違うだの、マウスホバーしろだのあらゆる記事が出てきましたが、結局は私の通し方が間違えてただけですw

というかseleniumのエラーはほぼほぼfindの通す先が何らかの原因で間違えている事が99パーセントでした（圧倒的偏見）
初心者の方は気をつけてください。

検索窓に指定ワードを入れて検索ボタンクリックするコードだけ一応最後に貼っておきます。
以上です。
from selenium import webdriver
from bs4 import BeautifulSoup
import chromedriver_binary
from time import sleep

options = webdriver.ChromeOptions()
options.add_argument('--no-sandbox') 
options.add_argument('--disable-dev-shm-usage')
browser = webdriver.Chrome('chromedriver',options=options)
url = "https://www.mercari.com/jp/"
browser.get(url)
sleep(2)
ITEM = 'ウィスキー山崎'

search_word = browser.find_elements_by_xpath("//input[@name='keyword']")[1]
search_word.send_keys(ITEM)
browser.find_element_by_css_selector('.sc-exAgwC.bdHDSo').click()
sleep(2)

　 Tweet
Qiitaで続きを読む

投稿日：2021-02-27T16:08:13+09:00

pythonをソースコードからUbuntuにインストールする

前置き

pythonをコンパイルする方法について色々記事はあふれているものの、
前提条件の違いでうまくいかず・・・

Ubuntu16.04のクリーンインストール状態から、
インストール完了までをまとめた。これでだいたいうまくいくはず。

環境

Ubuntu16.04 LTS server (64bit)をインストール直後の状態

ゴール

最新のpython3.9.2のインストール完了

環境の最新化

まず、パッケージリストを最新化します。

osoper@ubuntu1604:~$ sudo apt-get update

そして一括アップグレードします

osoper@ubuntu1604:~$ sudo apt-get upgrad

コンパイル環境を整える

pythonのソースコードのコンパイルに必要なパッケージを導入する

osoper@ubuntu1604:~$ sudo apt install build-essential \                         
> libbz2-dev libdb-dev \                                                        
> libreadline-dev libffi-dev \                                                  
> libgdbm-dev liblzma-dev \                                                     
> libncursesw5-dev libsqlite3-dev \                                             
> libssl-dev \                                                                  
> zlib1g-dev uuid-dev tk-dev

ソースコードの取得

osoper@ubuntu1604:~$ curl -O https://www.python.org/ftp/python/3.9.2/Python-3.9.2.tgz
% Total    % Received % Xferd  Average Speed   Time    Time     Time  Current
Dload  Upload   Total   Spent    Left  Speed
100 24.2M  100 24.2M    0     0  7701k      0  0:00:03  0:00:03 --:--:-- 7703k
osoper@ubuntu1604:~$ ls -l
合計 24808
-rw-rw-r-- 1 osoper osoper 25399571  2月 27 09:31 Python-3.9.2.tgz

ソースの解凍

osoper@ubuntu1604:~$ tar zxf Python-3.9.2.tgz
osoper@ubuntu1604:~$ ls -l
合計 24812                                                                      
drwxr-xr-x 17 osoper osoper     4096  2月 19 22:34 Python-3.9.2
-rw-rw-r--  1 osoper osoper 25399571  2月 27 09:31 Python-3.9.2.tgz

configure

コンパイルにはconfigure → make → make innstallと実施します。
コンパイルするファイルはたくさんあるので、一つ一つやると面倒です。
configureでMakefileというコンパイル計画のファイルを作って、
makeコマンドで計画にしたがって、コンパイルとインストールをすると思ってください。

configureコマンドはpythonのソースに含まれています。
makeはUbuntuのパッケージに含まれています。

osoper@ubuntu1604:~$ cd Python-3.9.2
osoper@ubuntu1604:~/Python-3.9.2$ ./configure --with-ensurepip=install
checking build system type... x86_64-pc-linux-gnu
checking host system type... x86_64-pc-linux-gnu
checking for python3.9... no
checking for python3... python3

(中略)

checking for --with-builtin-hashlib-hashes... md5,sha1,sha256,sha512,sha3,blake2
configure: creating ./config.status
config.status: creating Makefile.pre
config.status: creating Misc/python.pc
config.status: creating Misc/python-embed.pc
config.status: creating Misc/python-config.sh
config.status: creating Modules/ld_so_aix
config.status: creating pyconfig.h
creating Modules/Setup.local
creating Makefile


If you want a release build with all stable optimizations active (PGO, etc),
please run ./configure --enable-optimizations

「./configure --help」と打つことでオプションの詳細を確認可能です。
今回はpipのインストールオプションのみ含めました。(--with-ensurepip=install)
この場合、/usr/local/binにインストールされます。

コマンドが終わったところで、作成されたファイルを確認

osoper@ubuntu1604:~/Python-3.9.2$ ls -ltr
合計 2008
-rw-r--r--  1 osoper osoper 109891  2月 19 21:31 setup.py
-rw-r--r--  1 osoper osoper  45567  2月 19 21:31 pyconfig.h.in
-rw-r--r--  1 osoper osoper     82  2月 19 21:31 netlify.toml
drwxr-xr-x  2 osoper osoper   4096  2月 19 21:31 m4
-rwxr-xr-x  1 osoper osoper  15368  2月 19 21:31 install-sh
-rw-r--r--  1 osoper osoper 173556  2月 19 21:31 configure.ac
-rwxr-xr-x  1 osoper osoper 513139  2月 19 21:31 configure
-rwxr-xr-x  1 osoper osoper  36251  2月 19 21:31 config.sub
-rwxr-xr-x  1 osoper osoper  44166  2月 19 21:31 config.guess
-rw-r--r--  1 osoper osoper  13421  2月 19 21:31 aclocal.m4
drwxr-xr-x 23 osoper osoper   4096  2月 19 21:31 Tools
-rw-r--r--  1 osoper osoper  10132  2月 19 21:31 README.rst
drwxr-xr-x  3 osoper osoper   4096  2月 19 21:31 Python
drwxr-xr-x  2 osoper osoper   4096  2月 19 21:31 Programs
drwxr-xr-x  2 osoper osoper   4096  2月 19 21:31 PCbuild
drwxr-xr-x  6 osoper osoper   4096  2月 19 21:31 PC
drwxr-xr-x  4 osoper osoper   4096  2月 19 21:31 Objects
-rw-r--r--  1 osoper osoper  70514  2月 19 21:31 Makefile.pre.in
drwxr-xr-x  8 osoper osoper   4096  2月 19 21:31 Mac
drwxr-xr-x 34 osoper osoper   4096  2月 19 21:31 Lib
-rw-r--r--  1 osoper osoper  13925  2月 19 21:31 LICENSE
drwxr-xr-x  4 osoper osoper   4096  2月 19 21:31 Include
drwxr-xr-x  2 osoper osoper   4096  2月 19 21:31 Grammar
-rw-r--r--  1 osoper osoper    630  2月 19 21:31 CODE_OF_CONDUCT.md
drwxr-xr-x  4 osoper osoper   4096  2月 19 22:34 Parser
drwxr-xr-x 18 osoper osoper   4096  2月 19 22:34 Doc
-rwxrwxr-x  1 osoper osoper  42486  2月 27 09:42 config.status
-rw-rw-r--  1 osoper osoper  70214  2月 27 09:42 Makefile.pre
drwxr-xr-x  2 osoper osoper   4096  2月 27 09:42 Misc
-rw-rw-r--  1 osoper osoper  47695  2月 27 09:42 pyconfig.h
-rw-rw-r--  1 osoper osoper  79572  2月 27 09:42 Makefile
drwxr-xr-x 14 osoper osoper   4096  2月 27 09:42 Modules
-rw-rw-r--  1 osoper osoper 664138  2月 27 09:42 config.log

Makefileが存在することと、config.logが「configure: exit 0」で終わっていることを確認します。

make

シンプルにmakeとだけ、コマンドを打ちます。

osoper@ubuntu1604:~/Python-3.9.2$ make                                          
gcc -pthread -c -Wno-unused-result -Wsign-compare -DNDEBUG -g -fwrapv -O3 -Wall 
   -std=c99 -Wextra -Wno-unused-result -Wno-unused-parameter -Wno-missing-field-
initializers -Werror=implicit-function-declaration -fvisibility=hidden  -I./Incl
ude/internal  -I. -I./Include    -DPy_BUILD_CORE -o Programs/python.o ./Programs
/python.c                                                                       

(中略）

gcc -pthread     -Xlinker -export-dynamic -o Programs/_testembed Programs/_teste
mbed.o libpython3.9.a -lcrypt -lpthread -ldl  -lutil -lm   -lm
sed -e "s,@EXENAME@,/usr/local/bin/python3.9," < ./Misc/python-config.in >python
-config.py
LC_ALL=C sed -e 's,\$(\([A-Za-z0-9_]*\)),\$\{\1\},g' < Misc/python-config.sh >py
thon-config
osoper@ubuntu1604:~/Python-3.9.2$ echo $?
0

無事完了！！

make install

最後はインストール。ここだけsudoで実行するのを忘れずに！！

osoper@ubuntu1604:~/Python-3.9.2$ make installsudo
[sudo] osoper のパスワード:
if test "no-framework" = "no-framework" ; then \
    /usr/bin/install -c python /usr/local/bin/python3.9; \
else \
    /usr/bin/install -c -s Mac/pythonw /usr/local/bin/python3.9; \
fi
if test "3.9" != "3.9"; then \
    if test -f /usr/local/bin/python3.9 -o -h /usr/local/bin/python3.9; \
    then rm -f /usr/local/bin/python3.9; \
    fi; \

(中略)

Looking in links: /tmp/tmp2_tfnh2l
Processing /tmp/tmp2_tfnh2l/setuptools-49.2.1-py3-none-any.whl
Processing /tmp/tmp2_tfnh2l/pip-20.2.3-py2.py3-none-any.whl
Installing collected packages: setuptools, pip
Successfully installed pip-20.2.3 setuptools-49.2.1

Successfully installedと出て無事完了

確認

デフォルトの/usr/local/binにインストールされていることを確認

osoper@ubuntu1604:/usr/local/bin$ ls -l
合計 17276
lrwxrwxrwx 1 root root        8  2月 27 13:06 2to3 -> 2to3-3.9
-rwxr-xr-x 1 root root      101  2月 27 13:06 2to3-3.9
-rwxr-xr-x 1 root root      238  2月 27 13:06 easy_install-3.9
lrwxrwxrwx 1 root root        7  2月 27 13:06 idle3 -> idle3.9
-rwxr-xr-x 1 root root       99  2月 27 13:06 idle3.9
-rwxr-xr-x 1 root root      229  2月 27 13:06 pip3
-rwxr-xr-x 1 root root      229  2月 27 13:06 pip3.9
lrwxrwxrwx 1 root root        8  2月 27 13:06 pydoc3 -> pydoc3.9
-rwxr-xr-x 1 root root       84  2月 27 13:06 pydoc3.9
lrwxrwxrwx 1 root root        9  2月 27 13:06 python3 -> python3.9
lrwxrwxrwx 1 root root       16  2月 27 13:06 python3-config -> python3.9-config
-rwxr-xr-x 1 root root 17659504  2月 27 13:06 python3.9
-rwxr-xr-x 1 root root     3087  2月 27 13:06 python3.9-config

/usr/binのpythonの置き換え

/usr/binのpython3はデフォルトでインストールされている3.5にリンクされています。

osoper@ubuntu1604:/usr/local/bin$ python3 -V
Python 3.5.2

/usr/binのものが効いているようです。

osoper@ubuntu1604:/usr/bin$ ls -l python*
lrwxrwxrwx 1 root root       9  2月 26 20:22 python3 -> python3.5
-rwxr-xr-x 2 root root 4456208  1月 27 03:48 python3.5
-rwxr-xr-x 2 root root 4456208  1月 27 03:48 python3.5m
lrwxrwxrwx 1 root root      10  2月 26 20:22 python3m -> python3.5m

以下のコマンドでシンボリックリンクの置き換えをします。

osoper@ubuntu1604:~$ cd /usr/bin
osoper@ubuntu1604:/usr/bin$ sudo ln -nfs /usr/local/bin/python3.9 python3

確認して、完了！！

osoper@ubuntu1604:~$ ptyhopython3 -V
Python 3.9.2

参考

以下のサイトを参照しながら上記完了させました。
https://tech.chakapoko.com/python/dev/install-from-source.html
https://www.python.jp/install/ubuntu/index.html
https://qiita.com/kei0425/items/6b84938db2c22186fdbc

　 Tweet
Qiitaで続きを読む

投稿日：2021-02-27T16:02:30+09:00

pythonでクレカの確定明細から確定金額をLINEに通知する

目的

パートナーがいる方は共有でかかったお金をなんらかの形で管理しているかと思います。
今回はJCBのクレジットカード当月確定分の金額をLINEに送信するというプログラムを作成しました。

環境構築

windows8
anacondaをインストール
python3.7.5

ソース

ソースの説明をすると、
まずPhantomJSと呼ばれるプログラム上でブラウザの実行ができる環境を利用しています。
そしてブラウザの操作の部分はseleniumと呼ばれるライブラリを使用しています。

PhantomJSとseleniumでブラウザ操作してMYJCB画面の当月確定分の金額を取得して、
LINEのNotifyにリクエストを投げています。

これを毎月決まった日にいちいちログインせずとも自動実行させてかかった金額をパートナーに教えてあげられます。

kurekameisai.py

# -*- coding: utf-8 -*-
import urllib.request
from selenium import webdriver
import time
from selenium.webdriver.common.keys import Keys
import json
import requests

def serch():

    browser  = webdriver.PhantomJS()
    loginURL = "https://my.jcb.co.jp/Login"
    browser.get(loginURL)
    time.sleep(3)

    #sign-in
    username     = "" # ユーザー名
    password     = "" # パスワード
    secretAnswer = "" # 秘密の答え

    browser.find_element_by_id("userId").send_keys(username)
    browser.find_element_by_id("password").send_keys(password)
    browser.find_element_by_id("loginButtonAD").click()
    browser.find_element_by_id("form1:answer_").send_keys(secretAnswer)
    browser.find_element_by_id("form1:j_idt65").click()

    URL = "https://my.jcb.co.jp/iss-pc/member/details_inquiry/detail.html?detailMonth=1&output=web"
    # なぜか2回同じURLを指定すると目的のページへ繊維できる
    browser.get(URL)
    browser.get(URL)
    time.sleep(3)

    # 今月分の確定金額を返す
    return browser.find_element_by_class_name('price-02').text

def main():
    # LINE Notify Token
    access_token = '' # LINEのアクセストークン
    url          = 'https://notify-api.line.me/api/notify'

    headers = {
        'Authorization': 'Bearer {}'.format(access_token),
    }

    # LINEに送るメッセージを指定
    payload = {
        'message': 'リクルート今月支払' + serch(),
    }

    # request Notify
    response = requests.post(url, headers=headers, params=payload)
    #res      = json.loads(response.text)
    #print(res)

    return True

if __name__ == '__main__':
    main()

　 Tweet
Qiitaで続きを読む

投稿日：2021-02-27T15:50:19+09:00

Django rest framework にmodelを作る方法

1. models.pyにclassを作る
models.py
from django.db import models
class Character(models.Model):
    character = models.CharField(max_length=60)
    age = models.CharField(max_length=60)
    def __str__(self):
        return self.character
2.terminal上でcommandを実行する
(env) qiita  mysite % python manage.py makemigrations
Did you rename character.first to character.age (a CharField)? [y/N] y
Did you rename character.last to character.character (a CharField)? [y/N] y
Migrations for 'myapi':
  myapi/migrations/0003_auto_*********.py
    - Rename field first on character to age
    - Rename field last on character to character
(env) qiita mysite % python manage.py migrate       
Operations to perform:
  Apply all migrations: admin, auth, contenttypes, myapi, sessions
Running migrations:
  Applying myapi.0003_auto_********... OK
この前に他のfieldを削除していたので、このような内容になっているがpython manage.py makemigrations,python manage.py migrateを実行しokが出れば問題ない。

3.admin.pyにcharacterの設定
admin.py
from django.contrib import admin
from .models import Character

admin.site.register(Character)
このcodeを追加したら、python manage.py runserverを行う。
1.2.3の工程を行うことによって,Django rest frameworkにcharacterが追加される。

4.serializers.pyの作成
serializers.py
class CharacterSerializer(serializers.HyperlinkedModelSerializer):
    class Meta:
        model = Character
        fields = ('id', 'character', 'age')
serializers.pyというfileを新しく用意する。ここでは、fieldsの中にCharacterが持つことができる要素を追加することが出来る。今回はid,character,ageを設定した。なぜserializers.pyを作るのかというと、Django rest frameworkにデータを伝える際にjsonに変換しなければならないからである。
*今回の記事ではjsonには触れないことにする

5.views.py&urls.pyの設定
views.py
from rest_framework import viewsets

from .serializers import CharacterSerializer
from .models import Character

class CharacterViewSet(viewsets.ModelViewSet):
    queryset = Character.objects.all().order_by('character')
    serializer_class = CharacterSerializer
urls.py/mysite
from django.contrib import admin
from django.urls import path, include

urlpatterns = [
    path('admin/', admin.site.urls),
    path('', include('myapi.urls')),
]
urls.py/myapi
from django.urls import include, path
from rest_framework import routers
from . import views

router = routers.DefaultRouter()
router.register(r'characters', views.CharacterViewSet)


# Wire up our API using automatic URL routing.
# Additionally, we include login URLs for the browsable API.
urlpatterns = [
    path('', include(router.urls)),
    path('api-auth/', include('rest_framework.urls', namespace='rest_framework'))
]
views.py urls.pydでの設定を行うことによって画面にデータを表示させることが出来る。
*url.pyは２つあるので注意
*rest_frameworkの設定をしていないなら、あらかじめしておくことをおすすめする

python manage.py runserverを実行

urlにcharactersのurlが設定できていることを確認出来る。

7.実際にcharacterを追加してみる

Character listの中にデータが追加されている。このように追加できればmodel作成は完了である。

まとめ

今回はDjango rest framework へのmodelの追加を行った。model追加の注意点としては、urls.pyが２つあるため混合しないこと、commandの打ち忘れであると思う。またrest_frameworkを設定しなければ動かないので、その点も十分確認が必要である。

　 Tweet
Qiitaで続きを読む

投稿日：2021-02-27T15:47:55+09:00

【heroku デプロイ】アプリ新規作成と更新のやり方

【heroku デプロイ】新規と更新のやり方

herokuを使えば、コードを定期実行することができます。
無料なので、botとか作りたい時にオススメ。

備忘録としてメモ書き。

筆者もちょいちょい忘れることが多いので、
折角なので新規と更新のやり方をまとめることにした。

なお、更新は、たったの2行で済む。
terminal
$heroku login
$git push heroku master
デプロイ・新規

まずはインストール済かどうか確認
terminal
$git --version
$heroku -v
gitをインストール

herokuをインストール
terminal
$brew tap heroku/brew && brew install heroku
herokuにログイン
terminal
$heroku login
ブラウザでherokuのログイン画面が自動で立ち上がるので
ユーザー名とパスワードを入力してログイン。

herokuにアプリを作成
terminal
$heroku create アプリ名(重複作成できない)
ここで出力される***.gitをメモしておくこと。

runtime.txtとrequirements.txtを作成
runtime.txt
python-3.9.1
requirements.txt
appnope==0.1.2
argon2-cffi==20.1.0
asgiref==3.3.1
async-generator==1.10
attrs==20.3.0
autopep8==1.5.4
backcall==0.2.0
beautifulsoup4==4.9.3
bleach==3.2.1
bs4==0.0.1
cachetools==4.1.1
certifi==2020.11.8
////(省略)
herokuへアプリをデプロイ
terminal
$git init
$git remote add heroku (先程メモした***.git)
$git add .
$git commit -m "（メッセージ・コミット内容）"
$git push heroku master
これにてデプロイ完了。

Heroku Schedulerの設定

定時実行のHeroku Schedulerの設定を行う。
terminal
$heroku addons:add scheduler:standard
$heroku addons:open scheduler
ブラウザが開かれて設定。
※UTCが基準になっているため設定する時間は、
実行したい時間-9時間となるように設定すること。

デプロイ・更新

変更分をGitHubデスクトップでcommit,push。

herokuへログイン。
terminal
$heroku login
herokuにデプロイ。
terminal
$git push heroku master

　 Tweet
Qiitaで続きを読む

投稿日：2021-02-27T15:47:46+09:00

RDKit入門①：まずは環境構築

はじめに

RDKitの使い方について、自分の興味のある範囲から少しずつまとめていきます。
使い方の学習にあたっては「化学の新しいカタチ」さんの記事を主に参考にしています。
https://future-chem.com/

まずは環境構築から（とりあえず動けばいいという方向けです）。
(以下の内容は主にWindows 10での使用を想定しています)

Anacondaのインストール

まずはAnacondaをインストールします。
https://www.anaconda.com/products/individual
ページ下部にAnaconda Installerという部分があるので、お使いの環境に合わせてインストールを行います。

具体的な手順は以下のサイトを参考にしてください。
https://www.python.jp/install/anaconda/windows/install.html

RDKitのインストール

デフォルトではRDKitがインストールされていないため、まずはRDKitのインストールを行います。
Anaconda Prompt (Anaconda3)を開き、黒い画面が出たら以下の呪文を打ち込みます。
>conda config --add channels conda-forge
※RDKit を conda-forge 経由でインストールするためにチャンネルを追加

続いてRDKitのインストールを行います。
>conda install -c conda-forge rdkit
途中で
Proceed ([y]/n)?
と表示されることが何度かあると思いますが、yで続行します。

インストールできたかどうかの確認

まずはお好みの開発環境を開きます。
AnacondaをインストールするとJupyter NotebookやSpyderが一緒にインストールされているので、どちらか好みのソフトを開きましょう。

続いて以下の通りに打ち込んで実行します。
from rdkit import rdBase
print('rdkit version: ', rdBase.rdkitVersion)
エラーが出ずに以下のような表示があれば導入成功です。
（表示されるバージョンは導入時期等の環境によって異なります）
rdkit version:  2020.09.4

　 Tweet
Qiitaで続きを読む

投稿日：2021-02-27T15:37:16+09:00

【2021年版】python で ORM で DB操作

はじめに

技術の進歩は目覚ましいものです。
Web記事を検索すると、検索ボリュームの大きい結果から表示されるため、知らず知らずのうちに古い技術を使ってしまうことが多々あります。

そこで、2021年時点で、windows 環境で python でDB操作+OR Mapper した構成を書いておきたいと思います。

ツール説明

chocolatey Windows用パッケージ管理システム。

python3.9.2 python 本体。

poetry python のパッケージ管理システム。
pip は requirements.txt を手書きしないとダメだったが、npmやyarn の様に pyproject.toml を自動で更新してくれる。

mysqlalchemy OR Mapper。簡単なクラス定義で簡単にDB操作ができる。

alembic DB 構築/マイグレーションヘルパ。mysqlalchemy のクラス定義に沿ったスキーマをDBに構築。

※以後の説明のコードブロックの null ではじまるファイル名は記事でハイライトされる様に定義したファイル名で実際にはファイルを作っていません。

chocolatey

chocolatey
インストーラをダウンロードしてインストールしていたようなパッケージをコマンド一発でインストールできます。

管理者権限で PowerShell を開いて以下コマンド実行でインストールできます。
null.ps1
Set-ExecutionPolicy Bypass -Scope Process -Force; [System.Net.ServicePointManager]::SecurityProtocol = [System.Net.ServicePointManager]::SecurityProtocol -bor 3072; iex ((New-Object System.Net.WebClient).DownloadString('https://chocolatey.org/install.ps1'))
記事を書く時にググると新しいモノが見つかって微妙な気持ちになりますね。。。

scoop は未チェックでした。
Windows開発環境の構築をChocolateyからscoopに切り替える

python

chocolatey で簡単にインストールできます。
バージョン番号を指定しないと、インストール時点の最新版がインストールされます。
null.ps1
choco install python
poetry

pip を使ってインストールします。
pip はこれ以後利用しません。
null.ps1
py -m pip install poetry
poetry は仮想環境(virtualenv)を利用します。
以下設定をするとプロジェクト内に.venv ファイルを作成しモジュールの保存も行う様になります。(nodejs の node_modulesの様なフォルダ)
容量的にはPCに優しくないのですがこの設定をしないとモジュール参照の解決が面倒くさいのでした方がよいかなと思っています。
null.ps1
poetry config virtualenvs.in-project true
alembic, SQLAlchemy

alembic 以前は、SQLAlchemy-Migrate だったそうです。
SQLAlchemy の記事からたどってくと SQLAlchemy-Migrate にたどり着くのでどちらを使うかはググって判断してください。

poetry で、alembic, sqlalchemy をインストールします。
null.ps1
poetry init # 対話コンソールになるので適宜回答
poetry add alembic sqlalchemy
alembic

SQLAlchemy の class 定義と、DBを突き合わせて、テーブルを構築するのに必要なスクリプトの生成、実行が行えます。

初期化

最初に alembic init を実行し、DB構築の準備をします。
null.ps1
# alembic init {フォルダ名}
poetry run alembic init migrations
コマンドを実行すると、DB構築用のスクリプトと、migration 用のスクリプトを保存するフォルダが生成されます。
migrations/
  versions/
  env.py
  README
  script.py.mako
alembic.ini
生成された、alembic.ini のDB接続文字列を環境に合わせて修正します。
alembic.ini
# the output encoding used when revision files
# are written from script.py.mako
# output_encoding = utf-8

sqlalchemy.url = driver://user:pass@localhost/dbname
ORマッパーclass定義

このままだと、作るテーブルがないので適当にクラス定義します。
db/
  models.py
SQLAlchemy の Baseクラスから派生したクラスを定義します。
全てのテーブルに埋めたい created, modified などのフィールドを含むクラスを __abstract__ で定義し、そのクラスより派生すると少し楽になれるかもしれません。
models.py
from sqlalchemy.ext.declarative import declarative_base
from sqlalchemy.schema import Column
from sqlalchemy.schema import ForeignKey
from sqlalchemy.sql.functions import random
from sqlalchemy.sql.schema import UniqueConstraint
from sqlalchemy.sql.sqltypes import DATETIME
from sqlalchemy.types import Integer, String

from datetime import datetime

Base=declarative_base()

class BaseModel(Base):
    __abstract__ = True
    id = Column(Integer, primary_key=True, autoincrement=True)
    created = Column(DATETIME, default=datetime.now)
    modified = Column(DATETIME, default=datetime.now)

    def __init__(self):
        self.created = datetime.now
        self.modified = datetime.now

class User(BaseModel):
    """
    service users.
    """
    __tablename__ = "users"
    email = Column(String(255), unique=True)
    password = Column(String(255))

    def __init__(self, email, password):
        self.email = email
        self.password = password

class Match(BaseModel):
    __tablename__ = "matches"
    seed = Column(Integer, nullable=False)

    def __init__(self):
        self.seed = random.randint()

class MatchUser(BaseModel):
    __table_args__= ((UniqueConstraint("match_id", "user_id"), ))
    __tablename__ = "match_users"
    match_id = Column(Integer, ForeignKey("matches.id", onupdate="cascade", ondelete="cascade"))
    user_id = Column(Integer, ForeignKey("users.id"), nullable=False)

    def __init__(self, match_id, user_id):
        self.match_id = match_id
        self.user_id = user_id

class MatchTurn(BaseModel):
    __tablename__ = "match_turns"
    id = Column(Integer, primary_key=True, autoincrement=True)
    match_id = Column(Integer, ForeignKey("matches.id", onupdate="cascade", ondelete="cascade"))
    no = Column(Integer, nullable=False)

    def __init__(self, match_id, no):
        self.match_id = match_id
        self.no = no
model定義を参照する様に、migrations/env.py を編集

migrations/env.py を開くと、model の MetaData を定義する様にコメントが記載されているので、定義します。
migrations/env.py
# ★before
# add your model's MetaData object here
# for 'autogenerate' support
# from myapp import mymodel
# target_metadata = mymodel.Base.metadata
target_metadata = None
　↓先程定義した model のメタデータを定義
# ★after
# add your model's MetaData object here
from db.models import Base
target_metadata = Base.metadata
upgrade 作成

alembic revision でDB接続し、現在のDBのスキーマと models.pyの内容を比較して、スキーマ最新化に必要なスクリプトを作成し、migrations/versions に保存します。
null.ps1
# alembic revision --autogenerate -m {任意のバージョン番号}
poetry run alembic revision --autogenerate -m v0.01
upgrade 実行

alembic upgrade コマンドで、DBのスキーマを任意のバージョンにします。
null.ps1
poetry run alembic upgrade head
おわりに

細切れ記事は色々あるのですが、まとめ記事はないのでまとめました。
これだけ色々なものを入れたにも関わらず、割と短い記事で書き終わって、随分便利な世の中になってるなぁと思いました。
Java で同じアウトプットの記事を書こうと思ったら eclipse のインストールや設定も細かく解説が必要で、@ITあたりで全10回構成の記事にする物量になりそうだなと、なぜかムーアの法則に思いをはぜました。

ツール	説明
chocolatey	Windows用パッケージ管理システム。
python3.9.2	python 本体。
poetry	python のパッケージ管理システム。 pip は requirements.txt を手書きしないとダメだったが、npmやyarn の様に pyproject.toml を自動で更新してくれる。
mysqlalchemy	OR Mapper。簡単なクラス定義で簡単にDB操作ができる。
alembic	DB 構築/マイグレーションヘルパ。mysqlalchemy のクラス定義に沿ったスキーマをDBに構築。

　 Tweet
Qiitaで続きを読む

投稿日：2021-02-27T15:04:34+09:00

日付をリストにして返す関数

from datetime import timedelta
from datetime import datetime as dt

def datelist(start_str="2018-1-1", end_str="2018-12-31", input_format='%Y-%m-%d', output_format='%Y-%m-%d') -> list:
    start_dt = dt.strptime(start_str, input_format)
    end_dt = dt.strptime(end_str, input_format)
    days_num = (end_dt - start_dt).days + 1 # 最終日も含めたいので、+1

    result = map(lambda x:
                 (start_dt + timedelta(days=x)).strftime(output_format), range(days_num))
    return list(result) # ['2018-01-01', '2018-01-02',....]

　 Tweet
Qiitaで続きを読む

投稿日：2021-02-27T15:04:34+09:00

日付（文字列型）をリストにして返す関数

for文で回したいときにどうぞ。

from datetime import timedelta
from datetime import datetime as dt

def datelist(start_str="2018-1-1", end_str="2018-12-31", input_format='%Y-%m-%d', output_format='%Y-%m-%d') -> list:
    """引数のinput_format, output_formatはdatetime.strftimeで利用する形式"""
    start_dt = dt.strptime(start_str, input_format)
    end_dt = dt.strptime(end_str, input_format)
    days_num = (end_dt - start_dt).days + 1 # 最終日も含めたいので、+1

    result = map(lambda x:
                 (start_dt + timedelta(days=x)).strftime(output_format), range(days_num))
    return list(result) # ['2018-01-01', '2018-01-02',....]

　 Tweet
Qiitaで続きを読む

投稿日：2021-02-27T14:48:56+09:00

KerasでCallbackを使用する

はじめに

Kerasで学習する際に便利そうなコールバックがあったので使ってみました。
今回は下記のコールバックを使用してみます。

EarlyStopping

TensorBoard

CSVLogger

下記にKeras公式サイトのコールバックの説明があります。
https://keras.io/ja/callbacks/

EarlyStopping

監視対象の値が変化しなくなったときに学習を終了します。エポック数を多めに指定しても途中で終了してくれるので安心です。
ここでは、エポック数10回の間に損失値の変化が0.0001より小さければ、改善がみられないと判断して学習を終了するようにします。
es_cb = keras.callbacks.EarlyStopping(
    monitor='loss', min_delta=0.0001, patience=10, mode='auto')
TensorBoard

TensorBoardによる可視化を行います。
オプションがいろいろあるのですが、今回はログ出力先だけ指定して残りはデフォルト値のままとします。
tb_cb = keras.callbacks.TensorBoard(log_dir='./logs')
CSVLogger

エポックの結果をCSVファイルに出力してくれます。
csv_logger = keras.callbacks.CSVLogger('training.csv')
Pythonプログラム

前回と同様、一次関数を学習させます。
model.fit()で学習時にコールバックの指定を追加しています。
また、validation_dataを指定して、エポックごとにテストデータの検証も行うようにしています。
model.fit(
    x_train, y_train,
    epochs=500,
    callbacks=[es_cb, tb_cb, csv_logger],
    validation_data=(x_test, y_test))
プログラムの全体です。
import matplotlib.pyplot as plt
import numpy as np
from tensorflow import keras
from sklearn.model_selection import train_test_split

# Y = 2X + 3を求める関数とする。
x = np.linspace(0, 10, num=50)
y = 2 * x + 3

# トレーニングデータと検証データに分割
x_train, x_test, y_train, y_test = train_test_split(x, y, shuffle=False)

# ネットワークを作成
model = keras.models.Sequential([
    keras.layers.Dense(1, input_shape=(1,), activation="linear"),
])

# コールバックの作成
es_cb = keras.callbacks.EarlyStopping(
    monitor='loss', min_delta=0.0001, patience=10, mode='auto')
tb_cb = keras.callbacks.TensorBoard(log_dir='./logs')
csv_logger = keras.callbacks.CSVLogger('./training.csv')

# オプティマイザはSGD、損失関数はMSEを使用
model.compile(optimizer='sgd', loss='mse')

model.fit(
    x_train, y_train,
    epochs=500,
    callbacks=[es_cb, tb_cb, csv_logger],
    validation_data=(x_test, y_test))

print(model.get_weights())

plt.scatter(x, y, label='data', color='gray')
plt.plot(x_train, model.predict(x_train), label='train', color='blue')
plt.plot(x_test, model.predict(x_test), label='test', color='red')
plt.legend()
plt.show()
結果

エポック数に500を指定していますが、405エポックで学習が終了しました。

TensorBoardの表示

TensorBoardを起動します。
$ tensorboard --logdir=./logs

Serving TensorBoard on localhost; to expose to the network, use a proxy or pass --bind_all
TensorBoard 2.4.1 at http://localhost:6006/ (Press CTRL+C to quit)
ブラウザで http://localhost:6006/ にアクセスするとTensorBoardを見ることができます。
グラフのオレンジの線がトレーニングデータ、青の線がテストデータです。
学習とともに損失値が小さくなっているのがわかります。

CSVLoggerの結果

CSVLoggerで指定したCSVファイルもできています。
epoch,loss,val_loss
0,254.1975860595703,116.32344818115234
1,35.86260986328125,6.254454612731934
2,5.318000793457031,0.04576351121068001
3,1.8426451683044434,1.2428233623504639
4,1.295862078666687,2.55403733253479
5,1.1909117698669434,2.0331602096557617
6,1.181778073310852,2.214395761489868
7,1.1415034532546997,3.4069273471832275
8,1.1195648908615112,3.5103976726531982
9,1.0969243049621582,2.3636646270751953
10,1.0725418329238892,3.2535252571105957
11,1.0593643188476562,2.874397039413452
(以下略)
PandasとMatplotlibでグラフ化してみます。
最初の損失値が大きいので、4番目以降のエポックのデータを使ってグラフにします。
import pandas as pd
import matplotlib.pyplot as plt

df = pd.read_csv('training.csv', index_col='epoch')
df.iloc[3:].plot()
plt.legend()
plt.show()
TensorBoardと同じようなグラフを作成することができました。

おわりに

これでモデルを作成して、学習状況を確認する準備ができました。
次回はもっと複雑なデータを使った学習を行う予定です。

　 Tweet
Qiitaで続きを読む

投稿日：2021-02-27T14:41:11+09:00

【数理考古学】とある実数列(Real Sequance)の規定例②等比数列から乗法群へ

前回の投稿では「実数族(Real Family)」なる大分類を想定し、それに下属する(部分集合を構成する)整数族(Integer Family)の概念について考察しました。
【数理考古学】とある実数列の規定例①等差数列から加法整数群へ

こちらで最初に足掛かりとしたのは加減算に立脚する「(小学校の時に習った)等差数列」でした。今回足掛かりとするのは、同じく小学校の時に習った「乗除算に立脚する等比数列」と冪乗算となります。とはいえ…

等比数列…α=初項(First Ratio),r=公比(Common Rattio)

α^n(n=-Inf(inity)→0→α×r^{n-1},…,+Inf(inity))

冪乗算…α=根(Base,Root)

α^n(n=-Inf(inity)→0→+Inf(inity))=(-Inf(inity),…,α^{-x}=\frac{1}{α^x},…,α^{-1}=\frac{1}{α},α^{0}=\frac{α}{α}=1,α,α^2,α^3,…,+Inf(inity))

Rによる等比数列と等差数列の比較

c0<-seq(-5,5,length=11)

#等差数列(Arithmetic Sequence=算術数列)
fa<-function(a,d,n){a+d*(n-1)} 

#等比数列(Geometric Sequence=幾何数列)
fg<-function(a,r,n){a*r^(n-1)} 

#等差数列は初項1、公差1の時
#整数集合の添字と演算結果集合が一致する。
> c0
 [1] -5 -4 -3 -2 -1  0  1  2  3  4  5
> fa(1,1,c0)
 [1] -5 -4 -3 -2 -1  0  1  2  3  4  5

#等差数列で初項1で公差0の時と
#等比数列で初項0で公比0の時は
#演算結果集合がy=0で一致する。
> fg(1,0,c0)
 [1] 0 0 0 0 0 0 0 0 0 0 0
> fa(0,0,c0)
 [1] 0 0 0 0 0 0 0 0 0 0 0
#等比数列は理論上
#初項0,公比0の時もy=0に到達するが
#コンピューターはちゃんと計算してくれない。
> fg(0,0,c0)
 [1] NaN NaN NaN NaN NaN NaN   0   0   0   0   0
> 0*0^(1-1)
[1] 0
> 0*0^(0-1)
[1] NaN
> 0*0^0
[1] 0
> 0*0^-1
[1] NaN
> 0^-1
[1] Inf
> 0^-2
[1] Inf
> 0^-3
[1] Inf
> 0^-4
[1] Inf
> 0^Inf
[1] 0
#指数関数0^xの場合は逆に無限大に到達する。
> 0^c0
 [1] Inf Inf Inf Inf Inf   1   0   0   0   0   0

#形式的に等比数列の一般項の対数をとると
#log(αn)=log(a)+(n-1)×log(r)となり
#初項log(a),公差log(r)の等差数列と一致する。
fgl<-function(a,r,n){log(a)+(n-1)*log(r)}
> fgl(1,2,c0)
 [1] -4.1588831 -3.4657359 -2.7725887 -2.0794415 -1.3862944 -0.6931472  0.0000000  0.6931472
 [9]  1.3862944  2.0794415  2.7725887
> fa(log(1),log(2),c0)
 [1] -4.1588831 -3.4657359 -2.7725887 -2.0794415 -1.3862944 -0.6931472  0.0000000  0.6931472
 [9]  1.3862944  2.0794415  2.7725887

#ちなみに等比数列(初項1,公比2)と指数関数2^xは添字が一つズレている。
> fg(1,2,c0)
 [1]  0.015625  0.031250  0.062500  0.125000  0.250000  0.500000  1.000000  2.000000  4.000000
[10]  8.000000 16.000000
> 2^c0
 [1]  0.03125  0.06250  0.12500  0.25000  0.50000  1.00000  2.00000  4.00000  8.00000 16.00000
[11] 32.00000
> 2^(c0-1)
 [1]  0.015625  0.031250  0.062500  0.125000  0.250000  0.500000  1.000000  2.000000  4.000000
[10]  8.000000 16.000000

そう等差数列における奇数集合同様、例えば等比数列(初項1,公比2)と指数関数2^xも添字が一つズレるのです。

Rによる実装例

#等比数列(初項1,公比2)と指数関数2^x+1の比較
plot(c0,fg(1,2,c0),xlim=c(-5,5),type="l",ylim=c(0,16),main="Geometric Sequence",xlab="",ylab="")
par(new=T)
plot(c0,2^c0,xlim=c(-5,5),type="l",ylim=c(0,16),main="",xlab="",ylab="",col=rgb(0,0,1))
abline(v=1,col=rgb(1,0,0))
abline(v=0,col=rgb(1,0,0))
abline(h=1,col=rgb(1,0,0))
# 凡例を書き添える 。
legend("topleft", legend=c("Geometric Sequence(First Term=1,Comon Ratio=2)","Exponential Function y=2^x","x=0,1,y=1"), lty =c(1,1,1),col=c(rgb(0,0,0),rgb(0,0,1),rgb(1,0,0)))

どうやら等差数列同様、この辺りが頑張れる限界の模様ですね。

2.ネイピア族(Napier Famiry)の定義。

ここでまさかの人名推戴。「指数族」や「指数族」だと演算のイメージが強過ぎて元(Element)っぽくないので、あえてここで「常用対数表の父」に登場してもらう事にした次第です。
ジョン・ネイピア(John Napier,1550年~1617年) - Wikipedia

実際、この族の共通元は前回定義した「整数集合」の以下の写像となります。

-Inf(ity)→0\\
0→1\\
+Inf(ity)→+Inf(ity)

すると-1や+1は一体何処へ行ってしまうのでしょう？　もはや近似でしか計算出来ません。概ね1の場合は2(1+1)から、-1の場合は0(1-1)から計算を始めます。

1→exp(1)=(1+\frac{1}{n})^n=2.718282

Rによる作表例

#ヤコブ・ベルヌイの複利計算法に基づく算出方法
f0=function(x){(1+1/x)^x}
#グラフ化してみる。
plot(f0, xlim=c(0,50),ylim=c(0,3),lty =1,main="Natural logarithm", xlab="N", ylab="(1+1/N)^N")
#自然対数eと比較。
abline(h=exp(1))#exp(1)=2.718282...

-1→exp(-1)=(1-\frac{1}{n})^n=0.3678794

Rによる作表例

#オイラーの「ネイピアの対数表」に基づく算出方法
f0=function(x){(1-1/x)^x}
#グラフ化してみる。
plot(f0, xlim=c(0,50),ylim=c(0,0.5),lty =1,main="Natural logarithm", xlab="N", ylab="(1-1/N)^N")
#自然対数1/eと比較。
abline(h=exp(-1))#exp(-1)=0.3678794...

exp(1)とexp(-1)は当然逆数の関係にあり、反比例関数y=1/x上において「1×1の区画の次に面積が1となる座標の組み合わせ」としても知られています。

Rによる作表例

f0<-function(x){1/x}
plot(f0,asp=1,xlim=c(0,3),ylim=c(0,3),main="Inverse Proportional Formula")
#該当箇所の塗り潰し
sqx0<-seq(1,exp(1),length=11)
sqy0<-f0(sqx0)
polygon(
c(1,sqx0,exp(1)), #x
c(0,sqy0,0), #y
density=c(50), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=c(200,200,200)) 　#塗りつぶす色
sqx1<-seq(exp(-1),1,length=11)
sqy1<-f0(sqx1)
polygon(
c(0,0,exp(-1),sqx1,0), #x
c(1,exp(1),exp(1),sqy1,1), #y
density=c(50), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=c(200,200,200)) 　#塗りつぶす色

全体としてネイピア数exp(1)=2.718282を根とする冪乗算と計算結果が一致し、これを自然指数関数(Natural Exponential Function)exp(x)、その逆関数を自然対数関数(Natural Logarithm Function)log(x)と呼びます。全ての冪乗算は根の変換式によってこれに変換可能なので、族としての元はあくまで一つと考えて良いでしょう。
【初心者向け】指数・対数関数の発見とそれ以降の発展について。

log(a,base=b)=\frac{log(b,base=e)}{log(a,base=e)}

Rによる実装例

log(2,base=3)
[1] 0.6309298
log(2,base=4)/log(3,base=4)
[1] 0.6309298
> log(2)/log(3)
[1] 0.6309298

この対数尺の素晴らしいところは(射影元の整数族の尺度たる)均等尺上における掛け算が足し算に、割り算が引き算に、冪乗算が掛け算に置き換わる事です。近世におけるこの発見と常用対数表の登場により数学者や天文学者や物理学者の寿命が倍増したという話も。
【数理考古学】常用対数表を使った計算

Rによる計算例　1.43*5.93(掛け算→足し算)

> 1.43*5.93
[1] 8.4799
> log(1.43,base=10)
[1] 0.155336
> log(5.93,base=10)
[1] 0.7730547
> log(1.43,base=10)+log(5.93,base=10)
[1] 0.9283907
> 10^0.9283907
[1] 8.479899

pythonによる計算例　1.43*5.93(掛け算→足し算)

import numpy as np

print(1.43*5.93)
print(np.log10(1.43))
print(np.log10(5.93))
a=np.log10(1.43)+np.log10(5.93)
print(a)
print(10**a)
#出力結果
8.479899999999999
0.1553360374650618
0.7730546933642626
0.9283907308293244
8.4799

Rによる計算例 1.43/5.93(割り算→引き算)

> 1.43/5.93
[1] 0.2411467
> log(1.43,base=10)
[1] 0.155336
> log(5.93,base=10)
[1] 0.7730547
> log(1.43,base=10)-log(5.93,base=10)
[1] -0.6177187
> 10^-0.6177187
[1] 0.2411467

pythonによる計算例 1.43/5.93(割り算→引き算)

import numpy as np

print(1.43/5.93)
print(np.log10(1.43))
print(np.log10(5.93))
a=np.log10(1.43)-np.log10(5.93)
print(a)
print(10**a)
#出力結果
0.2411467116357504
0.1553360374650618
0.7730546933642626
-0.6177186558992007
0.24114671163575047

Rによる計算例 1034*2213(掛け算→足し算)

> 1034*2213
[1] 2288242
> log(1034,base=10)
[1] 3.014521
> log(2213,base=10)
[1] 3.344981
> log(1034,base=10)+log(2213,base=10)
[1] 6.359502
> log(1034*2213,base=10)
[1] 6.359502
> 10^6.359502
[1] 2288242

pythonによる計算例　1034*2213(掛け算→足し算)

import numpy as np

print(1034*2213)
print(np.log10(1034))
print(np.log10(2213))
a=np.log10(1034)+np.log10(2213)
print(a)
print(10**a)
#出力結果
2288242
3.0145205387579237
3.344981413927258
6.359501952685182
2288242.000000003

Rによる計算例　1034/2213(割り算→引き算)

> 1034/2213
[1] 0.467239
> log(1034,base=10)
[1] 3.014521
> log(2213,base=10)
[1] 3.344981
> log(1034,base=10)-log(2213,base=10)
[1] -0.3304609
> log(1034/2213,base=10)
[1] -0.3304609
> 10^-0.3304609
[1] 0.467239

pythonによる計算例　1034/2213(割り算→引き算)

import numpy as np

print(1034/2213)
print(np.log10(1034))
print(np.log10(2213))
a=np.log10(1034)-np.log10(2213)
print(a)
print(10**a)
#出力結果
0.46723904202440125
3.0145205387579237
3.344981413927258
-0.3304608751693343
0.4672390420244012

ネイピア族(Napier Famiry)の実数への漸近戦略。

しかし問題も生じました。冪乗算の定積分の式は素直に導出すると以下なのですが…

\int_{a}^{b}x^βdx=\frac{1}{β+1}×b^{β+1}-\frac{1}{β+1}×a^{β+1}

これがβ-1の時分母が0となり計算不能となってしまうのです。
【数理考古学】冪乗算の微積分

Rによる検証例

#Integrate(1→2)(x^β)dx
f0<-function(x)(2^(x+1))/(x+1)-1/(x+1)
f0(-1)

#確かに計算不能となる。
> f0(-1)
[1] NaN

#近似値(-1<a)
 f0(-1.1)
[1] 0.6696701
> f0(-1.01)
[1] 0.6907505
> f0(-1.001)
[1] 0.692907
> f0(-1.0001)
[1] 0.6931232
> f0(-1.00001)
[1] 0.6931448
> f0(-1.000001)
[1] 0.6931469
> f0(-1.0000001)
[1] 0.6931472
> f0(-1.00000001)
[1] 0.6931472

#近似値(a<-1)
> f0(-0.9)
[1] 0.7177346
> f0(-0.99)
[1] 0.695555
> f0(-0.999)
[1] 0.6933875
> f0(-0.9999)
[1] 0.6931712
> f0(-0.99999)
[1] 0.6931496
> f0(-0.999999)
[1] 0.6931474
> f0(-0.9999999)
[1] 0.6931472
> f0(-0.99999999)
[1] 0.6931472

#ちなみに正解はlog(2)=0.6931472となる。
> log(2)
[1] 0.6931472

反比例関数y=1/xのグラフでいうと以下の領域ですね。

Rによる作表例

f0<-function(x){1/x}
plot(f0,xlim=c(0,3),ylim=c(0,3),main="Inverse Proportional Formula")
#該当箇所の塗り潰し
sqx<-seq(1,2,length=11)
sqy<-f0(sqx)
polygon(
c(1,sqx,2), #x
c(0,sqy,0), #y
density=c(50), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=c(200,200,200)) 　#塗りつぶす色

ここで歴史的にはArctangentの収束先π/4を高速で計算したオイラー変換()の出番となります。「本当に一人？　ブルバキみたいな集団ペンネームじゃなくて?」と思うほど、オイラーの出番多過ぎ問題…
【数理考古学】オイラーの公式を導出したマクローリン級数の限界？

Rによる作表例

cx<-0:10
cy1<-c(0.6666667,0.8666667,0.7238095,0.8349206,0.7440115,0.8209346,0.754268,0.8130915,0.7604599,0.808079,0.7646007)
cy2<-c(0.6666667,0.7333333,0.7619048,0.7746032,0.7803752,0.7830392,0.7842824,0.7848674,0.7851445,0.7852765,0.7853396)
plot(cx,cy1,xlim=c(0,10),ylim=c(0.65,0.9),type="l",col=rgb(0,0,1),main="Leibniz Series & Eulerian Transformation", xlab="x", ylab="y")
par(new=T)#上書き指定
plot(cx,cy2,xlim=c(0,10),ylim=c(0.65,0.9),type="l",col=rgb(0,1,0),main="", xlab="", ylab="")
abline(h=pi/4,col=rgb(1,0,0))
legend("topright", legend=c("π/4=0.7853982","Leibniz","Euler"),lty=c(1,1,1),col=c(rgb(1,0,0),rgb(0,0,1),rgb(0,1,0)))

そして考え方のパラダイムシフトが起こります。任意の（すべての）正の実数はα×２^n(1≦α<2;nは整数)の形に表せるので,log(α×2^n)＝log(α)+n×log(2)と示せるのですが…・(ただしここにlog(3,base=2)が混ざり込む)。

Rによる検証例

> 2^0
[1] 1
> 2^1
[1] 2
> 2^0+2^1
[1] 3

#ところで
> 2^1.5849625
[1] 3
> log(3)/log(2)
[1] 1.584963
> log(3,base=2)
[1] 1.584963

#2^2
> 2^2
[1] 4
> 2^2+2^0
[1] 5
> 2^2+2^1
[1] 6

> 2^2+2^log(3,base=2)
[1] 7

#2^3
> 2^3
[1] 8

一覧表(8まで)

	Values	Explessions
1	1	2^0
2	2	2^1
3	3	2^0+2^1 / 2^log(3,base=2)
4	4	2^2
5	5	2^2+2^0
6	6	2^2+2^1
7	7	2^2+2^log(3,base=2)
8	8	2^3

target_values<-c("1","2","3","4","5","6","7","8")

target_explession<-c("2^0","2^1","2^0+2^1 / 2^log(3,base=2)","2^2","2^2+2^0","2^2+2^1","2^2+2^log(3,base=2)","2^3")

Regula_falsi04<-data.frame(Values=target_values,Explessions=target_explession)
library(xtable)
print(xtable(Regula_falsi04), type = "html")

つまりlog(2)の値さえ求めておけば,ここで示した近似式を用いて任意の正の実数xの自然対数log(x)の値を計算出来る事になる訳です。こうしてネイピア族も無事整数族と並び立つ形で「実数列そのものへの拡張」を果たす事になったのでした。
対数関数のTylor展開
 【無限遠点を巡る数理】等差数列と等比数列②基底関数概念の導入

Rによる検証例

#オイラー変換に従ったLog(2)の計算
> 2/3+2/3*(1/3)^3+2/5*(1/3)^5+2/7*(1/3)^7
[1] 0.6931348
> log(2)
[1] 0.6931472

#log(2)に基づく計算

#log(1)
> log(1)
[1] 0
> log(2)+log(1/2)
[1] 0
#log(3)
> log(3)
[1] 1.098612
> exp(log(3)-log(2))
[1] 1.5
> log(1.5)+log(2)
[1] 1.098612
#log(4)

> log(4)
[1] 1.386294
> log(2)*2
[1] 1.386294
> log(2^2)
[1] 1.386294

#log(5)

 > log(5)
[1] 1.609438

> exp(log(5)-log(2^2))
[1] 1.25
>log(1.25)+log(2^2)
[1] 1.609438

#log(6)
> log(6)
[1] 1.791759
> exp(log(6)-log(2^2))
[1] 1.5
> log(1.5)+log(2^2)
[1] 1.791759

#log(7)

> log(7)
[1] 1.94591
> exp(log(7)-log(2^2))
[1] 1.75
> log(1.75)+log(2^2)
[1] 1.94591

#log(8)

> log(8)
[1] 2.079442
> log(2)*3
[1] 2.079442
> log(2^3)
[1] 2.079442

一覧表(8まで)

	Numbers	Explessions	Values
1	log(1)	log(2^1)+log(1/2)	0
2	log(2)	log(2^1)	0.6931472
3	log(3)	log(1.5)+log(2^1)	1.098612
4	log(4)	log(2^2)	1.386294
5	log(5)	log(1.25)+log(2^2)	1.609438
6	log(6)	log(1.5)+log(2^2)	1.791759
7	log(7)	log(1.75)+log(2^2)	1.94591
8	log(8)	log(2^3)	2.079442

target_number<-c("log(1)","log(2)","log(3)","log(4)","log(5)","log(6)","log(7)","log(8)")

target_explession<-c("log(2^1)+log(1/2)","log(2^1)","log(3/2)+log(2^1)","log(2^2)","log(5/4)+log(2^2)","log(3/2)+log(2^2)","log(7/4)+log(2^2)","log(2^3)")

target_values<-c("0","0.6931472","1.098612","1.386294","1.609438","1.791759","1.94591","2.079442")

Regula_falsi04<-data.frame(Numbers=target_number,Explessions=target_explession,Values=target_values)
library(xtable)
print(xtable(Regula_falsi04), type = "html")

何故1と-1は特別なのか。

以下の投稿ではあたかも以下を自明の場合の様に扱ってしまいました。

-1=i^2=(0±1i)^2

【数理考古学】とある実数列の規定例①等差数列から加法整数群へ

せっかく等比数列の話が出たので少し掘り下げてみましょう。まず公比=1の時は1^x同様、ただの動かない点に過ぎません。

0<公比<1の時

純粋な1次元展開により０へ向けて収束します。

Rによる実装例

#振動関数(Mathematical Oscillation Function)
#公比D=0.8

MOF01<-function(index){
z0<-complex(real=0.8,imaginary=0)
f0<-function(x)z0^(2*x)
c0<-f0(index)
cx<-Re(c0)
cy<-Im(c0)
plot(cx,cy,asp=1,type="l",xlim=c(-1,1),ylim=c(-1,1),main="Mathematical Oscillation Function",xlab="X axis",ylab="Y axis")
text(cx,cy,"X",cex=2,col=rgb(0,1,0))
text(1,0,"1",cex=2,col=rgb(0,0,1))
text(0,0,"0",cex=2,col=rgb(0,0,1))
segments(0,0,cx,cy,col=rgb(0,1,0))
abline(h=0, col=c(200,200,200))
abline(v=0, col=c(200,200,200))
}

#アニメーション動作設定
Time_Code<-seq(0,8,length=30)
#アニメーション
library("animation")
saveGIF({
for (i in Time_Code){
　MOF01(i)
}
}, interval = 0.1, movie.name = "MOF36.gif")

公比>1の時

純粋な1次元展開により無限大に向けて発散します。

Rによる実装例

#振動関数(Mathematical Oscillation Function)
#公比D=1.2

MOF01<-function(index){
z0<-complex(real=1.2,imaginary=0)
f0<-function(x)z0^(2*x)
c0<-f0(index)
cx<-Re(c0)
cy<-Im(c0)
plot(cx,cy,asp=1,type="l",xlim=c(-3,3),ylim=c(-3,3),main="Mathematical Oscillation Function",xlab="X axis",ylab="Y axis")
text(cx,cy,"X",cex=2,col=rgb(0,1,0))
text(1,0,"1",cex=2,col=rgb(0,0,1))
text(0,0,"0",cex=2,col=rgb(0,0,1))
segments(0,0,cx,cy,col=rgb(0,1,0))
abline(h=0, col=c(200,200,200))
abline(v=0, col=c(200,200,200))
}

#アニメーション動作設定
Time_Code<-seq(0,8,length=30)
#アニメーション
library("animation")
saveGIF({
for (i in Time_Code){
　MOF01(i)
}
}, interval = 0.1, movie.name = "MOF37.gif")

公比=-1の時

X軸上から見ると-1と1の間を無限に往復し続ける様に見えます。

Rによる実装例(正方向Ver.)

#振動関数(Mathematical Oscillation Function)
#公比D=-1
#-1^xにi^2=-1を代入
#(0+1i)^2^x=(0+1i)^2x

MOF01<-function(index){
z0<-complex(real=0,imaginary=1)
f0<-function(x)z0^(2*x)
c0<-f0(index)
cx<-Re(c0)
cy<-Im(c0)
plot(cx,cy,asp=1,type="l",xlim=c(-1,1),ylim=c(-1,1),main="Mathematical Oscillation Function",xlab="X axis",ylab="Y axis")
text(cx,cy,"X",cex=2,col=rgb(0,1,0))
segments(0,0,cx,cy,col=rgb(0,1,0))
abline(h=0, col=rgb(1,0,0))
abline(v=0, col=rgb(1,0,0))
}

#アニメーション動作設定
Time_Code<-c(seq(-1,1,length=15),rev(seq(-1,1,length=15)))
#アニメーション
library("animation")
saveGIF({
for (i in Time_Code){
　MOF01(i)
}
}, interval = 0.1, movie.name = "MOF21.gif")

Rによる実装例(逆方向Ver.)

#振動関数(Mathematical Oscillation Function)
#公比D=-1
#-1^xにi^2=-1を代入
#(0+1i)^2^x=(0+1i)^2x

MOF01<-function(index){
z0<-complex(real=0,imaginary=-1)
f0<-function(x)z0^(2*x)
c0<-f0(index)
cx<-Re(c0)
cy<-Im(c0)
plot(cx,cy,asp=1,type="l",xlim=c(-1,1),ylim=c(-1,1),main="Mathematical Oscillation Function",xlab="X axis",ylab="Y axis")
text(cx,cy,"X",cex=2,col=rgb(0,1,0))
segments(0,0,cx,cy,col=rgb(0,1,0))
abline(h=0, col=rgb(1,0,0))
abline(v=0, col=rgb(1,0,0))
}

#アニメーション動作設定
Time_Code<-c(seq(-1,1,length=15),rev(seq(-1,1,length=15)))
#アニメーション
library("animation")
saveGIF({
for (i in Time_Code){
　MOF01(i)
}
}, interval = 0.1, movie.name = "MOF22.gif")

0>公比>-1の時

どんどん振幅の幅が狭まっていきます。

Rによる実装例

#振動関数(Mathematical Oscillation Function)
#公比D=-0.8

MOF01<-function(index){
z0<-complex(real=-0.8,imaginary=0)
f0<-function(x)z0^(2*x)
c0<-f0(index)
cx<-Re(c0)
cy<-Im(c0)
plot(cx,cy,asp=1,type="l",xlim=c(-1,1),ylim=c(-1,1),main="Mathematical Oscillation Function",xlab="X axis",ylab="Y axis")
text(cx,cy,"X",cex=2,col=rgb(0,1,0))
segments(0,0,cx,cy,col=rgb(0,1,0))
abline(h=0, col=rgb(1,0,0))
abline(v=0, col=rgb(1,0,0))
}

#アニメーション動作設定
Time_Code<-seq(0,8,length=90)
#アニメーション
library("animation")
saveGIF({
for (i in Time_Code){
　MOF01(i)
}
}, interval = 0.1, movie.name = "MOF24.gif")

公比<-1の時

どんどん振幅の幅が広がっていきます。

Rによる実装例

#振動関数(Mathematical Oscillation Function)
#公比D=-1.2

MOF01<-function(index){
z0<-complex(real=-1.2,imaginary=0)
f0<-function(x)z0^(2*x)
c0<-f0(index)
cx<-Re(c0)
cy<-Im(c0)
plot(cx,cy,asp=1,type="l",xlim=c(-3,3),ylim=c(-3,3),main="Mathematical Oscillation Function",xlab="X axis",ylab="Y axis")
text(cx,cy,"X",cex=2,col=rgb(0,1,0))
segments(0,0,cx,cy,col=rgb(0,1,0))
abline(h=0, col=rgb(1,0,0))
abline(v=0, col=rgb(1,0,0))
}

#アニメーション動作設定
Time_Code<-seq(0,8,length=90)
#アニメーション
library("animation")
saveGIF({
for (i in Time_Code){
　MOF01(i)
}
}, interval = 0.1, movie.name = "MOF25.gif")

そう、一点で留まってるのは1のみ、ちゃんと周回軌道を描くのは-1のみなんですね。

Rによる確認例

> (0-1i)*(0+1i)
[1] 1+0i
> (0+1i)*(0-1i)
[1] 1+0i
> (0-1i)*(0-1i)
[1] -1+0i
> (0+1i)*(0+1i)
[1] -1+0i

ここ数年取り組んできた「数についての考え方の総まとめ」その2。そんな感じで以下続報…

　 Tweet
Qiitaで続きを読む

投稿日：2021-02-27T12:52:22+09:00

Pyxelでの日本語の実装

注意

Qiitaで記事を書くのは初めてなのでご了承ください。

必要なライブラリ

cv2
Pyxel

準備

ダウンロード

8×8 ドット日本語フォント「美咲フォント」
のページのダウンロードから、PNG形式をダウンロードし、解凍します。
ここでは、ダウンロードしたフォルダを「misaki_font_data」として、実行ファイル下に置きます。

文字対応表作成

JIS X 0213コード表(全コード)
から、以下のように、表を全てコピーし、以下のように「code_table.txt」として保存します

code_table.txt

面区  点 JIS SJIS    EUC +0  +1  +2  +3  +4  +5  +6  +7  +8  +9  +A  +B  +C  +D  +E  +F
1面1区    0   2120    813F    A1A0        　 、 。 ,   .   ・ :   ;   ?   !   ゛ ゜ ´  `   ¨
16  2130    814F    A1B0    ^   ‾ _   ヽ ヾ ゝ ゞ 〃 仝 々 〆 〇 ー — ‐ /
32  2140    815F    A1C0    \   〜 ‖ |   … ‥ ‘ ’ “ ” (   )   〔 〕 [   ]
48  2150    816F    A1D0    {   }   〈 〉 《 》 「 」 『 』 【 】 +   − ±  ×
64  2160    8180    A1E0    ÷  =   ≠ <   >   ≦ ≧ ∞ ∴ ♂ ♀ °  ′ ″ ℃ ¥
80  2170    8190    A1F0    $   ¢  £  %   #   &   *   @   §  ☆ ★ ○ ● ◎ ◇ 

面区  点 JIS SJIS    EUC +0  +1  +2  +3  +4  +5  +6  +7  +8  +9  +A  +B  +C  +D  +E  +F
...

次にこれを実行します。

convert.py

edits = {#必要のない範囲のデータ　無くてもあっても変わらないので消しても〇
    2:[['〓','∈'],['∩','∧'],['∃','∠'],['∬','Å'],['¶','◯']],
    3:[[0,'0'],['9','A'],['Z','a'],['z',1]],
    4:[['ん',1]],
    5:[['ヶ',1]],
    #6:[['Ω','a'],['ω',1]],
    7:[['Я','а'],['я',1]],
    8:[['╂',1]],
    9:[[0,1]],
    10:[[0,1]],
    11:[[0,1]],
    12:[[0,1]],
    13:[['㎡','㊥']],
    14:[[0,1]],
    15:[[0,1]],
    47:[['腕',1]]
}

with open('./code_table.txt','r',encoding='utf-8') as f:#さきほど作成した「code_table.txt」を開いて文字列を取得します。
    s = f.read().replace('2面（第4水準漢字）','')#必要のない、「2面（第4水準漢字）」を取り除きます

    result_s = ""
    i = 1

    #コード表から文字だけを摘出します。
    for line in s.split('\n\n'):
        append_s = ""
        for l in line.split('\n')[1:]:
            append_s += ''.join(l.split('\t')[-16:])
        if i in edits:
            for r_0,r_1 in edits[i]:
                if type(r_0) == int:
                    r_0 *= len(append_s)
                else:
                    r_0 = append_s.find(r_0)+1
                if type(r_1) == int:
                    r_1 *= len(append_s)
                else:
                    r_1 = append_s.find(r_1)

                append_l = list(append_s)
                append_l[r_0:r_1] = " " * (r_1-r_0)

                append_s = ''.join(append_l)

        result_s += append_s.rstrip() + '\n'

        i += 1

    result_s = result_s[:result_s.find('熙')+1]

with open('./codes.txt','w',encoding='utf-8') as f:#「codes.txt」にresult_sを書き込みます
    f.write(result_s)

実行すると「codes.txt」というファイル名の文字対応表ができます。

表示

文字対応表と、PNG形式のフォントデータを参照して、Pyxelで日本語を表示します。

作成

draw.py

import pyxel as px
import cv2

with open('./codes.txt','r',encoding='utf-8') as f:#文字対応表を取得
    s = f.read()

fonts = [cv2.imread(f'./misaki_font_data/{file_name}.png') for file_name in ['misaki_gothic','misaki_gothic_2nd','misaki_mincho']]#各フォントのPNG形式データを取得

def text(x,y,txt,col,font=0,tategaki=False,width=256,height=256):#width,heightは、処理を軽くするために、描画領域を指定するのに使用します
    base_x = x
    base_y = y
    for char in txt:
        found = s.find(char)
        if found >= 0 and char != '\n' and -8 < x < width and -8 < y < height:
            sy = s[:found].count('\n')
            sx = s.split('\n')[sy].find(char)

            for i in range(8):
                for j in range(8):
                    if 128 > fonts[font][sy*8+j-1,sx*8+i-1][0]:
                        px.pset(x+i,y+j,col)

        if tategaki:
            y += 8
            if char == '\n':
                y = base_y
                x -= 8
        else:
            x += 8
            if char == '\n':
                x = base_x
                y += 8

class App:
    def __init__(self):
        px.init(256,128)
        px.run(self.update,self.draw)

    def update(self):
        if px.btnp(px.KEY_Q):
            px.quit()

    def draw(self):
        px.cls(0)
        text(0,0,"朝鮮民主主義人民共和国",7)#試しに「朝鮮民主主義人民共和国」と表示
        text(0,10,"なまむぎなまごめなまたまご",7)#試しに「なまむぎなまごめなまたまご」と表示

App()

実行結果

うまくいきました。
他にも縦書きやいろいろな文字を描画できます。
ツイッター

注意点

対応していない文字は、表示されず空白になります。
数字や記号などは、全角ではなく、半角で入力するようにしてください。

最後に

Pyxelでの日本語表示により、ゲーム作成の幅がすこしでも広がることを祈っております。
修正案、不具合などがあったらコメントしてください。

　 Tweet
Qiitaで続きを読む

投稿日：2021-02-27T12:29:38+09:00

ラズパイ＋超音波距離センサー＋カメラでおもちゃ（の原型）作り

カメラモジュールを購入したので，これを使った何か楽しめるものを作ろうと思いました．
そこで，人や物が近づいてきたら写真を撮影する，簡単なおもちゃを作ることにしました．

制作過程

使用した道具

今回は，以下の道具をを使用しました．

Raspberry Pi 4 Model B

ブレッドボード，T型GPIO拡張ボード，フラットリボンケーブル，ジャンパー線

カメラモジュール

HC-SR04超音波距離センサー

LED（黄）

220Ω抵抗

なお，LEDと抵抗は必須ではありませんが，しっかり動いているか確認できるようにするために用いています．

接続例

つなぎ方はいろいろあると思いますが，以下の図のように接続しました．

方針

今回の方針をわかりやすく整理するために，以下のようなフローチャートを作りました．（詳細な部分は省いています）

実際には途中でループを抜ける必要があるため，これにループを抜けるための処理を追加します．

結果

ソースコード
camera_sensor.py
import RPi.GPIO as GPIO
import time
from datetime import datetime
from picamera import PiCamera

# 各種変数を定義
trigPin = 16
echoPin = 18
ledPin = 11
MAX_DISTANCE = 220
timeOut = MAX_DISTANCE * 60
shootInterval = 5.0
catchDistance = 50.0

camera = PiCamera()

# 超音波が返ってくる時間を測定
def pulseIn(pin, level, timeOut):
    t0_sensor = time.time()
    while (GPIO.input(pin) != level):
        if ((time.time() - t0_sensor) > timeOut * 0.000001):
            return 0;
    t0_sensor = time.time()
    while (GPIO.input(pin) == level):
        if ((time.time() - t0_sensor) > timeOut * 0.000001):
            return 0;
    pulseTime = (time.time() - t0_sensor) * 1000000
    return pulseTime

# 物体との距離を計算
def getSonar():
    GPIO.output(trigPin, GPIO.HIGH)
    time.sleep(0.00001)
    GPIO.output(trigPin, GPIO.LOW)
    pingTime = pulseIn(echoPin, GPIO.HIGH, timeOut)
    distance = pingTime * 340.0 / 2.0 / 10000.0
    return distance

# 現在時刻を文字列として取得
def get_time_now(t1):
    today = datetime.fromtimestamp(t1)
    return today.strftime('%Y_%m_%d_%H_%M_%S')

# 準備
def setup():
    GPIO.setmode(GPIO.BOARD)
    GPIO.setup(trigPin, GPIO.OUT)
    GPIO.setup(echoPin, GPIO.IN)
    GPIO.setup(ledPin, GPIO.OUT)
    camera.start_preview()

# ループ処理
def loop():
    t0_camera = time.time()
    while True:
        distance = getSonar()
        t1 = time.time()
        if 0.0 < distance and distance < catchDistance:
            GPIO.output(ledPin, GPIO.HIGH)
            if (t1 - t0_camera) >= shootInterval:
                camera.capture('/home/pi/Desktop/images/%s.jpg'%(get_time_now(t1)))
                t0_camera = time.time()
        else:
            GPIO.output(ledPin, GPIO.LOW)
        print('The distance is: %2f cm'%(distance))
        time.sleep(0.5)

# 終了時の処理
def destroy():
    camera.stop_preview()
    GPIO.output(ledPin, GPIO.LOW)
    GPIO.cleanup()

if __name__ == '__main__':
    print('program is starting...')
    setup()
    try:
        loop()
    except KeyboardInterrupt:
        print('STOP!')
        destroy()
コードの説明

やや長いので，一部説明を省きます．

各種変数を定義
camera_sensor.py
trigPin = 16
echoPin = 18
ledPin = 11
MAX_DISTANCE = 220
timeOut = MAX_DISTANCE * 60
shootInterval = 5.0
catchDistance = 50.0

camera = PiCamera()
まずは，必要となるそれぞれの変数を定義します．今回は，MAX_DISTANCEで計測可能な最長距離を定めています．この場合，超音波が距離MAX_DISTANCEを往復するための時間timeOutは
timeOut = 2 * MAX_DISTANCE / 100 / 340 * 100000 ≒ MAX_DISTANCE * 58.8
となります．（わかりやすくするために58.8を60としています．また，音の時間にはすべて1000000を掛けています．）
また，ピンの番号はピンを指す位置により変わります．

距離の測定
camera_sensor.py
# 超音波が返ってくる時間を取得
def pulseIn(pin, level, timeOut):
    t0_sensor = time.time()
    while (GPIO.input(pin) != level):
        if ((time.time() - t0_sensor) > timeOut * 0.000001):
            return 0;
    t0_sensor = time.time()
    while (GPIO.input(pin) == level):
        if ((time.time() - t0_sensor) > timeOut * 0.000001):
            return 0;
    pulseTime = (time.time() - t0_sensor) * 1000000
    return pulseTime

# 物体との距離を計算
def getSonar():
    GPIO.output(trigPin, GPIO.HIGH)
    time.sleep(0.00001)
    GPIO.output(trigPin, GPIO.LOW)
    pingTime = pulseIn(echoPin, GPIO.HIGH, timeOut)
    distance = pingTime * 340.0 / 2.0 / 10000.0
    return distance
pulseIn(pin, level, timeOut)では，超音波が返ってくるまでの時間を取得します．GPIO_LOWが終わる時間とGPIO_HIGHが終わる時間の差を戻り値として返します．距離が任意の距離より離れている場合は，0を戻り値として返します．
また，getSonar()では，pulseIn(pin, level, timeOut)で取得した時間から距離(cm)を計算します．

現在時刻の取得
camera_sensor.py
# 現在時刻を文字列として取得
def get_time_now(t1):
    today = datetime.fromtimestamp(t1)
    return today.strftime('%Y_%m_%d_%H_%M_%S')
「UNIXエポックからの経過秒数」を「ローカルな日付と時刻」に変換します．その後，それらを文字列に変換します．

ループ
camera_sensor.py
# ループ処理
def loop():
    t0_camera = time.time()
    while True:
        distance = getSonar()
        t1 = time.time()
        if 0.0 < distance and distance < catchDistance:
            GPIO.output(ledPin, GPIO.HIGH)
            if (t1 - t0_camera) >= shootInterval:
                camera.capture('/home/pi/Desktop/images/%s.jpg'%(get_time_now(t1)))
                t0_camera = time.time()
        else:
            GPIO.output(ledPin, GPIO.LOW)
        print('The distance is: %2f cm'%(distance))
        time.sleep(0.5)
概ね上のフローチャートの通りです．ただし，distance = 0となった場合を考慮しています．

撮影した画像を保存するためのディレクトリを用意していない場合は，以下のコマンドを使いディレクトリを用意します．
$ cd Desktop
$ mkdir images
実行結果

想定通りの挙動をするか，実際に試してみます．

所々6秒間隔になっていますが，とりあえず成功です．

まとめ

感想

ほぼ思った通りに動かすことができてよかったです．

今後の展望

最後に，今回作ったおもちゃに付け足したい機能をまとめ，それに対する難易度を自分の主観で3段階で整理しました．（実際にやるかどうかは未定です）

やりたいこと難易度備考

距離によりLEDの色を変える ★ LEDの数を増やすだけ

録音機能を付ける ★★ マイクを用意する必要あり

Gmail等に通知を送る ★★★ 過程が多そう

~~見た目を整える~~ ~~★×99~~ ~~多分一番難しい~~

気になる点があれば，コメントでお知らせください

やりたいこと	難易度	備考
距離によりLEDの色を変える	★	LEDの数を増やすだけ
録音機能を付ける	★★	マイクを用意する必要あり
Gmail等に通知を送る	★★★	過程が多そう
~~見た目を整える~~	~~★×99~~	~~多分一番難しい~~

　 Tweet
Qiitaで続きを読む

投稿日：2021-02-27T11:59:12+09:00

"STOP: TOTAL NO. of ITERATIONS REACHED LIMIT."の解決法

はじめに

Pythonでロジスティック回帰（LogisticRegression）を用いた時，一応実行はできるが以下のような警告文が発生することがあった．
Python
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(X,y,random_state=0)
logreg = LogisticRegression()
logreg.fit(X_train,y_train)
print("Test score: {:.2f}".format(logreg.score(X_test,y_test)))
警告内容
STOP: TOTAL NO. of ITERATIONS REACHED LIMIT.
解決法

原因は，LogisticRegressionの最大反復回数に達しなかったことにあるようです．つまり，途中で処理が打ち切られているという事です．この最大反復回数はmax_iterで設定できます．この値を設定しない場合は，デフォルト値である1000が適用されるようです．そのため，max_iterの値を1000より大きくすることで，警告文が消えると考えられます．

max_iter適用例
Python
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(X,y,random_state=0)
logreg = LogisticRegression(max_iter=1500)
logreg.fit(X_train,y_train)
print("Test score: {:.2f}".format(logreg.score(X_test,y_test)))
今回の場合，最大反復回数を1500に設定したところ，警告文が消えましたが，処理内容によってこの値が異なると考えられます．

　 Tweet
Qiitaで続きを読む