- 投稿日:2021-03-14T23:59:12+09:00
カタラン数は素数羊の夢を見るか?
0. はじめに
本記事では組み合わせ論に頻出する重要な対象であるCatalan数の数論的な性質について簡単に解説します.
組み合わせ論的な解釈については他の方が書かれた良記事がたくさんありますので, そちらをご参考いただければと思います.
高度な数学はほとんど出てきませんので, 是非お気軽にご覧下さい.1. Catalan数の定義
ではまず本記事のテーマにであるCatalan数を定義しましょう.
以下の漸化式\begin{align} &C_{0} = 1, \\ &C_{n} = \sum_{k = 0}^{n - 1}C_{k}C_{n - 1 - k} \quad (n \geq 1) \end{align}で定まる整数列 $C_{n}$ を Catalan数 といいます.
以前三角関数に隠された組み合わせの秘密でご紹介したZig-Zag Number $Alt_{n}$ の漸化式によく似ていますね.1
後程ご紹介する一般項によってCatalan数を定義することもあるのですが, 漸化式として覚えておいた方が組み合わせ論的な解釈の理解をしやすいので, 本記事では漸化式によってCatalan数を定義しています.
組み合わせ論的解釈についてはWikipediaや高校数学の美しい物語様をご覧ください.また、上記定義によりCatalan数 $C_{n}$ は自然数となることが分かります.
2. 一般項と諸性質
本章ではCatalan数の一般項を求め, いくつかの簡単な公式や不等式を示します.
2.1. Catalan数の一般項
本節ではCatalan数の一般項を求めたいと思います.
しかし, 上記漸化式はそう簡単に解けそうではありませんよね.
こういう場合には母関数による議論に持ち込むと解ける場合があります.Catalan数 $C_{n}$ の母関数を
F(x) = \sum_{n = 0}^{\infty}C_{n}x^{n}と定義します.
すると, Catalan数の定義より,\begin{align} F(x) &= 1 + \sum_{n = 1}^{\infty}C_{n}x^{n} \\ &= 1 + \sum_{n = 1}^{\infty} \left(\sum_{k = 0}^{n - 1}C_{k}C_{n - 1- k}\right)x^{n} \\ &= 1 + \sum_{n = 0}^{\infty} \left(\sum_{k = 0}^{n}C_{k}C_{n - k}\right)x^{n + 1} \\ &= 1 + x\sum_{n = 0}^{\infty} \left(\sum_{k = 0}^{n}C_{k}C_{n - k}\right)x^{n} \\ &= 1 + xF(x)^{2} \end{align}より,
xF(x)^{2} - F(x) + 1 = 0つまり,
\left\{xF(x)\right\}^{2} - xF(x) + x = 0となります.
ここで $G(x) = xF(x)$ とおくと上記の等式は,G(x)^{2} - G(x) + x = 0であるからこれを $G(x)$ について解けば,
G(x) = \dfrac{1 - \sqrt{1 - 4x}}{2}となります. ただし, 二次方程式の解は $2$ つ出ますが, $G(0) = 0 \cdot F(0) = 0 \cdot 1 = 0$ より, 解は上の $1$ つに定まります.
さて今,
U(x) = \dfrac{1}{\sqrt{1 - 4x}}と定めると $G(x)$ は,
\begin{align} G(x) &= \dfrac{1 - (1 - 4x)U(x)}{2} \\ &= \dfrac{1 - U(x)}{2} + 2xU(x) \end{align}であり $U(x)$ は,
U(x) = \sum_{n = 0}^{\infty} \binom{2n}{n}x^{n}とTaylor展開できるので,
\begin{align} G(x) &= -\dfrac{1}{2}\sum_{n = 1}^{\infty}\binom{2n}{n}x^{n} + 2x\sum_{n = 0}^{\infty}\binom{2n}{n}x^{n} \\ &= \sum_{n = 0}^{\infty} \left\{2\binom{2n}{n} - \dfrac{1}{2}\binom{2(n + 1)}{n + 1}\right\}x^{n + 1} \\ &= \sum_{n = 0}^{\infty}\binom{2n}{n}x^{n + 1} \end{align}とできます. 従って, $G(x) = xF(x)$ だったことを思い出せば係数を比較することにより, Catalan数の一般項
C_{n} = \dfrac{1}{n + 1}\binom{2n}{n}\quad (n \geq 0)を得ることができました!
2.2. 簡単な応用
Catalan数の一般項を求めることができたので, この一般項を用いてCatalan数に関する簡単な漸化式や不等式を示すことができます.
まず, 定義とは別の漸化式を求めてみましょう.
$C_{n}$ の一般項表示より,\begin{align} C_{n + 1} &= \dfrac{1}{n + 2}\binom{2n + 2}{n + } \\ &= \dfrac{1}{n + 2} \dfrac{(2n + 2)!}{(n + 1)!(n + 1)!} \\ &= \dfrac{(2n + 2)(2n + 1)}{(n + 1)(n + 2)}C_{n} \\ &= \dfrac{4n + 2}{n + 2}C_{n} \end{align}となって,
C_{n + 1} = \dfrac{4n + 2}{n + 2}C_{n} \quad (n \geq 0)が成り立ちます.
またこの表示を用いることで数学的帰納法により, 不等式
C_{n} > n + 2 \quad (n \geq 4)を示すことができます.
是非挑戦してみてください.2.3. PythonプログラムによるCatalan数の計算
以下に, Catalan数を計算するためのPythonスクリプトを示しておきます.
Catalan数を返却する関数を $3$種類 定義しています.get_catalan.pyfrom sympy import catalan, binomial def get_catalan1(n): """ sympy.catalanで求めたCatalan数をそのまま返却する Parameters ---------- n : int 求めたいCatalan数のインデックス Returns ---------- Cn : int n番目のカタラン数 """ return catalan(n) def get_catalan2(n) : """ 定義の漸化式によって計算したCatalan数を返却する 再帰呼び出しによりとても重いので注意! Parameters ---------- n : int 求めたいCatalan数のインデックス Returns ---------- Cn : int n番目のカタラン数 """ if n == 0 or n == 1: return 1 else: return sum([get_catalan2(k) * get_catalan2(n - k - 1) for k in range(0, n)]) def get_catalan3(n): """ 一般項によって計算したCatalan数を返却する Parameters ---------- n : int 求めたいCatalan数のインデックス Returns ---------- Cn : int n番目のカタラン数 """ return binomial(2 * n, n) // (n + 1) if __name__ == '__main__': for n in range(1, 101): # ここでは1つ目の関数を採用 Cn = get_catalan1(n) print(f'n = {n} ---> Cn = {Cn}')3. Catalan数はいつ素数になるか?
ところで, Catalan数はいつ素数になるのでしょうか?
気になりますよね. 夜も寝られませんよね.
上のPythonスクリプトを元に確かめてみると, $0$ ~ $100$ の間では以下のようになります.n = 0 ---> Cn = 1 ,素数判定:False n = 1 ---> Cn = 1 ,素数判定:False n = 2 ---> Cn = 2 ,素数判定:True n = 3 ---> Cn = 5 ,素数判定:True n = 4 ---> Cn = 14 ,素数判定:False n = 5 ---> Cn = 42 ,素数判定:False n = 6 ---> Cn = 132 ,素数判定:False n = 7 ---> Cn = 429 ,素数判定:False n = 8 ---> Cn = 1430 ,素数判定:False n = 9 ---> Cn = 4862 ,素数判定:False n = 10 ---> Cn = 16796 ,素数判定:False n = 11 ---> Cn = 58786 ,素数判定:False n = 12 ---> Cn = 208012 ,素数判定:False n = 13 ---> Cn = 742900 ,素数判定:False n = 14 ---> Cn = 2674440 ,素数判定:False n = 15 ---> Cn = 9694845 ,素数判定:False n = 16 ---> Cn = 35357670 ,素数判定:False n = 17 ---> Cn = 129644790 ,素数判定:False n = 18 ---> Cn = 477638700 ,素数判定:False n = 19 ---> Cn = 1767263190 ,素数判定:False n = 20 ---> Cn = 6564120420 ,素数判定:False n = 21 ---> Cn = 24466267020 ,素数判定:False n = 22 ---> Cn = 91482563640 ,素数判定:False n = 23 ---> Cn = 343059613650 ,素数判定:False n = 24 ---> Cn = 1289904147324 ,素数判定:False n = 25 ---> Cn = 4861946401452 ,素数判定:False n = 26 ---> Cn = 18367353072152 ,素数判定:False n = 27 ---> Cn = 69533550916004 ,素数判定:False n = 28 ---> Cn = 263747951750360 ,素数判定:False n = 29 ---> Cn = 1002242216651368 ,素数判定:False n = 30 ---> Cn = 3814986502092304 ,素数判定:False n = 31 ---> Cn = 14544636039226909 ,素数判定:False n = 32 ---> Cn = 55534064877048198 ,素数判定:False n = 33 ---> Cn = 212336130412243110 ,素数判定:False n = 34 ---> Cn = 812944042149730764 ,素数判定:False n = 35 ---> Cn = 3116285494907301262 ,素数判定:False n = 36 ---> Cn = 11959798385860453492 ,素数判定:False n = 37 ---> Cn = 45950804324621742364 ,素数判定:False n = 38 ---> Cn = 176733862787006701400 ,素数判定:False n = 39 ---> Cn = 680425371729975800390 ,素数判定:False n = 40 ---> Cn = 2622127042276492108820 ,素数判定:False n = 41 ---> Cn = 10113918591637898134020 ,素数判定:False n = 42 ---> Cn = 39044429911904443959240 ,素数判定:False n = 43 ---> Cn = 150853479205085351660700 ,素数判定:False n = 44 ---> Cn = 583300119592996693088040 ,素数判定:False n = 45 ---> Cn = 2257117854077248073253720 ,素数判定:False n = 46 ---> Cn = 8740328711533173390046320 ,素数判定:False n = 47 ---> Cn = 33868773757191046886429490 ,素数判定:False n = 48 ---> Cn = 131327898242169365477991900 ,素数判定:False n = 49 ---> Cn = 509552245179617138054608572 ,素数判定:False n = 50 ---> Cn = 1978261657756160653623774456 ,素数判定:False n = 51 ---> Cn = 7684785670514316385230816156 ,素数判定:False n = 52 ---> Cn = 29869166945772625950142417512 ,素数判定:False n = 53 ---> Cn = 116157871455782434250553845880 ,素数判定:False n = 54 ---> Cn = 451959718027953471447609509424 ,素数判定:False n = 55 ---> Cn = 1759414616608818870992479875972 ,素数判定:False n = 56 ---> Cn = 6852456927844873497549658464312 ,素数判定:False n = 57 ---> Cn = 26700952856774851904245220912664 ,素数判定:False n = 58 ---> Cn = 104088460289122304033498318812080 ,素数判定:False n = 59 ---> Cn = 405944995127576985730643443367112 ,素数判定:False n = 60 ---> Cn = 1583850964596120042686772779038896 ,素数判定:False n = 61 ---> Cn = 6182127958584855650487080847216336 ,素数判定:False n = 62 ---> Cn = 24139737743045626825711458546273312 ,素数判定:False n = 63 ---> Cn = 94295850558771979787935384946380125 ,素数判定:False n = 64 ---> Cn = 368479169875816659479009042713546950 ,素数判定:False n = 65 ---> Cn = 1440418573150919668872489894243865350 ,素数判定:False n = 66 ---> Cn = 5632681584560312734993915705849145100 ,素数判定:False n = 67 ---> Cn = 22033725021956517463358552614056949950 ,素数判定:False n = 68 ---> Cn = 86218923998960285726185640663701108500 ,素数判定:False n = 69 ---> Cn = 337485502510215975556783793455058624700 ,素数判定:False n = 70 ---> Cn = 1321422108420282270489942177190229544600 ,素数判定:False n = 71 ---> Cn = 5175569924646105559418940193995065716350 ,素数判定:False n = 72 ---> Cn = 20276890389709399862928998568254641025700 ,素数判定:False n = 73 ---> Cn = 79463489365077377841208237632349268884500 ,素数判定:False n = 74 ---> Cn = 311496878311103321137536291518809134027240 ,素数判定:False n = 75 ---> Cn = 1221395654430378811828760722007962130791020 ,素数判定:False n = 76 ---> Cn = 4790408930363303911328386208394864461024520 ,素数判定:False n = 77 ---> Cn = 18793142726809884575211361279087545193250040 ,素数判定:False n = 78 ---> Cn = 73745243611532458459690151854647329239335600 ,素数判定:False n = 79 ---> Cn = 289450081175264899454283846029490767264392230 ,素数判定:False n = 80 ---> Cn = 1136359577947336271931632877004667456667613940 ,素数判定:False n = 81 ---> Cn = 4462290049988320482463241297506133183499654740 ,素数判定:False n = 82 ---> Cn = 17526585015616776834735140517915655636396234280 ,素数判定:False n = 83 ---> Cn = 68854441132780194707888052034668647142985206100 ,素数判定:False n = 84 ---> Cn = 270557451039395118028642463289168566420671280440 ,素数判定:False n = 85 ---> Cn = 1063353702922273835973036658043476458723103404520 ,素数判定:False n = 86 ---> Cn = 4180080073556524734514695828170907458428751314320 ,素数判定:False n = 87 ---> Cn = 16435314834665426797069144960762886143367590394940 ,素数判定:False n = 88 ---> Cn = 64633260585762914370496637486146181462681535261000 ,素数判定:False n = 89 ---> Cn = 254224158304000796523953440778841647086547372026600 ,素数判定:False n = 90 ---> Cn = 1000134600800354781929399250536541864362461089950800 ,素数判定:False n = 91 ---> Cn = 3935312233584004685417853572763349509774031680023800 ,素数判定:False n = 92 ---> Cn = 15487357822491889407128326963778343232013931127835600 ,素数判定:False n = 93 ---> Cn = 60960876535340415751462563580829648891969728907438000 ,素数判定:False n = 94 ---> Cn = 239993345518077005168915776623476723006280827488229600 ,素数判定:False n = 95 ---> Cn = 944973797977428207852605870454939596837230758234904050 ,素数判定:False n = 96 ---> Cn = 3721443204405954385563870541379246659709506697378694300 ,素数判定:False n = 97 ---> Cn = 14657929356129575437016877846657032761712954950899755100 ,素数判定:False n = 98 ---> Cn = 57743358069601357782187700608042856334020731624756611000 ,素数判定:False n = 99 ---> Cn = 227508830794229349661819540395688853956041682601541047340 ,素数判定:False n = 100 ---> Cn = 896519947090131496687170070074100632420837521538745909320 ,素数判定:False$n = 2, 3$ のとき以外は全て合成数になっていますね.
実は, Catalan数 $C_{n}$ が素数となるのは $n = 2, 3$ のときのみ であることが知られています.
本章ではこの事実を示しましょう.2まず, $0 \leq n \leq 4$ の範囲において素数となるのは $n = 2, 3$ のときのみであることが上記一覧よりわかります.
そこで, $n \geq 5$ において $C_{n}$ は素数にならないことを背理法で示しましょう.
背理法なので, ある自然数 $n_{0} \geq 5$ が存在して, $C_{n_{0}}$ が素数であると仮定します.
すると 2.2. 節で示した漸化式より,C_{n_{0} + 1} = \dfrac{4n_{0} + 2}{n_{0} + 2}C_{n_{0}}となります.
ここで 2.2. 節で示した不等式より $C_{n_{0}} > n_{0} + 2$ であることと $C_{n_{0}}$ が素数である仮定から, $C_{n_{0}}$ と $n_{0} + 2$ は互いに素となります.
よって, $n_{0} + 2$ は $4n_{0} + 2$ を割り切ることになります.
しかしこれは不等式3(n_{0} + 2) < 4n_{0} + 2 < 4(n_{0} + 2)が成り立つことに矛盾します.
従って, $5$ 以上の自然数 $n$ に対して $C_{n}$ は素数にならないため, $C_{n}$ が素数となるのは $n = 2, 3$ のときのみであることが示せました.4. Catalan擬素数とちょっとした展望
本章ではCatalan数が満たすある合同式を紹介し, それをもとにCatalan擬素数を定義します.
また, Catalan擬素数と双子素数の関係について少しだけ触れます.4.1. 素数とCatalan数が結びつく合同式
ここでは任意の奇素数 $p$ に対して成り立つ次の合同式
(-1)^{\frac{p - 1}{2}}C_{\frac{p - 1}{2}} \equiv 2 \quad (mod. p)を示します.
任意の自然数 $i$ に対して, $p - i \equiv -i \quad (mod. p)$ が成り立つという自明な事実を用いると,
\begin{align} (p - 1)! &= \left(p - 1\right)\left(p - 2\right) \cdots \left(p - \dfrac{p - 1}{2}\right)\dfrac{p - 1}{2} \cdots 2 \cdot 1 \\ & \equiv (-1)(-2) \cdots \left(- \dfrac{p - 1}{2}\right)\dfrac{p - 1}{2} \cdots 2 \cdot 1 \quad (mod. p)\\ & = ( - 1)^{\frac{p - 1}{2}}\left\{\left(\dfrac{p - 1}{2}\right)!\right\}^{2} \end{align}となります.
これとWilsonの定理 を用いると,\begin{align} (-1)^{\frac{p - 1}{2}}C_{\frac{p - 1}{2}} &= (-1)^{\frac{p - 1}{2}}\dfrac{2}{p + 1} \dfrac{(p - 1)!}{\left\{\left(\dfrac{p - 1}{2}\right)!\right\}^{2}} \\ &\equiv \dfrac{2}{p + 1} \quad (mod. p) \\ &\equiv 2 \quad (mod. p) \end{align}となって成立します.
4.2. Catalan擬素数と双子素数 (予告編)
4.1節では全ての奇素数に対して上記の合同式が成り立つことを示しました.
ではもう少し拡張して, 奇数の合成数のうち上記の合成を満たすものはどれくらいあるのでしょうか?
例えば, $1$ ~ $10000$ の間だとどれくらい存在するのでしょうか?
Pythonで簡単に試してみましょう.
ここではCatalan数の導出にはsympyの関数をそのまま使用しています.catalan_pseudoprime.pyfrom sympy import catalan, isprime def is_catalan_pseudoprime(n): """ 引数で指定した自然数が上の合同式を満たすかどうかをチェックする Parameters ---------- n : int チェック対象の自然数 Returns ---------- boolean 合同式を満たせばTrue, それ以外はFalse """ if n % 2 == 0 or isprime(n): return False k = (n - 1) // 2 return (pow(-1, k) * catalan(k)) % n == 2 if __name__ == '__main__': for n in range(1, 10001, 2): if is_catalan_pseudoprime(n): print(n)出力結果5907どうやら $10000$ 以下で上記合同式を満たす奇数の合成数は $5907$ のみのようです.
一般的に, 上記合同式を満たす奇数の合成数は Catalan擬素数 と呼ばれています.3現在判明しているCatalan擬素数は $5907, 1194649, 12327121$ のみです.
Catalan擬素数はかなりレアな数のようですね!実は, Catalan擬素数はMersenne数や双子素数と関係があります.
例えば, 双子素数の積で書けるCatalan擬素数は存在しないことが知られています.まだまだCatalan数の数論的性質には魅力がありそうです!
5. おわりに
本記事ではCatalan数について解説を行ってきました.
組み合わせ論でよく取り沙汰されるCatalan数ですが, 素数との絡みもあったりと数論的にもなかなか興味の尽きない対象ですね.
いずれ準備が済めば, 4.2. 節で触れた内容について1記事書きたいと思います.
そのときには是非ご覧くださいね!参考文献
- Aebi, Christian; Cairns, Grant (2008). "Catalan numbers, primes and twin primes" (PDF). Elemente der Mathematik. 63 (4): 153–164.
- 山本幸一. 順列・組合せと確率. 岩波書店, 2015
- 投稿日:2021-03-14T23:59:12+09:00
カタラン数は素数羊の夢を見るか??
0. はじめに
本記事では組み合わせ論に頻出する重要な対象であるCatalan数の数論的な性質について簡単に解説します.
組み合わせ論的な解釈については他の方が書かれた良記事がたくさんありますので, そちらをご参考いただければと思います.
高度な数学はほとんど出てきませんので, 是非お気軽にご覧下さい.1. Catalan数の定義
ではまず本記事のテーマであるCatalan数を定義しましょう.
以下の漸化式\begin{align} &C_{0} = 1, \\ &C_{n} = \sum_{k = 0}^{n - 1}C_{k}C_{n - 1 - k} \quad (n \geq 1) \end{align}で定まる整数列 $C_{n}$ を Catalan数 といいます.
以前三角関数に隠された組み合わせの秘密でご紹介したZig-Zag Number $Alt_{n}$ の漸化式によく似ていますね.1
後程ご紹介する一般項によってCatalan数を定義することもあるのですが, 漸化式として覚えておいた方が組み合わせ論的な解釈の理解をしやすいので, 本記事では漸化式によってCatalan数を定義しています.
組み合わせ論的解釈についてはWikipediaや高校数学の美しい物語様をご覧ください.また、上記定義によりCatalan数 $C_{n}$ は自然数となることが分かります.
2. 一般項と諸性質
本章ではCatalan数の一般項を求め, いくつかの簡単な公式や不等式を示します.
2.1. Catalan数の一般項
本節ではCatalan数の一般項を求めたいと思います.
しかし, 上記漸化式はそう簡単に解けそうではありませんよね.
こういう場合には母関数による議論に持ち込むと解ける場合があります.Catalan数 $C_{n}$ の母関数を
F(x) = \sum_{n = 0}^{\infty}C_{n}x^{n}と定義します.
すると, Catalan数の定義より,\begin{align} F(x) &= 1 + \sum_{n = 1}^{\infty}C_{n}x^{n} \\ &= 1 + \sum_{n = 1}^{\infty} \left(\sum_{k = 0}^{n - 1}C_{k}C_{n - 1- k}\right)x^{n} \\ &= 1 + \sum_{n = 0}^{\infty} \left(\sum_{k = 0}^{n}C_{k}C_{n - k}\right)x^{n + 1} \\ &= 1 + x\sum_{n = 0}^{\infty} \left(\sum_{k = 0}^{n}C_{k}C_{n - k}\right)x^{n} \\ &= 1 + xF(x)^{2} \end{align}より,
xF(x)^{2} - F(x) + 1 = 0つまり,
\left\{xF(x)\right\}^{2} - xF(x) + x = 0となります.
ここで $G(x) = xF(x)$ とおくと上記の等式は,G(x)^{2} - G(x) + x = 0であるからこれを $G(x)$ について解けば,
G(x) = \dfrac{1 - \sqrt{1 - 4x}}{2}となります. ただし, 二次方程式の解は $2$ つ出ますが, $G(0) = 0 \cdot F(0) = 0 \cdot 1 = 0$ より, 解は上の $1$ つに定まります.
さて今,
U(x) = \dfrac{1}{\sqrt{1 - 4x}}と定めると $G(x)$ は,
\begin{align} G(x) &= \dfrac{1 - (1 - 4x)U(x)}{2} \\ &= \dfrac{1 - U(x)}{2} + 2xU(x) \end{align}であり $U(x)$ は,
U(x) = \sum_{n = 0}^{\infty} \binom{2n}{n}x^{n}とTaylor展開できるので,
\begin{align} G(x) &= -\dfrac{1}{2}\sum_{n = 1}^{\infty}\binom{2n}{n}x^{n} + 2x\sum_{n = 0}^{\infty}\binom{2n}{n}x^{n} \\ &= \sum_{n = 0}^{\infty} \left\{2\binom{2n}{n} - \dfrac{1}{2}\binom{2(n + 1)}{n + 1}\right\}x^{n + 1} \\ &= \sum_{n = 0}^{\infty}\dfrac{1}{n + 1}\binom{2n}{n}x^{n + 1} \end{align}とできます. 従って, $G(x) = xF(x)$ だったことを思い出せば係数を比較することにより, Catalan数の一般項
C_{n} = \dfrac{1}{n + 1}\binom{2n}{n}\quad (n \geq 0)を得ることができました!
2.2. 簡単な応用
Catalan数の一般項を求めることができたので, この一般項を用いてCatalan数に関する簡単な漸化式や不等式を示すことができます.
まず, 定義とは別の漸化式を求めてみましょう.
$C_{n}$ の一般項表示より,\begin{align} C_{n + 1} &= \dfrac{1}{n + 2}\binom{2n + 2}{n + } \\ &= \dfrac{1}{n + 2} \dfrac{(2n + 2)!}{(n + 1)!(n + 1)!} \\ &= \dfrac{(2n + 2)(2n + 1)}{(n + 1)(n + 2)}C_{n} \\ &= \dfrac{4n + 2}{n + 2}C_{n} \end{align}となって,
C_{n + 1} = \dfrac{4n + 2}{n + 2}C_{n} \quad (n \geq 0)が成り立ちます.
またこの表示を用いることで数学的帰納法により, 不等式
C_{n} > n + 2 \quad (n \geq 4)を示すことができます.
是非挑戦してみてください.2.3. PythonプログラムによるCatalan数の計算
以下に, Catalan数を計算するためのPythonスクリプトを示しておきます.
Catalan数を返却する関数を $3$種類 定義しています.get_catalan.pyfrom sympy import catalan, binomial def get_catalan1(n): """ sympy.catalanで求めたCatalan数をそのまま返却する Parameters ---------- n : int 求めたいCatalan数のインデックス Returns ---------- Cn : int n番目のカタラン数 """ return catalan(n) def get_catalan2(n) : """ 定義の漸化式によって計算したCatalan数を返却する 再帰呼び出しによりとても重いので注意! Parameters ---------- n : int 求めたいCatalan数のインデックス Returns ---------- Cn : int n番目のカタラン数 """ if n == 0 or n == 1: return 1 else: return sum([get_catalan2(k) * get_catalan2(n - k - 1) for k in range(0, n)]) def get_catalan3(n): """ 一般項によって計算したCatalan数を返却する Parameters ---------- n : int 求めたいCatalan数のインデックス Returns ---------- Cn : int n番目のカタラン数 """ return binomial(2 * n, n) // (n + 1) if __name__ == '__main__': for n in range(1, 101): # ここでは1つ目の関数を採用 Cn = get_catalan1(n) print(f'n = {n} ---> Cn = {Cn}')3. Catalan数はいつ素数になるか?
ところで, Catalan数はいつ素数になるのでしょうか?
気になりますよね. 夜も寝られませんよね.
上のPythonスクリプトを元に確かめてみると, $0$ ~ $100$ の間では以下のようになります.n = 0 ---> Cn = 1 ,素数判定:False n = 1 ---> Cn = 1 ,素数判定:False n = 2 ---> Cn = 2 ,素数判定:True n = 3 ---> Cn = 5 ,素数判定:True n = 4 ---> Cn = 14 ,素数判定:False n = 5 ---> Cn = 42 ,素数判定:False n = 6 ---> Cn = 132 ,素数判定:False n = 7 ---> Cn = 429 ,素数判定:False n = 8 ---> Cn = 1430 ,素数判定:False n = 9 ---> Cn = 4862 ,素数判定:False n = 10 ---> Cn = 16796 ,素数判定:False n = 11 ---> Cn = 58786 ,素数判定:False n = 12 ---> Cn = 208012 ,素数判定:False n = 13 ---> Cn = 742900 ,素数判定:False n = 14 ---> Cn = 2674440 ,素数判定:False n = 15 ---> Cn = 9694845 ,素数判定:False n = 16 ---> Cn = 35357670 ,素数判定:False n = 17 ---> Cn = 129644790 ,素数判定:False n = 18 ---> Cn = 477638700 ,素数判定:False n = 19 ---> Cn = 1767263190 ,素数判定:False n = 20 ---> Cn = 6564120420 ,素数判定:False n = 21 ---> Cn = 24466267020 ,素数判定:False n = 22 ---> Cn = 91482563640 ,素数判定:False n = 23 ---> Cn = 343059613650 ,素数判定:False n = 24 ---> Cn = 1289904147324 ,素数判定:False n = 25 ---> Cn = 4861946401452 ,素数判定:False n = 26 ---> Cn = 18367353072152 ,素数判定:False n = 27 ---> Cn = 69533550916004 ,素数判定:False n = 28 ---> Cn = 263747951750360 ,素数判定:False n = 29 ---> Cn = 1002242216651368 ,素数判定:False n = 30 ---> Cn = 3814986502092304 ,素数判定:False n = 31 ---> Cn = 14544636039226909 ,素数判定:False n = 32 ---> Cn = 55534064877048198 ,素数判定:False n = 33 ---> Cn = 212336130412243110 ,素数判定:False n = 34 ---> Cn = 812944042149730764 ,素数判定:False n = 35 ---> Cn = 3116285494907301262 ,素数判定:False n = 36 ---> Cn = 11959798385860453492 ,素数判定:False n = 37 ---> Cn = 45950804324621742364 ,素数判定:False n = 38 ---> Cn = 176733862787006701400 ,素数判定:False n = 39 ---> Cn = 680425371729975800390 ,素数判定:False n = 40 ---> Cn = 2622127042276492108820 ,素数判定:False n = 41 ---> Cn = 10113918591637898134020 ,素数判定:False n = 42 ---> Cn = 39044429911904443959240 ,素数判定:False n = 43 ---> Cn = 150853479205085351660700 ,素数判定:False n = 44 ---> Cn = 583300119592996693088040 ,素数判定:False n = 45 ---> Cn = 2257117854077248073253720 ,素数判定:False n = 46 ---> Cn = 8740328711533173390046320 ,素数判定:False n = 47 ---> Cn = 33868773757191046886429490 ,素数判定:False n = 48 ---> Cn = 131327898242169365477991900 ,素数判定:False n = 49 ---> Cn = 509552245179617138054608572 ,素数判定:False n = 50 ---> Cn = 1978261657756160653623774456 ,素数判定:False n = 51 ---> Cn = 7684785670514316385230816156 ,素数判定:False n = 52 ---> Cn = 29869166945772625950142417512 ,素数判定:False n = 53 ---> Cn = 116157871455782434250553845880 ,素数判定:False n = 54 ---> Cn = 451959718027953471447609509424 ,素数判定:False n = 55 ---> Cn = 1759414616608818870992479875972 ,素数判定:False n = 56 ---> Cn = 6852456927844873497549658464312 ,素数判定:False n = 57 ---> Cn = 26700952856774851904245220912664 ,素数判定:False n = 58 ---> Cn = 104088460289122304033498318812080 ,素数判定:False n = 59 ---> Cn = 405944995127576985730643443367112 ,素数判定:False n = 60 ---> Cn = 1583850964596120042686772779038896 ,素数判定:False n = 61 ---> Cn = 6182127958584855650487080847216336 ,素数判定:False n = 62 ---> Cn = 24139737743045626825711458546273312 ,素数判定:False n = 63 ---> Cn = 94295850558771979787935384946380125 ,素数判定:False n = 64 ---> Cn = 368479169875816659479009042713546950 ,素数判定:False n = 65 ---> Cn = 1440418573150919668872489894243865350 ,素数判定:False n = 66 ---> Cn = 5632681584560312734993915705849145100 ,素数判定:False n = 67 ---> Cn = 22033725021956517463358552614056949950 ,素数判定:False n = 68 ---> Cn = 86218923998960285726185640663701108500 ,素数判定:False n = 69 ---> Cn = 337485502510215975556783793455058624700 ,素数判定:False n = 70 ---> Cn = 1321422108420282270489942177190229544600 ,素数判定:False n = 71 ---> Cn = 5175569924646105559418940193995065716350 ,素数判定:False n = 72 ---> Cn = 20276890389709399862928998568254641025700 ,素数判定:False n = 73 ---> Cn = 79463489365077377841208237632349268884500 ,素数判定:False n = 74 ---> Cn = 311496878311103321137536291518809134027240 ,素数判定:False n = 75 ---> Cn = 1221395654430378811828760722007962130791020 ,素数判定:False n = 76 ---> Cn = 4790408930363303911328386208394864461024520 ,素数判定:False n = 77 ---> Cn = 18793142726809884575211361279087545193250040 ,素数判定:False n = 78 ---> Cn = 73745243611532458459690151854647329239335600 ,素数判定:False n = 79 ---> Cn = 289450081175264899454283846029490767264392230 ,素数判定:False n = 80 ---> Cn = 1136359577947336271931632877004667456667613940 ,素数判定:False n = 81 ---> Cn = 4462290049988320482463241297506133183499654740 ,素数判定:False n = 82 ---> Cn = 17526585015616776834735140517915655636396234280 ,素数判定:False n = 83 ---> Cn = 68854441132780194707888052034668647142985206100 ,素数判定:False n = 84 ---> Cn = 270557451039395118028642463289168566420671280440 ,素数判定:False n = 85 ---> Cn = 1063353702922273835973036658043476458723103404520 ,素数判定:False n = 86 ---> Cn = 4180080073556524734514695828170907458428751314320 ,素数判定:False n = 87 ---> Cn = 16435314834665426797069144960762886143367590394940 ,素数判定:False n = 88 ---> Cn = 64633260585762914370496637486146181462681535261000 ,素数判定:False n = 89 ---> Cn = 254224158304000796523953440778841647086547372026600 ,素数判定:False n = 90 ---> Cn = 1000134600800354781929399250536541864362461089950800 ,素数判定:False n = 91 ---> Cn = 3935312233584004685417853572763349509774031680023800 ,素数判定:False n = 92 ---> Cn = 15487357822491889407128326963778343232013931127835600 ,素数判定:False n = 93 ---> Cn = 60960876535340415751462563580829648891969728907438000 ,素数判定:False n = 94 ---> Cn = 239993345518077005168915776623476723006280827488229600 ,素数判定:False n = 95 ---> Cn = 944973797977428207852605870454939596837230758234904050 ,素数判定:False n = 96 ---> Cn = 3721443204405954385563870541379246659709506697378694300 ,素数判定:False n = 97 ---> Cn = 14657929356129575437016877846657032761712954950899755100 ,素数判定:False n = 98 ---> Cn = 57743358069601357782187700608042856334020731624756611000 ,素数判定:False n = 99 ---> Cn = 227508830794229349661819540395688853956041682601541047340 ,素数判定:False n = 100 ---> Cn = 896519947090131496687170070074100632420837521538745909320 ,素数判定:False$n = 2, 3$ のとき以外は全て合成数になっていますね.
実は, Catalan数 $C_{n}$ が素数となるのは $n = 2, 3$ のときのみ であることが知られています.
本章ではこの事実を示しましょう.2まず, $0 \leq n \leq 4$ の範囲において素数となるのは $n = 2, 3$ のときのみであることが上記一覧よりわかります.
そこで, $n \geq 5$ において $C_{n}$ は素数にならないことを背理法で示しましょう.
背理法なので, ある自然数 $n_{0} \geq 5$ が存在して, $C_{n_{0}}$ が素数であると仮定します.
すると 2.2. 節で示した漸化式より,C_{n_{0} + 1} = \dfrac{4n_{0} + 2}{n_{0} + 2}C_{n_{0}}となります.
ここで 2.2. 節で示した不等式より $C_{n_{0}} > n_{0} + 2$ であることと $C_{n_{0}}$ が素数である仮定から, $C_{n_{0}}$ と $n_{0} + 2$ は互いに素となります.
よって, $n_{0} + 2$ は $4n_{0} + 2$ を割り切ることになります.
しかしこれは不等式3(n_{0} + 2) < 4n_{0} + 2 < 4(n_{0} + 2)が成り立つことに矛盾します.
従って, $5$ 以上の自然数 $n$ に対して $C_{n}$ は素数にならないため, $C_{n}$ が素数となるのは $n = 2, 3$ のときのみであることが示せました.4. Catalan擬素数とちょっとした展望
本章ではCatalan数が満たすある合同式を紹介し, それをもとにCatalan擬素数を定義します.
また, Catalan擬素数と双子素数の関係について少しだけ触れます.4.1. 素数とCatalan数が結びつく合同式
ここでは任意の奇素数 $p$ に対して成り立つ次の合同式
(-1)^{\frac{p - 1}{2}}C_{\frac{p - 1}{2}} \equiv 2 \quad (mod. p)を示します.
任意の自然数 $i$ に対して, $p - i \equiv -i \quad (mod. p)$ が成り立つという自明な事実を用いると,
\begin{align} (p - 1)! &= \left(p - 1\right)\left(p - 2\right) \cdots \left(p - \dfrac{p - 1}{2}\right)\dfrac{p - 1}{2} \cdots 2 \cdot 1 \\ & \equiv (-1)(-2) \cdots \left(- \dfrac{p - 1}{2}\right)\dfrac{p - 1}{2} \cdots 2 \cdot 1 \quad (mod. p)\\ & = ( - 1)^{\frac{p - 1}{2}}\left\{\left(\dfrac{p - 1}{2}\right)!\right\}^{2} \end{align}となります.
これとWilsonの定理 を用いると,\begin{align} (-1)^{\frac{p - 1}{2}}C_{\frac{p - 1}{2}} &= (-1)^{\frac{p - 1}{2}}\dfrac{2}{p + 1} \dfrac{(p - 1)!}{\left\{\left(\dfrac{p - 1}{2}\right)!\right\}^{2}} \\ &\equiv \dfrac{2}{p + 1} \quad (mod. p) \\ &\equiv 2 \quad (mod. p) \end{align}となって成立します.
4.2. Catalan擬素数と双子素数のかじり
4.1節では全ての奇素数に対して上記の合同式が成り立つことを示しました.
ではもう少し拡張して, 奇数の合成数のうち上記の合成を満たすものはどれくらいあるのでしょうか?
例えば, $1$ ~ $10000$ の間だとどれくらい存在するのでしょうか?
Pythonで簡単に試してみましょう.
ここではCatalan数の導出にはsympyの関数をそのまま使用しています.catalan_pseudoprime.pyfrom sympy import catalan, isprime def is_catalan_pseudoprime(n): """ 引数で指定した自然数が上の合同式を満たすかどうかをチェックする Parameters ---------- n : int チェック対象の自然数 Returns ---------- boolean 合同式を満たせばTrue, それ以外はFalse """ if n % 2 == 0 or isprime(n): return False k = (n - 1) // 2 return (pow(-1, k) * catalan(k)) % n == 2 if __name__ == '__main__': for n in range(1, 10001, 2): if is_catalan_pseudoprime(n): print(n)出力結果5907どうやら $10000$ 以下で上記合同式を満たす奇数の合成数は $5907$ のみのようです.
一般的に, 上記合同式を満たす奇数の合成数は Catalan擬素数 と呼ばれています.3現在判明しているCatalan擬素数は $5907$, $ 1194649$, $12327121$ のみです.
Catalan擬素数はかなりレアな数のようですね!実は, Catalan擬素数はMersenne数や双子素数と関係があります.
例えば, 双子素数の積で書けるCatalan擬素数は存在しないことが知られています.まだまだCatalan数の数論的性質には魅力がありそうです!
5. おわりに
本記事ではCatalan数について解説を行ってきました.
組み合わせ論でよく取り沙汰されるCatalan数ですが, 素数との絡みもあったりと数論的にもなかなか興味の尽きない対象ですね.
いずれ準備が済めば, 4.2. 節で触れた内容について1記事書きたいと思います.
そのときには是非ご覧くださいね!参考文献
- Aebi, Christian; Cairns, Grant (2008). "Catalan numbers, primes and twin primes" (PDF). Elemente der Mathematik. 63 (4): 153–164.
- 山本幸一. 順列・組合せと確率. 岩波書店, 2015
- 投稿日:2021-03-14T23:48:14+09:00
Pytorch-LightningのCheckpointでLAN内のminio(S3互換ストレージ)へモデルを保存する方法
概要
現在のpytorch-lightning(ver.1.2.3)では、S3への保存を行う際にendpointを指定できないため、LAN内にあるS3互換ストレージなどへ保存を行うことが出来ない。
以下のsetup_endpointを実行することで、fsspecモジュールへ強引にモンキーパッチを当ててエンドポイントを指定する。方法
- pytorch-lightning がクラウドストレージへのIOで使用している関数へモンキーパッチを当てEndpointを強引に指定する。
- 以下のコードをコピペしてsetup_endpointを実行するだけで可能。
コード
from typing import Any import gorilla import fsspec def apply_gorrila(function: Any, module: Any): patch = gorilla.Patch( module, function.__name__, function, settings=gorilla.Settings(allow_hit=True)) gorilla.apply(patch) def setup_endpoint(endpoint_url: str): def filesystem(protocol, **storage_options): if protocol == "s3": storage_options["client_kwargs"] = { "endpoint_url": endpoint_url, } original = gorilla.get_original_attribute(fsspec, 'filesystem') return original(protocol, **storage_options) def open_files(*args, **kwargs): kwargs["client_kwargs"] = { "endpoint_url": endpoint_url, } original = gorilla.get_original_attribute(fsspec.core, 'open_files') return original(*args, **kwargs) apply_gorrila(filesystem, fsspec) apply_gorrila(open_files, fsspec.core)
- 投稿日:2021-03-14T23:23:41+09:00
Linux で AirPods (その他 Bluetooth イヤホン) の音量を調節する
Linux で AirPods を使うと音量を最大にしても音が小さすぎます。
これは本来 AirPods などのワイヤレスイヤホンの音量は AVRCP という仕組みを使って調節しなければならないのが、Linux 側のサウンドサーバーがそれに対応していないことによるものです。コマンドラインから AirPods の音量を調節するスクリプト
Python で AVRCP を使って AirPods の音量を調節する簡単なスクリプトを作りました。
AirPods 以外の Bluetooth イヤホンでも使用できます。vol.py#!/usr/bin/env python3 import dbus import sys DBUS_OM_IFACE = 'org.freedesktop.DBus.ObjectManager' DBUS_PROP_IFACE = 'org.freedesktop.DBus.Properties' BLUEZ_SERVICE_NAME = 'org.bluez' BLUEZ_MT_IFACE = 'org.bluez.MediaTransport1' VOL_STEP = 5 def usage(): print("""Usage: {0} Show volume {0} <value> Set volume to <value> (0-127) {0} inc Increase volume {0} dec Decrease volume""".format(sys.argv[0]), file=sys.stderr) sys.exit(1) def main(): if len(sys.argv) > 2: usage() bus = dbus.SystemBus() om = dbus.Interface(bus.get_object(BLUEZ_SERVICE_NAME, '/'), DBUS_OM_IFACE) objects = om.GetManagedObjects() path = None for obj, props in objects.items(): if BLUEZ_MT_IFACE in props.keys(): path = obj break if path is None: print('No device exists', file=sys.stderr) sys.exit(1) vol_now = props[BLUEZ_MT_IFACE]['Volume'] if len(sys.argv) == 2: if sys.argv[1] == 'inc': vol = vol_now + VOL_STEP elif sys.argv[1] == 'dec': vol = vol_now - VOL_STEP elif sys.argv[1].isdecimal(): vol = sys.argv[1] else: usage() print('{} -> {}'.format(vol_now, vol)) obj = bus.get_object(BLUEZ_SERVICE_NAME, path) props = dbus.Interface(obj, DBUS_PROP_IFACE) props.Set(BLUEZ_MT_IFACE, 'Volume', dbus.types.UInt16(vol)) elif len(sys.argv) == 1: print(vol_now) if __name__ == '__main__': main()使い方
現在の音量を表示する
$ ./vol.py 20音量を設定する
0 から 127 までの値を指定できます。
$ ./vol.py 30 20 -> 30音量を上げる
$ ./vol.py inc 30 -> 35音量を下げる
$ ./vol.py dec 35 -> 30
- 投稿日:2021-03-14T22:55:26+09:00
Jetson Nanoをネットワークカメラ(grpc)にしたときの備忘録
はじめに
Jetson NanoにRaspberry Piカメラを接続し、ネットワークカメラのようなものを作りました。
Jetson Nano上で撮影、圧縮を行い、gRPCサーバで配信します。
また、systemdを用いてJetson Nano起動時に自動的に撮影機能・サーバ機能が起動するようにしました。
クライアント側からのリクエストで最新の撮影画像を取得できます。ソースコード
Githubにアップしています。
今回はサービス間通信に初めてgRPCを使ってみました。サーバ・クライアントともにpythonで実装しました。
gRPCでの実装自体はいろんなサイトで説明されているとおりでしたので、ここでは特に説明はしません。詰まったところ(備忘録)
実装時に悩んだところを備忘録的に書いておきます。
画像のエンコード・デコード
今回の実装では、Jetson Nano側で撮影したあと、OpenCVのimencode関数でJpg圧縮したものをgRPCで配信するようにしています。
encode_param = [int(cv2.IMWRITE_JPEG_QUALITY), 50] #imgはOpenCVの画像データ型 result, encimg = cv2.imencode('.jpg', img, encode_param) b64e = base64.b64encode(encimg)grpcのクライアント側でデータを受信したあと下記のコードでデコードしようとしましたがうまくいきませんでした。
#response.dataはgrpcで受信した画像データ jpg = base64.b64decode(response.data) img = cv2.imdecode(jpg, cv2.IMREAD_COLOR)正しく動作させるには一行、numpy.frombufferを挟む必要がありました。
jpg = base64.b64decode(response.data) jpg = np.frombuffer(jpg, dtype=np.uint8) img = cv2.imdecode(jpg, cv2.IMREAD_COLOR)この記事を参考にしました。
Systemd登録
Jetson Nanoの起動のたびに撮影・サーバスクリプトを実行するのは面倒なので、
電源投入後に自動でスクリプトが起動するようにSystemdにサービスを登録します。
下記のようなサービスを作成しました。[Unit] Description = camera daemon [Service] ExecStart = /opt/camera.sh Restart = always Type = simple [Install] WantedBy = multi-user.targetExecStartに記述したシェルスクリプトにはサーバスクリプト(jetson_nano_camera_server.py)の起動コマンドを記入しています。
#!/bin/bash python3 /path/to/jetson_nano_camera_server.pyこの状態でサービスを起動しステータスを確認すると、起動に失敗していました。
Loaded: loaded (/etc/systemd/system/camera.service; enabled; vendor preset: enabled) Active: failed (Result: exit-code) since Sun 2021-03-14 22:13:08 JST; 1min 55s ago Process: 7090 ExecStart=/opt/camera.sh (code=exited, status=1/FAILURE) Main PID: 7090 (code=exited, status=1/FAILURE)/var/log/syslogでログを確認したところ、次のようなエラーが出ていました。
Mar 14 22:13:08 xxxxxxxx camera.sh[7090]: Traceback (most recent call last): Mar 14 22:13:08 xxxxxxxx camera.sh[7090]: File "/path/to/jetson_nano_camera_server.py", line 7, in <module> Mar 14 22:13:08 xxxxxxxx camera.sh[7090]: import grpc Mar 14 22:13:08 xxxxxxxx camera.sh[7090]: ModuleNotFoundError: No module named 'grpc'pythonスクリプトのgprcのインポートで失敗しています。
camera.shを直接起動するとサーバは正常に起動するのに、systemdだと何故かうまく起動しませんでした。
grpcioはインストールしているはずなので、pip3 show grpcioでパッケージの情報を確認してみました。Name: grpcio Version: 1.36.1 Summary: HTTP/2-based RPC framework Home-page: https://grpc.io Author: The gRPC Authors Author-email: grpc-io@googlegroups.com License: Apache License 2.0 Location: /home/USER_NAME/.local/lib/python3.6/site-packages Requires: six Required-by: grpcio-toolsLocationがユーザディレクトリになっていました。もしかして?と思い、Systemdのサービスにユーザ名の項目を追加してみました。
[Unit] Description = camera daemon [Service] ExecStart = /opt/camera.sh Restart = always Type = simple User = USER_NAME [Install] WantedBy = multi-user.targetこの状態でサービスを起動、ステータスを確認すると、正常に起動していることを確認できました。
Loaded: loaded (/etc/systemd/system/camera.service; enabled; vendor preset: enabled) Active: active (running) since Sun 2021-03-14 22:35:16 JST; 8s ago Main PID: 9221 (camera.sh) Tasks: 19 (limit: 4183) CGroup: /system.slice/camera.service ├─9221 /bin/bash /opt/camera.sh └─9233 python3 /path/to/jetson_nano_camera_server.py再起動時に自動でサーバが起動することを確認できました。
終わりに
Jetson Nanoをネットワークカメラ化してみました。
gRPCによる通信、systemdでのサービスの設定などは興味がありつつも触れてこなかったところなので
わからないこともありましたがなんとか思った通りのものになりました。
- 投稿日:2021-03-14T21:45:08+09:00
【Python】Sideオブジェクト、Borderオブジェクトを使って罫線をひく。
pythonを使用してExcelファイルの操作を勉強しています。
本日の気づき(復習)は、罫線に関してです。
pythonでExcelを操作するため、openpyxlというパッケージを使用しています。今回は前回の復習(日報作成)から約一か月ということで(適当)
いままでの勉強内容を含め再度の復習もかねて、表に罫線を引きたいと思います。上記のようなブック「商品リストを」
こんな感じにしたいです。
今回の目標は
- 表の見出しやデータ量の増減に対応する。
- 表の位置がどこであっても対応する。
の二つです。
マージセルの操作関数
当初はWorksheet.iter_rowメソッドを使用してと考えていたのですが
公式に何かないかなとずるを考えだしたら・・・、ありました。
https://openpyxl.readthedocs.io/en/stable/styles.html#cell-styles-and-named-stylesfrom openpyxl.styles import Border, Side, PatternFill, Font, GradientFill, Alignment from openpyxl import Workbook def style_range(ws, cell_range, border=Border(), fill=None, font=None, alignment=None): top = Border(top=border.top) left = Border(left=border.left) right = Border(right=border.right) bottom = Border(bottom=border.bottom) first_cell = ws[cell_range.split(":")[0]] if alignment: ws.merge_cells(cell_range) first_cell.alignment = alignment rows = ws[cell_range] if font: first_cell.font = font for cell in rows[0]: cell.border = cell.border + top for cell in rows[-1]: cell.border = cell.border + bottom for row in rows: l = row[0] r = row[-1] l.border = l.border + left r.border = r.border + right if fill: for c in row: c.fill = fillフォントなどは今回使わないのですが、そのまま持ってきちゃいました。
目的の罫線を引くため、外枠の罫線設定を使用します。
対象範囲の縦線と横線を別に設定して引いていくという感じでしょうか。Sideオブジェクト
Side(color=RGB形式の色指定, border_style=線のスタイル)color引数は文字の時と同じですね。
border_style引数に関しては
- hair:極細
- thin:通常の太さ
- medium:通常と太線の中間
- thick:太線
- double:二重線
この辺はExcelと同じですね。
Borderオブジェクト
cell.border = Border(left=Sideオブジェクト, right=Sideオブジェクト, top=Sideオブジェクト, bottom=Sideオブジェクト)生成したSideオブジェクトを使用して、Borderオブジェクトを生成します。
そちらを、セルのborder属性に設定することで罫線を引く事が出来ます。こちらを踏まえて
最終的なコード
from openpyxl.styles import Border, Side, PatternFill, Font, GradientFill, Alignment from openpyxl import load_workbook # 公式にあるマージセルの操作関数 def style_range(ws, cell_range, border=Border(), fill=None, font=None, alignment=None): top = Border(top=border.top) left = Border(left=border.left) right = Border(right=border.right) bottom = Border(bottom=border.bottom) first_cell = ws[cell_range.split(":")[0]] if alignment: ws.merge_cells(cell_range) first_cell.alignment = alignment rows = ws[cell_range] if font: first_cell.font = font for cell in rows[0]: cell.border = cell.border + top for cell in rows[-1]: cell.border = cell.border + bottom for row in rows: l = row[0] r = row[-1] l.border = l.border + left r.border = r.border + right if fill: for c in row: c.fill = fill wb = load_workbook('商品リスト.xlsx') ws = wb.active # 各線のスタイルを設定 hair = Side(color='000000', border_style='hair') thin = Side(color='000000', border_style='thin') double = Side(color='000000', border_style='double') thick = Side(color='000000', border_style='thick') # 縦線の種類と位置を設定 border_ver_thin = Border(left=thin) border_ver_start = Border(left=thick) border_ver_end = Border(left=thin, right=thick) # 横線の種類と位置を設定 border_hor_hair = Border(top=hair) border_hor_thin = Border(top=thin) border_hor_double = Border(top=double) border_hor_thick = Border(top=thick) # 縦線を引く for col in range(ws.min_column, ws.max_column + 1): Alpha = ws.cell(row=ws.min_row, column=col).column_letter ver_range = Alpha + f'{ws.min_row}' + ':' + Alpha + f'{ws.max_row}' if col == ws.min_column: style_range(ws, ver_range, border=border_ver_start) elif col == ws.max_column: style_range(ws, ver_range, border=border_ver_end) style_range(ws, ver_range, border=border_ver_thin) # 横線を引く hor_start = ws.cell(row=ws.min_row, column=ws.min_column).column_letter hor_end = ws.cell(row=ws.min_row, column=ws.max_column).column_letter for row in range(ws.min_row, ws.max_row + 2): hor_range = hor_start + str(row) + ':' + hor_end + str(row) if row == ws.min_row or row == ws.max_row + 1: style_range(ws, hor_range, border=border_hor_thick) elif row == ws.min_row + 1: style_range(ws, hor_range, border=border_hor_double) elif (row - ws.min_row - 1) % 5 == 0: style_range(ws, hor_range, border=border_hor_thin) style_range(ws, hor_range, border=border_hor_hair) wb.save('商品リスト_傍線.xlsx')こんな感じになりました。
これから汎用性を高めたコードに変えていきたいのですが
今日は力尽きました・・・。
- 投稿日:2021-03-14T21:17:26+09:00
AWS DynamoDB テーブル一覧取得 メモ
テーブル一覧取得
resource
import boto3 dynamodb = boto3.resource('dynamodb') response = dynamodb.tables.all() print(type(response)) print(response) print('------------') for x in response: print(x, x._name, type(x))<class 'boto3.resources.collection.dynamodb.tablesCollection'> dynamodb.tablesCollection(dynamodb.ServiceResource(), dynamodb.Table) ------------ dynamodb.Table(name='TestTable1') TestTable1 <class 'boto3.resources.factory.dynamodb.Table'> dynamodb.Table(name='TestTable2') TestTable2 <class 'boto3.resources.factory.dynamodb.Table'>client
import boto3 dynamodb = boto3.client('dynamodb') response = dynamodb.list_tables() print(type(response)) print(response['TableNames'])<class 'dict'> ['TestTable1', 'TestTable2']参考記事
- 投稿日:2021-03-14T20:54:23+09:00
一般化した数独を作って解く ~PuLPで全ての解を出す~
数独のPuLPの例はありふれていますが, この記事では以下に挑戦します.
- 一般化して扱う
- 数独の問題生成をする
- 全ての解を出力する
- 最適解が複数ある場合でも, 通常PuLPでは1つの解しか返しません
- 他の問題にも応用できそう
PuLPクイック入門
PuLPは, (混合) 整数計画問題を解くことができるPythonライブラリです.
- 問題の定義:
m = pulp.LpProblem(name, sense)
name: モデルの名前. 任意の名前でOK.sense:pulp.LpMinimize(最小化問題)かpulp.LpMaximize(最大化問題)- 変数の定義:
pulp.LpVariable(name, lowBound, upBound, cat)
name: 変数の名前. 任意の名前でOKだが, 他の変数と重複してはいけない.lowBound: 下限値. 省略すると下限なし.upBound: 上限値. 省略すると上限なし.cat: 変数の種類. 文字列で指定する.
"Binary": 0, 1の二値変数."Integer": 整数変数."Continuous": 連続変数.- 目的関数の設定:
m += 式
- 例:
m += x+y
+=という表記がややこしいが, 目的関数を何度も設定すると上書きされるm.setObjective(式)だと思うとわかりやすい- 制約の書き方:
m += 条件式
- 制約が追加される
- 条件式で使える種類 (
!=,>,<は使えない)
式1 >= 式2式1 == 式2式1 <= 式2- 例:
m += x>=y
x>=yの制約が追加されます- 問題を解く:
m.solve()- 解いたあとのステータスを得る:
pulp.LpStatus[m.status]
"Undefined""Unbounded""Infeasible""Not Solved""Optimal"- 変数や目的関数の値を得る:
pulp.value(・)
- 変数の値:
pulp.value(変数)- 目的関数の値:
pulp.value(m.objective)- 便利な関数
pulp.lpSum(・): 合計をとるpulp.lpSum(係数, 変数): 内積をとるpulp.LpVariable.dicts(name, (iter1, iter2, ...), lowBound, upBound, cat): 変数を一気に作る
- 例:
vars = pulp.LpVariable.dicts("X", (range(3), range(4)))
f"X_{i}_{j}"の名前のついた変数が生成される(i=0,1,2, j=0,1,2,3)vars[i][j]のように各変数にアクセスできる
- numpyのように
vars[:, j]こういうアクセスができないので, このような表現を多用したいなら,vars = np.array([[pulp.LpVariable(f"X_{i}_{j}") for j in range(4)] for i in range(3)])で生成したほうがいい数独
数独はニコリの登録商標です (ナンプレとも呼ばれてます).
「各行, 各列, 3x3の枠内の数字は重複してはいけない」という条件のもと, 以下のような9x9のマスに1-9の数字を埋めていく問題です.---------------------------------------- | 5 | 2 9 | 4 | | 4 | 3 | 5 | | 2 | 7 | 6 8 | ---------------------------------------- | 6 | 4 1 | | | 7 | 8 5 | 1 2 | | 8 3 | 2 | 9 | ---------------------------------------- | 7 | 1 9 | 5 | | 6 | | 1 4 | | 5 | 6 | | ----------------------------------------今回はこの3x3のブロックを$m \times n$として一般化します.
盤面のサイズは$mn \times mn$とします. ($m=n=3$が普通の数独です)
たとえば, $m=2, n=3$ならこうなります.--------------------------- | 3 1 | 6 | | 5 | 1 2 | --------------------------- | 6 | 3 | | 4 2 | | --------------------------- | 2 3 | | | | | ---------------------------ソルバー
定式化
なにも考えずにやろうとすると, 盤面の変数行列を$X\in\{1,...,mn\}^2$として, たとえば行の制約を$X_{ij_1}\ne X_{ij_2} (j_1\ne j_2)$としたくなります.
しかし, $\ne$は使えないので別の表現をする必要があります.
- 変数: $X\in\{0,1\}^{mn \times mn \times mn}$
- $X_{ijk}$: 盤面$(i,j)$の値が $k+1$ であるなら $1$
- 添字は0始まりとしてます
- 定数: $P\in\{0,1,...,mn\}^{mn \times mn}$
- 与えられる問題を表す行列
- 0は空欄を表す
- 制約:
- $\displaystyle\sum_k X_{ijk}=1, \forall i,j$
- 1マスには1つの数字しか入らない
- $\displaystyle\sum_j X_{ijk}=1, \forall i,k$
- 行の数字は重複してはいけない
- $\displaystyle\sum_i X_{ijk}=1, \forall j,k$
- 列の数字は重複してはいけない
- $\displaystyle\sum_{i\le I<i+m,~j \le J<j+n}X_{IJk}=1, \forall i\in\{0,m,2m,...,mn\},j\in\{0,n,2n,...,mn\},k$
- $m \times n$ブロック内は重複してはいけない
- $X_{ij,P_{ij}-1}=1, \forall i,j, P_{ij}\ne 0$
- 与えられた数字を満たさないといけない
- 目的関数: なし
- あえて書くなら, 0 (定数)
コード
class Sudoku: """数独クラス""" def __init__(self, m, n): """考える小さいブロックのサイズ(m, n): 普通の数独ならm=3, n=3""" self.m = m self.n = n # 入る数字の最大数 self.max_num = m * n # ループ用 self.r = range(self.max_num) def init(self, problem): """与えられた問題を解くための初期化用関数 problem: 0が空欄をあらわすnp.ndarray(int) """ # 最適化問題 self.sudoku = pulp.LpProblem("sudoku", pulp.LpMinimize) # max_num x max_numの盤面の数を表す変数 self.board = np.array( [ [ [ pulp.LpVariable(f"board_{i}_{j}_{k}", cat="Binary") for k in self.r ] for j in self.r ] for i in self.r ] ) # 数字はどれか一つ for i in self.r: for j in self.r: self.sudoku += pulp.lpSum(self.board[i,j,:]) == 1 # 行に同じ数字が入ってはいけない for i in self.r: for k in self.r: self.sudoku += pulp.lpSum(self.board[i,:,k]) == 1 # 列に同じ数字が入ってはいけない for j in self.r: for k in self.r: self.sudoku += pulp.lpSum(self.board[:,j,k]) == 1 # 正方形の枠に同じ数字が入ってはいけない for i in range(0, self.max_num, self.m): for j in range(0, self.max_num, self.n): for k in self.r: self.sudoku += pulp.lpSum(self.board[i:i+self.m, j:j+self.n, k]) == 1 # 初期値をいれる for i in self.r: for j in self.r: if problem[i, j]:# 空欄でないとき self.sudoku += self.board[i, j, problem[i, j]-1] == 1定式化した表現を素直に書いただけです.
コード内では$X$をself.boardで表しています.すべての解を列挙する
先程の数独クラスで,
self.init(problem)してself.sudoku.solve()すれば解が得られますが, 1つしか得られません.
すべての解を列挙するためには, 一度出た解を再び出力しないような制約を加えて, 再び最適化する必要があります.得られた1つの解を$\tilde{X}$とします.
各マスには1つの数字しか入ってないので, 当然$\tilde{X}$の合計値は, $\displaystyle\sum_{ijk}\tilde{X}_{ijk}=(mn)^2$です.
別の解を得るためには, 「割り当てられた箇所の合計 $\le (mn)^2-1$」 という制約を追加します.
式で書くと,\sum_{ijk: \tilde{X}_{ijl}=1 } X_{ijl} \le (mn)^2-1この制約を加えることで, $\tilde{X}$の割り当てから, 最低でも1つは割り当てを変えなければいけなくなります.
def solve(self, problem): """ソルバー. 全ての解が順番に得られる problem: 0が空欄をあらわすnp.ndarray(int) """ self.init(problem) while True: self.sudoku.solve() if pulp.LpStatus[self.sudoku.status] != "Optimal": break answer = np.vectorize(pulp.value)(self.board) answer = np.where(answer)[2].reshape(self.max_num,self.max_num)+1 yield answer # 割り当てられた変数から最低でも1つ外すようにすることで別の解を探すようにする self.sudoku += pulp.lpSum([ self.board[i, j, k] for i in self.r for j in self.r for k in self.r if pulp.value(self.board[i, j, k]) == 1 ]) <= self.max_num * self.max_num-1これですべての解を列挙できるようになりました.
問題作成
作ったソルバーを使って数独の問題を作ります.
ここで, 問題とは, 解が存在し, 一意であるものと定義します.作った問題の解が一意であるかの判定は, すべての解を列挙する
self.solve(・)を使って表現します.
解の個数が2以上になった時点で一意ではありません.
解の個数が0なら解は存在しません.def is_unique(self, problem): """解が一意かどうか判定 True: 一意 False: 一意でない None: 解なし """ cnt = 0 for ans in self.solve(problem): cnt+=1 # 一意でない if cnt>=2: return False # 一意 if cnt==1: return True # 解なし return None単純な方法
空の盤面にランダムに数字を入れていき, ソルバーで解が一意かどうか判定しながら, 一意になるまで数字を追加します.
def create_problem_from_empty(self, try_num): """問題作成 (空の盤面にランダムに数字を入れていくバージョン) 実行速度遅い. """ # 空の盤面作成 problem = np.zeros((self.max_num, self.max_num), dtype=int) # 埋めていく for _ in range(try_num): print(">", end="") while True: i, j = np.random.randint(self.max_num, size=2) if not problem[i, j]: break # 盤面(i,j)を適当に埋める problem[i, j] = np.random.randint(self.max_num) + 1 is_unique = self.is_unique(problem) # 一意でないなら盤面を空白に戻す if is_unique is None: problem[i, j] = 0 continue # 一意なら終了 if is_unique: print("") return problem return None
try_numは埋める試行をする回数です. 十分大きな値を設定する必要があります.
単純で実装しやすいですが, はじめのうちはほとんど空欄の状態の数独を何度も解くことになるので, とても時間がかかります.
$??>10$からきつくなってきました.埋まった状態の盤面から穴を開けていく方法
この方法では, 最初に答えの盤面を用意してから空欄にしていきます.
ソルバーにとっては, ほとんど埋まった状態から解くことになり, 探索空間が少なく楽になります.
一方で, すべて埋まった盤面を用意するのが必要になります.
真面目にやると計算時間がやばいので, ヒューリスティックに埋めていきます.def __fill_rows(self, problem, i, try_num): """i行以降をランダムに埋める再帰関数 (埋まった状態の盤面作成用ヒューリスティック)""" if i >= self.max_num: return True for _ in range(try_num): if not self.__fill_vals(problem, i, 0, try_num): continue if self.__fill_rows(problem, i+1, try_num): return True return False def __fill_vals(self, problem, i, j, try_num): """i行目のj列以降をランダムに埋める再帰関数 (埋まった状態の盤面作成用ヒューリスティック)""" if j >= self.max_num: # 最後の列まで埋まったら return True for _ in range(try_num): problem[i, j] = np.random.randint(self.max_num)+1 # 重複判定 row = problem[i, :j+1] column = problem[:i+1, j] block = problem[i//m*m:i+1, j//n*n:(j//n+1)*n] zero_exist = (block == 0).any() if np.unique(row).shape[0] != row.shape[0] or \ np.unique(column).shape[0] != column.shape[0] or \ np.unique(block).shape[0]-zero_exist != (block != 0).sum(): continue # 重複したら別の数字をトライ if self.__fill_vals(problem, i, j+1, try_num): #次の値を埋めに行く return True problem[i, j] = 0 return False0行目から順番に埋めていきます.
「 $i$ 行以降を埋める」という動作は, 「 $i$ 行目を埋める」+「 $i+1$ 行目以降を埋める」という表現ができます. (再帰)
「 $i$ 行目の $j$ 列以降を埋める」という動作は, 「 $i$ 行目の $j$ 列目を埋める」+「 $i$ 行目の $j+1$ 列以降を埋める」という表現ができます. (再帰)
try_numは, その行を作る試行を行う回数, および, その値を埋める試行を行う回数です.
再帰で書くことで, 「この行何回試行してもうまくいかないな」となったら前の行に戻り前の行を疑って修正します.
ヒューリスティックなので, 失敗することもあります.次に, この埋められた盤面を使って問題を作ります.
def create_problem_from_fill(self, try_num, level=1): """問題作成 (埋まった状態から穴をあけていくバージョン) 最初に答えの盤面を作る必要がある. try_num: 答えの盤面作成で試行する回数. m*nくらいが良さそう. level: 穴あけ失敗許容回数 """ # 空の盤面作成 problem = np.zeros((self.max_num, self.max_num), dtype=int) # 盤面を全て埋める if not self.__fill_rows(problem, 0, try_num): return None cnt = 0 # 穴あけに失敗した回数 while True: print(">", end="") while True: i, j = np.random.randint(self.max_num, size=2) if problem[i, j]: break tmp = problem[i, j] # 盤面に穴をあける problem[i, j] = 0 if not self.is_unique(problem): # 一意でなくなったら値をもとに戻す problem[i, j] = tmp cnt += 1 if cnt >= level: break print("") return problem盤面に穴をあけて, 解いた結果, 一意ならOK.
一意でないなら値をもとに戻して終了します. (穴あけ失敗)
この穴あけ失敗回数の許容回数をlevelとしてます.
levelが大きくなると, なるべく空欄の多い問題を作ろうとするので, 問題の難易度が高くなります.実行結果
ちゃんと計算時間の平均とるの面倒なので, だいたいで書きます.
Intel(R) Core(TM) i5-8250U CPU @ 1.60GHz 1.80 GHzにて.問題作成時間:
m n 単純 穴あけ(level=1) 穴あけ(level=2) 2 3 2s-3s 1s-2s 2s-3s 3 3 15s-30s 3s-7s 6s-8s 3 4 3min 13s-15s 45s-52s 4 4 未実行 50s-60s 2min40s prologで実装したときはもう少し早かったのでかなり大きいサイズまでやれました.
prologソースのコメントに詳しく書いてます. (そもそもprolog知っている人どれくらいいるだろうか. )
こういう整数計画はprologの方が得意な気がする.
バックトラックで自動的にすべての解を出してくれるし.最後に自動生成した問題をいくつかおいておきます. やりたい方はどうぞ.
---------------------------------------- | 5 6 | 3 | | | 2 | | 6 | | 3 | 1 5 | 2 | ---------------------------------------- | | 8 | 3 | | 4 | | | | | 5 | 8 | ---------------------------------------- | 3 | 5 8 | 4 | | 6 | 9 2 | 1 | | 7 | 3 6 | | -------------------------------------------------------------------------------------------- | 7 4 | 10 9 | 3 1 | | | 7 1 2 | 10 | | 1 | 3 6 | | ---------------------------------------------------- | 5 | 2 | 9 10 11 | | 10 1 | 7 | 6 5 12 | | 12 8 | 6 9 | 4 | ---------------------------------------------------- | | 9 | 2 3 | | 3 8 | 11 12 10 | 5 | | | 3 5 | | ---------------------------------------------------- | 8 9 | 5 6 | 7 | | 5 12 | | 3 4 | | 3 | 8 10 | | ----------------------------------------------------
- 投稿日:2021-03-14T20:26:49+09:00
Pythonでクラスのインスタンス変数のメソッドをmockする
あるクラスがインスタンス変数として外部と通信するサーバーを持ち、その変数を利用しているメソッドをテストしたいという状況を考えます。
以下の例では、Clientクラスがself.serverを持ち、これを利用してJenkinsの次のビルドの番号を取得するget_next_build_numberメソッドを定義しています。client.pyfrom jenkins import Jenkins class Client: def __init__(self, url, username, password): self.server = Jenkins( url, username=username, password=password, ) def get_next_build_number(self, job_name): info = self.server.get_job_info(job_name) number = info["nextBuildNumber"] return numberテスト時には実際の通信を行いたくないため、
self.serverをモック化します。
単純にはclient = Client(test_url, test_user, test_pass) client.server = mock.MagicMock()で良さそうですが、
passwordが必要なためダミーでは認証エラーを吐いてしまいます。そこで、
Clientを継承してテスト用のクラスを定義し、そこでself.serverをモックに置き換えます。test_client.pyfrom unittest import mock from jenkins import Jenkins from src.client import Client class TestClient(Client): def __init__(self, test_number): mock_server = mock.MagicMock(spec=Jenkins) mock_server.get_job_info.return_value = {"nextBuildNumber": test_number} self.server = mock_server def test_get_next_build_number(): client = TestClient(1) assert client.get_next_build_number("") == 1これで通信やパスワードが必要な処理をモックに置き換え、
get_next_build_numberをテストすることができました。もしもっといい方法があれば教えて下さい……!
- 投稿日:2021-03-14T19:42:25+09:00
pythonファイルの先頭に数字を使うとSyntaxErrorになる
参考書の勉強で章ごとに5_7_3.pyとか使っていて、あるとき他のファイルからモジュールをインポートしようとしたらエラーになった。
from 5_7_2 import TwoLayerNet ==> from 5_7_2 import TwoLayerNet ^ SyntaxError: invalid syntaxファイル名を変えたりしてみると先頭に数字を使っていることがどうやら問題になっているっぽい
from twolayer572 import TwoLayerNet #こっちは実行できたまた先頭数字でもそれ単体で実行はできるけどimportしようとするとエラーになります。
- 投稿日:2021-03-14T19:32:56+09:00
ベイジアンネットワークを活用して因果探索を実装してみた
- 製造業出身のデータサイエンティストがお送りする記事
- 今回は、ベイジアンネットワークを活用して、因果探索を実装してみました。
はじめに
前回(統計的因果探索のLiNGAM)からの続きで、データから因果関係を推測するための機械学習技術の1つ「ベイジアンネットワーク」について整理しました。
細かい理論的な部分は省略します。ベイジアンネットワークとは
ベイジアンネットワークは条件付き確率をベースに、変数間のグラフ構造を表現したものです。
ベイジアンネットワークの中でも、依存関係を算出する方法はいくつかありますが、今回は以下の方法を実施しました。
- 独立性の検定により、変数間のスケルトン(方向のない依存関係)を特定
- V-structure,オリエンテーションルールにより一部のスケルトンに方向を付与
上記はPCアルゴリズムと呼ばれる手法で、簡単に実装することができました。
今回もUCI Machine Learning Repositoryで公開されているボストン住宅の価格データを用いて予測モデルを構築します。
pythonのコードは下記の通りです。
# 必要なライブラリーのインポート import pandas as pd import numpy as np import networkx as nx import os import matplotlib.pyplot as plt from sklearn.datasets import load_boston from pgmpy.models import BayesianModel from pgmpy.estimators import ConstraintBasedEstimator from pgmpy.estimators import BicScore次にデータを読み込みます。
# データセットの読込み boston = load_boston() # データフレームの作成 # 説明変数の格納 df = pd.DataFrame(boston.data, columns = boston.feature_names) # 目的変数の追加 df['MEDV'] = boston.target # データの中身を確認 df.head()次に、PCアルゴリズムは連続値は扱えないため、離散値へ変更します。
# 離散値に変更 df_discrete = df.copy() df_discrete['CRIM'] = pd.cut(df_discrete['CRIM'], 5) df_discrete['ZN'] = pd.cut(df_discrete['ZN'], 5) df_discrete['INDUS'] = pd.cut(df_discrete['INDUS'], 5) df_discrete['CHAS'] = pd.cut(df_discrete['CHAS'], 5) df_discrete['NOX'] = pd.cut(df_discrete['NOX'], 5) df_discrete['RM'] = pd.cut(df_discrete['RM'], 5) df_discrete['AGE'] = pd.cut(df_discrete['AGE'], 5) df_discrete['DIS'] = pd.cut(df_discrete['DIS'], 5) df_discrete['RAD'] = pd.cut(df_discrete['RAD'], 5) df_discrete['TAX'] = pd.cut(df_discrete['TAX'], 5) df_discrete['PTRATIO'] = pd.cut(df_discrete['PTRATIO'], 5) df_discrete['B'] = pd.cut(df_discrete['B'], 5) df_discrete['LSTAT'] = pd.cut(df_discrete['LSTAT'], 5) df_discrete['MEDV'] = pd.cut(df_discrete['MEDV'], 5) df_discrete.head()ここから、ライブラリー
pgmpyを用いてベイジアンネットワークを構築していきます。est = ConstraintBasedEstimator(df_discrete) skel, seperating_sets = est.estimate_skeleton(significance_level=0.01) print("Undirected edges: ", skel.edges()) pdag = est.skeleton_to_pdag(skel, seperating_sets) print("PDAG edges:", pdag.edges()) model = est.pdag_to_dag(pdag) print("DAG edges:", model.edges())各々算出されているものは下記を意味しております。
Undirected edgesは、方向性なしPDAG edgesは、部分的な方向性ありDAG edgesは、方向性あり得られた結果は下記です。
Undirected edges: [('ZN', 'DIS'), ('INDUS', 'NOX'), ('INDUS', 'TAX'), ('INDUS', 'PTRATIO'), ('NOX', 'DIS'), ('NOX', 'PTRATIO'), ('RM', 'MEDV'), ('AGE', 'LSTAT'), ('RAD', 'TAX'), ('RAD', 'PTRATIO'), ('TAX', 'PTRATIO'), ('LSTAT', 'MEDV')] PDAG edges: [('ZN', 'DIS'), ('INDUS', 'NOX'), ('INDUS', 'TAX'), ('INDUS', 'PTRATIO'), ('NOX', 'INDUS'), ('RM', 'MEDV'), ('AGE', 'LSTAT'), ('DIS', 'ZN'), ('DIS', 'NOX'), ('RAD', 'TAX'), ('RAD', 'PTRATIO'), ('TAX', 'INDUS'), ('TAX', 'RAD'), ('TAX', 'PTRATIO'), ('PTRATIO', 'INDUS'), ('PTRATIO', 'RAD'), ('LSTAT', 'AGE'), ('LSTAT', 'MEDV'), ('MEDV', 'RM'), ('MEDV', 'LSTAT')] DAG edges: [('INDUS', 'NOX'), ('INDUS', 'TAX'), ('INDUS', 'PTRATIO'), ('DIS', 'NOX'), ('DIS', 'ZN'), ('RAD', 'TAX'), ('RAD', 'PTRATIO'), ('TAX', 'PTRATIO'), ('LSTAT', 'AGE'), ('MEDV', 'RM'), ('MEDV', 'LSTAT')]上記で基本的な処理は終了ですが、可視化してみないと分かりにくいので可視化しました。
ただ、LiNGAMみたいに簡単に可視化してくれる方法がなかったため(あったら教えて欲しいです)、Undirected edges方向性なしと、DAG edges方向性ありだけ簡単に可視化しました。# Undirected edges(方向性なし)可視化 G = nx.Graph() G.add_nodes_from(df.columns) # ノード G.add_edges_from(skel.edges()) # 辺 nx.draw_circular(G, with_labels=True, arrowsize=30, node_size=800, alpha=0.3, font_weight='bold') plt.show()]: # DAG edges(方向性あり)可視化 DAG_model = BayesianModel(model.edges()) nx.draw_circular(DAG_model, with_labels=True, arrowsize=30, node_size=800, alpha=0.3, font_weight='bold') plt.show()さいごに
最後まで読んで頂き、ありがとうございました。
ベイジアンネットワークも結構簡単に利用できることが分かりました。可視化の部分は、いまいち良い感じに実装できていないので、今後の課題です。訂正要望がありましたら、ご連絡頂けますと幸いです。
- 投稿日:2021-03-14T19:29:27+09:00
Amazonの購入時刻をGmailの受信トレイから調べてみる
背景
Amazonで衝動買いする癖があるので購入時間を可視化していつ買っているかを把握することで気をつけたい。
- 何時に買っていることが多いか
- 何曜日に買っていることが多いか
手順
- Gmailの注文完了メールをGmail APIで抽出する
- 受信日時を取り出せるので時刻、曜日で集計し可視化する
準備
Gmail APIから自分用の
credentials.jsonをダウンロードして同じディレクトリに置く。APIの用意方法は以下を参照する。Gmail APIはPythonのライブラリが提供されているためそれを利用した。
実施(取得)
認証部分はサンプルとほぼ同じ。
「Amazon.co.jpでのご注文」の検索結果のリストを取得しそれぞれのメッセージ内容を参照している。pull.pyfrom __future__ import print_function import os.path from googleapiclient.discovery import build from google_auth_oauthlib.flow import InstalledAppFlow from google.auth.transport.requests import Request from google.oauth2.credentials import Credentials q = 'Amazon.co.jpでのご注文' email = 'test@gmail.com' SCOPES = ['https://www.googleapis.com/auth/gmail.readonly'] creds = None # 認証 if os.path.exists('token.json'): creds = Credentials.from_authorized_user_file('token.json', SCOPES) if not creds or not creds.valid: if creds and creds.expired and creds.refresh_token: creds.refresh(Request()) else: flow = InstalledAppFlow.from_client_secrets_file( 'credentials.json', SCOPES) creds = flow.run_local_server(port=0) with open('token.json', 'w') as token: token.write(creds.to_json()) # 注文取り出し service = build('gmail', 'v1', credentials=creds) results = service.users().messages().list(userId=email, q=q).execute() messages = results.get('messages', []) for message in messages: message_id = message.get('id') mail = service.users().messages().get(userId=email, id=message_id, format='minimal').execute() print(mail.get('internalDate'))実施(可視化)
結果から時刻情報と曜日情報のみ取り出し棒グラフで表示している。
draw.pyimport pandas as pd import matplotlib.pyplot as plt import numpy as np # 読み込み df = pd.read_csv('created_dates.txt', header=None) datetimes = pd.to_datetime(df[0], unit='ms') # 時刻情報だけのデータに変換 times = datetimes.dt.time times = pd.DataFrame(pd.to_datetime(times, format='%H:%M:%S', utc=True)) times.set_index(0, inplace=True) times.index = times.index.tz_convert('Asia/Tokyo') times[1] = 0 times = times.rename(columns={1: 'count'}, index={0: 'date'}) group = times.groupby(pd.Grouper(freq='60min')).count() # 曜日のデータに変換 weeks = pd.DataFrame(pd.to_datetime(datetimes, utc=True)).set_index(0) weeks.index = weeks.index.tz_convert('Asia/Tokyo') weekdays = weeks.index.weekday weekdays = pd.DataFrame(weekdays) weekdays[1] = 1 # 可視化 fig = plt.figure(figsize=(20,10)) ## 時間帯 x = group.index.strftime("%H:%M:%S") y = group ax = fig.add_subplot(2,1,1) ax.bar(x, group['count'], color="brown", align="center") ax.set_title('Every Hour') ax.set_xticks(x) ax.set_yticks(np.arange(0, y.max().item() )) ## 曜日 x = ["Sun","Mon","Tue","Wed","Thr","Fri","Sat"] y = weekdays.groupby(0).count()[1] ax2 = fig.add_subplot(2,1,2) ax2.bar(x, y, color="green", align="center") ax2.set_title('Every Date') ax2.set_xticks(x) ax2.set_yticks(np.arange(0, y.max() )) # 保存 fig.savefig("figure.png")結果
結論
- 週末に密集していると想いきや意外とまんべんなく買っている
- 寝る前の時間帯は危険
GitHubに実行環境をまとめてます。
- 投稿日:2021-03-14T19:29:27+09:00
Amazonの購入時刻をGmailの受信トレイから調べて可視化する
背景
Amazonで衝動買いする癖があるので購入時間を可視化していつ買っているかを把握することで気をつけたい。
- 何時に買っていることが多いか
- 何曜日に買っていることが多いか
手順
- Gmailの注文完了メールをGmail APIで抽出する
- 受信日時を取り出せるので時刻、曜日で集計し可視化する
準備
Gmail APIから自分用の
credentials.jsonをダウンロードして同じディレクトリに置く。APIの用意方法は以下を参照する。Gmail APIはPythonのライブラリが提供されているためそれを利用した。
実施(取得)
認証部分はサンプルとほぼ同じ。
「Amazon.co.jpでのご注文」の検索結果のリストを取得しそれぞれのメッセージ内容を参照している。pull.pyfrom __future__ import print_function import os.path from googleapiclient.discovery import build from google_auth_oauthlib.flow import InstalledAppFlow from google.auth.transport.requests import Request from google.oauth2.credentials import Credentials q = 'Amazon.co.jpでのご注文' email = 'test@gmail.com' SCOPES = ['https://www.googleapis.com/auth/gmail.readonly'] creds = None # 認証 if os.path.exists('token.json'): creds = Credentials.from_authorized_user_file('token.json', SCOPES) if not creds or not creds.valid: if creds and creds.expired and creds.refresh_token: creds.refresh(Request()) else: flow = InstalledAppFlow.from_client_secrets_file( 'credentials.json', SCOPES) creds = flow.run_local_server(port=0) with open('token.json', 'w') as token: token.write(creds.to_json()) # 注文取り出し service = build('gmail', 'v1', credentials=creds) results = service.users().messages().list(userId=email, q=q).execute() messages = results.get('messages', []) for message in messages: message_id = message.get('id') mail = service.users().messages().get(userId=email, id=message_id, format='minimal').execute() print(mail.get('internalDate'))出力値
internalDateにはUNIX時間でミリ秒まで記録されている。1556799xxx000 1556032xxx000 1556031xxx000 1555086xxx000 1554382xxx000 ...実施(可視化)
出力値から時刻情報と曜日情報のみ取り出し棒グラフで表示している。
draw.pyimport pandas as pd import matplotlib.pyplot as plt import numpy as np # 読み込み df = pd.read_csv('created_dates.txt', header=None) datetimes = pd.to_datetime(df[0], unit='ms') # 時刻情報だけのデータに変換 times = datetimes.dt.time times = pd.DataFrame(pd.to_datetime(times, format='%H:%M:%S', utc=True)) times.set_index(0, inplace=True) times.index = times.index.tz_convert('Asia/Tokyo') times[1] = 0 times = times.rename(columns={1: 'count'}, index={0: 'date'}) group = times.groupby(pd.Grouper(freq='60min')).count() # 曜日のデータに変換 weeks = pd.DataFrame(pd.to_datetime(datetimes, utc=True)).set_index(0) weeks.index = weeks.index.tz_convert('Asia/Tokyo') weekdays = weeks.index.weekday weekdays = pd.DataFrame(weekdays) weekdays[1] = 1 # 可視化 fig = plt.figure(figsize=(20,10)) ## 時間帯 x = group.index.strftime("%H:%M:%S") y = group ax = fig.add_subplot(2,1,1) ax.bar(x, group['count'], color="brown", align="center") ax.set_title('Every Hour') ax.set_xticks(x) ax.set_yticks(np.arange(0, y.max().item() )) ## 曜日 x = ["Sun","Mon","Tue","Wed","Thr","Fri","Sat"] y = weekdays.groupby(0).count()[1] ax2 = fig.add_subplot(2,1,2) ax2.bar(x, y, color="green", align="center") ax2.set_title('Every Date') ax2.set_xticks(x) ax2.set_yticks(np.arange(0, y.max() )) # 保存 fig.savefig("figure.png")結果
時刻では夜の23時、0時にピークを迎えている。曜日では大きく変わらないが金曜日に頻度が増えている。
結論
- 週末に密集していると思ったが意外とまんべんなく買っている
- 寝る前の時間帯は危険・・・!
GitHubに実行環境をまとめてます。
- 投稿日:2021-03-14T18:31:19+09:00
LambdaでAWS利用料のグラフをS3に保存し、Slackに通知する
はじめに
AWSアカウントの管理者になってから、ほぼ毎日Cost Explorerで利用料を確認し、料金の急増がないかをチェックしています。ただ、
- 手動での確認はやはり手間がかかり、もっと手軽な方法でやりたい
- 利用料の状況をチームメンバーにも共有し、コストの管理意識を芽生えてもらいたい
というニーズがあり、日々の利用料をSlackに通知するためのLambda関数を実装しました。
参考記事
まず、アーキテクチャとソースコードはこちらの記事を参考し、一部カスタマイズして作りました。(@hayao_kさん、ありがとうございました!)
日々のAWS請求額をグラフ付きでSlackに通知するただ、弊社のSlackワークスペースにおいては、ファイルアップロードのための
files:writeスコープが規則上認められていないため、アーキテクチャを一部変更し、Slackへの直接アップロードではなく、一度S3に保存したうえ、グラフのオブジェクトURLをリンクとしてSlackメッセージに貼り付けるという形にしました。実際のアーキテクチャは以下となります。
- CloudWatch Eventsによって指定の時間にLambda関数を呼び出す
- CloudWatchから
EstimatedChargesのメトリクス情報(データポイント)を取得- 取得したデータポイントに基づき、Lambda関数で利用料のグラフを生成
- 生成したグラフをS3バケットに保存 ? ここは参考記事からの変更点
- 利用料に関するメッセージを作成してSlackに送る(メッセージにグラフのURLも含める)
成果物のイメージ
また、メッセージにあるリンクをクリックすると、ブラウザ上でS3に保存されているグラフが表示されます。
実装の事前準備
Slack Incoming Webhooksを用意
S3バケットを用意
任意の端末からS3に保存されているグラフにアクセスしたい場合は、バケットのパブリックアクセスを有効化する必要がありますが、社外からのアクセスを回避したいので、バケットポリシーに弊社事業所のグローバルIPのみ許可します。
Lambda関数を作成
ランタイムは
Python 3.8
実行ロールは基本的な権限(CloudWatchにログ出力するための権限)で新規作成したうえ、再度IAMから当該ロールを編集し、下記2つのポリシーを追加します。
- CloudWatchReadOnlyAccess(手順2でCloudWatchからメトリクス情報を取得するため)
- 上記S3バケットへの操作権限(手順4でグラフをバケットに保存するため)
Lambda関数の中身(ソースコード)
バケットやWebhooksなどの情報は適宜書き換えるように。
lambda_function.pyimport base64 import boto3 import datetime import json import logging import os import requests from botocore.exceptions import ClientError logger = logging.getLogger() logger.setLevel(logging.INFO) client = None def get_cloudwatch_client(): global client client = boto3.client('cloudwatch', region_name='us-east-1') return client def get_metrics(start_time, end_time, client=None): if client is None: client = get_cloudwatch_client() try: response = client.get_metric_statistics( Namespace='AWS/Billing', MetricName='EstimatedCharges', Dimensions=[ { 'Name': 'Currency', 'Value': 'USD' } ], StartTime=start_time, EndTime=end_time, Period=21600, Statistics=['Maximum'] ) except ClientError as e: logger.error("Request failed: %s", e.response['Error']['Message']) else: return response def get_image(today, yesterday, diff, metrics, s3ObjKey, client=None): if client is None: client = get_cloudwatch_client() if diff > 0: title = ('Current Charges: $' + str(today) + ' / Increased $' + str(diff) + ' from Yesterday') min = yesterday * 0.7 max = today * 1.05 else: title = ('Current Charges: $' + str(today)) min = today * 0.7 max = yesterday * 1.05 widget_definition = json.dumps( { "width": 1280, "height": 800, "start": "-PT144H", "end": "PT0H", "timezone": "+0900", "view": "timeSeries", "stacked": True, "stat": "Maximum", "title": title, "metrics": [ ["AWS/Billing", "EstimatedCharges", "Currency", "USD"] ], "period": 43200, "annotations": { "horizontal": [ { "label": "Today", "value": today }, { "label": "Yesterday", "value": yesterday } ] }, "yAxis": { "left": { "label": "$", "min": (min), "max": (max) } }, } ) try: response = client.get_metric_widget_image( MetricWidget=widget_definition ) except ClientError as e: logger.error("Request failed: %s", e.response['Error']['Message']) else: s3 = boto3.resource('s3') bucket = s3.Bucket('xxxxxxxxxx') res = bucket.put_object(Body=( response["MetricWidgetImage"]), Key=s3ObjKey, ContentType='image/png') logger.info("Upload Image succeeded.") def build_payload(today_charge, diff, s3ObjUrl): payload = { "attachments": [ { "color": "good", "title": "AWS料金(クリックしてグラフを確認)", "title_link": s3ObjUrl, "fields": [ { "title": "対象AWSアカウント", "value": "`xxxxxxxxxxxx`", "short": False }, { "title": "本日まで利用した金額", "value": ":heavy_dollar_sign:" + str(today_charge), "short": True }, { "title": "昨日よりの増加量", "value": ":heavy_dollar_sign:" + str(diff), "short": True } ] } ] } return payload def lambda_handler(event, context): start_time = datetime.datetime.now() - datetime.timedelta(hours=30) end_time = datetime.datetime.now() logger.info('Metric Start Time: ' + str(start_time)) logger.info('Metric End Time: ' + str(end_time)) metrics = get_metrics(start_time, end_time) sorted_data = sorted(metrics['Datapoints'], key=lambda x: x['Timestamp']) logger.info("Sorted Data: %s", sorted_data) today_charge = sorted_data[-1]['Maximum'] yesterday_charge = sorted_data[0]['Maximum'] diff = round(today_charge - yesterday_charge, 2) targetAccount = 'xxxxxxxxxxxx' s3ObjKey = targetAccount + '/charge-graph-' + \ str((end_time + datetime.timedelta(hours=9)).date()) s3ObjUrl = 'https://xxxxxxxx.s3-ap-northeast-1.amazonaws.com/' + s3ObjKey get_image(today_charge, yesterday_charge, diff, metrics, s3ObjKey) payload = build_payload(today_charge, diff, s3ObjUrl) req = requests.post( 'https://hooks.slack.com/services/xxxxxxxxxxxxxxxx', data=json.dumps(payload)) try: req.raise_for_status() logger.info("Message posted.") return req.text except requests.RequestException as e: logger.error("Request failed: %s", e) return req最後に
Lambdaを実装し、データポイントの取得やグラフ(ウイジェット)生成のためのパラメータをチューニングして簡単なテストを済ませ、CloudWatchのイベントルールを設定したら終わりです。これで毎日Slackで料金のチェックや推移グラフを見ることができるようになりました。かなり便利です!
後日に余裕あったら
get_metric_statisticsとget_metric_widget_imageの仕様をまとめてみます。
- 投稿日:2021-03-14T18:09:44+09:00
GridSearchCV
GridSearchCV
機械学習のモデルには、モデルの初期値(ハイパーパラメータ)が存在する。
ハイパーパラメータは、モデルの予測精度に大きく影響を与えるので適切なパラメータを採用するためにチューニング作業。
その作業は、GridSearchCVを用いて、適切なパラメータの探索を行う。必要なライブラリーなどをインポートする
import numpy as np from sklearn.datasets import laod_iris from sklearn.model_selection import GridSearchCV from sklearn.liear_model import LogisticRegression iris=load_iris()ロジステック回帰のチューニング
model=LogisitcRegression() param_grid=[{"C":[1e-2,1e-1,1,1e1,1e2],panalty:["l1","l2]}] clf=GridSearcCV(model,param_grid,cv=5) clf.fit(X_train,y_train) best_params=clf.best_estimator_ best_score=clf.best_score_ print(best_params) print(best_score)modelを設定する
model=LogisticREgression()パラメータを設定する
param_grid=[{"C":[1e-2,1e-1,1,1e1,1e2],panalty:["l1","l2]}]グリッドサーチ
clf=GridSearcCV(model,param_grid,cv=5) clf.fit(X_train,y_train)GridSearch(モデル,パラメータ,交差検証)
最良モデルのパラメータとそのスコアを出力する
best_params=clf.best_estimator_ best_score=clf.best_score_ print(best_params) print(best_score)best_estimator_:データに対する最良のパラメータを出力する
best_score_:最良のスコアを出力する
- 投稿日:2021-03-14T18:07:59+09:00
PyAutoGUIとOpenCV画像認識を使いクリッカーゲームのBOT作成
Python PyAutoGUIとOpenCV画像認識を使いクリッカーゲームのBOT作成
やりたいこと自作のクリッカーゲームの自動化
※ サンプルではCookie Clicker の自動化を行った→ http://orteil.dashnet.org/cookieclicker/
- クッキーを自動でクリック
- 一定回数クリック後にCursurが購入可能かチェックし可能な場合、買う
- 1〜2を繰り返し行う
PyAutoGUIとopencv-pythonをインストール
PyAutoGUIドキュメント
opencv-pythonドキュメント
pip install pyautogui pip install opencv-pythonクッキーを自動でクリック
Cookie Clicker ブラウザ画面
絶対座標 200:400をクリック
クリック回数は0.5秒間隔で10回行うimport pyautogui def click(): pyautogui.click(x=200, y=400, clicks=10, interval=0.5, button='left') if __name__ == "__main__": click()Cursurが購入可能かチェック
最初にCursurの画像を取得
def screenshot_cursor(): screenshot = pyautogui.screenshot(region=(2226, 1242, 120, 120)) screenshot.save("images/cursor.png")購入可能時と購入不可能時の画像をそれぞれ取得
購入可能判定
2つ方法があった
PyAutoGUIのlocateOnScreenを使う
pyautogui.locateOnScreenを使う現在の画面に対象画像が存在する場合に座標が返る。
不一致はNULLconfidenceは一致率、今回は画像は同じで購入できない場合グレー画像かだけなので判定精度の調整が難しかった
0.9999で購入出来る場合は座標が返り、購入出来ない場合はNULLになったdef match_cursor_active(): rerturn pyautogui.locateOnScreen("images/cursor_active.png", confidence=.9999)OpenCVのmatchTemplateを使う
minVal, maxValで一致率が分かる
今回の画像の場合、購入できる画像は1.0, 1.0
購入できない場合は0.9970715045928955, 0.9970715045928955となったdef match_cv_cursor_active(): tmp = cv2.imread("images/cursor.png") cursor_active = cv2.imread("images/cursor_active.png") # 画像マッチング処理 result = cv2.matchTemplate(cursor_active, tmp, cv2.TM_CCORR_NORMED) minVal, maxVal, _, _ = cv2.minMaxLoc(result) if minVal < 1: return False return True備考:どちらも微妙なのでもっといい方法があれば教えて欲しい
色味判定などがいいのかもしれない
ぶっちゃけ今回の処理の場合、無条件でCursorクリックでも良いのだが...クリックして購入
def click_cursor(): pyautogui.click(x=1150, y=650, clicks=1, interval=0, button='left') if __name__ == "__main__": p = match_cursor_active() if p: click_cursor()全体のコード
クッキークリック10回を10回繰り返す処理にした
import time import cv2 import pyautogui def click(): pyautogui.click(x=200, y=400, clicks=10, interval=0.5, button='left') def click_cursor(): pyautogui.click(x=1150, y=650, clicks=1, interval=0, button='left') def screenshot_cursor(): screenshot = pyautogui.screenshot(region=(2226, 1242, 120, 120)) screenshot.save("images/cursor.png") def match_cursor_active(): return pyautogui.locateOnScreen("images/cursor_active.png", confidence=.9999) def match_cv_cursor_active(): tmp = cv2.imread("images/cursor.png") cursor_active = cv2.imread("images/cursor_active.png") # 画像マッチング処理 result = cv2.matchTemplate(cursor_active, tmp, cv2.TM_CCORR_NORMED) minVal, maxVal, _, _ = cv2.minMaxLoc(result) if minVal < 1: return False return True if __name__ == "__main__": max = 10 for loop in range(max): print(f"ループ回数:{loop}") click() p = match_cursor_active() if p: click_cursor() time.sleep(1)実行動画
以上、クリッカーゲーム攻略方法でした
いいね!と思ったら LGTM お願いします
【PR】プログラミング新聞リリースしました! → https://pronichi.com
【PR】週末ハッカソンというイベントやってます! → https://weekend-hackathon.toyscreation.jp/about/
- 投稿日:2021-03-14T17:48:20+09:00
Python: 適宜ファイルを差し替えながら大量のデータを書き込む
概要
大きなデータを書き込むときに、1つのファイルに書き込んでしまうと、読み込みのときに処理時間が膨大になったり、あるいはメモリのエラーで実行がそもそも不能になる可能性があります。
そこで、書き出し量がある一定量を超えたときに、出力ファイルを切り替えて、1ファイルが大きくならないようにするロジックを書くことがあるかもしれません。普通は主要処理の中に直接ロジックを書き込んだりすることも多いと思いますが、クラス化して使いやすくしました。
ファイル複数書き出しのクラス
コード
class FileWriter: def __init__(self, output_directory, path_format, threshold): self.output_directory = output_directory self.path_format = path_format self.threshold = threshold self.count = 0 self.total_count = 0 self.file_count = 0 self.file_object = None def write(self, string, count = 1): if self.file_object is None: self.file_count += 1 self.file_object = open(f"{self.output_directory}/{self.path_format.format(self.file_count)}", "w") self.file_object.write(string) self.count += count self.total_count += count if self.count >= self.threshold: self.file_object.close() self.file_object = None self.count = 0 def finish(self): if self.file_object is not None: self.file_object.close() self.file_object = None def __enter__(self): return self def __exit__(self, ex_type, ex_value, trace): self.finish()使い方
with の中で使います。書き込み用のディレクトリ (output_directory) を指定して、あとはひたすら write を実行していくだけです。 path_format に従ったファイル名で出力がされます。 write するたびに数値を与え、その合計が threshold を超えたら、ファイルの番号を1増やして新たに書き込みを始めていきます。
使ってみる
0 ~ 1023 までの数字を1行ずつ書いていきます。write に count の値を与えていないため、デフォルト値の1がカウント加算されます。カウントが threshold に指定している 100を超えたところで新しいファイルに移行し、書き込みを続けます。
with FileWriter("out", "single_{:04d}.txt", 100) as fw: for i in range(1024): fw.write(str(i) + "\n")これにより、 out/single_0001.txt ~ out/single_0011.txt というファイルに、数字が連番で書き出されます。
さて、1つの文章であるため、ファイルが分割されないように出力したいが、複数行の文字列であるため、行数分だけカウントは増やしたいということがあるかもしれません。そういう場合は len などを駆使しつつ、 write の引数 count に値を指定すればオーケーです。
with FileWriter("out", "multiple_{:04d}.txt", 100) as fw: values = [str(i) for i in range(40)] string = "\n".join(values) + "\n" for i in range(10): fw.write(string, len(values))0 ~ 39 までの数字を40行でまとめて書き出すため、100を超えるタイミング、つまり 40 * 3 = 120 のときにファイルが切り替わります。 out/multiple_0001.txt ~ out/multiple_0004.txt が出来上がります。
- 投稿日:2021-03-14T17:02:13+09:00
Django アプリケーション【Django つぶやきアプリ開発 #2】
0. はじめに
今回はアプリケーションとモデルについて説明していく。
前回環境を構築した続きからになる。
※powershellによるコマンドは全てtsubuyakiディレクトリ内で仮想環境を立ち上げて行う。1. プロジェクトとアプリケーション
前回はプロジェクトを作成したが、今回はアプリケーションを作成していく。実際に何らかの処理を行うものをアプリケーションと呼ぶ。例えば、ユーザーが商品を購入するためのアプリケーションや、商品在庫を管理するアプリケーションといった具合だ。そしてこれらをまとめたものがプロジェクトである。
アプリケーションの作成は以下を叩く。
python manage.py startapp post
python manage.py startapp "アプリケーション名"で任意のアプリケーションを作成することができる。2. アプリケーションの登録
アプリケーションを作成できても、実行できなければ意味がない。実行するためにアプリケーションを反映させる必要がある。
ユーザーが商品をお気に入りに入れる、ユーザーが商品を購入するなどの処理は作成したアプリケーション内のviews.pyというファイルに記載していく。まずはこの処理をアプリケーションに登録する必要がある。
作成したアプリケーションpostディレクトリ直下にurls.pyというファイルを作成する)。作成したファイルに以下を記述する。post/urls.pyfrom django.urls import path from . import views urlpatterns = [ path(), ]これで
urlpatternsのpath()内で呼び出したviewsの処理を呼び出すことができる。そしてこのファイルをプロジェクトに渡す。
プロジェクトディレクトリ直下にプロジェクト名と同じ名前のディレクトリがあるだろう。その中にurls.pyという名前のファイルがある。このファイルに先ほどのファイルを渡す。tsubuyaki/urls.pyfrom django.urls import path, include #追記 urlpatterns = [ path('admin/', admin.site.urls), #記載済み path('post/', include('post.urls')), #追記 ]まず始めに
import文、pathの後ろにincludeを追記する。これはpost/urls.pyファイル内のurlpatternsを読み込むために必要なライブラリだ。
そしてpath('admin/', admin.site.urls),と書いてある下にpath('post/', include('post.urls')),と追記することでファイルのパスを渡すことができる。
最後に作成したアプリケーションをプロジェクトに登録する。プロジェクトディレクトリ内にあるプロジェクトと同名のディレクトリ内に、settings.pyというファイルがある。このファイル内のINSTALLED_APPSというリストの先頭にアプリケーションを追記する。tsubuyaki/settings.pyINSTALLED_APPS = [ 'post', #追記 'django.contrib.admin',3. まとめ
以上でアプリケーションの作成、登録が完了だ。次回から実際につぶやきアプリの機能を作成していく。
- 投稿日:2021-03-14T16:25:18+09:00
【アニメーション入門】定番FuncAnimation関数で遊んでみた♬
これまで、この関係ではいくつか記事を書いてきましたが、今回のものが定番でしょう。
よく見ると、アニメーションのさせ方はいくつかに分類できるということに気が付いたのでそちらのまとめをします。
【参考】
①matplotlib のanimation を保存@はしくれエンジニアもどきのメモ
②matplotlibのanimation.FuncAnimationを用いて柔軟にアニメーション作成
③Animated line plot@matplotlib
④【シミュレーション入門】サイン波のマスゲーム♬やったこと
・簡単なアニメーション
・updateを使っている
・yeildを使う
・matplotlibの描画1
・FuncAnimation()関数の仕様
・FuncAnimation()関数の仕様を意識して描画する
・リサジュー図形を描く・簡単なアニメーション
たぶん一番簡単に動かしているコード
※このコード派生が見やすいので、比較のために全コード引用させていただきます
以下のコードでは、位相aを変化させてsin波を計算し、imでプロットし、それを配列imsに格納してanimationしています。
つまり、こういう風にプロットの集合を順次animationできるという例となっています。
簡単なアニメーションのコード
import numpy as np import matplotlib.pyplot as plt import matplotlib.animation as animation fig = plt.figure() x = np.arange(0, 10, 0.1) ims = [] for a in range(50): y = np.sin(x - a) im = plt.plot(x, y, "b") ims.append(im) ani = animation.ArtistAnimation(fig, ims) ani.save('sample.gif', writer='imagemagick')・updateを使っている
以下は、参考②のコードです。解説も丁寧にされているので詳細はそちらを見るといいと思います。
簡単に解説すると、上記ではいちいち計算しplotしていたものをupdate関数に入れて、これをFuncAnimation関数から呼び出すことにより描画しています。
考え方として、毎回前回の描画をplt.cla()で消去して描画するというパラパラ漫画の神髄を言っていると思います。
update関数利用の簡単なアニメーションのコード
import matplotlib.animation as anm import matplotlib.pyplot as plt import numpy as np fig = plt.figure(figsize = (10, 6)) x = np.arange(0, 10, 0.1) def update(i, fig_title, A): if i != 0: plt.cla() # 現在描写されているグラフを消去 pass y = A * np.sin(x - i) plt.plot(x, y, "r") plt.title(fig_title + 'i=' + str(i)) ani = anm.FuncAnimation(fig, update, fargs = ('Initial Animation! ', 2.0), \ interval = 100, frames = 132) ani.save("Sample1.gif", writer = 'imagemagick')・yeildを使う
以下のコードは、generator関数を利用しています。
generator関数利用の簡単なアニメーションのコード
import numpy as np import matplotlib.pyplot as plt from matplotlib.animation import FuncAnimation fig = plt.figure(figsize=(8, 8)) ax = plt.subplot(111, frameon=True) x = np.arange(0, 10, 0.1) y = np.sin(x) lin, = ax.plot(x,y,'ro') def gen(n): i = 0 n = n while i < n: y = np.sin(x-i) yield y i += 1 def update(num, data_, line): y1= next(data_) line.set_data(x,y1) data_ = gen(1000) N = 100 anim = FuncAnimation(fig, update, N, fargs=(data_, lin), interval=100) anim.save("Sample2.gif", writer = 'imagemagick')・matplotlibの描画1
matplotlibのサンプルとして、上記参考③に掲載されているもの。
animate()関数という上記のupdate()関数と同じ役割の関数において、初期化でplotしたlineに対して、line.set_ydataでデータ更新することにより、動画描画している。
※動画を滑らかに連続させるために2*np.piを加筆、
また、位相の変化の符号が異なるので逆方向に移動している
matplotlibの例の簡単なアニメーションのコード
import numpy as np import matplotlib.pyplot as plt import matplotlib.animation as animation fig, ax = plt.subplots() x = np.arange(0, 2*np.pi, 0.01) line, = ax.plot(x, np.sin(x)) def animate(i): line.set_ydata(np.sin(x + 2*np.pi*i / 50)) # update the data. return line, ani = animation.FuncAnimation( fig, animate, interval=20, blit=True, save_count=50) ani.save("animated_line_plot.gif")
上記のコードと比較すると、animate()関数にreturn line, が必要なのかと疑問を持ち以下のコードをやってみると、やはり動きました。
matplotlibの簡単なアニメーションのコードII
import numpy as np import matplotlib.pyplot as plt import matplotlib.animation as animation fig, ax = plt.subplots() x = np.arange(0, 2*np.pi, 0.01) line, = ax.plot(x, np.sin(x)) def animate(i): line.set_ydata(np.sin(x - 2*i*np.pi / 50)) # update the data. #return line, ani = animation.FuncAnimation( fig, animate, interval=20) #, blit=True) #, save_count=50) ani.save("animated_line_plot.gif")・FuncAnimation()関数の仕様
上記の特に最後の描画を理解するために、ここでアニメーション関数の仕様を見ておきましょう。
引数は、以下のようになっています。これらの引数に対して参考⑤で解説がありますので、それを掲載します。
class matplotlib.animation.FuncAnimation(fig, func, frames=None, init_func=None, fargs=None, save_count=None, *, cache_frame_data=True, **kwargs)[source]
【参考】
⑤matplotlib.animation.FuncAnimation
名称 引数 解説 fig Figure func callable 各フレームで呼び出す関数。最初の引数は、フレーム内の次の値になります。追加の位置引数は、fargsパラメーターを介して指定できます。必要な書式は次のとおりです。 def func(frame, *fargs) -> iterable_of_artists\textrm{blit == True}の場合、funcは、変更または作成されたすべてのアーティストの反復可能オブジェクトを返す必要があります。この情報は、図のどの部分を更新する必要があるかを決定するためにブリッティングアルゴリズムによって使用されます.blit == Falseの場合、戻り値は使用されません。その場合は省略できます。frames iterable, int, generator function, or None, optional funcとアニメーションの各フレームを渡すためのデータのソース ・反復可能である場合は、提供された値を使用するだけです。 iterableに長さがある場合、 save_count kwargをオーバーライドします。 ・整数の場合、range(frames)を渡すのと同じです ・ジェネレーター関数の場合、以下の書式が必要です。 def gen_function() -> obj・Noneの場合、itertools.countを渡すのと同じです。 これらすべての場合において、フレーム内の値はユーザー提供の関数に渡されるだけなので、どのタイプでもかまいません。init_func callable, optional 明確なフレームを描画するために使用される関数。指定しない場合は、フレームシーケンスの最初のアイテムから描画した結果が使用されます。この関数は、最初のフレームの前に1回呼び出されます。必要な書式は次のとおりです。 def init_func() -> iterable_of_artistsblit == Trueの場合、init_funcは、再描画されるアーティストの反復可能オブジェクトを返す必要があります。この情報は、図のどの部分を更新する必要があるかを決定するためにブリッティングアルゴリズムによって使用されます。 blit == Falseの場合、戻り値は使用されません。その場合は省略できます。fargs tuple or None, optional funcへの各呼び出しに渡す追加の引数。 save_count int, default: 100 フレームからキャッシュへの値の数のフォールバック。これは、フレーム数をフレームから推測できない場合、つまり、長さのないイテレータまたはジェネレータである場合にのみ使用されます。 interval int, default: 200 ミリ秒単位のフレーム間の遅延。 repeat_delay int, default: 0 繰り返しがTrueの場合、連続するアニメーションの実行間のミリ秒単位の遅延。 repeat bool, default: True フレームのシーケンスが完了したときにアニメーションが繰り返されるかどうか。 blit bool, default: False 描画を最適化するためにブリッティングが使用されているかどうか。注:ブリッティングを使用する場合、アニメーション化されたアーティストはzorderに従って描画されます。ただし、zorderに関係なく、以前のアーティストの上に描画されます。 cache_frame_data bool, default: True フレームデータをキャッシュするかどうか。フレームに大きなオブジェクトが含まれている場合は、キャッシュを無効にすると役立つ場合があります。 ・zorderって何よというのは、以下の参考⑥⑦から描画面をx-yとすると、z軸の表示順(前面-背面;数字0-)を決める数字だそうです。
以下は、参考⑦からの引用です。(番号の大きいほど、前面)
The default value depends on the type of the Artist:
Artist Z-order Images (AxesImage, FigureImage, BboxImage) 0 Patch, PatchCollection 1 Line2D, LineCollection (including minor ticks, grid lines) 2 Major ticks 2.01 Text (including axes labels and titles) 3 Legend 5 【参考】
⑥matplotlibの表示順に関する設定
⑦Zorder Demo@matplotlib・FuncAnimation()関数の仕様を意識して描画する
上記と同じようなサイン波を仕様を意識して描いて見ます。
【参考】
⑧【Matplotlib】FuncAnimationクラスを使用してグラフ内にアニメーションを描画するblit=Falseの場合
上の参考⑧のコードをサイン波出力に変更しています。
FuncAnimation関数の仕様を意識したアニメーションのコード
import numpy as np import matplotlib.pyplot as plt import matplotlib.animation as animation fig = plt.figure(figsize=(8, 6)) ax = fig.add_subplot(1, 1, 1) line,= ax.plot([], []) print("start") def gen_function(): """ ジェネレーター関数 """ x = [] y = [] for i in range(100): x0 = np.float(i*np.pi/50.) y0 = np.sin(x0) # ~~xの要素を逆順にする~~ x.append(x0) y.append(y0) for _x, _y in zip(x, y): yield [_x, _y] # 要素要素を戻り値として返す def init(): x = np.arange(0, 10, 0.1) y = np.sin(x) ax.set_xlim(0, 2*np.pi) ax.set_ylim(-1.1,1.1) line, = ax.plot(x, y, 'black') print("called?") def plot_func(frame): """ frame[0]: _xの要素 frame[1]: _yの要素 """ print(frame[0], frame[1]) ax.plot(frame[0],frame[1], 'ro') plt.pause(0.1) #パラパラ漫画となっている ani = animation.FuncAnimation( #blit = Falseの場合 fig=fig, func=plot_func, frames=gen_function, # ジェネレーター関数を設定 init_func=init, repeat=True, save_count = 100, ) ani.save("animated_line_plot_savecount150.gif") plt.show()blit=Trueの場合;zorderを意識して描く
zorderを使いこなすためにより仕様を意識して描画してみました。
zorderを利用の簡単なアニメーションのコード
import matplotlib.pyplot as plt from matplotlib.animation import FuncAnimation import numpy as np x_data = [] y_data = [] fig, ax = plt.subplots() line,= ax.plot([], [], 'ro', zorder = 1) #zorder=1背面 line_, = ax.plot([], [],zorder = 2, linewidth = 3) #zoder=2 前面 def gen_function(): x = [] y = [] for i in range(100): x0 = np.float(i*np.pi/50.) y0 = np.sin(x0) x.append(x0) y.append(y0) for _x, _y in zip(x, y): yield [_x, _y] # 要素要素を戻り値として返す def init(): """ 初期化関数 """ ax.set_xlim(0, 2*np.pi) # x軸固定 ax.set_ylim(-1.1, 1.1) # y軸固定 del (x_data[:], y_data[:]) # データを削除 return line, #line_, # 初期化されたプロットを返す def plot_func(frame): """ frameにはジェネレーター関数の要素が代入される frame: [_x, _y] """ x_data.append(frame[0]) #x_data =frame[0] y_data.append(frame[1]) #y_data = frame[1] line.set_data(x_data, y_data) # 繰り返しグラフを描画 line_.set_data(x_data, y_data) # 繰り返しグラフを描画 return line, #line_, # 更新されたプロットを返す anim = FuncAnimation( fig=fig, func=plot_func, frames=gen_function, init_func=init, interval=100, repeat=True, blit = True, save_count = 100, ) anim.save("anime_generator_savecount100_zorder_12_.gif") plt.show()ここで、line, はプロット描画、line_, は線描画です。
また、zorder=1は、zorder =2 より背面側に描画されます。そして、この場合、以下のline, とline_の返却のお作法が少なくとも4種類はあります。
return line, #line_, # 初期化されたプロットを返す
return line, #line_, # 更新されたプロットを返す
やってみると、以下の通りとなります。
・何も返さない⇒blit = Trueとしているのでエラーになります。
・line, line_, 両方返す line, line_, がzorder = 1, 2の場合
・line, line_, 両方返す line, line_, がzorder = 2, 1の場合
プロットが線に隠れなくなって一安心
・line, のみ 両方返す line, line_, がzorder = 2, 1の場合
このコードだと、この場合も上のものと全く同じanim.saveの画像が得られました。
実際の画面上でのplt.show()では上のblit=Falseと同じような描画が表れますが、保存されたgifは「・line, line_, 両方返す line, line_, がzorder = 2, 1の場合」と同じです。
さてということで、以下のように明示的にline_を外だしして、animationから外して描くこととしました。コードを見ると分かると思いますが、最初のline_の定義の所でまず描画します。そのあとは上記のコードと同一ですが、#line_.set_data(x_data, y_data)として、データの置き換えを実施しないこととしています。これを残しておくと、やはり上記と同じように描画上はサイン波の全体像は残りますが、保存されたものは「・line, line_, 両方返す line, line_, がzorder = 2, 1の場合」と同じです。
zorder利用の簡単なアニメーションのコードII
import matplotlib.pyplot as plt from matplotlib.animation import FuncAnimation import numpy as np x_data = [] y_data = [] fig, ax = plt.subplots() line,= ax.plot([], [], 'ro', zorder = 1) x = np.arange(0, 10, 0.1) y = np.sin(x) line_, = ax.plot(x, y,zorder = 2, linewidth = 3) def gen_function(): x = [] y = [] for i in range(100): x0 = np.float(i*np.pi/50.) y0 = np.sin(x0) # x.append(x0) y.append(y0) for _x, _y in zip(x, y): yield [_x, _y] # 要素要素を戻り値として返す def init(): """ 初期化関数 """ ax.set_xlim(0, 2*np.pi) # x軸固定 ax.set_ylim(-1.1, 1.1) # y軸固定 del (x_data[:], y_data[:]) # データを削除 return line, #line_, # 初期化されたプロットを返す def plot_func(frame): """ frameにはジェネレーター関数の要素が代入される frame: [_x, _y] """ x_data.append(frame[0]) #x_data =frame[0] y_data.append(frame[1]) #y_data = frame[1] line.set_data(x_data, y_data) # 繰り返しグラフを描画 #line_.set_data(x_data, y_data) # 繰り返しグラフを描画 return line, #line_, # 更新されたプロットを返す anim = FuncAnimation( fig=fig, func=plot_func, frames=gen_function, init_func=init, interval=100, repeat=True, blit = True, save_count = 150, ) anim.save("new_anime_generator_savecount100_zorder_12_both_.gif")ということで、元々やりたかったことが以下のように出来ました。
ちゃんと、定義通りに描画順序を正しく反映して、しかも元々やりたかったblit=Falseの場合と同じ描画が得られました。
・zorderを1,2とした場合
・zorderを2,1とした場合
・リサジュー図形を描く
FuncAnimationの仕様を意識して最初のサイン波の位相を動かす
リサジュー図形を描くためにx方向、y方向へ進行する波形を描画する
まずは、リサジュー図形のための、x方向、y方向へ進行する波形を表します。
上のままのコードをちょっと変更しました。
リサジュー図形のためのサイン波の簡単なアニメーションのコード
import matplotlib.pyplot as plt from matplotlib.animation import FuncAnimation import numpy as np x_data = [] y_data = [] fig, ax = plt.subplots() line,= ax.plot([], [], 'ro', zorder = 2) x = np.arange(-np.pi, np.pi, 0.1) y = np.pi*np.sin(x) line_, = ax.plot(x, y,zorder = 1, linewidth = 3) def gen_function(): x0 = np.arange(-np.pi, np.pi, 0.1) y0 = np.pi*np.sin(x) for i in range(100): y0 = np.pi*np.sin(x-i*np.pi/50) #毎回位相を変えて一周期分計算してyoに代入 yield [x0, y0] # 要素要素を戻り値として返す def init(): """ 初期化関数 """ ax.set_xlim(-np.pi-0.1, np.pi+0.1) # x軸固定 ax.set_ylim(-np.pi-0.1, np.pi+0.1) # y軸固定 del (x_data[:], y_data[:]) # データを削除 return line, line_, # 初期化されたプロットを返す def plot_func(frame): """ frameにはジェネレーター関数の要素が代入される frame: [_x, _y] """ x_data =frame[0] #frame[0]で1周期分のデータ y_data =frame[1] line.set_data(x_data, y_data) # 繰り返しグラフを描画 line_.set_data(y_data, x_data) # y方向への進行波 return line, line_, # 更新されたプロットを返す anim = FuncAnimation( fig=fig, func=plot_func, frames=gen_function, init_func=init, interval=100, repeat=True, blit = True, save_count = 150, ) anim.save("anime_generator_savecount100_zorder_21_ressajous_.gif") plt.show()リサジュー図形を描く
3つの図形を同時に描画します。見やすいようにx-, y-軸方向への進行波を線描画、ressajyousをプロットで描画します。
コードは以下のとおりです。
リサジュー図形のアニメーションのコード
import matplotlib.pyplot as plt from matplotlib.animation import FuncAnimation import numpy as np x_data = [] y_data = [] y1_data = [] fig, ax = plt.subplots() line,= ax.plot([], [], zorder = 2, linewidth = 3) x = np.arange(-np.pi, np.pi, 0.1) y = np.pi*np.sin(x) y1 = np.pi*np.sin(2*x) line_, = ax.plot(x, y1,zorder = 1, linewidth = 3) line_1, = ax.plot(y, y1,'ro', zorder = 3) def gen_function(): x0 = np.arange(-np.pi, np.pi, 0.1) for i in range(100): y0 = np.pi*np.sin(x-i*np.pi/50) y1 = np.pi*np.sin(2*(x-i*np.pi/50)+i*np.pi/50) #位相をずらす yield [x0, y0, y1] # 3要素を戻り値として返す def init(): """ 初期化関数 """ ax.set_xlim(-np.pi-0.1, np.pi+0.1) # x軸固定 ax.set_ylim(-np.pi-0.1, np.pi+0.1) # y軸固定 del (x_data[:], y_data[:], y1_data[:]) # データを削除 return line, line_, line_1, # 初期化されたプロットを返す def plot_func(frame): """ frameにはジェネレーター関数の要素が代入される frame: [_x, _y] """ x_data =frame[0] y_data =frame[1] y1_data =frame[2] line.set_data(x_data, y_data) # 繰り返しグラフを描画 line_.set_data(y1_data, x_data) line_1.set_data(y_data, y1_data) return line, line_, line_1, # 更新されたプロットを返す anim = FuncAnimation( fig=fig, func=plot_func, frames=gen_function, init_func=init, interval=100, repeat=True, blit = True, save_count = 150, ) anim.save("anime_generator_savecount100_zorder_21_ressajous_b.gif") plt.pause(10)リサジュー図形を描くII
今度は、リサジュー図形の説明の意味でx-, y- 方向へのサイン波上のプロットの(振幅、振幅)図つまりリサジューを描きます。
リサジュー図形のアニメーションのコードII
import matplotlib.pyplot as plt from matplotlib.animation import FuncAnimation import numpy as np x_data = [] y_data = [] y1_data = [] fig, ax = plt.subplots() line,= ax.plot([], [], zorder = 2, linewidth = 3) x = np.arange(-np.pi, np.pi, 0.01) y = np.pi*np.sin(x) y1 = np.pi*np.sin(2*x) line_, = ax.plot(x, y1,zorder = 1, linewidth = 1) line1_, = ax.plot(y, x,zorder = 1, linewidth = 1) line_1, = ax.plot([], [],'bo',markersize=12, zorder = 3.1) line_11, = ax.plot(y, y1, zorder = 3, linewidth = 2) line2,= ax.plot([], [], 'ro', zorder = 2) line_2, = ax.plot([], [], 'go',zorder = 1 ) def gen_function(): x_ = [] y_ = [] y1_ = [] for j in range(400): x0_ = np.float(j*np.pi/100.-np.pi) y0_ = np.pi*np.sin(2*x0_) y10_ = np.pi*np.sin(x0_) x_.append(x0_) y_.append(y0_) y1_.append(y10_) for _x, _y, _y1 in zip(x_, y_, y1_): yield [_x, _y, _y1] # 要素要素を戻り値として返す def init(): """ 初期化関数 """ ax.set_xlim(-np.pi-0.1, np.pi+0.1) # x軸固定 ax.set_ylim(-np.pi-0.1, np.pi+0.1) # y軸固定 del (x_data[:], y_data[:], y1_data[:] ) # データを削除 return line2, line_2, line_1, # 初期化されたプロットを返す def plot_func(frame): """ frameにはジェネレーター関数の要素が代入される frame: [_x, _y] """ x_data =frame[0] y_data =frame[1] y1_data = frame[2] line2.set_data(x_data, y_data) # 繰り返しグラフを描画 line_2.set_data(y1_data, x_data) line_1.set_data(y1_data, y_data) return line2, line_2, line_1, # 更新されたプロットを返す anim = FuncAnimation( fig=fig, func=plot_func, frames=gen_function, init_func=init, interval=100, repeat=True, blit = True, save_count = 200, ) anim.save("anime_generator_savecount100_zorder_21_ressajous_m.gif") plt.pause(10)まあ、通常のリサジュー図形の説明図を以下の通り出力できました。
上記の動いているうえで動かしたいところですが、変数が多くて混乱したので今日はここまでにしておきます。
以下の絵でもzorderが生きていると思います。
・勝手流
ここまでFuncAnimation関数を利用して描画の仕方をやってきましたが、参考④の記事のように自分で用意したものでも簡単なものは描画できます。
以下では、以前描画した常微分方程式の解の減衰振動をodeintで計算して描画しています。
減衰振動のアニメーションのコード
import matplotlib.animation as anm import matplotlib.pyplot as plt import numpy as np from scipy.integrate import odeint, simps def pend(y, t, b,c): theta, omega = y dydt = [omega, -c*omega-b*np.sin(theta)] return dydt b = 5 c = 0.05 #初期値y0=[theta0,omega0] y0 = [np.pi - 0.1, 0.0] #[0, 100]の範囲を1001の等間隔の時間tを生成 t = np.linspace(0, 100, 1001) #odeint(関数,初期値,時間,関数の定数) sol = odeint(pend, y0, t, args=(b,c)) fig = plt.figure(figsize = (18, 6)) ax1 = fig.add_subplot(1, 3, 1) ax2 = fig.add_subplot(1, 3, 2) ax3 = fig.add_subplot(1, 3, 3) xdata, ydata = [], [] ln1, = ax2.plot(x[0], p[0], 'b.') ln, = ax1.plot(t[0], sol[0,0], 'b.') ln2, = ax3.plot(t[0], sol[0,1], 'r.') ax2.set_xlim(-5, 5) ax2.set_ylim(-5, 5) ax1.set_xlim(-5, 100) ax1.set_ylim(-5, 5) ax3.set_xlim(-5, 100) ax3.set_ylim(-5, 5) def update(i, fig_title, A): y = sol[0:i, 0] y1 = sol[0:i, 1] ln1.set_data(x[0:i], p[0:i]) ln.set_data(t[0:i], y) ln2.set_data(t[0:i], y1) ax2.set_title(fig_title +'x-p i=' + str(i)) ax1.set_title(fig_title + 't-theta i=' + str(i)) ax3.set_title(fig_title + 't-omega i=' + str(i)) plt.pause(0.001) #return ln, ani = anm.FuncAnimation(fig, update, fargs = ('Initial Animation! ', 2.0), \ interval = 10, frames = 100) ani.save("Sample_odeint.gif", writer = 'imagemagick') plt.pause(10) frames = 1000 ps = 10 s = 0 for n in range(0,frames,ps): s+=ps num = s #%100 print(s, num) #,dataz) update(s,' ',A = 2.0) plt.pause(0.001) fig.savefig("simple_odeint.png") plt.close()ani.save("Sample_odeint.gif", writer = 'imagemagick')の描画
※容量の都合で1000フレーム中の初めの200フレームを保存しています。
そして、最後のfig.savefig("simple_odeint.png")は以下のとおりです。
※もちろん画面上は時々刻々変化するアニメーションになっています。
・animationのmethods
この辺りで、気になるものに以下の関数群があります。
一応、表は載せておきますが、saveとjupyter notebook上で描画させるHTML以外はあまり使っている例は見つけられませんでした。
HTMLの使い方は以下のとおりです。
ちなみに、上記のsaveでもwriter指定していましたが、実はwriter = 'imagemagick'がインストールしていない場合は以下のエラーが出て代替で'matplotlib.animation.PillowWriter'を利用しており、指定ない場合も出力されます。
MovieWriter imagemagick unavailable; trying to use <class 'matplotlib.animation.PillowWriter'> instead.
また、ffmpegのインストールは出来ましたが、mp4出力は成功していません。from matplotlib.animation import FFMpegWriter #anim.save("anime_generator_savecount100_zorder_12_.mp4") #, writer=FFMpegWriter, dpi = 80) writer = FFMpegWriter() anim.save("anime_generator_savecount100_zorder_12_.mp4", writer=writer) from IPython.display import HTML #for jupyter notebook HTML(anim.to_jshtml())
Methods __ init__(self, fig, func[, frames, ...]) Initialize self. new_frame_seq(self) Return a new sequence of frame information. new_saved_frame_seq(self) Return a new sequence of saved/cached frame information. save(self, filename[, writer, fps, dpi, ...]) Save the animation as a movie file by drawing every frame. to_html5_video(self[, embed_limit]) Convert the animation to an HTML5 tag. to_jshtml(self[, fps, embed_frames, ...]) Generate HTML representation of the animation new_frame_seq(self) Return a new sequence of frame information. new_saved_frame_seq(self) Return a new sequence of saved/cached frame information. まとめ
・アニメーションの定番FuncAnimation()関数で遊んでみた
・zorderの使い方と一般的なアニメーションを学んだ
・勝手に描画することにより、配列に格納した計算結果を使って、簡単にアニメーション出来ることも理解した・gen_function()のyieldで間引きも出来るが、次回の宿題とする
・リサジュー図形のより一般的な描画もやりきれなかったので次回の宿題とする
・多くのシミュレーションが可能となるのでやってみようと思う
- 投稿日:2021-03-14T16:11:45+09:00
エスケープシーケンスでターミナルにカラー表示するチートシート
こんなふうにテキストに色や下線を付けてターミナルで表示させるには、
Rubyなら
\e[...mでputs("ABC\e[4;31;44mDEF\e[0mGHI") puts("ABC\e[38;5;45mDEF\e[0mGHI")Perlなら
\e[...mでprint "ABC\e[4;31;44mDEF\e[0mGHI\n"; print "ABC\e[38;5;45mDEF\e[0mGHI\n";PHPなら
\e[...mでprint("ABC\e[4;31;44mDEF\e[0mGHI\n"); print("ABC\e[38;5;45mDEF\e[0mGHI\n");Bashなら
\e[...mでecho -e "ABC\e[4;31;44mDEF\e[0mGHI" echo -e "ABC\e[38;5;45mDEF\e[0mGHI"Pythonなら
\x1b[...mでprint("ABC\x1b[4;31;44mDEF\x1b[0mGHI"); print("ABC\x1b[38;5;45mDEF\x1b[0mGHI")Node.jsなら
\x1b[...mでconsole.log("ABC\x1b[4;31;44mDEF\x1b[0mGHI"); console.log("ABC\x1b[38;5;45mDEF\x1b[0mGHI");Scalaなら
\u001b[...mでprintln("ABC\u001b[4;31;44mDEF\u001b[0mGHI"); println("ABC\u001b[38;5;45mDEF\u001b[0mGHI");Javaなら
\033[...mまたは\u001b[...mでSystem.out.println("ABC\033[4;31;44mDEF\033[0mGHI"); System.out.println("ABC\033[38;5;45mDEF\033[0mGHI");
[とmの間の数字が色や装飾を表すパラメータです。パラメータが複数の場合はセミコロンで区切ります。上記サンプルであれば4は下線、31は赤文字、44は青背景、0はリセットです。
\e[4;31;44mは\e[4m\e[31m\e[44mとしても同じです。38と48は、セミコロン区切りで続くパラメータが必須で、詳細な色を指定できます。
装飾
パラメータ 効果 Windows Terminal Windows Tera Term Mac Terminal 1 太字(Bold) ○ △ ○ 2 細字(Faint, light font weight) ○ × ○ 3 斜体(Italic) △ △ △ 4 下線(Underline) ○ ○ ○ 5 点滅(Blink) ○ △ ○ 6 速い点滅(Rapid blink) × × × 7 背景色と文字色を入れ替える ○ ○ ○ 8 文字を隠す(Conceal) ○ × ○ 9 取り消し線(Strike) ○ × × ○:対応していそう
△:エスケープシーケンスに反応して変化はしているが、思ってたのとちがう
×:非対応8の文字を隠す効果は、対応している端末では、文字は見えませんが、マウスで選択すると文字が現れ、テキストをコピーできます。tmuxでもテキストをコピーできます。
Windows Terminal
WindowsのTera Term
MacのTerminal
色
色 標準の8色 明るい8色 256色 RGB 文字色 30~37 90~97 38;5;n 38;2;r;g;b 背景色 40~47 100~107 48;5;n 48;2;r;g;b 8色は下1桁で次の色を表します。
0 1 2 3 4 5 6 7 黒 赤 緑 黄 青 紫 水 白 256色のnは0~255の範囲で指定します。nを0~7にすると標準の8色と同じ色で、8~15にすると明るい8色と同じ色になります。
RGBのr, g, bの箇所も0~255の範囲で指定します。
WindowsのTera Termでは8色までしか対応していないようです。Windows TerminalとMacのTerminalは、256色もRGB指定も機能するようです。
Windows Terminal
WindowsのTera Term
MacのTerminal
リセット
パラメータ 効果 0 リセット 色や装飾の指定をすべて解除します。
この0は省略できます。Rubyなら
\e[mでリセットになります。サンプルコード
この記事の装飾と色のサンプル出力に使ったコードは以下です。Rubyです。
puts() def showcase1(str, text) "\e[#{str}m\\e[#{str}m#{text}\e[0m " end def showcase2(str) "\e[#{str}m\\e[#{str}m" + (" " * (8 - str.length)) + "\e[0m " end def showcase3(str, text) "\e[#{str}m#{text}\e[0m" end line = " " (1..9).each do |i| line += showcase1("#{i}", "いろは") end puts(line) puts() line1 = " " line2 = " " (0..7).each do |i| line1 += showcase2("#{30+i}") line2 += showcase2("#{40+i}") end puts(line1) puts(line2) line1 = " " line2 = " " (0..7).each do |i| line1 += showcase2("#{90+i}") line2 += showcase2("#{100+i}") end puts(line1) puts(line2) puts() (0..256).each do |i| if i % 8 == 0 line1 = " " line2 = " " end line1 += showcase2("38;5;#{i}") line2 += showcase2("48;5;#{i}") if i % 8 == 7 puts(line1) puts(line2) end end puts() (0..256).each do |i| if i % 64 == 0 line1 = " " end line1 += showcase3("48;2;0;255;#{i}", " ") if i % 64 == 63 puts(line1) end end puts()※エスケープシーケンスは、ほかにもカーソル移動や画面のクリアなどもできますが、本稿では色やテキストの装飾にとどめておきます。
- 投稿日:2021-03-14T16:07:38+09:00
Pythonライブラリ Cerberus によるバリデーション処理 メモ
Cerberusとは
- Pythonのオープンソースバリデーションライブラリ。
- 公式
準備
pip install cerberus利用方法
基本的な使い方
from cerberus import Validator # バリデーション対象パラメータのスキーマ定義し、バリデーターにセット schema = {'name': {'type': 'string'}, 'age': {'type': 'integer', 'min': 10}} v = Validator(schema) request_body = {'name': 'Little Joe', 'age': 5} # バリデーション実行 v.validate(request_body) >> False # エラー理由 v.errors >> {'age': ['min value is 10']}未定義のパラメータを許容する場合
v.allow_unknown = True独自ルールでバリデーションを行いたい場合
- リクエストボディに指定されたメールアドレスに対して正規表現でバリデーションを行う場合。
- 独自定義バリデータークラス:
extendedValidator.pyimport re from cerberus import Validator class ExtendedValidator(Validator): def _validate_email(self, email_address, field, value): if (email_address and not re.match('^[a-zA-Z0-9_.+-]+@[a-zA-Z0-9-]+\.[a-zA-Z0-9-.]+$', value)): self._error(field, 'invalid_email_address')
- バリデータにセットするスキーマ定義クラス:
const.py
- メールアドレスの基本バリデーションルールを定義する。
# setter制御用メタクラス class ConstMeta(type): def __setattr__(self, name, value): if name in self.__dict__: raise self.ConstError() self.__dict__[name] = value # スキーマ定数定義 class ValidatorConstClass(metaclass=ConstMeta): req_schema = { 'email_address': { 'type': 'string', 'required': True, 'empty': False, 'maxlength': 128, 'valid_email': True } }
- バリデーション処理実行クラス:
test.pyimport const from extendedValidator import ExtendedValidator ... # 独自定義したバリデーターをセット validator = ExtendedValidator(const.ValidatorConstClass.req_schema) # バリデーション実行 if not validator.validate(req_body): return {'result': 'validation_error', 'errors': validator.errors}参考情報
- 投稿日:2021-03-14T15:10:13+09:00
日本画と西洋画をAIで判別してみた
はじめまして。
美術鑑賞が趣味なのですが、日頃疑問に思ったことをきっかけに今回作成したアプリ
(https://jepic.herokuapp.com/) をブログにて共有させていただきます。目次
・動機と目的
・方法
・結果
・感想
・今後の課題と展望
・参考資料動機と目的
現代アートの場合、日本画なのか西洋画なのか区別がつかないものが増えてきたように感じます。
そもそも、浮世絵や印象派などといった古典的な日本画や西洋画と呼ばれているものをAIは識別
できるのか疑問に思い、今回このようなアプリを制作しました。
美術に興味がない人にも少しでも興味をもってもらえるような、美術に興味がある人にはAI面白いな
と思ってもらえるようなきっかけとなれば幸いです。方法
- 画像収集
- 画像選別
- 画像の水増し
- 画像の判定
画像収集
メトロポリタン美術館のopenaccessの画像 (https://github.com/metmuseum/openaccess)
を用いて、日本画と西洋画それぞれの画像収集を行いました。
画像ファイルが大きいため、Git LFS (https://git-lfs.github.com/)
をインストールしていない場合はまず、インストールする必要があります。
Git LFSインストール後、以下のコードでCSVの画像ファイルを取得します。画像収集1git lfs clone https://github.com/metmuseum/openaccess.gitCSVファイルを取得後、日本画と西洋画の画像収集を行いました。
下のコードは日本画の場合です。画像収集2import requests import urllib import json import pandas as pd import os import time # 作品マスターより、条件を指定し美術品を抽出 df_met = pd.read_csv('/content/drive/MyDrive/openaccess/MetObjects.csv') df_met_pd = df_met[df_met['Is Public Domain']==True] # パブリックドメインの作品を指定 df_met_pd_japan = df_met_pd[(df_met_pd['Culture']=='Japan')] # Culture: Japan df_met_pd_japan_paint = df_met_pd_japan[df_met_pd_japan['Classification']=='Paintings'] # Classification: Paintings # 対象美術品のIDが格納されたリストを作成 object_id_list = list(df_met_pd_japan_paint['Object ID']) # ObjectID確認用 # print(object_id_list) # 画像ダウンロードのための関数を定義 def download_file(url, path): try: with urllib.request.urlopen(url) as web_file, open(path, 'wb') as local_file: local_file.write(web_file.read()) except urllib.error.URLError as e: print(e) MET_API = 'https://collectionapi.metmuseum.org/public/collection/v1/objects/' target_image_key = 'primaryImageSmall' # 小さい方の画像キー directry = "metropdjp_img/" # 保存先ディレクトリ if not os.path.isdir(directry): os.makedirs(directry) for obj_id in object_id_list: target_url = MET_API + str(obj_id) res = requests.get(target_url) res_dict = json.loads(res.text) url = res_dict[target_image_key] file_path = directry + str(obj_id) + ".jpg" download_file(url, file_path) time.sleep(1) # サーバに負荷をかけすぎないよう1枚取得するごとに1秒停止画像選別
日本画の枚数が少なかったので、西洋画の枚数をできるだけ近い枚数になるよう、調整して
います。
なお絵画の中には文字が大部分を占める絵や、彫刻の一部に絵が描かれているものなど、
絵以外のものが大部分を占めているものは除外させていただきました。画像の水増し
日本画も西洋画も収集できた枚数が少なかったので、CNNのImageDataGeneratorを用いて
画像の水増しや、回転、反転、色彩を変えたりなどを行いました。
下のコードは日本画の場合です。画像の水増しimport os import glob import numpy as np from keras.preprocessing.image import ImageDataGenerator, load_img, img_to_array, array_to_img def draw_images(generator, x, dir_name, index): # 出力ファイルの設定 save_name = 'extened-' + str(index) g = generator.flow(x, batch_size=1, save_to_dir=output_dir, save_prefix=save_name, save_format='jpg') # 1つの入力画像から何枚拡張するかを指定 # g.next()の回数分拡張される for i in range(10): bach = g.next() if __name__ == '__main__': # 出力先ディレクトリの設定 output_dir = "/content/drive/MyDrive/metropdjpcn_img" if not(os.path.exists(output_dir)): os.mkdir(output_dir) # 拡張する画像群の読み込み images = glob.glob(os.path.join('/content/drive/MyDrive/metropdjp2_img', "*.jpg"))#ファイル名を指定 # 拡張する際の設定 generator = ImageDataGenerator( rotation_range=90, # 90°まで回転 width_shift_range=0.1, # 水平方向にランダムでシフト height_shift_range=0.1, # 垂直方向にランダムでシフト channel_shift_range=50.0, # 色調をランダム変更 shear_range=0.39, # 斜め方向(pi/8まで)に引っ張る horizontal_flip=True, # 垂直方向にランダムで反転 vertical_flip=True # 水平方向にランダムで反転 ) # 読み込んだ画像を順に拡張 for i in range(len(images)): img = load_img(images[i]) # 画像を配列化して転置a x = img_to_array(img) x = np.expand_dims(x, axis=0) # 画像の拡張 draw_images(generator, x, output_dir, i)画像の判定
VGG16を用いて日本画か西洋画かAIに判定してもらいました。
画像の判定import os import cv2 import numpy as np import matplotlib.pyplot as plt from tensorflow.keras.utils import to_categorical from tensorflow.keras.layers import Dense, Dropout, Flatten, Input from tensorflow.keras.applications.vgg16 import VGG16 from tensorflow.keras.models import Model, Sequential from tensorflow.keras import optimizers number = 100 path_japan = os.listdir('/content/drive/MyDrive/metropdjpcn_img/') path_europe = os.listdir('/content/drive/MyDrive/metropdeucn_img/') img_japan = [] img_europe = [] for i in range(len(path_japan)): img = cv2.imread('/content/drive/MyDrive/metropdjpcn_img/' + path_japan[i]) img = cv2.resize(img, (50,50)) img_japan.append(img) for i in range(len(path_europe)): img = cv2.imread('/content/drive/MyDrive/metropdeucn_img/' + path_europe[i]) img = cv2.resize(img, (50,50)) img_europe.append(img) X = np.array(img_japan + img_europe) y = np.array([0]*len(img_japan) + [1]*len(img_europe)) rand_index = np.random.permutation(np.arange(len(X))) X = X[rand_index] y = y[rand_index] X_train = X[:int(len(X)*0.8)] y_train = y[:int(len(y)*0.8)] X_test = X[int(len(X)*0.8):] y_test = y[int(len(y)*0.8):] y_train = to_categorical(y_train) y_test = to_categorical(y_test) input_tensor = Input(shape=(50, 50, 3)) vgg16 = VGG16(include_top=False, weights='imagenet', input_tensor=input_tensor) top_model = Sequential() top_model.add(Flatten(input_shape=vgg16.output_shape[1:])) top_model.add(Dense(256, activation='relu')) top_model.add(Dropout(0.5)) top_model.add(Dense(2, activation='softmax')) model = Model(inputs=vgg16.input, outputs=top_model(vgg16.output)) for layer in model.layers[:15]: layer.trainable = False model.compile(loss='categorical_crossentropy', optimizer=optimizers.SGD(lr=1e-4, momentum=0.9), metrics=['accuracy']) model.fit(X_train, y_train, batch_size=100, epochs=10, validation_data=(X_test, y_test)) def pred_picture(img): img = cv2.resize(img, (50, 50)) pred = np.argmax(model.predict(np.array([img]))) if pred == 0: return 'japan' else: return 'europe' img = cv2.imread('/content/drive/MyDrive/metropdjpcn_img/' + path_japan[0]) b,g,r = cv2.split(img) img = cv2.merge([r,g,b]) plt.imshow(img) plt.show() print(pred_picture(img)) pred_picture = os.listdir('/content/drive/MyDrive/metropdjpcn_img/') for i in range(len(path_japan)): img = cv2.imread('/content/drive/MyDrive/metropdjpcn_img/' + path_japan[i]) plt.imshow(img) plt.show() print(pred_picture(img)) pred_picture = os.listdir('/content/drive/MyDrive/metropdeucn_img/') for i in range(len(path_europe)): img = cv2.imread('/content/drive/MyDrive/metropdeucn_img/' + path_europe[i]) plt.imshow(img) plt.show() print(pred_picture(img))結果
幅広い年代の作品の絵画を用いたため、精度はあまり高くないかなと予想していたのですが、
予想していたよりもかなり高精度なものとなりました。結果58892288/58889256 [==============================] - 0s 0us/step Epoch 1/10 154/154 [==============================] - 561s 4s/step - loss: 1.5118 - accuracy: 0.8207 - val_loss: 0.1786 - val_accuracy: 0.9235 Epoch 2/10 154/154 [==============================] - 559s 4s/step - loss: 0.1701 - accuracy: 0.9334 - val_loss: 0.1624 - val_accuracy: 0.9522 Epoch 3/10 154/154 [==============================] - 556s 4s/step - loss: 0.1342 - accuracy: 0.9470 - val_loss: 0.1449 - val_accuracy: 0.9569 Epoch 4/10 154/154 [==============================] - 556s 4s/step - loss: 0.1374 - accuracy: 0.9505 - val_loss: 0.1121 - val_accuracy: 0.9627 Epoch 5/10 154/154 [==============================] - 551s 4s/step - loss: 0.0899 - accuracy: 0.9611 - val_loss: 0.1022 - val_accuracy: 0.9640 Epoch 6/10 154/154 [==============================] - 547s 4s/step - loss: 0.0730 - accuracy: 0.9691 - val_loss: 0.1013 - val_accuracy: 0.9671 Epoch 7/10 154/154 [==============================] - 548s 4s/step - loss: 0.0600 - accuracy: 0.9710 - val_loss: 0.0968 - val_accuracy: 0.9694 Epoch 8/10 154/154 [==============================] - 549s 4s/step - loss: 0.0521 - accuracy: 0.9746 - val_loss: 0.1032 - val_accuracy: 0.9723 Epoch 9/10 154/154 [==============================] - 554s 4s/step - loss: 0.0514 - accuracy: 0.9759 - val_loss: 0.0996 - val_accuracy: 0.9697 Epoch 10/10 154/154 [==============================] - 555s 4s/step - loss: 0.0388 - accuracy: 0.9814 - val_loss: 0.1007 - val_accuracy: 0.9705日本画は掛け軸の正解率が低く、それ以外は正解率が高かったです。
西洋画の正解率の高いものも低いものも共通点は見つけられなかったです。日本画の正解率の高かった絵画の例
日本画の正解率の低かった絵画の例
感想
日本画は掛け軸の割合が高かったので、かえって正解率が高くなるかと思いましたが、
逆の結果だったので驚きました。
西洋画で共通点が見つけられなかったのは残念ですが、今後画像の枚数を増やしたり、
印象派など会派別に分けてみると正解率との因果関係が見えてくるかもしれないと
感じました。今後の課題と展望
今後はさらに画像を収集し、より高精度なものにしていきたいです。
日本画は掛け軸の絵の部分だけ抽出したらどうなるのか、精度は変わるのか、挑戦したい
と思います。
制作した後でなんですが、そもそもジャポニスムが流行ってヨーロッパで日本風の作品が
生まれたり、日本の場合は中国から水墨画が伝わってきたりと、文化が混ざり合って今に
至っていると思われるので、現代アートで見分けがつきにくいというのは無理もないこと
なのかもしれません。
今後、現代アートでもどこの誰が作ったかAIが判定してくれるアプリが作れたらと思って
います。
ゆくゆくは描かれた絵が本物かどうかAIが判断するアプリを作りたいです。
その為にはまだまだ技術不足であり知識不足なので、日々精進してまいりたいと思います。参考資料
- 投稿日:2021-03-14T14:42:53+09:00
消息を断った潜水艦をベイズ推定で見つける
背景
1968年にアメリカ海軍の潜水艦スコーピオン号が消息を経ちました。この時の捜索に使われたのがベイズ推定を用いたベイズ捜索(Bayesian Search)です。飛行機やそのブラックボックスなどの捜索にも使われます。
変数定義
まず捜索エリアをセル分け定義します。ここでは簡易的に20x20のエリアとします。これに航路や最終報告された位置などの情報から、そのセルごとのあて推量の発見確率を、事前確率として以下のように確立分布で表現します。私の場合は正規分布で表現しました。赤いXは行方不明の捜索対象です。
ここで、以下のように変数を定義しておきます。
変数名 意味 $i$ セルのインデックス。上で示した捜索対象の場合$i=(16,10)$と表現する。 $Y_i$ iに捜索対象があるか否かの真値。ある場合1。ない場合0。 $\pi_i$ 上記のあて推量の事前確率。$P_r(Y_i=1)$ $Z_i$ iを捜索した結論。見つかった場合1。ない場合0。Yi=1であった場合に見つけられなかった場合も0。 $p_i$ iに捜索対象があった場合の発見確率。$P_r(Z_i=1|Y_i=1)$。この例ではどのセルも一律で0.1とする。実際には海底までの深さなどでセル毎に変更される。 $p_i$を定義している通り、この推定のポイントはそこに捜索対象があったとしても、捜索班の能力不足などにより見つけられない場合を考慮していることです。
さて、実際の捜索に移りましょう。捜索アルゴリズム
- $\pi_i$が最大となるインデックス$i$の示すセルを捜索セルとする。
- セル$i$にて捜索対象が見つかった場合終了。見つからなかった場合、以下の通りに$\pi$を更新。
$\pi_i \leftarrow \frac{(1-p_i)\pi_i}{1-p_i\pi_i} $
i以外のセルjに対しては:
$\pi_j \leftarrow \frac{\pi_j}{1-p_i\pi_i}$- 私の実装の場合、$\pi$がだんだん飽和し破綻したので、セル全体を合計して1.0になるように正規化しました。
- 1から繰り返し。
事前確率更新の様子
1000ステップを5ステップ飛ばしで描画させています。青い点がそのステップで捜索対象としたセルです。赤いXを捜索しても処理を終えていないのは、$p_i$が0.1だからです。10回に一回に捜索成功の判定となります。
見つけられたかどうかはあまり重要としていないので、最後まで示していません。時間が在る時に全探索とのパフォーマンス比較をやってみます。
考察
人間が
「だいたいここらへんにあるはず」
という推測情報を使って、そのあたりからなんとなく順繰り捜索する場合も、
「あれ、おかしいな。こんなに推測から外れている場所に在るわけ無いぞ。
またあのあたりから探すか」
という具合に、エリアを全捜索するのでは無く、ある程度捜索し終わったらまた予測地点から捜索をスタートするという動きになると思います。
ですので上記のGIF画像から、
ベイズ捜索はそれをより無駄なく合理的に行う方法なのだと思いました。上記のGIF結果を見ると、捜索点がセルの位置的にアチラコチラに触れているので、実際に捜索する場合は
セル内の捜索時間>>セル間の移動時間
でなければ、発見までの時間が無駄に長くなりますね。コード
以下に上げました。
参考文献
- 投稿日:2021-03-14T14:32:22+09:00
今回はデータ生成ツールの話・・
以前の検証以降・・・・
EqualumやSingleStore関連の投稿をしていると、データ生成部分だけ下さい!というお話を頂いたりする事が増え、また確かに良く考えると、有れば有ったで何かのお役に立てるかもしれない・・と思い立ち、データ生成部分に少し汎用性を持たせたバージョンを作成してみました。
まずは冒頭部分のカオスを修正します
大量に定義されていたメタデータ系情報をCSVファイルで作成し、それを別ファイルとして読み込む形にしたいと思います。
基本的には
import csv with open('CSV_File', 'r', encoding='utf-8-sig') as f: reader = csv.reader(f) for row in reader: print(row)の定番パターンをベースに実装します。
少し工夫が必要なのは、辞書形式にデータを準備する場合で、今回は以下のパターンをベースにしてみました。import csv Dict_Data = {} with open(CSV_File, 'r', encoding='utf_8_sig') as f: reader = csv.reader(f) Dict_Data = {rows[0]:rows[1] for rows in reader} print(Dict_Data)さて出来上がったのが・・・
CSVのカラムに合わせて修正して頂けば、ほぼ問題無く動くかと思います。また、今回のバージョンでは、基本的に以前の検証で使っていた、カテゴリ数5とかカテゴリ毎の商品数10個・・といった制限は外してあります(上の方の数字で調整してください)。また、これに伴って乱数のネタ元をnumpyに変更しています。
# coding: utf-8 # # 日本語版BIG DATA Generator # # Python 3版 # # 初期設定 import sys stdout = sys.stdout sys.stdout = stdout import datetime import pymysql.cursors import re import csv import numpy as np from numpy.random import * # テーブル名 Table_Name = "BIGDATA_TEST0_Table" # 書き込み用のカラム設定 DL0 = "ts, " # タイムスタンプ情報 DL1 = "Category, Product, Price, Units, Logistics, " # ビジネス情報 DL2 = "Card, Number, Payment, Tax, " # 支払い情報 DL3 = "User, Zip, Prefecture, Address, Area, Tel, Email, Point" # 顧客情報 # 生成するデータの数 Generate_Data = 1000000 # 途中経過のチェックポイント設定 Check_Point = 10 # 途中経過で生成されたSQL文を表示するか否か(0:表示しない 1:表示する) Display_SQL = 0 # CSVデータが5カラム毎のフォーマットなので5個飛びになります(必要に応じて変更) ID_Gap = 5 # 商品データの行数を定義(50個定義の場合は0−49で定義します) Data_Start = 0 # データのスタート行数(原則的に0を指定) Data_End = 49 # 投入データの総数から1を引いた数を指定) # 消費税率の設定(整数でパーセント表記) Tax_Data = 10 # 辞書のID(参照辞書を作成する際に利用) Area_List = 1 Logi_List = 2 # # データをランダムに行番号基準で選択して必要情報を返す # # 読み込んだCSVデータ列からランダムに商品情報を選択してデータを返します。 # 今回の改修で、読み込むCSVデータの行情報に対して、ランダムに0から始まる # データ番号でアクセスする形にしましたので、とりあえず選択対象を作成する!というノリで # CSVファイルを用意されればOKかと。 # def Pick_Up_Item(start, end, Data): RET_Data = [] ID = randint(start,end) * ID_Gap RET_Data.append(Data[ID]) # カテゴリ名 RET_Data.append(Data[ID + 1]) # 商品名 RET_Data.append(Data[ID + 2]) # 価格 RET_Data.append(Data[ID + 3]) # ポイント率 RET_Data.append(Data[ID + 4]) # 販売調整数(リアルっぽく見せる為) return(RET_Data) # # メタデータをCSV形式で読み込んで準備を行う # # CSVのフォーマット カテゴリー、 製品名、価格、 ポイント率、 販売調整係数 # def CSV_Data_Set1(CSV_File): RET_Data = [] with open(CSV_File, 'r', encoding='utf-8-sig') as f: reader = csv.reader(f) i = 0 for row in reader: RET_Data.append(row[i]) # カテゴリ名 RET_Data.append(row[i + 1]) # 商品名 RET_Data.append(row[i + 2]) # 価格 RET_Data.append(row[i + 3]) # ポイント率 RET_Data.append(row[i + 4]) # 販売調整数(リアルっぽく見せる為) return(RET_Data) # # 物流センターと地域名の辞書データをCSVファイルから作成する # # CSVのフォーマット 県名、 地域名、 物流センター名 # def CSV_Data_Set2(CSV_File, List_ID): RET_Data = {} with open(CSV_File, 'r', encoding='utf_8_sig') as f: reader = csv.reader(f) if List_ID == Area_List: RET_Data = {rows[0]:rows[1] for rows in reader} # 地域名辞書の作成 else: RET_Data = {rows[0]:rows[2] for rows in reader} # 配送センター辞書の作成 return(RET_Data) # # 此処からメインの処理になります # try: print("SingleStore上へのデータの生成を開始します。") print ("処理の開始 : " + datetime.datetime.now().strftime("%Y/%m/%d %H:%M:%S")) # Fakerの初期化 from faker import Faker fakegen = Faker('ja_JP') Faker.seed(fakegen.random_digit()) # 商品データをCSVファイルから読み込む Product_Data = CSV_Data_Set1('Product_Data.csv') # 地域名・配送センター名辞書をCSVフィルから作成 Area_Data = CSV_Data_Set2('Logi_Data.csv', Area_List) # 地域名辞書 Logi_Data = CSV_Data_Set2('Logi_Data.csv', Logi_List) # 物流センター名辞書 # SingleStoreとの接続 db = pymysql.connect(host = 'xxx.xxx.xxx.xxx', port=3306, user='xxxxxxxx', password='xxxxxxx', db='xxxxxxx', charset='utf8', cursorclass=pymysql.cursors.DictCursor) with db.cursor() as cursor: # 時間情報を生成する起点を確保 dt_now = datetime.datetime.now() # ループカウンターの初期化 Loop_Counter = 0 # 検証データの生成 while Loop_Counter < Generate_Data: # ts用のデータを生成 Sec = fakegen.random_digit() MIL_Sec = fakegen.random_digit() MIC_Sec = fakegen.random_digit() # 現実的なタイムスタンプ情報として利用します(秒単位でデータをズラしてBI等で使い易くする) ts_now = dt_now + datetime.timedelta(seconds=Sec, milliseconds=MIL_Sec, microseconds=MIC_Sec) dt_now = ts_now # 生成データを次回の起点に変更 # データをランダムに選択する(投入データ数は引数で定義可能) Select_Data = Pick_Up_Item(Data_Start, Data_End, Product_Data) # 所得した各情報を設定 Category = Select_Data[0] # カテゴリ名 Product = Select_Data[1] # 商品名 Price = Select_Data[2] # 価格 Point_Rate = Select_Data[3] # ポイント換算率 Real_Rate = Select_Data[4] # 販売数調整係数 # 購入数を設定(家電は原則的に1個単位(乾電池を除く)) if Real_Rate == '1': Units = 1 else: Units = randint(1, Real_Rate) # ポイントの計算を行いデータを設定 Point = int(Price) * Units * int(Point_Rate) / 100 # 支払い情報の設定 if str(fakegen.pybool()) == "True": Card = "現金" else: Card = fakegen.credit_card_provider() Number = fakegen.credit_card_number() if Card == "現金": Number = "N/A" # 支払い総額と消費税の設定 Payment = Units * int(Price) Tax = Payment * Tax_Data / 100 # 購入者情報の設定 User = fakegen.name() Zip = fakegen.zipcode() Address = fakegen.address() Tel = fakegen.phone_number() Email = fakegen.ascii_email() # 都道府県情報の抽出 pattern = u"東京都|北海道|(?:京都|大阪)府|.{2,3}県" m = re.match(pattern , Address) if m: Prefecture = m.group() # 地域名と物流センター名を県名から設定 Area = Area_Data.get(Prefecture) Logistics = Logi_Data.get(Prefecture) # SQLで使用するデータ列の作成 DV0 = str(ts_now)+"','" DV1 = Category + "','" + Product + "','" + str(Price) + "','" + str(Units) + "','" + Logistics + "','" DV2 = Card + "','" + Number + "','" + str(Payment) + "','" + str(Tax) + "','" DV3 = User + "','" + Zip + "','" + Prefecture + "','" + Address + "','" + Area + "','" + Tel + "','" + str(Email) + "','" + str(Point) SQL = "INSERT INTO " + Table_Name +"(" + DL0 + DL1 + DL2 + DL3 + ") VALUES('" + DV0 + DV1 + DV2 + DV3 + "')" # データベースへの書き込み cursor.execute(SQL) db.commit() # コンソールに生成データを表示 if Display_SQL == 1: print (SQL) # ループカウンタの更新 Loop_Counter = Loop_Counter + 1 # データの作成状況を表示 if (Loop_Counter % 10) == 0: print("途中経過: " + str(Loop_Counter) + " 個目のデータ作成を終了") except KeyboardInterrupt: print('!!!!! 割り込み発生 !!!!!') finally: # データベースコネクションを閉じる db.close() # 処理時間を表示して終了 print("今回生成したデータの総数 : " + str(Loop_Counter)) print("SingleStore上への指定されたデータ生成が終了しました。") print ("処理の終了 : " + datetime.datetime.now().strftime("%Y/%m/%d %H:%M:%S"))因みに、データテーブルを作成する部分は以前のものと同じです。
# coding: utf-8 # # 日本語版BIG DATA Generator # # Python 3版 # # # 初期設定 import sys stdout = sys.stdout sys.stdout = stdout import pymysql.cursors import datetime # テーブル名 Table_Name = "BIGDATA_TEST0_Table" # テーブル初期化 Table_Init = "DROP TABLE IF EXISTS " + Table_Name # テーブル定義 #DC0 = "id BIGINT AUTO_INCREMENT, ts TIMESTAMP(6) DEFAULT NOW(), " DC0 = "id BIGINT AUTO_INCREMENT, ts TIMESTAMP(6), " DC1 = "Category VARCHAR(20), Product VARCHAR(20), Price INT, Units INT, Logistics VARCHAR(20), " DC2 = "Card VARCHAR(40), Number VARCHAR(30), Payment INT, Tax INT, " DC3 = "User VARCHAR(20), Zip VARCHAR(10), Prefecture VARCHAR(10), Address VARCHAR(60), Area VARCHAR(10), Tel VARCHAR(15), Email VARCHAR(40), Point INT, " DC4 = "SHARD KEY (Area), PRIMARY KEY(id, Area)" try: print("SingleStore上へのテーブル作成処理を開始") print ("処理の開始 : " + datetime.datetime.now().strftime("%Y/%m/%d %H:%M:%S")) # SingleStoreに接続 db = pymysql.connect(host = 'xxx.xxx.xxx.xxx', port=3306, user='xxxxxxxx', password='xxxxxxxx', db='xxxxxxxx', charset='utf8', cursorclass=pymysql.cursors.DictCursor) # デモ用のテーブルの作成 Table_Create = "CREATE TABLE IF NOT EXISTS " + Table_Name + "(" + DC0 + DC1 + DC2 + DC3 + DC4 + ")" with db.cursor() as cursor: # 既存テーブルの初期化 cursor.execute(Table_Init) db.commit() # 新規にテーブルを作成 cursor.execute(Table_Create) db.commit() except KeyboardInterrupt: # 割り込み処理への対応 print('!!!!! 割り込み発生 !!!!!') finally: # データベースコネクションを閉じる db.close() # 処理時間を表示して終了 print("SingleStore上へのテーブル作成処理が終了") print ("処理の終了 : " + datetime.datetime.now().strftime("%Y/%m/%d %H:%M:%S"))CSVファイルの状況
CSVファイルをExcel等で適宜作成します。今回のカラム構造は
(A)商材カテゴリ
(B)商品名
(C)価格
(D)ポイント率(整数でパーセント数)
(E)販売調整係数(1回の最大販売数)
になります。この部分はPython内のパラメータと辻褄が合えば、変更利用が可能なように(多分・・(汗))作り変えましたので、いろいろなパターンでお使い頂けるかと思います(それに合わせてSQL定義文も忘れずに変更しておいてください)
地域名とそのエリアを配送するセンター名の参照辞書用CSVも同じ様に作成します。
同様に今回のカラム構造は
(A)県名
(B)地域名
(C)物流センター名
になります。
県名をキーに辞書参照を行う形で処理を行います。こちらも前述の商品系情報と同様に、柔軟な変更が可能ですので、随時必要な形に変更しPython側と辻褄を合わせてお使いください。
実行してみました・・・
これらのファイルを一つのディレクトリに格納して、いつものANACONDA環境で実行した結果が以下の通りです。
今回の纏め
今回は、今まで検証で使ってきたツールの整理整頓を行ってみました。出来るだけ横展開出来るように汎用性を持たせたつもりですが、引き続き改良していきたいと思います。
また特に、前回まで連続してご紹介してきた、MySQL互換で、マシン語レベルでSQL処理を実装している、”インメモリDBであるSingleStore環境での、動作検証やパフォーマンス確認等で使って頂ければ幸いです。
- 投稿日:2021-03-14T13:59:45+09:00
Pandasで世界の大学のランキングをソートする(excelデータ利用)no.7
Pandas についてシリーズで記事を書いています。(Pandas の基礎的な部分から書いていますので分からなくなった時は他のPandas関連の記事も参考にどうぞ)
今回の記事は第7回目の記事になります。
今回は、data.worldさんのサイトからWorld University Rankings 2019-20 という2019年から2020年の世界の大学ランキングについてのデータを使わせていただきます。
この記事を読めば
- condaでxlrd とopenpyxlをインストールする方法
- EXCELファイルを読み込む方法
- Seriesにpythonの機能を使う時の注意点
などが分かります
ではさっそく始めていきますね。
EXCELファイルを読み込む
今回読み込むデータは下記のexcel のデータになります
(※前回までは、CSVのデータを使っていました。)Pandas でEXCELファイルを読み込むには『xlrd』と『openpyxl』というライブラリーが必要であり、今回新たにインストールします
(Anaconda の使い方やconda でのライブラリーのインストール方法が分からない方はこちらの記事を参考にしてください。)
xlrdとopenpyxlをインストールする
xlrd とopenpyxlをインストールする前に、どの仮想環境にインストールするか決めてくださいね。
そしてまず、その仮想環境をactivate しましょう
(仮想環境って何?っていう人は こちらの記事 の『conda でenvironment を作る』という項目に書いています)
上記のスクショのように、あなたが今回ライブラリーをインストールしたい仮想環境が表示されていたらOKです。
確認後xlrd と openpyxl をインストールしましょう
conda install xlrd openpyxlとAnaconda Prompt に打ち込んでエンターキーを押してください。
するとインストールが始まり、最後に
Proceed([y]/n)?
と聞いてきますから 『y』をキーで打ち込みしょう
Anaconda Prompt に done と出れば無事にインストールができています。
EXCELファイルを読み込む
jupyter notebook でEXCELのデータを読み込みます。
import pandas as pd pd.readとread まで打ち込んだ時点で
Shift + Tab
を押すと選択肢が表示されます
今回はEXCELファイルを読み込みたいので『read_excel』を選択しましょう
CSVファイルを読み込み、DataFrame をSeries に変えた時と同じ要領で、EXCELのデータからSeriesのオブジェクトを作りましょう
※CSVファイルの読み込み方などが分からない方はこちらの記事を参考にどうぞ
下記のようにSeries のオブジェクトを作ることができました。
Python にビルトインされている機能を使う
EXCELデータからPandasのSeries オブジェクトを作った後は簡単でして、Python 自体の機能もSeries オブジェクトに使うことができます
例えば、トップ15位までの大学名を出したいのならpython でrangeを指定するときと同じやり方をします
(ちなみに今回作ったSeries は university_rank という変数に代入しています)
university_rank[:15]でトップ15校の世界の大学名を表示できました。
また今回のランキングに載っている大学名を下から順に15校並べたい時も
university_rank[-1:-15:-1]とすれば一番下に書かれた大学名から順番に表示されます
Python のA in [リスト]をSeries でも使える?
Python でリスト型データの中に、ある特定の文字列や数値が入っているかどうかを調べるのに
A in [リスト]を使いますよね
A がリストの中にあれば『True』を返してくれますし、無ければ『False』になります
例えば下記のスクショですと3はリストの中にあるのでTrue を返しています
では同じように、Series に対しても使えるでしょうか?
今回使っているデータの中に『"University of Tokyo"』が入っているのかな?と調べたい時。
結果は下のスクショのようになりました。
これは、(in Series名)にすると、その『index』をコンピューターが見て、その中に"University of Tokyo" があるかどうかを調べるからです。
そうではなく、あくまでもSeriesのvalueにあたる部分を調べたいのでSeriesの後ろに .values を付ける必要があります
そして"University of Tokyo" は13位に表示されていますので、True を返してくれます。
まとめ
今回の記事はこれくらいで終わりにします。<(_ _)>
Pandasシリーズの記事も7記事目になり、だんだんPandasでできることも多くなってきました。
また引き続き、紹介していきますね。
よろしくお願いしますっ!
- 投稿日:2021-03-14T13:39:44+09:00
Visual Studio CodeでC++, LaTeX, Pythonする(WSL2)
目次
- 概要
- Windows Subsystem for Linux 2
- Visual Studio Code
- C++
- LaTeX
- Python
1.概要
WSLの環境はあったが,
「WSL2で環境構築するぞ, うおお(無印と何が違うのかわかってない)」
となった. 結構困ったので自分用にメモしておく.
をめちゃくちゃ参考にした.
2.Windows Subsystem for Linux 2
Windows機で仮想的にLinuxを使うのに必要な, WSL(Windows Subsystem for Linux)のVer.2を入れる.
Microsoft公式の手動インストールをやる.2.1.Windows側の設定をする.
左下の窓マークを右クリック->「Windows PowerShell(管理者)(A)」で
dism.exe /online /enable-feature /featurename:Microsoft-Windows-Subsystem-Linux /all /norestartをコピペしてEnter
dism.exe /online /enable-feature /featurename:VirtualMachinePlatform /all /norestartもコピペして実行(上のとちょっと違う). ウィンドウはまだ消さない.
2.2.更新プログラムパッケージをダウンロード
x64用でダウンロード. 管理者許可もYes.
2.3.WSL2を使う設定
さっきのPowerShellで
wsl --set-default-version 2を実行.
2.4.Ubuntuをインストール
Microsoft Storeで「Ubuntu」と検索. 好きなバージョンを入手. ちな「Ubuntu 20.04 LTS」 にした.
2.5.Ubuntuの設定
~ここから実行はずっとUbuntu~
インストール出来たら, 起動(初回だけ時間がかかる). ユーザーネーム(適当に決める)を1回と, パスワード(表示されない)を2回入力する.
そのままだと, 海外経由で遅いので,sudo sed -i -e 's%http://.*.ubuntu.com%http://ftp.jaist.ac.jp/pub/Linux%g' /etc/apt/sources.listを実行して国内に変更する.
sudo apt upgradeを実行すると, 丁寧に時間をかけてアップグレードしてくれる. 続いて,
sudo apt updateも実行すると, 丁寧に時間をかけてアップデートしてくれる. これでWSL2は終わり!
3.Visual Studio Code
ヤバいメモ帳ことVisual Studio Code(VSCode)をいれます.
3.1.VSCodeインストール
VSCode公式からVSCodeのWindows版をダウンロード, インストール. 起動する.
3.2.拡張機能
「Ctrl」+「Shift」+「x」で出る検索窓から,
- Remote - WSL
- C/C++
- LaTeX Workshop
- Python
を検索して, それぞれインストール. 「再起動しろ!」といわれるので, 適宜してやる.
3.3.設定
「Ctrl」+「,」. 右上の紙がペロンとなっているアイコン「Open Settings (JASON)」を押す.
settings.json{ "files.eol": "\n", "terminal.integrated.shell.windows": "C:\\WINDOWS\\System32\\wsl.exe", }をコピペして保存.
4.C++
sudo apt install build-essentialを実行するだけ. 詳しくは
5.LaTeX
詳しくは
sudo apt install texlive-fullを実行. ひたすら待つ. 「Ctrl」+「k」, 「Ctrl」+「o」で「Windows (C:)」を選択し, 開く. 「New File」のアイコンから, 名前が「latex-tools.sh」で, 中身が
latex-tools.sh#!/bin/bash #Windows特有の c:/hoge/piyo → /mnt/c/hoge/piyo に書き換えてコマンドを実行するshellscript newArgs=() for arg in $@; do if [ ${arg:1:1} = : ]; then arg=/mnt/${arg:0:1}${arg#*:} fi newArgs+=( $arg ) done ${newArgs[@]}のファイルをC直下に保存. 「Ctrl」+「,」. 右上の紙がペロンとなっているアイコン「Open Settings (JASON)」を押す.
settings.json{ "files.eol": "\n", "terminal.integrated.shell.windows": "C:\\WINDOWS\\System32\\wsl.exe", "latex-workshop.latex.tools": [ { "name": "latexmk", "command": "wsl.exe", "args": [ "/mnt/c/latex-tools.sh", "latexmk", "-synctex=1", "-interaction=nonstopmode", "-file-line-error", "-pdf", "%DOC%" ] }, { "name": "pdflatex", "command": "wsl.exe", "args": [ "/mnt/c/latex-tools.sh", "pdflatex", "-synctex=1", "-interaction=nonstopmode", "-file-line-error", "%DOC%" ] }, { "name": "bibtex", "command": "wsl.exe", "args": [ "/mnt/c/latex-tools.sh", "bibtex", "%DOCFILE%" ] }, { "name":"ptex2pdf", "command": "wsl.exe", "args": [ "/mnt/c/latex-tools.sh", "ptex2pdf", "-l", "-ot", "-kanji=utf8 -synctex=1", "-interaction=nonstopmode", "%DOC%" ] }, { "name":"ptex2pdf (uplatex)", "command": "wsl.exe", "args": [ "/mnt/c/latex-tools.sh", "ptex2pdf", "-l", "-u", "-ot", "-kanji=utf8 -synctex=1", "-interaction=nonstopmode", "%DOC%" ] }, { "name": "pbibtex", "command": "wsl.exe", "args": [ "/mnt/c/latex-tools.sh", "pbibtex", "-kanji=utf8", "%DOCFILE%" ] } ], "latex-workshop.latex.recipes": [ { "name": "ptex2pdf", "tools": [ "ptex2pdf", ] }, { "name": "ptex2pdf (uplatex)", "tools": [ "ptex2pdf (uplatex)", ] }, { "name": "latexmk", "tools": [ "latexmk", ] }, { "name": "pdflatex", "tools": [ "pdflatex", ] }, { "name": "pdflatex -> bibtex -> pdflatex", "tools": [ "pdflatex", "bibtex", "pdflatex", ] }, { "name": "ptex2pdf -> pbibtex -> ptex2pdf", "tools": [ "ptex2pdf", "pbibtex", "ptex2pdf", ] }, { "name": "ptex2pdf (uplatex) -> pbibtex -> ptex2pdf (uplatex)", "tools": [ "ptex2pdf (uplatex)", "pbibtex", "ptex2pdf (uplatex)", ] }, ], "explorer.confirmDelete": false, "[latex]": { "editor.formatOnPaste": false, "editor.suggestSelection": "recentlyUsedByPrefix" }, "files.autoSave": "afterDelay", "workbench.startupEditor": "newUntitledFile" }に更新する.
6.Python
6.1.Anaconda3のインストール
anaconda公式から, Linux用(Windows用でない)の「64-Bit (x86) Installer」をダウンロード.
ubuntuでbash /mnt/c/Users/XXXX/Downloads/Anaconda3-(XXXXには, Windowsでのユーザー名が入る)まで入力して「Tab」を押すと, バージョンに合わせて
bash /mnt/c/Users/XXXX/Downloads/Anaconda3-2020.11-Linux-x86_64.shみたいな表示になるので実行. 指示に従ってAnaconda3をインストールする.
6.2.VcXsrvのインストール
画像の表示をする(今流行りの†GUI†)ために, VcXsrvをインストールする. sourceforge公式からダウンロードしたexeファイルを実行してインストール.
6.3.VcXsrvの設定
詳しくは
- VcXsrv のインストール(Windows 上)
- WSL2の導入とGUI環境の構築とsshfsしたものもgnome-openしたい!! [Ubuntu18.04/20.04]
- VcXsrv(Win版Xサーバー)を自動起動する方法
Xlaunchを起動して, 「ファイアーウォールがなんたら!」と警告がでたら, パブリック側を解除する. 基本デフォルトでポチポチしていくが, 「Extra settings」では, 最後の「Additional parameters for VcXsrv」欄に「-ac」を追加する. 毎回ポチるのは面倒なので, 自動化してしまう. 「Save configuration」をクリックして適当な場所に保存する. 「完了」. 左下の窓アイコンを右クリック「ファイル名を指定して実行(R)」で, 「shell:startup」を入力して「OK」. 右クリックから「新規作成」→「ショートカット」→「(さっき保存した場所)」で登録する.
6.4.パス設定
このままだといい感じに動かなかったので,
cdでホームディレクトリに移動し,
vi .bashrcを実行することで.bashrcを開く. 「i」を押すと編集モードになるので, 最後の行に
export PATH="/home/ZZZZ/anaconda3/bin:$PATH" export DISPLAY=$(cat /etc/resolv.conf | grep nameserver | awk '{print $2}'):0.0(ZZZZにはubuntuのユーザー名が入る)を追加. 「Esc」で離脱し,
:wqを実行することで, 保存終了できる.
source .bashrcを実行しておく.
- 投稿日:2021-03-14T13:39:44+09:00
Visual Studio CodeでC++, LaTeX, Python(GUI)する(WSL2)
目次
- 概要
- Windows Subsystem for Linux 2
- Visual Studio Code
- C++
- LaTeX
- Python
1.概要
WSLの環境はあったが,
「WSL2で環境構築するぞ, うおお(無印と何が違うのかわかってない)」
となった. 結構困ったので自分用にメモしておく.
をめちゃくちゃ参考にした.
2.Windows Subsystem for Linux 2
Windows機で仮想的にLinuxを使うのに必要な, WSL(Windows Subsystem for Linux)のVer.2を入れる.
Microsoft公式の手動インストールをやる.2.1.Windows側の設定をする.
左下の窓マークを右クリック->「Windows PowerShell(管理者)(A)」で
dism.exe /online /enable-feature /featurename:Microsoft-Windows-Subsystem-Linux /all /norestartをコピペしてEnter
dism.exe /online /enable-feature /featurename:VirtualMachinePlatform /all /norestartもコピペして実行(上のとちょっと違う). ウィンドウはまだ消さない.
2.2.更新プログラムパッケージをダウンロード
x64用でダウンロード. 管理者許可もYes.
2.3.WSL2を使う設定
さっきのPowerShellで
wsl --set-default-version 2を実行.
2.4.Ubuntuをインストール
Microsoft Storeで「Ubuntu」と検索. 好きなバージョンを入手. ちな「Ubuntu 20.04 LTS」 にした.
2.5.Ubuntuの設定
~ここから実行はずっとUbuntu~
インストール出来たら, 起動(初回だけ時間がかかる). ユーザーネーム(適当に決める)を1回と, パスワード(表示されない)を2回入力する.
そのままだと, 海外経由で遅いので,sudo sed -i -e 's%http://.*.ubuntu.com%http://ftp.jaist.ac.jp/pub/Linux%g' /etc/apt/sources.listを実行して国内に変更する.
sudo apt upgradeを実行すると, 丁寧に時間をかけてアップグレードしてくれる. 続いて,
sudo apt updateも実行すると, 丁寧に時間をかけてアップデートしてくれる. これでWSL2は終わり!
3.Visual Studio Code
ヤバいメモ帳ことVisual Studio Code(VSCode)をいれます.
3.1.VSCodeインストール
VSCode公式からVSCodeのWindows版をダウンロード, インストール. 起動する.
3.2.拡張機能
「Ctrl」+「Shift」+「x」で出る検索窓から,
- Remote - WSL
- C/C++
- LaTeX Workshop
- Python
を検索して, それぞれインストール. 「再起動しろ!」といわれるので, 適宜してやる.
3.3.設定
「Ctrl」+「,」. 右上の紙がペロンとなっているアイコン「Open Settings (JASON)」を押す.
settings.json{ "files.eol": "\n", "terminal.integrated.shell.windows": "C:\\WINDOWS\\System32\\wsl.exe", }をコピペして保存.
4.C++
sudo apt install build-essentialを実行するだけ. 詳しくは
5.LaTeX
詳しくは
sudo apt install texlive-fullを実行. ひたすら待つ. 「Ctrl」+「k」, 「Ctrl」+「o」で「Windows (C:)」を選択し, 開く. 「New File」のアイコンから, 名前が「latex-tools.sh」で, 中身が
latex-tools.sh#!/bin/bash #Windows特有の c:/hoge/piyo → /mnt/c/hoge/piyo に書き換えてコマンドを実行するshellscript newArgs=() for arg in $@; do if [ ${arg:1:1} = : ]; then arg=/mnt/${arg:0:1}${arg#*:} fi newArgs+=( $arg ) done ${newArgs[@]}のファイルをC直下に保存. 「Ctrl」+「,」. 右上の紙がペロンとなっているアイコン「Open Settings (JASON)」を押す.
settings.json{ "files.eol": "\n", "terminal.integrated.shell.windows": "C:\\WINDOWS\\System32\\wsl.exe", "latex-workshop.latex.tools": [ { "name": "latexmk", "command": "wsl.exe", "args": [ "/mnt/c/latex-tools.sh", "latexmk", "-synctex=1", "-interaction=nonstopmode", "-file-line-error", "-pdf", "%DOC%" ] }, { "name": "pdflatex", "command": "wsl.exe", "args": [ "/mnt/c/latex-tools.sh", "pdflatex", "-synctex=1", "-interaction=nonstopmode", "-file-line-error", "%DOC%" ] }, { "name": "bibtex", "command": "wsl.exe", "args": [ "/mnt/c/latex-tools.sh", "bibtex", "%DOCFILE%" ] }, { "name":"ptex2pdf", "command": "wsl.exe", "args": [ "/mnt/c/latex-tools.sh", "ptex2pdf", "-l", "-ot", "-kanji=utf8 -synctex=1", "-interaction=nonstopmode", "%DOC%" ] }, { "name":"ptex2pdf (uplatex)", "command": "wsl.exe", "args": [ "/mnt/c/latex-tools.sh", "ptex2pdf", "-l", "-u", "-ot", "-kanji=utf8 -synctex=1", "-interaction=nonstopmode", "%DOC%" ] }, { "name": "pbibtex", "command": "wsl.exe", "args": [ "/mnt/c/latex-tools.sh", "pbibtex", "-kanji=utf8", "%DOCFILE%" ] } ], "latex-workshop.latex.recipes": [ { "name": "ptex2pdf", "tools": [ "ptex2pdf", ] }, { "name": "ptex2pdf (uplatex)", "tools": [ "ptex2pdf (uplatex)", ] }, { "name": "latexmk", "tools": [ "latexmk", ] }, { "name": "pdflatex", "tools": [ "pdflatex", ] }, { "name": "pdflatex -> bibtex -> pdflatex", "tools": [ "pdflatex", "bibtex", "pdflatex", ] }, { "name": "ptex2pdf -> pbibtex -> ptex2pdf", "tools": [ "ptex2pdf", "pbibtex", "ptex2pdf", ] }, { "name": "ptex2pdf (uplatex) -> pbibtex -> ptex2pdf (uplatex)", "tools": [ "ptex2pdf (uplatex)", "pbibtex", "ptex2pdf (uplatex)", ] }, ], "explorer.confirmDelete": false, "[latex]": { "editor.formatOnPaste": false, "editor.suggestSelection": "recentlyUsedByPrefix" }, "files.autoSave": "afterDelay", "workbench.startupEditor": "newUntitledFile" }に更新する.
6.Python
6.1.Anaconda3のインストール
anaconda公式から, Linux用(Windows用でない)の「64-Bit (x86) Installer」をダウンロード.
ubuntuでbash /mnt/c/Users/XXXX/Downloads/Anaconda3-(XXXXには, Windowsでのユーザー名が入る)まで入力して「Tab」を押すと, バージョンに合わせて
bash /mnt/c/Users/XXXX/Downloads/Anaconda3-2020.11-Linux-x86_64.shみたいな表示になるので実行. 指示に従ってAnaconda3をインストールする.
6.2.VcXsrvのインストール
画像の表示をする(今流行りの†GUI†)ために, VcXsrvをインストールする. sourceforge公式からダウンロードしたexeファイルを実行してインストール.
6.3.VcXsrvの設定
詳しくは
- VcXsrv のインストール(Windows 上)
- WSL2の導入とGUI環境の構築とsshfsしたものもgnome-openしたい!! [Ubuntu18.04/20.04]
- VcXsrv(Win版Xサーバー)を自動起動する方法
Xlaunchを起動して, 「ファイアーウォールがなんたら!」と警告がでたら, パブリック側を解除する. 基本デフォルトでポチポチしていくが, 「Extra settings」では, 最後の「Additional parameters for VcXsrv」欄に「-ac」を追加する. 毎回ポチるのは面倒なので, 自動化してしまう. 「Save configuration」をクリックして適当な場所に保存する. 「完了」. 左下の窓アイコンを右クリック「ファイル名を指定して実行(R)」で, 「shell:startup」を入力して「OK」. 右クリックから「新規作成」→「ショートカット」→「(さっき保存した場所)」で登録する.
6.4.パス設定
このままだといい感じに動かなかったので,
cdでホームディレクトリに移動し,
vi .bashrcを実行することで.bashrcを開く. 「i」を押すと編集モードになるので, 最後の行に
export PATH="/home/ZZZZ/anaconda3/bin:$PATH" export DISPLAY=$(cat /etc/resolv.conf | grep nameserver | awk '{print $2}'):0.0(ZZZZにはubuntuのユーザー名が入る)を追加. 「Esc」で離脱し,
:wqを実行することで, 保存終了できる.
source .bashrcを実行しておく.
- 投稿日:2021-03-14T13:01:06+09:00
MSYS2 VSCode gccオプション設定プログラム
MSYS2で、Rustの開発環境が作れるようになった。
pacman -S mingw-w64-x86_64-rustこのRustは、rustupが含まれておらず、cargoを使い、MSYS2のgccコンパイラが使える。
Rustで画面を作ろうとすると、gtk-rsが簡単そうだ。
MSYS2でGTK3をインストールして
pacman -S mingw-w84-x86_64-gtk3
画面設計用のGladeも入れておけば、楽だろう。
pacman -S mingw-w64-x86_64-gladecargo側の設定で、cargo.tomlの[dependencies]にGTKを設定すれば、自動的にcrates(クエート)がダウンロードされる。
しかし、VSCodeで開発する際は、gccのコンパイルオプションを書くのが面倒くさい。
そこで、MSYS2に付属している、Pythonを使って、tasks.jsonなどに書き込むプログラムを書いてみた。
使い方
(1) main関数のvscodePath を設定する
(2) main関数のpkgList を設定する (ここでは、GTK3)
(3) setProperties関数のjsonName を設定する (ここでは、C/C++用)
(4) setTasks関数の"-mwindows"は、win10で、コンソール画面を非表示にできる gccオプションです。必要なければ、この行をコメントアウトしてください。
(5) 後は、実行するだけ (必要なパッケージは、何度 追加して実行しても、自動で重複削除しています)解説
MSYS2のtoolchainに付属のpkg-cofigコマンドを使って、必要な情報を得て、tasks.jsonとc_cpp_properties.jsonに書き込んでいます。
pkg-cofigコマンドは、MSYS2でインストールできる。
pacman -S mingw-w64-x86_64-toolchainこのプログラムは、gccコンパイラを使うのであれば、Rust以外でも使える。
パッケージ名を設定すれば、GTK以外でも、いろいろ使えるpyPkgConfig.py# This Python file uses the following encoding: utf-8 import sys import subprocess import os import json def getFlags(pkgList): ListA = [] for itemP in pkgList: result = subprocess.run(["pkg-config", "--cflags-only-I", itemP], encoding="utf-8", stdout=subprocess.PIPE) ListB = result.stdout.split() for itemB in ListB: itemB = setAbsPath("-I", itemB) ListA.append(itemB) ListA = uniList([], ListA) return ListA def getLibs(pkgList): ListA = [] for itemP in pkgList: result = subprocess.run(["pkg-config", "--libs", itemP], encoding="utf-8", stdout=subprocess.PIPE) ListB = result.stdout.split() for itemB in ListB: itemB = setAbsPath("-L", itemB) ListA.append(itemB) ListA = uniList([], ListA) return ListA def setAbsPath(head, Path): result = Path if head == Path[:2]: result = Path[2:] result = os.path.abspath(result) result = head + result return result def getFullPath(flagsList): List = [] for item in flagsList: if item[:2] == "-I": fullPath = item[2:] if os.path.isdir(fullPath): List.append(fullPath) List = uniList([], List) return List def getInculdePath(pathList): List = [] for item in pathList: fullPath = item lowPath = fullPath.lower() pos = lowPath.find("/include") if pos > 0: fullPath = fullPath[:pos + 8] fullPath = fullPath + "/**" List.append(fullPath) List = uniList([], List) return List def uniList(ListA, ListB): ListC = [] ListC = ListA for itemB in ListB: notFind = True for itemA in ListA: if itemA == itemB: notFind = False break if notFind: ListC.append(itemB) return ListC def setTasks(vscodePath, flagsList, libsList): jsonName = "/tasks.json" jsonPath = vscodePath + jsonName with open(jsonPath, mode="r", encoding="utf-8") as rf: jsonFile = json.load(rf) for item in jsonFile["tasks"]: itemList = item["args"] itemList = uniList([], itemList) itemList = uniList(itemList, flagsList) itemList = uniList(itemList, libsList) itemList = uniList(itemList, ["-mwindows"]) item["args"] = itemList with open(jsonPath, mode="w", encoding="utf-8") as wf: json.dump(jsonFile, wf, indent=4, ensure_ascii=False) def setProperties(vscodePath, incsList): jsonName = "/c_cpp_properties.json" jsonPath = vscodePath + jsonName with open(jsonPath, mode="r", encoding="utf-8") as rf: jsonFile = json.load(rf) for item in jsonFile["configurations"]: itemList = item["includePath"] itemList = uniList([], itemList) itemList = uniList(itemList, incsList) item["includePath"] = itemList with open(jsonPath, mode="w", encoding="utf-8") as wf: json.dump(jsonFile, wf, indent=4, ensure_ascii=False) def main(): vscodePath = "C:/work/hello/.vscode" pkgList = ["gtk+-3.0"] flgsList = getFlags(pkgList) libsList = getLibs(pkgList) pathList = getFullPath(flgsList) incsList = getInculdePath(pathList) setTasks(vscodePath, flgsList, libsList) setProperties(vscodePath, incsList) if __name__ == "__main__": main()GTK3を入れてみた。
tasks.json
{
"version": "2.0.0",
"tasks": [
{
"type": "cppbuild",
"label": "C/C++: gcc.exe アクティブなファイルのビルド",
"command": "C:\\msys64\\mingw64\\bin\\gcc.exe",
"args": [
"-g",
"${file}",
"-o",
"${fileDirname}\\${fileBasenameNoExtension}.exe",
"-IC:/msys64/mingw64/include/gtk-3.0",
"-IC:/msys64/mingw64/include/pango-1.0",
"-IC:/msys64/mingw64/include",
"-IC:/msys64/mingw64/include/glib-2.0",
"-IC:/msys64/mingw64/lib/glib-2.0/include",
"-IC:/msys64/mingw64/include/harfbuzz",
"-IC:/msys64/mingw64/include/freetype2",
"-IC:/msys64/mingw64/include/libpng16",
"-IC:/msys64/mingw64/include/fribidi",
"-IC:/msys64/mingw64/include/cairo",
"-IC:/msys64/mingw64/include/lzo",
"-IC:/msys64/mingw64/include/pixman-1",
"-IC:/msys64/mingw64/include/gdk-pixbuf-2.0",
"-IC:/msys64/mingw64/include/atk-1.0",
"-LC:/msys64/mingw64/lib",
"-lgtk-3",
"-lgdk-3",
"-lz",
"-lgdi32",
"-limm32",
"-lshell32",
"-lole32",
"-Wl,-luuid",
"-lwinmm",
"-ldwmapi",
"-lsetupapi",
"-lcfgmgr32",
"-lpangowin32-1.0",
"-lpangocairo-1.0",
"-lpango-1.0",
"-lharfbuzz",
"-latk-1.0",
"-lcairo-gobject",
"-lcairo",
"-lgdk_pixbuf-2.0",
"-lgio-2.0",
"-lgobject-2.0",
"-lglib-2.0",
"-lintl",
"-mwindows"
],
"options": {
"cwd": "${workspaceFolder}"
},
"problemMatcher": [
"$gcc"
],
"group": "build",
"detail": "コンパイラ: C:\\msys64\\mingw64\\bin\\gcc.exe"
}
]
}
環境設定により、完全な動作保証は、出来ていません。
- 投稿日:2021-03-14T12:48:22+09:00
【Django】管理サイトに自作した操作を追加する方法
前置き
サイト構築で試行錯誤していると、データにまとめて同じ操作を行いたい場面がちょこちょこ出てきます。デフォルトでは削除のみが用意されているので、それ以外の操作を行いたい場合は自分でadmin.pyを編集する必要があります。少し手こずったので、備忘録代わりに記録しておきます。
参考にさせていただいたサイト
コード
以下のようなモデルを想定します。私が実際に使っているモデルを簡易化したものです。
models.pyclass EnglishWord(models.Model): # 英語のスペル spell = models.CharField(max_length=30) # 難易度 difficulty = models.IntegerField(default=0)difficultyはユーザ側の行動により随時変化していきます。ここで、テストであれこれ弄ったデータをまとめてデフォルトの状態、すなわち0に戻す操作を追加します。
管理サイトの操作は、admin.pyで設定します。
admin.pyclass EnglishWordAdmin(admin.ModelAdmin): # 自作した操作を追加 actions = ['make_english_words_difficulty_zero'] # 自作した操作 def make_english_words_difficulty_zero(self, request, queryset): for english_word in queryset: english_word.difficulty = 0 english_word.save() # 管理サイト上での表示を決定 make_english_words_difficulty_zero.short_description = "英語の難易度を0にリセット"クラス内に追加したい操作を関数として書いて、actionsに登録。同時に管理サイト上でどのように表示するかを.short_descriptionで決定します。また、querysetからオブジェクトを読み込むことで、データを変更する操作が可能です。
まとめ
なにか分かりづらかったり、誤っていたらコメントの方へお願いします。集合知に感謝。
- 投稿日:2021-03-14T12:27:07+09:00
pythonでネタソートを自作してみた
初めに
随分前のものになるが、スターリンソートなるものを見た。
そして、これよりも計算量が少なるソートを考えてみた。その名も、切り捨てソート
計算量が少ないのかは知らんが。切り捨てソート
切り捨てソートとは強引にソート(昇順)にさせる。
その名の通り、昇順になっていない要素があったら、その後ろの値全てを粛正する。
昇順になってさえいればソートである。(暴論)def CutSort(L): R=[] imax=-1 for i in L: if imax<i: R.append(i) imax=i else:break return R入力:
[4,8,9,10,4,6,7,2]
出力:[4, 8, 9, 10]いい感じだ。
一つでも不適格なのがあるとその後ろを見ずにバッサリと切り捨てる。
なんと素晴らしいソートであろうか。こう考えるとまだ全体をみてやるスターリンソートのほうが優しいのかもしれない。


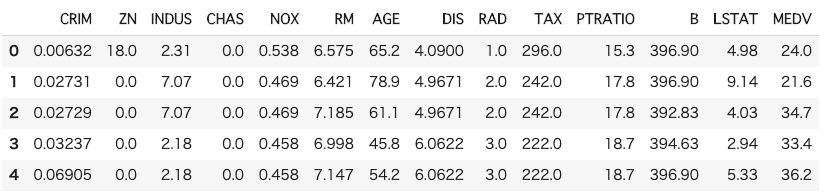





















































![A in [A, B, C, D, E].png](https://qiita-user-contents.imgix.net/https%3A%2F%2Fqiita-image-store.s3.ap-northeast-1.amazonaws.com%2F0%2F1011305%2F4570817a-602f-94ba-fd05-606d55ccfbb9.png?ixlib=rb-1.2.2&auto=format&gif-q=60&q=75&s=5943195a82ba9e586d4578e2c54068d9)


