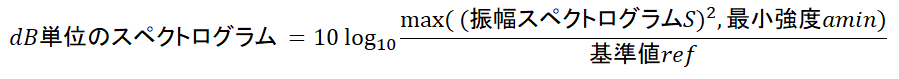- 投稿日:2020-07-05T23:24:51+09:00
WindowsPCが64ビットかどうかを確認する
- 投稿日:2020-07-05T23:20:00+09:00
python OpenCV で画像編集
OpenCVで文字の読み取り可能な画像へ編集する
import cv2 import numpy as np from IPython.display import display, Image def display_cv_image(image, format='.png'): decoded_bytes = cv2.imencode(format, image)[1].tobytes() display(Image(data=decoded_bytes)) img = cv2.imread("{画像ファイルpath}") display_cv_image(img) # グレイスケール化 gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY) # 二値化 ret,th1 = cv2.threshold(gray,200,255,cv2.THRESH_BINARY) display_cv_image(th1) contours, hierarchy = cv2.findContours(th1,cv2.RETR_TREE,cv2.CHAIN_APPROX_SIMPLE) # 面積の大きいもののみ選別 areas = [] for cnt in contours: area = cv2.contourArea(cnt) if area > 10000: epsilon = 0.1*cv2.arcLength(cnt,True) approx = cv2.approxPolyDP(cnt,epsilon,True) areas.append(approx) cv2.drawContours(img,areas,-1,(0,255,0),3) display_cv_image(img) img = cv2.imread("{画像ファイルpath}") dst = [] pts1 = np.float32(areas[0]) pts2 = np.float32([[600,300],[600,0],[0,0],[0,300]]) M = cv2.getPerspectiveTransform(pts1,pts2) dst = cv2.warpPerspective(img,M,(600,300)) display_cv_image(dst)
- 投稿日:2020-07-05T23:18:07+09:00
matplotlibでxticklabelsの色を個別に設定する
0.実現すること
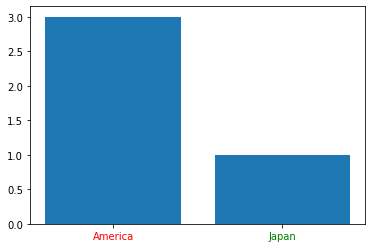
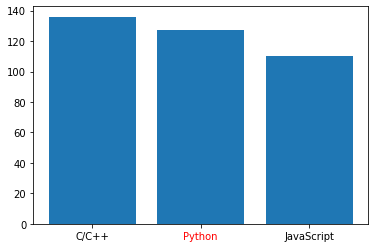
xticklabels(AmericaとかJapanの部分)の色を個別に設定する。1.Code
example.ipynbimport matplotlib.pyplot as plt # 描画領域の設定 fig, ax = plt.subplots() # xticklabelsとyvalueの設定(list) X = ["America", "Japan"] Y = [3, 1] # color 略記でもOK X_label_colors = ['r', 'green'] plt.bar(X, Y, align="center") # Xticklabelsとcolorを対応付ける(同数でなければならない) [t.set_color(i) for (i, t) in zip(X_label_colors, ax.xaxis.get_ticklabels())] plt.show()2.メモ
いくつかあるラベルの中で、特に目立たせたいラベルがあるときに使えそう。
example2.ipynbfig, ax = plt.subplots() X = ["C/C++", "Python", "JavaScript"] X_label_colors = ['black', 'red', 'black'] Y = [136, 127,110] plt.bar(X, Y, align="center") [t.set_color(i) for (i, t) in zip(X_label_colors, ax.xaxis.get_ticklabels())] plt.show()
- 投稿日:2020-07-05T23:13:41+09:00
ルービックキューブのソルバーライブラリ"kociemba"の使い方
はじめに
ルービックキューブの解法を計算してくれるライブラリkociembaの紹介&簡単な使い方を解説する記事です.
pythonには3Dグラフを描画するためのライブラリから麻雀のライブラリまで様々なものが存在します.今回紹介するのはルービックキューブの現在の状態から,全面を揃えるための解法を瞬時に計算してくれるライブラリです.
これから大学の授業等や夏休みの自由研究でルービックキューブのソルバーを探す人が,すぐにkociembaを見つけられるようにと思いこの記事を書きました.
kociembaを使った作品例
このライブラリのおかげで,「全自動でルービックキューブを解くロボット」を作ることができました.
Video: Automatic Rubik's Cube Solverkociembaとは?
もともとはルービックキューブを解くアルゴリズムKociemba's algorithmを考案した学者さんの名前です.本名をHerbert Kociembaと言うそうです.
自分は学科の制作課題のために,ルービックキューブを解くライブラリを探していていました.
実はルービックキューブを解くためのライブラリは他にもたくさんありますが,とてつもなく遅かったり,使い方がさっぱりわからない,といったものも多く,当時はどれを使うのが一番いいのか分からず苦労しました.そんな中,自分が試した中でこれが最も使いやすく,かつ計算も早かったのでこのライブラリを使用することにしました.インストール方法
自分の環境はUbuntu16.04 LTSでした.
pipで入れることができます.Python2.7, Python3.3+で確認済みのようですpip install kociembamacやubuntuなどUnixベースのOSを使っている人は以下のコマンドも必要なようです.
sudo apt-get install libffi-dev使い方
以下のように使います.記号の意味は後ほど解説します.
>>> import kociemba >>> kociemba.solve('DRLUUBFBRBLURRLRUBLRDDFDLFUFUFFDBRDUBRUFLLFDDBFLUBLRBD') u"D2 R' D' F2 B D R2 D2 R' F2 D' F2 U' B2 L2 U2 D R2 U"ルービックキューブの操作記法
軸は不動
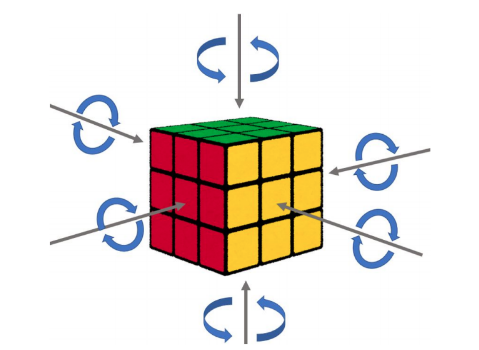
ルービックキューブができる人にとっては常識ですが,ルービックキューブの軸はどんなにネジ繰り回しても変わりません.以下の画像で,どう面を回しても,各面の中心のマスは動かないことが分かるかと思います.
この事実を利用すると,複雑に見える「ルービックキューブの状態」も,きちんと一意に決まる記号で表せることがわかります.
面の名前は中心マスの色で表す
各面の中心マスは動かないことがわかったので,どんなにバラバラな状態でも「中心が赤の面を回して」のように面を指定することができるようになりました.
回転角度も記号で表す
kociembaでは以下のように回転角度を表します.RはRedの面だとして,
R: 時計回りに90度 R': 反時計周りに90度 R2: 180度回転ソルバーへの入力方法
kociembaはどの向きで持っていようとも解けるように,各面を色ではなく(F(front), B(back), R(right), L(left), U(up), B(bottom))で表します.そこでまず,これらの記号と自分のルービックキューブの色の対応を以下のように決めます.当然,正面を向いた面の中心の色で対応付を決めます.
- F(正面)→白
- B(背面)→黄色
- ...
次に,以下の展開図をもとにどこの位置にどの色があるかを調べ上げます(ここは超大変).
例えば,一番上の
U1の位置に黄色があったとすれば,U1=Bとします.
最後に,U1, U2, U3, U4, U5, U6, U7, U8, U9, R1, R2, R3, R4, R5, R6, R7, R8, R9, F1, F2, F3, F4, F5, F6, F7, F8, F9, D1, D2, D3, D4, D5, D6, D7, D8, D9, L1, L2, L3, L4, L5, L6, L7, L8, L9, B1, B2, B3, B4, B5, B6, B7, B8, B9.の順番で文字列strを作り,kociemba.solve(str)を実行すれば,解が返ってきます.参考
- 投稿日:2020-07-05T23:00:19+09:00
AtCoder Beginner Contest 173 参戦記
AtCoder Beginner Contest 173 参戦記
直前まで寝ていて眠い、眠い. そのせいか A, B 問題解くのが遅かったし、しょうもない WA も出してしまった. まあ、体調管理も競技のうちなので、自分が悪い. 結果は青パフォだったのでヨシ!
ABC173A - Payment
2分半で突破. 書くだけ.
N = int(input()) if N % 1000 == 0: print(0) else: print(1000 - N % 1000)ABC173B - Judge Status Summary
4分で突破. 書くだけ.
N = int(input()) S = [input() for _ in range(N)] d = {'AC': 0, 'WA': 0, 'TLE': 0, 'RE': 0} for s in S: d[s] += 1 print('AC x', d['AC']) print('WA x', d['WA']) print('TLE x', d['TLE']) print('RE x', d['RE'])ABC173C - H and V
6分半で突破. 制約を見てビット全探索だと一目. 最近ビット全探索多くね? (まあ、今回は二重ループだけど)
from itertools import product H, W, K = map(int, input().split()) c = [input() for _ in range(H)] result = 0 for a in product([True, False], repeat=H): for b in product([True, False], repeat=W): t = 0 for y in range(H): if a[y]: continue for x in range(W): if b[x]: continue if c[y][x] == '#': t += 1 if t == K: result += 1 print(result)ABC173D - Chat in a Circle
14分で突破. WA1. N - 1 を N とかくチョンボ. 一つでもサンプルを試していればくらわなかったので猛省.
手でやってみると A を大きい順にソートしたものを a1, a2, ..., aN とした場合、a1 + a2 + a2 + a3 + a3 + ... となりそうだなと分かったので、それで提出したら AC した.
N = int(input()) A = list(map(int, input().split())) A.sort(reverse=True) result = 0 for i in range(N - 1): result += A[(i + 1) // 2] print(result)ABC173E - Multiplication 4
41分で突破. WA1. プラスルートの判別が間違っていた.
まず個数を見てプラスになるか、0になるか、マイナスになるかを考える. プラスの場合は絶対値が大きくなるように、マイナスの場合は絶対値が小さくなるように積算していけば良い. プラスの場合、マイナスの値は2個づつしか使えないことに注意.
N, K = map(int, input().split()) A = list(map(int, input().split())) m = 1000000007 a = [e for e in A if e > 0] b = [e for e in A if e < 0] c = [e for e in A if e == 0] # プラスルート if len(a) >= K - (min(K, len(b)) // 2) * 2: a.sort(reverse=True) b.sort() result = 1 i = 0 j = 0 k = 0 while k < K: if k < K - 1 and i < len(a) - 1 and j < len(b) - 1: x = a[i] * a[i + 1] y = b[j] * b[j + 1] if y >= x: result *= y result %= m j += 2 k += 2 else: result *= a[i] result %= m i += 1 k += 1 elif k < K - 1 and j < len(b) - 1: y = b[j] * b[j + 1] result *= y result %= m j += 2 k += 2 elif i < len(a): result *= a[i] result %= m i += 1 k += 1 elif j < len(b): result *= b[j] result %= m j += 1 k += 1 print(result) # 0 ルート elif len(c) != 0: print(0) # マイナスルート else: a.sort() b.sort(reverse=True) result = 1 i = 0 j = 0 k = 0 while k < K: if i < len(a) and j < len(b): if a[i] <= -b[i]: result *= a[i] result %= m i += 1 k += 1 else: result *= b[j] result %= m j += 1 k += 1 elif i < len(a): result *= a[i] result %= m i += 1 k += 1 elif j < len(b): result *= b[j] result %= m j += 1 k += 1 print(result)ABC173F - Intervals on Tree
解けず. O(N2) の解法しか思いつかなかった.
- 投稿日:2020-07-05T22:54:23+09:00
Python環境準備(venv初めて使う)
自分用メモ2です
Python環境づくり
会社で使っているPCはうまくいっていたAnacondaで
家のPCの環境作りをやろうとしたらうまく動かなかったので別の方法をトライWindows10 home
python インストール
https://www.python.org/downloads/windows/
~Windows x86-64 executable installer
を落としてインストール今日はVer.3.7.7にしてた
PATHは通し忘れたのでシステム環境変数のPATHに
C:~\Python\Python37
C:~\Python\Python37\Scripts
の2つを追加した
仮想環境 venvを使う
PowerShellで作業した
参考URL様
https://qiita.com/fiftystorm36/items/b2fd47cf32c7694adc2e
https://docs.python.org/ja/3/library/venv.html保存したい先へ移動
cd 環境を作るフォルダ名前を決めて環境作り→勝手に環境名のフォルダができる
python -m venv 環境名
アクティベート→ここで詰まる
.\環境名\Scripts\activate「このシステムではスクリプトの実行が無効になっているため」
とかなんとかでアクティベートできない参考URL様
https://toypool.hatenablog.com/entry/2019/02/08/142824
https://qiita.com/ryu22e/items/520b35db6a444d8289da上記にならって管理者権限でPowershellを起動しなおして
Set-ExecutionPolicy RemoteSignedYesで進める
再度アクティベートでうまいこと完了
.\環境名\Scripts\activate
Powershellの表示が
(環境名) ~
に変わったのでたぶんOKあとはpip install ***で色々揃えればいいのかな?
Visual studio codeでは作った環境のPythonに選びなおしたらうまく動いた
今日入れたモノ
numpy
opencv-python
pyrealsense2
open3d-python
pandas
matplotlib
seaborn
bokeh
- 投稿日:2020-07-05T22:25:00+09:00
Pythonのモジュールvenvについて
Venvについて
pythonの仮想環境をパッケージ化するモジュール。
例
プログラムAとB、ライブライXのversion1, versionが同じ環境動作している。
またプログラムAはversion1に、プログラムBはversion2に依存している場合を考える。
pythonでは一つの環境に同じライブラリの複数のバージョンを管理出来ない為、この時はプログラムA,Bのどちらか一方が正常に動作しなくなるはずです。
しかしVenvをモジュールを使用すれば、プログラムAの仮想環境にライブラリXのversion1、プログラムBの仮想環境にライブラリXのバージョン2を構築出来る。
上記のようにVenvを使えばプログラム毎に異なる仮想環境を構築できる。参考書籍
- 投稿日:2020-07-05T22:16:53+09:00
【感染症モデル入門】対数グラフを見てみると。。。第二波だ!?
二か月前はそろそろ終息だという予測を行ったが、
今回は、またまた感染拡大が東京と全国で発生しつつあるので、対数グラフを描いて、どの程度ヤバいのかを評価してみようと思う。
なお、利用したアプリやデータ収集方法(労働省ページから入手)は前回とほぼ同一です。前回の感染爆発は3月下旬から4月上旬に起こり(2週間程度の時間遅れがあるので、実際は3月中旬から4月上旬が感染ピークだった)、非常事態宣言も出されてどうにか終息した。
今回は、この非常事態宣言解除、そして東京アラート解除という終息宣言の後、やはりゆるみが出て今日に至ったようだ。東京の増加がヤバい
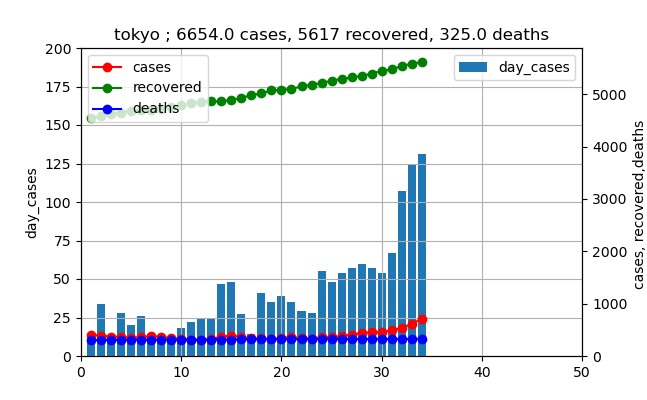
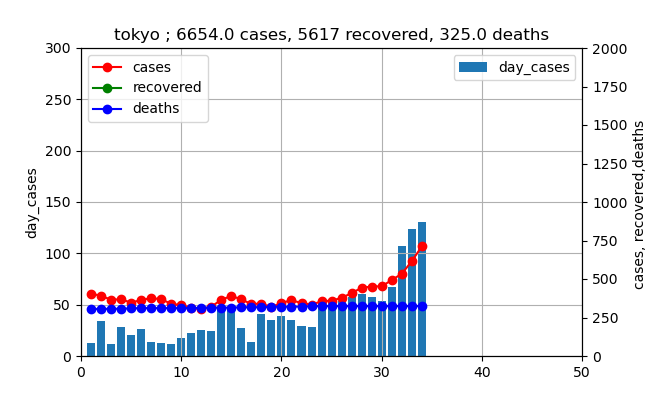
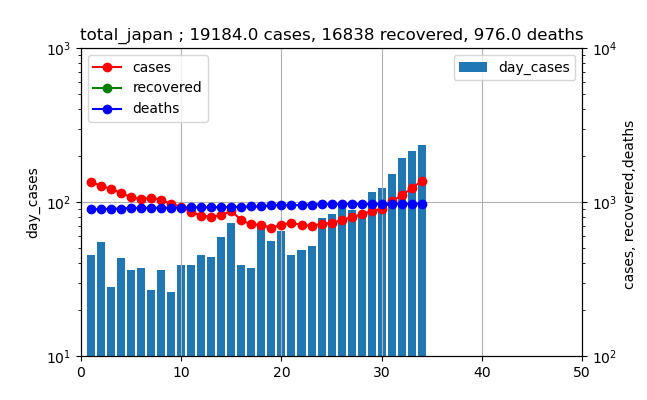
グラフで見ると以下のとおりです。(6月1日からの推移)
このグラフを見ると、新規感染数は徐々に増加しており、ついに100人を3日連続で超えてしまいました(本日も111人で4日連続になりました)。
しかし、実際の現在の患者数は赤いプロットが示すように、治癒数総数の緑のプロットに比較すると非常に小さいと言えます。
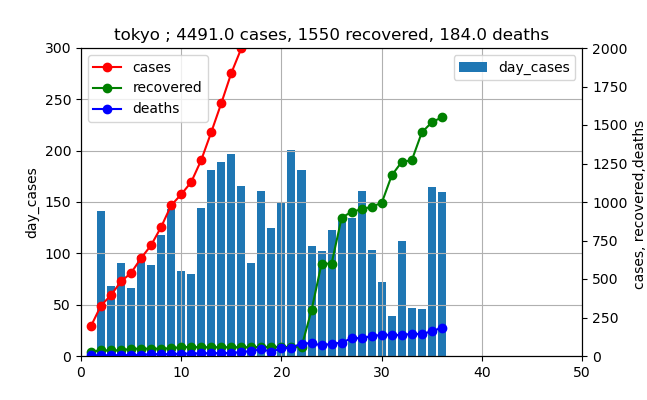
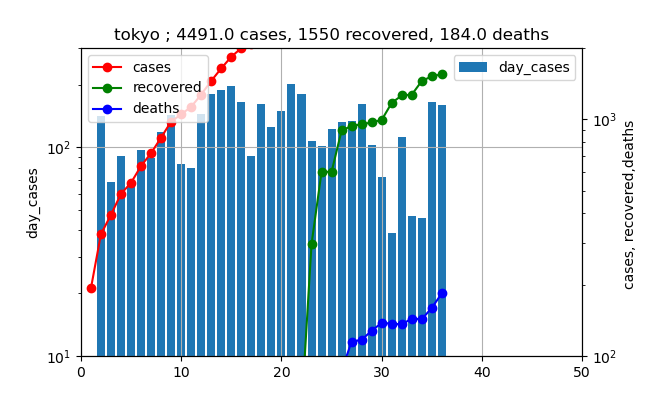
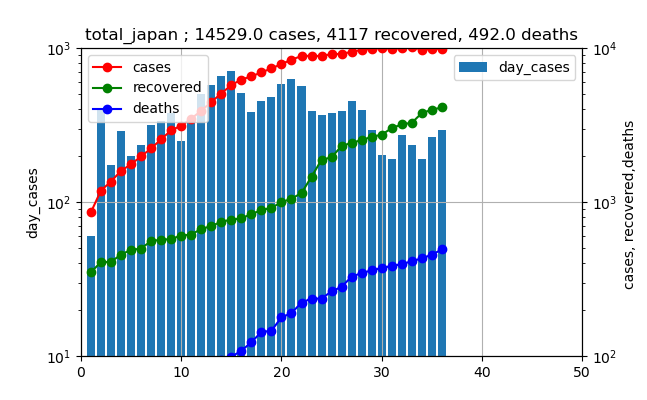
じゃ、このままでいいのかという議論をしたいと思います。そのために、前回の3月下旬から4月の感染数の推移がどうだったかを見てみましょう。(3月27日からの推移)
これを見ると、4月上旬のピーク時の値は200人程度だったことが分かります。
そして、上記のグラフをこれと同じスケールで表すと以下のようになります。
これを見ると、確かに棒グラフも増加し、さらに赤いプロットも急に増加しだしたが、まだまだ上図と比較すると少ないと思われます。
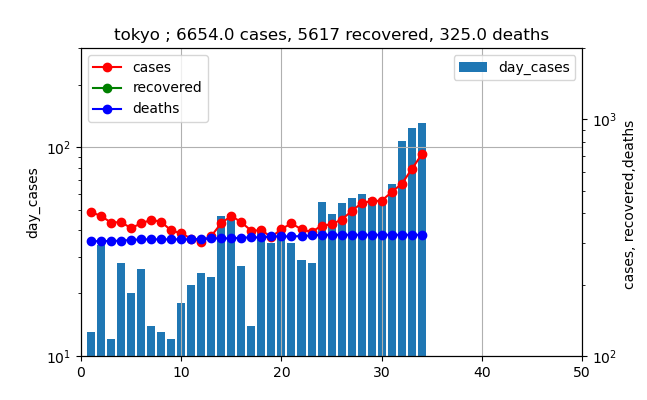
しかし、下のようにこれを対数プロットしてみるとどうでしょうか?
そして、現在は
これらの二つのグラフを比較すると、もう現在の棒グラフも赤いプロットも3月下旬から4月の爆発的な増加とほぼ同様なラインまで来ていることが分かります。
つまり、指数関数的な増加というのはそういうもので、あっという間に増加する傾向があります。今回の増加率は、たまたまだろうと思いますが、前回の増加率(傾き)と非常に似ています。つまり新規感染数は10倍/月程度の傾きを持っています。また、赤いプロットは10倍/2w程度の傾きです。
つまり、一月後には東京の新規感染数は1000人程度まで上がりそうです。その前に、赤いプロット、すなわち現存感染数であり、入院数に比例する数字ですが、二週間後程度で10000人レベルになりそうです。
二週間が重要な時間で、今なんらかの対策を打ったとしても、二週間はその対策が効果が出る前にやってきてしまいます。
ということで、これらのグラフを見るとこの傾向を減らすための、効果的な対策を早急に打つことが肝要だと思います。
※ただし、今は解放感から心が緩んだ為に発生したものと考えられるので、もう一度気持ちと行動をきちんと示す対策を打つことが必要たと思います実は全国もヤバい
当然、非常事態宣言解除は全国共通に実施されたものです。
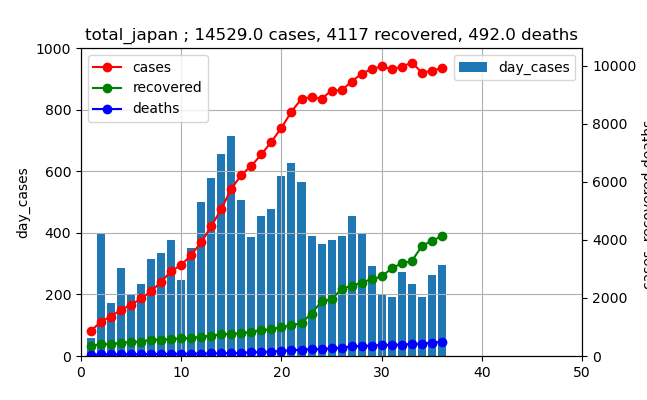
ということで、全国のデータを3月下旬から4月のデータと現在のデータを比較してみます。リニアスケールは以下のとおり
3月下旬から4月のデータ
現在のデータ
上記の比較では、まだまだ小さいので当分の間は大丈夫そうです。
しかし、これも対数プロットすると以下のように豹変します。
3月下旬から4月のデータ
現在のデータ
つまり、新規感染数が200を超えるということは、前回ピークの700位のレベルはあっという間、だいたい1週間位で達成してしまうでしょう
つまり、たぶん危険を察知して今後少しは鈍ってくると思われますが、新規感染数も感染者数も前回のピークを越えてくることが予測できます。問題はこの後の対策
問題は、この後の話です。
やはり、出来るだけ早く非常事態宣言を出して、初動対応するべきです。内容は経済を再度止める対策は必要ないと思います。
緩んだ気を引き締めて、一人一人が工夫して
・ソーシャルディスタンス
・集まらない
・マスク
・手洗い
・不要不急の移動自粛
・職場や遊戯場における3蜜回避
...
要は8割削減を再度目標にすべきだと思います。これまで培ってきたノウハウを発揮して、経済を回しながらより慎重な感染させない・感染しない対策を日々改善すればいいのだと思います。
そうでないと、今は若者中心の罹患者が高年齢層・基礎疾患持ちへ拡大して、最悪海外で遭遇しているような思わぬ犠牲者増を招くと考えられます。まとめ
・今起きている感染拡大を対数プロットして前回の感染拡大と比較した
・現在の感染拡大は既に第二波と呼べるスケールであり、放置すれば前回の感染拡大を超えると考えられる・感染症モデルでフィッティングしようと考えたが、第一波の余波が治癒数や死亡数として残っており、工夫しないと妥当な計算ができない
- 投稿日:2020-07-05T22:10:51+09:00
Python手遊び(CSVとPostgreSQL間での相互運用)
この記事、何?
ずっと前から考えていたこと。
プログラム上では変数に持つけど、ShutDownするからCSVとかにしたい。っていうか、横断検索考えると、DBに置きたい。でも、相互変換をいちいち書くのめんどい・・・列情報から最小限でテーブル作ってそこに値突っ込んで・・・とか考えてできたのがこれ。
つまり何作ったの?
まず、CSVファイルから列名を拾う。
さすがに各列の型を自動判別にしたくないので指定する。
まあ、目的は機械学習なので列の規定形式は倍精度浮動小数。なので、整数型とテキスト型の列を指定する。
で、それをもとにさっきとった列名からCREATE TABLE, INSERT INTOで突っ込む。
(まあ、INSERTはPandas使ってもいいけど、この流れを作っておいたほうがほかでいろいろやりやすいからね。)コード
# CalculateDescriptors.py import os import pandas as pd # 化合物を返す # I : SDFパス # O : 化合物オブジェクトリスト def get_mols(sdfpath): from rdkit import Chem mols = [mol for mol in Chem.SDMolSupplier(sdfpath) if mol is not None] return mols # 化合物の基本的な情報を返す [化合物名, 構造情報, 原子数, 結合数, SMILES, InChI] # I : 化合物オブジェクトリスト # O : 結果データ def get_values_base(mols): from rdkit import Chem columns = ['Name', 'Structure', 'Atoms', 'Bonds', 'SMILES', 'InChI'] values = list() for mol in mols: tmp = list() tmp.append(mol.GetProp('_Name')) tmp.append(Chem.MolToMolBlock(mol)) tmp.append(mol.GetNumAtoms()) tmp.append(mol.GetNumBonds()) tmp.append(Chem.MolToSmiles(mol)) tmp.append(Chem.MolToInchi(mol)) values.append(tmp) index = [i for i in range(len(mols))] df = pd.DataFrame(values, columns=columns, index=index) return df # 化合物の外部パラメータを返す # I : 化合物オブジェクトリスト # O : 結果データ def get_values_external(mols): from rdkit import Chem columns = ['ID', 'NAME', 'SOL', 'SMILES', 'SOL_classification'] values = list() for mol in mols: tmp = list() for column in columns: tmp.append(mol.GetProp(column)) values.append(tmp) columns = ['ext_' + column for column in columns] index = [i for i in range(len(mols))] df = pd.DataFrame(values, columns=columns, index=index) return df # 記述子を計算:RDKit # I : 化合物オブジェクトリスト # O : 結果データ def get_rdkit_descriptors(mols): from rdkit.Chem import AllChem, Descriptors from rdkit.ML.Descriptors import MoleculeDescriptors # RDKitの記述子の計算 # names = [mol.GetProp('_Name') for mol in mols] descLists = [desc_name[0] for desc_name in Descriptors._descList] calcs = MoleculeDescriptors.MolecularDescriptorCalculator(descLists) values = [calcs.CalcDescriptors(mol) for mol in mols] # DataFrameへ変換 index = [i for i in range(len(mols))] df = pd.DataFrame(values, columns=descLists, index=index) return df # 記述子を計算:mordred # I : 化合物オブジェクトリスト # O : 結果データ def get_mordred_descriptors(mols): # mordredの記述子の計算 from mordred import Calculator, descriptors calcs = Calculator(descriptors, ignore_3D=False) df = calcs.pandas(mols) df['index'] = [i for i in range(len(mols))] df.set_index('index', inplace=True) return df # 記述子を計算:CDK # I : SDFファイル # java実行ファイルパス # CDK jarファイルパス # O : 結果データ def get_cdk_descriptors(sdfpath, workfolderpath, java_path, cdk_jar_path): filepath = os.path.join(workfolderpath, 'tmp.csv') import subprocess command = f'{java_path} -jar {cdk_jar_path} -b {sdfpath} -t all -o {filepath}' print(command) subprocess.run(command, shell=False) df = pd.read_table(filepath) os.remove(filepath) return df # 主処理 def main(): data_folderpath = 'D:\\data\\python_data\\chem' sdfpath = os.path.join(data_folderpath, 'sdf\\solubility.test.20.sdf') csvpath = 'solubility.test.csv' java_path = 'C:\\Program Files\\Java\\jdk-14.0.1\\bin\\java.exe' workfolderpath = os.path.dirname(os.path.abspath(__file__)) cdk_jar_path = os.path.join(data_folderpath, 'jar\\CDKDescUI-1.4.6.jar') # 化合物取得 mols = get_mols(sdfpath) # 各値の取得 # (pythonライブラリ) dfs = list() for calcs in [get_values_base, get_values_external, get_rdkit_descriptors, get_mordred_descriptors]: dfs.append(calcs(mols)) # (jarファイル計算) dfs.append(get_cdk_descriptors(sdfpath, workfolderpath, java_path, cdk_jar_path)) # 全部結合 df = pd.concat(dfs, axis=1) df.to_csv('all_parameters.csv') print(df) # 起動処理 if __name__ == '__main__': main()も1個。
# CreateSQL.py import ReadCSVColumn # SQLを返す:DROP # I : テーブル名 # O : SQL def get_sql_drop_table(table_name): sql = f'DROP TABLE IF EXISTS {table_name}' return sql # SQLを返す:SELECT # I : テーブル名 # 列名リスト # O : SQL def get_sql_select(table_name, columns): sql = f''' SELECT {','.join(columns)} FROM {table_name} ''' return sql # SQLを返す:INSERT # I : テーブル名 # 列名リスト # O : SQL def get_sql_insert_table(table_name, columns): sql = f''' INSERT INTO {table_name} ( {','.join(columns)} ) VALUES ( {','.join(['%s' for column in columns])} ) ''' return sql # SQLを返す:CREATE TABLE # I : テーブル名 # 列名リスト # 列名リスト(再掲:整数型) # 列名リスト(再掲:テキスト型) # O : SQL def get_sql_create_table(table_name, columns, columns_int, columns_text): sql_columns = list() for column in columns: if column in columns_int: sql_columns.append(column + ' ' + 'integer') elif column in columns_text: sql_columns.append(column + ' ' + 'text') else: sql_columns.append(column + ' ' + 'double precision') sql = f''' CREATE TABLE {table_name} ( {','.join(sql_columns)} ) ''' return sql # 主処理 def main(): csvpath = 'solubility.test.csv' columns = ReadCSVColumn.get_columns_list(csvpath) columns_int = ['SampleID', 'Atoms', 'Bonds'] columns_text = ['SampleName', 'Structure', 'ID', 'NAME', 'SOL', 'SMILES', 'SOL_classification'] sql = get_sql_create_table('RDKit', columns, columns_int, columns_text) print(sql) # 起動処理 if __name__ == '__main__': main()あっ、も1個あった。
# ReadCSVColumn.py # テキストファイルを行のリスト形式で読み取る # I : ファイルパス # O : テキストリスト def get_lines_from_textfile(filepath): with open(filepath, 'r', encoding='utf-8') as f: lines = f.readlines() return lines # CSVパスリストから1行目を読み取り項目リストとして返す # I : CSVパス # O : 項目リスト def get_columns_list(csvpath): # 最終項目に改行がついていたので外す line_1st = get_lines_from_textfile(csvpath)[0] # 1行目の末尾に改行がつくので外す line_1st = line_1st.replace('\n', '') return line_1st.split(',') # 主処理 def main(): csvpath = 'solubility.test.csv' columns = get_columns_list(csvpath) for column in columns: print(column) # 起動処理 if __name__ == '__main__': main()これ全部動かすと初出のCSVと同型のテーブルをPostgreSQL上に作ってINSERTする、はず。
あとはDB上でマスタとJOINしてGROUP BYするなりご自由に。まあ・・・PostgreSQL上でPythonが動くならそれが一番いいと思うんだけどねぇ・・・
まあ、将来の課題ということで。感想
ようやくまともな枠ができかけたような気がする。
さて、次、もうちょっと本題に近いことをするよ。
- 投稿日:2020-07-05T21:54:24+09:00
[cx_Oracle入門](第11回) PL/SQLの実行の基本
連載目次
検証環境
- Oracle Cloud利用
- Oracle Linux 7.7 (VM.Standard2.1)
- Python 3.6
- cx_Oracle 8.0
- Oracle Database 19.5 (ATP, 1OCPU)
- Oracle Instant Client 18.5
無名PL/SQLの実行
無名PL/SQLの実行は、他のSQL文と同様、Cursorオブジェクトのexecute()メソッドで実行可能です。以下、サンプルです。サンプルの様に、バインド変数も利用可能です。
sample11a.pyimport cx_Oracle USERID = "admin" PASSWORD = "FooBar" DESTINATION = "atp1_low" SQL = """ begin :out_value := :in_value * 2; end; """ with cx_Oracle.connect(USERID, PASSWORD, DESTINATION) as connection: with connection.cursor() as cursor: outValue = cursor.var(int) cursor.execute(SQL, [outValue, 111]) print(outValue.getvalue())ストアドプロシージャの実行
ストアドプロシージャの実行は、下記2種類の実行方法があります。
Cursor.callproc()メソッドを使用
sample11b.pyimport cx_Oracle USERID = "admin" PASSWORD = "FooBar" DESTINATION = "atp1_low" SQL = """ create or replace procedure sample11b(in_value in number, out_value out number) is begin out_value := in_value * 2; end; """ with cx_Oracle.connect(USERID, PASSWORD, DESTINATION) as connection: with connection.cursor() as cursor: outValue = cursor.var(int) cursor.execute(SQL) cursor.callproc("sample11b", [222, outValue]) print(outValue.getvalue())下から2行目のように、最初の引数で呼び出したいストアドプロシージャの名前をstr型で指定してください。2番目の引数にはストアドプロシージャへの引数を、プロシージャの引数仕様に合わせて指定します。
Cursor.execute()メソッドを使用してSQLのCALL文を実行
sample11c.pyimport cx_Oracle USERID = "admin" PASSWORD = "FooBar" DESTINATION = "atp1_low" SQL = """ create or replace procedure sample11b(in_value in number, out_value out number) is begin out_value := in_value * 2; end; """ with cx_Oracle.connect(USERID, PASSWORD, DESTINATION) as connection: with connection.cursor() as cursor: outValue = cursor.var(int) cursor.execute(SQL) cursor.execute("call sample11b(:a, :b)", [333, outValue]) print(outValue.getvalue())プロシージャの引数をバインド変数として指定する必要があります。
callproc()とexecute()+CALLのどちらがよいかというと、callproc()の場合、DB APIのcallproc()は引数名を指定した引数の指定に対応していません。ただしcx_OracleではDB APIを拡張して対応しています。DB APIに厳密に対応したコーディングがしたい場合はexecute()+CALLとなります。とはいえ、cx_OracleはDB APIにない、独自拡張した仕様が結構ありますので、厳密に守るのも難しそうです。
逆に、コーディングのわかりやすさはcallproc()だと思います。また、CALL文でのストアドプロシージャやストアドファンクションの呼び出しは、callproc()と比べて微妙に仕様が異なる場合があるようです。こういった点が気になる場合はcallproc()の利用をお勧めいたします。ストアドファンクションの実行
ストアドプロシージャの実行は、下記2種類の実行方法があります。
Cursor.callfunc()メソッドを使用
sample11d.pyimport cx_Oracle USERID = "admin" PASSWORD = "FooBar" DESTINATION = "atp1_low" SQL = """ create or replace function sample11d(in_value in number) return number is begin return in_value * 2; end; """ with cx_Oracle.connect(USERID, PASSWORD, DESTINATION) as connection: with connection.cursor() as cursor: cursor.execute(SQL) returnValue = cursor.callfunc("sample11d", int, [111]) print(returnValue)下から2行目のように、関数を演算結果を戻すので、変数(サンプルのケースだとreturnValue)で受けています。
callfunc()メソッドの引数は、1つ目はファンクション名で、str型で渡す必要があります。2つ目は関数の戻り値のデータ型を指定します。3つ目は、関数の引数です。Cursor.execute()メソッドを使用してSQLのCALL文を実行
sample11e.pyimport cx_Oracle USERID = "admin" PASSWORD = "FooBar" DESTINATION = "atp1_low" SQL = """ create or replace function sample11d(in_value in number) return number is begin return in_value * 2; end; """ with cx_Oracle.connect(USERID, PASSWORD, DESTINATION) as connection: with connection.cursor() as cursor: outValue = cursor.var(int) cursor.execute(SQL) cursor.execute("call sample11d(:inValue) into :outValue", [222, outValue]) print(outValue.getvalue())基本的にはストアドプロシージャの実行と同様です。ストアドファンクションの場合は、戻り値を受けるためにINTO句が必要になる点、ご注意ください。
上記二つ実行方法ののどちらがよいかというと、基本的にはストアドファンクションと同様の考え方となります。違いは、DB APIにはcallfunc()が存在しない点です。
- 投稿日:2020-07-05T21:42:11+09:00
Python手遊び(記述子計算:真面目版)
この記事、何?
昔々、Python書き始めたころに化合物の記述子というものの計算を書いたことがある。
けど、まあ、見事に「Pnadasって何?」「っていうか、答え出るからいいよね?」って状態。
あれからだいぶたったので書き直してみた。そして、続投するDBへのI/Oへと続く。
まあ、手を入れるべきところは多いんだけど、「Done is better than perfect」ということで、いったんここで区切る。
概要
化合物の情報として、SDFファイルを用意する。
で、それをRDKitを使って、こんなやって変数化する。# 化合物取得 sdfpath = 'xxx.sdf' mols = get_mols(sdfpath)で、化合物ごとに「行」を構成し、何種類かの「列」を返す関数をいくつか作る。
やることは一緒なのでせっかくだから関数の形をそろえてみた。
ちなみに、戻り値の方はPandasのDataFrame型。
最近ようやく気づいたけど、これが便利。で、まとめてcsvとして出力。
コード
import os import pandas as pd # 化合物を返す # I : SDFパス # O : 化合物オブジェクトリスト def get_mols(sdfpath): from rdkit import Chem mols = [mol for mol in Chem.SDMolSupplier(sdfpath) if mol is not None] return mols # 化合物の基本的な情報を返す [化合物名, 構造情報, 原子数, 結合数, SMILES, InChI] # I : 化合物オブジェクトリスト # O : 結果データ def get_values_base(mols): from rdkit import Chem columns = ['Name', 'Structure', 'Atoms', 'Bonds', 'SMILES', 'InChI'] values = list() for mol in mols: tmp = list() tmp.append(mol.GetProp('_Name')) tmp.append(Chem.MolToMolBlock(mol)) tmp.append(mol.GetNumAtoms()) tmp.append(mol.GetNumBonds()) tmp.append(Chem.MolToSmiles(mol)) tmp.append(Chem.MolToInchi(mol)) values.append(tmp) index = [i for i in range(len(mols))] df = pd.DataFrame(values, columns=columns, index=index) return df # 化合物の外部パラメータを返す # I : 化合物オブジェクトリスト # O : 結果データ def get_values_external(mols): from rdkit import Chem columns = ['ID', 'NAME', 'SOL', 'SMILES', 'SOL_classification'] values = list() for mol in mols: tmp = list() for column in columns: tmp.append(mol.GetProp(column)) values.append(tmp) columns = ['ext_' + column for column in columns] index = [i for i in range(len(mols))] df = pd.DataFrame(values, columns=columns, index=index) return df # 記述子を計算:RDKit # I : 化合物オブジェクトリスト # O : 結果データ def get_rdkit_descriptors(mols): from rdkit.Chem import AllChem, Descriptors from rdkit.ML.Descriptors import MoleculeDescriptors # RDKitの記述子の計算 # names = [mol.GetProp('_Name') for mol in mols] descLists = [desc_name[0] for desc_name in Descriptors._descList] calcs = MoleculeDescriptors.MolecularDescriptorCalculator(descLists) values = [calcs.CalcDescriptors(mol) for mol in mols] # DataFrameへ変換 index = [i for i in range(len(mols))] df = pd.DataFrame(values, columns=descLists, index=index) return df # 記述子を計算:mordred # I : 化合物オブジェクトリスト # O : 結果データ def get_mordred_descriptors(mols): # mordredの記述子の計算 from mordred import Calculator, descriptors calcs = Calculator(descriptors, ignore_3D=False) df = calcs.pandas(mols) df['index'] = [i for i in range(len(mols))] df.set_index('index', inplace=True) return df # 記述子を計算:CDK # I : SDFファイル # java実行ファイルパス # CDK jarファイルパス # O : 結果データ def get_cdk_descriptors(sdfpath, workfolderpath, java_path, cdk_jar_path): filepath = os.path.join(workfolderpath, 'tmp.csv') import subprocess command = f'{java_path} -jar {cdk_jar_path} -b {sdfpath} -t all -o {filepath}' print(command) subprocess.run(command, shell=False) df = pd.read_table(filepath) os.remove(filepath) return df # 主処理 def main(): data_folderpath = 'D:\\data\\python_data\\chem' sdfpath = os.path.join(data_folderpath, 'sdf\\solubility.test.20.sdf') csvpath = 'solubility.test.csv' java_path = 'C:\\Program Files\\Java\\jdk-14.0.1\\bin\\java.exe' workfolderpath = os.path.dirname(os.path.abspath(__file__)) cdk_jar_path = os.path.join(data_folderpath, 'jar\\CDKDescUI-1.4.6.jar') # 化合物取得 mols = get_mols(sdfpath) # 各値の取得 # (pythonライブラリ) dfs = list() for calcs in [get_values_base, get_values_external, get_rdkit_descriptors, get_mordred_descriptors]: dfs.append(calcs(mols)) # (jarファイル計算) dfs.append(get_cdk_descriptors(sdfpath, workfolderpath, java_path, cdk_jar_path)) # 全部結合 df = pd.concat(dfs, axis=1) df.to_csv('all_parameters.csv') print(df) # 起動処理 if __name__ == '__main__': main()(出力:中略あり)
>python CalculateDescriptors.py 100%|██████████████████████████████████████████████████████████████████████████████████| 20/20 [00:01<00:00, 17.22it/s] ... Name Structure Atoms Bonds ... ALogP ALogp2 AMR nAcid 0 1 1\n RDKit 2D\n\n 6 5 0 0 0 ... 6 5 ... -0.3400 0.115600 26.1559 0 1 2 2\n RDKit 2D\n\n 7 6 0 0 0 ... 7 6 ... 1.2082 1.459747 33.4010 0 2 3 3\n RDKit 2D\n\n 5 4 0 0 0 ... 5 4 ... 0.7264 0.527657 23.4093 0 3 4 4\n RDKit 2D\n\n 6 6 0 0 0 ... 6 6 ... 0.4030 0.162409 25.0454 0 4 5 5\n RDKit 2D\n\n 5 4 0 0 0 ... 5 4 ... 1.4774 2.182711 25.1598 0 5 6 6\n RDKit 2D\n\n 7 7 0 0 0 ... 7 7 ... 1.4658 2.148570 35.8212 0 6 7 7\n RDKit 2D\n\n 8 7 0 0 0 ... 8 7 ... -0.2734 0.074748 30.1747 0 7 8 8\n RDKit 2D\n\n 8 8 0 0 0 ... 8 8 ... 1.5147 2.294316 40.0862 0 8 9 9\n RDKit 2D\n\n 9 9 0 0 0 ... 9 9 ... 2.7426 7.521855 43.8018 0 9 10 10\n RDKit 2D\n\n 9 10 0 0 0 ... 9 10 ... 0.8490 0.720801 41.1580 0 10 11 11\n RDKit 2D\n\n 10 10 0 0 0 ... 10 10 ... 2.1019 4.417984 48.7581 0 11 12 12\n RDKit 2D\n\n 12 12 0 0 0 ... 12 12 ... 0.1695 0.028730 52.1462 0 12 13 13\n RDKit 2D\n\n 14 15 0 0 0 ... 14 15 ... 2.5404 6.453632 69.2022 0 13 14 14\n RDKit 2D\n\n 12 13 0 0 0 ... 12 13 ... 2.0591 4.239893 58.2832 0 14 15 15\n RDKit 2D\n\n 12 13 0 0 0 ... 12 13 ... 2.8406 8.069008 57.7168 0 15 16 16\n RDKit 2D\n\n 14 16 0 0 0 ... 14 16 ... 2.4922 6.211061 67.3498 0 16 17 17\n RDKit 2D\n\n 16 18 0 0 0 ... 16 18 ... 3.3850 11.458225 75.9138 0 17 18 18\n RDKit 2D\n\n 18 21 0 0 0 ... 18 21 ... 3.0366 9.220940 85.5468 0 18 19 19\n RDKit 2D\n\n 18 21 0 0 0 ... 18 21 ... 3.0366 9.220940 85.5468 0 19 20 20\n RDKit 2D\n\n 14 16 0 0 0 ... 14 16 ... -0.5223 0.272797 60.8303 0 [20 rows x 2322 columns]あっ、SDFファイルに外部パラメータが5個あることを前提条件にしてしまっている・・・
そのうち直そう。。。それも込みで、RDKitの化合物情報から6つ、上記の外部パラメータが5個、RDKitから200個、CDKから286個、mordredから1824個で全部で2322個の値が取れました、という話・・・ん?1個違う?あっ、Indexか。なるほど。
感想
まあ、悪くないかも。
ほかにいろいろ作りたいものがあるのでもうちょっと出そろってから関数分けまじめに考えます。で、次の投稿に続く・・・と思う。
- 投稿日:2020-07-05T21:17:41+09:00
Djangoのテスト
はじめに
ここでは、Djangoにおけるテストについて解説していきます。
テスト対象
テスト対象は、以下のシンプルなブログ記事一覧ページとします。
project/urls.pyfrom django.contrib import admin from django.urls import include, path urlpatterns = [ path('admin/', admin.site.urls), path('blog/', include('blog.urls') ]blog/urls.pyfrom django.urls import path from . import views app_name = 'blog' urlpatterns = [ path('list/', views.PostList.as_view(), name='post_list') ]blog/models.pyfrom django.db import models class Post(models.model): title = models.CharField('タイトル', max_length=100) body = models.TextField('本文') created_at = models.DateTimeField('作成日時', auto_now_add=True) updated_at = models.DateTimeField('更新日時', auto_now=True) class Meta: ordering = ('-created_at') def __str__(self): return self.titleblog/views.pyfrom django.views import generic class PostList(generic.ListView): model = Post template_name = 'blog/post_list.html'blog/post_list.html{% for post in post_list %} <h1>{{ post.title }}</h1> <p>{{ post.body }}</p> {% endfor %}ファクトリークラスの作成
factory_boyを使うと、テスト用のレコードを作成することができます。blog/tests.pyimport factory from django.utils import timezone from .models import Post class PostFactory(factory.django.DjangoModelFactory): title = 'Sample post' body = 'This is a sample text.' created_at = timezone.now() updated_at = timezone.now() class Meta: model = Postここでは、
Postモデル用のファクトリークラスとして、PostFactoryを作成します。
titleやtextなどのデフォルト値を設定できます。テストの作成
blog/tests.pyfrom django.urls import reverse from django.test import TestCase class PostListTests(TestCase): def test_get_queryset(self): post_1 = PostFactory( title='First Post', body='This is the first post.' ) post_2 = PostFactory( title='Second Post', body='This is the second post.' ) res = self.client.get(reverse('blog:post_list')) self.assertTemplateUsed(res, 'blog/post_list.html') self.assertQuerysetEqual( res.context['post_list'], ['<Post: Second Post>', '<Post: First Post>'] ) self.assertEqual( res.context['post_list'][0].body, 'This is the first post.' ) self.assertEqual( res.context['post_list'][1].body, 'This is the second post.' )まず、上で作成した
PostFactoryを用いて、Postのレコードを作成します。
そして、記事一覧ページにアクセスした時のレスポンスを変数resに格納します。
resには、viewで作成されるcontextとしてpost_listが含まれますので、期待通りのquerysetが得られているかを確認します。
また、djangoのテストでは、views.pyで指定したHTMLテンプレートが使用されているかを確認するために、assertTemplateUsedが使えます。テストの実行
テストを実行するには、以下のコマンドを入力します。
$ python manage.py test (blog)最後にアプリケーション名を入れると、指定したアプリケーションでのみテストが実行されます。
まとめ
ここでは、djangoにおけるテストについて解説しました。
開発が進む中でバグを防止するためにもテストは重要です。
- 投稿日:2020-07-05T21:14:04+09:00
Pythonの音声処理ライブラリ【LibROSA】で音声読み込み⇒スペクトログラム変換・表示⇒位相推定して音声復元
LibROSAとは
- LibROSAはPythonの音声処理ライブラリです。
- 様々な音声処理を簡潔に記述できます。
- 今回は以下の音声処理の基本処理をまとめました。
- 音声の読み込み
- 周波数を指定して音声を読み込み
- Notebook上で、音声をプレーヤーで再生
- 音声波形のグラフを表示
- スペクトログラムへの変換
- STFTで音声からスペクトログラムへ変換
- 強度をdB単位に変換
- スペクトログラムのカラープロットを表示
- 音声を復元
- 逆STFTでスペクトログラムから音声を復元する場合
- 位相情報を推定して音声を復元する場合
初期化
import os from tqdm import tqdm import numpy as np import matplotlib.pyplot as plt import IPython.display from IPython.display import display import pandas as pd import librosa import librosa.display# pyplotのデフォルト値を設定 plt.rcParams.update({ 'font.size' : 10 ,'font.family' : 'Meiryo' if os.name == 'nt' else '' # Colabでは日本語フォントがインストールされてないので注意 ,'figure.figsize' : [10.0, 5.0] ,'figure.dpi' : 300 ,'savefig.dpi' : 300 ,'figure.titlesize' : 'large' ,'legend.fontsize' : 'small' ,'axes.labelsize' : 'medium' ,'xtick.labelsize' : 'small' ,'ytick.labelsize' : 'small' }) # ndarrayの表示設定 np.set_printoptions(threshold=0) # 可能ならndarrayを省略して表示 np.set_printoptions(edgeitems=1) # 省略時に1つの要素だけ表示音声の確認
読み込み
librosaに標準で入っている音声ファイルを読込みます。1
audio_path = librosa.util.example_audio_file(); audio_path出力'(ホームディレクトリなど)\\anaconda3\\lib\\site-packages\\librosa\\util\\example_data\\Kevin_MacLeod_-_Vibe_Ace.ogg'librosa.load() ドキュメント https://librosa.org/librosa/master/generated/librosa.core.load.html
y, sr = librosa.load(audio_path) # サンプリング周波数 22.05kHzで読み込み # y, sr = librosa.load(librosa.util.example_audio_file(), sr=None) # 元の音声ファイルのサンプリング周波数で読み込む場合 # y, sr = librosa.load(librosa.util.example_audio_file(), sr=4096) # 約4kHzでリサンプリングして読み込む場合 print([type(y), y.shape], [type(sr), sr])出力[<class 'numpy.ndarray'>, (1355168,)] [<class 'int'>, 22050]サンプリング周波数
srについて
-srはSampling Rate(サンプリング周波数)の略です。1秒間の音声を何個のデータで表すかを示します。(↑の例では22050データ/秒)
- 全データ数y.size=sr× 再生時間 が成り立ちます。
- srを指定しない場合、読み込んだファイルのサンプリング周波数に関わらず、22.05kHzにリサンプリングして読み込みます。 ← 【初見注意】
-sr=Noneを指定すると、元ファイルのサンプリング周波数で読み込みます。
-sr=値を指定すると、指定したサンプリング周波数で読み込みます。音声をプレーヤーで確認
- IPython.display.display() ドキュメント https://ipython.readthedocs.io/en/stable/api/generated/IPython.display.html#IPython.display.display
- IPython.display.Audio() ドキュメント https://ipython.readthedocs.io/en/stable/api/generated/IPython.display.html#IPython.display.Audio
音声はBase64エンコーディングしてJupyter Notebookに埋め込まれます。(重いので本記事では置き換えました)
display(IPython.display.Audio(y, rate=sr))librosa音声変換記事 https://t.co/CedmBGtHfS
— lilacs2039 (@lilacs2039) July 5, 2020
Vibe Ace (Kevin MacLeod) / CC BY 3.0 pic.twitter.com/eMkYzYU3af音声波形表示
librosa.display.waveplot() ドキュメント https://librosa.org/librosa/master/generated/librosa.display.waveplot.html
mpl_collection = librosa.display.waveplot(y, sr=sr) mpl_collection.axes.set(title="音声波形", ylabel="波形の振幅")出力[Text(0, 0.5, '波形の振幅'), Text(0.5, 1.0, '音声波形')]スペクトログラムへの変換
- 音声信号に「短時間フーリエ変換(Short-time Fourier transform : STFT)」を行うことでスペクトログラムが得られます。
- スペクトログラムとは、音声を周波数スペクトルの時間経過で示したものです。
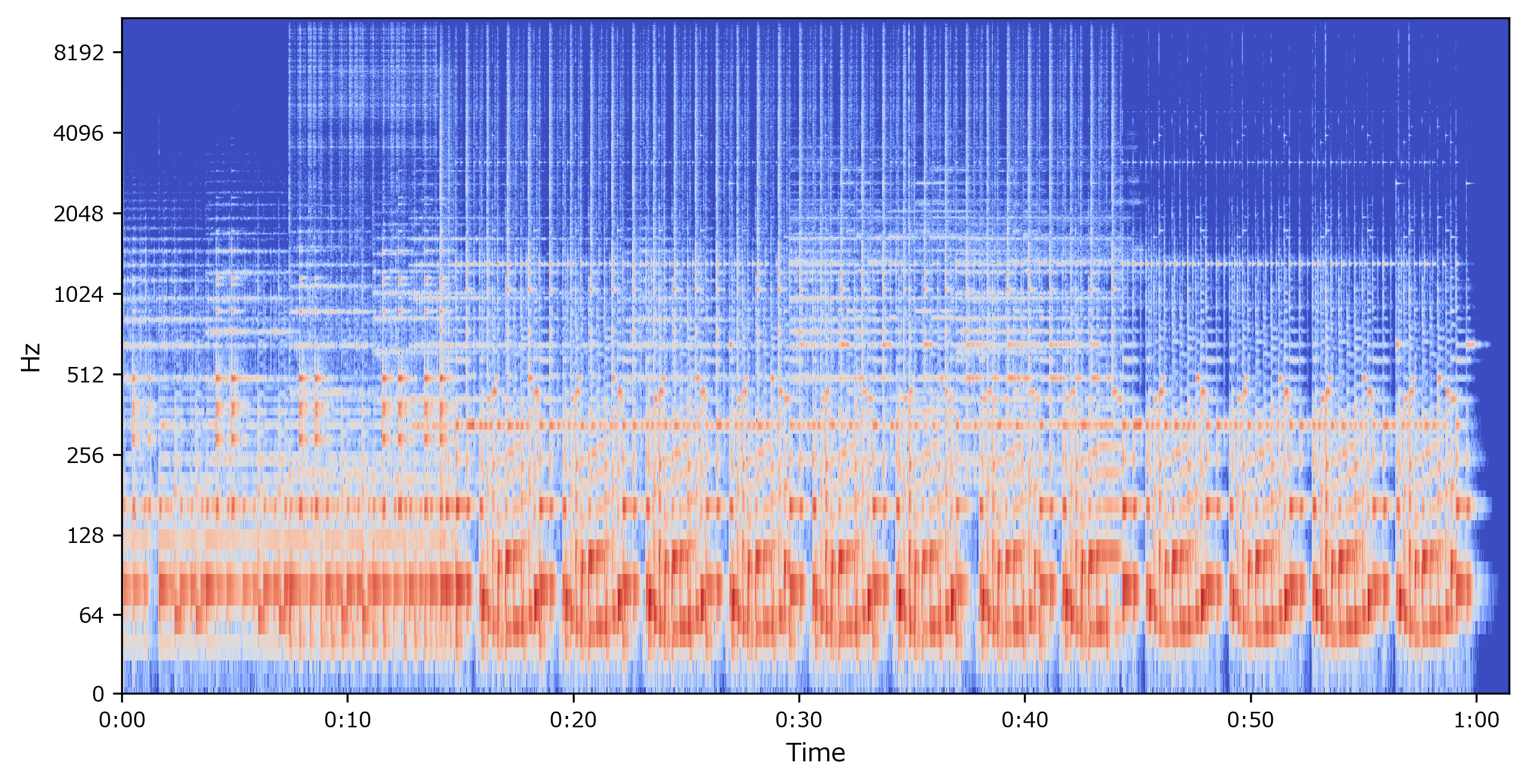
スペクトログラムの計算・表示
D = librosa.stft(y) # STFT S, phase = librosa.magphase(D) # 複素数を強度と位相へ変換 Sdb = librosa.amplitude_to_db(S) # 強度をdb単位へ変換 librosa.display.specshow(Sdb, sr=sr, x_axis='time', y_axis='log') # スペクトログラムを表示出力<matplotlib.axes._subplots.AxesSubplot at 0x1cb80c833c8>やっていること
STFT
- STFTの手順
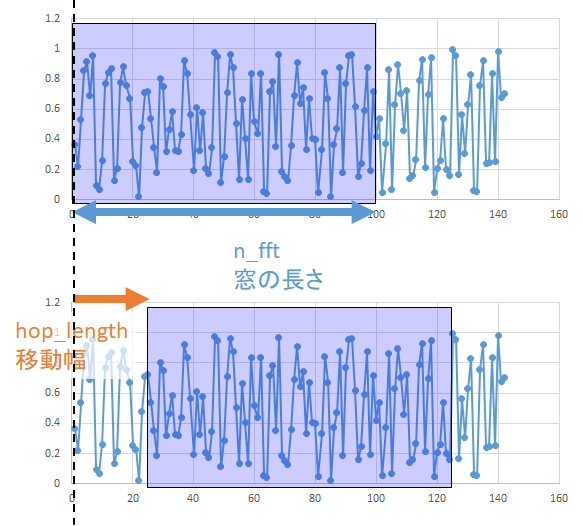
- 音声信号のある時間範囲を窓で区切ってフーリエ変換して、その時間範囲の周波数スペクトルを計算します。
- 窓をずらしながら繰り返すことで、周波数スペクトルの時間経過の行列
Dが得られます。- STFTの主なパラメータ
n_fft(窓の長さ)- デフォルト値は
2048hop_length(窓の移動幅)- デフォルト値は
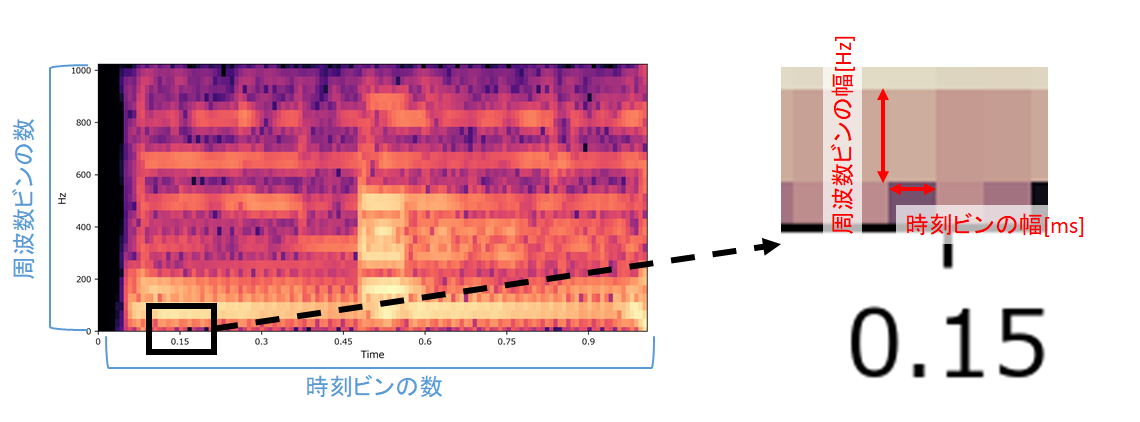
n_fft/4周波数ビン・時刻ビンの計算方法
スペクトログラム計算結果のイメージ
- 「周波数ビンの数」「時刻ビンの数」「周波数ビンの幅」「時刻ビンの幅」は以下のように計算できます。
- サンプリング定理から、音声の周波数はサンプリング周波数/2までしか表現できません。
デフォルト値において、
librosa.stft()は以下のような仕様になることがわかります。
- 0Hz~約11kHzの範囲を約1025分割して表現(周波数分解能は約10.76Hz)
- 1秒間を約43分割して表現(時間分解能は約23.26ms)
srやn_fftを調整して目標の分解能やデータサイズが実現できます。STFTの出力の行列
Dの確認librosa.stft() ドキュメント https://librosa.org/librosa/master/generated/librosa.core.stft.html
D = librosa.stft(y) # STFT print(type(D), D.shape) print(D)出力<class 'numpy.ndarray'> (1025, 2647) [[ 2.5802802e-03-0.j ... 7.2303657e-05-0.j] ... [-1.7063057e-07-0.j ... -5.1327298e-09-0.j]]
- STFTで得られた
Dは複素数の2次元ndarray ※ であることがわかります。※ 「2次元」ではなく「2階のテンソル」と呼ぶ方が正しいかもしれませんが、本記事では2次元で統一します。
複素数を強度と位相へ変換
複素数の行列
Dを、強度の行列Sと位相の行列phaseに変換します。
- librosa.magphase() ドキュメント https://librosa.org/librosa/master/generated/librosa.core.magphase.htmlS, phase = librosa.magphase(D) # 複素数を強度と位相へ変換
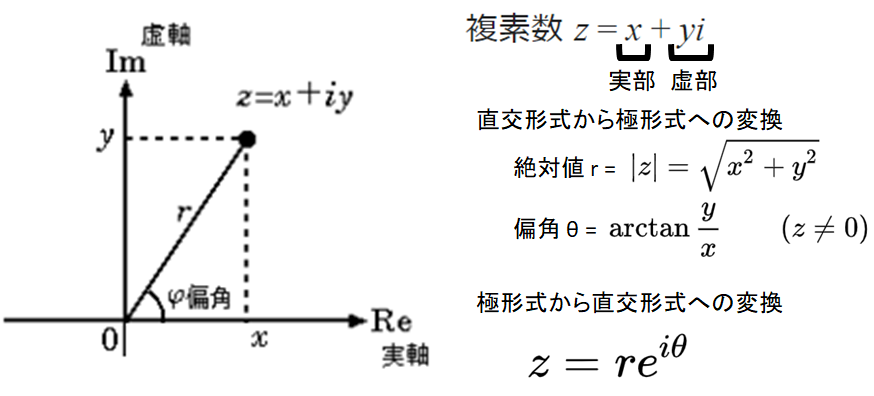
librosa.magphase(D)がやっていること
- STFTで得られた行列Dの複素数は直交形式ですが、スペクトログラムは極形式(絶対値 r: 強度, 偏角 θ: 位相)が望ましいです。
- そこで、複素数を「直交形式から極形式へ変換」しています。
- 参考:複素平面 ~ wikipedia https://ja.wikipedia.org/wiki/%E8%A4%87%E7%B4%A0%E5%B9%B3%E9%9D%A2
強度の行列
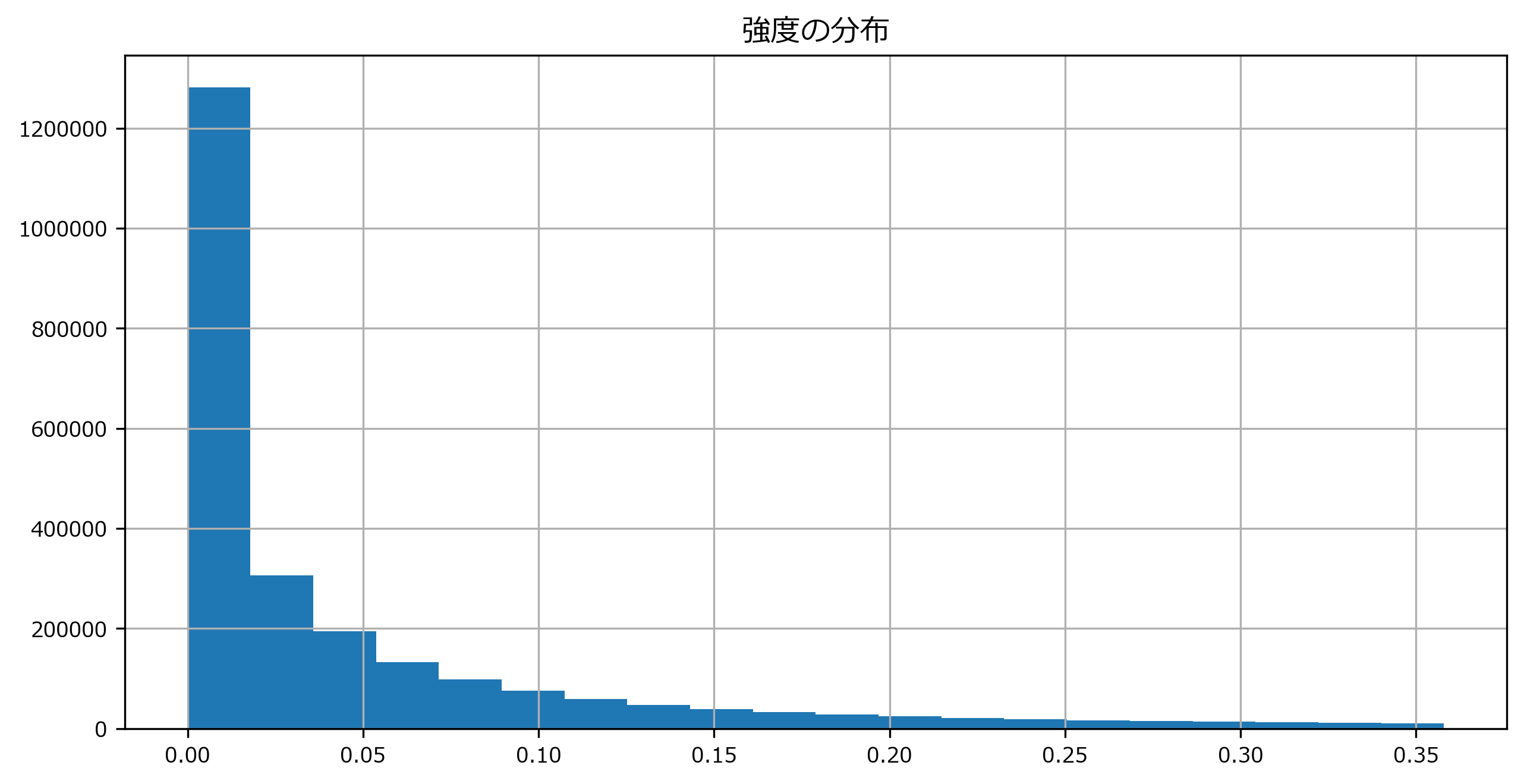
Sの確認print(type(S), S.shape) print(S)出力<class 'numpy.ndarray'> (1025, 2647) [[2.5802802e-03 ... 7.2303657e-05] ... [1.7063057e-07 ... 5.1327298e-09]]s = pd.DataFrame(S.flatten()) s.hist(bins=20, range=(s.min().values[0],s.quantile(0.9).values[0]) ) # Sの最小値~90%点までの分布を表示 plt.title("強度の分布")出力Text(0.5, 1.0, '強度の分布')強度の行列
Sは、2次元ndarrayで各要素は0より大きい実数であることがわかります。位相の行列
phaseの確認print(type(phase), phase.shape) print(phase)出力<class 'numpy.ndarray'> (1025, 2647) [[ 1.+0.000000e+00j ... 1.+0.000000e+00j] ... [-1.+8.742278e-08j ... -1.+8.742278e-08j]]p = pd.DataFrame(phase.flatten()).sample(n=1000) # 散布図にするにはデータ数多すぎなので、1000データをランダムサンプリング mpl_collection = plt.scatter(np.real(p), np.imag(p)) mpl_collection.axes.set(title="複素平面上の位相の散布図", xlabel="実部", ylabel="虚部", aspect='equal')出力[Text(0, 0.5, '虚部'), Text(0.5, 0, '実部'), Text(0.5, 1.0, '複素平面上の位相の散布図'), None]位相の行列
phaseは、2次元ndarrayで各要素は絶対値1, 偏角θの複素数であることがわかります。強度をdb単位へ変換
- スペクトログラムの強度が線形スケールで扱いづらい場合は、dB単位に変換して対数スケールで扱えるようにします。
- dB単位では、+20dBで(振幅)スペクトログラムの強度は10倍になります。
librosa.amplitude_to_db() ドキュメント https://librosa.org/librosa/master/generated/librosa.core.amplitude_to_db.html
Sdb = librosa.amplitude_to_db(S) # 強度をdb単位へ変換
librosa.amplitude_to_db()がやっていること下式で、振幅スペクトログラムをdB単位に変換します。
- 主なパラメータ
- 最小値
amin- 計算式のlogの中身が0のとき戻り値が-∞とならないように、最小値を指定
- デフォルト値 1e-5
- 基準値
ref- スペクトログラムの2乗 = refのとき、0dBとなるように変換する。
- デフォルト値 1
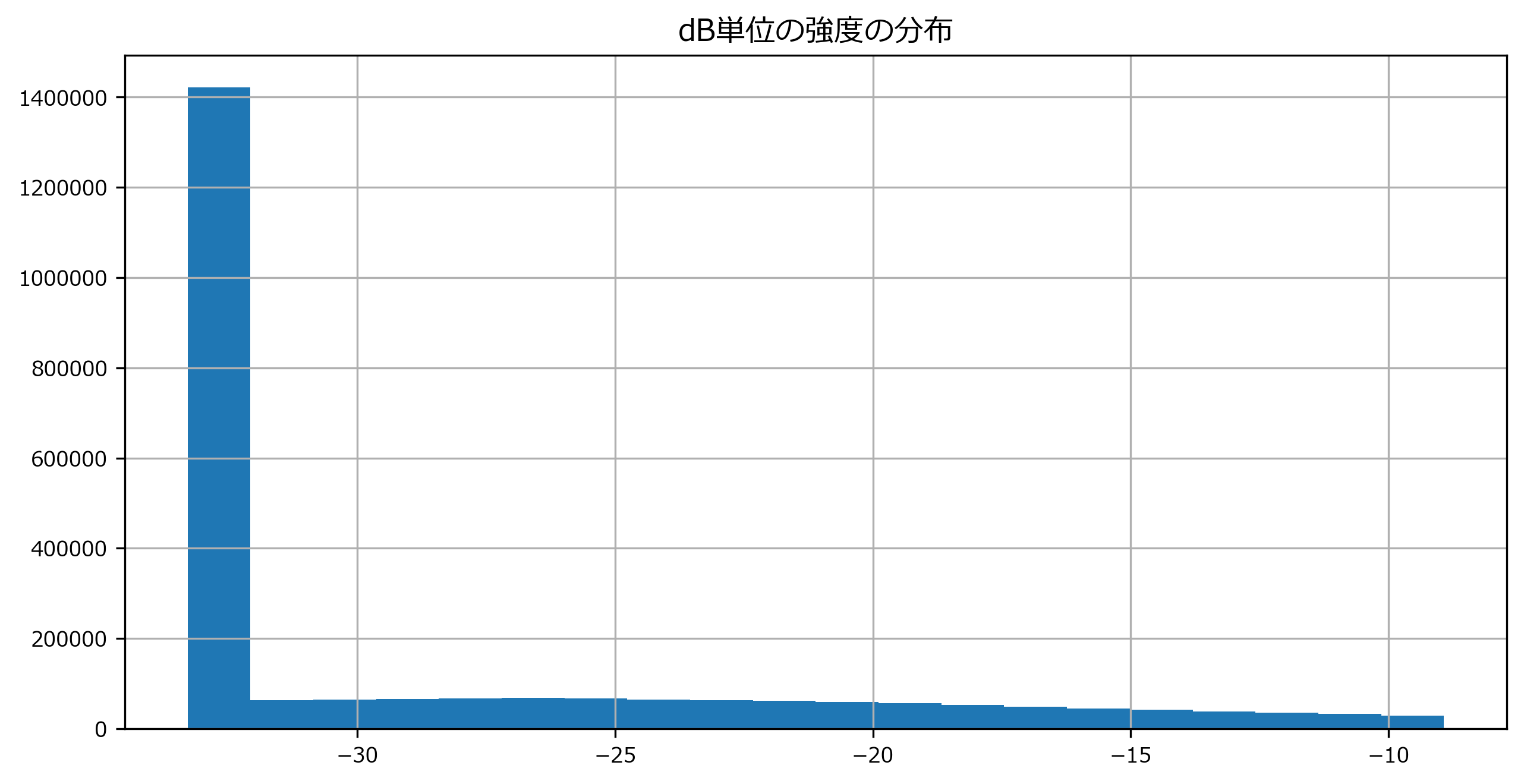
dB単位の強度の行列
Sdbの確認print(type(Sdb), Sdb.shape) print(Sdb)出力<class 'numpy.ndarray'> (1025, 2647) [[-33.29261 ... -33.29261] ... [-33.29261 ... -33.29261]]sdb = pd.DataFrame(Sdb.flatten()) sdb.hist(bins=20, range=(sdb.min().values[0], sdb.quantile(0.9).values[0]) ) # Sの最小値~90%点までの分布を表示 plt.title("dB単位の強度の分布")出力Text(0.5, 1.0, 'dB単位の強度の分布')スペクトログラムを表示
- 周波数と強さは線型目盛でも対数目盛でもよく、用途によって使い分けます。
librosa.display.specshow() ドキュメント https://librosa.org/librosa/master/generated/librosa.display.specshow.html
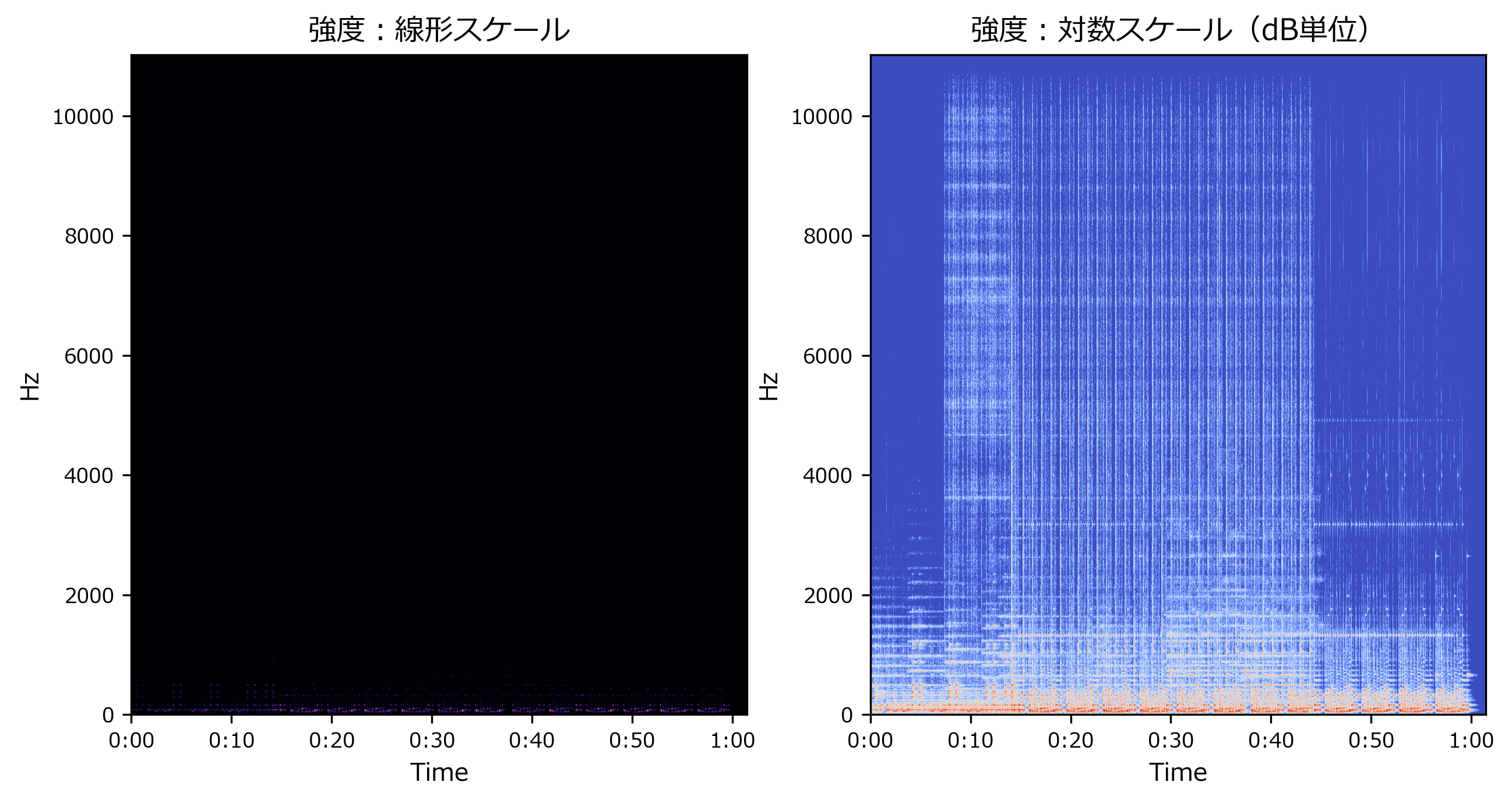
周波数:線形スケール
librosa.display.specshow()の引数に、y_axis='hz'を指定しますfig,axes = plt.subplots(nrows=1,ncols=2) axes[0].set_title("強度:線形スケール") librosa.display.specshow(S, sr=sr, x_axis='time', y_axis='hz', ax=axes[0]) axes[1].set_title("強度:対数スケール(dB単位)") librosa.display.specshow(Sdb, sr=sr, x_axis='time', y_axis='hz', ax=axes[1])出力<matplotlib.axes._subplots.AxesSubplot at 0x1cb81bed2c8>周波数:対数スケール
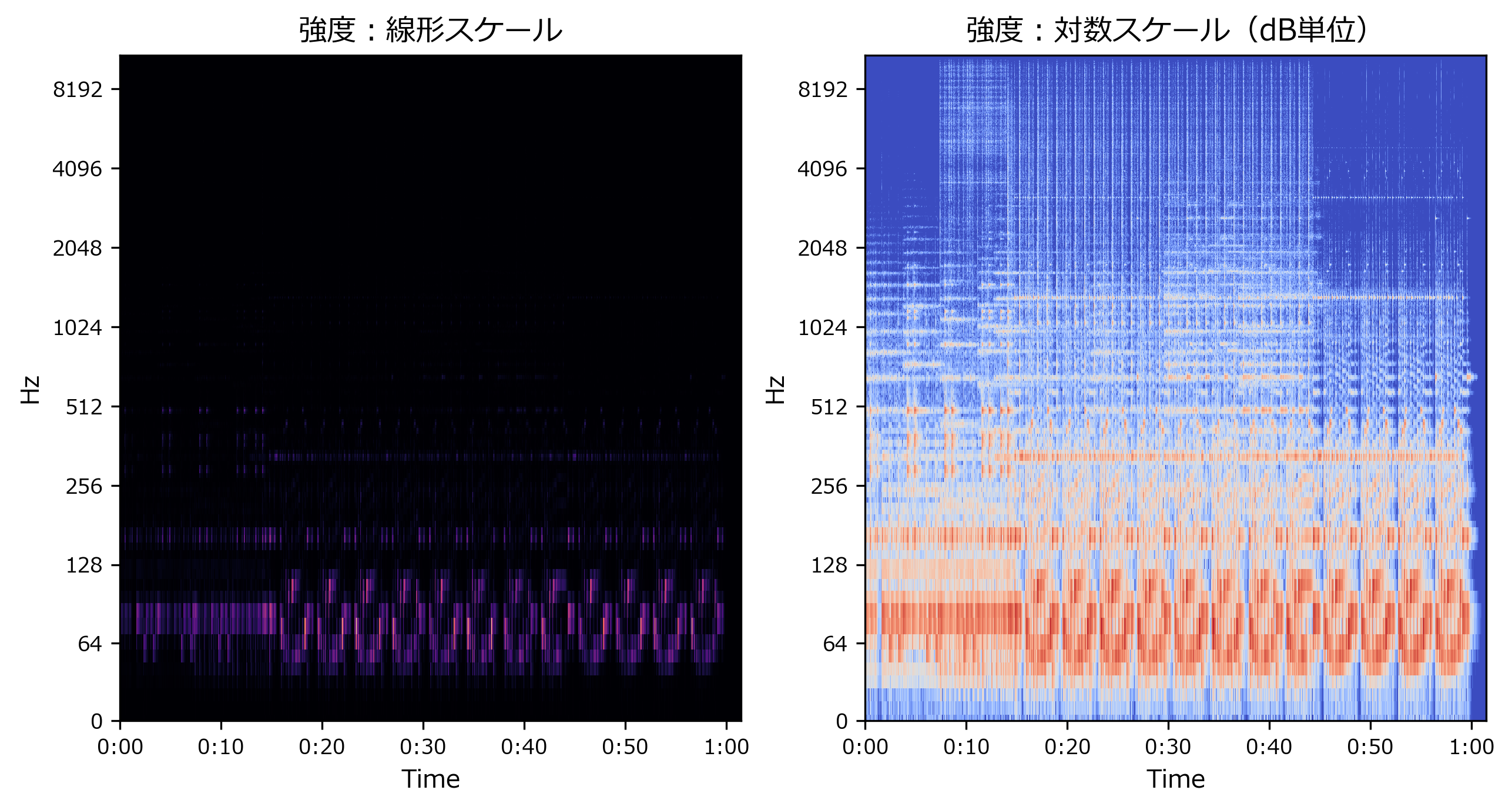
librosa.display.specshow()の引数に、y_axis='log'を指定しますfig,axes = plt.subplots(nrows=1,ncols=2) axes[0].set_title("強度:線形スケール") librosa.display.specshow(S, sr=sr, x_axis='time', y_axis='log', ax=axes[0]) axes[1].set_title("強度:対数スケール(dB単位)") librosa.display.specshow(Sdb, sr=sr, x_axis='time', y_axis='log', ax=axes[1])出力<matplotlib.axes._subplots.AxesSubplot at 0x1cb81ca9408>(おまけ)位相スペクトログラム
# 位相`phase`(直交形式)から偏角θを計算してカラープロット ax = librosa.display.specshow(np.arctan2(np.imag(phase), np.real(phase)), sr=sr, x_axis='time', y_axis='hz') ax.axes.set_ylabel("Phase") plt.title("位相スペクトログラム")出力Text(0.5, 1.0, '位相スペクトログラム')ランダムノイズのようにしか見えません。パターンを見出すのは難しそうです。
周波数・時間分解能の調整例
- やること
- 最初の60秒に対して、0~1kHzの範囲を時間分解能10ms程度で確認したい
手順
- 約2kHzでリサンプリング → n_fftを調整してSTFT、強度スペクトログラムを表示(周波数は線形スケール、強度はdB単位)
スペクトログラムのビン形状・分解能の予測値
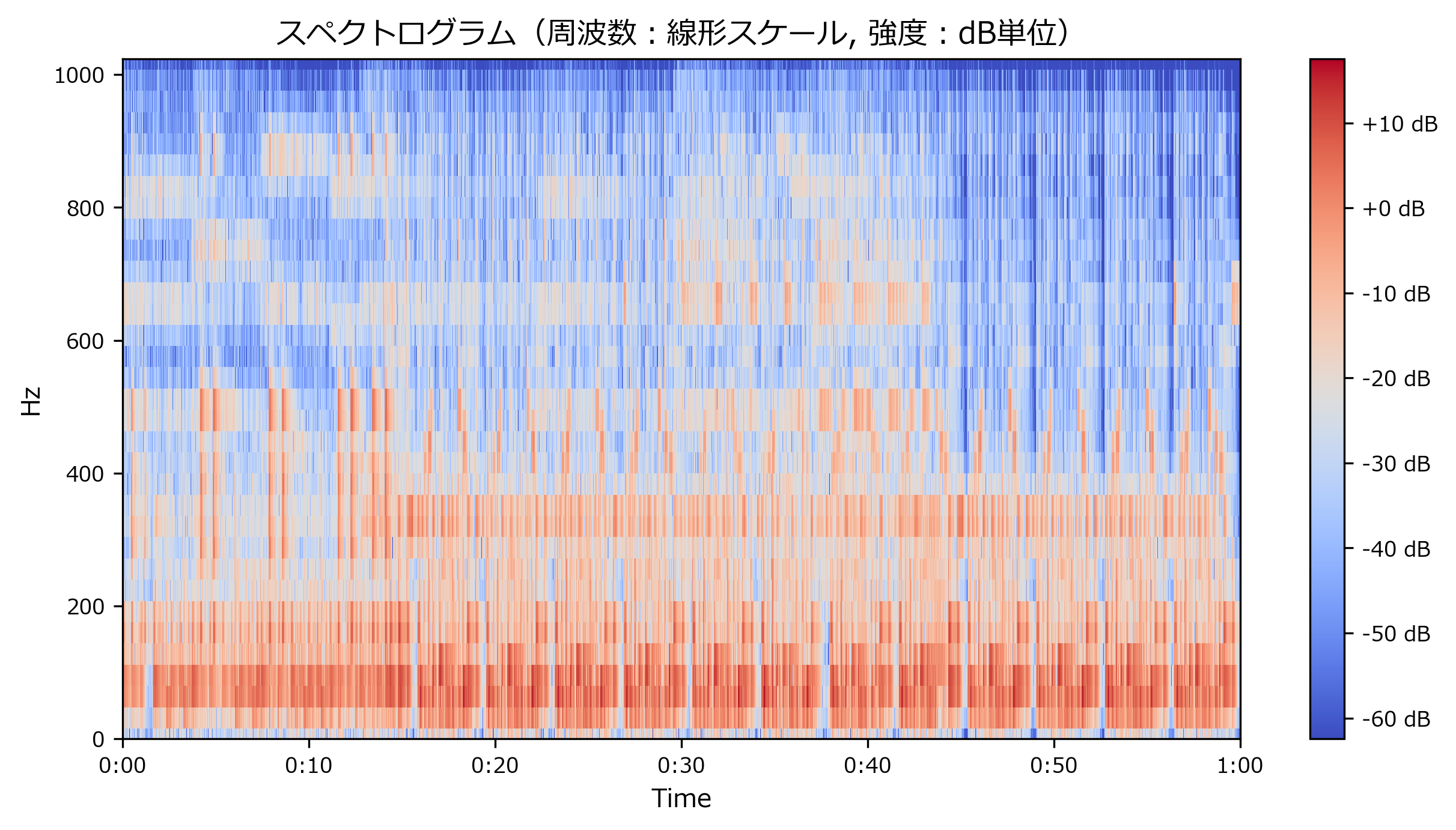
playtime2, sr2, n_fft2, hop_length2 = 60, 2048, 64, 64//4 # パラメータ y2 = librosa.resample(y[0:sr * playtime2],sr,sr2) D2 = librosa.stft(y2,n_fft=n_fft2, hop_length=hop_length2) # hop_lengthはデフォルト値と同じ計算にしたので、指定しなくても同じ。 S2, _ = librosa.magphase(D2) # 複素数を強度と位相へ変換 Sdb2 = librosa.amplitude_to_db(S2) # 強度をdb単位へ変換 tmp = librosa.display.specshow(Sdb2, sr=sr2, hop_length=hop_length2, x_axis='time', y_axis='hz') # スペクトログラムを表示 plt.title("スペクトログラム(周波数:線形スケール, 強度:dB単位)") plt.colorbar(format='%+2.0f dB')出力<matplotlib.colorbar.Colorbar at 0x1cbb67bec08>print("予測ビン形状 : \t", (33, 128 * playtime2)) print("実際のビン形状 :\t", Sdb2.shape)出力予測ビン形状 : (33, 7680) 実際のビン形状 : (33, 7681)スペクトログラムのビンの形状は、計算式で予測した値と大体あっていることが確認できます。
音声の復元
位相情報が使える場合:librosa.istft()
- 手順
- 下式で、強度
S,位相phaseから直交形式の複素数の行列Dへ変換- ISTFTでスペクトログラムを音声に復元します。
- 逆短時間フーリエ変換(Inverse short-time Fourier transform : ISTFT)
- librosa.istft() ドキュメント https://librosa.org/librosa/master/generated/librosa.core.istft.html?highlight=istft#librosa.core.istft
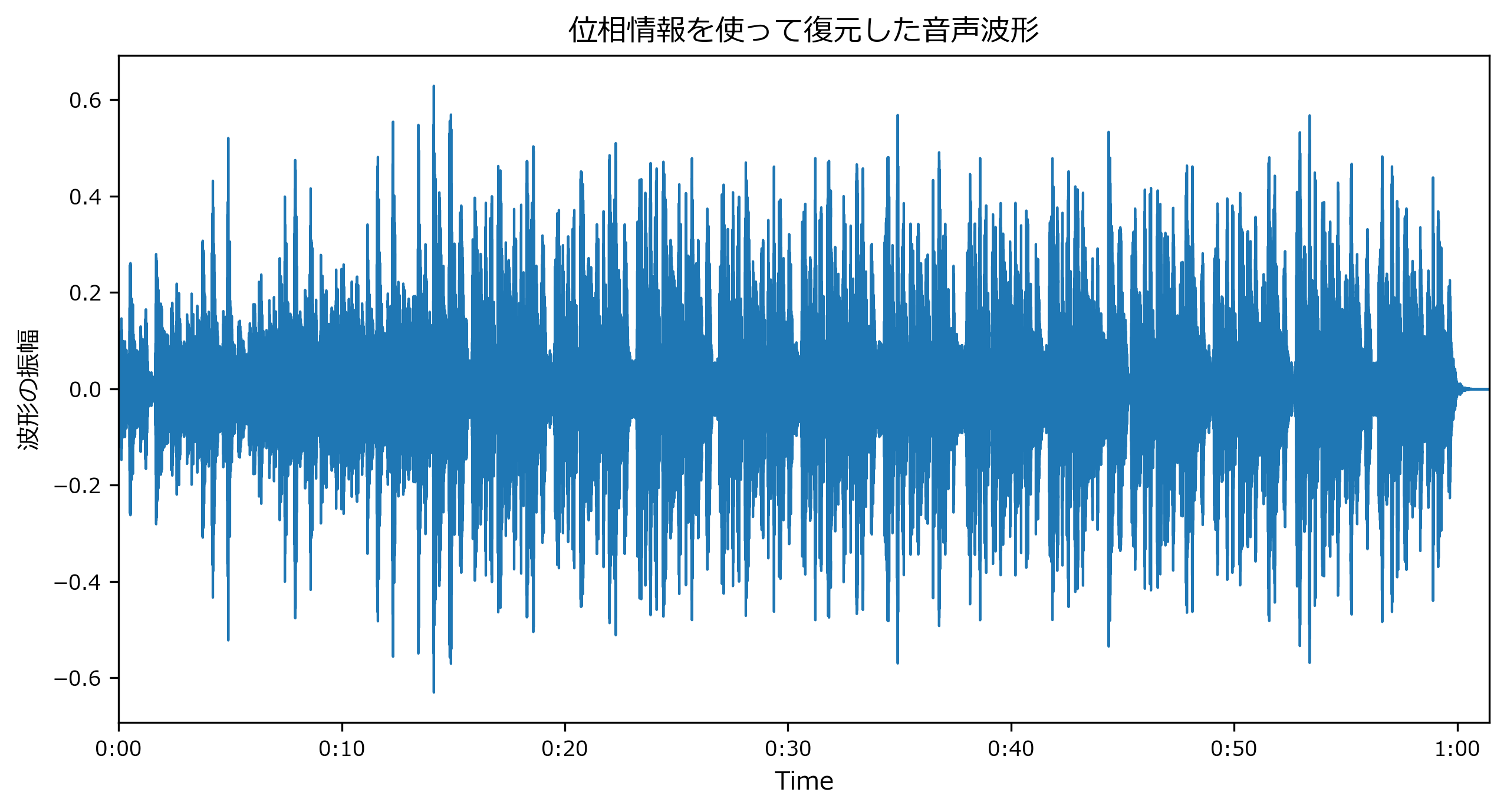
D = S * np.exp(1j*phase) # 直交形式への変換はlibrosaの関数ないみたいなので、自分で計算する。 y_inv = librosa.istft(D) display(IPython.display.Audio(y_inv, rate=sr)) mpl_collection = librosa.display.waveplot(y_inv, sr=sr) mpl_collection.axes.set(title="位相情報を使って復元した音声波形", ylabel="波形の振幅")出力[Text(0, 0.5, '波形の振幅'), Text(0.5, 1.0, '位相情報を使って復元した音声波形')]librosa音声変換記事 https://t.co/CedmBGtHfS
— lilacs2039 (@lilacs2039) July 5, 2020
Vibe Ace (Kevin MacLeod) / CC BY 3.0 pic.twitter.com/qaTaR4u7dtylim = ax.axes.set_ylim(); ylim # 次の比較用にy軸の範囲を保存出力(-0.6926389932632446, 0.6926389932632446)位相情報が使えない場合:griffinlim()で位相推定
位相情報なしで復元した場合
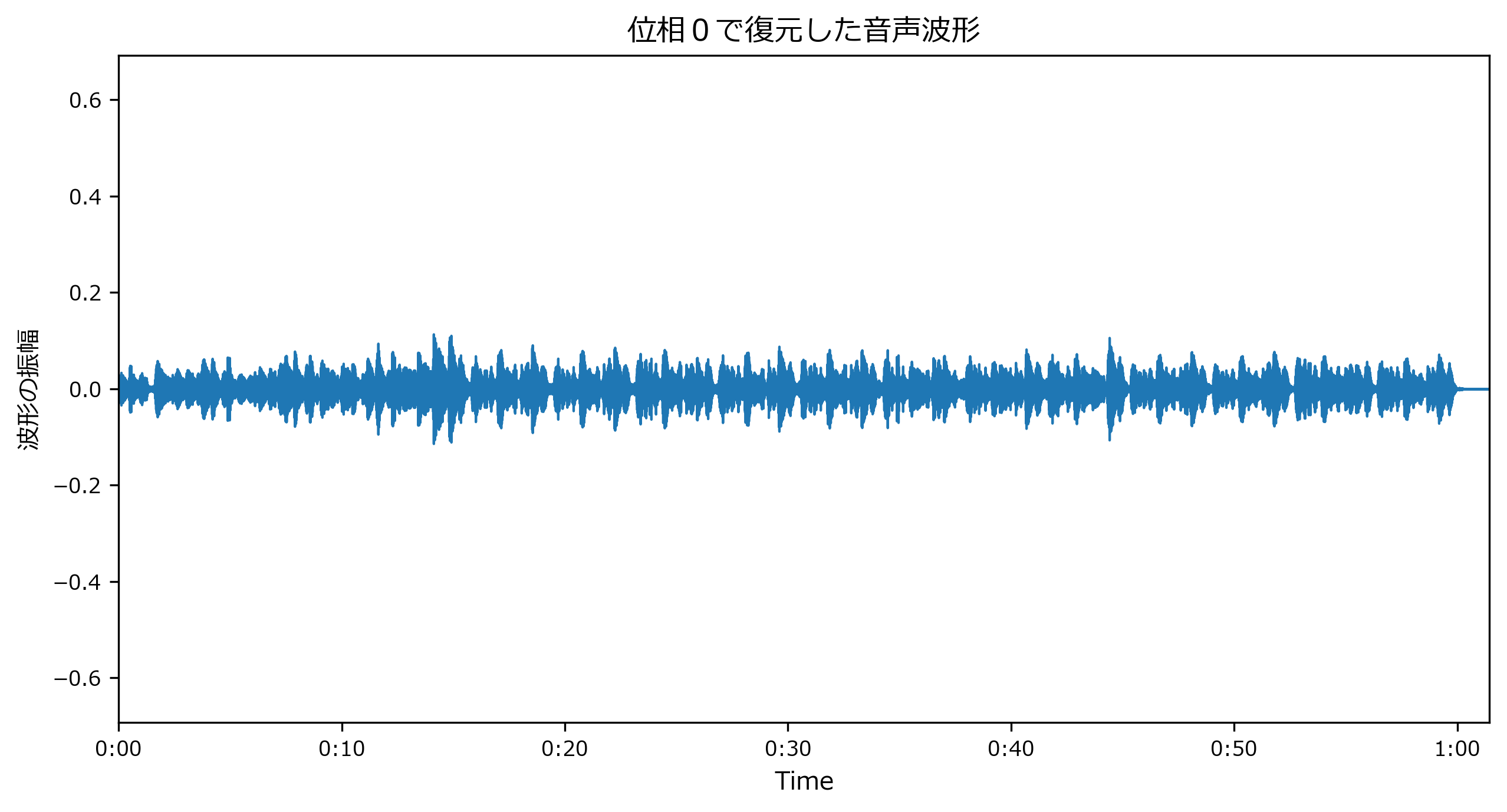
位相をすべてゼロとして直交形式の複素数の行列
Dへ変換した場合です。D = S * np.exp(np.zeros(S.shape)) y_inv = librosa.istft(D) display(IPython.display.Audio(y_inv, rate=sr)) mpl_collection = librosa.display.waveplot(y_inv, sr=sr) mpl_collection.axes.set(title="位相0で復元した音声波形", ylabel="波形の振幅") mpl_collection.axes.set_ylim(ylim);librosa音声変換記事 https://t.co/CedmBGtHfS
— lilacs2039 (@lilacs2039) July 5, 2020
Vibe Ace (Kevin MacLeod) / CC BY 3.0 pic.twitter.com/UzAxBfAFgt
- 音声の振幅が小さくなっています。聞いてみても何かヘンです。
griffinlim()で位相推定した場合
- librosa 0.7.x以降のバージョンでは
librosa.griffinlim()で、強度スペクトログラムのみから位相を推定して音声を復元できます。
- librosa.griffinlim() ドキュメント https://librosa.org/librosa/master/generated/librosa.core.griffinlim.html#librosa-core-griffinlim
- librosa 0.7.x 未満を使っているときは、issueから対象のソースコードをコピペして実行できます。(今回はこの方法です)
- Synthetic phase for inverse transforms #434
- https://github.com/librosa/librosa/issues/434#issuecomment-291266229
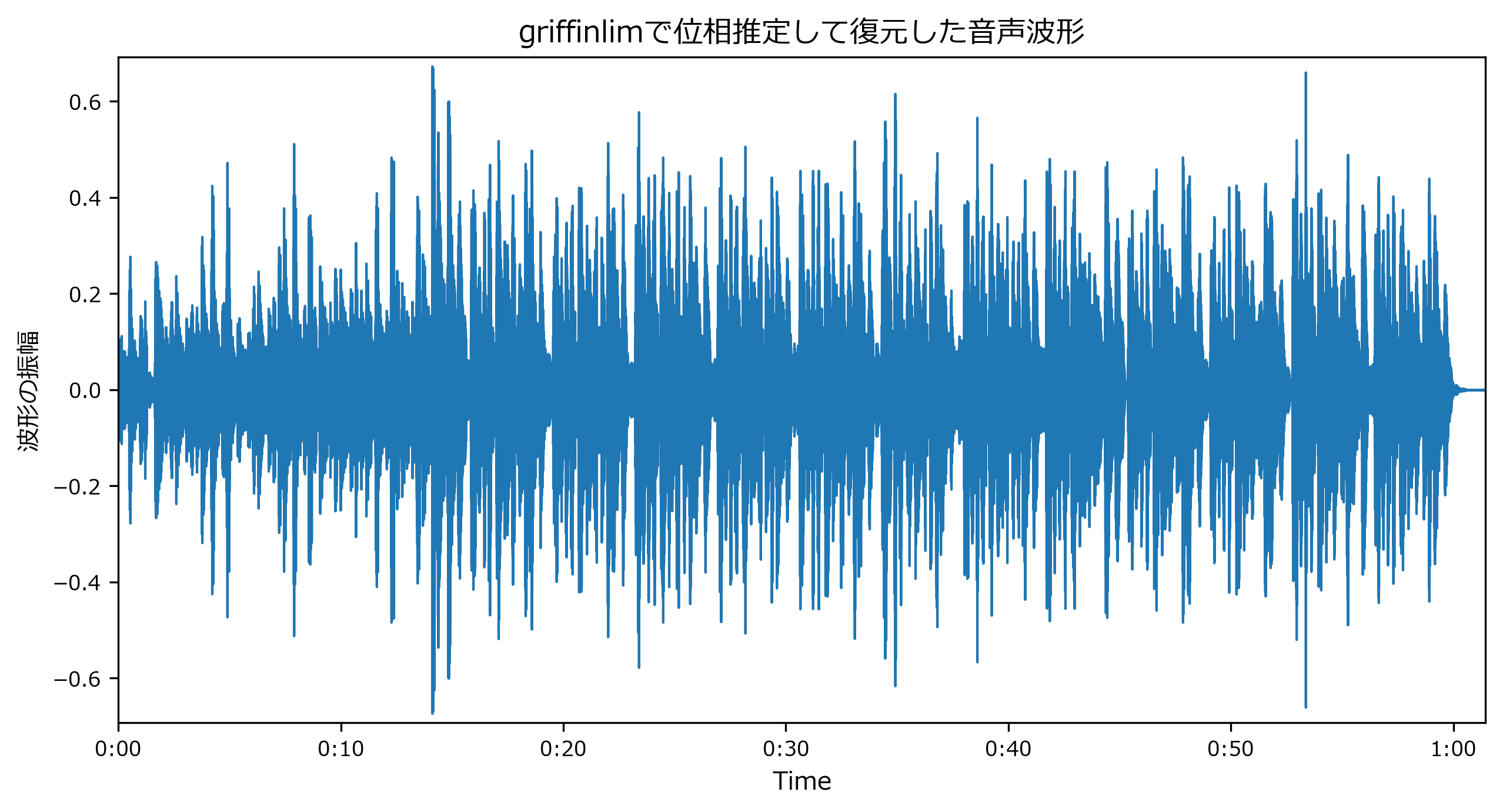
def griffinlim(spectrogram, n_iter = 100, window = 'hann', n_fft = 2048, hop_length = -1, verbose = False): if hop_length == -1: hop_length = n_fft // 4 angles = np.exp(2j * np.pi * np.random.rand(*spectrogram.shape)) t = tqdm(range(n_iter), ncols=100, mininterval=2.0, disable=not verbose) for i in t: full = np.abs(spectrogram).astype(np.complex) * angles inverse = librosa.istft(full, hop_length = hop_length, window = window) rebuilt = librosa.stft(inverse, n_fft = n_fft, hop_length = hop_length, window = window) angles = np.exp(1j * np.angle(rebuilt)) if verbose: diff = np.abs(spectrogram) - np.abs(rebuilt) t.set_postfix(loss=np.linalg.norm(diff, 'fro')) full = np.abs(spectrogram).astype(np.complex) * angles inverse = librosa.istft(full, hop_length = hop_length, window = window) return inverseprint("位相推定 開始") y_inv = griffinlim(S, verbose=True) print("位相推定 終了") display(IPython.display.Audio(y_inv, rate=sr)) mpl_collection = librosa.display.waveplot(y_inv, sr=sr) mpl_collection.axes.set(title="griffinlimで位相推定して復元した音声波形", ylabel="波形の振幅") mpl_collection.axes.set_ylim(ylim);出力位相推定 開始 100%|███████████████████████████████████████████████████| 100/100 [01:04<00:00, 1.55it/s, loss=376] 位相推定 終了librosa音声変換記事 https://t.co/CedmBGtHfS
— lilacs2039 (@lilacs2039) July 5, 2020
Vibe Ace (Kevin MacLeod) / CC BY 3.0 pic.twitter.com/k9M3LXCnGM
- 復元結果
- 聞いた感じは遜色なく復元できています。
- 音声波形はよく見ると、元の音声とは少し異なっています。
- 使いどころ
- 音声認識モデルの学習のためにデータオーグメンテーションでホワイトノイズを載せるなど、スペクトログラムで音声を編集してから、位相を推定して音声を復元することで、編集後の音声を聞いて確認することができます。
まとめ
- 音声処理ライブラリLibROSAを使って、音声の読み込み ⇒ スペクトログラムへの変換 ⇒ 音声の復元をしました。
Vibe Ace (Kevin MacLeod) / CC BY 3.0 ↩
- 投稿日:2020-07-05T21:09:32+09:00
ポートフォリオを作成するための学習項目
金融の情報システム部門で働いています。
社内SEのポジションですが、事務屋としての仕事の割合が多いです。
会話の中で技術的な話になることはあれど、実際に自分自身で何かを作ることがないため、これからの自分の立ち位置に非常に不安を抱えています。
なので、将来的な転職も選択肢に入れて、ポートフォリオを作成しようと考えています。
これまでに学習してきたこと、これから学習しようとしていることをまとめます。コンピュータサイエンス基礎
「令和02年 イメージ&クレバー方式でよくわかる 栢木先生の基本情報技術者教室 情報処理技術者試験」
大学生の頃に受験して合格しました。
もう何年も前の話なので、応用情報技術者試験をそのうち受けようかと考えています。Linux
「新しいLinuxの教科書」
後述するUdemyのDocker講座でもLinuxをコマンドの学習ができますが、改めて体系的に学ぼうと思います。HTML/CSS
「これから学ぶHTML/CSS 」
1年目の時にお世話になりました。
忘れてしまっていることも多いので、都度読み返すことになりそうです。JavaScript
「確かな力が身につくJavaScript「超」入門 第2版」
JavaScriptは全く未経験なのでこの機に勉強しようかと思います。Python
「独学プログラマー Python言語の基本から仕事のやり方まで」
これは1年目の時に学習しました。「Python2年生 スクレイピングのしくみ 体験してわかる!会話でまなべる!」
こちらは最近読みました。
非常にわかりやすかったです。
foliumを使って地図上にプロットできたときはちょっと感動しました。Django
「Python Django 超入門」
「独学プログラマー」の本を読んだ後にこちらを学習しました。
Webのチュートリアルなどもやってみたものの、自分自身でアプリを1から作ることはまだできていません。
これも、bootstrapでデザインを整えた時にちょっと感動しました。
チュートリアルではなく、1から再チャレンジします。Docker
米国AI開発者がゼロから教えるDocker講座
https://www.udemy.com/course/aidocker/
Udemyの動画講座です。学習は書籍の方が良いと思っていましたが、動画は画面の動きを見ながら学習できるのでわかりやすいです。
14時間というボリュームのある学習内容も、2倍速で視聴できるので素早く学習できます。
ちょうど今学習中です。入門Docker
https://y-ohgi.com/introduction-docker/
こちらもDockerの勉強ができます。
前述の動画講座は5000円ほどしますが、こちらは無料です。AWS
「Amazon Web Servicesインフラサービス活用大全 システム構築/自動化、データストア、高信頼化 impress top gearシリーズ」
AWSでアプリを動かすことができるまで経験しないと未経験では転職は厳しそうですし、
仮に採用されたとしても労働条件は良いものにならないだろうと思います。CircleCI
「いまさらだけどCircleCIに入門したので分かりやすくまとめてみた」
https://qiita.com/gold-kou/items/4c7e62434af455e977c2
何をするものなのかも正直知りません。
これから勉強していきます。
- 投稿日:2020-07-05T20:56:57+09:00
基礎数学
ライブラリ
- NumPy (ナンパイ) : 数値計算ライブラリ
- scikit-learn (サイキットラーン) : 機械学習全般に強いライブラリ
- SciPy (サイパイ) : 確率統計に強いライブラリ
- seaborn (シーボーン) : グラフを描くためのライブラリ
線形代数とは「ベクトルと行列を扱う分野」である
ベクトル : 数値を縦方向に並べる
行列 : 数値を縦横方向に並べる統計学
統計学とは得られているデータから法則性や知見を数学的に得る分野である
機械学習もある意味、統計学の中に含まれている
- 記述統計
- 手元のデータの分析を行う
- 代表値を計算する
- 傾向を分析する
- 推計統計
- 手元のデータの背後にある母集団の性質を予測する
- 特に機械学習と密接に関わっている
- データの基礎集計に使われる
- 選挙速報 (出口調査した有権者=標本、有権者全体=母集団)
- 視聴率
- 投稿日:2020-07-05T20:56:57+09:00
数学の基礎
ライブラリ
- NumPy (ナンパイ) : 数値計算ライブラリ
- scikit-learn (サイキットラーン) : 機械学習全般に強いライブラリ
- SciPy (サイパイ) : 確率統計に強いライブラリ
- seaborn (シーボーン) : グラフを描くためのライブラリ
線形代数とは「ベクトルと行列を扱う分野」である
ベクトル : 数値を縦方向に並べる
行列 : 数値を縦横方向に並べる統計学
統計学とは得られているデータから法則性や知見を数学的に得る分野である
機械学習もある意味、統計学の中に含まれている
- 記述統計
- 手元のデータの分析を行う
- 代表値を計算する
- 傾向を分析する
- 推計統計
- 手元のデータの背後にある母集団の性質を予測する
- 特に機械学習と密接に関わっている
- データの基礎集計に使われる
- 選挙速報 (出口調査した有権者=標本、有権者全体=母集団)
- 視聴率
- 投稿日:2020-07-05T19:37:15+09:00
Python 1次元でのDMD
はじめに
動的モード分解(Dynamic Mode Decomposition; DMD)というものが、2008年に発表されています12。DMDは主成分分析とフーリエ変換をあわせたような分解方法で、データを次元と時間方向の特徴に分離できる手法です。
参考にした解説記事は以下にあります。
- http://www.pyrunner.com/weblog/2016/07/25/dmd-python/
- https://iqujack-lequina.hatenablog.com/entry/2018/05/20/動的モード分解に関する覚書
- https://qiita.com/Miyabi1456/items/702f62c9bcd9c063d664
- https://qiita.com/harmegiddo/items/84552c32f4b75c26878a
DMDの固有値、固有ベクトルは複素数になり、固有値の複素成分で時間方向の分解を表します。ただ、1次元定在波だとうまく分離できない問題があります。説明は以下の記事にあります。
1次元データにあえてDMDを利用することはないと思いますが、Pythonコードが公開されていなかったので、参考までに記載します。うまく分解できない例と、できる例を示します。ベースとなる論文はTu 20143で、コードは、DMDの本のMatlabコードを参考にしています。
環境
Windows 10 home
Anaconda(Python 3.7.6)
Numpy(1.18.1)
分解対象
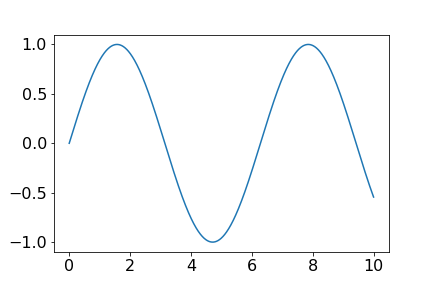
1次元のサイン波の数値データから周期を見つけます。周期は、複素数だと$1j$ですね。
$$
y = \sin(x)
$$
うまくいかないDMD例
うまくいかない例では、データが1次元しかないため、固有値が実数になり、複素数が出てきません。そのため、周期成分が分解できません。
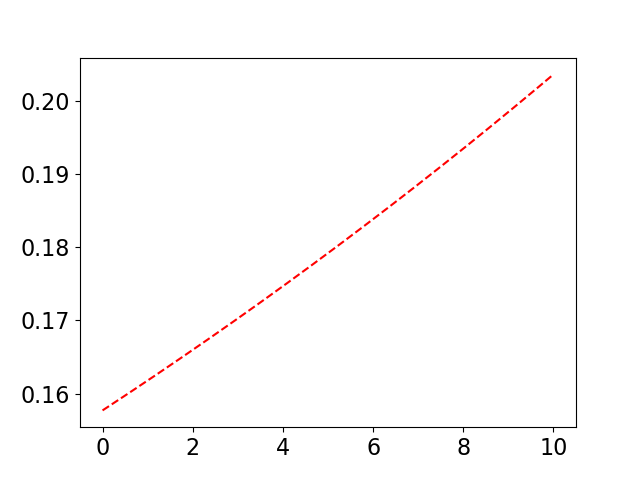
import numpy as np import numpy.linalg as LA import matplotlib.pyplot as plt %matplotlib inline t = np.arange(0, 10.01, 0.01) x = np.sin(t) dt = t[2] - t[1] #データ行列 X1 = x[:-1] X2 = x[1:] #SVD U,S,Vh = LA.svd(X1[np.newaxis,:],False) V = Vh.T #Aを左特異ベクトルで次元削減したAtilde Atilde = np.dot(np.dot(np.dot(U.T, X2[np.newaxis,:]), V), LA.inv(np.diag(S))) #Atilde の固有値と固有ベクトルを求める Lam, W = LA.eig(Atilde) print("固有値:",Lam)#Lam:1.00025541となって実数 #Atildeの固有ベクトルから、Aの固有ベクトルを求める Phi = np.dot(np.dot(np.dot(X2[np.newaxis,:], V), LA.inv(np.diag(S))), W) #離散型から連続型のexp(**)の**を求める Omega = np.log(Lam)/dt #OmegaとPhiから元の関数を復元する。 b = np.dot(LA.pinv(Phi * np.exp(Omega * t)).T, x) x_dmd = b * Phi * np.exp(Omega * t) plt.plot(t, x_dmd[0,:]) plt.show()うまくいくDMD例
説明記事で紹介されていますが、時間方向にデータをずらしたもので、もう一次元作り、2次元データにします。こうすることで、固有値に複素成分が出まして、数値データから、$\sin(x)$ が見つけられます。ただ、それだけです。
import numpy as np import numpy.linalg as LA import matplotlib.pyplot as plt %matplotlib inline t = np.arange(0, 10.01, 0.01) x = np.sin(t) dt = t[2] - t[1] #データ行列 #主な違いはここです。2次元にしています。 X_aug1 = np.array([x[:-2], x[1:-1]]) X_aug2 = np.array([x[1:-1], x[2:]]) #SVD U,S,Vh = LA.svd(X_aug1,False) V = Vh.conj().T #Aを左特異ベクトルで次元削減したAtilde #Uは複素共役をとって、転置行列にしてます。 Atilde = np.dot(np.dot(np.dot(U.conj().T, X_aug2), V), LA.inv(np.diag(S))) #Atilde の固有値と固有ベクトルを求める Lam, W = LA.eig(Atilde) print("固有値:", Lam)#Lam:[0.9995+0.00999983j 0.9995-0.00999983j]複素数 #Atildeの固有ベクトルから、Aの固有ベクトルを求める Phi = np.dot(np.dot(np.dot(X_aug2, V), LA.inv(np.diag(S))), W) #離散型から連続型のexp(**)の**を求める Omega = np.diag(np.log(Lam)/dt) print("Omega:", Omega)#念のため、1jになる #OmegaとPhiから元の関数を復元する。 #やっていることは1次元と変わらないですが、書き方が異なります。 b = np.dot(LA.pinv(Phi), X_aug1[:,0]) x_dmd = np.zeros([2,len(t)], dtype='complex') for i, _t in enumerate(t): x_dmd[:,i] = np.dot(np.dot(Phi, np.exp(Omega * _t)), b) plt.plot(t, x_dmd[0,:].real) plt.show()参考文献
P.J. Schmid, "Dynamic Mode Decomposition of numerical and experimental data", Proc., 61st Annual Meeting of the APS Division of Fluid Dynamics, 2008. ↩
P.J. Schmid, "Dynamic mode decomposition of numerical and experimental data", Journal of Fluid Mechanics, 2010. ↩
Tu, Rowley, Luchtenburg, Brunton, and Kutz, "On Dynamic Mode Decomposition: Theory and Applications", *American Institute of Mathematical Sciences, 2014. ↩
- 投稿日:2020-07-05T19:32:10+09:00
Rのpower.prop.test関数をpythonで実装する
- 適合度テストを設計するのに、サンプルサイズや検証力を求めたい
- Rのpower.prop.testという関数を使えば求められる
- 同じような関数をpythonでも使いたい…
ということで、練習としてRのpower.prop.test関数のソースコードを元にpythonで実装してみました。
引数の意味などはRの公式ドキュメントを参照してください。
コードは記事の最後に載せてます。使用例
サンプルサイズを求める
- グループ1は1%、グループ2は3%の確率でなんらかの効果がでると仮定
- 有意水準は0.05
- 検出力は0.8
- 片側検定
上記の条件を満たすためのサンプルの大きさnを求めます。
# python > params_dict = power_prop_test(p1=0.01, p2=0.03, power=0.8, sig_level=0.05, alternative="one_sided") Sample size: n = 604.845426012357 Probability: p1 = 0.01, p2 = 0.03 sig_level = 0.05, power = 0.8, alternative = one_sided NOTE: n is number in "each" group > print(params_dict) {'n': 604.845426012357, 'p1': 0.01, 'p2': 0.03, 'sig_level': 0.05, 'power': 0.8, 'alternative': 'one_sided'}Rで同じ値を渡した結果とほぼ一致します。
# R > power.prop.test(p1=0.01, p2=0.03, power=0.8, sig.level=0.05, alternative="one.sided") Two-sample comparison of proportions power calculation n = 604.8434 p1 = 0.01 p2 = 0.03 sig.level = 0.05 power = 0.8 alternative = one.sided NOTE: n is number in *each* group検出力を求める
次に、サンプルサイズn=1000のときの検出力(power)について同様に求めてみます。
#python > power_prop_test(n=1000, p1=0.01, p2=0.03, sig_level=0.05, alternative="one_sided") Sample size: n = 1000 Probability: p1 = 0.01, p2 = 0.03 sig_level = 0.05, power = 0.9398478094069961, alternative = one_sided NOTE: n is number in "each" group#R > power.prop.test(n=1000, p1=0.01, p2=0.03, sig.level=0.05, alternative="one.sided") Two-sample comparison of proportions power calculation n = 1000 p1 = 0.01 p2 = 0.03 sig.level = 0.05 power = 0.9398478 alternative = one.sided NOTE: n is number in *each* groupこちらもほとんど同じ値をとります。
補足
- python上でRを動かすPypeRなどで、直接Rの関数を呼び出したほうが簡単かも
- 初期値によっては収束せず、エラーを吐くかもしれません
読んでいただきありがとうございました。
使用したpower_prop_test関数
# 求めたいパラメーターをNoneにする # alternativeは"one_sided" "two_sided"のどちらかを選択 # 求めた各パラメータを辞書型で返します def power_prop_test(n=None, p1=None, p2=None, sig_level=0.05, power=None, alternative="one_sided", strict=False, tol=2.220446049250313e-16**0.25): from math import sqrt from scipy.stats import norm from scipy.optimize import brentq missing_params = [arg for arg in [n, p1, p2, sig_level, power] if not arg] num_none = len(missing_params) if num_none != 1: raise ValueError("exactly one of 'n', 'p1', 'p2', 'power' and 'sig.level'must be None") if sig_level is not None: if sig_level < 0 or sig_level > 1: raise ValueError("\"sig_level\" must be between 0 and 1") if power is not None: if power < 0 or power > 1: raise ValueError("\"power\" must be between 0 and 1") if alternative not in ["two_sided", "one_sided"]: raise ValueError("alternative must be \"two_sided\" or \"one_sided\"") t_side_dict = {"two_sided":2, "one_sided":1} t_side = t_side_dict[alternative] # compute power def p_body(p1=p1, p2=p2, sig_level=sig_level, n=n, t_side=t_side, strict=strict): if strict and t_side==2: qu = norm.ppf(1-sig_level/t_side) d = abs(p1-p2) q1 = 1-p1 q2 = 1-p2 pbar = (p1 + p2) / 2 qbar = 1 - pbar v1 = p1 * q1 v2 = p2 * q2 vbar = pbar * qbar power_value = (norm.cdf((sqrt(n) * d - qu * sqrt(2 * vbar))/sqrt(v1 + v2)) + norm.cdf(-(sqrt(n) * d + qu * sqrt(2 * vbar))/sqrt(v1 + v2))) return power_value else: power_value = norm.cdf((sqrt(n) * abs(p1 - p2) - (-norm.ppf(sig_level / t_side) * sqrt((p1 + p2) * (1 - (p1 + p2)/2)))) / sqrt(p1 * (1 - p1) + p2 * (1 - p2))) return power_value if power is None: power = p_body() # solve the equation for the None value argument elif n is None: def n_solver(x, power=power): return p_body(n=x) - power n = brentq(f=n_solver, a=1, b=1e+07, rtol=tol, maxiter=1000000) elif p1 is None: def p1_solver(x, power=power): return p_body(p1=x) - power try: p1 = brentq(f=p1_solver, a=0, b=p2, rtol=tol, maxiter=1000000) except: ValueError("No p1 in [0, p2] can be found to achive the desired power") elif p2 is None: def p2_solver(x, power=power): return p_body(p2=x) - power try: p2 = brentq(f=p2_solver, a=p1, b=1, rtol=tol, maxiter=1000000) except: VealueError("No p2 in [p1, 1] can be found to achive the desired power") elif sig_level is None: def sig_level_solver(x, power=power): return p_body(sig_level=x) - power try: sig_level = brentq(f=sig_level_solver, a=1e-10, b=1-1e-10, rtol=tol, maxiter=1000000) except: ValueError("No significance level [0,1] can be found to achieve the desired power") print(""" Sample size: n = {0} Probability: p1 = {1}, p2 = {2} sig_level = {3}, power = {4}, alternative = {5} NOTE: n is number in "each" group """.format(n, p1, p2, sig_level, power, alternative)) #各パラメーターは引数名をキーにもつ辞書で返される params_dict = {"n":n, "p1":p1, "p2":p2, "sig_level":sig_level, "power":power, "alternative":alternative} return params_dict
- 投稿日:2020-07-05T18:36:55+09:00
【統計学】ふつうのエンジニアが統計学の勉強を始めてみた- part2
はじめに
数学がちょっとデキル
ふつうのバックエンドエンジニアが
統計学を勉強してみたという話
今回やること
Jupyter Notebookを使って様々な統計量を計算する。
・合計値
・平均値
・標本分散
・不偏分散
・標準偏差
・最小値
・中央値
・最大値
今回使うライブラリ
import numpy as np import scipy as sp
サンプルデータ
# 魚のデータをテーマに記述統計を試してみる fish_data = np.array([2,3,3,4,4,4,4,5,5,6])
合計値を計算する
配列 fish_dataをscipy モジュールのsumメソッドに渡す。
結果をsum_valueに格納import numpy as np import scipy as sp fish_data = np.array([2,3,3,4,4,4,4,5,5,6]) # 合計値(sum_value)を出す sum_value = sp.sum(fish_data)
合計値に関する逸話(コラム)
雨の日で体育ができない為、教師が
少年に対して1~100までの数値を
全て足すことを課したところ
ものの数十秒で計算して結果を出したという。この少年は皆さんご存知
のちに数学と物理学の分野で偉人となるガウスさんです。
標本数を計算する
配列の長さを測ることで計算できる。
import numpy as np import scipy as sp fish_data = np.array([2,3,3,4,4,4,4,5,5,6]) # 標本の数 N を数える N = len(fish_data)
平均値を計算する
合計値 / 標本数で計算できる。
scipy を使うとmean メソッドで計算できる。import numpy as np import scipy as sp fish_data = np.array([2,3,3,4,4,4,4,5,5,6]) # 平均を出す sum_value / N avg = sp.mean(fish_data)
標本分散を計算する
「データが平均値からどれだけ離れているか」を表す指標
import numpy as np import scipy as sp fish_data = np.array([2,3,3,4,4,4,4,5,5,6]) # 平均を出す sum_value / N avg = sp.mean(fish_data) # 標本分散は英語で「Sample variance」 sigma = sp.sum((fish_data - avg)**2) / N
標本分散を計算する(2)
scipy を使うと簡単に標本分散を計算できる。
import numpy as np import scipy as sp fish_data = np.array([2,3,3,4,4,4,4,5,5,6]) # 標本分散 sigma を計算する # (scipy の varメソッドを使うと一発で計算できる) sigma = sp.var(fish_data , ddof = 0)
不偏分散を計算する
分散の値を過少に見積もってしまうバイアスがない分散
import numpy as np import scipy as sp fish_data = np.array([2,3,3,4,4,4,4,5,5,6]) # 平均を出す sum_value / N avg = sp.mean(fish_data) # 標本の数 N を数える N = len(fish_data) # 英語で「Unbiased distribution」 unb_dist = sp.sum((fish_data - avg)**2) / (N-1)
不偏分散を計算する(2)
scipy を使うと簡単に不偏分散を計算できる。
import numpy as np import scipy as sp fish_data = np.array([2,3,3,4,4,4,4,5,5,6]) unb_dist = sp.var(fish_data , ddof = 1)
標準偏差を計算する
「○○さんって偏差値いくつよ~」
「え、偏差値低い!!?」の偏差値ですね。不偏分散を平方することで求めることができます。
import numpy as np import scipy as sp fish_data = np.array([2,3,3,4,4,4,4,5,5,6]) # 平均を出す sum_value / N avg = sp.mean(fish_data) # 標本の数 N を数える N = len(fish_data) # 英語で「Unbiased distribution」 unb_dist = sp.sum((fish_data - avg)**2) / (N-1) # 標準偏差 英語で「standard deviation」 std_dev = sp.sqrt(unb_dist)
標準偏差を計算する(2)
scipy を使うと簡単に標準偏差を計算できる。
import numpy as np import scipy as sp fish_data = np.array([2,3,3,4,4,4,4,5,5,6]) # 不偏分散 を利用して標準偏差を計算する(ddof = 1) sp.std(fish_data,ddof = 1)
最小値
scipy を使うと簡単に最小値を計算できる。
一番ちっさい数値のことimport numpy as np import scipy as sp fish_data = np.array([2,3,3,4,4,4,4,5,5,6]) sp.amin(fish_data)
中央値
scipy を使うと簡単に中央値を計算できる。
中央値はサンプルの中でちょうど真ん中に位置する数値のことimport numpy as np import scipy as sp fish_data = np.array([2,3,3,4,4,4,4,5,5,6]) sp.median(fish_data)
最大値
scipy を使うと簡単に最大値を計算できる。
一番大きい数値のことimport numpy as np import scipy as sp fish_data = np.array([2,3,3,4,4,4,4,5,5,6]) sp.amax(fish_data)
まとめ
numpy と scipyが扱えれば
記述統計でよく使う統計量はおおよそいける。
だけれども、統計量それぞれの求め方は把握しておきましょう。
おわり
- 投稿日:2020-07-05T18:35:42+09:00
ゼロから始めるLeetCode Day77「1502. Can Make Arithmetic Progression From Sequence」
概要
海外ではエンジニアの面接においてコーディングテストというものが行われるらしく、多くの場合、特定の関数やクラスをお題に沿って実装するという物がメインである。
どうやら多くのエンジニアはその対策としてLeetCodeなるサイトで対策を行うようだ。
早い話が本場でも行われているようなコーディングテストに耐えうるようなアルゴリズム力を鍛えるサイトであり、海外のテックカンパニーでのキャリアを積みたい方にとっては避けては通れない道である。
と、仰々しく書いてみましたが、私は今のところそういった面接を受ける予定はありません。
ただ、ITエンジニアとして人並みのアルゴリズム力くらいは持っておいた方がいいだろうということで不定期に問題を解いてその時に考えたやり方をメモ的に書いていこうかと思います。
Python3で解いています。
前回
ゼロから始めるLeetCode Day76「3. Longest Substring Without Repeating Characters」A今はTop 100 Liked QuestionsのMediumを優先的に解いています。
Easyは全て解いたので気になる方は目次の方へどうぞ。Twitterやってます。
技術ブログ始めました!!
技術はLeetCode、Django、Nuxt、あたりについて書くと思います。こちらの方が更新は早いので、よければブクマよろしくお願いいたします!問題
1502. Can Make Arithmetic Progression From Sequence
難易度はEasy。最近追加された新しめの問題です。
Easyっぽくない問題なので是非解いてみてください。問題としては、数の配列
arrが与えられた時、連続する2つの要素間の差が同じであれば,数列は算術進行と呼ばれます。配列を再編成して算術進行を形成できる場合は
trueを返し,そうでない場合はfalseを返してください。Example 1:
Input: arr = [3,5,1]
Output: true
Explanation: We can reorder the elements as [1,3,5] or [5,3,1] with differences 2 and -2 respectively, between each consecutive elements.Example 2:
Input: arr = [1,2,4]
Output: false
Explanation: There is no way to reorder the elements to obtain an arithmetic progression.解法
class Solution: def canMakeArithmeticProgression(self, arr: List[int]) -> bool: arr.sort() length = len(arr) if length==2: return True difference = arr[1] - arr[0] for i in range(1, length): if arr[i] - arr[i - 1] != difference: return False return True # Runtime: 32 ms, faster than 100.00% of Python3 online submissions for Can Make Arithmetic Progression From Sequence. # Memory Usage: 13.9 MB, less than 100.00% of Python3 online submissions for Can Make Arithmetic Progression From Sequence.新しい問題でかつEasyなので両方100%の解答が出来ました。
最初に配列をソートします。
配列の長さが2の時のみ除外し、それ以外の場合は値の差をとったdifferenceとそれぞれのfor文で回した時の内容が異なる場合にはFalseを、それ以外の場合はTrueを返します。今回はここまで。お疲れ様でした。
- 投稿日:2020-07-05T18:33:23+09:00
mnistをロードしようとした時に出たエラーの対処法
初めに
先日、Tensorflow2に初めて触れまして、パターン認識のチュートリアル的立ち位置にあるmnistのデータセットで学習しようとしたのですが、その際にあったトラブルの解決法を書いていきます。
実行コード
f.pyimport tensorflow as tf mnist = tf.keras.datasets.mnist m_data=mnist.load_data()エラ〜コード
Exception: URL fetch failure on https://storage.googleapis.com/tensorflow/tf-keras-datasets/mnist.npz: None -- [SSL: CERTIFICATE_VERIFY_FAILED] certificate verify failed: unable to get local issuer certificate (_ssl.c:1108)
問題
sslに問題があってmnistのデータを取得できていないようです。
解決法
どうやらmacの標準のsslが対応していないために上記のエラーが起こっているようです。
私のMacの標準sslはLibreでしたのでopensslに変更してやります。
ターミナルで brew install openssl と入力してやればいいです。
しかし、これではまだsslはLibreのままです。
opensslに変更してやるには、opensslをインストールした際に
If you need to have openssl@1.1 first in your PATH run:
echo 'export PATH="/usr/local/opt/openssl@1.1/bin:$PATH"' >> ~/.zshrc
と表示されますので、いう通りに
echo 'export PATH="/usr/local/opt/openssl@1.1/bin:$PATH"' >> ~/.zshrc
のコードをコピペして実行します。
そしてその後、ターミナルを再起動し、 openssl versionと入力し、OpenSSL 1.1.1g 21 Apr 2020
のように表示されればOKです。
さらにこの後Pythonのフォルダにある
Install Certificates.command というファイルをクリックしてやると、無事にmnistがロードできるようになりました!参考記事
- 投稿日:2020-07-05T17:39:25+09:00
pythonで競技プログラミング
- 投稿日:2020-07-05T17:26:10+09:00
【ラビットチャレンジ(E資格)】応用数学
はじめに
2021/2/19・20に実施される日本ディープラーニング協会(JDLA)E資格合格を目指して、ラビットチャレンジを受講した際の学習記録です。
ラビットチャレンジは「現場で潰しが効くディープラーニング講座」の通学講座録画ビデオを編集した教材を活用したコースです。
質問等のサポートはありませんが、E資格受験のための格安(2020年6月時点での最安値)の講座です。第1章:線形代数
- スカラー
- だいたい、いわゆる普通の数
- +-×÷の演算が可能
- ベクトルに対する係数になれる
- ベクトル
- 「大きさ」と「向き」をもつ
- 矢印で図示される
- スカラーのセットで表示される
- 行列
- スカラーを表にしたもの
- ベクトルを並べたもの
単位行列と逆行列
かけても、かけられても相手が変化しない「1」のような行列を単位行列という。
$$ I = \begin{pmatrix}
1 & & \\
& 1 & \\
& & \ddots \
\end{pmatrix} $$
まるで逆数のような働きをする行列を逆行列という。
$$ AA^{-1} = A^{-1}A = I $$行列式の特徴
ある行列が2つの横ベクトルの組み合わせだと考えたとき、
$$ \begin{pmatrix}
a & b \\
c & d
\end{pmatrix} = \begin{pmatrix}
\vec{v_1} \\
\vec{v_2}
\end{pmatrix} $$
でつくられる平行四辺形の面積が逆行列の有無を判別する。
この面積を$ \begin{vmatrix}
a & b \\
c & d
\end{vmatrix} = \begin{vmatrix}
\vec{v_1} \\
\vec{v_2}
\end{vmatrix} $と表し行列式と呼ぶ。
$ \vec{v_1} = (a,b,c), \vec{v_2} = (a,b,c), \vec{v_3} = (a,b,c) $のとき、
$$ \begin{vmatrix}
\vec{v_1} \\
\vec{v_2} \\
\vec{v_3}
\end{vmatrix} = \begin{vmatrix}
a & b & c \\
d & e & f \\
g & h & i
\end{vmatrix} = \begin{vmatrix}
a & b & c \\
0 & e & f \\
0 & h & i
\end{vmatrix} + \begin{vmatrix}
0 & b & c \\
d & e & f \\
0 & h & i
\end{vmatrix} + \begin{vmatrix}
0 & b & c \\
0 & e & f \\
g & h & i
\end{vmatrix} = a \begin{vmatrix}
e & f \\
h & i
\end{vmatrix} - d \begin{vmatrix}
b & c \\
h & i
\end{vmatrix} + g \begin{vmatrix}
b & c \\
e & f
\end{vmatrix} $$n個のベクトルからできている行列式は、次の特徴を持つ。
- 同じ行ベクトルが含まれていると行列式はゼロ $$ \begin{vmatrix} \vec{v_1} \\ \vdots \\ \vec{w} \\ \vdots \\ \vec{w} \\ \vdots \\ \vec{v_n} \end{vmatrix} = 0 $$
- 1つのベクトルが $\lambda$ 倍されると行列式は $\lambda$ 倍される $$ \begin{vmatrix} \vec{v_1} \\ \vdots \\ \lambda\vec{v_i} \\ \vdots \\ \vec{v_n} \end{vmatrix} = \lambda \begin{vmatrix} \vec{v_1} \\ \vdots \\ \vec{v_i} \\ \vdots \\ \vec{v_n} \end{vmatrix} $$
- 他の成分が全部同じで $i$ 番目のベクトルだけが違った場合、行列式の足し合わせになる $$ \begin{vmatrix} \vec{v_1}\\ \vdots \\ \vec{v_i} + \vec{w} \\ \vdots \\ \vec{v_n} \end{vmatrix} = \begin{vmatrix} \vec{v_1} \\ \vdots \\ \vec{v_i} \\ \vdots \\ \vec{v_n} \end{vmatrix} + \begin{vmatrix} \vec{v_1} \\ \vdots \\ \vec{w} \\ \vdots \\ \vec{v_n} \end{vmatrix} $$
- 行を入れ替えると符号が変わる $$ \begin{vmatrix} \vec{v_1} \\ \vdots \\ \vec{v_s} \\ \vdots \\ \vec{v_t} \\ \vdots \\ \vec{v_n} \end{vmatrix} = - \begin{vmatrix} \vec{v_1} \\ \vdots \\ \vec{v_t} \\ \vdots \\ \vec{v_s} \\ \vdots \\ \vec{v_n} \end{vmatrix} $$
固有値と固有ベクトル
ある行列 $A$ に対して、以下のような式が成り立つ特殊なベクトル $\vec{x}$ と右辺の係数 $\lambda$ がある。
$$ A\vec{x} = \lambda\vec{x} $$
行列 $A$ とその特殊なベクトル $\vec{x}$ の積は、ただのスカラーの数 $\lambda$ とその特殊なベクトル $\vec{x}$ との積と同じ値になる。
この特殊なベクトル $\vec{x}$ とその係数 $\lambda$ を行列 $A$ に対する固有ベクトル、固有値という。固有値分解
ある実数を正方形に並べて作られた行列 $A$ が固有値 $\lambda_1,\lambda_2,…$ と固有ベクトル $\vec{v_1},\vec{v_2},…$ を持ったとする。この固有値を対角線上に並べた行列(それ以外の成分は0)
$$ A = \begin{pmatrix}
\lambda_1 & & \\
& \lambda_2 & \\
& & \ddots \
\end{pmatrix} $$
と、それに対応する固有ベクトルを並べた行列
$$ V = (\vec{v_1} \quad \vec{v_2} \quad …) $$
を用意したとき、それらは
$$ AV = VA $$
と関係付けられる。したがって
$$ A = VAV^{-1} $$
と変形できる。このように正方形の行列を上述の様な3つの行列の積に変形することを固有値分解という。この変形によって行列の累乗の計算が容易になる等の利点がある。特異値分解
正方行列以外でも固有値分解に似たことはできる。
$$ M \vec{v} = \sigma\vec{u} $$
$$ M^\top \vec{u} = \sigma\vec{v} $$
このような特殊な単位ベクトルがあるならば特異値分解できる。
$$ MV = US \qquad M^\top U = VS^\top $$
$$ M = USV^{-1} \qquad M^\top = VS^\top U^{-1} $$
これらの積は
$$ MM^\top = USV^{-1}VS^\top U^{-1} = USS^\top U^{-1} $$
つまり$ MM^\top $を固有値分解すれば、その左特異ベクトルと特異値の2乗が求められることがわかる。第2章:確率・統計
確率変数(random variable) $x$ :実際に実現された値(実現値)
$\hspace{112pt}$ …サイコロを投げて出た目とすると1〜6の整数値確率分布(probability distribution) $P(x)$ :実現値$x$がどれだけ選ばれやすいか
$\hspace{145pt}$ …サイコロの例では $P(1)=…=P(6)=\frac{1}{6}$条件付き確率
$$ P(Y=y|X=x) = \frac{P(Y=y,X=x)}{P(X=x)} $$
ある事象X=xが与えられた下で、Y=yとなる確率。独立な事象の同時確率
$$ P(X=x,Y=y) = P(X=x)P(Y=y)=P(Y=y,X=x) $$
ベイズの定理
$$ P(x|y) = \frac{P(y|x)P(x)}{\sum_x P(y|x)P(x)} $$
加法定理(全確率の法則) $P(y) = \sum_x P(x,y) = \sum_x P(y|x)P(x)$ を条件付き確率 $P(x|y) = \frac{P(x,y)}{P(y)} = \frac{P(y|x)P(x)}{P(y)}$ に用いると、得られる。期待値
- 期待値:その分布における確率変数の平均の値 or "ありえそう"な値 $$ E(f) = \sum_{k=1}^nP(X=x_k)f(X=x_k) $$ $\hspace{28pt}$ 連続する値なら… $$ \int P(X=x)f(X=x)dx $$
- 分散:データの散らばり具合 $$ Var(f) = E\Bigl(\bigl(f_{(X=x)}-E_{(f)}\bigl)^2\Bigl) = E\bigl(f^2_{(X=x)}\bigl)-\bigl(E_{(f)}\bigl)^2$$
- 共分散:2つのデータ系列の傾向の違い $$ Cov(f,g) = E\Bigl(\bigl(f_{(X=x)}-E(f)\bigl)\bigl(g_{(Y=y)}-E(g)\bigl)\Bigl) = E(fg)-E(f)E(g) $$
- 標準偏差:データの散らばり具合(分散は2乗してしまっているので元のデータと単位が違うので、平方根をとり単位を元に戻したもの) $$ \sigma = \sqrt{Var(f)} = \sqrt{E\bigl((f_{(X=x)}-E_{(f)})^2\bigl)} $$
様々な確率分布
- ベルヌーイ分布:2種類のみの結果しか得られないような試行の結果を表した分布(コイントスのイメージ) $$ P(x|\mu) = \mu^x(1-\mu)^{1-x} $$
- マルチヌーイ(カテゴリカル)分布:複数の種類の結果が得られるような試行の結果を表した分布(サイコロを転がすイメージ) $$ P(x|\mu) = \prod_{k=1}^K \mu_k^{x_k} $$
- 二項分布:ベルヌーイ分布の多試行版 $$ P(x|\lambda,n) = \frac{n!}{x!(n-x)!}\lambda^x(1-\lambda)^{n-x} $$
- ガウス分布:釣鐘型の連続分布 $$ N(x;\mu,\sigma^2) = \sqrt\frac{1}{2\pi\sigma^2}\exp\bigl(-\frac{1}{2\sigma^2}(x-\mu)^2\bigl) $$
第3章:情報理論
自己情報量
$$ I(x) = -\log{P(x)} $$
頻繁に起こる事象が観測されても、大した情報をもたらさない一方、珍しい事象ほど情報量は大きい。
そこで、確率の逆数 $\frac{1}{P(x)}$ が情報量の定義の候補となる。
しかし、独立な2現象 $x,y$ をそれぞれ観測して得た情報量は $\frac{1}{P(x)P(y)}$ ではなく、それぞれのもつ情報量の和となった方が自然な定義なので、対数をとる。
対数の底が2のとき、単位はビット(bit)。
対数の底がネイピア数 $e$ のとき、単位はナット(nat)。シャノンエントロピー(平均情報量)
$$ H(x) = E\bigl(I(x)\bigl) = -E\Bigl(\log\bigl(P(x)\bigl)\Bigl) = -\sum_x P(x)\log\bigl(P(x)\bigl) $$
自己情報量の期待値(自己情報量をすべての観測値で平均化したもの。カルバックライブラーダイバージェンス(Kullback-Leibler divergence)
$$ D_{KL}(P||Q) = E_x \Bigl[log\frac{P(x)}{Q(x)}\Bigl] = \sum_x P(x)\bigl(\log{P(x)}-\log{Q(x)}\bigl)$$
$Q$ という分布から、新たな $P$ という分布を見たときにどのぐらい情報が違うのかを表す指標。
一般にKLダイバージェンスは $Q$ に関する下に凸な関数で、 $P=Q$ のときのみ最小値 $D_{KL}(P||P)=0$ になる。
したがって、確かに分布間の距離のようなものであるが、 $P$ と $Q$ を入れ替た $D_{KL}(Q||P)$ は違う値になり本当の数学的な距離とは異なる。交差エントロピー(cross entropy)
$$ H(P,Q) = -E_{X \sim P} \log{Q(x)} = -\sum_xP(x)\log{Q(x)} $$
Qについての自己情報量をPの分布で平均することにより、2つの確率分布がどのぐらい離れているのかを表す指標。なお、確率分布 $P(x)$ と $Q(x)$ の交差エントロピーは、 $P(x)$ のエントロピーと $P(x)$ から見た $Q(x)$ のKLダイバージェンスを足し合わせたものになっている。
$$ \begin{align}
H(P,Q) &= -\sum_xP(x)\log{Q(x)} \\
&= -\sum_xP(x)\log{\frac{P(x)Q(x)}{P(x)}} \\
&= -\sum_xP(x)\bigl(\log{P(x)}+\log{Q(x)}-\log{P(x)}\bigl) \\
&= -\sum_xP(x)\log{P(x)} + \sum_xP(x)\bigl(\log{P(x)}-\log{Q(x)}\bigl) \\
&= H(P) + D_{KL}(P||Q) \\
\end{align} $$
- 投稿日:2020-07-05T17:21:06+09:00
AtCoder緑になるまでにやったこと、感想
Atcoderで緑に到達することができたので、勉強した内容と感想についてまとめたいと思います。何番煎じの内容か分かりませんが少しでもこれからAtcoderを始める人の助けになれば幸いです。
自己紹介
・化学系の大学院出身で社会人2年目、情報工学についてきちんと学んだことはありません。
・数学は理系大学院出身としては普通くらいの能力です。
・使用言語はPythonで,C++もコードを読んだりA,B問題の実装程度ならできます。
・プログラミングは社会人になってから勉強を始めました。(簡単なコードなら大学院時代にも書いていました)やったこと
過去問を解いているとレートが上がった、結局はそれだけなのですが効率をあげるために意識した2点についてまとめました。
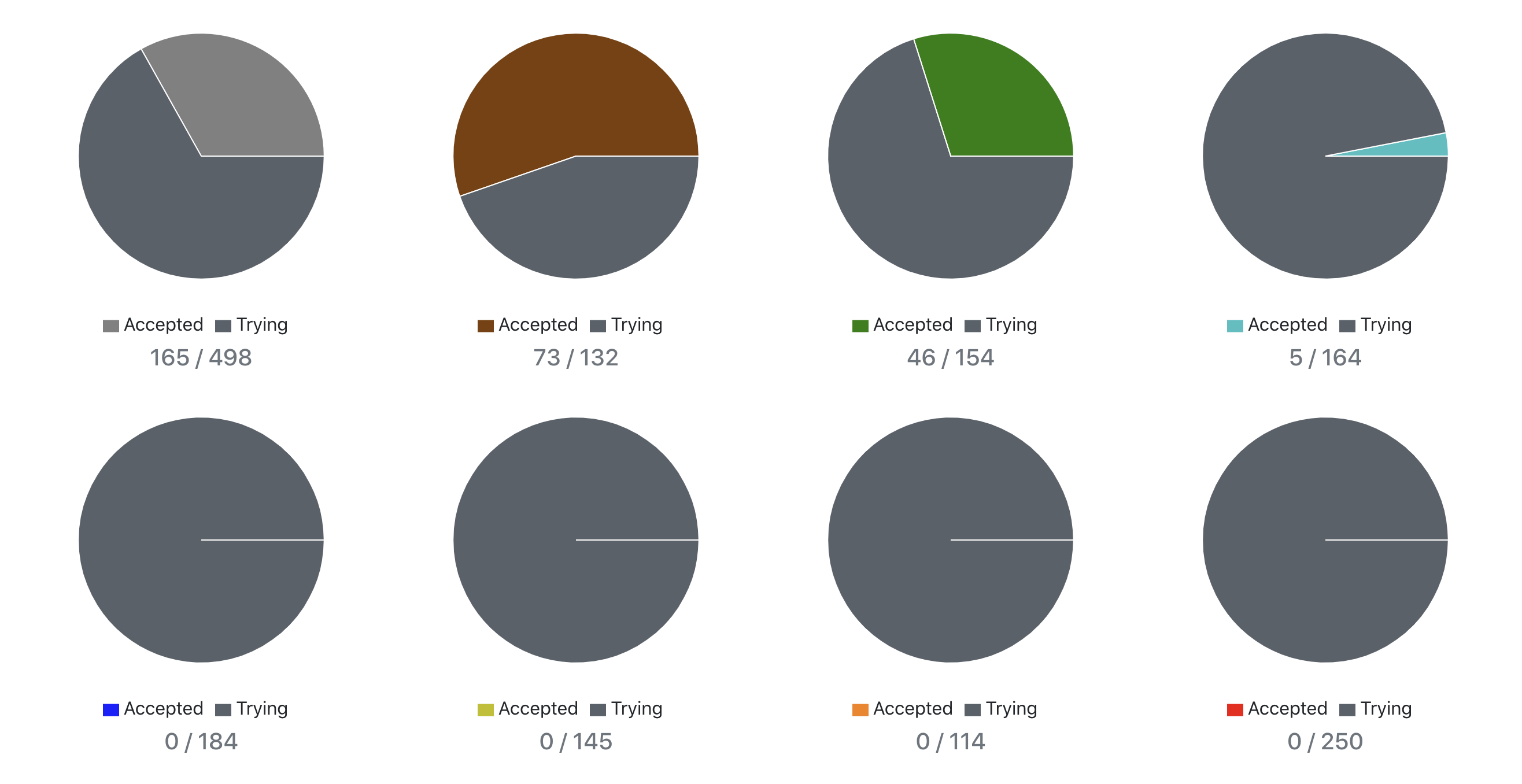
1. 適切な難易度の問題を解く
これは私が解いた過去問の実績です、特徴としては茶色問題の解いている比率が高い、水色問題の解いている比率が低い点かと考えています。灰色問題もそこそこ解いているように見えますが、これはC++の学習のため解いた問題が3割ほどありレートを上げる目的では解いていません。
このような実績になった理由として、緑レートに到達のできない段階では茶色問題に出るAtcoder頻出アルゴリズムについて正しく理解することがまず重要、水色問題は難しく学習の効率が悪い(その問題の本質を正しく理解できない)と考えたからです。緑色問題についてはレートが800近くなり茶色問題に苦労せず解けるようになってから取り組んでいます。2. 自分の学ぶべきアルゴリズムを理解する
他の方の緑到達記事にも書いてありますが、緑レートまでに理解すべきアルゴリズムは数で言えば10個程度です。10もあれば得意なもの、苦手なものが出てくると思います。苦手なものを重点的に勉強しましょう。ちなみに私は二分探索とDPが苦手です。。
アルゴリズムの勉強法として私は一度解いたことのある問題について実装を繰り返すという方法で勉強しました、理解していることと実装は別の問題なので実装の勉強は新しい問題を解くのとは別の方法でやることがいいのかもしれません。最後に
私はデータサイエンス分野に興味があり仕事でもそのような内容に携わっています。(kaggleへの取り組みについても書いてあるのでよければ読んでみてください。)
そのためもともとはアルゴリズムといったものには興味もありませんでしたし、業務にも活きないだろうと考えていました。しかし実際にAtcoderを通して学んでみるとアルゴリズムを考えることは面白いし、業務にも活きているなと感じます。計算量を意識したプログラミング、コーディングのスピード、バグの発見までの速度と行ったもので特に感じています。ですのでアルゴリズムに興味がないな、という方にもAtcoderのような競技プログラミングに一度は取り組んでみていただきたいなと思っています。
- 投稿日:2020-07-05T15:59:41+09:00
Django-TodoList②~詳細ページを表示してみよう~
はじめに
今回の記事では「TodoList」の詳細ページを表示していこうと思います。
前回までの記事にも目を通していただけるとスムーズに進められると思います。前回までの記事
↓
↓
↓
PycharmでDjangoでアプリケーションを作成する手順~準備編~urls.pyの編集
まずは'urls.py'にURLの繋ぎ込みを行っていきます。
アプリケーションの'urls.py'を開いてください。
(デフォルトでは用意されていないので作成していない方は、ターミナルに次のように打ち込んでください。)#アプリケーションディレクトリに移動 $ cd アプリケーション名 #今回は「todo」 #urls.pyの作成 $ touch urls.py'urls.py'を開いたら(作成できたら)、次のように追記してください。
from django.urls import path from .views import TodoList, TodoDetail urlpatterns = [ path('list/', TodoList.as_view()), path('detail/<int:pk>/', TodoDetail.as_view()), #詳細画面の繋ぎ込み ]'int:pk'とは、どのデータを表示するのか指定するものです。
あとで実際に入力しますが、URLの末尾に'detail/1/'と付け足すことで、1つ目のデータが表示されます。
ちなみに管理画面で一つ一つのデータの詳細を見ると、URL部分nの末尾に数字が表示されているのを確認できます。'TodoDetail.as_view'は’view.py’にある'TodoDetailクラスを持ってくると思ってもらえたら良いです。
view.pyの編集
次に'view.py'を編集していきます。
from django.shortcuts import render from django.views.generic import ListView, DetailView #DetailViewをインポート from .models import TodoModel class TodoList(ListView): template_name = 'list.html' model = TodoModel class TodoDetail(DetailView): #TodoDetailクラスを定義 template_name = 'detail.html' #'template'は'detail.html'を指定 model = TodoModel #モデルは'TodoModel'を指定前回の記事でも説明した通り、'views.py'は材料を集めるために動くものなので、'tempalte'とモデルの指定を行っています。
models.pyの編集
前回作成した'models.py'から少し変更を加えるので、次のように追記してください。
from django.db import models from django.utils import timezone class TodoModel(models.Model): title = models.CharField(max_length=50) content = models.TextField() deadline = models.DateTimeField(default=timezone.now)これで編集は完了です。
表示
それでは早速表示できているか確認していきましょう。
ターミナルに次のように打ち込んでください。
$ python manage.py runserverURLが表示されるのでそれをクリックするとブラウザに飛びます。
ブラウザに飛んだら、URLの末尾に'detal/1/'と付け足してください。そうすると一番最初に登録したデータの中身が表示されているのが確認できるはずです。
終わりに
今回は一つ一つのデータの詳細画面を表示することをしました。
今後も記事を追加していくので、参考にしていただければ幸いです。
- 投稿日:2020-07-05T15:52:54+09:00
誰に投票するかをくじ引きで決める
今日は都知事選ですね!
今年はすでに出来レースとなっていて、「誰に投票してもかわらないや」と思う人も多くいそうですし、投票率が下がるかもしれません。
https://www.amazon.co.jp/dp/4887597126
若者は、選挙に行かないせいで、四〇〇〇万円も損してる!? (ディスカヴァー携書) (日本語) 新書なんて本もありますが、
- 投票しない
- 白票を投じる
となりますと、
支持基盤を持った人たちがただ有利になるだけ、
つまり つまらない政治がずっと続く ことになるので是非投票したいですね。上記の書籍にもありますが、選びたい人がいない場合はエンピツ転がして選んでもいいんですよね。
目的は
- 投票率を上げる
- 候補者に支持基盤だよりにさせない
ことなので。
ただ、選びたい人がいなくても選びたくない人はいる、ということはあります。
候補者のリストを渡したらその中で一人を選んでくれる
といったプログラムを用意しました。given_lottery.pyimport secrets import sys def draw_lots(data=None): if data is None: return -1 lot_member = data.split(',') r = secrets.randbelow(len(lot_member)) return lot_member[r] if __name__ == '__main__': args = sys.argv print(draw_lots(args[1]))というくらいですね。
- 引数をカンマ区切りで分ける
- 0~要素数のなかでランダム値を出力する
- ランダム値でリストを引けば、名前が出力される
といった動きになります。
追記
コメントで「choice関数あるよ」と指摘を受けました。
というわけでリファクタリング。
import secrets import sys def draw_lots(data=None): if data is None: return -1 return secrets.choice(data.split(',')) if __name__ == '__main__': args = sys.argv print(draw_lots(args[1]))
- 引数をカンマ区切りで分ける
- ランダムに名前を出力
と、スッキリしましたね。
ソースファイルは
https://github.com/atworks/given-lottery
に置きました。あとは
> python .\given_lottery.py a,b,c,d,e eのように、カンマ区切りで文字列を渡したらランダムで1つを選んで出力します。
よい投票ライフを送りたいものです。
- 投稿日:2020-07-05T15:51:30+09:00
pip install が通らない場合のmodule install
要約
通常、pythonのmoduleは、「pip install module名」でインストールするが、セキュリティ等に阻まれて、「pip install module名」が効かない場合がある。例えば、会社PCなどで。その場合はwhlファイルをPypiからdownloadして「pip install whlファイル名」でインストールするか、圧縮ファイル (zip形式及びtar.gz形式のファイル) をdownloadして「python setup.py install」でインストールする。
材料及び方法
- Pypi (https://pypi.org/) の検索欄に対象モジュール名を入力する。
- 検索リストから対象モジュール名を選択する。
whlファイルまたはtar.gzファイルをダウンロードする。
対象モジュールファイルがダウンロードされたディレクトリに移動する。
tar.gzファイルは解凍する。
whlファイルの場合は、「pip install whlファイル名」を実行する。
tar.gz解凍の場合は、解凍されたフォルダに入って、「python setup.py install」を実行する。
依存するモジュールが無い場合はerrorが出るので、依存モジュールについても同様の手順でインストールする。
結果及び考察
当方法でpycaret実行環境を構築したときは、依存moduleのインストールが約100個必要だったので、ちゃんと効くpip installは偉大だなーと思いました。
- 投稿日:2020-07-05T15:02:49+09:00
[GCP] Cloud FunctionsでPythonプログラムを動作させるときの備忘録
Cloud FunctionsでPythonを動かそうとして何日も溶かしてしまったので、
未来の自分がこれ以上時間を溶かさないように残しておきます。ログ
処理が正常終了したときには print で出力したログも Cloud Logging から確認できますが、
例外が発生した時には except 句内の print は Cloud Logging に詳細が出力されずcrashという情報だけが残ります。
これではヒントが無く、どの処理でどういうエラーが出たのか全くわかりません。
logging モジュールを使うと出力したい場所でログがしっかり出力され、ログレベルに合わせて Cloud Logging の行ごとのアイコンも変わるので、使い勝手が良くなります。import logging import traceback def main(): try: # 処理 logger.info("output by logger") print("output by print") # 処理が正常終了すると出力される except: traceback.print_exc() # Cloud Loggingには出力されない logger.error("error by logger: ", exc_info=True) raiseGCP / Googleの他のサービスとの認証周り
ADC (https://cloud.google.com/docs/authentication/production?hl=ja) があるので、
google.auth.default()で credential 情報を取得できます。
認証先のサービスによってはCredentialのscope情報を付与したり、必要に応じた実行サービスアカウントへのロールの設定をしておきます。ローカルで開発する際は credential 情報を json ファイルで保存しておき、環境変数
GOOGLE_APPLICATION_CREDENTIALSに json ファイルのパスを指定するだけでgoogle.auth.default()の認証が通るので、ローカルと Cloud Functions での処理を分岐させる必要はありません。import google.auth from google.cloud import kms_v1 import gspread def spreadsheet(url): credentials, _ = google.auth.default(scopes=['https://spreadsheets.google.com/feeds','https://www.googleapis.com/auth/drive']) gc = gspread.authorize(credentials) return gc.open_by_url(url) def kms_client(): credentials, _ = google.auth.default() return kms_v1.KeyManagementServiceClient(credentials=credentials)Cloud Functions API から新規作成する際の 400 Bad Request エラーの原因調査
Python プログラムの Tips から少し話がそれますが、terraform を使って Cloud Functions に関数をデプロイするときにハマったので、合わせて残しておきます。
WebのGCPコンソールから関数を作成するときにはこの問題には当たらないとは思いますが、terraform で plan では問題なく差分が見れているのに apply すると
400 Bad Request INVALID_ARGUMENT The request has errors↑こんな感じのメッセージだけ出力されて、どの項目に不備があるのかわかりません。
terraformの場合、環境変数に
TF_LOG=debugを追加しても、得られる情報はあまり変わり有りません。
ただ、このTF_LOG=debugで出力されたリクエストボディの情報を控えておきます。cloud functions api の リファレンスページ の Try this API に
TF_LOG=debugで出力したリクエストボディを入力して EXECUTE してみると、400 Bad Request INVALID_ARGUMENT The request has errors以外にも不備のあるフィールド名と、不備の詳細が message に出力されると思います。定義済みの環境変数
毎回 print で出力して確認しているので、備忘録として出力をそのまま残しておきます。
environ({ 'PORT': '8080', 'X_GOOGLE_WORKER_PORT': '8091', 'NODE_ENV': 'production', 'X_GOOGLE_ENTRY_POINT': 'entrypoint', 'FUNCTION_TRIGGER_TYPE': 'HTTP_TRIGGER', 'GCLOUD_PROJECT': 'project_id', 'DEBIAN_FRONTEND': 'noninteractive', 'X_GOOGLE_FUNCTION_MEMORY_MB': '256', 'FUNCTION_TIMEOUT_SEC': '60', 'SUPERVISOR_INTERNAL_PORT': '8081', 'ENTRY_POINT': 'entrypoint', 'X_GOOGLE_LOAD_ON_START': 'false', 'X_GOOGLE_FUNCTION_REGION': 'asia-northeast1', 'X_GOOGLE_FUNCTION_VERSION': '1', 'WORKER_PORT': '8091', 'VIRTUAL_ENV': '/env', 'X_GOOGLE_GCP_PROJECT': 'project_id', 'CODE_LOCATION': '/user_code', 'PWD': '/user_code', 'X_GOOGLE_CONTAINER_LOGGING_ENABLED': 'false', 'FUNCTION_NAME': 'dummy_function', 'X_GOOGLE_CODE_LOCATION': '/user_code', 'FUNCTION_MEMORY_MB': '256', 'X_GOOGLE_FUNCTION_IDENTITY': 'dummy_service_account@project_id.iam.gserviceaccount.com', 'FUNCTION_IDENTITY': 'dummy_service_account@project_id.iam.gserviceaccount.com', 'FUNCTION_REGION': 'asia-northeast1', 'GCP_PROJECT': 'project_id', 'X_GOOGLE_FUNCTION_NAME': 'dummy_function', 'X_GOOGLE_SUPERVISOR_HOSTNAME': 'supervisor', 'HOME': '/tmp', 'SUPERVISOR_HOSTNAME': 'supervisor', 'PATH': '/env/bin:/usr/local/sbin:/usr/local/bin:/usr/sbin:/usr/bin:/sbin:/bin', 'X_GOOGLE_GCLOUD_PROJECT': 'project_id', 'X_GOOGLE_FUNCTION_TRIGGER_TYPE': 'HTTP_TRIGGER', 'X_GOOGLE_SUPERVISOR_INTERNAL_PORT': '8081', 'X_GOOGLE_FUNCTION_TIMEOUT_SEC': '60', 'LC_CTYPE': 'C.UTF-8', })まとめ
ログに有用な情報を出力できると不具合調査が楽になる。
認証周りはgoogle.authに頼って、サービスアカウントのロール設定で細かく制御する。まだまだハマリポイントありそうな予感しかしないが、勘所は掴んだ気でいます。
- 投稿日:2020-07-05T14:36:20+09:00
BeautifulSoupを用いて競馬データをスクレイピングする方法
目的
機械学習で競馬予想して回収率100%を目指す。
今回やること
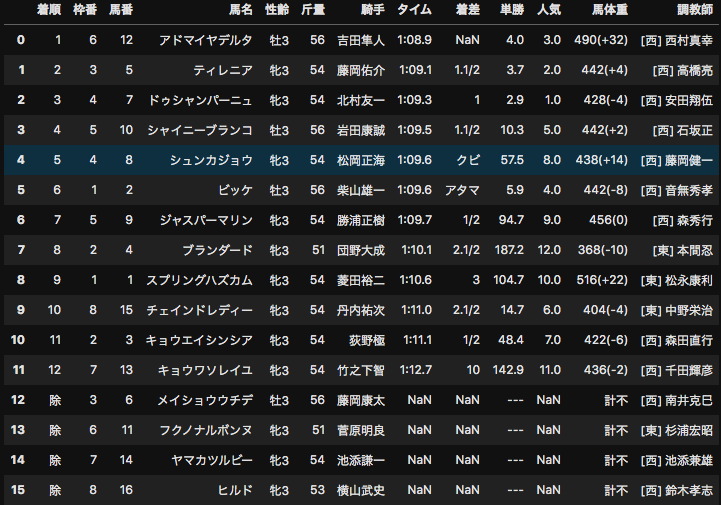
前回の記事で、netkeiba.comから2019年の全レース結果のデータをスクレイピングした。
今回はこれに加えて、レースの日付の情報や馬場の状態などのデータをスクレイピングしたい。
ソースコード
前回同様、race_idのリストを入れたらそれぞれのレースについてスクレイピング結果を辞書型で返してくれる関数を作る。
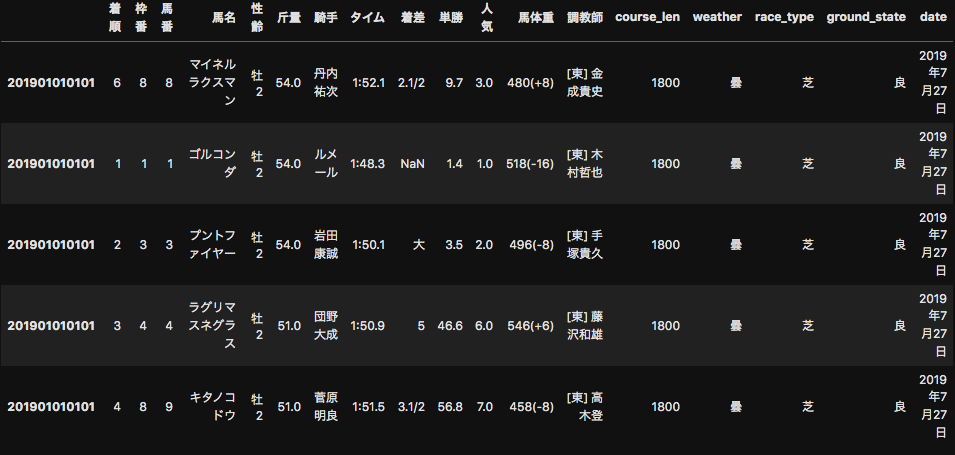
import requests from bs4 import BeautifulSoup import time from tqdm.notebook import tqdm import re def scrape_race_info(race_id_list): race_infos = {} for race_id in tqdm(race_id_list): try: url = "https://db.netkeiba.com/race/" + race_id html = requests.get(url) html.encoding = "EUC-JP" soup = BeautifulSoup(html.text, "html.parser") texts = ( soup.find("div", attrs={"class": "data_intro"}).find_all("p")[0].text + soup.find("div", attrs={"class": "data_intro"}).find_all("p")[1].text ) info = re.findall(r'\w+', texts) #Qiitaでバックスラッシュを打つとバグるので大文字にしてあります。 info_dict = {} for text in info: if text in ["芝", "ダート"]: info_dict["race_type"] = text if "障" in text: info_dict["race_type"] = "障害" if "m" in text: info_dict["course_len"] = int(re.findall(r"\d+", text)[0]) #ここも同様に大文字にしてます。 if text in ["良", "稍重", "重", "不良"]: info_dict["ground_state"] = text if text in ["曇", "晴", "雨", "小雨", "小雪", "雪"]: info_dict["weather"] = text if "年" in text: info_dict["date"] = text race_infos[race_id] = info_dict time.sleep(1) except IndexError: continue except Exception as e: print(e) break return race_infos前回スクレイピングしたデータからrace_id_listを作り、前回同様にDataFrame型にして元々のデータにmergeする。
race_id_list = results.index.unique() race_infos = scrape_race_info(race_id_list) for key in race_infos: race_infos[key].index = [key] * len(race_infos[key]) race_infos = pd.concat([pd.DataFrame(race_infos[key], index=[key]) for key in race_infos]) results = results.merge(race_infos, left_index=True, right_index=True, how='left')動画で詳しい解説をしています!
競馬予想で始めるデータ分析・機械学習
- 投稿日:2020-07-05T14:30:00+09:00
Flask実行時にModuleNotFoundError: No module named '***'の対策
問題
Pycharmで既存のプロジェクトにウェブサーバーを入れることにしました。ただ、既存のプロジェクトにサブパッケージとして、flaskプロジェクトを置きました。
そして、サブパッケージにcdして、falskサーバーを立ち上げて、ルーティングをアクセスする時に、以下のエラーが発生しました。
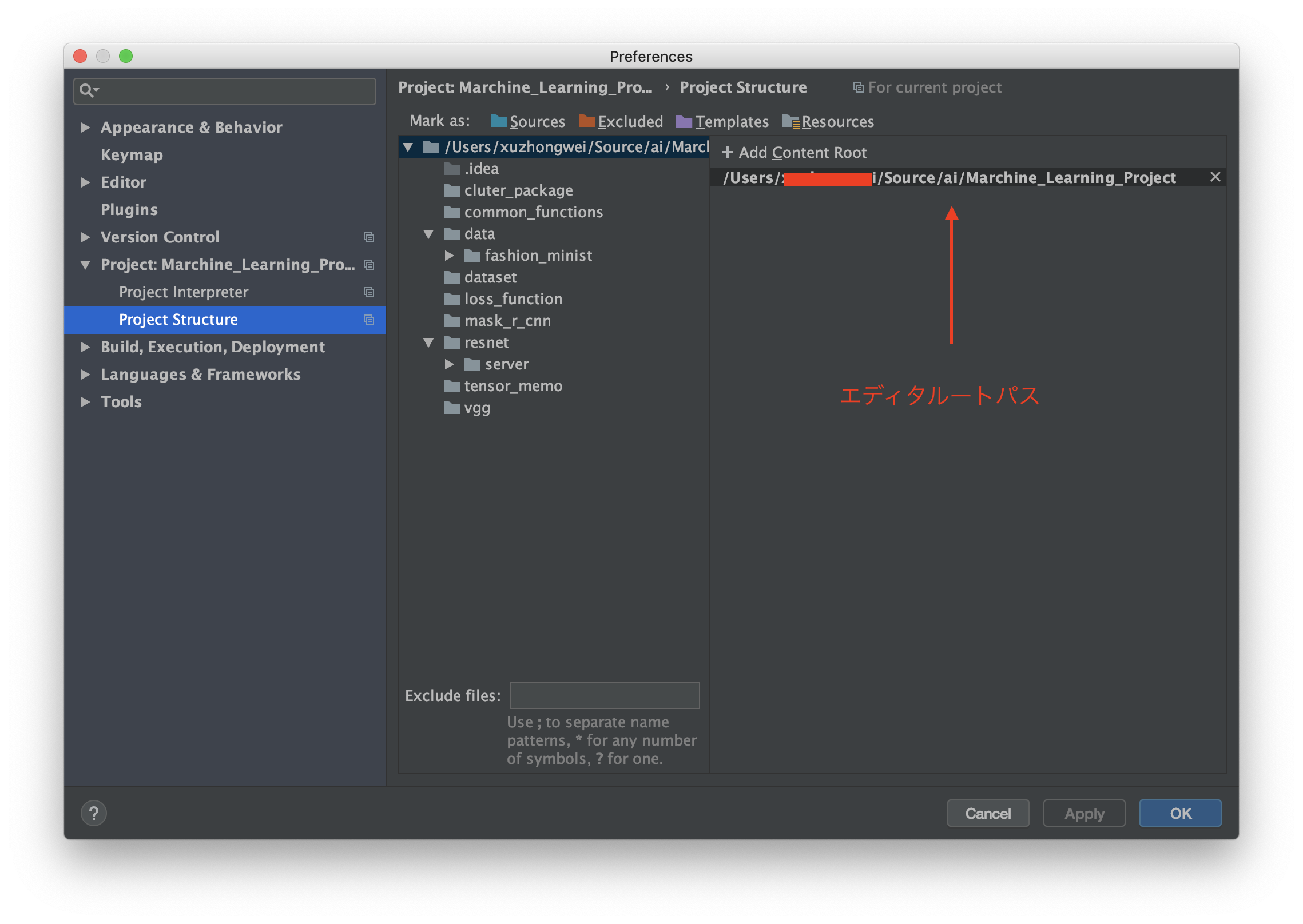
flask.cli.NoAppException lask.cli.NoAppException: While importing "Machine_Learning_Project.resnet.server.flaskr", an ImportError was raised: Traceback (most recent call last): File "/home/user/anaconda3/lib/python3.7/site-packages/flask/cli.py", line 240, in locate_app __import__(module_name) File "/home/user/Source/Machine_Learning_Project/resnet/server/flaskr/__init__.py", line 4, in <module> from resnet.server.flaskr.index import run_process_result, index_router ModuleNotFoundError: No module named 'resnet'エディターpycharmでは、import文にエラーがないですが、flaskサーバーにアクセスするときに、依存のパーケージを見つけれないえらーがウェブ側に表示されます。
原因
flaskサーバーを立ち上げるときに、いかのコマンドを実行しました。
cd /home/user/Source/Machine_Learning_Project/resnet/server flask runこのコマンドを実行するディレクトリのパスはflaskサーバーのルートパースになっています。
ルートパス:/home/user/Source/Machine_Learning_Project/resnet/server
flaskサーバーはこのパスしかわからないため、importされるパッケージをたどり着けるときに、このパスからたどり着けるしかできないです。
importされたパッケージは他のディレクトリにあるため、パッケージが見つからないエラーが発生しています
図のように、オレンジの部分はflaskサーバーのルートパースです。オレンジ部分以外なパッケージ(赤い部分)をimportする時に、当然見つからないエラーが発生します。
ずのように、エディターは赤い部分をルートパスとして指定するため、import分にエラーが表示されなかったです。解決法
falskサーバーにimportしたいパッケージの所在地を教えてあげれば、解決されます。
教える方法は以下のコードになります。import sys sys.path.append("/home/user/Source/Machine_Learning_Project")注意点としては、importしたいパッケージのimport文の前に置くべきです。